Округление в javascript: Math.round() — JavaScript | MDN

Math.floor(), Math.round(), Math.ceil() и Math.trunc() — JavaScript — Дока

1. Кратко
2. Как пишется
3. На практике
   1. Николай Лопин советует

Кратко

Скопировано

Объект Math содержит набор методов, который используется для округления чисел:

• round() — округление по обычным правилам;
• floor() — округление вниз;
• ceil() — округление вверх;
• trunc() — отбрасывание дробной части, не обращая внимания на знак аргумента.

Как пишется

Скопировано

Для обычного округления используйте Math.round():

console. log(Math.round(15.52))// 16console.log(Math.round(15.3))// 15
          console.log(Math.round(15.52))
// 16
console.log(Math.round(15.3))
// 15

Округление до ближайшего целого в большую сторону — Math.ceil():

console.log(Math.ceil(15.52))// 16console.log(Math.ceil(15.3))// 16
          console.log(Math.ceil(15.52))
// 16
console.log(Math.ceil(15.3))
// 16

Округление до ближайшего целого в меньшую сторону — Math.floor():

console.log(Math.floor(15.52))// 15console.log(Math.floor(15.3))// 15
          console.log(Math.floor(15.52))
// 15
console.log(Math.floor(15.3))
// 15
 

🛠 Используйте осторожно при работе с отрицательными числами:

console.log(Math.floor(-15.3))// -16
          console.log(Math.floor(-15.3))
// -16

Так происходит потому что -16 меньше, чем -15, а округление происходит в меньшую сторону.

Отбрасывание дробной части — Math.trunc()

console.log(Math.trunc(15.52))// 15console.log(Math.trunc(-15.3))// -15console.log(Math.trunc(0.123))// 0console.log(Math.trunc(-0.123))// -0
          console.log(Math.trunc(15.52))
// 15
console.log(Math.trunc(-15.3))
// -15
console.log(Math.trunc(0.123))
// 0
console.log(Math.trunc(-0.123))
// -0
 

На практике

Скопировано

Николай Лопин советует

Скопировано

🛠 Разные виды округления нужны в разных ситуациях:

• когда нужно разбить данные на страницы и посчитать общее количество страниц, используйте округление вверх: const totalPages =Math.ceil(totalItems / itemsPerPage).
• когда нужно выбрать случайный элемент массива, используйте округление вниз: Math.floor(Math.random() * array.length).

Если вы нашли ошибку, отправьте нам пул-реквест!

Во время отправки формы что-то пошло не так. Попробуйте ещё раз?

←

Объект Math

ctrl + alt + ←

→

Math.random()

ctrl + alt + →

Как округлить до целого? — efim360.ru

В JavaScript всё является объектами. Любой объект в JavaScript по цепочке прототипов приходит к «Глобальному Объекту» языка. У «Глобального Объекта» JavaScript есть свои собственные свойства-конструкторы. Одним из таких свойств является объект Math

Чтобы округлять дробные числа до целых нужно использовать конструктор Math и его собственные методы округления чисел:

• ceil( ) — округление до наибольшего целого
  
• floor( ) — округление до наименьшего целого
• round( ) — округление до ближайшего целого
• trunc() — округление до целого в сторону нуля

Напоминаю, что по правилам классической математики 0,5 округляется в большую сторону. Так работает метод round( ).

Примеры

В качестве примеров мы будем передавать в методы дробные числа.

Округление до наибольшего целого

Math.ceil(1.11)
2

Math.ceil(1.5)
2

Math.ceil(1.7)
2

Округление до наименьшего целого

Math.  floor(1.11)
1

Math.floor(1.5)
1

Math.floor(1.7)
1

Округление до ближайшего целого (как в математике)

Math.round(1.11)
1

Math.round(1.5)
2

Math.round(1.7)
2

Округление до целого в сторону нуля

Math.trunc(-11.1)
-11
Math.trunc(-11.6)
-11
Math.trunc(12.1)
12
Math.trunc(12.6)
12

Зачем нужно округлять дробные до целых?

Представьте, что где-то в логике алгоритма нужно найти середину массива? Если длина массива будет чётным числом, то при делении чётного числа на 2 мы всегда получим целое. А вот если длина массива будет нечётным числом, тогда деление на 2 вернёт нам дробное число.

Мы знаем, что в «правильных» массивах не бывает дробных индексов, а значит нам нужно будет явно указать какое-то целое, наиболее подходящее к серединному значению массива. Теперь вы знаете как можно округлить дробное до целого.

Где ещё можно применить округление до целого?

Почитайте решение одной из стандартных задач в языке JavaScript — Как проверить число на дробное?

Информационные ссылки

Стандарт ECMAScript — Раздел «21.3.2.10 Math.ceil ( x )» — https://tc39.es/ecma262/#sec-math.ceil

Стандарт ECMAScript — Раздел «21.3.2.16 Math.floor ( x )» — https://tc39.es/ecma262/#sec-math.floor

Стандарт ECMAScript — Раздел «21.3.2.28 Math.round ( x )» — https://tc39.es/ecma262/#sec-math.round

Руководство по округлению чисел в JavaScript

Math.round()

Метод Math.round() — самый простой способ округления чисел в JavaScript. Он округляет число до ближайшего целого числа, а это означает, что если число находится ровно посередине между двумя целыми числами, оно будет округлено в большую сторону. Этот метод прост и понятен, но может быть немного неточным при работе с большими числами. Например, если вы округлите число 1,5 до ближайшего целого числа, оно вернет 2, но если вы округлите число 1,6 до ближайшего целого числа, оно вернет 1. Это может привести к неожиданным результатам, если вы не будете осторожны.

Math.ceil()

Метод Math.ceil() аналогичен методу Math.round(), но всегда округляет число до ближайшего целого числа. Это означает, что если число находится ровно посередине между двумя целыми числами, оно всегда будет округляться в большую сторону. Этот метод полезен, если вы хотите, чтобы число всегда округлялось в большую сторону, но он может быть неточным, если вы имеете дело с большими числами. Например, если вы округлите число 1,5 до ближайшего целого числа, оно вернет 2, но если вы округлите число 1,6 до ближайшего целого числа, оно также вернет 2,9.0005

Math.floor()

Метод Math.floor() противоположен методу Math.ceil(). Он всегда округляет число до ближайшего целого числа. Это означает, что если число находится ровно посередине между двумя целыми числами, оно всегда будет округляться в меньшую сторону. Этот метод полезен, если вы хотите, чтобы число всегда округлялось в меньшую сторону, но он может быть неточным, если вы имеете дело с большими числами. Например, если вы округлите число 1,5 до ближайшего целого числа, оно вернет 1, но если вы округлите число 1,6 до ближайшего целого числа, оно также вернет 1,9.0005

Number.toFixed()

Метод Number.toFixed() немного сложнее других методов, но он может быть очень полезен при работе с большими числами. Этот метод позволяет вам указать количество знаков после запятой, до которого вы хотите округлить. Например, если вы хотите округлить число 1,5 до двух знаков после запятой, вы можете использовать для этого метод Number.toFixed(). Этот метод полезен, если вы хотите, чтобы число всегда округлялось до определенного числа знаков после запятой, но он может быть неточным, если вы имеете дело с большими числами.

Округление до ближайшего кратного

Иногда может потребоваться округлить число до ближайшего кратного другого числа. Например, если вы хотите округлить число до ближайшего кратного 10, вы можете использовать следующую формулу: Math.round(число / 10) * 10. Эта формула округлит число до ближайшего кратного 10. Этот метод полезно, если вы хотите, чтобы число всегда округлялось до ближайшего кратного другого числа, но может быть неточным, если вы имеете дело с большими числами.

Округление до ближайшей степени 10

Иногда вам может понадобиться округлить число до ближайшей степени 10. Например, если вы хотите округлить число до ближайшей степени 10, вы можете использовать следующую формулу: Math.pow(10, Math.round(Math.log10(число))). Эта формула округляет число до ближайшей степени 10. Этот метод полезен, если вы хотите, чтобы число всегда округлялось до ближайшей степени 10, но он может быть неточным, если вы имеете дело с большими числами.

Округление до ближайшего значащего числа

Иногда может потребоваться округлить число до ближайшего значащего числа. Например, если вы хотите округлить число до ближайшего значащего числа, вы можете использовать следующую формулу: Math.round(number * Math.pow(10, -Math.floor(Math.log10(number)))). Эта формула округляет число до ближайшего значащего числа. Этот метод полезен, если вы хотите, чтобы число всегда округлялось до ближайшего значащего числа, но он может быть неточным, если вы имеете дело с большими числами.

Округление до ближайшего целого числа, кратного другому числу

Иногда вам может понадобиться округлить число до ближайшего целого числа, кратного другому числу. Например, если вы хотите округлить число до ближайшего целого числа, кратного 10, вы можете использовать следующую формулу: Math.round(number / 10) * 10. Эта формула округлит число до ближайшего целого числа, кратного 10. Этот метод полезен, если вы хотите, чтобы число всегда округлялось до ближайшего целого числа, кратного другому числу, но он может быть неточным, если вы имеете дело с большими числами.

Округление до ближайшей целой степени другого числа

Иногда вам может понадобиться округлить число до ближайшей целой степени другого числа. Например, если вы хотите округлить число до ближайшей целой степени 10, вы можете использовать следующую формулу: Math.pow(10, Math.round(Math.log10(число))). Эта формула округляет число до ближайшей целой степени 10. Этот метод полезен, если вы хотите, чтобы число всегда округлялось до ближайшей целой степени другого числа, но он может быть неточным, если вы имеете дело с большими числа.

Округление до ближайшего целого числа другого числа

Иногда может потребоваться округлить число до ближайшего целого числа другого числа. Например, если вы хотите округлить число до ближайшего целого числа значащей цифры 10, вы можете использовать следующую формулу: Math.round(number * Math.pow(10, -Math.floor(Math.log10(number))). )). Эта формула округляет число до ближайшего целочисленного значащего разряда 10. Этот метод полезен, если вы хотите, чтобы число всегда округлялось до ближайшего целочисленного значащего разряда другого числа, но он может быть неточным, если вы имеете дело с большими числами.

Заключение

Округление чисел в JavaScript может быть непростой задачей, но немного потренировавшись, вы сможете быстро стать экспертом. В этом руководстве представлен обзор различных методов округления чисел в JavaScript, а также несколько советов и приемов, позволяющих извлечь из них максимальную пользу. Обладая необходимыми знаниями и практикой, вы можете легко стать экспертом по округлению чисел в JavaScript.

Пожалуйста, внимательно прочитайте этот отказ от ответственности перед тем, как начать пользоваться услугой. Используя эту услугу, вы подтверждаете, что вы полностью согласны и принимаете содержание этого заявления об отказе от ответственности. Вы можете отказаться от использования сервиса, если не согласны с данным отказом от ответственности. Этот документ создается автоматически на основе общедоступного контента в Интернете, захваченного Платформой машинного обучения для ИИ. Авторские права на информацию в этом документе, такую ​​как веб-страницы, изображения и данные, принадлежат их соответствующим авторам и издателям. Такой автоматически сгенерированный контент не отражает точку зрения или мнение Alibaba Cloud. Вы несете ответственность за определение законности, точности, подлинности, практичности и полноты содержания. Мы рекомендуем вам проконсультироваться со специалистом, если у вас есть какие-либо сомнения по этому поводу. Alibaba Cloud не несет ответственности за любые последствия использования вами контента без проверки. Если у вас есть отзывы или вы обнаружите, что в этом документе используется некоторый контент, в отношении которого у вас есть права и интересы, свяжитесь с нами по этой ссылке: https://www.alibabacloud.com/campaign/contact-us-feedback. Мы будем решать вопрос в соответствии с соответствующими правилами.

Глубокое погружение в JavaScript — числа с плавающей запятой и известные ошибки округления

Фото Федерико Респини на Unsplash

Введение

 > const num = 0,1 + 0,2
> console.log(num) // 0.30000000000000004 

Вы когда-нибудь пытались запустить приведенный выше фрагмент кода? Является ли ответ тем, что вы ожидали? Если нет, то этот пост может показаться вам интересным.

Во-первых, мы подробно рассмотрим, как очень большие и очень маленькие числа могут быть представлены в памяти компьютера, а также какой международный стандарт используется. Затем мы воспользуемся этим знанием и привяжем его к JavaScript, а также к тому, как наше новое знание может изменить то, как мы рассматриваем определенные конструкции JavaScript.

Проблема

Сайт с плавающей запятой-gui.de объясняет, почему числа с плавающей запятой действительно нужны в компьютерах. Это говорит что, поскольку память компьютера ограничена, компьютеры не могут хранить числа с бесконечная точность. Но какая точность нужна? И где это нужный? Сколько целых цифр (до запятой) и сколько цифры дроби

Рассмотрим три варианта использования:

• Инженер-строитель строит шоссе и измеряет длину дороги. К инженер, не важно ширина дороги 10 метров, или 10.0001 метр широкий, так как измерения, вероятно, не так точны в первом место.
• Инженер-электрик проектирует микросхему, где 0,0001 метра (или 0,1 миллиметры) огромная разница. Но тогда инженер-электрик никогда не должны иметь дело с расстояниями более 0,1 метра.
• Физик должен использовать скорость света (299 792 458 м/с) и Ньютона. гравитационная постоянная (около 0,00000000000667) вместе в одном расчет.

Инженер-строитель, инженер-электрик и физик каждый разные потребности, когда дело доходит до точности чисел, которые им нужно хранить. Но как эффективно хранить все эти числа в памяти компьютера? Имея фиксированное число целых чисел (до запятой) и дробных цифр (после запятой) совсем неэффективно из-за порядков величина разницы в числах, которые требуются для каждого из примеры использования, перечисленные выше.

Одним из решений этой проблемы, и, безусловно, наиболее распространенным, является число с плавающей запятой .

Краткая история

Арифметика с плавающей запятой и, следовательно, проблема 0.

В 1985 году IEEE стандартизировал плавающие точечная арифметика со стандартом IEEE 754. Стандарт решает множество проблем, возникающих из-за разнообразного набора реализаций с плавающей запятой в различных аппаратных и программных продуктах, и затрудняет надежное и переносимое использование с плавающей запятой.

Числа с плавающей запятой

В науке, когда мы имеем дело с действительно большими числа или очень маленькие числа, обычно эти числа представляются в научная нотация.

Например, постоянная Планка, которая связывает энергию, переносимую фотоном, к частоте фотона, это на самом деле маленькое число. Это:

0,000000000000000000000000006626068

Что в экспоненциальном представлении можно записать как:

6,626068 x 10 ^-34

Здесь мы перемещаем десятичную точку на 34 разряда, обозначаемую порядком величины .

Аналогично, постоянная Авогадро, которая связывает количество вещества в данного образца (измеряемого в молях), к количеству частиц в этом образце — это

602 300 000 000 000 000 000 000

Что в экспоненциальном представлении можно записать как:

6.023 x 10 ²³

Мы можем обобщить, как написаны научные обозначения:

M x 10 ^N

, который вы будете читать «M Times Ten, Rail to the to the

. сила н».

Эта научная запись, когда на нее ссылаются в смысле компьютерной арифметики, называется системой с плавающей запятой. в десятичной системе счисления, но мы также можем использовать экспоненциальное представление для представления чисел из двоичной системы счисления, например:

1,001011 x 2 ⁶

Двоичное число, представленное в научной записи.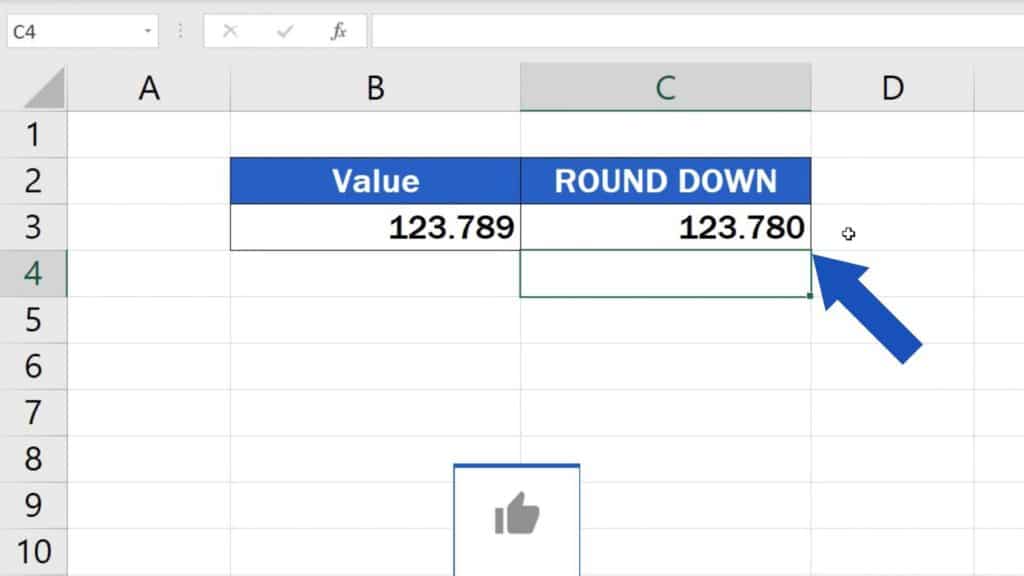 Это формат, в котором хранятся числа с плавающей запятой.

Числа с плавающей запятой — это двоичные числа, записанные в научном формат записи, и именно стандарт IEEE 754 стандартизировал, как эти числа с плавающей запятой будут храниться в памяти.

IEEE 754

 typeof NaN === "number" //true 

 if (typeof num === "number") {
  // сделай что-нибудь
} 

 if (typeof num === "number" && !Number.isNaN(num)) {
  // сделай что-нибудь
} 

 const a = 42 // Это число, хранящееся в памяти как значение с плавающей запятой. 
const b = 0.42 // Это также число, хранящееся в памяти как значение с плавающей запятой.
const c = 4e100 // Это тоже число, и тоже хранится в памяти как значение с плавающей запятой. 

 номера функцийCloseEnoughToEqual(n1, n2) {
  return Math.abs(n1 - n2) < Number.EPSILON
}
вар а = 0,1 + 0,2
вар б = 0,3
numberCloseEnoughToEqual(a, b) // истина
numberCloseEnoughToEqual(0.0000001, 0.0000002) // ложь 

 ;(42). toFixed() // "43"
;(42).toFixed(2) // "43.00"
константное число = 42,49
num.toFixed(1) // "42,6"
num.toFixed(3) // "42.490" 

 ;(1).toFixed() + (0.01).toFixed(1)