Целочисленное деление python – Числа: целые, вещественные, комплексные | Python 3 для начинающих и чайников

Содержание

Числа: целые, вещественные, комплексные | Python 3 для начинающих и чайников

Числа в Python 3: целые, вещественные, комплексные. Работа с числами и операции над ними.

Целые числа (int)

Числа в Python 3 ничем не отличаются от обычных чисел. Они поддерживают набор самых обычных математических операций:

x + y	Сложение
x — y	Вычитание
x * y	Умножение
x / y	Деление
x // y	Получение целой части от деления
x % y	Остаток от деления
-x	Смена знака числа
abs(x)	Модуль числа
divmod(x, y)	Пара (x // y, x % y)
x ** y	Возведение в степень
pow(x, y[, z])	x^y по модулю (если модуль задан)

Также нужно отметить, что целые числа в python 3, в отличие от многих других языков, поддерживают длинную арифметику (однако, это требует больше памяти).

>>> 255 + 34
289
>>> 5 * 2
10
>>> 20 / 3
6.666666666666667
>>> 20 // 3
6
>>> 20 % 3
2
>>> 3 ** 4
81
>>> pow(3, 4)
81
>>> pow(3, 4, 27)
0
>>> 3 ** 150
369988485035126972924700782451696644186473100389722973815184405301748249

Битовые операции

Над целыми числами также можно производить битовые операции

x \| y	Побитовое или
x ^ y	Побитовое исключающее или
x & y	Побитовое и
x << n	Битовый сдвиг влево
x >> y	Битовый сдвиг вправо
~x	Инверсия битов

Дополнительные методы

int.bit_length() — количество бит, необходимых для представления числа в двоичном виде, без учёта знака и лидирующих нулей.

>>> n = -37
>>> bin(n)
'-0b100101'
>>> n.bit_length()
6

int.to_bytes(length, byteorder, *, signed=False) — возвращает строку байтов, представляющих это число.

>>> (1024).to_bytes(2, byteorder='big')
b'\x04\x00'
>>> (1024).to_bytes(10, byteorder='big')
b'\x00\x00\x00\x00\x00\x00\x00\x00\x04\x00'
>>> (-1024).to_bytes(10, byteorder='big', signed=True)
b'\xff\xff\xff\xff\xff\xff\xff\xff\xfc\x00'
>>> x = 1000
>>> x.to_bytes((x.bit_length() // 8) + 1, byteorder='little')
b'\xe8\x03'

classmethod int.from_bytes(bytes, byteorder, *, signed=False) — возвращает число из данной строки байтов.

>>> int.from_bytes(b'\x00\x10', byteorder='big')
16
>>> int.from_bytes(b'\x00\x10', byteorder='little')
4096
>>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=True)
-1024
>>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=False)
64512
>>> int.from_bytes([255, 0, 0], byteorder='big')
16711680

Системы счисления

Те, у кого в школе была информатика, знают, что числа могут быть представлены не только в десятичной системе счисления. К примеру, в компьютере используется двоичный код, и, к примеру, число 19 в двоичной системе счисления будет выглядеть как 10011. Также иногда нужно переводить числа из одной системы счисления в другую. Python для этого предоставляет несколько функций:

int([object], [основание системы счисления]) — преобразование к целому числу в десятичной системе счисления. По умолчанию система счисления десятичная, но можно задать любое основание от 2 до 36 включительно.
bin(x) — преобразование целого числа в двоичную строку.
hex(х) — преобразование целого числа в шестнадцатеричную строку.

oct(х) — преобразование целого числа в восьмеричную строку.

Примеры:

>>> a = int('19') # Переводим строку в число
>>> b = int('19.5')  # Строка не является целым числом
Traceback (most recent call last):
  File "", line 1, in
ValueError: invalid literal for int() with base 10: '19.5'
>>> c = int(19.5)  # Применённая к числу с плавающей точкой, отсекает дробную часть
>>> print(a, c)
19 19
>>> bin(19)
'0b10011'
>>> oct(19)
'0o23'
>>> hex(19)
'0x13'
>>> 0b10011  # Так тоже можно записывать числовые константы
19
>>> int('10011', 2)
19
>>> int('0b10011', 2)
19

Вещественные числа (float)

Вещественные числа поддерживают те же операции, что и целые. Однако (из-за представления чисел в компьютере) вещественные числа неточны, и это может привести к ошибкам:

>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1
0.9999999999999999

Для высокой точности используют другие объекты (например Decimal и Fraction)).

Также вещественные числа не поддерживают длинную арифметику:

>>> a = 3 ** 1000
>>> a + 0.1
Traceback (most recent call last):
  File "", line 1, in
OverflowError: int too large to convert to float

Простенькие примеры работы с числами:

>>> c = 150
>>> d = 12.9
>>> c + d
162.9
>>> p = abs(d - c)  # Модуль числа
>>> print(p)
137.1
>>> round(p)  # Округление
137

Дополнительные методы

float.as_integer_ratio() — пара целых чисел, чьё отношение равно этому числу.

float.is_integer() — является ли значение целым числом.

float.hex() — переводит float в hex (шестнадцатеричную систему счисления).

classmethod float.fromhex(s) — float из шестнадцатеричной строки.

>>> (10.5).hex()
'0x1.5000000000000p+3'
>>> float.fromhex('0x1.5000000000000p+3')
10.5

Помимо стандартных выражений для работы с числами (а в Python их не так уж и много), в составе Python есть несколько полезных модулей.

Модуль math предоставляет более сложные математические функции.

>>> import math
>>> math.pi
3.141592653589793
>>> math.sqrt(85)
9.219544457292887

Модуль random реализует генератор случайных чисел и функции случайного выбора.

>>> import random
>>> random.random()
0.15651968855132303

Комплексные числа (complex)

В Python встроены также и комплексные числа:

>>> x = complex(1, 2)
>>> print(x)
(1+2j)
>>> y = complex(3, 4)
>>> print(y)
(3+4j)
>>> z = x + y
>>> print(x)
(1+2j)
>>> print(z)
(4+6j)
>>> z = x * y
>>> print(z)
(-5+10j)
>>> z = x / y
>>> print(z)
(0.44+0.08j)
>>> print(x.conjugate())  # Сопряжённое число
(1-2j)
>>> print(x.imag)  # Мнимая часть
2.0
>>> print(x.real)  # Действительная часть
1.0
>>> print(x > y)  # Комплексные числа нельзя сравнить
Traceback (most recent call last):
  File "", line 1, in
TypeError: unorderable types: complex() > complex()
>>> print(x == y)  # Но можно проверить на равенство
False
>>> abs(3 + 4j)  # Модуль комплексного числа
5.0
>>> pow(3 + 4j, 2)  # Возведение в степень
(-7+24j)

Также для работы с комплексными числами используется также модуль cmath.

pythonworld.ru

Python | Операции с числами

Операции с числами

Последнее обновление: 20.06.2017

Арифметические операции

Python поддерживает все распространенные арифметические операции:

+

Сложение двух чисел:
```
print(6 + 2)  # 8
```
—

Вычитание двух чисел:
```
print(6 - 2)  # 4
```
*

Умножение двух чисел:
```
print(6 * 2)  # 12
```
/

Деление двух чисел:
```
print(6 / 2)  # 3.0
```
//

Целочисленное деление двух чисел:
```

print(7 / 2)  # 3.5
print(7 // 2)  # 3
```
Данная операция возвращает целочисленный результат деления, отбрасывая дробную часть

Возведение в степень:


print(6 ** 2)  # Возводим число 6 в степень 2. Результат - 36

%

Получение остатка от деления:
```

print(7 % 2)  # Получение остатка от деления числа 7 на 2. Результат - 1
```
В данном случае ближайшее число к 7, которое делится на 2 без остатка, это 6. Поэтому остаток от деления равен 7 — 6 = 1

При последовательном использовании нескольких арифметических операций их выполнение производится в соответствии с их приоритетом. В начале выполняются операции с большим приоритетом. Приоритеты операций в порядке убывания приведены в следующей таблице.

Операции	Направление
**	Слева направо
* / // %	Слева направо
+ —	Слева направо

Пусть у нас выполняется следующее выражение:


number = 3 + 4 * 5 ** 2 + 7
print(number)  # 110

Здесь начале выполняется возведение в степень (5 ** 2) как операция с большим приоритетом, далее результат умножается на 4 (25 * 4), затем происходит сложение (3 + 100) и далее опять идет сложение (103 + 7).

Чтобы переопределить порядок операций, можно использовать скобки:


number = (3 + 4) * (5 ** 2 + 7)
print(number)  # 224

Следует отметить, что в арифметических операциях могут принимать участие как целые, так и дробные числа. Если в одной операции участвует целое число (int) и число с плавающей точкой (float), то целое число приводится к типу float.

Арифметические операции с присвоением

Ряд специальных операций позволяют использовать присвоить результат операции первому операнду:

+=

Присвоение результата сложения
-=

Присвоение результата вычитания
*=

Присвоение результата умножения
/=

Присвоение результата от деления
//=

Присвоение результата целочисленного деления
**=

Присвоение степени числа
%=

Присвоение остатка от деления

Примеры операций:


number = 10
number += 5
print(number)  # 15

number -= 3
print(number)  # 12

number *= 4
print(number)  # 48

Функции преобразования чисел

Ряд встроенных функций в Python позволяют работать с числами. В частности, функции int() и float() позволяют привести значение к типу int и float соответственно.

Например, пусть у нас будет следующий код:


first_number = "2"
second_number = 3
third_number = first_number + second_number

Мы ожидаем, что «2» + 3 будет равно 5. Однако этот код сгенерирует исключение, так как первое число на самом деле представляет строку. И чтобы все заработало как надо, необходимо привести строку к числу с помощью функции int():


first_number = "2"
second_number = 3
third_number = int(first_number) + second_number
print(third_number)	# 5

Аналогичным образом действует функция float(), которая преобразует в число с плавающей точкой. Но вообще с дробными числами надо учитывать, что результат операций с ними может быть не совсем точным. Например:


first_number = 2.0001
second_number = 5
third_number = first_number / second_number
print(third_number)	# 0.40002000000000004

В данном случае мы ожидаем получить число 0.40002, однако в конце через ряд нулей появляется еще какая-то четверка. Или еще одно выражение:

print(2.0001 + 0.1)  # 2.1001000000000003

В этот случае для округления результата мы можем использовать функцию round():


first_number = 2.0001
second_number = 0.1
third_number = first_number + second_number
print(round(third_number, 4))  # 2.1001

Первый параметр функции — округляемое число, а второй — сколько знаков после запятой должно содержать получаемое число.

Представление числа

При обычном определении числовой переменной она получает значение в десятичной системе. Но кроме десятичной в Python мы можем использовать двоичную, восьмеричную и шестнадцатеричную системы.

Для определения числа в двоичной системе перед его значением ставится 0 и префикс b:

x = 0b101 	# 101 в двоичной системе равно 5

Для определения числа в восьмеричной системе перед его значением ставится 0 и префикс o:

a = 0o11 	# 11 в восьмеричной системе равно 9

Для определения числа в шестнадцатеричной системе перед его значением ставится 0 и префикс x:

y = 0x0a		# a в шестнадцатеричной системе равно 10

И с числами в других системах измерения также можно проводить арифметические операции:


x = 0b101	# 5
y = 0x0a	# 10
z = x + y	# 15
print("{0} in binary {0:08b}   in hex {0:02x} in octal {0:02o}".format(z))

Для вывода числа в различных системах исчисления используются функция format, которая вызывается у строки. В эту строку передаются различные форматы. Для двоичной системы «{0:08b}», где число 8 указывает, сколько знаков должно быть в записи числа. Если знаков указано больше, чем требуется для числа, то ненужные позиции заполняются нулями. Для шестнадцатеричной системы применяется формат «{0:02x}». И здесь все аналогично — запись числа состоит из двух знаков, если один знак не нужен, то вместо него вставляется ноль. А для записи в восьмеричной системе испольуется формат «{0:02o}».

Результат работы скрипта:


15 in binary 00001111   in hex 0f   in octal 17

metanit.com

Интерактивный учебник языка Python

1. Целочисленная арифметика

Для целых чисел определены операции +, -, * и **. Операция деления / для целых чисел возвращает вещественное число (значение типа float). Также функция возведения в степень возвращает значение типа float, если показатель степени — отрицательное число.

Но есть и специальная операция целочисленного деления, выполняющегося с отбрасыванием дробной части, которая обозначается // (она соответствует операции div в Паскале). Она возвращает целое число: целую часть частного. Другая близкая ей операция − это операция взятия остатка от деления, обозначаемая % (она соответствует операции mod в Паскале). Например:

print(17 / 3)   # выведет 5.66666666667
print(17 // 3)  # выведет 5
print(17 % 3)   # выведет 2

2. Действительные числа

В этом разделе речь пойдет о действительных числах, имеющих тип float.

Обратите внимание, что если вы хотите считать с клавиатуры действительное число, то результат, возращаемый функцией input() необходимо преобразовывать к типу float:

1.492

x = float(input())
print(x)

Действительные (вещественные) числа представляются в виде чисел с десятичной точкой (а не запятой, как принято при записи десятичных дробей в русских текстах). Для записи очень больших или очень маленьких по модулю чисел используется так называемая запись «с плавающей точкой» (также называемая «научная» запись). В этом случае число представляется в виде некоторой десятичной дроби, называемой мантиссой, умноженной на целочисленную степень десяти (порядок). Например, расстояние от Земли до Солнца равно 1.496·10¹¹, а масса молекулы воды 2.99·10^-23.

Числа с плавающей точкой в программах на языке Питон, а также при вводе и выводе записываются так: сначала пишется мантисса, затем пишется буква e, затем пишется порядок. Пробелы внутри этой записи не ставятся. Например, указанные выше константы можно записать в виде 1.496e11 и 2.99e-23. Перед самим числом также может стоять знак минус.

Напомним, что результатом операции деления / всегда является действительное число (float), в то время как результатом операции // является целое число (int).

Преобразование действительных чисел к целому производится с округлением в сторону нуля, то есть int(1.7) == 1, int(-1.7) == -1.

3. Библиотека math

Для проведения вычислений с действительными числами язык Питон содержит много дополнительных функций, собранных в библиотеку (модуль), которая называется math.

Для использования этих функций в начале программы необходимо подключить математическую библиотеку, что делается командой

import math

Например, пусть мы хотим округлять вещественные числа до ближайшего целого числа вверх. Соответствующая функция ceil от одного аргумента вызывается, например, так: math.ceil(x) (то есть явно указывается, что из модуля math используется функция ceil). Вместо числа x может быть любое число, переменная или выражение. Функция возращает значение, которое можно вывести на экран, присвоить другой переменной или использовать в выражении:

import math

x = math.ceil(4.2)
y = math.ceil(4.8)
print(x)
print(y)

Другой способ использовать функции из библиотеки math, при котором не нужно будет при каждом использовании функции из модуля math указывать название этого модуля, выглядит так:

	from math import ceil
 
x = 7 / 2
y = ceil(x)
print(y)
или так:	from math import *
 
x = 7 / 2
y = ceil(x)
print(y)
Ниже приведен список основных функций модуля math. Более подробное описание
этих функций можно найти на сайте с документацией языка Питон.
Некоторые из перечисленных функций (int, round, abs)
являются стандартными и не требуют подключения модуля math для использования.
Функция Описание
Округление
int(x) Округляет число в сторону нуля. Это стандартная функция, для ее использования не нужно подключать
 модуль math.
round(x) Округляет число до ближайшего целого. Если дробная часть числа равна 0.5, то число округляется 
 до ближайшего четного числа.
pythontutor.ru
Как нам получить остаток от деления в Python 3?
Что представляет собой программа? Код и числа. Необходимые операции для чисел являются важным аспектом в программировании на любом языке. Какие же они бывают эти числа? Целочисленные, вещественные и комплексные. Для целых определены операции + , — , * , **. Для того чтобы получить остаток от деления Python и получить вещественное число, мы присваиваем знак \.
Из этой статьи вы узнаете:
Целые числа (int)
Вещественные числа (float)
Комплексные числа (из высшей математики)
Ребят, всем привет. Сегодня мы с вами поговорим о важной детали в программировании, о числах и взаимодействиях с ними.
Я открыл небольшой раздел «Примеры программ». В большей степени для себя. Так как хочу хранить в памяти как можно больше информации по строению кода. Для того чтобы быстро вспомнить, я решил выкладывать в ленте куски кода и примеры ПО.
Так что пользуйтесь, друзья.
Из истории. В V веке в Индии появилась система записи, которую мы знаем как арабские цифры и активно используем сейчас. Это был набор из 9 цифр от 1 до 9. Каждая цифра записывалась так, чтобы ей соответствовало количество углов. Например, в цифре 1 — один угол, в цифре 2 — два угла, в цифре 3 — три. И так до 9. Нуля еще не существовало, он появился позже. Вместо него просто оставляли пустое место.
Целые числа (int)
С целыми числами я думаю все понятно, обычные арифметические операции, остаток от деления, модуль числа и возведение в степень.
x + y Сложение
x — y Вычитание
x * y Умножение
x / y Деление
x // y Получение целой части от деления
x % y Остаток от деления
-x Смена знака числа
abs (x) Модуль числа
divmod (x, y) Пара (x // y, x % y)
x ** y Возведение в степень
pow (x, y[, z]) x^y по модулю (если модуль задан)
В среде разработки Arduino практически всё то же самое.
Вот то, что даст нам интерпретатор:
>>> 255 + 34 289 >>> 5 * 2 10 >>> 20 / 3 6.666666666666667 >>> 20 // 3 6 >>> 20 % 3 2 >>> 3 ** 4 81 >>> pow(3, 4) 81 >>> pow(3, 4, 27) 0 >>> 3 ** 150 369988485035126972924700782451696644186473100389722973815184405301748249
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 >>> 255 + 34
289
>>> 5 * 2
10
>>> 20 / 3
6.666666666666667
>>> 20 // 3
6
>>> 20 % 3
2
>>> 3 ** 4
81
>>> pow(3, 4)
81
>>> pow(3, 4, 27)
0
>>> 3 ** 150
369988485035126972924700782451696644186473100389722973815184405301748249
Вещественные числа (float)
То же самое что и целые, но имеют цифры после запятой. Мы можем манипулировать десятыми, сотыми и тысячными.
Сразу оговорюсь, с ними надо быть очень аккуратными и внимательными, так как такие числа могут давать погрешность и накопить ошибку.
Ответ интерпретатора:
>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 0.9999999999999999
>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1
0.9999999999999999
Слишком мега длинные числа интерпретатор не поддерживает.
>>> a = 3 ** 1000 >>> a + 0.1 Traceback (most recent call last):  File «», line 1, in OverflowError: int too large to convert to float
>>> a = 3 ** 1000
>>> a + 0.1
Traceback (most recent call last):
  File «», line 1, in
OverflowError: int too large to convert to float
Примеры с числами:
>>> c = 150 >>> d = 12.9 >>> c + d 162.9 >>> p = abs(d — c) # Модуль числа >>> print(p) 137.1 >>> round(p) # Округление 137
>>> c = 150
>>> d = 12.9
>>> c + d
162.9
>>> p = abs(d — c)  # Модуль числа
>>> print(p)
137.1
>>> round(p)  # Округление
137
Для работы с числами есть ещё полезные модули, помогающие в расчетах.
Модуль math предоставляет более сложные математические функции. Такие как квадратный корень, логарифмы, пи и т.д.
>>> import math >>> math.pi 3.141592653589793 >>> math.sqrt(85) 9.219544457292887
>>> import math
>>> math.pi
3.141592653589793
>>> math.sqrt(85)
9.219544457292887
И можно замутить любое случайное число с помощью модуля random. Я не до конца понимаю его значение, может кто использовал??
>>> import random >>> random.random() 0.15651968855132303
>>> import random
>>> random.random()
0.15651968855132303
И наконец…
Комплексные числа (из высшей математики)
В общих чертах код будет примерно таким:
>>> x = complex(1, 2) >>> print(x) (1+2j) >>> y = complex(3, 4) >>> print(y) (3+4j) >>> z = x + y >>> print(x) (1+2j) >>> print(z) (4+6j) >>> z = x * y >>> print(z) (-5+10j) >>> z = x / y >>> print(z) (0.44+0.08j) >>> print(x.conjugate()) # Сопряжённое число (1-2j) >>> print(x.imag) # Мнимая часть 2.0 >>> print(x.real) # Действительная часть 1.0 >>> print(x > y) # Комплексные числа нельзя сравнить Traceback (most recent call last):  File «», line 1, in TypeError: unorderable types: complex() > complex() >>> print(x == y) # Но можно проверить на равенство False >>> abs(3 + 4j) # Модуль комплексного числа 5.0 >>> pow(3 + 4j, 2) # Возведение в степень (-7+24j)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 >>> x = complex(1, 2)
>>> print(x)
(1+2j)
>>> y = complex(3, 4)
>>> print(y)
(3+4j)
>>> z = x + y
>>> print(x)
(1+2j)
>>> print(z)
(4+6j)
>>> z = x * y
>>> print(z)
(-5+10j)
>>> z = x / y
>>> print(z)
(0.44+0.08j)
>>> print(x.conjugate())  # Сопряжённое число
(1-2j)
>>> print(x.imag)  # Мнимая часть
2.0
>>> print(x.real)  # Действительная часть
1.0
>>> print(x > y)  # Комплексные числа нельзя сравнить
Traceback (most recent call last):
  File «», line 1, in
TypeError: unorderable types: complex() > complex()
>>> print(x == y)  # Но можно проверить на равенство
False
>>> abs(3 + 4j)  # Модуль комплексного числа
5.0
>>> pow(3 + 4j, 2)  # Возведение в степень
(-7+24j)
Если кто знает, скажите пожалуйста, в каких задачах применяются такие числа?
Подписывайтесь на новости блога. Если есть какие-то вопросы и предложения, вы знаете куда писать.
С уважением, ваш Гридин Семён
kip-world.ru
Как найти в Python остаток от деления?
Python – простой, современный язык для написания кода. Он обладает мощными библиотеками, способными вычислить любое выражение. Python выступает основным конкурентом для Matlab и Octave. Запустив в интерактивном режиме Python, остаток от деления пользователь сможет найти без труда. Но это еще не все! «Питон» может выступить мощным калькулятором.
Понятие оператора
Чтобы без труда найти в Python остаток от деления, нужно разобраться с некоторыми определениями. Оператор – знак или строка, позволяющие произвести математическое, побитовое, логическое и другое вычисление. Выражения или числа, вводимые пользователем, чтобы найти в Python 3 остаток от деления, тождественность сочетания или сравнения, называются операндами.
Разделяют следующие виды операторов:
арифметические;
побитовые;
логические;
операторы присваивания;
сравнения;
членства;
тождественности.
Проще говоря, в примере «15 — 5» оператором является знак «–», операндами – 15 и 5. Это арифметическая операция с целыми числами. Если взять к рассмотрению выражение «True and True», то оператором здесь выступает «and», а операндами – «True» и «True». Этот пример можно отнести к логическому типу.
Целые и вещественные числа. Математические операции и вывод результата
Если рассматривать математические операции над целыми и дробными числами, то операторами выступают +, -, *, /, **, //, %. С первыми тремя всё понятно. Они обозначают, соответственно, сложение, вычитание, умножение. Оператор «**» указывает на необходимость возведения в степень.
Знаки одинарного (/) и двойного (//) деления отличаются. Если первый выдает в решении вещественное число, то второй необходим для нахождения целой части от деления. К примеру, 9 // 4 = 2. Этот оператор соответствует функции div в Turbo Pascal. Но есть закономерность. Знак «/» выведет целое число как результат, если и делитель, и делимое – также целые. Чтобы найти в Python остаток от деления, нужно воспользоваться оператором «%». По аналогии с тем же «Турбо Паскалем» «%» сопоставим с функцией mod. К примеру, 9%2 = 1, т.е. в Python остаток от деления в данном случае равняется 1. Рассмотрим еще примеры.
Чтобы произвести деление без остатка, Python предлагает воспользоваться функцией divmod(х,у). В данном случае х – делимое, у – делитель. Для выражения divmod (9,3) программа выдаст следующий результат (3,0). Это означает, что целая часть от деления равняется 3, а остаток – 0.
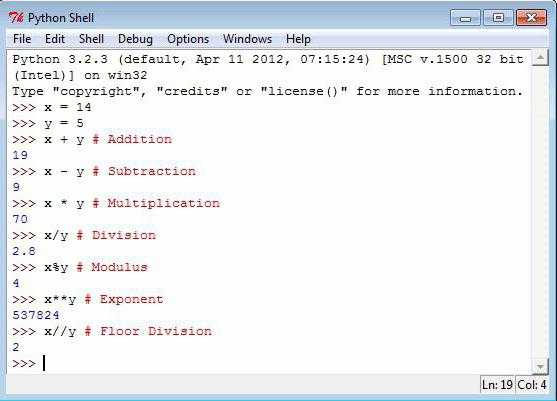
Математические операции можно выполнять без присваивания значения переменной. Тогда результат выдается автоматически. Если же код содержит присваивание переменной, то вывести результат на экран можно посредством оператора print.
Модуль math
Для удобства пользователей разработчики предлагают мощный модуль math, способный работать с любыми типами чисел и выполнять дополнительные функции.
Чтобы подключить библиотеку, нужно прописать в начале программного кода следующую строку: import math. Такая команда позволит подгрузить в программный код все функции, имеющиеся в модуле math. Тогда для подключения определенного блока из библиотеки нужно постоянно прописывать его. К примеру, x = math.ceil(5.6).
Если в программе будет часто использоваться один и тот же блок, то можно импортировать только его. К примеру, нужно произвести ряд округлений до ближайшего целого числа в большую сторону. Тогда код прописывается следующим образом: from math import ceil или from math import *. В обоих случаях дальнейший код по округлению результата не изменится.
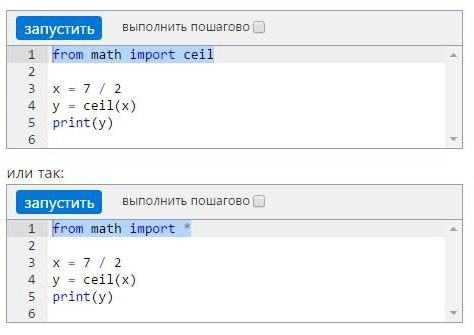
Стандартные функции арифметики в Python
Чтобы вычислить в Python остаток от целочисленного деления, не всегда нужно подгружать библиотеку math. Некоторые функции являются встроенными.
Встроенные функции Их назначение Примеры
 int(x)  Превращает вещественное число в целое, т.е.   дробная часть «отсекается».  int(5.3) >>> 5
 int(5.6) >>>5
 int(5.987) >>> 5
 round(x)  Происходит округление выражения до   ближайшего целого.  round(5.4) >>>5.0
 round(5.7) >>>6.0
 round(5.5) >>>6.0
 round(5.987)   >>>6.0
 round(x, n)  Используется для округления дробной части   до n знаков после запятой  round(5.8776,2)   >>>
 5.88
 round(5.9876,3)   >>>
 5.988
 abs(x)  Находит модуль выражения  abs(-7) >>>7
 abs(7.8) >>>7.8
 abs(-66.55)   >>>66.55
Функции, для которых необходимо подключение библиотеки (нужно изначально вписать from math import *), можно увидеть в следующей таблице.
Функции Их назначение
 ceil(x)  Функция необходима для округления числа до большего   целого («вверх»)
 floor(x)  Функция требуется, чтобы округлить число до меньшего   целого («вниз»)
 sqrt(x)  Вычисляет корень из числа
 log(x)  Необходима для нахождения логарифма. Если указать   основание, то и вычисление будет соответствующим.
 e  Выводит основание натурального логарифма
 sin(x)  Вычисление тригонометрических функций, где х выражен в   радианах
 cos(x)
 tan(x)
 asin(x)
 acos(x)
 atan(x)
 atan2(x,y)  Находит полярный угол точки, координаты которой задаются   х  и у
 degrees(x)  Необходима для преобразования угла из радиан в градусы
 radians(x)  Функция, необходимая для преобразования угла, заданного в   градусах, в радианы
 pi  Выводит значение константы π
В качестве примера ниже приведен код с использованием математических операторов.
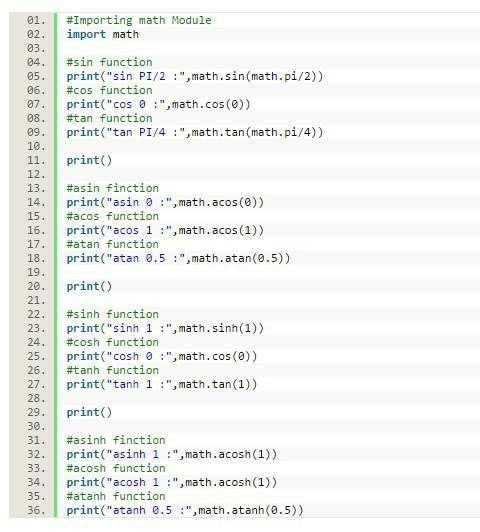
Результат выведен следующим образом.
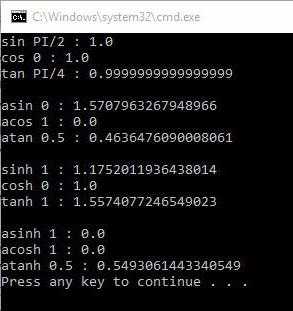
В модуле math гораздо больше функций. Здесь указаны наиболее встречающиеся.
fb.ru
Как выполнять математические действия с помощью операторов Python 3
 446В этом руководстве мы будем работать с двумя типами данных в Python – целыми числами (integer) и числами с плавающей точкой (floats):
Целые – числа без дробной части, которые могут быть положительными, отрицательными или нулём (…, -1, 0, 1, …).
С плавающей точкой – это числа, содержащие десятичную точку (например, 9.0 или -2.25).
В этой статье будут описаны операции с числовыми типами данных в Python.
 Оператор – это символ, которая обозначает операцию. Например, в математике знак плюса или + – это оператор сложения.
Мы рассмотрим схожие операторы, которые перешли в Python из математики. Но другие операторы специфичны именно для программирования.
Ниже представлена таблица с кратким обзором математических операторов, доступных в Python.
Операция Возвращаемое значение
x + y Сумма x и y.
x — y Разность x и y.
-x Изменение знака x.
+x Тождественность x.
x * y Произведение x и y.
x / y Частное от деления x на y.
x // y Частное от целочисленного деления x на y.
x % y Остаток от деления x / y.
x ** y x в степени y.
В Python операторы суммы и разности выполняют те же операции, что и в математике. Поэтому вы можете использовать этот язык программирования как калькулятор.
Рассмотрим некоторые примеры. Начнём с целых чисел:
Вывод
Вместо передачи целых чисел напрямую в функцию print мы можем инициализировать переменные для этих значений:
a = 88
b = 103
print(a + b)
Вывод
Целые числа могут быть как положительными, так и отрицательными. Поэтому можно добавлять отрицательные числа к положительным:
c = -36
d = 25
print(c + d)
Вывод
Прибавление работает аналогично и с числами с плавающей запятой:
e = 5.5
f = 2.5
print(e + f)
Вывод
Синтаксис разности тот же, что и для прибавления, за исключением того, что вместо оператора сложения (+) необходимо использовать оператор вычитания (-):
g = 75.67
h = 32
print(g - h)
Вывод
В этом примере мы вычитаем целое число из числа с плавающей точкой. Python возвратит число с плавающей точкой, если хотя бы одно из чисел выражения является числом с плавающей точкой.
Унарное математическое выражение состоит из одного элемента. В Python знаки плюса и минуса могут быть использованы как единичный оператор, чтобы вернуть тождественное значение (+) или сменить знак числа (-).
Знак плюса означает тождественное значение. Мы можем использовать его с положительными значениями:
Вывод
 
Когда мы используем знак плюса с отрицательным значением, он также вернёт значение тождественное данному. В этом случае он вернёт отрицательное значение:
Вывод
 
При использовании с отрицательным значением знак плюса возвращает то же отрицательное значение.
Минус (в отличие от знака плюса) изменяет знак числа. Поэтому при передаче положительного числа мы получим отрицательное значение:
Вывод
А когда мы используем минус в качестве унарного оператора с отрицательным значением, будет возвращено положительное число:
Вывод
Унарные арифметические операторы возвращают тождественное значение в случае с +i, или противоположное по знаку число в случае с -i.
Оператор, которые мы будем использовать в Python для умножения «*», а для деления «/». Пример умножения двух чисел с плавающей точкой в Python:
k = 100.1
l = 10.1
print(k * l)
Вывод
Когда вы выполняете деление в Python 3, частное всегда будет числом с плавающей точкой, даже если вы используете два целых числа:
m = 80
n = 5
print(m / n)
Вывод
Это одно из наиболее существенных отличий Python 2 от Python 3. В Python 3 результатом будет дробное число. Поэтому, когда вы используете оператора «/» для деления 11 на 2, возвращено будет 5.5. В Python 2 возвращаемое значение деления 11 / 2 было 5.
В Python 2 оператор «/» выполняет целочисленное деление, где частное x, а возвращаемое число – это наибольшее целое число, меньшее или равное x. Если вы выполните пример, приведённый выше, в Python 2, то получите 16 без десятичной точки.
В Python 3 для целочисленного деления можно использовать оператор «//». Выражение 100 // 40 вернёт значение 2.
Оператор % используется для деления по модулю, и возвращает остаток от деления, а не частное. Это полезно, например, для нахождения множителей числа.
Пример деления по модулю (с остатком):
o = 85
p = 15
print(o % p)
Вывод
 
В этом примере 85 делится на 15. Результат – 5 с остатком 10. Значение 10 выводится, поскольку оператор возвращает остаток от деления.
Если мы используем два числа с плавающей точкой для деления по модулю, число с плавающей точкой будет возвращено в качестве остатка:
q = 36.0
r = 6.0
print(o % p)
Вывод
 
В приведенном выше примере 36.0 делится на 6.0 без остатка, поэтому возвращается значение 0.0.
Оператор «**» в Python используется для возведения числа, расположенного слева от оператора в степень, указанную справа. То есть, в выражении 5 ** 3,  число 5 возводится в третью степень.
В математике часто используется выражение 5³. То есть 5 умножается на себя три раза. В Python мы получим тот же результат (125) выполнив 5 ** 3 или 5 * 5 * 5.
Пример с переменными:
s = 52.25
t = 7
print(s ** t)
1063173305051.292
Возведение числа с плавающей точкой 52.25 в степень 7 с помощью оператора ** приводит к выводу большого числа с плавающей точкой.
В Python операторы выполняются в порядке приоритета. Посмотрим на следующее выражение:
Умножение выполняется первым. Поэтому, если мы вызовем метод print(u), то получим следующее значение:
Вывод
Это потому, что 10 * 5 равно 50, а затем мы прибавляем 10, чтобы получить 60.
Если нужно было сложить 10 и 10, и умножить сумму на 5, то пришлось бы использовать скобки, как в математике:
u = (10 + 10) * 5
print(u)
Вывод
Оператор «=» присваивает значение, расположенное справа, переменной слева. Например, v = 23 присваивает значение числа 23 переменной v.
В программировании часто используют составные операторы присваивания. Они соединяют арифметический оператор с оператором «=». Поэтому для сложения мы используем оператор «+» с оператором «=», чтобы получить составной оператор «+=». Пример:
Вывод
Сначала мы задаём переменной w значение 5. Затем используем составной оператор присваивания +=, чтобы прибавить число справа, к переменной, расположенной слева, и присвоить результат переменной w.
Составные операторы присваивания часто используются в циклах for:
for x in range (0, 7):
    x *= 2
    print(x)
Вывод
При помощи for можно автоматизировать процесс использования оператора «*=». Он умножает переменную w на число 2, а затем присваивает полученный результат переменной w для следующей итерации цикла.
В Python предусмотрен составной оператор присваивания для каждой арифметической операции:
y += 1          # добавить число и присвоить результат
y -= 1          # отнять число и присвоить результат
y *= 2          # умножить на число и присвоить результат
y /= 3          # разделить на число и присвоить результат
y // = 5        # разделить без остатка на число и присвоить результат
y **= 2         # возвести в степень и присвоить результат
y %= 3          # вернуть остаток от деления и присвоить результат
Составные операторы присваивания полезны в тех случаях, когда переменная должна увеличиваться или уменьшаться с помощью инкремента. А также когда необходимо автоматизировать некоторый процесс в создаваемой программе.
В этой статье рассмотрены операторы, которые используются для математических операций с целыми и дробными десятичными числами.
 
 
 
 
Данная публикация представляет собой перевод статьи «How To Do Math in Python 3 with Operators» , подготовленной дружной командой проекта Интернет-технологии.ру
www.internet-technologies.ru
Использование целочисленного деления в Python — python
 Python2.7 автоматически использует подразделение / operator как целое (целое число), которое всегда будет производить целое число.
 Например:
 1/2 = 0
 3/4 = 0
 100/30 = 3
 Чтобы сделать float-разделение, вы должны иметь одно или оба значения как тип float.
 Как это:
Area = 1.0/2 * Base * Height # 1.0 is a float type, 1 is an integer type
 Результаты не то, что вы ожидали, так как Python оценивает выражения, используя целочисленное деление и порядок операций.
 Если вы оцениваете 16 * 12/2 в Python, Python интерпретирует это как (16 * 12)/2 или 192/2 = 96
 Если вы оцениваете 1/2 * 16 * 12, Python интерпретирует это как (((1/2) * 16) * 12)= (0 * 16) * 12
 Другие примеры:
  Area = Base * Height * (1.0/2.0)
 Python оценивает (1.0/2.0) первое это время, поскольку порядок операций диктует, что круглые скобки вычисляются в первую очередь. А так как 1.0 и 2.0 — это float, а не целые числа, Python отлично справляется с выполнением float-деления. Вы получите следующее:
Base * Height * (0.5)
= 192 * 0.5
= 96
 который дает вам то, что вы ожидаете.
 В противоположность:
Base * Height * (1/2)
= Base * Height * (0) # since 1/2 rounds down to 0 in integer division
= 192 * 0
= 0
 Альтернативное решение от Carpetsmoker:
from __future__ import division
 Эта строка даст вам поведение Python3.x в программе Python2.x, а Python3.x принимает / operator как float-деление, даже если оба значения являются целыми типами. Таким образом, после его импорта / становится оператором с плавающим делением.
>>> from __future__ import division
>>> 1/2
0.5
qaru.site
No related posts.

Целочисленное деление python – Числа: целые, вещественные, комплексные | Python 3 для начинающих и чайников

Числа: целые, вещественные, комплексные | Python 3 для начинающих и чайников

Целые числа (int)

Битовые операции

Дополнительные методы

Системы счисления

Вещественные числа (float)

Дополнительные методы

Комплексные числа (complex)

Python | Операции с числами

Операции с числами

Арифметические операции

Арифметические операции с присвоением

Функции преобразования чисел

Представление числа

Интерактивный учебник языка Python

1. Целочисленная арифметика

2. Действительные числа

3. Библиотека math

Как нам получить остаток от деления в Python 3?

Целые числа (int)

Вещественные числа (float)

Комплексные числа (из высшей математики)

Как найти в Python остаток от деления?

Понятие оператора

Целые и вещественные числа. Математические операции и вывод результата

Модуль math

Стандартные функции арифметики в Python

Как выполнять математические действия с помощью операторов Python 3

Использование целочисленного деления в Python — python

Добавить комментарий Отменить ответ

Рубрики

Рубрики

Функция	Описание
Округление
`int(x)`	Округляет число в сторону нуля. Это стандартная функция, для ее использования не нужно подключать модуль `math`.
`round(x)`	Округляет число до ближайшего целого. Если дробная часть числа равна 0.5, то число округляется до ближайшего четного числа.

Встроенные функции	Их назначение	Примеры
int(x)	Превращает вещественное число в целое, т.е. дробная часть «отсекается».	int(5.3) >>> 5 int(5.6) >>>5 int(5.987) >>> 5
round(x)	Происходит округление выражения до ближайшего целого.	round(5.4) >>>5.0 round(5.7) >>>6.0 round(5.5) >>>6.0 round(5.987) >>>6.0
round(x, n)	Используется для округления дробной части до n знаков после запятой	round(5.8776,2) >>> 5.88 round(5.9876,3) >>> 5.988
abs(x)	Находит модуль выражения	abs(-7) >>>7 abs(7.8) >>>7.8 abs(-66.55) >>>66.55

Функции	Их назначение
ceil(x)	Функция необходима для округления числа до большего целого («вверх»)
floor(x)	Функция требуется, чтобы округлить число до меньшего целого («вниз»)
sqrt(x)	Вычисляет корень из числа
log(x)	Необходима для нахождения логарифма. Если указать основание, то и вычисление будет соответствующим.
e	Выводит основание натурального логарифма
sin(x)	Вычисление тригонометрических функций, где х выражен в радианах
cos(x)
tan(x)
asin(x)
acos(x)
atan(x)
atan2(x,y)	Находит полярный угол точки, координаты которой задаются х и у
degrees(x)	Необходима для преобразования угла из радиан в градусы
radians(x)	Функция, необходимая для преобразования угла, заданного в градусах, в радианы
pi	Выводит значение константы π

Операция	Возвращаемое значение
x + y	Сумма x и y.
x — y	Разность x и y.
-x	Изменение знака x.
+x	Тождественность x.
x * y	Произведение x и y.
x / y	Частное от деления x на y.
x // y	Частное от целочисленного деления x на y.
x % y	Остаток от деления x / y.
x ** y	x в степени y.