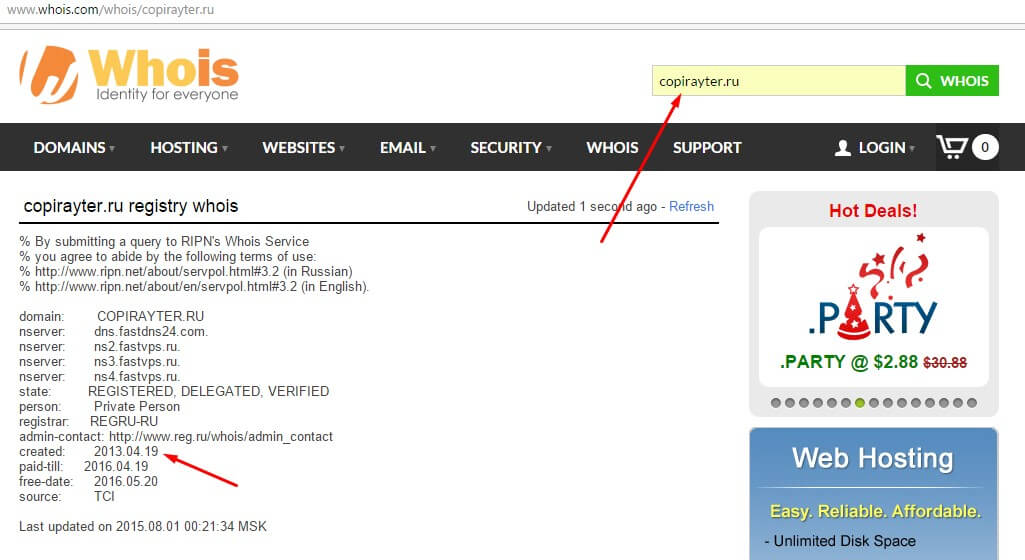
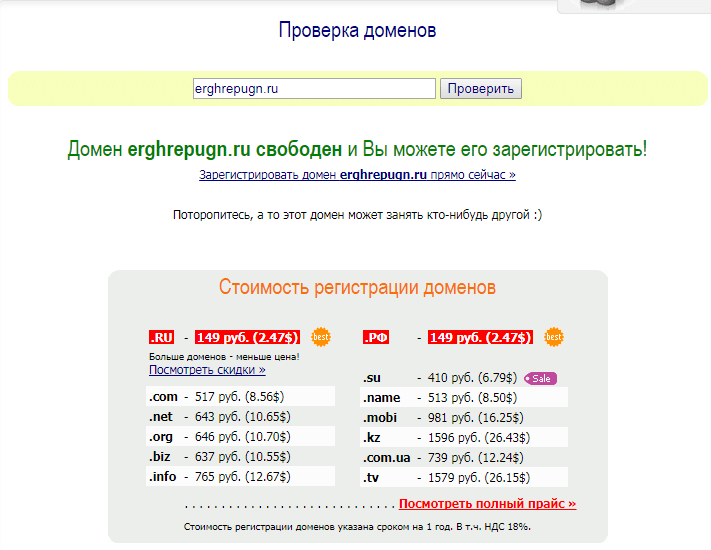
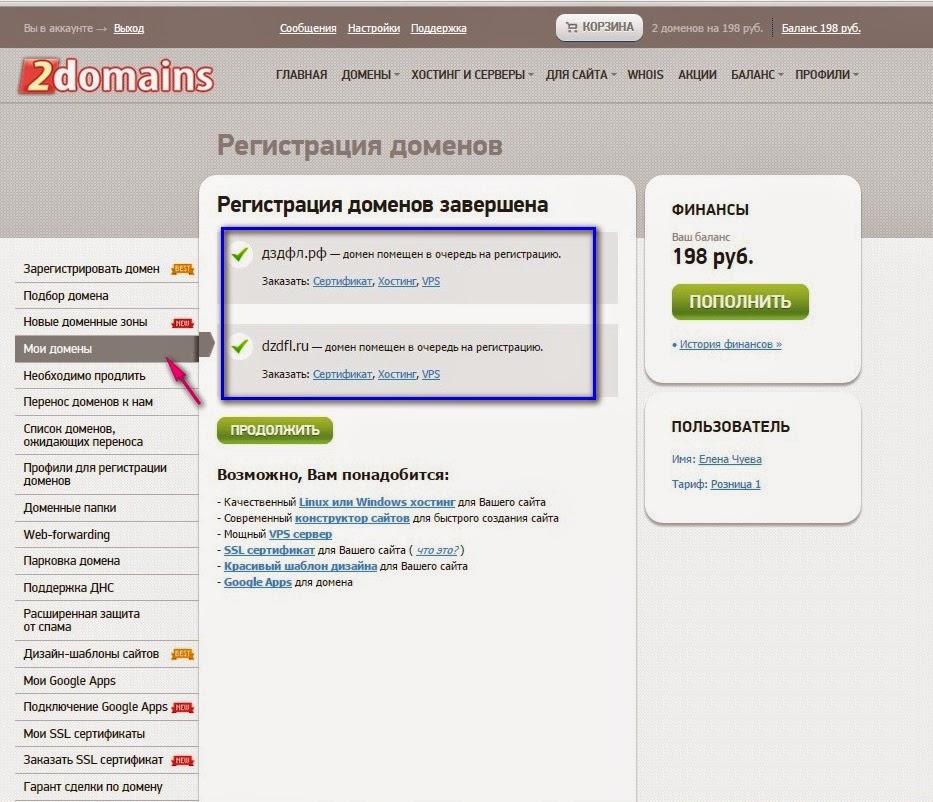
Whois сервис домена
Whois сервис — это сетевой протокол, который позволяет узнать основные данные о доменном имени (кто администратор и регистратор, срок регистрации и т.п.). Название происходит от английской фразы «who is» — «кто это».
Whois 🔎 — что это за услуга?
Протокол принадлежит ICANN — корпорации по управлению доменными именами и IP-адресам (ключевой регулятор доменной индустрии), которая аккредитует всех международных регистраторов. ICANN обеспечивает открытый доступ к данным Whois, а значит регистраторы обязаны делать общедоступной информацию о каждом новом зарегистрированном домене. В результате посмотреть её онлайн может каждый.
Единой базы зарегистрированных доменов не существует, поэтому протокол Whois агрегирует данные разных регистраторов. Компания REG.RU представляет свой сервис поиска данных о доменах Whois.
Для чего нужен Whois
С помощью Whois service можно увидеть сведения о домене, проверить IP-адрес сайта, узнать возраст домена и регистратора, посмотреть — чей домен и сайт, а также проверить свободные домены и многое другое.
- имя регистратора
- администратор сайта (может быть указан или скрыт, в зависимости от доменной зоны)
- срок, когда у домена истекает регистрация
- способы связи с администратором, если контактные данные открыты
- DNS-серверы
Так каждому становится доступна обширная информация о домене и сайте. Например, можно узнать владельца и посмотреть возраст домена. Но если о первом пункте скажет дата регистрации домена или создания сайта, то со вторым всё не так просто, так как владелец может воспользоваться услугой скрытия данных. Либо данные владельца могут быть скрыты согласно правилам доменной зоны. И тогда понять, кто хозяин сайта — невозможно.
Если нужно найти информацию о сайте по IP-адресу сайта, а не по домену, то следует воспользоваться Whois IP address service. В плане возможностей он абсолютно идентичен обычному Who ip.
Не многие знают, что такое простое действие, как проверка в Whois сервисе играет важную роль в информационной безопасности и помогает выявлять сайты-однодневки, фишинговые и прочие ресурсы, где мошенники могут украсть деньги или персональные данные пользователей. Если вы получили письмо с подозрительной ссылкой или попали на сомнительный ресурс — проверьте дату регистрации домена. Если информация о домене говорит о том, что адрес создан несколько дней, недель или месяцев назад — скорее всего это мошеннический ресурс.
Если вы получили письмо с подозрительной ссылкой или попали на сомнительный ресурс — проверьте дату регистрации домена. Если информация о домене говорит о том, что адрес создан несколько дней, недель или месяцев назад — скорее всего это мошеннический ресурс.
Как использовать сервис проверки домена
Проверить домен — очень просто. Нужно лишь ввести доменное имя или IP-адрес, а затем дождаться, когда система выведет на экран информацию о сайте. Строки с данными могут отличаться, в зависимости от регистраторов и доменных зон. Основные параметры:
- Domain Name Servers: Whois предоставляет сведения о DNS.
- State: актуальный статус домена.
- Person: если доменом владеет физлицо, то здесь будет информация о его администраторе (в некоторых доменных зонах она может быть скрыта).
- Org: если именем владеет юрлицо, то отобразится информация об организации.
- Registrar: компания, в которой зарегистрирован домен (регистратор).

- Admin-contact: контакты администратора.
- Created: дата регистрации доменного имени
- Paid-til: дата, когда регистрация завершится.
- Free-til: дата, когда адрес может освободится, если владелец его не продлит.
Для удобства проверки информации о доменных именах в REG.RU создан бот Whois в Telegram. Информация в нём аналогична Whois-сервису на сайте.
Похожие статьи:
Whois сервис. Информация о домене, местонахождение сайта и IP адреса
Whois сервис. Информация о домене, местонахождение сайта и IP адресаПолучите информацию о домене, местонахождение любого ресурса или IP адреса
Что такое WHOIS
Whois (от английского “who is” — «кто это») — интернет-сервис для поиска информации о сайте и проверки данных о доменном имени. Наш сервис Whois поможет узнать основные данные о доменном имени (кто администратор и регистратор, срок регистрации и т.
Чем поможет наш сервис
Whois позволяет узнать чей домен, сведения о домене или IP-адресе сайта. Это бывает нужно, чтобы узнать регистратора домена, выяснить, кому принадлежит домен и сайт, а также проверить свободные домены. Записи Whois могут различаться между регистраторами, но все они содержат обязательную информацию, а именно:
- название регистратора;
- дата регистрации;
- срок истечения регистрации домена;
- DNS серверы;
- контакты администратора домена, если они не скрыты настройками приватности.
Таким образом, Whois поможет узнать, сколько лет домену — об этом скажет дата регистрации домена или создания сайта, проверить доменное имя. Иногда также можно определить, кто хозяин сайта, размещённого на домене, но эта информация быть недоступна — многие регистраторы предлагают услугу частной регистрации и за дополнительную плату скрывают контакты администратора. Но стоит учесть, что все описанные выше данные относятся только к текущему периоду регистрации — вполне возможно, что до этого домен принадлежал другому лицу и впервые был зарегистрирован гораздо ранее.
Whois IP address service может искать информацию не по домену, а по IP-адресу сайта, но по функциональности он ничем не отличается от обычного запроса Whois. Но также предоставит информацию, которая полезна для
Как пользоваться WHOIS
Чтобы воспользоваться сервисом, просто введите в строку Whois любой домен или IP-адрес — после этого на экран выведется вся доступная информация о домене и сайте.
Записи Whois могут отличаться в зависимости от доменной зоны или регистратора.
Общая оценка: 4.7/5
Превосходно
На основе 50 отзывов
Игорь Малышев
18 янв. 2023
2023
Хороший виртуальный хостинг. Цена/качество на высоте, тех.поддержка в 90% случаях отвечает в течении 1 часа. Пока доволен.
Вячеслав Пустовит
5 июл. 2022
Пользуюсь хостингом уже около 6 месяцев. Как по мне очень хороший, удобный, быстрый и не дорогой хостинг. Все интуитивно понятно, в отличии от тех которыми пользовался до этого. В основном пользуюсь для размещения своего портфолио.
Руслан Маратович
14 мар. 2022
Прекрасный хостинг с демократичными ценами. С надёжностью проблем не возникало. Поддержка нормальная в целом.
Анвар Туракулов
5 мар. 2022
Хороший хостинг. Пользуюсь сервисом VDS. Поддержка нормальная, помогают. Благодарю за работу ребят
Алиса Штирц
31 дек. 2021
Самый топ хостинг потому что дешево и хорошо. Ни с доступностью сайта, ни с тех поддержкой проблем пока не было.
Роман Романов
29 сен. 2021
Пользуюсь больше года, наверное самый лучший облачный хостинг для моих сайтов. Поддержка отвечает очень быстро (точно быстрее, чем на хостингах, что пользовал ранее).
Екатерина Кутузова
13 июн. 2021
Очень довольна работой хостинга. Сравнить не с чем, но причины для смены провайдера нет.
Александр Продан
1 мар. 2021
Хорошие скоростные показатели, time to first byte ниже, чем на популярных других хостингах. Аптайм стремится к 100%, изредка только перезагружают сервера для обновления пакетов и зависимостей, вот недавно добавили php 8.
Макс Петриченко
15 янв. 2021
Друзья порекомендовали воспользоваться услугами этого хостинга. Пользуюсь уже около года, никаких серьезных проблем в работе у меня не возникало. Работает все стабильно и надежно. Приятные цены, отличная тех поддержка.
Роман Герасименко
23 окт. 2020
Действительно крутой хостинг. Очень выгодное и щедрое партнёрство, платят от 30% за приведенного клиента. И сам пользуюсь данным хостингом, скорость не сверхзвуковая, но для моих задач пойдёт.
Странице в разработке
Страница, на которую Вы собираетесь перейти находится в разработке.
Попробуйте позднее, наши специалисты уже работают над этим 🙂
Область и диапазон функций
Результаты обучения
- Найдите область определения функции, определяемой уравнением.
- Запишите домен и диапазон, используя стандартные обозначения.
- Поиск домена и диапазона по графику.
- Дайте домен и диапазон функций набора инструментов.
- График кусочно определенных функций.
Если вы настроены на фильм ужасов, вы можете посмотреть один из пяти самых популярных фильмов ужасов всех времен— Я Легенда , Ганнибал , Кольцо , Обида и Заклинание . На рис. 1 показана сумма в долларах, которую каждый из этих фильмов собрал в прокате, а также продажи билетов на фильмы ужасов в целом по годам. Обратите внимание, что мы можем использовать данные для создания функции суммы, заработанной каждым фильмом, или общих продаж билетов на все фильмы ужасов по годам. При создании различных функций с использованием данных мы можем идентифицировать различные независимые и зависимые переменные, а также анализировать данные и функции, чтобы определить домен и диапазон. В этом разделе мы исследуем методы определения области определения и диапазона таких функций.
При создании различных функций с использованием данных мы можем идентифицировать различные независимые и зависимые переменные, а также анализировать данные и функции, чтобы определить домен и диапазон. В этом разделе мы исследуем методы определения области определения и диапазона таких функций.
Рис. 1. На основе данных, собранных www.the-numbers.com.
Стандартная нотация для определения множеств
Существует несколько способов определения множеств чисел или математических объектов. Причина, по которой мы вводим это здесь, заключается в том, что нам часто нужно определить наборы чисел, которые составляют входы и выходы функции.
То, как мы записываем наборы, составляющие область и диапазон функций, часто зависит от того, как отношение или функция определены или представлены нам. Например, мы можем использовать списки для описания области функций, заданных в виде наборов упорядоченных пар. Если нам дано уравнение или график, мы можем использовать неравенства или интервалы для описания домена и диапазона.
В этом разделе мы представим стандартную нотацию, используемую для определения множеств, и дадим вам возможность попрактиковаться в написании множеств тремя способами: нотация неравенства, нотация построителя множеств и нотация интервала.
Рассмотрим набор [latex]\left\{x|10\le x<30\right\}[/latex], который описывает поведение [latex]x[/latex] в нотации конструктора наборов. Фигурные скобки [латекс]\{\}[/латекс] читаются как «набор», а вертикальная черта [латекс]|[/латекс] читается как «такой, что», поэтому мы должны читать [латекс]\ left\{x|10\le x<30\right\}[/latex] как «набор x -значений таких, что 10 меньше или равно [латекс]x[/латекс], и [латекс ]x[/latex] меньше 30».
В таблице ниже сравниваются обозначения неравенства, обозначения построителя наборов и обозначения интервалов.
| Обозначение неравенства | Набор-строитель Обозначение | Обозначение интервала | |
|---|---|---|---|
[латекс]5| [латекс]\{ч | 5 < ч\ле 10\}[/латекс] | [латекс](5,10][/латекс] | | |
| [латекс]5\le h<10[/латекс] | [латекс]\{ч | 5 \le h < 10\}[/латекс] | [латекс][5,10)[/латекс] | |
[латекс]5| [латекс]\{ч | 5 <ч <10\}[/латекс] | [латекс](5,10)[/латекс] | | |
| [латекс]ч<10[/латекс] | [латекс]\{ч | ч < 10\}[/латекс] | [латекс](-\infty,10)[/латекс] | |
| [латекс]h>10[/латекс] | [латекс]\{ч | ч > 10\}[/латекс] | [латекс](10,\infty)[/латекс] | |
| Все действительные числа | [латекс]\mathbf{R}[/латекс] | [латекс](−\infty,\infty)[/латекс] |
Чтобы объединить два интервала, используя нотацию неравенства или нотацию построителя множеств, мы используем слово «или». Как мы видели в предыдущих примерах, мы используем символ объединения [латекс]\чашка [/латекс] для объединения двух несвязанных интервалов. Например, объединение множеств [латекс]\лево\{2,3,5\право\}[/латекс] и [латекс]\лево\{4,6\право\}[/латекс] – это множество [латекс]\влево\{2,3,4,5,6\вправо\}[/латекс]. Это набор всех элементов, принадлежащих одному или другой (или оба) из исходных двух наборов. Для наборов с конечным числом таких элементов элементы не обязательно должны быть перечислены в порядке возрастания числового значения. Если исходные два набора имеют некоторые общие элементы, эти элементы должны быть перечислены только один раз в объединенном наборе. Для наборов действительных чисел на интервалах другим примером объединения является
Как мы видели в предыдущих примерах, мы используем символ объединения [латекс]\чашка [/латекс] для объединения двух несвязанных интервалов. Например, объединение множеств [латекс]\лево\{2,3,5\право\}[/латекс] и [латекс]\лево\{4,6\право\}[/латекс] – это множество [латекс]\влево\{2,3,4,5,6\вправо\}[/латекс]. Это набор всех элементов, принадлежащих одному или другой (или оба) из исходных двух наборов. Для наборов с конечным числом таких элементов элементы не обязательно должны быть перечислены в порядке возрастания числового значения. Если исходные два набора имеют некоторые общие элементы, эти элементы должны быть перечислены только один раз в объединенном наборе. Для наборов действительных чисел на интервалах другим примером объединения является
[latex]\left\{x|\text{ }|x|\ge 3\right\}=\left(-\infty ,-3\ right]\cup \left[3,\infty \right)[/latex]
В этом видео показано, как использовать нотацию интервала для описания множества.
com/embed/hqg85P0ZMZ4?feature=oembed&rel=0″ frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share» allowfullscreen=»» title=»Interval Notation»>В этом видео показано, как использовать нотацию Set-Builder для описания множества.
A Общее примечание: нотация построителя множеств и нотация интервалов
Нотация построителя наборов — это метод определения набора элементов, удовлетворяющих определенному условию. Оно принимает форму [латекс]\лево\{х|\текст{утверждение о}х\право\}[/латекс], которое читается как «множество всех [латекс]х[/латекс], таких, что утверждение о [латексе]х[/латексе] правда». Например,
[латекс]\влево\{х|4<х\ле 12\вправо\}[/латекс]
Интервальное обозначение — это способ описания наборов, включающих все действительные числа между нижним пределом, которые могут или не могут быть включенным, и верхний предел, который может быть включен или не включен. Значения конечной точки перечислены в скобках или круглых скобках. Квадратная скобка указывает на включение в набор, а скобка указывает на исключение из набора. Например,
Значения конечной точки перечислены в скобках или круглых скобках. Квадратная скобка указывает на включение в набор, а скобка указывает на исключение из набора. Например,
[латекс]\влево(4,12\вправо][/латекс]
Как: Имея линейный график, опишите набор значений, используя интервальную нотацию.0003
- Определите интервалы, которые необходимо включить в набор, определив, где толстая линия накладывается на реальную линию.
- В левом конце каждого интервала используйте [ для каждого конечного значения, которое должно быть включено в набор (сплошная точка), или ( для каждого исключенного конечного значения (незаштрихованная точка).
- В правом конце каждого интервала используйте ] для каждого конечного значения, которое должно быть включено в набор (закрашенная точка), или ) для каждого исключенного конечного значения (незаштрихованная точка).
- Используйте символ объединения [латекс]\чашка [/латекс], чтобы объединить все интервалы в один набор.

Пример: описание наборов на линии действительных чисел
Опишите интервалы значений, показанных ниже, используя нотацию неравенства, нотацию построителя множеств и нотацию интервала.
Показать раствор
Попробуйте
Учитывая приведенный ниже график, укажите графическое множество в
- слов
- нотация конструктора наборов
- обозначение интервала
Показать решение
В таблице ниже приведены сводные данные об обозначении интервалов.
Запись домена и диапазона по уравнению
В разделе «Функции и обозначения функций» мы познакомились с понятиями домена и диапазона . В этом разделе мы попрактикуемся в определении доменов и диапазонов для конкретных функций. Имейте в виду, что при определении доменов и диапазонов нам необходимо учитывать, что физически возможно или значимо в реальных примерах, таких как продажи билетов и год в приведенном выше примере с фильмом ужасов. Мы также должны рассмотреть, что математически разрешено. Например, мы не можем включать какое-либо входное значение, которое приводит к извлечению четного корня из отрицательного числа, если домен и диапазон состоят из действительных чисел. Или в функции, выраженной в виде формулы, мы не можем включить какое-либо входное значение в область определения, которая привела бы к делению на 0,9.0029
Мы также должны рассмотреть, что математически разрешено. Например, мы не можем включать какое-либо входное значение, которое приводит к извлечению четного корня из отрицательного числа, если домен и диапазон состоят из действительных чисел. Или в функции, выраженной в виде формулы, мы не можем включить какое-либо входное значение в область определения, которая привела бы к делению на 0,9.0029
Мы можем представить домен как «зону хранения», которая содержит «сырье» для «функциональной машины», а ассортимент — как еще одну «область хранения» для продуктов машины.
Мы можем записать домен и диапазон в интервальной нотации , которая использует значения в квадратных скобках для описания набора чисел. В обозначении интервала мы используем квадратную скобку [ когда набор включает конечную точку, и круглую скобку (, чтобы указать, что конечная точка либо не включена, либо интервал не ограничен. Например, если у человека есть 100 долларов, которые он может потратить, он или она нужно выразить интервал, который больше 0 и меньше или равен 100, и написать [латекс]\влево(0,\текст{ }100\вправо][/латекс]. Обозначение интервала мы обсудим более подробно позже.
Обозначение интервала мы обсудим более подробно позже.
Обратимся к поиску области определения функции, уравнение которой приведено. Часто для нахождения области определения таких функций необходимо запомнить три разные формы. Во-первых, если функция не имеет знаменателя или четного корня, подумайте, могут ли доменом быть все действительные числа. Во-вторых, если в уравнении функции есть знаменатель, исключите значения в области значений, при которых знаменатель равен нулю. В-третьих, если есть четный корень, рассмотрите возможность исключения значений, которые сделали бы подкоренное число отрицательным.
Прежде чем мы начнем, давайте рассмотрим правила записи интервалов:
- Первым записывается наименьший член интервала.
- Самый большой член в интервале пишется вторым после запятой.
- Круглые скобки ( или ) используются для обозначения того, что конечная точка не включена, что называется исключительным.
- Скобки [ или ] используются для указания того, что конечная точка включена, что называется включением.

Пример. Нахождение области определения функции как набора упорядоченных пар
Найдите область определения следующей функции: [латекс]\влево\{\влево(2,\текст{}10\вправо),\влево(3,\текст{}10\вправо),\влево(4, \text{ }20\right),\left(5,\text{ }30\right),\left(6,\text{ }40\right)\right\}[/latex] .
Показать раствор
Попробуйте
Найдите область определения функции:
[латекс]\влево\{\влево(-5,4\вправо),\влево(0,0\вправо),\влево(5,-4 \right),\left(10,-8\right),\left(15,-12\right)\right\}[/latex]
Показать решение
Как: Дана функция, записанная в виде уравнения, найти область определения. 9{3}[/латекс].Показать раствор
Практическое руководство. По заданной функции, записанной в виде уравнения, включающего дробную часть, найдите область определения.
- Определите входные значения.

- Определите любые ограничения на ввод. Если в формуле функции есть знаменатель, установите знаменатель равным нулю и найдите [latex]x[/latex] . Это значения, которые не могут быть введены в функцию.
- Запишите домен в форме интервала, исключив из домена любые ограниченные значения.
Пример. Нахождение области определения функции, содержащей знаменатель (рациональная функция)
Нахождение области определения функции [latex]f\left(x\right)=\dfrac{x+1}{2-x}[ /латекс].
Показать раствор
Попробуйте
Найдите область определения функции: [latex]f\left(x\right)=\dfrac{1+4x}{2x — 1}[/latex].
Показать раствор
Как: Для заданной функции, записанной в виде уравнения, включая четный корень, найти область определения.

- Определите входные значения.
- Поскольку имеется четный корень, исключите все действительные числа, которые приводят к отрицательному числу в подкоренном члене. Установите подкоренное число больше или равное нулю и найдите [латекс]х[/латекс].
- Решение(я) являются областью определения функции. Если возможно, запишите ответ в интервальной форме.
Пример: нахождение области определения функции с четным корнем
Найдите область определения функции [latex]f\left(x\right)=\sqrt{7-x}[/latex].
Показать решение
Попробуйте
Найдите домен функции [latex]f\left(x\right)=\sqrt{5+2x}[/latex].
Показать раствор
Q&A
Могут ли быть функции, в которых домен и диапазон вообще не пересекаются?
Да. Например, функция [latex]f\left(x\right)=-\frac{1}{\sqrt{x}}[/latex] имеет множество всех положительных действительных чисел в качестве области определения, но множество всех отрицательные действительные числа в качестве диапазона. Как более крайний пример, входы и выходы функции могут быть совершенно разными категориями (например, названия дней недели в качестве входов и числа в качестве выходов, как на графике посещаемости), в таких случаях домен и диапазон не имеют общих элементов.
Например, функция [latex]f\left(x\right)=-\frac{1}{\sqrt{x}}[/latex] имеет множество всех положительных действительных чисел в качестве области определения, но множество всех отрицательные действительные числа в качестве диапазона. Как более крайний пример, входы и выходы функции могут быть совершенно разными категориями (например, названия дней недели в качестве входов и числа в качестве выходов, как на графике посещаемости), в таких случаях домен и диапазон не имеют общих элементов.
ПОПРОБУЙТЕ
Когда вы определяете область определения функции, может помочь ее графическое изображение, особенно если у вас есть рациональное число или функция с четным корнем.
Сначала определите ограничения домена для следующих функций, затем нарисуйте каждую из них, чтобы проверить, согласуется ли ваш домен с графиком.
- [латекс]f(x) = \sqrt{2x-4}+5[/латекс]
- [латекс]g(x) = \dfrac{2x+4}{x-1}[/латекс]
Затем используйте онлайн-инструмент для построения графиков, чтобы оценить свою работу при обнаруженном вами ограничении домена. Какое значение функции дает вам графический калькулятор?
Какое значение функции дает вам графический калькулятор?
Как: Имея формулу для функции, определить домен и диапазон.
- Исключить из домена любые входные значения, которые приводят к делению на ноль.
- Исключить из домена любые входные значения, которые имеют недействительные (или неопределенные) числовые выходы.
- Используйте допустимые входные значения для определения диапазона выходных значений.
- Посмотрите на график функции и табличные значения, чтобы подтвердить фактическое поведение функции.
Пример: поиск домена и диапазона с помощью функций набора инструментов 9{3}-х[/латекс].
Показать раствор
Пример: поиск домена и диапазона
Найдите домен и диапазон [latex]f\left(x\right)=\dfrac{2}{x+1}[/latex].
Показать раствор
Пример: поиск домена и диапазона
Найдите домен и диапазон [latex]f\left(x\right)=2\sqrt{x+4}[/latex].
Показать раствор
Попробуйте
Найдите домен и диапазон [latex]f\left(x\right)=-\sqrt{2-x}[/latex].
Показать раствор
Определение домена и диапазона по графику
Другой способ определить домен и диапазон функций — использовать графики. Поскольку домен относится к набору возможных входных значений, домен графика состоит из всех входных значений, показанных на оси [latex]x[/latex]. Диапазон — это набор возможных выходных значений, которые показаны на оси [latex]y[/latex]. Имейте в виду, что если график выходит за пределы видимой части графика, домен и диапазон могут быть больше, чем видимые значения.
Мы можем заметить, что граф простирается по горизонтали от [латекс]-5[/латекс] вправо без границ, так что домен равен [латекс]\левый[-5,\infty \правый)[/латекс]. Вертикальный экстент графика — это все значения диапазона [latex]5[/latex] и ниже, поэтому диапазон равен [latex]\left(\mathrm{-\infty },5\right][/latex]. Обратите внимание, что домен и диапазон всегда записываются от меньших значений к большим или слева направо для домена и от нижней части графика к верхней части графика для диапазона.0029
Обратите внимание, что домен и диапазон всегда записываются от меньших значений к большим или слева направо для домена и от нижней части графика к верхней части графика для диапазона.0029
Пример: поиск домена и диапазона на графике
Найдите домен и диапазон функции [latex]f[/latex].
Показать раствор
Пример: определение области определения и диапазона по графику добычи нефти
Найдите область определения и диапазон функции [latex]f[/latex].
(кредит: изменение работы Управления энергетической информации США)
Показать решение
Попробуйте
Имея график, определите домен и диапазон, используя интервальную нотацию.
Показать решение
Вопросы и ответы
Могут ли домен и диапазон функции совпадать?
Да. Например, область определения и диапазон функции кубического корня — это множество всех действительных чисел.
Домен и диапазон функций инструментария
Теперь мы вернемся к нашему набору функций набора инструментов, чтобы определить домен и диапазон каждой из них.
Для постоянной функции [latex]f\left(x\right)=c[/latex] область определения состоит из всех действительных чисел; ограничений на ввод нет. Единственным выходным значением является константа [latex]c[/latex], поэтому диапазон представляет собой набор [latex]\left\{c\right\}[/latex], содержащий этот единственный элемент. В записи интервала это записывается как [латекс]\влево[с,с\право][/латекс], интервал, который начинается и заканчивается на [латекс]с[/латекс].
Для функции тождества [латекс]f\left(x\right)=x[/latex] ограничений на [latex]x[/latex] нет. { 2}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. Поскольку график не содержит отрицательных значений диапазона, диапазон состоит только из неотрицательных действительных чисел. 9{3}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. То же самое относится к вертикальному размеру графика, поэтому домен и диапазон включают все действительные числа.
{ 2}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. Поскольку график не содержит отрицательных значений диапазона, диапазон состоит только из неотрицательных действительных чисел. 9{3}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. То же самое относится к вертикальному размеру графика, поэтому домен и диапазон включают все действительные числа.
Для обратной функции [латекс]f\left(x\right)=\frac{1}{x}[/latex] мы не можем делить на 0, поэтому мы должны исключить 0 из области определения. Кроме того, 1, деленная на любое значение, никогда не может равняться 0, поэтому диапазон также не будет включать 0. В нотации построителя наборов мы могли бы также написать [латекс]\влево\{х|\текст{ }х\ne 0\вправо \}[/latex], множество всех вещественных чисел, не равных нулю. 9{2}}[/latex], мы не можем делить на [latex]0[/latex], поэтому мы должны исключить [latex]0[/latex] из домена.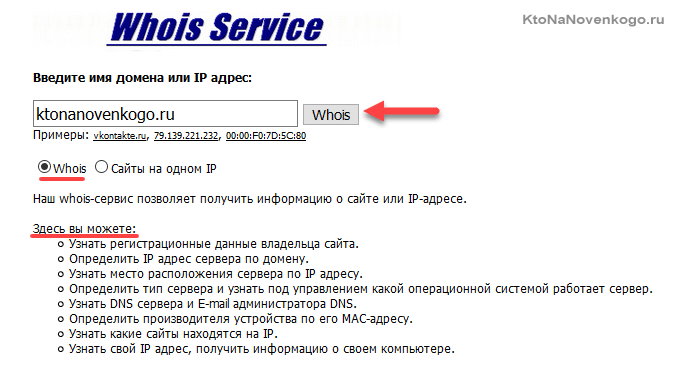 Также нет [latex]x[/latex], который может выдавать 0, поэтому 0 также исключается из диапазона. Обратите внимание, что выход этой функции всегда положителен из-за квадрата в знаменателе, поэтому диапазон включает только положительные числа.
Также нет [latex]x[/latex], который может выдавать 0, поэтому 0 также исключается из диапазона. Обратите внимание, что выход этой функции всегда положителен из-за квадрата в знаменателе, поэтому диапазон включает только положительные числа.
Для функции квадратного корня [latex]f\left(x\right)=\sqrt[]{x}[/latex] мы не можем извлечь квадратный корень из отрицательного действительного числа, поэтому домен должен быть 0 или выше. Диапазон также исключает отрицательные числа, поскольку квадратный корень из положительного числа [latex]x[/latex] определяется как положительный, хотя квадрат отрицательного числа [latex]-\sqrt{x}[/latex] также дает нам [латекс]x[/латекс].
Для функции кубического корня [latex]f\left(x\right)=\sqrt[3]{x}[/latex] домен и диапазон включают все действительные числа. Обратите внимание, что нет проблем с извлечением кубического корня или любого корня из нечетного целого числа из отрицательного числа, и результирующий результат будет отрицательным (это нечетная функция).
Попробуйте
Кусочно-определенные функции
Иногда мы сталкиваемся с функцией, которая требует более одной формулы для получения заданного результата. Например, в функциях инструментария мы ввели функцию абсолютного значения [latex]f\left(x\right)=|x|[/latex]. С доменом всех действительных чисел и диапазоном значений больше или равным 0, 9Абсолютное значение 0027
может быть определено как величина или модуль действительного числового значения независимо от знака. Это расстояние от 0 на числовой прямой. Все эти определения требуют, чтобы вывод был больше или равен 0.Если мы вводим 0 или положительное значение, вывод совпадает с вводом.
[латекс]f\left(x\right)=x\text{ if }x\ge 0[/latex]
Если мы вводим отрицательное значение, вывод будет противоположен вводу.
[латекс]f\left(x\right)=-x\text{ if }x<0[/latex]
Поскольку для этого требуются два разных процесса или части, функция абсолютного значения является примером кусочной функции .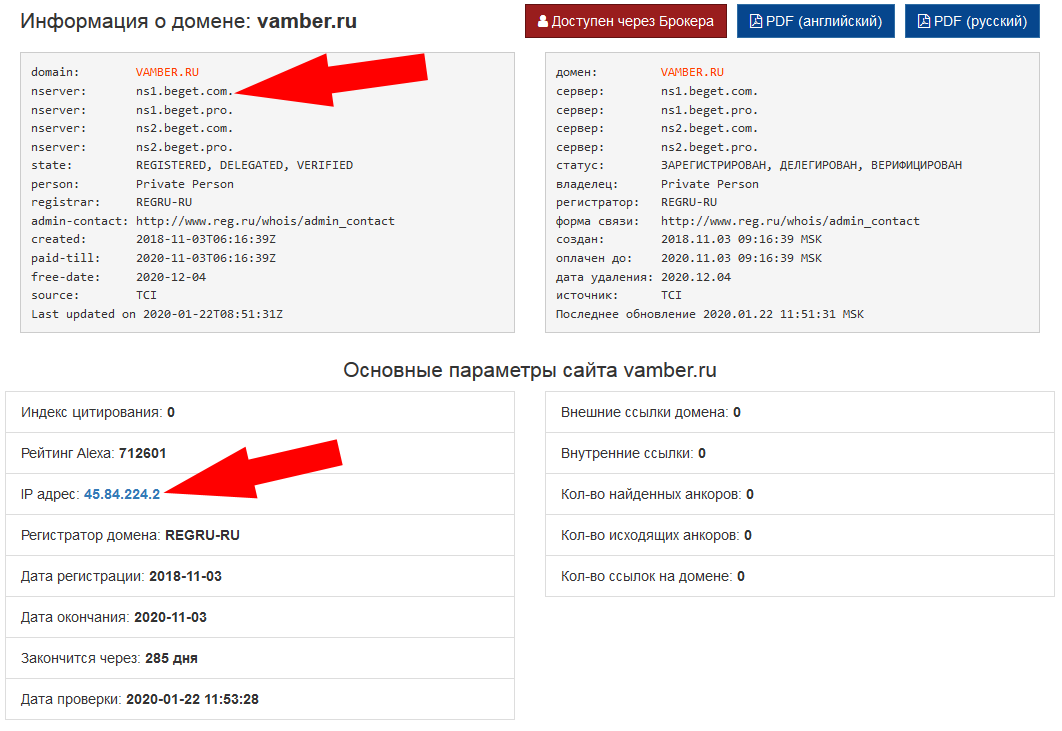 Кусочная функция — это функция, в которой используется более одной формулы для определения выходных данных для разных частей области.
Кусочная функция — это функция, в которой используется более одной формулы для определения выходных данных для разных частей области.
Мы используем кусочные функции для описания ситуаций, в которых правило или отношение изменяются, когда входное значение пересекает определенные «границы». Например, в бизнесе мы часто сталкиваемся с ситуациями, когда цена за единицу определенного товара снижается, когда количество заказанного товара превышает определенное значение. Налоговые скобки — еще один реальный пример кусочных функций. Например, рассмотрим простую налоговую систему, в которой доходы до [латекс]10 000 долларов[/латекс] облагаются налогом по ставке [латекс]10%[/латекс], а любой дополнительный доход облагается налогом по ставке [латекс]20%[/латекс]. . Налог на общий доход, [латекс] S[/латекс] , будет [латекс] 0,1 ш[/латекс], если [латекс]{S}\le$10 000[/латекс] и [латекс]1000 + 0,2 (с — 10 000 долларов США)[/latex] , если [латекс] S> 10 000 долларов США[/latex] .
A Общее примечание: кусочные функции
Кусочная функция — это функция, в которой для определения выходных данных используется более одной формулы. У каждой формулы есть свой домен, а домен функции представляет собой объединение всех этих меньших доменов. Обозначим эту идею следующим образом:
[латекс] f\left(x\right)=\begin{cases}\text{формула 1, если x находится в домене 1}\\ \text{формула 2, если x находится в домене 2}\\ \text{формула 3, если x находится в домене 3}\end{cases} [/latex]
В кусочной записи функция абсолютного значения равна
[латекс]|x|=\begin{cases}\begin{align}x&\text{ if }x\ge 0\\ -x&\text{ if }x<0\end{align}\end{cases }[/latex]
Как сделать: учитывая кусочную функцию, напишите формулу и определите домен для каждого интервала.
- Определите интервалы, для которых применяются разные правила.
- Определите формулы, описывающие, как вычислить выход из входа в каждом интервале.

- Используйте фигурные скобки и операторы if для записи функции.
Пример: написание кусочной функции
Музей взимает 5 долларов с человека за экскурсию с группой от 1 до 9 человек или фиксированную плату в размере 50 долларов за экскурсию с группой из 10 и более человек. Напишите функцию , связывающую количество людей [latex]n[/latex] со стоимостью [latex]C[/latex].
Показать раствор
Пример: Работа с кусочной функцией
Компания сотовой связи использует приведенную ниже функцию для определения стоимости [latex]C[/latex] в долларах за [latex]g[/latex] гигабайт передачи данных.
[латекс]C\left(g\right)=\begin{cases}\begin{align}{25} \hspace{2mm}&\text{ if }\hspace{2mm}{ 0 }<{ g } <{ 2 }\\ { 25+10 }\left(g - 2\right) \hspace{2mm}&\text{ if }\hspace{2mm}{ g}\ge{ 2 }\end{align}\ end{cases}[/latex]
Найдите стоимость использования 1,5 гигабайт данных и стоимость использования 4 гигабайт данных.
Показать раствор
Как сделать: по заданной кусочной функции нарисуйте график.
- Укажите на оси [latex]x[/latex] границы, определяемые интервалами на каждой части домена. 9{3} \hspace{2mm}&\text{ if }\hspace{2mm}{ x }<{-1 }\\ { -2 } \hspace{2mm}&\text{ if } \hspace{2mm}{ -1 }<{ x }<{ 4 }\\ \sqrt{x} \hspace{2mm}&\text{ if }\hspace{2mm}{ x }>{ 4 }\end{align}\end{cases }[/latex]
Показать решение
Попробуйте
Вы можете использовать онлайн-инструмент для построения графиков кусочно-определенных функций. Посмотрите это обучающее видео, чтобы узнать, как это сделать.
Постройте график следующей кусочной функции с помощью графического онлайн-инструмента.
 9{3} \hspace{2mm}&\text{ if }\hspace{2mm}{ x }<{-1 }\\ { -2 } \hspace{2mm}&\text{ if } \hspace{2mm}{ -1 }<{ x }<{ 4 }\\ \sqrt{x} \hspace{2mm}&\text{ if }\hspace{2mm}{ x }>{ 4 }\end{align}\end{cases }[/latex]
9{3} \hspace{2mm}&\text{ if }\hspace{2mm}{ x }<{-1 }\\ { -2 } \hspace{2mm}&\text{ if } \hspace{2mm}{ -1 }<{ x }<{ 4 }\\ \sqrt{x} \hspace{2mm}&\text{ if }\hspace{2mm}{ x }>{ 4 }\end{align}\end{cases }[/latex]Попробуйте
Вопросы и ответы
Можно ли применить более одной формулы кусочной функции к значению в домене?
Нет. Каждое значение соответствует одному уравнению в кусочной формуле.
Ключевые понятия
- Область определения функции включает в себя все действительные входные значения, которые не заставят нас выполнить неопределенную математическую операцию, такую как деление на ноль или извлечение квадратного корня из отрицательного числа.
- Область определения функции можно определить, перечислив входные значения набора упорядоченных пар.
- Область определения функции также можно определить, идентифицируя входные значения функции, записанные в виде уравнения.
- Интервальные значения, представленные на числовой прямой, могут быть описаны с использованием обозначения неравенства, обозначения построителя набора и обозначения интервала.

- Для многих функций домен и диапазон можно определить по графику.
- Понимание функций инструментария может быть использовано для определения домена и диапазона связанных функций.
- Кусочная функция описывается более чем одной формулой.
- График кусочной функции можно изобразить, используя каждую алгебраическую формулу в назначенной ей подобласти.
Глоссарий
- обозначение интервалов
- метод описания множества, включающего все числа между нижним пределом и верхним пределом; нижние и верхние значения указаны в скобках или круглых скобках, квадратная скобка указывает на включение в набор, а скобка указывает на исключение
- кусочная функция
- функция, в которой используется более одной формулы для определения выходных данных
- обозначение конструктора наборов
- метод описания множества по правилу, которому подчиняются все его члены; он принимает форму [латекс]\влево\{х|\текст{утверждение о}х\вправо\}[/латекс]
Домен и диапазон
Горячая математикадомен из функция ф ( Икс ) это набор всех значений, для которых определена функция, и диапазон функции – это множество всех значений, которые ф берет.

(В начальной школе вы, вероятно, называли домен замещающим набором, а диапазон — набором решений. Их также можно было назвать входом и выходом функции.)
Пример 1:
Рассмотрим функцию, показанную на схеме.
Здесь домен представляет собой набор { А , Б , С , Е } . Д не находится в домене, так как функция не определена для Д .
Ассортимент — это набор { 1 , 3 , 4 } . 2 не входит в диапазон, так как в домене нет буквы, которая сопоставляется с 2 .
Вы также можете говорить о домене связь , где один элемент в домене может быть сопоставлен более чем с одним элементом в диапазоне.

Пример 2:
Рассмотрим отношение { ( 0 , 7 ) , ( 0 , 8 ) , ( 1 , 7 ) , ( 1 , 8 ) , ( 1 , 9) , ( 2 , 10 ) } .
Здесь отношение задано как набор упорядоченных пар. Домен представляет собой набор Икс -координаты, { 0 , 1 , 2 } , а диапазон — это набор у -координаты, { 7 , 8 , 9, 10 } .
 Обратите внимание, что элементы домена
1
и
2
связаны с более чем одним элементом диапазона, так что это нет функция.
Обратите внимание, что элементы домена
1
и
2
связаны с более чем одним элементом диапазона, так что это нет функция.Но чаще, и особенно при работе с графиками на координатной плоскости, мы имеем дело с функциями, где каждый элемент области связан с одним элементом диапазона. (См. Проверка вертикальной линии .)
Пример 3:
Область определения функции
ф ( Икс ) «=» 1 Икс
все действительные числа, кроме нуля (поскольку при Икс «=» 0 , функция не определена: деление на ноль запрещено!).
Диапазон также включает все действительные числа, кроме нуля. Вы можете видеть, что на кривой есть некоторая точка для каждого у -значение кроме у «=» 0 .

Домены также можно указать явно, если есть значения, для которых функция может быть определена, но которые мы по каким-то причинам не хотим рассматривать.
Пример 4:
Следующие обозначения показывают, что область определения функции ограничена интервалом ( − 1 , 1 ) .
ф ( Икс ) «=» Икс 2 , − 1 < Икс < 1
График этой функции такой, как показано. Обратите внимание на незакрашенные кружки, которые показывают, что функция не определена в Икс «=» − 1 и Икс «=» 1 . у -значения варьируются от 0 вплоть до 1 (включая 0 , но не включая 1 ).





 9{3} \hspace{2mm}&\text{ if }\hspace{2mm}{ x }<{-1 }\\ { -2 } \hspace{2mm}&\text{ if } \hspace{2mm}{ -1 }<{ x }<{ 4 }\\ \sqrt{x} \hspace{2mm}&\text{ if }\hspace{2mm}{ x }>{ 4 }\end{align}\end{cases }[/latex]
9{3} \hspace{2mm}&\text{ if }\hspace{2mm}{ x }<{-1 }\\ { -2 } \hspace{2mm}&\text{ if } \hspace{2mm}{ -1 }<{ x }<{ 4 }\\ \sqrt{x} \hspace{2mm}&\text{ if }\hspace{2mm}{ x }>{ 4 }\end{align}\end{cases }[/latex]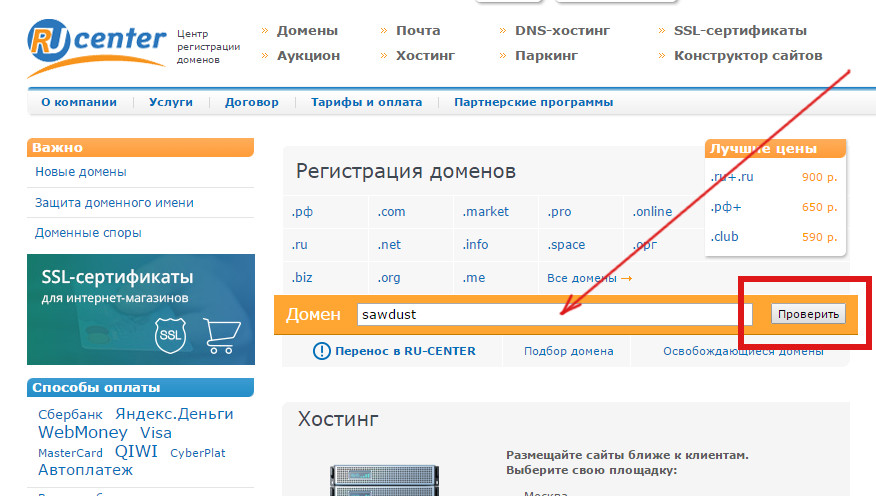
 Обратите внимание, что элементы домена
1
и
2
связаны с более чем одним элементом диапазона, так что это нет функция.
Обратите внимание, что элементы домена
1
и
2
связаны с более чем одним элементом диапазона, так что это нет функция.