Рекурсивные процедуры в языке Пролог | Практическая информатика
Рекурсия в большинстве языков программирования — это такой способ организации обработки данных, при котором программа (процедура) вызывает сама себя непосредственно, либо с помощью другой программы (процедуры).
Гравюра голландского художника Мориса Эшера «Рисующие руки» — одна из лучших иллюстраций понятия рекурсии. Всем известный стишок о попе и его собаке демонстрирует нам бесконечность рекурсивных вызовов. Используя рекурсию как прием программирования мы должны быть уверены, что рекурсивная процедура будет завершена.
В Прологе рекурсия встречается, когда предикат содержит цель, которая ссылается на саму себя. В рекурсивном правиле более сложные входные аргументы должны выражаться через менее сложные.
На примере уже имеющейся у нас базы данных объясним преимущества использования рекурсии и особенности рекурсивных правил. Пусть имеются следующие факты:
больше(слон, лошадь).больше(лошадь, осел). больше(осел, собака). больше(осел, обезьяна).
Выполним запрос к базе данных
?- больше(осел, собака). Yes
Цель больше(осел, собака) была достигнута потому, что этот факт был сообщен Прологу при загрузке базы. Теперь проверим, больше ли обезьяна слона?
?- больше(обезьяна, слон). No
Нет, не больше. Мы получили такой ответ, какой и ожидали: соответствующий запрос, а именно больше(обезьяна, слон) не подтвердился. Но, что случится, если мы зададим вопрос по-другому?
?- больше(слон, обезьяна). No
Таким образом, слоны не больше, чем обезьяны. Полученный результат совершенно не согласуется с нашими представлениями о мире, но если посмотреть на базу данных, то легко заметить, что в ней действительно ничего не сказано об отношениях между слонами и обезьянами. Однако, мы знаем, что слоны больше, чем лошади, которые в свою очередь больше, чем ослы, которые больше обезьян, поэтому слоны также должны быть больше, чем обезьяны.
Правильная интерпретация отрицательного ответа, данного Прологом, такова: информации, сообщенной системе, недостаточно для доказательства того, что слон больше обезьяны. Если мы захотим получить положительный ответ на запрос вида больше(слон, обезьяна), то мы должны обеспечить более точное описание мира. Одним из возможных способов решения этой проблемы является добавление отсутствующих фактов, например,
больше(слон, обезьяна).
Для нашего маленького примера это означает добавление еще 5 фактов. Однако гораздо лучшим решением будет добавление в программу нового отношения, которое мы назовем больше_2. Животное X больше, чем животное Y, если это определено как факт (первое правило) или существует животное Z, для которого определен факт, что животное X больше, чем животное Z и может быть показано, что животное Z больше, чем животное Y (второе правило). На Прологе это запишется так:
больше_2(X, Y) :- больше(X, Y). больше_2(X, Y) :- больше(X, Z), больше(Z, Y).
Если в цепочке участвуют не три, а большее число объектов, то придется добавить новые правила:
больше_2(X, Y) :- больше(X, Z1), больше(Z1, Z2), больше(Z2, Y). больше_2(X, Y) :- больше(X, Z1), больше(Z1, Z2), больше(Z2, Z3), больше(Z3, Y). ...
Эта программа длинна и работать будет далеко не всегда. Она сможет просматривать базу данных только до определенной глубины, задаваемой максимальным количеством подцелей в правилах.
Поэтому воспользуемся более корректной и элегантной формулировкой. Ключевая идея здесь — определить отношениебольше_2с помощью его самого. Теперь второе (и последнее!) правило выглядит так:
больше_2(X, Y) :- больше(X, Z), больше_2(Z, Y).
Таким образом, итоговая программа будет иметь вид
больше_2(X, Y) :- больше(X, Y). больше_2(X, Y) :- больше(X, Z), больше_2(Z, Y).
Обратите внимание на порядок подцелей во втором правиле: если их поменять местами, то в большинстве реализаций языка Пролог выполнение запроса к такой базе знаний приведет к сообщению об ошибке, аналогичному следующему:
ERROR: Out of local stack
Если теперь в запросе использовать предикат больше_2 вместо больше, то программа будет работать так, как и предполагалось:
?- больше_2(слон, обезьяна).Yes
Интерпретатор всегда просматривает базу данных сверху вниз. Поэтому он анализирует сначала первую фразу процедуры больше_2 и пытается унифицировать каждый аргумент запроса с соответствующим аргументом этой фразы. Это происходит при помощи сравнения запроса с началом правила больше_2(X, Y) (т. е. с его головой). После этого двум переменным присваиваются значения: X = слон и Y = обезьяна.
После конкретизации переменной некоторым термом это значение «закрепляется» за всеми случаями использования этой переменной в правиле. После унификации запроса с заголовком фразы интерпретатор переходит к обработке целей, содержащихся в теле этой фразы.
В данном случае Пролог не может найти в базе данных факта больше(слон, обезьяна) и переходит к рассмотрению второго правила. Оно гласит, что для того, чтобы получить ответ на вопрос больше_2(X,Y) (с фиксированными значениями переменных, то есть больше_2(слон, обезьяна)), Пролог должен ответить на два подвопросабольше(X, Z) и больше_2(Z, Y), опять же с соответствующими значениями переменных.
Любая рекурсивная процедура должна включать по крайней мере по одной из ниже перечисленных компонент.
- Нерекурсивную фразу, определяющую правило, применяемое в момент прекращения рекурсии.
- Рекурсивное правило, первая подцель которого вырабатывает новые значения аргументов, а вторая — рекурсивная подцель- использует эти значения.
Задание
Дана база данных «Родители», в которой предикат родитель(коля, андрей) означает, что Коля является родителем Андрея:
родитель(коля, андрей). родитель(андрей, саша). родитель(виктор, федор). родитель(виктор, петр). родитель(петр, елена).
Используя рекурсию, определите отношение предок/2 через отношение родитель/2. Будем говорить, что некоторый X является отдаленным предком некоторого Y, если между X и Y существует цепочка людей, связанных между собой отношением родитель — ребенок.
(курс 68 ч.) Ветвления. Использование двухшаговой детализации | Дополнительный материал к главе I (§§ 1
Планирование уроков на учебный год
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 9 классы | Планирование уроков на учебный год | Ветвления
Содержание урока
Ветвления
Пример задачи с двухшаговой детализацией
Дополнительный материал к главе I (§§ 1 — 7). Автоматизированные и автоматические системы управления
Дополнительный материал к главе I (§§ 1 — 7). Использование рекурсивных процедур
Компьютерный практикум ЦОР. Ветвление и последовательная детализация алгоритма
Компьютерный практикум ЦОР. Ветвление. Использование двухшаговой детализации
1.2.
 Использование рекурсивных процедур
Использование рекурсивных процедурВернемся к вопросу об использовании процедур при составлении программ управления исполнителями алгоритмов (см. § 5 нашего учебника). Но это будет особый вид процедур, которые называются рекурсивными процедурами.
Рекурсивной называется процедура, в которой имеется обращение к самой себе.
Не все учебные исполнители алгоритмов допускают использование рекурсивных процедур (рекурсии). Такая возможность имеется в учебной программе «Стрелочка», реализующей один из вариантов графического исполнителя алгоритмов (ГРИС). При программировании некоторых задач рекурсия может служить альтернативой циклу.
Приведем пример использования в программе для ГРИС «Стрелочка» рекурсивной процедуры вместо цикла.
Пусть начальное положения «Стрелочки» — произвольная точка в первой строке рабочего поля, направление «вправо» (рис. 1.16). Требуется построить линию, идущую из этой точки до правой границы области.
Рис. 1.16
Сначала приведем на языке «Стрелочки» программу, в которой используется цикл.
алгоритм ПУТЬ_1_0
Дано: исполнитель в точке А
Надо: воспроизвести образец
нач
пока впереди НЕ стена
нц
шаг
кц
кон
А теперь воспользуемся рекурсией, для чего опишем процедуру ЛИНИЯ_1.
алгоритм ПУТЬ_1_1
Дано: Исполнитель в точке А
Надо: Воспроизвести образец
нач
делай ЛИНИЯ_1
кон
процедура ЛИНИЯ_1
шаг
делай ЛИНИЯ_1
конец процедуры
В теле этой процедуры присутствует команда обращения к самой себе: делай ЛИНИЯ_1.
Пошаговое исполнение (трассировка) такой программы иллюстрируется следующей трассировочной таблицей в случае, если «Стрелочка» вначале располагается за два шага до стенки.
Трассировка алгоритма
В этом случае завершение исполнения алгоритма произойдет аварийным образом (ситуация НЕ МОГУ).
Дело в том, что в данном алгоритме мы имеем дело с бесконечно повторяющимся рекурсивным обращением к процедуре, что недопустимо. Количество обращений процедуры к самой себе при ее исполнении называется глубиной рекурсии. Глубина рекурсии должна быть конечной. Для исполнителя «Стрелочка» естественным ограничением количества обращений процедуры самой к себе может служить только достижение стены. Следовательно, рекурсивный вызов в процедуре надо поместить в команду ветвления, проверяющую условие достижения стены. Вот новый вариант алгоритма.
алгоритм ПУТЬ_1_2
Дано: Исполнитель в точке А
Надо: Воспроизвести образец
нач
делай ЛИНИЯ 2
кон
процедура ЛИНИЯ 2
если впереди НЕ стена
то
шаг
делай ЛИНИЯ 2
все
конец процедуры
Трассировка этого алгоритма представлена в следующей таблице:
Трассировка алгоритма
Поскольку в описании алгоритма присутствует «точка остановки» (условие окончания исполнения алгоритма), исполнитель «Стрелочка», дойдя до стены, остановится.
Возникает вопрос: а стоит ли пользоваться рекурсией, если задача решается с помощью цикла? Немного усложним исходную задачу: требуется построить линию, идущую из данной точки, до правой границы области, после чего исполнитель должен вернуться в исходную точку А.
При использовании рекурсии решение этой задачи запишется достаточно просто, в то время как циклический алгоритм для такой задачи построить невозможно.
алгоритм ПУТЬ_2
Дано: Исполнитель в точке А
Надо: Воспроизвести образец
нач
делай ЛИНИЯ_3
кон
процедура ЛИНИЯ З
если впереди НЕ стена
то
шаг
делай ЛИНИЯ_3
прыжок
иначе
поворот
поворот
все
конец процедуры
Трассировка алгоритма ПУТЬ_2 для исходного положения исполнителя за два шага до стенки показана в следующей таблице.
Трассировка алгоритма
Если при выполнении процедуры происходит рекурсивное обращение к ней самой, то это значит, что не произошел выход из этой процедуры при предыдущем обращении. Этот выход откладывается на будущее. Затем, после окончания рекурсивных обращений, все отложенные выходы отрабатываются в порядке, обратном порядку рекурсивных обращений. В приведенной программе отработка отложенных выходов начинается с выполнения команды поворот.
Таким образом, существуют задачи, для которых использование рекурсии позволяет получить достаточно компактную запись алгоритма, в то время как его «циклическая версия» может оказаться либо очень сложной, либо вообще не реализуемой.
Коротко о главном
Рекурсивной называется процедура, в которой имеется обращение к самой себе.
Использование рекурсии может быть эквивалентом использованию цикла.
Существуют задачи, для которых рекурсивное решение является наиболее оптимальным или единственно возможным.
Вопросы и задания
1. Что такое рекурсивная процедура?
2. В каком порядке происходит выход из последовательности рекурсивных обращений?
3. Попробуйте разобраться, какую задачу решает следующая программа, содержащая рекурсивную процедуру. Реализуйте ее в среде исполнителя «Стрелочка».
алгоритм ФИГУРА-1
Дано: Исполнитель в точке А
Надо: Воспроизвести образец
нач
делай ЛИНИЯ
поворот
поворот
поворот
шаг
шаг
кон
процедура ЛИНИЯ
если впереди НЕ стена
то
шаг
делай ЛИНИЯ
шаг
иначе
поворот
поворот
поворот
шаг
шаг
поворот
поворот
поворот
все
конец процедуры
4. Составьте программу с рекурсивной процедурой, по которой исполнитель, находящийся в произвольной точке поля, дойдет до стенки, затем повернется на 90 градусов по часовой стрелке и дойдет до конца этой стенки вдоль нее. В результате будет нарисован угол.
Составьте программу с рекурсивной процедурой, по которой исполнитель, находящийся в произвольной точке поля, дойдет до стенки, затем повернется на 90 градусов по часовой стрелке и дойдет до конца этой стенки вдоль нее. В результате будет нарисован угол.
Система основных понятий главы I
Следующая страница Компьютерный практикум ЦОР. Ветвление и последовательная детализация алгоритма
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного… Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит. Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования… Интересное: Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным… Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 10 из 35Следующая ⇒
Вернемся к вопросу об использовании процедур при составлении программ управления исполнителями алгоритмов (см.
Не все учебные исполнители алгоритмов допускают использование рекурсивных процедур (рекурсии). Такая возможность имеется в учебной программе «Стрелочка», реализующей один из вариантов графического исполнителя алгоритмов (ГРИС)* (*Единая коллекция цифровых образовательных ресурсов (ЕК ЦОР): http: //school-collection. edu. ru /). При программировании некоторых задач рекурсия может служить альтернативой циклу. Приведем пример использования в программе для ГРИС «Стрелочка» рекурсивной процедуры вместо цикла. Пусть начальное положения «Стрелочки» — произвольная точка в первой строке рабочего поля, направление «вправо» (рис. 1.16). Требуется построить линию, идущую из этой точки до правой границы области.
Сначала приведем на языке «Стрелочки» программу, в которой используется цикл.
алгоритмПУТЬ_1_0 Дано: исполнитель в точке А Надо: воспроизвести образец Нач покавпереди НЕ стена нц Шаг кц Кон А теперь воспользуемся рекурсией, для чего опишем процедуру ЛИНИЯ_1. алгоритм ПУТЬ_1_1 Дано: Исполнитель в точке А Надо: Воспроизвести образец Нач делай ЛИНИЯ1 Кон процедура ЛИНИЯ1 Шаг делайЛИНИЯ1 Конец процедуры
В теле этой процедуры присутствует команда обращения к самой себе: делай ЛИНИЯ1. Пошаговое исполнение (трассировка) такой программы иллюстрируется следующей трассировочной таблицей в случае, если «Стрелочка» вначале располагается за два шага до стенки.
Трассировка алгоритма
В этом случае завершение исполнения алгоритма произойдет аварийным образом (ситуация НЕ МОГУ). Дело в том, что в данном алгоритме мы имеем дело с бесконечно повторяющимся рекурсивным обращением к процедуре, что недопустимо. Количество обращений процедуры к самой себе при ее исполнении называется глубиной рекурсии. Глубина рекурсии должна быть конечной. Для исполнителя «Стрелочка» естественным ограничением количества обращений процедуры самой к себе может служить только достижение стены. Следовательно, рекурсивный вызов в процедуре надо поместить в команду ветвления, проверяющую условие достижения стены. Вот новый вариант алгоритма.
алгоритм ПУТЬ_1_2 Дано: Исполнитель в точке А Надо: Воспроизвести образец Нач делайЛИНИЯ 2 Кон процедураЛИНИЯ 2 если впереди НЕ стена то Шаг делай ЛИНИЯ 2 Все Конец процедуры
Трассировка этого алгоритма представлена в следующей таблице:
Трассировка алгоритма
Поскольку в описании алгоритма присутствует «точка остановки» (условие окончания исполнения алгоритма), исполнитель «Стрелочка», дойдя до стены, остановится.
Возникает вопрос: а стоит ли пользоваться рекурсией, если задача решается с помощью цикла? Немного усложним исходную задачу: требуется построить линию, идущую из данной точки, до правой границы области, после чего исполнитель должен вернуться в исходную точку А. При использовании рекурсии решение этой задачи запишется достаточно просто, в то время как циклический алгоритм для такой задачи построить невозможно.
алгоритм ПУТЬ_2 Дано: Исполнитель в точке А Надо: Воспроизвести образец Нач делай ЛИНИЯ_3 Кон
процедура ЛИНИЯ_3 если впереди НЕ стена то Шаг делай ЛИНИЯ_3 Прыжок Иначе Поворот Поворот Все Конец процедуры
Трассировка алгоритма ПУТЬ_2 для исходного положения исполнителя за два шага до стенки показана в следующей таблице.
Трассировка алгоритма
Если при выполнении процедуры происходит рекурсивное обращение к ней самой, то это значит, что не произошел выход из этой процедуры при предыдущем обращении. Этот выход откладывается на будущее. Таким образом, существуют задачи, для которых использование рекурсии позволяет получить достаточно компактную запись алгоритма, в то время как его «циклическая версия» может оказаться либо очень сложной, либо вообще не реализуемой.
Коротко о главном
Рекурсивной называется процедура, в которой имеется обращение к самой себе. Использование рекурсии может быть эквивалентом использованию цикла. Существуют задачи, для которых рекурсивное решение является наиболее оптимальным или единственно возможным.
Вопросы и задания
1. Что такое рекурсивная процедура? 2. В каком порядке происходит выход из последовательности рекурсивных обращений? 3.
алгоритмФИГУРА-1 Дано: Исполнитель в точке А Надо: Воспроизвести образец Нач делай ЛИНИЯ Поворот Поворот Поворот Шаг Шаг Кон
процедураЛИНИЯ если впереди НЕ стена то Шаг делай ЛИНИЯ Шаг Иначе Поворот Поворот Поворот Шаг Шаг Поворот Поворот Поворот Все Конец процедуры
4.
§8 Что такое программирование
Основные темы параграфа: ■кто такие программисты; ■что такое язык программирования; ■ что такое система программирования.
Кто такие программисты
Теперь вам предстоит ближе познакомиться еще с одним разделом информатики, который называется «Программирование».
Специалисты, профессионально занимающиеся программированием, называются программистами. Может возникнуть впечатление, что программисты теперь уже и не нужны! Но кто же тогда будет создавать все операционные системы, редакторы, графические пакеты, компьютерные игры и многое другое? Программисты, безусловно, нужны, причем задачи, которые им приходится решать, со временем становятся все сложнее. Программирование принято разделять на системное и прикладное. Системные программисты занимаются разработкой системного программного обеспечения: операционных систем, утилит и пр. В данной главе вы познакомитесь с простейшими правилами и приемами программирования, заглянете в эту актуальную и престижную профессиональную область.
⇐ Предыдущая567891011121314Следующая ⇒ Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций. |
Урок 6. Рекурсия: разделяй и властвуй
Разделяй и властвуй (англ. divide and conquer) в информатике — важная парадигма разработки алгоритмов, заключающаяся в рекурсивном разбиении решаемой задачи на две или более подзадачи того же типа, но меньшего размера, и комбинировании их решений для получения ответа к исходной задаче; разбиения выполняются до тех пор, пока все подзадачи не окажутся элементарными.
Википедия
- Что такое рекурсия
- Рекурсия и цикл
- Конечная рекурсия
- Рекурсия по значению переменной
- Разделяй и властвуй
- Что мы узнали и ещё немного
… и с удивлением обнаружил, что 10% моей аудитории наибольшие трудности испытывают в борьбе с концепцией рекурсивных процедур.Я был удивлён, ибо полагал, что рекурсия не сложна.
Из доклада Дейкстры от 1 марта 1999 года
Рекурсия — одна из самых важных идей в информатике, но её обычно рассматривают как одну из самых сложных частей программирования.
Кукарача вслед за Дейкстрой намерен развеять миф о сложности рекурсии, показать её простоту, красоту и полезность для решения задач.
Что такое рекурсия
Шёл я лесом, вижу мост, под мостом ворона мокнет. Взял её за хвост, положил на мост, пускай ворона сохнет. Шел я лесом, вижу мост, на мосту ворона сохнет. Взял её за хвост, положил под мост, пускай ворона мокнет…
Макс Фрай,
«Ворона на мосту»
Кукарача. Посмотри на эту программу. Что произойдёт, когда будет нажат зелёный флажок?
Антука.
Сначала выполнится процедура Подготовка —
исполнитель будет установлен у левого края сцены. Затем выполнится
процедура Поход.
Затем выполнится
процедура Поход.
Кукарача. И как же она выполнится?
Антука. Очень странная процедура, она «кусает» сама себя за хвост, вернее — за голову!
Кукарача. Это всё, что ты можешь сказать?
Антука. Подробности такие. Первая команда переместит усатого на 10 шагов вперёд. Вторая ничего не сделает — до края далеко. Следующая команда Поход. Укус за голову! Процедура вызывает саму себя. Что делать?
Кукарача. Исполнять!
Антука. Хорошо. Процедура Поход начинает выполняться заново. Первая команда переместит усатого ещё на 10 шагов. Вторая опять ничего не сделает — до края далеко. А следующая — снова Поход!
Кукарача. Что же произойдёт в итоге?
Что же произойдёт в итоге?
Антука. Кот будет смещаться вправо до края, затем команда развернёт его и он будет двигаться влево… Похоже получился необычный бесконечный цикл! И команда никогда не выполнится!
Кукарача. Это называется рекурсией! Процедура Поход — рекурсивная!
Рекурсивная процедура — это такая процедура, которая в процессе работы вызывает саму себя.
Рекурсия и цикл
Упал в рекурсию и больно стукнулся о дно стека.
Запись в больничном листе
программиста Сидорова
Антука. Получается, что рекурсия просто подменяет собой бесконечный цикл!
Кукарача. Это не так. Во-первых, рекурсия не всегда бесконечна (это хорошо!), а во-вторых, цикл и рекурсия работают по-разному: рекурсия во время работы тратит память компьютера (это плохо!), а цикл — нет!
Антука. На что же рекурсия расходует память?
На что же рекурсия расходует память?
Кукарача. При каждом обращении процедуры к самой себе интерпретатор запоминает в «последним пришёл — первым вышел»).»>стеке адрес возврата, чтобы продолжить работу программы, когда рекурсия закончится.
Антука. Зачем запоминать адрес возврата, если рекурсия никогда не заканчивается, и выполнять что-то после рекурсивного вызова не придётся?
Кукарача. Бесконечную рекурсию программисты не используют. Мы начали с неё для простоты. Это раз.
А теперь главное. Интерпретатор не разбирается, какой вызов происходит, рекурсивный или обычный. При вызове любой процедуры интерпретатор помещает адрес возврата в стек, чтобы правильно продолжить выполнение кода после завершения работы процедуры.
Антука. А почему в качестве хранилища возвратов используется стек?
Кукарача. При цепочке вызовов, первым должен сработать
последний адрес возврата, верно? Это согласуется с принципом
стека: «последним пришёл — первым вышел».
Вот почему стек идеально подходит для хранения адресов возврата.
При цепочке вызовов, первым должен сработать
последний адрес возврата, верно? Это согласуется с принципом
стека: «последним пришёл — первым вышел».
Вот почему стек идеально подходит для хранения адресов возврата.
Антука. Да, понятно. Действительно, рекурсия в отличие от цикла расходует память на стек.
Кукарача. И если рекурсия бесконечная, вся свободная память компьютера (его ОЗУ) может быстро исчерпаться, а это приведёт к краху работы интерпретатора.
Попробуй запустить программу, представленную ниже. В ней убраны медленные шаги исполнителя, и крах памяти наступает очень быстро:
Конечная рекурсия
Работает? Не ожидал!
Из записной книжки
программиста Сидорова
Антука. Хотелось бы увидеть пример конечной рекурсии.
Кукарача. Чтобы рекурсия остановилась, нужно предусмотреть в коде
рекурсивной процедуры проверку
на базовый случай — проверку условия,
при котором рекурсия заканчивается.
Чтобы рекурсия остановилась, нужно предусмотреть в коде
рекурсивной процедуры проверку
на базовый случай — проверку условия,
при котором рекурсия заканчивается.
Вот пример. Рекурсивные вызовы в процедуре заканчиваются, когда исполнитель касается красной «стены» (базовый случай):
Антука. Интересно, как будет работать стек возвратов при выполнении процедуры ?
Кукарача. При каждом рекурсивном вызове в стек возвратов будет помещаться адрес команды, следующей за рекурсивным вызовом. В нашем случае речь идёт о команде, следующей за командой по ветви ИНАЧЕ. Никаких команд там нет, что для интерпретатора равнозначно пустой команде.
Антука. А если за рекурсивным вызовом находятся какие-то команды?
Кукарача.
После завершения рекурсии
эти команды будут выполнены столько раз, сколько адресов
возврата накопилось в стеке. Группу команд, которая выполняется после завершения
рекурсии, в Роботландии традиционно называют
рекурсивной пружинкой.
Группу команд, которая выполняется после завершения
рекурсии, в Роботландии традиционно называют
рекурсивной пружинкой.
Проверим, как это работает, собрав такой код:
Антука. Значения переменных, после завершения работы программы, говорят о том, что двигаясь к стене, исполнитель выполнил команду 29 раз, а назад — только 28. Почему?
Кукарача. В момент, когда кот касается стены (базовый случай), рекурсия заканчивается, веточка ИНАЧЕ не срабатывает, следовательно, последняя команда в направлении «туда» не меняет стек возвратов, и в нём оказывается записей на одну меньше.
В точности уравнять движение «обратно» с движением «туда» можно, если вынести рекурсивную пружинку за условную команду:
Антука.
Попробую объяснить почему.
…
Рекурсия по значению переменной
Буратино дали три яблока. Два он съел. Сколько яблок осталось у Буратино? Думаете одно? Ничего подобного. Никто же не знает, сколько у него уже было яблок до этого. Мораль — обнуляйте переменные!
Из поучений
программиста Сидорова
Антука. Чтобы рекурсия закончилась, необходимо предусмотреть проверку на её окончание!
Кукарача. Да, верно. Во время рекурсии что-то должно меняться. И когда эти изменения приводят к особому состоянию (базовый случай), рекурсию надо остановить.
Антука. Самое изменчивое в программах — это переменные! Они поэтому так и называются!
Кукарача.
Верно! При помощи переменных (в том числе параметров процедур,
которые являются локальными переменными внутри процедуры)
чаще всего и управляют рекурсией. Решим для примера задачу о рисовании прямоугольной
спирали.
Решим для примера задачу о рисовании прямоугольной
спирали.
Задача. Прямоугольная спираль
Нарисовать спираль, такую как на рисунке.
Начальная точка: (0, −50)
Максимальная длина стороны: 200
Изменение длины: 10
Направление:
Решение
Антука. Попробую рассуждать «рекурсивно». Чтобы нарисовать спираль, нужно:
- Нарисовать сторону
- Повернуться
- И… ура! Рекурсия: нарисовать спираль с уменьшенной стороной
Перепишу этот рекурсивный план на псевдокоде:
ЭТО Спираль(сторона) Нарисовать прямую длиной сторона Повернуться // Нарисовать спираль с уменьшенной стороной Спираль(сторона-10) КОНЕЦ
Кукарача. Всё хорошо, кроме одного важного момента — у тебя получилась бесконечная рекурсия! Которая, к тому же, рано или поздно начнёт «рисовать» линии с отрицательной длиной!
Антука. Да, я забыл предусмотреть базовый случай!
Рекурсия должна закончится…
когда уменьшать сторону уже нельзя! Получается так:
Да, я забыл предусмотреть базовый случай!
Рекурсия должна закончится…
когда уменьшать сторону уже нельзя! Получается так:
ЭТО Спираль(сторона) ЕСЛИ сторона < 10 ТО ПУСТО // Базовый случай (делать ничего не надо) ИНАЧЕ // Рекурсивный случай { Нарисовать прямую длиной сторона Повернуться // Нарисовать спираль с уменьшенной стороной Спираль(сторона-10) } КОНЕЦ
Кукарача. Теперь всё хорошо. Соберём программу на Скретч по этому алгоритму:
Антука. Условная команда с пуcтой веточкой ТО смотрится некрасиво!
Кукарача. Согласен. Условную команду в полной форме можно заменить сокращённой:
Посмотрите, как будет выполняться программа.
Кукарача. А теперь интересный вопрос: как будет работать процедура, если рисование поставить за рекурсивным вызовом?
Антука. Пока идут рекурсивные вызовы, рисование откладывается при помощи стека
возвратов. Когда рекурсия закончится, отложенные фрагменты
(рекурсивная пружинка) сработают столько раз, сколько было
рекурсивных вызовов, и спираль будет нарисована.
Пока идут рекурсивные вызовы, рисование откладывается при помощи стека
возвратов. Когда рекурсия закончится, отложенные фрагменты
(рекурсивная пружинка) сработают столько раз, сколько было
рекурсивных вызовов, и спираль будет нарисована.
Кукарача. Важно отметить, что первой будет нарисована самая маленькая сторона спирали, так как ссылка на это рисование попала в стек последней.
Антука. Получается, что спираль будет раскручиваться (сторона увеличивается), а не закручиваться как раньше (сторона уменьшалась).
Кукарача. Верно. Спирали получатся, конечно, одинаковые, но они будут различно расположены по отношению к начальной точке, и рисоваться по-разному:
Посмотрите, как будет выполняться программа.
Разделяй и властвуй
Путник-друг, пойдём вместе. Ночь близка, звери кругом и огонь костра
может потухнуть. Но если мы согласимся разделить дозор ночи,
мы сохраним силы.
Ночь близка, звери кругом и огонь костра
может потухнуть. Но если мы согласимся разделить дозор ночи,
мы сохраним силы.
Елена Ивановна Рерих
Кукарача. Рекурсивные программы, которые мы собрали сегодня, интересны только в плане знакомства с рекурсией. Вместо рекурсии в этих программах лучше использовать цикл, ведь для работы цикла не нужна дополнительная память на стек возвратов.
Вот как, например, при помощи цикла записывается построение спирали:
Антука. Программа с циклом использует переменную X для хранения текущей стороны спирали, во всём остальном этот вариант не сложнее рекурсии, зато понятнее, и цикл не тратит память на стек возвратов! Рекурсия — забавная штука, но, вероятно, не очень полезная на практике!
Кукарача.
Здесь ты не прав! Существуют задачи, решить которые при помощи цикла
очень сложно, а рекурсивное решение простое и короткое.
Прежде, чем мы рассмотрим пример такой задачи, опишу общий принцип построения рекурсивных решений. Этот принцип можно озаглавить так: «разделяй и властвуй».
Разделяй и властвуй
Укажите параметр, по которому будет определяться окончание рекурсии. Затем опишите два шага:
- Базовый случай. Определяется значение параметра, при котором наступает простейший случай, и для него решение строится непосредственно. Это выход из рекурсии.
- Рекурсивный случай. Задача сводится к себе самой, но с другим значением параметра, таким, который приближает к базовому случаю.
Ну, а теперь…
Задача. Кривая Коха
Процесс построения выглядит следующим образом: берём
отрезок, разделяем на три равные части и заменяем средний интервал
равносторонним треугольником без этого сегмента. В результате
образуется ломаная, состоящая из четырёх звеньев
одинаковой длины по 1/3 от первоначального отрезка.
В результате
образуется ломаная, состоящая из четырёх звеньев
одинаковой длины по 1/3 от первоначального отрезка.
На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и так далее.
Требуется создать процедуру построения кривой Коха. Процедура должна иметь два параметра: длину начального отрезка и уровень. Кривая должна строиться из текущей точки в текущем направлении.
Решение
Параметр, который будет управлять рекурсией, понятен — это уровень.
| Базовый случай | Рекурсивный случай |
|---|---|
| уровень = 0 | уровень > 0 |
Тогда процедура будет выглядеть так:
Сначала построим решение для базового случая:
Затем строим решение для рекурсивного случая:
Антука. Потрясающе! Решение поражает своей простотой и буквальным соответствием
описанию кривой Коха!
Потрясающе! Решение поражает своей простотой и буквальным соответствием
описанию кривой Коха!
Кукарача. Хочу обратить внимание на то, что базовым уровнем можно считать сам отрезок, и тогда процедура упростится.
Антука. Здорово! А можно решить эту задачу при помощи цикла?
Кукарача. Да, это возможно, но потребует больших усилий! Приведу цитату Ли Колдуэлла (Leigh Caldwell) с сайта Stack Overflow, которая мне нравится:
Циклы могут ускорить работу программы. Рекурсия может ускорить работу программиста. Выбирайте, что важнее в вашей ситуации!
Отмечу, что кривая Коха является фракталом. Определение фрактала из Википедии:
Фрактал — множество, обладающее свойством
самоподобия (объект, в точности или приближённо совпадающий
с частью себя самого, то есть целое имеет ту же форму, что и одна
или более частей).
Антука. Мне пришла в голову идея построить из кривых Коха равносторонний треугольник! Получается красивая снежинка:
Кукарача. Фракталы часто используют для создания сложных реалистичных объектов на экране компьютера (например, в компьютерных играх), ведь эти объекты в реальной жизни, действительно, являются фракталами!
Примеры фракталов: кораллы, морские звёзды, кроны деревьев, кровеносная система человека, снежинки, облака, молнии…
Что мы узнали и ещё немного
Рекурсия — это самоповтор, включение некоторого объекта или события в самого себя, как части.
Рекурсивная процедура — это такая процедура, которая в процессе работы вызывает саму себя.
Перед выполнением любой процедуры (обычной или рекурсивной)
интерпретатор
предварительно
запоминает в
«последним пришёл — первым вышел»). «>стеке
адрес возврата.
«>стеке
адрес возврата.
В качестве хранилища адресов возврата используется стек по принципу работы этого хранилища «последним пришёл — первым вышел».
Рекурсия похожа на цикл, но в отличие от цикла во время своей работы расходует память на стек возвратов.
Чтобы рекурсия заканчивалась, надо в коде рекурсивной процедуры проверять базовый случай (выход из рекурсии) и правильно строить рекурсивный случай.
Базовый случай — это простейший вариант, при котором результат получается непосредственно.
Рекурсивный случай — это вызов процедуры самой себя, но с другими состояниями, которые приближают выполнение процедуры к базовому случаю.
Рекурсия с параметром. Принцип «Разделяй и властвуй»
Для рекурсивной процедуры нужно указать параметр, по которому будет
определяться окончание рекурсии. Затем собрать два шага:
Затем собрать два шага:
- Базовый случай. Определяется значение параметра, при котором наступает простейший случай, и для него решение строится непосредственно. Это выход из рекурсии.
- Рекурсивный случай. Задача сводится к себе самой, но с другим значением параметра, таким, который приближает к базовому случаю.
Терминальная и нетерминальная рекурсии
Терминал — это оконечное устройство, концевик. В частности, терминалом называют монитор (часто вместе с клавиатурой) как оконечное устройство компьютера для диалога с пользователем.
Раньше, когда работали на больших ЭВМ типа ЕС или БЭСМ, терминалы
(монитор+клавиатура) выносили в отдельные залы, где несколько
пользователей одновременно работали на отдельных терминалах с одной
ЭВМ. Иногда, такой терминал имел свой процессор и небольшую память. Таким образом, получалось, что терминал — это небольшой
компьютер. Но это не мешало ему быть терминалом, так как он работал
не самостоятельно, а служил оконечным устройством другой ЭВМ.
Таким образом, получалось, что терминал — это небольшой
компьютер. Но это не мешало ему быть терминалом, так как он работал
не самостоятельно, а служил оконечным устройством другой ЭВМ.
Терминальная рекурсия — это рекурсия-концевик, то есть, такая рекурсия, которая содержит рекурсивный вызов самым последним в своём логическом коде. После терминального рекурсивного вызова других команд в процедуре выполняться не должно.
Посмотрите на эту процедуру:
ЭТО вход ЕСЛИ условие ТО вход // рекурсивный случай ИНАЧЕ { … } // базовый случай КОНЕЦ
Кажется, что здесь рекурсия нетерминальная — ведь рекурсивный вызов вход стоит не самым последним.
Но это не так! Не важно, где стоит вызов, важно что после него
ничего не выполняется.
Вызов вход стоит в условной команде,
которая идёт последней, значит этот вызов терминальный.
А вот примеры нетерминальных рекурсий:
ЭТО вход1 ЕСЛИ условие ТО { вход1 команда } // рекурсивный случай ИНАЧЕ { … } // базовый случай КОНЕЦ ЭТО вход2 ЕСЛИ условие ТО { … } // базовый случай вход2 // нетерминальная рекурсия команда // рекурсивная пружинка КОНЕЦ
Нетерминальная рекурсия порождает отложенные команды, выполняемые после завершения рекурсии. Такие команды в Роботландии называют рекурсивными пружинками.
| Главная Контакты Случайная статья
|
gif» bgcolor=»#FDFCF7″/> | ||
|
Рекурсивное программирование В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная рекурсия), например, функция A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии. Число рекурсивных вызовов в каждый конкретный момент времени, называется текущим уровнем рекурсии. Основой для разработки рекурсивных алгоритмов служат, так называемые, рекуррентные соотношения (формулы), устанавливающие зависимость между результатами какого-либо действия на n-м шаге от результата аналогичных действий, полученных на предыдущем n-1-м шаге. Преимущество рекурсивного определения объекта заключается в том, что такое конечное определение теоретически способно описывать бесконечно большое число объектов. Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за счёт этого работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. ! Главное требование к рекурсивным процедурам заключается в том, что вызов рекурсивной процедуры должен выполнятся по условию, которое на каком-то уровне рекурсии станет ложным (т.к. бесконечной памяти не существует). Если условие истинно, то рекурсивный спуск продолжается. Когда оно становится ложным, то спуск заканчивается и начинается поочередный рекурсивный возврат из всех вызванных на данный момент копий рекурсивной процедуры. Структура рекурсивной процедуры может принимать 3 разные формы. 1. Форма с выполнением действий до рекурсивного вызова (с выполнением действий на рекурсивном спуске). 2. Форма с выполнением действий после рекурсивного вызова (с выполнением действий на рекурсивном возврате). 3. Форма с выполнением действий как до, так и после рекурсивного вызова (с выполнением действий как на рекурсивном спуске, так и на рекурсивном возврате). Все виды рекурсивных процедур находят применение на практике. Многие задачи, в том числе вычисления n!, безразличны к тому, какая используется форма рекурсивной процедуры. ! Однако есть классы задач, при решении которых требуется (программисту) сознательно управлять ходом работы рекурсивных процедур и функций.
Также имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного и/или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивается выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. Однако, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Scheme (диалект языка Lisp), описание которого содержит все необходимые сведения. Любую рекурсивную функцию можно заменить циклом и стеком.
|
|||
|
рекурсивная процедура — английский перевод
Рекурсивная сортировка | Recursive Sort |
Рекурсивная проверка. | Whether to do a recursive check. |
Так описывается рекурсивная часть этого теста. | This is how a recursive part of the test is described. |
Эта рекурсивная природа является бесконечной игрой. | That recursive nature is the infinite game. |
На приведенной ниже диаграмме изображена рекурсивная схема, являющаяся основой архитектуры Информационного центра | The following graphic illustrates the recursive scheme that is the foundation of the Clearing House architecture |
На приведенной ниже диаграмме изображена quot рекурсивная quot схема, являющаяся основой архитектуры Информационного центра | The following graphic illustrates the quot recursive quot scheme that is the foundation of the Clearing House architecture |
процедура процедура (порядок) назначения | Case 557 MAL 7 (1) 8 (1) 11 (3) (4) (5) Germany Bayerisches Oberstes Landesgericht 4Z SchH 13 99 (28 February 2000) |
Так, где у нас была рекурсивная функция, теперь мы просто будем иметь уравнения, которые упоминают друг друга. | So where we used to have a recursive function, now we’re just going to have equations that mention each other. |
Процедура | Procedures |
Процедура | Paragraph 7.2.4.4. |
ПРОЦЕДУРА | (vi) Woodwork supply |
Процедура. | Procedure. |
Процедура | Procedure for tests on flat test pieces. |
процедура | formal requirements |
Процедура | Direct programme assistance expenditure |
ПРОЦЕДУРА | Direct calibration method |
Процедура | Procedure. |
Процедура. | Procedures. |
Процедура | 31. |
процедура | courts |
Процедура | Procedure |
Процедура | For Notes see page 4. |
Процедура | C. Procedure |
ПРОЦЕДУРА | These claimants must submit |
Процедура | Topic Page |
процедура | procedure |
Процедура | Procedure |
ПРОЦЕДУРА | PROCEDURE |
Процедура | Procedure |
ПРОЦЕДУРА | The nature and purpose of the proceedings |
Процедура | Procedure to be followed |
Процедура | Modalities Procedure |
процедура | notice procedure |
Процедура | 2. |
. ПРОЦЕДУРА | II. PROCEDURE |
Процедура | 3. Procedure |
ПРОЦЕДУРА | Summary of the process |
Процедура | The Process |
Процедура! | Treatment. |
Можно сказать, хвост рекурсивная функция является функциональной формой цикла, и он выполняет так же, как эффективно, как и петли. | Could say a tail recursive function is the functional form of a loop, and it executes just as efficiently as a loop. |
Процедура представления жалоб (конфиденциальная процедура 1503)9. | There is likely to be a need for the advice of independent experts at some stages in the process (see further below) The complaint procedure (the 1503 confidential procedure). |
Наконец, надлежащая процедура это всего лишь процедура. | Finally, due process is just that a process. |
Процедура представления жалоб (конфиденциальная процедура 1503)9. | The complaint procedure (the 1503 confidential procedure). |
Наконец, надлежащая процедура это всего лишь процедура. | Finally, due process is just that a process. |
ПРОЦЕДУРА ЗАПРОСА | Inquiry ProcedurE |
Что рекурсивная хранимая процедура
1 отвечает на этот вопрос.
0 голосов
Связанные вопросы в базе данных
Хранимая процедура представляет собой набор … ПОДРОБНЕЕ
ответил 4 фев в базе данных по Неха • 8,920 баллов • 216 просмотров
- sql
- sql-сервер
- тскл
- хранимых процедур
Как в SQL Server 2000 вы. .. ПОДРОБНЕЕ
.. ПОДРОБНЕЕ
25 авг в базе данных по Китузз • 12 240 баллов • 45 просмотров
- хранимые процедуры
- SQL-сервер-2000
- sql-дроп
Хранимая процедура представляет собой набор … ПОДРОБНЕЕ
ответил 23 августа 2018 г. в базе данных по Кодирование по сердцу77 • 3720 баллов • 810 просмотров
- хранимые процедуры
Хранимая процедура представляет собой набор … ПОДРОБНЕЕ
ответил 6 сентября 2018 г. в базе данных по Кодирование по сердцу77 • 3720 баллов • 596 просмотров
- хранимые процедуры
Вы можете соединить свой код Java с … ПОДРОБНЕЕ
ответил 11 мая 2018 г. на Яве по Парт • 4 630 баллов • 935 просмотров
- ява
- база данных
- sql
На самом деле основных причин три:
Неэффективность в . .. ПОДРОБНЕЕ
.. ПОДРОБНЕЕ
ответил 7 сентября 2018 г. в базе данных по ДатаКинг99 • 8 240 баллов • 403 просмотра
- sql
- база данных
Одинарные кавычки используются для обозначения … ПОДРОБНЕЕ
ответил 11 сентября 2018 г. в базе данных по Кодирование по сердцу77 • 3720 баллов • 17 061 просмотр
- sql
- база данных
Такое использование кавычек называется разделителями… ПОДРОБНЕЕ
ответил 11 сентября 2018 г. в базе данных по Кодирование по сердцу77 • 3720 баллов • 254 просмотра
- sql
- база данных
Дублирование данных в базе — это… ПОДРОБНЕЕ
ответил 17 августа 2018 г. в базе данных по Саити • 6 380 баллов • 566 просмотров
- избыточность данных
Контрольная точка объявляет точку, до которой все . .. ПОДРОБНЕЕ
.. ПОДРОБНЕЕ
ответил 4 сентября 2018 г. в базе данных по Саити • 6 380 баллов • 1228 просмотров
- КПП
- база данных
- Все категории
- Апач Кафка (84)
- Апач Спарк (596)
- Лазурный (131)
- Большие данные Hadoop (1907)
- Блокчейн (1673)
- С# (124)
- С++ (268)
- Консультирование по вопросам карьеры (1060)
- Облачные вычисления (3356)
- Кибербезопасность и этичный взлом (145)
- Аналитика данных (1266)
- База данных (853)
- Наука о данных (75)
- DevOps и Agile (3500)
- Цифровой маркетинг (111)
- События и актуальные темы (28)
- IoT (Интернет вещей) (387)
- Ява (1178)
- Котлин (3)
- Администрирование Linux (384)
- Машинное обучение (337)
- Микростратегия (6)
- PMP (423)
- Power BI (516)
- Питон (3154)
- РПА (650)
- SalesForce (92)
- Селен (1569)
- Тестирование программного обеспечения (56)
- Таблица (608)
- Таленд (73)
- ТипСкрипт (124)
- Веб-разработка (2,999)
- Спросите нас о чем угодно! (66)
- Другие (1064)
- Мобильная разработка (46)
Подпишитесь на нашу рассылку и получайте персональные рекомендации.

Уже есть учетная запись? .
Каковы свойства рекурсивной процедуры? – AnswersAll
Содержание
Каковы свойства рекурсивной процедуры?
Недвижимость. Базовые критерии — должен быть хотя бы один базовый критерий или условие, чтобы при выполнении этого условия функция переставала вызывать себя рекурсивно. Прогрессивный подход. Рекурсивные вызовы должны развиваться таким образом, чтобы каждый раз, когда выполняется рекурсивный вызов, он приближался к базовым критериям.
Что такое рекурсия и рекурсивные процедуры должны иметь два свойства?
Рекурсия означает повторный вызов самой функции. Свойства: (1) Должен быть какой-то базовый случай, когда условие заканчивается. (2) Каждый рекурсивный вызов процедуры затрагивает меньший случай проблемы.
Какие существуют два типа рекурсивных функций?
Рекурсия в основном бывает двух типов в зависимости от того, вызывает ли функция сама себя из самой себя или несколько функций вызывают друг друга взаимно. Первый называется прямой рекурсией, а второй называется косвенной рекурсией. После этого вызова рекурсивная функция ничего не выполняет.
Первый называется прямой рекурсией, а второй называется косвенной рекурсией. После этого вызова рекурсивная функция ничего не выполняет.
Какие две фазы рекурсивного процесса?
Все рекурсивные функции работают в двух фазах — фаза намотки и фаза раскрутки. каждый экземпляр функции.
Что такое рекурсивная процедура?
Активная процедура, которая вызывается из самой себя или из другой активной процедуры, является рекурсивной процедурой. Такой вызов называется рекурсией. Процедура, вызываемая рекурсивно, должна иметь атрибут RECURSIVE, указанный в операторе PROCEDURE.
Что такое рекурсия и ее процесс?
Рекурсия — это метод компьютерного программирования, включающий использование процедуры, подпрограммы, функции или алгоритма, которые вызывают себя на шаге, имеющем условие завершения, так что последовательные повторения обрабатываются до критического шага, на котором выполняется условие, в которое момент времени остальная часть каждого повторения равна …
Каковы преимущества и недостатки рекурсии?
Преимущества/недостатки рекурсии #
- Для решения таких естественно рекурсивных задач, как Ханойская башня.

- Уменьшить ненужный вызов функции.
- Чрезвычайно полезно при применении одного и того же раствора.
- Рекурсия уменьшает длину кода.
- Это очень полезно при решении проблемы со структурой данных.
Каковы три ключевые особенности рекурсивного алгоритма?
Как и роботы Азимова, все рекурсивные алгоритмы должны подчиняться трем важным законам:
- Рекурсивный алгоритм должен вызывать сам себя, рекурсивно.
- Рекурсивный алгоритм должен иметь базовый случай.
- Рекурсивный алгоритм должен изменить свое состояние и перейти к базовому варианту.
Как работает множественная рекурсия?
Мы имеем дело с множественной рекурсией, когда активация метода может вызвать более одной рекурсивной активации одного и того же метода. Мы реализуем рекурсивный метод, который принимает положительное целое число n в качестве параметра и возвращает n-е число Фибоначчи. …
Что такое рекурсия и ее преимущества?
Сокращение ненужных вызовов функций. С помощью рекурсии можно легко решать проблемы, в то время как итеративное решение очень большое и сложное.
С помощью рекурсии можно легко решать проблемы, в то время как итеративное решение очень большое и сложное.
Что такое рекурсивное мышление?
1. Процесс решения больших задач путем их разбиения на более мелкие, более простые задачи, имеющие одинаковые формы. Узнайте больше в: Случайные процессы и визуальное восприятие: стохастическое искусство.
Какая польза от рекурсии?
Рекурсия предназначена для решения задач, которые можно разбить на более мелкие повторяющиеся задачи. Это особенно хорошо для работы с вещами, которые имеют много возможных ветвей и слишком сложны для итеративного подхода. Одним из хороших примеров этого может быть поиск в файловой системе.
Каковы два преимущества и недостатки рекурсии?
Преимущества/недостатки рекурсии #
- Код может быть легче писать.
- Для решения таких естественно рекурсивных задач, как Ханойская башня.
- Уменьшить ненужный вызов функции.

- Чрезвычайно полезно при применении одного и того же раствора.
- Рекурсия уменьшает длину кода.
Для чего нужна рекурсия?
Каковы правила рекурсии?
Подобно роботам Азимова, все рекурсивные алгоритмы должны подчиняться трем важным законам:
- Рекурсивный алгоритм должен иметь базовый случай.
- Рекурсивный алгоритм должен изменить свое состояние и перейти к базовому варианту.
- Рекурсивный алгоритм должен вызывать сам себя, рекурсивно.
Какие 2 случая всегда присутствуют в рекурсивном алгоритме?
Рекурсивная реализация всегда состоит из двух частей: базового случая, который является самым простым, наименьшим экземпляром проблемы, который не может быть подвергнут дальнейшей декомпозиции. Базовые случаи часто соответствуют пустоте — пустой строке, пустому списку, пустому множеству, пустому дереву, нулю и т. д.
В чем разница между прямой и косвенной рекурсией?
В прямой рекурсии только одна функция вызывается сама по себе. В косвенной рекурсии более одной функции заменяются другой функцией и количеством раз. прямая рекурсия делает накладные расходы.
В косвенной рекурсии более одной функции заменяются другой функцией и количеством раз. прямая рекурсия делает накладные расходы.
Зачем нужна рекурсия?
Что такое концепция рекурсии?
Рекурсия — это процесс определения проблемы (или решения проблемы) в терминах (более простой версии) самой себя. Например, мы можем определить операцию «найди дорогу домой» так: Если вы дома, перестаньте двигаться.
Что такое рекурсивный процесс?
«Рекурсивный» просто означает, что каждый шаг, который вы делаете в процессе написания, будет связан с другими шагами: например, после того, как вы набросаете эссе, вы немного проверите некоторые из ваших фактов — и если вы обнаружите, что у вас что-то не так, вы вернетесь к черновику и исправите это.
Использование рекурсии в хранимых процедурах
Использование рекурсии в хранимых процедурах
Основная концепция рекурсии проста: данный фрагмент кода вызывает сам себя до тех пор, пока не будет достигнуто некоторое граничное условие. Артур Фуллер демонстрирует, как использовать рекурсию в T-SQL.
Артур Фуллер демонстрирует, как использовать рекурсию в T-SQL.
Бесплатный информационный бюллетень TechRepublic по SQL Server, который доставляется каждый вторник, содержит практические советы, которые помогут вам лучше освоить эту мощную систему управления реляционными базами данных. Подпишитесь автоматически сегодня!
Рекурсия — одна из самых элегантных программных конструкций
по-моему. Я использовал его в десятках ситуаций и на нескольких языках программирования
. Основная концепция рекурсии проста: 90 361 фрагмент кода вызывает сам себя до тех пор, пока не будет достигнуто некоторое граничное условие. Я покажу вам, как использовать рекурсию в T-SQL, используя один из классических примеров рекурсии: вычисление факториала.
Факториал — это произведение любого числа на все меньшие
числа до двух. Например, факториал(10) равен
равно 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2. (Можно добавить * 1, но зачем
возиться?)
Следующий сценарий реализует алгоритм факториала:
Создать процедуру [dbo].[Factorial_AP]
(
@number integer,
@retval Integer output
)
как
Declare @in Integer
Declare @out integer
, если @number! = 1
. Начните
@INEGE @IN @INVER
@INVER
@INVER
@INVER
@INVER
@INEGER @INEGER @INEGER @INEGER
@number! = 1
. @Number – 1
EXEC Factorial_ap @In, @Out OUTPUT
SELECT @RetVal = @Number * @Out
END
ELSE
BEGIN
SELECT @RetVal = 1
END
RETURN
GO
Предполагая, что вы хотите вычислить факториал( n ), процедура вызовет себя ( n-2 ) раз. SQL Server допускает рекурсию
до глубины 32 вызовов, но при 13 вы столкнетесь с арифметическим переполнением.
Если вы предполагаете вычислять факториалы для больших чисел, то вам следует объявить
переменную как BigInt, а не как Integer. Это будет
позволяет вычислить факториал(20), что, кстати,
равно 2 432 902 008 176 640 000. Результаты увеличиваются в размере
Результаты увеличиваются в размере
так быстро, что factorial(21) ломает и эту реализацию
.
Каким бы красивым ни был алгоритм факториала, маловероятно, что
он пригодится вам в повседневном программировании. Тем не менее, он
лаконично иллюстрирует принцип рекурсии.
Практическое применение рекурсии
Существует много практических ситуаций, в которых рекурсия может
может быть ценным методом — среди них классическая задача программирования
под названием Bill of Materials. Эта проблема имеет как минимум два разных приложения
, в том числе:
- Учитывая
потребность в одном экземпляре объекта, подготовьте спецификацию
, необходимую для его создания. - Учитывая
конкретных уровней инвентаризации составляющих объектов, составляющих объект
, сколько объектов такого типа мы можем построить?
Предположим, что у нас есть объект O, который состоит из
четыре объекта X, три объекта Y и семь объектов Z. Поэтому для построения
Поэтому для построения
одного объекта O очевидно, что нам потребуется четыре объекта X, три объекта Y,
и семь объектов Z. Предположим, однако, что объекты Y и Z оба требуют
определенного количества объектов Q (например, винтов определенного диаметра, рисунка резьбы,
и рисунка головки). Затем мы должны посетить объекты Y и Z, определить количество
Q, которое им требуется, и посмотреть, есть ли у нас эта сумма в наличии. Если нет, мы не можем
построить объект O.
SQL Server 2000 не упрощает решение этой проблемы,
если вы заранее не знаете уровень рекурсии. Однако бета-версия SQL 2005 прошла
долгий путь решения этой проблемы. Гуру SQL Джо Селко
предлагает довольно умное решение этой проблемы, которое включает в себя отслеживание уровней
во время вставки строки. Его решение работает хорошо, но требует триггеров или эквивалентных механизмов
, которые обновляют столбцы уровня глубины при каждой вставке, обновлении,
или удалении. Посмотрите
Посмотрите
пример его метода, реализованного в Access. Вы можете легко портировать это
для SQL Server, а затем измените его в соответствии с вашими требованиями.
Я скоро вернусь к этой теме, чтобы проиллюстрировать значительные улучшения
, появившиеся в SQL Server 2005. Следите за обновлениями.
артурфуллер
Опубликовано: Изменено: Увидеть больше Управление данными Поделиться: Использование рекурсии в хранимых процедурах- Управление данными
Выбор редактора
- Изображение: Rawpixel/Adobe Stock
ТехРеспублика Премиум
Редакционный календарь TechRepublic Premium: ИТ-политики, контрольные списки, наборы инструментов и исследования для загрузки
Контент TechRepublic Premium поможет вам решить самые сложные проблемы с ИТ и дать толчок вашей карьере или новому проекту.

Персонал TechRepublic
Опубликовано: Изменено: Читать далее Узнать больше - Изображение: diy13/Adobe Stock
Программного обеспечения
Виндовс 11 22х3 уже здесь
Windows 11 получает ежегодное обновление 20 сентября, а также ежемесячные дополнительные функции. На предприятиях ИТ-отдел может выбирать, когда их развертывать.
Мэри Бранскомб
Опубликовано: Изменено: Читать далее Увидеть больше Программное обеспечение - Изображение: Кто такой Дэнни/Adobe Stock
Край
ИИ на переднем крае: 5 трендов, за которыми стоит следить
Edge AI предлагает возможности для нескольких приложений. Посмотрите, что организации делают для его внедрения сегодня и в будущем.
Меган Краус
Опубликовано: Изменено: Читать далее Увидеть больше - Изображение: яблоко
Программного обеспечения
Шпаргалка по iPadOS: все, что вы должны знать
Это полное руководство по iPadOS от Apple.
 Узнайте больше об iPadOS 16, поддерживаемых устройствах, датах выпуска и основных функциях с помощью нашей памятки.
Узнайте больше об iPadOS 16, поддерживаемых устройствах, датах выпуска и основных функциях с помощью нашей памятки.Персонал TechRepublic
Опубликовано: Изменено: Читать далее Увидеть больше Программное обеспечение - Изображение: Worawut/Adobe Stock
- Изображение: Bumblee_Dee, iStock/Getty Images
Программного обеспечения
108 советов по Excel, которые должен усвоить каждый пользователь
Независимо от того, являетесь ли вы новичком в Microsoft Excel или опытным пользователем, эти пошаговые руководства принесут вам пользу.

Персонал TechRepublic
Опубликовано: Изменено: Читать далее Увидеть больше Программное обеспечение
9 Рекурсия и циклы: процедуры и данные
← пред вверх следующая →
9 Рекурсия и циклы: процедуры и данные
Рекурсия – это акт самореференции. Когда мы говорим о
рекурсии в языках программирования, у нас может быть одна из (по крайней мере) двух
значения: рекурсия в данных и рекурсия в управлении (т.е.
поведения программы —
9.1 Рекурсивные и циклические данные
Рекурсия в данных может относиться к одной из двух вещей. Это может означать
относящийся к чему-то подобному или относящийся к
само то же самое.
Это может означать
относящийся к чему-то подобному или относящийся к
само то же самое.
Рекурсия того же вида приводит к тому, что мы традиционно называем рекурсивные данные. Например, дерево представляет собой рекурсивные данные. структура: каждая вершина может иметь несколько потомков, каждый из которых само дерево. Но если мы напишем процедуру обхода узлов дерево, мы ожидаем, что оно завершится без необходимости отслеживать, какое узлы, которые он уже посетил. Это конечные структуры данных.
Напротив, граф часто является циклическим данным: узел относится к другой узел, который может ссылаться на исходный. (Или для этого вопрос, узел может ссылаться непосредственно на себя.) Когда мы пересекаем график, при отсутствии каких-либо явных проверок того, что мы уже посетили, мы следует ожидать, что вычисление расходится, т. е. не завершается. Вместо этого графовым алгоритмам нужна память о том, что они посетили. избегать повторных обходов.
Добавление рекурсивных данных, таких как списки и деревья, к нашему языку
довольно просто. В основном нам требуются две вещи:
В основном нам требуются две вещи:
Возможность создавать составные структуры (например, узлы, которые есть ссылки на детей).
Возможность нижней части рекурсии (например, листьев).
Упражнение
Добавление списков и двоичных деревьев в качестве встроенных типов данных в программу язык.
Добавление циклических данных более тонко. Рассмотрим простейшую форму циклические данные, ячейка, ссылающаяся на себя:
Давайте попробуем определить это в Racket. Вот одна попытка:
(let ([b b]) b)
Но это не работает: b в правой части таблицы пусть не привязан. Легко увидеть, не обрушимся ли мы:
((Lambda (B) B) B) B). :
9’0004.
((лямбда (x) x) b) Отсутствие какой-то волшебной конструкции Racket, которой мы еще не seeЭта конструкция будет использоваться совместно, но практически ни в одном другом языке нет такого механизма записи, поэтому мы не будем останавливаться на это здесь. Фактически то, что мы изучаем, является основной идеей того, как на самом деле работает., становится ясно, что мы не можем создать циклическое значение в одном кадре. Вместо этого нам нужно сначала создать «место» для данных, затем обратитесь к этому месту внутри себя. использование «тогда» —
т. е. введение времени— должно предполагать операция мутации. Действительно, попробуем с коробками. Наш план таков. Во-первых, мы хотим создать коробку и привязать ее к какой-то идентификатор, скажем, b. Теперь мы хотим изменить содержимое коробка. Что мы хотим, чтобы он содержал? Отсылка к себе.
Как он получает эту ссылку? Используя имя, b, т.е. уже привязан к нему. Таким образом, мутация создает цикл:
(let ([b (box ‘dummy)]) (begin (set-box! b b) b)) 1 900 Мы вернемся к набору таких программ позже [ССЫЛКА]. А пока запустите его нетипизированный (#lang plai) язык.Когда вышеуказанная программа запущена, Racket печатает это как: #0=’#�#. Это обозначение на самом деле именно то, что нам нужно. Напомним, что #& — это то, как Racket печатает коробки. #0= (и аналогично для других чисел) так Racket называет части циклического данные. Таким образом, Racket говорит: «#0 привязан к ящику, чей содержимое равно #0#, т. е. все, что привязано к #0, т. е. сам».
Упражнение
Запустите аналогичную программу через интерпретатор для ящиков и сделайте уверен, что он производит циклическое значение.
Как это проверить?
Приведенная выше идея распространяется на другие типы данных. Таким же образом мы также может создавать циклические списки, графики и т.д. Центральная идея этот двухэтапный процесс: сначала назовите вакантное место; затем мутировать заполнитель, чтобы его содержимое было самим собой; чтобы получить «себя», используйте ранее связанное имя. Конечно, мы не должны ограничиваться «самоциклы»: у нас также могут быть взаимно циклические данные (где никто элемент является циклическим, но их комбинация является циклической).
9.2 Рекурсивные функции
В терминологии рекурсивная функция не является ссылкой на тот же вид функции, но скорее к той же функции сам. Полезно сначала убедиться, что мы сначала расширили язык с условными операторами (даже такими, которые проверяют только 0, как описано ранее: Добавление функций в язык), поэтому мы может писать нетривиальные программы, которые завершаются.
Теперь попробуем написать рекурсивный факториал:
(let ([fact (lambda (n) (if0 n 1 (* n (fact (- n 1)))))]) (fact 10 )) Но это вообще не работает! Внутренний факт дает несвязанное ошибка идентификатора, как и в нашем примере с циклическими данными.
Неудивительно, что мы должны столкнуться с той же ошибкой, потому что она имеет ту же причину. Наш традиционный механизм связывания не автоматически делать определения функций циклическими (действительно, в некоторых ранних языками программирования, они не были: по ошибке рекурсия была считается особенностью).Поскольку вы обычно пишут определения верхнего уровня, такого не встретишь проблема. На верхнем уровне каждая привязка неявно является переменной или коробка. В результате паттерн ниже более-менее автоматически ставится на месте для вас. Вот почему, когда вам нужен рекурсивный локальный привязка, вы должны использовать letrec или local, а не let. Вместо этого, если мы хотим рекурсия —
т. е. чтобы определение функции циклически ссылалось на сам — мы должны реализовать его вручную. Способы сделать это теперь ясны: проблема та же самая, которую мы диагностировано ранее, поэтому мы можем повторно использовать одно и то же решение. Мы снова должны выполните трехэтапный процесс: сначала создайте заполнитель, затем обратитесь к местозаполнитель, где мы хотим циклическую ссылку, и, наконец, мутировать заполнитель перед использованием.
Таким образом:
4056 46466 46466 46466 46466 46466 46466 46466 46466 46466 464619 464619 464619 464619 464619 464619 464619 464619 464619 464619 464619 46466 46466 46466 46466 4.
(пусть ([факт (коробка ‘пустышка)]) (Let ([Fact-Fun (Lambda (n) (if (Zero? N) 1 1 1 1 1 1 1 . ))))) (начало (SET-BOX! FACT-FUN) ((FACT UNBOX FACT)))) ))))))))))))))) даже не нужно развлечение фактами: я использовал эту привязку просто для ясности. Заметьте, потому что это не рекурсивно, и мы имеют идентификаторы, а не переменные, его использование может быть просто заменено его значением:
(Let ([Fact (Box ‘Dummy)]) (начало (Set-Box! Fact (LAMBDA! FACT (LAMBDA! FACT (LAMBDA! FACT (LAMBDA! FACT (LAMBD! ? N) 1 (*N (FACT UNBOX) (-N 1))))) (FACT UNBOX) 10)) (FACT UNBOX))) ISBO небольшая неприятность, связанная с необходимостью неоднократно распаковывать факт. В языке с переменными это было бы еще более бесшовный: Действительно, одно из применений переменных заключается в том, что они упростить обессахаривание вышеуказанного шаблона, вместо того, чтобы требовать каждое использование циклически связанного идентификатора должно быть распаковано. На с другой стороны, с небольшими дополнительными усилиями процесс обессахаривания может позаботьтесь и о распаковке.
(Let ([Fact ‘Dummy]) (Begin (SET! FACT (LAMBDA (N). 1 (* n (fact (- n 1)))))) (fact 10))) 9.3 Premature Observation
Our preceding discussion of this pattern shows a ясно темпоральный последовательность: создать, обновить, использовать. Мы можем захватить его в дешугаринге правило. Предположим, мы добавляем следующий новый синтаксис:
(корпус значения rec) В качестве примера его применения,
(rec fact 3333 (LAMBDA) (NAMPDA) (NAMPDA) (NAMPDA 1. 0573 (NAMPDA) (NAMPDA 10574 (NAMPDA) (NAMPDA
. n (fact (- n 1))))) 3333333333333 (LAMP (fact 10)) будет оцениваться как факториал 10. Этот новый синтаксис будет desugar to:
(let ([name (box ‘dummy)]) (begin (set-box! name value) тело)) Где мы предполагаем, что все ссылки на имя в значении и тело было переписано в (unbox name), или alternatively that we instead use variables:
(let ([name ‘dummy]) (begin (set! name value) body)) This естественно вызывает вопрос: а что, если они выйдут из строя? Самое интересное, что если мы попытаемся использовать name до того, как мы закончим обновлять его истинное значение? Затем наблюдаем состояние системы сразу после создания, то есть мы можем видеть заполнитель в необработанном виде.
The simplest example that demonstrates this is as follows:
(letrec ([x x]) x) or equivalently,
(local ([define x x]) x) заполнитель —
значение, которое никогда не предназначалось для публичного потребление. Это беспокоит, потому что, в конце концов, это законный значение, что означает, что его, вероятно, можно использовать, по крайней мере, в некоторых вычисления. Если разработчик получает доступ и использует его непреднамеренно, однако они эффективно вычисляют с ерундой. Обычно существует три решения этой проблемы:
Убедитесь, что значение достаточно скрыто, чтобы его можно было никогда не использовать в осмысленном контексте. Это означает такие значения, как 0 особенно плохи, и действительно, наиболее распространенные типы данных должны избегать.
Вместо этого язык может создать новый тип значения только для использования здесь. При переходе к любой другой операции это приведет к в ошибке.
Явно проверять каждое использование идентификатора на принадлежность это особое «преждевременное» значение. Пока это технически возможно, это накладывает огромный штраф на производительность программы. Таким образом, он обычно используется только в преподавании языков.
Разрешить использование конструктора рекурсии только в случае функции привязки, а затем убедитесь, что правая часть связывание синтаксически является функцией. К сожалению, это решение может быть немного радикальным, потому что оно не позволяет писать, т. Например, структуры для создания графиков.
9.4 Без явного состояния
Как вы, возможно, знаете, существует еще один способ определения рекурсивного функции (и, следовательно, рекурсивные данные), которые не используют явное мутационные операции.
Делай сейчас!
Вы уже видели, что происходит, когда мы пытаемся использовать просто пусть определить рекурсивную функцию.
Стараться. Подсказка: Замените больше. А потом еще немного. И более!
Получение рекурсии только из функций — замечательная идея, и я использую термин буквально. Это написано хорошо Даниэлем П. Фридманом и Маттиасом Феллейзеном в их книге, Маленький интриган. Читайте об этом в их образец главы онлайн.
Упражнение
Использует ли приведенное выше решение где-либо состояние? Неявно?
Рекурсия и фракталы – программирование для детей
Рекурсия
Концепция рекурсии впервые была представлена в главе LOGO , а затем в главе Math Applications . Напомним, Рекурсия — это процесс определения функции в терминах самой себя. Если функция вызывает сама внутри самой функции, функция называется рекурсивной функцией .
В этом разделе мы используем рекурсию с модулем черепахи для рисования многих интересных рисунков, таких как фракталы.
Прежде чем мы объясним, что такое фракталы, давайте определим, что такое самоподобие есть .
Что такое самоподобие?
Самоподобие форм – это когда формы подобны друг другу во всех масштабах (увеличение). То есть фигура считается самоподобной, если увеличенная часть небольшой части фигуры выглядит похожей (не идентичной) всей форме, частью которой является эта маленькая часть. Кроме того, если вы уменьшите масштаб всей фигуры, она будет похожа (не идентична) на каждую маленькую часть фигуры. Это свойство называется самоподобие . Это самоподобие встречается в природе, например, в листьях, ветвях деревьев, снежинках, спиралях сосновых шишек, брокколи и т. д.
Что такое фракталы?Фрактал — это геометрическая фигура, каждая часть которой является приблизительно уменьшенной копией всей фигуры. Каждая часть фрактала, независимо от того, насколько она увеличена (увеличена с помощью увеличительного стекла) или уменьшена, выглядит очень похожей на все изображение, а это означает, что каждая часть фрактального паттерна выглядит одинаково на всех уровнях увеличения .
Иными словами, фракталы — это паттерны, которые самоподобны в разных масштабах (увеличениях).
Фрактал — это бесконечный паттерн, основанный на повторяющемся паттерне, который бесконечно повторяется во все меньших масштабах. Фракталы создаются путем многократного повторения функции в постоянном цикле обратной связи с использованием рекурсии , которую мы изучали в Math Applications 9.0224 глава.
Фракталы состоят из самоподобных версий самих себя в меньших масштабах, которые сами состоят из меньших самоподобных версий самих себя, и так далее. Алгоритм фрактала начинается с желаемой размерности и использует рекурсию для уменьшения размерности на желаемый коэффициент на каждом шаге цикла рекурсии. Первый шаг рекурсии обозначается как глубина = 1, второй шаг рекурсии соответствует глубине = 2 и так далее. Мы можем продолжить рекурсию на любую желаемую глубину (навсегда, если пожелаем). Как правило, большинство программистов останавливаются на глубине = 3 или 4.
Узнайте больше о фракталах по ссылке ниже:
https://fractalfoundation.org/
http://en.wikipedia.org/wiki/Fractal
В этой главе мы создадим интересные фигуры с помощью рекурсии, используя:
- Шаблоны Коха
- Треугольник Серпинского
Кривая Коха
Одна из первых фрактальных кривых была описана шведским математиком Нильсом Фабианом Хельге фон Кохом в 1904 году. Эта фрактальная кривая названа кривой Коха в честь его имени. Кривые Коха допускают множество вариаций. Многие художники использовали кривые Коха для создания интересных форм и произведений искусства. Более подробная информация о кривых Коха находится по ссылке ниже.
Снежинка Коха
Снежинка Коха является примером фигуры, которая самоподобна , то есть выглядит одинаково в любом масштабе ( увеличение).
Самый простой способ объяснить, как рисовать снежинку, — это начать с прямой линии.
Возьмем линию длиной 300 пикселей. Первый шаг — разделить линию на три равные части по 100 пикселей каждая (см. шаг 0). Используя средний сегмент в качестве основы, мы рисуем равносторонний треугольник со стороной 100 пикселей, как показано в шаге 1). Затем основание треугольника удаляется, оставляя нам первую итерацию кривой Коха. См. шаг 1 (продолжение). Это изображение соответствует тому, что называется глубиной = 1. Теперь есть четыре прямые линии, каждая длиной 100 пикселей.
В шаге 2 мы повторяем ту же операцию на каждой из четырех линий, разделяя их на три равных сегмента и рисуя равносторонний треугольник на среднем сегменте каждой из четырех линий и удаляя основание каждого из четырех треугольников. Это показано на шаблоне Коха на шаге 2 (глубина = 2). Мы можем проделать ту же операцию с фигурой на шаге 2 и получить шаблон Коха глубины = 3. Это можно продолжать до бесконечности, чтобы получить более сложные шаблоны Коха.
Если вместо прямой линии мы начнем с равностороннего треугольника и проделаем описанную выше операцию с каждой из трех сторон равностороннего треугольника, мы получим Кривая Коха глубины = 1.
Операцию можно продолжить на каждой из полученных линий, чтобы получить более сложные узоры Коха.
Начиная с равностороннего треугольника, мы делим каждую сторону треугольника на три равные части. В средней части формируем равносторонний треугольник, выступающий из исходного треугольника под углом 60 градусов. Стороны этого нового треугольника составляют одну треть стороны треугольника, с которой мы начали. Затем мы удаляем основание этого нового маленького треугольника. Таким образом, исходная одна сторона треугольника была заменена четырьмя меньшими длинами, каждая из которых составляет одну треть стороны исходной длины стороны. Мы проделываем тот же процесс с двумя другими сторонами треугольника, с которого начали. Эта операция создает кривую Коха глубины = 1. Поскольку каждая сторона исходного треугольника была заменена четырьмя меньшими длинами, у нас есть 12 сторон на кривой Коха глубины = 1. Если мы повторим тот же процесс на каждой из 12 линий, мы получим кривую Коха глубины = 2.
Этот процесс можно продолжать до бесконечности, чтобы получить все более сложные кривые Коха.
В приведенной ниже программе используются функции модуля черепахи Python для рисования фрактальной кривой Коха. Программа использует функцию рекурсии для циклического выполнения кода, чтобы выполнять те же операции со строками, длина которых уменьшается при каждой итерации цикла. На каждой итерации цикла линии делятся на три равных сегмента, как описано выше.
ПРИМЕР ПРОГРАММЫ: КРИВАЯ КОХА СНЕЖИНКА
Имя программы: turtle_recursion_snowflake_final.py
###### ПРИМЕР ПРОГРАММЫ КРИВОЙ КОХА ###### ###### НАРИСУЕМ СНЕЖИНКУ КОХА ###### импортная черепаха screen = черепаха.Screen() # Создаем экран. screen.setup(480, 480) # Установить размер окна. ###### ЧЕРЕПАХА ФОРМА, СКОРОСТЬ, РАЗМЕР РУЧКИ, ЦВЕТ ###### TTL = черепаха.Черепаха() TTL.speed(10) # Установить скорость черепашки. 1 медленно, 10 быстро; 0 самый быстрый. TTL.color("red") # Установить цвет черепахи. TTL.pensize(2) #Установить ширину пера для рисования черепахи.TTL.shape("черепаха") ###### УСТАНОВИТЬ СТАРТОВУЮ ПОЗИЦИЮ ЧЕРЕПАХИ ###### TTL.penup() # Не позволяйте черепашке рисовать при перемещении в позицию (-160, 110). TTL.setposition(-170,110) TTL.pendown() # Разрешить черепашке рисовать. ###### ПЕРЕМЕННЫЕ ###### # Переменная 'length' - это длина стороны начального равностороннего треугольника. # Переменная 'length' делится на переменную 'lengthDivisor' на каждой итерации рекурсии. # Переменная 'recursionLevel' - это глубина кривой Коха. ###### ОПРЕДЕЛЕНИЕ ФРАКТАЛЬНОЙ ФУНКЦИИ Коха ###### # Нарисуйте фрактал Коха 'recursionLevel' и 'length'. № 1 def KochFractal (TTL, recursionLevel, length, lengthDivisor): if recursionLevel == 0: # recursionLevel = 0 является фрактальным базовым случаем. TTL.forward(length) # Это нарисует равносторонний треугольник. еще: длина = длина / длина делителя # Вызов функции KochFractal внутри самой функции - Рекурсия. # Нарисовать паттерн Коха одной трети «длины» и уменьшить «уровень рекурсии».
KochFractal(TTL, recursionLevel-1, length, lengthDivisor) TTL.left(60) #Повернуть черепаху влево на 60 градусов. KochFractal(TTL, recursionLevel-1, length, lengthDivisor) TTL.right(120) #Повернуть черепаху вправо на 120 градусов. KochFractal(TTL, recursionLevel-1, length, lengthDivisor) TTL.left(60) #Повернуть черепаху влево на 60 градусов. KochFractal(TTL, recursionLevel-1, length, lengthDivisor) ###### ИНИЦИАЛИЗАЦИЯ ФРАКТАЛЬНОЙ КОХА recursionLevel AND length ###### # Инициализировать переменную length, длину стороны равностороннего треугольника. length = 360 # Длина равностороннего треугольника = 360 пикселей. № 2 ###### ВЫЗОВ ФРАКТАЛЬНОЙ ФУНКЦИИ Коха ###### # Функция KochFractal рисует фрактал Коха для одной стороны треугольника. # Вызов функции KochFractal для первой стороны треугольника. KochFractal(TTL, 3, длина, 3) # 3 TTL.right(120) #Повернуть черепаху вправо на 120 градусов. # Вызов функции KochFractal для второй стороны треугольника.
KochFractal(TTL, 3, длина, 3) # 4 TTL.right(120) #Повернуть черепаху вправо на 120 градусов. # Вызов функции KochFractal для третьей стороны треугольника. KochFractal(TTL, 3, длина, 3) # 5 screen.exitonclick() # Выход
Вывод следующей программы.
Подробное объяснение программы:
1)
def KochFractal(TTL, recursionLevel, length, lengthDivisor):Шаг 1) определяет функцию KochFractal() с параметрами имя черепахи = TTL, уровень рекурсии, длина стороны треугольника и lengthDivisor (коэффициент деления на каждой итерации цикла рекурсии,.)
2)
length = 360Шаг 2) инициализирует переменную ‘length’, которая представляет собой длину стороны равностороннего треугольника . длина = 360 пикселей
3)
KochFractal(TTL, 3, length, 3)
TTL.right(120)#Поверните черепаху вправо на 120 градусов.Шаг 3) вызывает функцию KochFractal для первой стороны треугольника с аргументами recursionLevel = 3, lengthDivisor = 3.
«Длина определена как 360 на шаге 2). Затем он поворачивает черепаху вправо на 120 градусов.
4)
KochFractal(TTL, 3, length, 3)
TTL.вправо(120)#Поверните черепаху вправо на 120 градусов.Шаг 4) вызывает функцию KochFractal для второй стороны треугольника. Затем поворачивает черепаху вправо на 120 градусов.
5)
KochFractal(TTL, 3, length, 3)Шаг 5) вызывает функцию KochFractal для третьей стороны треугольника.
Фрактальное дерево рекурсии
В предыдущем разделе мы использовали модуль черепахи Python для рисования снежинки Коха с использованием рекурсии. В этом разделе мы будем использовать модуль черепахи и рекурсию для рисования дерева. Обратите внимание на самоподобие в каждой ветви дерева. В приведенном ниже примере используется программный поток, очень похожий на программу Koch Snowflake.
ПРИМЕР ПРОГРАММЫ: TURTLE RECURSION TREE FRACTAL
Название программы: turtle_recursion_tree_final.
py
Кредиты: адаптировано из
https://towardsdatascience.com/creating-fractals-with-python-d2b663786da5
ПРИМЕР РЕКУРСИИ ДЛЯ РИСОВАНИЯ ДЕРЕВА ###### # Кредиты: изменено с https://towardsdatascience.com/creating-fractals-with-python-d2b663786da6 # импортная черепаха screen = черепаха.Screen() # Создаем экран. screen.setup(320, 320) # Установить размер окна. ###### ЧЕРЕПАХА ФОРМА, СКОРОСТЬ, РАЗМЕР РУЧКИ, ЦВЕТ ###### TTL = черепаха.Черепаха() TTL.speed(0) # Установите скорость черепахи. 1 медленно, 10 быстро; 0 самый быстрый. TTL.color(«brown») # Установить цвет черепахи. TTL.pensize(1) #Установить ширину пера для рисования черепахи. ###### УСТАНОВИТЬ СТАРТОВУЮ ПОЗИЦИЮ ЧЕРЕПАХИ ###### TTL.penup() # Не позволяйте черепашке рисовать при перемещении в позицию (0, 110). TTL.setposition(0, -100) TTL.pendown() # Разрешить черепашке рисовать. TTL.hideturtle() TTL.setheading(90) ###### ПЕРЕМЕННЫЕ ###### # Переменная ‘branchLength’ — начальная длина ветви дерева. # Переменная ‘branchReduction’ вычитает из ‘branchLength’ в # каждую итерацию рекурсии.
# Переменная ‘recursionLevel’ — номер итерации рекурсии. ###### ОПРЕДЕЛИТЬ ФУНКЦИЮ treeFractal ###### # Рисуем фрактал с уровнем рекурсии, длиной ветки дерева, # уменьшение длины ветки для каждой итерации, и # угол, на который поворачивается ветвь на каждой итерации. def treeFractal (TTL, уровень рекурсии, длина ветви, сокращение ветви, угол): если уровень рекурсии == 0: TTL.fd(0) еще: длина ветки = длина ветки — сокращение ветки TTL.forward(Длина ветки) TTL.влево(угол) treeFractal (TTL, recursionLevel-1, branchLength, branchReduction, угол) TTL.вправо(угол * 2) treeFractal (TTL, recursionLevel-1, branchLength, branchReduction, угол) TTL.влево(угол) TTL.backward(длина ветки) # Вызвать функцию treeFractal со следующими параметрами. # Уровень рекурсии = 7; Длина ответвления = 50. # Сокращение числа ветвей на каждой итерации рекурсии = 5. # Поверните влево от прямого угла на 25 градусов. деревофрактал(TTL, 7, 45, 5, 25) screen.exitonclick() # Выход из экрана
Ниже приведен вывод программы.
Треугольник Серпинского
Треугольник Серпинского является самоподобным фракталом. Он состоит из равностороннего треугольника, из которого рекурсивно удаляются меньшие равносторонние треугольники (90 223 самоподобных 90 224 треугольника) в каждом цикле рекурсии. Этот процесс можно продолжать до бесконечности, постоянно уменьшая меньшие треугольники, удаляя из предыдущего шага рекурсии большие треугольники.
Фрактал треугольник Серпинского был впервые введен в 1915 by Вацлав Серпинский . См. Обогащение: фрактал в конце этой главы о вкладе Серпинского в фракталы.
Алгоритм построения треугольника Серпинского следующий:
- Начните с равностороннего треугольника.
- Найдите середины трех сторон треугольника.
- Соедините три средние точки. Это приведет к меньшему равностороннему треугольнику в середине, который выглядит перевернутым по сравнению с исходным треугольником.
Теперь у нас есть четыре треугольника — один в середине и по три в каждой из вершин треугольника, с которого мы начали.
- Снимите средний треугольник.
- Затем повторите тот же шаг для каждого из трех треугольников в вершинах исходного треугольника
- Мы можем продолжать этот процесс до бесконечности, чтобы получить все уменьшающиеся треугольники меньшего размера.
Следующая программа основана на описанном выше алгоритме.
Кредиты: Адаптировано из:
https://stackoverflow.com/questions/25772750/SierpinskiTrianglepinski-triangle-recursion-using-turtle-graphics
ПРИМЕР ПРОГРАММЫ: ТРЕУГОЛЬНИК СЕРПИНСКОГО ФРАКТАЛ
Имя программы: turtle_recursion_Sierpinski_final.py
# Треугольник Серпинского импортная черепаха screen = черепаха.Screen() # Создаем экран. screen.setup(320, 320) # Установить размер окна. ###### ЧЕРЕПАХА ФОРМА, СКОРОСТЬ, РАЗМЕР РУЧКИ, ЦВЕТ ###### TTL = черепаха.Черепаха() TTL.speed(1) # Установите скорость черепахи.1 медленно, 10 быстро; 0 самый быстрый. TTL.color("red") # Установить цвет черепахи. TTL.pensize(1) #Установить ширину пера для рисования черепахи. ###### УСТАНОВИТЬ СТАРТОВУЮ ПОЗИЦИЮ ЧЕРЕПАХИ ###### TTL.penup() # Не позволяйте черепашке рисовать при перемещении в позицию (0, 110). TTL.setposition(-100, -100) TTL.pendown() # Разрешить черепашке рисовать. ###### ПЕРЕМЕННЫЕ ###### # Переменная 'length' - начальная длина треугольника Серпинского. # Переменная 'angle' - это угол поворота черепахи. # Переменная 'recursionLevel' - номер итерации рекурсии. ###### ОПРЕДЕЛИТЬ ФУНКЦИЮ треугольника Серпинского ###### # Нарисовать фрактал с длиной треугольника, уровнем рекурсии и # угол, на который поворачивается черепаха. def SierpinskiTriangle (TTL, длина, уровень рекурсии, угол): if recursionLevel == 1: # Нарисовать треугольник. для я в диапазоне (3): TTL.fd(длина) TTL.влево(120) еще: Треугольник Серпинского (TTL, длина/2, уровень рекурсии-1, угол) TTL.
fd(длина/2) Треугольник Серпинского (TTL, длина/2, уровень рекурсии-1, угол) TTL.bk(длина/2) TTL.влево(угол) TTL.fd(длина/2) TTL.вправо(угол) Треугольник Серпинского (TTL, длина/2, уровень рекурсии-1, угол) TTL.влево(угол) TTL.bk(длина/2) TTL.вправо(угол) # Вызов функции SierpinskiTriangle с длиной треугольника = 200, # уровни рекурсии = 2, угол поворота черепахи = 60 градусов. Треугольник Серпинского(TTL, 200,3, 60) screen.exitonclick() # Выход из экрана
Ниже приведен вывод программы.
Рекурсия и FileSystemObject
На этой странице представлена концепция рекурсивных процедур и использует Scripting FileSystemObject как пример того, когда рекурсия может быть мощная техника программирования.Рекурсия — это метод программирования, который может упростить сложные задачи или выполнить задачи, которые невозможно выполнить любым другим способом. Проще говоря, процедура называется «рекурсивной», если она вызывает сам себя, почти всегда передавая себе параметр.
Это может показаться странно, что процедура может вызывать сама себя, а в языке нет ничего чтобы предотвратить это. Принципиально ничем не отличается процедура, вызывающая другую процедуру, и процедура, вызывающая саму себя.
Следует соблюдать осторожность с логикой рекурсивной процедуры. Должно быть некоторое условие, выполнение которого останавливает рекурсию. если вы не правильно управляйте рекурсией, вы окажетесь в бесконечном цикле. В своем В самой простой форме рекурсивная процедура выглядит примерно так:
Подпроцесс() Проц Конец субНедостаток здесь очевиден. Проц называть себя, которая называет себя, которая называет себя, навсегда. Здесь нет механизм побега. В конечном итоге эта процедура исчерпает ресурсы доступны для VBA во время выполнения, и VBA завершит процедуру с Недостаточно места в стеке Ошибка . В быстром примере VBA завершил рекурсия после примерно 6800 циклов. Это иллюстрирует в простейшие термины, что происходит без надлежащего escape-кода.
Процедура будет продолжать вызывать себя до того, как запустится среда выполнения VBA и завершит выполнение процесс. Обычно рекурсивная процедура инициируется другой процедурой. который обеспечивает начальное значение для рекурсивной процедуры. затем рекурсивная процедура изменяет этот параметр и вызывает сама себя. Когда некоторые условие выхода выполнено, рекурсивная процедура перестает вызывать себя, прокручивает процедуру «стек» и в конечном итоге возвращает процедура инициализации.
«Стек» — это структура данных, которая в нашем контексте используется для отслеживания какая процедура вызывает какую процедуру и где должно выполняться возобновить, когда процедура достигает своего завершения. «Стек» — это последних входящих, первая структура , и берет свое название от стопки обеденных тарелок. Вы всегда добавляете тарелки наверх стопки и всегда убираете тарелки. с вершины стека. Вы никогда не вставляете и не удаляете элементы из середины или дно стека. При использовании для отслеживания процедур «верхняя часть» стека всегда является выполняемой в данный момент процедурой.
Когда это процедура завершается, она удаляется или «извлекается» из стека, а затем вершина стека — это процедура, вызвавшая эту процедуру. Как процедуры вызываются, они «подталкиваются» на вершину стека, и когда процедура завершается, она «извлекается» из вершины стека и процедура, вызвавшая эту процедуру, теперь находится на вершине стека. в рекурсивной процедуры, показанной выше, процедура «Proc» «нажимается» на верхней части стека, но никогда не удаляется и не «выталкивается». Стек процедур в Возможности VBA ограничены. Как называет себя Proc, стек растет, потому что выхода из петли нет. Примерно при 6800 элементах стека стек заполнен до отказа, и VBA завершает все с помощью Вне Ошибка времени выполнения Stack Space .
Ниже показана правильно построенная рекурсивная процедура.
Тусклый Всего Пока Подзапуск() Всего = 0 Сумма Рекурсе 10 Debug.Print "DONE:" & CStr(Total) Конец сабвуфера Sub SumRecurse (N As Long) Всего = Всего + N Если N > 0 Тогда '''''''''''''''''''''''''' 'Вот, SumRecurse ' называет себя, проходя мимо ' N-1 в качестве параметра.'''''''''''''''''''''''''' Сумма рекурсе N - 1 Еще ''''''''''''''''''''''''''''''' ' Здесь N = 0, поэтому SumRecurse ' не называет себя. ''''''''''''''''''''''''''''''' Конец, если Конец суб
Этот код просто суммирует числа от 5 до 0, начиная с Запустить процедуру со значением из 5 и уменьшая это значение на 1 каждый раз SumRecurse вызывает сам. В этом коде есть механизм выхода для предотвращения петля от работы навсегда. Процедура запуска начинает рекурсивный процесс, вызывая SumRecurse передает его значение 5. SumRecurse процедура вызывает сама себя, передавая себе значение Н-1. Каждый раз, когда вызывает себя, он проходит N-1, поэтому значение N, как передано в каждом итерации рекурсивного цикла, уменьшается или уменьшается на 1. Когда N достигает 0, рекурсия завершается, и процесс перестает вызывать сам себя и отображает результат.
На самом деле вы никогда не использовали бы приведенный выше код — его можно было бы сделать больше просто с помощью цикла For или даже одной строки кода.
Тем не менее, это ввести понятие рекурсии.
Рекурсию можно использовать, когда вы не знаете во время разработки, как далеко рутина должна уйти. В качестве примера мы будем использовать FileSystemObject для вывода всех подкаталоги заданного каталога. Вы не знаете во время выполнения, сколько подпапки могут быть в данной папке, и вы не знаете, насколько глубоко вложенные папки вложены друг в друга. Папка может содержать вложенную папку, которая, в свою очередь, содержит вложенные папки, которые содержат вложенные папки и так далее. Код должен приспособить любую иерархию папок/подпапок, существующую во время выполнения время, которое вполне может не совпадать с тем, которое существует, когда код написано. Используя рекурсию, мы можем написать код, который может обрабатывать любое количество вложенные папки любого уровня.
Первый шаг — установить ссылку на среду выполнения сценариев. библиотека. В VBA перейдите в меню Tools , выберите References и прокрутите и проверьте запись «Среда выполнения сценариев Microsoft».
Следующий, объявить переменную уровня модуля с именем FSO типа Scripting.FileSystemObject.
Dim FSO как Scripting.FileSystemObjectЗатем создайте стартовую процедуру для кода. Эта процедура устанавливает исходная папка, папка, вложенную папку которой мы хотим вывести.
Sub StartListing () '''''''''''''''''''''''''''''''''''''' 'Это название ' папка, вложенные папки которой ' мы хотим перечислить. '''''''''''''''''''''''''''''''''''''' Dim TopFolderName как строка '''''''''''''''''''''''''''''''''''''' ' Это Scripting.Folder ' объект, представляющий ' папка с именем в TopFolderName. '''''''''''''''''''''''''''''''''''''' Dim TopFolderObj как Scripting.Folder '''''''''''''''''''''''''''''''''''''' «Это ячейка, в которой ' листинг начнется. '''''''''''''''''''''''''''''''''''''' Dim DestinationRange As Range TopFolderName = "C:\Test" '<<< ИЗМЕНИТЬ В ВАШУ ПАПКУ Установить DestinationRange = Worksheets(1).Range("A1") '''''''''''''''''''''''''''''''''''''' ' Если FSO не инициализирован, ' создать новый экземпляр FSO. '''''''''''''''''''''''''''''''''''''' Если ФСО ничто, то Установите FSO = New Scripting.FileSystemObject Конец, если '''''''''''''''''''''''''''''''''''''' ' Установите для нашей переменной TopFolderObj значение ' объект Folder представляет ' папка на диске, вложенные папки которой ' мы хотим перечислить. '''''''''''''''''''''''''''''''''''''' Установить TopFolderObj = FSO.GetFolder(TopFolderName) ListSubFolders OfFolder: = TopFolderObj, _ Диапазон назначения: = Диапазон назначения Конец суб
Пока эта процедура достаточно проста. Он создает новый экземпляр FileSystemObject при необходимости создает начальную ячейку для листинга и создает объект папки, представляющий папку на диске, вложенные папки которой мы хочу перечислить. Последним шагом этой процедуры является вызов процедуры с именем ListSubFolders.
Мы еще не написали эту процедуру. Процедура ListSubFolders выполнит всю работу по перечислению подпапок. Поскольку мы не знаем в во время разработки, какой будет наша начальная папка, и мы не знаем, что иерархия подпапок этой папки, мы должны написать процедуру для обработки любого количества подпапок, вложенных на любую глубину. Это делает его идеальный кандидат для рекурсивного решения. Процедура может называть себя как столько раз, сколько нужно, чтобы перечислить все подпапки.
Начнем с декларации Процедура ListSubFolders. Это показано ниже:
Sub ListSubFolders(OfFolder As Scripting.Folder, _ DestinationRange As Range)Это объявляет ListSubFolders чтобы принять объект папки сценариев и объект диапазона назначения. Объект OfFolder является объектом который представляет папку на диске, подпапки которой мы собираемся перечислить. Объект DestinationRange ссылается на ячейку на листе, где имя OffFolder будет написано. Полная процедура показана ниже:
Sub ListSubFolders(OfFolder As Scripting.Folder, _ DestinationRange как диапазон) '''''''''''''''''''''''''''''''''''''''''''''''''''''''' ''' ' Список подпапок ' Здесь перечислены все подпапки объекта OfFolder. 'Помещает полное имя папки OfFolder в диапазон ', на который ссылается DestinationRange. '''''''''''''''''''''''''''''''''''''''''''''''''''''''' ''' '''''''''''''''''''''''''''''''''''''' ' Это представляет одну подпапку ' в папке OfFolder. ' Мы используем это, чтобы перебрать ' все подпапки с For «Каждая петля. '''''''''''''''''''''''''''''''''''''' Dim SubFolder As Scripting.Folder '''''''''''''''''''''''''''''''''''''''''''' ' Вставьте имя OfFolder в 'Диапазон назначения. '''''''''''''''''''''''''''''''''''''''''''' DestinationRange.Value = OfFolder.Path '''''''''''''''''''''''''''''''''''''''''''' ' Point DestinationRange на одну строку вниз ' и один столбец вправо. Этот ' даст хороший вид с отступом ' иерархия папок.
'''''''''''''''''''''''''''''''''''''''''''' Установите DestinationRange = DestinationRange.Offset(1, 1) '''''''''''''''''''''''''''''''''''''''''''' ' Вот рекурсивная часть. Для каждого ' подпапка OfFolder, процедура ' вызывает себя, проходя в SubFolder и 'Диапазон назначения. В первый раз это ' называет себя, он проходит первый ' подпапка. Если в ЭТОЙ папке есть ' подпапки, эти подпапки будут ' подхватывается в петле ниже, и ' процедура будет вызывать себя для каждого ' подпапка. Этот процесс продолжается в течение ' настолько глубоко, насколько вложена подпапка. '''''''''''''''''''''''''''''''''''''''''' Для каждой подпапки в OfFolder.SubFolders ListSubFolders OfFolder:=Подпапка, _ Диапазон назначения: = Диапазон назначения Следующая подпапка '''''''''''''''''''''''''''''''''''''''''''''''' ' После того, как мы перечислили подпапку в ' OfFolder, переместите DestinationRange ' вниз на одну строку и назад на один столбец, чтобы ' слева, чтобы отразить, что мы закончили ' с такой глубиной папки/подпапки 'иерархия.
'''''''''''''''''''''''''''''''''''''''''''''''' Установить диапазон назначения = диапазон назначения (1, 0) Конец сабвуфера
Эта процедура сначала объявляет переменную с именем Подпапка типа Сценарии.Папка. Это будет представляют каждую подпапку Объект папки OfFolder, который передается процедуре. Позже мы будет использовать эту переменную в цикле For Each для получения каждой подпапки Папка. Далее мы поместите полное имя OfFolder в ячейке, на которую ссылается Диапазон назначения. Вслед за этим меняем DestinationRange для ссылки на одну строку вниз и на один столбец вправо от исходного положения. Это будет выполнить две вещи: (1) это гарантирует, что в следующий раз значение будет записывается в ячейку, на которую ссылается DestinationRange, он будет на одну строку ниже предыдущей записи и (2) он создает красивое представление иерархии подпапок с отступом. Каждая вложенная папка смещается на один столбец вправо и на одну строку вниз от своего родительская папка.
Следующий шаг — рекурсивная часть кода.
Для каждой подпапки в OfFolder.SubFolders ListSubFolders OfFolder:=Подпапка, _ Диапазон назначения: = Диапазон назначения Следующая подпапкаПри этом используется цикл For Each для получения ссылки на каждую подпапку внутри Папка. Для каждой подпапки находится в OfFolder, процедура вызывает себя для обработки этой папки (что в этом примере означает запись имени подпапки в DestinationRange), а затем циклы через , что подпапок папки, вызывая себя еще раз для каждой подпапка. Если вы внимательно проследите логический путь, вы увидите, что процедура ListSubFolders вызывается для каждой подпапки исходного TopFolderName, которое мы началось с в StartListing процедуры, независимо от того, насколько глубоко вложенными могут быть эти подпапки.
Наконец, мы меняем ссылку на DestinationДиапазон вниз на один строку и назад на один столбец влево, указывая, что мы закончили с этим уровнем иерархии подпапок.

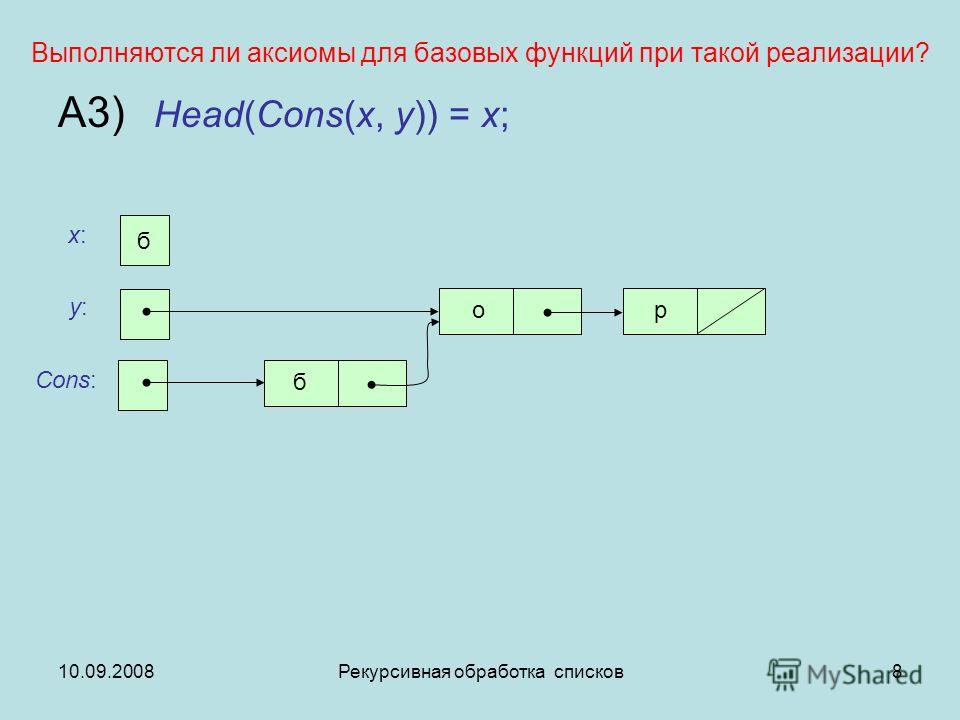
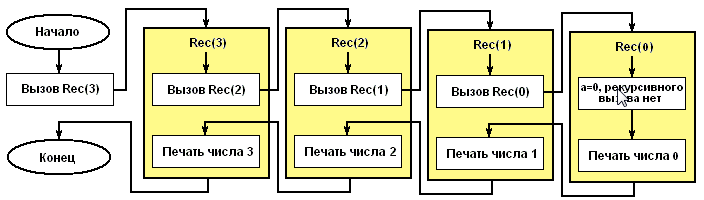 Yes
Yes
 ..
..
 § 5 нашего учебника). Но это будет особый вид процедур, которые называются рекурсивными процедурами.
§ 5 нашего учебника). Но это будет особый вид процедур, которые называются рекурсивными процедурами.
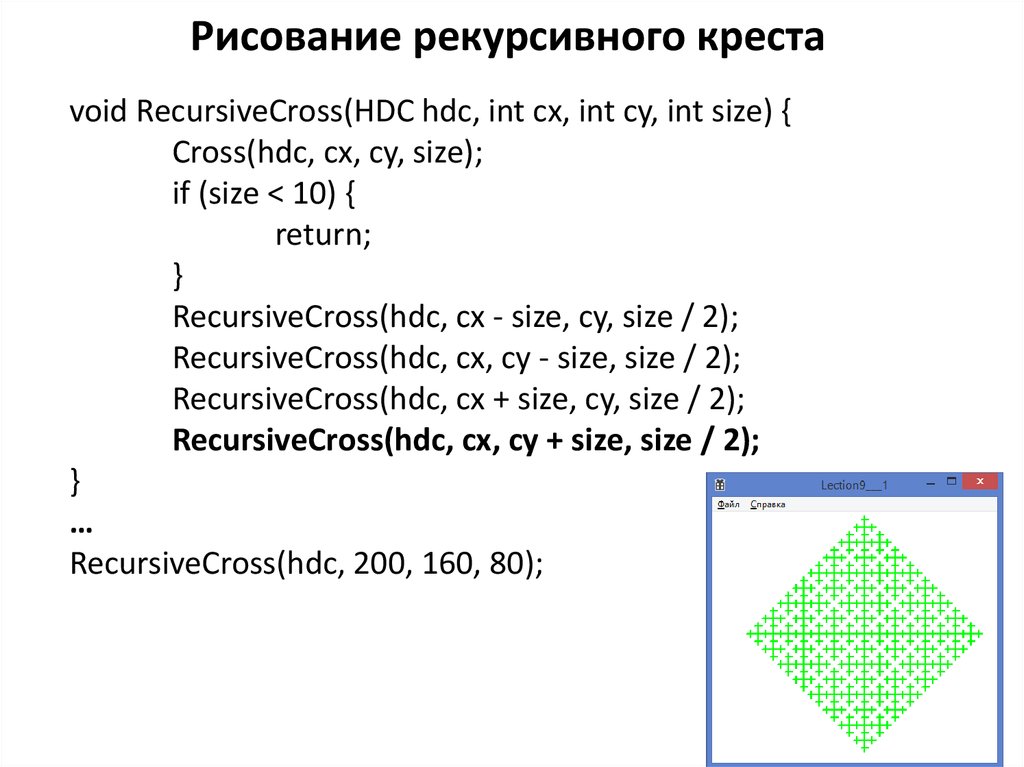 Выполнение программы завершится аварийно
Выполнение программы завершится аварийно

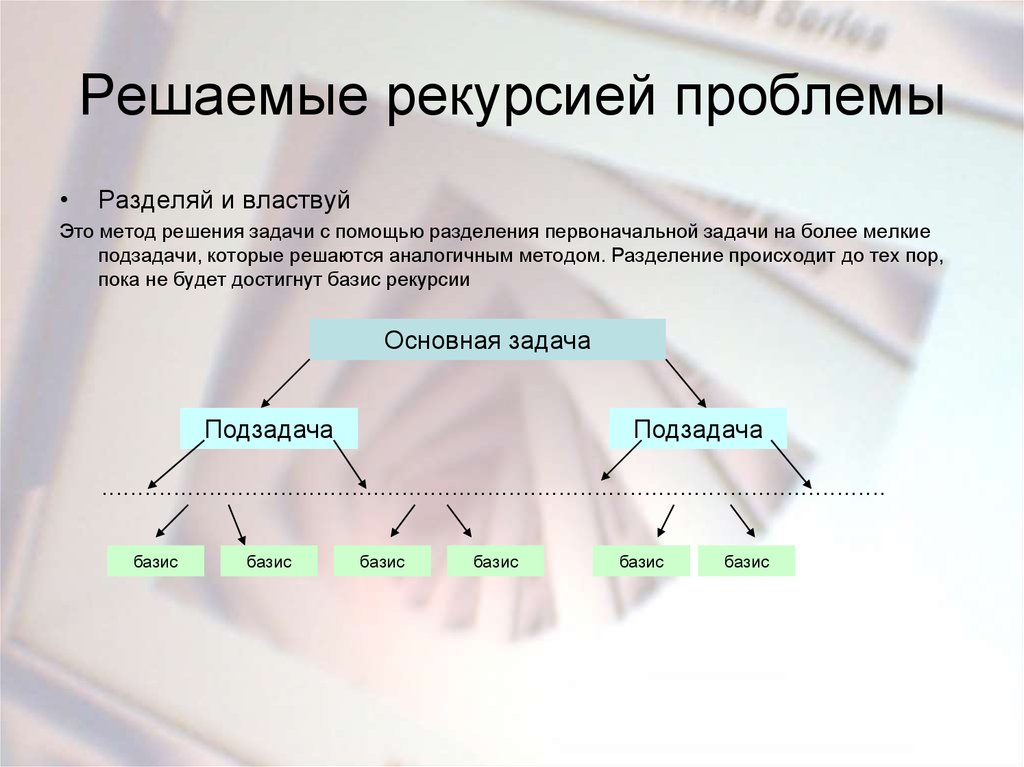
 Затем, после окончания рекурсивных обращений, все отложенные выходы отрабатываются в порядке, обратном порядку рекурсивных обращений. В приведенной программе отработка отложенных выходов начинается с выполнения команды поворот.
Затем, после окончания рекурсивных обращений, все отложенные выходы отрабатываются в порядке, обратном порядку рекурсивных обращений. В приведенной программе отработка отложенных выходов начинается с выполнения команды поворот. Попробуйте разобраться, какую задачу решает следующая программа, содержащая рекурсивную процедуру. Реализуйте ее в среде исполнителя «Стрелочка».
Попробуйте разобраться, какую задачу решает следующая программа, содержащая рекурсивную процедуру. Реализуйте ее в среде исполнителя «Стрелочка». Составьте программу с рекурсивной процедурой, по которой исполнитель, находящийся в произвольной точке поля, дойдет до стенки, затем повернется на 90 градусов по часовой стрелке и дойдет до конца этой стенки вдоль нее. В результате будет нарисован угол.
Составьте программу с рекурсивной процедурой, по которой исполнитель, находящийся в произвольной точке поля, дойдет до стенки, затем повернется на 90 градусов по часовой стрелке и дойдет до конца этой стенки вдоль нее. В результате будет нарисован угол. В первые годы существования ЭВМ для использования компьютера в любой области нужно было уметь программировать. В 1970-1980-х годах начинает развиваться прикладное программное обеспечение. Бурное распространение прикладного ПО произошло с появлением персональных компьютеров. Стало совсем не обязательным уметь программировать для того, чтобы воспользоваться компьютером. Люди, работающие на компьютерах, разделились на пользователей и программистов. В настоящее время пользователей гораздо больше, чем программистов.
В первые годы существования ЭВМ для использования компьютера в любой области нужно было уметь программировать. В 1970-1980-х годах начинает развиваться прикладное программное обеспечение. Бурное распространение прикладного ПО произошло с появлением персональных компьютеров. Стало совсем не обязательным уметь программировать для того, чтобы воспользоваться компьютером. Люди, работающие на компьютерах, разделились на пользователей и программистов. В настоящее время пользователей гораздо больше, чем программистов.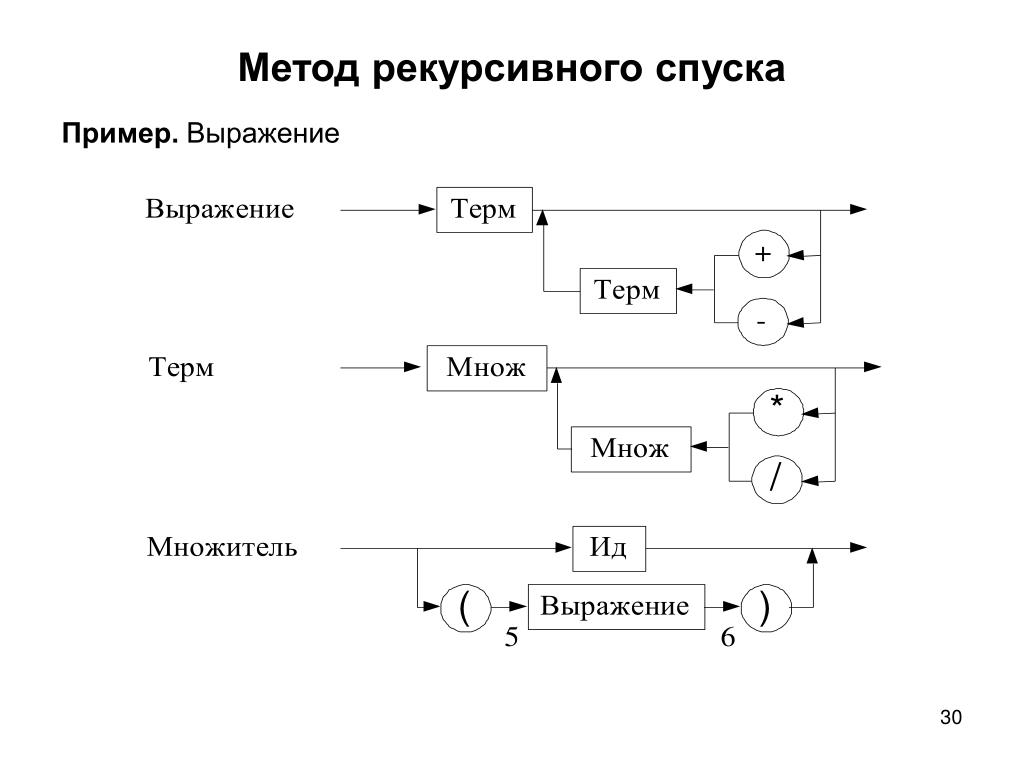 , а также систем программирования. Прикладные программисты создают прикладные программы: редакторы, табличные процессоры, игры, обучающие программы и др. Спрос на высококвалифицированных программистов, как системных, так и прикладных, очень большой.
, а также систем программирования. Прикладные программисты создают прикладные программы: редакторы, табличные процессоры, игры, обучающие программы и др. Спрос на высококвалифицированных программистов, как системных, так и прикладных, очень большой. ..
.. Я был удивлён, ибо полагал, что рекурсия не сложна.
Я был удивлён, ибо полагал, что рекурсия не сложна.
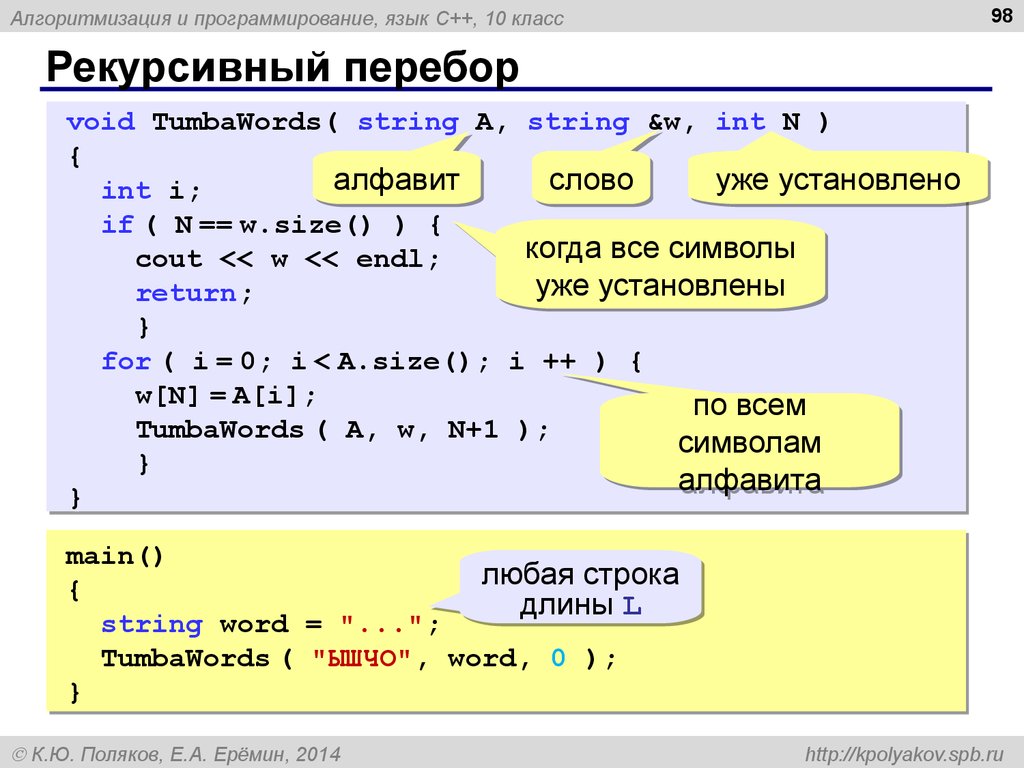 С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.
С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.
 Такими в частности являются задачи, использующие списковые и древовидные структуры данных.
Такими в частности являются задачи, использующие списковые и древовидные структуры данных.


 4.3 Procedure
4.3 Procedure Procedure
Procedure


 [Factorial_AP]
[Factorial_AP] 
 Узнайте больше об iPadOS 16, поддерживаемых устройствах, датах выпуска и основных функциях с помощью нашей памятки.
Узнайте больше об iPadOS 16, поддерживаемых устройствах, датах выпуска и основных функциях с помощью нашей памятки.
 :
: Как
он получает эту ссылку? Используя имя, b, т.е.
уже привязан к нему. Таким образом, мутация создает цикл:
Как
он получает эту ссылку? Используя имя, b, т.е.
уже привязан к нему. Таким образом, мутация создает цикл: Как это проверить?
Как это проверить?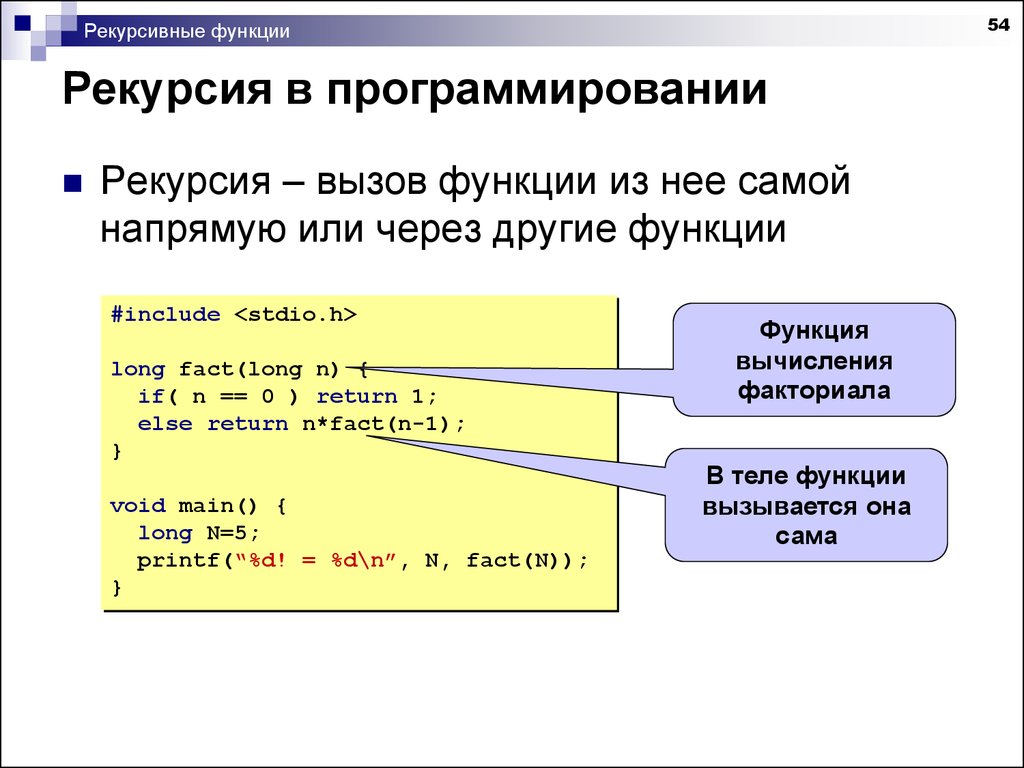
 Таким образом:
Таким образом: В языке с переменными это было бы еще более
бесшовный: Действительно, одно из применений переменных заключается в том, что они
упростить обессахаривание вышеуказанного шаблона, вместо того, чтобы требовать
каждое использование циклически связанного идентификатора должно быть распаковано. На
с другой стороны, с небольшими дополнительными усилиями процесс обессахаривания может
позаботьтесь и о распаковке.
В языке с переменными это было бы еще более
бесшовный: Действительно, одно из применений переменных заключается в том, что они
упростить обессахаривание вышеуказанного шаблона, вместо того, чтобы требовать
каждое использование циклически связанного идентификатора должно быть распаковано. На
с другой стороны, с небольшими дополнительными усилиями процесс обессахаривания может
позаботьтесь и о распаковке. 0573 (NAMPDA) (NAMPDA 10574 (NAMPDA) (NAMPDA
0573 (NAMPDA) (NAMPDA 10574 (NAMPDA) (NAMPDA
 Вместо этого язык может создать новый тип значения
только для использования здесь. При переходе к любой другой операции это приведет к
в ошибке.
Вместо этого язык может создать новый тип значения
только для использования здесь. При переходе к любой другой операции это приведет к
в ошибке. Стараться. Подсказка: Замените больше.
А потом еще немного. И более!
Стараться. Подсказка: Замените больше.
А потом еще немного. И более! Прежде чем мы объясним, что такое фракталы, давайте определим, что такое самоподобие есть .
Прежде чем мы объясним, что такое фракталы, давайте определим, что такое самоподобие есть .  Иными словами, фракталы — это паттерны, которые самоподобны в разных масштабах (увеличениях).
Иными словами, фракталы — это паттерны, которые самоподобны в разных масштабах (увеличениях). Узнайте больше о фракталах по ссылке ниже:
Узнайте больше о фракталах по ссылке ниже: Возьмем линию длиной 300 пикселей. Первый шаг — разделить линию на три равные части по 100 пикселей каждая (см. шаг 0). Используя средний сегмент в качестве основы, мы рисуем равносторонний треугольник со стороной 100 пикселей, как показано в шаге 1). Затем основание треугольника удаляется, оставляя нам первую итерацию кривой Коха. См. шаг 1 (продолжение). Это изображение соответствует тому, что называется глубиной = 1. Теперь есть четыре прямые линии, каждая длиной 100 пикселей.
Возьмем линию длиной 300 пикселей. Первый шаг — разделить линию на три равные части по 100 пикселей каждая (см. шаг 0). Используя средний сегмент в качестве основы, мы рисуем равносторонний треугольник со стороной 100 пикселей, как показано в шаге 1). Затем основание треугольника удаляется, оставляя нам первую итерацию кривой Коха. См. шаг 1 (продолжение). Это изображение соответствует тому, что называется глубиной = 1. Теперь есть четыре прямые линии, каждая длиной 100 пикселей. Операцию можно продолжить на каждой из полученных линий, чтобы получить более сложные узоры Коха.
Операцию можно продолжить на каждой из полученных линий, чтобы получить более сложные узоры Коха. Этот процесс можно продолжать до бесконечности, чтобы получить все более сложные кривые Коха.
Этот процесс можно продолжать до бесконечности, чтобы получить все более сложные кривые Коха. TTL.shape("черепаха")
###### УСТАНОВИТЬ СТАРТОВУЮ ПОЗИЦИЮ ЧЕРЕПАХИ ######
TTL.penup() # Не позволяйте черепашке рисовать при перемещении в позицию (-160, 110).
TTL.setposition(-170,110)
TTL.pendown() # Разрешить черепашке рисовать.
###### ПЕРЕМЕННЫЕ ######
# Переменная 'length' - это длина стороны начального равностороннего треугольника.
# Переменная 'length' делится на переменную 'lengthDivisor' на каждой итерации рекурсии.
# Переменная 'recursionLevel' - это глубина кривой Коха.
###### ОПРЕДЕЛЕНИЕ ФРАКТАЛЬНОЙ ФУНКЦИИ Коха ######
# Нарисуйте фрактал Коха 'recursionLevel' и 'length'. № 1
def KochFractal (TTL, recursionLevel, length, lengthDivisor):
if recursionLevel == 0: # recursionLevel = 0 является фрактальным базовым случаем.
TTL.forward(length) # Это нарисует равносторонний треугольник.
еще:
длина = длина / длина делителя
# Вызов функции KochFractal внутри самой функции - Рекурсия.
# Нарисовать паттерн Коха одной трети «длины» и уменьшить «уровень рекурсии».
TTL.shape("черепаха")
###### УСТАНОВИТЬ СТАРТОВУЮ ПОЗИЦИЮ ЧЕРЕПАХИ ######
TTL.penup() # Не позволяйте черепашке рисовать при перемещении в позицию (-160, 110).
TTL.setposition(-170,110)
TTL.pendown() # Разрешить черепашке рисовать.
###### ПЕРЕМЕННЫЕ ######
# Переменная 'length' - это длина стороны начального равностороннего треугольника.
# Переменная 'length' делится на переменную 'lengthDivisor' на каждой итерации рекурсии.
# Переменная 'recursionLevel' - это глубина кривой Коха.
###### ОПРЕДЕЛЕНИЕ ФРАКТАЛЬНОЙ ФУНКЦИИ Коха ######
# Нарисуйте фрактал Коха 'recursionLevel' и 'length'. № 1
def KochFractal (TTL, recursionLevel, length, lengthDivisor):
if recursionLevel == 0: # recursionLevel = 0 является фрактальным базовым случаем.
TTL.forward(length) # Это нарисует равносторонний треугольник.
еще:
длина = длина / длина делителя
# Вызов функции KochFractal внутри самой функции - Рекурсия.
# Нарисовать паттерн Коха одной трети «длины» и уменьшить «уровень рекурсии». KochFractal(TTL, recursionLevel-1, length, lengthDivisor)
TTL.left(60) #Повернуть черепаху влево на 60 градусов.
KochFractal(TTL, recursionLevel-1, length, lengthDivisor)
TTL.right(120) #Повернуть черепаху вправо на 120 градусов.
KochFractal(TTL, recursionLevel-1, length, lengthDivisor)
TTL.left(60) #Повернуть черепаху влево на 60 градусов.
KochFractal(TTL, recursionLevel-1, length, lengthDivisor)
###### ИНИЦИАЛИЗАЦИЯ ФРАКТАЛЬНОЙ КОХА recursionLevel AND length ######
# Инициализировать переменную length, длину стороны равностороннего треугольника.
length = 360 # Длина равностороннего треугольника = 360 пикселей. № 2
###### ВЫЗОВ ФРАКТАЛЬНОЙ ФУНКЦИИ Коха ######
# Функция KochFractal рисует фрактал Коха для одной стороны треугольника.
# Вызов функции KochFractal для первой стороны треугольника.
KochFractal(TTL, 3, длина, 3) # 3
TTL.right(120) #Повернуть черепаху вправо на 120 градусов.
# Вызов функции KochFractal для второй стороны треугольника.
KochFractal(TTL, recursionLevel-1, length, lengthDivisor)
TTL.left(60) #Повернуть черепаху влево на 60 градусов.
KochFractal(TTL, recursionLevel-1, length, lengthDivisor)
TTL.right(120) #Повернуть черепаху вправо на 120 градусов.
KochFractal(TTL, recursionLevel-1, length, lengthDivisor)
TTL.left(60) #Повернуть черепаху влево на 60 градусов.
KochFractal(TTL, recursionLevel-1, length, lengthDivisor)
###### ИНИЦИАЛИЗАЦИЯ ФРАКТАЛЬНОЙ КОХА recursionLevel AND length ######
# Инициализировать переменную length, длину стороны равностороннего треугольника.
length = 360 # Длина равностороннего треугольника = 360 пикселей. № 2
###### ВЫЗОВ ФРАКТАЛЬНОЙ ФУНКЦИИ Коха ######
# Функция KochFractal рисует фрактал Коха для одной стороны треугольника.
# Вызов функции KochFractal для первой стороны треугольника.
KochFractal(TTL, 3, длина, 3) # 3
TTL.right(120) #Повернуть черепаху вправо на 120 градусов.
# Вызов функции KochFractal для второй стороны треугольника. KochFractal(TTL, 3, длина, 3) # 4
TTL.right(120) #Повернуть черепаху вправо на 120 градусов.
# Вызов функции KochFractal для третьей стороны треугольника.
KochFractal(TTL, 3, длина, 3) # 5
screen.exitonclick() # Выход
KochFractal(TTL, 3, длина, 3) # 4
TTL.right(120) #Повернуть черепаху вправо на 120 градусов.
# Вызов функции KochFractal для третьей стороны треугольника.
KochFractal(TTL, 3, длина, 3) # 5
screen.exitonclick() # Выход
 «Длина определена как 360 на шаге 2). Затем он поворачивает черепаху вправо на 120 градусов.
«Длина определена как 360 на шаге 2). Затем он поворачивает черепаху вправо на 120 градусов. py
py # Переменная ‘recursionLevel’ — номер итерации рекурсии.
###### ОПРЕДЕЛИТЬ ФУНКЦИЮ treeFractal ######
# Рисуем фрактал с уровнем рекурсии, длиной ветки дерева,
# уменьшение длины ветки для каждой итерации, и
# угол, на который поворачивается ветвь на каждой итерации.
def treeFractal (TTL, уровень рекурсии, длина ветви, сокращение ветви, угол):
если уровень рекурсии == 0:
TTL.fd(0)
еще:
длина ветки = длина ветки — сокращение ветки
TTL.forward(Длина ветки)
TTL.влево(угол)
treeFractal (TTL, recursionLevel-1, branchLength, branchReduction, угол)
TTL.вправо(угол * 2)
treeFractal (TTL, recursionLevel-1, branchLength, branchReduction, угол)
TTL.влево(угол)
TTL.backward(длина ветки)
# Вызвать функцию treeFractal со следующими параметрами.
# Уровень рекурсии = 7; Длина ответвления = 50.
# Сокращение числа ветвей на каждой итерации рекурсии = 5.
# Поверните влево от прямого угла на 25 градусов.
деревофрактал(TTL, 7, 45, 5, 25)
screen.exitonclick() # Выход из экрана
# Переменная ‘recursionLevel’ — номер итерации рекурсии.
###### ОПРЕДЕЛИТЬ ФУНКЦИЮ treeFractal ######
# Рисуем фрактал с уровнем рекурсии, длиной ветки дерева,
# уменьшение длины ветки для каждой итерации, и
# угол, на который поворачивается ветвь на каждой итерации.
def treeFractal (TTL, уровень рекурсии, длина ветви, сокращение ветви, угол):
если уровень рекурсии == 0:
TTL.fd(0)
еще:
длина ветки = длина ветки — сокращение ветки
TTL.forward(Длина ветки)
TTL.влево(угол)
treeFractal (TTL, recursionLevel-1, branchLength, branchReduction, угол)
TTL.вправо(угол * 2)
treeFractal (TTL, recursionLevel-1, branchLength, branchReduction, угол)
TTL.влево(угол)
TTL.backward(длина ветки)
# Вызвать функцию treeFractal со следующими параметрами.
# Уровень рекурсии = 7; Длина ответвления = 50.
# Сокращение числа ветвей на каждой итерации рекурсии = 5.
# Поверните влево от прямого угла на 25 градусов.
деревофрактал(TTL, 7, 45, 5, 25)
screen.exitonclick() # Выход из экрана 
 Теперь у нас есть четыре треугольника — один в середине и по три в каждой из вершин треугольника, с которого мы начали.
Теперь у нас есть четыре треугольника — один в середине и по три в каждой из вершин треугольника, с которого мы начали. 1 медленно, 10 быстро; 0 самый быстрый.
TTL.color("red") # Установить цвет черепахи.
TTL.pensize(1) #Установить ширину пера для рисования черепахи.
###### УСТАНОВИТЬ СТАРТОВУЮ ПОЗИЦИЮ ЧЕРЕПАХИ ######
TTL.penup() # Не позволяйте черепашке рисовать при перемещении в позицию (0, 110).
TTL.setposition(-100, -100)
TTL.pendown() # Разрешить черепашке рисовать.
###### ПЕРЕМЕННЫЕ ######
# Переменная 'length' - начальная длина треугольника Серпинского.
# Переменная 'angle' - это угол поворота черепахи.
# Переменная 'recursionLevel' - номер итерации рекурсии.
###### ОПРЕДЕЛИТЬ ФУНКЦИЮ треугольника Серпинского ######
# Нарисовать фрактал с длиной треугольника, уровнем рекурсии и
# угол, на который поворачивается черепаха.
def SierpinskiTriangle (TTL, длина, уровень рекурсии, угол):
if recursionLevel == 1: # Нарисовать треугольник.
для я в диапазоне (3):
TTL.fd(длина)
TTL.влево(120)
еще:
Треугольник Серпинского (TTL, длина/2, уровень рекурсии-1, угол)
TTL.
1 медленно, 10 быстро; 0 самый быстрый.
TTL.color("red") # Установить цвет черепахи.
TTL.pensize(1) #Установить ширину пера для рисования черепахи.
###### УСТАНОВИТЬ СТАРТОВУЮ ПОЗИЦИЮ ЧЕРЕПАХИ ######
TTL.penup() # Не позволяйте черепашке рисовать при перемещении в позицию (0, 110).
TTL.setposition(-100, -100)
TTL.pendown() # Разрешить черепашке рисовать.
###### ПЕРЕМЕННЫЕ ######
# Переменная 'length' - начальная длина треугольника Серпинского.
# Переменная 'angle' - это угол поворота черепахи.
# Переменная 'recursionLevel' - номер итерации рекурсии.
###### ОПРЕДЕЛИТЬ ФУНКЦИЮ треугольника Серпинского ######
# Нарисовать фрактал с длиной треугольника, уровнем рекурсии и
# угол, на который поворачивается черепаха.
def SierpinskiTriangle (TTL, длина, уровень рекурсии, угол):
if recursionLevel == 1: # Нарисовать треугольник.
для я в диапазоне (3):
TTL.fd(длина)
TTL.влево(120)
еще:
Треугольник Серпинского (TTL, длина/2, уровень рекурсии-1, угол)
TTL. fd(длина/2)
Треугольник Серпинского (TTL, длина/2, уровень рекурсии-1, угол)
TTL.bk(длина/2)
TTL.влево(угол)
TTL.fd(длина/2)
TTL.вправо(угол)
Треугольник Серпинского (TTL, длина/2, уровень рекурсии-1, угол)
TTL.влево(угол)
TTL.bk(длина/2)
TTL.вправо(угол)
# Вызов функции SierpinskiTriangle с длиной треугольника = 200,
# уровни рекурсии = 2, угол поворота черепахи = 60 градусов.
Треугольник Серпинского(TTL, 200,3, 60)
screen.exitonclick() # Выход из экрана
fd(длина/2)
Треугольник Серпинского (TTL, длина/2, уровень рекурсии-1, угол)
TTL.bk(длина/2)
TTL.влево(угол)
TTL.fd(длина/2)
TTL.вправо(угол)
Треугольник Серпинского (TTL, длина/2, уровень рекурсии-1, угол)
TTL.влево(угол)
TTL.bk(длина/2)
TTL.вправо(угол)
# Вызов функции SierpinskiTriangle с длиной треугольника = 200,
# уровни рекурсии = 2, угол поворота черепахи = 60 градусов.
Треугольник Серпинского(TTL, 200,3, 60)
screen.exitonclick() # Выход из экрана
 Это может показаться
странно, что процедура может вызывать сама себя, а в языке нет ничего
чтобы предотвратить это. Принципиально ничем не отличается
процедура, вызывающая другую процедуру, и процедура, вызывающая саму себя.
Это может показаться
странно, что процедура может вызывать сама себя, а в языке нет ничего
чтобы предотвратить это. Принципиально ничем не отличается
процедура, вызывающая другую процедуру, и процедура, вызывающая саму себя. Процедура будет
продолжать вызывать себя до того, как запустится среда выполнения VBA и завершит выполнение
процесс. Обычно рекурсивная процедура инициируется другой процедурой.
который обеспечивает начальное значение для рекурсивной процедуры.
затем рекурсивная процедура изменяет этот параметр и вызывает сама себя. Когда некоторые
условие выхода выполнено, рекурсивная процедура перестает вызывать себя,
прокручивает процедуру «стек» и в конечном итоге возвращает
процедура инициализации.
Процедура будет
продолжать вызывать себя до того, как запустится среда выполнения VBA и завершит выполнение
процесс. Обычно рекурсивная процедура инициируется другой процедурой.
который обеспечивает начальное значение для рекурсивной процедуры.
затем рекурсивная процедура изменяет этот параметр и вызывает сама себя. Когда некоторые
условие выхода выполнено, рекурсивная процедура перестает вызывать себя,
прокручивает процедуру «стек» и в конечном итоге возвращает
процедура инициализации. Когда это
процедура завершается, она удаляется или «извлекается» из стека, а затем
вершина стека — это процедура, вызвавшая эту процедуру. Как процедуры
вызываются, они «подталкиваются» на вершину стека, и когда
процедура завершается, она «извлекается» из вершины стека и
процедура, вызвавшая эту процедуру, теперь находится на вершине стека. в
рекурсивной процедуры, показанной выше, процедура «Proc» «нажимается» на
верхней части стека, но никогда не удаляется и не «выталкивается». Стек процедур в
Возможности VBA ограничены. Как называет себя Proc, стек растет, потому что
выхода из петли нет. Примерно при 6800 элементах стека
стек заполнен до отказа, и VBA завершает все с помощью Вне
Ошибка времени выполнения Stack Space .
Когда это
процедура завершается, она удаляется или «извлекается» из стека, а затем
вершина стека — это процедура, вызвавшая эту процедуру. Как процедуры
вызываются, они «подталкиваются» на вершину стека, и когда
процедура завершается, она «извлекается» из вершины стека и
процедура, вызвавшая эту процедуру, теперь находится на вершине стека. в
рекурсивной процедуры, показанной выше, процедура «Proc» «нажимается» на
верхней части стека, но никогда не удаляется и не «выталкивается». Стек процедур в
Возможности VBA ограничены. Как называет себя Proc, стек растет, потому что
выхода из петли нет. Примерно при 6800 элементах стека
стек заполнен до отказа, и VBA завершает все с помощью Вне
Ошибка времени выполнения Stack Space . ''''''''''''''''''''''''''
Сумма рекурсе N - 1
Еще
'''''''''''''''''''''''''''''''
' Здесь N = 0, поэтому SumRecurse
' не называет себя.
'''''''''''''''''''''''''''''''
Конец, если
Конец суб
''''''''''''''''''''''''''
Сумма рекурсе N - 1
Еще
'''''''''''''''''''''''''''''''
' Здесь N = 0, поэтому SumRecurse
' не называет себя.
'''''''''''''''''''''''''''''''
Конец, если
Конец суб  Тем не менее, это
ввести понятие рекурсии.
Тем не менее, это
ввести понятие рекурсии. Следующий,
объявить переменную уровня модуля с именем FSO типа Scripting.FileSystemObject.
Следующий,
объявить переменную уровня модуля с именем FSO типа Scripting.FileSystemObject. Range("A1")
''''''''''''''''''''''''''''''''''''''
' Если FSO не инициализирован,
' создать новый экземпляр FSO.
''''''''''''''''''''''''''''''''''''''
Если ФСО ничто, то
Установите FSO = New Scripting.FileSystemObject
Конец, если
''''''''''''''''''''''''''''''''''''''
' Установите для нашей переменной TopFolderObj значение
' объект Folder представляет
' папка на диске, вложенные папки которой
' мы хотим перечислить.
''''''''''''''''''''''''''''''''''''''
Установить TopFolderObj = FSO.GetFolder(TopFolderName)
ListSubFolders OfFolder: = TopFolderObj, _
Диапазон назначения: = Диапазон назначения
Конец суб
Range("A1")
''''''''''''''''''''''''''''''''''''''
' Если FSO не инициализирован,
' создать новый экземпляр FSO.
''''''''''''''''''''''''''''''''''''''
Если ФСО ничто, то
Установите FSO = New Scripting.FileSystemObject
Конец, если
''''''''''''''''''''''''''''''''''''''
' Установите для нашей переменной TopFolderObj значение
' объект Folder представляет
' папка на диске, вложенные папки которой
' мы хотим перечислить.
''''''''''''''''''''''''''''''''''''''
Установить TopFolderObj = FSO.GetFolder(TopFolderName)
ListSubFolders OfFolder: = TopFolderObj, _
Диапазон назначения: = Диапазон назначения
Конец суб 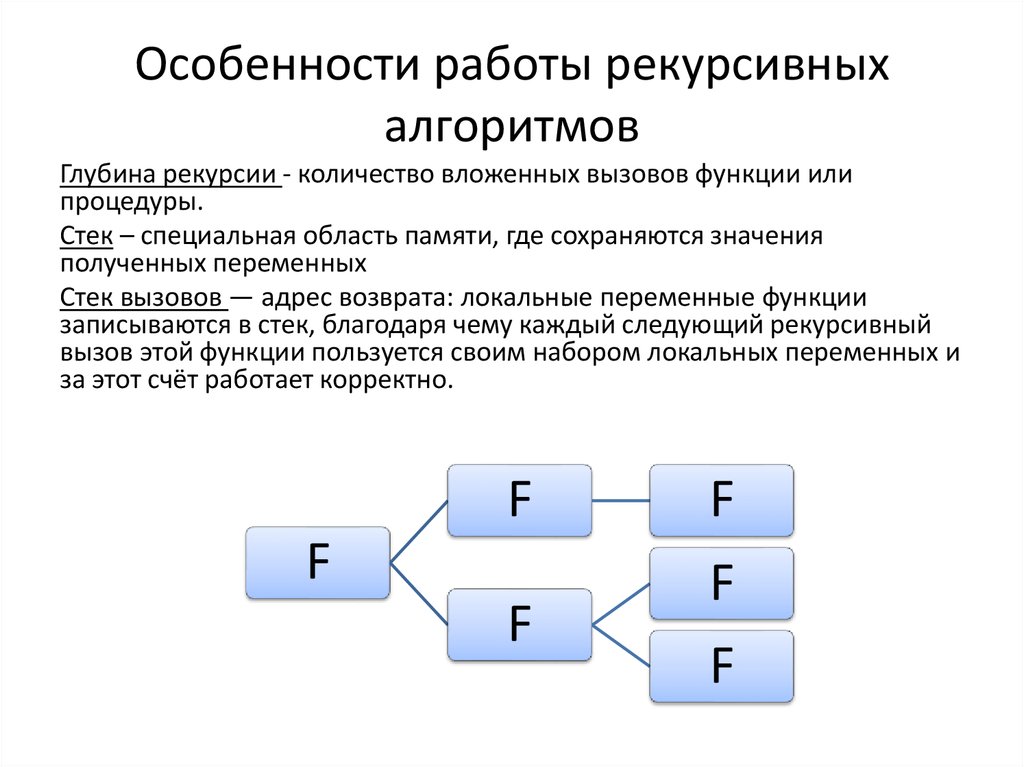 Мы еще не написали эту процедуру.
Процедура ListSubFolders
выполнит всю работу по перечислению подпапок. Поскольку мы не знаем в
во время разработки, какой будет наша начальная папка, и мы не знаем, что
иерархия подпапок этой папки, мы должны написать процедуру
для обработки любого количества подпапок, вложенных на любую глубину. Это делает его
идеальный кандидат для рекурсивного решения. Процедура может называть себя как
столько раз, сколько нужно, чтобы перечислить все подпапки.
Мы еще не написали эту процедуру.
Процедура ListSubFolders
выполнит всю работу по перечислению подпапок. Поскольку мы не знаем в
во время разработки, какой будет наша начальная папка, и мы не знаем, что
иерархия подпапок этой папки, мы должны написать процедуру
для обработки любого количества подпапок, вложенных на любую глубину. Это делает его
идеальный кандидат для рекурсивного решения. Процедура может называть себя как
столько раз, сколько нужно, чтобы перечислить все подпапки. Folder, _
DestinationRange как диапазон)
'''''''''''''''''''''''''''''''''''''''''''''''''''''''' '''
' Список подпапок
' Здесь перечислены все подпапки объекта OfFolder.
'Помещает полное имя папки OfFolder в диапазон
', на который ссылается DestinationRange.
'''''''''''''''''''''''''''''''''''''''''''''''''''''''' '''
''''''''''''''''''''''''''''''''''''''
' Это представляет одну подпапку
' в папке OfFolder.
' Мы используем это, чтобы перебрать
' все подпапки с For
«Каждая петля.
''''''''''''''''''''''''''''''''''''''
Dim SubFolder As Scripting.Folder
''''''''''''''''''''''''''''''''''''''''''''
' Вставьте имя OfFolder в
'Диапазон назначения.
''''''''''''''''''''''''''''''''''''''''''''
DestinationRange.Value = OfFolder.Path
''''''''''''''''''''''''''''''''''''''''''''
' Point DestinationRange на одну строку вниз
' и один столбец вправо. Этот
' даст хороший вид с отступом
' иерархия папок.
Folder, _
DestinationRange как диапазон)
'''''''''''''''''''''''''''''''''''''''''''''''''''''''' '''
' Список подпапок
' Здесь перечислены все подпапки объекта OfFolder.
'Помещает полное имя папки OfFolder в диапазон
', на который ссылается DestinationRange.
'''''''''''''''''''''''''''''''''''''''''''''''''''''''' '''
''''''''''''''''''''''''''''''''''''''
' Это представляет одну подпапку
' в папке OfFolder.
' Мы используем это, чтобы перебрать
' все подпапки с For
«Каждая петля.
''''''''''''''''''''''''''''''''''''''
Dim SubFolder As Scripting.Folder
''''''''''''''''''''''''''''''''''''''''''''
' Вставьте имя OfFolder в
'Диапазон назначения.
''''''''''''''''''''''''''''''''''''''''''''
DestinationRange.Value = OfFolder.Path
''''''''''''''''''''''''''''''''''''''''''''
' Point DestinationRange на одну строку вниз
' и один столбец вправо. Этот
' даст хороший вид с отступом
' иерархия папок. ''''''''''''''''''''''''''''''''''''''''''''
Установите DestinationRange = DestinationRange.Offset(1, 1)
''''''''''''''''''''''''''''''''''''''''''''
' Вот рекурсивная часть. Для каждого
' подпапка OfFolder, процедура
' вызывает себя, проходя в SubFolder и
'Диапазон назначения. В первый раз это
' называет себя, он проходит первый
' подпапка. Если в ЭТОЙ папке есть
' подпапки, эти подпапки будут
' подхватывается в петле ниже, и
' процедура будет вызывать себя для каждого
' подпапка. Этот процесс продолжается в течение
' настолько глубоко, насколько вложена подпапка.
''''''''''''''''''''''''''''''''''''''''''
Для каждой подпапки в OfFolder.SubFolders
ListSubFolders OfFolder:=Подпапка, _
Диапазон назначения: = Диапазон назначения
Следующая подпапка
''''''''''''''''''''''''''''''''''''''''''''''''
' После того, как мы перечислили подпапку в
' OfFolder, переместите DestinationRange
' вниз на одну строку и назад на один столбец, чтобы
' слева, чтобы отразить, что мы закончили
' с такой глубиной папки/подпапки
'иерархия.
''''''''''''''''''''''''''''''''''''''''''''
Установите DestinationRange = DestinationRange.Offset(1, 1)
''''''''''''''''''''''''''''''''''''''''''''
' Вот рекурсивная часть. Для каждого
' подпапка OfFolder, процедура
' вызывает себя, проходя в SubFolder и
'Диапазон назначения. В первый раз это
' называет себя, он проходит первый
' подпапка. Если в ЭТОЙ папке есть
' подпапки, эти подпапки будут
' подхватывается в петле ниже, и
' процедура будет вызывать себя для каждого
' подпапка. Этот процесс продолжается в течение
' настолько глубоко, насколько вложена подпапка.
''''''''''''''''''''''''''''''''''''''''''
Для каждой подпапки в OfFolder.SubFolders
ListSubFolders OfFolder:=Подпапка, _
Диапазон назначения: = Диапазон назначения
Следующая подпапка
''''''''''''''''''''''''''''''''''''''''''''''''
' После того, как мы перечислили подпапку в
' OfFolder, переместите DestinationRange
' вниз на одну строку и назад на один столбец, чтобы
' слева, чтобы отразить, что мы закончили
' с такой глубиной папки/подпапки
'иерархия. ''''''''''''''''''''''''''''''''''''''''''''''''
Установить диапазон назначения = диапазон назначения (1, 0)
Конец сабвуфера
''''''''''''''''''''''''''''''''''''''''''''''''
Установить диапазон назначения = диапазон назначения (1, 0)
Конец сабвуфера