Что такое Graph Search? / Хабр

За последний месяц мы успели пообщаться с более чем сотней людей которые ведут свой бизнес в Facebook и создают рекламные компании для повышения дохода своего бизнеса и охвата аудитории. Удивительно было узнать, что никто из них не знает о Graph Search и его возможностях.

Graph Search— это умный поиск в Facebook.

Когда друг вашего друга лайкает любимого исполнителя, комментирует пост, добавляется в группу, играет в игру то все такие действия записывается в библиотеку Social Graph и связываются с активностью всех остальных пользователей в Facebook. Маркетологи используют Graph Search как инструмент для поиска потенциальных покупателей и точечного таргетинга рекламных компаний или поиска полезных связей которые находятся в библиотеке Social Graph

Что Вы сможете с помощью Graph Search?
  • Определить своих потенциальных фанов
  • Узнать о любимых интересах и хобби потенциальных фанов
  • Узнать лайки и интересы ваших коллег по бизнесу
  • Украсть фанов у своих конкурентов
  • Найти потенциальных бизнес партнеров
  • Улучшить кчество и эффективность рекламных компаний

Начнём:

#0 Переключите интерфейс своего Facebook на английский “English (US)”, Graph Search не доступен на русском языке

Допустим что вы производите качественные изделия Dream Team

#1 Найдите страницы на которые подписаны ваши фаны.

Вы получите список страниц которые читают ваши потенциальные покупатели и страницы конкурентов. Указывайте в поиске страницу конкурента, если у вас мало фанов.

Запрос в Facebook:

  • Pages liked by people who like Dream Team Wear
  • Favorite pages of people who like Dream Team Wear

#2 Найдите интересы своих фанов

Вы сможете легко узнать больше о своих потенциальных покупателях без дебильных опросов, просто указажите в поиске страницу которая максимально подходит к вашей аудитории или выберите из списка выше

Запрос в Facebook:

  • Favorite interests of people who like don’t Take Fake

#3 Определите интересы лидеров мнений

Если лидер мнения лайкнит вашу страницу или еще лучше прокомментирует ваше предложение, то результаты будут намного лучше
Запрос в Facebook:

  • Interests liked by Artem Trawkin
  • Pages liked by Artem Trawkin

#4 Уточняйте запросы

Выбрав две страницы похожей категории вы еще больше удостоверитесь в интересах вашей аудитории

Запрос в Facebook:

  • Pages liked by people who like Dream Team Wear and From Ukraine With Love
  • Favorite interests of people who like don’t Take Fake and The new old

#5 Отсортируйте своих фанов

Вы также можете отделить интересы по полу, это будет полезно, если в вашей аудитории преобладает один пол.
Запрос в Facebook:

  • Favorite pages of females who like Dream Team Wear

#6 Отсортируйте конкурентов по категориям

Такой запрос позволяет отсортировать определенную категорию страничек с которыми связаны потенциальные покупатели. Один из наших любимых

Запрос в Facebook:

  • Pages about Clothing that are liked by people who like Dream Team Wear

#7 Узнайте возраст своих покупателей

Определите средний возраст фанов любой странички и найдите интересы для своей возрастной категории
Чтобы узнать возрастной диапазон ваших фанов перейдите по этой ссылке: https://www.facebook.com/buydreamteam/likes

Отсортируйте страницы потенциальных покупателей согласно возраста своих фанов или фанов конкурента

Запрос в Facebook:

  • Pages liked by people who are younger than 34 and older than 25 and like don’t Take Fake

#8 Отсортируйте интересы по локации

В каждом городе свои тренды, вы получите список интересов согласно аудитории из разных регионов

Запрос в Facebook:

  • Favorite interests of people who like The new old and live inOdessa, Ukraine

#9 Определите маршрут

Если ваш магазин находится где-то рядом с популярным кафе, парком или музеем, вы можете таргетировать рекламу на тех кто часто проходит мимо вашего бизнеса и чекинится у ваших соседях
Запрос в Facebook

  • Places near Креативний простір “Часопис” visited by people who like Taras Shevchenko National University of Kyiv

#10 Комбинируйте ваши запросы

Возможности Graph Search не ограничены, импровизируйте!
К примеру:

Как найти человека который рабоатет в компании c которой вы желаете сотрудничать?

  • People who work at Chooos
  • People who work at Chooos and visited gastroRock — гастрономический паб

Как найти страницы которые читают молодые программисты?

  • Pages liked by Engineers who like Mashable and TechCrunchand who are younger than 26 and older than 22

Какие группы вам стоит посетить?

  • Groups my friends are in
  • Groups people who like Dream Team Wear joined

Вы должны понимать, что поиск может быть не на 100% точным, активность пользователей которая скрыта их приватными настройками не будет учитываться.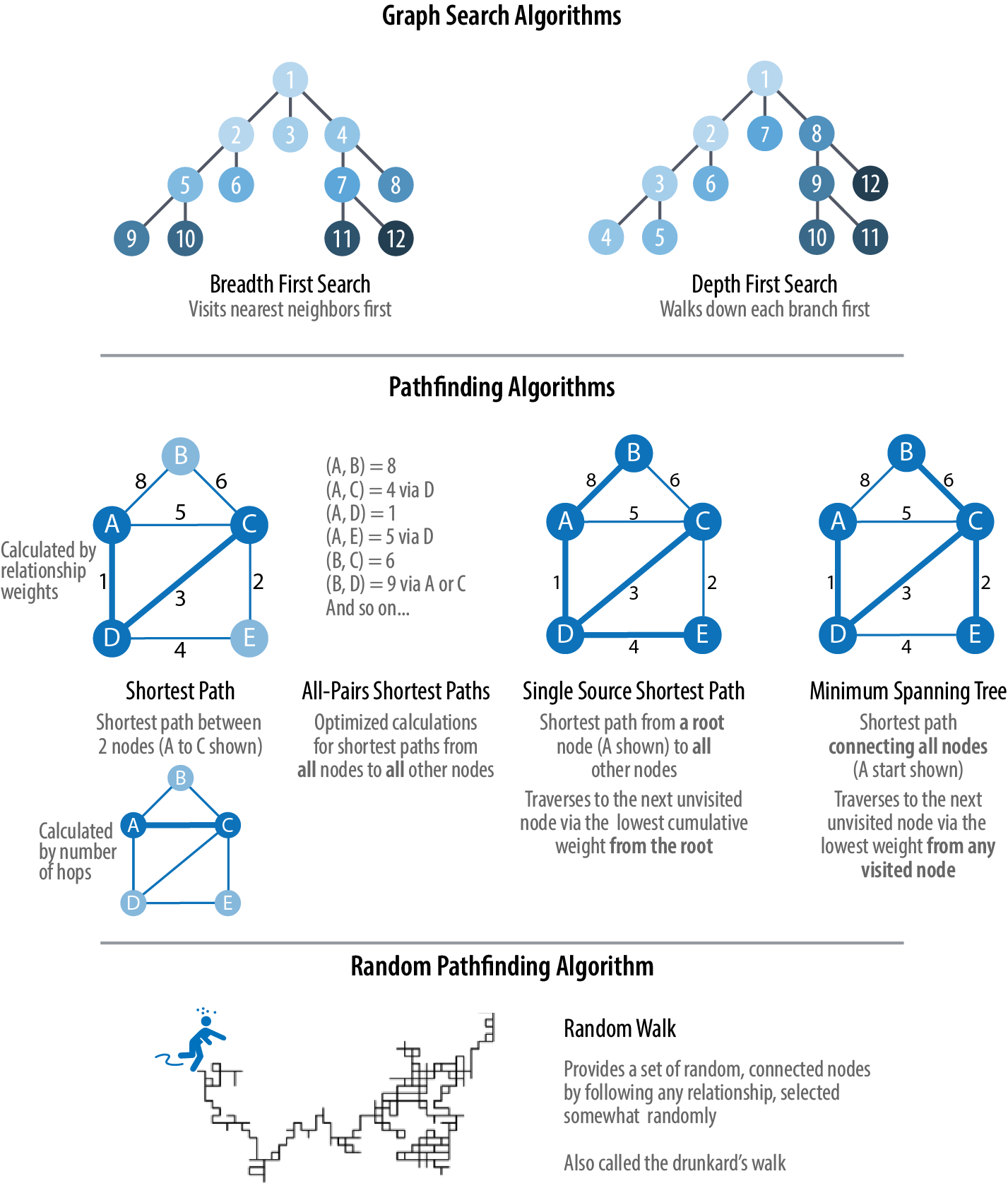

Этого будет достаточно чтобы изучить возможности Graph Search и интересы своих потенциальных покупателей.

5 способов использовать Graph Search по назначению — Соцсети на vc.ru

Если Facebook уже подарил вам возможность использования Graph Search, то вы можете не только спрятаться от него, но и хорошенько повеселиться.

Да, все запросы пока вводятся на английском, но уметь это делать надо в любом случае. Важно относиться к Graph Search не как к обычной строке поиска, а как к мощнейшему инструменту, способному изменить вашу жизнь.

Вот пять примеров того, как круто можно использовать Graph Search.

Найдите друзей с похожими интересами

Очень просто выяснить, кто из ваших друзей любит поняшек или передачу «Давай поженимся», но гораздо сложнее найти себе друга, который увлекается кёрлингом, как и вы.

Раньше надо было запостить статус типа «Ищу игроков в кёрлинг» или прошерстить профили всех своих знакомых в поисках заветного слова в поле «Интересы» или хотя бы соответствующих фотографий с камнями и швабрами.

А в Graph Search надо просто ввести «Friends who play curling» (или даже «…like curling»).

Мои друзья по кёрлингу не упарываются, приходится искать через одно рукопожатие

Кроме того, можно искать друзей, которые используют определённое приложение. Попробуйте «friends who use Bang with friends», например. Это полезно.

Устанавливайте связи с людьми из прошлого или будущего

Раньше приходилось использовать «Одноклассники», чтобы отыскать свою школьную любовь и наконец-таки воплотить в жизнь все мечты. Graph Search предлагает более элегантное решение.

Так, можно искать людей по месту жительства, нынешнему или прошлому, по школе, университету, бывшему месту работы. Так что запрос «People who finished MGIMO in 2009» (не забывайте про умное слово graduated from) выдаст вам ваших потенциальных однокурсников. Если заменить «friends» на «friends of my friends», можно найти вообще всех, с кем вы познакомились на пьянках в общаге.

«People named Kristina Egorova who live in Orel» позволит вам зайти с другой стороны. Кстати, если на Facebook ничего нет, то вам предложат результаты запроса из Bing.

И почему бы не ввести «female friends of my friends who are single and like My little pony»? Это же такой элегантный способ найти себе невесту!

Охотьтесь за фотографиями

Как же сложно найти фото своего друга или члена семьи из определённой поездки! Так много картинок постится в соцсети, и разобраться с ними становится всё сложнее и сложнее. Не беда, с этим поможет Graph Search.

Во-первых, нужно пропробовать ввести «Photos I like», чтобы вывести все картинки, которые вы когда-либо лайкали. Желательно, чтобы ваша девушка не сидела в этот момент рядом с вами — могут быть проблемы. К запросу можно добавить временной период.

Чтобы найти фото конкретного человека, введите «Photos of Boris Svidler», запрос можно бесконечно уточнять, конечно — «Photos of Boris Svidler from Baikal trip in 2003».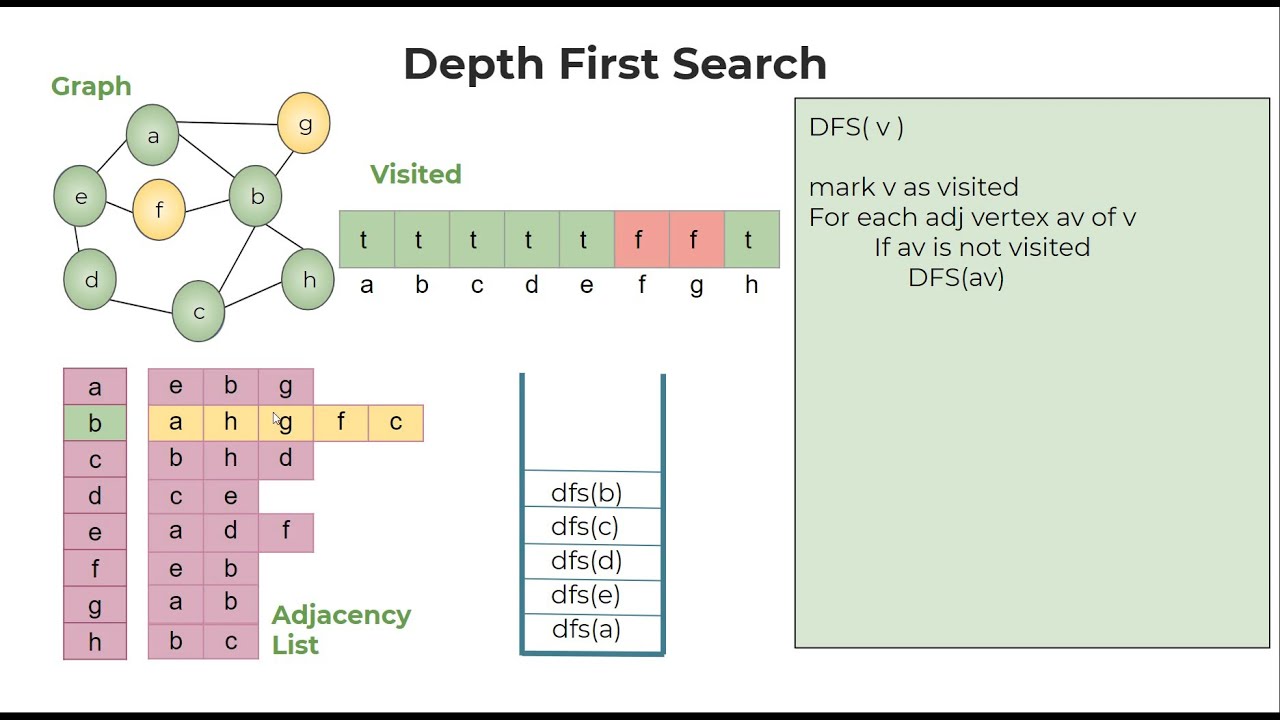


Ищите работу

Можно найти себе не только женщину или мужчину, но и человека, который может принять решение о приёме вас на работу. Может, вы не имеете его в списке друзей, но несколько общих знакомых — уже неплохое начало для начала трудовых отношений.

Запрос «People who work in Management and live in Silicon Valley» даст вам общее представление, скорее всего, придётся расширить его названиями компаний или более точным географическим положением.


Мне повезёт?

Возможно, вы заметили, что каждый раз появляется окошко, позволяющее модифицировать запрос. Там можно добавить пункты, о которых вы даже не задумывались — попробуйте, может, это сработает?

А внизу этого окна есть классная фраза «Discover Something New» — кажется, будто это рекламный слоган, а на деле это брат-близец кнопки «Мне повезёт» от Google.

Эта кнопка запускает случайный вариант поиска — наверняка вам попадётся что-то интересное! Кроме того, это отличный способ изучить все поисковые термины и категории.

Изучив синтаксис Graph Search и пользуясь подсказками, можно использовать этот поиск максимально эффективно.

Остаётся надеяться, что наш с вами общий друг, который занимается созданием главного российского конкурента Facebook, однажды всё-таки задумается о внедрении схожей технологии.

обходов графа

обходов графа

Темы:

  • трехцветный алгоритм
  • поиск в ширину
  • поиск в глубину
  • обнаружение цикла
  • топологическая сортировка
  • подключенных компонентов

Обход графа

Нам часто нужно решать задачи, которые можно выразить в терминах обхода или поиска по графу. Примеры включают:

  • Поиск всех доступных узлов (для сборки мусора)
  • Поиск наиболее доступного узла (поиск одиночной игры) или минимаксный наилучший достижимый узел (поиск игры для двух игроков)
  • Поиск наилучшего пути по графу (для маршрутизации и направлений карты)
  • Определение того, является ли граф DAG.
  • Топологическая сортировка графа.

Цель обхода графа, как правило, состоит в том, чтобы найти все достижимые узлы из заданного набора корневых узлов. В неориентированном графе мы проходим по всем ребрам; в в ориентированном графе мы следуем только внешним ребрам.

Трехцветный алгоритм

Абстрактно обход графа можно выразить в терминах триколора . алгоритм Дейкстры и др. В этом алгоритме узлы графа назначается один из трех цветов, которые могут меняться со временем:

  • Белые узлы — это необнаруженные узлы, которые еще не были замечены в текущем обходе и могут быть даже недоступны.
  • Черные узлы — это узлы, которые достижимы и с которыми выполняется алгоритм.
  • Серый узлы — это узлы, которые были обнаружены, но с которыми алгоритм еще не завершил работу. Эти узлы находятся на границе между белым и черным.

Ход работы алгоритма показан на следующем рисунке. Изначально черных узлов нет, а корни серые. Как Алгоритм прогрессирует, белые узлы превращаются в серые узлы, а серые узлы превращаются в черные узлы. В конце концов не осталось серых узлов и алгоритм готов.

Алгоритм всегда поддерживает ключевой инвариант: нет ребер из белые узлы к черным узлам. Это очевидно верно изначально, и потому что это true в конце, мы знаем, что любые оставшиеся белые узлы не могут быть достигнуты из черные узлы.

Псевдокод алгоритма выглядит следующим образом:

  1. Закрасьте все узлы белым цветом, кроме корневых узлов, которые окрашены в серый цвет.
  2. Пока существует какой-то серый узел n:
    • цвет некоторых белых преемников серого.
    • если n не имеет белых потомков, опционально покрасить n в черный цвет.

Этот алгоритм достаточно абстрактен, чтобы описать множество различных графов. обходы. Это позволяет конкретной реализации выбирать узел n из среди серых узлов; позволяет выбрать, каких и сколько белых преемников цвет серый, и это позволяет отсрочить окрашивание серых узлов в черный цвет. Мы говорим что такой алгоритм является недетерминированным потому что его поведение не полностью определен. Однако до тех пор, пока он работает с каждым выбранным серым узлом, любая реализация, которую можно описать в терминах этого алгоритма, завершится. Дальше, поскольку черно-белый инвариант сохраняется, он должен достигать всех достижимых узлов в графе.

Одно значение определения поиска по графу с точки зрения трехцветного алгоритма равно что трехцветный алгоритм работает даже при работе с серыми узлами одновременно, пока сохраняется черно-белый инвариант. мышление об этом инварианте, таким образом, помогает нам гарантировать, что любой обход графа, который мы Choose будет работать при распараллеливании, что становится все более важным.

Поиск в ширину

Поиск в ширину (BFS) — это алгоритм обхода графа, который исследует узлы в порядок их расстояния от корней, где расстояние определяется как минимальная длина пути от корня к узлу. Его псевдокод выглядит так:

// пусть s будет исходным узлом
граница = новая очередь()
пометить посещенный корень (установить root. distance = 0)
frontier.push(корень)
пока граница не пуста {
    Вершина v = граница.pop()
    для каждого преемника v' из v {
если v' не посещали {
граница.push(v')
пометить v' посещенным (v'.distance = v.distance + 1)
}
    }
}

Здесь белые узлы — это узлы, не отмеченные как посещенные, серые узлы — те, отмечены как посещенные и находятся на границе и , а черные узлы посещенные узлы больше не в граница . Вместо того, чтобы иметь посещенный флаг, мы можем отслеживать расстояние узла в поле v.distance . Когда обнаруживается новый узел, его расстояние устанавливается на единицу больше, чем у его предшественника против .

Когда граница представляет собой очередь в порядке поступления (FIFO), мы получаем поиск в ширину. Все узлы в очереди имеют минимальную длину пути внутри одного друг друга. В общем, есть набор узлов, которые нужно вытолкнуть, на некотором расстоянии k из исходника и еще набор элементов, позже в очереди на расстоянии k+1 .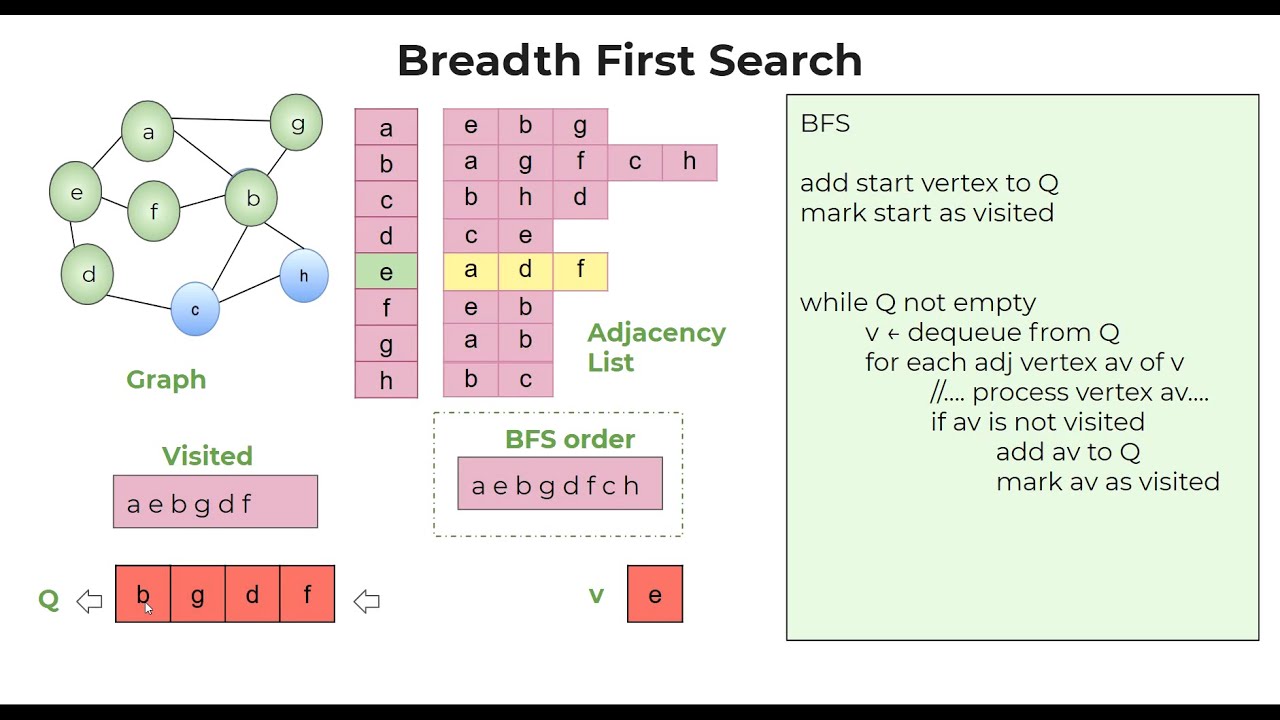 Каждый раз, когда новый узел помещается в очередь, она находится на расстоянии k+1 до тех пор, пока все узлы не будут находиться на расстоянии k исчезли, а к увеличились на единицу. Таким образом, вновь перемещенные узлы всегда на расстоянии не меньшем, чем любой другой серый узел.

Предположим, что мы запускаем этот алгоритм на следующем графе, предполагая, что что преемники посещаются в алфавитном порядке с любого заданного узла: :

В этом случае через очередь проходит следующая последовательность узлов: где каждый узел аннотируется его минимальным расстоянием от исходного узла A. Обратите внимание, что мы нажимаем на правую часть очереди и выталкиваем слева.

А0 В1 Д1 Е1 С2

Ясно, что узлы извлекаются в порядке расстояния: A, B, D, E, C. Это очень полезно. когда мы пытаемся найти кратчайший путь через граф к чему-либо. Когда очередь используется таким образом, она известна как рабочий список ; это держит трек оставшейся работы.

Поиск в глубину

Что, если бы мы заменили очередь FIFO стеком LIFO? В этом случае мы получаем совершенно другой порядок обхода. Предполагая, что преемники помещаются в стек в в обратном порядке в алфавитном порядке, последовательные состояния стека выглядят так:

А
Б Д Э
С Г Д
Д Э
Е

Со стеком поиск будет продолжаться от заданного узла настолько далеко, насколько это возможно. перед возвратом и рассмотрением других узлов в стеке. Например, узлу E пришлось ждать, пока не будут рассмотрены все узлы, достижимые из B и D. это поиск в глубину .

Более стандартный способ записи поиска в глубину — это рекурсивная функция, используя программный стек как стек выше. Мы начинаем с каждого узла белого цвета кроме начального узла и применить функцию DFS к стартовый узел:

DFS (вершина v) {
    отмечать v как посещенное
    установить цвет v на серый
    для каждого преемника v' из v {
если v' еще не посещен {
ДФС(v')
}
    }
    установить цвет v на черный
}

Вы можете думать об этом как о человеке, идущем по графику по стрелкам. и никогда не посещать узел дважды, кроме как при возврате, когда тупик достиг. Выполнение этого кода на графике выше дает следующий график раскраски в последовательности, которые напоминают, но немного отличаются от того, что мы видели с версией на основе стека:

Обратите внимание, что в любой момент времени существует единственный путь серых узлов. ведущий от начального узла и ведущий к текущему узлу против . Этот путь соответствует стеку в предыдущем реализации, хотя узлы в конечном итоге посещаются в другом порядке, потому что рекурсивный алгоритм помечает только одного преемника серым на время.

Последовательность вызовов DFS образует дерево. Это называется звонок дерево программы, а на самом деле любая программа имеет дерево вызовов. В этом случае дерево вызовов является подграфом исходного графа:

Алгоритм поддерживает состояние, которое пропорциональна размеру этого пути от корня. Это отличает DFS. из BFS, где количество состояний (размер очереди) соответствует размер периметра узлов на расстоянии к от начала узел. В обоих алгоритмах количество состояний может быть O(|V|). Для ДФС это происходит при поиске в связанном списке. Для BFS это происходит, когда поиск графа с большим количеством ветвлений, такого как бинарное дерево, потому что есть 2 k узлы на расстоянии k от корень. В сбалансированном двоичном дереве DFS поддерживает состояние, пропорциональное высота дерева или O(log |V|). Часто графики, которые мы хотим поиск больше похож на деревья, чем на связанные списки, поэтому DFS имеет тенденцию работать Быстрее.

Может быть не более |V| вызовы DFS_visit. И тело цикла на преемниках может быть выполнено не более чем |E| раз. Таким образом, асимптотическая характеристика DFS — это O(|V| + |E|), как и при поиске в ширину.

Если мы хотим выполнить поиск по всему графу, то одиночный рекурсивный обход может оказаться неэффективным. достаточно. Если бы мы начали обход с узла С, то пропустили бы все остальные узлы графа. Чтобы выполнить поиск в глубину всего график, мы вызываем DFS на произвольном непосещенном узле и повторяем до тех пор, пока каждый узел не был посещен. Например, рассмотрим исходный граф, расширенный двумя новыми узлы F и G:

DFS, начинающаяся с A, не будет искать все узлы. Предположим, мы затем выбираем F для начать с. Тогда мы достигнем всех узлов. Вместо того, чтобы построить только один дерева, являющегося подграфом исходного графа, мы получаем лес из двух деревьев:

Топологическая сортировка

Один из наиболее полезных алгоритмов работы с графами — топологическая сортировка. в котором узлы ациклического графа расположены в порядке, соответствующем края графа. Это удобно, когда вам нужно заказать набор элементы, где некоторые элементы не имеют ограничений по порядку относительно других элементы.

Например, предположим, что у вас есть набор задач для выполнения, но некоторые задачи должны быть выполнены до начала других задач. В каком порядке следует выполнять задания? Эту задачу можно решить, представив задачи как узел в графе, где есть ребро из задачи 1 в задачу 2, если задача 1 должна быть выполнена до задачи 2. Тогда топологическая разновидность график даст порядок, в котором задача 1 предшествует задаче 2. Очевидно, чтобы топологически отсортировать граф, он не может иметь циклов. Например, если вы готовили лазанью, вам может понадобиться выполнить задачи, описанные следующий график:

Есть некоторая гибкость в том, в каком порядке делать вещи, но ясно, что мы нужно сделать соус, прежде чем мы соберем лазанью. Топологическая сортировка будет найти некоторый порядок, который подчиняется этому и другим ограничениям порядка. Из конечно, невозможно топологически отсортировать граф с циклом в нем.

Ключевым наблюдением является то, что узел завершается (отмечается черным цветом) в конце концов. его потомки были отмечены черным цветом. Таким образом, узел, отмеченный черный позже должен появиться раньше при топологической сортировке. А обратный порядок обход генерирует узлы в обратном порядке топологический вид:

Алгоритм:

Выполните поиск в глубину по всему графу, начиная заново с непосещенный узел, если предыдущие начальные узлы не посещали каждый узел. Когда каждый узел будет готов (окрашен черным), наденьте его на голову изначально пустой список. Это явно требует времени, линейного по размеру график: O(|V| + |E|).

Например, в приведенном выше примере обхода узлы отмечены черным цветом. порядке C, E, D, B, A. Обратный порядок, мы получаем порядок A, B, D, E, C. Это топологический вид графа. Аналогично, в примере с лазаньей, предполагая, что что мы выбираем преемников сверху вниз, узлы отмечены черным цветом в порядке запекания, собрать лазанью, сделать соус, пожарить колбасу, отварить макароны, натереть сыр. Итак обратный порядок дает нам рецепт успешного приготовления лазаньи, даже несмотря на то, что успешные повара, скорее всего, будут делать что-то параллельно!

Обнаружение циклов

Поскольку узел заканчивается после своих потомков, цикл включает серый узел. указывая на одного из своих серых предков, который еще не закончился. Если один из преемники узла выделены серым цветом, должен быть цикл. Чтобы обнаружить циклы в графиках, поэтому выбираем произвольный белый узел и запускаем DFS. Если это завершится и остаются еще белые узлы, мы выбираем другой белый узел произвольно и повторить. В конце концов все узлы окрашены в черный цвет. Если в любое время мы последуем ребро к серому узлу, в графе есть цикл. Таким образом, циклы могут быть обнаружены в O(|V+E|) времени.

Классификация кромок

Мы можем классифицировать различные ребра графа на основе цвета узла. достигается, когда алгоритм следует за ребром. Вот расширенный (A – G) график с окрашенными краями, чтобы показать их классификацию.

Отметим, что классификация ребер зависит от того, какие деревья построены, и, следовательно, зависит от того, какой узел мы начинаем с и в каком порядке алгоритм выбирает преемников посещать.

Когда конечный узел отслеживаемого ребра белый, алгоритм выполняет рекурсивный вызов. Эти ребра называются края деревьев , показаны сплошным черным цветом стрелки.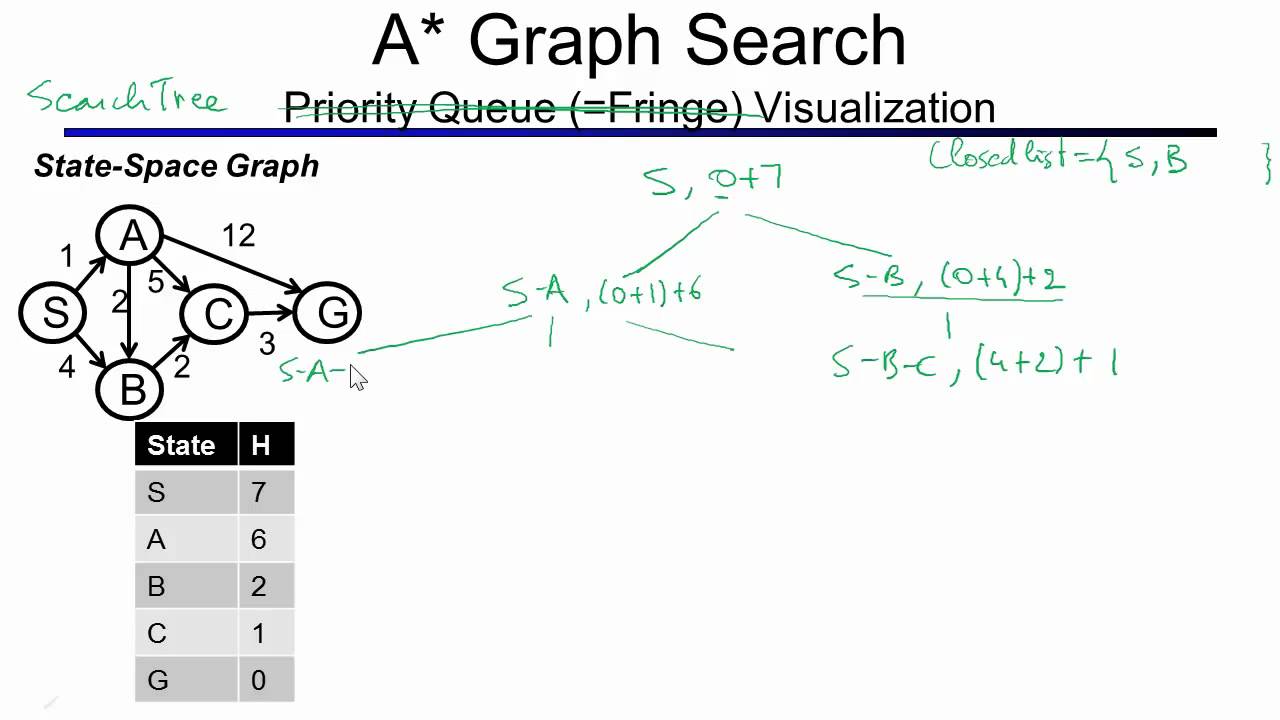 На этом рисунке граф выглядит по-другому, потому что узлы были перемещен, чтобы все края дерева шли вниз. Мы уже видели это дерево ребра показывают точную последовательность рекурсивных вызовов, выполненных во время обход.

Если место назначения следующего ребра выделено серым цветом, это назад. край , показан красным. Потому что есть только один серый путь узлы, задняя грань зацикливается на более раннем сером узле, создавая цикл. Граф имеет цикл тогда и только тогда, когда он содержит обратное ребро, когда пройдено из некоторого узла.

Если место назначения следующего ребра окрашено в черный цвет, это передний край или поперечный край . Это поперечное ребро, если он проходит между одним деревом и другим в лесу; в противном случае это передний край.

Обнаружение циклов

Часто бывает полезно знать, есть ли в графе циклы. Обнаруживать есть ли в графе циклы, мы выполняем поиск в глубину весь граф. Если при любом обходе найдено обратное ребро, граф содержит цикл.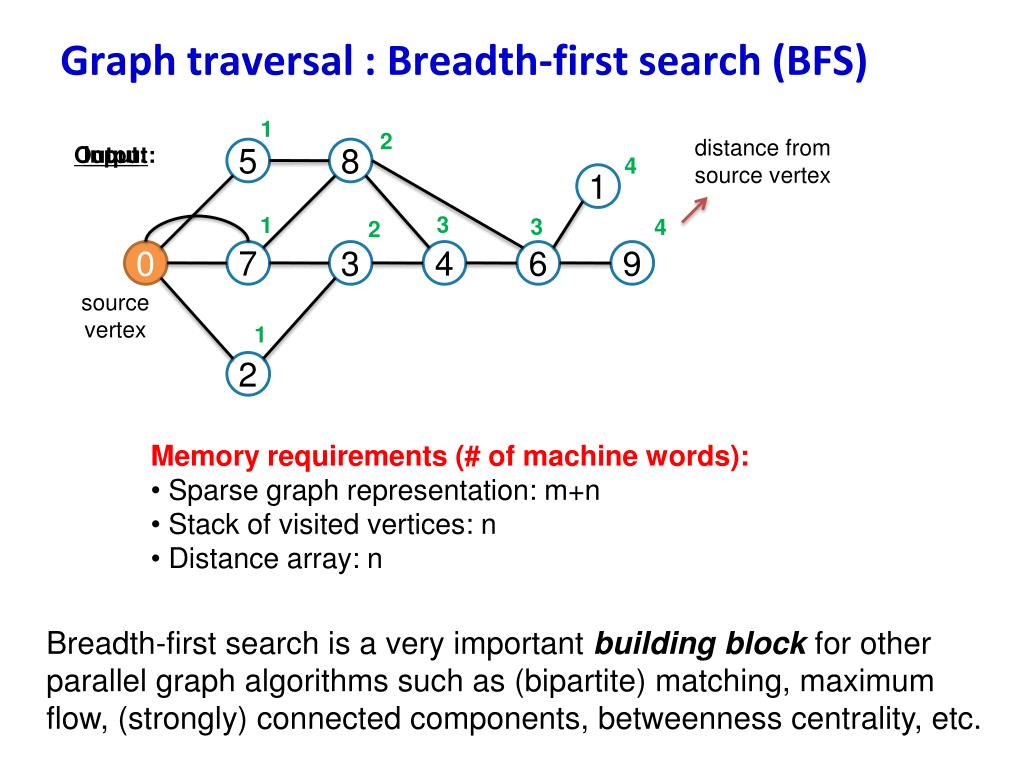 Если все узлы были посещены и ни один задний край не найдено, граф ацикличен.

Подключенные компоненты

Графики не нужно подключать, хотя мы рисовали связанных графов до сих пор. Граф связен, если существует путь между каждыми двумя узлами. Однако вполне возможно иметь график в котором нет пути от одного узла к другому узлу, даже следующие края назад. Для связности нам все равно в каком направлении идут ребра, так что мы могли бы также рассмотреть неориентированный граф. Подключенный компонент является подмножество S такое, что для любых двух соседних вершин v и v’, либо v и v’ оба принадлежат S, либо ни один из них.

Например, следующий неориентированный граф имеет три подключенные компоненты:

Проблема связанных компонентов состоит в том, чтобы определить, сколько компоненты составляют граф, и чтобы можно было найти для каждого узел в графе, к какому компоненту он принадлежит. Это может быть полезным способом решать задачи. Например, предположим что разные компоненты соответствуют разным задачам, которые необходимо сделано, и есть край между двумя компонентами, если они должны быть сделано в тот же день. Затем, чтобы узнать, каково максимальное количество дней, которые можно использовать для выполнения всех работ, нам нужно подсчитать компоненты.

Алгоритм:

Выполните поиск в глубину по графу. С началом каждого обхода создать новый компонент. Все вершины, достигнутые при обходе, принадлежат к этому компоненту. Количество обходов, выполненных во время поиска в глубину. поиск — это количество компонентов. Обратите внимание, что если граф направленный, то DFS должен следовать как по внутреннему, так и по внешнему краю.

Для ориентированных графов обычно более полезно определить строго подключенные компоненты . Сильно связный компонент (SCC) это максимальное подмножество вершин такое, что каждая вершина в множестве достижим из любого другого. Все циклы в графе являются частью одна и та же компонента сильной связности, а это означает, что каждый граф может быть рассматривается как DAG, состоящий из SCC. Благодаря Косараджу существует простой и эффективный алгоритм, который использует поиск в глубину дважды:

  1. Топологически отсортируйте узлы с помощью DFS. SCC будут появляться последовательно.
  2. Теперь пройдемся по транспонированному графу , но выберем новые (белые) корни в топологический порядок. Каждый новый подобход достигает отдельного SCC.

Например, рассмотрим следующий граф, который явно не является DAG:

Выполнение обхода в глубину, в котором нам случается выбирать потомков слева направо, и извлекая узлы в обратном порядке, мы получаем порядок 1, 4, 5, 6, 2, 3, 7. Обратите внимание, что SCC встречаются последовательно в этом порядке. Работа второй части Алгоритм заключается в определении границ.

На втором этапе мы начинаем с 1 и обнаруживаем, что у него нет предшественников, поэтому {1} ​​является первым ССС. Затем мы начинаем с 4 и обнаруживаем, что 5 и 6 достижимы через обратные ребра, поэтому второй SCC равен {4,5,6}. Начиная с 2, мы обнаруживаем {2,3}, а конечный SCC равен {7}. Результирующий DAG для SCC выглядит следующим образом:

Обратите внимание, что SCC также топологически сортируются этим алгоритмом.

Одним из неудобств этого алгоритма является то, что он требует способности ходить края назад. Алгоритм Тарьяна для определения сильно связанных компонентов лишь немного сложнее, но выполняет только один поиск в глубину. обход графа и только в прямом направлении.

См. Кормен, Лейзерсон и Ривест для получения более подробной информации.

Дополнительная литература

  • Каррано. Структуры данных и абстракции с помощью Java , Глава 31.
  • Кормен, Лейзерсон и Ривест. Введение в алгоритмы , Глава 23.

Заметки Эндрю Майерса, 19.04.12.

База данных графов

для начинающих: основы алгоритмов поиска графов

Когда Мухаммад ибн Муса аль-Хоразмий не был занят расстановкой книг, сбором просроченных штрафов и шиканьем детей (мы можем только предполагать) в библиотеке Дома Мудрости, он занимался еще несколькими побочными проектами: изобретением алгебры, популяризацией индо-арабская система счисления на Западе, помогая исламской астрономии повернуть новый угол и посрамив Птолемея обновленным списком координат примерно 2402 мест на земле.

Вероятно, он и представить себе не мог, что мы будем писать о нем в блоге 1200 лет спустя, но есть одна вещь, с пониманием которой у него не возникло бы особых проблем в том, что движет сегодняшним миром: алгоритмы. Это потому, что он , алгоритмы парня были названы в честь .

Работа Аль-Хорезми предшествовала миру графиков (изобретенному товарищем-супер-ботаником Эйлером) на 900 с лишним лет, так что, может быть, немногое из этого было бы для него новым, но он понял бы суть — просто как ты.

Это потому, что вам не нужно быть супер-ботаником, чтобы понять основы графовых алгоритмов, особенно когда они используются для поиска.

В этой серии блогов Базы данных графов для начинающих я познакомлю вас с основами технологии графов, предполагая, что у вас мало (или нет) знаний в этой области. За последние недели мы рассмотрели, почему технология графов — это будущее, почему взаимосвязанные данные важны, основы (и подводные камни) моделирования данных, почему важен язык запросов к базе данных, различия между императивными и декларативными языками запросов и прогнозным моделированием с использованием графа. теория.

На этой неделе мы обсудим различные алгоритмы поиска по графу и то, как они используются, в том числе алгоритм Дейкстры и алгоритм A*. Наше обсуждение будет сосредоточено на том, что алгоритмы поиска по графу делают для вас (и вашего бизнеса), не погружаясь слишком глубоко в математику теории графов.

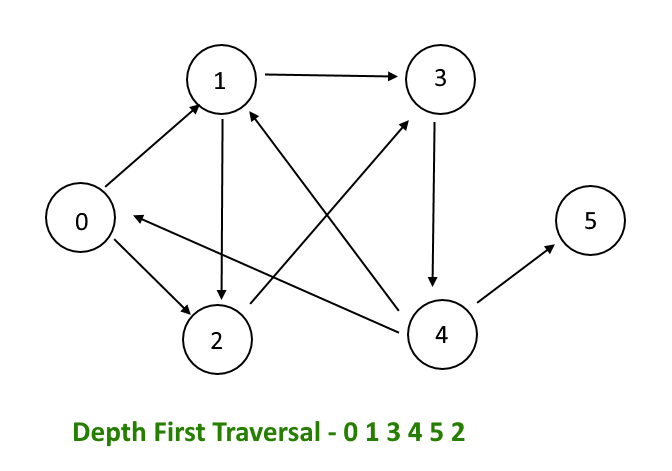
Алгоритмы поиска в глубину и ширину

Существует два основных типа алгоритмов поиска по графу: поиск в глубину и поиск в ширину.

Алгоритм первого типа перемещается от начального узла к некоторому конечному узлу, прежде чем повторять поиск по другому пути от того же начального узла, пока не будет получен ответ на запрос. Как правило, поиск в глубину является хорошим выбором при поиске отдельных фрагментов информации. Они также являются хорошим стратегическим выбором для общего обхода графа.

Самый классический или базовый уровень поиска в глубину — это неинформированный поиск, когда алгоритм ищет путь до тех пор, пока не достигнет конца графа, затем возвращается к начальному узлу и пробует другой путь.

Напротив, работа с семантически богатыми базами данных графов позволяет выполнять информированных поиска, которые выполняют досрочное прекращение поиска, если найдены узлы без совместимых исходящих отношений. В результате информированный поиск также имеет меньшее время выполнения.

(Для справки, запросы Cypher и обход графа Java обычно выполняют информированный поиск.)

Алгоритмы поиска в ширину выполняют поиск, исследуя граф по одному слою за раз. Они начинаются с узлов на один уровень в глубину от начального узла, за которыми следуют узлы на глубине два, затем на глубине три и так далее, пока не будет пройден весь граф. Вот так:

Как вы видите выше, поиск в ширину начинается с заданного узла (обозначен 0 ), а затем переходит к каждому узлу, который находится всего в одном переходе (обозначен 9).0089 1 ) до он перемещается к каждому узлу, который находится на расстоянии двух переходов ( 2 ). Затем, только после прохождения всех 2 узлов, он исследует еще один переход к узлам, отмеченным 3 .

Алгоритм Дейкстры

Подобно своим предшественникам-суперботаникам — аль-Хорезми и Эйлеру — Эдсгер Вайб Дейкстра отлично разбирался в алгоритмах и суперграфах. Вероятно, поэтому он изобрел алгоритм Дейкстры за двадцать минут . Как я уже сказал, супер-ботаник.

Цель алгоритма Дейкстры — провести поиск в ширину с более высоким уровнем анализа, чтобы найти кратчайший путь между двумя узлами в графе. Вот как это работает:

  1. Выберите начальный и конечный узлы и добавьте начальный узел к набору решаемых узлов со значением 0. Решаемые узлы — это набор узлов с кратчайшим известным путем от начального узла. Начальный узел имеет значение 0, потому что он находится на расстоянии 0 длины пути от самого себя.
  2. Пройдите в ширину от начального узла к его ближайшим соседям и запишите длину пути для каждого соседнего узла.
  3. Выберите кратчайший путь к одному из этих соседей и пометьте этот узел как решенный. В случае ничьей алгоритм Дейкстры выбирает случайным образом (предположительно, Ини, Мини, Мини, Моэ).
  4. Посетите ближайших соседей к набору решенных узлов и запишите длины пути от начального узла к этим новым соседям. Не посещайте никакие соседние узлы, которые уже были решены, так как мы уже знаем кратчайшие пути к ним.
  5. Повторяйте шаги 3 и 4, пока узел назначения не будет помечен как решенный.

Алгоритм Дейкстры эффективен, потому что он работает только с меньшим подмножеством возможных путей через граф (т. е. ему не нужно считывать через 90 293 все 90 294 ваших данных). После решения каждого узла известен кратчайший путь от начального узла, и все последующие пути строятся на этом знании.

Алгоритм Дейкстры часто используется для поиска кратчайших путей в реальном мире, например, для навигации и логистики. Давайте посмотрим на пример.

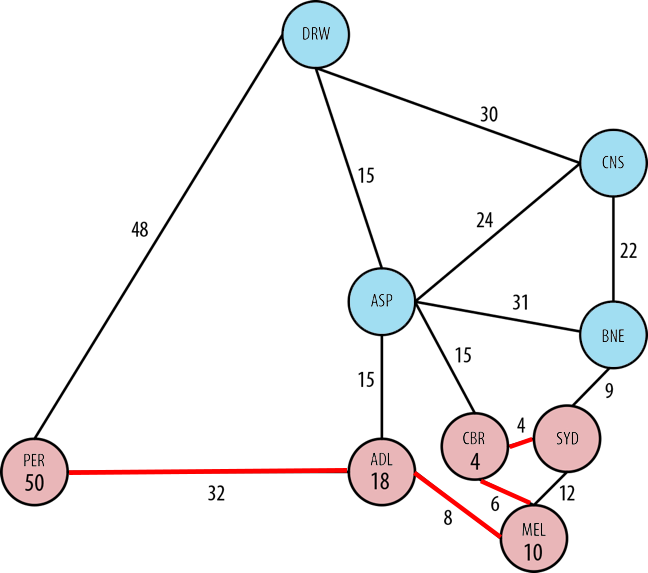
После всей их тяжелой работы аль-Хорезми и Эйлер собираются немного побаловать себя пунктом из своего списка желаний: старомодным путешествием по Австралии из Сиднея в Перт. Но, будучи супер-ботаниками-математиками, они хотят выбрать кратчайший путь и собираются использовать алгоритм Дейкстры, чтобы найти его.

Сидней является начальным узлом и немедленно решается со значением 0, так как наш знаменитый дуэт уже там.

Двигаясь в ширину, они смотрят на следующие города в одном прыжке от Сиднея: Брисбен, Канберра и Мельбурн.

Канберра — кратчайший путь в 4 часа, поэтому они считают это решенным. Они продолжают смотреть на остальную часть графа из своих решенных узлов (из Сиднея и из Канберры), рассматривая другие узлы и выбирая кратчайший путь. Оттуда Брисбен в 9 часов — следующий решенный узел.

Они идут дальше, выбирая между Мельбурном, Кэрнсом и Алис-Спрингс. Мельбурн — это кратчайший (общий) путь в 10 часов из Сиднея через Канберру, поэтому он становится их следующим решенным узлом.

Их следующие варианты соседних узлов (из уже решенных) — Аделаида, Кэрнс и Алис-Спрингс. В 18 часов из Сиднея через Канберру и Мельбурн Аделаида является следующим кратчайшим путем.

Следующие варианты — Перт (конечный пункт назначения), Алис-Спрингс и Кэрнс. Хотя на самом деле мы знаем, что в следующий раз они должны направиться прямо в Перт, аль-Хорезми и Эйлер все еще не знакомы со всей этой концепцией «Австралия вообще существует». Итак, они решают строго следовать алгоритму Дейкстры, несмотря ни на что (в конце концов, это то, что сделал бы компьютер).

В соответствии с алгоритмом Дейкстры Алис-Спрингс выбирается, потому что он имеет кратчайший путь (всего 19 часов против 50 часов).

Обратите внимание, что поскольку это поиск в ширину, алгоритм Дейкстры должен сначала искать все еще возможные пути, а не только первое решение, которое встречается. Именно по этому принципу Перт не сразу исключается как кратчайший путь.

Из Алис-Спрингс есть два варианта: Дарвин и Кэрнс. Последний составляет 31 час по сравнению с 34 часами первого, поэтому Кэрнс является следующим решенным узлом.

Единственный нерешенный узел, оставшийся от Кэрнса, — это Дарвин.

Из Дарвина они делают последний отрезок пути и прибывают в Перт, затратив 82 часа на этот исследованный путь.

Теперь, когда аль-Хорезми и Эйлер использовали алгоритм Дейкстры для решения всех возможных путей, они могут правильно сравнить два маршрута в Перт:

    • через Аделаиду ​​за 50 часов или
    • через Darwin за 82 часа

Соответственно, алгоритм Дейкстры выберет маршрут через Аделаиду ​​и будет считать Перт из Сиднея решенным при кратчайшем пути в 50 часов. Да начнется путешествие веков.

В итоге мы видим, что алгоритм использует ненаправленное исследование для получения результатов. Иногда это заставляет нас исследовать граф больше, чем интуитивно необходимо, поскольку алгоритм Дейкстры рассматривает каждый узел относительно изолированно и может в конечном итоге следовать путям, которые не вносят вклад в общий кратчайший путь.

Приведенный выше пример можно было бы улучшить, если бы при поиске использовалась какая-либо эвристика, как при поиске по первому наилучшему. Чтобы применить это в примере с дорожной поездкой, они могли бы выбрать направление на запад, а не на восток, и на юг, а не на север, что помогло бы избежать ненужных (мысленных) боковых поездок.

Алгоритм А*

Алгоритм A* улучшает алгоритм Дейкстры, комбинируя некоторые его элементы с элементами поиска наилучшего первого.

Произносится как «A-star», A* основан на наблюдении, что некоторые поисковые запросы являются информативными, что помогает нам лучше выбирать, какие пути пройти по графу. Подобно алгоритму Дейкстры, A* может выполнять поиск в большой области графа, но, как и поиск по первому наилучшему, A* использует эвристику для управления своим поиском.

Кроме того, в то время как алгоритм Дейкстры предпочитает искать узлы, близкие к текущей начальной точке, поиск по первому наилучшему отдает предпочтение узлам, расположенным ближе к месту назначения. A* уравновешивает два подхода, чтобы гарантировать, что на каждом уровне он выбирает узел с наименьшей общей стоимостью обхода.

Как показано в примере из предыдущего раздела, алгоритм Дейкстры может пропустить лучший маршрут при попытке завершить поиск.

Для получения дополнительной информации о том, как алгоритм A* используется на практике, обратитесь к главе 7 базы данных графов от O’Reilly Media.

Заключение

Алгоритмы поиска по графу помогают вам (или вашему дружелюбному компьютерному помощнику) перемещаться по набору данных графа наиболее эффективным способом. Но «наиболее эффективный» зависит от результатов, которые вы ищете — поиск в ширину не самый эффективный, если ваши результаты лучше подходят для запросов в глубину (и наоборот).

Здесь вам пригодятся ваши друзья-ботаники (или даже полезная электронная книга, если у вас нет друзей). Если они умны, они сопоставят правильный алгоритм графа с типом результатов, которые вы ищете.

Но теперь, когда они начинают говорить о широте, глубине и лучшем, вы можете сказать им, что знаете свою пятерку по Дейкстре, и это не ваше первое родео.

No related posts.