Логические и побитовые операции в Java
- Главная >
- Каталог >
- Java Стартовый >
- Логические операции в Java
Для прохождения теста нужно авторизироваться
Войти Регистрация
×
Вы открыли доступ к тесту! Пройти тест
Для просмотра полной версии видеокурса, онлайн тестирования и получения доступа к дополнительным учебным материалам купите курс Купить курс
Для просмотра всех видеокурсов ITVDN, представленных в Каталоге, а также для получения доступа к учебным материалам и онлайн тестированию купите подписку Купить подписку
№1
Введение в инфраструктуру Java
0:41:14
Материалы урокаДомашние заданияТестирование
Назначением данного урока является ознакомление с природой платформы Java, возможностями виртуальной машины Java (JVM), а также средствами разработки, которые применяются при построении Java-приложений на примере JetBrains IntelliJ IDEA. Выполняется обзор языков программирования и технологий, отличных от Java. На занятии рассматриваются простейшие примеры консольного приложения
Выполняется обзор языков программирования и технологий, отличных от Java. На занятии рассматриваются простейшие примеры консольного приложения
Читать дальше…
Машинная математика. Переменные и типы данных
1:04:19
Материалы урокаДомашние заданияТестированиеВ данном уроке рассматриваются основные системы счисления. Урок помогает научиться понимать двоичную и шестнадцатеричную системы счисления. Разъясняется понятие переменных и типов данных. Объясняются принципы выбора типа используемого при создании переменной.
Читать дальше…
Переменные и типы данных в Java
1:23:42
Материалы урокаДомашние заданияТестирование
В данном видео уроке Вы узнаете о назначение констант, основных арифметических операциях и операциях сравнения значений переменных. Демонстрируются примеры простого форматирования и вывода строк на экран.
Демонстрируются примеры простого форматирования и вывода строк на экран.
Читать дальше…
Условные конструкции Логические операции
0:48:34
Материалы урокаДомашние заданияТестированиеНа уроке рассматривается работа операторов ветвления их назначение, использование основных условных конструкции: if-else, тернарного оператора и switch-case.
Читать дальше…
Логические операции в Java
1:09:25
Данный урок посвящен рассмотрению таких понятий, как логические и побитовые операции. На занятии объясняется применение и использование операций конъюнкции, дизъюнкции, исключающего «или», логических операторов, операторов сдвига. Рассматриваются короткозамкнутые вычисления и теорема Де Моргана.
На занятии объясняется применение и использование операций конъюнкции, дизъюнкции, исключающего «или», логических операторов, операторов сдвига. Рассматриваются короткозамкнутые вычисления и теорема Де Моргана.
Читать дальше…
Циклические конструкции в Java
На уроке рассматривается работа циклических операторов (while, do-while, for) и применение операторов break и continue. Объясняется работа циклов Дейкстры и использование цикла «Паук».
Читать дальше…
Методы в Java
1:04:32
Материалы урокаДомашние заданияТестирование
Данный видео урок посвящен методам.
Читать дальше…
Методы и рекурсия в Java
0:55:10
Материалы урокаДомашние заданияТестированиеВ данном видеоуроке поговорим о том, где Вам может пригодиться рекурсия, а также рассмотрим перегрузку методов.
Читать дальше…
Массивы в Java
1:33:30
Материалы урокаДомашние заданияТестирование
На уроке рассматриваются примеры создания и использования массивов (одномерные, двумерные, трехмерные, зубчатые).
Читать дальше…
Следующий курс:
Видео курс Java Базовый для начинающих — онлайн обучение ITVDN
ПОКАЗАТЬ ВСЕ
основные темы, рассматриваемые на уроке
0:01:02
Логические и побитовые операции
0:02:00
Конъюнкция
0:04:40
Побитовое И
0:10:10
Дизъюнкция
0:11:40
Побитовое ИЛИ
0:14:15
Исключающее ИЛИ
0:15:32
Побитовое «Исключающее ИЛИ»
0:17:45
Отрицание
0:18:59
Побитовое отрицание
0:20:14
Изменение знака
0:21:54
Побитовые логические операции
0:27:50
Робота с портами(конъюнкция и дизъюнкция)
0:32:14
Исключающее ИЛИ (пример использования)
0:36:30
Логические операции
0:46:03
Операции сдвига
1:02:15
Короткозамкнутые вычисления
1:06:09
Теоремы Де Моргана
ПОКАЗАТЬ ВСЕ
ПОДРОБНЕЕ ПОДРОБНЕЕ ПОДРОБНЕЕ ПОДРОБНЕЕ ПОДРОБНЕЕ ПОДРОБНЕЕРегистрация через
✖или E-mail
Нажав на кнопку «Зарегистрироваться»,
Вы соглашаетесь с условиями использования.
Уже есть аккаунт
Получите курс бесплатно
✖
Вы выбрали курс для изучения
«»
Чтобы получить доступ к курсу, зарегистрируйтесь на сайте.
РЕГИСТРАЦИЯ
Спасибо за регистрацию
✖
Перейдите на почту и подтвердите Ваш аккаунт,
чтобы получить доступ ко всем
бесплатным урокам и вебинарам на сайте ITVDN.com
ПОДТВЕРДИТЬ ПОЧТУ НАЧАТЬ ОБУЧЕНИЕ
Спасибо за регистрацию
✖
Ваш аккаунт успешно подтвержден.
Начать обучение вы можете через Личный кабинет
пользователя или непосредственно на странице курса.
НАЧАТЬ ОБУЧЕНИЕ
Подтверждение аккаунта
На Ваш номер телефона было отправлено смс с кодом активации аккаунта. Пожалуйста, введите код в поле ввода.
Пожалуйста, введите код в поле ввода.
Отправить код еще раз
Изменить номер телефона
Ошибка
✖Обучение и трудоустройство Java-программистов от Junior до Senior
Битовые операции в Java.
Автор: Андрей Самойлов- Главная
- Статьи
Java позволяет манипулировать числами на битовом уровне, что означает работу с битами, из которых состоит число, а именно с его представлением в двоичной системе счисления. Что же такое система счисления вообще и двоичная система в частности?
Система счисления — символический метод
записи чисел, представление чисел с помощью письменных знаков. Количество цифр, используемых
в системе счисления, называется её «основанием».
Позиционные системы счисления — это системы счисления, в которых значение цифры напрямую зависит от её положения в числе.
Двоичная система счисления — позиционная система счисления с основанием 2. В двоичной системе счисления числа записываются с помощью двух символов (0 и 1).
Двоичная арифметика.
Таблица сложения
| + | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 10(перенос в старший разряд) |
Таблица вычитания
| — | 0 | 1 |
|---|---|---|
| 0 | 0 | д |
| 1 | (заём из старшего разряда) 1 |
0 |
Пример сложения «столбиком» (1410 + 510 = 1910 или 11102 + 1012 = 100112):
| + | 1 | 1 | 1 | 0 | |
|---|---|---|---|---|---|
| 1 | 0 | 1 | |||
| 1 | 0 | 0 | 1 | 1 | |
Таблица умножения
| × | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
Пример умножения «столбиком» (1410 * 510 = 7010 или 11102 * 1012 = 10001102):
| × | 1 | 1 | 1 | 0 | |||
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | |||||
| + | 1 | 1 | 1 | 0 | |||
| 1 | 1 | 1 | 0 | ||||
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | |
Эти операции работают с целочисленными типами данных
| Тип | Размер (бит) | Диапазон |
|---|---|---|
| byte | 8 бит | от -128 до 127 |
| short | 16 бит | от -32768 до 32767 |
| char | 16 бит | от 0 до 65535 |
| int | 32 бит | от -2147483648 до 2147483647 |
| long | 64 бит | от -9223372036854775808 до +9223372036854775807 |
Таблица истинности побитовых операций выглядит следующим образом
| A | B | A & B | A | B | A ^ B |
|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
Первые четыре оператора представляют собой применение битовых масок к аргументу в соответствие
с логическими функциями. Например, оператор & применяется для поиска элемента в HashMap по формуле
h & (length -1), где h — хэшкод элемента, а length — длина массива
Например, оператор & применяется для поиска элемента в HashMap по формуле
h & (length -1), где h — хэшкод элемента, а length — длина массива
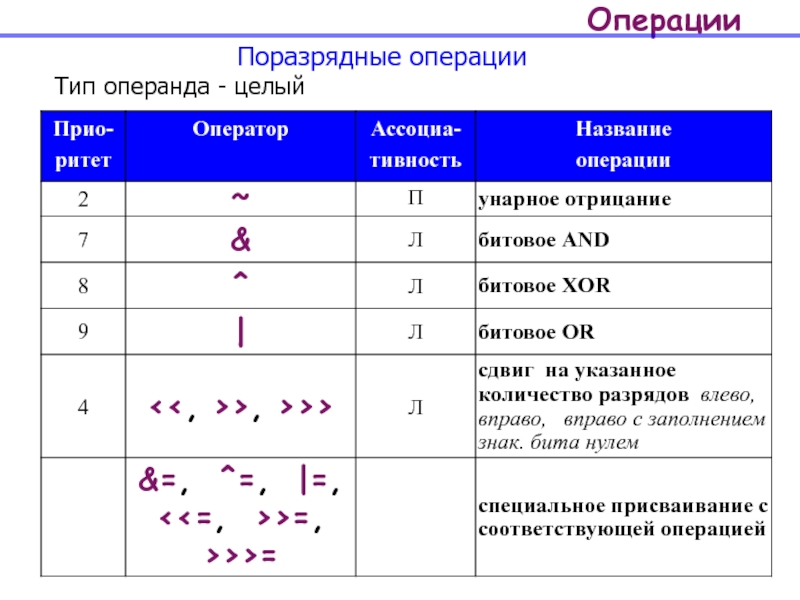
Наибольший интерес представляют операторы сдвига. Первым операндом оператора сдвига является число, которое нужно обработать, а вторым — количество бит, на которое следует выполнить сдвиг. Результатом операции сдвига является двоичное представление числа, сдвинутое в заданном направлении. Знаковые сдвиги также называют арифметическими, а беззнаковые — логическими.
Представление отрицательных чисел в Java.
Для хранения отрицательных чисел используется дополнительный код или второе дополнение (two’s complement). Положительное число преобразуется в отрицательное число путём инвертирования его бит с добавлением единицы.
Пример: Преобразование 32-битного числа 5 = 101:
Исходное число: 0000 0000 0000 0000 0000 0000 0000 0101
Инвертируем: 1111 1111 1111 1111 1111 1111 1111 1010
Прибавляем 1: 0000 0000 0000 0000 0000 0000 0000 0001
Результат: 1111 1111 1111 1111 1111 1111 1111 1011
Знаковый сдвиг влево (
Сдвигает двоичное представление первого операнда влево на количество бит,
заданное во втором операнде, знак числа сохраняется. Младшие(крайние правые) биты при этом заполняются нулями.
Соответствует умножению на 2.
Младшие(крайние правые) биты при этом заполняются нулями.
Соответствует умножению на 2.
Примеры:
27 (11011)
-5 (11111111111111111111111111111011)
Если число выходит за границы диапазона типа int, крайний бит теряется:
2 147 483 647 (1111111111111111111111111111111)
Почему не существует беззнакового(логического) сдвига влево? Потому что такой сдвиг не оказывает влияния на старший значащий бит(MSB) — крайний левый бит числа, изменяются только крайние правые биты. Кроме того, в процессорах семейства 8086 арифметический и логический сдвиг выполняют одну и ту же операцию.
Знаковый сдвиг вправо (>>)
Сдвигает двоичное представление первого операнда вправо на количество бит,
заданное во втором операнде, знак числа сохраняется. Старшие(крайние левые биты) заполняются нулями. Соответствует делению на 2:
Соответствует делению на 2:
24 (11000) >> 1 = 12 (1100)
-4 (11111111111111111111111111111100) >> 1 = -2 (11111111111111111111111111111110)
Беззнаковый сдвиг вправо(>>>)
Сдвигает двоичное представление первого операнда вправо на количество бит, заданное во втором операнде, знак числа не сохраняется. Для положительных чисел работает как деление:
24 (11000) >>> 1 = 12 (1100)
-24 (1111 1111 1111 1111 1111 1111 1110 1000) >>> 1 = 2147483636 (0111 1111 1111 1111 1111 1111 1111 0100)
Можно увидеть, что знаковый бит был заменён нулём
Особенности работы операторов сдвига
Операторы сдвига всегда возвращают тип int, даже если аргумент типа, например, byte. поэтому следующий код вернёт ошибку:
byte n = 27;
n = n
java: possible loss of precision
required: byte
ound: int
Устранить ошибку можно путём приведения к типу byte:
n = (byte) (n
Нельзя сдвинуть на количество бит, большее, чем разрядность операнда. При этом происходит неявное сокращение правого (кол-во бит) операнда.
При этом происходит неявное сокращение правого (кол-во бит) операнда.
Пример:
Если сдвинуть данное число на 32 бита, по идее, результат должен состоять из одних нулей, но на самом деле это не так:
-1 (11111111111111111111111111111111) >> 32 = -1 (11111111111111111111111111111111)
-1(11111111111111111111111111111111) >>> 32 = -1 (11111111111111111111111111111111)
Примеры применения битовых операций
- Ускорение операций умножения и деления чисел на два. Примеры можно увидеть в стандартной библиотеке jdk.
- Битовые поля(флаги). Пример пусть есть права на доступ — чтение, запись, выполнение. Их удобнее хранить не в трёх разных переменных, а в одной, устанавливая соответствующие биты.
- Алгоритмы шифрования и сжатия (например, Шифр Вернама построен на XOR).
- Работа с графикой.
- Работа с сетью.
 y; //XOR x and y
while (z != 0) {
//увеличим счётчик, если последняя двоичная цифра = 1
bitCount += z & 1;
z = z >> 1; //сдвигаем z на единицу вправо
}
return bitCount;
}
y; //XOR x and y
while (z != 0) {
//увеличим счётчик, если последняя двоичная цифра = 1
bitCount += z & 1;
z = z >> 1; //сдвигаем z на единицу вправо
}
return bitCount;
}Побитовые операторы в Java — Темы масштабирования
Обзор
Побитовые операторы являются одними из тех операторов, которые выполняют свои задачи на двоичном уровне непосредственно с двоичными цифрами (также известными как биты), наименьшей формой данных в компьютере или его данными. типы. Эти побитовые операторы являются более быстрым и эффективным способом взаимодействия с компьютерами для выполнения тяжелых вычислений за линейное время, поскольку они работают непосредственно с битами, а не через уровень абстракции программного обеспечения.
Эти побитовые операторы изменяют данные с постоянной временной сложностью и функционируют параллельно, делая их эффективными во всех системах, поэтому этот процесс изменения данных с помощью побитовых операторов называется Bit Manipulation .
 Почти все языки программирования должны будут работать с абстракциями данных (например, с объектами или переменными), а не с битами, которые они представляют. Однако для оптимизации производительности кода и уменьшения количества ошибок во многих сценариях требуется прямое манипулирование битами.
Почти все языки программирования должны будут работать с абстракциями данных (например, с объектами или переменными), а не с битами, которые они представляют. Однако для оптимизации производительности кода и уменьшения количества ошибок во многих сценариях требуется прямое манипулирование битами.Вот несколько примеров задач, требующих манипулирования битами или знания побитовых операторов:
- Низкоуровневое управление устройством
- Алгоритмы обнаружения и исправления ошибок
- Сжатие данных
- Алгоритмы шифрования
- Оптимизация
Область применения
Цель статьи:
- Подробно объяснить работу побитовых операторов.
- Обсудите операции И, ИЛИ, XOR, Дополнение, Сдвиг влево, Сдвиг вправо и Беззнаковый сдвиг вправо с примерами.
- Укажите случаи использования побитовых операторов в реальных жизненных ситуациях.
- Обсудите важные варианты использования побитовых операторов, таких как:
- Определить, является ли число четным или нечетным
- Преобразование строки из верхнего регистра в нижний и наоборот
- Определить количество установленных битов в числе
- Определить, установлен ли i-й бит числа
Введение в побитовые операторы в Java
На приведенном ниже рисунке показано количество шагов, необходимых для выполнения арифметических операций над десятичными и двоичными данными.

Вы можете видеть, на сколько шагов уменьшается нормальное представление при манипуляциях с битами.
Битовые манипуляции выполняются с помощью побитовых операторов для каждого бита числа отдельно и могут использоваться с любыми типами данных, такими как int, float, short, char и т. д.
Побитовые операторы работают с двоичным эквивалентом десятичные числа , т. е. операция выполняется над десятичными числами, и внутри эти операторы работают с отдельными битами бит за битом в соответствии с данными операциями:
- Сначала операнды преобразуются в двоичное представление
- Далее оператор применяется к каждому двоичному числу и вычисляется результат
- Наконец, результат преобразуется обратно в десятичное представление
Стандартные арифметические операторы выполняют операции над удобочитаемыми значениями (3+4), в то время как побитовые операторы непосредственно управляют низкоуровневыми данными.
Типы побитовых операторов Java в Java
9num2
Побитовое включение ИЛИ \ Побитовое дополнение ~ ~ num Побитовый сдвиг влево << num1 << num2 Побитовый сдвиг вправо >> num1 >> num2 Беззнаковый оператор сдвига вправо >>> num1>>>num2 Давайте пройдемся по всем этим операторам один за другим.

1. Побитовое И(&)
И (&) — это бинарный оператор, который сравнивает два двоичных операнда равной битовой длины (т. е. оба числа в их двоичной форме будут иметь одинаковую длину). Операнды преобразуются из десятичной формы в двоичную. Для каждого бита операция проверяет, равны ли оба бита 1 в обоих операндах. Если true, бит будет установлен в 1 в ответе. В противном случае результирующий бит устанавливается в 0. Вы можете понять эту операцию по арифметическое умножение . Поскольку умножение чего-либо на 0 заканчивается 0, сравнение И с любым 0 битом заканчивается 0.
Его таблица истинности:
Пример:
8), затем
Числа преобразуются в их двоичный эквивалент
а = 6 = 0110 (в двоичном формате) b = 8 = 1000 (в двоичном формате)
Затем над их бинарным представлением выполняется операция И.
0110 & 1000 ________ 0000 = 0 (в десятичном формате)
Полученное двоичное число преобразуется в десятичное и выводится пользователю как результат.

2. Побитовое ИЛИ(|)
Оператор ИЛИ (|) — это бинарный оператор, который принимает два операнда одинаковой длины, но сравнивает их следующим образом:
- Если любой соответствующий бит равен 1, ответ равен 1
- В противном случае ответ будет 0.
Другими словами, побитовое ИЛИ двух битов возвращает «1», если хотя бы один из битов равен 1. Вы можете понять из арифметическое сложение операция, добавление чего-либо с 0 приводит к тому же результату.
- Если два входных бита равны 0, выходной бит равен 0.
- Во всех остальных случаях это 1.
Его таблица истинности:
Пример:
Мы хотим выполнить операцию побитового ИЛИ 6 и 8 (6 | 8), затем
Числа преобразуются в их двоичный эквивалент
а = 6 = 0110 (в двоичном формате) b = 8 = 1000 (в двоичном формате)
Затем над их бинарным представлением выполняется операция ИЛИ.

0110 | 1000 ________ 1110 = 14 (в десятичной системе)
Полученное двоичное число преобразуется в десятичное и выводится пользователю как результат.
3. Сдвиг битов (>>,
<<, >>>)Сдвиг битов — это побитовая операция, при которой порядок ряда битов перемещается для эффективного выполнения математической операции. Битовый сдвиг сдвигает каждую цифру в двоичном представлении числа влево или вправо на столько пробелов, сколько указано вторым операндом. Эти операторы можно применять к целочисленным типам, таким как int, long, short, byte или char.
Существует три вида смены:
а. Сдвиг влево : << является оператором сдвига влево и отвечает потребностям как логических, так и арифметических сдвигов.
Пример:
б. Арифметический/знаковый сдвиг вправо : >> — это арифметический (или знаковый) оператор сдвига вправо.

Пример:
c. Логический/беззнаковый сдвиг вправо : >>> является логическим (или беззнаковым) оператором сдвига вправо. Он выполняет ту же операцию, что и оператор сдвига вправо, но его знак в операции не сохраняется.
Пример:
В Java все целочисленные типы данных имеют знак, а << и >> являются исключительно арифметическими сдвигами.
4. Побитовое дополнение (~)
Оператор побитового НЕ или дополнения просто означает отрицание каждого бита входного значения. Требуется только одно целое число. Все выборки 0 становятся 1, и все выборки 1 становятся 0. Другими словами, НЕ инвертируйте каждый входной бит. Этот перевернутый цикл называется дополнением битового ряда до 1.
Это делает число отрицательным, поскольку любая битовая последовательность, начинающаяся с 1, является отрицательной, так как здесь N = ~N всегда дает результат -(N+1). Поскольку система хранит данные в форме дополнения 2, это означает, что она хранит ~ N вот так.

Пример:
Мы хотим выполнить побитовое дополнение 6 (~6), затем
Представление числа в двоичном формате а = 6 => 0110 (в двоичном формате)
Теперь нам нужно найти ~6 (означает дополнение 1 к 6) 0000 0110 => 1111 1001 (поменять каждую единицу на 0 и наоборот) Итак, ~6 = 1111 1001, Здесь MSB (старший значащий бит) равен 1 (означает отрицательное значение). Тогда в памяти это будет представляться как комплимент 2 (Чтобы найти комплимент 2, сначала нужно найти комплимент 1, а затем добавить к нему 1.)
Нахождение комплимента 2 ~6, т.е. 1111 1001
- Преобразование обратно в десятичный формат. 0000 0111 => 7
На шаге 2: мы видели, что число отрицательное, поэтому окончательный ответ будет -7
Итак, ~6 === -7 (результат побитового дополнения)НЕ полезно для обращения чисел без знака к зеркальному значению на противоположной стороне от их средней точки.
 91000
________
1110 = 14 (в десятичной системе)
91000
________
1110 = 14 (в десятичной системе) Полученное двоичное число преобразуется в десятичное и выводится пользователю как результат.
- Исключающее ИЛИ используется для инвертирования выбранных отдельных битов в регистре или замены битовых комбинаций, которые показывают логические состояния.
- Широко используется в криптографии, а также для получения битов четности для проверки ошибок и отказоустойчивости.
- Первые побитовых операторов в Java работают с двоичными представлениями целых значений (long, int, short, char и byte) и возвращают целое число, тогда как логических операторов работают с логическими выражениями и возвращают логические значения (либо истинные или ложно).
- Кроме того, логические операторы всегда оценивают первое логическое выражение и, в зависимости от его результата и используемого оператора, могут оценивать или не оценивать второе.
 С другой стороны, побитовые операторы всегда оценивают оба операнда.
С другой стороны, побитовые операторы всегда оценивают оба операнда. - Наконец, логические операторы используются для получения решения на основе различных условий, тогда как побитовые операторы работают с битами и используют битовые манипуляции для получения результата.
- Побитовый оператор И представлен как &, а логический оператор И представлен как &&. Точно так же оператор побитового ИЛИ представлен как | а логический оператор ИЛИ представлен как ||.
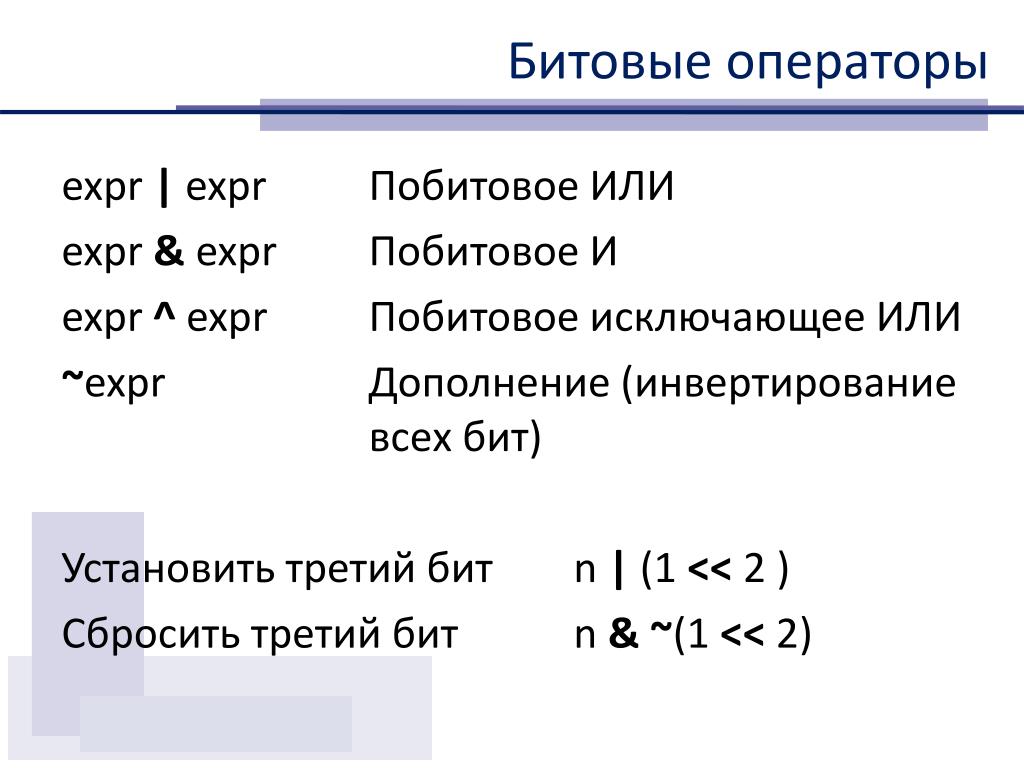
- У вас будут ситуации, когда вы захотите установить/очистить/переключить только один определенный бит регистра, не работая со всем регистром. Используя побитовые операторы, вы можете читать и выполнять операции ИЛИ/И/ИСКЛЮЧАЮЩЕЕ ИЛИ с подходящей маской, чтобы изменить только желаемую битовую позицию.
- Обычно побитовые операции быстрее, чем умножение/деление . Поэтому, если вы хотите умножить переменную x, скажем, на 9, вы сделаете (x<<3 + x), что может быть на несколько циклов быстрее, чем x*9 .

- Точно так же, если вы хотите использовать массив в качестве циклической очереди, было бы быстрее (и элегантнее) обрабатывать циклические проверки с побитовыми операциями. (размер вашего массива должен быть равен степени 2). Пример:
- Также, если вы хотите, чтобы флаг ошибки в программе содержал несколько кодов ошибок вместе для нескольких сценариев, каждый бит может содержать отдельное значение. Вы можете И с каждым отдельным кодом ошибки в качестве проверки. Одним из таких вариантов использования являются коды ошибок Unix.
- Также n-битная растровая карта может быть компактной структурой данных. Если вы хотите выделить пул ресурсов размером n, мы можем использовать n-биты для представления текущего состояния.
- В сжатии и шифровании, где оба они сильно зависят от побитовых алгоритмов. Посмотрите на пример алгоритма deflate — все в битах, а не в байтах. Например: кодирование Хаффмана (для сжатия) и стандарт шифрования данных (для шифрования) .
- Если результат побитовой операции ИЛИ с n при n|1 увеличивает значение n на 1, то оно четное, иначе нечетное.
- Возьмем число, num = 34 (представленное в битах , 100010).
 1 = 1010, что равно 10 в десятичном виде. Поскольку значение числа уменьшилось, num является нечетным.
1 = 1010, что равно 10 в десятичном виде. Поскольку значение числа уменьшилось, num является нечетным. - Наконец пусть num = 13 (представляет в битах 1101). Сейчас, 1101 | 1 = 1101, что равно 13 в десятичном виде. Поскольку значение числа не меняется, следовательно, число нечетное.
- ASCII-код буквы A равен 65 (в битах, 1000001), а 32 в битах равен 100000. 90 014
- Теперь ‘A’ & 32 = 65 & 32 = (1000001) | (100000) = 1100001 (97) и код ASCII для a также равен 97.
- Таким образом, после приведения числа 97 к char получается «a».
 Аналогично для других символов верхнего регистра эта операция дает соответствующий символ нижнего регистра.
Аналогично для других символов верхнего регистра эта операция дает соответствующий символ нижнего регистра. - Это работает благодаря следующим свойствам операции XOR:
Разница между логическими и побитовыми операторами
Между побитовыми и логическими операторами есть несколько различий.
Варианты использования и преимущества побитовых операторов в Java

Хитрости в побитовых операторах в Java
Всегда используйте побитовые операторы вместо арифметических операторов везде, где мы можем их использовать, потому что операции с побитовыми операторами в java намного быстрее, чем арифметические операторы. Это связано с тем, что операторы Bitwise работают непосредственно с битами, в то время как другие сначала преобразуют переменные или константы в биты, затем выполняют над ними операции, а затем снова преобразуют их обратно в десятичные значения, и поэтому это требует времени.
Давайте рассмотрим несколько примеров побитовых операций в Java: 91 увеличивает n на 1, если оно четное, иначе нечетное. Код: Вывод для приведенного выше кода: Объяснение: Временная сложность для всех трех побитовых операций равна O(1) . Как и в предыдущем примере, в этом также мы будем использовать побитовые операторы для преобразования в верхний или нижний регистр Теперь посмотрите на этот код: Вывод: Объяснение: 2. Измените символ на верхний или нижний регистр
Некоторые практические задачи по битовым операторам 9100001 = 1001111.
Теперь вы можете видеть, что оба числа меняются местами , то есть a становится 1001111 (79), а b становится 100001 (33).
2. Количество установленных битов в целом числе
В этой задаче мы будем использовать операторы И (&) и сдвиг вправо (>>), чтобы узнать количество установленных битов в числе. Всякий раз, когда мы вычисляем двоичное представление целочисленного значения, оно формируется как комбинация 0 и 1. Итак, цифра 1 известна как установленный бит, и в этом примере подсчитывается количество единиц в двоичном представлении десятичного числа.
Теперь рассмотрим следующий код:
Вывод:
Объяснение:
- В этой задаче мы просто повторяем число, пока оно не станет равным 0,90.
 014
014 - Внутри цикла проверяется, равен ли самый правый бит 1 или нет (используя операцию И), а затем удаляется самый правый бит с помощью оператора сдвига вправо.
- Мы удаляем крайний правый бит, чтобы иметь доступ к каждому биту заданного числа один за другим.
Давайте разберемся с этим шаг за шагом
Рассмотрим a = 79 (1001111).
Шаг 1: Проверьте, равен ли крайний правый бит 1 или нет, так как 1001111 и 1 равно 1, затем увеличьте счетчик setBits на 1 Шаг 3: . Продолжайте выполнять шаги 1 и 2, пока a не станет равным 0.
3. Убедитесь, что i
th бит числа равен 1 или 0В этой задаче мы узнаем, что i-й бит (начиная с 0-го бита с конца) любого числа равен 0 или 1, используя побитовые операторы AND(&) и сдвиг влево(<<).
Теперь рассмотрим следующий код:
Вывод:
Объяснение:
- Используемый выше метод называется битовой маскировкой.
 В этом подходе мы сначала создаем маску (на основе заданной задачи) и выполняем побитовую операцию маски с заданным числом.
В этом подходе мы сначала создаем маску (на основе заданной задачи) и выполняем побитовую операцию маски с заданным числом. - В этой задаче маска будет 1 << i, что в основном создает установленный бит в i-м индексе, сохраняя бит 0 во всех остальных индексах.
- После выполнения операции И, если результат равен 0, то i-й бит с конца равен 0, иначе 1.
Заключение
- Существуют различные побитовые операторы, такие как:
- И(&)
- ИЛИ(|)
- Дополнение (~)
- Битовый сдвиг (>>,<<,>>>) и 9)
- Побитовые операторы быстрее, чем стандартные арифметические операторы, работающие с десятичными числами. Это связано с тем, что он напрямую работает с битами, и в его случае не выполняются никакие вычисления преобразования.
- Логические и побитовые операции — это два разных типа операций. Первый работает с логическими типами данных, тогда как второй работает с битами.
- И побитовый оператор возвращает 1 тогда и только тогда, когда установлены оба бита.

- ИЛИ побитовый оператор возвращает 1, если хотя бы один из битов операнда установлен.
- Побитовый оператор XOR возвращает 1, если биты операнда противоположны по значению.
- Мы можем создавать маски для нацеливания на определенный бит в бинарной операции.
- Чтобы определить, является число нечетным или четным, мы можем использовать побитовые операторы, такие как AND , OR или XOR .
- Операторы в Java
Обработка битов в Java — операции побитового сдвига и битового сдвига
Java позволяет вам манипулировать целыми числами на уровне битов, что означает работу с определенными битами, которые представляют целое число. В некоторых случаях это может быть очень удобно.
Побитовые операторы
Вы, несомненно, знакомы с арифметическими операторами, такими как + — * / или %. Вы также наверняка знаете такие логические операторы, как & или |. Оказывается, есть еще один, немного менее известный набор операторов, которые манипулируют числами на уровне битов. Внутри каждое число хранится в двоичном формате — то есть 0 и 1.
Оказывается, есть еще один, немного менее известный набор операторов, которые манипулируют числами на уровне битов. Внутри каждое число хранится в двоичном формате — то есть 0 и 1.
Эти операторы могут выполняться над целочисленными типами и их вариантами, то есть
- байт (8 бит)
- короткий (16 бит)
- целое число (32 бита)
- длинный (64 бит)
- и даже символ (16 бит)
Унарный оператор побитового дополнения [~]
Это причудливое название в основном означает битовое отрицание. Он берет каждый бит числа и переворачивает его значение. То есть — 0 становится 1 и наоборот. Унарный означает, что ему нужен только один операнд. Оператор – это ~, и он ставится перед числом: 9.0005
~someVariable
или
Например, давайте использовать ~42:
- Двоичное представление числа 42 равно 101010.
- Поскольку 42 — это целое число, оно представляется как 32-битное значение, то есть 32 единицы или нули.

- Таким образом, все позиции слева от 101010 на самом деле заполнены нулями до 32 бит.
- То есть 00000000 00000000 00000000 00101010
- Перевернутое значение числа, указанного выше, тогда будет 11111111 11111111 11111111 11010101
Побитовое И [&]
В отличие от оператора побитового дополнения, другим побитовым операторам требуется два операнда.
A & B означает, что все биты обоих чисел сравниваются один за другим, и результирующее число вычисляется на основе значений битов из чисел A и B. Побитовое И похоже на логическое И в том смысле, что оно приводит к 1 только тогда, когда два сравниваемых бита равны 1. В противном случае это дает 0.
Например: 1010 и 1100 дадут 1000, поскольку первый бит слева является единственным, где оба операнда содержат 1. 9Б
Операторы битового сдвига
Сдвиг влево со знаком [
<<] Сдвиг влево со знаком принимает два операнда. Он берет битовую комбинацию первого операнда и сдвигает ее влево на количество разрядов, заданное вторым операндом. Например 5 << 3: Что происходит в этом случае - каждый бит в двоичном представлении целого числа 5 сдвигается на 3 позиции влево. Все места слева заполнены нулями. То есть: 9 н .
Он берет битовую комбинацию первого операнда и сдвигает ее влево на количество разрядов, заданное вторым операндом. Например 5 << 3: Что происходит в этом случае - каждый бит в двоичном представлении целого числа 5 сдвигается на 3 позиции влево. Все места слева заполнены нулями. То есть: 9 н .
Есть несколько дополнительных интересных аспектов:
- Несмотря на то, что вы можете использовать сдвиг byte, short или char, они преобразуются в 32-битное целое перед сдвигом
- Операторы битового сдвига никогда не выдают исключение
- Правый операнд (количество позиций для сдвига) уменьшается по модулю 32. То есть 5 <<35 эквивалентно 5 << 3.
Отрицательные целые числа в Java
На самом деле существует два типа сдвига вправо. Подписанные и неподписанные. Разница в том, как они обрабатывают отрицательные числа. Чтобы понять разницу, необходимо знать, как отрицательные числа представлены в Java. Двоичное представление само по себе не дает информации о том, является ли число отрицательным. Должно быть специальное правило, чтобы определить, как представлять отрицательные числа в двоичном формате. Существует несколько подходов к этой проблеме.
Должно быть специальное правило, чтобы определить, как представлять отрицательные числа в двоичном формате. Существует несколько подходов к этой проблеме.
Одно из решений состоит в том, что самый левый (самый значащий) бит является битом знака. Это означает, что его значение указывает, является ли число положительным или отрицательным. Однако у этого есть некоторые недостатки, такие как наличие двух способов представления нуля.
Java использует другой подход, который называется дополнением до двух . Отрицательные числа представляются путем инвертирования (переворачивания) всех битов с последующим добавлением 1. Тем не менее, если крайний левый бит равен 0, число положительное. В противном случае оно отрицательное. 9 n -1 в случае нечетных чисел.
Сдвиг вправо без знака [>>>]
В отличие от сдвига со знаком, беззнаковый сдвиг не учитывает знаковые биты, он просто сдвигает все биты вправо и дополняет результат нулями слева. Это означает, что для отрицательных чисел результат всегда положительный. Знаковые и беззнаковые сдвиги вправо имеют одинаковый результат для положительных чисел.
Знаковые и беззнаковые сдвиги вправо имеют одинаковый результат для положительных чисел.
Составные операторы присваивания
Java предлагает более короткий синтаксис для присваивания результатов арифметических или побитовых операций. Поэтому вместо того, чтобы писать это:
х = х + 1;
Вы можете использовать более короткую версию, которая будет обрабатывать как сложение, так и присваивание с помощью всего одного оператора:
x += 1;
Вы, вероятно, знакомы с составными операторами присваивания для арифметических операций, таких как += , -= или *= . Но в дополнение к этому Java также предлагает варианты побитовых операторов:
| Оператор | Пример | Эквивалентно | 95
|---|---|---|
| &= | х &= 5 | х = х и 5 |
| <<= | х <<= 5 | х = х << 5 |
| >>= | х >>= 5 | х = х >> 5 |
| >>>= | х >>>= 5 | х = х >>> 5 |
Обратите внимание, что для унарного оператора побитового дополнения [~] не существует составного оператора присваивания.

 y; //XOR x and y
while (z != 0) {
//увеличим счётчик, если последняя двоичная цифра = 1
bitCount += z & 1;
z = z >> 1; //сдвигаем z на единицу вправо
}
return bitCount;
}
y; //XOR x and y
while (z != 0) {
//увеличим счётчик, если последняя двоичная цифра = 1
bitCount += z & 1;
z = z >> 1; //сдвигаем z на единицу вправо
}
return bitCount;
} Почти все языки программирования должны будут работать с абстракциями данных (например, с объектами или переменными), а не с битами, которые они представляют. Однако для оптимизации производительности кода и уменьшения количества ошибок во многих сценариях требуется прямое манипулирование битами.
Почти все языки программирования должны будут работать с абстракциями данных (например, с объектами или переменными), а не с битами, которые они представляют. Однако для оптимизации производительности кода и уменьшения количества ошибок во многих сценариях требуется прямое манипулирование битами.



 91000
________
1110 = 14 (в десятичной системе)
91000
________
1110 = 14 (в десятичной системе)  С другой стороны, побитовые операторы всегда оценивают оба операнда.
С другой стороны, побитовые операторы всегда оценивают оба операнда.
 1 = 1010, что равно 10 в десятичном виде. Поскольку значение числа уменьшилось, num является нечетным.
1 = 1010, что равно 10 в десятичном виде. Поскольку значение числа уменьшилось, num является нечетным. Аналогично для других символов верхнего регистра эта операция дает соответствующий символ нижнего регистра.
Аналогично для других символов верхнего регистра эта операция дает соответствующий символ нижнего регистра. 014
014 В этом подходе мы сначала создаем маску (на основе заданной задачи) и выполняем побитовую операцию маски с заданным числом.
В этом подходе мы сначала создаем маску (на основе заданной задачи) и выполняем побитовую операцию маски с заданным числом.
