пишем свою «Матрицу» на Python
Изучать новое можно по-разному. Одним нравится сначала штудировать теорию, а потом применять её на практике. Другие предпочитают учиться исключительно на примерах, найденных на любимом Stackoverflow. А кто-то вообще загружает навыки управления вертолётом и технику боевых единоборств по выделенному каналу прямо в мозг.
В любом случае без практических упражнений не обойтись. После ускоренной загрузки знаний Нео всё равно должен пройти спарринг с Морфеусом, чтобы научиться применять терабайты загруженных навыков на практике. Только вот упражнения бывают разные. Одно дело — лихо взлететь под потолок и проломить балки восточного спортзала, и совсем другое — методично час за часом шлифовать своё мастерство.
Изображение: Wikimedia Commons
Определяем цели
Учебники программирования разнообразием примеров обычно не блещут. Встречаются, конечно, исключения, но в большинстве пособий упражнения похожи друг на друга и не особо интересны: создайте очередную адресную книгу, нарисуйте круг черепашкой, разработайте сайт магазина по продаже какой-нибудь «нужной» рекламной ерунды. Куда уж тут до достоверной имитации матрицы. Хотя…
Куда уж тут до достоверной имитации матрицы. Хотя…
Почему бы не взять всё это в свои руки и не начать придумывать упражнения самостоятельно? Да хоть бы и написать свою маленькую личную «Матрицу». Конечно, не ту, в которой будут небоскрёбы, стильные телефоны той эпохи и вездесущие непобедимые агенты Смиты. Для этого нам нужно ещё пару-тройку месяцев поучиться. Но любому начинающему программисту под силу написать модель культовой заставки со стекающими по экрану зелёными струйками цифр. Этим и займёмся.
Запрограммировать такую заставку можно практически на любом языке. Попробуем это сделать на «великом и могучем» Python.
Пишем техническое задание
Для начала определимся, что же мы хотим в итоге получить. Напишем сами себе небольшое техническое задание — всегда полезно. Подумайте про «Матрицу», и память сама подскажет образ — тёмное консольное окно, в котором будут стекать струйки зелёных цифр. Чтобы было интереснее, пусть они двигаются с разной скоростью. У каждой струйки должны быть начало — яркий зелёный ноль — и конец. Кстати, пусть скорости движения начала и конца струйки тоже будут разными и определяются случайным образом.
Кстати, пусть скорости движения начала и конца струйки тоже будут разными и определяются случайным образом.
Звучит не так и сложно. Теперь дело за малым — всего лишь написать код. Приступим.
Готовим инструменты
Как полагается, подключим все необходимые модули. Сначала стандартные:
import sys import random import time
Для работы с консолью Windows нам понадобятся модули bext и colorama. Как их установить с помощью pip, вы уже, наверняка, знаете. Нужно их подключить. Но сделаем это по всем правилам — с проверкой:
try:
import bext, colorama
except ImportError:
print ('Для запуска программы нужны модули bext и colorama.')
sys.exit ()Подготовим к работе консоль:
bext.title ('Matrix') # Меняем заголовок консольного окна
bext.clear () # Очищаем консольное окно
bext.hide () # Скрываем курсор в консольном окне
width, height = bext.size () # Получаем размер консольного окна
width -= 1
height -= 1Теперь осталось только завести константы с цветами для модуля colorama.
lgreen = colorama.Fore.LIGHTGREEN_EX green = colorama.Fore.GREEN
Windows — штука хитрая и противоречивая. Базовый цвет green в консоли — это тёмно-зелёный.
Изобретаем антиматерию
Теперь подумаем над самым главным вопросом: как же нам запрограммировать стекающие капли «Матрицы»? Каждая капля — это объект. Все капли разные, но ведут себя одинаково. Поэтому нам надо создать класс, в котором мы опишем основные действия с каплей и все её атрибуты.
Чтобы капли стекали с разной скоростью, зададим каждой из них случайный тайм-аут задержки — в шагах. Какие-то капли будут перемещаться на каждом шаге обновления нашей картинки, какие-то реже.
Как же быть с верхним концом струйки? Он должен «высыхать», причём со своей скоростью. Не будем придумывать ничего сложного. Пусть верхний конец тоже будет каплей, но чёрного цвета. Такая «капля» при перемещении будет не добавлять цифры, а наоборот стирать их. Получается прямо какая-то антикапля, антиматерия — красиво и стильно..files/image175.png)
Поскольку капля и антикапля ведут себя одинаково, запрограммируем их в одном классе.
Создаём капли
Итак, все действия с каплями и антикаплями мы будем выполнять в методах класса. Назовём его Drop и напишем метод создания объекта класса:
def __init__ (self):
self.x = random.randint (0, width) # Начальное положение по горизонтали
self.y = -1 # Начальное положение по вертикали - за верхней границей экрана
self.drop_type = random.randint (0, 1) # Тип: антикапля или капля
self.timeout = random.randint (0, 3) # Задержка до следующего перемещения
self.wait_count = random.randint (0, 3) # Счетчик паузыС атрибутами x и y всё понятно. Второй равен -1, чтобы капля раньше времени не показывалась на экране. Атрибуты timeout и wait_count нужны для обеспечения разной скорости падения капель. Первый задаёт постоянную скорость стекания, второй — итерационный счётчик.
Перемещаем капли
Теперь напишем метод перемещения капли с учётом её скорости.
def move (self):
if drop.wait_count < drop.timeout: # Пока рано перемещать
drop.wait_count += 1 # Увеличиваем счётчик паузы
return False
else: # Уже можно перемещать
drop.wait_count = 0 # Сбрасываем счётчик паузы
drop.y += 1 # Перемещаем каплю или антикаплю на шаг вниз
return TrueМетод возвращает логическое значение — факт перемещения капли. Или антикапли — всё равно.
Рисуем струйку
С перемещением разобрались. Настало время рисовать.
def draw (self):
if self.drop_type == 1:
symbol = str (random.randint (1, 9))
con_print (self.x, self.y, green, symbol)
self.zero_draw () # Рисуем яркий ноль
else:
con_print (self.x, self.y, green, ' ')Здесь мы вызываем два новых ещё не написанных метода: con_print и zero_draw. Первый будет выводить символ нужного цвета в указанное место консольного окна. Второй будет рисовать дополнительный яркий ноль в начале струйки.
Вот, собственно, и второй метод:
def zero_draw (self):
if (self.y < height):
con_print (self.x, self.y+1, lgreen, '0')Организуем перерождение капель
Мы уже поняли, что у нас получается не простая «Матрица», а философская. Посему, когда капли и антикапли будут достигать нижнего края экрана, заставим их переродиться. Они получат новую жизнь у верхней границы. Это будет стоить нам всего двух строк:
def renew (self):
self.__init__ ()Теперь у нас есть всё, что нужно. Класс Drop готов.
Выводим текст в консоль
Вырвемся за границы класса Drop и напишем две функции для вывода текста в консольное окно.
Если мы попытаемся напечатать что-то в нижнем правом углу консольного окна, то снизу автоматически добавится ещё одна строка. Ничего не поделаешь: в этом месте в нашей идеальной «Матрице» будет «битый пиксель»:
def is_rb_corner (x, y):
if x==width and y==height:
return True
else:
return FalseТеперь всё готово к тому, чтобы напечатать запрошенный символ в нужном месте.
def con_print (x, y, color, symbol):
if not is_rb_corner (x, y):
bext.goto (x, y)
sys.stdout.write (color)
print (symbol, end='')Собираем всё воедино
Все компоненты нашей будущей «Матрицы» готовы. Теперь осталось всё собрать вместе и запустить.
Создадим массив капель и антикапель (какого типа родится объект — дело случая).
drops = []
for i in range (1, width*2//3):
drop = Drop ()
drops.append (drop)И, наконец, самый главный цикл:
while True:
for drop in drops:
if drop.move (): # Проверяем перемещение элемента
drop.draw () # Отображаем элемент
if drop.y >= height: # Достигли дна
drop.renew () # Обновляем элемент
key = bext.getKey (blocking = False) # Проверяем, нажата ли клавиша
if key == 'esc': # Если нажата ESC, то выходим из программы
bext.clear ()
sys.
exit ()
time.sleep (0.02) # ЗадержкаВся программа целиком
import sys
import random
import time
# Подключаем дополнительные модули
try:
import bext, colorama
except ImportError:
print ('Для запуска программы нужны модули bext и colorama.')
sys.exit ()
class Drop:
def __init__ (self):
self.x = random.randint (0, width) # Начальное положение по горизонтали
self.y = -1 # Начальное положение по вертикали - за верхней границей экрана
self.drop_type = random.randint (0, 1) # Тип: антикапля или капля
self.timeout = random.randint (0, 3) # Задержка до следующего перемещения
self.wait_count = random.randint (0, 3) # Счетчик паузы
def renew (self):
self.__init__ ()
def move (self):
if drop.wait_count < drop.timeout: # Пока рано перемещать
drop.wait_count += 1 # Увеличиваем счётчик паузы
return False
else: # Уже можно перемещать
drop.

hide () # Скрываем курсор в консольном окне
width, height = bext.size () # Получаем размер консольного окна
width -= 1
height -= 1
green = colorama.Fore.GREEN
lgreen = colorama.Fore.LIGHTGREEN_EX
# Создаём массив капель и антикапель
drops = []
for i in range (1, width*2//3):
drop = Drop ()
drops.append (drop)
while True:
for drop in drops:
if drop.move (): # Проверяем перемещение элемента
drop.draw () # Отображаем элемент
if drop.y >= height: # Достигли дна
drop.renew () # Обновляем элемент
key = bext.getKey (blocking = False) # Проверяем, нажата ли клавиша
if key == 'esc': # Если нажата ESC, то выходим из программы
bext.clear ()
sys.exit ()
time.sleep (0.02) # ЗадержкаПредлагаю вам поэкспериментировать с этой программой. Попробуйте добавить к «Матрице» свои дополнительные необычные эффекты.
Линейная алгебра на Python. [Урок 1]. Задание Матрицы.
Эта статья открывает список уроков на тему “Линейная алгебра с примерами на Python“. Мы постараемся рассказать о базовых понятиях линейной алгебры, которые могут быть полезны тем, кто занимается машинным обучением и анализом данных, и будем сопровождать все это примерами на языке Python.
- Матрицы
- Виды матриц и способы их создания в Python
- Вектор-строка
- Вектор-столбец
- Квадратная матрица
- Диагональная матрица
- Единичная матрица
- Нулевая матрица
- Задание матрицы в общем виде
Матрицей в математике называют объект, записываемый в виде прямоугольной таблицы, элементами которой являются числа (могут быть как действительные, так и комплексные). Пример матрицы приведен ниже.
\(M\;=\;\begin{pmatrix}1&3&5\\7&2&4\end{pmatrix}\)
В общем виде матрица записывается так:
\(M=\begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\\a_{21}&a_{22}&…&a_{2n}\\…&…&…&…\\a_{m1}&a_{m2}&…&a_{mn}\end{pmatrix}\)
Представленная выше матрица состоит из i-строк и j-столбцов. Каждый ее элемент имеет соответствующее позиционное обозначение, определяемое номером строки и столбца на пересечении которых он расположен: \(a_{ij}\)- находится на i-ой строке и j-м столбце.
Важным элементом матрицы является главная диагональ, ее составляют элементы, у которых совпадают номера строк и столбцов.
Виды матриц и способы их создания в PythonМатрица в Python – это двумерный массив, поэтому задание матриц того или иного вида предполагает создание соответствующего массива. Для работы с массивами в Python используется тип данных список (англ. list). Но с точки зрения представления матриц и проведения вычислений с ними списки – не очень удобный инструмент, для этих целей хорошо подходит библиотека Numpy, ее мы и будем использовать в дальнейшей работе.
list). Но с точки зрения представления матриц и проведения вычислений с ними списки – не очень удобный инструмент, для этих целей хорошо подходит библиотека Numpy, ее мы и будем использовать в дальнейшей работе.
Напомним, для того, чтобы использовать библиотеку Numpy ее нужно предварительно установить, после этого можно импортировать в свой проект. По установке Numpy можно подробно прочитать в разделе “Установка библиотеки Numpy” из введения. Для того чтобы импортировать данный модуль, добавьте в самое начало программы следующую строку
import numpy as np
Если после импорта не было сообщений об ошибке, то значит все прошло удачно и можно начинать работу. Numpy содержит большое количество функций для работы с матрицами, которые мы будем активно использовать. Обязательно убедитесь в том, что библиотека установлена и импортируется в проект без ошибок.
Рассмотрим, различные варианты матриц и способы их задания в Python.
Вектором называется матрица, у которой есть только один столбец или одна строка. Более подробно свойства векторов, их геометрическая интерпретация и операции над ними будут рассмотрены в “Главе 2 Векторная алгебра”.
Вектор-строкаВектор-строка имеет следующую математическую запись.
\(v=(1\;2)\)
Такой вектор в Python можно задать следующим образом.
>>> v_hor_np = np.array([1, 2]) >>> print(v_hor_np ) [1 2]
Если необходимо создать нулевой или единичный вектор, то есть вектор, у которого все элементы нули либо единицы, то можно использовать специальные функции из библиотеки Numpy.
Создадим нулевую вектор-строку размера 5.
>>> v_hor_zeros_v1 = np.zeros((5,)) >>> print(v_hor_zeros_v1 ) [0. 0. 0. 0. 0.]
В случае, если требуется построить вектор-строку так, чтобы она сама являлась элементом какого-то массива, это нужно для возможности транспонирования матрицы (см. раздел “1.3 Транспонирование матрицы”), то данную задачу можно решить так.
раздел “1.3 Транспонирование матрицы”), то данную задачу можно решить так.
>>> v_hor_zeros_v2 = np.zeros((1, 5)) >>> print(v_hor_zeros_v2 ) [[0. 0. 0. 0. 0.]]
Построим единичную вектор-строку в обоих из представленных для нулевого вектора-строки форм.
>>> v_hor_one_v1 = np.ones((5,)) >>> print(v_hor_one_v1) [1. 1. 1. 1. 1.]
>>> v_hor_one_v2 = np.ones((1, 5)) >>> print(v_hor_one_v2) [[1. 1. 1. 1. 1.]]Вектор-столбец
Вектор-столбец имеет следующую математическую запись.
\(v=\begin{pmatrix}1\\2\end{pmatrix}\)
В общем виде вектор столбец можно задать следующим образом.
>>> v_vert_np = np.array([[1], [2]]) >>> print(v_vert_np) [[1] [2]]
Рассмотрим способы создания нулевых и единичных векторов-столбцов. Построим нулевой вектор-столбец.
Построим нулевой вектор-столбец.
>>> v_vert_zeros = np.zeros((5, 1)) >>> print(v_vert_zeros) [[0.] [0.] [0.] [0.] [0.]]
Единичный вектор-столбец можно создать с помощью функции ones().
>>> v_vert_ones = np.ones((5, 1)) >>> print(v_vert_ones) [[1.] [1.] [1.] [1.] [1.]]Квадратная матрица
Довольно часто, на практике, приходится работать с квадратными матрицами. Квадратной называется матрица, у которой количество столбцов и строк совпадает. В общем виде они выглядят так.
\(Msqr=\begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\\a_{21}&a_{22}&…&a_{2n}\\…&…&…&…\\a_{n1}&a_{n2}&…&a_{nn}\end{pmatrix}\)
Создадим следующую матрицу.
\(Msqr=\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}\)
В Numpy можно создать квадратную матрицу с помощью метода array().
>>> m_sqr_arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> print(m_sqr_arr) [[1 2 3] [4 5 6] [7 8 9]]
Как вы уже наверное заметили, аргументом функции np.array() является список Python, его можно создать отдельно и передать в функцию.
>>> m_sqr = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] >>> m_sqr_arr = np.array(m_sqr) >>> print(m_sqr_arr) [[1 2 3] [4 5 6] [7 8 9]]
Но в Numpy есть еще одни способ создания матриц – это построение объекта типа matrix с помощью одноименного метода. Задать матрицу можно в виде списка.
>>> m_sqr_mx = np.matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> print(m_sqr_mx) [[1 2 3] [4 5 6] [7 8 9]]
Также доступен стиль Matlab, когда между элементами ставятся пробелы, а строки разделяются точкой с запятой, при этом такое описание должно быть передано в виде строки.
>>> m_sqr_mx = np.matrix('1 2 3; 4 5 6; 7 8 9')
>>> print(m_sqr_mx)
[[1 2 3]
[4 5 6]
[7 8 9]]Диагональная матрицаОсобым видом квадратной матрицы является диагональная – это такая матрица, у которой все элементы, кроме тех, что расположены на главной диагонали, равны нулю.
\(Mdiag=\begin{pmatrix}a_{11}&0&…&0\\0&a_{22}&…&0\\…&…&…&…\\0&0&…&a_{nn}\end{pmatrix}\)
Диагональную матрицу можно построить вручную, задав только значения элементам на главной диагонали.
>>> m_diag = [[1, 0, 0], [0, 5, 0], [0, 0, 9]] >>> m_diag_np = np.matrix(m_diag) >>> print(m_diag_np) [[1 0 0] [0 5 0] [0 0 9]]
Библиотека Numpy предоставляет инструменты, которые могут упростить построение такой матрицы.
Первый вариант подойдет в том случае, если у вас уже есть матрица, и вы хотите сделать из нее диагональную. Создадим матрицу размера 3 3.
Создадим матрицу размера 3 3.
>>> m_sqr_mx = np.matrix('1 2 3; 4 5 6; 7 8 9')Извлечем ее главную диагональ.
>>> diag = np.diag(m_sqr_mx) >>> print(diag) [1 5 9]
Построим диагональную матрицу на базе полученной диагонали.
>>> m_diag_np = np.diag(np.diag(m_sqr_mx)) >>> print(m_diag_np) [[1 0 0] [0 5 0] [0 0 9]]
Второй вариант подразумевает построение единичной матрицы, ей будет посвящен следующий параграф.
Единичная матрицаЕдиничной матрицей называют такую квадратную матрицу, у которой элементы главной диагонали равны единицы, а все остальные нулю.
\(E=\begin{pmatrix}1&0&…&0\\0&1&…&0\\…&…&…&…\\0&0&…&1\end{pmatrix}\)
Создадим единичную матрицу на базе списка, который передадим в качестве аргумента функции matrix().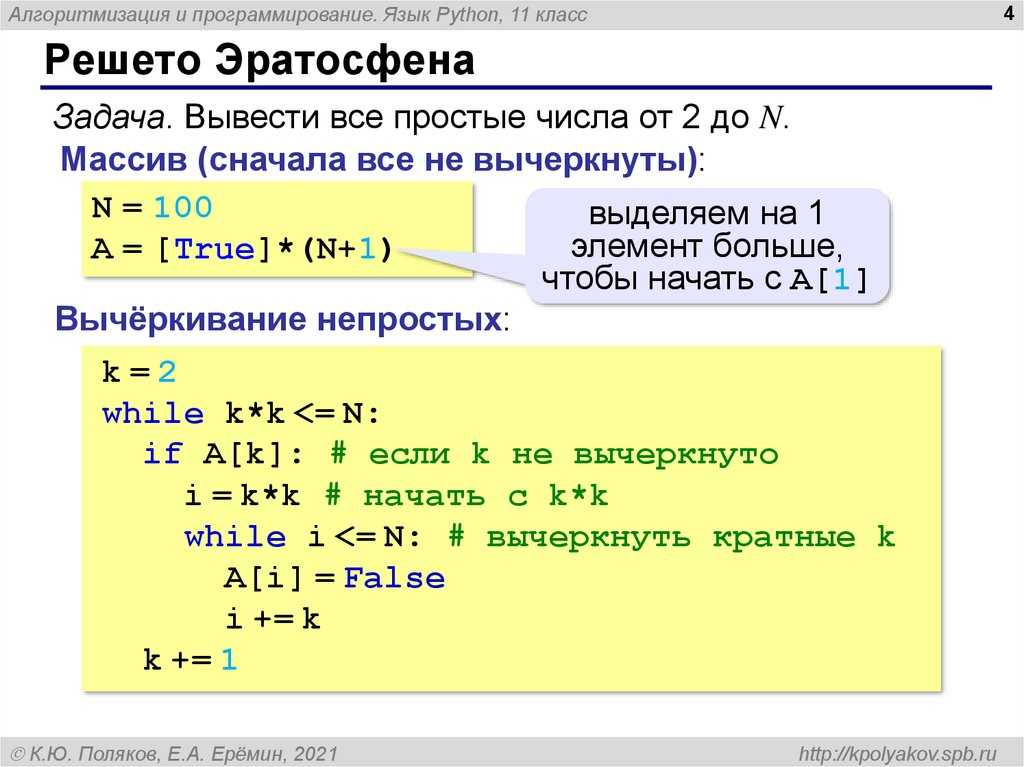
>>> m_e = [[1, 0, 0], [0, 1, 0], [0, 0, 1]] >>> m_e_np = np.matrix(m_e) >>> print(m_e_np) [[1 0 0] [0 1 0] [0 0 1]]
Такой способ не очень удобен, к счастью для нас, для построения такого типа матриц в библиотеке Numpy есть специальная функция – eye().
>>> m_eye = np.eye(3) >>> print(m_eye) [[ 1. 0. 0.] [ 0. 1. 0.] [ 0. 0. 1.]]
В качестве аргумента функции передается размерность матрицы, в нашем примере – это матрица 3 3. Тот же результат можно получить с помощью функции identity().
>>> m_idnt = np.identity(3) >>> print(m_idnt) [[ 1. 0. 0.] [ 0. 1. 0.] [ 0. 0. 1.]]Нулевая матрица
У нулевой матрицы все элементы равны нулю.
\(Z=\begin{pmatrix}0&0&…&0\\0&0&…&0\\…&…&…&…\\0&0&…&0\end{pmatrix}\)
Пример того, как создать такую матрицу с использованием списков, мы приводить не будем, он делается по аналогии с предыдущим разделом.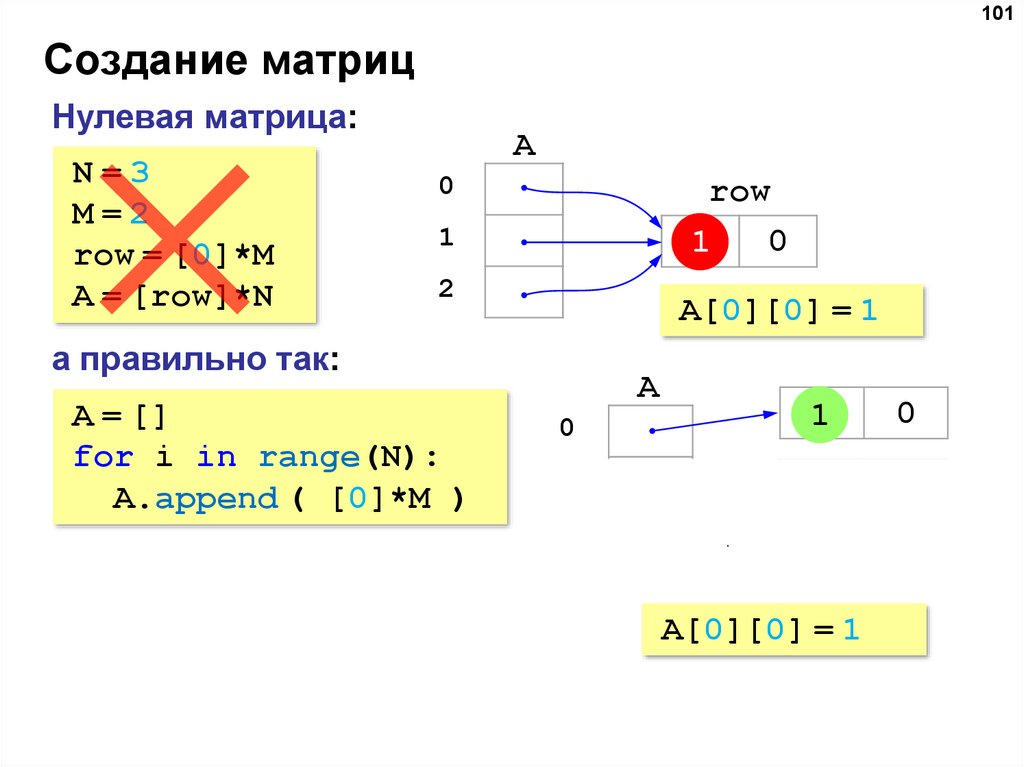 Что касается Numpy, то в составе этой библиотеки есть функция zeros(), которая создает нужную нам матрицу.
Что касается Numpy, то в составе этой библиотеки есть функция zeros(), которая создает нужную нам матрицу.
>>> m_zeros = np.zeros((3, 3)) >>> print(m_zeros) [[ 0. 0. 0.] [ 0. 0. 0.] [ 0. 0. 0.]]
В качестве параметра функции zeros() передается размерность требуемой матрицы в виде кортежа из двух элементов, первый из которых – число строк, второй – столбцов. Если функции zeros() передать в качестве аргумента число, то будет построен нулевой вектор-строка, это мы делали в параграфе, посвященном векторам.
Задание матрицы в общем видеЕсли у вас уже есть данные о содержимом матрицы, то создать ее можно используя списки Python или функцию matrix() из библиотеки Numpy.
>>> m_mx = np.matrix('1 2 3; 4 5 6')
>>> print(m_mx)
[[1 2 3]
[4 5 6]]Если же вы хотите создать матрицу заданного размера с произвольным содержимым, чтобы потом ее заполнить, проще всего для того использовать функцию zeros(), которая создаст матрицу заданного размера, заполненную нулями.
>>> m_var = np.zeros((2, 5)) >>> print(m_var) [[ 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0.]]P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
получение столбца и сложение — Нахождение максимального элемента
Матрица — это двумерный массив, состоящий из M строк и N столбцов. Матрицы часто используются в математических вычислениях. Программисты работают с матрицами в основном в научной области, однако их можно использовать и для других вещей, например, для быстрой генерации уровней в видео-игре.
Матрицы и библиотека NumPy
Программист может самостоятельно реализовать все функции для работы с матрицами: умножение, сложение, транспонирование и т. д. На Python это сделать гораздо проще, чем на более низкоуровневых языках, таких как C.
д. На Python это сделать гораздо проще, чем на более низкоуровневых языках, таких как C.
Но каждый раз писать одни и те же алгоритмы не имеет смысла, поэтому была разработана библиотека NumPy. Она используется для сложных научных вычислений и предоставляет программисту функции для работы с двумерными массивами.
Вместо того чтобы писать десятки строк кода для выполнения простых операций над матрицами, программист может использовать одну функцию из NumPy. Библиотека написана на Python, C и Фортране, поэтому функции работают даже быстрее, чем на чистом Python.
Подключение библиотеки NumPy
NumPy не встроена в интерпретатор Python, поэтому перед импортом её необходимо установить. Для этого в можно воспользоваться утилитой pip. Введите в консоле команду:
pip install numpy
Теперь, когда библиотека установлена, её можно подключить с помощью команды import. Для удобства переименуем numpy при импорте в np следующим образом:
import numpy as np
Ниже в примерах будет использован именно такой импорт, поэтому обращение к библиотеке будет через np, а не numpy!
Создание
Для создании матрицы используется функция array(). В функцию передаётся список. Вот пример создания, мы подаём в качестве аргумента функции двумерный список:
В функцию передаётся список. Вот пример создания, мы подаём в качестве аргумента функции двумерный список:
a = np.array([[3, 3, 3], [2, 5, 5]])
Вторым параметром можно задать тип элементов матрицы:
a = np.array([[3, 3, 3],[2, 5, 5]], int) print(a)
Тогда в консоль выведется:
[[3 3 3] [2 5 5]]
Обратите внимание, что если изменить int на str, то тип элементов изменился на строковый. Кроме того, при выводе в консоль NumPy автоматически отформатировал вывод, чтобы он выглядел как матрица, а элементы располагались друг под другом.
В качестве типов элементов можно использовать int, float, bool, complex, bytes, str, buffers. Также можно использовать и другие типы NumPy: логические, целочисленные, беззнаковые целочисленные, вещественные, комплексные. Вот несколько примеров:
- np.bool8 — логическая переменная, которая занимает 1 байт памяти.
- np.int64 — целое число, занимающее 8 байт.

- np.uint16 — беззнаковое целое число, занимающее 2 байта в памяти.
- np.float32 — вещественное число, занимающее 4 байта в памяти.
- np.complex64 — комплексное число, состоящее из 4 байтового вещественного числа действительной части и 4 байтов мнимой.
Вы также можете узнать размер матрицы, для этого используйте атрибут shape:
size = a.shape print(size) # Выведет (2, 3)
Первое число (2) — количество строк, второе число (3) — количество столбцов.
Нулевая матрица
Если необходимо создать матрицу, состоящую только из нулей, используйте функцию zeros():
a_of_zeros = np.zeros((2,2)) print(a_of_zeros)
Результат этого кода будет следующий:
[[0. 0.] [0. 0.]]
Получение строки, столбца и элемента
Чтобы получить строку двухмерной матрицы, нужно просто обратиться к ней по индексу следующим образом:
temp = a[0] print(temp) #Выведет [3 3 3]
Получить столбец уже не так просто. Используем срезы, в качестве первого элемента среза мы ничего не указываем, а второй элемент — это номер искомого столбца. Пример:
Используем срезы, в качестве первого элемента среза мы ничего не указываем, а второй элемент — это номер искомого столбца. Пример:
arr = np.array([[3,3,3],[2,5,5]], str) temp = arr[:,2] print(temp) # Выведет ['3' '5']
Чтобы получить элемент, нужно указать номер столбца и строки, в которых он находится. Например, элемент во 2 строке и 3 столбце — это 5, проверяем (помним, что нумерация начинается с 0):
arr = np.array([[3,3,3],[2,5,5]], str) temp = arr[1][2] print(temp) # Выведет 5
Умножение и сложение
Чтобы сложить матрицы, нужно сложить все их соответствующие элементы. В Python для их сложения используется обычный оператор «+».
Пример сложения:
arr1 = np.array([[3,3,3],[2,5,5]]) arr2 = np.array([[2,4,2],[1,3,8]]) temp = arr1 + arr2 print(temp)
Результирующая матрица будет равна:
[[ 5 7 5] [ 3 8 13]]
Важно помнить, что складывать можно только матрицы с одинаковым количеством строк и столбцов, иначе программа на Python завершится с исключением ValueError.
Умножение матриц сильно отличается от сложения. Не получится просто перемножить соответствующие элементы двух матриц. Во-первых, матрицы должны быть согласованными, то есть количество столбцов одной должно быть равно количеству строк другой и наоборот, иначе программа вызовет ошибку.
Умножение в NumPy выполняется с помощью метода dot().
Пример умножения:
arr1 = np.array([[3,3],[2,5]]) arr2 = np.array([[2,4],[1,3]]) temp = arr1.dot(arr2) print(temp)
Результат выполнения этого кода будет следующий:
[[ 9 21] [ 9 23]]
Как она получилась? Разберём число 21, его позиция это 1 строка и 2 столбец, тогда мы берем 1 строку первой матрицы и умножаем на 2 столбец второй. Причём элементы умножаются позиционно, то есть 1 на 1 и 2 на 2, а результаты складываются: [3,3] * [4,3] = 3 * 4 + 3 * 3 = 21.
Транспонированная и обратная
Транспонированная матрица — это матрица, у которой строки и столбцы поменялись местами. В библиотеки NumPy для транспонирования двумерных матриц используется метод transpose(). Пример:
В библиотеки NumPy для транспонирования двумерных матриц используется метод transpose(). Пример:
arr1 = np.array([[3,3],[2,5]]) temp = arr1.transpose() print(temp)
В результате получится матрица:
[[3 2] [3 5]]
Чтобы получить обратную матрицу, необходимо использовать модуль linalg (линейная алгебра). Используем функцию inv():
arr1 = np.array([[3,3],[2,5]]) temp = np.linalg.inv(arr1) print(temp)
Результирующая матрица будет равна:
[[ 0.55555556 -0.33333333] [-0.22222222 0.33333333]]
Получение максимального и минимального элемента
Чтобы получить максимальный или минимальный элемент, можно пройтись по всем элементам матрицы с помощью двух циклов for. Это стандартный алгоритм перебора, который известен почти каждому программисту:
arr = np.array([[3,3],[2,5]])
min = arr[0][0]
for i in range(arr.shape[0]):
for j in range(arr. shape[1]):
if min > arr[i][j]:
min = arr[i][j]
print("Минимальный элемент:", min) # Выведет "Минимальный элемент: 2"
shape[1]):
if min > arr[i][j]:
min = arr[i][j]
print("Минимальный элемент:", min) # Выведет "Минимальный элемент: 2"NumPy позволяет найти максимальный и минимальный элемент с помощью функций amax() и amin(). В качестве аргумента в функции нужно передать саму матрицу. Пример:
arr1 = np.array([[3,3],[2,5]])
min = np.amin(arr1)
max = np.amax(arr1)
print("Минимальный элемент:", min) # Выведет "Минимальный элемент: 2"
print("Максимальный элемент:", max) # Выведет "Максимальный элемент: 5"Как видим, результаты реализации на чистом Python и реализации с использованием библиотеки NumPy совпадают.
Заключение
На Python можно реализовать все необходимые функции для работы с матрицами. Чтобы упростить работу программистов, была создана библиотека NumPy. Она позволяет производить сложные математические вычисления легко и без ошибок, избавляя программиста от необходимости каждый раз писать один и тот же код.
Учебник на матрице Python — pythobyte.com
Автор оригинала: Pankaj Kumar.
Мы можем реализовать матрицу Python в форме 2-D списка или 2-D массив Отказ Для выполнения операций на Python Matrix нам нужно импортировать модуль Python Numpy.
Матрица Python важно в области статистики, обработки данных, обработки изображений и т. Д.
Создание матрицы Python
Матрица Python может быть создана с использованием одной из следующих методик:
- Используя списки
- С помощью метода Arange ()
- Используя Matrix () метод
1. Создание матрицы с использованием списков
numpy.array () Функция может быть использована для создания массива, использующего списки в качестве ввода к нему Отказ
Пример:
import numpy input_arr = numpy.array([[ 10, 20, 30],[ 40, 50, 60]]) print(input_arr)
Выход:
[[10 20 30] [40 50 60]]
Как видно выше, вывод представляет собой 2-D матрицу с заданным набором входов в виде списка.
2. Создание матрицы с использованием функции «Numpy.Arange ()»
numpy.arange () Функция вместе со входами списка можно использовать для создания матрицы в Python.
Пример:
import numpy print(numpy.array([numpy.arange(10,15), numpy.arange(15,20)]))
Выход:
[[10 11 12 13 14] [15 16 17 18 19]]
3. Создание матрицы с использованием функции «NUMPY.MATRIX ()»
numpy.matrix () Функция позволяет нам создать матрицу в Python.
Синтаксис:
numpy.matrix(input,dtype)
- Вход: ввод элементов для формирования матрицы.

- dtype: тип данных соответствующего выхода.
Пример:
import numpy as p
matA = p.matrix([[10, 20], [30, 40]])
print('MatrixA:\n', matA)
matB = p.matrix('[10,20;30,40]', dtype=p.int32) # Setting the data-type to int
print('\nMatrixB:\n', matB)
Выход:
MatrixA: [[10 20] [30 40]] MatrixB: [[10 20] [30 40]]
Добавление матрицы в Python
Работа добавления на матрицах может быть выполнена следующими способами:
- Традиционный метод
- Используя оператор ‘+’
1.
 Традиционный метод
Традиционный методВ этом традиционном методе мы в основном принимаем вход от пользователя, а затем выполните операцию сложения, используя для петлей (Треверс через элементы матрицы) и Оператор «+» Отказ
Пример:
import numpy as p
ar1 = p.matrix([[11, 22], [33, 44]])
ar2 = p.matrix([[55, 66], [77, 88]])
res = p.matrix(p.zeros((2,2)))
print('Matrix ar1 :\n', ar1)
print('\nMatrix ar2 :\n', ar2)
# traditional code
for x in range(ar1.shape[1]):
for y in range(ar2.shape[0]):
res[x, y] = ar1[x, y] + ar2[x, y]
print('\nResult :\n', res)
Примечание : Matrix.shape Возвращает размеры определенной матрицы.
Выход:
Matrix ar1 : [[11 22] [33 44]] Matrix ar2 : [[55 66] [77 88]] Result : [[ 66. 88.] [ 110. 132.]]
2. Использование оператора ‘+’
Этот метод обеспечивает лучшую эффективность кода, поскольку он уменьшает LOC (строки кода) и, таким образом, оптимизирует код.
Пример:
import numpy as p ar1 = p.matrix([[11, 22], [33, 44]]) ar2 = p.matrix([[55, 66], [77, 88]]) res = p.matrix(p.zeros((2,2))) print('Matrix ar1 :\n', ar1) print('\nMatrix ar2 :\n', ar2) res = ar1 + ar2 # using '+' operator print('\nResult :\n', res)
Выход:
Matrix ar1 : [[11 22] [33 44]] Matrix ar2 : [[55 66] [77 88]] Result : [[ 66 88] [110 132]]
Матричное умножение в Python
Умножение матрицы в Python может быть предоставлена с использованием следующих способов:
- Скалярный продукт
- Матричный продукт
Скалярный продукт
В скалярном продукте, Скаляр/постоянное значение умножается на каждый элемент матрицы.
‘*’ Оператор используется для умножения скалярного значения с элементами входных матриц.
Пример:
import numpy as p
matA = p.matrix([[11, 22], [33, 44]])
print("Matrix A:\n", matA)
print("Scalar Product of Matrix A:\n", matA * 10)
Выход:
Matrix A: [[11 22] [33 44]] Scalar Product of Matrix A: [[110 220] [330 440]]
Матричный продукт
Как уже упоминалось выше, мы можем использовать Оператор «*» только для скалярного умножения Отказ Для того, чтобы продолжить умножение Matrix, нам нужно использовать numpy. функция. dot ()
dot ()
numpy.dot () Функция берет Numpy массивы в качестве параметра Значения и выполняет умножение в соответствии с основными правилами умножения матрицы.
Пример:
import numpy as p
matA = p.matrix([[11, 22], [33, 44]])
matB = p.matrix([[2,2], [2,2]])
print("Matrix A:\n", matA)
print("Matrix B:\n", matB)
print("Dot Product of Matrix A and Matrix B:\n", p.dot(matA, matB))
Выход:
Matrix A: [[11 22] [33 44]] Matrix B: [[2 2] [2 2]] Dot Product of Matrix A and Matrix B: [[ 66 66] [154 154]]
Вычитание матрицы Python
‘-‘ Оператор используется для выполнения вычитания на матрице Python.
Пример:
import numpy as p
matA = p.matrix([[11, 22], [33, 44]])
matB = p.matrix([[2,2], [2,2]])
print("Matrix A:\n", matA)
print("Matrix B:\n", matB)
print("Subtraction of Matrix A and Matrix B:\n",(matA - matB))
Выход:
Matrix A: [[11 22] [33 44]] Matrix B: [[2 2] [2 2]] Subtraction of Matrix A and Matrix B: [[ 9 20] [31 42]]
Разделение матрицы Python
Скалярное разделение Может быть выполнен на элементах матрицы в Python, используя ‘/’ Оператор Отказ
Оператор «/» разделяет каждый элемент матрицы со скалярным/постоянным значением.
Пример :
import numpy as p
matB = p.matrix([[2,2], [2,2]])
print("Matrix B:\n", matB)
print("Matrix B after Scalar Division operation:\n",(matB/2))
Выход:
Matrix B: [[2 2] [2 2]] Matrix B after Scalar Division operation: [[ 1. 1.] [ 1. 1.]]
Транспонировать матрицу Python
Транспоминация матрицы в основном включает переворачивание матрицы над соответствующими диагоналами I. e. Это обменяет строки и столбцы входной матрицы. Ряды становятся колоннами и наоборот.
e. Это обменяет строки и столбцы входной матрицы. Ряды становятся колоннами и наоборот.
Например: давайте рассмотрим матрицу A с размерами 3 × 2 I.e 3 ряда и 2 столбцами. После выполнения операции транспонирования размеры матрицы A будут 2 × 3 I.e 2 ряда и 3 столбца.
Matrix.t В основном выполняет транспозью входной матрицы и производит Новая матрица в результате работы транспонирования.
Пример:
import numpy
matA = numpy.array([numpy.arange(10,15), numpy.arange(15,20)])
print("Original Matrix A:\n")
print(matA)
print('\nDimensions of the original MatrixA: ',matA.shape)
print("\nTranspose of Matrix A:\n ")
res = matA. T
print(res)
print('\nDimensions of the Matrix A after performing the Transpose Operation: ',res.shape)
T
print(res)
print('\nDimensions of the Matrix A after performing the Transpose Operation: ',res.shape)
Выход:
Original Matrix A: [[10 11 12 13 14] [15 16 17 18 19]] Dimensions of the original MatrixA: (2, 5) Transpose of Matrix A: [[10 15] [11 16] [12 17] [13 18] [14 19]] Dimensions of the Matrix A after performing the Transpose Operation: (5, 2)
В приведенном выше фрагменте кода я создал матрицу размеров 2 × 5 I.E. 2 ряда и 5 столбцов.
После выполнения операции транспонирования размеры результирующей матрицы составляют 5 × 2 I.e. 5 рядов и 2 столбцами.
Экспонент матрицы Python
Шкафчик на матрице рассчитывается элемент-мудрый I. E. Эффективность каждого элемента рассчитывается путем повышения элемента к мощности входного скалярного/постоянного значения.
E. Эффективность каждого элемента рассчитывается путем повышения элемента к мощности входного скалярного/постоянного значения.
Пример:
import numpy
matA = numpy.array([numpy.arange(0,2), numpy.arange(2,4)])
print("Original Matrix A:\n")
print(matA)
print("Exponent of the input matrix:\n")
print(matA ** 2) # finding the exponent of every element of the matrix
Выход:
Original Matrix A: [[0 1] [2 3]] Exponent of the input matrix: [[0 1] [4 9]]
В приведенном выше фрагменте кода мы обнаружили экспонант каждого элемента входной матрицы, подняв его до мощности 2.
Работа умножения Matrix с использованием Numpy Methods
Следующие методики могут быть использованы для размножения Numpy Matrix Matrix:
- Использование метода умножения ()
- Использование метода Matmul ()
- Использование метода DOT () – уже покрыто в этой статье
Способ 1: Использование метода умножения ()
numpy.multiply () Метод выполняет разумное умножение элемента на входной матрице.
Пример:
import numpy as p
matA = p.matrix([[10, 20], [30, 40]])
print('MatrixA:\n', matA)
matB = p.matrix('[10,20;30,40]', dtype=p.int32) # Setting the data-type to int
print('\nMatrixB:\n', matB)
print("Matrix multplication using numpy. matrix() method")
res = p.multiply(matA,matB)
print(res)
matrix() method")
res = p.multiply(matA,matB)
print(res)
Выход:
MatrixA: [[10 20] [30 40]] MatrixB: [[10 20] [30 40]] Matrix multplication using numpy.matrix() method [[ 100 400] [ 900 1600]]
Способ 2: Использование метода Matmul ()
numpy.matmul () Способ выполняет матричный продукт на входных матрицах.
Пример:
import numpy as p matA = p.matrix([[10, 20], [30, 40]]) print('MatrixA:\n', matA) matB = p.matrix('[10,20;30,40]', dtype=p.int32) # Setting the data-type to int print('\nMatrixB:\n', matB) print("Matrix multplication using numpy.matmul() method") res = p.matmul(matA,matB) print(res)
Выход:
MatrixA: [[10 20] [30 40]] MatrixB: [[10 20] [30 40]] Matrix multplication using numpy.matmul() method [[ 700 1000] [1500 2200]]
Я настоятельно рекомендую всем читателям пройти по-прежнему ниже учебное пособие, чтобы оказать тщательное понимание умножения Numpy Matrix: Обновление Numpy Matrix
Tumpy Matrix транспонимент
numpy.transose () Функция выполняет транспонирование на входной матрице и приводит к новой матрице.
Пример:
import numpy
matA = numpy.array([numpy.arange(10,15), numpy.arange(15,20)])
print("Original Matrix A:\n")
print(matA)
print('\nDimensions of the original MatrixA: ',matA.shape)
print("\nTranspose of Matrix A:\n ")
res = matA.transpose()
print(res)
print('\nDimensions of the Matrix A after performing the Transpose Operation: ',res.shape)
Выход:
Original Matrix A: [[10 11 12 13 14] [15 16 17 18 19]] Dimensions of the original MatrixA: (2, 5) Transpose of Matrix A: [[10 15] [11 16] [12 17] [13 18] [14 19]] Dimensions of the Matrix A after performing the Transpose Operation: (5, 2)
Рекомендуется прочитать: Numpy Matrix Transpose () Функция
Заключение
Таким образом, в этой статье мы поняли операции, выполненные на матрице Python, а также посмотрели на операции Numpy Matrix.
Рекомендации
- Матрица Python
- Numpy документация
- Python Numpy
100 NumPy задач | Python 3 для начинающих и чайников
100 (на самом деле, пока меньше) задач для NumPy, перевод английского варианта https://github.com/rougier/numpy-100
Импортировать NumPy под именем np
import numpy as np
Напечатать версию и конфигурацию
print(np.__version__) np.show_config()
Создать вектор (одномерный массив) размера 10, заполненный нулями
Z = np.zeros(10) print(Z)
Создать вектор размера 10, заполненный единицами
Z = np.ones(10) print(Z)
Создать вектор размера 10, заполненный числом 2.5
Z = np.full(10, 2.5) print(Z)
Как получить документацию о функции numpy.add из командной строки?
python3 -c "import numpy; numpy.info(numpy.add)"
Создать вектор размера 10, заполненный нулями, но пятый элемент равен 1
Z = np.zeros(10) Z[4] = 1 print(Z)
Создать вектор со значениями от 10 до 49
Z = np.arange(10,50) print(Z)
Развернуть вектор (первый становится последним)
Z = np.arange(50) Z = Z[::-1]
Создать матрицу (двумерный массив) 3×3 со значениями от 0 до 8
Z = np.arange(9).reshape(3,3) print(Z)
Найти индексы ненулевых элементов в [1,2,0,0,4,0]
nz = np.nonzero([1,2,0,0,4,0]) print(nz)
Создать 3×3 единичную матрицу
Z = np.eye(3) print(Z)
Создать массив 3x3x3 со случайными значениями
Z = np.random.random((3,3,3)) print(Z)
Создать массив 10×10 со случайными значениями, найти минимум и максимум
Z = np.random.random((10,10)) Zmin, Zmax = Z.min(), Z.max() print(Zmin, Zmax)
Создать случайный вектор размера 30 и найти среднее значение всех элементов
Z = np.random.random(30) m = Z.mean() print(m)
Создать матрицу с 0 внутри, и 1 на границах
Z = np.ones((10,10)) Z[1:-1,1:-1] = 0
Выяснить результат следующих выражений
0 * np.nan np.nan == np.nan np.inf > np.nan np.nan - np.nan 0.3 == 3 * 0.1
Создать 5×5 матрицу с 1,2,3,4 под диагональю
Z = np.diag(np.arange(1, 5), k=-1) print(Z)
Создать 8×8 матрицу и заполнить её в шахматном порядке
Z = np.zeros((8,8), dtype=int) Z[1::2,::2] = 1 Z[::2,1::2] = 1 print(Z)
Дан массив размерности (6,7,8). Каков индекс (x,y,z) сотого элемента?
print(np.unravel_index(100, (6,7,8)))
Создать 8×8 матрицу и заполнить её в шахматном порядке, используя функцию tile
Z = np.tile(np.array([[0,1],[1,0]]), (4,4)) print(Z)
Перемножить матрицы 5×3 и 3×2
Z = np.dot(np.ones((5,3)), np.ones((3,2))) print(Z)
Дан массив, поменять знак у элементов, значения которых между 3 и 8
Z = np.arange(11) Z[(3 < Z) & (Z <= 8)] *= -1
Создать 5×5 матрицу со значениями в строках от 0 до 4
Z = np.zeros((5,5)) Z += np.arange(5) print(Z)
Есть генератор, сделать с его помощью массив
def generate():
for x in xrange(10):
yield x
Z = np.fromiter(generate(),dtype=float,count=-1)
print(Z)Создать вектор размера 10 со значениями от 0 до 1, не включая ни то, ни другое
Z = np.linspace(0,1,12)[1:-1] print(Z)
Отсортировать вектор
Z = np.random.random(10) Z.sort() print(Z)
Проверить, одинаковы ли 2 numpy массива
A = np.random.randint(0,2,5) B = np.random.randint(0,2,5) equal = np.allclose(A,B) print(equal)
Сделать массив неизменяемым
Z = np.zeros(10) Z.flags.writeable = False Z[0] = 1
Дан массив 10×2 (точки в декартовой системе координат), преобразовать в полярную
Z = np.random.random((10,2)) X,Y = Z[:,0], Z[:,1] R = np.hypot(X, Y) T = np.arctan2(Y,X) print(R) print(T)
Заменить максимальный элемент на ноль
Z = np.random.random(10) Z[Z.argmax()] = 0 print(Z)
Создать структурированный массив с координатами x, y на сетке в квадрате [0,1]x[0,1]
Z = np.zeros((10,10), [('x',float),('y',float)])
Z['x'], Z['y'] = np.meshgrid(np.linspace(0,1,10),
np.linspace(0,1,10))
print(Z)Из двух массивов сделать матрицу Коши C (Cij = 1/(xi — yj))
X = np.arange(8) Y = X + 0.5 C = 1.0 / np.subtract.outer(X, Y) print(np.linalg.det(C))
Найти минимальное и максимальное значение, принимаемое каждым числовым типом numpy
for dtype in [np.int8, np.int32, np.int64]: print(np.iinfo(dtype).min) print(np.iinfo(dtype).max) for dtype in [np.float32, np.float64]: print(np.finfo(dtype).min) print(np.finfo(dtype).max) print(np.finfo(dtype).eps)
Напечатать все значения в массиве
np.set_printoptions(threshold=np.nan) Z = np.zeros((25,25)) print(Z)
Найти ближайшее к заданному значению число в заданном массиве
Z = np.arange(100) v = np.random.uniform(0,100) index = (np.abs(Z-v)).argmin() print(Z[index])
Создать структурированный массив, представляющий координату (x,y) и цвет (r,g,b)
Z = np.zeros(10, [ ('position', [ ('x', float, 1),
('y', float, 1)]),
('color', [ ('r', float, 1),
('g', float, 1),
('b', float, 1)])])
print(Z)Дан массив (100,2) координат, найти расстояние от каждой точки до каждой
import scipy.spatial Z = np.random.random((10,2)) D = scipy.spatial.distance.cdist(Z,Z) print(D)
Преобразовать массив из float в int
Z = np.arange(10, dtype=np.int32) Z = Z.astype(np.float32, copy=False)
Дан файл:
1,2,3,4,5 6,,,7,8 ,,9,10,11
Как прочитать его?
Z = np.genfromtxt("missing.dat", delimiter=",")Каков эквивалент функции enumerate для numpy массивов?
Z = np.arange(9).reshape(3,3) for index, value in np.ndenumerate(Z): print(index, value) for index in np.ndindex(Z.shape): print(index, Z[index])
Сформировать 2D массив с распределением Гаусса
X, Y = np.meshgrid(np.linspace(-1,1,10), np.linspace(-1,1,10)) D = np.hypot(X, Y) sigma, mu = 1.0, 0.0 G = np.exp(-((D - mu) ** 2 / (2.0 * sigma ** 2))) print(G)
Случайно расположить p элементов в 2D массив
n = 10 p = 3 Z = np.zeros((n,n)) np.put(Z, np.random.choice(range(n*n), p, replace=False), 1)
Отнять среднее из каждой строки в матрице
X = np.random.rand(5, 10) Y = X - X.mean(axis=1, keepdims=True)
Отсортировать матрицу по n-ому столбцу
Z = np.random.randint(0,10,(3,3)) n = 1 # Нумерация с нуля print(Z) print(Z[Z[:,n].argsort()])
Определить, есть ли в 2D массиве нулевые столбцы
Z = np.random.randint(0,3,(3,10)) print((~Z.any(axis=0)).any())
Дан массив, добавить 1 к каждому элементу с индексом, заданным в другом массиве (осторожно с повторами)
Z = np.ones(10) I = np.random.randint(0,len(Z),20) Z += np.bincount(I, minlength=len(Z)) print(Z)
Дан массив (w,h,3) (картинка) dtype=ubyte, посчитать количество различных цветов
w,h = 16,16 I = np.random.randint(0, 2, (h,w,3)).astype(np.ubyte) F = I[...,0] * 256 * 256 + I[...,1] * 256 + I[...,2] n = len(np.unique(F)) print(np.unique(I))
Дан четырехмерный массив, посчитать сумму по последним двум осям
A = np.random.randint(0,10, (3,4,3,4)) sum = A.reshape(A.shape[:-2] + (-1,)).sum(axis=-1) print(sum)
Найти диагональные элементы произведения матриц
# Slow version
np.diag(np.dot(A, B))
# Fast version
np.sum(A * B.T, axis=1)
# Faster version
np.einsum("ij,ji->i", A, B).Дан вектор [1, 2, 3, 4, 5], построить новый вектор с тремя нулями между каждым значением
Z = np.array([1,2,3,4,5]) nz = 3 Z0 = np.zeros(len(Z) + (len(Z)-1)*(nz)) Z0[::nz+1] = Z print(Z0)
Поменять 2 строки в матрице
A = np.arange(25).reshape(5,5) A[[0,1]] = A[[1,0]] print(A)
Рассмотрим набор из 10 троек, описывающих 10 треугольников (с общими вершинами), найти множество уникальных отрезков, составляющих все треугольники
faces = np.random.randint(0,100,(10,3))
F = np.roll(faces.repeat(2,axis=1),-1,axis=1)
F = F.reshape(len(F)*3,2)
F = np.sort(F,axis=1)
G = F.view( dtype=[('p0',F.dtype),('p1',F.dtype)] )
G = np.unique(G)
print(G)Дан массив C; создать массив A, что np.bincount(A) == C
C = np.bincount([1,1,2,3,4,4,6]) A = np.repeat(np.arange(len(C)), C) print(A)
Посчитать среднее, используя плавающее окно
def moving_average(a, n=3):
ret = np.cumsum(a, dtype=float)
ret[n:] = ret[n:] - ret[:-n]
return ret[n - 1:] / n
print(moving_average(np.arange(20), 3))Дан вектор Z, построить матрицу, первая строка которой (Z[0],Z[1],Z[2]), каждая последующая сдвинута на 1 (последняя (Z[-3],Z[-2],Z[-1]))
from numpy.lib import stride_tricks def rolling(a, window): shape = (a.size - window + 1, window) strides = (a.itemsize, a.itemsize) return stride_tricks.as_strided(a, shape=shape, strides=strides) Z = rolling(np.arange(10), 3) print(Z)
Инвертировать булево значение, или поменять знак у числового массива без создания нового
Z = np.random.randint(0,2,100) np.logical_not(arr, out=arr) Z = np.random.uniform(-1.0,1.0,100) np.negative(arr, out=arr)
Рассмотрим 2 набора точек P0, P1 описания линии (2D) и точку р, как вычислить расстояние от р до каждой линии i (P0[i],P1[i])
def distance(P0, P1, p):
T = P1 - P0
L = (T**2).sum(axis=1)
U = -((P0[:,0] - p[...,0]) * T[:,0] + (P0[:,1] - p[...,1]) * T[:,1]) / L
U = U.reshape(len(U),1)
D = P0 + U * T - p
return np.sqrt((D**2).sum(axis=1))
P0 = np.random.uniform(-10,10,(10,2))
P1 = np.random.uniform(-10,10,(10,2))
p = np.random.uniform(-10,10,( 1,2))
print(distance(P0, P1, p))Дан массив. Написать функцию, выделяющую часть массива фиксированного размера с центром в данном элементе (дополненное значением fill если необходимо)
Написать функцию, выделяющую часть массива фиксированного размера с центром в данном элементе (дополненное значением fill если необходимо)
Z = np.random.randint(0,10, (10,10)) shape = (5,5) fill = 0 position = (1,1) R = np.ones(shape, dtype=Z.dtype)*fill P = np.array(list(position)).astype(int) Rs = np.array(list(R.shape)).astype(int) Zs = np.array(list(Z.shape)).astype(int) R_start = np.zeros((len(shape),)).astype(int) R_stop = np.array(list(shape)).astype(int) Z_start = (P - Rs//2) Z_stop = (P + Rs//2)+Rs%2 R_start = (R_start - np.minimum(Z_start, 0)).tolist() Z_start = (np.maximum(Z_start, 0)).tolist() R_stop = np.maximum(R_start, (R_stop - np.maximum(Z_stop-Zs,0))).tolist() Z_stop = (np.minimum(Z_stop,Zs)).tolist() r = [slice(start,stop) for start,stop in zip(R_start,R_stop)] z = [slice(start,stop) for start,stop in zip(Z_start,Z_stop)] R[r] = Z[z] print(Z) print(R)
Посчитать ранг матрицы
Z = np.random.uniform(0,1,(10,10)) rank = np.linalg.matrix_rank(Z)
Найти наиболее частое значение в массиве
Z = np.random.randint(0,10,50) print(np.bincount(Z).argmax())
Извлечь все смежные 3×3 блоки из 10×10 матрицы
Z = np.random.randint(0,5,(10,10)) n = 3 i = 1 + (Z.shape[0] - n) j = 1 + (Z.shape[1] - n) C = stride_tricks.as_strided(Z, shape=(i, j, n, n), strides=Z.strides + Z.strides) print(C)
Создать подкласс симметричных 2D массивов (Z[i,j] == Z[j,i])
# Note: only works for 2d array and value setting using indices
class Symetric(np.ndarray):
def __setitem__(self, (i,j), value):
super(Symetric, self).__setitem__((i,j), value)
super(Symetric, self).__setitem__((j,i), value)
def symetric(Z):
return np.asarray(Z + Z.T - np.diag(Z.diagonal())).view(Symetric)
S = symetric(np.random.randint(0,10,(5,5)))
S[2,3] = 42
print(S)Рассмотрим множество матриц (n,n) и множество из p векторов (n,1). Посчитать сумму p произведений матриц (результат имеет размерность (n,1))
p, n = 10, 20 M = np.ones((p,n,n)) V = np.ones((p,n,1)) S = np.tensordot(M, V, axes=[[0, 2], [0, 1]]) print(S) # It works, because: # M is (p,n,n) # V is (p,n,1) # Thus, summing over the paired axes 0 and 0 (of M and V independently), # and 2 and 1, to remain with a (n,1) vector.
Дан массив 16×16, посчитать сумму по блокам 4×4
Z = np.ones((16,16))
k = 4
S = np.add.reduceat(np.add.reduceat(Z, np.arange(0, Z.shape[0], k), axis=0),
np.arange(0, Z.shape[1], k), axis=1)Написать игру «жизнь»
def iterate(Z):
# Count neighbours
N = (Z[0:-2,0:-2] + Z[0:-2,1:-1] + Z[0:-2,2:] +
Z[1:-1,0:-2] + Z[1:-1,2:] +
Z[2: ,0:-2] + Z[2: ,1:-1] + Z[2: ,2:])
# Apply rules
birth = (N == 3) & (Z[1:-1,1:-1]==0)
survive = ((N == 2) | (N == 3)) & (Z[1:-1,1:-1] == 1)
Z[...] = 0
Z[1:-1,1:-1][birth | survive] = 1
return Z
Z = np.random.randint(0,2,(50,50))
for i in range(100):
print(Z)
Z = iterate(Z)Найти n наибольших значений в массиве
Z = np.arange(10000) np.random.shuffle(Z) n = 5 print (Z[np.argpartition(-Z,n)[:n]])
Построить прямое произведение массивов (все комбинации с каждым элементом)
def cartesian(arrays):
arrays = [np.asarray(a) for a in arrays]
shape = map(len, arrays)
ix = np.indices(shape, dtype=int)
ix = ix.reshape(len(arrays), -1).T
for n, arr in enumerate(arrays):
ix[:, n] = arrays[n][ix[:, n]]
return ix
print(cartesian(([1, 2, 3], [4, 5], [6, 7])))Даны 2 массива A (8×3) и B (2×2). Найти строки в A, которые содержат элементы из каждой строки в B, независимо от порядка элементов в B
A = np.random.randint(0,5,(8,3)) B = np.random.randint(0,5,(2,2)) C = (A[..., np.newaxis, np.newaxis] == B) rows = (C.sum(axis=(1,2,3)) >= B.shape[1]).nonzero()[0] print(rows)
Дана 10×3 матрица, найти строки из неравных значений (например [2,2,3])
Z = np.random.randint(0,5,(10,3)) E = np.logical_and.reduce(Z[:,1:] == Z[:,:-1], axis=1) U = Z[~E] print(Z) print(U)
Преобразовать вектор чисел в матрицу бинарных представлений
I = np.array([0, 1, 2, 3, 15, 16, 32, 64, 128], dtype=np.uint8) print(np.unpackbits(I[:, np.newaxis], axis=1))
Дан двумерный массив. Найти все различные строки
Z = np.random.randint(0, 2, (6,3)) T = np.ascontiguousarray(Z).view(np.dtype((np.void, Z.dtype.itemsize * Z.shape[1]))) _, idx = np.unique(T, return_index=True) uZ = Z[idx] print(uZ)
Даны векторы A и B, написать einsum эквиваленты функций inner, outer, sum и mul
# Make sure to read: http://ajcr.net/Basic-guide-to-einsum/
np.einsum('i->', A) # np.sum(A)
np.einsum('i,i->i', A, B) # A * B
np.einsum('i,i', A, B) # np.inner(A, B)
np.einsum('i,j', A, B) # np.outer(A, B)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Матрица Python и введение в NumPy
В этой статье мы узнаем о матрицах Python с использованием вложенных списков и пакета NumPy.
Матрица — это двумерная структура данных, в которой числа расположены в строках и столбцах. Например:
Эта матрица представляет собой матрицу 3×4 (произносится как «три на четыре»), поскольку она имеет 3 строки и 4 столбца.
Python Matrix
Python не имеет встроенного типа для матриц. Однако мы можем рассматривать список списка как матрицу. Например:
А = [[1, 4, 5],
[-5, 8, 9]]
Мы можем рассматривать этот список как матрицу, имеющую 2 строки и 3 столбца.
Обязательно изучите списки Python, прежде чем продолжить эту статью.
Давайте посмотрим, как работать с вложенным списком.
А = [[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]]
печать("А=", А)
print("A[1] =", A[1]) # 2-я строка
print("A[1][2] =", A[1][2]) # 3-й элемент 2-й строки
print("A[0][-1] =", A[0][-1]) # Последний элемент 1-й строки
столбец = []; # пустой список
для строки в A:
столбец.добавлять (строка [2])
print("3-й столбец =", столбец)
Когда мы запустим программу, вывод будет:
А = [[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]] А[1] = [-5, 8, 9, 0] А[1][2] = 9 А[0][-1] = 12 3-й столбец = [5, 9, 11]
Вот еще несколько примеров, связанных с матрицами Python с использованием вложенных списков.
- Добавить две матрицы
- Транспонировать матрицу
- Умножить две матрицы
Использование вложенных списков в качестве матрицы подходит для простых вычислительных задач, однако есть лучший способ работы с матрицами в Python с использованием пакета NumPy.
NumPy Array
NumPy — это пакет для научных вычислений, поддерживающий мощные объекты N-мерного массива. Прежде чем вы сможете использовать NumPy, вам необходимо установить его. Для получения дополнительной информации,
- Посетите: Как установить NumPy?
- Если вы используете Windows, загрузите и установите дистрибутив Python anaconda. Он поставляется с NumPy и несколькими другими пакетами, связанными с наукой о данных и машинным обучением.
После установки NumPy его можно импортировать и использовать.
NumPy предоставляет многомерный массив чисел (который на самом деле является объектом). Возьмем пример:
импортировать numpy как np а = np.массив ([1, 2, 3]) print(a) # Вывод: [1, 2, 3] print(type(a)) # Вывод:
Как видите, класс массива NumPy называется ndarray .
Как создать массив NumPy?
Существует несколько способов создания массивов NumPy.
1. Массив целых, вещественных и комплексных чисел
импортировать numpy как np A = np.массив ([[1, 2, 3], [3, 4, 5]]) печать(А) A = np.array([[1.1, 2, 3], [3, 4, 5]]) # Массив чисел с плавающей запятой печать(А) A = np.array([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив комплексных чисел печать(А)
Когда вы запустите программу, вывод будет:
[[1 2 3] [3 4 5]] [[1.1 2. 3. ] [3. 4. 5. ]] [[1.+0.j 2.+0.j 3.+0.j] [3.+0.к 4.+0.к 5.+0.к]]
2. Массив нулей и единиц
импортировать numpy как np zeors_array = np.zeros ((2, 3)) печать (zeors_array) ''' Выход: [[0. 0. 0.] [0. 0. 0.]] ''' one_array = np.ones( (1, 5), dtype=np.int32 ) // указание dtype print(ones_array) # Вывод: [[1 1 1 1 1]]
Здесь мы указали dtype до 32 бит (4 байта). Следовательно, этот массив может принимать значения от -2 -31 до 2 -31 -1 .
3. Использование arange() и shape()
импортировать numpy как np
A = np.arange(4)
печать('А =', А)
B = np.arange(12).reshape(2, 6)
печать('В =', В)
'''
Выход:
А = [0 1 2 3]
В = [[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]]
'''
Узнайте больше о других способах создания массива NumPy.
Операции с матрицами
Выше мы привели 3 примера: сложение двух матриц, умножение двух матриц и транспонирование матрицы. Раньше мы использовали вложенные списки для написания этих программ. Давайте посмотрим, как мы можем выполнить ту же задачу, используя массив NumPy.
Добавление двух матриц
Мы используем оператор + для добавления соответствующих элементов двух матриц NumPy.
импортировать numpy как np A = np.массив ([[2, 4], [5, -6]]) B = np.массив([[9, -3], [3, 6]]) C = A + B # поэлементное сложение печать(С) ''' Выход: [[11 1] [ 8 0]] '''
Умножение двух матриц
Чтобы умножить две матрицы, мы используем метод dot() . Узнайте больше о том, как работает numpy.dot.
Примечание: * используется для умножения массивов (умножения соответствующих элементов двух массивов), а не умножения матриц.
импортировать numpy как np A = np.массив ([[3, 6, 7], [5, -3, 0]]) B = np.массив ([[1, 1], [2, 1], [3, -3]]) С = А. точка (В) печать(С) ''' Выход: [[ 36 -12] [-1 2]] '''
Транспонирование матрицы
Мы используем numpy.transpose для вычисления транспонирования матрицы.
импортировать numpy как np A = np.массив ([[1, 1], [2, 1], [3, -3]]) печать (A.transpose()) ''' Выход: [[ 1 2 3] [ 1 1 -3]] '''
Как видите, NumPy значительно облегчил нашу задачу.
Доступ к элементам матрицы, строкам и столбцам
Доступ к элементам матрицы
Подобно спискам, мы можем получить доступ к элементам матрицы, используя индекс. Начнем с одномерного массива NumPy.
импортировать numpy как np
А = np.массив ([2, 4, 6, 8, 10])
print("A[0] =", A[0]) # Первый элемент
print("A[2] =", A[2]) # Третий элемент
print("A[-1] =", A[-1]) # Последний элемент
Когда вы запустите программу, вывод будет:
А[0] = 2 А[2] = 6 А[-1] = 10
Теперь давайте посмотрим, как мы можем получить доступ к элементам двумерного массива (который в основном является матрицей).
импортировать numpy как np
A = np.массив([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
# Первый элемент первой строки
печать("А[0][0] =", А[0][0])
# Третий элемент второй строки
печать("А[1][2] =", А[1][2])
# Последний элемент последней строки
print("А[-1][-1] =", А[-1][-1])
Когда мы запустим программу, вывод будет:
А[0][0] = 1 А[1][2] = 9 А[-1][-1] = 19
Доступ к строкам матрицы
импорт numpy как np A = np.массив([[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]]) print("A[0] =", A[0]) # Первая строка print("A[2] =", A[2]) # Третья строка print("A[-1] =", A[-1]) # Последняя строка (в данном случае 3-я строка)
Когда мы запустим программу, вывод будет:
А[0] = [1, 4, 5, 12] А[2] = [-6, 7, 11, 19] А[-1] = [-6, 7, 11, 19]
Доступ к столбцам матрицы
импорт numpy как np
A = np.массив([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[:,0] =",A[:,0]) # Первый столбец
print("A[:,3] =", A[:,3]) # Четвертый столбец
print("A[:,-1] =", A[:,-1]) # Последний столбец (в данном случае 4-й столбец)
Когда мы запустим программу, вывод будет:
А[:,0] = [ 1 -5 -6] А[:,3] = [12 0 19] А[:,-1] = [12 0 19]
Если вы не знаете, как работает приведенный выше код, прочтите раздел о нарезке матрицы в этой статье.
Нарезка матрицы
Нарезка одномерного массива NumPy аналогична списку. Если вы не знаете, как работает нарезка для списка, посетите статью Понимание нотации срезов в Python.
Если вы не знаете, как работает нарезка для списка, посетите статью Понимание нотации срезов в Python.
Возьмем пример:
импортировать numpy как np буквы = np.array([1, 3, 5, 7, 9, 7, 5]) # элементы с 3-го по 5-й print(letters[2:5]) # Вывод: [5, 7, 9] # элементы с 1-го по 4-й print(letters[:-5]) # Вывод: [1, 3] # от 6-го до последнего элемента print(letters[5:]) # Вывод:[7, 5] # от 1-го до последнего элемента print(letters[:]) # Вывод:[1, 3, 5, 7, 9, 7, 5] # обращение списка print(letters[::-1]) # Вывод:[5, 7, 9, 7, 5, 3, 1]
Теперь давайте посмотрим, как мы можем разрезать матрицу.
импортировать numpy как np
A = np.массив([[1, 4, 5, 12, 14],
[-5, 8, 9, 0, 17],
[-6, 7, 11, 19, 21]])
print(A[:2, :4]) # две строки, четыре столбца
''' Выход:
[[ 1 4 5 12]
[-5 8 9 0]]
'''
print(A[:1,]) # первая строка, все столбцы
''' Выход:
[[ 1 4 5 12 14]]
'''
print(A[:,2]) # все строки, второй столбец
''' Выход:
[ 5 9 11 ]
'''
print(A[:, 2:5]) # все строки, с третьего по пятый столбец
'''Выход:
[[ 5 12 14]
[ 9 0 17 ]
[11 19 21]]
'''
Как видите, использование NumPy (вместо вложенных списков) значительно упрощает работу с матрицами, и мы даже не коснулись основ. Мы предлагаем вам подробно изучить пакет NumPy, особенно если вы пытаетесь использовать Python для обработки и анализа данных.
Мы предлагаем вам подробно изучить пакет NumPy, особенно если вы пытаетесь использовать Python для обработки и анализа данных.
Ресурсы NumPy, которые могут оказаться полезными:
- Учебное пособие по NumPy
- Ссылка NumPy
Как создать матрицу в Python
В этом руководстве по Python мы обсудим , как создать матрицу в Python . Кроме того, мы увидим следующие темы:
- Что такое матрица в python ?
- Как создать матрицу в python с помощью пользовательского ввода
- Создать пустую матрицу с помощью NumPy в python
- Как создать матрицу в Python 3
- Как выполнить умножение матриц в Python
- Как создать матрицу с помощью цикла for в Python
- Как создать матрицу в Python с помощью списка
- Умножить 8 строк, Матрица с 1 столбцом и 1 строкой, 8 столбцов, чтобы получить 8 строк.
Что такое матрица в питоне?
- Матрица Python представляет собой двумерный прямоугольный массив данных, хранящихся в строках и столбцах.

- Горизонтальные записи в матрице называются «строками», а вертикальные — «столбцами».
- Если в матрице r строк и c столбцов, то порядок матрицы определяется как r x c .
- Данные, хранящиеся в матрице, могут быть строками, числами и т. д.
- В матрице данные упорядочены по строкам и столбцам.
- Матрица — важная структура данных для математических и научных расчетов.
- В Python нет встроенного типа для матриц, поэтому мы можем рассматривать список из списка как матрицу.
Вам может понравиться файл копии Python (примеры) и перекрестная таблица в Python Pandas.
Как создать матрицу в Python с помощью пользовательского ввода
Давайте посмотрим , как создать матрицу в Python :
- В Python существует популярная библиотека под названием NumPy .
- Для работы с NumPy нам необходимо его установить.
 Команда для установки NumPy — «pip install NumPy» .
Команда для установки NumPy — «pip install NumPy» . - Чтобы использовать NumPy в коде, мы должны импортировать его как ‘ импортировать NumPy как np’ .
- Матрица создается с помощью функции NumPy.matrix() .
- Мы возьмем пользовательский ввод для матрицы, а затем отобразим матрицу на выходе.
Пример:
импортировать numpy как np
a = int(input("Введите количество строк:"))
b = int(input("Введите количество столбцов:"))
print("Введите число в одну строку через пробел:")
val = список (карта (целое, ввод (). Разделить ()))
матрица = np.array(val).reshape(a,b)
печать (матрица) После написания приведенного выше кода (как создать матрицу в Python с использованием пользовательского ввода), как только вы напечатаете «матрица» , вывод будет выглядеть как «[[2 4] [6 3]] » . Здесь np.array().reshape() используется для печати матрицы.
Вы можете обратиться к приведенному ниже снимку экрана , как создать матрицу в python, используя пользовательский ввод .
Как создать матрицу в Python с помощью пользовательского вводаСоздать пустую матрицу с помощью NumPy в Python
Здесь мы увидим , как создать пустую матрицу с помощью NumPy в Python .
Чтобы создать пустую матрицу, мы сначала импортируем NumPy как np , а затем используем np.empty() для создания пустой матрицы.
Пример:
импортировать numpy как np м = np.пусто((0,0)) print(m)
После написания приведенного выше кода (создайте пустую матрицу с помощью NumPy в python), как только вы напечатаете «m» , вывод будет выглядеть как «[ ] » . Здесь матрица np.empty() из 0 строк и 0 столбцов используется для создания пустой матрицы в python.
Вы можете обратиться к приведенному ниже снимку экрана , создав пустую матрицу, используя NumPy в python .
Как создать матрицу в python 3
Сначала мы импортируем numpy как np , а затем создадим матрицу, используя numpy.matrix() . Таким образом, матрица может быть создана в python.
Пример:
импортировать numpy как np
m = np.matrix([[3, 4], [5, 2]])
print('Matrix is:\n', m) После написания приведенного выше кода (как создать матрицу в Python 3), как только вы напечатаете «m» , вывод будет выглядеть как «[[ 3 4] [5 2]] ” . Здесь np.matrix() используется для печати матрицы и возвращает матрицу.
Вы можете обратиться к приведенному ниже снимку экрана , как создать матрицу в Python 3 .
Как создать матрицу в python 3Как сделать умножение матриц в python
Умножение матриц — это операция, которая принимает две матрицы в качестве входных данных. Чтобы получить поэлементное умножение, мы можем использовать функцию np.multiply() .
Чтобы получить поэлементное умножение, мы можем использовать функцию np.multiply() .
Пример:
импортировать numpy как np мат1 = np.matrix ([[2, 5], [4, 1]]) мат2 = np.matrix ([[6, 5], [4, 7]]) matrix_result = np.multiply (mat1, mat2) print(matrix_result)
После написания приведенного выше кода (как сделать умножение матриц в python), как только вы напечатаете «matrix_result» , то вывод будет выглядеть как «[[12 25] [16 7]]». Здесь np.multiply() используется для умножения двух матриц, и после умножения будет получена одна матрица.
Вы можете обратиться к приведенному ниже снимку экрана, как выполнить умножение матриц в python.
Как сделать умножение матриц в pythonКак создать матрицу, используя цикл for в python
Давайте посмотрим , как создать матрицу, используя цикл for в python .
Для создания матрицы с использованием цикла for нам необходимо принять пользовательский ввод. Матрица состоит из списков, которые создаются и назначаются столбцам и строкам, а цикл for используется для строк и столбцов.
Матрица состоит из списков, которые создаются и назначаются столбцам и строкам, а цикл for используется для строк и столбцов.
Пример:
c_size = int(input("Введите размер столбца: "))
r_size = int(input("Введите размер строки: "))
х = []
у = []
для j в диапазоне (0, c_size):
у.добавлять(0)
для i в диапазоне (0, r_size):
х. добавить (у)
print(x) После написания приведенного выше кода (как создать матрицу с помощью цикла for в python), как только вы напечатаете «x» , то вывод будет выглядеть как «[[0, 0, 0], [0, 0, 0], [0, 0, 0]]». Здесь пользователь вводит размер строки и столбца и добавляет столбец к каждой строке. Матрица будет напечатана в качестве вывода.
Вы можете обратиться к приведенному ниже снимку экрана, как создать матрицу, используя цикл for в python .
Как создать матрицу, используя цикл for в PythonКак создать матрицу в Python, используя список
Давайте посмотрим , как создать матрицу в Python, используя список ?
Мы можем создать матрицу в Python, используя вложенный список. Сначала мы будем импортировать NumPy , а затем мы можем использовать np.array() , используя список, который даст вывод в виде матрицы.
Сначала мы будем импортировать NumPy , а затем мы можем использовать np.array() , используя список, который даст вывод в виде матрицы.
Пример:
импортировать numpy как np мат = np.массив ([[1, 3, 2], [5, 6, 4]]) print(mat)
После написания приведенного выше кода (как создать матрицу в Python с помощью списка), как только вы напечатаете «mat» , вывод будет выглядеть как «[[1 3 2] [5 6 4]]». Здесь np.array() используется для создания матрицы с использованием списка и выдает матрицу в качестве вывода.
Вы можете обратиться к приведенному ниже снимку экрана, как создать матрицу в Python, используя список
Как создать матрицу в Python, используя список 8 столбцов, чтобы получить 8 строк В этом разделе мы узнаем, как умножить 8 строк, 1 столбец матрицы и 1 строку, 8 столбцов, чтобы получить 8 строк. Вот графическое представление этой темы.
- На изображении выше у нас есть 8 строк с 1 столбцом, которые мы должны умножить на 1 строку с 8 столбцами.
- Основное правило умножения матриц: «количество строк в первой матрице должно быть равно количеству столбцов во второй матрице», и в данном случае это правило выполняется, поэтому мы можем приступить к умножению.
- Каждый элемент первой матрицы будет умножен на каждый элемент второй матрицы. Вот иллюстрация умножения на матрицу в Python.
- В основном существует 3 способа реализации умножения матриц в Python.
- numpy.dot() метод
- с использованием оператора @ на 2 матрицах.
- Метод tf.matmul() в Tensorflow
- Метод Numpy dot используется для нахождения произведения двух массивов.
- Существует тонкая разница между массивом и матрицей. Поэтому, если вы видите ошибку при выполнении умножения двумя другими методами, попробуйте
метод numpy.. Это даст вам правильные результаты без каких-либо ошибок. dot()
dot() - Вот синтаксис для использования метода
numpy.dot()в Python.
импортировать numpy как np np.dot(matrix1, matrix2)
- Здесь матрица1 и матрица2 — это матрицы, которые перемножаются друг с другом. Мы не создали их в синтаксисе, но они доступны в приведенном ниже примере.
- Другим решением является использование оператора « @ » в Python. 9Оператор 0238 @ ‘ используется в качестве знака для умножения матриц в Python.
- Обратите внимание, что это работает только с матрицами, а не с массивами.
- Вот синтаксис для использования @ для умножения матриц в Python.
матрица1 @ матрица2
- Третье решение использует тензорный поток. Tensorflow — это расширенный инструмент, используемый с Python и R для предварительных вычислений.
- Имеет различные встроенные модули, ускоряющие расчет сложных алгоритмов.

- Если вы имеете дело с большими матрицами, вы можете сократить время вычислений, используя модуль tensorflow tf.matmul() в tensorflow python.
- Вот синтаксис для выполнения матричного умножения с использованием Python Tensorflow
импортировать тензорный поток как tf tf.matmul(matrix1, matrix2)
Вот реализация матричного умножения 1 строки 8 столбцов и 8 строк 1 столбца на Python Jupyter Notebook.
Вам могут понравиться следующие руководства по Python:
- Модификаторы доступа Python + примеры
- Python Чтение CSV-файла и запись CSV-файла
- Python Массив с примерами
- Хэш-таблица в Python
- Блочный отступ в Python
- Как отобразить календарь в Python
- 4 калькулятор в Python
- Регулярные выражения в Python
- Операторы сравнения Python
- Учебное пособие по пространству имен Python
В этом учебном пособии по Python мы узнали о как сделать матрицу в питоне . Кроме того, мы рассмотрели следующие темы:
Кроме того, мы рассмотрели следующие темы:
- Что такое матрица в python?
- Как создать матрицу в Python с помощью пользовательского ввода
- Создать пустую матрицу с помощью NumPy в Python
- Как создать матрицу в Python 3
- Как выполнить умножение матриц в Python
- Как создать матрицу с помощью for loop в python
- Как создать матрицу в Python, используя список
- Умножьте 8-строчную матрицу с 1 столбцом и 1-строчную 8-столбцовую матрицу, чтобы получить 8-строчную.
Bijay Kumar
Python — один из самых популярных языков в Соединенных Штатах Америки. Я давно работаю с Python и имею опыт работы с различными библиотеками на Tkinter, Pandas, NumPy, Turtle, Django, Matplotlib, Tensorflow, Scipy, Scikit-Learn и т. д. У меня есть опыт работы с различными клиентами в таких странах, как США, Канада, Великобритания, Австралия, Новая Зеландия и т. д. Проверьте мой профиль.
Enjoysharepoint.com/
| Проверить, все ли матричные элементы вдоль заданной оси оцениваются как True. |
| Проверяет, имеет ли какой-либо элемент массива вдоль заданной оси значение True. |
| Индексы максимальных значений по оси. |
| Индексы минимальных значений по оси. |
| Возвращает индексы, которые будут разбивать этот массив. |
| Возвращает индексы для сортировки этого массива. |
| Копия массива, приведенная к указанному типу. |
| Поменять местами байты элементов массива |
| Используйте индексный массив для создания нового массива из набора вариантов. |
| Возвращает массив, значения которого ограничены |
| Возвращает выбранные срезы этого массива вдоль заданной оси. |
| Комплексно-сопряженные все элементы. |
| Вернуть комплексно-сопряженное число поэлементно. |
| Вернуть копию массива. |
| Возвращает совокупное произведение элементов по заданной оси. |
| Возвращает совокупную сумму элементов по заданной оси. |
| Возврат указанных диагоналей. |
| Дамп массива в указанный файл. |
| Возвращает пиксель массива в виде строки. |
| Заполните массив скалярным значением. |
| Вернуть сглаженную копию матрицы. |
| Вернуть себя как объект |
| Вернуть себя как сглаженный |
| Возвращает (комплексное) сопряженное транспонирование self . |
| Возвращает (мультипликативный) инверсию обратимого self . |
| Возвращает транспонирование матрицы. |
| Возвращает поле заданного массива определенного типа. |
| Скопируйте элемент массива в стандартный скаляр Python и верните его. |
| Вставка скаляра в массив (скаляр преобразуется в dtype массива, если возможно) |
| Возвращает максимальное значение по оси. |
| Возвращает среднее значение элементов матрицы по заданной оси. |
| Возвращает минимальное значение по оси. |
| Возвратите массив с теми же данными, просмотренными с другим порядком байтов. |
| Возвращает индексы ненулевых элементов. |
| Переупорядочивает элементы в массиве таким образом, чтобы значение элемента в k-й позиции было в позиции, в которой оно было бы в отсортированном массиве. |
| Возвращает произведение элементов массива по заданной оси. |
| Размах (максимум-минимум) значения по заданной оси. |
| Установить |
| Возвращает сглаженную матрицу. |
| Повтор элементов массива. |
| Возвращает массив, содержащий те же данные с новой формой. |
| Изменение формы и размера массива на месте. |
| Возвращает a с округлением каждого элемента до заданного числа десятичных знаков. |
| Найдите индексы, в которые элементы v должны быть вставлены в a для сохранения порядка. |
| Поместите значение в указанное место в поле, определяемом типом данных. |
| Установить флаги массива WRITEABLE, ALIGNED, WRITEBACKIFCOPY соответственно. |
| Сортировка массива на месте. |
| Возврат возможно измененной матрицы. |
| Возвращает стандартное отклонение элементов массива по заданной оси. |
| Возвращает сумму элементов матрицы по заданной оси. |
| Вернуть вид массива с осью 1 и осью 2 , переставленными местами. |
| Возвращает массив, сформированный из элементов и по заданным индексам. |
| Создание байтов Python, содержащих необработанные байты данных в массиве. |
| Запись массива в файл в текстовом или двоичном виде (по умолчанию). |
| Вернуть матрицу в виде (возможно, вложенного) списка. |
| Псевдоним совместимости для |
| Возвращает сумму по диагоналям массива. |
| Возвращает вид массива с транспонированными осями. |
| Возвращает дисперсию элементов матрицы по заданной оси. |
| Новый вид массива с теми же данными. |
Транспонирование, умножение, массивы NumPy Примеры
Что такое матрица Python?
Матрица Python — это специализированный двумерный прямоугольный массив данных, хранящихся в строках и столбцах. Данные в матрице могут быть числами, строками, выражениями, символами и т. д. Матрица — одна из важных структур данных, которую можно использовать в математических и научных расчетах.
Из этого руководства по Python вы узнаете:
- Что такое матрица Python?
- Как работают матрицы Python?
- Создайте матрицу Python, используя тип данных вложенного списка
- Чтобы прочитать данные внутри Python Matrix, используя список.

- Пример 2: Чтобы прочитать последний элемент из каждой строки.
- Пример 3: Печать строк в матрице
- Добавление матриц с использованием вложенного списка
- Умножение матриц с использованием вложенного списка
- Создание матрицы Python с использованием массивов из пакета Python Numpy
- Матричная операция с использованием Numpy.Array()
- Доступ к матрице NumPy
Как работают матрицы Python?
Данные внутри двумерного массива в матричном формате выглядят следующим образом:
Шаг 1)
Он показывает матрицу 2×2. Он имеет две строки и 2 столбца. Данные внутри матрицы являются числами. Строка1 имеет значения 2,3, а строка2 имеет значения 4,5. Столбцы, т. е. col1, имеют значения 2,4, а col2 — значения 3,5.
Шаг 2)
Показывает матрицу 2×3. Он имеет две строки и три столбца. Данные внутри первой строки, т. е. row1, имеют значения 2, 3, 4, а row2 — значения 5, 6, 7. Столбцы col1 имеют значения 2,5, col2 имеют значения 3,6, а col3 имеют значения 4,7.
Столбцы col1 имеют значения 2,5, col2 имеют значения 3,6, а col3 имеют значения 4,7.
Точно так же вы можете хранить свои данные внутри матрицы nxn в Python. Многие операции могут быть выполнены с матричным сложением, вычитанием, умножением и т. д.
В Python нет простого способа реализовать матричный тип данных.
Матрица Python использует массивы, и то же самое можно реализовать.
- Создайте матрицу Python, используя тип данных вложенного списка
- Создание матрицы Python с использованием массивов из пакета Python Numpy
Создание матрицы Python с использованием типа данных вложенного списка
В Python массивы представляются с использованием типа данных списка. Итак, теперь мы будем использовать список для создания матрицы Python.
Мы создадим матрицу 3×3, как показано ниже:
- Матрица имеет 3 строки и 3 столбца.
- Первая строка в формате списка будет следующей: [8,14,-6]
- Вторая строка в списке будет: [12,7,4]
- Третья строка в списке будет: [-11,3,21]
Матрица внутри списка со всеми строками и столбцами показана ниже:
Список = [[Row1],
[Ряд 2],
[Строка 3]
. ..
[РядN]]
..
[РядN]]
Таким образом, в соответствии с приведенной выше матрицей тип списка с данными матрицы выглядит следующим образом:
M1 = [[8, 14, -6], [12,7,4], [-11,3,21]]
Для чтения данных внутри Python Matrix с помощью списка.
Мы будем использовать матрицу, определенную выше. Пример будет читать данные, печатать матрицу, отображать последний элемент из каждой строки.
Пример: для печати матрицы
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
#Чтобы распечатать матрицу
печать(M1)
Вывод:
Матрица M1 = [[8, 14, -6], [12, 7, 4], [-11, 3, 21]]
Пример 2: Чтобы прочитать последний элемент из каждой строки.
М1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
длина_матрицы = длина (M1)
#Чтобы прочитать последний элемент из каждой строки.
для i в диапазоне (matrix_length):
печать (M1[i][-1])
Вывод:
-6 4 21
Пример 3: Печать строк в матрице
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
длина_матрицы = длина (M1)
#Чтобы напечатать строки в матрице
для i в диапазоне (matrix_length):
печать (M1 [я])
Вывод:
[8, 14, -6] [12, 7, 4] [-11, 3, 21]
Добавление матриц с помощью вложенного списка
Мы можем легко добавить две заданные матрицы. Матрицы здесь будут в виде списка. Давайте поработаем над примером, который позаботится о добавлении данных матриц.
Матрицы здесь будут в виде списка. Давайте поработаем над примером, который позаботится о добавлении данных матриц.
Матрица 1:
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
Матрица 2 :
M2 = [[3, 16, -6],
[9,7,-4],
[-1,3,13]]
Последняя инициализирует матрицу, в которой будет храниться результат M1 + M2.
Матрица 3 :
M3 = [[0,0,0],
[0,0,0],
[0,0,0]]
Пример: добавление матриц
Для добавления матриц будет использоваться цикл for, который будет проходить по обеим заданным матрицам.
М1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
М2 = [[3, 16, -6],
[9,7,-4],
[-1,3,13]]
М3 = [[0,0,0],
[0,0,0],
[0,0,0]]
длина_матрицы = длина (M1)
#Чтобы добавить матрицы M1 и M2
для i в диапазоне (len (M1)):
для k в диапазоне (len (M2)):
M3[i][k] = M1[i][k] + M2[i][k]
#Распечатать матрицу
print("Сумма матриц M1 и M2 = ", M3)
Вывод:
Сумма матриц M1 и M2 = [[11, 30, -12], [21, 14, 0], [-12, 6, 34]]
Умножение матриц с использованием вложенного списка
Чтобы умножить матрицы, мы можем использовать цикл for для обеих матриц, как показано в коде ниже:
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
М2 = [[3, 16, -6],
[9,7,-4],
[-1,3,13]]
М3 = [[0,0,0],
[0,0,0],
[0,0,0]]
длина_матрицы = длина (M1)
#Для умножения матриц M1 и M2
для i в диапазоне (len (M1)):
для k в диапазоне (len (M2)):
M3[i][k] = M1[i][k] * M2[i][k]
#Распечатать матрицу
print("Умножение матриц M1 и M2 = ", M3)
Вывод:
Умножение матриц M1 и M2 = [[24, 224, 36], [108, 49, -16], [11, 9, 273]]
Создание матрицы Python с использованием массивов из пакета Python Numpy
Библиотека Python Numpy помогает работать с массивами. Numpy обрабатывает массив немного быстрее, чем список.
Numpy обрабатывает массив немного быстрее, чем список.
Для работы с Numpy его необходимо сначала установить. Следуйте инструкциям ниже, чтобы установить Numpy.
Шаг 1)
Команда для установки Numpy:
pip install NumPy
Шаг 2)
Чтобы использовать Numpy в своем коде, его необходимо импортировать.
import NumPy
Шаг 3)
Вы также можете импортировать NumPy, используя псевдоним, как показано ниже:
import NumPy as np
матрица питона.
Пример: массив в Numpy для создания матрицы Python
импортировать numpy как np M1 = np.массив([[5, -10, 15], [3, -6, 9], [-4, 8, 12]]) печать(M1)
Вывод:
[[ 5 -10 15] [ 3 -6 9] [-4 8 12]]
Матричная операция с использованием Numpy.Array()
Матричная операция, которую можно выполнить, — это сложение, вычитание, умножение, транспонирование, чтение строк, столбцов матрицы, нарезка матрицы и т. д. Во всех примерах мы собирается использовать метод array().
д. Во всех примерах мы собирается использовать метод array().
Сложение матрицы
Чтобы выполнить сложение матрицы, мы создадим две матрицы с помощью numpy.array() и добавим их с помощью оператора (+).
Пример:
импортировать numpy как np M1 = np.array([[3, 6, 9], [5, -10, 15], [-7, 14, 21]]) M2 = np.array([[9, -18, 27], [11, 22, 33], [13, -26, 39]]) М3 = М1 + М2 печать(M3)
Вывод:
[[ 12 -12 36] [ 16 12 48 ] [ 6 -12 60]]
Вычитание матрицы
Чтобы выполнить вычитание матрицы, мы создадим две матрицы с помощью numpy.array() и вычтем их с помощью оператора (-).
Пример:
импортировать numpy как np M1 = np.array([[3, 6, 9], [5, -10, 15], [-7, 14, 21]]) M2 = np.array([[9, -18, 27], [11, 22, 33], [13, -26, 39]]) М3 = М1 - М2 печать(M3)
Вывод:
[[ -6 24 -18] [-6-32-18] [-20 40 -18]]
Умножение матриц
Сначала создадим две матрицы, используя numpy. arary(). Чтобы умножить их, вы можете использовать метод numpy dot(). Numpy.dot() — это точечный продукт матриц M1 и M2. Numpy.dot() обрабатывает двумерные массивы и выполняет умножение матриц.
arary(). Чтобы умножить их, вы можете использовать метод numpy dot(). Numpy.dot() — это точечный продукт матриц M1 и M2. Numpy.dot() обрабатывает двумерные массивы и выполняет умножение матриц.
Пример:
импортировать numpy как np M1 = np.массив ([[3, 6], [5, -10]]) M2 = np.массив ([[9, -18], [11, 22]]) М3 = М1.точка(М2) печать(M3)
Вывод:
[[ 93 78] [-65-310]]
Транспонирование матрицы
Транспонирование матрицы вычисляется путем преобразования строк в столбцы и столбцов в строки. Функцию transpose() из Numpy можно использовать для вычисления транспонирования матрицы.
Пример:
импортировать numpy как np M1 = np.массив([[3, 6, 9], [5, -10, 15], [4,8,12]]) M2 = M1.транспонировать() печать(М2)
Вывод:
[[ 3 5 4] [ 6 -10 8] [ 9 15 12]]
Нарезка матрицы
Нарезка вернет вам элементы из матрицы на основе заданного начального/конечного индекса.
- Синтаксис для нарезки – [начало:конец]
- Если начальный индекс не указан, он считается равным 0.
 Например, [:5] означает, что он равен [0:5].
Например, [:5] означает, что он равен [0:5]. - Если конец не передан, он будет считаться длиной массива.
- Если начало/конец имеют отрицательные значения, то нарезка будет выполняться с конца массива.
Прежде чем мы приступим к срезу матрицы, давайте сначала поймем, как применить срез к простому массиву.
импортировать numpy как np массив = np.массив ([2,4,6,8,10,12,14,16]) print(arr[3:6]) # напечатает элементы с 3 по 5 print(arr[:5]) # напечатает элементы от 0 до 4 print(arr[2:]) # напечатает элементы от 2 до длины массива. print(arr[-5:-1]) # будет печатать с конца, т.е. от -5 до -2 print(arr[:-1]) # будет печатать с конца, т.е. от 0 до -2
Вывод:
[8 10 12] [ 2 4 6 8 10 ] [ 6 8 10 12 14 16] [ 8 10 12 14 ] [ 2 4 6 8 10 12 14]
Теперь реализуем нарезку матрицы. Для выполнения среза матрицы
синтаксис будет M1[начало_строки:конец_строки, начало_столбца:конец_столбца]
- Первое начало/конец будет для строки, т.
 е. для выбора строк матрицы.
е. для выбора строк матрицы. - Второе начало/конец будет для столбца, т.е. для выбора столбцов матрицы.
Матрица M1 t, которую мы собираемся использовать, выглядит следующим образом:
M1 = np.массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
Всего 4 ряда. Индекс начинается с 0 до 3. 0 -я -я строка — это [2,4,6,8,10], 1 -я -я строка — это [3,6,9,-12,-15], за которой следуют 2 -й -й и 3-й -й -й.
Матрица M1 имеет 5 столбцов. Индекс начинается от 0 до 4. Столбец 0 th имеет значения [2,3,4,5], столбцы 1 st имеют значения [4,6,8,-10], за которыми следуют 2 -й , 3-й -й , 4-й -й -й и 5-й -й -й.
Вот пример, показывающий, как получить данные строк и столбцов из матрицы с помощью срезов. В примере мы печатаем строки 1 st и 2 nd , а для столбцов нам нужны первый, второй и третий столбцы. Чтобы получить этот вывод, мы использовали: M1[1:3, 1:4]
Чтобы получить этот вывод, мы использовали: M1[1:3, 1:4]
Пример:
import numpy as np
M1 = np.массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[1:3, 1:4]) # Для 1:3 это даст первую и вторую строку.
#Столбцы будут взяты с первого по третий.
Вывод:
[[ 6 9 -12] [ 8 12 16]]
Пример: для печати всех строк и третьих столбцов
импортировать numpy как np
M1 = np.массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[:,3]) # Это напечатает все строки и данные третьего столбца.
Вывод:
[ 8 -12 16 -20]
Пример: для печати первой строки и всех столбцов
импортировать numpy как np
M1 = np.массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[:1,]) # Будет напечатана первая строка и все столбцы
Вывод:
[[ 2 4 6 8 10]]
Пример: для печати первых трех строк и первых двух столбцов
импортировать numpy как np M1 = np.массив([[2, 4, 6, 8, 10], [3, 6, 9, -12, -15], [4, 8, 12, 16, -20], [5, -10, 15, -20, 25]]) печать (M1 [: 3,: 2])
Вывод:
[[2 4] [3 6] [4 8]]
Доступ к матрице NumPy
Мы видели, как работает нарезка. Принимая это во внимание, мы узнаем, как получить строки и столбцы из матрицы.
Для печати строк матрицы
В примере будут напечатаны строки матрицы.
Пример:
импортировать numpy как np M1 = np.массив([[3, 6, 9], [5, -10, 15], [4,8,12]]) print(M1[0]) # первая строка print(M1[1]) # вторая строка print(M1[-1]) # -1 напечатает последнюю строку
Вывод:
[3 6 9] [ 5 -10 15] [ 4 8 12]
Чтобы получить последнюю строку, вы можете использовать индекс или -1. Например, матрица имеет 3 строки:
, поэтому M1[0] даст вам первую строку,
M1[1] даст вам вторую строку
M1[2] или M1[-1] даст вам третий ряд или последний ряд.
Для печати столбцов матрицы
импортировать numpy как np M1 = np.массив([[2, 4, 6, 8, 10], [3, 6, 9, -12, -15], [4, 8, 12, 16, -20], [5, -10, 15, -20, 25]]) print(M1[:,0]) # Будет напечатан первый столбец print(M1[:,3]) # Будет напечатан третий столбец print(M1[:,-1]) # -1 даст вам последний столбец
Вывод:
[2 3 4 5] [ 8 -12 16 -20] [ 10 -15 -20 25]
Резюме:
- Матрица Python представляет собой специализированный двумерный прямоугольный массив данных, хранящихся в строках и столбцах. Данные в матрице могут быть числами, строками, выражениями, символами и т. д. Матрица — одна из важных структур данных, которую можно использовать в математических и научных расчетах.
- В Python нет простого способа реализовать матричный тип данных. Матрица Python может быть создана с использованием типа данных вложенного списка и библиотеки numpy.
- Библиотека Python Numpy помогает работать с массивами. Numpy обрабатывает массив немного быстрее, чем список.
- Матричная операция, которую можно выполнить, это сложение, вычитание, умножение, транспонирование, чтение строк, столбцов матрицы, разрезание матрицы и т.
 д.
д. - Чтобы добавить две матрицы, вы можете использовать numpy.array() и добавить их с помощью оператора (+).
- Чтобы умножить их, вы можете использовать метод numpy dot(). Numpy.dot() — это точечный продукт матриц M1 и M2. Numpy.dot() обрабатывает двумерные массивы и выполняет умножение матриц.
- Транспонирование матрицы вычисляется путем преобразования строк в столбцы и столбцов в строки. Функцию transpose() из Numpy можно использовать для вычисления транспонирования матрицы.
- Разрезание матрицы вернет вам элементы на основе заданного начального/конечного индекса.
Инициализировать матрицу в Python — GeeksforGeeks
Существует много способов объявить двумерный массив с заданным количеством строк и столбцов. Давайте посмотрим на некоторые из них, а также на небольшие, но хитрые уловы, которые их сопровождают.
: Мы можем сделать это, используя понимание списка, функцию конкатенации оператора * и несколько других способов.
Method 0: 2 list comprehensions
Python3
|
Выход
матрица размерности 3 x 2 равна [[0, 0], [0, 0], [0, 0]] модифицированная матрица [[1, 2], [3, 4], [5, 6]] адрес (мат [0] [0]) = 11094304, адрес (мат [0] [1]) = 11094336 адрес (мат [1] [0]) = 11094368, адрес (мат [1] [1]) = 11094400 адрес (мат [2] [0]) = 11094432, адрес (мат [2] [1]) = 11094464
Метод 1: 1 понимание списка внутри и 1 операция объединения снаружи0062 = 3
cols = 2
mat = [[ 0 for _ in range (cols )]] * rows
print (f 'matrix with dimension {rows} x {cols} is {mat}' )
mat[ 0 ][ 0 ], mat[ 0 ][ 1 ] = 1 , 2
mat[ 1 ][ 0 ], MAT [ 1 ] [ 1 ] = 3 , 4 7662 , 4 7662 , 4 7662 . 
], матовый[ 2 ] [ 1 ] = 5 , 6
Печать (F 'Modied . print (f 'addr(mat[0][0]) = {id(mat[0][0])}, addr(mat[0][1]) = {id(mat[0] [1])}' )
print (f 'addr(mat[1][0]) = {id(mat[1][0])}, addr(mat[1 ][1]) = {id(mat[1][1])}' )
print (f 'addr(mat[2][0]) = {id(mat[2][0])}, addr(mat[2][1]) = {id(mat[2][1])}' )
Выходная
матрица размерностью 3 x 2 равна [[0, 0], [0, 0], [0 , 0]] модифицированная матрица [[5, 6], [5, 6], [5, 6]] адрес (мат [0] [0]) = 11094432, адрес (мат [0] [1]) = 11094464 адрес (мат [1] [0]) = 11094432, адрес (мат [1] [1]) = 11094464 адрес (мат [2] [0]) = 11094432, адрес (мат [2] [1]) = 11094464
Method 2: 1 list comprehension outside and 1 concatenation operation inside
Python3
968) [ 0 ], mat[ 0 ][ 1 ] = 1 , 2 161 161 161 161 161 2 |
Выход
матрица размером 3 x 2 [[ 0, 0], [0, 0], [0, 0]] модифицированная матрица [[1, 2], [3, 4], [5, 6]] адрес (мат [0] [0]) = 11094304, адрес(мат[0][1]) = 11094336 адрес (мат [1] [0]) = 11094368, адрес (мат [1] [1]) = 11094400 адрес (мат [2] [0]) = 11094432, адрес (мат [2] [1]) = 11094464
Method 3: 2 concatenation operations
Python3
|
Выход
матрица размерности 3 х 2 равно [[0, 0], [0, 0], [0, 0]] модифицированная матрица [[5, 6], [5, 6], [5, 6]] адрес (мат [0] [0]) = 11094432, адрес(мат[0][1]) = 11094464 адрес (мат [1] [0]) = 11094432, адрес (мат [1] [1]) = 11094464 адрес (мат [2] [0]) = 11094432, адрес (мат [2] [1]) = 11094464
Здесь мы видим, что результаты Метода 1 и Метода 3 *неожиданны*.
Мы ожидали, что все строки в мате будут разными после того, как мы присвоим им 1,2,3,4,5,6 соответственно. Но в Method1 и Method3 все они равны [5,6]. Это показывает, что, по сути, mat[0],mat[1] и mat[2] ссылаются на одну и ту же память, что можно увидеть, проверив их адреса с помощью функции id в python. 93 возможности организации понимания списка и оператора конкатенации. Это упражнение я оставляю читателю для выполнения.
Если вы работаете с numpy, мы можем сделать это, используя метод изменения формы.
Python3
|
Создание матрицы в Python — Java2Blog
Содержание
- Использование списков для создания матрицы в Python
- Использование вложенных списков для создания матрицы
- Использование цикла for для создания матрицы
- Использование массивов numpy для создания матрицы в Python
- Использование функции numpy.array() для создания матрицы в Python
- Использование функции numpy.matrix() для создания матрицы в Python
- Использование функции numpy.reshape() для создания матрицы в Python
- Использование функции numpy.append() для создания матрицы в Python
В мире программирования матрицы представлены в виде двумерных массивов, используемых для представления данных в строках и столбцах. Они используются в различных математических и статистических операциях и сохраняют свою форму. Матрица с равным количеством строк и столбцов называется квадратной матрицей.
Они используются в различных математических и статистических операциях и сохраняют свою форму. Матрица с равным количеством строк и столбцов называется квадратной матрицей.
Чтобы создать матрицу в Python, мы можем использовать массивы или списки numpy . В этой статье мы обсудим, как создать матрицу в Python.
Использование списков для создания матрицы в Python
Список также хранит набор элементов в определенных позициях. Список может хранить элементы разных типов в одном списке, и математические операции нельзя применять непосредственно к списку.
Мы можем использовать его для создания матрицы в Python.
Использование вложенных списков для создания матрицы
Вложенный список — это список внутри списка, который можно использовать для создания матрицы в Python.
Ниже показан очень простой пример.
m = [[4,1,2],[7,5,3],[9,6,9]] для i в m: print(i) 9000 |
Выход:
Выход
[4, 1, 2] [7, 5, 3] [9, 1, 2] [7, 5, 3] [9, 1, 2] [7, 5, 3], 6 , 9 ]
|
В приведенном выше примере мы создали простой вложенный список, представляющий матрицу.
Обратите внимание, что мы не распечатывали список напрямую. Это сделано потому, что список будет напечатан в одной строке. Вот почему мы перебираем каждую строку по отдельности. Мы также можем сделать это более аккуратно с помощью функции join() .
См. код ниже.
м = [[4,1,2],[7,5,3],[9,6,9]] for i in m: print(' '.join(str(i)))
|
Output:
output
[ 4 , 1 , 2 ] [ 7 , 5 , 3 ] [ 9 , 6 , 9 ]
|
m = [[4,8,9] для i в диапазоне (3)] для i в m: (я)))
|
Output:
output
[ 4 , 8 , 9 ] [ 4 , 8 , 9 ] [ 4 , 8 , 9 ]
|
Этот метод берет один список и преобразует его в матрицу требуемой формы.
Существует еще один способ использования цикла для для создания матрицы в Python.
Например,
1 2 3 4 5 6 7 8 10 0003 11 | 9000 2 | для i в диапазоне (0,3): для j в диапазоне (0,3): lst. m.append(lst) 90 lst = 90 002 0 [0 002] в m:print(' '.join(str(i)))
|
Выход:
Выход
[0, 0, 0] [0, 0, 0] [0, 0, 0] [0, 0, 0] [0, 0, 0] [0, 0, 0] . |
В приведенном выше примере
- Сначала мы инициализировали два пустых списка. Один будет действовать как строка, а другой — как окончательная матрица.
- Запускаем вложенный цикл. Внутренний цикл добавляет элемент в список
lst. - Во внешнем цикле
lstдобавляется к матричному спискуmв виде строки. - Затем мы инициализируем
lstкак пустой список, и цикл повторяется снова для следующей строки.
Этот метод очень удобен, если мы хотим получить ввод от пользователя для каждого элемента в списке. Для этого нам нужно просто запросить ввод во внутреннем цикле перед добавлением элемента в список
Для этого нам нужно просто запросить ввод во внутреннем цикле перед добавлением элемента в список lst .
Окончательный список, рассмотренный в приведенных выше примерах, может быть напрямую преобразован в массив numpy с использованием функции numpy.array() или numpy.matrix() . Эти методы будут рассмотрены ниже.
Использование массивов
numpy для создания матрицы в Python Массив numpy используется для хранения набора элементов одного типа. Однако мы можем применять математические операции непосредственно к массиву, и они могут эффективно хранить более длинную последовательность данных. Вот почему считается лучшим подходом использовать numpy массивы для матриц в Python.
Давайте обсудим различные методы создания матрицы в Python с использованием массивов numpy .
Использование функции
numpy.array() для создания матрицы в Python Мы можем создать двумерный массив numpy с помощью функции numpy. в Python. array()
array()
Например,
1 2 3 4 5 6 |
импортировать numpy как np m = np.array([[4,1,2],[7,5,3],[9,6,9]]) print("Матрица : \n", m) print("Dimensions: \n", m.shape)
|
Output:
output
1 2 3 4 5 6 7 8 |
Матрица: [[4 1 2] [7 5 3] [9 6 9]] Размеры: (3, 3)
|
В приведенном выше примере мы создали простую матрицу на Python. Мы проверили это, отобразив форму матрицы, которая показывает, что это двумерный массив с 3 столбцами и 3 строками.
Использование функции
numpy. matrix()
matrix() для создания матрицы в Python Функция numpy.matrix() используется для возврата двумерного массива. Работает аналогично numpy.array() функция, обсуждавшаяся ранее.
Например,
1 2 3 4 5 6 | Импорт Numpy As NP | . ,2],[7,5,3],[9,6,9]]) print("Матрица: \n", m) print("Размеры: \n", m.shape)
|
Вывод:
вывод
1 2 3 4 5 6 7 8 | MATRIX: | [40003 9062 [4 1000 2. ]
Использование
Numpy. Reshape ()
Reshape () Функция для создания матрицы в Python 9142 111111111111111111111111111111111111111111111111111111111111111111111111111111111. . () также можно использовать для создания матрицы в Python. Эту функцию можно использовать для изменения формы массива. Мы можем использовать его, чтобы изменить форму одномерного массива на двумерный массив без изменения его элементов.
См. приведенный ниже код.
1 2 3 4 5 6 | Импорт Numpy as NP M = NP.Array (4,1,1,1,1,1,1,1,10002 5,3,9,6,9]]).reshape(3,3) print("Матрица: \n", m) print("Размеры: \n", m.shape)
|
Выход:
Выход
1 2 3 4 5 6 7 8 | Матрикс: [[4 1 2] [7 5 3] [9 [9 2] [7 5 3] [9 [[4 1 2] [7 5 3] [9 [[4 1 2] [7 5 3] ]] Размеры: (3, 3)
|
Давайте обсудим, что произошло в приведенном выше примере.
- У нас был одномерный массив, состоящий всего из девяти элементов.
- Функция
reshape()изменила это на двумерный массив с формой(3,3). - Все элементы были расположены в матрице с 3 строками и 3 столбцами.
Обратите внимание, что мы должны быть осторожны с количеством элементов в массиве перед изменением его формы. Поскольку матрица формы (3,3) будет иметь 9 элементов, приведенный выше пример не будет работать, если общее количество элементов в одномерном массиве не равно 9.
Использование функции
numpy.append() для создания матрицы в Python Мы можем использовать numpy.append() 9Функция 0062 для создания матрицы в Python из существующего массива. Мы достигаем этого путем добавления строк в существующий массив.
См. код ниже.
1 2 3 4 5 6 7 | Импорт Numpy As NP M = NP. новый = np.append(m,[[7,5,3],[9,6,9]], ось = 0) print("Матрица: \n", новый) print("Dimensions: \n", new.shape)
|
Output:
output
1 2 3 4 5 6 7 8 | Матрица: [[4 1 2] [7 5 3] [9 6 9]] Размеры: (3, 3) |
В приведенном выше примере
- У нас был одномерный массив с именем
m, содержащий в общей сложности три элемента. - Мы использовали функцию
append(), чтобы добавить еще две строки в существующий массив и создать новый массив с именемnew. - Параметр
осиуказан как0в функцииappend(), поскольку мы хотим добавить элементы в виде строк.




 shape[1]):
if min > arr[i][j]:
min = arr[i][j]
print("Минимальный элемент:", min) # Выведет "Минимальный элемент: 2"
shape[1]):
if min > arr[i][j]:
min = arr[i][j]
print("Минимальный элемент:", min) # Выведет "Минимальный элемент: 2" array([[ 10, 20, 30],[ 40, 50, 60]])
print(input_arr)
array([[ 10, 20, 30],[ 40, 50, 60]])
print(input_arr)
 array([numpy.arange(10,15), numpy.arange(15,20)]))
array([numpy.arange(10,15), numpy.arange(15,20)]))

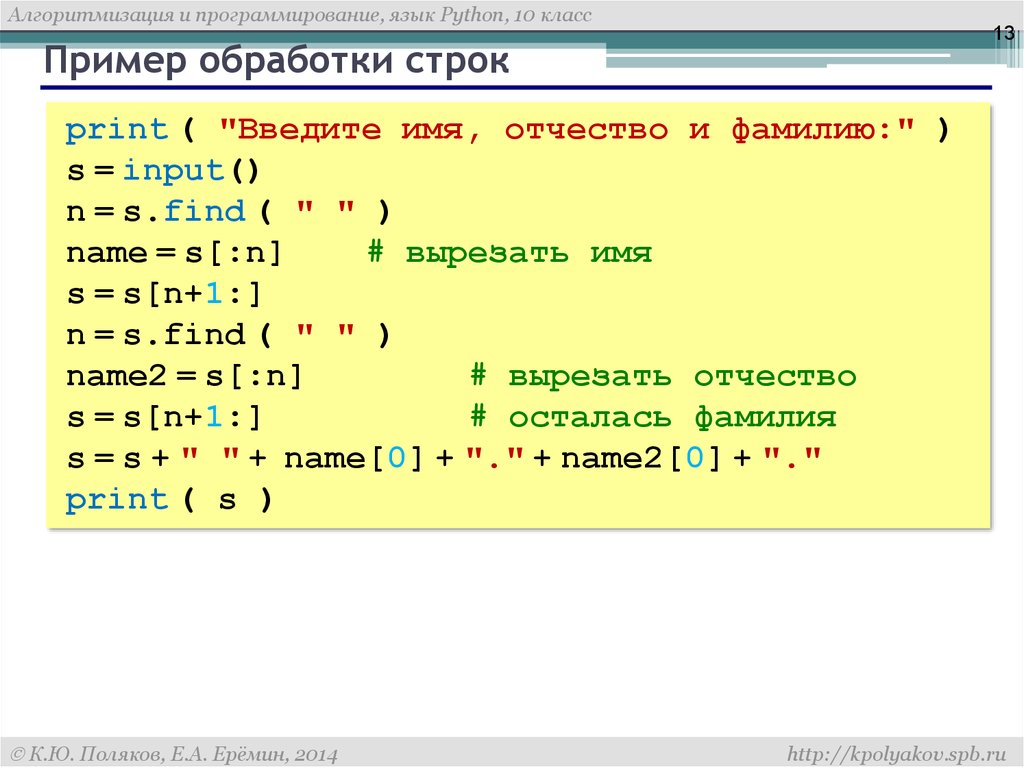 matrix([[11, 22], [33, 44]])
ar2 = p.matrix([[55, 66], [77, 88]])
res = p.matrix(p.zeros((2,2)))
print('Matrix ar1 :\n', ar1)
print('\nMatrix ar2 :\n', ar2)
res = ar1 + ar2 # using '+' operator
print('\nResult :\n', res)
matrix([[11, 22], [33, 44]])
ar2 = p.matrix([[55, 66], [77, 88]])
res = p.matrix(p.zeros((2,2)))
print('Matrix ar1 :\n', ar1)
print('\nMatrix ar2 :\n', ar2)
res = ar1 + ar2 # using '+' operator
print('\nResult :\n', res)
 T
print(res)
print('\nDimensions of the Matrix A after performing the Transpose Operation: ',res.shape)
T
print(res)
print('\nDimensions of the Matrix A after performing the Transpose Operation: ',res.shape)
 matrix() method")
res = p.multiply(matA,matB)
print(res)
matrix() method")
res = p.multiply(matA,matB)
print(res)
 matrix([[10, 20], [30, 40]])
print('MatrixA:\n', matA)
matB = p.matrix('[10,20;30,40]', dtype=p.int32) # Setting the data-type to int
print('\nMatrixB:\n', matB)
print("Matrix multplication using numpy.matmul() method")
res = p.matmul(matA,matB)
print(res)
matrix([[10, 20], [30, 40]])
print('MatrixA:\n', matA)
matB = p.matrix('[10,20;30,40]', dtype=p.int32) # Setting the data-type to int
print('\nMatrixB:\n', matB)
print("Matrix multplication using numpy.matmul() method")
res = p.matmul(matA,matB)
print(res)
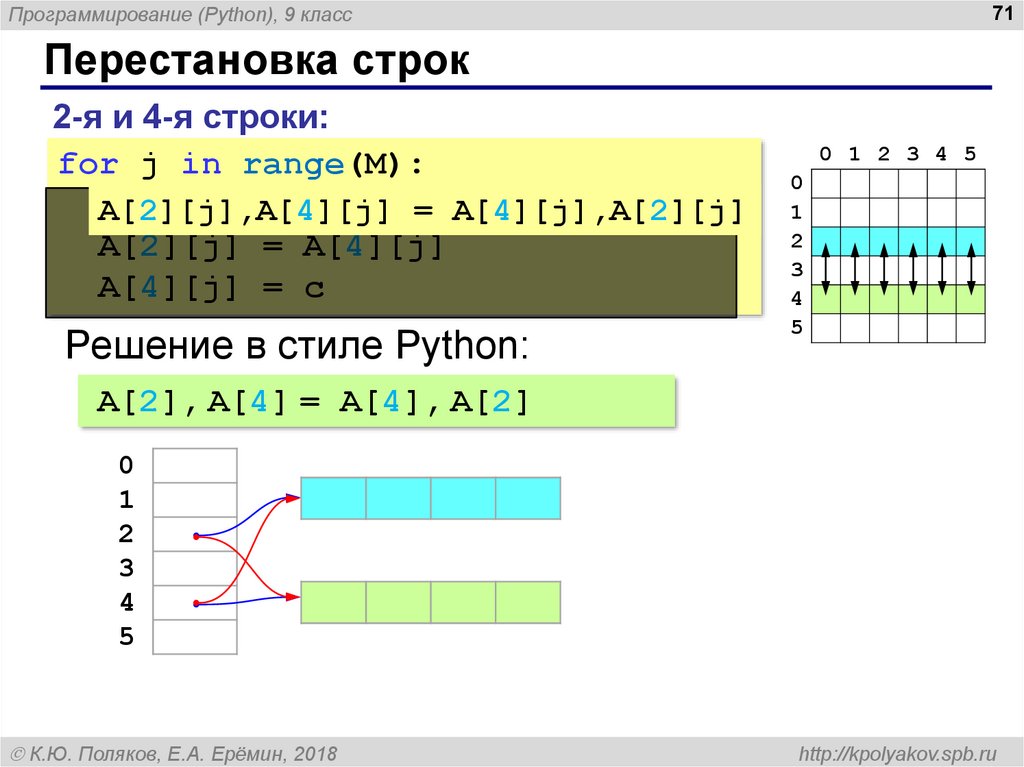 zeros(10)
Z[4] = 1
print(Z)
zeros(10)
Z[4] = 1
print(Z) ones((10,10))
Z[1:-1,1:-1] = 0
ones((10,10))
Z[1:-1,1:-1] = 0 zeros((5,5))
Z += np.arange(5)
print(Z)
zeros((5,5))
Z += np.arange(5)
print(Z)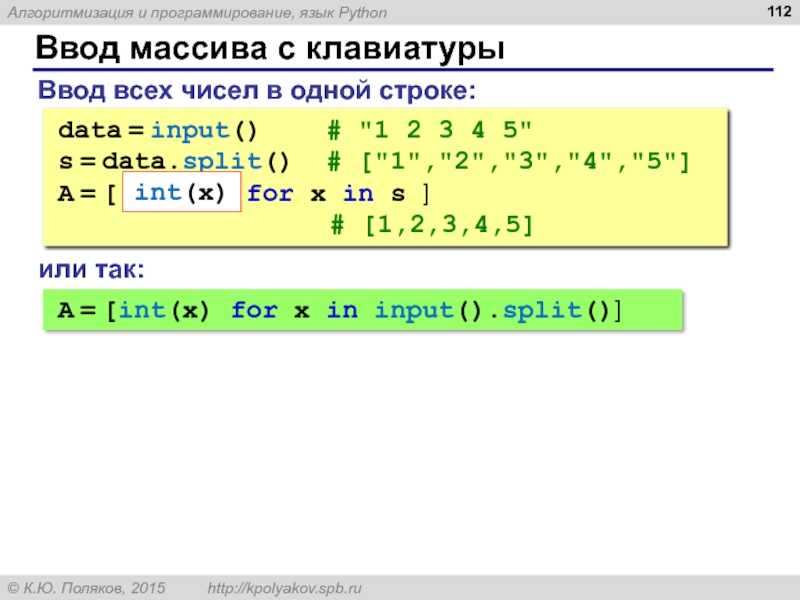 random.random(10)
Z[Z.argmax()] = 0
print(Z)
random.random(10)
Z[Z.argmax()] = 0
print(Z) arange(100)
v = np.random.uniform(0,100)
index = (np.abs(Z-v)).argmin()
print(Z[index])
arange(100)
v = np.random.uniform(0,100)
index = (np.abs(Z-v)).argmin()
print(Z[index]) arange(9).reshape(3,3)
for index, value in np.ndenumerate(Z):
print(index, value)
for index in np.ndindex(Z.shape):
print(index, Z[index])
arange(9).reshape(3,3)
for index, value in np.ndenumerate(Z):
print(index, value)
for index in np.ndindex(Z.shape):
print(index, Z[index]) ones(10)
I = np.random.randint(0,len(Z),20)
Z += np.bincount(I, minlength=len(Z))
print(Z)
ones(10)
I = np.random.randint(0,len(Z),20)
Z += np.bincount(I, minlength=len(Z))
print(Z)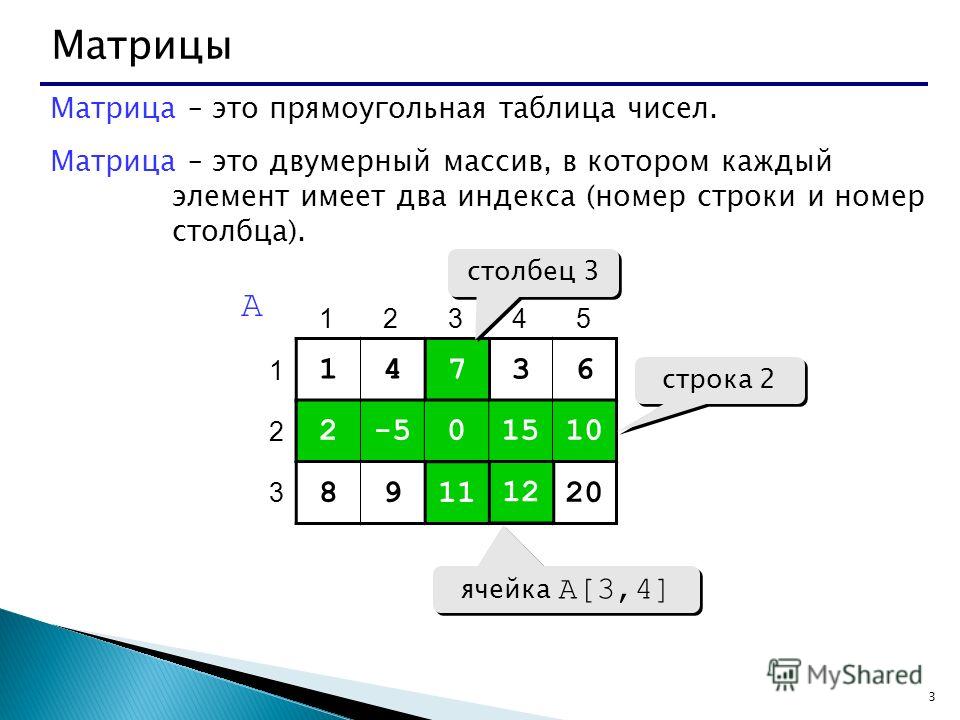 arange(25).reshape(5,5)
A[[0,1]] = A[[1,0]]
print(A)
arange(25).reshape(5,5)
A[[0,1]] = A[[1,0]]
print(A) lib import stride_tricks
def rolling(a, window):
shape = (a.size - window + 1, window)
strides = (a.itemsize, a.itemsize)
return stride_tricks.as_strided(a, shape=shape, strides=strides)
Z = rolling(np.arange(10), 3)
print(Z)
lib import stride_tricks
def rolling(a, window):
shape = (a.size - window + 1, window)
strides = (a.itemsize, a.itemsize)
return stride_tricks.as_strided(a, shape=shape, strides=strides)
Z = rolling(np.arange(10), 3)
print(Z)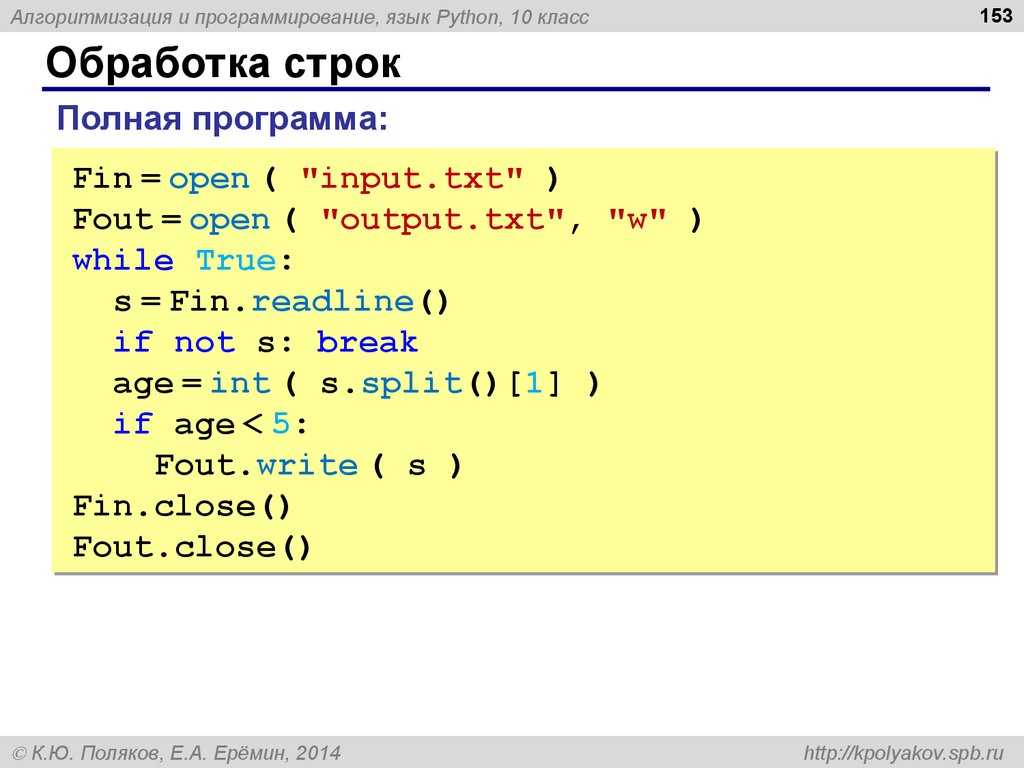 random.randint(0,10,50)
print(np.bincount(Z).argmax())
random.randint(0,10,50)
print(np.bincount(Z).argmax()) ones((p,n,1))
S = np.tensordot(M, V, axes=[[0, 2], [0, 1]])
print(S)
# It works, because:
# M is (p,n,n)
# V is (p,n,1)
# Thus, summing over the paired axes 0 and 0 (of M and V independently),
# and 2 and 1, to remain with a (n,1) vector.
ones((p,n,1))
S = np.tensordot(M, V, axes=[[0, 2], [0, 1]])
print(S)
# It works, because:
# M is (p,n,n)
# V is (p,n,1)
# Thus, summing over the paired axes 0 and 0 (of M and V independently),
# and 2 and 1, to remain with a (n,1) vector.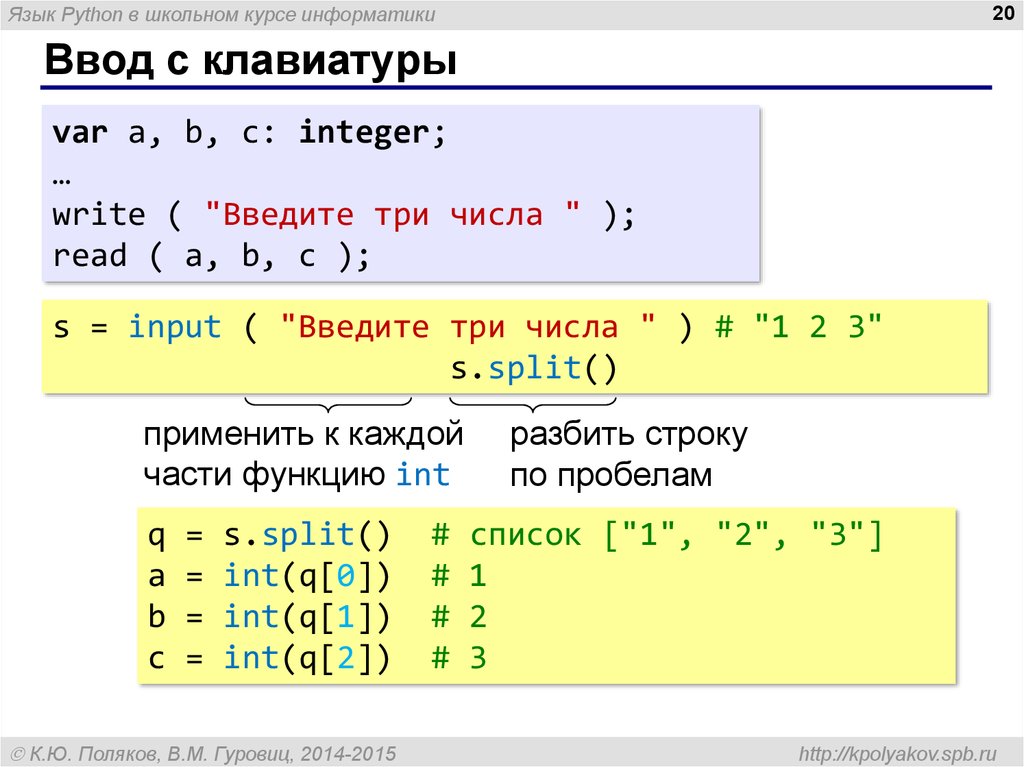 arange(10000)
np.random.shuffle(Z)
n = 5
print (Z[np.argpartition(-Z,n)[:n]])
arange(10000)
np.random.shuffle(Z)
n = 5
print (Z[np.argpartition(-Z,n)[:n]]) array([0, 1, 2, 3, 15, 16, 32, 64, 128], dtype=np.uint8)
print(np.unpackbits(I[:, np.newaxis], axis=1))
array([0, 1, 2, 3, 15, 16, 32, 64, 128], dtype=np.uint8)
print(np.unpackbits(I[:, np.newaxis], axis=1)) Создание массивов функцией array()
Создание массивов функцией array() Конечно, мы можем все это сделать
также через функцию array, используя механизм генерации списков,
например, так:
Конечно, мы можем все это сделать
также через функцию array, используя механизм генерации списков,
например, так:

 Использовать их
достаточно просто. Например, так:
Использовать их
достаточно просто. Например, так:
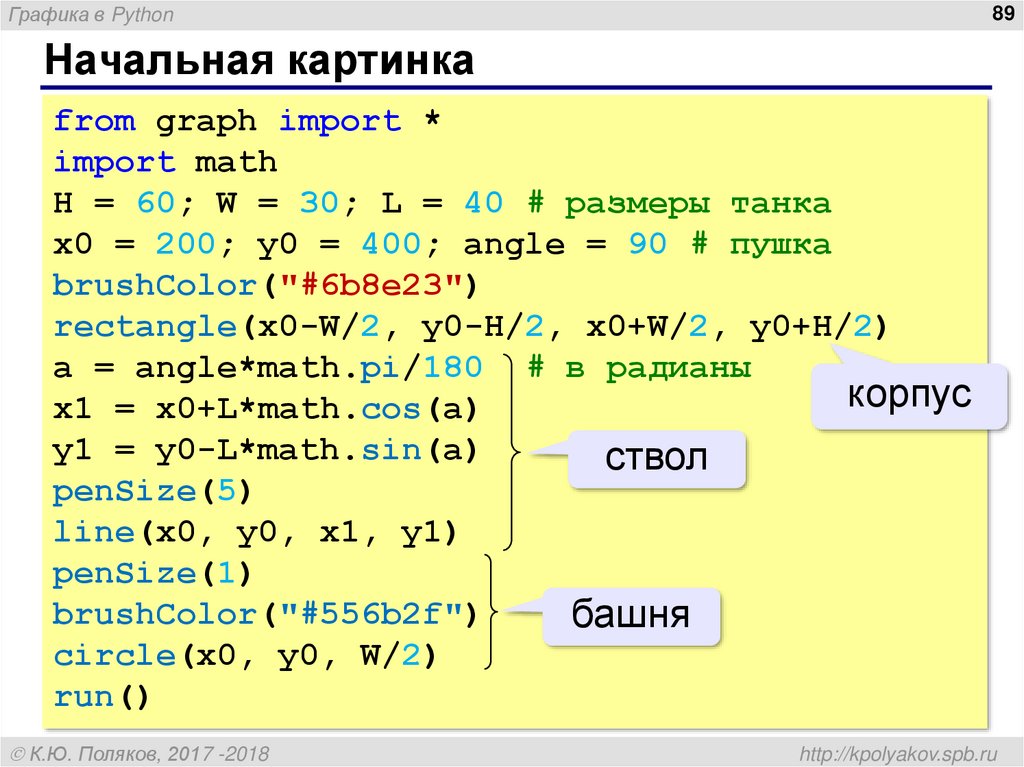

 mat('1, 2, 3, 4') # то же самое: создает матрицу 1x4 из строки
np.mat('1 2; 3 4') # возвращает матрицу 2x2
mat('1, 2, 3, 4') # то же самое: создает матрицу 1x4 из строки
np.mat('1 2; 3 4') # возвращает матрицу 2x2 Например:
Например:
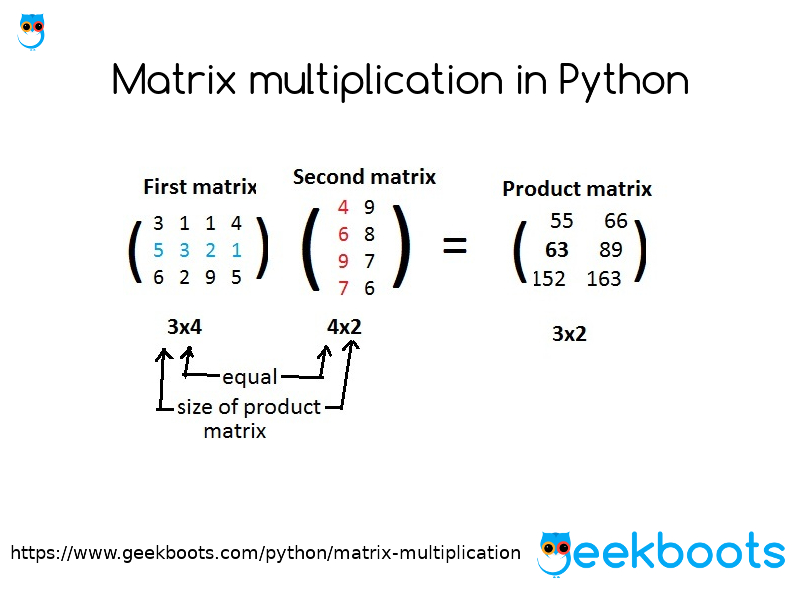 vander([1,2,3]) # матрица Вандермонда 3x3
vander([1,2,3]) # матрица Вандермонда 3x3
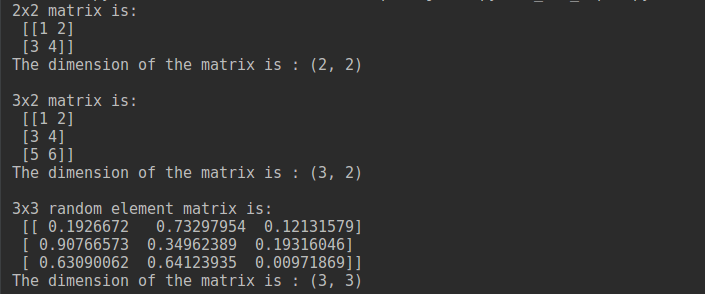
 А здесь мы сразу получаем готовый
массив значений функции косинуса. Это работает гораздо быстрее циклов в Python.
А здесь мы сразу получаем готовый
массив значений функции косинуса. Это работает гораздо быстрее циклов в Python.

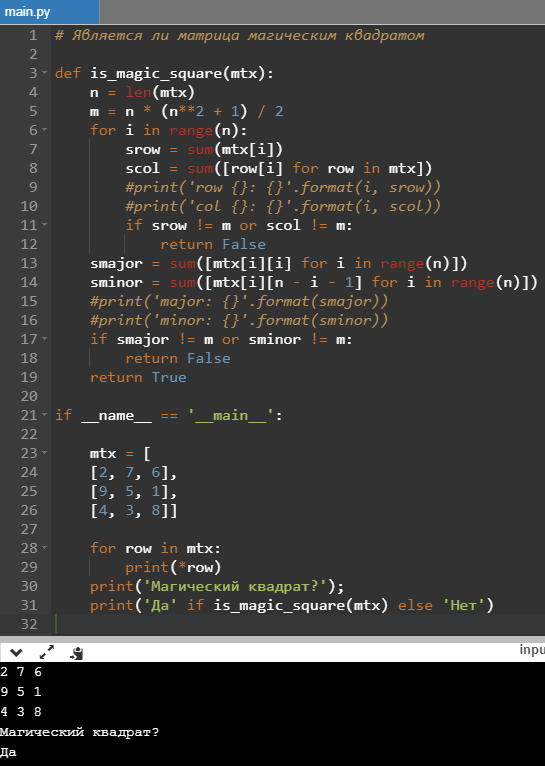

 copy(a)
copy(a) fromfunction(lambda x, y: x*100+y, (2, 2))
fromfunction(lambda x, y: x*100+y, (2, 2)) fromstring('1, 2, 3', dtype='int16', sep= ',')
fromstring('1, 2, 3', dtype='int16', sep= ',') Базовые математические операции над массивами | NumPy уроки
Базовые математические операции над массивами | NumPy уроки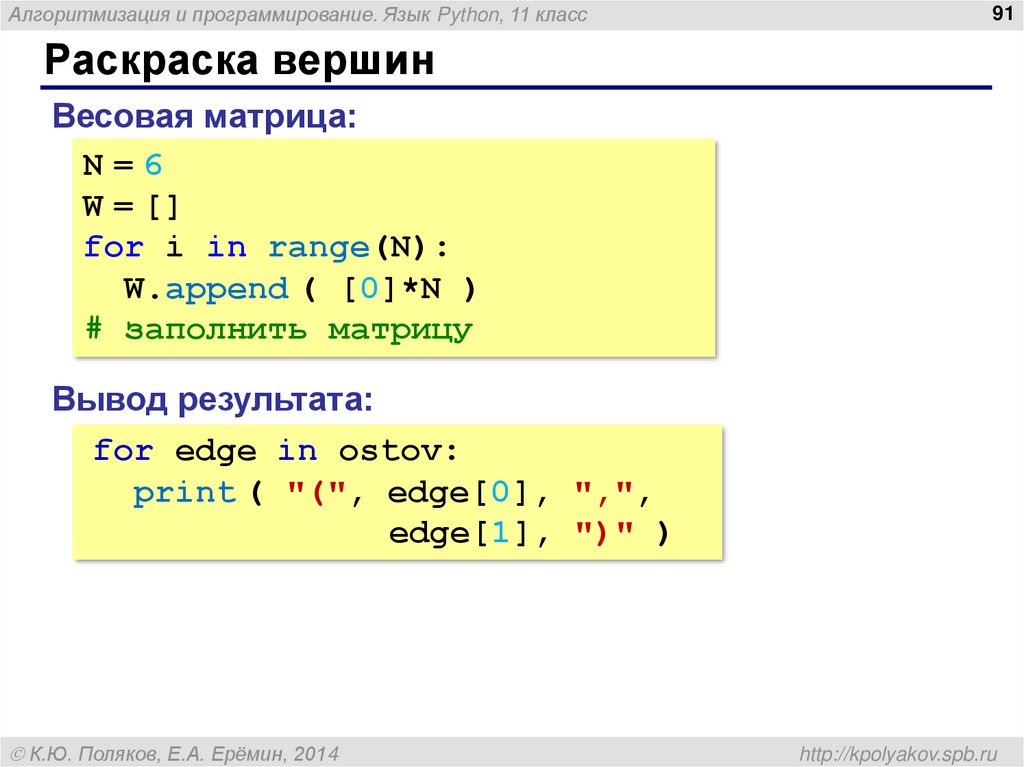 массив ([1, 2, 3])
print(a) # Вывод: [1, 2, 3]
print(type(a)) # Вывод:
массив ([1, 2, 3])
print(a) # Вывод: [1, 2, 3]
print(type(a)) # Вывод:  int32 ) // указание dtype
print(ones_array) # Вывод: [[1 1 1 1 1]]
int32 ) // указание dtype
print(ones_array) # Вывод: [[1 1 1 1 1]]
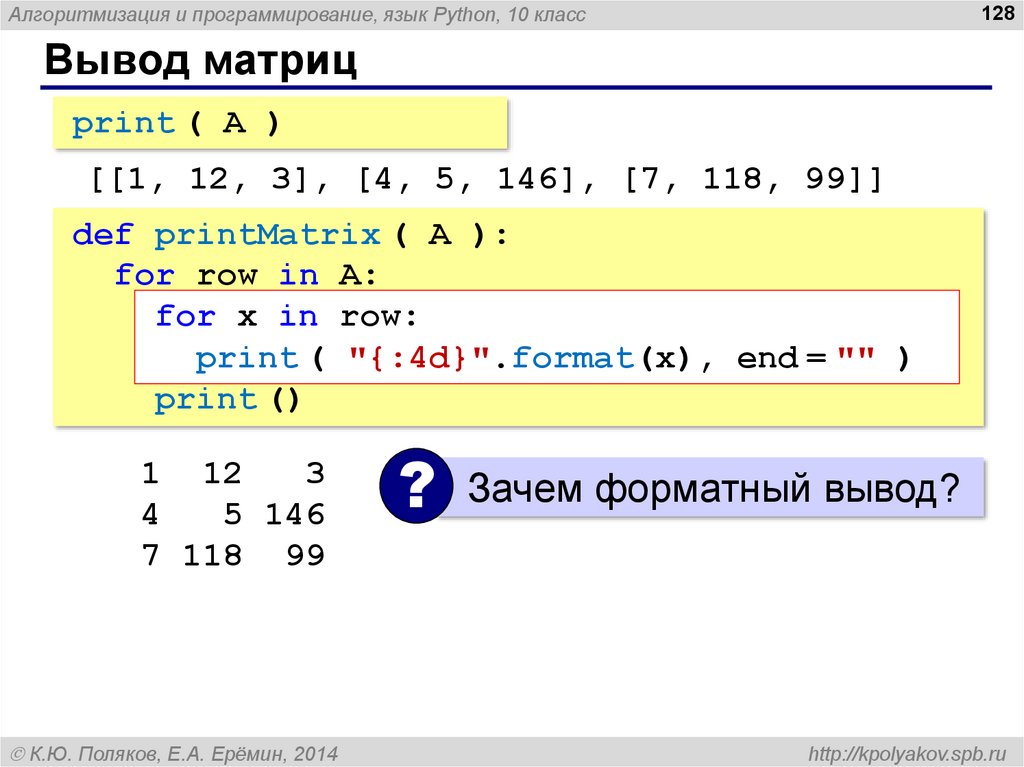 массив([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[0] =", A[0]) # Первая строка
print("A[2] =", A[2]) # Третья строка
print("A[-1] =", A[-1]) # Последняя строка (в данном случае 3-я строка)
массив([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[0] =", A[0]) # Первая строка
print("A[2] =", A[2]) # Третья строка
print("A[-1] =", A[-1]) # Последняя строка (в данном случае 3-я строка) 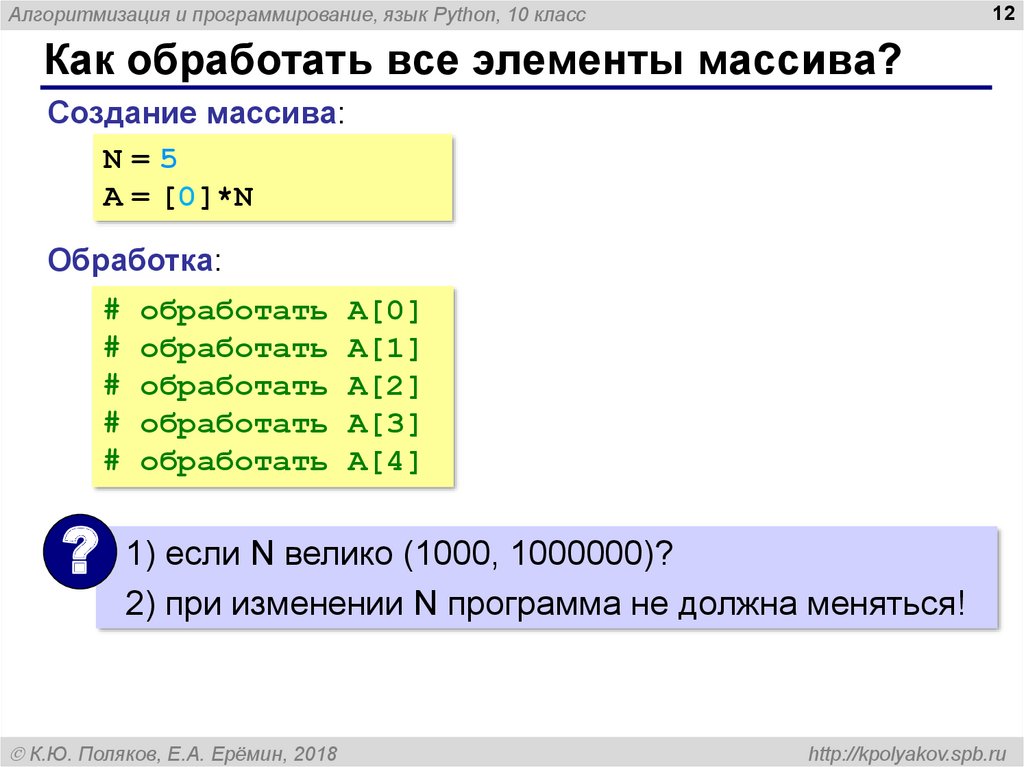
 Команда для установки NumPy — «pip install NumPy» .
Команда для установки NumPy — «pip install NumPy» .