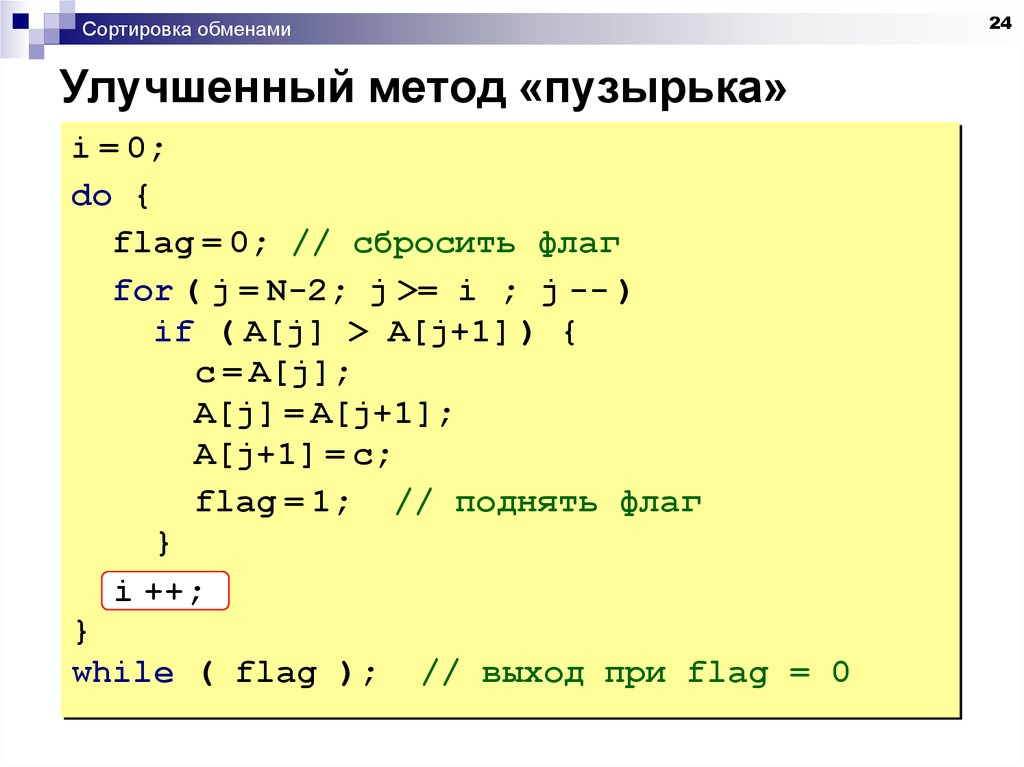
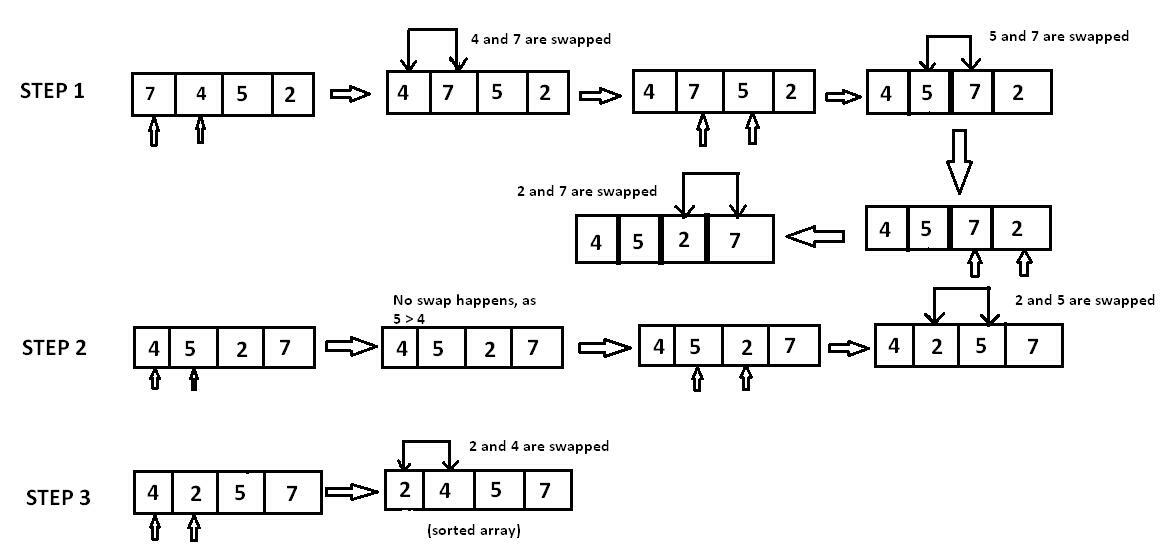
java — метод пузырька где ошибка?
Вопрос задан
Изменён 6 лет 6 месяцев назад
Просмотрен 136 раз
public class BubbleSorter {
public static void sort (int[] arr) {
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length ; j++) {
if (arr[j] > arr[j + 1]) {
int t = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = t;
}
}
}
}
}
1
В условии второго цикла измени for (int j = 0; j < arr.length; j++) на for (int j = 0; j < arr.. Потому что при j < arr.length идет выход за пределы массива.
Ошибка в том, что при обращении к j + 1 элементу массива arr, Вы выходите за его пределы.
Пусть, например, arr.length == 10, тогда при j = 9 Вы попытаетесь обратиться к элементу arr[9 + 1] = arr[10], однако последний элемент массива arr – это arr[9].
ArrayIndexOutOfBoundsException возникает из-за выхода за пределы массива, у вас во втором цикле, где на последней итерации arr[j + 1] будет arr[arr.lenght], то есть ошибка, вышли за предел arr.
Измените вложенный цикл
for (int j = 0; j < arr.length ; j++)
на этот
for (int j = 0; j < arr.length - i - 1 ; j++)
Решили проблему с выходом за пределы массива, теперь на последней итерации
arr[j + 1]будетarr[arr.
lenght - 1]Не делаем лишних проверок с уже отсортированными элементами(для каждого нового i, массив, который нужно отсортировать, меньше на 1)
lenght - 1]Зарегистрируйтесь или войдите
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Основные виды сортировок и примеры их реализации
На собеседованиях будущим стажёрам-разработчикам дают задания на знание структур данных и алгоритмов — в том числе сортировок.
Академия Яндекса и соавтор специализации «Искусство разработки на современном C++» Илья Шишков составили список для подготовки с методами сортировки, примерами их реализации и гифками, чтобы лучше понять, как они работают.
Пузырьковая сортировка и её улучшения
Сортировка пузырьком
Сортировка пузырьком — один из самых известных алгоритмов сортировки. Здесь нужно последовательно сравнивать значения соседних элементов и менять числа местами, если предыдущее оказывается больше последующего. Таким образом элементы с большими значениями оказываются в конце списка, а с меньшими остаются в начале.
Этот алгоритм считается учебным и почти не применяется на практике из-за низкой эффективности: он медленно работает на тестах, в которых маленькие элементы (их называют «черепахами») стоят в конце массива. Однако на нём основаны многие другие методы, например, шейкерная сортировка и сортировка расчёской.
Сортировка перемешиванием (шейкерная сортировка)
Шейкерная сортировка отличается от пузырьковой тем, что она двунаправленная: алгоритм перемещается не строго слева направо, а сначала слева направо, затем справа налево.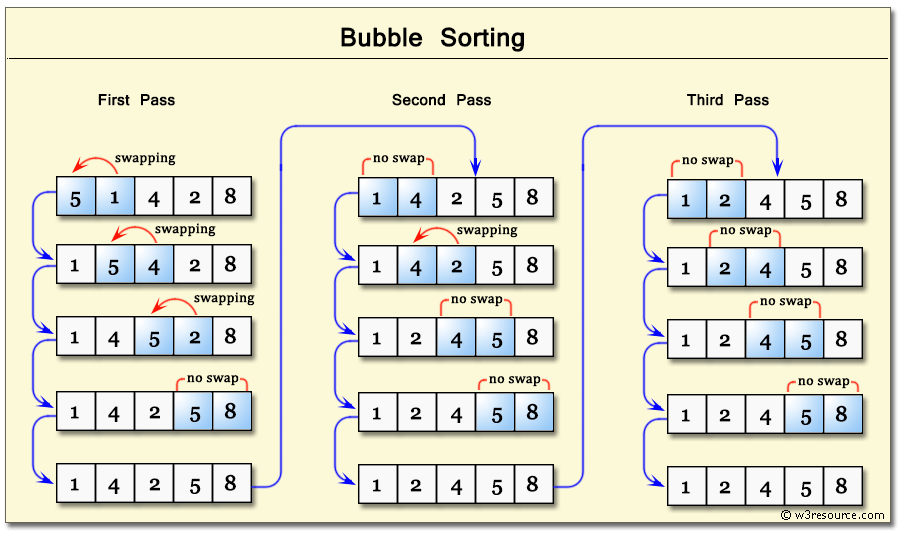
Сортировка расчёской
Сортировка расчёской — улучшение сортировки пузырьком. Её идея состоит в том, чтобы «устранить» элементы с небольшими значения в конце массива, которые замедляют работу алгоритма. Если при пузырьковой и шейкерной сортировках при переборе массива сравниваются соседние элементы, то при «расчёсывании» сначала берётся достаточно большое расстояние между сравниваемыми значениями, а потом оно сужается вплоть до минимального.
Первоначальный разрыв нужно выбирать не случайным образом, а с учётом специальной величины — фактора уменьшения, оптимальное значение которого равно 1,247. Сначала расстояние между элементами будет равняться размеру массива, поделённому на 1,247; на каждом последующем шаге расстояние будет снова делиться на фактор уменьшения — и так до окончания работы алгоритма.
Простые сортировки
Сортировка вставками
При сортировке вставками массив постепенно перебирается слева направо. При этом каждый последующий элемент размещается так, чтобы он оказался между ближайшими элементами с минимальным и максимальным значением.
Сортировка выбором
Сначала нужно рассмотреть подмножество массива и найти в нём максимум (или минимум). Затем выбранное значение меняют местами со значением первого неотсортированного элемента. Этот шаг нужно повторять до тех пор, пока в массиве не закончатся неотсортированные подмассивы.
Эффективные сортировки
Быстрая сортировка
Этот алгоритм состоит из трёх шагов. Сначала из массива нужно выбрать один элемент — его обычно называют опорным. Затем другие элементы в массиве перераспределяют так, чтобы элементы меньше опорного оказались до него, а большие или равные — после. А дальше рекурсивно применяют первые два шага к подмассивам справа и слева от опорного значения.
Быструю сортировку изобрели в 1960 году для машинного перевода: тогда словари хранились на магнитных лентах, а сортировка слов обрабатываемого текста позволяла получить переводы за один прогон ленты, без перемотки назад.
Сортировка слиянием
Сортировка слиянием пригодится для таких структур данных, в которых доступ к элементам осуществляется последовательно (например, для потоков).
Здесь массив разбивается на две примерно равные части и каждая из них сортируется по отдельности. Затем два отсортированных подмассива сливаются в один.
Пирамидальная сортировка
При этой сортировке сначала строится пирамида из элементов исходного массива. Пирамида (или двоичная куча) — это способ представления элементов, при котором от каждого узла может отходить не больше двух ответвлений. А значение в родительском узле должно быть больше значений в его двух дочерних узлах.
Пирамидальная сортировка похожа на сортировку выбором, где мы сначала ищем максимальный элемент, а затем помещаем его в конец. Дальше нужно рекурсивно повторять ту же операцию для оставшихся элементов.
Пузырьковая сортировка – Алгоритм, исходный код, временная сложность 02
Часть 5. Сортировка пузырькомЧасть 6. Быстрая сортировка
Часть 7. Сортировка слиянием
Часть 8. Heapsort
Часть 9. Сортировка подсчетом Информационный бюллетень
, чтобы немедленно получать информацию о новых частях.
)
Эта статья является частью серии «Алгоритмы сортировки: Полное руководство» и…
- объясняет, как работает пузырьковая сортировка,
- представляет исходный код пузырьковой сортировки,
- объясняет, как получить его временную сложность
- , и проверяет, соответствует ли производительность собственной реализации ожидаемому поведению во время выполнения в соответствии с временной сложностью.
Исходный код всех статей этой серии можно найти в моем GitHub-репозитории.
Алгоритм пузырьковой сортировки
При пузырьковой сортировке (иногда «пузырьковой сортировке») два последовательных элемента сравниваются друг с другом и, если левый элемент больше правого, меняются местами.
Эти операции сравнения и замены выполняются слева направо для всех элементов. Поэтому после первого прохода самый большой элемент располагается крайним справа. Или лучше: самое позднее после первого прохода — возможно, он пришел туда раньше.
Вы повторяете этот процесс до тех пор, пока в одной итерации больше не будет подкачки.
Пример пузырьковой сортировки
В следующих визуализациях я показываю, как сортировать массив [6, 2, 4, 9, 3, 7] с помощью пузырьковой сортировки:
Подготовка
– и правильная, отсортированная часть. Правая часть вначале пуста:
Итерация 1
Сравниваем первые два элемента, 6 и 2, и, поскольку 6 меньше, меняем местами элементы:
Теперь сравниваем второй элемент с третьим, т. е. 6 с 4. Они тоже в неправильном порядке и поэтому меняются местами:
Сравниваем третий с четвертым элементом, т. е. 6 с 9. 6 меньше 9, поэтому нам не нужно менять местами эти два элемента.
Четвертый и пятый элементы, 9 и 3, нужно снова поменять местами:
И, наконец, пятый и шестой элементы, 9 и 7, нужно поменять местами. После этого первая итерация завершена.
9 достигло своей конечной позиции, и мы перемещаем границу между областями на одно поле влево:
В следующей итерации эта граница показывает нам, до какой позиции должны сравниваться элементы.
Кстати, граница области существует только в оптимизированной версии пузырьковой сортировки. В исходном варианте он отсутствует. Следовательно, на каждой итерации сравнение выполняется без необходимости до конца массива.
Итерация 2
Мы снова начинаем с начала массива и сравниваем 2 с 4. Они расположены в правильном порядке и их не нужно менять местами.
То же самое относится к 4 и 6.
Однако 6 и 3 нужно поменять местами, чтобы они были в правильном порядке:
6 и 7 в правильном порядке и не должны быть поменялся местами. Нам не нужно дальше сравнивать, так как 9 уже находится в отсортированной области.
Наконец, мы снова перемещаем границу области на одну позицию влево, чтобы нам больше не приходилось смотреть на два последних элемента, 7 и 9.
Итерация 3
Снова начинаем с начала массива. 2 и 4 расположены правильно друг к другу. 4 и 3 нужно поменять местами:
4 и 6 не нужно менять местами. 7 и 9 уже отсортированы.
Итак, эта итерация уже закончена, и мы перемещаем границу области влево:
Итерация 4
Начнем снова с начала массива. В несортированной области ни 2 и 3, ни 3 и 4 не нужно менять местами. Теперь все элементы отсортированы, и мы можем закончить алгоритм.
Происхождение имени
Когда мы анимируем операции замены из предыдущего примера, элементы постепенно поднимаются в свои целевые позиции — подобно пузырям, отсюда и название «Пузырьковая сортировка»:
Пузырьковая сортировка Исходный код Java
Ниже вы найдете оптимизированную реализацию пузырьковой сортировки, описанную выше.
В первой итерации самый большой элемент перемещается в крайнее правое положение. Во второй итерации второй по величине перемещается на предпоследнюю позицию. И так далее. Поэтому на каждой итерации нам приходится сравнивать на один элемент меньше, чем на предыдущей итерации.
(В примере из предыдущего раздела я представил это границей области, которая перемещается на одну позицию влево после каждой итерации.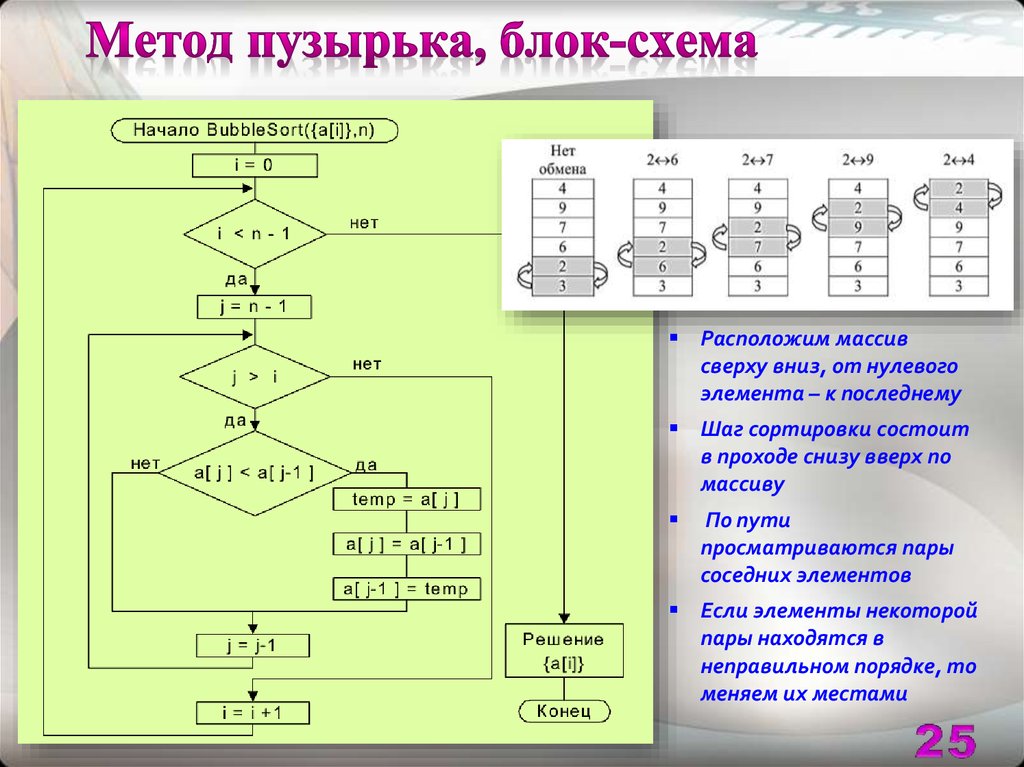
)
Поэтому во внешнем цикле мы уменьшаем значение max , начиная с elements.length - 1 , на единицу в каждой итерации.
Затем внутренний цикл сравнивает два элемента друг с другом до позиции max и меняет их местами, если левый элемент больше правого.
Если в ходе итерации не было заменено ни одного элемента (т. е. swapped равен false ), алгоритм завершается преждевременно.
открытый класс BubbleSortOpt1 { общедоступная статическая недействительная сортировка (элементы int []) { for (int max = elements.length - 1; max > 0; max--) { логическое значение заменено = ложь; for (int i = 0; i < max; i++) { int слева = элементы[i]; int справа = элементы[i + 1]; если (слева > справа) { элементы[i + 1] = слева; элементы[i] = справа; заменено = верно; } } если (!swapped) перерыв; } } } Язык кода: Java (java)
Показанный код немного отличается от класса BubbleSortOpt1 в репозитории GitHub.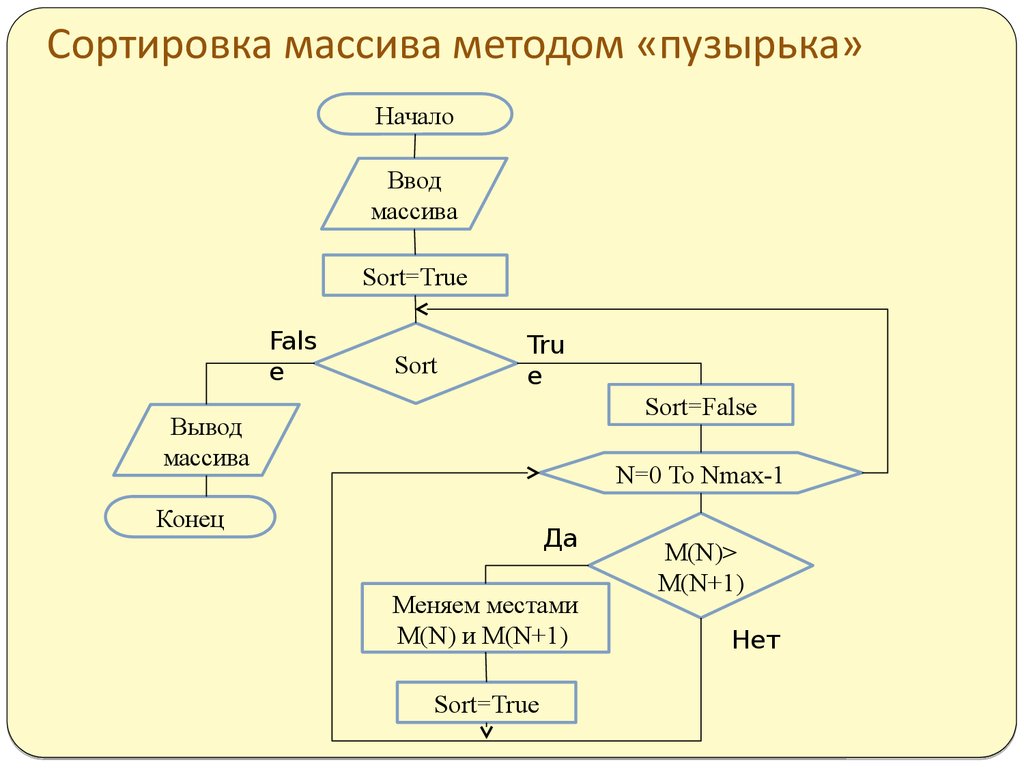
Неоптимизированный алгоритм, который сравнивает элементы до конца на каждой итерации, можно найти в классе BubbleSort.
В классе BubbleSortOpt2 вы найдете теоретически еще более оптимизированный алгоритм. После итерации n th возможно, что будут отсортированы не только последние n элементов, но и больше — в зависимости от того, как элементы были расположены изначально.
Следовательно, этот вариант не уменьшает max на 1, а после каждой итерации устанавливает max на позицию последнего замененного элемента. Однако тест CompareBubbleSorts показывает, что на практике этот вариант работает медленнее:
----- Результаты после 50 итераций ----- BubbleSort -> самый быстрый: 772,6 мс, медиана: 790,3 мс BubbleSortOpt1 -> самый быстрый: 443,2 мс, медиана: 452,7 мс BubbleSortOpt2 -> самое быстрое: 497,0 мс, медиана: 510,0 мс Язык кода: открытый текст (открытый текст)
Полный вывод тестовой программы можно найти в файле TestResults_BubbleSort_Algorithms.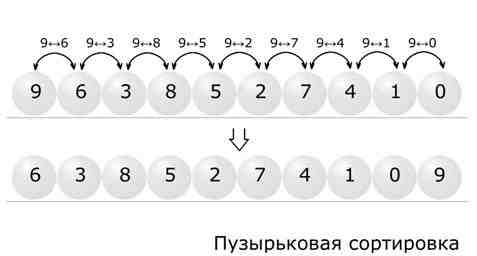
log.
Почему вторая оптимизированная версия медленнее? Я предполагаю, что это потому, что сохранение и многократное (в пределах одной итерации) обновление позиции последнего замененного элемента намного дороже, чем изменение
Время пузырьковой сортировки Сложность
Обозначим через n количество элементов, подлежащих сортировке. В приведенном выше примере n = 6 .
Два вложенных цикла предполагают, что мы имеем дело с квадратичным временем, т. е. с временной сложностью* O(n²) . Это будет иметь место, если оба цикла повторяются до значения, которое линейно растет с n .
Для пузырьковой сортировки это не так просто доказать, как для сортировки вставками или сортировки выбором.
С помощью пузырьковой сортировки мы должны исследовать лучший , худший и средний случай отдельно. Мы сделаем это в следующих подразделах.
* Я объясняю термины «временная сложность» и «большая нотация O» в этой статье, используя примеры и диаграммы.
Временная сложность в наилучшем случае
Давайте начнем с самого простого случая: если числа уже отсортированы в порядке возрастания, алгоритм на первой итерации определит, что никакие пары чисел не нужно менять местами, и немедленно прекратит работу.
Алгоритм должен выполнить n-1 сравнений; поэтому:
Временная сложность пузырьковой сортировки в наилучшем случае: O(n)
Временная сложность в наихудшем случае
Я продемонстрирую наихудший случай на примере. Предположим, мы хотим отсортировать массив по убыванию [6, 5, 4, 3, 2, 1] с помощью пузырьковой сортировки.
В первой итерации самый большой элемент, номер 6, перемещается из крайнего левого угла в крайний правый. Я пропустил пять отдельных шагов (поменяв местами пары 6/5, 6/4, 6/3, 6/2, 6/1) на рисунке:
Во второй итерации второй по величине элемент, цифра 5, перемещается из крайнего левого положения через четыре промежуточных шага на предпоследнюю позицию:
через три промежуточных шага.
В четвертой итерации число 3 перемещается – за два отдельных шага – в конечную позицию:
И, наконец, 2 и 1 меняются местами:
Итак, всего у нас есть 5 + 4 + 3 + 2 + 1 = 15 операций сравнения и обмена.
Мы также можем рассчитать это следующим образом:
Шесть элементов умножить на пять операций сравнения и обмена; делим на два, так как в среднем по всем итерациям половина элементов сравнивается и переставляется местами: :
n × (n – 1) × ½
При умножении получаем:
½ (n² – n)
Наивысшая степень числа n в этом термине n² ; поэтому:
Временная сложность пузырьковой сортировки в наихудшем случае: O(n²)
Средняя временная сложность
К сожалению, среднюю временную сложность пузырьковой сортировки нельзя — в отличие от большинства других алгоритмов сортировки — объяснить в показательный способ.
Не доказывая этого математически (это вышло бы за рамки данной статьи), можно грубо сказать, что в среднем происходит примерно вдвое меньше обменных операций, чем в худшем случае, поскольку примерно половина элементов находится в правильное положение относительно соседнего элемента.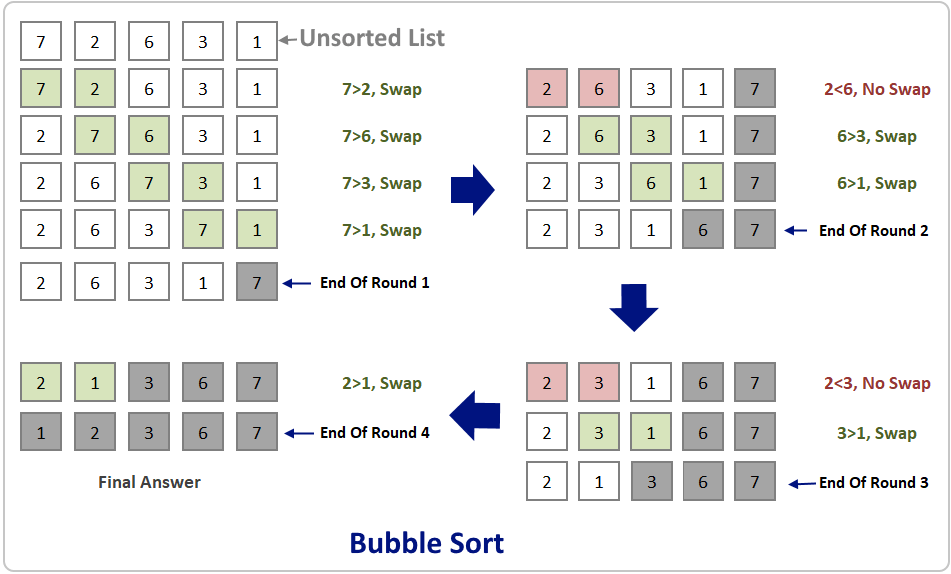
Таким образом, количество обменных операций:
¼ (n² – n)
Все становится еще сложнее с количеством операций сравнения, которое составляет (источник: эта статья в немецкой Википедии; в английской версии этого нет):
½ ( n² — n × ln(n) — (𝛾 + ln(2) — 1) × n) + O(√n)
В обоих терминах наивысшая степень n снова равна n² ; поэтому:
Средняя временная сложность случая пузырьковой сортировки: O(n²)
Время выполнения Java пузырьковой сортировки Пример
Проверим теорию тестом! В репозитории GitHub вы найдете программу UltimateTest, которая тестирует сортировку пузырьком (и все другие алгоритмы сортировки, представленные в этой серии статей) по следующим критериям:
- для размеров массивов, начиная с 1024 элементов, удваиваясь после каждой итерации. пока мы не достигнем размера массива 536 870 912 (= 2 29 ) или процесс сортировки не займет больше 20 секунд;
- для несортированных, восходящих и нисходящих предварительно отсортированных элементов;
- с двумя прогревочными раундами, чтобы дать компилятору HotSpot достаточно времени для оптимизации кода.
Вся процедура повторяется до тех пор, пока мы не прервем программу. После каждой итерации программа отображает медиану всех предыдущих результатов измерений.
Вот результат сортировки пузырьком после 50 итераций:
| n | не отсортировано | по убыванию | по возрастанию | 109309… | … | … |
|---|---|---|---|---|---|---|
| 8,192 | 61,73 мс | 35,18 мс | 0,004 мс | 16 84294,64 мс | 141,16 мс | 0,008 мс |
| 32 768 | 1272,07 мс | 566,39 мс | 0,015 мс | |||
| 65536 | 5196,82 мс | 1 1 19911|||||
| 131 072 | 20 903,54 мс | 9 068,25 мс | 0,060 мс | |||
| 262 144 | – | – 1 900 | ||||
. .. | … | … | … | |||
| 536 870 912 | – | – | 192,509 мс |
| n | Перестановки несортированные | Перестановки по убыванию | Сравнения несортированные | Сравнения по убыванию | 107 306… | … | . .. | .. . 31 854 | 65 280 | 32 893 | 32 895 |
|---|---|---|---|---|
| 512 | 128 340 | 261 632 | 130 767 | 131 327 |
| 1 047 552 | 524 475 | 524 799 | ||
| 2 048 | 2 111 762 4 0311 | 03112 097 546 | 2 098 175 | |
| … | … | … | … | … |
Результаты подтверждают предположение: с несортированными элементами у нас примерно вдвое меньше операций обмена и немного меньше сравнений, чем с элементами, отсортированными по убыванию.
Почему пузырьковая сортировка быстрее для элементов, отсортированных в порядке убывания, чем для несортированных элементов?
Как возможно, что пузырьковая сортировка работает намного быстрее с элементами, отсортированными в порядке убывания, чем с элементами, упорядоченными случайным образом, несмотря на вдвое большее количество операций обмена?
Причину этого несоответствия можно найти в «предсказании ветвей»:
Если элементы отсортированы по убыванию, то результат операции сравнения если (слева > справа) всегда равно true в несортированной области и всегда false в отсортированной области.
Если предсказание ветвления предполагает, что результат сравнения всегда такой же, как и результат предыдущего сравнения, то это предположение всегда верно — за одним единственным исключением: на границе области. Это позволяет большую часть времени полностью использовать конвейер инструкций ЦП.
С другой стороны, с несортированными данными невозможно сделать надежные прогнозы относительно результата сравнения, поэтому конвейер часто приходится удалять и заполнять заново.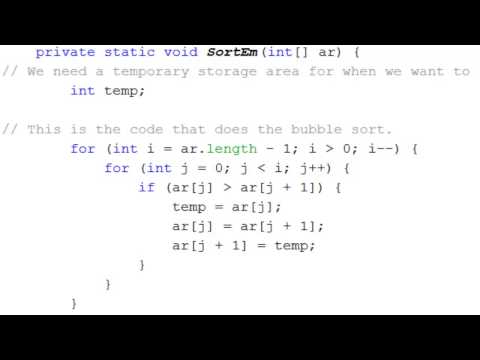
Другие характеристики пузырьковой сортировки
В этом разделе рассматриваются пространственная сложность, стабильность и возможность распараллеливания пузырьковой сортировки.
Space Сложность пузырьковой сортировки
Пузырьковая сортировка не требует дополнительного места в памяти, кроме переменной цикла max и вспомогательных переменных , замененных местами , слева и справа .
Таким образом, пространственная сложность сортировки пузырьком составляет O(1) .
Стабильность пузырьковой сортировки
При постоянном сравнении двух соседних элементов друг с другом и замене их местами только в том случае, если левый элемент больше правого, элементы с одним и тем же ключом никогда не могут поменяться местами относительно друг друга.
Для этого потребуется, чтобы два элемента поменялись местами в более чем одной позиции (как это происходит при сортировке выбором).
С пузырьковой сортировкой это невозможно. Таким образом,
Пузырьковая сортировка является стабильным алгоритмом сортировки.
Распараллеливание пузырьковой сортировки
Существует два подхода к распараллеливанию пузырьковой сортировки:
Подход 1 «Сортировка нечетных-четных»
Вы параллельно сравниваете первый со вторым элементом, третий с четвертым, пятый с шестым и т.д. и меняете местами соответствующие элементы, если левый больше правого.
Затем вы сравниваете второй элемент с третьим, четвертый с пятым, шестой с седьмым и так далее.
Эти два шага чередуются до тех пор, пока элементы не перестанут меняться местами ни на одном шаге:
Этот алгоритм также называется «Сортировка нечетных-четных».
Исходный код можно найти в классе BubbleSortParallelOddEven в репозитории GitHub.
Синхронизация между шагами (потоки не могут начинаться с шага, пока все потоки не завершат предыдущий шаг) реализована с помощью Phaser.
Подход 2 «Разделяй и властвуй»
Вы делите массив для сортировки на столько областей («разделов»), сколько доступно ядер ЦП.
Теперь вы выполняете одну итерацию пузырьковой сортировки во всех разделах параллельно. Дождитесь завершения всех потоков, а затем сравните последний элемент одного раздела с первым элементом следующего раздела. Когда все потоки завершены, процесс начинается снова.
Повторяйте эти шаги до тех пор, пока элементы не перестанут меняться во всех потоках:
Исходный код алгоритма можно найти в классе BubbleSortParallelDivideAndConquer в репозитории GitHub.
Опять же, Phaser используется для синхронизации потоков. На самом деле большая часть кода обоих алгоритмов одинакова, поскольку массив также делится на разделы для четно-нечетного подхода. Я переместил общий код в абстрактный базовый класс BubbleSortParallelSort.
Параллельная пузырьковая сортировка: производительность
Я сравниваю производительность параллельных вариантов с упомянутым выше тестом CompareBubbleSorts.
Вот результат для параллельных алгоритмов по сравнению с самым быстрым последовательным вариантом
----- Результаты после 50 итераций----- BubbleSortOpt1 -> самый быстрый: 443,2 мс, медиана: 452,7 мс BubbleSortParallelOddEven -> самый быстрый: 62,6 мс, медиана: 68,6 мс BubbleSortParallelDivideAndConquer ->самое быстрое: 126,8 мс, медиана: 145,7 мс Язык кода: открытый текст (открытый текст)
Вариант «нечет-чет» на моем 6-ядерном процессоре (12 виртуальных ядер с Hyper-threading) и с 20 000 несортированных элементов, таким образом, в 6,6 раза быстрее, чем последовательная версия.
Подход «разделяй и властвуй» всего в 3,1 раза быстрее. Вероятно, это связано с тем, что каждый поток выполняет только одно сравнение на втором подэтапе итерации. Это контрастирует с относительно высокими усилиями по синхронизации, требуемыми фазовращателем.
Резюме
Пузырьковая сортировка — это простой в реализации, стабильный алгоритм сортировки с временной сложностью O(n²) в среднем и худшем случаях и O(n) в лучшем случае.
Вы найдете больше алгоритмов сортировки в этом обзоре всех алгоритмов сортировки и их характеристик в первой части серии статей.
Пузырьковая сортировка была последним простым методом сортировки в этой серии статей; в следующей части мы войдем в область эффективных методов сортировки, начиная с быстрой сортировки.
Если вам понравилась статья, не стесняйтесь поделиться ею, используя одну из кнопок «Поделиться» в конце. Вы хотите, чтобы я информировал вас по электронной почте, когда я публикую новую статью? Затем нажмите здесь, чтобы подписаться на информационный бюллетень HappyCoders.
Что такое пузырьковая сортировка? | Определение и обзор
Пузырьковая сортировка — это базовый алгоритм для упорядочивания строки чисел или других элементов в правильном порядке. Метод работает, проверяя каждый набор соседних элементов в строке слева направо, меняя их позиции, если они не в порядке. Затем алгоритм повторяет этот процесс до тех пор, пока он не сможет просмотреть всю строку и не найдет двух элементов, которые нужно поменять местами.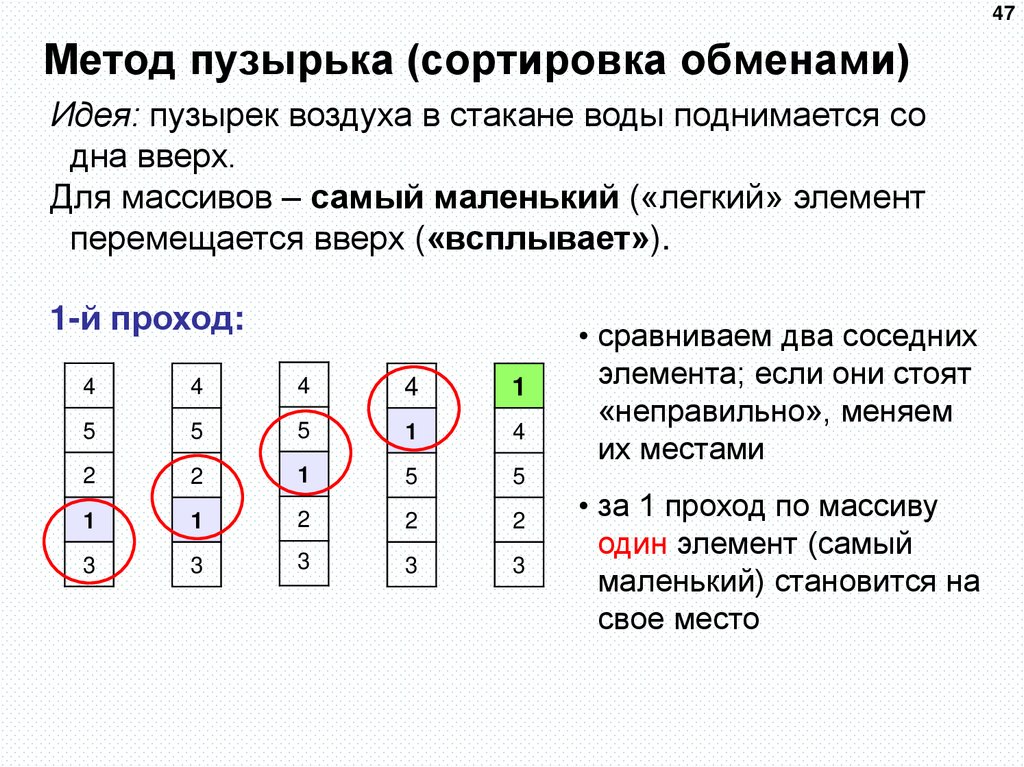
Как выглядит сортировка пузырьком?
Если программист или аналитик хочет упорядочить последовательность чисел в порядке возрастания, метод пузырьковой сортировки будет выглядеть так, как показано на рисунке.
Алгоритм будет просматривать два элемента за раз, переставлять те, которые еще не расположены в порядке возрастания слева направо, а затем продолжать циклически проходить всю последовательность, пока не завершит проход без переключения номеров.
Как программисты используют пузырьковую сортировку?
Программисты используют пузырьковую сортировку, чтобы упорядочить последовательность чисел в правильном порядке. Поскольку это самый простой тип алгоритма сортировки, пузырьковая сортировка редко используется в реальных компьютерных науках. Его наиболее распространенное использование для программистов включает следующее:
1. Способ изучения базовой сортировки
Пузырьковая сортировка работает как метод обучения новых программистов сортировке наборов данных, потому что алгоритм прост для понимания и реализации.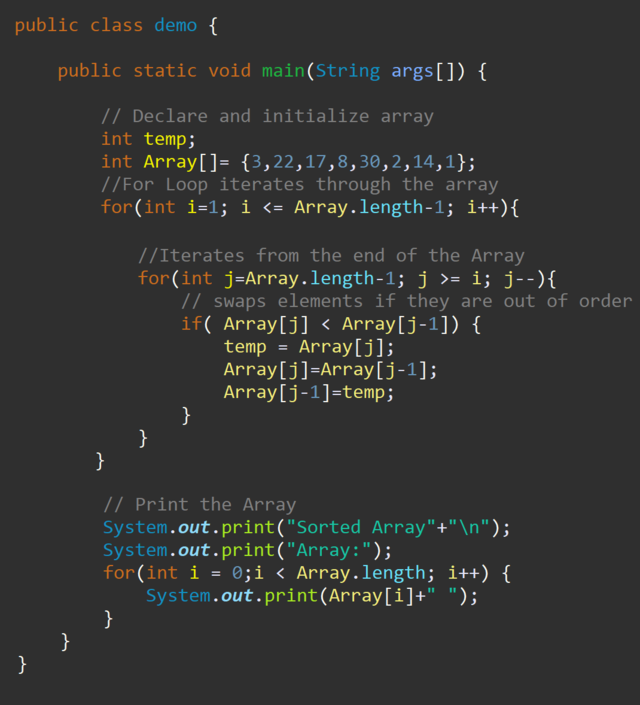
2. Методика сортировки крошечных наборов данных
Поскольку приходится многократно циклически перебирать весь набор элементов, сравнивая только два соседних элемента за раз, пузырьковая сортировка не оптимальна для более массивных наборов данных. Но он может хорошо работать при сортировке небольшого количества элементов.
3. Методология сортировки наборов данных, которые в основном уже упорядочены
Наконец, некоторые компьютерщики и аналитики данных используют этот алгоритм для окончательной проверки наборов данных, которые, по их мнению, уже почти отсортированы.
Как менеджеры по продукции могут использовать пузырьковую сортировку?
Одна из самых важных и сложных обязанностей менеджера по продукту — взвесить конкурирующие инициативы и решить, на чем сосредоточить ограниченное время и ресурсы команды.
Например, продуктовые команды взвешивают затраты и преимущества элементов невыполненной работы, чтобы решить, какие элементы займут место в дорожной карте продукта.