Numpy обратная матрица: матрицы и операции над ними

Клон NumPy / Хабр

Небольшой модуль для работы с массивами в Python без использования сторонних библиотек (клон NumPy, но только на чистом Python).

Домашним заданием в университете задали написать программу, которая вычисляет нормы и разложения матрицы, но запретили использовать сторонние библиотеки. В выборе языка программирования не ограничивали. Я выбрал python (что было ошибкой, т.к. он намного медленнее Java и C/C++) и соответственно мне нельзя использовать NumPy. В процессе пришлось написать функции выполнения операций с массивами, функции нахождения миноров, определителя и тд. В итоге получилась мини библиотека для работы с массивами.

Мой код, написанный на чистом питоне намного медленнее NumPy, который производит вычисления на C и Fortran (плюс мой код не оптимизирован).

Что может МатЛОЛ:

• Сумма, разность и произведение матриц
• Произведение матрицы на число
• Транспонирование матрицы
• Минора матрицы
• Определитель матрицы
• Обратная матрица
• Союзная матрица
• Число обусловленности матрицы
• Первая, вторая (не доработана), Евклидова и бесконечная нормы матрицы
• Решение уравнения AX = B
• LU разложение
• Разложение Холецкого
• Метод Зейделя

Примеры использования MathLOL

# from mathlol import *
from mathlol import mathlol

matrix = mathlol()
matrix. set([[1, 2, 3],
           [4, 5, 6],
           [7, -8, 9]])
matrix.get() # Возвращает матрицу

matrix * 2 # Произведение элементов матрицы на 2
A = [[0, 0, 0],
    [0, 1, 0],
    [0, 0, 0]]
# Произведение 2 матриц
matrix.dot(A)
matrix * A
matrix.transposition() # Транспонирование матрицы
matrix.minor(i = 0, j = 0) # Минор матрицы
matrix.determinant() # Определитель матрицы
matrix.inverse() # Обратная матрица
L, U = matrix.lu() # LU разложение
matrix.seidel(b = [[5.0], [9.0], [1.0]]) # Метод Зейделя

vector = mathlol()
vector.set([1, 2, 3, 4, 5])
vector.checkvector() # Проверяет, является ли матрица вектором
vector.norm1_vector()
vector.norm2_vector()
vector.norm3_vector()

Производительность MathLOL

from mathlol import mathlol
import time
import random
import matplotlib. pyplot as plt
# Создаём набор данных
data = {}
for i in range(10, 110, 10):
    array = []
    for i_ in range(i):
        temp = []
        for j_ in range(i):
            temp.append(random.randint(-100, 100))
        array.append(temp)
    data[i] = array
# Производим вычисления и измеряем скорость
mlol_dot = {}
for key in data.keys():
    matrix = mathlol()
    matrix.set(matrix = data[key])
    
    start = time.process_time()
    result = matrix * matrix
    end = time.process_time() - start
    
    mlol_dot[key] = end
# Строим график
plt.plot(mlol_dot.keys(), mlol_dot.values())
plt.title("MathLOL \nПроизведение матриц")
plt.xlabel("Размер матрицы (NxN)")
plt.ylabel("Время (сек)")

Скорость вычисления произведений матриц размера от 100×100 до 1000×1000

Сравним скорости вычислений numpy и mathlol. К сожалению, mathlol очень сильно уступал в скорости и я решил взять для numpy матрицы размеров от 100×100 до 1000×1000, а для mathlol от 10×10 до 100×100.

MathLOL вычислил произведение матрицы 100×100 на саму себя за 0.16 секунды, а NumPy вычислил произведение матрицы 1000×1000 на саму себя за 0.002 (!!!) секунды. Разница просто огромная.

У нас стояла задача просто реализовать различные функции для работы с матрицами, что мы и сделали, но программа с большими матрицами работает не так быстро как хотелось бы. Осталось доработать программу, добавить еще несколько функций (например, функция для вычисления числа Тодда), буду признателен если посмотрите код, укажете на ошибки и возможно поможете доработать код.

На этом все, код и примеры выложены на гитхабе.

P.S. В процессе написания статьи мне захотелось поэкспериментировать и встроить в свой модуль C/C++. Займусь этим в ближайшее время и посмотрим насколько удастся приблизиться к производительности NumPy.

python — Построить обратную матрицу методом Гаусса

У вас несколько ошибок в коде.

1. Вы конструируете правую часть как np.matrix, поэтому после np. hstack вы получаете тоже объект типа np.matrix. Это очень специальный вид массивов. В частности, итератор m возвращает не одномерные строки чисел, а двумерные массивы формы (1,6). В результате row[nrow] оказывается не числом, а одномерным массивом.

   В numpy есть специальная функция для построения единичной матрицы:

   np.eye(n) строит единичную матрицу размером n x n. Поэтому вам лучше конструировать m как m = np.hstack((matrix_origin, np.eye(len(matrix_origin)))

2. Вы инициализировали n как число колонок в m: m = m.shape[1]. Но тогда вот эта строчка неверна: for row_ in range(k - 1, -1, -1) — у вас нет строк с номерами 5,4,3. Если n определяет число строк, то нужно присваивать вот так: n = m.shape[0]

3. Но в таком случае сломается ваш код выделения правой части np.

   hsplit(m, n // 2)[1]. Я предлагаю использовать индексирование вместо hsplit: m[:, n:].copy() есть двумерный массив, каждая строка которого есть строка из m начиная с элемента с номером n, то есть элементы №№ 3,4 и 5. Как раз правая часть матрицы m. Метод copy() вызывается для того, чтобы не держать указатель на m, в противном случае m будет висеть в памяти до тех пор, пока «жив» указатель на результат функции inverse_matrix

После исправления этих ошибок получится что-то вроде

def inverse_matrix(matrix_origin):
    """
    Функция получает на вход матрицу, затем добавляет к ней единичную матрицу, 
    проводит элементарные преобразования по строкам с первоначальной, добиваясь получения слева единичной матрицы.
    В этом случае справа окажется матрица, которая является обратной к заданнй первоначально 
    """
    # Склеиваем 2 матрицы: слева - первоначальная, справа - единичная
    n = matrix_origin.  shape[0]
    m = np.hstack((matrix_origin, np.eye(n)))
    
    for nrow, row in enumerate(m):
        # nrow равен номеру строки
        # row содержит саму строку матрицы
        divider = row[nrow] # диагональный элемент
        # делим на диагональный элемент:
        row /= divider
        # теперь вычитаем приведённую строку из всех нижележащих строк:
        for lower_row in m[nrow+1:]:
            factor = lower_row[nrow] # элемент строки в колонке nrow
            lower_row -= factor*row # вычитаем, чтобы получить ноль в колонке nrow
    # обратный ход:
    for k in range(n - 1, 0, -1):
        for row_ in range(k - 1, -1, -1):
            if m[row_, k]:
                # 1) Все элементы выше главной диагонали делаем равными нулю
                m[row_, :] -= m[k, :] * m[row_, k]
    return m[:,n:].copy()

Результат инвертирования вашей матрицы

array([[ 0.04128819,  0.09805945,  0.08980182],
       [ 0.15689513, -0.08790039, -0.01401625],
       [ 0.1734104 , -0.  18025555,  0.206115  ]])

Я добавил jupyter notebook со своим вариантом, он быстрее на 10-15% за счёт выбора операций индексирования.

NumPy Inverse

« Матрицы » — это фундаментальный инструмент для обработки данных, машинного обучения и линейной алгебры в Python. Они хранят числа в виде сетки и позволяют выполнять различные операции, такие как решение уравнений и преобразование данных. Иногда нам может понадобиться обратить эффект матрицы, найдя ее обратную. Обращение матрицы может помочь нам решить систему линейных уравнений. Для обращения матрицы в Python используется библиотека « numpy ».

В этой статье на нескольких примерах объясняется, как использовать «numpy» для обращения матрицы.

Что такое обратная матрица?

Математически матрица представляет собой массив строк и столбцов чисел, символов или уравнений. Обратные матрицы — это новые матрицы, которые производят единичную матрицу путем их умножения на исходные заданные матрицы. Квадратная матрица, содержащая «единицы» по диагонали и «нули» в других местах, является единичной матрицей.

Как инвертировать матрицу, используя «numpy»?

Библиотека « numpy » предоставляет простую функцию « inv() » для инвертирования матрицы. Эта функция принимает на вход матрицу и возвращает обратную.

Синтаксис

numpy.linalg.inv(a)

В приведенном выше синтаксисе параметр « a » соответствует инвертируемой матрице.

Примечание : обратная матрица не применима/функциональна для всех типов матриц. Она такова, что если данная матрица вырожденная, т. е. ее определитель равен « ноль », он не имеет обратного. В таких случаях функция « inv() » вызовет исключение « LinAlgError ».

Пример 1. Вычисление обратной матрицы «2×2»

Возьмем простую матрицу «2×2» и вычислим ее обратную, используя «numpy»:

import numpy
value_a = numpy.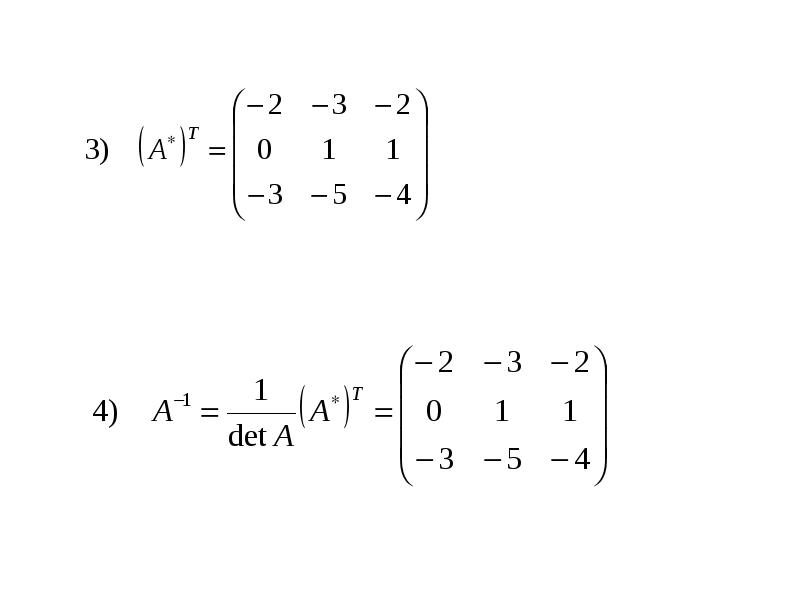 array([[52, 22], [43 , 24]])
print(‘Данная матрица: \n’,value_a)
inv_a = numpy.linalg.inv(value_a)
print(‘Обратная матрица: \n’,inv_a)

В приведенном выше коде создается матрица « 2×2 », и функция « inv() » модуля « numpy.linalg » используется для вычисления ее обратной.

Результат

Фрагмент вывода показывает обратную матрицу заданной матрицы.

Пример 2. Вычисление обратной матрицы «3×3»

Возьмем матрицу «3×3» и вычислим ее обратную, используя «numpy»:

import numpy
value_1 = numpy.array([[52, 32, 14], [24, 25, 36], [27, 28, 29]])
print(‘Данная матрица: \n’,value_1)
inv_1 = numpy.linalg.inv(value_1)
print(‘\nОбратная матрица: \n ‘,inv_1)

Приведенные выше строки кода создали матрицу « 3×3 » и вычислили ее обратную с помощью функции « inv() ».

Вывод

Приведенный выше вывод возвращает обратную матрицу «3×3».

Пример 3. Вычисление обратной «сингулярной матрицы»

Возьмем сингулярную матрицу и попробуем вычислить ее обратную:

)

В приведенном выше блоке кода функция « numpy.linalg.inv() » принимает сингулярную матрицу и возвращает ошибку « LinAlgError » после вычисления обратной.

Выходные данные

Из приведенного выше вывода следует, что обратная матрица не вычислялась, поскольку данная матрица является единственной.

Альтернативный подход: найти обратную матрицу с помощью библиотеки «scipy» Давайте разберемся с этим на примере ниже.

Пример

Следующий код использует функцию « linalg.inv() » библиотеки « scipy » для получения обратной матрицы:

import numpy
from s cipy импорт linalg
value_a = numpy. matrix([[27, 32,],[43, -25]])
print(‘Данная матрица: \n’,value_a)
value_b = linalg.inv(value_a)
print(‘\nОбратная матрица: \n’,value_b)

  90 007

В этом коде функция « linalg.inv() » библиотеки « numpy » используется для поиска обратной указанной матрицы.

Результат

Этот результат возвращает обратную матрицу заданной матрицы.

Заключение

Инверсия матриц — жизненно важная частая операция в линейной алгебре, и «numpy» предлагает простую функцию « inv() ” для этой цели. В этой статье обсуждалось, как инвертировать матрицу с помощью «numpy», используя функцию «inv()». Библиотека « scipy » содержит функцию с именем « linalg.inv() », которую также можно использовать для поиска обратной данной матрицы. Демонстрируются различные примеры нахождения обратной матрицы с разными размерами, включая сингулярную матрицу.

Numpy linalg.

Шрея Бозе / 22 января 2023 г.

Научные расчеты иногда могут быть чрезвычайно утомительными, особенно когда они включают матрицы огромных размеров и сложные значения. Numerical Python или просто библиотека Numpy уже содержат встроенные функции, включающие матрицы и линейную алгебру, которые делают вычисления быстрее и точнее. В этой статье мы разберем и рассмотрим работу одной из таких функций, а именно linalg.inv.

Читайте также: NumPy linalg.matrix_power: вычисление мощности квадратной матрицы

Функция Linalg.inv

Функция NumPy linalg.inv , которую можно использовать для определения мультипликативной обратной матрицы порядка n. Мультипликативная обратная матрица — это величина, обратная регулярной матрице, как обратная величина любого другого числа в арифметике. Обратная матрица помогает нам найти неизвестные переменные в системе линейных уравнений, используя матричный метод и формулу, приведенную ниже:

AX = B => X = A ^-1 B

где A= матрица коэффициентов, A ^-1 обратная матрица коэффициентов, X матрица, содержащая неизвестные переменные, а B матрица ординат или определителей.

Также читайте: NumPy linalg.det – Вычисление определителя заданного массива

Необходимое условие и формула обратной матрицы: ноль, |А| !=0, то есть матрица невырожденная. Это свойство матрицы часто называют обратимостью. Матрица, для которой существует обратная, называется обратимой матрицей.

Формула для нахождения обратной матрицы приведена ниже:

A ^-1 = (сопряженная матрица A) / | А |

Если мы умножим матрицу A ранга n на обратную A ^-1 , то получим единичную матрицу ранга n. Ниже показана единичная матрица 3-го порядка:

Синтаксис функции numpy.linalg.inv():

Функция имеет следующий синтаксис:

linalg.inv(A)

Параметры: A : (тип данных = ndarray или arraylike) Это матрица, обратную которой необходимо найти.

Возвращает: Ainv : (тип данных = тот же, что и у A) Это инверсия A .

Выдает: LinAlgError: Если матрица не квадратная или невырожденная.

Пример 1. Нахождение обратной матрицы

Давайте рассмотрим первый пример, в котором мы просто найдем обратную матрицу с помощью функции.

# Импортируем необходимый пакет
импортировать numpy как py
  
# Берем матрицу 3-го порядка
A = py.массив([[2, 3, 4],
              [-3, -3, -2],
              [-2, 1, -1]])
# Вычисление обратной заданной матрицы
Ainv= py.linalg.inv(A)
print("обратная матрица = ", Ainv)
 

Вывод кода будет следующим:

обратная матрица = [[-0,2173913 -0,30434783 -0,26086957]
 [-0,04347826 -0,26086957 0,34782609]
 [ 0,39130435 0,34782609 -0,13043478]]
 

#импорт необходимых модулей
импортировать numpy как py
# Берем пользовательский ввод для матрицы
Row = int(input("Введите номер строки для матрицы:"))
Col = int(input("Введите количество столбцов для матрицы:"))
# Инициализация матрицы
А= []
print("Введите записи для A построчно:")
for i in range(Row): #for цикл для записей строки
    запись =[]
    for j in range(Col): #for цикл для записей столбца
         entry. append(int(input()))
    A.добавлять(запись)
print("матрица A =")
печать(А)
# Вычисление обратной заданной матрицы
Ainv= py.linalg.inv(A)
print("обратная матрица = ", Ainv)
 

Введите номер строки для матрицы: 4
Введите количество столбцов для матрицы: 4
Введите записи для A построчно:
2
5
0
8
1
4
2
6
7
8
9
3
1
5
7
8
матрица A =
[[2, 5, 0, 8], [1, 4, 2, 6], [7, 8, 9, 3], [1, 5, 7, 8]]
обратная матрица = [[ 0,96089385 -1,91620112 0,07821229 0,44692737]
 [-1,03351955 2,3575419 0,06703911 -0,75977654]
 [-0,00558659-0,27374302 0,01117318 0,20670391]
 [ 0,53072626 -0,99441341 -0,06145251 0,36312849]]