Как получить остаток от деления в java
Арифметические операторы
В следующей таблице перечислены основные арифметические операторы (или операции), применяемые в языке Java:
| Операция | Описание |
| + | Сложение (а также унарный плюс) |
| — | Вычитание (а также унарный минус) |
| * | Умножение |
| / | Деление |
| % | Деление по модулю |
Рассмотрим некоторые правила работы с арифметическими операторами:
- Выражения вычисляются слева направо, если не добавлены круглые скобки или одни операции имеют более высокий приоритет.
- Операции * , / , и % имеют более высокий приоритет чем + и — .
Арифметические операторы над целочисленными значениями
Например, в этом коде, переменные a и b будут иметь разные значения:
Унарные операции сложения и вычитания
- Операция унарного вычитания изменяет знак своего единственного операнда.

- Операция унарного сложения просто возвращает значение своего операнда. Она в принципе не является необходимой, но возможна.
Деление целочисленных чисел в Java
Когда операция деления выполняется над целочисленным типом данных, ее результат не будет содержать дробный компонент. Это деление без остатка в Java:
Результат выполнения этой программы:
Арифметические операторы над переменными типа char
Операнды арифметических операторов должны иметь числовой тип. Арифметические операторы нельзя выполнять над логическими типами данных, но допускается над типами данных char , поскольку в Java этот тип, по существу, является разновидностью типа int . Например:
Или как в следующем примере:
Деление по модулю в Java
Оператор деления по модулю — обозначается символом % . Этот оператор возвращает остаток от деления первого числа на второй в Java. При делении целого числа результатом будет так же целое число:
2. Составные арифметические операции с присваиванием
| Операция | Описание |
| += | Сложение с присваиванием |
| -= | Вычитание с присваиванием |
| *= | Умножение с присваиванием |
| /= | Деление с присваиванием |
| %= | Деление по модулю с присваиванием |
В Java имеются специальные операции, объединяющие арифметические операторы с операцией присваивания.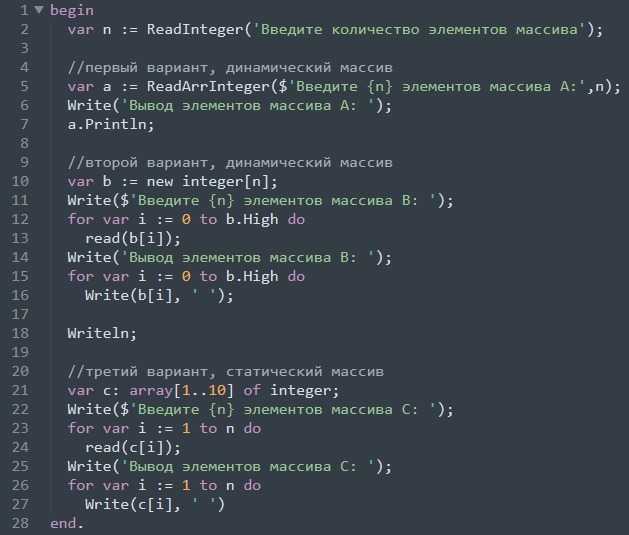 Рассмотрим следующее выражение:
Рассмотрим следующее выражение:
B Java эту операцию можно записать следующим образом:
Составные операции с присваиванием позволяют не только уменьшить объем кода, но и позволяют выполнять автоматическое преобразование чего не делают обычные операции:
Основы
Как и в любом языке программирования, в языке Java резервируются определенные слова, которые компилятор распознает как особые. Их нельзя использовать для именования конструкций Java: переменных, методов и т.д. Список ключевых слов не слишком велик:
| abstract | assert | boolean | break | byte |
| case | catch | char | class | const |
| continue | default | do | double | else |
| enum | extends | final | finally | float |
| for | goto | if | implements | import |
| instanceof | int | interface | long | native |
| new | package | private | protected | public |
| return | short | static | strictfp | super |
| switch | synchronized | this | throw | throws |
| transient | try | void | volatile | while |
Формально слова true, false и null не входят в число ключевых слов, но их тоже нельзя использовать в качестве имён переменных. Обратите внимание, что Android Studio выделяет ключевые слова в редакторе кода особым цветом (синтаксическая подсветка).
Обратите внимание, что Android Studio выделяет ключевые слова в редакторе кода особым цветом (синтаксическая подсветка).
Переменные
Переменные используются для хранения данных. Переменные сначала должны быть объявлены, и только после этого ими можно пользоваться.
Как следует из названия, переменные могут меняться (точнее их значения). Проведём аналогию с кошачьим приютом. Котов привозят в приют, потом добрые люди забирают котов из него. Получается, что коты постоянно меняются, а приют остаётся.
Переменные могут быть двух видов
- примитивные типы: int, float, double, char и другие, которые представляют собой числа, символы
- объекты, которые представляют классы
Список переменных примитивных типов рассматривается в следующей статье.
Переменной можно присвоить начальное значение (инициализировать) через знак равенства и указанием значения. Указываемое значение должно подходить типу, который вы указали для переменной. Для объявления нескольких переменных одного типа можно использовать запятые:
Также возможна динамическая инициализация. Вам нужно только проследить, чтобы вычисляемое выражение соответствовало переменной.
Вам нужно только проследить, чтобы вычисляемое выражение соответствовало переменной.
В некоторых случаях нужно, чтобы переменная не менялась, в этом случае переменная называется константой и имеет ключевое слово final.
Переменные имеют свою область видимости. Она может быть доступна только внутри метода, цикла, класса. Подобная защита уменьшает риск ошибок от несанкционированного доступа или изменений от чужого кода. Также следует помнить, что внутри блока переменные можно объявить в любом месте, но они становятся допустимыми только после объявления. Если ситуация будет обратной, то конструкция будет бессмысленной и вам не разрешат так делать:
Переменные создаются при входе в их область видимости и уничтожаются при выходе из неё. Иными словами, переменная утратит своё значение сразу после выхода из области видимости. Поэтому, переменные, которые объявлены внутри метода, не будут хранить свои значения между обращениями к этому методу.
Если объявление переменной содержит инициализацию, то инициализация будет повторяться при каждом вхождении в блок, в котором она объявлена. Допустим, у нас есть блок:
Допустим, у нас есть блок:
При каждом вхождении в цикл переменной присваивается снова и снова значение 42. И хотя потом переменной присваивается значение 54, оно теряется при повторном вхождении в блок.
Блоки бывают вложенными, но тем не менее во внутреннем блоке нельзя объявлять переменные с тем же именем, что и во внешней области:
Оператор присваивания
Оператором присваивания является одиночный знак равенства (=):
Тип переменная должен соответствовать типу выражение. Оператор присваивания можно использовать в виде цепочки присваивания:
Оператор присваивания берёт значение правого выражения. Поэтому выражение z = 9 будет равно 9, после чего оно присваивается переменной y, а затем — переменной x.
Помните, что в сравнении используется другой оператор ==, а не оператор присваивания.
Комментарии
В Java используются три вида комментариев. Многострочные комментарии начинаются с символов /* и заканчиваются символами */. Однострочные комментарии начинаются с комбинации символов //. Причем, однострочный комментарий можно использовать не только на отдельной строке, но и после оператора.
Однострочные комментарии начинаются с комбинации символов //. Причем, однострочный комментарий можно использовать не только на отдельной строке, но и после оператора.
Начинающим программистам необходимо писать комментариев как можно больше, так как, вернувшись к своему коду через месяц-другой, вы с трудом вспомните, что вы тут нашкодили накодили.
Существует ещё третий тип комментариев для создания самодокументирующего кода (комментарий документации). Но это отдельная тема для разговора.
В студии создание и управление комментариями можно упростить через меню Code. Там вы найдёте такие команды как Comment With Line Comment, Comment With Block Comment. Попробуйте самостоятельно разобраться с ними.
Backdoor!
С помощью комментария злобные программисты могут внедрить закладку в разрабатываемый софт. Если в комментариях программы использовать Unicode для переноса строки и после нее написать свой код, то IDE (Android Studio) будет отображать это как комментарий, но код будет выполняться.
На первый взгляд, код не должен выполняться. Но это не так. Можете проверить.
\u000a — это Unicode-символ переноса строки (он же \n). Сначала производится декодирование, а потом уже разбор самого кода. Получается, что сначала произойдёт перенос, а потом будет напечатан рабочий код. Следующий пример тоже рабочий.
Стиль оформления кода
Существует негласные правила оформления стиля при написании кода. Старайтесь их придерживаться. Также запоминайте оформление кода в документации и справочниках. Например, принято записывать имена классов с большой буквы (class JavaQuickCourseActivity). Если имя состоит из нескольких слов, то каждое слово в имени также начинается с большой буквы. Использовать символы подчеркивания или тире нежелательно (Java_Quick_Course_Activity или Java-Quick-Course-Activity).
Для методов и переменных используется такой же формат, только первый символ записывается с маленькой буквы, например, resultButton.
Константы принято писать только большими буквами — IDD_LIST_NAMES. В этом случае одного взгляда достаточно, чтобы сразу определить, что перед вами константа.
В этом случае одного взгляда достаточно, чтобы сразу определить, что перед вами константа.
На первых порах вам этого достаточно.
Операторы
Как и везде, в Java есть операторы сложения (+), вычитания (-), умножения (*), деления (/), которые применимы к числам.
| Оператор | Пример использования | Описание |
|---|---|---|
| + | a + b | Сложение а и b (также унарный плюс) |
| + | +a | Преобразование a в переменную типа int, если это переменная типа byte, short или char |
| — | a – b | Вычитание b из а (также унарный минус) |
| — | -a | Арифметическая инверсия а |
| * | a * b | Умножение а на b |
| / | a / b | Деление a на b |
| % | a % b | Вычисление остатка от деления а на b (деление по модулю) |
| ++ | a++ | Приращение а на 1 с предварительным вычислением значения а (инкремент) |
| ++ | ++a | Приращение а на 1 с последующим вычислением значения а |
| — | a— | Уменьшение а на 1 с предварительным вычислением значения а (декремент) |
| — | —a | Уменьшение а на 1 с последующим вычислением значения а |
| += | a += b | Краткая форма записи a = a + b (сложение с присваиванием) |
| -= | a -= b | Краткая форма записи a = a – b (вычитание с присваиванием) |
| *= | a *= b | Краткая форма записи a = a * b (умножение с присваиванием) |
| /= | a /= b | Краткая форма записи a = a / b (деление с присваиванием) |
| %= | a %= b | Краткая форма записи a = a % b (деление по модулю с присваиванием) |
Операнды арифметических операторов должны иметь числовой тип. Нельзя использовать их к логическим типам. Можно применять к типам char, который по сути можно представлять как тип int.
Нельзя использовать их к логическим типам. Можно применять к типам char, который по сути можно представлять как тип int.
Для строк можно использовать только операции + и +=. Умножать, вычитать и делить слова нельзя. Обратите внимание, что при сложении слов «мышь»+»мышь» получается не «мыши», как предположил мой кот Рыжик, а «мышьмышь». На самом деле символ + при работе со строками называется не сложением, а конкатенацией.
Оператор деления по модулю
Существует оператор, вычисляющий остаток от деления нацело (%). Чтобы запомнить данный знак, обратите внимание на наклонную черту, как в обычном делении, которую окружают два нолика. Деление нацело обрезает, а не округляет результат.
Если 42 разделить по модулю на 10, то получим значение 2, а если 42.56 разделить по модулю на 10, то получим 2.5600000000000023:
Деление по модулю очень удобно использовать для разбивки числа на части. Предположим вам надо получить последние две цифры 2013 года. Вот как можно это сделать:
Вот как можно это сделать:
Вот и другой пример. Предположим, у вас есть фильм «Кот в сапогах», продолжительность которого равна 135 минутам. Чтобы разбить это число на часы и минуты, нужно применить такой код:
В результате получим ответ: Кот в сапогах идёт 2 часа 15 минут.
Обратите внимание, что переменная minutes всегда будет содержать числа в диапазоне от 0 до 59.
Стоит запомнить одну особенность. При делении большого числа на меньшее, например (5 % 4), понятно, что остаток будет 1. При делении по модулю меньших чисел 0, 1, 2, 3 на число 4 получатся те же значения 0, 1, 2, 3.
Напоследок, остаётся сказать, что делить на 0 нельзя. У вас будет выводиться сообщение об ошибке либо на этапе компиляции, либо во время работы программы.
В задачнике есть упражнения с применением данного оператора: 1, 2
Приоритет
Если вы не прогуливали уроки математики, то знаете, что в сложных выражениях скобки позволяют определить порядок вычислений. Например, в выражении 2 + 3 * 4 сначала идет умножение, а потом сложение. Расставив скобки, мы можем сначала сложить два числа, а потом умножить:
Например, в выражении 2 + 3 * 4 сначала идет умножение, а потом сложение. Расставив скобки, мы можем сначала сложить два числа, а потом умножить:
Кстати, использование скобок не влияет на производительность программы. Поэтому можете не стесняться и расставлять их побольше.
Укороченная форма записи
В Java также можно использовать укороченную форму записи, чтобы одновременно произвести операцию и присвоение. Для укороченной записи используется оператор с последующим знаком равенства. Например, чтобы прибавить число 7 к переменной x и присвоить результат этой же переменной, используйте команду x += 7. Это справедливо и для других операторов:
Укороченная форма записи не только сокращает объём и время написания кода, но и работает более эффективно (хотя доказательств не знаю).
Автоувеличение и автоуменьшение на единицу
Очень часто вам придется увеличивать или уменьшать значение переменной на единицу. Поэтому существует специальные операторы увеличения (инкремента) и уменьшения (декремента). Для инкремента используются два плюса (++), а для декремента два минуса (—).
Для инкремента используются два плюса (++), а для декремента два минуса (—).
Данные операторы существуют в двух версиях — префиксной и постфиксной. Префиксный инкремент или декремент значит, что ++ или — записываются перед переменной или выражением.
В этом случае сначала выполняется операция, а затем выдается результат.
При постфиксном инкременте или декременте оператор записывается после переменной или выражения:
Здесь сначала выдается значение, и лишь затем выполняется операция.
Например, мы хотим ежегодно увеличивать возраст кота в анкете:
Данный код аналогичен более длинному варианту:
В простых выражениях особой разницы в постфиксной и префиксной формами нет, но в сложных выражениях может играть существенную роль. Поэтому не рекомендую использовать этот способ в выражениях, чтобы не запутаться самому. Пишите код проще.
Инкремент и декремент применяется только к значениям переменных, к числу применять этот способ нельзя.
По ссылке или по значению
У нас есть класс Cat
Попробуем, используя этот класс, передать объект Cat в метод и посмотреть, что получится:
Как получить остаток от деления в java
6 сентября 2014 Мария (admin)
В уроке 8 мы затронули логические операторы, они нам были необходимы для формирования логического выражения в условиях if. Этот урок будет посвящен математике в Java, и поэтому мы рассмотрим подробнее арифметические операторы и частично возможности класса Math.
Этот урок будет посвящен математике в Java, и поэтому мы рассмотрим подробнее арифметические операторы и частично возможности класса Math.
Но для начала, выясним, что же такое операторы. Операторы это специальные символы, отвечающие за ту или иную операцию, например сложение, умножение, сравнение. Все операторы в Java можно разбить на 4 класса — арифметические, битовые, операторы сравнения и логические.
Арифметические операторы в JavaДля стандартных арифметических операций, таких как сложение, вычитание, умножение, деление в Java используются традиционные символы, к которым мы привыкли со школы:
Примечание: при операции деления, если оба аргумента являются целыми числами, то в результате получим целое число. Дробная часть, если такая имеется, отбросится. Если хотим получить число с дробной частью, то нужно, чтобы один из аргументов был типа double. Это можно указать в самом выражении при помощи добавления после числа . 0 или .d. Пример:
0 или .d. Пример:
В Java также имеется специальный оператор %, обозначающий остаток от делния.
Пример использования: дан массив целых чисел, вывести на консоль только те числа, которые делятся на 3.
Операции с присваиванием
Рассмотрим задачу вывода на экран 10 первых четных чисел чисел
мы можем записать сокращенно
+= это оператор сложения с присваиванием. Подобные операторы есть для всех основных 5 операций, рассмотренных выше
Пример использования: Найти факториал числа 7.
Инкрементирование и декрементирование
Инкремент, обозначается ++ и увеличивает значение переменной на единицу. Декремент обозначается — и уменьшает значение на единицу. С инкрементом и декрементом мы часто встречаемся в цикле for.
Инкремент и декремент бывают двух форм
Различие префиксной и постфиксной формы проявляется только тогда, когда эти операции присутствуют в выражениях. Если форма префиксная, то сначала произойдет увеличение (или уменьшение) переменной на единицу, а потом с новым значением будет произведены дальнейшие вычисления. Если форма постфиксная, то расчет выражения будет происходить со старым значением переменной, а переменная увеличится (или уменьшится) на единицу после вычисления выражения. Пример
Если форма постфиксная, то расчет выражения будет происходить со старым значением переменной, а переменная увеличится (или уменьшится) на единицу после вычисления выражения. Пример
В первом случае сначала переменная a увеличится на 1, потом произойдет вычисление всего выражения. Во втором случае произойдет вычисление выражения при старом значении b = 3, и после вычисления b увеличится на 1, на результат в postfix это уже не повлияет.
Если вы поняли принцип работы постфиксного и префиксного инкремента/декремента, то предлагаю решить в уме такую задачу:
Вопрос: чему в итоге равны x и y? После того, как вы сделали предположение, проверьте его в java.
Задача со зведочкой. Дан код:
Какие числа будут выведены на экран? Почему? Разобраться самостоятельно.
Примечание: инкремент и декремент применяются только к переменной. Выражение вида 7++ считается недопустимым.
Математические функции и константы (класс Math)Для решения задач нередко требуется использование математических функций. В Java такие функции включены в класс Math. Для того, чтобы использовать методы класса Math, нужно подключить его в начале .java файла с вашим кодом.
В Java такие функции включены в класс Math. Для того, чтобы использовать методы класса Math, нужно подключить его в начале .java файла с вашим кодом.
Часто используемые математические функции
- sqrt(a) — извлекает квадратный корень из числа а.
- pow(a, n) — a возводится в степень n.
- sin(a), cos(a), tan(a) — тригонометрические функции sin, cos и tg угла a указанного в радианах.
- asin(n), acos(n), atan(n) — обратные тригонометрические функции, возвращают угол в радианах.
- exp(a) — возвращает значение экспоненты, возведенной в степень a.
- log(a) — возвращает значение натурального логарифма числа a.
- log10(a) — возвращает значение десятичного логарифма числа a.
- abs(a) — возвращает модуль числа a.

- round(a) — округляет вещественное число до ближайшего целого.
Константы
- PI — число «пи», с точностью в 15 десятичных знаков.
- E — число «e»(основание экспоненциальной функции), с точностью в 15 десятичных знаков.
- Дан массив целых чисел, найти среди элементов массива числа, которые делятся на 3 и на 6
- Посчитать среднее арифметическое чисел в массиве
- Известны катеты прямоугольного треугольника, найти его площадь и периметр
- Даны два целых числа, найти их наибольший общий делитель и наименьшее общее кратное
- Даны радиус вращения и высота конуса, вычислить объем конуса.
Категория: Уроки Java
Как вычислить остаток от деления в java
Деление по модулю в Java
Ещё со школы мы знакомы с таким понятием как обычное деление:
С этим все понятно. А что же это за «зверь» такой, деление по модулю ? И звучит то так угрожающе. А на самом деле всё очень и очень просто. Давайте разбираться.
А на самом деле всё очень и очень просто. Давайте разбираться.
Что Вам нужно понимать:
- Деление по модулю – это оператор
Как работает оператор сложения, вычитания и т.д. наверняка Вы уже знаете. А вот за что отвечает деление по модулю поймёте буквально через пару минут. Немного терпения.
- Деление по модулю обозначается вот таким знаком: %
- Деление по модулю иногда называют mod. То есть если увидите название mod, знайте, речь идет об операторе деление по модулю.
- В чём суть оператора? Деление по модулю даёт остаток от деления.
Давайте посмотрим на примерах как это работает.
Пример №1Необходимо разделить 9 на 4, используя:
- обычное деление, как нас учили в школе
- деление по модулю
Логику работы оператора деления по модулю Вы уже поняли. Самое время попробовать запустить пример на своём компьютере:
Если Вы запустите этот код на своём компьютере, то в консоль будет выведено такое число:
Пример №2Необходимо разделить 17 на 5, используя:
- обычное деление, как нас учили в школе
- деление по модулю
И пробуем теперь запустить программу на компьютере:
Если Вы запустите этот код на своём компьютере, то в консоль будет выведено такое число:
Пример №3Необходимо разделить 21 на 7, используя:
- обычное деление, как нас учили в школе
- деление по модулю
И пробуем теперь запустить программу на компьютере:
Если Вы запустите этот код на своём компьютере, то в консоль будет выведено такое число:
Пример №4Необходимо разделить 7. 6 на 2.9, используя:
6 на 2.9, используя:
- обычное деление, как нас учили в школе
- деление по модулю
И пробуем теперь запустить программу на компьютере:
Если Вы запустите этот код на своём компьютере, то в консоль будет выведено число, близкое к 1.8. Например, Вы можете увидеть какое-то такое число: 1.7999999999999998. Из-за определённых особенностей Java, которые мы будем с Вами рассматривать позже в других статьях, на разных компьютерах число будет немного отличаться. Но оно будет близкое по значению к 1.8
Итак, как Вы уже поняли, оператор деления по модулю вычисляет остаток от деления.
- Применяется к таким типам переменных:
- Byte, short, Int, long – целочисленный тип переменных
- Float, Double – числа с плавающей точкой
- Отрицательные и положительные числа
Есть небольшой нюанс при использовании оператора деления по модулю с отрицательными и положительными числами.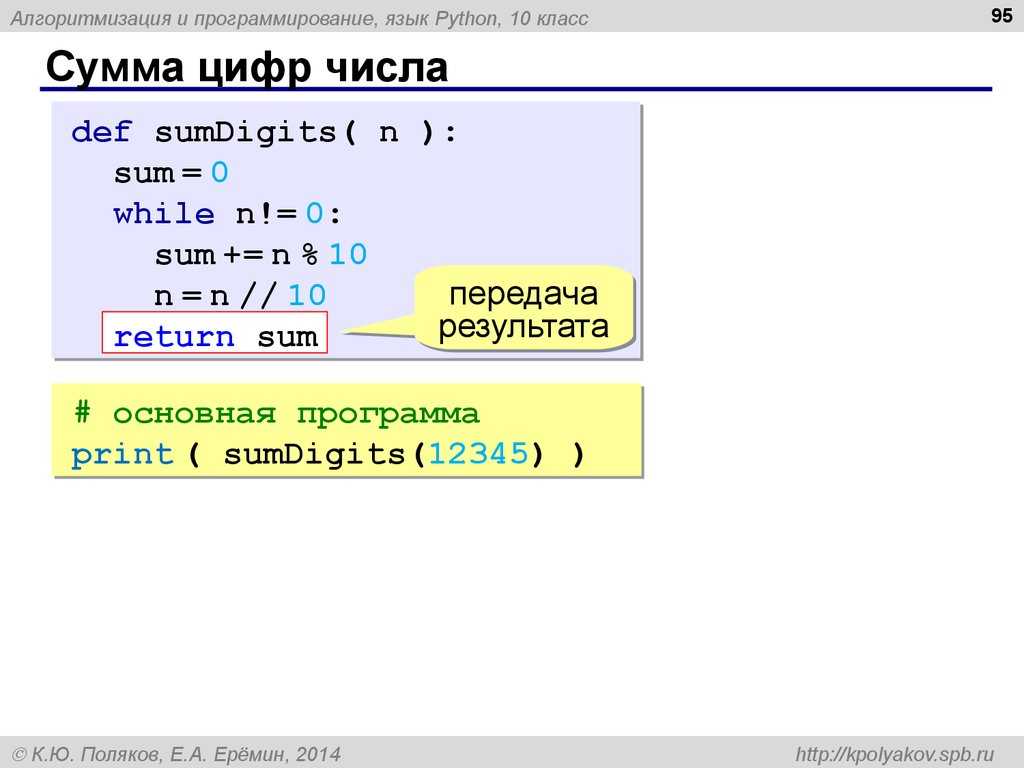
Работает простое правило:
- Отбрасываете знак минуса
- Делите числа как обычно
- А далее, если первое число (делимое), было со знаком минус, к результату добавляете знак минус.
И пробуем теперь запустить программу на компьютере — один из описанных выше примеров:
Как вычислить остаток от деления в java
6 сентября 2014 Мария (admin)
В уроке 8 мы затронули логические операторы, они нам были необходимы для формирования логического выражения в условиях if. Этот урок будет посвящен математике в Java, и поэтому мы рассмотрим подробнее арифметические операторы и частично возможности класса Math.
Но для начала, выясним, что же такое операторы. Операторы это специальные символы, отвечающие за ту или иную операцию, например сложение, умножение, сравнение. Все операторы в Java можно разбить на 4 класса — арифметические, битовые, операторы сравнения и логические.
Для стандартных арифметических операций, таких как сложение, вычитание, умножение, деление в Java используются традиционные символы, к которым мы привыкли со школы:
Примечание: при операции деления, если оба аргумента являются целыми числами, то в результате получим целое число. Дробная часть, если такая имеется, отбросится. Если хотим получить число с дробной частью, то нужно, чтобы один из аргументов был типа double. Это можно указать в самом выражении при помощи добавления после числа .0 или .d. Пример:
В Java также имеется специальный оператор %, обозначающий остаток от делния.
Пример использования: дан массив целых чисел, вывести на консоль только те числа, которые делятся на 3.
Операции с присваиванием
Рассмотрим задачу вывода на экран 10 первых четных чисел чисел
мы можем записать сокращенно
+= это оператор сложения с присваиванием. Подобные операторы есть для всех основных 5 операций, рассмотренных выше
Пример использования: Найти факториал числа 7.
Инкрементирование и декрементирование
Инкремент, обозначается ++ и увеличивает значение переменной на единицу. Декремент обозначается — и уменьшает значение на единицу. С инкрементом и декрементом мы часто встречаемся в цикле for.
Инкремент и декремент бывают двух форм
Различие префиксной и постфиксной формы проявляется только тогда, когда эти операции присутствуют в выражениях. Если форма префиксная, то сначала произойдет увеличение (или уменьшение) переменной на единицу, а потом с новым значением будет произведены дальнейшие вычисления. Если форма постфиксная, то расчет выражения будет происходить со старым значением переменной, а переменная увеличится (или уменьшится) на единицу после вычисления выражения. Пример
В первом случае сначала переменная a увеличится на 1, потом произойдет вычисление всего выражения. Во втором случае произойдет вычисление выражения при старом значении b = 3, и после вычисления b увеличится на 1, на результат в postfix это уже не повлияет.
Если вы поняли принцип работы постфиксного и префиксного инкремента/декремента, то предлагаю решить в уме такую задачу:
Вопрос: чему в итоге равны x и y? После того, как вы сделали предположение, проверьте его в java.
Задача со зведочкой. Дан код:
Какие числа будут выведены на экран? Почему? Разобраться самостоятельно.
Примечание: инкремент и декремент применяются только к переменной. Выражение вида 7++ считается недопустимым.
Математические функции и константы (класс Math)Для решения задач нередко требуется использование математических функций. В Java такие функции включены в класс Math. Для того, чтобы использовать методы класса Math, нужно подключить его в начале .java файла с вашим кодом.
Часто используемые математические функции
- sqrt(a) — извлекает квадратный корень из числа а.
- pow(a, n) — a возводится в степень n.
- sin(a), cos(a), tan(a) — тригонометрические функции sin, cos и tg угла a указанного в радианах.

- asin(n), acos(n), atan(n) — обратные тригонометрические функции, возвращают угол в радианах.
- exp(a) — возвращает значение экспоненты, возведенной в степень a.
- log(a) — возвращает значение натурального логарифма числа a.
- log10(a) — возвращает значение десятичного логарифма числа a.
- abs(a) — возвращает модуль числа a.
- round(a) — округляет вещественное число до ближайшего целого.
Константы
- PI — число «пи», с точностью в 15 десятичных знаков.
- E — число «e»(основание экспоненциальной функции), с точностью в 15 десятичных знаков.
- Дан массив целых чисел, найти среди элементов массива числа, которые делятся на 3 и на 6
- Посчитать среднее арифметическое чисел в массиве
- Известны катеты прямоугольного треугольника, найти его площадь и периметр
- Даны два целых числа, найти их наибольший общий делитель и наименьшее общее кратное
- Даны радиус вращения и высота конуса, вычислить объем конуса.

Категория: Уроки Java
Оператор mod — остаток от деления. Что такое mod?
Оператор mod обозначается символом % и является оператором деления по модулю. Он возвращает остаток от деления 1-го операнда на 2-й и широко используется в разных языках программирования для решения ряда задач.
Оператор mod в Java
В Java operator mod может работать как с целыми числами (byte/int/short/long), так и с плавающей точкой (byte/int/short/long). Давайте приведём пример работы оператора mod при делении:
После выполнения этой программы вы получите результат следующего вида:
Как видим, оператор mod — это прекрасный способ найти остаток от деления. Зачем это может понадобиться на практике? Например, при нахождении кратности числа и определении, является ли некоторое число, введённое с клавиатуры, чётным. Также с помощью оператора mod можно узнать, делится ли одно число на другое без остатка или определить последнюю цифру числа. В общем, оператор mod очень полезен при решении различных задач по программированию.
Оператор mod в SQL
Не менее интересно использование mod в базах данных. Аналогично, mod находит остаток от деления. При этом вместо mod можно задействовать операцию %, делающую то же самое. Синтаксис в SQL следующий:
Но можно написать и иначе, используя % :
Давайте приведём пример использования mod в базах данных. Вот, например, таблица numbers:
Найдём остаток от деления столбца number на три:
В результате запрос SQL выберет следующие строки:
Но, как мы уже говорили выше, этот же запрос можно без проблем переписать:
Операция взятия остатка от деления в Java
Я уже однажды расписывал операции в Java. В этой статье я акцентрирую внимание на операцию взятия остатка от деления, так как её работа отличается в различных языках программирования и иногда порождает недопонимание.
Операция взятия остатка % в Java работает не только с целыми числами, но и с числами с плавающей точкой.
Для целых чисел операция взятия остатка работает по такому принципу, что результат операции будет таким, что будет выполняться равенство:
Это равенство действует даже в том случае, если левый операнд будет наименьшим отрицательным числом для своего типа, а операнд в правой части будет равен -1 (тогда результатом будет 0).
Результатом операции взятия остатка для целых чисел в Java может быть отрицательное число только в том случае, если левый операнд будет отрицательным числом, а также результат может быть положительным только в том случае, если операнд в левой части будет положительным числом.
Если в правой части операции взятия остатка для целочисленных операндов в Java стоит 0, то результатом будет ArithmeticException .
Примеры работы операции взятия остатка для целочисленных операндов (выполнено в JShell):
Как я уже говорил, в Java операция взятия остатка % работает и с числами с плавающей точкой ( float и double ). Согласно спецификации языка Java операция взятия остатка для чисел с плавающей точкой работает не так, как это принято в IEEE 754, но если очень нужно то можно использовать метод Math . IEEEremainder .
IEEEremainder .
В Java операция взятия остатка % работает согласно следующим правилам:
- Если один из операндов равен NaN, то результат операции будет NaN.
- Если результат не NaN, то знаком результата будет знак операнда в левой части.
- Если операнд в левой части Infinity, или операнд в правой части равен нулю, или выполняются оба условия, то результат будет равен операнду в левой части.
- Если операнд в левой части конечен, а операнд в правой части Infinity, то результат будет равен операнду в левой части.
- Если операнд в левой части равен нулю, а операнд в правой части конечен, то результат будет равен операнду в левой части.
- Во всех остальных случаях результат r взятия остатка от операнда n при делении на d определяется по математической формуле r = n — (d × q), где q будет целым числом, которое отрицательно только в случае, если n / d отрицательно, и положительно, если n / d положительно, и его размер максимально возможный, но не превышающий отношение n и d.
 Пример: 0,5 ÷ 0,3 = 1,6, тогда q будет положительным, так как 1,6 положительно, а наибольший размер, не превышающий 1,6 будет 1, то q = 1, а значит r = 0,5 — (0,3 × 1) = 0,2.
Пример: 0,5 ÷ 0,3 = 1,6, тогда q будет положительным, так как 1,6 положительно, а наибольший размер, не превышающий 1,6 будет 1, то q = 1, а значит r = 0,5 — (0,3 × 1) = 0,2.
Операция взятия остатка для чисел с плавающей точкой никогда не приводит к возникновению Exception-ов.
Циклы while и for . Объектно-ориентированное программирование на Java. Платформа Java SE
Давайте представим, что мы хотим разделить целое число m на другое целое число n.
И мы хотим получить результат целочисленного деления, то есть самое большое количество раз, которое n вписывается в m.
Например, целочисленное деление 7 на 2, равно 3, потому что 2 по 3 раза, это 6.
Остаток равен 1.
И представьте себе, что у нас нет встроенной операции, которая выполняет эту операцию для нас.
Поэтому нам нужно сделать повторяемые вычитания.
И если нам удастся вычесть 2 из 7 три раза, это означает, что целочисленное деление равно 3.
Целочисленное деление y и целочисленный остаток x соответствуют формуле, m равно y умножить на n плюс x.
Предположим, что нам даны целые числа m и n.
А в x сохраняется оставшееся значение после вычитаний.
Итак, давайте начнем с x равно m.
y содержит результат целочисленного деления.
Мы инициализируем y 0 и приращиваем y на 1 каждый раз, когда мы вычитаем n из x.
И мы продолжаем вычитать n из x, пока x не меньше n.
Если x больше или равно n, мы вычитаем n из x и увеличим y на 1.
Таким образом, эта программа делает то, что мы хотим, но тут есть проблема.
Мы не знаем, сколько операторов if мы должны добавить.
Потому что это зависит от фактических значений m и n.
Например, с 7 и 2, это будет три выражения if.
При других входных данных это должно быть другое число if выражений.
В Java эту проблему решает оператор while.
Теперь эта программа делает то же самое, что и прежде, повторяет выражение, пока выполняется условие.
Но теперь у нас есть одно большое преимущество.
Выражения повторяются столько раз, сколько это необходимо, автоматически.
Но теперь вы должны быть очень осторожны при написании условия while.
Потому что есть опасность войти в бесконечный цикл, если условие while никогда не прекратится.
Преимущество цикла while заключается в том, что нам не нужно заранее знать, сколько раз мы должны что-либо повторять.
Мы повторяем, пока не будет достигнута цель, выраженная логическим условием.
Иногда, однако, мы знаем, сколько раз нам нужно что-либо повторить.
Это легко реализовать подсчетом.
Хитрость заключается в том, чтобы ввести счетчик.
Это целочисленная переменная, которую мы обновляем на каждой итерации.
Здесь существует три важных элемента: величина, с которой мы хотим начать, значение в конце и шаг между значениями.
Здесь мы начинаем с 0 и заканчиваем 3. И шаг 1.
Поэтому мы выполняем четыре итерации для i равного 0, 1, 2 и 3.
Теперь, помимо подсчета, мы можем захотеть что-то сделать в теле цикла.
В этом случае предположим, что у нас есть другая переменная, n, которую мы хотим умножать на 2 при каждой итерации.
Так как такого рода подсчет используется часто, в Java для этого есть специальная конструкция.
А именно, цикл for.
Этот цикл объединяет три важных момента для переменной счетчика:
Ее инициализацию, условие остановки, и выражение обновления.
Имейте в виду, что обновление выполняется после того, как выполняется тело цикла, а не раньше.
Для цикла for скобки являются обязательными, а также две точки с запятой внутри.
Фигурные скобки необходимы только в том случае, если есть более одного выражения в теле цикла.
Но это хорошая практика, чтобы всегда писать их.
Однако иногда желательно выполнить тело цикла хотя бы один раз, даже если в начальный момент условное выражение ложно.
Иначе говоря, существуют ситуации, когда проверку условия прерывания цикла желательно выполнять в конце цикла, а не в его начале.
И в Java есть именно такой цикл: do-while.
Этот цикл всегда выполняет тело цикла хотя бы один раз, так как его условное выражение проверяется в конце цикла.
В приведенном примере тело цикла выполняется до первой проверки условия завершения.
Мы уже видели оператор break в выражении switch.
Но оператор break также может прерывать любой цикл.
Предположим, у вас есть цикл.
И иногда желательно немедленно завершить цикл, не проверяя условие.
В таких случаях используется оператор break.
Оператор break немедленно завершает цикл, и управление программой переходит к следующему выражению, следующему за циклом.
Оператор break почти всегда используется вместе с выражением if else.
Также иногда желательно не прервать цикл, а пропустить код тела цикла и перейти к следующей итерации.
Оператор continue пропускает текущую итерацию цикла и когда выполняется оператор continue, управление программой переходит к концу цикла.
Затем проверяется условие, которое управляет циклом.
Оператор continue также почти всегда используется вместе с выражением if else.
Данный текст является ознакомительным фрагментом.
Арифметические операторы в java — ПК журнал
Рейтинг статьиЗагрузка…
Арифметические операторы
1. Основные арифметические операторы Java
В следующей таблице перечислены основные арифметические операторы (или операции), применяемые в языке Java:
| Операция | Описание |
| + | Сложение (а также унарный плюс) |
| — | Вычитание (а также унарный минус) |
| * | Умножение |
| / | Деление |
| % | Деление по модулю |
Рассмотрим некоторые правила работы с арифметическими операторами:
- Выражения вычисляются слева направо, если не добавлены круглые скобки или одни операции имеют более высокий приоритет.

- Операции * , / , и % имеют более высокий приоритет чем + и — .
Арифметические операторы над целочисленными значениями
Например, в этом коде, переменные a и b будут иметь разные значения:
Унарные операции сложения и вычитания
- Операция унарного вычитания изменяет знак своего единственного операнда.
- Операция унарного сложения просто возвращает значение своего операнда. Она в принципе не является необходимой, но возможна.
Деление целочисленных чисел в Java
Когда операция деления выполняется над целочисленным типом данных, ее результат не будет содержать дробный компонент. Это деление без остатка в Java:
Результат выполнения этой программы:
Арифметические операторы над переменными типа char
Операнды арифметических операторов должны иметь числовой тип. Арифметические операторы нельзя выполнять над логическими типами данных, но допускается над типами данных char , поскольку в Java этот тип, по существу, является разновидностью типа int . Например:
Например:
Или как в следующем примере:
Деление по модулю в Java
Оператор деления по модулю — обозначается символом % . Этот оператор возвращает остаток от деления первого числа на второй в Java. При делении целого числа результатом будет тоже целое число:
2. Составные арифметические операции с присваиванием
| Операция | Описание |
| += | Сложение с присваиванием |
| -= | Вычитание с присваиванием |
| *= | Умножение с присваиванием |
| /= | Деление с присваиванием |
| %= | Деление по модулю с присваиванием |
В Java имеются специальные операции, объединяющие арифметические операторы с операцией присваивания. Рассмотрим следующее выражение:
B Java эту операцию можно записать следующим образом:
Составные операции с присваиванием позволяют не только уменьшить объем кода, но и позволяют выполнять автоматическое преобразование чего не делают обычные операции:
9.
 Java — Основные операторы языка
Java — Основные операторы языкаJava предоставляет богатый набор операторов для управления переменными. Все операторы Java можно разделить на следующие группы:
- арифметические операторы;
- операторы сравнения;
- побитовые операторы;
- логические операторы;
- операторы присваивания;
- прочие операторы.
Содержание
Арифметические операторы
Арифметические операторы — используются в математических выражениях таким же образом, как они используются в алгебре. Предположим, целая переменная A равна 10, а переменная B равна 20. В следующей таблице перечислены арифметические операторы в Java:
| Оператор | Описание | Пример |
| + | Складывает значения по обе стороны от оператора | A + B даст 30 |
| — | Вычитает правый операнд из левого операнда | A — B даст -10 |
| * | Умножает значения по обе стороны от оператора | A * B даст 200 |
| / | Оператор деления делит левый операнд на правый операнд | B / A даст 2 |
| % | Делит левый операнд на правый операнд и возвращает остаток | B % A даст 0 |
| ++ | Инкремент — увеличивает значение операнда на 1 | B++ даст 21 |
| — | Декремент — уменьшает значение операнда на 1 | B— даст 19 |
Пример
Следующий простой пример показывает программно арифметические операторы. Скопируйте и вставьте следующий java-код в файл test.java, скомпилируйте и запустить эту программу:
Скопируйте и вставьте следующий java-код в файл test.java, скомпилируйте и запустить эту программу:
Это произведет следующий результат:
Операторы сравнения
Есть следующие операторы сравнения, поддерживаемые на языке Java. Предположим, переменная A равна 10, а переменная B равна 20. В следующей таблице перечислены реляционные операторы или операторы сравнения в Java:
| Оператор | Описание | Пример |
| == | Проверяет, равны или нет значения двух операндов, если да, то условие становится истинным | (A == B) — не верны |
| != | Проверяет, равны или нет значения двух операндов, если значения не равны, то условие становится истинным | (A != B) — значение истинна |
| > | Проверяет, является ли значение левого операнда больше, чем значение правого операнда, если да, то условие становится истинным | (A > B) — не верны |
| = | Проверяет, является ли значение левого операнда больше или равно значению правого операнда, если да, то условие становится истинным | (A >= B) — значение не верны |
| > (сдвиг вправо) | Бинарный оператор сдвига вправо. Значение правых операндов перемещается вправо на количество бит, заданных левых операндом. Значение правых операндов перемещается вправо на количество бит, заданных левых операндом. | A >> 2 даст 15, который является 1111 |
| >>> (нулевой сдвиг вправо) | Нулевой оператор сдвига вправо. Значение левых операндов перемещается вправо на количество бит, заданных правым операндом, а сдвинутые значения заполняются нулями. | A >>> 2 даст 15, который является 0000 1111 |
Пример
Следующий простой пример показывает, программно побитовые операторы в Java. Скопируйте и вставьте следующий java-код в файл test.java, скомпилируйте и запустить эту программу:
Будет получен следующий результат:
Логические операторы
Предположим, логическая переменная A имеет значение true, а переменная B хранит false. В следующей таблице перечислены логические операторы в Java:
| Оператор | Описание | Пример |
| && | Называется логический оператор «И». Если оба операнда являются не равны нулю, то условие становится истинным | (A && B) — значение false |
| || | Называется логический оператор «ИЛИ».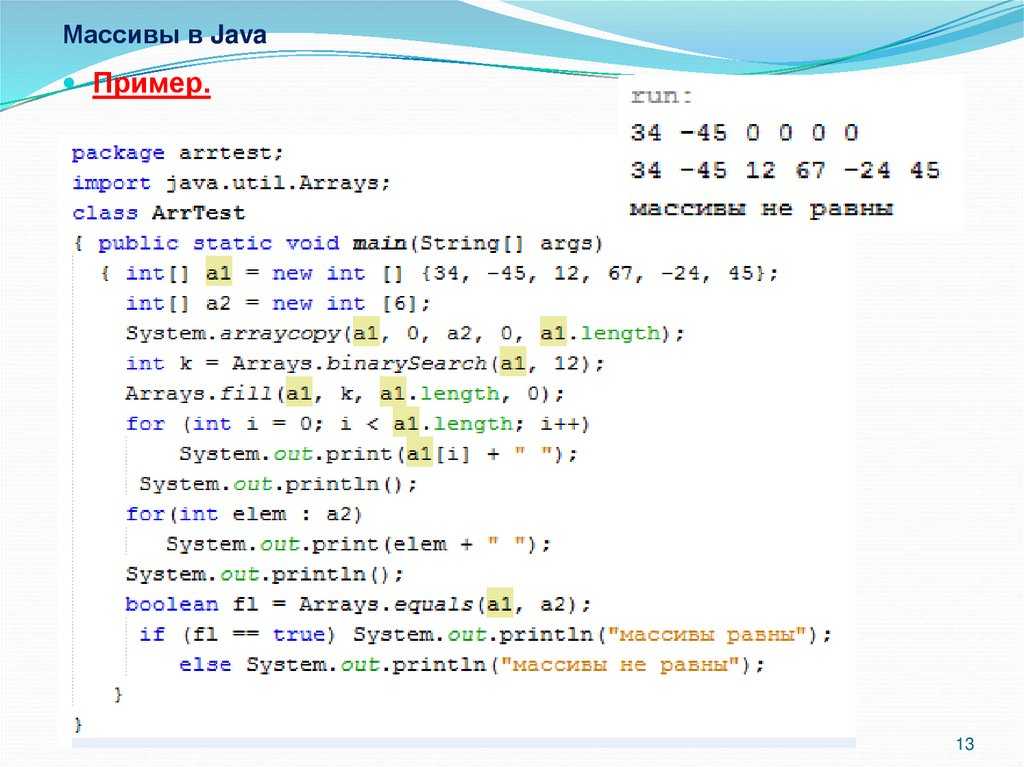 Если любой из двух операндов не равен нулю, то условие становится истинным Если любой из двух операндов не равен нулю, то условие становится истинным | (A || B) — значение true |
| ! | Называется логический оператор «НЕ». Использование меняет логическое состояние своего операнда. Если условие имеет значение true, то оператор логического «НЕ» будет делать false | !(A && B) — значение true |
Пример
Следующий простой пример показывает, программно логические операторы в Java. Скопируйте и вставьте следующий java-код в файл test.java, скомпилируйте и запустить эту программу:
Это произведет следующий результат:
Операторы присваивания
Существуют следующие операторы присваивания, поддерживаемые языком Java:
| Оператор | Описание | Пример |
| = | Простой оператор присваивания, присваивает значения из правой стороны операндов к левому операнду | C = A + B, присвоит значение A + B в C |
| += | Оператор присваивания «Добавления», он присваивает левому операнду значения правого | C += A, эквивалентно C = C + A |
| -= | Оператор присваивания «Вычитания», он вычитает из правого операнда левый операнд | C -= A, эквивалентно C = C — A |
| *= | Оператор присваивания «Умножение», он умножает правый операнд на левый операнд | C * = A эквивалентно C = C * A |
| /= | Оператор присваивания «Деление», он делит левый операнд на правый операнд | C /= A эквивалентно C = C / A |
| %= | Оператор присваивания «Модуль», он принимает модуль, с помощью двух операндов и присваивает его результат левому операнду | C %= A, эквивалентно C = C % A |
| >= | Оператор присваивания «Сдвиг вправо» | C >>= 2, это как C = C >> 2 |
| &= | Оператор присваивания побитового «И» («AND») | C &= 2, это как C = C & 2 |
| ^= | Оператор присваивания побитового исключающего «ИЛИ» («XOR») | C ^= 2, это как C = C ^ 2 |
| |= | Оператор присваивания побитового «ИЛИ» («OR») | C |= 2, это как C = C | 2 |
Пример
Следующий простой пример показывает, программно логические операторы в Java. Скопируйте и вставьте следующий java-код в файл test.java, скомпилируйте и запустить эту программу:
Скопируйте и вставьте следующий java-код в файл test.java, скомпилируйте и запустить эту программу:
Будет получен следующий результат:
Прочие операторы
Есть несколько других операторов, поддерживаемых языком Java.
Тернарный оператор или условный оператор (?:)
Тернарный оператор — оператор, который состоит из трех операндов и используется для оценки выражений типа boolean. Тернарный оператор в Java также известен как условный оператор. Этот. Цель тернарного оператора или условного оператора заключается в том, чтобы решить, какое значение должно быть присвоено переменной. Оператор записывается в виде:
Пример
Ниже приведен пример:
Будет получен следующий результат:
Оператор instanceof
Оператор instanceof — проверяет, является ли объект определенного типа (типа класса или типа интерфейса) и используется только для переменных ссылочного объекта. Оператор instanceof записывается в виде:
Примеры
Если переменная ссылочного объекта в левой части оператора проходит проверку для класса/типа интерфейса на правой стороне, результатом будет значение true. Ниже приведен пример и описание оператора instanceof:
Ниже приведен пример и описание оператора instanceof:
Будет получен следующий результат:
Этот оператор по-прежнему будет возвращать значение true, если сравниваемый объект является совместимым с типом на право назначения. Ниже приводится еще один пример:
Будет получен следующий результат:
Приоритет операторов в Java
Приоритет операторов определяет группирование терминов в выражении. Это влияет как вычисляется выражение. Некоторые операторы имеют более высокий приоритет, чем другие; например оператор умножения имеет более высокий приоритет, чем оператор сложения:
Например, x = 7 + 3 * 2. Здесь x присваивается значение 13, не 20, потому что оператор «*» имеет более высокий приоритет, чем «+», так что сначала перемножается «3 * 2», а затем добавляется «7».
В таблице операторы с наивысшим приоритетом размещаются в верхней части, и уровень приоритета снижается к нижней части таблицы. В выражении высокий приоритет операторов в Java будет оцениваться слева направо.
Операторы Java
В этой статье вы узнаете о различных типах операторов Java и их синтаксисе.
Операторы это специальные символы, которые осуществляют операции над операндами ( переменными и значениями ). Например, « + » это оператор, который производит сложение.
Сейчас вы узнаете, как использовать операторы, чтобы манипулировать переменными.
Операторы присваивания
Используются в Java , чтобы присвоить значения переменным. Например,
Оператор « = » присваивает значение справа от себя переменной, находящейся слева. В примере переменной age присвоено значение 5 .
Пример 1: оператор присваивания
Когда вы запустите программу, на экран выведется:
Арифметические операторы
Арифметические операторы Java используются, чтобы производить математические операции сложения, вычитания умножения и так далее.
| Оператор | Значение |
|---|---|
| + | Сложение (также используется для конкатенации строк) |
| — | Вычитание |
| * | Умножение |
| / | Деление |
| % | Остаток от деления |
Пример 2: Арифметические операторы
Когда вы запустите программу, на экран выведется:
В примере с оператором деления Java , приведенном выше, использованные операнды – переменные. Кроме этого могут использоваться символьные значения. Например:
Кроме этого могут использоваться символьные значения. Например:
Оператор « + » также может быть использован, чтобы соединить ( конкатенировать ) две строки или больше.
Пример 3: Арифметический оператор
Когда вы запустите программу, на экран выведется:
Унарные операторы
Унарный оператор Java производит операцию только над одним операндом.
| Оператор | Значение |
| + | Унарный плюс (не нужен, так как числа положительные и без него). |
| — | Унарный минус; инвертирует знак выражения. |
| ++ | Оператор инкремента; увеличивает значение на 1. |
| — | Оператор декремента; уменьшает значение на 1. |
| ! | Оператор логического отрицания; инвертирует значение булевой переменной. |
Пример 4: Унарный оператор
Когда вы запустите программу, на экран выведется:
В Java можно использовать операторы « ++ » и « — » в качестве префикса и постфикса.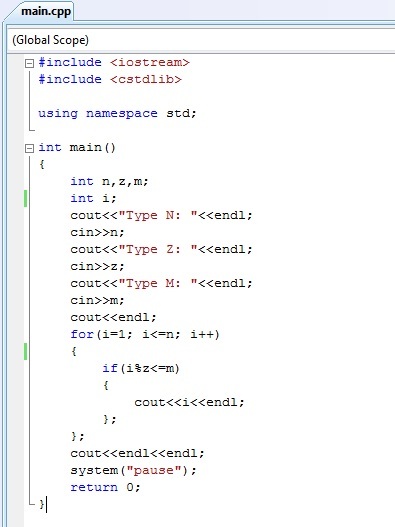 Оператор « ++ » увеличивает значение на 1 , а « — » уменьшает значение на 1 .
Оператор « ++ » увеличивает значение на 1 , а « — » уменьшает значение на 1 .
Есть большая разница в использовании операторов Java инкремента и декремента в префиксе и в постфиксе. Рассмотрим пример:
Пример 5: Унарный оператор
Когда вы запустите программу, на экран выведется:
Когда выполняется выражение System.out.println(number++) , первым вычисляется изначальное значение. Переменная number увеличивается только после этого. Поэтому вы получите на выходе 5.2 . Далее, когда выполняется System.out.println(number) , показывается значение 6.2 .
Тем не менее, когда выполняется System.out.println(++number) , number увеличивается на 1 перед тем, как будет выведено на экран. Так же обстоят дела и с оператором Java декремента.
Операторы равенства и отношений
Операторы равенства и отношений проверяют, является ли операнд больше, меньше, равен, неравен второму и так далее. Получаемый результат равен true или false .
| Оператор | Описание | Пример |
| == | равен | 5 == 3 результат false |
| != | неравен | 5 != 3 результат true |
| > | Больше | 5 > 3 результат true |
| = | Больше или равен | 5 >= 5 результат true |
| Java , на экран выведется: |
Здесь мы использовали оператор « > », чтобы проверить, больше ли number1 , чем number2 .
Так как number2 больше, чем number1 , результатом выражения number1 > number2 будет false .
Кроме операторов отношений, есть оператор сравнения типов instanceof , который сравнивает объект и определенный тип.
Оператор instanceof
Пример оператора instanceof .
Когда вы запустите программу, на экран выведется true . Это происходит от того, что test — экземпляр класса String .
Логические операторы
Java логические операторы || ( условное-ИЛИ (OR) ) и && ( условное-И (AND) ) совершают операции над булевыми выражениями. Вот как они работают.
| Оператор | Описание | Пример |
| || | условное-ИЛИ; true если хотя бы одно из булевых выражений истинно (true) | false || true результат — true |
| && | условное-И; истинно если все булевы выражения истинны (true). | false && true результат — false |
Пример 8: Логические операторы
Когда вы запустите программу, на экран выведется:
Тернарный оператор
Условный оператор или тернарный оператор Java « ? :» — это сокращение выражения if-then-else . 5
5
Данная публикация представляет собой перевод статьи « Java Operators » , подготовленной дружной командой проекта Интернет-технологии.ру
Арифметические операторы в java
В уроке 8 мы затронули логические операторы, они нам были необходимы для формирования логического выражения в условиях if. Этот урок будет посвящен математике в Java, и поэтому мы рассмотрим подробнее арифметические операторы и частично возможности класса Math.
Но для начала, выясним, что же такое операторы. Операторы это специальные символы, отвечающие за ту или иную операцию, например сложение, умножение, сравнение. Все операторы в Java можно разбить на 4 класса — арифметические, битовые, операторы сравнения и логические.
Арифметические операторы в JavaДля стандартных арифметических операций, таких как сложение, вычитание, умножение, деление в Java используются традиционные символы, к которым мы привыкли со школы:
Примечание: при операции деления, если оба аргумента являются целыми числами, то в результате получим целое число. Дробная часть, если такая имеется, отбросится. Если хотим получить число с дробной частью, то нужно, чтобы один из аргументов был типа double. Это можно указать в самом выражении при помощи добавления после числа .0 или .d. Пример:
Дробная часть, если такая имеется, отбросится. Если хотим получить число с дробной частью, то нужно, чтобы один из аргументов был типа double. Это можно указать в самом выражении при помощи добавления после числа .0 или .d. Пример:
В Java также имеется специальный оператор %, обозначающий остаток от делния.
Пример использования: дан массив целых чисел, вывести на консоль только те числа, которые делятся на 3.
Операции с присваиванием
Рассмотрим задачу вывода на экран 10 первых четных чисел чисел
мы можем записать сокращенно
+= это оператор сложения с присваиванием. Подобные операторы есть для всех основных 5 операций, рассмотренных выше
Пример использования: Найти факториал числа 7.
Инкрементирование и декрементирование
Инкремент, обозначается ++ и увеличивает значение переменной на единицу. Декремент обозначается — и уменьшает значение на единицу. С инкрементом и декрементом мы часто встречаемся в цикле for.
Инкремент и декремент бывают двух форм
Различие префиксной и постфиксной формы проявляется только тогда, когда эти операции присутствуют в выражениях. Если форма префиксная, то сначала произойдет увеличение (или уменьшение) переменной на единицу, а потом с новым значением будет произведены дальнейшие вычисления. Если форма постфиксная, то расчет выражения будет происходить со старым значением переменной, а переменная увеличится (или уменьшится) на единицу после вычисления выражения. Пример
Если форма префиксная, то сначала произойдет увеличение (или уменьшение) переменной на единицу, а потом с новым значением будет произведены дальнейшие вычисления. Если форма постфиксная, то расчет выражения будет происходить со старым значением переменной, а переменная увеличится (или уменьшится) на единицу после вычисления выражения. Пример
В первом случае сначала переменная a увеличится на 1, потом произойдет вычисление всего выражения. Во втором случае произойдет вычисление выражения при старом значении b = 3, и после вычисления b увеличится на 1, на результат в postfix это уже не повлияет.
Если вы поняли принцип работы постфиксного и префиксного инкремента/декремента, то предлагаю решить в уме такую задачу:
Вопрос: чему в итоге равны x и y? После того, как вы сделали предположение, проверьте его в java.
Задача со зведочкой. Дан код:
Какие числа будут выведены на экран? Почему? Разобраться самостоятельно.
Примечание: инкремент и декремент применяются только к переменной. Выражение вида 7++ считается недопустимым.
Выражение вида 7++ считается недопустимым.
Для решения задач нередко требуется использование математических функций. В Java такие функции включены в класс Math. Для того, чтобы использовать методы класса Math, нужно подключить его в начале .java файла с вашим кодом.
Оценка статьи:
Загрузка…
Adblock
detector
Циклический сдвиг массива java
При передаче в метод 0-го сдвига нужно вернуть исходный массив без изменений. А если больше или равен длине массива, то использовать остаток от деления.
А если больше или равен длине массива, то использовать остаток от деления.
Не так давно стартовал очередной курс Java на одном небезызвестном образовательном портале. И вот, моим студентам досталась задача по работе с массивами. Статья в первую очередь для них, но и для интересующихся, конечно же 🙂 Отдельное спасибо [email protected] за комментарий по поводу массива с чётным количеством элементов и чётным размером сдвига. Я переписал алгоритм и обновил статью.
Я переписал алгоритм и обновил статью.
Итак, задача сформулирована следующим образом
Написать метод, которому на вход подается одномерный массив и число n (может быть положительным, или отрицательным), при этом метод должен сместить все элементы массива на n позиций. Для усложнения задачи нельзя пользоваться вспомогательными массивами.
Усложняющее условие было введено потому, что можно решить задачу при помощи разделения массивов. В таком случае решение состоит в том, чтобы «отрезать» от массива кусок длиной n справа или слева (в зависимости от того, как n сравнивается с 0) и «прикрепить» отрезанную часть обратно с другой стороны. Это довольно дешёвый алгоритм, который имеет сложность O(n), но он будет требовать дополнительной памяти для хранения временного массива размера n. Поскольку такое решение самое простое, да и не особенно подходит под условие задачи, то мы перейдём сразу к более сложной алгоритмизации.
Разумеется, после первых подходов многие студенты находят следующее довольно логичное и вполне корректное решение. Оно весьма популярно на различных сайтах, описывающих циклический сдвиг. Суть его в том, что любой сдвиг можно представить в качестве n сдвигов на 1 ячейку. Сдвиг на 1 ячейку довольно просто реализуется циклом. В итоге, если изобразить это Java-методом, получается примерно такой метод:
Оно весьма популярно на различных сайтах, описывающих циклический сдвиг. Суть его в том, что любой сдвиг можно представить в качестве n сдвигов на 1 ячейку. Сдвиг на 1 ячейку довольно просто реализуется циклом. В итоге, если изобразить это Java-методом, получается примерно такой метод:
public static int [ ] shiftArray ( int [ ] incomingArray, int shift ) <
// Любой сдвиг больше длины массива можно оптимизировать до меньшего сдвига
// через деление по модулю
int finalShift ;
if ( shift > incomingArray. length ) <
shift = Math . abs ( shift % incomingArray. length ) ;
>
else <
finalShift = shift ;
>
// в зависимости от знака сдвига движение будет происходить
// слева направо при положительном сдвиге
// справа налево при отрицательном
if ( shift > 0 ) <
for ( int n = 0 ; n shift ; n ++ ) <
// убираем первый элемент в буфер, а на его место ставим хвостовой элемент
int buffer = incomingArray [ 0 ] ;
myArray [ 0 ] = incomingArray [ incomingArray.
// циклично сдвигаем весь массив
for ( int j = 1 ; j incomingArray. length — 1 ; j ++ ) <
incomingArray [ incomingArray. length — j ] = incomingArray [ incomingArray. length — j — 1 ] ;
>
// ставим буферный элемент в 1 ячейку
incomingArray [ 1 ] = buffer ;
>
>
else if ( shift 0 ) <
for ( int i = 0 ; i > shift ; n — ) <
int buffer = incomingArray [ incomingArray. length — 1 ] ;
incomingArray [ incomingArray. length — 1 ] = incomingArray [ 0 ] ;
for ( int j = 1 ; j incomingArray. length — 1 ; j ++ ) <
>
incomingArray [ incomingArray. length — 2 ] = buffer ;
>
>
>
Хочу отметить, что такое решение имеет место, и оно применимо. Но мы же решаем алгоритмическую задачу, поэтому неплохо бы поговорить о том, какую сложность будет иметь приведенный алгоритм. Если опустить процесс вычислений буферных элементов и обмена ими между ячейками, то сложность алгоритма сводится к O(N * M), где N — размер входного массива, а M — величина сдвига. Очевидно, что для |M| = 1 (т.е. M = -1 или M = 1) сложность снизится до O(N). Это частный случай.
Очевидно, что для |M| = 1 (т.е. M = -1 или M = 1) сложность снизится до O(N). Это частный случай.
Теперь давайте подумаем, что же тут не так. На самом деле, если мы знаем величину сдвига (а мы её знаем), то вполне можно вычислить, какой элемент будет следующим. Это говорит о том, что можно создать жонглирующий алгоритм следующего вида:
- Получаем нулевой элемент и кладем его в буфер
- Начинаем цикл от 0 до длины массива включительно (это обусловлено тем, что в момент, когда мы дойдём до последнего элемента, он будет помещен в буфер, из которого его надо восстановить на месте нулевого элемента, чем полностью закольцевать сдвиг)
- Дальше мы меняем местами элементы, исходя из размера шага. Например, для шага 3 и массива длиной 7 мы сначала поменяем элементы 0, 3, 6. Затем — 1, 4, 2. И так далее.
Если рассмотреть наборы изменяемых элементов, то мы увидим, что количество таких наборов, внутри которых мы будем итеративно менять местами элементы, будет равно наименьшему общему делителю для размера массива и размера сдвига. К примеру, для массива из 12 элементов при сдвиге 3 мы будем иметь три набора смещаемых элементов.
К примеру, для массива из 12 элементов при сдвиге 3 мы будем иметь три набора смещаемых элементов.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
— 1, 4, 7, 10
— 2, 5, 8, 11
— 3, 6, 9, 12
4 5 6 7 8 9 10 11 12 1 2 3
Поскольку эти наборы независимы, то при перестановке в них элементов местами мы не нарушим общий порядок следования элементов.
В реализации нужно учитывать и то, что сдвиг может идти как влево, так и вправо.
Теперь мы можем написать реализацию нашего алгоритма
public class moves <
public static void main ( String [ ] args ) <
int [ ] in1 = < 5 , 3 , 7 , 2 , 9 , 13 , 42 >;
int [ ] out1 = moves ( in1, — 2 ) ;
printOut ( out1 ) ;
int [ ] in2 = < 5 , 3 , 7 , 2 , 9 , 13 , 42 , 43 , 45 , 46 >;
int [ ] out2 = moves ( in2, 2 ) ;
printOut ( out2 ) ;
int [ ] in3 = < 5 , 3 , 7 , 2 , 9 , 13 , 42 , 143 >;
int [ ] out3 = moves ( in3, 5 ) ;
printOut ( out3 ) ;
int [ ] in4 = < 5 , 3 , 7 , 2 , 9 , 42 , 43 , 45 , 46 >;
int [ ] out4 = moves ( in4, 0 ) ;
printOut ( out4 ) ;
>
/**
* Main method, shifts array
* @param incoming — user array
* @param delta — shift value
* @return int[] result array
*/
static int [ ] moves ( int [ ] incoming, int delta ) <
int currentIndex, movedIndex, buffer ;
for ( int i = 0 ; i greatestCommonDivisor ( delta, incoming. length ) ; i ++ ) <
length ) ; i ++ ) <
buffer = incoming [ i ] ;
if ( delta > 0 ) <
while ( true ) <
movedIndex = currentIndex + delta ;
if ( movedIndex >= incoming. length )
movedIndex = movedIndex — incoming. length ;
if ( movedIndex == i )
break ;
incoming [ currentIndex ] = incoming [ movedIndex ] ;
currentIndex = movedIndex ;
>
>
else if ( delta 0 ) <
while ( true ) <
movedIndex = currentIndex + delta ;
if ( movedIndex 0 )
movedIndex = incoming. length + movedIndex ;
if ( movedIndex == i )
break ;
incoming [ currentIndex ] = incoming [ movedIndex ] ;
currentIndex = movedIndex ;
>
>
incoming [ currentIndex ] = buffer ;
>
/**
* Simple printout
* @param incomingArray user array
*/
public static void printOut ( int [ ] incomingArray ) <
for ( int item : incomingArray ) <
System . out . print ( item + » » ) ;
>
/**
* Finding the GCD in recoursive function
* @param a — first element
* @param b — second element
* @return int GCD
*/
static int greatestCommonDivisor ( int a, int b )
<
if ( b == 0 )
return a ;
else
return greatestCommonDivisor ( b, a % b ) ;
>
>
Как и в прошлый раз, мы можем пренебречь расчетами индексов. И в конечном итоге мы получаем сложность алгоритма, которая зависит исключительно от длины массива, т.е. O(N). И эта сложность не будет меняться в зависимости от исключительных ситуаций, что как минимум не хуже предыдущего алгоритма, а для сдвигов, больших, чем единица, лучше.
И в конечном итоге мы получаем сложность алгоритма, которая зависит исключительно от длины массива, т.е. O(N). И эта сложность не будет меняться в зависимости от исключительных ситуаций, что как минимум не хуже предыдущего алгоритма, а для сдвигов, больших, чем единица, лучше.
Надеюсь, приведенные измышления будут для Вас полезны. Буду рад критике и комментариям!
Дочитавшим до конца, картинка де мотиватор 🙂
Я новичок в java и у меня возник данный вопрос. Опишу ситуацию: есть двумерный массив типа int 9 на 9, и есть метод, который делает циклический сдвиг в одномерном массиве на заданное количество элементов.
Первое что я сделал это инициализировал первую строку двумерного массива числами от 1 до 9.
После чего я, сделав сдвиг на один элемент, записал то что получится в 4-ю строчку двумерного массива.
Но тут и возникла проблема: когда функция возвращает сдвинутый массив и записывает его в 4-ю строчку почему-то сдвигается и нулевая строчка, и они, по сути, просто дублирую друг друга. Как я понимаю, они просто ссылаются на одно и тоже место в памяти, и тут возникает вопрос: почему нельзя таким образом проинициализировать строки в массиве?
Как я понимаю, они просто ссылаются на одно и тоже место в памяти, и тут возникает вопрос: почему нельзя таким образом проинициализировать строки в массиве?
Сложение, вычитание и другая математика в Kotlin
Проще всего разобраться с операциями можно с помощью арифметики. Операция сложения берет два числа и преобразует их в сумму. Операция вычитания берет два числа и преобразует их в разность. Во всех приложениях вы найдете простую арифметику — от подсчета количества лайков до расчета правильного размера и положения кнопки или окна — числа и правда везде!
Содержание статьи
- Простые математические операции в Kotlin
- Десятичные числа в Kotlin
- Операция для получения остатка в Kotlin
- Операции смещения в Kotlin
- Порядок операций в Kotlin
В этом разделе вы узнаете о различных арифметических операциях, которые предлагает Kotlin. В следующих уроках мы разберем операции для типов, отличных от чисел.
Простые математические операции в Kotlin
Все операции в Kotlin используют символ, известный как оператор, для указания типа осуществляемой операции. Рассмотрим четыре арифметические операции, с которым вы знакомы с первого класса: сложение, вычитание, умножение и деление.
Рассмотрим четыре арифметические операции, с которым вы знакомы с первого класса: сложение, вычитание, умножение и деление.
Для данных операций в Kotlin используются следующие операторы:
- Сложение:
+ - Вычитание:
- - Умножение:
* - Деление:
/
Данные операторы используются следующим образом:
2 + 6 10 — 2 2 * 4 24 / 3
2 + 6 10 — 2 2 * 4 24 / 3 |
Каждая из данных строчек является выражением. У выражения есть значение. В данных случаях у всех четырех выражений одинаковые значения: 8. Вы набираете код для выполнения операций по аналогии с написанием примеров на бумаге.
В IDE вы увидите значения выражений в выводе на консоли с помощью команды println():
Если хотите, можете убрать пробелы возле оператора:
Разницы нет. Вы можете даже использовать варианты с пробелами и без вперемежку. К примеру:
К примеру:
2+6 // OK 2 + 6 // OK 2 +6 // OK 2+ 6 // OK
2+6 // OK 2 + 6 // OK 2 +6 // OK 2+ 6 // OK |
Однако зачастую удобнее читать выражения с пробелами возле оператора.
Десятичные числа в Kotlin
Во всех операциях выше использовались целые числа, которые относятся к типу integer. Однако не все числа целые.
Рассмотрим следующий пример:
22 / 7
22 / 7 |
Результатом данной операции будет число 3. Это потому что, если вы используете в выражении только целые числа, Kotlin сделает результат также целым числом. В данном случае результат округляется до ближайшего целого числа.
Вы можете указать Kotlin, что нужно использовать десятичные числа, записав их в следующей форме:
22.0 / 7.0
22. |
На этот раз результатом будет число 3.142857142857143.
Операция для получения остатка % в Kotlin
Четыре операции, с которыми мы работали до сих пор, легко понять, потому что вы с ними хорошо знакомы в жизни. В Kotlin также есть более сложные операции, которые вы можете использовать. Это стандартные математические операции, только менее распространенные. Рассмотрим их.
Сначала разберем операцию остатка, или операцию по модулю. При делении числителя на знаменатель — результатом будет целое число, а также остаток. Этот остаток и является результатом операции по модулю. Например, 10 по модулю 3 равно 1, потому что 3 трижды переходит в 10 с остатком 1.
В Kotlin оператором остатка является символ %, который используется следующим образом:
28 % 10
28 % 10 |
В данном случае результатом будет число 8, которое является остатком при делении 28 на 10. Если вам нужно посчитать то же самое, используя десятичные числа, это можно сделать следующим образом:
Если вам нужно посчитать то же самое, используя десятичные числа, это можно сделать следующим образом:
28.0 % 10.0
28.0 % 10.0 |
Результат идентичен % без десятичных чисел, что можно увидеть на выводе при использовании указателя формата:
println(«%.0f».format(28.0 % 10.0))
println(«%.0f».format(28.0 % 10.0)) |
Операции смещения в Kotlin
Операции правого и левого смещения (Shift) принимают двоичную форму десятичного числа и смещают цифры налево или направо соответственно. Затем они возвращают десятичную форму нового двоичного числа.
К примеру, десятичное число 14 в бинарном виде будет состоять из восьми цифр — 00001110. Смещение на два пункта влево приведет к числу 00111000, которое равно 56 в десятичной системе.
Далее дана схема того, что происходит во время операции смещения:
Цифры, которые приходят на замену пустым местам, становятся 0. Отсеченные числа будут потеряны. Смещение вправо аналогично, но цифры сдвигаются в правую часть. Функции Kotlin для данных двух операций являются следующими:
Отсеченные числа будут потеряны. Смещение вправо аналогично, но цифры сдвигаются в правую часть. Функции Kotlin для данных двух операций являются следующими:
- Смещение влево:
shl - Смещение вправо:
shr
Это инфиксные функции, которые помещаются между операндами, чтобы вызов функции выглядел как операция. Позже мы подробнее рассмотрим инфиксные функции в Kotlin.
Далее дан пример:
1 shl 3 32 shr 2
1 shl 3
32 shr 2 |
Оба значения равны 8.
Одна из причин использования смещений — облегчить умножение или деление на числа во второй степени. Обратите внимание, что сдвиг влево на единицу — это то же самое, что умножение на два, сдвиг влево на два — это то же самое, что умножение на четыре и так далее. Со смещением вправо ситуация аналогична.
Раньше код часто использовал этот трюк, потому что сдвиг битов для CPU намного проще, чем сложная арифметика умножения и деления. Следовательно, код был быстрее при использовании смещения. Однако в наши дни процессоры намного быстрее, и компиляторы могут даже преобразовывать умножение и деление на числа во второй степени в сдвиги.
Следовательно, код был быстрее при использовании смещения. Однако в наши дни процессоры намного быстрее, и компиляторы могут даже преобразовывать умножение и деление на числа во второй степени в сдвиги.
Порядок выполнения операций в Kotlin
Высока вероятность, что при вычислении значений вам нужно будет использовать много различных операций. Далее дан пример того, как это можно сделать в Kotlin:
((8000 / (5 * 10)) — 32) shr (29 % 5)
((8000 / (5 * 10)) — 32) shr (29 % 5) |
Обратите внимание на использование скобок, у которых в Kotlin две цели: сделать код понятным для чтения и устранить неоднозначность.
Рассмотрим пример:
350 / 5 + 2
350 / 5 + 2 |
Результат будет равен 72 (350 делится на 5, а потом прибавляется 2) или 50 (350 делится на 7)? Те, кто хорошо учился в школе, наверняка с уверенностью воскликнут «72»! И будут абсолютно правы!
Kotlin использует так называемый приоритет операторов. Оператор деления (
Оператор деления (/) имеет более высокий приоритет, чем оператор сложения (+), поэтому в этом примере код сначала выполняет операцию деления.
Если вы хотите, чтобы Kotlin сначала выполнял сложение, то есть возвращал 50, вы можете использовать круглые скобки, например:
350 / (5 + 2)
350 / (5 + 2) |
Правила приоритета аналогичны тому, что вы изучали в школе по математике. У умножения и деления более высокий, чем у сложения и вычитания.
The Remainder Operator работает с двойниками в Java — The Renegade Coder
Я преподаю в OSU почти два года, и меня всегда поражало, как многому я учусь у своих студентов. Например, в прошлом у меня были студенты, которые писали странные фрагменты кода, которые я не понимал. На данный момент, даже после более чем 300 постов в блогах, нескольких видеороликов на YouTube и даже сбора фрагментов кода с более чем 100 языков, можно подумать, что я все это видел. Ну, недавно я видел студента, использующего оператор остатка (
Ну, недавно я видел студента, использующего оператор остатка ( % ) в парном разряде, и с тех пор я совсем не был прежним.
Содержание
Остаток против оператора модуля
Прежде чем я начну рассказ, я хотел бы остановиться и провести различие между оператором остатка и оператором модуля. В Java нет оператора модуля . Вместо этого % — оператор остатка. Для положительных чисел они функционально эквивалентны. Однако, как только мы начнем играть с отрицательными числами, мы увидим удивительную разницу.
Я уже немного рассказывал об этой разнице в статье про шифрование RSA. Тем не менее, я нашел еще один отличный источник, в котором сравнивается оператор «по модулю» в различных языках, включая Java, Python, PHP и C. Например, если мы возьмем 3 % 5 , мы получим 3, потому что 5 вообще не входит в 3. Если мы начнем играть с отрицательными числами, результаты будут аналогичными. Например, если мы возьмем 3 % -5 , мы все равно получим три, потому что это все, что осталось.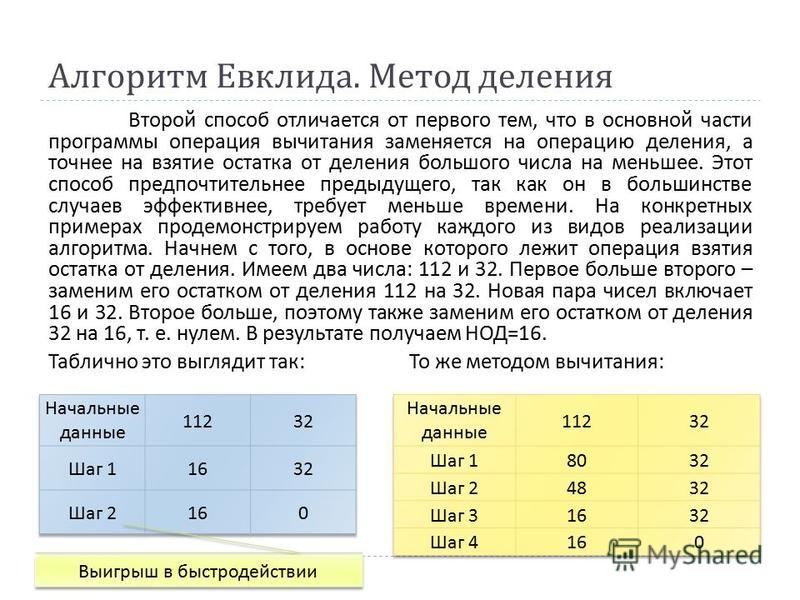
Между тем, если мы изменим сценарий и сделаем дивиденд отрицательным (в конце концов, остаток является побочным продуктом деления), мы начнем видеть отрицательные остатки. Например, -3 % 5 возвращает -3. Аналогично, -3 % -5 возвращает -3.
Обратите внимание, что во всех этих примерах мы получаем одни и те же результаты с некоторыми вариациями знака. Другими словами, с оператором остатка нас не слишком интересуют знаки. Все, что мы хотим знать, это сколько раз одно число входит в другое число. Затем мы смотрим на делимое, чтобы определить знак.
С другой стороны, у оператора по модулю немного больше нюансов. Во-первых, операнд справа определяет диапазон возможных возвращаемых значений. Если это значение положительное, результат будет положительным. Это немного отличается от нашего оператора остатка.
Между тем, левый операнд определяет направление, в котором мы циклически перемещаемся по диапазону возможных значений. Естественно, это идеально согласуется с оператором остатка, когда оба значения имеют одинаковый знак. К сожалению, в любых других обстоятельствах они совершенно разные:
К сожалению, в любых других обстоятельствах они совершенно разные:
| Expression | Java (Remainder) | Python (MOD) |
|---|---|---|
3 % 5 | 3 | 3 |
3 % -5 | 3 | -2 |
-3 % 5 | -3 | 2 |
-3 % -5 | -3 | -3 |
Оператор остатка для двойных чисел
Когда мы думаем об операторе остатка, мы часто предполагаем, что он работает исключительно с целыми числами — по крайней мере, до недавнего времени я так понимал. Как оказалось, оператор остатка на самом деле работает с числами с плавающей запятой, и в этом есть смысл.
Вдохновение
Ранее в этом месяце я работал со студентом в лаборатории, который попросил их написать программу обмена монет. В частности, эта программа должна была принимать от пользователя несколько центов и выводить номиналы в американской валюте (например, доллары, полдоллара, четверти, десять центов, пятаки и пенни).
В частности, эта программа должна была принимать от пользователя несколько центов и выводить номиналы в американской валюте (например, доллары, полдоллара, четверти, десять центов, пятаки и пенни).
Если вы думаете о том, как решить эту проблему, я дам вам подсказку: вы можете использовать жадный подход. Другими словами, сначала выберите самую большую монету и подсчитайте, сколько из них делится на ваше текущее количество центов. Если вы все сделаете правильно, вам даже не понадобится поток управления. Однако вы можете немного почистить свой код с помощью массива и цикла. Поскольку мне лень писать решение на Java, вот как оно может выглядеть на Python:
цента = 150
доллары = центы // 100
центов %= 100
половина_долларов = центов // 50
центов %= 50
четверти = центы // 25
центов %= 25
десять центов = центы // 10
центов %= 10
никель = центов // 5
центов %= 5
пенни = центы
print(f'{доллары}, {полдоллары}, {четверти}, {даймы}, {пятак}, {пенни}') Во всяком случае, у меня был студент, который интерпретировал центы как доллары и центы. Другими словами, они позволяют своему пользователю вводить суммы в долларах, например, 1,50 доллара, а не 150 центов. Честно говоря, это не так уж и много. Все, что нам нужно сделать, это умножить сумму в долларах на 100 и добавить оставшиеся центы, чтобы получить целое число.
Другими словами, они позволяют своему пользователю вводить суммы в долларах, например, 1,50 доллара, а не 150 центов. Честно говоря, это не так уж и много. Все, что нам нужно сделать, это умножить сумму в долларах на 100 и добавить оставшиеся центы, чтобы получить целое число.
Но это не то, что сделал этот ученик. Вместо этого они рассматривали каждое достоинство как двойное (то есть действительное число). Затем они продолжили использовать оператор остатка без каких-либо последствий. Проще говоря, я был ошеломлен. В конце концов, как это могло сработать? Вы вычисляете остаток только от деления в большую сторону, верно? В противном случае у вас останется десятичная дробь и ничего не останется — по крайней мере, я так думал.
Использование удвоения
Если бы мы переписали приведенную выше программу, используя доллары и центы, мы могли бы получить что-то вроде следующего:
цента = 1,50 доллары = центы // 1 центов %= 1 половина_долларов = центов // 0,50 центов% = 0,50 четверти = центы // 0,25 центов% = 0,25 десять центов = центы // 0,10 центов %= .1 никель = центы // 0,05 центов% = 0,05 пенни = центы // 0,01 print(f'{доллары}, {половина_долларов}, {четверть}, {даймс}, {пятак}, {пенни}')
И если мы запустим это, мы получим точно такой же результат, как и раньше: один доллар и полдоллара. Как это возможно?
Как оказалось, вычисление остатка с использованием десятичных дробей вполне допустимо. Все, что нам нужно сделать, это вычислить, сколько раз наше делимое идет полностью на в наш делитель. Например, 0,77 % 0,25 «в идеале» даст 0,02, потому что это максимально близкое значение, которое мы можем получить к 0,77, не переходя больше.
Предостережения
Узнав, что можно взять остаток от десятичной дроби, я сразу же удивился, почему я не знал об этом раньше. Конечно, быстрый поиск в Google покажет вам всевозможные ошибочные действия, которые могут возникнуть.
Например, в предыдущем примере я утверждал, что 0,02 будет остатком от 0,77 и 0,25, и это будет вроде как. Видите ли, в большинстве языков программирования значения с плавающей запятой по умолчанию имеют определенную точность, которая определяется базовой двоичной архитектурой. Другими словами, существуют десятичные числа, которые не могут быть представлены в двоичном виде. Одно из этих чисел является результатом нашего выражения выше:
Видите ли, в большинстве языков программирования значения с плавающей запятой по умолчанию имеют определенную точность, которая определяется базовой двоичной архитектурой. Другими словами, существуют десятичные числа, которые не могут быть представлены в двоичном виде. Одно из этих чисел является результатом нашего выражения выше:
>>> 0,77 % 0,25 0,020000000000000018
При работе с действительными числами мы постоянно сталкиваемся с подобными проблемами. В конце концов, есть удивительное количество десятичных значений, которые не могут быть представлены в двоичном виде. В результате мы получаем сценарии, в которых ошибки округления могут привести к сбою нашего алгоритма изменений. Чтобы доказать это, я переписал приведенное выше решение, чтобы вычислить сдачу для первых 200 центов:
для i в диапазоне (200):
центов = (i//100) + (i/100) % 1
ожидаемый = центы
доллары = центы // 1
центов %= 1
половина_долларов = центов // 0,50
центов% = 0,50
четверти = центы // 0,25
центов% = 0,25
десять центов = центы // 0,10
центов %= . 1
никель = центы // 0,05
центов% = 0,05
пенни = центы // 0,01
фактический = доллары + полдоллара * 0,50 + четверти * 0,25 + десять центов * 0,10 + пятак * 0,05 + пенни * 0,01
печать (f'{ожидаемый}: {фактический}')
1
никель = центы // 0,05
центов% = 0,05
пенни = центы // 0,01
фактический = доллары + полдоллара * 0,50 + четверти * 0,25 + десять центов * 0,10 + пятак * 0,05 + пенни * 0,01
печать (f'{ожидаемый}: {фактический}')
Для вашего здравомыслия я не буду выводить результаты, но поделюсь несколькими суммами в долларах, где этот алгоритм дает сбой: при вычислении пенни: .03 % .01 )
.09 % .05 ) .013 .11 % .14 терпит неудачу при вычислении десятицентовиков: .12 % .1 ) .15 % .1 ) Уже сейчас мы начинаем видеть тревожную часть этих расчеты становятся жертвой ошибок округления. Только за первые 16 центов мы не можем произвести точную сдачу в 50% случаев (без учета 0). Это не здорово!
Это не здорово!
Кроме того, многие ошибки начинают повторяться. Другими словами, я подозреваю, что эта проблема усугубляется с увеличением количества центов, поскольку при этом увеличивается вероятность ошибок округления. Конечно, я пошел дальше и модифицировал программу еще раз, чтобы измерить частоту ошибок:
ошибки = 0
для я в диапазоне (1000000):
центов = (i//100) + (i/100) % 1
ожидаемый = центы
доллары = центы // 1
центов %= 1
половина_долларов = центов // 0,50
центов% = 0,50
четверти = центы // 0,25
центов% = 0,25
десять центов = центы // 0,10
центов %= .1
никель = центы // 0,05
центов% = 0,05
пенни = центы // 0,01
фактический = доллары + полдоллара * 0,50 + четверти * 0,25 + десять центов * 0,10 + пятак * 0,05 + пенни * 0,01
ошибки += 0 если ожидаемо == актуально иначе 1
print(f"{(ошибки/1000000) * 100}% ОШИБКА") Теперь я должен предварить, что этот фрагмент кода сравнивает действительные числа, используя == , что обычно считается плохой практикой. В результате мы можем считать несколько «правильных» решений неправильными. Тем не менее, я думаю, что это достаточно хорошая оценка на данный момент.
В результате мы можем считать несколько «правильных» решений неправильными. Тем не менее, я думаю, что это достаточно хорошая оценка на данный момент.
Когда я запустил его, я обнаружил, что 53,850699999999996% всех расчетов изменений были неверными. По иронии судьбы, даже в моем вычислении ошибки была проблема с округлением.
Следует ли использовать оператор остатка для двойных значений?
На данный момент мы должны задаться вопросом, имеет ли смысл использовать оператор остатка для двойных чисел в Java. В конце концов, если ошибки округления являются такой проблемой, кто вообще может доверять результатам?
Лично моя интуиция подсказала бы избегать этой операции любой ценой. Тем не менее, я немного покопался, и есть несколько способов обойти эту проблему. Например, мы могли бы попробовать выполнить арифметику в другой базе, используя класс, который представляет значения с плавающей запятой в виде строки целых чисел (например, класс Decimal в Python или класс BigDecimal в Java).
Конечно, у такого рода классов есть свои проблемы с производительностью, и невозможно избежать ошибок округления по основанию 10. В конце концов, основание 10 не может представлять такие значения, как одна треть. Тем не менее, вы добьетесь гораздо большего успеха с оставшимся оператором.
В конце концов, я лично не сталкивался с этим сценарием, и я сомневаюсь, что вы тоже столкнетесь. Конечно, если вы здесь, скорее всего, вы столкнулись именно с этой проблемой. К сожалению, у меня нет большого решения для вас.
В любом случае, спасибо, что заглянули. Если вы нашли эту статью интересной, подумайте о том, чтобы поделиться ею. Если вы хотите, чтобы в ваш почтовый ящик попадало больше подобного контента, зайдите на мою страницу с информационным бюллетенем и оставьте свой адрес электронной почты. Кроме того, вы можете поддержать The Renegade Coder, став покровителем или совершив одну из этих странных вещей.
Пока вы здесь, ознакомьтесь с одной из следующих статей по теме:
- Камень, ножницы, бумага с использованием модульной арифметики
- Еще один способ изучить рекурсию
- Разница между заявлениями и выражениями
В противном случае, спасибо, что нашли время, чтобы проверить мой сайт! Я ценю это.
Будучи учеником на протяжении всей жизни и стремящимся учителем, я обнаружил, что не все предметы имеют одинаковое значение. В результате некоторые темы могут остаться незамеченными из-за нехватки времени или других обязательств. Лично я нахожу эти потерянные артефакты довольно забавными для обсуждения. Вот почему я решил запустить целую серию, чтобы сделать именно это. Добро пожаловать в Coding Tangents, сборник статей, посвященных граничным темам разработки программного обеспечения.
В этой серии я расскажу о темах, которые, как мне кажется, интересовали многих моих учеников, но никогда не имели возможности их изучить. Во многих случаях это предметы, которые, как мне кажется, заслуживают большего внимания в классе. Например, вы когда-нибудь получали формальное объяснение модификаторов доступа? Как насчет управления пакетами? Управление версиями?
В некоторых случаях студенты вынуждены изучать эти предметы самостоятельно. Естественно, это создает почву для заблуждений, которые становятся популярными на онлайн-форумах, таких как Stack Overflow и Reddit. В этой серии я надеюсь вернуться к основам, где эти темы могут быть рассмотрены во всей их полноте.
Естественно, это создает почву для заблуждений, которые становятся популярными на онлайн-форумах, таких как Stack Overflow и Reddit. В этой серии я надеюсь вернуться к основам, где эти темы могут быть рассмотрены во всей их полноте.
← Предыдущий пост: [#10] [#12]: Следующий пост →
Recent Posts
link to Understanding Short Circuit Evaluation in Software DesignПонимание оценки короткого замыкания в разработке программного обеспечения
Когда дело доходит до организации вашей логики в программе, одним из инструментов, который может сделать для вас много тяжелой работы, является оценка короткого замыкания. В этой статье я расскажу немного о...
Продолжить чтение
ссылка на Я, наконец, разобрался с модулем и системой пакетов PythonНаконец-то я разобрался с модулем Python и системой пакетов
Учиться писать код на Python очень весело, но вы можете обнаружить, что жизнь становится намного сложнее, когда вы начинаете экспериментировать с более сложными проектами. Давайте поговорим о модулях Python и системе пакетов.
Давайте поговорим о модулях Python и системе пакетов.
Продолжить чтение
Модуль: Глоссарий Java
В Java вы берете остаток с помощью оператора %. % неофициально называется модулем оператора (иногда называемого модом или по модулю), хотя математики и серьезные компьютерщики умоляли бы чтобы отличаться, это оператор остатка, а не модуль. JLS (спецификация языка Java) правильно относится к это как оператор остатка.К счастью, деление Java имеет евклидово свойство, а именно когда вы умножаете частное на делитель и добавляете остаток, вы получаете обратно дивиденд. Когда вы запрашиваете % 3 в Java, вы можете быть изумлен тем, что иногда получаю ответ за пределами диапазона 0..2. См. правила знака остатка/модуля. Будьте особенно осторожны, когда объединение случайных чисел в меньший диапазон с помощью оператора %.
Отрицательные операнды
Модуль Java ведет себя, ну, странно. В Java знак остатка следует за делимым, а не за делителем как и следовало ожидать. % может дать отрицательный результат
даже с положительным делителем. Будьте особенно осторожны при подборе случайных чисел
в меньший диапазон с оператором модуля, например. wheel.nextInt() % 3 даст вам числа -2 ..
+2, а не 0..2, как можно было бы ожидать.
% может дать отрицательный результат
даже с положительным делителем. Будьте особенно осторожны при подборе случайных чисел
в меньший диапазон с оператором модуля, например. wheel.nextInt() % 3 даст вам числа -2 ..
+2, а не 0..2, как можно было бы ожидать.Например, когда вы вычисляете день недели, беря day_number % 7 в Java вы будете поражены, иногда получая отрицательный ответ вне диапазона 0 .. 6, а именно при дивиденд отрицательный. Смотри правила знаков. Ява дивизия усеченное деление.
Смешанные базовые расчеты
Оператор модуля полезен во времени расчет, т. грамм. сколько дней, часов, минут, секунд, миллисекунд 112 233 445 566 778 899 миллисекунд? Проще перейти от дней, часов, минут и секунд к миллисекундам. Вы просто умножаете каждый компонент на static final long MILLISECONDS_PER_DAY = 24 * 60 * 60 * 1000L;
static final long MILLISECONDS_PER_HOUR = 60 * 60 * 1000L;
static final long MILLISECONDS_PER_MINUTE = 60 * 1000L;
static final long MILLISECONDS_PER_SECOND = 1000L;
длинные миллисекунды = дни * MILLISECONDS_PER_DAY + часы * MILLISECONDS_PER_HOUR
+ минут * MILLISECONDS_PER_MINUTE
+ секунд * MILLISECONDS_PER_SECOND
+ миллисекунды; Это довольно упрощенный ответ на проблему. Более сложные ответы см.
Календарь.
Более сложные ответы см.
Календарь.Вы можете использовать подобную логику для работы с другими дурацкими смешанными базовыми системами, такими как широта и долгота с ее градусами, минутами и секундами, ярдами, футами и дюймами или тонн, фунтов и унций. APL (язык программирования) имеет встроенные операторы для аккуратной обработки. В Яве вы должны кодировать преобразования от руки.
Остаток, модуль и деление часто определяются причудливым образом на компьютерных языках, часто для того, чтобы его можно было быстро и легко реализовать на авторском оборудовании. Java имеет %, оператор остатка, но не имеет встроенного оператора модуля или функции.| Знаки | отдел / | Остаток % | Модуль |
|---|---|---|---|
| + + | 7/4 = 1 | 7 % 4 = 3 | 7 mod 4 = 3 |
| - + | -7 / 4 = -1 | -7 % 4 = -3 | -7 мод 4 = 1 |
| + - | 7 / -4 = -1 | 7 % -4 = 3 | 7 мод -4 = -1 |
| - - | -7 / -4 = +1 | -7 % -4 = -3 | -7 mod -4 = -3 |
Оттачивание интуиции
Изучив закономерности в следующие три таблицы % остатка Java, mod математический модуль и / целочисленное деление, у вас будет лучшее представление о том, как они Работа. Обратите внимание, что для Java% знак делителя не имеет значения. Знак
результат следует за знаком делимого. Примечание для математического модуля, результат
всегда в диапазоне 0..divisor-1 для положительных делителей, независимо от знака
делимое и результат всегда находятся в диапазоне divisor+1..0 для отрицательного
делителей независимо от знака делимого. % и модуль дают то же самое
получается при совпадении знаков делимого и делителя. Интересно отметить, как
сложные симметрии и повторения.
Обратите внимание, что для Java% знак делителя не имеет значения. Знак
результат следует за знаком делимого. Примечание для математического модуля, результат
всегда в диапазоне 0..divisor-1 для положительных делителей, независимо от знака
делимое и результат всегда находятся в диапазоне divisor+1..0 для отрицательного
делителей независимо от знака делимого. % и модуль дают то же самое
получается при совпадении знаков делимого и делителя. Интересно отметить, как
сложные симметрии и повторения.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Получение цифр числа, любая система счисления
Модуль можно использовать для разбить число на цифры, десятичную, шестнадцатеричную или любую другую базу.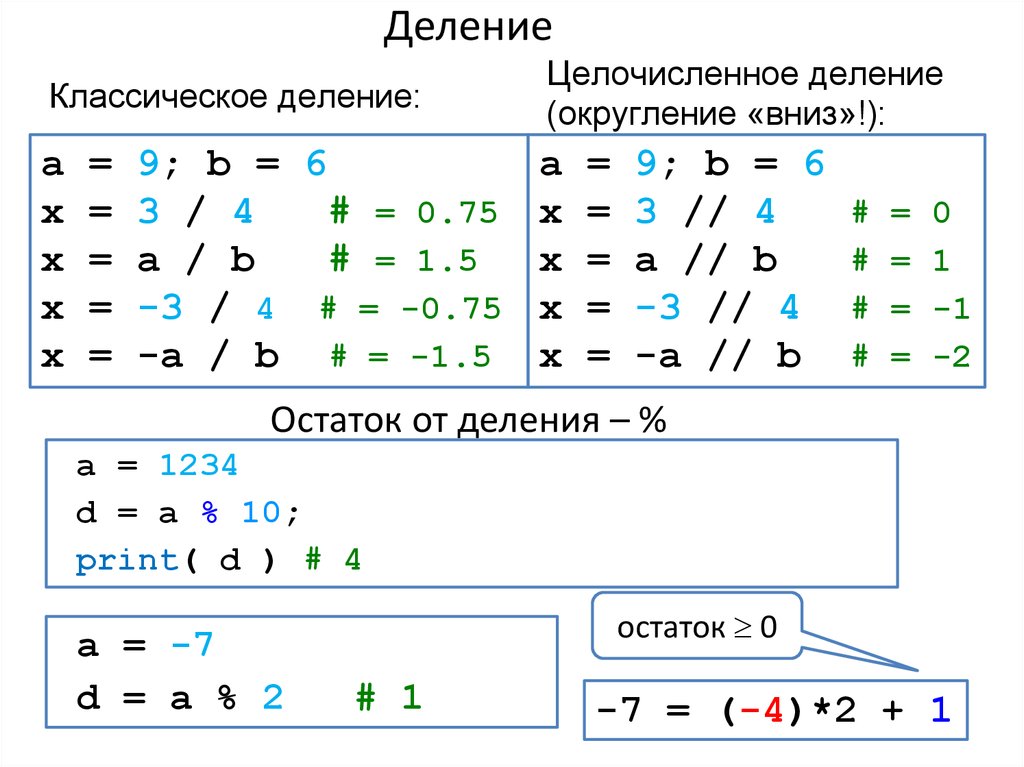
Чет или нечет?
Вы можете сказать, является ли int четный или нечетный, глядя на его остаток, модуль 2:логическое значение даже = x % 2 == 0; логический нечетный = х % 2 != 0;Обратите внимание, что этот аналогичный код, который вы часто видите, будет работать для , а не . отрицательные числа:
логическое значение даже = x % 2 == 0; логический нечетный = x% 2 == 1; // не работает для отрицательных xСуществует более быстрый способ вычислить их, маскируя младший бит:
логическое значение даже = ( x & 1 ) == 0; логический нечетный = ( x & 1 ) != 0;Код может быть еще быстрее, если вы хотите получить число 0 или 1 в качестве результата, скажем, для индексирование массива вместо логического значения:
целое нечетное = х & 1;
Каждый n-й
Допустим, вы хотели что-то сделать каждый четвертый линия, напр. вставить пробел, цветную полосу, галочку…Другое использование
Модуль можно использовать при вычислении следующего свободного круга. буфер с беличьей клеткой.
буфер с беличьей клеткой.int nextbuf = (thisbuf + 1) % запаса;Модуль можно использовать для преобразования смещения в файл в номер фрагмента и смещение. внутри этого куска.
int recordNumber = fileOffset / blockSize; int recordOffset = fileOffset % blockSize;
Плавающая точка %
% также определен для работы с плавающие и двойные операнды, хотя это использование довольно редко. Результат операции остатка с плавающей запятой, вычисленный оператором %, не совпадает с результатом, полученным остатком
операция, определяемая плавающим кодом IEEE 754.
стандарт точки. IEEE (Институт инженеров по электротехнике и электронике) 754 остатка
операция вычисляет остаток от деления округления, а не деления усечения.
% в операциях с плавающей запятой ведет себя аналогично
оператор целочисленного остатка; это можно сравнить с библиотечной функцией C
мод. IEEE 754 остаточная операция может быть вычислена библиотечной подпрограммой Math. IEEEостаток. (Обратите внимание на нарушение именования
соглашения.)
IEEEостаток. (Обратите внимание на нарушение именования
соглашения.)
Узнать больше
JLS : % оператор
JLS : порядок оценки выражения
*
+
++
--
/
абсолютное значение
Предложение Бали по переопределению того, как работает %
деление
с плавающей запятой
смешанная база
оператор
Документация JDK 19 — Домашняя страница
- Домашняя страница
- Ява
- Ява SE
- 19
Обзор
- Прочтите меня
- Примечания к выпуску
- Что нового
- Руководство по миграции
- Загрузить JDK
- Руководство по установке
- Формат строки версии
Инструменты
- Технические характеристики инструментов JDK
- Руководство пользователя JShell
- Руководство по JavaDoc
- Руководство пользователя средства упаковки
Язык и библиотеки
- Обновления языка
- Основные библиотеки
- HTTP-клиент JDK
- Учебники по Java
- Модульный JDK
- Руководство программиста API бортового регистратора
- Руководство по интернационализации
Технические характеристики
- Документация API
- Язык и ВМ
- Имена стандартных алгоритмов безопасности Java
- банка
- Собственный интерфейс Java (JNI)
- Инструментальный интерфейс JVM (JVM TI)
- Сериализация
- Проводной протокол отладки Java (JDWP)
- Спецификация комментария к документации для стандартного доклета
- Прочие характеристики
Безопасность
- Руководство по безопасному кодированию
- Руководство по безопасности
Виртуальная машина HotSpot
- Руководство по виртуальной машине Java
- Настройка сборки мусора
Управление и устранение неполадок
- Руководство по устранению неполадок
- Руководство по мониторингу и управлению
- Руководство по JMX
Client Technologies
- Руководство по специальным возможностям Java
Реализации евклидова деления
Примечание: Эта статья была переведена с помощью автоматического переводчика и одного проход был сделан, чтобы удалить самые большие ошибки.
Если вы хотите сделать эту статью читабельной, вы можете сообщать мне об ошибках перевода (слово, предложение, абзац) по связавшись со мной по адресу электронной почты внизу страницы. Спасибо
Принцип
В этой статье обсуждается евклидово деление, фундаментальный предмет, представляющий
отправной точкой для всех вопросов, связанных с простыми числами и факторизацией целых чисел.
Евклидово деление со сложением, вычитанием и умножением является одним из четырех основных
операции над целыми числами. Его цель состоит в том, чтобы попытаться оставить заданную группу элементов справедливой.
относительно ограничения, характеризуемого числом.
Например, пакет с 12 шариками, которые можно раздать трем людям, или бабушкин торт.
разрезать на 8 порций, пока нас 6 за столом.
Мы считаем, что в этой статье мы работаем с положительными целыми числами (набор N натуральных чисел), таким образом, это
справедливое распределение иногда невозможно без появления «половинок», «четвертей»,
"третье лицо" или другое. .. Например, 3 мяча, которые нужно распределить между 2 людьми, дают каждому по 1 мячу.
и мы не пытаемся отрезать последнее... Этот остаток нераспределенный откладывается, это остаток.
.. Например, 3 мяча, которые нужно распределить между 2 людьми, дают каждому по 1 мячу.
и мы не пытаемся отрезать последнее... Этот остаток нераспределенный откладывается, это остаток.
Обратите внимание, что на рациональных числах (множество Q) и так далее на действительных числах (очень грубо плавающие числа)
распространение возможно, но может дать что-то с трудом представимое в реальной жизни,
например 10/3 = 3,3333... это означает от 3 до бесконечности, в них сложно разрезать торт
условия...
С математической точки зрения определение евклидова деления натуральных чисел
выглядит следующим образом:
Пусть a и b целые числа и b отлично от 0, существует единственная пара (q, r) целых чисел
такие как:
- а = бк + р
- г < б
Примечание 1 : Мы находим это понятие справедливого распределения с помощью термина «bq» и
остаток с термином "r".
Примечание 2 : Для целых чисел (набор Z целых чисел, положительных и отрицательных) мы имеем почти
такое же определение. Только второе условие меняется и становится |r| < |б|.
Только второе условие меняется и становится |r| < |б|.
Об имени на условиях евклидова деления «a = bq + r» имеем:
- а это дивиденд
- b это делитель
- q - это частное
- р остаток
Проведение испытаний
В этой статье мы представим некоторые известные реализации евклидова деления и сравните их, чтобы увидеть, какие из них наиболее эффективны и быстрее. Но оценить время и столкнуться с результатами, у нас должна быть небольшая тестовая программа, которая будет измерять время различные реализации деления, а также проверьте три следующих критерия, чтобы избежать предвзятость в тестировании:
- Тестовые наборы должны быть согласованными: одно деление составляет миллисекунду, если мы проверяем только одно подразделение, мы не можем извлечь соответствующую информацию, потому что времени слишком мало. Мы будем поэтому делайте прогоны в 20 миллионов делений.
- Наборы тестов должны быть одинаковыми для каждой реализации: для сравнения двух реализаций
евклидова деления, он обязательно будет использовать тот же набор тестов, потому что деление с
разные методы на разные номера не интересны.

- Создайте несколько наборов тестов с разными свойствами: идея состоит в том, чтобы протестировать реализации разделение на наборы, имеющие разные свойства, с целью выдвижения сильных и слабых сторон реализации.
Класс Java EuclideTestCaseGenerator отвечает за создание наборов тестов. Этот
будет создавать наборы в соответствии с 3 методами: один с именем «случайный» будет брать случайным образом числа a (
дивиденд) и b (делитель) между 1 и 1000 миллиардов, другой называется «A > B» idem для
«случайный», за исключением того, что a обязательно больше, чем b, и последний назван «custom», такой же, как случайный
с а > 4*b.
Наконец, Java-класс EuclideBench является оркестратором для запуска реализаций
Евклидово деление. Реализации должны реализовывать (как java) интерфейс IEuclide.
источник
Первая реализация
Самый простой способ вычислить евклидово деление опирается на его определение: «сколько
раз я могу поставить b в ?». Это приводит к простому и относительно короткому алгоритму. состоящий из вычитания столько раз, сколько это может быть b (делитель) a (делимое), пока не получите
остаток меньше b.
состоящий из вычитания столько раз, сколько это может быть b (делитель) a (делимое), пока не получите
остаток меньше b.
public long [] euclid( long a, long b) {
long r = a;
long q = 0;
в то время как (r >= b) {
r = r - b;
q = q + 1;
}
long [] евклид = { q, r };
возврат евклид;
}
На данный момент у нас нет никаких элементов сравнения с другими реализациями, но
поверьте метод наивен :).
Все, что мы видим в этом алгоритме, — это риск не результата, когда a слишком велико по сравнению с b.
потому что переменная r в инструкции "r = r - b" не уменьшается достаточно быстро. Сложность
алгоритма равен O(a).
источник
Вторая реализация
Чтобы улучшить первую реализацию, может быть интересно закодировать десятичное деление, которое мы
учиться в школе. А для тех, кто не помнит, как это работает, по простой схеме
это намного лучше, чем длинная речь, чтобы запомнить метод. .. позаботьтесь о том, чтобы схема показала
как выучить молодой французский. По тому уголку света, где вы изучали положение
цифры и визуальные изменения, но общие принципы остаются прежними:
.. позаботьтесь о том, чтобы схема показала
как выучить молодой французский. По тому уголку света, где вы изучали положение
цифры и визуальные изменения, но общие принципы остаются прежними:
т.е. 87 = 7 * 12 + 3
На уровне реализации метод состоит в умножении b (делитель) на 10 несколько
раз меньше, чем a (делимое), то делаем деление идентично первому
реализации и, наконец, снова с дивидендом остатка от деления
предыдущий шаг.
общедоступный длинный [] евклид( длинный a, длинный b) {
длинный r = а;
long q = 0;
длинное n = 1;
long aux = 0;
в то время как (r >= b) {
в то время как (b * n <= a) {
n *= 10;
}
n /= 10;
aux = b * n;
в то время как (r >= aux) {
r = r - aux;
q = q + n;
}
a = r;
n = 1;
}
long [] евклид = { q, r };
возврат евклид;
}
В этой статье мы будем приводить результаты в виде трех таблиц, представляющих прогон
на каждом из трех тестовых наборов (случайный, A > B и A > 4 * B). Важно видеть, что
направление чтения сверху вниз и алгоритмы должны сравниваться только в
контекст пробега. Здесь мы случайно взяли 40 миллионов чисел (2 умножить на 20 миллионов) и
рассчитал время, необходимое наивному и десятичному алгоритму для выполнения 20 миллионов евклидовых
дивизии (это пробег 1). Затем мы взяли другие числа, такие как A > B, и повторили 20
миллион делений (прогон 2), затем то же самое для A > 4 * B (прогон 3).
Важно видеть, что
направление чтения сверху вниз и алгоритмы должны сравниваться только в
контекст пробега. Здесь мы случайно взяли 40 миллионов чисел (2 умножить на 20 миллионов) и
рассчитал время, необходимое наивному и десятичному алгоритму для выполнения 20 миллионов евклидовых
дивизии (это пробег 1). Затем мы взяли другие числа, такие как A > B, и повторили 20
миллион делений (прогон 2), затем то же самое для A > 4 * B (прогон 3).
Все это говорит о том, что мало интереса сравнивать два отдельных прогона, потому что наборы данных
отличается, хотя верно то, что мы видим, что время увеличивается между 3 прогонами, этот рост
трудно поддается количественной оценке.
Посмотрим, что будет.
| Случайный | А > В | А > 4 * В | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Работа/проверка | n1 / 150660990 | n2 / 2 | 702 | n3 / 1221575580 | ||||||
| Наивный | 1,437 | 2,281 | 5,375 | |||||||
| Десятичный | 2,0 | +0,563 | 2,984 | +0,703 | 4. 032 032 | -1,343 | ||||
Эта вторая реализация показывает, что наивный метод работает быстрее, когда мы берем случайные значения.
или когда a (делимое) больше, чем b (делитель), потому что алгоритм очень прост
и иди быстро. К минусам, когда b в 4 раза меньше, чем a, производительность меняется на обратную и десятичная дробь
метод становится намного быстрее.
В тестовом примере A > B мы можем задаться вопросом, почему выигрыш отсутствует просто потому, что тестовый набор
неадекватный! Проблема возникает из-за распределения чисел при случайной стрельбе. За
например, если мы выберем число от 0 до 1000, у нас будет 890,99% шанс попасть в 4-значный
число (результаты можно экстраполировать на n цифр), на 4-значных числах мы имеем отношения a / b
очень низкий, поэтому результат A > B неубедителен. Добавляя условие A > 4 * B, мы
искусственно увеличить соотношение, и мы ясно видим выигрыш.
Второй алгоритм меньше зависит от отношения a/b, потому что мы начинаем с умножения на
10 б столько раз, сколько необходимо, чтобы оказаться ближе к а. источник
источник
Третья реализация
Чтобы оптимизировать время вычисления евклидова деления, мы изменим стратегию на
реализация алгоритма, основанного на дихотомии. Этот метод позволяет очень быстро найти
значение, используя старую добрую пословицу «разделяй и властвуй».
Здесь дихотомический поиск будет сосредоточен на значении q (частное). Подход состоит
первый шаг к ограничению q, затем многократно разрезая этот интервал на две равные части и выбирая
интервал содержит q.
Следует отметить, что эти операции по границе и разрезанию будут выполняться со степенью 2
или, другими словами, мы используем бинарные операции, облегчающие работу компьютера. 9n
Критерии дихотомии следующие:
- Если b * ((альфа + бета) / 2) <= a, то альфа = (альфа + бета) / 2
- Если b * ((альфа + бета)/2) > а, то бета = (альфа + бета)/2
И это работает! Шаг за шагом мы приближаемся (и находим) частное q. Для большего
подробности, включая математическую демонстрацию метода, см. во французской Википедии.
статья о Евклидовом
деление (раздел бинарного метода). К сожалению, не нашел на английском языке.
во французской Википедии.
статья о Евклидовом
деление (раздел бинарного метода). К сожалению, не нашел на английском языке.
public long [] euclide( long a, long b) {
long n = 0;
long aux = b;
if (a < b) {
long [] euclide = { 0, a };
вернуть евклид;
}
в то время как (aux <= a) {
aux = (aux << 1);
n++;
}
long alpha = (1 << (n - 1));
длинный бета = (1 << n);
в то время как (n-- > 0) {
aux = (альфа + бета) >> 1;
если ((aux * b) <= a) {
alpha = aux;
} else {
beta = aux;
}
}
long [] евклид = { альфа, а - (b * альфа) };
возврат евклид;
}
И мы улучшаем производительность. ..
..
С подходом дихотомии мы чувствуем, что "пробел" преодолен. Поскольку десятичный метод позволяет
большой выигрыш при условии, что a (дивиденд) очень велик по сравнению с b
(делитель), здесь создается впечатление обобщённого выигрыша на всех наборах тестов. А это
нормально, потому что мы прошли log2(a).
источник
| Случайный | А > В | А > 4 * В | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Работа/проверка | n4 / 198332981 | n5 / 3 | 967 | n6 / 13002 | ||||||
| Наивный | 1,578 | 2,75 | 5,921 | |||||||
| Десятичный | 2,0 | +0,422 | 3,0 | +0,25 | 4,032 | -1,889 | ||||
| Бинарная дихотомия | 1,375 | -0,625 | 2,015 | -0,985 | 3,297 | -0,735 | ||||
Четвертая реализация
Всегда стремясь к производительности, мы делаем большой скачок назад в истории цивилизации. так как собираемся вдохновить из технического подразделения в Древнем Египте на реализацию четвертого
алгоритма Евклидова деления.
так как собираемся вдохновить из технического подразделения в Древнем Египте на реализацию четвертого
алгоритма Евклидова деления.
Вопрос: Были ли все египтяне во времена фараонов потенциальными учеными-компьютерщиками?
Никто не знает, кроме их методов умножения
и деление
полагался в основном на числа разложения в степени 2, чтобы выполнить эти 2 операции.
В основном они рассуждали в двоичном формате, чтобы иметь возможность умножать и делить.
- Насчет умножения, целью было преобразовать в бинарный первый оператор (см.
Википедия для этого преобразования), а затем построить таблицу степеней 2, умноженных на
второй оператор (легко, просто умножьте на 2 второй оператор столько раз, сколько хотите), и
наконец, суммируя значения в таблице как «где установлен бит».
Пример с 18 * 9 = ? 18 (двоичный) 9 * 2 (n раз) 0 9 1 18 there is 1, we pick 0 36 0 72 1 144 there is 1, мы выбираем Итак, 18 + 144 = 162 = 18 * 9. 
- Что касается деления, то египтяне использовали тот же принцип, но в обратном порядке.
Они начали с построения таблицы степеней числа 2, умноженного на делитель (всегда с умножение на 2) до тех пор, пока не получится число больше а (делимое). Затем они восстанавливают "результат в двоичном виде" путем выбора числа, такие как их сложения не превышают a. Этот выбор, начиная с наибольшего числа (самый старший бит).Пример 218 / 6 = ? n 6 * 2 (n times) Addition 5 192 192 we pick because 192 < 218 4 96 X we don't pick Потому что 192 + 96 = 288 ET 288> 218 3 48 x Мы не выбираем, потому что 192 + 48> 218 2 24 216 Мы выбираем, потому что 1 24 216 2 2 = 36, остаток r равен 2 (218 - 116). 
Большинство сайтов в Интернете говорят о разделении Египта как об историческом подходе, а не как о Информатика. Таким образом, мы находим принцип работы и много информации, описывающей предмет. в текстовом виде. К минусам мы не видели примера реализации алгоритма, но это не мешает неважно, просто сделай это!
общедоступный длинный [] евклид( длинных а, длинных б) {
длинных n = 0;
long p = b;
if (a < b) {
long [] euclide = { 0, a };
вернуть евклид;
}
в то время как (p <= a) {
p = (p << 1);
n++;
}
p = (p >> 1);
н--;
long q = (1 << n);
long aux = p; 9n, но и цикл «пока (n > 0)» в центре программы. По сути, эти два алгоритма эквивалентны, один можно переписать в другой. sourceЧто касается производительности, мы снова получаем большую скорость.
 Конечно, не так сильно, как изменение от
от десятичного до дихотомического, но выигрыш в 0,2 с (кроме случайного) в среднем является почетным.
Конечно, не так сильно, как изменение от
от десятичного до дихотомического, но выигрыш в 0,2 с (кроме случайного) в среднем является почетным.Направление чтения по пробегу (и сверху вниз).
Не сравнивайте два отдельных запуска.Случайный А > В А > 4 * В Работа/проверка n7 / 162438146 n8 / 313167294 n9 / 1211389641 Наивный 1.406 2,781 5,5 Десятичный 2,016 +0,61 3,0 +0,219 3,828 -1,672 Бинарная дихотомия 1,39 -0,626 2,0 -1,0 3,015 -0,813 Двоичный египетский 1,36 -0,03 1,781 -0,219 2,719 -0,296 Пятая реализация
А вот последняя реализация евклидова деления, это метод бинарной дихотомии, дополненной методом Горнера.

По сути, это просто более изящная переписка египетской дивизии (четвертой реализации), который сам по себе эквивалентен третьему (если следовать...).public long [] евклид( long a, long b) {
long r = a;
long q = 0;
длинное n = 0;
long aux = b;
в то время как (aux <= a) {
aux = (aux << 1);
n++;
}
в то время как (n > 0) {
aux = (aux >> 1);
н--;
q = (q << 1);
if (r >= aux) {
r = r - aux;
q++;
}
}
long [] евклид = { q, r };
возврат евклид;
}По производительности на нашем старом тестовом компьютере AMD 3200 2 Ghz хуже, чем реализации египетской дивизии, посмотреть, нет ли на других машинах (или др. языки) у нас есть и эта разница.
источникНаправление чтения по пробегу (и сверху вниз). 




 Пример: 0,5 ÷ 0,3 = 1,6, тогда q будет положительным, так как 1,6 положительно, а наибольший размер, не превышающий 1,6 будет 1, то q = 1, а значит r = 0,5 — (0,3 × 1) = 0,2.
Пример: 0,5 ÷ 0,3 = 1,6, тогда q будет положительным, так как 1,6 положительно, а наибольший размер, не превышающий 1,6 будет 1, то q = 1, а значит r = 0,5 — (0,3 × 1) = 0,2.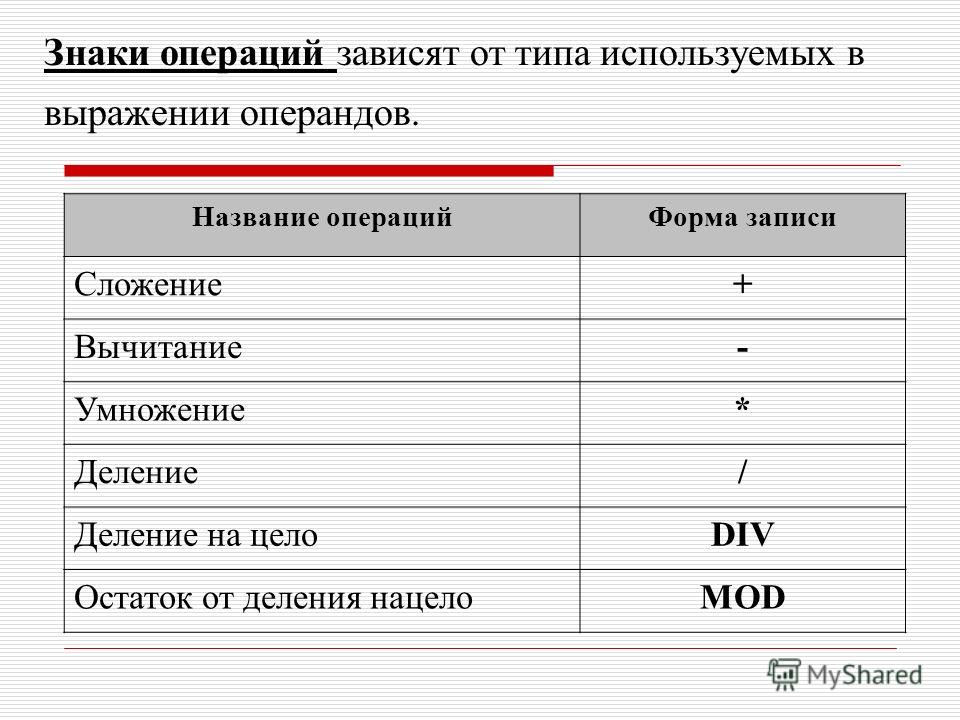
 0 / 7.0
0 / 7.0 1
никель = центы // 0,05
центов% = 0,05
пенни = центы // 0,01
print(f'{доллары}, {половина_долларов}, {четверть}, {даймс}, {пятак}, {пенни}')
1
никель = центы // 0,05
центов% = 0,05
пенни = центы // 0,01
print(f'{доллары}, {половина_долларов}, {четверть}, {даймс}, {пятак}, {пенни}')  1
никель = центы // 0,05
центов% = 0,05
пенни = центы // 0,01
фактический = доллары + полдоллара * 0,50 + четверти * 0,25 + десять центов * 0,10 + пятак * 0,05 + пенни * 0,01
печать (f'{ожидаемый}: {фактический}')
1
никель = центы // 0,05
центов% = 0,05
пенни = центы // 0,01
фактический = доллары + полдоллара * 0,50 + четверти * 0,25 + десять центов * 0,10 + пятак * 0,05 + пенни * 0,01
печать (f'{ожидаемый}: {фактический}')
