Инженерная графика методичка — Стр 2
11
1 ОСНОВЫ ВЕКТОРНОЙ ГРАФИКИ
Как известно из курса лекций по компьютерной графике, различают растровую и векторную графику.
Изображения в растровой графике представлены в виде массива цифр. Основным элементом изображения является точка. При экранном изображении эта точка называется пикселем (от английского выражения picture element — pixel). В цифровом изображении каждая точка растра (пиксель) представлена единственным параметром — цветом. Именно это имеется в виду, когда рассматривается понятие «значение пикселя».
Необходимо различать технический и математический растры. Технический растр — целочисленная решетка на плоскости. Например, так реализуется изображение на экране монитора как частный случай.
Вданном учебно-методическом руководстве речь будет идти только о векторной графике.
Изображения в векторной графике создаются математическими формулами, а не координатами точек, как в растровой графике. Основу изображений в векторной графике создают векторы или контуры.
Для описания контуров в программах редактирования векторной графики применяют так называемые кривые Безье — параметрические кривые третьего порядка.
Вкачестве формулы, которая была бы достаточно простой (с точки зрения математика), универсальной (с точки зрения программиста) и геометрически наглядной (с точки зрения пользователя — художника или дизайнера), чаще всего используется упомянутая кривая Безье. На самом деле, это целое семейство кривых, из которых используется частный случай с кубической степенью, т.е. кривая третьего порядка, описываемая следующим параметрическим уравнением:
R(t) = Po(l – t)3 + P1t(l – t)2 + P2t2(l – t) + Р3t3, где 0 < t < 1.
12
Такую кривую можно построить, если известны координаты четырех точек, называемых контрольными.
Из четырех контрольных точек кривая проходит только через две, поэтому эти точки называются опорными — anchor points (иначе они называются узлами (nodes), поскольку «связывают» элементарные кривые друг с другом, чтобы образовать сложный единый контур).
Две другие контрольные точки не лежат на кривой, но их расположение определяет кривизну кривой, поэтому эти точки иначе называются управляющими точками, а линии, соединяющие управляющую и опорную точки, управляющей линией (в просторечии их именуют «рычагами»). Кривая Безье является гладкой кривой, т.е. она не имеет разрывов и непрерывно заполняет отрезок между начальной и конечной точками.
Кривая начинается в первой опорной точке, касаясь отрезка своей управляющей линии, и заканчивается в последней опорной точке, также касаясь отрезка своей управляющей линии. Это позволяет гладко соединять две кривые Безье друг с другом: управляющие линии располагаются вдоль одной прямой, которая является касательной к получившейся кривой.
Основными объектами векторной графики являются: примитивы (линия, круг, эллипс и др.), составные объекты и различные заливки.
Примитив — объект, создаваемый, редактируемый и уничтожаемый одной командой.
Сегменты могут иметь прямолинейную или криволинейную формы.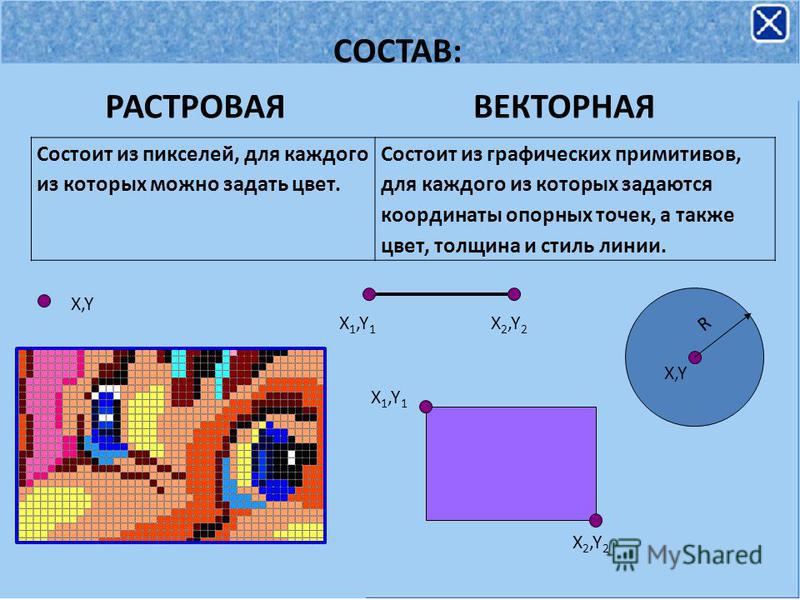 Форма сегмента определяется типом ограничивающих его узлов, которые могут быть гладкими или угловыми. В гладком узле контур образует плавный перегиб, в то время как в угловом — излом. Если сегмент хотя бы с одной стороны будет ограничен гладким узлом, он будет криволинейным. С другой стороны, чтобы сегмент был прямолинейным, он должен быть ограничен с обеих сторон только угловыми узлами. Различают также еще два типа узлов. Узел Безье — вершина, подобная гладкой, но позволяющая управлять кривизной сегментов при входе и выходе из нее. Для этого она снабжается касательными векторами с маркерами (квадратиками) на концах. У вершин Безье касательные векторы всегда лежат на одной прямой, а расстояние маркеров от
Форма сегмента определяется типом ограничивающих его узлов, которые могут быть гладкими или угловыми. В гладком узле контур образует плавный перегиб, в то время как в угловом — излом. Если сегмент хотя бы с одной стороны будет ограничен гладким узлом, он будет криволинейным. С другой стороны, чтобы сегмент был прямолинейным, он должен быть ограничен с обеих сторон только угловыми узлами. Различают также еще два типа узлов. Узел Безье — вершина, подобная гладкой, но позволяющая управлять кривизной сегментов при входе и выходе из нее. Для этого она снабжается касательными векторами с маркерами (квадратиками) на концах. У вершин Безье касательные векторы всегда лежат на одной прямой, а расстояние маркеров от
13
вершины можно изменять. При этом перемещение одного маркера приводит к центрально-симметричному перемещению другого. Вершина Безье с изломом — отличается тем, что касательные векторы не связаны друг с другом и маркеры можно перемещать независимо.
Замкнутые контуры (например, многоугольные, эллиптические и т.
Любые контуры могут иметь обводку. Контур — понятие математическое, и толщины он не имеет. Чтобы сделать контур видимым, ему придают обводку — линию заданной толщины и цвета, проведенную строго по контуру. По умолчанию всем новопостроенным линиям задается одинаковая толщина, однако по желанию обводку можно изменить — создать пунктирную, градиентную или художественную.
Любое векторное изображений состоит из множества контуров. Можно представить его в виде иерархического дерева.
1.На самом нижнем уровне расположены узлы и отрезки
линий.
2. Выше расположены сегменты. Сегменты позволяют изменять не только положение конечных узлов, но изменять форму сегмента.
Выше расположены сегменты. Сегменты позволяют изменять не только положение конечных узлов, но изменять форму сегмента.
3.Далее располагаются контуры — любая геометрическая фигура, представляющая собой очертания объекта. Как указывалось, контуры могут быть замкнутыми или открытыми, а также иметь заливку.
4.Объекты, представляющие собой различные векторные формы (каркасы, поверхности, тела).
5.Вершиной является само изображение, представленное совокупностью перечисленных выше объектов.
В программе редактирования векторных рисунков линии, фигуры и текст задаются математическими выражениями, что да-
14
ет возможность автоматически настраивать их на максимальное разрешение устройства вывода, идет ли речь о лазерном принтере или фотонаборном аппарате. Программа посылает на принтер математические выражения, которые переводятся в изображение на бумаге или пленке. Иными словами, принтер преобразует математические выражения в распечатываемые пиксели. По сравнению с экраном разрешение принтера намного выше.
Еще одно преимущество векторных рисунков состоит в том, что для них не требуется много места на диске. Объем файла векторного рисунка зависит только от количества и сложности объектов, составляющих этот рисунок, поэтому его размер, в отличие от растрового рисунка, практически не влияет на этот объем. Векторный рисунок сада, в котором прорисованы сотни листиков и лепестков, занимает во много раз больше места на диске, чем огромный плакат с изображением всего лишь трех прямоугольников. Кроме того, описание цветовых характеристик не сильно увеличивает размер файла, поскольку данные о цвете идентичны для всего объекта.
Контуры, заливки и обводки — основа построения векторного изображения. Все компоненты векторного изображения описываются математически, а значит — абсолютно точно. Чем большее количество контуров содержится в изображении, тем оно выглядит более живым и детализированным. Однако с другой стороны, чем больше контуров, тем больше вычислений необходимо произвести для построения изображения, т.к. после каждого внесенного изменения все изображение полностью пересчитывается.
Однако с другой стороны, чем больше контуров, тем больше вычислений необходимо произвести для построения изображения, т.к. после каждого внесенного изменения все изображение полностью пересчитывается.
Векторные изображения не в состоянии обеспечить близкую к оригиналу реалистичность, но они компактны, и поскольку состоят из «реализованных математических моделей», то допускают свободное масштабирование совершенно без потери качества. Преимуществом векторных изображений является также их легкое редактирование.
Самым существенным недостатком векторной графики является программная зависимость, поскольку не существует принципиальной возможности создать стандартный единый фор-
15
мат, который бы позволял свободно открывать любой векторный документ в любой векторной программе.
Следует иметь в виду, что современные программные продукты часто не являются чисто растровыми или векторными редакторами. Например, векторный редактор Corel Draw имеет инструменты для работы с растровыми изображениями, а также может использовать подключаемые (plug-ins) инструменты.
16
2 ОБЩИЕ СВЕДЕНИЯ О СИСТЕМЕ КОМПАС 3D V8 LT
Система КОМПАС-3D LT предназначена для выполнения учебных проектно-конструкторских работ в различных отраслях деятельности. Различают три варианта проектов — чертеж, фрагмент и деталь.
Деталь — модель изделия, изготавливаемого из однородного материала, без применения сборочных операций. Файл детали имеет расширение .m3d.
Чертеж — основной тип графического документа в КОМ- ПАС-3D. Чертеж содержит графическое изображение изделия, основную надпись, рамку, иногда — дополнительные объекты оформления (знак неуказанной шероховатости, технические требования и т.д.). Чертеж КОМПАС-3D всегда содержит один лист заданного пользователем формата. В файле чертежа КОМПАС3D могут содержаться не только чертежи (в понимании ЕСКД), но и схемы, плакаты и прочие графические документы. Файл чертежа имеет расширение .cdw.
Фрагмент — вспомогательный тип графического документа в КОМПАС-3D. Фрагмент отличается от чертежа отсутствием рамки, основной надписи и других объектов оформления конструкторского документа. Он используется для хранения изображений, которые не нужно оформлять как отдельный лист (эскизные прорисовки, разработки и т.д.). Кроме того, во фрагментах также хранятся созданные типовые решения для последующего использования в других документах. Файл фрагмента имеет расширение .frw.
Фрагмент отличается от чертежа отсутствием рамки, основной надписи и других объектов оформления конструкторского документа. Он используется для хранения изображений, которые не нужно оформлять как отдельный лист (эскизные прорисовки, разработки и т.д.). Кроме того, во фрагментах также хранятся созданные типовые решения для последующего использования в других документах. Файл фрагмента имеет расширение .frw.
Приведенный далее материал является лишь кратким руководством по пользованию Компас 3D V8 LT и не требует никакой отчетности. Варианты выполнения задания в Компас 3D V8 LT приведены в конце руководства.
Начальным этапом является создание детали. Для открытия проекта нажмите левой кнопкой на пиктограмму Создать ,
выберите Деталь , интерфейс Компас 3D V8 LT представлен на рисунке 1.
17
Зона заголовка | Падающее меню |
Стандартная панель инструментов Главная панель Дерево построения
Компактная
инструментальная
панель
Рабочее поле
Строка состояния
Рисунок 1
Компас 3D V8 LT позволяет создавать пользовательский интерфейс. Для этого следует выбрать в падающем меню пункт
Для этого следует выбрать в падающем меню пункт
Сервис — Настройка интерфейса… — Панели инструментов,
рисунок 2. Активизируйте инструментальную панель Геометрия. Появившуюся на рабочем поле плавающую панель можно закрепить, например, слева от дерева построений.
Можно добавить в любую панель необходимые кнопки, Для этого надо указать закладкуКоманды диалогового окна, рисунок 2.
Для добавления кнопок в панели инструментов надо «перетащить» команду на нужную панель.
Состав Компактной панели зависит от типа активного документа.
18
Рисунок 2
Основным инструментом работы в Компас 3D V8 LT является курсор манипулятора (мыши). Курсор может перемещаться по рабочему полю с различным шагом. Изменить шаг можно в панели свойств .
В процессе работы с графическими документами вы можете отменять выполненные действия. Отмененные действия могут, в свою очередь, быть повторены. Количество запоминаемых для отмены команд вы можете задать при настройке системы. Для отмены используется кнопка Отменить , для возврата — кноп-
Для отмены используется кнопка Отменить , для возврата — кноп-
ка Повторить .
Для удаления объектов достаточно просто их выделить (объект подсвечивается зеленым) и нажать кнопку Delete.
Для редактирования без использования команд объект или объекты выделяются. Для перемещения надо просто навести курсор на выделенные объекты и, не отпуская левую клавишу, «перетащить» их на нужное место.
Для копирования выполнить вышеуказанные действия с нажатой клавишей Ctrl.
Для изменения размеров объектов или их положения на рабочем поле надо выполнить процедуру перетаскивания с выделенными вершинами.
19
Можно выполнить редактирование в панели состояния, если при щелчке правой кнопкой мыши выбрать в контекстном меню пункт Редактировать.
Управлять изображением можно с помощью кнопок панели Вид . Это кнопки — Увеличить размер изображения рамкой, Увеличить масштаб изображения, Уменьшить масштаб изображения, Текущий масштаб. — Кнопка динамического приближения/отдаления и кнопка показать все . Но наиболее удобным способом управления изображением является использования колесика скроллинга мыши. Вращение колесика приближает/отдаляет изображение, а нажатие на кнопку скроллинга позволяет панорамировать изображение.
Но наиболее удобным способом управления изображением является использования колесика скроллинга мыши. Вращение колесика приближает/отдаляет изображение, а нажатие на кнопку скроллинга позволяет панорамировать изображение.
В процессе работы с графическим документом постоянно возникает необходимость точно установить курсор в некоторую точку (начало координат, центр окружности, конец отрезка и т.п.), иными словами, выполнить привязку к уже существующим точкам или объектам. Без такой привязки невозможно создать точный чертеж.
КОМПАС-3D LT предоставляет возможности привязок к характерным точкам (пересечение, граничные точки, центр и т.д.) и объектам (по нормали, по направлениям осей координат).
Предусмотрены две разновидности привязки — глобальная (действующая по умолчанию) и локальная (однократная).
Глобальная привязка (если она установлена) постоянно действует при вводе и редактировании объектов. Например, если включена глобальная привязка к пересечениям, то при вводе каждой точки система автоматически будет выполнять поиск ближайшего пересечения в пределах апертуры (ловушки) курсора. Можно установить несколько глобальных привязок.
Можно установить несколько глобальных привязок.
Локальную привязку требуется всякий раз вызывать заново. Чтобы воспользоваться локальной привязкой при построении или редактировании графического объекта, раскройте меню кнопки Локальная привязка (это вынесенная на панель Глобальные привязки кнопка последней использовавшейся локальной привязки)
и вызовите из него нужную команду, рисунок 3.
20
Рисунок 3
Команды для выполнения многих часто используемых действий можно вызвать из контекстного меню. Эти меню появляются на экране при нажатии правой кнопки мыши. Состав меню будет разным для различных ситуаций. В нем будут собраны наиболее типичные для данного момента работы команды, рисунок 4.
Рисунок 4
Во время работы с документами КОМПАС-3D LT пользователь выполняет различные операции над объектами — редактирует их, копирует, перемещает, поворачивает и так далее.
⇐ Предыдущая30313233343536373839Следующая ⇒ «Лестничный» эффект появляется при увеличении ___________ изображения.
. Примитивами в векторной графике именуют …
Решение:
⇐ Предыдущая30313233343536373839Следующая ⇒
|
Векторная графика — ГИС Вики
| Эта статья нуждается в дополнительных ссылках для проверки. Пожалуйста, помогите улучшить эту статью, добавив надежные ссылки. Материал без источника может быть оспорен и удален. (январь 2008 г.) |
 Растровые изображения основаны на пикселях и, таким образом, масштабируются с потерей четкости, в то время как векторные изображения можно масштабировать до бесконечности без ухудшения качества.
Растровые изображения основаны на пикселях и, таким образом, масштабируются с потерей четкости, в то время как векторные изображения можно масштабировать до бесконечности без ухудшения качества.Векторная графика — это использование геометрических примитивов, таких как точки, линии, кривые и фигуры или многоугольники, основанные на математических уравнениях, для представления изображений в компьютерной графике.
Форматы векторной графики дополняют растровую графику, которая представляет собой представление изображений в виде массива пикселей, как это обычно используется для представления фотографических изображений. [1] В некоторых случаях рекомендуется работать с векторными инструментами и форматами, а в случаях, когда лучше всего работать с растровыми инструментами и форматами. Бывают случаи, когда оба формата объединяются. Понимание преимуществ и ограничений каждой технологии и взаимосвязи между ними, скорее всего, приведет к эффективному и действенному использованию инструментов.
Содержание
- 1 Обзор
- 1.1 Редактирование векторной графики
- 1.2 Стандарты
- 1.3 Приложения
- 2 Мотивация
- 3 Типичные примитивные объекты
- 4 Векторные операции
- 5 Печать
- 6 Векторная иллюстрация
- 7 3D-моделирование
- 8 форматов
- 9 См. также
- 10 Каталожные номера
Обзор
Компьютерные дисплеи состоят из сетки небольших прямоугольных ячеек, называемых пикселями. Картинка строится из этих ячеек. Чем меньше и ближе друг к другу ячейки, тем лучше качество изображения, но тем больше размер файла, необходимого для хранения данных. Если количество пикселей остается постоянным, размер каждого пикселя будет увеличиваться, и изображение при увеличении становится зернистым (пиксельным), поскольку разрешение глаза позволяет ему различать отдельные пиксели.
Файлы векторной графики хранят линии, формы и цвета, из которых состоит изображение, в виде математических формул. Программа векторной графики использует эти математические формулы для построения изображения на экране, создавая изображение наилучшего возможного качества с учетом разрешения экрана. Математические формулы определяют, где должны быть размещены точки, составляющие изображение, для достижения наилучших результатов при отображении изображения. Поскольку эти формулы могут создавать изображение, масштабируемое до любого размера и детализации, качество изображения определяется только разрешением дисплея, а размер файла векторных данных, генерирующих изображение, остается неизменным. Печать изображения на бумаге обычно дает более четкий вывод с более высоким разрешением, чем печать его на экране, но может использовать точно такой же файл векторных данных.
Программа векторной графики использует эти математические формулы для построения изображения на экране, создавая изображение наилучшего возможного качества с учетом разрешения экрана. Математические формулы определяют, где должны быть размещены точки, составляющие изображение, для достижения наилучших результатов при отображении изображения. Поскольку эти формулы могут создавать изображение, масштабируемое до любого размера и детализации, качество изображения определяется только разрешением дисплея, а размер файла векторных данных, генерирующих изображение, остается неизменным. Печать изображения на бумаге обычно дает более четкий вывод с более высоким разрешением, чем печать его на экране, но может использовать точно такой же файл векторных данных.
Редактирование векторной графики
Программное обеспечение для векторной графики используется для создания и редактирования векторной графики. Изображение может быть изменено путем редактирования экранных объектов, которые затем сохраняются как модификации математических формул. Математические операторы в программном обеспечении могут использоваться для растягивания, скручивания и окрашивания составных объектов на изображении или на всем изображении, и эти инструменты интуитивно понятны пользователю через графический интерфейс пользователя компьютера. Созданное изображение экрана можно сохранить в виде растрового/растрового файла или сгенерировать растровое изображение любого разрешения из векторного файла для использования на любом устройстве.
Математические операторы в программном обеспечении могут использоваться для растягивания, скручивания и окрашивания составных объектов на изображении или на всем изображении, и эти инструменты интуитивно понятны пользователю через графический интерфейс пользователя компьютера. Созданное изображение экрана можно сохранить в виде растрового/растрового файла или сгенерировать растровое изображение любого разрешения из векторного файла для использования на любом устройстве.
Размер генерируемого файла будет зависеть от требуемого разрешения, но размер векторного файла, генерирующего растровый/растровый файл, всегда останется неизменным. Таким образом, легко преобразовать векторный файл в ряд форматов растровых/растровых файлов, но сделать это в обратном направлении гораздо сложнее, особенно если требуется последующее редактирование векторного изображения. Может оказаться преимуществом сохранить изображение, созданное из исходного векторного файла, в виде растрового или растрового формата, потому что разные системы имеют разные (и несовместимые) векторные форматы, а некоторые могут вообще не поддерживать векторную графику.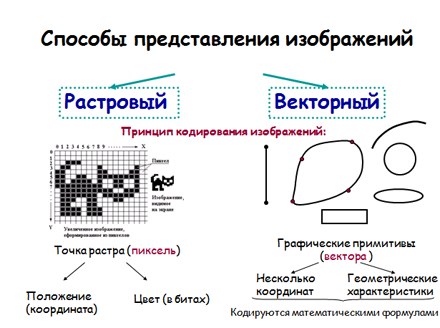 Однако после преобразования файла из векторного формата он, вероятно, станет больше и потеряет преимущество масштабируемости без потери разрешения. Также больше нельзя будет редактировать отдельные части изображения как отдельные объекты.
Однако после преобразования файла из векторного формата он, вероятно, станет больше и потеряет преимущество масштабируемости без потери разрешения. Также больше нельзя будет редактировать отдельные части изображения как отдельные объекты.
Векторные форматы не всегда подходят для работы с графикой. Например, цифровые устройства, такие как камеры и сканеры, производят растровую графику, которую нецелесообразно преобразовывать в векторную, поэтому для этого типа работы редактор будет работать с пикселями, а не с рисованием объектов, определяемых математическими формулами. Комплексные графические инструменты будут объединять изображения из векторных и растровых источников и могут предоставлять инструменты редактирования для обоих, поскольку некоторые части изображения могут быть получены с камеры, а другие могут быть нарисованы с использованием векторных инструментов.
Стандарты
Стандартом W3C для векторной графики является SVG. Стандарт сложен, и его принятие было относительно медленным, по крайней мере, частично из-за коммерческих интересов. Многие веб-браузеры теперь имеют некоторую поддержку рендеринга данных svg, но полные реализации стандарта все еще сравнительно редки.
Многие веб-браузеры теперь имеют некоторую поддержку рендеринга данных svg, но полные реализации стандарта все еще сравнительно редки.
Приложения
Одним из первых применений векторных графических дисплеев была система ПВО США SAGE. Системы векторной графики были изъяты из системы управления воздушным движением в США только в 1999 году и, вероятно, до сих пор используются в военных и специализированных системах. Векторная графика также использовалась на TX-2 в лаборатории Линкольна Массачусетского технологического института пионером компьютерной графики Иваном Сазерлендом для запуска его программы Sketchpad в 1963 году.
Последующие системы векторной графики, большинство из которых итерировались через динамически изменяемые сохраненные списки инструкций по рисованию, включают GT40 от Digital. [2] Была домашняя игровая система, которая использовала векторную графику под названием Vectrex, а также различные аркадные игры, такие как Asteroids и Space Wars . Дисплеи области хранения, такие как Tektronix 4014, могут отображать векторные изображения, но не могут изменять их без предварительного стирания дисплея.
Дисплеи области хранения, такие как Tektronix 4014, могут отображать векторные изображения, но не могут изменять их без предварительного стирания дисплея.
Современные дисплеи с векторной графикой иногда можно увидеть на лазерных световых шоу, где два быстро движущихся зеркала X-Y используются для быстрого рисования фигур и текста на экране.
Термин «векторная графика» в основном используется сегодня в контексте двумерной компьютерной графики. Это один из нескольких режимов, которые художник может использовать для создания изображения на растровом дисплее. Другие режимы включают текст, мультимедиа и 3D-рендеринг. Практически весь современный 3D-рендеринг выполняется с использованием расширений методов 2D-векторной графики. Плоттеры, используемые в техническом рисовании, до сих пор рисуют векторы прямо на бумаге.
Мотивация
Например, рассмотрим круг радиусом r . Основные части информации, необходимые программе для рисования этого круга:
- указание на то, что нужно нарисовать круг
- радиус р
- расположение центральной точки окружности
- стиль и цвет линии штриха (возможно, прозрачный)
- стиль и цвет заливки (возможно, прозрачный)
Преимущества этого стиля рисования по сравнению с растровой графикой:
- Этот минимальный объем информации приводит к гораздо меньшему размеру по сравнению с большими растровыми изображениями (размер представления не зависит от размеров объекта), хотя часто говорят, что векторной графике с небольшим размером файла недостает детализация по сравнению с реальной фотографией.

- Соответственно, можно бесконечно увеличивать, например. дуга окружности, и она остается гладкой. С другой стороны, многоугольник, представляющий кривую, покажет, что на самом деле он не изогнут.
- При увеличении масштаба линии и кривые не должны расширяться пропорционально. Часто ширина либо не увеличена, либо менее пропорциональна. С другой стороны, неправильные кривые, представленные простыми геометрическими фигурами, можно сделать пропорционально шире при увеличении, чтобы они выглядели гладкими и не похожими на эти геометрические фигуры.
- Параметры объектов сохраняются и впоследствии могут быть изменены. Это означает, что перемещение, масштабирование, вращение, заливка и т. д. не ухудшают качество рисунка. Более того, обычно размеры указываются в аппаратно-независимых единицах, что приводит к наилучшей возможной растеризации на растровых устройствах.
- С трехмерной точки зрения рендеринг теней с векторной графикой также намного более реалистичен, поскольку тени можно абстрагировать в лучи света, из которых они формируются.
 Это позволяет создавать фотореалистичные изображения и визуализацию.
Это позволяет создавать фотореалистичные изображения и визуализацию.
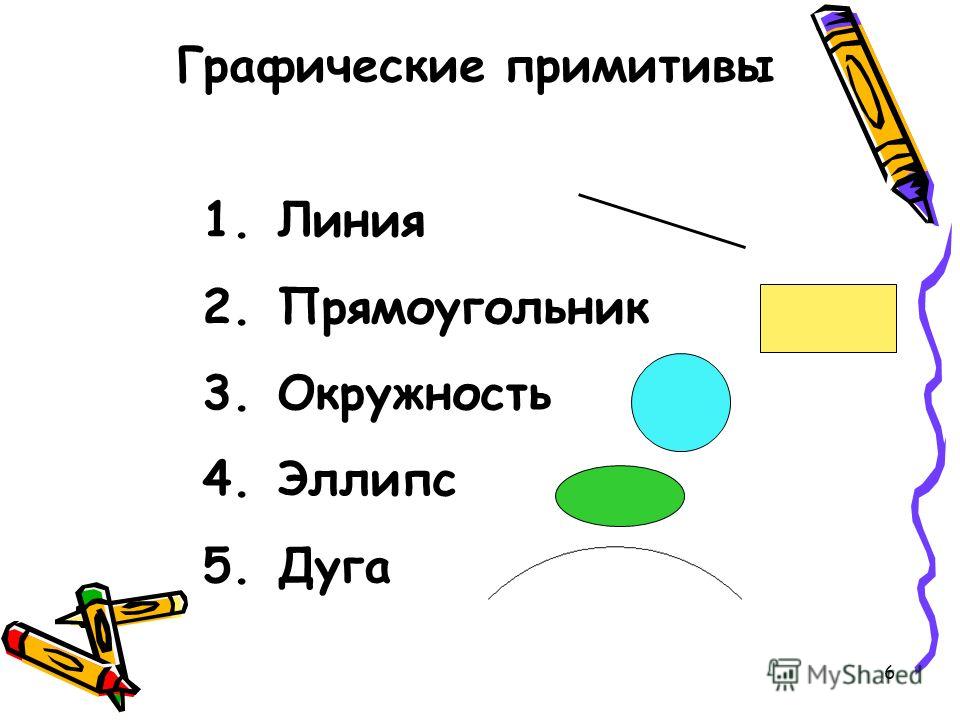
Типовые объекты-примитивы
- Линии и полилинии
- Полигоны
- Круги и эллипсы
- Кривые Безье
- Безигоны
- Текст (в форматах компьютерных шрифтов, таких как TrueType, где каждая буква создается из кривых Безье)
Этот список не является полным. Существуют различные типы кривых (сплайны Катмулла-Рома, NURBS и т. д.), которые полезны в определенных приложениях.
Часто растровое изображение рассматривается как примитивный объект. С концептуальной точки зрения он ведет себя как прямоугольник.
Векторные операции
Редакторы векторной графики обычно допускают вращение, перемещение, зеркальное отображение, растяжение, наклон, преобразования, изменение z-порядка и объединение примитивов в более сложные объекты.
Более сложные преобразования включают операции над множествами, а не над замкнутыми формами (объединение, разность, пересечение и т. д.).
д.).
Векторная графика идеально подходит для простых или составных рисунков, которые должны быть независимыми от устройства или не должны достигать фотореализма. Например, языки описания страниц PostScript и PDF используют модель векторной графики.
Печать
Векторная графика — ключ к печати. Поскольку рисунок состоит из ряда математических кривых, он будет печататься очень четко даже при изменении размера. Например, можно распечатать векторный логотип на небольшом листе копировальной бумаги, а затем увеличить тот же векторный логотип до размера рекламного щита и сохранить такое же четкое качество. Растровая графика с низким разрешением будет чрезмерно размытой или пикселизированной, если ее увеличить с размера визитной карточки до размера рекламного щита.
Если мы рассматриваем типографские знаки как изображения, то те же соображения, которые мы сделали для графики, применимы даже к составлению письменного текста для печати (набору). Старые наборы символов хранились в виде растровых изображений, поэтому для достижения максимального качества печати их нужно было использовать только при заданном разрешении; эти форматы шрифтов считаются немасштабируемыми. Высококачественная типографика в настоящее время основана на рисунках символов (шрифтах), которые обычно хранятся в виде векторной графики и, как таковые, масштабируются до любого размера. Примерами этих векторных форматов для символов являются шрифты Postscript и шрифты TrueType.
Высококачественная типографика в настоящее время основана на рисунках символов (шрифтах), которые обычно хранятся в виде векторной графики и, как таковые, масштабируются до любого размера. Примерами этих векторных форматов для символов являются шрифты Postscript и шрифты TrueType.
Векторная иллюстрация
Векторная иллюстрация — популярная техника многих цифровых иллюстраторов по всему миру. Одними из величайших всемирно известных художников в этой области являются Джон Бургерман, Каталина Эстрада, Петра Стефанкова, Натан Юревичюс, Дж. Отто Сейбольд, Лео Бланшетт и другие.
3D-моделирование
В компьютерной 3D-графике наиболее распространены векторизованные представления поверхности (растровые изображения могут использоваться для специальных целей, таких как текстурирование поверхности, данные высотного поля и рельефное отображение). В младших классах простые сетки полигонов используются для представления геометрических деталей в приложениях, где важны интерактивная частота кадров или простота. На высоком уровне, когда кто-то готов пожертвовать более длительным временем рендеринга для повышения качества и точности изображения, используются представления гладких поверхностей, такие как пятна Безье, NURBS или поверхности Subdivision. Однако можно добиться гладкой визуализации поверхности полигональной сетки с помощью алгоритмов затенения, таких как Фонг и Гуро.
На высоком уровне, когда кто-то готов пожертвовать более длительным временем рендеринга для повышения качества и точности изображения, используются представления гладких поверхностей, такие как пятна Безье, NURBS или поверхности Subdivision. Однако можно добиться гладкой визуализации поверхности полигональной сетки с помощью алгоритмов затенения, таких как Фонг и Гуро.
Форматы
Основная статья: Векторные форматы
Одним из примеров формата векторной графики является SVG (Scalable Vector Graphics), открытый стандарт, созданный и разработанный консорциумом World Wide Web для удовлетворения потребностей (и попыток нескольких корпораций) для универсального, скриптового и универсального векторного формата для Интернета и других целей. Другим примером является VML, предложенный стандарт, принятый Microsoft. Возможно, формат AI, собственный формат Adobe Illustrator, также является стандартным для векторной графики.
Формат файла SWF Adobe (ранее Macromedia) также представляет собой векторный контейнер, используемый для хранения анимации. Таким образом, веб-страницы, созданные во Flash, могут быть увеличены до размера монитора любого размера с сохранением того же качества графики.
Таким образом, веб-страницы, созданные во Flash, могут быть увеличены до размера монитора любого размера с сохранением того же качества графики.
См. также
- Adobe Illustrator
- Инкскейп
- Каир (графика)
- Антизернистая геометрия
- Картонная техника
- Компьютерное проектирование
- Электронные карты
- Графическое программное обеспечение
- Обзор формата графического файла
- GXL (язык обмена графическими данными)
- Список редакторов векторной графики
- Список языков разметки векторной графики
- Растр в вектор
- Шейп-файл
- Черепаха графика
- Векторная игра
- Редактор векторной графики
- Масштабируемая векторная графика (SVG)
- Язык векторной разметки (VML)
- Векторный монитор
- Вексель
- Каркасная модель
Каталожные номера
- ↑ Айра Гринберг (2007).
 Обработка: творческое кодирование и вычислительное искусство . Апресс. ISBN 159059617X. http://books.google.com/books?id=WTl_7H5HUZAC&pg=PA115&dq=raster+vector+graphics+photographic&lr=&as_brr=0&ei=llOVR5LKCJL0iwGZ8-ywBw&sig=YEjfPOYSUDIf1CUbL5S5Jbzs7M8.
Обработка: творческое кодирование и вычислительное искусство . Апресс. ISBN 159059617X. http://books.google.com/books?id=WTl_7H5HUZAC&pg=PA115&dq=raster+vector+graphics+photographic&lr=&as_brr=0&ei=llOVR5LKCJL0iwGZ8-ywBw&sig=YEjfPOYSUDIf1CUbL5S5Jbzs7M8. - ↑ «Графический терминал DEC GT40» . http://www.brouhaha.com/~eric/retrocomputing/dec/gt40/. Проверено в 2009 г.-05-06.
Введение в компьютерную графику. Раздел 1.2. Элементы трехмерной графики
Раздел 1.2
Когда мы обращаемся к трехмерной графике, мы обнаруживаем, что наиболее распространенные подходы имеют более
общего с векторной графикой, чем с растровой графикой.
То есть содержимое изображения указывается в виде списка геометрических объектов.
Метод называется геометрическим моделированием. Отправная точка
состоит в том, чтобы построить «искусственный трехмерный мир» как набор простых геометрических фигур, расположенных в
трехмерное пространство. Объекты могут иметь атрибуты, которые в сочетании с
глобальные свойства мира, определяющие внешний вид объектов. Часто набор основных фигур очень ограничен и может включать только точки, отрезки и т.
и треугольники. Можно построить более сложную форму, такую как многоугольник или сфера.
аппроксимируется как набор более основных форм, если он сам не рассматривается
быть основным. Чтобы сделать двухмерное изображение сцены,
сцена проецируется из трех измерений
вплоть до двух измерений. Проекция эквивалентна
фотографирование места происшествия. Давайте посмотрим, как все это работает в
немного подробнее.
Часто набор основных фигур очень ограничен и может включать только точки, отрезки и т.
и треугольники. Можно построить более сложную форму, такую как многоугольник или сфера.
аппроксимируется как набор более основных форм, если он сам не рассматривается
быть основным. Чтобы сделать двухмерное изображение сцены,
сцена проецируется из трех измерений
вплоть до двух измерений. Проекция эквивалентна
фотографирование места происшествия. Давайте посмотрим, как все это работает в
немного подробнее.
Во-первых, геометрия…. Мы начинаем с пустого трехмерного пространства или «мира». Конечно, это пространство существует только концептуально, но оно полезно думать о нем как о реальном и иметь возможность визуализировать его в уме. Пространство нуждается система координат, которая связывает каждую точку в пространстве с тремя числами, обычно называют координатами x , y и z точки. Эта система координат называется «мировыми координатами».
Мы хотим построить сцену внутри мира, состоящую из геометрических объектов. Например,
мы можем указать отрезок линии в сцене, указав координаты двух его конечных точек,
и мы можем указать треугольник, задав координаты трех его вершин. Самое маленькое здание
блоки, с которыми нам приходится работать, такие как отрезки и треугольники, называются
геометрические примитивы. Разная графика
системы делают доступными различные наборы примитивов, но во многих случаях только самые основные
формы, такие как линии и треугольники, считаются примитивными. Сложная сцена может содержать
большое количество примитивов, и было бы очень сложно создать сцену
давая явные координаты для каждого отдельного примитива. Решение, как у любого программиста
следует сразу же догадаться, заключается в объединении примитивов в повторно используемые компоненты.
Например, для сцены с несколькими автомобилями мы могли бы создать геометрическую
модель колеса. Автомобиль можно смоделировать как четыре колеса вместе с моделями
другие компоненты. И тогда мы могли бы использовать несколько копий модели автомобиля в
сцена.
Например,
мы можем указать отрезок линии в сцене, указав координаты двух его конечных точек,
и мы можем указать треугольник, задав координаты трех его вершин. Самое маленькое здание
блоки, с которыми нам приходится работать, такие как отрезки и треугольники, называются
геометрические примитивы. Разная графика
системы делают доступными различные наборы примитивов, но во многих случаях только самые основные
формы, такие как линии и треугольники, считаются примитивными. Сложная сцена может содержать
большое количество примитивов, и было бы очень сложно создать сцену
давая явные координаты для каждого отдельного примитива. Решение, как у любого программиста
следует сразу же догадаться, заключается в объединении примитивов в повторно используемые компоненты.
Например, для сцены с несколькими автомобилями мы могли бы создать геометрическую
модель колеса. Автомобиль можно смоделировать как четыре колеса вместе с моделями
другие компоненты. И тогда мы могли бы использовать несколько копий модели автомобиля в
сцена. Обратите внимание, что после создания геометрической модели ее можно использовать в качестве
компонент в более сложных моделях. Это называется иерархическим моделированием.
Обратите внимание, что после создания геометрической модели ее можно использовать в качестве
компонент в более сложных моделях. Это называется иерархическим моделированием.
Предположим, мы построили модель колеса из геометрических примитивов.
Когда это колесо перемещается в нужное положение в модели автомобиля, координаты
все его примитивы должны быть скорректированы. Итак, что именно мы получили, построив
колесо? Дело в том, что все координаты в колесе корректируются аналогично . То есть, чтобы поместить колесо в автомобиль, нам достаточно
указать одну регулировку, которая применяется ко всему колесу. Тип «корректировка»
которое используется, называется геометрическим преобразованием (или геометрическим преобразованием).
трансформация). Геометрическое преобразование
используется для настройки размера, ориентации и положения геометрического объекта. При изготовлении
модель автомобиля, строим одно колесо . Затем мы применяем четыре различных
преобразуется в модель колеса, чтобы добавить четыре копии колеса к автомобилю. Точно так же мы можем добавить в сцену несколько автомобилей, применяя различные преобразования.
на ту же модель автомобиля.
Точно так же мы можем добавить в сцену несколько автомобилей, применяя различные преобразования.
на ту же модель автомобиля.
Три самых основных вида геометрического преобразования называются масштабированием, вращения и перевода. Масштабирующее преобразование используется для установки размера объекта, то есть для его увеличения или уменьшения. по какому-то определенному фактору. Преобразование вращения используется для установки ориентации объекта путем поворота его на некоторый угол. относительно какой-то определенной оси. Трансляционное преобразование используется для установки положения объекта, сместив его на заданную величину от исходного положения. В этой книге мы встретимся с этими преобразованиями сначала в двух измерениях, где они легче понять. Но именно в 3D-графике они становятся по-настоящему необходимыми.
Далее, внешний вид…. Геометрические фигуры сами по себе не очень интересны. Вы должны быть в состоянии
установить их внешний вид. Это делается путем присвоения атрибутов
к геометрическим объектам. Очевидным атрибутом является цвет, но получение реалистичного
внешний вид оказывается намного сложнее, чем просто указать цвет
для каждого примитива. В 3D-графике вместо цвета обычно говорят о
материал. Термин материал здесь относится к свойствам, которые определяют
собственный внешний вид поверхности. По сути, это означает, что поверхность
взаимодействует со светом, попадающим на поверхность. Свойства материала могут включать основные
цвет, а также другие свойства, такие как блеск, шероховатость и прозрачность.
Очевидным атрибутом является цвет, но получение реалистичного
внешний вид оказывается намного сложнее, чем просто указать цвет
для каждого примитива. В 3D-графике вместо цвета обычно говорят о
материал. Термин материал здесь относится к свойствам, которые определяют
собственный внешний вид поверхности. По сути, это означает, что поверхность
взаимодействует со светом, попадающим на поверхность. Свойства материала могут включать основные
цвет, а также другие свойства, такие как блеск, шероховатость и прозрачность.
Одним из наиболее полезных свойств материала является текстура.
В самых общих чертах текстура — это способ варьирования свойств материала от точки к точке.
на поверхности. Чаще всего текстура используется для разных цветов.
точки. Это часто делается с использованием 2D-изображения в качестве текстуры. Изображение может быть нанесено на поверхность
чтобы изображение выглядело так, как будто оно «нарисовано» на поверхности.
Однако текстура также может относиться к изменению значений таких вещей, как прозрачность или
«болтливость». Текстуры позволяют нам добавлять детали к сцене, не используя огромное количество
геометрические примитивы; вместо этого вы можете использовать меньшее количество текстурированных примитивов.
Текстуры позволяют нам добавлять детали к сцене, не используя огромное количество
геометрические примитивы; вместо этого вы можете использовать меньшее количество текстурированных примитивов.
Материал является неотъемлемым свойством объекта, но фактический внешний вид объект также зависит от среды, в которой объект просматривается. В реальном мире вы ничего не видите, если в окружающей среде нет света. То же самое и в 3D-графике: вам нужно добавить имитацию освещения. к сцене. В сцене может быть несколько источников света. Каждый источник света может иметь свой собственный цвет, интенсивность и направление или положение. Свет от этих источников будет затем взаимодействуйте со свойствами материала объектов в сцене. Поддержка для освещение в графической системе может варьироваться от довольно простого до очень сложного и вычислительно интенсивный.
Наконец, изображение…. В общем, конечной целью 3D-графики является создание 2D-изображений 3D-мира.
Преобразование из 3D в 2D включает в себя просмотр и
проекция. Мир выглядит иначе, если смотреть с разных
точки зрения. Чтобы настроить точку зрения, нам нужно указать позицию зрителя
и направление, в котором смотрит зритель. Также необходимо указать
направление «вверх», направление, которое будет указывать вверх на конечном изображении.
Это можно рассматривать как размещение «виртуальной камеры» в сцене. Однажды
точка зрения настроена, мир, видимый с этой точки зрения, может быть спроецирован в
2D. Проекция аналогична съемке с помощью камеры.
Мир выглядит иначе, если смотреть с разных
точки зрения. Чтобы настроить точку зрения, нам нужно указать позицию зрителя
и направление, в котором смотрит зритель. Также необходимо указать
направление «вверх», направление, которое будет указывать вверх на конечном изображении.
Это можно рассматривать как размещение «виртуальной камеры» в сцене. Однажды
точка зрения настроена, мир, видимый с этой точки зрения, может быть спроецирован в
2D. Проекция аналогична съемке с помощью камеры.
Последним шагом в 3D-графике является присвоение цвета отдельным пикселям в 2D изображение. Этот процесс называется растеризацией, и весь процесс создания изображения называется рендерингом. сцена.
Во многих случаях конечной целью является не создание одного изображения, а
анимация, состоящая из последовательности изображений, показывающих мир
в разное время. В анимации есть небольшие изменения по сравнению с одним изображением в
последовательность к следующей. Почти любой аспект сцены может измениться во время анимации.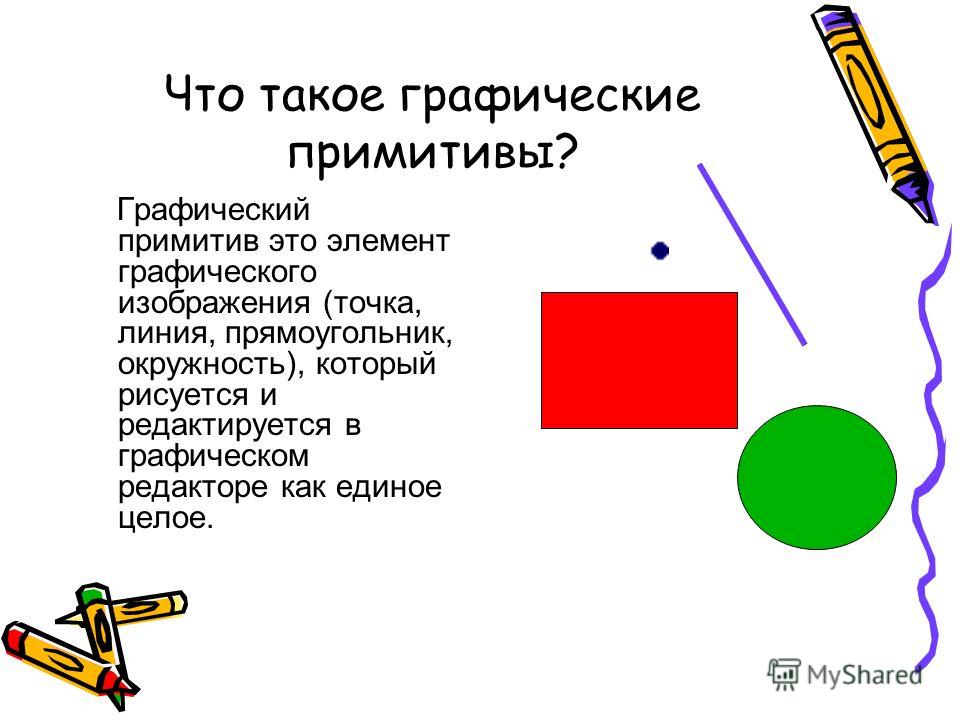

 ○ растрового ○ векторного
○ растрового ○ векторного д.), именуемых «примитивами».
д.), именуемых «примитивами». ..
..
 Ознакомить студентов с основными культуральными характеристиками микроорганизмов и методами определения…
Ознакомить студентов с основными культуральными характеристиками микроорганизмов и методами определения…
 Это позволяет создавать фотореалистичные изображения и визуализацию.
Это позволяет создавать фотореалистичные изображения и визуализацию. Обработка: творческое кодирование и вычислительное искусство . Апресс. ISBN 159059617X. http://books.google.com/books?id=WTl_7H5HUZAC&pg=PA115&dq=raster+vector+graphics+photographic&lr=&as_brr=0&ei=llOVR5LKCJL0iwGZ8-ywBw&sig=YEjfPOYSUDIf1CUbL5S5Jbzs7M8.
Обработка: творческое кодирование и вычислительное искусство . Апресс. ISBN 159059617X. http://books.google.com/books?id=WTl_7H5HUZAC&pg=PA115&dq=raster+vector+graphics+photographic&lr=&as_brr=0&ei=llOVR5LKCJL0iwGZ8-ywBw&sig=YEjfPOYSUDIf1CUbL5S5Jbzs7M8.