#10. Двусвязный список. Структура и основные операции
Курс по структурам данных: https://stepik.org/a/134212
Смотреть материал на видео
На этом занятии мы познакомимся с новой структурой данных – двусвязными списками. Если вы хорошо понимаете, как работает односвязный список, то вся основа у вас уже есть, так как двусвязный список – это все тот же односвязный, только каждый элемент имеет ссылки next и prev на следующий и предыдущий элементы. Во всем остальном он идентичен односвязному.
Также мы имеем здесь
два указателя: head – на первый элемент списка; tail – на последний.
В результате, можно очень быстро обрабатывать первые и последние элементы,
например, делать добавление элементов в начало списка или вконец, а также
удалять их. У граничных объектов указатель prev и next принимают
значения NULL. Так можно
определять первый и последний элементы списка.
(Помимо значения NULL можно
использовать любую другую предопределенную величину, например, None если программа
пишется на Python).
Добавление элементов в начало и конец двусвязного списка
Я думаю, что структура двухсвязного списка вам понятна. Давайте теперь рассмотрим базовые операции работы с этой структурой данных. И начнем с операции добавления элементов в начало и конец списка.
Предположим, что в списке два объекта и мы хотим добавить новый в его конец:
Вначале создается новый элемент в памяти компьютера, на который ведет временная ссылка ptr. Затем, ссылка next последнего объекта списка должна вести на этот новый объект. Для этого достаточно присвоить ссылке адрес нового элемента:
tail.next = ptr
Далее необходимо ссылке prev нового элемента присвоить адрес последнего элемента списка:
ptr.prev = tail
И последнее, указатель tail переместить на новый последний элемент списка:
tail = ptr
Скорость работы
этой операции составляет O(1) и часто реализуется командой push_back().
По аналогии выполняется добавление нового элемента в начало двусвязного списка. Создается новый объект, на который ссылается указатель ptr. Затем, ссылка prev первого объекта должна вести на добавляемый элемент:
head.prev = ptr
Ссылка next добавляемого элемента должна вести на объект head:
ptr.next = head
И указатель head перемещаем на объект ptr:
head = ptr
Вот так, достаточно просто выполняется добавление нового элемента в начало двусвязного списка. Скорость выполнения этой операции с точки зрения О большого составляет O(1) и часто реализуется командой push_front().
Доступ к произвольному элементу двусвязного списка
Давайте теперь
посмотрим, как осуществляется доступ к произвольному элементу в двусвязном
списке. Предположим, имеется список из нескольких элементов и указатели head и tail, которые
ссылаются на первый и последний элементы этого списка.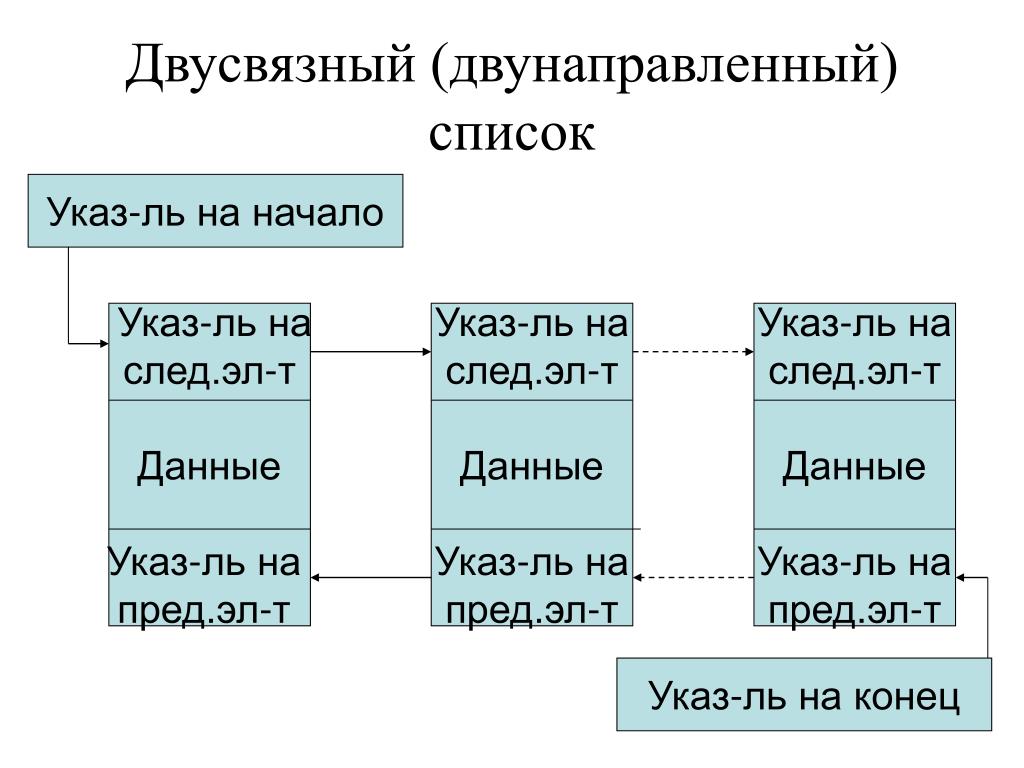
То есть, через указатель ptr мы сейчас обращаемся к первому элементу и можем, например, прочитать его данные командой:
value = ptr.data
Чтобы перейти к следующему второму элементу необходимо переместить указатель ptr на него. Сделать это можно очень просто с помощью указателя next первого объекта:
ptr = ptr.next
Получаем доступ ко второму элементу списка. Можем записывать и считывать из него данные:
ptr.data = new_value
По аналогии, для перехода к следующему третьему элементу, снова выполняем команду:
ptr = ptr.next
и указатель ptr ссылается на третий элемент. И так можно проходить по всем элементам списка до последнего.
С точки зрения О
большого объем вычислений для перехода к произвольному k-му элементу
списка составляет O(n), где n – общее число
элементов в списке.
Но у двусвязных списков есть важное преимущество по сравнению с односвязными списками: мы можем перемещаться по элементам в обе стороны (и вправо и влево). Когда выполняется команда:
ptr = ptr.next
то осуществляется переход вправо. А с помощью команды:
ptr = ptr.prev
влево. В частности, это несколько упрощает некоторые операции, например, удаление промежуточных элементов.
Вставка элемента в двусвязный список
Но сначала мы рассмотрим вставку нового элемента в произвольную позицию двусвязного списка. Предположим, в списке имеется три элемента и мы хотим вставить новый элемент после второго, на который ссылается указатель left:
Затем, создается
новый объект в памяти устройства, на который ссылается временный указатель ptr.
Все что нам
осталось – это настроить связи между соседними элементами относительно
вставляемого. Для этого создадим еще один временный указатель right, который будет
ссылаться на следующий элемент после left:
right = left.next
В результате мы имеем ссылки left и right на соседние объекты относительно вставляемого.
Сформируем новые связи между элементами. Первые две связи между объектом left и ptr, очевидно, создаются командами:
left.next = ptr
ptr.prev = left
А следующие две (между right и ptr) командами:
right.prev = ptr
ptr.next = right
Все, новый элемент вставлен в двусвязный список после объекта left. Разумеется, в реальных программах нужно дополнительно проверять, чтобы объекты left и right существовали, прежде чем обращаться к указателям next и prev этих объектов.
Вычислительная
сложность непосредственно вставки нового элемента, составляет O(1).
Но здесь
нужно учитывать, что прежде необходимо получить ссылку на объект left, после которого
вставляется новый элемент. А эта операция выполняется за O(n). Поэтому, в
общем случае, вставка нового элемента в двусвязный список имеет сложность O(n). И часто
реализуется командой insert().
Удаление промежуточных элементов
Следующая операция – удаление промежуточных элементов. Предположим, имеется список из четырех элементов и мы хотим удалить третий. На него ведет указатель node:
Первым шагом нам нужно получить ссылки на соседние объекты относительно удаляемого. Это можно сделать командами:
left = node.prev
right = node.next
Затем, освободить память, занимаемую объектом node. Например, в C++ это делается командой:
delete node
В некоторых
других языках, таких как Python, эту операцию берет на себя
сборщик мусора, когда на объект не ведет никаких внешних ссылок.
Осталось только изменить связи у объектов left и right (связать их между собой). Делается это очень просто. Ссылка next объекта left должна вести на объект right:
left.next = right
А ссылка prev объекта right на left:
right.prev = left
Все, связи настроены и удаление промежуточного элемента выполнено. Вычислительная сложность самой операции удаления составляет O(1). С учетом поиска удаляемого элемента – O(n). А сама команда часто называется erase().
Удаление первого и последнего элементов
В заключение этого занятия отдельно рассмотрим алгоритмы удаления первого и последнего элемента двусвязного списка.
Предположим, в списке имеется четыре элемента и мы собираемся удалить первый. Тогда создадим временный указатель ptr, который будет ссылаться на следующий (второй) элемент:
ptr = head.
next
И у этого второго элемента указатель prev приравняем значению NULL:
ptr.prev = NULL
Затем, освободим память, занимаемую первым элементом head. В С++ это делается с помощью оператора delete:
delete head
И переместим указатель head на второй элемент, который теперь стал первым:
head = ptr
Вот общий принцип удаления первого элемента в двусвязном списке. Вычислительная сложность этого алгоритма составляет O(1) и часто реализуется командой pop_front().
По аналогии выполняется удаление последнего элемента. Вначале формируем временный указатель ptr на предыдущий объект списка:
ptr = tail.prev
Затем, указатель next объекта ptr приравниваем значению NULL:
ptr.next = NULL
Освобождаем память из под последнего элемента:
delete tail
И устанавливаем указатель tail на новый последний элемент:
tail = ptr
Вычислительная
сложность этого алгоритма составляет O(1) и часто реализуется командой pop_back().
Заключение
Подведем общие итоги этого занятия. Самые быстрые операции – это добавление элементов в начало и конец списка, а также удаление последних элементов. Остальные операции имеют сложность O(n).
|
Команда |
Big O |
|
|
Добавление в начало |
push_front() |
O(1) |
|
Добавление в конец |
push_back() |
O(1) |
|
Удаление с конца |
pop_back() |
O(1) |
|
Удаление с начала |
pop_front() |
O(1) |
|
Вставка элемента |
insert() |
O(n) |
|
Удаление промежуточных элементов |
erase() |
O(n) |
|
Доступ к элементу |
at() |
O(n) |
На следующем
занятии мы продолжим эту тему и посмотрим на пример реализации односвязного
списка на языке программирования.
Курс по структурам данных: https://stepik.org/a/134212
Видео по теме
#1. О большое (Big O) — верхняя оценка сложности алгоритмов
#2. О большое (Big O). Случаи логарифмической и факториальной сложности
#3. Статический массив. Структура, его преимущества и недостатки
#4. Примеры реализации статических массивов на C++
#5. Динамический массив. Принцип работы
#6. Реализация динамического массива на Python
#7. Реализация динамического массива на С++ с помощью std::vector
#8. Односвязный список. Структура и основные операции
#9. Делаем односвязный список на С++
#10. Двусвязный список. Структура и основные операции
#11. Делаем двусвязный список на С++
#12. Двусвязный список (list) в STL на С++
#13.
Очереди типов FIFO и LIFO
#14. Очередь collections.deque на Python
#15. Очередь deque библиотеки STL языка C++
#16. Стек. Структура и принцип работы
#17. Реализация стека на Python и C++
#18. Бинарные деревья. Начало
#19. Бинарное дерево. Способы обхода и удаления вершин
#20. Реализация бинарного дерева на Python
#21. Множества (set). Операции над множествами
#22. Множества set и multiset в C++
#23. Контейнер map библиотеки STL в C++
#24. Префиксное (нагруженное, Trie) дерево. Ассоциативные массивы
#25. Хэш-таблицы. Что это такое и как работают
#26. Хэш-функции. Универсальное хэширование
#27. Метод открытой адресации.
Двойное хэширование
#28. Использование хэш-таблиц в Python и С++
Реализация двусвязного списка C++
Двусвязный список — это структурная концепция C++, состоящая из одного или нескольких узлов. Один узел должен состоять из трех частей: данных, ссылки на предыдущий узел и следующего следующего узла. Говорят, что самый первый узел является «головным» узлом, который используется для доступа ко всему связанному списку. Самый последний узел связанного списка всегда имеет значение NULL. Если вы новичок в этой концепции и ищете аутентичные ресурсы для получения знаний, то это руководство для вас.Начнем эту статью с создания нового файла C++. Мы должны создать его с помощью терминального запроса «touch». После создания файла наша следующая задача — открыть его и написать код на C++. Для открытия вы можете использовать любой встроенный редактор Ubuntu 20.04, такой как текстовый редактор, редактор vim или редактор Gnu nano. Итак, мы используем инструкцию «nano» в нашей оболочке, чтобы открыть в ней файл double.
cc.
Пример 01:
Давайте создадим базовый пример кода C++ для создания двусвязного списка. После открытия файла мы добавили файл iostream. Будет использоваться стандартное пространство имен C++. После этого мы создали структуру узла под названием «Узел» с некоторыми ее элементами. Он содержит целочисленную переменную «d» в качестве части данных. Затем мы определили три новые структуры узлов. Узел «p» показывает предыдущий узел, «n» показывает следующий узел, а головной узел «h» указан как NULL в качестве другого узла.
Теперь приведенная выше структура бесполезна, пока мы не добавим и не покажем некоторые узлы в программном коде. Мы используем функцию add() для получения данных узла из функции main(). В его первой строке мы создали новый узел «новый узел», используя структуру «Узел» и назначив ему память, равную размеру «Узел». Символы знака «->» используются для ссылки на части узла, т. е. «следующий», «предыдущий», «данные» и т. д. Таким образом, мы обращались к данным нового узла с помощью -> sing и добавляли данные, переданные функцией main() в параметре «nd», в переменную «d» нового узла.
Предыдущий узел нового узла будет инициализирован NULL, а его следующий узел будет «головой». Оператор «if» здесь проверяет, что значение заголовка «h» не равно NULL. Если значение «h» не равно NULL, это сделает предыдущий узел «головного» узла новым узлом. Кроме того, голова также будет новым узлом, то есть будет иметь значение нового узла.
А вот и функция «show()» для отображения созданного узла. Внутри него мы создали узел «ptr» и сделали его «головой». Цикл «пока» здесь для подтверждения того, что значение «ptr» не равно NULL. Пока условие выполняется, оператор cout будет отображать данные, добавленные пользователем, таким же, но противоположным образом. Теперь следующим из узлов «ptr» станет «ptr».
Вот наша функция main(), с которой начинается выполнение. Мы вызвали функцию «добавить» 4 раза, чтобы создать новый узел и добавить данные в переменную «d» нового узла. Оператор cout показывает нам, что мы будем вызывать функцию «show», чтобы отобразить все добавленные нами узлы.
Теперь пришло время скомпилировать этот код C++ в компиляторе Ubuntu g++ для языка C++. При запуске кода с «./a.out» мы отобразили данные 4 узлов в противоположном порядке, т. Е. мы добавили в порядке 4, 12, 2, 7, и он возвращается в порядке 7, 2, 12, 4, показывая последнюю подачу первой порядок.
Пример 02:
Рассмотрим еще один пример двусвязного списка. Создал структуру «Узел» с той же переменной «d», следующим узлом «n» и предыдущим узлом «p».
Теперь мы использовали функцию Frontpush() для вставки узла в начале с его данными, то есть головным узлом. Мы создали внутри него новый узел, то есть «newNode», используя синтаксис структуры «Node*». После этого мы ссылаемся на его данные «d», его следующий узел, который будет «головой», и предыдущий узел, который будет NULL. Оператор «if» использовался для проверки того, что значение заголовка не равно NULL. Если заголовок уже не «NULL», мы должны сделать предыдущий заголовок новым узлом, и заголовок будет указывать на новый узел.
Функция afterpush() предназначена для вставки нового узла после уже созданного узла. Оператор «if» проверит, равен ли предыдущий узел NULL или нет, и отобразит это с помощью «cout». Новый узел был сформирован, и данные будут вставлены в «d». «Следующий» из нового станет следующим из предыдущего, а следующий из предыдущего станет новым узлом. Предыдущее из нового само станет предыдущим. Если следующий из новых не равен NULL, мы сделаем следующий из новых, который также является следующим из новых, новым узлом.
Теперь мы будем использовать функцию «Endpush», чтобы вставить новый узел в конец связанного списка. Создан новый узел, и данные, переданные функцией main(), присваиваются «d», а следующий из новых равен NULL. Мы храним голову временно. «Если» проверит, пуст ли связанный список, и сделает новый узел «головным». «Пока» будет проходить по связанному списку, если связанный список уже не пуст. Поскольку «temp» — это наш последний узел, мы назначили следующий temp «new». Предыдущее или новое присваивается «temp».
Метод delete () использует разные операторы «если» для замены следующего и предыдущего узла del-node и головного узла. Наконец, функция «free» используется для освобождения памяти del-узла.
Функция show() этой программы снова используется для вывода двусвязного списка.
Функция main() начинает выполнение с инициализации головного узла значением NULL. Функция «Endpush» вызывается для вставки узла в конец путем передачи «head» и 5 в качестве данных. Frontpush() используется дважды, чтобы добавить узел в начало связанного списка. После повторного использования «endpush()» мы дважды использовали «Afterpush()». Функции show() и «Delete()» используются одна за другой, в то время как «delete» используется для удаления каждого последнего узла из связанного списка, и show() отображает это.
Компиляция и выполнение показывают связанный список от начала до конца, то есть после удаления каждого узла.
Вывод
В этой статье объясняются простые примеры кода для создания двусвязного списка на C++ при использовании системы Ubuntu 20.
04 Linux. Мы также рассмотрели способы вставки узла в начало и конец связанного списка и вставки после уже созданного узла, т. е. между ними. Функция удаления каждый раз удаляла каждый узел из связанного списка.
Двусвязный список Программа на C
Обзор
Двусвязный список — это вариант односвязного списка, в котором обход по списку возможен в обоих направлениях: вперед и назад. Каждый узел в списке хранит данные, указатель на следующий узел и указатель на предыдущий узел.
Область применения
В этой статье рассказывается о двусвязном списке в C, необходимости двусвязного списка, операциях над двусвязным списком и реализации двусвязного списка на языке программирования C.
Введение
Двусвязный список представляет собой сложную структуру данных и является расширенной версией структуры данных односвязного списка. Двусвязный список — это связанная структура данных, состоящая из записей, называемых узлами , которые последовательно связаны друг с другом с помощью указателей в виде цепочки.
Каждый узел в двусвязном списке хранит данные, указатель на следующий узел в последовательности и указатель на предыдущий узел в последовательности. Эти указатели называются next и previous соответственно. Этот указатель хранит адрес памяти следующего и предыдущего указателя в последовательности. Специальный указатель узла заголовок используется для обозначения начала двусвязного списка. Предыдущий указатель в головном узле и следующий указатель в последнем узле двусвязного списка указывают на контрольное значение или признак конца. В языке программирования C это сигнальное значение является нулевым указателем. Мы можем выполнять множество операций над двусвязным списком, таких как вставка нового узла в список в определенной позиции, удаление узла в указанной позиции из списка и отображение списка из голова узел до конца.
Синтаксис
Каждый узел представляет собой двусвязный список на C, в котором хранятся данные, следующий указатель и предыдущий указатель.
Мы можем реализовать программу двусвязного списка на C, используя следующий синтаксис узла. Для простоты предположим, что данные представляют собой целочисленное значение.
Для написания программы двусвязного списка на C нам необходимо определить следующие компоненты:
- Узел — Это базовая единица двусвязного списка. Узлы связаны друг с другом с помощью указателей для создания двусвязного списка. Каждый узел хранит элемент данных, следующий указатель и предыдущий указатель.
- Next Pointer — хранит адрес следующего узла в последовательности в двусвязном списке.
- Предыдущий указатель — хранит адрес предыдущего узла в последовательности в двусвязном списке.
- Данные — хранит значение данных узла.
- Заголовок — представляет собой начало двусвязного списка.
Двусвязный список содержит указатели на предыдущий узел и следующий узел в последовательности.
это самое большое преимущество двусвязного списка перед односвязным списком. Всякий раз, когда приложению требуется навигация в обоих направлениях, нам нужен двусвязный список.
Например, программу двусвязного списка на C можно использовать в веб-браузере для управления навигацией по ссылкам. Всякий раз, когда пользователь щелкает новую гиперссылку, ссылка вставляется в конец двусвязного списка. Теперь, если пользователь хочет переходить между ссылками туда-сюда, то эту возможность можно реализовать движением вперед-назад указателя головы в двусвязном списке.
Двусвязный список — это структура данных, которая содержит узлы в определенной последовательности. Он содержит головной указатель, указывающий на начало двусвязного списка. Узлы реализованы с использованием структуры на языке программирования C. Каждая структура хранит указатель на следующий узел в последовательности и указатель на предыдущий узел в последовательности. Кроме того, он также хранит данные в каждом узле.
В языке программирования C мы храним данные типа int для простоты объяснения. Однако любой тип данных может храниться в каждом узле. Контрольное значение в языке программирования C равно NULL. Он используется для указания на конец связанного списка.
Двусвязный список хранит дополнительный предыдущий указатель и, следовательно, потребляет больше памяти, чем односвязный список. Каждый узел содержит указатель на предыдущий узел и следующий узел в последовательности. Более того, мы должны поддерживать головной указатель, указывающий на начало двусвязного списка. Этот указатель используется для таких операций, как вставка, удаление, обход и т. д. Дополнительный указатель, поддерживаемый в каждом узле, делает такие операции, как вставка и удаление, более дорогими. Ниже представлено представление в памяти двусвязного списка. Контрольное значение, используемое в C, является нулевым указателем NULL. Указывает на конец связанного списка.
Рассмотрим двусвязный список, показанный на изображении выше.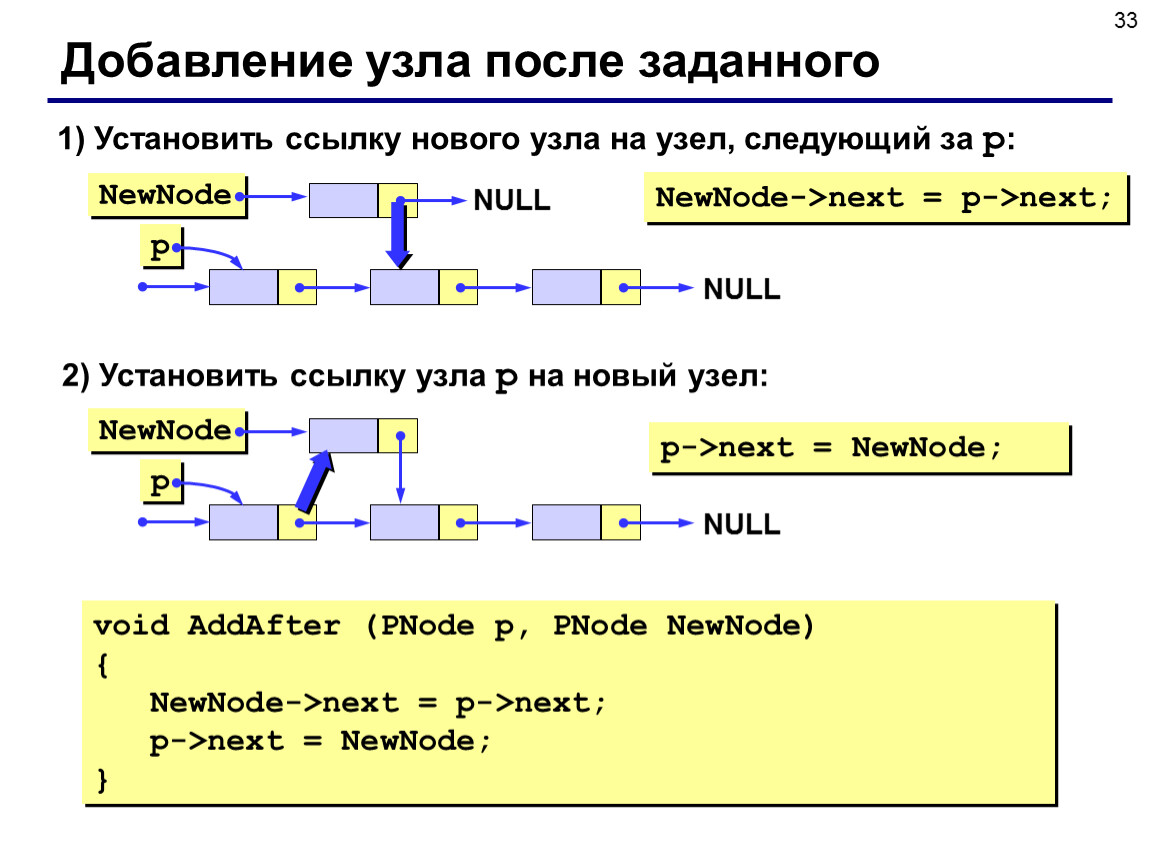
Каждый узел в двусвязном списке представлен с использованием адреса памяти, и адрес указывает на структуру Node, в которой хранятся данные, следующий указатель и предыдущий указатель.
Над двусвязным списком можно выполнять множество операций. Метод и выполнение каждой операции мы обсудим ниже, далее в статье.
Обход
Обход означает посещение каждого узла связанного списка, начиная с указателя на начало и заканчивая концом списка. Обычно это делается для выполнения определенной операции, такой как отображение данных каждого узла или поиск узла и т. д.
Вставка
Мы можем вставить новый узел в двусвязный список в любую позицию. Существует четыре основных сценария вставки узла в двусвязный список:
- Вставка в начале : В этом случае новый узел вставляется перед двусвязным списком. Указатель Head обновляется, чтобы указывать на только что добавленный узел.
- Вставка в конец : В этом случае новый узел вставляется в конец двусвязного списка.
Никаких изменений для указателя головы не требуется. - Вставка после данного узла : В этом случае, имея указатель на узел в двусвязном списке, нам нужно вставить новый узел после узла, указатель на который нам дан.
- Вставка перед заданным узлом : В этом случае при наличии указателя на узел цель состоит в том, чтобы вставить новый узел перед узлом, на который указан указатель.
Никаких изменений для указателя головы не требуется.Удаление
Удаление означает удаление узла из двусвязного списка и сохранение его структуры после операции. Возможны три случая удаления узла из двусвязного списка:
- Удаление в начале : Узел в начале двусвязного списка удаляется. Указатель головы обновляется, чтобы указывать на следующий узел удаленного узла. Удаляемый узел удаляется из памяти.
- Удаление в конце : Удаляется последний узел двусвязного списка.
- Удаление узла в заданной позиции : В этом случае нам нужно удалить узел в указанной позиции из двусвязного списка.
Поиск
Поиск узла включает сравнение данных каждого узла в двусвязном списке с элементом, заданным для поиска. Как правило, в качестве вывода возвращается расположение узла в связанном списке или адрес узла. Этот адрес можно использовать для доступа к тому же узлу, если это необходимо. Если такого узла нет, то в качестве вывода возвращается NULL.
Алгоритм
Новый узел добавляется перед двусвязным списком. Этот новый узел становится новым указателем головы.
- Шаг 1: Создайте новый узел с элементом данных. Назовем этот узел как new_nodenew\_nodenew_node.
- Шаг 2 : Назначить следующий указатель new_nodenew\_nodenew_node на голову.
- Шаг 3: Если указатель заголовка не равен NULL, то присвойте указатель prev заголовка узлу new_nodenew\_nodenew_node.
- Шаг 4: Наконец, обновите указатель заголовка.
Пример
Рассмотрим связанный список с 3 узлами 1⟷2⟷31 \longleftrightarrow 2 \longleftrightarrow 31⟷2⟷3.
Теперь мы хотим добавить узел с данными 0 впереди.
Во-первых, мы создаем новый узел с данными 0 и назначаем следующий указатель нового узла на головной указатель.
Теперь мы назначаем указатель prev головы новому узлу.
Наконец, мы обновляем указатель головы.
Примечание: Мы передаем указатель на головной указатель в функцию insertAtFront. Если мы этого не сделаем, то указатель заголовка будет обновляться локально только внутри функции.
Реализация
Анализ сложности
Временная сложность —
Чтобы добавить новый узел впереди, мы обновляем только постоянное количество указателей, поэтому временная сложность составляет O(1)O(1)O(1).
Временная сложность: O(1)O(1)O(1)
Пространственная сложность —
Чтобы добавить новый узел впереди, мы только создаем указатель на новый узел. Дополнительная память не требуется, поэтому пространственная сложность составляет O(1)O(1)O(1).
Космическая сложность: O(1)O(1)O(1)
Алгоритм
Чтобы добавить новый узел в конец двусвязного списка, нам сначала нужно выполнить итерацию до конца связанного списка, а затем добавить новый узел.
- Шаг 1: Создайте временный указатель ptrptrptr. Инициализируйте его указателем головы.
- Шаг 2: Пока ptr→nextptr \rightarrow nextptr→next не равен NULL, перейти к следующему узлу ptr→nextptr \rightarrow nextptr→next.
- Шаг 3: Теперь создайте новый узел с данными new_nodenew\_nodenew_node.
- Шаг 4: Назначьте ptr→nextptr \rightarrow nextptr→next для new_nodenew\_nodenew_node и назначьте new_node→prevnew\_node \rightarrow prevnew_node→prev для ptrptrptr.
Пример
Рассмотрим связанный список с 3 узлами 1⟷2⟷31 \longleftrightarrow 2 \longleftrightarrow 31⟷2⟷3. Теперь мы хотим добавить узел с данными 4 в конце.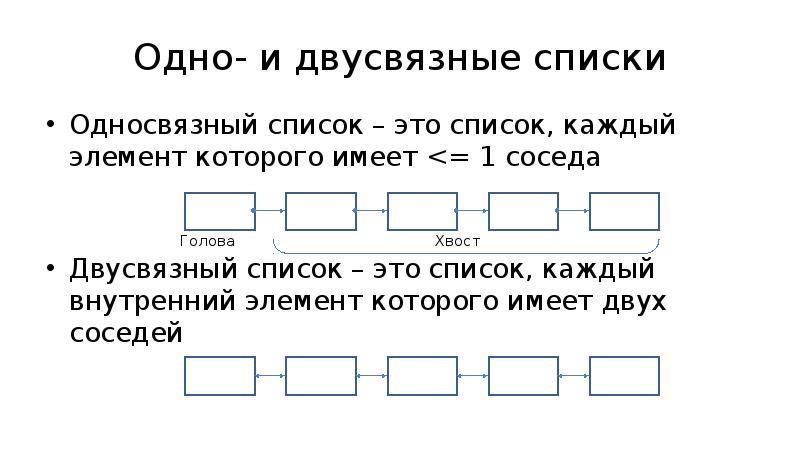
Сначала мы переходим к последнему узлу, используя указатель currcurrcurr, и присваиваем следующий указатель currcurrcurr новому узлу.
Теперь мы обновляем указатель prev нового узла.
Реализация
Анализ сложности
Временная сложность —
Когда мы добавляем новый узел в конец двусвязного списка, мы итерируем от указателя головы до последнего узла, поэтому временная сложность равна O(N )O(N)O(N), где NNN — количество узлов, присутствующих в списке.
Временная сложность: O(N)O(N)O(N)
Пространственная сложность —
В реализации мы используем постоянный объем пространства для указателей и создания объекта нового узла, поэтому пространственная сложность O(1)O(1)O(1).
Пространство Сложность: O(1)O(1)O(1)
Алгоритм
В этом случае нам дан узел узелузелузел, после которого мы должны вставить новый узел.
- Шаг 1: Создайте новый узел new_nodenew\_nodenew_node с указанными данными.
- Шаг 2: Назначить новый_узел→следующий новый\_узел \стрелка вправо следующийновый_узел→рядом с узлом→следующий узел \стрелка вправо следующийузел→следующий.
- Шаг 3: Назначить узел→следующий узел \стрелка вправо следующий узел→рядом с новый_узелновый_узелновый_узел.
- Шаг 4: Назначьте новый_узел→предыдущийновый\_узел \стрелка вправо предыдущий_узел→предыдущий узелузелузел.
- Шаг 5: Если new_node→nextnew\_node \rightarrow nextnew_node→next не равно NULL, тогда назначьте new_node→next→prevnew\_node \rightarrow next \rightarrow prevnew_node→next→prev новому_узлуnew\_nodenew_node.
Пример
Рассмотрим связанный список с 3 узлами 1⟷2⟷41 \longleftrightarrow 2 \longleftrightarrow 41⟷2⟷4. Теперь мы хотим добавить узел с данными 3 после второго узла.
Нам также дан указатель на второй узел.
Сначала мы обновим следующий указатель нового узла до следующего указателя данного узла. Затем мы присваиваем следующий указатель данного узла новому узлу.
Наконец, мы обновляем указатели prev нового узла и следующего узла.
Реализация
Анализ сложности
Временная сложность —
В реализации мы делаем постоянное количество изменений указателя, поэтому сложность O(1)O(1)O(1).
Время Сложность: O(1)O(1)O(1)
Сложность пространства —
В реализации нам требуется постоянное количество указателей и объектов нового узла, поэтому сложность пространства равна
О(1)О(1)О(1).
Пространство Сложность: O(1)O(1)O(1)
Алгоритм
В этом случае нам дан узел nodenodenode, перед которым мы должны вставить новый узел.
- Шаг 1: Создайте новый узел new_nodenew\_nodenew_node с указанными данными.
- Шаг 2: Назначить новый_узел→следующий новый\_узел \стрелка вправо следующий новый_узел→рядом с узломузел.
- Шаг 3: Если node→prevnode \rightarrow prevnode→prev не равно NULL, тогда назначьте node→prev→nextnode \rightarrow prev \rightarrow nextnode→prev→next к new_nodenew\_nodenew_node и new_node→prevnew\_node \rightarrow prevnew_node→ предыдущий к узлу→предыдущий узел \стрелка вправо предыдущий узел→пред.
- Шаг 4: Если node→prevnode \rightarrow prevnode→prev равно NULL, то обновите указатель заголовка, когда мы вставляем узел в начале списка.
- Шаг 5: Обновить node→prevnode \rightarrow prevnode→prev до new_nodenew\_nodenew_node.
Реализация
Анализ сложности
Временная сложность —
В реализации мы делаем постоянное количество изменений указателя, поэтому сложность составляет O(1)O(1)O(1).
Временная сложность: O(1)O(1)O(1)
Пространственная сложность —
В реализации нам требуется постоянное количество указателей и объектов нового узла, поэтому пространственная сложность равна О(1)О(1)О(1).
Пространственная сложность: O(1)O(1)O(1)
Алгоритм
- Шаг 1: Инициализировать указатель currcurrcurr на указатель headhead.
- Шаг 2: Если указатель заголовка не равен NULL, то увеличивается указатель заголовка.
- Шаг 3: Сделайте указатель currcurrcurr равным NULL и освободите память.
Пример
Рассмотрим связанный список с 3 узлами 1⟷2⟷31 \longleftrightarrow 2 \longleftrightarrow 31⟷2⟷3. Теперь мы хотим удалить узел впереди.
В этом случае мы просто обновляем указатель заголовка на следующий указатель заголовка и удаляем первый узел в последовательности.
Окончательная последовательность: 2⟷32 \longleftrightarrow 32⟷3
Реализация
Анализ сложности
Сложность времени —
позволяя узлу впереди, следовательно, временная сложность O(1)O(1)O(1).
Временная сложность: O(1)O(1)O(1)
Пространственная сложность —
В реализации мы используем только постоянный объем памяти для указателя currcurrcurr, поэтому пространственная сложность равна O (1)О(1)О(1).
Пространственная сложность: O(1)O(1)O(1)
Алгоритм
- Шаг 1: Инициализировать указатель currcurrcurr на указатель headhead.
- Шаг 2: Пока значение curr→nextcurr \rightarrow nextcurr→next не равно NULL, увеличьте указатель currcurrcurr.
- Шаг 3: Обновить curr→prev→nextcurr \rightarrow prev \rightarrow nextcurr→prev→next как NULL и curr→prevcurr \rightarrow prevcurr→prev как NULL.
- Шаг 4: Сделать указатель currcurrcurr равным NULL и освободить память.
Пример
Рассмотрим связанный список с 3 узлами 1⟷2⟷31 \longleftrightarrow 2 \longleftrightarrow 31⟷2⟷3.
Теперь мы хотим удалить узел в конце.
Сначала мы переходим к последнему узлу, используя указатель currcurrcurr. Теперь мы присваиваем curr→nextcurr \rightarrow nextcurr→next как NULL.
Наконец, мы удаляем текущий узел.
Реализация
Анализ сложности
Временная сложность —
В реализации мы итерируем до конца двусвязного списка, следовательно, временная сложность составляет O(N)O(N)O(N).
Временная сложность: O(N)O(N)O(N)
Пространственная сложность —
В реализации мы используем постоянное количество указателей, поэтому пространственная сложность O(1)O (1)О(1).
Пространство Сложность: O(1)O(1)O(1)
Алгоритм
В этом случае мы должны удалить узел с указанным индексом positionpositionposition.
- Шаг 1: Если positionpositionposition равно 1, то мы удаляем передний узел.
- Шаг 2: Итерировать указатель currcurrcurr до тех пор, пока position>1position > 1position>1.
- Шаг 3: Теперь нам нужно удалить узел currcurrcurr и соединить curr→prevcurr \rightarrow prevcurr→prev и curr→nextcurr \rightarrow nextcurr→next.
- Шаг 4: Назначить curr→prev→nextcurr \rightarrow prev \rightarrow nextcurr→prev→next to curr→nextcurr \rightarrow nextcurr→next и curr→next→prevcurr \rightarrow next \rightarrow prevcurr→next→prev to curr→ предыдущая \правая стрелка предыдущая→пред.
- Шаг 5: Сделайте указатель currcurrcurr равным NULL и освободите память.
Пример
Рассмотрим связанный список с 3 узлами 1⟷2⟷31 \longleftrightarrow 2 \longleftrightarrow 31⟷2⟷3. Теперь мы хотим удалить второй узел в списке.
Сначала идем ко второму узлу по указателю currcurrcurr.
Далее мы соединяем предыдущий узел currcurrcurr и следующий узел узла currcurrcurr.
Наконец, мы удаляем текущий узел.
Реализация
Анализ сложности
Временная сложность —
В реализации мы итерируем до позиции>1позиция>1позиция>1. В худшем случае мы можем в конечном итоге перебрать весь список, следовательно, временная сложность будет O(N)O(N)O(N), где N — количество узлов в связанном списке.
Временная сложность: O(N)O(N)O(N)
Пространственная сложность —
В реализации мы используем только постоянный объем памяти для указателя currcurrcurr, поэтому пространственная сложность равна О(1)О(1)О(1).
Пространство Сложность: O(1)O(1)O(1)
Результат:
Преимущества
- Двусвязный список можно просматривать как в прямом, так и в обратном направлении.
- В случае вставки, если задан узел, после которого должен быть вставлен новый узел, то время, затрачиваемое в случае двусвязного списка, равно O(1).
