Рекурсивной: Что такое рекурсия, рекурсивный и итеративный процесс в программировании

Что такое рекурсия, рекурсивный и итеративный процесс в программировании

В этой статье разбираемся, какой бывает рекурсия, как с ее помощью можно решать задачи и что такое рекурсивные функции.

• Рекурсия vs рекурсивный или итеративный процесс: в чем разница
• Методы решения задач с помощью рекурсии
• В чем отличие рекурсивного процесса от итеративного
• Что такое рекурсивные функции и в чем особенность их применения
• Что такое хвостовая рекурсия

Вы читаете обновленную и улучшенную версию нашей старой статьи

Рекурсия vs рекурсивный или итеративный процесс: в чем разница

Рекурсия — это функция, которая вызывает саму себя, но с другими значениями параметров.

На самом деле понятия рекурсии и процесса никак не связаны. Рекурсия — просто абстрактная концепция, которую можно наблюдать в природе, в математике и в других областях. Такая же абстрактная, как, например, музыкальная гармония.

Теперь давайте поговорим о компьютерах. Для выполнения задач им нужны инструкции. Когда компьютер выполняет набор инструкций — это процесс. Ваш работающий сейчас браузер — тоже процесс. Простой цикл, выводящий на экран десять раз число «42» — также процесс.

Некоторые задачи можно решать рекурсивно, то есть использовать концепцию, когда что-то является частью самого себя, в инструкциях. В частности, функция может быть частью самой себя, то есть вызывать саму себя.

Читайте также: Что такое callback-функция в JavaScript?

Методы решения задач с помощью рекурсии

Есть два метода решения задач с использованием рекурсии: рекурсивный процесс и итеративный процесс. Рекурсия в них не отличается: в каждом из подходов функция вызывает саму себя, рекурсивно. Отличаются способы использования идеи рекурсии.

Давайте продолжим аналогию с музыкальной гармонией и подумаем про фортепиано. При написании музыки используем эту концепцию — «гармонию звуков». Можно придумать разные способы: рассчитывать частоты звуков — ноты — математическими формулами или рассчитывать правильные расстояния между клавишами.

В детстве я научился находить правильные расстояния между клавишами на фортепиано, и получал гармоничные комбинации звуков, но понятия не имел, что это за ноты. А профессиональный музыкант знает теорию и подбирает гармонию другими методами. В любом случае, гармония есть гармония, эта концепция не меняется, меняются лишь способы ее использования.

В чем отличие рекурсивного процесса от итеративного

Рекурсивный процесс на каждом шаге рекурсии говорит «я это запомню и потом посчитаю». «Потом» наступает в самом конце.

• Если рекурсивный процесс считает факториал 6, то ему нужно запомнить 5 чисел, чтобы посчитать их в самом конце, когда уже никуда не деться и рекурсивно двигаться вниз больше нельзя
• Когда мы находимся в очередном вызове функции, то где-то снаружи этого вызова в памяти хранятся эти запомненные числа

На этой картинке видно, как растет использование памяти: процессу нужно запоминать все больше и больше чисел

Рекурсивный процесс — это процесс с отложенным вычислением.

Итеративный процесс постоянно говорит «я сейчас посчитаю все что можно и продолжу» на каждом шаге рекурсии. Ему не нужно ничего запоминать вне вызова, он всегда все считает в первый возможный момент. Каждый шаг рекурсии может существовать в изоляции от прошлых, потому что вся информация передается последовательно.

• Когда итеративный процесс считает факториал 6, то ему не нужно запоминать числа. Нужно лишь считать и передавать результат дальше, в новый вызов
• Когда мы находимся в очередном вызове функции, снаружи этого вызова в памяти ничего не нужно запоминать

А на этой картинке видно, что использование памяти не растет.

Подытожим в шуточной форме. Рекурсивный процесс — это чувак, который все дела откладывает на вечер пятницы. В течение недели у него мало работы, а в пятницу завал. Но ему так нравится.

Итеративный процесс — это чувак, который все делает при первой возможности. У него работа равномерно распределена по неделе, а пятница — просто обычный день, но последний.

Что такое рекурсивные функции и в чем особенность их применения

Рекурсивные функции — это те функции, которые используют итеративный процесс. Для каждого рекурсивного вызова в стек вызовов записывается вся информация, связанная с этим вызовом, вроде параметров функции и ее локальных переменных, адреса возврата в точку вызова.

Для рекурсивной функции выделяется дополнительная область памяти — лексический контекст функции, область видимости —, которая обслуживает рекурсивный вызов. Так как это стек вызовов, то контексты предыдущих рекурсивных вызовов также продолжают занимать память.

Достижение большой глубины рекурсии, или же, недостижение терминального условия выхода из рекурсии, приводит к переполнению стека, так как он ограничен в размерах, и аварийному завершению всей программы.

Читайте также: Как проверить качество кода: функциональное и нефункциональное тестирование

В контексте каждого рекурсивного вызова такой функции хранится вся необходимая информация для его успешного выполнения.

Он самодостаточен и никак не зависит от предыдущих контекстов. Помните, что этот чувак ничего не откладывает на потом, на вечер пятницы?

В наших практиках на Хекслете мы реализовывали такое поведение благодаря использованию аккумулятора acc, который передается в качестве аргумента из одного вызова в другой и накапливает в себе результат вычисления необходимого значения.

Получается, что, грубо говоря, на каком бы по уровню вложенности рекурсивном вызове мы не находились, все предыдущие уже не имеют значения и являются «бесполезной обузой», нагружающей память. Это распространяется в том числе и на самый последний рекурсивный вызов, где срабатывает терминальное условие. Он готов вернуть готовое вычисленное значение из функции сразу, ему не нужны для этого предыдущие контексты в стеке.

Что такое хвостовая рекурсия

Как использовать преимущества итеративного процесса и одновременно избавиться от недостатка рекурсивных функций, то есть от неумолимого роста использования памяти? Можно избавить процесс от заполнения стека «ненужными» контекстами предыдущих вызовов и обеспечить прямой возврат из функции при достижении терминального условия.

Для этого служит так называемая оптимизация хвостовой рекурсии (Tail call optimization). Итеративный процесс, который мы рассмотрели, как раз можно отнести к хвостовой рекурсии. Благодаря оптимизации состояния стека, она придает итеративному процессу вид «плоской» итерации. Так исключается его переполнение из-за большой глубины рекурсии.

Хвостовая рекурсия и ее оптимизация широко используется при написании программ на функциональных языках программирования.

Никогда не останавливайтесь: В программировании говорят, что нужно постоянно учиться даже для того, чтобы просто находиться на месте. Развивайтесь с нами — на Хекслете есть сотни курсов по разработке на разных языках и технологиях

Рекурсивное название небольшой статьи о рекурсии / Хабр

Практика преподавания и изучения программирования преимущественно на базе императивных языков (включая объектно-ориентированные императивные языки) приводит к тому, что такой фундаментальный алгоритмический механизм, как рекурсия, остаётся плохо понятным многими программистами и порождает заблуждения, транслируемые в популярной культуре.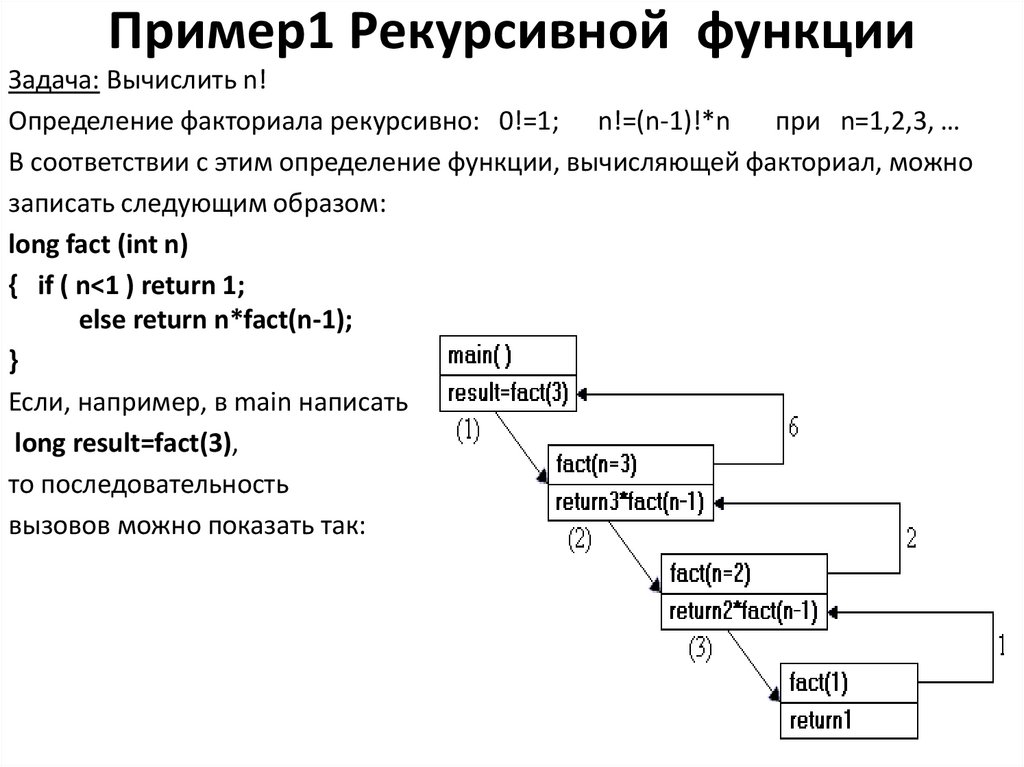 Попытаемся внести в вопрос немного ясности и изложить некоторые свои мысли по этому поводу.

Что такое рекурсия?

Что такое рекурсия в бытовом понимании? Это решение задачи через сведение её к самой себе в более простых условиях.

Допустим, мы туристы, и перед нами стоит задача попытаться найти в доставшемся нам рюкзаке с едой банку тушёнки. Проверим, пустой ли рюкзак. Если пустой, задача решена, тушёнки нет. Иначе вынимаем из рюкзака первый попавшийся предмет. Если это банка тушёнки, задача решена, тушёнка найдена. Иначе повторяем весь наш алгоритм для имеющегося теперь у нас полегчавшего рюкзака с оставшимся содержимым, и результат решения задачи при этом откладывается на следующий шаг.

Этот пример рекурсии поймёт и маленький ребёнок, а программисты заметят, что это по существу задача поиска элемента в односвязном списке.

Рекурсия сама по себе представляет просто один из возможных способов описания повторяющихся действий. Цикл всегда может быть описан в виде рекурсии. Рекурсия может быть описана в виде конечного числа циклов, но это иногда может потребовать дополнительной структуры данных, хранящей последовательность рекурсивных вызовов.

Определения

Формально введём некоторые определения. Вопрос далеко не нов, поэтому возьмём определения из достаточно академичных источников, таких как [Friedman1975] и [Хювёнен1990]. В математике рекурсия рассматривается в теории рекурсивных функций, являющейся одним из формализмов теории алгоритмов, поэтому определения многих терминов имеют базу в виде очень чётко заданных математических понятий.

Рекурсия – использование самого себя. Также для простоты словом рекурсия называют рекурсивный вызов.

Рекурсивный вызов – прямой или опосредованный вызов функцией самой себя.

Простая рекурсия – рекурсивный вызов, встречающийся не более одного раза в каждой ветви кода функции. Чандра в [Chandra1972] показал, что простая рекурсия всегда может быть сведена компилятором к итеративному циклу, в дальнейшем этот результат был улучшен, что описано ниже.

Терминальная ветвь – ветвь кода рекурсивной функции, завершающая его без дальнейших рекурсивных вызовов.

Бесконечная рекурсия – последовательность рекурсивных вызовов, никогда не выходящая на терминальную ветвь.

Параллельная рекурсия – рекурсия, встречающаяся несколько раз в одной ветви кода функции.

Взаимная рекурсия – вызов двумя или более функциями друг друга.

Рекурсия по значению – рекурсивный вызов, определяющий результат функции.

Рекурсия по аргументам – рекурсивный вызов, участвующий в вычислении аргументов функции.

Рекурсия высокого порядка – случай, когда в определении функции рекурсивный вызов является аргументом вызова этой же самой функции. Обратите внимание, что рекурсия высокого порядка не имеет никакого отношения к функциям высокого порядка. При помощи рекурсии порядка N могут быть описаны вычисления в N+1 вложенных циклах, однако обратное не всегда верно.

Порядок рекурсии – уровень, на котором находится вызов в рекурсии высокого порядка. Обычные используемые на практике случаи рекурсии содержат рекурсивные вызовы нулевого порядка.

Стилизованная рекурсивная функция – некий специальный вид рекурсивной функции нулевого порядка, более общий, чем простая рекурсия, и удовлетворяющий семи довольно замысловато сформулированным требованиям, описанным в статье [Friedman1975] (желающие могут прочитать их по ссылке ниже, страницы 4-5 статьи). Авторы показывают, что стилизованная рекурсивная функция всегда может быть сведена компилятором к итеративному циклу.

Далее приведены строго не определённые понятия.

Хвостовая рекурсия – простая рекурсия, рекурсивный вызов в которой находится в конце кода функции. Многие источники в интернете называют хвостовой рекурсией только такие вызовы, которые непосредственно предшествуют возврату из функции (назовём это хвостовой рекурсией I), в то время как другие интерпретируют хвостовую рекурсию более широко, понимая её как однократный рекурсивный вызов где-либо в последней линейной ветке кода (назовём это хвостовой рекурсией II), или как простую рекурсию. По любому определению, хвостовая рекурсия является частным случаем простой рекурсии.

Оптимизация хвостовой рекурсии, или оптимизация хвостового вызова – преобразование транслятором хвостового вызова функции (необязательно рекурсивного) в линейный (циклический) код. Здесь опять-таки широк диапазон интерпретаций, начиная от простой замены пары команд call/ret на jmp (которая в том числе устраняет хвостовую рекурсию I) и заканчивая более сложными оптимизациями хвостовой рекурсии II и простой рекурсии.

Применение определений

Наш бытовой пример с тушёнкой в рюкзаке представлял собой простую рекурсию с двумя терминальными ветвями и хвостовой рекурсией. Заметим, что рекурсивный код всегда начинается с терминальных ветвей, иначе исполнение программы погрузится в бесконечную рекурсию и никогда до них не дойдёт.

Напишем псевдокод на языке Лисп для наших туристов, чтобы они точно понимали, что делать, проснувшись утром голодными и не помнящими, что у них в рюкзаках:

(defun ищемТушёнку (рюкзак)
  (cond 
    ((null рюкзак) nil)
    ((тушёнка? (car рюкзак)) (car рюкзак))
    (t (ищемТушёнку (cdr рюкзак)))))

Здесь мы определили функцию ищемТушёнку от параметра-списка рюкзак. Её тело состоит из условного оператора cond

, имеющего две терминальные и одну рекурсивную ветку. Рюкзак проверяется на пустоту, затем первый элемент рюкзака (car рюкзак) проверяется специальным предикатом, не тушёнка ли это, затем по третьей ветви, которая предваряется тождественно истинным к этому моменту условием t, уходим на рекурсивный вызов с остатком списка (cdr рюкзак).

Если есть желание довести дело до компьютерного исполняемого кода, определим также наш предикат:

(defun тушёнка? (x) (eq x 'тушёнка))

Прямо в таком виде это можно ввести в GNU Common Lisp или SBCL и искать тушёнку.

(ищемТушёнку '(носки хлеб учебникЛиспа штопор
               тушёнка смартфон ноутбук
               шишка шишка кирпич носовойПлаток
               нож кредитка конфета бумажка
               зубочистка непонятныйМусор))
ТУШЁНКА

Код здесь написан в чисто функциональном стиле, не содержит переменных и присваиваний, что эффективно с точки зрения распределения памяти в статической секции и в куче.

Эффективность рекурсии

Многие программисты считают, что рекурсия неэффективна, так как поедает место на стеке, и ей не место в продуктовом коде. Так ли это?

Безусловно, всякий инструмент нужно применять по назначению, и для перебора чисел от 1 до N, наверное, не надо использовать рекурсивный вызов. Тем не менее, так ли ужаcна рекурсия по сравнению с итерированным циклом?

Современные 64-разрядные системы программирования обычно без труда позволяют распределять до гигабайтов адресного пространства в стековой памяти. Этого хватит буквально на миллиарды вложенных рекурсивных вызовов. Вряд ли когда-нибудь вам понадобится рекурсия такой глубины, и даже если да, то основной проблемой, скорее всего, станет процессорное время, а не стековая память. Цикл с содержательным смыслом на миллиард итераций – это дело серьёзное. Тем не менее, проблема со стеком всё-таки есть, и о ней необходимо помнить.

Однако, как следует из приводившихся выше определений, всякая стилизованная рекурсия и тем более всякая простая рекурсия приводима к виду итеративного цикла.

Многие трансляторы об этом знают, в большем или меньшем объёме.

Часто использующимся в компиляторах приёмом оптимизации является оптимизация хвостовой рекурсии, или tail call (tail recursion) optimization. Многим программистам известно, что обычно трансляторы преобразуют хвостовую рекурсию I в эквивалентный цикл, поэтому такая задача, как наш поиск в рюкзаке, после оптимизации не будет занимать место на стеке по мере продвижения в глубины рюкзака.

Однако, интернет полон мнений, что способность компилятора к оптимизации хвостовой рекурсии исчерпывается заменой пары команд call/ret на команду jmp. Поэтому, якобы, даже обычная функция факториала в виде

(defun fact (n)
  (cond
    ((zerop n) 1)
    (t (* n (fact (- n 1))))))

непригодна к оптимизации и вызовет разрушительный рост стека, так как после рекурсивного вызова остаётся выполнить ещё умножение, и код функции, таким образом, не представляет собой хвостовую рекурсию I. Дальше разделяющие такое мнение люди предлагают «оптимизировать» этот факториал, передавая умножаемые значения вторым параметром.

В действительности, например, у [Penman2018] разобран пример компиляции соответствующего кода в C/C++ и показано, что хвостовая рекурсия II оптимизируется и заменяется на цикл современным компилятором. Попытки выполнить такую оптимизацию вручную ни к чему не приводят на уровне машинного кода и только затрудняют понимание исходного текста.

В общем-то, уже на уровне здравого смысла понятно, что вычисления, записанные в коде после вызова хвостовой рекурсии II, можно переместить из эпилога получаемого цикла в пролог его следующей итерации, чем свести задачу к хвостовой рекурсии I.

На практике оказывается, что компиляторы популярных для вычислений языков (Си/Си++, Фортран) как правило, обеспечивают глубокую оптимизацию хвостовой рекурсии при включённой оптимизации. Трансляторы Лиспа оптимизируют хвостовую рекурсию в разной степени. Трансляторы Джавы и Питона не оптимизирует хвостовую рекурсию по принципиальным соображениям, так как разработчики считают важным сохранять исходную трассировку вызовов.

Оптимизация некоторых рекурсивных вычислительных процессов также может может быть достигнута путём применения механизма мемоизации.

Наконец, вновь надо вернуться к обстоятельству, что уже значение (fact 1000) занимает целый экран цифрами получившегося числа, а в стеке набирается всего 1000 элементов.

Кошмары высокого порядка

Рассмотрим теперь действительно не оптимизируемую автоматически рекурсивную функцию, например, крайне вычислительно ёмкую функцию Аккермана с рекурсией первого порядка, быстро уходящей на огромную глубину. Цитируется по [Хювяйнен1990]:

(defun аккерман (m n)
  (cond
    ((= m 0) (+ n 1))
    ((= n 0) (аккерман (- m 1) 1))
    (t (аккерман (- m 1) (аккерман m (- n 1))))))

Значение (аккерман 4 1) считается на моём компьютере в SBCL за 16 секунд с занятым стеком менее 4 мегабайт, то есть стек расходуется со скоростью 256 килобайт в секунду. Таким образом, 4-гигабайтного стека хватило бы на 4.5 часа вычислений рекурсивной функции, ничего по существу не делающей, кроме углубления своей рекурсии. (Для завершённости заметим, что значение (аккерман 4 2) вычислить брутфорсом через её рекурсивное определение пока не в человеческих силах, хотя имеется более быстрый альтернативный алгоритм [Grossman1988]; и полагаем совершенно невероятным, чтобы кому-либо в практических целях понадобился вычислительный процесс, описываемый рекурсией второго и более порядка).

Вывод

Так как это статья о рекурсии, то вывод заключается в том, что выводы представлены в самой этой статье о рекурсии.

Литература

[Хювёнен1990] Э. Хювёнен, Й. Сеппянен. Мир Лиспа. М.: Мир, 1990.

[Chandra1972] A. Chandra. Efficient compilation of linear recursive programs. Stanford AI project, STAN‑CS-72–282, 1972.

[Friedman1975] D. Friedman, D. Wise. Unwinding stylized recursions into iterations // Indiana Univ., 1975.

[Grossman1988] J. Grossman, R. Zeitman. An inherently iterative computation of Ackermann’s function // Theoretical Computer Science Vol. 57 Issues 2-3, May 1988, pp. 327-330

[Penman2018] T. Penman. Tail Call Optimisation and C / C++

Рекурсивное определение и значение — Merriam-Webster

ре · курсивный ri-ˈkər-siv 

1

: рекурсии, относящейся к ней или включающей ее

рекурсивная функция в компьютерной программе

2

: относящаяся к процедуре, которая может повторяться бесконечно, или составляющая ее

рекурсивное правило в грамматике

рекурсивно наречие

рекурсивность существительное

Примеры предложений

Недавние примеры в Интернете Любовь, общение, интеллектуальные дебаты и эстетическое влечение — вот те течения, которые формируют его рекурсивное движение . — Саидия Хартман, The New Yorker , 3 марта 2023 г. Ад оказывается в ловушке рекурсивных циклов историй Mail. — Эд Йонг, Discover Magazine , 25 декабря 2010 г. Такие триповые, рекурсивных игр были основным продуктом trompe l’oeil. — Сьюзен Таллман, 9 лет.0027 The New York Review of Books , 29 декабря 2022 г. Рекурсивный сюжет о прелюбодеянии кажется шуткой об ожиданиях, возлагаемых на сложный, перегруженный теорией системный роман, который критики так часто воспринимают как предсказательный, опережающий свое время или богоподобный в своей памяти о вещах прошлого. — Ханна Голд, The New Yorker , 16 ноября 2022 г. Другие рекурсивных фраз включают музыку, связанную с Вирджинией, которую Кларисса подслушивает из церковного хора. — Джошуа Бароне, 9 лет.0027 New York Times , 21 ноября 2022 г. Крайне правый пузырь Твиттера во всей его рекурсивной ярости частично виноват. — ПРОВОДНАЯ , 17 ноября 2022 г. Во время обучения вороны получали гранулы птичьего корма или мучных червей за успешное формирование рекурсивных последовательностей, согласно Wall Street Journal. — Уилл Салливан, Smithsonian Magazine , 14 ноября 2022 г. Одно из животных сгенерировало рекурсивных последовательностей примерно в половине испытаний. — Дайана Квон, Scientific American , 2 ноября 2022 г. Узнать больше

Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «рекурсивный». Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.

История слов

Этимология

ранее, «повторяющееся неоднократно», от латинского recursus, причастие прошедшего времени от recurrere «бежать назад, бежать в обратном направлении, вернуться» + -ive; в заданных смыслах как перевод немецкого rekurrent или rekursiv — больше в recur

Первое известное использование

1934, в значении, определенном в смысле 1

Путешественник во времени

Первое известное использование рекурсивного было в 1934 году

Другие слова того же года рекурсия

рекурсивный

рекурсивное определение

Посмотреть другие записи поблизости

Процитировать эту запись «Рекурсивный».

Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/recursive. По состоянию на 9 марта 2023 г. Последнее обновление: 6 марта 2023 г. — Обновлены примеры предложений

Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы!

Merriam-Webster без сокращений

заискивать

См. Определения и примеры »

Получайте ежедневно по электронной почте Слово дня!

---

Что было первым?

• горячий прием или холодный прием ?

• холодный прием горячий дубль

Вы знаете, как это выглядит. .. но как это называется?

ПРОЙДИТЕ ТЕСТ

Сможете ли вы составить 12 слов из 7 букв?

ИГРАТЬ

Рекурсивное определение и значение | Словарь.com

• Основные определения
• Викторина
• Связанное содержимое
• Подробнее о рекурсии
• Примеры

Показывает уровень оценки в зависимости от сложности слова.

[ ri-kur-siv ]

/ rɪˈkɜr sɪv /

Сохранить это слово!

См. синонимы слова «рекурсивный» на сайте Thesaurus.com

Показывает уровень оценки в зависимости от сложности слова.

---

прилагательное

относящееся к правилу или процедуре, которые можно применять повторно, или использующие их.

Математика, Информатика. относящийся к математическому процессу рекурсии или использующий его: рекурсивная функция; рекурсивная процедура.

ВИКТОРИНА

ВСЕ ЗА(U)R ЭТОГО БРИТАНСКОГО ПРОТИВ. АМЕРИКАНСКИЙ АНГЛИЙСКИЙ ВИКТОРИНА

Между тем, как люди говорят по-английски в США и Великобритании, огромная разница. Способны ли ваши языковые навыки определить разницу? Давай выясним!

Вопрос 1 из 7

Правда или ложь? Британский английский и американский английский различаются только сленговыми словами.

Происхождение рекурсивного

Впервые записано в 1935–1940 гг.; recurs(ion) + -ive

ДРУГИЕ СЛОВА ОТ recursive

recursive·ly, adverbre·cur·siveness, существительное

Слова рядом с recursive

recursive F, recurring, recurring decimal, recursion, recursion формула, рекурсия, рекурсивное определение, рекурсивная функция, рекурсивная подпрограмма, изгиб, изгиб

Dictionary.com Unabridged На основе Random House Unabridged Dictionary, © Random House, Inc. , 2023 г.

ПОДРОБНЕЕ О РЕКУРСИИ

Что означает

рекурсивный ?

Что-то рекурсивное зациклено, особенно таким образом, что процесс может повторяться.

Рекурсивный имеет очень специфические значения в математике, компьютерном программировании и лингвистике, но в каждом случае он включает некоторую форму повторения, особенно когда часть последовательности или формулы опирается на предыдущие части. Такой процесс называется рекурсия .

Пример: Программа является рекурсивной: как только она завершает свою функцию поиска, она автоматически начинает сначала.

Откуда взялось

рекурсивное ?

Рекурсивный существует как минимум с конца 1700-х годов. Оно происходит от комбинации латинского recursiōn-, , что означает «бегущий назад», и суффикса прилагательного -ive . Его форма существительного, рекурсия , был зарегистрирован с начала 1600-х годов. Бит -curs- в recursive происходит от слова, означающего бежать, которое также встречается в таких словах, как . Таким образом, вы можете думать о рекурсивном как о значении , повторно запускающем .

Рекурсивный изначально просто означал «постоянно повторяющийся», но к середине 1900-х годов он приобрел специальный математический смысл. Математический смысл относится к применению функции к ее собственным значениям для создания бесконечной последовательности значений. Уравнение, которое дает нам знаменитую последовательность Фибоначчи, является таким процессом.

Это математическое использование привело к вычислительному применению рекурсивных алгоритмов: процессов, которые решают большую проблему, решая меньшие версии проблемы. В лингвистике рекурсивных элементов — это те, которые повторяются по некоторому шаблону. Например, плохой в Он плохой, плохой человек есть рекурсивное , как и конструкция существительного-глагола в Она сказала, что он думал, что мы знали, что она считает это плохой идеей .

Если вы еще не совсем понимаете рекурсивный , было бы неплохо прочитать эту статью еще раз с самого начала (и рекурсивный !).

Знаете ли вы…?

Как

рекурсивное используется в реальной жизни?

Рекурсивный чаще всего используется в контексте компьютерного программирования. В более общем смысле он используется для описания ситуаций, связанных с циклом.

Я определенно добавляю свой сайт-портфолио в качестве одного из своих проектов на моем сайте-портфолио 🙂.

Рекурсивное нечто 😋

— И Ф Е Д И Л И ⚡ (@SauceCodee) 8 декабря 2019 г.

К сожалению, крупные телепремии по-прежнему чрезвычайно важны для определения основных показателей того, как выглядит «хороший» фильм. Это рекурсивное явление.

— Дана Шварц (@DanaSchwartzzz) 9 декабря 2019 г.

Мать Мадонны тоже была Мадонной, поэтому представьте картину эпохи Возрождения под названием «Мадонна с младенцем», которая представляет собой рекурсивное изображение поп-звезды 80-х, держащей уменьшенную версию себя, которая держит уменьшенную версию себя, которая держит уменьшенную версию себя. … pic.twitter.com/FTG25JWPRY

— ВРЕМЯ СКАНЕР (@timescanner) 4 декабря 2019 г.

Какое из следующих слов не соответствует общему значению рекурсивного ?

A. циклический
B. повторяющийся
C. рекуррентный
D. завершающий

Слова, относящиеся к рекурсивному

циклический, циклический, рекуррентный, повторяющийся, периодический, итеративный, повторяющийся

Как использовать рекурсивный в предложении

• Дэн читал статью Хаузера-Хомски-Фитча так: язык рекурсивен.

  Говорить — значит бросать друг в друга вымышленные миры — Выпуск 89: Темная сторона|Кевин Бергер|9 сентября 2020|Наутилус

• строить вещи все больше и больше.

  Разговоры — это бросание вымышленных миров друг в друга — Выпуск 89: Темная сторона | Кевин Бергер | 9 сентября, 2020|Наутилус

• Просто он считает иерархическую структуру плоской, и поэтому Пираха не использует этот массивный рекурсивный прием.

  Говорить — значит бросать друг в друга вымышленные миры — Выпуск 89: Темная сторона|Кевин Бергер|9 сентября 2020 г.|Наутилус

• Участников исследования обучали составлять два набора символов в рекурсивных паттернах.

  Обезьяны могут иметь общие с людьми ключевые навыки, связанные с грамматикой|Брюс Бауэр|26 июня 2020 г.|Новости науки

• Одно из двух животных оказалось в среднем более склонным к формированию новых рекурсивных последовательностей, чем примерно три четверти дошкольников и примерно половина жителей боливийских деревень.

  Обезьяны могут иметь общие с людьми ключевые навыки грамматики|Брюс Бауэр|26 июня 2020|Новости науки

• С тех пор на Ирак обрушились черные миазмы рекурсивной мести.

  No related posts.