Что такое рекурсия, рекурсивный и итеративный процесс в программировании
В этой статье разбираемся, какой бывает рекурсия, как с ее помощью можно решать задачи и что такое рекурсивные функции.
- Рекурсия vs рекурсивный или итеративный процесс: в чем разница
- Методы решения задач с помощью рекурсии
- В чем отличие рекурсивного процесса от итеративного
- Что такое рекурсивные функции и в чем особенность их применения
- Что такое хвостовая рекурсия
Вы читаете обновленную и улучшенную версию нашей старой статьи
Рекурсия vs рекурсивный или итеративный процесс: в чем разница
Рекурсия — это функция, которая вызывает саму себя, но с другими значениями параметров.
На самом деле понятия рекурсии и процесса никак не связаны. Рекурсия — просто абстрактная концепция, которую можно наблюдать в природе, в математике и в других областях. Такая же абстрактная, как, например, музыкальная гармония.
Теперь давайте поговорим о компьютерах. Для выполнения задач им нужны инструкции. Когда компьютер выполняет набор инструкций — это процесс. Ваш работающий сейчас браузер — тоже процесс. Простой цикл, выводящий на экран десять раз число «42» — также процесс.
Некоторые задачи можно решать рекурсивно, то есть использовать концепцию, когда что-то является частью самого себя, в инструкциях. В частности, функция может быть частью самой себя, то есть вызывать саму себя.
Читайте также: Что такое callback-функция в JavaScript?
Методы решения задач с помощью рекурсии
Есть два метода решения задач с использованием рекурсии: рекурсивный процесс и итеративный процесс. Рекурсия в них не отличается: в каждом из подходов функция вызывает саму себя, рекурсивно. Отличаются способы использования идеи рекурсии.
Давайте продолжим аналогию с музыкальной гармонией и подумаем про фортепиано. При написании музыки используем эту концепцию — «гармонию звуков». Можно придумать разные способы: рассчитывать частоты звуков — ноты — математическими формулами или рассчитывать правильные расстояния между клавишами.
Можно придумать разные способы: рассчитывать частоты звуков — ноты — математическими формулами или рассчитывать правильные расстояния между клавишами.
В детстве я научился находить правильные расстояния между клавишами на фортепиано, и получал гармоничные комбинации звуков, но понятия не имел, что это за ноты. А профессиональный музыкант знает теорию и подбирает гармонию другими методами. В любом случае, гармония есть гармония, эта концепция не меняется, меняются лишь способы ее использования.
В чем отличие рекурсивного процесса от итеративного
Рекурсивный процесс на каждом шаге рекурсии говорит «я это запомню и потом посчитаю». «Потом» наступает в самом конце.
- Если рекурсивный процесс считает факториал 6, то ему нужно запомнить 5 чисел, чтобы посчитать их в самом конце, когда уже никуда не деться и рекурсивно двигаться вниз больше нельзя
- Когда мы находимся в очередном вызове функции, то где-то снаружи этого вызова в памяти хранятся эти запомненные числа
На этой картинке видно, как растет использование памяти: процессу нужно запоминать все больше и больше чисел
Рекурсивный процесс — это процесс с отложенным вычислением.
Итеративный процесс постоянно говорит «я сейчас посчитаю все что можно и продолжу» на каждом шаге рекурсии. Ему не нужно ничего запоминать вне вызова, он всегда все считает в первый возможный момент. Каждый шаг рекурсии может существовать в изоляции от прошлых, потому что вся информация передается последовательно.
- Когда итеративный процесс считает факториал 6, то ему не нужно запоминать числа. Нужно лишь считать и передавать результат дальше, в новый вызов
- Когда мы находимся в очередном вызове функции, снаружи этого вызова в памяти ничего не нужно запоминать
А на этой картинке видно, что использование памяти не растет.
Подытожим в шуточной форме. Рекурсивный процесс — это чувак, который все дела откладывает на вечер пятницы. В течение недели у него мало работы, а в пятницу завал. Но ему так нравится.
Итеративный процесс — это чувак, который все делает при первой возможности. У него работа равномерно распределена по неделе, а пятница — просто обычный день, но последний.
Что такое рекурсивные функции и в чем особенность их применения
Рекурсивные функции — это те функции, которые используют итеративный процесс. Для каждого рекурсивного вызова в стек вызовов записывается вся информация, связанная с этим вызовом, вроде параметров функции и ее локальных переменных, адреса возврата в точку вызова.
Для рекурсивной функции выделяется дополнительная область памяти — лексический контекст функции, область видимости —, которая обслуживает рекурсивный вызов. Так как это стек вызовов, то контексты предыдущих рекурсивных вызовов также продолжают занимать память.
Достижение большой глубины рекурсии, или же, недостижение терминального условия выхода из рекурсии, приводит к переполнению стека, так как он ограничен в размерах, и аварийному завершению всей программы.
Читайте также: Как проверить качество кода: функциональное и нефункциональное тестирование
В контексте каждого рекурсивного вызова такой функции хранится вся необходимая информация для его успешного выполнения. Он самодостаточен и никак не зависит от предыдущих контекстов. Помните, что этот чувак ничего не откладывает на потом, на вечер пятницы?
Он самодостаточен и никак не зависит от предыдущих контекстов. Помните, что этот чувак ничего не откладывает на потом, на вечер пятницы?
В наших практиках на Хекслете мы реализовывали такое поведение благодаря использованию аккумулятора acc, который передается в качестве аргумента из одного вызова в другой и накапливает в себе результат вычисления необходимого значения.
Получается, что, грубо говоря, на каком бы по уровню вложенности рекурсивном вызове мы не находились, все предыдущие уже не имеют значения и являются «бесполезной обузой», нагружающей память. Это распространяется в том числе и на самый последний рекурсивный вызов, где срабатывает терминальное условие. Он готов вернуть готовое вычисленное значение из функции сразу, ему не нужны для этого предыдущие контексты в стеке.
Что такое хвостовая рекурсия
Как использовать преимущества итеративного процесса и одновременно избавиться от недостатка рекурсивных функций, то есть от неумолимого роста использования памяти? Можно избавить процесс от заполнения стека «ненужными» контекстами предыдущих вызовов и обеспечить прямой возврат из функции при достижении терминального условия.
Для этого служит так называемая оптимизация хвостовой рекурсии (Tail call optimization). Итеративный процесс, который мы рассмотрели, как раз можно отнести к хвостовой рекурсии. Благодаря оптимизации состояния стека, она придает итеративному процессу вид «плоской» итерации. Так исключается его переполнение из-за большой глубины рекурсии.
Хвостовая рекурсия и ее оптимизация широко используется при написании программ на функциональных языках программирования.
Никогда не останавливайтесь: В программировании говорят, что нужно постоянно учиться даже для того, чтобы просто находиться на месте. Развивайтесь с нами — на Хекслете есть сотни курсов по разработке на разных языках и технологиях
Рекурсивные вычислительные системы
М. Б. Игнатьев, Ю. Е. Шейнин, Санкт-Петербургский государственный университет аэрокосмического приборостроения
Истоки разработки
В феврале 1972 г. на базе кафедры технической кибернетики в Ленинградском институте авиационного приборостроения (ЛИАП) была создана кафедра вычислительных систем и сетей, возглавил которую д.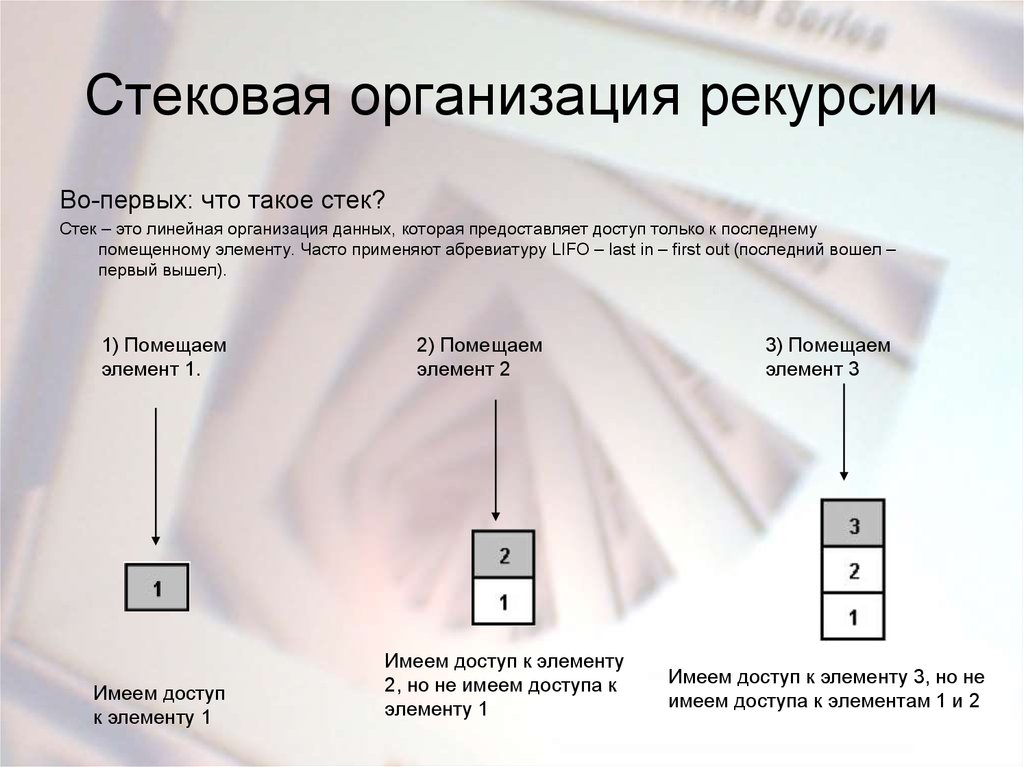 т. н. М. Б. Игнатьев – один из авторов этих строк. С момента своего основания эта кафедра помимо традиционных направлений исследования в области робототехники стала развивать новое направление, связанное с разработкой развивающихся вычислительных систем нетрадиционной архитектуры.
т. н. М. Б. Игнатьев – один из авторов этих строк. С момента своего основания эта кафедра помимо традиционных направлений исследования в области робототехники стала развивать новое направление, связанное с разработкой развивающихся вычислительных систем нетрадиционной архитектуры.
В тот период в Советском Союзе шла борьба между двумя тенденциями дальнейшего развития вычислительной техники. Первая ориентировалась на проведение и совершенствование собственных разработок, таких, как серии машин БЭСМ, «Урал» и др. Вторая нацеливалась на использование зарубежного опыта, прежде всего копирование машин фирмы ИБМ.
Необходимо отметить, что в это время фирма ИБМ занимала практически монопольное положение в сфере производства ЭВМ и их продвижения на рынок, нередко при этом грубо нарушая законы о монополиях и ведя судебные процессы как в США, так и за рубежом. Этот монополизм проявлялся и в компьютерной литературе – там описывались машины ИБМ и почти ничего не говорилось о машинах конкурирующих фирм, например, Контрол Дейта Корпорейшен, Бэрроуз и др. В машинах же фирмы ИБМ реализовывалась классическая неймановская архитектура, которая в целом ряде ситуаций уже не могла удовлетворить потребителей.
В машинах же фирмы ИБМ реализовывалась классическая неймановская архитектура, которая в целом ряде ситуаций уже не могла удовлетворить потребителей.
В этой ситуации наша молодая кафедра, выделившаяся из кафедры технической кибернетики ЛИАП в феврале 1972 г., решила развивать нетрадиционные многопроцессорные вычислительные системы, которые в перспективе могли обеспечить более высокую производительность и надежность. Для нас такое решение было продолжением работ в области цифровых дифференциальных анализаторов, которые являлись многопроцессорными специализированными рекурсивными структурами с обратными связями, высокопроизводительными и надежными за счет введения избыточности методом избыточных переменных, который ранее был нами разработан [1, 2, 4–9]. Важный шаг был сделан доцентом ЛИАП В. А. Торгашевым, предложившим распространить и развить эти принципы на универсальные вычислительные машины. В итоге и родилась концепция рекурсивных машин, которая получила поддержку Государственного Комитета СССР по науке и технике в Москве и Института кибернетики во главе с академиком В. М. Глушковым в Киеве. Сложился коллектив из москвичей, которых представлял В. А. Мясников, киевлян, руководимых В. М. Глушковым, и ленинградцев с общим центром в ЛИАП.
М. Глушковым в Киеве. Сложился коллектив из москвичей, которых представлял В. А. Мясников, киевлян, руководимых В. М. Глушковым, и ленинградцев с общим центром в ЛИАП.
Наиболее ярко предложенная нами концепция была представлена в докладе на международном конгрессе ИФИП в Стокгольме в 1974 г. [10]. Этот доклад сделал М. Б. Игнатьев; советская делегация отнеслась к докладу очень холодно, зато иностранцы приветствовали доклад, который фактически ниспровергал компьютерные авторитеты и традиционную архитектуру и провозглашал нетрадиционную рекурсивную архитектуру. Так впервые советская компьютерная разработка была анонсирована на международной арене, что привлекло к ней внимание многих. Итогом этой акции явилось, во-первых, включение работы в программу ГКНТ с выделением финансирования на создание экспериментального образца рекурсивной машины; во-вторых, заключение соглашения с фирмой Контрол Дейта о создании образца рекурсивной машины на основе предложенных нами архитектурных решений; в-третьих, предоставление в наше распоряжение самой лучшей для того времени элементной базы и средств отладки. Руководителем рабочей группы по сотрудничеству с фирмой Контрол Дейта Корпорейшен стал М. Б. Игнатьев, который и в дальнейшем в этом качестве развивал проект по рекурсивной машине, и, в частности, занимался покупкой машины Сайбер для Ленинградского научного центра АН СССР.
Руководителем рабочей группы по сотрудничеству с фирмой Контрол Дейта Корпорейшен стал М. Б. Игнатьев, который и в дальнейшем в этом качестве развивал проект по рекурсивной машине, и, в частности, занимался покупкой машины Сайбер для Ленинградского научного центра АН СССР.
На базе этой машины фактически организовался сначала Ленинградский научно-исследовательский вычислительный центр, а потом и Ленинградский институт информатики и автоматизации АН СССР.
Следует отметить, это было время некоторого потепления советско-американских отношений, сопровождавшееся и расширением научного сотрудничества, именно в этот период реализовывался, например, проект Союз-Апполон. Таким образом, в результате стечения благоприятных обстоятельств нам удалось развернуть деятельность по реальному созданию рекурсивной машины. Закипела работа, в которой принимали участие многие сотрудники нашей кафедры – В. А. Торгашев, В. И. Шкиртиль, С. В. Горбачев, В. Б. Смирнов, В. М. Кисельников, А. М. Лупал, Ю. Е. Шейнин и многие другие. В результате к началу 1979 г. были изготовлены многие блоки машины, и в том же году экспериментальный образец рекурсивной машины был предъявлен государственной комиссии во главе с академиком А. А. Дородницыным.
Е. Шейнин и многие другие. В результате к началу 1979 г. были изготовлены многие блоки машины, и в том же году экспериментальный образец рекурсивной машины был предъявлен государственной комиссии во главе с академиком А. А. Дородницыным.
В специальном Постановлении ГКНТ СССР и Комиссии Президиума Совета Министров СССР от 14.09.1979 г. за №472/276 отмечалось, что «запуск первого в мире экспериментального образца многопроцессорной рекурсивной машины высокой производительности и надежности является достижением мирового уровня». Были разработаны планы дальнейшего развития этой работы, но в декабре 1979-го советские войска вошли в Афганистан, и правительство США разорвало все научно-технические связи с СССР, в том числе и контакты по линии фирмы Контрол Дейта, что нанесло нам большой ущерб. Но начатая работа продолжалась, хотя к этому времени наш коллектив разделился – часть сотрудников во главе с В. А. Торгашевым в январе 1980 г. перешла в только что образованный Ленинградский научно-исследовательский вычислительный центр АН СССР, другая часть продолжала работать на нашей кафедре над созданием различных модификаций многопроцессорных систем. Отдел рекурсивных машин был создан в Институте кибернетики в Киеве. Таковы внешние контуры этой пионерской работы.
Отдел рекурсивных машин был создан в Институте кибернетики в Киеве. Таковы внешние контуры этой пионерской работы.
Принципы организации рекурсивных машин и систем
В математике существует большой раздел – рекурсивные функции [3]. Долгое время термин «рекурсия» употреблялся математиками, не будучи чётко определённым. Его приблизительный интуитивный смысл можно описать следующим образом. Значение искомой функции Ф в произвольной точке Х (под точкой подразумевается набор значений аргументов) определяется, вообще говоря, через значения этой же функции в других точках Н, которые в каком-то смысле предшествуют Х. Само слово «рекурсия» означает возвращение [17]. Рекурсивные функции – это вычислимые функции. По сути дела все вычислимые на компьютерах функции – это рекурсивные функции, но разные компьютерные архитектуры по-разному ведут вычислительные процессы. Чем лучше соответствует структура компьютера структуре задач, тем меньше затраты памяти и времени. Так что когда мы говорим о рекурсивных машинах, мы говорим о соответствии структур машины и решаемых задач, а так как задачи бывают разные, то структура машин должна гибко подстраиваться к структурам задач. Математика в настоящее время погружена в программирование, и в программировании рекурсивные операции распространены.
Так что когда мы говорим о рекурсивных машинах, мы говорим о соответствии структур машины и решаемых задач, а так как задачи бывают разные, то структура машин должна гибко подстраиваться к структурам задач. Математика в настоящее время погружена в программирование, и в программировании рекурсивные операции распространены.
ЭВМ выступает как средство материализации логико-математических преобразований. ЭВМ являет собой иллюстрацию концепции потенциальной осуществимости, поскольку при отсутствии ограничений на время работы и емкость памяти любая ЭВМ в состоянии провести любые вычисления. Конкретное же протекание процессов вычисления проявляется лишь на уровне организации преобразований информации (задействуются конкретные регистры, коммутаторы, процессоры, линии передачи данных в определенном порядке и сочетании и т. д.). С этой точки зрения архитектура ЭВМ – это её структура в состоянии (процессе) реализации алгоритма, т. е. как бы ожившая структура. Философской основой такого представления является теория отражения, раскрывающая отображение категорий и явлений одной природы (числа, алгоритмы) на объекты другой природы (физические элементы, сигналы). Причем это отображение взаимно неоднозначно – алгоритму аj может соответствовать множество архитектур {А} и обратно – архитектуре Аj непосредственно не соответствует какой-либо алгоритм аj. Специфика взаимодействия {а} и {А} раскрывает глубинные свойства диалектического процесса развития математики и вычислительной техники как частного случая взаимодействия абстрактного и конкретного. Как отмечает С. А Яновская, «лицо машинной математики все более зависит от развития философских и логических оснований математики» [23]. Не представляется возможным непротиворечивая формализация отображения {а} -> {А} из-за его неоднозначности. Поэтому построить соответствующую аксиоматическую теорию проектирования ЭВМ не представляется возможным [24].
Причем это отображение взаимно неоднозначно – алгоритму аj может соответствовать множество архитектур {А} и обратно – архитектуре Аj непосредственно не соответствует какой-либо алгоритм аj. Специфика взаимодействия {а} и {А} раскрывает глубинные свойства диалектического процесса развития математики и вычислительной техники как частного случая взаимодействия абстрактного и конкретного. Как отмечает С. А Яновская, «лицо машинной математики все более зависит от развития философских и логических оснований математики» [23]. Не представляется возможным непротиворечивая формализация отображения {а} -> {А} из-за его неоднозначности. Поэтому построить соответствующую аксиоматическую теорию проектирования ЭВМ не представляется возможным [24].
Когда мы формулировали принципы организации рекурсивных машин, мы исходили из потребностей развития вычислительных машин и систем. Мы получили множество авторских свидетельств [13, 14, 15 и др. ], это был интересный творческий процесс и с точки зрения достоверности сделанного тогда, в 1974–1979 гг., стоило бы полностью воспроизвести наш доклад на конгрессе ИФИП в Стокгольме [10]. Он содержал анализ недостатков машин традиционной архитектуры, ревизию принципов фон Неймана, принципы архитектуры рекурсивных машин, основные особенности языка рекурсивных машин, фрагментарное описание рекурсивной машины.
], это был интересный творческий процесс и с точки зрения достоверности сделанного тогда, в 1974–1979 гг., стоило бы полностью воспроизвести наш доклад на конгрессе ИФИП в Стокгольме [10]. Он содержал анализ недостатков машин традиционной архитектуры, ревизию принципов фон Неймана, принципы архитектуры рекурсивных машин, основные особенности языка рекурсивных машин, фрагментарное описание рекурсивной машины.
В качестве иллюстрации рекурсивной структуры можно привести систему 3М – модульную микропроцессорную систему [18]. Система 3М строится из модулей трех типов – операционных, коммуникационных и интерфейсных. Операционные модули выполняют основную работу по обработке данных, реализации объектов математической памяти, процессов определения готовности и выполнения операторов программы на внутреннем языке. Коммуникационный модуль предназначен для реализации коммуникационной системы – установления логического соединения между модулями, обмена информацией между модулями, поиска в системе ресурсов запрошенного типа. Интерфейсные модули подключаются к внешним устройствам своими блоками ввода-вывода. Вопросы организации обмена информацией с внешним миром имеют большое значение для существенно многопроцессорных систем, оказывают значительное влияние на их фактические характеристики. Различные классы задач требуют разной интенсивности обмена с внешними устройствами. Вычислительная система должна обеспечивать построение таких ее конфигураций для каждого конкретного применения, которые бы обладали оптимальными для этого применения характеристиками по вводу-выводу. Система 3М обеспечивает инкрементное наращивание вычислительной мощности до любого необходимого значения путем подключения дополнительных блоков без внесения изменений в имеющуюся систему и ее программное обеспечение как на этапе разработки системы, так и в ходе ее эксплуатации. Методология проектирования и реализации системы 3М базируется на рассмотрении вычислительной системы как иерархии виртуальных машин. Система 3М имеет рекурсивно-организованную многоуровневую структуру.
Интерфейсные модули подключаются к внешним устройствам своими блоками ввода-вывода. Вопросы организации обмена информацией с внешним миром имеют большое значение для существенно многопроцессорных систем, оказывают значительное влияние на их фактические характеристики. Различные классы задач требуют разной интенсивности обмена с внешними устройствами. Вычислительная система должна обеспечивать построение таких ее конфигураций для каждого конкретного применения, которые бы обладали оптимальными для этого применения характеристиками по вводу-выводу. Система 3М обеспечивает инкрементное наращивание вычислительной мощности до любого необходимого значения путем подключения дополнительных блоков без внесения изменений в имеющуюся систему и ее программное обеспечение как на этапе разработки системы, так и в ходе ее эксплуатации. Методология проектирования и реализации системы 3М базируется на рассмотрении вычислительной системы как иерархии виртуальных машин. Система 3М имеет рекурсивно-организованную многоуровневую структуру. Рекурсивность структуры состоит в том, что структура всякой модификации системы задается рекурсивным определением. Динамически меняющиеся в ходе вычислений виртуальные процессы требуют постоянной динамической реконфигурации связей между модулями. В настоящее время реализуются системы, содержащие тысячи и миллионы процессоров.
Рекурсивность структуры состоит в том, что структура всякой модификации системы задается рекурсивным определением. Динамически меняющиеся в ходе вычислений виртуальные процессы требуют постоянной динамической реконфигурации связей между модулями. В настоящее время реализуются системы, содержащие тысячи и миллионы процессоров.
Экспериментальная реализация параллельных вычислительных систем для динамических параллельных вычислений
Ниже в хронологическом порядке рассматриваются экспериментальные образцы, разработанные начиная с 1974 года.
1979 год
Первой параллельной ВС на микропроцессорных СБИС стал разработанный в 1979 г. экспериментальный четырехпроцессорный образец Рекурсивной ЭВМ (РВМ).
Структура экспериментального образца микропроцессорной РВМ
Экспериментальный образец РВМ включал два вычислительных модуля, один коммуникационный модуль и интерфейсный модуль (процессор ввода-вывода). Его структура представлена на рис. 1. Построенный на секционных микропроцессорах, он показал принципиальную возможность создания модульных параллельных ВС с распределенной архитектурой, с распределенными параллельными вычислениями. Их эффективная поддержка реализовывалась в архитектуре и структуре модулей параллельной ВС – вычислительных модулях, реализовывавших собственно вычисления и новые механизмы децентрализованного управления; в коммуникационных модулях, аппаратно-микропрограммно реализовывавших протоколы коммуникационной системы для взаимодействия параллельных процессов, идущих в вычислительных модулях. Операторы внутреннего языка РВМ – языка высокого уровня, соответствовали среднегранулярным, микропрограммно-реализованным процессам обработки информации. Управляющие операторы внутреннего языка реализовывали основные механизмы управления параллельными вычислениями на уровне сети таких операторов.
Их эффективная поддержка реализовывалась в архитектуре и структуре модулей параллельной ВС – вычислительных модулях, реализовывавших собственно вычисления и новые механизмы децентрализованного управления; в коммуникационных модулях, аппаратно-микропрограммно реализовывавших протоколы коммуникационной системы для взаимодействия параллельных процессов, идущих в вычислительных модулях. Операторы внутреннего языка РВМ – языка высокого уровня, соответствовали среднегранулярным, микропрограммно-реализованным процессам обработки информации. Управляющие операторы внутреннего языка реализовывали основные механизмы управления параллельными вычислениями на уровне сети таких операторов.
1982–1985 гг.
Диплом ГКНТ СССР за разработку высокопроизводительных рекурсивных многопроцессорных комплексов
По результатам испытаний экспериментального образца микропроцессорной ВС были организованы работы по созданию высокопроизводительных параллельных ЭВМ – Рекурсивных ЭВМ. Они проводились в сотрудничестве ИК и ЛИАП с привлечением ряда промышленных организаций.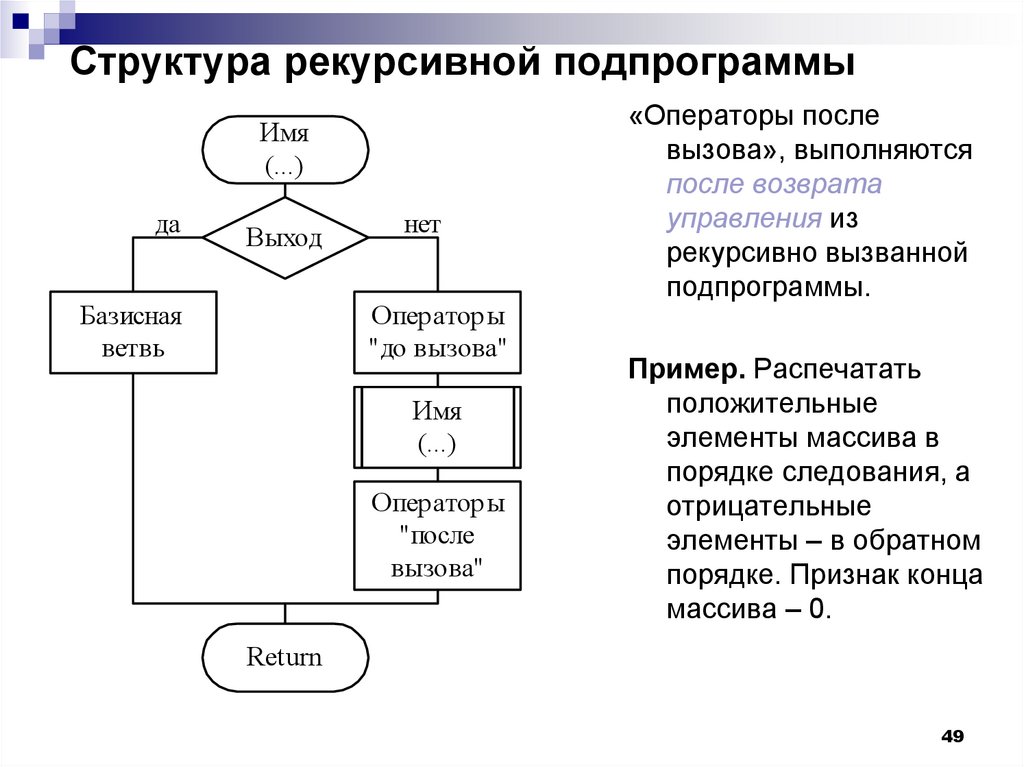 В Институте кибернетики АН УССР создавался образец большого вычислительного комплекса – макроконвейерного вычислительного комплекса для решения больших задач, в ЛИАП (ныне СПбГУАП) – модульная масштабируемая параллельная ВС «Система 3М» на микропроцессорной элементной базе. Было создано два параллельных ВС – большая макроконвейерная ВС класса mainframe для вычислений большой разрядности (64–128 разрядов), с перспективами масштабирования на уровень суперкомпьютерных ВС, – в ИК АН УССР, и в ЛИАП – модульная масштабируемая микропроцессорная ВС «Система 3М», для решения задач с разрядностью 16–32 разряда. Работа было высокого оценена государственной комиссией ГКНТ СССР (рис. 2).
В Институте кибернетики АН УССР создавался образец большого вычислительного комплекса – макроконвейерного вычислительного комплекса для решения больших задач, в ЛИАП (ныне СПбГУАП) – модульная масштабируемая параллельная ВС «Система 3М» на микропроцессорной элементной базе. Было создано два параллельных ВС – большая макроконвейерная ВС класса mainframe для вычислений большой разрядности (64–128 разрядов), с перспективами масштабирования на уровень суперкомпьютерных ВС, – в ИК АН УССР, и в ЛИАП – модульная масштабируемая микропроцессорная ВС «Система 3М», для решения задач с разрядностью 16–32 разряда. Работа было высокого оценена государственной комиссией ГКНТ СССР (рис. 2).
Проект 32-процессорной микропроцессорной параллельной ВС «Система 3М»
В проекте «Системы 3М» большое внимание уделялось модульности и масштабируемости. Общая структура проекта «Системы 3М» приведена на рис. 3, который иллюстрирует топологию этой системы. Структура разработанной параллельной ВС включала 32 вычислительных модуля, 16 коммуникационных модулей. Модульная структура с рекурсивно определяемой топологией связи обеспечивала масштабирование параллельной ВС путем увеличения числа модулей при сохранении как структуры модулей, так и системного и прикладного ПО.
Модульная структура с рекурсивно определяемой топологией связи обеспечивала масштабирование параллельной ВС путем увеличения числа модулей при сохранении как структуры модулей, так и системного и прикладного ПО.
Структура экспериментального образца параллельной ВС «Система 3М»
Поддержка свойства масштабируемости в системных механизмах распределенной ОС и коммуникационных модулей позволяет создавать на типовых узлах ограниченной номенклатуры программно-совместимые параллельные ВС с широким диапазоном характеристик по производительности, объему памяти и пропускной способности ввода-вывода (использовалось три типа модулей – вычислительные модули, коммуникационные модули и интерфейсные модули).
Общий вид экспериментального образца параллельной ВС «Система 3М»
Был создан экспериментальный образец «Системы 3М» (рис. 4, 5), разработано его системное ПО, проведен большой комплекс исследований и экспериментов по решению на нем прикладных задач различного класса.
1986–1988 г.

Развитие микропроцессорной техники, создание все более мощных микропроцессоров и достаточно производительных микропроцессорных узлов на их основе, освоение их серийного производства и применение для широкого круга задач поставили вопрос о создании параллельных ВС на основе серийно выпускаемых микропроцессорных модулей, в том числе для систем специального назначения.
При реализациях параллельных ВС на готовых микропроцессорных узлах (спустя десятилетие этот подход получил название COTS – Commercial Off The Shelf) функциям и свойствам ВМ уровня логической структуры на уровне физической структуры наиболее полно будет соответствовать пара ВМ – терминальный коммуникационный модуль (ТКМ). Комбинация ВМ-ТКМ дает основу для реализации полного набора функций ВМ. ТКМ в таких системах подключается на системную (локальную) шину серийного микропроцессорного узла (Q-bus, VME, PCI) и занимает место коммуникационного контроллера (КК).
Параллельная ВС на базе серийных микроЭВМ «Электроника 81Б»
Параллельная ВС такого класса была разработана нами на основе серийной микроЭВМ «Электроника 81Б», пригодных и для возимых, и для бортовых применений (рис. 6). На стандартную системную шину (для «Электроники 81Б» – шина Q-bus) в качестве КК подключается специальная относительно несложная плата, реализующая высокоскоростной дуплексный внутрисистемный интерфейс параллельной ВС. Учитывая ограниченный диапазон масштабируемости для разрабатывавшихся параллельных ВС, а также целевые области применения, в данном проекте параллельной ВС (название «РВМС» – Распределенная мультипроцессорная ВС) была принята линия на перенос сложности реализации внутрисистемных протоколов с КК вычислительных модулей на коммуникационные модули. Для РМВС в качестве КМ был разработан специализированный коммуникационный транспьютерный модуль РТ841. Аппаратно-микропрограммная реализация внутрисистемных протоколов нижнего уровня, доступный микропрограммный уровень и специализированные на логическую обработку параллельные блоки при достаточно высокой тактовой частоте позволили сбалансировать характеристики коммуникационной системы на базе такого ТКМ с максимальной пропускной способностью, которую могут обеспечить вычислительные модули на базе «Электроники 81Б», в конфигурациях до 8 вычислительных модулей на один КМ.
6). На стандартную системную шину (для «Электроники 81Б» – шина Q-bus) в качестве КК подключается специальная относительно несложная плата, реализующая высокоскоростной дуплексный внутрисистемный интерфейс параллельной ВС. Учитывая ограниченный диапазон масштабируемости для разрабатывавшихся параллельных ВС, а также целевые области применения, в данном проекте параллельной ВС (название «РВМС» – Распределенная мультипроцессорная ВС) была принята линия на перенос сложности реализации внутрисистемных протоколов с КК вычислительных модулей на коммуникационные модули. Для РМВС в качестве КМ был разработан специализированный коммуникационный транспьютерный модуль РТ841. Аппаратно-микропрограммная реализация внутрисистемных протоколов нижнего уровня, доступный микропрограммный уровень и специализированные на логическую обработку параллельные блоки при достаточно высокой тактовой частоте позволили сбалансировать характеристики коммуникационной системы на базе такого ТКМ с максимальной пропускной способностью, которую могут обеспечить вычислительные модули на базе «Электроники 81Б», в конфигурациях до 8 вычислительных модулей на один КМ. Большие конфигурации (до 18 ВМ) комплексируются с использованием 3 КМ, объединенных в полносвязанную структуру, где удельная пропускная способность КС (пропускная способность на 1 ВМ) остается в том же диапазоне, что и для базовой мультипроцессорной конфигурации с одним ВМ. Для созданного в ЛИАП экспериментального образца РМВС (конфигурация с 8 ВМ и 1 КМ) была разработана распределенная ОС, система программирования на языке Си, система отладки с распределенным отладочным монитором («РОМ») [25]. Операционная система РМВС послужила прообразом разработанной в 90-х годах операционной системы НевОС . Опыт создания системы параллельного программирования для РМВС, ее применения для программирования достаточно больших программных комплексов послужили отправной точкой для постановки работ по системам визуального параллельного программирования, создания в последующие годы языка и системы программирования ВИЗА.
Большие конфигурации (до 18 ВМ) комплексируются с использованием 3 КМ, объединенных в полносвязанную структуру, где удельная пропускная способность КС (пропускная способность на 1 ВМ) остается в том же диапазоне, что и для базовой мультипроцессорной конфигурации с одним ВМ. Для созданного в ЛИАП экспериментального образца РМВС (конфигурация с 8 ВМ и 1 КМ) была разработана распределенная ОС, система программирования на языке Си, система отладки с распределенным отладочным монитором («РОМ») [25]. Операционная система РМВС послужила прообразом разработанной в 90-х годах операционной системы НевОС . Опыт создания системы параллельного программирования для РМВС, ее применения для программирования достаточно больших программных комплексов послужили отправной точкой для постановки работ по системам визуального параллельного программирования, создания в последующие годы языка и системы программирования ВИЗА.
1989–1992 гг.
Другая линия развития параллельных ВС, объединяющая разработку специальной структуры ВМ с использованием в качестве его ядра СБИС микропроцессора с фиксированной системой команд, была предложена для отечественных проектов 32-разрядных микропроцессоров новой архитектуры, создававшихся в конце 80-х – начале 90-х годов. В качестве ядра ВМ были рассмотрены (совместно с НПО «Элас», Зеленоград) микропроцессор «Салют» – микропроцессор, разрабатывавшийся для бортовых ВК перспективных космических аппаратов, и микропроцессор «Эль-90» – микропроцессорная реализация архитектуры «Эльбрус» (совместно с Институтом точной механики и вычислительной техники). И в том и в другом микропроцессорном наборе имелись возможности интеграции в структуру ядра ВМ специализированного коммуникационного контроллера и расширения базовой системой команд некоторой формой экстракодов. Структура ВМ на базе МП «Салют» приведена на рис. 7.
В качестве ядра ВМ были рассмотрены (совместно с НПО «Элас», Зеленоград) микропроцессор «Салют» – микропроцессор, разрабатывавшийся для бортовых ВК перспективных космических аппаратов, и микропроцессор «Эль-90» – микропроцессорная реализация архитектуры «Эльбрус» (совместно с Институтом точной механики и вычислительной техники). И в том и в другом микропроцессорном наборе имелись возможности интеграции в структуру ядра ВМ специализированного коммуникационного контроллера и расширения базовой системой команд некоторой формой экстракодов. Структура ВМ на базе МП «Салют» приведена на рис. 7.
Структура вычислительного модуля на базе микропроцессорного набора «Салют»
Учитывая вариант включения функцией ТКМ в перечень прямо аппаратно-программно реализуемых в ВМ функций (с исключением ТКМ как самостоятельного компонента физической структуры) и в духе транспьютерных технологий можно считать такое «поглощение» ТКМ вычислительным модулем наиболее перспективным вариантом. Это позволило погрузить в архитектуру вычислительных модулей КК для внутрисистемных коммуникаций в параллельной ВС, реализовать алгоритмы КС с высокой эффективностью. Оценки и моделирование свидетельствовали, что достижимые в таких системах показатели задержки доставки сообщений между ВМ (L), накладных расходов ЦП ВМ на передачу сообщения (o), интервал между последовательно передаваемыми сообщениями (g) сбалансированы с характеристиками производительности вычислительного ядра ВМ. Расширение системы команд экстракодами управления процессами позволяло в два-три раза снизить накладные расходы на переключение процессов s, снизить показатель o.
Оценки и моделирование свидетельствовали, что достижимые в таких системах показатели задержки доставки сообщений между ВМ (L), накладных расходов ЦП ВМ на передачу сообщения (o), интервал между последовательно передаваемыми сообщениями (g) сбалансированы с характеристиками производительности вычислительного ядра ВМ. Расширение системы команд экстракодами управления процессами позволяло в два-три раза снизить накладные расходы на переключение процессов s, снизить показатель o.
1992–1994 гг.
Развитие в мире транспьютерных технологий определило интерес отечественной промышленности к этому классу ВС и направление ряда наших проектов в области параллельных ВС. Проведенные исследования и эксперименты с транспьютерными модулями на основе транспьютеров Т805 показало преимущества глубокой интеграции механизмов управления процессами, мультипрограммного режима работы транспьютера как компонента параллельной ВС с распределенной архитектурой. В то же время были видны и преимущества наших подходов с инкапсулированием последовательных программ внутри процессов – целостных компонентов параллельной схемы программы, с более высоким уровнем сервиса КС и используемых в ней протоколов, развитых средств сегментации и управления памятью в архитектуре ВМ.
В то же время были видны и преимущества наших подходов с инкапсулированием последовательных программ внутри процессов – целостных компонентов параллельной схемы программы, с более высоким уровнем сервиса КС и используемых в ней протоколов, развитых средств сегментации и управления памятью в архитектуре ВМ.
Структура макета транспьютерной БВС на серийных транспьютерных модулях («гиперТРАМАах»)
Выводы наших исследований были подтверждены и практикой развития самих транспьютерных технологий, появлением нового поколения транспьютеров – Т9000. Т9000 развивал транспьютерные архитектуры именно в тех направлениях, которые указывались нами как ограничения семейства Т800, имевшиеся в наших архитектурных и структурных решениях в указанных выше проектах. Хотя и в Т9000 мы не увидели полного набора искомых функциональных возможностей для системной поддержки динамических параллельных вычислений в параллельных ВС с распределенной архитектурой, в целом они давали хорошую основу для построения параллельных ВС.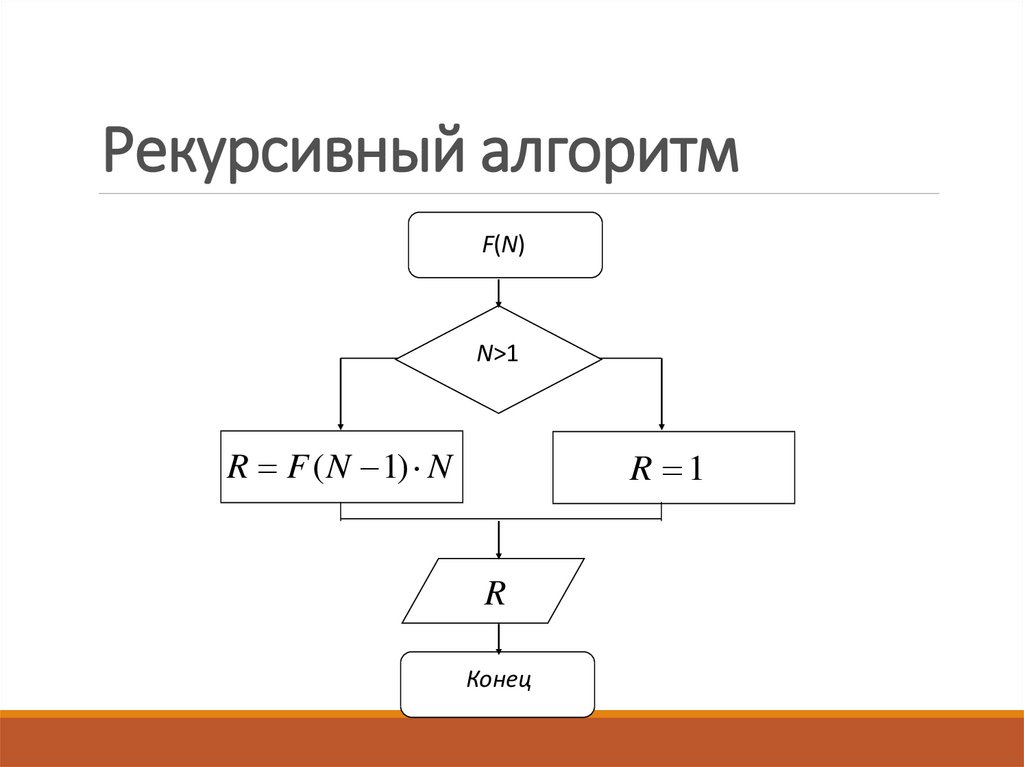 Недостающие механизмы реализовывались на них программно в ядре ОС с приемлемой эффективностью. Нами был разработан проект параллельной ВС на транспьютерах. Структура макета такой параллельной ВС показана на рис. 8.
Недостающие механизмы реализовывались на них программно в ядре ОС с приемлемой эффективностью. Нами был разработан проект параллельной ВС на транспьютерах. Структура макета такой параллельной ВС показана на рис. 8.
Кластерная ВС на серийных высокопроизводительных системных блоках и сетевых средствах
Следующим этапом работы стал проект высокопроизводительной кластерной ВС с масштабируемой конфигурацией, реализованный полностью на серийных технических средствах: системных блоках ПЭВМ, серийных сетевых контроллерах и коммутаторах с диапазоном производительности от 10 до 100 Гфлоп при стоимости порядка 0,3 долл. за 1 Мфлоп (300 долл. за 1 Гфлоп, оценки по техническим характеристикам микропроцессоров на июнь 2001 г.). На рис. 9 и 10 представлены структуры 8-и 36-процессорных конфигураций кластерной ВС.
Структура кластерной ВС на серийных системных блоках и сетевых средствах
Разработка параллельных кластерных ВС лежит в русле основных современных тенденций создания высокопроизводительных вычислительных средств (СВТ) широкого применения для решения современных сложных нерегулярных вычислительных задач [26].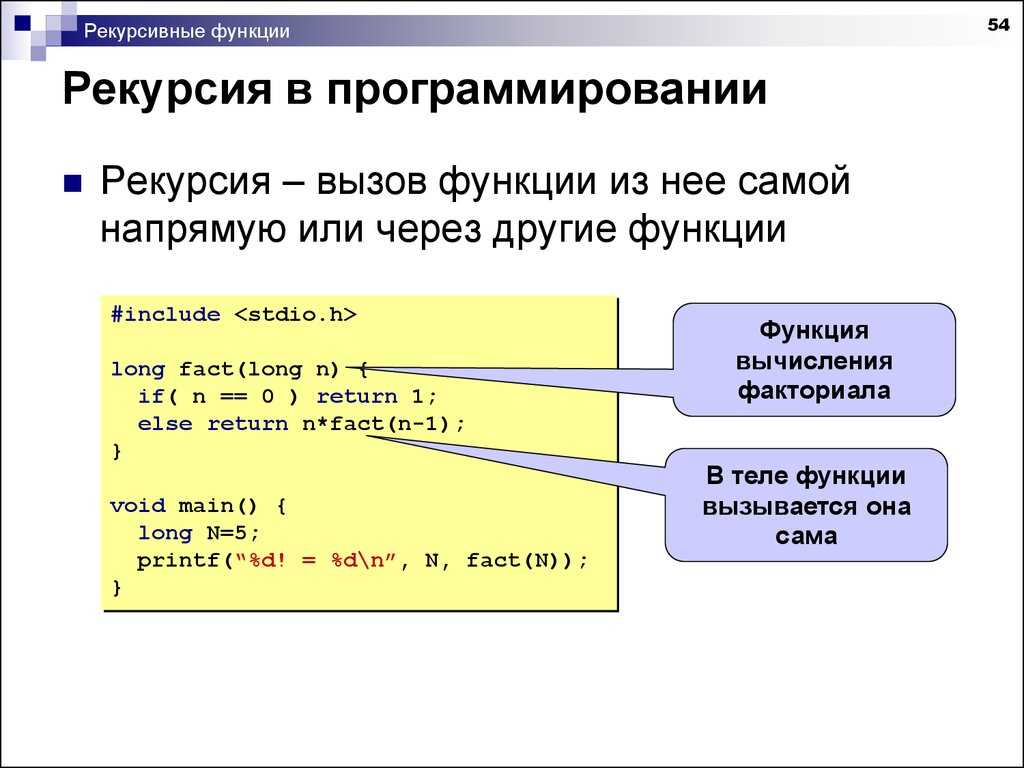 С другой стороны, для нас это возврат на новом этапе к созданию параллельных ВС на основе серийно выпускаемых блоков вычислительной техники, который был нами апробирован в параллельной ВС на микроЭВМ «Электроника 81Б».
С другой стороны, для нас это возврат на новом этапе к созданию параллельных ВС на основе серийно выпускаемых блоков вычислительной техники, который был нами апробирован в параллельной ВС на микроЭВМ «Электроника 81Б».
Однако в отличие от предыдущего проекта на «Электроника 81Б» проект кластерных ВС строился с ориентацией на создание СВТ широкого применения, где кроме показателя абсолютной производительности ВС важное значение имеют технико-экономические характеристики, удельная стоимость достигаемой производительности. Это определяет отличия в подходах к проектированию кластерной ВС, ориентацию на максимальное использование серийных (за счет этого – дешевых) технических средств для реализации физического уровня параллельной ВС. Если в проекте параллельной ВС на микроЭВМ «Электроника 81Б» готовым компонентом были микроЭВМ – основа ВМ параллельной ВС, а средства реализации коммуникационной системы были специальной разработки, то проект кластерной ВС использует готовые, серийно выпускаемые технические средства и в качестве основы построения КС. Средства реализации КС составляют существенную часть затрат на построение кластерных ВС. Например, Томас Стерлинг оценивает приемлемый уровень расходов на КС кластерной системы как 25–30% всех расходов на аппаратуру кластерной ВС [27].
Средства реализации КС составляют существенную часть затрат на построение кластерных ВС. Например, Томас Стерлинг оценивает приемлемый уровень расходов на КС кластерной системы как 25–30% всех расходов на аппаратуру кластерной ВС [27].
Такой подход в нашем проекте стал возможен благодаря существенным сдвигам в развитии архитектуры и структуры сетевых средств, методов их взаимодействия с ЭВМ, которые стали реальностью со времени создания нашей параллельной ВС на «Электронике 81Б». Выросли технико-экономические характеристики средств локальных сетей массового применения. Сетевые контроллеры Fast Ethernet для шины PCI стали массовой продукцией по цене 15–35 долл., стоимость сетевых контроллеров Gigabit Ethernet с тысяч долларов уменьшилась до сотен долларов.
В сетевых средствах массового производства произошел переход от моноканальных архитектур, с использованием физической или логической шины (концентраторы) к архитектурам с коммутацией кадров. Замена моноканала на коммутатор с масштабируемой структурой позволяет варьировать пропускную способность КС с ростом числа абонентов – ВМ, иметь низкие значения задержек передачи сообщений L и сохранять их при росте числа ВМ в кластерной ВС.
Кроме того, построенная на коммутаторах структура ЛВС (а в кластерной ВС – ее КС) переводит все связи между узлами физической структуры параллельной ВС в категорию каналов «точка – точка» как на физическом, так и на канальном уровне. Это позволило во многих серийно выпускаемых сетевых блоках перейти на дуплексный режим работы канала подключения КК в ВМ к сетевой инфраструктуре, что дает почти двойное увеличение пропускной способности стыка ВМ с КС.
Ранее в нашем проекте параллельной ВС на «Электронике 81Б» были реализованы все эти возможности, только на базе коммуникационных средств специальной разработки. Теперь же можно использовать серийные, существенно более дешевые блоки. Конечно, пока не все из тех средств архитектурной поддержки, которые нужны для параллельных ВС, мы можем найти в сетевых средствах современных локальных сетей. Однако потери от их программной эмуляции – это плата за дешевизну серийных средств и таким образом всей кластерной ВС в целом.
Другая оборотная сторона применения серийных средств локальных сетей для КС – ограниченная масштабируемость кластерных ВС на серийных технических средствах (в данном контексте – сетевых средств).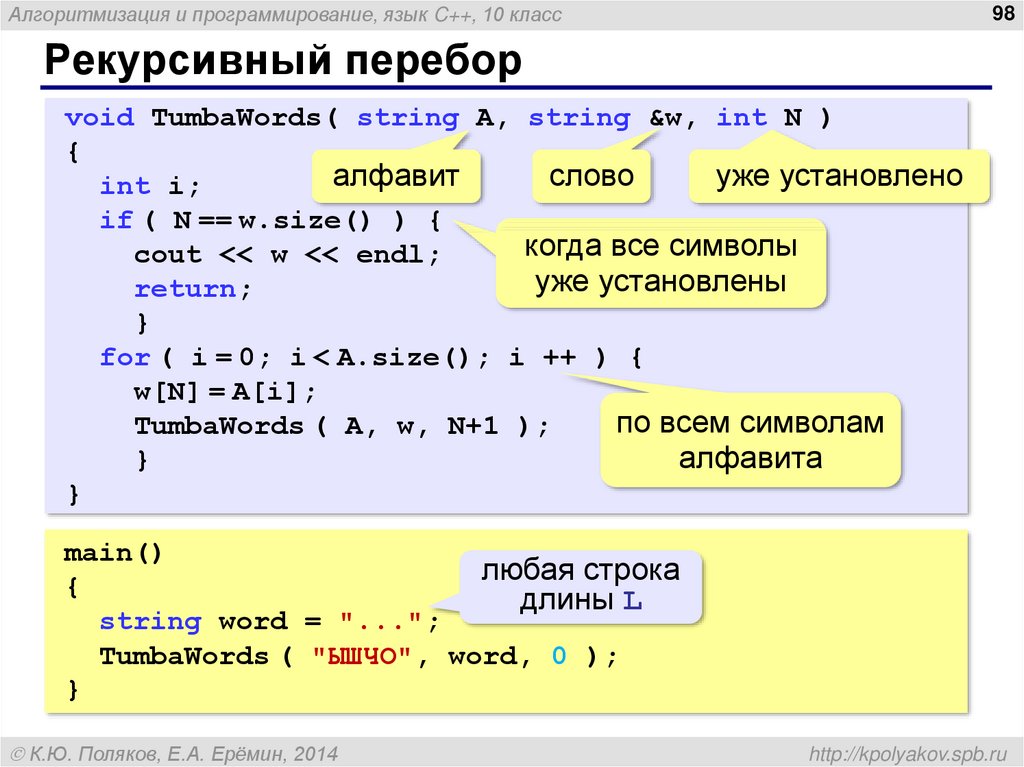 Для малых конфигураций кластерных ВС (например, с одним коммутатором средней стоимости) удельная пропускная способность КС на одного абонента, показатели L, o, g, будут определяться тем, что позволяют получить используемые технические средства ВМ, узла параллельной кластерной ВС – сетевого контроллера, системного блока. Наращивание конфигурации в пределах, определяемых заложенными в серийный коммутатор возможностями наращивания (stackable switches) и комплексирования с другими коммутаторами по каналам повышенной пропускной способности (например, каналов Gigabit Ethernet для коммутаторов FastEthernet), позволяет не ухудшать эти показатели при масштабировании системы. Так, удельные показатели КС 36-процессорной конфигурации кластерной ВС (рис. 10) будут практически такими же, как и для 8-процессорной конфигурации (рис. 8).
Для малых конфигураций кластерных ВС (например, с одним коммутатором средней стоимости) удельная пропускная способность КС на одного абонента, показатели L, o, g, будут определяться тем, что позволяют получить используемые технические средства ВМ, узла параллельной кластерной ВС – сетевого контроллера, системного блока. Наращивание конфигурации в пределах, определяемых заложенными в серийный коммутатор возможностями наращивания (stackable switches) и комплексирования с другими коммутаторами по каналам повышенной пропускной способности (например, каналов Gigabit Ethernet для коммутаторов FastEthernet), позволяет не ухудшать эти показатели при масштабировании системы. Так, удельные показатели КС 36-процессорной конфигурации кластерной ВС (рис. 10) будут практически такими же, как и для 8-процессорной конфигурации (рис. 8).
36-процессорная кластерная ВС
Конечно, можно поставить и тысячу, и десять тысяч системных блоков ПЭВМ и соединить их некоторой структурой КС с сетью из коммутаторов и кабелей между ними. В мире известны десятки кластерных ВС с числом процессоров больше тысячи. Однако для каждого из имеющегося на рынке набора серийных сетевых блоков будут свои ограничения на возможность масштабирования структуры сети с сохранением удельной пропускной способности на один абонент КС. Дальнейшее увеличение числа абонентов сети ведет к уменьшению пропускной способности КС в расчете на одного абонента, к росту показателей L, o, g, критичных для функционирования параллельной ВС. И такая кластерная ВС будет работоспособна, и она сможет решать задачи. Однако все на большем числе задач будут расти потери ресурса процессорного времени и падать эффективная производительность. Эти факторы и приводят к тому, что эффективная производительность кластерных ВС (real applications performance – RAP) оценивается как 5–15% от их пиковой производительности (Peak Advertised Performance, PAP) [28]. Для сравнения: у лучше сбалансированных профессиональных высокопроизводительных ВК – малопроцессорных ВК из векторных процессоров – это соотношение оценивается как 30–50%.
В мире известны десятки кластерных ВС с числом процессоров больше тысячи. Однако для каждого из имеющегося на рынке набора серийных сетевых блоков будут свои ограничения на возможность масштабирования структуры сети с сохранением удельной пропускной способности на один абонент КС. Дальнейшее увеличение числа абонентов сети ведет к уменьшению пропускной способности КС в расчете на одного абонента, к росту показателей L, o, g, критичных для функционирования параллельной ВС. И такая кластерная ВС будет работоспособна, и она сможет решать задачи. Однако все на большем числе задач будут расти потери ресурса процессорного времени и падать эффективная производительность. Эти факторы и приводят к тому, что эффективная производительность кластерных ВС (real applications performance – RAP) оценивается как 5–15% от их пиковой производительности (Peak Advertised Performance, PAP) [28]. Для сравнения: у лучше сбалансированных профессиональных высокопроизводительных ВК – малопроцессорных ВК из векторных процессоров – это соотношение оценивается как 30–50%.
Наконец, большое значение имеет появление поддержки архитектуры виртуального интерфейса (Virtual Interface Architecture, VIA) в архитектуре коммуникационных контроллеров и сопровождающих их драйверах для серийных ОС (в нашем случае – для ОС Linux). Один из авторов настоящей статьи, Шейнин Ю. Е., был участником (contributing member) международной рабочей группы, разрабатывавшей и исследовавшей спецификацию VIA. Качественно новый уровень организации взаимодействия ПО, выполняющегося на центральном процессоре ВМ, с коммуникационным контроллером позволяет существенно снизить накладные расходы o и задержки передачи сообщений L. Так, накладные расходы o удается сократить до 4 мкс [29]. В нашей кластерной ВС мы используем сетевые контроллеры типа Intel Pro 100 с драйверами M-VIA для ОС Linux.
Еще лучшие характеристики можно получать при использовании коммуникационной среды, построенной по технологии АТМ [30]. Для этой технологии также серийно выпускаются и КК, и коммутаторы. Однако современный рынок СВТ сложился таким образом, что сетевые средства по технологии АТМ не получили столь массового распространения, как современные технологии Ethernet. В результате сетевые узлы и блоки не стали столь массовой продукцией и цены на них существенно, в несколько раз выше.
Однако современный рынок СВТ сложился таким образом, что сетевые средства по технологии АТМ не получили столь массового распространения, как современные технологии Ethernet. В результате сетевые узлы и блоки не стали столь массовой продукцией и цены на них существенно, в несколько раз выше.
Перспективы развития вычислительных систем
Высокопроизводительные вычислительные средства давно стали ключевым аспектом развития науки и техники. Компьютерное моделирование широко используется в естественных науках для исследования явлений и процессов реального мира, в прикладных дисциплинах – для анализа и оптимизации инженерных решений. Прогнозируется дальнейший рост значимости компьютерного моделирования вычислительных экспериментов для развития фундаментальных и прикладных наук, прогресса в инженерных дисциплинах разного профиля, перехода от натурных экспериментов к исследованиям на компьютерных моделях. Яркий пример – замена ядерных взрывов на компьютерное моделирование и вычислительные эксперименты.
Представление о широте спектра задач для массово-параллельных систем и типовых классов вычислительных алгоритмов дает их сводка на рис. 11 [33]. Очевидно, что это сегодняшнее представление является лишь малой частью тех задач, которые придется решать массово-параллельным системам в ближайшее десятилетие.
Перспективные задачи для массово-параллельных ВС
Сформировались и получили признание дисциплины, базирующиеся на высокопроизводительной компьютерной обработке и моделировании: вычислительная метеорология (моделирование погодных и климатических процессов), астрономия и астрофизика (исследование звезд, суперновых, нейтронных звезд, космология), вычислительная физика, вычислительная химия (Computational Chemistry), молекулярное моделирование (Molecular Modelling) и др.
Наряду с ними развиваются новые научные дисциплины, новые отрасли знаний [33]: вычислительная экономика (Computational Economics), вычислительная логика (Computational Logic), вычислительная экология (Computational Ecology), биоинформатика (Bioinformatics), вычислительная лингвистика (Computational Linguistics), вычислительная электроника (Computational Electronics) и др.
Не меньшее значение придается расширению применения методов и технологий суперкомпьютерной обработки данных в новых сферах, за рамками традиционно научных и инженерных областей, для улучшения сервисов для широких слоев населения и накопления знаний человеческим обществом. Базирующиеся на суперкомпьютерных возможностях обработки информации «интеллектуальные» экспертные системы смогут оперативно вырабатывать оптимальные решения в различных областях – от здравоохранения до прогноза поведения рынков.
Растет значение высокопроизводительных вычислительных средств в задачах непосредственного управления оборудованием и системами, которые имеют критический характер для нормального функционирования и самого существования человеческого общества.
Массово-параллельные вычисления с терафлоповой и петафлоповой (1015) производительностью необходимы и в сложных приборных комплексах. Источники рентгеновского излучения в исследовательских центрах, гигагерцовые NMR-системы, ускорители элементарных частиц, аэродинамические трубы и другие научные приборные комплексы генерируют огромные потоки данных, сотни мегабайт в секунду и более [35, 36]. Все эти данные требуют сложной обработки и комплексного анализа [37, 38]. Дальнейшее развитие и методик экспериментальных научных исследований, и научных приборных комплексов требует анализа поступающих с приборов потоков данных в реальном времени так, чтобы по их результатам учеными мог контролироваться, модифицироваться и управляться ход самого научного эксперимента.
Еще более захватывающая научная проблема, обещающая качественно-новые возможности научных исследований, – непосредственная интеграция приборных комплексов для проведения экспериментов и массово-параллельных суперкомпьютерных вычислительных средств, ведущих в реальном времени моделирование лежащих в основе проводимого эксперимента физических, химических и т. п. процессов. При этом появляется возможность прямого взаимодействия эксперимента, теории и научных представлений исследователей (scientific insight), их взаимовлияния в единой интерактивной среде научных исследований.
п. процессов. При этом появляется возможность прямого взаимодействия эксперимента, теории и научных представлений исследователей (scientific insight), их взаимовлияния в единой интерактивной среде научных исследований.
Перспективные задачи характеризуются большими размерностями обрабатываемых массивов данных, большими объемами вычислений, требуют огромных вычислительных ресурсов [39]. Среди перечисленных выше типовых задач многие относятся к задачам большой вычислительной интенсивности (computation intensive), объем вычислений которых растет значительно быстрее роста размерности задачи и быстрее роста объема обрабатываемых данных. Например, даже для традиционной задачи умножения матриц многие известные алгоритмы параллельного умножения матриц требуют O(N3) операций вычислений и O(N2) пересылок данных [40]. Для широкого класса задач трехмерного моделирования физических систем отмечен рост вычислительной сложности (объема вычислений) как n4, при росте объема требуемой памяти как n3. В вычислительной химии имеется большое число задач, вычислительная сложность которых характеризуется как n5, n7, n! и др.
В вычислительной химии имеется большое число задач, вычислительная сложность которых характеризуется как n5, n7, n! и др.
В этих условиях достигнутый терафлоповый (1012 операций с плавающей запятой в секунду) уровень производительности суперкомпьютерных систем является недостаточным. Уже сегодня есть реальные, актуальные и готовые к решению задачи, требующие производительности в десятки и сотни терафлоп, ясны постановки ряда задач, требующие производительности в 1000 терафлоп. На повестке дня – создание в ближайшее десятилетие вычислительных систем с производительностью, измеряемой в петафлопах – 1015 операций в секунду, которые уже называют петафлоповыми компьютерами (Petaflop Computers). По оценкам PITAC (Консультативного совета по информационным технологиям при президенте США) задача создания петафлоповых суперкомпьютеров должна быть решена к 2007 г. [41].
Вычислительные машины предназначены для решения задач.
Общая схема решения задач имеет вид Ячел -> Яос ->Япр ->Ямаш -> Ярез, где Ячел – формулировка задачи на естественном языке, Яос – формулировка задачи на языке основных соотношений, Япр – формулировка задачи на языке программирования, Ямаш – формулировка задачи на машинном языке, Ярез – формулировка задачи на языке результата в виде графиков, таблиц, изображений, текстов, звуков и т. п.
К сожалению, для большинства задач имеется только формулировка на естественном языке, множество задач плохо формализованы. Поэтому актуальным является переход от описания на естественном языке к описанию на языке основных соотношений; лингвокомбинаторное моделирование является одним из способов такой формализации [22]. В результате такой формализации порождаются рекурсивные структуры со структурированной неопределенностью. Таким образом, рекурсивная структура машин должна включать три составляющих – явления, смыслы и структурированную неопределенность, которые наличествуют в любой задаче.
Таким образом, рекурсивная структура машин должна включать три составляющих – явления, смыслы и структурированную неопределенность, которые наличествуют в любой задаче.
Литература
- А. А. Воронов, А. Р. Гарбузов, Б. Л. Ермилов, М. Б. Игнатьев, Г. Н. Соколов, Ян Си Зен. Цифровые аналоги для систем автоматического управления. Изд. АН СССР, 1960.
- М. Б. Игнатьев. Голономные автоматические системы. Л.–М., Изд. АН СССР, 1963.
- А. И. Мальцев. Алгоритмы и рекурсивные функции. М., 1965.
- М. Б. Игнатьев. О совместном использовании принципов введения избыточности и обратной связи для построения ультраустойчивых систем. Труды Ш Всесоюзного совещания по автоматическому управлению, т. 1. Изд. АН СССР, 1968.
- М. Б. Игнатьев. Метод избыточных переменных для функционального кодирования цифровых автоматов. Сб. «Теория автоматов», №4. Киев, ИК АН УССР, 1969.
- М. Б. Игнатьев. О лингвистическом подходе к анализу и синтезу сложных систем. Тезисы Межвузовской научно-технической конференции «Техническая кибернетика».
 Изд. МВТУ, 1969.
Изд. МВТУ, 1969. - М. Б. Игнатьев. Избыточность в многоцелевых системах. Труды IV симпозиума по проблеме избыточности. Л., 1970.
- М. Б. Игнатьев, Ф. М. Кулаков, А. М. Покровский. Алгоритмы управления роботами-манипуляторами. М., Машиностроение, 1972. США, Вирджиния пресс, 1973.
- Г. С. Бритов, М. Б. Игнатьев, Л. А. Мироновский, Ю. М. Смирнов. Управление вычислительными процессами. ЛГУ, 1973.
- V. Glushkov, M. Ignatyev, V. Miasnikov, V. Torgashev. Recursive machines and computing technology. Proceedings IFIP-74, computer hardware and architecture, p. 65–70, Stockholm, August 5–10, 1974.
- М. Б. Игнатьев, В. А. Мясников, А. М. Покровский. Программное управление оборудованием. Изд. 2-е. М., Машиностроение, 1984.
- М. Б. Игнатьев, В. А. Мясников, В. А. Торгашев. Рекурсивные вычислительные машины. Препринт №12. ИТМ и ВТ АН СССР, 1977.
- М. Б. Игнатьев, В. М. Кисельников, В. А. Торгашев, В. Б. Смирнов. Ассоциативное запоминающее устройство. А.
 с. 4844562. Опубл. в Б. И., №34, 1975.
с. 4844562. Опубл. в Б. И., №34, 1975. - А. А. Бекасова, С. В. Горбачев, М. Б. Игнатьев, В. А. Мясников, В. А. Торгашев. Процессор с микропрограммным управлением. А. с. 814118 с приоритетом от 18.10.1979.
- С. В. Горбачев, М. Б. Игнатьев, В. М. Кисельников, В. А. Мясников, В. А. Торгашев. Многопроцессорная вычислительная система. А. с. 962965 с приоритетом от 27 августа 1974. Опубл. в Б. И., №36, 1982.
- М. Б. Игнатьев, В. А. Мясников, В. В. Фильчаков. Организация вычислительного процесса при решении прикладных задач на многопроцессорной системе с рекурсивной организацией. Журнал АН УССР, сер. Кибернетика, 1984, №3, с. 30–37.
- Рекурсия. Ст. в Математической энциклопедии, т. 4. М, 1984, с. 962–966.
- В. А. Мясников, М. Б. Игнатьев, А. А. Кочкин, Ю. Е. Шейнин. Микропроцессоры – системы программирования и отладки. М., Энергоатомиздат, 1985.
- С. В. Горбачев, М. Б. Игнатьев, Ю. Е. Шейнин. Рекурсивные ЭВМ массового применения. Тезисы 11-й Всесоюзной конференции по актуальным проблемам информатики и вычислительной техники.
 Ереван, АН Армянской ССР, 1987.
Ереван, АН Армянской ССР, 1987. - М. Б. Игнатьев, Я. Комора. Обобщенная параметрическая модель реализации локально-рекурсивных структур в трехмерных интегральных схемах. ДАН СССР, 1991, т. 320, №5, с. 1058–1062.
- М. Б. Игнатьев, В. В. Фильчаков, Л. Г. Осовецкий. Активные методы обеспечения надежности алгоритмов и программ. Политехника, 1992.
- М. Б. Игнатьев. Лингвокомбинаторное моделирование плохо формализованных систем. Информационно-управляющие системы, 2003, №6, с. 34–37.
- С. А. Яновская. Методологические проблемы науки. М, 1972.
- П. Г. Суворова. Диалектика абстрактного и конкретного в понятии «архитектура ЭВМ». Сб. «Новые идеи в философии науки и научном познании». Под ред. Ю. И. Мирошникова. Екатеринбург, 2002.
- Т. Е. Аладова, М. Б. Игнатьев, Ю. Е. Шейнин. Распределенный монитор для отладки программного обеспечения мультипроцессорных систем. Микропроцессорные средства и системы, 1990, №5, с. 49–56.
- High Performance Cluster Computing: Architectures and Systems.
 Rajkumar Buyya (editor), ISBN 0–13–013784–7, Prentice Hall PTR, NJ, USA, 1999, v.1, 2.
Rajkumar Buyya (editor), ISBN 0–13–013784–7, Prentice Hall PTR, NJ, USA, 1999, v.1, 2. - Th. Sterling. The Future of Cluster Interconnects: Infiniband or Ethernet. A Beowulf Perspective. Panel Presentation at IEEE Cluster 2000 Conference.
- G. Bell, J. Gray. High Performance Computing: Crays, Clusters, and Centers. What Next? Microsoft Research, Technical Report MSR-TR-2001–76, 2001. 7 p.
- Ph. Buonadonna, A. Geweke, D. Culler. An Implementation and Analysis of the Virtual Interface Architecture. Proceedings of SC98, Orlando, Florida, November 1998. 9 p.
- S. Gorbachev, E. Gontcharova, M. Ignatiev, Y. E. Sheynin. Distributed High Performance Computing Over ATM Networks. In: Proceedings of the High Performance Computing (HPC ’98), ASTC’98 Conference, Boston, USA, April 1998, p. 216–221.
- М. Б. Игнатьев, Ю. Е. Шейнин. 25 лет со времени создания рекурсивной вычислительной машины высокой производительности и надежности и проблемы параллельных вычислений.
 Доклад на пленарном заседании 23-й международной конференции по школьной информатике и проблемам устойчивого развития, Санкт-Петербург, 16 апреля 2004 г.
Доклад на пленарном заседании 23-й международной конференции по школьной информатике и проблемам устойчивого развития, Санкт-Петербург, 16 апреля 2004 г. - G. G. Weigand. Petaflop II. The ASCI Challenge. Petaflops II. 2nd Conference on Enabling Technologies for Peta(fl)ops Computing. Santa Barbara, California, USA, February 1999.
- R. Stevens. Applications for PetaFLOPS. Petaflops II. 2nd Conference on Enabling Technologies for Peta(fl)ops Computing. Santa Barbara, California, USA, February 1999.
- J. Bashor. Researchers Achieve One Teraflop Performance With Supercomputer Simulation Of Magnetism. Berkeley Research News, 1998, November 9.
- W. E. Johnston. Real-Time Widely Distributed Instrumentation Systems. The Grid: Blueprint for a New Computing Infrastructure. Ed. by Ian Foster and Carl Kesselman. Morgan Kaufmann. Pubs. August 1998.
- W. E. Johnston e. a. High-Speed Distributed Data Handling for On-Line Instrumentation Systems. Proceedings of ACM/IEEE SC97: High Performance Networking and Computing.
 Nov., 1997.
Nov., 1997. - William E. Johnston e. a. High-Speed Distributed Data Handling for High-Energy and Nuclear Physics. Invited lecture (W. Johnston) at the 1997 CERN School of Computing, Pruhonice (Prague), Czech Republic. 17–30 August 1997. Published in the «Proceedings of the 1997 CERN School of Computing.» Also published in the proceedings of Computing in High Energy Physics, Berlin, Germany. April, 1997.
- W. Johnston e. a. Real-Time Generation and Cataloguing of Large Data-Objects in Widely Distributed Environments. International Journal of Digital Libraries May, 1998.
- D. H. Bailey. Petaflops Algorithms. Petaflops II. 2nd Conference on Enabling Technologies for Peta(fl)ops Computing. Santa Barbara, California, USA, February 1999.
- J. Choi. A New Parallel Matrix Multiplication Algorithm on Distributed-Memory Concurrent Computers. Center for Research on Parallel Computation, Rice University, September 1997, CRPC-TR97758, 19 р.
- Information Technology Research: Investing in Our Future.
 PITAC – Report to the President, February 24, 1999.
PITAC – Report to the President, February 24, 1999.
Статья опубликована 08.12.2005 г.
8. Рекурсивные функции
Рекурсивные функции очень хорошо иллюстрируют понятие алгоритма. Если рассуждать упрощенно, то для рекурсивной функции должен существовать алгоритм, вычисляющей ее значения. Вообще говоря, большая часть известных числовых функций являются рекурсивными.
Полезно вспомнить, как определяются Элементарные функции. Вначале рассматривается несколько классов функций: алгебраические, тригонометрические, показательные, логарифмические. Элементарная функция определяется как Суперпозиция (или сложная функция) этих функций.
Рекурсивные функции строятся аналогичным образом.
Обратите внимание, что все функции в данном параграфе определены на множестве . Если это необходимо, в обозначении функции верхний индекс указывает число переменных. Так, функция зависит от переменных. Таким образом, .
Рассмотрим вначале примитивно-рекурсивные функции.
Простейшие примитивно-рекурсивные функции Задаются следующим образом.
· Функция следования задается формулой: (или ).
· Функция аннулирования задается формулой: .
· Функция тождества определяется следующим образом: , то есть эта функция произвольному -мерному вектору сопоставляет его -ю координату.
Из простейших примитивно-рекурсивных функций можно получить примитивно-рекурсивные функции с помощью следующих двух операторов.
· Оператор суперпозиции. Пусть , , , …, – примитивно-рекурсивные функции. Тогда функция
Получена с помощью оператора суперпозиции.
Оператор суперпозиции – это оператор построения сложной функции. Если мы умеем вычислять функции , , …, и , то значения функции могут быть получены последовательным вычислением значений функций , , …, на некотором наборе значений переменных , и вычислением значения функции на наборе значений , , …,
Пример. Функция получается суперпозицией функций 0(X) и S(X): . Аналогичным образом можно получить функции вида для всех значений N.
Аналогичным образом можно получить функции вида для всех значений N.
· Оператор примитивной рекурсии из известных примитивно-рекурсивных функций и позволяет строить новую функцию . Так,
,
.
Тогда функция получена с помощью оператора примитивной рекурсии, что выражается обозначением .
Таким образом, сначала (при фиксированных значениях ) определяется значение функции при , а затем каждое следующее значение функции (зависящее от ) выражается через предыдущее значение (зависящее от ).
Пусть . Тогда функция есть постоянная. Обозначим ее следующим образом: . Функция зависит от двух переменных. Обозначим ее так: . Тогда
,
.
Для произвольного получаем (обозначения , , , …, вводятся в предположении, что набор фиксирован):
,
,
,
. . . . . . . . . . . . . . . . . .
.
. . . . . . . . . . . . . . . . . .
Пример. Даны функции и . Определим функцию , полученную из данных функций по схеме примитивной рекурсии.
Решение. Найдем значения функции .
,
;
;
.
Можно предположить, что .
Докажем последнюю формулу методом математической индукции по переменной .
1. Проверим формулу при .
, то есть при формула верна.
2. Допустим, что предположение индукции верно при , то есть, верна формула .
Докажем, что предположение индукции верно при , то есть, верна формула . Выразим с помощью схемы примитивной рекурсии.
.
Таким образом, на основании метода математической индукции формула доказана для всех .
Теперь строго определим примитивно-рекурсивные функции.
Определение. 1) Простейшие примитивно-рекурсивные функции примитивно-рекурсивны.
2) Примитивно-рекурсивными являются функции, полученные из примитивно-рекурсивных функций с помощью операторов суперпозиции и (или) примитивной рекурсии.
3) Функция является примитивно-рекурсивной тогда и только тогда, когда это следует из 1) и 2).
Пример. Покажем, что функция примитивно-рекурсивна.
Покажем, что функция примитивно-рекурсивна.
Доказательство. , , следовательно, функция должна зависеть от одной переменной, а функция – от трех. Пользуясь заданием функции, найдем ее значения:
.
То есть .
Таким образом, функция получена по схеме примитивной рекурсии () из примитивно-рекурсивных функций, следовательно, сама является примитивно-рекурсивной.
Примитивно-рекурсивными, в частности, являются следующие функции: , , , , , ,
Операция минимизации по -ой переменной функции обозначается следующим образом: , и определяется так.
Рассмотрим уравнение относительно :
. (1)
Это уравнение решается подбором, вместо переменной последовательно подставляются 0,1,2,… При этом возможны случаи.
· На некотором шаге левая часть соотношения (1) не определена. Следовательно, на наборе операция минимизации не определена.
· На каждом шаге левая часть соотношения (1) определена, но равенство не выполняется ни при каких значениях . Следовательно, на наборе операция минимизации не определена.
Следовательно, на наборе операция минимизации не определена.
· Левая часть соотношения (1) определена при , но при равенство не выполняется, а при выполняется. В этом случае число считается значением операции минимизации на наборе .
Пример. [13]. Найти функции, получаемые из данной числовой функции с помощью оператора минимизации по каждой ее переменной.
Решение. Минимизируем функцию по переменной . Рассмотрим уравнение
. (2)
1. Если , , то при подстановке получаем верное равенство.
2. Если , то левая часть равенства (2) не определена.
3. Если , , то при подстановке в левой части равенства (2) появляется выражение , не имеющее смысла, и в этом случае операция минимизации не определена.
4. Если , то получаем равенство . Оно имеет смысл при , то есть , что рассмотрено в первом пункте, и при , то есть . При равенство не имеет смысла.
Таким образом,
Минимизируем функцию по переменной . Рассмотрим уравнение
.
Это уравнение на самом первом шаге, при подстановке вместо нуля теряет смысл, значит, операция минимизации по второй переменной нигде не определена.
Минимизируем функцию по переменной . Рассмотрим уравнение
. (3)
Если левая часть соотношения (3) имеет смысл и равенство (3) выполнено, то оно выполнено и при подстановке в это соотношение переменной на первом шаге, то есть при . В остальных случаях значение операции минимизации не определено.
Определение. Частично-рекурсивной функцией называется числовая функция, получаемая за конечное число шагов из простейших примитивно-рекурсивных функций с помощью операторов суперпозиции, примитивной рекурсии и минимизации.
Определение. Числовая функция называется Общерекурсивной, если она частично-рекурсивна и всюду определена.
Определение. Функция называется Эффективно вычислимой, если существует алгоритм, позволяющий вычислить ее значения.
В данном определении алгоритм понимается в интуитивном значении, следовательно, интуитивным является и понятие эффективно вычислимой функции.
Имеет место следующий тезис.
Тезис Черча. Каждая интуитивно вычислимая функция является частично-рекурсивной.
Тезис является недоказуемым, так как он связывает нестрогое понятие интуитивно вычислимой функции и строгое математическое понятие частично-рекурсивной функции.
Тезис может быть опровергнут построением примера интуитивно вычислимой, но не частично-рекурсивной функции.
| < Предыдущая | Следующая > |
|---|
Рекурсия в Python
Сумма чисел от 1 до n
Если бы я хотел узнать сумму чисел от 1 до n, где n — натуральное число, я мог бы посчитать вручную 1 + 2 + 3 + 4 + … + (несколько часов спустя) + n. А можно просто написать цикл for:
n = 0
for i in range (1, n+1):
n += iИли использовать рекурсию:
def recursion(n): if n == 1: return 1 return n + recursion(n - 1)
У рекурсии есть несколько преимуществ в сравнении с первыми двумя методами. Рекурсия занимает меньше времени, чем выписывание 1 + 2 + 3 на сумму от 1 до 3.
Рекурсия занимает меньше времени, чем выписывание 1 + 2 + 3 на сумму от 1 до 3.
Для recusion(4) рекурсия может работать в обратную сторону:
Вызов функций: (4 -> 4 + 3 -> 4 + 3 + 2 -> 4 + 3 + 2 + 1 -> 10)
Принимая во внимание, что цикл [for] работает строго вперед: (1 -> 1 + 2 -> 1 + 2 + 3 -> 1 + 2 + 3 + 4 -> 10). Иногда рекурсивное решение проще, чем итеративное решение. Это очевидно при реализации обращения связанного списка.
Как и когда происходит рекурсия
Рекурсия появляется когда вызов функции повторно вызывает ту же функцию до завершения первоначального вызова функции. Например, рассмотрим известное математическое выражение x! (т.е. факториал). Факториал определяется для всех неотрицательных целых чисел следующим образом:
Если число равно 0, то будет 1.
В противном случае ответом будет то, что число умножается на факториал на единицу меньше этого числа.
В Python наивная реализация факториала может быть определена как функция следующим образом:
def factorial(n): if n == 0: return 1 else: return n * factorial(n - 1)
Иногда функции рекурсии трудно понять, поэтому давайте рассмотрим поэтапно.
Рассмотрим выражение factorial(3). Эта и все остальные вызовы функций создают новую среду. Среда представляет собой таблицу, которая сопоставляет идентификаторы (например, n, factorial, print и т.д.) с их соответствующими значениями.
В любой момент времени вы можете получить доступ к текущей среде с помощью locals(). В первом вызове функции единственная локальная переменная, которая определяется n = 3.Поэтому locals() будет показывать {"n": 3}. Так как n == 3, возвращаемое значение становится n * factorial(n - 1).
На следующем этапе ситуация может немного запутаться. Глядя на наше новое выражение, мы уже знаем, что такое n. Однако мы еще не знаем, что такое factorial(n - 1).
Во-первых, n - 1 принимает значение 2.Затем 2 передаётся factorial как значение для n. Поскольку это новый вызов функции, создаётся вторая среда для хранения нового n.
Пусть A — первое окружение, а B — второе окружение. A всё ещё существует и равен {"n": 3} , однако B (что равно {"n": 2}) является текущей средой. Если посмотреть на тело функции, возвращаемое значение, опять же, n * factorial(n - 1).
Не определяя это выражение, заменим его на исходное выражение return. Делая это, мы мысленно отбрасываем B, поэтому не забудьте заменить n соответственно (т.е. ссылки на B n заменены на n - 1) который использует A n ). Теперь исходное обратное выражение становится n * ((n - 1) * factorial((n - 1) - 1)). Подумайте, почему так?
Теперь давайте определим factorial((n - 1) - 1)). Так как A n == 3, мы пропускаем 1 через factorial. Поэтому мы создаем новую среду C, которая равна {"n": 1}. Мы снова возвращаем значение n * factorial(n - 1). Итак, заменим исходный
Итак, заменим исходный factorial((n - 1) - 1)) выражения return аналогично тому, как раньше мы скорректировали исходное выражение return. Исходное выражение теперь n * ((n - 1) * ((n - 2) * factorial((n - 2) - 1))).
Почти закончили. Теперь нам нужно оценить factorial((n - 2) - 1). На этот раз мы пропустим через 0. Следовательно, должно получиться 1.
Теперь давайте проведём нашу последнюю замену. Исходное выражение return теперь n * ((n - 1) * ((n - 2) * 1)). Напомню, что исходное выражение возврата оценивается под A , выражение становится 3 * ((3 - 1) * ((3 - 2) * 1)). Здесь получается 6.
Чтобы убедиться, что это правильный ответ, вспомните, что 3! == 3 * 2 * 1 == 6. Прежде чем читать дальше, убедитесь, что вы полностью понимаете концепцию среды и то, как они применяются к рекурсии.
Утверждение, if n == 0: return 1, называется базовым случаем. Потому что это не рекурсия. Базовый случай необходим, без него вы столкнетесь с бесконечной рекурсией. С учетом сказанного, если у вас есть хотя бы один базовый случай, у вас может быть столько случаев, сколько вы хотите. Например, можно записать факториал таким образом:
Базовый случай необходим, без него вы столкнетесь с бесконечной рекурсией. С учетом сказанного, если у вас есть хотя бы один базовый случай, у вас может быть столько случаев, сколько вы хотите. Например, можно записать факториал таким образом:
def factorial(n):
if n == 0:
return 1
elif n == 1:
return 1
else:
return n * factorial(n - 1)У вас может также быть несколько случаев рекурсии, но мы не будем вдаваться в подробности, потому что это редкий случай, и его трудно мысленно обрабатывать.
Вы также можете иметь «параллельные» рекурсивные вызовы функций. Например, рассмотрим последовательность Фибоначчи, которая определяется следующим образом:
- Если число равно 0, то ответ равен 0.
- Если число равно 1, то ответ равен 1.
В противном случае ответ представляет собой сумму двух предыдущих чисел Фибоначчи.
Мы можем определить это следующим образом:
def fib(n):
if n == 0 or n == 1:
return n
else:
return fib(n - 2) + fib(n - 1)
Я не буду разбирать эту функцию также тщательно, как и с factorial(3), но окончательное значение возврата fib(5) эквивалентно следующему (синтаксически недействительному) выражению:
(
fib((n - 2) - 2)
+
(
fib(((n - 2) - 1) - 2)
+
fib(((n - 2) - 1) - 1)
)
)
+
(
(
fib(((n - 1) - 2) - 2)
+
fib(((n - 1) - 2) - 1)
)
+
(
fib(((n - 1) - 1) - 2)
+
(
fib((((n - 1) - 1) - 1) - 2)
+
fib((((n - 1) - 1) - 1) - 1)
)
)
)Решением (1 + (0 + 1)) + ((0 + 1) + (1 + (0 + 1))) будет 5.
Теперь давайте рассмотрим еще несколько терминов:
Tail call — это просто вызов рекурсивной функции, который является последней операцией и должна быть выполнена перед возвратом значения. Чтобы было понятно, return foo(n - 1) — это хвост вызова, но return foo(n - 1) + 1 не является (поскольку операция сложения будет последней операцией).
Оптимизация хвоста вызова (TCO или tail cost optimization) — это способ автоматического сокращения рекурсии в рекурсивных функциях.
Устранение хвоста вызова (TCE или tail cost elimination) — это сокращение хвостового вызова до выражения, которое может быть оценено без рекурсии. TCE — это тип TCO.
Оптимизация хвоста вызова может пригодиться по нескольким причинам:
Интерпретатор может снизить объём памяти, занятый средами. Поскольку ни у кого нет неограниченной памяти, чрезмерные рекурсивные вызовы функций приведут к переполнению стека.
Интерпретатор может уменьшить количество переключателей кадров стека.
В Python нет TCO по нескольким причинам, поэтому для обхода этого ограничения можно использовать другие методы. Выбор используемого метода зависит от варианта использования. Интуитивно понятно, что factorial и fib можно относительно легко преобразовать в итеративный код следующим образом:
def factorial(n):
product = 1
while n > 1:
product *= n
n -= 1
return product
def fib(n):
a, b = 0, 1
while n > 0:
a, b = b, a + b
n -= 1
return aОбычно это самый эффективный способ устранения рекурсии вручную, но для более сложных функций может быть трудно.
Другим полезным инструментом является декодер lru_cache, который можно использовать для уменьшения количества лишних вычислений.
Теперь вы знаете, как избежать рекурсии в Python, но когда её нужно использовать? Ответ «не часто». Все рекурсивные функции могут быть реализованы итеративно. Это просто вопрос, как именно сделать. Однако есть редкие случаи, когда можно использовать рекурсию. Рекурсия распространена в Python, когда ожидаемые вводы не вызовут значительного количества вызовов рекурсивных функций.
Однако есть редкие случаи, когда можно использовать рекурсию. Рекурсия распространена в Python, когда ожидаемые вводы не вызовут значительного количества вызовов рекурсивных функций.
Если вы интересуетесь рекурсией, стоит изучить функциональные языки, такие как Scheme или Haskell. На таких языках рекурсия намного полезней.
Хотя приведённый выше пример последовательности Фибоначчи, хорошо показывает, как применять определение в python и позже использовать кэш lru, при этом он имеет неэффективное время работы, из-за того, что выполняет 2 рекурсивных вызова. Количество вызовов функции растет экспоненциально до n.
В таком случае лучше использовать линейную рекурсию:
def fib(n):
if n <= 1:
return (n,0)
else:
(a, b) = fib(n - 1)
return (a + b, a)Но у этого примера есть проблема в возвращении пары числе вместо одного. Это показывает, что не всегда стоит использовать рекурсию.
Исследование дерева с рекурсией
Допустим, у нас есть такое дерево:
root
- A
- AA
- AB
- B
- BA
- BB
- BBAЕсли мы хотим перечислить все имена элементов, мы можем сделать это с помощью простого цикла for. У нас есть функция
У нас есть функция get_name(), которая возвращает строку с именем узла, функция get_children(), которая возвращает список всех подузлов данного узла в дереве, и функция get_root() для получить корневой узел.
root = get_root(tree)
for node in get_children(root):
print(get_name(node))
for child in get_children(node):
print(get_name(child))
for grand_child in get_children(child):
print(get_name(grand_child))
# Выводит: A, AA, AB, B, BA, BB, BBAЭтот код работает хорошо и быстро, но что если под-узлы получили свои под-узлы? И эти под-узлы могут иметь больше под-узлов … Что если вы не знаете заранее, сколько их будет? Решением этой проблемы будет использование рекурсии.
def list_tree_names(node):
for child in get_children(node):
print(get_name(child))
list_tree_names(node=child)
list_tree_names(node=get_root(tree))
# Выводит: A, AA, AB, B, BA, BB, BBA
Возможно, вы не хотите вывести, а вернуть список всех имён узлов. Это можно сделать с помощью передачи прокручиваемого списка в качестве параметра.
Это можно сделать с помощью передачи прокручиваемого списка в качестве параметра.
def list_tree_names(node, lst=[]):
for child in get_children(node):
lst.append(get_name(child))
list_tree_names(node=child, lst=lst)
return lst
list_tree_names(node=get_root(tree))
# returns ['A', 'AA', 'AB', 'B', 'BA', 'BB', 'BBA']Увеличение максимальной глубины рекурсии
Существует предел глубины возможной рекурсии, который зависит от реализации Python. Когда предел достигнут, возникает исключение RuntimeError:
RuntimeError: Maximum Recursion Depth Exceeded
Пример программы, которая может вызвать такую ошибку:
def cursing(depth):
try:
cursing(depth + 1) # actually, re-cursing
except RuntimeError as RE:
print('I recursed {} times!'.format(depth))
cursing(0)
# Out: I recursed 1083 times!Можно изменить предел глубины рекурсии с помощью
sys.setrecursionlimit(limit)
Чтобы проверить текущие параметры лимита, нужно запустить:
sys.getrecursionlimit()
Если запустить тот же метод выше с новым пределом, мы получаем
sys.setrecursionlimit(2000) cursing(0) # Out: I recursed 1997 times!
В Python 3.5 ошибка стала называться RecursionError, которая является производной от RuntimeError.
Хвостовая рекурсия — как не надо делать
Хвостовая рекурсия — частный случай рекурсии, при котором любой рекурсивный вызов является последней операцией перед возвратом из функции.
Вот пример обратного отсчета, написанного с использованием хвостовой рекурсии:
def countdown(n):
if n == 0:
print("Blastoff!")
else:
print(n)
countdown(n-1)
Любое вычисление, которое может быть выполнено с использованием итерации, также может быть выполнено с использованием рекурсии. Вот версия find_max, написанная с использованием хвостовой рекурсии:
def find_max(seq, max_so_far):
if not seq:
return max_so_far
if max_so_far < seq[0]:
return find_max(seq[1:], seq[0])
else:
return find_max(seq[1:], max_so_far)
Хвостовую рекурсию лучше не использовать, поскольку компилятор Python не обрабатывает оптимизацию для хвостовых рекурсивных вызовов. В таких случаях рекурсивное решение использует больше системных ресурсов, чем итеративное.
В таких случаях рекурсивное решение использует больше системных ресурсов, чем итеративное.
Оптимизация хвостовой рекурсии с помощью интроспекции стека
По умолчанию рекурсивный стек Python не превышает 1000 кадров. Это ограничение можно изменить, установив sys.setrecursionlimit(15000) который быстрее, однако этот метод потребляет больше памяти. Вместо этого мы также можем решить проблему рекурсии хвоста, используя интроспекцию стека.
#!/usr/bin/env python2.4
# Эта программа показыает работу декоратора, который производит оптимизацию хвостового вызова. Он делает это, вызывая исключение, если оно является его прародителем, и перехватывает исключения, чтобы вызвать стек.
import sys
class TailRecurseException:
def __init__(self, args, kwargs):
self.args = args
self.kwargs = kwargs
# Эта программа показыает работу декоратора, который производит
# оптимизацию хвостового вызова. Он делает это, вызывая исключение, если
# оно является его прародителем, и перехватывает исключения, чтобы
# подделать оптимизацию хвоста Эта функция не работает, если функция
# декоратора возвращается без хвоста. def tail_call_optimized(g):
def func(*args, **kwargs):
f = sys._getframe()
if f.f_back and f.f_back.f_back \
and f.f_back.f_back.f_code == f.f_code:
raise TailRecurseException(args, kwargs)
else:
while 1:
try:
return g(*args, **kwargs)
except TailRecurseException as e:
args = e.args
kwargs = e.kwargs
func.__doc__ = g.__doc__
return func
def tail_call_optimized(g):
def func(*args, **kwargs):
f = sys._getframe()
if f.f_back and f.f_back.f_back \
and f.f_back.f_back.f_code == f.f_code:
raise TailRecurseException(args, kwargs)
else:
while 1:
try:
return g(*args, **kwargs)
except TailRecurseException as e:
args = e.args
kwargs = e.kwargs
func.__doc__ = g.__doc__
return funcЧтобы оптимизировать рекурсивные функции, мы можем использовать декоратор @tail_call_optimized для вызова нашей функции. Вот несколько примеров общей рекурсии с использованием декоратора, описанного выше:
Факториальный пример:
# "calculate a factorial"
@tail_call_optimized
def factorial(n, acc=1):
if n == 0:
return acc
return factorial(n-1, n*acc)
print(factorial(10000))
# печатает очень большое число
# и не достигает лимита рекурсии.
Пример Фибоначчи:
@tail_call_optimized
def fib(i, current = 0, next = 1):
if i == 0:
return current
else:
return fib(i - 1, next, current + next)
print(fib(10000))
# также выводит большое число,
# но не доходит до лимита рекурсииЧтобы выйти из рекурсии, нужно ввести команду stopCondition.
Исходная переменная должна быть передана рекурсивной функции, чтобы сохранить её.
Рекурсивный подход — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Рекурсивный подход обычно предпочитается итеративному в тех случаях, когда рекурсия более естественно отражает математическую сторону задачи и приводит к программе, которая проще для понимания и отладки. Другой причиной для выбора рекурсивного решения является то, что итеративное решение может не быть очевидным. [1]
Рекурсивный подход полезен прежде всего для алгоритмов на графах ( см. разд. [2]
Обычно рекурсивный подход предпочитают итеративному, если он более естественно отражает задачу и ее результаты, то есть более нагляден и легче отлаживается. Другая причина предпочтения рекурсивного решения состоит в том, что итеративное решение может не быть очевидным. [3]
Используя рекурсивный подход, аналогичный программе 13. 6, реализуйте операции construct, search и insert для таблиц символов, в основе которых лежат структуры данных в виде сбалансированных по высоте ( AVL) деревьев.
[4]
6, реализуйте операции construct, search и insert для таблиц символов, в основе которых лежат структуры данных в виде сбалансированных по высоте ( AVL) деревьев.
[4]
Используя RB-представление и рекурсивный подход, аналогичный программе 13.6, реализуйте операции construct, search и insert для таблиц символов, в основе которых лежат структуры данных в виде восходящих сбалансированных 2 — 3-де-ревьев. [5]
Используя RB-представление и рекурсивный подход, аналогичный программе 13.6, реализуйте операции construct, search и insert для таблиц символов, в основе которых лежат структуры данных в виде восходящих сбалансированных 2 — 3 — 4-деревьев. Совет: код может выглядеть аналогично программе 13.6, но должен выполнять операции в другом порядке. [6]
Используя RB — представление и рекурсивный подход, аналогичный программе ] 3.6, ревизуйте операции construct t № urch к / iufrt ии та & шц t и мнило в, ь основе которых лежат структуры данных ь виде вое ходя а дик сбгизнснршнишмк деревьев, С и: кат может ьыглддеть анпогичтю программе 13, ft, nn выполнять операции в другом порядке. [7]
[7]
Некоторые неприятности могут поджидать любителей рекурсивного подхода к написанию функции. Возможны, в принципе, ситуации, когда рекурсивные вызовы переполнят внутренний стек данных сопроцессора, рассчитанный на восемь уровней рекурсии, и возникнет сбой программы. [8]
Решение не всякой проблемы выигрывает от использования рекурсивного подхода, а порой и невозможно применить рекурсию. Однако если Вы в состоянии управлять списком LIFO в любом виде, то Ваша задача по существу является рекурсивной. Даже в том случае, когда рекурсия невозможна, целесообразно выполнить первоначальный вариант в виде рекурсивной программы, затем отбросить рекурсию, моделируя LIFO-память с помощью Ваших собственных связанных списков или индексированных структур данных. Полученная в результате программа будет гораздо яснее и проще для понимания, чем в случае ее разработки с пустого места. [9]
Программа, иллюстрирующая области действия ( часть 2 из 2. [10]
[10] |
Сначала мы рассмотрим рекурсию обобщенно, а затем исследуем несколько программ, содержащих рекурсивные функции. Рекурсивные подходы к решению задач имеют ряд общих элементов. Для решения задачи вызывается рекурсивная функция. Фактически функция знает решение только простейшего случая ( случаев), или так называемого основного случая. Если функция вызывается для решения основного случая, то она просто возвращает результат. Если функция вызывается для решения более сложной проблемы, функция делит задачу на две обобщенных части: часть, для которой функция имеет способ решения, и часть, для которой функция решения не имеет. Чтобы сделать рекурсию возможной, последняя часть должна быть похожа на первоначальную задачу, но она должна быть более простым, или редуцированным ее вариантом. Поскольку эта новая задача похожа на первоначальную, функция запускает ( вызывает) свою новую копию, чтобы продолжить решение меньшей задачи. Этот процесс называется рекурсивным вызовом или шагом рекурсии.
[11]
Этот процесс называется рекурсивным вызовом или шагом рекурсии.
[11]
Эту программу было бы трудно понять без двух уровней абстракции, разработанных для ее реализации. Несложно убедиться, что рекурсивный подход реализует ротации, изображенные на рис. 13.17; затем можно убедиться, что программа реализует высокоуровневый алгоритм в 2 — 3 — 4-деревьях — разделяет 4-узлы на пути вниз по дереву, а затем вставляет новый элемент в 2 — или 3-узел в месте завершения пути поиска в нижней части дерева. [12]
Лисп входит в число наиболее значимых и долговечных языков программирования. Его влияние на исследования в области искусственного интеллекта и технологии знаний особенно проявилось в интерактивном программировании, методах функционального программирования, в распространении в программировании идей рекурсивного подхода, а также в том, что многие идеи в последствии были включены Китайский в более новые языки программирования. [13]
Страницы: 1
Рекурсивная модель — Энциклопедия по экономике
Пример рекурсивной модели [c. 300]
300]Независимо от того, хотим ли мы оценить одно из уравнений системы или же намерены оценить каждое уравнение модели, мы оказываемся в ситуации, когда ни обыкновенный метод наименьших квадратов, ни его модификации, рассмотренные в главах о модели, состоящей из одного уравнения, в общем случае не обеспечивают удовлетворительную процедуру оценивания. Если обыкновенный метод наименьших квадратов применяется к уравнению модели, в которое обычно будут входить несколько текущих значений эндогенных переменных, то придется одну из них выбрать в качестве зависимой переменной для данного уравнения. Тогда оставшиеся (одно или несколько) текущие значения эндогенных переменных, участвующие в этом соотношении, будут, вообще говоря, коррелировать с возмущающим воздействием и поэтому оценки, найденные обыкновенным методом наименьших квадратов, окажутся смещенными и несостоятельными. Только в случае рекурсивных моделей обыкновенный метод наименьших квадратов, как мы увидим в параграфе 13.1, дает нам оптимальный способ оценивания. [c.375]
[c.375]
Мы уже знаем, что трудности при оценивании систем одновременных уравнений возникают из-за корреляции между возмущениями и эндогенными переменными и поэтому нам теперь необходимо убедиться в том, что специальные свойства рекурсивной модели позволяют эти трудности преодолеть. [c.376]
X2. таблица 431 Распределенный лаг 292 Регрессия трех переменных 63 Рекурсивные модели 375 [c.441]
Большинство используемых финансовых моделей имеют рекурсивный и/или параллельный характер. Рекурсивность означает, что для решения очередного уравнения в его правую часть вместо переменной подставляется предыдущее уравнение, решенное относительно этой переменной, и т. д. [c.300]
Рекурсивными являются модели, в которых неправильные конфигурации повторяются при [c.44]
Если из модели исключить тождество дохода, число предопределенных переменных модели уменьшится на 1 (из модели будет исключена переменная G,). Число эндогенных переменных модели также снизится на единицу — переменная Y, станет экзогенной. В правых частях функции потребления и функции денежного рынка будут находиться только предопределенные переменные. Функция инвестиций постулирует зависимость эндогенной переменной I, от эндогенной переменной г, (которая зависит только от предопределенных переменных) и предопределенной переменной /,.]. Таким образом, мы получим рекурсивную систему. Ее параметры можно оценивать обычным МНК, и нет необходимости исследования системы уравнения на идентификацию.
[c.121]
В правых частях функции потребления и функции денежного рынка будут находиться только предопределенные переменные. Функция инвестиций постулирует зависимость эндогенной переменной I, от эндогенной переменной г, (которая зависит только от предопределенных переменных) и предопределенной переменной /,.]. Таким образом, мы получим рекурсивную систему. Ее параметры можно оценивать обычным МНК, и нет необходимости исследования системы уравнения на идентификацию.
[c.121]
Однако если зависимая переменная у одного уравнения выступает в виде фактора х в другом уравнении, то исследователь может строить модель в виде системы рекурсивных уравнений [c.179]
Как уже отмечалось, не все эконометрические модели имеют вид системы одновременных уравнений. Так, широкий класс функций спроса на ряд потребительских товаров часто представляет собой рекурсивную систему, в которой с уравнениями можно работать последовательно и проблемы одновременного оценивания не возникают. [c.212]
Здесь j указывает на объясняющую переменную, связь которой с объясняемой переменной / раскрывается в структурной модели, к пробегает по подмножеству всех переменных, непосредственно влияющих на j-ю переменную (на графе эти вершины связаны с вершиной / дугами). Соотношение (4.20) справедливо для любой рекурсивной системы.
[c.221]
Соотношение (4.20) справедливо для любой рекурсивной системы.
[c.221]
Формальное содержание этого подхода заключается в гипотезе о полностью специфицированной линейной рекурсивной причинной модели, оценке ее параметров, а затем использовании этих значений для воспроизведения эмпирической корреляционной матрицы. Основная идея процедуры — это положение о том, что модель, которая не воспроизводит эмпирических корреляций, должна быть отвергнута. [c.222]
Второй ситуацией является случай с неизвестным каузальным приоритетом среди переменных. Допустим, что мы имеем набор переменных, для которых не известен каузальный порядок причина-следствие, и имеются две гипотезы, каждая по-своему устанавливающая его, постулируя отсутствие тех или иных возможных отношений. Описываемый подход может быть применен как для сравнения этих теорий, так и для их отбрасывания. Заметим, что в процедуре сравнения одна модель-гипотеза может оказаться лучше другой, но никогда — правильной. Более того, если одна из гипотез близка к тому, чтобы описываться полной рекурсивной системой, то обычно она работает, лучше воспроизводя корреляционную матрицу, и, естественно, будет выбираться как более удачная, даже если она весьма далека от истины. [c.223]
[c.223]
Модель включает как рекурсивные, так и одновременно решаемые уравнения, причем наличие последних позволяет учесть и некоторые обратные связи процесса энергопотребления. Это делает модель адекватной реальным взаимосвязям, что, в свою очередь, повышает надежность и достоверность прогнозных расчетов. [c.201]
Необходимость рассматривать системы, отличные от рекурсивных, возникает в связи с тем, что исследователь обычно располагает некоторыми усредненными (агрегированными) данными. Например, данные о рыночной конъюнктуре могут быть усреднены по недельным или месячным периодам. Предположим, что известны величины Pt — средняя цена за неделю t и Qt — средний объем ежедневных продаж за неделю /. Если считать время реакции рынка, как и раньше, равным одному дню, то соотношение Pt = a0 + a j. + UL вряд ли можно признать разумным. В этой ситуации рассмотренная в 14.1 модель представляется более естественной. [c.414]
МОДЕЛЬ РЕКУРСИВНАЯ — одна из эконометрических моделей, в которой причинно-следственные связи эндогенных переменных находятся в строгой односторонней последовательности. В данной модели матрица параметров представлена в виде треугольника, а отклонения случайных величин не находятся в прямой или обратной корреляции.
[c.385]
В данной модели матрица параметров представлена в виде треугольника, а отклонения случайных величин не находятся в прямой или обратной корреляции.
[c.385]
Это модель, в которой текущие значения одного множества переменных определяют текущие значения первого. Простейший пример модели рекурсивной имеет следующий вид [c.385]
Одним из случаев успешного применения МНК для оценки структурных коэффициентов модели является его использование для рекурсивных (треугольных) моделей. В этих моделях эндогенные переменные последовательно (рекурсивно) связаны друг с другом. А именно, первая эндогенная переменная YI зависит лишь от экзогенных переменных Хь i = 1, 2,. .., m и случайного отклонения Si. Вторая эндогенная переменная Y2 определяется лишь значениями экзогенных переменных Х i = 1, 2,. .., m случайным отклонением 82, а также эндогенной переменной YI. Третья эндогенная переменная Y3 зависит от тех же переменных, что и Y2, случайного отклонения з, а также от предыдущих эндогенных переменных (Yi, Y2) и т. д.
[c.326]
д.
[c.326]
Рекурсивность функции оптимизации. В результате анализа было выявлено, что модель оптимизации ассортимента, как правило, предполагает с учетом ограничений увеличить долю той продукции, которая имеет наибольшую маржинальную рентабельность или какой-либо коэффициент перспективности или привлекательности, и на этом оптимизационные расчеты заканчиваются. Однако увеличение объема реализации требует либо снижения цены, либо увеличения затрат на продвижение. Поэтому, вполне возможно, стремление увеличить объем реализации будет сопровождаться снижением рентабельности, что в свою очередь может потребовать пересмотра оптимальной структуры. Поскольку обычно в оптимизационную модель не закладываются затраты на достижение определенного уровня рентабельности, объема реализации (так как неизвестно, каким будет этот оптимальный объем реализации), то расчетный теоретический уровень прибыли является на практике не достижимым при существенных расчетных изменениях структуры ассортимента. Разрешение данного противоречия следует проводить путем имитации возможных затрат на достижение определенного объема реализации продукции.
[c.39]
Разрешение данного противоречия следует проводить путем имитации возможных затрат на достижение определенного объема реализации продукции.
[c.39]
Раздумывая над этими рекурсивными моделями, заливами внутри заливов, Мандельброт назвал этот феномен «фрактально-стью». Что интересно в отношении фракталов, так это то, что они показывают, что система может постоянно повторять свои модели в различных масштабах или шкалах. Другими словами, является самомоделируемой. [c.62]
Рекурсивная модель (re ursive model) — динамическая модель, обладающая математическим свойством рекурсии, т. е. если даны, например, все переменные модели до момента (t— 1), то модель обеспечивает и получение одного за другим значений переменных для t, по ним для (t+1) и т. д. — Прим. научи, ред. [c.62]
Для предсказания волатильности при помощи GAR H можно использовать рекурсивную модель следующего вида [c.361]
Величины Ut и Vt обозначают накопленные за неделю возмущения. Без введения дополнительных переменных эта модель оказывается теперь даже неидентифицируемой, однако если бы идентифицирующие ее переменные и существовали, то мы убедились бы, что в общем случае вынужденное агрегирование по временнь ш периодам может превратить чисто рекурсивную модель в полностью одновременную со всеми вытекающими отсюда проблемами ее оценивания. [c.379]
[c.379]
Рассмотрим подразделение hevrolet. Система I может включать различные производственные цехи. Система II будет координировать взаимодействие производственных цехов, система III — размещать инвестиции на модернизацию различных цехов. Система IV будет рассматривать вопрос о том, нужны ли новые производственные методы или модели. Система V будет решать, когда вводить новые модели или производственные методы. Рекурсивные уровни опускаются вниз до определенного уровня в зависимости от того, что предпочтет индивид, который должен выполнять поставленные задачи (системы I, II и III), — поменять работу или получить новые знания (системы IV и V). [c.302]
Фрактальная геометрия, она же — рекурсивная геометрия — геометрия динамических форм, моделей, которые обладают математическим свойством рекурсии. Это значит, что если даны, например, все переменные модели до момента (t-1), то модель обеспечивает и получение одного за другим значений переменных для t, по ним — для (t+1) и тд. Вообще, рекурсия (re urren e) — в общем смысле вычисление функции по определенному алгоритму. Примерами таких алгоритмов являются рекуррентные формулы, выводящие вычисления заданного члена последовательности (чаще всего числовой) из вычисления нескольких предыдущих ее членов. Например, если X1=2,Xk+1=2Xk+2, то задана числовая последовательность 2,4,10,22…
[c.3]
Вообще, рекурсия (re urren e) — в общем смысле вычисление функции по определенному алгоритму. Примерами таких алгоритмов являются рекуррентные формулы, выводящие вычисления заданного члена последовательности (чаще всего числовой) из вычисления нескольких предыдущих ее членов. Например, если X1=2,Xk+1=2Xk+2, то задана числовая последовательность 2,4,10,22…
[c.3]
На основании собственного опыта я разработал довольно интересную гипотезу о фондовых рынках я постулировал, что фондовый рынок при адаптации теории научного метода Поппера действует во многом так же, как и я, с той лишь разницей, что он не знает, что так поступает. Другими словами, он выбирает некий тезис и проверяет его когда он оказывается ошибочным, как это обычно и бывает, он проверяет другой тезис. Это и вызывает колебания на рынке. Такой процесс происходит на разных уровнях, а получаемые модели являются рекурсивными, как и фракталы Мандельброта10. [c.44]
И последнее модель может быть включена в качестве составной части в многосетевую среду принятия решений, а полученная общая производительность — измеряться, исходя из заданного решающего правила (см. [290]). Наконец, более динамичные подходы можно получить, используя рекурсивные сети с механизмами обратной связи.
[c.227]
[290]). Наконец, более динамичные подходы можно получить, используя рекурсивные сети с механизмами обратной связи.
[c.227]
Для формальной верификации гипотез необходимо соответствие между графом и системой уравнений, его описывающей. Алгебраическая система, соответствующая графу без контуров (петель), является рекурсивной системой, позволяющей рекур-рентно определять значения входящих в нее переменных. В такой системе в уравнения для признака xt включаются все переменные, за исключением расположенных выше его по графу связей. Формулировка гипотез в структуре рекуррентной модели обычно не вызывает затруднений при использовании данных в динамике. Если же анализируются статистические данные, то следует учитывать зависимость системы от ее прошлых состояний. [c.213]
Паутинообразная модель ( obweb) в теории цены является рекурсивной. [c.425]
СВЯЗИ В СИСТЕМЕ. Определений термина связь — десятки. Самое общее таково это то, что объединяет элементы системы в одно целое. Связи между элементами системы могут быть жесткими (таковы они обычно в технике) и гибкими, изменяющя-мися в процессе функционирования системы, — таковы они в экономике, в живых существах, в обществе. С точки зрения кибернетики связь— это процесс обмена информацией, который регулирует поведение систем (т. е. управляет ими). Наиболее важными считаются следующие виды связей обратные, рекурсивные, синерги-ческие (т. е. усиливающие) и циклические. В экономико-математической модели они выражаются через уравнения связи или неравенства связи
[c.51]
Связи между элементами системы могут быть жесткими (таковы они обычно в технике) и гибкими, изменяющя-мися в процессе функционирования системы, — таковы они в экономике, в живых существах, в обществе. С точки зрения кибернетики связь— это процесс обмена информацией, который регулирует поведение систем (т. е. управляет ими). Наиболее важными считаются следующие виды связей обратные, рекурсивные, синерги-ческие (т. е. усиливающие) и циклические. В экономико-математической модели они выражаются через уравнения связи или неравенства связи
[c.51]
Вместе с тем учтённый в модели Леонтьева принцип формирования цен мирового рынка в какой-то мере отражает процессы, происходящие в реальности. Вопрос в том, как относиться к этим процессам считать ли их естественными и заслуживающими дальнейшего распространения или, наоборот, противодействующими прогрессу и требующи.ми замены. Ответ может быть получен при изучении свойств динамич. рекурсивно-балансовой модели, требующей изменяющихся цен. Они вводятся в такие модели как оценки баланса прошлого года. Если бы в проекте Будущее мировой экономики была осуществлена динамизация модели, то использованный метод определения цен привёл бы к реализации долгосрочной стратегии развития, основанной на принципе сравнительных издержек. Выигрыш от такой стратегии получает сильнейший из внешнеторговых партнёров, поскольку остальные деформируют структуру своего х-ва в соответствии с его интересами. При введении оптимизации в долгосрочные модели, опирающиеся на межотраслевой баланс, стратегия сравнительных издержек, в силу к-рой каждый регион должен специализироваться на том, что он умеет производить лучше в данный момент, становится господствующей, а возможности выбора иной стратегии долгосрочного развития практически исключаются. Проекция подобного подхода на региональную структуру способ-па породить лишь наиболее нереалистич. рекомендации по размещению нроиз-ва и разделению труда между
[c.616]
Они вводятся в такие модели как оценки баланса прошлого года. Если бы в проекте Будущее мировой экономики была осуществлена динамизация модели, то использованный метод определения цен привёл бы к реализации долгосрочной стратегии развития, основанной на принципе сравнительных издержек. Выигрыш от такой стратегии получает сильнейший из внешнеторговых партнёров, поскольку остальные деформируют структуру своего х-ва в соответствии с его интересами. При введении оптимизации в долгосрочные модели, опирающиеся на межотраслевой баланс, стратегия сравнительных издержек, в силу к-рой каждый регион должен специализироваться на том, что он умеет производить лучше в данный момент, становится господствующей, а возможности выбора иной стратегии долгосрочного развития практически исключаются. Проекция подобного подхода на региональную структуру способ-па породить лишь наиболее нереалистич. рекомендации по размещению нроиз-ва и разделению труда между
[c.616]
Следовательно, нам достаточно освоить только эту рекурсивную процедуру, с тем чтобы любой руководитель предприятия, владеющий общей ситуацией на предприятии и в подразделениях, а также знающий цели и задачи предприятия, смог без особого труда создать подобную модель (Модель2) применительно к предприятию в целом. [c.322]
[c.322]
Рекурсивный алгоритм экспоненциального скользящего среднего выглядит так для каждой точки данных коэффициент (с), определяющий эффективную длину скользящего среднего (m), умножается на значение данной точки данных и к результату прибавляется разность 1,0 — с, умноженная на текущее значение скользящего среднего, что и дает новое значение. Коэффициент с приравнивается к2,0/(т+1),где т— период скользящей средней. Чанд в 1992 г. модифицировал данный алгоритм. В его модели значение коэффициента с не является константой, а зависит от текущей волатильности рынка — громкости рынка, выраженной в виде стандартного отклонения цен за некоторое количество последних точек данных. Поскольку стандартное отклонение сильно варьируется на разных рынках и показатель волатильности должен быть относительным, Чанд предложил делить наблюдаемое стандартное отклонение для каждой точки на среднее значение стандартного отклонения для всех точек в имеющемся образце данных. Для каждого бара коэффициент 2,0/(т + 1)) рассчитывается заново, умножаясь на относительную волатильность, таким образом получается скользящее среднее с периодом, динамически подстраивающимся под активность рынка. [c.134]
[c.134]
И главный фактор успеха здесь — это понимание того, что такое рациональное инвестиционное поведение, плюс качественная и количественная математическая модель такого поведения. Много сил в науке было отдано тому, чтобы описать рациональный инвестиционный выбор (например, через функцию инвестиционной полезности). Однако, если исследование аспектов рационального инвестиционного поведения не опирается на детальный анализ фондового рынка и макроэкономической обстановки в стране, где осуществляются инвестиции, то такой анализ рационального инвестиционного поведения является бесполезным. А в такой постановке задача практически не звучит. Приятным исключением является подход, применяемый компанией Latti e Finan ial [129], где прослеживается детальная модельная связь между макроэкономическими факторами и количественными оценками тенденций фондового рынка. Но здесь другая крайность слишком велика в моделях [129] доля механистического понимания связей на макро- и микроуровне, когда возникает прямой соблазн рекурсивного прогнозирования , где будущее с точностью до вероятностно расред елейного случайного сигнала определяется настоящим. Фактор рационализации выбора совершенно выпадает из моделей такого сорта.
[c.95]
Фактор рационализации выбора совершенно выпадает из моделей такого сорта.
[c.95]
Рекурсивное определение и значение | Dictionary.com
- Лучшие определения
- Викторина
- Связанный контент
- Подробнее о рекурсивном
- Примеры
Показывает уровень оценки в зависимости от сложности слова.
[ ri-kur-siv ]
/ rɪˈkɜr sɪv /
Сохранить это слово!
См. синонимы слова «рекурсивный» на Thesaurus.com
Показывает уровень оценки в зависимости от сложности слова.
прилагательное
, относящееся к правилу или процедуре, которые можно применять повторно, или использующие их.
Математика, Вычислительная техника. относящийся к математическому процессу рекурсии или использующий его: рекурсивная функция; рекурсивная процедура.
ВИКТОРИНА
Сыграем ли мы в «ДОЛЖЕН» ПРОТИВ. «ДОЛЖЕН» ВЫЗОВ?
Должны ли вы пройти этот тест на «должен» или «должен»? Это должно оказаться быстрым вызовом!
Вопрос 1 из 6
Какая форма используется для указания обязательства или обязанности кого-либо?
Происхождение рекурсивного
Впервые записано в 1935–1940 гг.; рекурс(ион) + -ive
ДРУГИЕ СЛОВА ИЗ рекурсивный
рекурсивный лы, наречие курсивность, существительноеСлова рядом рекурсивный
повторяющийся, повторяющийся десятичный, рецидивирующая цифровая фиброма детства, рекурсия, формула рекурсии, рекурсия, рекурсивное определение, рекурсивная функция, рекурсивная подпрограмма, рекурсия, рекурсия
Dictionary.com Unabridged Основано на словаре Random House Unabridged Dictionary, © Random House, Inc., 2022 г.
ПОДРОБНЕЕ О РЕКУРСИИ
Что означает
рекурсивный ? Что-то рекурсивное зациклено, особенно таким образом, что процесс может повторяться.
Рекурсивный имеет очень специфические значения в математике, компьютерном программировании и лингвистике, но в каждом случае он включает некоторую форму повторения, особенно когда часть последовательности или формулы опирается на предыдущие части. Такой процесс называется рекурсия .
Пример: Программа является рекурсивной: как только она завершает свою функцию поиска, она автоматически начинает сначала.
Откуда
рекурсивное ? Рекурсивный существует как минимум с конца 1700-х годов. Оно происходит от комбинации латинского recursiōn-, , что означает «бегущий назад», и суффикса прилагательного -ive . Его форма существительного, рекурсия , был записан с начала 1600-х годов. Бит -curs- в recursive происходит от слова, означающего бежать, которое также встречается в таких словах, как . Таким образом, вы можете думать о рекурсивном как о повторном выполнении .
Рекурсивный первоначально просто означало «постоянно повторяющийся», но к середине 1900-х годов он приобрел специальный математический смысл. Математический смысл относится к применению функции к ее собственным значениям для создания бесконечной последовательности значений. Уравнение, которое дает нам знаменитую последовательность Фибоначчи, является таким процессом.
Это математическое использование привело к вычислительному применению рекурсивных алгоритмов: процессов, которые решают большую проблему, решая меньшие версии проблемы. В лингвистике рекурсивных элементов — это те, которые повторяются по некоторому шаблону. Например, плохой в Он плохой, плохой человек — это рекурсивное , как и конструкция существительного-глагола в Она сказала, что он думал, что мы знали, что она считает это плохой идеей .
Если вы еще не до конца понимаете рекурсивное , было бы неплохо прочитать эту статью еще раз с начала (и рекурсивное !).
Знаете ли вы…?
Как
рекурсивное используется в реальной жизни?Рекурсивный чаще всего используется в контексте компьютерного программирования. В более общем смысле он используется для описания ситуаций, связанных с циклом.
Я определенно добавляю свой сайт-портфолио в качестве одного из своих проектов на моем сайте-портфолио 🙂.
Рекурсивное нечто 😋
— И Ф Е Д И Л И ⚡ (@SauceCodee) 8 декабря 2019 г.
К сожалению, крупные телевизионные награды по-прежнему чрезвычайно важны для определения основных показателей того, как выглядит «хороший» фильм. Это рекурсивное явление.
— Дана Шварц (@DanaSchwartzzz) 9 декабря 2019 г.
Мать Мадонны тоже была Мадонной, поэтому представьте картину эпохи Возрождения под названием «Мадонна с младенцем», которая представляет собой рекурсивное изображение поп-звезды 80-х, держащей уменьшенную версию себя, которая держит уменьшенную версию себя, которая держит уменьшенную версию себя.
… pic.twitter.com/FTG25JWPRY
— ВРЕМЯ СКАНЕР (@timescanner) 4 декабря 2019 г.
Какое из следующих слов не соответствует общему значению рекурсивного ?
A. циклический
B. повторяющийся
C. рекуррентный
D. завершающийСлова, относящиеся к рекурсивному
циклический, циклический, рекуррентный, повторяющийся, периодический, итеративный, повторяющийся
Как использовать рекурсивный в предложении
Для этого вам понадобится так называемая рекурсивная процедура — что-то, что позволит вам повторно использовать и строить вещи все более и более масштабными способами.
Говорить — значит бросать друг в друга вымышленные миры — Выпуск 89: Темная сторона|Кевин Бергер|9 сентября 2020|Наутилус
Просто он думает, что иерархическая структура плоская, и поэтому Пираха не использует этого массивного рекурсивного устройства.
Разговоры — это бросание вымышленных миров друг в друга — выпуск 89: Темная сторона|Кевин Бергер|9 сентября 2020 г.
|Наутилус
То, как Дэн читал статью Хаузера-Хомски-Фитча, — это рекурсия языка.
Говорить — значит бросать друг в друга вымышленные миры — Выпуск 89: Темная сторона|Кевин Бергер|9 сентября 2020 г.|Наутилус
Участников исследования обучали составлять из двух наборов символов рекурсивные шаблоны.
Обезьяны могут иметь общие с людьми ключевые навыки, связанные с грамматикой|Брюс Бауэр|26 июня 2020 г.|Новости науки
Одно из двух животных оказалось в среднем более склонным к формированию новых рекурсивных последовательностей, чем примерно три четверти дошкольников и примерно половина жителей боливийских деревень.
Обезьяны могут иметь общие с людьми навыки грамматики|Брюс Бауэр|26 июня 2020|Новости науки
С тех пор на Ирак обрушились черные миазмы рекурсивной мести.
Что бы ты ни делал, кто-то умрет. Короткая история о невозможном выборе в Ираке|Натан Брэдли Бети|31 августа 2014 г.
|DAILY BEAST 9Определение 0015
в кембриджском словаре английского языка
Примеры рекурсии
рекурсии
Хитрость в том, что эти три вещи подпитывают друг друга, иногда рекурсивно способами.
Из проводного
Несмотря на наше незнание причин, антидепрессанты остаются незаменимым бальзамом для миллионов людей, позволяющим им вырваться из замкнутого круга горя.
Из проводного
Рекурсивное мышление имеет решающее значение для всех человеческих групп; рекурсии в языке нет.
От NPR
Он говорит, что первый может избежать проблемы, не запуская рекурсивного , но что насчет второго?
Из Арс Техника
Их подход к рекурсивному обобщению из краудсорсинга имеет интригующий потенциал.
Из Phys.Org
Их трудно остановить, потому что они часто направляются через рекурсивных провайдеров.
Из Арс Техника
Но «самое забавное в этом определении то, что рекурсивно », — говорит он.
Из Phys.Org
Вычислительная эффективность была улучшена за счет отказа от традиционного рекурсивного поиска .
Из Кембриджского корпуса английского языка
Надо сначала переделать рекурсивные определения типов как неподвижные точки так называемых базовых функторов.
Из Кембриджского корпуса английского языка
Здесь необходимо упомянуть еще один аспект ленивых рекурсивных типов данных.
Из Кембриджского корпуса английского языка
Теперь мы можем определить рекурсивный -алгоритм на основе этой двухфазной спецификации и доказать его правильность.
Из Кембриджского корпуса английского языка
Это позволяет избежать написания явных пунктов «обработки исключений» для каждого рекурсивного вызова gfpt.
Из Кембриджского корпуса английского языка
Все рекурсивные вызовы сохраняют сжимаемость и замыкание типов аргументов.
Из Кембриджского корпуса английского языка
В оставшейся части этого раздела рассматриваются еще два варианта алгоритма gfp, которые более точно соответствуют хорошо известным алгоритмам подтипирования для рекурсивных типов.
Из Кембриджского корпуса английского языка
Любые ограничения, исключающие этот пример, должны исключать примитивные рекурсивные типы экземпляров; трудно понять, что останется при таких ограничениях.
Из Кембриджского корпуса английского языка
Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Переводы recursive
на китайский (традиционный)
回歸的, 遞迴的…
Подробнее
на китайском (упрощенном)
回归的, 递归的…
Подробнее
Нужен переводчик?
Получите быстрый бесплатный перевод!
Как произносится рекурсивное ?
Обзор
повторяющийся
повторяющийся
повторяющийся номер
рекурсия
рекурсивный
рекурсивно БЕТА
изогнутый БЕТА
отвод
бунтующий
Проверьте свой словарный запас с помощью наших веселых викторин по картинкам
- {{randomImageQuizHook.
copyright1}}
- {{randomImageQuizHook.copyright2}}
Авторы изображений
Попробуйте пройти викторину прямо сейчас
Слово дня
осмотр достопримечательностей
деятельность по посещению интересных мест, особенно людьми, находящимися в отпуске
Об этом
Блог
Безграничная энергия и сила (язык энергии, часть 2)
Подробнее
Новые слова
Громовая лихорадка
В список добавлено больше новых слов
Наверх
Содержание
EnglishExamplesTranslations
Изучайте Haskell во благо!
- Синтаксис в функциях
- Оглавление
- Функции высшего порядка
Привет, рекурсия!
Мы кратко упоминали рекурсию в предыдущей главе.
В этой главе мы более подробно рассмотрим рекурсию, почему она важна для Haskell и как мы можем найти очень краткие и элегантные решения проблем, думая рекурсивно.
Если вы до сих пор не знаете, что такое рекурсия, прочтите это предложение. Ха-ха! Просто шучу! На самом деле рекурсия — это способ определения функций, в котором функция применяется внутри своего собственного определения. Определения в математике часто даются рекурсивно. Например, последовательность Фибоначчи определяется рекурсивно. Во-первых, мы определяем первые два числа Фибоначчи нерекурсивно. Мы говорим, что F(0) = 0 и F(1) = 1 , что означает, что 0-е и 1-е числа Фибоначчи равны 0 и 1 соответственно. Тогда мы говорим, что для любого другого натурального числа это число Фибоначчи является суммой двух предыдущих чисел Фибоначчи. Так F(n) = F(n-1) + F(n-2) . Таким образом, F(3) равно F(2) + F(1) , что равно (F(1) + F(0)) + F(1) . Поскольку теперь мы подошли только к нерекурсивно определенным числам Фибоначчи, мы можем с уверенностью сказать, что F(3) равно 2.
Наличие одного или двух элементов в определении рекурсии, определенных нерекурсивно (например, F(0) и F(1) здесь) также называется краевым условием и важно, если вы хотите, чтобы ваша рекурсивная функция завершилась. Если бы мы не определили F(0) и F(1) не рекурсивно, вы никогда не получите решения ни для одного числа, потому что вы достигнете 0, а затем перейдете к отрицательным числам. Внезапно вы бы сказали, что Ф(-2000) это Ф(-2001) + Ф(-2002) и конца этому не видно!
Рекурсия важна для Haskell, потому что, в отличие от императивных языков, вы выполняете вычисления в Haskell, объявляя, что что-то есть , а не объявляя , как вы это получаете. Вот почему в Haskell нет циклов while или for, и вместо этого нам много раз приходится использовать рекурсию, чтобы объявить, что что-то есть.
Maximum awesome
Функция Maximum принимает список объектов, которые можно заказать (например, экземпляры класса типов Ord), и возвращает самый большой из них.
Подумайте, как бы вы реализовали это императивным способом. Вы, вероятно, настроили бы переменную для удержания максимального значения на данный момент, а затем перебрали бы элементы списка, и если элемент больше, чем текущее максимальное значение, вы бы заменили его этим элементом. Максимальное значение, которое остается в конце, является результатом. Вау! Слишком много слов для описания такого простого алгоритма!
Теперь давайте посмотрим, как мы определяем его рекурсивно. Мы могли бы сначала установить граничное условие и сказать, что максимум одноэлементного списка равен единственному элементу в нем. Тогда мы можем сказать, что максимум более длинного списка — это голова, если голова больше, чем максимум хвоста. Если максимум хвоста больше, ну, тогда это максимум хвоста. Вот и все! Теперь давайте реализуем это на Haskell.
максимум' :: (Ord a) => [a] -> a максимум' [] = ошибка "максимум пустого списка" максимум' [х] = х максимум' (x:xs) | х > максхвост = х | в противном случае = maxTail где maxTail = максимум' xsКак видите, сопоставление с образцом отлично сочетается с рекурсией! В большинстве императивных языков нет сопоставления с образцом, поэтому вам приходится делать много операторов if else для проверки краевых условий.
Здесь мы просто выкладываем их как шаблоны. Итак, первое краевое условие говорит, что если список пуст, произойдет сбой! Имеет смысл, потому что каков максимум пустого списка? Я не знаю. Второй шаблон также устанавливает краевое условие. В нем говорится, что если это одноэлементный список, просто верните единственный элемент.
Теперь действие происходит в третьем шаблоне. Мы используем сопоставление с образцом, чтобы разделить список на голову и хвост. Это очень распространенная идиома при выполнении рекурсии со списками, так что привыкайте к ней. Мы используем привязку , где , чтобы определить maxTail как максимум остального списка. Затем мы проверяем, больше ли голова максимума остального списка. Если да, то возвращаем голову. В противном случае мы возвращаем максимум остатка списка.
Давайте возьмем пример списка чисел и проверим, как это будет работать на них: [2,5,1]. Если мы назовем максимальное значение для этого, первые два шаблона не будут совпадать. Будет третий, и список будет разделен на 2 и [5,1].
, где пункт хочет знать максимум [5,1], поэтому мы идем по этому маршруту. Он снова соответствует третьему шаблону, и [5,1] разбивается на 5 и [1]. Опять же, предложение where хочет знать максимум [1]. Поскольку это граничное условие, возвращается 1. Наконец! Таким образом, поднимаясь на один шаг вверх, сравнивая 5 с максимальным значением [1] (которое равно 1), мы, очевидно, возвращаемся к 5. Итак, теперь мы знаем, что максимум [5,1] равен 5. Мы снова поднимаемся на один шаг, где у нас было 2 и [5,1]. Сравнивая 2 с максимальным числом [5,1], равным 5, мы выбираем 5.
Еще более понятный способ написать эту функцию — использовать макс. Если вы помните, max — это функция, которая принимает два числа и возвращает большее из них. Вот как мы могли бы переписать максимум, используя max:
максимум' :: (Ord a) => [a] -> a максимум' [] = ошибка "максимум пустого списка" максимум' [х] = х максимум' (x:xs) = max x (максимум' xs)Элегантно! По сути, максимум списка — это максимум первого элемента и максимум хвоста.
Еще несколько рекурсивных функций
Теперь, когда мы знаем, как вообще мыслить рекурсивно, давайте реализуем несколько функций, используя рекурсию. Во-первых, мы реализуем replicate. replicate принимает Int и некоторый элемент и возвращает список, содержащий несколько повторений одного и того же элемента. Например, репликация 3 5 возвращает [5,5,5]. Давайте подумаем о краевом условии. Я предполагаю, что краевое условие равно 0 или меньше. Если мы попытаемся воспроизвести что-то ноль раз, он должен вернуть пустой список. Также для отрицательных чисел, потому что это не имеет смысла.
replicate' :: (Num i, Ord i) => i -> a -> [a] реплицировать n x | нМы использовали здесь защитные элементы вместо шаблонов, потому что мы проверяем логическое условие. Если n меньше или равно 0, вернуть пустой список. В противном случае верните список, в котором x является первым элементом, а затем x повторяется n-1 раз в качестве хвоста. В конце концов, часть (n-1) приведет к тому, что наша функция достигнет граничного состояния.

Примечание: Num не является подклассом Ord. Это означает, что то, что составляет число, на самом деле не должно соответствовать порядку. Вот почему мы должны указывать ограничения класса Num и Ord при выполнении сложения или вычитания, а также сравнения.
Далее мы реализуем дубль. Он берет определенное количество элементов из списка. Например, take 3 [5,4,3,2,1] вернет [5,4,3]. Если мы попытаемся взять 0 или меньше элементов из списка, мы получим пустой список. Также, если мы попытаемся взять что-нибудь из пустого списка, мы получим пустой список. Обратите внимание, что это два граничных условия. Итак, давайте запишем это:
взять' :: (Num i, Ord i) => i -> [a] -> [a] взятый _ | п <= 0 = [] возьми' _ [] = [] возьми' n (x:xs) = x : возьми' (n-1) xsПервый шаблон указывает, что если мы попытаемся взять 0 или отрицательное число элементов, мы получим пустой список. Обратите внимание, что мы используем _ для соответствия списку, потому что в данном случае нам все равно, что это такое.
Также обратите внимание, что мы используем охрану, но без другой части. Это означает, что если n окажется больше 0, сопоставление не будет выполнено до следующего шаблона. Второй шаблон указывает на то, что если мы попытаемся взять что-либо из пустого списка, мы получим пустой список. Третий шаблон разбивает список на голову и хвост. А затем мы утверждаем, что если взять n элементов из списка, получится список, в котором x является началом, а затем список, который берет n-1 элемент из хвоста в качестве хвоста. Попробуйте на листе бумаги записать, как будет выглядеть оценка, если мы попытаемся взять, скажем, 3 из [4,3,2,1].
reverse просто переворачивает список. Подумайте о краевом условии. Что это? Да ладно... это пустой список! Перевернутый пустой список равен самому пустому списку. Хорошо. А как насчет остального? Ну, вы могли бы сказать, что если мы разделим список на голову и хвост, перевернутый список будет равен перевернутому хвосту, а затем голове в конце.
обратный' :: [а] -> [а] обратный' [] = [] реверс' (x:xs) = реверс' xs ++ [x]Вот так!
Поскольку Haskell поддерживает бесконечные списки, наша рекурсия не обязательно должна иметь краевое условие.
Но если у него его нет, он либо будет продолжать что-то бесконечно взбивать, либо создавать бесконечную структуру данных, например бесконечный список. Преимущество бесконечных списков в том, что мы можем обрезать их, где захотим. Repeat принимает элемент и возвращает бесконечный список, содержащий только этот элемент. Рекурсивная реализация этого очень проста, смотрите.
повторить' :: а -> [а] повторить' х = х:повторить хВызов повтора 3 даст нам список, который начинается с 3, а затем имеет бесконечное количество троек в конце. Таким образом, вызов repeat 3 будет оцениваться как 3:repeat 3, то есть 3:(3:repeat 3), то есть 3:(3:(3:repeat 3)), и т. д. Repeat 3 никогда не завершит вычисление, тогда как take 5 (повторить 3) даст нам список из пяти троек. По сути, это похоже на репликацию 5 3.
.zip берет два списка и сжимает их вместе. zip [1,2,3] [2,3] возвращает [(1,2),(2,3)], потому что он усекает более длинный список, чтобы он соответствовал длине более короткого.
Как насчет того, чтобы заархивировать что-то с пустым списком? Ну, тогда мы получаем пустой список. Итак, вот наше граничное условие. Однако zip принимает в качестве параметров два списка, поэтому на самом деле существует два граничных условия.
zip' :: [a] -> [b] -> [(a,b)] zip' _ [] = [] zip' [] _ = [] zip' (x:xs) (y:ys) = (x,y):zip' xs ysПервые два шаблона говорят, что если первый список или второй список пусты, мы получаем пустой список. В третьем говорится, что два заархивированных списка эквивалентны соединению их головок в пары, а затем присоединению застегнутых хвостов. Заархивирование [1,2,3] и ['a','b'] в конечном итоге попытается заархивировать [3] с помощью []. Срабатывают шаблоны граничных условий, и поэтому результат будет (1,'a'):(2,'b'):[], который точно такой же, как [(1,'a'),(2,'b ')].
Реализуем еще одну стандартную библиотечную функцию — elem. Он принимает элемент и список и проверяет, есть ли этот элемент в списке. Пограничным условием, как и в большинстве случаев со списками, является пустой список.
Мы знаем, что пустой список не содержит элементов, поэтому в нем точно нет нужных нам дроидов.
elem' :: (Eq a) => a -> [a] -> Bool элемент а [] = Ложь элемент а (x:xs) | а == х = Истина | в противном случае = элемент xsДовольно просто и ожидаемо. Если голова не является элементом, мы проверяем хвост. Если мы достигнем пустого списка, результатом будет False.
Быстрее, сортируйте!
У нас есть список предметов, которые можно сортировать. Их тип является экземпляром класса типов Ord. А теперь мы хотим их рассортировать! Есть очень классный алгоритм сортировки, который называется quicksort. Это очень умный способ сортировки предметов. Хотя для реализации быстрой сортировки в императивных языках требуется более 10 строк, в Haskell реализация намного короче и элегантнее. Quicksort стал своего рода детищем Haskell. Поэтому давайте реализуем его здесь, хотя реализация быстрой сортировки в Haskell считается очень дрянной, потому что все делают это, чтобы продемонстрировать, насколько элегантен Haskell.
Итак, сигнатура типа будет quicksort :: (Ord a) => [a] -> [a]. Никаких сюрпризов. Краевое состояние? Пустой список, как и ожидалось. Отсортированный пустой список — это пустой список. Теперь перейдем к основному алгоритму: отсортированный список — это список, в котором все значения меньше (или равны) началу списка впереди (и эти значения отсортированы), затем идет заголовок списка в конце списка. средний, а затем идут все значения, которые больше головы (они также отсортированы). Обратите внимание, что в этом определении мы сказали, что сортирует два раза, так что нам, вероятно, придется сделать рекурсивный вызов дважды! Также обратите внимание, что мы определили его с помощью глагола is для определения алгоритма вместо того, чтобы говорить , сделай это, сделай то, затем сделай то... . В этом прелесть функционального программирования! Как мы собираемся фильтровать список, чтобы получить только те элементы, которые меньше головы нашего списка, и только те элементы, которые больше? Перечислите понимания.
Итак, давайте погрузимся и определим эту функцию.
quicksort :: (Ord a) => [a] -> [a] быстрая сортировка [] = [] быстрая сортировка (x:xs) = пусть smallSorted = quicksort [a | а <- xs, а <= х] bigSorted = быстрая сортировка [a | а <- хз, а > х] в сортировке поменьше ++ [x] ++ по сортировке побольшеДавайте сделаем небольшой тестовый запуск, чтобы увидеть, правильно ли он себя ведет.
ghci> быстрая сортировка [10,2,5,3,1,6,7,4,2,3,4,8,9] [1,2,2,3,3,4,4,5,6,7,8,9,10] ghci> quicksort "быстрая коричневая лиса перепрыгивает через ленивую собаку" "abcdeeefghhijklmnoooopqrrsttuuvwxyz"Буйя! Это то, о чем я говорю! Итак, если у нас есть, скажем, [5,1,9,4,6,7,3] и мы хотим его отсортировать, этот алгоритм сначала возьмет голову, которая равна 5, а затем поместит ее в середину двух списков, которые меньше и больше его. Итак, в какой-то момент у вас будет [1,4,3] ++ [5] ++ [9,6,7]. Мы знаем, что после полной сортировки списка число 5 останется на четвертом месте, так как есть на 3 числа меньше его и на 3 числа больше его.
Теперь, если мы отсортируем [1,4,3] и [9,6,7], у нас будет отсортированный список! Мы сортируем два списка, используя одну и ту же функцию. В конце концов, мы разобьем его настолько, что дойдем до пустых списков, а пустой список уже каким-то образом отсортирован в силу того, что он пуст. Вот иллюстрация:
Элемент, который находится на месте и больше не будет двигаться, отображается оранжевым цветом. Если вы прочитаете их слева направо, вы увидите отсортированный список. Хотя мы решили сравнивать все элементы с головами, мы могли использовать любой элемент для сравнения. В быстрой сортировке элемент, с которым вы сравниваете, называется опорным элементом. Они здесь зеленые. Мы выбрали голову, потому что ее легко получить путем сопоставления с образцом. Элементы, которые меньше, чем опорная точка, выделены светло-зеленым цветом, а элементы, превышающие опорную точку, — темно-зеленым. Желтоватый градиент представляет собой применение быстрой сортировки.
Рекурсивное мышление
До сих пор мы использовали довольно много рекурсии, и, как вы, наверное, заметили, здесь есть закономерность.
Обычно вы определяете пограничный случай, а затем определяете функцию, которая делает что-то между некоторым элементом и функцией, применяемой к остальным. Неважно, список это, дерево или любая другая структура данных. Сумма — это первый элемент списка плюс сумма остальных элементов списка. Произведением списка является первый элемент списка, умноженный на произведение остальной части списка. Длина списка равна единице плюс длина конца списка. Экцетера, екчетера ...
Конечно, у них тоже есть пограничные случаи. Обычно крайним случаем является некоторый сценарий, когда рекурсивное приложение не имеет смысла. При работе со списками пограничным случаем чаще всего является пустой список. Если вы имеете дело с деревьями, пограничным случаем обычно является узел, у которого нет потомков.
Аналогично, когда вы имеете дело с числами рекурсивно. Обычно это связано с некоторым числом и измененной функцией, применяемой к этому числу. Ранее мы выполнили функцию факториала, и это произведение числа на факториал этого числа минус один.
Такое рекурсивное приложение не имеет смысла с нулем, потому что факториалы определены только для положительных целых чисел. Часто значение пограничного случая оказывается тождеством. Идентичность для умножения равна 1, потому что если вы умножаете что-то на 1, вы получаете это что-то обратно. Также при суммировании списков мы определяем сумму пустого списка как 0, а 0 является идентификатором для добавления. В быстрой сортировке пограничным случаем является пустой список, а идентификатор также является пустым списком, потому что, если вы добавите пустой список в список, вы просто получите исходный список обратно.
Итак, когда вы пытаетесь придумать рекурсивный способ решения проблемы, подумайте о том, когда рекурсивное решение неприменимо, и посмотрите, можно ли использовать это как пограничный случай, подумайте об идентичностях и подумайте, не сломаете ли вы кроме параметров функции (например, списки обычно разбиваются на начало и конец с помощью сопоставления с образцом) и в какой части вы будете использовать рекурсивный вызов.
- Синтаксис в функциях
- Оглавление
- Функции высшего порядка
Уникальность человеческого рекурсивного мышления
Эта статья из выпуска
май-июнь 2007 г.
Том 95, номер 3
Страница 240
DOI: 10.1511/2007.65.240
- Недоступно для покупки
- Посмотреть выпуск
Однажды во время посещения Киото я наткнулся на ворота с табличкой, написанной кандзи. Я спросил гида, что это значит, и он ответил, что это можно перевести как «Не выставлять счета». Нужно только быть умеренно проницательным, чтобы понять, что сам знак является счетом и, таким образом, нарушает свое собственное сообщение.
Чтобы предотвратить размещение таких счетов, мы могли бы рассмотреть возможность размещения еще одного знака с надписью «Не размещать счета «Не размещать счета». Но это, в свою очередь, является счетом, поэтому, возможно, нам нужен еще один знак, который говорит: «Не размещайте счета без счетов». Проблема, как я уверен, теперь вы понимаете, заключается в том, что этот процесс приводит к бесконечной последовательности знаков, которые охватывают не только ворота, но и всю вселенную, поскольку каждая купюра длиннее предыдущей. Лучше, может быть, просто позволить людям приклеить несколько купюр на ворота.
Peter M. Corr/Alamy
Ad Right
Самореферентные счета являются примерами рекурсии. Другой пример взят из анонимной пародии на первую строчку печально известного романа Эдварда Бульвер-Литтона « Пол Клиффорд :
». Ночь была темная и ненастная, и мы сказали капитану: «Расскажи нам сказку!» И вот что рассказал капитан: «Была темная и ненастная ночь, и мы сказали капитану: «Расскажи нам историю!» И вот что рассказал капитан: «Темно было…»С вычислительной точки зрения рекурсия — это процесс, который вызывает сам или который вызывает аналогичный процесс.
В примере «Не выставлять счета» знак, хотя и невольно, отсылает к самому себе, тогда как в пародии на роман Бульвер-Литтон история в рассказе та же история.
Как вариант, можно привести определение в словарном стиле:
Пожалуй, лучше не останавливаться на этом.
Я полагаю, что рекурсия является вездесущим свойством человеческого разума и, возможно, основной характеристикой, отличающей наш вид от всех других существ на планете. Рекурсия — хорошо известное свойство языка, но я утверждаю, что это явление применимо и к ряду других предположительно человеческих областей, включая «теорию разума», мысленные путешествия во времени, производство, концепцию «я» и, возможно, даже религию.
Грамматические правила языка используют рекурсию для создания бесконечного разнообразия потенциальных предложений, которые мы можем произнести и понять. Возможно, самым простым примером является предложение, состоящее из предложений, в соответствии с правилом, которое может быть выражено как
S → S + S
, где стрелка является символом для , можно переписать как и S означает для предложение .
Правила перезаписи в этой форме — обычный способ показать, как устроен язык. Это конкретное правило, примененное дважды, создает следующее предложение, найденное в книге А. А. Милна 9.0065 Винни-Пух : "Дождь лил, лил и лил." Этот пример, тем не менее, довольно тривиален, поскольку он просто сводится к повторению, по-видимому, чтобы создать ощущение, что дождь шел довольно долго, вызывая у Пятачка некоторую скуку.
Рекурсия может быть намного сложнее, чем простое повторение, и она используется в человеческом языке для уточнения или усложнения высказывания. Например, мы можем разбить предложения на фразы, а затем применить рекурсивные правила, чтобы прикрепить фразы к фразам или встроить фразы во фразы. Существуют именное словосочетание (NP), глагольное словосочетание (VP) и предложное словосочетание (PP).
Во время визита в издательство в Хоуве, Англия, издатель встретил меня маловероятной фразой: «Рибена стекает по люстрам». (Рибена — торговая марка ароматизированного напитка в Соединенном Королевстве, и он действительно стекал со светильников.
) Здесь предложение сначала разбивается на NP («Рибена») и VP («стекает вниз»). люстры»). Но сам VP состоит из глагола («текет») плюс PP («вниз по люстрам»), который, в свою очередь, состоит из предлога («вниз») плюс NP («по люстрам»). Таким образом, предложение можно разобрать с точки зрения следующих правил перезаписи:
1. S → NP + VP
2. NP → существительное
3. VP → глагол + PP
4. PP → предлог + NPПрименительно к более сложным предложениям такие правила включают рекурсию. Например, NP может включать в себя aPP , , который, в свою очередь, может включать NP . В принципе, можно многократно повторять правила 2 и 4. Если бы издатель не был в какой-то панике, он мог бы уточнить: «Рибена стекает по люстрам на ковер рядом с моим столом». (наверху была детская).
Дети быстро учатся ценить силу рекурсии (если не Рибены), о чем свидетельствуют следующие предложения из известного детского рассказа «Дом, который построил Джек»:
1.Это дом, который построил Джек .
2. Это солод, который лежал в доме, который построил Джек.
3. Это крыса, которая съела солод, который лежал в доме, который построил Джек.
4. Это кошка, которая убила крысу, съевшую солод, который лежал в доме, который построил Джек.
5. Это собака, которая беспокоила кошку, которая убила крысу, которая ела солод, который лежал в доме, который построил Джек.И так далее. Важно понимать, что речь идет не просто о добавлении несвязанных элементов. Новые предложения постепенно добавляются в начале, а остальная часть предложения все больше определяет существительное. В четвертом предложении, например, речь идет именно о той кошке, которая убила крысу, съевшую солод, и так далее. Кошка, убившая крысу, которая не ела солод, который лежал в доме, который построил Джек, просто не годится.
Том Данн
Предложения в «Доме, который построил Джек» являются примерами так называемой конечной рекурсии , в которой рекурсивное правило вызывается в конце.
Четвертое предложение, например, начинается с предложения «Это кот», но затем добавляется относительное предложение «который убил крысу», чтобы определить кота. В этом относительном предложении упоминается крыса, а для определения крысы добавляется еще одно относительное предложение, «которые ели солод», и так далее. В принципе можно добавлять рекурсивные элементы до бесконечности или до тех пор, пока ваша кратковременная память не сможет больше удерживать.
Другим видом рекурсии является центрально-вложенная рекурсия , в которой составляющие встраиваются в составляющие. Например, в третьем предложении «Дом, который построил Джек» можно сделать подлежащим предложение солод, а не крысу, и таким образом вставить относительное предложение, описывающее солод, в предложение о солоде: Солод, который съела крыса, лежал в доме, который построил Джек.
Такие встроенные словосочетания, как в этом предложении, встречаются часто. Но если фразы встроены во встроенные фразы, все может усложниться.
Например, давайте превратим четвертое предложение в предложение с солодом: Солод, который съела крыса, убитая котом, лежал в доме, который построил Джек. Теперь попробуйте пятое предложение: Солод, который съела крыса, которую съела кошка, которую беспокоила собака, лежал в доме, который построил Джек. Ты все еще следишь за мной?
Этот последний пример совершенно грамматичен, но более чем на один уровень рекурсии с вложенным центром трудно следовать по психологическим, а не лингвистическим причинам. Встраивание в центр требует запоминающего устройства, такого как стек указателей, указывающих, где взять процедуру после завершения встроенного компонента. Это не так уж плохо, если есть только одна встроенная структура, поскольку в памяти может храниться один указатель, показывающий, где взять исходную процедуру. При множественном встраивании вам необходимо отслеживать несколько указателей, что может привести к перерасходу рабочей памяти. Примеры предложений с более чем одним уровнем встраивания в центр редко встречаются в естественном дискурсе.
В недавней статье Science психолог Марк Д. Хаузер из Гарвардского университета и его коллеги предположили, что рекурсия является основной характеристикой, которая отличает человеческий язык от всех других форм общения животных. Шимпанзе и бонобо обучались форме языка, иногда известной как протоязык , с некоторыми характеристиками человеческого языка, включая использование символов для представления объектов или действий и некоторую способность комбинировать символы для создания новых значений. Однако нет никаких доказательств того, что эти обезьяны используют эти символы (или комбинации символов) рекурсивным образом, чтобы создать что-то подобное неограниченному набору значений, который можем создать мы, люди.
По крайней мере, на первый взгляд, песни, издаваемые некоторыми птицами, кажутся сложными для человеческого языка. Американские орнитологи Джек П. Хейлман и Миллисент С. Фикен однажды утверждали, что крики синиц имеют вычислимый синтаксис и поэтому квалифицируются как «язык».
Эти крики состоят из четырех качественно различных звуков, которые мы можем обозначить A, B, C и D . Эти элементы всегда находятся в одном и том же порядке, хотя любой элемент может повторяться любое количество раз или может быть вообще опущен. Последовательности ABCD, B, BD, AAABBCCCD являются законными. Хотя такие последовательности весьма разнообразны, они не предполагают рекурсии, кроме простого повторения элементов. В отличие от человеческого языка, последовательности могут быть определены с помощью так называемой грамматики конечных состояний , в которой выбор элемента в любой точке последовательности может быть указан предшествующим элементом. Таким образом, B может следовать за A, или B , может быть первым в последовательности, но никогда не может следовать за 9.0065 C или D . Конечно, птицы вполне могли использовать более сложные правила, но нам не нужно предполагать большего, чем то, что они просто переходили от одного элемента к другому, без какой-либо оценки того, что было до или после.
Напротив, человеческий язык включает в себя объединение составляющих во фразы и создание предложений по рекурсивным правилам, согласно которым фразы могут быть определены в терминах фраз, и каждый элемент в последовательности вносит свой вклад в грамматическую конструкцию.
Том Данн
Нейроэтолог Тимоти К. Гентнер из Калифорнийского университета в Сан-Диего и его коллеги недавно заявили, что европейские скворцы могут анализировать последовательности звуков, состоящие из целых четырех уровней рекурсии, встроенной в центр. Скворцов учили различать последовательности звуков, составленные из восьми звуков, классифицированных как погремушки, A, , и восьми звуков, классифицированных как трели , B . Последовательности генерировались либо грамматикой с конечным числом состояний, в которой 9Последовательности 0065 AB просто повторялись до четырех раз (как в AB, ABAB, ABABAB или ABABABAB ), или в которых пар AB встроены в пары AB с четырьмя уровнями рекурсии (как в AB, AABB, AAABBB, и AAAABBBB ).
Фактические выборы A и B были сгенерированы случайным образом, так что птицы не могли просто выучить определенные последовательности. Некоторые, но не все, птицы научились отличать такие последовательности друг от друга, а также от последовательностей, не подчиняющихся правилам, что свидетельствует о способности понимать рекурсию.
Проблема здесь в том, что скворцам не нужно анализировать рекурсивные последовательности в соответствии с правилом рекурсии. Более простое решение состоит в том, чтобы просто подсчитать количество последовательных A и количество последовательных B и принять последовательность как принадлежащую к рекурсивной категории, если эти два числа равны. Такая стратегия, вероятно, не выходит за рамки вычислительных возможностей скворца. Существует множество свидетельств наличия у птиц чувства числа. Например, знаменитый африканский серый попугай Алекс, воспитанный Ирэн Пепперберг из Гарвардского университета, умеет считать до шести и понимает понятия «одинаковое» и «различное».
Скворцы также известны своими замысловатыми песнями, предполагающими сложное воспроизведение и восприятие последовательностей. Говорят, что заключительная часть Концерта для фортепиано с оркестром соль мажор Моцарта, K. 453, основана на песне его любимого скворца. Однако нет никаких указаний на то, что песни скворцов, хотя и моцартовские, рекурсивны. Следует также помнить, что даже люди испытывают значительные трудности при разборе предложений, в которых количество встроенных фраз превышает два.
Опять же, мы не знаем, что на самом деле происходит в уме скворца, но экономия требует, чтобы мы приняли более простое объяснение их поведения. Задача показать, что любой нечеловеческий вид может либо создавать, либо анализировать рекурсивные комбинации элементов, остается.
Рекурсия не ограничивается языком, но применима и к другим аспектам человеческого мышления. Одна из них известна как «теория разума», которая относится к способности представить, что может происходить в уме другого человека.
Ментальные процессы мышления, познания, восприятия или чувства можно рассматривать как теорию разума нулевого порядка, и, вероятно, они являются общими для многих видов. Они не рекурсивны. Теория сознания первого порядка относится к мышлению, знанию, восприятию или чувству того, что другие мыслят, знают, воспринимают или чувствуют и, следовательно, являются рекурсивными. Это подразумевается такими утверждениями, как «Я думаю, вы, должно быть, думаете, что я идиот» или «Тед думает, что Алиса хочет, чтобы Фред перестал ее доставать».
Том Данн
Способны ли на это нечеловеческие виды? Откуда мы могли знать? Проблема в том, что язык сам по себе хорошо приспособлен для выражения рекурсивных идей, и без языка трудно проверить теорию сознания. До сих пор ни одно животное, кроме человека, не показало нам, что у него есть система коммуникации, достаточно мощная, чтобы раскрыть теорию разума, поэтому мы должны полагаться на нелингвистические тесты.
Один из таких тестов включает в себя тактический обман, когда одно животное выполняет какое-то действие, основанное на оценке того, что другое животное может думать или что оно может видеть. Молодой шимпанзе может подождать, пока доминирующий самец не отвлечется, прежде чем воровать еду. В более сложном примере молодой павиан-самец может увидеть, как другой павиан ест кукурузу. Он кричит в притворном страхе, и его мать приходит и прогоняет другого бабуина. Затем молодой бабуин захватывает кукурузу. Вопрос здесь в том, знал ли на самом деле молодой бабуин, что будет в голове у его матери, когда он закричит, или это поведение было просто усвоено методом проб и ошибок.
Психологи Ричард Бирн и Эндрю Уайтен из Университета Сент-Эндрюс в Файфе, Шотландия, собрали примеры возможного тактического обмана из наблюдений, сделанных приматологами в полевых условиях, и тщательно отфильтровали те, которые могли бы зависеть от простых проб и ошибок. Из общего числа 253 случаев проверку прошли только 26 наблюдений.
Было 12 экземпляров от обычных шимпанзе и по три от бонобо, горилл и орангутангов. Также прошло еще пять экземпляров от мангабеев, близких родственникам бабуинов. Тем не менее Бирн и Уайтэн предположили, что истинный тактический обман, требующий теории разума, может быть ограничен человеческими существами и человекообразными обезьянами, и даже среди последних доказательства не очень убедительны. Напротив, поиск по запросу «тактический обман» в поисковой системе Google дает примерно 967 000 ответов, большинство из которых касаются человеческих войн.
Cognitive Evolution Group, University of Louisiana at Lafayette
Были предложены и другие тесты для нечеловеческих видов, но результаты едва ли более убедительны. Например, психолог Даниэль Повинелли и его коллеги из Университета Луизианы в Лафайете показали, что шимпанзе с такой же вероятностью будут выпрашивать еду у человека с завязанными глазами или с ведром на голове, как и у того, кто может видеть, предполагая, что шимпанзе неспособны к рекурсивному пониманию того, может ли видеть другой человек.
Майкл Томаселло из Института эволюционной антропологии Макса Планка и его коллеги утверждают, что шимпанзе на самом деле умнее и при некоторых обстоятельствах понимают то, что видят другие, хотя авторы признают, что «шимпанзе не обладают полноценным человеческим разумом». как теория разума».
Если есть сомнения в том, что человекообразные обезьяны способны к теории разума первого порядка, то нет никаких оснований предполагать, что они способны к более высоким порядкам. Человеческие дела легко впадают во многие порядки теории разума, что хорошо показано в литературе и театре. В романе Джейн Остин «Гордость и предубеждение» Элизабет Беннет думает что Дарси думает что она думает он слишком резко думает о своей семье. Или в шекспировской Двенадцатая ночь , Мария предвидит что сэр Тоби с нетерпением предвидит что Оливия будет судить Мальволио абсурдно дерзок по отношению к предположим что она желает его 50066 себе 60 9065 считает своим поклонником Каждое выделенное курсивом слово после первого указывает на другой уровень рекурсии.
Теория разума может даже быть предпосылкой для религиозной веры, по словам эволюционного психолога Робина Данбара из Ливерпульского университета. Представление о добром Боге, который наблюдает за нами, наказывает и допускает нас на Небеса, если мы достаточно добродетельны, зависит от понимания того, что другие существа — в данном случае сверхъестественные — могут иметь мысли и эмоции, подобные человеческим. . Действительно, Данбар полагает, что может потребоваться несколько порядков рекурсии, поскольку религия — это социальная деятельность, зависящая от общих убеждений.
Необходимый рекурсивный цикл работает примерно так: я полагаю что вы думаете что я верю что есть боги, которые намерены влиять на наше будущее, потому что они понимают чего мы желаем . Это рекурсия пятого порядка. Сам Данбар, должно быть, достиг рекурсии шестого порядка, если он предполагает все это, и если вы предполагаете, что он это делает, то вы достигли рекурсии седьмого порядка.
Назовите это "Седьмое небо", если хотите.
Вера в то, что у человека есть собственные мысли, является теорией разума относительно самого себя. Философ Рене Декарт известен фразой « cogito, ergo sum», , хотя на самом деле он написал « Je pense, donc je suis» — «Я мыслю, следовательно, существую». Декарт принял это за основное доказательство своего собственного существования, потому что, даже если он сомневался в этом, сомнение было формой мышления, так что его действительное существование не вызывало сомнений. Фраза принципиально рекурсивна, поскольку подразумевает не просто мышление, а мышление о мышлении. Тот факт, что мы можем осознавать наше собственное мышление (и не только наши собственные мысли), подразумевает понятие «я».
Том Данн
Один из способов выяснить, имеют ли животные представление о себе, — это зеркальный тест, впервые разработанный в 1970 году психологом Гордоном Г. Гэллапом-младшим, ныне работающим в Государственном университете Нью-Йорка в Олбани.
Клеймо ставится на животное таким образом, что его можно рассмотреть только в зеркале. Тогда возникает вопрос, попытается ли животное удалить метку или иным образом покажет, что оно понимает, что метка находится на его собственном теле. Данные свидетельствуют о том, что только дельфины, человекообразные обезьяны и слоны проходят тест, что означает, что у них есть представление о себе. Однако результаты противоречивы, потому что они могут означать не более чем то, что эти животные понимают, что объект в зеркале соответствует их собственному физическое «я», , но это не означает, что они понимают, что физическое «я» способно к мыслям или желаниям.
Чтобы быть правильно рекурсивным, должно быть задействовано понятие самости, то есть не просто знание того, что кто-то является физическим объектом, но знание того, что кто-то знает, или знание того, что у него есть ментальные состояния. Существует мало свидетельств того, что это относится к любому нечеловеческому виду.
Еще один способ проверить концепцию себя — это осознание того, что человек может существовать в разные моменты времени.
Например, мы можем вспомнить, о чем мы думали или что переживали вчера, что опять-таки является рекурсивным процессом. Это указывает на то, что мы можем не только понять, что у нас есть мыслительные процессы в настоящем, но и то, что они у нас были в прошлом и будут в будущем. Расширяя изречение Декарта, мы могли бы сказать: «Я думал, следовательно, я был» и «Я буду думать, следовательно, я буду». Концепция себя может быть расширена во времени.
Представление о себе в прошлом зависит от памяти. По словам канадского нейробиолога Энделя Тульвинга, существует два вида сознательной памяти. Семантическая память относится к вашему хранилищу знаний о мире, таких как знание того, что Веллингтон — столица Новой Зеландии, или что температура кипения воды составляет 100 градусов по Цельсию. Эпизодическая память относится к конкретным эпизодам вашей жизни, которые вы можете пережить в уме. Вы, вероятно, помните то, что делали вчера, не просто как последовательность фактов, а как события, которые вы можете осознать и воспроизвести в уме.
Такие воспоминания, в отличие от семантических воспоминаний, рекурсивны, потому что они включают в себя ментальные ссылки на ваше прежнее ментальное «я». Восстановление семантических воспоминаний подразумевает то, что Тулвинг называет 9.0065 ноэтическое осознание , которое является просто знанием, тогда как восстановление эпизодических воспоминаний подразумевает аутоноэтическое осознание , которое является самопознанием.
Тульвинг также утверждал, что эпизодическая память уникальна для людей. Это не отрицает, что у других видов есть память, часто поразительная. Например, среди птиц, которые прячут пищу, кедровка Кларка является одной из самых плодовитых, храня семена в тысячах мест и извлекая их с высокой, но не идеальной точностью. Однако это не означает, что птица помнит сам процесс тайника пищи; скорее, он может просто помнить, где находится еда. Мне кажется, я знаю значения десятков тысяч слов, но, за очень немногими исключениями, я не могу вспомнить эпизоды, в которых я впервые столкнулся с этими словами.
Умные эксперименты, проведенные Николой Клейтон и ее коллегами из Кембриджского университета, показали, что по крайней мере один вид птиц, западная кустарниковая сойка, может обладать более подробной памятью, чем можно было предположить. Птицы могут помнить, где они хранили определенные предметы, такие как черви или орехи, и они найдут то или иное в зависимости от того, как долго они были спрятаны. Как правило, они предпочитают червей, но будут избегать ночных ползунов в пользу орехов, если черви были спрятаны слишком долго и, следовательно, вероятно, разложились и стали неприятными на вкус. Это означает, что сойки знают что было закэшировано, где было закешировано и когда закэшировано. Эти три условия, известные как критерии WWW , , были признаны некоторыми достаточными доказательствами существования эпизодической памяти у кустарниковой сойки — смиренная мысль. Тем не менее, это может быть недостаточным доказательством того, что птицы вновь переживают процесс тайника.
Память о том, где был кэширован продукт питания, может содержать метку времени, эквивалентную «сроку годности», которая указывает, как долго продукт был кэширован, но это не обязательно должно включать в себя конкретную память для самого эпизода кэширования.
У приматов больше шансов продемонстрировать мысленное путешествие во времени, чем у птиц, особенно у наших ближайших нечеловеческих родственников, шимпанзе и бонобо. Немецко-американский психолог Вольфганг Келер, известный своими экспериментами над шимпанзе во время дислокации на Канарских островах во время Первой мировой войны, заметил, что, несмотря на все свои импровизационные способности, шимпанзе плохо представляли прошлое или будущее. Работа, проведенная за последние 50 лет по обучению языковому общению шимпанзе и бонобо, не дает особых оснований сомневаться в этом выводе. До сих пор нет ни свидетельств приобретения времени, ни какого-либо ощущения, что эти животные сообщают о конкретных прошлых событиях или возможных будущих.
Психолог Томас Саддендорф из Университета Квинсленда утверждал, что эпизодическая память является лишь частью более общей способности к мысленным путешествиям во времени , что включает в себя путешествие как в воображаемое будущее, так и в вспоминаемое прошлое. Пациенты с амнезией, которые теряют эпизодическую память, также теряют ощущение возможных будущих событий, и дети, кажется, понимают концепции прошлого и будущего примерно в одно и то же время, в возрасте четырех лет. В самом деле, эпизодическая память может функционировать не столько как запись прошлого, сколько как хранилище информации о событиях, которое может предоставить своего рода словарь для генерации будущих событий. Возможно, это объясняет, почему эпизодическая память одновременно и ненадежна, и неполна, и часто является проклятием для судов. В случаях амнезии обычно теряются эпизодические, а не семантические воспоминания. Неважно, что эпизодическая память неполна и хрупка, если она предоставляет достаточно информации для создания правдоподобных и эффективных будущих сценариев.
Ведь для нас важно будущее, а не прошлое.
Возможно, не будет преувеличением сказать, что люди одержимы временем, когда мы размышляем о прошлом и планируем свое будущее. Мы измеряем время в секундах, минутах, часах, днях, неделях, месяцах, годах, десятилетиях, веках, тысячелетиях, эрах и эонах. Мы измеряем его как в прошлое, так и в будущее. Мы экстраполируем его за пределы нашей собственной жизни, вплоть до Большого Взрыва, который, как говорят, создал Вселенную. С течением времени мы понимаем смерть, и, возможно, поэтому мы обращались к религиям за обещанием загробной жизни. Время создает стресс, поскольку сроки приближаются, но мы также можем обратиться ко времени, чтобы исцелить наши беды. Когда Виола в Двенадцатая ночь , переодевшись мужчиной, оказывается в безвыходной ситуации, она говорит: "О Время, ты должен распутать это, а не я; Это слишком тугой узел для меня, чтобы завязать!"
Сам язык пропитан временем. We use many prepositions, such as at , about , around , between , across , against , from , to and through , to apply to time as well as пробел, а некоторые, такие как с или с по ограничены измерением времени.
Использование времени позволяет нам включать время в язык, даже рекурсивным образом. Например, прошедшее совершенное время, как в «Я уже поел», относится к событию, которое находится дальше в прошлом, чем какое-то опорное время в прошлом, в то время как будущее совершенное, как в «Он прибудет», относится к событию. что-то, что будет в прошлом в какой-то момент в будущем.
Какой бы ни была способность нечеловеческих животных мысленно путешествовать во времени, можно с уверенностью сказать, что еще раз генеративный, рекурсивный способ, которым мы представляем себе события во времени, по-видимому, превосходит все, что было продемонстрировано или даже намекнуто в наших исследованиях. ближайшие родственники приматов.
Другим примером рекурсии, вероятно, заимствованным из языка, является счет. Используя рекурсивные правила, люди могут считать бесконечно. Все, что вам нужно, это конечный набор цифр и несколько простых правил, которые вы можете использовать для перехода от одного числа к другому.
Теперь мы знаем, что многие виды животных умеют считать, но они могут делать это точно лишь до некоторого небольшого значения. Даже это не является строгим подсчетом, но ближе к человеческой способности субитизации , , которая является способностью перечислять с первого взгляда количество до четырех. Кроме того, наша способность перечислять без фактического подсчета становится все более неточной по мере увеличения фактического числа. Вы можете оценить количество людей, посетивших лекцию, примерно в 75 человек, а аудиторию футбольного матча — в 15 000 человек, но ни в том, ни в другом случае вы вряд ли будете точны. Счет, однако, может обеспечить идеальную точность до любого числа, хотя, конечно, это может занять много времени. Счет — еще одна иллюстрация того, как рекурсивные принципы могут значительно увеличить силу и возможности человеческого разума. В более общем смысле человеческие вычисления рекурсивны. Программисты используют подпрограммы, которые вызывают подпрограммы, а на моем ноутбуке есть папки, содержащие папки, содержащие папки.
Фотография предоставлена Яном Каннеллом и Кэролайн Раби.
Использование и производство инструментов может также включать рекурсивные компоненты. Использование инструментов само по себе не является исключительно человеческим. Шимпанзе используют камни для раскалывания орехов и веток для извлечения термитов из своих нор; они даже изготавливают «копья», чтобы пронзить добычу. Обезьяны-капуцины — исключительные пользователи инструментов, использующие предметы различными способами для достижения своих целей. Они используют палки, чтобы загребать еду, складывают коробки, чтобы добраться до еды, и даже бросают предметы в людей. Новокаледонские вороны обдирают и формируют листья пандануса или сооружают веточки с крючками на концах, чтобы доставать личинок из нор. Но люди, несомненно, являются самыми искусными производителями и пользователями инструментов.
Том Данн
Американский сравнительный психолог Бенджамин Б.
Бек, специалист по поведению при изготовлении орудий труда, однажды заметил, что «человек — единственное животное, которое, как было замечено, использует орудие для изготовления орудий». Это снова подразумевает рекурсию. Современная технология по крайней мере повторяется, если не всегда действительно рекурсивна; рассмотрим сборочные линии, которые начались с Ford Model T. Тем не менее есть колеса внутри колес, двигатели внутри двигателей, компьютеры внутри компьютеров. В конце концов, возможно, мы сможем затопить земной шар продуктами нашей рекурсии.
Люди вполне могут быть уникальны в своих попытках найти критерии, определяющие нашу собственную уникальность — мы мыслим уникально, поэтому мы уникальны. Среди характеристик, которые часто называют уникальными человеческими, — язык, теория разума, концепция познающего себя, эпизодическая память, ментальное путешествие во времени, создание инструментов, которые делают инструменты, и счет. Я утверждаю, что все они уникальны из-за человеческой способности к рекурсивному мышлению.
Психологи-эволюционисты утверждают, что основные характеристики человеческого разума развились в течение плейстоцена, периода от 1,8 миллиона лет до 10 000 лет назад. В эту эпоху наши предки-гоминиды были охотниками-собирателями, и социальные связи и общение стали необходимыми для выживания. Согласно психологам-эволюционистам, таким как Леда Космидес и Джон Туби из Калифорнийского университета в Санта-Барбаре, разум развивался модульным образом, со специфическими модулями, посвященными определенным функциям, таким как язык, теория разума, обнаружение измен и романтическая любовь. Поскольку рекурсия применима к нескольким областям, маловероятно, что это явление представляет собой модуль в том смысле, в котором этот термин используют эволюционные психологи. Я скорее предполагаю, что это способ вычисления, который может быть применен к нескольким различным ментальным областям.
Том Данн
Примерно два миллиона лет назад и на протяжении плейстоцена мозг наших предков-гоминидов резко увеличился в размерах, став примерно в три раза больше, чем ожидалось у приматов того же размера.
Американский зоолог Ричард Д. Александер предположил, что не только социальные связи были необходимы для выживания во враждебной среде (вместе с кошками-убийцами и другими опасностями), но также и то, что наши предки сталкивались с растущей конкуренцией со стороны себе подобных. Это привело к безудержным циклам макиавеллизма, которым противостояли социальные связи и механизмы обнаружения и изгнания нахлебников, что привело к таким сложным, но в основе своей социальным явлениям, как язык, теория разума, религия и войны. Именно это сложное исчисление социальных дел, возможно, привело к выбору более крупного мозга со способностью к рекурсивным нейронным системам.
Расширение лобных долей, в частности, могло быть особенно важным. Известно, что лобные доли участвуют в языке, теории разума, эпизодической памяти и умственном путешествии во времени, и эти рекурсивные способности могут также зависеть от того факта, что люди, по сравнению с другими приматами, проходят более длительный период роста.
Чтобы соответствовать общему образцу приматов, человеческие дети должны рождаться в возрасте около 18 месяцев, а не 9 месяцев. Но, как известно любой матери, это было бы невозможно, учитывая размер родовых путей. Мозг новорожденного шимпанзе составляет около 60 % веса взрослого человека, тогда как мозг новорожденного человека составляет лишь около 24 %. Наше затянувшееся детство означает, что человеческий мозг претерпевает большую часть своего роста, подвергаясь внешним воздействиям, и поэтому точно настроен на окружающую среду.
Патриция М. Гринфилд из Калифорнийского университета в Лос-Анджелесе задокументировала, как у детей примерно в одно и то же время развиваются иерархические представления как о языке, так и о манипулировании объектами. Точно так же, как они начинают объединять слова во фразы, а затем использовать эти фразы как единицы для объединения в предложения, они начинают комбинировать объекты, такие как гайки и болты, а затем использовать комбинации в качестве объектов для дальнейших манипуляций.
Гринфилд утверждает, что оба действия зависят от области, соответствующей области Брока, той части коры головного мозга, которая в первую очередь отвечает за производство речи, в левой части мозга. Далее она предполагает, что эта связь между языком и иерархическими манипуляциями сохраняется и во взрослом возрасте, ссылаясь на свидетельство того, что люди с афазией Брока также плохо воспроизводят рисунки иерархических древовидных структур, состоящих из линий.
Однако в ходе дальнейшего развития структуры лобных долей, участвующие в рекурсии, могут дифференцироваться. Гринфилд также ссылается на свидетельство того, что в выборке умственно отсталых детей некоторые из них умели строить иерархию, но плохо владели грамматикой, в то время как у других наблюдалась обратная картина. Она связывает эти результаты с нейрофизиологическими данными о том, что одна и та же область мозга может в равной степени участвовать в обеих функциях до двухлетнего возраста. После этого возраста наблюдается усиление дифференциации в окрестностях области Брока, так что верхняя область участвует в физическом манипулировании объектами, а соседняя нижняя область организует грамматику.
Анализ Гринфилда может быть широко применим в отношении развития и дифференциации ряда рекурсивных навыков, включая язык, теорию сознания, эпизодическую память, понимание времени и манипулирование объектами. Все эти навыки, кажется, появляются в раннем детстве, когда мозг растет. Критический период постнатального роста является как эволюционным, так и эволюционным феноменом. Вероятно, он начал проявляться как характеристика рода Homo 9.0066 около двух миллионов лет назад и управляет тем, как дети приобретают навыки. Этот расширенный шаблон роста выводит нас за пределы простых ассоциативных сетей к более динамичным процессорам, которые могут анализировать иерархические структуры и рекурсивно использовать правила.
Хотя рекурсивные навыки кажутся несколько диссоциируемыми, их совместное развитие и, возможно, совместное развитие могут быть связаны. Например, появление рекурсивного синтаксиса могло быть обусловлено эволюционным отбором именно потому, что он соответствует рекурсивной структуре теории сознания и позволял нашим предкам передавать свои макиавеллистские мысли — без сомнения, своим сообщникам, а не соперникам.
Теория разума может по-разному включаться в язык, позволяя нам модулировать нашу речь в соответствии с психическим состоянием слушателя. Рекурсивное понимание времени, возможно, имело решающее значение для эволюции самого языка, который прекрасно приспособлен для описания событий в разные моменты времени и в местах, отличных от настоящего. Таким образом, рекурсия — это свойство, которое влияет на раннее развитие базовых навыков, предоставляя нам гибкость и креативность, которые характеризуют человеческий разум.
- Александр Р. Д. 1989. Эволюция человеческой психики. В году Человеческая революция: поведенческие и биологические взгляды на происхождение современных людей, изд. . П. Мелларс и К. Стрингер. Принстон, Нью-Джерси: Издательство Принстонского университета.
- Баркоу, Дж., Л. Космидес и Дж. Туби, ред. 1992. Адаптированный разум: эволюционная психология и формирование культуры . Нью-Йорк: Издательство Оксфордского университета.
- Бек, Б.
Б. 1980. Поведение орудий животных: использование и производство орудий животными . Нью-Йорк: Garland STPM Press.
- Бирн, Р. В. и А. Уайтэн. 1990. Тактический обман приматов: база данных 1990 года. Отчет Предстоятеля 27:1-10.
- Клейтон, Н. С., Т. Дж. Басси и А. Дикинсон. 2003. Могут ли животные помнить прошлое и планировать будущее? Nature Reviews Neuroscience 4:685-691.
- Corballis, MC 2003. Рекурсия как ключ к человеческому разуму. В году от спаривания к ментальности: оценка эволюционной психологии , изд. К. Стерельный и Дж. Фитнес, стр. 155-171. Нью-Йорк: Психология Пресс.
- Corballis, MC В печати. Рекурсия, язык и скворцы. Когнитивные науки .
- Данбар, Р. 2004. Человеческая история . Лондон: Фабер и Фабер.
- Gallup, GG, Jr. 1982. Самосознание и появление разума у приматов. Американский журнал приматологии 2: 237-248.
- Гентнер, Т.
К., К. М. Фенн, Д. Марголиаш и Х. К. Нусбаум. 2006. Рекурсивное изучение синтаксических моделей певчими птицами. Природа 440:1204-1207.
- Гринфилд, П. М. 1991. Язык, инструменты и мозг: онтогенез и филогенез иерархически организованного последовательного поведения. Науки о поведении и мозге, 14 , 531-595.
- Хейлман, Дж. С. и М. С. Фикен. 1986. Комбинаторное общение животных с вычислимым синтаксисом: вызов цыпленка-ди квалифицируется структурной лингвистикой как «язык». Поведение животных 34:1899-1901.
- Хаузер, М. Д., Н. Хомский и У. Т. Фитч. 2002. Языковой факультет: что это такое, у кого он есть и как он развивался? Наука 298:1569-1579.
- Келер, В. 1925. Менталитет обезьян . Нью-Йорк: Рутледж и Кеган Пол.
- Повинелли, Д. Дж. и Дж. Вонк. 2003. Разум шимпанзе: подозрительно человеческий? Тенденции в когнитивных науках 7:157-160.
- Суддендорф Т. и М. К. Корбаллис. 1997.
Ментальное путешествие во времени и эволюция человеческого разума. Монографии по генетической, социальной и общей психологии 123:133-167.
- Суддендорф Т. и М. К. Корбаллис. Под давлением. Эволюция предвидения: что такое мысленное путешествие во времени и уникально ли оно для людей? Науки о поведении и мозге .
- Tomasello, M., J. Call and B. Hare, 2003. Шимпанзе понимают психологические состояния — вопрос в том, какие именно и в какой степени? Тенденции в когнитивных науках 7:153-156.
- Тулвинг, Э. 1983. Элементы эпизодической памяти . Лондон: Издательство Оксфордского университета.
Recursive Labs Visual Engagement Tools
Перенесите личное взаимодействие с клиентами в цифровой мир
В эпоху цифровых технологий ваш веб-сайт или мобильное приложение являются вашим основным местом работы. Ваша домашняя страница — это витрина вашего магазина. А ваши агенты по обслуживанию клиентов — это улыбающиеся лица, которые привлекают клиентов и заставляют их возвращаться.
Recursive Labs не требует загрузки, готовые к соблюдению требований инструменты совместного просмотра и совместного использования экрана в сочетании с беспрепятственным видеочатом, который можно развернуть с помощью экранной подсказки, SMS-сообщения или текстового чата, означает, что даже самый сложный процесс продажи или заявки на обслуживание могут быть решены в кратчайшие сроки. в реальном времени. Безопасная работа бок о бок с вашим клиентом является отличительной чертой расширенного онлайн-обслуживания клиентов.
Сегодняшние клиенты не хотят просто обслуживаться. Они хотят быть обрученными.
Общайтесь лицом к лицу с любым клиентом в любой точке мира с помощью любого устройства. Ваша команда может вернуться к дням, когда вы оказывали руководство от человека к человеку. Мы создали нашу платформу с учетом интересов предприятий, поэтому вместе мы можем предложить совместные и полностью совместимые пути клиентов для любой отрасли. Оптимизируйте свои цифровые взаимодействия уже сегодня.
Увеличивайте доход, сохраняйте клиентов и повышайте удовлетворенность клиентов с помощью наших интерфейсов для совместной работы с клиентами.
Совместный просмотр и демонстрация экрана в реальном времени
Краткий обзор целей KPI в реальном времени:
Увеличение доходов в Интернете
Устранение повторных вызовов
Повышение удовлетворенности клиентов
Уменьшить среднее время обработки
Снижение нормы прибыли
Видеочат Relate
Краткий обзор целей KPI Relate:
Повышение разрешения при первом вызове
Повышение удовлетворенности клиентов
Увеличение коэффициента конверсии
Уменьшить среднее время обработки
Минимизируйте усилия клиента
Relate SMS Краткий обзор целей KPI:
Уменьшить количество кренов грузовика
Увеличить разрешение первого вызова
Сокращение пробега и расходов на топливо
Повышение удовлетворенности поставщиков
Уменьшить среднее время обработки
Запрос входящего видеочата в прямом эфире
Запрос прямых целевых показателей KPI:
Повышение удовлетворенности клиентов
Увеличение коэффициента конверсии
Уменьшить разочарование клиентов
Сократить среднее время обработки
Минимизируйте усилия клиента
Сокращение циклов продаж
Запись записи сеанса
Краткий обзор целевых показателей KPI:
Повышение компетенции должностных обязанностей
Уменьшить среднее время обучения
Улучшение передачи обучения
Повышение рейтинга Net Promoter Score
Упрощение процессов соответствия
Банковское дело и финансы
Менее половины клиентов банков, опрошенных J.
D. Power в 2022 году, считают, что связаться с представителем службы поддержки легко. Современные потребители осуществляют банковские операции онлайн, и их самой большой проблемой стало решение проблем с обслуживанием клиентов. Хватит запутанных справочных статей и вялых очередей заявок в службу поддержки! Поддержка совместного просмотра в реальном времени позволяет вашим обученным экспертам знакомить клиентов с формами, приложениями и заявлениями.
Отредактируйте любой экранный элемент из представления вашего агента, чтобы данные клиентов всегда были защищены и конфиденциальны. Добавляйте комментарии в прямом эфире на общем экране, доступном только для просмотра, или сотрудничайте, заполняя поля от имени вашего клиента.
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Привод преобразований технических продуктов
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Сокращение отказа от онлайн-форм и приложений
Помогите клиентам ориентироваться в сложных документах
Включить службу консьержа
Обеспечьте такой же отличный сервис, как и в лобби банка
Повышение разрешения при первом вызове (FCR)
Поднимите показатель Net Promoter за счет более счастливых пользователей
Свяжитесь с финансовыми экспертами лицом к лицу
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Call-Center-as-a-Service
Совместные и объединенные пути клиентов сокращают вашу воронку продаж, стимулируют конверсии для сложных технических продаж и улучшают вашу CRM за счет большего количества завершенных записей.
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Предоставьте своему отделу продаж возможность совместного просмотра с покупателями в вашем интернет-магазине, чтобы просматривать технические характеристики, выделять товары для перекрестных продаж и поддерживать связь клиентов с вашим брендом, а не с вашим конкурентом!
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Увеличьте CSAT, добавив индивидуальный подход
Предложите взаимодействие с клиентами следующего поколения
Станьте лидером в технологии контакт-центров
Выполнять больше вызовов с низким временем обработки
Сокращение количества отказов с личным чатом
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Розничная торговля и электронная коммерция
Совместные и объединенные пути клиентов сокращают вашу воронку продаж, стимулируют конверсию для сложных технических продаж и улучшают вашу CRM за счет большего количества закрытых записей.
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Предоставьте своему отделу продаж возможность совместного просмотра с покупателями в вашем интернет-магазине, чтобы просматривать технические характеристики, выделять товары для перекрестных продаж и поддерживать связь клиентов с вашим брендом, а не с вашим конкурентом!
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Персонализация циклов взаимодействия с клиентом
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Оставайтесь с пользователями, чтобы снизить количество отказов от корзины
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Телекоммуникационные и ИТ-услуги
Совместные и объединенные пути клиентов сокращают вашу воронку продаж, стимулируют конверсии для сложных технических продаж и улучшают вашу CRM за счет большего количества закрытых записей.
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Предоставьте своему отделу продаж возможность совместного просмотра с покупателями в вашем интернет-магазине, чтобы просматривать технические характеристики, выделять товары для перекрестных продаж и поддерживать связь клиентов с вашим брендом, а не с вашим конкурентом!
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Устранение препятствий воронки продаж с помощью живого чата
Предлагайте индивидуальную поддержку продаж на страницах продукта
Предлагать видеочат без загрузок
Объясните сложные сервисные предложения за несколько минут
Узнавайте больше данных о лидах до контакта
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Выездная служба
Совместные и объединенные пути клиентов сокращают вашу воронку продаж, стимулируют конверсию для сложных технических продаж и улучшают вашу CRM за счет большего количества закрытых записей.
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Предоставьте своему отделу продаж возможность совместного просмотра с покупателями в вашем интернет-магазине, чтобы просматривать технические характеристики, выделять товары для перекрестных продаж и поддерживать связь клиентов с вашим брендом, а не с вашим конкурентом!
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Увеличение разрешения первого вызова (FCR)
Удалите ненужные тележки
Соедините полевых техников с передовыми экспертами
Поддерживайте движение вашего флота с помощью мгновенной связи
Более эффективное использование ресурсов на местах
Тратьте меньше времени на ввод, больше времени на исправление
Повышение эффективности выездного обслуживания на любом устройстве
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Страхование
Предложения, дополнительные услуги и варианты полиса могут сбивать с толку. Безопасный сеанс совместного просмотра с новыми и существующими клиентами в вашем приложении или на вашем веб-сайте без загрузки означает, что ваши независимые агенты всегда на расстоянии одного клика.
Агенты и брокеры могут построчно просматривать сложные формы вместе с клиентами с помощью простой в использовании визуальной платформы взаимодействия с клиентами, которая доступна по простой ссылке, QR-коду или тексту.
Персонализируйте пути клиентов
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Познакомьте пользователей с котировками, политиками и документами
Ускорьте процесс рассмотрения претензий с помощью Relate SMS
Свяжитесь с агентами и брокерами лицом к лицу
Выделяйте услуги и преимущества на экране
Повышение ежемесячной скорости связывания с помощью персонализации
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Здравоохранение
Медицинские работники каждый день работают с конфиденциальной информацией и должны соответствовать строгим требованиям HIPAA. Программное обеспечение для совместного просмотра в реальном времени готово к соблюдению требований и позволяет скрывать любые данные, элементы или элементы, которые вы диктуете, от того, чтобы они когда-либо попадали на экран вашего сервисного агента.
Медицинские работники и специалисты по выставлению счетов могут помочь новичкам разобраться в сложных формах, инструкциях по лекарствам и амбулаторных документах, помогая ориентироваться прямо на экране.
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Удовлетворить растущий спрос на телемедицину
Ознакомьтесь с рекомендациями и документами по лекарствам
Проводить пациентов через длинные инструкции
Подключайтесь в любом месте, на любом устройстве
Выделение экранных инструкций и примечаний
Снизить порог для пользователей, не разбирающихся в технологиях
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Автомобилестроение
Совместные и объединенные пути клиентов сокращают вашу воронку продаж, стимулируют конверсию для сложных технических продаж и улучшают вашу CRM за счет большего количества закрытых записей.
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Предоставьте своему отделу продаж возможность совместного просмотра с покупателями в вашем интернет-магазине, чтобы просматривать технические характеристики, выделять товары для перекрестных продаж и поддерживать связь клиентов с вашим брендом, а не с вашим конкурентом!
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Преобразование привода технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Подключение удаленных магазинов и дилерских центров
Пусть эксперты заглянут под капот, где угодно
Диагностика и решение технических проблем быстрее
Меньше потерянного времени повышает эффективную норму труда
Решите больше проблем при первом звонке
Персонализация циклов взаимодействия с клиентом
Сократить воронку продаж
Привод преобразований технических изделий
Расширение возможностей вашего отдела продаж
Уменьшить норму прибыли
Мгновенный переход со страницы на встречу
Уменьшите количество брошенных корзин, оставаясь с пользователями
По данным Trust Pilot, сайты электронной коммерции могут повысить коэффициент конверсии на целых 8% за счет персонализированного взаимодействия с клиентами.
Recursive Labs Suite: совместный просмотр, видеочат, совместное использование камеры и многое другое
Индивидуальное руководство ускоряет заполнение онлайн-документов, приложений и покупок.
Визуальное взаимодействие с клиентами, которое интегрируется с вашей CRM
Наши удобные для соблюдения нормативных требований бесплатные визуальные инструменты взаимодействия с клиентами были созданы для предприятий, использующих основные платформы CRM и VCC, такие как Salesforce, Zendesk, Microsoft Dynamics, Amazon Connect и Five9. . Мы также масштабируемся до предприятий любого размера! Запустить собственную CRM? Без проблем. Мы можем предоставить наш открытый API, чтобы вы могли создавать собственные коннекторы.
Мобильное приложение готово
Хотите добавить в свое мобильное приложение визуальное взаимодействие с клиентами следующего поколения? Наш мобильный SDK упрощает развертывание наших сервисов и их настройку в соответствии с уникальными требованиями среды вашего приложения.
Запланируйте звонок, чтобы узнать больше!
Привлекайте клиентов с помощью нового уровня обслуживания и поддержки
Нет загрузок. Никаких подписок. Нет имен пользователей.
Просто нажмите, подключитесь и безопасно просматривайте или делитесь экраном с вашими клиентами на любом устройстве.
Recursive Sans & Mono
Созданный для максимальной универсальности, контроля и производительности, Recursive представляет собой изменяемый шрифт с пятью осями. Это позволяет вам выбирать из широкого спектра предопределенных стилей или набирать именно то, что вы хотите для каждой из его осей: Monospace, Casual, Weight, Slant и Cursive . Используя все преимущества технологии вариативных шрифтов, Recursive предлагает беспрецедентный уровень гибкости благодаря одному файлу шрифта.
Recursive черпает вдохновение в повседневном рисовании одним мазком, стилистически гибком и энергичном стиле письма кистью.
Адаптируя эту эстетическую основу к системе типов, Recursive разработан, чтобы преуспеть в цифровых интерактивных средах. Это делает шрифт идеальным для широкого спектра применений, включая приложения с большим объемом данных, техническую документацию и редакторы кода.
Recursive создан с учетом адаптивности и разнообразия, предлагая полную систему типов, но гарантируя, что каждый стиль может идеально сочетаться со своими братьями и сестрами. Имея так много возможных вариаций в своих подсемействах, насыщенности и стилях, Recursive позволяет использовать дюжину комбинаций шрифтов, которые обеспечивают достаточный контраст, чтобы четко определить типографские роли, сохраняя при этом связный голос.
Этот шрифт представлен в двух практичных и хорошо читаемых подсемействах: Sans и Mono. Благодаря оси Monospace (
MONO) оба этих подсемейства можно использовать в одном файле шрифта. Вы даже можете выбрать пользовательские экземпляры, которые являются полупропорциональными или полумоноширинными.Разумеется, вертикальные показатели, такие как высота строки, высота заглавной буквы и высота по оси x, являются общими для всей оси Monospace . Это позволяет создавать гармоничные и эффективные макеты даже при смешивании различных пропорций, например, в приложениях с большим объемом данных и технической документации.
Рекурсивный шрифт Sans создан для дизайна текста и пользовательского интерфейса. В то время как его пропорциональные символы обеспечивают удобное чтение в размерах текста, его самые тяжелые веса идеально подходят для создания резких заголовков с узкими интервалами.
Recursive Mono создан для кода. Его символы имеют одинаковую ширину для четкости и идеального выравнивания. Это особенно полезно для использования в задачах программирования и проектирования с большими объемами данных, но также дает творческие возможности в типографике дисплея.
Символы в обоих подсемействах, Sans и Mono, сохраняют одинаковую ширину во всех стилях шрифта, независимо от значений, установленных на осях Weight, Casual, Slant и Cursive .
Таким образом, вы можете использовать Recursive для создания анимированных переходов шрифтов, не нарушая макет элементов пользовательского интерфейса, таких как меню и кнопки.
Recursive использует свою ось Casual (
CASL), чтобы предложить диапазон индивидуальности, позволяющий получить правильный тон для любого контекста. Вдоль этой оси формы букв подстраиваются по кривизне штриха, контрасту и концам, чтобы перейти от прочного, рационального Линейный в дружелюбный, энергичный Повседневный . Все стили по этой оси предназначены для обеспечения высокой читаемости при средних размерах и размерах текста. При размерах дисплея наиболее эффективно использовать любой конец оси Casual .Линейные стили (
CASL 0) имеют слегка сглаженные края и простые открытые формы. Это оптимизирует удобочитаемость и позволяет лучше сосредоточиться на плотной информации, такой как длинный текст и сложный код.Casual (
CASL 1) перекликается с мягкими и волнистыми мазками повседневной вывески, но упрощает эти формы для создания яркого и привлекательного тона.Это делает его идеальным для веб-заголовков, фрагментов кода и интерфейсов командной строки.
Recursive поставляется в широком диапазоне весов, от светлого (
300) до сверхтяжелого черного (900). Вы можете выбрать один из семи предопределенных весов или установить пользовательское значение через его Weight (wght) ось. А поскольку Recursive поддерживает согласованные формы букв по всей оси Weight , он обеспечивает плавную анимацию между любым из его различных весов.В Recursive наклонные и курсивные формы букв можно контролировать отдельно. Ось Slant (
slnt) определяет угол наклона букв, а ось Cursive (CRSV) позволяет настроить способ замены курсивных букв вдольslnt.Курсивные буквы Recursive (
CRSV 1) заменяют знакомые «римские» формы букв курсивными вариантами, такими как одноэтажные «a» и «g». По умолчанию Recursive автоматически применяет эти альтернативы курсиву при установке оси Slant (slnt) за пределами-14.Это обеспечивает плавные анимированные переходы от нормального шрифта к наклонному с наклоном до 13,99°, а также «настоящий курсив» с курсивными буквами под углом 14°. Также можно использовать наклонные римские (
slnt -15, CRSV 0), прямой курсив (slnt 0 , CRSV 1) или установите пользовательские значения на обеих осях, чтобы получить больше возможностей для экспериментов.В качестве вариативного шрифта Recursive дает вам детальный контроль над каждым из его стилей. Тем не менее, он также поставляется с 64 предопределенными стилями, к которым легко получить доступ через меню шрифтов. Названные именованными экземплярами¹ , они работают так же, как и обычные статические шрифты.
¹ Именованный экземпляр: предопределенное место в пространстве дизайна вариативного шрифта, подобное «статическим экземплярам», знакомым по традиционным цифровым шрифтам.
Чтобы удовлетворить потребности в глобальном общении, Recursive поддерживает широкий спектр языков на основе латиницы, включая вьетнамский.
Он также поставляется с расширенным набором валют, символов, дробей и стрелок.
Абенаки, афан оромо, афар, африкаанс, албанский, эльзасский, амис, анута, арагонский, аранский, арумынский, аррернте, арванитский (латиница), астурийский, атаял, аймара, азербайджанский, башкирский (латиница), баскский, белорусский (латиница) ), бемба, биколь, бислама, боснийский, бретонский, креольский язык Кабо-Верде, каталонский, кебуано, чаморро, чавакано, чичева, чикасо, кимбрийский, кофан, корнуоллский, корсиканский, крик, крымскотатарский (латиница), хорватский, чешский, датский, даванский, делавэрский, дхолуо, дреху, голландский, английский, эсперанто, эстонский, фарерский, фиджийский, филиппинский, финский, народный, французский, фризский, фриульский, гагаузский (латиница), галисийский, ганда, генуэзский, немецкий, гикуйю, гуньянди, гренландский (Kalaallisut), гваделупский креольский, гвичин, гаитянский креольский, хан, гавайский, хилигайнон, хопи, хотчан (латиница), венгерский, исландский, идо, игбо, илокано, индонезийский, интерглосса, интерлингва, ирландский, истро-румынский, итальянский , ямайский, яванский (латиница), джерриайс, кайнганг, кала-лагау я, капампанган (латиница), какчикель, каракалпак (латиница) ин), карельский (латиница), кашубский, киконго, киньярванда, кирибати, кирунди, клингонский, курдский (латиница), ладинский, латинский, латинский sine Flexione, латышский, литовский, ложбанский, ломбардский, нижнесаксонский, люксембургский, масаи, махува, малайский, мальтийский, мэнский, маори, маркизский, мегленорумынский, мериам мир, мирандский, могавк, молдавский, монтанье, черногорский, муррин-патха, нагамский креольский, науатль, ндебеле, неаполитанец, нгиямбаа, ниуэ, нунгар, норвежский, новиальный, Западный, окситанский, древнеисландский, древнескандинавский, онипот, ошивамбо, осетинский (латиница), палауский, папиаменто, пьемонтский, польский, португальский, потаватоми, кекчи, кечуа, раротонганский, румынский, ретороманский, ротокас, саамский (инари-саамский) ), саамы (луле-саамы), саамы (северные саамы), саамы (южные саамы), самоанский, санго, сарамакский, сардинский, шотландский гэльский, сербский (латиница), сери, сейшельский креольский, шауни, шона, сицилийский, силезский, словацкий , словенский, словио (латиница), сомалийский, сербский (нижнесербский), сербский (верхнесербский), сото (северный), сото (южный) р-н), испанский, срананский, сунданский (латиница), суахили, свази, шведский, тагальский, таитянский, тетум, ток-писин, токелау, тонга, чилуба, тсонга, тсвана, тумбука, турецкий, туркменский (латиница), тувалуанский, цоциль, узбекский (латиница), венецианский, вепсский, вьетнамский, волапюк, выро, валлисийский, валлонский, варай-варай, варлпири, вайуу, валлийский, вик-мунгкан, вираджури, волоф, шаванте, коса, япский, йинджибарнди, сапотек, зарма, зазаки , Зулу, Зуни
А
A
латинская заглавная буква a (u+0041)
А
À
латинская заглавная буква а с запятой (u+00c0)
А
Á
латинская заглавная буква a с акутом (u+00c1)
Â
Â
латинская заглавная буква a с циркумфлексом (u+00c2)
Ã
Ã
латинская заглавная буква a с тильдой (u+00c3)
Ä
Ä
латинская заглавная буква а с диэрезисом (u+00c4)
Å
Å
латинская заглавная буква a с кольцом вверху (u+00c5)
А
À
латинская заглавная буква а с макроном (u+0100)
Ă
Â
латинская заглавная буква a с сокращением (u+0102)
Ą
Ą
латинская заглавная буква а с огонеком (u+0104)
Ǻ
Ǻ
латинская заглавная буква a с кольцом вверху и акут (u+01fa)
Ȁ
Ȁ
латинская заглавная буква а с двойной гравировкой (u+0200)
Ȃ
Ȃ
латинская заглавная буква a с перевернутым сокращением (u+0202)
Ạ
Ạ
латинская заглавная буква a с точкой внизу (u+1ea0)
Ả
Ả
латинская заглавная буква a с крючком вверху (u+1ea2)
Ấ
Ấ
латинская заглавная буква a с циркумфлексом и акутом (u+1ea4)
Ầ
Ầ
латинская заглавная буква a с циркумфлексом и гравировкой (u+1ea6)
Ẩ
Ẩ
латинская заглавная буква a с циркумфлексом и крючком вверху (u+1ea8)
Ẫ
Ẫ
латинская заглавная буква a с циркумфлексом и тильдой (u+1eaa)
Ậ
Ậ
латинская заглавная буква a с циркумфлексом и точкой внизу (u+1eac)
Ắ
Ắ
латинская заглавная буква a с сокращением и акутом (u+1eae)
Ằ
Ằ
латинская заглавная буква a с краткой и серьезной (u+1eb0)
Ẳ
Ẳ
латинская заглавная буква a с кратким и крючком вверху (u+1eb2)
Ẵ
Ẵ
латинская заглавная буква a с бреве и тильдой (u+1eb4)
Ặ
Ặ
латинская заглавная буква a с краткой и точкой внизу (u+1eb6)
Б
B
латинская заглавная буква b (u+0042)
С
C
латинская заглавная буква c (u+0043)
Ç
Ç
латинская заглавная буква c с седилью (u+00c7)
Ć
→
латинская заглавная буква c с острым знаком (u+0106)
Ĉ
Ĉ
латинская заглавная буква c с циркумфлексом (u+0108)
Ċ
Ċ
латинская заглавная буква c с точкой над ней (u+010a)
Ч
Č
латинская заглавная буква c с кароном (u+010c)
Ḉ
Ḉ
латинская заглавная буква c с седилью и акут (u+1e08)
Д
D
латинская заглавная буква d (u+0044)
Ď
Ď
латинская заглавная буква d с кароном (u+010e)
Ḍ
латинская заглавная буква d с точкой внизу (u+1e0c)
Ḏ
Ḏ
латинская заглавная буква d с чертой внизу (u+1e0e)
Е
E
латинская заглавная буква e (u+0045)
Э
È
латинская заглавная буква e с запятой (u+00c8)
Э
É
латинская заглавная буква e с акутом (u+00c9)
Ê
Ê
латинская заглавная буква e с циркумфлексом (u+00ca)
Ë
Ë
латинская заглавная буква e с диэрезисом (u+00cb)
Э
Ē
латинская заглавная буква e с макроном (u+0112)
Ĕ
Ĕ
латинская заглавная буква e с сокращением (u+0114)
Э
Ė
латинская заглавная буква e с точкой над ней (u+0116)
Ę
Ø
латинская заглавная буква e с огонеком (u+0118)
Ě
Ě
латинская заглавная буква e с кароном (u+011a)
Ȅ
Ȅ
латинская заглавная буква e с двойной гравировкой (u+0204)
Ȇ
Ȇ
латинская заглавная буква e с перевернутым сокращением (u+0206)
Ḕ
Ḕ
латинская заглавная буква e с макроном и гравировкой (u+1e14)
Ḗ
Ḗ
латинская заглавная буква e с макроном и акутом (u+1e16)
Ḝ
Ḝ
латинская заглавная буква e с cedilla и breve (u+1e1c)
Ẹ
Ẹ
латинская заглавная буква e с точкой внизу (u+1eb8)
Ẻ
Ẻ
латинская заглавная буква e с крючком вверху (u+1eba)
Ẽ
Ẽ
латинская заглавная буква e с тильдой (u+1ebc)
Ế
Ế
латинская заглавная буква e с циркумфлексом и акутом (u+1ebe)
Ề
Ề
латинская заглавная буква e с циркумфлексом и гравировкой (u+1ec0)
Ể
Ể
латинская заглавная буква e с циркумфлексом и крючком вверху (u+1ec2)
Ễ
Ễ
латинская заглавная буква e с циркумфлексом и тильдой (u+1ec4)
Ệ
Ệ
латинская заглавная буква e с циркумфлексом и точкой внизу (u+1ec6)
Ф
F
латинская заглавная буква f (u+0046)
грамм
G
латинская заглавная буква g (u+0047)
ГРАММ
Ü
латинская заглавная буква g с циркумфлексом (u+011c)
ГРАММ
Ğ
латинская заглавная буква g с сокращением (u+011e)
ГРАММ
Ġ
латинская заглавная буква g с точкой над ней (u+0120)
ГРАММ
Ģ
латинская заглавная буква g с седилью (u+0122)
Ǧ
Ǧ
латинская заглавная буква g с кароном (u+01e6)
ГРАММ
№
латинская заглавная буква g с макроном (u+1e20)
ЧАС
H
латинская заглавная буква h (u+0048)
ЧАС
Ĥ
латинская заглавная буква h с циркумфлексом (u+0124)
ЧАС
Ḥ
латинская заглавная буква h с точкой внизу (u+1e24)
ЧАС
Ḫ
латинская заглавная буква h с краткой аббревиатурой внизу (u+1e2a)
я
I
латинская заглавная буква i (u+0049)
Я
Ì
латинская заглавная буква i с запятой (u+00cc)
Я
Н
латинская заглавная буква i с острым знаком (u+00cd)
Я
Î
латинская заглавная буква i с циркумфлексом (u+00ce)
Я
Ï
латинская заглавная буква i с диэрезисом (u+00cf)
Я
è
латинская заглавная буква i с тильдой (u+0128)
Я
Ī
латинская заглавная буква i с макроном (u+012a)
Я
Ĭ
латинская заглавная буква i с сокращением (u+012c)
Я
Į
латинская заглавная буква i с огонеком (u+012e)
Я
İ
латинская заглавная буква i с точкой над ней (u+0130)
Ȉ
Ȉ
латинская заглавная буква i с двойной гравировкой (u+0208)
Ȋ
Ȋ
латинская заглавная буква i с перевернутой краткостью (u+020a)
Я
Ḯ
латинская заглавная буква i с диэрезисом и острым (u+1e2e)
Я
Ỉ
латинская заглавная буква i с крючком вверху (u+1ec8)
Я
Ị
латинская заглавная буква i с точкой внизу (u+1eca)
Дж
J
латинская заглавная буква j (u+004a)
Ĵ
ô
латинская заглавная буква j с циркумфлексом (u+0134)
К
K
латинская заглавная буква k (u+004b)
Ķ
Ķ
латинская заглавная буква k с седилью (u+0136)
л
L
латинская заглавная буква l (u+004c)
Ĺ
№
латинская заглавная буква l с акутом (u+0139)
Ļ
Ļ
латинская заглавная буква l с седильей (u+013b)
Ľ
Ľ
латинская заглавная буква l с кароном (u+013d)
Ḷ
№
латинская заглавная буква l с точкой внизу (u+1e36)
Ḻ
Ḻ
латинская заглавная буква l с чертой внизу (u+1e3a)
М
M
латинская заглавная буква m (u+004d)
Ṃ
Ṃ
латинская заглавная буква m с точкой внизу (u+1e42)
Н
N
латинская заглавная буква n (u+004e)
С
Ñ
латинская заглавная буква n с тильдой (u+00d1)
Ń
Ń
латинская заглавная буква n с острым знаком (u+0143)
Ņ
№
латинская заглавная буква n с седилью (u+0145)
Ň
Ň
латинская заглавная буква н с кароном (u+0147)
Ṅ
Ṅ
латинская заглавная буква n с точкой над ней (u+1e44)
Ṇ
Ṇ
латинская заглавная буква n с точкой внизу (u+1e46)
Ṉ
Ṉ
латинская заглавная буква n с чертой ниже (u+1e48)
О
O
латинская заглавная буква o (u+004f)
Ò
Ò
латинская заглавная буква o с запятой (u+00d2)
О
О
латинская заглавная буква o с острым знаком (u+00d3)
Ô
Ô
латинская заглавная буква o с циркумфлексом (u+00d4)
Õ
Õ
латинская заглавная буква o с тильдой (u+00d5)
О
Ö
латинская заглавная буква o с диэрезисом (u+00d6)
О
Ō
латинская заглавная буква o с макроном (u+014c)
Ŏ
Ŏ
латинская заглавная буква o с краткостью (u+014e)
Ő
Ő
латинская заглавная буква o с двойным ударением (u+0150)
Ơ
Ơ
латинская заглавная буква o с рогом (u+01a0)
Ǫ
Ǫ
латинская заглавная буква o с огонеком (u+01ea)
Ȍ
Ȍ
латинская заглавная буква o с двойной гравировкой (u+020c)
Ȏ
Ȏ
латинская заглавная буква o с перевернутым сокращением (u+020e)
Ȫ
Ȫ
латинская заглавная буква o с диэрезисом и макроном (u+022a)
Ȭ
Ȭ
латинская заглавная буква o с тильдой и макроном (u+022c)
Ȱ
Ȱ
латинская заглавная буква o с точкой над ней и макроном (u+0230)
Ṍ
Ṍ
латинская заглавная буква o с тильдой и акусом (u+1e4c)
Ṏ
Ṏ
латинская заглавная буква o с тильдой и диэрезисом (u+1e4e)
Ṑ
Ṑ
латинская заглавная буква o с макроном и грависом (u+1e50)
Ṓ
Ṓ
латинская заглавная буква o с макроном и акутом (u+1e52)
Ọ
Ọ
латинская заглавная буква o с точкой внизу (u+1ecc)
Ỏ
Ỏ
латинская заглавная буква o с крючком вверху (u+1ece)
Ố
Ố
латинская заглавная буква o с циркумфлексом и акутом (u+1ed0)
Ồ
Ồ
латинская заглавная буква o с циркумфлексом и гравировкой (u+1ed2)
Ổ
Ổ
латинская заглавная буква o с циркумфлексом и крюком вверху (u+1ed4)
Ỗ
Ỗ
латинская заглавная буква o с циркумфлексом и тильдой (u+1ed6)
Ộ
Ộ
латинская заглавная буква o с циркумфлексом и точкой внизу (u+1ed8)
Ớ
Ớ
латинская заглавная буква o с рогом и акут (u+1eda)
Ờ
Ờ
латинская заглавная буква o с рогом и могилой (u+1edc)
Ở
Ở
латинская заглавная буква o с рогом и крючком вверху (u+1ede)
Ỡ
Ỡ
латинская заглавная буква o с рожком и тильдой (u+1ee0)
Ợ
Ợ
латинская заглавная буква o с рогом и точкой внизу (u+1ee2)
п
P
латинская заглавная буква p (u+0050)
Вопрос
Q
латинская заглавная буква q (u+0051)
р
R
латинская заглавная буква r (u+0052)
Р
Ŕ
латинская заглавная буква r с акутом (u+0154)
Р
Ŗ
латинская заглавная буква r с седилью (u+0156)
Р
Ø
латинская заглавная буква r с кароном (u+0158)
Ȑ
Ȑ
латинская заглавная буква r с двойной гравировкой (u+0210)
Ȓ
Ȓ
латинская заглавная буква r с перевернутым сокращением (u+0212)
Р
Ṛ
латинская заглавная буква r с точкой внизу (u+1e5a)
Р
Ṟ
латинская заглавная буква r с чертой внизу (u+1e5e)
С
S
латинская заглавная буква s (u+0053)
Ś
Ś
латинская заглавная буква s с острым знаком (u+015a)
О
Ŝ
латинская заглавная буква s с циркумфлексом (u+015c)
Ş
Ş
латинская заглавная буква s с седильей (u+015e)
Ш
Š
латинская заглавная буква s с кароном (u+0160)
Ș
Ș
латинская заглавная буква s с запятой внизу (u+0218)
Ṡ
Ṡ
латинская заглавная буква s с точкой над ней (u+1e60)
Ṣ
Ṣ
латинская заглавная буква s с точкой внизу (u+1e62)
Ṥ
Ṥ
латинская заглавная буква s с острым знаком и точкой сверху (u+1e64)
Ṧ
Ṧ
латинская заглавная буква s с кароном и точкой над ней (u+1e66)
Ṩ
Ṩ
латинская заглавная буква s с точкой внизу и точкой вверху (u+1e68)
Т
T
латинская заглавная буква t (u+0054)
Ţ
Ţ
латинская заглавная буква t с седильей (u+0162)
Ť
Ť
латинская заглавная буква t с кароном (u+0164)
ц
Ț
латинская заглавная буква t с запятой внизу (u+021a)
Ṭ
Ṭ
латинская заглавная буква t с точкой внизу (u+1e6c)
Ṯ
Ṯ
латинская заглавная буква t с чертой ниже (u+1e6e)
U
U
латинская заглавная буква u (u+0055)
Ù
Ù
латинская заглавная буква u с запятой (u+00d9)
Ú
У
латинская заглавная буква u с острым знаком (u+00da)
Û
Û
латинская заглавная буква u с циркумфлексом (u+00db)
О
Ü
латинская заглавная буква u с диэрезисом (u+00dc)
Ũ
×
латинская заглавная буква u с тильдой (u+0168)
Ū
Ū
латинская заглавная буква u с макроном (u+016a)
Ŭ
Ŭ
латинская заглавная буква u с сокращением (u+016c)
Ů
Ů
латинская заглавная буква u с кольцом вверху (u+016e)
Ű
Ű
латинская заглавная буква u с двойным ударением (u+0170)
Ų
Ų
латинская заглавная буква u с огонеком (u+0172)
я
Ư
латинская заглавная буква u с рогом (u+01af)
Ȕ
Ȕ
латинская заглавная буква u с двойной гравировкой (u+0214)
Ȗ
Ȗ
латинская заглавная буква u с перевернутым сокращением (u+0216)
Ṹ
Ṹ
латинская заглавная буква u с тильдой и акусом (u+1e78)
Ṻ
Ṻ
латинская заглавная буква u с макроном и диэрезисом (u+1e7a)
Ụ
Ụ
латинская заглавная буква u с точкой внизу (u+1ee4)
Ủ
Ủ
латинская заглавная буква u с крючком вверху (u+1ee6)
Ứ
Ứ
латинская заглавная буква u с рогом и акусом (u+1ee8)
Ừ
Ừ
латинская заглавная буква u с рогом и могилой (u+1eea)
Ử
Ử
латинская заглавная буква u с рогом и крючком вверху (u+1eec)
Ữ
Ữ
латинская заглавная буква u с рожком и тильдой (u+1eee)
Ự
Ự
латинская заглавная буква u с рогом и точкой внизу (u+1ef0)
В
V
латинская заглавная буква v (u+0056)
Вт
W
латинская заглавная буква w (u+0057)
Ŵ
Ŵ
латинская заглавная буква w с циркумфлексом (u+0174)
Ẁ
Ẁ
латинская заглавная буква w с запятой (u+1e80)
Ẃ
Ẃ
латинская заглавная буква w с острым знаком (u+1e82)
Ẅ
Ẅ
латинская заглавная буква w с диэрезисом (u+1e84)
Икс
X
латинская заглавная буква x (u+0058)
Д
Д
латинская заглавная буква y (u+0059)
Ý
Ý
латинская заглавная буква y с акутом (u+00dd)
Ŷ
Ŷ
латинская заглавная буква y с циркумфлексом (u+0176)
Ÿ
Ÿ
латинская заглавная буква y с диэрезисом (u+0178)
Ȳ
Ȳ
латинская заглавная буква y с макроном (u+0232)
Ẏ
Ẏ
латинская заглавная буква y с точкой над ней (u+1e8e)
Ỳ
Ỳ
латинская заглавная буква y с запятой (u+1ef2)
Ỵ
Ỵ
латинская заглавная буква y с точкой внизу (u+1ef4)
Ỷ
Ỷ
латинская заглавная буква y с крючком вверху (u+1ef6)
Ỹ
Ỹ
латинская заглавная буква y с тильдой (u+1ef8)
Z
Z
латинская заглавная буква z (u+005a)
Ź
№
латинская заглавная буква z с острым знаком (u+0179)
Ż
Ż
латинская заглавная буква z с точкой над ней (u+017b)
Ž
Ž
латинская заглавная буква z с кароном (u+017d)
Ẓ
Ẓ
латинская заглавная буква z с точкой внизу (u+1e92)
Æ
Æ
латинская заглавная буква ae (u+00c6)
Ǽ
Ǽ
латинская заглавная буква ae с острым знаком (u+01fc)
Ð
Ð
латинская заглавная буква eth (u+00d0)
Ø
Ø
латинская заглавная буква o со штрихом (u+00d8)
Ǿ
Ǿ
латинская заглавная буква o со штрихом и острым ударом (u+01fe)
Þ
Þ
латинская заглавная буква шип (u+00de)
Đ
Đ
латинская заглавная буква d со штрихом (u+0110)
ЧАС
æ
латинская заглавная буква h со штрихом (u+0126)
IJ
IJ
латинская заглавная лигатура ij (u+0132)
латинская заглавная лигатура ij с острым знаком (u+e133)
Ŀ
№
латинская заглавная буква l с точкой в середине (u+013f)
Ł
Ł
латинская заглавная буква l со штрихом (u+0141)
Ŋ
Ŋ
латинская заглавная англ (u+014a)
О
Œ
латинская заглавная лигатура oe (u+0152)
Ŧ
Ŧ
латинская заглавная буква t со штрихом (u+0166)
Ə
Ə
латинская заглавная буква шва (u+018f)
Ɲ
Ɲ
латинская заглавная буква n с левым крючком (u+019d)
DŽ
DŽ
латинская заглавная буква dz с кароном (u+01c4)
LJ
LJ
латинская заглавная буква lj (u+01c7)
NJ
NJ
латинская заглавная буква nj (u+01ca)
SS
ẞ
латинская заглавная буква диез s (u+1e9e)
Ом
Ом
9Знак 2516 Ом (u+2126)
а
а
латинская строчная а (u+0061)
а
à
строчная латинская буква a с запятой (u+00e0)
а
á
латинская строчная буква а с акутом (u+00e1)
â
â
строчная латинская буква a с циркумфлексом (u+00e2)
г
ã
строчная латинская буква a с тильдой (u+00e3)
ä
ä
латинская строчная буква а с диэрезисом (u+00e4)
å
å
строчная латинская буква a с кольцом вверху (u+00e5)
а
ā
строчная латинская буква a с макроном (u+0101)
ă
ă
латинская строчная буква а с сокращением (u+0103)
ą
±
строчная латинская буква а с огонеком (u+0105)
ǻ
ǻ
строчная латинская буква a с кольцом вверху и акут (u+01fb)
ȁ
ȁ
строчная латинская буква а с двойной запятой (u+0201)
ȃ
ȃ
строчная латинская буква а с перевернутым сокращением (u+0203)
ạ
ạ
строчная латинская буква a с точкой внизу (u+1ea1)
ả
ả
строчная латинская буква a с крючком вверху (u+1ea3)
ấ
ấ
строчная латинская буква a с циркумфлексом и акутом (u+1ea5)
ầ
ầ
строчная латинская буква a с циркумфлексом и гравировкой (u+1ea7)
ẩ
ẩ
строчная латинская буква a с циркумфлексом и крючком вверху (u+1ea9)
ẫ
ẫ
строчная латинская буква a с циркумфлексом и тильдой (u+1eab)
ậ
ậ
строчная латинская буква a с циркумфлексом и точкой внизу (u+1ead)
ắ
или
строчная латинская буква а с кратким и острым (u+1eaf)
ằ
ằ
строчная латинская буква a с аббревиатурой (u+1eb1)
ẳ
ẳ
строчная латинская буква a с кратким и крючком вверху (u+1eb3)
ẵ
ẵ
строчная латинская буква a с бреве и тильдой (u+1eb5)
ặ
ặ
строчная латинская буква a с кратким обозначением и точкой внизу (u+1eb7)
б
b
латинская строчная b (u+0062)
с
c
строчная латинская буква c (u+0063)
ç
и
строчная латинская буква c с седилью (u+00e7)
ć
ć
строчная латинская буква c с акутом (u+0107)
Э
ĉ
строчная латинская буква c с циркумфлексом (u+0109)
ċ
ċ
строчная латинская буква c с точкой над ней (u+010b)
ч
č
строчная латинская буква c с кароном (u+010d)
ḉ
ḉ
строчная латинская буква c с седилью и акут (u+1e09)
д
d
латинская строчная d (u+0064)
д
№
латинская строчная буква d с символом Caron (u+010f)
ḍ
ḍ
латинская строчная буква d с точкой внизу (u+1e0d)
ḏ
ḏ
латинская строчная буква d с чертой внизу (u+1e0f)
е
e
строчная латинская буква e (u+0065)
э
и
латинская строчная буква е с запятой (u+00e8)
э
é
строчная латинская буква e с акутом (u+00e9)
э
ê
строчная латинская буква e с циркумфлексом (u+00ea)
ë
ë
латинская строчная буква e с диэрезисом (u+00eb)
Э
ē
латинская строчная буква e с макроном (u+0113)
ĕ
ĕ
строчная латинская буква e с кратким (u+0115)
Э
ė
строчная латинская буква e с точкой над ней (u+0117)
я
ę
латинская строчная буква e с огонеком (u+0119)
э
ě
латинская строчная буква e с символом карона (u+011b)
ȅ
ȅ
латинская строчная буква e с двойной запятой (u+0205)
ȇ
ȇ
строчная латинская буква e с перевернутым сокращением (u+0207)
ḕ
ḕ
латинская строчная буква e с макроном и гравировкой (u+1e15)
ḗ
ḗ
латинская строчная буква e с макроном и акутом (u+1e17)
ḝ
ḝ
строчная латинская буква e с седилью и бреве (u+1e1d)
ẹ
ẹ
латинская строчная буква e с точкой внизу (u+1eb9)
ẻ
ẻ
строчная латинская буква e с крючком вверху (u+1ebb)
ẽ
ẽ
строчная латинская буква e с тильдой (u+1ebd)
ế
ế
латинская строчная буква e с циркумфлексом и акутом (u+1ebf)
ề
ề
латинская строчная буква e с циркумфлексом и гравировкой (u+1ec1)
ể
ể
латинская строчная буква e с циркумфлексом и крючком вверху (u+1ec3)
ễ
ễ
латинская строчная буква e с циркумфлексом и тильдой (u+1ec5)
ệ
ệ
латинская строчная буква e с циркумфлексом и точкой внизу (u+1ec7)
ф
f
строчная латинская буква f (u+0066)
грамм
g
строчная латинская буква g (u+0067)
грамм
ĝ
строчная латинская буква g с циркумфлексом (u+011d)
грамм
ß
латинская строчная буква g с кратким (u+011f)
грамм
á
строчная латинская буква g с точкой над ней (u+0121)
грамм
ģ
латинская строчная буква g с седилью (u+0123)
ǧ
ǧ
латинская строчная буква g с кароном (u+01e7)
грамм
ḡ
латинская строчная буква g с макроном (u+1e21)
час
h
латинская строчная h (u+0068)
час
ĥ
строчная латинская буква h с циркумфлексом (u+0125)
час
ḥ
строчная латинская буква h с точкой внизу (u+1e25)
час
ḫ
строчная латинская буква h с краткой аббревиатурой внизу (u+1e2b)
я
i
латинская строчная i (u+0069)
я
х
латинская строчная буква i с гравировкой (u+00ec)
я
í
строчная латинская буква i с акутом (u+00ed)
я
î
строчная латинская буква i с циркумфлексом (u+00ee)
я
ï
латинская строчная буква i с диэрезисом (u+00ef)
я
ĩ
строчная латинская буква i с тильдой (u+0129)
я
ī
строчная латинская буква i с макроном (u+012b)
я
ĭ
строчная латинская буква i с сокращением (u+012d)
я
į
строчная латинская буква i с огонеком (u+012f)
ȉ
ȉ
строчная латинская буква i с двойной запятой (u+0209)
ȋ
ȋ
строчная латинская буква i с перевернутым сокращением (u+020b)
я
ḯ
строчная латинская буква i с диэрезисом и акутом (u+1e2f)
я
ỉ
строчная латинская буква i с крючком вверху (u+1ec9)
я
ị
строчная латинская буква i с точкой внизу (u+1ecb)
Дж
j
строчная латинская буква j (u+006a)
ĵ
х
строчная латинская буква j с циркумфлексом (u+0135)
к
k
строчная латинская буква k (u+006b)
ķ
ķ
строчная латинская буква k с седилью (u+0137)
л
l
строчная латинская буква l (u+006c)
ĺ
→
латинская строчная буква l с акутом (u+013a)
ļ
ļ
строчная латинская буква l с седилью (u+013c)
ľ
ľ
строчная латинская буква l с кароном (u+013e)
ḷ
ḷ
строчная латинская буква l с точкой внизу (u+1e37)
ḻ
ḻ
строчная латинская буква l с чертой внизу (u+1e3b)
м
m
строчная латинская буква m (u+006d)
ṃ
ṃ
латинская строчная буква m с точкой внизу (u+1e43)
н
n
латинская строчная n (u+006e)
с
–
строчная латинская буква n с тильдой (u+00f1)
ń
ń
латинская строчная буква n с акутом (u+0144)
ņ
ņ
латинская строчная буква n с седилью (u+0146)
ň
№
латинская строчная буква н с символом карона (u+0148)
ṅ
ṅ
строчная латинская буква n с точкой над ней (u+1e45)
ṇ
ṇ
строчная латинская буква n с точкой внизу (u+1e47)
ṉ
ṉ
строчная латинская буква n с чертой внизу (u+1e49)
о
o
латинская строчная o (u+006f)
ò
ò
строчная латинская буква o с запятой (u+00f2)
о
—
строчная латинская буква o с акутом (u+00f3)
ô
ô
строчная латинская буква o с циркумфлексом (u+00f4)
х
х
строчная латинская буква o с тильдой (u+00f5)
ö
ö
строчная латинская буква o с диэрезисом (u+00f6)
о
ō
строчная латинская буква o с макроном (u+014d)
ŏ
ŏ
строчная латинская буква o с краткостью (u+014f)
ő
ő
строчная латинская буква o с двойным ударением (u+0151)
ơ
ơ
строчная латинская буква o с рожком (u+01a1)
ǫ
ǫ
строчная латинская буква o с огонеком (u+01eb)
ȍ
ȍ
строчная латинская буква o с двойной гравировкой (u+020d)
ȏ
ȏ
строчная латинская буква o с перевернутым сокращением (u+020f)
ȫ
ȫ
строчная латинская буква o с диэрезисом и макроном (u+022b)
ȭ
ȭ
строчная латинская буква o с тильдой и макроном (u+022d)
ȱ
ȱ
строчная латинская буква o с точкой над ней и макроном (u+0231)
ṍ
ṍ
строчная латинская буква o с тильдой и акусом (u+1e4d)
ṏ
ṏ
строчная латинская буква o с тильдой и диэрезисом (u+1e4f)
ṑ
ṑ
строчная латинская буква o с макроном и грависом (u+1e51)
ṓ
ṓ
строчная латинская буква o с макроном и акутом (u+1e53)
ọ
ọ
строчная латинская буква o с точкой внизу (u+1ecd)
ỏ
ỏ
строчная латинская буква o с крючком вверху (u+1ecf)
ố
ố
латинская строчная буква o с циркумфлексом и акутом (u+1ed1)
ồ
ồ
латинская строчная буква o с циркумфлексом и гравировкой (u+1ed3)
ổ
ổ
строчная латинская буква o с циркумфлексом и крючком вверху (u+1ed5)
ỗ
ỗ
строчная латинская буква o с циркумфлексом и тильдой (u+1ed7)
ộ
ộ
латинская строчная буква o с циркумфлексом и точкой внизу (u+1ed9)
ớ
ớ
строчная латинская буква o с рогом и акут (u+1edb)
ờ
ờ
строчная латинская буква o с рогом и могилой (u+1edd)
ở
ở
строчная латинская буква o с рожком и крючком вверху (u+1edf)
ỡ
ỡ
строчная латинская буква o с рожком и тильдой (u+1ee1)
ợ
ợ
строчная латинская буква o с рогом и точкой внизу (u+1ee3)
п
p
строчная латинская буква p (u+0070)
д
q
латинская строчная q (u+0071)
р
r
латинская строчная буква r (u+0072)
р
ŕ
латинская строчная буква r с акутом (u+0155)
р
ŗ
латинская строчная буква r с седилью (u+0157)
р
Ø
строчная латинская буква r с символом карона (u+0159)
ȑ
ȑ
латинская строчная буква r с двойной гравировкой (u+0211)
ȓ
ȓ
латинская строчная буква r с перевернутым сокращением (u+0213)
р
ṛ
латинская строчная буква r с точкой внизу (u+1e5b)
р
ṟ
латинская строчная буква r с чертой внизу (u+1e5f)
с
с
латинская строчная буква с (u+0073)
с
ś
латинская строчная буква s с акутом (u+015b)
ш
ŝ
латинская строчная буква s с циркумфлексом (u+015d)
с
ş
строчная латинская буква s с седилью (u+015f)
ш
š
латинская строчная буква s с кароном (u+0161)
ș
ș
строчная латинская буква s с запятой внизу (u+0219)
ṡ
ṡ
латинская строчная буква s с точкой над ней (u+1e61)
с
ṣ
латинская строчная буква s с точкой внизу (u+1e63)
ṥ
ṥ
латинская строчная буква s с акутом и точкой над ней (u+1e65)
ṧ
ṧ
латинская строчная буква s с кароном и точкой над ней (u+1e67)
ṩ
ṩ
латинская строчная буква s с точкой внизу и точкой вверху (u+1e69)
т
t
строчная латинская буква t (u+0074)
ţ
ţ
строчная латинская буква t с седилью (u+0163)
ť
ť
строчная латинская буква t с кароном (u+0165)
ц
ț
латинская строчная буква t с запятой внизу (u+021b)
т
ṭ
латинская строчная буква t с точкой внизу (u+1e6d)
ṯ
ṯ
латинская строчная буква t с чертой внизу (u+1e6f)
ẗ
ẗ
латинская строчная буква t с диэрезисом (u+1e97)
ты
u
латинская строчная буква u (u+0075)
ù
ù
латинская строчная буква u с запятой (u+00f9)
ú
ú
латинская строчная буква u с акутом (u+00fa)
û
û
латинская строчная буква u с циркумфлексом (u+00fb)
ü
ü
латинская строчная буква u с диэрезисом (u+00fc)
ũ
ũ
латинская строчная буква u с тильдой (u+0169)
ū
ū
латинская строчная буква u с макроном (u+016b)
ŭ
–
строчная латинская буква u с краткостью (u+016d)
.
..
…
строчная латинская буква u с кольцом вверху (u+016f)
ű
ű
латинская строчная буква u с двойным ударением (u+0171)
ų
ų
латинская строчная буква u с огонеком (u+0173)
ư
ư
латинская строчная буква u с рогом (u+01b0)
ȕ
ȕ
латинская строчная буква u с двойной запятой (u+0215)
ȗ
ȗ
латинская строчная буква u с перевернутым сокращением (u+0217)
р
№
строчная латинская буква u с тильдой и акут (u+1e79)
ṻ
ṻ
латинская строчная буква u с макроном и диэрезисом (u+1e7b)
ụ
ụ
латинская строчная буква u с точкой внизу (u+1ee5)
ủ
ủ
латинская строчная буква u с крючком вверху (u+1ee7)
ứ
ứ
латинская строчная буква u с рогом и акутом (u+1ee9)
ừ
ừ
латинская строчная буква u с рогом и могилой (u+1eeb)
ử
ử
строчная латинская буква u с рожком и крючком вверху (u+1eed)
ữ
ữ
латинская строчная буква u с рожком и тильдой (u+1eef)
ự
ự
латинская строчная буква u с рогом и точкой внизу (u+1ef1)
в
v
латинская строчная v (u+0076)
ж
w
строчная латинская буква w (u+0077)
ŵ
х
строчная латинская буква w с циркумфлексом (u+0175)
ẁ
ẁ
латинская строчная буква w с запятой (u+1e81)
ẃ
ẃ
латинская строчная буква w с акутом (u+1e83)
ẅ
ẅ
латинская строчная буква w с диэрезисом (u+1e85)
Икс
x
строчная латинская буква x (u+0078)
у
y
латинская строчная y (u+0079)
ý
ý
латинская строчная буква y с акутом (u+00fd)
ÿ
ÿ
латинская строчная буква y с диэрезисом (u+00ff)
ŷ
ŷ
латинская строчная буква y с циркумфлексом (u+0177)
ȳ
ȳ
строчная латинская буква y с макроном (u+0233)
ẏ
ẏ
латинская строчная буква y с точкой над ней (u+1e8f)
ỳ
ỳ
латинская строчная буква y с запятой (u+1ef3)
ỵ
ỵ
латинская строчная буква y с точкой внизу (u+1ef5)
ỷ
ỷ
латинская строчная буква y с крючком вверху (u+1ef7)
ỹ
ỹ
латинская строчная буква y с тильдой (u+1ef9)
г
z
латинская строчная буква z (u+007a)
ź
ź
латинская строчная буква z с акутом (u+017a)
ż
ż
строчная латинская буква z с точкой над ней (u+017c)
ž
ž
латинская строчная буква z с кароном (u+017e)
ẓ
ẓ
латинская строчная буква z с точкой внизу (u+1e93)
SS
ß
латинская строчная диез s (u+00df)
æ
æ
строчная латинская буква ae (u+00e6)
ǽ
ǽ
строчная латинская буква ae с акутом (u+01fd)
ð
ð
строчная латинская буква eth (u+00f0)
ø
ø
строчная латинская буква o со штрихом (u+00f8)
ǿ
ǿ
строчная латинская буква o со штрихом и акут (u+01ff)
þ
þ
латинская строчная буква шип (u+00fe)
д
đ
строчная латинская буква d со штрихом (u+0111)
час
ħ
строчная латинская буква h со штрихом (u+0127)
я
ı
латинская строчная без точки i (u+0131)
я
№
латинская малая лигатура ij (u+0133)
малая латинская лигатура ij с острым знаком (u+e132)
ĸ
№
латинская строчная буква кра (u+0138)
ŀ
ŀ
строчная латинская буква l с точкой в середине (u+0140)
ł
ł
строчная латинская буква l с чертой (u+0142)
ʼn
ʼn
строчная латинская буква n с предшествующим апострофом (u+0149)
ŋ
ŋ
латинская строчная eng (u+014b)
œ
–
малая латинская лигатура oe (u+0153)
ŧ
ŧ
латинская строчная буква t со штрихом (u+0167)
dž
dž
латинская строчная буква dz с кароном (u+01c6)
lj
lj
строчная латинская буква lj (u+01c9)
nj
nj
строчная латинская буква nj (u+01cc)
ȷ
ȷ
латинская строчная без точки j (u+0237)
я
ə
латинская строчная буква schwa (u+0259)
ɲ
ɲ
латинская строчная буква n с левым крючком (u+0272)
π
π
греческая строчная буква пи (u+03c0)
Dž
Dž
латинская заглавная буква d со строчной буквой z и символом знака (u+01c5)
Lj
Lj
латинская заглавная буква l со строчной буквой j (u+01c8)
Nj
Nj
латинская заглавная буква n со строчной буквой j (u+01cb)
ff
ff
малая латинская лигатура ff (u+fb00)
фи
fi
малая латинская лигатура fi (u+fb01)
ffi
ffi
малая латинская лигатура ffi (u+fb03)
ʹ
ʹ
буква модификатора штрих (u+02b9)
ʺ
ʺ
буква модификатора двойное штрих (u+02ba)
`
ʻ
буква-модификатор превратилась в запятую (u+02bb)
ʾ
ʾ
буква-модификатор правое полукольцо (u+02be)
ʿ
ʿ
буква-модификатор левое полукольцо (u+02bf)
ˈ
ˈ
вертикальная буква-модификатор (u+02c8)
ˉ
ˉ
буква-модификатор макрон (u+02c9)
ˊ
ˊ
буква-модификатор острого ударения (u+02ca)
ˋ
ˋ
буква-модификатор с серьезным ударением (u+02cb)
ˌ
ˌ
буква-модификатор нижняя вертикальная черта (u+02cc)
ª
ª
женский порядковый номер (u+00aa)
º
º
порядковый номер мужского рода (u+00ba)
0
цифра ноль (u+0030)
1
1
цифра один (u+0031)
2
2
цифра два (u+0032)
3
3
цифра три (u+0033)
4
4
цифра четыре (u+0034)
5
5
цифра пять (u+0035)
6
6
цифра шесть (u+0036)
7
7
цифра семь (u+0037)
8
8
цифра восемь (u+0038)
9
9
цифра девять (u+0039)
¹
№
верхний индекс один (u+00b9)
²
²
верхний индекс два (u+00b2)
³
³
верхний индекс три (u+00b3)
¼
¼
вульгарная дробь одна четверть (u+00bc)
½
½
вульгарная дробь половина (u+00bd)
¾
¾
вульгарная дробь три четверти (u+00be)
⁰
⁰
нулевой верхний индекс (u+2070)
⁴
⁴
верхний индекс четыре (u+2074)
⁵
⁵
верхний индекс пять (u+2075)
⁶
⁶
верхний индекс шесть (u+2076)
⁷
⁷
верхний индекс семь (u+2077)
⁸
⁸
верхний индекс восемь (u+2078)
⁹
⁹
верхний индекс девять (u+2079)
₀
₀
нулевой индекс (u+2080)
₁
₁
индекс один (u+2081)
₂
₂
индекс два (u+2082)
₃
₃
нижний индекс три (u+2083)
₄
₄
индекс четыре (u+2084)
₅
₅
индекс пять (u+2085)
₆
₆
индекс шесть (u+2086)
₇
₇
индекс семь (u+2087)
₈
₈
индекс восемь (u+2088)
₉
₉
индекс девять (u+2089)
⅓
⅓
вульгарная дробь одна треть (u+2153)
⅔
⅔
вульгарная дробь две трети (u+2154)
⅛
⅛
вульгарная дробь одна восьмая (u+215b)
⅜
⅜
вульгарная дробь три восьмых (u+215c)
⅝
⅝
вульгарная дробь пять восьмых (u+215d)
⅞
⅞
вульгарная дробь семь восьмых (u+215e)
_
_
нижняя строка (u+005f)
-
-
дефис-минус (u+002d)
-
‐
дефис (u+2010)
‒
‒
цифра тире (u+2012)
–
–
в тире (u+2013)
—
—
длинное тире (u+2014)
―
―
Турник (у+2015)
(
(
левая скобка (u+0028)
)
)
правая скобка (u+0029)
[
[
левая квадратная скобка (u+005b)
]
]
правая квадратная скобка (u+005d)
{
{
левая фигурная скобка (u+007b)
}
}
правая фигурная скобка (u+007d)
⟨
⟨
математическая левая угловая скобка (u+27e8)
⟩
⟩
математическая правая угловая скобка (u+27e9)
#
#
Знак номера (u+0023)
%
%
знак процента (u+0025)
‰
‰
Знак промилле (u+2030)
'
'
апостроф (u+0027)
"
"
кавычки (u+0022)
‘
‘
левая одинарная кавычка (u+2018)
’
’
правая одинарная кавычка (u+2019)
“
"
левая двойная кавычка (u+201c)
”
”
правая двойная кавычка (u+201d)
‚
‚
одинарная нижняя 9-кавычка (u+201a)
„
„
двойная нижняя 9-кавычка (u+201e)
‹
‹
одинарная левая кавычка (u+2039)
›
›
одинарная правая кавычка (u+203a)
«
«
двойная кавычка, указывающая влево (u+00ab)
»
»
правая двойная кавычка (u+00bb)
*
*
звездочка (u+002a)
†
†
кинжал (u+2020)
‡
‡
двойной кинжал (u+2021)
·
·
средняя точка (u+00b7)
•
•
пуля (u+2022)
…
…
горизонтальное многоточие (u+2026)
.

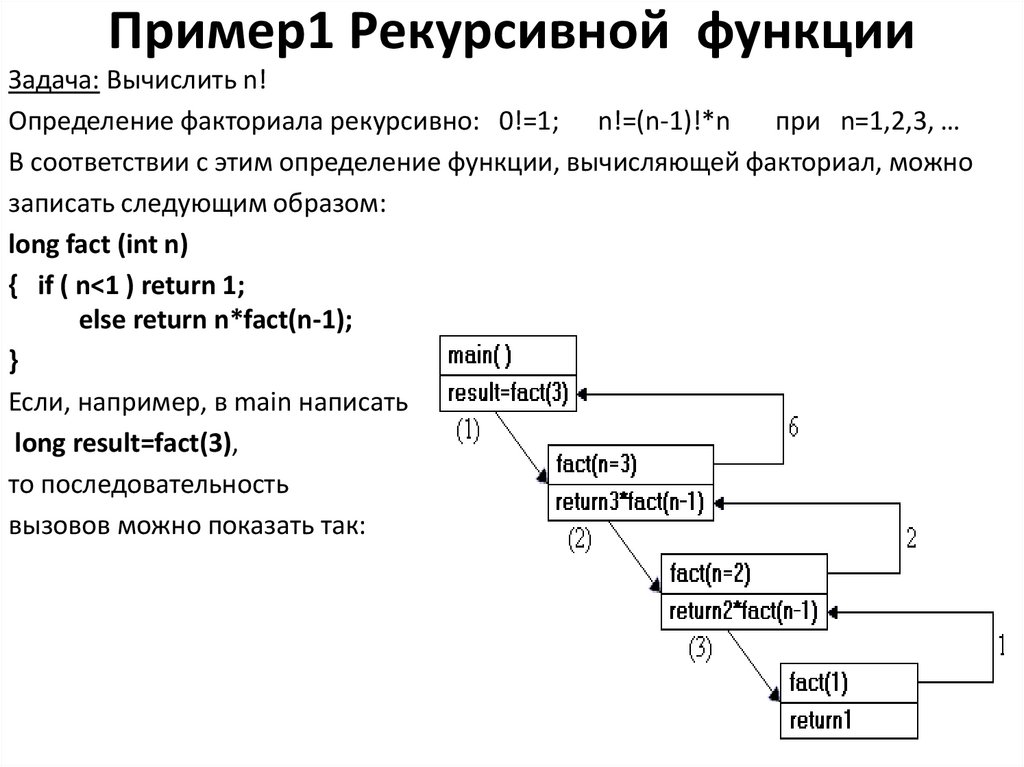 Изд. МВТУ, 1969.
Изд. МВТУ, 1969. с. 4844562. Опубл. в Б. И., №34, 1975.
с. 4844562. Опубл. в Б. И., №34, 1975.