Рекурсивность что это: рекурсивность | Перевод рекурсивность?

РЕКУРСИВНЫЙ — Что такое РЕКУРСИВНЫЙ?

Слово состоит из 11 букв: первая р, вторая е, третья к, четвёртая у, пятая р, шестая с, седьмая и, восьмая в, девятая н, десятая ы, последняя й,

Слово рекурсивный английскими буквами(транслитом) — rekrsivnyi

• Буква р встречается 2 раза. Слова с 2 буквами р
• Буква е встречается 1 раз. Слова с 1 буквой е
• Буква к встречается 1 раз. Слова с 1 буквой к
• Буква у встречается 1 раз. Слова с 1 буквой у
• Буква с встречается 1 раз. Слова с 1 буквой с
• Буква и встречается 1 раз. Слова с 1 буквой и
• Буква в встречается 1 раз. Слова с 1 буквой в
• Буква н встречается 1 раз. Слова с 1 буквой н
• Буква ы встречается 1 раз. Слова с 1 буквой ы
• Буква й встречается 1 раз. Слова с 1 буквой й

Рекурсивный

Рекурсивный (от лат. recursio — возвращение) — возвращающий к прошлому, к предшествующему; рекурсивные функции — функции, значения которых для данного аргумента вычисляются с помощью значений для предшествующих аргументов.

Начала современного естествознания. — 2006

Рекурсивный МНК

Также получающиеся в результате применения рекурсивного МНК (рекурсивные остатки) используются при тестировании стабильности параметров модели.

ru.wikipedia.org

Рекурсивный заем

Рекурсивный заем (1) Заем, при котором уполномочивающее лицо, или гарант, несет ответственность в случае, если должник не производит платежа.

(2) Заем…

Финансово-инвестиционный словарь. — 2002

Рекурсивный язык

В математической логике и информатике рекурсивный язык — тип формального языка, также называемый разрешимым или разрешимым по Тьюрингу. Класс всех рекурсивных языков часто обозначается через R…

ru.wikipedia.org

Рекурсивная модель

Рекурсивная модель [recursive model] — динамическая модель, обладающая математическим свойством рекурсии. Это значит, что если даны, например, все переменные модели до момента (t-1)…

slovar-lopatnikov.ru

РЕКУРСИВНАЯ МОДЕЛЬ [recursive model] — динамическая модель, обладающая математическим свойством рекурсии. Это значит, что если даны, напр., все переменные модели до момента (t–1)…

Лопатников. — 2003

Рекурсивный акроним

Рекурсивный акроним — акроним (иногда бэкроним), который ссылается на себя. В среде компьютерных хакеров стало традиционным выбирать акронимы и аббревиатуры, которые косвенно или напрямую ссылаются на себя.

ru.wikipedia.org

РЕКУРСИВНЫЙ АКРОНИМ. Акроним (иногда бэкроним), который ссылается на себя. В среде компьютерных хакеров стало традиционным выбирать акронимы и аббревиатуры, которые косвенно или напрямую ссылаются на себя.

Бизнес-словарь

Рекурсивное определение

Рекурсивное определение или индуктивное определение определяет сущность в терминах её самой (то есть рекурсивно), хотя и полезным способом. Для того, чтобы это было возможно, определение в любом данном случае должно быть хорошо-основанным.

..

ru.wikipedia.org

РЕКУРСИВНОЕ ОПРЕДЕЛЕНИЕ — часто применяемый в математике способ задания функций, при к-ром значение искомой функции в данной точке определяется через ее значения в предшествующих точках (при подходящем отношении предшествования).

Математическая энциклопедия. — 1977-1985

РЕКУРСИВНАЯ ТЕОРИЯ МНОЖЕСТВ

РЕКУРСИВНАЯ ТЕОРИЯ МНОЖЕСТВ — раздел тео-рии рекурсивных функций, в к-ром рассматриваются и классифицируются подмножества натуральных чисел с алгоритмич. точки зрения, а также исследуются структуры, возникающие в результате такой классификации.

Математическая энциклопедия. — 1977-1985

РЕКУРСИВНЫЕ ФУНКЦИИ И ПРЕДИКА́ТЫ

РЕКУРСИВНЫЕ ФУНКЦИИ И ПРЕДИКА́ТЫ — один из важнейших для оснований математики и математич. логики классов понятий, служащих уточнениями содержат. понятий эффективно вычислимой арифметической функции и эффективно разрешимого арифметического предиката…

Философская энциклопедия

Рекурсивная функция (теория вычислимости)

Рекурсивные функции (от позднелатинского recursio — возвращение), название, закрепившееся за одним из наиболее распространённых вариантов уточнения общего понятия арифметического алгоритма, т.е. такого алгоритма…

БСЭ. — 1969—1978

Термин рекурсивная функция в теории вычислимости используется для обозначения трёх классов функций примитивно рекурсивные функции; общерекурсивные функции; частично рекурсивные функции. Последние совпадают с классом вычислимых по Тьюрингу функций.

ru.wikipedia.org

РЕКУРСИВНАЯ ФУНКЦИЯ — ч а с т и ч н о р е к у р с и в н а я ф у н к ц и я,- одно из математич. уточнений интуитивного понятия вычислимой функции, определяемое следующим образом.

Математическая энциклопедия. — 1977-1985

Русский язык

Рекурси́вный; кр. ф. -вен, -вна.

Орфографический словарь. — 2004

---

• Слова из слова «рекурсивный»
• Слова на букву «р»
• Слова, начинающиеся на «ре»
• Слова c буквой «й» на конце
• Слова c «ый» на конце
• Слова, начинающиеся на «рек»
• Слова, начинающиеся на «реку»
• Слова, оканчивающиеся на «ный»
• Слова, заканчивающиеся на «вный»

1. рекуперация
2. рекуррентный
3. рекурсивные
4. рекурсивный
5. рекурсия
6. релаксант
7. релаксатор

Рекурсивная сложность техносоциальных систем как фактор

Рекурсивная сложность техносоциальных систем как фактор
разрастания социальных рисков

________________________

Орлов Д.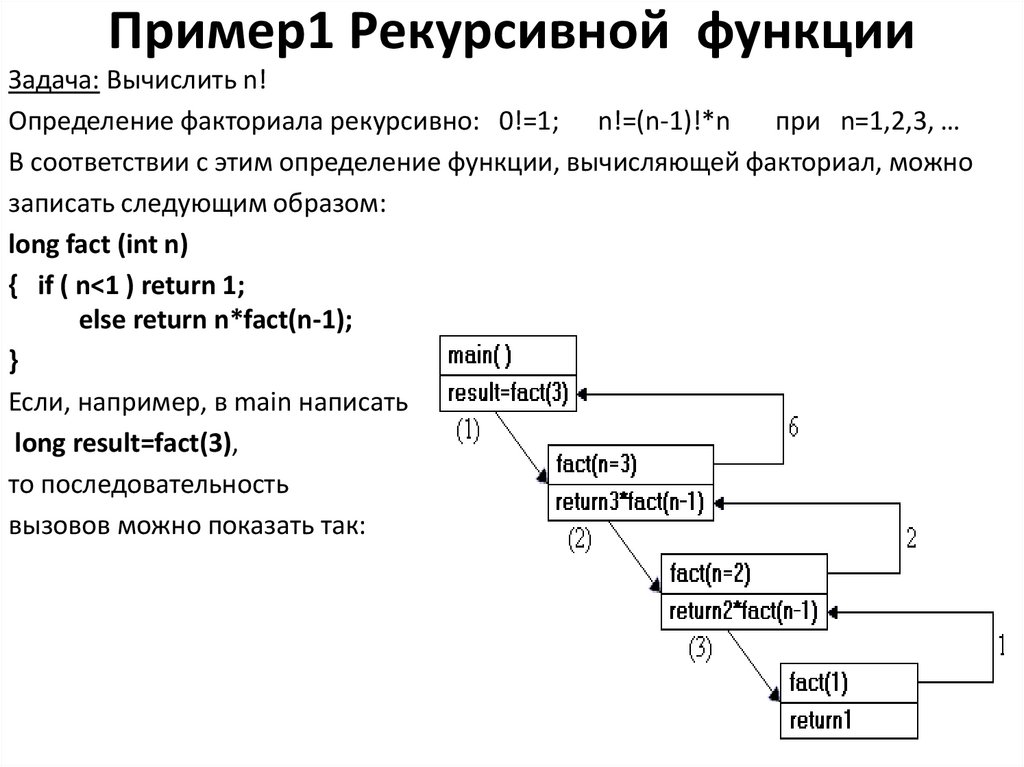 Е.

Статья рекомендована Н.И. Кузнецовой 28.07.2014 г.

Аннотация

В статье рассматривается проблема непрогнозируемого разрастания современных сложных систем (финансовых рынков, социальных сетей интернета и др.), показывается нерелевантность традиционных инструментов социального и кибернетического их описания. Опираясь на положения системной теории Н. Лумана, автор предлагает переориентировать исследовательский фокус на поиск рекурсивных моделей сложных техносоциальных объектов.

Ключевые слова: техносоциальные системы, социальные риски, социальные сети, рекурсивные модели.

Исследовательский интерес программистов и социологов все больше привлекают «непокорные» техносоциальные системы, которые непрогнозируемо разрастаются, а их динамика не поддается описанию традиционными средствами моделирования. Такое поведение характерно, к примеру, для современных финансовых рынков и социальных сетей интернета. Динамика разрастания этих и подобных им объектов характеризуется свойством аутопоэзиса, при котором в объекте замыкается рекурсивная петля – безостановочный процесс примыкания последующей операции к предшествующей.

При этом объект сам (из себя) надстраивает этажи собственной сложности, опираясь на свой же структурный ресурс [1]. В таких случаях отклик системы на заданное воздействие трудно предсказать, а в сколько-нибудь отдаленной перспективе возможности прогнозирования будущего таких систем практически сводятся к нулю [2]. Непрозрачность поведения подобных систем провоцирует многочисленные социальные риски.

Сложный объект обычно характеризуется наличием сетевой структуры. К метафоре ризоматической сети обращается, к примеру, теоретик постмодерна Ж. Делез [3]. Однако в контексте исследования современных сложных систем наиболее продуктивными представляются результаты, полученные парижской школой объект-центричной социологии (Б. Латур, М. Каллон, К. Кнорр-Цетин) [1].

Б. Латур использует понятие сети при исследовании науки как особой системы убеждений людей [4]. В науке имеет место конкуренция сетей убеждений. Сеть в понимании Латура – это растущий и трансформирующийся объект, который выстраивается, сталкивается с другими сетями, побеждает или проваливается. Главное в победе сети – это затвердевание определенного утверждения, превращение его в «черный ящик». Латур – признанный автор акторно-сетевой теории (Actor-Network Theory – ANT) и один из лидеров целого направления современной социологии – наука, техника и общество (Science, Technology and Society – STS). Сеть убеждения в науке, узлами которой являются люди, вещи, тексты и т.д., также может быть отнесена к техносоциальным системам наподобие интернета и финансового рынка. Латур утверждает: вещи способны давать отпор теоретику, стремящемуся описать взаимодействия классическими средствами по формуле Э. Дюркгейма – «социальное объясняется через социальное» [5]. Теоретик неизбежно сталкивается с непокорностью объекта, которую нельзя понять и объяснить одними только социальными причинами. Дело в том, что вещи (объекты) вписаны в социальные отношения, наряду с людьми, как самостоятельные акторы.

К. Кнорр-Цетин и У. Брюггер одними из первых обратили внимание на то, что взаимодействие людей и объектов (программного оборудования, финансовых потоков, средств осуществления транзакций и т. д.) фондового рынка существенно искажается, когда описывается традиционными инструментами социологии. Этот тип разрастающейся связи – трейдеры-объекты, как оказалось, нельзя адекватно отобразить, принимая в расчет одни лишь социальные причины, придавая тем самым социальному фактору исключительное и всеобъемлющее значение [6]. Авторы «Рынка как объекта привязанности» тщательно анализируют взаимодействие трейдеров через биржевые компьютерные терминалы, посредством которых осуществляются сделки. В качестве эмпирической базы исследования был выбран торговый зал Швейцарского банка (Swiss Bank). Применительно к теме настоящей статьи важно выделить, по меньшей мере, три вывода по итогам исследования.

1. Рынок как объект ни одним игроком не может быть понят во всей полноте, он непрерывно разворачивает свою структуру.

2. Субъект (трейдер) вовлекается в объект (рынок) и не располагает управляющим уровнем. Он не столько управляет объектом, сколько встраивается в него – стремится своими действиями «продавить» рынок.

3. «Продавливая» рынок, трейдеры антропоморфизируют его, приписывая всей системе, в которую они вовлечены, свойства живого человекоразмерного объекта, который всегда недостаточен, незавершен и всегда находится в процессе становления. При этом с точки зрения невовлеченного стороннего наблюдателя трейдеры, казалось бы, выполняют вполне определенную задачу: необходимо заработать максимум для инвестора, получить максимальный бонус, устранить последствия неудачных сделок и т. д.

Пространственные границы рынка размыты и эфемерны. Сделка может быть заключена в любой точке земного шара, а время, в течение которого перенаправляются денежные потоки, измеряется секундами. При этом, с одной стороны, фиксируется деформация ценностных установок участников торгов, с другой – провоцируются глобальные социальные риски, в значительной степени затрагивающие экономику и благополучие целых государств. Еще одно важное обстоятельство, отмеченное исследователями, – сопротивление рынка попыткам описать его по схеме Input/Output – предсказуемого выхода в ответ на заданный вход. Таким образом, классические инструменты моделирования поведения данного и подобных ему объектов оказываются в лучшем случае малоэффективными. Попытаемся ответить на вопрос, почему так происходит?

В недрах классической науки в XVII–XVIII вв. сформировался принцип линейной причинности. Линейная причинность предполагает, что взаимная игра причин и следствий строго определена. Наука на этом этапе стремится к целостному объяснению мира, которое включает природу, человека и общество. П. Лаплас, утверждая детерминированность мира, писал: «Мы должны рассматривать настоящее состояние вселенной как следствие ее предшествующего состояния и как причину последующего» [7, с. 9]. Это положение по сей день сохраняет силу в отношении простых систем, для которых «достаточно полагать, что суммарные свойства их частей исчерпывающе определяют свойства целого» [8, с. 37]. Сам по себе принцип детерминизма не отрицает существования сложных объектов. Однако сложность (или усложнение) рассматривается в ее агрегативном значении, когда, зная внутреннюю схему объекта и принцип его работы, можно его разобрать и собрать заново, можно гарантировать его поведение (Output) в зависимости от тех или иных способов воздействия на него (Input).

В середине XX в. возникает новая парадигма исследования, стремящаяся, так же как и классическая наука XVII–XVIII вв., к целостному и согласованному объяснению мира. Речь идет о системном подходе. В отличие от классического естествознания, системный подход включает в рассмотрение объекты, в которых присутствует обратная связь. Первые попытки построения общей теории систем осуществляются приблизительно в одно время с появлением кибернетики Н. Винера и относятся к 1940–1950-м годам. Кибернетика не является вариантом общей теории систем, однако общесистемный и кибернетический способы описания объектов имеют много общих черт. В первую очередь это нацеленность на согласованное (в пределе – формализованное) описание систем различной природы.

Помимо кибернетики, в середине XX столетия появляются общая теория систем Л. фон Берталанфи, теория социальных систем Т. Парсонса и др. близкие им концепции. Однако именно кибернетика получила наибольшую известность как всеобщая теория управления. На основе положений кибернетики, базирующихся на развитом математическом аппарате (теория графов, теория автоматов, математическая логика, теория информации), стало возможным построение прикладных математических моделей. В кибернетике и общей теории систем рождается представление об эмерджентности – особом целостном качестве объекта-системы, не сводимом и не выводимом из составляющих его элементов. Кибернетика успешно применяется в задачах описания искусственных машин. Тем не менее неразрешимой проблемой для нее остается описание сложных социальных и техносоциальных систем, которые в большинстве случаев не позволяют применить к себе понятийную конструкцию Input/Output. Кибернетика Винера определяла ценностный ресурс информации как возможность расширения управления. Отсюда известное выражение: «Кто обладает информацией, тот управляет миром». Э. Морен показывает ряд недостатков кибернетики 1950–1960-х годов, среди которых особо выделяет недостижимость антропосоциальной сложности в рамках этой теории. Появившись как образ «антропосоциальной мегамашины», кибернетика пыталась описать сознание и общество в терминах искусственной машины. «Кибернетика обрела свою форму, – пишет Морен, – в контексте господствовавших в то время способов мышления и действия, а не просто доминировала над ними. После того как в своем понятии машины кибернетика вышла за пределы редукционизма, который разлагал целое на его элементы, она развернула такой редукционизм, который сводит все живые или природные существа-машины к модели искусственной машины… У кибернетики отсутствует фундамент. Ей не хватает принципа сложности» [9, с. 306].

С указанными недостатками, по-видимому, связаны трудности кибернетического подхода в описании социальных систем. Эти трудности выражаются в несоответствии кибернетической модели моделируемому объекту. Модель должна включать то существенное, что встроено в моделируемый объект, т.е. быть адекватной объекту. Нетрудно заметить, что иррелевантными природе объекта могут быть не только кибернетические, но и экономические модели. Например, ряд моделей прогнозирования рыночной ситуации базируется на предположении о рациональном поведении участников рынка. Однако жизнь людей не сводится лишь к удовлетворению экономических интересов, и их поведение далеко не всегда рационально. Н. Талеб, рассматривая подходы к моделированию экономических систем, утверждает, что в ортодоксальной экономической теории рациональность превратилась в «смирительную рубашку» [10]. Идеи максимизации и оптимизации экономических интересов, которые легли в основу большинства моделей рынка, не оправдали себя на практике. Такая оптимизация является ярким примером «стерильного моделирования».

Исследуя динамику рынка, Б. Мандельброт приводит в качестве примера американский экономический кризис 1987 г., когда в день пика обвала цен 27 октября ценовые котировки скакали, «как безумные», и стоимость американской экономики уменьшалась на 100 млн. долларов в секунду в течение самого критического часа торгов [11, с. 155]. Мандельброт указывает, что очень сложно определить фатальную пусковую причину обвала цен. Рынок – объект с турбулентной динамикой. Он демонстрирует пример системы, в которой, наряду с обратной связью, присутствует особенный механизм, не схватываемый привычными понятиями сети, обратной связи и входа/выхода.

Таким образом, механизмы развития/эволюции техносоциальных объектов не описываются средствами классического детерминистского анализа. Во-первых, они характеризуются выстраиванием собственных уровней сложности. Во-вторых, они непрозрачны для наблюдателя, желающего найти в них целостный причинно-следственный механизм. В-третьих, они способны к взрывной, турбулентной активности. Возможно, именно здесь результаты, полученные Х. фон Фёрстером, могут дать толчок к поиску новых путей описания сложности. Х. фон Фёрстер разрабатывал проблему поведения «нетривиальной машины», которая способна подключать собственное состояние при ответе на внешнее воздействие [12]. В «кибернетике 2-го порядка» фон Фёрстера ключевым становится понятие рекурсии. Система, в которой запущен рекурсивный процесс, обладает собственным типом детерминации. Она отвечает на внешние воздействия (или игнорирует их) в соответствии с собственной динамикой. Для такой системы характерна сложная (не лапласовская) причинность. Дальнейшее развитие идеи рекурсии выразилось в концепции аутопоэзиса, нашедшей отражение в работах чилийских нейробиологов У. Матураны и Ф. Варелы, а также в системной теории немецкого социолога Н. Лумана.

Луман рассматривает систему не как совокупность элементов и отношений, а как единство, образуемое и поддерживаемое за счет рекурсивного присоединения операций [13]. Предложенный Луманом теоретический аппарат, с нашей точки зрения, весьма продуктивен для поиска возможностей моделирования сложных аутопоэзных объектов. В теории Лумана коммуникация рекурсивно присоединяется к коммуникации, однако это (конкретное) продолжение коммуникации вовсе не гарантировано предшествующими присоединениями. Оно всегда несет в себе неопределенность (по определению Лумана – осуществляется в соответствии с принципом двойной контингенции). Слово «контингентность» (contingency) близко по значению к русскому слову «случайность», но не совпадает с ним: оно накладывает запрет как на невозможное, так и на гарантированное событие будущего. Аналогично на финансовом рынке сделка присоединяется к сделке. В теории Лумана граница системы не определяется вещественно, а проходит по контуру операций. Рынок также не имеет строго выраженных физических границ. Его границы определяются операционально – системой сделок по покупке и продаже. Этот ряд сопоставлений можно продолжить. Однако необходимо выделить ключевое понятие, используемое Луманом, – аутопоэзис (т.е. самостроительство) систем. Понятие аутопоэзиса вначале разрабатывалось в биологии и применялось для различения живой клетки и неживых систем [14]. Система, в которой запущена рекурсивная петля, достигнув определенного уровня сложности, начинает выстраивать свои операции в соответствии с собственной динамикой. Сложность финансового рынка и интернет-коммуникаций позволяет сделать предположение о самозапуске аутопоэзиса в этих системах [2, 15].

Одним из инструментов описания сложности рекурсивных оперативно замкнутых систем могут стать фрактальные структуры Б. Мандельброта [11]. Фрактал – это рекурсивная структура, в чем-то подобная схеме нетривиальной машины и механизму присоединения операций в операционально замкнутой системе. В рамках этого математического направления, возможно, удастся разработать мощные инструменты прикладной математики, которые обеспечат продвижение в описании сложных объектов.

Однако между фракталом и динамикой аутопоэзной системы есть различие. Фрактал строится из базовой формулы, базового порождающего правила. «Предложенный Н. Луманом подход, – пишет Е.Н. Ивахненко, – не приемлет метафор возврата к первоначалу, поиска естественных констант или установление apriori в раскрытии сложности самовозрастающих (аутопойезис) биологических объектов, социального порядка, коммуникативных приращений» [2, с. 93]. Луман также говорит о бесперспективности попыток четкой фиксации будущего состояния аутопоэзной системы. Для такой системы характерна динамика эволюционного дрейфа и отсутствие линейной причинности. При этом вводимое им понятие двойной контингенции как некоторого горизонта возможностей представляется достаточно продуктивным для моделирования [16].

Таким образом, современные социальные теории отвечают на запрос на новые модели описания техносоциальных объектов. Усложнение, эволюция и, как итог, запуск аутопоэзиса в этих объектах смещают фокус их моделирования с захвата управляющего уровня на коммуникативное включение в рекурсивную динамику. Новые исследовательские стратегии и модели должны указывать способы выявления социальных рисков, провоцируемых рекурсивно разрастающейся сложностью, и находить адекватные способы блокировки наиболее опасных для общества последствий такого разрастания.

Литература

1. Ивахненко Е.Н. Аутопойезис информационных объектов // Информационное общество. 2009. № 1. С. 34–41.

2. Ивахненко Е.Н. Социология встречается со сложностью // Вестник РГГУ. Серия «Философские науки. Религиоведение». 2013. № 11. С. 90–101.

3. Делёз Ж., Гваттари Ф. Тысяча плато. Капитализм и шизофрения. М.: Астрель, 2010.

4. Латур Б. Наука в действии. СПб.: Изд-во Европ. ун-та в С.-Петербурге, 2013.

5. Латур Б. Когда вещи дают сдачи: возможный вклад «исследований науки» в общественные науки // Вестник МГУ. Сер. «Философия». 2003. № 3. С. 9–34.

6. Кнорр-Цетин К., Брюггер У. Рынок как объект привязанности: исследование постсоциальных отношений на финансовых рынках // Социология вещей. Сб. статей. М.: Издательский дом «Территория будущего», 2006. С. 309–341.

7. Лаплас П. Опыт философии теории вероятностей: Пер. с фр. М.: Книжный дом «Либроком», 2011.

8. Степин В.С. Исторические типы научной рациональности в их отношении к проблеме сложности // Синергетическая парадигма. Синергетика инновационной сложности. М.: Прогресс-Традиция, 2011.

9. Морен Э. Метод. Природа природы. М.: «Канон+», 2013.

10. Талеб Н. Черный лебедь. Под знаком непредсказуемости. М.: КоЛибри, 2009.

11. Мандельброт Б., Хадсон Р. (Не)послушные рынки. Фрактальная революция в финансах. М.: Вильямс, 2006.

12. Foerster H. von. Cybernetics of Cybernetics. Urbana Illinois: University of Illinois Press (Biological Computer Laboratory), 1974a.

13. Луман Н. Введение в системную теорию. М.: Логос, 2007.

14. Матурана У., Варела Ф. Древо познания. М.: Прогресс-традиция, 2001.

15. Лавренчук Е.А. Аутопойезис социальных сетей интернет-коммуникаций // Вестник РГГУ. Серия «Философия. Социология». 2009. № 12. С. 48–56.

16. Ивахненко Е.Н., Аттаева Л.И. Изменение стратегий осмысления сложного: от метафизики и целерациональности к коммуникативной контингентности // Известия Смоленского государственного университета. 2011. № 4. С. 353–366.

____________________________

ОРЛОВ Дмитрий Евгеньевич

Аспирант кафедры социальной философии философского факультета Российского государственного гуманитарного университета

---

&copy Информационное общество, 2014 вып. 5-6, с. 28-33.

Что такое рекурсия в программировании?

Что вы подразумеваете под рекурсией?

Рекурсия означает «решение проблемы с использованием решения меньших подзадач (меньшая версия той же проблемы)» или «определение проблемы с точки зрения самой себя». Это широко используемая идея в структурах данных и алгоритмах для решения сложных задач путем их разбиения на более простые. В этом блоге мы поймем основные концепции рекурсии и поможем вам усовершенствовать один из важнейших навыков решения проблем в структурах данных и алгоритмах.

Рекурсия часто встречается в математике, где мы можем найти множество примеров выражений, записанных через самих себя. Например, вычисление значения nth факториала и nth чисел Фибоначчи является одним из лучших примеров. Но рекурсия — это такая же концепция программирования!

• Нахождение n-го факториала: n! = п * (п — 1)!
• Нахождение n-го числа Фибоначчи: F(n) = F(n — 1) + F(n — 2)

Как рекурсия работает в реальной жизни?

Предположим, вы стоите в длинной очереди людей. Сколько человек стоит прямо за вами в очереди?

Правила

• Один человек может видеть только человека, стоящего прямо впереди и сзади. Так что нельзя просто оглянуться назад и сосчитать.
• Каждому человеку разрешено задавать вопросы человеку, стоящему спереди или сзади. Как мы можем решить эту задачу рекурсивно?

Решение

Как работает рекурсия в программировании?

В терминах программирования рекурсия — это функция, вызывающая саму себя до тех пор, пока «базовое условие» не станет истинным для получения правильного вывода.

 пустая функция (размер ввода)
{
    базовый вариант
    .. .. ...
    функция (меньший размер ввода) // рекурсивный вызов
    .. .. ...
}
основной ()
{
    ... .. ...
    функция (размер ввода)
    ... .. ...
} 

Другими словами: чтобы решить проблему, мы решаем проблему, которая является меньшим экземпляром той же проблемы, а затем используем решение этого меньшего экземпляра для решения исходной проблемы. Чтобы рекурсивный алгоритм работал, меньшие подзадачи должны в конечном итоге прийти к базовому случаю.

Проще говоря, любой рекурсивный алгоритм состоит из двух частей: базового случая и рекурсивной структуры.

Базовый случай

Базовый случай — это завершающее условие, при котором функция немедленно возвращает результат. Это наименьшая версия задачи, для которой мы уже знаем решение.

Рекурсивная структура  

Рекурсивная структура — это идея разработать решение проблемы путем решения ее меньших подзадач, т. е. той же задачи, но для меньшего размера входных данных. Мы продолжаем вызывать ту же проблему для меньших размеров ввода, пока не достигнем базового случая рекурсии.

Этапы решения проблемы с использованием рекурсии

• Определить базовый случай: подумайте о наименьшей версии проблемы и запишите решение.
• Определить рекурсивную структуру: предположим, что у нас есть функция для решения задачи с заданным размером входных данных. Здесь нам нужно подумать: как мы могли бы использовать решение задачи для меньшего размера входных данных, чтобы решить задачу для заданного размера входных данных?
• Объедините базовый вариант и рекурсивную структуру, чтобы получить полное решение проблемы.

Идеи, о которых следует помнить при работе с рекурсией

• Наш код должен охватывать все допустимые экземпляры меньших размеров ввода.
• У нас должен быть правильный базовый случай, который не делает рекурсивных вызовов.
• Когда мы делаем рекурсивный вызов, он должен вызвать меньший экземпляр и перейти к базовому варианту.
• Если у нас есть правильная рекурсивная структура и базовый случай, то рекурсия решит проблему за нас. Это «рекурсивный прыжок веры», когда мы не должны беспокоиться о промежуточных шагах рекурсивных вызовов. Думать!

Основные примеры рекурсивных функций

Вычисление суммы двух чисел с помощью рекурсии

 sum(x, y)
= х, если (у == 0)
= 1 + сумма (x, y - 1), if(y > 0) 

Вычислить произведение двух чисел с помощью рекурсии

 product(x, y)
= 0, если (у == 0)
= сумма (x, произведение(x, y - 1), if(y > 0) 

Вычислить степень двух чисел с помощью рекурсии

 мощность(x, y)
= 1, если (у == 0)
= произведение (х, мощность (х, у - 1), если (у > 0) 

Понимание рекурсии через нахождение n-го факториала

Факториал неотрицательного целого числа представляет собой произведение всех целых чисел, меньших или равных n. Например. факториал числа 5 равен 1 * 2 * 3 * 4 * 5 = 120

Рекурсивная структура

Согласно математическому определению факториала числа n, мы можем написать:

 n!
= n * (n - 1) * (n - 2) *….* 2 * 1
= п * (п - 1)!
=> n-й факториал = n * (n - 1)-й факториал 

Если мы вычислим значение (n — 1)th  факториал, мы можем легко вычислить значение n-го  факториала. Это означает, что мы можем решить проблему размера входных данных n с меньшей проблемой размера входных данных (n — 1) . Другими словами, мы можем решить эту проблему, используя идею рекурсии!

Предположим, что функции fact(n) и fact(n — 1) возвращают значение n-го и (n — 1)th факториала соответственно, тогда мы можем написать следующую рекурсивную структуру:

 факт(n) = n * факт(n - 1) 

Базовый случай

В каждом рекурсивном решении должно быть завершающее условие или базовый случай, при котором наша рекурсия непосредственно даст нам результаты, не разбивая ее снова на подзадача. Если мы посмотрим на приведенную выше рекурсивную структуру, то обнаружим за сценой следующую цепочку рекурсивных вызовов:

 факт(n)
= п * факт (п - 1)
= n * (n - 1) * факт (n - 2)
... и так далее
= n * (n - 1) * (n - 2) * ... * 4 * 3 * 2 * факт (1)
= n * (n - 1) * (n - 2) * ... * 4 * 3 * 2 * 1 * факт (0) 

Факториал отрицательного числа не определен, поэтому fact(0) — это наименьшая версия факториальной задачи, в которой наша рекурсия завершится и вернет значение напрямую. Таким образом, n = 0 — это базовый случай, который вернет значение 1.

Рекурсивный псевдокод n-го факториала

 int fact(int n)
{
    если (п == 0)
        вернуть 1
    вернуть n * факт (n - 1)
} 

Как работает рекурсия в фоновом режиме?

Если мы нарисуем поток рекурсии для факториальной программы, можно обнаружить такую ​​закономерность: факт(0) вызывается последним, но он возвращает значение первым. Точно так же мы сначала вызываем fact(n), но возвращаем значение последним. Вы нашли Last In First Out (LIFO) заказов на рекурсивные вызовы и возвращаемые значения? Да, вы правильно поняли! За кулисами компилятор использует структуру данных стека для имитации рекурсии и получения правильного вывода. Мы называем этот стек: Call Stack!

• Порядок рекурсивных вызовов: от большей проблемы к меньшей

  факт (n) -> факт (n — 1) -> … -> факт (i) -> … -> факт (1) -> факт (0)

• Порядок возвращаемых значений: от меньшей проблемы к большей проблеме

  факт(0) -> факт(1) -> …-> факт(i) -> … -> факт(n — 1) -> факт(n)

Как идея стека вызовов работает в рекурсии?

• Информация о выполнении рекурсивной функции хранится в стеке вызовов. Он содержит сведения о выполнении: текущее состояние потока управления функцией, локальные переменные и другую внутреннюю информацию. Когда любая функция вызывается из main(), ей выделяется память в стеке.
• Во время рекурсии, когда функция вызывает ту же функцию для меньшего размера входных данных, ей выделяется память, и она помещается на вершину стека вызовов.
• Память для вызываемой функции выделяется поверх памяти, выделенной для вызывающей функции, и для каждого вызова функции создается другая копия локальных переменных.
• Когда достигается базовый вариант, функция возвращает свое значение функции, которой она была вызвана, память освобождается, и процесс продолжается.

Визуализация для вычисления fact(5) с использованием рекурсии

Примеры некоторых известных рекурсивных алгоритмов l], A[r]) + reverse(A, l+1, r-1)

Базовый случай: если (l >= r), то вернуть

Рекуррентное соотношение: T(n) = T(n — 2 ) + c, Временная сложность = O(n)

Нахождение НОД двух чисел

Рекурсивная структура: НОД(a, b) = НОД(b, a mod b), здесь a > b 9n)

Алгоритм бинарного поиска

Рекурсивная структура: binarySearch(A[], l, r, k)

 - если A[mid] = k, вернуть mid
- если (A[mid] > k), binarySearch(A[], l, mid - 1, k)
- if (A[mid] < k), binarySearch(A[], mid + 1, r, k) 

Базовый случай: Если (l > r), то вернуть -1

Рекуррентное соотношение: T(n) = T(n/2) + c, временная сложность = O(log n)

Алгоритм сортировки слиянием

Рекурсивная структура: mergeSort (A[], l, r)

 - сортировка слиянием (A, l, mid)
- сортировка слиянием (A, середина+1, г)
- merge(A, l, mid, r) 

Базовый случай: если (l == r), то возврат. Это случай одноэлементного массива.

Рекуррентное соотношение: T(n) = 2 T(n/2) + cn, временная сложность = O(n log n)

Алгоритм быстрой сортировки

Рекурсивная структура: quickSort(A[], l, r )

 - стержень = перегородка (A, l, r)
- быстрая сортировка (A, l, стержень - 1)
- quickSort(A, pivot + 1, r) 

Базовый случай: если (l >= r), то возврат.

Рекуррентное соотношение: T(n) = Сумма (от i = 0 до n - 1) [T(i) + T(n - i - 1)]/ n, временная сложность = O(nlogn) [Анализ среднего случая]

Реверс связанного списка

Рекурсивная структура: reverseList(заголовок узла)

 - Оставшийся узел = reverseList(head->next)
- голова->следующая->следующая = голова
- голова->следующий = NULL
- вернуть оставшиеся 

Базовый случай: если (head == NULL || head->next == NULL), вернуть заголовок

Рекуррентное соотношение: T(n) = T(n - 1) + c, временная сложность = O (н)

Обход двоичного дерева в обратном порядке

Рекурсивная структура: postorder(root)

 - postorder(root->left)
- postorder(корень->право)
- Посетите корень 

Базовый случай: if(root == NULL), затем возврат

Рекуррентное соотношение: T(n) = T(n - 1) + c, временная сложность = O(n)

Распечатать все перестановка заданной строки

Рекурсивная структура: permute(S[], l, r)

 for(i = l to r)
{
    своп(S[l], S[i])
    переставить (S, l + 1, r)
    своп(S[l], S[i])
} 

Базовый случай: if(l == r) then print(A)

Рекуррентное соотношение: T(n) = сумма (i = 0 to n - 1) [T(n - i) + c], временная сложность = O(n!)

Ошибка переполнения стека в рекурсии

Когда мы вызываем рекурсивную функцию, адрес возврата и аргументы помещаются в стек вызовов. Стек конечен, поэтому, если рекурсия слишком глубокая, вы в конечном итоге исчерпаете место в стеке. Это также называется переполнением стека в рекурсии. В некоторых ситуациях, если рекурсивная функция является хвостовой рекурсией, некоторые компиляторы могут оптимизировать рекурсивный вызов, превратив его в переход. Популярные причины ошибки переполнения стека:

• Рекурсивная функция написана с отсутствующим базовым регистром.
• Рекурсивный вызов функции с неправильным базовым регистром.

Распространенные ошибки в рекурсивных реализациях

Вот два распространенных случая, когда рекурсивная реализация может пойти не так:

• Базовый случай полностью отсутствует или для задачи требуется более одного базового случая, но не все базовые случаи покрыты .
• Рекурсивный шаг не сводится к меньшей подзадаче, поэтому рекурсия не сходится.

Ищите их при отладке. С другой стороны, бесконечный цикл в итеративной реализации обычно становится ошибкой переполнения стека в рекурсивной реализации. Глючная рекурсивная программа дает сбой быстрее!

Анализ рекурсивных алгоритмов

Основная идея рекурсивного анализа: вычислить общее количество операций, выполняемых рекурсией при каждом рекурсивном вызове, и суммировать, чтобы получить общую временную сложность. Поэтому, когда рекурсия выполняет постоянную операцию при каждом рекурсивном вызове, мы просто подсчитываем общее количество рекурсивных вызовов. В противном случае анализ будет немного математическим, если количество операций при каждом рекурсивном вызове зависит от размера входных данных.

В целом существует несколько методов анализа рекурсии: метод подстановки, метод дерева рекурсии и основная теорема.

• Метод рекурсивного дерева — один из самых популярных и фундаментальных подходов к анализу, в котором мы определяем рекуррентное отношение, рисуем рекурсивное дерево, вычисляем стоимость каждого уровня и суммируем уровень за уровнем, чтобы получить общую временную сложность.
• Метод подстановки представляет собой простую идею: мы записываем функцию рекуррентного отношения в терминах размера входных данных и подставляем значение меньшего размера входных данных, чтобы получить математический ряд в терминах n. Этот метод лучше всего работает для некоторых простых рекурсивных функций, но математические ряды могут быть сложными для вычисления некоторых функций.
• Основная теорема — один из самых популярных методов, который можно применять только для анализа алгоритмов «разделяй и властвуй».

Изучите этот блог, чтобы узнать об анализе рекурсии : Анализ рекурсии в структуре данных и алгоритмах

Рекурсия против. Итерация

• Как итерация, так и рекурсия включают повторение: Итерация явно использует структуру повторения, а рекурсия достигает повторения посредством повторяющихся вызовов метода.
• Итерация и рекурсия включают случай завершения: итерация завершается, когда условие цикла становится ложным, а рекурсия завершается, когда распознается базовый случай.
• Итерация и рекурсия могут происходить бесконечно: бесконечный цикл возникает с итерацией, если условие цикла всегда становится истинным. Но бесконечная рекурсия возникает, если шаг рекурсии не уменьшает проблему таким образом, который сходится в базовом случае.
• Рекурсия повторно вызывает вызовы методов для решения более мелких проблем, и, следовательно, возникают дополнительные затраты на вызовы методов. Это может дорого обойтись как процессорному времени, так и объему памяти.

Дополнительные сведения см. в этом блоге: Сравнение итерации и рекурсии

Применение рекурсии при решении задач

• Подход «разделяй и властвуй»
• Решение алгоритмов поиска и сортировки
• Решение задач динамического программирования
• Решение проблем с помощью поиска с возвратом
• Решение проблем связанных списков
• Решение проблем дерева с помощью DFS
• Решение проблем с графами с помощью DFS
• Разработка алгоритмов аппроксимации

Концепции для дальнейшего изучения

• Типы рекурсии
• Хвостовая рекурсия и рекурсивная оптимизация
• Идея функционального программирования

Задачи кодирования для практики с использованием рекурсии

• Задача Иосифа Флавия
• Проблема переполнения
• Алгоритм быстрого выбора для нахождения k-го наименьшего элемента
• Рекурсивный обход бинарного дерева
• Найти все возможные комбинации K чисел от 1 до n
• Найти k-й наименьший элемент двух отсортированных массивов
• Медиана двух отсортированных массивов
• Проблема N-ферзя
• Алгоритм Карацубы

Ссылки на содержимое

• Алгоритмы CLRS
• Руководство по разработке алгоритмов Стивена Скиены

Наслаждайтесь обучением, Наслаждайтесь программированием, Наслаждайтесь алгоритмами!

Что такое рекурсия в программировании?

Что такое рекурсия??

Рекурсия — это способ решения проблем с помощью меньших версий одной и той же проблемы. Мы решаем проблему через меньшие подзадачи, пока не достигнем тривиальной версии проблемы, то есть базового случая.

«Чтобы понять рекурсию, нужно сначала понять рекурсию».

Другими словами, рекурсивная функция — это функция, которая вызывает себя до тех пор, пока «базовое условие» не станет истинным, и выполнение не прекратится. Рекурсивная функция состоит из двух частей:

1. Базовый вариант
2. Рекурсивная структура

Любая рекурсивная функция будет выглядеть как

 функция(arg1,arg2,....)
{
    если (условие базового случая)
    {
        // Базовый вариант
    }
    // Рекурсивная структура
    
} 

Базовый вариант : с наименьшая версия проблемы, для которой мы уже знаем решение, или завершающее условие, при котором функция может немедленно вернуть результат.

Рекурсивная структура: Поиск решения проблемы через решение ее более мелких подзадач. Здесь функция должна называть себя чтобы разбить текущую проблему на более простой уровень.

Давайте возьмем пример задачи обратного отсчета, чтобы понять базовый случай и рекурсивную структуру.

Пример рекурсии 1: задача обратного отсчета

Вам нужно вывести числа от N до 1 в порядке убывания.

Рекурсивная структура

В рекурсивной структуре мы разбиваем решение задачи на решение меньших версий той же задачи. Итак, здесь мы можем вывести N на первом шаге и вызвать ту же функцию для вывода оставшихся N -1 чисел.

Печать чисел от N до 1 = печать (N) + Печать чисел от N-1 до 1

Исходная задача: печать чисел от N до 1
Меньшая подзадача: печать чисел от N-1 до 1

 => обратный отсчет (N) = печать (N) + обратный отсчет (N-1) 

Теперь цепочка вызова функции должна где-то остановиться. Просто подумайте, что может быть базовым для вышеуказанного решения?

Базовый вариант

Обратный отсчет нужно остановить после печати 1. Поэтому нам нужно написать базовое условие, чтобы остановить выполнение программы.

 пустой обратный отсчет (целое число)
{
    если ( n < 1 ) // Базовый случай
    {
        return // останавливает выполнение оператором return. 
    }
} 

Теперь нам просто нужно объединить рекурсивную структуру и базовый случай, чтобы написать полную рекурсивную реализацию вышеуказанной проблемы.

Псевдокод

 пустой обратный отсчет (целое число)
{
    if(n < 1) // Базовый случай
    {
        возвращаться
    }
    печать (н)
    обратный отсчет (n-1) // Рекурсивный
} 

Блок-схема программы

Критические идеи для размышления!

• Подумайте о рекурсивном решении для печати чисел в порядке возрастания (от 1 до N).

Пример рекурсии 2: Факторная проблема

Нам нужно найти энный факториал. Факториал числа – это произведение чисел от 1 до n (включительно). Например, факториал 4 равен 1*2*3*4 = 24.

Рекурсивная структура

Согласно определению факториала, мы можем описать решение задачи через решение ее меньшей подзадачи.

Нахождение n-го факториала = n * нахождение (n-1)-го факториала

Исходная задача: найти n-й факториал
Меньшая подзадача: найти (n-1)-й факториал

 факт(n) = n * факт(n-1) 

Базовый вариант

Теперь подумайте о базовом случае, когда функция будет напрямую давать вам результаты, не разбивая ее снова на подзадачи.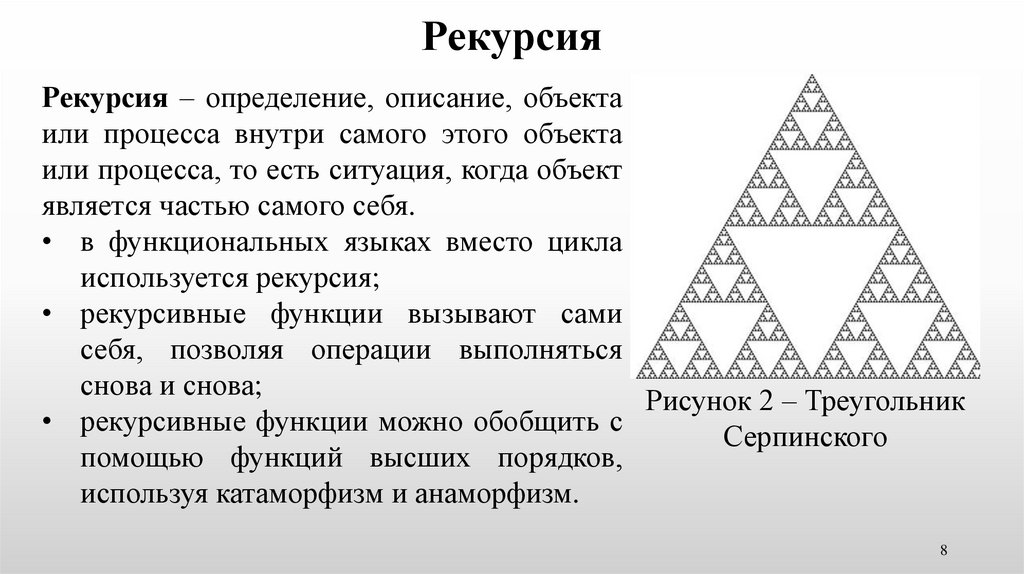

 факт(5)
= 5 * факт (4)
= 5 * 4 * факт (3)
= 5 * 4 * 3 * факт (2)
= 5 * 4 * 3 * 2 * факт (1)
= 5 * 4 * 3 * 2 * 1 * факт (0) 

Факториал отрицательного числа не определен, поэтому факт(0) — это наименьшая версия факториальной задачи, на которой наше решение завершится.

Здесь n = 0 — это базовый случай, который вернет 1. Так как 0! = 1

Ход программы

Псевдокод

 на самом деле (целое число)
{
    if(n == 0) // Базовый случай
    {
        вернуть 1
    }
    
    return n*fact(n-1) // Рекурсивная структура
} 

Критические идеи для размышления

Возьмите задачу «Перевернуть строку» и подумайте о ее рекурсивном решении с помощью описанного выше мыслительного процесса.

Некоторые известные рекурсивные алгоритмы

Нахождение n-го числа Фибоначчи

 Рекурсивная структура
фибоначчи (n) = фибоначчи (n-1) + фибоначчи (n-2)
Базовый вариант
если (n <= 1) вернуть n.
Здесь у нас есть 2 базовых случая: fib(0) = 0 и fib(1) = 1 

Нахождение НОД двух чисел

 Рекурсивная структура
НОД(а, Ь) = НОД(Ь, модуль Ь)
Здесь мы предполагаем, что а > b
Базовый вариант
НОД(а, 0) = а 

Перевернуть массив

 Рекурсивная структура
обратный массив (А, л, г)
- поменять местами(А[л], А[г])
- reverseArray(A, l+1, r-1)
Базовый вариант
Если (l >= r), то вернуть (думаю!) 

Бинарный поиск

 Рекурсивная структура
Двоичный поиск(A[],l,r,k)
- середина = l + (r-l)/2
- если (A[mid] > k), то вызвать BinarySearch(A[],l,mid-1,k)
- если (A[mid] < k), то вызвать BinarySearch(A[], mid+1, r, k)
Базовый вариант
Если (l > r), то вернуть -1.  Это случай безуспешного поиска (Подумай!) 

Сортировка слиянием

 Рекурсивная структура
mergeSort(A[],l,r)
- середина = l+(r-l)/2
- Рекурсивная сортировка первой половины: mergeSort(A, l, mid)
- Рекурсивная сортировка второй половины: mergeSort(A, mid+1, r)
- Объединить две отсортированные половины: merge(A, l, mid, r)
Базовый вариант
Если (l == r), то возврат. Это случай одного элемента (думаю!) 

Быстрая сортировка

 Рекурсивная структура
быстрая сортировка (A [], l, r)
- стержень = раздел (A, l, r)
- быстрая сортировка (A, l, стержень - 1)
- быстрая сортировка (A, точка опоры + 1, r)
Базовый вариант
если (l >= r), то возврат.
Здесь у нас есть два базовых случая: (l > r) и (l == r) 

Последовательный обход бинарного дерева

 Рекурсивная структура
В порядке (корень)
- Обход левого поддерева: Inorder(root->left)
- Посетите корень
- Обход правого поддерева: Inorder(root->right)
Базовый вариант
если (корень == NULL), то вернуть 

Вывести все перестановки заданной строки

 Рекурсивная структура
перестановка (строка A, l, r)
для (я = от л до г)
- поменять местами(А[1], А[i])
- переставить(A,l+1,r)
- поменять местами(А[1], А[i])
Базовый вариант
если(l == r), то выведите(A)(Подумай!) 

Самая длинная общая подпоследовательность

 Рекурсивная структура
lcs(X, Y, m, n)
- если (X[m-1] == Y[n-1]), вернуть 1 + lcs(X, Y, m-1, n-1)
- иначе вернуть max (lcs(X, Y, m, n-1), lcs(X, Y, m-1, n))
 
Базовый вариант
если (m == 0 || n == 0), то вернуть 0 

Идея стека рекурсивных вызовов

Если мы наблюдаем приведенный выше поток выполнения рекурсии, становится виден один шаблон: факт (0) вызывается последним, но сначала возвращается значение. Точно так же мы сначала вызываем fact(n), но возвращаем значение последним. (Думать!)

Порядок выполнения вызова функции

 факт(n)-> факт(n-1)...-> факт(i)->...-> факт(1)-> факт(0) 

Порядок, в котором функции возвращают значения

 факт(0)-> факт(1)...-> факт(i)->...-> факт(n-1)-> факт(n) 

Вышеупомянутая идея похожа на порядок «последний пришел — первый ушел» (LIFO). Вот некоторые ключевые идеи, связанные с выполнением рекурсии:

• Для выполнения рекурсивных функций компилятор использует "Стек вызовов" который основан на структуре данных стека.
• Когда программа вызывает функцию, ей выделяется память, и она помещается на вершину стека вызовов.
• Память для вызываемой функции выделяется поверх памяти, выделенной для вызывающей функции, и для каждого вызова функции создается другая копия локальных переменных.
• Когда базовый случай достигнут, функция возвращает свое значение функции, которой она вызывается, и память освобождается, и процесс продолжается.

Если вы не знакомы с структура данных стека , предположим стопку книг. Здесь вы можете добавлять по одной книге за раз. Затем, когда нужно взять из него один, вы можете взять только то, что находится на вершине стека.

Давайте посмотрим на стек вызовов для факториала на примере

Как приступить к решению проблемы с помощью рекурсии?

Чтобы решить любую проблему рекурсивно, просто попробуйте следовать этому мыслительному процессу, это облегчит решение рекурсивной структуры и базовых случаев:

1. Как мы можем решить ту же проблему, используя решение ее более мелких подзадач?
2. Не беспокойтесь о решении мелких подзадач, потому что рекурсия позаботится об этом!
3. Напишите рекурсивную структуру с параметром функции и правильными граничными условиями.
4. Определите базовые случаи, то есть наименьшую версию проблемы, для которой вы уже знаете решение. Что произойдет, если вы выберете неправильный базовый вариант или не напишете базовый вариант? (Думать!)
5. Понимание природы подзадач важно для рекурсивных решений. Например :

• Разделяй и властвуй: Решение проблем с помощью более чем одной подзадачи и подзадачи независимы.
• Динамическое программирование: Решение проблем с помощью более чем одной подзадачи и подзадачи зависят

Применение рекурсии

• Решение проблем с массивами и связанными списками
• Решение проблем с деревьями
• Решение задач с графами
• Решение проблем методом «разделяй и властвуй»
• Решение проблем с помощью динамического программирования
• Решение проблем с помощью исчерпывающего поиска и поиска с возвратом
• Известные алгоритмы сортировки, такие как быстрая сортировка, сортировка слиянием
• Разработка алгоритмов аппроксимации

Зачем нам нужна рекурсия?

Вот некоторые преимущества использования рекурсии:

• Рекурсивное решение часто чище, чем итеративное решение. Мы часто встречаем случаи, когда ~50 строк цикла for можно сократить до ~5–10 строк рекурсии.
• В некоторых случаях более естественно «мыслить рекурсивно» . Рекурсия — это самый ясный и простой способ решения проблем в структурах данных, таких как деревья, где рекурсивная структура проста для понимания.
• Есть некоторые проблемы, которые довольно сложно или невозможно решить с помощью Итерация.
• Рекурсия естественным образом разбивает проблемы на более мелкие, независимые подзадачи, что значительно облегчает решение. распараллеливать .

  No related posts.