Рекурсия это в программировании – Рекурсия. Тренировочные задачи / Habr

📌 Рекурсия — это… 🎓 Что такое Рекурсия?

Рекурсивное изображение экрана Визуальная форма рекурсии страницы Википедии

Реку́рсия — процесс повторения элементов самоподобным образом. Например, если два зеркала установить друг напротив друга, то возникающие в них вложенные отражения суть одна из форм бесконечной рекурсии.

Термин «рекурсия» используется в различных специальных областях знаний — от лингвистики до логики, но наиболее широкое применение находит в математике и информатике. В математике и информатике рекурсия имеет отношение к методу определения функций: рекурсивно заданная функция в своём определении содержит себя, в частности, рекурсивной является функция, заданная рекуррентной формулой. Таким образом, можно одним выражением дать бесконечный набор способов вычисления функции, определить множество объектов через самого себя с использованием ранее заданных частных определений.

С рекурсией тесно связана математическая индукция: она является естественным способом доказательства свойств функций на натуральных числах, рекурсивно заданных через свои меньшие значения.

В математике

В программировании

Функции

В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная или косвенная рекурсия), например, функция вызывает функцию , а функция  — функцию . Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.

Преимущество рекурсивного определения объекта заключается в том, что такое конечное определение теоретически способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.

Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за счёт этого работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого, обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.

Имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивается выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. Однако, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Scheme (диалект языка Lisp), описание которого содержит все необходимые сведения.

Любую рекурсивную функцию можно заменить циклом и стеком.

Данные

Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):

 struct element_of_list
 {
   element_of_list *next; /* ссылка на следующий элемент того же типа */
   int data; /* некие данные */
 };

Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.

В физике

Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из уменьшающихся отражений зеркал.

Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.

В лингвистике

См. также: Рекурсия (лингвистика)

Способность языка порождать вложенные предложения и конструкции. Базовое предложение «кошка съела мышь» может быть за счёт рекурсии расширено как Ваня догадался, что кошка съела мышь, далее как Катя знает, что Ваня догадался, что кошка съела мышь и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку. Однако, в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Дэниэл Эверетт (англ.)^[1].

В культуре

Большая часть шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода, например, известно высказывание:

«чтобы понять рекурсию, нужно сначала понять рекурсию».

Весьма популярна шутка о рекурсии, напоминающая словарную статью:

Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:

• рассказ про Йона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки»:

Нашёл следующие краткие сведения:
«СЕПУЛЬКИ — важный элемент цивилизации ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКАРИИ».

Я последовал этому совету и прочёл:
«СЕПУЛЬКАРИИ — устройства для сепуления (см.)».
Я поискал «Сепуление»; там значилось:
«СЕПУЛЕНИЕ — занятие ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКИ».

Лем С. «Звёздные дневники Ийона Тихого. Путешествие четырнадцатое.»

• Рассказ из «Кибериады» о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).
• Рекурсивные акронимы: GNU (GNU Not Unix), PHP (PHP: Hypertext Preprocessor) и т. д.

См. также

Примечания

3dic.academic.ru

📌 Рекурсия — это… 🎓 Что такое Рекурсия?

Рекурсивное изображение экрана Визуальная форма рекурсии страницы Википедии

Реку́рсия — процесс повторения элементов самоподобным образом. Например, если два зеркала установить друг напротив друга, то возникающие в них вложенные отражения суть одна из форм бесконечной рекурсии.

Термин «рекурсия» используется в различных специальных областях знаний — от лингвистики до логики, но наиболее широкое применение находит в математике и информатике. В математике и информатике рекурсия имеет отношение к методу определения функций:

рекурсивно заданная функция в своём определении содержит себя, в частности, рекурсивной является функция, заданная рекуррентной формулой. Таким образом, можно одним выражением дать бесконечный набор способов вычисления функции, определить множество объектов через самого себя с использованием ранее заданных частных определений.

С рекурсией тесно связана математическая индукция: она является естественным способом доказательства свойств функций на натуральных числах, рекурсивно заданных через свои меньшие значения.

В математике

В программировании

Функции

В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная или косвенная рекурсия), например, функция вызывает функцию , а функция  — функцию . Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.

Преимущество рекурсивного определения объекта заключается в том, что такое конечное определение теоретически способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.

Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за счёт этого работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого, обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.

Имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивается выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. Однако, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Scheme (диалект языка Lisp), описание которого содержит все необходимые сведения.

Любую рекурсивную функцию можно заменить циклом и стеком.

Данные

Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):

 struct element_of_list
 {
   element_of_list *next; /* ссылка на следующий элемент того же типа */
   int data; /* некие данные */
 };

Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.

В физике

Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из уменьшающихся отражений зеркал.

Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.

В лингвистике

См. также: Рекурсия (лингвистика)

Способность языка порождать вложенные предложения и конструкции. Базовое предложение «кошка съела мышь» может быть за счёт рекурсии расширено как Ваня догадался, что кошка съела мышь, далее как Катя знает, что Ваня догадался, что кошка съела мышь и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку. Однако, в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Дэниэл Эверетт (англ.)^[1].

В культуре

Большая часть шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода, например, известно высказывание: «чтобы понять рекурсию, нужно сначала понять рекурсию».

Весьма популярна шутка о рекурсии, напоминающая словарную статью:

Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:

• рассказ про Йона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки»:

Нашёл следующие краткие сведения:
«СЕПУЛЬКИ — важный элемент цивилизации ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКАРИИ».
Я последовал этому совету и прочёл:
«СЕПУЛЬКАРИИ — устройства для сепуления (см.)».
Я поискал «Сепуление»; там значилось:
«СЕПУЛЕНИЕ — занятие ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКИ».

Лем С. «Звёздные дневники Ийона Тихого. Путешествие четырнадцатое.»

• Рассказ из «Кибериады» о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).
• Рекурсивные акронимы: GNU (GNU Not Unix), PHP (PHP: Hypertext Preprocessor) и т. д.

См. также

Примечания

dis.academic.ru

Рекурсия

Материал из Seo Wiki — Поисковая Оптимизация и Программирование

Реку́рсия — метод определения класса объектов или методов предварительным заданием одного или нескольких (обычно простых) его базовых случаев или методов, а затем заданием на их основе правила построения определяемого класса, ссылающегося прямо или косвенно на эти базовые случаи.

Другими словами, рекурсия — способ общего определения объекта или действия через себя, с использованием ранее заданных частных определений. Рекурсия используется, когда можно выделить самоподобие задачи.

Определение в логике, использующее рекурсию, называется индуктивным (см., например, Натуральное число).

Примеры

• Метод Гаусса — Жордана для решения Системы линейных алгебраических уравнений является рекурсивным.
• Факториал целого неотрицательного числа <math>n</math> обозначается <math>n!</math> и определяется как

  <math>n!=n\times(n-1)!</math> при <math>n>0</math> и <math>n!=1</math> при <math>n=0</math>

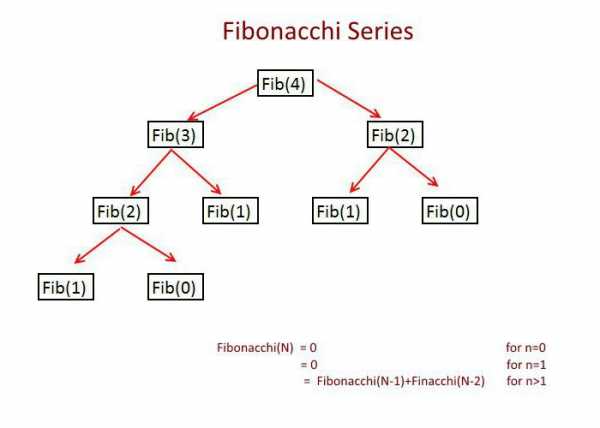
• Числа Фибоначчи определяются с помощью рекуррентного соотношения:

  Первое и второе числа Фибоначчи равны 1

  Для <math>n>2</math>, <math>n-e</math> число Фибоначчи равно сумме <math>(n-1)</math>-го и <math>(n-2)</math>-го чисел Фибоначчи

• Практически все геометрические фракталы задаются в форме бесконечной рекурсии. (например, треугольник Серпинского).
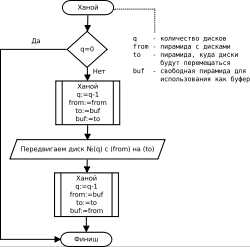
• Задача «Ханойские башни». Её содержательная постановка такова:

  В одном из буддийских монастырей монахи уже тысячу лет занимаются перекладыванием колец. Они располагают тремя пирамидами, на которых надеты кольца разных размеров. В начальном состоянии 64 кольца были надеты на первую пирамиду и упорядочены по размеру. Монахи должны переложить все кольца с первой пирамиды на вторую, выполняя единственное условие — кольцо нельзя положить на кольцо меньшего размера. При перекладывании можно использовать все три пирамиды. Монахи перекладывают одно кольцо за одну секунду. Как только они закончат свою работу, наступит конец света.

  Рекурсивный вариант решения задачи можно описать так:

Алгоритм по передвижению башни, алгоритм передвинет нужное количество дисков из пирамиды «источник» на пирамиду «задание» используя «запасную» пирамиду.

Если число дисков равно одному, тогда:

• Передвиньте диск из источника в задание

В противном случае:

• Рекурсивно передвиньте все диски кроме одного из источника в запас, используя задание как запас
• Передвиньте оставшийся диск из источника в задание
• Передвиньте все диски из запаса в задание используя источник как запас

Рекурсия в программировании

Функции

В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная рекурсия), например, функция <math>A</math> вызывает функцию <math>B</math>, а функция <math>B</math> — функцию <math>A</math>. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.

Преимущество рекурсивного определения объекта заключается в том, что такое конечное определение теоретически способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.

Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за этот счёт работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого, обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.

Впрочем, имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного и/или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивается выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. Однако, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Scheme (диалект языка Lisp), описание которого содержит все необходимые сведения.

Данные

Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):

 class element_of_list
 {
   element_of_list *next; /* ссылка на следующий элемент того же типа */
   int data; /* некие данные */
 };

Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.

Рекурсия в физике

Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из затухающих отражений зеркал.

Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.

Рекурсия в лингвистике

Способность языка порождать вложенные предложения и конструкции. Базовое предложение кошка съела мышь может быть за счет рекурсии расширено как Ваня догадался, что кошка съела мышь, далее как Катя знает, что Ваня догадался, что кошка съела мышь и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку (хотя в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Д. Эверетт). О рекурсии в лингвистике, ее разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е. А. Лодатко «Рекурсивные лингвистические структуры» (см.: Рекурсивные лингвистические структуры)

Цитаты

Юмор

Большая часть всех шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода. Известные высказывания: ‘Чтобы понять рекурсию, нужно сначала понять рекурсию’, ‘Чтобы что-то сделать, надо что-то сделать’ и т. д. Весьма популярна шутка о рекурсии, напоминающая словарную статью:

Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:

• Рассказ про Йона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки»:

Нашёл следующие краткие сведения:
«СЕПУЛЬКИ — важный элемент цивилизации ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКАРИИ».
Я последовал этому совету и прочёл:
«СЕПУЛЬКАРИИ — устройства для сепуления (см.)».
Я поискал «Сепуление»; там значилось:
«СЕПУЛЕНИЕ — занятие ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКИ».

Лем С. «Звёздные дневники Ийона Тихого. Путешествие четырнадцатое.»

• Рассказ из «Кибериады» о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).

Русская народная сказка-песня «У попа была собака…» являет пример рекурсии:

У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:

«У попа была собака, он её любил,

Она съела кусок мяса, он её убил,

В землю закопал,

Надпись написал:

«У попа была собака, он её любил,

Она съела кусок мяса, он её убил,

В землю закопал,

Надпись написал:

…

В поисковой системе Google, при запросе «рекурсия» выскакивает надпись «Возможно, вы имели в виду: рекурсия».

См. также

Примечания

Ссылки

• Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1

www.sbup.com

рекурсия — Викисловарь

В Википедии есть страница «Рекурсия (значения)».

Содержание

• 1 Русский
  • 1.1 Морфологические и синтаксические свойства
  • 1.2 Произношение
  • 1.3 Семантические свойства
    • 1.3.1 Значение
    • 1.3.2 Синонимы
    • 1.3.3 Антонимы
    • 1.3.4 Гиперонимы
    • 1.3.5 Гипонимы
  • 1.4 Родственные слова
  • 1.5 Этимология
  • 1.6 Фразеологизмы и устойчивые сочетания
  • 1.7 Перевод

Морфологические и синтаксические свойства[править]

падеж	ед. ч.	мн. ч.
Им.	реку́рсия	реку́рсии
Р.	реку́рсии	реку́рсий
Д.	реку́рсии	реку́рсиям
В.	реку́рсию	реку́рсии
Тв.	реку́рсией реку́рсиею	реку́рсиями
Пр.	реку́рсии	реку́рсиях

ре-ку́р-си·я

Существительное, неодушевлённое, женский род, 1-е склонение (тип склонения 7a по классификации А. А. Зализняка).

Корень: -рекурс-; суффикс: -иj; окончание: -я.

Произношение[править]

• МФА: [rʲɪˈkursʲɪɪ̯ə]

Семантические свойства[править]

Значение[править

ru.wiktionary.org

Рекурсия Википедия

Рекурсивное изображение экрана Визуальная форма рекурсии страницы Википедии

Реку́рсия — определение, описание, изображение какого-либо объекта или процесса внутри самого этого объекта или процесса, то есть ситуация, когда объект является частью самого себя. Термин «рекурсия» используется в различных специальных областях знаний — от лингвистики до логики, но наиболее широкое применение находит в математике и информатике.

В математике[ | ]

В математике рекурсия имеет отношение к методу определения функций и числовых рядов: рекурсивно заданная функция определяет своё значение через обращение к себе самой с другими аргументами. При этом возможно два варианта:

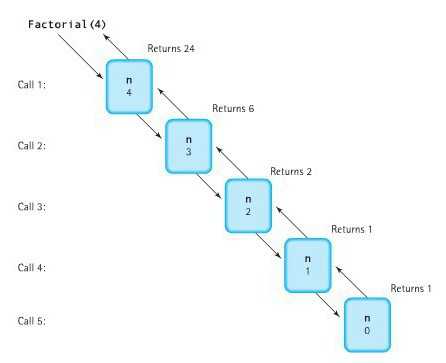
• Конечная рекурсивная функция. Она задаётся таким образом, чтобы для любого конечного аргумента за конечное число рекурсивных обращений привести к одному из отдельно определённых частных случаев, вычисляемых без рекурсии. Классический пример: рекурсивно-определённый факториал целого неотрицательного числа:

ru-wiki.ru

Рекурсия — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Реку́рсия — определение, описание, изображение какого-либо объекта или процесса внутри самого этого объекта или процесса, то есть ситуация, когда объект является частью самого себя. Термин «рекурсия» используется в различных специальных областях знаний — от лингвистики до логики, но наиболее широкое применение находит в математике и информатике.

В математике

В математике рекурсия имеет отношение к методу определения функций и числовых рядов: рекурсивно заданная функция определяет своё значение через обращение к себе самой с другими аргументами. При этом возможно два варианта:

• Конечная рекурсивная функция. Она задаётся таким образом, чтобы для любого конечного аргумента за конечное число рекурсивных обращений привести к одному из отдельно определённых частных случаев, вычисляемых без рекурсии. Классический пример: рекурсивно-определённый факториал целого неотрицательного числа: <math>n!=\begin{cases}n\cdot(n-1)!,&n>0\\1,&n=0\end{cases}</math>. Здесь каждое следующее рекурсивное обращение делается с аргументом, меньшим на единицу. Поскольку n, по определению, целое неотрицательное число, через n рекурсивных обращений вычисление функции гарантированно придёт к частному случаю <math>0!=1</math>, на котором рекурсия прекратится. Таким образом, несмотря на рекурсивность определения, вычисление функции для любого аргумента из области определения окажется конечным.
• Бесконечная рекурсивная функция. Она задаётся в виде обращения к самой себе во всех случаях (по крайней мере, для некоторых из аргументов). Подобным образом могут задаваться бесконечные ряды, бесконечные непрерывные дроби и так далее. Практическое вычисление точного значения здесь, естественно, невозможно, поскольку потребует бесконечного времени. Требуемый результат находится аналитическими методами. Тем не менее, если речь идёт не о получении абсолютно точного значения, а о вычислении заданного приближения искомого значения, то тут в некоторых случаях возможно прямое использование рекурсивного определения: вычисления по нему ведутся до тех пор, пока необходимая точность не будет достигнута. Примером может служить один из вариантов разложения числа Эйлера:

<math>e = 2+\cfrac{2}{2+\cfrac{3}{3+\cfrac{4}{4+\ldots}}}\; = 2+f(2)</math>, где <math>f(n)=\cfrac{n}{n+f(n+1)}</math>

Прямой расчёт по приведённой формуле вызовет бесконечную рекурсию, но можно доказать, что значение f(n) при возрастании n стремится к единице (поэтому, несмотря на бесконечность ряда, значение числа Эйлера конечно). Для приближённого вычисления значения e достаточно искусственно ограничить глубину рекурсии некоторым наперёд заданным числом и по достижении его использовать вместо <math>f(n)</math> единицу.

Другим примером рекурсии в математике является числовой ряд, заданный рекуррентной формулой, когда каждый следующий член ряда вычисляется как результат функции от n предыдущих членов. Таким образом с помощью конечного выражения (представляющего собой совокупность реккурентной формулы и набора значений для первых n членов ряда) может даваться определение бесконечного ряда.

С рекурсией тесно связана математическая индукция: она является естественным способом доказательства свойств функций на натуральных числах, рекурсивно заданных через свои меньшие значения.

В математике отдельно рассматривается класс так называемых «примитивно рекурсивных» функций. Определение примитивно рекурсивной функции также рекурсивно, оно задаёт набор примитивных функций и набор правил; функция является примитивно рекурсивной, если она может быть представлена как комбинация примитивно рекурсивных функций, образованная по этим правилам.

Примеры рекурсии в математике:

<math>A(m,\;n)=\begin{cases}n+1,&m=0;\\A(m-1,\;1),&m>0,\;n=0;\\A(m-1,\;A(m,\;n-1)),&m>0,\;n>0.\end{cases}</math>

В программировании

Функции

В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная или косвенная рекурсия), например, функция <math>A</math> вызывает функцию <math>B</math>, а функция <math>B</math> — функцию <math>A</math>. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии. Рекурсивная программа позволяет описать повторяющееся или даже потенциально бесконечное вычисление, причём без явных повторений частей программы и использования циклов.

Структурно рекурсивная функция на верхнем уровне всегда представляет собой команду ветвления (выбор одной из двух или более альтернатив в зависимости от условия (условий), которое в данном случае уместно назвать «условием прекращения рекурсии»), имеющей две или более альтернативные ветви, из которых хотя бы одна является рекурсивной и хотя бы одна — терминальной. Рекурсивная ветвь выполняется, когда условие прекращения рекурсии ложно, и содержит хотя бы один рекурсивный вызов — прямой или опосредованный вызов функцией самой себя. Терминальная ветвь выполняется, когда условие прекращения рекурсии истинно; она возвращает некоторое значение, не выполняя рекурсивного вызова. Правильно написанная рекурсивная функция должна гарантировать, что через конечное число рекурсивных вызовов будет достигнуто выполнение условия прекращения рекурсии, в результате чего цепочка последовательных рекурсивных вызовов прервётся и выполнится возврат.

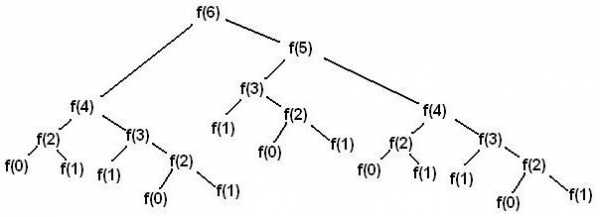
Помимо функций, выполняющих один рекурсивный вызов в каждой рекурсивной ветви, бывают случаи «параллельной рекурсии», когда на одной рекурсивной ветви делается два или более рекурсивных вызова. Параллельная рекурсия типична при обработке сложных структур данных, таких как деревья. Простейший пример параллельно-рекурсивной функции — вычисление ряда Фибоначчи, где для получения значения n-го члена необходимо вычислить (n-1)-й и (n-2)-й.

Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за счёт этого работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов.

Вопрос о желательности использования рекурсивных функций в программировании неоднозначен: с одной стороны, рекурсивная форма может быть структурно проще и нагляднее, в особенности, когда сам реализуемый алгоритм по сути рекурсивен. Кроме того, в некоторых декларативных или чисто функциональных языках (таких как Пролог или Haskell) просто нет синтаксических средств для организации циклов, и рекурсия в них — единственный доступный механизм организации повторяющихся вычислений. С другой стороны, обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии. Так, широко распространённый в учебной литературе пример рекурсивного вычисления факториала является, скорее, примером того, как не надо применять рекурсию, так как приводит к достаточно большой глубине рекурсии и имеет очевидную реализацию в виде обычного циклического алгоритма.

Имеется специальный тип рекурсии, называемый «хвостовой рекурсией» (структура рекурсивного алгоритма такова, что рекурсивный вызов является последней выполняемой операцией в функции, а его результат непосредственно возвращается в качестве результата функции). Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивается выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. Однако далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Scheme (диалект языка Lisp), описание которого содержит все необходимые сведения.

Теоретически, любую рекурсивную функцию можно заменить циклом и стеком. Однако такая модификация, как правило, бессмысленна, так как приводит лишь к замене автоматического сохранения контекста в стеке вызовов на ручное выполнение тех же операций с тем же расходом памяти. Исключением может быть ситуация, когда рекурсивный алгоритм приходится моделировать на языке, в котором рекурсия запрещена.

Доказательство корректности программ

В отличие от явно-циклических программ, для доказательства корректности рекурсивных нет необходимости искусственно вводить инвариант. Аналитическое доказательство корректности рекурсивной функции сводится к методу математической индукции, то есть к доказательству следующих утверждений:

1. Корректность использования рекурсивного обращения. Доказывается, что результат, вычисляемый в любой рекурсивной ветви функции, будет верным при условии, что соответствующие рекурсивные вызовы, в свою очередь, вернут верный результат.
2. Корректность всех терминальных ветвей. Доказывается, что все терминальные ветви возвращают верные значения. Как правило, это доказывается элементарно, так как терминальные ветви обычно никаких вычислений не содержат.
3. Достижимость терминальной ветви для любого корректного набора параметров после конечного числа рекурсивных вызовов. Доказывается, что изменение параметров вызова функции, которое производится при рекурсивном обращении, через конечное число рекурсивных вызовов приведёт к одному из наборов параметров, для которых задана терминальная ветвь.

Из суммы первого и второго утверждений следует, что в случае достижения терминальной ветви (а это значит — во всех случаях, когда вычисление функции окажется конечным) функция вернёт правильный результат. Третье положение доказывает, что конечным будет любое вычисление. Следовательно, любой вызов функции с корректными параметрами вернёт правильный результат (с очевидной оговоркой — если глубина рекурсии не окажется настолько большой, что вызовет переполнение памяти).

Данные

Рекурсивное определение данных возникает тогда, когда структура данных (запись, объект) содержит вложенный объект, структурно аналогичный самому себе или (что бывает чаще) ссылку на такой же объект. Преимущество рекурсивного определения объекта заключается в том, что такое конечное определение способно описать потенциально бесконечную структуру данных. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):

 struct element_of_list
 {
   element_of_list *next; /* ссылка на следующий элемент того же типа */
   int data; /* некие данные */
 };

Поскольку бесконечное число вложенных объектов невозможно разместить в конечной памяти, в реальности такие рекурсивно-определённые структуры всегда конечны. В заключительных (терминальных) ячейках обычно записываются пустые указатели, являющиеся одновременно флагами, указывающими программе, обрабатывающей структуру, что достигнут её конец.

Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных. В последние годы стала популярной концепция так называемых «ленивых вычислений», согласно которой данные, обрабатываемые программой, вычисляются лишь тогда, когда в них возникает необходимость. Реализация этой концепции привела к появлению в некоторых языках (Haskell, Python) возможности описывать потенциально-бесконечные, в том числе рекурсивные последовательности без явного ограничения на порождение объектов и свободно работать с ними.

В физике

Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из уменьшающихся отражений зеркал.

Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.

В лингвистике

Способность языка порождать вложенные предложения и конструкции. Базовое предложение «кошка съела мышь» может быть за счёт рекурсии расширено как «Ваня догадался, что кошка съела мышь», далее как «Катя знает, что Ваня догадался, что кошка съела мышь» и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку. Однако, в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Дэниэл Эверетт (англ.)^[1].

В культуре

Данный раздел имеет чрезмерный объём или содержит маловажные подробности.Если вы не согласны с этим, пожалуйста, покажите в тексте существенность излагаемого материала. В противном случае раздел может быть удалён. Подробности могут быть на странице обсуждения.

Большая часть шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода, например, известно высказывание: «чтобы понять рекурсию, нужно сначала понять рекурсию».

Весьма популярна шутка о рекурсии, напоминающая словарную статью:

Тема рекурсии присутствует во многих рассказах и очерках аргентинского писателя Хорхе Луиса Борхеса.

Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:

• рассказ про Ийона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки»:

Нашёл следующие краткие сведения:
«СЕПУЛЬКИ — важный элемент цивилизации ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКАРИИ».
Я последовал этому совету и прочёл:
«СЕПУЛЬКАРИИ — устройства для сепуления (см.)».
Я поискал «Сепуление»; там значилось:
«СЕПУЛЕНИЕ — занятие ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКИ».

Лем С. «Звёздные дневники Ийона Тихого. Путешествие четырнадцатое.»

• Рассказ из «Кибериады» о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).
• Рекурсивные акронимы: GNU (GNU Not Unix), PHP (PHP: Hypertext Preprocessor), WINE (Wine Is Not an Emulator) и т. д.
• Герб Российской Федерации является рекурсивно-определённым графическим объектом: в правой лапе изображённого на нём двуглавого орла зажат скипетр, который венчается уменьшенной копией герба. Так как на этом гербе в правой лапе орла также находится скипетр, получается бесконечная рекурсия.
• Рассказ Генри Каттнера «Порочный круг».

См. также

Напишите отзыв о статье «Рекурсия»

Примечания

1. ↑ О рекурсии в лингвистике, её разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е. А. Лодатко [www.relga.ru/Environ/WebObjects/tgu-www.woa/wa/Main?textid=2148&level1=main&level2=articles «Рекурсивные лингвистические структуры»]

Ссылки

• www.russika.ru/ef.php?s=4585

К:Википедия:Статьи без источников (тип: не указан)

Отрывок, характеризующий Рекурсия

Он читал и читал всё, что попадалось под руку, и читал так что, приехав домой, когда лакеи еще раздевали его, он, уже взяв книгу, читал – и от чтения переходил ко сну, и от сна к болтовне в гостиных и клубе, от болтовни к кутежу и женщинам, от кутежа опять к болтовне, чтению и вину. Пить вино для него становилось всё больше и больше физической и вместе нравственной потребностью. Несмотря на то, что доктора говорили ему, что с его корпуленцией, вино для него опасно, он очень много пил. Ему становилось вполне хорошо только тогда, когда он, сам не замечая как, опрокинув в свой большой рот несколько стаканов вина, испытывал приятную теплоту в теле, нежность ко всем своим ближним и готовность ума поверхностно отзываться на всякую мысль, не углубляясь в сущность ее. Только выпив бутылку и две вина, он смутно сознавал, что тот запутанный, страшный узел жизни, который ужасал его прежде, не так страшен, как ему казалось. С шумом в голове, болтая, слушая разговоры или читая после обеда и ужина, он беспрестанно видел этот узел, какой нибудь стороной его. Но только под влиянием вина он говорил себе: «Это ничего. Это я распутаю – вот у меня и готово объяснение. Но теперь некогда, – я после обдумаю всё это!» Но это после никогда не приходило.
Натощак, поутру, все прежние вопросы представлялись столь же неразрешимыми и страшными, и Пьер торопливо хватался за книгу и радовался, когда кто нибудь приходил к нему.
Иногда Пьер вспоминал о слышанном им рассказе о том, как на войне солдаты, находясь под выстрелами в прикрытии, когда им делать нечего, старательно изыскивают себе занятие, для того чтобы легче переносить опасность. И Пьеру все люди представлялись такими солдатами, спасающимися от жизни: кто честолюбием, кто картами, кто писанием законов, кто женщинами, кто игрушками, кто лошадьми, кто политикой, кто охотой, кто вином, кто государственными делами. «Нет ни ничтожного, ни важного, всё равно: только бы спастись от нее как умею»! думал Пьер. – «Только бы не видать ее , эту страшную ее ».

В начале зимы, князь Николай Андреич Болконский с дочерью приехали в Москву. По своему прошедшему, по своему уму и оригинальности, в особенности по ослаблению на ту пору восторга к царствованию императора Александра, и по тому анти французскому и патриотическому направлению, которое царствовало в то время в Москве, князь Николай Андреич сделался тотчас же предметом особенной почтительности москвичей и центром московской оппозиции правительству.
Князь очень постарел в этот год. В нем появились резкие признаки старости: неожиданные засыпанья, забывчивость ближайших по времени событий и памятливость к давнишним, и детское тщеславие, с которым он принимал роль главы московской оппозиции. Несмотря на то, когда старик, особенно по вечерам, выходил к чаю в своей шубке и пудренном парике, и начинал, затронутый кем нибудь, свои отрывистые рассказы о прошедшем, или еще более отрывистые и резкие суждения о настоящем, он возбуждал во всех своих гостях одинаковое чувство почтительного уважения. Для посетителей весь этот старинный дом с огромными трюмо, дореволюционной мебелью, этими лакеями в пудре, и сам прошлого века крутой и умный старик с его кроткою дочерью и хорошенькой француженкой, которые благоговели перед ним, – представлял величественно приятное зрелище. Но посетители не думали о том, что кроме этих двух трех часов, во время которых они видели хозяев, было еще 22 часа в сутки, во время которых шла тайная внутренняя жизнь дома.
В последнее время в Москве эта внутренняя жизнь сделалась очень тяжела для княжны Марьи. Она была лишена в Москве тех своих лучших радостей – бесед с божьими людьми и уединения, – которые освежали ее в Лысых Горах, и не имела никаких выгод и радостей столичной жизни. В свет она не ездила; все знали, что отец не пускает ее без себя, а сам он по нездоровью не мог ездить, и ее уже не приглашали на обеды и вечера. Надежду на замужество княжна Марья совсем оставила. Она видела ту холодность и озлобление, с которыми князь Николай Андреич принимал и спроваживал от себя молодых людей, могущих быть женихами, иногда являвшихся в их дом. Друзей у княжны Марьи не было: в этот приезд в Москву она разочаровалась в своих двух самых близких людях. М lle Bourienne, с которой она и прежде не могла быть вполне откровенна, теперь стала ей неприятна и она по некоторым причинам стала отдаляться от нее. Жюли, которая была в Москве и к которой княжна Марья писала пять лет сряду, оказалась совершенно чужою ей, когда княжна Марья вновь сошлась с нею лично. Жюли в это время, по случаю смерти братьев сделавшись одной из самых богатых невест в Москве, находилась во всем разгаре светских удовольствий. Она была окружена молодыми людьми, которые, как она думала, вдруг оценили ее достоинства. Жюли находилась в том периоде стареющейся светской барышни, которая чувствует, что наступил последний шанс замужества, и теперь или никогда должна решиться ее участь. Княжна Марья с грустной улыбкой вспоминала по четвергам, что ей теперь писать не к кому, так как Жюли, Жюли, от присутствия которой ей не было никакой радости, была здесь и виделась с нею каждую неделю. Она, как старый эмигрант, отказавшийся жениться на даме, у которой он проводил несколько лет свои вечера, жалела о том, что Жюли была здесь и ей некому писать. Княжне Марье в Москве не с кем было поговорить, некому поверить своего горя, а горя много прибавилось нового за это время. Срок возвращения князя Андрея и его женитьбы приближался, а его поручение приготовить к тому отца не только не было исполнено, но дело напротив казалось совсем испорчено, и напоминание о графине Ростовой выводило из себя старого князя, и так уже большую часть времени бывшего не в духе. Новое горе, прибавившееся в последнее время для княжны Марьи, были уроки, которые она давала шестилетнему племяннику. В своих отношениях с Николушкой она с ужасом узнавала в себе свойство раздражительности своего отца. Сколько раз она ни говорила себе, что не надо позволять себе горячиться уча племянника, почти всякий раз, как она садилась с указкой за французскую азбуку, ей так хотелось поскорее, полегче перелить из себя свое знание в ребенка, уже боявшегося, что вот вот тетя рассердится, что она при малейшем невнимании со стороны мальчика вздрагивала, торопилась, горячилась, возвышала голос, иногда дергала его за руку и ставила в угол. Поставив его в угол, она сама начинала плакать над своей злой, дурной натурой, и Николушка, подражая ей рыданьями, без позволенья выходил из угла, подходил к ней и отдергивал от лица ее мокрые руки, и утешал ее. Но более, более всего горя доставляла княжне раздражительность ее отца, всегда направленная против дочери и дошедшая в последнее время до жестокости. Ежели бы он заставлял ее все ночи класть поклоны, ежели бы он бил ее, заставлял таскать дрова и воду, – ей бы и в голову не пришло, что ее положение трудно; но этот любящий мучитель, самый жестокий от того, что он любил и за то мучил себя и ее, – умышленно умел не только оскорбить, унизить ее, но и доказать ей, что она всегда и во всем была виновата. В последнее время в нем появилась новая черта, более всего мучившая княжну Марью – это было его большее сближение с m lle Bourienne. Пришедшая ему, в первую минуту по получении известия о намерении своего сына, мысль шутка о том, что ежели Андрей женится, то и он сам женится на Bourienne, – видимо понравилась ему, и он с упорством последнее время (как казалось княжне Марье) только для того, чтобы ее оскорбить, выказывал особенную ласку к m lle Bоurienne и выказывал свое недовольство к дочери выказываньем любви к Bourienne.
Однажды в Москве, в присутствии княжны Марьи (ей казалось, что отец нарочно при ней это сделал), старый князь поцеловал у m lle Bourienne руку и, притянув ее к себе, обнял лаская. Княжна Марья вспыхнула и выбежала из комнаты. Через несколько минут m lle Bourienne вошла к княжне Марье, улыбаясь и что то весело рассказывая своим приятным голосом. Княжна Марья поспешно отерла слезы, решительными шагами подошла к Bourienne и, видимо сама того не зная, с гневной поспешностью и взрывами голоса, начала кричать на француженку: «Это гадко, низко, бесчеловечно пользоваться слабостью…» Она не договорила. «Уйдите вон из моей комнаты», прокричала она и зарыдала.
На другой день князь ни слова не сказал своей дочери; но она заметила, что за обедом он приказал подавать кушанье, начиная с m lle Bourienne. В конце обеда, когда буфетчик, по прежней привычке, опять подал кофе, начиная с княжны, князь вдруг пришел в бешенство, бросил костылем в Филиппа и тотчас же сделал распоряжение об отдаче его в солдаты. «Не слышат… два раза сказал!… не слышат!»
«Она – первый человек в этом доме; она – мой лучший друг, – кричал князь. – И ежели ты позволишь себе, – закричал он в гневе, в первый раз обращаясь к княжне Марье, – еще раз, как вчера ты осмелилась… забыться перед ней, то я тебе покажу, кто хозяин в доме. Вон! чтоб я не видал тебя; проси у ней прощенья!»
Княжна Марья просила прощенья у Амальи Евгеньевны и у отца за себя и за Филиппа буфетчика, который просил заступы.
В такие минуты в душе княжны Марьи собиралось чувство, похожее на гордость жертвы. И вдруг в такие то минуты, при ней, этот отец, которого она осуждала, или искал очки, ощупывая подле них и не видя, или забывал то, что сейчас было, или делал слабевшими ногами неверный шаг и оглядывался, не видал ли кто его слабости, или, что было хуже всего, он за обедом, когда не было гостей, возбуждавших его, вдруг задремывал, выпуская салфетку, и склонялся над тарелкой, трясущейся головой. «Он стар и слаб, а я смею осуждать его!» думала она с отвращением к самой себе в такие минуты.

В 1811 м году в Москве жил быстро вошедший в моду французский доктор, огромный ростом, красавец, любезный, как француз и, как говорили все в Москве, врач необыкновенного искусства – Метивье. Он был принят в домах высшего общества не как доктор, а как равный.
Князь Николай Андреич, смеявшийся над медициной, последнее время, по совету m lle Bourienne, допустил к себе этого доктора и привык к нему. Метивье раза два в неделю бывал у князя.
В Николин день, в именины князя, вся Москва была у подъезда его дома, но он никого не велел принимать; а только немногих, список которых он передал княжне Марье, велел звать к обеду.
Метивье, приехавший утром с поздравлением, в качестве доктора, нашел приличным de forcer la consigne [нарушить запрет], как он сказал княжне Марье, и вошел к князю. Случилось так, что в это именинное утро старый князь был в одном из своих самых дурных расположений духа. Он целое утро ходил по дому, придираясь ко всем и делая вид, что он не понимает того, что ему говорят, и что его не понимают. Княжна Марья твердо знала это состояние духа тихой и озабоченной ворчливости, которая обыкновенно разрешалась взрывом бешенства, и как перед заряженным, с взведенными курками, ружьем, ходила всё это утро, ожидая неизбежного выстрела. Утро до приезда доктора прошло благополучно. Пропустив доктора, княжна Марья села с книгой в гостиной у двери, от которой она могла слышать всё то, что происходило в кабинете.
Сначала она слышала один голос Метивье, потом голос отца, потом оба голоса заговорили вместе, дверь распахнулась и на пороге показалась испуганная, красивая фигура Метивье с его черным хохлом, и фигура князя в колпаке и халате с изуродованным бешенством лицом и опущенными зрачками глаз.
– Не понимаешь? – кричал князь, – а я понимаю! Французский шпион, Бонапартов раб, шпион, вон из моего дома – вон, я говорю, – и он захлопнул дверь.
Метивье пожимая плечами подошел к mademoiselle Bourienne, прибежавшей на крик из соседней комнаты.
– Князь не совсем здоров, – la bile et le transport au cerveau. Tranquillisez vous, je repasserai demain, [желчь и прилив к мозгу. Успокойтесь, я завтра зайду,] – сказал Метивье и, приложив палец к губам, поспешно вышел.
За дверью слышались шаги в туфлях и крики: «Шпионы, изменники, везде изменники! В своем доме нет минуты покоя!»
После отъезда Метивье старый князь позвал к себе дочь и вся сила его гнева обрушилась на нее. Она была виновата в том, что к нему пустили шпиона. .Ведь он сказал, ей сказал, чтобы она составила список, и тех, кого не было в списке, чтобы не пускали. Зачем же пустили этого мерзавца! Она была причиной всего. С ней он не мог иметь ни минуты покоя, не мог умереть спокойно, говорил он.
– Нет, матушка, разойтись, разойтись, это вы знайте, знайте! Я теперь больше не могу, – сказал он и вышел из комнаты. И как будто боясь, чтобы она не сумела как нибудь утешиться, он вернулся к ней и, стараясь принять спокойный вид, прибавил: – И не думайте, чтобы я это сказал вам в минуту сердца, а я спокоен, и я обдумал это; и это будет – разойтись, поищите себе места!… – Но он не выдержал и с тем озлоблением, которое может быть только у человека, который любит, он, видимо сам страдая, затряс кулаками и прокричал ей:
– И хоть бы какой нибудь дурак взял ее замуж! – Он хлопнул дверью, позвал к себе m lle Bourienne и затих в кабинете.
В два часа съехались избранные шесть персон к обеду. Гости – известный граф Ростопчин, князь Лопухин с своим племянником, генерал Чатров, старый, боевой товарищ князя, и из молодых Пьер и Борис Друбецкой – ждали его в гостиной.
На днях приехавший в Москву в отпуск Борис пожелал быть представленным князю Николаю Андреевичу и сумел до такой степени снискать его расположение, что князь для него сделал исключение из всех холостых молодых людей, которых он не принимал к себе.
Дом князя был не то, что называется «свет», но это был такой маленький кружок, о котором хотя и не слышно было в городе, но в котором лестнее всего было быть принятым. Это понял Борис неделю тому назад, когда при нем Ростопчин сказал главнокомандующему, звавшему графа обедать в Николин день, что он не может быть:
– В этот день уж я всегда езжу прикладываться к мощам князя Николая Андреича.
– Ах да, да, – отвечал главнокомандующий. – Что он?..
Небольшое общество, собравшееся в старомодной, высокой, с старой мебелью, гостиной перед обедом, было похоже на собравшийся, торжественный совет судилища. Все молчали и ежели говорили, то говорили тихо. Князь Николай Андреич вышел серьезен и молчалив. Княжна Марья еще более казалась тихою и робкою, чем обыкновенно. Гости неохотно обращались к ней, потому что видели, что ей было не до их разговоров. Граф Ростопчин один держал нить разговора, рассказывая о последних то городских, то политических новостях.
Лопухин и старый генерал изредка принимали участие в разговоре. Князь Николай Андреич слушал, как верховный судья слушает доклад, который делают ему, только изредка молчанием или коротким словцом заявляя, что он принимает к сведению то, что ему докладывают. Тон разговора был такой, что понятно было, никто не одобрял того, что делалось в политическом мире. Рассказывали о событиях, очевидно подтверждающих то, что всё шло хуже и хуже; но во всяком рассказе и суждении было поразительно то, как рассказчик останавливался или бывал останавливаем всякий раз на той границе, где суждение могло относиться к лицу государя императора.
За обедом разговор зашел о последней политической новости, о захвате Наполеоном владений герцога Ольденбургского и о русской враждебной Наполеону ноте, посланной ко всем европейским дворам.
– Бонапарт поступает с Европой как пират на завоеванном корабле, – сказал граф Ростопчин, повторяя уже несколько раз говоренную им фразу. – Удивляешься только долготерпению или ослеплению государей. Теперь дело доходит до папы, и Бонапарт уже не стесняясь хочет низвергнуть главу католической религии, и все молчат! Один наш государь протестовал против захвата владений герцога Ольденбургского. И то… – Граф Ростопчин замолчал, чувствуя, что он стоял на том рубеже, где уже нельзя осуждать.
– Предложили другие владения заместо Ольденбургского герцогства, – сказал князь Николай Андреич. – Точно я мужиков из Лысых Гор переселял в Богучарово и в рязанские, так и он герцогов.
– Le duc d’Oldenbourg supporte son malheur avec une force de caractere et une resignation admirable, [Герцог Ольденбургский переносит свое несчастие с замечательной силой воли и покорностью судьбе,] – сказал Борис, почтительно вступая в разговор. Он сказал это потому, что проездом из Петербурга имел честь представляться герцогу. Князь Николай Андреич посмотрел на молодого человека так, как будто он хотел бы ему сказать кое что на это, но раздумал, считая его слишком для того молодым.

wiki-org.ru

No related posts.