Рекурсия — Википедия
Рекурсивное изображение экрана Визуальная форма рекурсии страницы ВикипедииРеку́рсия — определение, описание, изображение какого-либо объекта или процесса внутри самого этого объекта или процесса, то есть ситуация, когда объект является частью самого себя. Термин «рекурсия» используется в различных специальных областях знаний — от лингвистики до логики, но наиболее широкое применение находит в математике и информатике.
В математике

В математике рекурсия имеет отношение к методу определения функций и числовых рядов: рекурсивно заданная функция определяет своё значение через обращение к себе самой с другими аргументами. При этом возможно два варианта:
- Конечная рекурсивная функция. Она задаётся таким образом, чтобы для любого конечного аргумента за конечное число рекурсивных обращений привести к одному из отдельно определённых частных случаев, вычисляемых без рекурсии. Классический пример: рекурсивно-определённый факториал целого неотрицательного числа: n!={n⋅(n−1)!,n>01,n=0{\displaystyle n!={\begin{cases}n\cdot (n-1)!,&n>0\\1,&n=0\end{cases}}}. Здесь каждое следующее рекурсивное обращение делается с аргументом, меньшим на единицу. Поскольку
- Бесконечная рекурсивная функция. Она задаётся в виде обращения к самой себе во всех случаях (по крайней мере, для некоторых из аргументов). Подобным образом могут задаваться бесконечные ряды, бесконечные непрерывные дроби и так далее. Практическое вычисление точного значения здесь, естественно, невозможно, поскольку потребует бесконечного времени. Требуемый результат находится аналитическими методами. Тем не менее, если речь идёт не о получении абсолютно точного значения, а о вычислении заданного приближения искомого значения, то тут в некоторых случаях возможно прямое использование рекурсивного определения: вычисления по нему ведутся до тех пор, пока необходимая точность не будет достигнута. Примером может служить разложение в непрерывную дробь числа
- e=2+22+33+44+…=2+f(2){\displaystyle e=2+{\cfrac {2}{2+{\cfrac {3}{3+{\cfrac {4}{4+\ldots }}}}}}\;=2+f(2)}, где f(n)=nn+f(n+1){\displaystyle f(n)={\cfrac {n}{n+f(n+1)}}}
- Прямой расчёт по приведённой формуле вызовет бесконечную рекурсию, но можно доказать, что значение f(n) при возрастании n стремится к единице (поэтому, несмотря на бесконечность ряда, значение числа Эйлера конечно). Для приближённого вычисления значения e достаточно искусственно ограничить глубину рекурсии некоторым наперёд заданным числом и по достижении его использовать вместо f(n){\displaystyle f(n)} единицу.
Другим примером рекурсии в математике является числовая последовательность, заданная рекуррентной формулой, когда каждый следующий член последовательности вычисляется как результат функции от n предыдущих членов. Таким образом с помощью конечного выражения (представляющего собой совокупность рекуррентной формулы и набора значений для первых n членов ряда) может даваться определение бесконечной последовательности.
С рекурсией тесно связана математическая индукция: она является естественным способом доказательства свойств функций на натуральных числах, рекурсивно заданных через свои меньшие значения.
В математике отдельно рассматривается класс так называемых «примитивно рекурсивных» функций. Определение примитивно рекурсивной функции также рекурсивно, оно задаёт набор примитивных функций и набор правил; функция является примитивно рекурсивной, если она может быть представлена как комбинация примитивно рекурсивных функций, образованная по этим правилам.
Примеры рекурсии в математике:
- A(m,n)={n+1,m=0;A(m−1,1),m>0,n=0;A(m−1,A(m,n−1)),m>0,n>0.{\displaystyle A(m,\;n)={\begin{cases}n+1,&m=0;\\A(m-1,\;1),&m>0,\;n=0;\\A(m-1,\;A(m,\;n-1)),&m>0,\;n>0.\end{cases}}}
В программировании
Функции
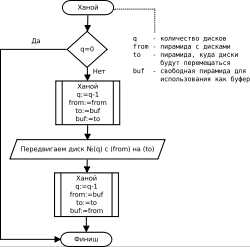
В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная или косвенная рекурсия), например, функция A{\displaystyle A} вызывает функцию B{\displaystyle B}, а функция B{\displaystyle B} — функцию A{\displaystyle A}. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии. Рекурсивная программа позволяет описать повторяющееся или даже потенциально бесконечное вычисление, причём без явных повторений частей программы и использования циклов.
Структурно рекурсивная функция на верхнем уровне всегда представляет собой команду ветвления (выбор одной из двух или более альтернатив в зависимости от условия (условий), которое в данном случае уместно назвать «условием прекращения рекурсии»), имеющую две или более альтернативные ветви, из которых хотя бы одна является рекурсивной и хотя бы одна —
Помимо функций, выполняющих один рекурсивный вызов в каждой рекурсивной ветви, бывают случаи «параллельной рекурсии», когда на одной рекурсивной ветви делается два или более рекурсивных вызова. Параллельная рекурсия типична при обработке сложных структур данных, таких как деревья. Простейший пример параллельно-рекурсивной функции — вычисление ряда Фибоначчи, где для получения значения n-го члена необходимо вычислить (n-1)-й и (n-2)-й.
Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за счёт этого работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов.
Вопрос о желательности использования рекурсивных функций в программировании неоднозначен: с одной стороны, рекурсивная форма может быть структурно проще и нагляднее, в особенности, когда сам реализуемый алгоритм по сути рекурсивен. Кроме того, в некоторых декларативных или чисто функциональных языках (таких как Пролог или Haskell) просто нет синтаксических средств для организации циклов, и рекурсия в них — единственный доступный механизм организации повторяющихся вычислений. С другой стороны, обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии. Так, широко распространённый в учебной литературе пример рекурсивного вычисления факториала является, скорее, примером того, как
Имеется специальный тип рекурсии, называемый «хвостовой рекурсией» (структура рекурсивного алгоритма такова, что рекурсивный вызов является последней выполняемой операцией в функции, а его результат непосредственно возвращается в качестве результата функции). Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивается выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. Однако далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Scheme (диалект языка Lisp), описание которого содержит все необходимые сведения.
Теоретически, любую рекурсивную функцию можно заменить циклом и стеком. Однако такая модификация, как правило, бессмысленна, так как приводит лишь к замене автоматического сохранения контекста в стеке вызовов на ручное выполнение тех же операций с тем же расходом памяти. Исключением может быть ситуация, когда рекурсивный алгоритм приходится моделировать на языке, в котором рекурсия запрещена.
Доказательство корректности программ
В отличие от явно-циклических программ, для доказательства корректности рекурсивных нет необходимости искусственно вводить инвариант. Аналитическое доказательство корректности рекурсивной функции сводится к методу математической индукции, то есть к доказательству следующих утверждений:
- Корректность рекурсивного обращения. Доказывается, что результат, вычисляемый в любой рекурсивной ветви функции, будет верным при условии, что параметры функции заданы корректно и соответствующие рекурсивные вызовы вернут верный результат.
- Корректность всех терминальных ветвей. Доказывается, что все терминальные ветви возвращают верные значения. Как правило, это доказательство тривиально, так как терминальные ветви обычно никаких вычислений не содержат.
- Достижимость терминальной ветви для любого корректного набора параметров после конечного числа рекурсивных вызовов. Доказывается, что изменение параметров вызова функции, которое производится при рекурсивном обращении, через конечное число рекурсивных вызовов приведёт к одному из наборов параметров, для которых существует терминальная ветвь.
Из суммы первого и второго утверждений следует, что в случае достижения терминальной ветви (а это значит — во всех случаях, когда вычисление функции окажется конечным) функция вернёт правильный результат. Третье положение доказывает, что конечным будет любое вычисление. Следовательно, любой вызов функции с корректными параметрами вернёт правильный результат (с очевидной «технической» оговоркой — если глубина рекурсии не окажется настолько большой, что вызовет переполнение памяти).
Данные
Рекурсивное определение данных возникает тогда, когда структура данных (запись, объект) содержит вложенный объект, структурно аналогичный самому себе или (что бывает чаще) ссылку на такой же объект. Преимущество рекурсивного определения объекта заключается в том, что такое конечное определение способно описать потенциально бесконечную структуру данных. Подобные структуры используются при описании списков и графов. Пример описания списка (C):
struct element_of_list
{
struct element_of_list *next; /* указатель на следующий элемент того же типа */
int data; /* некие данные */
};
Поскольку бесконечное число вложенных объектов невозможно разместить в конечной памяти, в реальности такие рекурсивно-определённые структуры всегда конечны. В заключительных (терминальных) ячейках обычно записываются пустые указатели, являющиеся одновременно флагами, указывающими программе, обрабатывающей структуру, что достигнут её конец.
Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных. В последние годы стала популярной концепция так называемых «ленивых вычислений», согласно которой данные, обрабатываемые программой, вычисляются лишь тогда, когда в них возникает необходимость. Реализация этой концепции привела к появлению в некоторых языках (Haskell, Python) возможности описывать потенциально-бесконечные, в том числе рекурсивные последовательности без явного ограничения на порождение объектов и свободно работать с ними.
В физике
Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из уменьшающихся отражений зеркал.
Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.
В лингвистике
В лингвистике рекурсией называют способность языка порождать вложенные предложения и конструкции. Базовое предложение «кошка съела мышь» может быть за счёт рекурсии расширено как «Ваня догадался, что кошка съела мышь», далее как «Катя знает, что Ваня догадался, что кошка съела мышь» и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку. Однако в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Дэниэл Эверетт (англ.)[1].
В культуре
Данный раздел имеет чрезмерный объём или содержит маловажные подробности. Если вы не согласны с этим, пожалуйста, покажите в тексте существенность излагаемого материала. В противном случае раздел может быть удалён. Подробности могут быть на странице обсуждения. |
Большая часть шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода, например, известно высказывание: «чтобы понять рекурсию, нужно сначала понять рекурсию».
Весьма популярна шутка о рекурсии, напоминающая словарную статью:
- рекурсия
- см. рекурсия
Тема рекурсии присутствует во многих рассказах и очерках аргентинского писателя Хорхе Луиса Борхеса.
Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:
- рассказ про Ийона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки»:
Нашёл следующие краткие сведения:
«СЕПУЛЬКИ — важный элемент цивилизации ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКАРИИ».
Я последовал этому совету и прочёл:
«СЕПУЛЬКАРИИ — устройства для сепуления (см.)».
Я поискал «Сепуление»; там значилось:
«СЕПУЛЕНИЕ — занятие ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКИ».Лем С. «Звёздные дневники Ийона Тихого. Путешествие четырнадцатое.»
 Рекурсивный герб России
Рекурсивный герб России- Рассказ из «Кибериады» о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).
- Рекурсивные акронимы: GNU (GNU Not Unix), PHP (PHP: Hypertext Preprocessor), WINE (Wine Is Not an Emulator) и т. д.
- Герб Российской Федерации является рекурсивно-определённым графическим объектом: в правой лапе изображённого на нём двуглавого орла зажат скипетр, который венчается уменьшенной копией герба. Так как на этом гербе в правой лапе орла также находится скипетр, получается бесконечная рекурсия.
- Рассказ Генри Каттнера «Порочный круг».
- Стихотворение детского поэта Андрея Усачева «Жучок»
- Стихотворение М. Ю. Лермонтова «Сон»
- Поисковая система Google при запросе «рекурсия» выводит надпись «Возможно, вы имели в виду: рекурсия»
См. также
Примечания
Ссылки
wikipedia.green
Обсуждение:Рекурсия — Википедия
Господа. Сейчас наблюдается некоторая война правок относительно необходимости рекурсии в статье про рекурсию. Я бы предложил несколько вариантов:
- оставить статью без рекурсивных ссылок
- рекурсия в цитате [1].
- рекурсия в см. также [2].
- рекурсия в первичном определении [3]
George Shuklin 13:55, 22 мая 2006 (UTC)
- Георгий, боюсь я Вам покажусь ужасно занудным, но, возможно Вам стоит просто подготовить статью о рекурсии для абсурдопедии (наверняка с Вашим тону=ким чувством юмора статья получится отличная), а отсюда дать ссылку на неё. Тогда и овцы будут сыты и волки целы. MaxiMaxiMax 14:05, 22 мая 2006 (UTC)
- Оставить без ссылок пока кто-нибудь не придумает, зачем они нужны. В указанном виде — ссыкли бессмысленны и ничего не иллюстрируют, только запутывают читателя. Может быть в википедии и можно отыскать понятия определённые рекурсивно, но это надо постараться. —Amoses @ 14:12, 22 мая 2006 (UTC)
- Думаю, что существуют статьи, рекурсивно ссылающиеся друг на друга в определении, но это нужно исправлять, а не культивировать. MaxiMaxiMax 14:16, 22 мая 2006 (UTC)
- Оставить без ссылок пока кто-нибудь не придумает, зачем они нужны. В указанном виде — ссыкли бессмысленны и ничего не иллюстрируют, только запутывают читателя. Может быть в википедии и можно отыскать понятия определённые рекурсивно, но это надо постараться. —Amoses @ 14:12, 22 мая 2006 (UTC)
- Рекурсивных ссылок не надо. Лучше поставить ссылку на Y-комбинатор. Lispnik 14:16, 22 мая 2006 (UTC)
По обсуждению в жожо решил взять часть статьи из английской вики. George Shuklin 14:22, 22 мая 2006 (UTC)
- Весь этот юмор относится к вырожденному случаю «дурной», «бесконечной» рекурсии. Надо это отметить, а то он действительно как-то дескридитирует идею индукции. —Amoses @ 14:38, 22 мая 2006 (UTC)
Я таки это сделал! В статье есть ссылка на саму статью, и к такому виду, думаю, возражений не будет. ^_^George Shuklin 14:42, 22 мая 2006 (UTC)
(на правах псевдовиртуала 🙂 В принципе, рекурсивная ссылка в статье о рекурсии вещь довольно остроумная, и, вероятно, нелишняя. Но эта рекурсия должна быть явно выражена. Т.е. я бы сделал
- либо единственную рекурсивную ссылку в разделе Cм. также: Рекурсия (NB: не «Рекурсивное определение рекурсии»)
- либо сделал ссылки на каждой интерации слова рекурсия — «чтоб дошло :)»
Все спрорные варианты — не выражены, поэтому я не вижу в них смысла — их мало кто заметит. Grain 14:49, 22 мая 2006 (UTC)
- «Рекурсия — см. Рекурсия» — это каноничный анекдот-определение. Оставить. Oal 23:25, 22 мая 2006 (UTC)
«Реку́рсия — метод определения класса объектов или методов предварительным заданием одного или нескольких (обычно простых) его базовых случаев или методов, а затем заданием на их основе правила построения определяемого класса, ссылающегося прямо или косвенно на эти базовые случаи.» — вот потому вас и называют тем нехорошим словом, которое ваш фильтор правок не пропускает, это же надо так «просто» и «понятно» обьяснить банальный круговорот и возвращение к началу… Не всякий петрик на такое способен… Black Baron95.165.108.178 03:48, 15 июля 2010 (UTC)
В чём будет заключаться показательность такого примера ? (Не вдаваясь в суть предмета) Что конкретно будет иллюстрировать такая ссылка ? Как сейчас, в разделе юмор — наверное, можно… —Kaganer 18:48, 22 мая 2006 (UTC)
«Рассказ о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей». Хмм… а это случайно не Шекли? —ajvol 20:15, 22 мая 2006 (UTC)
- Нет. Там серия про роботов просветлённых, мудрейших и т.д. Наткнусь, напишу точные названия. (Шекли не доводит до настоящего абсурда 🙂 George Shuklin 21:21, 22 мая 2006 (UTC)
Наглядный пример рекурсии :)[править код]
[4] 🙂 Edward Chernenko 17:06, 27 мая 2006 (UTC)
Предлагаю вставить код программы на русском, как в 1С, вычисляющей факториал заданного числа. Очень наглядно! Wormantson 11:23, 19 апреля 2007 (UTC)
- Только в виде ОЧЕНЬ короткого псевдо-кода/алгоритма. Например
- Чтобы найти факториал Числа Х
- Если Х=1 то факториал равен 1
- Если Х не равен 1 то найти факториал числа (Х-1) и умножить на Х.
- Так нагляднее, потому-что не все знают языки програмирования, а так понятнее, и все могут выполнить такой алгоритм даже без компьютера.—Hq3473 17:36, 19 апреля 2007 (UTC)
А факториал таки рекуррентная, а не рекурсивная функция. И совсем не яркий пример рекурсии. 78.29.11.13 16:23, 9 сентября 2010 (UTC)
Предлогаю или убрать код в ActionScript в викиучебник, или переписать псеводо-кодом. 90%(а то и больше) читателей все равно не поймут, а википедия не учебник по ActionScriptу.—Hq3473 03:15, 23 мая 2007 (UTC)
- Вперёд, переписывай. Ужé две недели прошло с твоего предложения, и никто не возразил. —Mithgol the Webmaster 06:57, 6 июня 2007 (UTC)
- Сделано.—Hq3473 02:19, 7 июня 2007 (UTC)
Рекурсия в программировании[править код]
«В программировании рекурсия — вызов функции или процедуры из неё же самой (обычно с другими значениями входных параметров), непосредственно или через другие функции (например, функция А вызывает функцию B, а функция B — функцию A).»
Предлагаю заменить на:
В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная рекурсия),например, функция А вызывает функцию B, а функция B — функцию A.
1) «обычно с другими значениями входных параметров» — не принципиально для определения, параметров может и не быть.
2) функция А может вызывать процедуру В, а та в свою очередь А и наоборот.
—tim2 09:24, 11 ноября 2007 (UTC)
- Уточнение «процедура» это ИМХО излишне, т.к. разделение искуственное и введено в преимущественно в паскале (зачем?). Вообще, если не рассматривать сторонние эффекты, в рамках концепции функций один и тот же набор параметров должен приводить к одному и тому же поведению (т.е. зацикливанию). Использование внешнего хранилища информации для управления рекурсией в общем случае эквивалентно просто расширению списка аргументов. #!George Shuklin 10:32, 11 ноября 2007 (UTC)
- Зачем в Паскале…: чтобы не возвращать результата, когда он не нужен…
- внешнее хранилище — все-таки не параметр (хотя можно обобщить и так, многим будет непонятно), кроме того, процедура может запрашивать функцию, которая, например, считывает следующее имя из FAT на HD, т.о. процедура будет рекурсивно «шарить» по дереву директорий, не зацикливаясь; или запрашивать таймер, или генератор случайных чисел…(Таймер и генератор тоже можно обобщить как «внешнее хранилище», но стоит ли? 😉 Для определения это не принципиально, как и то, какой вид подпрограммы (функция или процедура) вызывается. ИМХО, запись «функции (процедуры)» короче, чем «функции или процедуры», и не требует, при повторном появлении слова, снова писать «функции или процедуры». Иначе следовало бы записать:
- «В программировании рекурсия — вызов функции или процедуры из неё же самой (обычно с другими значениями входных параметров), непосредственно или через другие функции или процедуры (например, функция или процедура А вызывает функцию или процедуру B, а функция или процедура B — функцию или процедуру A).»
- Разговор всего лишь о форме (о словах) — по существу определения предлагаю лишь одно уточнение: добавить слова «простая рекурсия» и «сложная рекурсия» (см.выше).—tim2 11:29, 13 ноября 2007 (UTC)
- Прошло время, но возражений больше не последовало. Если все согласны, я исправляю через несколько дней определение на предложенное здесь.—tim2 14:25, 2 декабря 2007 (UTC)
- Сделано. —tim2 02:44, 27 декабря 2007 (UTC)
Мне кажется, что рекурсия — почти исключительно программистский термин (ну, и ещё лингвистика подходит, только имеет свой оттенок), а остальные примеры и области притянуты за уши. Например, Фибоначчи и факториал — это не рекурсия, а рекуррентные последовательности. Это уж от способа вычисления получается — итеративность или рекурсивность. Определение натурального числа — не рекурсия, а индукция. Про физику вообще молчу (зачем обратную связь втянули в эту статью — непонятно). Предлагаю исключить лишнее. infovarius 12:17, 22 марта 2008 (UTC) Полностью согласен, мусорка, а не статья. 78.29.11.13 09:35, 18 сентября 2010 (UTC)
Возможно, аноним пытается сказать, что в рамках ограниченного количества доступной оперативной памяти, о бесконечности в программировании речи идти не может. Может, как-то поправить на «потенциально бесконечное» или как-то так? —Illythr (Толк?) 14:42, 30 августа 2009 (UTC)
- Рекурсия — она бывает не только в программах для компьютеров с конечным объемом памяти. В математике и computer science есть понятие рекурсивного типа данных — где рекурсия используется для задания бесконечного множества объектов. Множества всех возможных двоичных деревьев, например. — X7q 14:53, 30 августа 2009 (UTC)
- Верно, но раздел называется «Рекурсия в программировании». 🙂 Может, просто приписать «теоретически»? —Illythr (Толк?) 14:58, 30 августа 2009 (UTC)
- Да, я тоже думаю с «теоретически» было бы правильнее. — X7q 07:14, 31 августа 2009 (UTC)
- «Бесконечную» рекурсию можно организовать и с конечным стеком, было бы желание. 91.207.100.2 07:41, 16 июня 2011 (UTC)
- Верно, но раздел называется «Рекурсия в программировании». 🙂 Может, просто приписать «теоретически»? —Illythr (Толк?) 14:58, 30 августа 2009 (UTC)
Уважаемые участники!
По неопытности я добавил в разделе «Рекурсия:Ссылки» ссылку на «Recursive Curve Maker» без регистрации и без предварительного обсуждения. Это программа построения рекурсивных кривых Гильберта, Серпинского и произвольных кривых с симметрией от 3 до 16-ого порядка. В пакете 90(180) наглядных примеров, с возможностью сохранять построенные кривые в формате BMP (ч.б. и цв.), создавать и отредактировать кривые. В программе такие кривые могут сгенерированы также со случайной закономерностью. Имеет медленный режим для наглядного показа вычерчивания рекурсивной кривой.
Мне кажется это хорошая демонстрация самого понятия рекурсии и рекурсивных объектов (кривых, фракталей). Что и предлагаю обсудить на предмет добавления ссылки в разделах «Рекурсия» и «Фракталь».
Эту программу я написал специально для внука как игру, с целью обучения. Написана она на Pascal-е в среде Delphi.Эта программа не коммерческая и свободно может распространяться.
С уважением —Vahram Mekhitarian 16:20, 10 декабря 2011 (UTC)
- Считаю, что в википедии не место для ссылок на exe’шники на бесплатных хостингах от непонятно кого. Там могут быть и вирусы, и трояны и все что угодно. И мир не только вокруг одной windows вертится. — X7q 16:29, 10 декабря 2011 (UTC)
- Даже если рядом есть исходник (не заметил его на вашем сайте, впрочем), все равно лучше не ссылаться — мало ли что с exe’шником после компиляции могли сделать. В том числе даже и без участия человека — некоторые вирусы могут сами к чужим .exeшникам прицепляться. — X7q 16:40, 10 декабря 2011 (UTC)
В математике — путаница[править код]
В первом абзаце —
Конечная рекурсивная функция. … Классический пример: рекурсивно-определённый факториал… Здесь каждое следующее рекурсивное обращение делается с аргументом, меньшим на единицу.
В конце раздела написано
Другим примером рекурсии в математике является числовая последовательность, заданная рекуррентной формулой,
Этот «другой» пример — повтор того, о чем говорится в первом абзаце. Mx1024 (обс.) 17:53, 23 октября 2017 (UTC)
ru.wikipedia.org
Что такое рекурсия в программировании – рекурсивный алгоритм
Тренировочные задачи на рекурсию
В этом листке собраны тренировочные задачи. Их решение необязательно, но рекомендуется тем, кто плохо освоил задачи на рекурсию. Также в этом листке есть несколько довольно сложных задач, которые могут быть интересны всем. Задачи из этого листка не учитываются при выставлении оценок.
Задачи можно сдавать на языках C++ и Python, поэтому если вы хотите попрактиковаться в другом языке, то тоже можете сдавать задачи.
В задачах этого листка нельзя использовать циклы и массивы. Также могут быть и другие ограничения в каких-то конкретных задачах (например, запрет использования строк в арифметических задачах, запрет использования срезов в решениях на питоне).
Задачи проверяются только автоматически и сразу же получают OK при прохождении всех тестов. Однако, если при последующей проверке кода будет выявлено нарушение вышеизложенных требований или будут другие замечания к решению, статус OK может быть изменен.
A: От 1 до n
Дано натуральное число \(n\). Выведите все числа от 1 до \(n\).
B: От A до B
Даны два целых числа A и В (каждое в отдельной строке). Выведите все числа от A до B включительно, в порядке возрастания, если , или в порядке убывания в противном случае.
C: Функция Аккермана
В теории вычислимости важную роль играет функция Аккермана \(A(m, n)\), определенная следующим образом: \[ A(m, n) = \begin{cases} n + 1 & m = 0\\ A(m — 1, 1)& m > 0, n = 0\\ A(m — 1, A(m, n — 1))& m > 0, n > 0\\ \end{cases} \]
Даны два целых неотрицательных числа \(m\) и \(n\), каждое в отдельной строке. Выведите \(A(m, n)\).
D: Точная степень двойки
Дано натуральное число N. Выведите слово , если число N является точной степенью двойки, или слово в противном случае.
Операцией возведения в степень пользоваться нельзя!
E: Сумма цифр числа
Дано натуральное число N. Вычислите сумму его цифр.
При решении этой задачи нельзя использовать строки, списки, массивы (ну и циклы, разумеется).
F: Цифры числа справа налево
Дано натуральное число N. Выведите все его цифры по одной, в обратном порядке, разделяя их пробелами или новыми строками.
При решении этой задачи нельзя использовать строки, списки, массивы (ну и циклы, разумеется). Разрешена только рекурсия и целочисленная арифметика.
G: Цифры числа слева направо
Дано натуральное число N. Выведите все его цифры по одной, в обычном порядке, разделяя их пробелами или новыми строками.
При решении этой задачи нельзя использовать строки, списки, массивы (ну и циклы, разумеется). Разрешена только рекурсия и целочисленная арифметика.
H: Проверка числа на простоту
Дано натуральное число \(n>1\). Проверьте, является ли оно простым. Программа должна вывести слово , если число простое и , если число составное. Алгоритм должен иметь сложность \(O(\sqrt{n})\).
Указание. Понятно, что задача сама по себе нерекурсивна, т.к. проверка числа \(n\) на простоту никак не сводится к проверке на простоту меньших чисел. Поэтому нужно сделать еще один параметр рекурсии: делитель числа, и именно по этому параметру и делать рекурсию.
I: Разложение на множители
Дано натуральное число \(n>1\). Выведите все простые делители этого числа в порядке неубывания с учетом кратности. Алгоритм должен иметь сложность \(O(\sqrt{n})\).
J: Палиндром
Дано слово, состоящее только из строчных латинских букв. Проверьте, является ли это слово палиндромом. Выведите или .
При решении этой задачи нельзя пользоваться циклами, в решениях на питоне нельзя использовать срезы с шагом, отличным от 1.
| Ввод | Вывод |
|---|---|
| radar | YES |
| yes | NO |
K: Вывести нечетные числа последовательности
Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Выведите все нечетные числа из этой последовательности, сохраняя их порядок.
В этой задаче нельзя использовать глобальные переменные и передавать какие-либо параметры в рекурсивную функцию. Функция получает данные, считывая их с клавиатуры. Функция не возвращает значение, а сразу же выводит результат на экран. Основная программа должна состоять только из вызова этой функции.
L: Вывести члены последовательности с нечетными номерами
Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Выведите первое, третье, пятое и т.д. из введенных чисел. Завершающий ноль выводить не надо.
В этой задаче нельзя использовать глобальные переменные и передавать какие-либо параметры в рекурсивную функцию. Функция получает данные, считывая их с клавиатуры. Функция не возвращает значение, а сразу же выводит результат на экран. Основная программа должна состоять только из вызова этой функции.
M: Максимум последовательности
Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите наибольшее значение числа в этой последовательности.
В этой задаче нельзя использовать глобальные переменные и передавать какие-либо параметры в рекурсивную функцию. Функция получает данные, считывая их с клавиатуры. Функция возвращает единственное значение: максимум считанной последовательности. Гарантируется, что последовательность содержит хотя бы одно число (кроме нуля).
N: Среднее значение последовательности
Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите среднее значение элементов этой последовательности (без учета последнего нуля).
В этой задаче нельзя использовать глобальные переменные. Функция получает данные, считывая их с клавиатуры, а не получая их в виде параметра. В программе на языке Python функция возвращает кортеж из пары чисел: число элементов в последовательности и их сумма. В программе на языке C++ результат записывается в две переменные, которые передаются в функцию по ссылке.
Гарантируется, что последовательность содержит хотя бы одно число (кроме нуля).
| Ввод | Вывод |
|---|---|
| 1 7 9 0 | 5.666666666666667 |
O: Второй максимум
Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите значение второго по величине элемента в этой последовательности, то есть элемента, который будет наибольшим, если из последовательности удалить наибольший элемент.
В этой задаче нельзя использовать глобальные переменные. Функция получает данные, считывая их с клавиатуры, а не получая их в виде параметра. В программе на языке Python функция возвращает результат в виде кортежа из нескольких чисел и функция вообще не получает никаких параметров. В программе на языке C++ результат записывается в переменные, которые передаются в функцию по ссылке. Других параметров, кроме как используемых для возврата значения, функция не получает.
Гарантируется, что последовательность содержит хотя бы два числа (кроме нуля).
| Ввод | Вывод |
|---|---|
| 1 7 9 0 | 7 |
| 1 2 2 1 0 | 2 |
P: Количество элементов, равных максимуму
Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите, какое количество элементов этой последовательности, равны ее наибольшему элементу.
В этой задаче нельзя использовать глобальные переменные. Функция получает данные, считывая их с клавиатуры, а не получая их в виде параметра.
В программе на языке Python функция возвращает результат в виде кортежа из нескольких чисел и функция вообще не получает никаких параметров. В программе на языке C++ результат записывается в переменные, которые передаются в функцию по ссылке. Других параметров, кроме как используемых для возврата значения, функция не получает.
Гарантируется, что последовательность содержит хотя бы одно число (кроме нуля).
| Ввод | Вывод |
|---|---|
| 1 7 9 0 | 1 |
| 1 3 3 1 0 | 2 |
Q: Количество единиц
Дана последовательность натуральных чисел (одно число в строке), завершающаяся двумя числами 0 подряд. Определите, сколько раз в этой последовательности встречается число 1. Числа, идущие после двух нулей, необходимо игнорировать.
В этой задаче нельзя использовать глобальные переменные и параметры, передаваемые в функцию. Функция получает данные, считывая их с клавиатуры, а не получая их в виде параметров.
R: Треугольная последовательность
Дана монотонная последовательность, в которой каждое натуральное число k встречается ровно k раз: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, …
По данному натуральному n выведите первые n членов этой последовательности. Попробуйте обойтись только одним циклом for.
| Ввод | Вывод |
|---|---|
| 2 | 1 2 |
| 5 | 1 2 2 3 3 |
S: Заданная сумма цифр
Даны натуральные числа \(k\) и \(s\). Определите, сколько существует \(k\)-значных натуральных чисел, сумма цифр которых равна \(d\). Запись натурального числа не может начинаться с цифры 0.
В этой задаче можно использовать цикл для перебора всех цифр, стоящих на какой-либо позиции.
T: Без двух нулей
Даны числа \(a\) и \(b\). Определите, сколько существует последовательностей из \(a\) нулей и \(b\) единиц, в которых никакие два нуля не стоят рядом.
U: Разворот числа
Дано число \(n\), десятичная запись которого не содержит нулей. Получите число, записанное теми же цифрами, но в противоположном порядке.
При решении этой задачи нельзя использовать циклы, строки, списки, массивы, разрешается только рекурсия и целочисленная арифметика.
Фунция должна возвращать целое число, являющееся результатом работы программы, выводить число по одной цифре нельзя.
steptosleep.ru
Рекурсия в программировании
 Рекурсии представляют собой довольно интересные события, однако в программировании они являются особенной важностью в отдельных случаях. У людей, которые впервые сталкиваются с ними, часто возникают проблемы с их пониманием.
Рекурсии представляют собой довольно интересные события, однако в программировании они являются особенной важностью в отдельных случаях. У людей, которые впервые сталкиваются с ними, часто возникают проблемы с их пониманием.
Как правило, это связано с обширной сферой потенциального использования самого термина в зависимости от контекста, в котором «рекурсия» применяется. Однако можно надеяться, что данная статья позволит избежать различных недоразумений или непониманий.
Что означает термин «рекурсия»?
Слово «рекурсия» обладает целым спектром значений, которые связаны с областью, где оно используется. Универсальным обозначением является то, что данный термин представляет собой определения, изображения, описания объектов либо процессов в самих объектах. Они наблюдаются тогда, когда объект выступает частью самого себя. В различных науках, таких как математика, программирование, физика и других по-своему определяется рекурсия. Практическое использование она находит в работе информационных систем, а также физических экспериментах.
Что означает рекурсия в программировании?
Рекурсивными ситуациями в программировании называют такие моменты, когда процедура или функция программы вызываются самостоятельно. В данном случае нет ничего странного. Необходимо отметить, что рекурсии не вызывает сложностей, и в отдельных случаях способны заменить циклы. При правильном задании компьютеру вызова процедуры или функции он просто начинает ее выполнять. Рекурсия способна быть конечной или бесконечной.
Чтобы первая перестала самостоятельно себя вызывать, в ней же должны быть условия прекращения. Ними могут выступать уменьшение значения переменной, в результате чего при достижении конкретного значения осуществляется остановка вызова и завершение программы/переход к последующему коду. Все зависит от необходимости достичь определенных целей. Бесконечная рекурсия предусматривает то, что она будет вызываться до тех пор, пока будет функционировать компьютер или программа.
Кроме того, существует организация сложной рекурсии, которая происходит при использовании двух функций. Например, есть А и Б. Функция А предусматривает в своем коде вызов Б, который, в свою очередь, говорит компьютеру о необходимости выполнения А. Сложные рекурсии являются выходом из целого ряда сложных логических ситуаций, которые возникают в компьютерной логике. Если пользователь хорошо знаком с программными циклами, он, наверняка, уже замечал схожесть между ними, а также рекурсией. Таким образом, они на самом деле способны осуществлять похожие или аналогичные задания.
При помощи рекурсии можно выполнять имитацию работы цикла. Это, как правило, полезно в том случае, когда сами циклы применять не очень удобно. Схема программной реализации не особо отличается у различных высокоуровневых языков программирования. Однако рекурсия в «Паскале», в С или другом языке программирования обладает своими особенностями. Ее можно с успехом реализовать и в низкоуровневых языках, к примеру, «Ассемблера», однако это несколько проблематично и требует больших затрат по времени.
Деревья рекурсии Что означает «дерево» в программировании? Оно представляет собой конечное множество, которое состоит как минимум из одного узла.
Должны соблюдаться следующие условия:
• присутствует начальный специальный узел, который является корнем всего дерева.
• остальных узлов насчитывается количество, отличное от нуля.
Они отличаются от попарно непересекающихся подмножеств и тоже являются деревом. Данные формы организации имеют названия поддеревьев главного дерева. Таким образом, деревья включают поддеревья, содержащие еще деревья, однако их меньше, чем предыдущее дерево. Такая ситуация продолжается до того момента, пока в одном узле не останется возможность продвинуться дальше. Это и будет означать окончание рекурсии. Существует еще один нюанс, который связан со схематическим изображением. Итак, обыкновенные деревья растут снизу вверх, однако в программировании они изображаются наоборот. Узлы, которые не имеют продолжения, являются конечными узлами. Чтобы обеспечить удобство обозначения, применяется генеалогическая терминология (предки, дети).
Зачем она используется в программировании?
Рекурсия нашла свое применение в программировании при решении множества сложных задач. Если требуется совершить лишь один вызов, наиболее оптимальным вариантом является использование интеграционного цикла, однако при двух и более повторах, во избежание построения цепочки и обеспечение их выполнения в виде дерева, применяются рекурсивные ситуации. Что касается широкого класса задач, такая организация вычислительного процесса считается самой удачной с точки зрения потребления ресурсов.
Таким образом, рекурсия в «Паскале» или другом высокоуровневом языке программирования является вызовом функции или процедуры до выполнения условий. Причем количество внешних вызовов не имеет значение. Таким образом, в программе может быть лишь одно обращение к подпрограмме, однако выполняться оно будет до конкретного момента, который определен заранее. Это так называемый аналог цикла с собственной спецификой использования.
Различие рекурсии в различных языках программирования
Конечно, рекурсия имеет общую схему реализации и определенное использование в каждом отдельном случае, однако в программировании она обладает собственными особенностями. Иногда это приводит к некоторым трудностям в процессе поиска требуемого материала. Так или иначе, всегда необходимо помнить: когда язык программирования вызывает функции или процедуры, это означает, что и вызов рекурсии вполне осуществим. Ее отличия, которые имеют первостепенное значение, проявляются во время использования низких и высоких языков программирования.
Как правило, это связано с возможностями программной реализации. Исполнение в результате зависит от того, какую задачу следует решить, в соответствии с ней и пишется рекурсия. Стоит отметить, что функции и процедуры применяются различные, однако их цель всегда одна. Она заключается в том, чтобы заставить вызвать самих себя.
Рекурсия – это просто. Возможно, для начинающих ее понять поначалу будет сложно. Именно поэтому требуются примеры рекурсии или один из них. Необходимо привести пример из бытовой жизни, который способен лучше всего понять саму суть данного механизма достижения целей в области программирования. Понадобится взять два или больше зеркал, установить их таким способом, чтобы в одном отражались все остальные. В таком случае можно увидеть, что зеркала отображают себя многократно, обеспечивая эффект бесконечности. Таким образом, рекурсия представляет собой отражения. Как видно из примера, представленного выше, их будет множество.
Из всего вышесказанного можно сделать вывод, что понять рекурсию просто, для этого необходимо лишь желание. При изучению материалов по программированию, можно понять, что рекурсия является легко выполнимой задачей.
bezwindowsa.ru
это что? Рекурсия в программировании (примеры)
Рекурсии являются интересными событиями сами по себе, но в программировании они представляют особенную важность в отдельных случаях. Впервые сталкиваясь с ними, довольно значительное количество людей имеют проблемы с их пониманием. Это связано с огромным полем потенциального применения самого термина в зависимости от контекста, в котором «рекурсия» используется. Но можно надеяться, что эта статья поможет избежать возможного недоразумения или непонимания.
Что такое «рекурсия» вообще?
 Слово «рекурсия» имеет целый спектр значений, которые зависят от области, в которой оно применяется. Универсальное обозначение является таким: рекурсии — это определения, изображения, описания объектов или процессов в самих объектах. Возможны они только в тех случаях, когда объект является частью самого себя. По-своему определяют рекурсию математика, физика, программирование и ряд других научных дисциплин. Практическое применение она нашла в работе информационных систем и физических экспериментах.
Слово «рекурсия» имеет целый спектр значений, которые зависят от области, в которой оно применяется. Универсальное обозначение является таким: рекурсии — это определения, изображения, описания объектов или процессов в самих объектах. Возможны они только в тех случаях, когда объект является частью самого себя. По-своему определяют рекурсию математика, физика, программирование и ряд других научных дисциплин. Практическое применение она нашла в работе информационных систем и физических экспериментах.Что подразумевают под рекурсией в программировании?
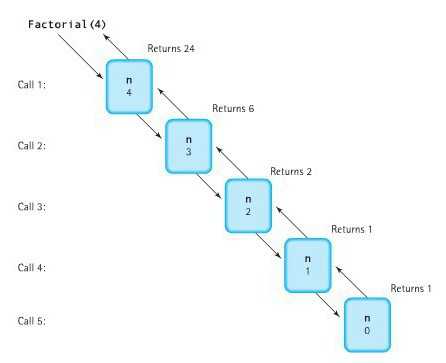 Рекурсивными ситуациями, или рекурсией в программировании, называют моменты, когда процедура или функция программы вызывает саму себя. Как бы странно для тех, кто начал изучать программирование, это ни звучало, здесь нет ничего странного. Следует запомнить, что рекурсии – это не сложно, и в отдельных случаях они заменяют циклы. Если компьютеру правильно задать вызов процедуры или функции, он просто начнёт её выполнять.
Рекурсивными ситуациями, или рекурсией в программировании, называют моменты, когда процедура или функция программы вызывает саму себя. Как бы странно для тех, кто начал изучать программирование, это ни звучало, здесь нет ничего странного. Следует запомнить, что рекурсии – это не сложно, и в отдельных случаях они заменяют циклы. Если компьютеру правильно задать вызов процедуры или функции, он просто начнёт её выполнять.Рекурсия может быть конечной или бесконечной. Для того чтобы первая прекратила сама себя вызывать, в ней же должны быть условия прекращения. Это может быть уменьшение значения переменной и при достижении определённого значения остановка вызова и завершение программы/переход к последующему коду, в зависимости от потребностей достичь определённых целей. Под бесконечной рекурсией подразумевают, что она будет вызываться, пока будет работать компьютер или программа, в которой она работает.
Возможна также организация сложной рекурсии с помощью двух функций. Допустим, есть А и Б. Функция А имеет в своем коде вызов Б, а Б, в свою очередь, указывает компьютеру на необходимость выполнить А. Сложные рекурсии – это выход из целого ряда сложных логических ситуаций для компьютерной логики.
Если читающий эти строки изучал программные циклы, то он, наверное, уже заметил схожесть между ними и рекурсией. В целом они действительно могут выполнять похожие или идентичные задания. С помощью рекурсии удобно делать имитацию работы цикла. Особенно это полезно там, где сами циклы использовать не очень удобно. Схема программной реализации не сильно различается у разных высокоуровневых языков программирования. Но всё же рекурсия в «Паскале» и рекурсия в С или другом языке имеет свои особенности. Может она быть успешно реализована и в низкоуровневых языках вроде «Ассемблера», но это является более проблематичным и затратным по времени.
Деревья рекурсии
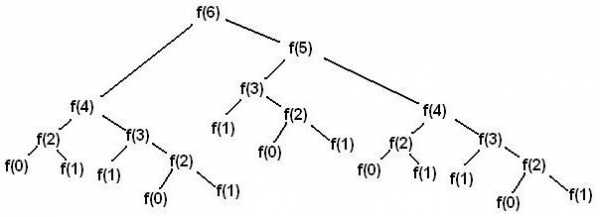 Что такое «дерево» в программировании? Это конечное множество, состоящее как минимум из одного узла, который:
Что такое «дерево» в программировании? Это конечное множество, состоящее как минимум из одного узла, который:- Имеет начальный специальный узел, который называют корнем всего дерева.
- Остальные узлы находятся в количестве, отличном от нуля, попарно непересекающихся подмножеств, при этом они тоже являются деревом. Все такие формы организации называют поддеревьями главного дерева.
Другими словами: деревья содержат поддеревья, которые содержат ещё деревья, но в меньшем количестве, чем предыдущее дерево. Так продолжается до тех пор, пока в одном из узлов не останется возможности продвигаться далее, и это будет обозначать конец рекурсии. Есть ещё один нюанс насчет схематического изображения: обычные деревья растут снизу вверх, а в программировании они рисуются наоборот. Узлы, не имеющие продолжения, называются конечными узлами. Для удобства обозначения и для удобства используется генеалогическая терминология (предки, дети).
Зачем она применяется в программировании?
 Своё применение рекурсия в программировании нашла в решении целого ряда сложных задач. Если необходимо сделать только один вызов, то более легким является применение интеграционного цикла, но при двух и более повторах, чтобы избежать построения цепочки и сделать их выполнение в виде дерева, и применяются рекурсивные ситуации. Для широкого класса задач организация вычислительного процесса таким способом является наиболее оптимальной с точки зрения потребления ресурсов. Так, рекурсия в «Паскале» или другом любом высокоуровневом языке программирования представляет собой вызов функции или процедуры до выполнения условий, независимо от количества внешних вызовов. Другими словами, в программе может быть только одно обращение к подпрограмме, но происходить оно будет до определённого заранее момента. В некотором роде это аналог цикла со своей спецификой использования.
Своё применение рекурсия в программировании нашла в решении целого ряда сложных задач. Если необходимо сделать только один вызов, то более легким является применение интеграционного цикла, но при двух и более повторах, чтобы избежать построения цепочки и сделать их выполнение в виде дерева, и применяются рекурсивные ситуации. Для широкого класса задач организация вычислительного процесса таким способом является наиболее оптимальной с точки зрения потребления ресурсов. Так, рекурсия в «Паскале» или другом любом высокоуровневом языке программирования представляет собой вызов функции или процедуры до выполнения условий, независимо от количества внешних вызовов. Другими словами, в программе может быть только одно обращение к подпрограмме, но происходить оно будет до определённого заранее момента. В некотором роде это аналог цикла со своей спецификой использования.Отличия рекурсии в различных языках программирования
Несмотря на общую схему реализации и конкретное применение в каждом отдельном случае, рекурсия в программировании имеет свои особенности. Это может привести к сложности во время поиска необходимого материала. Но всегда следует помнить: если язык программирования вызывает функции или процедуры, значит, и вызов рекурсии — дело осуществимое. Но наиболее значимые её отличия проявляются при использовании низких и высоких языков программирования. Особенно это касается возможностей программной реализации. Исполнение в конечном итоге зависит от того, какая задача поставлена, в соответствии с ней и пишется рекурсия. Функции и процедуры используются разные, но их цель всегда одна – заставить вызвать самих себя.
Рекурсия – это легко. Как просто запомнить содержание статьи?
 Для начинающих понять её, может быть, поначалу сложно, поэтому нужны примеры рекурсии или хотя бы один. Поэтому следует привести небольшой пример из бытовой жизни, который поможет понять саму суть этого механизма достижения целей в программировании. Возьмите два или больше зеркал, поставьте их так, чтобы в одном отображались все остальные. Можно увидеть, что зеркала отображают себя многократно, создавая эффект бесконечности. Вот рекурсии — это, образно говоря, отражения (их будет множество). Как видите, понять несложно, было бы желание. А изучая материалы по программированию, далее можно понять, что рекурсия – это ещё и очень легко выполнимая задача.
Для начинающих понять её, может быть, поначалу сложно, поэтому нужны примеры рекурсии или хотя бы один. Поэтому следует привести небольшой пример из бытовой жизни, который поможет понять саму суть этого механизма достижения целей в программировании. Возьмите два или больше зеркал, поставьте их так, чтобы в одном отображались все остальные. Можно увидеть, что зеркала отображают себя многократно, создавая эффект бесконечности. Вот рекурсии — это, образно говоря, отражения (их будет множество). Как видите, понять несложно, было бы желание. А изучая материалы по программированию, далее можно понять, что рекурсия – это ещё и очень легко выполнимая задача.fb.ru
О пользе рекурсии
О пользе рекурсииЭту заметку о пользе рекурсии я написал после прочтения соответствующей части книги С. Макконнелла «Совершенный код». Книга прекрасная, но, на мой взгляд, автор совершенно напрасно обещает уволить сотрудника, использующего рекурсию. Мне рекурсия помогала много раз, и я видел множество превосходных примеров её использования.
В заметке я буду рассматривать рекурсию на классическом примере — вычисление факториала. На более сложных зачах эффект от использования рекурсии (как положительный, так и отрицательный) может оказаться на много больше.
Компактность записи
Итак, давайте сравним записи функций, вычисляющих факториал с использованием рекурсии и без использования рекурсии. Оказывается, слухи о громоздкости рекурсии во многом преувеличены.
Небольшое замечание: для краткости, все мои реализации (и рекурсивные и не рекурсивные) будут достаточно просты. Например, я не буду проверять корректность входных данных (отрицательное число, вообще не число). Вопросов надёжности кода я коснусь чуть ниже.
# пример 1
# вычисление факториала на языке Python без рекурсии
def fac(n):
f = 1
i = 2
while i <= n:
f *= i
i += 1
return f
Многие могут сказать, что функция чрезмерно усложнена
добавлением переменной i. Чуть ниже, я поясню, зачем
я это сделал, а пока приведу классический вариант:
# пример 2
# Python; без рекурсии; классика
def fac(n):
f = 1
while n > 1:
f *= n
n -= 1
return f
У такого подхода есть один важный недостаток, к нему мы скоро вернёмся. А пока давайте посмотрим на рекурсивные реализации.
Сперва классическая реализация с рекурсией, всё на том же Python:
# пример 3
# Python; с рекурсией; классика
def fac(n):
if n == 0:
return 1
else:
return n * fac(n-1)
Обратите внимание, на сколько близко эта запись перекликается с математическим определение факториала.
Можно сэкономить одну строчку:
# пример 4 (экономичная запись примера 3)
# Python; с рекурсией; классика
def fac(n):
if n == 0:
return 1
return n * fac(n-1)
Ту же самую мысль можно записать ещё компактней
# пример 5 (одно-строчная запись примера 3)
def fac(n): return (1 if n == 0 else n * fac(n-1))
Этот пример работает только в Python 2.5 и старше.
Приведу два примера на Haskell:
-- пример 7
-- запись примера 3 на Haskell
fac n = if n == 0
then 1
else n * fac (n-1)
Приведу ещё один, более компактный, но вполне понятный для неподготовленного читателя:
-- пример 8
-- реализация рекурсивного вычисления факториала
-- на Haskell; дополнительно компактности удалось
-- достичь за счёт использования клозов (от clause)
fac 0 = 1
fac n = n * fac (n-1)
Можно приводить ещё множество реализаций вычисления факториала, но мне кажется, что приведённых примеров достаточно, чтобы развеять миф о том, что рекурсивные реализации громоздки.
На мой взгляд, дело обстоит противоположным образом: в тех случаях, где рекурсия оправдана, она позволяет значительно сократить объём кода и сделать его на много понятней.
Как же можно повысить понятность кода, используя рекурсию?
Неизменяемость переменных
При программировании бывает полезно придерживаться концепции неизменяемости переменных (многие языки программирования вообще не допускают изменения переменных). Это позволяет убить сразу много зайцев:
- во-первых, вы избавляетесь от сайд-эффектов (side effect) — побочных эффектов, связанных с тем, что одна и та же переменная принимает разные значения в разные моменты времени;
- во-вторых, вы можете легко проверять данные на корректность; это достаточно делать один раз и все проверки можно группировать, скажем, в начале функции; это повышает не только надёжность кода, но и его читабельность, а так же, позволяет ничего не забыть;
- в-третьих, вы существенно повышаете читабельность кода, так как читающему не надо просматривать весь код, чтобы отследить эволюцию переменной; ему достаточно найти то место, где переменной присвоено значение, а дальше он может быть уверен, что это значение не изменится.
Давайте рассмотрим эти аспекты подробней.
Избавление от сайд-эффектов (side effect)
Рассмотрим рекурсивную и не рекурсивную реализацию. Повторю их здесь.
Не рекурсивная (одна из, она мне нравится больше; почему — поясню ниже)
# пример 1
# вычисление факториала на языке Python без рекурсии
def fac(n):
f = 1
i = 2
while i <= n:
f *= i
i += 1
return f
Тут мы видим сразу две изменяемые переменные — f и i.
Причём i оказывает влияние на f в одном месте, а изменяет
своё значение — в другом. Это потенциальный источник
ошибок такого вида:
# пример 1 с ошибкой
def fac(n):
f = 1
i = 2
while i <= n:
i += 1 # Ошибка
f *= i # Порядок выполнения операций не верный
return f
Даже в таком тривиальном коде заметить ошибку не легко. С увеличением объёма кода, находить ошибки, связанные с побочными эффектам, становится очень сложно.
Самое неприятное в таких ошибках то, что компилятор или интерпретатор, в большинстве случаев, ничего не заподозрит; с его точки зрения, код абсолютно правильный. Чтобы найти такую ошибку, вам придётся кропотливо вычитывать весь код (или не менее кропотливо работать в отладчике, или читать километровые файлы детальных протоколов, одно другого не слаще), следя за всеми изменениями переменных, отслеживая множество вариантов развития событий, учитывая возможную много-поточность выполнения операций… Весь этот ад появляется только потому, что переменные в нашей программе изменяемые и одно действие наводит побочный эффект на другое действие.
Вариант с рекурсией полностью избавлен от этого недостатка (приведу его здесь снова):
# пример 3
# Python; с рекурсией; классика
def fac(n):
if n == 0:
return 1
else:
return n * fac(n-1)
В процессе выполнения функции fac ни одна переменная не изменяется.
Это обстоятельство может сильно упростить чтение и понимание кода.
Неизменяемость переменных даёт ещё одно ценное преимущество: у каждой переменной появляется вполне определённое назначение, которое не может быть изменено.
Лёгкость проверки корректности значений
Так как значения не изменяются, их можно легко проверять на корректность. Причём все проверки можно группировать, не опасаясь, что переменная изменится к моменту, когда над ней будут производиться какие-то действия.
Строго говоря, проверка становится вполне естественной веткой в существующем алгоритме. Вот модифицированный пример 3:
# пример 3 с проверкой значений на "не-отрицательность"
def fac(n):
if n == 0:
return 1
if n > 0:
return n * fac(n-1)
else:
return 'ERROR'
Чтобы реализовать аналогичную проверку в не рекурсивном варианте кода (примеры 1 и 2), пришлось бы добавить отдельный проверяющий механизм. И это не случайно, причины кроются в различном подходе к работе с данными. К этим различиям я ещё вернусь в секции «»Данные, управляемые программами» против «программ, управляемых данными»».
Однозначность назначения каждой переменной
Действительно, если переменные сохраняют свои значения, то и их назначение остаётся строго неизменным. В сочетании с удачными именами это обстоятельство может оказать неоценимую помощь при чтении и отладке кода.
Взгляните ещё раз на рекурсивный пример 3: переменная n сохраняет единственное назначение.
Чтобы идея была понятней, давайте введём ещё одну переменную (конечно же, она тоже будет неизменяемой):
# пример 3 с дополнительно переменной
def fac(n):
if n == 0:
f = 1
else:
f = n * fac(n-1)
return f
Теперь переменных две и их смысл одинаков везде, где они используются: n — аргумент, f — факториал n (и ни что иное).
Теперь пришло время объяснить, почему мне так не симпатичен пример 2 (приведу его здесь снова):
# пример 2
# Python; без рекурсии; классика
def fac(n):
f = 1 # первое использование f
while n > 1:
f *= n # второе использование f
n -= 1
return f # третье использование f
Здесь переменная f используется трижды, и все три раза
она имеет разный смысл:
- первый раз — начальное значение — фиксированная константа;
- второй раз она используется как аккумулятор для хранения промежуточных результатов;
- трети раз — это искомое значение — факториал n.
Этот код — прекрасный образец того, как можно максимально эффективно запутывать программу, используя одну и ту же переменную в разных качествах.
Конечно, в данном случае, прочитать программу не сложно,
но если она будет решать более сложную задачу,
содержать тысячи строк, а переменная f будет
не одна и будет не скаляром… Понять замысел программиста
станет очень сложно.
И снова, источник всех бед только то, что переменная f — изменяемая.
«Данные, управляемые программами» против «программ, управляемых данными»
Существует два подхода к обработке данных, имеющих фундаментальные различия.
Первый — «программа управляет данными». Это наиболее простой и общеизвестный способ взаимодействия с данными. Если данные просты, то он позволяет без труда обрабатывать их, но если данные сложны (например, это некие конструкции, допускающие многократные вложения: HTML, XML, PostScript или просто программа на некотором языке высокого уровня), то алгоритму приходится обрабатывать множество возможных вариантов. Одна из наибольших проблем — обработка ошибок. Чтобы точно диагностировать ошибку, приходится рассматривать множество вариантов во множестве мест кода. Группировка проверок может значительно помочь программисту, но такой подход таит потенциальную опасность того, что значение изменится где-то между проверкой его корректности и его использованием.
Создавая такой код, очень легко что-то упустить и создать «дырку» — такой код, который будет работать непредусмотренным образом, если получит непредусмотренные автором данные. То есть злоумышленник сможет скомбинировать такие входные данные, которые заставят код работать не так, как задумывал автор.
Второй подход — «данные управляют программой». Этот подход используется в функциональных языках программирования и наиболее чисто реализован (на мой взгляд) в XSLT.
При написании кода в этом стиле, вы не создаёте алгоритм, вы не описываете последовательность действий. Вы пишете набор «формул», которые потом будут применяться к входным данным для получения результата. В момент написания вы не знаете в каком порядке будут выполняться инструкции, которые вы кодируете; потому, что вы не знаете, какие данные будет обрабатывать ваша программа. Но благодаря тому, что все ваши переменные являются неизменяемыми, вы можете не волноваться о порядке выполнения команд.
Давайте я приведу чуть-модифицированный вариант третьего примера:
# пример 3 (чуть модифицированный)
def fac(n):
if n == 0: return 1
if n != 0: return n * fac(n-1)
Такая запись делает более очевидным тот факт, что функция fac не кодирует никакого алгоритма; она не определяет последовательность
действий. В ней записано два утверждения:
если n равно нулю, то результат -- 1
если n не равно нуля, то результат -- выражение
Эти строки можно выполнять в любом порядке. Для программиста не важно в каком порядке они будут отрабатываться. Он может отладить каждую ветку отдельно, а потом объединить их, не опасаясь сайд-эффектов. То, какая именно ветка будет работать, определятся входными данными. Поэтому подход и называется «данные управляют программой».
Подход, когда данные управляют программой даёт множество преимуществ, основными из которых являются: лёгкость понимания кода и простота написания обработчиков ложных данных, независимость одних частей кода от других. Но главное, такой подход не позволяет программисту создавать «дырки».
Рекурсия расточительна
«More computing sins are committed in the name of efficiency
(without necessarily achieving it) than for any other single
reason — including blind stupidity.»
— W. A. Wulf
«We should forget about small efficiencies, say about 97%
of the time: premature optimization is the root of all evil.»
— C. A. R. Hoare
Это правда. Очень существенным недостатком рекурсии, является её расточительность.
Но думая о производительности, всегда следует помнить, что обычно, процедуры, вызываемые часто и принимающие на себя большую нагрузку, составляют не большую часть программы. Остальные части могут быть спроектированы, жертвуя производительностью в пользу облегчения сопровождения и модификации и повышения надёжности кода.
Приведу один пример. Допустим вы разрабатываете программу-архиватор. Понятно, что процедура архивирования должна работать максимально быстро, чтобы не заставлять пользователя ждать. Но так же ясно, что пользователь не будет генерировать тысячи кликов мышкой или нажатий клавиш в секунду, разрешение экрана, скорее всего, не превысит миллион на миллион пикселей, а объём параметров командной строки не будет измеряться мегабайтами. То есть, для части кода, отвечающей за интерфейс, производительность не так существенна.
С другой стороны, алгоритм архивирования вряд ли изменится, и если он написан хорошо, то его доработка и развитие не понадобится. Этого нельзя сказать об интерфейсе, здесь совершенству нет предела. В таком случае, код, описывающий интерфейс, должен быть понятным, простым и легко наращиваться.
Любая программа (и комплексы программ тоже) имеет не так уж много мест, в которых оптимизация действительно нужна. В большинстве же случаев, оптимизация не даёт выигрыша в производительности, но затрудняет дальнейшее развитие программы.
Учитывая это обстоятельство, можно достаточно смело говорить о том, что использование рекурсии противопоказано лишь в немногих случаях. А в большинстве случаев использование рекурсии вполне допустимо, и при разумном применении, рекурсия может сослужить хорошую службу.
Кроме того, не надо забывать про хвостовую рекурсию. Нашу рекурсивную процедуру вычисления факториала можно записать так:
def fac(n, a=None):
if a is None:
a = 1
if n < 2:
return a
return fac(n - 1, a * n)
Мы мало что изменили. Фактически, мы просто поменяли порядок умножения. Но теперь мы получили вычисление факториала с хвостовой рекурсией.
Она характерна тем, что после рекурсивного вызова не выполняется никаких
действий (наш предыдущий вариант таким свойством не обладал). В этом
случае компилятор может превратить рекурсию в цикл. В gcc это сделает
уже -O2-оптимизация. То есть, мы получили рекурсию без дополнительных
накладных расходов.
Конечно, далеко не всегда удаётся переформулировать рекурсию в виде концевой.
Рекурсия позволяет создавать код с неизменяемыми переменными, что
- делает код более читабельным,
- защищает от ошибок типа «действия выполнены в не верном порядке», «использована не-инициализированная переменная» и других аналогичных,
- облегчает организацию контроля корректности входных данных,
- позволяет читать код с любого места, не просматривая его весь, отслеживая все изменения переменной,
- облегчает отладку.
В некоторых случаях, рекурсия позволяет более ясно сформулировать идею алгоритма; например, это относится к алгоритму быстрой сортировки — quicksort — который рекурсивен по своей природе.
Но, конечно, использовать рекурсию следует разумно. Нужно учитывать то, что часто (не всегда) она ведёт к большим расходам стека и некоторому снижению производительности.
Кроме того, прибегая к рекурсии, надо понимать, какую выгоду вы можете от неё получить, и стремиться максимизировать выгоду и минимизировать вклад отрицательных качеств рекурсии.
В любом случае, существует множество языков, в которых рекурсия — единственное средство, для выполнения многих действий. К таким языкам относятся не только «экзотические» функциональные языки, такие как Haskell, но и средства более широкого применения: XSLT-процессоры, макро-процессор m4 (основа системы autoconf и многих систем конфигурирования), и другие средства. Такое «тяготение» к рекурсии — не следствие ограниченности этих языков; напротив, эти языки специально оптимизированы для использования рекурсии; они активно эксплуатируют факт неизменяемости переменных и способны выполнить множество оптимизаций, избавляя программиста от многих забот.
Отправить
www.michurin.net
Рекурсия — WiKi
В математике рекурсия имеет отношение к методу определения функций и числовых рядов: рекурсивно заданная функция определяет своё значение через обращение к себе самой с другими аргументами. При этом возможно два варианта:
- Конечная рекурсивная функция. Она задаётся таким образом, чтобы для любого конечного аргумента за конечное число рекурсивных обращений привести к одному из отдельно определённых частных случаев, вычисляемых без рекурсии. Классический пример: рекурсивно-определённый факториал целого неотрицательного числа: n!={n⋅(n−1)!,n>01,n=0{\displaystyle n!={\begin{cases}n\cdot (n-1)!,&n>0\\1,&n=0\end{cases}}} . Здесь каждое следующее рекурсивное обращение делается с аргументом, меньшим на единицу. Поскольку n, по определению, целое неотрицательное число, через n рекурсивных обращений вычисление функции гарантированно придёт к частному случаю 0!=1{\displaystyle 0!=1} , на котором рекурсия прекратится. Таким образом, несмотря на рекурсивность определения, вычисление функции для любого аргумента из области определения окажется конечным.
- Бесконечная рекурсивная функция. Она задаётся в виде обращения к самой себе во всех случаях (по крайней мере, для некоторых из аргументов). Подобным образом могут задаваться бесконечные ряды, бесконечные непрерывные дроби и так далее. Практическое вычисление точного значения здесь, естественно, невозможно, поскольку потребует бесконечного времени. Требуемый результат находится аналитическими методами. Тем не менее, если речь идёт не о получении абсолютно точного значения, а о вычислении заданного приближения искомого значения, то тут в некоторых случаях возможно прямое использование рекурсивного определения: вычисления по нему ведутся до тех пор, пока необходимая точность не будет достигнута. Примером может служить разложение в непрерывную дробь числа e:
- e=2+22+33+44+…=2+f(2){\displaystyle e=2+{\cfrac {2}{2+{\cfrac {3}{3+{\cfrac {4}{4+\ldots }}}}}}\;=2+f(2)} , где f(n)=nn+f(n+1){\displaystyle f(n)={\cfrac {n}{n+f(n+1)}}}
- Прямой расчёт по приведённой формуле вызовет бесконечную рекурсию, но можно доказать, что значение f(n) при возрастании n стремится к единице (поэтому, несмотря на бесконечность ряда, значение числа Эйлера конечно). Для приближённого вычисления значения e достаточно искусственно ограничить глубину рекурсии некоторым наперёд заданным числом и по достижении его использовать вместо f(n){\displaystyle f(n)} единицу.
Другим примером рекурсии в математике является числовая последовательность, заданная рекуррентной формулой, когда каждый следующий член последовательности вычисляется как результат функции от n предыдущих членов. Таким образом с помощью конечного выражения (представляющего собой совокупность рекуррентной формулы и набора значений для первых n членов ряда) может даваться определение бесконечной последовательности.
С рекурсией тесно связана математическая индукция: она является естественным способом доказательства свойств функций на натуральных числах, рекурсивно заданных через свои меньшие значения.
В математике отдельно рассматривается класс так называемых «примитивно рекурсивных» функций. Определение примитивно рекурсивной функции также рекурсивно, оно задаёт набор примитивных функций и набор правил; функция является примитивно рекурсивной, если она может быть представлена как комбинация примитивно рекурсивных функций, образованная по этим правилам.
Примеры рекурсии в математике:
- A(m,n)={n+1,m=0;A(m−1,1),m>0,n=0;A(m−1,A(m,n−1)),m>0,n>0.{\displaystyle A(m,\;n)={\begin{cases}n+1,&m=0;\\A(m-1,\;1),&m>0,\;n=0;\\A(m-1,\;A(m,\;n-1)),&m>0,\;n>0.\end{cases}}}
Функции
В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная или косвенная рекурсия), например, функция A{\displaystyle A} вызывает функцию B{\displaystyle B} , а функция B{\displaystyle B} — функцию A{\displaystyle A} . Количество вложенных вызовов функции или процедуры называется глубиной рекурсии. Рекурсивная программа позволяет описать повторяющееся или даже потенциально бесконечное вычисление, причём без явных повторений частей программы и использования циклов.
Структурно рекурсивная функция на верхнем уровне всегда представляет собой команду ветвления (выбор одной из двух или более альтернатив в зависимости от условия (условий), которое в данном случае уместно назвать «условием прекращения рекурсии»), имеющую две или более альтернативные ветви, из которых хотя бы одна является рекурсивной и хотя бы одна — терминальной. Рекурсивная ветвь выполняется, когда условие прекращения рекурсии ложно, и содержит хотя бы один рекурсивный вызов — прямой или опосредованный вызов функцией самой себя. Терминальная ветвь выполняется, когда условие прекращения рекурсии истинно; она возвращает некоторое значение, не выполняя рекурсивного вызова. Правильно написанная рекурсивная функция должна гарантировать, что через конечное число рекурсивных вызовов будет достигнуто выполнение условия прекращения рекурсии, в результате чего цепочка последовательных рекурсивных вызовов прервётся и выполнится возврат.
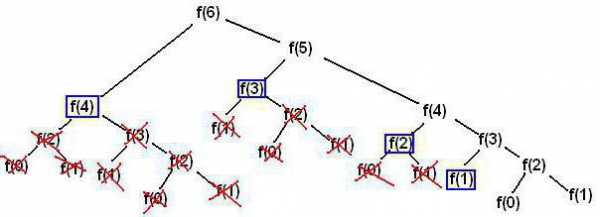
Помимо функций, выполняющих один рекурсивный вызов в каждой рекурсивной ветви, бывают случаи «параллельной рекурсии», когда на одной рекурсивной ветви делается два или более рекурсивных вызова. Параллельная рекурсия типична при обработке сложных структур данных, таких как деревья. Простейший пример параллельно-рекурсивной функции — вычисление ряда Фибоначчи, где для получения значения n-го члена необходимо вычислить (n-1)-й и (n-2)-й.
Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за счёт этого работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов.
Вопрос о желательности использования рекурсивных функций в программировании неоднозначен: с одной стороны, рекурсивная форма может быть структурно проще и нагляднее, в особенности, когда сам реализуемый алгоритм по сути рекурсивен. Кроме того, в некоторых декларативных или чисто функциональных языках (таких как Пролог или Haskell) просто нет синтаксических средств для организации циклов, и рекурсия в них — единственный доступный механизм организации повторяющихся вычислений. С другой стороны, обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии. Так, широко распространённый в учебной литературе пример рекурсивного вычисления факториала является, скорее, примером того, как не надо применять рекурсию, так как приводит к достаточно большой глубине рекурсии и имеет очевидную реализацию в виде обычного циклического алгоритма.
Имеется специальный тип рекурсии, называемый «хвостовой рекурсией» (структура рекурсивного алгоритма такова, что рекурсивный вызов является последней выполняемой операцией в функции, а его результат непосредственно возвращается в качестве результата функции). Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивается выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. Однако далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Scheme (диалект языка Lisp), описание которого содержит все необходимые сведения.
Теоретически, любую рекурсивную функцию можно заменить циклом и стеком. Однако такая модификация, как правило, бессмысленна, так как приводит лишь к замене автоматического сохранения контекста в стеке вызовов на ручное выполнение тех же операций с тем же или большим расходом памяти. Исключением может быть ситуация, когда рекурсивный алгоритм приходится моделировать на языке, в котором рекурсия запрещена.
Доказательство корректности программ
В отличие от явно-циклических программ, для доказательства корректности рекурсивных нет необходимости искусственно вводить инвариант. Аналитическое доказательство корректности рекурсивной функции сводится к методу математической индукции, то есть к доказательству следующих утверждений:
- Корректность рекурсивного обращения. Доказывается, что результат, вычисляемый в любой рекурсивной ветви функции, будет верным при условии, что параметры функции заданы корректно и соответствующие рекурсивные вызовы вернут верный результат.
- Корректность всех терминальных ветвей. Доказывается, что все терминальные ветви возвращают верные значения. Как правило, это доказательство тривиально, так как терминальные ветви обычно никаких вычислений не содержат.
- Достижимость терминальной ветви для любого корректного набора параметров после конечного числа рекурсивных вызовов. Доказывается, что изменение параметров вызова функции, которое производится при рекурсивном обращении, через конечное число рекурсивных вызовов приведёт к одному из наборов параметров, для которых существует терминальная ветвь.
Из суммы первого и второго утверждений следует, что в случае достижения терминальной ветви (а это значит — во всех случаях, когда вычисление функции окажется конечным) функция вернёт правильный результат. Третье положение доказывает, что конечным будет любое вычисление. Следовательно, любой вызов функции с корректными параметрами вернёт правильный результат (с очевидной «технической» оговоркой — если глубина рекурсии не окажется настолько большой, что вызовет переполнение памяти).
Данные
Рекурсивное определение данных возникает тогда, когда структура данных (запись, объект) содержит вложенный объект, структурно аналогичный самому себе или (что бывает чаще) ссылку на такой же объект. Преимущество рекурсивного определения объекта заключается в том, что такое конечное определение способно описать потенциально бесконечную структуру данных. Подобные структуры используются при описании списков и графов. Пример описания списка (C):
struct element_of_list
{
struct element_of_list *next; /* указатель на следующий элемент того же типа */
int data; /* некие данные */
};
Поскольку бесконечное число вложенных объектов невозможно разместить в конечной памяти, в реальности такие рекурсивно-определённые структуры всегда конечны. В заключительных (терминальных) ячейках обычно записываются пустые указатели, являющиеся одновременно флагами, указывающими программе, обрабатывающей структуру, что достигнут её конец.
Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных. В последние годы стала популярной концепция так называемых «ленивых вычислений», согласно которой данные, обрабатываемые программой, вычисляются лишь тогда, когда в них возникает необходимость. Реализация этой концепции привела к появлению в некоторых языках (Haskell, Python) возможности описывать потенциально-бесконечные, в том числе рекурсивные последовательности без явного ограничения на порождение объектов и свободно работать с ними.
ru-wiki.org
