Содержание

Построение сложных выражений—ArcMap | Документация

Доступно с лицензией Spatial Analyst.

  • Правила сложных выражений

Одним из наиболее ценных качеств Алгебры карт является возможность создания выражения, включающего несколько операторов и инструментов. Сочетание нескольких операторов и инструментов в одном выражении облегчает моделирование сложных взаимодействий и позволяет сократить общее время обработки. Сложные выражения не ограничены функциональностью инструментов модуля ArcGIS Spatial Analyst; они могут включать инструменты из любых других наборов инструментов. При построении сложных выражений необходимо соблюдать определенные правила взаимодействия.

Правила сложных выражений

  • В сложных выражениях только результат слева от знака равенства становится Растровым объектом.
  • Последовательность выполнения операторов в выражении определяется скобками и уровнем предшествования используемых операторов. , |) и/или операторов отношений (<, <=, >, >=, ==, !=), необходимо использовать скобки. Например, скобки должны быть в следующем выражении: (a>2) & (a<5).
     
    outRas = (Raster("a") > 2 ) & ( Raster("a") < 5)
    Более подробно:

    Для некоторых выражений требуются не скобки, а другая форма записи. Например, выражение a < b < c не будет выполнено, а добавление скобок изменит его смысл. Для успешного выполнения этого выражения его необходимо переписать в виде (a < b) & (b < c).

  • В сложных выражениях можно совместно использовать операторы, переменные. числа и инструменты.
    outRas = Sin("inras1") + Raster("inras2") + 8

    const = 10
outRas = Raster("inras1") + 2 * const
  • Все правила, относящиеся к использованию скобок в выражениях, созданных из операторов, равно действительны для выражений, созданных из инструментов и операторов. Инструмент или оператор в наиболее глубоко вложенных скобках будет обработан первым.
    num = 10
outRas = (ZonalStatistics((Raster("inras2") + Raster("inras3")),
                         "Value", "valueras", "MAXIMUM") - num ) / 8

    В приведенном выше выражении сумма inras2 и inras3 служит входными данными для инструмента Зональная статистика (Zonal Statistics). Значение num затем вычитается перед операцией деления.

  • В последовательности выражений результат одного выражения может быть входными данными в последующем выражении.
    outAdd = Raster("inras1") + Raster("inras2")
outRas = FocalStatistics(outAdd, NbrCircle(5, "Map"), "MEAN")

    В приведенном выше примере outAdd – это растровый объект, созданный путем сложения inras1 и inras2. Поскольку outAdd является переменной, его не нужно заключать в кавычки при использовании в качестве входных данных для последующего инструмента Фокальная статистика.

  • Любой инструмент можно встроить в другой, независимо от того, является ли результат растром или классом пространственных объектов Выходные данные встроенного инструмента используются в качестве входных для принимающего инструмента.
    outdistance = EucDistance(ContourList("elevation", "#", [1500]))
    В этом примере выходные данные инструмента Изолинии по значениям используются в качестве входных для инструмента Евклидово расстояние .
    dist = EucDistance(arcpy.Select_analysis("schools", "#", "Pop>2000"))
    В приведенном выше примере выходные данные инструмента Выборка из набора инструментов Анализ используются в качестве входных для инструмента Евклидово расстояние.
    Примечание:

    Поскольку встроенный инструмент создает выходные данные, которые являются лишь промежуточными в большом рабочем процессе, выходной аргумент может быть заменен хэш-символом «#», что позволит инструменту создать уникальный путь и имя для этих временных выходных данных. Использование хэш-символа обсуждается более подробно в секции Выходные данные инструмента раздела справки Использование инструментов в Python.

  • Чтобы использовать дополнительные выходные данные инструмента в выражении, необходимо указать имя набора данных или переменную, представляющую набор данных.
    costDist = CostDistance("source", "in_cost", 15000, "out_bklink") 
costOut = CostPath("dest", costDist, "out_bklink")
    В приведенном выше примере дополнительный выходной растр направления является выходными данными в рабочей области с именем «out_bklink».
    bklink = "C:/results/out_bklink"
costDist = CostDistance("source", "in_cost", 15000, bklink) 
costOut = CostPath("dest", costDist, bklink)
    В приведенном выше примере растр направления определяется переменной перед выполнением инструмента. Переменная указывает местоположение и имя выходного растра обратной ссылки.

Связанные разделы

Урок математики во 2-м классе «Сложные выражения без скобок с действиями разных степеней и порядок выполнения в них действий»

Цели:

  • Формировать у учащихся умение находить значения сложных выражений без скобок, содержащих действия разных ступеней.
  • Совершенствовать умение работать с задачей.
  • Развивать наблюдательность, умение сравнивать, анализировать.
  • Воспитывать у учащихся нравственно-этические качества: доброжелательность, волю, интерес, тактичность и т.д.

Ход урока

1. Организационный момент

Долгожданный дан звонок.

Начинается урок.

2. Актуализация опорных знаний

Учитель: Сегодня на уроке математики мы:

– проведем математическую разминку;
– получим новые знания;
– продолжим работу с задачами.

(Запись на доске.)

– Предлагаю начать урок с математической разминки.

28 276 25 22

– Ребята, что вы можете сказать о данных числах?

(- натуральные числа;
– 28, 25, 22 – двузначные числа, а 276 – трехзначное число;
– 276 – “лишнее” число;
– в записи каждого числа использована цифра “2”)

– Запишите, пожалуйста, двузначные числа в тетрадь.

– Что вы заметили? (Есть ли в числовом ряду какая-то закономерность?)

(- числа расположены в порядке уменьшения;
– каждое следующее число на 3 меньше, чем предыдущее).

– Можно ли продолжить записанный ряд, сохраняя закономерность? (Да.

28, 25, 22, 19, 16, 13, 10, 7, 4, 1)

– Назовите однозначные числа. (7, 4, 1) Используя эти числа, я составила следующее выражение: 1 + 7 • 4

– Что вы можете о нем сказать? Письменно найдите значение данного выражения.

3. Постановка учебной проблемы

Учащиеся записывают варианты решения примера в тетради, а затем выносят их на доску:

1 + 7 • 4 = 8 • 4 = 32
1 + 7 • 4 = 1 + 28 = 29

– Сравните полученные записи.

– Что вы заметили? (Оба выражения одинаковые, а имеют различные знания)

– Давайте разберемся, кто же прав?

– Почему возникло затруднение? (Вычисления делали по-разному)

– Сравните выражения: в 1-ом выражении – действия одной ступени, во 2-ом выражении – действия двух ступеней.

– Значит, какой вопрос возникает? Чего мы еще не знаем? Какую проблему необходимо решить на уроке?

(Мы не знаем, в каком порядке выполняют действия разных ступеней в выражении без скобок.)

– Сформулируйте тему урока. (Порядок выполнения действий разных ступеней в сложных выражениях без скобок.)

4. Открытие новых знаний

– Как же поступить с данным выражением? Поработайте в группах и попробуйте найти верное решение.

1) Заменить действие “•” на действие “+” и найти правильный ответ.
2) Сравнить полученные результаты с правильным ответом, выбрать правильное решение.

– Так в каком же порядке выполняют действия разных ступеней в выражениях без скобок? Сделайте вывод.

(Чтобы выполнить действия разных ступеней в выражениях без скобок, нужно сначала сделать действие “•”, а затем “+”.)

– Сравните свое правило с тем, что дано в учебнике на странице № 108.

– Чтобы лучше запомнить это правило, давайте построим схему:

« • » и « : » « + » и « – »

– О чем мы не договорили? (Сначала выполняются по порядку все действия…)

5. Первичное закрепление

– Давайте посмотрим, как вы поняли новое правило. Укажите порядок действий в записанных выражениях.

68 – 28 : 4 5 • 2 + 24 : 3
63 + 9 • 3 71 – 7 • 3

– Найдите значение этих выражений. (“Сильные” ребята выполняют самостоятельно, “слабые” – с комментированием у доски).

– Кому было легко справиться с заданием? У кого возникли затруднения? В чем?

– Так в каком же порядке выполняют действия разных ступеней в выражениях без скобок? (Повторение правила)

Физкульминутка

1, 2, 3, 4, 5!
Все умеем мы считать.
Отдыхать умеем тоже.
Руки за спину положим,
Голову поднимем выше
И легко – легко подышим.
Поднимаем руки класс – это раз.
Повернулась голова – это 2.
Руки вниз, вперед смотри – это 3.
Руки в стороны пошире развернули на 4.
Самого себя обнять – это 5.
Всем ребятам дружно сесть – это 6.

6. Самостоятельная работа с проверкой в классе

– А сейчас предлагаю вам выполнить небольшую самостоятельную работу:

I. Выберите выражение, в котором правильно указан порядок действий:

– Проверка.

– Почему выбрали именно третье выражение? (Потому что здесь по порядку выполняется действие “ • ”, а затем по порядку “ + ” и “ — ”.)

II. Самостоятельно расставьте порядок действий и найдите значения выражений:

45 : 9 + 2 • 4
9 • 2 – 5 • 3 + 27
(36 + 12) : 8 + 7

(Взаимопроверка в паре. )

– Вам удалось найти значения всех выражений? (Возникли трудности при решении третьего примера).

– Почему? (Не знакомы с порядком выполнения действий в выражениях со скобками).

– На следующем уроке математики мы познакомимся с порядком выполнения действий в выражениях со скобками, содержащих действия одной или разных ступеней.

III. Задание для тех, кто быстро справится с 1-м и 2-м заданием:

– Запишите из 1-ого задания выражения, в которых допущены ошибки, правильно расставьте порядок действий и найдите значения данных выражений.

– Проверка.

Итог

– Так в каком же порядке выполняют действия разных ступеней в выражениях без скобок?

7. Повторение ранее изученного материала

– Прочитайте текст:

Витрину магазина украшают 27 мягких игрушек, а механических в 3 раза меньше, чем мягких.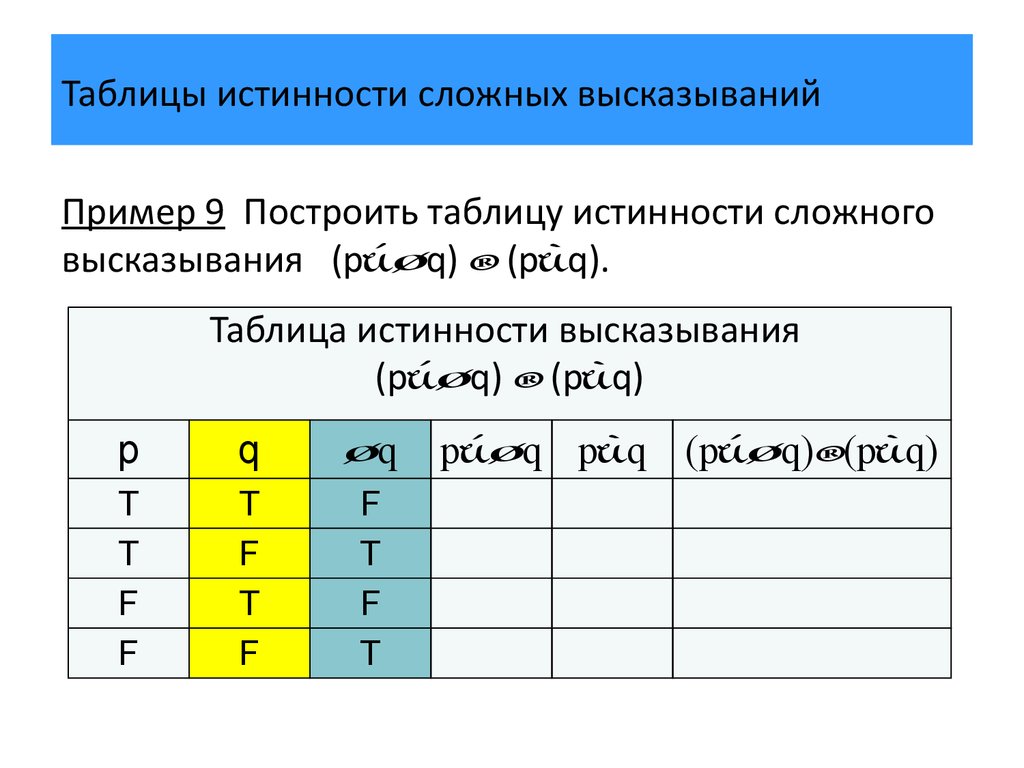

– Можно ли назвать этот текст задачей? Почему?

– Дополните текст так, чтобы получилась простая задача.

(Витрину магазина украшают 27 мягких игрушек, а механических в 3 раза меньше, чем мягких. Сколько механических игрушек украшают витрину магазина?)

– Решите задачу. (27 : 3 = 9 (иг.).)

– А теперь дополните этот текст так, чтобы получилась составная задача.

(Витрину магазина украшают 27 мягких игрушек, а механических в 3 раза меньше, чем мягких. Сколько всего игрушек украшают витрину магазина?)

– Решите эту задачу.

(27 : 3 + 27 = 36 (иг.))

– Пригодилось ли вам умение выполнять действия разных ступеней в выражениях без скобок? (Да.)

8. Итог урока. Рефлексия

– Наш урок подошел к концу.

– Какое же открытие вы сделали на уроке? (Научились выполнять действия разных ступеней в выражениях без скобок?)

– Только ли при решении выражений необходимы эти знания? ( Нет. Они нужны и при решении задач.)

– Что вам кажется самым главным на этом уроке?

– Кто испытал затруднения на уроке и в чем?

– В чем причина?

– Кто запомнил, какое открытие нас ждет на следующем уроке? (Познакомимся с порядком выполнения действий в выражениях со скобками, содержащих действия одной или разных ступеней.)

– Что больше всего понравилось в уроке?

– А мне понравилось, как вы сегодня работали на уроке. Спасибо!

Выражения

Выражение — это любое сочетание чисел, букв и знаков операций. Можно сказать, что вся математика состоит из выражений.

Выражения бывают двух видов: числовые и буквенные.

Числовые выражения состоят из чисел и знаков математических операций. Например, следующие выражения являются числовыми:

Буквенные выражения помимо чисел и знаков операций содержат ещё и буквы. Например, следующие выражения являются буквенными:

Буквы, которые содержатся в буквенных выражениях, называются переменными. Запомните это раз и навсегда! Спросите любого школьника что такое переменная — этот вопрос поставит его в ступор, несмотря на то что он будет решать сложные задачи по математике, не зная что это такое. А между тем, переменная это фундаментальное понятие, без понимания которого математику невозможно изучать.

Под словом «изучать» мы подразумеваем самостоятельное чтение соответствующей литературы  и способность понимать, что там написано. А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.

Поскольку понятие переменной очень важно, остановимся на нём подробнее. Посмотрите внимательно на слово «переменная». Ничего не напоминает? Слово «переменная» происходит от слов «меняться», «изменить», «изменить своё значение». Переменная в математике всегда выражена какой-то буквой. Например, запишем следующее выражение:

a + 5

Это буквенное выражение. Здесь одна переменная a.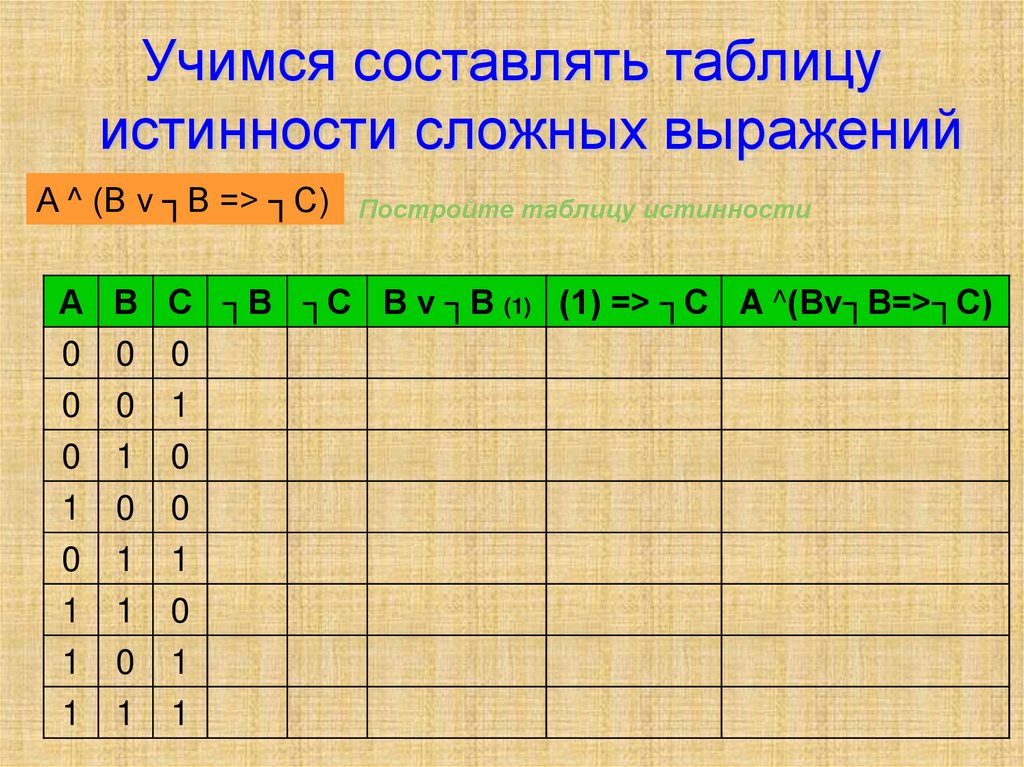 Поскольку она является переменной, значит может изменить свое значение в любой момент времени. Изменить значение может любой: вы, учитель, ваш товарищ, кто угодно. Например, давайте изменим значение этой переменной. Присвоим ей значение 5. Для этого запишем саму переменную, затем поставим знак равенства и запишем 5

a = 5 

Что случится в результате этого? Значение переменной a, то есть 5 отправится в главное выражение a + 5, и подставится вместо a.

Значение переменной a подставляется в исходное выражение.

В результате имеем: 5 + 5 = 10

Конечно, мы рассмотрели простейшее выражение. На практике встречаются более сложные выражения, в которых присутствуют дроби, степени, корни и скобки. Выглядит это устрашающе. На самом деле ничего страшного. Главное понять сам принцип.

В учебниках часто встречаются задания следующего содержания: найдите значение выражения x + 10, при x = 5. Такие задания как раз и требуют, чтобы вместо переменной подставили её значение. Давайте выполним это задание. Значение переменной x равно 5. Подставляем эту пятёрку в исходное выражение x + 10 и получаем 5 + 10 = 15.

Значение переменной x подставляется в выражение x + 10

Переменная это своего рода контейнер, где хранится значение. Переменные удобны тем, что они позволяют, не приводя примеров доказывать теоремы, записывать различные формулы и законы.

Вспомните второй урок «Основные операции». Чтобы понять сложение мы привели пример 5 + 2 = 7 и сказали, что числа 5 и 2 являются слагаемыми, а число 7 — суммой. Но мы могли бы понять эту тему и без примера, если бы воспользовались буквенным выражением. Обозначили бы слагаемые любыми буквами, например a и b, а сумму обозначили бы как с. Тогда у нас получилось бы выражение с тремя переменными a + b = c, и мы бы сказали, что a и b — это слагаемые, c — сумма.

Имея выражение a + b = c, можно пользоваться им, подставляя вместо переменных a и b любые числа. А переменная c будет получать своё значение автоматически, в зависимости от того, какие числа будут подставлены вместо a и b

В качестве практики можете выполнить следующее задание. Дано выражение a + b = c. Найдите его значение, если a = 10, b = 6. Переменная c получит своё значение автоматически. Ответ запишите следующим образом: при a = 10 и b = 6, переменная c равна такому-то числу.

Решение:

a + b = c

10 + 6 = 16

Ответ: при a = 10 и b = 6, переменная c равна 16.

Значение выражения

Фраза «выполнить действие» означает выполнить одну из операций действия.

В учебниках младших классов часто можно встретить задания следующего содержания: выполнить действия, и далее перечисляются примеры, которые нужно решить. Когда перед вами подобное задание, вы сразу должны понимать, что от вас требуют решить пример. В народе это звучит как «решить пример«, но если быть более  грамотным, то надо говорить «найти значение выражения». Решить пример и найти значение выражения это фактически одно и то же.

Например, дано выражение 10 + 6, и от нас требуют найти значение этого выражения. Это означает, что нам нужно решить данный пример. Поставить знак равенства = и записать ответ:

10 + 6 = 16

Сумма 16, которая получилась в результате и называется значением выражения 10 + 6.

Значение выражения — это результат выполнения действий, содержащихся в выражении.

Рассмотрим еще примеры:

  • 16 это значение выражения 4 × 4, поскольку 4 × 4 = 16
  • 20 это значение выражения 10 + 10, поскольку 10 + 10 = 20
  • 5 это значение выражения 10 ÷ 2, поскольку 10 ÷ 2 = 5

Задания для самостоятельного решения

Задание 1. Найдите значение выражения 5 + x при x = 4

Показать решение

Задание 2. Найдите значение выражения a + 3 при a = 7

Показать решение

Задание 3. Найдите значение выражения a + a + a при a = 10

Показать решение

Задание 4. Найдите значение выражения a + b при a = 10 и b = 20

Показать решение

Задание 5. Найдите значение выражения b + b + b при b = 5

Показать решение

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано

7.3 Упрощение сложных рациональных выражений — Алгебра среднего уровня 2e

Цели обучения

К концу этого раздела вы сможете:

  • Упростите сложное рациональное выражение, записав его в виде деления
  • Упростите сложное рациональное выражение с помощью ЖК-дисплея

Приготовься 7.

7

Прежде чем начать, пройдите этот тест на готовность.

Упрощение: 35910.35910.
Если вы пропустили эту проблему, просмотрите пример 1.27.

Приготовься 7,8

Упрощение: 1−1342+4·5,1−1342+4·5.
Если вы пропустили эту проблему, просмотрите пример 1.31.

Приготовься 7,9

Решите: 12x+14=18,12x+14=18.
Если вы пропустили эту проблему, просмотрите пример 2.9.

Упростите сложное рациональное выражение, записав его в виде деления

Сложные дроби — это дроби, в которых числитель или знаменатель содержит дробь. Ранее мы упрощали сложные дроби, подобные этим:

3458x2xy63458x2xy6

В этом разделе мы упростим сложные рациональные выражения, которые являются рациональными выражениями с рациональными выражениями в числителе или знаменателе.

Комплексное рациональное выражение

Комплексное рациональное выражение — это рациональное выражение, в котором числитель и/или знаменатель содержат рациональное выражение.

Вот несколько сложных рациональных выражений:

4y-38y2-91x+1yxy-yx2x+64x-6-4×2-364y-38y2-91x+1yxy-yx2x+64x-6-4×2-36

Помните, мы всегда исключаем значения, при которых любой знаменатель равен нулю.

Мы будем использовать два метода для упрощения сложных рациональных выражений.

Ранее в этой главе мы уже видели это сложное рациональное выражение.

6×2-7x+24x-82×2-8x+3×2-5x+66×2-7x+24x-82×2-8x+3×2-5x+6

Мы заметили, что дроби говорят нам делить, поэтому переписали это как задачу деления:

(6×2−7x+24x−8)÷(2×2−8x+3×2−5x+6).(6×2−7x+24x−8)÷(2×2−8x+3×2−5x+6).

Затем мы умножили первое рациональное выражение на обратное второму, точно так же, как мы делаем это при делении двух дробей.

Это один из способов упростить сложные рациональные выражения. Мы следим за тем, чтобы комплексное рациональное выражение имело форму, в которой одна дробь находится над другой дробью. Затем мы пишем это так, как если бы мы делили две дроби.

Пример 7,24

Упростите сложное рациональное выражение, записав его в виде деления: 6x−43×2−16,6x−43×2−16.

Решение

6x-43×2-166x-43×2-16
Перепишите сложную дробь в виде деления. 6x−4÷3×2−166x−4÷3×2−16
Перепишите как произведение первого умножения на
, обратное второму.		 6x-4·x2-1636x-4·x2-163
Фактор. 3·2x−4·(x−4)(x+4)33·2x−4·(x−4)(x+4)3
Умножить. 3·2(x−4)(x+4)3(x−4)3·2(x−4)(x+4)3(x−4)
Удалить общие множители. 3·2(x−4)(x+4)3(x−4)3·2(x−4)(x+4)3(x−4)
Упрощение. 2(х+4)2(х+4)

Существуют ли значения x , которые нельзя допускать? Исходное комплексное рациональное выражение имело знаменатели x−4x−4 и x2−16.x2−16. Это выражение было бы неопределенным, если x=4x=4 или x=-4.x=-4.

Попытайся 7,47

Упростите сложное рациональное выражение, записав его в виде деления: 2×2−13x+1,2×2−13x+1.

Попытайся 7,48

Упростите сложное рациональное выражение, записав его в виде деления: 1×2−7x+122x−4,1×2−7x+122x−4.

Полосы дробей действуют как символы группировки. Итак, чтобы следовать порядку действий, мы максимально упрощаем числитель и знаменатель, прежде чем мы сможем выполнить деление.

Пример 7,25

Упростите сложное рациональное выражение, записав его в виде деления: 13+1612−13,13+1612−13.

Решение
Упростите числитель и знаменатель.
Найдите ЖК-дисплей и сложите дроби в числителе.
Найдите ЖК-дисплей и вычтите дроби в знаменателе
.
Упростите числитель и знаменатель.
Перепишите сложное рациональное выражение в виде задачи на деление
.
Умножьте первое на обратное значение второго.
Упрощение. 3

Попытайся 7,49

Упростите сложное рациональное выражение, записав его в виде деления: 12+2356+112,12+2356+112.

Попытайся 7,50

Упростите сложное рациональное выражение, записав его в виде деления: 34−1318+56,34−1318+56.

Мы следуем той же процедуре, когда комплексное рациональное выражение содержит переменные.

Пример 7,26

Как упростить сложное рациональное выражение с помощью деления

Упростите сложное рациональное выражение, записав его в виде деления: 1x+1yxy-yx.1x+1yxy-yx.

Решение

Попытайся 7,51

Упростите сложное рациональное выражение, записав его в виде деления: 1x+1y1x−1y. 1x+1y1x−1y.

Попытайся 7,52

Упростите сложное рациональное выражение, записав его в виде деления: 1a+1b1a2−1b21a+1b1a2−1b2.

Здесь мы суммируем шаги.

Как

Упростите сложное рациональное выражение, записав его в виде деления.
  1. Шаг 1. Упростите числитель и знаменатель.
  2. Шаг 2. Перепишите сложное рациональное выражение в виде задачи на деление.
  3. Шаг 3. Разделите выражения.

Пример 7,27

Упростите сложное рациональное выражение, записав его в виде деления: n−4nn+51n+5+1n−5.n−4nn+51n+5+1n−5.

Решение
Упростите числитель и знаменатель.
Найдите общий знаменатель числителя и
знаменателя.
Упростите числители.
Вычесть рациональные выражения в числителе и
добавить в знаменателе.
Упрощение. (Теперь у нас есть одно рациональное выражение на
одно рациональное выражение.)
Переписать как деление дроби.
Умножьте первый раз на обратную величину второго.
Фактор любых выражений, если это возможно.
Удалить общие множители.
Упрощение.

Попытайся 7,53

Упростите сложное рациональное выражение, записав его в виде деления: b−3bb+52b+5+1b−5.b−3bb+52b+5+1b−5.

Попытайся 7,54

Упростите сложное рациональное выражение, записав его в виде деления: 1−3c+41c+4+c3.1−3c+41c+4+c3.

Упростите сложное рациональное выражение с помощью ЖК-дисплея

Мы «очищали» дроби, умножая их на ЖКИ, когда решали уравнения с дробями. Мы можем использовать эту стратегию здесь, чтобы упростить сложные рациональные выражения. Умножим числитель и знаменатель на ЖК всех рациональных выражений.

Давайте посмотрим на сложное рациональное выражение, которое мы упростили одним способом в примере 7. 25. Здесь мы упростим это, умножив числитель и знаменатель на LCD. Когда мы умножаем на LCDLCDLCDLCD, мы умножаем на 1, поэтому значение остается прежним.

Пример 7,28

Упростите сложное рациональное выражение с помощью ЖКИ: 13+1612−13,13+1612−13.

Решение
LCD всех дробей в целом выражении равен 6.
Очистите дроби, умножив числитель и знаменатель
на этот ЖК-дисплей.
Распределить.
Упрощение.

Попытайся 7,55

Упростите сложное рациональное выражение с помощью ЖКИ: 12+15110+15.12+15110+15.

Попытайся 7,56

Упростите сложное рациональное выражение с помощью ЖК-дисплея: 14+3812−516,14+3812−516.

Мы будем использовать тот же пример, что и в примере 7.26. Решите, какой метод работает лучше для вас.

Пример 7,29

Как упростить сложное рациональное выражение с помощью ЖК-дисплея

Упростите сложное рациональное выражение с помощью ЖК-дисплея: 1x+1yxy-yx.1x+1yxy-yx.

Решение

Попытайся 7,57

Упростите сложное рациональное выражение с помощью ЖК-дисплея: 1a+1bab+ba. 1a+1bab+ba.

Попытайся 7,58

Упростите сложное рациональное выражение с помощью ЖК-дисплея: 1×2−1y21x+1y.1×2−1y21x+1y.

Как

Упростите сложное рациональное выражение с помощью ЖК-дисплея.
  1. Шаг 1. Найдите ЖК всех дробей в сложном рациональном выражении.
  2. Шаг 2. Умножьте числитель и знаменатель на LCD.
  3. Шаг 3. Упростите выражение.

Обязательно начните с факторизации всех знаменателей, чтобы найти ЖК-дисплей.

Пример 7.30

Упростите сложное рациональное выражение с помощью ЖК-дисплея: 2x+64x−6−4×2−36,2x+64x−6−4×2−36.

Решение
Найдите ЛК всех дробей в комплексном рациональном выражении
. ЖК-дисплей равен x2-36=(x+6)(x-6)x2-36=(x+6)(x-6).
Умножьте числитель и знаменатель на ЖК-дисплей.
Упростите выражение.
Распределить в знаменателе.
Упрощать.
Упрощение.
Чтобы упростить знаменатель, распределите
и объедините подобные члены.
Фактор знаменателя.
Удалить общие множители.
Упрощение.
Обратите внимание, что больше нет общих делителей
для числителя и знаменателя.

Попытайся 7,59

Упростите сложное рациональное выражение с помощью ЖК-дисплея: 3x+25x-2-3×2-4,3x+25x-2-3×2-4.

Попытайся 7,60

Упростите сложное рациональное выражение с помощью ЖКИ: 2x−7−1x+76x+7−1×2−49,2x−7−1x+76x+7−1×2−49.

Обязательно сначала разложите знаменатели. Действуйте осторожно, так как математика может запутаться!

Пример 7.31

Упростите сложное рациональное выражение с помощью ЖКИ: 4м2-7м+123м-3-2м-4,4м2-7м+123м-3-2м-4.

Решение
Найдите ЛП всех дробей в сложном рациональном выражении
.
ЖК-дисплей (м-3)(м-4).(м-3)(м-4).
Умножьте числитель и знаменатель
на ЖК-дисплей.
Упрощение.
Упрощение.
Распределить.
Объедините похожие термины.

Попытайся 7,61

Упростите сложное рациональное выражение с помощью ЖК-дисплея: 3×2+7x+104x+2+1x+5,3×2+7x+104x+2+1x+5.

Попытайся 7,62

Упростите сложное рациональное выражение с помощью ЖК-дисплея: 4yy+5+2y+63yy2+11y+30.4yy+5+2y+63yy2+11y+30.

Пример 7,32

Упростите сложное рациональное выражение с помощью ЖК-дисплея: yy+11+1y-1.yy+11+1y-1.

Решение
Найдите ЛКД всех дробей в сложном рациональном выражении.
ЖК-дисплей (y+1)(y−1).(y+1)(y−1).
Умножьте числитель и знаменатель на ЖК-дисплей.
Распределите в знаменателе и упростите.
Упрощение.
Упростите знаменатель и оставьте факторизованным числитель
.
Разложите знаменатель на множители и удалите множители
, общие с числителем.
Упрощение.

Попытайся 7,63

Упростите сложное рациональное выражение с помощью ЖК-дисплея: xx+31+1x+3.xx+31+1x+3.

Попытайся 7,64

Упростите сложное рациональное выражение с помощью ЖК-дисплея: 1+1x−13x+1.1+1x−13x+1.

СМИ

Получите доступ к этому онлайн-ресурсу, чтобы получить дополнительные инструкции и попрактиковаться в сложных дробях.

  • Сложные дроби

Раздел 7.3 Упражнения

Практика ведет к совершенству

Упростите сложное рациональное выражение, записав его в виде деления

В следующих упражнениях упростите каждое сложное рациональное выражение, записав его в виде деления.

151.

2аа+44а2а2-162аа+44а2а2-16

152.

3bb-5b2b2-253bb-5b2b2-25

153.

5c2+5c−1410c+75c2+5c−1410c+7

154.

8d2+9d+1812d+68d2+9d+1812d+6

155.

12+5623+7912+5623+79

156.

12+3435+71012+3435+710

157.

23−1934+5623−1934+56

158.

12−1623+3412−1623+34

159.

нм+1n1n-нмнм+1n1n-нм

160.

1p+pqqp-1q1p+pqqp-1q

161.

1r+1t1r2−1t21r+1t1r2−1t2

162.

2v+2w1v2−1w22v+2w1v2−1w2

163.

х-2хх+31х+3+1х-3х-2хх+31х+3+1х-3

164.

у-2уу-42у-4+2у+4у-2уу-42у-4+2у+4

165.

2-2а+31а+3+а22-2а+31а+3+а2

166.

4+4b-51b-5+b44+4b-51b-5+b4

Упрощение сложного рационального выражения с помощью ЖК-дисплея

В следующих упражнениях упростите каждое сложное рациональное выражение с помощью ЖК-дисплея.

167.

13+1814+11213+1814+112

168.

14+1916+11214+1916+112

169.

56+29718−1356+29718−13

170.

16+41535−1216+41535−12

171.

cd+1d1d-dccd+1d1d-dc

172.

1m+mnnm−1n1m+mnnm−1n

173.

1p+1q1p2−1q21p+1q1p2−1q2

174.

2r+2t1r2−1t22r+2t1r2−1t2

175.

2x+53x−5+1×2−252x+53x−5+1×2−25

176.

5y−43y+4+2y2−165y−43y+4+2y2−16

177.

5z2−64+3z+81z+8+2z−85z2−64+3z+81z+8+2z−8

178.

3с+6+5с-61с2-36+4с+63с+6+5с-61с2-36+4с+6

179.

4a2−2a−151a−5+2a+34a2−2a−151a−5+2a+3

180.

5b2−6b−273b−9+1b+35b2−6b−273b−9+1b+3

181.

5c+2−3c+75cc2+9c+145c+2−3c+75cc2+9c+14

182.

6d−4−2d+72dd2+3d−286d−4−2d+72dd2+3d−28

183.

2+1п-35п-32+1п-35п-3

184.

nn-23+5n-2nn-23+5n-2

185.

мм+54+1м-5мм+54+1м-5

186.

7+2q−21q+27+2q−21q+2

В следующих упражнениях упростите каждое сложное рациональное выражение, используя любой метод.

187.

34−2712+51434−2712+514

188.

vw+1v1v-vwvw+1v1v-vw

189.

2а+41а2-162а+41а2-16

190.

3b2−3b−405b+5−2b−83b2−3b−405b+5−2b−8

191.

3m+3n1m2−1n23m+3n1m2−1n2

192.

2r−91r+9+3r2−812r−91r+9+3r2−81

193.

х-3хх+23х+2+3х-2х-3хх+23х+2+3х-2

194.

уу+32+1у−3уу+32+1у−3

Письменные упражнения

195.

В этом разделе вы научились упрощать сложную дробь 3x+2xx2−43x+2xx2−4 двумя способами: переписать ее как задачу на деление или умножить числитель и знаменатель на LCD. Какой метод вы предпочитаете? Почему?

196.

Эфраим хочет начать упрощать сложную дробь 1a+1b1a-1b1a+1b1a-1b, сокращая переменные в числителе и знаменателе, 1a+1b1a-1b.1a+1b1a-1b. Объясните, что не так с планом Эфраима.

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.

ⓑ После просмотра контрольного списка, как вы думаете, хорошо ли вы подготовились к следующему разделу? Почему или почему нет?

Комплексные алгебраические выражения и… Пошаговое решение математических задач

6.5  Сложные алгебраические выражения

  Выражение, которое содержит различные комбинации сложения, вычитания, умножения и деления с рациональными выражениями, называется сложным алгебраическим выражением. . Примеры сложных алгебраических выражений:

  (1/x+1/y)/(x+y),(1/(x+2)-1/x)/(1+2/x) и (4-x)/(x+3 )+x/(x+3)÷(x)/(x-3)

  В таком выражении, как (1/x+1/y)/(x+y), крупная дробная черта является символом включение. Выражение можно записать следующим образом:

  (1/x+1/y)/(x+y)=(1/x+1/y)÷(x+y)

Аналогично, (1/(x +2)-1/x)/(1+2/x)=(1/(x+2)-1/x)÷(x+2/x)

  Упростите, работая с числителем и знаменателем отдельно, как если бы они были в скобках. Сделайте числитель одной дробью и знаменатель одной дробью. Затем разделите. 92)

   Второй метод заключается в том, чтобы найти НОК знаменателей дробей как в исходном числителе, так и в исходном знаменателе, а затем умножить и числитель, и знаменатель на этот НОК.

  (1/x+1/y)/(x+y)=(1/x+1/y)/((x+y)/1)  x у 1  МОК=xy

  =((1/x+1/y)xy))/(((x+y)/1)xy)=(1/x*xy+1/y*xy)/(( x+y)xy)

  ==1/(xy)

  (1/(x+2)-1/x)/((1+2)/x)=((1/(x+2) -1/х)*х(х+2))/((1+2/х)*х(х+2)  х х+2  НОК=х(х+2)

  =

92)

  Каждый из только что описанных методов действителен. Иногда один из них проще в использовании, чем другой, но выбор за вами.

  В таком выражении, как

  (4-x)/(x+3)+x/(x+3)÷x/(x-3)

  правила порядка операций указывают, что деление быть сделано в первую очередь.

  (4-x)/(x+3)+x/(x+3)÷x/(x-3)

  =(4-x)/(x+3)+x/(x+3) )*(x-3)/x

  =(4-x)/(x+3)+(x-3)/(x+3)

  =(4-x+x-3)/(x +3)

  =1/(x+3) 92))(x+y)(x-y)

  =

  =((x-y)-(x+y))/(2y)

  =(x-y-x-y)/(2y)

  )/=(-2y) (2 года)

  =-1

Давайте посмотрим, как наш математический решатель решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.

Решите аналогичную задачуВведите свою собственную задачу

6.6  Пропорции с приложениями

  Рассмотрите утверждение: «В этом университете на каждые три студентки приходится два студента мужского пола». Означает ли это, что есть только 5 студентов, 2 из которых мужчины и 3 женщины? Не очень вероятно. Предположим, что шансы на скачки на Old Blue составляют 10 к 1. Если Old Blue выиграет, и вы поставите 2 доллара, что вы выиграете?

  Это примеры соотношений. Отношение – это сравнение двух чисел, обычно записываемое как a:b или a/b. Соотношение студентов-мужчин и женщин можно записать как 2:3 или 2/3. Отношение выплаты в долларах к ставке в долларах на Old Blue будет 10:1 или 10/1.

  Нас интересуют пропорции. Пропорция – это уравнение, в котором два отношения равны. Примеры:

  3/4=6/8, 10/1=x/2, (3n)/(5n)=3/5 и (x+3)/2=(x-5)/4

Верна ли пропорция 6/10=9/15? Один из способов ответить на этот вопрос — сократить обе дроби.

  6/10==3/5 и 9/15==3/5

  Итак, 6/10=9/15 верно.

  Еще одна техника состоит в том, чтобы записать 6*15=10*9 или 6*15=90 и 10*9=90. Мы говорим, что произведение крайностей равно произведению средств. Следующий формат можно использовать для определения крайних и средних значений пропорции.

    

  a и d (первый и четвертый члены) называются крайними; b и c (2-й и 3-й члены) называются средними.

  Если a/b=c/d, то a*d=b*c

  Эту связь можно показать следующим образом.

    a/b=c/d

  a/b*(bd)/1=c/d*(bd)/1  Умножьте обе части на bd.

    Упрощение.

  a*d=b*c

  Если один или несколько терминов неизвестны, необходимо решить уравнение, чтобы найти значение неизвестного, представленного в терминах. Первый шаг должен состоять в том, чтобы найти произведение средних и крайних значений и приравнять их друг к другу.

Примеры

Решение следующих пропорций для неизвестного числа

1. 12/15 = 8/x

12x = 15*8

(12x)/12 = (15*8)/12

x == 10

или, уменьшая 12/15 с первого до 4/5:

12/15 = 8/x

4/5 = 8/x

4x = 5*8

(4x)/4 = 40/ 4

   x=10

  2. (x+3)/2=(x-5)/4

   4(x+3)=2(x-5)

 0  2×1+12

   4x+12-2x-12=2x-10-2x-12

2x = -22

(2x)/2 = -22/2

x = -11

Проверка:

(-11+3)/2 = (-11-5)/4

   -8/2=-16/4

   -4=-4

Давайте посмотрим, как наш решатель уравнений решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.

Решить подобную задачуВведите свою проблему

  Пропорции естественным образом возникают в повседневных проблемах. Например, если шины продаются по цене 2 за 75 долларов, но вам нужно 5 новых шин, сколько вы заплатите за 5 шин? Установка пропорции дает:

  

(2 шины)/(75 долларов)=(5 шин)/(x долларов) или (75 долларов)/(х долларов)=(2 шины)/(5 шин)
числители совпадают по типу, а знаменатели совпадают по типу числители соответствуют, а знаменатели соответствуют

Решение,

2/75 = 5/x

2x = 5*75

(2x)/2 = 375/2

x = 187,50 $0005

  Стоимость 5 шин составит 187,50 долларов США.

Пример

   1. На чертеже здания в масштабе архитектора 1/2 дюйма соответствует 12 футам. Что представляют собой 3 дюйма?

Решение:

(1/2 дюйма)/(12 футов) = (3 дюйма)/(x футов)

1/2x = 3*12

2*1/2x = = 3*12

2*1/2x = 3* 36*2

   x=72

  Три дюйма равны 72 футам.

Калькулятор упрощения сложных выражений

Дом
Многочлены
Нахождение наибольшего общего делителя
Факторинг трехчленов
Функция абсолютного значения
Краткий обзор полиномов факторинга
Решение уравнений с одним радикальным членом
Добавление дробей
Вычитание дробей
Метод ФОЛЬГИ
График сложных неравенств
Решение абсолютных неравенств
Сложение и вычитание многочленов
Использование наклона
Решение квадратных уравнений
Факторинг
Свойства умножения показателей степени
Завершение квадрата
Решение систем уравнений методом подстановки
Объединение подобных радикальных терминов
Исключение с помощью умножения
Решение уравнений
Теорема Пифагора 1
Нахождение наименьших общих кратных
Умножение и деление в экспоненциальном представлении
Сложение и вычитание дробей
Решение квадратных уравнений
Сложение и вычитание дробей
Умножение на 111
Добавление дробей
Умножение и деление рациональных чисел
Умножение на 50
Решение линейных неравенств с одной переменной
Упрощение кубических корней, содержащих целые числа
График сложных неравенств
Простые трехчлены как произведения двучленов
Написание линейных уравнений в форме пересечения наклона
Решение линейных уравнений
Линии и уравнения
Пересечения параболы
Функция абсолютного значения
Решение уравнений
Решение сложных линейных неравенств
Комплексные номера
Разложение на множители разности двух квадратов
Умножение и деление рациональных выражений
Сложение и вычитание радикалов
Умножение и деление чисел со знаком
Решение систем уравнений
Факторизация противоположности GCF
Умножение специальных многочленов
Свойства показателей
Научное обозначение
Умножение рациональных выражений
Сложение и вычитание рациональных выражений с отличающимися знаменателями
Умножение на 25
Десятичные дроби
Решение квадратных уравнений путем заполнения квадрата
Частное правило для показателей степени
Упрощение квадратных корней
Умножение и деление рациональных выражений
Независимые, противоречивые и зависимые системы уравнений
склонов
Графические линии на координатной плоскости
Графические функции
Силы десяти
Свойство нулевой мощности экспонентов
Вершина параболы
Рационализация знаменателя
Тест факторизуемости для квадратных трехчленов
Трехчленные квадраты
Решение двухшаговых уравнений
Решение линейных уравнений, содержащих дроби
Умножение на 125
Свойства экспоненты
Умножение дробей
Сложение и вычитание рациональных выражений с одинаковым знаменателем
Квадратные выражения — заполнение квадратов
Сложение и вычитание смешанных чисел с разными знаменателями
Решение формулы для заданной переменной
Факторинг трехчленов
Умножение и деление дробей
Умножение и деление комплексных чисел в полярной форме
Уравнения мощности и их графики
Решение линейных систем уравнений путем замены
Решение полиномиальных уравнений с помощью факторинга
Законы экспонентов
индекс casa mÃo
Системы линейных уравнений
Свойства рациональных показателей
Мощность произведения и мощность частного
Факторизация различий идеальных квадратов
Деление дробей
Разложение полинома на множители путем нахождения GCF
Графики линейных уравнений
шагов факторинга
Свойство умножения показателей степени
Решение систем линейных уравнений с тремя переменными
Решение экспоненциальных уравнений
Нахождение НОК набора одночленов
 
  • Expression
  • Equation
  • Inequality
  • Contact us
  • Simplify
  • Factor
  • Expand
  • GCF
  • LCM
  • Solve
  • Graph
  • System
  • Решить
  • График
  • Система
  • Математический решатель на вашем сайте

Калькулятор упрощения сложных выражений
Похожие темы:
задачи по алгебре для 6 класса скачать | ответы в рабочей тетради по алгебре холла 2 | алгебра 2 ответа | алгебра эстафеты | Алгебра 10 класс | алгебра+сложение кубов | кубический корень из многочленов | графический метод квадратного уравнения или линейного уравнения | упростить с помощью факторинга | «решатель задач» «расширенное исчисление» математика скачать | экспонента квадратного корня | дайте мне алгебру 1 ответов | квадратный бином ti 89| математика для чайников логарифмическая

Автор Сообщение
Чонана

Дата регистрации: 28. 08.2004
Откуда: США [из Лондона, Англия]

Размещено: Четверг, 28 декабря, 07:08
Привет ребята. Я изучаю коррекционную алгебру. Я очень люблю математику с детства. К сожалению, я дошел до того, что больше не могу решать упражнения по алгебре в одиночку. У меня был частный учитель математики, который до сих пор помогал мне с домашним заданием, но мне пришлось заплатить много денег, и мне пришлось сказать ему, чтобы он больше не приходил. Сегодня мы изучали кое-что новое: калькулятор упрощенных сложных выражений, и когда я пришел домой с урока, я заметил, что не могу сделать домашнее задание по математике, и это меня испугало. Я также до сих пор не понимаю радикалов и системы уравнений. Что мне теперь делать? Я люблю математику и не хочу плохих оценок.
Наверх
Вофий Тимидов

Дата регистрации: 06.07.2001
Откуда: Болгария

Размещено: Четверг, 28 декабря, 20:15
Алгебратор — настоящая жемчужина, которая может помочь вам с Алгеброй 2. Поскольку я не был силен в базовой математике, один из моих классных наставников предложил мне попробовать Алгебратор, и, основываясь на его совете, я поискал его в Интернете, купил и начал использовать. Это. Это было просто необычно. Если вы внимательно будете следовать каждому предложенному там примеру по Алгебре 2, вы определенно освоите основные принципы вычитания дробей и подобия сторон-углов за несколько часов.
Наверх
cmithy_dnl

Зарегистрирован: 08.01.2002
Откуда: Австралия

Размещено: Пятница, 29 декабря, 11:12
Я обнаружил несколько подходящих программ. Я их проверил. Алгебратор оказался наиболее подходящим для квадратичных неравенств, подобия треугольников и преобразования единиц. Это было также легко управлять. Это вело меня шаг за шагом к ответу, а не просто давало решение. Таким образом, я тоже научился объяснять проблемы. К тому времени, когда я закончил с этим, я научился решать проблемы. Я нашел их полезными для предварительной алгебры, алгебры 2 и промежуточной алгебры, которые помогли мне в моих классах алгебры. Может быть, это как раз то, что вы ищете. Почему бы не попробовать это?
Наверх
т-в

Дата регистрации: 13.06.2007
Откуда: Калифорния, США

Размещено: Суббота, 30 декабря, 18:25
Похоже, что-то, что мне нужно купить прямо сейчас. Любые ссылки для заказа этой программы через Интернет?
Наверх
Момэпи

Зарегистрирован: 22.07.2004
Откуда: Ирландия

Размещено: Воскресенье, 31 декабря, 07:41
Вы можете загрузить это программное обеспечение с https://mathsite.org/adding-fractions.html. Доступно несколько демоверсий, чтобы убедиться, что это то, что вам нужно, и если вы сочтете это полезным, вы можете получить лицензионную версию за небольшую сумму.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *