Основные структуры данных. Матчасть. Азы / Хабр
Все чаще замечаю, что современным самоучкам очень не хватает матчасти. Все знают языки, но мало основы, такие как типы данных или алгоритмы. Немного про типы данных.
Еще в далеком 1976 швейцарский ученый Никлаус Вирт написал книгу Алгоритмы + структуры данных = программы.
40+ лет спустя это уравнение все еще верно. И если вы самоучка и надолго в программировании пробегитесь по статье, можно по диагонали. Можно код кофе.
В статье так же будут вопросы, которое вы можете услышать на интервью.
Что такое структура данных?
Структура данных — это контейнер, который хранит данные в определенном макете. Этот «макет» позволяет структуре данных быть эффективной в некоторых операциях и неэффективной в других.
Какие бывают?
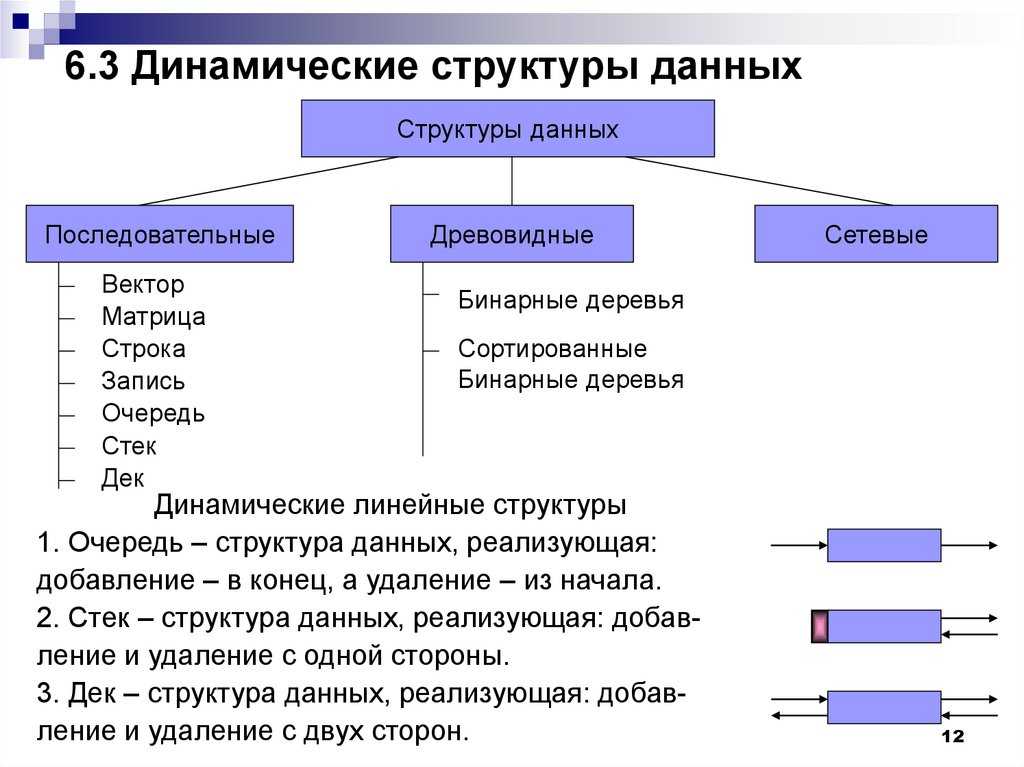
Линейные, элементы образуют последовательность или линейный список, обход узлов линеен. Примеры: Массивы. Связанный список, стеки и очереди.
Примеры: Массивы. Связанный список, стеки и очереди.
Нелинейные, если обход узлов нелинейный, а данные не последовательны. Пример: граф и деревья.
Основные структуры данных.
- Массивы
- Стеки
- Очереди
- Связанные списки
- Графы
- Деревья
- Префиксные деревья
Массивы
Массив — это самая простая и широко используемая структура данных. Другие структуры данных, такие как стеки и очереди, являются производными от массивов.
Изображение простого массива размера 4, содержащего элементы (1, 2, 3 и 4).
Каждому элементу данных присваивается положительное числовое значение (индекс), который соответствует позиции элемента в массиве. Большинство языков определяют начальный индекс массива как 0.
Бывают
Одномерные, как показано выше.
Многомерные, массивы внутри массивов.
Основные операции
- Insert-вставляет элемент по заданному индексу
- Get-возвращает элемент по заданному индексу
- Delete-удаление элемента по заданному индексу
- Size-получить общее количество элементов в массиве
Вопросы
- Найти второй минимальный элемент массива
- Первые неповторяющиеся целые числа в массиве
- Объединить два отсортированных массива
- Изменение порядка положительных и отрицательных значений в массиве
Стеки
Стек — абстрактный тип данных, представляющий собой список элементов, организованных по принципу LIFO (англ. last in — first out, «последним пришёл — первым вышел»).
Это не массивы. Это очередь. Придумал Алан Тюринг.
Примером стека может быть куча книг, расположенных в вертикальном порядке. Для того, чтобы получить книгу, которая где-то посередине, вам нужно будет удалить все книги, размещенные на ней.
Изображение стека, в три элемента (1, 2 и 3), где 3 находится наверху и будет удален первым.
Основные операции
- Push-вставляет элемент сверху
- Pop-возвращает верхний элемент после удаления из стека
- isEmpty-возвращает true, если стек пуст
- Top-возвращает верхний элемент без удаления из стека
Вопросы
- Реализовать очередь с помощью стека
- Сортировка значений в стеке
- Реализация двух стеков в массиве
- Реверс строки с помощью стека
Очереди
Подобно стекам, очередь — хранит элемент последовательным образом. Существенное отличие от стека – использование FIFO (First in First Out) вместо LIFO.
Пример очереди – очередь людей. Последний занял последним и будешь, а первый первым ее и покинет.
Изображение очереди, в четыре элемента (1, 2, 3 и 4), где 1 находится наверху и будет удален первым
Основные операции
- Enqueue—) — вставляет элемент в конец очереди
- Dequeue () — удаляет элемент из начала очереди
- isEmpty () — возвращает значение true, если очередь пуста
- Top () — возвращает первый элемент очереди
Вопросы
- Реализовать cтек с помощью очереди
- Реверс первых N элементов очереди
- Генерация двоичных чисел от 1 до N с помощью очереди
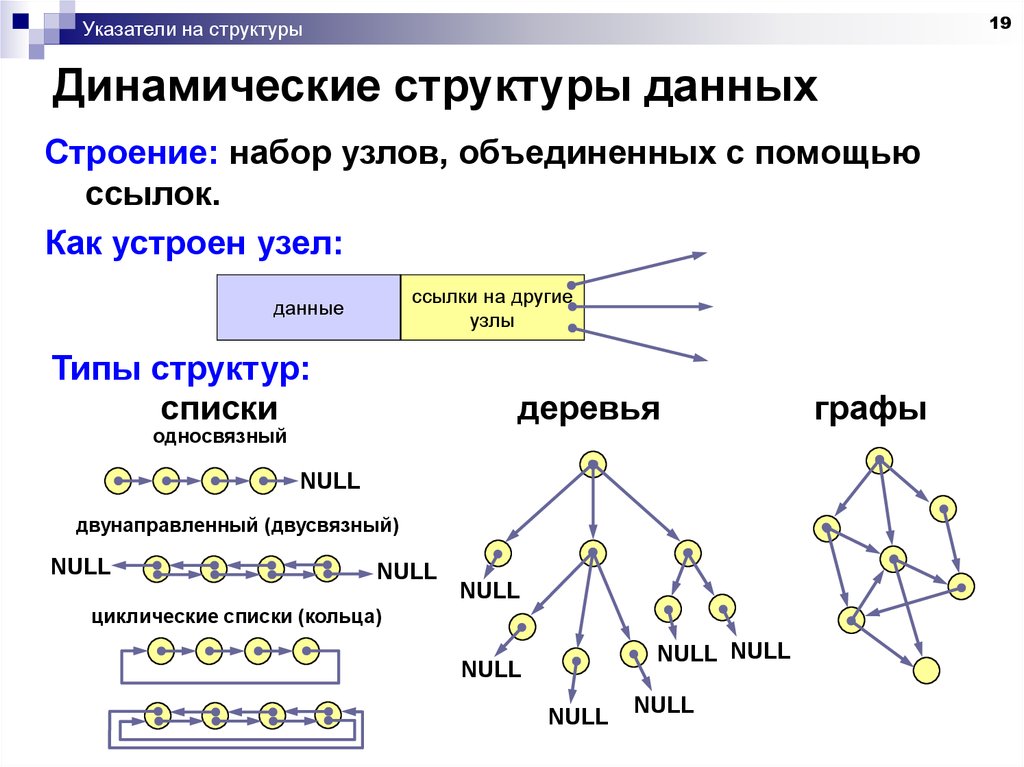
Связанный список
Связанный список – массив где каждый элемент является отдельным объектом и состоит из двух элементов – данных и ссылки на следующий узел.
Принципиальным преимуществом перед массивом является структурная гибкость: порядок элементов связного списка может не совпадать с порядком расположения элементов данных в памяти компьютера, а порядок обхода списка всегда явно задаётся его внутренними связями.
Бывают
Однонаправленный, каждый узел хранит адрес или ссылку на следующий узел в списке и последний узел имеет следующий адрес или ссылку как NULL.
1->2->3->4->NULL
Двунаправленный, две ссылки, связанные с каждым узлом, одним из опорных пунктов на следующий узел и один к предыдущему узлу.
NULL<-1<->2<->3->NULL
Круговой, все узлы соединяются, образуя круг. В конце нет NULL. Циклический связанный список может быть одно-или двукратным циклическим связанным списком.
1->2->3->1
Самое частое, линейный однонаправленный список. Пример – файловая система.
Основные операции
- InsertAtEnd — Вставка заданного элемента в конец списка
- InsertAtHead — Вставка элемента в начало списка
- Delete — удаляет заданный элемент из списка
- DeleteAtHead — удаляет первый элемент списка
- Search — возвращает заданный элемент из списка
- isEmpty — возвращает True, если связанный список пуст
Вопросы
- Реверс связанного списка
- Определение цикла в связанном списке
- Возврат N элемента из конца в связанном списке
- Удаление дубликатов из связанного списка
Графы
Граф-это набор узлов (вершин), которые соединены друг с другом в виде сети ребрами (дугами).
Бывают
Ориентированный, ребра являются направленными, т.е. существует только одно доступное направление между двумя связными вершинами.
Смешанные
Встречаются в таких формах как
- Матрица смежности
- Список смежности
Общие алгоритмы обхода графа
- Поиск в ширину – обход по уровням
- Поиск в глубину – обход по вершинам
Вопросы
- Реализовать поиск по ширине и глубине
- Проверить является ли граф деревом или нет
- Посчитать количество ребер в графе
- Найти кратчайший путь между двумя вершинами
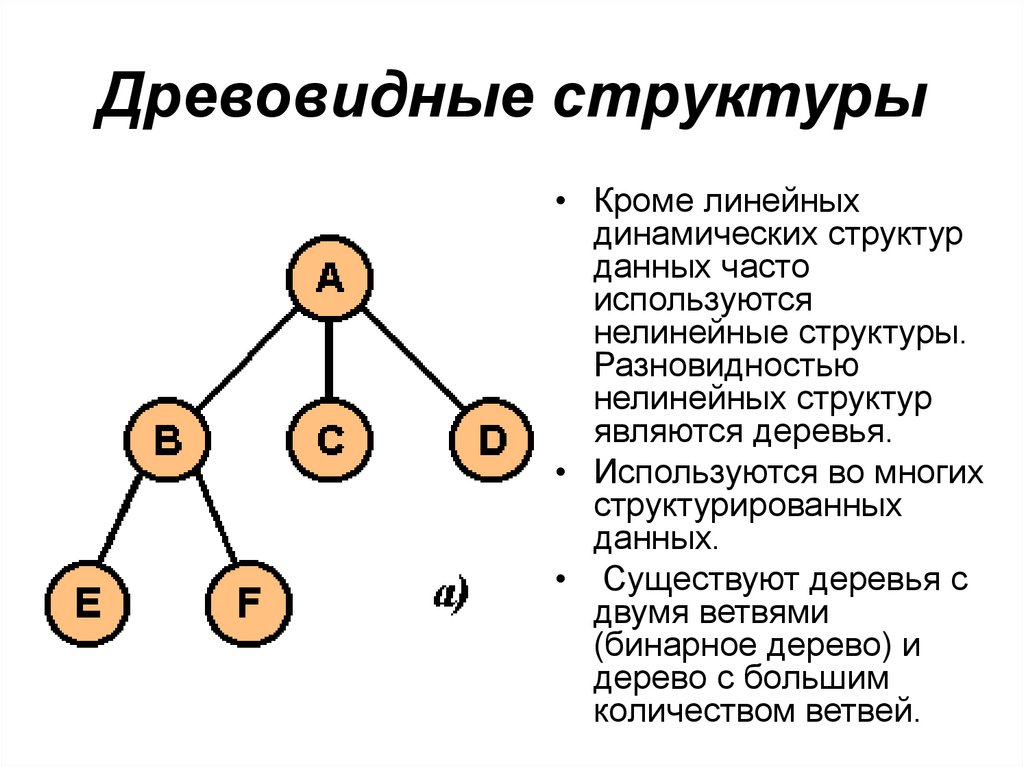
Деревья
Дерево-это иерархическая структура данных, состоящая из узлов (вершин) и ребер (дуг). Деревья по сути связанные графы без циклов.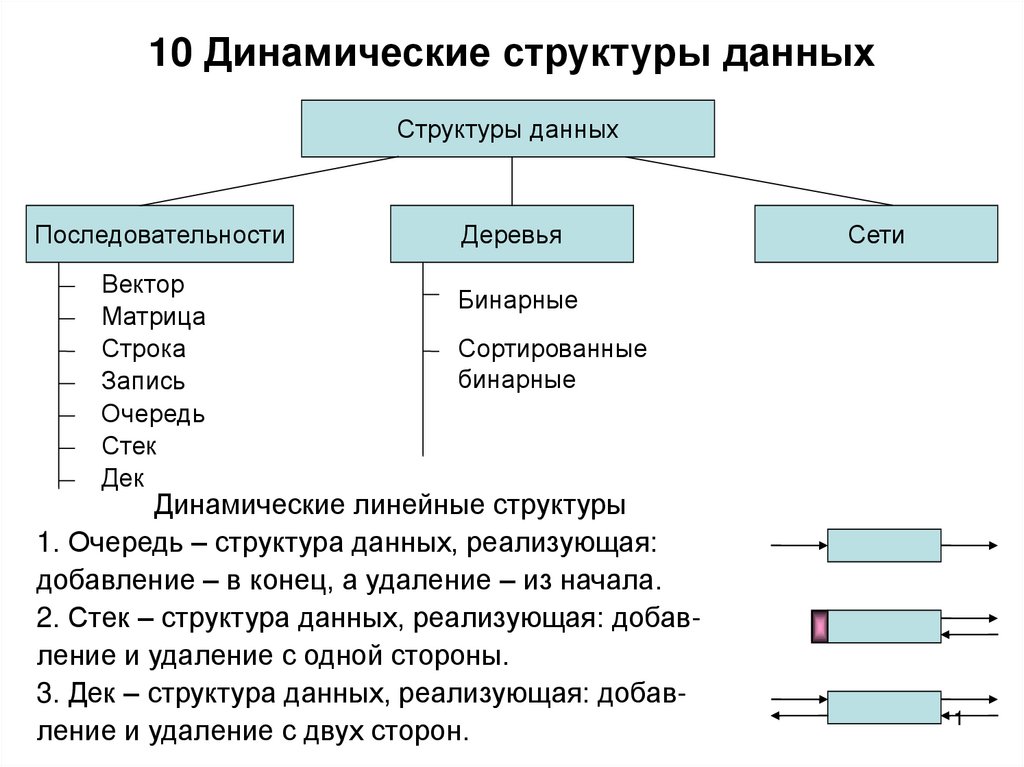
Древовидные структуры везде и всюду. Дерево скилов в играх знают все.
Простое дерево
Типы деревьев
- N дерево
- Сбалансированное дерево
- Бинарное дерево
- Дерево Бинарного Поиска
- AVL дерево
- 2-3-4 деревья
Бинарное дерево самое распространенное.
«Бинарное дерево — это иерархическая структура данных, в которой каждый узел имеет значение (оно же является в данном случае и ключом) и ссылки на левого и правого потомка. » — Procs
Три способа обхода дерева
- В прямом порядке (сверху вниз) — префиксная форма.
- В симметричном порядке (слева направо) — инфиксная форма.
- В обратном порядке (снизу вверх) — постфиксная форма.
Вопросы
- Найти высоту бинарного дерева
- Найти N наименьший элемент в двоичном дереве поиска
- Найти узлы на расстоянии N от корня
- Найти предков N узла в двоичном дереве
Trie ( префиксное деревое )
Разновидность дерева для строк, быстрый поиск.
Вот как такое дерево хранит слова «top», «thus» и «their».
Слова хранятся сверху вниз, зеленые цветные узлы «p», «s» и «r» указывают на конец «top», «thus « и «their» соответственно.
Вопросы
- Подсчитать общее количество слов
- Вывести все слова
- Сортировка элементов массива с префиксного дерева
- Создание словаря T9
Хэш таблицы
Хэширование — это процесс, используемый для уникальной идентификации объектов и хранения каждого объекта в заранее рассчитанном уникальном индексе (ключе).
Объект хранится в виде пары «ключ-значение», а коллекция таких элементов называется «словарем». Каждый объект можно найти с помощью этого ключа.
По сути это массив, в котором ключ представлен в виде хеш-функции.
Эффективность хеширования зависит от
- Функции хеширования
- Размера хэш-таблицы
- Метода борьбы с коллизиями
Пример сопоставления хеша в массиве.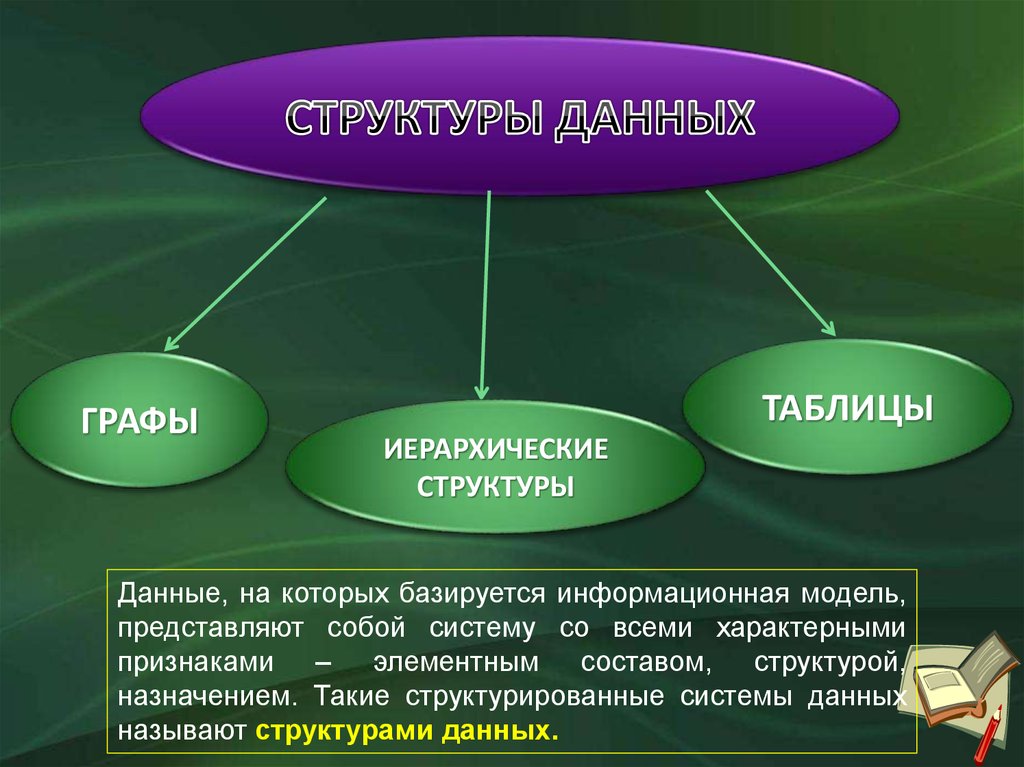 Индекс этого массива вычисляется через хэш-функцию.
Индекс этого массива вычисляется через хэш-функцию.
Вопросы
- Найти симметричные пары в массиве
- Найти, если массив является подмножеством другого массива
- Описать открытое хеширование
Список ресурсов
- medium.freecodecamp.org/the-top-data-structures-you-should-know-for-your-next-coding-interview-36af0831f5e3
- www.geeksforgeeks.org/commonly-asked-data-structure-interview-questions-set-1
- prog-cpp.ru/data-list
- habr.com/post/267855
- habr.com/post/273687
- habr.com/post/150732
- ruhighload.com/%D0%A7%D1%82%D0%BE+%D1%82%D0%B0%D0%BA%D0%BE%D0%B5+%D1%85%D0%B5%D1%88-%D1%82%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D1%8B+%D0%B8+%D0%BA%D0%B0%D0%BA+%D0%BE%D0%BD%D0%B8+%D1%80%D0%B0%D0%B1%D0%BE%D1%82%D0%B0%D1%8E%D1%82
- ru.wikipedia.org
Вместо заключения
Матчасть так же интересна, как и сами языки.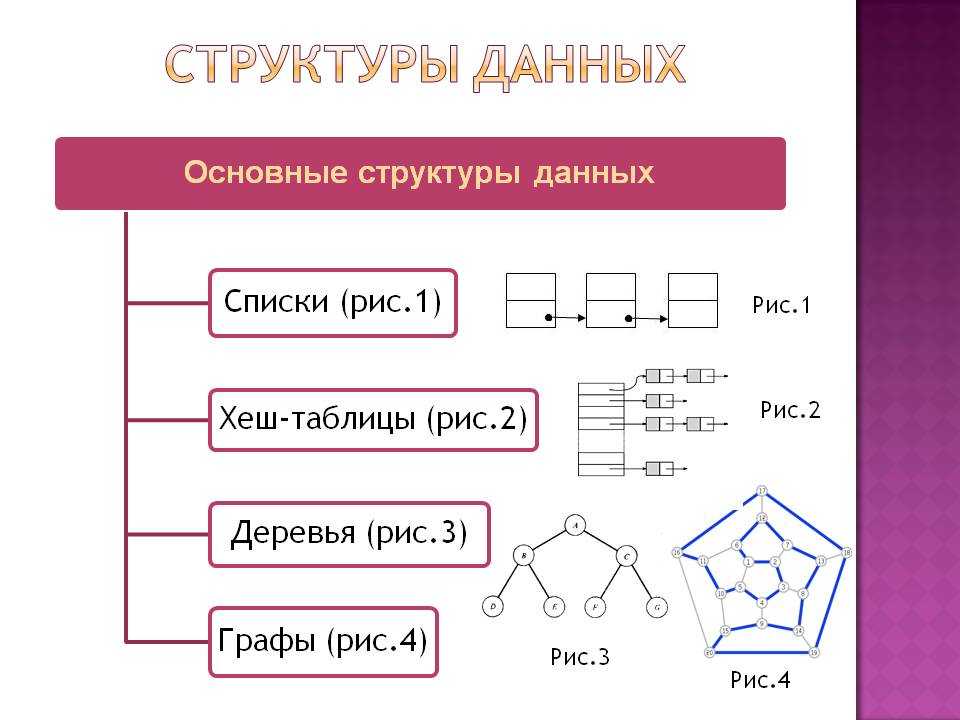 Возможно, кто-то увидит знакомые ему базовые структуры и заинтересуется.
Возможно, кто-то увидит знакомые ему базовые структуры и заинтересуется.
Спасибо, что прочли. Надеюсь не зря потратили время =)
PS: Прошу извинить, как оказалось, перевод статьи уже был тут и очень недавно, я проглядел.
Если интересно, вот она, спасибо Hokum, буду внимательнее.
10 типов структур данных, которые нужно знать + видео и упражнения / Хабр
Екатерина Малахова, редактор-фрилансер, специально для блога Нетологии адаптировала статью Beau Carnes об основных типах структур данных.
«Плохие программисты думают о коде. Хорошие программисты думают о структурах данных и их взаимосвязях», — Линус Торвальдс, создатель Linux.
Структуры данных играют важную роль в процессе разработки ПО, а еще по ним часто задают вопросы на собеседованиях для разработчиков. Хорошая новость в том, что по сути они представляют собой всего лишь специальные форматы для организации и хранения данных.
В этой статье я покажу вам 10 самых распространенных структур данных. Для каждой из них приведены видео и примеры их реализации на JavaScript. Чтобы вы смогли попрактиковаться, я также добавил несколько упражнений из бета-версии новой учебной программы freeCodeCamp.
Обратите внимание, что некоторые структуры данных включают временную сложность в нотации «большого О». Это относится не ко всем из них, так как иногда временная сложность зависит от реализации. Если вы хотите узнать больше о нотации «большого О», посмотрите это видео от Briana Marie.
В статье я привожу примеры реализации этих структур данных на JavaScript: они также пригодятся, если вы используете низкоуровневый язык вроде С. В многие высокоуровневые языки, включая JavaScript, уже встроены реализации большинства структур данных, о которых пойдет речь. Тем не менее, такие знания станут серьезным преимуществом при поиске работы и пригодятся при написании высокопроизводительного кода.
Связные списки
Связный список — одна из базовых структур данных. Ее часто сравнивают с массивом, так как многие другие структуры можно реализовать с помощью либо массива, либо связного списка. У этих двух типов есть преимущества и недостатки.
Ее часто сравнивают с массивом, так как многие другие структуры можно реализовать с помощью либо массива, либо связного списка. У этих двух типов есть преимущества и недостатки.
Так устроен связный список
Связный список состоит из группы узлов, которые вместе образуют последовательность. Каждый узел содержит две вещи: фактические данные, которые в нем хранятся (это могут быть данные любого типа) и указатель (или ссылку) на следующий узел в последовательности. Также существуют двусвязные списки: в них у каждого узла есть указатель и на следующий, и на предыдущий элемент в списке.
Основные операции в связном списке включают добавление, удаление и поиск элемента в списке.
Пример реализации на JavaScript
Временная сложность связного списка ╔═══════════╦═════════════════╦═══════════════╗ ║ Алгоритм ║Среднее значение ║ Худший случай ║ ╠═══════════╬═════════════════╬═══════════════╣ ║ Space ║ O(n) ║ O(n) ║ ║ Search ║ O(n) ║ O(n) ║ ║ Insert ║ O(1) ║ O(1) ║ ║ Delete ║ O(1) ║ O(1) ║ ╚═══════════╩═════════════════╩═══════════════╝
Упражнения от freeCodeCamp
- Work with Nodes in a Linked List
- Create a Linked List Class
- Remove Elements from a Linked List
- Search within a Linked List
- Remove Elements from a Linked List by Index
- Add Elements at a Specific Index in a Linked List
- Create a Doubly Linked List
- Reverse a Doubly Linked List
Стеки
Стек — это базовая структура данных, которая позволяет добавлять или удалять элементы только в её начале.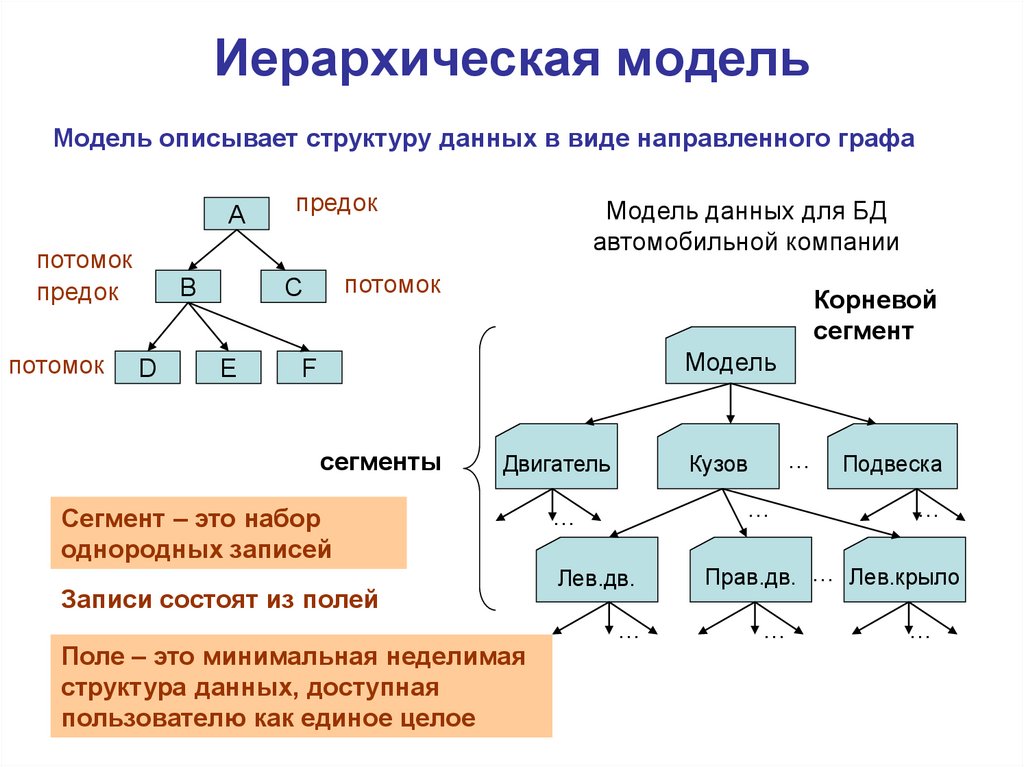 Она похожа на стопку книг: если вы хотите взглянуть на книгу в середине стека, сперва придется убрать лежащие сверху.
Она похожа на стопку книг: если вы хотите взглянуть на книгу в середине стека, сперва придется убрать лежащие сверху.
Стек организован по принципу LIFO (Last In First Out, «последним пришёл — первым вышел») . Это значит, что последний элемент, который вы добавили в стек, первым выйдет из него.
Так устроен стек
В стеках можно выполнять три операции: добавление элемента (push), удаление элемента (pop) и отображение содержимого стека (pip).
Пример реализации на JavaScript
Временная сложность стека ╔═══════════╦═════════════════╦═══════════════╗ ║ Алгоритм ║Среднее значение ║ Худший случай ║ ╠═══════════╬═════════════════╬═══════════════╣ ║ Space ║ O(n) ║ O(n) ║ ║ Search ║ O(n) ║ O(n) ║ ║ Insert ║ O(1) ║ O(1) ║ ║ Delete ║ O(1) ║ O(1) ║ ╚═══════════╩═════════════════╩═══════════════╝
Упражнения от freeCodeCamp
- Learn how a Stack Works
- Create a Stack Class
Очереди
Эту структуру можно представить как очередь в продуктовом магазине. Первым обслуживают того, кто пришёл в самом начале — всё как в жизни.
Первым обслуживают того, кто пришёл в самом начале — всё как в жизни.
Так устроена очередь
Очередь устроена по принципу FIFO (First In First Out, «первый пришёл — первый вышел»). Это значит, что удалить элемент можно только после того, как были убраны все ранее добавленные элементы.
Очередь позволяет выполнять две основных операции: добавлять элементы в конец очереди (enqueue) и удалять первый элемент (dequeue).
Пример реализации на JavaScript
Временная сложность очереди ╔═══════════╦═════════════════╦═══════════════╗ ║ Алгоритм ║Среднее значение ║ Худший случай ║ ╠═══════════╬═════════════════╬═══════════════╣ ║ Space ║ O(n) ║ O(n) ║ ║ Search ║ O(n) ║ O(n) ║ ║ Insert ║ O(1) ║ O(1) ║ ║ Delete ║ O(1) ║ O(1) ║ ╚═══════════╩═════════════════╩═══════════════╝
Упражнения от freeCodeCamp
- Create a Queue Class
- Create a Priority Queue Class
- Create a Circular Queue
Множества
Так выглядит множество
Множество хранит значения данных без определенного порядка, не повторяя их. Оно позволяет не только добавлять и удалять элементы: есть ещё несколько важных функций, которые можно применять к двум множествам сразу.
Оно позволяет не только добавлять и удалять элементы: есть ещё несколько важных функций, которые можно применять к двум множествам сразу.
- Объединение комбинирует все элементы из двух разных множеств, превращая их в одно (без дубликатов).
- Пересечение анализирует два множества и создает еще одно из тех элементов, которые присутствуют в обоих изначальных множествах.
- Разность выводит список элементов, которые есть в одном множестве, но отсутствуют в другом.
- Подмножество выдает булево значение, которое показывает, включает ли одно множество все элементы другого множества.
Пример реализации на JavaScript
Упражнения от freeCodeCamp
- Create a Set Class
- Remove from a Set
- Size of the Set
- Perform a Union on Two Sets
- Perform an Intersection on Two Sets of Data
- Perform a Difference on Two Sets of Data
- Perform a Subset Check on Two Sets of Data
- Create and Add to Sets in ES6
- Remove items from a set in ES6
- Use .
 has and .size on an ES6 Set
has and .size on an ES6 Set - Use Spread and Notes for ES5 Set() Integration
Map
Map — это структура, которая хранит данные в парах ключ/значение, где каждый ключ уникален. Иногда её также называют ассоциативным массивом или словарём. Map часто используют для быстрого поиска данных. Она позволяет делать следующие вещи:
- добавлять пары в коллекцию;
- удалять пары из коллекции;
- изменять существующей пары;
- искать значение, связанное с определенным ключом.
Так устроена структура map
Пример реализации на JavaScript
Упражнения от freeCodeCamp
- Create a Map Data Structure
- Create an ES6 JavaScript Map
Хэш-таблицы
Так работают хэш-таблица и хэш-функция
Хэш-таблица — это похожая на Map структура, которая содержит пары ключ/значение. Она использует хэш-функцию для вычисления индекса в массиве из блоков данных, чтобы найти желаемое значение.
Обычно хэш-функция принимает строку символов в качестве вводных данных и выводит числовое значение. Для одного и того же ввода хэш-функция должна возвращать одинаковое число. Если два разных ввода хэшируются с одним и тем же итогом, возникает коллизия. Цель в том, чтобы таких случаев было как можно меньше.
Таким образом, когда вы вводите пару ключ/значение в хэш-таблицу, ключ проходит через хэш-функцию и превращается в число. В дальнейшем это число используется как фактический ключ, который соответствует определенному значению. Когда вы снова введёте тот же ключ, хэш-функция обработает его и вернет такой же числовой результат. Затем этот результат будет использован для поиска связанного значения. Такой подход заметно сокращает среднее время поиска.
Пример реализации на JavaScript
Временная сложность хэш-таблицы ╔═══════════╦═════════════════╦═══════════════╗ ║ Алгоритм ║Среднее значение ║ Худший случай ║ ╠═══════════╬═════════════════╬═══════════════╣ ║ Space ║ O(n) ║ O(n) ║ ║ Search ║ O(1) ║ O(n) ║ ║ Insert ║ O(1) ║ O(n) ║ ║ Delete ║ O(1) ║ O(n) ║ ╚═══════════╩═════════════════╩═══════════════╝
Упражнения от freeCodeCamp
- Create a Hash Table
Двоичное дерево поиска
Двоичное дерево поиска
Дерево — это структура данных, состоящая из узлов.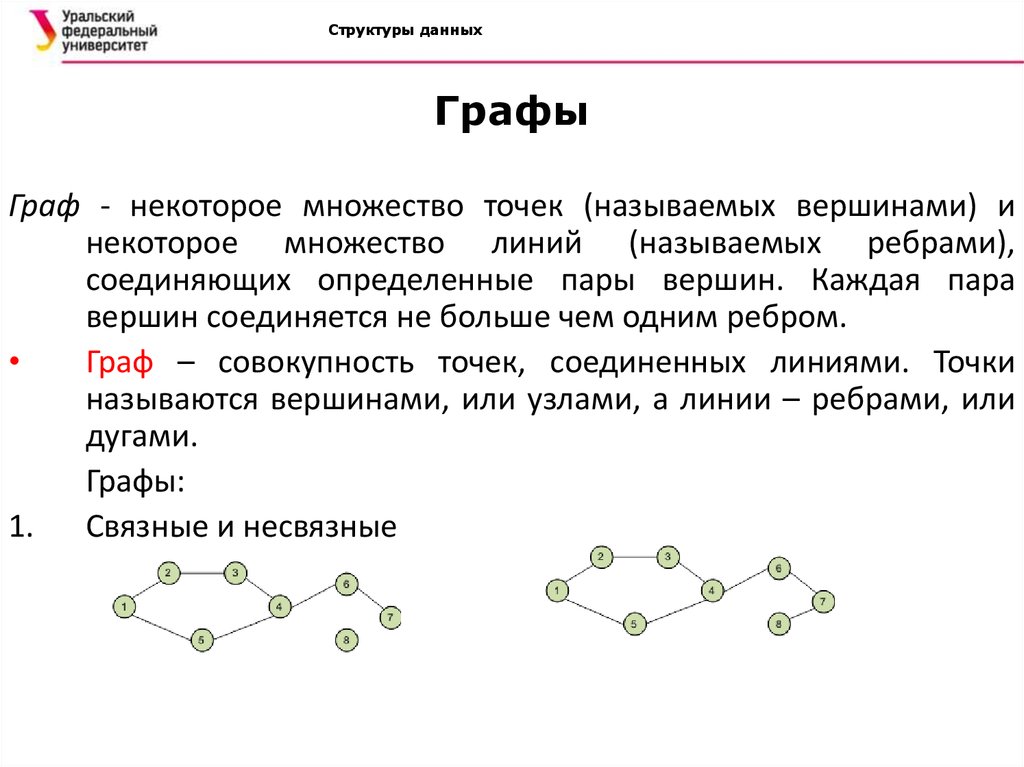 Ей присущи следующие свойства:
Ей присущи следующие свойства:
- Каждое дерево имеет корневой узел (вверху).
- Корневой узел имеет ноль или более дочерних узлов.
- Каждый дочерний узел имеет ноль или более дочерних узлов, и так далее.
У двоичного дерева поиска есть два дополнительных свойства:
- Каждый узел имеет до двух дочерних узлов (потомков).
- Каждый узел меньше своих потомков справа, а его потомки слева меньше его самого.
Двоичные деревья поиска позволяют быстро находить, добавлять и удалять элементы. Они устроены так, что время каждой операции пропорционально логарифму общего числа элементов в дереве.
Пример реализации на JavaScript
Временная сложность двоичного дерева поиска ╔═══════════╦═════════════════╦══════════════╗ ║ Алгоритм ║Среднее значение ║Худший случай ║ ╠═══════════╬═════════════════╬══════════════╣ ║ Space ║ O(n) ║ O(n) ║ ║ Search ║ O(log n) ║ O(n) ║ ║ Insert ║ O(log n) ║ O(n) ║ ║ Delete ║ O(log n) ║ O(n) ║ ╚═══════════╩═════════════════╩══════════════╝
Упражнения от freeCodeCamp
- Find the Minimum and Maximum Value in a Binary Search Tree
- Add a New Element to a Binary Search Tree
- Check if an Element is Present in a Binary Search Tree
- Find the Minimum and Maximum Height of a Binary Search Tree
- Use Depth First Search in a Binary Search Tree
- Use Breadth First Search in a Binary Search Tree
- Delete a Leaf Node in a Binary Search Tree
- Delete a Node with One Child in a Binary Search Tree
- Delete a Node with Two Children in a Binary Search Tree
- Invert a Binary Tree
Префиксное дерево
Префиксное (нагруженное) дерево — это разновидность дерева поиска. Оно хранит данные в метках, каждая из которых представляет собой узел на дереве. Такие структуры часто используют, чтобы хранить слова и выполнять быстрый поиск по ним — например, для функции автозаполнения.
Оно хранит данные в метках, каждая из которых представляет собой узел на дереве. Такие структуры часто используют, чтобы хранить слова и выполнять быстрый поиск по ним — например, для функции автозаполнения.
Так устроено префиксное дерево
Каждый узел в языковом префиксном дереве содержит одну букву слова. Чтобы составить слово, нужно следовать по ветвям дерева, проходя по одной букве за раз. Дерево начинает ветвиться, когда порядок букв отличается от других имеющихся в нем слов или когда слово заканчивается. Каждый узел содержит букву (данные) и булево значение, которое указывает, является ли он последним в слове.
Посмотрите на иллюстрацию и попробуйте составить слова. Всегда начинайте с корневого узла вверху и спускайтесь вниз. Это дерево содержит следующие слова: ball, bat, doll, do, dork, dorm, send, sense.
Пример реализации на JavaScript
Упражнения от freeCodeCamp
- Create a Trie Search Tree
Двоичная куча
Двоичная куча — ещё одна древовидная структура данных.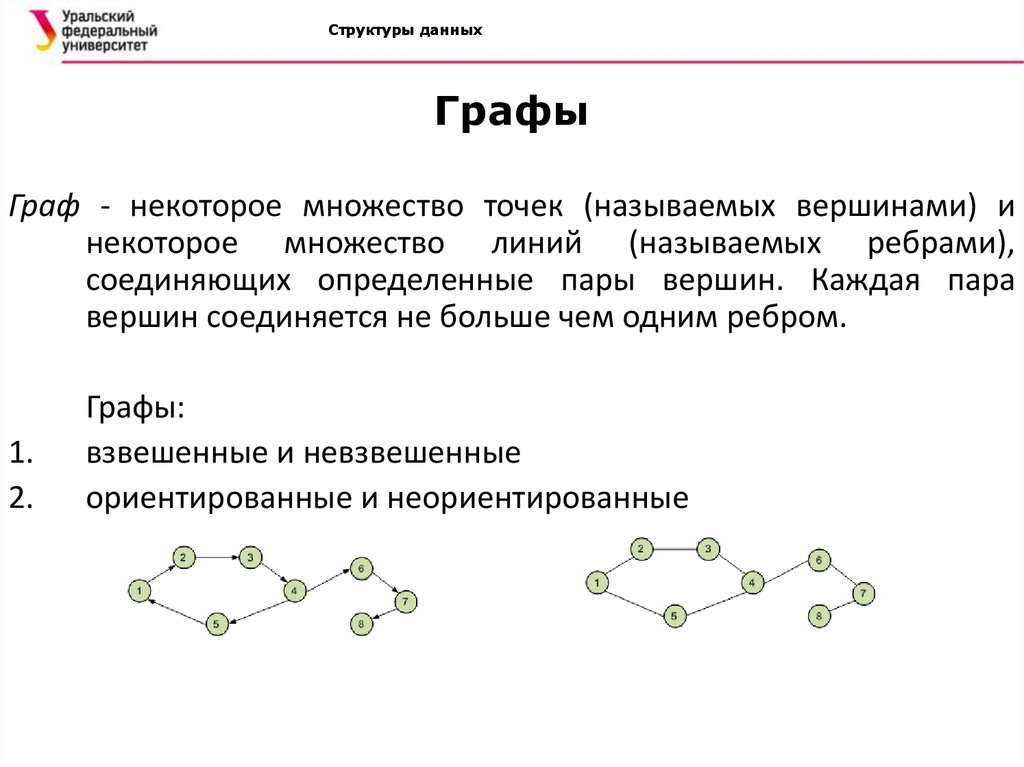 В ней у каждого узла не более двух потомков. Также она является совершенным деревом: это значит, что в ней полностью заняты данными все уровни, а последний заполнен слева направо.
В ней у каждого узла не более двух потомков. Также она является совершенным деревом: это значит, что в ней полностью заняты данными все уровни, а последний заполнен слева направо.
Так устроены минимальная и максимальная кучи
Двоичная куча может быть минимальной или максимальной. В максимальной куче ключ любого узла всегда больше ключей его потомков или равен им. В минимальной куче всё устроено наоборот: ключ любого узла меньше ключей его потомков или равен им.
Порядок уровней в двоичной куче важен, в отличие от порядка узлов на одном и том же уровне. На иллюстрации видно, что в минимальной куче на третьем уровне значения идут не по порядку: 10, 6 и 12.
Пример реализации на JavaScript
Временная сложность двоичной кучи ╔═══════════╦══════════════════╦═══════════════╗ ║ Алгоритм ║ Среднее значение ║ Худший случай ║ ╠═══════════╬══════════════════╬═══════════════╣ ║ Space ║ O(n) ║ O(n) ║ ║ Search ║ O(n) ║ O(n) ║ ║ Insert ║ O(1) ║ O(log n) ║ ║ Delete ║ O(log n) ║ O(log n) ║ ║ Peek ║ O(1) ║ O(1) ║ ╚═══════════╩══════════════════╩═══════════════╝
Упражнения от freeCodeCamp
- Insert an Element into a Max Heap
- Remove an Element from a Max Heap
- Implement Heap Sort with a Min Heap
Граф
Графы — это совокупности узлов (вершин) и связей между ними (рёбер).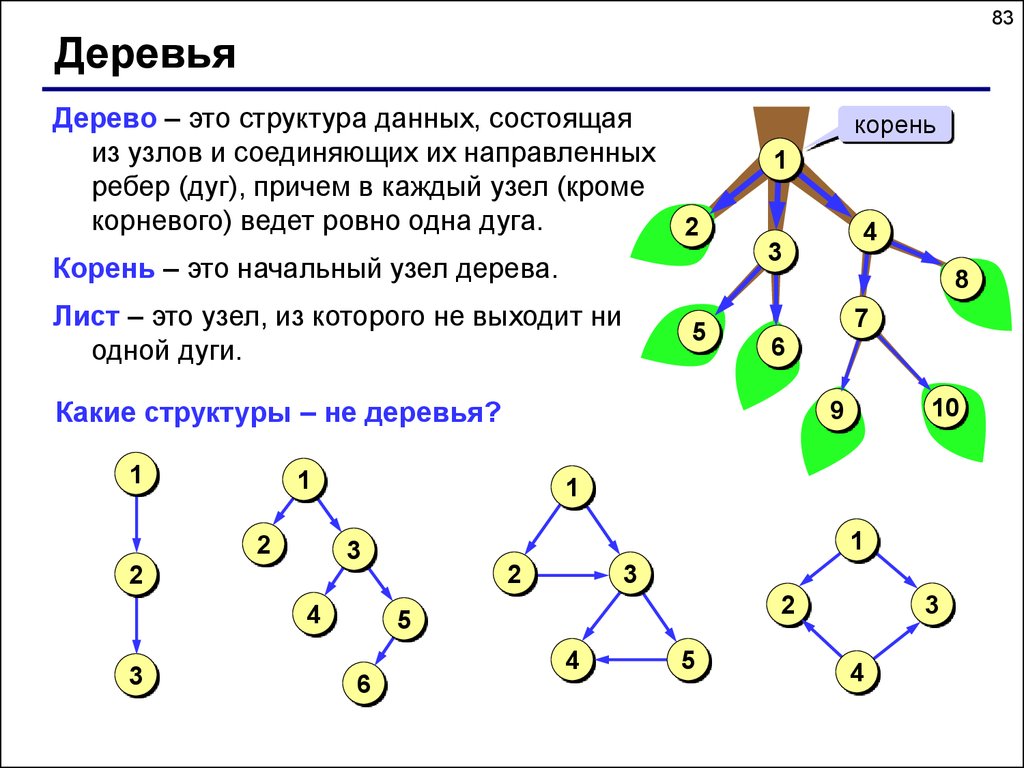 Также их называют сетями.
Также их называют сетями.
По такому принципу устроены социальные сети: узлы — это люди, а рёбра — их отношения.
Графы делятся на два основных типа: ориентированные и неориентированные. У неориентированных графов рёбра между узлами не имеют какого-либо направления, тогда как у рёбер в ориентированных графах оно есть.
Чаще всего граф изображают в каком-либо из двух видов: это может быть список смежности или матрица смежности.
Граф в виде матрицы смежности
Список смежности можно представить как перечень элементов, где слева находится один узел, а справа — все остальные узлы, с которыми он соединяется.
Матрица смежности — это сетка с числами, где каждый ряд или колонка соответствуют отдельному узлу в графе. На пересечении ряда и колонки находится число, которое указывает на наличие связи. Нули означают, что она отсутствует; единицы — что связь есть. Чтобы обозначить вес каждой связи, используют числа больше единицы.
Существуют специальные алгоритмы для просмотра рёбер и вершин в графах — так называемые алгоритмы обхода. К их основным типам относят поиск в ширину (breadth-first search) и в глубину (depth-first search). Как вариант, с их помощью можно определить, насколько близко к корневому узлу находятся те или иные вершины графа. В видео ниже показано, как на JavaScript выполнить поиск в ширину.
К их основным типам относят поиск в ширину (breadth-first search) и в глубину (depth-first search). Как вариант, с их помощью можно определить, насколько близко к корневому узлу находятся те или иные вершины графа. В видео ниже показано, как на JavaScript выполнить поиск в ширину.
Пример реализации на JavaScript
Временная сложность списка смежности (графа) ╔═══════════════╦════════════╗ ║ Алгоритм ║ Время ║ ╠═══════════════╬════════════╣ ║ Storage ║ O(|V|+|E|) ║ ║ Add Vertex ║ O(1) ║ ║ Add Edge ║ O(1) ║ ║ Remove Vertex ║ O(|V|+|E|) ║ ║ Remove Edge ║ O(|E|) ║ ║ Query ║ O(|V|) ║ ╚═══════════════╩════════════╝
Упражнения от freeCodeCamp
- Introduction to Graphs
- Adjacency List
- Adjacency Matrix
- Incidence Matrix
- Breadth-First Search
- Depth-First Search
Узнать больше
Если до этого вы никогда не сталкивались с алгоритмами или структурами данных, и у вас нет какой-либо подготовки в области ИТ, лучше всего подойдет книга Grokking Algorithms. В ней материал подан доступно и с забавными иллюстрациями (их автор — ведущий разработчик в Etsy), в том числе и по некоторым структурам данных, которые мы рассмотрели в этой статье.
В ней материал подан доступно и с забавными иллюстрациями (их автор — ведущий разработчик в Etsy), в том числе и по некоторым структурам данных, которые мы рассмотрели в этой статье.
От редакции Нетологии
Нетология проводит набор на курсы по Big Data:
1. Программа «Big Data: основы работы с большими массивами данных»
Для кого: инженеры, программисты, аналитики, маркетологи — все, кто только начинает вникать в технологию Big Data.
- введение в историю и основы технологии;
- способы сбора больших данных;
- типы данных;
- основные и продвинутые методы анализа больших данных;
- основы программирования, архитектуры хранения и обработки для работы с большими массивами данных.
Формат занятий: онлайн.
Подробности по ссылке → http://netolo.gy/dJd
2. Программа «Data Scientist»
Для кого: специалисты, работающие или собирающиеся работать с Big Data, а также те, кто планирует построить карьеру в области Data Science.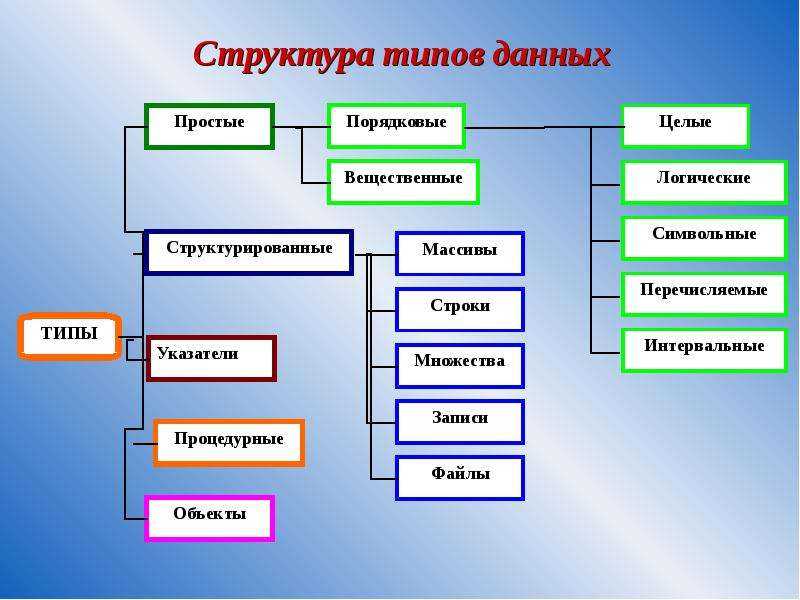 Для обучения необходимо владеть как минимум одним из языков программирования (желательно Python) и помнить программу по математике старших классов (а лучше вуза).
Для обучения необходимо владеть как минимум одним из языков программирования (желательно Python) и помнить программу по математике старших классов (а лучше вуза).
Темы курса:
- экспресс-обучение основным инструментам, Hadoop, кластерные вычисления;
- деревья решений, метод k-ближайших соседей, логистическая регрессия, кластеризация;
- уменьшение размерности данных, методы декомпозиции, спрямляющие пространства;
- введение в рекомендательные системы;
- распознавание изображений, машинное зрение, нейросети;
- обработка текста, дистрибутивная семантика, чатботы;
- временные ряды, модели ARMA/ARIMA, сложные модели прогнозирования.
Формат занятий: офлайн, г. Москва, центр Digital October. Преподают специалисты из Yandex Data Factory, Ростелеком, «Сбербанк-Технологии», Microsoft, OWOX, Clever DATA, МТС.
Подробности по ссылке.
Введение в структуры данных — GeeksforGeeks
ЧТО ТАКОЕ СТРУКТУРА ДАННЫХ?В информатике структура данных — это способ организации и хранения данных в компьютерной программе, обеспечивающий доступ к ним и эффективное их использование.
Структуры данных предоставляют средства управления большими объемами данных, обеспечивая эффективный поиск, сортировку, вставку и удаление данных.
Структуры данных можно разделить на два типа: примитивные структуры данных и непримитивные структуры данных. Примитивные структуры данных — это самые основные структуры данных, доступные в языке программирования, такие как целые числа, числа с плавающей запятой, символы и логические значения. Непримитивные структуры данных — это сложные структуры данных, построенные с использованием примитивных типов данных, таких как массивы, связанные списки, стеки, очереди, деревья, графики и хэш-таблицы.
Выбор структуры данных для конкретной задачи зависит от типа и объема обрабатываемых данных, операций, которые необходимо выполнить с данными, и требований к эффективности программы. Эффективное использование структур данных может значительно повысить производительность программы, сделав ее быстрее и эффективнее с точки зрения использования памяти.
Структура данных — это особый способ организации данных в компьютере, обеспечивающий их эффективное использование. Идея состоит в том, чтобы уменьшить пространственную и временную сложность различных задач.
Выбор хорошей структуры данных позволяет эффективно выполнять множество важных операций. Эффективная структура данных также требует минимального объема памяти и времени выполнения для обработки структуры.
Dat
Структуры а являются важным понятием в информатике и программировании. Вот несколько причин, почему они важны:- Эффективная обработка данных: Структуры данных обеспечивают способ организации и хранения данных таким образом, чтобы обеспечить эффективный поиск, обработку и хранение данных. Например, использование хеш-таблицы для хранения данных может обеспечить постоянный доступ к данным.
- Управление памятью: Правильное использование структур данных может помочь уменьшить использование памяти и оптимизировать использование ресурсов.
 Например, использование динамических массивов позволяет более эффективно использовать память, чем использование статических массивов.
Например, использование динамических массивов позволяет более эффективно использовать память, чем использование статических массивов. - Повторное использование кода: Структуры данных могут использоваться в качестве строительных блоков в различных алгоритмах и программах, что упрощает повторное использование кода.
- Абстракция: Структуры данных обеспечивают уровень абстракции, который позволяет программистам сосредоточиться на логической структуре данных и операциях, которые можно с ними выполнять, а не на деталях того, как данные хранятся и обрабатываются.
- Схема алгоритма: Многие алгоритмы для эффективной работы полагаются на определенные структуры данных. Понимание структур данных имеет решающее значение для разработки и реализации эффективных алгоритмов.
В целом, структуры данных необходимы для эффективного и действенного управления данными и манипулирования ими. Они являются фундаментальной концепцией информатики и широко используются в программировании и разработке программного обеспечения.
Структура данных и синтез алгоритма связаны друг с другом. Представление данных должно быть простым для понимания, чтобы разработчик и пользователь могли эффективно реализовать операцию.
Структуры данных обеспечивают простой способ организации, поиска, управления и хранения данных. Вот список необходимых данных.
- Эффективный доступ к данным и управление ими: Структуры данных обеспечивают быстрый доступ к данным и управление ими. Например, массив обеспечивает постоянный доступ к элементам с использованием их индекса, а хеш-таблица обеспечивает быстрый доступ к элементам на основе их ключа. Без структур данных программам пришлось бы искать данные последовательно, что приводило бы к снижению производительности.
- Управление памятью: Структуры данных позволяют эффективно использовать память за счет динамического выделения и освобождения памяти. Например, связанный список может динамически выделять память для каждого элемента по мере необходимости, а не заранее выделять фиксированный объем памяти.
 Это помогает избежать потери памяти и обеспечивает эффективное управление памятью.
Это помогает избежать потери памяти и обеспечивает эффективное управление памятью. - Повторное использование кода : Структуры данных можно повторно использовать в различных программах и проектах. Например, общую структуру данных стека можно использовать в нескольких программах, требующих функционирования LIFO (последним пришел — первым вышел), без необходимости каждый раз переписывать один и тот же код.
- Оптимизация алгоритмов: Структуры данных помогают оптимизировать алгоритмы, обеспечивая эффективный доступ к данным и манипулирование ими. Например, бинарное дерево поиска обеспечивает быстрый поиск и вставку элементов, что делает его идеальным для реализации алгоритмов поиска и сортировки.
- Масштабируемость: Структуры данных позволяют программам эффективно обрабатывать большие объемы данных. Например, хэш-таблица может хранить большие объемы данных, обеспечивая при этом быстрый доступ к элементам на основе их ключа.

Структуры данных можно разделить на два основных типа: примитивные структуры данных и непримитивные структуры данных.
Примитивные структуры данных: это самые основные структуры данных, которые обычно встроены в языки программирования. Примеры включают:
Integer
Float
Character
Boolean
Double
Void
Непримитивные структуры данных: Это сложные структуры данных, построенные с использованием примитивных типов данных. Непримитивные структуры данных можно разделить на следующие типы:
Массивы: Набор элементов одного типа данных, хранящихся в смежных ячейках памяти.
Связанные списки: Набор элементов, соединенных ссылками или указателями.
Стеки: Совокупность элементов, которые следуют принципу «последним пришел – первым вышел» (LIFO).
Очереди: Набор элементов, которые следуют принципу «первым пришел – первым обслужен» (FIFO).
Деревья: Иерархическая структура данных, состоящая из узлов, соединенных ребрами.
Графики: Нелинейная структура данных, состоящая из узлов и ребер.
Хэш-таблицы: Структура данных, в которой данные хранятся ассоциативным образом с использованием хэш-функции.
Кучи: Специализированная древовидная структура данных, удовлетворяющая свойству кучи.
Попыток: Древовидная структура данных, используемая для хранения ассоциативных массивов, где ключами являются строки.
Наборы: Коллекция уникальных элементов.
Карты: Абстрактный тип данных, в котором хранятся пары ключ-значение.
Выбор структуры данных зависит от решаемой задачи и операций, выполняемых с данными. Различные структуры данных имеют разные сильные и слабые стороны и подходят для разных сценариев. Понимание различных типов структур данных и их характеристик важно для эффективной разработки и реализации алгоритмов.
- Линейная структура данных
- Нелинейная структура данных.
- Линейная структура данных — это тип структуры данных, в которой элементы данных расположены в последовательном порядке, и каждый элемент имеет уникального предшественника и преемника, за исключением первого и последние элементы. Линейные структуры данных являются одномерными и могут проходиться последовательно от первого до последнего элемента.
- Элементы расположены в одном измерении, известном также как линейное измерение.
- Пример: списки, стек, очередь и т. д.
- A Нелинейная структура данных – это тип структуры данных, в котором элементы данных расположены не в последовательном порядке. , и у каждого элемента может быть один или несколько предшественников и потомков. Нелинейные структуры данных могут представлять сложные отношения между элементами данных, такими как иерархии, сети и графики.

- Элементы располагаются в измерениях один-много, много-один и много-много.
- Пример: дерево, график, таблица и т. д. элементов данных, хранящихся в непрерывной памяти места. Идея состоит в том, чтобы хранить несколько элементов одного типа вместе. Это упрощает вычисление положения каждого элемента, просто добавляя смещение к базовому значению, т. е. местонахождению в памяти первого элемента массива (обычно обозначается именем массива).
2. Связанные списки : Как и массивы, связанный список представляет собой линейную структуру данных. В отличие от массивов, элементы связанного списка не хранятся в непрерывном месте; элементы связаны с помощью указателей.
3. Стек : Стек — это линейная структура данных, которая следует определенному порядку выполнения операций. Порядок может быть LIFO (последним пришел, первым ушел) или FILO (первый пришел последним).
 В стеке все операции вставки и удаления разрешены только в одном конце списка.
В стеке все операции вставки и удаления разрешены только в одном конце списка.В основном со стеком выполняются три основные операции:
- Инициализация : Сделать стек пустым.
- Push: Добавляет элемент в стек. Если стек заполнен, говорят, что это состояние переполнения.
- Pop: Удаляет элемент из стека. Элементы выталкиваются в обратном порядке, в котором они выдвигались. Если стек пуст, говорят, что это состояние Underflow.
- Peek or Top: Возвращает верхний элемент стека.
- isEmpty: Возвращает true, если стек пуст, иначе false.
4. Очередь : Как и стек, очередь представляет собой линейную структуру, которая следует определенному порядку выполнения операций. Порядок – «первым пришел – первым обслужен» (FIFO). В очередь элементы вставляются с одного конца и удаляются с другого конца.
 Хорошим примером очереди является любая очередь потребителей ресурса, в которой потребитель, пришедший первым, обслуживается первым. Разница между стеками и очередями заключается в удалении. В стеке мы удаляем последний добавленный элемент; в очереди мы удаляем элемент, добавленный последним.
Хорошим примером очереди является любая очередь потребителей ресурса, в которой потребитель, пришедший первым, обслуживается первым. Разница между стеками и очередями заключается в удалении. В стеке мы удаляем последний добавленный элемент; в очереди мы удаляем элемент, добавленный последним.В очереди в основном выполняются следующие четыре основные операции:
- Постановка в очередь: Добавляет элемент в очередь. Если очередь заполнена, то говорят, что это состояние переполнения.
- Удаление из очереди: Удаляет элемент из очереди. Элементы выталкиваются в том же порядке, в котором они выдвигаются. Если очередь пуста, говорят, что это состояние Underflow.
- Спереди: Получить первый предмет из очереди.
- Сзади: Получить последний элемент из очереди.
5. Двоичное дерево : В отличие от массивов, связанных списков, стеков и очередей, которые представляют собой линейные структуры данных, деревья являются иерархическими структурами данных.
 Двоичное дерево — это древовидная структура данных, в которой каждый узел имеет не более двух дочерних элементов, называемых левым дочерним элементом и правым дочерним элементом. Реализуется в основном с помощью Links.
Двоичное дерево — это древовидная структура данных, в которой каждый узел имеет не более двух дочерних элементов, называемых левым дочерним элементом и правым дочерним элементом. Реализуется в основном с помощью Links.Двоичное дерево представлено указателем на самый верхний узел в дереве. Если дерево пусто, то значение root равно NULL. Узел двоичного дерева содержит следующие части.
1. Данные 2. Указатель на левый дочерний элемент 3. Указатель на правый дочерний элемент
6. Двоичное дерево поиска : Двоичное дерево поиска — это двоичное дерево со следующими дополнительными свойствами:
- Левая часть корневого узла содержит меньше ключей, чем корневой узел ключ.
- Правая часть корневого узла содержит ключи, большие, чем ключ корневого узла.
- В двоичном дереве нет повторяющихся ключей.
Двоичное дерево, обладающее следующими свойствами, известно как двоичное дерево поиска (BST).

7. Куча : Куча — это специальная структура данных на основе дерева, в которой дерево является полным двоичным деревом. Как правило, кучи могут быть двух типов:
- Max-Heap: В Max-Heap ключ, присутствующий в корневом узле, должен быть наибольшим среди ключей, присутствующих во всех его дочерних узлах. Одно и то же свойство должно быть рекурсивно истинным для всех поддеревьев в этом двоичном дереве.
- Минимальная куча: В минимальной куче ключ, присутствующий в корневом узле, должен быть минимальным среди ключей, присутствующих во всех его дочерних узлах. Одно и то же свойство должно быть рекурсивно истинным для всех поддеревьев в этом двоичном дереве.
8. Хеширование структуры данных : Хеширование — это важная структура данных, предназначенная для использования специальной функции, называемой хеш-функцией, которая используется для сопоставления заданного значения с определенным ключом для более быстрого доступа к элементам.
 Эффективность отображения зависит от эффективности используемой хэш-функции.
Эффективность отображения зависит от эффективности используемой хэш-функции.Пусть хеш-функция H(x) сопоставляет значение x с индексом x%10 в массиве. Например, если список значений равен [11, 12, 13, 14, 15], он будет храниться в позициях {1, 2, 3, 4, 5} в массиве или хеш-таблице соответственно.
9. Матрица : Матрица представляет собой набор чисел, расположенных в порядке строк и столбцов. Элементы матрицы необходимо заключать в круглые скобки или скобки.
Ниже показана матрица из 9 элементов.
10. Trie : Trie является эффективной информационной структурой данных. Используя Trie, сложность поиска можно довести до оптимального предела (длина ключа). Если мы храним ключи в бинарном дереве поиска, для хорошо сбалансированного BST потребуется время, пропорциональное M * log N, где M — максимальная длина строки, а N — количество ключей в дереве.
Применение структур данных: Используя Trie, мы можем искать ключ за время O(M). Однако штраф связан с требованиями к хранилищу Trie.
Используя Trie, мы можем искать ключ за время O(M). Однако штраф связан с требованиями к хранилищу Trie.- Массивы : Массивы используются для хранения набора однородных элементов памяти. Они обычно используются для реализации других структур данных, таких как стеки и очереди, а также для представления матриц и таблиц.
- Связанные списки : Связанные списки используются для хранения набора разнородных элементов с динамическим выделением памяти. Они обычно используются для реализации стеков, очередей и хеш-таблиц.
- Деревья : Деревья используются для представления иерархических структур данных, таких как файловые системы, организационные диаграммы и сетевые топологии. Двоичные деревья поиска обычно используются для реализации словарей и таблиц символов.
- Графики : Графики используются для представления сложных взаимосвязей между элементами данных, такими как социальные сети, транспортные сети и компьютерные сети.
 Они обычно используются для реализации алгоритмов кратчайшего пути и алгоритмов обхода графа.
Они обычно используются для реализации алгоритмов кратчайшего пути и алгоритмов обхода графа. - Хэш таблицы : Хэш-таблицы используются для реализации ассоциативных массивов, в которых хранятся пары ключ-значение. Они обеспечивают быстрый доступ к элементам данных на основе своих ключей.
- Стеки : Стеки используются для хранения набора элементов в порядке LIFO (последний пришел — первый ушел). Они обычно используются для реализации функций отмены-возврата, рекурсивных вызовов функций и оценки выражений.
- Очереди : Очереди используются для хранения набора элементов в порядке поступления (FIFO). Они обычно используются для реализации очередей ожидания, очередей сообщений и планирования заданий.
Введение в линейные структуры данных
Линейные структуры данных — это структуры данных, в которых элементы данных хранятся в линейной последовательности.
 К ним относятся:
К ним относятся:- Массивы : Набор элементов, хранящихся в смежных ячейках памяти.
- Связанные списки: Набор узлов, каждый из которых содержит элемент и ссылку на следующий узел.
- Стеки : Набор элементов в порядке «последний пришел — первый ушел» (LIFO).
- Очереди : Набор элементов в порядке поступления (FIFO).
- Линейные структуры данных используются во многих компьютерных приложениях, таких как поиск, сортировка и обработка данных. Они обеспечивают эффективный доступ к данным, но могут потребовать дополнительной памяти для хранения указателей между элементами.
Структура данных — это особый способ организации данных в компьютере, обеспечивающий их эффективное использование. Идея состоит в том, чтобы уменьшить пространственную и временную сложность различных задач. Ниже представлен обзор некоторых популярных линейных структур данных.
1.
 Массив
Массив
2. Связанный список
3. Стек
4. Очередь0
3 Массив 09 Массив — это структура данных, используемая для хранения однородных элементов в смежных местах. Размер массива должен быть указан перед сохранением данных.
Пусть размер массива равен n. Время доступа: O(1) [Это возможно, потому что элементы хранятся в смежных местах] Время поиска: O(n) для последовательного поиска: O (log n) для двоичного поиска [если массив отсортирован] Время вставки: O(n) [Наихудший случай возникает, когда вставка происходит в начале массива и требует сдвига всех элементов] Время удаления: O(n) [Наихудший случай возникает, когда удаление происходит в начале массива и требует смещения всех элементов]Пример: Например, предположим, что мы хотим сохранить оценки всех учеников в классе, мы можем использовать массив для их хранения.
 Это помогает сократить использование ряда переменных, поскольку нам не нужно создавать отдельную переменную для оценок по каждому предмету. Доступ ко всем меткам можно получить, просто пройдясь по массиву.
Это помогает сократить использование ряда переменных, поскольку нам не нужно создавать отдельную переменную для оценок по каждому предмету. Доступ ко всем меткам можно получить, просто пройдясь по массиву.Преимущества массивов:
- Постоянный доступ: Массивы обеспечивают постоянный доступ к элементам с использованием их индекса, что делает их хорошим выбором для реализации алгоритмов, которым требуется быстрый доступ к элементам.
- Распределение памяти: Массивы хранятся в смежных ячейках памяти, что делает распределение памяти эффективным.
- Простота реализации. Массивы просты в реализации и могут использоваться с базовыми конструкциями программирования, такими как циклы и условные операторы.
Недостатки массивов:
- Фиксированный размер: Массивы имеют фиксированный размер, поэтому после их создания размер нельзя изменить. Это может привести к перерасходу памяти, если массив слишком велик, или динамическому изменению размера, если массив слишком мал.

- Медленная вставка и удаление: Вставка или удаление элементов в массиве может быть медленным, особенно если операция должна выполняться в середине массива. Это требует смещения всех элементов, чтобы освободить место для нового элемента или заполнить пробел, оставленный удаленным элементом.
- Промахи в кэше: Массивы могут страдать от промахов в кэше, если доступ к элементам осуществляется не в последовательном порядке, что может привести к снижению производительности.
- Таким образом, массивы — хороший выбор для задач, где требуется постоянный доступ к элементам и эффективное выделение памяти, но их недостатки следует учитывать для задач, где важны динамическое изменение размера и быстрые операции вставки/удаления.
Связанный список
Связанный список представляет собой линейную структуру данных (подобную массивам), где каждый элемент является отдельным объектом. Связанный список состоит из двух элементов: данных и ссылки на следующий узел.
 Ссылка на следующий узел задается с помощью указателей, а данные являются значением узла. Каждый узел содержит данные и ссылки на другие узлы. Это упорядоченный набор элементов данных, называемый узлом, и линейный порядок поддерживается указателями. Он имеет преимущество перед массивом по количеству узлов, т.е. размер связанного списка не является фиксированным и может увеличиваться и уменьшаться по мере необходимости, в отличие от массивов.
Ссылка на следующий узел задается с помощью указателей, а данные являются значением узла. Каждый узел содержит данные и ссылки на другие узлы. Это упорядоченный набор элементов данных, называемый узлом, и линейный порядок поддерживается указателями. Он имеет преимущество перед массивом по количеству узлов, т.е. размер связанного списка не является фиксированным и может увеличиваться и уменьшаться по мере необходимости, в отличие от массивов.Типы связанных списков:
1. Односвязный список: В этом типе связанного списка каждый узел хранит адрес или ссылку следующего узла в списке, а последний узел имеет следующий адрес или ссылку как NULL. Например, 1->2->3->4->NULL2. Двойной связанный список: В этом типе связанного списка с каждым узлом связаны две ссылки. Одна из ссылок указывает на следующий узел. и один к предыдущему узлу. Преимущество этой структуры данных в том, что мы можем перемещаться в обоих направлениях, а для удаления нам не нужно иметь явный доступ к предыдущему узлу.
 Например. NULL<-1<->2<->3->NULL
Например. NULL<-1<->2<->3->NULL 3. Циклический связанный список: Циклический связанный список — это связанный список, в котором все узлы соединены в круг. В конце нет NULL. Циклический связанный список может быть одинарным циклическим связным списком или дважды циклическим связанным списком. Преимущество этой структуры данных в том, что любой узел можно сделать начальным узлом. Это полезно при реализации циклических очередей в связном списке. Например. 1->2->3->1 [Следующий указатель последнего узла указывает на первый]
4. Циклический двусвязный список: Циклический двусвязный список представляет собой комбинацию двусвязного списка и циклического связанного списка. Это означает, что этот связанный список является двунаправленным и содержит два указателя, причем последний указатель указывает на первый указатель.
Время доступа к элементу: O(n) Время поиска элемента: O(n) Вставка элемента: O(1) [Если мы находимся в позиции где мы должны вставить элемент] Удаление элемента: O(1) [Если мы знаем адрес узла перед узлом, который будет удален]Пример: Рассмотрим предыдущий пример, где мы создали массив оценок учеников.
 Теперь, если в курс добавляется новый предмет, его оценки также добавляются в массив оценок. Но размер массива был фиксированным, и он уже заполнен, поэтому он не может добавить новый элемент. Если мы создадим массив размером намного больше, чем количество субъектов, возможно, что большая часть массива останется пустой. Мы уменьшаем потери пространства. Создается связанный список, который добавляет узел только при введении нового элемента. Вставки и удаления также становятся проще благодаря связному списку.
Теперь, если в курс добавляется новый предмет, его оценки также добавляются в массив оценок. Но размер массива был фиксированным, и он уже заполнен, поэтому он не может добавить новый элемент. Если мы создадим массив размером намного больше, чем количество субъектов, возможно, что большая часть массива останется пустой. Мы уменьшаем потери пространства. Создается связанный список, который добавляет узел только при введении нового элемента. Вставки и удаления также становятся проще благодаря связному списку.
Один большой недостаток связанного списка — не допускается произвольный доступ. С массивами мы можем получить доступ к i-му элементу за время O(1). В связанном списке это занимает Θ(i) времени.Преимущества связанных списков:
- Динамический размер: Связанные списки имеют динамический размер, поэтому они могут увеличиваться или уменьшаться по мере необходимости без потери памяти.
- Эффективная вставка и удаление. Связанные списки обеспечивают эффективные операции вставки и удаления, поскольку необходимо обновить только указатели на предыдущий и следующий узлы.

- Удобство использования кеша. Связанные списки могут быть удобными для кеша, поскольку они обеспечивают линейный доступ к элементам, что может привести к лучшему использованию кеша и повышению производительности.
Недостатки связанных списков:
- Медленный доступ. Связанные списки не обеспечивают постоянный доступ к элементам по индексу, поэтому доступ к элементу в середине списка может быть медленным.
- Больше накладных расходов на память: Связные списки требуют больше накладных расходов на память по сравнению с массивами, так как каждый элемент в списке хранится как узел, который содержит значение и указатель на следующий узел.
- Сложнее реализовать: Связанные списки сложнее реализовать, чем массивы, поскольку они требуют использования указателей и связанных структур данных.
- Таким образом, связанные списки являются хорошим выбором для задач, где важны динамический размер и эффективные операции вставки/удаления, но их недостатки следует учитывать для задач, где необходим постоянный доступ к элементам.

Стек
Стек или LIFO (последний вошел, первый вышел) — это абстрактный тип данных, который служит набором элементов с двумя основными операциями: push, которая добавляет элемент в набор, и pop, который удаляет последний добавленный элемент. В стеке обе операции push и pop выполняются на одном и том же конце, который находится на вершине стека. Это может быть реализовано с использованием как массива, так и связанного списка.
Вставка : O(1) Удаление: O(1) Время доступа: O(n) [наихудший случай] Вставка и удаление разрешены на одном конце.
Пример: Стеки используются для обслуживания вызовов функций (функция, вызванная последней, должна завершить выполнение первой), мы всегда можем убрать рекурсию с помощью стеков. Стеки также используются в тех случаях, когда нам нужно перевернуть слово, проверить наличие сбалансированных скобок и в редакторах, где слово, которое вы набрали последним, удаляется первым при использовании операции отмены.
 Точно так же реализовать функциональность возврата в веб-браузерах.
Точно так же реализовать функциональность возврата в веб-браузерах.Операции с первичным стеком:
- void push(int data): При выполнении этой операции элемент вставляется в стек.
- int pop(): При выполнении этой операции элемент удаляется из вершины стека и возвращается.
Вспомогательные операции стека:
- int top(): Эта операция вернет последний вставленный элемент, который находится вверху, не удаляя его.
- int size(): Эта операция вернет размер стека, т. е. общее количество элементов, присутствующих в стеке.
- int isEmpty(): Эта операция указывает, пуст стек или нет.
- int isFull() : Эта операция указывает, заполнен стек или нет.
Типы стеков:
- Стек регистров: Этот тип стека также является элементом памяти, присутствующим в блоке памяти, и может обрабатывать только небольшой объем данных.
 Высота стека регистров всегда ограничена, так как размер стека регистров очень мал по сравнению с памятью.
Высота стека регистров всегда ограничена, так как размер стека регистров очень мал по сравнению с памятью. - Стек памяти: Этот тип стека может обрабатывать большой объем данных памяти. Высота стека памяти является гибкой, поскольку он занимает большой объем данных памяти.
Преимущества стеков:
- Порядок LIFO (последним пришел, первым ушел): стеки позволяют сохранять и извлекать элементы в порядке LIFO, что полезно для реализации таких алгоритмов, как поиск в глубину.
- Эффективные операции: стеки обеспечивают эффективные операции push-and-pop, поскольку требуется обновить только верхний элемент.
- Простота реализации: стеки можно легко реализовать с помощью массивов или связанных списков, что делает их простой структурой данных для понимания и использования.
Недостатки стеков:
- Фиксированный размер: Стеки имеют фиксированный размер, поэтому они могут страдать от переполнения, если добавляется слишком много элементов, или недостаточного количества, если удаляется слишком много элементов.

- Ограниченные операции: стеки допускают только операции push, pop и peek (доступ к верхнему элементу), поэтому они не подходят для реализации алгоритмов, требующих постоянного доступа к элементам или эффективных операций вставки и удаления.
- Несбалансированные операции: стеки могут стать несбалансированными, если операции вталкивания и извлечения выполняются неравномерно, что приводит к переполнению или недостатку заполнения.
- Таким образом, стеки являются хорошим выбором для задач, где важен порядок LIFO и эффективные операции push и pop, но их недостатки следует учитывать для задач, требующих динамического изменения размера, постоянного доступа к элементам или более сложных операций.
Очередь
Очередь или FIFO (первым пришел, первым обслужен) — это абстрактный тип данных, который служит набором элементов с двумя основными операциями: постановка в очередь, процесс добавления элемента в набор. (Элемент добавляется с обратной стороны) и исключить из очереди процесс удаления первого добавленного элемента.
 (Элемент снимается с лицевой стороны). Это может быть реализовано с использованием как массива, так и связанного списка.
(Элемент снимается с лицевой стороны). Это может быть реализовано с использованием как массива, так и связанного списка.Вставка : O(1) Удаление: O(1) Время доступа: O(n) [худший случай]
Пример: Очередь, как следует из названия, представляет собой структуру данных, построенную в соответствии с очередями автобусной остановки или поезда, где человек, стоящий впереди очереди ( стоящий дольше всех) тот, кто первым получит билет. Таким образом, любая ситуация, когда ресурсы распределяются между несколькими пользователями и обслуживаются в порядке очереди. Примеры включают планирование ЦП, планирование дисков. Другое применение очереди — когда данные передаются асинхронно (данные не обязательно принимаются с той же скоростью, что и отправляются) между двумя процессами. Примеры включают буферы ввода-вывода, каналы, файловый ввод-вывод и т. д.
Основные операции с очередью:
- void enqueue(int data): вставляет элемент в конец очереди, т.
 е. в конец очереди.
е. в конец очереди. - int dequeue(): эта операция удаляет и возвращает элемент, находящийся в начале очереди.
Вспомогательные операции над очередью:
- int front(): Эта операция возвращает элемент в начало, не удаляя его.
- int Rear(): Эта операция возвращает элемент в конце, не удаляя его.
- int isEmpty(): Эта операция указывает, пуста ли очередь или нет.
- int size(): Эта операция возвращает размер очереди, т. е. общее количество содержащихся в ней элементов.
Типы очередей:
- Простая очередь: Простая очередь, также известная как линейная очередь, представляет собой самую простую версию очереди. Здесь вставка элемента, т. е. операция постановки в очередь, происходит на заднем конце, а удаление элемента, т. е. операция удаления из очереди, происходит на переднем конце.

- Циклическая очередь: В циклической очереди элемент очереди действует как круговое кольцо. Работа циклической очереди аналогична линейной очереди, за исключением того факта, что последний элемент соединяется с первым элементом. Его преимущество в том, что память используется лучше. Это связано с тем, что если есть пустое место, то есть если в определенной позиции в очереди нет элемента, то элемент может быть легко добавлен в эту позицию.
- Приоритетная очередь: Эта очередь является особым типом очереди. Его особенность в том, что он упорядочивает элементы в очереди на основе некоторого приоритета. Приоритет может быть чем-то, где элемент с наибольшим значением имеет приоритет, поэтому он создает очередь с убывающим порядком значений. Приоритет также может быть таким, что элемент с наименьшим значением получает наивысший приоритет, поэтому, в свою очередь, он создает очередь с возрастающим порядком значений.
- Dequeue: Dequeue также известен как Double Ended Queue.
 Как следует из названия, это означает, что элемент может быть вставлен или удален с обоих концов очереди, в отличие от других очередей, в которых это можно сделать только с одного конца. Из-за этого свойства он может не подчиняться свойству First In First Out.
Как следует из названия, это означает, что элемент может быть вставлен или удален с обоих концов очереди, в отличие от других очередей, в которых это можно сделать только с одного конца. Из-за этого свойства он может не подчиняться свойству First In First Out.
Преимущества очередей:
- Порядок FIFO (первым пришел, первым обслужен): Очереди позволяют сохранять и извлекать элементы в порядке FIFO, что полезно для реализации таких алгоритмов, как поиск в ширину. .
- Эффективные операции. Очереди обеспечивают эффективную постановку в очередь и удаление из очереди, поскольку необходимо обновлять только начало и конец очереди.
- Динамический размер: Очереди могут динамически увеличиваться, поэтому их можно использовать в ситуациях, когда количество элементов неизвестно или может меняться со временем.
Недостатки очередей:
- Ограниченные операции: Очереди допускают только операции постановки в очередь, удаления из очереди и просмотра (доступ к переднему элементу), поэтому они не подходят для реализации алгоритмов, требующих постоянного доступа к элементам или эффективной вставки.
 и операции удаления.
и операции удаления. - Медленный произвольный доступ: Очереди не допускают постоянный доступ к элементам по индексу, поэтому доступ к элементу в середине очереди может быть медленным.
- Кэш недружественный: Очереди могут быть недружественными к кэшу, так как элементы извлекаются в другом порядке, чем они сохраняются, что может привести к плохому использованию кэша и производительности.
Таким образом, очереди
Обзор структур данных | Набор 2 (двоичное дерево, BST, куча и хэш)
Эта статья предоставлена Abhiraj Smit . Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше.
Преимущества линейных структур данных:
- Эффективный доступ к данным: Элементы могут быть легко доступны по их положению в последовательности.
- Динамическое изменение размера: Линейные структуры данных могут динамически регулировать свой размер по мере добавления или удаления элементов.

- Простота реализации: Линейные структуры данных можно легко реализовать с помощью массивов или связанных списков.
- Универсальность : Линейные структуры данных могут использоваться в различных приложениях, таких как поиск, сортировка и обработка данных.
- Простые алгоритмы : Многие алгоритмы, используемые в линейных структурах данных, просты и понятны.
Недостатки линейных структур данных:
- Ограниченный доступ к данным : Доступ к элементам, не сохраненным в конце или начале последовательности, может занять много времени.
- Накладные расходы памяти : Поддержание связей между элементами в связанных списках и указателями в стеках и очередях может потреблять дополнительную память.
- Сложные алгоритмы : Некоторые алгоритмы, используемые в линейных структурах данных, такие как поиск и сортировка, могут быть сложными и занимать много времени.

- Неэффективное использование памяти : Линейные структуры данных могут привести к неэффективному использованию памяти, если в распределении памяти есть промежутки.
- Не подходит для определенных операций : Линейные структуры данных могут не подходить для операций, требующих постоянного произвольного доступа к элементам, таких как поиск элемента в большом наборе данных.
Важные моменты:
Ниже приведены некоторые важные моменты, затронутые во введении в линейные структуры данных:Определение и типы: Линейные структуры данных — это тип структуры данных, в которой элементы хранятся в линейной последовательности. Наиболее распространенными типами линейных структур данных являются массивы, связанные списки, стеки и очереди.
- Массивы : Массивы представляют собой набор элементов, хранящихся в смежных ячейках памяти. Он обеспечивает постоянный доступ к элементам, но замедляет операции вставки и удаления.

- Связанные списки: Связанные списки представляют собой набор элементов, где каждый элемент хранится как узел и связан со следующим узлом через указатель. Связанные списки имеют динамический размер и обеспечивают эффективные операции вставки и удаления.
- Стеки : Стеки — это тип структуры данных, в которой элементы хранятся и извлекаются в порядке «последний пришел — первый ушел» (LIFO). Это полезно для реализации таких алгоритмов, как поиск в глубину.
- Очереди : Очереди — это тип структуры данных, в которой элементы хранятся и извлекаются в порядке поступления и поступления (FIFO). Это полезно для реализации таких алгоритмов, как поиск в ширину.
- Временная сложность: Временная сложность операций, таких как вставка, удаление и поиск в линейных структурах данных, зависит от типа используемой структуры данных. Временная сложность каждой операции должна учитываться при выборе структуры данных для конкретной задачи.


 has and .size on an ES6 Set
has and .size on an ES6 Set Структуры данных предоставляют средства управления большими объемами данных, обеспечивая эффективный поиск, сортировку, вставку и удаление данных.
Структуры данных предоставляют средства управления большими объемами данных, обеспечивая эффективный поиск, сортировку, вставку и удаление данных. Структура данных — это особый способ организации данных в компьютере, обеспечивающий их эффективное использование. Идея состоит в том, чтобы уменьшить пространственную и временную сложность различных задач.
Структура данных — это особый способ организации данных в компьютере, обеспечивающий их эффективное использование. Идея состоит в том, чтобы уменьшить пространственную и временную сложность различных задач. Например, использование динамических массивов позволяет более эффективно использовать память, чем использование статических массивов.
Например, использование динамических массивов позволяет более эффективно использовать память, чем использование статических массивов. Это помогает избежать потери памяти и обеспечивает эффективное управление памятью.
Это помогает избежать потери памяти и обеспечивает эффективное управление памятью.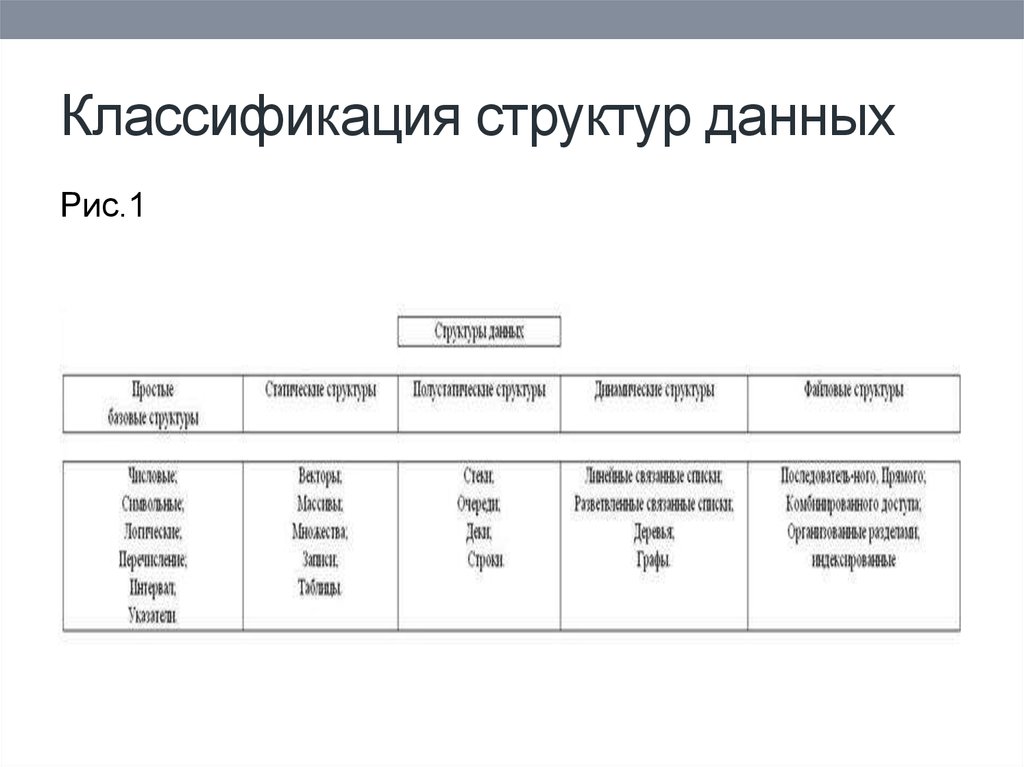
 В стеке все операции вставки и удаления разрешены только в одном конце списка.
В стеке все операции вставки и удаления разрешены только в одном конце списка.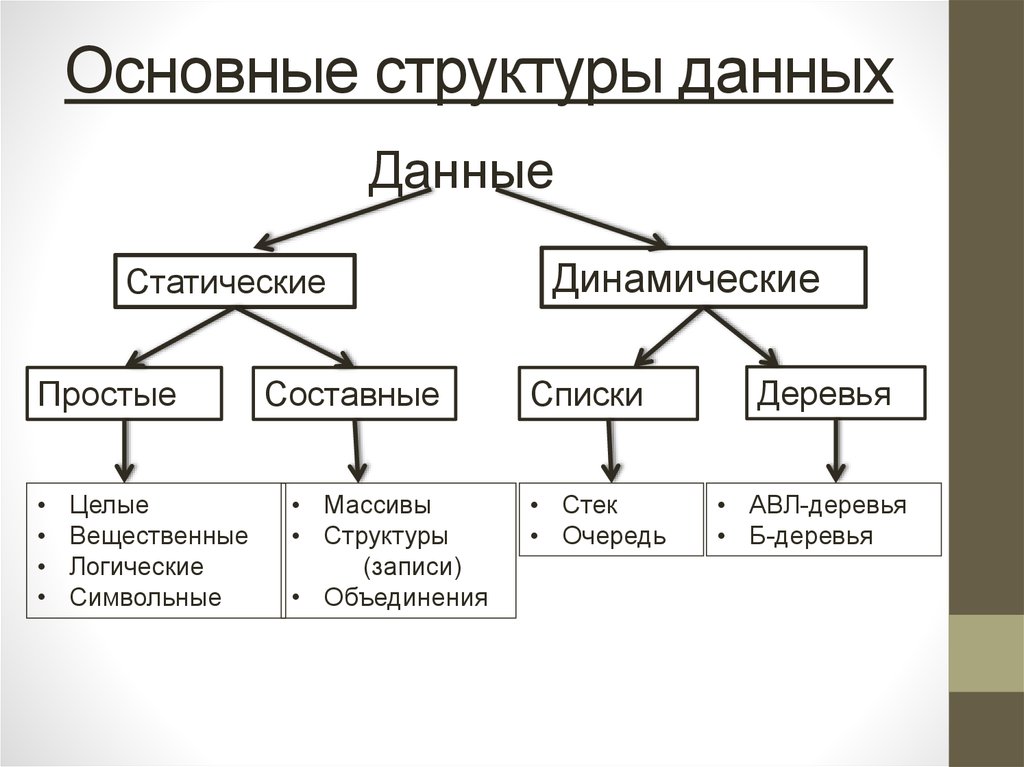 Хорошим примером очереди является любая очередь потребителей ресурса, в которой потребитель, пришедший первым, обслуживается первым. Разница между стеками и очередями заключается в удалении. В стеке мы удаляем последний добавленный элемент; в очереди мы удаляем элемент, добавленный последним.
Хорошим примером очереди является любая очередь потребителей ресурса, в которой потребитель, пришедший первым, обслуживается первым. Разница между стеками и очередями заключается в удалении. В стеке мы удаляем последний добавленный элемент; в очереди мы удаляем элемент, добавленный последним.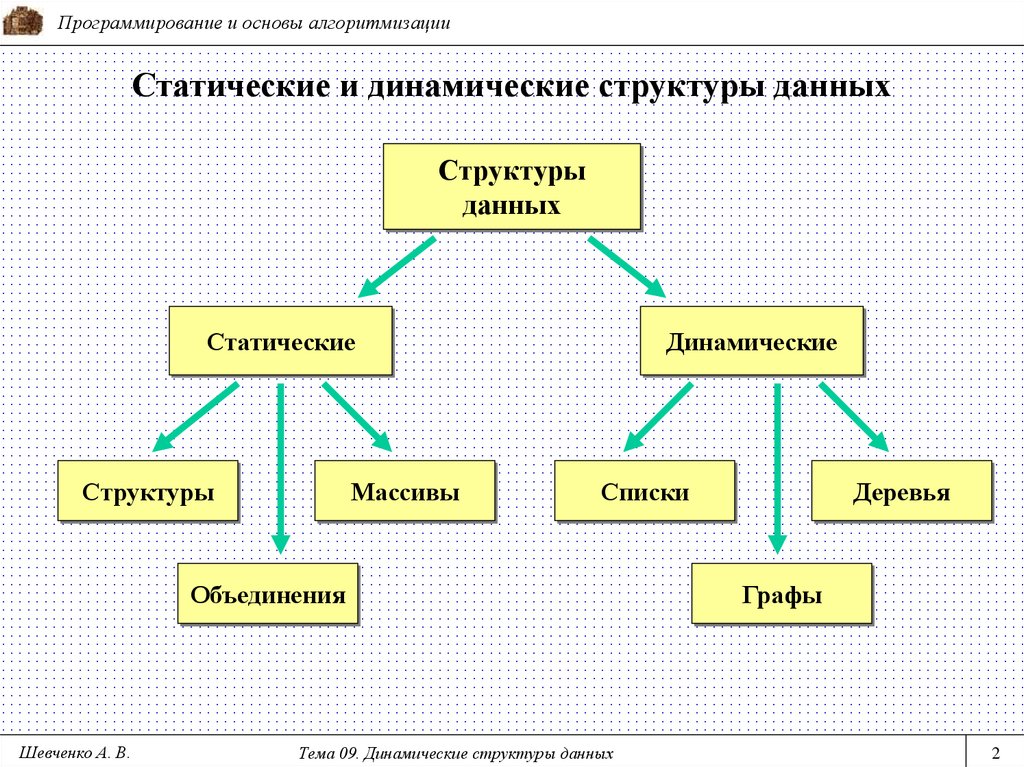 Двоичное дерево — это древовидная структура данных, в которой каждый узел имеет не более двух дочерних элементов, называемых левым дочерним элементом и правым дочерним элементом. Реализуется в основном с помощью Links.
Двоичное дерево — это древовидная структура данных, в которой каждый узел имеет не более двух дочерних элементов, называемых левым дочерним элементом и правым дочерним элементом. Реализуется в основном с помощью Links.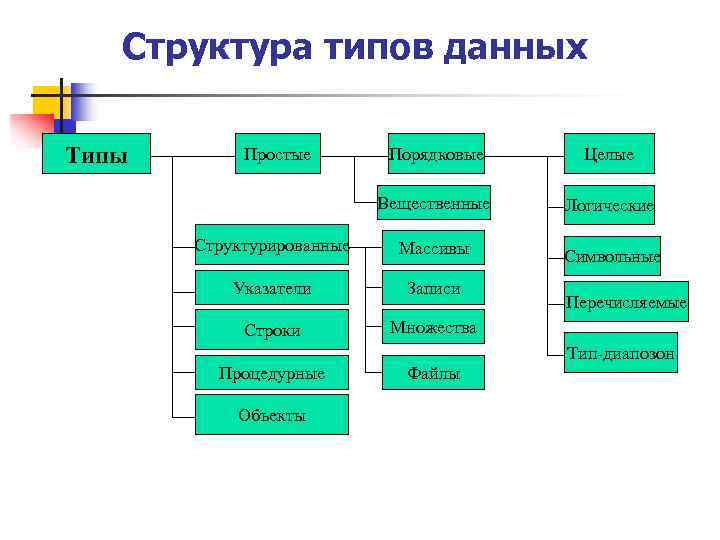
 Эффективность отображения зависит от эффективности используемой хэш-функции.
Эффективность отображения зависит от эффективности используемой хэш-функции.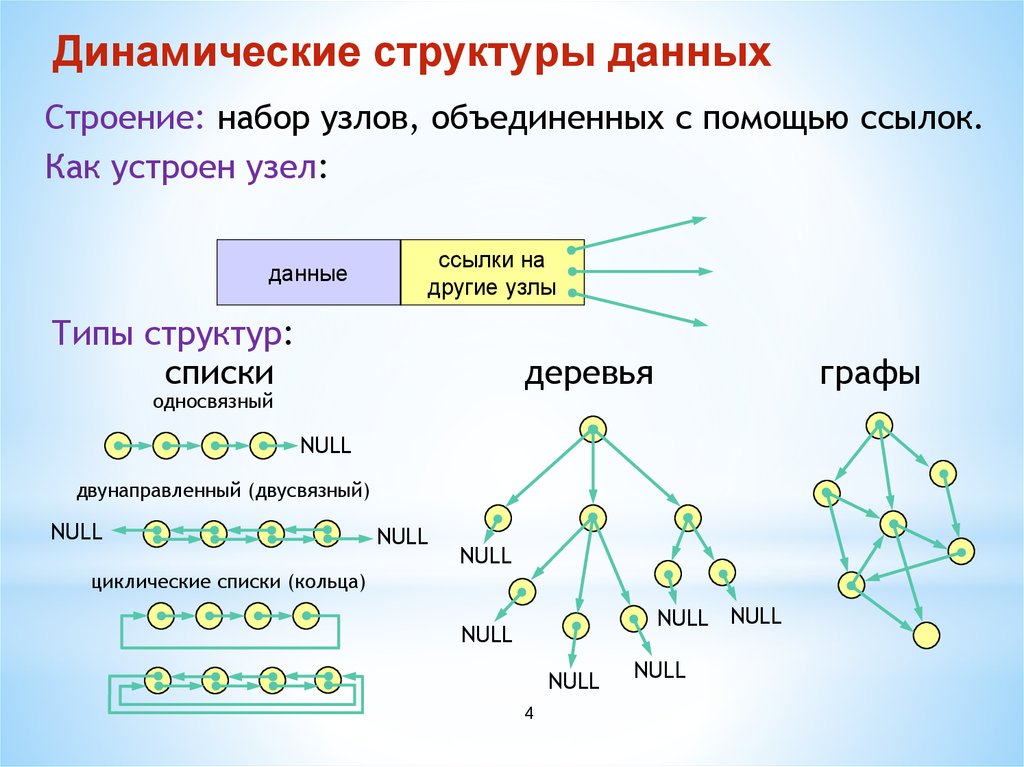 Используя Trie, мы можем искать ключ за время O(M). Однако штраф связан с требованиями к хранилищу Trie.
Используя Trie, мы можем искать ключ за время O(M). Однако штраф связан с требованиями к хранилищу Trie.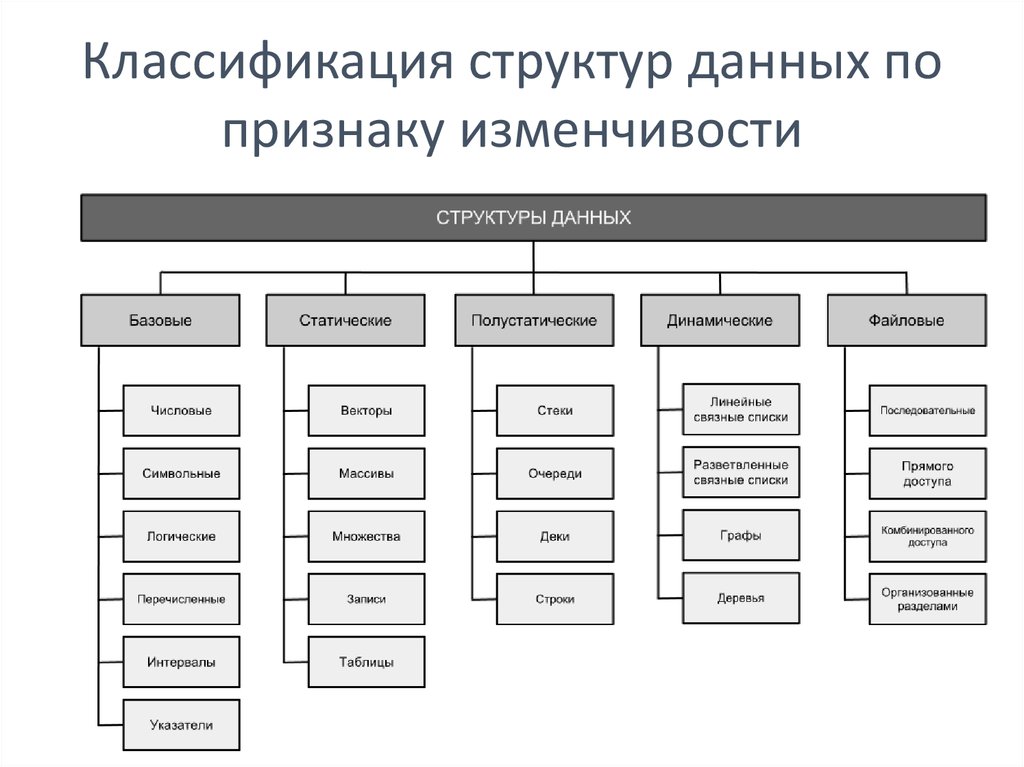 Они обычно используются для реализации алгоритмов кратчайшего пути и алгоритмов обхода графа.
Они обычно используются для реализации алгоритмов кратчайшего пути и алгоритмов обхода графа.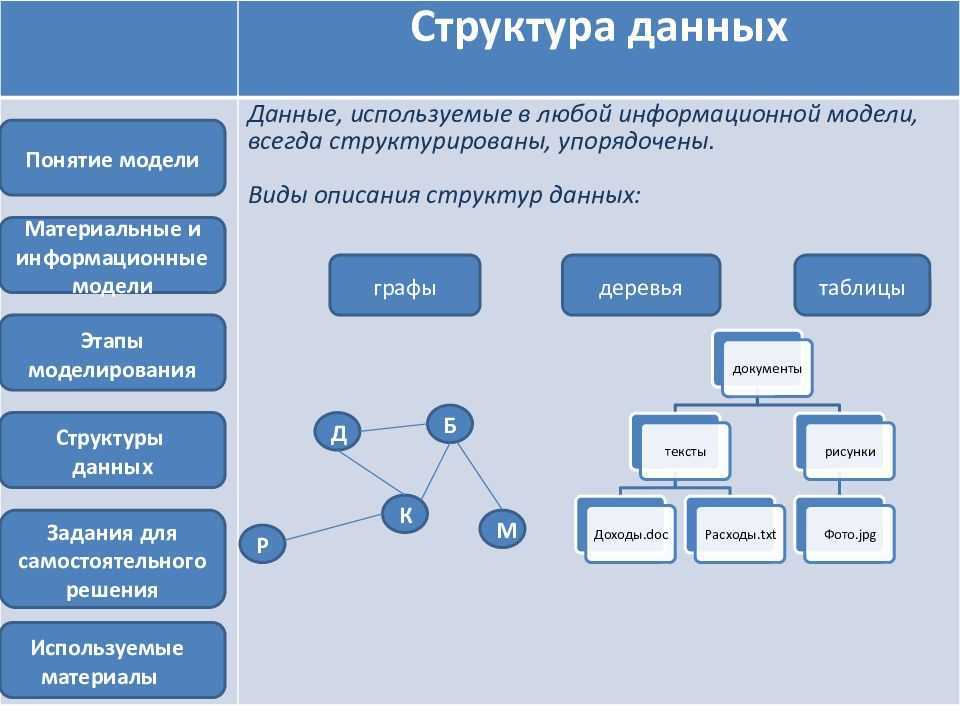 К ним относятся:
К ним относятся: Массив
Массив  Это помогает сократить использование ряда переменных, поскольку нам не нужно создавать отдельную переменную для оценок по каждому предмету. Доступ ко всем меткам можно получить, просто пройдясь по массиву.
Это помогает сократить использование ряда переменных, поскольку нам не нужно создавать отдельную переменную для оценок по каждому предмету. Доступ ко всем меткам можно получить, просто пройдясь по массиву.
 Ссылка на следующий узел задается с помощью указателей, а данные являются значением узла. Каждый узел содержит данные и ссылки на другие узлы. Это упорядоченный набор элементов данных, называемый узлом, и линейный порядок поддерживается указателями. Он имеет преимущество перед массивом по количеству узлов, т.е. размер связанного списка не является фиксированным и может увеличиваться и уменьшаться по мере необходимости, в отличие от массивов.
Ссылка на следующий узел задается с помощью указателей, а данные являются значением узла. Каждый узел содержит данные и ссылки на другие узлы. Это упорядоченный набор элементов данных, называемый узлом, и линейный порядок поддерживается указателями. Он имеет преимущество перед массивом по количеству узлов, т.е. размер связанного списка не является фиксированным и может увеличиваться и уменьшаться по мере необходимости, в отличие от массивов. Например. NULL<-1<->2<->3->NULL
Например. NULL<-1<->2<->3->NULL  Теперь, если в курс добавляется новый предмет, его оценки также добавляются в массив оценок. Но размер массива был фиксированным, и он уже заполнен, поэтому он не может добавить новый элемент. Если мы создадим массив размером намного больше, чем количество субъектов, возможно, что большая часть массива останется пустой. Мы уменьшаем потери пространства. Создается связанный список, который добавляет узел только при введении нового элемента. Вставки и удаления также становятся проще благодаря связному списку.
Теперь, если в курс добавляется новый предмет, его оценки также добавляются в массив оценок. Но размер массива был фиксированным, и он уже заполнен, поэтому он не может добавить новый элемент. Если мы создадим массив размером намного больше, чем количество субъектов, возможно, что большая часть массива останется пустой. Мы уменьшаем потери пространства. Создается связанный список, который добавляет узел только при введении нового элемента. Вставки и удаления также становятся проще благодаря связному списку. 

 Точно так же реализовать функциональность возврата в веб-браузерах.
Точно так же реализовать функциональность возврата в веб-браузерах. Высота стека регистров всегда ограничена, так как размер стека регистров очень мал по сравнению с памятью.
Высота стека регистров всегда ограничена, так как размер стека регистров очень мал по сравнению с памятью.
 (Элемент снимается с лицевой стороны). Это может быть реализовано с использованием как массива, так и связанного списка.
(Элемент снимается с лицевой стороны). Это может быть реализовано с использованием как массива, так и связанного списка.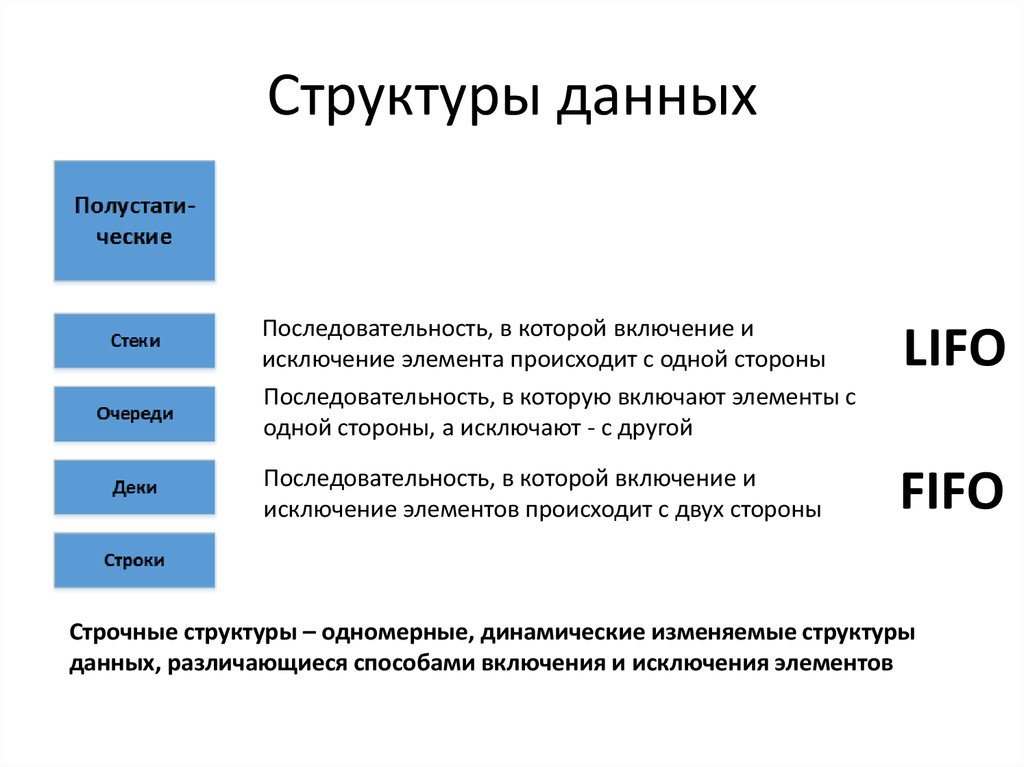 е. в конец очереди.
е. в конец очереди. 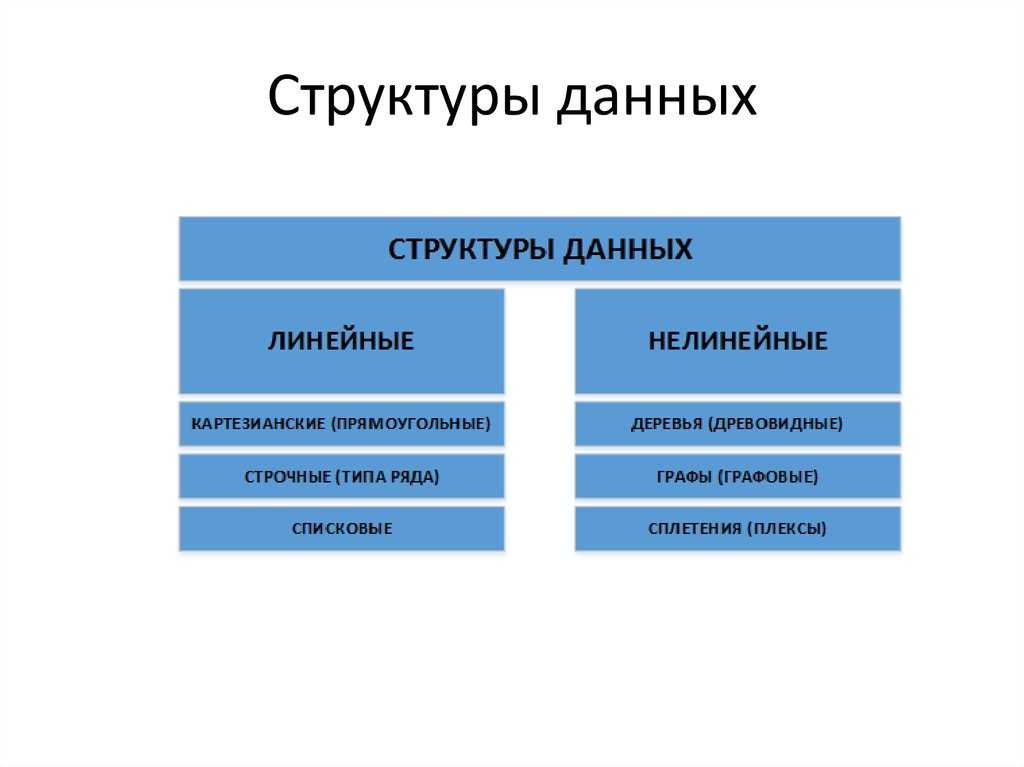
 Как следует из названия, это означает, что элемент может быть вставлен или удален с обоих концов очереди, в отличие от других очередей, в которых это можно сделать только с одного конца. Из-за этого свойства он может не подчиняться свойству First In First Out.
Как следует из названия, это означает, что элемент может быть вставлен или удален с обоих концов очереди, в отличие от других очередей, в которых это можно сделать только с одного конца. Из-за этого свойства он может не подчиняться свойству First In First Out.  и операции удаления.
и операции удаления.