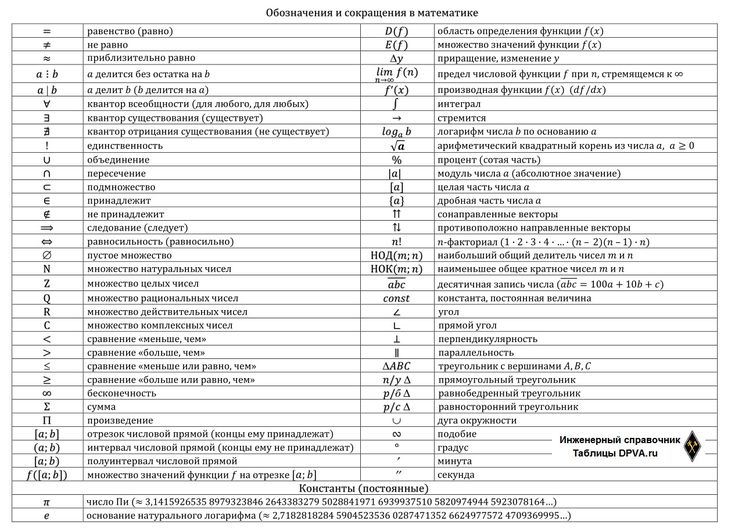
Таблица знаков в геометрии и их значения: пересечение, подобие
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Знаки и символы в геометрии
Ниже представлена таблица с основными математическими символами и знаками, которые используются в геометрии с 7 класса и старше.
| Знак | Название | Значение/описание | Пример |
| ∠ | угол | фигура, состоящая из двух лучей и вершины | ∠ABC = 30° |
| ru/wp-content/uploads/2020/01/ostr-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ostr-ugol.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/ostr-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ostr-ugol.png" />»> | острый угол | угол от 0 до 90 градусов | ∠AOB = 60° |
| ru/wp-content/uploads/2020/01/pryamoy-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/pryamoy-ugol.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/pryamoy-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/pryamoy-ugol.png" />»> | прямой угол | угол, равный 90 граусам | ∠AOB = 90° |
| ru/wp-content/uploads/2020/01/tupoy-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/tupoy-ugol.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/tupoy-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/tupoy-ugol.png" />»> | тупой угол | угол от 90 до 180 градусов | ∠AOB = 120° |
| ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" class="stbSkipLazy aligncenter size-full" width="80" height="240" data-full="https://microexcel.ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" class="stbSkipLazy aligncenter size-full" width="80" height="240" data-full="https://microexcel.ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" />»> | развернутый угол | угол, равный 180 градусам | ∠AOB = 180° |
| ° (или deg) | градус | единица измерения угла, равна 1/360 окружности | 45° |
| ′ | минута | единица измерения угла, 1° = 60′ | α = 70°59′ |
| ″ | секунда | единица измерения угла, 1′ = 60″ | α = 70°59′59″ |
| ru/wp-content/uploads/2020/01/line-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/line-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-exc.png" />»> | линия | бесконечная прямая без начала и конца | |
| ru/wp-content/uploads/2020/01/line-segment-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-segment-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/line-segment-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-segment-exc.png" />»> | отрезок | участок на прямой между точками A и B | |
| ru/wp-content/uploads/2020/01/ray-exc.png" class="stbSkipLazy aligncenter size-full" width="35" height="35" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ray-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/ray-exc.png" class="stbSkipLazy aligncenter size-full" width="35" height="35" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ray-exc.png" />»> | луч | бесконечная прямая, имеющая начало в точке A, но не имеющая конца | |
| ru/wp-content/uploads/2020/01/arc-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/arc-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/arc-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/arc-exc.png" />»> | дуга | дуга, образованная между точками A и B | |
| ⊥ | перпендикулярность | линии (прямые), расположенные под углом 90° по отношению друг к другу | AC ⊥ BC |
| || | параллельность | непересекающиеся прямые (линии) | AB || CD |
| ∩ | пересечение | множество одинаковых элементов, принадлежащих как множеству A, так и B | A ∩ B |
| ∈ / ∉ | принадлежность/ непринадлежность | элемент является/не является элементом заданного множества | a ∈ S |
| ≅ | конгуэнтность | эквивалентность геометрических форм и размеров | ∆ABC ≅ ∆XYZ |
| ~ | подобие | та же форма, но разные размеры | ∆ABC ~ ∆XYZ |
| Δ | треугольник | фигура треугольника | ΔABC ≅ ΔBCD |
| |x-y| | дистанция | дистанция между точками X и Y | | x-y | = 5 |
| π | константа «Пи» | отношение длины окружности к диаметру круга, π = C/d | 141592654…</nobr>» data-order=»<nobr>π = 3.141592654…</nobr>»>π = 3.141592654… |
| рад (rad) или c | радиан | единица измерения угла | 360° = 2π c |
microexcel. ru
ru
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Формулы геометрии.
 Площади фигур — материалы для подготовки к ЕГЭ и ОГЭ по Математике
Площади фигур — материалы для подготовки к ЕГЭ и ОГЭ по МатематикеЧтобы решать задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Начнем с квадрата.
Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна произведению его длины и ширины.
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне. Она также равна произведению его сторон на синус угла между ними.
Для площади треугольника есть целых 5 формул. И все они применяются в задачах ЕГЭ.
1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:
2) Она также равна половине произведения его сторон на синус угла между ними:
3) По формуле Герона, где полупериметр.
4) Также площадь треугольника равна произведению его полупериметра на радис вписанной окружности, S = pr.
5) Еще один способ. Площадь треугольника равна произведению его сторон, деленному на 4 радиуса описанной окружности,
Есть и другие формулы для площади треугольника. Но для решения заданий ЕГЭ, и первой, и второй части, достаточно этих пяти.
Площадь прямоугольного треугольника равна половине произведения его катетов. Она также равна половине произведения гипотенузы на высоту, проведенную к этой гипотенузе:
Площадь правильного треугольника равна квадрату его стороны, умноженному на и деленному на 4:
Площадь трапеции равна произведению полусуммы оснований на высоту,
Также можно сказать, что площадь трапеции равна произведению ее средней линии на высоту,
Площадь произвольного четырехугольника равна половине произведения его диагоналей на синус угла между ними,
Площадь ромба равна произведению квадрата его стороны на синус угла ромба. Она также равна половине произведения диагоналей:
Площадь круга равна произведению числа и квадрата радиуса круга.
Ее также можно записать как произведение числа и квадрата диаметра круга, деленного на 4:
Вспомним важные свойства площадей фигур.
- Равные фигуры имеют равные площади.
- Если фигура составлена из нескольких фигур, не имеющих общих внутренних точек, то ее площадь равна сумме площадей этих фигур.
Пример. Найдем площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1см1см.
Решение:
Найдем площадь фигуры на рисунке как сумму площадей нескольких фигур.
На рисунке это три треугольника и трапеция, указаны их площади. Тогда площадь фигуры равна 10 + 3,5 + 1,5 + 3 = 18.
Ответ: 18.
3. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Треугольники АВС и на рисунке называются подобными.
У треугольника все стороны в k раз длиннее, чем у треугольника АВС. Высота треугольника в k раз длиннее, чем высота треугольника АВС. Тогда площадь треугольника в раз больше, чем площадь треугольника АВС.
Тогда площадь треугольника в раз больше, чем площадь треугольника АВС.
4. На рисунке показаны треугольники АВС и BCD, имеющие общую высоту. Отношение площадей этих треугольников равно отношению АС к CD:
5. Треугольники АВС и АЕС на рисунке имеют одинаковое основание и разные высоты.
Отношение площадей этих треугольников равно отношению их высот:
6. Медиана треугольника делит его на два равновеликих, то есть равных по площади, треугольника.
На рисунке СМ — медиана треугольника АВС. Площади треугольников АСМ и ВСМ равны.
7. Три медианы треугольника делят его на шесть равных по площади треугольников.
На рисунке все 6 треугольников, из которых состоит треугольник АВС, имеют равные лощади.
Задачи ЕГЭ и ОГЭ по теме: Площади фигур.
Задача 1. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен
Решение:
Площадь треугольника равна половине произведения его сторон на синус угла между ними. Поэтому
Поэтому
Ответ: 24.
Задача 2. Площадь треугольника ABC равна 4, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.
Решение:
Так как DE и АВ параллельны, треугольники CDE и САВ подобны с коэффициентом подобия Площади подобных фигур относятся как квадрат коэффициента подобия. Тогда
Ответ: 1.
Задача 3. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?
Решение:
Выразим площадь двумя способами:
Тогда
Ответ: 6.
Задача 4. Площадь треугольника ABC равна 10, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.
Решение:
Треугольник CDE подобен треугольнику CAB с коэффициентом Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому
Следовательно, .
Ответ: 7,5.
Задача 5. В параллелограмме ABCD AB = 3, AD = 21, . Найдите большую высоту параллелограмма.
Решение:
Большая высота — это DH, потому что проведена к меньшей стороне. Из треугольника АDН:
Ответ: 18.
Задача 6. Найдите площадь квадрата, если его диагональ равна 1.
Решение:
Квадрат — это частный случай ромба. Площадь квадрата равна половине произведения его диагоналей. Поэтому она равна 0,5.
Ответ: 0,5.
Задача 7. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.
Решение:
Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2a. Площадь прямоугольника равна тогда одна из сторон равна 3, а другая 6. Периметр P = 2 · 3 + 2 · 6 = 18.
Ответ: 18.
Задача 8.
Решение:
Площадь параллелограмма равна произведению его сторон на синус угла между ними. Площадь прямоугольника равна произведению длины на ширину. Пусть одна сторона параллелограмма и прямоугольника равна вторая равна а острый угол параллелограмма равен Тогда площадь параллелограмма равна а площадь прямоугольника равна
По условию площадь прямоугольника вдвое больше:
Следовательно,
Ответ: 30.
Задача 9. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
Решение:
Площадь параллелограмма равна произведению его основания на высоту, проведенную к этому основанию. Пусть высоты равны соответственно a и b. Тогда S = 5 · a = 10 · b = 40. Поэтому a = 8, b = 4. Большая высота равна 8.
Ответ: 8.
Задача 10. Найдите площадь ромба, если его высота равна 2, а острый угол 30
Решение:
Площадь ромба равна произведению квадрата его стороны на синус угла ромба. С другой стороны, площадь ромба равна произведению его основания на высоту, проведенную к этому основанию. Пусть сторона ромба равна
Получим уравнение:
Корень уравнения a = 4, поэтому
Ответ: 8.
Задача 11. Найдите площадь ромба, если его диагонали равны 4 и 12.
Решение:
Площадь ромба равна половине произведения его диагоналей.
Ответ: 24.
Задача 12. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
Решение:
Трапеция равнобедренная, значит,
Тогда по теореме Пифагора из треугольника ADH:
Ответ: 160.
Задача 13.
Решение:
Проведем высоту CH. Треугольник CHB — прямоугольный, в нем
Треугольник CHB — прямоугольный, в нем
значит, он также равнобедренный, CH = HB = 4.
Ответ: 16.
Задача 14. Высота трапеции равна 5, площадь равна 75. Найдите среднюю линию трапеции.
Решение:
Средняя линия трапеции равна полусумме оснований. Выразим её из формулы площади трапеции:
Ответ: 15.
Задача 15. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту. Пусть высота равна h, тогда
Из этого уравнения получим: h = 4.
Рассмотрим прямоугольный треугольник, гипотенузой которого является боковая сторона трапеции, равная 8, а катетом — высота трапеции. Длина катета равна половине гипотенузы, следовательно, он лежит напротив угла
Ответ: 30.
Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Задача 16. Найдем площадь четырехугольника на рисунке.
Решение:
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным 5. Высоты этих треугольников равны 2 и 3. Тогда площадь четырёхугольника равна сумме площадей двух треугольников:
Ответ: 12,5.
В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Задача 17. Найдем площадь треугольника, изображенного на клетчатой бумаге.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной 5 и трёх прямоугольных треугольников. Видите их на рисунке? Получаем:
Ответ: 10,5.
Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.
Задача 18.
Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.
Решение:
На этом рисунке мы видим часть круга. Площадь всего круга равна так как Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R = 1), а длина дуги данного сектора равна 2, следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Ответ: 1.
Формула Пика
Покажем, как вычислять площадь фигуры, изображенной на координатной плоскости, с помощью формулы Пика.
Задача 19. Найдите площадь многоугольника АВСDE, изображенного на рисунке.
Первый способ:
Площадь многоугольника ABCDE равна сумме площадей треугольника BCD, трапеции BKDE и треугольника AKE.
Имеем:
Второй способ — применить формулу Пика.
Назовем точку координатной плоскости целочисленной, если обе ее координаты — целые числа. На нашем рисунке это точки на пересечениях линий, разделяющих клетчатую бумагу на клетки.
На нашем рисунке это точки на пересечениях линий, разделяющих клетчатую бумагу на клетки.
Площадь многоугольника с целочисленными вершинами равна
.
Здесь В — количество целочисленных точек внутри многоугольника, Г — количество целочисленных точек на границе многоугольника.
Главное — аккуратно посчитать. На нашем рисунке
В = 24 (показаны зеленым),
Г = 8 (показаны красным),
S = 24 + — 1 = 27.
Ответ: 27.
Таблица символов юникода для Вашего сайта
- Информация о материале
- Lesl.ru
- Просмотров: 10563
|
Таблица символов юникода может быть полезна тем, кто создаёт, администрирует или продвигает сайт. Символы, приведённые ниже, могут быть использованы как в Title страниц, так и Description. В зависимости от поисковой системы сниппет будет образован с помощью одного или сразу двух этих метаданных. Экспериментируйте и привлекайте больше посетителей, увеличивайте заходы на сайт и количество «продаж»! |
||
ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ
■ □ ▢ ▣ ▤ ▥ ▦ ▧ ▨ ▩ ▪ ▫ ▬ ▭ ▮ ▯ ▰ ▱ ▲ △ ▴ ▵ ▶ ▷ ► ▻ ▼ ▽ ▾ ▿ ◀ ◁ ◄ ◅ ◆ ◇ ◈ ◉ ◊ ○ ◌ ◍ ◎ ● ◐ ◑ ◒ ◓ ◔ ◕ ◖ ◗ ◘ ◙ ◚ ◛ ◜ ◝ ◞ ◟ ◠ ◡ ◢ ◣ ◤ ◥ ◦ ◧ ◨ ◩ ◪ ◫ ◬ ◭ ◮ ◯ ░ ▒ ▓ █ ❏ ❐ ❑ ❒
ЧИСЛА И НУМЕРАЦИЯ
① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩ ⑪ ⑫ ⑬ ⑭ ⑮ ⑯ ⑰ ⑱ ⑲ ⑳ ⑴ ⑵ ⑶ ⑷ ⑸ ⑹ ⑺ ⑻ ⑼ ⑽ ⑾ ⑿ ⒀ ⒁ ⒂ ⒃ ⒄ ⒅ ⒆ ⒇ ⒈ ⒉ ⒊ ⒋ ⒌ ⒍ ⒎ ⒏ ⒐ ⒑ ⒒ ⒓ ⒔ ⒕ ⒖ ⒗ ⒘ ⒙ ⒚ ⒛ ⒜ ⒝ ⒞ ⒟ ⒠ ⒡ ⒢ ⒣ ⒤ ⒥ ⒦ ⒧ ⒨ ⒩ ⒪ ⒫ ⒬ ⒭ ⒮ ⒯ ⒰ ⒱ ⒲ ⒳ ⒴ ⒵ Ⓐ Ⓑ Ⓒ Ⓓ Ⓔ Ⓕ Ⓖ Ⓗ Ⓘ Ⓙ Ⓚ Ⓛ Ⓜ Ⓝ Ⓞ Ⓟ Ⓠ Ⓡ Ⓢ Ⓣ Ⓤ Ⓥ Ⓦ Ⓧ Ⓨ Ⓩ ⓐ ⓑ ⓒ ⓓ ⓔ ⓕ ⓖ ⓗ ⓘ ⓙ ⓚ ⓛ ⓜ ⓝ ⓞ ⓟ ⓠ ⓡ ⓢ ⓣ ⓤ ⓥ ⓦ ⓧ ⓨ ⓩ ⓪ ⓿ ❶ ❷ ❸ ❹ ❺ ❻ ❼ ❽ ❾ ❿ ⓫ ⓬ ⓭ ⓮ ⓯ ⓰ ⓱ ⓲ ⓳ ⓴
ПАЛОЧКИ, ЧЁРТОЧКИ И КРЕСТИКИ
─ ━ │ ┃ ┄ ┅ ┆ ┇ ┈ ┉ ┊ ┋ ┌ ┍ ┎ ┏ ┐ ┑ ┒ ┓ └ ┕ ┖ ┗ ┘ ┙ ┚ ┛ ├ ┝ ┞ ┟ ┠ ┡ ┢ ┣ ┤ ┥ ┦ ┧ ┨ ┩ ┪ ┫ ┬ ┭ ┮ ┯ ┰ ┱ ┲ ┳ ┴ ┵ ┶ ┷ ┸ ┹ ┺ ┻ ┼ ┽ ┾ ┿ ╀ ╁ ╂ ╃ ╄ ╅ ╆ ╇ ╈ ╉ ╊ ╋ ╌ ╍ ╎ ╏ ═ ║ ╒ ╓ ╔ ╕ ╖ ╗ ╘ ╙ ╚ ╛ ╜ ╝ ╞ ╟ ╠ ╡ ╢ ╣ ╤ ╥ ╦ ╧ ╨ ╩ ╪ ╫ ╬ ╭ ╮ ╯ ╰ ╱ ╲ ╳ ╴ ╵ ╶ ╷ ╸ ╹ ╺ ╻ ╼ ╽ ╾ ╿ ▀ ▁ ▂ ▃ ▄ ▅ ▆ ▇ █ ▉ ▊ ▋ ▌ ▍ ▎ ▏ ▐ ░ ▒ ▓ ▔ ▕
СИМВОЛЫ КВАДРАТИКОВ, СТРЕЛОЧЕК, КОЛБОЧЕК
■ □ ▢ ▣ ▤ ▥ ▦ ▧ ▨ ▩ ▪ ▫ ▬ ▭ ▮ ▯ ▰ ▱ ▲ △ ▴ ▵ ▶ ▷ ▸ ▹ ► ▻ ▼ ▽ ▾ ▿ ◀ ◁ ◂ ◃ ◄ ◅ ◆ ◇ ◈ ◉ ◊ ○ ◌ ◍ ◎ ● ◐ ◑ ◒ ◓ ◔ ◕ ◖ ◗ ◘ ◙ ◚ ◛ ◜ ◝ ◞ ◟ ◠ ◡ ◢ ◣ ◤ ◥ ◦ ◧ ◨ ◩ ◪ ◫ ◬ ◭ ◮ ◯ ◽ ◾
МАТЕМАТИКА,ФИЗИКА
ℂ ℃ ℄ ℅ ℆ ℇ ℈ ℉ ℊ ℋ ℌ ℍ ℎ ℏ ℐ ℑ ℒ ℓ ℔ ℕ № ℗ ℘ ℙ ℚ ℛ ℜ ℝ ℞ ℟ ℠ ℡ ™ ℣ ℤ ℥ Ω ℧ ℨ ℩ K Å ℬ ℭ ℮ ℯ ℰ ℱ Ⅎ ℳ ℴ ⅓ ⅔ ⅕ ⅖ ⅗ ⅘ ⅙ ⅚ ⅛ ⅜ ⅝ ⅞ ⅟ ℵ ℶ ℷ ℸ ⅍ ⅎ Ⅽ Ⅾ Ⅿ∀ ∁ ∂ ∃ ∄ ∅ ∆ ∇ ∈ ∉ ∊ ∋ ∌ ∍ ∎ ∏ ∐ ∑ − ∓ ∔ ∕ ∖ ∗ ∘ ∙ √ ∛ ∜ ∝ ∞ ∟ ∠ ∡ ∢ ∣ ∤ ∥ ∦ ∧ ∨ ∩ ∪ ∫ ∬ ∭ ∮ ∯ ∰ ∱ ∲ ∳ ∴ ∵ ∶ ∷ ∸ ∹ ∺ ∻ ∼ ∽ ∾ ∿ ≀ ≁ ≂ ≃ ≄ ≅ ≆ ≇ ≈ ≉ ≊ ≋ ≌ ≍ ≎ ≏ ≐ ≑ ≒ ≓ ≔ ≕ ≖ ≗ ≘ ≙ ≚ ≛ ≜ ≝ ≞ ≟ ≠ ≡ ≢ ≣ ≤ ≥ ≦ ≧ ≨ ≩ ≪ ≫ ≬ ≭ ≮ ≯ ≰ ≱ ≲ ≳ ≴ ≵ ≶ ≷ ≸ ≹ ≺ ≻ ≼ ≽ ≾ ≿ ⊀ ⊁ ⊂ ⊃ ⊄ ⊅ ⊆ ⊇ ⊈ ⊉ ⊊ ⊋ ⊌ ⊍ ⊎ ⋐ ⋑ ⋒ ⋓ ⋔ ⋕ ⋖ ⋗ ⋘ ⋙ ⋚ ⋛ ⋜ ⋝ ⋞ ⋟ ⋠ ⋡ ⋢ ⋣ ⋤ ⋥ ⋦ ⋧ ⋨ ⋩ ⋪ ⋫ ⋬ ⋭ ⋮ ⋯ ⋰ ⋱ ⋲ ⋳ ⋴ ⋵ ⋶ ⋷ ⋸ ⋹ ⋺ ⋻ ⋼ ⋽ ⋾ ⋿ ⌀
РИМСКИЕ ЧИСЛА
ⅰ ⅱ ⅲ ⅳ ⅴ ⅵ ⅶ ⅷ ⅸ ⅹ ⅺ ⅻ ⅼ Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ Ⅺ Ⅻ Ⅼ
ЗНАКИ ЗАДИАКА
♈ ♉ ♊ ♋ ♌ ♍ ♎ ♏ ♐ ♑ ♒ ♓
ЦВЕТЫ
⚜ ✥ ✤ ✻ ✼ ✽ ✾ ❀ ✿ ❁ ❃ ❇ ❈ ❉ ❊ ❋ ⚘ ☘
СЕРДЕЧКИ
❦ ❧ ☙ ❥ ❣ ♡ ♥ ❤ ➳ ღ
СТРЕЛКИ, УКАЗАТЕЛИ
← ↑ → ↓ ↔ ↕ ↖ ↗ ↘ ↙ ↚ ↛ ↜ ↝ ↞ ↟ ↠ ↡ ↢ ↣ ↤ ↥ ↦ ↧ ↨ ↩ ↪ ↫ ↬ ↭ ↮ ↯ ↰ ↱ ↲ ↳ ↴ ↵ ↶ ↷ ↸ ↹ ↺ ↻ ↼ ↽ ↾ ↿ ⇀ ⇁ ⇂ ⇃ ⇄ ⇅ ⇆ ⇇ ⇈ ⇉ ⇊ ⇋ ⇌ ⇍ ⇎ ⇏ ⇐ ⇑ ⇒ ⇓ ⇔ ⇕ ⇖ ⇗ ⇘ ⇙ ⇚ ⇛ ⇜ ⇝ ⇞ ⇟ ⇠ ⇡ ⇢ ⇣ ⇤ ⇥ ⇦ ⇧ ⇨ ⇩ ⇪ ⇫ ⇬ ⇭ ⇮ ⇯ ⇰ ⇱ ⇲ ⇳ ⇴ ⇵ ⇶ ⇷ ⇸ ⇹ ⇺ ⇻ ⇼ ⇽ ⇾ ⇿ ⊲ ⊳ ⊴ ⊵ ⊶ ⊷ ⊸ ⊹ ⊺ ⊻ ⊼ ⊽ ⊾ ⊿ ⋀ ⋁ ⋂ ⋃ ⋄ ⋅ ⋆ ⋇ ⋈ ⋉ ⋊ ⋋ ⋌ ⋍ ⋎ ⋏ ⌁ ⌂ ⌃ ⌄ ⌅ ⌆ ⌇ ⌈ ⌉ ⌊ ⌋ ⌌ ⌍ ⌎ ⌏ ⌐ ⌑ ⌒ ⌓ ⌔ ⌕ ⌖ ⌗ ⌘ ⌙ ⌚ ⌛ ⌜ ⌝ ⌞ ⌟ ⌠ ⌡ ⌢ ⌣ ⌤ ⌥ ⌦ ⌧ ⏎ ⏏ ⟶ ⟷ ⟸ ⟹ ⟺ ⟻ ⟼ ⟽ ⟾ ⟿ ⤀ ⤁ ⤂ ⤃ ⤄ ⤅ ⤆ ⤇ ⤈ ⤉ ⤊ ⤋ ⤌ ⤍ ⤎ ⤏ ⤐ ⤑ ⤒ ⤓ ⤔ ⤕ ⤖ ⤗ ⤘ ⤙ ⤚ ⤛ ⤜ ⤝ ⤞ ⤟ ⤠ ⤡
ШАХМАТНЫЕ ФИГУРЫ, МАСТИ, НОТЫ
♕ ♖ ♗ ♘ ♙ ♚ ♛ ♜ ♝ ♞ ♟ ♠ ♡ ♢ ♣ ♤ ♥ ♦ ♧ ♩ ♪ ♫ ♬ ♭ ♮ ♯
ТЕЛЕФОНЫ, Е-МАЙЛЫ, КАНЦЕЛЯРИЯ
℡ ⌕ ☎ ☏ ✆ @ ✉ ☕ ✁ ✂ ✃ ✄ ✍ ✎ ✏ ✐ ✑ ✒ ⌦ ⌫ ⌧ ㍶
СПЕЦИАЛЬНЫЕ СИМВОЛЫ
☀ ☁ ☂ ☃ ☄ ★ ☆ ☇ ☈ ☉ ☊ ☋ ☌ ☍ ☎ ☏ ☐ ☑ ☒ ☓ ☔ ☕ ☖ ☗ ☘ ☙ ☚ ☛ ☜ ☝ ☞ ☟ ☠ ☡ ☢ ☣ ☤ ☥ ☦ ☧ ☨ ☩ ☪ ☫ ☬ ☭ ☮ ☯ ☰ ☱ ☲ ☳ ☴ ☵ ☶ ☷ ♮ ♯ ♰ ♱ ✁ ✂ ✃ ✄ ✆ ✇ ✈ ✉ ✌ ✍ ✎ ✏ ✐ ✑ ✒ ✓ ✔ ✕ ✖ ✗ ✘ ✙ ✚ ✛ ✜ ✝ ✞ ✟ ✠ ✡✢ ✣ ✤ ✥ ✦ ✧ ✩ ✪ ✫ ✬ ✭ ✮ ✯ ✰ ✱ ✲ ✳ ✴ ✵ ✶ ✷ ✸ ✹ ✺ ✻ ✼ ✽ ✾ ✿ ❀ ❁ ❂ ❃ ❄ ❅ ❆ ❇ ❈ ❉ ❊ ❋ ❍ ❏ ❐ ❑ ❒ ❖ ❡ ❢ ❣ ❤ ❥ ❦ ❧ ❘ ❙ ❚ ❛ ❜ ❝ ❞ ➱ ➲ ➳ ➴ ➵ ➶ ➷ ➸ ➘ ➙ ➚ ➛ ➜ ➝ ➞ ➟ ➠ ➡ ➢ ➣ ➤ ➥ ➦ ➧ ➨ ➩ ➪ ➫ ➬ ➭ ➮ ➯ ➔ ???? ➹ ➺ ➻ ➼ ➽ ➾ ⟠ ⟡ ⟦ ⟧ ⟨ ⟩ ⟪ ⟫ ⟰ ⟱ ⟲ ⟳ ⟴ ⟵ ஆ இ ஐ ஓ ண ன ஹ ௫ ஞ ௵ ௸ ஊ ௹ ௺ ௐ ඐ ඇ ජ ණ ඏ බ ෆ ឈ ឱ ណ ឃ ៚ ៙ ⚢ ⚣ ⚤ ⚥ ⚦ ⚧ ⚨ ⚩ ☪ ☫ ☬ ☥ ⚳ ⚴ ⚵ ⚶ ⚷ ⚸ ♆ ⚕ ⚚ ☤ ♩ ♪ ♫ ♬ ♭ ♮ ♯ ☚ ☛ ☜ ☝ ☞ ☟ ☝ ☑ ✅ ✓ ✔ ✖ ✗ ✘ ☑ ☒ ☀ ☁ ☂ ☔ ☇ ☭ ☢ ⚑ ☭ ☮ ⚠ ⚡ ♨ ⚒ ⚓ ⚔ ⚛ ☣ ⌚ ⌛ ⚐ ☘ ✌ ✇ ∞ © ☠ ✉ ☯ ☭ ? $ £ ¢ ₽ ⭐
Надеемся, что данные коды (кодировки) символов Юникода помогут Вам при провдвижении сайта. В противном случае Вы всегда можете доверить это дело специалистам — команде LESL.RU.
В противном случае Вы всегда можете доверить это дело специалистам — команде LESL.RU.
Если Вы хотите заказать продвижение сайта у команды LESL.RU, вышлите нам на почту [email protected] Ваш сайт для предварительного анализа. Мы изучим тему и составим индивидуальное предложение по продвижению, исходя из тематики сайта и его региона.
Полезные статьи
11 апреля, 2022
Как администрировать сайт на…
Подробнее…
16 марта, 2022
Как создать презентацию в…
Подробнее…
05 июля, 2021
Как сделать сниппет для…
Подробнее. ..
..
14 ноября, 2020
Бэкап сайта. Что это…
Подробнее…
08 апреля, 2020
Обложка для Ютуба. Размер…
Подробнее…
10 марта, 2020
Маркетинг-кит компании. Создание, цена…
Подробнее…
04 марта, 2020
Как собрать семантическое ядро
Подробнее…
10 января, 2020
Презентация торгового центра
Подробнее. ..
..
29 октября, 2019
Вопросы начинающего владельца сайта
Подробнее…
18 сентября, 2019
Профессиональный подход в создании…
Подробнее…
13 июня, 2019
Презентация магазина для арендодателя
Подробнее…
13 мая, 2019
Как правильно выбрать доменное…
Подробнее. ..
..
06 мая, 2019
Презентация ресторана для арендодателя.…
Подробнее…
27 февраля, 2019
Какой выбрать хостинг для…
Подробнее…
06 февраля, 2019
Способы создания мультиязычного сайта
Подробнее…
21 января, 2019
Самостоятельное оформление ВКонтакте и…
Подробнее. ..
..
19 января, 2019
80 золотых правил копирайтинга
Подробнее…
13 декабря, 2018
Сколько стоит изготовление презентации…
Подробнее…
22 ноября, 2018
Презентация строительной компании. Примеры…
Подробнее…
07 ноября, 2018
Как сделать 3D-фотографию в…
Подробнее. ..
..
Таблица символов по геометрии
Геометрия и тригонометрия – это разделы математики, связанные с геометрическими фигурами и углами треугольников. В следующем списке перечислены некоторые из наиболее заметных символов в этих темах, а также их использование и значение.
Для удобства чтения эти символы сгруппированы по функциям в таблицы. Другие полные списки математических символов — с разбивкой по темам и типам — также можно найти на соответствующих страницах ниже (или на панели навигации).
В геометрии точки и линии образуют основу более сложных геометрических фигур, таких как треугольники, окружности, четырехугольники и многоугольники. В следующей таблице приведены некоторые из наиболее заметных символов, связанных с ними, а также значение каждого символа и пример.
Таблица символов по геометрии:
| Символ | Имя символа | Значение / определение | Пример |
|---|---|---|---|
| ∠ | угол | образован двумя лучами | ∠ABC = 30° |
| измеренный угол | АВС = 30° | ||
| сферический угол | АОВ = 30° | ||
| ∟ | прямой угол | = 90° | α = 90° |
| ° | степень | 1 оборот = 360° | α = 60° |
| град | степень | 1 оборот = 360 градусов | α = 60 градусов |
| ′ | простой | угловых минут, 1° = 60′ | α = 60°59′ |
| ″ | двойной штрих | угловых секунд, 1′ = 60″ | α = 60°59′59″ |
| строка | бесконечная линия | ||
| АВ | сегмент линии | линия из пункта А в пункт Б | |
| луч | линия, начинающаяся с точки А | ||
| дуга | дуга из точки А в точку В | = 60° | |
| ⊥ | перпендикулярно | перпендикулярных линий (угол 90°) | AC ⊥ БК |
| ∥ | параллельно | параллельных линий | АВ ∥ CD |
| ≅ | соответствует | эквивалентность геометрических фигур и размера | ∆АВС ≅ ∆XYZ |
| ~ | сходство | одинаковые формы, но разные размеры | ∆АВС ~ ∆XYZ |
| Δ | треугольник | треугольник | ΔАВС ≅ ΔBCD |
| | х — у | | расстояние | расстояние между точками x и y | | х — у | = 5 |
| № | постоянная Пи | π = 3,141592654. .. ..— отношение длины окружности к диаметру круга | с = π ⋅ d = 2⋅ π ⋅ r |
| рад | радиан | радиан Единица измерения угла | 360° = 2π рад |
| с | радиан | радиан Единица измерения угла | 360° = 2π с |
| град | град/гон | градусный угловой блок | 360° = 400 град |
| г | град/гон | градусный угловой блок | 360° = 400 г |
Символы алгебры »
В настоящее время у нас есть около 5611 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и преподавателей, дизайнеров и просто для всех.
Вы можете найти на этой странице финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы автокредита и калькуляторы лизинга, калькуляторы процентов, калькуляторы выплат, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, калькуляторы финансов, калькуляторы подоходного налога , калькуляторы сложных процентов, калькулятор зарплаты, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор ИМТ, калькуляторы калорий, калькулятор жировых отложений, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, калькулятор процентов, генератор случайных чисел, калькулятор треугольника, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор среднего балла, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генератор паролей калькулятор преобразования tor и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebook (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook). Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)
Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)
Есть много очень полезных бесплатных онлайн-инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или пришлете нам какие-либо предложения по другим инструментам, которые придут вам на ум. Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или нуждается в лучшем переводе, сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.
Ниже перечислены наиболее часто используемые многими пользователями по всему миру.
- Бесплатные онлайн-калькуляторы и инструменты
- Калькуляторы часовых поясов/часов/дат
- Бесплатные онлайн-калькуляторы преобразования единиц
- Бесплатные онлайн-инструменты для веб-дизайна
- Бесплатные онлайн-инструменты для электричества и электроники
- Математика 1 Инструменты
- 0 Текст Онлайн-инструменты
- PDF Tools
- Code
- Экология
- Others
- Бесплатные онлайн-загрузчики для социальных сетей
- Numbers
- Algebra
- Trigonometry
- Probability & Statistics
- Calculus & analysis
- Mathematical symbols
- Algebra symbols
- Asterisk sign
- Basic math symbols
- Calculus symbols
- Division sign
- Equals sign
- Geometry symbols
- Greek alphabet
- Символ бесконечности
- Символ бесконечности ALT-код
- Символ бесконечности в MS Word
- Символ бесконечности на Facebook
- Символ бесконечной бесконечности на клавиатуре
- Символ бесконечности на MAC
- — это бесконечность.
 Реальное число
Реальное число - Логические символы
- Минус Знак
- Умножение Dot 9033 Статистические символы
- Знак времени
И мы все еще развиваемся. Наша цель — стать универсальным сайтом для людей, которым нужно быстро рассчитать или найти быстрый ответ для основных конверсий.
Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Поэтому все наши инструменты и сервисы абсолютно бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый из них строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите малейшую ошибку — ваш вклад чрезвычайно ценен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.
Нашли ошибку? Дайте нам знать!
Мы получили ваше сообщение, мы свяжемся с вами в ближайшее время.
Ой! Что-то пошло не так, обновите страницу и повторите попытку.
Идентификатор страницы: 1625
Список символов геометрии и тригонометрии
Геометрия и тригонометрия — разделы математики, связанные с геометрическими фигурами и углами треугольников. В следующем списке перечислены некоторые из наиболее заметных символов в этих темах, а также их использование и значение.
В целях удобочитаемости эти символы классифицируются по их функциям в таблицы. Другие полные списки математических символов — с разбивкой по темам и типам — также можно найти на соответствующих страницах ниже (или на панели навигации).
Содержание
Предпочитаете версию в формате PDF?
Получите основную сводку математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX.
Да. Это было бы полезно.
Символы, относящиеся к точкам/линиям
В геометрии точек и линий образуют основу более сложных геометрических фигур, таких как треугольники, окружности, четырехугольники и многоугольники. В следующей таблице приведены некоторые из наиболее заметных символов, связанных с ними, а также значение каждого символа и пример.
В следующей таблице приведены некоторые из наиболее заметных символов, связанных с ними, а также значение каждого символа и пример.
| Символ Название | Пояснение | Пример | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| $A$, $B$, $C$, $D$, $P$, $Q$, $R$, $S$ | Переменные для точек | Если $P_1 =P_2$, то $\overline{P_1 Q} = \overline{P_2 Q}$. | |||||||||
| $ \ ell $ | Переменная для строк | $ \ ell_1 \ parallel \ ell_2 $ | |||||||||
| $ \ OverleftrightRow {ab} $ | 696666666 ($ 9027 | 66666 ($ 9027 | 66666 ($ 9027 | 6666 ($ | 6666 ($ | 6666 ($ | 6666 ($ | 6666 ($ | 9 | ). и $B$ | $\overleftrightarrow{AB}=\overleftrightarrow{BA}$ |
| $\overline{AB}$ | Отрезок между точками $A$ и $B$ | $\overline{AB} \cong \overline{PQ}$ | |||||||||
| $\overrightarrow{AB}$ | Луч из точки $A $ до точки $B$ | $\overrightarrow{AB} \ne \overrightarrow{BA}$ | |||||||||
| $|AB|$ | Расстояние от точки $A$ до точки $B$ | $| до нашей эры | \le \\ |AB| + |AC|$ | |||||||||
| $\ell_1 \parallel \ell_2$ | Строки $\ell_1$ и $\ell_2$ равны parallel | Если $\square ABCD$ — параллелограмм, то $\overline{AB} \parallel \overline{CD}$. 2.$ 2.$ | |||||||||
| $\ell_1 \not\perp \ell_2$ | Линии $\ell_1$ и $\ell_2$ неперпендикулярны | Если $\overline{AB} \not\perp \overline{BC} $, то $\square ABCD$ не является прямоугольником. |
Символы, связанные с углом
Угол по существу соответствует «открытию» геометрической фигуры, количественное определение которого приводит к значительному развитию геометрии и тригонометрии. В следующей таблице приведены некоторые из наиболее заметных символов, связанных с углами, а также значение каждого символа и пример. 9{\prime\prime} = \left(\dfrac{38}{60}\right)’$
Символы, связанные с окружностью
точек окружности можно рассматривать как равноудаленные друг от друга точку и часто играет решающую роль в развитии евклидовой геометрии и тригонометрии. В следующей таблице приведены некоторые из наиболее заметных символов, связанных с кругом, а также их соответствующее значение и пример.
В следующей таблице приведены некоторые из наиболее заметных символов, связанных с кругом, а также их соответствующее значение и пример.
| Название символа | Объяснение | Пример | |
|---|---|---|---|
| $ $ | Variable для Circle (или $ ). одинаковый радиус, то они равны. | ||
| $\odot P$ | Окружность с центром вокруг точки $P$ | Если $P \ne Q$, то $\odot P \ne \odot Q$. | |
| $r$ | Радиус окружности | $r = \sqrt{\dfrac{A}{\pi}}$ | |
| $d$ | Диаметр окружности | $d =2r$ 90 $C$Окружность окружности | $C=2\pi r$ |
| $\overparen{AB}$ | Сегмент дуги между точками $A$ и $B$ 2 \overline{AB}$ — это диаметр, тогда $\overparen{AB}$ будет соответствовать полуокружности. |
Тригонометрические функции
В тригонометрии многие функции используются для связи углов внутри прямоугольного треугольника с его различными длинами или отношениями . В следующей таблице описаны некоторые из наиболее распространенных функций этой категории, а также их соответствующее использование и примеры.
| Имя символа | Объяснение | Пример |
|---|---|---|
| $\sin \theta$ | 9{-1}x$ Функция арктангенса (арктангенс) | $\displaystyle \lim_{x \to \infty} \arctan x = \dfrac{\pi}{2}$ |
- Sine function
- Cosine function
- Tangent function
- Cosecant function
- Secant function
- Cotangent function
В элементарной геометрии большая часть исследования вращается вокруг анализа многоугольников , многогранников и других трехмерных фигур . В следующей таблице приведены некоторые из наиболее заметных символов в этих категориях, а также соответствующее значение и использование каждого символа.
В следующей таблице приведены некоторые из наиболее заметных символов в этих категориях, а также соответствующее значение и использование каждого символа.
| Обозначение Название | Объяснение | Пример | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $\triangle ABC$ | $C$7$s, $Avertices 0027| $\треугольник ABC \sim \треугольник A’B’C’$ | | |||||||||||
| $\square ABCD$ | Квадрат / Четырехугольники с вершинами $A$, $B$, $C$ и $ D$ | Если $\overline{AB} \parallel \overline{CD}$, то $\square ABCD$ является трапецией. | |||||||||||
| $ \ pi $ (Capital Pi) | Переменная для плоскостей | $ \ pi_1 \ parallel \ pi_2 $ | |||||||||||
| $ f \ f ‘$ | |||||||||||||
| $ f \ f’ $ | . вычислить $F’$ | $\triangle ABC \sim \triangle PQR$ | |||||||||||
| $F \nsim F’$ | Фигура $F$ не похожа на фигуру $F’$ | Так как $F$ правильный пятиугольник и $F’$ не является $F \nsim F’$. | |||||||||||
| $F \cong F’$ | Фигура $F$ конгруэнтна фигуре $F’$ | $\triangle ABC \cong \triangle A’B’C’$ $\implies \overline {AB} \cong \overline{A’B’}$ | |||||||||||
| $F \ncong F’$ | Цифра $F$ равна не соответствует фигуре $F’$ | $\квадрат ABCD \nsim \\ \квадрат A’B’C’D’ \ подразумевает \\ \квадрат ABCD \ncong \\ \квадрат A’B’C’D ‘ $ | |||||||||||
| $\varphi$ (phi) | Золотое сечение | $\varphi = \dfrac{1 + \sqrt{5}}{2} \ приблизительно 1,618$ | h 90 | Высота треугольника/четырехугольника/ Трехмерные фигуры | Поскольку $h = 5$, $A=\dfrac{5 \cdot 3}{2}$. | ||||||||
| $b$ | Основание треугольника/четырехугольника | Для тупоугольного треугольника $b$ соответствует расширенному основанию треугольника. | |||||||||||
| $l$ | Длина прямоугольника/прямоугольного тела | Когда $l=10$, $A= 10 \cdot 20$. | |||||||||||
| $ W $ | Ширина Прямоугольника/Прямоугольное твердое вещество | $ A = LW $ | |||||||||||
| $ P $ | PERIMET| $V$ | Количество вершин в многограннике | Для куба $V = 8$. | $E$ | Количество ребер в многограннике | Вообще говоря, $E \ge V$ для многогранников. | $F$ | Количество граней в многограннике | Для тетраэдра $F=4$. | $\chi$ (chi) | Эйлерова характеристика | Для выпуклых многогранников $\chi = V-E + F = \\ 2.$ | |
На следующих рисунках показаны 5 платоновых тел (правильные, выпуклые многогранники) вместе с соответствующим количеством вершин, ребер и граней.
- Тетраэдр $(V= 4, E= 6, \\ F=4, \chi=2)$
- Куб $(V=8, E=12, \\ F=6, \ chi=2)$
- Октаэдр $(V=6, E=12, \\ F=8, \chi=2)$
- Додекаэдр $(V=20, E=30, F=12 , \chi= 2)$
- Икосаэдр $(V=12, E=30, F=20, \chi=2)$
Основной список символов см. в разделе Математические символы. Списки символов, классифицированных по , типу и по теме , см. на соответствующих страницах ниже.
в разделе Математические символы. Списки символов, классифицированных по , типу и по теме , см. на соответствующих страницах ниже.
Предпочитаете версию в формате PDF?
Получите основную сводку математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX.
Да. Это было бы полезно.
Дополнительные ресурсы
- Полное руководство по изучению высшей математики : Автономная система из 10 принципов для эффективного изучения высшей математики, мышления и решения задач
- Полное справочное руководство по LaTeX : Полное справочное руководство, чтобы сделать процесс LaTeXing более эффективным и менее болезненным
- 10 заповедей обучения высшей математике : Иллюстрированное веб-руководство по 10 масштабируемым правилам изучения высшей математики
- Полный глоссарий жаргона высшей математики : Обзор высшей математики в 106 терминах
Геометрические символы — схема, использование и часто задаваемые вопросы
В астрономии геометрические фигуры помогают понять расположение различных планет, Солнечной системы и разные звезды. Наши планеты круглые. Орбиты овальные. Многие геометрические принципы и машины используются в астрономии. Многие важные расчеты и открытия, сделанные в астрономии, возможны с помощью геометрии. Геометрия разработана, чтобы быть эффективным руководством для измерения скорости, местоположения, объема и длины небесных тел. Астрономия занимается изучением этих объектов, а геометрия помогает определить ширину и расположение атмосферы.
Наши планеты круглые. Орбиты овальные. Многие геометрические принципы и машины используются в астрономии. Многие важные расчеты и открытия, сделанные в астрономии, возможны с помощью геометрии. Геометрия разработана, чтобы быть эффективным руководством для измерения скорости, местоположения, объема и длины небесных тел. Астрономия занимается изучением этих объектов, а геометрия помогает определить ширину и расположение атмосферы.
Геометрия — это наука о формах. Он широко подразделяется на два типа: плоскостная геометрия и объемная геометрия. Планиметрия имеет дело с двумерными фигурами, такими как квадраты, круги, прямоугольники, треугольники и многие другие. Принимая во внимание, что геометрия твердого тела занимается изучением трехмерных форм, таких как куб, прямоугольный параллелепипед, цилиндр, конус, сфера и многие другие.
Изучение этой формы необходимо для нахождения длины, ширины, площади, объема, периметра и многих других терминов.
В математике нам снова и снова нужны определенные термины для решения задач. Становится трудно повторно писать полные термины, поэтому обнаруживаются сокращения для этих терминов, и это называется символом.
Становится трудно повторно писать полные термины, поэтому обнаруживаются сокращения для этих терминов, и это называется символом.
Есть много символов, связанных с этими терминами.
Символы геометрии используются изо дня в день для обозначения длины, ширины, площади, объема, углов и т. д. На этом занятии мы изучим введение в символы геометрии и важную таблицу символов геометрии
Вот таблица символов геометрии . Это поможет вам запомнить этот символ на кончике пальца.
Таблица символов геометрии
Рассмотрим различные символы и связанные с ними значения
Geometry Symbols Chart
Symbol | Symbol Name | Meaning | Example | |||||||||||
∠ | Angle | formed двумя лучами | ∠PQR = 400 | |||||||||||
∡ | измеренный угол | измеренный угол между двумя углами0003 | ∡PQR = 70º | |||||||||||
⊾ | Angle | formed by two rays | ∠PQR = 60º | |||||||||||
∟ | Right angle | Два луча образуют угол 90º | ↑PQR = 90º | |||||||||||
º | градуса | градуса | градуля 9003 | 9 | градуса 9003 | 9003градуса | 9 | градуса | 9 | градуса | 9003. | ∠PQR = 60º | ||
‘ | Arcminute | 1º = 60′ | ∠PQR = 40º49′ | |||||||||||
“ | Arcsecond | 1 ‘= 60 ” | ↑PQR = 50º49’30” | |||||||||||
AB | СЕГМИГИ | .0003 | Line AB with endpoints A and B | |||||||||||
\[\overleftrightarrow{AB}\] | Line | infinite line | A line AB infinite in both the directions | |||||||||||
\[\overrightarrow{AB}\] | луч | Прямая, начинающаяся из точки А | Прямая, бесконечно проходящая через точку В0003 | |||||||||||
⊥ | perpendicular | perpendicular lines (90º angle) | BC ⊥ AB (read as AB perpendicular to AB) | |||||||||||
⟂̷
| Не перпендикулярно | Линии не перпендикулярны друг другу | BC ⟂̷ AB (читается как BC не перпендикулярно AB) | |||||||||||
≅ | congruent to | equivalence of two triangles | ∆PQR ≅ ∆XYZ (read as ∆PQR congruent to ∆XYZ) | |||||||||||
∥ | parallel | параллельные линии | AB || CD (читается, что линии AB и CD параллельны) | |||||||||||
∦ | Не параллельно | Non-parallel lines | AB∦CD ( read as AB and cd are non-parallel lines) | |||||||||||
Δ | Triangle | The shape of the triangle | ΔABC ≅ ΔPQR | |||||||||||
□ | Quadrilateral | The shape of any quadrilateral | □ABCD | |||||||||||
~ | Similarity | same shapes, but not of the same size | ∆ABC ~ ∆PQR (read as a∆ABC is similar to ∆PQR) | |||||||||||
π | Константа PI | π = 3,141592654… ИЛИ 22/7 — это отношение окружности к диаметру круга | C = πd = 2πr | |||||||||||
Расстояние | расстояние между точками x и y | | х–у | = 3 | ||||||||||||
rad | radians | radians angle unit | 360° = 2π rad | |||||||||||
c | radians | radians angle unit | 360° = 2π c | |||||||||||
град | град/гон | grads angle unit | 360° = 400 grad | |||||||||||
g | gradians/gons | grads angle unit | 3600 = 400g |
Это очень важная таблица геометрических символов, которая поможет вам в решении задач. Запоминание этой диаграммы символов геометрии очень важно.
Запоминание этой диаграммы символов геометрии очень важно.
Еще несколько общих символов
(изображение будет загружено в ближайшее время)
(Изображение будет загружено в ближайшее время)
Помимо упомянутых выше есть более распространенные символы, связанные с геометрией.
Вышеприведенный рисунок представляет собой неправильный пятиугольник, многоугольник с пятью сторонами.
Давайте взглянем на некоторые используемые символы:
Углы обычно обозначаются дугой, если это острый или тупой угол, или полуквадратом, если это прямой угол. углы
Буквы A, B, C, D и E — это вершины фигуры, которую можно обозначить любыми алфавитами. Пересечение двух прямых является вершиной.
Засечки оранжевого цвета на сторонах фигуры указывают, что две стороны конгруэнтны. Стороны, на которых отмечен этот знак, равны. Засечки также называются «метками штриховки». Например, сторона AB конгруэнтна стороне DE. А сторона BC равна стороне CD.
Например, сторона AB конгруэнтна стороне DE. А сторона BC равна стороне CD.
Символ угла ‘∠’ чаще всего используется для описания любого угла. Угол ABC выражается как ∠ABC. Средний алфавит здесь является вершиной угла. Вы описываете, следовательно, мы можем также написать это как ∠B. А если вы хотите написать меру угла, то она пишется как m∠ABC или m∠B. Вместо того, чтобы снова и снова писать слово «мера», мы можем просто написать для него слово «м».
Например, нам нужно указать меру угла ABC, которую мы можем записать как
м∠ABC = 1200
Или
м∠B = 1200
Запись таким образом упрощается при решении задач.
Геометрия в домашней деятельности и домашнем хозяйстве
Удивительно, но математика играет важную роль в искусстве кулинарии. Есть полезные инструменты, такие как мерные чашки, мерные ложки и весы, которые помогут в приготовлении пищи. Однако при приготовлении пищи и выпечке требуется некоторый фон измерений, дроби и геометрия. Повара должны иметь возможность измерять и измерять ингредиенты, время приготовления, а также регулировать и измерять температуру приготовления. Точки, линии, углы, кривые, двухмерные формы, объемы и масштабы составляют основу домашнего дизайна и геометрии.
Повара должны иметь возможность измерять и измерять ингредиенты, время приготовления, а также регулировать и измерять температуру приготовления. Точки, линии, углы, кривые, двухмерные формы, объемы и масштабы составляют основу домашнего дизайна и геометрии.
В видеоиграх используется геометрия, чтобы помочь зрителям ощутить глубину и движение. Другие развлекательные мероприятия, такие как сборка наборов, строительство пандусов для скейтборда или создание Lego, требуют геометрии. Геометрия позволяет определить, как формы и фигуры сочетаются друг с другом, чтобы максимизировать эффективность и визуальную привлекательность. Выстегивание требует геометрии, чтобы ваше белье было сбалансированным и визуально привлекательным. Таким образом, ясно, что геометрия влияет на нас даже в самых основных деталях нашей жизни. Независимо от формы, это помогает нам понять определенные события и повысить уровень жизни.
Почему дельта означает разницу или изменение статистики по сравнению с другим символом?
Существует как минимум четыре различных признака различия или изменения в математике, все они основаны на слове «различие».
d используется в качестве отправной точки для гибкости, чтобы показать бесконечную разницу в гибкости. Официально он показывает «разницу», которая связана с разницей, поскольку разница стремится к нулю. Это первая буква слова «отличие» или «различие».
Δ используется в качестве отправной точки для переменных, чтобы указать относительную изменчивость переменных. Оно происходит от греческого слова Διαφορά, означающего «различие».
Δ используется в качестве начала переменной, чтобы показать небольшую разницу в переменной. В отличие от Δx, δx обычно считается очень малым. Оно также происходит от греческого слова διαφορά, означающего «различие».
∂ — это вариант вышеприведенного, используемый в многомерном исчислении для обозначения «частичной вариации».


 Символы юникода позволяют выделять ссылку на Ваш сайт в выдаче поисковых систем Яндекс, Гугл. Однако использование этих символов должно быть продуманным, чтобы не получить обратный эффект.
Символы юникода позволяют выделять ссылку на Ваш сайт в выдаче поисковых систем Яндекс, Гугл. Однако использование этих символов должно быть продуманным, чтобы не получить обратный эффект. Реальное число
Реальное число 92$
92$ 0003
0003