Как транспонировать матрицу в Python (с библиотеками и без них)
Перевод статьи «Transpose a Matrix».
Сегодня мы хотим разобрать, как транспонировать матрицу в Python. Однако сначала давайте рассмотрим, что представляет из себя матрица сама по себе и в чём заключается процесс транспонирования.
Итак, матрица состоит из строк и столбцов. Создать матрицу можно по-разному, но самый простой способ – использовать вложенные списки, как показано ниже:
matrix = [[1, 2, 4], [31, 17, 15]]
Внутренние списки представляют собой строки, а каждый элемент внутри списка называется столбцом. Итак, в приведенном выше примере у нас есть две строки и три столбца, т.е. мы имеем дело с матрицей 2 на 3. Стоит помнить, что индексация Python начинается с нуля.
Транспонирование матрицы означает, что мы меняем строки на столбцы или столбцы на строки. Теперь давайте обсудим различные методы транспонирования матрицы.
Теперь давайте обсудим различные методы транспонирования матрицы.
Метод 1. Транспонирование матрицы с помощью NumPy transpose()
Первый метод, который мы разберем, — это использование библиотеки NumPy. NumPy в основном работает с массивами в Python, а для транспонирования мы можем вызвать метод transpose().
Давайте разберем всё по порядку. Для начала нам нужно импортировать модуль NumPy как np.
Дальше, в ячейке номер [25] мы создаем массив NumPy с именем arr_matrix.
В ячейке номер [26] мы вызываем метод transpose() для нашей матрицы – объекта arr_matrix, который мы создали ранее.
В ячейке номер [27] мы выводим на экран исходную матрицу arr_matrix.
А в ячейке номер [28] – транспонированную матрицу arr_transpose. Можем заметить, что в результате мы получили именно то, что нам было нужно – транспонированную матрицу.
Метод 2. Использование метода numpy.
 transpose()
transpose()Мы также можем транспонировать матрицу в Python с помощью numpy.transpose(). При этом мы передаем матрицу в метод transpose() в качестве аргумента.
В ячейке номер [29] мы создаем матрицу, используя массив NumPy, с именем arr_matrix.
Далее мы передаем arr_matrix в метод transpose() и сохраняем результат в новую переменную arr_transpose.
В ячейке номер [31] мы печатаем исходную матрицу arr_matrix.
А дальше мы выводим на экран транспонированную матрицу arr_transpose. Получаем результат аналогичный тому, что получили в первом примере.
Метод 3. Транспонирование матрицы с использованием библиотеки SymPy
Применение библиотеки SymPy – это еще один подход к транспонированию матрицы. Эта библиотека использует символьную математику для решения алгебраических задач.
Сначала нам, конечно же, нужно импортировать библиотеку SymPy. Она не поставляется вместе с Python по умолчанию, поэтому вы должны установить её в своей системе, иначе код не будет работать.
В ячейке номер [34] мы создаем матрицу с помощью библиотеки sympy.
Дальше, в ячейке [35], мы вызываем transpose (T) при помощи точечного оператора и сохраняем результаты в новую переменную sympy_transpose.
В ячейке номер [36] мы печатаем исходную матрицу matrix. А в ячейке номер [37] – транспонированную матрицу sympy_transpose. Как видим, у нас получилась транспонированная матрица.
Метод 4. Транспонирование матрицы с использованием вложенного цикла
В Python матрицу можно транспонировать и без применения каких-либо библиотек. Для этого нам придется использовать вложенные циклы.
Мы создаем одну матрицу, а затем вторую (того же размера, что и первая) — для сохранения результатов после транспонирования. При этом важно отметить, что мы далеко не всегда знаем размерность исходной матрицы. Поэтому матрицу для результата мы создаем не напрямую, а используя размер исходной.
В ячейке номер [38] мы создаем матрицу и выводим ее на экран.
В следующей ячейке мы применяем «питонический» способ узнать размерность транспонированной матрицы, используя исходную. А именно — используем генератор списков со вложенными циклами for.
В ячейке [40] мы запускаем два цикла for. Внешний цикл предназначен для строк, а вложенный – для столбцов.
В ячейке номер [41] мы выводим исходную матрицу Matrix. А в ячейке [42] — транспонированную матрицу trans_Matrix.
Метод 5. Использование генератора списка
Следующий метод, который мы разберем, — это использование генератора списка. Этот метод похож на предыдущий с использованием вложенных циклов, но он более «питонический». Можно сказать, что это более продвинутый способ транспонирования матрицы в одной строке кода без использования библиотек.
Сначала мы создаем матрицу m, используя вложенные списки.
Затем в ячейке номер [44] мы используем вложенные циклы, как и в предыдущем примере. Однако здесь мы делаем это в одну строчку, используя генератор списков.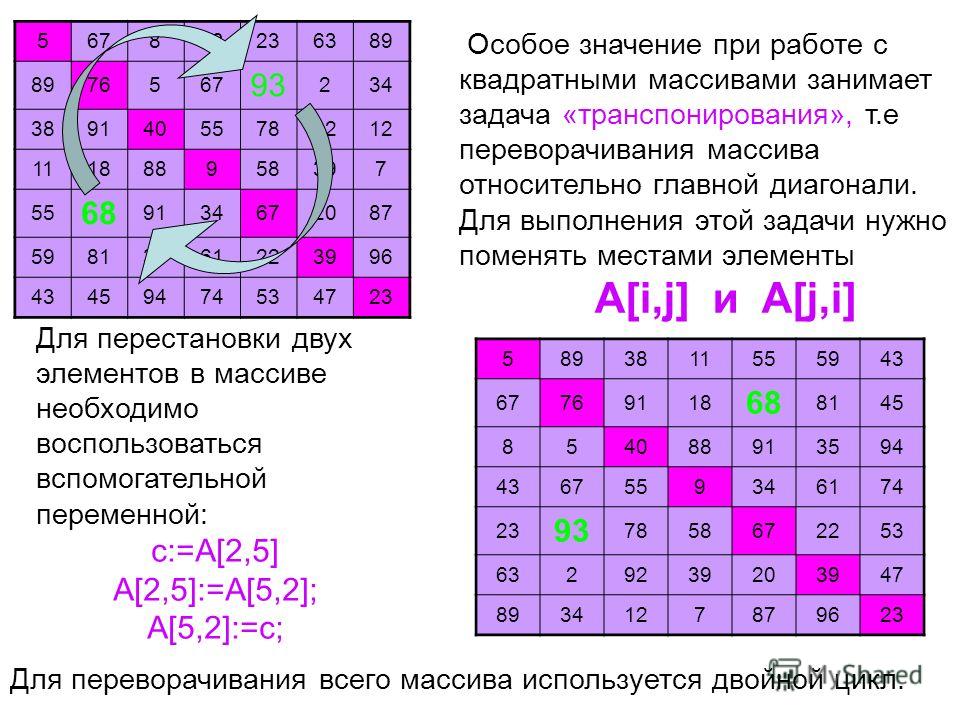 Более того, тут нет никакой необходимости менять индексы
Более того, тут нет никакой необходимости менять индексы [j] [i] местами, как мы это делали в предыдущий раз.
В следующей ячейке мы выводим исходную матрицу m. После этого в ячейке номер [42] выводим транспонированную матрицу trans_m. Как видим, желаемый результат получен.
Метод 6. Транспонирование матрицы с помощью pymatrix
Pymatrix – ещё одна облегченная библиотека для матричных операций в Python. Мы можем выполнить транспонирование и с её помощью.
В ячейке номер [43] мы импортируем библиотеку pymatrix. Она не поставляется вместе с Python по умолчанию, поэтому, чтобы код работал корректно, нужно установить ее в своей системе перед использованием.
Затем при помощи библиотеки pymatrix мы создаем матрицу (в ячейке [44]).
В ячейке номер [45] вызываем метод trans() для нашей матрицы и сохраняем результаты в новую переменную pymatrix_transpose.
Потом мы выводим на экран исходную матрицу matrix. А в ячейке номер [47] выводим уже транспонированную матрицу
А в ячейке номер [47] выводим уже транспонированную матрицу pymatrix_transpose. Как видим, код отработал правильно.
Метод 7. Использование метода zip
Zip – еще один метод транспонирования матрицы.
В ячейке номер [63] мы создаем новую матрицу, используя вложенные списки.
В ячейке номер [64] мы передаем матрицу в zip с помощью оператора *. Мы вызываем каждую строку, а затем преобразуем эту строку в новый список, который становится транспонированной матрицей.
Заключение
Итак, сегодня мы рассмотрели, как транспонировать матрицу в Python. Мы разобрали различные методы, которые могут помочь нам в транспонировании матрицы (с использованием библиотек и без них).
Мы также познакомились с несколькими новыми библиотеками, такими как pymatrix и sympy.
Надеемся, теперь у вас не осталось вопросов о том, как транспонировать матрицу. Более того, вы можете выбрать наиболее подходящий способ для решения этой задачи.
Линейная алгебра на Python.
 [Урок 2].Транспонирование Матрицы
[Урок 2].Транспонирование МатрицыВ этом уроке мы рассмотрим операцию “транспонирование матрицы” и как она выполняется на Python. Также разберем на примерах свойства этой операции.
Транспонирование матрицыТранспонирование матрицы – это процесс замены строк матрицы на ее столбцы, а столбцов соответственно на строки. Полученная в результате матрица называется транспонированной. Символ операции транспонирования – буква T.
➣ Численный пример
Для исходной матрицы:
Транспонированная будет выглядеть так:
➤ Пример на Python
Решим задачу транспонирования матрицы на Python. Создадим матрицу A:
>>> A = np.matrix('1 2 3; 4 5 6')
>>> print(A)
[[1 2 3]
[4 5 6]]Транспонируем матрицу с помощью метода transpose():
>>> A_t = A.transpose() >>> print(A_t) [[1 4] [2 5] [3 6]]
Существует сокращенный вариант получения транспонированной матрицы, он очень удобен в практическом применении:
>>> print(A.T) [[1 4] [2 5] [3 6]]
Рассмотрим на примерах свойства транспонированных матриц. Операции сложения и умножение матриц, а также расчет определителя более подробно будут рассмотрены в последующих уроках.
Свойство 1. Дважды транспонированная матрица равна исходной матрице:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2 3; 4 5 6')
>>> print(A)
[[1 2 3]
[4 5 6]]
>>> R = (A.T).T
>>> print(R)
[[1 2 3]
[4 5 6]]Свойство 2. Транспонирование суммы матриц равно сумме транспонированных матриц:
➣ Численный пример
➤Пример на Python
>>> A = np.matrix('1 2 3; 4 5 6') >>> B = np.matrix('7 8 9; 0 7 5') >>> L = (A + B).T >>> R = A.T + B.T >>> print(L) [[ 8 4] [10 12] [12 11]] >>> print(R) [[ 8 4] [10 12] [12 11]]
Свойство 3
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> L = (A.dot(B)).T
>>> R = (B.T).dot(A.T)
>>> print(L)
[[19 43]
[22 50]]
>>> print(R)
[[19 43]
[22 50]]В данном примере, для умножения матриц, использовалась функция dot() из библиотеки
Свойство 4. Транспонирование произведения матрицы на число равно произведению этого числа на транспонированную матрицу:
Транспонирование произведения матрицы на число равно произведению этого числа на транспонированную матрицу:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2 3; 4 5 6')
>>> k = 3
>>> L = (k * A).T
>>> R = k * (A.T)
>>> print(L)
[[ 3 12]
[ 6 15]
[ 9 18]]
>>> print(R)
[[ 3 12]
[ 6 15]
[ 9 18]]Свойство 5. Определители исходной и транспонированной матрицы совпадают:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> A_det = np.linalg.det(A)
>>> A_T_det = np.linalg.det(A.T)
>>> print(format(A_det, '.9g'))
-2
>>> print(format(A_T_det, '.9g'))
-2Ввиду особенностей Python при работе с числами с плавающей точкой, в данном примере вычисления определителя рассматриваются только первые девять значащих цифр после запятой (за это отвечает параметр ‘.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Python Программа для поиска транспонирования матрицы
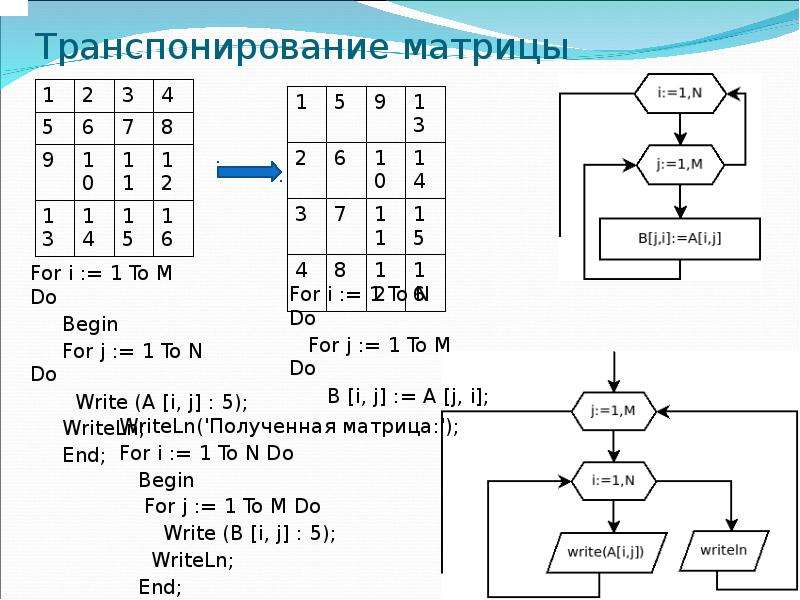
Транспонирование матрицы получается путем замены строк на столбцы и столбцов на строки. Другими словами, транспонирование A[][] получается путем замены A[i][j] на A[j][i].
Для квадратной матрицы: Приведенная ниже программа находит транспонирование A[][] и сохраняет результат в B[][], мы можем изменить N для другого измерения.
Python3
N = 4
по умолчанию транспонировать (A,B): 90 019 для i в диапазоне (N): для j в диапазоне (N): B[i][j] 90 019 = А[j][i]
А = 1 , 1 , 1 , 1 9001 9 ], [ 2 , 2 , 2 , 2 ], [ 3 , 9001 9 3 , 3 , 3 ], [ 4 , 4 , 4 , 4 9001 9 ]]
= A[:][:]
транспонировать (A, B)
напечатать ( "Матрица результата" ) для i в диапазоне (N): для j в диапазоне (N): печать (B[i][j], " " , end = '') print () 90 003 |
Результирующая матрица 1 2 3 4 2 2 3 4 3 3 3 4 4 4 4 4
Временная сложность: O(n 2 )
Вспомогательное пространство: O(n 2 )
Для прямоугольной матрицы: ниже программа находит транспонирование A[][] и сохраняет результат в Б[][].
Python3
M = 3 N = 4
деф транспонировать (A, B):
для i в диапазоне (N): 900 18 для j в диапазоне (M): B[i][j] = A[j][i]
A = [ [ 1 , 1 , 1 , 1 , 2 , 2 ], [ 3 , 3 , 3 , 3 ]] 90 002 B = [[ 0 для x в диапазоне (M)] для y в диапазоне (N)] 900 03
транспонировать (A, B)
печать ( "Матрица результатов" ) для i в диапазоне (N ): для j в диапазон (M): печать (B[i][j], " " , конец = 9002 0 |
Результирующая матрица 1 2 3 1 2 3 1 2 3 1 2 3
Временная сложность : O(n*m)
Вспомогательное пространство : O(n*m)
На месте для квадратной матрицы:
Python3
N = 4
def транспонировать (A):
для i в диапазон (N): для j в диапазон (i + 1 , N): A[i][j], A[j][i] = A[j][i], A[i][j]
A = [ [ 1 , 1 , 1 , 1 ], 9 0020 "Измененная матрица" ) для i в диапазоне (N): для j в 900 19 диапазон (N): печать (A[i] [j], " " , конец = '') печать () 9 0003 |
Модифицированная матрица является 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4
Временная сложность : O(n 2 )
Вспомогательное пространство : O(1)
Пожалуйста, обратитесь к полной статье о программе, чтобы найти транспонирование матрицы для получения более подробной информации!
Подход №4: Использование zip()
В этом подходе zip(*matrix) используется для «разархивирования» строк матрицы и группировки соответствующих элементов вместе. Оператор * используется для передачи строк матрицы в качестве отдельных аргументов функции zip(). Полученные кортежи затем преобразуются обратно в списки с использованием понимания списка.
Оператор * используется для передачи строк матрицы в качестве отдельных аргументов функции zip(). Полученные кортежи затем преобразуются обратно в списки с использованием понимания списка.
Алгоритм
1. Определите транспонируемую матрицу.
2. Используйте функцию zip(), чтобы сгруппировать соответствующие элементы каждой строки вместе и создать из них кортежи.
3. Преобразуйте каждый кортеж обратно в список, используя генератор списка.
4. Сохраните полученный список списков как транспонированную матрицу.
5. Распечатайте исходную и транспонированную матрицы.
Python3
матрица = [[ 1 , 1 , 1 , 1 ], 9001 8 [ 2 , 2 , 2 , 2 ], [ 3 , 3 900 19 , 3 , 3 ], [ 4 , 4 , 4 , 4 ]]
транспонировать = [ список (строка) для ряд в zip ( * матрица)] 9 0019 печать ( "Исходная матрица:" ) для ряд в матрица: печать (строка)
печать ( "Транспонированная матрица:" ) для строка в транспонировать: печать (строка) |
Исходная матрица: [1, 1, 1, 1] [2, 2, 2, 2] [3, 3, 3, 3] [4, 4, 4, 4] Транспонированная матрица: [1, 2, 3, 4] [1, 2, 3, 4] [1, 2, 3, 4] [1, 2, 3, 4] 92 элемента.Кроме того, мы создаем временные кортежи в процессе транспонирования, но они отбрасываются после преобразования обратно в списки.
МЕТОД 5: Использование спискового понимания
ПОДХОД:
В этой программе показано, как найти транспонирование заданной матрицы с помощью спискового понимания.
АЛГОРИТМ:
1.Инициализируйте 2D-список A с заданными значениями матрицы.
2.Создайте новый результат двумерного списка, используя вложенное понимание списка.
3. Во внутреннем анализе списка выполните итерацию по строкам A и извлеките i-й элемент из каждой строки.
4.Добавьте извлеченные элементы в виде строки в список результатов.
5. Распечатайте результирующую матрицу, перебирая каждую строку и соединяя элементы пробелом.Python3
A = [[ 1 , 900 19 1 , 1 , 1 ], [ 2 , 2 , 2 , 2 ], [ 3 , 3 , 3 , 3 ], [ 90 019 4 , 4 , 4 , 4 ]]
результат = [[строка[i] для строка 90 019 в A] для i в диапазон ( len (A[ 0 ]))]
для ряд 900 19 в результат: напечатать ( T. |

 transpose()
>>> print(A_t)
[[1 4]
[2 5]
[3 6]]
transpose()
>>> print(A_t)
[[1 4]
[2 5]
[3 6]] matrix('1 2 3; 4 5 6')
>>> B = np.matrix('7 8 9; 0 7 5')
>>> L = (A + B).T
>>> R = A.T + B.T
>>> print(L)
[[ 8 4]
[10 12]
[12 11]]
>>> print(R)
[[ 8 4]
[10 12]
[12 11]]
matrix('1 2 3; 4 5 6')
>>> B = np.matrix('7 8 9; 0 7 5')
>>> L = (A + B).T
>>> R = A.T + B.T
>>> print(L)
[[ 8 4]
[10 12]
[12 11]]
>>> print(R)
[[ 8 4]
[10 12]
[12 11]] Кроме того, мы создаем временные кортежи в процессе транспонирования, но они отбрасываются после преобразования обратно в списки.
Кроме того, мы создаем временные кортежи в процессе транспонирования, но они отбрасываются после преобразования обратно в списки.  Транспонирование матрицы в python может быть реализовано различными способами, такими как вложенные циклы, понимание вложенного списка, функция zip() и функция transpose() библиотеки NumPy.
Транспонирование матрицы в python может быть реализовано различными способами, такими как вложенные циклы, понимание вложенного списка, функция zip() и функция transpose() библиотеки NumPy.  Если количество строк N и количество столбцов M . Тогда мы говорим, что матрица представляет собой матрицу N x M .
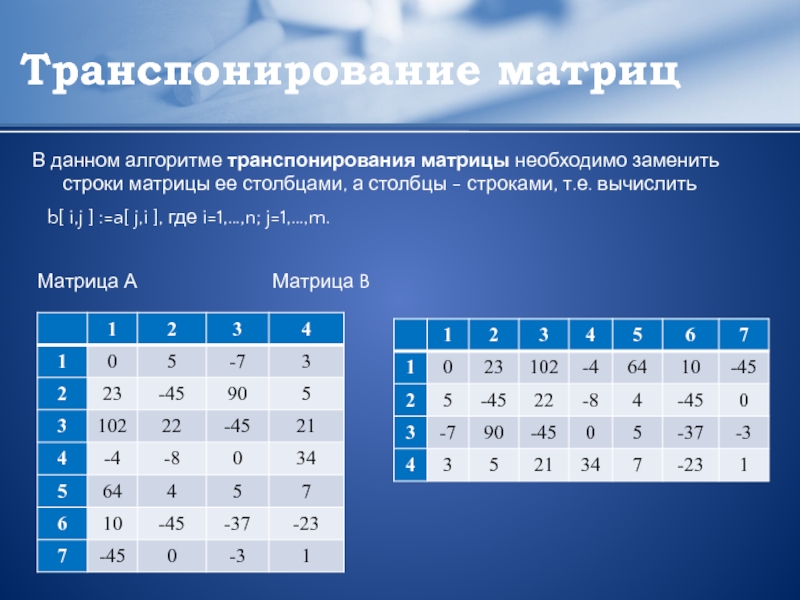
Обратитесь к изображению ниже, чтобы увидеть, как матрица представлена с помощью индексов.
Если количество строк N и количество столбцов M . Тогда мы говорим, что матрица представляет собой матрицу N x M .
Обратитесь к изображению ниже, чтобы увидеть, как матрица представлена с помощью индексов.  Транспонирование матрицы будет выглядеть так, как показано ниже:
Транспонирование матрицы будет выглядеть так, как показано ниже:

 Мы будем использовать функцию transpose() библиотеки NumPy. Давайте посмотрим код для лучшего понимания.
Мы будем использовать функцию transpose() библиотеки NumPy. Давайте посмотрим код для лучшего понимания.