Хеширование строк – Полиномиальные хеши и их применение / Habr

Содержание

Хэширование в строковых задачах — Алгоритмика

Хэш — это какая-то функция, сопоставляющая объектам какого-то множества числовые значения из ограниченного промежутка.

«Хорошая» хэш-функция:

Быстро считается — за линейное от размера объекта время;
Имеет не очень большие значения — влезающие в 64 бита;
«Детерминированно-случайная» — если хэш может принимать $n$ различных значений, то вероятность того, что хэши от двух случайных объектов совпадут, равна примерно $\frac{1}{n}$.

Обычно хэш-функция не является взаимно однозначной: одному хэшу может соответствовать много объектов. Такие функции называют сюръективными.

Для некоторых задач удобнее работать с хэшами, чем с самими объектами. Пусть даны $n$ строк длины $m$, и нас просят $q$ раз проверять произвольные две на равенство. Вместо наивной проверки за $O(q \cdot n \cdot m)$, мы можем посчитать хэши всех строк, сохранить, и во время ответа на запрос сравнивать два числа, а не две строки.

Применения в реальной жизни

Чек-суммы. Простой и быстрый способ проверить целостность большого передаваемого файла — посчитать хэш-функцию на стороне отправителя и на стороне получателя и сравнить.
Хэш-таблица. Класс unordered_set из STL можно реализовать так: заведём $n$ изначально пустых односвязных списков. Возьмем какую-нибудь хэш-функцию $f$ с областью значений $[0, n)$. При обработке .insert(x) мы будем добавлять элемент $x$ в $f(x)$-тый список. При ответе на .find(x) мы будем проверять, лежит ли $x$-тый элемент в $f(x)$-том списке. Благодаря «равномерности» хэш-функции, после $k$ добавлений ожидаемое количество сравнений будет равно $\frac{k}{n}$ = $O(1)$ при правильном выборе $n$.

Мемоизация. В динамическом программировании нам иногда надо работать с состояниями, которые непонятно как кодировать, чтобы «разгладить» в массив. Пример: шахматные позиции. В таком случае нужно писать динамику рекурсивно и хранить подсчитанные значения в хэш-таблице, а для идентификации состояния использовать его хэш.
Проверка на изоморфизм. Если нам нужно проверить, что какие-нибудь сложные структуры (например, деревья) совпадают, то мы можем придумать для них хэш-функцию и сравнивать их хэши аналогично примеру со строками.
Криптография . Правильнее и безопаснее хранить хэши паролей в базе данных вместо самих паролей — хэш-функцию нельзя однозначно восстановить.
Поиск в многомерных пространствах. Детерминированный поиск ближайшей точки среди $m$ точек в $n$-мерном пространстве быстро не решается. Однако можно придумать хэш-функцию, присваивающую лежащим рядом элементам одинаковые хэши, и делать поиск только среди элементов с тем же хэшом, что у запроса.

Хэшируемые объекты могут быть самыми разными: строки, изображения, графы, шахматные позиции, просто битовые файлы.

Сегодня же мы остановимся на строках.

Полиномиальное хэширование

Лайфхак: пока вы не выучили все детерминированные строковые алгоритмы, научитесь пользоваться хэшами.

Будем считать, что строка — это последовательность чисел от $1$ до $m$ (размер алфавита). В C++ char это на самом деле тоже число, поэтому можно вычитать из символов минимальный код и кастовать в число: int x = (int) (c - 'a' + 1).

Определим прямой полиномиальный хэш строки как значение следующего многочлена:

\[ h_f = (s_0 + s_1 k + s_2 k^2 + \ldots + s_n k^n) \mod p \]

Здесь $k$ — произвольное число больше размера алфавита, а $p$ — достаточно большой модуль, вообще говоря, не обязательно простой.

Его можно посчитать за линейное время, поддерживая переменную, равную нужной в данный момент степени $k$:

Можем ещё определить обратный полиномиальный хэш:

\[ h_b = (s_0 k^n + s_1 k^{n-1} + \ldots + s_n) \mod p \]

Его преимущество в том, что можно написать на одну строчку кода меньше:

Автору проще думать об обычных многочленах, поэтому он будет везде использовать прямой полиномиальный хэш и обозначать его просто буквой $h$.

Зачем это нужно?

Используя тот факт, что хэш это значение многочлена, можно быстро пересчитывать хэш от результата выполнения многих строковых операций.

Например, если нужно посчитать хэш от конкатенации строк $a$ и $b$ (т. е. $b$ приписали в конец строки $a$), то можно просто хэш $b$ домножить на $k^{|a|}$ и сложить с хэшом $a$:

\[ h(ab) = h(a) + k^{|a|} \cdot h(b) \]

Удалить префикс строки можно так:

\[ h(b) = \frac{h(ab) — h(a)}{k^{|a|}} \]

А суффикс — ещё проще:

\[ h(a) = h(ab) — k^{|a|} \cdot h(b) \]

В задачах нам часто понадобится домножать $k$ в какой-то степени, поэтому имеет смысл предпосчитать все нужные степени и сохранить в массиве:

Как это использовать в реальных задачах? Пусть нам надо отвечать на запросы проверки на равенство произвольных подстрок одной большой строки. Подсчитаем значение хэш-функции для каждого префикса:

Теперь с помощью этих префиксных хэшей мы можем определить функцию, которая будет считать хэш на произвольном подотрезке:

\[ h(s[l:r]) = \frac{h_r-h_l}{k^l} \]

Деление по модулю возможно делать только при некоторых k и mod (а именно — при взаимно простых). В любом случае, писать его долго, и мы это делать не хотим.

Для нашей задачи не важно получать именно полиномиальный хэш — главное, чтобы наша функция возвращала одинаковый многочлен от одинаковых подстрок. Вместо приведения к нулевой степени приведём многочлен к какой-нибудь достаточно большой — например, к $n$-ной. Так проще — нужно будет домножать, а не делить.

\[ \hat{h}(s[l:r]) = k^{n-l} (h_r-h_l) \]

Теперь мы можем просто вызывать эту функцию от двух отрезков и сравнивать числовое значение, отвечая на запрос за $O(1)$.

Упражнение. Напишите то же самое, но используя обратный полиномиальный хэш — этот способ тоже имеет право на существование, и местами он даже проще. Обратный хэш подстроки принято считать и использовать в стандартном виде из определения, поскольку там нет необходимости в делении.

Лайфхак. Если взять обратный полиномиальный хэш короткой строки на небольшом алфавите с $k=10$, то числовое значение хэша строки будет наглядно соотноситься с самой строкой:

\[ h(abacaba)=1213121 \]

Этим удобно пользоваться при дебаге.

Примеры задач

Количество разных подстрок. Посчитаем хэши от всех подстрок за $O(n^2)$ и добавим их все в std::set. Чтобы получить ответ, просто вызовем set.size().

Поиск подстроки в строке. Можно посчитать хэши от шаблона (строки, которую ищем) и пройтись «окном» размера шаблона по тексту, поддерживая хэш текущей подстроки. Если хэш какой-то из этих подстрок совпал с хэшом шаблона, то мы нашли нужную подстроку. Это называется алгоритмом Рабина-Карпа.

Сравнение строк (больше-меньше, а не только равенство). У любых двух строк есть какой-то общий префикс (возможно, пустой). Сделаем бинпоиск по его длине, а дальше сравним два символа, идущие за ним.

Палиндромность подстроки. Можно посчитать два массива — обратные хэши и прямые. Проверка на палиндром будет заключаться в сравнении значений hash_substring() на первом массиве и на втором.

Количество палиндромов. Можно перебрать центр палиндрома, а для каждого центра — бинпоиском его размер. Проверять подстроку на палиндромность мы уже умеем. Как и всегда в задачах на палиндромы, случаи четных и нечетных палиндромов нужно обрабатывать отдельно.

Хранение строк в декартовом дереве

Если для вас всё вышеперечисленное тривиально: можно делать много клёвых вещей, если «оборачивать» строки в декартово дерево. В вершине дерева можно хранить символ, а также хэш подстроки, соответствующей её поддереву. Чтобы поддерживать хэш, нужно просто добавить в upd() пересчёт хэша от конкатенации трёх строк — левого сына, своего собственного символа и правого сына.

Имея такое дерево, мы можем обрабатывать запросы, связанные с изменением строки: удаление и вставка символа, перемещение и переворот подстрок, а если дерево персистентное — то и копирование подстрок. При запросе хэша подстроки нам, как обычно, нужно просто вырезать нужную подстроку и взять хэш, который будет лежать в вершине-корне.

Если нам не нужно обрабатывать запросы вставки и удаления символов, а, например, только изменения, то можно использовать и дерево отрезков вместо декартова.

Вероятность ошибки и почему это всё вообще работает

У алгоритмов, использующих хэширование, есть один неприятный недостаток: недетерминированность. Если мы сгенерируем бесконечное количество примеров, то когда-нибудь нам не повезет, и программа отработает неправильно. На CodeForces даже иногда случаются взломы решений, использующих хэширование — можно в оффлайне сгенерировать тест против конкретного решения.

Событие, когда два хэша совпали, а не должны, называется коллизией. Пусть мы решаем задачу определения количества различных подстрок — мы добавляем в set $O(n^2)$ различных случайных значений в промежутке $[0, m)$. Понятно, что если произойдет коллизия, то мы какую-то строку не учтем и получим WA. Насколько большим следует делать $m$, чтобы не бояться такого?

Выбор констант

Практическое правило: если вам нужно хранить $n$ различных хэшей, то безопасный модуль — это число порядка $10 \cdot n^2$. Обоснование — см. парадокс дней рождений.

Не всегда такой можно выбрать один — если он будет слишком большой, будут происходить переполнения. Вместо этого можно брать два или даже три модуля и считать много хэшей параллельно.

Можно также брать модуль $2^{64}$. У него есть несколько преимуществ:

Он большой — второй модуль точно не понадобится.
С ним ни о каких переполнениях заботиться не нужно — если все хранить в unsigned long long, процессор сам автоматически сделает эти взятия остатков при переполнении.
С ним хэширование будет быстрее — раз переполнение происходит на уровне процессора, можно не выполнять долгую операцию %.

Всё с этим модулем было прекрасно, пока не придумали тест против него. Однако, его добавляют далеко не на все контесты — имейте это в виду.

В выборе же $k$ ограничения не такие серьезные:

Она должна быть чуть больше размера словаря — иначе можно изменить две соседние буквы и получить коллизию.
Она должна быть взаимно проста с модулем — иначе в какой-то момент всё может занулиться.

Главное — чтобы значения $k$ и модуля не знал человек, который генерирует тесты.

Парадокс дней рождений

В группе, состоящей из 23 или более человек, вероятность совпадения дней рождения хотя бы у двух людей превышает 50%.

Более общее утверждение: в мультимножество нужно добавить $\Theta(\sqrt{n})$ случайных чисел от 1 до n, чтобы какие-то два совпали.

Первое доказательство (для любителей матана). Пусть $f(n, d)$ это вероятность того, что в группе из $n$ человек ни у кого не совпали дни рождения. Будем считать, что дни рождения распределены независимо и равномерно в промежутке от $1$ до $d$.

\[ f(n, d) = (1-\frac{1}{d}) \times (1-\frac{2}{d}) \times … \times (1-\frac{n-1}{d}) \]

Попытаемся оценить $f$:

\[ \begin{aligned} e^x & = 1 + x + \frac{x^2}{2!} + \ldots & \text{(ряд Тейлора для экспоненты)} \\ & \simeq 1 + x & \text{(аппроксимация для $|x| \ll 1$)} \\ e^{-\frac{n}{d}} & \simeq 1 — \frac{n}{d} & \text{(подставим $\frac{n}{d} \ll 1$)} \\ f(n, d) & \simeq e^{-\frac{1}{d}} \times e^{-\frac{2}{d}} \times \ldots \times e^{-\frac{n-1}{d}} & \\ & = e^{-\frac{n(n-1)}{2d}} & \\ & \simeq e^{-\frac{n^2}{2d}} & \\ \end{aligned} \]

Из последнего выражения более-менее понятно, что вероятность $\frac{1}{2}$ достигается при $n \approx \sqrt{d}$ и в этой точке изменяется очень быстро.

Второе доказательство (для любителей теорвера). Введем $\frac{n(n-1)}{2}$ индикаторов — по одному для каждой пары людей $(i, j)$ — каждый будет равен единице, если дни рождения совпали. Ожидание и вероятность каждого индикатора равна $\frac{1}{d}$.

Обозначим за $X$ число совпавших дней рождений. Его ожидание равно сумме ожиданий этих индикаторов, то есть \(\frac{n (n-1)}{2} \cdot \frac{

algorithmica.org

Что значит хеш. Вычисление хеша в цикле. Хеширование строк переменной длины

И т. п.). Выбор той или иной хеш-функции определяется спецификой решаемой задачи. Простейшими примерами хеш-функций могут служить контрольная сумма или CRC .

В общем случае однозначного соответствия между исходными данными и хеш-кодом нет. Поэтому существует множество массивов данных, дающих одинаковые хеш-коды — так называемые коллизии . Вероятность возникновения коллизий играет немаловажную роль в оценке «качества» хеш-функций.

Контрольные суммы

Несложные, крайне быстрые и легко реализуемые аппаратно алгоритмы, используемые для защиты от непреднамеренных искажений, в том числе ошибок аппаратуры.

По скорости вычисления в десятки и сотни раз быстрее, чем криптографические хеш-функции, и значительно проще в аппаратной реализации.

Платой за столь высокую скорость является отсутствие криптостойкости — легкая возможность подогнать сообщение под заранее известную сумму. Также обычно разрядность контрольных сумм (типичное число: 32 бита) ниже, чем криптографических хешей (типичные числа: 128, 160 и 256 бит), что означает возможность возникновения непреднамеренных коллизий.

Простейшим случаем такого алгоритма является деление сообщения на 32- или 16- битные слова и их суммирование, что применяется, например, в TCP/IP .

Как правило, к такому алгоритму предъявляются требования отслеживания типичных аппаратных ошибок, таких, как несколько подряд идущих ошибочных бит до заданной длины. Семейство алгоритмов т. н. «циклический избыточных кодов » удовлетворяет этим требованиям. К ним относится, например, CRC32 , применяемый в аппаратуре ZIP.

Криптографические хеш-функции

Среди множества существующих хеш-функций принято выделять криптографически стойкие , применяемые в криптографии . Криптостойкая хеш-функция прежде всего должна обладать стойкостью к коллизиям двух типов:

Применение хеширования

Хеш-функции также используются в некоторых структурах данных — хеш-таблицаx и декартовых деревьях . Требования к хеш-функции в этом случае другие:

хорошая перемешиваемость данных
быстрый алгоритм вычисления

Сверка данных

В общем случае это применение можно описать, как проверка некоторой информации на идентичность оригиналу, без использования оригинала. Для сверки используется хеш-значение проверяемой информации. Различают два основных направления этого применения:

Проверка на наличие ошибок

Например, контрольная сумма может быть передана по каналу связи вместе с основным текстом. На приёмном конце, контрольная сумма может быть рассчитана заново и её можно сравнить с переданным значением. Если будет обнаружено расхождение, то это значит, что при передаче возникли искажения и можно запросить повтор.

Бытовым аналогом хеширования в данном случае может служить приём, когда при переездах в памяти держат количество мест багажа. Тогда для проверки не нужно вспоминать про каждый чемодан, а достаточно их посчитать. Совпадение будет означать, что ни один чемодан не потерян. То есть, количество мест багажа является его хеш-кодом.

Проверка парольной фразы

В большинстве случаев парольные фразы не хранятся на целевых объектах, хранятся лишь их хеш-значения. Хранить парольные фразы нецелесообразно, так как в случае несанкционированного доступа к файлу с фразами злоумышленник узнает все парольные фразы и сразу сможет ими воспользоваться, а при хранении хеш-значений он узнает лишь хеш-значения, которые не обратимы в исходные данные, в данном случае в парольную фразу. В ходе процедуры аутентификации вычисляется хеш-значение введённой парольной фразы, и сравнивается с сохранённым.

Примером в данном случае могут служить ОС GNU/Linux и Microsoft Windows XP . В них хранятся лишь хеш-значения парольных фраз из учётных записей пользователей.

Ускорение поиска данных

Например, при записи текстовых полей в базе данных может рассчитываться их хеш код и данные могут помещаться в раздел, соответствующий этому хеш-коду. Т

offlink.ru

Кольцевой хеш — Википедия

Кольцевой хеш

(англ. rolling hash) — хеш-функция, обрабатывающая вход в рамках некоторого окна. Получение значения хеш-функции для сдвинутого окна в таких функциях является дешевой операцией. Для пересчета значения требуется знать лишь предыдущее значение хеша, значение входных данных, которые остались за пределами окна, и значение данных, которые попали в окно. Другими словами, если x=h(a1a2⋯an){\displaystyle x=h(a_{1}a_{2}\cdots a_{n})} представляет собой хеш последовательности a1a2⋯an{\displaystyle a_{1}a_{2}\cdots a_{n}}, то хеш h(a2a3⋯anan+1){\displaystyle h(a_{2}a_{3}\cdots a_{n}a_{n+1})} для «сдвинутой» последовательности a2a3⋯anan+1{\displaystyle a_{2}a_{3}\cdots a_{n}a_{n+1}} может быть получен с помощью легко вычислимой функции f(x,a1,an+1){\displaystyle f(x,a_{1},a_{n+1})}.

Возможность быстрого «сдвига» хеша накладывает некоторые ограничения на теоретические гарантии. В частности, показано^[1], что семейства кольцевых хешей не могут быть 3-независимыми^[en]; максимум — универсальными или 2-независимыми^[en]. Впрочем, для большинства приложений достаточно универсальности (даже приблизительной).

Кольцевой хеш применяется для поиска подстроки в алгоритме Рабина — Карпа, для вычисления хешей N-грамм в тексте^[2], а также в программе rsync для сравнения двоичных файлов (используется кольцевая версия adler-32).

В алгоритме Рабина — Карпа часто используется простой полиномиальный кольцевой хеш, построенный на операциях умножения и сложения

[3]^[4]:

h(a1a2⋯an)=(a1xn−1+a2xn−2+a3xn−3+⋯+anx0)modq{\displaystyle h(a_{1}a_{2}\cdots a_{n})=(a_{1}x^{n-1}+a_{2}x^{n-2}+a_{3}x^{n-3}+\cdots +a_{n}x^{0}){\bmod {q}}}.

Чтобы избежать использования целочисленной арифметики произвольной точности, используется арифметика в кольце вычетов по модулю q{\displaystyle q}, умещающемуся в одно машинное слово. Выбор констант x{\displaystyle x} и q{\displaystyle q} очень важен для получения качественного хеша. В исходном варианте хеша предполагалось, что q{\displaystyle q} должно быть случайно выбранным простым числом, а x=2{\displaystyle x=2}.^[3] Но ввиду того, что алгоритм выбора случайного простого числа не такой простой, предпочитают использовать вариант хеша, в котором q{\displaystyle q} является фиксированным простым числом, а x{\displaystyle x} выбирается случайно из диапазона {0,1,…,q−1}{\displaystyle \{0,1,\ldots ,q-1\}}. Дитзфелбингер и др.^[4] показали, что такой вариант хеша имеет те же теоретические характеристики, что и исходный. В частности, вероятность совпадения значений хешей двух различных строк a1a2⋯an{\displaystyle a_{1}a_{2}\cdots a_{n}} и b1b2⋯bn{\displaystyle b_{1}b_{2}\cdots b_{n}} не превосходит 1/nc{\displaystyle 1/n^{c}}, если a1,…,an{\displaystyle a_{1},\ldots ,a_{n}} и b1,…,bn{\displaystyle b_{1},\ldots ,b_{n}} представляют собой целые числа из диапазона [0,q){\displaystyle [0,q)}, q>nc+1{\displaystyle q>n^{c+1}} и x{\displaystyle x} выбирается действительно случайно.

Удаление старых входных символов и добавление новых производится путём прибавления или вычитания первого или последнего члена формулы (по модулю q{\displaystyle q}). Для удаления члена a1xn−1{\displaystyle a_{1}x^{n-1}} хранят заранее посчитанное значение xn−1modq{\displaystyle x^{n-1}{\bmod {q}}}. Сдвиг окна производится путём домножения всего многочлена h(a1a2⋯an){\displaystyle h(a_{1}a_{2}\cdots a_{n})} на x{\displaystyle x} либо делением на x{\displaystyle x} (если q{\displaystyle q} простое, то в кольце вычетов возможно вместо деления производить умножение на обратную величину). На практике удобнее всего полагать q=231−1{\displaystyle q=2^{31}-1} или q=261−1{\displaystyle q=2^{61}-1} для, соответственно, 32- и 64-битовых машинных слов (это так называемые простые числа Мерсенна). В таком случае операция взятия модуля может быть выполнена на многих компьютерах с помощью быстрых операций побитового сдвига и сложения^[5]. Другой возможный выбор — значения q=232−5{\displaystyle q=2^{32}-5} или q=264−59{\displaystyle q=2^{64}-59}, для которых тоже существуют быстрые алгоритмы взятия остатка от деления на q{\displaystyle q} (при этом диапазон допустимых значений x{\displaystyle x} немного сужают)^[6]. Частое заблуждение — полагать q=232{\displaystyle q=2^{32}}. Существуют семейства строк, на которых хеш с q=2L{\displaystyle q=2^{L}} будет всегда давать множество коллизий, независимо от выбора L{\displaystyle L}.^[7] Эти и другие дальнейшие детали реализации и теоретического анализ полиномиального хеша можно найти в статье об алгоритме Рабина — Карпа.

Данный хеш похож на обычный полиномиальный хеш, но все вычисления в нём производятся в конечном поле GF(2L){\displaystyle \mathrm {GF} (2^{L})}. Обычно L{\displaystyle L} выбирается равным 64. Элементы поля — это числа 0,1,…,2L−1{\displaystyle 0,1,\ldots ,2^{L}-1}. Сложение в поле реализуется с помощью операции побитового исключающего «или» ⊕{\displaystyle \oplus }, а умножение выполняется с помощью операции a⋆b{\displaystyle a\star b}, которая сначала беспереносно умножает^[en] a{\displaystyle a} на b{\displaystyle b}, а потом берёт остаток от «беспереносного» деления результата на некоторый выбранный фиксированный элемент q∈{2L,2L+1,…,2L+1−1}{\displaystyle q\in \{2^{L},2^{L}+1,\ldots ,2^{L+1}-1\}} (беспереносным делением здесь названа операция обратная беспереносному умножению). Элемент q=2i1+2i2+⋯+2ik{\displaystyle q=2^{i_{1}}+2^{i_{2}}+\cdots +2^{i_{k}}} должен быть выбран так, что L=i1>i2>⋯>ik≥0{\displaystyle L=i_{1}>i_{2}>\cdots >i_{k}\geq 0} и xi1+xi2+⋯+xi0{\displaystyle x^{i_{1}}+x^{i_{2}}+\cdots +x^{i_{0}}} — это неприводимый многочлен над полем GF(2){\displaystyle GF(2)} (на поле GF(2L){\displaystyle \mathrm {GF} (2^{L})} часто смотрят как на множество многочленов над полем GF(2){\displaystyle \mathrm {GF} (2)} по модулю произвольного неприводимого многочлена степени L{\displaystyle L}). Например, можно положить q=264+24+23+2+1{\displaystyle q=2^{64}+2^{4}+2^{3}+2+1}^[8]. Тогда хеш вычисляется следующим образом^[4]:

h(a1a2⋯an)=(a1⋆xn−1)⊕(a2⋆xn−2)⊕⋯⊕(an−1⋆x)⊕an{\displaystyle h(a_{1}a_{2}\cdots a_{n})=(a_{1}\star x^{n-1})\oplus (a_{2}\star x^{n-2})\oplus \cdots \oplus (a_{n-1}\star x)\oplus a_{n}},

где x{\displaystyle x} — это случайно выбранное на этапе инициализации хеша число из диапазона {0,1,…,2L−1}{\displaystyle \{0,1,\ldots ,2^{L}-1\}}, а xm{\displaystyle x^{m}} — это короткая запись для x⋆x⋆⋯⋆x{\displaystyle x\star x\star \cdots \star x}, где x{\displaystyle x} повторён m{\displaystyle m} раз. С помощью основной теоремы алгебры можно показать, что вероятность коллизии хешей двух различных строк длины n{\displaystyle n} не превосходит n/2L{\displaystyle n/2^{L}}. Показано^[8], что на современных процессорах Intel и AMD вся необходимая для хеша арифметика над полем GF(2L){\displaystyle \mathrm {GF} (2^{L})} может быть эффективно вычислена с помощью инструкций из расширения CLMUL^[en].

Пусть h′{\displaystyle h’} — какой-то хеш, который отображает символы a1,…,an{\displaystyle a_{1},\ldots ,a_{n}} хешируемой строки в L{\displaystyle L}-битовые числа (обычно L=32{\displaystyle L=32} или L=64{\displaystyle L=64}). Хеш циклическими полиномами определяется следующим образом^[2]:

h(a1a2⋯an)=sn−1(h′(a1))⊕sn−2(h′(a2))⊕⋯⊕s(h′(an−1))⊕h′(an),{\displaystyle h(a_{1}a_{2}\cdots a_{n})=s^{n-1}(h'(a_{1}))\oplus s^{n-2}(h'(a_{2}))\oplus \cdots \oplus s(h'(a_{n-1}))\oplus h'(a_{n}),}

где ⊕{\displaystyle \oplus } — это операция побитового исключающего «или», а si(x){\displaystyle s^{i}(x)} — это операция циклического сдвига L{\displaystyle L}-битового числа x{\displaystyle x} на i{\displaystyle i} битов влево. Несложно показать, что данный хеш кольцевой:

h(a2a3…an+1)=s(h(a1a2…an))⊕sn(h′(a1))⊕h′(an+1).{\displaystyle h(a_{2}a_{3}\ldots a_{n+1})=s(h(a_{1}a_{2}\ldots a_{n}))\oplus s^{n}(h'(a_{1}))\oplus h'(a_{n+1}).}

Главное преимущество этого хеша в том, что он использует только быстрые побитовые операции доступные на многих современных компьютерах. Качество хеша напрямую зависит от выбора функции h′{\displaystyle h’}. Лемире и Касер^[1] доказали, что если функция h′{\displaystyle h’} выбирается случайно из семейства независимых хеш-функций^[en], то вероятность совпадения хешей двух различных строк длины n{\displaystyle n} не превосходит 1/2L−n+1{\displaystyle 1/2^{L-n+1}}. Это накладывает определённые ограничения на диапазон задач, в которых данный хеш может использоваться. Во-первых, длина хешируемых строк должна быть меньше L{\displaystyle L}. Для алгоритмов хеширования общего назначения это условие может быть проблемой, но, например, для хеширования n{\displaystyle n}-грамм, где n{\displaystyle n} обычно не превосходит 16, такое ограничение является естественным (в случае n{\displaystyle n}-грамм роль символов играют отдельные лексемы текста). Во-вторых, выбор семейства независимых функций h′{\displaystyle h’} в некоторых случаях тоже может быть проблемой. Для байтового алфавита свойством независимости обладает семейство функций h′{\displaystyle h’}, закодированных таблицей из 256-и различных случайных L{\displaystyle L}-битовых чисел (выбор функции — это заполнение таблицы). Для хеширования n{\displaystyle n}-грамм можно присваивать различные случайные L{\displaystyle L}-битовые числа различным лексемам (обычно число разных лексем в таких задачах относительно невелико) и такое семейство хеш-функций h′{\displaystyle h’} тоже имеет свойство независимости.

Данный хеш применим только в специальном случае, когда символы хешируемой строки a1a2⋯an{\displaystyle a_{1}a_{2}\cdots a_{n}} суть числа 0 и 1. Идея хеша в том, чтобы смотреть на входную строку a1a2⋯an{\displaystyle a_{1}a_{2}\cdots a_{n}} как на многочлен A(x)=a1xn−1⊕a2xn−2⊕⋯⊕an−1x⊕anx0{\displaystyle A(x)=a_{1}x^{n-1}\oplus a_{2}x^{n-2}\oplus \cdots \oplus a_{n-1}x\oplus a_{n}x^{0}} над полем GF(2){\displaystyle \mathrm {GF} (2)}, а сам хеш представляет собой взятие остатка от деления A(x){\displaystyle A(x)} на случайно выбранный на этапе инициализации хеша неприводимый многочлен P(x){\displaystyle P(x)} степени L{\displaystyle L} над полем GF(2){\displaystyle \mathrm {GF} (2)}. По существу это та же процедура, что используется в CRC. Рассмотрим её более подробно.

Результат хеширования строки a1a2⋯an{\displaystyle a_{1}a_{2}\cdots a_{n}} — это последовательность битов b

ru.wikipedia.org

Совсем просто про минимальное идеальное хеширование, основанное на графах / Habr

Представим, что перед нами стоит классическая задача получить данные по какому-то ключу. Причем количество данных и их ключей заранее известно.

Как решать подобную задачу?

Если количество пар ключ-значение заведомо невелико, то бывает смысл просто захардкодить. Но если таких значений много миллионов?

Можно просто перебором пройтись по списку пока не встретится нужное значение ключа. Но тогда сложность будет линейная O(N), что, в данном случае, должно расстроить любого инженера. А какая сложность алгоритма тогда требуется? Которая не зависит от количества данных и выполняется за фиксированное время, т. е. с константной сложностью O(1).

Как можно получать данные за фиксированное время?

Хеширование

Если расположить данные в памяти последовательно, то зная смещение, где находится нужная информация, можно получать доступ, который не будет зависеть от изначального количества данных.

Другими словами, нам надо найти способ преобразовывать ключ в смещение, где будут находиться данные. Смещение — это просто целое число: [0, n — 1], где n — количество сохраняемых значений.

На помощь приходят хеш-функции, задача которых как раз заключается в преобразовании ключей в целые числа. Такие числа могут быть интерпретированы как смещения, по которым сохраняют данные.

Но, к сожалению, хеш-функции порождают коллизии, то есть два разных ключа могут давать одинаковое смещение.

Исходя из задачи, у нас фиксированное и заранее известное количество данных, что дает возможность избежать подобных проблем.

Идеальное хеширование

Идеальная хеш-функция (Perfect Hash Function) — это такая хеш-функция, которая преобразует заранее известное статическое множество ключей в диапазон целых чисел [0, m — 1] без коллизий, т. е. один ключ соответствует только одному уникальному значению. А если количество результирующих значений такое же как и количество входящих ключей, такая функция называется Минимальной Идеальной Хеш-функцией (Minimal Perfect Hash Function).

Рассмотрим пример минимальной идеальной хеш-функции основанной на случайных графах.

Давайте пофантазируем и представим, что каждый ключ соответствует одному уникальному ребру, и, соответственно, двух вершин.
Тогда ключ может быть представлен в виде такого примитивного графа:

Рис 1. Граф, где ребро соответсвует ключу и описывается через две вершины.

Так как ключ представлен в виде ребра, а ребро всегда соединяет как минимум(потому что бывают еще гиперграфы) две вершины, значит искомая функция может выглядеть примерно так:

h(key) = g(node1, node2)

где h(key) — это минимальная идеальная хеш-функция, значение которой описывает ребро, key — ключ, g() — некая пока неизвестная функция зависящая от вершин графа node1 и node2. Так как они должны зависеть от ключа, то получается

h(key) = g(f1(key), f2(key))

По сути для f1 и f2 можно выбрать любые хеш-функции, которые будут применяться для одного ключа.

Осталось определить неизвестную функцию g(), которая описывает взаимосвязь двух узлов f1(key), f2(key) и ребро.

Вот здесь начинаются фокусы

Для простоты определим значение ребра как сумма значений узлов, соединяющиеся этим ребром.
Так как ребро соответствует только одному ключу, то это и есть искомое значение, результат минимальной идеальной функции.

h(key) = (g1(f1(key)) + g2(f2(key))) mod m

где h(key) — это значение ребра, f1(key) — это первый узел графа, g1() — значение этого узла, f2(key) — второй узел, g2() — значение второго узла, m — количество ребер.

Если еще проще, то

значение минимальной идеальной функции = (значение узла 1 + значения узла 2) mod количество ребер.

Рис 2. Представление одного ключа в графе.

Другими словами, чтобы определить номера узлов используется хеш-функции, и часто бывают коллизии, поэтому один узел может содержать множество ребер.

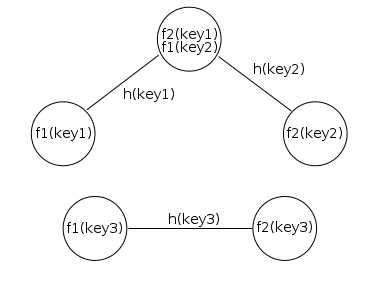
Рис 3. Коллизии в хеш-функциях порождают несколько ребер на одной вершине. Так же вершины одного ключа могут не соеденяться с вершинами другого ключа.

Вот где соль

Определившись как взаимосвязаны узлы графа с их ребрами, мы сперва определяем значения ребер h(key) (это просто инкрементный индекс), которые будут заведомо уникальны, а потом подбираем значения узлов.

Например, значение последующего узла можно посчитать так:

g2(f2(key)) = h(key) — g1(f1(key))

или

значение узла 2 = значение ребра — значения узла 1

Осталось только пройтись по графу, взять 0 за начальное значение первого узла подграфа и посчитать все остальные.

К сожалению, данный подход не работает если граф получился зацикленным. Так как нет способа заранее гарантировать незацикленность графа, то в случае обнаружения зацикленности придется перерисовать граф с другими хеш-функциями.

Зациклинность лучше всего проверять удалением вершин с только одним ребром. Если вершины останутся, то граф зациклен.

На простом примере

Теперь пришел черед описать сам алгоритм на примере.

Задача: Имеется множество ключей состоящих из названий 12 месяцев. Необходимо создать минимальную идеальную хеш-функцию, где каждый месяц транслируется в только одно уникальное целое число в диапазоне [0, 11].

1. Проходим по всем ключам и добавляем вершины и ребра. Для этого выбираем две хеш-функии f1 и f2.

Например:
Для ключа jan получаем номер первого узла f1(jan) := 4 и номер второго узла f2(jan) := 13
Для ключа feb, f1(feb) := 0, f2(feb) := 17
и так далее.

2. Проверяем получился ли граф зацикленным, если да, то повторяем шаг №1 заново и при этом меняем хеш функции f1/f2.
Вероятность появления цикла в графе зависит от количества возможных вершин. Поэтому введем понятие как фактор размера графа. Количество узлов определяется как:

m = c * n

где m — количество узлов в графе, с — константный фактор размера, n — количество ключей.

3. В случае успешного создания незацикленного графа, надо пройтись по всем узлам и посчитать их значение по формуле

g2(f2(key)) = h(key) — g1(f1(key))

или

значение дочернего узла = индекс ребра — значение узла предка

Например, присваиваем узлу с номером 0 значение 0 и идем по его ребру с индексом 6:

g2(13) = 6 — 0 = 6, узел с номером 13 получает значение 6 и т. д.

В результате имеем такой граф.

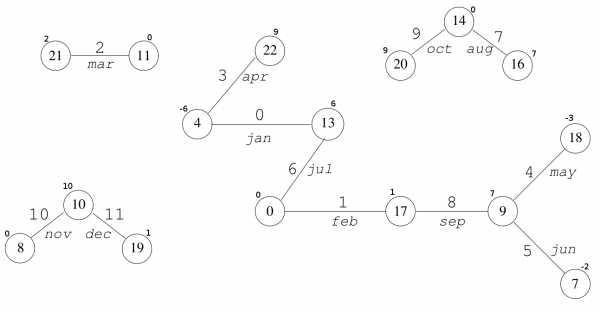
Рис 4. Результирующий граф, где ключами выступают имена месяцев и использованы случайные хеш-функции для получения номеров вершин. Числа возле узлов есть значение узла.

Лукап

Допустим нам надо получить уникальный индекс по ключу sep.
Используем те же хеш-функции, которые были использованы для создания графа:

f1(sep) := 17
f2(sep) := 9

Получив номера вершин, складываем их значения:

h(sep) = (g(17) + g(9)) mod 12 = (1 + 7) mod 12 = 8

Данный алгоритм называется CHM и реализован в библиотеке CMPH.
И как можно убедиться, создание хеш-таблицы имеет линейную сложность O(N), а поиск индекса по ключу — константную O(1).

Послесловие

А вы помните бородатую задачку от гугл?
Как скопировать однонаправленный список за линейное время, если узел списка выглядит так?

struct list_node
{
    list_node* next;
    list_node* random;
};

И решение предполагалось склонировать узлы, чтобы по две копии узла было подряд, а потом разделить этот списк с копиями нод на два списка, в каждом по копии. В итоге сложность получается линейная.

А теперь представьте в вашем расположении минимальная идеальная хеш-функция, которая может сохранить по указателю его индекс в списке и по индексу сохранять указатель. И решить задачу можно будет так:

1. Проходим список, получаем массив указателей нод и их индекс.
2. Создаем минимальные идеальные хеш-функции для указателей нод.
3. Создаем новый список, получаем массив индексов нод и их указателей.
4. Создаем другие идеальные функции для индексов второго списка, что бы по индексу получить адрес.
5. Проходим новый список, и получаем адрес старой ноды, по нему получаем индекс, а по второй хеш-функции получаем адрес уже во втором списке по индексу.

В итоге список будет скопирован за линейное время.
Хотя, конечно, идея продублировать ноды и разделить потом на два списка, красивее и быстрее.

Спасибо за усилия.

Почитать

1. Z.J. Czech, G. Havas, and B.S. Majewski. An optimal algorithm for generating minimal perfect hash functions., Information Processing Letters, 43(5):257-264, 1992.
2. Minimal Perfect Hash Functions — Introduction.
3. mphf — Моя реализация CHM на C++.

habr.com

Хеширование – что это и зачем

Криптографические хеш-функции — незаменимый и повсеместно распространенный инструмент, используемый для выполнения целого ряда задач, включая аутентификацию, проверку целостности данных, защиту файлов и даже обнаружение зловредного ПО. Существует масса алгоритмов хеширования, отличающихся криптостойкостью, сложностью, разрядностью и другими свойствами. Считается, что идея хеширования принадлежит сотруднику IBM, появилась около 50 лет назад и с тех пор не претерпела принципиальных изменений. Зато в наши дни хеширование обрело массу новых свойств и используется в очень многих областях информационных технологий.

Что такое хеш?

Если коротко, то криптографическая хеш-функция, чаще называемая просто хешем, — это математический алгоритм, преобразовывающий произвольный массив данных в состоящую из букв и цифр строку фиксированной длины. Причем при условии использования того же типа хеша длина эта будет оставаться неизменной, вне зависимости от объема вводных данных. Криптостойкой хеш-функция может быть только в том случае, если выполняются главные требования: стойкость к восстановлению хешируемых данных и стойкость к коллизиям, то есть образованию из двух разных массивов данных двух одинаковых значений хеша. Интересно, что под данные требования формально не подпадает ни один из существующих алгоритмов, поскольку нахождение обратного хешу значения — вопрос лишь вычислительных мощностей. По факту же в случае с некоторыми особо продвинутыми алгоритмами этот процесс может занимать чудовищно много времени.

Как работает хеш?

Например, мое имя — Brian — после преобразования хеш-функцией SHA-1 (одной из самых распространенных наряду с MD5 и SHA-2) при помощи онлайн-генератора будет выглядеть так: 75c450c3f963befb912ee79f0b63e563652780f0. Как вам скажет, наверное, любой другой Брайан, данное имя нередко пишут с ошибкой, что в итоге превращает его в слово brain (мозг). Это настолько частая опечатка, что однажды я даже получил настоящие водительские права, на которых вместо моего имени красовалось Brain Donohue. Впрочем, это уже другая история. Так вот, если снова воспользоваться алгоритмом SHA-1, то слово Brain трансформируется в строку 97fb724268c2de1e6432d3816239463a6aaf8450. Как видите, результаты значительно отличаются друг от друга, даже несмотря на то, что разница между моим именем и названием органа центральной нервной системы заключается лишь в последовательности написания двух гласных. Более того, если я преобразую тем же алгоритмом собственное имя, но написанное уже со строчной буквы, то результат все равно не будет иметь ничего общего с двумя предыдущими: 760e7dab2836853c63805033e514668301fa9c47.

Впрочем, кое-что общее у них все же есть: каждая строка имеет длину ровно 40 символов. Казалось бы, ничего удивительного, ведь все введенные мною слова также имели одинаковую длину — 5 букв. Однако если вы захешируете весь предыдущий абзац целиком, то все равно получите последовательность, состоящую ровно из 40 символов: c5e7346089419bb4ab47aaa61ef3755d122826e2. То есть 1128 символов, включая пробелы, были ужаты до строки той же длины, что и пятибуквенное слово. То же самое произойдет даже с полным собранием сочинений Уильяма Шекспира: на выходе вы получите строку из 40 букв и цифр. При всем этом не может существовать двух разных массивов данных, которые преобразовывались бы в одинаковый хеш.

Вот как это выглядит, если изобразить все вышесказанное в виде схемы:

Для чего используется хеш?

Отличный вопрос. Однако ответ не так прост, поскольку криптохеши используются для огромного количества вещей.

Для нас с вами, простых пользователей, наиболее распространенная область применения хеширования — хранение паролей. К примеру, если вы забыли пароль к какому-либо онлайн-сервису, скорее всего, придется воспользоваться функцией восстановления пароля. В этом случае вы, впрочем, не получите свой старый пароль, поскольку онлайн-сервис на самом деле не хранит пользовательские пароли в виде обычного текста. Вместо этого он хранит их в виде хеш-значений. То есть даже сам сервис не может знать, как в действительности выглядит ваш пароль. Исключение составляют только те случаи, когда пароль очень прост и его хеш-значение широко известно в кругах взломщиков. Таким образом, если вы, воспользовавшись функцией восстановления, вдруг получили старый пароль в открытом виде, то можете быть уверены: используемый вами сервис не хеширует пользовательские пароли, что очень плохо.

Вы даже можете провести простой эксперимент: попробуйте при помощи специального сайта произвести преобразование какого-нибудь простого пароля вроде «123456» или «password» из их хеш-значений (созданных алгоритмом MD5) обратно в текст. Вероятность того, что в базе хешей найдутся данные о введенных вами простых паролях, очень высока. В моем случае хеши слов «brain» (8b373710bcf876edd91f281e50ed58ab) и «Brian» (4d236810821e8e83a025f2a83ea31820) успешно распознались, а вот хеш предыдущего абзаца — нет. Отличный пример, как раз для тех, кто все еще использует простые пароли.

Еще один пример, покруче. Не так давно по тематическим сайтам прокатилась новость о том, что популярный облачный сервис Dropbox заблокировал одного из своих пользователей за распространение контента, защищенного авторскими правами. Герой истории тут же написал об этом в твиттере, запустив волну негодования среди пользователей сервиса, ринувшихся обвинять Dropbox в том, что он якобы позволяет себе просматривать содержимое клиентских аккаунтов, хотя не имеет права этого делать.

Впрочем, необходимости в этом все равно не было. Дело в том, что владелец защищенного копирайтом контента имел на руках хеш-коды определенных аудио- и видеофайлов, запрещенных к распространению, и занес их в черный список хешей. Когда пользователь предпринял попытку незаконно распространить некий контент, автоматические сканеры Dropbox засекли файлы, чьи хеши оказались в пресловутом списке, и заблокировали возможность их распространения.

Где еще можно использовать хеш-функции помимо систем хранения паролей и защиты медиафайлов? На самом деле задач, где используется хеширование, гораздо больше, чем я знаю и тем более могу описать в одной статье. Однако есть одна особенная область применения хешей, особо близкая нам как сотрудникам «Лаборатории Касперского»: хеширование широко используется для детектирования зловредных программ защитным ПО, в том числе и тем, что выпускается нашей компанией.

Как при помощи хеша ловить вирусы?

Примерно так же, как звукозаписывающие лейблы и кинопрокатные компании защищают свой контент, сообщество создает черные списки зловредов (многие из них доступны публично), а точнее, списки их хешей. Причем это может быть хеш не всего зловреда целиком, а лишь какого-либо его специфического и хорошо узнаваемого компонента. С одной стороны, это позволяет пользователю, обнаружившему подозрительный файл, тут же внести его хеш-код в одну из подобных открытых баз данных и проверить, не является ли файл вредоносным. С другой — то же самое может сделать и антивирусная программа, чей «движок» использует данный метод детектирования наряду с другими, более сложными.

Криптографические хеш-функции также могут использоваться для защиты от фальсификации передаваемой информации. Иными словами, вы можете удостовериться в том, что файл по пути куда-либо не претерпел никаких изменений, сравнив его хеши, снятые непосредственно до отправки и сразу после получения. Если данные были изменены даже всего на 1 байт, хеш-коды будут отличаться, как мы уже убедились в самом начале статьи. Недостаток такого подхода лишь в том, что криптографическое хеширование требует больше вычислительных мощностей или времени на вычисление, чем алгоритмы с отсутствием криптостойкости. Зато они в разы надежнее.

Кстати, в повседневной жизни мы, сами того не подозревая, иногда пользуемся простейшими хешами. Например, представьте, что вы совершаете переезд и упаковали все вещи по коробкам и ящикам. Погрузив их в грузовик, вы фиксируете количество багажных мест (то есть, по сути, количество коробок) и запоминаете это значение. По окончании выгрузки на новом месте, вместо того чтобы проверять наличие каждой коробки по списку, достаточно будет просто пересчитать их и сравнить получившееся значение с тем, что вы запомнили раньше. Если значения совпали, значит, ни одна коробка не потерялась.

www.kaspersky.ru

Хеширование (скрытие) строк в Python

Прежде всего, позвольте мне сказать, что вы не можете гарантировать уникальные результаты. Если вы хотите получить уникальные результаты для всех строк в юниверсе, вам лучше сохранить самую строку (или сжатую версию).

Подробнее об этом за секунду. Сначала сделаем хэши.

путь hashlib

Вы можете использовать любой из основных криптографических хэшей для хэша строки с несколькими шагами:

>>> import hashlib
>>> sha = hashlib.sha1("I am a cat")
>>> sha.hexdigest()
'576*************************************'

У вас есть выбор между SHA1, SHA224, SHA256, SHA384, SHA512 и MD5 в отношении встроенных модулей.

Какая разница между этими хэш-алгоритмами?

Функция хеша работает, беря данные переменной длины и превращая их в данные фиксированной длины.

Фиксированная длина, в случае каждого из алгоритмов SHA, встроенных в hashlib, — это количество бит, указанное в имени (за исключением sha1, которое составляет 160 бит). Если вам нужна большая уверенность в том, что две строки не попадут в одно и то же ведро (то же значение хэша), выберите хеш с большим дайджестом (фиксированная длина).

В отсортированном порядке это размеры дайджеста, с которыми вы должны работать:

Algorithm Digest Size (in bits)
md5 128
sha1 160
sha224 224
sha256 256
sha384 384
sha512 512

Чем больше дайджест, тем меньше вероятность столкновения, если ваша хеш-функция стоит соли.

Подождите, как насчет `hash()`?

Встроенная функция hash() возвращает целые числа, которые также могут быть просты в использовании для цели. Однако есть проблемы.

>>> hash('moo')
6387157653034356308

Если ваша программа будет запущена в разных системах, вы не можете быть уверены, что hash вернет ту же самую вещь. На самом деле, я работаю на 64-битном поле, используя 64-битный Python. Эти значения будут сильно отличаться от 32-битного Python.
Для Python 3.3+, как указано @gnibbler, hash() рандомизируется между прогонами. Он будет работать в течение одного прогона, но почти наверняка не будет работать в разных версиях вашей программы (вытаскивая из упомянутого текстового файла).

Почему hash() будет построен таким образом? Ну, встроенный хэш существует по одной конкретной причине. Хэш-таблицы/словари/поиск таблиц в памяти. Не для криптографического использования, а для дешевых поисков во время выполнения.

Не используйте hash(), используйте hashlib.

qa-help.ru

Что такое Хэширование? Под капотом блокчейна / Habr

Очень многие из вас, наверное, уже слышали о технологии блокчейн, однако важно знать о принципе работы хэширования в этой системе. Технология Блокчейн является одним из самых инновационных открытий прошлого века. Мы можем так заявить без преувеличения, так как наблюдаем за влиянием, которое оно оказало на протяжении последних нескольких лет, и влиянием, которое оно будет иметь в будущем. Для того чтобы понять устройство и предназначение самой технологии блокчейн, сначала мы должны понять один из основных принципов создания блокчейна.

Так что же такое хэширование?

Простыми словами, хэширование означает ввод информации любой длины и размера в исходной строке и выдачу результата фиксированной длины заданной алгоритмом функции хэширования. В контексте криптовалют, таких как Биткоин, транзакции после хэширования на выходе выглядят как набор символов определённой алгоритмом длины (Биткоин использует SHA-256).

Input- вводимые данные, hash- хэш

Посмотрим, как работает процесс хэширования. Мы собираемся внести определенные данные. Для этого, мы будем использовать SHA-256 (безопасный алгоритм хэширования из семейства SHA-2, размером 256 бит).

Как видите, в случае SHA-256, независимо от того, насколько объёмные ваши вводимые данные (input), вывод всегда будет иметь фиксированную 256-битную длину. Это крайне необходимо, когда вы имеете дело с огромным количеством данных и транзакций. Таким образом, вместо того, чтобы помнить вводимые данные, которые могут быть огромными, вы можете просто запомнить хэш и отслеживать его. Прежде чем продолжать, необходимо познакомиться с различными свойствами функций хэширования и тем, как они реализуются в блокчейн.

Криптографические хэш-функции

Криптографическая хэш-функция — это специальный класс хэш-функций, который имеет различные свойства, необходимые для криптографии. Существуют определенные свойства, которые должна иметь криптографическая хэш-функция, чтобы считаться безопасной. Давайте разберемся с ними по очереди.

Свойство 1: Детерминированние
Это означает, что независимо от того, сколько раз вы анализируете определенный вход через хэш-функцию, вы всегда получите тот же результат. Это важно, потому что если вы будете получать разные хэши каждый раз, будет невозможно отслеживать ввод.

Свойство 2: Быстрое вычисление
Хэш-функция должна быть способна быстро возвращать хэш-вход. Если процесс не достаточно быстрый, система просто не будет эффективна.

Свойство 3: Сложность обратного вычисления
Сложность обратного вычисления означает, что с учетом H (A) невозможно определить A, где A – вводимые данные и H(А) – хэш. Обратите внимание на использование слова “невозможно” вместо слова “неосуществимо”. Мы уже знаем, что определить исходные данные по их хэш-значению можно. Возьмем пример.

Предположим, вы играете в кости, а итоговое число — это хэш числа, которое появляется из кости. Как вы сможете определить, что такое исходный номер? Просто все, что вам нужно сделать, — это найти хэши всех чисел от 1 до 6 и сравнить. Поскольку хэш-функции детерминированы, хэш конкретного номера всегда будет одним и тем же, поэтому вы можете просто сравнить хэши и узнать исходный номер.

Но это работает только тогда, когда данный объем данных очень мал. Что происходит, когда у вас есть огромный объем данных? Предположим, вы имеете дело с 128-битным хэшем. Единственный метод, с помощью которого вы должны найти исходные данные, — это метод «грубой силы». Метод «грубой силы» означает, что вам нужно выбрать случайный ввод, хэшировать его, а затем сравнить результат с исследуемым хэшем и повторить, пока не найдете совпадение.

Итак, что произойдет, если вы используете этот метод?

Лучший сценарий: вы получаете свой ответ при первой же попытке. Вы действительно должны быть самым счастливым человеком в мире, чтобы это произошло. Вероятность такого события ничтожна.
Худший сценарий: вы получаете ответ после 2 ^ 128 — 1 раз. Это означает, что вы найдете свой ответ в конце всех вычислений данных (один шанс из 340282366920938463463374607431768211456)
Средний сценарий: вы найдете его где-то посередине, поэтому в основном после 2 ^ 128/2 = 2 ^ 127 попыток. Иными словами, это огромное количество.

Таким образом, можно пробить функцию обратного вычисления с помощью метода «грубой силы», но потребуется очень много времени и вычислительных ресурсов, поэтому это бесполезно.

Свойство 4: Небольшие изменения в вводимых данных изменяют хэш
Даже если вы внесете небольшие изменения в исходные данные, изменения, которые будут отражены в хэше, будут огромными. Давайте проверим с помощью SHA-256:

Видите? Даже если вы только что изменили регистр первой буквы, обратите внимание, насколько это повлияло на выходной хэш. Это необходимая функция, так как свойство хэширования приводит к одному из основных качеств блокчейна – его неизменности (подробнее об этом позже).

Свойство 5: Коллизионная устойчивость
Учитывая два разных типа исходных данных A и B, где H (A) и H (B) являются их соответствующими хэшами, для H (A) не может быть равен H (B). Это означает, что, по большей части, каждый вход будет иметь свой собственный уникальный хэш. Почему мы сказали «по большей части»? Давайте поговорим об интересной концепции под названием «Парадокс дня рождения».

Что такое парадокс дня рождения?
Если вы случайно встречаете незнакомца на улице, шанс, что у вас совпадут даты дней рождений, очень мал. Фактически, если предположить, что все дни года имеют такую же вероятность дня рождения, шансы другого человека, разделяющего ваш день рождения, составляют 1/365 или 0,27%. Другими словами, он действительно низкий.

Однако, к примеру, если собрать 20-30 человек в одной комнате, шансы двух людей, разделяющих тот же день, резко вырастает. На самом деле, шанс для 2 человек 50-50, разделяющих тот же день рождения при таком раскладе.

Как это применяется в хэшировании?
Предположим, у вас есть 128-битный хэш, который имеет 2 ^ 128 различных вероятностей. Используя парадокс дня рождения, у вас есть 50% шанс разбить коллизионную устойчивость sqrt (2 ^ 128) = 2 ^ 64.

Как вы заметили, намного легче разрушить коллизионную устойчивость, нежели найти обратное вычисление хэша. Для этого обычно требуется много времени. Итак, если вы используете такую функцию, как SHA-256, можно с уверенностью предположить, что если H (A) = H (B), то A = B.

Свойство 6: Головоломка
Свойства Головоломки имеет сильнейшее воздействие на темы касающиеся криптовалют (об этом позже, когда мы углубимся в крипто схемы). Сначала давайте определим свойство, после чего мы подробно рассмотрим каждый термин.

Для каждого выхода «Y», если k выбран из распределения с высокой мин-энтропией, невозможно найти вводные данные x такие, что H (k | x) = Y.

Вероятно, это, выше вашего понимания! Но все в порядке, давайте теперь разберемся с этим определением.

В чем смысл «высокой мин-энтропии»?
Это означает, что распределение, из которого выбрано значение, рассредоточено так, что мы выбираем случайное значение, имеющее незначительную вероятность. В принципе, если вам сказали выбрать число от 1 до 5, это низкое распределение мин-энтропии. Однако, если бы вы выбрали число от 1 до бесконечности, это — высокое распределение мин-энтропии.

Что значит «к|х»?
«|» обозначает конкатенацию. Конкатенация означает объединение двух строк. Например. Если бы я объединила «голубое» и «небо», то результатом было бы «голубоенебо».
Итак, давайте вернемся к определению.

Предположим, у вас есть выходное значение «Y». Если вы выбираете случайное значение «К», невозможно найти значение X, такое, что хэш конкатенации из K и X, выдаст в результате Y.

Еще раз обратите внимание на слово «невозможно», но не исключено, потому что люди занимаются этим постоянно. На самом деле весь процесс майнинга работает на этом (подробнее позже).

Примеры криптографических хэш-функций:

MD 5: Он производит 128-битный хэш. Коллизионная устойчивость была взломана после ~2^21 хэша.
SHA 1: создает 160-битный хэш. Коллизионная устойчивость была взломана после ~2^61 хэша.
SHA 256: создает 256-битный хэш. В настоящее время используется в Биткоине.
Keccak-256: Создает 256-битный хэш и в настоящее время используется Эфириуме.

Хэширование и структуры данных.
Структура данных — это специализированный способ хранения данных. Если вы хотите понять, как работает система «блокчейн», то есть два основных свойства структуры данных, которые могут помочь вам в этом:

1. Указатели
2. Связанные списки

Указатели
В программировании указатели — это переменные, в которых хранится адрес другой переменной, независимо от используемого языка программирования.

Например, запись int a = 10 означает, что существует некая переменная «a», хранящая в себе целочисленное значение равное 10. Так выглядит стандартная переменная.

Однако, вместо сохранения значений, указатели хранят в себе адреса других переменных. Именно поэтому они и получили свое название, потому как буквально указывают на расположение других переменных.

Связанные списки
Связанный список является одним из наиболее важных элементов в структурах данных. Структура связанного списка выглядит следующим образом:

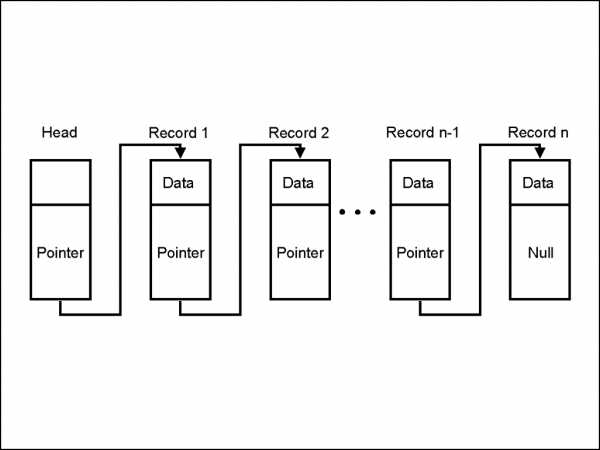
*Head – заголовок; Data – данные; Pointer – указатель; Record – запись; Null – ноль

Это последовательность блоков, каждый из которых содержит данные, связанные со следующим с помощью указателя. Переменная указателя в данном случае содержит адрес следующего узла, благодаря чему выполняется соединение. Как показано на схеме, последний узел отмечен нулевым указателем, что означает, что он не имеет значения.

Важно отметить, что указатель внутри каждого блока содержит адрес предыдущего. Так формируется цепочка. Возникает вопрос, что это значит для первого блока в списке и где находится его указатель?

Первый блок называется «блоком генезиса», а его указатель находится в самой системе. Выглядит это следующим образом:

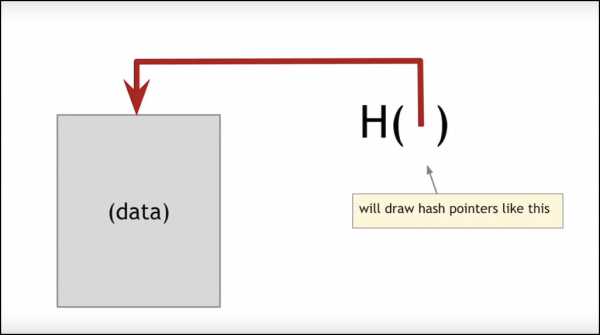
*H ( ) – Хэшированные указатели изображаются таким образом

Если вам интересно, что означает «хэш-указатель», то мы с радостью поясним.
Как вы уже поняли, именно на этом основана структура блокчейна. Цепочка блоков представляет собой связанный список. Рассмотрим, как устроена структура блокчейна:

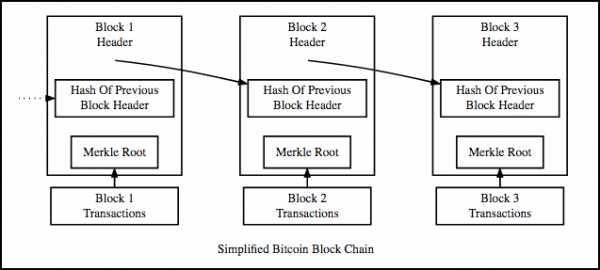
* Hash of previous block header – хэш предыдущего заголовка блока; Merkle Root – Корень Меркла; Transactions – транзакции; Simplified Bitcoin Blockchain – Упрощенный блокчейн Биткоина.

Блокчейн представляет собой связанный список, содержащий данные, а так же указатель хэширования, указывающий на предыдущий блок, создавая таким образов связную цепочку. Что такое хэш-указатель? Он похож на обычный указатель, но вместо того, чтобы просто содержать адрес предыдущего блока, он также содержит хэш данных, находящихся внутри предыдущего блока. Именно эта небольшая настройка делает блокчейн настолько надежным. Представим на секунду, что хакер атакует блок 3 и пытается изменить данные. Из-за свойств хэш-функций даже небольшое изменение в данных сильно изменит хэш. Это означает, что любые незначительные изменения, произведенные в блоке 3, изменят хэш, хранящийся в блоке 2, что, в свою очередь, изменит данные и хэш блока 2, а это приведет к изменениям в блоке 1 и так далее. Цепочка будет полностью изменена, а это невозможно. Но как же выглядит заголовок блока?

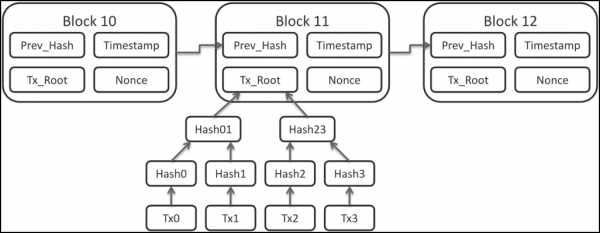
* Prev_Hash – предыдущий хэш; Tx – транзакция; Tx_Root – корень транзакции; Timestamp – временная отметка; Nonce – уникальный символ.

Заголовок блока состоит из следующих компонентов:

· Версия: номер версии блока
· Время: текущая временная метка
· Текущая сложная цель (См. ниже)
· Хэш предыдущего блока
· Уникальный символ (См. ниже)
· Хэш корня Меркла

Прямо сейчас, давайте сосредоточимся на том, что из себя представляет хэш корня Меркла. Но до этого нам необходимо разобраться с понятием Дерева Меркла.

Что такое Дерево Меркла?

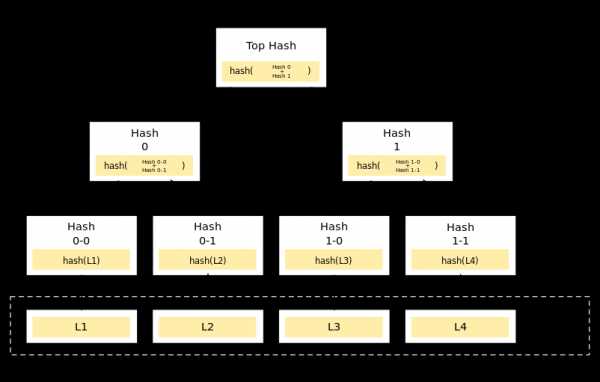
Источник: Wikipedia

На приведенной выше диаграмме показано, как выглядит дерево Меркла. В дереве Меркла каждый нелистовой узел является хэшем значений их дочерних узлов.

Листовой узел: Листовые узлы являются узлами в самом нижнем ярусе дерева. Поэтому, следуя приведенной выше схеме, листовыми будут считаться узлы L1, L2, L3 и L4.

Дочерние узлы: Для узла все узлы, находящиеся ниже его уровня и которые входят в него, являются его дочерними узлами. На диаграмме узлы с надписью «Hash 0-0» и «Hash 0-1» являются дочерними узлами узла с надписью «Hash 0».

Корневой узел: единственный узел, находящийся на самом высоком уровне, с надписью «Top Hash» является корневым.

Так какое же отношение Дерево Меркла имеет к блокчейну?
Каждый блок содержит большое количество транзакций. Будет очень неэффективно хранить все данные внутри каждого блока в виде серии. Это сделает поиск какой-либо конкретной операции крайне громоздким и займет много времени. Но время, необходимое для выяснения, на принадлежность конкретной транзакции к этому блоку или нет, значительно сокращается, если Вы используете дерево Меркла.

Давайте посмотрим на пример на следующем Хэш-дереве:

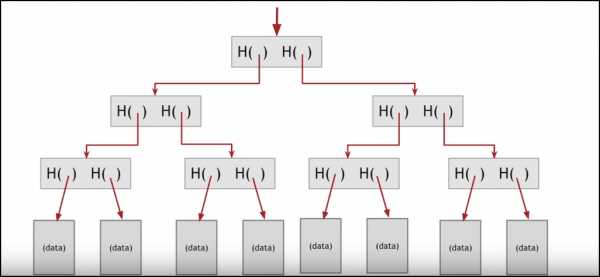
Изображение предоставлено проектом: Coursera

Теперь предположим, я хочу узнать, принадлежат ли эти данные блоку или нет:

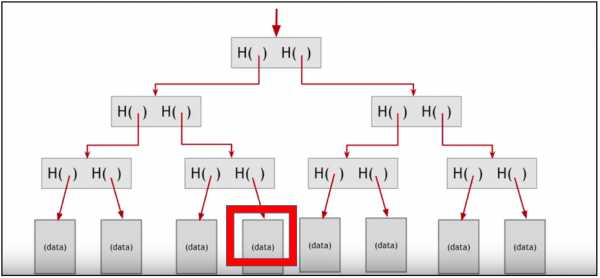
Вместо того, чтобы проходить через сложный процесс просматривания каждого отдельного процесса хэша, а также видеть принадлежит ли он данным или нет, я просто могу отследить след хэша, ведущий к данным:

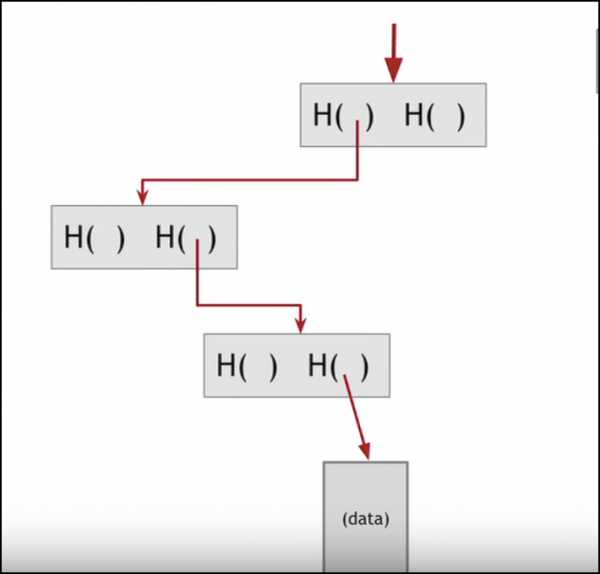
Это значительно сокращает время.

Хэширование в майнинге: крипто-головоломки.
Когда мы говорим «майнинг», в основном, это означает поиск нового блока, который будет добавлен в блокчейн. Майнеры всего мира постоянно работают над тем, чтобы убедиться, что цепочка продолжает расти. Раньше людям было проще работать, используя для майнинга лишь свои ноутбуки, но со временем они начали формировать «пулы», объединяя при этом мощность компьютеров и майнеров, что может стать проблемой. Существуют ограничения для каждой криптовалюты, например, для биткоина они составляют 21 миллион. Между созданием каждого блока должен быть определенный временной интервал заданный протоколом. Для биткоина время между созданием блока занимает всего 10 минут. Если бы блокам было разрешено создаваться быстрее, это привело бы к:

Большому количеству коллизий: будет создано больше хэш-функций, которые неизбежно вызовут больше коллизий.
Большому количеству брошенных блоков: Если много майнеров пойдут впереди протокола, они будут одновременно хаотично создавать новые блоки без сохранения целостности основной цепочки, что приведет к «осиротевшим» блокам.

Таким образом, чтобы ограничить создание блоков, устанавливается определенный уровень сложности. Майнинг чем-то напоминает игру: решаешь задачу – получаешь награду. Усиление сложности делает решение задачи намного сложнее и, следовательно, на нее затрачивается большее количество времени.WRT, которая начинается с множества нулей. При увеличении уровня сложности, увеличивается количество нулей. Уровень сложности изменяется после каждого 2016-го блока.

Процесс Майнинга

Примечание: в этом разделе мы будем говорить о выработке биткоинов.
Когда протокол Биткоина хочет добавить новый блок в цепочку, майнинг – это процедура, которой он следует. Всякий раз, когда появляется новый блок, все их содержимое сначала хэшируется. Если подобранный хэш больше или равен, установленному протоколом уровню сложности, он добавляется в блокчейн, а все в сообществе признают новый блок.

Однако, это не так просто. Вам должно очень повезти, чтобы получить новый блок таким образом. Так как, именно здесь присваивается уникальный символ. Уникальный символ (nonce) — это одноразовый код, который объединен с хэшем блока. Затем эта строка вновь меняется и сравнивается с уровнем сложности. Если она соответствует уровню сложности, то случайный код изменяется. Это повторяется миллион раз до тех пор, пока требования не будут наконец выполнены. Когда же это происходит, то блок добавляется в цепочку блоков.

Подводя итоги:

• Выполняется хэш содержимого нового блока.
• К хэшу добавляется nonce (специальный символ).
• Новая строка снова хэшируется.
• Конечный хэш сравнивается с уровнем сложности, чтобы проверить меньше он его или нет
• Если нет, то nonce изменяется, и процесс повторяется снова.
• Если да, то блок добавляется в цепочку, а общедоступная книга (блокчейн) обновляется и сообщает нодам о присоединении нового блока.
• Майнеры, ответственные за данный процесс, награждаются биткоинами.

Помните номер свойства 6 хэш-функций? Удобство использования задачи?
Для каждого выхода «Y», если k выбран из распределения с высокой мин-энтропией, невозможно найти вход x таким образом, H (k | x) = Y.

Так что, когда дело доходит до майнинга биткоинов:

• К = Уникальный символ
• x = хэш блока
• Y = цель проблемы

Весь процесс абсолютно случайный, основанный на генерации случайных чисел, следующий протоколу Proof Of Work и означающий:

Решение задач должно быть сложным.
Однако проверка ответа должна быть простой для всех. Это делается для того, чтобы убедиться, что для решения проблемы не использовались недозволенные методы.

Что такое скорость хэширования?
Скорость хэширования в основном означает, насколько быстро эти операции хэширования происходят во время майнинга. Высокий уровень хэширования означает, что в процессе майнинга участвуют всё большее количество людей и майнеров, и в результате система функционирует нормально. Если скорость хэширования слишком высокая, уровень сложности пропорционально увеличивается. Если скорость хэша слишком медленная, то соответственно, уровень сложности уменьшается.

Вывод

Хэширование действительно является основополагающим в создании технологии блокчейн. Если кто-то хочет понять, что такое блокчейн, он должен начать с того, чтобы понять, что означает хэширование.