Python 3.9 При заполнении двумерного массива кортежами, в какой-то момент вместо записи в одну ячейку, происходит заполнение многих (python, python-3.x, массивы, матрицы) / husl.ru
Вопрос по глюку заполнения двумерной матрицы в Python 3.9.
В двух вложенных циклах, пэлементно заполняю двумерный массив. В какой-то момент, происходит необъяснимая запись сразу во всё продолжение ряда (множество ячеек). Вот распечатка массива, сначала всё работает правильно, каждый раз в одной ячейке появляется новый элемент. А затем приходит глюк.
--- [None, None, None, None, None, (2041, 2042), (2043, 2044), (2045, 2046), (2047, 2048), (2049, 2050)] --- [None, None, None, None, None, (2051, 2052), (2053, 2054), (2055, 2056), (2057, 2058), None] --- [None, None, None, None, None, None, None, None, None, None] --- [None, None, None, None, None, None, None, None, None, None] --- [None, None, None, None, None, None, None, None, None, None] --- [None, None, None, None, None, None, None, None, None, None] --- [None, None, None, None, None, None, None, None, None, None] --- [None, None, None, None, None, None, None, None, None, None] --- [None, None, None, None, None, None, None, None, None, None] --- [None, None, None, None, None, None, None, None, None, None]
Записался элемент (2057, 2058)
--- [None, None, None, None, None, (2041, 2042), (2043, 2044), (2045, 2046), (2047, 2048), (2049, 2050)] --- [None, None, None, None, None, (2051, 2052), (2053, 2054), (2055, 2056), (2057, 2058), (2059, 2060)] --- [None, None, None, None, None, None, None, None, None, None] --- [None, None, None, None, None, None, None, None, None, None] --- [None, None, None, None, None, None, None, None, None, None] --- [None, None, None, None, None, None, None, None, None, None] --- [None, None, None, None, None, None, None, None, None, None] --- [None, None, None, None, None, None, None, None, None, None] --- [None, None, None, None, None, None, None, None, None, None] --- [None, None, None, None, None, None, None, None, None, None] Записался элемент (2059, 2060) --- [None, None, None, None, None, (2041, 2042), (2043, 2044), (2045, 2046), (2047, 2048), (2049, 2050)] --- [None, None, None, None, None, (2051, 2052), (2053, 2054), (2055, 2056), (2057, 2058), (2059, 2060)] --- [None, None, None, None, None, (2061, 2062), None, None, None, None] --- [None, None, None, None, None, (2061, 2062), None, None, None, None] --- [None, None, None, None, None, (2061, 2062), None, None, None, None] --- [None, None, None, None, None, (2061, 2062), None, None, None, None] --- [None, None, None, None, None, (2061, 2062), None, None, None, None] --- [None, None, None, None, None, (2061, 2062), None, None, None, None] --- [None, None, None, None, None, (2061, 2062), None, None, None, None] --- [None, None, None, None, None, (2061, 2062), None, None, None, None]
Вот оно! (2061, 2062) расползся вниз по непонятным причинам!!! И так продолжается с каждой дальнейшей итерацией
--- [None, None, None, None, None, (2041, 2042), (2043, 2044), (2045, 2046), (2047, 2048), (2049, 2050)] --- [None, None, None, None, None, (2051, 2052), (2053, 2054), (2055, 2056), (2057, 2058), (2059, 2060)] --- [None, None, None, None, None, (2061, 2062), (2063, 2064), None, None, None] --- [None, None, None, None, None, (2061, 2062), (2063, 2064), None, None, None] --- [None, None, None, None, None, (2061, 2062), (2063, 2064), None, None, None] --- [None, None, None, None, None, (2061, 2062), (2063, 2064), None, None, None] --- [None, None, None, None, None, (2061, 2062), (2063, 2064), None, None, None] --- [None, None, None, None, None, (2061, 2062), (2063, 2064), None, None, None] --- [None, None, None, None, None, (2061, 2062), (2063, 2064), None, None, None] --- [None, None, None, None, None, (2061, 2062), (2063, 2064), None, None, None]
Вот кусок кода, где появляется глюк:
def draw_cubes(): # добавляю фигуру в стэк кубиков global figure print("draw cubes start") for line in CUBES: print("Fom the beginning:", line) for i, line in enumerate(figure.figure_map): for j, element in enumerate(line): if figure.figure_map[i][j] == '1': y = figure.y - i x = figure.x + j # Именно это присвоение ГЛЮЧИТ, но не сразу CUBES[-y-1][x] = draw_cube_element(y, x, "green", "yellow") #Распечатываю массив для отладки for l in CUBES: print("---", l)
Подробнее. Игра Тетрис. Все кубики хранятся в матрице CUBES соответствующей размеру стакана (10х10) изначально заполненной None в каждой ячейке. Когда в ячейку попадает кубик, туда прописывается Id элемента canvas. Всё прекрасно работает, но когда Id достигают района 2000+, вдруг, при записи элемента в одну ячейку, он записывается во все оставшиеся ячейки по «y».
Наглядно это видно в консольном выводе:
Для отладки распечатывается массив CUBES при каждом добавлении элемента в ячейку.
Играя в игру с тестовой фигурой 5х4, четырежды расставляя её по краям, на пятый раз, глюк проявляется.
Помогите разобраться, пожалуйста.
Весь код:
from tkinter import *
import time
import random
GLASS_WIDTH = 10
GLASS_HEIGHT = 10
BLOCK_SIZE = 30
START_X = 3
START_Y = 3
CUBES = []
for i in range(GLASS_HEIGHT):
row = []
for j in range(GLASS_WIDTH):
row.append(None)
CUBES.append(row)
empty_cubes_line = []
for i in range(GLASS_WIDTH):
empty_cubes_line.append(None)
# разные варианты фигур
'''FIGURE_TYPES = [['10',
'10',
'11'], ['1'], ['110',
'011'], ['111']]'''
# фигура для отладки
FIGURE_TYPES = [['11111',
'11111',
'11111',
'11111']]
def make_figure_choice():
the_choice = random.randrange(len(FIGURE_TYPES))
return FIGURE_TYPES[the_choice]
class Figure:
def __init__(self):
self.figure_map = make_figure_choice()
self.x = START_X
self.
y = START_Y
self.block_list = []
def rotate_left(self):
m = len(self.figure_map)
n = len(self.figure_map[0])
new_matrix = [[self.figure_map[j][i] for j in range(m)] for i in range(n-1, -1, -1)]
self.figure_map = new_matrix
def rotate_right(self):
m = len(self.figure_map)
n = len(self.figure_map[0])
new_matrix = [[self.figure_map[j][i] for j in range(m-1, -1, -1)] for i in range(n)]
self.figure_map = new_matrix
def move_left(self):
self.x = self.x - 1
def move_right(self):
self.x = self.x + 1
def move_down(self):
self.y += 1
figure = Figure()
tk = Tk()
tk.title("Тетрис")
tk.resizable(0, 0)
tk.wm_attributes("-topmost", 1)
canvas = Canvas(tk, width=GLASS_WIDTH * BLOCK_SIZE, height=GLASS_HEIGHT * BLOCK_SIZE, bd=0, highlightthickness=0)
canvas.pack()
tk.update()
GAME_ON = True
def draw_figure():
global GAME_ON
if check_collision():
GAME_ON = False
if len(figure.

remove(line)
CUBES.append(empty_cubes_line)
# Перерисовываю все кубики (удаляю старые, рисую новые) если было удаление линии
if to_redraw:
for i, line in enumerate(reversed(CUBES)):
for j, item in enumerate(line):
if item is not None:
delete_cube_element(item)
id1, id2 = draw_cube_element(i, j, 'red', 'orange')
CUBES[-i-1][j] = (id1, id2)
print(-i-1, j)
time.sleep(0.2)
tk.update_idletasks()
tk.update()
make_new_figure()
def make_new_figure():
global GAME_ON
figure.x = START_X
figure.y = START_Y
if check_collision():
GAME_ON = False
figure.figure_map = make_figure_choice()
draw_figure()
def delete_cube_element(element):
canvas.delete(element[0])
canvas.delete(element[1])
def draw_cube_element(i, j, fill1, fill2):
id1 = canvas.create_rectangle(j * BLOCK_SIZE, i * BLOCK_SIZE,
j * BLOCK_SIZE + BLOCK_SIZE, i * BLOCK_SIZE + BLOCK_SIZE,
fill=fill1)
id2 = canvas.
create_rectangle(j * BLOCK_SIZE + 2, i * BLOCK_SIZE + 2,
j * BLOCK_SIZE + BLOCK_SIZE - 2, i * BLOCK_SIZE + BLOCK_SIZE - 2,
fill=fill2)
return id1, id2
def check_collision():
for i, line in enumerate(figure.figure_map):
for j, item in enumerate(line):
if figure.figure_map[i][j] == '1':
if figure.x + j >= GLASS_WIDTH or figure.x + j < 0 or figure.y >= GLASS_HEIGHT:
return True
if figure.y - i >0 and CUBES[-figure.y+i-1][figure.x + j] is not None:
return True
return False
def check_borders(movement_type):
if movement_type == 'Right':
if check_collision():
figure.move_left()
if movement_type == 'Left':
if check_collision():
figure.move_right()
if movement_type == 'Up':
# Если есть наложение, то двигаю фигуру влево (столько раз сколько длинна фигуры)
for i in range(len(figure. figure_map[0])-1):
if check_collision():
figure.move_left()
# Если смещение влево не помогло...
if check_collision():
# возвращаю фигуру на место
for i in range(len(figure.figure_map[0]) - 1):
figure.move_right()
# Двигаю фигуру вправо, вдруг там свободно
for i in range(len(figure.figure_map[0])):
if check_collision():
figure.move_right()
# возвращаю обратно, если не вышло
if check_collision():
for i in range(len(figure.figure_map[0])):
figure.move_left()
figure.rotate_right()
if movement_type == 'Down':
# Если есть наложение, то двигаю фигуру влево (столько раз сколько длинна фигуры)
for i in range(len(figure.figure_map[0]) - 1):
if check_collision():
figure.move_left()
# Если смещение влево не помогло...
if check_collision():
# возвращаю фигуру на место
for i in range(len(figure.
figure_map[0])-1):
if check_collision():
figure.move_left()
# Если смещение влево не помогло...
if check_collision():
# возвращаю фигуру на место
for i in range(len(figure.figure_map[0]) - 1):
figure.move_right()
# Двигаю фигуру вправо, вдруг там свободно
for i in range(len(figure.figure_map[0])):
if check_collision():
figure.move_right()
# возвращаю обратно, если не вышло
if check_collision():
for i in range(len(figure.figure_map[0])):
figure.move_left()
figure.rotate_right()
if movement_type == 'Down':
# Если есть наложение, то двигаю фигуру влево (столько раз сколько длинна фигуры)
for i in range(len(figure.figure_map[0]) - 1):
if check_collision():
figure.move_left()
# Если смещение влево не помогло...
if check_collision():
# возвращаю фигуру на место
for i in range(len(figure. figure_map[0]) - 1):
figure.move_right()
# Двигаю фигуру вправо, вдруг там свободно
for i in range(len(figure.figure_map[0])):
if check_collision():
figure.move_right()
# возвращаю обратно, если не вышло
if check_collision():
for i in range(len(figure.figure_map[0])):
figure.move_left()
figure.rotate_left()
if check_collision():
figure.y = figure.y - 1
return True
return False
def new_coordinates(event):
if event == "no_button":
movement_type = "d"
figure.move_down()
else:
movement_type = event.keysym
if movement_type == "Up":
figure.rotate_left()
if movement_type == "Down":
figure.rotate_right()
if movement_type == "Left":
figure.move_left()
if movement_type == "Right":
figure.move_right()
if movement_type == "d":
figure.
figure_map[0]) - 1):
figure.move_right()
# Двигаю фигуру вправо, вдруг там свободно
for i in range(len(figure.figure_map[0])):
if check_collision():
figure.move_right()
# возвращаю обратно, если не вышло
if check_collision():
for i in range(len(figure.figure_map[0])):
figure.move_left()
figure.rotate_left()
if check_collision():
figure.y = figure.y - 1
return True
return False
def new_coordinates(event):
if event == "no_button":
movement_type = "d"
figure.move_down()
else:
movement_type = event.keysym
if movement_type == "Up":
figure.rotate_left()
if movement_type == "Down":
figure.rotate_right()
if movement_type == "Left":
figure.move_left()
if movement_type == "Right":
figure.move_right()
if movement_type == "d":
figure. move_down()
if check_borders(movement_type):
draw_cubes()
else:
draw_figure()
canvas.bind_all("<KeyPress-Left>", new_coordinates)
canvas.bind_all("<KeyPress-Right>", new_coordinates)
canvas.bind_all("<KeyPress-Up>", new_coordinates)
canvas.bind_all("<KeyPress-Down>", new_coordinates)
canvas.bind_all("<KeyPress-d>", new_coordinates)
'''while GAME_ON:
draw_figure()
new_coordinates("no_button")
#tk.update_idletasks()
#tk.update()
time.sleep(0.5)'''
tk.mainloop()
move_down()
if check_borders(movement_type):
draw_cubes()
else:
draw_figure()
canvas.bind_all("<KeyPress-Left>", new_coordinates)
canvas.bind_all("<KeyPress-Right>", new_coordinates)
canvas.bind_all("<KeyPress-Up>", new_coordinates)
canvas.bind_all("<KeyPress-Down>", new_coordinates)
canvas.bind_all("<KeyPress-d>", new_coordinates)
'''while GAME_ON:
draw_figure()
new_coordinates("no_button")
#tk.update_idletasks()
#tk.update()
time.sleep(0.5)'''
tk.mainloop()
Линейная алгебра на Python. [Урок 1]. Задание Матрицы.
Эта статья открывает список уроков на тему “Линейная алгебра с примерами на Python“. Мы постараемся рассказать о базовых понятиях линейной алгебры, которые могут быть полезны тем, кто занимается машинным обучением и анализом данных, и будем сопровождать все это примерами на языке Python.
МатрицыМатрицей в математике называют объект, записываемый в виде прямоугольной таблицы, элементами которой являются числа (могут быть как действительные, так и комплексные). Пример матрицы приведен ниже.
Пример матрицы приведен ниже.
\(M\;=\;\begin{pmatrix}1&3&5\\7&2&4\end{pmatrix}\)
В общем виде матрица записывается так:
\(M=\begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\\a_{21}&a_{22}&…&a_{2n}\\…&…&…&…\\a_{m1}&a_{m2}&…&a_{mn}\end{pmatrix}\)
Представленная выше матрица состоит из i-строк и j-столбцов. Каждый ее элемент имеет соответствующее позиционное обозначение, определяемое номером строки и столбца на пересечении которых он расположен: \(a_{ij}\)- находится на i-ой строке и j-м столбце.
Важным элементом матрицы является главная диагональ, ее составляют элементы, у которых совпадают номера строк и столбцов.
Виды матриц и способы их создания в PythonМатрица в Python – это двумерный массив, поэтому задание матриц того или иного вида предполагает создание соответствующего массива. Для работы с массивами в Python используется тип данных список (англ. list). Но с точки зрения представления матриц и проведения вычислений с ними списки – не очень удобный инструмент, для этих целей хорошо подходит библиотека Numpy, ее мы и будем использовать в дальнейшей работе.
list). Но с точки зрения представления матриц и проведения вычислений с ними списки – не очень удобный инструмент, для этих целей хорошо подходит библиотека Numpy, ее мы и будем использовать в дальнейшей работе.
Напомним, для того, чтобы использовать библиотеку Numpy ее нужно предварительно установить, после этого можно импортировать в свой проект. По установке Numpy можно подробно прочитать в разделе “Установка библиотеки Numpy” из введения. Для того чтобы импортировать данный модуль, добавьте в самое начало программы следующую строку
import numpy as np
Если после импорта не было сообщений об ошибке, то значит все прошло удачно и можно начинать работу. Numpy содержит большое количество функций для работы с матрицами, которые мы будем активно использовать. Обязательно убедитесь в том, что библиотека установлена и импортируется в проект без ошибок.
Рассмотрим, различные варианты матриц и способы их задания в Python.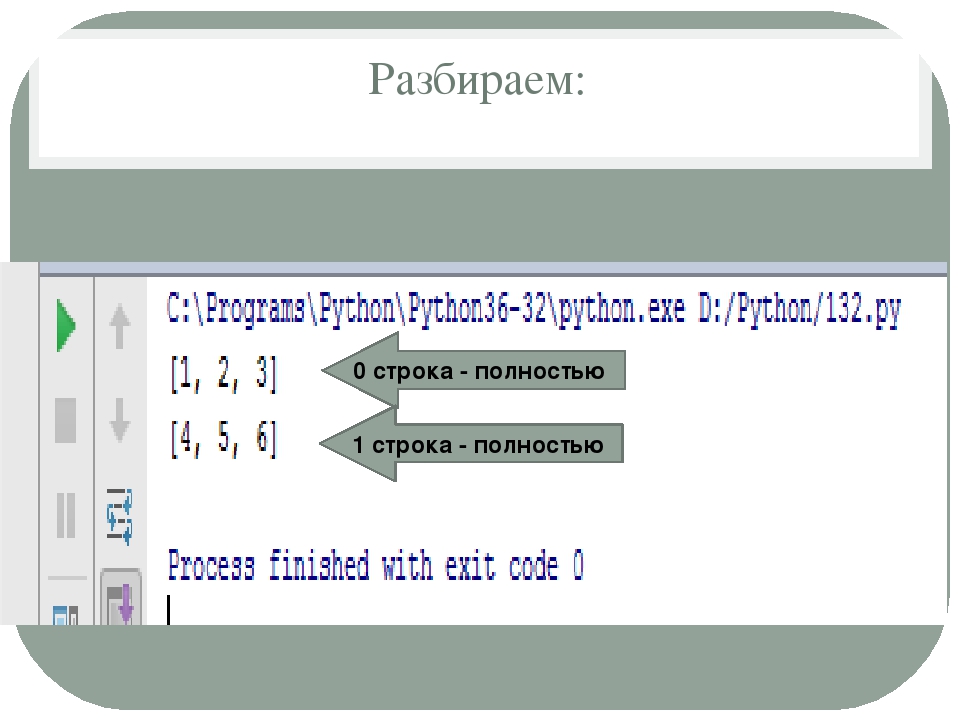
Вектором называется матрица, у которой есть только один столбец или одна строка. Более подробно свойства векторов, их геометрическая интерпретация и операции над ними будут рассмотрены в “Главе 2 Векторная алгебра”.
Вектор-строкаВектор-строка имеет следующую математическую запись.
\(v=(1\;2)\)
Такой вектор в Python можно задать следующим образом.
>>> v_hor_np = np.array([1, 2]) >>> print(v_hor_np ) [1 2]
Если необходимо создать нулевой или единичный вектор, то есть вектор, у которого все элементы нули либо единицы, то можно использовать специальные функции из библиотеки Numpy.
Создадим нулевую вектор-строку размера 5.
>>> v_hor_zeros_v1 = np.zeros((5,)) >>> print(v_hor_zeros_v1 ) [0. 0. 0. 0. 0.]
В случае, если требуется построить вектор-строку так, чтобы она сама являлась элементом какого-то массива, это нужно для возможности транспонирования матрицы (см. раздел “1.3 Транспонирование матрицы”), то данную задачу можно решить так.
раздел “1.3 Транспонирование матрицы”), то данную задачу можно решить так.
>>> v_hor_zeros_v2 = np.zeros((1, 5)) >>> print(v_hor_zeros_v2 ) [[0. 0. 0. 0. 0.]]
Построим единичную вектор-строку в обоих из представленных для нулевого вектора-строки форм.
>>> v_hor_one_v1 = np.ones((5,)) >>> print(v_hor_one_v1) [1. 1. 1. 1. 1.]
>>> v_hor_one_v2 = np.ones((1, 5)) >>> print(v_hor_one_v2) [[1. 1. 1. 1. 1.]]Вектор-столбец
Вектор-столбец имеет следующую математическую запись.
\(v=\begin{pmatrix}1\\2\end{pmatrix}\)
В общем виде вектор столбец можно задать следующим образом.
>>> v_vert_np = np.array([[1], [2]]) >>> print(v_vert_np) [[1] [2]]
Рассмотрим способы создания нулевых и единичных векторов-столбцов. Построим нулевой вектор-столбец.
Построим нулевой вектор-столбец.
>>> v_vert_zeros = np.zeros((5, 1)) >>> print(v_vert_zeros) [[0.] [0.] [0.] [0.] [0.]]
Единичный вектор-столбец можно создать с помощью функции ones().
>>> v_vert_ones = np.ones((5, 1)) >>> print(v_vert_ones) [[1.] [1.] [1.] [1.] [1.]]Квадратная матрица
Довольно часто, на практике, приходится работать с квадратными матрицами. Квадратной называется матрица, у которой количество столбцов и строк совпадает. В общем виде они выглядят так.
\(Msqr=\begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\\a_{21}&a_{22}&…&a_{2n}\\…&…&…&…\\a_{n1}&a_{n2}&…&a_{nn}\end{pmatrix}\)
Создадим следующую матрицу.
\(Msqr=\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}\)
В Numpy можно создать квадратную матрицу с помощью метода array().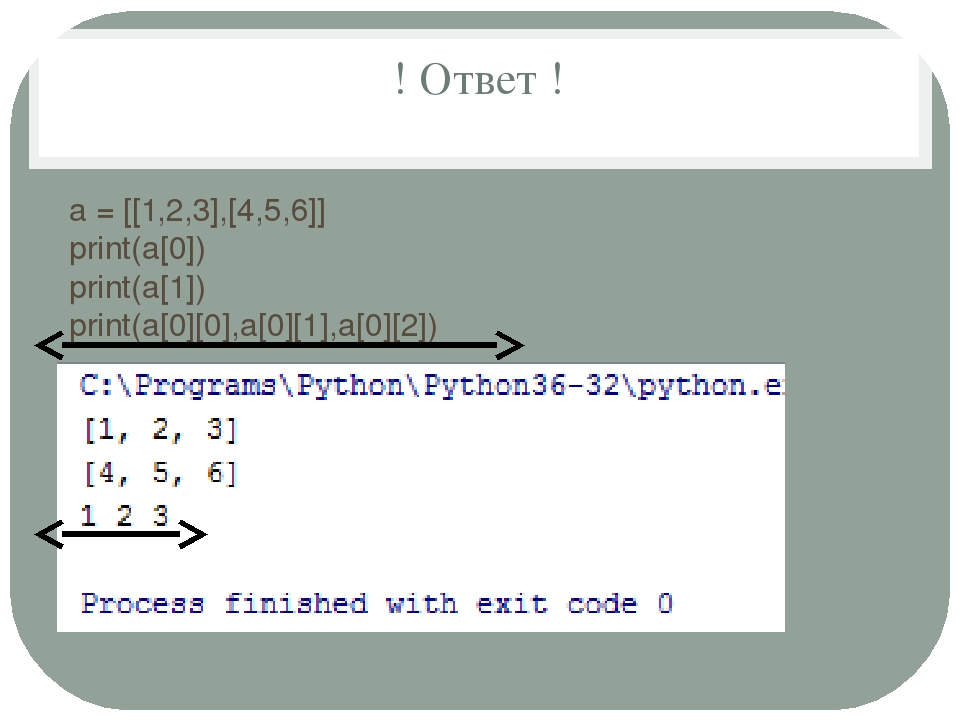
>>> m_sqr_arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> print(m_sqr_arr) [[1 2 3] [4 5 6] [7 8 9]]
Как вы уже наверное заметили, аргументом функции np.array() является список Python, его можно создать отдельно и передать в функцию.
>>> m_sqr = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] >>> m_sqr_arr = np.array(m_sqr) >>> print(m_sqr_arr) [[1 2 3] [4 5 6] [7 8 9]]
Но в Numpy есть еще одни способ создания матриц – это построение объекта типа matrix с помощью одноименного метода. Задать матрицу можно в виде списка.
>>> m_sqr_mx = np.matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> print(m_sqr_mx) [[1 2 3] [4 5 6] [7 8 9]]
Также доступен стиль Matlab, когда между элементами ставятся пробелы, а строки разделяются точкой с запятой, при этом такое описание должно быть передано в виде строки.
>>> m_sqr_mx = np.matrix('1 2 3; 4 5 6; 7 8 9')
>>> print(m_sqr_mx)
[[1 2 3]
[4 5 6]
[7 8 9]]Диагональная матрицаОсобым видом квадратной матрицы является диагональная – это такая матрица, у которой все элементы, кроме тех, что расположены на главной диагонали, равны нулю.
\(Mdiag=\begin{pmatrix}a_{11}&0&…&0\\0&a_{22}&…&0\\…&…&…&…\\0&0&…&a_{nn}\end{pmatrix}\)
Диагональную матрицу можно построить вручную, задав только значения элементам на главной диагонали.
>>> m_diag = [[1, 0, 0], [0, 5, 0], [0, 0, 9]] >>> m_diag_np = np.matrix(m_diag) >>> print(m_diag_np) [[1 0 0] [0 5 0] [0 0 9]]
Библиотека Numpy предоставляет инструменты, которые могут упростить построение такой матрицы.
Первый вариант подойдет в том случае, если у вас уже есть матрица, и вы хотите сделать из нее диагональную. Создадим матрицу размера 3 3.
Создадим матрицу размера 3 3.
>>> m_sqr_mx = np.matrix('1 2 3; 4 5 6; 7 8 9')Извлечем ее главную диагональ.
>>> diag = np.diag(m_sqr_mx) >>> print(diag) [1 5 9]
Построим диагональную матрицу на базе полученной диагонали.
>>> m_diag_np = np.diag(np.diag(m_sqr_mx)) >>> print(m_diag_np) [[1 0 0] [0 5 0] [0 0 9]]
Второй вариант подразумевает построение единичной матрицы, ей будет посвящен следующий параграф.
Единичная матрицаЕдиничной матрицей называют такую квадратную матрицу, у которой элементы главной диагонали равны единицы, а все остальные нулю.
\(E=\begin{pmatrix}1&0&…&0\\0&1&…&0\\…&…&…&…\\0&0&…&1\end{pmatrix}\)
Создадим единичную матрицу на базе списка, который передадим в качестве аргумента функции matrix().
>>> m_e = [[1, 0, 0], [0, 1, 0], [0, 0, 1]] >>> m_e_np = np.matrix(m_e) >>> print(m_e_np) [[1 0 0] [0 1 0] [0 0 1]]
Такой способ не очень удобен, к счастью для нас, для построения такого типа матриц в библиотеке Numpy есть специальная функция – eye().
>>> m_eye = np.eye(3) >>> print(m_eye) [[ 1. 0. 0.] [ 0. 1. 0.] [ 0. 0. 1.]]
В качестве аргумента функции передается размерность матрицы, в нашем примере – это матрица 3 3. Тот же результат можно получить с помощью функции identity().
>>> m_idnt = np.identity(3) >>> print(m_idnt) [[ 1. 0. 0.] [ 0. 1. 0.] [ 0. 0. 1.]]Нулевая матрица
У нулевой матрицы все элементы равны нулю.
\(Z=\begin{pmatrix}0&0&…&0\\0&0&…&0\\…&…&…&…\\0&0&…&0\end{pmatrix}\)
Пример того, как создать такую матрицу с использованием списков, мы приводить не будем, он делается по аналогии с предыдущим разделом. Что касается Numpy, то в составе этой библиотеки есть функция zeros(), которая создает нужную нам матрицу.
Что касается Numpy, то в составе этой библиотеки есть функция zeros(), которая создает нужную нам матрицу.
>>> m_zeros = np.zeros((3, 3)) >>> print(m_zeros) [[ 0. 0. 0.] [ 0. 0. 0.] [ 0. 0. 0.]]
В качестве параметра функции zeros() передается размерность требуемой матрицы в виде кортежа из двух элементов, первый из которых – число строк, второй – столбцов. Если функции zeros() передать в качестве аргумента число, то будет построен нулевой вектор-строка, это мы делали в параграфе, посвященном векторам.
Задание матрицы в общем видеЕсли у вас уже есть данные о содержимом матрицы, то создать ее можно используя списки Python или функцию matrix() из библиотеки Numpy.
>>> m_mx = np.matrix('1 2 3; 4 5 6')
>>> print(m_mx)
[[1 2 3]
[4 5 6]]Если же вы хотите создать матрицу заданного размера с произвольным содержимым, чтобы потом ее заполнить, проще всего для того использовать функцию zeros(), которая создаст матрицу заданного размера, заполненную нулями.
>>> m_var = np.zeros((2, 5)) >>> print(m_var) [[ 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0.]]P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 | #include <stdio. |
Генераторы списков в Python
В языке программирования Python существует специальная синтаксическая конструкция, которая позволяет по определенным правилам создавать заполненные списки. Такие конструкции называются генераторами списков. Их удобство заключается в более короткой записи программного кода, чем если бы создавался список обычным способом.
Такие конструкции называются генераторами списков. Их удобство заключается в более короткой записи программного кода, чем если бы создавался список обычным способом.
Например, надо создать список, заполненный натуральными числами до определенного числа. «Классический» способ будет выглядеть примерно так:
>>> a = [] >>> for i in range(1,15): ... a.append(i) ... >>> a [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]
На создание списка ушло три строчки кода. Генератор же сделает это за одну:
>>> a = [i for i in range(1,15)] >>> a [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]
Здесь конструкция [i for i in range(1,15)] является генератором списка. Вся конструкция заключается в квадратные скобки, что как бы говорит, что будет создан список. Внутри квадратных скобок можно выделить три части: 1) что делаем с элементом (в данном случае ничего не делаем, просто добавляем в список), 2) что берем (в данном случае элемент i), 3) откуда берем (здесь из объекта range). Части отделены друг от друга ключевыми словами
Части отделены друг от друга ключевыми словами for и in.
Рассмотрим такой пример:
>>> a = [2,-2,4,-4,7,5] >>> b = [i**2 for i in a] >>> b [4, 4, 16, 16, 49, 25]
В данном случае в генераторе списка берется каждый элемент из списка a и возводится в квадрат. Таким образом, 1) что делаем — возводим элемент в квадрат, 2) что берем — элемент, 3) откуда берем — из списка a.
>>> a = {1:10, 2:20, 3:30}
>>> b = [i*a[i] for i in a]
>>> b
[10, 40, 90]
Здесь берется ключ из словаря, а в генерируемый список добавляется произведение ключа на его значение.
>>> a = {1:10, 2:20, 3:30}
>>> b = [[i,a[i]] for i in a]
>>> b
[[1, 10], [2, 20], [3, 30]]
>>> c = [j for i in b for j in i]
>>> c
[1, 10, 2, 20, 3, 30]
В этом примере генерируемый список b состоит из вложенных списков. Если бы в генераторе были опущены квадратные скобки в выражении
Если бы в генераторе были опущены квадратные скобки в выражении [i,a[i]], то произошла бы ошибка. Если все же надо получить одноуровневый список из ключей и значений словаря, надо взять каждый вложенный список и из него взять каждый элемент. Это достигается за счет вложенной конструкции for, что демонстрируется в строчке c = [j for i in b for j in i]. «Классический» синтаксис для заполнения списка c выглядел бы так:
>>> c = [] >>> for i in b: ... for j in i: ... c.append(j) ... >>> c [1, 10, 2, 20, 3, 30]
В конец генератора можно добавлять конструкцию if. Например, надо из строки извлечь все цифры:
>>> a = "lsj94ksd231 9" >>> b = [int(i) for i in a if '0'<=i<='9'] >>> b [9, 4, 2, 3, 1, 9]
Или заполнить список числами, кратными 30 или 31:
>>> a = [i for i in range(30,250) ... if i%30 == 0 or i%31 == 0] >>> a [30, 31, 60, 62, 90, 93, 120, 124, 150, 155, 180, 186, 210, 217, 240, 248]
Таким образом, генераторы позволяют создавать списки легче и быстрее. Однако заменить ими достаточно сложные конструкции не получится.
Однако заменить ими достаточно сложные конструкции не получится.
Python — 2D Array — CoderLessons.com
Двумерный массив — это массив внутри массива. Это массив массивов. В этом типе массива положение элемента данных обозначается двумя индексами вместо одного. Таким образом, он представляет собой таблицу со строками и столбцами данных. В приведенном ниже примере двумерного массива обратите внимание, что каждый элемент массива также является массивом.
Рассмотрим пример записи температуры 4 раза в день, каждый день. Иногда записывающий инструмент может быть неисправен, и мы не можем записать данные. Такие данные за 4 дня могут быть представлены в виде двумерного массива, как показано ниже.
Day 1 - 11 12 5 2 Day 2 - 15 6 10 Day 3 - 10 8 12 5 Day 4 - 12 15 8 6
Вышеуказанные данные могут быть представлены в виде двумерного массива, как показано ниже.
T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]]
Доступ к значениям в двумерном массиве
Элементы данных в двух десятичных массивах могут быть доступны с использованием двух индексов. Один индекс ссылается на основной или родительский массив, а другой индекс ссылается на позицию элемента данных во внутреннем массиве. Если мы упомянем только один индекс, тогда весь внутренний массив будет напечатан для этой позиции индекса. Пример ниже иллюстрирует, как это работает.
Один индекс ссылается на основной или родительский массив, а другой индекс ссылается на позицию элемента данных во внутреннем массиве. Если мы упомянем только один индекс, тогда весь внутренний массив будет напечатан для этой позиции индекса. Пример ниже иллюстрирует, как это работает.
from array import * T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]] print(T[0]) print(T[1][2])
Когда приведенный выше код выполняется, он дает следующий результат —
[11, 12, 5, 2] 10
Чтобы распечатать весь двумерный массив, мы можем использовать python for loop, как показано ниже. Мы используем конец строки, чтобы распечатать значения в разных строках.
from array import *
T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]]
for r in T:
for c in r:
print(c,end = " ")
print()Когда приведенный выше код выполняется, он дает следующий результат —
11 12 5 2 15 6 10 10 8 12 5 12 15 8 6
Вставка значений в двумерный массив
Мы можем вставить новые элементы данных в определенную позицию, используя метод insert () и указав индекс.
В приведенном ниже примере новый элемент данных вставляется в позиции индекса 2.
from array import *
T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]]
T.insert(2, [0,5,11,13,6])
for r in T:
for c in r:
print(c,end = " ")
print()Когда приведенный выше код выполняется, он дает следующий результат —
11 12 5 2 15 6 10 0 5 11 13 6 10 8 12 5 12 15 8 6
Обновление значений в двумерном массиве
Мы можем обновить весь внутренний массив или некоторые конкретные элементы данных внутреннего массива, переназначив значения с помощью индекса массива.
from array import *
T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]]
T[2] = [11,9]
T[0][3] = 7
for r in T:
for c in r:
print(c,end = " ")
print()Когда приведенный выше код выполняется, он дает следующий результат —
11 12 5 7 15 6 10 11 9 12 15 8 6
Удаление значений в двумерном массиве
Мы можем удалить весь внутренний массив или некоторые конкретные элементы данных внутреннего массива, переназначив значения с помощью метода del () с index. Но если вам нужно удалить определенные элементы данных в одном из внутренних массивов, используйте процесс обновления, описанный выше.
Но если вам нужно удалить определенные элементы данных в одном из внутренних массивов, используйте процесс обновления, описанный выше.
from array import *
T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]]
del T[3]
for r in T:
for c in r:
print(c,end = " ")
print()Когда приведенный выше код выполняется, он дает следующий результат —
PYTHON. Двумерные массивы — Информатика Эксперт
PYTHON. Двумерные массивы. Двумерные массивы или матрица — это набор однотипных данных, имеющий общее имя, доступ к элементам которого осуществляется по двум индексам. В языке программирования Python таблицу можно представить в виде списка строк, каждый элемент которого является в свою очередь списком, например, чисел. Приведём таблицу, в которой создаётся числовая таблица из двух строк и трех столбцов, с которой производятся различные действия.
Представим таблицу в виде кода:
a = [[1, 2, 3], [4, 5, 6]] print(a[0]) print(a[1]) b = a[0] print(b) print(a[0][2]) a[0][1] = 7 print(a) print(b) b[2] = 9 print(a[0]) print(b)
a = [[1, 2, 3], [4, 5, 6]] print(a[0]) print(a[1]) b = a[0] print(b) print(a[0][2]) a[0][1] = 7 print(a) print(b) b[2] = 9 print(a[0]) print(b) |
Здесь первая строка списка a[0] является списком из чисел [1, 2, 3]. То есть
То есть a[0][0] == 1, значение a[0][1] == 2, a[0][2] == 3, a[1][0] == 4, a[1][1] == 5, a[1][2] == 6.
Продемонстрируем, как выводить двумерный массив, используя это удобное свойство цикла for:
a = [[1, 2, 3, 4], [5, 6], [7, 8, 9]] for row in a: for elem in row: print(elem, end=’ ‘) print()
a = [[1, 2, 3, 4], [5, 6], [7, 8, 9]] for row in a: for elem in row: print(elem, end=’ ‘) print() |
Естественно, для вывода одной строки можно воспользоваться методом join():
for row in a: print(‘ ‘.join([str(elem) for elem in row]))
for row in a: print(‘ ‘. |
Пусть программа получает на вход двумерный массив в виде n строк, каждая из которых содержит m чисел, разделенных пробелами. Считать их можно следующим образом:
# в первой строке ввода идёт количество строк массива n = int(input()) a = [] for i in range(n): a.append([int(j) for j in input().split()])
# в первой строке ввода идёт количество строк массива n = int(input()) a = [] for i in range(n): a.append([int(j) for j in input().split()]) |
Можно сделать то же самое и при помощи генератора:
# в первой строке ввода идёт количество строк массива n = int(input()) a = [[int(j) for j in input().split()] for i in range(n)]
# в первой строке ввода идёт количество строк массива n = int(input()) a = [[int(j) for j in input(). |
Для создания двумерных массивов можно использовать вложенные генераторы, разместив генератор списка, являющегося строкой, внутри генератора всех строк. Напомним, что сделать список из n строк и m столбцов можно при помощи генератора, создающего список из n элементов, каждый элемент которого является списком из m нулей:
[[0] * m for i in range(n)]
[[0] * m for i in range(n)] |
Но при этом внутренний список также можно создать при помощи, например, такого генератора: [0 for j in range(m)]. Вложив один генератор в другой, получим вложенные генераторы:
[[0 for j in range(m)] for i in range(n)]
[[0 for j in range(m)] for i in range(n)] |
Но если число 0 заменить на некоторое выражение, зависящее от i (номер строки) и j (номер столбца), то можно получить список, заполненный по некоторой формуле.
Например, пусть нужно задать следующий массив (для удобства добавлены дополнительные пробелы между элементами):
0 0 0 0 0 0 0 1 2 3 4 5 0 2 4 6 8 10 0 3 6 9 12 15 0 4 8 12 16 20
0 0 0 0 0 0 0 1 2 3 4 5 0 2 4 6 8 10 0 3 6 9 12 15 0 4 8 12 16 20 |
В этом массиве n = 5 строк, m = 6 столбцов, и элемент в строке i и столбце jвычисляется по формуле: a[i][j] = i * j.
Для создания такого массива можно использовать генератор:
[[i * j for j in range(m)] for i in range(n)]
[[i * j for j in range(m)] for i in range(n)] |
Python | Правильное использование 2D-массивов / списков
Python предоставляет множество способов создания двумерных списков / массивов. Однако необходимо знать различия между этими способами, поскольку они могут создавать сложности в коде, которые может быть очень трудно отследить. Начнем с рассмотрения распространенных способов создания 1d массива размера N, инициализированного нулями.
Однако необходимо знать различия между этими способами, поскольку они могут создавать сложности в коде, которые может быть очень трудно отследить. Начнем с рассмотрения распространенных способов создания 1d массива размера N, инициализированного нулями.
Метод 1a
|
Метод 1b
|
Расширяя вышесказанное, мы можем определять двумерные массивы следующими способами.
Метод 2a
|
[[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [ 0, 0, 0, 0, 0]]
Метод 2b
|
[[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [ 0, 0, 0, 0, 0]]
Метод 2c
|
[[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [ 0, 0, 0, 0, 0]]
Оба способа дают, казалось бы, тот же результат, что и сейчас. Давайте изменим один из элементов в массиве метода 2a и метода 2b.
|
[1, 0, 0, 0, 0] [1, 0, 0, 0, 0] [1, 0, 0, 0, 0] [1, 0, 0, 0, 0] [1, 0, 0, 0, 0] [1, 0, 0, 0, 0] [0, 0, 0, 0, 0] [0, 0, 0, 0, 0] [0, 0, 0, 0, 0] [0, 0, 0, 0, 0]
Мы ожидаем, что только первый элемент первой строки изменится на 1, но первый элемент каждой строки изменится на 1 в методе 2a. Это своеобразное функционирование связано с тем, что Python использует неглубокие списки, которые мы попытаемся понять.
Это своеобразное функционирование связано с тем, что Python использует неглубокие списки, которые мы попытаемся понять.
В методе 1a Python не создает 5 целочисленных объектов, а создает только один целочисленный объект, и все индексы массива arr указывают на один и тот же объект int, как показано.
Если мы присваиваем 0-й индекс другому целому числу, например 1, то создается новый целочисленный объект со значением 1, а затем 0-й индекс теперь указывает на этот новый объект int, как показано ниже
Точно так же, когда мы создаем двумерный массив как «arr = [[0] * cols] * rows», мы, по сути, продолжаем приведенную выше аналогию.
1. Создается только один целочисленный объект.
2. Создается один 1d список, и все его индексы указывают на один и тот же объект int в точке 1.
3. Теперь arr [0], arr [1], arr [2]…. arr [n-1] все указывают на один и тот же объект списка выше в пункте 2.
Указанную выше настройку можно визуализировать на изображении ниже.
Теперь давайте изменим первый элемент в первой строке «arr» на
arr [0] [0] = 1
=> arr [0] указывает на единственный объект списка, который мы создали выше.(Помните, что arr [1], arr [2]… arr [n-1] тоже указывают на один и тот же объект списка)
=> Присвоение arr [0] [0] создаст новый объект int со значением 1 и arr [0] [0] теперь будет указывать на этот новый объект int. (как и arr [1] [0], arr [2] [0]… arr [n-1] [0])
Это хорошо видно на изображении ниже.
Итак, когда 2d массивы создаются таким образом, изменение значений в определенной строке повлияет на все строки, поскольку по существу существует только один целочисленный объект и только один объект списка, на который ссылаются все строки массива.
Как и следовало ожидать, отследить ошибки, вызванные таким использованием мелких списков, сложно. Следовательно, лучший способ объявить 2d-массив —
|
В отличие от метода 2a, этот метод создает 5 отдельных объектов списка. Один из способов проверить это — использовать оператор «is», который проверяет, относятся ли два операнда к одному и тому же объекту.
Один из способов проверить это — использовать оператор «is», который проверяет, относятся ли два операнда к одному и тому же объекту.
|
Внимание компьютерщик! Укрепите свои основы с помощью курса Python Programming Foundation и изучите основы.
Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS .
Урок 10 — Многомерные списки в Python
Основные моменты урока
Вам нужен краткий справочник по многомерному списки на Python вместо полного урока? Вот он:
Укороченная инициализация 2D-массива:
кино = [
[0, 0, 0, 0, 1],
[0, 0, 0, 1, 1],
[0, 0, 1, 1, 1],
[0, 0, 0, 1, 1],
[0, 0, 0, 0, 1]
] Запись 1 на позиции [1] [0] :
кино [1] [0] = 1
Чтение значения (теперь 1 ) в позиции [1] [0] :
{PYTHON}
кино = [
[0, 0, 0, 0, 1],
[0, 0, 0, 1, 1],
[0, 0, 1, 1, 1],
[0, 0, 0, 1, 1],
[0, 0, 0, 0, 1]
]
кинотеатр [1] [0] = 1
печать (кино [1] [0]) Печать всего 2D-массива:
Создание пустого 2D-массива заданного размера:
{PYTHON}
кино = []
для j в диапазоне (5):
столбец = []
для i в диапазоне (5):
столбец.добавить (0)
cinema.append (столбец)
для колонки в кино:
для элемента в столбце:
print (item, end = "")
Распечатать()
Хотите узнать больше? Полный урок по этой теме приводится ниже.
На предыдущем уроке «Строки в Python — Split» мы узнали, как использовать split () строковый метод. Сегодняшнее руководство — это в основном бонус, когда
речь идет об основных конструкциях Python. Мы обсудим то, что мы называем многомерным
списки (массивы). По сути, вы можете сразу перейти к следующему уроку,
однако я настоятельно рекомендую вам закончить этот, чтобы вы могли понять
остальные техники.В конце концов, это еще только основы.
Мы обсудим то, что мы называем многомерным
списки (массивы). По сути, вы можете сразу перейти к следующему уроку,
однако я настоятельно рекомендую вам закончить этот, чтобы вы могли понять
остальные техники.В конце концов, это еще только основы.
Мы уже работали с одномерными списками, которые можно представить как ряд ящиков в памяти нашего компьютера.
(Список из восьми номеров можно увидеть в изображение)
Хотя это не слишком часто, иногда вы можете встретить многомерные списки. Особенно, если речь идет об игровых приложениях.
Двумерный список
Хорошим представлением двумерного списка является сетка, потому что технически это один.Практическое применение двумерных списков было бы их использование хранить свободные места в кинотеатре. Вот наглядное представление о том, что Я имею в виду:
(видим свободные места в кинотеатре на картинке)
Конечно, в реальной жизни кинотеатр был бы больше, но этот список вполне подходит. В качестве примера.
В качестве примера. 0 означает, что сиденье доступно, 1 стоит
для того, что нет. Позже мы могли добавить 2 для зарезервированных мест.
и так далее.Было бы более уместно создать наш собственный тип данных (называемый
enumerable) для этих состояний, но мы вернемся к этому позже. А пока будем работать
с числами.
В Python мы объявляем 2D-массив (список) как список списков:
cinema = []
для j в диапазоне (5):
столбец = []
для i в диапазоне (5):
column.append (0)
cinema.append (столбец) Вначале создаем пустой одномерный список. Затем мы генерируем 5 дополнительных списков (столбцов), используя цикл для , заполните каждый
список с 5 нулями с помощью вложенного цикла и добавить список в
исходный список как новый элемент.
Первое число указывает количество столбцов, второе — количество столбцов.
строк, мы могли бы рассматривать это и наоборот, например, матрицы в
в математике на первом месте стоит количество строк.
Мы только что создали таблицу, полную нулей.
Заполнение данных
Давайте теперь заполним кинозал 1 сек, как вы можете видеть на
изображение выше. Поскольку мы будем ленивы, как и положено хорошим программистам, воспользуемся для циклов для создания строки 1 с Для доступа к элементу 2D-списка
мы должны ввести две координаты.
кино [2] [2] = 1
для i в диапазоне (1, 4):
cinema [i] [3] = 1
для i в диапазоне (5):
cinema [i] [4] = 1 Выход
Мы будем печатать список, используя цикл, как и раньше. Нам понадобится 2 петли для
2d список, первый будет перебирать столбцы, а второй —
ряды. Как настоящие программисты, мы не будем указывать количество строк и столбцов.
прямо в цикл, потому что он может измениться в будущем. Мы знаем len () , поэтому мы можем легко спросить, сколько столбцов в
внешний список и сколько элементов во внутреннем.Мы должны иметь в виду
внешний список может быть пустым.
Мы вложим циклы по порядку, чтобы внешний цикл проходил по строкам. а внутренний — над столбцами текущей строки. После печати строки мы должен разорвать линию. Оба контура должны иметь разные управляющие переменные:
. {PYTHON}
кино = []
для j в диапазоне (5):
столбец = []
для i в диапазоне (5):
column.append (0)
cinema.append (столбец)
кино [2] [2] = 1
для i в диапазоне (1, 4):
cinema [i] [3] = 1
для i в диапазоне (5):
cinema [i] [4] = 1
cols = len (кино)
строки = 0
если cols:
rows = len (кино [0])
для j в диапазоне (строки):
для я в диапазоне (столбцы):
print (cinema [i] [j], end = "")
печать () Результат:
Консольное приложение 00000 00000 00100 01110 11111
N-мерные массивы
Иногда бывает полезно создать список с еще большим количеством измерений. Мы можем
все хоть представляют себе 3Д список. Добавляя аналогию с кино, мы скажем, что наш
имеет несколько этажей или, как правило, больше комнат. Тогда визуализация будет выглядеть
как это:
Мы можем
все хоть представляют себе 3Д список. Добавляя аналогию с кино, мы скажем, что наш
имеет несколько этажей или, как правило, больше комнат. Тогда визуализация будет выглядеть
как это:
Мы можем создать 3D-массив так же, как мы создали 2D-массив:
кинотеатров = []
для k в диапазоне (5):
кино = []
для j в диапазоне (5):
столбец = []
для i в диапазоне (5):
column.append (0)
cinema.append (столбец)
cinemas.append (кино) Приведенный выше код создает трехмерный массив, который вы видели на картинке.Мы можем получить к нему доступ через индексаторы, квадратные скобки, как и раньше, но теперь нужно ввести 3 координаты.
кинотеатров [3] [2] [1] = 1
Укороченная инициализация многомерных списков
Я также упомяну, что даже многомерные списки можно инициализировать с помощью значения напрямую (код создает и инициализирует переполненный кинозал, когда вы можно увидеть на картинке):
кино = [
[0, 0, 0, 0, 1],
[0, 0, 0, 1, 1],
[0, 0, 1, 1, 1],
[0, 0, 0, 1, 1],
[0, 0, 0, 0, 1]
] (Список в этом коде вращается, поскольку мы определяем столбцы, которые объявлены
здесь строками).
Зубчатые массивы
В некоторых случаях нам даже не нужно «тратить» память на всю таблицу. Вместо этого мы можем создавать неровные многомерные списки.
Мы можем создать его либо с помощью циклов, либо с помощью сокращенной инициализации ( код ниже создает список с зазубринами из картинки):
jagged_list = [
[15, 2, 8, 5, 3],
[3, 3, 7],
[9, 1, 16, 13],
[],
[5]
] Тогда мы напечатали бы это так:
{PYTHON}
jagged_list = [
[15, 2, 8, 5, 3],
[3, 3, 7],
[9, 1, 16, 13],
[],
[5]
]
для столбца в jagged_list:
для элемента в столбце:
print (item, end = "")
печать () В заключение хочу добавить, что некоторые люди, не умеющие пользоваться
правильно использовать 2D-списки или словари для хранения нескольких наборов данных
единое целое. например представьте, что мы хотим сохранить длину, ширину и высоту
из пяти сотовых телефонов. Хотя вы можете подумать, что 3D-список лучше всего подходит для
ситуации, это может быть осуществлено с помощью обычного одномерного списка (в частности, списка
объекты типа
например представьте, что мы хотим сохранить длину, ширину и высоту
из пяти сотовых телефонов. Хотя вы можете подумать, что 3D-список лучше всего подходит для
ситуации, это может быть осуществлено с помощью обычного одномерного списка (в частности, списка
объекты типа Телефон ). Мы рассмотрим все это в
курс объектно-ориентированного программирования. Если вы чувствуете, что все еще можете использовать
Больше практики, попробуйте упражнения для этого урока.
В следующем уроке «Кортежи, множества и словари в Python» мы рассмотрим основные математические функции.
Python — многомерные массивы или матрицы
Многомерные массивы или матрицы
Существуют ситуации, когда требуются многомерные массивы или матрицы. Во многих языках (Java, COBOL, BASIC) это понятие многомерность достигается за счет предварительного объявления размеров (и ограничение размеров каждого измерения). В Python они обрабатываются несколько проще.
Если вам нужна более сложная обработка, чем мы показываем
в этом разделе вам понадобится Python Цифровой модуль , также известный как NumPy . Это проект Source Forge, и его можно
найдено по адресу
Это проект Source Forge, и его можно
найдено по адресу https://numpy.sourceforge.net/ .
Давайте посмотрим на простую двухмерную сводную таблицу. Когда бросая две кости, есть 36 возможных исходов. Мы можем свести эти в двухмерной таблице с одним кубиком в рядах и одним кубиком в столбцы:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
В Python можно реализовать многомерную таблицу, подобную этой. как последовательность последовательностей.Таблица — это последовательность строк. Каждая строка представляет собой
последовательность отдельных ячеек. Это позволяет нам использовать математические
обозначение. Где математик мог бы сказать A i, j , в Python мы можем сказать
как последовательность последовательностей.Таблица — это последовательность строк. Каждая строка представляет собой
последовательность отдельных ячеек. Это позволяет нам использовать математические
обозначение. Где математик мог бы сказать A i, j , в Python мы можем сказать А [i] [j] . В Python нам нужна строка i из таблицы A и столбца j из этой строки.
Это очень похоже на список из кортеж мы обсуждали в разделе «Списки кортежей».
Пример списка списков. Мы можем построить таблицу, используя вложенный список. В В следующем примере создается таблица как последовательность последовательностей, а затем заполняет каждую ячейку таблицы.
table = [[0 для i в диапазоне (6)] для j в диапазоне (6)]
таблица печати
для d1 в диапазоне (6):
для d2 в диапазоне (6):
таблица [d1] [d2] = d1 + d2 + 2
таблица печати
Эта программа выдала следующий результат.
[[0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0]] [[2, 3, 4, 5, 6, 7], [3, 4, 5, 6, 7, 8], [4, 5, 6, 7, 8, 9], [5, 6, 7, 8, 9, 10], [6, 7, 8, 9, 10, 11], [7, 8, 9, 10, 11, 12]]
Эта программа сделала две вещи.Он создал таблицу размером шесть на шесть нули. Затем он заполнил его каждой возможной комбинацией двух кубиков. Это не самый эффективный способ сделать это, но мы хотим проиллюстрировать несколько техник на простом примере. Мы посмотрим на каждую половину деталь.
Первая часть этой программы создает и печатает 6-элементную список , названный таблица ; каждый предмет
в таблице находится 6-элементный список нулей. Оно использует
понимание списка для создания объекта для каждого значения j в диапазоне от 0 до 6.Каждый из объектов — это список нулей, по одному для каждого значения i в диапазоне от 0 до 6. После этой инициализации
распечатана двумерная таблица нулей.
После этой инициализации
распечатана двумерная таблица нулей.
Понимание можно читать от внутреннего к внешнему, как
обычное выражение. Внутренний список , [0
for i in range (6)] , создает простой список из шести нулей. Внешний список , [[...] для
j in range (6)] создает шесть копий этих внутренних лист с.
Затем вторая часть этой программы перебирает все
комбинации двух кубиков, заполняющие каждую ячейку таблицы. Это
выполняется в виде двух вложенных петель, по одной петле на каждую из двух игральных костей. Внешний
Перечисляет все значения одного кубика, d1 . Петля
Перечисляет все значения второго кубика, d2 .
Обновление каждой ячейки включает выбор строки с стол [d1] ; это список из 6
значения. Конкретная ячейка в этом списке —
выбран ... [d2] . Мы устанавливаем эту ячейку на число выпавших
на кубике: d1 + d2 + 2 .
Дополнительные примеры. Печатный список г. list s немного трудно читать. Следующее
цикл отобразит таблицу в более удобочитаемой форме.
>>>для строки в таблице:...печатный ряд...[2, 3, 4, 5, 6, 7] [3, 4, 5, 6, 7, 8] [4, 5, 6, 7, 8, 9] [5, 6, 7, 8, 9, 10] [6, 7, 8, 9, 10, 11] [7, 8, 9, 10, 11, 12]
В качестве упражнения мы предоставим читателю возможность добавить некоторые функции
к этому, чтобы напечатать заголовки столбцов и строк вместе с содержимым.Как
подсказка, значение "% 2d"% строка операция может быть полезна для получения числовых преобразований фиксированного размера.
Явные значения индекса. Подведем итоги нашей таблицы бросков кубиков и накопим
таблица частот. Мы будем использовать простой список из 13 сегментов (пронумерованных
от 0 до 12) для частоты каждого броска кубика. Мы видим, что
бросок кубика 2 происходит только один раз в нашей матрице, поэтому мы расширим это
Мы видим, что
бросок кубика 2 происходит только один раз в нашей матрице, поэтому мы расширим это fq [2] будет иметь значение 1. Давайте посетим каждую ячейку в
матрицу и накапливают таблицу частот.
Есть альтернатива этому подходу. Вместо того, чтобы вырезать каждую последовательность строк, мы могли бы использовать явные индексы и искать каждый индивидуальное значение с целочисленным индексом в последовательность.
fq = 13 * [0]
для i в диапазоне (6):
для j в диапазоне (6):
c = таблица [i] [j]
fq [c] + = 1
Мы инициализируем таблицу частот, fq , как список из 13 нулей.
Внешний цикл устанавливает для переменной i значение
значения от 0 до 5.Внутренний цикл устанавливает переменную j к значениям от 0 до 5.
Мы используем значение индекса i для выбора строки
из таблицы, а значение индекса j для выбора
столбец из этой строки. Это значение
Это значение c . Мы тогда
накапливать частоты встречаемости в таблице частот, fq .
Это выглядит очень математически и формально. Однако Python дает нам альтернатива, которая может быть несколько проще.
Использование итераторов списков вместо значений индекса. Поскольку наша таблица представляет собой список списков, мы можем использовать силу из для заявление, чтобы пройти через элементы без использования индекса.
fq = 13 * [0]
печать fq
для строки в таблице:
для c в строке:
fq [c] + = 1
print fq [2:]
Мы инициализируем таблицу частот, fq , как список из 13 нулей.
Внешний цикл устанавливает переменную row для каждого
элемент исходной таблицы переменной. Этот
разбивает таблицу на отдельные строки, каждая из которых представляет собой 6-элементную список .
Внутренний цикл устанавливает переменную c для каждого
значение столбца в строке. Это разбивает строку на
индивидуальные ценности.
Это разбивает строку на
индивидуальные ценности.
Мы подсчитываем фактическое возникновение каждого значения, c используя значение в качестве индекса в таблице частот, fq . Увеличение значения частоты на 1.
Математические матрицы. Мы используем технику явного индекса для управления математически определенные матричные операции. Матричные операции выполнены более четко с этим стилем явных операций с индексами.Мы покажем сложение матриц в качестве примера, а умножение матриц оставьте как упражнение в следующем разделе.
m1 = [[1, 2, 3, 0], [4, 5, 6, 0], [7, 8, 9, 0]]
m2 = [[2, 4, 6, 0], [1, 3, 5, 0], [0, -1, -2, 0]]
m3 = [4 * [0] для i в диапазоне (3)]
для i в диапазоне (3):
для j в диапазоне (4):
m3 [i] [j] = m1 [i] [j] + m2 [i] [j]
В этом примере мы создали две входные матрицы, м1 и м² , каждая три на четыре. Мы
инициализировал третью матрицу, м3 , до трех строк по четыре
нули, используя понимание. Затем мы перебрали все строки (используя
переменная
Затем мы перебрали все строки (используя
переменная и ) и все столбцы (используя j переменная) и вычислила сумму м1 и м² .
Python предоставляет ряд модулей для обработки таких обработка. В Части IV «Компоненты, модули и пакеты» мы рассмотрим модули, чтобы получить больше информации. сложная матричная обработка.
6.2. Подробнее о двумерных массивах — документация python_for_ss 0.1.1
В этом разделе мы обсудим некоторые из , использующие 2D-массивов, уделяя особое внимание их роли в представлении математических отношения.Мы также рассмотрим некоторые более сложные аспекты типа данных.
Необходимость в 2D-массивах очевидна, если вы взяли линейную алгебру.
учебный класс. Они соответствуют математическому объекту, называемому матрицей .
Одно из применений матриц — решение систем уравнений, но
это действительно только царапины на поверхности. Более фундаментальное приложение
для специалиста по данным, они могут представить все, что известно о
единый набор данных. Обычно каждая строка представляет собой элемент (индивидуальный или
событие в данных), а запись в каждом столбце — ее значение для
конкретный атрибут.Например, предположим, что в каждом номере отеля есть
лампы, столы, стулья и кровати, но в разном количестве. Мы можем
представляют инвентарь предметов в 5-комнатной гостинице с матрицей 5х4 (5
строки, 4 столбца) следующим образом:
Обычно каждая строка представляет собой элемент (индивидуальный или
событие в данных), а запись в каждом столбце — ее значение для
конкретный атрибут.Например, предположим, что в каждом номере отеля есть
лампы, столы, стулья и кровати, но в разном количестве. Мы можем
представляют инвентарь предметов в 5-комнатной гостинице с матрицей 5х4 (5
строки, 4 столбца) следующим образом:
6 3 4 1 5 2 3 2 8 3 6 2 5 1 3 1 10 4 7 2
Итак, первый ряд представляет собой комнату с 6 лампами, 3 столами, 4 стульями и 1 сп. Теперь, если мы представим стоимость каждого элемента в виде 1D-массива стоимости (или вектор ), чтобы использовать математический термин:
, где цены упорядочены так же, как в наших столбцах выше: лампы расходы, стоимость стола, стоимость стула и стоимость кровати.Затем мы можем вычислить Стоимость за номер составляет:
room_matrix = \ np.array ( [[6, 3, 4, 1], [5, 2, 3, 2], [8, 3, 6, 2], [5, 1, 3, 1], [10, 4, 7, 2]]) cost_vector = np.array ([40, 175, 90, 450])
печать room_matrix print cost_vector распечатать room_matrix.dot (cost_vector)
[[6 3 4 1] [5 2 3 2] [8 3 6 2] [5 1 3 1] [10 4 7 2]] [40 175 90 450] [1575 1720 2285 1095 2630]
Математическое имя метода точек , который вычисляет
Стоимость номера составляет , умножение матриц .
У массивов много атрибутов.
печать a.shape распечатать a.ndim напечатать a.dtype.name распечатать a.itemsize распечатать a.size тип печати (а) напечатать np.ndarray
(3, 5) 2 int64 8 15 <тип 'numpy.ndarray'> <тип 'numpy.ndarray'> [6 7 8] <тип 'numpy.ndarray'>
b = np.array ([6, 7, 8]) печать b тип печати (b) б
[6 7 8] <тип 'numpy.ndarray'>
Последовательность последовательностей может использоваться для определения 2D-массива, но поскольку внутренние последовательности — это строки таблицы, все они должны быть одинаковой длины.
b = np.array ([(1.5,2,3), (4,5,6)]) б
массив ([[1.5, 2., 3.],
[4., 5., 6.]])
Массивы также могут содержать комплексные числа, но помните, что для этого требуется два количества для определения одного комплексного числа:
c = np.array ([[1,2], [3,4]], dtype = complex) c
массив ([[1. + 0.j, 2. + 0.j],
[3. + 0.j, 4. + 0.j]])
Очень удобный способ заполнения массива — начать с массива содержащие все 0 или 1, а затем обновить содержимое:
массив ([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
Индексирование работает так же, как и с обычными последовательностями Python, за исключением того, что теперь есть два аспекта, о которых стоит беспокоиться
------------------------------------------------- -------------------------- IndexError Traceback (последний вызов последним)в () ----> 1 х [3,0] IndexError: индекс 3 находится за пределами оси 0 с размером 3
Assigment работает так же, как и с последовательностями Python, за исключением того, что теперь работает в двух измерениях
массив ([[0., 0., 0., 0.], [0., 0., 3., 0.], [0., 0., 0., 0.]])
X = np. нули ((3,4))
ctr = 0
(строки, столбцы) = X.shape
для я в диапазоне (строки):
для j в диапазоне (столбцы):
ctr + = 1
X [i, j] + = ctr * 10
Икс
массив ([[10., 20., 30., 40.],
[50., 60., 70., 80.],
[90., 100., 110., 120.]])
Намного более быстрый и естественный способ создать тот же массив:
X = np.arange (10,130,10) .reshape ((3,4)) Икс
массив ([[10, 20, 30, 40],
[50, 60, 70, 80],
[90, 100, 110, 120]])
Следующее выражение дает вторую строку X
Следующее выражение дает 3-й столбец X :
Обратите внимание, что столбцы и строки — это всего лишь одномерные массивы; их ничто не идентифицирует как векторы-строки или векторы-столбцы.
Для удобства numpy позволяет пропустить : , если вам нужна строка.
Другими словами, следующие два выражения являются синонимами.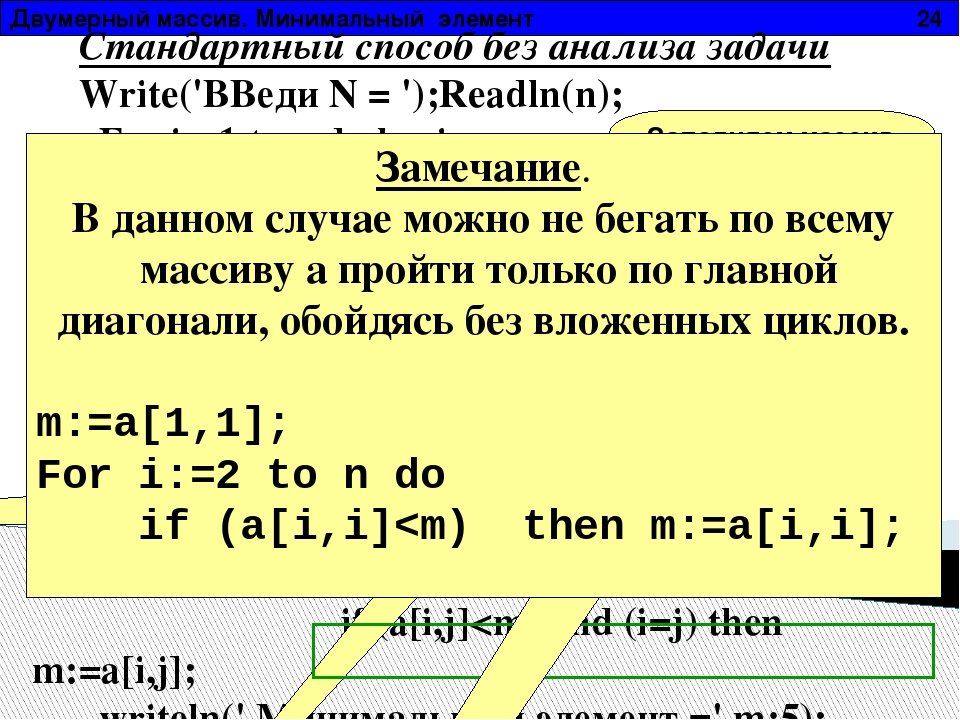 Обратите внимание, что вы нужен
Обратите внимание, что вы нужен : , если вам нужен столбец.
[50. 60. 70. 80.] [50, 60, 70, 80.]
print X [1 ,:], X [1,:]. Shape напечатать X [:, 1]
[50 60 70 80] (4,) [20 60 100]
Теперь давайте возьмем часть столбца или строки. Первые два элемента
второй столбец X , за которым следуют первые два элемента второго
ряд X :
печать X напечатать X [1,: 2] напечатать X [: 2,1]
[[10 20 30 40] [50 60 70 80] [90 100 110 120]] [50 60] [20 60]
Теперь давайте возьмем подмассив 2×2, состоящий из верхнего левого угла
размером X , затем следует центральная часть последних двух рядов.
печать X напечатать X [: 2,: 2] напечатать X [1:, 1: 3]
[[10 20 30 40] [50 60 70 80] [90 100 110 120]] [[10 20] [50 60]] [[60 70] [100 110]]
Транспонирование массива иногда является хорошим способом получить 2D-массив, который вы
действительно хотите. Перестановка массива
Перестановка массива M называется M.T , а
определение таково, что
Итак, если M — это массив m x n , то M.T — это n x m множество.Посмотрите на X.T и проверьте эти определения. м -й ряд X становится м -й колонной X.T . Колонна н -я X становится n -й строкой X.T .
печать X Распечатать распечатать X.T напечатайте X [1,2], X.T [2,1]
[[10 20 30 40] [50 60 70 80] [90 100 110 120]] [[10 50 90] [20 60 100] [30 70 110] [40 80 120]] 70 70
Есть также 3D-массивы, которые имеют третье измерение; каждая позиция по третьему измерению определяет 2D-массив.
A = np.arange (24) .reshape ((2,3,4)) А
массив ([[[0, 1, 2, 3],
[4, 5, 6, 7],
[8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
В двумерном массиве единственный индексный срез представляет собой строку или столбец (одномерный массив). В
3D-массив, срез с одним индексом — это 2D-массив. В качестве примеров
Предлагаем ниже, 3D-массивы представляют собой жесткую структуру данных.
думать, и они обычно используются для очень специфических приложений,
например, представление цветных изображений (3 слоя 2D-представления,
по одному для каждой интенсивности красно-зелено-синего цвета).
В
3D-массив, срез с одним индексом — это 2D-массив. В качестве примеров
Предлагаем ниже, 3D-массивы представляют собой жесткую структуру данных.
думать, и они обычно используются для очень специфических приложений,
например, представление цветных изображений (3 слоя 2D-представления,
по одному для каждой интенсивности красно-зелено-синего цвета).
массив ([[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]])
массив ([[3, 7, 11],
[15, 19, 23]]))
массив ([[8, 9, 10, 11],
[20, 21, 22, 23]])
6.2.1. 3. Поэлементные арифметические операции
Мы отметили выше важный факт о массивах, который отличает их от списки: арифметические операции могут выполняться с массивами как если бы они были числами. Мы обсудим это немного подробнее прямо в этом разделе.
Прежде всего отметим, что арифметические операции, такие как
сложение и умножение между
два массива хорошо определены, если массивы встречаются
определенные ограничения. Если у них то же самое
форма, сложение и умножение всегда
четко определенный.
Если у них то же самое
форма, сложение и умножение всегда
четко определенный.
импортировать numpy как np a = np.array ([20,30,40,50]) b = np.arange (4) распечатать печать b
В следующем примере мы проиллюстрируем широковещательную передачу . Поэлементно операции расширены для применения между массивами и объектами, которые не массивы или между массивами, которые не одинаковой формы.o например, 2 * a (a — массив выше) возвращает массив который содержит все элементы умноженного на 2
массив ([40, 60, 80, 100])
Это работает путем «трансляции» 2 в массив того же размера, что и a, а затем выполнение поэлементного преобразования двух массивов.
Поэлементная арифметика также работает с 2D массивы, часто довольно интуитивно.
A = np.array ([[1,1],
[0,1]])
B = np.array ([[2,0],
[3,4]])
A * B # поэлементное произведение
Вы можете перемножить два массива одинаковой формы, как мы это делали с a и b выше, но вы не можете полагаться на широковещательную рассылку, чтобы выяснить
что делать с несоответствующими размерами массивов. В общем, добавление массивов
разного размера вместе не получится:
В общем, добавление массивов
разного размера вместе не получится:
c = np.array ([2,3]) с * а
------------------------------------------------- -------------------------- ValueError Traceback (последний вызов последним)в () 1 c = np.array ([2,3]) ----> 2 с * а ValueError: операнды не могут транслироваться вместе с фигурами (2,) (4,)
Но иногда есть разумный способ примените операцию вдоль некоторого измерения 2D-массива.Рассмотрим:
a = np.array ([20,30,40,50]) c = np.arange (8) .reshape ((2,4)) c
массив ([[0, 1, 2, 3],
[4, 5, 6, 7]])
массив ([[20, 31, 42, 53],
[24, 35, 46, 57]])
Тот же принцип вещания применяется к Булевы тесты, которые преобразуются в поэлементные операций, в результате чего получается массив логических значений. Мы вернемся к этому вопросу ниже.
массив ([True, True, False, False], dtype = bool)
6.
 2.2. Поэлементные логические операции, маскирование
2.2. Поэлементные логические операции, маскированиеВыше мы отмечали, что идея поэлементных операций распространяется на Булевы тесты.
Как правило, применение логического теста к массиву возвращает массив значений истинности того же размера, что и исходный множество. Так же, как
добавляет 3 к каждому элементу массива X , поэтому
возвращает массив значений истинности, который сообщает нам, какие элементы X больше 2.
импортировать numpy как np X = np.array ([1,5,2,7,9,4,3, -6]) распечатать X напечатать X> = 3
[1 5 2 7 9 4 3–6] [Ложь Истина Ложь Истина Истина Истина Истина Ложь]
Одно из наиболее важных применений Логические массивы заключаются в том, что они может индексировать другие массивы.Это будет всегда работает, когда логический массив одинаков shape как индексируемый массив. Итак, в простейшем случае:
Это возвращает в точности элементы X, которые больше или равны
3.
Мы могли бы сделать то же самое с пониманием списка, но массив вычисление выше намного быстрее:
Причина, по которой X [X> = 3] работает, связана с базовым фактом массива
индексирование мы еще не сделали явным. Любой логический массив Y из
правильную длину можно использовать для индексации массива X, если X и Y одинаковы
длина.
Случайный, но важный пример. Предположим, у нас есть массив длиной 8 и мы хотим получить доступ к первому, третьему и седьмому элементам. Вот как сделайте это с помощью логического массива:
X = np.arange (8) + 1 Y = np.array ([True, False, True, False, False, False, True, False]) распечатать X X [Y]
булевых массивов также можно использовать для подсчета количества элементов в
массив, удовлетворяющий некоторому ограничению. Логическое значение True обрабатывается как
1 с арифметическими операциями
а логическое значение False равно 0, поэтому при суммировании логического массива учитывается
количество Истин. Следующее выражение правильно подсчитывает количество
элементы в
Следующее выражение правильно подсчитывает количество
элементы в X , которые больше или равны 3.
Однако в этом случае использование операции с массивом составляет примерно на порядок менее эффективен, чем естественный Пифоническая идиома.
len ([x вместо x в X, если x> 3])
Подробнее об операциях с массивами и эффективности ниже. Это непростая тема.
Логические операции работают более или менее должным образом на 2D-массивах:
импортировать numpy как np y = np.оранжевый (35) .reshape (5,7) у> 3
массив ([[Ложь, Ложь, Ложь, Ложь, Истина, Истина, Истина],
[Верно, Верно, Верно, Верно, Верно, Верно, Верно],
[Верно, Верно, Верно, Верно, Верно, Верно, Верно],
[Верно, Верно, Верно, Верно, Верно, Верно, Верно],
[True, True, True, True, True, True, True]], dtype = bool)
Обратите внимание, что этот логический массив сохраняет форму 5×7 y .
Но если мы используем его для индексации элементов y , результат должен быть 1D
массив:
массив ([4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34])
Теперь предположим, что у нас есть массив данных с 4 столбцами, но мы только
хотите сохранить первый, второй и четвертый столбцы.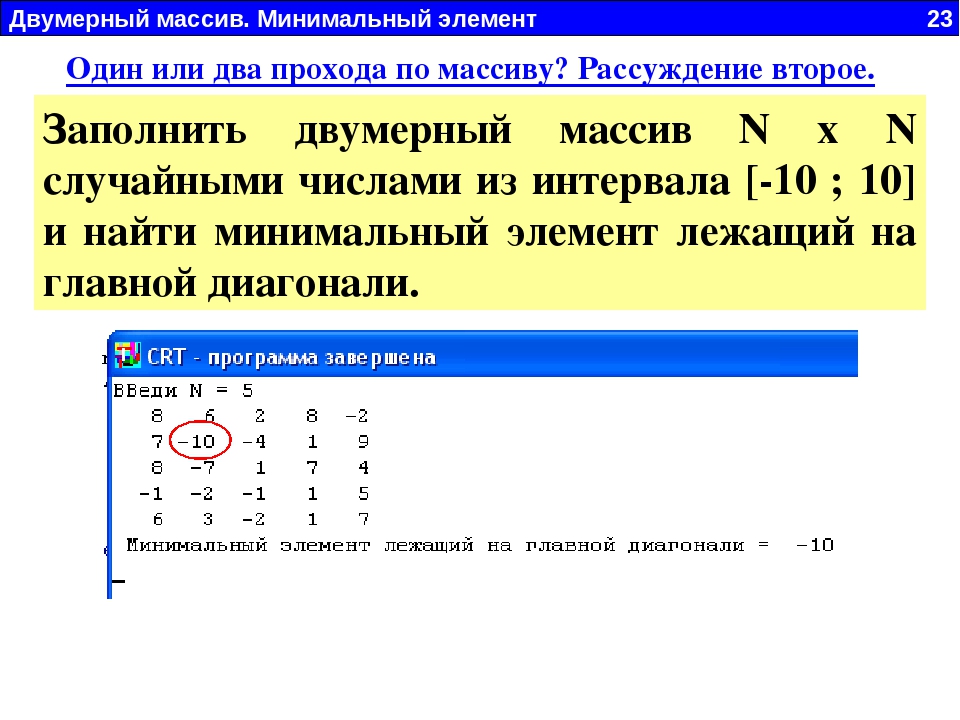 Вот простой способ
для этого с помощью логического массива:
Вот простой способ
для этого с помощью логического массива:
X = np.arange (8) .reshape ((2,4)) + 1 распечатать X print X [:, np.array ([True, True, False, True])]
[[1 2 3 4] [5 6 7 8]] [[1 2 4] [5 6 8]]
Теперь логические массивы и логическое маскирование — отличная функция, но она иногда вызывают у вас горе, если вы забываете, что что-то является массивом и что логический тест часто возвращает массив значений истинности вместо значения истины.
Python вернет ошибку, если вы попытаетесь использовать массив, в котором логическое значение
ожидаемое значение.Наиболее частая ошибка такого рода — , если — п.
------------------------------------------------- -------------------------- ValueError Traceback (последний вызов последним)в () ----> 1, если y: 2 печати "привет" ValueError: истинное значение массива с более чем одним элементом неоднозначно. Используйте a. any () или a.all ()
И результат любого логического теста, который можно интерпретировать как поэлементная операция вызовет ту же ошибку:
------------------------------------------------- -------------------------- ValueError Traceback (последний вызов последним)в () ----> 1, если y == 0: 2 печати "привет" ValueError: истинное значение массива с более чем одним элементом неоднозначно.Используйте a.any () или a.all ()
Тест - , однако, не вызывает эту ошибку, потому что не может
интерпретировать как поэлементную операцию:
Обратной стороной этого является то, что вы должны знать, чтобы ожидать различных видов
результаты с == и - это , когда речь идет о массивах.
[[Ложь Ложь Ложь Ложь Ложь] [Ложь Ложь Ложь Ложь Ложь Ложь] [Ложь Ложь Ложь Ложь Ложь Ложь] [Ложь Ложь Ложь Ложь Ложь Ложь] [Ложь Ложь Ложь Ложь Ложь Ложь]]
6.
 2.3. Данные в виде массивов
2.3. Данные в виде массивовМногие модули Python, которые предоставляют данные, делают это в виде массива. Как Например, мы загружаем знаменитый набор данных iris , созданный Эдгаром Андерсоном. и прославился в статье Рональда Фишера.
из sklearn.datasets import load_iris данные = load_iris () особенности = данные ['данные'] цель = данные ['цель']
Переменная features — это массив numpy :
print features.shape print features.ndim особенности печати.dtype.name print features.size тип печати (особенности) функции печати [: 10]
(150, 4) 2 float64 600 <тип 'numpy.ndarray'> [[5,1 3,5 1,4 0,2] [4,9 3. 1,4 0,2] [4,7 3,2 1,3 0,2] [4,6 3,1 1,5 0,2] [5. 3,6 1,4 0,2] [5,4 3,9 1,7 0,4] [4,6 3,4 1,4 0,3] [5. 3,4 1,5 0,2] [4,4 2,9 1,4 0,2] [4,9 3,1 1,5 0,1]]
Последнее, что напечатано, — это первые 10 строк из элементов . Этот массив
представляет данные об ирисах. Каждая строка представляет разные диафрагмы и
дает 4 измерения для этого экземпляра.Итак, есть 150 экземпляров ириса;
с 4 измерениями для каждого, это 600 элементов данных в массиве
(
Каждая строка представляет разные диафрагмы и
дает 4 измерения для этого экземпляра.Итак, есть 150 экземпляров ириса;
с 4 измерениями для каждого, это 600 элементов данных в массиве
( функций. Размер ). Данные используются для классификационных исследований.
Давайте применим то, что мы только что узнали, чтобы выбрать кератиновое подмножество данных. Первое число в каждой строке представляет чашелистиков длиной этого конкретный образец ириса. Давайте найдем все радужки в наборе данных длина чашелистика 5,
Сначала мы получаем вектор для первого столбца и используем его для создания Логический вектор, определяющий, какие строки имеют 5.0 в первом столбце.
first_col = features [:, 0] напечатать first_col == 5.0
[Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Верно Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Истина Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Истина Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Истина Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Истина Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь Ложь]
Затем мы используем только что созданный логический массив для индексации строк,
в сочетании с : , чтобы указать, что нам нужны все столбцы.
функций [first_col == 5.0 ,:]
массив ([[5., 3.6, 1.4, 0.2],
[5., 3.4, 1.5, 0.2],
[5., 3., 1.6, 0.2],
[5., 3.4, 1.6, 0.4],
[5., 3.2, 1.2, 0.2],
[5., 3.5, 1.3, 0.3],
[5., 3.5, 1.6, 0.6],
[5., 3.3, 1.4, 0.2],
[5., 2., 3.5, 1.],
[5., 2.3, 3.3, 1.]])
Таким образом, только 10 растений из 150 имеют длину чашелистиков 5.
Конечно, мы можем сделать все это за один шаг с тем же результатом:
функций [features [:, 0] == 5.0 ,:]
массив ([[5., 3.6, 1.4, 0.2],
[5., 3.4, 1.5, 0.2],
[5., 3., 1.6, 0.2],
[5., 3.4, 1.6, 0.4],
[5., 3.2, 1.2, 0.2],
[5., 3.5, 1.3, 0.3],
[5., 3.5, 1.6, 0.6],
[5., 3.3, 1.4, 0.2],
[5., 2., 3.5, 1.],
[5., 2.3, 3.3, 1.]])
Так как здесь мы индексируем строки, : также можно не указывать:
функций [features [:, 0] == 5.0]
массив ([[5., 3,6, 1,4, 0,2], [5., 3.4, 1.5, 0.2], [5., 3., 1.6, 0.2], [5., 3.4, 1.6, 0.4], [5., 3.2, 1.2, 0.2], [5., 3.5, 1.3, 0.3], [5., 3.5, 1.6, 0.6], [5., 3.3, 1.4, 0.2], [5., 2., 3.5, 1.], [5., 2.3, 3.3, 1.]])
Более интересное использование индексации логических массивов — найти все
ирисы определенного класса, используя переменную target , определенную, когда
мы загрузили данные; target — это массив, содержащий класс каждого
радужная оболочка в наборе данных:
тип печати (цель) цель печати.форма набор для печати (цель) функции печати [0], цель [0] функции печати [90], цель [90]
<тип 'numpy.ndarray'> (150,) set ([0, 1, 2]) [5,1 3,5 1,4 0,2] 0 [5,5 2,6 4,4 1,2] 1
Как видно из распечаток, цель представляет собой одномерный массив (вектор )
длина 150, содержащая только значения 0,1 и 2. Это три
классы, к которым может принадлежать ирис. Ровно столько же записей
в целевом массиве , так как в массиве
Ровно столько же записей
в целевом массиве , так как в массиве функций есть строки.За
любой диафрагмы, ее индекс строки в массиве функций является индексом ее
класс в мишени . Выше мы напечатали функции и целевой класс
для ирисов 0 и 90.
Мы можем воспользоваться этой структурой, чтобы найти все ирисы класса
1 очень качественно. Обратите внимание, что target == 1 — это логический массив
длина 150.
массив ([Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь,
Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь,
Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь,
Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь,
Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь,
Ложь, Ложь, Ложь, Ложь, Ложь, Истина, Истина, Истина, Истина,
Верно, Верно, Верно, Верно, Верно, Верно, Верно, Верно, Верно
Верно, Верно, Верно, Верно, Верно, Верно, Верно, Верно, Верно
Верно, Верно, Верно, Верно, Верно, Верно, Верно, Верно, Верно,
Верно, Верно, Верно, Верно, Верно, Верно, Верно, Верно, Верно,
Верно, Верно, Верно, Верно, Верно, Верно, Верно, Верно, Верно,
Истина, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь,
Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь,
Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь,
Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь,
Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь, Ложь,
False, False, False, False, False, False], dtype = bool)
Чтобы найти радужные оболочки класса 1, мы просто используем этот логический массив для
укажите нужные строки в массиве features array:
массив ([[7., 3.2, 4.7, 1.4], [6.4, 3.2, 4.5, 1.5], [6.9, 3.1, 4.9, 1.5], [5.5, 2.3, 4., 1.3], [6.5, 2.8, 4.6, 1.5], [5.7, 2.8, 4.5, 1.3], [6.3, 3.3, 4.7, 1.6], [4.9, 2.4, 3.3, 1.], [6,6, 2,9, 4,6, 1,3], [5.2, 2.7, 3.9, 1.4], [5., 2., 3.5, 1.], [5.9, 3., 4.2, 1.5], [6., 2.2, 4., 1.], [6.1, 2.9, 4.7, 1.4], [5.6, 2.9, 3.6, 1.3], [6.7, 3.1, 4.4, 1.4], [5.6, 3., 4.5, 1.5], [5.8, 2.7, 4.1, 1.], [6.2, 2.2, 4.5, 1.5], [5.6, 2.5, 3.9, 1.1], [5.9, 3.2, 4.8, 1.8], [6.1, 2.8, 4., 1.3], [6.3, 2.5, 4.9, 1.5], [6.1, 2.8, 4.7, 1.2], [6.4, 2.9, 4.3, 1.3], [6.6, 3., 4.4, 1.4], [6,8, 2,8, 4,8, 1,4], [6.7, 3., 5., 1.7], [6., 2.9, 4.5, 1.5], [5.7, 2.6, 3.5, 1.], [5.5, 2.4, 3.8, 1.1], [5.5, 2.4, 3.7, 1.], [5.8, 2.7, 3.9, 1.2], [6., 2.7, 5.1, 1.6], [5.4, 3., 4.5, 1.5], [6., 3.4, 4.
5, 1.6], [6,7, 3,1, 4,7, 1,5], [6.3, 2.3, 4.4, 1.3], [5.6, 3., 4.1, 1.3], [5.5, 2.5, 4., 1.3], [5.5, 2.6, 4.4, 1.2], [6.1, 3., 4.6, 1.4], [5.8, 2.6, 4., 1.2], [5., 2.3, 3.3, 1.], [5.6, 2.7, 4.2, 1.3], [5.7, 3., 4.2, 1.2], [5.7, 2.9, 4.2, 1.3], [6.2, 2.9, 4.3, 1.3], [5.1, 2.5, 3., 1.1], [5.7, 2.8, 4.1, 1.3]])
Теперь предположим, что мы хотим просто увидеть чашелистиков длиной (столбец 0) ирисы целевого класса 1 и сравните их с длиной чашелистиков ирисы целевого класса 0, чтобы убедиться, что длина чашелистиков является хорошим способом говоря два класса отдельно. Мы могли бы сделать:
функций печати [target == 1,0] функции печати [target == 0,0]
[7.6,4 6,9 5,5 6,5 5,7 6,3 4,9 6,6 5,2 5,9 6. 6,1 5,6 6,7 5,6 5,8 6,2 5,6 5,9 6,1 6,3 6,1 6,4 6,6 6,8 6,7 6. 5,7 5,5 5,5 5,8 6. 5,4 6. 6,7 6,3 5,6 5,5 5,5 6,1 5,8 5. 5,6 5,7 5,7 6,2 5,1 5,7] [5,1 4,9 4,7 4,6 5,4 4,6 5.4,4 4,9 5,4 4,8 4,8 4,3 5,8 5,7 5,4 5,1 5,7 5,1 5,4 5,1 4,6 5,1 4,8 5. 5,2 5,2 4,7 4,8 5,4 5,2 5,5 4,9 5,5 4,9 4,4 5,1 5,5 4,4 5,1 4,8 5,1 4,6 5,3 5.]
И хотя есть некоторое совпадение, мы видим, что есть тенденция к значение столбца 0 в цели 1 должно быть выше, чем в целевом классе 0.
6.2.4. Операции с массивами
Некоторые операции выполняются поэлементно, некоторые нет. Те, которых нет, те, которые имеет смысл применять к массиву в целом. Давай приготовим массив:
a = np.array ([[1.0, 2.0], [3.0, 4.0], [8.0,5.0]]) а
массив ([[1., 2.],
[3., 4.],
[8., 5.]])
Теперь транспонируем . То есть мы будем менять строки и столбцы. Вместо массива 3×2 мы получаем массив 2×3.
массив ([[1., 3., 8.],
[2., 4., 5.]])
Итак, транспонируем операцию с массивом. Это применимо к массиву в целом, не элемент за элементом, а в результате возвращает массив.
Чтобы получить доступ к тому же элементу в b , теперь нам нужно поменять местами строку и столбец
индексы
распечатать [2,0] напечатать b [0,2]
Другой пример операции с массивом — матричное произведение , или скалярное произведение . Это математически важная операция, требующая
два массива и возвращает массив. Вы можете найти его определение в
Википедия, если вам интересно.
Это математически важная операция, требующая
два массива и возвращает массив. Вы можете найти его определение в
Википедия, если вам интересно.
массив ([[5., 11., 18.],
[11., 25., 44.],
[18., 44., 89.]])
Мораль: при программировании с использованием массивов важно знать, какие
операции могут применяться поэлементно, а какие нет. Различие
не всегда полностью предсказуемо. Выше мы видели, что == — это
Логическая операция, которая применяется поэлементно к массиву, но равно ,
другая логическая операция — нет.
6.2.5. Косинус
Один из способов измерения сходства между двумя массивами x и y .
взять их косинус. Название этой меры сходства весьма
подходящее. Косинус x и y является мерой геометрического
косинус угла между ними. Это 1, когда этот угол равен 0 (т. Е. x и y идентичны по направлению) и -1, когда векторы
точки в противоположных направлениях, и 0, когда векторы ортогональны (
не разделяйте компонент ни в каком направлении). Он вычисляется путем взятия
скалярное произведение единичных векторов, указывающих в том же направлении, что и
Он вычисляется путем взятия
скалярное произведение единичных векторов, указывающих в том же направлении, что и x и y . Для этого разделим x и y на их евклидову матрицу.
length ( LA.norm в коде ниже) и возьмите скалярное произведение
полученные результаты.
импортировать numpy как np
импортировать numpy.linalg как LA
x = np.array ([3,4])
y = np.array ([4,3])
def find_unit_vector (x):
вернуть x / LA.norm (x, ord = 2)
def косинус (x, y):
возврат (find_unit_vector (x)).точка (find_unit_vector (y))
Максимально возможное значение косинуса для двух векторов составляет 1,0 .
Максимально возможное значение достигается при сравнении вектора x сама с собой x . Таким образом, ничто не может быть более похоже на x , чем x .
себе. Уф. Это обнадеживает.
LA.norm (find_unit_vector (x))
6.2.6.
 Зачем нужны массивы?
Зачем нужны массивы? время импорта
импортировать numpy как np
py_sec = timeit.timeit ('сумма (x * x для x в xrange (1000))',
число = 10000)
np_sec = timeit.timeit ('на. dot (на)',
setup = "импортировать numpy как np; na = np.arange (1000)",
число = 10000)
print ("Нормальный Python:% f sec"% py_sec)
print ("NumPy:% f sec"% np_sec)
Нормальный Python: 0,840633 сек. NumPy: 0,019618 сек.Массивы
обеспечивают все виды удобства индексирования для доступа к данным, которые
действительно табличный . Табличные данные — это данные, для которых есть веские основания
быть представленным в таблице; то есть есть веская причина подумать о
строки как единое целое, и хороший повод рассматривать столбцы как единицы.И поэтому есть веские основания полагать, что мы могли бы захотеть применить некоторые
вычислительные операции для столбцов и строк. Мы исследуем эти идеи
немного больше в будущем задании.
Как мы увидим, все виды данных в основном представляют собой таблицы. Но хотя
это очень важно. Возможно, это не главная причина, по которой так много
ученые, инженеры и аналитики данных используют numpy и другие
инструменты программирования, такие как matlab и R , которые предоставляют таблицы, или матриц (математическое название аналогичной концепции), как
фундаментальная структура данных.Основная причина — вычислительная эффективность.
Имея единую структуру данных с предсказуемыми типами и поэлементно
основные арифметические операции позволяют писать очень эффективно
способы выполнения более сложных операций. Приведенный выше фрагмент кода
демонстрирует это путем сравнения времени между двумя способами
вычисление суммы квадратов от 0 до 999 включительно; первый
используется при вычислении переменной normal_py_sec , является обычным
Способ вычисления такой суммы на языке Python: приготовьте контейнер с теорией. целые числа, возведите каждое из них в квадрат и просуммируйте результат.Второй, хранящийся в
varibale
целые числа, возведите каждое из них в квадрат и просуммируйте результат.Второй, хранящийся в
varibale np_sec , использует массивы numpy. На самом деле есть очень
важная математическая операция скалярное произведение , которое умножает все
соответствующие элементы двух векторов (поэлементно) и суммирует результат.
Используя эту предварительно скомпилированную быструю математическую операцию , мы ускоряем код на
коэффициент около 80 на моей машине, и ваши результаты в различных домашних
машины будут разные, но примерно в том же масштабе.
Обратите внимание, что массивы numpy сами по себе не помогают.В коде
фрагмент ниже, мы умножаем массив na на себя и суммируем
результат. Этот код на самом деле на медленнее, чем на базовый код Python,
потому что он оплачивает накладные расходы на создание массива numpy , но не
использовать его, используя правильную оптимизированную операцию. Урок здесь
это кодирование, чтобы максимально использовать преимущества numpy может быть непросто, но если у вас есть веская причина быть эффективным,
определенно стоит поэкспериментировать. Это начинается с знания
о видах встроенных функций, специфичных для массивов, которые предлагает
Это начинается с знания
о видах встроенных функций, специфичных для массивов, которые предлагает numpy .
naive_np_sec = timeit.timeit ('сумма (на * на)',
setup = "импортировать numpy как np; na = np.arange (1000)",
число = 10000)
print ("Наивный NumPy:% f sec"% naive_np_sec)
Наивный NumPy: 1,382197 сек
Python Упражнение: создает двумерный массив
Условие Python: Упражнение 11 с Решением
Напишите программу Python, которая принимает на вход две цифры m (строка) и n (столбец) и генерирует двумерный массив.Значение элемента в i-й строке и j-м столбце массива должно быть i * j.
Примечание:
i = 0,1 .., m-1
j = 0,1, n-1.
Изображение:
Пример раствора:
Код Python:
row_num = int (input («Введите количество строк:»))
col_num = int (input ("Введите количество столбцов:"))
multi_list = [[0 для столбца в диапазоне (col_num)] для строки в диапазоне (row_num)]
для строки в диапазоне (row_num):
для столбца в диапазоне (col_num):
multi_list [строка] [столбец] = строка * столбец
печать (multi_list)
Пример вывода:
Введите количество строк: 3 Введите количество столбцов: 4 [[0, 0, 0, 0], [0, 1, 2, 3], [0, 2, 4, 6]]
Схема:
org/WebPageElement/Heading»> Визуализировать выполнение кода Python:
Следующий инструмент визуализирует, что делает компьютер, шаг за шагом, когда он выполняет указанную программу:
Редактор кода Python:
Есть другой способ решить эту проблему? Разместите свой код (и комментарии) через Disqus.
Предыдущая: Напишите программу на Python, которая выполняет итерацию целых чисел от 1 до 50. Для кратных трем выведите «Fizz» вместо числа, а для кратных пяти выведите «Buzz». Для чисел, кратных трем и пяти, выведите «FizzBuzz».
Далее: Напишите программу Python, которая принимает последовательность строк (пустую строку для завершения) в качестве входных данных и печатает строки в качестве выходных (все символы в нижнем регистре).
Python: советы дня
Python: объединение словарей
dict1 = {'a': 1, 'b': 2}
dict2 = {'b': 3, 'c': 4}
dict3 = {'c': 5, 'd': 6}
объединено = {** dict1, ** dict2, ** dict3}
печать (объединено)
Выход:
{'a': 1, 'b': 3, 'c': 5, 'd': 6}
2D-массивов в Python | Реализация массивов в Python
Добро пожаловать в этот учебник по Python, в котором мы узнаем о 2D-массивах в Python.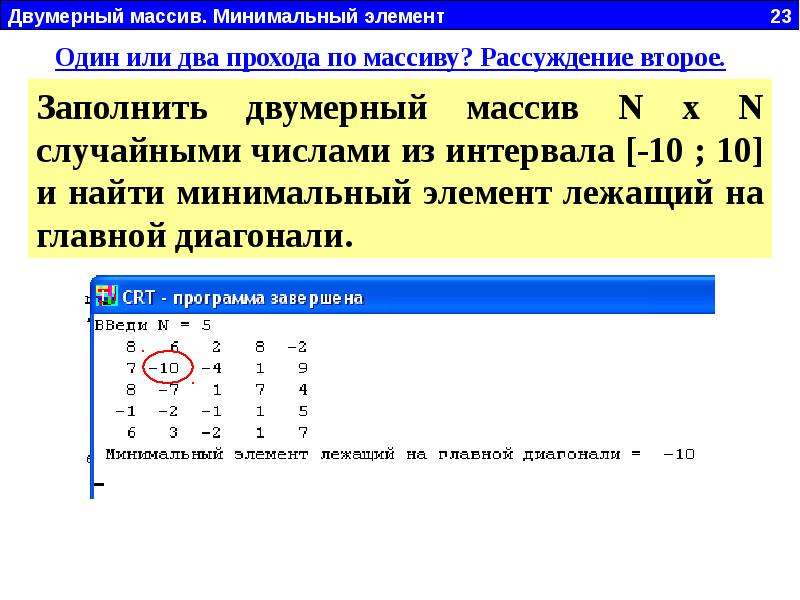 Вся статья разбита на несколько тем с учетом потока. В этой статье будут рассмотрены следующие указатели:
Вся статья разбита на несколько тем с учетом потока. В этой статье будут рассмотрены следующие указатели:
Итак, затяните ремни безопасности, и давайте начнем с этой статьи о 2D-массивах в Python.
2D-массивы в Python Что такое массивы ?Итак, прежде чем углубляться в реализацию массива, сначала давайте посмотрим, что же на самом деле представляют собой массивы!
Массив — это линейная структура данных, которая содержит упорядоченный набор элементов одного типа в последовательной ячейке памяти.Итак, массив — это структура данных, которая используется для линейного хранения элементов одного типа в памяти.
На каждом языке программирования массив представлен как Array_name [index]. Индекс — это число, указывающее номер ячейки определенного элемента в ячейке памяти. Поскольку он использует последовательную память, номера индексов также являются непрерывными. Совершенно очевидно, что индексация массива начинается с 0 и заканчивается n-1, где n — размер массива.
Переходим к статье о 2D-массивах в Python.
Как массивы определяются и используются в Python?Итак, мы все знаем, что массивы не представлены как отдельный объект в python, но мы можем использовать объект списка для определения и использования его как массива.
Например, рассмотрим массив из десяти чисел: A = {1,2,3,4,5}
Синтаксис, используемый для объявления массива:
array_name = []
Если вы хотите инициализировать его значениями, вы можете использовать:
имя_массива = [значение1, значение2, значение3, значение n]
Для обхода массива мы используем индексацию, например, если мы хотим получить значение 2, мы используем
имя_массива [расположение значения 2, начиная с 0]
Переходим к статье о 2D-массивах в Python.
Преимущества использования списка как массива Использование списка для описания массива дает множество преимуществ.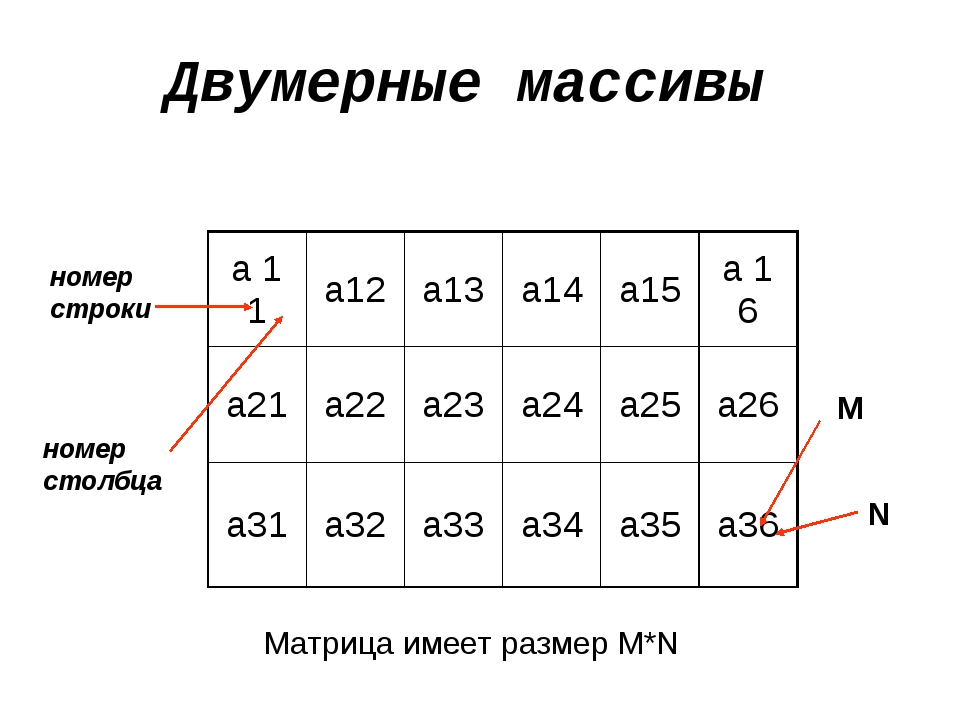 Он не только поддерживает основные операции с массивом, но также имеет некоторые дополнительные операции:
Он не только поддерживает основные операции с массивом, но также имеет некоторые дополнительные операции:
- Он поддерживает нарезку. Посредством нарезки мы можем нарезать наш массив по любым размерам.
- Поддерживает отрицательную индексацию. Теперь вы можете использовать array_name [-1], чтобы получить последний элемент, и аналогично -2 дает второй последний элемент.
- Он имеет встроенные функции для хранения, обновления и управления данными.
- Может хранить разноподобные элементы вместе. Имеет перегруженный оператор + и *.
Таким образом, list предоставляет мощный способ реализации массивов.
Переходим к статье о 2D-массивах в Python.
Что такое двумерный массив и как его создать с помощью объекта списка ? А вот и самая важная часть; Двумерный массив. От фреймов данных машинного обучения до матриц, наиболее широко используемый массив — это двумерный массив.
В основном двумерный массив определяется как массив массивов. Это может показаться немного запутанным, но давайте просто поймем, что это значит.
Это может показаться немного запутанным, но давайте просто поймем, что это значит.
На данный момент мы видели массив, содержащий данные типа [1, 2, 3, 4, 5], которые можно интерпретировать как линию в координатной геометрии, если эти точки должны быть нанесены на график. Что, если я скажу, что у меня есть данные о 5 учениках по 5 предметам:
- Студент 1 = [98, 95, 92, 99, 78]
- Студент 2 = [95, 85, 68, 48, 45]
- Студент 3 = [98, 95, 92, 99, 25]
- Студент 4 = [98, 72, 58, 99, 75]
- Студент 5 = [98, 95, 92, 99, 48]
Сейчас у вас может быть пять разных списков для хранения этих данных, но это будет неэффективно и, честно говоря, не очень хорошая конструкция для использования списка.Более того, это возможно даже для небольших данных, но что мы будем делать в случае 100000 студентов? Ясно, что эта конструкция неприемлема для хорошего программиста.
На помощь приходят двумерные массивы. Что, если мы сможем сохранить эти пять массивов студентов в массиве? Что ж, можем! Вот что означает массив массивов. Мы будем хранить эти массивы внутри самого массива. Поскольку, если вы строите эти элементы с учетом их геометрических точек, вам потребуются две плоскости для них (а именно x и y), что называется 2-мерным массивом или двухмерным массивом.
Мы будем хранить эти массивы внутри самого массива. Поскольку, если вы строите эти элементы с учетом их геометрических точек, вам потребуются две плоскости для них (а именно x и y), что называется 2-мерным массивом или двухмерным массивом.
Двумерный массив для того же будет:
student_data = [[98, 95, 92, 99, 78], [95, 85, 68, 48, 45], [98, 95, 92, 99] , 25], [98, 72, 58, 99, 75], [98, 95, 92, 99, 48]]
Для доступа к элементам мы будем использовать два индекса, первый индекс для определения местоположения списка, где наш элемент сохраняется и второй индекс для определения местоположения элемента в этом списке.
Например, мы хотим получить доступ к отметке студента 3 по предмету 4, тогда мы можем получить к ней доступ, используя
student_data [2] [3]
Примечание. Мы использовали индекс № 2 для местоположения 3, потому что индексирование начинается с 0
Переходим к статье о 2D-массивах в Python.
Как вставить элементы в двумерный массив? Теперь, когда мы узнали, как создавать, инициализировать и перемещаться по элементам двухмерного массива. Теперь посмотрим, как элементы хранятся в двумерном массиве.
Теперь посмотрим, как элементы хранятся в двумерном массиве.
Подумайте, если мы хотим сохранить результаты ученика 6 в этом двумерном массиве, тогда мы можем использовать встроенную функцию append ().
Пример
student6 = [56, 89, 48, 96, 45]
И мы хотим сохранить его в student_data, тогда
student_data.append (student6)
Они добавят элементы в последнюю позицию 2-го массива. Таким образом, в основном общий синтаксис:
имя_массива.append (имя_списка_to_add)
Предположим, студент2 сдал дополнительный экзамен по предмету 6, тогда его оценки также должны быть включены. Так что и здесь мы можем использовать ту же функцию добавления.
Но синтаксис для вставки элемента:
Имя_массива [index_of_sub_array] .append (element_to_add)
Используя указанный выше синтаксис, если мы хотим вставить 98 оценок, полученных студентом2, мы можем использовать указанный выше синтаксис как:
student_data [1].append (98)
Переходим к статье о 2D-массивах в Python.
Как обновить элементы двумерного массива?Итак, до сих пор мы видели, как создать наш двумерный массив, как его инициализировать и заполнить данными, а также как вставить элементы в любую позицию двумерного массива. Теперь перейдем к следующей важной теме, касающейся обновления элементов двумерного массива.
Чтобы понять это, давайте продолжим на примере student_data.
Теперь предположим, что студент 3 сдал повторный экзамен по предмету 5 и получил 98 баллов, теперь эти повышенные оценки необходимо обновить.Итак, как мы можем этого добиться? Мы можем просто добиться этого с помощью оператора присваивания.
student_data [2] [4] = 98
Как вы можете видеть, 25 было увеличено до 98.
Итак, обобщенный синтаксис для обновления любого элемента двухмерного массива:
Array_name [index_of_sub_array] [index_of_element_to_update] = new_value
С их помощью вы можете обновлять элементы один за другим. Но что, если вы хотите обновить всю успеваемость ученика? Тогда редактирование каждой записи — это кропотливая задача.Таким образом, несмотря на редактирование элементов по одному, мы можем изменить весь массив информации.
Но что, если вы хотите обновить всю успеваемость ученика? Тогда редактирование каждой записи — это кропотливая задача.Таким образом, несмотря на редактирование элементов по одному, мы можем изменить весь массив информации.
Допустим, данные student1 были введены неправильно и теперь их необходимо обновить, поэтому мы можем создать новый массив mark_sheet для student1, а затем обновить соответствующий список. Совершенно очевидно, что когда мы заменяем массив в целом, нам не требуется [index_of_element_to_update], поэтому новый обобщенный синтаксис для обновления всего массива будет следующим:
Array_name [index_of_sub_array] = new_sub_array
Например, оценка student1 были введены неправильно, и новые отметки будут 45, 78, 96, 78, 85.
Тогда то же самое можно обновить следующим образом:
student1 = [45, 78, 96, 78, 85]
student_data [0] = student1
Вы можете увидеть, как был обновлен весь массив.
Перемещение с этой статьей
Как удалить элементы двумерного массива?Теперь давайте посмотрим, как мы можем удалить любые элементы двумерного массива. Предположим, студент 4 покинул школу, и его запись должна быть удалена, тогда нам придется удалить всю его запись, или мы можем сказать массив.Итак, чтобы удалить элементы объекта списка, мы используем функцию pop.
Итак, чтобы удалить данные student4, мы можем сделать следующее:
student_data.pop (3)
Обобщенный синтаксис:
имя_массива.pop (index_of_sub_array_to_remove)
Однако в некоторых сценариях удаление конкретный элемент вместо полного массива. Мы можем добиться того же, используя функцию pop.
Считайте, что студент 1 не зарегистрирован по предмету 2, тогда его запись по предмету 2 должна быть удалена.Итак, чтобы удалить запись subject2 для student1,
student_data [0] .pop (1)
Таким образом, обобщенный синтаксис для удаления элемента 2-мерного массива будет:
Array_name [index_of_sub_array] .pop (index_of_sub_array] .pop (index_of_element_to_relement_to_
Таким образом, вы можете выполнять любые операции с двумерным массивом в Python. Мы начали с понимания массивов, затем мы увидели, как можно эффективно выполнять каждую операцию. Мы рассмотрели все, от создания до обновления двумерных массивов. Это Абхишек !, снова поймает вас всех в следующей статье этой серии.
Примечание:
Индексирование начинается с 0, а не с 1
Таким образом, мы подошли к концу этой статьи о «2D-массивах в Python». С ростом популярности вырос спрос и в таких областях, как машинное обучение, искусственный интеллект, наука о данных и т. Д. Чтобы улучшить свои навыки, зарегистрируйтесь в программе сертификации по питону edureka и начните свое обучение.
Есть вопросы? Упомяните их в комментариях. Мы свяжемся с вами в ближайшее время.
NumPy — Анализ данных с помощью Python
NumPy — это библиотека Python для обработки многомерных массивов. Он содержит как структуры данных, необходимые для хранения массивов и доступа к ним, так и операции и функции для вычислений с использованием этих массивов. Хотя массивы обычно используются для хранения чисел, можно хранить и другие типы данных, например строки. В отличие от списков в ядре Python, основная структура данных NumPy, массив, должен иметь один и тот же тип данных для всех своих элементов.В
однородность массивов позволяет оптимизировать функции, которые используют массивы в качестве входных и выходных данных.
Он содержит как структуры данных, необходимые для хранения массивов и доступа к ним, так и операции и функции для вычислений с использованием этих массивов. Хотя массивы обычно используются для хранения чисел, можно хранить и другие типы данных, например строки. В отличие от списков в ядре Python, основная структура данных NumPy, массив, должен иметь один и тот же тип данных для всех своих элементов.В
однородность массивов позволяет оптимизировать функции, которые используют массивы в качестве входных и выходных данных.
Есть несколько применений многомерных массивов в анализе данных. Например, их можно использовать для:
- хранить матрицы, решать системы линейных уравнений, находить собственные значения / векторы, находить разложения матриц и решать другие задачи, знакомые из линейной алгебры
- хранит данные многомерных измерений. Например, элемент
a [i, j]в 2-мерном массиве может хранить температуру \ (t_ {ij} \), измеренную в координатах i, j на 2-мерной поверхности.
- изображений и видео могут быть представлены в виде массивов NumPy:
- полутоновое изображение может быть представлено как двумерный массив
- цветное изображение может быть представлено как трехмерное изображение, третье измерение содержит компоненты цвета красный, зеленый и синий
- цветное видео может быть представлено в виде четырехмерного массива
- двухмерная таблица может хранить последовательность из выборок , и каждая выборка может быть разделена на признаков .Например, мы можем измерять погодные условия один раз в день, и эти условия могут включать температуру, направление и скорость ветра, а также количество дождя. Затем у нас будет один образец в день, и его характеристиками будут температура, ветер и дождь. В стандартном представлении такого типа табличных данных строки соответствуют выборкам, а столбцы соответствуют к особенностям. Мы видим больше подобных данных в главах о Pandas и Scikit-learn.
В этой главе мы рассмотрим:
- Создание массивов
- Типы и атрибуты массивов
- Доступ к массивам с индексированием и нарезкой
- Изменение формы массивов
- Объединение и разделение массивов
- Быстрые операции с массивами
- Агрегаты массивов
- Правила операций с двоичными массивами
- Матричные операции, известные из линейной алгебры
Мы начинаем с импорта библиотеки NumPy, и мы используем для нее стандартное сокращение np .
Создание массивов
Есть несколько способов создания массивов NumPy. Один из способов — предоставить (вложенный) список в качестве параметра конструктору массива :
np.array ([1,2,3]) # одномерный массив
Обратите внимание, что отсутствие скобок в приведенном выше выражении, т.е. вызов np.array (1,2,3) приведет к ошибке.
Двумерный массив может быть задан перечислением строк массива:
нп.массив ([[1,2,3], [4,5,6]])
массив ([[1, 2, 3],
[4, 5, 6]])
Точно так же трехмерный массив можно описать как список списков списков:
np.array ([[[1,2], [3,4]], [[5,6], [7,8]]])
массив ([[[1, 2],
[3, 4]],
[[5, 6],
[7, 8]]])
Есть несколько вспомогательных функций для создания массивов распространенных типов:
array ([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0. ]])
]])
Чтобы указать, что элементы — это int s вместо float s, используйте параметр dtype :
np.zeros ((3,4), dtype = int)
array ([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]])
Аналогично единиц инициализирует все элементы в один, полный инициализирует все элементы до указанного значения, а пусто оставляет элементы неинициализированными:
массив ([[1., 1., 1.],
[1., 1., 1.]])
np.full ((2,3), fill_value = 7)
массив ([[7, 7, 7],
[7, 7, 7]])
массив ([[6.246e-310, 1.02713165e-316, 0.00000000e + 000,
0,00000000e + 000],
[0.00000000e + 000, 0.00000000e + 000, 8.70018274e-313,
9.27487698e-317]])
Функция eye создает единичную матрицу, то есть матрица с элементами по диагонали устанавливается в единицу, а недиагональные элементы равны нулю:
array ([[1, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 0, 1]])
Функция arange работает так же, как функция range , но создает массив вместо списка.
Для нецелочисленных диапазонов лучше использовать linspace :
np.linspace (0, np.pi, 5) # Равномерно распределенный диапазон с 5 элементами
массив ([0., 0.78539816, 1.57079633, 2.35619449, 3.14159265])
При linspace не нужно вычислять длину шага, вместо этого нужно указать желаемое количество элементов. По умолчанию конечная точка включается в результат, в отличие от и .
Массивы со случайными элементами
Для тестирования наших программ мы можем использовать в качестве входных данных реальные данные.Однако реальные данные не всегда доступны, и для их сбора может потребоваться время. Вместо этого мы могли бы генерировать случайные числа для использования в качестве замены. Они могут быть очень легко сгенерированы с помощью NumPy и могут быть взяты из нескольких разных дистрибутивов, из которых мы упоминаем ниже лишь некоторые. Случайные данные могут имитировать реальные данные лучше, чем, например, диапазоны или постоянные массивы. Иногда нам также нужны случайные числа в наших программах, чтобы выбрать подмножество
реальные данные (выборка). NumPy может легко создавать массивы желаемой формы, заполненные случайными числами.Ниже приведены несколько примеров.
Иногда нам также нужны случайные числа в наших программах, чтобы выбрать подмножество
реальные данные (выборка). NumPy может легко создавать массивы желаемой формы, заполненные случайными числами.Ниже приведены несколько примеров.
np.random.random ((3,4)) # Элементы равномерно распределяются из полуоткрытого интервала [0.0,1.0)
массив ([[0,521, 0,58179893, 0,47661561, 0,39423081], [0,581, 0,32964409, 0,07077432, 0,238916], [0,78337758, 0,07423979, 0,87106393, 0,3
58]])np.random.normal (0, 1, (3,4)) # Элементы обычно распределяются со средним значением 0 и стандартным отклонением 1массив ([[- 0.1655536, 0,84389534, -0,3337582, -1,88533703], [0,26776494, 0,28465075, 0,23800085, -0,93539492], [-0,51372478, 0,74807735, 0,840, -0,14310498]])np.random.randint (-2, 10, (3,4)) # Элементы представляют собой равномерно распределенные целые числа из полуоткрытого интервала [-2,10)массив ([[8, 4, 3, -2], [2, -2, 4, 5], [5, 9, 5, -2]])Иногда бывает полезно иметь возможность воссоздавать одни и те же данные при каждом запуске нашей программы.
Например, если в нашей программе есть ошибка, которая проявляется только при определенных входных данных, то для отладки нашей программы она должна вести себя детерминированно. Мы можем создавать случайные числа детерминированно, если всегда начинаем с одной и той же начальной точки. Эта начальная точка обычно является целым числом, и мы называем ее начальным значением . Пример использования:
np.random.seed (0) print (np.random.randint (0, 100, 10)) печать (np.random.normal (0, 1, 10))[44 47 64 67 67 9 83 21 36 87] [1.26611853 -0,50587654 2,54520078 1,08081191 0,48431215 0,578 -0,18158257 1,41020463 -0,37447169 0,27519832]Если вы запустите вышеуказанную ячейку несколько раз, она всегда будет давать одни и те же числа, в отличие от предыдущих примеров. Попробуйте перезапустить их сейчас!
Вызов
np.random.seedинициализирует глобальный генератор случайных чисел . Все вызовыnp.random.,random
np.random.normalи т. Д. Используют этот глобальный генератор случайных чисел.Однако можно создать новые генераторы случайных чисел и использовать их для выборки случайных чисел из распределения. Пример использования:new_generator = np.random.RandomState (seed = 123) # RandomState - это класс, поэтому мы передаем начальное значение его конструктору new_generator.randint (0, 100, 10)массив ([66, 92, 98, 17, 83, 57, 86, 97, 96, 47])Вы увидите, что они используются позже в материалах и в упражнениях, просто чтобы мы могли согласовать, что такое случайные входные данные.Как еще мы могли договориться о том, правильный результат или нет, если мы не можем договориться о вводе!
Типы и атрибуты массивов
Массив имеет несколько атрибутов:
ndimсообщает количество измерений,shapeсообщает размер в каждом измерении,sizeсообщает количество элементов, аdtypeсообщает тип элемента.Давайте создадим вспомогательную функцию для изучения этих атрибутов:
def info (имя, a): print (f "{name} имеет тусклый {a.ndim}, shape {a.shape}, size {a.size} и dtype {a.dtype}: ") печать (а)b = np.array ([[1,2,3], [4,5,6]]) info ("b", b)b имеет dim 2, shape (2, 3), size 6 и dtype int64: [[1 2 3] [4 5 6]]c = np.array ([b, b]) # Создает трехмерный массив info ("c", c)c имеет dim 3, shape (2, 2, 3), size 12 и dtype int64: [[[1 2 3] [4 5 6]] [[1 2 3] [4 5 6]]]d = np.array ([[1,2,3,4]]) # вектор-строка info ("d", d)d имеет dim 2, shape (1, 4), size 4 и dtype int64: [[1 2 3 4]]Обратите внимание, как Python распечатал трехмерный массив.Общие правила печати n-мерного массива как вложенного списка:
- последнее измерение печатается слева направо,
- предпоследний печатается сверху вниз,
- остальные также печатаются сверху вниз, причем каждый фрагмент отделен от следующего пустой строкой.

Индексирование, нарезка и изменение формы
Индексирование
Одномерный массив ведет себя как список в Python:
a = np.array ([1,4,2,7,9,5]) печать (a [1]) печать (a [-2])
Для многомерного массива индекс представляет собой кортеж, разделенный запятыми, а не одно целое число:
б = нп.массив ([[1,2,3], [4,5,6]]) печать (б) print (b [1,2]) # индекс строки 1, индекс столбца 2 print (b [0, -1]) # индекс строки 0, индекс столбца -1
# Как и в случае со списками, возможно изменение через индексацию b [0,0] = 10 печать (б)
Обратите внимание, что если вы даете только один индекс многомерному массиву, он индексирует первое измерение массива, то есть строки. Например:
print (b [0]) # Первая строка print (b [1]) # Вторая строка
Нарезка
Нарезка работает аналогично спискам, но теперь у нас могут быть срезы разных размеров:
печать (а) печать (a [1: 3]) print (a [:: - 1]) # Оборачивает массив
[1 4 2 7 9 5] [4 2] [5 9 7 2 4 1]
печать (б) print (b [:, 0]) печать (b [0 ,:]) print (b [:, 1:])
[[10 2 3] [4 5 6]] [10 4] [10 2 3] [[2 3] [5 6]]
Мы даже можем назначить срез:
Распространенная идиома - извлекать строки или столбцы из массива:
print (b [:, 0]) # Первый столбец print (b [1 ,:]) # Вторая строка
Изменение формы
При изменении формы массива количество его элементов остается прежним, но они интерпретируются заново, чтобы иметь другую форму. Примером этого является интерпретация одномерного массива как двухмерного массива:
Примером этого является интерпретация одномерного массива как двухмерного массива:
a = np.arange (9)
anew = a.reshape (3,3)
info ("заново", заново)
информация ("а", а)
заново имеет dim 2, shape (3, 3), size 9 и dtype int64: [[0 1 2] [3 4 5] [6 7 8]] a имеет dim 1, shape (9,), size 9 и dtype int64: [0 1 2 3 4 5 6 7 8]
d = np.arange (4) # 1d массив
dr = d.reshape (1,4) # вектор-строка
dc = d.reshape (4,1) # вектор-столбец
info ("d", d)
информация ("доктор", доктор)
info ("dc", dc)
d имеет dim 1, shape (4,), size 4 и dtype int64: [0 1 2 3] dr имеет dim 2, shape (1, 4), size 4 и dtype int64: [[0 1 2 3]] dc имеет dim 2, shape (4, 1), size 4 и dtype int64: [[0] [1] [2] [3]]
Обратите внимание, что 1d-массив и векторы строк и столбцов, которые представляют собой 2d-массивы, являются принципиально разными объектами, даже если они выглядят одинаково.Они ведут себя по-разному, когда мы комбинируем или иным образом оперируем массивами разных форм, как мы увидим в следующем разделе и далее в этом материале.
Альтернативный синтаксис для создания, например, векторов столбцов или строк - использование ключевого слова np.newaxis . Иногда это проще или естественнее, чем с методом reshape :
info ("d", d)
info ("дроу", d [:, np.newaxis])
info ("дроу", d [np.newaxis,:])
info ("dcol", d [:, np.newaxis])
d имеет dim 1, shape (4,), size 4 и dtype int64: [0 1 2 3] drow имеет dim 2, shape (4, 1), size 4 и dtype int64: [[0] [1] [2] [3]] drow имеет dim 2, shape (1, 4), size 4 и dtype int64: [[0 1 2 3]] dcol имеет dim 2, shape (4, 1), size 4 и dtype int64: [[0] [1] [2] [3]]
Напишите две функции, get_rows и get_columns , которые получают в качестве параметра двумерный массив.Они должны вернуть список строк и столбцов массива соответственно. Строки и столбцы должны быть одномерными массивами. Вы можете использовать в своем решении операцию транспонировать , которая переворачивает строки в столбцы. Транспонирование выполняется методом
Транспонирование выполняется методом T :
a = np.random.randint (0, 10, (4,4)) печать (а) печать (a.T)
[[0 1 9 9] [0 4 7 3] [2 7 2 0] [0 4 5 5]] [[0 0 2 0] [1 4 7 4] [9 7 2 5] [9 3 0 5]]
Протестируйте свое решение в основной функции.Пример использования:
a = np.array ([[5, 0, 3, 3], [7, 9, 3, 5], [2, 4, 7, 6], [8, 8, 1, 6]]) get_rows (а) [массив ([5, 0, 3, 3]), массив ([7, 9, 3, 5]), массив ([2, 4, 7, 6]), массив ([8, 8, 1, 6 ])] get_columns (а) [массив ([5, 7, 2, 8]), массив ([0, 9, 4, 8]), массив ([3, 3, 7, 1]), массив ([3, 5, 6, 6 ])]
Объединение, разделение и складывание массивов
Есть два способа объединения нескольких массивов в один больший массив: объединить и стек . Concatenate принимает n-мерные массивы и возвращает n-мерный массив, тогда как стек принимает n-мерные массивы и возвращает n + 1-мерный массив. Несколько примеров из них:
Несколько примеров из них:
a = np.arange (2)
b = np.arange (2,5)
print (f "a имеет форму {a.shape}: {a}")
print (f "b имеет форму {b.shape}: {b}")
np.concatenate ((a, b)) # объединение 1d массивов
a имеет форму (2,): [0 1] b имеет форму (3,): [2 3 4]
c = np.arange (1,5) .reshape (2,2)
print (f "c имеет форму {c.shape}: ", c, sep =" \ n ")
np.concatenate ((c, c)) # объединение 2d массивов
c имеет форму (2, 2): [[1 2] [3 4]]
массив ([[1, 2],
[3, 4],
[1, 2],
[3, 4]])
По умолчанию concatenate объединяет массивы по оси 0. Чтобы объединить массивы по горизонтали, добавьте параметр axis = 1 :
np.concatenate ((c, c), ось = 1)
массив ([[1, 2, 1, 2],
[3, 4, 3, 4]])
Если вы хотите объединить массивы с разными размерами, например, чтобы добавить новый столбец в 2-мерный массив, вы должны сначала изменить форму массивов, чтобы они имели одинаковое количество измерений:
print ("Новая строка:")
печать (нп. объединить ((c, a.reshape (1,2))))
print ("Новый столбец:")
print (np.concatenate ((c, a.reshape (2,1)), ось = 1))
объединить ((c, a.reshape (1,2))))
print ("Новый столбец:")
print (np.concatenate ((c, a.reshape (2,1)), ось = 1))
Новая строка: [[1 2] [3 4] [0 1]] Новый столбец: [[1 2 0] [3 4 1]]
Используйте стек для создания массивов более высокой размерности из массивов более низкой размерности:
массив ([[2, 3, 4],
[2, 3, 4]])
массив ([[2, 2],
[3, 3],
[4, 4]])
Обратная операция объединения - это разбиение .Его аргумент указывает либо количество равных частей, на которые делится массив, либо явно указывает точки останова.
d = np.arange (12) .reshape (6,2)
print ("d:")
печать (d)
d1, d2 = np.split (d, 2)
print ("d1:")
печать (d1)
print ("d2:")
печать (d2)
d: [[0 1] [2 3] [4 5] [6 7] [8 9] [10 11]] d1: [[0 1] [2 3] [4 5]] d2: [[6 7] [8 9] [10 11]]
d = np.arange (12) .reshape (2,6)
print ("d:")
печать (d)
parts = np. split (d, (2,3,5), axis = 1)
для i, p в перечислении (части):
print ("часть% i:"% i)
печать (p)
split (d, (2,3,5), axis = 1)
для i, p в перечислении (части):
print ("часть% i:"% i)
печать (p)
d: [[0 1 2 3 4 5] [6 7 8 9 10 11]] часть 0: [[0 1] [6 7]] часть 1: [[2] [8]] часть 2: [[3 4] [9 10]] часть 3: [[5] [11]]
Создайте функцию get_row_vectors , которая возвращает список строк из входного массива формы (n, m) , но на этот раз строки должны иметь форму (1, m) .Точно так же создайте функцию get_columns_vectors , которая возвращает список столбцов (каждый имеет форму (n, 1) ) входной матрицы.
Пример: для входной матрицы 2x3
результат должен быть
векторов строк:
[массив ([[5, 0, 3]]), массив ([[3, 7, 9]]])]
Векторы столбцов:
[массив ([[5],
[3]]),
массив ([[0],
[7]]),
массив ([[3],
[9]])]
Приведенный выше вывод - это в основном просто возвращенные списки, напечатанные с print .Только некоторые пробелы изменены, чтобы он выглядел лучше. Выход не проверял.
Выход не проверял.
Создайте функцию diamond , которая возвращает двумерный целочисленный массив, где 1 образуют ромбовидную форму. Остальные номера - 0 . Функция должна получить параметр, указывающий длину стороны ромба. Сделайте это, используя eye и , объединяющие функции NumPy и нарезки массива.
Пример использования:
принт (ромб (3)) [[0 0 1 0 0] [0 1 0 1 0] [1 0 0 0 1] [0 1 0 1 0] [0 0 1 0 0]] печать (ромб (1)) [[1]]
Быстрые вычисления с использованием универсальных функций
Помимо обеспечения способа хранения и доступа к многомерным массивам, NumPy также предоставляет несколько процедур для выполнения над ними вычислений.Одна из причин популярности NumPy заключается в том, что эти вычисления могут быть очень эффективными, намного более эффективными, чем то, что обычно делает Python. Самым большим узким местом в эффективности являются циклы, которые можно повторять миллионы, миллиарды или даже больше раз. Петли должны быть максимально эффективными. Что замедляет циклы в Python как
тот факт, что Python - это язык с динамической типизацией. Это означает, что в каждом выражении Python выяснил типы аргументов операций.Рассмотрим следующий цикл:
Петли должны быть максимально эффективными. Что замедляет циклы в Python как
тот факт, что Python - это язык с динамической типизацией. Это означает, что в каждом выражении Python выяснил типы аргументов операций.Рассмотрим следующий цикл:
L = [1, 5.2, «ab»]
L2 = []
для x в L:
L2.append (x * 2)
печать (L2)
На каждой итерации этого цикла Python выясняет тип переменной x, которая в этом примере может быть int, float или string, и в зависимости от этого типа вызывает другую функцию для выполнения «умножения» на два. . Что делает NumPy эффективным, так это требование, чтобы каждый элемент в массиве был одного типа. Эта однородность массивов позволяет создавать векторизованные операции , которые работают не с отдельными элементами, а с массивами (или подмассивами).Предыдущий Пример использования векторизованных операций NumPy показан ниже.
a = np.array ([2.1, 5.0, 17.2]) а2 = а * 2 печать (a2)
Поскольку каждая итерация использует идентичные операции, только данные отличаются, это может быть скомпилировано в машинный язык, а затем выполнено за один раз, что позволяет избежать динамической типизации Python. Операция вектора имени происходит от линейной алгебры, где сложение двух векторов \ (v = (v_1, v_2, \ ldots, v_d) \) и \ (w = (w_1, w_2, \ ldots, w_d) \) определяется элементом -в случае как \ (v + w = (v_1 + w_1, v_2 + w_2, \ ldots, v_d + w_d) \).
Операция вектора имени происходит от линейной алгебры, где сложение двух векторов \ (v = (v_1, v_2, \ ldots, v_d) \) и \ (w = (w_1, w_2, \ ldots, w_d) \) определяется элементом -в случае как \ (v + w = (v_1 + w_1, v_2 + w_2, \ ldots, v_d + w_d) \).
В дополнение к этому есть несколько математических функций, определенных в векторной форме. Основные арифметические операции: сложение + , вычитание -, отрицание -, умножение * , деление /, деление по полу // , возведение в степень ** и остаток % .
Можно объединить в более сложные выражения. Пример:
b = np.array ([- 1, 3.2, 2.4]) печать (-a ** 2 * b)
Также определены несколько других математических функций. Несколько примеров из них можно найти ниже.
печать (np.abs (b)) печать (np.cos (b)) печать (np.exp (b)) печать (np.log2 (np.abs (b)))
[1. 3.2 2.4] [0,54030231 -0,99829478 -0,73739372] [0,36787944 24,5325302 11,02317638] [0.1.67807191 1.26303441]
В номенклатуре NumPy эти векторные операции называются ufuncs (универсальные функции).
Агрегации: макс., Мин., Сумма, среднее, стандартное отклонение…
Агрегации позволяют нам сжать информацию в массиве до нескольких чисел.
np.random.seed (0)
a = np.random.randint (-100, 100, (4,5))
печать (а)
print (f "Минимум: {a.min ()}, максимум: {a.max ()}")
print (f "Сумма: {a.sum ()}")
print (f "Среднее: {a.mean ()}, стандартное отклонение: {a.std ()}")
[[72 -53 17 92-33] [95 3-91-79-64] [-13-30-12 40-42] [93-61-13 74-12]] Минимум: -91, максимум: 95 Сумма: -17 Среднее: -0.85, стандартное отклонение: 58.39886557117355
Вместо агрегирования по всему массиву мы можем агрегировать также только по определенным осям:
np.random.seed (9)
b = np.random.randint (0, 10, (3,4))
печать (б)
print ("Суммы столбцов:", b.sum (axis = 0))
print ("Суммы строк:", b.sum (axis = 1))
[[5 6 8 6] [1 6 4 8] [1 8 5 1]] Суммы в столбцах: [7 20 17 15] Суммы строк: [25 19 15]
Обратите внимание, что большинство функций агрегирования в NumPy имеют соответствующие методы. Кроме того, в языке Python есть встроенные функции
Кроме того, в языке Python есть встроенные функции , сумма , мин. , макс. , любой и все для последовательностей. Убедитесь, что вы случайно не использовали их для массивов, так как они могут иметь немного другую семантику и будут работать значительно медленнее, чем функции и методы NumPy.
| Функция Python | Функция NumPy | Метод NumPy |
|---|---|---|
| сумма | нп.сумма | а.сум |
| нп.прод | а.прод | |
| нп. Среднее | a.mean | |
| нп.стд | a.std | |
| нп.вар | а.вар | |
| мин. | нм / мин | а мин |
| макс | нм макс. | а. Макс. |
нп. Аргмин Аргмин | a.argmin | |
| нп.argmax | a.argmax | |
| нп. Средний | ||
| np. Процентиль | ||
| любой | нп. Любой | a.any |
| все | нп. Всего | а. Все |
Давайте измерим, насколько более медленная функция Python sum по сравнению с эквивалентом NumPy при агрегировании по массиву:
a = np.arange (1000) % timeit np.сумма (а)
3,76 мкс ± 28,4 нс на цикл (среднее ± стандартное отклонение из 7 прогонов, 100000 циклов в каждом)
90,6 мкс ± 140 нс на цикл (среднее ± стандартное отклонение из 7 прогонов, по 10000 циклов в каждом)
Скорость NumPy частично связана с тем, что его массивы должны иметь один и тот же тип для всех элементов. Это требование допускает некоторые эффективные оптимизации.
Записать функцию vector_lengths , которая получает в качестве параметра двумерный массив формы (n, m).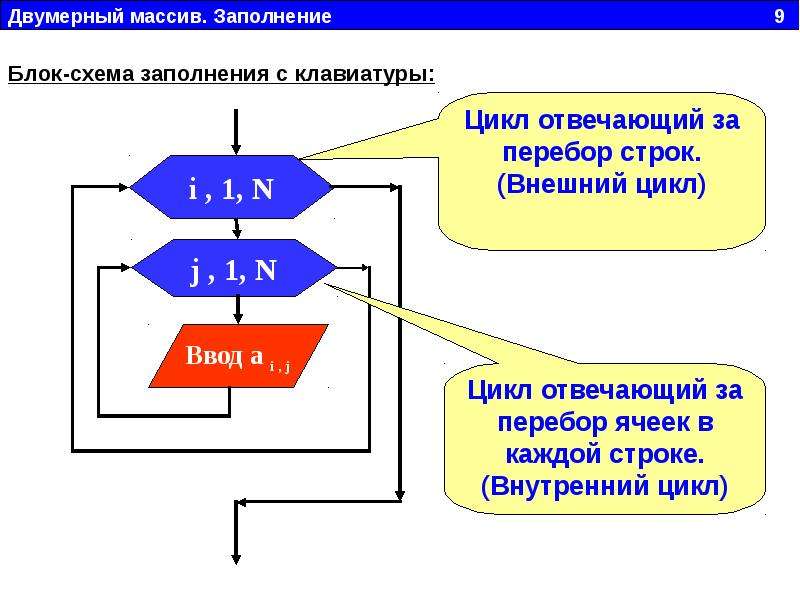 Каждая строка в этом массиве соответствует вектору.Функция должна возвращать массив формы (n,), который имеет длину каждого вектора во входных данных. Длина определяется обычной евклидовой нормой. Ни в коем случае не используйте петли в своем решении. Вместо этого используйте векторизованные операции. Вы должны использовать как минимум
Каждая строка в этом массиве соответствует вектору.Функция должна возвращать массив формы (n,), который имеет длину каждого вектора во входных данных. Длина определяется обычной евклидовой нормой. Ни в коем случае не используйте петли в своем решении. Вместо этого используйте векторизованные операции. Вы должны использовать как минимум np.sum и np.sqrt функции. Вы не можете использовать функцию scipy.linalg.norm . Проверьте свою функцию в основной функции.
Пусть x и y m-мерные векторы. Угол \ (\ alpha \) между двумя векторами определяется уравнением \ (\ cos_ {xy} (\ alpha): = \ frac {\ langle x, y \ rangle} {|| x || || y | |} \), где угловые скобки обозначают внутренний продукт, и \ (|| x ||: = \ sqrt {\ langle x, x \ rangle} \).
Запись функции vector_angles , которая получает два массива X и Y с одинаковой формой (n, m) в качестве параметров. Каждая строка в массивах соответствует вектору. Функция должна возвращать вектор формы (n,) с соответствующими углами между векторами X и Y в градусах, а не в радианах. Опять же, не используйте циклы, а используйте векторизованные операции.
Опять же, не используйте циклы, а используйте векторизованные операции.
Примечание: функция np.arccos определена только в домене [-1.0,1.0]. Если вы попытаетесь вычислить np.arccos (1.000000001) , произойдет сбой. Подобные ошибки могут возникать из-за использования конечной точности в численных вычислениях. Заставить аргумент находиться в правильном диапазоне (метод clip ).
Протестируйте свое решение в основной программе.
Радиовещание
Мы видели, что NumPy позволяет выполнять операции с массивами поэлементно. Но NumPy также позволяет выполнять бинарные операции, которые не требуют, чтобы два массива имели одинаковую форму. Например, мы можем добавить 4 ко всем элементам массива с помощью следующего выражения:
нп.arange (3) + np.array ([4])
Фактически, поскольку массив только с одним элементом, скажем 4, можно рассматривать как скаляр 4, NumPy допускает следующее выражение, которое эквивалентно приведенному выше:
Чтобы понять, какие операции разрешены, то есть какие формы двух массивов совместимы с , может быть полезно подумать, что перед выполнением двоичной операции NumPy пытается растянуть массивы, чтобы они имели одинаковую форму. Например, в приведенном выше примере NumPy сначала растянул массив
Например, в приведенном выше примере NumPy сначала растянул массив np.array ([4]) (или скаляр 4) в массив np.array ([4,4,4]) , а затем выполняет поэлементное сложение. В NumPy это растяжение называется , вещание .
Массивы аргументов, конечно, могут иметь более высокие измерения, как показывает следующий пример:
а = np.full ((3,3), 5)
b = np.arange (3)
print ("a:", a, sep = "\ n")
print ("b:", b)
print ("a + b:", a + b, sep = "\ n")
а: [[5 5 5] [5 5 5] [5 5 5]] b: [0 1 2] а + б: [[5 6 7] [5 6 7] [5 6 7]]
В этом примере второй аргумент сначала транслировался в массив
нп.массив ([[0, 1, 2],
[0, 1, 2],
[0, 1, 2]])
массив ([[0, 1, 2],
[0, 1, 2],
[0, 1, 2]])
, после чего было выполнено сложение. И может оказаться, что оба массива аргументов нужно транслировать, как в следующем примере:
a = np.arange (3) b = np.arange (3) .reshape ((3,1)) информация ("а", а) info ("b", b) информация ("a + b", a + b)
a имеет dim 1, shape (3,), size 3 и dtype int64: [0 1 2] b имеет dim 2, shape (3, 1), size 3 и dtype int64: [[0] [1] [2]] a + b имеет dim 2, shape (3, 3), size 9 и dtype int64: [[0 1 2] [1 2 3] [2 3 4]]
Чтобы увидеть, какие аргументы передавались перед двоичной операцией, функция np.broadcast_arrays можно использовать:
Broadcasted_a, Broadcasted_b = np.broadcast_arrays (a, b)
информация ("Broadcasted_a", Broadcasted_a)
информация ("Broadcasted_b", Broadcasted_b)
Broadcasted_a имеет dim 2, shape (3, 3), size 9 и dtype int64: [[0 1 2] [0 1 2] [0 1 2]] Broadcasted_b имеет dim 2, shape (3, 3), size 9 и dtype int64: [[0 0 0] [1 1 1] [2 2 2]]
Итак, транслировались оба массива, но по-разному. Теперь давайте рассмотрим правила работы трансляции.
- Все входные массивы с
ndimменьше, чем входной массив с наибольшимndim, имеют добавленные единицы к их формам.
- Размер в каждом измерении выходной формы является максимальным из всех входных размеров в этом измерении.
- Входные данные могут использоваться в вычислениях, если их размер в конкретном измерении либо совпадает с выходным размером в этом измерении, либо имеет значение точно 1.
- Если входной размер имеет размер 1 в своей форме, первая запись данных в этом измерении будет использоваться для всех вычислений по этому измерению.Другими словами, шаговый механизм ufunc просто не будет шагать по этому измерению (шаг будет равен 0 для этого измерения).
Наконец, пример ситуации, когда два массива несовместимы:
a = np.array ([1,2,3])
b = np.array ([4,5])
пытаться:
a + b # Это не работает, так как нарушает правило 3 выше.
кроме ValueError как e:
import sys
печать (е, файл = sys.stderr)
операнды не могли транслироваться вместе с формами (3,) (2,)
Запись функции multiplication_table , которая получает положительное целое число n в качестве параметра. Функция должна возвращать массив с формой (n, n). Элемент с индексом
Функция должна возвращать массив с формой (n, n). Элемент с индексом (i, j) должен быть i * j . Не используйте для петель! В своем решении положитесь на трансляцию, функцию np.arange , операторы изменения формы и векторизации. Пример использования:
печать (таблица_множения (4)) [[0 0 0 0] [0 1 2 3] [0 2 4 6] [0 3 6 9]]
Резюме (неделя 2)
- Мы узнали, как можно использовать регулярные выражения для задания регулярных наборов строк
- Мы знаем, как узнать, соответствует ли строка регулярному выражению
- Мы знаем, как извлекать фрагменты текста, соответствующие RE
- Мы можем заменить совпадения с RE другой строкой
- Мы можем читать (и записывать) текстовый файл построчно или весь файл одновременно
- Мы также знаем, как указать кодировку файла.Кодировка utf-8 очень распространена и может представлять почти каждый символ или символ любого (естественного) языка
- Параметры программы находятся в массиве
sys., и мы можем вернуть значение из программы с помощью функции argv
argv sys.exit - Файловые потоки
sys.stdin,sys.stdoutиsys.stderrпозволяют выполнять базовый текстовый ввод и вывод в программу и из нее - Каждое значение в Python - это объект
- Классы - это определяемые пользователем типы данных, они сообщают, как создавать экземпляры (объекты) этого типа
- Связь между объектами и классами:
isinstance - Связь между классами:
issubclass
- Исключения сигнализируют об исключительных ситуациях, не обязательно об ошибках
- Мы знаем, как перехватывать и вызывать исключения
- Эффективность NumPy основана на том факте, что одни и те же операции могут выполняться быстро над элементами, если все элементы имеют один и тот же тип.Это так называемые векторизованные операции
- Мы знаем, как создавать, изменять форму, выполнять базовый доступ, комбинировать, разделять и агрегировать массивы







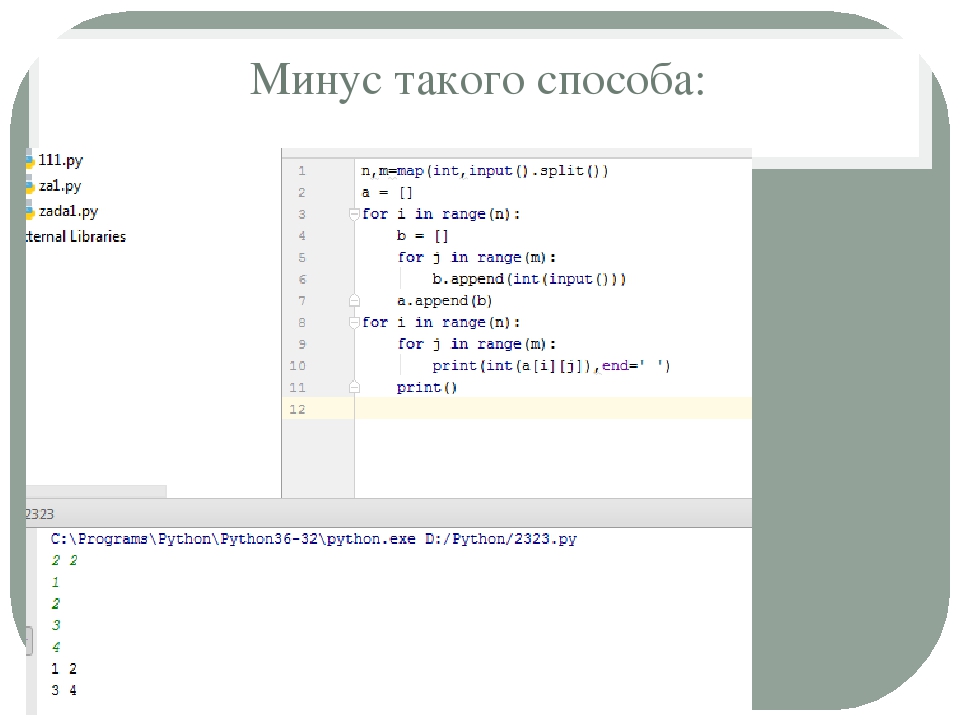 figure_map[0])-1):
if check_collision():
figure.move_left()
# Если смещение влево не помогло...
if check_collision():
# возвращаю фигуру на место
for i in range(len(figure.figure_map[0]) - 1):
figure.move_right()
# Двигаю фигуру вправо, вдруг там свободно
for i in range(len(figure.figure_map[0])):
if check_collision():
figure.move_right()
# возвращаю обратно, если не вышло
if check_collision():
for i in range(len(figure.figure_map[0])):
figure.move_left()
figure.rotate_right()
if movement_type == 'Down':
# Если есть наложение, то двигаю фигуру влево (столько раз сколько длинна фигуры)
for i in range(len(figure.figure_map[0]) - 1):
if check_collision():
figure.move_left()
# Если смещение влево не помогло...
if check_collision():
# возвращаю фигуру на место
for i in range(len(figure.
figure_map[0])-1):
if check_collision():
figure.move_left()
# Если смещение влево не помогло...
if check_collision():
# возвращаю фигуру на место
for i in range(len(figure.figure_map[0]) - 1):
figure.move_right()
# Двигаю фигуру вправо, вдруг там свободно
for i in range(len(figure.figure_map[0])):
if check_collision():
figure.move_right()
# возвращаю обратно, если не вышло
if check_collision():
for i in range(len(figure.figure_map[0])):
figure.move_left()
figure.rotate_right()
if movement_type == 'Down':
# Если есть наложение, то двигаю фигуру влево (столько раз сколько длинна фигуры)
for i in range(len(figure.figure_map[0]) - 1):
if check_collision():
figure.move_left()
# Если смещение влево не помогло...
if check_collision():
# возвращаю фигуру на место
for i in range(len(figure. figure_map[0]) - 1):
figure.move_right()
# Двигаю фигуру вправо, вдруг там свободно
for i in range(len(figure.figure_map[0])):
if check_collision():
figure.move_right()
# возвращаю обратно, если не вышло
if check_collision():
for i in range(len(figure.figure_map[0])):
figure.move_left()
figure.rotate_left()
if check_collision():
figure.y = figure.y - 1
return True
return False
def new_coordinates(event):
if event == "no_button":
movement_type = "d"
figure.move_down()
else:
movement_type = event.keysym
if movement_type == "Up":
figure.rotate_left()
if movement_type == "Down":
figure.rotate_right()
if movement_type == "Left":
figure.move_left()
if movement_type == "Right":
figure.move_right()
if movement_type == "d":
figure.
figure_map[0]) - 1):
figure.move_right()
# Двигаю фигуру вправо, вдруг там свободно
for i in range(len(figure.figure_map[0])):
if check_collision():
figure.move_right()
# возвращаю обратно, если не вышло
if check_collision():
for i in range(len(figure.figure_map[0])):
figure.move_left()
figure.rotate_left()
if check_collision():
figure.y = figure.y - 1
return True
return False
def new_coordinates(event):
if event == "no_button":
movement_type = "d"
figure.move_down()
else:
movement_type = event.keysym
if movement_type == "Up":
figure.rotate_left()
if movement_type == "Down":
figure.rotate_right()
if movement_type == "Left":
figure.move_left()
if movement_type == "Right":
figure.move_right()
if movement_type == "d":
figure.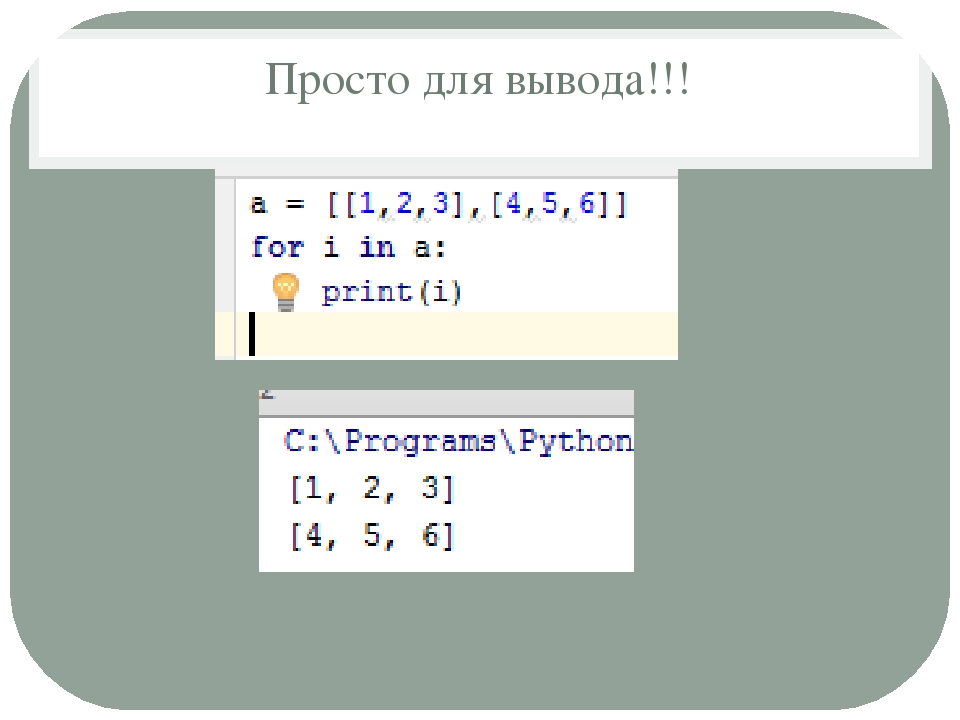 move_down()
if check_borders(movement_type):
draw_cubes()
else:
draw_figure()
canvas.bind_all("<KeyPress-Left>", new_coordinates)
canvas.bind_all("<KeyPress-Right>", new_coordinates)
canvas.bind_all("<KeyPress-Up>", new_coordinates)
canvas.bind_all("<KeyPress-Down>", new_coordinates)
canvas.bind_all("<KeyPress-d>", new_coordinates)
'''while GAME_ON:
draw_figure()
new_coordinates("no_button")
#tk.update_idletasks()
#tk.update()
time.sleep(0.5)'''
tk.mainloop()
move_down()
if check_borders(movement_type):
draw_cubes()
else:
draw_figure()
canvas.bind_all("<KeyPress-Left>", new_coordinates)
canvas.bind_all("<KeyPress-Right>", new_coordinates)
canvas.bind_all("<KeyPress-Up>", new_coordinates)
canvas.bind_all("<KeyPress-Down>", new_coordinates)
canvas.bind_all("<KeyPress-d>", new_coordinates)
'''while GAME_ON:
draw_figure()
new_coordinates("no_button")
#tk.update_idletasks()
#tk.update()
time.sleep(0.5)'''
tk.mainloop()
 h>
int** AllocMat(int n, int m);
void InputA (int **a, int n, int m );
void OutputA (int **a, int n, int m );
void bubble (int **a, int a2);
void main()
{
int n,m;
int a[n][m];
printf("input n & m");
scanf("%d %d", &n, &m);
int** a= AllocMat(n, m);
InputA(a,n,m);
int c=n*m;
int* b[c];
int* b=Transformation(a, b, m, n)
OutputA(a,n,m);
void bubble (a, a2)
OutputA2(a,n,m);
}
int** AllocMat(int n, int m)
{
int* p = new int[n*m];
int** a = new int*[n];
for(int i=0; i<n; i++)
{
a[i] = p + i*m;
}
return a;
}
void InputA (int **a, int n, int m ) //ввод матрицы
{
for (int i=0; i<n; i++)
{
for (int j=0; j<m; j++)
{
printf ("A[%d][%d]=",i,j);
scanf_s("%d", &a[i][j]);
}
}
}
void OutputA (int **a, int n, int m ) //вывод матрицы
{
for (int i=0; i<n; i++)
{
for (int j=0; j<m; j++)
{
printf ("%d ",a[i][j]);
}
printf("\n");
_getch();
}
}
void Transformation(int** a, int* b, int m, int n)
{
for ( i = 0; i < m; i ++ )
for ( j = 0; j < n; j ++ )
b[i*n+j] = a[i][j];
}
void Bubble(int b)
{
int temp;
for (int i=0; i<c-1; i++)
for (int j=0; j<i; j++)
{
if (b[j]>b[j+1])
{
temp=b[j];
b[j]=b[j+1];
b[j+1]=temp;
}
}
/* void Filling (int** a, n, m )
for (int i = m - 1; i >= 0; i--)
{
if ((n - i)%2 != 0)// если столбец нечётный (если считать справа налево)
{
for (int j = 0; j < n; j++)
{
}// заполняем столбец сверху вниз
}
else
{
for (int j = n - 1; j >= 0; j--)
{
}//заполняем столбец снизу вверх
}
}
/*
}
}
h>
int** AllocMat(int n, int m);
void InputA (int **a, int n, int m );
void OutputA (int **a, int n, int m );
void bubble (int **a, int a2);
void main()
{
int n,m;
int a[n][m];
printf("input n & m");
scanf("%d %d", &n, &m);
int** a= AllocMat(n, m);
InputA(a,n,m);
int c=n*m;
int* b[c];
int* b=Transformation(a, b, m, n)
OutputA(a,n,m);
void bubble (a, a2)
OutputA2(a,n,m);
}
int** AllocMat(int n, int m)
{
int* p = new int[n*m];
int** a = new int*[n];
for(int i=0; i<n; i++)
{
a[i] = p + i*m;
}
return a;
}
void InputA (int **a, int n, int m ) //ввод матрицы
{
for (int i=0; i<n; i++)
{
for (int j=0; j<m; j++)
{
printf ("A[%d][%d]=",i,j);
scanf_s("%d", &a[i][j]);
}
}
}
void OutputA (int **a, int n, int m ) //вывод матрицы
{
for (int i=0; i<n; i++)
{
for (int j=0; j<m; j++)
{
printf ("%d ",a[i][j]);
}
printf("\n");
_getch();
}
}
void Transformation(int** a, int* b, int m, int n)
{
for ( i = 0; i < m; i ++ )
for ( j = 0; j < n; j ++ )
b[i*n+j] = a[i][j];
}
void Bubble(int b)
{
int temp;
for (int i=0; i<c-1; i++)
for (int j=0; j<i; j++)
{
if (b[j]>b[j+1])
{
temp=b[j];
b[j]=b[j+1];
b[j+1]=temp;
}
}
/* void Filling (int** a, n, m )
for (int i = m - 1; i >= 0; i--)
{
if ((n - i)%2 != 0)// если столбец нечётный (если считать справа налево)
{
for (int j = 0; j < n; j++)
{
}// заполняем столбец сверху вниз
}
else
{
for (int j = n - 1; j >= 0; j--)
{
}//заполняем столбец снизу вверх
}
}
/*
}
} join([str(elem) for elem in row]))
join([str(elem) for elem in row])) split()] for i in range(n)]
split()] for i in range(n)] )
)  )
)  )
)  :
:  array ([40, 175, 90, 450])
array ([40, 175, 90, 450])
 array ([(1.5,2,3), (4,5,6)])
б
array ([(1.5,2,3), (4,5,6)])
б
 , 0., 0., 0.],
[0., 0., 3., 0.],
[0., 0., 0., 0.]])
, 0., 0., 0.],
[0., 0., 3., 0.],
[0., 0., 0., 0.]])
 any () или a.all ()
any () или a.all ()
 , 3,6, 1,4, 0,2],
[5., 3.4, 1.5, 0.2],
[5., 3., 1.6, 0.2],
[5., 3.4, 1.6, 0.4],
[5., 3.2, 1.2, 0.2],
[5., 3.5, 1.3, 0.3],
[5., 3.5, 1.6, 0.6],
[5., 3.3, 1.4, 0.2],
[5., 2., 3.5, 1.],
[5., 2.3, 3.3, 1.]])
, 3,6, 1,4, 0,2],
[5., 3.4, 1.5, 0.2],
[5., 3., 1.6, 0.2],
[5., 3.4, 1.6, 0.4],
[5., 3.2, 1.2, 0.2],
[5., 3.5, 1.3, 0.3],
[5., 3.5, 1.6, 0.6],
[5., 3.3, 1.4, 0.2],
[5., 2., 3.5, 1.],
[5., 2.3, 3.3, 1.]])
 , 3.2, 4.7, 1.4],
[6.4, 3.2, 4.5, 1.5],
[6.9, 3.1, 4.9, 1.5],
[5.5, 2.3, 4., 1.3],
[6.5, 2.8, 4.6, 1.5],
[5.7, 2.8, 4.5, 1.3],
[6.3, 3.3, 4.7, 1.6],
[4.9, 2.4, 3.3, 1.],
[6,6, 2,9, 4,6, 1,3],
[5.2, 2.7, 3.9, 1.4],
[5., 2., 3.5, 1.],
[5.9, 3., 4.2, 1.5],
[6., 2.2, 4., 1.],
[6.1, 2.9, 4.7, 1.4],
[5.6, 2.9, 3.6, 1.3],
[6.7, 3.1, 4.4, 1.4],
[5.6, 3., 4.5, 1.5],
[5.8, 2.7, 4.1, 1.],
[6.2, 2.2, 4.5, 1.5],
[5.6, 2.5, 3.9, 1.1],
[5.9, 3.2, 4.8, 1.8],
[6.1, 2.8, 4., 1.3],
[6.3, 2.5, 4.9, 1.5],
[6.1, 2.8, 4.7, 1.2],
[6.4, 2.9, 4.3, 1.3],
[6.6, 3., 4.4, 1.4],
[6,8, 2,8, 4,8, 1,4],
[6.7, 3., 5., 1.7],
[6., 2.9, 4.5, 1.5],
[5.7, 2.6, 3.5, 1.],
[5.5, 2.4, 3.8, 1.1],
[5.5, 2.4, 3.7, 1.],
[5.8, 2.7, 3.9, 1.2],
[6., 2.7, 5.1, 1.6],
[5.4, 3., 4.5, 1.5],
[6., 3.4, 4.
, 3.2, 4.7, 1.4],
[6.4, 3.2, 4.5, 1.5],
[6.9, 3.1, 4.9, 1.5],
[5.5, 2.3, 4., 1.3],
[6.5, 2.8, 4.6, 1.5],
[5.7, 2.8, 4.5, 1.3],
[6.3, 3.3, 4.7, 1.6],
[4.9, 2.4, 3.3, 1.],
[6,6, 2,9, 4,6, 1,3],
[5.2, 2.7, 3.9, 1.4],
[5., 2., 3.5, 1.],
[5.9, 3., 4.2, 1.5],
[6., 2.2, 4., 1.],
[6.1, 2.9, 4.7, 1.4],
[5.6, 2.9, 3.6, 1.3],
[6.7, 3.1, 4.4, 1.4],
[5.6, 3., 4.5, 1.5],
[5.8, 2.7, 4.1, 1.],
[6.2, 2.2, 4.5, 1.5],
[5.6, 2.5, 3.9, 1.1],
[5.9, 3.2, 4.8, 1.8],
[6.1, 2.8, 4., 1.3],
[6.3, 2.5, 4.9, 1.5],
[6.1, 2.8, 4.7, 1.2],
[6.4, 2.9, 4.3, 1.3],
[6.6, 3., 4.4, 1.4],
[6,8, 2,8, 4,8, 1,4],
[6.7, 3., 5., 1.7],
[6., 2.9, 4.5, 1.5],
[5.7, 2.6, 3.5, 1.],
[5.5, 2.4, 3.8, 1.1],
[5.5, 2.4, 3.7, 1.],
[5.8, 2.7, 3.9, 1.2],
[6., 2.7, 5.1, 1.6],
[5.4, 3., 4.5, 1.5],
[6., 3.4, 4. 5, 1.6],
[6,7, 3,1, 4,7, 1,5],
[6.3, 2.3, 4.4, 1.3],
[5.6, 3., 4.1, 1.3],
[5.5, 2.5, 4., 1.3],
[5.5, 2.6, 4.4, 1.2],
[6.1, 3., 4.6, 1.4],
[5.8, 2.6, 4., 1.2],
[5., 2.3, 3.3, 1.],
[5.6, 2.7, 4.2, 1.3],
[5.7, 3., 4.2, 1.2],
[5.7, 2.9, 4.2, 1.3],
[6.2, 2.9, 4.3, 1.3],
[5.1, 2.5, 3., 1.1],
[5.7, 2.8, 4.1, 1.3]])
5, 1.6],
[6,7, 3,1, 4,7, 1,5],
[6.3, 2.3, 4.4, 1.3],
[5.6, 3., 4.1, 1.3],
[5.5, 2.5, 4., 1.3],
[5.5, 2.6, 4.4, 1.2],
[6.1, 3., 4.6, 1.4],
[5.8, 2.6, 4., 1.2],
[5., 2.3, 3.3, 1.],
[5.6, 2.7, 4.2, 1.3],
[5.7, 3., 4.2, 1.2],
[5.7, 2.9, 4.2, 1.3],
[6.2, 2.9, 4.3, 1.3],
[5.1, 2.5, 3., 1.1],
[5.7, 2.8, 4.1, 1.3]])
 4,4 4,9 5,4 4,8 4,8 4,3 5,8
5,7 5,4 5,1 5,7 5,1 5,4 5,1 4,6 5,1 4,8 5. 5,2 5,2 4,7
4,8 5,4 5,2 5,5 4,9 5,5 4,9 4,4 5,1 5,5 4,4 5,1
4,8 5,1 4,6 5,3 5.]
4,4 4,9 5,4 4,8 4,8 4,3 5,8
5,7 5,4 5,1 5,7 5,1 5,4 5,1 4,6 5,1 4,8 5. 5,2 5,2 4,7
4,8 5,4 5,2 5,5 4,9 5,5 4,9 4,4 5,1 5,5 4,4 5,1
4,8 5,1 4,6 5,3 5.]
 append (98)
append (98)  pop (index_of_sub_array] .pop (index_of_element_to_relement_to_
pop (index_of_sub_array] .pop (index_of_element_to_relement_to_ 
 ]])
]])
 Например, если в нашей программе есть ошибка, которая проявляется только при определенных входных данных, то для отладки нашей программы она должна вести себя детерминированно. Мы можем создавать случайные числа детерминированно, если всегда начинаем с одной и той же начальной точки. Эта начальная точка обычно является целым числом, и мы называем ее начальным значением . Пример использования:
Например, если в нашей программе есть ошибка, которая проявляется только при определенных входных данных, то для отладки нашей программы она должна вести себя детерминированно. Мы можем создавать случайные числа детерминированно, если всегда начинаем с одной и той же начальной точки. Эта начальная точка обычно является целым числом, и мы называем ее начальным значением . Пример использования: random
random  Давайте создадим вспомогательную функцию для изучения этих атрибутов:
Давайте создадим вспомогательную функцию для изучения этих атрибутов:
 объединить ((c, a.reshape (1,2))))
print ("Новый столбец:")
print (np.concatenate ((c, a.reshape (2,1)), ось = 1))
объединить ((c, a.reshape (1,2))))
print ("Новый столбец:")
print (np.concatenate ((c, a.reshape (2,1)), ось = 1))
 split (d, (2,3,5), axis = 1)
для i, p в перечислении (части):
print ("часть% i:"% i)
печать (p)
split (d, (2,3,5), axis = 1)
для i, p в перечислении (части):
print ("часть% i:"% i)
печать (p)
 1.67807191 1.26303441]
1.67807191 1.26303441]
 arange (3) .reshape ((3,1))
информация ("а", а)
info ("b", b)
информация ("a + b", a + b)
arange (3) .reshape ((3,1))
информация ("а", а)
info ("b", b)
информация ("a + b", a + b)

 argv
argv