SavePearlHarbor | Ещё одна копия хабора
Сегодняшний мир становится все сложнее с каждым днем, и системы, с которыми нам приходится сталкиваться, становятся все более разветвленными и разнообразными. При этом, мы всегда сталкиваемся с множеством различных целей, которые должны быть учтены и достигнуты одновременно. Как же нам разобраться в этой сложности и принимать обоснованные решения?
В этом нам поможет понятие эффективности Парето. Именно оно играет ключевую роль в анализе многокритериальных систем. Этот принцип был впервые сформулирован итальянским экономистом Вильфредо Парето в начале 20-го века и означает, что если нет такого решения, которое бы улучшило одну из целей, не ухудшив при этом другие, то такое решение считается эффективным с точки зрения Парето.
Вильфредо Парет
Теоретические основы анализа многокритериальных систем
Многокритериальные системы — это системы, в которых существует несколько целей, которые могут быть взаимоисключающими или взаимосвязанными. Каждая цель представляет собой определенный критерий, и анализ таких систем направлен на оптимизацию или нахождение компромиссных решений между этими целями. Особенностью многокритериальных систем является сложность в выборе оптимального решения, так как удовлетворение одной цели может привести к ухудшению другой.
Каждая цель представляет собой определенный критерий, и анализ таких систем направлен на оптимизацию или нахождение компромиссных решений между этими целями. Особенностью многокритериальных систем является сложность в выборе оптимального решения, так как удовлетворение одной цели может привести к ухудшению другой.
Формальные инструменты теории многокритериальной оптимизации
Формальные инструменты теории многокритериальной оптимизации представляют собой математические методы и алгоритмы, которые позволяют находить оптимальные решения в многокритериальных системах. Эти методы помогают решить сложную задачу с учетом влияния каждого критерия на другие и определить оптимальные компромиссные решения.
Один из ключевых методов теории многокритериальной оптимизации — это построение множества Парето. Множество Парето представляет собой набор всех компромиссных решений, которые удовлетворяют принципу Парето — нет такого решения, которое бы улучшило хотя бы одну из целей, не ухудшив при этом другие.
Для построения множества Парето используются различные методы многокритериальной оптимизации, такие как:
Метод эффективного многокритериального программирования (Efficient Multi-Objective Programming, EMOP): Этот метод основан на решении задачи оптимизации сразу нескольких критериев с помощью математических моделей и алгоритмов. EMOP позволяет найти все компромиссные решения на границе Парето и определить их эффективность с точки зрения каждого критерия.
Методы негативных взвешиваний (Weighted Sum Method): В этом подходе каждому критерию присваивается весовой коэффициент, отражающий его относительную важность. Затем оптимизируется линейная комбинация критериев с учетом весов, что позволяет найти оптимальные компромиссные решения.
Методы эволюционной оптимизации: Эволюционные алгоритмы, такие как генетические алгоритмы и алгоритмы роя частиц, также применяются для решения задач многокритериальной оптимизации.
 Они основаны на идеях биологической эволюции и позволяют находить оптимальные решения на границе Парето путем постепенного улучшения и отбора решений.
Они основаны на идеях биологической эволюции и позволяют находить оптимальные решения на границе Парето путем постепенного улучшения и отбора решений.
Важным аспектом формальных инструментов теории многокритериальной оптимизации является возможность интерпретации результатов. Множество Парето предоставляет информацию о компромиссных решениях и позволяет принять взвешенные решения в зависимости от предпочтений принимающего решение лица или организации.
Построение множества Парето и его интерпретации
Для построения множества Парето применяются различные методы многокритериальной оптимизации, такие как метод эффективного многокритериального программирования (EMOP), методы негативных взвешиваний, а также эволюционные алгоритмы. Давайте рассмотрим каждый метод подробнее и приведем примеры построения множества Парето.
Метод эффективного многокритериального программирования (EMOP): EMOP позволяет найти все компромиссные решения на границе Парето с помощью математических моделей и алгоритмов оптимизации.

Для примера рассмотрим следующую функцию с двумя критериями:
def target_function(x, y): return x**2 + y**2, (x-2)**2 + (y-2)**2
Эта функция имеет два критерия, и мы хотим найти оптимальные решения с помощью EMOP.
Для построения графика используем библиотеку matplotlib и numpy:
import numpy as np import matplotlib.pyplot as plt def target_function(x, y): return x**2 + y**2, (x-2)**2 + (y-2)**2 # Создаем сетку точек для анализа x = np.linspace(0, 4, 100) y = np.linspace(0, 4, 100) X, Y = np.meshgrid(x, y) # Вычисляем значения критериев для каждой точки Z1, Z2 = target_function(X, Y) # Строим график с использованием цветной маркировки точек на границе Парето plt.contourf(X, Y, Z1, cmap='Blues', levels=50, alpha=0.7) plt.contourf(X, Y, Z2, cmap='Oranges', levels=50, alpha=0.7) # Находим точки на границе Парето и помечаем их красным цветом efficient_frontier = [] for i in range(len(x)): for j in range(len(y)): Z1_val, Z2_val = target_function(x[i], y[j]) is_efficient = True for k in range(len(x)): for l in range(len(y)): if target_function(x[k], y[l])[0] < Z1_val and target_function(x[k], y[l])[1] < Z2_val: is_efficient = False break if not is_efficient: break if is_efficient: efficient_frontier.append([x[i], y[j]]) efficient_frontier = np.array(efficient_frontier) plt.scatter(efficient_frontier[:, 0], efficient_frontier[:, 1], color='red', label='Граница Парето') # Добавляем подписи и легенду plt.xlabel('Критерий 1') plt.ylabel('Критерий 2') plt.title('График множества Парето с помощью EMOP') plt.legend() # Показываем график plt.show()
Этот код создаст график с двумя критериями, на котором красными точками будут отмечены точки на границе Парето, найденные с помощью метода эффективного многокритериального программирования (EMOP).
График
Вы можете изменить функцию цели target_function и поэкспериментировать с различными критериями и их взаимосвязью для получения интересующих вас результатов.
Метод негативного взвешивания: в методах негативных взвешиваний каждому критерию присваивается весовой коэффициент, отражающий его относительную важность. Оптимизация производится путем линейной комбинации критериев с учетом их весов. Предположим, что у нас есть три критерия: стоимость, качество и время производства. Каждый критерий имеет свой весовой коэффициент, который отражает его значимость.
________________ | C | Q | T | Вес ---------------- | 3 | 4 | 2 | 0.4 | 2 | 5 | 3 | 0.3 | 4 | 3 | 1 | 0.2
В данном примере, C — стоимость, Q — качество, T — время производства. У каждого решения указаны значения по каждому критерию. Весовые коэффициенты указывают, насколько важен каждый критерий.
Итог = (0.4 * C) + (0.3 * Q) + (0.2 * T)
Метод негативных взвешиваний позволит нам определить оптимальные компромиссные решения, учитывая предпочтения по каждому критерию.
Эволюционные методы оптимизации: эволюционные алгоритмы, такие как генетические алгоритмы и алгоритмы роя частиц, также применяются для построения множества Парето. Они основаны на принципах биологической эволюции и позволяют находить оптимальные решения на границе Парето путем постепенного улучшения и отбора решений.
Давайте рассмотрим пример использования генетического алгоритма для построения множества Парето в задаче оптимизации с двумя критериями. В данном примере мы будем использовать библиотеку DEAP (Distributed Evolutionary Algorithms in Python) для реализации генетического алгоритма.
Убедитесь, что у вас установлена библиотека deap, иначе выполните установку с помощью pip install deap.
import random import numpy as np import matplotlib.pyplot as plt from deap import algorithms, base, creator, tools # Определение функции цели и критериев def target_function(x, y): return x**2 + y**2, (x-2)**2 + (y-2)**2 # Определение минимизирующего типа задачи creator.create("FitnessMin", base.Fitness, weights=(-1.0, -1.0)) # Определение типа индивида (решения) creator.create("Individual", np.ndarray, fitness=creator.FitnessMin) toolbox = base.Toolbox() # Определение диапазона значений для переменных x и y BOUND_LOW, BOUND_UP = 0.0, 4.0 # Определение функции для инициализации индивидов def create_individual(): return np.random.uniform(BOUND_LOW, BOUND_UP, 2) # Определение функции для оценки индивидов (присваивание значений целевой функции) def evaluate_individual(individual): return target_function(*individual), # Регистрация функций для работы с генетическим алгоритмом toolbox.register("individual", create_individual) toolbox.register("population", tools.
initRepeat, list, toolbox.individual) toolbox.register("evaluate", evaluate_individual) toolbox.register("mate", tools.cxBlend, alpha=0.5) # Блендовское скрещивание toolbox.register("mutate", tools.mutGaussian, mu=0, sigma=0.2, indpb=0.2) # Гауссова мутация toolbox.register("select", tools.selNSGA2) # NSGA-II - алгоритм многокритериальной оптимизации def main(): random.seed(42) # Создание начальной популяции population = toolbox.population(n=50) # Оценка популяции fitnesses = list(map(toolbox.evaluate, population)) for ind, fit in zip(population, fitnesses): ind.fitness.values = fit # Запуск генетического алгоритма NGEN = 50 # Количество поколений for gen in range(NGEN): offspring = algorithms.varAnd(population, toolbox, cxpb=0.5, mutpb=0.1) fits = toolbox.map(toolbox.evaluate, offspring) for ind, fit in zip(offspring, fits): ind.fitness.values = fit population = toolbox.select(offspring, k=len(population)) # Извлечение оптимальных решений с границы Парето pareto_front = tools. selPareto(population, k=1) # Вывод оптимальных решений print("Оптимальные решения на границе Парето:") for solution in pareto_front: print(f"X: {solution[0]:.2f}, Y: {solution[1]:.2f}") # Построение графика X, Y = np.meshgrid(np.linspace(BOUND_LOW, BOUND_UP, 100), np.linspace(BOUND_LOW, BOUND_UP, 100)) Z1, Z2 = target_function(X, Y) plt.contourf(X, Y, Z1, cmap='Blues', levels=50, alpha=0.7) plt.contourf(X, Y, Z2, cmap='Oranges', levels=50, alpha=0.7) plt.scatter(*zip(*pareto_front), color='red', label='Граница Парето') plt.xlabel('Критерий 1') plt.ylabel('Критерий 2') plt.title('График множества Парето с помощью генетического алгоритма') plt.legend() plt.show() if __name__ == "__main__": main()
selPareto(population, k=1) # Вывод оптимальных решений print("Оптимальные решения на границе Парето:") for solution in pareto_front: print(f"X: {solution[0]:.2f}, Y: {solution[1]:.2f}") # Построение графика X, Y = np.meshgrid(np.linspace(BOUND_LOW, BOUND_UP, 100), np.linspace(BOUND_LOW, BOUND_UP, 100)) Z1, Z2 = target_function(X, Y) plt.contourf(X, Y, Z1, cmap='Blues', levels=50, alpha=0.7) plt.contourf(X, Y, Z2, cmap='Oranges', levels=50, alpha=0.7) plt.scatter(*zip(*pareto_front), color='red', label='Граница Парето') plt.xlabel('Критерий 1') plt.ylabel('Критерий 2') plt.title('График множества Парето с помощью генетического алгоритма') plt.legend() plt.show() if __name__ == "__main__": main()В этом примере мы определяем функцию target_function, которая представляет собой два критерия оптимизации. Затем мы используем библиотеку DEAP для создания генетического алгоритма. Генетический алгоритм запускается в цикле по заданному количеству поколений, после чего мы извлекаем оптимальные решения на границе Парето и строим график с помощью библиотеки matplotlib.
При выполнении этого кода вы получите график с двумя критериями, на котором красными точками будут отмечены решения на границе Парето, найденные с помощью генетического алгоритма. Вы можете изменять параметры генетического алгоритма и функции target_function для решения других задач с множественными критериями.
Построение компромиссных решений
Компромиссы помогают учесть разнообразные интересы и предпочтения заинтересованных сторон, а также находить устойчивые решения при наличии конфликтующих целей.
Методы агрегации целей и их роль в определении компромиссных решений:
Методы агрегации целей представляют собой способы объединения различных критериев или целей в единую функцию, которая позволяет сравнивать различные решения на основе их множественных критериев. Когда имеется множество критериев, каждый из которых может быть важен по-разному, необходимо учесть их вклад в итоговое решение. Методы агрегации целей помогают найти компромиссное решение, балансирующее между разными критериями, что позволяет удовлетворить интересы различных заинтересованных сторон.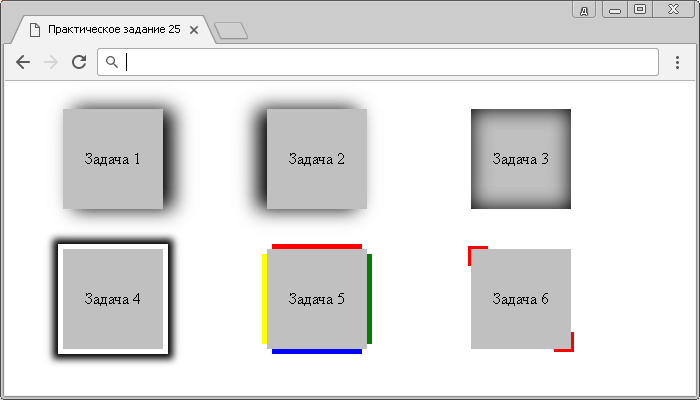
Рассмотрим некоторые из основных методов агрегации целей:
Взвешенная сумма (Weighted Sum): Это один из самых простых методов агрегации целей, где каждый критерий умножается на соответствующий ему весовой коэффициент, а затем полученные значения суммируются. Весовые коэффициенты отражают относительную важность каждого критерия. Такой метод прост в реализации и интерпретации, однако он не всегда учитывает взаимосвязи между критериями и может привести к субъективности при выборе весов.
Мультипликативная агрегация (Multiplicative Aggregation): При данном подходе значения каждого критерия умножаются на соответствующий им весовой коэффициент, а затем полученные значения перемножаются. Такой метод учитывает взаимосвязи между критериями, так как высокое значение одного критерия может компенсировать низкое значение другого. Однако он также требует аккуратного выбора весов, чтобы избежать искажения результатов.
Методы линейного программирования (Linear Programming Methods): Методы линейного программирования позволяют сформировать оптимальное решение на основе критериев и ограничений задачи.
 Они позволяют находить компромиссные решения, удовлетворяющие ограничениям и предпочтениям. Такие методы могут быть полезны при наличии сложных ограничений или большого количества критериев.
Они позволяют находить компромиссные решения, удовлетворяющие ограничениям и предпочтениям. Такие методы могут быть полезны при наличии сложных ограничений или большого количества критериев.
Использование методов агрегации целей в определении компромиссных решений позволяет найти баланс между различными критериями и выбрать решения, которые наилучшим образом соответствуют различным интересам и требованиям. Однако следует помнить, что выбор метода агрегации и определение весовых коэффициентов — это сложный процесс, который требует тщательного анализа и обсуждения с заинтересованными сторонами.
Использование весовых коэффициентов и их влияние на результаты анализа:
Весовые коэффициенты отражают относительную важность каждого критерия в принятии решения и позволяют определить, насколько каждый критерий влияет на итоговый результат анализа. Правильный выбор весовых коэффициентов помогает учесть различные предпочтения и интересы заинтересованных сторон, что позволяет найти баланс между различными критериями и построить компромиссные решения.
Рассмотрим ключевые аспекты использования весовых коэффициентов и их влияния на результаты анализа:
Определение весовых коэффициентов: Выбор весовых коэффициентов может быть основан на различных подходах. Некоторые из них включают:
Экспертное мнение: Заинтересованные стороны и эксперты могут определить весовые коэффициенты на основе своего опыта и знаний о системе и критериях.
Аналитические методы: Существуют аналитические методы, такие как метод анализа иерархий (AHP), которые позволяют определить весовые коэффициенты путем сравнения критериев по их значимости и предпочтительности.
Использование данных: Некоторые методы определения весовых коэффициентов основаны на анализе статистических данных и взаимосвязей между критериями.
Влияние на результаты анализа: Выбор весовых коэффициентов может существенно повлиять на итоговые результаты анализа и определение компромиссных решений.
 Если один из критериев сильно взвешен (имеет большой вес), то решение будет сильно зависеть от этого критерия. С другой стороны, если все критерии имеют примерно одинаковый вес, компромиссное решение будет более равномерным по отношению к разным критериям.
Если один из критериев сильно взвешен (имеет большой вес), то решение будет сильно зависеть от этого критерия. С другой стороны, если все критерии имеют примерно одинаковый вес, компромиссное решение будет более равномерным по отношению к разным критериям.Субъективность и неопределенность: Выбор весовых коэффициентов часто остается субъективным и может зависеть от личных предпочтений и мнений принимающего решение. Это может привести к различным результатам при различных интерпретациях значимости критериев. Важно обсуждать и обосновывать выбор весов с заинтересованными сторонами и экспертами, чтобы уменьшить влияние субъективности.
Чувствительность к изменениям: Изменение весовых коэффициентов может привести к изменению компромиссных решений. Это может быть полезно для оценки влияния каждого критерия на итоговый результат и анализа чувствительности решений к изменениям.
Определение эффективности Парето
Как определить эффективность Парето на основе множества Парето? Этот аспект анализа играет ключевую роль в принятии обоснованных и компромиссных решений в условиях множественных целей.
Методы определения эффективности Парето на основе множества Парето
позволяют выявить оптимальные компромиссные решения, которые соответствуют принципу Парето, а именно, решения, которые невозможно улучшить по всем критериям одновременно без ухудшения других. Давайте рассмотрим некоторые из основных методов определения эффективности Парето и приведем практические примеры их применения.
Математическое программирование:
Математическое программирование включает в себя различные методы оптимизации, такие как линейное программирование (ЛП) и нелинейное программирование (НЛП). Один из способов определения эффективности Парето — это решение многокритериальной оптимизационной задачи с использованием математического программирования. В результате такой оптимизации получается множество Парето, которое содержит все эффективные решения.
Пример: Предположим, у нас есть задача оптимизации производства, и мы имеем два критерия: максимизировать производство продукции и минимизировать затраты. Математическое программирование позволит нам найти все решения, которые обеспечивают оптимальное соотношение между производством и затратами, и составляют множество Парето.
Математическое программирование позволит нам найти все решения, которые обеспечивают оптимальное соотношение между производством и затратами, и составляют множество Парето.
Необходимые условия:
Другой подход к определению эффективности Парето — это установление необходимых условий для решения, чтобы оно считалось эффективным Парето. Это позволяет уменьшить пространство поиска оптимальных решений и упростить процесс анализа.
Предположим, у нас есть задача оптимизации производства, и нашей целью является максимизация производства продукции при ограниченных ресурсах. Необходимым условием для эффективного Парето решения может быть требование, что затраты на производство не превышают определенного значения. Таким образом, мы можем исключить из рассмотрения решения, которые не удовлетворяют этому условию и сосредоточиться на более перспективных вариантах.
Итеративные методы:
Итеративные методы представляют собой алгоритмы, которые позволяют последовательно улучшать решения на множестве Парето, чтобы найти оптимальные компромиссы.
К примеру у нас есть задача выбора оптимальной логистической схемы для доставки грузов. Критерии включают время доставки и стоимость. Итеративный метод может начать с одного решения и последовательно улучшать его, двигаясь по множеству Парето к оптимальному решению, которое обеспечивает оптимальное сочетание времени и стоимости доставки.
Часть 3: Определение эффективности Парето
В этой части статьи мы углубимся в анализ многокритериальных систем и узнаем, как определить эффективность Парето на основе множества Парето. Этот аспект анализа играет ключевую роль в принятии обоснованных и компромиссных решений в условиях множественных целей.
Методы определения эффективности Парето на основе множества Парето:
Эффективность Парето связана с идеей того, что некоторые решения нельзя улучшить по одному критерию без ухудшения другого. Таким образом, решение считается эффективным Парето, если не существует другого решения, которое бы было лучше по всем критериям одновременно. При анализе многокритериальных систем, часто строятся графики, называемые «графиками Парето» или «множеством Парето», которые представляют собой множество эффективных решений.
При анализе многокритериальных систем, часто строятся графики, называемые «графиками Парето» или «множеством Парето», которые представляют собой множество эффективных решений.
Методы определения эффективности Парето включают:
Математическое программирование: Применение различных методов оптимизации, таких как линейное программирование, нелинейное программирование или другие подходы, чтобы найти все эффективные решения, составляющие множество Парето.
Необходимые условия: Определение критериев, которые должны быть выполнены для решения, чтобы оно считалось эффективным Парето. Это помогает сократить пространство поиска оптимальных решений и ускорить процесс анализа.
Интерпретация результатов анализа множества Парето и выбор наилучших решений:
После того, как мы определили множество Парето, наступает этап интерпретации результатов. Важно понимать, что множество Парето не предоставляет одно единственное оптимальное решение, а представляет собой набор компромиссных вариантов с разными уровнями предпочтений по критериям. На этом этапе, заинтересованные стороны должны учитывать свои потребности и приоритеты для принятия обоснованных решений.
На этом этапе, заинтересованные стороны должны учитывать свои потребности и приоритеты для принятия обоснованных решений.
Основные шаги при интерпретации результатов:
Приоритеты: Определение, какие критерии являются наиболее важными для системы или задачи, и отбираются решения, которые лучше всего соответствуют этим приоритетам. Это позволяет сфокусироваться на ключевых аспектах исследуемой системы.
Риски: Решения на множестве Парето могут быть различными по степени устойчивости к возможным изменениям условий или рисковым событиям. Необходимо выбрать решения, которые обладают достаточной степенью устойчивости и минимизируют потенциальные риски. Это особенно важно в сложных и динамичных системах.
Сравнение эффективности Парето с другими методами анализа систем с множественными целями
Сравнение эффективности Парето с другими методами анализа систем с множественными целями позволяет лучше понять преимущества и ограничения данного подхода.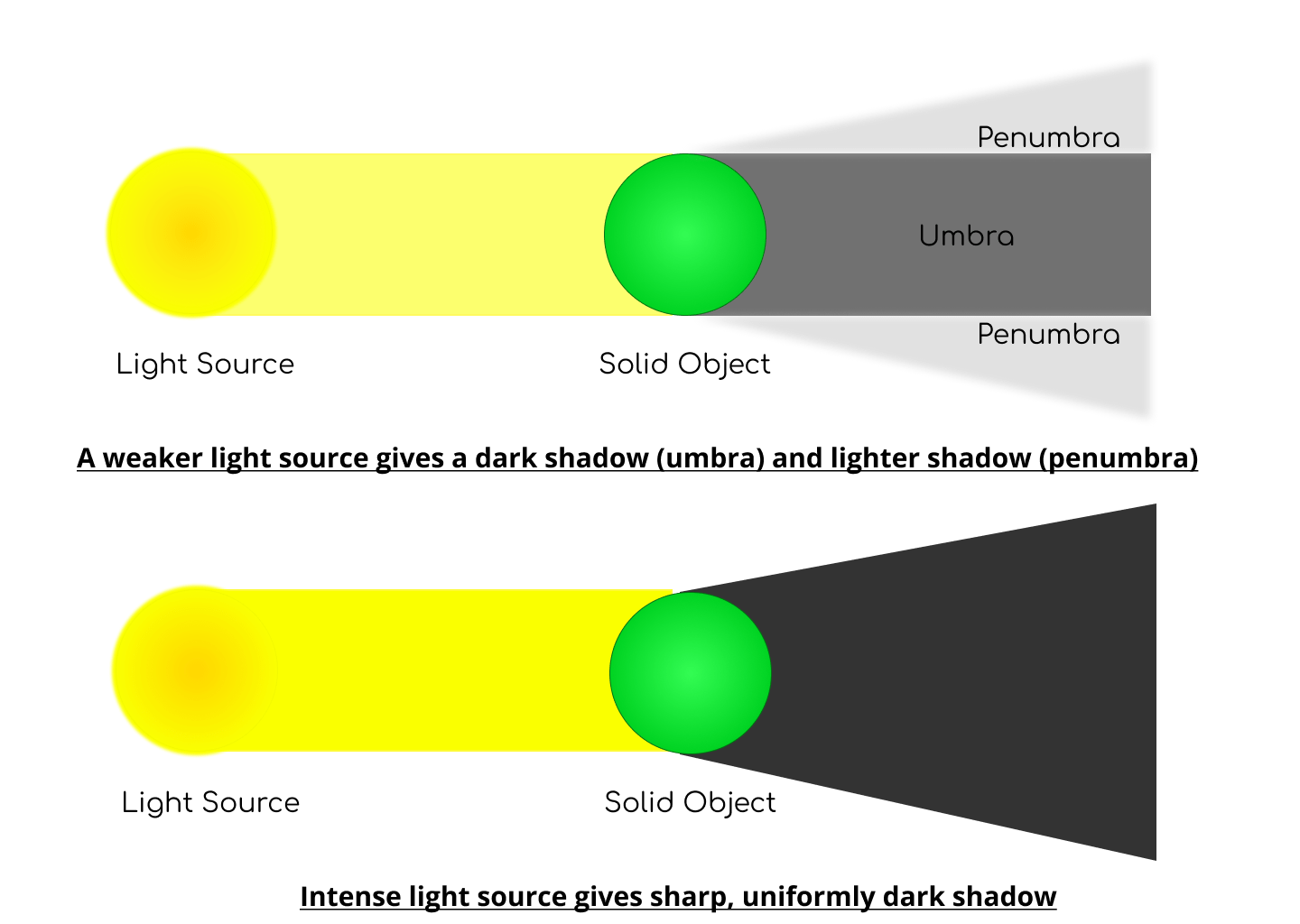 Рассмотрим некоторые из основных методов и их сравнение с эффективностью Парето:
Рассмотрим некоторые из основных методов и их сравнение с эффективностью Парето:
Методы уступки (Trade-off approach):
Методы уступки используются для принятия решений в условиях множественных целей, но они не учитывают принцип Парето. Вместо того чтобы искать компромиссные решения на множестве Парето, методы уступки обычно выбирают одно единственное оптимальное решение, которое наиболее соответствует приоритетам и весам критериев. Это может привести к упущению других важных компромиссов и неучету альтернативных вариантов.
В отличие от методов уступки, эффективность Парето предоставляет множество компромиссных решений, а не единственное оптимальное. Это позволяет более полно учитывать разнообразие интересов и предпочтений заинтересованных сторон, что делает подход Парето более гибким и адаптивным.
Лексикографическая оптимизация:
Лексикографическая оптимизация является методом, при котором критерии упорядочиваются по приоритетам. Оптимизация происходит последовательно по критериям в порядке установленных приоритетов. Такой подход не обязательно приводит к эффективным Парето решениям, так как улучшение по одному критерию может привести к ухудшению другого.
Оптимизация происходит последовательно по критериям в порядке установленных приоритетов. Такой подход не обязательно приводит к эффективным Парето решениям, так как улучшение по одному критерию может привести к ухудшению другого.
В отличие от лексикографической оптимизации, эффективность Парето позволяет рассматривать все критерии одновременно и искать компромиссные решения на основе их взаимозависимости. Это делает подход Парето более полезным при анализе сложных систем с взаимосвязанными критериями.
Анализ чувствительности:
Анализ чувствительности позволяет оценить, как изменения в значениях критериев влияют на результаты принятия решений. Этот метод помогает понять, насколько устойчивы решения к изменениям условий и параметров.
Эффективность Парето также учитывает чувствительность решений, но в рамках множества Парето. Оптимальные компромиссные решения в множестве Парето обладают разной степенью устойчивости к изменениям, что позволяет выбирать более надежные и устойчивые варианты.
Практический пример
В данном практическом примере мы рассмотрим задачу выбора оптимального автомобиля, учитывая различные критерии, такие как цена, расход топлива и производительность. Мы построим множество Парето и определим компромиссные решения на основе эффективности Парето.
Допустим, у нас есть следующие данные об автомобилях:
# Импортируем необходимые библиотеки import matplotlib.pyplot as plt import numpy as np # Данные об автомобилях (Цена, Расход топлива, Производительность) cars = { 'Car A': (30000, 8, 200), 'Car B': (25000, 7, 180), 'Car C': (32000, 9, 220), 'Car D': (28000, 6, 190), 'Car E': (33000, 9.5, 210), 'Car F': (27000, 7.5, 180) } # Преобразуем данные в массивы numpy для удобства работы prices = np.array([cars[car][0] for car in cars]) fuel_consumptions = np.array([cars[car][1] for car in cars]) performances = np.array([cars[car][2] for car in cars]) # Нормализуем данные (масштабируем значения критериев от 0 до 1) normalized_prices = (prices - np. min(prices)) / (np.max(prices) - np.min(prices)) normalized_fuel_consumptions = (fuel_consumptions - np.min(fuel_consumptions)) / (np.max(fuel_consumptions) - np.min(fuel_consumptions)) normalized_performances = (performances - np.min(performances)) / (np.max(performances) - np.min(performances))
min(prices)) / (np.max(prices) - np.min(prices)) normalized_fuel_consumptions = (fuel_consumptions - np.min(fuel_consumptions)) / (np.max(fuel_consumptions) - np.min(fuel_consumptions)) normalized_performances = (performances - np.min(performances)) / (np.max(performances) - np.min(performances)) Теперь, когда у нас есть данные об автомобилях и мы их нормализовали, давайте построим множество Парето с помощью графика на плоскости «Цена — Расход топлива»:
# Построим множество Парето pareto_front = [] for i in range(len(cars)): if all((normalized_prices[i] <= normalized_prices[j] and normalized_fuel_consumptions[i] <= normalized_fuel_consumptions[j]) for j in range(len(cars))): pareto_front.append(i) # Построим график plt.figure(figsize=(10, 6)) plt.scatter(normalized_prices, normalized_fuel_consumptions, label='Автомобили', color='blue') plt.scatter(normalized_prices[pareto_front], normalized_fuel_consumptions[pareto_front], label='Множество Парето', color='red') plt.xlabel('Нормализованная Цена') plt.ylabel('Нормализованный Расход топлива') plt.title('Множество Парето: Цена - Расход топлива') plt.legend() plt.grid() plt.show()
Построенный график
Полученный график покажет все рассматриваемые автомобили на плоскости «Цена — Расход топлива» синими точками, а точки, которые образуют множество Парето, будут выделены красным.
Теперь, давайте также построим график для плоскости «Цена — Производительность»:
# Построим множество Парето для плоскости "Цена - Производительность" pareto_front_performance = [] for i in range(len(cars)): if all((normalized_prices[i] <= normalized_prices[j] and normalized_performances[i] >= normalized_performances[j]) for j in range(len(cars))): pareto_front_performance.append(i) # Построим график plt.figure(figsize=(10, 6)) plt.scatter(normalized_prices, normalized_performances, label='Автомобили', color='blue') plt.scatter(normalized_prices[pareto_front_performance], normalized_performances[pareto_front_performance], label='Множество Парето', color='red') plt.xlabel('Нормализованная Цена') plt.ylabel('Нормализованная Производительность') plt.title('Множество Парето: Цена - Производительность') plt.legend() plt.grid() plt.show()
Полученный график
Теперь у нас есть два графика, каждый из которых показывает множество Парето в различных плоскостях «Цена — Расход топлива» и «Цена — Производительность». Множество Парето представляет собой компромиссные решения, которые обеспечивают наилучшие результаты по двум критериям одновременно. Это позволяет нам лучше понять, какие автомобили являются оптимальными выборами при учете различных критериев и ограничений.
Заключение
Анализ многокритериальных систем с использованием методов эффективности Парето представляет собой мощный и гибкий подход к принятию компромиссных решений. Он позволяет находить оптимальные варианты, которые сочетают лучшие характеристики по различным критериям и обеспечивают баланс интересов различных заинтересованных сторон.
Материал подготовлен в преддверии старта специализации «Системный аналитик и Бизнес аналитик». По ссылке вы сможете узнать о курсе подробнее и зарегистрироваться на бесплатный вебинар: «Нефункциональные требованиями глазами бизнес-аналитика».
По ссылке вы сможете узнать о курсе подробнее и зарегистрироваться на бесплатный вебинар: «Нефункциональные требованиями глазами бизнес-аналитика».
Как добавить внутренние тени текста в GIMP
В GIMP нет простой опции, позволяющей одним щелчком мыши добавить внутреннюю тень текста , но в этом руководстве мы покажем, как можно добиться этого эффекта, при котором текст выглядит так, как если бы он был вырезан из страницы.
Любой, кто привык работать с Adobe Photoshop , знает, что внутренняя тень текста легко наносится с помощью стилей слоев, но GIMP не предлагает сопоставимой функции. Чтобы добавить внутреннюю тень к тексту в GIMP, вам нужно выполнить несколько отдельных шагов, и это может показаться немного сложным для менее опытных пользователей.
Однако этот процесс относительно прост, поэтому даже новым пользователям GIMP не составит труда следовать этому руководству. Помимо достижения общей цели — научить вас добавлять внутреннюю текстовую тень, вы также познакомитесь с использованием слоев, масок слоев и применением размытия, одного из многих эффектов фильтра по умолчанию, которые поставляются с GIMP.
Помимо достижения общей цели — научить вас добавлять внутреннюю текстовую тень, вы также познакомитесь с использованием слоев, масок слоев и применением размытия, одного из многих эффектов фильтра по умолчанию, которые поставляются с GIMP.
Если у вас установлена копия GIMP, вы можете начать работу с руководством.
Первый шаг — открыть пустой документ и добавить к нему текст. Перейдите в « Файл» > « Создать» и в диалоговом окне « Создать новое изображение » установите размер изображения в соответствии с вашими требованиями и нажмите « ОК» .
Когда документ откроется, выберите поле « Цвет фона», чтобы открыть палитру цветов, установите нужный цвет фона и нажмите «ОК».
Теперь перейдите в Edit > Fill with BG Color, чтобы залить фон нужным цветом.
Теперь установите цвет переднего плана на цвет текста и выберите инструмент «Текст» на панели инструментов .

Выберите пустую страницу и в текстовом редакторе GIMP введите текст, с которым вы хотите работать. Вы можете использовать элементы управления в палитре параметров инструмента, чтобы изменить шрифт и размер шрифта.
Далее вы продублируете этот слой и растеризуете его, чтобы сформировать основу внутренней тени. Перейдите в Слой > Дублировать слой .
Щелкните правой кнопкой мыши на новом слое и выберите Discard Text Information, чтобы растеризовать его.
Верхний текстовый слой необходимо переместить на несколько пикселей вверх и влево, чтобы он был смещен относительно текста ниже. Выберите инструмент «Перемещение» на панели инструментов и выделите черный текст на странице. Теперь вы можете использовать клавиши со стрелками на клавиатуре, чтобы переместить черный текст немного влево и вверх.

- Фактическая величина, на которую вы перемещаете слой, будет зависеть от размера вашего текста — чем он больше, тем больше вам придется его перемещать. Например, если вы работаете с относительно небольшим текстом, возможно, для кнопки на веб-странице, вы можете перемещать текст только на один пиксель в каждом направлении.
- Наш пример — больший размер, чтобы сделать сопровождающий экран немного более четким (хотя этот метод наиболее эффективен при меньших размерах), и поэтому мы переместили черный текст на два пикселя в каждом направлении.
Затем щелкните правой кнопкой мыши нижний текстовый слой в палитре слоев и выберите « Альфа для выделения» .
Вы увидите контур «марширующих муравьев», и если вы щелкнете верхний текстовый слой в палитре «Слои» и перейдете в « Правка» > « Очистить» , большая часть черного текста будет удалена.

Перейдите к Select > None, чтобы удалить выделение «походные муравьи».
Убедитесь, что верхний слой в палитре слоев выделен, а затем перейдите в « Фильтры» > « Размытие» > « Размытие по Гауссу» . В открывшемся диалоговом окне Размытие по Гауссу убедитесь, что значок цепочки рядом с радиусом размытия не поврежден (щелкните его, если он есть), чтобы оба поля ввода изменились одновременно. Теперь вы можете выбрать стрелки вверх и вниз рядом с полями ввода по горизонтали и вертикали, чтобы изменить степень размытия. Количество будет варьироваться в зависимости от размера текста, над которым вы работаете. Для текста меньшего размера может быть достаточно размытия в один пиксель, но для текста большего размера используйте 3 пикселя.
 Когда сумма установлена, выберитеOK .
Когда сумма установлена, выберитеOK .Наконец, вы можете сделать размытый слой похожим на внутреннюю текстовую тень, используя функцию « Альфа для выделения» и маску слоя .
Если вы работаете с текстом небольшого размера, вам, вероятно, не нужно будет перемещать размытый слой, но когда вы работаете с более крупным текстом, вы можете выбрать инструмент «Перемещение» и сместить слой вниз и вправо. на один пиксель в каждом направлении.
Теперь щелкните правой кнопкой мыши нижний текстовый слой в палитре «Слои» и выберите « Альфа для выделения» .
Затем щелкните правой кнопкой мыши верхний слой и выберите « Добавить маску слоя», чтобы открыть диалоговое окно « Добавить маску слоя ». В этом диалоговом окне выберите « Выбор» перед выбором « Добавить» .

- Это скрывает любой размытый слой, который выходит за границы текстового слоя, так что создается впечатление внутренней тени текста.
Тень коробки | Webflow University
Домашняя страница урока
Тень окна
Домашняя страница урока
Все уроки
Используйте тени блока, чтобы добавить глубины внутри или снаружи границ элемента.
layout-design
У этого видео старый пользовательский интерфейс. Скоро будет обновленная версия!
Это видео содержит стороннюю интеграцию, поэтому пользовательский интерфейс может быть устаревшим. Посетите их документацию для получения актуальной информации!
В этом уроке:
- Тени перехода
- Создание границ с тенями блока
Тени перехода
Вы можете добавить переходы к теням блока, чтобы взаимодействие с ними было плавным. Например, вы можете добавить к элементу эффект наведения, который сделает цвет тени блока темнее. Вот шаги:
Например, вы можете добавить к элементу эффект наведения, который сделает цвет тени блока темнее. Вот шаги:
- Добавьте тень к элементу и стилю с черным цветом и непрозрачностью 20%
- В меню Состояния выберите При наведении курсора
- Настройте тень окна так, чтобы она имела непрозрачность 55 %
- Вернитесь в меню Состояния и выберите Нет (обычный)
- В нижней части панели стилей , ниже 9 0021 Эффекты добавьте переход и выберите Тень коробки из списка
- Установите время перехода или оставьте значение по умолчанию 200 мс0021 Состояние None и состояние Hover . Без перехода в 200 мс эффект наведения будет резко переключаться между уровнями непрозрачности. Вы можете стилизовать состояния наведения или нажатия с помощью тени блока, как хотите.
Создание границ с помощью теней
Вы можете добавить несколько теней к одному элементу для создания уникальных визуальных эффектов.

Узнайте больше о тенях и других эффектах .
Вот пример создания тонкой границы и тени с использованием нескольких теней:
- Добавьте внешнюю тень и установите Размытие и Расстояние на 0 пикселей и Размер на 1 пиксель
- Установите цвет тени rgba(0,0,0,0.1 ) — черный с непрозрачностью 10 %
- Добавьте вторую внешнюю тень. Установите Размытие на 8 пикселей и Расстояние на 2 пикселя.
- Установить также цвет rgba(0,0,0,0.1)
0%
Пройти тест еще раз
Перейдите к соответствующим урокам, чтобы узнать больше:
Введение в HTML/CSSБлок, который содержит другие блоки внутри, называется __, а блоки внутри другого блока называются __
«родительский элемент»; «детские элементы»
«братские элементы»; «сестринские элементы»
«материнский элемент»; «детские элементы»
«командный элемент»; «элементы-члены»
0%
Повторить тест
Перейдите к соответствующим урокам, чтобы узнать больше:
Введение в HTML/CSSПоля можно использовать для.
 ..
..Создание пространства внутри блока
Создание пространства между блоками
Создание границ вокруг элемента
Удаление отступов
0%
Пройдите тест еще раз
Перейдите к соответствующим урокам, чтобы узнать больше:
Введение в HTML/CSSЕсли вы перетащите элемент на пустой холст в Webflow, куда он будет автоматически помещен?
В левом верхнем углу холста
В правом верхнем углу холста
Точно там, где вы его уронили
В центре холста
0%
Пройти тест еще раз
Перейдите к соответствующим урокам, чтобы узнать больше:
Введение в HTML/CSS 901 05Какое свойство CSS влияет на внешний вид элемента?
Поле
Граница
Отступы
Размер
0%
Повторить тест
Перейдите к соответствующим урокам, чтобы узнать больше:
Введение в HTML/CSS. 30%
Пройти тест еще раз
Перейдите к соответствующим урокам, чтобы узнать больше:
Введение в HTML/CSSКак ящики ведут себя в Интернете по умолчанию?
Они ведут себя так, как будто они в слайд-шоу.
 Каждая коробка располагается там, где вы ее опускаете на слайде
Каждая коробка располагается там, где вы ее опускаете на слайдеОни ведут себя как колода карт. Каждый блок перекрывает другой
Они ведут себя как сетка. Блоки расположены в строках и столбцах
Они ведут себя как текстовый документ. Блоки начинаются в верхнем левом углу, и каждый блок переходит на следующую строку, когда достигает правого края
0%
Повторить тест
Перейдите к соответствующим урокам, чтобы узнать больше:
Введение в HTML/CSSПочему понимание блочной модели имеет решающее значение в веб-разработке?
Помогает при создании сложных анимаций
Помогает определить цветовую схему веб-сайта
Позволяет точно контролировать размер элементов и расстояние между ними
Помогает при оптимизации производительности веб-сайта
0%
Пройти тест еще раз 9 0003
Чтобы узнать больше, перейдите к соответствующим урокам:
Введение в HTML/CSSКакую роль блочная модель играет в адаптивном дизайне?
Управляет размером шрифта элементов на разных размерах экрана
Определяет, как мы читаем на веб-странице
Обеспечивает гибкие макеты для разных размеров экрана
Обеспечивает совместимость со старыми веб-браузерами
0%
Пройти тест еще раз
Перейдите к соответствующим урокам, чтобы узнать больше:
In tro to HTML/CSSЧто такое блочная модель в веб-разработке?
Блочная модель формирует основу того, как элементы размещаются и проектируются на веб-странице
Блочная модель — это язык программирования
Блочная модель — это стандартный способ создания анимации
Блочная модель — это стандартный протокол для работы в сети
Оценка HTML/CSS
0%
Пройти тест еще раз
Перейдите к соответствующим урокам, чтобы узнать больше:
Введение в HTML/ CSSЧто в CSS означает точка в начале селектора?
Представляет тег HTML
Обозначает селектор ID
Обозначает селектор класса
Идентифицирует селектор периода
Оценка HTML/CSS
0%
Пройти тест еще раз
Перейдите к соответствующим урокам, чтобы узнать больше:
Введение в HTML/CSS цель CSS в веб-разработке?Для определения структуры и содержания веб-страниц
Для обработки на стороне сервера
Для управления стилем и макетом веб-страниц
Для обеспечения интерактивности на веб-страницах
Оценка HTML/CSS
0%
Повторное тестирование
Перейдите к соответствующим урокам, чтобы узнать больше:
Введение в HTML/CSSВ чем преимущество использования классов в CSS?
Классы позволяют стилизовать все элементы с помощью этого класса одновременно
Классы управляют содержимым веб-страницы
Классы выполняют задачи обработки на стороне сервера
Классы обеспечивают интерактивность и анимацию на веб-страницах
Оценка HTML/CSS
0%
Повторить тест
Перейдите к соответствующим урокам, чтобы узнать больше:
Введение в HTML/CSSЧто такое HTML?
Язык гипертекстовых мультимедиа
Язык разметки HyperTransfer
Язык разметки гиперссылок
Язык разметки гипертекста
Оценка HTML/CSS
0%
Пройти тест еще раз
Перейдите к соответствующим урокам, чтобы узнать больше:
Введение в HTML/CSSДля чего используются теги HTML?
Для определения структуры и содержания веб-страниц
Для обработки на стороне сервера
Для управления внешним видом и компоновкой веб-страниц
Для обеспечения интерактивности на веб-страницах
Оценка HTML/CSS
0% 9 0011
Пройдите тест еще раз
Перейдите к соответствующим урокам, чтобы узнать больше:
Введение в HTML/CSSЧто означает CSS?
Каскадные таблицы стилей
Креативные таблицы стилей
Центральные таблицы стилей
Таблицы стилей контента
Оценка HTML/CSS
0%
Повторное тестирование
Перейдите к соответствующим урокам, чтобы узнать больше:
Введение в HTML/CSSКакой элемент HTML используется для определения элемента абзаца?
HTML/CSS оценка
0%
Повторите тест
Перейдите к соответствующим урокам, чтобы узнать больше:
Введение в HTML/CSSКак называются различные типы HTML-элементов?
Классы
Таблицы стилей
Теги
Функции
Оценка HTML/CSS
0%
Пройти тест еще раз
Перейти к связанным урокам, чтобы узнать больше:
Введение в HTML/CSSЧто лучше всего описывает HTML?
HTML — это структура и содержимое страницы
HTML — стиль страницы
HTML — классы на странице
HTML — взаимодействие страницы
Содержание shadow Chapter
Abstract
Этот документ содержит определение «тени блока».
 свойство, которое было удалено из фона CSS3 и
Модуль границ пока не стабилизируется.
свойство, которое было удалено из фона CSS3 и
Модуль границ пока не стабилизируется.Это обрывочный редакционный черновик, абсолютно нестабильный, и не имеет никакого официального статуса. Относитесь к нему так, как если бы вы приклейте записку на стол редактора.
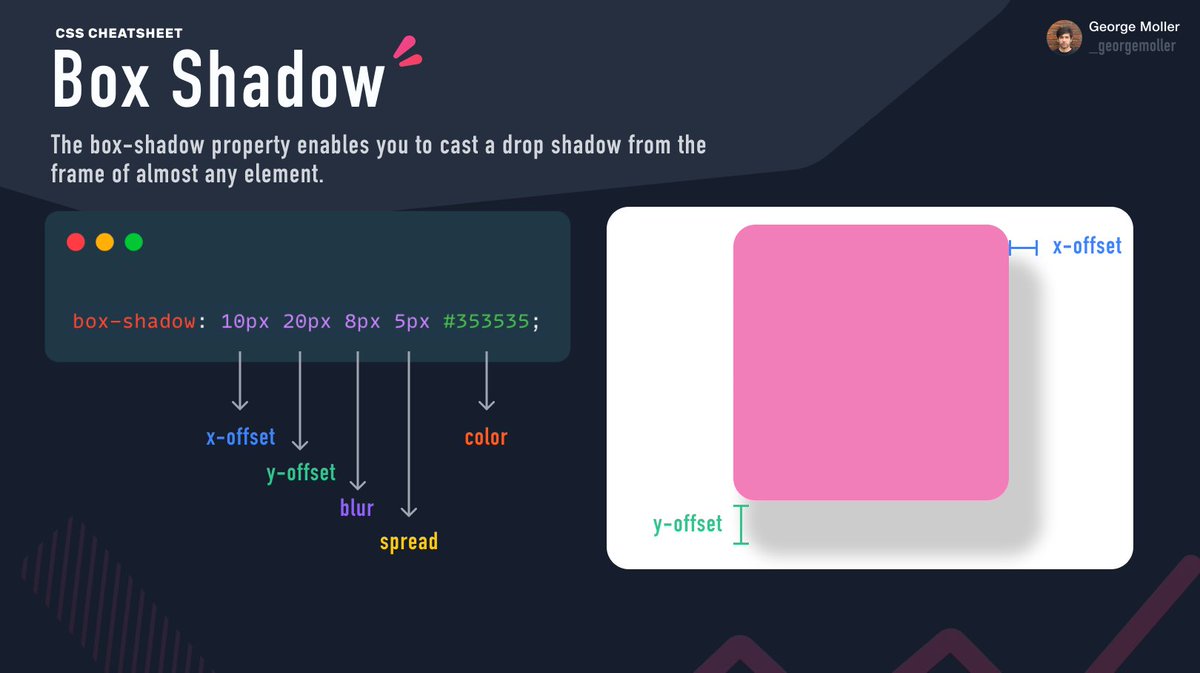
Свойство box-shadow
Имя: коробка-тень Значение: нет | <тень> [ , <тень> ]* Начальный номер: нет Применяется к: все элементы Унаследовано: нет Проценты: Н/Д СМИ: визуальный Расчетное значение: любая становится абсолютной; вычисляется любой цвет; в противном случае, как указано Свойство box-shadow прикрепляет одну или несколько теней к коробке.
 Свойство представляет собой список теней, разделенных запятыми, каждая из которых указана
на 2-4 значения длины, необязательный цвет и необязательную «вставку»
ключевое слово. Пропущенные длины равны 0, пропущенные цвета являются цветом, выбранным UA.
Свойство представляет собой список теней, разделенных запятыми, каждая из которых указана
на 2-4 значения длины, необязательный цвет и необязательную «вставку»
ключевое слово. Пропущенные длины равны 0, пропущенные цвета являются цветом, выбранным UA.Где
<тень> = вставка? && [ <длина> {2,4} && <цвет> ? ]Компоненты каждого
- Первая длина — это горизонтальное смещение тени. А положительное значение рисует тень, смещенную вправо от коробка, отрицательная длина влево.
- Вторая длина — это вертикальное смещение. Положительное значение смещает тень вниз, отрицательную вверх.
- Третья длина — это радиус размытия. Отрицательные значения не допустимый. Если он равен 0, тень резкая, в противном случае чем больше значение, тем сильнее размыта тень. Точного алгоритма нет. указано.
- Четвертая длина — это радиус разброса.
 Положительные значения вызывают
тень должна расти во всех направлениях по указанному радиусу.
Отрицательные значения заставляют тень сжиматься. Тень не должна
изменять форму при применении радиуса разброса: острые углы должны
оставаться острым.
Положительные значения вызывают
тень должна расти во всех направлениях по указанному радиусу.
Отрицательные значения заставляют тень сжиматься. Тень не должна
изменять форму при применении радиуса разброса: острые углы должны
оставаться острым. - Цвет — цвет тени.
- Ключевое слово »inset», если оно присутствует, изменяет тень от внешней тени (та, которая затеняет коробку на холст, как бы приподнятый над холстом) во внутреннюю тень (тот, который затеняет холст на коробке, как если бы коробка была разрезана выходит из полотна и смещается за него).
Внешняя тень блока отбрасывает тень, как если бы рамка элемента были непрозрачны. Тень рисуется только за пределами края границы: это не рисуется внутри рамки элемента.
Внутренняя тень блока отбрасывает тень, как будто все, что находится за пределами отступа края были непрозрачны. Внутренняя тень рисуется только внутри края заполнения: он не рисуется за пределами поля заполнения элемента.

Если поле имеет ненулевой радиус границы, тень округляется таким же образом.
Это все еще обсуждается. Пожалуйста, присылайте комментарии на www-style.
Однако, если у коробки есть border-image, тени рисуются иначе: они маскируются изображением границы вместо области границы следующим образом.
- Для внешней тени тень создается в предположении, что padding box непрозрачен, а затем комбинирует его с изображением границы для создания маски альфа-канала для тени. Значения спреда интерпретируется как увеличение размера поля заполнения и вызывает маска границы изображения должна быть соответственно изменена. Результирующая тень рисуется только за пределами отступа. коробка.
- Для внутренней тени тень создается в предположении, что все
за пределами поля границы непрозрачно, а затем комбинируя это с
border-image для создания маски альфа-канала для тени. Значения спреда
интерпретируются как уменьшение размера рамки и вызывают
маска границы изображения должна быть соответственно изменена.
 Результирующая тень рисуется только внутри границ рамки.
Результирующая тень рисуется только внутри границ рамки.
Если UA не может создавать тени, учитывающие прозрачность и частично прозрачные аспекты бордюрного изображения, оно не должно создавать вообще тень. UA может игнорировать значения спреда при отрисовке тени для рамки-изображения.
Если элемент имеет несколько полей, все они получают тени, но тени рисуются только там, где также должны быть нарисованы границы, см. «box-break».
Эффекты тени применяются спереди назад: первая тень сверху, а остальные слои позади. Тени не влияют макет и может перекрывать другие блоки или их тени. С точки зрения укладки контексты и порядок рисования, внешние тени элемента рисуются непосредственно под фоном этого элемента и внутренние тени элемент рисуется непосредственно над фоном этого элемента (ниже границ и изображения границы, если таковые имеются).
Тени никогда не влияют на макет и не вызывают прокрутку или увеличение размер прокручиваемой области.

Ниже приведены несколько примеров оранжевого блока с синей окантовкой. получает тень.
граница: 5 пикселей сплошной синий; цвет фона: оранжевый; ширина: 144 пикселя; высота: 144 пикселя;
радиус границы: 20 пикселей;
радиус границы: 0;
коробка-тень: RGBA(0,0,0,0,4) 10 пикселей 10 пикселей;
тень коробки: RGBA(0,0,0,0,4) 10 пикселей 10 пикселей вставка
тень коробки: RGBA(0,0,0,0,4) 10 пикселей 10 пикселей 0 10px /* разворот */
тень коробки: RGBA(0,0,0,0,4) 10 пикселей 10 пикселей 0 10px /* разворот */ вставка
Свойство »box-shadow» применяется к псевдоэлементу »::first-letter», но не псевдоэлемент »::first-line».


 Они основаны на идеях биологической эволюции и позволяют находить оптимальные решения на границе Парето путем постепенного улучшения и отбора решений.
Они основаны на идеях биологической эволюции и позволяют находить оптимальные решения на границе Парето путем постепенного улучшения и отбора решений.

 selPareto(population, k=1) # Вывод оптимальных решений print("Оптимальные решения на границе Парето:") for solution in pareto_front: print(f"X: {solution[0]:.2f}, Y: {solution[1]:.2f}") # Построение графика X, Y = np.meshgrid(np.linspace(BOUND_LOW, BOUND_UP, 100), np.linspace(BOUND_LOW, BOUND_UP, 100)) Z1, Z2 = target_function(X, Y) plt.contourf(X, Y, Z1, cmap='Blues', levels=50, alpha=0.7) plt.contourf(X, Y, Z2, cmap='Oranges', levels=50, alpha=0.7) plt.scatter(*zip(*pareto_front), color='red', label='Граница Парето') plt.xlabel('Критерий 1') plt.ylabel('Критерий 2') plt.title('График множества Парето с помощью генетического алгоритма') plt.legend() plt.show() if __name__ == "__main__": main()
selPareto(population, k=1) # Вывод оптимальных решений print("Оптимальные решения на границе Парето:") for solution in pareto_front: print(f"X: {solution[0]:.2f}, Y: {solution[1]:.2f}") # Построение графика X, Y = np.meshgrid(np.linspace(BOUND_LOW, BOUND_UP, 100), np.linspace(BOUND_LOW, BOUND_UP, 100)) Z1, Z2 = target_function(X, Y) plt.contourf(X, Y, Z1, cmap='Blues', levels=50, alpha=0.7) plt.contourf(X, Y, Z2, cmap='Oranges', levels=50, alpha=0.7) plt.scatter(*zip(*pareto_front), color='red', label='Граница Парето') plt.xlabel('Критерий 1') plt.ylabel('Критерий 2') plt.title('График множества Парето с помощью генетического алгоритма') plt.legend() plt.show() if __name__ == "__main__": main() Они позволяют находить компромиссные решения, удовлетворяющие ограничениям и предпочтениям. Такие методы могут быть полезны при наличии сложных ограничений или большого количества критериев.
Они позволяют находить компромиссные решения, удовлетворяющие ограничениям и предпочтениям. Такие методы могут быть полезны при наличии сложных ограничений или большого количества критериев. Если один из критериев сильно взвешен (имеет большой вес), то решение будет сильно зависеть от этого критерия. С другой стороны, если все критерии имеют примерно одинаковый вес, компромиссное решение будет более равномерным по отношению к разным критериям.
Если один из критериев сильно взвешен (имеет большой вес), то решение будет сильно зависеть от этого критерия. С другой стороны, если все критерии имеют примерно одинаковый вес, компромиссное решение будет более равномерным по отношению к разным критериям. min(prices)) / (np.max(prices) - np.min(prices)) normalized_fuel_consumptions = (fuel_consumptions - np.min(fuel_consumptions)) / (np.max(fuel_consumptions) - np.min(fuel_consumptions)) normalized_performances = (performances - np.min(performances)) / (np.max(performances) - np.min(performances))
min(prices)) / (np.max(prices) - np.min(prices)) normalized_fuel_consumptions = (fuel_consumptions - np.min(fuel_consumptions)) / (np.max(fuel_consumptions) - np.min(fuel_consumptions)) normalized_performances = (performances - np.min(performances)) / (np.max(performances) - np.min(performances))  xlabel('Нормализованная Цена') plt.ylabel('Нормализованный Расход топлива') plt.title('Множество Парето: Цена - Расход топлива') plt.legend() plt.grid() plt.show()
xlabel('Нормализованная Цена') plt.ylabel('Нормализованный Расход топлива') plt.title('Множество Парето: Цена - Расход топлива') plt.legend() plt.grid() plt.show()  xlabel('Нормализованная Цена') plt.ylabel('Нормализованная Производительность') plt.title('Множество Парето: Цена - Производительность') plt.legend() plt.grid() plt.show()
xlabel('Нормализованная Цена') plt.ylabel('Нормализованная Производительность') plt.title('Множество Парето: Цена - Производительность') plt.legend() plt.grid() plt.show() 


 Когда сумма установлена, выберитеOK .
Когда сумма установлена, выберитеOK .

 ..
.. Каждая коробка располагается там, где вы ее опускаете на слайде
Каждая коробка располагается там, где вы ее опускаете на слайде свойство, которое было удалено из фона CSS3 и
Модуль границ пока не стабилизируется.
свойство, которое было удалено из фона CSS3 и
Модуль границ пока не стабилизируется. Свойство представляет собой список теней, разделенных запятыми, каждая из которых указана
на 2-4 значения длины, необязательный цвет и необязательную «вставку»
ключевое слово. Пропущенные длины равны 0, пропущенные цвета являются цветом, выбранным UA.
Свойство представляет собой список теней, разделенных запятыми, каждая из которых указана
на 2-4 значения длины, необязательный цвет и необязательную «вставку»
ключевое слово. Пропущенные длины равны 0, пропущенные цвета являются цветом, выбранным UA.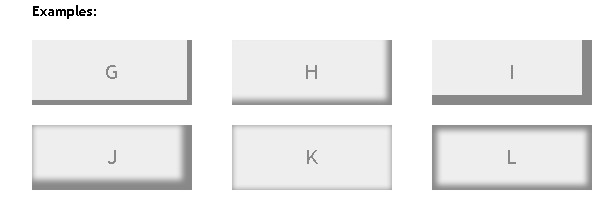 Положительные значения вызывают
тень должна расти во всех направлениях по указанному радиусу.
Отрицательные значения заставляют тень сжиматься. Тень не должна
изменять форму при применении радиуса разброса: острые углы должны
оставаться острым.
Положительные значения вызывают
тень должна расти во всех направлениях по указанному радиусу.
Отрицательные значения заставляют тень сжиматься. Тень не должна
изменять форму при применении радиуса разброса: острые углы должны
оставаться острым.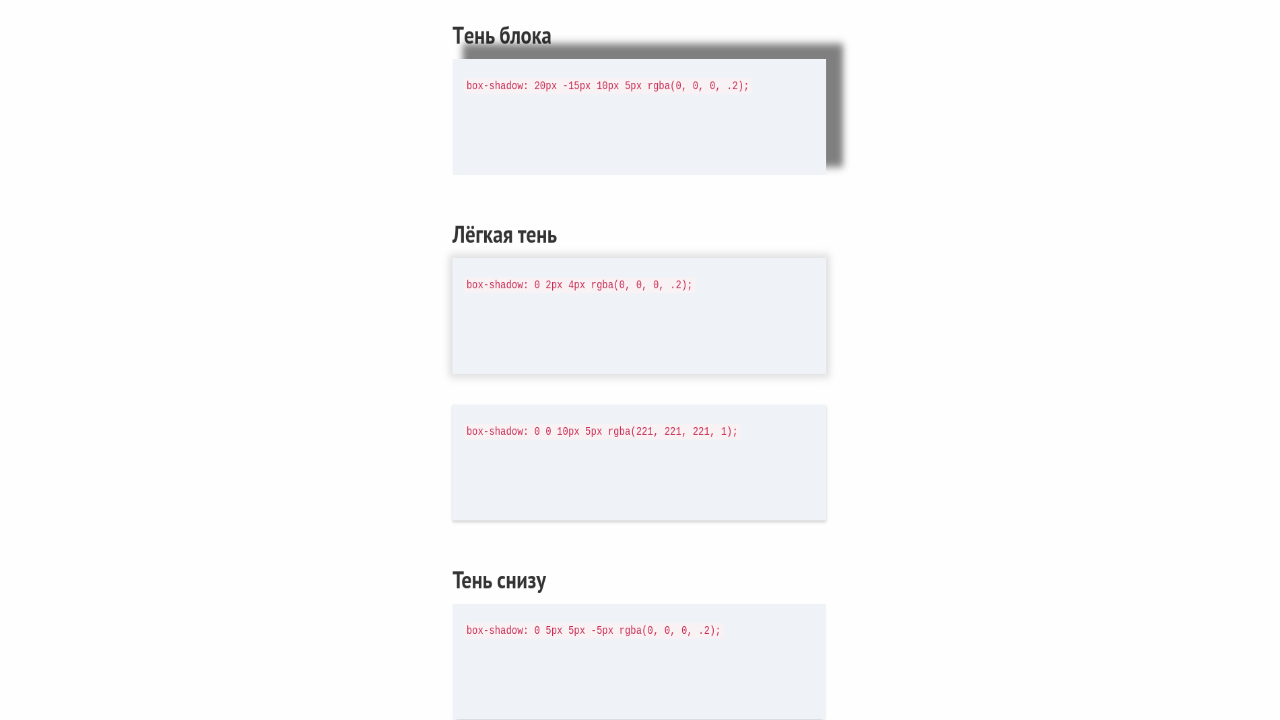
 Результирующая тень рисуется только внутри границ рамки.
Результирующая тень рисуется только внутри границ рамки.
