Содержание

Digital Chip

Все данные в языке Си имеют свой тип. Переменные определенных типов занимают в памяти какое-то место, разное в зависимости от типа. В Си нет четкого закрепления количества памяти за определенными типами. Это отдано на реализацию конкретного компилятора под конкретную платформу. Например, переменная типа int в одном компиляторе может занимать в памяти 16 бит, в другом — 32 бита, в третьем — 8 бит. Все определяет конкретный компилятор. Правда, все стремятся к универсализации, и в основном в большинстве компиляторов тип int, например, занимает 2 байта, а тип char — один.

Я в последнее время немного затупил, не мог вспомнить, сколько байт занимает тип double в AVR-GCC. Обычно при программировании контроллеров работаешь с целочисленными типами, типа int и char, а к типам с плавающей точкой прибегаешь не часто, в связи с их ресурсоемкостью.

Поэтому, на будущее, оставлю себе здесь памятку с указанием размеров занимаемой памяти типами данных для компилятора AVR-GCC и диапазон изменения переменных этого типа.

Типы данных в языке Си для компилятора AVR-GCC

ТипРазмер в
байтах (битах)		Интервал изменения
char1 (8)-128 .. 127
unsigned char1 (8)0 .. 255
signed char1 (8)-128 .. 127
int2 (16)-32768 .. 32767
unsigned int2 (16)0 .. 65535
signed int2 (16)-32768 .. 32767
short int2 (16)-32768 .. 32767
unsigned short int2 (16)0 .. 65535
signed short int2 (16)-32768 . . 32767
long int
4 (32)-2147483648 .. 2147483647
unsigned long int4 (32)0 .. 4294967295
signed long int4 (32)-2147483648 .. 2147483647
float4 (32)3.4Е-38 .. 3.4Е+38
double4 (32)3.4Е-38 .. 3.4Е+38
long double10 (80)3.4Е-4932 .. 3.4Е+4932

[stextbox id=»warning» caption=»Обратите внимание»]Реализация типа double в AVR-GCC отступает от стандарта. По стандарту double занимает 64 бита. В AVR-GCC переменная этого типа занимает 32 бита, и соответственно, она эквивалентна переменной с типом

float![/stextbox]

В дополнение к этому, в библиотеках AVR-GCC введено несколько производных от стандартных типов. Они описаны в файле stdint.h. Сделано это, наверно, для улучшения наглядности и уменьшения текста программ (ускорения их написания :)). Вот табличка соответствия:

Производные типы от стандартных в языке Си для компилятора AVR-GCC

Производный типСтандартный тип
int8_tsigned char
uint8_t
unsigned char
int16_tsigned int
uint16_tunsigned int
int32_tsigned long int
uint32_tunsigned long int
int64_tsigned long long int
uint64_tunsigned long long int

Тип Void

В языке Си есть еще один тип — тип void. Void используется для указания, что функция не возвращает ничего в качестве результата, или не принимает на вход никаких параметров. Этот тип не применяется для объявления переменных, соответственно он не занимает места в памяти.

Одинарная или двойная точность? / Хабр

Введение

В научных вычислениях мы часто используем числа с плавающей запятой (плавающей точкой). Эта статья представляет собой руководство по выбору правильного представления числа с плавающей запятой. В большинстве языков программирования есть два встроенных вида точности: 32-битная (одинарная точность) и 64-битная (двойная точность). В семействе языков C они известны как

float и double, и здесь мы будем использовать именно такие термины. Есть и другие виды точности: half, quad и т. д. Я не буду заострять на них внимание, хотя тоже много споров возникает относительно выбора half vs float или double vs quad. Так что сразу проясним: здесь идёт речь только о 32-битных и 64-битных числах IEEE 754.

Статья также написана для тех из вас, у кого много данных. Если вам требуется несколько чисел тут или там, просто используйте double и не забивайте себе голову!

Статья разбита на две отдельные (но связанные) дискуссии: что использовать для хранения ваших данных и что использовать при вычислениях. Иногда лучше хранить данные во float, а вычисления производить в double.

Если вам это нужно, в конце статьи я добавил небольшое напоминание, как работают числа с плавающей запятой. Не стесняйтесь сначала прочитать его, а потом возвращайтесь сюда.

Точность данных

У 32-битных чисел с плавающей запятой точность примерно 24 бита, то есть около 7 десятичных знаков, а у чисел с двойной точностью — 53 бита, то есть примерно 16 десятичных знаков. Насколько это много? Вот некоторые грубые оценки того, какую точность вы получаете в худшем случае при использовании float и double для измерения объектов в разных диапазонах:

Масштаб Одинарная точность Двойная точность
Размер комнаты микрометр радиус протона
Окружность Земли 2,4 метра нанометр
Расстояние до Солнца 10 км толщина человеческого волоса
Продолжительность суток 5 миллисекунд пикосекунда
Продолительность столетия 3 минуты микросекунда
Время от Большого взрыва тысячелетие минута

(пример: используя double, мы можем представить время с момента Большого взрыва с точностью около минуты).

Итак, если вы измеряете размер квартиры, то достаточно float. Но если хотите представить координаты GPS с точностью менее метра, то понадобится

double.

Почему всегда не хранить всё с двойной точностью?

Если у вас много оперативной памяти, а скорость выполнения и расход аккумулятора не являются проблемой — вы можете прямо сейчас прекратить чтение и использовать double. До свидания и хорошего вам дня!

Если же память ограничена, то причина выбора float вместо double проста: он занимает вдвое меньше места. Но даже если память не является проблемой, сохранение данных во float может оказаться значительно быстрее. Как я уже упоминал, double занимает в два раза больше места, чем

float, то есть требуется в два раза больше времени для размещения, инициализации и копирования данных, если вы используете double. Более того, если вы считываете данные непредсказуемым образом (случайный доступ), то с double у вас увеличится количество промахов мимо кэша, что замедляет чтение примерно на 40% (судя по практическому правилу O(√N), что подтверждено бенчмарками).

Влияние на производительность вычислений с одинарной и двойной точностью

Если у вас хорошо подогнанный конвейер с использованием SIMD, то вы сможете удвоить производительность FLOPS, заменив double

на float. Если нет, то разница может быть гораздо меньше, но сильно зависит от вашего CPU. На процессоре Intel Haswell разница между float и double маленькая, а на ARM Cortex-A9 разница большая. Исчерпывающие результаты тестов см. здесь.

Конечно, если данные хранятся в double, то мало смысла производить вычисления во float. В конце концов, зачем хранить такую точность, если вы не собираетесь её использовать? Однако обратное неправильно: может быть вполне оправдано хранить данные во float, но производить некоторые или все вычисления с двойной точностью.

Когда производить вычисления с увеличенной точностью

Даже если вы храните данные с одинарной точностью, в некоторых случаях уместно использовать двойную точность при вычислениях.

6) чисел, то теряются шесть десятичных знаков (а у float их всего семь!). Решение простое: вместо этого выполнять вычисления в формате double:

float sum(float* values, long long count)
{
    double sum = 0;
    for (long long i = 0; i < count; ++i) {
        sum += values[i];
    }
    return (float)sum;
}

Скорее всего, этот код будет работать так же быстро, как и первый, но при этом не будет теряться точность. Обратите внимание, что вовсе не нужно хранить числа в

double, чтобы получить преимущества увеличенной точности вычислений!

Пример

Предположим, что вы хотите точно измерить какое-то значение, но ваше измерительное устройство (с неким цифровым дисплеем) показывает только три значимых разряда. Измерение переменной десять раз выдаёт следующий ряд значений:

3.16, 3.15, 3.16, 3.18, 3.15, 3.11, 3.14, 3.11, 3.14, 3.15

Чтобы увеличить точность, вы решаете сложить результаты измерений и вычислить среднее значение. В этом примере используется число с плавающей запятой в base-10, у которого точность составляет точно семь десятичных знаков (похоже на 32-битный

float). С тремя значимыми разрядами это даёт нам четыре дополнительных десятичных знака точности:

3.160000 +
3.150000 +
3.160000 +
3.180000 +
3.150000 +
3.110000 +
3.140000 +
3.110000 +
3.140000 +
3.150000 =
31.45000

В сумме уже четыре значимых разряда, с тремя свободными. Что если сложить сотню таких значений? Тогда мы получим нечто вроде такого:

314.4300

Всё ещё остались два неиспользованных разряда. Если суммировать тысячу чисел?

3140.890

Десять тысяч?

31412.87

Пока что всё хорошо, но теперь мы используем все десятичные знаки для точности. Продолжим складывать числа:

31412.87 +
    3.11 =
31415.98

Заметьте, как мы сдвигаем меньшее число, чтобы выровнять десятичный разделитель. У нас больше нет запасных разрядов, и мы опасно приблизились к потере точности. Что если сложить сто тысяч значений? Тогда добавление новых значений будет выглядеть так:

314155.6  +
     3.12 =
314158.7

Обратите внимание, что последний значимый разряд данных (2 в 3.12) теряется. Вот теперь потеря точности действительно происходит, поскольку мы непрерывно будем игнорировать последний разряд точности наших данных. Мы видим, что проблема возникает после сложения десяти тысяч чисел, но до ста тысяч. У нас есть семь десятичных знаков точности, а в измерениях имеются три значимых разряда. Оставшиеся четыре разряда — это четыре порядка величины, которые выполняют роль своеобразного «числового буфера». Поэтому мы можем безопасно складывать четыре порядка величины = 10000 значений без потери точности, но дальше возникнут проблемы. Поэтому правило следующее:

Если в вашем числе с плавающей запятой P разрядов (7 для float, 16 для double) точности, а в ваших данных S разрядов значимости, то у вас остаётся P-S разрядов для манёвра и можно сложить 10^(P-S) значений без проблем с точностью. (16-3) = 10 000 000 000 000 значений без проблем с точностью.

(Существуют численно стабильные способы сложения большого количества значений. Однако простое переключение с float на double гораздо проще и, вероятно, быстрее).

Выводы


  • Не используйте лишнюю точность при хранении данных.
  • Если складываете большое количество данных, переключайтесь на двойную точность.

Приложение: Что такое число с плавающей запятой?

Я обнаружил, что многие на самом деле не вникают, что такое числа с плавающей запятой, поэтому есть смысл вкратце объяснить. Я пропущу здесь мельчайшие детали о битах, INF, NaN и поднормалях, а вместо этого покажу несколько примеров чисел с плавающей запятой в base-10. Всё то же самое применимо к двоичным числам.

Вот несколько примеров чисел с плавающей запятой, все с семью десятичными разрядами (это близко к 32-битному float).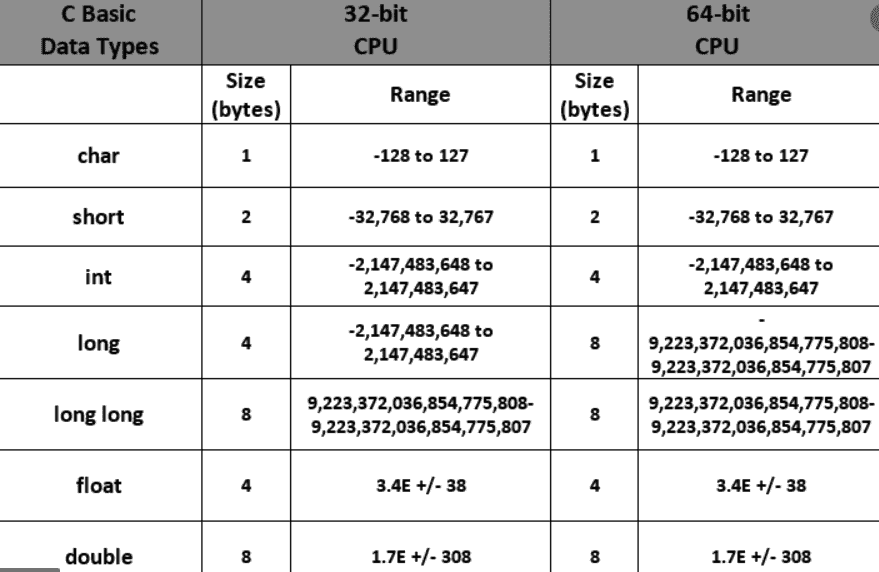 -3 =
3.141593 + 0.0001111111 =
3.141593 + 0.000111 =
3.141704

Заметьте, как мы сдвинули некоторые из значимых десятичных знаков, чтобы запятые совпадали. Другими словами, мы теряем точность, когда складываем числа разных величин.

Размер типов данных в C

Типы данных — одна из наиболее важных функций языка программирования C. Мы используем типы данных с функциями и переменными для определения того, какие данные они обычно содержат. Эти данные могут быть символом или значением некоторого типа. Также могут быть различные наборы символов или наборы значений. Язык C предлагает очень широкий спектр всех типов данных, и каждый из них может содержать уникальный тип данных с некоторым заранее определенным диапазоном.

В этой статье мы более подробно рассмотрим размер типов данных в C в соответствии с программой GATE для CSE (Computer Science Engineering). Читайте дальше, чтобы узнать больше.

Содержание

  • Типы типов данных в C
  • Первичные типы данных
    • Размер первичных типов данных
    • Размер символа
    • Короткий целочисленный размер
    • Размер длинного целого числа
      • Что отличает диапазон для беззнаковых и знаковых типов?
      • Дополнение 1S
      • Дополнение 2S
  • Типы данных с плавающей запятой
    • Нормализованная форма
    • Денормализованная форма
      • Резюме
  • Производные типы данных
  • Практические проблемы с размером типов данных в C
  • Часто задаваемые вопросы

Типы типов данных в C

Язык программирования C имеет два основных типа данных:

  • Первичный
  • Производный

Первичные типы данных

Первичные типы данных в основном являются стандартными типами данных, которые определяет язык C. Язык определяет четыре основных типа данных в программировании. Это:

char – по своей природе являются однобайтовыми. Тип данных char может содержать один символ в локальном наборе символов.

float – это типы одинарной точности с плавающей запятой.

инт – это целые числа. Обычно они отражают естественный размер целого числа на хост-компьютере.

double – это типы с плавающей запятой двойной точности.

Кроме того, к базовым типам данных можно применять различное количество квалификаторов. Длинные и короткие квалификаторы, применяемые к целым числам, окажутся такими:

.

счетчик длинных чисел;

короткий инт ш;

*Обратите внимание, что мы можем опустить слово int в объявлениях такого типа.

Размер первичных типов данных

Вот список всех первичных типов данных:

Тип Диапазон Размер (в байтах)
беззнаковый символ от 0 до 255 1
подписанный символ или символ от -128 до +127 1
целое число без знака 0 до 65535 2
подписанное целое число или целое число -32 768 до +32767 2
короткое целое без знака 0 до 65535 2
со знаком короткое целое или короткое целое -32 768 до +32767 2
длинное целое без знака от 0 до +4 294 967 295 4
подписанное длинное целое или длинное целое от -2 147 483 648 до +2 147 483 647 4
длинный двойной 3. 4E-4932 до 1.1E+4932 10
двойной 1.7E-308 до 1.7E+308 8
поплавок от 3.4E-38 до 3.4E+38 4

Размер и диапазон типов данных во многом зависят от компилятора. Однако код, компилируемый компилятором, предназначен для некоторых конкретных типов микроконтроллеров или микропроцессоров. Один единственный компилятор может обеспечить поддержку нескольких целей или процессоров. Затем компилятор определяет размер доступных типов данных на основе выбранной цели. Проще говоря, размер любого типа данных напрямую зависит от компилятора вместе с целевым процессором (для которого генерация кода происходит с помощью компилятора).

В приведенной выше таблице предполагается 16-битный компилятор. Это означает, что генерация кода компилятора будет для 16-битного целевого процессора. Целое число, как правило, является естественным размером для любого процессора или машины. В таблице, упомянутой выше, целое число имеет ширину 16 бит или 2 байта. Таким образом, компилятор также имеет ширину 16 бит или 2 байта. Если бы компилятор был 32-битным, размер типа int был бы примерно 32-битным или 4 байта. Однако это может происходить не каждый раз. Также возможно, что размер целого числа составляет 32 бита или 4 байта для 64-битного процессора. Это полностью зависит от типа компилятора.

Давайте рассмотрим пример целочисленного типа данных:

внутр.темп.; // переменная temp может хранить целочисленные значения

(как отрицательные, так и положительные)

темп = 50;

темп = -50;

подписанный временный интервал; // переменная temp может хранить целочисленные значения

(как отрицательные, так и положительные)

темп = 987654;

темп = -987654;

беззнаковый интервал времени; // переменная «temp» способна хранить целочисленные значения

(только положительный)

темп = 87654;

темп = -8; // Данное присвоение неверно

Размер символа

Размер как беззнакового, так и подписанного char всегда равен 1 байту, независимо от того, какой компилятор мы используем.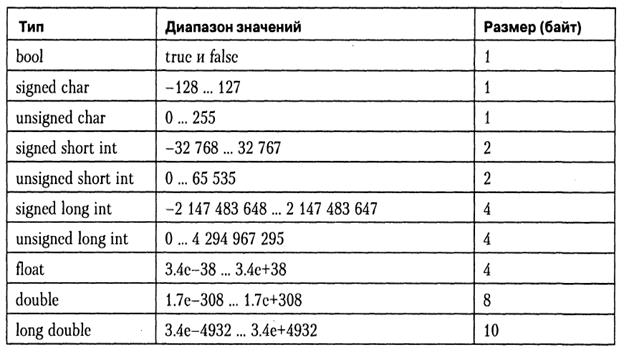 Здесь знаковый символ может содержать отрицательные значения. Таким образом, определенный диапазон здесь составляет от -128 до +127. Но беззнаковый символ может содержать только положительные значения. Таким образом, диапазон таких символов составляет от 0 до 255. Эти типы символьных данных могут хранить символы ASCII или числа, эквивалентные символам ASCII.

Размер короткого целого числа

В большинстве компиляторов размер как целых чисел без знака, так и целых чисел со знаком составляет около 2 байт.

Размер длинного целого числа

Размер длинных целых чисел без знака и со знаком зависит от типа используемого компилятора. Размер обычно составляет около 32 бит или 4 байта для 16/32-битного компилятора. Тем не менее, это зависит от того, какой компилятор мы используем.

Нет спецификации размеров типов данных в соответствии со стандартом C, кроме символьных. По определению C:

Каждый компилятор может выбрать подходящий размер для собственного оборудования. Он подвергается только одному ограничению: длинные должны быть не менее 32 бит, целые и короткие — не менее 16 бит, короткие не длиннее, чем целые, а целые не длиннее, чем длинные.

Чем отличается диапазон для беззнаковых и знаковых типов?

Хотя размер любого типа данных без знака и знака одинаков, они оба имеют разные диапазоны значений для хранения в любой переменной. Почему? Это связано с тем, что числа со знаком представлены в форме дополнения до 2 в любом процессоре или машине. Например, представление числа -23 в виде дополнения до 2 будет выглядеть так:

(десятичный) 23 <-> (двоичный) 10111

Дополнение до 1

Дополнение числа 10111 до 1 будет равно – 111111111111111111111111111111111111111111111111111111111101000

Здесь общее количество единиц, добавляемых перед фактическим числом, во многом зависит от размера машины или целевого процессора. Поскольку машина, с которой мы здесь имеем дело, является 64-битной машиной, мы добавили столько единиц, чтобы итоговое число также стало 64-битным числом.

Проще говоря, дополнение до единицы — это, по сути, инвертированная версия фактического числа. 0 преобразуются в 1, а 1 в 0.

Дополнение до двойки

Дополнение до 2 в основном является дополнением до 1 + 1, то есть

111111111111111111111111111111111111111111111111111111111101000 + 1:

111111111111111111111111111111111111111111111111111111111101001 <-> (десятичный) -23

Некоторые расчеты на компьютере помогут вам проверить этот результат здесь.

Давайте рассмотрим пример знакового символа, способного хранить числа в диапазоне от -128 до +127. Теперь мы все знаем, что и беззнаковый, и подписанный char могут хранить в себе всего 8 бит данных.

Итак, если предположить, что мы пытаемся сохранить число -190 в 8-битном переменном символе, то процессор будет обрабатывать это число следующим образом:

(десятичный) 190 <-> (двоичный) 10111110 : 8 бит

Дополнение до 1 для значения 190: (Двоичный) 01000001 : 8 бит

Дополнение до 2 для значения 190: (Двоичный) 01000010 : 8 бит

(Двоичный) 01000010 <-> (Десятичный) 66

Интерпретация номеров символов компьютером будет следующей:

(1) Старший бит: Знак числа [0: Положительный, 1: Отрицательный], 7-0 Биты: 1000010: [66] Фактические данные

Это означает, что всякий раз, когда мы пытаемся сохранить число, превышающее определенный диапазон, это число в конечном итоге будет округлено в меньшую сторону. Таким образом, мы получили результат 256-19.0 равно 66. Здесь 256 — это, по сути, максимальное значение, которое может хранить беззнаковое число символов.

Теперь давайте рассмотрим еще один пример того, как мы можем сохранить число -126 в переменной типа данных char.

(десятичный) 126 <-> (двоичный) 01111110

Дополнение до 1 126: (Двоичный) 10000001 : 8-бит

Дополнение до 2 для 126: (Двоичный) 10000010 : 8-бит

(Двоичный) 10000010 <-> (Десятичный) -126

Если вы хотите проверить полученные результаты, вы можете выполнить обратные вычисления. Здесь число отрицательное, так как старший бит равен 1. Кроме того, 0000010 — это остальные 7 бит. Таким образом, дополнение числа до 2 будет: ~0000010 = 1111101 = (десятичное) 126

Если мы объединим число и знак здесь, мы получим результат: (десятичный) -126

Та же самая концепция подходит как для беззнаковых, так и для целых типов данных со знаком.

Подводя итог, можно сказать, что и беззнаковые, и знаковые числа имеют одинаковое определение размера данных в C. Однако числа со знаком представляются в форме дополнения до 2, а старший бит двоичного числа представляет знак этого числа. Поскольку двоичная 1 (дополнительный 1 бит) предназначена для идентификации данного числа как отрицательного, общий диапазон чисел со знаком намного меньше, чем диапазон чисел без знака.

Ваш процессор обрабатывает отрицательные числа, поэтому вам не нужно заботиться о них отдельно. Просто убедитесь, что вы присваиваете допустимое число переменной со знаком, которая попадает в определенный диапазон. Если вы этого не сделаете, назначенный номер в конечном итоге будет усечен.

Типы данных с плавающей запятой

Язык C определяет два основных типа данных для хранения дробных чисел или чисел с плавающей запятой. Это двойной или поплавок . Можно легко применить длинные квалификаторы к двойнику. Таким образом, мы получаем еще один тип — long double.

В компьютерной системе формат IEEE-754 представляет числа с плавающей запятой. -3 = 1,375D.

Здесь бит знака в основном представляет знак числа, где S=1 — отрицательное число, а S=0 — положительное число. В упомянутом выше примере S=1. Таким образом, число отрицательное. Это означает, что число будет -1,375D.

Фактическая экспонента в нормализованной форме будет E-127 (это так называемое смещение-127 или избыток-127). Это потому, что человек должен представлять как отрицательные, так и положительные показатели. В случае 8-битного E, который находится в диапазоне от 0 до 255, фактическая экспонента чисел от -127 до 128 может быть обеспечена избыточной схемой -127. Например, в упомянутом примере E-127=129-127=2D.

2. Денормализованная форма

У нормализованной формы есть серьезные проблемы. Например, он использует неявное значение, которое приводит к 1 вместо дроби. Таким образом, нормализованная форма не может представлять ноль как число, начинающееся с 1. Денормализованная форма в основном предназначена для представления числа ноль, а также других чисел. -126 = 0,9-126 тогда будет оцениваться как очень маленькое число. Нам нужно представить денормализованную форму, используя E=0 и F=0. Они также могут представлять чрезвычайно отрицательные и положительные числа, близкие к нулевому значению.

(c) В случае E = 255 будут представлены некоторые специальные значения, например, NaN (относится не к числу) и ±INF (отрицательная и положительная бесконечность).

Производные типы данных

Они также известны как определяемые пользователем типы. Этот тип данных является производным от первичного типа данных, поэтому он известен как производные типы данных. Но они способны хранить набор различных значений вместо хранения одного единственного значения. Объединения, структуры, массивы и перечисления являются одними из наиболее распространенных в языке C.

Практические задачи по размеру типов данных в C

1. Размер char равен 1 байту, если char:

А. Подпись

Б. Без знака

С. Оба

Д. Нет. Это больше 1 байта.

Ответ – C. Оба

2. Тип данных int отражает естественный размер _________ на _____________.

А. целое число, программа

B. Целое число , хост-компьютер

C. с плавающей запятой, главная машина

D. с плавающей запятой, программа

Ответ – B. Целое число , хост-компьютер

3. Диапазон и размер типа данных варьируются между различными:

А. Компиляторы

B. Операционные системы

С. Оба

Д. Нет

Ответ – C. Оба

Часто задаваемые вопросы

Q1

Что отличает диапазон для беззнаковых и подписанных типов?

Хотя размер любого типа данных без знака и знака одинаков, они оба имеют разные диапазоны значений, которые можно сохранить в любой переменной. Почему? Это связано с тем, что числа со знаком представлены в форме дополнения до 2 в любом процессоре или машине. Например, представление числа -23 в виде дополнения до 2 будет выглядеть так:
(Десятичный) 23 <-> (Двоичный) 10111

Q2

Почему мы используем плавающие типы данных?

Язык C определяет два основных типа данных для хранения дробных чисел или чисел с плавающей запятой. Они бывают двойными или плавающими. Можно легко применить длинные квалификаторы к двойнику. Таким образом, мы получаем еще один тип — long double.
В компьютерной системе формат IEEE-754 представляет числа с плавающей запятой. Большинство современных процессоров и процессоров принимают этот формат. Он имеет два основных представления:
1. 32-битная одинарная точность
2. 64-битная двойная точность

Продолжайте учиться и следите за обновлениями, чтобы получать последние обновления об экзамене GATE, а также о критериях приемлемости GATE, GATE 2023, допускной карточке GATE, программе GATE для CSE (компьютерная инженерия), примечаниях GATE CSE, вопроснике GATE CSE и многом другом.

Также исследуйте,

  • Константы в C
  • Двойной тип данных в C
  • Перечислимый тип данных в C
  • Приоритет операторов и ассоциативность в C

сравнение — Размер типов данных C на разных машинах и sizeof(complex long double)

спросил

Изменено 13 лет, 2 месяца назад

Просмотрено 5к раз

Кто-нибудь знает веб-сайт или статью, где сравнивались размеры типов данных C на разных машинах? Меня интересуют значения некоторых «больших» машин, таких как System z или аналогичный.

А: Существует ли верхняя граница байтов, которую может иметь самый большой собственный тип данных на на любой машине , и всегда ли он имеет тип complex long double ?

Редактировать: я не уверен, но используют ли данные регистра SIMD преимущества кеша ЦП? Типы данных, которые будут храниться в специальном блоке и не использовать кеш L1/L2/L, меня не интересуют.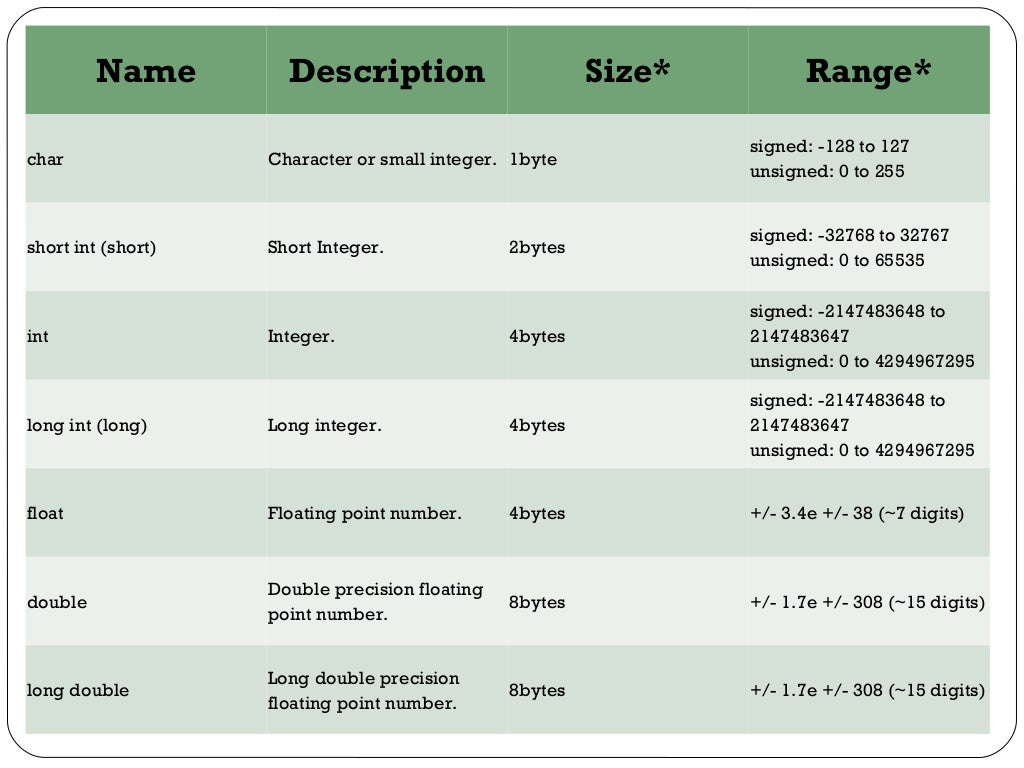 Будут проверены только типы {char, short, int, long, long long, float, double, long double, _Bool, void *} (и с _Complex).

  • c
  • сравнение
  • типы
  • размер

2

Размер типа данных C не зависит от платформы компьютера. Это зависит от реализации компилятора. Два разных компилятора на одной и той же аппаратной платформе могут по-разному реализовывать базовые типы, что приводит к совершенно разным размерам.

Также следует учитывать тот факт, что такие стандартные типы, как size_t не обязательно будут представлены доступными для пользователя типами, такими как unsigned int . Вполне допустимо и возможно, что size_t может быть реализовано через специфичный для реализации беззнаковый тип неизвестного размера и диапазона.

Кроме того, теоретически (и педантично) язык C не имеет «самого большого» типа с точки зрения размера . Спецификация языка C не дает абсолютно никаких гарантий в отношении относительных размеров основных типов. Язык C дает гарантии только относительного содержит представляемых значений каждого типа. Например, язык гарантирует, что диапазон int не меньше диапазона short . Однако, поскольку [почти] любой тип может содержать произвольное количество битов заполнения, теоретически размер объекта типа short может быть больше, чем размер объекта типа int . Это, конечно, очень экзотическая ситуация.

Однако на практике можно ожидать, что long long int — самый большой целочисленный тип, а long double — самый большой тип с плавающей запятой. Вы также можете включить в рассмотрение сложные типы, если хотите.

4

Вы упомянули «родные» типы данных, но обратите внимание, что комплекс не определен спецификацией C и, следовательно, не является родным типом. Нативные типы для C: char , int , float , double и 9.0497 недействителен .

Размер типа данных обычно определяется базовой платформой, а также компилятором. Стандарт C определяет минимальный диапазон для этих типов и определяет несколько относительных отношений ( long int должен быть не меньше обычного int и т. д.). Нет простого способа определить абсолютный размер любого типа без его тестирования.

Когда я работаю с новой платформой, и я не знаю конкретных размеров типов данных, я пишу короткое приложение, которое выводит результат размер для всех стандартных типов C. Существуют также заголовки, такие как stdint.h , которые предоставляют типы данных, размер которых можно доверять.

Нет верхней границы размера типа данных. Стандарт C определяет char как «достаточно большой для хранения любого члена набора символов выполнения».

No related posts.