URL и хэширование — API. Yandex Safe Browsing
Списки Safe Browsing состоят из префиксов хэшей SHA-256 произвольной длины (от 4 до 32 байт), которые соответствуют URL интернет-ресурсов, представляющих угрозу для пользователя. Чтобы проверить наличие URL в списке (в локальной базе или на сервере), вычислите префикс хэша. Для этого:
Приведите URL к каноническому виду.
Создайте выражения для хоста и пути.
Вычислите хэш полной длины и префикс хэша.
Пример реализации на языке Golang.
Выполните поиск по локальной базе списков Safe Browsing. Если префикс хэша найден, отправьте его в запросе.
URL должен соответствовать стандарту RFC 2396. URL в интернационализированных доменных именах (IDN), например .рф, нужно конвертировать в ASCII методом Punycode. URL должен содержать компонент пути, то есть завершаться слешем: например, https://yandex..
Чтобы привести URL к каноническому виду:
Удалите знаки табуляции
0x09и перевода строки0x0dи0x0a.Удалите якорь. Например,
https://yandex.ru/#anchorсократите доhttps://yandex.ru/.Отдельно обработайте:
- Хост
Удалите точки в начале и в конце.
Замените несколько последовательных точек на одну.
Если имя хоста — IP-адрес, приведите его в вид четырех десятичных чисел, разделенных точкой.
Приведите к нижнему регистру.
- Путь
Примечание. Не применяйте эти действия к параметрам запроса.
Удалите последовательность символов
/.и замените ./
.//./на/.Замените несколько последовательных слешей на один.
Экранируйте все ASCII-символы младше 32 и старше 127, а также
#и%. Используйте шестнадцатеричную запись в верхнем регистре.
Пример
| Исходный URL | Канонический вид |
|---|---|
http://host/%25%32%35 | http://host/%25 |
http://host/%25%32%35%25%32%35 | http://host/%25%25 |
http://host/%2525252525252525 | http://host/%25 |
http://host/asdf%25%32%35asd | http://host/asdf%25asd |
http://host/%%%25%32%35asd%% | http://host/%25%25%25asd%25%25 |
http://%32%31%33%2e%31%38%30%2e%32%31%30%2e5/%2e%73%65%63%75%72%65%2f%77%77%77%2e%6d%6f%69%6b%72%75%67%2e%72%75/ | http://213. |
http://3279880203/smth | http://195.127.0.11/smth |
http://www.yandex.ru/smth/.. | http://www.yandex.ru/ |
www.yandex.ru | http://www.yandex.ru/ |
http://www.zlo.com/smth#ancor | http://www.zlo.com/smth |
http://www.YANdex.ru/ | http://www.yandex.ru/ |
http://www.yandex.ru.../ | http://www. |
http://www.yandex.ru/m\ta\rp\ns | http://www.yandex.ru/maps |
http://zlo.com/smth#more#again | http://zlo.com/smth |
http://\x01\x80.com/ | http://%01%80.com/ |
http://www.hostport.com:1234/ | http://www.hostport.com/ |
http://www.yandex.ru/ | http://www.yandex.ru/ |
http:// probel.ru/ | http://%20probel. |
http://host.com//dvaslesha?more//slashes | http://host.com/dvaslesha?more//slashes |
После того как URL приведен к канонической форме, создайте:
Выражения для хоста и пути.
Комбинации этих выражений.
- Выражения для хоста
Сформируйте не более 5 различных строк:
Полное имя хоста.
До 4 имен хоста, начиная с последних пяти компонент и последовательно удаляя первую компоненту. Домен верхнего уровня можно пропустить. Эти строки не нужно создавать, если имя хоста — IP-адрес.
- Выражения для пути
Сформируйте не более 6 различных строк:
Полный путь с параметрами запроса.
Полный путь без параметров запроса.

4 пути, начиная с корня и последовательно добавляя компонент пути с закрывающим слешем.
- Комбинации
Сформируйте до 30 различных комбинаций выражений для хоста и пути. Эти комбинации должны включать только имя хоста и путь; схема (протокол), имя пользователя, пароль и порт нужно исключить. Если в URL есть параметры запроса, по крайней мере одна комбинация должна содержать полный путь и параметры запроса.
- Пример
Для URL
http://a.b.c/1/2.html?param=1нужно сформировать следующие строки:a.b.c/1/2.html?param=1 a.b.c/1/2.html a.b.c/ a.b.c/1/ b.c/1/2.html?param=1 b.c/1/2.html b.c/ b.c/1/
Для URL
http://a.b.c.d.e.f.g/1.htmlнужно сформировать следующие строки:a.b.c.d.e.f.g/1.html a.b.c.d.e.f.g/ (Вариант b.c.d.e.f.g нужно пропустить, потому что используются только последние пять компонент имени хоста и полное имя хоста) c.
 d.e.f.g/1.html
c.d.e.f.g/
d.e.f.g/1.html
d.e.f.g/
e.f.g/1.html
e.f.g/
f.g/1.html
f.g/
d.e.f.g/1.html
c.d.e.f.g/
d.e.f.g/1.html
d.e.f.g/
e.f.g/1.html
e.f.g/
f.g/1.html
f.g/Для URL
http://1.2.3.4/1/нужно сформировать следующие строки:1.2.3.4/1/ 1.2.3.4/
После того, как комбинации из выражений для хоста и пути сформированы, вычислите для каждой из них хэш SHA256 полной длины.
Затем вычислите префикс для каждого хэша полной длины. Префикс хэша состоит из 4–32 байт.
Примеры из стандарта FIPS-180-4:
- Хэш для строки
abc - Хэш для строки
abcdbcdecdefdefgefghfghighijhijkijkljklmklmnlmnomnopnopq
Была ли статья полезна?
Как работает хэш-алгоритм SHA-2 (SHA 256)? Разбираем на примере
Автор Мария Багулина
SHA-2 (Secure Hash Algorithm 2) — одно из самых популярных семейств алгоритмов хеширования. В этой статье мы разберём каждый шаг алгоритма SHA-256, принадлежащего к SHA-2, и покажем, как он работает на реальном примере.
В этой статье мы разберём каждый шаг алгоритма SHA-256, принадлежащего к SHA-2, и покажем, как он работает на реальном примере.
Что такое хеш-функция?
Если вы хотите узнать больше о хеш-функциях, можете почитать Википедию. Но чтобы понять, о чём пойдёт речь, давайте вспомним три основные цели хеш-функции:
- обеспечить проверку целостности (неизменности) данных;
- принимать ввод любой длины и выводить результат фиксированной длины;
- необратимо изменить данные (ввод не может быть получен из вывода).
SHA-2 и SHA-256
SHA-2 — это семейство алгоритмов с общей идеей хеширования данных. SHA-256 устанавливает дополнительные константы, которые определяют поведение алгоритма SHA-2. Одной из таких констант является размер вывода. «256» и «512» относятся к соответствующим размерам выходных данных в битах.
Мы рассмотрим пример работы SHA-256.
SHA-256 «hello world». Шаг 1. Предварительная обработка
1. Преобразуем «hello world» в двоичный вид:
01101000 01100101 01101100 01101100 01101111 00100000 01110111 01101111 01110010 01101100 01100100
2. Добавим одну единицу:
Добавим одну единицу:
01101000 01100101 01101100 01101100 01101111 00100000 01110111 01101111 01110010 01101100 01100100 1
3. Заполняем нулями до тех пор, пока данные не станут кратны 512 без последних 64 бит (в нашем случае 448 бит):
01101000 01100101 01101100 01101100 01101111 00100000 01110111 01101111 01110010 01101100 01100100 10000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
4. Добавим 64 бита в конец, где 64 бита — целое число с порядком байтов big-endian, обозначающее длину входных данных в двоичном виде. В нашем случае 88, в двоичном виде — «1011000».
01101000 01100101 01101100 01101100 01101111 00100000 01110111 01101111 01110010 01101100 01100100 10000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 01011000
Теперь у нас есть ввод, который всегда будет без остатка делиться на 512.
Шаг 2. Инициализация значений хеша (h)
Создадим 8 значений хеша. Это константы, представляющие первые 32 бита дробных частей квадратных корней первых 8 простых чисел: 2, 3, 5, 7, 11, 13, 17, 19.
h0 := 0x6a09e667 h2 := 0xbb67ae85 h3 := 0x3c6ef372 h4 := 0xa54ff53a h5 := 0x510e527f h5 := 0x9b05688c h6 := 0x1f83d9ab h7 := 0x5be0cd19
Шаг 3. Инициализация округлённых констант (k)
Создадим ещё немного констант, на этот раз их 64. Каждое значение — это первые 32 бита дробных частей кубических корней первых 64 простых чисел (2–311).
0x428a2f98 0x71374491 0xb5c0fbcf 0xe9b5dba5 0x3956c25b 0x59f111f1 0x923f82a4 0xab1c5ed5 0xd807aa98 0x12835b01 0x243185be 0x550c7dc3 0x72be5d74 0x80deb1fe 0x9bdc06a7 0xc19bf174 0xe49b69c1 0xefbe4786 0x0fc19dc6 0x240ca1cc 0x2de92c6f 0x4a7484aa 0x5cb0a9dc 0x76f988da 0x983e5152 0xa831c66d 0xb00327c8 0xbf597fc7 0xc6e00bf3 0xd5a79147 0x06ca6351 0x14292967 0x27b70a85 0x2e1b2138 0x4d2c6dfc 0x53380d13 0x650a7354 0x766a0abb 0x81c2c92e 0x92722c85 0xa2bfe8a1 0xa81a664b 0xc24b8b70 0xc76c51a3 0xd192e819 0xd6990624 0xf40e3585 0x106aa070 0x19a4c116 0x1e376c08 0x2748774c 0x34b0bcb5 0x391c0cb3 0x4ed8aa4a 0x5b9cca4f 0x682e6ff3 0x748f82ee 0x78a5636f 0x84c87814 0x8cc70208 0x90befffa 0xa4506ceb 0xbef9a3f7 0xc67178f2
Шаг 4.
 Основной цикл
Основной циклСледующие шаги будут выполняться для каждого 512-битного «куска» входных данных. Наша тестовая фраза «hello world» довольно короткая, поэтому «кусок» всего один. На каждой итерации цикла мы будем изменять значения хеш-функций h0–h7, чтобы получить окончательный результат.
Шаг 5. Создаём очередь сообщений (w)
1. Копируем входные данные из шага 1 в новый массив, где каждая запись является 32-битным словом:
01101000011001010110110001101100 01101111001000000111011101101111 01110010011011000110010010000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000001011000
2. Добавляем ещё 48 слов, инициализированных нулями, чтобы получить массив
Добавляем ещё 48 слов, инициализированных нулями, чтобы получить массив w[0…63]:
01101000011001010110110001101100 01101111001000000111011101101111 01110010011011000110010010000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000001011000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 ... ... 00000000000000000000000000000000 00000000000000000000000000000000
3. Изменяем нулевые индексы в конце массива, используя следующий алгоритм:
Изменяем нулевые индексы в конце массива, используя следующий алгоритм:
- For
ifromw[16…63]:s0 = (w[i-15] rightrotate 7) xor (w[i-15] rightrotate 18) xor (w[i-15] righthift 3)s1 = (w[i-2] rightrotate 17) xor (w[i-2] rightrotate 19) xor (w[i-2] righthift 10)w [i] = w[i-16] + s0 + w[i-7] + s1
Давайте посмотрим, как это работает для w[16]:
w[1] rightrotate 7: 01101111001000000111011101101111 -> 11011110110111100100000011101110 w[1] rightrotate 18: 01101111001000000111011101101111 -> 00011101110110111101101111001000 w[1] rightshift 3: 01101111001000000111011101101111 -> 00001101111001000000111011101101 s0 = 11011110110111100100000011101110 XOR 00011101110110111101101111001000 XOR 00001101111001000000111011101101 s0 = 11001110111000011001010111001011 w[14] rightrotate 17: 00000000000000000000000000000000 -> 00000000000000000000000000000000 w[14] rightrotate19: 00000000000000000000000000000000 -> 00000000000000000000000000000000 w[14] rightshift 10: 00000000000000000000000000000000 -> 00000000000000000000000000000000 s1 = 00000000000000000000000000000000 XOR 00000000000000000000000000000000 XOR 00000000000000000000000000000000 s1 = 00000000000000000000000000000000 w[16] = w[0] + s0 + w[9] + s1 w[16] = 01101000011001010110110001101100 + 11001110111000011001010111001011 + 00000000000000000000000000000000 + 00000000000000000000000000000000 // сложение рассчитывается по модулю 2^32 w[16] = 00110111010001110000001000110111
Это оставляет нам 64 слова в нашей очереди сообщений (w):
01101000011001010110110001101100 01101111001000000111011101101111 01110010011011000110010010000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000000000000 00000000000000000000000001011000 00110111010001110000001000110111 10000110110100001100000000110001 11010011101111010001000100001011 01111000001111110100011110000010 00101010100100000111110011101101 01001011001011110111110011001001 00110001111000011001010001011101 10001001001101100100100101100100 01111111011110100000011011011010 11000001011110011010100100111010 10111011111010001111011001010101 00001100000110101110001111100110 10110000111111100000110101111101 01011111011011100101010110010011 00000000100010011001101101010010 00000111111100011100101010010100 00111011010111111110010111010110 01101000011001010110001011100110 11001000010011100000101010011110 00000110101011111001101100100101 10010010111011110110010011010111 01100011111110010101111001011010 11100011000101100110011111010111 10000100001110111101111000010110 11101110111011001010100001011011 10100000010011111111001000100001 11111001000110001010110110111000 00010100101010001001001000011001 00010000100001000101001100011101 01100000100100111110000011001101 10000011000000110101111111101001 11010101101011100111100100111000 00111001001111110000010110101101 11111011010010110001101111101111 11101011011101011111111100101001 01101010001101101001010100110100 00100010111111001001110011011000 10101001011101000000110100101011 01100000110011110011100010000101 11000100101011001001100000111010 00010001010000101111110110101101 10110000101100000001110111011001 10011000111100001100001101101111 01110010000101111011100000011110 10100010110101000110011110011010 00000001000011111001100101111011 11111100000101110100111100001010 11000010110000101110101100010110
Шаг 6.
 Цикл сжатия
Цикл сжатия- Инициализируем переменные
a, b, c, d, e, f, g, hи установим их равными текущим значениям хеша соответственно.h0, h2, h3, h4, h5, h5, h6, h7. - Запустим цикл сжатия, который будет изменять значения a…h . Цикл выглядит следующим образом:
for i from 0 to 63S1 = (e rightrotate 6) xor (e rightrotate 11) xor (e rightrotate 25)ch = (e and f) xor ((not e) and g)temp1 = h + S1 + ch + k[i] + w[i]S0 = (a rightrotate 2) xor (a rightrotate 13) xor (a rightrotate 22)maj = (a and b) xor (a and c) xor (b and c)temp2 := S0 + majh = gg = ff = ee = d + temp1d = cc = bb = aa = temp1 + temp2
Давайте пройдём первую итерацию. 32:
32:
a = 0x6a09e667 = 01101010000010011110011001100111
b = 0xbb67ae85 = 10111011011001111010111010000101
c = 0x3c6ef372 = 00111100011011101111001101110010
d = 0xa54ff53a = 10100101010011111111010100111010
e = 0x510e527f = 01010001000011100101001001111111
f = 0x9b05688c = 10011011000001010110100010001100
g = 0x1f83d9ab = 00011111100000111101100110101011
h = 0x5be0cd19 = 01011011111000001100110100011001
e rightrotate 6:
01010001000011100101001001111111 -> 11111101010001000011100101001001
e rightrotate 11:
01010001000011100101001001111111 -> 01001111111010100010000111001010
e rightrotate 25:
01010001000011100101001001111111 -> 10000111001010010011111110101000
S1 = 11111101010001000011100101001001 XOR 01001111111010100010000111001010 XOR 10000111001010010011111110101000
S1 = 00110101100001110010011100101011
e and f:
01010001000011100101001001111111
& 10011011000001010110100010001100 =
00010001000001000100000000001100
not e:
01010001000011100101001001111111 -> 10101110111100011010110110000000
(not e) and g:
10101110111100011010110110000000
& 00011111100000111101100110101011 =
00001110100000011000100110000000
ch = (e and f) xor ((not e) and g)
= 00010001000001000100000000001100 xor 00001110100000011000100110000000
= 00011111100001011100100110001100
// k[i] is the round constant
// w[i] is the batch
temp1 = h + S1 + ch + k[i] + w[i]
temp1 = 01011011111000001100110100011001 + 00110101100001110010011100101011 + 00011111100001011100100110001100 + 1000010100010100010111110011000 + 01101000011001010110110001101100
temp1 = 01011011110111010101100111010100
a rightrotate 2:
01101010000010011110011001100111 -> 11011010100000100111100110011001
a rightrotate 13:
01101010000010011110011001100111 -> 00110011001110110101000001001111
a rightrotate 22:
01101010000010011110011001100111 -> 00100111100110011001110110101000
S0 = 11011010100000100111100110011001 XOR 00110011001110110101000001001111 XOR 00100111100110011001110110101000
S0 = 11001110001000001011010001111110
a and b:
01101010000010011110011001100111
& 10111011011001111010111010000101 =
00101010000000011010011000000101
a and c:
01101010000010011110011001100111
& 00111100011011101111001101110010 =
00101000000010001110001001100010
b and c:
10111011011001111010111010000101
& 00111100011011101111001101110010 =
00111000011001101010001000000000
maj = (a and b) xor (a and c) xor (b and c)
= 00101010000000011010011000000101 xor 00101000000010001110001001100010 xor 00111000011001101010001000000000
= 00111010011011111110011001100111
temp2 = S0 + maj
= 11001110001000001011010001111110 + 00111010011011111110011001100111
= 00001000100100001001101011100101
h = 00011111100000111101100110101011
g = 10011011000001010110100010001100
f = 01010001000011100101001001111111
e = 10100101010011111111010100111010 + 01011011110111010101100111010100
= 00000001001011010100111100001110
d = 00111100011011101111001101110010
c = 10111011011001111010111010000101
b = 01101010000010011110011001100111
a = 01011011110111010101100111010100 + 00001000100100001001101011100101
= 01100100011011011111010010111001Все расчёты выполняются ещё 63 раза, изменяя переменные а…h. В итоге мы должны получить следующее:
В итоге мы должны получить следующее:
h0 = 6A09E667 = 01101010000010011110011001100111 h2 = BB67AE85 = 10111011011001111010111010000101 h3 = 3C6EF372 = 00111100011011101111001101110010 h4 = A54FF53A = 10100101010011111111010100111010 h5 = 510E527F = 01010001000011100101001001111111 h5 = 9B05688C = 10011011000001010110100010001100 h6 = 1F83D9AB = 00011111100000111101100110101011 h7 = 5BE0CD19 = 01011011111000001100110100011001 a = 4F434152 = 001001111010000110100000101010010 b = D7E58F83 = 011010111111001011000111110000011 c = 68BF5F65 = 001101000101111110101111101100101 d = 352DB6C0 = 000110101001011011011011011000000 e = 73769D64 = 001110011011101101001110101100100 f = DF4E1862 = 011011111010011100001100001100010 g = 71051E01 = 001110001000001010001111000000001 h = 870F00D0 = 010000111000011110000000011010000
Шаг 7. Изменяем окончательные значения
После цикла сжатия, но ещё внутри основного цикла, мы модифицируем значения хеша, добавляя к ним соответствующие переменные a…h. 32.
32.
h0 = h0 + a = 10111001010011010010011110111001 h2 = h2 + b = 10010011010011010011111000001000 h3 = h3 + c = 10100101001011100101001011010111 h4 = h4 + d = 11011010011111011010101111111010 h5 = h5 + e = 11000100100001001110111111100011 h5 = h5 + f = 01111010010100111000000011101110 h6 = h6 + g = 10010000100010001111011110101100 h7 = h7 + h = 11100010111011111100110111101001
Шаг 8. Получаем финальный хеш
И последний важный шаг — собираем всё вместе.
digest = h0 append h2 append h3 append h4 append h5 append h5 append h6 append h7
= B94D27B9934D3E08A52E52D7DA7DABFAC484EFE37A5380EE9088F7ACE2EFCDE9Готово! Мы выполнили каждый шаг SHA-2 (SHA-256) (без некоторых итераций).
Алгоритм SHA-2 в виде псевдокода
Если вы хотите посмотреть на все шаги, которые мы только что сделали, в виде псевдокода, то вот пример:
Пояснения: Все переменные беззнаковые, имеют размер 32 бита и при вычислениях суммируются по модулю 232 message — исходное двоичное сообщение m — преобразованное сообщение Инициализация переменных (первые 32 бита дробных частей квадратных корней первых восьми простых чисел [от 2 до 19]): h0 := 0x6a09e667 h2 := 0xbb67ae85 h3 := 0x3c6ef372 h4 := 0xa54ff53a h5 := 0x510e527f h5 := 0x9b05688c h6 := 0x1f83d9ab h7 := 0x5be0cd19 Таблица констант (первые 32 бита дробных частей кубических корней первых 64 простых чисел [от 2 до 311]): k[ 0..63 ] := 0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5, 0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174, 0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da, 0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967, 0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85, 0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070, 0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3, 0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2 Предварительная обработка: m := message ǁ [единичный бит] m := m ǁ [k нулевых бит], где k — наименьшее неотрицательное число, такое что (L + 1 + K) mod 512 = 448, где L — число бит в сообщении (сравнима по модулю 512 c 448) m := m ǁ Длина(message) — длина исходного сообщения в битах в виде 64-битного числа с порядком байтов от старшего к младшему Далее сообщение обрабатывается последовательными порциями по 512 бит: разбить сообщение на куски по 512 бит для каждого куска разбить кусок на 16 слов длиной 32 бита (с порядком байтов от старшего к младшему внутри слова): w[ 0.
.15 ] Сгенерировать дополнительные 48 слов: для i от 16 до 63 s0 := (w[i-15] rightrotate 7) xor (w[i-15] rightrotate 18) xor (w[i-15] rightshift 3) s1 := (w[i- 2] rightrotate 17) xor (w[i- 2] rightrotate 19) xor (w[i- 2] rightshift 10) w[i] := w[i-16] + s0 + w[i-7] + s1 Инициализация вспомогательных переменных: a := h0 b := h2 c := h3 d := h4 e := h5 f := h5 g := h6 h := h7 Основной цикл: для i от 0 до 63 S1 := (e rightrotate 6) xor (e rightrotate 11) xor (e rightrotate 25) ch := (e and f) xor ((not e) and g) temp1 := h + S1 + ch + k[i] + w[i] S0 := (a rightrotate 2) xor (a rightrotate 13) xor (a rightrotate 22) maj := (a and b) xor (a and c) xor (b and c) temp2 := S0 + maj h := g g := f f := e e := d + temp1 d := c c := b b := a a := temp1 + temp2 Добавить полученные значения к ранее вычисленному результату: h0 := h0 + a h2 := h2 + b h3 := h3 + c h4 := h4 + d h5 := h5 + e h5 := h5 + f h6 := h6 + g h7 := h7 + h Получить итоговое значение хеша SHA-2: digest := hash := h0 append h2 append h3 append h4 append h5 append h5 append h6 append h7
Перевод статьи «How SHA-2 Works Step-By-Step (SHA-256)»
PHP: Хеширование паролей — Manual
Change language: EnglishBrazilian PortugueseChinese (Simplified)FrenchGermanJapaneseRussianSpanishTurkishOther
Submit a Pull Request Report a Bug
В этом разделе разъясняются причины, стоящие за хешированием паролей в целях
безопасности, а также эффективные методы хеширования.
- Почему я должен хешировать пароли пользователей в моем приложении?
- Почему популярные хеширующие функции, такие как md5 и sha1 не подходят для паролей?
- Если популярные хеширующие функции не подходят, как же я тогда должен хешировать свои пароли?
- Что такое соль?
- Как я должен хранить свою соль?
- Почему я должен хешировать пароли пользователей в моем приложении?
Хеширование паролей является одним из самых основных соображений безопасности, которые необходимо сделать, при разработке приложения, принимающего пароли от пользователей. Без хеширования, пароли, хранящиеся в базе вашего приложения, могут быть украдены, например, если ваша база данных была скомпрометирована, а затем немедленно могут быть применены для компрометации не только вашего приложения, но и аккаунтов ваших пользователей на других сервисах, если они не используют уникальных паролей.

Применяя хеширующий алгоритм к пользовательским паролям перед сохранением их в своей базе данных, вы делаете невозможным разгадывание оригинального пароля для атакующего вашу базу данных, в то же время сохраняя возможность сравнения полученного хеша с оригинальным паролем.
Важно заметить, однако, что хеширование паролей защищает их только от компрометирования в вашем хранилище, но не обязательно от вмешательства вредоносного кода в вашем приложении.
- Почему популярные хеширующие функции, такие как md5() и sha1() не подходят для паролей?
Такие хеширующие алгоритмы как MD5, SHA1 и SHA256 были спроектированы очень быстрыми и эффективными. При наличии современных технологий и оборудования, стало довольно просто выяснить результат этих алгоритмов методом «грубой силы» для определения оригинальных вводимых данных.

Из-за той скорости, с которой современные компьютеры могут «обратить» эти хеширующие алгоритмы, многие профессионалы компьютерной безопасности строго не рекомендуют использовать их для хеширования паролей.
- Если популярные хеширующие функции не подходят, как же я тогда должен хешировать свои пароли?
При хешировании паролей существует два важных соображения: это стоимость вычисления и соль. Чем выше стоимость вычисления хеширующего алгоритма, тем больше времени требуется для взлома его вывода методом «грубой силы».
PHP предоставляет встроенное API хеширования паролей, которое безопасно работает и с хешированием и с проверкой паролей.
Другой возможностью является функция crypt(), которая поддерживает несколько алгоритмов хеширования. При использовании этой функции вы можете быть уверенным, что выбранный вами алгоритм доступен, так как PHP содержит собственную реализацию каждого поддерживаемого алгоритма, даже в случае, если какие-то из них не поддерживаются вашей системой.

При хешировании паролей рекомендуется применять алгоритм Blowfish, который также используется по умолчанию в API хеширования паролей, так как он значительно большей вычислительной сложности, чем MD5 или SHA1, при этом по-прежнему гибок.
Учтите, что, если вы используете функцию crypt() для проверки пароля, то вам нужно предостеречь себя от атак по времени, применяя сравнение строк, которое занимает постоянное время. Ни операторы PHP == и ===, ни функция strcmp() не являются таковыми. Функция же password_verify() как раз делает то, что нужно. Настоятельно рекомендуется использовать встроенное API хеширования паролей, если есть такая возможность.
- Что такое соль?
Криптографическая соль представляет собой данные, которые применяются в процессе хеширования для предотвращения возможности разгадать оригинальный ввод с помощью поиска результата хеширования в списке заранее вычисленных пар ввод-хеш, известном также как «радужная» таблица.

Более простыми словами, соль — это кусочек дополнительных данных, которые делают ваши хеши намного более устойчивыми к взлому. Существует много онлайн-сервисов, предоставляющих обширные списки заранее вычисленных хешей вместе с их оригинальным вводом. Использование соли делает поиск результирующего хеша в таком списке маловероятным или даже невозможным.
password_hash() создаёт случайную соль в случае, если она не была передана, и чаще всего это наилучший и безопасный выбор.
- Как я должен хранить свою соль?
При использовании функции password_hash() или crypt(), возвращаемое значение уже содержит соль как часть созданного хеша. Это значение нужно хранить как есть в вашей базе данных, так как оно содержит также информацию о хеширующей функции, которая использовалась, и может быть непосредственно передано в функции password_verify() или crypt() при проверке пароля.

Следующая диаграмма показывает формат возвращаемого значения функциями crypt() или password_hash(). Как можно видеть, они содержат полную информацию об алгоритме и соли, требуемых для будущей проверки пароля.
+add a note
User Contributed Notes 4 notes
up
down
144
alf dot henrik at ascdevel dot com ¶
8 years ago
For starters, speed IS an issue with MD5 in particular and also SHA1. I've written my own MD5 bruteforce application just for the fun of it, and using only my CPU I can easily check a hash against about 200mill. hash per second. The main reason for this speed is that you for most attempts can bypass 19 out of 64 steps in the algorithm. For longer input (> 16 characters) it won't apply, but I'm sure there's some ways around it. So on essence: Oh, and I can see there's someone mentioning MD5 and rainbow tables. If you read the numbers here, I hope you realize how incredibly stupid and useless rainbow tables have become in terms of MD5. Unless the input to MD5 is really huge, you're just not going to be able to compete with GPUs here. By the time a storage media is able to produce far beyond 3TB/s, the CPUs and GPUs will have reached much higher speeds. As for SHA1, my belief is that it's about a third slower than MD5. I can't verify this myself, but it seems to be the case judging the numbers presented for MD5 and SHA1. The moral here: I feel like I should comment some of the clams being posted as replies here. 8 = 7,21389578984e+15 combinations.
8 = 7,21389578984e+15 combinations.
With 100 billion per second it would then take 7,21389578984e+15 / 3600 = ~20 hours to figure out what it actually says. Keep in mind that you'll need to add the numbers for 1-7 characters as well. 20 hours is not a lot if you want to target a single user.
There's a reason why newer hash algorithms are specifically designed not to be easily implemented on GPUs. The issue with speeds is basically very much the same here as well.
The issue with speeds is basically very much the same here as well.
Please do as told. Don't every use MD5 and SHA1 for hasing passwords ever again. We all know passwords aren't going to be that long for most people, and that's a major disadvantage. Adding long salts will help for sure, but unless you want to add some hundred bytes of salt, there's going to be fast bruteforce applications out there ready to reverse engineer your passwords or your users' passwords.
up
down
27
swardx at gmail dot com ¶
6 years ago
https://nakedsecurity.sophos.com/2013/11/20/serious-security-how-to-store-your-users-passwords-safely/ Serious Security: How to store your users’ passwords safely In summary, here is our minimum recommendation for safe storage of your users’ passwords: Use a strong random number generator to create a salt of 16 bytes or longer. Whatever you do, don’t try to knit your own password storage algorithm. A great read..
Feed the salt and the password into the PBKDF2 algorithm.
Use HMAC-SHA-256 as the core hash inside PBKDF2.
Perform 20,000 iterations or more. (June 2016.)
Take 32 bytes (256 bits) of output from PBKDF2 as the final password hash.
Store the iteration count, the salt and the final hash in your password database.
Increase your iteration count regularly to keep up with faster cracking tools.
up
down
2
tamas at microwizard dot com ¶
1 year ago
The reason of salting is to avoid using rainbow tables (sorry guys this is the only reason) because it speeds up (shortcuts) the "actual" processing power. PHP salting functions returns all the needed information for checking passwords, therfore this information should be treated as constant from farther point of view. It is also a target for rainbow tables (sure: for much-much larger ones). What is the solution? Yes, it will make problems for hackers. He/she needs to understand your system. No speed up for password cracking will work for him/her without reimplementing your whole system. This is my two cent. While I am reading the comments some old math lessons came into my mind and started thinking. Using constants in a mathematical algorythms do not change the complexity of the algorythm itself.
(((Longer stored hashes AND longer password increases complexity of cracking NOT adding salt ALONE.)))
The solution is to store password hash and salt on different places.
The implementation is yours. Every two different places will be good enough.
up
down
4
fluffy at beesbuzz dot biz ¶
10 years ago
Also, hash algorithms such as md5 are for the purpose of generating a digest and checking if two things are probably the same as each other; they are not intended to be impossible to generate a collision for. Even if an underlying password itself requires a lot of brute forcing to determine, that doesn't mean it will be impossible to find some other bit pattern that generates the same hash in a trivial amount of time. As such: please, please, PLEASE only use salted hashes for password storage. There is no reason to implement your own salted hash mechanism, either, as crypt() already does an excellent job of this. The security issue with simple hashing (md5 et al) isn't really the speed, so much as the fact that it's idempotent; two different people with the same password will have the same hash, and so if one person's hash is brute-forced, the other one will as well. This facilitates rainbow attacks. Simply slowing the hash down isn't a very useful tactic for improving security. It doesn't matter how slow and cumbersome your hash algorithm is - as soon as someone has a weak password that's in a dictionary, EVERYONE with that weak password is vulnerable.
This facilitates rainbow attacks. Simply slowing the hash down isn't a very useful tactic for improving security. It doesn't matter how slow and cumbersome your hash algorithm is - as soon as someone has a weak password that's in a dictionary, EVERYONE with that weak password is vulnerable.
+add a note
Хэш-функция в повседневной жизни — NTA на vc.
 ru
ruИзвестно, что хэш-функция создает уникальный цифровой отпечаток из исходной информации. Итоговое хэширования информации называют хэш-суммой или просто хэшем.
3130 просмотров
Как же это работает? Хэш-функция берет определенную информацию, например, часть текста или пароль от вашего аккаунта, это может быть даже отдельный файл и преобразует эту информацию в строку определенной длины. Эта строка всегда будет иметь одинаковую длину вне зависимости от того, какого размера была входная информация. Существует достаточно много различных хеш- алгоритмов. Например, слово bitcoin, пропущенное через хэш алгоритм sha-256 будет выглядеть вот так.
Хэш-функции очень сильно отличаются от обычного шифрования.
Зашифровав какую-либо информацию через алгоритм AES вы всегда с помощью парольной фразы сможете ее расшифровать. Хэш-функции работают только в одну сторону. Пропустив какую-либо информацию через хэш-функцию, например, свой пароль, вы не сможете получить исходное значение информации, зная значение хэша. Это одно из требований к хэш-функциям. Хэш-функция должна быть однонаправленная. Позже мы разберем пример, для чего это нужно.
Это одно из требований к хэш-функциям. Хэш-функция должна быть однонаправленная. Позже мы разберем пример, для чего это нужно.
Второе основное требование для хэш-функций — фиксированный размер получаемого хэша, вне зависимости от введенной информации. Сейчас перед вами таблица с несколькими исходными данными и хэшами.
Как видите исходная информация разной длины, однако хэш имеет одинаковую длину. В любом из случаев следующее требование к хэш-функции — уникальность получаемого кэша и практически полное отсутствие коллизии. Что это значит? Это значит, что два разных набора информации не могут выдать одинаковое значение хэша.
Коллизии существуют для большинства хеш-функций, но в надежных хеш- функциях частота возникновения коллизии близка к теоретическому минимуму. Например, хэш-функция md5 сейчас стала абсолютно не устойчива к коллизии.
Компьютеры стали настолько мощные, что найти коллизию за приемлемое время не составит труда. Прямо сейчас в интернете можно найти генератор к коллизии для хэш-функции md5. Чуть позже мы объясним, как коллизии могут быть использованы злоумышленникам. Хэш-функция также должна быть быстрой и быстро хэшировать исходную информацию. Но, это так же является и уязвимостью для «брутфорса», так чем быстрее работает хэш-функция, тем больше она уязвима для полного перебора. Для хорошей криптографической хэш-функции также важно наличие лавинного эффекта. Что это значит? Это значит, что при изменении даже одного байта в исходной информации, полученный хеш поменяется кардинально.
Чуть позже мы объясним, как коллизии могут быть использованы злоумышленникам. Хэш-функция также должна быть быстрой и быстро хэшировать исходную информацию. Но, это так же является и уязвимостью для «брутфорса», так чем быстрее работает хэш-функция, тем больше она уязвима для полного перебора. Для хорошей криптографической хэш-функции также важно наличие лавинного эффекта. Что это значит? Это значит, что при изменении даже одного байта в исходной информации, полученный хеш поменяется кардинально.
Как же будет выглядеть идеальная криптографическая хэш-функция? Идеалом криптографической хэш-функции можно считать ту функцию, которой присущи следующие пять свойств:
- Детерминированность — одинаковые входные данные всегда дают одинаковое значение хэша.
- Высокая скорость вычисления хэш-функций из любого сообщения.
- Однонаправленность — невозможно получить исходное сообщение, зная его хэш, за исключением попыток полного перебора.

- Наличие лавинного эффекта – минимальное изменение в исходном сообщении приводит к кардинальному изменению хэша.
- Невозможность найти одинаковое значение хэша для двух разных сообщений.
Давайте рассмотрим простой пример, как используются хэш-функции, когда вы
регистрируетесь, например, в Вконтакте или другой социальной сети. Ваш логин и пароль пропускается через определенную хэш-функцию и значения хэша записываются в базу данных. После регистрации, когда вы используете логин и пароль для входа они опять пропускаются через хэш-функцию, и значение хэша сравнивается с тем значением хэша, которое было записано в базу данных.
Изначально, после вашей регистрации, если значения совпадают, система вас авторизует. Если значение хэша не совпадают, то выскакивает уведомление о том, что логин или пароль неверный. Здесь мы возвращаемся к основному требованию хэш-функции — однонаправленности. Потенциальные злоумышленники, взломав базу данных какой-то социальной сети получат значений хэшей, но не чистые логины и пароли. Именно из-за того, что хэш-функция однонаправленная, из нее нельзя получить исходные данные, такие как пароль и логин пользователя.
Именно из-за того, что хэш-функция однонаправленная, из нее нельзя получить исходные данные, такие как пароль и логин пользователя.
Тем не менее злоумышленник, получив хэши все-таки сможет узнать пароль некоторых пользователей. Для этого используется атака по «радужным» таблицам.
Злоумышленники используют заранее вычисленные хэши для простых и часто используемых паролей и сравнивают хэши в таблице с полученными хэшами из базы данных социальной сети. Но тут появляется одна такая проблема: если некоторые пользователи устанавливают одинаковый пароль, итоговый хэш паролей получается тоже одинаковый. Вы можете сказать, что маловероятно что кто-то будет использовать одинаковый пароль. Однако, вот таблицы самых популярных паролей за 2020 год которые используют пользователи в социальных сетях и других сервисах.
Чтобы не было проблем с одинаковым хешем, когда несколько пользователей используют одинаковый пароль, используется «соль».
Что такое «соль»? «Соль»- это строка данных которая пропускается через хэш-функции вместе с паролем.
Использование «соли» при хэшировании гарантирует то, что даже при одинаковых паролях значение хэша будет разное. Допустим, если Алиса и Боб используют одинаковый пароль qwerty. Хэш этих паролей будут кардинально отличаться из-за того, что была использована «соль».
В интернете есть огромное количество уже прочитанных заранее хэшей. Для самых популярных паролей, например, на сайте «crackstation» можно проверить, как это работает. Для начала давайте пропустим самый часто используемый пароль qwerty через хэш-функцию sha-256.
Получаем значение хэша. Это значение хэша вставляем на сайт «crackstation» и получаем результат qwerty. Это не значит, что хэш-функцию обратили и вычислили исходное значение. Это значит, что у этого сайта есть база данных с уже прочитанными хэшами для каждого простого и часто используемого пароля.
Но использование «соли» не гарантирует полную защиту от атак злоумышленников. Злоумышленники все еще могут перебирать значение хэша через «брутфорс» или же полный перебор.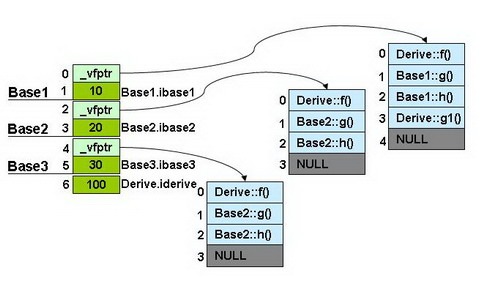 Злоумышленникам понадобится больше времени, так как надо будет перебирать еще и все возможные значения «соли». Но теоретически это возможно, так как основное требование хэш-функции — скорость хэширования. А как мы упоминали ранее, скорость хеширования не всегда является преимуществом, особенно когда это касается хранения паролей, чтобы защититься от «брутфорса».
Злоумышленникам понадобится больше времени, так как надо будет перебирать еще и все возможные значения «соли». Но теоретически это возможно, так как основное требование хэш-функции — скорость хэширования. А как мы упоминали ранее, скорость хеширования не всегда является преимуществом, особенно когда это касается хранения паролей, чтобы защититься от «брутфорса».
Так используются специально замедленные хэш-функции, на вычисление которых уходит больше времени, чем на вычисление стандартных функций. Это функции: decrypt, sckrypt или argon2. Их использование для хранения паролей полностью нейтрализует возможный «брутфорс» (Brute-force Attack). Такие функции используются для создания секретного ключа, который состоит из пароля пользователя, «соли», и дополнительного параметра cost. Параметр cost необходим для защиты от «радужных таблиц».
Параметр cost определяет количество циклов, через который будет пропущена исходная информация и это замедляет процесс хэширования. Таким образом, атака полного перебора становится невозможной, так как процесс хэширования сильно замедлен и за приемлемое время не получится перебрать достаточное количество паролей и всевозможных комбинаций «соли».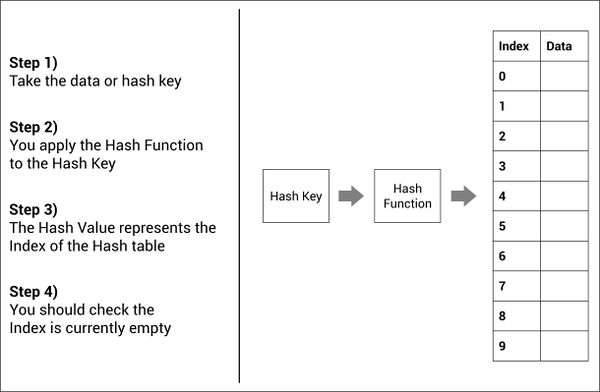
Со временем компьютеры станут мощнее и атаки полного перебора на этот алгоритм смогут быстрее достигать своей цели. Для защиты от этого необходимо просто увеличить параметр cost, который определяет количество циклов.
Чем больше циклов, тем больше времени потребуется для хеширования исходной информации.
Давайте рассмотрим метод защиты данных, который используют сервис dropbox. Изначально dropbox берёт пароль пользователя и пропускают его через определенную простую хэш-функцию без использования «соли». И затем полученный хэш пропускается через функцию BCrypt с использованием «соли» и параметр cost величиной в 10 циклов. Это защищает от брутфорса (Brute-force Attack). Так в конечном итоге вся эта информация шифруется алгоритмом шифрования aes. Злоумышленнику придется вскрывать все эти слои защиты, чтобы добраться до нужной ему информации.
Однако, стоит отметить что слабые пароли все равно уязвимы. Длинный и надежный
Пароль, пропущенный через простую хэш-функция md5 будет сложнее подобрать
чем пароль из 6 символов, но пропущенный через функцию BCrypt с параметром cost в 25 циклов.
Хранение и защита паролей не единственная сфера где применяются хэш-функции. Они также применяются для проверки целостности файлов, как было сказано ранее. При малейшем изменении исходного файла его хэш-сумма кардинально изменяется. Как это может быть использовано? Самый простой пример: проверка программного обеспечения, скаченного с сайта разработчика. Большинство разработчиков программного обеспечения рядом со ссылкой на скачивание программы размещают хэш-сумму каждого из файлов. После загрузки ПО на свой компьютер, пользователь может сравнить хэши и убедиться в том, что файлы подлинные и не подвергались изменению. Это может быть также использовано для передачи файлов между двумя людьми, когда необходимо убедиться в том, что в процессе передачи файлов он не был изменен. Но здесь при использовании надежных или устаревших хэш-функций имеет место быть коллизионная атака, когда два разных документа имеют одинаковый хеш.
Как происходит коллизионная атака. Приведём пример. Ева создает два разных документа «а» и «б» имеющих одинаковое значение хэш суммы. Предположим, что Ева хочет обмануть Боба, выдав свой документ за документ Алисы. Ева отсылает документ Алисе, которая доверяет содержанию данного документа, подписывает его хэш и отсылает подпись Еве. Ева прикрепляет подпись документа «а» к документу «б» затем отправляет подпись и документ Бобу утверждая, что Алиса подписала этот документ. Поскольку электронная подпись сверяет лишь значение хэша документа «б», Боб не узнает о подмене.
Предположим, что Ева хочет обмануть Боба, выдав свой документ за документ Алисы. Ева отсылает документ Алисе, которая доверяет содержанию данного документа, подписывает его хэш и отсылает подпись Еве. Ева прикрепляет подпись документа «а» к документу «б» затем отправляет подпись и документ Бобу утверждая, что Алиса подписала этот документ. Поскольку электронная подпись сверяет лишь значение хэша документа «б», Боб не узнает о подмене.
С надежным криптографическими хэш-функциями такое провернуть невозможно, но с устаревший md5 это реально осуществить.
Хэш-функции также используются и в блокчейне, каждая транзакция в блокчейне биткоина содержит информацию о получателе и отправителе. О сумме транзакций, времени её отправки и так далее. Вся эта информация хэшируется и образуется «транзакшин ID». «Транзакшин ID» это хэш-сумма, которая используется для ее идентификации и проверки того, что эта транзакция произошла. Хэши также используются и в блоках в блокчейне. Каждый блок блокчейна, биткоина, содержит свой хэш и хэш предыдущего блока, что образует связанную цепочку.
Пример применения хэширования паролей в Python с помощью модуля BCrypt.
Модуль bcrypt в PyPi предлагает удобную реализацию BCrypt, которую мы можем установить через pip:
pip install bcrypt
После того, как установили BCrypt с помощью pip, вы можете импортировать его в свой проект:
import bcrypt
Возьмем «Passwordnew» в качестве примера пароля, чтобы показать его в использование BCrypt:
pwd = ‘Passwordnew’ bytePwd = password.encode(‘utf-8’)
Хешируем зашифрованный пароль с помощью BCrypt:
# Generate salt mySalt = bcrypt.gensalt() # Hash password hash = bcrypt.hashpw(bytePwd, mySalt)
Проверим, будет ли текстовый пароль допустимым паролем для нового хэша, который создали в примере:
print(bcrypt.checkpw(password, hash)) # Output: True
Таким образом, для наглядности был проиллюстрирован процесс хеширования пароля на примере BCrypt.
Надеюсь, что у вас сложилось представление о том, что такое хэш-функция, как работает алгоритм хэширования и как это можно использовать.
Хеширование — Криптография
Хеширование (иногда «хэширование», англ. hashing) — преобразование по детерминированному алгоритму входного массива данных произвольной длины в выходную битовую строку фиксированной длины. Такие преобразования также называются хеш-функциями или функциями свёртки, а их результаты называют хешем, хеш-кодом или сводкой сообщения(англ. message digest). Хеширование применяется для построения ассоциативных массивов, поиска дубликатов в сериях наборов данных, построения достаточно уникальных идентификаторов для наборов данных, контрольное суммирование с целью обнаружения случайных или намеренных ошибок при хранении или передаче, для хранения паролей в системах защиты (в этом случае доступ к области памяти, где находятся пароли, не позволяет восстановить сам пароль), при выработке электронной подписи (на практике часто подписывается не само сообщение, а его хеш-образ). В общем случае однозначного соответствия между исходными данными и хеш-кодом нет в силу того, что количество значений хеш-функций меньше, чем вариантов входного массива; существует множество массивов с разным содержимым, но дающих одинаковые хеш-коды — так называемые коллизии. Вероятность возникновения коллизий играет немаловажную роль в оценке качества хеш-функций. Существует множество алгоритмов хеширования с различными свойствами (разрядность, вычислительная сложность, криптостойкость и т. п.). Выбор той или иной хеш-функции определяется спецификой решаемой задачи. Простейшими примерами хеш-функций могут служить контрольная сумма или CRC. ИсторияДональд Кнут относит первую систематическую идею хеширования к сотруднику IBM Хансу Петеру Луну (нем. Hans Peter Luhn), предложившему хеш-кодирование в январе 1953 года. В 1956 году Арнольд Думи (англ. Arnold Dumey) в своей работе «Computers and automation» первым представил концепцию хеширования таковой, какой её знает большинство программистов сейчас. Первой серьёзной работой, связанной с поиском в больших файлах, была статья Уэсли Питерсона (англ. W. Wesley Peterson) в IBM Journal of Research and Development 1957 года, в которой он определил открытую адресацию, а также указал на ухудшение производительности при удалении. Спустя шесть лет была опубликована работа Вернера Бухгольца (нем. Werner Buchholz), в которой проведено обширное исследование хеш-функций. В течение нескольких последующих лет хеширование широко использовалось, однако не было опубликовано никаких значимых работ. В 1967 году хеширование в современном значении упомянуто в книге Херберта Хеллермана «Принципы цифровых вычислительных систем». В 1968 году Роберт Моррис (англ. Robert Morris) опубликовал в Communications of the ACM большой обзор по хешированию, эта работа считается ключевой публикацией, вводящей понятие о хешировании в научный оборот и закрепившей ранее применявшийся только в жаргоне специалистов термин «хеш». До начала 1990-х годов в русскоязычной литературе в качестве эквивалента термину «хеширование» благодаря работам Андрея Ершова использовалось слово «расстановка», а для коллизий использовался термин «конфликт» (Ершов использовал «расстановку» с 1956 года, в русскоязычном издании книги Вирта «Алгоритмы и структуры данных» 1989 года также используется термин «расстановка»). Предлагалось также назвать метод русским словом «окрошка». Однако ни один из этих вариантов не прижился, и в русскоязычной литературе используется преимущественно термин «хеширование».[3] Виды хеш-функцийХорошая хеш-функция должна удовлетворять двум свойствам:
Предположим, для определённости, что количество ключей , а хеш-функция имеет не более различных значений: В качестве примера «плохой» хеш-функции можно привести функцию с , которая десятизначному натуральном числу сопоставляет три цифры выбранные из середины двадцатизначного квадрата числа . Однако существует несколько более простых и надежных методов, на которых базируются многие хеш-функции. Хеш-функции, основанные на деленииПервый метод заключается в том, что мы используем в качестве хеша остаток от деления на , где — это количество всех возможных хешей: При этом очевидно, что при чётном значение функции будет чётным, при чётном , и нечётным — при нечётном, что может привести к значительному смещению данных в файлах. Также не следует использовать в качестве степень основания счисления компьютера, так как хеш-код будет зависеть только от нескольких цифр числа , расположенных справа, что приведет к большому количеству коллизий. На практике обычно выбирают простое — в большинстве случаев этот выбор вполне удовлетворителен. Ещё следует сказать о методе хеширования, основанном на делении на полином по модулю два. В данном методе также должна являться степенью двойки, а бинарные ключи () представляются в виде полиномов. В этом случае в качестве хеш-кода берутся значения коэффциентов полинома, полученного как остаток от деления на заранее выбранный полином степени : При правильном выборе такой способ гарантирует отсутствие коллизий между почти одинаковыми ключами.[3] Мультипликативная схема хешированияВторой метод состоит в выборе некоторой целой константы , взаимно простой с , где — количество представимых машинным словом значений (в компьютерах IBM PC ). Тогда можем взять хеш-функцию вида: В этом случае, на компьютере с двоичной системой счисления, является степенью двойки и будет состоять из старших битов правой половины произведения . Среди преимуществ этих двух методов стоит отметь, что они выгодно используют то, что реальные ключи неслучайны, например в том случае если ключи представляют собой арифметическую прогрессию (допустим последовательность имён «ИМЯ1», «ИМЯ2», «ИМЯ3»). Одной из вариаций данного метода является хеширование Фибоначчи, основанное на свойствах золотого сечения. В качестве здесь выбирается ближайшее к целое число, взаимно простое с Хеширование строк переменной длиныВышеизложенные методы применимы и в том случае, если нам необходимо рассматривать ключи, состоящие из нескольких слов или ключи переменной длины. Например можно скомбинировать слова в одно при помощи сложения по модулю или операции «исключающее или». Одним из алгоритмов, работающих по такому принципу является хеш-функция Пирсона. Хеширование Пирсона (англ. Pearson hashing) — алгоритм, предложенный Питером Пирсоном (англ. Peter Pearson) для процессоров с 8-битными регистрами, задачей которого является быстрое вычисление хеш-кода для строки произвольной длины. Алгоритм можно описать следующим псевдокодом, который получает на вход строку и использует таблицу перестановок Среди преимуществ алгоритма следует отметить:
В качестве альтернативного способа хеширования ключей, состоящих из символов (), можно предложить вычисление Идеальное хешированиеИдеальной хеш-функцией (англ. Perfect hash function) называется такая функция, которая отображает каждый ключ из набора в множество целых чисел без коллизий. Описание
Идеальное хеширование применяется в тех случаях, когда мы хотим присвоить уникальный идентификатор ключу, без сохранения какой-либо информации о ключе. Одним из наиболее очевидных примеров использования идеального (или скорее k-идеального) хеширования является ситуация, когда мы располагаем небольшой быстрой памятью, где размещаем значения хешей, связанных с данными хранящимися в большой, но медленной памяти. Причем размер блока можно выбрать таким, что необходимые нам данные, хранящиеся в медленной памяти, будут получены за один запрос. Подобный подход используется, например, в аппаратных маршрутизаторах. Также идеальное хеширование используется для ускорения работы алгоритмов на графах, в тех случаях, когда представление графа не умещается в основной памяти. Универсальное хешированиеУниверсальным хешированием (англ. Universal hashing) называется хеширование, при котором используется не одна конкретная хеш-функция, а происходит выбор из заданного семейства по случайному алгоритму. Использование универсального хеширования обычно обеспечивает низкое число коллизий. Универсальное хеширование имеет множество применений, например, в реализации хеш-таблиц и криптографии. ОписаниеПредположим, что мы хотим отобразить ключи из пространства в числа . На входе алгоритм получает некоторый набор данных и размерностью , причем неизвестный заранее. Как правило целью хеширования является получение наименьшего числа коллизий, чего трудно добиться используя какую-то определенную хеш-функцию. В качестве решения такой проблемы можно выбирать функцию случайным образом из определенного набора, называемого универсальным семейством . |
Безопасное хэширование паролей | Руководство по PHP
За последние 24 часа нас посетили 7457 программистов и 661 робот. Сейчас ищут 165 программистов …
Сейчас ищут 165 программистов …
Вернуться к: ЧАВО
В этом разделе разъясняются причины, стоящие за хэшированием паролей в целях безопасности, а также эффективные методы хэширования.
- Почему я должен хэшировать пароли пользователей в моем приложении?
- Почему популярные хэширующие функции, такие как md5 и sha1 не подходят для паролей?
- Если популярные хэширующие функции не подходят, как же я тогда должен хэшировать свои пароли?
- Что такое соль?
- Как я должен хранить свою соль?
- Почему я должен хэшировать пароли пользователей в моем приложении?
Хэширование паролей является одним из самых базовых соображений безопасности, которые необходимо сделать, при разработке приложения, принимающего пароли от пользователей.
 Без хэширования, пароли, хранящиеся в базе вашего приложения,
могут быть украдены, например, если ваша база данных была скомпрометирована,
а затем немедленно могут быть применены для компрометации не только вашего
приложения, но и аккаунтов ваших пользователей на других сервисах, если
они не используют уникальных паролей.
Без хэширования, пароли, хранящиеся в базе вашего приложения,
могут быть украдены, например, если ваша база данных была скомпрометирована,
а затем немедленно могут быть применены для компрометации не только вашего
приложения, но и аккаунтов ваших пользователей на других сервисах, если
они не используют уникальных паролей.Применяя хэширующий алгоритм к пользовательским паролям перед сохранением их в своей базе данных, вы делаете невозможным разгадывание оригинального пароля для атакующего вашу базу данных, в то же время сохраняя возможность сравнения полученного хэша с оригинальным паролем.
Важно заметить, однако, что хэширование паролей защищает их только от компрометирования в вашем хранилище, но не обязательно от вмешательства вредоносного кода в вашем приложении.
- Почему популярные хэширующие функции, такие как md5() и sha1() не подходят для паролей?
Такие хэширующие алгоритмы как MD5, SHA1 и SHA256 были спроектированы очень быстрыми и эффективными.
 При наличии современных технологий и
оборудования, стало довольно просто выяснить результат этих алгоритмов методом
«грубой силы» для определения оригинальных вводимых данных.
При наличии современных технологий и
оборудования, стало довольно просто выяснить результат этих алгоритмов методом
«грубой силы» для определения оригинальных вводимых данных.Из-за той скорости, с которой современные компьютеры могут «обратить» эти хэширующие алгоритмы, многие профессионалы компьютерной безопасности строго не рекомендуют использовать их для хэширования паролей.
- Если популярные хэширующие функции не подходят, как же я тогда должен хэшировать свои пароли?
При хэшировании паролей существует два важных соображения: это стоимость вычисления и соль. Чем выше стоимость вычисления хэширующего алгоритма, тем больше времени требуется для взлома его вывода методом «грубой силы».
PHP 5.5 предоставляет встроенное API хэширования паролей, которое безопасно работает и с хэшированием и с проверкой паролей.
 Также есть
» PHP библиотека совместимости,
доступная с PHP 5.3.7.
Также есть
» PHP библиотека совместимости,
доступная с PHP 5.3.7.Другой возможностью является функция crypt(), которая поддерживает несколько алгоритмов хэширования в PHP 5.3 и новее. При использовании этой функции вы можете быть уверенным, что выбранный вами алгоритм доступен, так как PHP содержит собственную реализацию каждого поддерживаемого алгоритма, даже в случае, если какие-то из них не поддерживаются вашей системой.
При хэшировании паролей рекомендуется применять алгоритм Blowfish, который также используется по умолчанию в API хэширования паролей, так как он значительно большей вычислительной сложности, чем MD5 или SHA1, при этом по-прежнему гибок.
Учтите, что, если вы используете функцию crypt() для проверки пароля, то вам нужно предостеречь себя от атак по времени, применяя сравнение строк, которое занимает постоянное время. Ни операторы PHP == и ===, ни функция strcmp() не являются таковыми.
 Функция же password_verify() как раз делает то, что нужно.
Настоятельно рекомендуется использовать
встроенное API хэширования паролей,
если есть такая возможность.
Функция же password_verify() как раз делает то, что нужно.
Настоятельно рекомендуется использовать
встроенное API хэширования паролей,
если есть такая возможность.
- Что такое соль?
Криптографическая соль представляет собой данные, которые применяются в процессе хэширования для предотвращения возможности разгадать оригинальный ввод с помощью поиска результата хэширования в списке заранее вычисленных пар ввод-хэш, известном также как «радужная» таблица.
Более простыми словами, соль — это кусочек дополнительных данных, которые делают ваши хэши намного более устойчивыми к взлому. Существует много онлайн-сервисов, предоставляющих обширные списки заранее вычисленных хэшей вместе с их оригинальным вводом. Использование соли делает поиск результирующего хэша в таком списке маловероятным или даже невозможным.

password_hash() создает случайную соль в случае, если она не была передана, и чаще всего это наилучший и безопасный выбор.
- Как я должен хранить свою соль?
При использовании функции password_hash() или crypt(), возвращаемое значение уже содержит соль как часть созданного хэша. Это значение нужно хранить как есть в вашей базе данных, так как оно содержит также информацию о хэширующей функции, которая использовалась, и может быть непосредственно передано в функции password_verify() или crypt() при проверке пароля.
Следующая диаграмма показывает формат возвращаемого значения функциями crypt() или password_hash(). Как можно видеть, они содержат полную информацию об алгоритме и соли, требуемых для будущей проверки пароля.
Вернуться к: ЧАВО
Хеш-функция в C | Типы методов разрешения конфликтов
В этой статье есть краткое примечание о хешировании (хэш-таблица и хэш-функция). Наиболее важной концепцией является «поиск», который определяет временную сложность. Чтобы уменьшить временную сложность по сравнению с любой другой концепцией хеширования структуры данных, которая в среднем имеет время O (1), а в худшем случае это займет время O (n).
Наиболее важной концепцией является «поиск», который определяет временную сложность. Чтобы уменьшить временную сложность по сравнению с любой другой концепцией хеширования структуры данных, которая в среднем имеет время O (1), а в худшем случае это займет время O (n).
Хэширование — это метод с более быстрым доступом к элементам, который сопоставляет заданные данные с меньшим ключом для сравнения. В общем, в этом методе ключи отслеживаются с помощью хеш-функции в таблицу, известную как хеш-таблица.
Что такое хеш-функция?
Хеш-функция — это функция, использующая операцию постоянного времени для сохранения и извлечения значения из хэш-таблицы, которое применяется к ключам как целые числа и используется в качестве адреса для значений в хеш-таблице.
Типы хеш-функции В C
Типы хеш-функций объясняются ниже:
1. Метод деления
В этом методе хеш-функция зависит от остатка от деления.
Пример: элементы, которые должны быть помещены в хеш-таблицу, равны 42,78,89,64, и возьмем размер таблицы равным 10.
Хэш (ключ) = элементы % размера таблицы;
2 = 42 % 10;
8 = 78 % 10;
9 = 89 % 10;
4 = 64 % 10;
Табличное представление можно увидеть следующим образом:
2. Метод среднего квадрата
В этом методе в качестве индекса используется средняя часть квадратного элемента.
Элементы для размещения в хеш-таблице: 210, 350, 99 890 и размер таблицы 100.
210* 210 = 44100, индекс = 1, так как средняя часть результата (44 1 00) равна 1.
350* 350 = 122500, индекс = 25 так как средняя часть результата (12 25 00) равна 25.
99* 99 = 9801, индекс = 80 так как средняя часть результата (9 80 1) равна 80.
890* 890 = 792100, индекс = 21, так как средняя часть результата (79 21 00) равна 21.
3. Метод сложения цифр
В этом методе элемент, который должен быть помещен в таблицу, является хеш-ключом, который получается путем разделения элементов на различные части, а затем объединения частей путем выполнения некоторых простых математических операций.
Размещаемые элементы: 23576623, 34687734.
- хеш (ключ) = 235+766+23 = 1024
- хеш-ключ) = 34+68+77+34 = 213
Предположим, что в этих типах хэширования у нас есть числа от 1 до 100 и размер хеш-таблицы = 10. Элементы = 23, 12, 32
Хэш (ключ) = 23 % 10 = 3;
Хэш (ключ) = 12 % 10 = 2 ;
Хэш (ключ) = 32 % 10 = 2 ;
Из приведенного выше примера обратите внимание, что оба элемента 12 и 32 указывают на 2-е место в таблице, где невозможно записать оба в одно и то же место, такая проблема известна как коллизия. Чтобы избежать подобных проблем, можно использовать некоторые методы хеш-функций.
Типы методов разрешения коллизий
Давайте обсудим типы методов разрешения коллизий:
1. Цепочка
В этом методе, как следует из названия, он обеспечивает цепочку блоков для записи в таблице, содержащей две записи элементов. . Таким образом, всякий раз, когда происходят такие столкновения, поля действуют как связанный список.
Пример: 23, 12, 32 с размером таблицы 10.
Хэш (ключ) = 23 % 10 = 3;
Хэш (ключ) = 12 % 10 = 2 ;
Хэш (ключ) = 32 % 10 =2 ;
2. Открытая адресация
- Линейное зондирование
Это еще один метод решения проблем столкновений. Как следует из названия, всякий раз, когда возникает коллизия, два элемента должны быть помещены в одну и ту же запись в таблице, но с помощью этого метода мы можем искать следующее пустое место или запись в таблице и размещать второй элемент. Это снова может привести к другой проблеме; если мы не находим пустую запись в таблице, это приводит к кластеризации. Таким образом, это известно как проблема кластеризации, которая может быть решена следующим методом.
Пример: 23, 12, 32 с размером таблицы 10
Хэш (ключ) = 23 % 10 = 3;
Хэш (ключ) = 12 % 10 =2 ;
Хэш (ключ) = 32 % 10 =2 ;
На этой диаграмме 12 и 32 могут быть помещены в одну и ту же запись с индексом 2, но таким способом они располагаются линейно.
- Квадратичное измерение
Этот метод решает проблему кластеризации при линейном зондировании. В этом методе хэш-функция с хеш-ключом рассчитывается как хэш (ключ) = (хеш (ключ) + x * x) % размера таблицы (где x = 0, 1, 2…).
Пример: 23, 12, 32 с размером таблицы 10
Хэш (ключ) = 23 % 10 = 3;
Хэш (ключ) = 12 % 10 =2 ;
Хэш (ключ) = 32 % 10 =2 ;
Здесь мы видим, что 23 и 12 могут быть легко размещены, но 32 не могут, так как снова 12 и 32 имеют одну и ту же запись с одним и тем же индексом в таблице, согласно этому методу хэш (ключ) = (32 + 1*1) % 10 = 3. Но в этом случае запись таблицы с индексом 3 помещается в 23, поэтому мы должны увеличить значение x на 1. Хэш (ключ) = (32 + 2 * 2) % 10 = 6. Итак теперь мы можем поместить 32 в запись с индексом 6 в таблице.
- Двойное хеширование
В этом методе мы должны вычислить 2 хеш-функции, чтобы решить проблему коллизий. Первый рассчитывается с помощью простого метода деления. Второй должен удовлетворять двум правилам; он не должен быть равен 0, и записи должны проверяться.
Второй должен удовлетворять двум правилам; он не должен быть равен 0, и записи должны проверяться.
- 1 (ключ) = ключ % размера таблицы.
- 2 (ключ) = p – (ключ по модулю p), где p — простые числа < размера таблицы.
Пример: 23, 12, 32 с размером таблицы 10
Хэш (ключ) = 23 % 10 = 3;
Хэш (ключ) = 12 % 10 =2 ;
Хэш (ключ) = 32 % 10 =2 ;
Здесь снова элемент 32 можно поместить с помощью hash3 (ключ) = 5 – (32 % 5) = 3. Таким образом, 32 можно поместить в индекс 5 в таблице, которая пуста, так как нам нужно перепрыгнуть через 3 записи. разместить его.
Заключение
Хеширование — один из важных методов поиска данных, обеспечиваемый очень эффективными и быстрыми методами с использованием хеш-функций и хеш-таблиц. Каждый элемент можно искать и размещать с помощью различных методов хеширования. Этот метод намного быстрее, чем любая другая структура данных с точки зрения временного коэффициента.
Рекомендуемые статьи
Это руководство по функции хеширования в C. Здесь мы обсудили краткий обзор, типы хеш-функций в C и методы разрешения коллизий в деталях. Вы также можете просмотреть другие наши рекомендуемые статьи, чтобы узнать больше:
- Хеширование в СУБД
- Процесс шифрования
- Хеш-функция в Java
- Хеш-функция в PHP
Введение в хэш-таблицы в C | Беннет Бьюкенен
Если вы знакомы с языками сценариев, такими как Python или Ruby, вы помните типы данных, известные как массивы и словари. Ниже приведен краткий пример способов доступа к данным в этих типах данных. Массив характеризуется упорядоченной серией элементов, а словарь характеризуется элементами с парными отношениями ключ-значение.
Обратите внимание, как использование словаря позволяет нам извлекать данные, используя сопоставление ключ-значение словаря. В этом посте мы построим хэш-таблица , использующая этот метод хранения данных. Как мы увидим, эта структура данных позволяет извлекать данные более эффективно, чем обычный индексированный массив. Таким образом, хэш-таблица представляет собой структуру данных с элементами массива с ключами.
Как мы увидим, эта структура данных позволяет извлекать данные более эффективно, чем обычный индексированный массив. Таким образом, хэш-таблица представляет собой структуру данных с элементами массива с ключами.
В отличие от Python, с его возможностью использовать встроенный тип данных словаря, в C у нас есть только индексированные массивы для работы. Таким образом, чтобы создать хэш-таблицу , нам потребуется получить данные с помощью функций, использующих индексированные массивы. Для этого мы создадим простой массив длиной n , где n — это количество элементов в нашей хеш-таблице . Кроме того, каждый из элементов массива должен иметь два атрибута: ключ и значение . Таким образом, мы в конечном итоге сможем запрашивать хеш-таблицу на основе атрибута ключа и возвращать связанные данные значения .
Прежде чем перейти к подробному объяснению того, как мы этого добьемся, давайте рассмотрим основную функцию, которую мы будем использовать. Здесь мы видим четыре функции, которые мы напишем для построения наших хэш-таблица : ht_create(), ht_put(), ht_get(), и ht_free() . Все фрагменты кода для этого хэша таблицы можно найти здесь.
Здесь мы видим четыре функции, которые мы напишем для построения наших хэш-таблица : ht_create(), ht_put(), ht_get(), и ht_free() . Все фрагменты кода для этого хэша таблицы можно найти здесь.
Первое, что нам нужно сделать, это определить структуры двух компонентов, которые мы будем использовать для создания хеш-таблицы . W e назовет эти две структуры List и HashTable . List определяет элемент хеш-таблицы , который имеет два указателя на наши строковые данные: ключ и значение . У него также есть указатель next на объект типа List (достаточно сказать, что наш указатель next облегчит получение наших данных). Вторая структура HashTable определяет саму хэш-таблицу , которая имеет целое число без знака размера и массив элементов списка .
Определив наши структуры, мы напишем функцию ht_create() , который выделяет память, необходимую для HashTable длины размера.
Теперь, когда мы создали нашу хэш-таблицу , нам понадобится способ заполнить ее элементами списка . Чтобы определить, какой индекс будет иметь какой-либо конкретный ключ , необходимо будет определить функцию. Это послужит двоякой цели: назначению индекса для нового ключа и извлечению индекса ранее существовавшего ключа 9.0206 .
Мы напишем функцию ht_put() , которая создает новый элемент в нашей хеш-таблице , выделяя память для нового элемента List с именем node и назначая строки, переданные функции, ключу . и значение , r соответственно. Теперь, когда у нас есть новый узел , давайте создадим функцию node_handler() , которая вставляет наши элементы в список. Мы хотим, чтобы эта функция в первую очередь вставляла элемент в заданный индекс массива, но она также должна обрабатывать случай, когда индекс уже содержит данные, хранящиеся в этом месте — случай, известный как 9. 0205 столкновение . В таком случае мы создадим связанный список 90 205 90 206 элементов данных, чтобы мы могли перебирать их и находить соответствующие данные. Теперь в игру вступает указатель next нашей структуры List , поскольку мы устанавливаем его так, чтобы он указывал на ранее существовавшие данные . Теперь мы можем использовать этот указатель для вставки нового элемента списка в начало связанного списка . Таким образом, мы получаем цепочку из 90 205 элементов списка 90 206 в этом индексе массива, последний из которых указывает на NULL.
0205 столкновение . В таком случае мы создадим связанный список 90 205 90 206 элементов данных, чтобы мы могли перебирать их и находить соответствующие данные. Теперь в игру вступает указатель next нашей структуры List , поскольку мы устанавливаем его так, чтобы он указывал на ранее существовавшие данные . Теперь мы можем использовать этот указатель для вставки нового элемента списка в начало связанного списка . Таким образом, мы получаем цепочку из 90 205 элементов списка 90 206 в этом индексе массива, последний из которых указывает на NULL.
Наконец, мы можем определить функцию ht_get() , которая извлекает данные из хеш-таблицы , как в нашем словаре Python. Это возьмет нашу хеш-таблицу с ключом в качестве параметра и будет искать в определенном индексе массива элемент списка с ключом . Если он найден, то он любезно вернет значение этого элемента .
Наша первоначальная цель достигнута, но наша работа еще не завершена. К настоящему моменту мы выделили 72 байта памяти для нашей программы, поэтому давайте не забудем освободить эту память, чтобы избежать утечек памяти.
К настоящему моменту мы выделили 72 байта памяти для нашей программы, поэтому давайте не забудем освободить эту память, чтобы избежать утечек памяти.
Если вы хотите увидеть код в действии, вы можете клонировать репозиторий, содержащий файлы учебника, и перейти в каталог. Скомпилируйте программу с файлами, которые мы исследовали, и запустите исполняемый файл. Инструмент, который мне нравится использовать для отслеживания использования памяти моей программой, называется valgrind, поэтому мы будем использовать его, чтобы узнать, как программа использует память. Эти файлы были протестированы с использованием Ubuntu 14.04.
$ git clone https://github.com/bennettbuchanan/holbertonschool-low_level_programming$ cd holbertonschool-low_level_programming/example_hash_table/$ gcc -Wall -Wextra -Werror -pedantic main.c ht_put.c ht_create.c hash.c ht_get. c ht_free.c$ valgrind ./a.out
На выходе мы получаем букву C, и valgrind сообщает нам, что утечки памяти невозможны, потому что C — это весело . Спасибо, что следите за нами!
Спасибо, что следите за нами!
Get-FileHash (Microsoft.PowerShell.Utility) — PowerShell | Microsoft Узнайте
Обратная связь Редактировать
Твиттер LinkedIn Фейсбук Эл. адрес
- № по каталогу
- Модуль:
- Microsoft.PowerShell.Утилита
Вычисляет хеш-значение для файла с использованием указанного хеш-алгоритма.
Синтаксис
Get-FileХэш [-Путь] <Строка[]> [[-Алгоритм] ] [ ]
Get-FileХэш [-LiteralPath] <Строка[]> [[-Алгоритм] ] [ ]
Get-FileХэш [-InputStream] <поток> [[-Алгоритм] ] [ ]
Описание
Командлет Get-FileHash вычисляет хеш-значение для файла с помощью указанного хэш-алгоритма. Хэш-значение — это уникальное значение, соответствующее содержимому файла. Вместо того, чтобы идентифицировать
содержимое файла по его имени, расширению или другому обозначению, хеш присваивает уникальный
значение к содержимому файла. Имена файлов и расширения могут быть изменены без изменения
содержимое файла и без изменения хеш-значения. Точно так же содержимое файла может быть
изменены без изменения имени или расширения. Однако изменение даже одного символа в
содержимое файла изменяет хеш-значение файла.
Хэш-значение — это уникальное значение, соответствующее содержимому файла. Вместо того, чтобы идентифицировать
содержимое файла по его имени, расширению или другому обозначению, хеш присваивает уникальный
значение к содержимому файла. Имена файлов и расширения могут быть изменены без изменения
содержимое файла и без изменения хеш-значения. Точно так же содержимое файла может быть
изменены без изменения имени или расширения. Однако изменение даже одного символа в
содержимое файла изменяет хеш-значение файла.
Назначение хеш-значений — предоставить криптографически безопасный способ проверки того, что содержимое
файла не были изменены. Хотя некоторые алгоритмы хеширования, включая MD5 и SHA1, больше не
считается защищенным от атак, цель алгоритма безопасного хэширования — сделать невозможным
изменить содержимое файла — либо случайно, либо в результате злонамеренной или несанкционированной попытки — и
поддерживать одно и то же значение хеш-функции. Вы также можете использовать хеш-значения, чтобы определить, имеют ли два разных файла
точно такое же содержание. Если хэш-значения двух файлов идентичны, содержимое файлов
также идентичны.
Если хэш-значения двух файлов идентичны, содержимое файлов
также идентичны.
По умолчанию командлет Get-FileHash использует алгоритм SHA256, хотя любой алгоритм хеширования,
поддерживается целевой операционной системой.
Примеры
Пример 1. Вычисление хэш-значения для файла
В этом примере используется командлет Get-FileHash для вычисления хэш-значения для /etc/apt/sources.list файл. Используемый хэш-алгоритм по умолчанию, SHA256 . Выход
передается в список форматов 9Командлет 0388 для форматирования вывода в виде списка.
Get-FileHash /etc/apt/sources.list | Список форматов Алгоритм: SHA256 Хэш: 3CBCFDDEC145E3382D592266BE193E5BE53443138EE6AB6CA09FF20DF609E268 Путь: /etc/apt/sources.list
Пример 2. Вычисление хеш-значения для файла ISO
В этом примере используется командлет Get-FileHash и алгоритм SHA384 для вычисления хэш-значения
для файла ISO, который администратор загрузил из Интернета. Вывод направляется в
Вывод направляется в Format-List Командлет для форматирования вывода в виде списка.
Get-FileHash C:\Users\user1\Downloads\Contoso8_1_ENT.iso -Алгоритм SHA384 | Список форматов Алгоритм: SHA384 Хэш: 20AB1C2EE19FC96A7C66E33917D191A24E3CE9DAC99DB7C786ACCE31E559144FEAFC695C58E508E2EBBC9D3C96F21FA3 Путь: C:\Users\user1\Downloads\Contoso8_1_ENT.iso
Пример 3. Вычисление хеш-значения потока
В этом примере мы используем System.Net.WebClient для загрузки пакета из
Страница выпуска Powershell. Релиз
страница также документирует хэш SHA256 каждого файла пакета. Мы можем сравнить опубликованное значение хеша
с тем, что мы вычисляем с Get-FileHash .
$wc = [System.Net.WebClient]::new() $pkgurl = 'https://github.com/PowerShell/PowerShell/releases/download/v6.2.4/powershell_6.2.4-1.debian.9_amd64.deb' $publishedHash = '8E28E54D601F0751922DE24632C1E716B4684876255CF82304A9B19E89A9CCAC' $FileHash = Get-FileHash-InputStream($wc.OpenRead($pkgurl)) $FileHash.Hash -eq $publishedHash True
Пример 4. Вычисление хэша строки
PowerShell не предоставляет командлет для вычисления хэша строки. Тем не менее, вы можете написать
строку в поток и используйте InputStream параметр Get-FileHash для получения хеш-значения.
$stringAsStream = [System.IO.MemoryStream]::new()
$writer = [System.IO.StreamWriter]::new($stringAsStream)
$writer.write("Привет, мир")
$писатель.Flush()
$stringAsStream.Position = 0
Get-FileHash -InputStream $stringAsStream | Хеш Select-Object
Хэш
----
64EC88CA00B268E5BA1A35678A1B5316D212F4F366B2477232534A8AECA37F3C Параметры
-Алгоритм
-InputStream
-LiteralPath
-Path
Входные данные
Строка
Командлету Get-FileHash можно передать строку, содержащую путь к одному или нескольким файлам.
Выводы
Microsoft. Powershell.Utility.FileHash
Powershell.Utility.FileHash
Get-FileHash возвращает объект, представляющий путь к указанному файлу, значение
вычисленный хэш и алгоритм, используемый для вычисления хеша.
- Список форматов
Обратная связь
Отправить и просмотреть отзыв для
Этот продукт Эта страница
Просмотреть все отзывы о странице
хеш-таблиц — Cprogramming.com
Эрик Су
Хэш-таблицы являются эффективной реализацией структуры данных массива с ключами, структура, иногда известная как ассоциативный массив или карта. Если вы работаете в C++ вы можете воспользоваться контейнером карты STL для массивов с ключами, реализованных с использованием бинарных деревьев, но эта статья познакомит вас с теорией того, как хэш-таблица работает.
Массивы с ключами и массивы с индексами
Одним из самых больших недостатков такого языка, как C, является отсутствие
массивы с ключами. В обычном массиве C (также называемом индексированным массивом) единственный способ
для доступа к элементу будет использоваться его порядковый номер. Чтобы найти элемент 50 из
массив с именем «сотрудники», вы должны получить к нему доступ следующим образом:
В обычном массиве C (также называемом индексированным массивом) единственный способ
для доступа к элементу будет использоваться его порядковый номер. Чтобы найти элемент 50 из
массив с именем «сотрудники», вы должны получить к нему доступ следующим образом:
сотрудники[50];
Однако в массиве с ключами вы можете связать каждый элемент с «ключом», который может быть любым, от имени до номера модели продукта. Таким образом, если у вас есть массив записей сотрудников с ключами, вы можете получить доступ к записи сотрудника «Джон Браун» следующим образом:
. сотрудники["Браун, Джон"];
Одна из основных форм массива с ключами называется хеш-таблицей. В хеш-таблице ключ используется для поиска элемента вместо номера индекса. Так как хеш-таблица должен быть закодирован с использованием индексированного массива, должен быть какой-то способ преобразование ключа в порядковый номер. Этот способ называется функцией хеширования.
Хеш-функции
Хеш-функция может быть чем угодно. Как устроена хеш-функция
на самом деле кодируется в зависимости от ситуации, но обычно хеш-функция
должен возвращать значение на основе ключа и размера массива хеширования
таблица построена на. Кроме того, есть одна важная вещь, которую иногда упускают из виду.
что хэш-функция должна возвращать одно и то же значение каждый раз, когда ей дается
тот же ключ.
Как устроена хеш-функция
на самом деле кодируется в зависимости от ситуации, но обычно хеш-функция
должен возвращать значение на основе ключа и размера массива хеширования
таблица построена на. Кроме того, есть одна важная вещь, которую иногда упускают из виду.
что хэш-функция должна возвращать одно и то же значение каждый раз, когда ей дается
тот же ключ.
Допустим, вы хотите организовать список примерно из 200 адресов по именам людей. фамилии. Хеш-таблица была бы идеальной для такого рода вещей, так что вы можете получить доступ к записям с фамилиями людей в качестве ключей.
Во-первых, мы должны определить размер используемого массива. Давайте воспользуемся массивом из 260 элементов, чтобы на каждую букву алфавита приходилось в среднем около 10 пробелов элементов.
Теперь нам нужно создать функцию хеширования. Во-первых, давайте создадим связь между буквами и цифрами:
А --> 0 Б --> 1 С --> 2 Д --> 3 ... и так далее до Z --> 25.
Самый простой способ организовать хеш-таблицу на основе первой буквы фамилии.
Так как у нас 260 элементов, мы можем умножить первую букву фамилии на 10. Таким образом, когда дается такой ключ, как «Смит», ключ будет преобразован в индекс 180 (S — это 19-я буква имени). алфавита, поэтому S --> 18 и 18 * 10 = 180).
Поскольку мы используем простую функцию для быстрого создания индексного номера и используем тот факт, что индексный номер можно использовать для прямого доступа к элементу, время доступа к хеш-таблице довольно мало. Связанный список ключей и элементов не будет таким быстрым, поскольку вам придется искать каждую пару ключ-элемент.
Столкновения и обработка столкновений
Проблемы, конечно, возникают, когда у нас есть фамилии с одинаковой первой буквой. Таким образом, «Вебстер» и «Уитни» будут соответствовать одному и тому же порядковому номеру, 22. Подобная ситуация, когда два ключа отправляются в одно и то же место в массиве, называется коллизией. Если вы пытаетесь вставить элемент, вы можете обнаружить, что пространство уже заполнено другим элементом.
Конечно, вы можете попытаться просто создать огромный массив и таким образом сделать коллизии почти невозможными, но тогда это лишает смысла использование хеш-таблицы. Одним из преимуществ хеш-таблицы является то, что она быстрая и маленькая.
Обработка коллизий с открытой адресацией
Самый простой алгоритм обработки коллизий известен как метод открытой адресации или метод закрытого хеширования. Когда вы добавляете элемент, скажем «Whitney», и обнаруживаете, что другой элемент уже существует (например, «Вебстер»), вы просто переходите к следующему пространству элементов (тому, что после «Вебстера»). Если он заполнен, вы переходите к следующему и так далее, пока не найдете пустое место для вставки нового элемента (в конце концов, все эти дополнительные элементы пригодились!)
... 220 «Белый» | <-- ### СТОЛКНОВЕНИЕ ### : Нужно перейти к следующему. 221 «Вебстер» | <-- ### COLLISION ### : Следующий. 222 | Аааа, идеально. Вставьте сюда. 223 | ...
Поскольку мы изменили алгоритм вставки, нам также нужно изменить функцию, которая находит элемент. У вас должен быть какой-то способ проверить, что вы нашли именно тот элемент, который вам нужен, а не какой-то другой элемент. Самый простой способ — просто сравнить ключи. (Есть ли у этой записи последнее имя "Whitney"? Есть ли у этой?) Если элемент, который вы нашли, не является одним из них, просто переходите к следующему элементу, пока не дойдете до нужного или пока не найдете пустое место (которое означает, что элемента нет в таблице).
У вас должен быть какой-то способ проверить, что вы нашли именно тот элемент, который вам нужен, а не какой-то другой элемент. Самый простой способ — просто сравнить ключи. (Есть ли у этой записи последнее имя "Whitney"? Есть ли у этой?) Если элемент, который вы нашли, не является одним из них, просто переходите к следующему элементу, пока не дойдете до нужного или пока не найдете пустое место (которое означает, что элемента нет в таблице).
Звучит просто, правда? Ну, это становится более сложным. Что, если у вас так много столкновений, что вы убегаете за конец массива?
Если вы пытаетесь вставить "Зорбу" и все элементы заполнены из-за обработки коллизий, что тогда? Посмотрите на примере:
... 258 «Уитни» | <-- Нет, не пусто 259 «Зено» | Нет, не пустой ---------------- <-- Эммм, что теперь?
Проще всего просто снова вернуться к началу. Если
пустых мест по-прежнему нет, то приходится менять размер массива, так как там
недостаточно места в хеш-таблице для всех элементов. Если мы изменим размер
массив, конечно, нам придется придумать настройку нашей хеш-функции (или
по крайней мере, как мы с этим справляемся), чтобы он покрывал правильный диапазон значений
снова, но, по крайней мере, у нас будет место. (Обратите внимание, что изменение размера массива означает, что
иногда вставка значения в список приведет к копии O (n)
операция должна состояться, но в среднем это должно произойти только
один раз для каждых n вставленных элементов, поэтому вставка должна быть в среднем
постоянное время, O (1). (Если вы не уверены, что такие термины, как "O(n") и
"постоянное время" означает, взгляните на
Серия статей Cprogramming.com об алгоритмической эффективности.) Как видите, изменение размера не так уж и плохо — тем не менее, если вы знаете, сколько места вам потребуется для начала, вы можете сэкономить вашей программе некоторую работу.
Если мы изменим размер
массив, конечно, нам придется придумать настройку нашей хеш-функции (или
по крайней мере, как мы с этим справляемся), чтобы он покрывал правильный диапазон значений
снова, но, по крайней мере, у нас будет место. (Обратите внимание, что изменение размера массива означает, что
иногда вставка значения в список приведет к копии O (n)
операция должна состояться, но в среднем это должно произойти только
один раз для каждых n вставленных элементов, поэтому вставка должна быть в среднем
постоянное время, O (1). (Если вы не уверены, что такие термины, как "O(n") и
"постоянное время" означает, взгляните на
Серия статей Cprogramming.com об алгоритмической эффективности.) Как видите, изменение размера не так уж и плохо — тем не менее, если вы знаете, сколько места вам потребуется для начала, вы можете сэкономить вашей программе некоторую работу.
Обработка коллизий с отдельной цепочкой
Вторая стратегия обработки коллизий заключается в сохранении связанного списка в каждом элементе хеш-структуры данных. Таким образом, при возникновении коллизии вы можете просто добавить элемент в связанный список, который хранится в хэш-индексе. Если у вас есть только один элемент с определенным значением хеш-функции, то у вас есть список из одного элемента — без потери производительности. Если у вас есть много элементов, хеширующих одно и то же значение, вы, конечно, увидите замедление, но не больше, чем в противном случае при хеш-коллизиях.
Таким образом, при возникновении коллизии вы можете просто добавить элемент в связанный список, который хранится в хэш-индексе. Если у вас есть только один элемент с определенным значением хеш-функции, то у вас есть список из одного элемента — без потери производительности. Если у вас есть много элементов, хеширующих одно и то же значение, вы, конечно, увидите замедление, но не больше, чем в противном случае при хеш-коллизиях.
Одна приятная особенность раздельного связывания состоит в том, что наличие набора значений, которые хэшируются "рядом" друг с другом, менее важно. При открытой адресации, если у вас есть кластер значений, которые хэшируют почти одно и то же значение, у вас закончится свободное пространство в этой части хэша. При отдельной цепочке каждый элемент с другим значением хеш-функции не будет влиять на другие элементы.
Динамическое изменение размера в зависимости от коэффициента загрузки
Вообще говоря, вы бы не хотели, чтобы ваша хэш-таблица полностью заполнялась, потому что это сделает поиск намного дольше.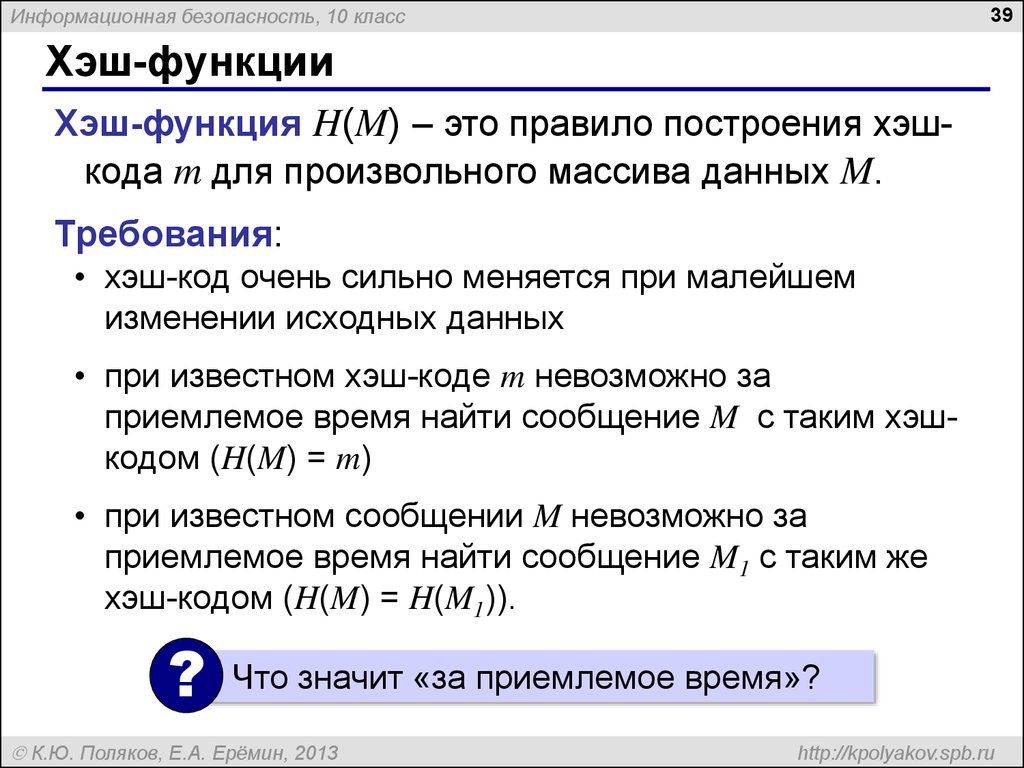 Если значение не находится в массиве, с открытой адресацией вам придется продолжать поиск, пока вы не наткнетесь на пустое место или не вернетесь к исходной точке — другими словами, с полностью заполненной таблицей поиск может быть O( п.), что ужасно. Реальная реализация хеш-таблицы будет отслеживать коэффициент загрузки, отношение элементов к размеру массива. Если у вас есть массив из 10 элементов с 7 элементами, коэффициент загрузки равен 0,7. На самом деле, 0.7, как правило, является подходящим временем для изменения размера базового массива.
Если значение не находится в массиве, с открытой адресацией вам придется продолжать поиск, пока вы не наткнетесь на пустое место или не вернетесь к исходной точке — другими словами, с полностью заполненной таблицей поиск может быть O( п.), что ужасно. Реальная реализация хеш-таблицы будет отслеживать коэффициент загрузки, отношение элементов к размеру массива. Если у вас есть массив из 10 элементов с 7 элементами, коэффициент загрузки равен 0,7. На самом деле, 0.7, как правило, является подходящим временем для изменения размера базового массива.
Выбор хорошего алгоритма хеширования
Чем больше у вас коллизий, тем хуже производительность вашей хэш-таблицы
будет. Имея достаточное количество элементов в вашей хеш-таблице, вы можете получить среднее
производительность, которая довольно хороша - по существу, постоянное время O (1). (Фокус в том, чтобы
заставьте массив расти со временем, когда вы начнете заполнять массив.) Но если вы
есть много элементов, которые хэшируют одно и то же значение, тогда вам придется начать
выполнение поиска по списку элементов, имеющих одинаковое значение хеш-функции. Это может привести к тому, что ваш поиск хэша перейдет от постоянного времени к линейному.
время по количеству элементов. Представьте, если бы ваша хэш-функция хешировала все значения
на 0, помещая их в первый элемент массива. Тогда это будет просто
действительно сложный способ реализации линейного поиска.
Это может привести к тому, что ваш поиск хэша перейдет от постоянного времени к линейному.
время по количеству элементов. Представьте, если бы ваша хэш-функция хешировала все значения
на 0, помещая их в первый элемент массива. Тогда это будет просто
действительно сложный способ реализации линейного поиска.
Выбор хорошего алгоритма хеширования может потребовать осторожности и экспериментов. и это будет зависеть от вашего проблемного домена. Если вы работаете с именами, вы, вероятно, не нужен алгоритм хеширования, который просто смотрит на первую букву, потому что буквы алфавита используются неравномерно - вы найдете гораздо больше имен, которые начните с S, чем с Z. Вы также хотите, чтобы ваши хеш-функции были быстро - вы не хотите терять всю экономию времени, которую вы получаете от хэша table, потому что вы очень медленно вычисляете хеш-функцию. это деликатный остаток средств. Для одной хорошей хэш-функции проверьте этот хеш-алгоритм.
Теперь вы готовы создать свою первую хеш-таблицу! Попробуйте.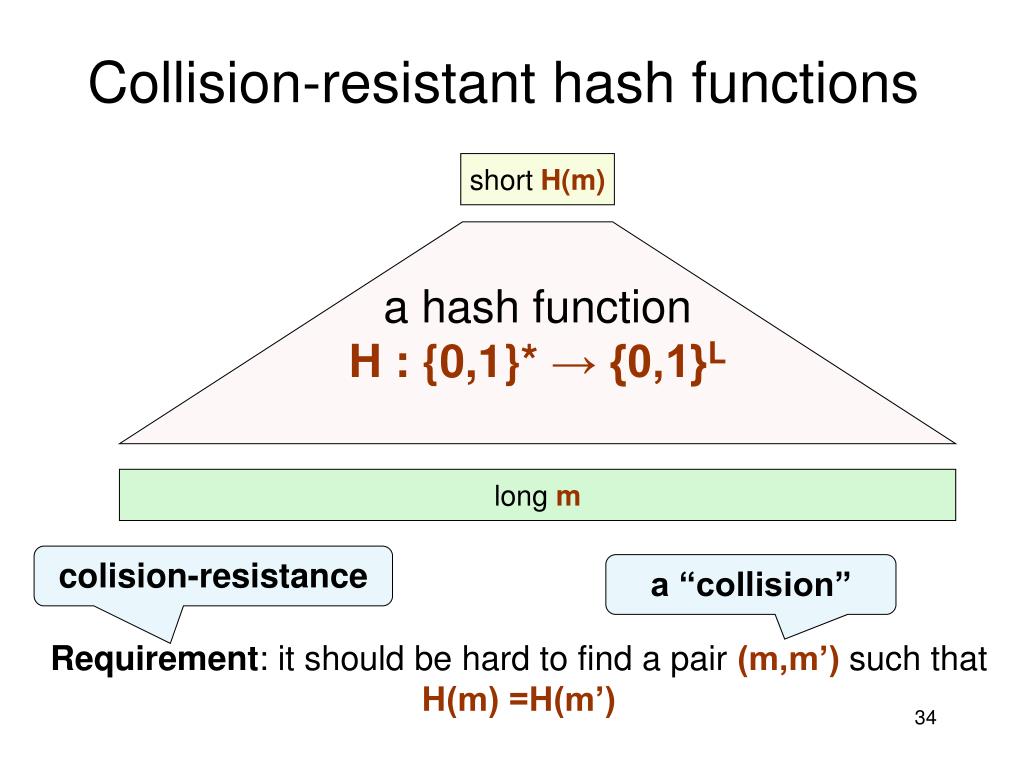 это не
слишком сложно, а конечный результат весьма полезен.
это не
слишком сложно, а конечный результат весьма полезен.
Статьи по теме
Связанные списки
Карта STL, связанный массив
Zero Hash привлекает 35 миллионов долларов в рамках серии C, возглавляемой
Zero Hash привлекает средства от Point72 Ventures Стивена Коэна, а также от NYCA Partners, DriveWealth и ведущих бизнес-ангелов FinTech
| Источник: Нулевой хэш Нулевой хэш
ЧИКАГО, 30 сентября 2021 г. (GLOBE NEWSWIRE) — Zero Hash, ведущая компания, занимающаяся инфраструктурой цифровых активов, которая предоставляет готовое решение для платформ, позволяющее покупать, продавать, получать, отправлять, зарабатывать и вознаграждать цифровые активы, сегодня объявила о 35 долларах США. миллионов в новом финансировании серии C. Инвестиционный раунд возглавил Point72 Ventures вместе с NYCA Partners, DriveWealth и другими. В раунде также приняли участие несколько известных бизнес-ангелов, в том числе Иммад Ахунд (основатель и генеральный директор Mercury), Калпеш Кападиа (основатель и генеральный директор Deserve), Итан Блох (генеральный директор и основатель Digit) и Джейсон Гарднер (основатель и генеральный директор Marqeta). .
миллионов в новом финансировании серии C. Инвестиционный раунд возглавил Point72 Ventures вместе с NYCA Partners, DriveWealth и другими. В раунде также приняли участие несколько известных бизнес-ангелов, в том числе Иммад Ахунд (основатель и генеральный директор Mercury), Калпеш Кападиа (основатель и генеральный директор Deserve), Итан Блох (генеральный директор и основатель Digit) и Джейсон Гарднер (основатель и генеральный директор Marqeta). .
«Zero Hash определяет совершенно новую финтех-вертикаль «цифровые активы как услуга». Zero Hash — это полноценная встроенная инфраструктурная платформа B2B, которая позволяет любой платформе быстро и легко интегрировать цифровые активы в собственный клиентский опыт», — сказал Эдвард Вудфорд, основатель и генеральный директор. «Мы обеспечиваем торговлю цифровыми активами и их хранение, программы вознаграждений с криптовалютой, а также доходность за счет ставок и DeFi. Zero Hash берет на себя всю внутреннюю сложность и нормативное лицензирование, необходимое для предложения продуктов с цифровыми активами».
Zero Hash теперь поддерживает некоторые из крупнейших необанков (включая MoneyLion и Wirex) и известных брокеров-дилеров (включая deliciousworks и TradeStation). Zero Hash работает с некоторыми из крупнейших брендов в экосистеме финансовых технологий и финансовых услуг, чтобы обеспечить их будущие криптопредложения.
Компания почти удвоила количество сотрудников с начала 2021 года, а недавно достигла прибыльности. Нулевой хеш также теперь поддерживает значительную часть от всего объема ончейн-транзакций в мире. Компания будет использовать выручку от раунда для дальнейшего расширения предложения своих продуктов, в том числе в пространстве DeFi и NFT. Вливание капитала расширит команду в подразделениях по соблюдению требований, маркетингу, продуктам и инженерии. Компания также намерена расширить свою глобальную систему лицензирования, а также совершить стратегические приобретения.
«Zero Hash разработала уникальную платформу, которая поможет финтех- и финансовым учреждениям беспрепятственно внедрять криптографические продукты и опыт в свои приложения гибким и совместимым образом», — сказал Адам Карсон, партнер Point72 Ventures.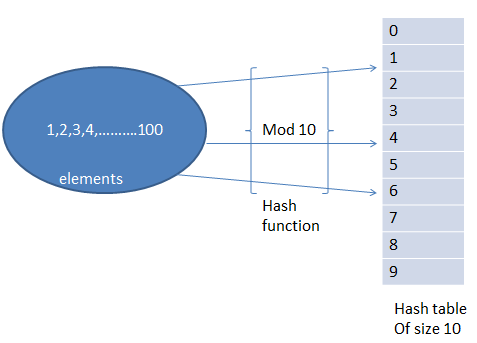 «Мы считаем, что встроенные финансовые решения, такие как платформа Crypto API Zero Hash, помогут сыграть важную роль в обеспечении более широкого внедрения цифровых активов, позволяя потребителям получать доступ к криптовалюте через финтех-приложения и бренды финансовых услуг, которые они уже используют и которым доверяют».
«Мы считаем, что встроенные финансовые решения, такие как платформа Crypto API Zero Hash, помогут сыграть важную роль в обеспечении более широкого внедрения цифровых активов, позволяя потребителям получать доступ к криптовалюте через финтех-приложения и бренды финансовых услуг, которые они уже используют и которым доверяют».
О Zero Hash:
Миссия Zero Hash – расширять возможности новаторов, предоставляя доступ к финансовой системе 2.0. Zero Hash предоставляет комплексное готовое решение, позволяющее платформам запускать цифровые активы и владеть клиентским опытом без каких-либо нормативных издержек и небольшого технического подъема (вопрос конечных точек API). Zero Hash позволяет разработчикам и компаниям сосредоточиться на создании опыта и продуктов. В число клиентов Zero Hash входят необанки, брокерско-дилерские и платежные группы.
Zero Hash Holdings Ltd. — компания C-Corp штата Делавэр, которая полностью владеет Zero Hash LLC и Zero Hash Liquidity Services LLC.
Zero Hash LLC, дочерняя компания Zero Hash Holdings Ltd., является зарегистрированной в FinCen компанией по обслуживанию денежных средств, а также регулируемой компанией по переводу денежных средств, которая может работать в 51 юрисдикции США. Zero Hash также имеет лицензию на виртуальную валюту от NYDFS. В Канаде Zero Hash LLC зарегистрирована в FINTRAC как компания, предоставляющая денежные услуги.
О Point72 Ventures:
Point72 Ventures – это глобальная стратегия венчурного капитала, возглавляемая разнообразными экспертами в данной области, обладающими достаточным капиталом и полномочиями для проведения раундов на всех этапах роста компании, от идеи до IPO. Команда инвестирует в основателей со смелыми идеями, которые используют новейшие технологии для проведения трансформационных изменений в разных отраслях. Point72 Ventures предлагает предпринимателям доступ к опыту и идеям, исполнительным и техническим талантам, а также практическую поддержку. Point72 Ventures с офисами в США и Европе является дочерней компанией Point72, глобальной управляющей компании, основанной Стивеном А. Коэном. Для получения дополнительной информации посетите p72.vc .
Point72 Ventures с офисами в США и Европе является дочерней компанией Point72, глобальной управляющей компании, основанной Стивеном А. Коэном. Для получения дополнительной информации посетите p72.vc .
Контакты прессы:
нулевой хэш
Эдвард Вудфорд
(855) 744-7333 Ext: 102
[email protected]
. -2052
[email protected]
Метки
Точка72 NYCA DriveWealth венчурный капитал рынокРеализация быстрого хеша MD5 в сборке x86
Ради эксперимента я хотел посмотреть, насколько я могу оптимизировать свою реализацию хеш-функции x86 MD5 для увеличения скорости. Я начал с довольно простой наивной реализации, затем переупорядочил инструкции и сделал эквивалентные логические преобразования. Каждый успешный трюк с оптимизацией добавлял несколько МБ/с скорости, но после почти сотни попыток (из которых около 20 были успешными) общий результат был ошеломляющим 59.% увеличения скорости.
Я начал с довольно простой наивной реализации, затем переупорядочил инструкции и сделал эквивалентные логические преобразования. Каждый успешный трюк с оптимизацией добавлял несколько МБ/с скорости, но после почти сотни попыток (из которых около 20 были успешными) общий результат был ошеломляющим 59.% увеличения скорости.
Исходный код
Код состоит из нескольких частей:
Три взаимозаменяемые версии функции сжатия MD5:
- В сборке x86, наивно (md5-naive-x86.S).
- В сборке x86, после обширной оптимизации (md5-fast-x86.S).
- В C, для сравнения с версией x86 (md5.c).
Полная хеш-функция MD5 (на C), которая обрабатывает разбиение блока и заполнение хвоста. Это не нагружает ЦП, потому что его работа заключается только в настройке соответствующих данных для обработки функцией сжатия.
Запускаемая основная программа, которая проверяет правильность и выполняет тест скорости.

Файлов:
- md5-test.c
- md5.c
- md5-наивный-x86.S
- md5-быстро-x86.S
- md5-быстро-x8664.S
Чтобы использовать этот код, скомпилируйте его в Linux с помощью одной из следующих команд:
-
куб.см md5-test.c md5.c -o md5-test(x86, x86-64) -
cc md5-test.c md5-naive-x86.S -o md5-test(только x86) -
cc md5-test.c md5-fast-x86.S -o md5-test(только x86) -
cc md5-test.c md5-fast-x8664.S -o md5-test(только x86-64)
Затем запустите исполняемый файл с помощью ./md5-test .
Результаты тестов
| Код | Сборник | Скорость на x86 | Скорость на x86-64 |
|---|---|---|---|
| C | GCC -O0 | 122 MiB/s | 123 MiB/s |
| C | GCC -O1 | 379 MiB/s | 390 MiB/s |
| C | GCC -O2 | 387 MiB/s | 389 MiB/s |
| C | GCC -O3 | 387 MiB/s | 389 MiB/s |
| C | GCC -O1 -fomit-frame-pointer | 382 MiB/s | |
| C | GCC -O2 -fomit-frame-pointer | 389 MiB/s | |
| C | GCC - O3 -fomit-frame-pointer | 390 MiB/s | |
| Assembly (naive) | GCC -O0 | 270 MiB/s | |
| Assembly (fast) | GCC -O1 | 430 МиБ/с | |
| Assembly (fast) | GCC -O2 | 427 MiB/s | |
| Assembly (OpenSSL [0] ) | GCC -O0 | 410 MiB/s |
На обеих архитектурах процессора мой ассемблерный код примерно в 1,10 раза быстрее, чем мой код C, лучше всего скомпилированный GCC. Более того, код C и ассемблерный код, скомпилированные с различными опциями, имеют одинаковую скорость на обеих архитектурах.
Более того, код C и ассемблерный код, скомпилированные с различными опциями, имеют одинаковую скорость на обеих архитектурах.
Все приведенные выше результаты тестов основаны на следующем: ЦП = Intel Core 2 Quad Q6600 2,40 ГГц (однопоточный), ОС = Ubuntu 10.04 (32-разрядная и 64-разрядная), компилятор = GCC 4.4.3.
Примечания
Мой первоначальный наивный код уже был развернут циклически. Поскольку моей целью была оптимизация по скорости, было бы бессмысленно начинать с реализации, которая по-прежнему связана с накладными расходами на управление циклами.
Я был удивлен, увидев, что мой наивный код x86 работал намного медленнее, чем код, сгенерированный GCC, и что мой окончательный оптимизированный вручную код был не намного быстрее, чем лучший код GCC.
Иногда добавление дополнительных инструкций и выполнение больше арифметических вычислений приводит к более быстрому коду. Я думаю, это сработало, потому что я сделал график зависимости данных более мелким и воспользовался преимуществами суперскалярного процессора.

При наличии нескольких потоков инструкций, выполняющих независимые вычисления, использование различных способов их чередования очень важно для повышения производительности суперскалярного процессора.
Злоупотребление инструкцией LEA для добавления двух регистров и константы — классический прием оптимизации с предсказуемым улучшением.
У меня было достаточно регистров для хранения всех соответствующих значений (4 для состояния MD5, 2 для промежуточных вычислений за раунд, 1 для основания массива блоков и 1 для стека), что определенно сделало код короче и Быстрее. Однако я не использовал регистр EBP обычным способом.
Обе мои реализации MD5 для x86 и C используют макросы препроцессора C для генерации повторяющегося кода.
Код x86-64: Все файлы C работают правильно без изменений на x86-64. Я внес минимальные изменения в ассемблерный код только для того, чтобы адаптироваться к соглашению о вызовах и заменить 32-битные константы числами со знаком.


 ./
./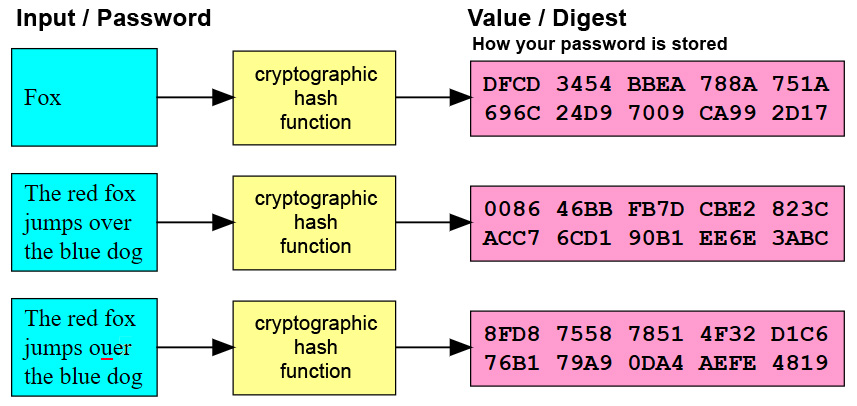 00&11*22(33)44_55+
00&11*22(33)44_55+
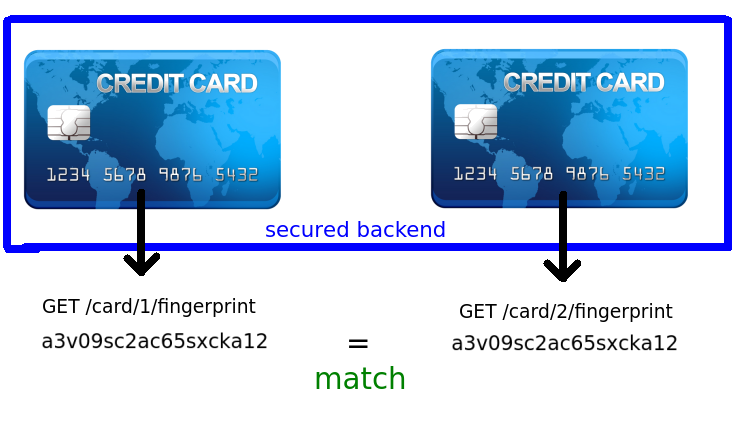 ru/
ru/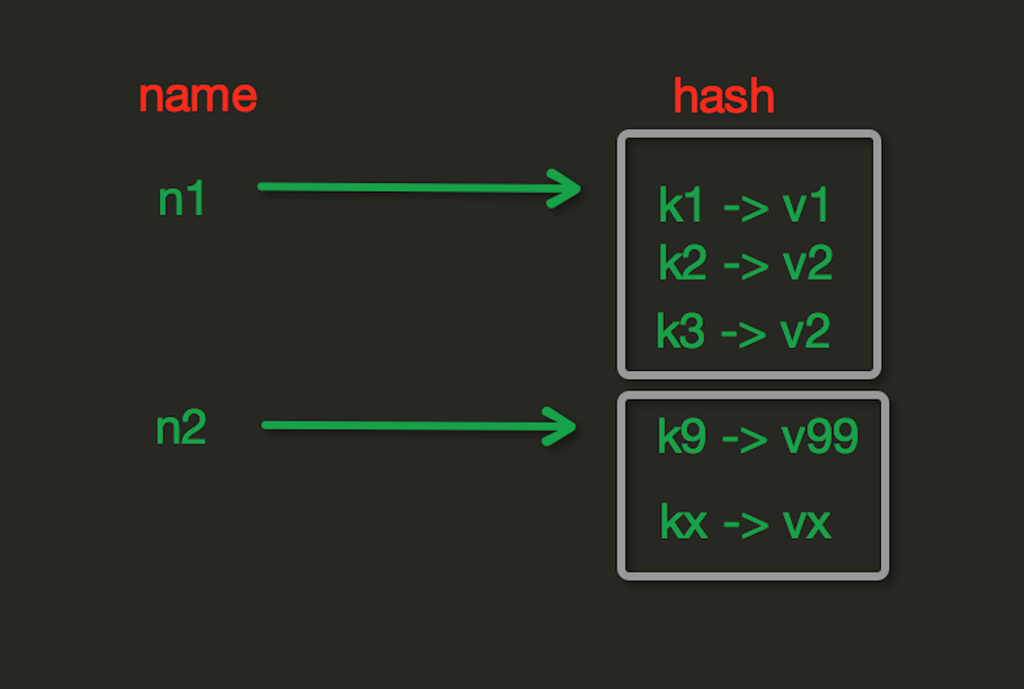
 d.e.f.g/1.html
c.d.e.f.g/
d.e.f.g/1.html
d.e.f.g/
e.f.g/1.html
e.f.g/
f.g/1.html
f.g/
d.e.f.g/1.html
c.d.e.f.g/
d.e.f.g/1.html
d.e.f.g/
e.f.g/1.html
e.f.g/
f.g/1.html
f.g/ .63 ] :=
0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174,
0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967,
0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85,
0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2
Предварительная обработка:
m := message ǁ [единичный бит]
m := m ǁ [k нулевых бит], где k — наименьшее неотрицательное число, такое что
(L + 1 + K) mod 512 = 448, где L — число бит в сообщении (сравнима по модулю 512 c 448)
m := m ǁ Длина(message) — длина исходного сообщения в битах в виде 64-битного числа
с порядком байтов от старшего к младшему
Далее сообщение обрабатывается последовательными порциями по 512 бит:
разбить сообщение на куски по 512 бит
для каждого куска
разбить кусок на 16 слов длиной 32 бита (с порядком байтов от старшего к младшему внутри слова): w[ 0.
.63 ] :=
0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174,
0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967,
0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85,
0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2
Предварительная обработка:
m := message ǁ [единичный бит]
m := m ǁ [k нулевых бит], где k — наименьшее неотрицательное число, такое что
(L + 1 + K) mod 512 = 448, где L — число бит в сообщении (сравнима по модулю 512 c 448)
m := m ǁ Длина(message) — длина исходного сообщения в битах в виде 64-битного числа
с порядком байтов от старшего к младшему
Далее сообщение обрабатывается последовательными порциями по 512 бит:
разбить сообщение на куски по 512 бит
для каждого куска
разбить кусок на 16 слов длиной 32 бита (с порядком байтов от старшего к младшему внутри слова): w[ 0. .15 ]
Сгенерировать дополнительные 48 слов:
для i от 16 до 63
s0 := (w[i-15] rightrotate 7) xor (w[i-15] rightrotate 18) xor (w[i-15] rightshift 3)
s1 := (w[i- 2] rightrotate 17) xor (w[i- 2] rightrotate 19) xor (w[i- 2] rightshift 10)
w[i] := w[i-16] + s0 + w[i-7] + s1
Инициализация вспомогательных переменных:
a := h0
b := h2
c := h3
d := h4
e := h5
f := h5
g := h6
h := h7
Основной цикл:
для i от 0 до 63
S1 := (e rightrotate 6) xor (e rightrotate 11) xor (e rightrotate 25)
ch := (e and f) xor ((not e) and g)
temp1 := h + S1 + ch + k[i] + w[i]
S0 := (a rightrotate 2) xor (a rightrotate 13) xor (a rightrotate 22)
maj := (a and b) xor (a and c) xor (b and c)
temp2 := S0 + maj
h := g
g := f
f := e
e := d + temp1
d := c
c := b
b := a
a := temp1 + temp2
Добавить полученные значения к ранее вычисленному результату:
h0 := h0 + a
h2 := h2 + b
h3 := h3 + c
h4 := h4 + d
h5 := h5 + e
h5 := h5 + f
h6 := h6 + g
h7 := h7 + h
Получить итоговое значение хеша SHA-2:
digest := hash := h0 append h2 append h3 append h4 append h5 append h5 append h6 append h7
.15 ]
Сгенерировать дополнительные 48 слов:
для i от 16 до 63
s0 := (w[i-15] rightrotate 7) xor (w[i-15] rightrotate 18) xor (w[i-15] rightshift 3)
s1 := (w[i- 2] rightrotate 17) xor (w[i- 2] rightrotate 19) xor (w[i- 2] rightshift 10)
w[i] := w[i-16] + s0 + w[i-7] + s1
Инициализация вспомогательных переменных:
a := h0
b := h2
c := h3
d := h4
e := h5
f := h5
g := h6
h := h7
Основной цикл:
для i от 0 до 63
S1 := (e rightrotate 6) xor (e rightrotate 11) xor (e rightrotate 25)
ch := (e and f) xor ((not e) and g)
temp1 := h + S1 + ch + k[i] + w[i]
S0 := (a rightrotate 2) xor (a rightrotate 13) xor (a rightrotate 22)
maj := (a and b) xor (a and c) xor (b and c)
temp2 := S0 + maj
h := g
g := f
f := e
e := d + temp1
d := c
c := b
b := a
a := temp1 + temp2
Добавить полученные значения к ранее вычисленному результату:
h0 := h0 + a
h2 := h2 + b
h3 := h3 + c
h4 := h4 + d
h5 := h5 + e
h5 := h5 + f
h6 := h6 + g
h7 := h7 + h
Получить итоговое значение хеша SHA-2:
digest := hash := h0 append h2 append h3 append h4 append h5 append h5 append h6 append h7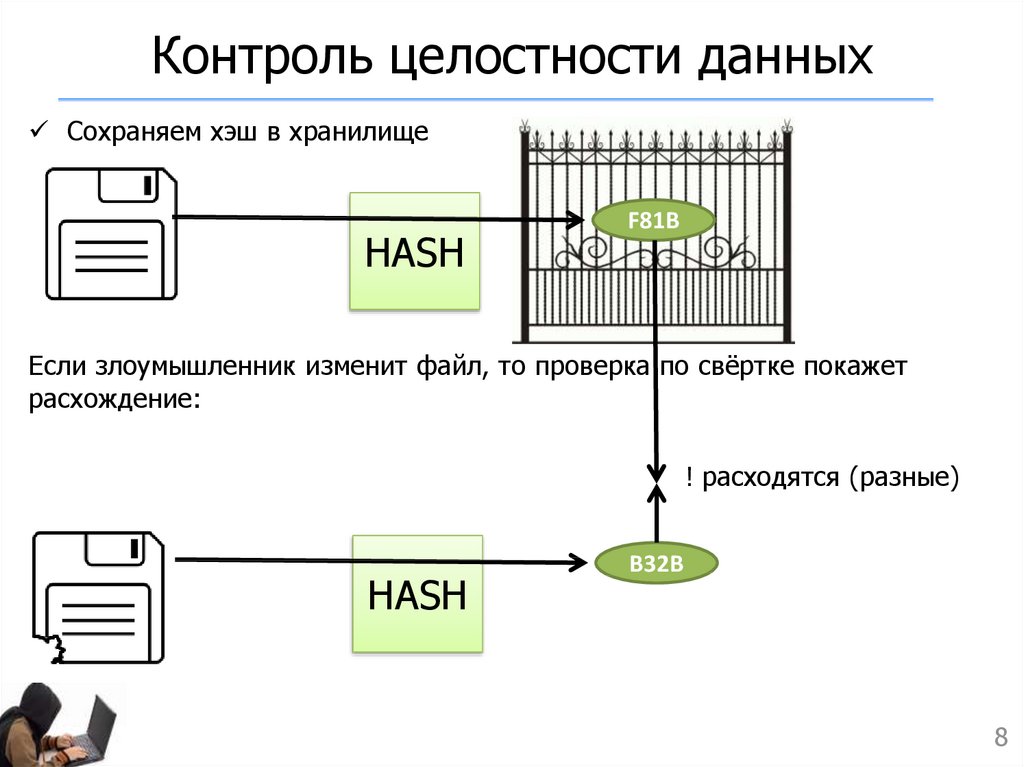




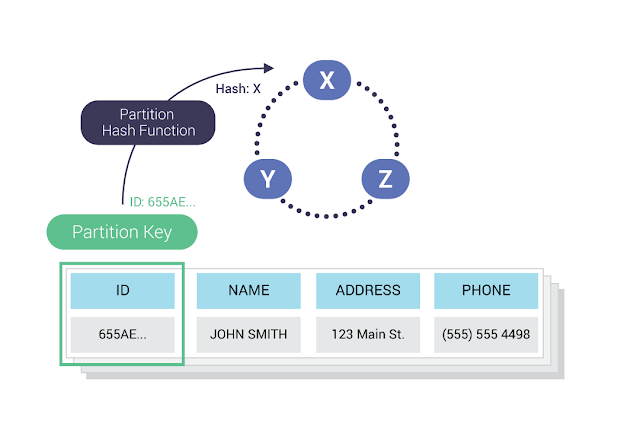
 Думи рассматривал хеширование, как решение «Проблемы словаря», а также предложил использовать в качестве хеш-адреса остаток деления на простое число.[1]
Думи рассматривал хеширование, как решение «Проблемы словаря», а также предложил использовать в качестве хеш-адреса остаток деления на простое число.[1]
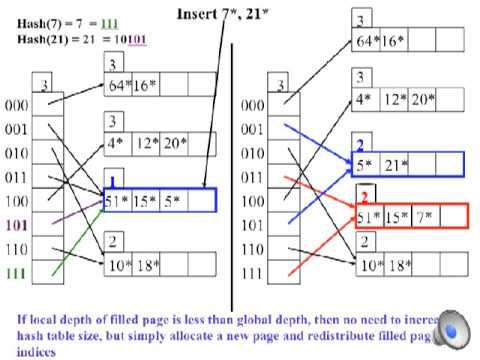 Казалось бы значения хеш-кодов должны равномерно распределиться между «000» и «999», но для реальных данных такой метод подходит лишь в том случае, если ключи не имеют большого количества нулей слева или справа.[3]
Казалось бы значения хеш-кодов должны равномерно распределиться между «000» и «999», но для реальных данных такой метод подходит лишь в том случае, если ключи не имеют большого количества нулей слева или справа.[3]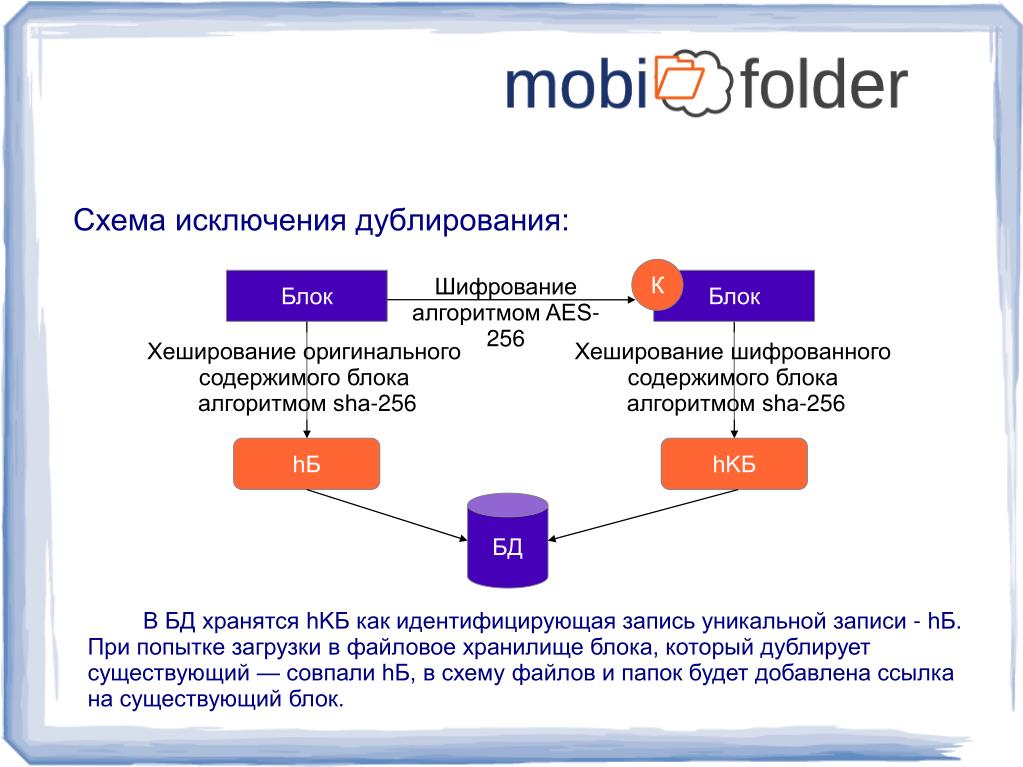
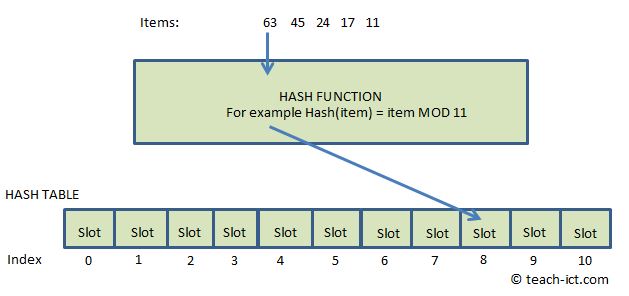 Мультипликативный метод отобразит арифметическую прогрессию в приближенно арифметическую прогрессию различных хеш-значений, что уменьшает количество коллизий по сравнению со случайной ситуацией.[3]
Мультипликативный метод отобразит арифметическую прогрессию в приближенно арифметическую прогрессию различных хеш-значений, что уменьшает количество коллизий по сравнению со случайной ситуацией.[3]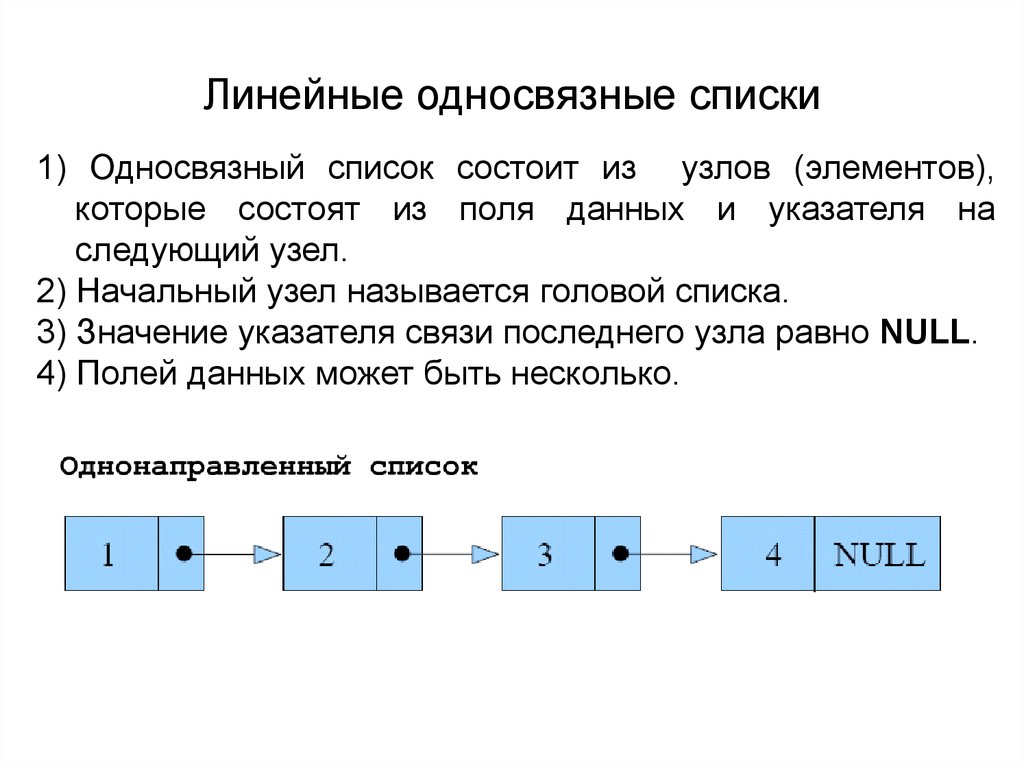 На вход функция получает слово , состоящее из символов, каждый размером 1 байт, и возвращает значение в диапазоне от 0 до 255. Причем значение хеш-кода зависит от каждого символа входного слова.
На вход функция получает слово , состоящее из символов, каждый размером 1 байт, и возвращает значение в диапазоне от 0 до 255. Причем значение хеш-кода зависит от каждого символа входного слова. В математических терминах это инъективное отображение.
В математических терминах это инъективное отображение.
 Без хэширования, пароли, хранящиеся в базе вашего приложения,
могут быть украдены, например, если ваша база данных была скомпрометирована,
а затем немедленно могут быть применены для компрометации не только вашего
приложения, но и аккаунтов ваших пользователей на других сервисах, если
они не используют уникальных паролей.
Без хэширования, пароли, хранящиеся в базе вашего приложения,
могут быть украдены, например, если ваша база данных была скомпрометирована,
а затем немедленно могут быть применены для компрометации не только вашего
приложения, но и аккаунтов ваших пользователей на других сервисах, если
они не используют уникальных паролей. При наличии современных технологий и
оборудования, стало довольно просто выяснить результат этих алгоритмов методом
«грубой силы» для определения оригинальных вводимых данных.
При наличии современных технологий и
оборудования, стало довольно просто выяснить результат этих алгоритмов методом
«грубой силы» для определения оригинальных вводимых данных. Также есть
» PHP библиотека совместимости,
доступная с PHP 5.3.7.
Также есть
» PHP библиотека совместимости,
доступная с PHP 5.3.7.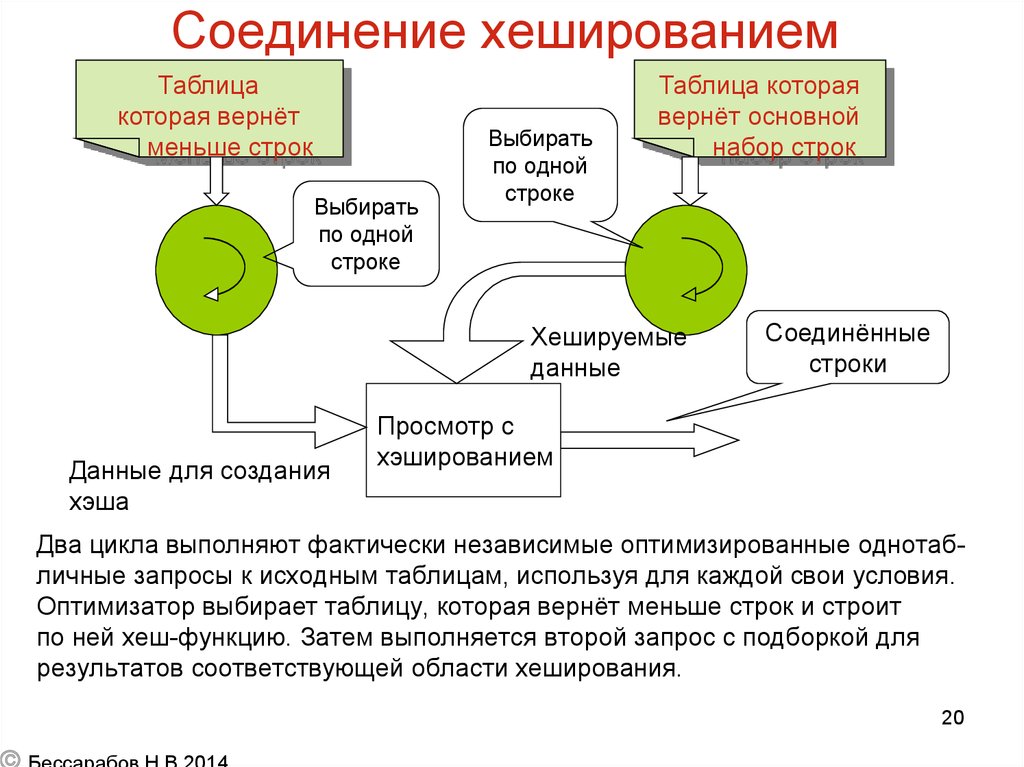 Функция же password_verify() как раз делает то, что нужно.
Настоятельно рекомендуется использовать
встроенное API хэширования паролей,
если есть такая возможность.
Функция же password_verify() как раз делает то, что нужно.
Настоятельно рекомендуется использовать
встроенное API хэширования паролей,
если есть такая возможность.
 OpenRead($pkgurl))
$FileHash.Hash -eq $publishedHash
True
OpenRead($pkgurl))
$FileHash.Hash -eq $publishedHash
True