Хеширование – что это и зачем
Криптографические хеш-функции — незаменимый и повсеместно распространенный инструмент, используемый для выполнения целого ряда задач, включая аутентификацию, проверку целостности данных, защиту файлов и даже обнаружение зловредного ПО. Существует масса алгоритмов хеширования, отличающихся криптостойкостью, сложностью, разрядностью и другими свойствами. Считается, что идея хеширования принадлежит сотруднику IBM, появилась около 50 лет назад и с тех пор не претерпела принципиальных изменений. Зато в наши дни хеширование обрело массу новых свойств и используется в очень многих областях информационных технологий.
Что такое хеш?
Если коротко, то криптографическая хеш-функция, чаще называемая просто хешем, — это математический алгоритм, преобразовывающий произвольный массив данных в состоящую из букв и цифр строку фиксированной длины. Причем при условии использования того же типа хеша длина эта будет оставаться неизменной, вне зависимости от объема вводных данных. Криптостойкой хеш-функция может быть только в том случае, если выполняются главные требования: стойкость к восстановлению хешируемых данных и стойкость к коллизиям, то есть образованию из двух разных массивов данных двух одинаковых значений хеша. Интересно, что под данные требования формально не подпадает ни один из существующих алгоритмов, поскольку нахождение обратного хешу значения — вопрос лишь вычислительных мощностей. По факту же в случае с некоторыми особо продвинутыми алгоритмами этот процесс может занимать чудовищно много времени.
Как работает хеш?
Например, мое имя — Brian — после преобразования хеш-функцией SHA-1 (одной из самых распространенных наряду с MD5 и SHA-2) при помощи онлайн-генератора будет выглядеть так: 75c450c3f963befb912ee79f0b63e563652780f0. Как вам скажет, наверное, любой другой Брайан, данное имя нередко пишут с ошибкой, что в итоге превращает его в слово brain (мозг). Это настолько частая опечатка, что однажды я даже получил настоящие водительские права, на которых вместо моего имени красовалось Brain Donohue. Впрочем, это уже другая история. Так вот, если снова воспользоваться алгоритмом SHA-1, то слово Brain трансформируется в строку 97fb724268c2de1e6432d3816239463a6aaf8450. Как видите, результаты значительно отличаются друг от друга, даже несмотря на то, что разница между моим именем и названием органа центральной нервной системы заключается лишь в последовательности написания двух гласных. Более того, если я преобразую тем же алгоритмом собственное имя, но написанное уже со строчной буквы, то результат все равно не будет иметь ничего общего с двумя предыдущими: 760e7dab2836853c63805033e514668301fa9c47.
Впрочем, кое-что общее у них все же есть: каждая строка имеет длину ровно 40 символов. Казалось бы, ничего удивительного, ведь все введенные мною слова также имели одинаковую длину — 5 букв. Однако если вы захешируете весь предыдущий абзац целиком, то все равно получите последовательность, состоящую ровно из 40 символов: c5e7346089419bb4ab47aaa61ef3755d122826e2. То есть 1128 символов, включая пробелы, были ужаты до строки той же длины, что и пятибуквенное слово. То же самое произойдет даже с полным собранием сочинений Уильяма Шекспира: на выходе вы получите строку из 40 букв и цифр. При всем этом не может существовать двух разных массивов данных, которые преобразовывались бы в одинаковый хеш.
Вот как это выглядит, если изобразить все вышесказанное в виде схемы:
Для чего используется хеш?
Отличный вопрос. Однако ответ не так прост, поскольку криптохеши используются для огромного количества вещей.
Для нас с вами, простых пользователей, наиболее распространенная область применения хеширования — хранение паролей. К примеру, если вы забыли пароль к какому-либо онлайн-сервису, скорее всего, придется воспользоваться функцией восстановления пароля. В этом случае вы, впрочем, не получите свой старый пароль, поскольку онлайн-сервис на самом деле не хранит пользовательские пароли в виде обычного текста. Вместо этого он хранит их в виде хеш-значений. То есть даже сам сервис не может знать, как в действительности выглядит ваш пароль. Исключение составляют только те случаи, когда пароль очень прост и его хеш-значение широко известно в кругах взломщиков. Таким образом, если вы, воспользовавшись функцией восстановления, вдруг получили старый пароль в открытом виде, то можете быть уверены: используемый вами сервис не хеширует пользовательские пароли, что очень плохо.
Вы даже можете провести простой эксперимент: попробуйте при помощи специального сайта произвести преобразование какого-нибудь простого пароля вроде «123456» или «password» из их хеш-значений (созданных алгоритмом MD5) обратно в текст. Вероятность того, что в базе хешей найдутся данные о введенных вами простых паролях, очень высока. В моем случае хеши слов «brain» (8b373710bcf876edd91f281e50ed58ab) и «Brian» (4d236810821e8e83a025f2a83ea31820) успешно распознались, а вот хеш предыдущего абзаца — нет. Отличный пример, как раз для тех, кто все еще использует простые пароли.
Еще один пример, покруче. Не так давно по тематическим сайтам прокатилась новость о том, что популярный облачный сервис Dropbox заблокировал одного из своих пользователей за распространение контента, защищенного авторскими правами. Герой истории тут же написал об этом в твиттере, запустив волну негодования среди пользователей сервиса, ринувшихся обвинять Dropbox в том, что он якобы позволяет себе просматривать содержимое клиентских аккаунтов, хотя не имеет права этого делать.
Впрочем, необходимости в этом все равно не было. Дело в том, что владелец защищенного копирайтом контента имел на руках хеш-коды определенных аудио- и видеофайлов, запрещенных к распространению, и занес их в черный список хешей. Когда пользователь предпринял попытку незаконно распространить некий контент, автоматические сканеры Dropbox засекли файлы, чьи хеши оказались в пресловутом списке, и заблокировали возможность их распространения.
Где еще можно использовать хеш-функции помимо систем хранения паролей и защиты медиафайлов? На самом деле задач, где используется хеширование, гораздо больше, чем я знаю и тем более могу описать в одной статье. Однако есть одна особенная область применения хешей, особо близкая нам как сотрудникам «Лаборатории Касперского»: хеширование широко используется для детектирования зловредных программ защитным ПО, в том числе и тем, что выпускается нашей компанией.
Как при помощи хеша ловить вирусы?
Примерно так же, как звукозаписывающие лейблы и кинопрокатные компании защищают свой контент, сообщество создает черные списки зловредов (многие из них доступны публично), а точнее, списки их хешей. Причем это может быть хеш не всего зловреда целиком, а лишь какого-либо его специфического и хорошо узнаваемого компонента. С одной стороны, это позволяет пользователю, обнаружившему подозрительный файл, тут же внести его хеш-код в одну из подобных открытых баз данных и проверить, не является ли файл вредоносным. С другой — то же самое может сделать и антивирусная программа, чей «движок» использует данный метод детектирования наряду с другими, более сложными.
Криптографические хеш-функции также могут использоваться для защиты от фальсификации передаваемой информации. Иными словами, вы можете удостовериться в том, что файл по пути куда-либо не претерпел никаких изменений, сравнив его хеши, снятые непосредственно до отправки и сразу после получения. Если данные были изменены даже всего на 1 байт, хеш-коды будут отличаться, как мы уже убедились в самом начале статьи. Недостаток такого подхода лишь в том, что криптографическое хеширование требует больше вычислительных мощностей или времени на вычисление, чем алгоритмы с отсутствием криптостойкости. Зато они в разы надежнее.
Кстати, в повседневной жизни мы, сами того не подозревая, иногда пользуемся простейшими хешами. Например, представьте, что вы совершаете переезд и упаковали все вещи по коробкам и ящикам. Погрузив их в грузовик, вы фиксируете количество багажных мест (то есть, по сути, количество коробок) и запоминаете это значение. По окончании выгрузки на новом месте, вместо того чтобы проверять наличие каждой коробки по списку, достаточно будет просто пересчитать их и сравнить получившееся значение с тем, что вы запомнили раньше. Если значения совпали, значит, ни одна коробка не потерялась.
Что такое Хэширование? Под капотом блокчейна / Хабр
Очень многие из вас, наверное, уже слышали о технологии блокчейн, однако важно знать о принципе работы хэширования в этой системе. Технология Блокчейн является одним из самых инновационных открытий прошлого века. Мы можем так заявить без преувеличения, так как наблюдаем за влиянием, которое оно оказало на протяжении последних нескольких лет, и влиянием, которое оно будет иметь в будущем. Для того чтобы понять устройство и предназначение самой технологии блокчейн, сначала мы должны понять один из основных принципов создания блокчейна.Так что же такое хэширование?
Input- вводимые данные, hash- хэш
Посмотрим, как работает процесс хэширования. Мы собираемся внести определенные данные. Для этого, мы будем использовать SHA-256 (безопасный алгоритм хэширования из семейства SHA-2, размером 256 бит).
Как видите, в случае SHA-256, независимо от того, насколько объёмные ваши вводимые данные (input), вывод всегда будет иметь фиксированную 256-битную длину. Это крайне необходимо, когда вы имеете дело с огромным количеством данных и транзакций. Таким образом, вместо того, чтобы помнить вводимые данные, которые могут быть огромными, вы можете просто запомнить хэш и отслеживать его. Прежде чем продолжать, необходимо познакомиться с различными свойствами функций хэширования и тем, как они реализуются в блокчейн.
Криптографические хэш-функции
Криптографическая хэш-функция — это специальный класс хэш-функций, который имеет различные свойства, необходимые для криптографии. Существуют определенные свойства, которые должна иметь криптографическая хэш-функция, чтобы считаться безопасной. Давайте разберемся с ними по очереди.
Свойство 1: Детерминированние
Это означает, что независимо от того, сколько раз вы анализируете определенный вход через хэш-функцию, вы всегда получите тот же результат. Это важно, потому что если вы будете получать разные хэши каждый раз, будет невозможно отслеживать ввод.
Свойство 2: Быстрое вычисление
Хэш-функция должна быть способна быстро возвращать хэш-вход. Если процесс не достаточно быстрый, система просто не будет эффективна.
Свойство 3: Сложность обратного вычисления
Сложность обратного вычисления означает, что с учетом H (A) невозможно определить A, где A – вводимые данные и H(А) – хэш. Обратите внимание на использование слова “невозможно” вместо слова “неосуществимо”. Мы уже знаем, что определить исходные данные по их хэш-значению можно. Возьмем пример.
Предположим, вы играете в кости, а итоговое число — это хэш числа, которое появляется из кости. Как вы сможете определить, что такое исходный номер? Просто все, что вам нужно сделать, — это найти хэши всех чисел от 1 до 6 и сравнить. Поскольку хэш-функции детерминированы, хэш конкретного номера всегда будет одним и тем же, поэтому вы можете просто сравнить хэши и узнать исходный номер.
Но это работает только тогда, когда данный объем данных очень мал. Что происходит, когда у вас есть огромный объем данных? Предположим, вы имеете дело с 128-битным хэшем. Единственный метод, с помощью которого вы должны найти исходные данные, — это метод «грубой силы». Метод «грубой силы» означает, что вам нужно выбрать случайный ввод, хэшировать его, а затем сравнить результат с исследуемым хэшем и повторить, пока не найдете совпадение.
Итак, что произойдет, если вы используете этот метод?
- Лучший сценарий: вы получаете свой ответ при первой же попытке. Вы действительно должны быть самым счастливым человеком в мире, чтобы это произошло. Вероятность такого события ничтожна.
- Худший сценарий: вы получаете ответ после 2 ^ 128 — 1 раз. Это означает, что вы найдете свой ответ в конце всех вычислений данных (один шанс из 340282366920938463463374607431768211456)
- Средний сценарий: вы найдете его где-то посередине, поэтому в основном после 2 ^ 128/2 = 2 ^ 127 попыток. Иными словами, это огромное количество.
Таким образом, можно пробить функцию обратного вычисления с помощью метода «грубой силы», но потребуется очень много времени и вычислительных ресурсов, поэтому это бесполезно.
Свойство 4: Небольшие изменения в вводимых данных изменяют хэш
Даже если вы внесете небольшие изменения в исходные данные, изменения, которые будут отражены в хэше, будут огромными. Давайте проверим с помощью SHA-256:
Видите? Даже если вы только что изменили регистр первой буквы, обратите внимание, насколько это повлияло на выходной хэш. Это необходимая функция, так как свойство хэширования приводит к одному из основных качеств блокчейна – его неизменности (подробнее об этом позже).
Свойство 5: Коллизионная устойчивость
Учитывая два разных типа исходных данных A и B, где H (A) и H (B) являются их соответствующими хэшами, для H (A) не может быть равен H (B). Это означает, что, по большей части, каждый вход будет иметь свой собственный уникальный хэш. Почему мы сказали «по большей части»? Давайте поговорим об интересной концепции под названием «Парадокс дня рождения».
Что такое парадокс дня рождения?
Если вы случайно встречаете незнакомца на улице, шанс, что у вас совпадут даты дней рождений, очень мал. Фактически, если предположить, что все дни года имеют такую же вероятность дня рождения, шансы другого человека, разделяющего ваш день рождения, составляют 1/365 или 0,27%. Другими словами, он действительно низкий.
Однако, к примеру, если собрать 20-30 человек в одной комнате, шансы двух людей, разделяющих тот же день, резко вырастает. На самом деле, шанс для 2 человек 50-50, разделяющих тот же день рождения при таком раскладе.
Как это применяется в хэшировании?
Предположим, у вас есть 128-битный хэш, который имеет 2 ^ 128 различных вероятностей. Используя парадокс дня рождения, у вас есть 50% шанс разбить коллизионную устойчивость sqrt (2 ^ 128) = 2 ^ 64.
Как вы заметили, намного легче разрушить коллизионную устойчивость, нежели найти обратное вычисление хэша. Для этого обычно требуется много времени. Итак, если вы используете такую функцию, как SHA-256, можно с уверенностью предположить, что если H (A) = H (B), то A = B.
Свойство 6: Головоломка
Свойства Головоломки имеет сильнейшее воздействие на темы касающиеся криптовалют (об этом позже, когда мы углубимся в крипто схемы). Сначала давайте определим свойство, после чего мы подробно рассмотрим каждый термин.
Для каждого выхода «Y», если k выбран из распределения с высокой мин-энтропией, невозможно найти вводные данные x такие, что H (k | x) = Y.
Вероятно, это, выше вашего понимания! Но все в порядке, давайте теперь разберемся с этим определением.
В чем смысл «высокой мин-энтропии»?
Это означает, что распределение, из которого выбрано значение, рассредоточено так, что мы выбираем случайное значение, имеющее незначительную вероятность. В принципе, если вам сказали выбрать число от 1 до 5, это низкое распределение мин-энтропии. Однако, если бы вы выбрали число от 1 до бесконечности, это — высокое распределение мин-энтропии.
Что значит «к|х»?
«|» обозначает конкатенацию. Конкатенация означает объединение двух строк. Например. Если бы я объединила «голубое» и «небо», то результатом было бы «голубоенебо».
Итак, давайте вернемся к определению.
Предположим, у вас есть выходное значение «Y». Если вы выбираете случайное значение «К», невозможно найти значение X, такое, что хэш конкатенации из K и X, выдаст в результате Y.
Еще раз обратите внимание на слово «невозможно», но не исключено, потому что люди занимаются этим постоянно. На самом деле весь процесс майнинга работает на этом (подробнее позже).
Примеры криптографических хэш-функций:
- MD 5: Он производит 128-битный хэш. Коллизионная устойчивость была взломана после ~2^21 хэша.
- SHA 1: создает 160-битный хэш. Коллизионная устойчивость была взломана после ~2^61 хэша.
- SHA 256: создает 256-битный хэш. В настоящее время используется в Биткоине.
- Keccak-256: Создает 256-битный хэш и в настоящее время используется Эфириуме.
Хэширование и структуры данных.
Структура данных — это специализированный способ хранения данных. Если вы хотите понять, как работает система «блокчейн», то есть два основных свойства структуры данных, которые могут помочь вам в этом:
1. Указатели
2. Связанные списки
Указатели
В программировании указатели — это переменные, в которых хранится адрес другой переменной, независимо от используемого языка программирования.
Например, запись int a = 10 означает, что существует некая переменная «a», хранящая в себе целочисленное значение равное 10. Так выглядит стандартная переменная.
Однако, вместо сохранения значений, указатели хранят в себе адреса других переменных. Именно поэтому они и получили свое название, потому как буквально указывают на расположение других переменных.
Связанные списки
Связанный список является одним из наиболее важных элементов в структурах данных. Структура связанного списка выглядит следующим образом:
*Head – заголовок; Data – данные; Pointer – указатель; Record – запись; Null – ноль
Это последовательность блоков, каждый из которых содержит данные, связанные со следующим с помощью указателя. Переменная указателя в данном случае содержит адрес следующего узла, благодаря чему выполняется соединение. Как показано на схеме, последний узел отмечен нулевым указателем, что означает, что он не имеет значения.
Важно отметить, что указатель внутри каждого блока содержит адрес предыдущего. Так формируется цепочка. Возникает вопрос, что это значит для первого блока в списке и где находится его указатель?
Первый блок называется «блоком генезиса», а его указатель находится в самой системе. Выглядит это следующим образом:
*H ( ) – Хэшированные указатели изображаются таким образом
Если вам интересно, что означает «хэш-указатель», то мы с радостью поясним.
Как вы уже поняли, именно на этом основана структура блокчейна. Цепочка блоков представляет собой связанный список. Рассмотрим, как устроена структура блокчейна:
* Hash of previous block header – хэш предыдущего заголовка блока; Merkle Root – Корень Меркла; Transactions – транзакции; Simplified Bitcoin Blockchain – Упрощенный блокчейн Биткоина.
Блокчейн представляет собой связанный список, содержащий данные, а так же указатель хэширования, указывающий на предыдущий блок, создавая таким образов связную цепочку. Что такое хэш-указатель? Он похож на обычный указатель, но вместо того, чтобы просто содержать адрес предыдущего блока, он также содержит хэш данных, находящихся внутри предыдущего блока. Именно эта небольшая настройка делает блокчейн настолько надежным. Представим на секунду, что хакер атакует блок 3 и пытается изменить данные. Из-за свойств хэш-функций даже небольшое изменение в данных сильно изменит хэш. Это означает, что любые незначительные изменения, произведенные в блоке 3, изменят хэш, хранящийся в блоке 2, что, в свою очередь, изменит данные и хэш блока 2, а это приведет к изменениям в блоке 1 и так далее. Цепочка будет полностью изменена, а это невозможно. Но как же выглядит заголовок блока?
* Prev_Hash – предыдущий хэш; Tx – транзакция; Tx_Root – корень транзакции; Timestamp – временная отметка; Nonce – уникальный символ.
Заголовок блока состоит из следующих компонентов:
· Версия: номер версии блока
· Время: текущая временная метка
· Текущая сложная цель (См. ниже)
· Хэш предыдущего блока
· Уникальный символ (См. ниже)
· Хэш корня Меркла
Прямо сейчас, давайте сосредоточимся на том, что из себя представляет хэш корня Меркла. Но до этого нам необходимо разобраться с понятием Дерева Меркла.
Что такое Дерево Меркла?
Источник: Wikipedia
На приведенной выше диаграмме показано, как выглядит дерево Меркла. В дереве Меркла каждый нелистовой узел является хэшем значений их дочерних узлов.
Листовой узел: Листовые узлы являются узлами в самом нижнем ярусе дерева. Поэтому, следуя приведенной выше схеме, листовыми будут считаться узлы L1, L2, L3 и L4.
Дочерние узлы: Для узла все узлы, находящиеся ниже его уровня и которые входят в него, являются его дочерними узлами. На диаграмме узлы с надписью «Hash 0-0» и «Hash 0-1» являются дочерними узлами узла с надписью «Hash 0».
Корневой узел: единственный узел, находящийся на самом высоком уровне, с надписью «Top Hash» является корневым.
Так какое же отношение Дерево Меркла имеет к блокчейну?
Каждый блок содержит большое количество транзакций. Будет очень неэффективно хранить все данные внутри каждого блока в виде серии. Это сделает поиск какой-либо конкретной операции крайне громоздким и займет много времени. Но время, необходимое для выяснения, на принадлежность конкретной транзакции к этому блоку или нет, значительно сокращается, если Вы используете дерево Меркла.
Давайте посмотрим на пример на следующем Хэш-дереве:
Изображение предоставлено проектом: Coursera
Теперь предположим, я хочу узнать, принадлежат ли эти данные блоку или нет:
Вместо того, чтобы проходить через сложный процесс просматривания каждого отдельного процесса хэша, а также видеть принадлежит ли он данным или нет, я просто могу отследить след хэша, ведущий к данным:
Это значительно сокращает время.
Хэширование в майнинге: крипто-головоломки.
Когда мы говорим «майнинг», в основном, это означает поиск нового блока, который будет добавлен в блокчейн. Майнеры всего мира постоянно работают над тем, чтобы убедиться, что цепочка продолжает расти. Раньше людям было проще работать, используя для майнинга лишь свои ноутбуки, но со временем они начали формировать «пулы», объединяя при этом мощность компьютеров и майнеров, что может стать проблемой. Существуют ограничения для каждой криптовалюты, например, для биткоина они составляют 21 миллион. Между созданием каждого блока должен быть определенный временной интервал заданный протоколом. Для биткоина время между созданием блока занимает всего 10 минут. Если бы блокам было разрешено создаваться быстрее, это привело бы к:
- Большому количеству коллизий: будет создано больше хэш-функций, которые неизбежно вызовут больше коллизий.
- Большому количеству брошенных блоков: Если много майнеров пойдут впереди протокола, они будут одновременно хаотично создавать новые блоки без сохранения целостности основной цепочки, что приведет к «осиротевшим» блокам.
Таким образом, чтобы ограничить создание блоков, устанавливается определенный уровень сложности. Майнинг чем-то напоминает игру: решаешь задачу – получаешь награду. Усиление сложности делает решение задачи намного сложнее и, следовательно, на нее затрачивается большее количество времени.WRT, которая начинается с множества нулей. При увеличении уровня сложности, увеличивается количество нулей. Уровень сложности изменяется после каждого 2016-го блока.
Процесс Майнинга
Примечание: в этом разделе мы будем говорить о выработке биткоинов.
Когда протокол Биткоина хочет добавить новый блок в цепочку, майнинг – это процедура, которой он следует. Всякий раз, когда появляется новый блок, все их содержимое сначала хэшируется. Если подобранный хэш больше или равен, установленному протоколом уровню сложности, он добавляется в блокчейн, а все в сообществе признают новый блок.
Однако, это не так просто. Вам должно очень повезти, чтобы получить новый блок таким образом. Так как, именно здесь присваивается уникальный символ. Уникальный символ (nonce) — это одноразовый код, который объединен с хэшем блока. Затем эта строка вновь меняется и сравнивается с уровнем сложности. Если она соответствует уровню сложности, то случайный код изменяется. Это повторяется миллион раз до тех пор, пока требования не будут наконец выполнены. Когда же это происходит, то блок добавляется в цепочку блоков.
Подводя итоги:
• Выполняется хэш содержимого нового блока.
• К хэшу добавляется nonce (специальный символ).
• Новая строка снова хэшируется.
• Конечный хэш сравнивается с уровнем сложности, чтобы проверить меньше он его или нет
• Если нет, то nonce изменяется, и процесс повторяется снова.
• Если да, то блок добавляется в цепочку, а общедоступная книга (блокчейн) обновляется и сообщает нодам о присоединении нового блока.
• Майнеры, ответственные за данный процесс, награждаются биткоинами.
Помните номер свойства 6 хэш-функций? Удобство использования задачи?
Для каждого выхода «Y», если k выбран из распределения с высокой мин-энтропией, невозможно найти вход x таким образом, H (k | x) = Y.
Так что, когда дело доходит до майнинга биткоинов:
• К = Уникальный символ
• x = хэш блока
• Y = цель проблемы
Весь процесс абсолютно случайный, основанный на генерации случайных чисел, следующий протоколу Proof Of Work и означающий:
- Решение задач должно быть сложным.
- Однако проверка ответа должна быть простой для всех. Это делается для того, чтобы убедиться, что для решения проблемы не использовались недозволенные методы.
Что такое скорость хэширования?
Скорость хэширования в основном означает, насколько быстро эти операции хэширования происходят во время майнинга. Высокий уровень хэширования означает, что в процессе майнинга участвуют всё большее количество людей и майнеров, и в результате система функционирует нормально. Если скорость хэширования слишком высокая, уровень сложности пропорционально увеличивается. Если скорость хэша слишком медленная, то соответственно, уровень сложности уменьшается.
Вывод
Хэширование действительно является основополагающим в создании технологии блокчейн. Если кто-то хочет понять, что такое блокчейн, он должен начать с того, чтобы понять, что означает хэширование.
Хеширование — это… Что такое Хеширование?
Хеш-функция, отображающая множество имён в множество натуральныых чиселХеширование (иногда «хэширование», англ. hashing) — преобразование по детерменированному алгоритму входного массива данных произвольной длины в выходную битовую строку фиксированной длины. Такие преобразования также называются хеш-функциями или функциями свёртки, а их результаты называют хешем, хеш-кодом или сводкой сообщения (англ. message digest). Если у двух строк хеш-коды разные, строки гарантированно различаются, если одинаковые — строки, вероятно, совпадают.
Хеширование применяется для построения ассоциативных массивов, поиска дубликатов в сериях наборов данных, построения достаточно уникальных идентификаторов для наборов данных, контрольное суммирование с целью обнаружения случайных или намеренных ошибок при хранении или передаче, для хранения паролей в системах защиты (в этом случае доступ к области памяти, где находятся пароли, не позволяет восстановить сам пароль), при выработке электронной подписи (на практике часто подписывается не само сообщение, а его хеш-образ).
В общем случае однозначного соответствия между исходными данными и хеш-кодом нет в силу того, что количество значений хеш-функций меньше, чем вариантов входного массива; существует множество массивов с разным содержимым, но дающих одинаковые хеш-коды — так называемые коллизии. Вероятность возникновения коллизий играет немаловажную роль в оценке качества хеш-функций.
Существует множество алгоритмов хеширования с различными свойствами (разрядность, вычислительная сложность, криптостойкость и т. п.). Выбор той или иной хеш-функции определяется спецификой решаемой задачи. Простейшими примерами хеш-функций могут служить контрольная сумма или CRC.
История
Дональд Кнут относит первую систематическую идею хеширования к сотруднику IBM Хансу Петеру Луну (нем. Hans Peter Luhn), предложившему хеш-кодирование в январе 1953 года.
В 1956 году Арнольд Думи (англ. Arnold Dumey) в своей работе «Computers and automation» первым представил концепцию хеширования таковой, какой её знает большинство программистов сейчас. Думи рассматривал хеширование, как решение «Проблемы словаря», а также предложил использовать в качестве хеш-адреса остаток деления на простое число.[1]
Первой серьёзной работой, связанной с поиском в больших файлах, была статья Уэсли Питерсона (англ. W. Wesley Peterson) в IBM Journal of Research and Development 1957 года, в которой он определил открытую адресацию, а также указал на ухудшение производительности при удалении. Спустя шесть лет был опубликована работа Вернера Бухгольца (нем. Werner Buchholz), в которой проведено обширное исследование хеш-функций. В течение нескольких последующих лет хеширование широко использовалось, однако не было опубликовано никаких значимых работ.
В 1967 году хеширование в современном значении упомянуто в книге Херберта Хеллермана «Принципы цифровых вычислительных систем»[2]. В 1968 году Роберт Моррис (англ. Robert Morris) опубликовал в Communications of the ACM большой обзор по хешированию, эта работа считается ключевой публикацией, вводящей понятие о хешировании в научный оборот и закрепившей ранее применявшийся только в жаргоне специалистов термин «хеш».
До начала 1990-х годов в русскоязычной литературе в качестве эквивалента термину «хеширование» благодаря работам Андрея Ершова использовалось слово «расстановка», а для коллизий использовался термин «конфликт» (Ершов использовал «расстановку» с 1956 года, в русскоязычном издании книги Вирта «Алгоритмы и структуры данных» 1989 года также используется термин «расстановка»). Предлагалось также назвать метод русским словом «окрошка». Однако ни один из этих вариантов не прижился, и в русскоязычной литературе используется преимущественно термин «хеширование».[3]
Виды хеш-функций
Хорошая хеш-функция должна удовлетворять двум свойствам:
- Быстро вычисляться;
- Минимизировать количество коллизий
Предположим, для определённости, что количество ключей , а хеш-функция имеет не более различных значений:
В качестве примера «плохой» хеш-функции можно привести функцию с , которая десятизначному натуральном числу сопоставляет три цифры выбранные из середины двадцатизначного квадрата числа . Казалось бы значения хеш-кодов должны равномерно распределиться между «000» и «999», но для реальных данных такой метод подходит лишь в том случае, если ключи не имеют большого количества нулей слева или справа.[3]
Однако существует несколько более простых и надежных методов, на которых базируются многие хеш-функции.
Хеш-функции основанные на делении
Первый метод заключается в том, что мы используем в качестве хеша остаток от деления на , где это количество всех возможных хешей:
При этом очевидно, что при чётном значение функции будет чётным, при чётном , и нечётным — при нечётном, что может привести к значительному смещению данных в файлах. Также не следует использовать в качестве степень основания счисления компьютера, так как хеш-код будет зависеть только от нескольких цифр числа , расположенных справа, что приведет к большому количеству коллизий. На практике обычно выбирают простое — в большинстве случаев этот выбор вполне удовлетворителен.
Ещё следует сказать о методе хеширования, основанном на делении на полином по модулю два. В данном методе также должна являться степенью двойки, а бинарные ключи () представляются в виде полиномов. В этом случае в качестве хеш-кода берутся значения коэффциентов полинома, полученного как остаток от деления на заранее выбранный полином степени :
При правильном выборе такой способ гарантирует отсутствие коллизий между почти одинаковыми ключами.[3]
Мультипликативная схема хеширования
Второй метод состоит в выборе некоторой целой константы , взаимно простой с , где — количество представимых машинным словом значений (в компьютерах IBM PC ). Тогда можем взять хеш-функцию вида:
В этом случае, на компьютере с двоичной системой счисления, является степенью двойки и будет состоять из старших битов правой половины произведения .
Среди преимуществ этих двух методов стоит отметь, что они выгодно используют то, что реальные ключи неслучайны, например в том случае если ключи представляют собой арифметическую прогрессию (допустим последовательность имён «ИМЯ1», «ИМЯ2», «ИМЯ3»). Мультипликативный метод отобразит арифметическую прогрессию в приближенно арифметическую прогрессию различных хеш-значений, что уменьшает количество коллизий по сравнению со случайной ситуацией.[3]
Одной из вариаций данного метода является хеширование Фибоначчи, основанное на свойствах золотого сечения. В качестве здесь выбирается ближайшее к целое число, взаимно простое с [3]
Хеширование строк переменной длины
Вышеизложенные методы применимы и в том случае, если нам необходимо рассматривать ключи, состоящие из нескольких слов или ключи переменной длины. Например можно скомбинировать слова в одно при помощи сложения по модулю или операции «исключающее или». Одним из алгоритмов, работающих по такому принципу является хеш-функция Пирсона.
Хеширование Пирсона (англ. Pearson hashing) — алгоритм, предложенный Питером Пирсоном (англ. Peter Pearson) для процессоров с 8-битными регистрами, задачей которого является быстрое вычисление хеш-кода для строки произвольной длины. На вход функция получается слово , состоящее из символов, каждый размером 1 байт, и возвращает значение в диапазоне от 0 до 255. Причем значение хеш-кода зависит от каждого символа входного слова.
Алгоритм можно описать следующим псевдокодом, который получает на вход строку и использует таблицу перестановок
h := 0
for each c in W loop
index := h xor c
h := T[index]
end loop
return h
Среди преимуществ алгоритма следует отметить:
- Простоту вычисления;
- Не существует таких входных данных, для которых вероятность коллизии наибольшая;
- Возможность модификации в идеальную хеш-функцию.[4]
В качестве альтернативного способа хеширования ключей, состоящих из символов (), можно предложить вычисление
- [3]
Идеальное хеширование
Идеальной хеш-функцией (англ. Perfect hash function) называется такая функция, которая отображает каждый ключ из набора в множество целых чисел без коллизий. В математических терминах это инъективное отображение.
Описание
- Функция называется идеальной хеш-функцией для , если она инъективна на ;
- Функция называется минимальной идеальной хеш-функцией для , если она является ИХФ и ;
- Для целого , функция называется -идеальной хеш-функцией (k-PHF) для если для каждого имеем .
Идеальное хеширование применяется в тех случаях, когда мы хотим присвоить уникальный идентификатор ключу, без сохранения какой-либо информации о ключе. Одним из наибоее очевидных примеров использования идеального (или скорее k-идеального) хеширования является ситуация, когда мы распологаем небольшой быстрой памятью, где размещаем значения хешей, связанных с данными хранящимися в большой, но медленной памяти. Причем размер блока можно выбрать таким, что необходимые нам данные, хранящиеся в медленной памяти, будут получены за один запрос. Подобный подход используется, например, в аппаратных маршрутизаторах. Также идеальное хеширование используется для ускорения работы алгоритмов на графах, в тех случаях, когда представление графа не умещается в основной памяти. [5]
Универсальное хеширование
Универсальным хешированием (англ. Universal hashing) называется хеширование, при котором используется не одна конкретная хеш-функция, а происходит выбор из заданного семейства по случайному алгоритму. Использование универсального хеширования обычно обеспечивает низкое число коллизий. Универсальное хеширование имеет множество применений, например, в реализации хеш-таблиц и криптографии.
Описание
Предположим, что мы хотим отобразить ключи из пространства в числа . На входе алгоритм получает некоторый набор данных и размерностью , причем неизвестный заранее. Как правило целью хеширования является получение наименьшего числа коллизий, чего трудно добиться используя какую-то определенную хеш-функцию.
В качестве решения такой проблемы можно выбирать функцию случайным образом из определенного набора, называемого универсальным семейством .[6]
Методы борьбы с коллизиями
Как уже говорилось выше, коллизией (иногда конфликтом[1] или столкновением) хеш-функции называются такие два входных блока данных, которые дают одинаковые хеш-коды.
В хеш-таблицах
Большинство первых работ описывающих хеширование было посвящено методам борьбы с коллизиями в хеш-таблицах, так как хеш-функции применялись для поиска в больших файлах. Существует два основных метода используемых в хеш-таблицах:
- Метод цепочек(метод прямого связывания)
- Метод открытой адресации
Первый метод заключается в поддержке связных списков, по одному на каждое значение хеш-функции. В списке хранятся ключи, дающие одинаковое значение хеш-кодов. В общем случае, если мы имеем ключей и списков, средний размер списка будет и хеширование приведет к уменьшению среднего количества работы по сравнению с последовательным поиском примерно в раз.
Второй метод состоит в том, что в массиве таблицы хранятся пары ключ-значение. Таким образом мы полностью отказываемся от ссылок и просто просматриваем записи таблицы, пока не найдем нужный ключ или пустую позицию. Последовательность, в которой просматриваются ячейки таблицы называется последовательностью проб.[3]
Криптографическая соль
Существует несколько способов для защиты от подделки паролей и подписей, работающих даже в том случае, если криптоаналитику известны способы построения коллизий для используемой хеш-функции. Одним из таких методов является добавление криптографической соли (строки случайных данных) к входным данным (иногда «соль» добавляется и к хеш-коду), что значительно затрудняет анализ итоговых хеш-таблиц. Данный метод, к примеру, используется для хранения паролей в UNIX-подобных операционных системах.
Применение хеш-функций
Хеш-функции широко используются в криптографии, а также во многих структурах данных — хеш-таблицаx, фильтрах Блума и декартовых деревьях.
Криптографические хеш-функции
Среди множества существующих хеш-функций принято выделять криптографически стойкие, применяемые в криптографии, так как на них накладываются дополнительные требования. Для того чтобы хеш-функция считалась криптографически стойкой, она должна удовлетворять трем основным требованиям, на которых основано большинство применений хеш-функций в криптографии:
- Необратимость: для заданного значения хеш-функции m должно быть вычислительно неосуществимо найти блок данных , для которого .
- Стойкость к коллизиям первого рода: для заданного сообщения M должно быть вычислительно неосуществимо подобрать другое сообщение N, для которого .
- Стойкость к коллизиям второго рода: должно быть вычислительно неосуществимо подобрать пару сообщений , имеющих одинаковый хеш.
Данные требования не являются независимыми:
- Обратимая функция нестойка к коллизиям первого и второго рода.
- Функция, нестойкая к коллизиям первого рода, нестойка к коллизиям второго рода; обратное неверно.
Следует отметить, что не доказано существование необратимых хеш-функций, для которых вычисление какого-либо прообраза заданного значения хеш-функции теоретически невозможно. Обычно нахождение обратного значения является лишь вычислительно сложной задачей.
Атака «дней рождения» позволяет находить коллизии для хеш-функции с длиной значений n битов в среднем за примерно вычислений хеш-функции. Поэтому n-битная хеш-функция считается криптостойкой, если вычислительная сложность нахождения коллизий для неё близка к .
Для криптографических хеш-функций также важно, чтобы при малейшем изменении аргумента значение функции сильно изменялось (лавинный эффект). В частности, значение хеша не должно давать утечки информации даже об отдельных битах аргумента. Это требование является залогом криптостойкости алгоритмов хеширования, хеширующих пользовательский пароль для получения ключа.[7]
Хеширование часто используется в алгоритмах электронно-цифровой подписи, где шифруется не само сообщение, а его хеш-код, что уменьшает время вычисления, а также повышает криптостойкость. Также в большинстве случаев, вместо паролей хранятся значения их хеш-кодов.
Контрольные суммы
Несложные, крайне быстрые и легко осуществимые аппаратные алгоритмы, используемые для защиты от непреднамеренных искажений, в том числе ошибок аппаратуры. С точки зрения математики является хеш-функцией, которая вычисляет контрольный код, применяемый для обнаружения ошибок при передаче и хранении информации
По скорости вычисления в десятки и сотни раз быстрее, чем криптографические хеш-функции, и значительно проще в аппаратном исполнении.
Платой за столь высокую скорость является отсутствие криптостойкости — лёгкая возможность подогнать сообщение под заранее известную сумму. Также обычно разрядность контрольных сумм (типичное число: 32 бита) ниже, чем криптографических хешей (типичные числа: 128, 160 и 256 бит), что означает возможность возникновения непреднамеренных коллизий.
Простейшим случаем такого алгоритма является деление сообщения на 32- или 16- битные слова и их суммирование, что применяется, например, в TCP/IP.
Как правило, к такому алгоритму предъявляются требования отслеживания типичных аппаратных ошибок, таких, как несколько подряд идущих ошибочных бит до заданной длины. Семейство алгоритмов т. н. «циклических избыточных кодов» удовлетворяет этим требованиям. К ним относится, например, CRC32, применяемый в устройствах Ethernet и в формате сжатия данных ZIP.
Контрольная сумма, например, может быть передана по каналу связи вместе с основным текстом. На приёмном конце, контрольная сумма может быть рассчитана заново и её можно сравнить с переданным значением. Если будет обнаружено расхождение, то это значит, что при передаче возникли искажения и можно запросить повтор.
Бытовым аналогом хеширования в данном случае может служить приём, когда при переездах в памяти держат количество мест багажа. Тогда для проверки не нужно вспоминать про каждый чемодан, а достаточно их посчитать. Совпадение будет означать, что ни один чемодан не потерян. То есть, количество мест багажа является его хеш-кодом. Данный метод легко дополнить до защиты от фальсификации передаваемой информации (метод MAC). В этом случае хеширование производится криптостойкой функцией над сообщением, объединенным с секретным ключом, известным только отправителю и получателю сообщения. Таким образом, криптоаналитик не сможет восстановить код по перехваченному сообщению и значению хеш-функции, то есть, не сможет подделать сообщение (См. имитозащита).
Геометрическое хеширование
Геометрическое хеширование (англ. Geometric hashing) – широко применяемый в компьтерной графике и вычислительной геометрии метод для решения задач на плоскости или в трёхмерном пространстве, например для нахождения ближайших пар в множестве точек или для поиска одинаковых изображений. Хеш-функция в данном методе обычно получает на вход какое-либо метрическое пространство и разделяет его, создавая сетку из клеток. Таблица в данном случае является массивом с двумя или более индексами и называется файл сетки(англ. Grid file). Геометрическое хеширование также применяется в телекоммуникациях при работе с многомерными сигналами.[8]
Ускорение поиска данных
Хеш-таблицей называется структура данных, позволяющая хранить пары вида (ключ,хеш-код) и поддерживающая операции поиска, вставки и удаления элемента. Задачей хеш-таблиц является ускорение поиска, например, при записи текстовых полей в базе данных может рассчитываться их хеш код и данные могут помещаться в раздел, соответствующий этому хеш-коду. Тогда при поиске данных надо будет сначала вычислить хеш-код текста и сразу станет известно, в каком разделе их надо искать, то есть, искать надо будет не по всей базе, а только по одному её разделу (это сильно ускоряет поиск).
Бытовым аналогом хеширования в данном случае может служить помещение слов в словаре по алфавиту. Первая буква слова является его хеш-кодом, и при поиске мы просматриваем не весь словарь, а только нужную букву.
Примечания
- ↑ 1 2 Никлаус Вирт.Алгоритмы и структуры данных
- ↑ Herbert Hellerman. Digital Computer System Principles. N.Y.: McGraw-Hill, 1967, 424 pp.
- ↑ 1 2 3 4 5 6 7 Дональд Кнут. Искусство программирования
- ↑ Pearson, Peter K. (June 1990), ««Fast Hashing of Variable-Length Text Strings»», Communications of the ACM Т. 33 (6): 677, doi:10.1145/78973.78978, <http://portal.acm.org/citation.cfm?id=78978>
- ↑ Djamal Belazzougui, Fabiano C. Botelho, Martin Dietzfelbinger (2009). «Hash, displace, and compress» (PDF) (Springer Berlin / Heidelberg). Проверено 2011-08-11.
- ↑ Miltersen, Peter Bro Universal Hashing (PDF). Архивировано из первоисточника 24 июня 2009.
- ↑ Брюс Шнаейр, Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си
- ↑ Wolfson, H.J. & Rigoutsos, I (1997). Geometric Hashing: An Overview. IEEE Computational Science and Engineering, 4(4), 10-21.
Литература
- Брюс Шнайер «Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си». — М.: Триумф, 2002. — ISBN 5-89392-055-4
- Дональд Кнут Искусство программирования, том 3. Сортировка и поиск = The Art of Computer Programming, vol.3. Sorting and Searching. — 2-е изд. — М.: «Вильямс», 2007. — С. 824. — ISBN 0-201-89685-0
- Никлаус Вирт «Алгоритмы и структуры данных». — М.: Мир, 1989. — ISBN 5-03-001045-9
Ссылки
Что такое хеш и хэширование простыми словами.: spayte — LiveJournal
Сегодня у нас на очереди хеш. Что это такое? Зачем он нужен? Почему это слово так часто используется в интернете применительно к совершенно разным вещам? Имеет ли это какое-то отношение к хештегам или хешссылкам? Где применяют хэш, как вы сами можете его использовать? Что такое хэш-функция и хеш-сумма? Причем тут коллизии?
«>Все это (или почти все) вы узнаете из этой маленькой заметки. Поехали…
Что такое хеш и хэширование простыми словами
Слово хеш происходит от английского «hash», одно из значений которого трактуется как путаница или мешанина. Собственно, это довольно полно описывает реальное значение этого термина. Часто еще про такой процесс говорят «хеширование», что опять же является производным от английского hashing (рубить, крошить, спутывать и т.п.).
Появился этот термин в середине прошлого века среди людей занимающихся обработках массивов данных. Хеш-функция позволяла привести любой массив данных к числу заданной длины. Например, если любое число (любой длинны) начать делить много раз подряд на одно и то же простое число, то полученный в результате остаток от деления можно будет называть хешем. Для разных исходных чисел остаток от деления (цифры после запятой) будет отличаться.
Для обычного человека это кажется белибердой, но как ни странно в наше время без хеширования практически невозможна работа в интернете. Так что же это такая за функция? На самом деле она может быть любой (приведенный выше пример это не есть реальная функция — он придуман мною чисто для вашего лучшего понимания принципа). Главное, чтобы результаты ее работы удовлетворяли приведенным ниже условиям.
Зачем нужен хэш
Смотрите, еще пример. Есть у вас текст в файле. Но на самом деле это ведь не текст, а массив цифровых символов (по сути число). Как вы знаете, в компьютерной логике используются двоичные числа (ноль и единица). Они запросто могут быть преобразованы в шестнадцатиричные цифры, над которыми можно проводить математические операции. Применив к ним хеш-функцию мы получим на выходе (после ряда итераций) число заданной длины (хеш-сумму).
Если мы потом в исходном текстовом файле поменяем хотя бы одну букву или добавим лишний пробел, то повторно рассчитанный для него хэш уже будет отличаться от изначального (вообще другое число будет). Доходит, зачем все это нужно? Ну, конечно же, для того, чтобы понять, что файл именно тот, что и должен быть. Это можно использовать в целом ряде аспектов работы в интернете и без этого вообще сложно представить себе работу сети.
Где и как используют хеширование
Например, простые хэш-функции (не надежные, но быстро рассчитываемые) применяются при проверке целостности передачи пакетов по протоколу TCP/IP (и ряду других протоколов и алгоритмов, для выявления аппаратных ошибок и сбоев — так называемое избыточное кодирование). Если рассчитанное значение хеша совпадает с отправленным вместе с пакетом (так называемой контрольной суммой), то значит потерь по пути не было (можно переходить к следующему пакету).
А это, ведь на минутку, основной протокол передачи данных в сети интернет. Без него никуда. Да, есть вероятность, что произойдет накладка — их называют коллизиями. Ведь для разных изначальных данных может получиться один и тот же хеш. Чем проще используется функция, тем выше такая вероятность. Но тут нужно просто выбирать между тем, что важнее в данный момент — надежность идентификации или скорость работы. В случае TCP/IP важна именно скорость. Но есть и другие области, где важнее именно надежность.
Похожая схема используется и в технологии блокчейн, где хеш выступает гарантией целостности цепочки транзакций (платежей) и защищает ее от несанкционированных изменений. Благодаря ему и распределенным вычислениям взломать блокчен очень сложно и на его основе благополучно существует множество криптовалют, включая самую популярную из них — это биткоин. Последний существует уже с 2009 год и до сих пор не был взломан.
Более сложные хеш-функции используются в криптографии. Главное условие для них — невозможность по конечному результату (хэшу) вычислить начальный (массив данных, который обработали данной хеш-функцией). Второе главное условие — стойкость к коллизиями, т.е. низкая вероятность получения двух одинаковых хеш-сумм из двух разных массивов данных при обработке их этой функцией. Расчеты по таким алгоритмам более сложные, но тут уже главное не скорость, а надежность.
Так же хеширование используется в технологии электронной цифровой подписи. С помощью хэша тут опять же удостоверяются, что подписывают именно тот документ, что требуется. Именно он (хеш) передается в токен, который и формирует электронную цифровую подпись. Но об этом, я надеюсь, еще будет отдельная статья, ибо тема интересная, но в двух абзацах ее не раскроешь.
Для доступа к сайтам и серверам по логину и паролю тоже часто используют хеширование. Согласитесь, что хранить пароли в открытом виде (для их сверки с вводимыми пользователями) довольно ненадежно (могут их похитить). Поэтому хранят хеши всех паролей. Пользователь вводит символы своего пароля, мгновенно рассчитывается его хеш-сумма и сверяется с тем, что есть в базе. Надежно и очень просто. Обычно для такого типа хеширования используют сложные функции с очень высокой криптостойкостью, чтобы по хэшу нельзя было бы восстановить пароль.
Какими свойствами должна обладать хеш-функция
Хочу систематизировать кое-что из уже сказанного и добавить новое.
- Как уже было сказано, функция эта должна уметь приводить любой объем данных (а все они цифровые, т.е. двоичные, как вы понимаете) к числу заданной длины (по сути это сжатие до битовой последовательности заданной длины хитрым способом).
- При этом малейшее изменение (хоть на один бит) входных данных должно приводить к полному изменению хеша.
- Она должна быть стойкой в обратной операции, т.е. вероятность восстановления исходных данных по хешу должна быть весьма низкой (хотя последнее сильно зависит от задействованных мощностей)
- В идеале она должна иметь как можно более низкую вероятность возникновения коллизий. Согласитесь, что не айс будет, если из разных массивов данных будут часто получаться одни и те же значения хэша.
- Хорошая хеш-функция не должна сильно нагружать железо при своем исполнении. От этого сильно зависит скорость работы системы на ней построенной. Как я уже говорил выше, всегда имеется компромисс между скорость работы и качеством получаемого результата.
- Алгоритм работы функции должен быть открытым, чтобы любой желающий мог бы оценить ее криптостойкость, т.е. вероятность восстановления начальных данных по выдаваемому хешу.
Хеш — это маркер целостности скачанных в сети файлов
Где еще можно встретить применение этой технологии? Наверняка при скачивании файлов из интернета вы сталкивались с тем, что там приводят некоторые числа (которые называют либо хешем, либо контрольными суммами) типа:
CRC32: 7438E546
MD5: DE3BAC46D80E77ADCE8E379F682332EB
SHA-1: 332B317FB97126B0F79F7AF5786EBC51E5CC82CF
Что это такое? И что вам с этим всем делать? Ну, как правило, на тех же сайтах можно найти пояснения по этому поводу, но я не буду вас утруждать и расскажу в двух словах. Это как раз и есть результаты работы различных хеш-функций (их названия приведены перед числами: CRC32, MD5 и SHA-1).
Зачем они вам нужны? Ну, если вам важно знать, что при скачивании все прошло нормально и ваша копия полностью соответствует оригиналу, то нужно будет поставить на свой компьютер программку, которая умеет вычислять хэш по этим алгоритмам (или хотя бы по некоторым их них).
После чего прогнать скачанные файлы через эту программку и сравнить полученные числа с приведенными на сайте. Если совпадают, то сбоев при скачивании не было, а если нет, то значит были сбои и есть смысл повторить закачку заново.
Популярные хэш-алгоритмы сжатия
- CRC32 — используется именно для создания контрольных сумм (так называемое избыточное кодирование). Данная функция не является криптографической. Есть много вариаций этого алгоритма (число после CRC означает длину получаемого хеша в битах), в зависимости от нужной длины получаемого хеша. Функция очень простая и нересурсоемкая. В связи с этим используется для проверки целостности пакетов в различных протоколах передачи данных.
- MD5 — старая, но до сих пор очень популярная версия уже криптографического алгоритма, которая создает хеш длиной в 128 бит. Хотя стойкость этой версии на сегодняшний день и не очень высока, она все равно часто используется как еще один вариант контрольной суммы, например, при скачивании файлов из сети.
- SHA-1 — криптографическая функция формирующая хеш-суммы длиной в 160 байт. Сейчас идет активная миграция в сторону SHA-2, которая обладает более высокой устойчивостью, но SHA-1 по-прежнему активно используется хотя бы в качестве контрольных сумм. Но она так же по-прежнему используется и для хранения хешей паролей в базе данных сайта (об этом читайте выше).
- ГОСТ Р 34.11-2012 — текущий российский криптографический (стойкий к взлому) алгоритм введенный в работу в 2013 году (ранее использовался ГОСТ Р 34.11-94). Длина выходного хеша может быть 256 или 512 бит. Обладает высокой криптостойкостью и довольно хорошей скоростью работы. Используется для электронных цифровых подписей в системе государственного и другого документооборота.
HashTab — вычисление хеша для любых файлов на компьютере
Раз уж зашла речь о программе для проверки целостности файлов (расчета контрольных сумм по разным алгоритмам хеширования), то тут, наверное, самым популярным решением будет HashTab.
Она бесплатна для личного некоммерческого использования и покрывает с лихвой все, что вам может понадобиться от подобного рода софта. После ее скачивания и установки запускать ничего не надо. Просто кликаете правой кнопкой мыши по нужному файлу в Проводнике (или ТоталКомандере) и выбираете самый нижний пункт выпадающего меню «Свойства»:
В открывшемся окне перейдите на вкладку «Хеш-суммы файлов», где будут отображены контрольные суммы, рассчитанные по нужным вам алгоритмам хэширования (задать их можно нажав на кнопку «Настройки» в этом же окне). По умолчанию отображаются три самых популярных:
Чтобы не сравнивать контрольные суммы визуально, можно числа по очереди вставить в рассположенное ниже поле (со знаком решетки) и нажать на кнопку «Сравнить файл».
Как видите, все очень просто и быстро. А главное эффективно.
Хеш — что это такое и как хэш-функция помогает решать вопросы безопасности в интернете
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Хочу продолжить серию статей посвященных различным терминам, которые не всегда могут быть понятны без дополнительных пояснений. Чуть ранее я рассказывал про то, что значит слово кликбейт и что такое хост, писал про IP и MAC адреса, фишинг и многое другое.


Сегодня у нас на очереди хеш. Что это такое? Зачем он нужен? Почему это слово так часто используется в интернете применительно к совершенно разным вещам? Имеет ли это какое-то отношение к хештегам или хешссылкам? Где применяют хэш, как вы сами можете его использовать? Что такое хэш-функция и хеш-сумма? Причем тут коллизии?
Все это (или почти все) вы узнаете из этой маленькой заметки. Поехали…
Что такое хеш и хэширование простыми словами
Слово хеш происходит от английского «hash», одно из значений которого трактуется как путаница или мешанина. Собственно, это довольно полно описывает реальное значение этого термина. Часто еще про такой процесс говорят «хеширование», что опять же является производным от английского hashing (рубить, крошить, спутывать и т.п.).
Появился этот термин в середине прошлого века среди людей занимающихся обработках массивов данных. Хеш-функция позволяла привести любой массив данных к числу заданной длины. Например, если любое число (любой длинны) начать делить много раз подряд на одно и то же простое число (это как?), то полученный в результате остаток от деления можно будет называть хешем. Для разных исходных чисел остаток от деления (цифры после запятой) будет отличаться.
Для обычного человека это кажется белибердой, но как ни странно в наше время без хеширования практически невозможна работа в интернете. Так что же это такая за функция? На самом деле она может быть любой (приведенный выше пример это не есть реальная функция — он придуман мною чисто для вашего лучшего понимания принципа). Главное, чтобы результаты ее работы удовлетворяли приведенным ниже условиям.
Зачем нужен хэш
Смотрите, еще пример. Есть у вас текст в файле. Но на самом деле это ведь не текст, а массив цифровых символов (по сути число). Как вы знаете, в компьютерной логике используются двоичные числа (ноль и единица). Они запросто могут быть преобразованы в шестнадцатиричные цифры, над которыми можно проводить математические операции. Применив к ним хеш-функцию мы получим на выходе (после ряда итераций) число заданной длины (хеш-сумму).
Если мы потом в исходном текстовом файле поменяем хотя бы одну букву или добавим лишний пробел, то повторно рассчитанный для него хэш уже будет отличаться от изначального (вообще другое число будет). Доходит, зачем все это нужно? Ну, конечно же, для того, чтобы понять, что файл именно тот, что и должен быть. Это можно использовать в целом ряде аспектов работы в интернете и без этого вообще сложно представить себе работу сети.
Где и как используют хеширование
Например, простые хэш-функции (не надежные, но быстро рассчитываемые) применяются при проверке целостности передачи пакетов по протоколу TCP/IP (и ряду других протоколов и алгоритмов, для выявления аппаратных ошибок и сбоев — так называемое избыточное кодирование). Если рассчитанное значение хеша совпадает с отправленным вместе с пакетом (так называемой контрольной суммой), то значит потерь по пути не было (можно переходить к следующему пакету).
А это, ведь на минутку, основной протокол передачи данных в сети интернет. Без него никуда. Да, есть вероятность, что произойдет накладка — их называют коллизиями. Ведь для разных изначальных данных может получиться один и тот же хеш. Чем проще используется функция, тем выше такая вероятность. Но тут нужно просто выбирать между тем, что важнее в данный момент — надежность идентификации или скорость работы. В случае TCP/IP важна именно скорость. Но есть и другие области, где важнее именно надежность.
Похожая схема используется и в технологии блокчейн, где хеш выступает гарантией целостности цепочки транзакций (платежей) и защищает ее от несанкционированных изменений. Благодаря ему и распределенным вычислениям взломать блокчен очень сложно и на его основе благополучно существует множество криптовалют, включая самую популярную из них — это биткоин. Последний существует уже с 2009 год и до сих пор не был взломан.
Более сложные хеш-функции используются в криптографии. Главное условие для них — невозможность по конечному результату (хэшу) вычислить начальный (массив данных, который обработали данной хеш-функцией). Второе главное условие — стойкость к коллизиями, т.е. низкая вероятность получения двух одинаковых хеш-сумм из двух разных массивов данных при обработке их этой функцией. Расчеты по таким алгоритмам более сложные, но тут уже главное не скорость, а надежность.
Так же хеширование используется в технологии электронной цифровой подписи. С помощью хэша тут опять же удостоверяются, что подписывают именно тот документ, что требуется. Именно он (хеш) передается в токен, который и формирует электронную цифровую подпись. Но об этом, я надеюсь, еще будет отдельная статья, ибо тема интересная, но в двух абзацах ее не раскроешь.
Для доступа к сайтам и серверам по логину и паролю тоже часто используют хеширование. Согласитесь, что хранить пароли в открытом виде (для их сверки с вводимыми пользователями) довольно ненадежно (могут их похитить). Поэтому хранят хеши всех паролей. Пользователь вводит символы своего пароля, мгновенно рассчитывается его хеш-сумма и сверяется с тем, что есть в базе. Надежно и очень просто. Обычно для такого типа хеширования используют сложные функции с очень высокой криптостойкостью, чтобы по хэшу нельзя было бы восстановить пароль.
Какими свойствами должна обладать хеш-функция
Хочу систематизировать кое-что из уже сказанного и добавить новое.
- Как уже было сказано, функция эта должна уметь приводить любой объем данных (а все они цифровые, т.е. двоичные, как вы понимаете) к числу заданной длины (по сути это сжатие до битовой последовательности заданной длины хитрым способом).
- При этом малейшее изменение (хоть на один бит) входных данных должно приводить к полному изменению хеша.
- Она должна быть стойкой в обратной операции, т.е. вероятность восстановления исходных данных по хешу должна быть весьма низкой (хотя последнее сильно зависит от задействованных мощностей)
- В идеале она должна иметь как можно более низкую вероятность возникновения коллизий. Согласитесь, что не айс будет, если из разных массивов данных будут часто получаться одни и те же значения хэша.
- Хорошая хеш-функция не должна сильно нагружать железо при своем исполнении. От этого сильно зависит скорость работы системы на ней построенной. Как я уже говорил выше, всегда имеется компромисс между скорость работы и качеством получаемого результата.
- Алгоритм работы функции должен быть открытым, чтобы любой желающий мог бы оценить ее криптостойкость, т.е. вероятность восстановления начальных данных по выдаваемому хешу.
Хеш — это маркер целостности скачанных в сети файлов
Где еще можно встретить применение этой технологии? Наверняка при скачивании файлов из интернета вы сталкивались с тем, что там приводят некоторые числа (которые называют либо хешем, либо контрольными суммами) типа:
CRC32: 7438E546 MD5: DE3BAC46D80E77ADCE8E379F682332EB SHA-1: 332B317FB97126B0F79F7AF5786EBC51E5CC82CF
Что это такое? И что вам с этим всем делать? Ну, как правило, на тех же сайтах можно найти пояснения по этому поводу, но я не буду вас утруждать и расскажу в двух словах. Это как раз и есть результаты работы различных хеш-функций (их названия приведены перед числами: CRC32, MD5 и SHA-1).
Зачем они вам нужны? Ну, если вам важно знать, что при скачивании все прошло нормально и ваша копия полностью соответствует оригиналу, то нужно будет поставить на свой компьютер программку, которая умеет вычислять хэш по этим алгоритмам (или хотя бы по некоторым их них).
После чего прогнать скачанные файлы через эту программку и сравнить полученные числа с приведенными на сайте. Если совпадают, то сбоев при скачивании не было, а если нет, то значит были сбои и есть смысл повторить закачку заново.
Популярные хэш-алгоритмы сжатия
- CRC32 — используется именно для создания контрольных сумм (так называемое избыточное кодирование). Данная функция не является криптографической. Есть много вариаций этого алгоритма (число после CRC означает длину получаемого хеша в битах), в зависимости от нужной длины получаемого хеша. Функция очень простая и нересурсоемкая. В связи с этим используется для проверки целостности пакетов в различных протоколах передачи данных.
- MD5 — старая, но до сих пор очень популярная версия уже криптографического алгоритма, которая создает хеш длиной в 128 бит. Хотя стойкость этой версии на сегодняшний день и не очень высока, она все равно часто используется как еще один вариант контрольной суммы, например, при скачивании файлов из сети.
- SHA-1 — криптографическая функция формирующая хеш-суммы длиной в 160 байт. Сейчас идет активная миграция в сторону SHA-2, которая обладает более высокой устойчивостью, но SHA-1 по-прежнему активно используется хотя бы в качестве контрольных сумм. Но она так же по-прежнему используется и для хранения хешей паролей в базе данных сайта (об этом читайте выше).
- ГОСТ Р 34.11-2012 — текущий российский криптографический (стойкий к взлому) алгоритм введенный в работу в 2013 году (ранее использовался ГОСТ Р 34.11-94). Длина выходного хеша может быть 256 или 512 бит. Обладает высокой криптостойкостью и довольно хорошей скоростью работы. Используется для электронных цифровых подписей в системе государственного и другого документооборота.
HashTab — вычисление хеша для любых файлов на компьютере
Раз уж зашла речь о программе для проверки целостности файлов (расчета контрольных сумм по разным алгоритмам хеширования), то тут, наверное, самым популярным решением будет HashTab.
Она бесплатна для личного некоммерческого использования и покрывает с лихвой все, что вам может понадобиться от подобного рода софта. После ее скачивания и установки запускать ничего не надо. Просто кликаете правой кнопкой мыши по нужному файлу в Проводнике (или ТоталКомандере) и выбираете самый нижний пункт выпадающего меню «Свойства»:
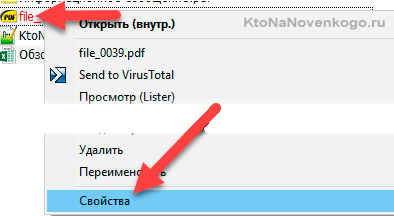

В открывшемся окне перейдите на вкладку «Хеш-суммы файлов», где будут отображены контрольные суммы, рассчитанные по нужным вам алгоритмам хэширования (задать их можно нажав на кнопку «Настройки» в этом же окне). По умолчанию отображаются три самых популярных:
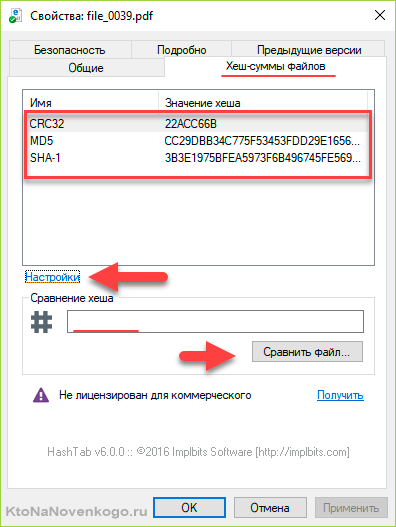

Чтобы не сравнивать контрольные суммы визуально, можно числа по очереди вставить в рассположенное ниже поле (со знаком решетки) и нажать на кнопку «Сравнить файл».
Как видите, все очень просто и быстро. А главное эффективно.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Использую для заработка
Рубрика: ЧАстые ВОпросыУниверсальное и идеальное хеширование / Блог компании OTUS. Онлайн-образование / Хабр
Начинаем неделю с полезного материала приуроченного к запуску курса «Алгоритмы для разработчиков». Приятного прочтения.1. Обзор
Хеширование — отличный практический инструмент, с интересной и тонкой теорией. Помимо использования в качестве словарной структуры данных, хеширование также встречается во многих различных областях, включая криптографию и теорию сложности. В этой лекции мы опишем два важных понятия: универсальное хеширование (также известное как универсальные семейства хеш-функций) и идеальное хеширование.
Материал, освещенный в этой лекции, включает в себя:
- Формальная постановка и общая идея хеширования.
- Универсальное хеширование.
- Идеальное хеширование.
2. Вступление
Мы рассмотрим основную проблему со словарем, которую мы обсуждали до этого, и рассмотрим две версии: статическую и динамическую:
- Статическая: дано множество элементов S, мы хотим хранить его таким образом, чтобы можно было быстро выполнять поиск.
- Например, фиксированный словарь.
- Динамическая: здесь у нас есть последовательность запросов на вставку, поиск и, возможно, удаление. Мы хотим сделать все это эффективно.
Для первой проблемы мы могли бы использовать отсортированный массив и двоичный поиск. Для второй мы могли бы использовать сбалансированное дерево поиска. Однако хеширование дает альтернативный подход, который зачастую является самым быстрым и удобным способом решения этих проблем. Например, предположим, что вы пишете программу для AI-поиска и хотите хранить ситуации, которые вы уже разрешили (позиции на доске или элементы пространства состояний), чтобы не повторять те же вычисления, при столкновении с ними снова. Хеширование обеспечивает простой способ хранения такой информации. Также существует множество применений в криптографии, сетях, теории сложности.
3. Основы хеширования
Формальная постановка для хеширования заключается в следующем.
- Ключи принадлежат некоторому большому множеству U. (Например, представьте, что U — набор всех строк длиной не более 80 символов ascii.)
- Есть некоторое множество ключей S в U, которое нам на самом деле нужно (ключи могут быть как статическими, так и динамическими). Пусть N = |S|. Представьте, что N гораздо меньше, чем размер U. Например, S — это множество имен учеников в классе, которое намного меньше, чем 128^80.
- Мы будем выполнять вставки и поиск с помощью массива A некоторого размера M и хеш-функции h: U → {0,…, М — 1}. Дан элемент x, идея хеширования состоит в том, что мы хотим хранить его в A[h(x)]. Обратите внимание, что если бы U было маленьким (например, 2-символьные строки), то можно было бы просто сохранить x в A[x], как в блочной сортировке. Проблема в том, что U большое, поэтому нам нужна хеш-функция.
- Нам нужен метод для разрешения коллизий. Коллизия — это когда h(x) = h(y) для двух разных ключей x и y. В этой лекции мы будем обрабатывать коллизии, определяя каждый элемент A как связанный список. Есть ряд других методов, но для проблем, на которых мы сосредоточимся здесь, это самый подходящий. Этот метод называется методом цепочек. Чтобы вставить элемент, мы просто помещаем его в начало списка. Если h — хорошая хеш-функция, то мы надеемся, что списки будут небольшими.
Одним из замечательных свойств хеширования является то, что все словарные операции невероятно просты в реализации. Чтобы выполнить поиск ключа x, просто вычислите индекс i = h(x) и затем идите по списку в A[i], пока не найдете его (или не выйдете из списка). Чтобы вставить, просто поместите новый элемент в верхней части его списка. Чтобы удалить, нужно просто выполнить операцию удаления в связанном списке. Теперь мы переходим к вопросу: что нам нужно для достижения хорошей производительности?
Желательные свойства. Основные желательные свойства для хорошей схемы хеширования:
- Ключи хорошо рассредоточены, чтобы у нас не было слишком много коллизий, так как коллизии влияют на время выполнения поиска и удаления.
- M = O(N): в частности, мы бы хотели, чтобы наша схема достигла свойства (1) без необходимости, чтобы размер таблицы M был намного больше, чем число элементов N.
- Функция h должна быстро вычисляться. В нашем сегодняшнем анализе мы будем рассматривать время для вычисления h(x) как константу. Тем не менее, стоит помнить, что она не должна быть слишком сложной, потому что это влияет на общее время выполнения.
Учитывая это, время поиска элемента x равно O(размер списка A[h(x)]). То же самое верно для удалений. Вставки занимают время O(1) независимо от длины списков. Итак, мы хотим проанализировать, насколько большими получаются эти списки.
Базовая интуиция: один из способов красиво распределить элементы — это распределить их случайным образом. К сожалению, мы не можем просто использовать генератор случайных чисел, чтобы решить, куда направить следующий элемент, потому что тогда мы никогда не сможем найти его снова. Итак, мы хотим, чтобы h было чем-то «псевдослучайным» в некотором формальном смысле.
Сейчас мы изложим некоторые плохие новости, а затем некоторые хорошие.
Утверждение 1 (Плохие новости) Для любой хэш-функции h, если |U| ≥ (N −1) M +1, существует множество S из N элементов, которые все хешируются в одном месте.
Доказательство: по принципу Дирихле. В частности, чтобы рассмотреть контрапозиции, если бы каждое местоположение имело не более N — 1 элементов U, хэширующих его, то U мог бы иметь размер не более M (N — 1).
Отчасти поэтому хэширование кажется таким загадочным — как можно утверждать, что хэширование хорошо, если для любой хэш-функции вы можете придумать способы ее предотвращения? Один из ответов заключается в том, что существует множество простых хеш-функций, которые хорошо работают на практике для типичных множеств S. Но что, если мы хотим получить хорошую гарантию наихудшего случая?
Вот ключевая идея: давайте использовать рандомизацию в нашей конструкции h, по аналогии с рандомизированной быстрой сортировкой. (Само собой разумеется, h будет детерминированной функцией). Мы покажем, что для любой последовательности операций вставки и поиска (нам не нужно предполагать, что набор вставленных элементов S является случайным), если мы выберем h таким вероятностным способом, производительность h в этой последовательности будет хорошо в ожидании. Таким образом, это та же самая гарантия, что и в рандомизированной быстрой сортировке или ловушках. В частности, это идея универсального хеширования.
Как только мы разработаем эту идею, мы будем использовать ее для особенно приятного приложения под названием «идеальное хеширование».
4. Универсальное хеширование
Определение 1. Рандомизированный алгоритм H для построения хеш-функций h: U → {1, …, М}
универсален, если для всех x != y в U имеем
Мы также можем сказать, что множество H хеш-функций является универсальным семейством хеш-функций, если процедура «выбрать h ∈ H наугад» универсальна. (Здесь мы отождествляем множество функций с равномерным распределением по множеству.)
Теорема 2. Если H универсален, то для любого множества S ⊆ U размера N, для любого x ∈ U (например, который мы могли бы искать), если мы строим h случайным образом в соответствии с H, ожидаемое число коллизий между х и другими элементами в S не более N/M.
Доказательство: у каждого y ∈ S (y != x) есть не более 1 / M шанса столкновения с x по определению «универсального». Так,
- Пусть Cxy = 1, если x и y сталкиваются, и 0 в противном случае.
- Пусть Cx обозначает общее количество столкновений для x. Итак, Cx = Py∈S, y != x Cxy.
- Мы знаем, что E [Cxy] = Pr (x и y сталкиваются) ≤ 1 / M.
- Таким образом, по линейности ожидания E [Cx] = Py E [Cxy] <N / M.
Теперь мы получаем следующее следствие.
Следствие 3. Если H универсален, то для любой последовательности операций L вставки, поиска и удаления, в которых в системе одновременно может быть не более M элементов, ожидаемая общая стоимость L операций для случайного h ∈ H равна только O (L) (просмотр времени для вычисления h как константы).
Доказательство: для любой данной операции в последовательности ее ожидаемая стоимость постоянна по теореме 2, поэтому ожидаемая общая стоимость L операций равна O (L) по линейности ожидания.
Вопрос: можем ли мы на самом деле построить универсальную H? Если нет, то это все довольно бессмысленно. К счастью, ответ — да.
4.1. Создание универсального хеш-семейства: матричный метод
Допустим, ключи имеют длину u-бит. Скажем, размер таблицы M равен степени 2, поэтому индекс длиной b-битов с M = 2b.
Что мы сделаем, это выберем h в качестве случайной матрицы 0/1 b-by-u и определим h (x) = hx, где мы добавим mod 2. Эти матрицы короткие и толстые. Например:
Утверждение 4. Для x != y Prh [h (x) = h (y)] = 1 / M = 1 / 2b.
Доказательство: во-первых, что означает умножение h на x? Мы можем думать об этом как о добавлении некоторых из столбцов h (делая векторное сложение mod 2), где 1 бит в x указывает, какие из них добавить. (например, мы добавили 1-й и 3-й столбцы h выше)
Теперь возьмем произвольную пару ключей x, y такую, что x != y. Они должны где-то отличаться, так что, скажем, они различаются по i-й координате, а для конкретности скажем xi = 0 и yi = 1. Представьте, что сначала мы выбрали все h, кроме i-го столбца. По оставшимся выборкам i-го столбца h (x) является фиксированным. Однако каждая из 2b различных настроек i-го столбца дает различное значение h (y) (в частности, каждый раз, когда мы переворачиваем бит в этом столбце, мы переворачиваем соответствующий бит в h (y)). Таким образом, есть точно 1 / 2b шанс, что h (x) = h (y).
Существуют и другие методы построения универсальных хеш-семейств, основанных также на умножении простых чисел (см. Раздел 6.1).
Следующий вопрос, который мы рассмотрим: если мы исправим множество S, сможем ли мы найти хеш-функцию h такую, что все поиски будут иметь постоянное время? Ответ — да, и это приводит к теме идеального хеширования.
5. Идеальное хеширование
Мы говорим, что хеш-функция является идеальной для S, если все поиски происходят за O(1). Вот два способа построения идеальных хеш-функций для заданного множества S.
5.1 Метод 1: решение в пространстве O(N2)
Скажем, мы хотим иметь таблицу, размер которой квадратичен по размеру N нашего словаря S. Тогда вот простой метод построения идеальной хеш-функции. Пусть H универсален и M = N2. Тогда просто выберите случайный h из H и попробуйте! Утверждение состоит в том, что есть по крайней мере 50% шанс, что у нее не будет коллизий.
Утверждение 5. Если H универсален и M = N2, то Prh∼H (нет коллизий в S) ≥ 1/2.
Доказательство:
• Сколько пар (x, y) есть в S? Ответ:
• Для каждой пары вероятность их столкновения составляет ≤ 1 / M по определению универсальности.
• Итак, Pr (существует коллизия) ≤ / M <1/2.
Это как другая сторона «парадокса дня рождения». Если количество дней намного больше, чем количество людей в квадрате, то есть разумный шанс, что ни у одной пары не будет одинакового дня рождения.
Итак, мы просто выбираем случайную h из H, и если возникают какие-либо коллизии, мы просто выбираем новую h. В среднем нам нужно будет сделать это только дважды. Теперь, что если мы хотим использовать только пространство O(N)?
5.2 Метод 2: решение в пространстве O(N)
Вопрос о том, можно ли достичь идеального хеширования в пространстве O(N), был в течение некоторого времени открытым: «Должны ли таблицы быть отсортированы?». То есть для фиксированного набора можно получить постоянное время поиска только с линейным пространством? Была серия все более и более сложных попыток, пока, наконец, она не была решена с использованием хорошей идеи универсальных хеш-функций в двухуровневой схеме.
Способ заключается в следующем. Сначала мы будем хэшировать в таблицу размера N, используя универсальное хеширование. Это приведет к некоторым коллизиям (если только нам не повезет). Однако затем мы перехешируем каждую корзину, используя метод 1, возводя в квадрат размер корзины, чтобы получить нулевые коллизии. Таким образом, схема состоит в том, что у нас есть хеш-функция первого уровня h и таблица A первого уровня, а затем N хеш-функций второго уровня h2,…, hN и N таблицы второго уровня A1,…, А.Н… Чтобы найти элемент x, мы сначала вычисляем i = h (x), а затем находим элемент в Ai [hi (x)]. (Если бы вы делали это на практике, вы могли бы установить флаг так, чтобы вы делали второй шаг, только если на самом деле были коллизии с индексом i, а в противном случае просто помещали бы сам x в A [i], но давайте не будем об этом беспокоиться здесь .)
Скажем, хеш-функция h хеширует n элементов S в местоположение i. Мы уже доказывали (анализируя метод 1), что мы можем найти h2,…, hN, так что общее пространство, используемое во вторичных таблицах, равно Pi (ni) 2. Осталось показать, что мы можем найти функцию первого уровня h такую, что Pi (ni) 2 = O (N). На самом деле, мы покажем следующее:
Теорема 6. Если мы выберем начальную точку h из универсального множества H, то
Pr[X
i
(ni)2 > 4N] < 1/2.Доказательство. Докажем это, показав, что E [Pi (ni) 2]
Теперь, хитрый трюк заключается в том, что один из способов подсчитать это количество — подсчитать количество упорядоченных пар, у которых возникает коллизия, включая коллизии с самим собой. Например, если корзина имеет {d, e, f}, то у d возникнет коллизия с каждым из {d, e, f}, у e возникнет коллизия с каждым из {d, e, f}, и у f возникнет коллизия с каждым из {d, e, f}, поэтому мы получаем 9. Итак, мы имеем:
E[X
i
(ni)2] = E[X
x
X
y
Cxy] (Cxy = 1 if x and y collide, else Cxy = 0)
= N +X
x
X
y6=x
E[Cxy]
≤ N + N(N − 1)/M (where the 1/M comes from the definition of universal)
< 2N. (since M = N)
Итак, мы просто пробуем случайное h из H, пока не найдем такое, что Pi n2 i
6. Дальнейшее обсуждение
6.1 Еще один метод универсального хеширования
Вот еще один метод построения универсальных хеш-функций, который немного более эффективен, чем матричный метод, приведенный ранее.
В матричном методе мы рассматривали ключ как вектор битов. В этом методе вместо этого мы будем рассматривать ключ x как вектор целых чисел [x1, x2,…, xk] с единственным требованием, чтобы каждый xi находился в диапазоне {0, 1,…, М-1}. Например, если мы хешируем строки длиной k, то xi может быть i-м символом (если размер нашей таблицы не менее 256) или i-й парой символов (если размер нашей таблицы не менее 65536). Кроме того, мы будем требовать, чтобы размер нашей таблицы M был простым числом. Чтобы выбрать хеш-функцию h, мы выберем k случайных чисел r1, r2,…, рк из {0, 1,…, M — 1} и определить:
h(x) = r1x1 + r2x2 + . . . + rkxk mod M.Доказательство того, что этот метод универсален, строится точно так же, как доказательство матричного метода. Пусть x и y два разных ключа. Мы хотим показать, что Prh (h (x) = h (y)) ≤ 1 / M. Поскольку x != y, должен быть случай, когда существует некоторый индекс i такой, что xi != yi. Теперь представьте, что сначала вы выбрали все случайные числа rj для j != i. Пусть h ′ (x) = Pj6 = i rjxj. Итак, выбрав ri, мы получим h (x) = h ′ (x) + rixi. Это означает, что у нас возникает коллизия между x и y именно тогда, когда
h′(x) + rixi = h′(y) + riyi mod M, or equivalently when
ri(xi − yi) = h′(y) − h′(x) mod M.Поскольку M — простое, деление на ненулевое значение mod M является допустимым (каждое целое число от 1 до M −1 имеет мультипликативный обратный по модулю M), что означает, что существует ровно одно значение ri по модулю M, для которого выполняется приведенное выше уравнение истина, а именно ri = (h ′ (y) — h ′ (x)) / (xi — yi) mod M. Таким образом, вероятность этого происшествия равна точно 1 / M.
6.2 Другое использование хеширования
Предположим, у нас есть длинная последовательность элементов, и мы хотим увидеть, сколько разных элементов находятся в списке. Есть ли хороший способ сделать это?
Одним из способов является создать хеш-таблицу, а затем сделать один проход по последовательности, сделав для каждого элемента поиск и затем вставку, если его еще нет в таблице. Количество отдельных элементов — это просто количество вставок.
А теперь, что если список действительно огромен и у нас нет места для его хранения, но нам подойдёт приблизительный ответ. Например, представьте, что мы являемся маршрутизатором и наблюдаем, как проходит много пакетов, и мы хотим (приблизительно) увидеть, сколько существует различных IP-адресов источника.
Вот хорошая идея: скажем, у нас есть хеш-функция h, которая ведет себя как случайная функция, и давайте представим, что h (x) — действительное число от 0 до 1. Одна вещь, которую мы можем сделать, это просто отслеживать минимальный хеш стоимость произведена до сих пор (поэтому у нас не будет таблицы вообще). Например, если ключи 3,10,3,3,12,10,12 и h (3) = 0,4, h (10) = 0,2, h (12) = 0,7, то мы получим 0,2.
Дело в том, что если мы выберем N случайных чисел в [0, 1], ожидаемое значение минимума будет 1 / (N + 1). Кроме того, есть хороший шанс, что он довольно близок (мы можем улучшить нашу оценку, запустив несколько хеш-функций и взяв медиану минимумов).
Вопрос: зачем использовать хеш-функцию, а не просто выбирать случайное число каждый раз? Это потому, что мы заботимся о количестве различных элементов, а не только об общем количестве элементов (эта проблема намного проще: просто используйте счетчик…).
Друзья, была ли эта статья полезной для вас? Пишите в комментарии и присоединяйтесь ко дню открытых дверей, который пройдет уже 25 апреля.
Что такое хеш и для чего он нужен?
Что такое хеш?Хеш-функцией называется математическое преобразование информации в короткую, определенной длины строку.
Зачем это нужно?Анализ при помощи хеш-функций часто используют для контроля целостности важных файлов операционной системы, важных программ, важных данных. Контроль может производиться как по необходимости, так и на регулярной основе.
Как это делается?Вначале определяют, целостность каких файлов нужно контролировать. Для каждого файла производится вычисления значения его хеша по специальному алгоритму с сохранением результата. Через необходимое время производится аналогичный расчет и сравниваются результаты. Если значения отличаются, значит информация содержащаяся в файле была изменена.
Какими характеристиками должна обладать хеш-функция?
- должна уметь выполнять преобразования данных произвольной длины в фиксированную;
- должна иметь открытый алгоритм, чтобы можно было исследовать её криптостойкость;
- должна быть односторонней, то есть не должно быть математической возможности по результату определить исходные данные;
- должна «сопротивляться» коллизиям, то есть не должна выдавать одинаковых значений при разных входных данных;
- не должна требовать больших вычислительных ресурсов;
- при малейшем изменении входных данных результат должен существенно изменяться.
Какие популярные алгоритмы хеширования?В настоящее время используются следующие хеш-функции:
- CRC– циклический избыточный код или контрольная сумма. Алгоритм весьма прост, имеет большое количество вариаций в зависимости от необходимой выходной длины. Не является криптографическим!
- MD5 – очень популярный алгоритм. Как и его предыдущая версия MD4 является криптографической функцией. Размер хеша 128 бит.
- SHA-1 – также очень популярная криптографическаяфункция. Размер хеша 160 бит.
- ГОСТ Р 34.11-94 – российский криптографический стандарт вычисления хеш-функции. Размер хеша 256 бит.
Когда эти алгоритмы может использовать системный администратор? Часто при скачивании какого-либо контента, например программ с сайта производителя, музыки, фильмов или другой информации присутствует значение контрольных сумм, вычисленных по определенному алгоритму. Из соображений безопасности после скачивания необходимо провести самостоятельное вычисление хеш-функции и сравнить значение с тем, что указано на сайте или в приложении к файлу. Делали ли вы когда-нибудь такое?
Чем удобнее рассчитывать хеш?Сейчас существует большое количество подобных утилит как платных, так и свободных для использования. Мне лично понравилась HashTab . Во-первых, утилита при установке встраивается в виде вкладки в свойства файлов, во-вторых, позволяет выбирать большое количество алгоритмов хеширования, а в третьих является бесплатной для частного некоммерческого использования.
Что есть российского? Как было сказано выше в России есть стандарт хеширования ГОСТ Р 34.11-94, который повсеместно используется многими производителями средств защиты информации. Одним из таких средств является программа фиксации и контроля исходного состояния программного комплекса «ФИКС». Эта программа является средством контроля эффективности применения СЗИ.
ФИКС (версия 2.0.1) для Windows 9x/NT/2000/XP
- Вычисление контрольных сумм заданных файлов по одному из 5 реализованных алгоритмов.
- Фиксация и последующий контроль исходного состояния программного комплекса.
- Сравнение версий программного комплекса.
- Фиксация и контроль каталогов.
- Контроль изменений в заданных файлах (каталогах).
- Формирование отчетов в форматах TXT, HTML, SV.
- Изделие имеет сертификат ФСТЭК по НДВ 3 № 913 до 01 июня 2013 г.
А как на счет ЭЦП? Результат вычисленияхеш-функции вместе с секретным ключом пользователя попадает на вход криптографического алгоритма, где и рассчитывается электронно-цифровая подпись. Строго говоря, хеш-функция не является частью алгоритма ЭЦП, но часто это делается специально, для того, чтобы исключить атаку с использованием открытого ключа.
В настоящее время многие приложения электронной коммерции позволяют хранить секретный ключ пользователя в закрытой области токена (ruToken, eToken) без технической возможности извлечения его оттуда. Сам токен имеет весьма ограниченную область памяти, измеряемую в килобайтах. Для подписания документа нет никакой возможности передать документ в сам токен, а вот передать хеш документа в токен и на выходе получить ЭЦП очень просто.
Безопасность— разница между хешированием пароля и его шифрованием
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
Введение в последовательное хеширование. Что такое последовательное хеширование? Как это… | by Тейва Харсаньи

С развитием распределенных архитектур, последовательного хеширования стали мейнстримом. Но что это такое и чем он отличается от стандартного алгоритма хеширования? Каковы точные мотивы этого?
Сначала опишем основные понятия. Затем мы углубимся в существующие алгоритмы, чтобы понять проблемы, связанные с согласованным хешированием.
Хеширование
Хеширование — это процесс преобразования данных произвольного размера в значений фиксированного размера . Каждый существующий алгоритм имеет свою спецификацию:
- MD5 выдает 128-битные хеш-значения.
- SHA-1 создает 160-битные хеш-значения.
- и т. Д.
Хеширование имеет множество применений в информатике. Например, одно из этих приложений называется контрольной суммой. Чтобы проверить целостность набора данных, можно использовать алгоритм хеширования.Сервер хеширует набор данных и указывает хеш-значение клиенту. Затем клиент хеширует свою версию набора данных и сравнивает хеш-значения. Если они равны, целостность должна быть проверена.
Здесь важно «следует». Наихудший сценарий — это коллизия . Конфликт — это когда два разных фрагмента данных имеют одинаковое хеш-значение . Давайте возьмем реальный пример, определив следующую функцию хеширования: для данного человека она возвращает дату его рождения (день и месяц рождения).Парадокс дня рождения говорит нам, что если в комнате всего 23 человека, вероятность того, что у двух человек будет один и тот же день рождения (следовательно, столкновение), составляет более 50%. Следовательно, функция дня рождения, вероятно, не является хорошей функцией хеширования.
Плохая функция хешированияВ качестве быстрого введения в хеширование важно понять, что основная идея заключается в распределении значений по домену . Например:
- MD5 распределяет значения по 128-битной области пространства
- Хеш-таблица (или хэш-карта), поддерживаемая массивом из 32 элементов, имеет внутреннюю хеш-функцию, которая распределяет значения по любому индексу (от 0 до 31) .
Распределение нагрузки
Распределение нагрузки можно определить как процесс распределения нагрузки между узлами. Термин узел здесь взаимозаменяем с сервером или экземпляром. Это вычислительная единица.
Балансировка нагрузки — это один из примеров распределения нагрузки. Речь идет о распределении набора задач по набору ресурсов. Например, мы используем балансировку нагрузки для распределения запросов API между экземплярами веб-сервера.
Когда дело доходит до данных, мы предпочитаем использовать термин сегментирование .Осколок базы данных — это горизонтальный раздел данных в базе данных. Типичный пример — база данных, разделенная на три сегмента, где каждый сегмент имеет подмножество общих данных.
Балансировка нагрузки и сегментирование имеют общие проблемы. Распределение данных равномерно , например, чтобы гарантировать, что узел не перегружен по сравнению с другими. В некотором контексте балансировка нагрузки и сегментирование также должны поддерживать связь задач или данных с одним и тем же узлом:
- Если нам нужно сериализовать, обрабатывать одну за одной операции для данного потребителя, мы должны направить запрос к тому же самому узлу. узел.
- Если нам нужно распространить данные, мы должны знать, какой шард является владельцем определенного ключа.
Знакомо? В этих двух примерах мы распределяем значения по домену. Будь то задача, распространяемая на серверные узлы или данные на осколок базы данных, мы находим идею, связанную с хешированием. Это причина, по которой хеширование можно использовать в сочетании с распределением нагрузки. Посмотрим как.
Mod-n хеширование
Принцип mod-n хеширования следующий.Каждый ключ хешируется с использованием хеш-функции для преобразования входных данных в целое число. Затем мы выполняем вычисление по модулю в зависимости от количества узлов.
Рассмотрим конкретный пример с 3 узлами. Здесь нам нужно распределить нагрузку между этими узлами на основе идентификатора ключа. Каждый ключ хешируется, затем мы выполняем операцию по модулю:
Преимущество этого подхода — отсутствие состояния. Нам не нужно сохранять какое-либо состояние, чтобы напоминать нам, что foo был направлен на узел 2. Тем не менее, нам нужно знать, сколько узлов настроено для применения операции по модулю.
Тогда как этот механизм работает в случае увеличения или уменьшения масштаба (добавления или удаления узлов)? Если мы добавим еще один узел, операция по модулю теперь будет основана на 4 вместо 3:
Как мы видим, ключи foo и baz больше не связаны с одним и тем же узлом. При хешировании mod-n нет никаких гарантий сохранения согласованности в ассоциации ключ / узел. Это проблема? Может.
Что, если мы реализуем хранилище данных с использованием сегментирования и на основе стратегии mod-n для распределения данных? Если мы масштабируем количество узлов, нам нужно выполнить операцию перебалансировки .В предыдущем примере перебалансировка означает:
- Перемещение
fooс узла 2 на узел 0. - Перемещение
bazс узла 2 на узел 3.
Теперь, что произойдет, если мы сохраним миллионы или даже миллиарды данных и что нам нужно перебалансировать почти все? Как мы понимаем, это был бы тяжелый процесс. Следовательно, мы должны изменить нашу технику распределения нагрузки, чтобы гарантировать, что после перебалансировки:
- Распределение останется равным равномерному , насколько это возможно, на основе нового количества узлов.
- Количество ключей, которые необходимо перенести, должно быть ограничено. В идеале это было бы только 1 / n процентов ключей, где n — количество узлов.
Это и есть цель согласованных алгоритмов хеширования .
Однако термин «последовательный» может несколько сбивать с толку. Я встречал инженеров, которые предполагали, что такие алгоритмы продолжают связывать данный ключ с одним и тем же узлом, даже несмотря на масштабируемость. Это не вариант.Он должен быть последовательным до определенного момента, чтобы обеспечить равномерное распределение.
Теперь пора заняться некоторыми решениями.
Rendezvous был первым алгоритмом, когда-либо предложенным для решения нашей проблемы. Хотя в первоначальном исследовании, опубликованном в 1996 году, термин «согласованное хеширование» не упоминался, оно все же дает решение описанных нами проблем. Давайте посмотрим на одну возможную реализацию на Go:
Как это работает? Мы проходим каждый узел и вычисляем его хеш-значение. Хеш-значение возвращается функцией hash , которая производит целое число на основе ключа (нашего ввода) и идентификатора узла (самый простой подход — хешировать конкатенацию двух строк).Затем мы возвращаем узел с наибольшим значением хеш-функции. Это причина, по которой алгоритм также известен как хеширование с наивысшим случайным весом.
Основным недостатком рандеву является его временная сложность O ( n ), где n — количество узлов. Это очень эффективно, если нам нужно ограниченное количество узлов. Тем не менее, если мы начнем обслуживать тысячи узлов, это может вызвать проблемы с производительностью.
Следующий алгоритм был выпущен в 1997 году Karger et al. В этом документе.В этом исследовании впервые упоминается термин согласованное хеширование.
Он основан на кольце (массив с сквозным соединением). Хотя это самый популярный алгоритм последовательного хеширования (или, по крайней мере, самый известный), принцип не всегда хорошо понимается. Давайте погрузимся в это.
Первая операция — создание кольца. Кольцо имеет фиксированную длину. В нашем примере мы разбиваем его на 12 частей:
Затем мы размещаем наши узлы. В нашем примере мы определим N0 , N1 и N2 .
Узлы пока распределяются равномерно. Мы вернемся к этому вопросу позже.
Затем пора посмотреть, как представлять ключи. Во-первых, нам нужна функция f , которая возвращает индекс кольца (от 0 до 11) на основе ключа. Для этого мы можем использовать хеширование mod-n. Поскольку длина кольца постоянна, это не доставит нам никаких проблем.
В нашем примере мы определим 3 ключа: a , b и c . Наносим f на каждую.Предположим, у нас есть следующие результаты:
Следовательно, мы можем расположить ключи на кольце следующим образом:
Как связать данный ключ с узлом? Основная логика — двигаться вперед на . Из заданного ключа мы возвращаем первый узел, который мы находим следующим при продвижении вперед:
В этом примере мы связываем a с N1 , b и c с N2 .
Теперь давайте посмотрим, как выполняется ребалансировка .Определяем еще один узел N3 . Где мы должны его разместить? Больше нет места, чтобы общее распределение было однородным. Стоит ли реорганизовать узлы? Нет, иначе мы бы перестали быть последовательными, не так ли? Чтобы разместить узел, мы повторно используем ту же хеш-функцию f , которую мы ввели. Вместо того, чтобы вызывать с помощью ключа, его можно вызывать с идентификатором узла. Таким образом, положение нового узла определяется случайным образом.
Тогда возникает один вопрос: что нам делать с и , поскольку следующий узел больше не N1 :
Решение следующее: мы должны изменить его ассоциацию и получить , а будет связан с N3 :
Как мы обсуждали ранее, идеальный алгоритм должен перебалансировать 1 / n в среднем процентов ключей.В нашем примере, когда мы добавляем четвертый узел, у нас должно быть 25% возможных ключей, повторно связанных с N3 . Так ли это?
-
N0из индексов с 8 по 12: 33,3% от общего числа ключей -
N1из индексов со 2 по 4: 16,6% от общего количества ключей -
N2из индексов с 4 по 8: 33,3% от общего числа ключей Всего ключей -
N3от индексов 0 до 2: 16,6% от общего количества ключей
Распределение неравномерное.Как мы можем это улучшить? Решение заключается в использовании виртуальных узлов .
Предположим, что вместо размещения одной точки на узел мы можем расположить три. Также нам нужно определить три разные функции хеширования. Каждый узел хешируется трижды, так что мы получаем три разных индекса:
Мы можем применить тот же алгоритм, двигаясь вперед. Тем не менее, ключ будет связан с узлом независимо от виртуального узла, с которым он встретился.
В этом примере распределение теперь будет следующим:
-
N0: 33.3% -
N1: 25% -
N2: 41,6%
Чем больше виртуальных узлов мы определяем для каждого узла, тем более равномерным должно быть распределение. В среднем, при 100 виртуальных узлах на сервер стандартное распределение составляет около 10%. С 1000 это около 3,2%.
Этот механизм также полезен, если у нас есть узлы с разным размером. Например, если узел сконфигурирован так, чтобы теоретически обрабатывать в два раза большую нагрузку, чем другие, мы могли бы развернуть вдвое больше виртуальных узлов.
Тем не менее, основным недостатком виртуальных узлов является объем памяти. Если нам придется обслуживать тысячи серверов, потребуются мегабайты памяти.
Прежде чем двигаться дальше, интересно отметить, что иногда алгоритм можно существенно улучшить, изменив небольшую часть. Так обстоит дело, например, с алгоритмом, опубликованным Google в 2017 году, который называется согласованное хеширование с ограниченными нагрузками. Эта версия основана на той же идее кольца, которую мы описали. Тем не менее, их подход состоит в том, чтобы выполнить небольшую перебалансировку при при любом обновлении (добавлен / удален новый ключ или узел).Эта версия превосходит исходную с точки зрения стандартного отклонения за счет наихудшей временной сложности.
В 2007 году два инженера из Google опубликовали хеш-код перехода. По сравнению с алгоритмом на основе кольца эта реализация «не требует хранилища, работает быстрее и лучше справляется с равномерным разделением ключевого пространства между сегментами и равномерным распределением рабочей нагрузки при изменении количества сегментов» . Иными словами, это улучшает распределение рабочей нагрузки между узлами (корзина — это та же концепция, что и узел) без каких-либо дополнительных затрат памяти.
Вот алгоритм на C ++ (7 строк кода 🤯):
В кольцевом согласованном хэше с 1000 виртуальными узлами стандартное отклонение составило около 3,2%. В хэше с согласованным переходом нам больше не нужна концепция виртуальных узлов. Тем не менее, стандартное отклонение остается менее 0,0000001%.
Но есть одно ограничение. Узлы должны быть пронумерованы последовательно . Если у нас есть список серверов foo , bar и baz , мы не сможем удалить, например, bar .Тем не менее, если мы настроим хранилище данных, мы можем применить алгоритм для получения индекса сегментов на основе общего количества сегментов. Следовательно, согласованный хэш-код может быть полезен в контексте сегментирования, но не для балансировки нагрузки.
Поскольку теперь у нас есть некоторый опыт последовательного хеширования, давайте сделаем шаг назад и посмотрим, какой будет идеальный алгоритм:
- Только 1 / n процентов ключей будут переназначены в среднем, где n — это количество узлов.
- A O ( n ) сложность пространства, где n — количество узлов.
- A O (1) временная сложность для вставки / удаления узла и для каждого поиска ключа.
- Минимальное стандартное отклонение, чтобы гарантировать, что узел не перегружен по сравнению с другим.
- Это позволит связать вес с узлом, чтобы справиться с разным размером узла.
- Это позволит произвольным именам узлов (не пронумерованным последовательно) поддерживать как балансировку нагрузки, так и сегментирование.
К сожалению, такого алгоритма не существует. Основываясь на том, что мы видели:
- Rendezvous имеет линейную временную сложность на поиск.
- Кольцевой согласованный хэш имеет плохое минимальное стандартное отклонение без концепции виртуальных узлов. С виртуальными узлами сложность пространства равна O ( n * v ) с n количеством узлов и v количеством виртуальных узлов на узел.
- Согласованный хэш перехода не имеет постоянной временной сложности и не поддерживает произвольные имена узлов.
Тема все еще открыта, и есть недавние исследования, на которые стоит обратить внимание. Например, последовательный хэш с несколькими зондами, выпущенный в 2005 году.Он поддерживает сложность пространства O (1). Тем не менее, чтобы достичь стандартного отклонения ε, требуется время O (1 / ε) на поиск. Например, если мы хотим достичь стандартного отклонения менее 0,5%, потребуется хеширование ключа примерно 20 раз. Следовательно, мы можем получить минимальное стандартное отклонение, но с более высокой временной сложностью поиска.
Как мы уже говорили во введении, последовательные алгоритмы хеширования стали широко распространенными. Сейчас он используется в бесчисленных системах, таких как MongoDB, Cassandra, Riak, Akka и т. Д.будь то в контексте балансировки нагрузки или распределения данных. Тем не менее, как это часто бывает в информатике, у каждого решения есть компромиссы.
Говоря о компромиссах, если вам нужно продолжение, вы можете взглянуть на отличный пост, написанный Дамианом Грыски:
Некоторые другие ресурсы, на которые стоит обратить внимание:
.Безопасность— Является ли «двойное хеширование» пароля менее безопасным, чем его однократное хеширование?
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Загрузка…
.python — что такое хеширование функций (трюк с хешированием)?
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
