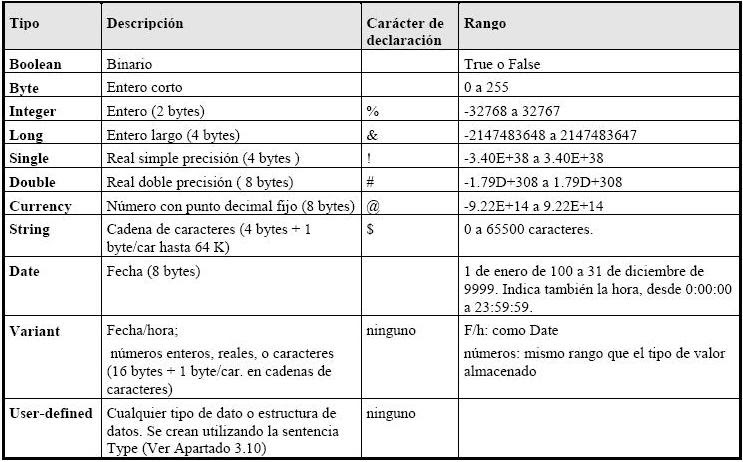
Тип данных Integer — Visual Basic
Twitter LinkedIn Facebook Адрес электронной почты
- Статья
- Чтение занимает 3 мин
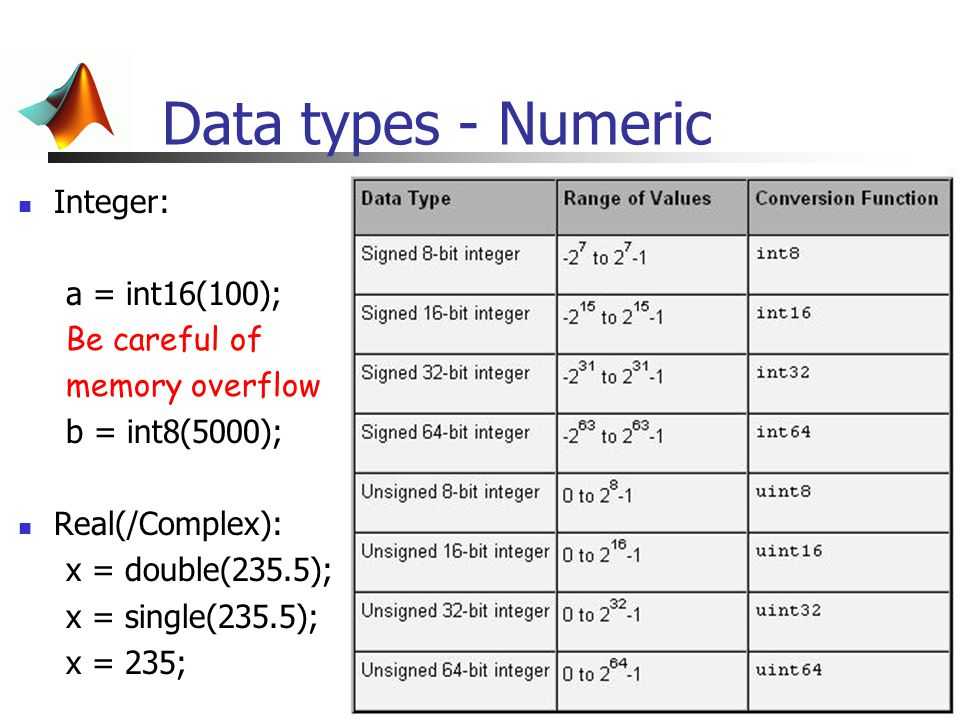
Содержит 32-разрядные (4-байтовые) целые числа со знаком в диапазоне от -2 147 483 648 до 2 147 483 647.
Тип данных Integer обеспечивает оптимальную производительность на 32-разрядных процессорах. Другие целочисленные типы загружаются в память и сохраняются в памяти с более низкой скоростью.
Значение по умолчанию для типа Integer — 0.
Можно объявить и инициализировать Integer переменную, назначив ей десятичный литерал, шестнадцатеричный литерал, восьмеричный литерал или (начиная с Visual Basic 2017) двоичный литерал. Если целочисленный литерал выходит за пределы диапазона Integer (то есть, если он меньше Int32.MinValue или больше Int32.MaxValue), возникает ошибка компиляции.
В следующем примере целые числа, равные 90 946 и представленные в виде десятичного, шестнадцатеричного и двоичного литерала, назначаются значениям Integer.
Dim intValue1 As Integer = 90946 Console.WriteLine(intValue1) Dim intValue2 As Integer = &h26342 Console.WriteLine(intValue2) Dim intValue3 As Integer = &B0001_0110_0011_0100_0010 Console.WriteLine(intValue3) ' The example displays the following output: ' 90946 ' 90946 ' 90946
WriteLine(intValue3)
' The example displays the following output:
' 90946
' 90946
' 90946
Примечание
Вы используете префикс &H обозначает шестнадцатеричный литерал, префикс &b или &B обозначающий двоичный литерал, а также префикс &o или &O обозначающий восьмеричный литерал. У десятичных литералов префиксов нет.
Начиная с Visual Basic 2017 г., вы также можете использовать символ подчеркивания в _качестве разделителя цифр для повышения удобочитаемости, как показано в следующем примере.
Dim intValue1 As Integer = 90_946 Console.WriteLine(intValue1) Dim intValue2 As Integer = &H0001_6342 Console.WriteLine(intValue2) Dim intValue3 As Integer = &B0001_0110_0011_0100_0010 Console.WriteLine(intValue3) ' The example displays the following output: ' 90946 ' 90946 ' 90946
Начиная с Visual Basic 15.
5, вы также можете использовать символ подчеркивания (_) в качестве ведущего разделителя между префиксом и шестнадцатеричными, двоичными или восьмеричных цифрами. Пример:
Dim number As Integer = &H_C305_F860
Чтобы использовать символ подчеркивания в качестве ведущего разделителя, необходимо добавить следующий элемент в файл проекта Visual Basic (*.vbproj):
<PropertyGroup> <LangVersion>15.5</LangVersion> </PropertyGroup>
Дополнительные сведения см. в разделе «Выбор версии языка Visual Basic».
Числовые литералы также могут включать Iсимвол типа для обозначения Integer типа данных, как показано в следующем примере.
Dim number = &H_035826I
Советы по программированию
Вопросы взаимодействия. Если вы работаете с компонентами, не написанными для платформа .NET Framework, таких как объекты automation или COM, помните, что
Integerв других средах используется другая ширина данных (16 битов). При передаче 16-разрядного аргумента такому компоненту в новом коде Visual Basic следует объявить его как Integer.Расширение. Тип данных
Integerможно расширить доLong,Decimal,SingleилиDouble. Это означает, что типIntegerможно преобразовать в любой из этих типов без возникновения ошибки System.OverflowException.Символы типов. При добавлении к литералу символа типа литерала
Iпроизводится принудительное приведение литерала к типу данныхInteger. При добавлении символа идентификатора типа%к любому идентификатору производится принудительное приведение этого идентификатора к типуТип Framework. В .NET Framework данный тип соответствует структуре System.Int32.
При передаче 16-разрядного аргумента такому компоненту в новом коде Visual Basic следует объявить его как Диапазон
При попытке присвоить целочисленной переменной значение, лежащее за пределами диапазона данного типа, возникает ошибка.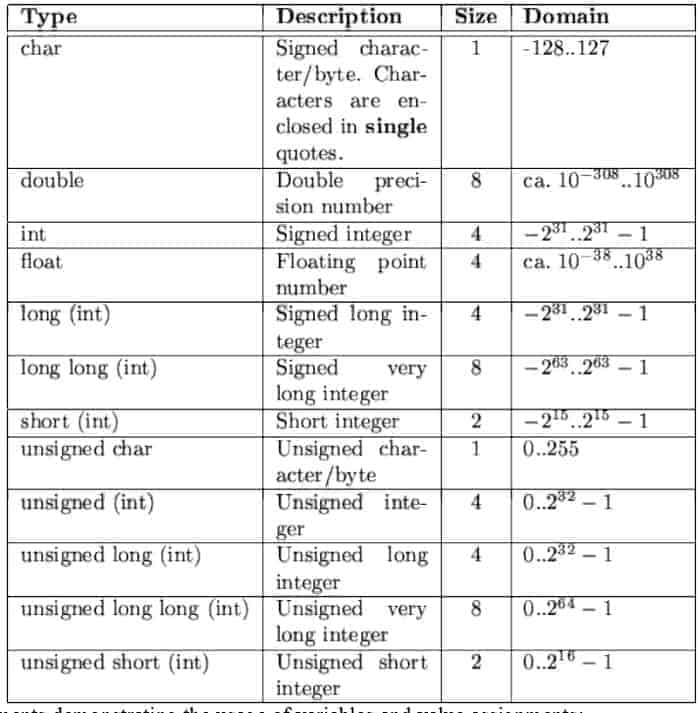
При попытке задать дробное значение оно округляется вверх или вниз до ближайшего целого значения. Если число находится точно посередине между двумя целыми числами, значение округляется до ближайшего четного целого. Такое поведение минимизирует ошибки округления, происходящие от постоянного округления среднего значения в одном направлении. В следующем коде приведены примеры округления.
' The valid range of an Integer variable is -2147483648 through +2147483647. Dim k As Integer ' The following statement causes an error because the value is too large. k = 2147483648 ' The following statement sets k to 6. k = 5.9 ' The following statement sets k to 4 k = 4.5 ' The following statement sets k to 6 ' Note, Visual Basic uses banker’s rounding (toward nearest even number) k = 5.5
См. также раздел
- System.Int32
- Типы данных
- Тип данных Long
- Тип данных Short
- Type Conversion Functions
- Сводка по преобразованию
- Эффективное использование типов данных
Слово integer — English for me
ˈɪntɪdʒə
than the number of non-zero positive integers being added together?
чем число отличных от нуля положительных целых чисел, сложенных вместе?
Поделиться
Перевод:
Noun:
целое
нечто целое
Adjective:
целый
Фразы:
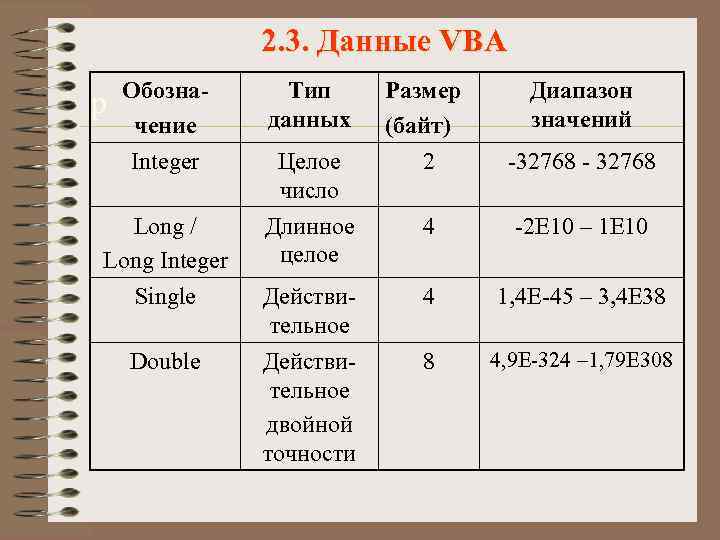целочисленное программированиеinteger constant — целочисленная константа
integer number — целое число
integer operand — циклочисленный операнд
integer operation — целочисленная операция
integer ordinal — целочисленное порядковое число
integer-valued parameter — целочисленный параметр
integer part — целая часть (числа)
partition of integer — разбиение целого числа
integer polyhedron — целочисленный многогранник
Показать все
Примеры:
Three is a positive integer.
— Три — это положительное целое число.
6 is an integer, but 6.4 is not. — Число 6 является целым, а 6,4 — нет.
An integer is a number that is not a fraction. — Целым называется число, которое не является дробью.
Both 10 and -10 are integers. — Как 10, так и -10 являются целыми числами.
integer vitae: blameless in life ; innocent
Gaussian integer: a complex number of the form a + bi where a and b are integers
greatest-integer function: the function that assigns to each real number the greatest integer less than or equal to the number
everyone number figure count everything emblem component sum symbol rate member character arm total price group cost amount
перевод на русский, синонимы, антонимы, произношение, примеры предложений, транскрипция, значение, словосочетания
I have come to believe that for Ramanujan, every single positive integer is one of his personal friends. | Я пришел к пониманию, что для Рамануджана каждое положительное целое число является одним из близких друзей. |
The number of hash functions, k, must be a positive integer . | Число хэш — функций, k, должно быть положительным целым числом . |
Assume that s > 1 is the smallest positive integer which is the product of prime numbers in two different ways. | Предположим, что s > 1 — наименьшее положительное целое число , которое является произведением простых чисел двумя различными способами. |
To keep things simple, let us assume that a is a positive integer . | Чтобы упростить задачу, предположим, что a — положительное целое число . |
In order to prove the lemma, we must introduce the binomial theorem, which states that for any positive integer n,. | Чтобы доказать лемму, мы должны ввести биномиальную теорему, которая утверждает, что для любого положительного целого числа n,. |
So p − 1 = km for some positive integer m and then. | Итак, p — 1 = km для некоторого положительного целого числа m и затем. |
This implies that the difference between 1 and x is less than the inverse of any positive integer . | Это означает, что разница между 1 и x меньше, чем обратная величина любого положительного целого числа . |
Also, every positive integer is the sum of at most 548 ninth powers;. | Кроме того, каждое положительное целое число является суммой не более 548 девятых степеней;. |
The principal quantum number n describes the energy of the electron and is always a positive integer . | Основное квантовое число n описывает энергию электрона и всегда является положительным целым числом . |
In fact, it can be any positive integer , but for reasons discussed below, large numbers are seldom encountered. | Фактически, это может быть любое положительное целое число , но по причинам, рассмотренным ниже, большие числа встречаются редко. |
However, these squares on the diagonal have positive integer sides that are smaller than the original squares. | Однако эти квадраты на диагонали имеют положительные целочисленные стороны, которые меньше, чем исходные квадраты. |
For larger positive integer values of n, the correct result is given by the binomial theorem. | Для больших положительных целых значений n правильный результат дается биномиальной теоремой. |
A number is said to be normal in base b if, for every positive integer n, all possible strings n digits long have density b−n. | Число считается нормальным в базе b, если для каждого положительного целого числа n все возможные строки n цифр длиной имеют плотность b — n. |
If it can be proved that if a decimal of the form 0.b1b2b3… is a positive integer , then it must be 0.999…, which is then the source of the 9s in the theorem. | Если можно доказать, что если десятичное число вида 0.b1b2b3… является положительным целым числом , то оно должно быть 0,999…, который затем является источником 9s в теореме. |
If any pi = qj then, by cancellation, s/pi = s/qj would be another positive integer , different from s, which is greater than 1 and also has two distinct factorizations. | Если какое — либо pi = qj, то при отмене s/pi = s/qj будет другим положительным целым числом , отличным от s, которое больше 1 и также имеет две различные факторизации. |
As a result, there is no smallest positive integer with multiple prime factorizations, hence all positive integers greater than 1 factor uniquely into primes. | В результате не существует наименьшего положительного целого числа с множественными простыми факторизациями, следовательно, все положительные целые числа , превышающие 1 фактор, однозначно делятся на простые числа . |
Sidney Kravitz has shown that for k a positive integer , Q a prime exceeding 2k, and. | Сидней Кравиц показал, что для k положительное целое число , Q простое число , превышающее 2k, и. |
A highly composite number is a positive integer with more divisors than any smaller positive integer has. | Очень сложное число — это положительное целое число с большим числом делителей, чем любое меньшее положительное целое число . |
In number theory, a pernicious number is a positive integer such that the Hamming weight of its binary representation is prime. | В теории чисел пагубное число — это положительное целое число , такое, что вес Хэмминга его двоичного представления является простым. |
There is no case of more than three, because every fourth consecutive positive integer is divisible by 4 = 2×2 and therefore not squarefree. | Здесь нет случая больше трех, потому что каждое четвертое подряд положительное целое число делится на 4 = 2×2 и поэтому не является бесквадратным. |
In number theory, an odious number is a positive integer that has an odd number of 1s in its binary expansion. | В теории чисел одиозное число — это положительное целое число , которое имеет нечетное число 1s в своем двоичном разложении. |
In number theory, a hemiperfect number is a positive integer with a half-integral abundancy index. | Например, токсичная изоляция обычно сжигается медной проволокой, чтобы получить доступ к металлу. |
A positive integer n is a powerful number if, for every prime factor p of n, p2 is also a divisor. | Положительное целое число n является мощным числом , если для каждого простого множителя p из n p2 также является делителем. |
In mathematics, a superperfect number is a positive integer n that satisfies. | В математике, суперсовершенными число — положительное целое число N, которое удовлетворяет. |
So, when talking of the square root of a positive integer , this is the positive square root that is meant. | Итак, когда речь идет о квадратном корне из положительного целого числа , то имеется в виду именно этот положительный квадратный корень. |
Lagrange found that the representation of the square root of any non-square positive integer as a continued fraction is periodic. | Лагранж обнаружил, что представление квадратного корня любого неквадратичного положительного целого числа в виде непрерывной дроби является периодическим. |
At the time of its introduction, it was the largest specific positive integer ever to have been used in a published mathematical proof. | На момент его введения это было самое большое конкретное положительное целое число , когда — либо использовавшееся в опубликованном математическом доказательстве. |
A rational number is a number that can be expressed as a fraction with an integer numerator and a positive integer denominator. | Рациональное число — это число , которое может быть выражено в виде дроби с целочисленным числителем и положительным целочисленным знаменателем. |
Lagrange’s four-square theorem states that every positive integer can be written as the sum of at most four square numbers. | Теорема Лагранжа о четырех квадратах гласит, что каждое положительное целое число может быть записано как сумма не более четырех квадратных чисел. |
A positive or negative integer representing the day of the month from 1 to 31. | Положительное или отрицательное целое число в диапазоне от 1 до 31, представляющее день месяца. |
A positive or negative integer representing the month of the year from 1 to 12 (January to December). | Положительное или отрицательное целое число в диапазоне от 1 (январь) до 12 (декабрь), представляющее месяц года. |
For integer or positive index α the Bessel function of the first kind may be defined with the alternating series. | Для целого или положительного индекса α функция Бесселя первого рода может быть определена с помощью чередующихся рядов. |
Equivalently, if the positive triangular root n of x is an integer , then x is the nth triangular number. | Аналогично, если положительный треугольный корень n из x является целым числом , то x — это N — е треугольное число . |
Let x be a real number with 0 positive odd integer . | Пусть x — вещественное число с 0 положительное нечетное целое число . |
A Goldbach number is a positive even integer that can be expressed as the sum of two odd primes. | Число Гольдбаха — это положительное четное целое число , которое может быть выражено как сумма двух нечетных простых чисел. |
Corresponding signed integer values can be positive , negative and zero; see signed number representations. | Соответствующие целочисленные значения со знаком могут быть положительными , отрицательными и нулевыми; см. представление чисел со знаком. |
A prime number is an integer greater than 1 that is not the product of two smaller positive integers . | Простое число — это целое число , большее 1, которое не является произведением двух меньших положительных целых чисел. |
Целое число: простое определение и использование
Определения статистики >
Содержание:
- Определение
- Абсолютное значение
- Целочисленное программирование
Целое число включает целые числа и отрицательные целые числа. Целые числа могут быть положительными, отрицательными или нулевыми. Например: 1, -1, 0, 101 и -101.
Набору целых чисел часто присваивается символ Z , а Z определяется как
{…, -3, -2, -1, 0, 1, 2, 3,…}
Существует бесконечное количество целых чисел.
Их можно упорядочить, поместив в числовую строку; число справа всегда больше числа слева.
Числовая линия, показывающая расстояние между -1 и 1.
Абсолютное значение целого числа — это расстояние от этого числа до начала координат (0). Поскольку и 3, и -3 отстоят на 3 единицы (шага) от начала отсчета, абсолютное значение обоих чисел равно 3.
Абсолютное значение -3 равно 3, потому что это три пробела от нуля на числовой прямой.
Знак
Знак (-) для всех целых чисел слева от начала координат (0) равен (-), а для всех чисел справа (+). Отрицательные целые числа — это числа со знаком (-), а положительные — со знаком (+). Целые положительные числа можно записывать без знака.
Сложение и вычитание
Чтобы сложить два целых числа с одинаковым знаком, сложите абсолютные значения и присвойте сумме тот же знак, что и у обоих значений.
Например: (-4) + (-7) = -(4 + 7)= – 11,
Чтобы сложить два целых числа с разными знаками, найдите разницу в абсолютных значениях и присвойте разнице тот же знак, что и число с наибольшим абсолютным значением.
Например: (-5) + (3)
- Найдите абсолютные значения (5 и 3).
- Найдите разницу между 5 и 3 (5 – 3 = 2).
- Найдите знак наибольшего абсолютного значения. -5 имеет отрицательный знак.
- Добавьте знак из шага 3 к разнице, найденной на шаге 2. Результат равен -2.
Вычитание означает прибавление к противоположному .
Например:
Вычитая -2 из 10, получаем:
10 – – 2 = 10 + 2 (2 противоположно -2) = 12.
Вычитая 2 из 10 получаем:
10 + (-2) = 8.
Когда целое число прибавляется или вычитается из другого, результатом всегда является целое число.
Умножение
Чтобы умножить целое число, умножьте абсолютное значение. Если два перемножаемых целых числа имеют одинаковый знак, результат положительный. Если два целых числа имеют разные знаки, результат будет отрицательным.
При умножении одного целого числа на другое всегда получается целое число.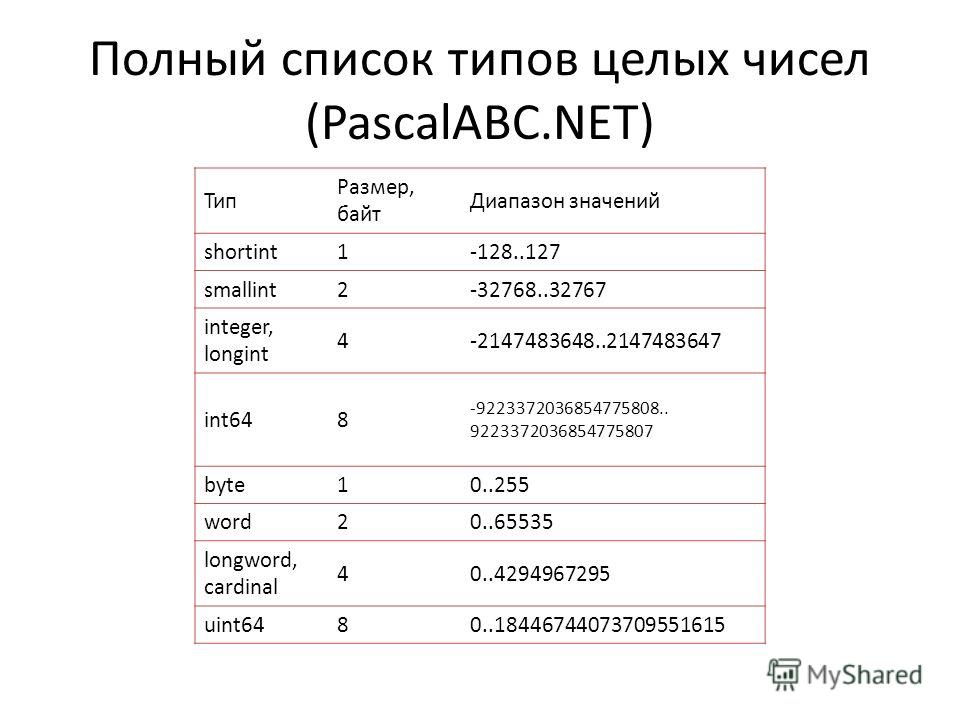
Но когда одно делится на другое, результат может быть целым числом, а может и не быть. Например, если 3/3 = 1 и 8/4 = 2 и являются целыми числами, то 3/4 и 8/5 таковыми не являются.
Задачи целочисленного программирования (IP) представляют собой тип задачи осуществимости или математической оптимизации, в которой некоторые (или все) переменные ограничены целыми значениями.
- Если все переменные ограничены целыми числами, проблема IP называется Проблема чистого целочисленного программирования (IP).
- Если переменные представляют собой смесь обязательных целых чисел и других, не имеющих такого ограничения, задача IP называется смешанной задачей IP .
- Если целые числа ограничены 0 или 1, проблема называется чистой или смешанной&mdas; Задача двоичного целочисленного программирования .
Иногда термин IP используется для обозначения целочисленного линейного программирования , типа программирования, в котором и целевая функция, и любые нецелочисленные ограничения являются линейными.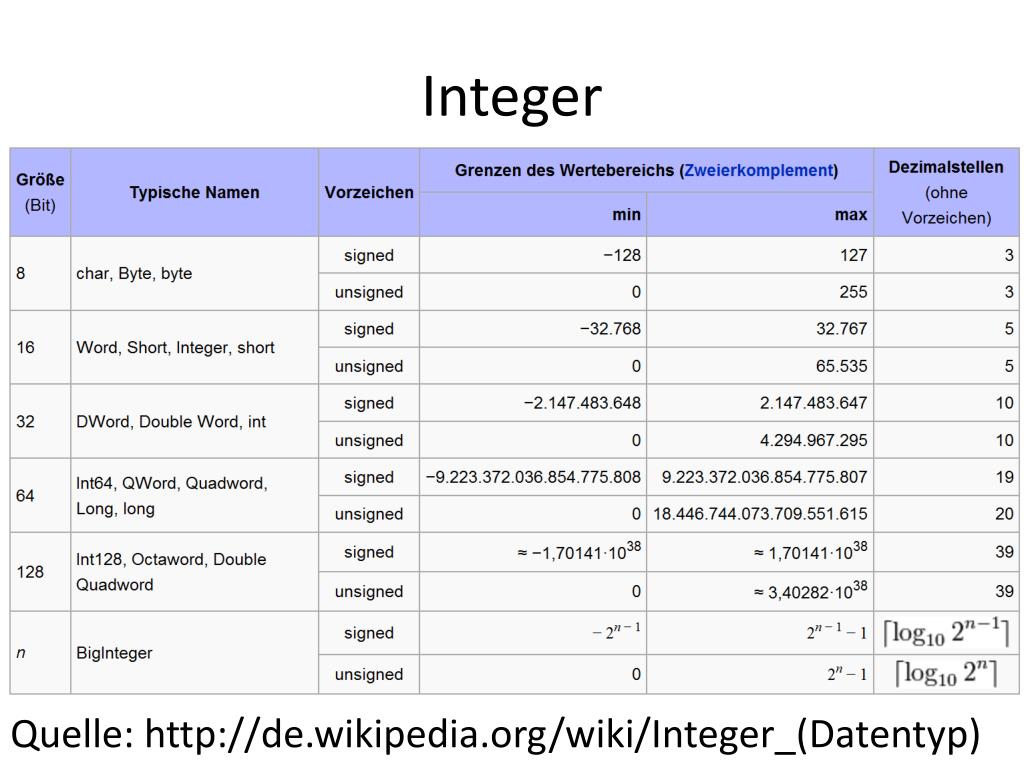
Моделирование с помощью IP-проблем
Когда же используются IP-задачи? Часто для моделирования реальных задач, где значения, естественно, ограничены целыми числами. Например, если мы смоделировали производство компьютеров на фабрике в Китае с помощью простых моделей линейного программирования, мы могли бы прийти к плану выпуска 2067,4 компьютеров в месяц. Это «.4» не имеет интуитивного смысла; как фабрика может производить 40% компьютеров (хотя я полагаю, что они могут остановить линию, когда эта 0,4 часть компьютера будет закончена!). Мы можно было бы округлить до , но было бы лучше, если бы это было целое число.
Иногда нецелочисленные переменные имеют еще меньше смысла. Например, модель линейного программирования, назначающая учителей в определенные города, может рекомендовать разместить 0,7 учителя в одном городе и 0,5 — в другом. Нам нужен способ создания моделей, учитывающих целые числа некоторых или всех переменных.
Формулировка и решение задач IP
Формулировка IP обычно сложнее, чем формулировка простых линейных программ.
Хотя есть некоторые хитрости, главное – практика.
Не существует алгоритмов общего назначения, эффективных с точки зрения вычислений, для решения ИП, аналогичных тем, которые используются для линейных программ. Вместо этого вы обычно должны выбирать между универсальными, неэффективными в вычислительном отношении методами решения или разрабатывать алгоритм специального назначения, который может решить только эту конкретную проблему.
Ссылки
- MathWorks, Inc. IP. Получено с
https://www.mathworks.com/discovery/integer-programming.html 5 мая 2018 г. - Центр знаний IBM. Что такое ИП? Получено с https://www.ibm.com/support/knowledgecenter/SSSA5P_12.6.1/ilog.odms.ide.help/OPL_Studio/opllanguser/topics/opl_languser_shortTour_IP_what.html 5 мая 2018 г.
- Бизли, Дж. Э. Примечания по исследованию операций: Программирование. Получено с http://people.brunel.ac.uk/~mastjjb/jeb/or/ip.html 5 мая 2018 г. .
- Положительные и отрицательные. http://web.cerritos.edu/dford/SitePages/Math_40/Math50Lesson6.pdf. Проверено 19 июня 2018 г. .
- Дворскак, Б. Сложение и вычитание. https://mypages.iit.edu/~smart/dvorber/lesson4.htm Дата обращения 19 июня 2018 г.
http://web.cerritos.edu/dford/SitePages/Math_40/Math50Lesson6.pdf. Проверено 19 июня 2018 г. УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Целое число, абсолютное значение: простое определение и примеры, программирование» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/integer/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста Связаться с нами .
Что такое целое число? (с картинками)
`;
Брендан МакГиган
Целое число — это то, что более известно как целое число. Оно может быть положительным, отрицательным или числом ноль, но оно должно быть целым. В некоторых случаях определение целого числа будет исключать число ноль или даже набор отрицательных чисел, но это не так распространено, как более широкое использование этого термина. Целые числа — это числа, с которыми люди больше всего знакомы, и они играют решающую роль практически во всей математике.
Чтобы понять, что такое целое число, то есть чем оно отличается от простого «числа», мы должны взглянуть на другие наборы чисел, которые могут существовать. Многие из этих наборов пересекаются с целочисленным набором в некоторых областях, а некоторые практически идентичны. Другие имеют очень мало общего с любыми целыми числами — такие числа, как правило, гораздо менее знакомы большинству людей.
Подмножество положительных целых чисел, вероятно, является самым старым набором чисел.
Эту группу часто называют набором счетных чисел, поскольку это числа, используемые для подсчета вещей и идей. Числа в положительном наборе — это все целые числа выше нуля. Таким образом, набор будет указан как {1, 2, 3, 4…} и так далее до бесконечности. Как и само множество целых чисел, положительные целые числа бесконечны. Поскольку люди считали с тех пор, как мы знаем, этот набор также существовал в течение очень долгого времени. Хотя, возможно, не было известно, что он бесконечен, набор был по существу тем же самым.
Очень тесно связанным набором является набор всех неотрицательных целых чисел.
Этот набор идентичен набору положительных целых чисел, за исключением того, что он также включает ноль. Исторически число ноль было нововведением, появившимся вскоре после того, как счетные числа получили широкое распространение.
Оба этих набора можно назвать набором натуральных чисел. Некоторые математики предпочитают исключать ноль из натуральных чисел, в то время как другие считают полезным его включение. Если мы рассмотрим более всеобъемлющее определение, мы сможем определить целое число как любой член множества натуральных чисел, а также их отрицательные аналоги.
Помимо целого числа, мы находим другие наборы, которые являются более сложными.
Следующей логической прогрессией является множество всех рациональных чисел. Рациональное число — это любое число, которое можно рассматривать как отношение двух целых чисел. Это означает, что само целое число будет рациональным — 2/2 — это отношение, но оно также просто равно 1, а 8/2 — это тоже отношение, и тоже равно 4. Это также означает, что дроби — это рациональные числа — 3. /4 не целое, а рациональное число.
Следующим шагом будет набор действительных чисел. Их проще всего описать как любое число, которое можно разместить на числовой прямой. Это будет включать любое целое число, а также любое рациональное число, поскольку дроби могут быть помещены в числовую строку.
Кроме того, оно включает числа, которые не могут быть выражены просто как отношение между двумя числами — например, квадратный корень из двух дает бесконечную строку цифр после запятой, поэтому его никогда нельзя адекватно описать как рациональное число. но это реальное число.
Последний набор чисел, с которым обычно имеют дело, — это набор комплексных чисел. Эти числа не имеют фактического места на числовой прямой, но, тем не менее, используются во многих математических процессах. Комплексные числа включают мнимую составляющую, обычно обозначаемую как 9.0022 i , где i 2 равно -1.
Существует множество различных типов чисел, и каждое из них занимает свое место в мире математики и во многих дисциплинах, в которых оно используется. Целое число лучше всего можно описать как тем, что оно есть, так и тем, чем оно не является. Это любое целое положительное число от единицы до бесконечно большого числа. Целое число — это число ноль. Это любое целое отрицательное число, от отрицательного до бесконечно большого отрицательного числа. Это не любое число, которое имеет остаток после запятой. Целое число не является особым действительным числом, таким как пи или 9.0022 е . И это не сложное или иррациональное число.
Целые числа — определение, примеры и правила .
Примеры включают -3, 0 и 2.В математике целых чисел — это числа, которые не содержат дробей или десятичных знаков. Набор включает ноль, натуральные числа (счетные числа) и их аддитивные инверсии (отрицательные целые числа). Примеры целых чисел включают -5, 0 и 7. Здесь есть все, что вам нужно знать о целых числах, включая их примеры и их правила сложения, вычитания, умножения и деления.
Что такое целые числа?
Целые числа — это числа без десятичных знаков и дробей. Но, в отличие от целых чисел, целые числа включают отрицательные числа. Типичные символы для набора целых чисел включают заглавную букву Z, а также версии этой буквы, выделенные жирным шрифтом на доске или полужирным шрифтом. Набор Z = {…, -3, -2, -1, 0, 1, 2, 3, …}. Это счетно бесконечное множество. Все целые числа являются как рациональными, так и действительными числами.
Примеры целых и нецелых чисел
Integers include:
- Negative integers
- Zero
- Positive integers
So, examples of integers are:
- -57
- -13
- -1
- 0
- 5
- 124
Примеры чисел, которые не являются целыми числами:
- 1/3
- 0,45
- -22. 6
- 132.4
- -1/2
- √ 3
- PI
- 3 I 9007 3
- PI
- 3 1 I0023
- 7 ⅚
6Сложение и вычитание
Правила сложения и вычитания целых чисел по сути являются правилами работы с положительными и отрицательными числами.
Сложение двух чисел с одинаковыми знаками дает ответ с тем же знаком. При сложении целых чисел противоположных знаков ответ имеет знак большего значения.При сложении двух целых чисел с одинаковым знаком ответ имеет тот же знак. Например:
- 1 + 3 = 4
- (-4) + (-3) = -7
- 4 + 0 = 4
- 0 + (-2) = -2
Сложение целых чисел с разными знаками работает так же, как вычитание целых чисел. Ответ имеет тот же знак, что и число с большим значением. Обратите внимание, что когда вы вычитаете отрицательное целое число, это то же самое, что прибавлять его положительное значение. Например:
- (-7) + 2 = -5, что также равно 2 – 7
- 4 + (-8) = 4 – 8 = -4
- 3 – (-2) = 3 + 2 = 5
- (-5) – (-3) = (-5) + 3 = -2, что также равно 3 – 5
- 8 – 0 = 8
Умножение и деление
Правила умножения и деления просты:
- Если оба целых числа положительные, ответ положительный.
- Если оба целых числа отрицательные, ответ положительный. Два отрицательных знака компенсируют друг друга.
- Если числа имеют разные знаки, ответ отрицательный.
- При сложении или делении нескольких чисел суммируйте, сколько положительных и сколько отрицательных. Если число отрицательных знаков нечетное, ответ также отрицательный. В противном случае он положителен.
- Умножение любого целого числа на 0 равно 0.
- Деление на ноль равно бесконечности или неопределенности (в зависимости от типа выполняемых вами математических операций).
- Умножение двух целых чисел дает другое целое число, но это не правило деления.
Вот примеры умножения и деления целых чисел.
- 4 x 5 = 20
- (-2) x (-3) = 6
- (-6) x 3 = -18
- 7 x (-2) = -14
- 2 x (-3) ) x 4 = -24
- (-2) x 2 x (-3) = 12
- 12 / 2 = 6
- (-2) / 6 = -1/3
- (-10) / 5 = -2
- 14 / (-7) = -2
- (-6) / (-2) = 3
Правила и свойства целых чисел
К алгебраическим свойствам целых чисел относятся: идентификационный элемент
Обратите внимание, что целые числа замкнуты при вычитании, но не замкнуты при делении.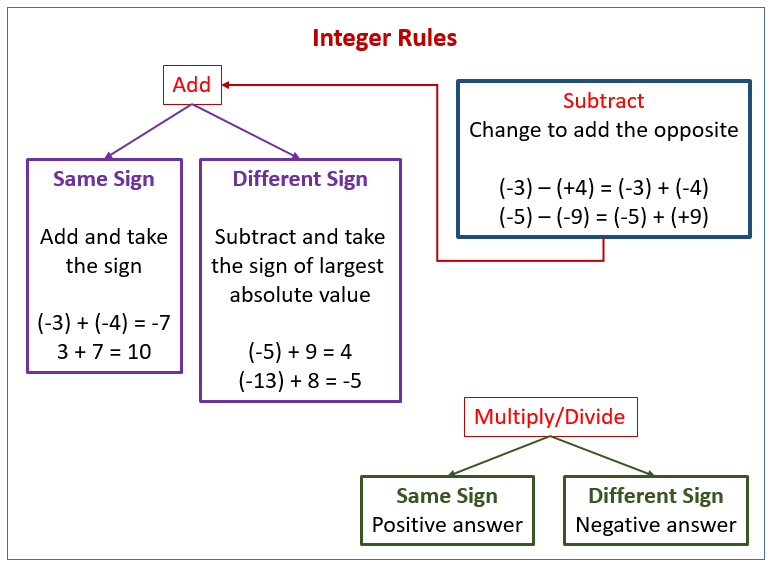
Другими словами, если вы разделите одно целое число на другое, ответ не обязательно будет другим целым числом. Например, 2, деленное на 4, равно 1/2 или 0,5 (не целому числу). Деление целого числа на ноль не определено.
Вот краткое описание этих свойств.
| Сложение/вычитание | Умножение/деление | |
|---|---|---|
| Замыкание | a + b = целое число; a – b = целое число | a x b = целое число; не закрытый для разделения |
| Элемент идентификации | а + 0 = а; а – 0 = а | а + 1 = а; a ÷ 1 = a |
| Ассоциативное свойство | a + (b + c) = (a + b) + c; а – (б – в) – (а – б) – в | a x (b x c) = (a x b) x c |
| Коммутативное свойство | .(a + b) x c = (a x c) + (b x c) | |
| Обратные элементы | a + (-a) = 0 | -1 и 1 только обратимые целые числа. |
| Без делителей нуля | Если a x b = 0, то a = 0 и/или b = 0 |
(a x b) + (a x c) иСсылки
- Clapham, Christopher; Николсон, Джеймс (2014). Краткий Оксфордский математический словарь (5-е изд.). Издательство Оксфордского университета. ISBN 978-0-19-967959-1.
- Фробишер, Лен (1999). Номер «Учимся преподавать: Пособие для учащихся и учителей начальной школы» . Серия Стэнли Торнса «Преподавание начальной математики». Нельсон Торнс. ISBN 978-0-7487-3515-0.
- Голдрей, Дерек (1998). Классическая теория множеств: управляемое независимое исследование (1-е изд.). Бока-Ратон, Флорида: Chapman & Hall/CRC.
