Исправление изогнутых линий на фотографиях. Дисторсия.
Исправление изогнутых линий на фотографиях. Дисторсия.
Дисторсия — аберрация оптических систем, при которой линейное увеличение изменяется по полю зрения. Световые лучи, проходя через центр линзы, сходятся в точке, расположенной дальше от линзы, чем лучи, которые проходят через ее края.
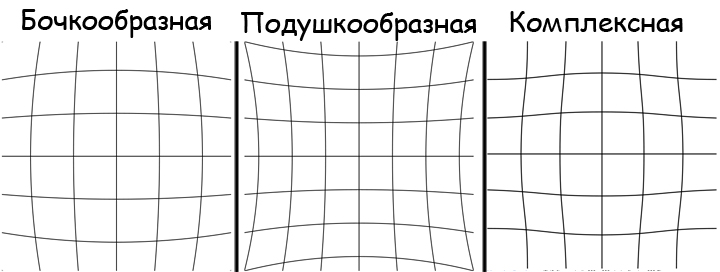
Дисторсия может быть отрицательной — «бочкообразной», особенно она выражена у широкоугольных объективов, и положительной — «подушкообразной». Положительная дисторсия чаще встречается у телеобъективов.
Чаще всего проявлению бочкообразной дисторсии способствует применение минимального фокусного расстояния (зума), подушкообразной, соответственно, применение максимального фокусного расстояния.
Способы борьбы с дисторсией
- Производители объективов применяют асферические линзы — специальные линзы с изогнутой поверхностью, позволяющей скорректировать искажения.

- По возможности избегать съемки на минимальном и максимальном фокусных расстояниях.
- Помещать снимаемый объект ближе к центру, где искажений нет, или они менее выражены. Затем кадрированием отсечь зоны с наибольшими искажениями.
- Исправить дисторсию в графическом редакторе.
Мы предлагаем простой способ исправления дисторсии в программе Perspective Pilot.
Вы можете, перемещая ползунок, выпрямить изогнутые линии по краям кадра. Также, после проведения калибровки фотоаппарата, дисторсию можно исправлять в автоматическом режиме. Подробнее читайте на страничке программы.
Наверх
Коррекция дисторсии, Исправление перспективы в программе Photoshop
Эти два фильтра программы Adobe Photoshop CS5 действуют похожим образом: один исправляет перспективу изображение, другой — накладывает изображение на трехмерную поверхность.
Фильтр Коррекция дисторсии
Находится в меню
Иногда фильтр справляется таким образом с задачей, иногда нет. Если автокоррекции не получилось, переходите на вкладку Заказная. Если Вы поставите галочку напротив пункта Сетка, то сможете выравнивать изображение точно по горизонтальным или вертикальным линиям сетки.
Можно устранять вогнутые или выпуклые искажения, можно исправлять перспективу по вертикали и горизонтали, можно также изменять угол изображения, если на нем у Вас завален горизонт.
Кроме того, с помощью фильтра Коррекция дисторсии можно избавиться от автоматических аберраций — цветных полос вдоль контрастных переходов. Увеличиваете изображение, и смотрите на контрастные участки изображения. Если есть аберрация — двигаете ползунки так, чтобы она исчезла.
Увеличиваете изображение, и смотрите на контрастные участки изображения. Если есть аберрация — двигаете ползунки так, чтобы она исчезла.
Также можно убрать, или наоборот усилить эффект виньетирования, передвигая бегунок в пункте
Также можно выбрать инструмент Перемещение сетки, он в окне фильтра находится слева, третий сверху значок. С помощью этого инструмента можно перемещать сетку, чтобы поставить ее у прямолинейных объектов, и выставить изображение точно так, как нужно.
Фильтр Исправление перспективы
Находится в меню Фильтр — Исправление перспективы. С помощью этого фильтра можно накладывать изображение на трехмерные поверхности. Например, можно сделать новую обложку для книги, или сделать трехмерную открытку.
Для использования фильтра открываете в программе Adobe Photoshop CS5 изображение, которое нужно разместить на поверхности, и объект с поверхностью, на которую изображение будет размещено. Например, открываете книгу и изображение, которое будет на обложке книги.
Выделяете изображение, копируете его, можно с помощью Ctrl + C, и переходите на объект с трехмерной поверхностью. Точками определяете места, на которые лягут углы изображения, то есть отмечаете четыре места, на которые лягут углы изображения. Если область создана правильно, то появится синяя сетка, если неправильно — сетка будет красной.
Затем вставляете изображение. Можно для этого нажать Ctrl + V.
С помощью горячих клавиш Ctrl + T Вы можете подогнать изображение точно под трехмерную плоскость. Выполнив подгонку, нажимаете ОК.
Видео о том, как с помощью фильтра Коррекция дисторсии исправить перспективу на изображение, и о том, как с помощью фильтра Исправление перспективы сделать трехмерную открытку
Более подробные сведения Вы можете получить в разделах «Все курсы» и «Полезности», в которые можно перейти через верхнее меню сайта. В этих разделах статьи сгруппированы по тематикам в блоки, содержащие максимально развернутую (насколько это было возможно) информацию по различным темам.
В этих разделах статьи сгруппированы по тематикам в блоки, содержащие максимально развернутую (насколько это было возможно) информацию по различным темам.
Также Вы можете подписаться на блог, и узнавать о всех новых статьях.
Подписаться на блог: Дорога к Бизнесу за Компьютером
Проголосуйте и поделитесь с друзьями анонсом статьи на Facebook:
Автоматическая коррекция дисторсии в Camera Raw
В предыдущих версиях Camera Raw были доступны лишь некоторые параметры коррекции дисторсии, но теперь многие стандартные дефекты объектива можно исправлять автоматически. Это достигается благодаря считыванию метаданных файла (в них указывается модель камеры и объектива, которыми был сделан снимок) и применению готовых профилей. Все выполняется чрезвычайно быстро и требует установки буквально одного флажка, но что делать, если для вашего фотоаппарата или объектива нет профилей, либо в изображении отсутствуют метаданные, либо применяемый профиль вас не устраивает? Ответы на эти вопросы будут даны ниже.
А все потому, что, как я уже упоминал, программа считывает метаданные снимка, определяя тип фотоаппарата и объектива, которые использовались при съемке, а затем находит в своей базе данных соответствующий профиль и применяет его для коррекции изображения.

Шаг 3
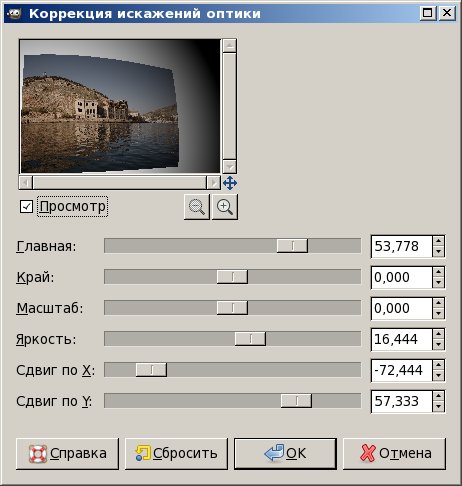
Что же делать в том случае, если для снимка не найден профиль или метаданные отсутствуют (например, требуется обработать отсканированное изображение или файл, скопированный из другого документа)? Взгляните на показанную здесь иллюстрацию. Модулю Camera Raw не удалось найти профиль для данного изображения, поэтому в раскрывающемся списке Маке (Производитель) в разделе Lens Profile (Профиль объектива) выбрано значение None (Нет). При этом раскрывающиеся списки Model (Модель) и Profile (Профиль) неактивны. Вам просто нужно подсказать программе, какое оборудование использовалось при съемке (если это известно), или, на худой конец, выбрать тип оборудования наугад.
Попробуйте различные варианты и посмотрите, какой из них лучше подходит. (В принципе программа редко ошибается с выбором оптимального варианта. Но иногда бывает так, что я получаю лучшие результаты, когда выбираю совсем не тот объектив, которым сделал снимок.) В данном случае я указал объектив Fisheye-Nikkor 10.5mm. Шаг 5 Предыдущие снимки были сделаны объективом «рыбий глаз» с фокусным расстоянием 10,5 мм. Теперь рассмотрим ситуацию, в которой дисторсия настолько сильна, что встроенного профиля недостаточно для коррекции изображения.
 Кажется, будто здание и башня на снимке «заваливаются» к центру, особенно башня, которая слишком наклонена вправо. Подобная проблема типична для фотоаппаратов с полноразмерной матрицей при съемке широкоугольным объективом (в данном случае использовался объектив 28-300 мм с фокусным расстоянием 28 мм). Здесь проявляется не только искажение перспективы, но и виньетирование (затемнение) по всем четырем углам, а кроме того, снимок недодержан и недостаточно контрастен.
Удалось лишь передать атмосферу таинственности и тумана, но в целом снимок пока что плохой.
Шаг 6
Начнем с быстрой настройки экспозиции и контраста, чтобы потом не отвлекаться. Для этого достаточно сделать всего несколько щелчков мышью. Когда снимок выглядит недодержанным и «плоским» (недостаточно контрастным), лучше всего воспользоваться кнопкой Auto (Авто).
Кажется, будто здание и башня на снимке «заваливаются» к центру, особенно башня, которая слишком наклонена вправо. Подобная проблема типична для фотоаппаратов с полноразмерной матрицей при съемке широкоугольным объективом (в данном случае использовался объектив 28-300 мм с фокусным расстоянием 28 мм). Здесь проявляется не только искажение перспективы, но и виньетирование (затемнение) по всем четырем углам, а кроме того, снимок недодержан и недостаточно контрастен.
Удалось лишь передать атмосферу таинственности и тумана, но в целом снимок пока что плохой.
Шаг 6
Начнем с быстрой настройки экспозиции и контраста, чтобы потом не отвлекаться. Для этого достаточно сделать всего несколько щелчков мышью. Когда снимок выглядит недодержанным и «плоским» (недостаточно контрастным), лучше всего воспользоваться кнопкой Auto (Авто). Снимок уже улучшился, но пока это только начальная точка. Добавьте больше контраста, перетащив ползунок Contrast (Контрастность) к отметке +20, а затем перетащите ползунок Blacks (Затемнение) к отметке -50, чтобы тени не выглядели размытыми, и, наконец, перетащите ползунок Clarity (Четкость) вправо (я остановился на отметке +71, чтобы проявить достаточно деталей).
 Виньетирование по краям все еще осталось, но сейчас мы его устраним.
Шаг 7
Перейдите к панели Lens Corrections (Коррекция дисторсии) и установите флажок Enable Lens Profile Corrections (Разрешить коррекцию профиля объектива) на вкладке Profile (Профиль). Программа проверяет метаданные снимка и, если в базе данных удается найти соответствующий профиль объектива, автоматически исправляет снимок. В данном случае удалось выровнять фундамент здания, немного выправить перспективу фасада и устранить виньетирование по краям. Результат снова улучшился, но этого мало. Линия фундамента оказалась недостаточно ровной, поэтому я отрегулировал степень коррекции, перетащив ползунок Distortion (Искажение) к отметке 113.
Шаг 8
Если незначительные настройки профиля объектива не помогают (на иллюстрации к предыдущему шагу хорошо видно, что здания по-прежнему «заваливаются»), откройте вкладку Manual (Ручной режим) и выполните нужные преобразования вручную.
Виньетирование по краям все еще осталось, но сейчас мы его устраним.
Шаг 7
Перейдите к панели Lens Corrections (Коррекция дисторсии) и установите флажок Enable Lens Profile Corrections (Разрешить коррекцию профиля объектива) на вкладке Profile (Профиль). Программа проверяет метаданные снимка и, если в базе данных удается найти соответствующий профиль объектива, автоматически исправляет снимок. В данном случае удалось выровнять фундамент здания, немного выправить перспективу фасада и устранить виньетирование по краям. Результат снова улучшился, но этого мало. Линия фундамента оказалась недостаточно ровной, поэтому я отрегулировал степень коррекции, перетащив ползунок Distortion (Искажение) к отметке 113.
Шаг 8
Если незначительные настройки профиля объектива не помогают (на иллюстрации к предыдущему шагу хорошо видно, что здания по-прежнему «заваливаются»), откройте вкладку Manual (Ручной режим) и выполните нужные преобразования вручную. (Примечание: преобразования, выполняемые на вкладке Manual, добавляются к настройкам, заданным на вкладке Profile.) В данном случае требуется устранить вертикальное искажение перспективы.
(Примечание: преобразования, выполняемые на вкладке Manual, добавляются к настройкам, заданным на вкладке Profile.) В данном случае требуется устранить вертикальное искажение перспективы. Перетаскивайте ползунок Vertical (По вертикали) влево, наблюдая за положением башни. Она должна стать строго вертикальной (мне пришлось перетащить ползунок к отметке -43). Подобное изменение перспективы приведет к появлению в нижних углах изображения пустых областей с серой заливкой, но этот дефект мы вскоре устраним. На данном этапе нам удалось решить хотя бы проблему «падающей башни». Шаг 9 Щелкните на кнопке Open Image (Открыть изображение), чтобы открыть полученное изображение (с пустыми областями по углам) в программе Photoshop. Очевидно, что для устранения проблем с выравниванием программе пришлось немного сжать изображение. Это привело к небольшому искажению пропорций зданий. Чтобы восстановить исходные пропорции, а заодно убрать пустые области с серой заливкой, воспользуйтесь инструментом Rectangular Marquee (Прямоугольная область), который вызывается клавишей <М>, и протащите его указатель по изображению, удерживая нажатой кнопку мыши.
 Рамка выделения должна дойти до нижнего края изображения над пустой областью.
Рамка выделения должна дойти до нижнего края изображения над пустой областью. Теперь нажмите комбинацию клавиш <Ctrl+T>, чтобы включить режим свободного трансформирования. Потяните центральный нижний маркер вниз, чтобы заполнить серый промежуток, как показано на иллюстрации. Нажмите клавишу <Enter> (<Return>), чтобы заблокировать изменения, а затем нажмите <Ctrl+D>, чтобы снять выделение. Теперь здание не кажется сжатым. Шаг 10 Что касается двух треугольных промежутков по краям, то есть два варианта. 1. Проще всего кадрировать изображение так, чтобы удалить серые края. Для этого нажмите клавишу <C> для выбора инструмент Crop (Рамка), растяните рамку по фотографии так, чтобы промежутки остались вне области выделения, и нажмите клавишу <Enter> (<Return>). 2.
Второй метод, основанный на заливке с учетом содержимого, гораздо эффективнее. Выберите инструмент Magic Wand (Волшебная палочка) и щелкните на сером участке слева, чтобы выделить его, а затем щелкните на сером участке справа при нажатой клавише <Shift>.
 В меню Selects > Modify (Выделение > Модификация) выполните команду Expand (Расширить) и в диалоговом окне Expand Selection (Расширить область) введите значение 4. (Заливка с учетом содержимого работает лучше, если расширить выделение на 4 пикселя.)
Шаг 11
Нажмите клавишу <Backspace> (<Delete>), чтобы открыть диалоговое окно Fill (Заполнить). Только учтите, что изображение должно быть сведенным. Если оно располагается на отдельном слое, нажатие клавиши не сработает, и придется выполнить команду Edit > Fill (Редактирование > Выполнить заливку). Убедитесь в том, что в раскрывающемся списке Use (Использовать) выбрано значение Content-Aware (С учетом содержимого). Щелкните на кнопке ОК и позвольте программе сделать всю работу за вас.
В меню Selects > Modify (Выделение > Модификация) выполните команду Expand (Расширить) и в диалоговом окне Expand Selection (Расширить область) введите значение 4. (Заливка с учетом содержимого работает лучше, если расширить выделение на 4 пикселя.)
Шаг 11
Нажмите клавишу <Backspace> (<Delete>), чтобы открыть диалоговое окно Fill (Заполнить). Только учтите, что изображение должно быть сведенным. Если оно располагается на отдельном слое, нажатие клавиши не сработает, и придется выполнить команду Edit > Fill (Редактирование > Выполнить заливку). Убедитесь в том, что в раскрывающемся списке Use (Использовать) выбрано значение Content-Aware (С учетом содержимого). Щелкните на кнопке ОК и позвольте программе сделать всю работу за вас. Конечно, кое-где произошло дублирование деталей, но на 98% результат меня устраивает. Конец уже близок! Нажмите комбинацию клавиш <Ctrl+D>, чтобы отменить выделение треугольных областей.
 Шаг 12
Башня слева уже не «заваливается», но выглядит немного сплюснутой. Давайте применим еще один быстрый прием. Снова воспользуйтесь инструментом Rectangular Marquee (Прямоугольная область) и обведите башню рамкой, захватив при этом немного пространства вокруг (нам нужно скрыть старый фрагмент, чтобы он не был виден). Нажмите комбинацию клавиш <Ctrl+J>, чтобы скопировать выделенную область на отдельный слой, и нажмите комбинацию клавиш <Ctrl+T>, включив режим свободного трансформирования.
Шаг 13
Удерживая нажатой клавишу <Ctrl>, перетащите правый верхний маркер рамки вверх, чтобы выпрямить башню (как показано на иллюстрации). Не исключено, что в результате башня станет выше, чем нужно, поэтому в конце отпустите клавишу <Ctrl> и перетащите центральный верхний маркер немного вниз. Пока режим свободного трансформирования активен, перейдите к панели Layers (Слои) и уменьшите непрозрачность верхнего слоя, чтобы под ним была видна исходная башня.
Шаг 12
Башня слева уже не «заваливается», но выглядит немного сплюснутой. Давайте применим еще один быстрый прием. Снова воспользуйтесь инструментом Rectangular Marquee (Прямоугольная область) и обведите башню рамкой, захватив при этом немного пространства вокруг (нам нужно скрыть старый фрагмент, чтобы он не был виден). Нажмите комбинацию клавиш <Ctrl+J>, чтобы скопировать выделенную область на отдельный слой, и нажмите комбинацию клавиш <Ctrl+T>, включив режим свободного трансформирования.
Шаг 13
Удерживая нажатой клавишу <Ctrl>, перетащите правый верхний маркер рамки вверх, чтобы выпрямить башню (как показано на иллюстрации). Не исключено, что в результате башня станет выше, чем нужно, поэтому в конце отпустите клавишу <Ctrl> и перетащите центральный верхний маркер немного вниз. Пока режим свободного трансформирования активен, перейдите к панели Layers (Слои) и уменьшите непрозрачность верхнего слоя, чтобы под ним была видна исходная башня. Это позволит совместить их изображения.
Это позволит совместить их изображения. Только не забудьте потом вернуть непрозрачность к отметке 100%. Теперь нажмите клавишу <Enter> (<Return>), чтобы заблокировать трансформацию. Можно ли считать такой прием «жульничеством»? Я вас умоляю! Его не стоит применять, если вы фотожурналист, снимающий репортажи для службы новостей. Если же вы, как и я, просто пытаетесь делать красивые фотографии, пользуйтесь им на здоровье. Шаг 14 Финальный шаг заключается в существенном усилении резкости полученного изображения. Выполните в меню Filter > Sharpen (Фильтр > Усиление резкости) команду Unsharp Mask (Контурная резкость). В поле Amount (Эффект) задайте значение от 90 до 100%, увеличьте значение радиуса до отметки 1.5 и выставьте значение Threshold (Изогелия) на отметку 3. Это значительное усиление резкости, но когда имеешь дело с фотографией, в которой столько деталей, резкости мало не бывает. Щелкните на кнопке ОК, чтобы завершить работу по коррекции дисторсии.
 На следующей странице показаны исходное и отредактированное изображения.
На следующей странице показаны исходное и отредактированное изображения.
Исправление сильной дисторсии / «рыбьего глаза» вручную: overquantum — LiveJournal
Фотографии и видео, снятые широкоугольными объективами, имеют эффект «рыбий глаз», который иногда хочется исправить.Обычные средства, типа Photoshop-а, с сильной дисторсией могут не справиться или результат не будет «прямолинейным» (ортоскопическим).
Например, фото с квадрокоптера Xiro Xplorer V имеют примерно втрое большие искажения, чем может исправить Photoshop.
Больше возможностей даёт инструмент Barrel Distortion из программного пакета ImageMagick.
Однако для правильного использования этого инструмента необходимо задать 3 или 4 параметра искажения, что не очень просто.
Если для камеры не нашлось параметров в PTlens/Hugin/LensFun, то остаётся только подбирать или вычислять параметры искажения.
В документации на ImageMagick прелагается использовать Hugin, однако инструкция выглядит запутанной. Насколько я понимаю, требуется снять прямоугольную решётку дважды и отметить на снимках несколько десятков точек.
Но очень неплохой результат можно получить и самостоятельно. Для этого достаточно сфотографировать один прямолинейный объект по возможности на всю ширину кадра и снять с него координаты 5 точек.
В моём случае оказалось достаточно линии горизонта, проходящей вблизи верхнего края кадра.
Для рассчёта параметров из координат можно воспользоваться подготовленным мною инструментом defish_calc.
Для работы инструмента необходим Excel и add-in «Solver» (также известный как надстройка «Поиск решения»).
1) Задайте размеры изображения — в поля B11 и B12
2) Задайте координаты от 5 до 10 точек (в B21:C30), которые лежат на одной линии, прямолинейной в реальности. Координаты можно взять как минимум с помощью Paint.
3) Запустите Solver на минимизацию поля L9 с подбором параметров I10:I14 (ограничения не требуются).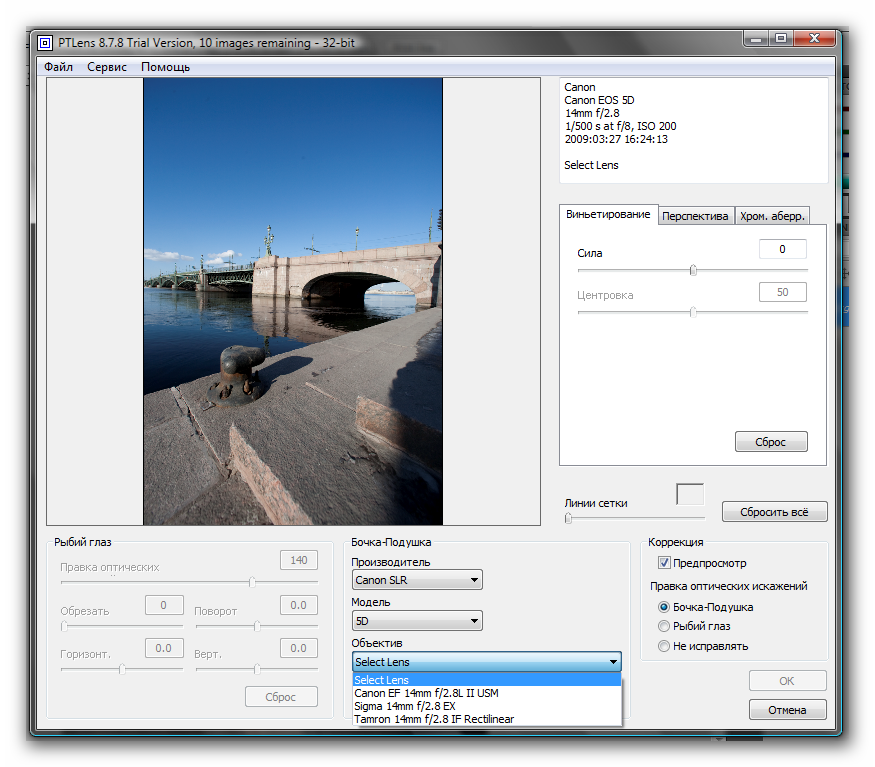
4) Результирующие числа a,b,c (в ячейках I10-I12) дадут параметры для Barrel Distortion.
В ячейке K15 вы получите почти готовую командную строку для преобразования картинки с помощью ImageMagick (вместо imput.jpg надо подставить имя файла и т.д.)
Примечания:
* По-умолчанию Barrel Distortion с 3 параметрами сохраняет на месте круг, касающийся краёв снимка, диаметр этого круга равен минимальному из габаритных размеров снимка (для горизонтальных кадров — высоте).
Углы исходного изображения при этом уходят за края и теряются.
Если вы хотите, например, сохранить всю ширину исходного горизонтального снимка, можно использовать Barrel Distortion с 4 параметрами. Для этого задайте в поля B15:B16 коордианты точки, которую нужно «зафиксировать» (для сохранения ширины это будет X=0 и Y=половина высоты снимка). После запуска «Solver» 4й искомый параметр — d (поле I16).
* Если после работы «Solver»-а отображаются статус NOK («Norm» получился больше 3 или «Norm of rounded» (L12) больше нуля или «Max difference» (L13) больше 1), значит параметры искажения подобраны недостаточно хорошо.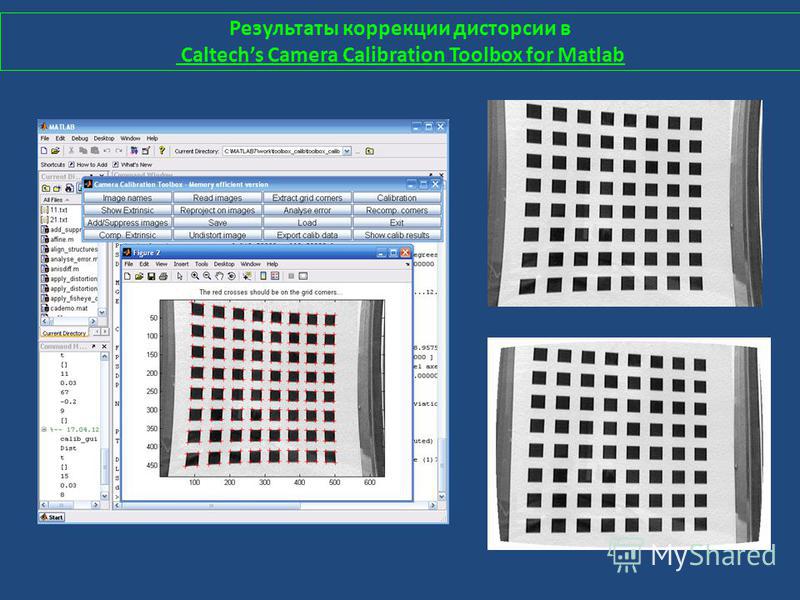 Этому может быть 2 причины:
Этому может быть 2 причины:
1) Указанные 5-10 точек не лежат на самом деле на прямой линии
2) Дисторсия снимка слишком сильная и Barrel Distortion не справляется
* Рисунок «Line and frame distortion» позволяет оценить прямолинейность восстановленной линии (Restored line) и какая часть (синяя рамка) исходного снимка (красная рамка) останется на исправленном изображении. Там где синяя рамка выходит за края красной — в исправленном снимке будет заполнение.
* Рисунок «Distorted line — measured and calculated» позволяет визуально оценить точность воспроизведения искажения с помощью Barrel Distortion. Красные кружки и синие крестики должны все совпадать.
График «Distortion function» показывает кривую функции R(r)
* Если Excel есть, а «Solver» использовать не получается, можно попробовать подобрать параметры a,b,c,p,q вручную, меняя их по одному всё более мелкими шагами в сторону уменьшения Norm. Достаточно довести «Norm of rounded» (L12) до нуля.
Насколько я вижу, онлайновые сервисы пока не предоставляют функционала аналогичного Solver для нелинейных уравнений. 2 )
2 )
Эту функцию необходимо минимизировать подбором неизвестных a,b,c,p,q
Если задать более 5 точек, то можно оценить точность нахождения параметров.
Полученные параметры Barrel Distortion для Xiro Xplorer V:
1) Для фотографий (4320х3240 или иного 4:3)
«0.0602051521391688 -0.186821319369571 -0.133623072628317»
2) Для фотографий (4320х3240 или иного 4:3) с сохранением ширины кадра
«0.151765060326058 -0.374280001474025 -0.21055353708688 1.58638531648197»
3) Для видео (1920х1080 или иного 16:9)
«0.0169891758465488 -0.0771539753571165 -0.0850908340028834»
4) Для видео (1920х1080 или иного 16:9) с сохранением ширины кадра
«0.0642398867473021 -0.211314302852179 -0.157126620422966 1.58625195846726»
Ещё примеры использования этих параметров для фотографий из сети. Примечательно, что все они сделаны по одному и тому же набору параметров (№1), снятых с моего снимка.
А это пример моделирования видеокадра с сохранением ширины (набор параметров №4 выше):
Субъективно:
1) Все фотографии лучше смотрятся после корректировки искажения.
2) В большинстве случаев корректировка искажения не делает видео лучше или хуже.
3) Корректировка делает лучше видеосъёмку с видом вниз или если в кадре видна только земля и объекты на ней.
4) В случае поворотов камеры при стоянии на месте, скорректированная видеосъёмка получается хуже (объекты увеличиваются при движении к краю кадра и уменьшаются при движении к центру).
В планах — подготовка инструмента для более точной калибровки по нескольким прямолинейным объектам.
Другие инструменты и полезные ссылки по дисторсии и корректировке:
1) DEFISHEYE script from Fred Weinhaus
2) Инструкция для Fisheye-Hemi
3) Field of View Calculator
4) Are there any free or better alternatives to Fisheye-Hemi?
Manual defisheye with ImageMagick for Xiro Xplorer V
Коррекция дисторсии и других оптических искажений в Camera RAW
Коррекция дисторсии – это вкладка правой панели конвертера Camera RAW, которая предназначена для исправления оптических искажений объектива. Любой объектив имеет аберрации, которые ухудшают качество изображения. На этой вкладке можно исправить дисторсию, хроматическую аберрацию и геометрические искажения. Посмотрим, как это делается.
Любой объектив имеет аберрации, которые ухудшают качество изображения. На этой вкладке можно исправить дисторсию, хроматическую аберрацию и геометрические искажения. Посмотрим, как это делается.
Перейти на вкладку «Коррекция дисторсии» можно либо кликнув по пиктограмме с изображением линз, либо нажав комбинацию клавиш Ctrl+Alt+6. Перед вами появятся 3 вкладки: «Профиль», позволяющий учесть особенности вашего объектива, «Цветность» — для компенсации хроматической аберрации, и «Ручной режим» с регуляторами для исправления геометрических искажений и коррекции виньетирования.
Коррекция профиля объективаПроизводится на вкладке «Профиль». Большинство современных объективов оснащены микропроцессорами, которые передают информацию о типе объектива, фокусном расстоянии, диафрагме, дистанции фокусировки, зуме, и некоторую другую, которая записывается в метаданные EXIF файла фотографии. Если у вас объектив с микропроцессором и фотоаппарат той же марки, что и объектив (о выборе фотоаппарата и объектива можно прочитать в специальных статьях на нашем сайте), то вы можете использовать автоматическую коррекцию профиля объектива.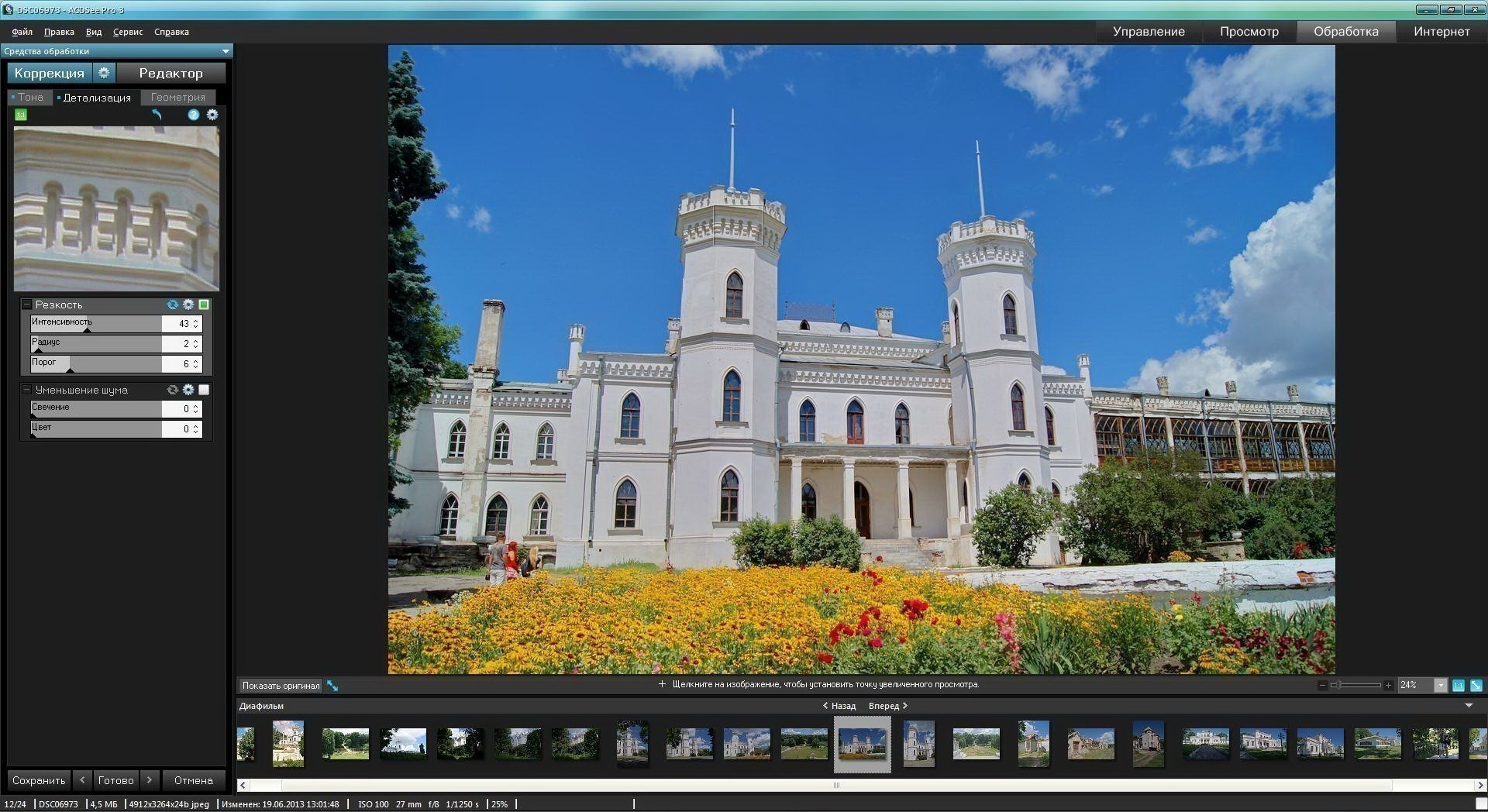
Нажимаете галочку «Разрешить коррекцию профиля объектива» и конвертер автоматически учитывает все особенности именно вашей оптики. Компания Adobe постоянно собирает всю самую свежую информацию обо всей выпускаемой в мире фотографической технике, поэтому вероятность того, что ваша модель объектива есть в базе данных программы, очень велика.
Посмотрите, как конвертер справился с коррекцией оптических искажений на этой фотографии. Слева фото без коррекции, справа – с исправленной геометрией. Это хорошо видно по ограждению набережной на переднем плане (показано стрелкой):
Под установкой профиля объектива находятся регуляторы степени коррекции геометрических искажений и виньетирования. Если автоматическая коррекция дисторсии вас не устраивает, то вы можете ее усилить или ослабить, а если заметно виньетирование по краям, то подкорректировать и его. В нашем примере виньетирования не видно, а коррекция дисторсии была проведена правильно, что и бывает в большинстве случаев, поэтому дополнительно мы исправлять ничего не будем.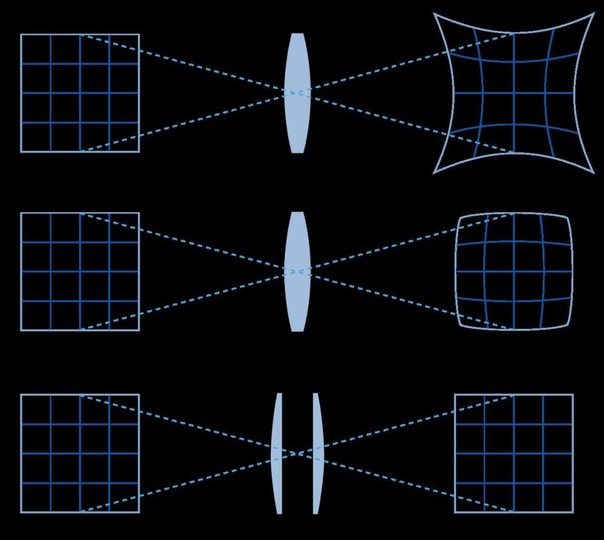
Если программа не смогла идентифицировать ваш объектив, то его можно выбрать вручную из раскрывающегося списка моделей объективов и брендов производителей фототехники. Это бывает при использовании объективов сторонних фирм, но список их довольно большой, и в нем присутствуют самые известные и популярные марки, так что и в этом случае выбрать объектив вам, скорее всего, удастся.
Коррекция хроматических аберрацийЕе можно сделать на вкладке «Цветность». Хроматическая аберрация – это радуга, особенно хорошо заметная в местах с высоким контрастом. Возникает из-за различной степени преломления света различных длин волн. Современные объективы неплохо ее компенсируют, но, тем не менее, при увеличении масштаба просмотра хроматизм бывает очень заметным и весьма неприятным.
Это хорошо видно на фотографии зимнего леса, где на правом снимке показан увеличенный фрагмент контрастного изображения на краю кадра. Слева видна зеленая часть спектра, а справа – фиолетовая:
Такие аберрации надо обязательно убирать, поскольку они не только портят снимок, но и крайне отрицательно сказываются при печати фотографий. Для этого в конвертере Camera RAW предусмотрены автоматический и ручной инструменты. И, надо заметить, что это тот редкий случай, когда автоматический режим дает великолепные результаты, поэтому рекомендую вам пользоваться именно им. Нажимаем галочку «Удалить хроматическую аберрацию», и вот вам результат:
Для этого в конвертере Camera RAW предусмотрены автоматический и ручной инструменты. И, надо заметить, что это тот редкий случай, когда автоматический режим дает великолепные результаты, поэтому рекомендую вам пользоваться именно им. Нажимаем галочку «Удалить хроматическую аберрацию», и вот вам результат:
То же самое можно сделать вручную, передвигая соответствующие регуляторы. Для этого сначала выбираем цветовой диапазон для коррекции, сдвигая или раздвигая движки цветового фона с нажатой клавишей Alt (при этом корректируемый участок будет выделяться черным цветом), а затем корректируем степень коррекции регуляторами степени воздействия. Результат мы получим такой же, как и при автоматической коррекции, но потратим драгоценное время. В случае, если автоматика вас чем то не устраивает, можете пользоваться ручным режимом.
Ручная коррекция геометрических искаженийДелается на вкладке «Ручной режим». Здесь можно скорректировать положительную или отрицательную дисторсию, вертикальные и горизонтальные искажения перспективы, повернуть изображение, и если при этом изменился размер холста, то изменить масштаб.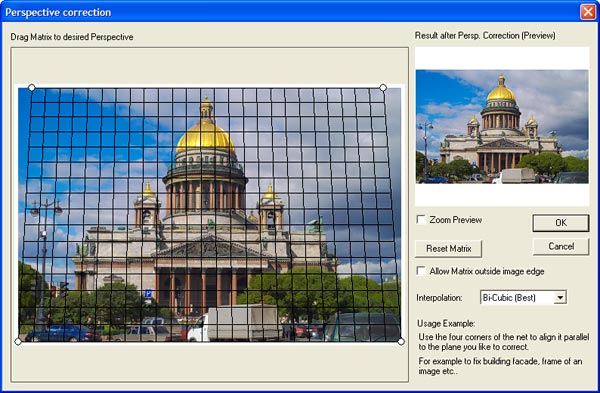 Кроме этого, есть возможность сделать осветляющее или затемняющее виньетирование. Посмотрите, как это получилось на изображении, снятом широкоугольным объективом:
Кроме этого, есть возможность сделать осветляющее или затемняющее виньетирование. Посмотрите, как это получилось на изображении, снятом широкоугольным объективом:
Наклонные линии стали вертикальными, при этом пришлось увеличить масштаб для компенсации изменений размера холста. Виньетирование можно было и не делать, но для примера я его тоже немного добавил.
Теперь вы знаете, как пользоваться вкладкой «Коррекция дисторсии», которая предоставляет несколько очень полезных инструментов для улучшения качества ваших фотографий.
Особенности коррекции оптических искажений в цифровой фотографии
The article talks about the distortion correction in digital images, as well as cases where correction is used to solve applied problems.
Любой объектив вносит искажения в формируемое им изображение. Чем дороже оптика, тем меньше искажений. Но полностью избавиться от них невозможно.
- Виньетирование — затемнение изображения по краям кадра.

- Хроматические аберрации — «расслоение» изображения по цветовым каналам из-за различных углов преломления у света с разной длиной волны. Проявляется в виде цветного ореола вокруг контрастных мест.
- Дисторсия — искривление изображения, вызванное неравномерным линейным увеличением при отклонении от оптической оси. Из-за дисторсии прямые линии на кадре становятся изогнутыми.
С развитием цифровой техники появилась возможность строить математические модели оптических искажений и исправлять их. Помимо общего повышения качества фотографий, расчет и устранение аберраций критически необходимы для решения множества практических задач, таких как компьютерное зрение (CV — Computer Vision), фотограмметрия, объединение нескольких фотографий и создание панорам. Точные расчеты на основании фотографий без коррекции искажений невозможны.
С точки зрения различных расчетов наиболее важным является исправление дисторсии. виньетированием и хроматическими аберрации зачастую можно либо пренебречь, либо они исправляются некоторыми камерами прямо в процессе съемки, если камера знает калибровки для текущего объектива.
Существует несколько математических моделей, описывающих дисторсию. Пожалуй, самой популярной моделью является PTLens, изначально разработанная доктором Хельмутом Дерша (Helmut Dersch) в Panorama Tools. На данный момент эта модель является основной в библиотеке LensFun. В свою очередь эту библиотеку используют множество популярных открытых фоторедакторов — UFRaw, Darktable, Rawstudio, Digikam/Kipi, GimpLensfun, Photivo и оболочка для создания панорам Hugin. Библиотека имеет постоянно пополняемую базу объективов, которая облегчает исправление искажений. Однако есть возможность и самостоятельно создать профиль для своего объектива.
Немного особняком стоит библиотека компьютерного зрения OpenCV, которая использует свою собственную математическую модель, описывающую дисторсию. Ту же самую модель использует и Blender для реконструкции и привязки живого видео к 3D-сцене.
Проблема заключается в том, что LensFun не поддерживает модель дисторсии, используемую в OpenCV. Да и при наличии такой поддержки, прямой конвертации одной модели в другую добиться невозможно. Поэтому на данный момент нет возможности использовать обширную базу объективов и инструменты для профилирования при работе с видео в Blender и в других разработках, использующих библиотеку OpenCV. Перспективной выглядит идея подбора коэффициентов одной модели на основании коэффициентов другой модели методом наименьших квадратов — например, при помощи библиотеки ceres-solver.
Поэтому на данный момент нет возможности использовать обширную базу объективов и инструменты для профилирования при работе с видео в Blender и в других разработках, использующих библиотеку OpenCV. Перспективной выглядит идея подбора коэффициентов одной модели на основании коэффициентов другой модели методом наименьших квадратов — например, при помощи библиотеки ceres-solver.
Редакторы фотографий, как правило, могут использовать только уже готовые данные калибровки объективов. Сшиватель панорам Hugin или Blender могут подбирать приблизительные коэффициенты для коррекции дисторсии в процессе своей работы. Такое поведение обусловлено работой сразу с несколькими фотографиями (или видео), которые позволяют сопоставлять между собой разные ракурсы. Тем не менее, предварительная аккуратная калибровка объектива специальными мишенями позволяет повысить точность расчетов, качество результата и снизить суммарные трудозатраты.
| Метки: |
Коррекция искажения линзы
Домой Пожертвовать Новый Поиск Галерея Практические инструкции Ссылки Семинары О нас Контакт
Исправление
Искажение объектива
© 2010
KenRockwell. com
com
От камера | Ствол искажения исправлены @ +6.00 |
Исправлено трапецеидальное искажение и бочкообразное искажение.
Корректирующий Перспектива
Корректирующий Боковая хроматическая аберрация и цветная бахрома
ВВЕДЕНИЕ
Это тривиально с Photoshop CS2, CS3, CS4 и CS5. Эта особенность отсутствует в более ранние версии Photoshop, но я объясню, как это сделать с ними внизу.
Это
работает с любым изображением, JPG, RAW, сканированием пленки и т. д.
д.
ПРИМЕР ВЫШЕ
Вот что этот фильтр, бесплатно включенный в Photoshop CS2 и более поздних версий, может сделать плохое изображение с цифровой камеры.
Исходное изображение, вверху слева, снято камерой Nikon D70 с объективом 18–70 мм, установленным на 18 мм. На 18 мм у 18-70 мм есть не только ствол. искажение, оно имеет сложное бочкообразное искажение, которое трудно верный.Как видите, даже этот нелинейный вид бочкообразного искажения очень хорошо исправлено. Большинство других линз поправить еще проще. Я выбрал это как самый сложный пример, который мне удалось найти.
Бочка Искажение — вот что сделало верхнюю часть отеля изогнутой. В исправленном изображение, сделанное установкой ползунка, который я объясню ниже на +6.00, крыша сейчас прям.
Мост
любители были бы счастливы просто поправить изогнутые линии
вне. Профессионалы тоже хотят фиксировать вертикали. Так как
Я направил камеру вверх, здание выглядит так, будто оно падает
назад. Я подробно описываю, как исправить сходящуюся перспективу
линии на финальном большом изображении здесь.
Профессионалы тоже хотят фиксировать вертикали. Так как
Я направил камеру вверх, здание выглядит так, будто оно падает
назад. Я подробно описываю, как исправить сходящуюся перспективу
линии на финальном большом изображении здесь.
Photoshop CS2, CS3, CS4 и CS5
От в меню вверху экрана в CS2 просто выберите: ФИЛЬТР> ИСКАЖЕНИЕ > КОРРЕКЦИЯ ОБЪЕКТИВА.Быть уверенным чтобы включить сетку для справки.
Начиная с CS5, он находится в ФИЛЬТР> КОРРЕКЦИЯ ОБЪЕКТИВА.
Есть Есть три способа выбрать величину коррекции:
1.) Введите его в поле «Удалить искажение» или
.2.) Переместите ползунок или
3.)
Используйте Удалить искажение
Инструмент (D) в верхнем левом углу экрана. Выберите его и возьмите
середина искаженной строки.Перетащите его, пока он не станет правильным. Релиз.
Выберите его и возьмите
середина искаженной строки.Перетащите его, пока он не станет правильным. Релиз.
Почувствуйте бесплатно для точной настройки по своему усмотрению.
Мост Для линз нужны значения только от +5 до -3, так что не беспокойтесь. В моем тесты линз Я сейчас перечисляю значения, которые нужно ввести в поле, чтобы спасти нас все время.
Хит Хорошо, когда вы закончите точную настройку. Вуаля!
Перед Photoshop CS2
Назад в темные дни Photoshop CS и до того, как я обычно использовали команду «Spherize» в разделе ФИЛЬТР> ИСКАЖЕНИЕ > СФЕРИЗИРОВАТЬ.Сначала увеличьте размер холста на 50–100%, чтобы исправить весь образ.
КОМПЛЕКСНЫЕ ИСКАЖЕНИЯ
CS2’s
Фильтр отлично работает для простых линейных искажений первого порядка. Они просто изгибают линии в широкие кривые.
Они просто изгибают линии в широкие кривые.
Подробнее сложные искажения сгибают линии в более сложные формы, такие как усы. Фильтр искажения линзы CS2 не может исправить их полностью.
Для сложное искажение, которое вы можете попробовать стороннего производителя инструменты, которые я объясняю здесь, такие как DxO и бесплатные инструменты панорамы.
Помогите мне помочь вам наверх
Я поддерживаю свою растущую семью через этот веб-сайт, как бы безумно это ни казалось.
Самая большая помощь — это использование любой из этих ссылок на Adorama, Amazon, B&H, eBay, Ritz, Calumet и J&R и
когда вы получите свои вкусности. Это ничего не стоит вам и является самым большим источником поддержки для этого сайта, а значит, и для моей семьи. eBay — это всегда азартная игра, но во всех других местах всегда лучшие цены и лучшие услуги, поэтому я использовал их еще до того, как появился этот веб-сайт. Всем рекомендую лично .
Всем рекомендую лично .
Если вы найдете это страница столь же полезна, как книга, которую вам, возможно, пришлось купить, или семинар, который вы можете пришлось принять, не стесняйтесь помогать мне продолжать помогать всем.
Если вы получили свое снаряжение по одной из моих ссылок или помогли другим способом, вы — семья. Такие замечательные люди, как вы, позволяют мне постоянно добавлять на этот сайт. Спасибо!
Если вы еще не помогли, помогите и подумайте о том, чтобы помочь мне подарком в размере 5 долларов.00.
Поскольку эта страница защищена авторским правом и официально зарегистрирована, изготовление копий, особенно в виде распечаток для личного пользования, является незаконным. Если вы хотите сделать распечатку для личного использования, вам предоставляется одноразовое разрешение только в том случае, если вы заплатите 5 долларов США за распечатку или ее часть.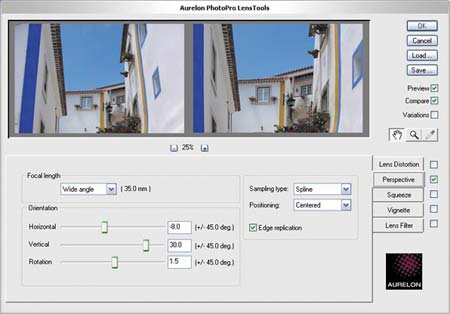 Спасибо!
Спасибо!
Спасибо за чтение!
Мистер и миссис Кен Рокуэлл, Райан и Кэти.
Домой Пожертвовать Новый Поиск Галерея Практические инструкции Ссылки Семинары О нас Контакты
Коррекция радиального искажения изображения на основе модели деления
1.
Введение
Искажение линзы обычно подразделяется на три типа: радиальное искажение, децентрализованное искажение и искажение тонкой призмы. 1 — 4 На практике для большинства линз радиальная составляющая искажения является преобладающей. 5 , 6 Это может выглядеть как бочкообразное искажение или подушкообразное искажение. Радиальное искажение изгибает прямые линии в дуги окружности, 6 , нарушая основную инвариантность, сохраненную в модели камеры-обскуры, в которой прямые в мире отображаются в прямые линии в плоскости изображения.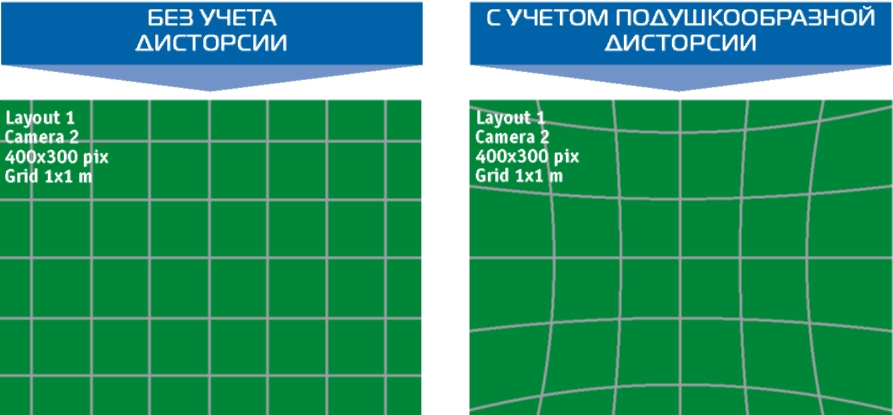 7 Радиальное искажение — наиболее значительный вид искажения в современных камерах. 5 , 8
7 Радиальное искажение — наиболее значительный вид искажения в современных камерах. 5 , 8
Методы, используемые для получения параметров в функции радиального искажения для исправления искаженных изображений, можно условно разделить на две основные категории: метод нескольких ракурсов 9 — 14 и одиночный просмотр метод. 6 , 7 , 15 , 16 Для метода множественных представлений наиболее широко используемым программным обеспечением для автономной калибровки является набор инструментов, предоставленный Жан-Ивом Буге. 17 Он может обрабатывать калибровку после импорта изображения с моделью искажения объектива, которая включает семь параметров, которых достаточно для большинства типов камер. Хотя тот факт, что для метода множественных представлений не требуются особые условия в сцене, например прямые линии, что дает ему широкий спектр применений, недостатком этого метода является то, что он требует нескольких изображений, которые недоступны в много случаев, чтобы провести процесс. 6 В последние десятилетия в исследованиях было предложено множество методов оценки радиальных искажений. 18 — 26 Бухари и Дейли 21 предложили метод автоматической оценки радиального искажения на основе метода отвеса. Они сравнили статистический анализ того, как различные методы подбора круга способствуют точной оценке параметров искажения. Они обеспечивают качественные результаты на большом количестве сложных реальных изображений. Альварес и др. 22 , 23 предложили алгебраический подход к оценке параметров искажения линзы на основе исправления линий на изображении.Параметры дисторсии объектива получаются путем минимизации полинома с четырьмя степенями от нескольких переменных. Искажение объектива оценивается с помощью модели разделения с использованием одного параметра, что позволяет сформулировать проблему в схеме преобразования Хафа, добавив параметр искажения для лучшего выделения прямых линий из изображения.
6 В последние десятилетия в исследованиях было предложено множество методов оценки радиальных искажений. 18 — 26 Бухари и Дейли 21 предложили метод автоматической оценки радиального искажения на основе метода отвеса. Они сравнили статистический анализ того, как различные методы подбора круга способствуют точной оценке параметров искажения. Они обеспечивают качественные результаты на большом количестве сложных реальных изображений. Альварес и др. 22 , 23 предложили алгебраический подход к оценке параметров искажения линзы на основе исправления линий на изображении.Параметры дисторсии объектива получаются путем минимизации полинома с четырьмя степенями от нескольких переменных. Искажение объектива оценивается с помощью модели разделения с использованием одного параметра, что позволяет сформулировать проблему в схеме преобразования Хафа, добавив параметр искажения для лучшего выделения прямых линий из изображения. 24 — 26 Камеры RGB-D, такие как Microsoft Kinect, стали очень широко использоваться в приложениях перцепционных вычислений. Чтобы использовать весь потенциал устройств RGB-D, необходимо выполнить калибровку для определения внутренних и внешних параметров датчиков цвета и глубины, а также для уменьшения искажения линз и глубины.Ранние работы по калибровке устройств RGB-D включают метод Эрреры 27 и метод Смизека. 28
24 — 26 Камеры RGB-D, такие как Microsoft Kinect, стали очень широко использоваться в приложениях перцепционных вычислений. Чтобы использовать весь потенциал устройств RGB-D, необходимо выполнить калибровку для определения внутренних и внешних параметров датчиков цвета и глубины, а также для уменьшения искажения линз и глубины.Ранние работы по калибровке устройств RGB-D включают метод Эрреры 27 и метод Смизека. 28
В этом исследовании наш метод, основанный на использовании искаженных прямых линий, попадает во вторую категорию. Метод работает с одним изображением, на котором существуют как минимум три искаженные прямые линии, и не требует калибровочного шаблона. Модель Brown 29 — 33 чаще всего используется для описания искажения объектива, и лучше всего подходит для объективов с небольшими искажениями.Однако, когда искажение становится большим, оно может быть неудовлетворительным. Мы используем модель деления Фицгиббона 9 радиального искажения с одним параметром. Модель деления способна выразить большие искажения гораздо более низкого порядка. Хартли и Канг утверждали, что обычное предположение, что центр искажения находится в центре изображения, небезопасно. 13 Наш метод также вычисляет центр радиального искажения, что важно для получения оптимальных результатов.
Мы используем модель деления Фицгиббона 9 радиального искажения с одним параметром. Модель деления способна выразить большие искажения гораздо более низкого порядка. Хартли и Канг утверждали, что обычное предположение, что центр искажения находится в центре изображения, небезопасно. 13 Наш метод также вычисляет центр радиального искажения, что важно для получения оптимальных результатов.
Остальная часть этого документа построена следующим образом.Раздел 2 описывает модель искажения и оценку параметров искажения. В гл. 3 представлено подробное количественное исследование оценки производительности как на синтетических, так и на реальных изображениях. Наконец, в этой статье приводятся выводы в разд. 4.
2.
Методология
2.1.
Модели искажения
Модель Брауна, которая чаще всего используется для описания искажения линзы, может быть записана как
Eq. (1)
{xu = (xd − x0) (1 + k1rd2 + k2rd4 + k3rd6 + ⋯) + (1 + p3rd2 + ⋯) {p1 [rd2 + 2 (xd − x0) 2] + 2p2 (xd − x0) ( yd − y0)}, yu = (yd − y0) (1 + k1rd2 + k2rd4 + k3rd6 + ⋯) + (1 + p3rd2 + ⋯) {p2 [rd2 + 2 (yd − y0) 2] + 2p1 (xd − x0) (yd − y0)}, где (xu, yu) и (xd, yd) — соответствующие координаты неискаженной точки и искаженной точки на изображении соответственно.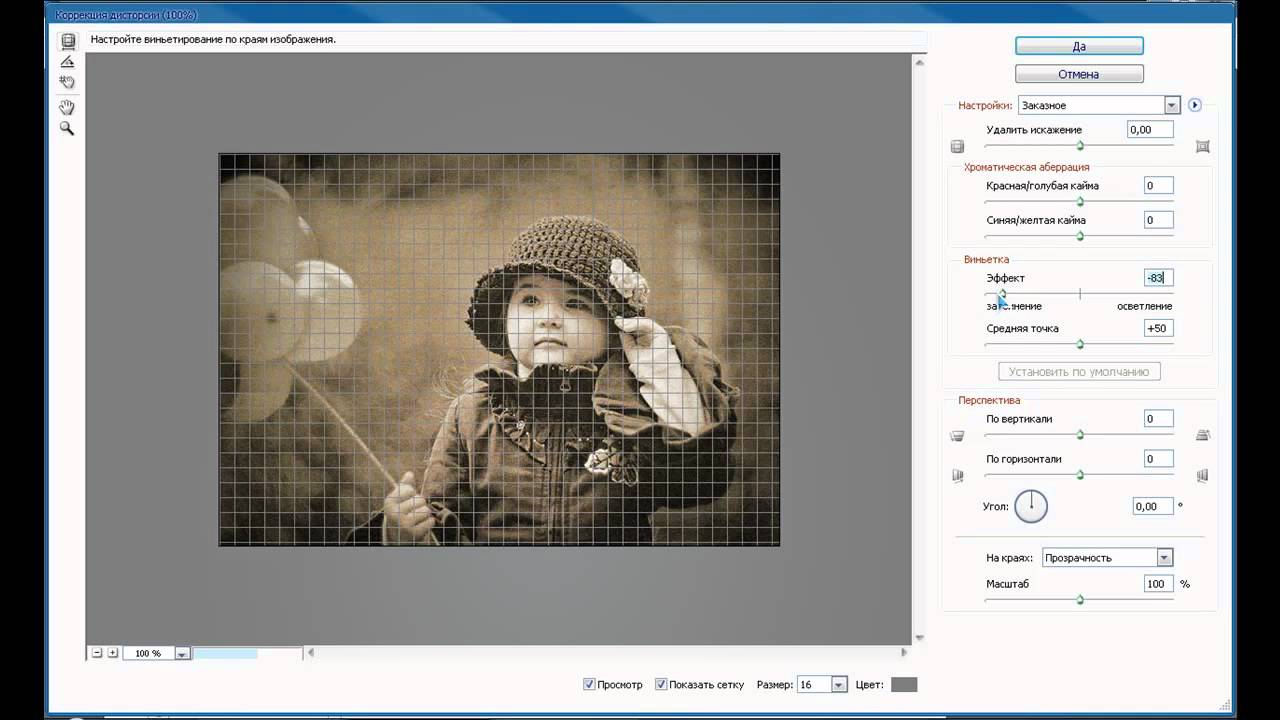 rd = (xd − x0) 2+ (yd − y0) 2 — евклидово расстояние от искаженной точки до центра искажения (x0, y0).
rd = (xd − x0) 2+ (yd − y0) 2 — евклидово расстояние от искаженной точки до центра искажения (x0, y0).Согласно Чжану, 5 радиальная деформация является преобладающей. Наиболее часто используемую модель радиальных искажений можно записать как
Eq. (2)
{xu = xd (1 + λ1rd2 + λ2rd4 + ⋯), yu = yd (1 + λ1rd2 + λ2rd4 + ⋯), предполагая, что искаженный центр (x0, y0) является центром изображения. Эта модель лучше всего подходит для объективов с небольшими искажениями. Однако, когда искажение становится большим, оно может быть неудовлетворительным, и на практике необходимо учитывать многие другие факторы. 6Фитцгиббон 9 предложил модель разделения как
Eq. (3)
{xu = xd1 + λ1rd2 + λ2rd4 + ⋯, yu = yd1 + λ1rd2 + λ2rd4 + ⋯. Наиболее заметным преимуществом модели деления над моделью Брауна является то, что она способна выразить большие искажения гораздо более низкого порядка. В частности, для многих камер достаточно одного параметра. 9 , 10 В нашем исследовании мы используем модель деления на один параметр
9 , 10 В нашем исследовании мы используем модель деления на один параметр
Eq. (4)
{xu = xd1 + λrd2, yu = yd1 + λrd2.2.2.
Искажение прямой линии
В рамках модели разделения одного параметра искаженное изображение прямой линии можно рассматривать как дугу окружности. 6 Уравнение прямой линии выражается как
Из уравнения. (4) имеем
Ур. (6)
Axd1 + λrd2 + Byd1 + λrd2 + C = 0, тогда мы получаем уравнение кругаEq. (7)
xd2 + yd2 + ACλxd + BCλyd + 1λ = 0.Если (x0, y0) является центром радиального искажения, мы имеем
Eq. (8)
(xd − x0) 2+ (yd − y0) 2 + ACλ (xd − x0) + BCλ (yd − y0) + 1λ = 0.Пусть D = ACλ − 2×0, E = BCλ − 2y0, F = x02 + y02 − ACλx0 − BCλy0 + 1λ, тогда мы имеем
Eq. (9)
xd2 + yd2 + Dxd + Eyd + F = 0 иуравнение. (10)
x02 + y02 + Dx0 + Ey0 + F − 1λ = 0. Уравнение (9) указывает, что группа параметров (D, E, F) может быть определена путем подгонки окружности к дуге, которая извлекается из изображение. Дуга окружности на изображении проецируется из прямой линии мира. Выделив не менее трех дуг и определив три группы параметров (D, E, F), центр искажения можно оценить, решив линейные уравнения
Дуга окружности на изображении проецируется из прямой линии мира. Выделив не менее трех дуг и определив три группы параметров (D, E, F), центр искажения можно оценить, решив линейные уравненияEq.(11)
{(D1 − D2) x0 + (E1 − E2) y0 + (F1 − F2) = 0, (D1 − D3) x0 + (E1 − E3) y0 + (F1 − F3) = 0, и оценка λ можно получить изEq. (12)
λ = 1×02 + y02 + Dx0 + Ey0 + F. При извлечении более трех дуг из изображения и определении этих параметров (D, E, F) параметр (x0, y0, λ) может быть получен на основе по схеме Левенберга – Марквардта (LM). Хотя этот метод требует наличия в изображении как минимум трех искаженных линий, он может справиться с ситуацией, в которой обнаруживается меньше линий, путем добавления большего количества изображений, снятых той же камерой с разными углами захвата.Пока в сцене присутствует линия, этот метод применим.2.3.
Метод подгонки окружности
Чтобы найти дуги, мы сначала извлекаем ребра с помощью оператора Кэнни. Затем мы отслеживаем все граничные точки, связанные с начальной точкой. От заданной начальной точки мы отслеживаем в одном направлении, сохраняя координаты краевых точек в массиве и маркируя пиксели в краевом изображении. Когда больше не найдено связанных точек, мы возвращаемся к начальной точке и отслеживаем в обратном направлении.Наконец, выполняется проверка общего количества найденных точек кромки, и кромка игнорируется, если она слишком короткая.
От заданной начальной точки мы отслеживаем в одном направлении, сохраняя координаты краевых точек в массиве и маркируя пиксели в краевом изображении. Когда больше не найдено связанных точек, мы возвращаемся к начальной точке и отслеживаем в обратном направлении.Наконец, выполняется проверка общего количества найденных точек кромки, и кромка игнорируется, если она слишком короткая.
После начального процесса идентификации дуги для каждой результирующей дуги присваивается первоначальное предположение параметров, за которым следует итерационный нелинейный метод наименьших квадратов LM для получения оптимизированных параметров. Подгонка Таубина используется для первоначального предположения. 34 Он использует четыре параметра для определения круга: a (x2 + y2) + bx + cy + d = 0, с a 0. Центр круга равен (−b2a, −c2a), а радиус равен r = (- b2a) 2 + (- c2a) 2 − da.Он минимизирует целевую функцию Ω (a, b, c, d) = ∑i = 1N (axi2 + ayi2 + bxi + cyi + d2) при условии, что 4a2z‾ + 4abx‾ + 4acy‾ + b2 + c2 = 1, где x¯ — среднее значение x-координат точек, y‾ — среднее значение y-координат точек, а z¯ = 1NΣi = 1N (xi2 + yi2).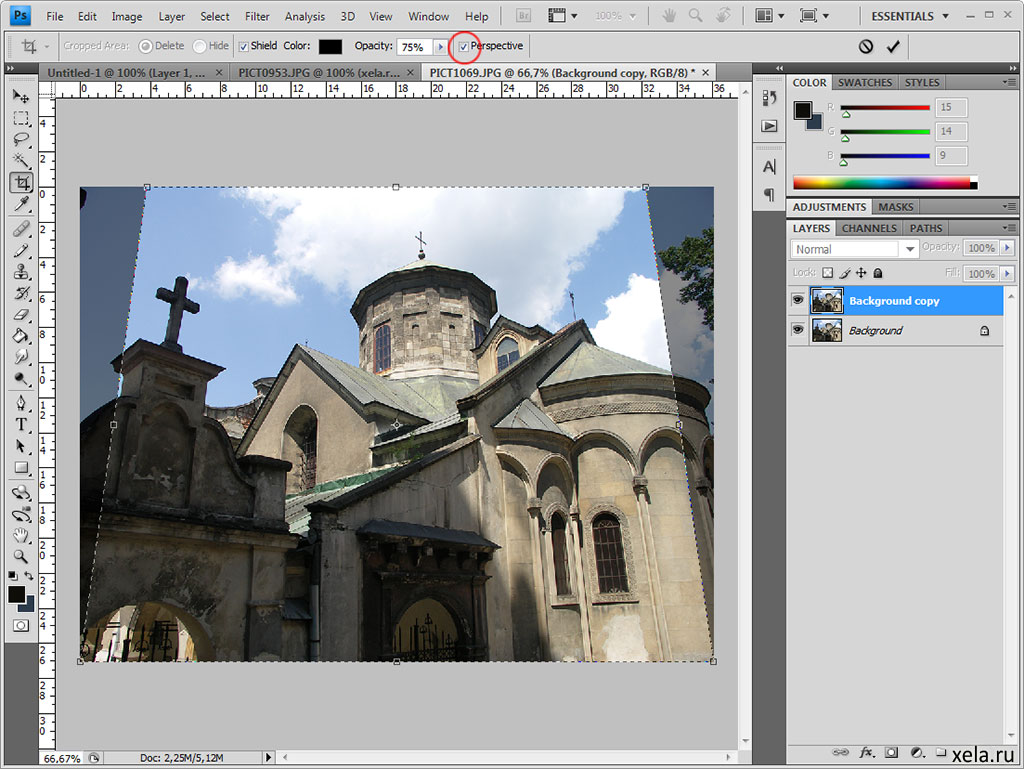 Целевая функция для LM fit 35 равна Ω (xc, yc, r) = ∑i = 1N (ri − r) 2, где ri = (xi − xc) 2+ (yi − yc) 2.
Целевая функция для LM fit 35 равна Ω (xc, yc, r) = ∑i = 1N (ri − r) 2, где ri = (xi − xc) 2+ (yi − yc) 2.
3.
Результат и обсуждение
Эксперименты проводились как на синтетических, так и на реальных изображениях. Проведена оценка эффективности предложенного подхода.Мы используем энтропию Хафа для оценки качества восстановления искаженных синтетических изображений. Преобразование Хафа — это метод, позволяющий находить линии на изображениях. 36 В основе техники лежит преобразование прямой в точку в пространстве Хафа. Линия представлена единственной точкой в двумерном (2-D) пространстве Хафа ρ × θ, в котором значения этих точек меняются. В нашем случае указанный порог устанавливается эмпирически как 0,3 * макс (пространство Хафа) для получения всех пиков, которые представляют линии.Прямая линия на искаженном изображении рассматривается как дуга окружности, и мы используем только значения θ для измерения прямолинейности. Итак, преобразуйте двумерное пространство Хафа ρ × θ в одномерное (1-D) θ пространство, суммируя значения ρ для каждого θ, тогда энтропия Хафа определяется как
Eq.
 (13) H = −b = 1Binsp (Hb) log2 [p (Hb)], где Bins — это количество дискретных интервалов θ (мы устанавливаем Bins = 180), а p (Hb) — значение вероятности.
(13) H = −b = 1Binsp (Hb) log2 [p (Hb)], где Bins — это количество дискретных интервалов θ (мы устанавливаем Bins = 180), а p (Hb) — значение вероятности.3.1.
Тесты на синтетических изображениях
Изображение размером 640 × 480 пикселей, как показано на рис.1, использовалось как исходное изображение (H = 1). Синтетические изображения генерируются из исходного изображения с заданной информацией о параметрах искажения (x0, y0, λ). Мы провели три серии экспериментов с синтетическими изображениями.
Рис. 1
Исходное изображение и соответствующие одномерные преобразования Хафа.
3.1.1.
Varying λ
В первой серии синтетические изображения получаются с параметрами искажения (320,240, λ), с изменяющимися λ на разных уровнях (от крайних подушкообразных до бочкообразных искажений).Для положительного λ (подушкообразного искажения) размер синтетических изображений больше 640 × 480 пикселей, а центр искажения отличается от известных параметров (x0, y0, λ). Для отрицательного λ (бочкообразного искажения) размер синтетических изображений составляет 640 × 480 пикселей, а центр искажения фиксируется на (320, 240). Синтетические изображения, исправленные изображения и соответствующие одномерные преобразования Хафа показаны на рис. 2. Для крайнего случая λ≥5.0 × 10−6 мы отображаем только точки, для которых rd2≤1 / (4λ), в результате получается круглая допустимая область вокруг центра изображения.
Для отрицательного λ (бочкообразного искажения) размер синтетических изображений составляет 640 × 480 пикселей, а центр искажения фиксируется на (320, 240). Синтетические изображения, исправленные изображения и соответствующие одномерные преобразования Хафа показаны на рис. 2. Для крайнего случая λ≥5.0 × 10−6 мы отображаем только точки, для которых rd2≤1 / (4λ), в результате получается круглая допустимая область вокруг центра изображения.
Рис. 2
Коррекция синтетических изображений (с разными λ). (а) Для положительных λ. Первый столбец: искаженные изображения на разных уровнях λ. Второй столбец: соответствующие одномерные преобразования Хафа первого столбца. Третий столбец: исправленные изображения первого столбца. Четвертый столбец: соответствующие одномерные преобразования Хафа третьего столбца. (б) При отрицательном λ. Первый столбец: искаженные изображения на разных уровнях λ. Второй столбец: соответствующие одномерные преобразования Хафа первого столбца. Третий столбец: исправленные изображения первого столбца.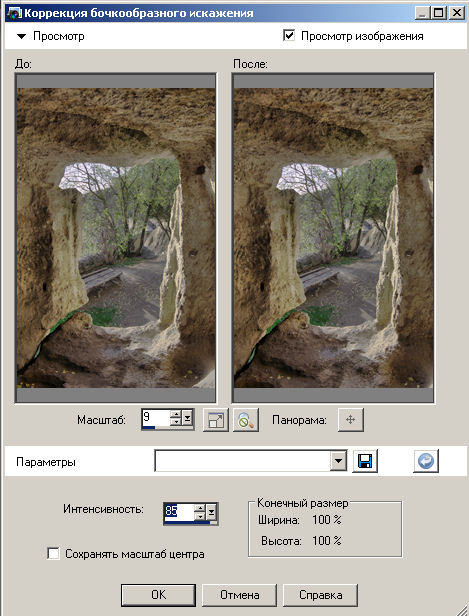 Четвертый столбец: соответствующие одномерные преобразования Хафа третьего столбца.
Четвертый столбец: соответствующие одномерные преобразования Хафа третьего столбца.
Как показано на рис. 2, предложенный метод очень хорошо работает для всех параметров искажения в тестовом интервале и удаляет радиальные искажения изображения с высокой точностью. Оценочные результаты параметров искажения и энтропии Хафа скорректированных изображений показаны в таблице 1. Первоначальная оценка извлекает только три дуги, которые имеют максимальное искажение, а оценка, основанная на методе LM, извлекает шестнадцать дуг, которые также имеют максимальное искажение.Dis — евклидово расстояние между истинным (x0, y0) и оценкой (x0, y0). Rel — относительная ошибка для λ, т.е. | (λestimate − λtrue) / λtrue |. Dis, λestimate и Rel можно найти в Таблице 1.
Таблица 1
Оценочные результаты синтетических изображений из Рис. 2.
| λtrue | Первоначальная оценка | Оценка методом LM | H | ||||
|---|---|---|---|---|---|---|---|
| λ расчет | Отн. | Dis | λ расчет | Отн. | Dis | ||
| 1.0 × 10-5 | 0,999777183 × 10-5 | 2,2817 × 10-4 | 0,6704 | 0,99993718 × 10-5 | 6,282 × 10-5 | 0,7208 | 0,9911 |
| 5,0 × 10– 6 | 5.0006619 × 10-6 | 1,3237 × 10-4 | 0,7185 | 5.0002084 × 10-6 | 4,169 × 10-5 | 0,7043 | 0,9710 |
| 1,0 × 10-6 | 1.000 × 10-6 | 7,8688 × 10-4 | 0,6429 | 0,9996487 × 10-6 | 3.5131 × 10−4 | 1.1189 | 1 |
| 8.0 × 10−7 | 7.978815 × 10−7 | 2,64816 × 10−3 | 0.9011 | 8.002692 × 10−7 | 3.3644 × 10− 4 | 0,9705 | 1 |
| 6,0 × 10–7 | 6,007668 × 10–7 | 1,27806 × 10–3 | 1,4614 | 6,002536 × 10–7 | 4,2261 × 10–4 | 0,6508 | 1 |
| 4,0 × 10-7 | 4,025 900 × 10-7 | 6.47499 × 10−3 | 4,2259 | 3.999954 × 10−7 | 1,146 × 10−5 | 3,0141 | 1 |
| 2,0 × 10−7 | 2,068505 × 10−7 | 3,425237 × 10− 2 | 3.9462 | 1.995506 × 10−7 | 2.24694 × 10−3 | 6.4786 | 1 |
| −2.0 × 10−7 | −2.056167 × 10−7 | 2.808350 × 10−2 | 11,7907 | −2,011946 × 10−7 | 5,97300 × 10−3 | 7,3833 | 1 |
| −4.0 × 10−7 | −3,951756 × 10−7 | 1,206111 × 10−2 | 6,5535 | −3,966594 × 10−7 | 8,35147 × 10−3 | 1,9250 | 1 |
| −6,0 × 10−7 | −6,062686 × 10−7 | 1,044762 × 10−2 | 3,8644 | −6,025610 × 10−7 | 4,26833 × 10−3 | 1.6750 | 1 |
| −8,0 × 10−7 | −7,919760 × 10−7 | 1.003003 × 10−2 | 3,4495 | −8,008144 × 10−7 | 1.01804 × 10−3 | 1,1657 | 1 |
| −1,0 × 10−6 | −1,0014953 × 10−6 | 1,49534 × 10−3 | 0,8899 | −0,9995671 × 10−6 | 4,3291 × 10−4 | 0,7946 | 1 |
| −5,0 × 10−6 | −4,9972071 × 10−6 | 5,5859 × 10−4 | 1,0859 | −5,0008469 × 10−6 | 1,6937 × 10−4 | 0,9439 | 1 |
| −1,0 × 10−5 | −0,995460 12 × 10−5 | 4.53988 × 10-3 | 0,3783 | -1,00022696 × 10-5 | 2,2696 × 10-4 | 0,5654 | 1 |
Из таблицы 1 мы можем видеть, что предлагаемый подход дает убедительные параметры искажения, которые очень близки к истинным параметрам искажения, используемым для создания синтетических изображений. Этот метод очень надежен даже в крайних случаях. Таблица 1 также показывает, что метод LM дает лучшие оценки, чем методы трех дуг. Хотя метод LM может немного увеличить Dis, он резко снизил Rel.Результаты с точки зрения относительной ошибки оценки для λ в Таблице 1 достаточно ясно показывают, что наш метод чрезвычайно точен при оценке λ, оценочные результаты Rel, основанные на методе LM, находятся в диапазоне от 10-3 до 10-5. Отн увеличивается, когда λ приближается к нулю, что отражает следующий фактор: поскольку истинное значение чрезвычайно мало, небольшие отклонения между оценочными и истинными значениями параметров приводят к относительно большим ошибкам. Таблица 1 довольно четко показывает, что расчетные результаты Dis на основе метода LM составляют менее 8 пикселей.Кроме того, в случае | λ | ≥6,0 × 10−7 Dis меньше 2 пикселей. Энтропия Хафа всегда равна 1, за исключением крайнего случая λ≥5.0 × 10−6. В этом случае мы отображаем только те точки, для которых rd2≤1 / (4λ) [см. Рис. 2 (a)]. θ всегда равно 0 (или 90) в пространстве Хафа даже в крайнем случае λ≥5.0 × 10−6, что показывает, что наш метод устойчив. Реальные изображения не могут содержать слишком много искаженных прямых линий. К счастью, результаты в таблице 1 достаточно ясно показывают, что первоначальная оценка извлекает только три дуги, которые имеют удовлетворительную точность.
3.1.2.
Изменяющийся центр искажения
Во второй серии синтетические изображения получают с искажением, зафиксированным на умеренном уровне бочкообразного искажения (λ = -1,0 × -6), при изменении центра искажения. Синтетические изображения, скорректированные изображения и соответствующие одномерные преобразования Хафа представлены на рис. 3. Dis, λestimate и Rel можно найти в таблице 2.
Рис. 3
Коррекция синтетических изображений (с разными искажениями центр). Первый столбец: искаженные изображения.Второй столбец: соответствующие одномерные преобразования Хафа первого столбца. Третий столбец: исправленные изображения первого столбца. Четвертый столбец: соответствующие одномерные преобразования Хафа третьего столбца.
Таблица 2
Оценочные результаты синтетических изображений из Рис. 3.
| (x0, y0) true | Начальная оценка | Оценка методом LM | H | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| λestimate | Rel | (x0, y0) оценка | Dis | λ оценка | Rel | (x0, y0) оценка | Dis | ||||
| (300, 220) | −0.9993661 × 10-6 | 6,3387 × 10-4 | (302,0406, 220,5043) | 2,1019 | −0,9997905 × 10-6 | 2,0946 × 10-4 | (301,1228, 219,5050) | 1,2 | |||
| (300, 260) | −0,9997047 × 10−6 | 2,9529 × 10−4 | (301,7350, 259,7820) | 1,7486 | −1,0000697 × 10−6 | 6,974 × 10−5 | (300.9076, 259.0131) | 1.3408 | 1 | ||
| (340, 220) | -1.0040027 × 10-6 | 4,00267 × 10-3 | (337,1097, 219.6016) | 2,9176 | -1,0002655 × 10-6 | 2,6555 × 10-4 | (338,4051, 219,1870) | 1,70 | |||
| (340, 260) | −1,0036289 × 10−6 | 3,62891 × 10−3 | (337,0461, 258,7703) | 3,1997 | −0,9997154 × 10−6 | 2,84518 × 10−4 | (337,7498, 259,1804) | 2,3948 | 1 | ||
| (240, 160) | -1.0012700 × 10–6 | 1,27000 × 10–3 | (239,0277, 159,8959) | 0,9778 | −0,9996601 × 10-6 | 3,3993 × 10–4 | (237,9878, 158,7605) | (237,9878, 158,7605) | (237,9878, 158,7605) | (237,9878, 158,7605) | |
| (240, 320) | −0,9969717 × 10−6 | 3,02829 × 10−3 | (239,9595, 319,4118) | 0,5896 | −1,0000098 × 10−6 | 9,84 × 10−6 | (238.2006, 320.1384) | 1.8048 | 1 | ||
| (400, 160) | -1.0028122 × 10-6 | 2,81218 × 10-3 | (399,3107, 159,8861) | 0,6987 | −0,9998814 × 10-6 | 1,1862 × 10-4 | (398,1673, 159,2641) | 1,97 | |||
| (400, 320) | -1,0023331 × 10-6 | 2,33315 × 10-3 | (398,8879, 317,7069) | 2,5486 | -1,0000925 × 10-6 | 9,248 × 10-5 | (398,1597, 319,5542) | 1,8935 | 1 | ||
Как показано на рис.3, предложенный метод очень хорошо работает для всех параметров искажения в тестовом интервале и с высокой точностью устраняет радиальные искажения изображения. Из таблицы 2 видно, что наш метод дает хорошие результаты по параметру искажения (x0, y0, λ). Результаты с точки зрения относительной ошибки оценки для λ в таблице 2 достаточно ясно показывают, что наш метод чрезвычайно точен при оценке λ, а также для оценочных результатов Rel, основанных на методе LM, в диапазоне от 10-4 до 10-6. Расчетные результаты Dis по методу LM составляют менее 3 пикселей.Энтропия Хафа всегда равна 1, что показывает надежность нашего метода.
3.1.3.
Сравнение с другим методом
Чтобы оценить точность нашего метода, мы сравнили его с методом, разработанным Alvarez et al. 22 , 23 Alvarez et al. развернули демонстрационный веб-сайт 37 для своего метода, который позволяет пользователям отправлять изображение для устранения искажения после ручного выбора на нем искаженных линий. Для честного сравнения, как в методе Альвареса, так и в нашем методе использовались одни и те же три линии.Синтетическое изображение было сгенерировано из исходного изображения с заданной информацией о параметрах искажения (320, 240, λ = -1,0 × 10-6). Синтетическое изображение, исправленные изображения и соответствующие одномерные преобразования Хафа представлены на рис. 4. Dis, (x0, y0) оценка и H можно найти в таблице 3. По сравнению с исходным изображением (рис. 1) , содержание исправленного изображения [Рис. 4 (b)], созданное с помощью метода Альвареса, будет уменьшено, а содержимое исправленного изображения [Рис. 4 (c)], полученный из предложенного метода, без изменений.Как показано на рис. 4, предлагаемый метод превосходит метод Альвареса с точки зрения визуальных качеств. Из Таблицы 3 мы можем количественно увидеть, что предложенный метод резко снизил Dis, а энтропия Хафа равна исходному изображению. Более того, по сравнению с методом Альвареса, который требует ручного вмешательства для выбора искаженных прямых линий, предлагаемый метод требует гораздо меньшего времени обработки.
Рис. 4
(a) Синтетическое изображение и соответствующие одномерные преобразования Хафа.(b) Исправленное изображение (a), созданное с помощью метода Альвареса и соответствующих одномерных преобразований Хафа. (c) Исправленное изображение (a), которое сгенерировано из предложенного метода и соответствующих одномерных преобразований Хафа.
Таблица 3
Сравнение результатов синтетического изображения с рис. 4.
| Алгоритм | (x0, y0) оценка | Dis | H |
|---|---|---|---|
| Alvarez et al. | (330.0076, 235.0030) | 11.1858 | 1.7206 |
| Предложено | (319,6754, 239,1714) | 0,8899 | 1 |
3.2.
Тесты на реальных изображениях
Исходные протестированные реальные изображения и исправленные изображения показаны на рис. 5, исходное изображение (a) — (g) получено с веб-сайта Image Processing on Line. 38 Из Рис. 5 мы, очевидно, можем наблюдать искажение (слева в паре), а также коррекцию (справа в паре). Эти результаты продемонстрировали, что на восстановленных изображениях было успешно устранено радиальное искажение.Он показывает надежность и точность предлагаемого подхода в коррекции радиальных искажений.
Рис. 5
Коррекция реальных изображений. Некоторые прямые в мире линии были помечены прямыми красными линиями на исправленном изображении, показывая сильные точки схода. (a) (b) (c) (d) (g) здание, (e) спальня, (f) солнечная электростанция и (h) потолок коридора.
Для количественной оценки мы сравнили предложенный метод с методом Чжана 5 и методом Альвареса.Для метода Чжана он должен использовать калибровочный образец (шахматную доску с черно-белыми квадратами) для оценки внутренних параметров камеры, поэтому его процесс занимает гораздо больше времени. Для сравнения метода Альвареса и предлагаемого метода были взяты те же три искаженные линии. Реальное изображение, исправленные изображения и соответствующие одномерные преобразования Хафа представлены на рис. 6. Как и ожидалось, предлагаемый метод превосходит метод Чжана и метод Альвареса с точки зрения визуальных качеств.По сравнению с методом Чжана, который включает калибровку камеры, и методом Альвареса, который требует ручного вмешательства для выбора искаженных прямых линий, предлагаемый метод намного быстрее с точки зрения времени обработки. Распределение вероятностей в 1-D θ пространстве Хафа на рис. 6 (d) показывает, что наш метод намного более однороден при 0 и 180 градусах по сравнению с методами на рис. 6 (б) и 6 (в). Это означает, что предложенный метод дает более удовлетворительный результат по устранению радиального искажения изображения.
Фиг.6
(a) Реальное изображение и соответствующие одномерные преобразования Хафа. (b) Исправленное изображение (a), созданное с помощью метода Чжана и соответствующих одномерных преобразований Хафа. (c) Исправленное изображение (a), созданное с помощью метода Альвареса и соответствующих одномерных преобразований Хафа. (d) Исправленное изображение (a), которое сгенерировано из предложенного метода и соответствующих одномерных преобразований Хафа.
4.
Выводы
В этой статье мы предложили подход для исправления радиального искажения изображения, вызванного линзой.Этот метод работает с одним изображением и не требует специального калибровочного шаблона. Экспериментальные результаты показали значительное достижение в исправлении радиального искажения изображения как в синтетических, так и в реальных изображениях. Основные результаты исследования можно резюмировать по трем аспектам. (1) Предлагаемый метод точен и надежен при оценке радиальной дисторсии. Это чрезвычайно полезно во многих приложениях, особенно в тех, где созданная человеком среда содержит множество строк. Хотя предлагаемый метод требует наличия в изображении как минимум трех искаженных линий, он может справиться с ситуацией, в которой обнаруживается меньше линий, путем добавления большего количества изображений, снятых той же камерой с разными углами захвата.Предлагаемый метод применим до тех пор, пока в сцене присутствует линия. (2) Количественная оценка предполагаемых параметров радиального искажения была достигнута с помощью определенной меры энтропии Хафа, основанной на распределении вероятностей в 1-D θ пространстве Хафа. (3) Методика Таубина показала свой положительный эффект при первоначальном предположении параметров дуги. Это значительно улучшило скорость сходимости в процессе итеративного нелинейного метода наименьших квадратов LM для расчета параметров дуги.
Благодарности
Эта работа была поддержана Национальным фондом естественных наук Китая (грант № 51575388).
Ссылки
4.
F. Wu et al., « Методика калибровки панорамной камеры для исследования глубокого космоса по круговым маркерам », Acta Opt. Син., 33 (11), 1115002 (2013). http://dx.doi.org/10.3788/AOS GUXUDC 0253-2239 Google Scholar9.
A. W. Fitzgibbon, « Одновременная линейная оценка геометрии нескольких ракурсов и искажения объектива ,» в Proc.конференции 2001 IEEE Computer Society Conf. по компьютерному зрению и распознаванию образов (CVPR ’01), 125 –132 (2001). http://dx.doi.org/10.1109/CVPR.2001.910.
Д. Клаус и А. В. Фитцгиббон, « Рациональная модель искажения объектива для обычных камер », в конференции IEEE Computer Society Conf. по компьютерному зрению и распознаванию образов (CVPR ’05), 213 –219 (2005). http: //dx.doi.org / 10.1109 / CVPR.2005.43 Google Scholar29.
Д. К. Браун, « Децентрализация искажений линз ,» Фотометрический англ., 32 (3), 444 –462 (1966). Google Scholar30.
Д. К. Браун, « Калибровка камеры ближнего действия », Фотография. Eng., 37 (8), 855 –866 (1971). Google Scholar31.
Дж. Г. Фрайер и Д. К. Браун, « Искажение объектива для фотограмметрии с близкого расстояния ,» Фотография.Англ. Пульт Сенс., 52 (1), 51 –58 (1986). Google Scholar34.
Г. Таубин, « Оценка плоских кривых, поверхностей и неплоских пространственных кривых, определяемых неявными уравнениями, с приложениями для сегментации изображений по краям и диапазонам », IEEE Trans. Pattern Anal. Мах. Интел., 13 (11), 1115 –1138 (1991). http://dx.doi.org/10.1109/34.103273 ITPIDJ 0162-8828 Google Scholar35.
Н.Чернов, Круговая и линейная регрессия: подгонка окружностей и линий методом наименьших квадратов, Chapman & Hall / CRC, Бока-Ратон, Флорида (2010). Google ScholarБиография
Фанлу Ву получил степень бакалавра в Школе оптоэлектронной инженерии Чанчуньского университета науки и технологий в 2011 году и степень магистра в Университете Китайской академии наук, Китай, в 2014 году. В настоящее время он защищает докторскую диссертацию в Школе точного приборостроения и оптоэлектроники при Тяньцзиньском университете, Китай.Его исследовательские интересы включают калибровку камеры, мозаику изображений и реконструкцию изображений со сверхвысоким разрешением.
Хун Вэй получила докторскую степень в Бирмингемском университете в 1996 году. Она работала научным сотрудником в рамках спонсируемого Hewlett Packard проекта систем CMOS-камер высокого разрешения. Она также работала научным сотрудником в финансируемом EPSRC проекте Фарадея, модель из фильмов. Она поступила в Университет Рединга в 2000 году. В настоящее время ее исследовательские интересы включают интеллектуальное компьютерное зрение и его приложения для изображений с дистанционным зондированием и распознавания лиц (биометрические).
Сянцзюнь Ван получил степени бакалавра, магистра и доктора наук в области точных измерительных технологий и инструментов в Тяньцзиньском университете, Китай, в 1980, 1985 и 1990 годах, соответственно. В настоящее время он является профессором и директором исследовательской группы систем точных измерений в Тяньцзиньском университете. Его исследовательские интересы включают фотоэлектрические датчики и тестирование, компьютерное зрение, анализ изображений, MOEMS и MEMS.
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или уточнить у системного администратора.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Коррекция искажений в зависимости от угла проекции в высокоскоростной рентгеновской компьютерной томографии на базе усилителя изображения
Геометрические искажения неизбежны в помещениях, где используются усилители рентгеновского изображения.Когда картина наведенного искажения изменяется со временем, каждый записанный кадр должен быть соответствующим образом скорректирован, что имеет место, например, в случае традиционной визуализации с помощью С-образной дуги. Это демонстрирует потребность в надежных и простых в использовании методах коррекции, зависящих от угла проекции. В настоящей работе мы демонстрируем такой динамический подход, основанный на корреляции цифровых изображений (DIC). Мы проверяем метод на установке для высокоскоростной рентгеновской томографии, где переменные искажения вызваны неоднородным распределением ферромагнитных компонентов в стадии вращения образца.Сравнивая идеальные положения металлических бусинок в прямолинейном шаблоне и их положения на скорректированных рентгенограммах этого шаблона, мы вывели минимальное количество кадров, необходимых для оценки изменяющегося поведения искажения во время полного вращения столика. Затем этот метод был проверен в алгоритме калибровки геометрии для томографической установки, а также в томографической реконструкции. Перед применением любой коррекции искажения записанные изображения страдают в среднем от среднего и максимального искажения 11.12 пикселей (1,56 мм) и 42,79 пикселей (6,10 мм) соответственно. Из наших экспериментов мы пришли к выводу, что трех проекций, выбранных с интервалом 120 °, достаточно для исправления любого кадра, записанного под промежуточным углом, со средней и максимальной остаточными ошибками соответственно ниже 0,48 пикселя (0,068 мм) и 1,68 пикселя (0,240 мм). при использовании 14-дюймового усилителя изображения, покрывающего поле зрения 292 мм и 292 мм. Эти результаты означают уменьшение средней и максимальной ошибок искажения не менее 96%, независимо от угла проецирования.Затем результаты показали повышенную точность калибровки геометрии системы, что привело к уменьшению размытия краев и лучшему контрасту, а также к сохранению формы при томографической реконструкции. Это демонстрирует, что новый метод точен и надежен, а благодаря общедоступности программного обеспечения DIC он очень доступен и прост в использовании.
Коррекция радиального искажения
Коррекция радиального искаженияСОДЕРЖАНИЕ — Индекс — Следующий
Коррекция радиальных искажений
Современные объективы для фотоаппаратов относительно свободны от геометрических искажений.Однако всегда есть небольшой остаток даже с самыми дорогими линзами.
Радиальное искажение:
Радиальное искажение наиболее заметны при съемке вертикальных структур, имеющих прямые линии, которые затем кажутся изогнутыми. Такое искажение проявляется наиболее заметно, когда самый широкий угол (кратчайшее фокусное расстояние) выбирается либо с фиксированным, либо с зум-объективом. Это может быть адекватно исправлено путем применения простого полиномиального преобразования из-за Математик и астроном 19-го века Филипп Людвиг фон Зайдель (1821-1896), опубликованная им в 1856 году, требующая трех констант. влияющие на содержимое изображения в зависимости от расстояния до центр и симметричный относительно него, отсюда и название радиальное искажение.Полное обсуждение с полной математической базой дано по этой ссылке
Калибровка:
Эти константы могут вычисляться путем фотографирования конструкции или мишени, содержащей известные прямые линии как по вертикали, так и по горизонтали. Они зависят от фокусное расстояние объектива относительно длины диагонали датчика изображения и варьируются от объектива к объективу. Для камер с сменные линзы, для каждой линзы требуется отдельная калибровка и для выбора типичных фокусных расстояний относительно заданного камера.Для менее дорогой цифровой камеры с несменным объектив, калибровка требуется только для выбора фокусных расстояний.
Эта программа обращается к базе данных PTLens.dat для исправления искажений. Использовать последние записи в базе данных, вы должны приобрести лицензию в Страница покупки по адресу http://epaperpress.com/ptlens . Обновления базы данных можно найти на странице загрузки того же сайта. Инструкция по установке лицензии в RadCor находится в файле readme. что сопровождает лицензию.Если у вас есть вопросы по связаться с базой данных Тома Ниманна ( http://epaperpress.com/whoami ).
Из-за множества камеры и объективы на рынке, которые постоянно пополняются, Невозможно создать профиль для каждой камеры и каждого объектива. Поэтому эта программа предлагает простые инструменты для калибровки любых комбинация камеры и объектива, если доступно подходящее изображение. Здесь процесс называется ручной коррекции. .
Хроматическая аберрация:
Некоторые более дешевые камеры имеют искажения, которые зависят от цвета.Это хроматический аберрация. В этой программе предлагается возможность выбора поправочные константы для красной, зеленой и синей составляющих изображение калибровки цвета в опции хроматической коррекции .
В дополнение к радиальные искажения и хроматические аберрации, есть и другие типы искажения объектива, влияющие на качество и геометрию изображения, не радиально симметричны. Этот тип искажения (тангенциальный) в этой программе не исправлено, так как обычно мало по сравнению при этом из-за радиального искажения линз на типичном изображении разрешения цифровых фотоаппаратов.Перспективное искажение, которое вводится камерой, направленной под углом на интересующий объект, будет рассмотрен в другой программе.
Виньетирование:
Если раздача света по сторонам изображения не то же самое, что и ближе к в центре эти части изображения кажутся темнее. Программа может исправить простое симметричное радиальное виньетирование, иногда присутствует под очень широкими углами или при использовании бленды объектива.
Коррекция искажения широкоугольного объектива | Путеводитель по наружной фотографии
Сверхширокоугольные объективы часто вызывают искажение линз.Важно иметь программу постпроизводства, которая решает проблему. В этом видео профессиональный фотограф на открытом воздухе Ян Плант проведет вас через свой собственный процесс постпродакшена и расскажет, как исправить искажения объектива.
Ян предпочитает Adobe Lightroom в качестве процессора обработки фотографий и органайзера изображений. Он объясняет, что эта программа редактирования дает вам несколько инструментов для коррекции неизбежного бочкообразного искажения, которое вы получаете на изображениях, снятых с помощью сверхширокоугольного объектива. В качестве примера коррекции искажения объектива он импортирует фотографию высоких деревьев, сделанную с низкого уровня, стволы изогнуты от искажения.Модуль Lens Correction в Lightroom выбирает марку и модель его камеры и объектива, автоматически выпрямляет кривые деревья, а также корректирует виньетирование.
Для своего следующего шага он переходит к модулю Transform, чтобы исправить искажение перспективы. В разделе «Ограничить кадрирование» он демонстрирует, что вы можете вносить коррективы, используя различные ползунки, включая вертикальный, горизонтальный, поворот, аспект и масштаб. Но Ян напоминает вам, что эти типы коррекции искажения линз субъективны и основаны на художественном видении вашего собственного изображения.
Он показывает вам свое сверхширокоугольное изображение горы с белыми шапками и соснами на переднем плане. Однако деревья наклоняются, вызывая искажение. В Lightroom он открывает модуль «Включить коррекцию профиля» и исправляет искажения краев. Затем он использует инструмент «Преобразование» и вносит коррективы с помощью инструмента «Вертикаль», который исправляет искажения в деревьях, но снижает разрешение. С помощью инструментов «Смещение по оси Y» и «Смещение по оси X» он корректирует потерянные части изображения.Чтобы уменьшить или расширить изображение, он также покажет вам, как использовать инструмент «Масштаб».
Присоединяйтесь к профессиональному стрелку Яну Планту за его компьютером, чтобы познакомить вас с методами и примерами, которые покажут вам, как использовать коррекцию искажения объектива в Lightroom.
Смотрите все видео в нашем Ультра-широкоугольном курсе:
Сверхширокий пейзаж — предварительный просмотр курса
Введение в сверхширокоугольную фотографию
Когда использовать сверхширокоугольный объектив
Съемка на близком и дальнем расстоянии с помощью сверхширокоугольного объектива
Сложение фокусировки с помощью сверхширокоугольного объектива
Как предотвратить блики объектива
Съемка интерьеров с помощью сверхширокоугольного объектива
Ретуширование сгруппированных изображений в фокусе
Настройка штатива для использования на уровне земли
Совмещение экспозиций с помощью Photoshop
Коррекция искажений широкоугольным объективом
Что такое искажение объектива?
В фотографии есть два типа искажений: оптические и перспективные.И то, и другое приводит к некоторой деформации изображений — одни слегка, а другие очень заметно. В то время как оптическое искажение вызвано оптической конструкцией линз (и поэтому часто называется «искажением объектива»), перспективное искажение вызвано положением камеры относительно объекта или положением объекта в кадре изображения. И, безусловно, важно различать эти типы искажений и идентифицировать их, так как вы довольно часто увидите их все на фотографии.Цель этой статьи — подробно объяснить каждый тип искажения с иллюстрациями и примерами изображений.
Мы рассмотрим три различных типа оптических искажений, а затем обсудим прямолинейный и криволинейный характер широкоугольных объективов. В заключение мы покажем, как искажение перспективы влияет на изображения, как показано в таблице содержания ниже.
Оптическое искажение
В фотографии искажение обычно относится к оптической аберрации, которая деформирует и изгибает физически прямые линии и заставляет их выглядеть кривыми на изображениях, поэтому такое искажение также обычно называют «криволинейным» (подробнее об этом ниже).Оптическое искажение возникает в результате оптической конструкции, когда используются специальные линзы для уменьшения сферических и других аберраций. Короче говоря, оптическое искажение — это ошибка объектива.
Существует три известных типа оптического искажения — баррель, подушечка для иголок и усы / усы (также известные как волнистые и сложные). Давайте рассмотрим каждый из них более подробно, но прежде чем мы это сделаем, давайте взглянем на объектив с нулевым искажением:
Такие «идеальные» объективы очень редки, поскольку большинство объективов страдают по крайней мере от одного вида искажений, описанного ниже.Очень хорошие объективы имеют линзы, которые значительно уменьшают искажение там, где оно незаметно для наших глаз. Многие зум-объективы, особенно суперзумы, такие как Nikon 18-200mm VR, страдают от нескольких типов искажений, таких как цилиндрический и подушкообразный при разных фокусных расстояниях.
Бочкообразное искажение
Когда прямые линии изогнуты внутрь в форме бочонка, этот тип аберрации называется «бочкообразным искажением». Обычно бочкообразное искажение наблюдается на широкоугольных объективах, потому что поле зрения объектива намного шире, чем размер датчика изображения, и, следовательно, его необходимо «сжать», чтобы он поместился.В результате прямые линии заметно загнуты внутрь, особенно к крайним краям рамы. Вот пример сильного бочкообразного искажения:
Обратите внимание, что линии появляются прямо в самом центре кадра и только начинают отклоняться от центра. Это связано с тем, что изображение по оптической оси (т. Е. В центре линзы) совпадает, но его увеличение уменьшается по направлению к углам.
Бочкообразное искажение обычно присутствует на большинстве широкоугольных объективов с постоянным фокусным расстоянием и многих зум-объективов с относительно коротким фокусным расстоянием.Степень искажения может варьироваться в зависимости от расстояния от камеры до объекта. Даже стандартные 50-миллиметровые объективы с постоянным фокусным расстоянием могут потенциально давать бочкообразное искажение на близком расстоянии. Бочкообразное искажение можно значительно уменьшить за счет использования компенсирующих оптических элементов, но полностью устранить такое искажение практически невозможно. Некоторые объективы, такие как Nikon 14-24mm f / 2.8G, имеют ряд таких элементов компенсации искажений, которые значительно увеличивают как вес, так и размер объектива. Вот почему широкоугольные объективы обычно больше и тяжелее стандартных / обычных объективов.
Исправление деформации ствола обычно довольно простой процесс. Программное обеспечение для постобработки, такое как Lightroom и Photoshop, а также многие другие сторонние инструменты могут легко исправить проблемы с бочкообразным искажением, если у объектива есть поддерживающий профиль в базе данных. Поскольку все линзы индивидуальны, такие данные профиля линзы должны быть тщательно проверены в лабораторных условиях и созданы. Я написал подробную статью, описывающую этот процесс, в моей статье «Коррекция линз в Lightroom».
Подушкообразное искажение
Подушкообразное искажение — полная противоположность бочкообразного искажения — прямые линии изогнуты наружу от центра.Этот тип искажения обычно наблюдается на телеобъективах и возникает из-за увеличения изображения по направлению к краям кадра от оптической оси. На этот раз поле зрения меньше, чем размер датчика изображения, и поэтому его необходимо «растянуть», чтобы соответствовать размеру. В результате прямые линии кажутся вытянутыми вверх в углах, как показано ниже:
Подушкообразное искажение также является очень распространенной аберрацией, особенно для зум-объективов. Дорогие супертелеобъективы с постоянным фокусным расстоянием имеют компенсирующие элементы, которые могут значительно снизить подушкообразное искажение до незначительного уровня, но большинство потребительских и даже профессиональных зум-объективов, таких как Nikon 80-400 мм VR, страдают от подушкообразного искажения.Фактически, подушкообразное искажение может быть очень сильным для объективов потребительского уровня, что вы быстро заметите на изображениях.
Важно отметить, что большинство зум-объективов, которые меняют фокусное расстояние от широкоугольного до стандартного или телефото, обычно страдают от бочкообразного искажения на самых коротких фокусных расстояниях, которое постепенно переходит в подушкообразное искажение к самому длинному концу. Хорошим примером такого поведения является Nikon 18-300mm VR, который начинается с сильного бочкообразного искажения на 18 мм, затем быстро переключается на подушкообразное искажение на 28 мм и остается таким до 300 мм.
Как и бочкообразное искажение, подушкообразное искажение также можно легко исправить с помощью программного обеспечения для постобработки, такого как Lightroom и Photoshop. Профили линз, встроенные в Lightroom и Camera RAW, позволяют полностью устранить его одним щелчком мыши.
Искажение усов
Самым отвратительным из радиальных искажений является искажение усов, которое я иногда называю «волнистым» искажением. По сути, это комбинация бочкообразного искажения и подушкообразного искажения.Прямые линии выглядят изогнутыми внутрь к центру кадра, а затем изгибаются наружу в крайних углах, как показано ниже:
Это причина, по которой искажение усов часто называют «сложным» искажением, поскольку его характеристики действительно сложные и может быть довольно болезненным. Хотя этот тип искажения потенциально можно исправить, для этого часто требуется специальное программное обеспечение. Вы не можете просто использовать встроенные инструменты в Lightroom и Photoshop, если уже не создан определенный профиль объектива для борьбы с таким искажением.Если вы попытаетесь справиться с таким искажением, как бочкообразное, вы в конечном итоге еще больше изогнете крайние углы. И если вы попытаетесь компенсировать подушкообразное искажение, вы в конечном итоге изогнете его для еще более сильного бочкообразного искажения к центру.
Некоторые старые объективы, а также некоторые современные линзы имеют искажение типа усов. Хорошим примером этого является объектив Nikon 18-35mm f / 3.5-4.5D, который демонстрирует довольно неприятный случай искажения усов.
Прямолинейные и криволинейные линзы
Некоторые объективы имеют оптическую «прямолинейность» (например, Nikon 14mm f / 2.8D и Canon EF 14mm f / 2.8L II USM), где они дают прямые линии, не сгибая их (напоминая человеческое зрение), в то время как другие линзы, такие как линзы «рыбий глаз», спроектированы так, чтобы быть «криволинейными». Прямолинейные линзы обычно растягивают объекты, чтобы они выглядели прямыми, особенно по краям кадра. Криволинейные же линзы ничего не растягивают, но сильно искажают изображение, изгибая прямые линии (как в дверных глазках). Взгляните на следующие образцы изображений, которые демонстрируют эффекты как прямолинейной, так и криволинейной линзы:
Как видите, забор на образце криволинейной линзы выглядит неестественно изогнутым — это потому, что я сфотографировал его с помощью объектива типа «рыбий глаз» (криволинейного).Изображение справа — это то, что вы видели бы через прямолинейный объектив — забор выглядит прямым и естественным, как если бы вы видели его своими глазами. Размер ограждения, который кажется большим перед кадром и уменьшается на больших расстояниях, является искажением перспективы (см. Ниже), не имеющим ничего общего с оптическим искажением.
Прямолинейное и криволинейное словоблудие объектива обычно применяется только к широкоугольным объективам.
Искажения перспективы
До сих пор мы говорили только об оптических искажениях.Другой тип искажения, который часто наблюдается на изображениях, — это искажение перспективы. В отличие от оптического искажения, оно не имеет ничего общего с оптикой объектива и, следовательно, не является ошибкой объектива. При проецировании трехмерного пространства на двухмерное изображение, если объект находится слишком близко к камере, он может казаться непропорционально большим или искаженным по сравнению с объектами на заднем плане. Это вполне нормальное явление, и вы легко можете увидеть это собственными глазами. Если вы возьмете меньший объект, например, ваш мобильный телефон, а затем поднесете его очень близко к глазам, он будет казаться большим по сравнению, например, с вашим телевизором с большим экраном на заднем плане (и чем дальше ваш телефон от телевизора, тем меньше будет телевизор. отображаются относительно вашего телефона).То же самое может произойти при фотографировании любого объекта, в том числе людей.
Например, если вы фотографируете человека с близкого расстояния сверхширокоугольным объективом, его нос, глаза и губы могут казаться нереально большими, а уши могут выглядеть очень маленькими или даже полностью исчезать с изображения. Взгляните на следующие фотографии объекта, снятого с помощью широкоугольного объектива с очень близкого расстояния:
Слева: при очень близком расстоянии лицо объекта выглядит непропорциональноСправа: немного отодвигаясь и центрируя голову объекта, проблема решается. но посмотрите, что он сделал с телом объекта — плечи выглядят огромными по сравнению с остальным телом.
Посмотрите на размер его головы на левой фотографии — она кажется непропорционально большой по сравнению с его телом. Его глаза, нос и губы очень увеличены, а уши карликовые.
Это та часть, которая, кажется, сбивает с толку многих фотографов — связь (или ее отсутствие) фокусного расстояния с искажением перспективы. Вы можете услышать, как некоторые фотографы говорят, что для фотографирования людей следует использовать более длинные фокусные расстояния, иначе они будут искажаться из-за короткого фокусного расстояния объектива.Это в основном ложное утверждение, потому что у линз нет перспективы. За исключением объективов типа «рыбий глаз», все объективы имеют одинаковую перспективу — перспективу определяет расстояние от камеры до объекта, а не фокусное расстояние. Создается иллюзия разного ракурса линз, потому что с большим фокусным расстоянием вам нужно стоять подальше от объекта, чтобы кадрировать их таким же образом. Если бы вы встали на таком же расстоянии, объект выглядел бы точно так же! Поэтому, если вы возьмете объектив 50 мм и объектив 85 мм, между ними нет разницы в перспективе, если вы стоите в одном месте и держите расстояние от объекта до камеры на одном и том же.Да, объект определенно будет казаться меньше с объективом 50 мм из-за более короткого фокусного расстояния / более широкого поля зрения, но перспектива и пропорции будут одинаковыми для обоих. Таким образом, преимущество линз с более длинным фокусным расстоянием в таких случаях — это возможность увеличить объект в кадре, сохраняя при этом нормальную перспективу. Телеобъективы не исправляют искажение перспективы волшебным образом — они заставляют вас отодвинуться от объекта, что и меняет перспективу.
Взгляните на следующую фотографию красного автомобиля:
NIKON D3S + 14-24mm f / 2.8 @ 14 мм, ISO 200, 1/125, f / 8.0Автомобиль выглядит полностью искаженным, потому что я стоял очень близко к нему и фотографировал его широкоугольным объективом (Nikon 14-24 мм). Обратите внимание, что левая часть автомобиля выглядит непропорционально большой — даже левый свет выглядит примерно на 50% больше, чем правый, хотя вы знаете, что они одинакового размера. Автомобиль занимает большую часть кадра, и все на заднем плане выглядит относительно маленьким. Если бы я использовал обычный объектив и стоял на том же месте, у меня бы получилась только часть автомобиля, занимающая весь кадр.Тем не менее, если бы я обрезал оба изображения для одного и того же поля зрения, сильно обрезав широкоугольный снимок, эффект искажения перспективы был бы одинаковым для обоих.
Вот еще один пример искажения перспективы:
NIKON D800E + 35mm f / 1.4 @ 35mm, ISO 100, 1/200, f / 11.0На этом изображении улицы в центре Сан-Франциско четыре этажа здания слева и справа они выглядят больше, чем 48-этажная пирамида Трансамерики (длинное здание вдали), хотя на самом деле они намного меньше, если поставить их рядом.Поскольку я использовал широкоугольный объектив, я смог показать передние здания намного больше, чем они есть на самом деле.
Приведенные выше примеры перспективного искажения известны как «широкоугольное» или «расширенное» искажение. Существует еще один вид искажения перспективы, противоположный широкоугольному искажению — это искажение «телефото» или искажение «сжатия». Компрессионное искажение возможно только с телеобъективами, потому что для этого требуется, чтобы фотограф оставался на большом расстоянии по отношению к объекту, из-за чего очень удаленные объекты кажутся больше, чем они есть по сравнению с «нормальной» перспективой.
И, наконец, случай сходящихся линий. Когда датчик камеры не совсем параллелен фотографируемому объекту, например зданию, он создает изображение, которое сначала может показаться неестественным из-за его «наклонного» эффекта, как показано ниже:
NIKON D800E + Zeiss Distagon T * 1.4 / 35 ZF.2 @ 35 мм, ISO 100, 1/320, f / 8.0Однако это совершенно естественная перспектива без искажений, потому что ваши глаза будут видеть это точно так же. Производители линз предлагают линзы с «управлением перспективой» или «наклоном-сдвигом», чтобы справиться с этой конкретной ситуацией, но результат на самом деле получается неестественным, поскольку в реальной жизни это выглядит не так, когда мы смотрим вверх.Взгляните на приведенные ниже примеры до (слева) и после (справа) изменения управления перспективой:
Изображение слева — это то, как вы бы увидели его своими глазами, если бы вы стояли там, а изображение справа — то, что объектив с управлением перспективой / наклоном-сдвигом будет работать с изображением после того, как оно будет выровнено по зданию.
Вот еще пара примеров сходящихся линий, когда одна часть изображения кажется намного больше другой просто потому, что она ближе:
NIKON D800E + 35mm f / 1.4 @ 35 мм, ISO 100, 1/320, f / 8,0 NIKON D800E + 24-70 мм f / 2,8 @ 32 мм, ISO 200, 1/40, f / 11,0Опять же, все это не является результатом искажения — это естественная перспектива!
И, наконец, еще один пример искажения перспективы с участием людей:
NIKON D800E + 14-24 мм f / 2,8 @ 14 мм, ISO 100, 1/50, f / 4,0Обратите внимание, как воздушные шары в центре кадра выглядят естественно , а головы жениха и шафера имеют форму яйца.



 Для зум-объективов, щелкните правой кнопкой мыши ( Cmd+клик на Mac ) и выберите наиболее подходящее фокусное расстояние. Если вы не можете найти свой профиль объектива, нажмите кнопку « Поиск в Интернете », чтобы найти профили, загруженные другими фотографами. Если вы хотите сохранить профиль для дальнейшего использования, нажмите на выпадающее меню « Профили объектива » ( всплывающее меню на Mac ) и выберите « Сохранить онлайн-профиль локально ».
Для зум-объективов, щелкните правой кнопкой мыши ( Cmd+клик на Mac ) и выберите наиболее подходящее фокусное расстояние. Если вы не можете найти свой профиль объектива, нажмите кнопку « Поиск в Интернете », чтобы найти профили, загруженные другими фотографами. Если вы хотите сохранить профиль для дальнейшего использования, нажмите на выпадающее меню « Профили объектива » ( всплывающее меню на Mac ) и выберите « Сохранить онлайн-профиль локально ». Инструменты « Перемещение сетки », « Рука » и « Лупа » помогут более удобно задать настройки;
Инструменты « Перемещение сетки », « Рука » и « Лупа » помогут более удобно задать настройки; Многие проблемы, такие как искажение перспективны, легче исправить с помощью сетки;
Многие проблемы, такие как искажение перспективны, легче исправить с помощью сетки; Подушкообразное искажение — обратный эффект, при котором прямые линии вогнуты вовнутрь.
Подушкообразное искажение — обратный эффект, при котором прямые линии вогнуты вовнутрь.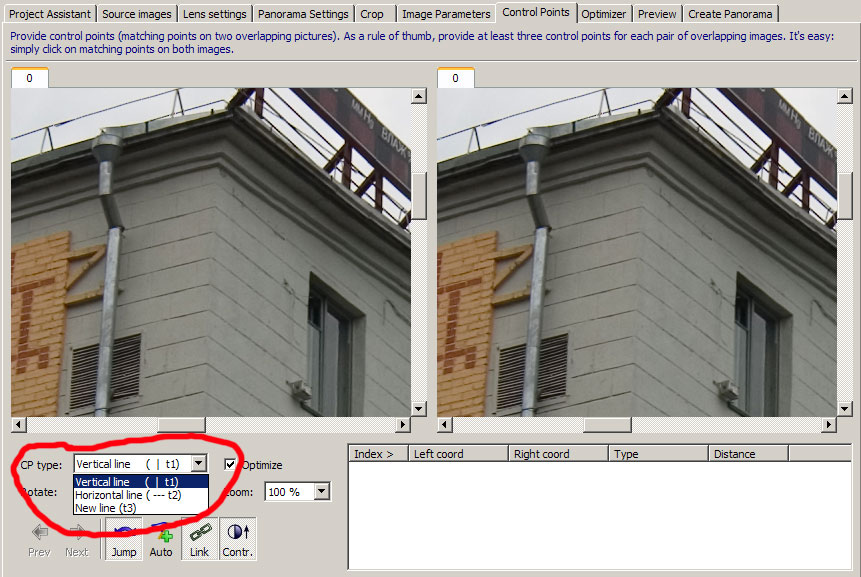 Сетка изображения для настройки этого фильтра позволяет упростить эти исправления и сделать их аккуратнее, чем при использовании команды «Трансформирование».
Сетка изображения для настройки этого фильтра позволяет упростить эти исправления и сделать их аккуратнее, чем при использовании команды «Трансформирование».

 )
)

 Чтобы совместить сетку с линиями изображения, ее можно передвинуть с помощью инструмента «Перемещение сетки» .
Чтобы совместить сетку с линиями изображения, ее можно передвинуть с помощью инструмента «Перемещение сетки» . В этом случае используйте команду «Загрузить настройки» .)
В этом случае используйте команду «Загрузить настройки» .) Шум отсканированных изображений может быть вызван сенсором сканера. Часто на сканированных изображениях проявляется зерно пленки.
Шум отсканированных изображений может быть вызван сенсором сканера. Часто на сканированных изображениях проявляется зерно пленки. чтобы в объектив поместилось всё здание, а не только нижняя его часть).
чтобы в объектив поместилось всё здание, а не только нижняя его часть).
 На рисунке показан схематичный пример этих искажений:
На рисунке показан схематичный пример этих искажений:
 Для этого выберите инструмент «Перемещение сетки» (Move Grid Tool), расположенный в левой части диалогового окна, и мышкой и перетащите сетку:
Для этого выберите инструмент «Перемещение сетки» (Move Grid Tool), расположенный в левой части диалогового окна, и мышкой и перетащите сетку: