Изучаем матрицы в питоне и массивы NumPy в Python
Матрица — это двухмерная структура данных, в которой числа расположены в виде строк и столбцов. Например:
Эта матрица является матрицей три на четыре, потому что она состоит из 3 строк и 4 столбцов.
Python не имеет встроенного типа данных для матриц. Но можно рассматривать список как матрицу. Например:
A = [[1, 4, 5],
[-5, 8, 9]]
Этот список является матрицей на 2 строки и 3 столбца.
Обязательно ознакомьтесь с документацией по спискам Python, прежде чем продолжить читать эту статью.
Давайте посмотрим, как работать с вложенным списком.
A = [[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]]
print("A =", A)
print("A[1] =", A[1]) # вторая строка
print("A[1][2] =", A[1][2]) # третий элемент второй строки
print("A[0][-1] =", A[0][-1]) # последний элемент первой строки
column = []; # пустой список
for row in A:
column.append(row[2])
print("3rd column =", column)
Когда мы запустим эту программу, результат будет следующий:
A = [[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]] A [1] = [-5, 8, 9, 0] A [1] [2] = 9 A [0] [- 1] = 12 3-й столбец = [5, 9, 11]
Использование вложенных списков в качестве матрицы подходит для простых вычислительных задач. Но в Python есть более эффективный способ работы с матрицами – NumPy .
Но в Python есть более эффективный способ работы с матрицами – NumPy .
NumPy — это расширение для научных вычислений, которое поддерживает мощный объект N-мерного массива. Прежде чем использовать NumPy, необходимо установить его. Для получения дополнительной информации,
- Ознакомьтесь: Как установить NumPy Python?
- Если вы работаете в Windows, скачайте и установите дистрибутив anaconda Python. Он поставляется вместе с NumPy и другими расширениями.
После установки NumPy можно импортировать и использовать его.
NumPy предоставляет собой многомерный массив чисел (который на самом деле является объектом). Давайте рассмотрим приведенный ниже пример:
import numpy as np a = np.array([1, 2, 3]) print(a) # Вывод: [1, 2, 3] print(type(a)) # Вывод: <class 'numpy.ndarray'>
Как видите, класс массива NumPy называется ndarray.
Существует несколько способов создания массивов NumPy.
import numpy as np A = np.array([[1, 2, 3], [3, 4, 5]]) print(A) A = np.array([[1.1, 2, 3], [3, 4, 5]]) # Массив чисел с плавающей запятой print(A) A = np.array([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив составных чисел print(A)
Когда вы запустите эту программу, результат будет следующий:
[[1 2 3] [3 4 5]] [[1.1 2. 3.] [3. 4. 5.]] [[1. + 0.j 2. + 0.j 3. + 0.j] [3. + 0.j 4. + 0.j 5. + 0.j]]
import numpy as np zeors_array = np.zeros( (2, 3) ) print(zeors_array) ''' Вывод: [[0. 0. 0.] [0. 0. 0.]] ''' ones_array = np.ones( (1, 5), dtype=np.int32 ) // указание dtype print(ones_array) # Вывод: [[1 1 1 1 1]]
Здесь мы указали dtype — 32 бита (4 байта). Следовательно, этот массив может принимать значения от -2-31 до 2-31-1.
import numpy as np
A = np.arange(4)
print('A =', A)
B = np.arange(12).reshape(2, 6)
print('B =', B)
'''
Вывод:
A = [0 1 2 3]
B = [[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]]
'''
Узнайте больше о других способах создания массива NumPy .
Выше мы привели пример сложение, умножение матриц и транспонирование матрицы. Мы использовали вложенные списки, прежде чем создавать эти программы. Рассмотрим, как выполнить ту же задачу, используя массив NumPy.
Мы используем оператор +, чтобы сложить соответствующие элементы двух матриц NumPy.
import numpy as np A = np.array([[2, 4], [5, -6]]) B = np.array([[9, -3], [3, 6]]) C = A + B # сложение соответствующих элементов print(C) ''' Вывод: [[11 1] [ 8 0]] '''
Чтобы умножить две матрицы, мы используем метод dot(). Узнайте больше о том, как работает numpy.dot .
Примечание: * используется для умножения массива (умножения соответствующих элементов двух массивов), а не умножения матрицы.
import numpy as np A = np.array([[3, 6, 7], [5, -3, 0]]) B = np.array([[1, 1], [2, 1], [3, -3]]) C = a.dot(B) print(C) ''' Вывод: [[ 36 -12] [ -1 2]] '''
Мы используем numpy.transpose для вычисления транспонирования матрицы.
import numpy as np A = np.array([[1, 1], [2, 1], [3, -3]]) print(A.transpose()) ''' Вывод: [[ 1 2 3] [ 1 1 -3]] '''
Как видите, NumPy значительно упростил нашу задачу.
Также можно получить доступ к элементам матрицы, используя индекс. Начнем с одномерного массива NumPy.
import numpy as np
A = np.array([2, 4, 6, 8, 10])
print("A[0] =", A[0]) # Первый элемент
print("A[2] =", A[2]) # Третий элемент
print("A[-1] =", A[-1]) # Последний элемент
Когда вы запустите эту программу, результат будет следующий:
A [0] = 2 A [2] = 6 A [-1] = 10
Теперь выясним, как получить доступ к элементам двухмерного массива (который в основном представляет собой матрицу).
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
# Первый элемент первой строки
print("A[0][0] =", A[0][0])
# Третий элемент второй строки
print("A[1][2] =", A[1][2])
# Последний элемент последней строки
print("A[-1][-1] =", A[-1][-1])
Когда мы запустим эту программу, результат будет следующий:
A [0] [0] = 1 A [1] [2] = 9 A [-1] [- 1] = 19
import numpy as np A = np.array([[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]]) print("A[0] =", A[0]) # Первая строка print("A[2] =", A[2]) # Третья строка print("A[-1] =", A[-1]) # Последняя строка (третья строка в данном случае)
Когда мы запустим эту программу, результат будет следующий:
A [0] = [1, 4, 5, 12] A [2] = [-6, 7, 11, 19] A [-1] = [-6, 7, 11, 19]
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[:,0] =",A[:,0]) # Первый столбец
print("A[:,3] =", A[:,3]) # Четвертый столбец
print("A[:,-1] =", A[:,-1]) # Последний столбец (четвертый столбец в данном случае)
Когда мы запустим эту программу, результат будет следующий:
A [:, 0] = [1 -5 -6] A [:, 3] = [12 0 19] A [:, - 1] = [12 0 19]
Если вы не знаете, как работает приведенный выше код, прочтите раздел «Разделение матрицы».
Разделение одномерного массива NumPy аналогично разделению списка. Рассмотрим пример:
import numpy as np letters = np.array([1, 3, 5, 7, 9, 7, 5]) # с 3-го по 5-ый элементы print(letters[2:5]) # Вывод: [5, 7, 9] # с 1-го по 4-ый элементы print(letters[:-5]) # Вывод: [1, 3] # с 6-го до последнего элемента print(letters[5:]) # Вывод:[7, 5] # с 1-го до последнего элемента print(letters[:]) # Вывод:[1, 3, 5, 7, 9, 7, 5] # список в обратном порядке print(letters[::-1]) # Вывод:[5, 7, 9, 7, 5, 3, 1]
Теперь посмотрим, как разделить матрицу.
import numpy as np
A = np.array([[1, 4, 5, 12, 14],
[-5, 8, 9, 0, 17],
[-6, 7, 11, 19, 21]])
print(A[:2, :4]) # две строки, четыре столбца
''' Вывод:
[[ 1 4 5 12]
[-5 8 9 0]]
'''
print(A[:1,]) # первая строка, все столбцы
''' Вывод:
[[ 1 4 5 12 14]]
'''
print(A[:,2]) # все строки, второй столбец
''' Вывод:
[ 5 9 11]
'''
print(A[:, 2:5]) # все строки, с третьего по пятый столбец
''' Вывод:
[[ 5 12 14]
[ 9 0 17]
[11 19 21]]
'''
Использование NumPy вместо вложенных списков значительно упрощает работу с матрицами. Мы рекомендуем детально изучить пакет NumPy, если вы планируете использовать Python для анализа данных.
Мы рекомендуем детально изучить пакет NumPy, если вы планируете использовать Python для анализа данных.
Данная публикация является переводом статьи «Python Matrices and NumPy Arrays» , подготовленная редакцией проекта.
100 NumPy задач | Python 3 для начинающих и чайников
100 (на самом деле, пока меньше) задач для NumPy, перевод английского варианта https://github.com/rougier/numpy-100
Импортировать NumPy под именем np
Напечатать версию и конфигурацию
print(np.__version__) np.show_config()
Создать вектор (одномерный массив) размера 10, заполненный нулями
Z = np.zeros(10) print(Z)
Создать вектор размера 10, заполненный единицами
Создать вектор размера 10, заполненный числом 2.5
Z = np.full(10, 2.5) print(Z)
Как получить документацию о функции numpy.add из командной строки?
python3 -c "import numpy; numpy.info(numpy.add)"
Создать вектор размера 10, заполненный нулями, но пятый элемент равен 1
Z = np.zeros(10) Z[4] = 1 print(Z)
Создать вектор со значениями от 10 до 49
Z = np.arange(10,50) print(Z)
Развернуть вектор (первый становится последним)
Z = np.arange(50) Z = Z[::-1]
Создать матрицу (двумерный массив) 3×3 со значениями от 0 до 8
Z = np.arange(9).reshape(3,3) print(Z)
Найти индексы ненулевых элементов в [1,2,0,0,4,0]
nz = np.nonzero([1,2,0,0,4,0]) print(nz)
Создать 3×3 единичную матрицу
Создать массив 3x3x3 со случайными значениями
Z = np.random.random((3,3,3)) print(Z)
Создать массив 10×10 со случайными значениями, найти минимум и максимум
Z = np.random.random((10,10)) Zmin, Zmax = Z.min(), Z.max() print(Zmin, Zmax)
Создать случайный вектор размера 30 и найти среднее значение всех элементов
Z = np.random.random(30) m = Z.mean() print(m)
Создать матрицу с 0 внутри, и 1 на границах
Z = np.ones((10,10)) Z[1:-1,1:-1] = 0
Выяснить результат следующих выражений
0 * np.nan np.nan == np.nan np.inf > np.nan np.nan - np.nan 0.3 == 3 * 0.1
Создать 5×5 матрицу с 1,2,3,4 под диагональю
Z = np.diag(np.arange(1, 5), k=-1) print(Z)
Создать 8×8 матрицу и заполнить её в шахматном порядке
Z = np.zeros((8,8), dtype=int) Z[1::2,::2] = 1 Z[::2,1::2] = 1 print(Z)
Дан массив размерности (6,7,8). Каков индекс (x,y,z) сотого элемента?
print(np.unravel_index(100, (6,7,8)))
Создать 8×8 матрицу и заполнить её в шахматном порядке, используя функцию tile
Z = np.tile(np.array([[0,1],[1,0]]), (4,4)) print(Z)
Перемножить матрицы 5×3 и 3×2
Z = np.dot(np.ones((5,3)), np.ones((3,2))) print(Z)
Дан массив, поменять знак у элементов, значения которых между 3 и 8
Z = np.arange(11) Z[(3 < Z) & (Z <= 8)] *= -1
Создать 5×5 матрицу со значениями в строках от 0 до 4
Z = np.zeros((5,5)) Z += np.arange(5) print(Z)
Есть генератор, сделать с его помощью массив
def generate():
for x in xrange(10):
yield x
Z = np.fromiter(generate(),dtype=float,count=-1)
print(Z)Создать вектор размера 10 со значениями от 0 до 1, не включая ни то, ни другое
Z = np.linspace(0,1,12)[1:-1] print(Z)
Отсортировать вектор
Z = np.random.random(10) Z.sort() print(Z)
Проверить, одинаковы ли 2 numpy массива
A = np.random.randint(0,2,5) B = np.random.randint(0,2,5) equal = np.allclose(A,B) print(equal)
Сделать массив неизменяемым
Z = np.zeros(10) Z.flags.writeable = False Z[0] = 1
Дан массив 10×2 (точки в декартовой системе координат), преобразовать в полярную
Z = np.random.random((10,2)) X,Y = Z[:,0], Z[:,1] R = np.hypot(X, Y) T = np.arctan2(Y,X) print(R) print(T)
Заменить максимальный элемент на ноль
Z = np.random.random(10) Z[Z.argmax()] = 0 print(Z)
Создать структурированный массив с координатами x, y на сетке в квадрате [0,1]x[0,1]
Z = np.zeros((10,10), [('x',float),('y',float)])
Z['x'], Z['y'] = np.meshgrid(np.linspace(0,1,10),
np.linspace(0,1,10))
print(Z)Из двух массивов сделать матрицу Коши C (Cij = 1/(xi — yj))
X = np.arange(8) Y = X + 0.5 C = 1.0 / np.subtract.outer(X, Y) print(np.linalg.det(C))
Найти минимальное и максимальное значение, принимаемое каждым числовым типом numpy
for dtype in [np.int8, np.int32, np.int64]: print(np.iinfo(dtype).min) print(np.iinfo(dtype).max) for dtype in [np.float32, np.float64]: print(np.finfo(dtype).min) print(np.finfo(dtype).max) print(np.finfo(dtype).eps)
Напечатать все значения в массиве
np.set_printoptions(threshold=np.nan) Z = np.zeros((25,25)) print(Z)
Найти ближайшее к заданному значению число в заданном массиве
Z = np.arange(100) v = np.random.uniform(0,100) index = (np.abs(Z-v)).argmin() print(Z[index])
Создать структурированный массив, представляющий координату (x,y) и цвет (r,g,b)
Z = np.zeros(10, [ ('position', [ ('x', float, 1),
('y', float, 1)]),
('color', [ ('r', float, 1),
('g', float, 1),
('b', float, 1)])])
print(Z)Дан массив (100,2) координат, найти расстояние от каждой точки до каждой
import scipy.spatial Z = np.random.random((10,2)) D = scipy.spatial.distance.cdist(Z,Z) print(D)
Преобразовать массив из float в int
Z = np.arange(10, dtype=np.int32) Z = Z.astype(np.float32, copy=False)
Дан файл:
1,2,3,4,5 6,,,7,8 ,,9,10,11
Как прочитать его?
Z = np.genfromtxt("missing.dat", delimiter=",")Каков эквивалент функции enumerate для numpy массивов?
Z = np.arange(9).reshape(3,3) for index, value in np.ndenumerate(Z): print(index, value) for index in np.ndindex(Z.shape): print(index, Z[index])
Сформировать 2D массив с распределением Гаусса
X, Y = np.meshgrid(np.linspace(-1,1,10), np.linspace(-1,1,10)) D = np.hypot(X, Y) sigma, mu = 1.0, 0.0 G = np.exp(-((D - mu) ** 2 / (2.0 * sigma ** 2))) print(G)
Случайно расположить p элементов в 2D массив
n = 10 p = 3 Z = np.zeros((n,n)) np.put(Z, np.random.choice(range(n*n), p, replace=False), 1)
Отнять среднее из каждой строки в матрице
X = np.random.rand(5, 10) Y = X - X.mean(axis=1, keepdims=True)
Отсортировать матрицу по n-ому столбцу
Z = np.random.randint(0,10,(3,3)) n = 1 # Нумерация с нуля print(Z) print(Z[Z[:,n].argsort()])
Определить, есть ли в 2D массиве нулевые столбцы
Z = np.random.randint(0,3,(3,10)) print((~Z.any(axis=0)).any())
Дан массив, добавить 1 к каждому элементу с индексом, заданным в другом массиве (осторожно с повторами)
Z = np.ones(10) I = np.random.randint(0,len(Z),20) Z += np.bincount(I, minlength=len(Z)) print(Z)
Дан массив (w,h,3) (картинка) dtype=ubyte, посчитать количество различных цветов
w,h = 16,16 I = np.random.randint(0, 2, (h,w,3)).astype(np.ubyte) F = I[...,0] * 256 * 256 + I[...,1] * 256 + I[...,2] n = len(np.unique(F)) print(np.unique(I))
Дан четырехмерный массив, посчитать сумму по последним двум осям
A = np.random.randint(0,10, (3,4,3,4)) sum = A.reshape(A.shape[:-2] + (-1,)).sum(axis=-1) print(sum)
Найти диагональные элементы произведения матриц
# Slow version
np.diag(np.dot(A, B))
# Fast version
np.sum(A * B.T, axis=1)
# Faster version
np.einsum("ij,ji->i", A, B).Дан вектор [1, 2, 3, 4, 5], построить новый вектор с тремя нулями между каждым значением
Z = np.array([1,2,3,4,5]) nz = 3 Z0 = np.zeros(len(Z) + (len(Z)-1)*(nz)) Z0[::nz+1] = Z print(Z0)
Поменять 2 строки в матрице
A = np.arange(25).reshape(5,5) A[[0,1]] = A[[1,0]] print(A)
Рассмотрим набор из 10 троек, описывающих 10 треугольников (с общими вершинами), найти множество уникальных отрезков, составляющих все треугольники
faces = np.random.randint(0,100,(10,3))
F = np.roll(faces.repeat(2,axis=1),-1,axis=1)
F = F.reshape(len(F)*3,2)
F = np.sort(F,axis=1)
G = F.view( dtype=[('p0',F.dtype),('p1',F.dtype)] )
G = np.unique(G)
print(G)Дан массив C; создать массив A, что np.bincount(A) == C
C = np.bincount([1,1,2,3,4,4,6]) A = np.repeat(np.arange(len(C)), C) print(A)
Посчитать среднее, используя плавающее окно
def moving_average(a, n=3):
ret = np.cumsum(a, dtype=float)
ret[n:] = ret[n:] - ret[:-n]
return ret[n - 1:] / n
print(moving_average(np.arange(20), 3))Дан вектор Z, построить матрицу, первая строка которой (Z[0],Z[1],Z[2]), каждая последующая сдвинута на 1 (последняя (Z[-3],Z[-2],Z[-1]))
from numpy.lib import stride_tricks def rolling(a, window): shape = (a.size - window + 1, window) strides = (a.itemsize, a.itemsize) return stride_tricks.as_strided(a, shape=shape, strides=strides) Z = rolling(np.arange(10), 3) print(Z)
Инвертировать булево значение, или поменять знак у числового массива без создания нового
Z = np.random.randint(0,2,100) np.logical_not(arr, out=arr) Z = np.random.uniform(-1.0,1.0,100) np.negative(arr, out=arr)
Рассмотрим 2 набора точек P0, P1 описания линии (2D) и точку р, как вычислить расстояние от р до каждой линии i (P0[i],P1[i])
def distance(P0, P1, p):
T = P1 - P0
L = (T**2).sum(axis=1)
U = -((P0[:,0] - p[...,0]) * T[:,0] + (P0[:,1] - p[...,1]) * T[:,1]) / L
U = U.reshape(len(U),1)
D = P0 + U * T - p
return np.sqrt((D**2).sum(axis=1))
P0 = np.random.uniform(-10,10,(10,2))
P1 = np.random.uniform(-10,10,(10,2))
p = np.random.uniform(-10,10,( 1,2))
print(distance(P0, P1, p))Дан массив. Написать функцию, выделяющую часть массива фиксированного размера с центром в данном элементе (дополненное значением fill если необходимо)
Написать функцию, выделяющую часть массива фиксированного размера с центром в данном элементе (дополненное значением fill если необходимо)
Z = np.random.randint(0,10, (10,10)) shape = (5,5) fill = 0 position = (1,1) R = np.ones(shape, dtype=Z.dtype)*fill P = np.array(list(position)).astype(int) Rs = np.array(list(R.shape)).astype(int) Zs = np.array(list(Z.shape)).astype(int) R_start = np.zeros((len(shape),)).astype(int) R_stop = np.array(list(shape)).astype(int) Z_start = (P - Rs//2) Z_stop = (P + Rs//2)+Rs%2 R_start = (R_start - np.minimum(Z_start, 0)).tolist() Z_start = (np.maximum(Z_start, 0)).tolist() R_stop = np.maximum(R_start, (R_stop - np.maximum(Z_stop-Zs,0))).tolist() Z_stop = (np.minimum(Z_stop,Zs)).tolist() r = [slice(start,stop) for start,stop in zip(R_start,R_stop)] z = [slice(start,stop) for start,stop in zip(Z_start,Z_stop)] R[r] = Z[z] print(Z) print(R)
Посчитать ранг матрицы
Z = np.random.uniform(0,1,(10,10)) rank = np.linalg.matrix_rank(Z)
Найти наиболее частое значение в массиве
Z = np.random.randint(0,10,50) print(np.bincount(Z).argmax())
Извлечь все смежные 3×3 блоки из 10×10 матрицы
Z = np.random.randint(0,5,(10,10)) n = 3 i = 1 + (Z.shape[0] - n) j = 1 + (Z.shape[1] - n) C = stride_tricks.as_strided(Z, shape=(i, j, n, n), strides=Z.strides + Z.strides) print(C)
Создать подкласс симметричных 2D массивов (Z[i,j] == Z[j,i])
# Note: only works for 2d array and value setting using indices
class Symetric(np.ndarray):
def __setitem__(self, (i,j), value):
super(Symetric, self).__setitem__((i,j), value)
super(Symetric, self).__setitem__((j,i), value)
def symetric(Z):
return np.asarray(Z + Z.T - np.diag(Z.diagonal())).view(Symetric)
S = symetric(np.random.randint(0,10,(5,5)))
S[2,3] = 42
print(S)Рассмотрим множество матриц (n,n) и множество из p векторов (n,1). Посчитать сумму p произведений матриц (результат имеет размерность (n,1))
p, n = 10, 20 M = np.ones((p,n,n)) V = np.ones((p,n,1)) S = np.tensordot(M, V, axes=[[0, 2], [0, 1]]) print(S) # It works, because: # M is (p,n,n) # V is (p,n,1) # Thus, summing over the paired axes 0 and 0 (of M and V independently), # and 2 and 1, to remain with a (n,1) vector.
Дан массив 16×16, посчитать сумму по блокам 4×4
Z = np.ones((16,16))
k = 4
S = np.add.reduceat(np.add.reduceat(Z, np.arange(0, Z.shape[0], k), axis=0),
np.arange(0, Z.shape[1], k), axis=1)Написать игру «жизнь»
def iterate(Z):
# Count neighbours
N = (Z[0:-2,0:-2] + Z[0:-2,1:-1] + Z[0:-2,2:] +
Z[1:-1,0:-2] + Z[1:-1,2:] +
Z[2: ,0:-2] + Z[2: ,1:-1] + Z[2: ,2:])
# Apply rules
birth = (N == 3) & (Z[1:-1,1:-1]==0)
survive = ((N == 2) | (N == 3)) & (Z[1:-1,1:-1] == 1)
Z[...] = 0
Z[1:-1,1:-1][birth | survive] = 1
return Z
Z = np.random.randint(0,2,(50,50))
for i in range(100):
print(Z)
Z = iterate(Z)Найти n наибольших значений в массиве
Z = np.arange(10000) np.random.shuffle(Z) n = 5 print (Z[np.argpartition(-Z,n)[:n]])
Построить прямое произведение массивов (все комбинации с каждым элементом)
def cartesian(arrays):
arrays = [np.asarray(a) for a in arrays]
shape = map(len, arrays)
ix = np.indices(shape, dtype=int)
ix = ix.reshape(len(arrays), -1).T
for n, arr in enumerate(arrays):
ix[:, n] = arrays[n][ix[:, n]]
return ix
print(cartesian(([1, 2, 3], [4, 5], [6, 7])))Даны 2 массива A (8×3) и B (2×2). Найти строки в A, которые содержат элементы из каждой строки в B, независимо от порядка элементов в B
A = np.random.randint(0,5,(8,3)) B = np.random.randint(0,5,(2,2)) C = (A[..., np.newaxis, np.newaxis] == B) rows = (C.sum(axis=(1,2,3)) >= B.shape[1]).nonzero()[0] print(rows)
Дана 10×3 матрица, найти строки из неравных значений (например [2,2,3])
Z = np.random.randint(0,5,(10,3)) E = np.logical_and.reduce(Z[:,1:] == Z[:,:-1], axis=1) U = Z[~E] print(Z) print(U)
Преобразовать вектор чисел в матрицу бинарных представлений
I = np.array([0, 1, 2, 3, 15, 16, 32, 64, 128], dtype=np.uint8) print(np.unpackbits(I[:, np.newaxis], axis=1))
Дан двумерный массив. Найти все различные строки
Z = np.random.randint(0, 2, (6,3)) T = np.ascontiguousarray(Z).view(np.dtype((np.void, Z.dtype.itemsize * Z.shape[1]))) _, idx = np.unique(T, return_index=True) uZ = Z[idx] print(uZ)
Даны векторы A и B, написать einsum эквиваленты функций inner, outer, sum и mul
# Make sure to read: http://ajcr.net/Basic-guide-to-einsum/
np.einsum('i->', A) # np.sum(A)
np.einsum('i,i->i', A, B) # A * B
np.einsum('i,i', A, B) # np.inner(A, B)
np.einsum('i,j', A, B) # np.outer(A, B)Библиотека NumPy в Python матрицы в питон
В этом уроке мы разберём действия с матрицами в модуле NumPy в Python Питон.
NumPy это модуль для Python, предназначенный для научных расчётов. NumPy позволяет использовать в Питоне математические функции, такие как работа с матрицами, векторами, все тригонометрические функции, возведение в экспоненту и действия с логарифмами. NumPy в Питон позволяет работать с матрицами гораздо быстрее, чем стандартные алгоритмы работы с матрицами.
Для более удобного использования NumPy импортируем этот модуль, используя постфикс as np.
import numpy as np
as np означает, что когда мы вызываем процедуры и функции из NumPy в Python, перед названиями этих процедур и функций вместо numpy мы будем писать np. Это позволит не только удобнее писать код, но и быстрее читать его. Например, вместо numpy.array([1, 2]) мы будем писать np.array([1, 2]).
Матрицы в NumPy в Питоне задаются с помощью команды np.array([]). В круглых скобках находится сам массив, в квадратных скобках находятся элементы массива.
Пример. Задание одномерного массива в python
import numpy as np
arr = np.array([1, 2])
Матрица в Python задаётся с помощью двумерного массива. Матрица это таблица состоящая из строк и столбцов. Двумерный массив задаётся с помощью той же команды, что и одномерный массив.
Пример. Задание матрицы двумерного массива и вывод различных его элементов на экран в python
import numpy as np
matrix = np.array([ [‘first’, ‘second’], [‘third’, ‘fourth’] ])
print(matrix[0, 0])
print(matrix[1, 1])
print(matrix[0, 0]) выведет первый элемент из первого массива внутри – first. print(matrix[1, 1]) выведет второй элемент внутреннего второго массива – fourth.
NumPy в Питоне может выполнять различные действия с матрицами, такие как сложение, умножение, возведение матрицы в степень и вычисление определителя матрицы.
Для сложения матриц в Питоне не используются никакие команды, матрицы в Python складываются так же, как и числа.
Пример. Сложение матриц.
import numpy as np
matrix1 = np.array([ [3, 5, 1], [8, 7, 2] ])
matrix2 = np.array([ [5, 3, 4], [1, 10, 9] ])
total = matrix1 + matrix2
print(total)
NumPy в Питоне позволяет складывать только матрицы одинаковых размеров.
Матрицы складываются с помощью сложения всех элементов массива с одинаковыми индексами. Матрица с суммами этих элементов является результатом сложения.
Умножение матрицы на вектор в Python выполняется с помощью команды A.dot(B), где A и B это матрицы. Для выполнения умножения в Питоне нужно, чтобы количество столбцов матрицы A было равно количеству строк матрицы B.
Пример. Умножение матрицы на вектор в python
import numpy as np
a = np.array([ [2, 1], [2, 2], [4, 3] ])
b = np.array([ [1], [3] ])
total = a.dot(b)
print(total)
Умножение вектора на матрицу определено только тогда, когда число столбцов матрицы равно числу строк вектора. В этом примере была рассмотрена матрица размером 3×2 и вектор-строка размером 2×1. Число столбцов матрицы (2) равно числу строк вектора (2). В результате умножения матрицы на вектор получается вектор, у кторого число строк равно числу строк матрицы
Определитель матрицы в Python вычисляется с помощью с помощью команды
np.linalg.det(A), где A это квадратная матрица. У квадратной матрицы количество строк равно количеству столбцов.
Пример. Вычисление определителя матрицы в python
import numpy as np
a = np.array([ [2, 1], [4, 3] ])
print(np.linalg.det(a))
Определитель может быть вычислен только для матриц с одинаковым количеством строк и столбцов – квадратных матриц. В этом примере с матрицей размерами 2×2 определитель матрицы равен разнице произведений диагоналей (2 * 3 – 1 * 4 = 2.0)
Умножение матрицы на матрицу в Питоне выполняется с помощью команды A.dot(B), где A и B это матрицы. Умножение определено, если количество столбцов A равно количеству строк B.
Пример. Умножение матрицы на матрицу в python
import numpy as np
a = np.array([ [2, 1, 3], [2, 2, 4] ])
b = np.array([ [1, 1], [3, 2], [2, 4] ])
total = a.dot(b)
print(total)
Чтобы умножение было определено, количество столбцов первой матрицы должно быть равно количеству строк второй матрицы. В этом примере умножаются матрицы размерами 2×3 и 3×2, результатом умножения является матрица размером 2×2.
Возведение матрицы в степень в Питоне выполняется с помощью команды np.linalg.matrix_power(A, P), где A – квадратная матрица, P – степень, в которую возводится матрица, допускаются только целочисленные степени. Возводить в степень можно только квадратные матрицы, так как количество строк должно быть равно количеству столбцов матрицы.
Пример. Возведение матрицы в степень в python
import numpy as np
a = np.array([[1, 3], [2, 1]])
result = np.linalg.matrix_power(a, 2)
print(result)
Для решения системы двух линейных уравнений нужно задать два массива. Один массив будет содержать коэффициенты для x и y в каждом уравнении, второй массив будет содержать правые части уравнений. Для решения линейных уравнений используется команда в Python np.linalg.solve(матрица левой части, вектор правой части)
Решение системы линейных уравнений в python
import numpy as np
a = np.array([[1, 2], [3, 2]])
b = np.array([5, 6])
result = np.linalg.solve(a, b)
print(result)
Эта программа на Python решает два линейных уравнения.
1x + 2y = 5
3x + 2y = 6
Для вычисления экспоненты числа или массива в Питоне используется команда np.5], где e это основание натурального логарифма.
Вернуться к содержанию Следующая тема Графики функций и поверхностей в Python
Полезно почитать по теме матрицы и массивы в python:
Матрицы в python
Массивы в python
Поделиться:
Создание матрицы python без использования numpy или чего-либо еще и максимальной суммы строк и столбцов
Хотите создать матрицу, как показано ниже в python
[[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16]]
но не зная, как это сделать, я попробовал понять список, как показано ниже
[[y+x for y in range(4)] for x in range(4)]
что дает результат, как показано ниже
[[0, 1, 2, 3], [1, 2, 3, 4], [2, 3, 4, 5], [3, 4, 5, 6]]
а также хочу напечатать строку с максимальной суммой и столбцы с максимальной суммой.
Заранее спасибо
python matrixПоделиться Источник Chethu 31 августа 2016 в 12:57
4 ответа
- Найти суммы строк для подмножества столбцов матрицы
Вот матрица 10 х 12: mat <- matrix(runif(120, 0, 1), 10) Я пытаюсь найти суммы столбцов для подмножеств матрицы (в частности, суммы столбцов для столбцов с 1 по 4, с 5 по 8 и с 9 по 12) по строкам. Желаемым результатом будет матрица 10 х 3. Я попробовал подходы из этого ответа , используя…
- Numpy расположение памяти строк/столбцов матрицы
Numpy nd-массивы выкладываются как непрерывные 1-d массивы. Этот разговор stack overflow ( копирование байтов в Python из массива Numpy в строку или bytearray ) предполагает, что индексация строк матриц является ‘views’ в исходном массиве и что никакие новые объекты массива не выделяются в памяти…
4
[[x * 4 + y + 1 for y in range(4)] for x in range(4)]
что эквивалентно:
[[(x << 2) + y for y in range(1, 5)] for x in range(4)]
Вот небольшой ориентир:
import timeit
def f1():
return [[x * 4 + y + 1 for y in range(4)] for x in range(4)]
def f2():
return [[(x << 2) + y for y in range(1, 5)] for x in range(4)]
def f3():
a = range(1, 5)
return [[(x << 2) + y for y in a] for x in range(4)]
N = 5000000
print timeit.timeit('f1()', setup='from __main__ import f1', number=N)
print timeit.timeit('f2()', setup='from __main__ import f2', number=N)
print timeit.timeit('f3()', setup='from __main__ import f3', number=N)
# 13.683984791
# 13.4605276559
# 9.65608339037
# [Finished in 36.9s]
Где мы можем заключить, что оба метода f1 & f2 дают почти одинаковую производительность. Так что было бы хорошим выбором вычислить внутренний range(1,5) только один раз, как f3
Поделиться BPL 31 августа 2016 в 13:00
3
Функция range принимает 3 аргумента start, end и step . Вы можете использовать один диапазон с шагом 4, а другой — для создания вложенных списков с использованием внешнего диапазона.
>>> [[i for i in range(i, i+4)] for i in range(1, 17, 4)]
[[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16]]
вот еще один способ с одним range :
>>> main_range = range(1, 5)
>>> [[i*j + (i-1)*(4-j) for j in main_range] for i in main_range]
[[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16]]
А вот и Numpythonic подход:
>>> n = 4
>>> np.split(np.arange(1, n*n + 1), np.arange(n ,n*n, n))
[array([1, 2, 3, 4]), array([5, 6, 7, 8]), array([ 9, 10, 11, 12]), array([13, 14, 15, 16])]
Поделиться Kasravnd 31 августа 2016 в 13:00
1
попробовать это,
In [1]: [range(1,17)[n:n+4] for n in range(0, len(range(1,17)), 4)]
Out[1]: [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16]]
Поделиться Rahul K P 31 августа 2016 в 13:08
0
Это может быть быстрым решением
[([x-3,x-2,x-1,x]) for x in range(1,17) if x%4 ==0]
Но что вы подразумеваете под максимальной суммой столбцов и строк
Поделиться kunal_mehta_the_great 31 августа 2016 в 13:31
Похожие вопросы:
Numpy: получить все комбинации строк и столбцов данной матрицы
Есть ли какой-нибудь простой способ получить с помощью numPy (или любой другой библиотеки python) комбинацию строк и столбцов данной матрицы? Например, если я приведу эту матрицу: A = np.array(…
Все диагональные элементы матрицы NXN без использования numpy в python
Попытка получить все диагональные элементы матрицы NXN без использования numpy, Это отличается от Get diagonal без использования numpy в Python Пожалуйста, не помечайте как дубликат. Вот мой…
Как найти длину (или размеры, Размер) матрицы numpy в python?
Для матрицы numpy в python from numpy import matrix A = matrix([[1,2],[3,4]]) Как я могу найти длину строки (или столбца) этой матрицы? Аналогично, как я могу узнать количество строк или столбцов?…
Найти суммы строк для подмножества столбцов матрицы
Вот матрица 10 х 12: mat <- matrix(runif(120, 0, 1), 10) Я пытаюсь найти суммы столбцов для подмножеств матрицы (в частности, суммы столбцов для столбцов с 1 по 4, с 5 по 8 и с 9 по 12) по…
Numpy расположение памяти строк/столбцов матрицы
Numpy nd-массивы выкладываются как непрерывные 1-d массивы. Этот разговор stack overflow ( копирование байтов в Python из массива Numpy в строку или bytearray ) предполагает, что индексация строк…
Как вычислить евклидово расстояние между всеми парами векторов столбцов для данной матрицы без использования циклов? (используя только numpy)
Как указано в заголовке, мне нужно вычислить евклидово расстояние между всеми возможными парами векторных столбцов данной матрицы без использования циклов и только с помощью numpy. Это дает…
numpy python — одновременное нарезание строк и столбцов
У меня есть матрица numpy с размером 130 X 13. Допустим, я хочу выбрать определенный набор строк, удовлетворяющих условию, и подмножество столбцов — trainx[trainy==label,[0,6]] Приведенный выше код…
Как получить строки матрицы без использования каких-либо циклов в numpy или tensorflow?
У меня есть матрица, и я хочу прочитать в каждой строке матрицы и использовать tf.nn.top_k, чтобы найти верхние значения k для каждой строки. Как бы я получил каждую строку матрицы без использования…
Numpy 1D массив: Матрица строк или столбцов по умолчанию?
В следующем коде я создаю массив 2 numpy. Один — 1D, а другой-2D. Когда я транспонирую массив 1D, он остается прежним. Он не меняется от матрицы строк к матрице столбцов. Когда я транспонирую массив…
Выполнение суммы строк и суммы столбцов в списке списков в python
Я хочу вычислить сумму строк и сумму столбцов матрицы в python; однако из-за требований infosec я не могу использовать какие-либо внешние библиотеки. Итак, чтобы создать матрицу, я использовал…
Векторы и матрицы в инструментарии Numpy
Содержание страницы
Векторы и матрицы
Здравствуйте и вновь добро пожаловать на занятия по теме «Инструментарий Numpy на языке Python».
В этой статье мы подробнее рассмотрим векторы, а также поговорим о матрицах.
Вы уже видели, насколько массивы Numpy похож на векторы: мы можем проводить над ними такие операции, как их сложение, умножение на скаляр, выполнять поэлементные операции вроде возведения в квадрат. А что с матрицами? Матрицу можно рассматривать как двухмерный массив. Согласно другому представлению, её также можно рассматривать как список списков. Действительно, можно использовать список списков, чтобы определить матрицу. Попробуем так и сделать.
Итак, первый список будет иметь элементы 1 и 2, второй список – элементы 3 и 4. Обратите внимание, что списки должны иметь одинаковую длину.
M = np.array([ [1,2], [3,4] ])
Считается, что первый индекс – это строка, второй – столбец. Для сравнения создадим также настоящий список списков:
L = [ [1,2], [3,4] ]
Допустим, мы хотим получить элемент матрицы, скажем, единицу. В списке Python сначала индексируется строка, что даёт нам первый список, содержащий 1 и 2:
L[0]
Итак, теперь у нас есть 1 и 2. Нам нужен первый элемент из этого списка, поэтому
L[0][0]
и получаем 1. Заметьте, то же самое можно сделать и с помощью массива Numpy:
M[0][0]
Это также даёт нам 1. Но есть и сокращённая запись, похожая на MATLAB, с использованием запятой:
M[0,0]
И это также даёт нам 1. Так несколько удобнее, поскольку нужно набрать на символ меньше.
Обратите внимание, что в Numpy есть тип данных, который так и называется – матрица:
M2 = np.matrix([ [1,2], [3,4] ])
Получилась матрица. Во многом матрица схожа с массивом Numpy, но есть и отличия. В большинстве случаев используются просто массивы Numpy; в действительности даже официальная документация фактически рекомендует не пользоваться матрицами. Поэтому в данном курсе мы не будем заострять на них своё внимание. Увидев матрицу, имеет смысл преобразовать её в массив. Это можно сделать с помощью команды
A = np.array(M2)
В результате получим ту же матрицу, но в виде массива. Обратите внимание, что, хоть это и массив, мы можем пользоваться удобными матричными операциями, например транспонированием:
A.T
В результате получается транспонированная матрица A.
Резюмируем. Мы показали, что матрица на самом деле является лишь двухмерным массивом Numpy, а вектор – одномерным массивом Numpy. Таким образом, матрица на самом деле является двухмерным вектором. Обобщая, можно считать матрицу двухмерным математическим объектом, содержащим числа, а вектор – одномерным математическим объектом, также содержащим числа. Иногда встречается представление вектора в виде двухмерного объекта. Например, в учебниках по математике может указываться вектор-столбец размерности 3×1 и вектор-строка размерности 1×3. Временами мы также будем представлять их в таком виде в Numpy, но наличие двух размерностей делает такой объект более похожим на матрицу, что может сбить с толку. В таком случае просто помните, что обсуждаются лишь две вещи – одномерные и двухмерные массивы.
Создание матриц для работы с ними
Существуют некоторые различные способы генерации массивов данных.
Иногда нужны несколько массивов просто чтобы попрактиковаться – как в этом курсе. Один из способов вы уже видели, когда я воспользовался массивом Numpy для создания списка, например
np.array([1,2,3])
Заметьте, это не очень удобно, поскольку приходится вручную вставлять каждый элемент. А если нужен массив с сотней элементов? А если нужно, чтобы он содержал случайные числа? Поэтому в данной лекции будет показано, как можно создавать массивы.
Прежде всего я покажу, как создать массив, состоящих из одних нулей. Это делается с помощью функции zeros с указанием длины:
Z = np.zeros(10)
Это даёт вектор с 10 элементами, состоящий из нулей. Можно создать и матрицу размерности 10×10, состоящую из одних нулей:
Z = np.zeros((10, 10))
В результате получаем 100 нулей в матрице размерности 10×10. Обратите внимание, что функция по-прежнему принимает лишь один аргумент – кортеж, содержащий каждую размерность. Есть эквивалентная функция, создающая массив из одних единиц. К примеру,
O = np.ones((10, 10))
Получилась матрица размерности 10×10, состоящая из одних единиц.
Теперь предположим, что нам нужен ряд случайных числен. Для этого можно воспользоваться функцией np.random.random. Создадим, к примеру, массив случайных чисел размерности 10×10:
R = np.random.random((10,10))
Получился набор случайных чисел в матрице размерностью 10×10. Бросается в глаза, что все числа больше 0 и меньше 1. Это связано с тем, что когда речь идёт о случайных числах, имеется в виду распределение вероятностей, откуда и возникли случайные числа. Данная конкретная функция случайных чисел даёт нам равномерно распределённые числа между 0 и 1. А если нам нужны числа с гауссовым распределением? В Numpy есть функция и для этого. Давайте попробуем. Называется она random.randn. Вновь-таки, возьмём размерность 10×10:
G = np.random.randn((10×10))
И у нас ничего не получилось – требуются целые числа. Сама функция правильна, но мы указали неправильный аргумент. Дело в том, что, как ни странно, функция randn библиотеки Numpy воспринимает каждую размерность как отдельный аргумент, в то время как все остальные упоминавшиеся функции принимают кортежи. Поэтому правильно вставлять – только для функции randn! – каждую размерность по отдельности:
G = np.random.randn(10,10)
Теперь всё работает. Мы имеем числа с гауссовым распределением, средним значением 0 и дисперсией 1. Массивы Numpy также предоставляют удобные функции для вычисления этих статистических величин. Так, команда
G.mean()
даёт нам среднее значение, а команда
G.var()
позволяет получить дисперсию.
Как видим, полученные числа весьма близки к истинным значениям.
Произведение матриц
Что интересно в произведениях матриц при изучении линейной алгебры, – так это то, что обычно называется умножением матриц. Умножение матриц имеет специальное требование: внутренние размерности двух умножаемых матриц должны совпадать. Так, если у нас есть матрица A размерности 2×3 и матрица B размерности 3×3, то мы можем умножить A на B, поскольку внутренняя размерность равна 3. Однако мы не можем умножить B на A, поскольку внутренняя размерность левого множителя равна 3, а внутренняя размерность правого равна 2.
Возникает вопрос: для чего существует такое требование при умножении матриц? Рассмотрим определение операции умножения матриц:
То есть ij-й элемент матрицы C равен сумме произведений всех соответствующих элементов из i-й строки матрицы A и j-го столбца матрицы B. Другими словами, ij-й элемент матрицы C равен скалярному произведению i-й строки матрицы A и j-го столбца матрицы B. В связи с этим обычно используется функция dot библиотеки Numpy:
C = A.dot(B)
Это и будет умножением матриц.
Как в математике, так и в программировании часто встречается операция поэлементного умножения. В случае векторов мы уже видели, что для этого используется звёздочка (*). Как можно догадаться, в случае двухмерных массивов звёздочка также производит поэлементное умножение. Это означает, что при использовании звёздочки в случае многомерных массивов оба массива должны иметь в точности одинаковую размерность. Это может показаться странным, ведь в других языках звёздочка действительно означает настоящее умножение матриц. Но нужно просто запомнить, что для Numpy звёздочка означает поэлементное умножение, а функция dot – умножение матриц. Также сбивать с толку может то обстоятельство, что при записи математических уравнений нет даже чётко определённого символа для операции поэлементного умножения. Так, некоторые пользуются кружком с точкой внутри, а некоторые – кружком с крестиком внутри. Похоже, в математике просто не существует стандартной записи для данной операции, хотя она часто возникает в машинному обучении в связи с необходимостью использовать градиенты.
Другие операции с матрицами
В данном подразделе, я покажу вам некоторые другие операции с матрицами, которые позволяет библиотека Numpy. При этом предполагается, что вы уже знакомы с ними из курса линейной алгебры, а потому это будет скорее демонстрация того, как их реализовать в Numpy.
Начнём с нахождения обратной матрицы. Вначале создадим матрицу:
A = np.array([[1,2],[3,4]])
Воспользуемся функцией inv модуля linalg:
Ainv = np.linalg.inv(A)
Мы получили обратную матрицу. Чтобы проверить правильность ответа, умножим матрицу, обратную A, на саму А:
Ainv.dot(A)
В результате имеем единичную матрицу. Можем сделать и наоборот, умножив матрицу А на обратную ей:
A.dot(Ainv)
И тоже получаем единичную матрицу.
Следующее – нахождение определителя матрицы. Это можно сделать с помощью команды
np.linalg.det(A)
Как и ожидалось, получаем ответ -2.
Иногда нужна диагональ матрицы, для этого используется команда
np.diag(A)
В результате имеем диагональные элементы в виде вектора. В других случаях у нас есть вектор чисел, представляющий диагональ матрицы, остальные элементы которой считаются равными нулю. Чтобы представить такой вектор в виде двухмерного массива, можно воспользоваться этой же функцией. Например,
np.diag([1,2])
Получим 1 и 2 на диагонали, а остальные элементы – нули.
Это надо запомнить: если подставить двухмерный массив в функцию diag, то получим одномерный массив из диагональных элементов; если же подставить одномерный массив, то получится двухмерный массив, в котором все внедиагональные элементы равны нулю, а первоначальный массив располагается на главной диагонали матрицы.
Бывает, что у нас есть два вектора, а нам нужно выполнить внешнее произведение. В частности, внешнее произведение возникает, когда мы вычисляем ковариацию ряда векторов-образцов. Мы уже знакомы с поэлементным произведением, для которого используется звёздочка, и скалярным произведением, для чего используется функция dot. Напомню, что скалярное произведение также называется внутренним произведением.
Итак, создадим два вектора:
a = np.array([1,2])
b = np.array([3,4])
Внешнее произведение вычисляется по команде
np.outer(a, b)
Можете проверить правильность ответа. Обратите внимание, что можно выполнить и внутреннее произведение с помощью команды
np.inner(a, b)
Это даст тот же ответ, что и при использовании команды
a.dot(b)
Каким из этих способов пользоваться – сугубо на ваше усмотрение.
Другая распространённая операция – нахождение следа матрицы. Это сумма элементов матриц, расположенных на главной диагонали. Заметьте, что мы можем выполнить эту операцию, используя уже имеющиеся сведения:
np.dialog(A).sum()
Получим ожидаемый ответ 5. Но в Numpy для этого есть и соответствующая функция:
np.trace(A)
И мы опять-таки получаем 5.
И последнее, что мы обсудим, – это собственные значения и собственные векторы. Если вы не проходили их в курсе линейной алгебры, то, вероятно, вам следует углубить свои знания по этому предмету. Но сейчас я просто покажу, как всё это делается в коде, поэтому если вы не знаете, что такое собственные значения и собственные векторы, просто пропустите эту часть.
Часто возникает необходимость вычислить собственные значения и собственные векторы симметричной матрицы, такой как ковариационная матрица набора данных. Создадим случайным образом определённые данные размерности 100×3 с гауссовым распределением:
X = np.random.randn(100,3)
Обратите внимание: считается, что каждый пример – это строка, а каждый признак – это столбец, поэтому для данного конкретного вымышленного набора данных у нас имеется 100 примеров и 3 признака. Разумеется, в Numpy уже есть функция для вычисления ковариации. Опробуем её:
cov = np.cov(X)
Проверим размерность ковариационной матрицы, чтобы убедиться, что всё правильно.
cov.shape
Получилось, что размерность равна 100×100. Это неправильная размерность, должно быть 3×3, ведь наши данные имеют размерность 3. Попробуем ещё раз, транспонировав X:
cov = np.cov(X.T)
Теперь размерность 3×3. Нужно помнить, что при вычислении ковариационной матрицы данных необходимо её сначала транспонировать.
Для вычисления собственных значений и собственных векторов есть две функции – eig и eigh. Eigh предназначена только для симметричных и эрмитовых матриц. Если вы никогда не изучали линейную алгебру комплексных чисел, не беспокойтесь о том, что такое эрмитова матрица. Симметричной называется матрица, которая, будучи транспонированной, остаётся равной сама себе:
То есть ij-й элемент матрицы C равен сумме произведений всех соответствующих элементов из i-й строки матрицы A и j-го столбца матрицы B. Другими словами, ij-й элемент матрицы C равен скалярному произведению i-й строки матрицы A и j-го столбца матрицы B. В связи с этим обычно используется функция dot библиотеки Numpy:
C = A.dot(B)
Это и будет умножением матриц.
Как в математике, так и в программировании часто встречается операция поэлементного умножения. В случае векторов мы уже видели, что для этого используется звёздочка (*). Как можно догадаться, в случае двухмерных массивов звёздочка также производит поэлементное умножение. Это означает, что при использовании звёздочки в случае многомерных массивов оба массива должны иметь в точности одинаковую размерность. Это может показаться странным, ведь в других языках звёздочка действительно означает настоящее умножение матриц. Но нужно просто запомнить, что для Numpy звёздочка означает поэлементное умножение, а функция dot – умножение матриц. Также сбивать с толку может то обстоятельство, что при записи математических уравнений нет даже чётко определённого символа для операции поэлементного умножения. Так, некоторые пользуются кружком с точкой внутри, а некоторые – кружком с крестиком внутри. Похоже, в математике просто не существует стандартной записи для данной операции, хотя она часто возникает в машинному обучении в связи с необходимостью использовать градиенты.
Другие операции с матрицами
В данном подразделе, я покажу вам некоторые другие операции с матрицами, которые позволяет библиотека Numpy. При этом предполагается, что вы уже знакомы с ними из курса линейной алгебры, а потому это будет скорее демонстрация того, как их реализовать в Numpy.
Начнём с нахождения обратной матрицы. Вначале создадим матрицу:
A = np.array([[1,2],[3,4]])
Воспользуемся функцией inv модуля linalg:
Ainv = np.linalg.inv(A)
Мы получили обратную матрицу. Чтобы проверить правильность ответа, умножим матрицу, обратную A, на саму А:
Ainv.dot(A)
В результате имеем единичную матрицу. Можем сделать и наоборот, умножив матрицу А на обратную ей:
A.dot(Ainv)
И тоже получаем единичную матрицу.
Следующее – нахождение определителя матрицы. Это можно сделать с помощью команды
np.linalg.det(A)
Как и ожидалось, получаем ответ -2.
Иногда нужна диагональ матрицы, для этого используется команда
np.diag(A)
В результате имеем диагональные элементы в виде вектора. В других случаях у нас есть вектор чисел, представляющий диагональ матрицы, остальные элементы которой считаются равными нулю. Чтобы представить такой вектор в виде двухмерного массива, можно воспользоваться этой же функцией. Например,
np.diag([1,2])
Получим 1 и 2 на диагонали, а остальные элементы – нули.
Это надо запомнить: если подставить двухмерный массив в функцию diag, то получим одномерный массив из диагональных элементов; если же подставить одномерный массив, то получится двухмерный массив, в котором все внедиагональные элементы равны нулю, а первоначальный массив располагается на главной диагонали матрицы.
Бывает, что у нас есть два вектора, а нам нужно выполнить внешнее произведение. В частности, внешнее произведение возникает, когда мы вычисляем ковариацию ряда векторов-образцов. Мы уже знакомы с поэлементным произведением, для которого используется звёздочка, и скалярным произведением, для чего используется функция dot. Напомню, что скалярное произведение также называется внутренним произведением.
Итак, создадим два вектора:
a = np.array([1,2])
b = np.array([3,4])
Внешнее произведение вычисляется по команде
np.outer(a, b)
Можете проверить правильность ответа. Обратите внимание, что можно выполнить и внутреннее произведение с помощью команды
np.inner(a, b)
Это даст тот же ответ, что и при использовании команды
a.dot(b)
Каким из этих способов пользоваться – сугубо на ваше усмотрение.
Другая распространённая операция – нахождение следа матрицы. Это сумма элементов матриц, расположенных на главной диагонали. Заметьте, что мы можем выполнить эту операцию, используя уже имеющиеся сведения:
np.dialog(A).sum()
Получим ожидаемый ответ 5. Но в Numpy для этого есть и соответствующая функция:
np.trace(A)
И мы опять-таки получаем 5.
И последнее, что мы обсудим, – это собственные значения и собственные векторы. Если вы не проходили их в курсе линейной алгебры, то, вероятно, вам следует углубить свои знания по этому предмету. Но сейчас я просто покажу, как всё это делается в коде, поэтому если вы не знаете, что такое собственные значения и собственные векторы, просто пропустите эту часть.
Часто возникает необходимость вычислить собственные значения и собственные векторы симметричной матрицы, такой как ковариационная матрица набора данных. Создадим случайным образом определённые данные размерности 100×3 с гауссовым распределением:
X = np.random.randn(100,3)
Обратите внимание: считается, что каждый пример – это строка, а каждый признак – это столбец, поэтому для данного конкретного вымышленного набора данных у нас имеется 100 примеров и 3 признака. Разумеется, в Numpy уже есть функция для вычисления ковариации. Опробуем её:
cov = np.cov(X)
Проверим размерность ковариационной матрицы, чтобы убедиться, что всё правильно.
cov.shape
Получилось, что размерность равна 100×100. Это неправильная размерность, должно быть 3×3, ведь наши данные имеют размерность 3. Попробуем ещё раз, транспонировав X:
cov = np.cov(X.T)
Теперь размерность 3×3. Нужно помнить, что при вычислении ковариационной матрицы данных необходимо её сначала транспонировать.
Для вычисления собственных значений и собственных векторов есть две функции – eig и eigh. Eigh предназначена только для симметричных и эрмитовых матриц. Если вы никогда не изучали линейную алгебру комплексных чисел, не беспокойтесь о том, что такое эрмитова матрица. Симметричной называется матрица, которая, будучи транспонированной, остаётся равной сама себе:
Эрмитова же матрица – это матрица, которая остаётся равной сама себе, будучи сопряжённой:
Как известно, ковариационная матрица является симметричной, поэтому можно использовать функцию eigh. Её и попробуем:
np.linalg.eigh(cov)
В результате получаем кортежи. Первый содержит три собственных значения, а второй – собственные векторы, представленные в столбцах. Попробуем теперь с обычной функцией eig:
np.linalg.eig(cov)
Получаем тот же ответ. Обратите внимание, что обычная функция eig хоть и даёт тот же ответ, но полученные собственные значения и соответствующие собственные векторы могут размещаться в другом порядке. В данном конкретном случае порядок тот же, но есть вероятность, что он может поменяться.
На этом лекция заканчивается. Она довольно короткая, поскольку была создана для тех, кто уже знаком с математическим аппаратом, но ещё не знает, как его реализовать в Numpy.
Решение системы линейных уравнений
В заключение мы рассмотрим последнюю из самых распространённых операций с матрицами – решение системы линейных уравнений.
Напомню, что система линейных уравнений имеет вид
где A – матрица, x – вектор-столбец искомых значений, b – вектор чисел. Решение, конечно же, состоит в умножении обоих частей уравнений на матрицу, обратную A:
Это корректная операция, поскольку предполагается, что A является квадратной матрицей, что значит, что она обратима. Тогда x имеет единственное решение. Другими словами, если размерность x равна D, то у нас есть D уравнений с D неизвестными.
Тут не должно возникнуть никаких сложностей, поскольку у нас уже есть весь инструментарий, необходимый для такого рода вычислений. Вы уже видели, как находится обратная матрица и как производить умножение матриц, а именно эти две вещи нам и нужны.
Решим пример. A у нас будет матрицей
Это корректная операция, поскольку предполагается, что A является квадратной матрицей, что значит, что она обратима. Тогда x имеет единственное решение. Другими словами, если размерность x равна D, то у нас есть D уравнений с D неизвестными.
Тут не должно возникнуть никаких сложностей, поскольку у нас уже есть весь инструментарий, необходимый для такого рода вычислений. Вы уже видели, как находится обратная матрица и как производить умножение матриц, а именно эти две вещи нам и нужны.
Решим пример. A у нас будет матрицей
b у нас будет вектором [1, 2]:
b = np.array([1, 2])
Решением будет
x = np.linalg.inv(A).dot(b)
Итак, решением являются числа 0 и 0,5. Для проверки попробуйте решить этот пример вручную.
Конечно же, ввиду очень частого проведения такого рода вычислений, есть способ и получше – с помощью функции с соответствующим названием solve. Поэтому можно записать
x = np.linalg.solve(A, b)
И получим тот же ответ.
Если вы когда-либо прежде писали код в MATLAB, то могли заметить, что при попытке использовать метод inv MATLAB выдаёт предупреждение и сообщает, что есть и более эффективный способ вычислений. В MATLAB он называется не solve, но по сути это тот же самый алгоритм, и он действительно куда более эффективен и точен. Поэтому если у вас когда-нибудь возникнет необходимость решить подобного рода уравнение, никогда не пользуетесь inv. Всегда используйте solve.
Текстовая задача
Давайте разберём несложный пример, чтобы попрактиковаться в использовании функции solve.
Итак, поставим задачу. На небольшой ярмарке входная плата составляет 1,5 доллара для ребёнка и 4 доллара для взрослого. Однажды за день ярмарку посетило 2200 человек; при этом было собрано 5050 долларов входной платы. Сколько детей и сколько взрослых посетили ярмарку в этот день?
Итак, обозначим количество детей через X1, а количество взрослых – через X2. Мы знаем, что
Мы также знаем, что
Мы также знаем, что
Обратите внимание, что это линейное уравнение, где A равно:
а b равно :
а b равно :
Подставим эти значения в Numpy и найдём решение:
A = np.array([[1,1], [1.5,4]])
b = np.array([2200, 5050])
np.linalg.solve(A, b)
Получаем ответ: 1500 детей и 700 взрослых. Попробуйте также решить это уравнение вручную, чтобы проверить ответ.
Копии и представления массивов | NumPy
Вы, может быть уже заметили, что некоторые функции, что-то делают с массивом, возвращают какой-то результат, но при этом с исходным массивом ничего не происходит. Например:
>>> a = np.arange(18).reshape(3, 6)
>>> a
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17]])
>>>
>>> a.T
array([[ 0, 6, 12],
[ 1, 7, 13],
[ 2, 8, 14],
[ 3, 9, 15],
[ 4, 10, 16],
[ 5, 11, 17]])
>>>
>>> a # Исходный массив не изменился
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17]])Дело в том, что в NumPy существует два понятия: копия массива и представление массива. Попробуем разобраться на примерах.
>>> a = np.arange(18).reshape(3, 6)
>>>
>>> b = a
>>> c = a.T
>>>
>>> # Можно подумать, что b и c - это
... # другие массивы, другие объекты, но
...
>>> a[0][0] = 777777
>>> a
array([[777777, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[ 12, 13, 14, 15, 16, 17]])
>>>
>>> b
array([[777777, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[ 12, 13, 14, 15, 16, 17]])
>>>
>>> c
array([[777777, 6, 12],
[ 1, 7, 13],
[ 2, 8, 14],
[ 3, 9, 15],
[ 4, 10, 16],
[ 5, 11, 17]]) Вот здесь у новичков и начинаются: путаница, непонимание и ошибки. Хотя все довольно просто. Итак, когда мы выполнили присваивание b = a, то на самом деле никакого копирования данных не произошло. То есть в памяти компьютера по прежнему находится один массив, а переменные a и b на самом деле даже не переменные, а указатели, которые указывают на одни и те же данные в памяти. Именно поэтому обращаясь по разным указателям к одним и тем же данным мы видим одно и то же.
Хорошо, a и b — это указатели. Как быть с переменной с? По сути это тоже указатель, который ссылается на туже самую область памяти с данными, на которую ссылаются a и b, но представлены эти данные в другой форме. Поэтому в NumPy и существует понятие — представление массива. Действительно, одни и те же данные могут быть представлены в разной форме:
>>> a = np.arange(18).reshape(3, 6)
>>> b = a.reshape(2, 9)
>>> c = a.reshape(2, 3, 3)
>>>
>>> a
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17]])
>>>
>>> b
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8],
[ 9, 10, 11, 12, 13, 14, 15, 16, 17]])
>>>
>>> c
array([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9, 10, 11],
[12, 13, 14],
[15, 16, 17]]])
>>>
>>> # Но если изменить один элемент через а
... # то это отразится во всех представлениях
...
>>> a[0][0] = 7777777
>>>
>>> b
array([[7777777, 1, 2, 3, 4, 5, 6,
7, 8],
[ 9, 10, 11, 12, 13, 14, 15,
16, 17]])
>>>
>>> c
array([[[7777777, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9, 10, 11],
[ 12, 13, 14],
[ 15, 16, 17]]])
>>> Более того, раз все представления ссылаются на одни и те же данные то изменение элементов в одном представлении отразится на всех других представлениях и даже указателях, которые указывают на те же самые данные:
>>> b[0][0] = 1111111
>>> c[0][1][0] = 222222
>>>
>>> b
array([[1111111, 1, 2, 222222, 4, 5, 6,
7, 8],
[ 9, 10, 11, 12, 13, 14, 15,
16, 17]])
>>>
>>> c
array([[[1111111, 1, 2],
[ 222222, 4, 5],
[ 6, 7, 8]],
[[ 9, 10, 11],
[ 12, 13, 14],
[ 15, 16, 17]]])
>>>
>>> a
array([[1111111, 1, 2, 222222, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[ 12, 13, 14, 15, 16, 17]])Мы можем говорить о копировании, только если данные в памяти физически скопировались в другое место. И как мы убедились, простое присваивание не выполняет такого копирования. Еще мы теперь знаем, что одни и те же данные могут иметь разные представления. Но путаница еще сохраняется, не так ли?
Всё равно непонятно, как теперь правильно выражаться говоря о коде NumPy? И вообще, существует ли в самом NumPy какая-нибудь терминологии на этот случай? Давайте разберемся окончательно и закрепим все это на примерах.
10.1. Присваиванием массивы не копируются
Простое присваивание не делает никаких копий массива — это первое о чем нужно помнить. Да, по началу это кажется странной прихотью создателей NumPy (или самого Python), но если бы это было не так, то нам пришлось бы работать с памятью напрямую, либо самостоятельно беспокоиться об использовании памяти. Поэтому отсутствие автоматического копирования при присваивании — небольшая плата за простоту и легкость Python.
>>> # Давайте создадим массив с именем "a"
...
>>> a = np.arange(12)
>>> # Теперь мы можем сказать: 'У нас есть массив "а"!'
...
>>> a
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
>>>
>>> # Теперь сделаем копию массива "а"
...
>>> b = a
>>> # Казалось бы, что у нас теперь 2 массива
...
>>> a
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
>>> b
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
>>>
>>> b is a # Однако массив "b" это массив "a"
True
>>> # Более того это один и тот же объект:
...
>>> id(a)
2968935744
>>> id(b)
2968935744
>>>
>>> id(a) == id(b)
True Самое любопытное, что массивы a и b это действительно один и тот же массив, то есть не просто одни и те же данные, но и тип данных.
>>> a.dtype # Тип элементов массива "а"
dtype('int32')
>>> b.dtype # Тип элементов массива "b"
dtype('int32')
>>>
>>> a.dtype = np.float64 # Меняем тип элементов массива "а"
>>> a.dtype
dtype('float64')
>>> b.dtype # Тип элементов массива "b" так же меняется
dtype('float64') В таких ситуациях, даже с математической точки зрения, мы можем говорить, что у нас действительно есть два массива: массив a и массив b, но мы должны обязательно уточнять (и помнить сами), что это в самом прямом смысле один и тот же массив.
10.2. Копирование массивов
Довольно часто, необходимо сделать полную копию массива и метод copy позволяет сделать это, причем скопировать не только данные массива но и все его свойства.
>>> a = np.arange(12).reshape(2,6)
>>> a
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]])
>>>
>>> b = a.copy()
>>> b
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]])
>>>
>>> b == a # Все элементы массивов равны
array([[ True, True, True, True, True, True],
[ True, True, True, True, True, True]], dtype=bool)
>>>
>>> b is a # Но теперь это уже не один и тот же объект
False
>>>
>>> # Теперь, это разные объекты даже в памяти
...
>>> id(a)
2968935824
>>> id(b)
2968935624
>>>
>>> id(a) == id(b)
False
>>>
>>> a[0][0] = 7777777 # Изменения в одном не отразятся на другом
>>> a
array([[7777777, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]])
>>> b
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]])
>>>
>>> a.dtype
dtype('int32')
>>> b.dtype # Массив "b" скопировал даже тип элементов
dtype('int32')
>>> a.dtype = np.int16 # Изменим тип элементов массива "а"
>>> a.dtype
dtype('int16')
>>> b.dtype # Тип элементов массива "b" не меняется
dtype('int32') Вот теперь, если мы говорим о массивах a и b, то мы говорим о реальных копиях: у них одинаковые данные, но это не одни и те же данные. Когда мы говорим или слышим, что массив b — это копия массива a, то именно это и подразумевается в терминологии NumPy.
10.3. Представления массивов
Теперь мы знаем, что простое присваивание не выполняет копирования массивов. Если нам нужна копия, то мы можем легко сделать ее с помощью метода copy. Однако, бывают случаи когда копия массива не нужна, а нужен тот же самый массив но с другими размерами — другое представление исходного массива.
Для таких нужд NumPy предоставляет метод ndarray.view(). Этот метод создает новый объект массива, который просматривает данные исходного массива, но изменение размеров одного массива не повлечет изменение размеров другого.
>>> a = np.arange(12)
>>> a
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
>>>
>>> b = a
>>> b
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
>>>
>>> a.shape = 3, 4 # Меняем размеры массива "а"
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>>
>>> b # Размеры массива "b" так же изменились
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>>
>>> # Теперь создадим представление массива "а"
...
>>> c = a.view()
>>> c
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>>
>>> a.shape = 2, 6 # Изменим размеры массива "а"
>>> a
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]])
>>>
>>> c # Размеры массива "с" не изменились
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>>
>>> # Но массив "с" просматривает те же данные что и "а"
... # Изменение элементов в "а" отразится на массиве "с"
...
>>> a[0][0] = 11111
>>> c
array([[11111, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> # А изменение элементов в "с" отразится на массиве "а"
>>> c[0][0] = 77777
>>> a
array([[77777, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]])Как правило, функции меняющие форму и порядок элементов в массивах возвращают именно представление, а не копию массива:
>>> a = np.arange(8)
>>> b = a.reshape(2,4) # Массив "b" - это представление массива "а"
>>> c = b.T # А вот массив "с" - это представление массива "b"
>>>
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7])
>>> b
array([[0, 1, 2, 3],
[4, 5, 6, 7]])
>>> c
array([[0, 4],
[1, 5],
[2, 6],
[3, 7]])
>>>
>>> # Все три массива просматривают одни и те же данные
...
>>> c[0][0] = 77777
>>>
>>> c
array([[77777, 4],
[ 1, 5],
[ 2, 6],
[ 3, 7]])
>>> b
array([[77777, 1, 2, 3],
[ 4, 5, 6, 7]])
>>> a
array([77777, 1, 2, 3, 4, 5, 6, 7])Срезы массивов — это тоже представления массивов:
>>> a = np.arange(12)
>>> a
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
>>>
>>> b = a[0:12:2]
>>> b
array([ 0, 2, 4, 6, 8, 10])
>>>
>>> c = a[1:12:2]
>>> c
array([ 1, 3, 5, 7, 9, 11])
>>>
>>> # Все три массива просматривают одни и те же данные
...
>>> b[:] = 0
>>>
>>> b
array([0, 0, 0, 0, 0, 0])
>>> a
array([ 0, 1, 0, 3, 0, 5, 0, 7, 0, 9, 0, 11])
>>>
>>> c[:] = -1
>>> c
array([-1, -1, -1, -1, -1, -1])
>>>
>>> a
array([ 0, -1, 0, -1, 0, -1, 0, -1, 0, -1, 0, -1]) Если мы говорим, что массив b — это представление массива a, то подразумевается, что независимо от формы и вида массива b он состоит из тех же данных в памяти, что и массив a. Поэтому изменение элементов в одном из них повлечет изменение соответствующих элементов в другом.
Расшифровка матрицы путаницы
Дата публикации Jul 22, 2019
В случае проблемы классификации, имеющей только одну точность классификации, может не дать вам полную картину. Таким образом, матрица путаницы или матрица ошибок используется для суммирования производительности алгоритма классификации.
фотоДжошуа СортинонаUnsplashВычисление матрицы путаницы может дать вам представление о том, где модель классификации верна и какие ошибки она допускает.
Путаница путаница используется для проверки производительности модели классификации на наборе тестовых данных, для которых известны истинные значения. Большинство показателей эффективности, таких как точность, отзыв, рассчитываются из матрицы путаницы.
Эта статья направлена на:
1. Что такое матрица путаницы и зачем она нужна?
2. Как рассчитать путаницу для двухклассовой задачи классификации на примере кошки-собаки.
3. Как создать путаницу в Python & R.
4. Краткое изложение и интуиция о различных мерах: точность, отзыв, точность и специфика
Матрица путаницы предоставляет сводку прогнозирующих результатов в задаче классификации. Правильные и неправильные прогнозы суммируются в таблице со своими значениями и разбиваются по каждому классу.
Матрица путаницы для двоичной классификацииМы не можем полагаться на одно значение точности в классификации, когда классы не сбалансированы. Например, у нас есть набор данных из 100 пациентов, 5 из которых имеют диабет, а 95 здоровы. Однако, если наша модель только предсказывает класс большинства, то есть все 100 человек здоровы, даже если у нас точность классификации составляет 95%. Поэтому нам нужна матрица путаницы.
Давайте возьмем пример:
У нас всего 10 кошек и собак, и наша модель предсказывает, кошка это или нет.
Фактические значения = [«собака», «кошка», «собака», «кошка», «собака», «собака», «кошка», «собака», «кошка», «собака» »]
Прогнозируемые значения = [«собака», «собака», «собака», «собака», «собака», «собака», «кошка», «кошка», «кошка», «кошка»]
Помните, мы описываем прогнозируемые значения как положительные / отрицательные, а фактические значения как истинные / ложные.
Определение терминов:
Настоящий позитив: вы предсказали позитив, и это правда. Вы предсказали, что животное — это кошка, и это действительно так.
True Negative: вы предсказали отрицательный результат, и это правда. Вы предсказали, что животное — это не кошка, и на самом деле это не так (это собака).
Ложный положительный результат (ошибка типа 1). Вы предсказали положительный результат, и это неверно. Вы предсказали, что животное — это кошка, но на самом деле это не так (это собака).
Ложное отрицание (ошибка типа 2). Вы прогнозировали отрицательное значение, и оно ложно. Вы предсказали, что животное не кошка, но на самом деле это так.
Точность классификации:
Точность классификации определяется соотношением:
Напомним (Чувствительность ака):
Напомним, определяется как отношение общего количества правильно классифицированных положительных классов к общему количеству положительных классов. Или из всех положительных классов, сколько мы предсказали правильно. Отзыв должен быть высоким.
Точность:
Точность определяется как отношение общего количества правильно классифицированных положительных классов к общему количеству предсказанных положительных классов. Или из всех прогнозирующих положительных классов, сколько мы предсказали правильно. Точность должна быть высокой.
Уловка, чтобы помнить:дозрение имеетдоДиктивные результаты в знаменателе.
F-оценка или F1-оценка:
Сложно сравнивать две модели с разными Precision и Recall. Поэтому, чтобы сделать их сопоставимыми, мы используем F-Score. Это Гармоническое Средство Точности и Вспомнить. По сравнению с арифметическим средним, гармоническое среднее наказывает более экстремальные значения. F-оценка должна быть высокой.
Специфичность:
Специфичность определяет долю фактических негативов, которые правильно определены.
Пример для интерпретации матрицы путаницы:
Давайте вычислим матрицу путаницы, используя приведенный выше пример с кошкой и собакой:
Точность классификации:
Точность = (TP + TN) / (TP + TN + FP + FN) = (3 + 4) / (3 + 4 + 2 + 1) = 0,70
Отзыв:Напомним, дает нам представление о том, когда на самом деле да, как часто он предсказывает да.
Напомним = TP / (TP + FN) = 3 / (3 + 1) = 0,75
Точность:Точность говорит нам о том, когда он предсказывает, да, как часто это правильно.
Точность = TP / (TP + FP) = 3 / (3 + 2) = 0,60
F-оценка:
F-оценка = (2 * Recall * Precision) / (Recall + Presision) = (2 * 0,75 * 0,60) / (0,75 + 0,60) = 0,67
Специфичность:
Специфичность = TN / (TN + FP) = 4 / (4 + 2) = 0,67
Давайте используем и коды Python, и R, чтобы понять приведенный выше пример с собакой и кошкой, который поможет вам лучше понять, что вы узнали о матрице путаницы до сих пор.
ПИТОН:Сначала давайте возьмем код Python для создания матрицы путаницы. Мы должны импортировать модуль матрицы путаницы из библиотеки sklearn, которая помогает нам генерировать матрицу путаницы
Ниже приведена реализация приведенного выше объяснения в Python:
Код PythonOUTPUT ->Confusion Matrix :
[[3 1]
[2 4]]
Accuracy Score : 0.7
Classification Report :
precision recall f1-score supportcat 0.60 0.75 0.67 4
dog 0.80 0.67 0.73 6micro avg 0.70 0.70 0.70 10
macro avg 0.70 0.71 0.70 10
weighted avg 0.72 0.70 0.70 10
Р:Давайте теперь используем R-код для создания матрицы путаницы. Мы будем использовать библиотеку карет в R для вычисления матрицы путаницы.
Код ROUTPUT ->Confusion Matrix and Statistics Reference
Prediction 0 1
0 4 1
1 2 3Accuracy : 0.7
95% CI : (0.3475, 0.9333)
No Information Rate : 0.6
P-Value [Acc > NIR] : 0.3823Kappa : 0.4Mcnemar's Test P-Value : 1.0000Sensitivity : 0.6667
Specificity : 0.7500
Pos Pred Value : 0.8000
Neg Pred Value : 0.6000
Prevalence : 0.6000
Detection Rate : 0.4000
Detection Prevalence : 0.5000
Balanced Accuracy : 0.7083'Positive' Class : 0
- Точность — это насколько вы уверены в своих истинных положительных сторонах. Вспомните, насколько вы уверены, что не пропускаете ни одного позитива.
- выберитеОтзывесли возникновениеложные негативы недопустимы / недопустимы.Например, в случае диабета у вас было бы больше ложных срабатываний (ложных срабатываний) вместо сохранения ложных отрицательных.
- выберитеточностьесли хочешь быть побольшеуверен в своих истинных позитивах, Например, в случае спам-писем вы бы предпочли иметь несколько спам-писем в вашем почтовом ящике, а не обычные электронные письма в вашем ящике для спама. Вы хотели бы быть уверены, что электронная почта X является спамом, прежде чем мы поместим ее в ящик для спама.
- выберитеспецифичностьесли хочешьпокрыть все истинные негативы,то есть мы не хотим ложных срабатываний или ложных срабатываний. Например, в случае теста на наркотики, при котором все люди с положительным тестом немедленно попадут в тюрьму, вы не хотели бы, чтобы кто-либо без наркотиков отправлялся в тюрьму.
Мы можем сделать вывод, что:
- Значение точности 70% означает, что идентификация 3 из каждых 10 кошек неверна, а 7 — правильна.
- Точность 60% означает, что метка 4 из каждых 10 кошек — это не кошка (то есть собака), а 6 — кошки.
- Напомним, что значение 70% означает, что 3 из каждых 10 кошек в действительности пропущены нашей моделью, а 7 правильно определены как кошки.
- Значение специфичности, равное 60%, означает, что 4 из каждых 10 собак (то есть не кошек) в действительности помечены как кошки, а 6 — как собаки.
Если у вас есть какие-либо комментарии или вопросы, не стесняйтесь оставлять свои отзывы ниже. Вы всегда можете связаться со мной поLinkedIn,
Оригинальная статья
Манипуляции с матрицей в Python — GeeksforGeeks
В Python матрица может быть реализована как 2D-список или 2D-массив. Формирование матрицы из последнего дает дополнительные функции для выполнения различных операций в матрице. Эти операции и массив определены в модуле « numpy ».
Операция с матрицей:
1. add (): — Эта функция используется для выполнения поэлементного сложения матрицы .
2. subtract (): — Эта функция используется для вычитания элементов матрицы .
3. DivX (): — Эта функция используется для выполнения поэлементного матричного деления .
|
Выход:
Поэлементное сложение матрицы: [[8 10] [13 15]] Поэлементное вычитание матрицы: [[-6-6] [-5 -5]] Поэлементное деление матрицы: [[0.14285714 0,25] [0,44444444 0,5]]
4. multiply (): — Эта функция используется для выполнения поэлементного умножения матриц .
5. dot (): — Эта функция используется для вычисления матричного умножения , а не поэлементного умножения .
|
Выход:
Поэлементное умножение матрицы: [[7 16] [36 50]] Произведение матриц: [[25 28] [73 82]]
6. sqrt (): — Эта функция используется для вычисления квадратного корня из каждого элемента матрицы.
7. sum (x, axis): — Эта функция используется для сложения всех элементов в матрице . Необязательный аргумент «ось» вычисляет сумму столбцов , если ось равна 0, и сумму строк , если ось , равна 1 .
8. «T»: — Этот аргумент используется для транспонирования указанной матрицы.
|
Выход:
Элементный квадратный корень равен: [[1. 1.41421356] [2. 2.23606798]] Суммирование всех матричных элементов: 34 Суммирование всей матрицы по столбцам: [16 18] Суммирование всей матрицы по строкам: [15 19] Транспонирование данной матрицы: [[1 4] [2 5]]
Автор статьи Manjeet Singh 100 🙂 .Если вам нравится GeeksforGeeks, и вы хотели бы внести свой вклад, вы также можете написать статью с помощью provide.geeksforgeeks.org или отправить ее по электронной почте на [email protected]. Посмотрите, как ваша статья появляется на главной странице GeeksforGeeks, и помогите другим гикам.
Пожалуйста, напишите комментарий, если вы обнаружите что-то неправильное, или если вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше.
Внимание компьютерщик! Укрепите свои основы с помощью курса Python Programming Foundation и изучите основы.
Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS . И чтобы начать свое путешествие по машинному обучению, присоединитесь к курсу Машинное обучение — базовый уровень
Получите матричный ввод от пользователя в Python
Матрица— это не что иное, как прямоугольное расположение данных или чисел. Другими словами, это прямоугольный массив данных или чисел. Горизонтальные записи в матрице называются «строками», а вертикальные записи называются «столбцами».Если матрица содержит r строк и c столбцов, то порядок матрицы равен r x c . Каждая запись в матрице может быть целочисленной, плавающей или даже комплексной.
Примеры:
// Матрица 3 x 4
1 2 3 4
М = 4 5 6 7
6 7 8 9
// матрица 2 x 3 в Python
A = ([2, 5, 7],
[4, 7, 9])
// Матрица 3 x 4 в Python, где записи представляют собой числа с плавающей запятой
B = ([1.0, 3,5, 5,4, 7,9],
[9.0, 2.5, 4.2, 3.6],
[1.5, 3.2, 1.6, 6.5]) В Python мы можем использовать пользовательскую матрицу ввода по-разному. Некоторые методы для матрицы пользовательского ввода в Python показаны ниже:
Код # 1:
|
Вывод:
Введите количество строк: 2 Введите количество столбцов: 3 Введите записи по строкам: 1 2 3 4 5 6 1 2 3 4 5 6
Один вкладыш:
|
Код # 2: Использование функции map () и Numpy .
В Python существует популярная библиотека под названием NumPy . Эта библиотека является фундаментальной библиотекой для любых научных вычислений. Он также используется для многомерных массивов, и, поскольку мы знаем, что матрица — это прямоугольный массив, мы будем использовать эту библиотеку для матрицы пользовательского ввода.
|
Выход:
Введите количество строк: 2 Введите количество столбцов: 2 Введите записи в одну строку через пробел: 1 2 3 1 [[1 2] [3 1]]
Внимание компьютерщик! Укрепите свои основы с помощью курса Python Programming Foundation и изучите основы.
Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS . И чтобы начать свое путешествие по машинному обучению, присоединяйтесь к Машинное обучение — курс базового уровня
Матрицы в Python
Python известен своей аккуратностью и удобством чтения и обработки данных. Существуют различные методы обработки данных в Python, такие как использование словарей, кортежей, матриц и т. Д. В этом руководстве вы узнаете о матрицах и их функциях.
Что такое матрица в Python?
Это двухмерная (двумерная) структура данных. В реальных проектах и при моделировании реальных данных вы должны хранить данные в последовательном или табличном формате. Предположим, вы хотите сохранить данные трех сотрудников трех разных отделов. В табличном формате это будет выглядеть примерно так:
| Идентификатор сотрудника | Имя сотрудника | Отдел сотрудника |
|---|---|---|
| 1001A | Ray | Технический руководитель |
| 2004B | Менеджер Карлос | 900|
| 3100A | Alex | Ведущий разработчик |
В Python эти таблицы называются двумерными массивами, которые также называются матрицами.Python дает нам возможность представлять эти данные в виде списков.
Пример:
val = [['1001A', 'Ray', 'Technical Head'], ['2004B', 'Karlos', 'Manager'], ['3100A', 'Alex', 'Lead Разработчик ']] В приведенном выше фрагменте кода val представляет матрицу 3 X 3, состоящую из трех строк и трех столбцов.
Создание матрицы в Python
Python позволяет разработчикам реализовывать матрицы, используя вложенный список. Списки могут быть созданы, если вы поместите все элементы или элементы, начинающиеся с ‘[‘ и заканчивающиеся ‘]’ (квадратные скобки), и разделяете каждый элемент запятой.
val = [['Дэйв', 101,90,95],
['Alex', 102,85,100],
['Ray', 103,90,95]] Динамическое создание матриц в Python
Можно создать матрицу тревоги, перечислив набор элементов (скажем, n), а затем связав каждый из элементов с другим Одномерный список из m элементов. Вот фрагмент кода для этого:
n = 3
м = 3
val = [0] * n
для x в диапазоне (n):
val [x] = [0] * m
print (val) Вывод программы будет:
[[0, 0, 0], [0, 0, 0], [0, 0, 0]]
Доступ к элементам матриц
Есть разные методы получения элементов матрицы в Python.
i) Индекс списка : Для доступа к элементам матрицы вы должны использовать квадратные скобки после имени переменной с номером строки и столбца, например: val [row_no] [col_no]
val = [ ['Дэйв', 101,90,95], ['Алекс', 102,85,100], ['Рэй', 103,90,95]]
печать (val [2])
print (val [0] [1]) Вывод:
['Ray', 103,90,95] 101
ii) Отрицательное индексирование : Python также предоставляет функцию индексации с отрицательными значениями в квадратных скобках для последовательного доступа к значениям.При отрицательной индексации -1 относится к последнему элементу матрицы, -2 — к второму последнему и продолжается.
val = [['Dave', 101,90,95], ['Alex', 102,85,100], ['Ray', 103,90,95]]
печать (val [-2])
print (val [-1] [- 2]) Вывод:
['Alex', 102,85,100] 90
Работа с матрицами Numpy: первая удобная ссылка
Иева Зарина, разработчик программного обеспечения, Nordigen.
В начале, когда я начал работать с обработкой естественного языка, я использовал списки Python по умолчанию.Но довольно скоро, после более масштабных экспериментов и большего количества данных, у меня заканчивается оперативная память. Списки Python не оптимизированы для пространства памяти, поэтому на Numpy.
Numpy — это де-факто инструмент ndarray для научной экосистемы Python.
Массивы Numpy очень похожи на C — обычно вы создаете массив нужного размера заранее, а затем заполняете его. Слияние и добавление не рекомендуется, поскольку Numpy создаст один пустой массив размером с объединяемые массивы, а затем просто скопирует в него содержимое.
Вот несколько способов манипулирования массивами Numpy (ndarray):
Создать ndarray
Некоторые способы создания матриц numpy:
импортировать numpy как np список = [1, 2, 3] c = np.asarray (список)
- Создайте ndarray размером , который вам нужен, заполненный единицами, нулями или случайными значениями:
# Элементы массива как ndarray c = np.array ([1, 2, 3]) # Форма массива 2x2 2d для массивов в формате (строки, столбцы) shape = (2, 2) # Случайные значения c = np.пустой (форма) d = np.ones (форма) e = np.zeros (форма)
# Создание ndarray из списка c = np.array ([[1., 2.,], [1., 2.]]) # Создание нового массива в форме c, заполненного 0 d = np.empty_like (c)
Ломтик
Иногда мне нужно выбрать только часть из всех столбцов или строк в 2-мерной матрице. Например, матрицы:
a = np.asarray ([[1,1,2,3,4], # 1-я строка
[2,6,7,8,9], # 2-я строка
[3,6,7,8,9], # 3-й ряд
[4,6,7,8,9], # 4-й ряд
[5,6,7,8,9] # 5-й ряд
])
б = нп.asarray ([[1,1],
[1,1]])
# Выберите строку в формате a [начало: конец], если начало или конец опущены, это означает весь диапазон.
y = a [: 1] # 1-я строка
y = a [0: 1] # 1-я строка
y = a [2: 5] # выбрать строки с 3-й по 5-ю строку
# Выберите столбец в формате a [начало: конец, номер_столбца]
x = a [:, -1] # -1 означает первый с конца
x = a [:, 1: 3] # выберите столбцы со 2-го по 3-й
Объединить массивы
Объединение массивов numpy — , не рекомендуется , потому что внутренне numpy создаст пустой большой массив, а затем скопирует в него содержимое.Лучше всего сначала создать желаемый размер, а затем просто заполнить его. Однако иногда слияния не избежать. В этом случае numpy имеет несколько встроенных функций :
Конкатенация
1d массивов:
a = np.array ([1, 2, 3]) b = np.array ([5, 6]) напечатать np.concatenate ([a, b, b]) # >> [1 2 3 5 6 5 6]
2d массивов:
a2 = np.array ([[1, 2], [3, 4]]) # axis = 0 - объединить по строкам распечатать np.объединить ((a2, b), ось = 0) # >> [[1 2] # [3 4] # [5 6]] # axis = 1 - объединить по столбцам, но сначала нужно транспонировать b: б.Т # >> [[5] # [6]] np.concatenate ((a2, b.T), ось = 1) # >> [[1 2 5] # [3 4 6]]
Добавить — добавить значения в конец массива
1d массивов:
# 1d массивы напечатать np.append (a, a2) # >> [1 2 3 1 2 3 4] распечатать np.добавить (а, а) # >> [1 2 3 1 2 3]
2d массивов — оба массива должны соответствовать форме строк:
печать np.append (a2, b, axis = 0) # >> [[1 2] # [3 4] # [5 6]] напечатать np.append (a2, b.T, axis = 1) # >> [[1 2 5] # [3 4 6]]
Hstack (стек по горизонтали) и vstack (стек по вертикали)
1d массивов:
напечатать np.hstack ([a, b]) # >> [1 2 3 5 6] распечатать np.vstack ([a, a]) # >> [[1 2 3] # [1 2 3]]
2d массивов:
print np.hstack ([a2, a2]) # массивы должны соответствовать форме # >> [[1 2 1 2] # [3 4 3 4]] напечатать np.vstack ([a2, b]) # >> [[1 2] # [3 4] # [5 6]]
Типы в ndarray
Без значения с плавающей запятой по умолчанию numpy может содержать все распространенные типы . Если любое из чисел в массиве является плавающим, все числа будут преобразованы в число с плавающей запятой:
а = нп.массив ([1, 2, 3.3]) распечатать # >> [1. 2. 3.3]
Но вы можете легко привести тип к int, float или другому:
a = np.array ([1, 2, 3.3]) распечатать # >> [1. 2. 3.3] напечатать a.astype (int) # >> [1 2 3]
Строковые массивы необходимо создать как массивы с типом S1 для строки длиной 1, S2 для длины 2 и так далее. numpy.chararray () создает массив с этим типом. Вам нужно указать форму массива и itemsize — длину каждой строки.
chararray = np.chararray ([3,3], itemsize = 3) chararray [:] = 'abc' # присвоение значения всем полям печать chararray # >> [['abc' 'abc' 'abc'] # ['abc' 'abc' 'abc'] # ['abc' 'abc' 'abc']]
Чтение / запись в файл
Запишите массив numpy в файл с помощью numpy.savetext () в текстовой форме и загрузите его с помощью numpy.loadtext ():
a2 = np.array ([
[1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1],
[1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1],
[1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1],
[1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1],
[1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1],
[1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1]
])
нп.savetxt ('test.txt', a2, delimiter = ',')
a2_new = np.loadtxt ('test.txt', delimiter = ',')
Запись разреженных матриц
Однако в машинном обучении, если у вас есть большая разреженная матрица (с большим количеством значений, равных 0), чтение и запись больших матриц выполняется быстрее, а файл меньше, если вы используете формат svmlight :
из sklearn.datasets import dump_svmlight_file, load_svmlight_file
матрица = [
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2],
[1, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 1, 2],
[1, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 1, 2]
]
ярлыки = [1,1,1,1,1,2,2]
dump_svmlight_file (матрица, метки, 'svmlight.txt ', zero_based = True)
# Файл выглядит так:
# 1 0: 1 13: 1 14: 2
# 1 0: 1 13: 1 14: 2
# 1 0: 1 13: 1 14: 2
# 1 0: 1 13: 1 14: 2
# 1 0: 1 13: 1 14: 2
# 2 0: 1 5: 3 13: 1 14: 2
# 2 0: 1 5: 3 13: 1 14: 2
svm_loaded = load_svmlight_file ('svmlight.txt', zero_based = True)
Используйте .toarray (), чтобы вернуть матрицу из формата сжатых разреженных строк svmlight:
svm_loaded [0] .toarray () # элемент матрицы с индексом 0 svm_loaded [1] # ярлыков в индексе 1
Подводя итог, в этом посте было рассмотрено, как:
- создать массивы numpy,
- массивов срезов,
- объединить массивы,
- базовых типов массивов numpy,
- чтение и запись массивов в файл,
- чтение и запись разреженных матриц в формат svmlight.
Это было просто введение в numpy-матрицы о том, как начать работу и как выполнять базовые манипуляции. Дополнительную информацию можно найти в этом руководстве MIT, а также в официальной документации.
Биография: Иева Зарина — разработчик программного обеспечения в Nordigen.
Оригинал. Размещено с разрешения.
Связанный:
1. Векторы, матрицы и массивы
Обсуждение
Частая ситуация в машинном обучении — огромное количество данные; однако большинство элементов данных — нули.Например, представьте матрицу, в которой столбцы — это каждый фильм на Netflix, а строки каждый пользователь Netflix, а значения — сколько раз пользователь смотрел именно этот фильм. В этой матрице были бы десятки тысяч столбцов и миллионов строк! Однако, поскольку большинство пользователей не смотрят в большинстве фильмов подавляющее большинство элементов было бы нулевым.
Разреженные матрицы хранят только ненулевые элементы и принимают все другие значения будет равно нулю, что приведет к значительной экономии вычислительных ресурсов.В нашем решение, мы создали массив NumPy с двумя ненулевыми значениями, затем преобразовал его в разреженную матрицу. Если мы рассмотрим разреженную матрицу, мы можем видите, что сохраняются только ненулевые значения:
# Просмотр разреженной матрицыпечать(matrix_sparse)
(1, 1) 1 (2, 0) 3
Есть несколько типов разреженных матриц. Однако в матрицах сжатых разреженных строк (CSR), (1, 1) и (2, 0) представляют (с нулевым индексом) индексы ненулевых значений 1 и 3 , соответственно.Например, элемент 1 находится во второй строке и втором столбце. Мы можем увидеть преимущество разреженных матриц, если мы создадим гораздо большую матрицу с большим количеством нулевых элементов, а затем сравним эту большую матрицу с нашей исходной разреженной матрицей:
# Создать большую матрицуmatrix_large=np.массив([[0,0,0,0,0,0,0,0,0,0],[0,1,0,0,0,0,0,0,0,0],[3,0,0,0,0,0,0,0,0,0]])# Создать матрицу сжатых разреженных строк (CSR)matrix_large_sparse=sparse.csr_matrix(matrix_large)
# Просмотр исходной разреженной матрицыпечать(matrix_sparse)
(1, 1) 1 (2, 0) 3
# Увеличить разреженную матрицупечать(matrix_large_sparse)
(1, 1) 1 (2, 0) 3
Как мы видим, несмотря на то, что мы добавили намного больше нулевых элементов в большую матрицу, ее разреженное представление в точности совпадает с нашей исходной разреженной матрицей.То есть добавление нулевых элементов не изменило размер разреженной матрицы.
Как уже упоминалось, существует много различных типов разреженных матриц, таких как в виде сжатого разреженного столбца, списка списков и словаря ключей. Хотя объяснение различных типов и их значения вне рамок этой книги, стоит отметить, что пока есть нет «лучшего» типа разреженной матрицы, есть значимые различия между их, и мы должны осознавать, почему мы выбираем один тип над другим.
Как реализовать матрицы в Python с помощью NumPy?
Матрицы используются как математический инструмент для различных целей в реальном мире. В этой статье мы обсудим все, что есть о Матрицах в Python, используя знаменитую библиотеку NumPy, в следующем порядке:
БОНУС : Собираем все вместе — код Python для решения системы линейных уравнений
Давайте начнем с Матрицы в Python.
Что такое NumPy и когда его использовать?NumPy — это библиотека Python, позволяющая легко выполнять численные вычисления с использованием одномерных и многомерных массивов и матриц.Как следует из названия, NumPy отлично справляется с численными расчетами. Многие библиотеки науки о данных, такие как Pandas , Scikit-learn , SciPy , matplotlib, и т. Д., Зависят от NumPy. Он является неотъемлемой частью современных приложений для обработки данных, написанных на Python.
Многие вычисления линейной алгебры легко решить с помощью NumPy. Линейная алгебра — это основной математический инструмент, используемый во многих алгоритмах машинного обучения .Следовательно, подробное знание NumPy поможет вам в создании библиотек или расширении существующих библиотек машинного обучения.
NumPy предоставляет:
- мощный объект N-мерного массива, называемый ndarray
- Функции вещания
- Инструменты для интеграции кода C / C ++ и Fortran
- Полезная линейная алгебра, преобразование Фурье и возможности случайных чисел
Сейчас Давайте продолжим с нашими матрицами в Python и посмотрим, как создать матрицу.
Создание матрицы в NumPy Создание матрицы с использованием списков## Import numpy импортировать numpy как np ## Создайте двумерный массив numpy, используя списки Python arr = np.массив ([[1, 2, 3], [4, 5, 6]]) print (arr)
np.array используется для создания массива NumPy из списка. Массивы NumPy имеют тип ndarray.
Результатом вышеупомянутой программы является:
Она представляет собой двумерную матрицу, где входом в np.array () является список списков [[1, 2, 3], [4, 5, 6]]. Каждый список в родительском списке образует строку в матрице.
Создание матрицы с использованием диапазоновnp.arange () может генерировать последовательность чисел с указанием начала и конца.
## Генерация чисел от (начало) до (конец-1) ## Здесь start = 0 ## конец = 5 ## Сгенерирован массив NumPy от 0 до 4 print (np.arange (0,5))
Вышеупомянутый оператор выводит следующий одномерный массив:
Чтобы сгенерировать 2D-матрицу, мы можем использовать np.arange () внутри списка. Мы передаем этот список в np.array (), что делает его двумерным массивом NumPy.
print (np.array ([np.arange (0,5), np.arange (5,10)]))
Вышеупомянутый оператор выводит следующий 2D-массив:
Форма массива NumPyМы называем любой объект NumPy массивом N-измерений.В математике это называется N-размерной матрицей. У каждого объекта NumPy ndarray можно запросить его форму. Форма — это кортеж в формате (n_rows, n_cols)
Следующий фрагмент печатает форму матрицы
## Использование примера из приведенного выше раздела для создания матрицы с использованием диапазонов arr_2d = np.array ([np.arange (0,5), np.arange (5,10)]) print (arr_2d.shape)
Вывод:
(2, 5) означает, что матрица имеет 2 строки и 5 столбцов
Матрица заполнена нулями и единицами Заполнение нули:## Создайте матрицу формы (3, 4), заполненную нулями ## По умолчанию числа типа float64 генерируются, если не указано печать (нп.нули ((3, 4)))
Вывод:
По умолчанию в массиве генерируются числа с плавающей запятой, если не указано иное.
Заполнение единицами:## Создайте матрицу формы (2, 2), заполненную единицами ## Здесь мы указали dtype = np.int16, который просит NumPy сгенерировать целые числа print (np.ones ((2, 2), dtype = np.int16))
Вывод:
При генерации матрицы с единицами есть поворот, мы передали дополнительный параметр dtype = нп.int16. Это заставляет функцию np.ones генерировать целые числа, а не значение с плавающей запятой по умолчанию. Этот дополнительный параметр также может быть передан в np.zeros
Матричные операции и примеры ДобавлениеВ приведенном ниже примере объясняются два типа сложения:
- Скалярное сложение
- Матричное сложение
импортировать numpy как np ## Сгенерировать две матрицы mat_2d_1 = np.array ([np.arange (0,3), np.arange (3,6)]) mat_2d_2 = нп.массив ([np.arange (6,9), np.arange (9,12)])print («Матрица1: n», mat_2d_1) print («Матрица2: n», mat_2d_2) ## Добавьте 1 к каждому элементу в mat_2d_1 и распечатайте его print («Скалярное сложение: n», mat_2d_1 + 1) ## Добавьте две матрицы выше поэлементно print («Поэлементное сложение двух матриц одинакового размера: n», mat_2d_1 + mat_2d_2)
Вывод:
ВычитаниеВычитание аналогично сложению. Нам просто нужно изменить операцию со сложения на вычитание.
импортировать numpy как np
## Сгенерировать две матрицы
mat_2d_1 = np.array ([np.arange (0,3), np.arange (3,6)])
mat_2d_2 = np.array ([np.arange (6,9), np.arange (9,12)])
print ("Матрица1: n", mat_2d_1)
print ("Матрица2: n", mat_2d_2)
## Вычтите 1 из каждого элемента в mat_2d_1 и распечатайте его
print («Скалярное сложение: n», mat_2d_1 - 1)
## Вычтите две матрицы выше поэлементно
print («Поэлементное вычитание двух матриц одинакового размера: n», mat_2d_1 - mat_2d_2) Вывод:
ПроизведениеМожно выполнить два типа умножения или операции над произведением Матрицы NumPy
- Скалярное произведение: скалярное значение умножается на все элементы матрицы
- Точечное произведение: это произведение двух матриц в соответствии с правилами умножения матриц.См. В разделе «Умножение матриц» правила умножения матриц.
импортировать numpy как np
## Сгенерируйте две матрицы формы (2,3) и (3,2), чтобы мы могли найти
## скалярное произведение
mat_2d_1 = np.array ([np.arange (0,3), np.arange (3,6)])
mat_2d_2 = np.array ([np.arange (0,2), np.arange (2,4), np.arange (4,6)])
## Печать форм и матриц
print ("Матрица1: n", mat_2d_1)
print ("Matrix1 shape: n", mat_2d_1.shape)
print ("Матрица2: n", mat_2d_2)
print ("Matrix2 shape: n", mat_2d_2.shape)
## Умножьте каждый элемент на 2 в mat_2d_1 и распечатайте его
print («Скалярное произведение: n», mat_2d_1 * 2)
## Найдите произведение двух приведенных выше матриц с помощью скалярного произведения
print ("Точечный продукт: n", np.точка (mat_2d_1, mat_2d_2))
ВАЖНО : Обратите внимание, что оператор * используется только для скалярного умножения. Однако для умножения матриц мы используем функцию np.dot (), которая принимает в качестве аргумента два 2D-массива NumPy.
Выход:
ДелениеПоэлементное скалярное деление может быть выполнено с помощью оператора деления /
импортировать numpy как np
## Сгенерировать матрицу формы (2,3)
mat_2d = нп.массив ([np.arange (0,3), np.arange (3,6)])
## Распечатать матрицу
print ("Матрица: n", mat_2d)
## Элементное деление на скаляр
print («Скалярное деление: n», mat_2d / 2)
Выход:
ЭкспонентаЭлементная экспонента может быть найдена с помощью оператора **
импортировать numpy как np
## Сгенерировать матрицу формы (2,3)
mat_2d = np.array ([np.arange (0,3), np.arange (3,6)])
## Распечатать матрицу
print ("Матрица: n", mat_2d)
## Найдите показатель степени по элементам i.е. возвести каждый элемент в матрицу в степень 2
print ("Матрица в степени 2: n", mat_2d ** 2)
Вывод:
Транспонирование- транспонирование матрицы — это новая матрица , строки которой являются столбцами исходной матрицы A ( 310 ) матрица становится (3, 2) матрицей в форме
- Numpy имеет свойство для каждого объекта ndarray, который хранит транспонирование матрицы.Нам не нужно использовать какой-либо специальный оператор, чтобы найти транспонирование матрицы.
- matrix.T обеспечивает транспонирование матрицы в NumPy
- Нижеприведенный фрагмент демонстрирует операцию транспонирования
импортировать numpy как np
## Сгенерировать матрицу формы (2,3)
mat_2d = np.array ([np.arange (0,3), np.arange (3,6)])
## Распечатать матрицу
print ("Матрица: n", mat_2d)
## Транспонирование матрицы
print ("Транспонировать n", mat_2d.T)
Вывод:
Нарезка матрицы- Слой матрицы выбирает подматрицу.Python предоставляет прекрасный синтаксис для индексирования и нарезки матриц.
- Нарезка использует следующий синтаксис:
- матрица [диапазон индекса строки, диапазон индекса столбца, номер шага]
- Диапазоны индекса строки и столбца соответствуют стандартному синтаксису Python Начальный индекс: конечный индекс
- Выбранный диапазон всегда от начало индекса до (конечный индекс — 1) при запуске кода
импортировать numpy как np
# Создать матрицу
mat_2d = нп.массив ([np.arange (0,3), np.arange (3,6)])
print ("Матрица: n", mat_2d)
# Нарезать, чтобы получить вторую строку в матрице
print ("Нарезано: n", mat_2d [1 :,:])
Вывод:
- Выбор диапазона строк 1: означает выбор индекса строки 1 до последней строки
- Индекс диапазона столбцов: означает выбор всех столбцов в выбранном диапазоне строк
импортировать numpy как np
# Создать матрицу
mat_2d = нп.массив ([np.arange (0,3), np.arange (3,6)])
print ("Матрица: n", mat_2d)
# Срез, чтобы получить последний столбец в матрице
print ("Нарезанный: n", mat_2d [:, 2:])
Выход:
- Выбор диапазона строк: означает выбор всех строк
- Индекс диапазона столбцов 2: означает выбор всех столбцов, начиная с индекса 2 до конца
импортировать numpy как np
# Создать матрицу
mat_2d = нп.массив ([np.arange (0,4), np.arange (4,8), np.arange (8,12), np.arange (12,16)])
print ("Матрица: n", mat_2d)
# Нарежьте, чтобы получить (2, 2) подматрицу в центре mat_2d
# т.е.
# [[5 6]
# [9 10]]
print ("Нарезано: n", mat_2d [1: 3, 1: 3])
Вывод:
- Выбор диапазона строк 1: 3 выбирает строки с индексами от 1 до 2 включительно
- Выбор диапазона столбцов 1: 3 выбирает столбцы с индексами с 1 по 2 включительно
Система уравнений
- Матричная запись для решения системы уравнений:
- X = np.точка ((инверсия A), B)
- Где:
- X = вектор неизвестных
- A = Коэффициенты на LHS
- B = Значения на RHS
- Например, рассмотрим ниже линейную систему уравнений:
- x + y + z = 1
2x + 4y + z = -2
x — y + z = 0 - можно представить в виде матриц как:
- X = [xyz] вектор неизвестных
A = [[1 1 1]
[2 4 1]
[1 -1 1]]
B = [1-2 0]
- Использование упомянутой матричной формулы выше, мы можем решить систему уравнений следующим образом:
импортировать numpy как np
## A = (3,3) матрица
А = np.массив ([[1,1,1], [2,4,1], [1, -1,1]])
## B = (3,1) матрица
B = np.array ([1, -2, 0]). T
## X = Inv (A) .B = (3, 1) в форме
X = np.dot (np.linalg.inv (A), B)
print ("Решение: n", X)
Вывод:
Где, x = -4,5, y = 0,5 и z = 5,0
На этом мы подошли к концу нашей статьи. Надеюсь, вы поняли, что такое матрицы в Python.
Чтобы получить более глубокие знания о Python и его различных приложениях, вы можете записаться на обучение Python Certification Training в режиме реального времени с круглосуточной поддержкой и пожизненным доступом.
Есть к нам вопрос? Пожалуйста, укажите это в разделе комментариев блога «Матрицы в Python», и мы свяжемся с вами в ближайшее время.
Разреженные матрицы (scipy.sparse) — SciPy v1.6.3 Справочное руководство
Пакет SciPy 2-D разреженной матрицы для числовых данных.
Содержание
Классы разреженных матриц
| Матрица с разреженными строками блоков |
| Разреженная матрица в формате COOrdinate. |
| Сжатая матрица с разреженными столбцами |
| Сжатая матрица разреженных строк |
| Разреженная матрица с DIAgonal хранилищем |
| Разреженная матрица на основе словаря ключей. |
| Построчный список списков разреженная матрица |
| Этот класс предоставляет базовый класс для всех разреженных матриц. |
Функции
Построение разреженных матриц:
| Разреженная матрица с единицами по диагонали |
| Матрица идентичности в разреженном формате |
| произведение кронекера разреженных матриц А и Б |
| сумма кронекера разреженных матриц A и B |
| Постройте разреженную матрицу из диагоналей. |
| Возвращает разреженную матрицу по диагонали. |
| Постройте блочно-диагональную разреженную матрицу из предоставленных матриц. |
| Вернуть нижнюю треугольную часть матрицы в разреженном формате |
| Вернуть верхнюю треугольную часть матрицы в разреженном формате |
| Построить разреженную матрицу из разреженных субблоков |
| Сложить разреженные матрицы по горизонтали (по столбцам) |
| Укладывать разреженные матрицы вертикально (по строкам) |
| Создает разреженную матрицу заданной формы и плотности с равномерно распределенными значениями. |
| Создает разреженную матрицу заданной формы и плотности со случайно распределенными значениями. |
Сохранение и загрузка разреженных матриц:
| Сохранение разреженной матрицы в файл в формате |
| Загрузить разреженную матрицу из файла в формате |
Инструменты с разреженной матрицей:
| Возвращает индексы и значения ненулевых элементов матрицы |
Определение разреженных матриц:
Информация об использовании
Доступно семь типов разреженных матриц:
csc_matrix: сжатый формат разреженных столбцов
csr_matrix: сжатый формат разреженных строк
bsr_matrix: Формат разреженных строк блока
lil_matrix: Формат списка списков
dok_matrix: Формат словаря ключей
coo_matrix: COOrdinate формат (также известный как IJV, триплетный формат)
dia_matrix: DIA Угловой формат
Для эффективного построения матрицы используйте dok_matrix или lil_matrix.Класс lil_matrix поддерживает базовую нарезку и причудливую индексацию с помощью синтаксис аналогичен массивам NumPy. Как показано ниже, формат COO также может использоваться для эффективного построения матриц. Несмотря на их сходство с массивами NumPy, категорически не рекомендуется использовать NumPy функции непосредственно на этих матрицах, потому что NumPy может некорректно преобразовать их для вычислений, приводящих к неожиданным (и неверным) результатам. если ты хотите применить функцию NumPy к этим матрицам, сначала проверьте, есть ли в SciPy собственная реализация для данного класса разреженной матрицы, или преобразует разреженная матрица в массив NumPy (e.g., используя метод toarray () class) перед применением метода.
Для выполнения таких манипуляций, как умножение или инверсия, сначала преобразовать матрицу в формат CSC или CSR. Формат lil_matrix: на основе строк, поэтому преобразование в CSR эффективно, тогда как преобразование в CSC меньше так.
Все преобразования между форматами CSR, CSC и COO эффективны, операции с линейным временем.
Матрица векторного произведения
Чтобы произвести векторное произведение между разреженной матрицей и вектором, просто используйте метод matrix dot , как описано в его строке документации:
>>> импортировать numpy как np >>> от scipy.разреженный импорт csr_matrix >>> A = csr_matrix ([[1, 2, 0], [0, 0, 3], [4, 0, 5]]) >>> v = np.array ([1, 0, -1]) >>> A.dot (v) массив ([1, -3, -1], dtype = int64)
Предупреждение
Начиная с NumPy 1.7, np.dot не знает о разреженных матрицах, поэтому его использование приведет к неожиданным результатам или ошибкам. Вместо этого сначала должен быть получен соответствующий плотный массив:
>>> np.dot (A.toarray (), v) массив ([1, -3, -1], dtype = int64)
, но тогда все преимущества в производительности будут потеряны.
Формат CSR особенно подходит для быстрых матричных векторных произведений.
Пример 1
Создайте lil_matrix размером 1000×1000 и добавьте к нему несколько значений:
>>> из scipy.sparse import lil_matrix >>> из scipy.sparse.linalg import spsolve >>> из импорта numpy.linalg решить, норма >>> из numpy.random import rand
>>> A = lil_matrix ((1000, 1000)) >>> A [0,: 100] = rand (100) >>> A [1, 100: 200] = A [0,: 100] >>> А.setdiag (ранд (1000))
Теперь преобразуйте его в формат CSR и решите A x = b для x:
>>> A = A.tocsr () >>> b = rand (1000) >>> x = spsolve (A, b)
Преобразуйте его в плотную матрицу и решите, и убедитесь, что результат то же самое:
>>> x_ = решить (A.toarray (), b)
Теперь мы можем вычислить норму ошибки с помощью:
>>> ошибка = норма (х-х_) >>> эрр <1e-10 Правда
Он должен быть маленьким 🙂
Пример 2
Построить матрицу в формате COO:
>>> из scipy import sparse >>> из массива импорта numpy >>> I = массив ([0,3,1,0]) >>> J = массив ([0,3,1,2]) >>> V = массив ([4,5,7,9]) >>> А = разреженный.coo_matrix ((V, (I, J)), shape = (4,4))
Обратите внимание, что индексы не нужно сортировать.
Дублирующиеся (i, j) записи суммируются при преобразовании в CSR или CSC.
>>> I = массив ([0,0,1,3,1,0,0]) >>> J = массив ([0,2,1,3,1,0,0]) >>> V = массив ([1,1,1,1,1,1,1]) >>> B = sparse.coo_matrix ((V, (I, J)), shape = (4,4)). Tocsr ()
Это полезно для построения матриц жесткости и массы методом конечных элементов.
Дополнительная информация
Индексы столбцов CSR не обязательно отсортированы.Аналогично для строки CSC индексы. Используйте методы .sorted_indices () и .sort_indices (), когда отсортированные индексы обязательны (например, при передаче данных в другие библиотеки).
.

 array([[1, 1], [2, 1], [3, -3]])
print(A.transpose())
'''
Вывод:
[[ 1 2 3]
[ 1 1 -3]]
'''
array([[1, 1], [2, 1], [3, -3]])
print(A.transpose())
'''
Вывод:
[[ 1 2 3]
[ 1 1 -3]]
'''
 array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[0] =", A[0]) # Первая строка
print("A[2] =", A[2]) # Третья строка
print("A[-1] =", A[-1]) # Последняя строка (третья строка в данном случае)
array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[0] =", A[0]) # Первая строка
print("A[2] =", A[2]) # Третья строка
print("A[-1] =", A[-1]) # Последняя строка (третья строка в данном случае)
 array([1, 3, 5, 7, 9, 7, 5])
# с 3-го по 5-ый элементы
print(letters[2:5]) # Вывод: [5, 7, 9]
# с 1-го по 4-ый элементы
print(letters[:-5]) # Вывод: [1, 3]
# с 6-го до последнего элемента
print(letters[5:]) # Вывод:[7, 5]
# с 1-го до последнего элемента
print(letters[:]) # Вывод:[1, 3, 5, 7, 9, 7, 5]
# список в обратном порядке
print(letters[::-1]) # Вывод:[5, 7, 9, 7, 5, 3, 1]
array([1, 3, 5, 7, 9, 7, 5])
# с 3-го по 5-ый элементы
print(letters[2:5]) # Вывод: [5, 7, 9]
# с 1-го по 4-ый элементы
print(letters[:-5]) # Вывод: [1, 3]
# с 6-го до последнего элемента
print(letters[5:]) # Вывод:[7, 5]
# с 1-го до последнего элемента
print(letters[:]) # Вывод:[1, 3, 5, 7, 9, 7, 5]
# список в обратном порядке
print(letters[::-1]) # Вывод:[5, 7, 9, 7, 5, 3, 1]
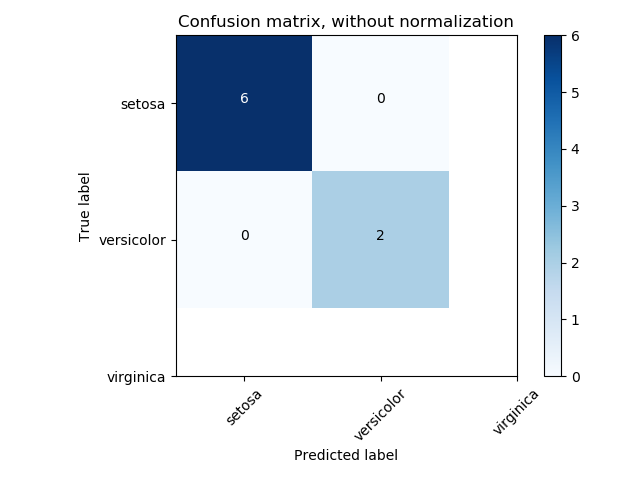 zeros(10)
Z[4] = 1
print(Z)
zeros(10)
Z[4] = 1
print(Z)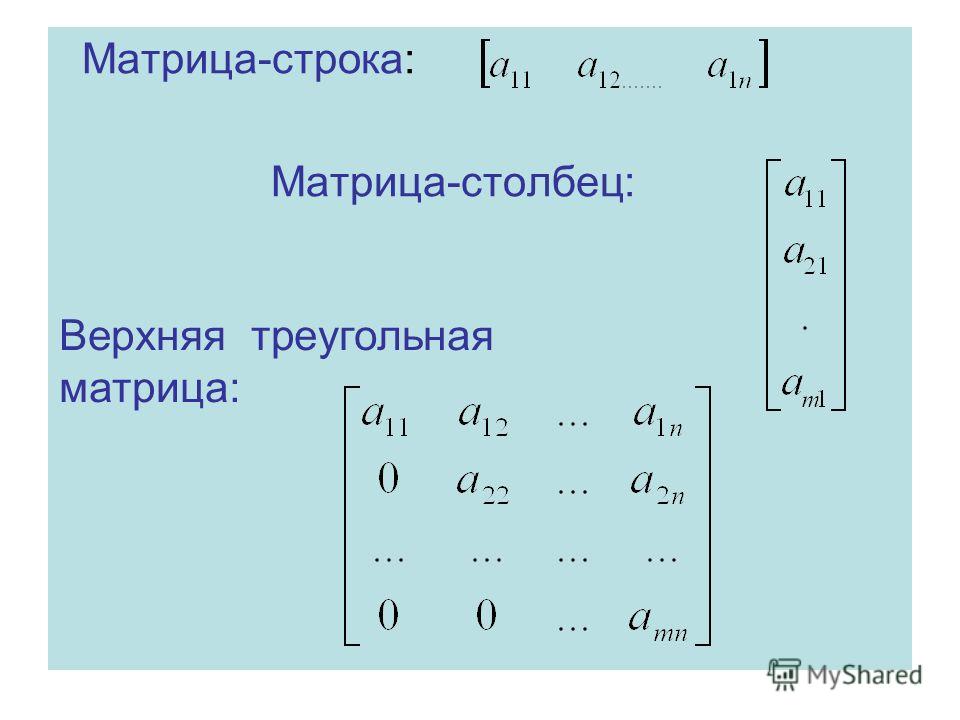 ones((10,10))
Z[1:-1,1:-1] = 0
ones((10,10))
Z[1:-1,1:-1] = 0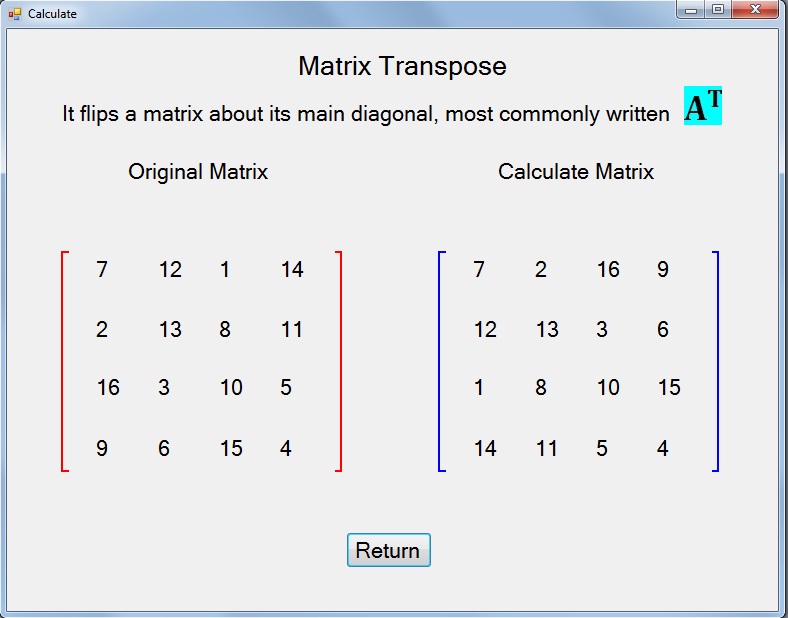 zeros((5,5))
Z += np.arange(5)
print(Z)
zeros((5,5))
Z += np.arange(5)
print(Z) random.random(10)
Z[Z.argmax()] = 0
print(Z)
random.random(10)
Z[Z.argmax()] = 0
print(Z)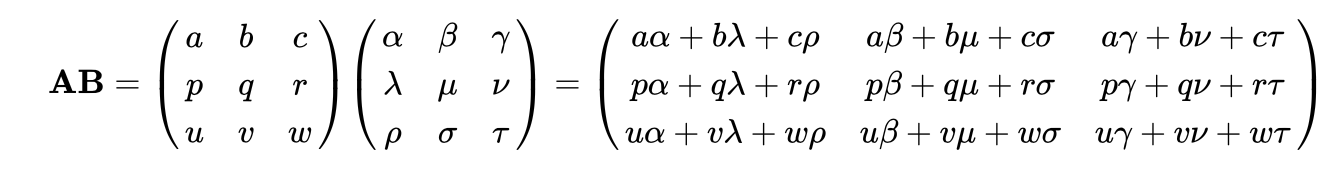 arange(100)
v = np.random.uniform(0,100)
index = (np.abs(Z-v)).argmin()
print(Z[index])
arange(100)
v = np.random.uniform(0,100)
index = (np.abs(Z-v)).argmin()
print(Z[index]) arange(9).reshape(3,3)
for index, value in np.ndenumerate(Z):
print(index, value)
for index in np.ndindex(Z.shape):
print(index, Z[index])
arange(9).reshape(3,3)
for index, value in np.ndenumerate(Z):
print(index, value)
for index in np.ndindex(Z.shape):
print(index, Z[index])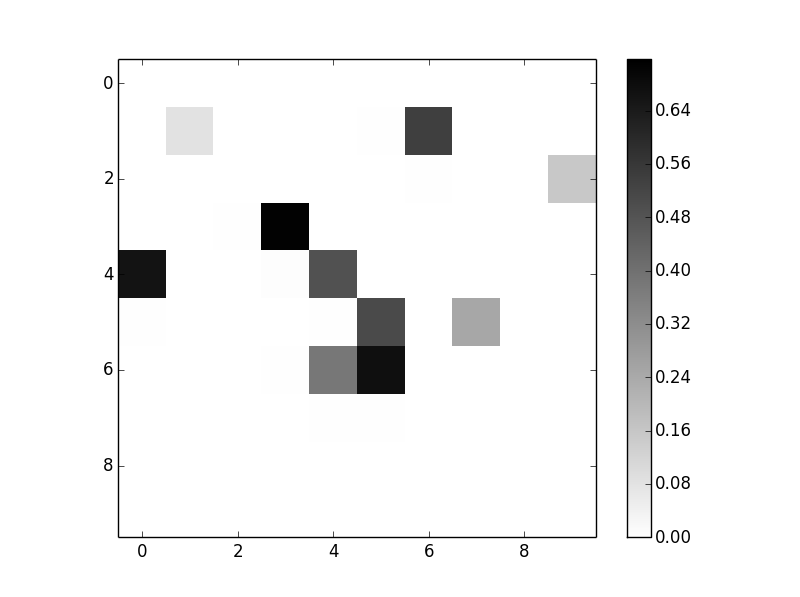 ones(10)
I = np.random.randint(0,len(Z),20)
Z += np.bincount(I, minlength=len(Z))
print(Z)
ones(10)
I = np.random.randint(0,len(Z),20)
Z += np.bincount(I, minlength=len(Z))
print(Z) arange(25).reshape(5,5)
A[[0,1]] = A[[1,0]]
print(A)
arange(25).reshape(5,5)
A[[0,1]] = A[[1,0]]
print(A)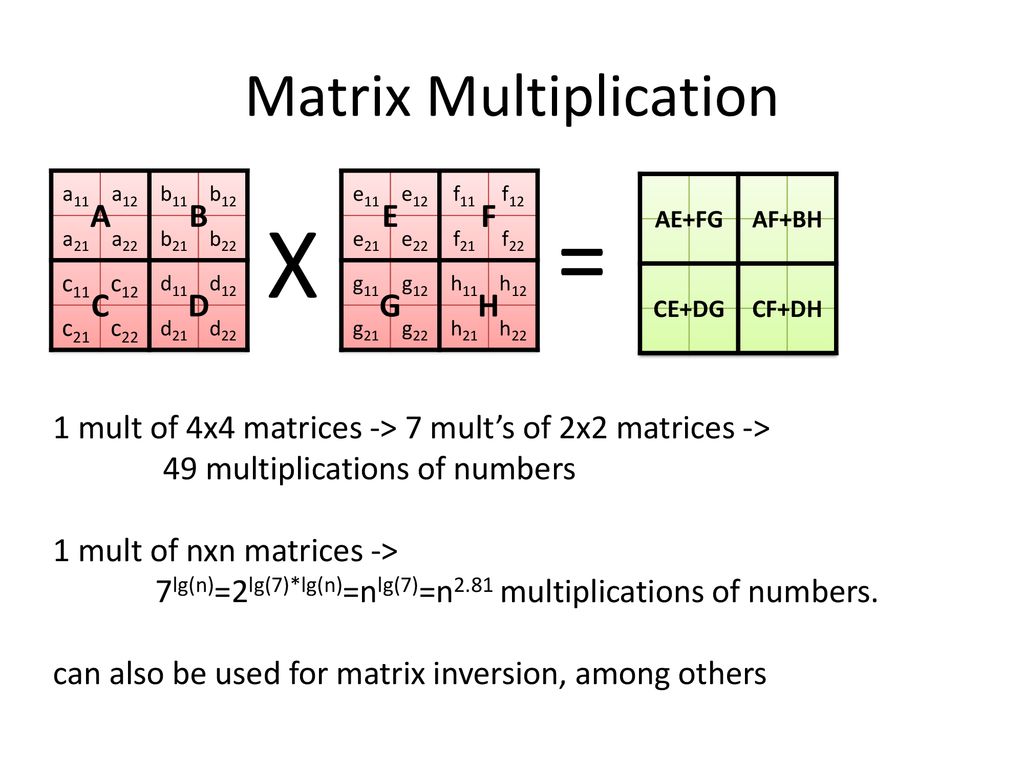 lib import stride_tricks
def rolling(a, window):
shape = (a.size - window + 1, window)
strides = (a.itemsize, a.itemsize)
return stride_tricks.as_strided(a, shape=shape, strides=strides)
Z = rolling(np.arange(10), 3)
print(Z)
lib import stride_tricks
def rolling(a, window):
shape = (a.size - window + 1, window)
strides = (a.itemsize, a.itemsize)
return stride_tricks.as_strided(a, shape=shape, strides=strides)
Z = rolling(np.arange(10), 3)
print(Z) random.randint(0,10,50)
print(np.bincount(Z).argmax())
random.randint(0,10,50)
print(np.bincount(Z).argmax()) ones((p,n,1))
S = np.tensordot(M, V, axes=[[0, 2], [0, 1]])
print(S)
# It works, because:
# M is (p,n,n)
# V is (p,n,1)
# Thus, summing over the paired axes 0 and 0 (of M and V independently),
# and 2 and 1, to remain with a (n,1) vector.
ones((p,n,1))
S = np.tensordot(M, V, axes=[[0, 2], [0, 1]])
print(S)
# It works, because:
# M is (p,n,n)
# V is (p,n,1)
# Thus, summing over the paired axes 0 and 0 (of M and V independently),
# and 2 and 1, to remain with a (n,1) vector. arange(10000)
np.random.shuffle(Z)
n = 5
print (Z[np.argpartition(-Z,n)[:n]])
arange(10000)
np.random.shuffle(Z)
n = 5
print (Z[np.argpartition(-Z,n)[:n]])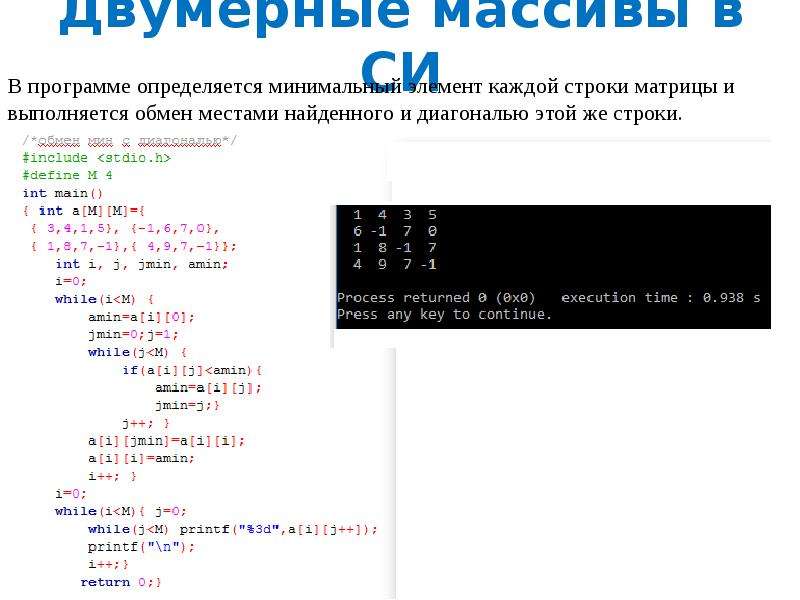 array([0, 1, 2, 3, 15, 16, 32, 64, 128], dtype=np.uint8)
print(np.unpackbits(I[:, np.newaxis], axis=1))
array([0, 1, 2, 3, 15, 16, 32, 64, 128], dtype=np.uint8)
print(np.unpackbits(I[:, np.newaxis], axis=1))