Изучаем матрицы в питоне и массивы NumPy в Python
0 ∞ 1
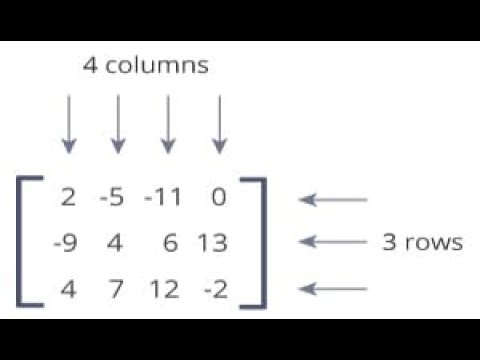
Матрица — это двухмерная структура данных, в которой числа расположены в виде строк и столбцов. Например:
Эта матрица является матрицей три на четыре, потому что она состоит из 3 строк и 4 столбцов.
- Матрицы в Python
- NumPy массивы в Python
- Как создать массив NumPy?
- Массив целых чисел, чисел с плавающей точкой и составных чисел
- Массив нулей и единиц
- Использование arange() и shape()
- Операции с матрицами
- Сложение двух матриц или сумма элементов массива Python
- Умножение двух матриц Python
- Транспонирование матрицы питон
- Доступ к элементам матрицы, строкам и столбца
- Доступ к элементам матрицы
- Доступ к строкам матрицы
- Доступ к столбцам матрицы
- Разделение матрицы
Python не имеет встроенного типа данных для матриц. Но можно рассматривать список как матрицу. Например:
Но можно рассматривать список как матрицу. Например:
A = [[1, 4, 5],
[-5, 8, 9]]
Этот список является матрицей на 2 строки и 3 столбца.
Обязательно ознакомьтесь с документацией по спискам Python, прежде чем продолжить читать эту статью.
Давайте посмотрим, как работать с вложенным списком.
A = [[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]]
print("A =", A)
print("A[1] =", A[1]) # вторая строка
print("A[1][2] =", A[1][2]) # третий элемент второй строки
print("A[0][-1] =", A[0][-1]) # последний элемент первой строки
column = []; # пустой список
for row in A:
column.append(row[2])
print("3rd column =", column)
Когда мы запустим эту программу, результат будет следующий:
A = [[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]] A [1] = [-5, 8, 9, 0] A [1] [2] = 9 A [0] [- 1] = 12 3-й столбец = [5, 9, 11]
Использование вложенных списков в качестве матрицы подходит для простых вычислительных задач. Но в Python есть более эффективный способ работы с матрицами – NumPy .
NumPy — это расширение для научных вычислений, которое поддерживает мощный объект N-мерного массива. Прежде чем использовать NumPy, необходимо установить его. Для получения дополнительной информации,
- Ознакомьтесь: Как установить NumPy Python?
- Если вы работаете в Windows, скачайте и установите дистрибутив anaconda Python. Он поставляется вместе с NumPy и другими расширениями.
После установки NumPy можно импортировать и использовать его.
NumPy предоставляет собой многомерный массив чисел (который на самом деле является объектом). Давайте рассмотрим приведенный ниже пример:
import numpy as np a = np.array([1, 2, 3]) print(a) # Вывод: [1, 2, 3] print(type(a)) # Вывод: <class 'numpy.ndarray'>
Как видите, класс массива NumPy называется ndarray.
Существует несколько способов создания массивов NumPy.
import numpy as np A = np.array([[1, 2, 3], [3, 4, 5]]) print(A) A = np.array([[1.1, 2, 3], [3, 4, 5]]) # Массив чисел с плавающей запятой print(A) A = np.array([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив составных чисел print(A)
Когда вы запустите эту программу, результат будет следующий:
[[1 2 3] [3 4 5]] [[1.1 2. 3.] [3. 4. 5.]] [[1. + 0.j 2. + 0.j 3. + 0.j] [3. + 0.j 4. + 0.j 5. + 0.j]]
import numpy as np zeors_array = np.zeros( (2, 3) ) print(zeors_array) ''' Вывод: [[0. 0. 0.] [0. 0. 0.]] ''' ones_array = np.ones( (1, 5), dtype=np.int32 ) // указание dtype print(ones_array) # Вывод: [[1 1 1 1 1]]
Здесь мы указали dtype — 32 бита (4 байта). Следовательно, этот массив может принимать значения от -2-31 до 2-31-1.
import numpy as np
A = np.arange(4)
print('A =', A)
B = np.arange(12).reshape(2, 6)
print('B =', B)
'''
Вывод:
A = [0 1 2 3]
B = [[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]]
'''
Узнайте больше о других способах создания массива NumPy .
Выше мы привели пример сложение, умножение матриц и транспонирование матрицы. Мы использовали вложенные списки, прежде чем создавать эти программы.
Мы используем оператор +, чтобы сложить соответствующие элементы двух матриц NumPy.
import numpy as np A = np.array([[2, 4], [5, -6]]) B = np.array([[9, -3], [3, 6]]) C = A + B # сложение соответствующих элементов print(C) ''' Вывод: [[11 1] [ 8 0]] '''
Чтобы умножить две матрицы, мы используем метод dot(). Узнайте больше о том, как работает numpy.dot .
Примечание: * используется для умножения массива (умножения соответствующих элементов двух массивов), а не умножения матрицы.
import numpy as np A = np.array([[3, 6, 7], [5, -3, 0]]) B = np.array([[1, 1], [2, 1], [3, -3]]) C = a.dot(B) print(C) ''' Вывод: [[ 36 -12] [ -1 2]] '''
Мы используем numpy.transpose для вычисления транспонирования матрицы.
import numpy as np A = np.array([[1, 1], [2, 1], [3, -3]]) print(A.transpose()) ''' Вывод: [[ 1 2 3] [ 1 1 -3]] '''
Как видите, NumPy значительно упростил нашу задачу.
Также можно получить доступ к элементам матрицы, используя индекс. Начнем с одномерного массива NumPy.
import numpy as np
A = np.array([2, 4, 6, 8, 10])
print("A[0] =", A[0]) # Первый элемент
print("A[2] =", A[2]) # Третий элемент
print("A[-1] =", A[-1]) # Последний элемент
Когда вы запустите эту программу, результат будет следующий:
A [0] = 2 A [2] = 6 A [-1] = 10
Теперь выясним, как получить доступ к элементам двухмерного массива (который в основном представляет собой матрицу).
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
# Первый элемент первой строки
print("A[0][0] =", A[0][0])
# Третий элемент второй строки
print("A[1][2] =", A[1][2])
# Последний элемент последней строки
print("A[-1][-1] =", A[-1][-1])
Когда мы запустим эту программу, результат будет следующий:
A [0] [0] = 1 A [1] [2] = 9 A [-1] [- 1] = 19
import numpy as np A = np.array([[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]]) print("A[0] =", A[0]) # Первая строка print("A[2] =", A[2]) # Третья строка print("A[-1] =", A[-1]) # Последняя строка (третья строка в данном случае)
Когда мы запустим эту программу, результат будет следующий:
A [0] = [1, 4, 5, 12] A [2] = [-6, 7, 11, 19] A [-1] = [-6, 7, 11, 19]
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[:,0] =",A[:,0]) # Первый столбец
print("A[:,3] =", A[:,3]) # Четвертый столбец
print("A[:,-1] =", A[:,-1]) # Последний столбец (четвертый столбец в данном случае)
Когда мы запустим эту программу, результат будет следующий:
A [:, 0] = [1 -5 -6] A [:, 3] = [12 0 19] A [:, - 1] = [12 0 19]
Если вы не знаете, как работает приведенный выше код, прочтите раздел «Разделение матрицы».
Разделение одномерного массива NumPy аналогично разделению списка. Рассмотрим пример:
import numpy as np letters = np.array([1, 3, 5, 7, 9, 7, 5]) # с 3-го по 5-ый элементы print(letters[2:5]) # Вывод: [5, 7, 9] # с 1-го по 4-ый элементы print(letters[:-5]) # Вывод: [1, 3] # с 6-го до последнего элемента print(letters[5:]) # Вывод:[7, 5] # с 1-го до последнего элемента print(letters[:]) # Вывод:[1, 3, 5, 7, 9, 7, 5] # список в обратном порядке print(letters[::-1]) # Вывод:[5, 7, 9, 7, 5, 3, 1]
Теперь посмотрим, как разделить матрицу.
import numpy as np
A = np.array([[1, 4, 5, 12, 14],
[-5, 8, 9, 0, 17],
[-6, 7, 11, 19, 21]])
print(A[:2, :4]) # две строки, четыре столбца
''' Вывод:
[[ 1 4 5 12]
[-5 8 9 0]]
'''
print(A[:1,]) # первая строка, все столбцы
''' Вывод:
[[ 1 4 5 12 14]]
'''
print(A[:,2]) # все строки, второй столбец
''' Вывод:
[ 5 9 11]
'''
print(A[:, 2:5]) # все строки, с третьего по пятый столбец
''' Вывод:
[[ 5 12 14]
[ 9 0 17]
[11 19 21]]
'''
Использование NumPy вместо вложенных списков значительно упрощает работу с матрицами. Мы рекомендуем детально изучить пакет NumPy, если вы планируете использовать Python для анализа данных.
Мы рекомендуем детально изучить пакет NumPy, если вы планируете использовать Python для анализа данных.
Вадим Дворниковавтор-переводчик статьи «Python Matrices and NumPy Arrays»
Дайте знать, что вы думаете по этой теме материала в комментариях. За комментарии, дизлайки, отклики, лайки, подписки низкий вам поклон!
Изучаем матрицы в питоне и массивы NumPy в Python
0 ∞ 1
Матрица — это двухмерная структура данных, в которой числа расположены в виде строк и столбцов. Например:
Эта матрица является матрицей три на четыре, потому что она состоит из 3 строк и 4 столбцов.
- Матрицы в Python
- NumPy массивы в Python
- Как создать массив NumPy?
- Массив целых чисел, чисел с плавающей точкой и составных чисел
- Массив нулей и единиц
- Использование arange() и shape()
- Операции с матрицами
- Сложение двух матриц или сумма элементов массива Python
- Умножение двух матриц Python
- Транспонирование матрицы питон
- Доступ к элементам матрицы, строкам и столбца
- Доступ к элементам матрицы
- Доступ к строкам матрицы
- Доступ к столбцам матрицы
- Разделение матрицы
Python не имеет встроенного типа данных для матриц. Но можно рассматривать список как матрицу. Например:
Но можно рассматривать список как матрицу. Например:
A = [[1, 4, 5],
[-5, 8, 9]]
Этот список является матрицей на 2 строки и 3 столбца.
Обязательно ознакомьтесь с документацией по спискам Python, прежде чем продолжить читать эту статью.
Давайте посмотрим, как работать с вложенным списком.
A = [[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]]
print("A =", A)
print("A[1] =", A[1]) # вторая строка
print("A[1][2] =", A[1][2]) # третий элемент второй строки
print("A[0][-1] =", A[0][-1]) # последний элемент первой строки
column = []; # пустой список
for row in A:
column.append(row[2])
print("3rd column =", column)
Когда мы запустим эту программу, результат будет следующий:
A = [[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]] A [1] = [-5, 8, 9, 0] A [1] [2] = 9 A [0] [- 1] = 12 3-й столбец = [5, 9, 11]
Использование вложенных списков в качестве матрицы подходит для простых вычислительных задач. Но в Python есть более эффективный способ работы с матрицами – NumPy .
NumPy — это расширение для научных вычислений, которое поддерживает мощный объект N-мерного массива. Прежде чем использовать NumPy, необходимо установить его. Для получения дополнительной информации,
- Ознакомьтесь: Как установить NumPy Python?
- Если вы работаете в Windows, скачайте и установите дистрибутив anaconda Python. Он поставляется вместе с NumPy и другими расширениями.
После установки NumPy можно импортировать и использовать его.
NumPy предоставляет собой многомерный массив чисел (который на самом деле является объектом). Давайте рассмотрим приведенный ниже пример:
import numpy as np a = np.array([1, 2, 3]) print(a) # Вывод: [1, 2, 3] print(type(a)) # Вывод: <class 'numpy.ndarray'>
Как видите, класс массива NumPy называется ndarray.
Существует несколько способов создания массивов NumPy.
import numpy as np A = np.array([[1, 2, 3], [3, 4, 5]]) print(A) A = np.array([[1.1, 2, 3], [3, 4, 5]]) # Массив чисел с плавающей запятой print(A) A = np.array([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив составных чисел print(A)
Когда вы запустите эту программу, результат будет следующий:
[[1 2 3] [3 4 5]] [[1.1 2. 3.] [3. 4. 5.]] [[1. + 0.j 2. + 0.j 3. + 0.j] [3. + 0.j 4. + 0.j 5. + 0.j]]
import numpy as np zeors_array = np.zeros( (2, 3) ) print(zeors_array) ''' Вывод: [[0. 0. 0.] [0. 0. 0.]] ''' ones_array = np.ones( (1, 5), dtype=np.int32 ) // указание dtype print(ones_array) # Вывод: [[1 1 1 1 1]]
Здесь мы указали dtype — 32 бита (4 байта). Следовательно, этот массив может принимать значения от -2-31 до 2-31-1.
import numpy as np
A = np.arange(4)
print('A =', A)
B = np.arange(12).reshape(2, 6)
print('B =', B)
'''
Вывод:
A = [0 1 2 3]
B = [[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]]
'''
Узнайте больше о других способах создания массива NumPy .
Выше мы привели пример сложение, умножение матриц и транспонирование матрицы. Мы использовали вложенные списки, прежде чем создавать эти программы. Рассмотрим, как выполнить ту же задачу, используя массив NumPy.
Рассмотрим, как выполнить ту же задачу, используя массив NumPy.
Мы используем оператор +, чтобы сложить соответствующие элементы двух матриц NumPy.
import numpy as np A = np.array([[2, 4], [5, -6]]) B = np.array([[9, -3], [3, 6]]) C = A + B # сложение соответствующих элементов print(C) ''' Вывод: [[11 1] [ 8 0]] '''
Чтобы умножить две матрицы, мы используем метод dot(). Узнайте больше о том, как работает numpy.dot .
Примечание: * используется для умножения массива (умножения соответствующих элементов двух массивов), а не умножения матрицы.
import numpy as np A = np.array([[3, 6, 7], [5, -3, 0]]) B = np.array([[1, 1], [2, 1], [3, -3]]) C = a.dot(B) print(C) ''' Вывод: [[ 36 -12] [ -1 2]] '''
Мы используем numpy.transpose для вычисления транспонирования матрицы.
import numpy as np A = np.array([[1, 1], [2, 1], [3, -3]]) print(A.transpose()) ''' Вывод: [[ 1 2 3] [ 1 1 -3]] '''
Как видите, NumPy значительно упростил нашу задачу.
Также можно получить доступ к элементам матрицы, используя индекс. Начнем с одномерного массива NumPy.
import numpy as np
A = np.array([2, 4, 6, 8, 10])
print("A[0] =", A[0]) # Первый элемент
print("A[2] =", A[2]) # Третий элемент
print("A[-1] =", A[-1]) # Последний элемент
Когда вы запустите эту программу, результат будет следующий:
A [0] = 2 A [2] = 6 A [-1] = 10
Теперь выясним, как получить доступ к элементам двухмерного массива (который в основном представляет собой матрицу).
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
# Первый элемент первой строки
print("A[0][0] =", A[0][0])
# Третий элемент второй строки
print("A[1][2] =", A[1][2])
# Последний элемент последней строки
print("A[-1][-1] =", A[-1][-1])
Когда мы запустим эту программу, результат будет следующий:
A [0] [0] = 1 A [1] [2] = 9 A [-1] [- 1] = 19
import numpy as np A = np.array([[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]]) print("A[0] =", A[0]) # Первая строка print("A[2] =", A[2]) # Третья строка print("A[-1] =", A[-1]) # Последняя строка (третья строка в данном случае)
Когда мы запустим эту программу, результат будет следующий:
A [0] = [1, 4, 5, 12] A [2] = [-6, 7, 11, 19] A [-1] = [-6, 7, 11, 19]
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[:,0] =",A[:,0]) # Первый столбец
print("A[:,3] =", A[:,3]) # Четвертый столбец
print("A[:,-1] =", A[:,-1]) # Последний столбец (четвертый столбец в данном случае)
Когда мы запустим эту программу, результат будет следующий:
A [:, 0] = [1 -5 -6] A [:, 3] = [12 0 19] A [:, - 1] = [12 0 19]
Если вы не знаете, как работает приведенный выше код, прочтите раздел «Разделение матрицы».
Разделение одномерного массива NumPy аналогично разделению списка. Рассмотрим пример:
import numpy as np letters = np.array([1, 3, 5, 7, 9, 7, 5]) # с 3-го по 5-ый элементы print(letters[2:5]) # Вывод: [5, 7, 9] # с 1-го по 4-ый элементы print(letters[:-5]) # Вывод: [1, 3] # с 6-го до последнего элемента print(letters[5:]) # Вывод:[7, 5] # с 1-го до последнего элемента print(letters[:]) # Вывод:[1, 3, 5, 7, 9, 7, 5] # список в обратном порядке print(letters[::-1]) # Вывод:[5, 7, 9, 7, 5, 3, 1]
Теперь посмотрим, как разделить матрицу.
import numpy as np
A = np.array([[1, 4, 5, 12, 14],
[-5, 8, 9, 0, 17],
[-6, 7, 11, 19, 21]])
print(A[:2, :4]) # две строки, четыре столбца
''' Вывод:
[[ 1 4 5 12]
[-5 8 9 0]]
'''
print(A[:1,]) # первая строка, все столбцы
''' Вывод:
[[ 1 4 5 12 14]]
'''
print(A[:,2]) # все строки, второй столбец
''' Вывод:
[ 5 9 11]
'''
print(A[:, 2:5]) # все строки, с третьего по пятый столбец
''' Вывод:
[[ 5 12 14]
[ 9 0 17]
[11 19 21]]
'''
Использование NumPy вместо вложенных списков значительно упрощает работу с матрицами. Мы рекомендуем детально изучить пакет NumPy, если вы планируете использовать Python для анализа данных.
Мы рекомендуем детально изучить пакет NumPy, если вы планируете использовать Python для анализа данных.
Вадим Дворниковавтор-переводчик статьи «Python Matrices and NumPy Arrays»
Дайте знать, что вы думаете по этой теме материала в комментариях. За комментарии, дизлайки, отклики, лайки, подписки низкий вам поклон!
Python — Матрица — GeeksforGeeks
Здесь мы обсудим различные способы формирования матрицы с помощью Python. В этом руководстве мы также обсудим различные операции, которые можно выполнять с матрицей. мы также рассмотрим внешний модуль Numpy для формирования матрицы и его операции в Python.
Что такое матрица?
Матрица представляет собой набор чисел, расположенных в виде прямоугольного массива в строках и столбцах. В области техники, физики, статистики и графики матрицы широко используются для выражения поворотов изображения и других типов преобразований.
Матрица называется матрицей размера m на n и обозначается символом «m x n» , если имеется m строк и n столбцов.
Создание простой матрицы с использованием Python
Метод 1: Создание матрицы со списком из списков
Здесь мы собираемся создать матрицу с использованием списка списков.
Python3
|
Выход:
Матрица = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]9001 5 Способ 2 : получение ввода матрицы от пользователя в Python
Здесь мы берем ряд строк и столбцов от пользователя и печатаем матрицу.
Python3
|
Вывод:
Введите количество строк:2 Введите количество столбцов: 2 Введите записи построчно: 5 6 7 8 5 6 7 8
Временная сложность: O(n*n)
Вспомогательное пространство: O(n*n)
Метод 3.
 Создание матрицы с использованием понимания списка
Создание матрицы с использованием понимания спискаПредставление списка — это элегантный способ определения и создания списка в Python, используют функцию диапазона для печати 4 строк и 4 столбцов.
Python3
|
Вывод:
[[0, 1, 2, 3], [0, 1, 2, 3], [0, 1, 2, 3], [0, 1, 2, 3]]
Присвоение значения в матрице
Способ 1: присвоить значение отдельной ячейке в матрице
Здесь мы заменяем и присваиваем значение отдельной ячейке (1 строка и 1 столбец = 11) в матрице.
Python3
|
Вывод:
[[1, 2, 3 ], [4, 11 , 6], [7, 8, 9]]
Способ 2.
 Присвоение значения отдельной ячейке с использованием отрицательного индексирования в матрице
Присвоение значения отдельной ячейке с использованием отрицательного индексирования в матрицеЗдесь мы заменяем и присваиваем значение отдельной ячейке (-2 строки и -1 столбца = 21) в матрице.
Python3
|
Вывод:
[[1, 2, 3], [4, 5, 21 ], [7, 8, 9 ]]
Доступ к значению в матрице
Метод 1: доступ к значениям матрицы
Здесь мы получаем доступ к элементам матрицы, передавая ее строку и столбец.
Python3
|
Вывод:
Матрица в 1 строке и 3 столбцах = 3 Матрица с 3 строками и 3 столбцами = 9
Метод 2: доступ к значениям матрицы с использованием отрицательной индексации
Здесь мы получаем доступ к элементам матрицы, передавая ее строку и столбец с отрицательной индексацией.
Python3
|
Вывод:
8
Математические операции с матрицей в Python
Пример 1.
 Добавление значений в матрицу с помощью цикла for в Python
Добавление значений в матрицу с помощью цикла for в PythonЗдесь мы добавляем две матрицы, используя цикл for в Python.
Python3
|
Вывод:
[10, 10, 10] [10, 10, 10] [10, 10, 10]
Временная сложность: O(n*n)
Вспомогательное пространство: O(n*n)
Пример 2: Добавление и вычитание значений в матрице с пониманием списка
Выполнение основного сложения и вычитание с использованием понимания списка.
Python3
| 9 0106
Выход:
Добавление матрицы [10, 10, 10] [10, 10, 10] [10, 10, 10] Матричное вычитание [-8, -6, -4] [-2, 0, 2] [4, 6, 8]
Временная сложность: O(n*n)
Вспомогательное пространство: O(n*n)
Пример 3: Программа Python для умножения и деления двух матриц
Выполнение базового умножения и деления с использованием цикла Python.
Python3
90 003 900 26 печать 9 0026
|
Вывод:
Умножение матриц [9, 16, 21] [24, 25, 24] [21, 16, 9] Матричный отдел [0, 0, 0] [0, 1, 1] [2, 4, 9]
Временная сложность: O(n*n)
Вспомогательное пространство: O(n*n)
Транспонирование в матрице
Пример: Программа Python для транспонирования матрицы с использованием цикла
Транспонирование матрицы достигается заменой строк на столбцы и столбцов на строки. Другими словами, транспонирование A[][] получается путем замены A[i][j] на A[j][i].
Другими словами, транспонирование A[][] получается путем замены A[i][j] на A[j][i].
Python3
|
Вывод:
[9, 6, 3] [8, 5, 2] [7, 4, 1]
Временная сложность: O(n*n)
Вспомогательное пространство: O(n*n)
Матрица с использованием Numpy
Создание матрицы с использованием Numpy
Здесь мы создаем массив Numpy с помощью numpy. random и случайный модуль.
random и случайный модуль.
Python3
|
Выход: 90 011
[[2 7 5] [8 5 1] [8 4 6]]
Матричные математические операции в Python с использованием Numpy
Здесь мы рассмотрим различные математические операции, такие как сложение, вычитание, умножение и деление, с использованием Numpy.
Python3
печать (numpy.subtract(x, у))
|
Вывод:
Поэлементное сложение матрицы является : [[ 8 10] [13 15]] Поэлементное вычитание матрицы: [[-6 -6] [-5 -5]] Поэлементное умножение матрицы: [[ 7 16] [36 50]] Поэлементное деление матрицы: [[0,14285714 0,25 ] [0,44444444 0,5 ]]
Точечное и перекрестное произведение с матрицей
Здесь мы найдем внутреннее, внешнее и перекрестное произведение матриц и векторов, используя NumPy в Python.
Python3
|
Выход:
Скалярное произведение двух массивов: [[ 30 24 18] [ 84 69 54 ] [138 114 90]] Перекрестное произведение двух массивов: [[-10 20 -10] [-10 20 -10] [-10 20 -10]]
Транспонирование матрицы в Python с использованием Numpy
Чтобы выполнить операцию транспонирования в матрице, мы можем использовать метод numpy.transpose().
Python3
|
Вывод:
[[1 4][2 5][3 6]]
Создать пустую матрицу с NumPy в Python
Инициализация пустой массив, используя функцию np.zeros().
Python3
|
Матрица 2x2: [[0 0] [0 0]] Матрица 3x3: [[0.0. 0.] [0. 0. 0.] [0. 0. 0.]]
Нарезка в матрице с использованием Numpy
Нарезка — это процесс выбора определенных строк и столбцов из матрицы и последующего создания новой матрицы путем удаления всех невыбранных элементов. В первом примере мы печатаем всю матрицу, во втором мы передаем 2 в качестве начального индекса, 3 в качестве последнего индекса и скачок индекса в качестве 1. То же самое используется в следующем принте, мы только изменили индекс перейти к 2.
Python3
|
9 0010 Вывод:
[[ 6 8 10] [ 9 -12 15] [ 12 16 20 ] [ 15 -20 25]] Разрезание третьей строки — второй столбец: [16] Нарезка третьей строки — третьего столбца: [20]
Удаление строк и столбцов с помощью Numpy
Здесь мы пытаемся удалить строки с помощью функции np. delete(). В коде мы сначала пытались удалить 0 th ряд, затем мы попытались удалить 2 й ряд, а затем 3 й ряд.
delete(). В коде мы сначала пытались удалить 0 th ряд, затем мы попытались удалить 2 й ряд, а затем 3 й ряд.
Python3
|
Вывод:
данные после удаления 0-й строки: [[ 9 -12 15] [ 12 16 20 ] [ 15 -20 25]] данные после удаления 1-й строки: [[ 6 8 10] [ 12 16 20 ] [ 15 -20 25]] данные после удаления 2-й строки: [[ 6 8 10] [ 9 -12 15] [ 15 -20 25]]
Добавить строку/столбцы в массив Numpy
Мы добавили еще один столбец в позицию 4 th , используя np. hstack.
hstack.
Python3
|
Вывод:
результирующий массив [[ 6 8 10 1] [ 9 -12 15 2] [ 15 -20 25 3]]
Примеры транспонирования, умножения, массивов NumPy
Что такое матрица Python?
Матрица Python — это специализированный двумерный прямоугольный массив данных, хранящихся в строках и столбцах.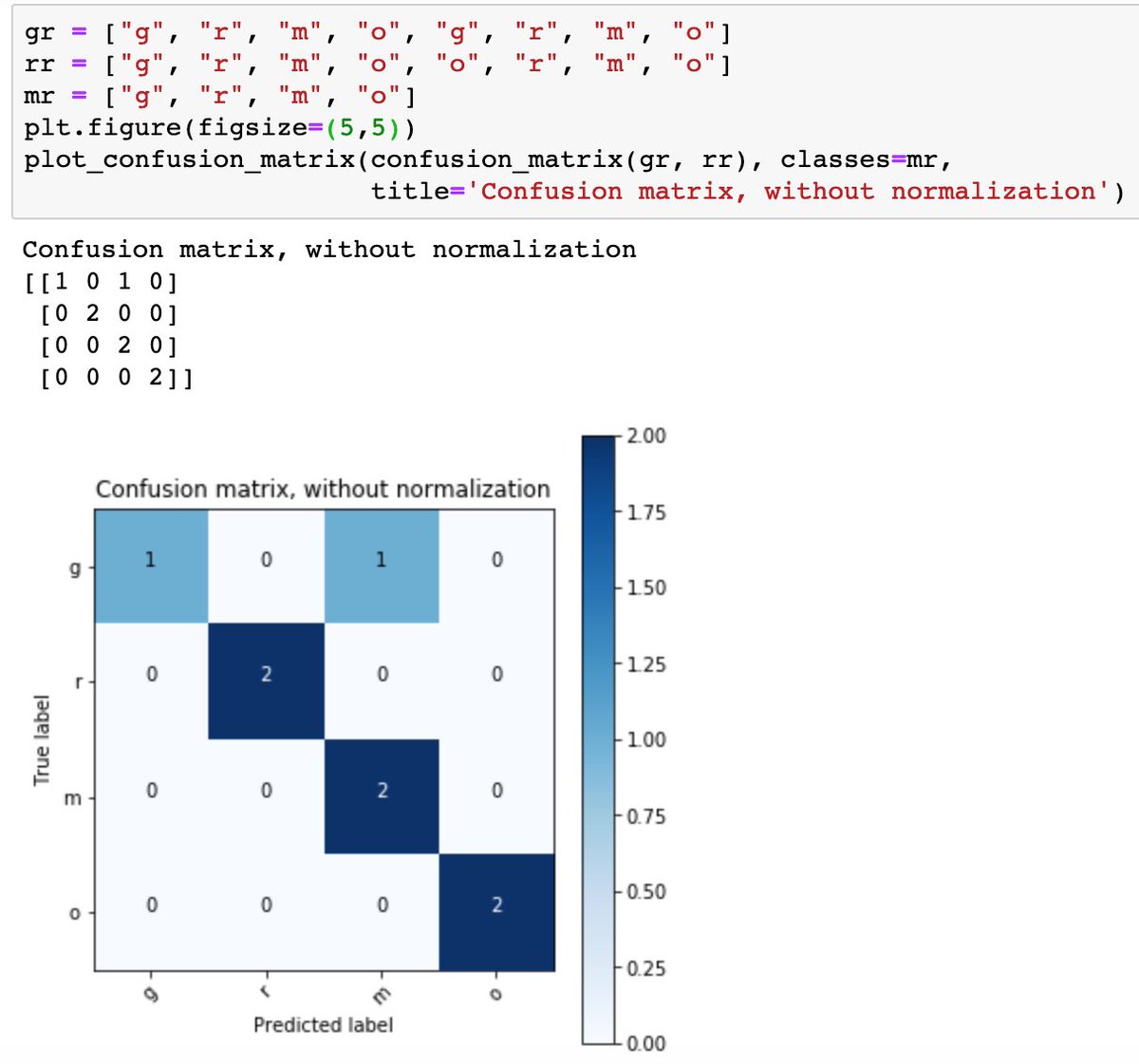 Данные в матрице могут быть числами, строками, выражениями, символами и т. д. Матрица — одна из важных структур данных, которую можно использовать в математических и научных расчетах.
Данные в матрице могут быть числами, строками, выражениями, символами и т. д. Матрица — одна из важных структур данных, которую можно использовать в математических и научных расчетах.
Из этого руководства по Python вы узнаете:
- Что такое матрица Python?
- Как работают матрицы Python?
- Создание матрицы Python с использованием типа данных вложенного списка
- Чтобы прочитать данные внутри Python Matrix, используя список.
- Пример 2: Чтобы прочитать последний элемент из каждой строки.
- Пример 3: Печать строк в матрице
- Добавление матриц с использованием вложенного списка
- Умножение матриц с использованием вложенного списка
- Создание матрицы Python с использованием массивов из пакета Python Numpy
- Матричная операция с использованием Numpy.Array()
- Доступ к матрице NumPy
Как работают матрицы Python?
Данные внутри двумерного массива в матричном формате выглядят следующим образом:
Шаг 1)
Он показывает матрицу 2×2.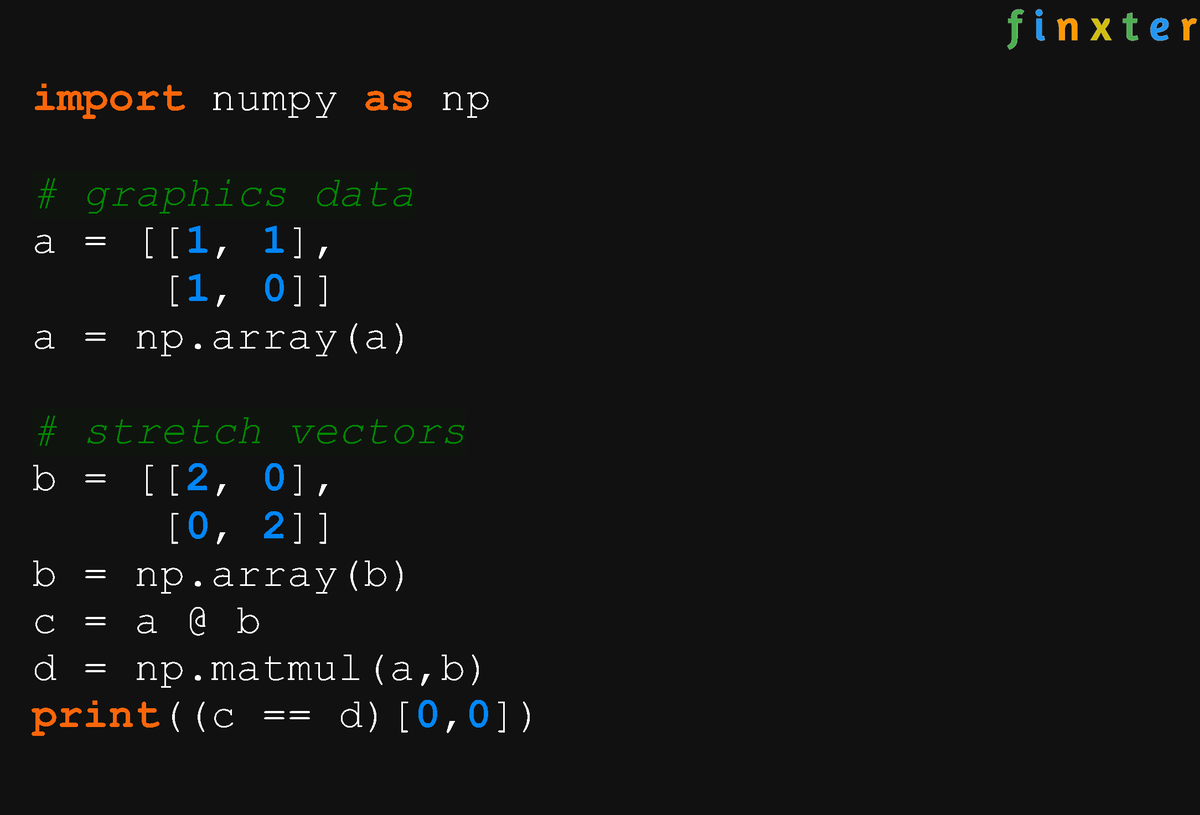 Он имеет две строки и 2 столбца. Данные внутри матрицы являются числами. Строка1 имеет значения 2,3, а строка2 имеет значения 4,5. Столбцы, т. е. col1, имеют значения 2,4, а col2 — значения 3,5.
Он имеет две строки и 2 столбца. Данные внутри матрицы являются числами. Строка1 имеет значения 2,3, а строка2 имеет значения 4,5. Столбцы, т. е. col1, имеют значения 2,4, а col2 — значения 3,5.
Шаг 2)
Показывает матрицу 2×3. Он имеет две строки и три столбца. Данные внутри первой строки, т. е. row1, имеют значения 2, 3, 4, а row2 — значения 5, 6, 7. Столбцы col1 имеют значения 2,5, col2 имеют значения 3,6, а col3 имеют значения 4,7.
Точно так же вы можете хранить свои данные внутри матрицы nxn в Python. Многие операции могут быть выполнены с матричным сложением, вычитанием, умножением и т. д.
В Python нет простого способа реализации матричного типа данных.
Матрица Python использует массивы, и то же самое можно реализовать.
- Создание матрицы Python с использованием типа данных вложенного списка
- Создание матрицы Python с использованием массивов из пакета Python Numpy
Создание матрицы Python с использованием типа данных вложенного списка
В Python массивы представляются с использованием типа данных списка. Итак, теперь мы будем использовать список для создания матрицы Python.
Итак, теперь мы будем использовать список для создания матрицы Python.
Мы создадим матрицу 3×3, как показано ниже:
- Матрица состоит из 3 строк и 3 столбцов.
- Первая строка в формате списка будет следующей: [8,14,-6]
- Вторая строка в списке будет: [12,7,4]
- Третья строка в списке будет: [-11,3,21]
Матрица внутри списка со всеми строками и столбцами показана ниже:
Список = [[Row1],
[Ряд 2],
[Строка 3]
...
[РядN]]
Таким образом, в соответствии с приведенной выше матрицей тип списка с матричными данными выглядит следующим образом:
М1 = [[8, 14, -6], [12,7,4], [-11,3,21]]
Для чтения данных внутри Python Matrix с помощью списка.
Мы будем использовать матрицу, определенную выше. Пример будет читать данные, печатать матрицу, отображать последний элемент из каждой строки.
Пример: для печати матрицы
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
#Чтобы распечатать матрицу
печать(M1)
Вывод:
Матрица M1 = [[8, 14, -6], [12, 7, 4], [-11, 3, 21]]
Пример 2: Чтобы прочитать последний элемент из каждой строки.

М1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
длина_матрицы = длина (M1)
#Чтобы прочитать последний элемент из каждой строки.
для i в диапазоне (matrix_length):
печать (M1[i][-1])
Вывод:
-6 4 21
Пример 3: Печать строк в матрице
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
длина_матрицы = длина (M1)
#Чтобы напечатать строки в матрице
для i в диапазоне (matrix_length):
печать (M1 [я])
Вывод:
[8, 14, -6] [12, 7, 4] [-11, 3, 21]
Добавление матриц с помощью вложенного списка
Мы можем легко добавить две заданные матрицы. Матрицы здесь будут в виде списка. Давайте поработаем над примером, который позаботится о добавлении данных матриц.
Матрица 1:
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
Матрица 2 :
M2 = [[3, 16, -6],
[9,7,-4],
[-1,3,13]]
Последняя инициализирует матрицу, в которой будет храниться результат M1 + M2.
Матрица 3 :
M3 = [[0,0,0],
[0,0,0],
[0,0,0]]
Пример: добавление матриц
Для добавления матриц будет использоваться цикл for, который будет проходить по обеим заданным матрицам.
М1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
М2 = [[3, 16, -6],
[9,7,-4],
[-1,3,13]]
М3 = [[0,0,0],
[0,0,0],
[0,0,0]]
длина_матрицы = длина (M1)
#Чтобы добавить матрицы M1 и M2
для i в диапазоне (len (M1)):
для k в диапазоне (len (M2)):
M3[i][k] = M1[i][k] + M2[i][k]
#Распечатать матрицу
print("Сумма матриц M1 и M2 = ", M3)
Вывод:
Сумма матриц M1 и M2 = [[11, 30, -12], [21, 14, 0], [-12, 6, 34]]
Умножение матриц с использованием вложенного списка
Чтобы умножить матрицы, мы можем использовать цикл for для обеих матриц, как показано в коде ниже:
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
М2 = [[3, 16, -6],
[9,7,-4],
[-1,3,13]]
М3 = [[0,0,0],
[0,0,0],
[0,0,0]]
длина_матрицы = длина (M1)
#Для умножения матриц M1 и M2
для i в диапазоне (len (M1)):
для k в диапазоне (len (M2)):
M3[i][k] = M1[i][k] * M2[i][k]
#Распечатать матрицу
print("Умножение матриц M1 и M2 = ", M3)
Вывод:
Умножение матриц M1 и M2 = [[24, 224, 36], [108, 49, -16], [11, 9, 273]]
Создание матрицы Python с использованием массивов из пакета Python Numpy
Библиотека Python Numpy помогает работать с массивами. Numpy обрабатывает массив немного быстрее, чем список.
Numpy обрабатывает массив немного быстрее, чем список.
Для работы с Numpy его необходимо сначала установить. Следуйте инструкциям ниже, чтобы установить Numpy.
Шаг 1)
Команда для установки Numpy:
pip install NumPy
Шаг 2)
Чтобы использовать Numpy в своем коде, его необходимо импортировать.
import NumPy
Шаг 3)
Вы также можете импортировать Numpy, используя псевдоним, как показано ниже:
import NumPy as np
создать матрица питона.
Пример: массив в Numpy для создания матрицы Python
импортировать numpy как np M1 = np.массив([[5, -10, 15], [3, -6, 9], [-4, 8, 12]]) печать(M1)
Вывод:
[[ 5 -10 15] [ 3 -6 9] [-4 8 12]]
Матричная операция с использованием Numpy.Array()
Матричная операция, которую можно выполнить, — это сложение, вычитание, умножение, транспонирование, чтение строк, столбцов матрицы, нарезка матрицы и т. д. Во всех примерах мы собирается использовать метод array().
д. Во всех примерах мы собирается использовать метод array().
Сложение матрицы
Чтобы выполнить сложение матрицы, мы создадим две матрицы с помощью numpy.array() и добавим их с помощью оператора (+).
Пример:
импортировать numpy как np M1 = np.array([[3, 6, 9], [5, -10, 15], [-7, 14, 21]]) M2 = np.array([[9, -18, 27], [11, 22, 33], [13, -26, 39]]) М3 = М1 + М2 печать(M3)
Вывод:
[[ 12 -12 36] [ 16 12 48 ] [ 6 -12 60]]
Вычитание матрицы
Чтобы выполнить вычитание матрицы, мы создадим две матрицы с помощью numpy.array() и вычтем их с помощью оператора (-).
Пример:
импортировать numpy как np M1 = np.array([[3, 6, 9], [5, -10, 15], [-7, 14, 21]]) M2 = np.array([[9, -18, 27], [11, 22, 33], [13, -26, 39]]) М3 = М1 - М2 печать(M3)
Вывод:
[[ -6 24 -18] [-6-32-18] [-20 40 -18]]
Умножение матриц
Сначала создадим две матрицы, используя numpy. arary(). Чтобы умножить их, вы можете использовать метод numpy dot(). Numpy.dot() — это точечный продукт матриц M1 и M2. Numpy.dot() обрабатывает двумерные массивы и выполняет умножение матриц.
arary(). Чтобы умножить их, вы можете использовать метод numpy dot(). Numpy.dot() — это точечный продукт матриц M1 и M2. Numpy.dot() обрабатывает двумерные массивы и выполняет умножение матриц.
Пример:
импортировать numpy как np M1 = np.массив ([[3, 6], [5, -10]]) M2 = np.массив ([[9, -18], [11, 22]]) М3 = М1.точка(М2) печать(M3)
Вывод:
[[ 93 78] [-65-310]]
Транспонирование матрицы
Транспонирование матрицы вычисляется путем преобразования строк в столбцы и столбцов в строки. Функцию transpose() из Numpy можно использовать для вычисления транспонирования матрицы.
Пример:
импортировать numpy как np M1 = np.массив([[3, 6, 9], [5, -10, 15], [4,8,12]]) M2 = M1.транспонировать() печать(М2)
Вывод:
[[ 3 5 4] [ 6 -10 8] [ 9 15 12]]
Нарезка матрицы
Нарезка вернет вам элементы из матрицы на основе заданного начального/конечного индекса.
- Синтаксис для нарезки – [начало:конец]
- Если начальный индекс не указан, он считается равным 0.
 Например, [:5], это означает как [0:5].
Например, [:5], это означает как [0:5]. - Если конец не передан, он будет считаться длиной массива.
- Если начало/конец имеют отрицательные значения, то нарезка будет выполняться с конца массива.
Прежде чем мы приступим к срезу матрицы, давайте сначала разберемся, как применить срез к простому массиву.
импортировать numpy как np массив = np.массив ([2,4,6,8,10,12,14,16]) print(arr[3:6]) # напечатает элементы с 3 по 5 print(arr[:5]) # напечатает элементы от 0 до 4 print(arr[2:]) # напечатает элементы от 2 до длины массива. print(arr[-5:-1]) # будет печатать с конца, т.е. от -5 до -2 print(arr[:-1]) # будет печатать с конца, т.е. от 0 до -2
Вывод:
[8 10 12] [ 2 4 6 8 10 ] [ 6 8 10 12 14 16] [ 8 10 12 14 ] [ 2 4 6 8 10 12 14]
Теперь реализуем нарезку матрицы. Для выполнения среза матрицы
синтаксис будет M1[начало_строки:конец_строки, начало_столбца:конец_столбца]
- Первое начало/конец будет для строки, т.
 е. для выбора строк матрицы.
е. для выбора строк матрицы. - Второе начало/конец будет для столбца, т.е. для выбора столбцов матрицы.
Матрица M1 t, которую мы собираемся использовать, выглядит следующим образом:
M1 = np.массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
Всего 4 ряда. Индекс начинается с 0 до 3. Строка 0 th — это [2,4,6,8,10], строка 1 st — это [3,6,9,-12,-15], за которой следуют 2 -й и 3 -й .
Матрица M1 имеет 5 столбцов. Индекс начинается от 0 до 4. Столбец 0 th имеет значения [2,3,4,5], столбцы 1 st имеют значения [4,6,8,-10], за которыми следуют 2 -й , 3-й -й , 4-й -й и 5-й -й -й.
Вот пример, показывающий, как получить данные строк и столбцов из матрицы с помощью срезов. В примере мы печатаем строки 1 st и 2 nd , а для столбцов нам нужны первый, второй и третий столбцы. Чтобы получить этот вывод, мы использовали: M1[1:3, 1:4]
Чтобы получить этот вывод, мы использовали: M1[1:3, 1:4]
Пример:
import numpy as np
M1 = np.массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[1:3, 1:4]) # Для 1:3 это даст первую и вторую строку.
#Столбцы будут взяты с первого по третий.
Вывод:
[[ 6 9 -12] [ 8 12 16]]
Пример: для печати всех строк и третьих столбцов
импортировать numpy как np
M1 = np.массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[:,3]) # Это напечатает все строки и данные третьего столбца.
Вывод:
[8-12 16-20]
Пример: для печати первой строки и всех столбцов
импортировать numpy как np
M1 = np.массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[:1,]) # Будет напечатана первая строка и все столбцы
Вывод:
[[ 2 4 6 8 10]]
Пример: для печати первых трех строк и первых двух столбцов
импортировать numpy как np M1 = np.массив([[2, 4, 6, 8, 10], [3, 6, 9, -12, -15], [4, 8, 12, 16, -20], [5, -10, 15, -20, 25]]) печать (M1 [: 3,: 2])
Вывод:
[[2 4] [3 6] [4 8]]
Доступ к матрице NumPy
Мы видели, как работает нарезка. Принимая это во внимание, мы узнаем, как получить строки и столбцы из матрицы.
Для печати строк матрицы
В примере будут напечатаны строки матрицы.
Пример:
импортировать numpy как np M1 = np.array([[3, 6, 9], [5, -10, 15], [4,8,12]]) print(M1[0]) # первая строка print(M1[1]) # вторая строка print(M1[-1]) # -1 напечатает последнюю строку
Вывод:
[3 6 9] [ 5 -10 15] [ 4 8 12]
Чтобы получить последнюю строку, вы можете использовать индекс или -1. Например, матрица имеет 3 строки:
, поэтому M1[0] даст вам первую строку,
M1[1] даст вам вторую строку
M1[2] или M1[-1] даст вам третий ряд или последний ряд.
Для печати столбцов матрицы
импортировать numpy как np M1 = np.массив([[2, 4, 6, 8, 10], [3, 6, 9, -12, -15], [4, 8, 12, 16, -20], [5, -10, 15, -20, 25]]) print(M1[:,0]) # Будет напечатан первый столбец print(M1[:,3]) # Будет напечатан третий столбец print(M1[:,-1]) # -1 даст вам последний столбец
Вывод:
[2 3 4 5] [ 8 -12 16 -20] [ 10 -15 -20 25]
Сводка:
- Матрица Python представляет собой специализированный двумерный прямоугольный массив данных, хранящихся в строках и столбцах. Данные в матрице могут быть числами, строками, выражениями, символами и т. д. Матрица — одна из важных структур данных, которую можно использовать в математических и научных расчетах.
- В Python нет простого способа реализовать матричный тип данных. Матрица Python может быть создана с использованием типа данных вложенного списка и библиотеки numpy.
- Библиотека Python Numpy помогает работать с массивами. Numpy обрабатывает массив немного быстрее, чем список.
- Матричная операция, которую можно выполнять, это сложение, вычитание, умножение, транспонирование, чтение строк, столбцов матрицы, разрезание матрицы и т.


 array([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив составных чисел
print(A)
array([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив составных чисел
print(A)
 array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[0] =", A[0]) # Первая строка
print("A[2] =", A[2]) # Третья строка
print("A[-1] =", A[-1]) # Последняя строка (третья строка в данном случае)
array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[0] =", A[0]) # Первая строка
print("A[2] =", A[2]) # Третья строка
print("A[-1] =", A[-1]) # Последняя строка (третья строка в данном случае)
 array([1, 3, 5, 7, 9, 7, 5])
# с 3-го по 5-ый элементы
print(letters[2:5]) # Вывод: [5, 7, 9]
# с 1-го по 4-ый элементы
print(letters[:-5]) # Вывод: [1, 3]
# с 6-го до последнего элемента
print(letters[5:]) # Вывод:[7, 5]
# с 1-го до последнего элемента
print(letters[:]) # Вывод:[1, 3, 5, 7, 9, 7, 5]
# список в обратном порядке
print(letters[::-1]) # Вывод:[5, 7, 9, 7, 5, 3, 1]
array([1, 3, 5, 7, 9, 7, 5])
# с 3-го по 5-ый элементы
print(letters[2:5]) # Вывод: [5, 7, 9]
# с 1-го по 4-ый элементы
print(letters[:-5]) # Вывод: [1, 3]
# с 6-го до последнего элемента
print(letters[5:]) # Вывод:[7, 5]
# с 1-го до последнего элемента
print(letters[:]) # Вывод:[1, 3, 5, 7, 9, 7, 5]
# список в обратном порядке
print(letters[::-1]) # Вывод:[5, 7, 9, 7, 5, 3, 1]
 array([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив составных чисел
print(A)
array([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив составных чисел
print(A)
 array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[0] =", A[0]) # Первая строка
print("A[2] =", A[2]) # Третья строка
print("A[-1] =", A[-1]) # Последняя строка (третья строка в данном случае)
array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[0] =", A[0]) # Первая строка
print("A[2] =", A[2]) # Третья строка
print("A[-1] =", A[-1]) # Последняя строка (третья строка в данном случае)
 array([1, 3, 5, 7, 9, 7, 5])
# с 3-го по 5-ый элементы
print(letters[2:5]) # Вывод: [5, 7, 9]
# с 1-го по 4-ый элементы
print(letters[:-5]) # Вывод: [1, 3]
# с 6-го до последнего элемента
print(letters[5:]) # Вывод:[7, 5]
# с 1-го до последнего элемента
print(letters[:]) # Вывод:[1, 3, 5, 7, 9, 7, 5]
# список в обратном порядке
print(letters[::-1]) # Вывод:[5, 7, 9, 7, 5, 3, 1]
array([1, 3, 5, 7, 9, 7, 5])
# с 3-го по 5-ый элементы
print(letters[2:5]) # Вывод: [5, 7, 9]
# с 1-го по 4-ый элементы
print(letters[:-5]) # Вывод: [1, 3]
# с 6-го до последнего элемента
print(letters[5:]) # Вывод:[7, 5]
# с 1-го до последнего элемента
print(letters[:]) # Вывод:[1, 3, 5, 7, 9, 7, 5]
# список в обратном порядке
print(letters[::-1]) # Вывод:[5, 7, 9, 7, 5, 3, 1]
 append(
append(  array([[
array([[  multiply(x,y)) 9 0027
multiply(x,y)) 9 0027 dot(X, Д)
dot(X, Д)  transpose(matrix))
transpose(matrix))  0. 0.]
[0. 0. 0.]
[0. 0. 0.]]
0. 0.]
[0. 0. 0.]
[0. 0. 0.]] 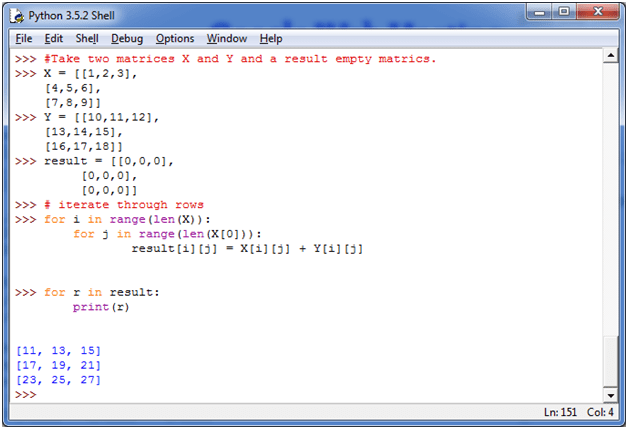 delete(a,
delete(a,  Например, [:5], это означает как [0:5].
Например, [:5], это означает как [0:5].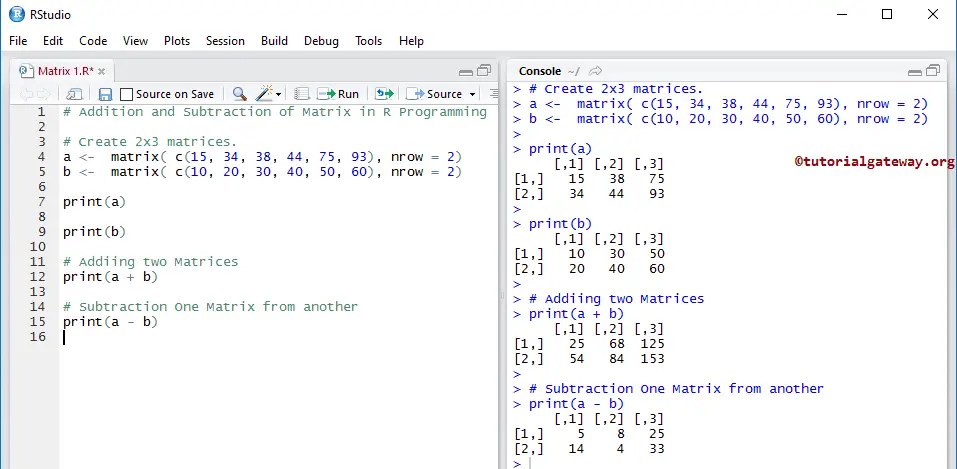 е. для выбора строк матрицы.
е. для выбора строк матрицы. массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
печать (M1 [: 3,: 2])
массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
печать (M1 [: 3,: 2])
 массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[:,0]) # Будет напечатан первый столбец
print(M1[:,3]) # Будет напечатан третий столбец
print(M1[:,-1]) # -1 даст вам последний столбец
массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[:,0]) # Будет напечатан первый столбец
print(M1[:,3]) # Будет напечатан третий столбец
print(M1[:,-1]) # -1 даст вам последний столбец