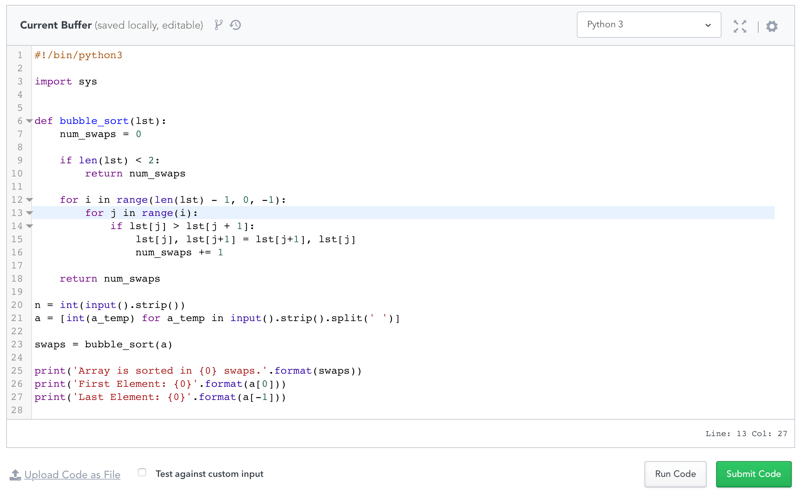
Сортировка пузырьком. Язык Python
Сортировка пузырьком — это метод сортировки массивов и списков путем последовательного сравнения и обмена соседних элементов, если предшествующий оказывается больше последующего.
В процессе выполнения данного алгоритма элементы с большими значениями оказываются в конце списка, а элементы с меньшими значениями постепенно перемещаются по направлению к началу списка. Образно говоря, тяжелые элементы падают на дно, а легкие медленно всплывают подобно пузырькам воздуха.
В сортировке методом пузырька количество итераций внешнего цикла определяется длинной списка минус единица, так как когда второй элемент становится на свое место, то первый уже однозначно минимальный и находится на своем месте.
Количество итераций внутреннего цикла зависит от номера итерации внешнего цикла, так как конец списка уже отсортирован, и выполнять проход по этим элементам смысла нет.
Пусть имеется список [6, 12, 4, 3, 8].
За первую итерацию внешнего цикла число 12 переместится в конец.
- 6 > 12? Нет
- 12 > 4? Да. Меняем местами
- 12 > 3? Да. Меняем местами
- 12 > 8? Да. Меняем местами
Результат: [6, 4, 3, 8, 12]
За вторую итерацию внешнего цикла число 8 переместиться на предпоследнее место. Для этого потребуется 3 сравнения:
- 6 > 4? Да. Меняем местами
- 6 > 3? Да. Меняем местами
- 6 > 8? Нет
Результат: [4, 3, 6, 8, 12]
На третьей итерации внешнего цикла исключаются два последних элемента. Количество итераций внутреннего цикла равно двум:
- 4 > 3? Да. Меняем местами
- 4 > 6? Нет
Результат: [3, 4, 6, 8, 12]
На четвертой итерации внешнего цикла осталось сравнить только первые два элемента, поэтому количество итераций внутреннего равно единице:
- 3 > 4? Нет
Результат: [3, 4, 6, 8, 12]
Реализация сортировки пузырьком с помощью циклов for
from random import randint
N = 10
a = []
for i in range(N):
a.
append(randint(1, 99))
print(a)
for i in range(N-1):
for j in range(N-i-1):
if a[j] > a[j+1]:
a[j], a[j+1] = a[j+1], a[j]
print(a)
append(randint(1, 99))
print(a)
for i in range(N-1):
for j in range(N-i-1):
if a[j] > a[j+1]:
a[j], a[j+1] = a[j+1], a[j]
print(a)Пример выполнения кода:
[63, 80, 62, 69, 71, 37, 12, 90, 19, 67] [12, 19, 37, 62, 63, 67, 69, 71, 80, 90]
С помощью циклов while
from random import randint
N = 10
a = []
for i in range(N):
a.append(randint(1, 99))
print(a)
i = 0
while i < N - 1:
j = 0
while j < N - 1 - i:
if a[j] > a[j+1]:
a[j], a[j+1] = a[j+1], a[j]
j += 1
i += 1
print(a)Функция сортировки пузырьком на Python
from random import randint
def bubble(array):
for i in range(N-1):
for j in range(N-i-1):
if array[j] > array[j+1]:
buff = array[j]
array[j] = array[j+1]
array[j+1] = buff
N = 10
a = []
for i in range(N):
a.append(randint(1, 99))
print(a)
bubble(a)
print(a)Больше задач в PDF
Пузырьковая сортировка на Python и С# OTUS
В этом материале мы поговорим про алгоритм сортировки пузырьком (Bubble sort).
Для примера попробуем отсортировать массив вручную, после чего напишем код для сортировки пузырьком на языке программирования Python и Си шарп.
Описание алгоритма
В процессе сортировки пузырьком происходит попарное сравнение соседних элементов массива, начиная с нулевого. После первой итерации самое большое число окажется на месте последнего, причем в дальнейших итерациях это значение уже задействоваться не будет (по сути, мы получим n-1 сравнений). Далее алгоритм находит второй по величине элемент, который ставится на предпоследнее место, потом третий и пр. В результате на месте нулевого элемента (не забываем, что нумерация в массиве начинается с нуля) окажется наименьшее число, а на месте последнего элемента – наибольшее. То есть мы можем сказать, что элементы от большего к меньшему «всплывают» по аналогии с пузырьками.
Проговорим алгоритм еще раз:
- Текущий элемент сравнивается с последующим.
- Если последующий меньше или больше, они меняются местами.
- Когда сортировка заканчивается, алгоритм прекращает работу, иначе снова происходит переход на шаг № 1.
Важно понимать, что при реализации сортировки применяют 2 цикла: основной и вложенный (внутренний цикл). По результатам одного прохода внутреннего цикла самый большой элемент смещается в конец массива, тогда как самый маленький перемещается к началу (на одну позицию).
Рассмотрим пример
Представьте, что у нас есть следующий массив:
7 2 9 4 1 0
В процессе первой итерации мы возьмем нулевой элемент (это 7) и сравним его с соседним. Так как семь больше двух, числа меняются своими местами. То есть массив меняется:
2 7 9 4 1 0
Потом происходит сравнение второго и третьего числа. Так как изначально 9 больше семи, то семь остается на месте. Далее 9 последовательно сравнивается с остальными значениями и таким образом постепенно перемещается в самый конец массива (так как числа, большего, чем 9, в массиве нет, девятка занимает заслуженное последнее место).
2 7 4 1 0 9
Первая итерация закончена, количество шагов уменьшилось на 1 (n-1), то есть 9 находится там, где надо. Больше это число не затрагивается.
Во второй итерации все опять начинается с нулевого элемента массива (в нашем случае это двойка) с последующими сравнениями и перемещениями. В результате массив будет выглядеть следующим образом:
2 4 1 0 7 9
И так далее. Итоговый вид массива после сортировки по методу пузырьком вы можете видеть ниже:
0 1 2 4 7 9
Как видите, ничего сложного в этом нет.
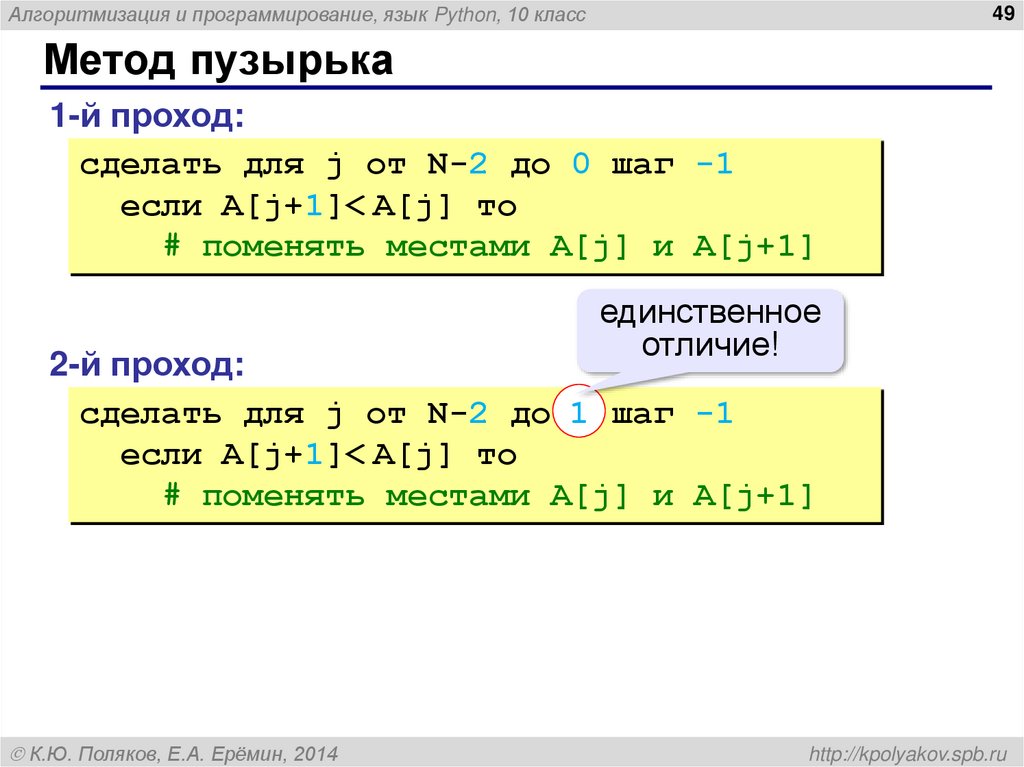
Реализация на Си шарп
Чтобы реализовать сортировку пузырьком, сначала над создать саму функцию сортировки, которая будет располагаться в итоге перед функцией main:
static int[] BubbleSort(int[] mas)
{
int temp;
for (int i = 0; i < mas.Length; i++)
{
for (int j = i + 1; j < mas.
Length; j++)
{
if (mas[i] > mas[j])
{
temp = mas[i];
mas[i] = mas[j];
mas[j] = temp;
}
}
}
return mas;
}
Итоговый код будет выглядеть следующим образом:
Реализация на Python
Теперь давайте попробуем выполнить сортировку пузырьком c «Пайтон»:
По материалам:
- https://all-python.ru/primery/puzyryok.html;
- https://csharp.webdelphi.ru/sortirovka-massiva-c-algoritm-sortirovka-puzyrkom/;
- https://vscode.ru/prog-lessons/sortirovka-metodom-puzyirka-c-sharp.html.
Программа Python для пузырьковой сортировки
Улучшить статью
Сохранить статью
- Уровень сложности: Easy
- Последнее обновление: 13 июн, 2022
Улучшить статью
Сохранить статью
Пузырьковая сортировка — это простейший алгоритм сортировки, который работает путем повторной замены соседних элементов, если они расположены в неправильном порядке.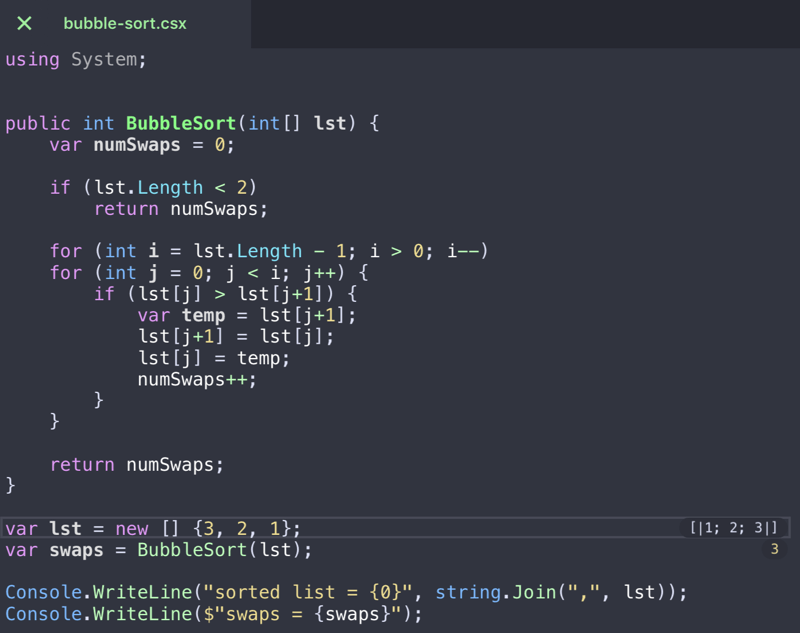
Python3
):
, 12 , 22 , 11 , 90 ] 90 ] 9033. 0032 bubbleSort(arr)
Печать ( " % D" % ARR [I], END = " ) " ) "" ) " ) |
0033 1 
0034 
Если первое значение выше второго значения, первое значение занимает позицию второго значения, а второе значение занимает позицию первого значения. Если первое значение меньше второго, то замена не производится.
Получите следующий элемент в списке, затем повторите процесс, выполненный на шаге 3, пока все значения не будут размещены в правильном порядке возрастания.
Итерация завершается, и инициируется следующая до тех пор, пока процесс не будет завершен, как показано в приведенном ниже примере пузырьковой сортировки.
Код ничего не выводит.
Код ничего не выводит
Алгоритм выполняет минимальное количество выполнений, которое выражается как [Big-Omega] Ω(n)