Неразрывный пробел – правила для авторов.

Что такое неразрывный пробел и для чего он нужен знают не все опытные авторы, а о новичках и говорить не приходится. 

Зачем нужен необычный пробел


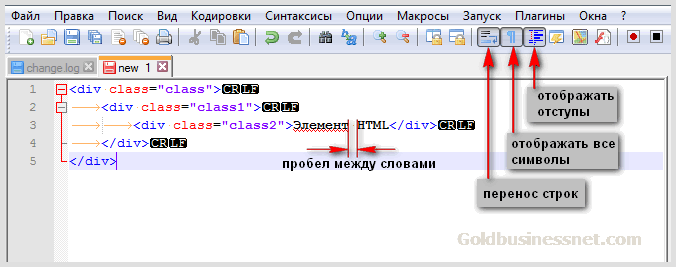
Многие если и слышали об этом понятии, то их знания ограничиваются тем, что MS Word при наборе чисел с разделителями групп разрядов автоматически меняет обычный пробел на неразрывный. В обычном режиме это незаметно, увидеть отличие можно лишь в специальном режиме работы программы, включить который можно, нажав на кнопку ¶ на панели инструментов.

Неразрывный пробел нужен для того, чтобы перенос с одной строки на другую был правильным. Не секрет, что текстовые редакторы и браузеры автоматически переносят текст на новую строку, когда в текущей место исчерпано. При этом руководствуются они вовсе не правилами русского языка. Неразрывный пробел нужен для того, чтобы запретить в этом месте делать перенос строки.

Когда нужен неразрывный пробел


1.  Разделение групп разрядов

Как уже показано выше, при разделении разрядов между собой пробелом нужно использовать его неразрывный вариант.

2. Инициалы и фамилии

Если инициалы на одной строке, а фамилия на другой, это как минимум некрасиво. Чтобы уменьшить вероятность неверного переноса, некоторые редакторы советуют не ставить пробел между инициалами. Однако правильнее разделить их неразрывными пробелами.

3. Сокращения

К ним относятся словосочетания и фразы

4. Слово-сокращение и имя собственное

5. Единица измерения, счетное слово, спецзнак и связанное число

Еще случаи, когда понадобится неразрывный пробел:

1. При вставке в текст тире.

Хорошо пробел перед знаком делать неразрывным, а после него обычным.

2. Бинарные математические операции

Здесь так же перед математическим знаком используется неразрывный пробел, а после него обычный.

3. Неразрывным пробелом стоит отделять от предыдущих слов одно- и двухбуквенные союзы, предлоги и слова: и, а, но, же, бы, ли, в, с, ты, я и т. д.

Как вставить в текст


Вы можете решить, что правильно использовать пробелы обязан тот, кто будет публиковать текст. Однако уважающий себя и своих заказчиков автор сразу вставляет в текст правильные пробелы.

Вставляем неразрывный пробел в текстовом редакторе

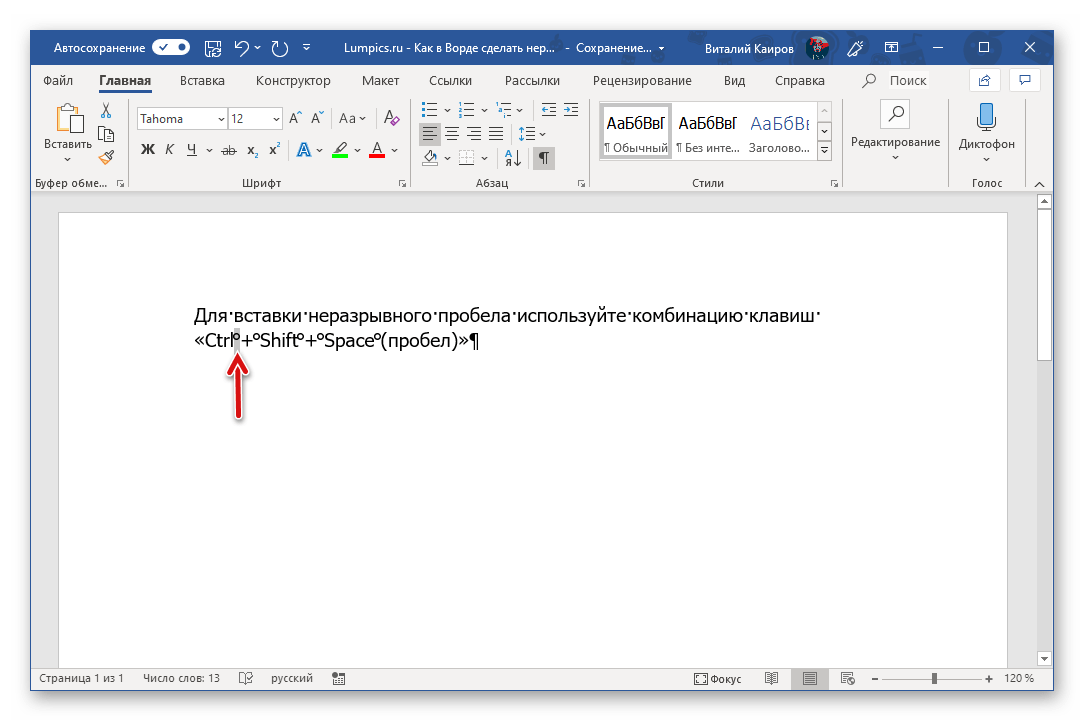
В этом поможет сочетание клавиш Alt+255 или: 

Также можно найти данную функцию на панели Word: 

Чтобы контролировать употребление пробела, стоит завести привычку набирать и вычитывать тексты в режиме, когда показаны все непечатаемые символы. Иначе «на глаз» отличить обычный пробел от неразрывного не получится.

Неразрывный пробел в html


Если вам попался ответственный автор, то неразрывные пробелы в тексте уже проставлены, и вам остается только заменить их на соответствующий код –   

Делать это придется вручную — при копировании текста в визуальный редактор неразрывные пробелы последний заменит на обычные.

Неразрывный пробел и СЕО


Иногда специалисты по продвижению категорично настроены против использования в тексте html-тегов неразрывного пробела и переноса строки (<br />), мотивируя такой подход тем, что это мешает продвижению. Это не совсем верно. Поисковики вполне нормально обрабатывают эти теги, если они вставлены правильно. Затрудняет продвижение неверное использование, например &nbsp; или nbsp; (без &).

The following two tabs change content below.

  • Об авторе
  • Последние публикации

Секрет 12. Неразрывный пробел в презентации – Эффективная работа в MS Office

На уроке 1 я рассказала вам, что такое неразрывный пробел в Word’е.

Так как строки образуются автоматически, то не редкость, когда в конце одной строки болтается число, а в начале следующей строки ‒ размерность. Так же ужасно смотрится предлог в гордом одиночестве и частицы «не» и «ни». Чтобы связать два слова  «цепью» используют неразрывный пробел.

Неразрывный пробел образуется одновременным нажатием клавиш Shift+Ctrl+пробел:

И если в тексте документа эти случаи вполне терпимы, то в презентациях просто недопустимы в силу особенностей восприятия (см. Д3 Свойства восприятия).

Кстати, хочу заметить, что высококвалифицированные полиграфисты никогда не допустят одиночных предлогов и разорванных числового значения с размерностью, как на приведённом мной примере. Вот вам несколько ссылок:

  • https://studopedia.ru/4_51586_pravila-nabora-i-verstki.html,
  • http://www.creajob.com/ar8416ru-minikodeks-verstki1-ehlementarnye-pravila-tipografiki.html,

Вы скажете, что в Point’е никаких неразрывных пробелов нет. И будете абсолютно правы! И тем не менее…

По окончании урока вы сможете:

  1. Искусственно образовать новую строчку в тексте слайда
  2. Искусственно вставить на разрывный пробел в текст слайда

Скачайте учебную презентацию тут. Откройте учебную презентацию. На самом первом слайде вы увидите, что в предложении два предлога «в» находятся в конце строчек:

1. Новая строчка в тексте слайда

Шаг 1. Вставьте разрыв строки перед первым предлогом «в»:

  1. Подведите курсор-стрелку перед предлогом «в» пока не появится текстовый курсор
  2. Щёлкните ЛМ
  3. Одновременно нажмите клавиши Shift+Enter

Получаем такую картину:

Шаг 2. Теперь выделяем текстовый блок и меняем размер шрифта (двойной щелчок ЛМ по тексту → лента Главная → группа команд Шрифт → кнопка выпадающего меню размера шрифта → размер шрифта 24 или другой на ваше усмотрение):

Получили, что получили:

Как видите, искусственное образование новой строчки далеко не панацея.

Конечно, я пользуюсь приёмом искусственного образования строчки. Но только на последней стадии форматирования презентации, когда дальнейших правок не предвидится.

А теперь попробуем неразрывный пробел.

2. Неразрывный пробел в тексте слайда

Шаг 1. Выделите текст слайда (тройной щелчок ЛМ по тексту)

Шаг 2. Скопируйте текст в буфер обмена (лента Главная → группа команд Буфер обмена → кнопка Скопировать, можно Вырезать):

Шаг 3. Откройте новый документ Word и вставьте содержимое буфера обмена (лента Главная → группа команд Буфер обмена → команда Вставить):

Обратите внимание на непечатаемый символ «Разрыв строки» после слова «поступает» и перед предлогом «в».

Понять и запомнить!И в Word’е и в Point’е есть непечатаемые символы. Но…

В Word’е мы можем включить режим непечатаемых символов и увидеть эти символы.

В Point’е нет режима непечатаемых символов, поэтому мы увидеть эти символы не можем.

Мне очень недостаёт режима непечатаемых символов в Point’е!

Шаг 4. Удалите непечатаемый символ «Разрыв строки» (выделяем непечатаемый символ → клавиша Delete):

Шаг 5. Поставьте неразрывный пробел после предлогов «в» (выделите пробел → одновременное нажатие клавиш на клавиатуре Shift+Ctrl+пробел):

  1. первый предлог «в»

Обратили внимание, что непечатаемый символ «Пробел» изменился на кружок непечатаемого символа «Неразрывный пробел?

  1. второй предлог «в»

Шаг 6. Выделите текст (см. урок 2) тройным щелчком

ЛМ и скопируйте в буфер обмена (лента Главная → группа команд Буфер обмена → команда Копировать):

Возвращаемся в Point (надеюсь, вы его не закрыли?). Я буду работать в своей презентации, но можно открыть новую презентацию – это не важно.

Шаг 7. Выделите заполнитель (см. Секрет 6) с текстом (подведите курсор к границе заполнителя → как только курсор превратится в крестик с разнонаправленными стрелками щёлкните ЛМ) и вставьте содержимое буфера обмена (лента Главная → группа команд Буфер обмена → команда Вставить):То есть мы заменили содержимое заполнителя на содержимое буфера обмена.

Я даже вставила содержимое буфера обмена дважды и получила такую картину:

Теперь нам надо убедиться, что мы перенесли из документа в презентацию непечатаемые символы «Неразрывный пробел».

Шаг 8. Задайте первому абзацу размер шрифта 20 пт, а второму абзацу – 28 пт (выделяем абзац → лента Главная → группа команд Шрифт → кнопка выпадающего меню Размер шрифта):

Как видите, теперь совершенно неважно, как вы будете изменять текст – предлог «в» всегда будут идти в связке со следующим словом.

Я уже слышу возражения, что сделать таким образом неразрывный пробел для всех предлогов долго, что начальство торопит, времени нет.

На это меня два возражения:

Во-первых, давайте уважать наших клиентов и делать для них презентации высшего качества.

А во-вторых, заменить в Word’е простые пробелы в предлогах, союзах, частицах «не» и «ни» на неразрывные пробелы можно ОДНОМОМЕНТНО! Для этого нужно знать возможности команды Заменить и понимать язык подстановочных символов. А это уже немного попозже. Я обязательно расскажу вам об этой замечательной возможности Word’а, но полагаю, что в один урок мы не уложимся.

Теперь вы сможете:

  1. Искусственно образовать новую строчку в тексте слайда
  2. Искусственно вставить неразрывный пробел в текст слайда

общая топология — Как аксиомизировать понятие «непрерывное пространство»?

Вот что я думаю об этом вопросе и как бы я ответил на него сейчас:

В дальнейшем я буду использовать «непрерывный» в смысле «достаточно непрерывный, чтобы аналитик мог заинтересоваться им или найти его интересным» и , а не в смысле «морфизма между топологическими пространствами»; последнее значение, очевидно, гораздо более общее. Однако я считаю, что первый смысл лучше отражает интуицию неспециалиста в отношении слова «непрерывный», а также то, что имел в виду Рисс. Действительно, некоторые считают, что анализ состоит из «точной формулировки интуитивных понятий … непрерывности» или изучения «непрерывных изменений». Только первый смысл термина «непрерывный» имеет смысл в этих контекстах, а второй — нет.

Функциональный анализ часто преподается как продолжение реального и/или комплексного анализа, а в некоторой степени и является фактическим. В какой-то степени это различие имеет значение только для элементарного анализа, поскольку проблемы в этой области неизбежно приводят к рассмотрению функциональных пространств.

Что объединяет эти изучаемые пространства? Что все они являются топологическими векторными пространствами над $\mathbb{R}$ или $\mathbb{C}$, часто с несколькими совместимыми/интересными топологиями на выбор. (Если мы хотим включить изучение многообразий/дифференциальной геометрии, то нужно абстрагироваться далее к «пространствам, которые локально гомеоморфны топологическим векторным пространствам над $\mathbb{R}/\mathbb{C}$.)

Кто-то может возразить, что не нужна «алгебраическая» структура для определения пространств, соответствующих интуитивному понятию «непрерывность», и что топологическая структура должна быть всем, что необходимо.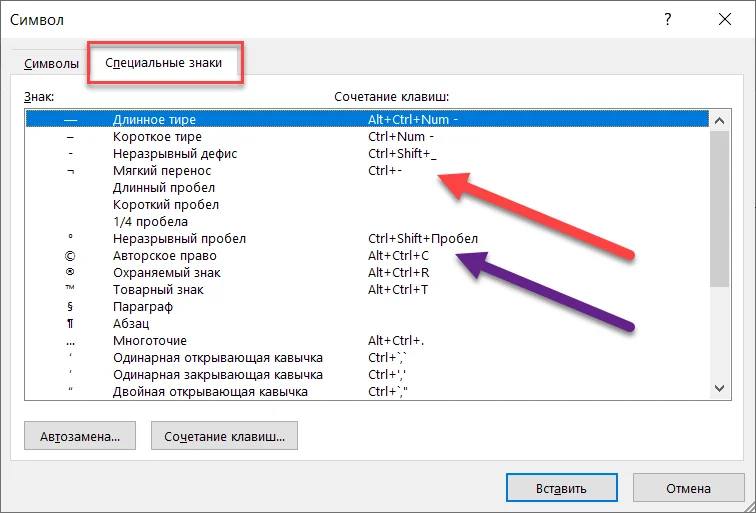 Однако у меня есть несколько ответов на это:

  1. Помните, что топологическое понятие непрерывности не соответствует интуитивному понятию, передаваемому использованием слова «непрерывный» в повседневной речи.

  2. Алгебраическое условие быть векторным пространством над $\mathbb{R}$ или $\mathbb{C}$ можно рассматривать как означающее, что пространство «хорошо играет» с $\mathbb{R}$ и $\ матбб{С}$. Поскольку эти два пространства в каком-то смысле являются простейшими из возможных пространств, для которых нам не нужно беспокоиться о том, что последовательности Коши не сходятся, любое пространство, которое хорошо сочетается с ними, с большей вероятностью будет соответствовать нашему интуитивному предположению, что последовательность Коши «должна» сходиться. .

  3. Если мы хотим включить функциональные пространства, нам нужно ограничиться векторными пространствами, потому что почти любое функциональное пространство, которое может нас заинтересовать (как аналитика), является векторным пространством.

  4. Ограничение не имеет большого значения, когда мы обобщаем пространства, которые «локально гомеоморфны топологическим векторным пространствам над $\mathbb{R}/\mathbb{C}$», плюс, естественно, вводит некоторые необходимые механизмы иметь четко определенные касательные пространства. И я думаю, что касательные пространства также хорошо соответствуют нашему интуитивному понятию непрерывности (которое иногда называют гладкостью) — например, в точке конуса, где нет четко определенной касательной плоскости, мы говорим, что она «заостренная», но не гладко».

  5. Помните, что быть топологическим векторным пространством не означает иметь смесь топологических и алгебраических структур — эти две структуры должны быть совместимыми друг с другом, а это значит, что они должны до некоторой степени усиливать друг друга. Таким образом, в некоторой степени цель части векторного пространства состоит в том, чтобы просто наложить дополнительные топологические условия.

  6. Есть много важных топологических свойств, которые соответствуют нашему интуитивному понятию «непрерывный», которые следуют из их (топологической) структуры векторного пространства, я обрисую это более подробно ниже.

  7. Эмпирически говоря, большинство топологических контрпримеров к интуитивному понятию «непрерывного пространства», которые я нашел на $\pi$-базе, либо не были векторными пространствами (или если они были, то они не были векторными пространствами над $\mathbb {R}$ или $\mathbb{C}$) либо были векторными пространствами, но имели топологию, которая либо не совместима со структурой векторного пространства, либо не связана с ней естественным образом. Это навело меня на мысль, что здесь происходит что-то фундаментальное.

Однако самым сильным аргументом в пользу наложения алгебраических условий является следующий:

Топология группы определяется ее системой окрестностей идентичности. В частности, системы окрестностей в каждой точке гомеоморфны друг другу.

Таким образом, то, что может показаться абстрактным условием, на самом деле сводится к интуитивному, почти геометрическому: каждая точка пространства, рассматриваемая локально, неразличима.

Тот факт, что это неверно для общих топологических пространств, делает их интересными объектами для изучения; однако это не обязательно соответствует интуитивным представлениям о «непрерывности».

Однако я добавлю одно чисто топологическое условие: «непрерывное» пространство также должно быть $T1$. Это происходит по крайней мере по двум причинам:

  1. Как я уже говорил в другом месте, для пространства, которое является «непрерывным» в интуитивном смысле, наиболее естественно иметь замкнутые точки и не иметь открытых точек. Это должно означать, в частности, что каждая точка в пространстве имеет единственную систему окрестностей (различимую в топологии), множество предельных точек замкнуто и что пространство не опирается ни на одну точку для своей «непрерывности» (т. мы все еще имеем открытый набор при удалении любой отдельной точки). Эти предположения делают пространство гораздо лучше управляемым с точки зрения предельной сходимости, а также по своей сути исключают из рассмотрения многие примеры «дискретных» или «полудискретных» пространств.

  2. Несколько очень важных топологических следствий следуют только для топологических векторных пространств, которые также являются $T1$, и это допущение безопасно делать в анализе, поэтому многие авторы (например, Рудин) обычно делают это.

Давайте начнем выводить хорошие свойства, которые составят суть моего аргумента.

  1. Любое такое пространство не просто $T1$, а на самом деле вполне регулярно и имеет на нем однородную структуру. Оба они также часто считаются соответствующими интуитивному понятию непрерывности; мы получаем их бесплатно на основе относительно слабых аксиом.

  2. Каждое такое пространство не только автоматически локально линейно связно, но и локально дугово связно, поскольку хаусдорфовость и локально линейная связность подразумевают локально дуговую связность. Другими словами, он автоматически имеет множество кривых (топологических 1-многообразий) в качестве подмножеств, что также хорошо соответствует нашему интуитивному понятию «непрерывности».

  3. Каждое такое пространство (кроме тривиального) несчетно, т.е. имеет «мощность континуума «, потому что любое линейно-связное пространство, состоящее более чем из двух точек, является несчетным.

  4. Поскольку пространство хаусдорфово, каждый предел уникален! Следовательно, эти пространства особенно хороши для изучения пределов. В результате каждое компактное подмножество также замкнуто в этих пространствах, опять же в соответствии с интуицией.

  5. Этой структуры уже достаточно, чтобы определить понятие ограниченности: https://en.wikipedia.org/wiki/Bounded_set_(topological_vector_space). Хотя «непрерывное пространство» должно быть в некотором смысле «деформируемым», оно не должно быть произвольно деформируемым без изменения своего «характера». Ограниченность множеств обеспечивает хороший инвариант для рассмотрения во многих контекстах.

  6. Такое пространство дискретно тогда и только тогда, когда оно тривиально, что прекрасно согласуется с интуицией.

Все это без навязывания метрики! Это означает, что мы по-прежнему получаем много хороших свойств, но все еще имеем достаточную общность, рассматривая неметризуемые пространства, представляющие интерес для анализа (например, слабая * топология).

Однако другой хороший аргумент в пользу этих пространств, соответствующих интуиции, относится к метрическим пространствам. В частности, эти пространства метризуемы тогда и только тогда, когда они имеют счетные базы окрестностей. Это дает очень простой и легкий критерий, определяющий, является ли пространство этого типа метризуемым, что, вообще говоря, неверно. Более того, этот критерий очень хорошо соответствует интуиции, возникающей при рассмотрении «шаров радиуса 1/n и n», которые мы можем использовать для локальных баз соседства в евклидовых пространствах. Наконец, каждое такое метризуемое пространство этого типа является пространством Бэра по теореме Бэра о категориях.

Короче говоря, эти пространства методом проб и ошибок естественным образом выделились в качестве основных объектов изучения в анализе и дифференциальной топологии/геометрии, и они обладают большинством, если не всеми, свойствами, которые можно было бы связать с интуитивным понятием «непрерывное пространство». Они также включают в себя все стандартные примеры, которые приходят на ум, в том числе топологические многообразия и все наиболее широко изучаемые функциональные пространства (согласно Википедии).

Более подробно см. другие мои вопросы: Какова мотивация топологической аксиомы произвольного объединения? Заметим, что ни сепарабельность, ни вторая счетность для этих пространств, о которых я упоминал вообще, не имеют места, и что первая счетность имеет место тогда и только тогда, когда пространство метризуемо.

Существуют ли какие-либо свойства «по умолчанию», которые справедливы почти для всех топологических пространств в анализе? (Комментарии несколько полезны).

https://math.stackexchange.com/questions/1836475/t-f-properties-of-every-non-тривиальный-топологический-вектор-пространство-над-mathbbr

Следствие теоремы Биркгофа Какутани: первый счетный топологический вектор пробелы

Можно ли определить связность пути без использования единичного интервала? (Ответ на этот вопрос приводит к аргументу, что связность по путям не является слишком сильным свойством, чтобы просить пространство иметь его.)

Является ли каждый (нетривиальный) путь, связанный с пространством, несчетным?

Зачем изучать не-T1 топологические пространства? В принципе любое пространство, отличное от T1, не представляет интереса для анализа, за исключением некоторых операторных алгебр, но я не вижу сильной мотивации хотеть включать все операторные алгебры/спектры как принадлежащие интуитивному понятию «непрерывное пространство», даже если они полезны для их изучения.

ОБНОВЛЕНИЕ: На с. 36, глава 2 книги Ли Введение в топологические многообразия , в нем указано, что

Самая важная особенность пространств с первой счетностью состоит в том, что это пространства, в которых последовательности достаточны для обнаружения большинства топологических свойств.

Это утверждение становится более точным в контексте непрерывных пространств, как я определил их выше, по сравнению с общими топологическими пространствами.

Например, метрическое пространство компактно тогда и только тогда, когда оно секвенциально компактно. Непрерывное пространство метризуемо тогда и только тогда, когда оно счетно. Первое счетное пространство счетно компактно тогда и только тогда, когда оно секвенциально компактно. Следовательно, счетная компактность, секвенциальная компактность и актуальная компактность совпадают в непрерывном пространстве тогда и только тогда, когда оно счетно сначала. Это лучше согласуется с интуицией.

Еще более идеальным результатом было бы показать, что непрерывное пространство является секвенциальным пространством тогда и только тогда, когда оно первично счетно. Однако в настоящее время я недостаточно знаю о последнем, чтобы подтвердить или опровергнуть это. Тем не менее, обычное направление импликации верно, а именно то, что первая счетность влечет секвенциальность, таким образом, секвенциальная непрерывность и непрерывность совпадают для всех метризуемых = первой счетных непрерывных пространств.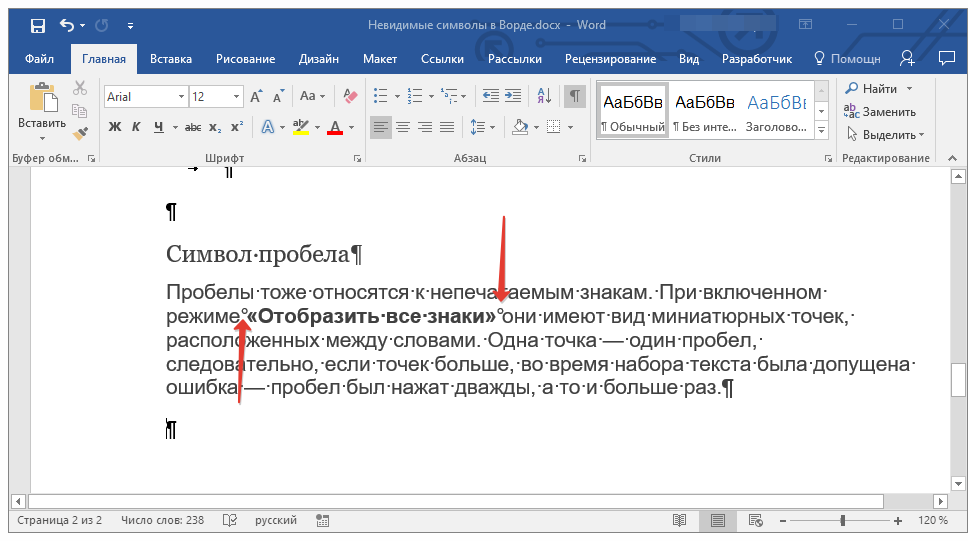

Было бы также неплохо найти некоторую связь между непрерывными пространствами и пространствами Фреше-Урысона: последовательная непрерывность против непрерывности. 9{\ infty} \ psi ( x ) \ влево | х \ право \ угол \ mathrm {~ d} х \end{выровнено} где $\psi ( x)$ задает компонент $\left| \psi \right\rangle $ связан с базисным вектором $\влево| х\вправо\угол $. К сожалению, ничего из вышеперечисленного никогда не определяется, и поэтому мне интересно, как это объясняется математически, т.е.

  1. Что такое непрерывное гильбертово пространство?
  2. Как понимать приведенный выше интеграл (поскольку это, по-видимому, не обычный интеграл Римана)?
  3. Когда приведенный выше интеграл корректно определен?

Было бы здорово, если бы кто-нибудь ответил на некоторые из этих вопросов или указал мне соответствующую литературу. Заранее спасибо!

Редактировать: Документ, который я читаю, взят из лекции, которую я посещаю, здесь соответствующая часть, которая знакомит с непрерывными гильбертовыми пространствами:

Бесконечные непрерывные измерения .

No related posts.