Массивы NumPy | NumPy
3.1. Прежде чем читать
Нужно немного знать Python. Причем «немного» означает действительно немного и вовсе не означает, что перед чтением данного руководства вам нужно досконально изучить этот язык. Открытой вкладки с официальным руководством окажется вполне достаточно.
Все примеры выполнены в консоли IDE Spyder дистрибутива Anaconda на Python версии 3.5. и NumPy версии 1.14.0. Приводимые примеры так же будут работать в любом другом дистрибутиве Python 3.х версии и последней версией пакета NumPy. Но если некоторые примеры все же не работают, то ознакомьтесь с официальной документацией вашего дистрибутива, возможно причина связана с его особенностями.
Например, если в своем дистрибутиве вы обнаружили последнюю версию IDE Spyder, то в ней нет Python консоли, к которой привыкают многие новички, учившиеся экспериментировать с кодом в IDLE. При этом новичкам может так же показаться, что и все примеры, представленные здесь, тоже лучше выполнять в Python консоли. Но нет, Python консоль использовалась автором лишь по техническим причинам, которые связаны с редактурой, версткой и дизайном кода. Консоль IPython имеет гораздо больше преимуществ.
3.2. Основы
Главный объект NumPy — это однородный многомерный массив. Чаще всего это одномерная последовательность или двумерная таблица, заполненные элементами одного типа, как правило числами, которые проиндексированы кортежем положительных целых чисел. В NumPy, элементы этого кортежа называются осями, а число осей рангом.
Что бы перейти к примерам, сначала выполним импорт пакета:
>>> import numpy as np Импортирование numpy под псевдонимом np уже стало общепринятой, негласной, договоренностью, можно сказать, традицией.
Теперь мы може приступить к примерам. Способов создания массивов NumPy довольно много, но мы начнем с самого тривиального — создание массива из заполненного вручную списка Python:
>>> a = np.array([11, 22, 33, 44, 55, 66, 77, 88, 99])
>>>
>>> a
array([11, 22, 33, 44, 55, 66, 77, 88, 99])Теперь у нас есть одномерный массив (словосочетание «ранг массива» вряд ли приживется в русском языке), т.е. у него всего одна ось вдоль которой происходит индексирование его элементов.

Получить доступ к числу 33 можно привычным способом:
>>> a[2]
33В общем-то, можно подумать, что ничего интересного и нет в этих массивах, но на самом деле это только начало кроличьей норы. Оцените:
>>> a[[7, 0, 3, 3, 3, 0, 7]]
array([88, 11, 44, 44, 44, 11, 88])Вместо одного индекса, указан целый список индексов. А вот еще любопытный пример, теперь вместо индекса укажем логическое выражение:
>>> a[a > 50]
array([55, 66, 77, 88, 99])>>> 2*a + 10
array([ 32, 54, 76, 98, 120, 142, 164, 186, 208])
>>>
>>> np.sin(a)**2 + np.cos(a)**2
array([1., 1., 1., 1., 1., 1., 1., 1., 1.])Векторизованные — означает, что все арифметические операции и математические функции выполняются сразу над всеми элементами массивов. А это в свою очередь означает, что нет никакой необходимости выполнять вычисления в цикле. В случае одномерного массива, можно подумать, что это не такой уж бонус, ведь есть генераторы. Но давайте перейдем к двумерным массивам:
>>> a = np.arange(12)
>>> a
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
>>>
>>> a = a.reshape(3, 4)
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]]) Сейчас мы создали массив с помощью функции np.arange(), которая во многом аналогична функции range() языка Python. Затем, мы изменили форму массива с помощью метода reshape(), т.е. на самом деле создать этот массив мы могли бы и одной командой:
>>> a = np.arange(12).reshape(3, 4)
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])Визуально, данный массив выглядит следующим образом:

Глядя на картинку, становится понятно, что первая ось (и индекс соответственно) — это строки, вторая ось — это столбцы. Т.е. получить элемент 9 можно простой командой:
>>> a[2][1] # равносильно команде a[2, 1]
9Снова можно подумать, что ничего нового — все как в Python. Да, так и есть, и, это круто! Еще круто, то что NumPy добавляет к удобному и привычному синтаксису Python, весьма удобные трюки, например — транслирование массивов:
>>> b = [2, 3, 4, 5]
>>>
>>> a*b
array([[ 0, 3, 8, 15],
[ 8, 15, 24, 35],
[16, 27, 40, 55]]) В данном примере, без всяких циклов (и генераторов), мы умножили каждый столбец из массива b. Т.е. мы как бы транслировали (в какой-то степени можно сказать — растянули) массив b по массиву a.
То же самое мы можем проделать с каждой строкой массива a:
>>> c = [[10], [20], [30]]
>>>
>>> a + c
array([[10, 11, 12, 13],
[24, 25, 26, 27],
[38, 39, 40, 41]]) В данном случае мы просто прибавили к массиву a массив-столбец c. И получили, то что хотели. Сейчас мы не будем подробно рассматривать механизм транслирования — это тема другой главы. Вместо этого я хочу отметить, что при работе с двумерными или трехмерными массивами, особенно с массивами большей размерности, становится очень важным удобство работы с элементами массива, которые расположены вдоль отдельных измерений — его осей.
Например, у нас есть двумерный массив и мы хотим узнать его минимальные элементы по строкам и столбцам. Для начала создадим массив из случайных чисел и пусть, для нашего удобства, эти числа будут целыми:
>>> a = np.random.randint(0, 15, size = (4, 6)) >>> a array([[ 9, 12, 5, 3, 1, 7], [ 2, 12, 10, 11, 14, 9], [ 4, 4, 9, 11, 5, 2], [12, 8, 6, 8, 9, 3]])
Минимальный элемент в данном массиве это:
>>> a.min()
1А вот минимальные элементы по столбцам и строкам:
>>> a.min(axis = 0) # минимальные элементы по столбцам
array([2, 4, 5, 3, 1, 2])
>>>
>>> a.min(axis = 1) # минимальные элементы по строкам
array([1, 2, 2, 3])Такое поведение заложено практически во все функции и методы NumPy:
>>> a.mean(axis = 0) # среднее по столбцам
array([6.75, 9. , 7.5 , 8.25, 7.25, 5.25])
>>>
>>> np.std(a, axis = 1) # стандартное отклонение по строкам
array([3.67045259, 3.77123617, 3.13138237, 2.74873708])Чтож, мы рассмотрели одномерные и двумерные массивы, а так же некоторые трюки NumPy. Но данный пакет позиционируется прежде всего как научный инструмент. Что насчет вычислений, их скорости и занимаемой памяти?
Для примера, создадим трехмерный массив:
>>> a = np.arange(48).reshape(4, 3, 4) >>> a array([[[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]], [[12, 13, 14, 15], [16, 17, 18, 19], [20, 21, 22, 23]], [[24, 25, 26, 27], [28, 29, 30, 31], [32, 33, 34, 35]], [[36, 37, 38, 39], [40, 41, 42, 43], [44, 45, 46, 47]]])
Почему именно трехмерный? На самом деле реальный мир вовсе не ограничивается таблицами, векторами и матрицами. Еще существуют тензоры, кватернионы, октавы. А некоторые данные, гораздо удобнее представлять именно в трехмерном и четырехмерном представлении, например, биржевые торги по всем инструментам, лучше всего представлять в трехмерном виде, а торги нескольких бирж в четырехмерном. Конечно, такими сложными вычислениями занимается очень небольшое количество людей, но надо отметить, что именно эти люди двигают науку и индустрию вперед. Да и слово «сложное» можно считать синонимом «интересное. Поэтому… что-то мы отвлеклись… вот наш трехмерный массив:

Визуализация (и хорошее воображение) позволяет сразу догадаться, как устроена индексация трехмерных массивов. Например, если нам нужно вытащить из данного массива число 31, то достаточно выполнить:
>>> a[2][1][3] # или a[2, 1, 3]
31Но, что если мы хотим узнать побольше об этом массиве. В самом деле, у массивов есть целый ряд важных атрибутов. Например, количество осей массива (его размерность), которую при работе с очень большими массивами, не всегда легко увидеть:
>>> a.ndim
3 Массив a действительно трехмерный. Но иногда становится интересно, а на сколько же большой массив перед нами. Например, какой он формы, т.е. сколько элементов расположено вдоль каждой оси? Ответить позволяет метод ndarray.shape:
>>> a.shape
(4, 3, 4) Метод ndarray.size просто возвращает общее количество элементов массива:
>>> a.size
48Еще может встать такой вопрос — сколько памяти занимает наш массив? Иногда даже возникает такой вопрос — влезет ли результирующий массив после всех вычислений в оперативную память? Что бы на него ответить надо знать, сколько «весит» один элемент массива:
>>> a.itemsize # эквивалентно ndarray.dtype.itemsize
4 ndarray.itemsize возвращает размер элемента в байтах. Теперь мы можем узнать сколько «весит» наш массив:
>>> a.size*a.itemsize
192Итого — 192 байта. На самом деле, размер занимаемой массивом памяти, зависит не только от количества элементов в нем, но и от испльзуемого типа данных:
>>> a.dtype
dtype('int32') dtype('int32') — означает, что используется целочисленный тип данных, в котором для хранения одного числа выделяется 32 бита памяти. Но если мы выполним какие-нибудь вычисления с массивом, то тип данных может измениться:
>>> b = a/3.14
>>>
>>> b
array([[[ 0. , 0.31847134, 0.63694268, 0.95541401],
[ 1.27388535, 1.59235669, 1.91082803, 2.22929936],
[ 2.5477707 , 2.86624204, 3.18471338, 3.50318471]],
[[ 3.82165605, 4.14012739, 4.45859873, 4.77707006],
[ 5.0955414 , 5.41401274, 5.73248408, 6.05095541],
[ 6.36942675, 6.68789809, 7.00636943, 7.32484076]],
[[ 7.6433121 , 7.96178344, 8.28025478, 8.59872611],
[ 8.91719745, 9.23566879, 9.55414013, 9.87261146],
[10.1910828 , 10.50955414, 10.82802548, 11.14649682]],
[[11.46496815, 11.78343949, 12.10191083, 12.42038217],
[12.7388535 , 13.05732484, 13.37579618, 13.69426752],
[14.01273885, 14.33121019, 14.64968153, 14.96815287]]])
>>>
>>>
>>> b.dtype
dtype('float64') Теперь у нас есть еще один массив — массив b и его тип данных 'float64' — вещественные числа (числа с плавающей точкой) длинной 64 бита. А его размер:
>>> b.size*b.itemsize
384 Тогда массив a — 192 байта, массив b — 384 байта. А в общем, получается, 576 байт — что очень мало для современных объемов оперативной памяти, но и реальные объемы данных, которые сейчас приходится обрабатывать совсем немаленькие.
Мы с вами собирались ответить на вопросы производительности вычислений в NumPy, но это тоже тема отдельной главы. Могу лишь сказать, что на самом деле скорость вычислений, очень сильно зависит от того кода, который вы пишите. Например, частое копирование и присваивание массивов, приводит к бесполезному потреблению памяти, а работа универсальных функций NumPy без дополнительных настроек, особенно в циклах, так же может выполняться несколько медленнее. В общем задача по использованию всего вычислительного потенциала программного обеспечения и железа, не такая уж и простая, но определенно решаемая задача.
3.3. Напоследок
Если вы новичок, то очень скоро поймете, что в использовании NumPy так же прост как и Python. Но, рано или поздно, дело дойдет до сложных задач и вот тогда начнется самое интересное: документации не хватает, ничего не гуглится, а бесчисленные «почти» подходящие советы приводят к необъяснимым сверхъестественным последствиям. Что делать в такой ситуации?
- гуглить упорнее и спускаться к самому дну поисковой выдачи;
- гуглить на английском языке, потому что, на английском информации на порядки больше чем на русском;
- если не помог пункт 2, то это означает, что вы просто маньяк какой-то, и что бы решить свою маниакальную задачу, вам придется гуглить на китайском языке, потому что на китайском информации на порядки больше чем на английском.
Это шутка и серьезная рекомендация одновременно. Но, если говорить абсолютно серьезно, то просто придерживайтесь здравого смысла. Где этот здравый смысл начинается, а где заканчивается в конкретной задаче сказать очень трудно. import this вам в помощь:
>>> import this
The Zen of Python, by Tim Peters
Beautiful is better than ugly.
Explicit is better than implicit.
Simple is better than complex.
Complex is better than complicated.
Flat is better than nested.
Sparse is better than dense.
Readability counts.
Special cases aren't special enough to break the rules.
Although practicality beats purity.
Errors should never pass silently.
Unless explicitly silenced.
In the face of ambiguity, refuse the temptation to guess.
There should be one-- and preferably only one --obvious way to do it.
Although that way may not be obvious at first unless you're Dutch.
Now is better than never.
Although never is often better than *right* now.
If the implementation is hard to explain, it's a bad idea.
If the implementation is easy to explain, it may be a good idea.
Namespaces are one honking great idea -- let's do more of those!Если вы раньше пользовались R или matlab, то вас тоже ожидает много приятных сюрпризов, по крайней мере один — придется меньше стучать по клавиатуре.




pyprog.pro
NumPy в Python. Часть 1 / Habr
Предисловие переводчика
Доброго времени суток, Хабр. Запускаю цикл статей, которые являются переводом небольшого мана по numpy, ссылочка. Приятного чтения.
Введение
NumPy это open-source модуль для python, который предоставляет общие математические и числовые операции в виде пре-скомпилированных, быстрых функций. Они объединяются в высокоуровневые пакеты. Они обеспечивают функционал, который можно сравнить с функционалом MatLab. NumPy (Numeric Python) предоставляет базовые методы для манипуляции с большими массивами и матрицами. SciPy (Scientific Python) расширяет функционал numpy огромной коллекцией полезных алгоритмов, таких как минимизация, преобразование Фурье, регрессия, и другие прикладные математические техники.
Установка
Если у вас есть Python(x, y) (Примечание переводчика: Python(x, y), это дистрибутив свободного научного и инженерного программного обеспечения для численных расчётов, анализа и визуализации данных на основе языка программирования Python и большого числа модулей (библиотек)) на платформе Windows, то вы готовы начинать. Если же нет, то после установки python, вам нужно установить пакеты самостоятельно, сначала NumPy потом SciPy. Установка доступна здесь. Следуйте установке на странице, там всё предельно понятно.
Немного дополнительной информации
Сообщество NumPy и SciPy поддерживает онлайн руководство, включающие гайды и туториалы, тут: docs.scipy.org/doc.
Импорт модуля numpy
Есть несколько путей импорта. Стандартный метод это — использовать простое выражение:
>>> import numpyТем не менее, для большого количества вызовов функций numpy, становиться утомительно писать numpy.X снова и снова. Вместо этого намного легче сделать это так:
>>> import numpy as npЭто выражение позволяет нам получать доступ к numpy объектам используя np.X вместо numpy.X. Также можно импортировать numpy прямо в используемое пространство имен, чтобы вообще не использовать функции через точку, а вызывать их напрямую:
>>> from numpy import *Однако, этот вариант не приветствуется в программировании на python, так как убирает некоторые полезные структуры, которые модуль предоставляет. До конца этого туториала мы будем использовать второй вариант импорта (import numpy as np).
Массивы
Главной особенностью numpy является объект array. Массивы схожи со списками в python, исключая тот факт, что элементы массива должны иметь одинаковый тип данных, как float и int. С массивами можно проводить числовые операции с большим объемом информации в разы быстрее и, главное, намного эффективнее чем со списками.
Создание массива из списка:
a = np.array([1, 4, 5, 8], float)
>>> a
array([ 1., 4., 5., 8.])
>>> type(a)
<class 'numpy.ndarray'>Здесь функция array принимает два аргумента: список для конвертации в массив и тип для каждого элемента. Ко всем элементам можно получить доступ и манипулировать ими также, как вы бы это делали с обычными списками:
>>> a[:2]
array([ 1., 4.])
>>> a[3]
8.0
>>> a[0] = 5.
>>> a
array([ 5., 4., 5., 8.])Массивы могут быть и многомерными. В отличии от списков можно задавать команды в скобках. Вот пример двумерного массива (матрица):
>>> a = np.array([[1, 2, 3], [4, 5, 6]], float)
>>> a
array([[ 1., 2., 3.],
[ 4., 5., 6.]])
>>> a[0,0]
1.0
>>> a[0,1]
2.0Array slicing работает с многомерными массивами аналогично, как и с одномерными, применяя каждый срез, как фильтр для установленного измерения. Используйте «:» в измерении для указывания использования всех элементов этого измерения:
>>> a = np.array([[1, 2, 3], [4, 5, 6]], float)
>>> a[1,:]
array([ 4., 5., 6.])
>>> a[:,2]
array([ 3., 6.])
>>> a[-1:, -2:]
array([[ 5., 6.]])Метод shape возвращает количество строк и столбцов в матрице:
>>> a.shape
(2, 3)Метод dtype возвращает тип переменных, хранящихся в массиве:
>>> a.dtype
dtype('float64')Тут float64, это числовой тип данных в numpy, который используется для хранения вещественных чисел двойной точности. Так как же float в Python.
Метод len возвращает длину первого измерения (оси):
a = np.array([[1, 2, 3], [4, 5, 6]], float)
>>> len(a)
2Метод in используется для проверки на наличие элемента в массиве:
>>> a = np.array([[1, 2, 3], [4, 5, 6]], float)
>>> 2 in a
True
>>> 0 in a
FalseМассивы можно переформировать при помощи метода, который задает новый многомерный массив. Следуя следующему примеру, мы переформатируем одномерный массив из десяти элементов во двумерный массив, состоящий из пяти строк и двух столбцов:
>>> a = np.array(range(10), float)
>>> a
array([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])
>>> a = a.reshape((5, 2))
>>> a
array([[ 0., 1.],
[ 2., 3.],
[ 4., 5.],
[ 6., 7.],
[ 8., 9.]])
>>> a.shape
(5, 2)Обратите внимание, метод reshape создает новый массив, а не модифицирует оригинальный.
Имейте ввиду, связывание имен в python работает и с массивами. Метод copy используется для создания копии существующего массива в памяти:
>>> a = np.array([1, 2, 3], float)
>>> b = a
>>> c = a.copy()
>>> a[0] = 0
>>> a
array([0., 2., 3.])
>>> b
array([0., 2., 3.])
>>> c
array([1., 2., 3.])Списки можно тоже создавать с массивов:
>>> a = np.array([1, 2, 3], float)
>>> a.tolist()
[1.0, 2.0, 3.0]
>>> list(a)
[1.0, 2.0, 3.0]Можно также переконвертировать массив в бинарную строку (то есть, не human-readable форму). Используйте метод tostring для этого. Метод fromstring работает в для обратного преобразования. Эти операции иногда полезны для сохранения большого количества данных в файлах, которые могут быть считаны в будущем.
>>> a = array([1, 2, 3], float)
>>> s = a.tostring()
>>> s
'\x00\x00\x00\x00\x00\x00\xf0?\x00\x00\x00\x00\x00\x00\x00@\x00\x00\x00\x00\x00\x00\x08@'
>>> np.fromstring(s)
array([ 1., 2., 3.])Заполнение массива одинаковым значением.
>>> a = array([1, 2, 3], float)
>>> a
array([ 1., 2., 3.])
>>> a.fill(0)
>>> a
array([ 0., 0., 0.])Транспонирование массивов также возможно, при этом создается новый массив:
>>> a = np.array(range(6), float).reshape((2, 3))
>>> a
array([[ 0., 1., 2.],
[ 3., 4., 5.]])
>>> a.transpose()
array([[ 0., 3.],
[ 1., 4.],
[ 2., 5.]])Многомерный массив можно переконвертировать в одномерный при помощи метода flatten:
>>> a = np.array([[1, 2, 3], [4, 5, 6]], float)
>>> a
array([[ 1., 2., 3.],
[ 4., 5., 6.]])
>>> a.flatten()
array([ 1., 2., 3., 4., 5., 6.])
Два или больше массивов можно сконкатенировать при помощи метода concatenate:
>>> a = np.array([1,2], float)
>>> b = np.array([3,4,5,6], float)
>>> c = np.array([7,8,9], float)
>>> np.concatenate((a, b, c))
array([1., 2., 3., 4., 5., 6., 7., 8., 9.])Если массив не одномерный, можно задать ось, по которой будет происходить соединение. По умолчанию (не задавая значения оси), соединение будет происходить по первому измерению:
>>> a = np.array([[1, 2], [3, 4]], float)
>>> b = np.array([[5, 6], [7,8]], float)
>>> np.concatenate((a,b))
array([[ 1., 2.],
[ 3., 4.],
[ 5., 6.],
[ 7., 8.]])
>>> np.concatenate((a,b), axis=0)
array([[ 1., 2.],
[ 3., 4.],
[ 5., 6.],
[ 7., 8.]])
>>>
np.concatenate((a,b), axis=1)
array([[ 1., 2., 5., 6.],
[ 3., 4., 7., 8.]])В заключении, размерность массива может быть увеличена при использовании константы newaxis в квадратных скобках:
>>> a = np.array([1, 2, 3], float)
>>> a
array([1., 2., 3.])
>>> a[:,np.newaxis]
array([[ 1.],
[ 2.],
[ 3.]])
>>> a[:,np.newaxis].shape
(3,1)
>>> b[np.newaxis,:]
array([[ 1., 2., 3.]])
>>> b[np.newaxis,:].shape
(1,3)Заметьте, тут каждый массив двумерный; созданный при помощи newaxis имеет размерность один. Метод newaxis подходит для удобного создания надлежаще-мерных массивов в векторной и матричной математике.
На этом у нас конец первой части перевода. Спасибо за внимание.
habr.com
Матрицы и массивы NumPy в Python
Матрица — это двухмерная структура данных, в которой числа расположены в виде строк и столбцов. Например:

Эта матрица является матрицей три на четыре, потому что она состоит из 3 строк и 4 столбцов.
Python не имеет встроенного типа данных для матриц. Но можно рассматривать список как матрицу. Например:
A = [[1, 4, 5],
[-5, 8, 9]]
Этот список является матрицей на 2 строки и 3 столбца.

Обязательно ознакомьтесь с документацией по спискам Python, прежде чем продолжить читать эту статью.
Давайте посмотрим, как работать с вложенным списком.
A = [[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]]
print("A =", A)
print("A[1] =", A[1]) # вторая строка
print("A[1][2] =", A[1][2]) # третий элемент второй строки
print("A[0][-1] =", A[0][-1]) # последний элемент первой строки
column = []; # пустой список
for row in A:
column.append(row[2])
print("3rd column =", column)
Когда мы запустим эту программу, результат будет следующий:
A = [[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]] A [1] = [-5, 8, 9, 0] A [1] [2] = 9 A [0] [- 1] = 12 3-й столбец = [5, 9, 11]
Использование вложенных списков в качестве матрицы подходит для простых вычислительных задач. Но в Python есть более эффективный способ работы с матрицами – NumPy .
NumPy — это расширение для научных вычислений, которое поддерживает мощный объект N-мерного массива. Прежде чем использовать NumPy, необходимо установить его. Для получения дополнительной информации,
- Ознакомьтесь: Как установить NumPy?
- Если вы работаете в Windows, скачайте и установите дистрибутив anaconda Python. Он поставляется вместе с NumPy и другими расширениями.
После установки NumPy можно импортировать и использовать его.
NumPy предоставляет собой многомерный массив чисел (который на самом деле является объектом). Давайте рассмотрим приведенный ниже пример:
import numpy as np a = np.array([1, 2, 3]) print(a) # Вывод: [1, 2, 3] print(type(a)) # Вывод: <class 'numpy.ndarray'>
Как видите, класс массива NumPy называется ndarray.
Существует несколько способов создания массивов NumPy.
import numpy as np A = np.array([[1, 2, 3], [3, 4, 5]]) print(A) A = np.array([[1.1, 2, 3], [3, 4, 5]]) # Массив чисел с плавающей запятой print(A) A = np.array([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив составных чисел print(A)
Когда вы запустите эту программу, результат будет следующий:
[[1 2 3] [3 4 5]] [[1.1 2. 3.] [3. 4. 5.]] [[1. + 0.j 2. + 0.j 3. + 0.j] [3. + 0.j 4. + 0.j 5. + 0.j]]
import numpy as np zeors_array = np.zeros( (2, 3) ) print(zeors_array) ''' Вывод: [[0. 0. 0.] [0. 0. 0.]] ''' ones_array = np.ones( (1, 5), dtype=np.int32 ) // указание dtype print(ones_array) # Вывод: [[1 1 1 1 1]]
Здесь мы указали dtype — 32 бита (4 байта). Следовательно, этот массив может принимать значения от -2-31 до 2-31-1.
import numpy as np
A = np.arange(4)
print('A =', A)
B = np.arange(12).reshape(2, 6)
print('B =', B)
'''
Вывод:
A = [0 1 2 3]
B = [[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]]
'''
Узнайте больше о других способах создания массива NumPy .
Выше мы привели пример сложение, умножение матриц и транспонирование матрицы. Мы использовали вложенные списки, прежде чем создавать эти программы. Рассмотрим, как выполнить ту же задачу, используя массив NumPy.
Мы используем оператор +, чтобы сложить соответствующие элементы двух матриц NumPy.
import numpy as np A = np.array([[2, 4], [5, -6]]) B = np.array([[9, -3], [3, 6]]) C = A + B # сложение соответствующих элементов print(C) ''' Вывод: [[11 1] [ 8 0]] '''
Чтобы умножить две матрицы, мы используем метод dot(). Узнайте больше о том, как работает numpy.dot .
Примечание: * используется для умножения массива (умножения соответствующих элементов двух массивов), а не умножения матрицы.
import numpy as np A = np.array([[3, 6, 7], [5, -3, 0]]) B = np.array([[1, 1], [2, 1], [3, -3]]) C = a.dot(B) print(C) ''' Вывод: [[ 36 -12] [ -1 2]] '''
Мы используем numpy.transpose для вычисления транспонирования матрицы.
import numpy as np A = np.array([[1, 1], [2, 1], [3, -3]]) print(A.transpose()) ''' Вывод: [[ 1 2 3] [ 1 1 -3]] '''
Как видите, NumPy значительно упростил нашу задачу.
Также можно получить доступ к элементам матрицы, используя индекс. Начнем с одномерного массива NumPy.
import numpy as np
A = np.array([2, 4, 6, 8, 10])
print("A[0] =", A[0]) # Первый элемент
print("A[2] =", A[2]) # Третий элемент
print("A[-1] =", A[-1]) # Последний элемент
Когда вы запустите эту программу, результат будет следующий:
A [0] = 2 A [2] = 6 A [-1] = 10
Теперь выясним, как получить доступ к элементам двухмерного массива (который в основном представляет собой матрицу).
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
# Первый элемент первой строки
print("A[0][0] =", A[0][0])
# Третий элемент второй строки
print("A[1][2] =", A[1][2])
# Последний элемент последней строки
print("A[-1][-1] =", A[-1][-1])
Когда мы запустим эту программу, результат будет следующий:
A [0] [0] = 1 A [1] [2] = 9 A [-1] [- 1] = 19
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[0] =", A[0]) # Первая строка
print("A[2] =", A[2]) # Третья строка
print("A[-1] =", A[-1]) # Последняя строка (третья строка в данном случае)
Когда мы запустим эту программу, результат будет следующий:
A [0] = [1, 4, 5, 12] A [2] = [-6, 7, 11, 19] A [-1] = [-6, 7, 11, 19]
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[:,0] =",A[:,0]) # Первый столбец
print("A[:,3] =", A[:,3]) # Четвертый столбец
print("A[:,-1] =", A[:,-1]) # Последний столбец (четвертый столбец в данном случае)
Когда мы запустим эту программу, результат будет следующий:
A [:, 0] = [1 -5 -6] A [:, 3] = [12 0 19] A [:, - 1] = [12 0 19]
Если вы не знаете, как работает приведенный выше код, прочтите раздел «Разделение матрицы».
Разделение одномерного массива NumPy аналогично разделению списка. Рассмотрим пример:
import numpy as np letters = np.array([1, 3, 5, 7, 9, 7, 5]) # с 3-го по 5-ый элементы print(letters[2:5]) # Вывод: [5, 7, 9] # с 1-го по 4-ый элементы print(letters[:-5]) # Вывод: [1, 3] # с 6-го до последнего элемента print(letters[5:]) # Вывод:[7, 5] # с 1-го до последнего элемента print(letters[:]) # Вывод:[1, 3, 5, 7, 9, 7, 5] # список в обратном порядке print(letters[::-1]) # Вывод:[5, 7, 9, 7, 5, 3, 1]
Теперь посмотрим, как разделить матрицу.
import numpy as np
A = np.array([[1, 4, 5, 12, 14],
[-5, 8, 9, 0, 17],
[-6, 7, 11, 19, 21]])
print(A[:2, :4]) # две строки, четыре столбца
''' Вывод:
[[ 1 4 5 12]
[-5 8 9 0]]
'''
print(A[:1,]) # первая строка, все столбцы
''' Вывод:
[[ 1 4 5 12 14]]
'''
print(A[:,2]) # все строки, второй столбец
''' Вывод:
[ 5 9 11]
'''
print(A[:, 2:5]) # все строки, с третьего по пятый столбец
''' Вывод:
[[ 5 12 14]
[ 9 0 17]
[11 19 21]]
'''
Использование NumPy вместо вложенных списков значительно упрощает работу с матрицами. Мы рекомендуем детально изучить пакет NumPy, если вы планируете использовать Python для анализа данных.
Данная публикация представляет собой перевод статьи «Python Matrices and NumPy Arrays» , подготовленной дружной командой проекта Интернет-технологии.ру
www.internet-technologies.ru
Учебник по NumPy — Визуализация примеров для быстрого изучения
Пакет NumPy является незаменимым помощником Python. Он тянет на себе анализ данных, машинное обучение и научные вычисления, а также существенно облегчает обработку векторов и матриц. Некоторые ведущие пакеты Python используют NumPy как основной элемент своей инфраструктуры. К их числу относятся scikit-learn, SciPy, pandas и tenorflow. Помимо возможности разобрать по косточкам числовые данные, умение работать с NumPy дает значительное преимущество при отладке более сложных сценариев библиотек.
Содержание

В данной статье будут рассмотрены основные способы использования NumPy на примерах, а также типы представления данных (таблицы, картинки, текст и так далее) перед их последующей подачей модели машинного обучения.
Создание массивов NumPy
Можно создать массив NumPy (он же ndarray), передав ему список Python, используя np.array(). В данном случае Python создает массив, который выглядит следующим образом:
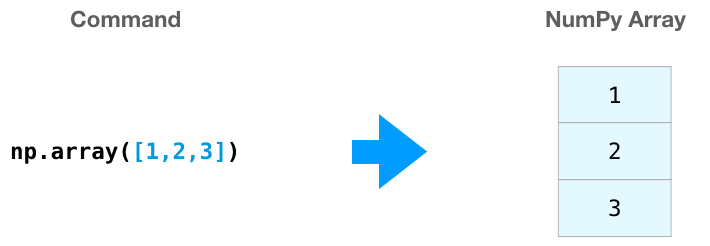
Нередки случаи, когда необходимо, чтобы NumPy инициализировал значения массива.
Мы собрали ТОП Книг для Python программиста которые помогут быстро изучить язык программирования Python. Список книг: Книги по PythonДля этого NumPy использует такие методы, как ones(), zeros() и random.random(). Требуется просто передать им количество элементов, которые необходимо сгенерировать:
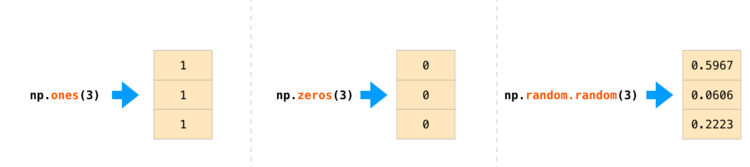
После создания массивов можно манипулировать ими довольно любопытными способами.
Арифметические операции над массивами NumPy
Создадим два массива NumPy и продемонстрируем выгоду их использования.
Массивы будут называться data и ones:

При сложении массивов складываются значения каждого ряда. Это сделать очень просто, достаточно написать data + ones:
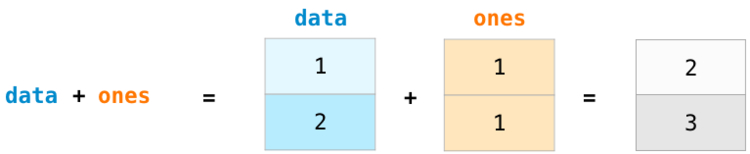
Новичкам может прийтись по душе тот факт, что использование абстракций подобного рода не требует написания циклов for с вычислениями. Это отличная абстракция, которая позволяет оценить поставленную задачу на более высоком уровне.
Помимо сложения, здесь также можно выполнить следующие простые арифметические операции:

Довольно часто требуется выполнить какую-то арифметическую операцию между массивом и простым числом. Ее также можно назвать операцией между вектором и скалярной величиной. К примеру, предположим, в массиве указано расстояние в милях, и его нужно перевести в километры. Для этого нужно выполнить операцию data * 1.6:

Как можно увидеть в примере выше, NumPy сам понял, что умножить на указанное число нужно каждый элемент массива. Данный концепт называется трансляцией, или broadcating. Трансляция бывает весьма полезна.
Индексация массива NumPy
Массив NumPy можно разделить на части и присвоить им индексы. Принцип работы похож на то, как это происходит со списками Python.

Агрегирование в NumPy
Дополнительным преимуществом NumPy является наличие в нем функций агрегирования:

Функциями min(), max() и sum() дело не ограничивается.
К примеру:
mean()позволяет получить среднее арифметическое;prod()выдает результат умножения всех элементов;stdнужно для среднеквадратического отклонения.
Это лишь небольшая часть довольно обширного списка функций агрегирования в NumPy.
Использование нескольких размерностей NumPy
Все перечисленные выше примеры касаются векторов одной размерности. Главным преимуществом NumPy является его способность использовать отмеченные операции с любым количеством размерностей.
Создание матриц NumPy на примерах
Созданные в следующей форме списки из списков Python можно передать NumPy. Он создаст матрицу, которая будет представлять данные списки:

Упомянутые ранее методы ones(), zeros() и random.random() можно использовать так долго, как того требует проект.
Достаточно только добавить им кортеж, в котором будут указаны размерности матрицы, которую мы создаем.

Арифметические операции над матрицами NumPy
Матрицы можно складывать и умножать при помощи арифметических операторов (+ - * /). Стоит, однако, помнить, что матрицы должны быть одного и того же размера. NumPy в данном случае использует операции координат:

Арифметические операции над матрицами разных размеров возможны в том случае, если размерность одной из матриц равно одному. Это значит, что в матрице только один столбец или один ряд. В таком случае для выполнения операции NumPy будет использовать правила трансляции:

dot() Скалярное произведение NumPy
Главное различие с обычными арифметическими операциями здесь в том, что при умножении матриц используется скалярное произведение. В NumPy каждая матрица может использовать метод dot(). Он применяется для проведения скалярных операций с рассматриваемыми матрицами:

На изображении выше под каждой фигурой указана ее размерность. Это сделано с целью отметить, что размерности обеих матриц должны совпадать с той стороны, где они соприкасаются. Визуально представить данную операцию можно следующим образом:

Индексация матрицы NumPy
Операции индексации и деления незаменимы, когда дело доходит до манипуляции с матрицами:
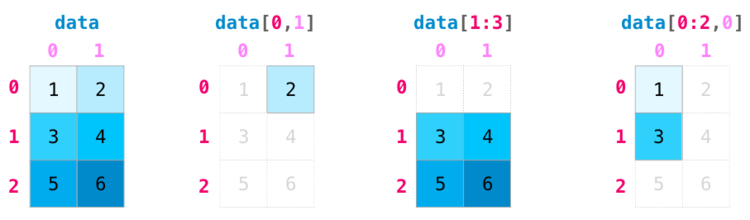
Агрегирование матриц NumPy
Агрегирование матриц происходит точно так же, как агрегирование векторов:

Используя параметр axis, можно агрегировать не только все значения внутри матрицы, но и значения за столбцами или рядами.

Транспонирование и изменение формы матриц в numpy
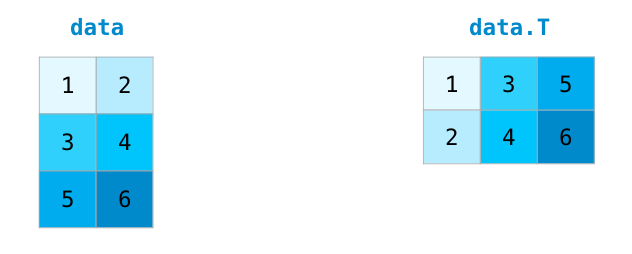
Нередки случаи, когда нужно повернуть матрицу. Это может потребоваться при вычислении скалярного произведения двух матриц. Тогда возникает необходимость наличия совпадающих размерностей. У массивов NumPy есть полезное свойство под названием T, что отвечает за транспонирование матрицы.
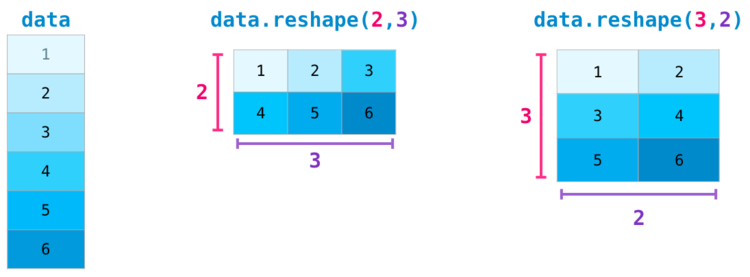
Некоторые более сложные ситуации требуют возможности переключения между размерностями рассматриваемой матрицы. Это типично для приложений с машинным обучением, где некая модель может запросить определенную форму вывода, которая является отличной от формы начального набора данных. В таких ситуациях пригодится метод reshape() из NumPy. Здесь от вас требуется только передать новые размерности для матрицы. Для размерности вы можете передать -1, и NumPy выведет ее верное значение, опираясь на данные рассматриваемой матрицы:
Еще больше размерностей NumPy
NumPy может произвести все вышеперечисленные операции для любого количества размерностей. Структура данных, расположенных центрально, называется ndarray, или n-мерным массивом.

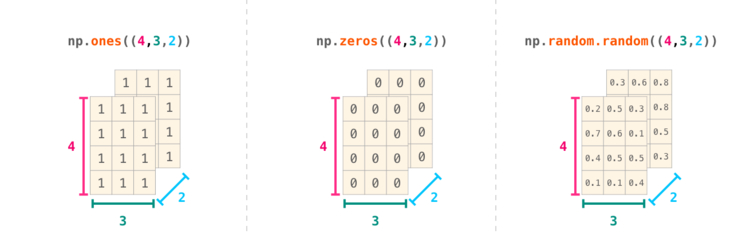
В большинстве случаев для указания новой размерности требуется просто добавить запятую к параметрам функции NumPy:
На заметку: Стоит иметь в виду, что при выводе 3-мерного массива NumPy результат, представленный в виде текста, выглядит иначе, нежели показано в примере выше. Порядок вывода n-мерного массива NumPy следующий — последняя ось зацикливается быстрее всего, а первая медленнее всего. Это значит, что вывод
np.ones((4,3,2))будет иметь вид:
array([[[1., 1.], [1., 1.], [1., 1.]], [[1., 1.], [1., 1.], [1., 1.]], [[1., 1.], [1., 1.], [1., 1.]], [[1., 1.], [1., 1.], [1., 1.]]])
array([[[1., 1.], [1., 1.], [1., 1.]],
[[1., 1.], [1., 1.], [1., 1.]],
[[1., 1.], [1., 1.], [1., 1.]],
[[1., 1.], [1., 1.], [1., 1.]]]) |
Примеры работы с NumPy
Подытожим все вышесказанное. Вот несколько примеров полезных инструментов NumPy, которые могут значительно облегчить процесс написания кода.
Математические формулы NumPy
Необходимость внедрения математических формул, которые будут работать с матрицами и векторами, является главной причиной использования NumPy. Именно поэтому NumPy пользуется большой популярностью среди представителей науки. В качестве примера рассмотрим формулу среднеквадратичной ошибки, которая является центральной для контролируемых моделей машинного обучения, что решают проблемы регрессии:
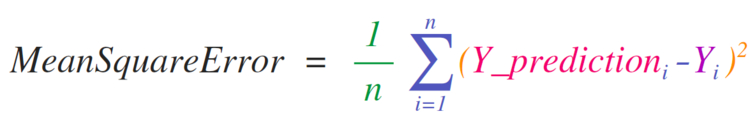
Реализовать данную формулу в NumPy довольно легко:

Главное достоинство NumPy в том, что его не заботит, если predictions и labels содержат одно или тысячи значение (до тех пор, пока они оба одного размера). Рассмотрим пример, последовательно изучив четыре операции в следующей строке кода:

У обоих векторов predictions и labels по три значения. Это значит, что в данном случае n равно трем. После выполнения указанного выше вычитания мы получим значения, которые будут выглядеть следующим образом:

Затем мы можем возвести значения вектора в квадрат:

Теперь мы вычисляем эти значения:

Таким образом мы получаем значение ошибки некого прогноза и score за качество модели.
Представление данных NumPy
Задумайтесь о всех тех типах данных, которыми вам понадобится оперировать, создавая различные модели работы (электронные таблицы, изображения, аудио и так далее). Очень многие типы могут быть представлены как n-мерные массивы:
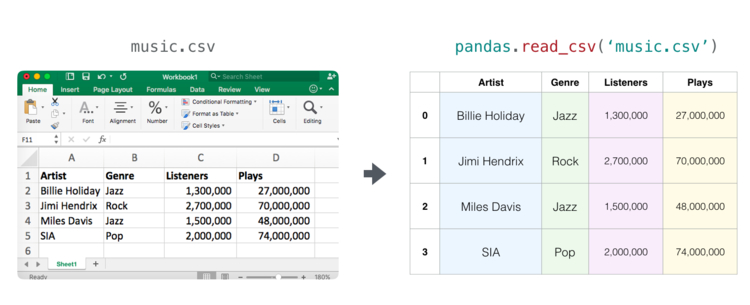
Таблицы NumPy — примеры использования таблиц
Таблица значений является двумерной матрицей. Каждый лист таблицы может быть отдельной переменной. Для работы с таблицами в Python чаще всего используется pandas.DataFrame, что задействует NumPy и строит поверх него.
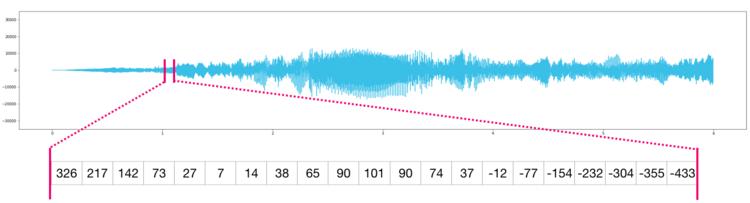
Аудио и временные ряды в NumPy
По сути аудио файл — это одномерный массив семплов. Каждый семпл представляет собой число, которое является крошечным фрагментов аудио сигнала. Аудио CD-качества может содержать 44 100 семплов в секунду, каждый из которых является целым числом в промежутке между -32767 и 32768. Это значит, что десятисекундный WAVE-файл CD-качества можно поместить в массив NumPy длиной в 10 * 44 100 = 441 000 семплов.
Хотите извлечь первую секунду аудио? Просто загрузите файл в массив NumPy под названием audio, после чего получите audio[: 44100].
Фрагмент аудио файла выглядит следующим образом:
То же самое касается данных временных рядов, например, изменения стоимости акций со временем.
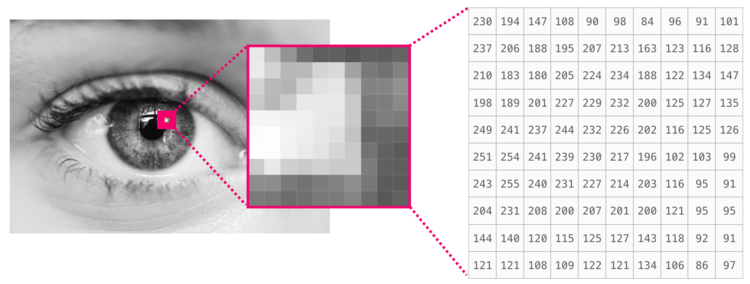
Обработка изображений в NumPy
Изображение является матрицей пикселей по размеру (высота х ширина).
Если изображение черно-белое, то есть представленное в полутонах, каждый пиксель может быть представлен как единственное число. Обычно между 0 (черный) и 255 (белый). Хотите обрезать квадрат размером 10 х 10 пикселей в верхнем левом углу картинки? Просто попросите в NumPy image[:10, :10].
Вот как выглядит фрагмент изображения:
Если изображение цветное, каждый пиксель представлен тремя числами. Здесь за основу берется цветовая модель RGB — красный (R), зеленый (G) и синий (B).
В данном случае нам понадобится третья размерность, так как каждая клетка вмещает только одно число. Таким образом, цветная картинка будет представлена массивом ndarray с размерностями: (высота х ширина х 3).

Обработка текста в NumPy на примерах
Когда дело доходит до текста, подход несколько меняется. Цифровое представление текста предполагает создание некого python словаря, то есть инвентаря всех уникальных слов, которые бы распознавались моделью, а также векторно (embedding step). Попробуем представить в цифровой форме цитату из стихотворения арабского поэта Антара ибн Шаддада, переведенную на английский язык:
“Have the bards who preceded me left any theme unsung?”
Перед переводом данного предложения в нужную цифровую форму модель должна будет проанализировать огромное количество текста. Здесь можно обработать небольшой набор данный, после чего использовать его для создания словаря из 71 290 слов.

Предложение может быть разбито на массив токенов, что будут словами или частями слов в зависимости от установленных общих правил:

Затем в данной таблице словаря вместо каждого слова мы ставим его id:

Однако данные id все еще не обладают достаточным количеством информации о модели как таковой. Поэтому перед передачей последовательности слов в модель токены/слова должны быть заменены их векторными представлениями. В данном случае используется 50-мерное векторное представление Word2vec.

Здесь ясно видно, что у массива NumPy есть несколько размерностей [embedding_dimension x sequence_length]. На практике все выглядит несколько иначе, однако данное визуальное представление более понятно для разъяснения общих принципов работы.
Для лучшей производительности модели глубокого обучения обычно сохраняют первую размерность для пакета. Это происходит из-за того, что тренировка модели происходит быстрее, если несколько примеров проходят тренировку параллельно. Здесь особенно полезным будет reshape(). Например, такая модель, как BERT, будет ожидать ввода в форме: [batch_size, sequence_length, embedding_size].
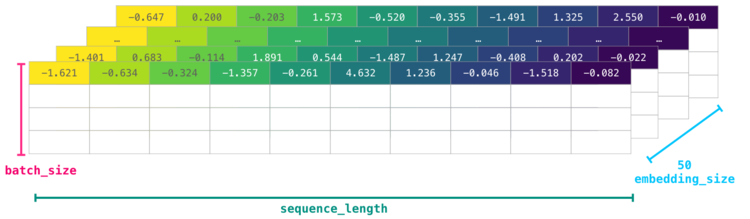
Теперь мы получили числовой том, с которым модель может работать и делать полезные вещи. Некоторые строки остались пустыми, однако они могут быть заполнены другими примерами, на которых модель может тренироваться или делать прогнозы.
(На заметку: Поэма, строчку из которой мы использовали в примере, увековечила своего автора в веках. Будучи незаконнорожденным сыном главы племени от рабыни, Антара ибн Шаддан мастерски владел языком поэзии. Вокруг исторической фигуры поэта сложились мифы и легенды, а его стихи стали частью классической арабской литературы).
python-scripts.com
array | NumPy
numpy.array(object, dtype=None, copy=True, order='K', subok=False, ndmin=0)
Функция array() создает массив NumPy.
- Параметры:
- object — подобный массиву объект
- Список или кортеж, а так же лбая функция или объект с методом, возвращаеющие список или кортеж.
- dtype — тип данных NumPy (необязательный)
- Определяет тип данных выходного массива.
- copy — False или True (необязательный)
- Если этот параметр установлен в True (по умолчанию), то объект копируется. В противном случае копирование происходит только если: метод
__array__объекта возвращает копию, еслиobjectявляется вложенной последовательностью, если треуется доступ к определенным параметрам массива (dtype, order и т.д.) - order — ‘K’, ‘A’, ‘C’ или ‘F’ (необязательный)
- Этот параметр определяет в каком порядке массивы должны храниться в памяти: строчном C-стиле или столбчатом стиле Fortran. Если object не является массивом NumPy, то созданный массив будет находиться в памяти в строковом С порядке, если указать флаг ‘F’, то будет храниться в столбчатом порядке ‘Fortran’. Если object — это массив NumPy, то флаг ‘K’ либо сохраняет порядок исходного массива либо устанавливает самый близкий по структуре; флаг ‘A’ установит макет памяти выходного массива в ‘F’ если массив
objectявляется смежным со столбчатым стилем Fortran, в противном случае макет памяти будет установлен в ‘C’. По умолчанию флаг установлен в значение ‘K’. - subok- True или False (необязательный)
- Если параметр установлен в значение True (установлено по умодчанию в False), то выходной массив будет использовать тип подкласса массива
object, если False то тип массива базового класса. - ndmin- целое число (необязательный)
- Определяет минимальное количество измерений результирующего массива, которое, по мере необходимости, будет прикреплено к его форме для удовлетворения этого требования.
- Возвращает:
- результат — массив NumPy
- Массив удовлетворяющий всем указанным требованиям.
Замечание
Довольно большое значение имеет параметр order, который отвечает за порядок хранения массива в памяти. В некоторых ситуациях этот порядок может изменяться, что в редких случаях может приводить к ошибкам. Например при выполении транспонирования массива порядок ‘C’ может измениться на порядок ‘F’:
>>> a = np.array([[1, 2], [1, 2]])
>>> a
array([[1, 2],
[1, 2]])
>>>
>>> b = a.T # Присвоим массиву 'b' транспонированную матрицу 'a'
>>> b
array([[1, 1],
[2, 2]])
>>>
>>> # Теперь проверим порядок хранения в памяти
...
>>> a.flags
C_CONTIGUOUS : True
F_CONTIGUOUS : False
OWNDATA : True
WRITEABLE : True
ALIGNED : True
UPDATEIFCOPY : False
>>>
>>> b.flags
C_CONTIGUOUS : False
F_CONTIGUOUS : True
OWNDATA : False
WRITEABLE : True
ALIGNED : True
UPDATEIFCOPY : False Как видно, массив a до транспонирования имел C_CONTIGUOUS : True и F_CONTIGUOUS : False т.е. был организован в C-стиле, после транспонирования он сменился на стиль Fortran: C_CONTIGUOUS : False и F_CONTIGUOUS : True.
Если параметр order установлен в значение ‘A’ и в качестве object указан массив с порядком отличным от ‘F’ или ‘C’, то результирующий массив не всегда будет иметь ожидаемый флаг ‘C’. В редких случаях это так же может приводить к ошибкам.
Примеры
>>> import numpy as np
>>>
>>> np.array([1, 2, 3, 4, 5, 6, 7])
array([1, 2, 3, 4, 5, 6, 7])
>>>
>>>
>>> # Если элементы разного типа, то все они приводятся к наиболее общему:
... np.array([1, 1, 2, 2, 3.14, 3.14])
array([ 1. , 1. , 2. , 2. , 3.14, 3.14])
>>>
>>> np.array([1+1j, 1+1j, 2, 2, 3.14, 3.14])
array([ 1.00+1.j, 1.00+1.j, 2.00+0.j, 2.00+0.j, 3.14+0.j, 3.14+0.j])
>>>
>>>
>>> np.array([[1, 2], [3, 4]]) # Двумерный массив
array([[1, 2],
[3, 4]])
>>> # Создание трехмерного массива
>>> np.array([[[1, 1], [2, 2]],
... [[3, 3], [4, 4]],
... [[5, 5], [6, 6]]])
array([[[1, 1],
[2, 2]],
[[3, 3],
[4, 4]],
[[5, 5],
[6, 6]]])
>>>
>>>
>>> # Создание массива у которого минимум 2 измерения:
... a = np.array([1, 3, 5], ndmin = 2)
>>> a
array([[1, 3, 5]])
>>>
>>>
>>> # Указание типа данных массива:
... np.array([[1, 2], [3, 4]], dtype = complex)
array([[ 1.+0.j, 2.+0.j],
[ 3.+0.j, 4.+0.j]])
>>>
>>>
>>> # Создание структурированного массива:
... y = np.array([(1, 1), (2, 4), (3, 9), (4, 16)], dtype = [('x','i2'),('f_x','f4')])
>>> y['x']
array([1, 2, 3, 4], dtype=int16)
>>> y['f_x']
array([ 1., 4., 9., 16.], dtype=float32)
>>>
>>>
>>> # Создание массивов с использованием подклассов:
... np.array(np.mat('1 1 1; 2 2 2; 3 3 3'))
array([[1, 1, 1],
[2, 2, 2],
[3, 3, 3]])
>>>
>>> np.array(np.mat('1 1 1; 2 2 2; 3 3 3'), subok = True)
matrix([[1, 1, 1],
[2, 2, 2],
[3, 3, 3]]) 



pyprog.pro
Numpy | Создание массива
Создание массива с использованием List: массивы используются для хранения нескольких значений в одной переменной. Python не имеет встроенной поддержки массивов, но вместо этого можно использовать списки Python.
Пример :
обр = [1, 2, 3, 4, 5] arr1 = ["гиков", "для", "гиков"]
# Python программа для создания
# массив
# Создание массива с использованием списка
обр = [1, 2, 3, 4, 5]
ибо я в обр:
печать (я)
Выход:
1 2 3 4 5
Создание массива с использованием функций массива:
Функция array (тип данных, список значений) используется для создания массива с типом данных и списком значений, указанным в его аргументах.
Пример :
# Python-код для демонстрации работы
# array ()
# импорт "массива" для операций с массивами
импортировать массив
# инициализация массива со значениями массива
# инициализирует массив со знаком целыми числами
arr = array.array ('i', [1, 2, 3])
# печать исходного массива
print ("Новый созданный массив:", end = "")
для i в диапазоне (0,3):
print (arr [i], end = "")
печать ("/ r")
Выход:
Новый созданный массив: 1 2 3 1 5
Создание массива с использованием numpy методов:
NumPy предлагает несколько функций для создания массивов с начальным заполнителем. Это сводит к минимуму необходимость выращивания массивов, дорогостоящей операции. Например: np.zeros , np.empty и т. Д.
numpy.empty (shape, dtype = float, order = ‘C’) : вернуть новый массив заданной формы и типа со случайными значениями.
# Python Программирование, иллюстрирующее
# numpy.empty метод
импортировать NumPy как Компьютерщик
b = geek.empty (2, dtype = int)
печать ("Матрица b: / n", b)
a = geek.empty ([2, 2], dtype = int)
печать ("/ nMatrix a: / n", a)
c = geek.empty ([3, 3])
печать ("/ nMatrix c: / n", c)
Выход :
Матрица б: [0 1079574528] Матрица а: [[0 0] [0 0]] Матрица а: [[0. 0. 0.] [0. 0. 0.] [0. 0. 0.]]
numpy.zeros (shape, dtype = None, order = ‘C’) : вернуть новый массив заданной формы и типа с нулями.
# Программа Python, иллюстрирующая
# numpy.zeros метод
импортировать NumPy как Компьютерщик
b = geek.zeros (2, dtype = int)
печать ("Матрица b: / n", b)
a = geek.zeros ([2, 2], dtype = int)
печать ("/ nMatrix a: / n", a)
c = geek.zeros ([3, 3])
печать ("/ nMatrix c: / n", c)
Выход :
Матрица б: [0 0] Матрица а: [[0 0] [0 0]] Матрица с: [[0. 0. 0.] [0. 0. 0.] [0. 0. 0.]]
Перестройка массива: Мы можем использовать reshape метод , чтобы изменить массив. Рассмотрим массив с формой (a1, a2, a3,…, aN). Мы можем изменить его и преобразовать в другой массив с формой (b1, b2, b3,…, bM).
Единственное обязательное условие: a1 x a2 x a3… x aN = b1 x b2 x b3… x bM. (т.е. оригинальный размер массива остается неизменным.)
numpy.reshape (array, shape, order = ‘C’) : формирует массив без изменения данных массива.
# Программа Python, иллюстрирующая
# numpy.reshape () метод
импортировать NumPy как Компьютерщик
array = geek.arange (8)
печать («Исходный массив: / n», массив)
# массив формы с 2 строками и 4 столбцами
array = geek.arange (8) .reshape (2, 4)
print ("/ narray, измененный с 2 строками и 4 столбцами: / n", массив)
# массив формы с 2 строками и 4 столбцами
array = geek.arange (8) .reshape (4, 2)
print ("/ narray, измененный с 2 рядами и
4 столбца: / n ", массив) # Создает массив 3D массив = geek.arange (8) .reshape (2, 2, 2) print (" / nОригинальный массив преобразован в 3D: / n ", массив) Выход :
Исходный массив: [0 1 2 3 4 5 6 7] массив изменен с 2 рядами и 4 столбцами: [[0 1 2 3] [4 5 6 7]] массив изменен с 2 рядами и 4 столбцами: [[0 1] [2 3] [4 5] [6 7]] Исходный массив преобразован в 3D: [[[0 1] [2 3]] [[4 5] [6 7]]]
Для создания последовательностей чисел NumPy предоставляет функцию, аналогичную диапазону, которая возвращает массивы вместо списков.
arange возвращает равномерно распределенные значения в заданном интервале. размер шага указан.
linspace возвращает равномерно распределенные значения в заданном интервале. номер нет элементов возвращаются.
arange ([start,] stop [, step,] [, dtype]) : возвращает массив с равномерно расположенными элементами в соответствии с интервалом. Упомянутый интервал наполовину открыт, т.е. [Старт, Стоп)
# Python Программирование, иллюстрирующее
# numpy.arange метод
импортировать NumPy как Компьютерщик
print ("A / n", geek.arange (4) .reshape (2, 2), "/ n")
print ("A / n", geek.arange (4, 10), "/ n")
print ("A / n", geek.arange (4, 20, 3), "/ n")
Выход :
[[0 1] [2 3]] [4 5 6 7 8 9] [4 7 10 13 16 19]
numpy.linspace (start, stop, num = 50, endpoint = True, retstep = False, dtype = None) : возвращает числовые пробелы равномерно по интервалу. Похоже на расположение, но вместо шага используется номер образца.
# Python Программирование, иллюстрирующее
# numpy.linspace метод
импортировать NumPy как Компьютерщик
# restep установлен в True
print ("B / n", geek.linspace (2.0, 3.0, num = 5, retstep = True), "/ n")
# Чтобы оценить sin () на большом расстоянии
x = geek.linspace (0, 2, 10)
print ("A / n", geek.sin (x))
Выход :
В (массив ([2., 2.25, 2.5, 2.75, 3.]), 0,25) [0. 0,22039774 0,42995636 0,6183698 0,77637192 0,8961922 0,9719379 0,9998386 0,9786557 0,90929743]
Свести массив: мы можем использовать метод сглаживания, чтобы получить копию массива, свернутого в одно измерение. Он принимает аргумент заказа. Значением по умолчанию является «C» (для основного ряда строк). Используйте ‘F’ для основного порядка столбца.
numpy.ndarray.flatten (order = ‘C’) : Возвращает копию массива, свернутого в одно измерение.
# Программа Python, иллюстрирующая # numpy.flatten () метод импортировать NumPy как Компьютерщик array = geek.array ([[1, 2], [3, 4]]) # используя метод flatten array.flatten () печать (массив) #using толстый метод array.flatten ( 'F') печать (массив)
Выход :
[1, 2, 3, 4] [1, 3, 2, 4]
Методы создания массива в Numpy
| функция | Описание |
|---|---|
| пустой () | Вернуть новый массив заданной формы и типа без инициализации записей |
| empty_like () | Возврат нового массива с той же формой и типом, что и у данного массива. |
| глаз () | Вернуть двумерный массив с единицами по диагонали и нулями в других местах. |
| тождество () | Вернуть массив идентификаторов |
| из них () | Вернуть новый массив заданной формы и типа, заполненный |
| ones_like () | Возвратите массив из тех же формы и типа, что и данный массив |
| Нули () | Вернуть новый массив заданной формы и типа, заполненный нулями |
| zeros_like () | Вернуть массив нулей с той же формой и типом, что и данный массив |
| full_like () | Вернуть полный массив с той же формой и типом, что и данный массив. |
| Массив () | Создать массив |
| asarray () | Преобразовать ввод в массив |
| asanyarray () | Преобразуйте входные данные в ndarray, но передайте подклассы ndarray через |
| ascontiguousarray () | Вернуть непрерывный массив в памяти (порядок C) |
| asmatrix () | Интерпретировать входные данные как матрицу |
| копия () | Вернуть копию массива данного объекта |
| frombuffer () | Интерпретировать буфер как одномерный массив |
| из файла() | Построить массив из данных в текстовом или двоичном файле |
| fromfunction () | Построить массив, выполнив функцию над каждой координатой |
| fromiter () | Создать новый одномерный массив из итерируемого объекта |
| fromstring () | Новый одномерный массив, инициализированный из текстовых данных в строке |
| loadtxt () | Загрузить данные из текстового файла |
| arange () | Вернуть равномерно распределенные значения в заданном интервале |
| LINSPACE () | Возвратите равномерно распределенные числа за указанный интервал |
| logspace () | Возвращайте числа, равномерно распределенные в логарифмическом масштабе |
| geomspace () | Вернуть числа, равномерно распределенные в логарифмическом масштабе (геометрическая прогрессия) |
| meshgrid () | Вернуть координатные матрицы из координатных векторов |
| MGRID () | Экземпляр nd_grid, который возвращает плотную многомерную сетку |
| ogrid () | Экземпляр nd_grid, который возвращает открытую многомерную сетку |
| Diag () | Извлечь диагональ или построить диагональный массив |
| diagflat () | Создайте двумерный массив со сглаженным входом в виде диагонали |
| три () | Массив с единицами на и ниже заданной диагонали и нулями в других местах |
| TRIL () | Нижний треугольник массива |
| triu () | Верхний треугольник массива |
| Vander () | Генерация матрицы Вандермонда |
| мат() | Интерпретировать входные данные как матрицу |
| BMAT () | Построить матричный объект из строки, вложенной последовательности или массива |
adsense2code6
espressocode.top
append | NumPy
numpy.append(a, values, axis=None)
Функция append() добавляет элементы в конец массива.
- Параметры:
- a — подобный массиву объект
- Любой объект который может быть преобразован в массив NumPy. Указанные элементы будут добавляться к копии данного объекта.
- values — подобный массиву объект
- Любой объект который может быть преобразован в массив NumPy, который будет добавлен к a. Значение данного параметра должно иметь туже форму, что и a по всем осям, за исключением той, вдоль которой идет добавление. Если параметр axis не указан то значения могут быть любой формы, так как будут сжаты до одной оси перед добавлением.
- axis — целое число (необязательный)
- Определяет ось, в конец которой выполняется добавление. По умолчанию axis = None, что соответствует сжиманию a и values до одной оси и созданию так же одномерного результирующего массива.
- Возвращает:
- ndarray — массив NumPy
- Копия входного массива a с добавленными значениями values в конец указанной оси.
Примеры
>>> import numpy as np
>>>
>>> a = np.array([1, 2, 3, 4])
>>>
>>> np.append(a, 0)
array([1, 2, 3, 4, 0])
>>>
>>> np.append(a, [5, 6, 7, 8, 9])
array([1, 2, 3, 4, 5, 6, 7, 8, 9])
>>>
>>>
>>> b = np.array([[2, 3], [5, 7]])
>>>
>>> np.append(b, [[11, 13]], axis = 0)
array([[ 2, 3],
[ 5, 7],
[11, 13]])
>>>
>>> np.append(b, [[11, 13]], axis = 1) # Приведет к ошибке
>>>
>>> # Ошибка вызвана тем что формы массивов должны
... # совпадать по всем осям, кроме той, что указана в axis:
... b.shape, np.array([[11, 13]]).shape
((2, 2), (1, 2))
>>>
>>> np.append(b, [[11], [13]], axis = 1)
array([[ 2, 3, 11],
[ 5, 7, 13]])
>>>
>>> np.append(b, [[11, 17], [13, 19]], axis = 1)
array([[ 2, 3, 11, 17],
[ 5, 7, 13, 19]])
>>>
>>> np.append(b, [[11, 17, 23], [13, 19, 29]], axis = 1)
array([[ 2, 3, 11, 17, 23],
[ 5, 7, 13, 19, 29]]) 



pyprog.pro
