Умножение матриц NumPy: начните за 5 минут
NumPy — популярная библиотека Python, которая предлагает ряд мощных математических функций. Библиотека широко используется в количественных областях, таких как наука о данных, машинное обучение и глубокое обучение. Мы можем использовать NumPy для выполнения сложных математических вычислений, таких как умножение матриц.
Умножение матриц может помочь нам быстро приблизиться к очень сложным вычислениям. Он может помочь нам в теории сетей, линейных системах уравнений, моделировании населения и многом другом. В этом руководстве мы рассмотрим некоторые основные вычисления с умножением матриц NumPy.
Содержание
- Что такое NumPy?
- Установка и импорт NumPy
- Что такое матрица NumPy?
- Методы умножения матриц NumPy
- Скалярное умножение или скалярное произведение с numpy.dot
- Матричный продукт с numpy.matmul
- Поэлементное умножение матриц с помощью numpy.multiply
- Подведение итогов и следующие шаги
Что такое NumPy?
NumPy — это библиотека Python с открытым исходным кодом, которую мы можем использовать для выполнения высокоуровневых математических операций с массивами, матрицами, линейной алгеброй, анализом Фурье и т. Д. Библиотека NumPy очень популярна в научных вычислениях, науках о данных и машинном обучении. NumPy совместим с популярными библиотеками данных, такими как pandas, matplotlib и Scikit-learn. Это намного быстрее, чем списки Python, потому что он объединяет более быстрые коды, такие как C и C ++, в Python. Он также разбивает наши задачи на несколько частей и обрабатывает каждую часть одновременно.
Д. Библиотека NumPy очень популярна в научных вычислениях, науках о данных и машинном обучении. NumPy совместим с популярными библиотеками данных, такими как pandas, matplotlib и Scikit-learn. Это намного быстрее, чем списки Python, потому что он объединяет более быстрые коды, такие как C и C ++, в Python. Он также разбивает наши задачи на несколько частей и обрабатывает каждую часть одновременно.
Установка и импорт NumPy
Прежде чем мы начнем, убедитесь, что у нас установлен NumPy. Если у вас уже есть Python, вы можете установить NumPy с помощью одной из следующих команд:
conda install numpy
или
pip install numpy
Чтобы импортировать NumPy в наш код Python, мы можем использовать следующую команду:
import numpy as np
Что такое матрица NumPy?
Матрица — это двумерный массив. Каждый элемент в массиве имеет два индекса. Давайте посмотрим на пример в NumPy:
import numpy as np
A = [[6, 7],
[8, 9]]
print(np.
array(A) [0,0])
В приведенном выше коде, мы имеем матрицу A [[6, 7], [8, 9]]. Мы запрашиваем элемент, указанный в (0,0), и наш результат возвращается 6. Когда мы хотим определить форму нашей матрицы, мы используем количество строк по количеству столбцов. Это означает, что матрица A имеет форму 2×2.
Теперь давайте взглянем на несколько различных методов умножения матриц NumPy.
Методы умножения матриц NumPy
Есть три основных способа выполнить умножение матрицы NumPy:
- np.dot(array a, array b): возвращает скалярное произведение или скалярное произведение двух массивов
- np.matmul(array a, array b): возвращает матричное произведение двух массивов
- np.multiply(array a, array b): возвращает поэлементное матричное умножение двух массивов
Давайте подробнее рассмотрим каждый из трех методов:
Скалярное умножение или скалярное произведение с numpy.dot
Скалярное умножение — это простая форма умножения матриц, это просто число, как 1, 2или 3.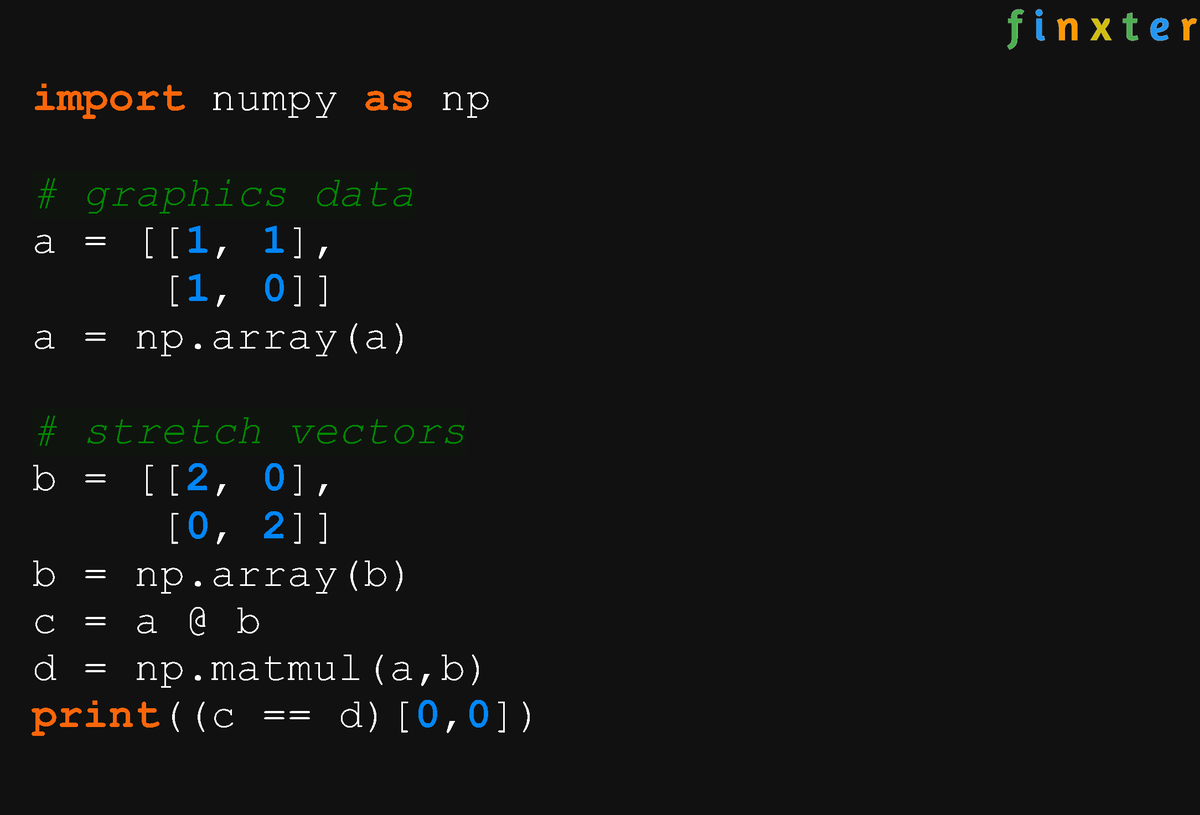 При скалярном умножении мы умножаем скаляр на матрицу. Каждый элемент в матрице умножается на скаляр, в результате чего выходные данные имеют ту же форму, что и исходная матрица.
При скалярном умножении мы умножаем скаляр на матрицу. Каждый элемент в матрице умножается на скаляр, в результате чего выходные данные имеют ту же форму, что и исходная матрица.
При скалярном умножении порядок не имеет значения. Мы получим один и тот же результат независимо от того, умножаем ли мы скаляр на матрицу или матрицу на скаляр.
Давайте посмотрим на пример:
import numpy as np
A = 5
B = [[6, 7],
[8, 9]]
print(np.dot(A,B))
Теперь давайте умножим двумерную матрицу на другую двумерную матрицу. При умножении двух матриц порядок имеет значение. Это означает, что матрица A, умноженная на матрицу B, не то же самое, что матрица B, умноженная на матрицу A.
Прежде чем мы начнем, давайте посмотрим на визуальное представление того, как выполняется умножение.
import numpy as np
A = [[6, 7],
[8, 9]]
B = [[1, 3],
[5, 7]]
print(np.dot(A,B))
print(«———-«)
print(np.
dot(B,A))
Примечание. Важно отметить, что мы можем перемножить две матрицы только в том случае, если количество столбцов в первой матрице равно количеству строк во второй матрице.
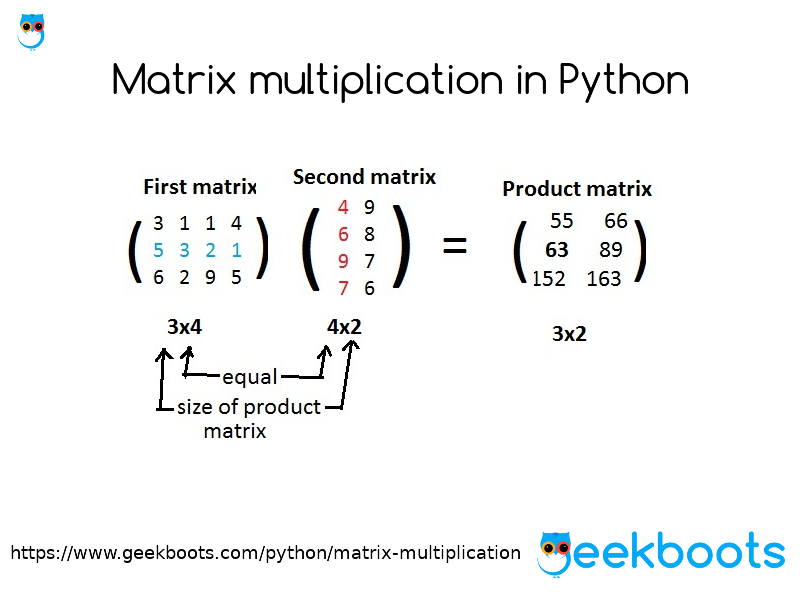
Матричный продукт с numpy.matmul
matmul()Функция дает нам матрицу произведение двух 2-й массивов. С помощью этого метода мы не можем использовать скалярные значения для нашего ввода. Если один из наших аргументов представляет собой одномерный массив, функция преобразует его в матрицу, добавляя 1 к его измерению. Он удаляется после завершения умножения.
Если один из наших аргументов больше 2-d, функция рассматривает его как стек матриц в последних двух индексах. Этот matmul()метод отлично подходит для случаев, когда мы не уверены в размерах наших матриц.
Давайте посмотрим на несколько примеров:
Умножение двумерного массива на другой двумерный массив
import numpy as np
A = [[2, 4],
[6, 8]]
B = [[1, 3],
[5, 7]]
print(np.
matmul(A,B))
Умножение двумерного массива на одномерный массив
import numpy as np
A = [[5, 0],
[0, 5]]
B = [5, 2]
print(np.matmul(A,B))
Один массив с размерами больше 2-х
import numpy as np
A = np.arange(8).reshape(2, 2, 2)
B = np.arange(4).reshape(2, 2)
print(np.matmul(A,B))
Поэлементное умножение матриц с помощью numpy.multiply
numpy.multiply()Метод принимает две матрицы в качестве входных данных и выполняет поэлементное умножение на них. Поэлементное умножение, или произведение Адамара, умножает каждый элемент первой матрицы на эквивалентный элемент во второй матрице. При использовании этого метода обе матрицы должны иметь одинаковые размеры.
Давайте посмотрим на пример:
import numpy as np
A = np.array([[1, 3, 5, 7, 9], [2, 4, 6, 8, 10]])
B = np.array([[1, 2, 3, 4, 5], [5, 4, 3, 2, 1]])
print(np.
multiply(A,B))
Мы можем передать в numpy.multiply()метод определенные строки, столбцы или подматрицы. Размеры строк, столбцов или подматриц, которые мы передаем в качестве наших операндов, должны быть одинаковыми. Давайте посмотрим на пример:
import numpy as np
A = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]])
B = np.array([[11, 12, 13, 14, 15], [16, 17, 18, 19, 20]])
print(np.multiply(A[ 0,:], B[ 1,: ]))
print(«———-«)
print(np.multiply(A[ 1,:], B[ 0,:]))
Подведение итогов и следующие шаги
Поздравляем с вашими первыми шагами в умножении матриц NumPy! Это сложная, но важная часть линейной алгебры. Это помогает нам лучше понять различные аспекты науки о данных, машинного обучения, глубокого обучения и других распространенных областей. Еще многое предстоит узнать о NumPy и матрицах. Вот некоторые рекомендуемые темы для обсуждения:
- Транспонирование матрицы NumPy
- Массивы NumPy (ndarray)
- NumPy векторизация
python — Задача на умножение матриц с использованием NumPy
Вопрос задан
Изменён 6 месяцев назад
Просмотрен 93 раза
Всем привет, изучаю возможности NumPy. Не пойму, правда, тут моя математика просела окончательно или понимание Python.
Не пойму, правда, тут моя математика просела окончательно или понимание Python.
Введите через пробел 16 чисел, создайте из них вектор. Преобразуйте вектор в матрицу А размера 4 на 4 любым способом. Найдите натуральное число x из диапазона [1, 9], для которого матрица вида
x 0 0 0
0 x 0 0
0 0 x 0
0 0 0 x
при умножении на матрицу A увеличит всё её элементы в 3 раза. Выведите на экран произведение матриц.
Мое начало кода:
import numpy as np
data=input('Enter 16 numbers using space: ')
lst=list(map(int, data.split(' ')))
a=np.array(lst).reshape(4,4)
b=a*3
Дальше думала сделать что-то вроде деления матриц, но запуталась + в ответе матрица далеко не диагональная получается:
from numpy.linalg import inv b_inv=inv(b) c=a*b_inv print(c)
Помогите разобраться, пожалуйста)
- python
- numpy
- матрицы
Значение x отыскивается в уме и не зависит от другой матрицы.
* в NumPy означает поэлементное умножение массивов. Вам нужен оператор @.import numpy as np a = np.array(range(16)).reshape(4, 4) print(a) b = 3 * np.eye(4) print(b) c = a @ b print(c)
$ python matrices.py [[ 0 1 2 3] [ 4 5 6 7] [ 8 9 10 11] [12 13 14 15]] [[3. 0. 0. 0.] [0. 3. 0. 0.] [0. 0. 3. 0.] [0. 0. 0. 3.]] [[ 0. 3. 6. 9.] [12. 15. 18. 21.] [24. 27. 30. 33.] [36. 39. 42. 45.]]
Зарегистрируйтесь или войдите
Регистрация через GoogleОтправить без регистрации
ПочтаНеобходима, но никому не показывается
Отправить без регистрации
ПочтаНеобходима, но никому не показывается
By clicking “Отправить ответ”, you agree to our terms of service and acknowledge that you have read and understand our privacy policy and code of conduct.
numpy.matmul — Руководство NumPy v1.24
- numpy.matmul( x1 , x2 , /, out=None , * , cast=’same_kind’ , order=’K’ , dtype=Нет , субок = True [ подпись , extobj , оси , ось ]) =
Произведение матриц двух массивов.
- Параметры:
- x1, x2 array_like
Входные массивы, скаляры не допускаются.
- out ndarray, необязательный
Местоположение, в котором сохраняется результат. Если он предусмотрен, он должен иметь форма, соответствующая подписи
- **kwargs
Другие аргументы, содержащие только ключевые слова, см.
 документы ufunc.
документы ufunc.Новое в версии 1.16: теперь обрабатывает ufunc kwargs
- Возвращает:
- y ndarray
Матричный продукт входных данных. Это скаляр только тогда, когда оба x1, x2 являются одномерными векторами.
- Повышение:
- ValueError
Если последний размер x1 не совпадает с размером предпоследнее измерение x2 .
Если передается скалярное значение.
См. также
-
vdot Комплексно-сопряженное скалярное произведение.
-
тензордот Суммирование произведений по произвольным осям.
-
einsum Соглашение Эйнштейна о суммировании.
-
точка альтернативный матричный продукт с другими правилами вещания.
Примечания
Поведение зависит от аргументов следующим образом.

Если оба аргумента являются двумерными, они умножаются, как обычно матрицы.
Если любой из аргументов имеет значение N-D, N > 2, он рассматривается как стек матрицы, находящиеся в последних двух индексах, и транслируются соответственно.
Если первый аргумент одномерный, он преобразуется в матрицу с помощью добавляя 1 к своим размерам. После умножения матриц предшествующая 1 удаляется.
Если второй аргумент одномерный, он преобразуется в матрицу с помощью добавление 1 к его размерам. После умножения матриц добавленная 1 удаляется.
матмулотличается отточкапо двум важным параметрам:Умножение на скаляры не допускается, вместо этого используйте
*.Стеки матриц передаются вместе, как если бы матрицы были элементы, соблюдающие подпись
(н,к),(к,м)->(н,м):>>> a = np.ones([9, 5, 7, 4]) >>> c = np.
 ones([9, 5, 4, 3])
>>> np.dot(a, c).shape
(9, 5, 7, 9, 5, 3)
>
ones([9, 5, 4, 3])
>>> np.dot(a, c).shape
(9, 5, 7, 9, 5, 3)
>
Функция matmul реализует семантику оператора
@введен в Python 3.5 после PEP 465 .По возможности использует оптимизированную библиотеку BLAS (см.
numpy.linalg).Примеры
Для двумерных массивов это матричное произведение:
>>> a = np.array([[1, 0], ... [0, 1]]) >>> b = np.array([[4, 1], ... [2, 2]]) >>> np.matmul(а, б) массив([[4, 1], [2, 2]])Для 2-D, смешанного с 1-D, результат обычный.
>>> a = np.array([[1, 0], ... [0, 1]]) >>> b = np.массив ([1, 2]) >>> np.matmul(а, б) массив ([1, 2]) >
Вещание обычное для стеков массивов
>>> a = np.arange(2 * 2 * 4).reshape((2, 2, 4)) >>> b = np.arange(2 * 2 * 4).reshape((2, 4, 2)) >>> np.matmul(a,b).shape (2, 2, 2) >>> np.
 matmul(a, b)[0, 1, 1]
98
>>> сумма(а[0, 1, :] * b[0, :, 1])
98
matmul(a, b)[0, 1, 1]
98
>>> сумма(а[0, 1, :] * b[0, :, 1])
98
Вектор, вектор возвращает скалярное скалярное произведение, но ни один аргумент комплексно-сопряженный:
>>> np.matmul([2j, 3j], [2j, 3j]) (-13+0j)
Скалярное умножение вызывает ошибку.
>>> np.matmul([1,2], 3) Traceback (последний последний вызов): ... ValueError: matmul: входному операнду 1 не хватает размеров...
Оператор
@может использоваться как сокращение дляnp.matmulна ндаррейс.>>> x1 = np.массив([2j, 3j]) >>> x2 = np.array([2j, 3j]) >>> х1 @ х2 (-13+0j)
Новое в версии 1.10.0.
Начните работу за 5 минут
Главная/Блог/Программирование/Умножение матриц NumPy: начните за 5 минут
03 сентября 2021 г. — 5 мин чтения
Эрин Шаффер
NumPy — популярная библиотека Python, предлагающая ряд мощных математических функций. Библиотека широко используется в количественных областях, таких как наука о данных, машинное обучение и глубокое обучение.
Умножение матриц NumPy может помочь нам быстро получить приближенные значения для очень сложных вычислений. Это может помочь нам с теорией сетей, линейными системами уравнений, моделированием населения и многим другим. В этом руководстве мы рассмотрим некоторые базовые вычисления с умножением матриц NumPy и матричными операциями.
Начнем!
Мы рассмотрим :
- Что такое NumPy?
- Что такое матрица NumPy?
- Методы умножения матриц NumPy
- Завершение и следующие шаги
Что такое NumPy?
NumPy — это библиотека Python с открытым исходным кодом, которую мы можем использовать для выполнения высокоуровневых математических операций с массивами, матрицами, линейной алгеброй, анализом Фурье и многим другим. Библиотека NumPy очень популярна в научных вычислениях, науке о данных и машинном обучении. NumPy совместим с различными типами данных и другими популярными библиотеками данных, такими как pandas, matplotlib и Scikit-learn. это намного быстрее, чем Python перечисляет , потому что он интегрирует более быстрые коды, такие как C и C++, в Python. Он также разбивает наши задачи на несколько частей и обрабатывает каждую часть одновременно.
NumPy совместим с различными типами данных и другими популярными библиотеками данных, такими как pandas, matplotlib и Scikit-learn. это намного быстрее, чем Python перечисляет , потому что он интегрирует более быстрые коды, такие как C и C++, в Python. Он также разбивает наши задачи на несколько частей и обрабатывает каждую часть одновременно.
Установка и импорт NumPy
Прежде чем мы начнем, убедитесь, что у нас установлен NumPy. Если у вас уже есть Python, вы можете установить NumPy с помощью одной из следующих команд:
conda install numpy
pip install numpy
Чтобы импортировать NumPy в наш код Python, мы можем использовать следующую команду:
импортировать numpy как np
Если вы хотите изучить структуры данных Python, начните с этого полезного руководства по Python!
Что такое матрица NumPy?
Матрица — это двумерный массив. Каждый элемент массива имеет два индекса. Давайте рассмотрим пример в NumPy:
Каждый элемент массива имеет два индекса. Давайте рассмотрим пример в NumPy:
импортировать numpy как np
A = [[6, 7],
[8, 9]]
print(np.array(A) [0,0])
В приведенном выше коде у нас есть матрица A [[6, 7], [8, 9]] . Мы запрашиваем элемент, заданный по адресу (0,0) , и наш вывод возвращает 6 . Когда мы хотим определить форму нашей матрицы, мы используем количество строк по количеству столбцов. Это означает, что матрица A имеет форму 2×2.
Теперь давайте рассмотрим несколько различных методов умножения матриц NumPy.
Методы умножения матриц NumPy
Существует три основных способа выполнения умножения матриц NumPy:
-
np.dot(массив a, массив b): возвращает скаляр или скалярное произведение двух массивов -
np.matmul(массив a, массив b): возвращает матричное произведение двух массивов -
np.: возвращает поэлементное матричное умножение двух массивов multiply(массив a, массив b)
multiply(массив a, массив b)
Давайте подробнее рассмотрим каждый из трех методов с учебным пособием NumPy по каждому из них:
Скалярное умножение или скалярное произведение с numpy.dot
Скалярное умножение — это простая форма матричного умножения. Скаляр — это просто число, например 1 , 2 или 3 . При скалярном умножении мы умножаем скаляр на матрицу . Каждый элемент в матрице умножается на скаляр, в результате чего на выходе получается та же форма, что и у исходной матрицы.
При скалярном умножении порядок не имеет значения . Мы получим один и тот же результат, умножим ли мы скаляр на матрицу или матрицу на скаляр.
Давайте рассмотрим пример:
импортировать numpy как np
A = 5
B = [[6, 7],
[8, 9]]
print(np.dot (А ,B))
Теперь давайте умножим двумерную матрицу на другую двумерную матрицу.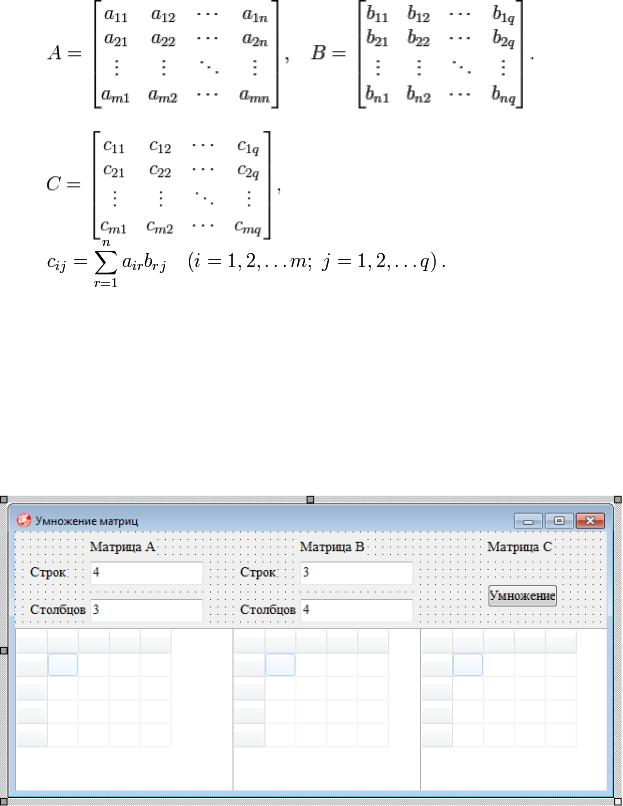 При умножении двух матриц порядок имеет значение . Это означает, что матрица A, умноженная на матрицу B, не совпадает с матрицей B, умноженной на матрицу A.
При умножении двух матриц порядок имеет значение . Это означает, что матрица A, умноженная на матрицу B, не совпадает с матрицей B, умноженной на матрицу A.
Прежде чем мы начнем, давайте посмотрим на визуализацию того, как выполняется умножение.
импортировать numpy как np
A = [[6, 7],
[8, 9]]
B = [[1, 3],
[5, 7]]
print(np .dot(A,B))
print("----------")
print(np.dot(B,A))
Примечание . Важно отметить, что мы можем умножать две матрицы только в том случае, если количество столбцов в первой матрице равно количеству строк во второй матрице.
Матричный продукт с numpy.matmul
9Функция 0108 matmul() дает нам матричное произведение двух двумерных массивов. С помощью этого метода мы не можем использовать скалярные значения для нашего ввода. Если один из наших аргументов является одномерным массивом, функция преобразует его в матрицу NumPy, добавляя 1 к его размерности. Это удаляется после выполнения умножения.
Это удаляется после выполнения умножения.
Если один из наших аргументов больше 2-d, функция рассматривает его как стек матриц по двум последним индексам. Метод matmul() отлично подходит для случаев, когда мы не уверены в том, какими будут размеры наших матриц.
Рассмотрим несколько примеров:
Умножение двумерного массива на другой двумерный массив
import numpy as np
A = [[2, 4],
[6, 8]]
B = [[1, 3],
[5, 7]]
print(np.matmul(A,B))
Умножение двумерного массива на одномерный массив
импортировать numpy как np
A = [[5, 0],
[0, 5]]
B = [5, 2]
print(np.matmul(A,B))
Один массив с размерами больше 2-d
импортировать numpy как np
A = np.arange(8).reshape(2, 2, 2)
B = np.arange(4). reshape(2, 2)
print(np.matmul(A,B))
Поэлементное умножение матриц с numpy.
 multiply
multiply Метод numpy.multiply() принимает две матрицы в качестве входных данных и выполняет элемент -мудрое умножение на них. Поэлементное умножение, или произведение Адамара, умножает каждый элемент первой матрицы NumPy на эквивалентный элемент второй матрицы. При использовании этого метода обе матрицы должны иметь одинаковые размеры.
Давайте рассмотрим пример:
импортировать numpy как np
A = np.array([[1, 3, 5, 7, 9], [2, 4, 6, 8, 10]])
B = np.array([[1, 2, 3, 4, 5], [5, 4, 3, 2, 1]])
print(np.multiply(A,B))
Мы может передавать определенные строки, столбцы или подматрицы методу numpy.multiply(). Размеры строк, столбцов или подматриц, которые мы передаем в качестве наших операндов, должны быть одинаковыми. Давайте рассмотрим пример:
импортировать numpy как np
A = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]])
B = np.array([[11, 12, 13, 14, 15], [16, 17, 18, 19, 20]])
print(np.
multiply(A[0,:], B[1,:]))
print("---- ------")
print(np.multiply(A[ 1,:], B[ 0,:]))
Завершение и следующие шаги
Поздравляем с первыми шагами с матрицей NumPy умножение! Это сложная, но важная часть линейной алгебры. Это помогает нам углубить наше понимание различных аспектов науки о данных, машинного обучения, глубокого обучения и других распространенных областей. Нам еще многое предстоит узнать о NumPy и матрицах.
Ниже приведены некоторые рекомендуемые темы для обсуждения:
Транспонирование матрицы NumPy
Массивы NumPy (
ndarray)Векторизация NumPy
numpy.ndarrayиndarrayобъектыМногомерные массивы
Хотите начать работу с Python? Ознакомьтесь с планом обучения Educative от нуля до героя на Python . Этот практический путь обучения поможет вам овладеть навыками, необходимыми для извлечения информации из данных с использованием мощного ассортимента популярных библиотек Python.

 array(A) [0,0])
array(A) [0,0]) dot(B,A))
dot(B,A)) matmul(A,B))
matmul(A,B)) multiply(A,B))
multiply(A,B))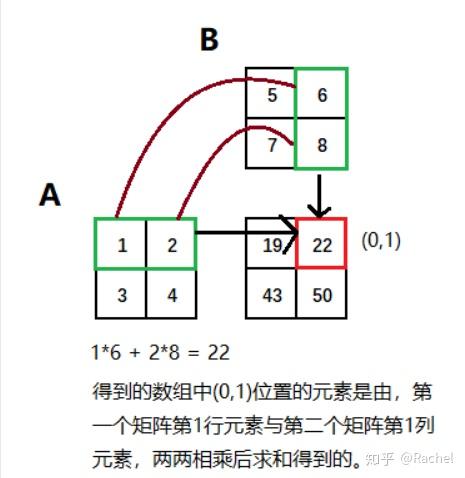 документы ufunc.
документы ufunc.
 ones([9, 5, 4, 3])
>>> np.dot(a, c).shape
(9, 5, 7, 9, 5, 3)
>
ones([9, 5, 4, 3])
>>> np.dot(a, c).shape
(9, 5, 7, 9, 5, 3)
> matmul(a, b)[0, 1, 1]
98
>>> сумма(а[0, 1, :] * b[0, :, 1])
98
matmul(a, b)[0, 1, 1]
98
>>> сумма(а[0, 1, :] * b[0, :, 1])
98
 multiply(массив a, массив b)
multiply(массив a, массив b)  multiply(A[0,:], B[1,:]))
multiply(A[0,:], B[1,:]))