Линейная алгебра на Python. [Урок 5]. Обратная матрица и ранг матрицы
Пятый урок посвящен нахождению обратной матрицы, ее свойствам, а также определению ранга матрицы
- Обратная матрица
- Ранг матрицы
Обратной матрицей A-1 матрицы A называют матрицу, удовлетворяющую следующему равенству:
где – E это единичная матрица.
Для того, чтобы у квадратной матрицы A была обратная матрица необходимо и достаточно чтобы определитель |A| был не равен нулю. Введем понятие союзной матрицы. Союзная матрица A* строится на базе исходной A путем замены всех элементов матрицы A на их алгебраические дополнения.
Исходная матрица:
Союзная ей матрица A*:
Транспонируя матрицу A*, мы получим так называемую присоединенную матрицу A*T:
Теперь, зная как вычислять определитель и присоединенную матрицу, мы можем определить матрицу A-1, обратную матрице A:
➣ Численный пример
Пример вычисления обратной матрицы. Пусть дана исходная матрица A, следующего вида:
Пусть дана исходная матрица A, следующего вида:
Для начала найдем определитель матрицы A:
Как видно из приведенных вычислений, определитель матрицы не равен нулю, значит у матрицы A есть обратная. Построим присоединенную матрицу, для этого вычислим алгебраические дополнения для каждого элемента матрицы A:
Союзная матрица будет иметь следующий вид:
Присоединенная матрица получается из союзной путем транспонирования:
Находим обратную матрицу:
➤ Пример на Python
Решим задачу определения обратной матрицы на Python. Для получения обратной матрицы будем использовать функцию
>>> A = np.matrix('1 -3; 2 5')
>>> A_inv = np.linalg.inv(A)
>>> print(A_inv)
[[ 0.45454545 0.27272727]
[-0.18181818 0.09090909]]Рассмотрим свойства обратной матрицы.
Свойство 1. Обратная матрица обратной матрицы есть исходная матрица:
Обратная матрица обратной матрицы есть исходная матрица:
➤Пример на Python
>>> A = np.matrix('1. -3.; 2. 5.')
>>> A_inv = np.linalg.inv(A)
>>> A_inv_inv = np.linalg.inv(A_inv)
>>> print(A)
[[1. -3.]
[2. 5.]]
>>> print(A_inv_inv)
[[1. -3.]
[2. 5.]]Свойство 2. Обратная матрица транспонированной матрицы равна транспонированной матрице от обратной матрицы:
➤ Пример на Python
>>> A = np.matrix('1. -3.; 2. 5.')
>>> L = np.linalg.inv(A.T)
>>> R = (np.linalg.inv(A)).T
>>> print(L)
[[ 0.45454545 -0.18181818]
[ 0.27272727 0.09090909]]
>>> print(R)
[[ 0.45454545 -0.18181818]
[ 0.27272727 0.09090909]]Свойство 3. Обратная матрица произведения матриц равна произведению обратных матриц:
➤ Пример на Python
Ранг матрицы>>> A = np. matrix('1. -3.; 2. 5.') >>> B = np.matrix('7. 6.; 1. 8.') >>> L = np.linalg.inv(A.dot(B)) >>> R = np.linalg.inv(B).dot(np.linalg.inv(A)) >>> print(L) [[ 0.09454545 0.03272727] [-0.03454545 0.00727273]] >>> print(R) [[ 0.09454545 0.03272727] [-0.03454545 0.00727273]]
Ранг матрицы является еще одной важной численной характеристикой. Рангом называют максимальное число линейно независимых строк (столбцов) матрицы. Линейная независимость означает, что строки (столбцы) не могут быть линейно выражены через другие строки (столбцы). Ранг матрицы можно найти через ее миноры, он равен наибольшему порядку минора, который не равен нулю. Существование ранга у матрицы не зависит от того квадратная она или нет.
Вычислим ранг матрицы с помощью Python. Создадим единичную матрицу:
>>> m_eye = np.eye(4) >>> print(m_eye) [[1. 0. 0. 0.] [0. 1. 0.0.] [0. 0. 1. 0.] [0. 0. 0. 1.]]
Ранг такой матрицы равен количеству ее столбцов (или строк), в нашем случае ранг будет равен четырем, для его вычисления на
>>> rank = np.linalg.matrix_rank(m_eye) >>> print(rank) 4
Если мы приравняем элемент в нижнем правом углу к нулю, то ранг станет равен трем:
>>> m_eye[3][3] = 0 >>> print(m_eye) [[1. 0. 0. 0.] [0. 1. 0. 0.] [0. 0. 1. 0.] [0. 0. 0. 0.]] >>> rank = np.linalg.matrix_rank(m_eye) >>> print(rank) 3P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
NumPy, часть 4: linalg | Python 3 для начинающих и чайников
В прошлых частях мы разбирались с основными операциями над массивами и randomом в NumPy. Теперь же мы приступим к более серьёзным вещам, которые есть в NumPy. Первый на очереди у нас модуль numpy.linalg, позволяющий делать многие операции из линейной алгебры.
Возведение в степень
linalg.matrix_power(M, n) — возводит матрицу в степень n.
Разложения
linalg.cholesky(a) — разложение Холецкого.
linalg.qr(a[, mode]) — QR разложение.
linalg.svd(a[, full_matrices, compute_uv]) — сингулярное разложение.
Некоторые характеристики матриц
linalg.eig(a) — собственные значения и собственные векторы.
linalg.norm(x[, ord, axis]) — норма вектора или оператора.
linalg.cond(x[, p]) — число обусловленности.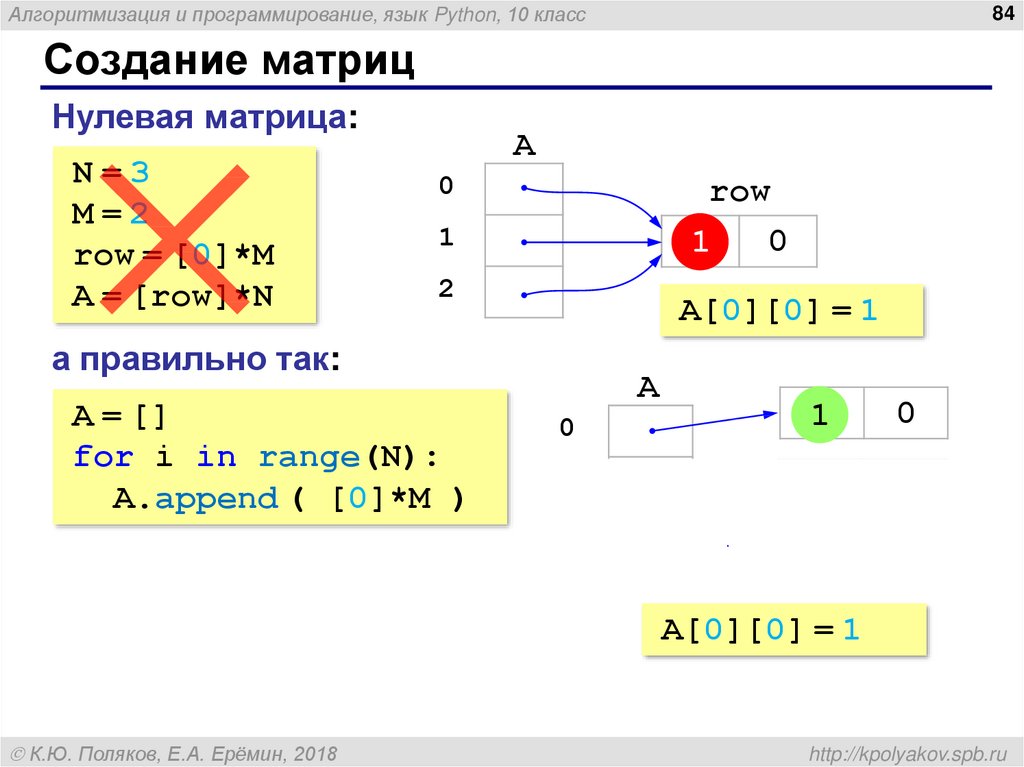
linalg.det(a) — определитель.
linalg.slogdet(a) — знак и логарифм определителя (для избежания переполнения, если сам определитель очень маленький).
Системы уравнений
linalg.solve(a, b) — решает систему линейных уравнений Ax = b.
linalg.tensorsolve(a, b[, axes]) — решает тензорную систему линейных уравнений Ax = b.
linalg.lstsq
linalg.inv(a) — обратная матрица.
Замечания:
- linalg.LinAlgError — исключение, вызываемое данными функциями в случае неудачи (например, при попытке взять обратную матрицу от вырожденной).
- Подробная документация, как всегда, на английском: https://docs.scipy.org/doc/numpy/reference/routines.linalg.html
- Массивы большей размерности в большинстве функций linalg интерпретируются как набор из нескольких массивов нужной размерности. Таким образом, можно одним вызовом функции проделывать операции над несколькими объектами.

>>> a = np.arange(18).reshape((2,3,3))
>>> a
array([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9, 10, 11],
[12, 13, 14],
[15, 16, 17]]])
>>> np.linalg.det(a)
array([ 0., 0.])Для вставки кода на Python в комментарий заключайте его в теги <pre><code>Ваш код</code></pre>
Свежее
- Модуль csv — чтение и запись CSV файлов
- Создаём сайт на Django, используя хорошие практики. Часть 1: создаём проект
- Онлайн-обучение Python: сравнение популярных программ
Категории
- Книги о Python
- GUI (графический интерфейс пользователя)
- Курсы Python
- Модули
- Новости мира Python
- NumPy
- Обработка данных
- Основы программирования
- Примеры программ
- Типы данных в Python
- Видео
- Python для Web
- Работа для Python-программистов
Полезные материалы
- Сделай свой вклад в развитие сайта!
- Самоучитель Python
- Карта сайта
- Отзывы на книги по Python
- Реклама на сайте
Мы в соцсетях
Как инвертировать матрицу с помощью NumPy
Улучшить статью
Сохранить статью
- Уровень сложности: Easy
- Последнее обновление: 18 авг, 2020
Улучшить статью
Сохранить статью
Обратная матрица — это просто обратная матрица, как это делается в обычной арифметике для одного числа, которое используется для решения уравнений для нахождения значений неизвестных переменных.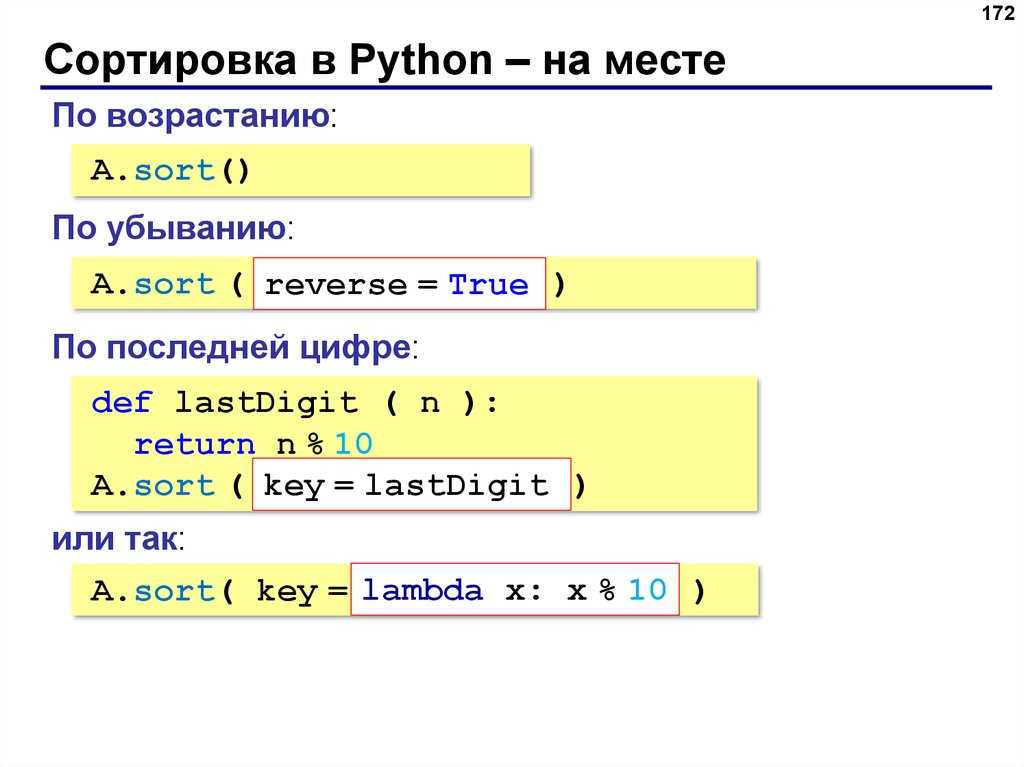 Обратная матрица — это та матрица, которая при умножении на исходную матрицу дает единичную матрицу. Обратная матрица существует, только если матрица равна неединственное число, т. е. определитель не должен быть равен 0 . Используя определитель и сопряженное, мы можем легко найти обратную квадратную матрицу, используя приведенную ниже формулу:
Обратная матрица — это та матрица, которая при умножении на исходную матрицу дает единичную матрицу. Обратная матрица существует, только если матрица равна неединственное число, т. е. определитель не должен быть равен 0 . Используя определитель и сопряженное, мы можем легко найти обратную квадратную матрицу, используя приведенную ниже формулу:
, если det(A) != 0
A -1 = прил(А)/прил(А)
еще
«Инверс не существует» Уравнение Матрикса
Где,
A -1 :
B: Матрица решений
Обратная матрица с использованием NumPy
Python предоставляет очень простой метод вычисления обратной матрицы. Функция numpy.linalg.inv() , доступная в модуле python NumPy, используется для вычисления обратной матрицы.
Синтаксис:
numpy.
linalg.inv ( a ) Параметр
Параметр0024
a: Инвертируемая матрица
Возвраты:
Обратная матрица a .
Example 1:
Python
, - 2 , 5 ], |
Output:
[[ 0.17647059-0,00326797 -0,02287582] [ 0,05882353 -0,13071895 0,08496732] [-0.11764706 0.1503268 0.05228758]]
Example 2:
Python
[ 4 , - 2 , 5 , 1 ], |
Output:
[[ 0.13368984 0,10695187 0,02139037 -0,09090909] [-0,00229183 0,02673797 0,14820474 -0,12987013] [-0,12987013 0,18181818 0,06493506 -0,02597403] [ 0,11000764 -0,28342246 -0,11382735 0,23376623]]
Пример 3:
Python
|

 matrix('1. -3.; 2. 5.')
>>> B = np.matrix('7. 6.; 1. 8.')
>>> L = np.linalg.inv(A.dot(B))
>>> R = np.linalg.inv(B).dot(np.linalg.inv(A))
>>> print(L)
[[ 0.09454545 0.03272727]
[-0.03454545 0.00727273]]
>>> print(R)
[[ 0.09454545 0.03272727]
[-0.03454545 0.00727273]]
matrix('1. -3.; 2. 5.')
>>> B = np.matrix('7. 6.; 1. 8.')
>>> L = np.linalg.inv(A.dot(B))
>>> R = np.linalg.inv(B).dot(np.linalg.inv(A))
>>> print(L)
[[ 0.09454545 0.03272727]
[-0.03454545 0.00727273]]
>>> print(R)
[[ 0.09454545 0.03272727]
[-0.03454545 0.00727273]] 0.]
[0. 0. 1. 0.]
[0. 0. 0. 1.]]
0.]
[0. 0. 1. 0.]
[0. 0. 0. 1.]]
 linalg.inv ( a ) Параметр
linalg.inv ( a ) Параметр linalg.inv(A))
linalg.inv(A))  linalg.inv(A))
linalg.inv(A))  LINLG.INV (A))
LINLG.INV (A)) 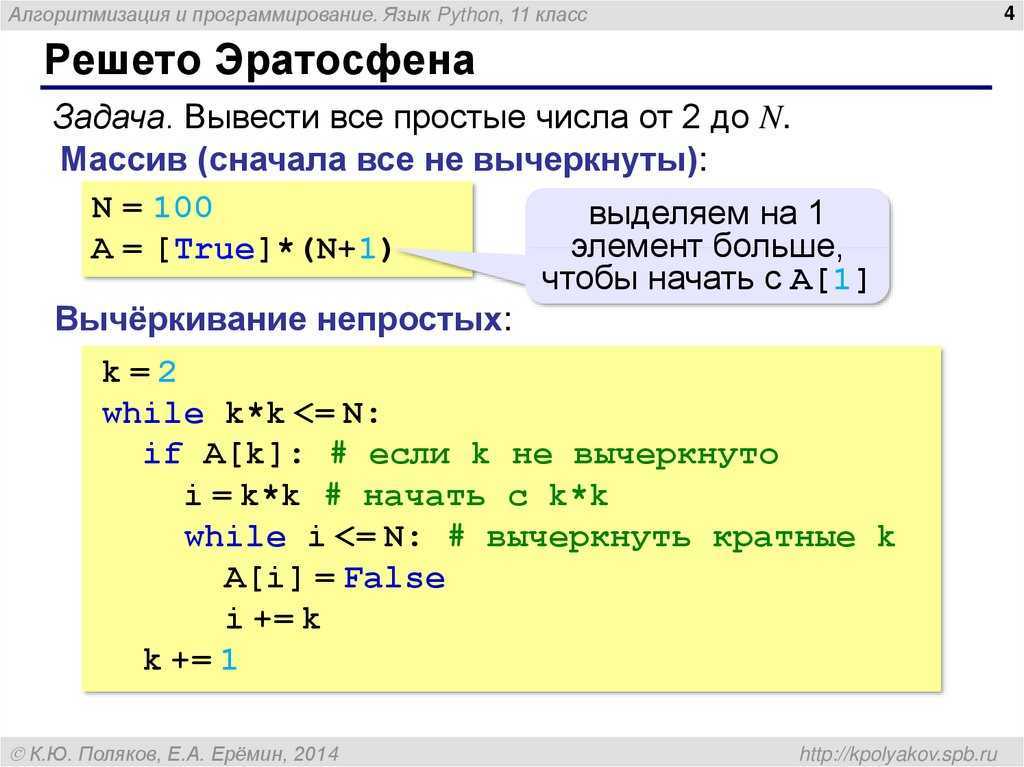
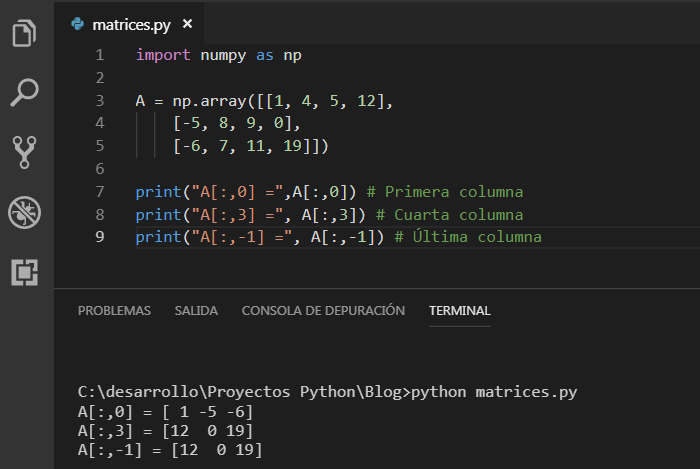 linalg.inv (обработка)
linalg.inv (обработка)
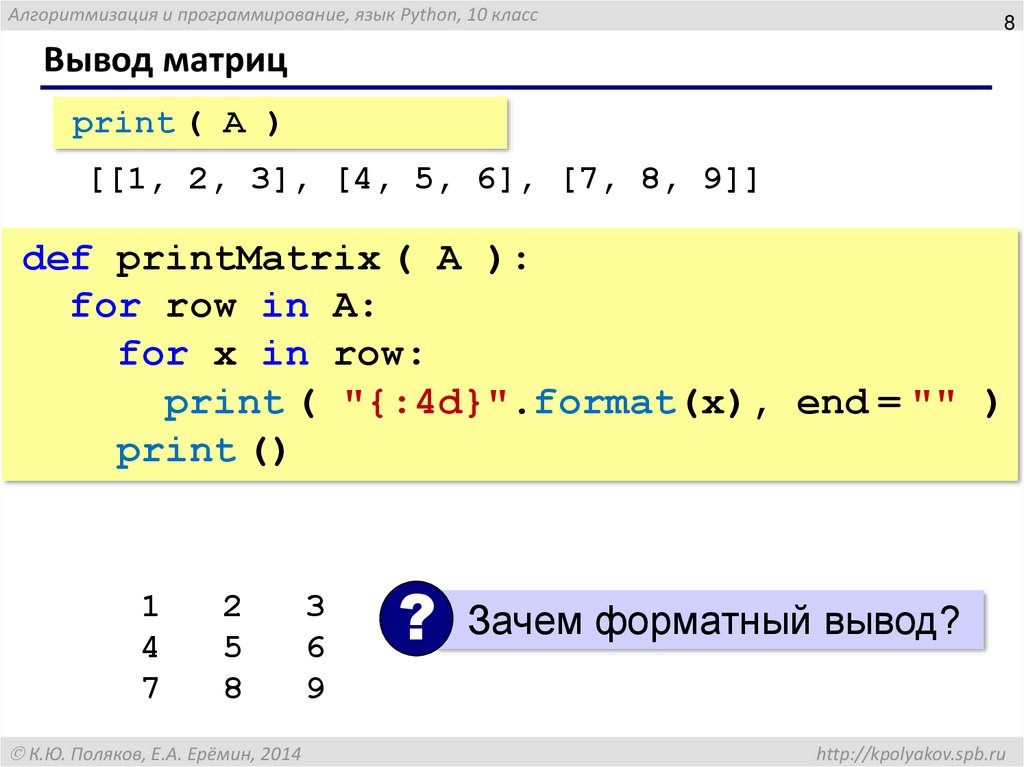 Функция помогает пользователю проверить, что
Функция помогает пользователю проверить, что 