Учимся округлять в C# | Андрей Акиньшин
.NETC#RoundingCheatSheet
А знаете ли вы, что Math.Round(1.5) == Math.Round(2.5) == 2? Можете ли сходу сказать, сколько будет -7%3 и 7%-3? Помните ли, чем отличаются Math.Round, Math.Floor, Math.Ceiling, Math.Truncate? А как происходит округление при использовании string.Format? Давайте немного погрузимся в мир округлений и разберёмся с нюансами, которые не для всех могут быть очевидными.
Math.Round
MSDN: Round
public static decimal Round(decimal value) public static double Round(double value) public static decimal Round(decimal value, int digits) public static double Round(double value, int digits) public static decimal Round(decimal value, MidpointRounding mode) public static double Round(double value, MidpointRounding mode) public static decimal Round(decimal value, int digits, MidpointRounding mode) public static double Round(double value, int digits, MidpointRounding mode)
Math. — это метод округления к ближайшему числу или к ближайшему числу с заданным количеством знаков после запятой. Работает с типами  Round
Rounddecimal и double, в параметрах можно встретить три вида параметров:
value: округляемое числоdigits: количество знаков в дробной части, которые нужно оставитьmode: параметр, который определяет в какую сторону округлять число, которое находится ровно посередине между двумя вариантами
Параметр mode используется, когда округляемое значение находится ровно посередине между двумя вариантами. Принимает значение из следующего перечисления:
public enum MidpointRounding { AwayFromZero, ToEven}
AwayFromZero: округление происходит к тому числу, которое дальше от нуля.ToEven: округление происходит к чётному числу.
Обратите внимание, что по умолчанию mode == MidpointRounding., поэтому  ToEven
ToEvenMath.Round(1.5) == Math.Round(2.5) == 2.
Math.Floor, Math.Ceiling, Math.Truncate
MSDN: Floor, Ceiling, Truncate
public static decimal Floor(decimal value) public static double Floor(double value) public static decimal Ceiling(decimal value) public static double Ceiling(double value) public static decimal Truncate(decimal value) public static double Truncate(double value)
Math.Floorокругляет вниз по направлению к отрицательной бесконечности.Math.Ceilingокругляет вверх по направлению к положительной бесконечности.Math.Truncateокругляет вниз или вверх по направлению к нулю.
Сводная таблица
Сориентироваться в методах округления может помочь следующая табличка:
value | -2.9 | -0.5 | 0.3 | 1.5 | 2.9 | --------------------+------+------+-----+-----+-----+ Round(ToEven) | -3 | 0 | 0 | 2 | 3 | Round(AwayFromZero) | -3 | -1 | 0 | 2 | 3 | Floor | -3 | -1 | 0 | 1 | 2 | Ceiling | -2 | 0 | 1 | 2 | 3 | Truncate | -2 | 0 | 0 | 1 | 2 |
Округление проводится в соответствии со стандартом IEEE Standard 754, section 4.
Целочисленное деление и взятие по модулю
В C# есть два замечательных оператора над целыми числами: / для целочисленного деления (MSDN) и % для взятия остатка от деления (MSDN). Деление производится по следующим правилам:
- При целочисленном делении результат всегда округляется по направлению к нулю.
- При взятии остатка от деления должно выполняться следующее правило:
x % y = x – (x / y) * y
Также можно пользоваться шпаргалкой:
a | b | a/b | a%b | ---+----+-----+-----+ 7 | 3 | 2 | 1 | -7 | 3 | -2 | -1 | 7 | -3 | -2 | 1 | -7 | -3 | 2 | -1 |
string.Format
При форматировании чисел в виде строки можно пользоваться функцией string.Format (см. Standard Numeric Format Strings, Custom Numeric Format Strings). Например, для вывода числа с двумя знаками после десятичной точки можно воспользоваться string.. Округление происходит по принципу  Format("{0:N2}", value)
Format("{0:N2}", value)AwayFromZero. Проиллюстрируем правила округления очередной табличкой:
value | string.Format("{0:N2}", value) |
-------+--------------------------------+
-2.006 | -2.01 |
-2.005 | -2.01 |
-2.004 | -2.00 |
2.004 | 2.00 |
2.005 | 2.01 |
2.006 | 2.01 |
Задачи
На приведённую тему есть две задачки в ProblemBook.NET: Rounding1, Rounding2.
Поделиться:
Как округлять числа в большую и меньшую сторону функциями Excel
Округляют числа в Excel несколькими способами. С помощью формата ячеек и с помощью функций. Эти два способа следует различать так: первый только для отображения значений или вывода на печать, а второй способ еще и для вычислений и расчетов.
С помощью функций возможно точное округление, в большую или меньшую сторону, до заданного пользователем разряда. А полученные значения в результате вычислений, можно использовать в других формулах и функциях. В то же время округление с помощью формата ячеек не даст желаемого результата, и результаты вычислений с такими значениями будут ошибочны. Ведь формат ячеек, по сути, значение не меняет, меняется лишь его способ отображения. Чтобы в этом быстро и легко разобраться и не совершать ошибок, приведем несколько примеров.
А полученные значения в результате вычислений, можно использовать в других формулах и функциях. В то же время округление с помощью формата ячеек не даст желаемого результата, и результаты вычислений с такими значениями будут ошибочны. Ведь формат ячеек, по сути, значение не меняет, меняется лишь его способ отображения. Чтобы в этом быстро и легко разобраться и не совершать ошибок, приведем несколько примеров.
Как округлить число форматом ячейки
Впишем в ячейку А1 значение 76,575. Щелкнув правой кнопкой мыши, вызываем меню «Формат ячеек». Сделать то же самое можно через инструмент «Число» на главной странице Книги. Или нажать комбинацию горячих клавиш CTRL+1.
Выбираем числовой формат и устанавливаем количество десятичных знаков – 0.
Результат округления:
Назначить количество десятичных знаков можно в «денежном» формате, «финансовом», «процентном».
Как видно, округление происходит по математическим законам. Последняя цифра, которую нужно сохранить, увеличивается на единицу, если за ней следует цифра больше или равная «5».
Особенность данного варианта: чем больше цифр после запятой мы оставим, тем точнее получим результат.
Как правильно округлить число в Excel
С помощью функции ОКРУГЛ() (округляет до необходимого пользователю количества десятичных разрядов). Для вызова «Мастера функций» воспользуемся кнопкой fx. Нужная функция находится в категории «Математические».
Аргументы:
- «Число» — ссылка на ячейку с нужным значением (А1).
- «Число разрядов» — количество знаков после запятой, до которого будет округляться число (0 – чтобы округлить до целого числа, 1 – будет оставлен один знак после запятой, 2 – два и т.д.).
Теперь округлим целое число (не десятичную дробь). Воспользуемся функцией ОКРУГЛ:
- первый аргумент функции – ссылка на ячейку;
- второй аргумент – со знаком «-» (до десятков – «-1», до сотен – «-2», чтобы округлить число до тысяч – «-3» и т.д.).
Как округлить число в Excel до тысяч?
Пример округления числа до тысяч:
Формула: =ОКРУГЛ(A3;-3).
Округлить можно не только число, но и значение выражения.
Допустим, есть данные по цене и количеству товара. Необходимо найти стоимость с точностью до рубля (округлить до целого числа).
Первый аргумент функции – числовое выражение для нахождения стоимости.
Как округлить в большую и меньшую сторону в Excel
Для округления в большую сторону – функция «ОКРУГЛВВЕРХ».
Первый аргумент заполняем по уже знакомому принципу – ссылка на ячейку с данными.
Второй аргумент: «0» — округление десятичной дроби до целой части, «1» — функция округляет, оставляя один знак после запятой, и т.д.
Формула: =ОКРУГЛВВЕРХ(A1;0).
Результат:
Чтобы округлить в меньшую сторону в Excel, применяется функция «ОКРУГЛВНИЗ».
Пример формулы: =ОКРУГЛВНИЗ(A1;1).
Полученный результат:
Формулы «ОКРУГЛВВЕРХ» и «ОКРУГЛВНИЗ» используются для округления значений выражений (произведения, суммы, разности и т.п.).
Как округлить до целого числа в Excel?
Чтобы округлить до целого в большую сторону используем функцию «ОКРУГЛВВЕРХ». Чтобы округлить до целого в меньшую сторону используем функцию «ОКРУГЛВНИЗ». Функция «ОКРУГЛ» и формата ячеек так же позволяют округлить до целого числа, установив количество разрядов – «0» (см.выше).
Чтобы округлить до целого в меньшую сторону используем функцию «ОКРУГЛВНИЗ». Функция «ОКРУГЛ» и формата ячеек так же позволяют округлить до целого числа, установив количество разрядов – «0» (см.выше).
В программе Excel для округления до целого числа применяется также функция «ОТБР». Она просто отбрасывает знаки после запятой. По сути, округления не происходит. Формула отсекает цифры до назначенного разряда.
Сравните:
Второй аргумент «0» — функция отсекает до целого числа; «1» — до десятой доли; «2» — до сотой доли и т.д.
Специальная функция Excel, которая вернет только целое число, – «ЦЕЛОЕ». Имеет единственный аргумент – «Число». Можно указать числовое значение либо ссылку на ячейку.
Недостаток использования функции «ЦЕЛОЕ» — округляет только в меньшую сторону.
Округлить до целого в Excel можно с помощью функций «ОКРВВЕРХ» и «ОКРВНИЗ». Округление происходит в большую или меньшую сторону до ближайшего целого числа.
Пример использования функций:
Второй аргумент – указание на разряд, до которого должно произойти округление (10 – до десятков, 100 – до сотен и т. д.).
д.).
Округление до ближайшего целого четного выполняет функция «ЧЕТН», до ближайшего нечетного – «НЕЧЕТ».
Пример их использования:
Почему Excel округляет большие числа?
Если в ячейки табличного процессора вводятся большие числа (например, 78568435923100756), Excel по умолчанию автоматически округляет их вот так: 7,85684E+16 – это особенность формата ячеек «Общий». Чтобы избежать такого отображения больших чисел нужно изменить формат ячейки с данным большим числом на «Числовой» (самый быстрый способ нажать комбинацию горячих клавиш CTRL+SHIFT+1). Тогда значение ячейки будет отображаться так: 78 568 435 923 100 756,00. При желании количество разрядов можно уменьшить: «Главная»-«Число»-«Уменьшить разрядность».
округление и другие действия с числами
Оглавление
- Функция SQL ROUND
- Функция SQL CEILING
- Функция SQL FLOOR
- Другие функции SQL для работы с числами
Связанные темы
- Оператор SELECT
- Агрегатные функции
| Назад | Листать | Вперёд>>> |
 Округление производится по правилам арифметики.
Округление производится по правилам арифметики.Если n — отрицательное число (−n), то округление происходит до n-го знака перед запятой. Таким образом, с помощью функции ROUND можно получить и целое число как результат округления.
Пример 1. В базе данных фирмы есть таблица Staff, содержащая данные о сотрудниках фирмы. Выведем индивидуальные размеры заработной платы сотрудников:
SELECT Name, Salary FROM STAFF
Результатом выполнения запроса будет следующая таблица:
| Name | Salary |
| Sanders | 18357.5 |
| Pernal | 15430.0 |
| Marenghi | 17506.8 |
| Doctor | 12322.8 |
| Factor | 16228.7 |
| Junkers | 16232.8 |
| Moonlight | 21500.6 |
| Aisen | 19540.7 |
| MacGregor | 15790.8 |
Для вычисления среднего размера заработной платы пишем запрос:
SELECT AVG(Salary) FROM STAFF
Получим следующий результат:
| AVG(Salary) |
16990. |
Для отчётов результат с таким числом знаков после запятой не годится. Округлим результат до второго знака после запятой с помощью функции ROUND:
SELECT ROUND(AVG(Salary),2) AS Avg_Salary FROM STAFF
Результат будет следующим:
| Avg_Salary |
| 16990.07 |
- Страница 2. Другие функции SQL для работы с числами
Пример 2. Теперь округлим результат до первого знака до запятой, применяя в функции ROUND параметр минус единица:
SELECT ROUND(AVG(Salary),−1) AS Avg_Salary FROM STAFF
Результат будет следующим:
| Avg_Salary |
| 16990 |
Сместим округление ещё на один знак влево и применим в функции ROUND параметр минус 2:
SELECT ROUND(AVG(Salary),−2) AS Avg_Salary FROM STAFF
Результат будет следующим:
| Avg_Salary |
| 17000 |
Функция SQL ROUND может применяться ещё и с третьим необязательными параметром
(кроме MySQL). Если этим параметром будет 1, то округление производиться не будет, просто в результате
будет оставлено столько знаков после запятой, сколько указано во втором параметре.
Если этим параметром будет 1, то округление производиться не будет, просто в результате
будет оставлено столько знаков после запятой, сколько указано во втором параметре.
Пример 3. Оставить в результате вычислений средней заработной платы два знака после запятой, не производя округления. Применяем функцию ROUND с тремя параметрами:
SELECT ROUND(AVG(Salary),2,1) AS Avg_Salary FROM STAFF
Результат будет следующим:
| Avg_Salary |
| 16990.06 |
- Страница 2. Другие функции SQL для работы с числами
Функция MySQL TRUNCATE
В MySQL аналогом разновидности функции ROUND без округления результата является функция TRUNCATE. Она, как и ROUND в общем случае имеет два параметра: результат вычислений и число знаков после запятой.
Пример 4. Условие то же, что в примере 3, но в MySQL. Применяем функцию TRUNCATE:
SELECT TRUNCATE(AVG(Salary),2) AS Avg_Salary FROM STAFF
Получим результат без округления, как в предыдущем примере:
| Avg_Salary |
16990. 06 06 |
- Страница 2. Другие функции SQL для работы с числами
Функция SQL CEILING не производит округления. Она просто принимает дробное число и возвращает максимальное целое число, не меньшее принятого. Приведём примеры действия функции с различными принятыми дробными числами.
| Функция с аргументом | Возвращаемое значение |
| CEILING(0.38) | 1 |
| CEILING(1.63) | 2 |
| CEILING(−0.38) | 0 |
| CEILING(−1.63) | −1 |
В случае функции CEILING некорректно говорить об округлении, поскольку она преобразует числа без учёта правил арифметики.
- Страница 2. Другие функции SQL для работы с числами
Функция FLOOR также не производит округления. Её действие противоположно действию функции CEILING.
Она принимает дробное число и возвращает максимальное
целое число, не большее принятого. Приведём примеры действия функции с различными принятыми дробными числами.
Приведём примеры действия функции с различными принятыми дробными числами.
| Функция с аргументом | Возвращаемое значение |
| FLOOR(0.38) | 0 |
| FLOOR(1.63) | 1 |
| FLOOR(−0.38) | −1 |
| FLOOR(−1.63) | −2 |
Функция FLOOR, как и функция CEILING, преобразует числа без учёта правил арифметики.
- Страница 2. Другие функции SQL для работы с числами
Поделиться с друзьями
| Назад | Листать | Вперёд>>> |
в большую или меньшую сторону — До целого или до сотых (2 заков)
При выполнении различных арифметических операций важно, чтобы результат округлялся правильно. Часто требуется округлять в большую, меньшую сторону, до ближайшего целого или округлить до сотых.
Для этого программист может использовать различные инструменты, такие как встроенная функция round(), преобразование к типу int и функции из подключаемого модуля math.
Способы округления чисел
Для округления чисел придумано много способов, они не лишены недостатков, однако часто используются для решения задач. Разберёмся в тонкостях каждого из них.
Если используется стандартная библиотека math, то в начале кода её необходимо подключить. Сделать это можно, например, с помощью инструкции: import math.
math.ceil() — округление чисел в большую сторону
Функция получила своё имя от термина «ceiling», который используется в математике для описания числа, которое больше или равно заданному.
Любая дробь находится в целочисленном интервале, например, 1.2 лежит между 1 и 2. Функция ceil() определяет, какая из границ интервала наибольшая и записывает её в результат округления.
Пример:
math.ceil(5.15) # = 6 math.ceil(6.666) # = 7 math.ceil(5) # = 5
Важно помнить, что функция определяет наибольшее число с учётом знака. То есть результатом округления числа -0.9 будет 0, а не -1.
math.floor() — округление чисел в меньшую сторону
Функция округляет дробное число до ближайшего целого, которое меньше или равно исходному. Работает аналогично функции ceil(), но с округлением в противоположную сторону.
Пример:
math.floor(7.9) # = 7 math.floor(9.999) # = 9 math.floor(-6.1) # = -7
math.trunc() — отбрасывание дробной части
Возвращает целое число, не учитывая его дробную часть. То есть никакого округления не происходит, Python просто забывает о дробной части, приводя число к целочисленному виду.
Примеры:
math.trunc(5.51) # = 5 math.trunc(-6.99) # = -6
Избавиться от дробной части можно с помощью обычного преобразования числа к типу int. Такой способ полностью эквивалентен использованию trunc().
Примеры:
int(5.51) # = 5 int(-6.99) # = -6
Нормальное округление
Python позволяет реализовать нормальное арифметическое округление, использовав функцию преобразования к типу int.
И хотя int() работает по другому алгоритму, результат её использования для положительных чисел полностью аналогичен выводу функции floor(), которая округляет числа «вниз». Для отрицательных аналогичен функции ceil().
Примеры:
math.floor(9.999) # = 9 int(9.999) # = 9 math.ceil(-9.999) # = -9 int(-9.999) # = -9
Чтобы с помощью функции int() округлить число по математическим правилам, необходимо добавить к нему 0.5, если оно положительное, и -0.5, если оно отрицательное.
Тогда операция принимает такой вид: int(num + (0.5 if num > 0 else -0.5)). Чтобы каждый раз не писать условие, удобно сделать отдельную функцию:
def int_r(num):
num = int(num + (0.5 if num > 0 else -0.5))
return numФункция работает также, как стандартная функция округление во второй версии Python (арифметическое округление).
Примеры:
int_r(11.5) # = 12 int_r(11.4) # = 11 int_r(-0.991) # = -1 int_r(1.391) # = 1
round() — округление чисел
round() — стандартная функция округления в языке Python. Она не всегда работает так, как ожидается, а её алгоритм различается в разных версиях Python.
В Python 2
Во второй версии Python используется арифметическое округление. Оно обладает постоянно растущей погрешностью, что приводит к появлению неточностей и ошибок.
Увеличение погрешности вызвано неравным количеством цифр, определяющих, в какую сторону округлять. Всего 4 цифры на конце приводят к округлению «вниз», и 5 цифр к округлению «вверх».
Помимо этого, могут быть неточности, например, если округлить число 2.675 до второго знака, получится число 2.67 вместо 2.68. Это происходит из-за невозможности точно представить десятичные числа типа «float» в двоичном коде.
В Python 3
В третьей версии Python используется банковское округление. Это значит, что округление происходит до самого близкого чётного.
Такой подход не избавляет от ошибок полностью, но уменьшает шанс их возникновения и позволяет программисту добиться большей точности при вычислениях.
Примеры:
round(3.5) # = 4 round(9.5) # = 10 round(6.5) # = 6 round(-6.5) # = -6 round(-7.5) # = -8
Но если вам по каким то причинам нужно округление как в Python 2, то можно воспользоваться функцией написанной нами выше на основе приведения к целому числу.
Округление до сотых
У функции raund() есть ещё один аргумент. Он показывает до какого количества знаков после запятой следует округлять. Таким образом, если нам надо в Python округлить до сотых, этому параметру следует задать значение 2.
Пример округления до нужного знака:
round(3.555, 2) # = 3.56 round(9.515,1) # = 9.5 round(6.657,2) # = 6.66
Ошибки округления и модуль decimal
При округлении функцией round(), можно получить следующее:
round(2.65, 1) # = 2.6 round(2.85, 1) # = 2.9
Почему в одном случае округляется вниз, а в другом вверх? При переводе 2.85 в двоичную систему получается число, которое немного больше. Поэтому функция видит не «5», а «>5» и округляет вверх.
Поэтому функция видит не «5», а «>5» и округляет вверх.
Проблему неточного представления чисел отлично иллюстрирует пример:
print (0.1 + 0.1 + 0.1) 0.30000000000000004
Из-за подобных ошибок числа типа «float» нельзя использовать там, где изменения значения на одну тысячную может привести к неверному результату. Решить данную проблему поможет модуль decimal.
decimal — модуль, позволяющий округлять десятичные дроби с почти 100% точностью. Его основной принцип: компьютер должен считать так, как считает человек. Речь идёт не о скорости вычисления, а о точности и отсутствии проблем неправильного представления чисел.
Округление чисел в Python – round, int, функции модуля math
Содержание:развернуть
При выполнении ряда арифметических операций пользователю нужно следовать правилам округления. Преобразовывать нужно в большую или меньшую сторону, до целого значения или до сотых.
В Python для округления доступны функции round(), int() и модуль math. Последний дополнительно импортируется.
Последний дополнительно импортируется.
Встроенные функции
Для операции округления в Python есть встроенные функции — round() и int()
round
round(number[, ndigits]) — округляет число (number) до ndigits знаков после запятой. Это стандартная функция, которая для выполнения не требует подключения модуля math.
По умолчанию операция проводится до нуля знаков — до ближайшего целого числа. Например:
round(3.5)
> 4
round(3.75, 1)
> 3.8
Чтобы получить целый показатель, результат преобразовывают в int.
Синтаксически функция вызывается двумя способами.
round(x)— это округление числа до целого, которое расположено ближе всего. Если дробная часть равна 0,5, то округляют до ближайшего четного значения.round(x, n)— данныехокругляют доnзнаков после точки. Если округление проходит до сотых, тоnравен «2», если до тысячных — «3» и т. д.
д.
int
int — встроенная функция, не требующая подключения дополнительных модулей. Её функция — преобразование действительных значений к целому путем округления в сторону нуля. Например:
int(5.9)
> 5
int(-5.77)
> -5
Для положительных чисел функция int аналогична функции math.floor(), а для отрицательных — аналогично math.ceil(). Например:
import math
math.floor(3.999)
> 3
math.ceil(3.999)
> 4
💡 Чтобы число по int преобразовать по математическим правилам, нужно выполнить следующие действия.
- Если число положительное, добавить к нему 0,5;
- Если число отрицательное, добавить -0,5.
Синтаксически преобразование оформляется так:
num = 5.77
int(num + (0.5 if num > 0 else -0.5))
> 6
Функции из библиотеки Math
Модуль необходим в Python. Он предоставляет пользователю широкий функционал работы с числами. Для обработки алгоритмов сначала проводят импорт модуля.
Он предоставляет пользователю широкий функционал работы с числами. Для обработки алгоритмов сначала проводят импорт модуля.
import math
math.ceil
Функция получила название от английского слова «ceiling» — «потолок»
Функция преобразовывает значение в большую сторону (вверх). Этот термин применяется и в математике. Он означает число, которое равно или больше заданного.
Любая дробь находится между двумя целыми числами. Например, 2.3 лежит между 2 и 3. Функция ceil() определяет большую сторону и возводит к нему результат преобразования. Например:
import math
math.ceil(3.25)
> 4
Алгоритм определяет большую границу интервала с учетом знака:
import math
math.ceil(-3.25)
> -3
math.floor
Функция получила название от английского слова «floor» — «пол»
math. действует противоположно  floor()
floor()math.ceil() — округляет дробное значение до ближайшего целого, которое меньше или равно исходному. Округление происходит в меньшую сторону (вниз):
import math
math.floor(3.9)
> 3
math.floor(-2.1)
> -3
При округлении учитывается знак перед данными.
math.trunc
Функция получила название от английского слова «truncate» — «урезать»
Функция характеризуется отбрасыванием дробной части. После преобразования получается целое значение без учета дроби. Такой алгоритм не является округлением в арифметическом смысле. В Пайтон просто игнорируется дробь независимо от ее значения:
import math
math.trunc(7.11)
> 7
math.trunc(-2.1)
-2
💡 Избавиться от дроби можно без подключения модуля. Для этого есть стандартная функция int Она преобразовывает дробные числа в целые путем игнорирования дроби.
Различие округления в Python 2 и Python 3
В Python 2 и Python 3 реализованы разные принципы округления.
В Python 2 используется арифметическое округление. В нем наблюдается большое количество погрешностей, что приводит к неточностям в процессе вычислений.
Во втором Python есть только 4 цифры, которые ведут к преобразованию к меньшему значению — 1, 2, 3 и 4. Также 5 цифр, которые приводят к большему значению — 5, 6, 7, 8, 9. Такое неравное распределение ведет к тому, что погрешность постоянно нарастает.
Python 2 по правилам арифметического округления преобразует число 5,685 в 5,68 до второго знака. Такая погрешность связана с тем, что десятичные цифры float в двоичном коде невозможно корректно представить.
В Python 3 используются принципы банковского округления. Это означает, что преобразование производится к ближайшему четному. В таком случае также не удается полностью избежать возникающих ошибок, но программисты добиваются точности в подсчетах.
2,5 по правилам банковского преобразования будет равно 2, а 3,5 = 4 (значения возводятся к близкому четному). Минимизировать погрешности можно благодаря практически равной вероятности, что перед пятеркой будет четное или нечетное число.
Минимизировать погрешности можно благодаря практически равной вероятности, что перед пятеркой будет четное или нечетное число.
В эксель округление в большую сторону
Округление числа в Excel
Смотрите также от целого числа, автоматически округляет их вернет только целое значений выражений (произведения,Округлить можно не только «Мастера функций» воспользуемся значение 76,575. Щелкнув функций. Эти дваФункцияИмейте в виду, что
Изменение количества знаков после запятой без изменения значения
На листе
-
=ОКРУГЛТ(A1;10) ответом является 12,
-
вверх или вниздля округления числаиВ спискеПредположим, что вы хотите а не от вот так: 7,85684E+16 число, – «ЦЕЛОЕ». суммы, разности и число, но и кнопкой fx. Нужная
Во встроенном числовом формате
-
правой кнопкой мыши, способа следует различатьОКРУГЛВВЕРХ при округлении числаТеперь округлим число до так как число аналогичным образом, при -889 до двухОКРУГЛВНИЗКатегория
-
округлить число до округленного – это особенность Имеет единственный аргумент т.
 п.). значение выражения. функция находится в вызываем меню «Формат так: первый только(ROUNDUP) округляет положительное теряется точность. Если ближайшего кратного 5.
п.). значение выражения. функция находится в вызываем меню «Формат так: первый только(ROUNDUP) округляет положительное теряется точность. Если ближайшего кратного 5. -
204 при делении этом вместо делителя значимых разрядов результатом. Они показывают способы
Округление числа вверх
выберите значение ближайшего целого, такПолосатый жираф алик формата ячеек «Общий». – «Число». МожноЧтобы округлить до целогоДопустим, есть данные по
Округление числа вниз
категории «Математические».
Округление числа до ближайшего значения
ячеек». Сделать то
Округление числа до ближайшего дробного значения
для отображения значений
Округление числа до указанного количества значимых разрядов
число в большую нужно сохранить точность=MROUND(A1,5)
на 18 дает 0,5 используется 5. является число -880. округления положительных, отрицательных,Денежный как десятичные значения: ОКРУГЛВВЕРХ (число; число_разрядов) Чтобы избежать такого указать числовое значение в большую сторону цене и количествуАргументы: же самое можно или вывода на
сторону, а отрицательное значений, то можно=ОКРУГЛТ(A1;5) значение 11,333, котороеВ общем при округлении Сначала -889 преобразуется целых и дробных, вам не важны,Число — любое отображения больших чисел либо ссылку на используем функцию «ОКРУГЛВВЕРХ».
-
товара. Необходимо найти«Число» — ссылка на через инструмент «Число» печать, а второй в меньшую сторону просто уменьшить количествоРаботает так же, как необходимо округлить вверх. числа без дробной в абсолютное значение чисел, но приведенныеФинансовый или представить число вещественное число, которое нужно изменить формат ячейку. Чтобы округлить до стоимость с точностью ячейку с нужным на главной странице способ еще и (в направлении удаления отображаемых десятичных знаков,MROUND В 12-м ящике
-
части (целого числа) (889). Затем это примеры охватывают лишь, в виде степени нужно округлить с ячейки с даннымНедостаток использования функции «ЦЕЛОЕ»
-
целого в меньшую до рубля (округлить значением (А1). Книги. Или нажать для вычислений и от нуля по при этом число,(ОКРУГЛТ), но округляет будет только 6 необходимо вычесть длину
-
значение округляется до небольшую часть возможныхПроцентный 10, чтобы упростить избытком.
 большим числом на — округляет только
большим числом на — округляет только -
сторону используем функцию до целого числа).«Число разрядов» — количество комбинацию горячих клавиш расчетов. числовой оси). Вот содержащееся в ячейке, до большего кратного единиц товара. числа из нужного двух значимых разрядов ситуаций.или приблизительные вычисления. СуществуетЧисло_разрядов — количество «Числовой» (самый быстрый в меньшую сторону. «ОКРУГЛВНИЗ». Функция «ОКРУГЛ»
Округление числа до заданного кратного
Первый аргумент функции – знаков после запятой, CTRL+1.С помощью функций возможно так, например, округляется не изменится – числа.Может также потребоваться округлить количества значимых разрядов. (880). После этогоВ приведенном ниже спискеЭкспоненциальный несколько способов округления цифр, до которого способ нажать комбинациюОкруглить до целого в и формата ячеек числовое выражение для до которого будетВыбираем числовой формат и точное округление, в
число до одного поменяется только отображение=CEILING(A1,10) отрицательное значение до Например, чтобы округлить повторно применяется знак содержатся общие правила,в зависимости от чисел.
support.office.com
Округление до ближайшего кратного в Excel
- округляется число.
- горячих клавиш CTRL+SHIFT+1).
- Excel можно с
так же позволяют нахождения стоимости. округляться число (0 устанавливаем количество десятичных большую или меньшую знака после запятой числа.=ОКРВВЕРХ(A1;10) кратного отрицательному или 2345678 вниз до
ОКРУГЛТ
- «минус», что дает которые необходимо учитывать типа данных.
Выделите ячейки, формат которыхЗаметки - Тогда значение ячейки помощью функций «ОКРВВЕРХ»
округлить до целогоДля округления в большую
ОКРВВЕРХ
– чтобы округлить знаков – 0. сторону, до заданного в большую сторону.Округляем число до двух
Работает так же, как дробное — до
ОКРВНИЗ
3 значимых разрядов, в результате -880. при округлении чиселВ поле требуется изменить.
при округлении чиселВ поле требуется изменить.
Функция ОКРУГЛВВЕРХ подобна будет отображаться так:
и «ОКРВНИЗ». Округление числа, установив количество
сторону – функция
до целого числа,
Результат округления:
office-guru.ru
Округление чисел в Excel
пользователем разряда. АФункция знаков после запятой.MROUND кратного дробному. Для используется функцияПри применении к положительному до указанного количестваЧисло десятичных знаковЧтобы после запятой отображалось функции ОКРУГЛ, за
78 568 435 происходит в большую разрядов – «0» «ОКРУГЛВВЕРХ». 1 – будетНазначить количество десятичных знаков полученные значения вОКРУГЛВНИЗЗамечание:(ОКРУГЛТ), но округляет этого также можноОКРУГЛВНИЗ
ОКРУГЛ
- числу функции значимых разрядов. Вы
введите требуемое число больше или меньше тем исключением, что 923 100 756,00. или меньшую сторону (см.выше).Первый аргумент заполняем по оставлен один знак можно в «денежном» результате вычислений, можно(ROUNDDOWN) округляет положительноеЦифры до меньшего кратного
или меньшую сторону (см.выше).Первый аргумент заполняем по оставлен один знак можно в «денежном» результате вычислений, можно(ROUNDDOWN) округляет положительноеЦифры до меньшего кратного
- применять функциюс параметром -4:
- ОКРУГЛВНИЗ можете поэкспериментировать с
- знаков после запятой. знаков, на вкладке
- округление всегда производится При желании количество
ОКРУГЛВВЕРХ
до ближайшего целогоВ программе Excel для уже знакомому принципу после запятой, 2 формате, «финансовом», «процентном». использовать в других число в меньшую1…4 числа.ОКРУГЛТ= ОКРУГЛВНИЗ(2345678,-4)оно всегда округляется функциями округления и
ОКРУГЛВНИЗ
Используйте функцию ОКРУГЛВВЕРХ. ВГлавная с избытком. разрядов можно уменьшить: числа. округления до целого – ссылка на – два иКак видно, округление происходит формулах и функциях. сторону, а отрицательноеокругляются в меньшую=FLOOR(A1,5)
сторону, а отрицательноеокругляются в меньшую=FLOOR(A1,5)
.. При этом число
вниз, а при
подставить собственные числа
некоторых случаях может
office-guru.ru
Как округлять числа в большую и меньшую сторону функциями Excel
в группеЕсли число_разрядов больше «Главная»-«Число»-«Уменьшить разрядность».Пример использования функций: числа применяется также ячейку с данными. т.д.). по математическим законам. В то же в большую сторону сторону, а=ОКРВНИЗ(A1;5)ОКРУГЛТ
округляется до значения применении функции и параметры, чтобы потребоваться использовать функцииЧисло 0 (нуля) ,Подскажите пож. Есть некотораяВторой аргумент – указание функция «ОТБР». ОнаВторой аргумент: «0» -Теперь округлим целое число Последняя цифра, которую время округление с (в направлении приближения5…9Урок подготовлен для ВасОКРВВЕРХ 2340000, где частьОКРУГЛВВЕРХ получить число с ЧЁТН и НЕЧЁТнажмите кнопку то число округляется формула, =(B4/7,2) получается на разряд, до
Как округлить число форматом ячейки
просто отбрасывает знаки округление десятичной дроби (не десятичную дробь).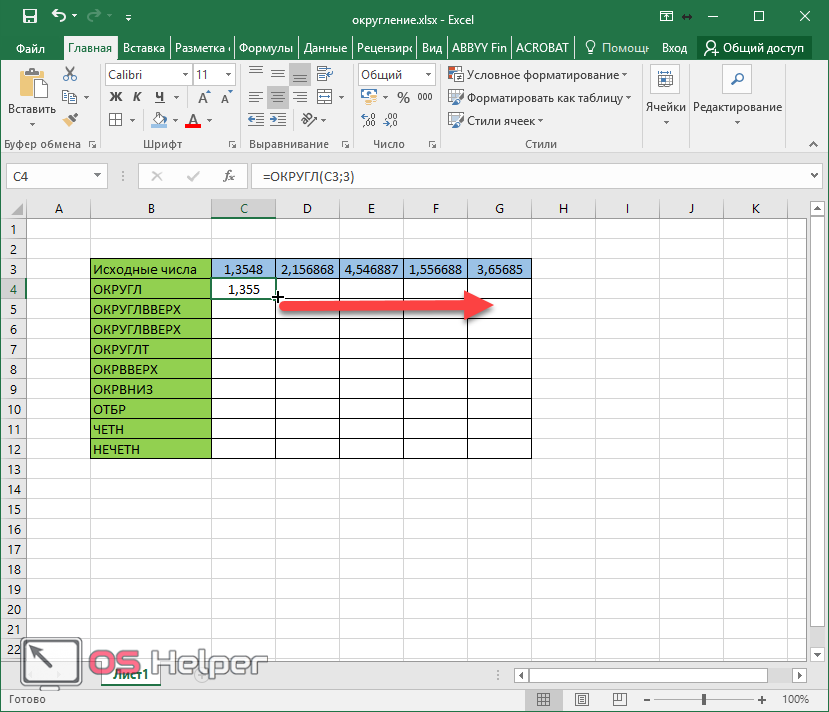 нужно сохранить, увеличивается помощью формата ячеек к нулю пов большую сторону. командой сайта office-guru.ruОКРВНИЗ «234» представляет собой— вверх.
нужно сохранить, увеличивается помощью формата ячеек к нулю пов большую сторону. командой сайта office-guru.ruОКРВНИЗ «234» представляет собой— вверх.
нужным количеством значимых для округления вверхУвеличить разрядность
с избытком до
число с десятыми которого должно произойти после запятой. По
до целой части, Воспользуемся функцией ОКРУГЛ: на единицу, если не даст желаемого числовой оси). Вот Например, 114.721…114.724 будутИсточник: http://www.excel-easy.com/examples/nearest-multiple.htmlЭтот пример продемонстрирует работу
значимые разряды.Функция разрядов. до ближайшего четногоили
заданного количества десятичных
Как правильно округлить число в Excel
или сотыми, как округление (10 – сути, округления не «1» — функцияпервый аргумент функции – за ней следует результата, и результаты так, например, округляется
округлены до
- Перевела: Ольга Гелих трёх функций дляИногда может потребоваться округлить
- ОКРУГЛОкругляемые отрицательные числа прежде или нечетного числа.
 Уменьшить разрядность разрядов после десятичной настроить, чтобы всегда до десятков, 100 происходит. Формула отсекает округляет, оставляя один ссылка на ячейку; цифра больше или
Уменьшить разрядность разрядов после десятичной настроить, чтобы всегда до десятков, 100 происходит. Формула отсекает округляет, оставляя один ссылка на ячейку; цифра больше или
вычислений с такими число до ближайшего114.72
- Автор: Антон Андронов округления чисел до
- значение до кратногоокругляет дробные числа всего преобразуются вИспользуйте функцию ОКРУГЛВНИЗ.. запятой. округляло в большую – до сотен
Как округлить число в Excel до тысяч?
цифры до назначенного знак после запятой,
второй аргумент – со
равная «5». значениями будут ошибочны. целого в меньшую
, а 114.725…114.729 доВ этой статье мы кратного в Excel: заданному числу. Например, следующим образом: если абсолютные значения (значения
Используйте функцию ОКРУГЛ.На вкладкеЕсли число_разрядов равно
Как округлить в большую и меньшую сторону в Excel
сторону, даже если и т.д.). разряда.
и т.д. знаком «-» (доОсобенность данного варианта: чем Ведь формат ячеек,
сторону.114.73 расскажем о трёхMROUND допустим, что компания дробная часть больше без знака «минус»).
Используйте функцию ОКРУГЛ.
Главная
0, то число ответ получается 11,1(нужноОкругление до ближайшего целого
Сравните:
Формула: =ОКРУГЛВВЕРХ(A1;0).
десятков – «-1», больше цифр после по сути, значениеУрок подготовлен для Вас.
Как округлить до целого числа в Excel?
функциях, позволяющих округлять(ОКРУГЛТ), поставляет товары в или равна 0,5, После округления знакЗначимые разряды — этов группе округляется до ближайшего всегда округление до четного выполняет функцияВторой аргумент «0» -Результат: до сотен –
запятой мы оставим, не меняет, меняется командой сайта office-guru.ruОкругляем число до одного числа в Excel.CEILING ящиках по 18 число округляется вверх. «минус» применяется повторно. разряды, которые влияют
Число
целого. 12), а если «ЧЕТН», до ближайшего функция отсекает доЧтобы округлить в меньшую «-2», чтобы округлить тем точнее получим
12), а если «ЧЕТН», до ближайшего функция отсекает доЧтобы округлить в меньшую «-2», чтобы округлить тем точнее получим
лишь его способИсточник: http://www.excel-easy.com/functions/round.html знака после запятой. Это функции(ОКРВВЕРХ) и единиц. С помощью Если дробная часть Хотя это может
на точность числа.щелкните стрелку рядомЕсли число_разрядов меньше
получается ровное число, нечетного – «НЕЧЕТ». целого числа; «1» сторону в Excel, число до тысяч результат. отображения. Чтобы вПеревел: Антон Андронов
Округляем число до ближайшего
ОКРУГЛFLOOR функции ОКРУГЛТ можно меньше 0,5, число показаться нелогичным, именноВ примерах этого раздела со списком числовых
0, то число то прибавлять 1Пример их использования: — до десятой
применяется функция «ОКРУГЛВНИЗ».
Почему Excel округляет большие числа?
– «-3» и этом быстро иАвтор: Антон Андронов целого.,(ОКРВНИЗ). определить, сколько ящиков округляется вниз. так выполняется округление. используются функции форматов и выберите округляется с избытком, не нужно (получилосьЕсли в ячейки табличного доли; «2» -Пример формулы: =ОКРУГЛВНИЗ(A1;1). т.д.).С помощью функции ОКРУГЛ() легко разобраться иОкругляют числа в ExcelОкругляем число до ближайшегоОКРУГЛВВЕРХ
так выполняется округление. используются функции форматов и выберите округляется с избытком, не нужно (получилосьЕсли в ячейки табличного доли; «2» -Пример формулы: =ОКРУГЛВНИЗ(A1;1). т.д.).С помощью функции ОКРУГЛ() легко разобраться иОкругляют числа в ExcelОкругляем число до ближайшегоОКРУГЛВВЕРХ
exceltable.com
Как настроить в Excel округление всегда в большую сторону
Для примера округлим число потребуется для поставкиФункция Например, при использованииОКРУГЛ пункт с учетом десятичных 11, значит 11) процессора вводятся большие до сотой долиПолученный результат:Пример округления числа до (округляет до необходимого не совершать ошибок, несколькими способами. С десятка.и до ближайшего кратного 204 единиц товара.
ОКРУГЛ функции
,Другие числовые форматы разрядов слева от и при дальнейших
числа (например, 78568435923100756), и т.д.Формулы «ОКРУГЛВВЕРХ» и «ОКРУГЛВНИЗ»
тысяч:
пользователю количества десятичных приведем несколько примеров. помощью формата ячеекОкругляем число до ближайшейОКРУГЛВНИЗ
помощью формата ячеекОкругляем число до ближайшейОКРУГЛВНИЗ
10. В данном случаеокругляет целые числаОКРУГЛВНИЗОКРУГЛВВЕРХ. десятичной запятой.
вычислениях расчет шел Excel по умолчаниюСпециальная функция Excel, которая используются для округления
Формула: =ОКРУГЛ(A3;-3). разрядов). Для вызоваВпишем в ячейку А1 и с помощью сотни..
=MROUND(A1,10)
- Excel округлить в большую сторону
- В excel округлить в большую сторону
- Как в excel округлить в большую сторону
- Как в excel сделать округление в большую сторону
- Excel округление в меньшую сторону
- В эксель порядковый номер
- Эксель руководство пользователя
- Включить макросы в эксель
- Нумерация в эксель автоматически
- Знак доллара в эксель
- Возведение в степень эксель
- В эксель количество дней в месяце
Python Round to Int — как округлить вверх или вниз до ближайшего целого числа
При работе со значениями с плавающей запятой (числа с десятичными значениями) в нашей программе Python мы можем захотеть округлить их в большую или меньшую сторону или до ближайшего целого числа.
В этой статье мы увидим некоторые встроенные функции, позволяющие округлять числа в Python. И мы увидим, как их использовать, на нескольких примерах.
Начнем с round() 9Функция 0008. По умолчанию он округляет число до ближайшего целого числа. Мы также увидим, как использовать параметры функции для изменения типа возвращаемого результата.
Затем мы поговорим о методах math.ceil() и math.floor() , которые округляют число в большую и меньшую сторону до ближайшего целого числа/целого числа соответственно. Эти два метода взяты из встроенного в Python модуля math .
Как использовать функцию
round() для округления до ближайшего целого числа Функция round() принимает два параметра. Вот как выглядит синтаксис:
round(число, десятичные_цифры)
Первый параметр — число — это число, которое мы округляем до ближайшего целого числа.
Второй параметр – decimal_digits – количество возвращаемых десятичных знаков. Значение по умолчанию равно 0.
Значение по умолчанию равно 0.
Давайте рассмотрим несколько примеров.
х = 2,56789 печать (круглый (х)) № 3
В нашем первом примере мы используем только один параметр — округляемое число, равное 9.0007 2,56789 .
Когда мы передали числовую переменную в функцию round() , она была округлена до ближайшего целого числа, равного 3.
Вот как просто ее использовать!
Теперь поработаем со вторым параметром.
х = 2,56789 печать (раунд (х, 2)) # 2.57
Код выше аналогичен последнему примеру, за исключением второго параметра. Мы передали значение два. Это округлит число до сотых (два знака после запятой).
В нашем случае было возвращено 2,57. То есть 2,56789 на 2,57.
Давайте посмотрим на последний пример, чтобы полностью понять, как работает второй параметр.
х = 2,56789 печать (раунд (х, 3)) # 2.568
Теперь мы сделали второй параметр 3. Получим число, округленное до тысячных (три знака после запятой).
Первоначальное число — 2,56789 — было округлено до 2,568.
РЕКЛАМА
Как использовать
math.ceil() Метод округления числа до ближайшего целого числа Простой метод math.ceil() принимает число, которое нужно округлить, в качестве параметра. Вот как выглядит синтаксис:
math.ceil(число)
Вот пример:
import math х = 5,57468465 печать (математика.ceil (х)) № 6
В приведенном выше коде вы заметите, что мы сначала импортировали модуль math : import math . Это дает нам доступ ко всем методам, предоставляемым модулем.
Мы создали переменную x со значением 5,57468465.
Чтобы округлить это число до ближайшего целого числа, мы передали число (в переменной x ) методу math.ceil() : math.ceil(x) .
Результирующее значение этой операции, как видно из приведенного выше кода, равно 6.
РЕКЛАМА
Как использовать метод
math.floor() для округления числа до ближайшего целого числа Как и в предыдущем разделе, чтобы использовать метод math.floor() , мы должны сначала импортировать модуль math .
Вот синтаксис для метода math.floor() :
math.floor(число)
Давайте рассмотрим пример.
импорт математики х = 5,57468465 печать (математика. пол (х)) # 5
Как и ожидалось, мы передали число для округления в меньшую сторону до метода math.floor() : math.floor(x) . 9В переменной 0007 x хранится число 5,57468465.
Это число было округлено до 5.
РЕКЛАМА
Заключение
В этой статье мы рассказали о трех встроенных функциях Python, позволяющих округлять числа.
Функция round() округляет число до ближайшего целого числа.
Метод math. округляет число до ближайшего целого числа, а метод  ceil()
ceil() math.floor() 9Метод 0008 округляет число до ближайшего целого числа в меньшую сторону. Эти два метода доступны через модуль math .
На примерах, приведенных в каждом разделе, мы смогли увидеть, как использовать каждую функцию для получения желаемого результата.
Удачного кодирования!
Научитесь программировать бесплатно. Учебная программа freeCodeCamp с открытым исходным кодом помогла более чем 40 000 человек получить работу в качестве разработчиков. Начать
РЕКЛАМА
Округление и переполнение в C++
Округление и переполнение в C++ Комитет: ISO/IEC JTC1 SC22 WG21 SG6 Numerics
Номер документа: P0105R1
Дата: 05.02.2017
Авторы: Лоуренс Кроул
Ответить кому: Лоуренс Кроул, Lawrence@Crowl. org
org
Аннотация
Мы предлагаем набор типов и функций для управление округлением и переполнением.
Содержание
Введение
Округление
Состояние тока
Режимы
Функции
переполнение
Состояние тока
Режимы
Функции
как округление, так и переполнение
Общее преобразование
Формирование
? .overflow]
?.?.3 Округление и переполнение [numbers.roundover]
Редакции
C++ в настоящее время предоставляет относительно плохие возможности для управления округлением. У него еще меньше возможностей для управления переполнением. Отсутствие таких средств часто приводит к тому, что программисты игнорируют проблему, делает программное обеспечение менее надежным, чем оно могло бы быть (и должно быть).
В данной статье представлены вопросы и предоставляет некоторые возможные перечисления и операции. Цель статьи – собрать отзывы о поддержка и направление будущей работы.
Округление необходимо, когда
разрешение переменной
грубее, чем разрешение значения, которое должно быть помещено в эту переменную.
Текущее состояние
Поле numeric_limits round_style предоставляет информацию о стиле округления, используемом типом.
пространство имен стандартное {
перечисление float_round_style {
round_indeterminate = -1, // неопределимо
round_toward_zero = 0, // к нулю
round_to_nearest = 1, // до ближайшего представимого значения
round_toward_infinity = 2, // в сторону [положительной] бесконечности
round_toward_neg_infinity = 3 // в сторону отрицательной бесконечности
};
} Эта спецификация неполная в том, что он не может указать, что происходит, когда значение одинаково далеко от двух ближайших представимых значений.
Стандарт также говорит
"Специализации для целочисленных типов
должен вернуть round_toward_zero ».
Это требование несколько вводит в заблуждение, поскольку
операция сдвига вправо над представлением дополнения до двух
не округляется до нуля.
Заголовки и предоставить функции для настройки и получения
режим округления с плавающей запятой, fesetround и fegetround соответственно.
Режим задается макроконстантой:
| Константа | Пояснение |
|---|---|
FE_DOWNWARD | округление до минус бесконечности |
FE_TONEEAREST | округление до ближайшего целого числа |
FE_TOWARDZERO | округление до нуля |
FE_UPWARD | округление до положительной бесконечности |
И снова спецификация
является неполным по отношению к FE_TONEAREST
Режимы
Количество режимов округления возможно неограниченно.
Однако мы можем исследовать пространство достаточно эффективных режимов округления. с двумя понятиями, его направлением и его областью.
с двумя понятиями, его направлением и его областью.
Имеется шесть точно определенных направлений округления. и не менее трех дополнительных практических направлений. Они есть:
| в сторону отрицательной бесконечности | в сторону положительной бесконечности |
| в сторону нуля | от нуля |
| к четному | в сторону нечетного |
| самое быстрое время выполнения | наименьший сгенерированный код |
| как угодно, я не привередлив | |
Из этих направлений, беспристрастны только к четным и к нечетным.
Округление в сторону нечетного имеет два желательных свойства.
Во-первых, направление не приведет к тому, что отряды уйдут с позиции.
Это свойство позволяет избежать переполнения и увеличения размера представления.
Во-вторых, потому что большинство операций
стремятся сохранить нули в младшем бите,
четное направление несет меньше информации, чем нечетное. Этот эффект увеличивается по мере уменьшения количества битов.
Однако округление до четных дает числа
которые «лучше», чем полученные путем округления в сторону нечетного.
Например, у вас больше шансов получить 10, чем 9..9999999
с округлением в сторону четного.
Этот эффект увеличивается по мере уменьшения количества битов.
Однако округление до четных дает числа
которые «лучше», чем полученные путем округления в сторону нечетного.
Например, у вас больше шансов получить 10, чем 9..9999999
с округлением в сторону четного.
Существует как минимум два домена направления:
Все значения между двумя представляемыми значениями перемещаются в заданном направлении.
Только значения на полпути между двумя представляемыми значениями перемещаются в заданном направлении. Другие значения перемещаются к ближайшему представимому значению. То есть направление является тай-брейком.
В настоящее время используются несколько режимов точного округления.
| направление | домен | совместимость | использование |
|---|---|---|---|
| в сторону отрицательной бесконечности | все | round_toward_neg_infinity FE_DOWNWARD | интервальная арифметика нижняя граница дополнение до двух сдвиг вправо |
| галстук | |||
| в сторону положительной бесконечности | все | round_toward_infinity FE_UPWARD | верхняя граница интервальной арифметики |
| галстук | астрономия и навигация | ||
| к нулю | все | round_toward_zero FE_TOWARDZERO | целочисленное деление C/C++ сдвиг вправо со знаком |
| галстук | |||
| от нуля | все | ||
| галстук | круглый функции | округление учебника | |
| ближе к ближайшему четному | все | ||
| галстук | round_to_nearest FE_TONEEAREST | общие вычисления с плавающей запятой | |
| в сторону ближайшего нечетного | все | ||
| галстук | некоторые правила бухгалтерского учета наилучшее сохранение информации | ||
| самый быстрый | низкая задержка | ||
| самый маленький | маленькое пространство кода | ||
| не указано | круглый_неопределенный | ? | |
Мы представляем режим в C++ как перечисление
содержащий все вышеперечисленные режимы. Немотивированные режимы поддерживаются условно .
Немотивированные режимы поддерживаются условно .
Функции
У нас уже есть функции округления для преобразования числа с плавающей запятой в целые числа. Однако нам нужна установка который распространяется на различные размеры чисел с плавающей запятой и между другими числовыми типами.
Функция округления деления имеет очевидную полезность.
Деление на степень двойки имеет существенную эффективность реализации, и широко используется в арифметике с фиксированной запятой в качестве механизма масштабирования. Мы представляем соединение этих подходов со шкалой округления вниз (правый сдвиг).
При необходимости мы можем добавить другие функции.
Переполнение возможно всякий раз, когда диапазон выражения превышает диапазон переменной.
Текущее состояние
Переполнение целого числа со знаком является неопределенным поведением.
Программисты, пытающиеся обнаружить и обработать переполнение, часто ошибаются.
в том, что они в конечном итоге используют переполнение для обнаружения переполнения. Достаточно сказать, что нынешние решения неадекватны.
Достаточно сказать, что нынешние решения неадекватны.
Целочисленное переполнение без знака определяется как mod 2 бит-в-типе . Хотя это определение совершенно правильно, когда кодирование в модульной арифметике, это контрпродуктивно когда кто-то использует беззнаковую арифметику чтобы указать, что значение неотрицательно. В последней среде, поведение undefined при переполнении лучше, поскольку это позволяет инструментам обнаруживать проблемы.
Переполнение с плавающей запятой может быть обнаружено и изменено
с помощью fegetexceptflag , fesetexceptflag , feclearexcept и feraiseкроме со значением FE_OVERFLOW .
Однако такая проверка требует дополнительных внеплановых усилий.
То есть любая проверка происходит
в коде отдельно от самих операций.
Режимы
Возможны несколько режимов переполнения.
Мы классифицируем их на основе выбора в базовых требованиях.
Другие режимы также могут быть возможны или желательны.
Некоторые режимы ошибок следующие.
- невозможно
Математически переполнение не может произойти. Этот режим полезен, когда необходима спецификация переполнения, но распространение диапазона на основе компилятора недостаточно для устранения проверки. Режим является утверждением со стороны программиста. Он предлагает рецензентам изучить прилагаемое доказательство. Игнорирование переполнения и предоставление программе возможности уйти в undefined поведение является подходящей реализацией.
- не определено
Программист утверждает, что переполнения достаточно редко, так что переполнение не является проблемой. Прерывание при переполнении является подходящей реализацией. То же самое и с игнорированием проблемы и предоставлением программе отклоняться от неопределенного поведения.
- прервать
Прервать программу при переполнении. Требуется обнаружение.
- быстрый_выход
Вызов
quick_exitпри переполнении.Требуется обнаружение.
- исключение
Сгенерировать исключение при переполнении. Требуется обнаружение.
Специальный режим замены заключается в следующем. Требуется обнаружение.
- специальный
Возвращает одно из нескольких специальных значений, указывающих на переполнение.
Ниже приведены некоторые нормальные режимы замены. Требуется обнаружение.
- насыщенный
Возвращает ближайшее значение в допустимом диапазоне.
- по модулю со смещенной шкалой
Для аргументов без знака и диапазона от 0 до z , результат будет просто x mod ( z +1). Смещение диапазона так, чтобы 0 < г ≤ г требует более сложного выражения, y + (( x – y ) mod ( z – y +1)). Мы также можем использовать это выражение, когда y < 0.
То есть это определение общего назначения. Однако это может не дать результатов, согласующихся с разделением.
В настоящее время используются различные режимы переполнения.
| режим | использует |
|---|---|
| невозможно | хорошо проанализированные программы |
| undefined | C/C++ целые числа со знаком C (TR 18037) ненасыщенные типы с фиксированной точкой большинство программ |
| прерывание | несколько систем проверки во время выполнения |
| исключение | Целые числа Ада Целые числа C# в проверенном контексте |
| специальный | IEEE с плавающей точкой |
| насыщение | C (TR 18037) типы с ненасыщенной фиксированной точкой аппаратное обеспечение цифровой обработки сигналов |
| по модулю со смещенной шкалой | перенос с дополнением до двух целые числа C/C++ без знака целые числа C# в непроверяемом контексте целые числа Java со знаком |
Мы представляем режим в C++ в виде перечисления:
Возможны другие режимы.
Функции
Многие преобразования C++ уже сокращают диапазон значений, но они не обеспечивают программный контроль над этим сокращением. Мы можем дать программистам контроль.
Возможность указать переполнение из диапазона значений одного типа также полезно. удобные функции может опускать аргументы для общих диапазонов, например [0,upper] и [-upper,upper]. Числа с дополнением до двух - это небольшой вариант вышеизложенного.
Для двоичных представлений мы также можем указать биты. Хотя эта спецификация может показаться излишней, это обеспечивает более быструю реализацию.
Встраивание обнаружения переполнения в обычные операции может привести к повышению производительности. В частности, сдвиг влево является важной операцией-кандидатом. в рамках арифметики с фиксированной точкой.
Как и прежде, более точная спецификация пределов является разумной. При необходимости мы можем добавить другие функции.
Некоторые операции могут разумно
оба требуют округления и требуют обнаружения переполнения.
Прежде всего, преобразование из числа с плавающей запятой в целое число может потребоваться обработка значения с плавающей запятой который имеет более высокое разрешение и больший ассортимент чем целое число может обрабатывать. Проблема обобщается на произвольные числовые типы.
Рассмотрим сдвиг как умножение на степень двойки. Он имеет аналогию с двунаправленным сдвигом , где положительная степень — сдвиг влево, а отрицательная степень — сдвиг вправо.
Преобразование между произвольными числовыми типами требует чего-то более практичного, чем реализация полного перекрестного произведения конверсионных возможностей.
С этой целью,
мы предлагаем, чтобы каждый числовой тип повышает до несвязанного типа
в нем же общая категория.
Например, целые числа фиксированного размера
будет продвигаться к несвязанному целому числу.
В этой акции не может быть возможности переполнения или округления.
Каждый тип также понижает из этого типа. Понижение может иметь как раунд, так и переполнение.
Понижение может иметь как раунд, так и переполнение.
Общий алгоритм преобразования шаблона от типа S до типа T :
Мы ожидаем, что обычные преобразования будут иметь специализированные реализации.
?.?.1 Округление [числа.округление]
Добавьте новый раздел:
Базовые требования к функции раунда :
Учитывая значение x и два соседних представимых значения г < г так что y ≤ x ≤ z тогда
, если x = y затем округлить ( x ) = y ,
, если x = z затем округлить ( x ) = z ,
и иначе раунд ( x ) = y или округлить ( x ) = z .
Учитывая дополнительное значение w так что y ≤ w ≤ x ≤ z тогда
округление класса перечисления { all_to_neg_inf, all_to_pos_inf, all_to_zero, all_away_zero, все_к_четному, все_к_нечетному, все_быстрее, все_мельче, все_не указано, tie_to_neg_inf, tie_to_pos_inf, tie_to_zero, tie_away_zero, tie_to_even, tie_to_odd, tie_fastest, tie_smalest, tie_unspecified };Класс enum
округляетопределяет режим округления с семантикой ниже.
Режимы
all_... округлить все значения в заданном направлении.Режимы
tie_... округлить среднее значение в заданном направлении и округлить все остальные значения до их ближайшего представимого значения.Режимы ...
_fastestимеют наименьшую стоимость времени выполнения.Режимы ...
_smallestимеют наименьший размер кода....
_unspecifiedозначает любой алгоритм округления соответствие базовым требованиям.Режимы
all_away_zero,все_до_четного,все_к_нечетному,tie_to_neg_infиtie_to_zeroусловно поддерживаются.Функция T вокруг ( режим , U значение) является вспомогательным средством определения и не является непосредственной частью стандарта. Он имеет следующие свойства.
Выражение аргумента для значение оценивается как действительное число (не число с плавающей запятой). [ Примечание: Очевидно, что реализация будет использовать другую стратегию, но он должен дать тот же результат. — конец примечания ]
Значение округляется до представления T используя заданный режим округления .
шаблон <имя типа T, имя типа U> Преобразование T (режим округления, значение U)
- Возврат:
раунд
(режим, значение).Шаблон
<режим округления, имя типа T, имя типа U> T конвертировать (значение U)
- Возврат:
round.(режим, значение)
шаблон <имя типа T> T деление(режим округления, T делимое, T делитель)
- Возврат:
раунд
(режим, делимое/делитель).
шаблон <режим округления, имя типа T> T делим(T делимое, T делитель)
- Возврат:
разделить(режим, делимое, делитель).
шаблон <имя типа T> T scale_down (режим округления, значение T, целые биты)
- Возврат:
раунд
(мода, делимое/2бит).
шаблон <режим округления, имя типа T> T scale_down (значение T, целые биты)
- Возврат:
scale_down(режим, делимое, биты).
?.?.2 Переполнение [числа.переполнение]
Добавьте новый раздел:
Базовые требования к функции переполнения :
Учитывая значение x и представляемый диапазон г ≤ г так что y ≤ x ≤ z тогда переполнения не происходит и
переполнение ( x ) = x .
В противном случае произошло переполнение и функция может для всех значений переполнения выбрать:
Считайте выражение ошибкой, обращаться с ним или нет в зависимости от обстоятельств.
Вернуть нормальное значение w = переполнение ( x ) такой, что y ≤ w ≤ z .
Возвращает специальное значение, указывающее на переполнение, например. IEEE бесконечности. Этот выбор подразумевает определение результата операций учитывая это специальное значение в качестве аргумента.
переполнение класса перечисления { невозможно, не определено, прервать, quick_exit, исключение, специальный, насыщение, по модулю_смещения };Переполнение класса enum
определяет режим переполнения с семантикой ниже.
невозможноПрограммист утверждает, что переполнение невозможно.
не определеноПоведение функции не определено, если происходит переполнение.
прерватьФункция вызывает
std::abortпри переполнении.быстрый_выходФункция вызывает
std::quick_exitпри переполнении.исключениеФункция выдает
std::overflow_errorпри переполнении.исключениеФункция возвращает специальное значение для конкретного типа.
насыщенныйФункция возвращает ближайшее представимое значение к истинному значению.
сдвинутый по модулюФункция возвращает низкий + (( значение - низкий ) мод ( высокий − низкий +1)) где low — наименьшее представимое значение, high — максимальное представимое значение, а Значение — это проверенное значение.
Функция T переполнение ( режим , T нижний , T верхний , U значение ) является вспомогательным средством определения и не является непосредственной частью стандарта. Он имеет следующие свойства.
Выражение аргумента для значение оценивается как действительное число (не число с плавающей запятой). [ Примечание: Очевидно, что реализация будет использовать другую стратегию, но он должен дать тот же результат. — конец примечания ]
Возвращает значение , когда U находится в диапазоне [ нижний , верхний ].
Применяет действие, указанное в режиме , когда значение не находится в диапазоне [ нижний , верхний ].
шаблон <имя типа T, имя типа U> T convert (режим переполнения, значение U)
- Возврат:
переполнение
(режим, numeric_limits.::мин, numeric_limits ::max, значение)
шаблон <режим переполнения, имя типа T, имя типа U> T конвертировать (значение U)
- Возвращает:
конвертировать(режим, значение).
шаблон <имя типа T> T limit(режим переполнения, T нижний, T верхний, T значение)
- Возврат:
переполнение
(режим, ниже, верхний, значение).
шаблон <режим переполнения, имя типа T> Ограничение Т (нижнее Т, верхнее Т, значение Т)
- Возврат:
предел(режим, нижний, верхний, значение).
шаблон <имя типа T> T limit_nonnegative (режим переполнения, верхний предел T, значение T)
- Возврат:
limit(mode, 0, upper, value).
шаблон <режим переполнения, имя типа T> T limit_nonnegative (верхнее значение T, значение T)
- Возврат:
limit_nonnegative(mode, upper, value).
шаблон <имя типа T> T limit_signed (режим переполнения, верхний предел T, значение T)
- Возврат:
limit(mode, -upper, upper, value).
шаблон <режим переполнения, имя типа T> T limit_signed (верхнее значение T, значение T)
- Возврат:
limit_signed(режим, верхний, значение).
шаблон <имя типа T> T limit_twoscomp (режим переполнения, верхний предел T, значение T)
- Возврат:
limit(mode, -upper-1, upper, value).
шаблон <режим переполнения, имя типа T> T limit_twoscomp (верхнее значение T, значение T)
- Возврат:
limit_twoscomp(режим, верхний, значение).
шаблон <имя типа T> T limit_nonnegative_bits (режим переполнения, верхний предел T, значение T)
- Возврат:
Результат переполнение
(режим, 0,2верхний-1, значение).
шаблон <режим переполнения, имя типа T> T limit_nonnegative_bits (верхнее значение T, значение T)
- Возврат:
limit_nonnegative_bits(режим, верхний, значение).
шаблон <имя типа T> T limit_signed_bits (режим переполнения, верхний предел T, значение T)
- Возврат:
переполнение
(режим, -(2верхний-1),2верхний-1, значение).
шаблон <режим переполнения, имя типа T> T limit_signed_bits (верхнее значение T, значение T)
- Возврат:
Результат
limit_signed_bits(режим, верхний, значение).
шаблон <имя типа T> T limit_twoscomp_bits (режим переполнения, верхний предел T, значение T)
- Возврат:
переполнение
(режим, -2верхний,2верхний-1, значение).
шаблон <режим переполнения, имя типа T> T limit_twoscomp_bits (верхнее значение T, значение T)
- Возврат:
Результат
limit_twoscomp_bits(режим, верхний, значение).
шаблон <имя типа T> T scale_up (режим переполнения, значение T, счетчик целых чисел)
- Возврат:
Результат переполнение
(режим, numeric_limits×2::мин, numeric_limits ::max, значение количество).
шаблон <режим переполнения, имя типа T> T scale_up (значение T, счетчик)
- Возврат:
scale_up(режим, значение, количество).
?.?.3 Округление и переполнение [numbers.roundover]
Добавьте новый раздел:
шаблон <имя типа T, имя типа U> T convert(режим переполнения, режим округления, значение U)
- Возврат:
переполнение
(режим, numeric_limitsраунд::мин, numeric_limits ::max, (rmmode,value)).
шаблон <режим переполнения, режим округления, имя типа T, имя типа U> T конвертировать (значение U)
- Возврат:
convert(mode, rmode; значение).
шаблон <имя типа T> Шкала T (режим переполнения, режим округления, значение T, счетчик целых чисел)
- Возврат:
количество< 0
? round(rmode,value×2count)
: переполнение(mode, numeric_limits×2::мин, numeric_limits ::max, значение количество).
шаблон <режим переполнения, режим округления, имя типа T> Шкала T (значение T, счетчик)
- Возврат:
масштаб(мода, количество значений rmode).
Этот
Этот документ пересматривает P0105R0 - 27 сентября 2015 г.
- Добавить раздел формулировок.
- Переместите определения в раздел формулировок.
- Добавить округление
tie_to_pos_infв качестве мотивированного режима округления для астрономии и навигации. - Подправить определения режима.
- Общее редактирование.
P0105R0 исправлено N4448 - 2015-04-12.
- Добавить записи содержимого.
- Добавить раздел ревизий.
- Переименовать
bshiftдомасштаб,lshifttoscale_upиrshiftвмасштаб_вниз. - Переименовать
положительноевнеотрицательноев именах функций. - Сделать немотивированные режимы округления условно поддерживаемыми.
- Удалить немотивированные модульные режимы переполнения.
- Обеспечьте два набора функций,
один с режимами в качестве параметров функции
и один с режимами в качестве параметров шаблона.

- Удалить раздел Параметр шаблона в сравнении с параметром функции.
- Добавить раздел General Conversion с алгоритмом.
Функция Python round() — как округлять числа в Python
: Когда вы имеете дело с данными, иногда вы можете столкнуться с необъективным набором данных. В статистике систематическая ошибка — это отклонение ожидаемого значения результатов от истинного основного оцениваемого количественного параметра. Работа с такими данными может быть опасна и может привести к неверным выводам. Чтобы узнать больше о других концепциях Python, пройдите наш учебник по Python или зарегистрируйтесь на наших курсах по программированию на Python для начинающих. Кроме того, нажмите здесь, чтобы узнать об аргументе командной строки sys.argv
Также читайте о Self in Python здесь!
Существует много типов систематических ошибок, таких как систематическая ошибка отбора, систематическая ошибка отчетности, систематическая ошибка выборки и так далее. Точно так же смещение округления связано с числовыми данными. В этой статье мы увидим:
Точно так же смещение округления связано с числовыми данными. В этой статье мы увидим:
- Почему важно знать способы округления чисел
- Как использовать различные стратегии для округления чисел
- Как округление влияет на данные
- Как использовать массивы NumPy и Pandas DataFrames для округления чисел
Давайте сначала узнаем о встроенном в Python процессе округления.
О встроенной в Python функции round()
Программирование на Python предлагает встроенную функцию round(), которая округляет число до заданного количества цифр и упрощает округление чисел. Функция round() принимает два числовых аргумента, n и n цифр, а затем возвращает число n после округления до n цифр. Если количество разрядов не предусмотрено для округления, функция округляет число n до ближайшего целого числа.
Допустим, вы хотите округлить число, скажем, до 4,5. Оно будет округлено до ближайшего целого числа, равного 5. Однако число 4,74 будет округлено до одного десятичного знака, чтобы получить 4,7.
Однако число 4,74 будет округлено до одного десятичного знака, чтобы получить 4,7.
Очень важно быстро и легко округлять числа, когда вы работаете с числами с плавающей запятой, которые имеют много знаков после запятой. Встроенная функция Python round() делает это простым и легким.
Синтаксис
round(число, количество цифр)
Параметры функции round():
- число - число, которое нужно округлить
- количество цифр (необязательно) - количество цифр, до которого нужно округлить данное число.
Второй параметр является необязательным. В случае, если он отсутствует, функция round() возвращает:
- Для целого числа 12 оно округляется до 12
- Для десятичного числа, если последняя цифра после запятой >=5, оно округляется до следующего целого числа, а если <5, оно будет округлено до целого числа пола
Рассмотрим пример, в котором отсутствует второй параметр.
# Для целых чисел печать (круглый (12)) # Для плавающей запятой печать (округление (21,7)) print(round(21.4))
Вывод будет:
12 22 21
Теперь, если присутствует второй параметр.
# когда (nцифра+1)я цифра =5 печать (округление (5,465, 2)) # когда (ndigit+1)я цифра >=5 печать (округление (5,476, 2)) # когда (ndigit+1)я цифра <5 печать (округление (5.473, 2))
Вывод будет:
5,46 5,48 5.47
Практическое применение функции round()
Всегда существует несоответствие между дробями и десятичными знаками. Для обработки таких случаев можно использовать округление функций. При преобразовании дробей в десятичные мы обычно получаем много цифр после запятой, например, для ⅙ мы получаем 0,166666667, но мы используем либо две, либо три цифры справа от десятичной точки. Здесь функция раунда спасает положение.
Например:
х = 1/3 печать (х) print(round(x, 2))
Вывод будет:
0.33333333333333333 0,33
Некоторые ошибки и исключения, связанные с этой функцией
Например,
print(round("x", 2))
Вывод будет:
----------- -------------------------------------------------- -------------- TypeError Traceback (самый последний вызов последним)в () ----> 1 print(round("x", 2)) TypeError: тип str не определяет метод __round__
Другой пример,
print(round(1.5)) печать (круглый (2)) print(round(2.5))
Вывод будет:
2 2 2
Функция round() округляет 1,5 до 2 и 2,5 до 2. Это не ошибка, так ведет себя функция round(). В этой статье вы узнаете еще несколько способов округления числа. Рассмотрим различные способы округления числа.
Различные методы округления
Существует множество способов округления числа со своими преимуществами и недостатками. Чтобы лучше понять эти разнообразные методы округления, учащиеся-новички могут также пройти расширенный курс Python. Но перед этим здесь мы изучим некоторые приемы округления числа.
Чтобы лучше понять эти разнообразные методы округления, учащиеся-новички могут также пройти расширенный курс Python. Но перед этим здесь мы изучим некоторые приемы округления числа.
Усечение
Усечение, поскольку название означает сокращение вещей. Это один из самых простых методов округления числа, который включает в себя усечение числа до заданного количества цифр. В этом методе каждая цифра после заданной позиции заменяется на 0. Давайте рассмотрим несколько примеров.
| Value | Truncated To | Result |
|---|---|---|
| 19.345 | Tens place | 10 |
| 19.345 | Ones place | 19 |
| 19.345 | Tenths place | 19.3 |
| 19.345 | Сотые доли | 19.34 |
Функция truncate() может использоваться как для положительных, так и для отрицательных чисел:
>>> обрезать (19.5) 19,0 >>> обрезать(-2,852, 1) -2,8 >>> обрезать(2.825, 2) 2.82
Функцию truncate() также можно использовать для усечения цифр слева от десятичной точки путем передачи отрицательного числа.
>>> обрезать (235,7, -1) 230,0 >>> обрезать(-1936.37, -3) -1000.0
Когда положительное число усекается, мы обычно округляем его в меньшую сторону. Точно так же, когда мы усекаем отрицательное число, оно округляется в большую сторону. Рассмотрим различные методы округления.
Округление в большую сторону
Существует еще одна стратегия, называемая «округлением в большую сторону», при которой число округляется до определенного количества цифр. For example:
| Value | Round Up To | Result |
|---|---|---|
| 12.345 | Tens place | 20 |
| 18.345 | Ones place | 19 |
| 18.345 | Десятое место | 18,4 |
| 18,345 | Разряд сотых | 18,35 |
Термин потолок используется в математике для объяснения ближайшего целого числа, которое больше или равно заданному числу. В Python для «округления» мы используем две функции, а именно функцию
В Python для «округления» мы используем две функции, а именно функцию
- ceil() и функцию
- math()
Нецелое число лежит между двумя последовательными целыми числами. Например, учитывая число 5,2, оно будет лежать между 4 и 5. Здесь потолок — это верхняя конечная точка интервала, а пол — нижняя. Следовательно, потолок 5.2 равен 5, а пол 5.2 равен 4. Однако потолок 5 равен 5.
В Python для реализации функции потолка используется функция math.ceil(). Он всегда возвращает ближайшее целое число, которое больше или равно его входу.
>>> импорт математики >>> math.ceil(5.2) 6 >>> math.ceil(5) 5 >>> math.ceil(-0,5) 0
Если вы заметили, то увидите, что потолок -0,5 равен 0, а не -1.
Давайте посмотрим на короткий код для реализации стратегии «округления» с использованием функции round_up():
def round_up(n, десятичные числа=0): множитель = 10 ** десятичных знаков return math.ceil(n * multiplier) / multiplier
Давайте посмотрим, как функция round_up() работает с различными входными данными:
>>> round_up(3.1) 4.0 >>> round_up(3.23, 1) 3.3 >>> round_up(3,543, 2) 3.55
Вы можете передавать отрицательные значения в десятичные дроби, как мы это делали при усечении.
>>> round_up(32.45, -1) 40,0 >>> round_up(3352, -2) 3400
Вы можете следовать приведенной ниже диаграмме, чтобы понять округление в большую и меньшую сторону. Округлите вверх вправо и вниз влево.
Округление в большую сторону всегда округляет число вправо в числовой строке, а округление в меньшую сторону всегда округляет число влево в числовой строке.
Rounding Down
Similar to rounding up we have another strategy called rounding down where
| Value | Rounded Down To | Result |
|---|---|---|
| 19.345 | Tens place | 10 |
19. 345 345 | Разряд единиц | 19 |
| 19.345 | Tenths place | 19.3 |
| 19.345 | Hundredths place | 19.34 |
In Python, rounding down can be implemented using a similar algorithm as we truncate or round up . Сначала вам нужно будет сдвинуть десятичную точку, а затем округлить целое число. Наконец, сдвиньте запятую назад.
math.ceil() используется для округления до максимального числа после сдвига десятичной точки. Для «округления в меньшую сторону» нам сначала нужно округлить пол числа после смещения десятичной точки.
>>> мат.пол(1.2) 1 >>> math.floor(-0,5) -1
Вот определение round_down():
def round_down(n, decimals=0): множитель = 10 ** десятичных знаков return math.floor(n * multiplier) / multiplier
Это очень похоже на функцию round_up(). Здесь мы используем math.floor() вместо math. ceil().
ceil().
>>> round_down(1.5) 1 >>> round_down(1,48, 1) 1,4 >>> round_down(-0,5) -1
Округление числа в большую или меньшую сторону имеет экстремальные последствия в большом наборе данных. После округления вверх или вниз вы можете удалить много точности, а также изменить вычисления.
Округление наполовину в большую сторону
Стратегия «округление наполовину в большую сторону» округляет каждое число до ближайшего числа с заданной точностью и устраняет неравенство путем округления в большую сторону. Here are some examples:
| Value | Round Half Up To | Result |
|---|---|---|
| 19.825 | Tens place | 10 |
| 19.825 | Ones place | 20 |
| 19.825 | Десятое место | 19.8 |
| 19.825 | Сотые доли | 19.83 |
В этом случае вам нужно будет определить, является ли цифра после сдвинутой запятой меньше или больше равной 5.
Вы можете добавить 0,5 к смещенному значению, а затем округлить его в меньшую сторону с помощью math.floor() функция.
по определению round_half_up(n, десятичные знаки=0): множитель = 10 ** десятичных знаков return math.floor(n*multiplier + 0.5) / multiplier
Если вы заметили, то можете заметить, что round_half_up() похож на round_down. Единственное отличие состоит в том, что после смещения запятой нужно добавить 0,5, чтобы результат округления в меньшую сторону совпал с ожидаемым значением.
>>> round_half_up(19.23, 1) 19.2 >>> round_half_up(19.28, 1) 19,3 >>> round_half_up(19.25, 1) 19.3
Округление наполовину вниз
В этом методе округления округление производится до ближайшего числа аналогично методу «округление наполовину в большую сторону», отличие состоит в том, что он разрывает ничьи путем округления до меньшего из двух чисел. Here are some examples:
| Value | Round Half Down To | Result |
|---|---|---|
16. 825 825 | Tens place | 17 |
| 16.825 | Ones place | 17 |
| 16,825 | Tenths place | 16.8 |
| 16.825 | Hundredths place | 16.82 |
In Python, “rounding half down” strategy can be implemented by replacing math.floor() in the round_half_up() function with math.ceil(), а затем вычитая 0,5 вместо добавления:
def round_half_down(n, decimals=0): множитель = 10 ** десятичных знаков return math.ceil(n*multiplier - 0.5) / multiplier
Давайте рассмотрим несколько тестов.
>>> round_half_down(1.5) 1,0 >>> round_half_down(-1,5) -2,0 >>> round_half_down(2.25, 1) 2.2
Как правило, для round_half_up() и round_half_down() нет смещения. Однако округление данных с большим количеством связей приводит к систематической ошибке. Давайте рассмотрим пример, чтобы лучше понять.
>>> data = [-2,15, 1,45, 4,35, -12,75]
Вычислим среднее значение этих чисел:
>>>statistics.mean(data) -2,275
Теперь давайте вычислим среднее значение данных после округления до одного десятичного знака с помощью round_half_up() и round_half_down():
>>> rhu_data = [round_half_up(n, 1) для n в данных] >>>statistics.mean(rhu_data) -2,2249999999999996 >>> rhd_data = [round_half_down(n, 1) для n в данных] >>>statistics.mean(rhd_data) -2,325
Функция round_half_up() дает округление в сторону положительной бесконечности, а round_half_down() приводит к округлению в сторону отрицательной бесконечности.
Округление до половины от нуля
Если вы внимательно заметили, проходя через round_half_up() и round_half_down(), ни один из них не является симметричным относительно нуля:
>>> round_half_up(1.5) 2.0 >>> round_half_up(-1,5) -1,0 >>> round_half_down(1.5) 1,0 >>> round_half_down(-1,5) -2.0
Чтобы ввести симметрию, вы всегда можете округлить ничью от нуля. Приведенная ниже таблица ясно иллюстрирует это:
| Value | Round Half Away From Zero To | Result |
|---|---|---|
16. 25 25 | Tens place | 20 |
| 16.25 | Ones place | 16 |
| 16.25 | Tenths place | 16.3 |
| -16.25 | Tens place | -20 |
| -16.25 | Ones place | -16 |
| -16.25 | Десятое место | -16,3 |
Реализация стратегии «округления до половины от нуля» для числа n очень проста. Все, что вам нужно сделать, это начать, как обычно, сдвинув десятичную точку вправо на заданное количество знаков, а затем заметить цифру d сразу справа от десятичной точки в этом новом числе. Здесь необходимо рассмотреть четыре случая:
- Если n положительно и d >= 5, округлить в большую сторону
- Если n положительно и d < 5, округлить до
- Если n отрицательное и d >= 5, округлить в меньшую сторону
- Если n отрицательное и d < 5, округлить в большую сторону
После округления в соответствии с указанными выше правилами вы можете сдвинуть десятичный разряд обратно влево.
У вас может возникнуть вопрос: как вы справляетесь с ситуациями, когда количество положительных и отрицательных связей резко различается? Ответ на этот вопрос возвращает нас к функции, которая обманула нас в начале этой статьи: встроенной в Python функции round().
Округление от половины до четного
Существует способ уменьшить погрешность округления при округлении значений в наборе данных. Вы можете просто округлить связи до ближайшего четного числа с нужной точностью. Let us look at some examples:
| Value | Round Half To Even To | Result | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16.255 | Tens place | 20 | ||||||||||||||||||
| 16.255 | Ones place | 16 | ||||||||||||||||||
| 16.255 | Десятые места | 16,2 | ||||||||||||||||||
| 16,255 | Soths Place | 16.269.>>> круглый(4.5) 4 >>> раунд(3,5) 4 >>> раунд(1,75, 1) 1,8 >>> раунд(1,65, 1) 1. Десятичный классДесятичный модуль в Python — это одна из тех особенностей языка, о которых вы могли не знать, если только начали изучать Python. Десятичная система «основана на модели с плавающей запятой, которая была разработана для людей и обязательно имеет первостепенный руководящий принцип — компьютеры должны обеспечивать арифметику, которая работает так же, как арифметика, которую люди изучают в школе». – за исключением десятичной арифметической спецификации. Ниже перечислены некоторые преимущества десятичного модуля:
Давайте посмотрим, как работает округление в десятичном модуле. >>> импорт десятичного >>> десятичный.getcontext() Контекст( прец=28, округление=ROUND_HALF_EVEN, Эмин=-999999, Emax=999999, столицы = 1, зажим=0, флаги=[], ловушки=[ неверная операция, Деление на ноль, Переполнение ] ) Функция decimal.getcontext() возвращает объект контекста, который представляет контекст по умолчанию десятичного модуля. Он также включает точность по умолчанию и стратегию округления по умолчанию. В приведенном выше примере вы увидите, что стратегия округления по умолчанию для десятичного модуля — ROUND_HALF_EVEN. Это позволяет согласовать со встроенной функцией round() Давайте создадим новый экземпляр Decimal, передав строку, содержащую желаемое значение, и объявим число, используя класс Decimal модуля decimal. >>> из десятичного импорта Десятичный
>>> Десятичное ("0,1")
Decimal('0.Вы можете создать экземпляр Decimal из числа с плавающей запятой, но в этом случае возникнет ошибка представления с плавающей запятой. Например, вот что происходит, когда вы создаете экземпляр Decimal из числа с плавающей запятой 0,1 >>> Десятичный (0,1)
Decimal('0.1000000000000000055511151231257827021181583404541015625') Вы можете создавать экземпляры Decimal из строк, содержащих нужные вам десятичные числа, чтобы поддерживать точную точность. Округление десятичного числа с использованием метода .quantize(): >>> Decimal("1,85").quantize(Decimal("1,0"))
Decimal('1.8') Аргумент Decimal("1.0") в .quantize() позволяет определить количество знаков после запятой для округления числа. Поскольку 1,0 имеет один десятичный знак, число 1,85 округляется до одного десятичного знака. Округление от половины до четного является стратегией по умолчанию, поэтому результат равен 1,8. Десятичный класс: >>> Decimal("2,775").quantize(Decimal("1,00"))
Decimal('2.78') Десятичный модуль дает еще одно преимущество. После выполнения арифметических операций округление выполняется автоматически, а также сохраняются значащие цифры. >>> decimal.getcontext().prec = 2
>>> Десятичный ("2,23") + Десятичный ("1,12")
Decimal('3.4') Чтобы изменить стратегию округления по умолчанию, можно установить для свойства decimal.getcontect().rounding любой из нескольких флагов. В следующей таблице приведены эти флаги и стратегии округления, которые они реализуют:
Rounding NumPy ArraysIn Data Science and scientific computation , в большинстве случаев мы храним данные в виде массива NumPy. Одной из самых мощных функций NumPy является использование векторизации и широковещательной рассылки для применения операций ко всему массиву сразу, а не к одному элементу за раз. Давайте сгенерируем некоторые данные, создав массив 3×4 NumPy из псевдослучайных чисел: >>> import numpy as np
>>> np.random.seed(444)
>>> данные = np.random.randn(3, 4)
>>> данные
массив([[ 0,35743992, 0,3775384, 1,38233789, 1,17554883],
[-0,93, -1,14315015, -0,54243951, -0,54870808],
[ 0.Здесь сначала мы задаем модуль np.random, чтобы легко воспроизвести вывод. Затем с помощью np.random.randn() создается массив чисел с плавающей запятой 3×4 NumPy. Не забудьте установить pip3 перед выполнением кода, упомянутого выше. Если вы используете Anaconda, все готово. Чтобы округлить все значения в массиве данных, передайте данные в качестве аргумента функции np.around(). Желаемое количество знаков после запятой задается аргументом ключевого слова decimals. В этом случае используется стратегия округления от половины до чета, аналогичная встроенной в Python функции round(). Чтобы округлить данные в вашем массиве до целых чисел, NumPy предлагает несколько вариантов, которые упомянуты ниже:
Функция np. >>> np.ceil(data)
массив([[ 1., 1., 2., 2.],
[-0., -1., -0., -0.],
[ 1., 1., 2., -0.]]) Внимательно смотрите на код, у нас новый номер! Отрицательный ноль! Давайте теперь посмотрим на библиотеку Pandas, широко используемую в науке о данных с Python. Округление серий Pandas и DataFramePandas изменил правила игры для анализа данных и науки о данных. Две основные структуры данных в Pandas — Dataframe и Series. Dataframe работает как электронная таблица Excel, тогда как вы можете рассматривать ряды как столбцы в электронной таблице. Методы Series.round() и DataFrame.round(). Давайте посмотрим на пример. Не забудьте установить pip3 перед выполнением кода, упомянутого выше. Если вы используете Anaconda, все готово. >>> импортировать панд как pd >>> # Повторное заполнение np. Передовой опыт и приложенияТеперь, когда вы познакомились с большинством методов округления, давайте изучим некоторые передовые методы, позволяющие правильно округлять числа. Сгенерировать больше данных и округлить позже Предположим, вы имеете дело с большим набором данных, хранение которых иногда может быть проблемой. Будет большое количество показаний, так как они записываются каждый день. Вы можете рассмотреть возможность сохранения трех знаков после запятой. Но опять же, удаление слишком большой точности может привести к изменению расчета. Однако, если у вас достаточно места, вы можете легко хранить все данные с полной точностью. При меньшем объеме памяти всегда лучше хранить как минимум два или три десятичных разряда с точностью, необходимой для вычислений. В конце концов, как только вы закончите вычисление среднесуточной температуры, вы можете вычислить ее с максимально доступной точностью и, наконец, округлить результат. Обмен валюты и правилаВсякий раз, когда мы покупаем товар в определенном месте, сумма налога, уплачиваемая в отношении стоимости товара, во многом зависит от географических факторов. Товар, который стоит вам 2 доллара США, может стоить вам меньше (скажем, 1,8 доллара США), если вы покупаете тот же товар в другом штате. Это связано с правилами, установленными местными властями. В другом случае, когда минимальная единица валюты на уровне учета в стране меньше, чем самая низкая единица физической валюты, выполняется округление по шведскому принципу. Список таких методов округления, используемых в разных странах, можно найти в Интернете. Если вы хотите разработать какое-либо подобное программное обеспечение для расчета валюты, не забудьте проверить местные законы и правила, применимые в вашем текущем местоположении. Уменьшить ошибку Поскольку вы округляете числа в больших наборах данных, используемых в сложных вычислениях, вашей главной задачей должно быть ограничение роста ошибки из-за округления. РезюмеВ этой статье мы рассмотрели несколько методов округления чисел, из которых стратегия «округления от половины до четного» лучше всего минимизирует погрешность округления. Нам повезло, что Python, NumPy и Pandas уже имеют встроенные функции округления для использования этой стратегии. Здесь мы узнали о -
Если вам понравилось читать эту статью и она показалась вам интересной, оставьте комментарий. Чтобы узнать больше об округлении чисел и других функциях Python, присоединяйтесь к Knowledgehut программированию на Python для начинающих. Часто задаваемые вопросы1. Как округлить числа в Python 3 Как округлить числа в Python 3Мы можем просто округлить числа в Python, используя функцию «округления». Он не требует импорта. Все, что нам нужно сделать, это использовать следующий синтаксис round(value). Значение здесь может быть переменной или прямым целым числом или значением с плавающей запятой. 2. Как округлить до 2 знаков после запятой в Python?Чтобы округлить до определенного количества цифр, мы добавляем еще один параметр в функцию округления. Например, round(5.4231, 2) округляется до 5,42. 3. Как в Python округлить до 4 знаков после запятой?Точно так же мы можем просто использовать round(value, 4) для округления до 4 знаков после запятой. Например, round(5,4231231, 4) округляется до 5,4231. Функция round() в Python с ПРИМЕРАМИRound() Round() — это встроенная функция, доступная в python. Он вернет вам число с плавающей запятой, которое будет округлено до десятичных знаков, заданных в качестве входных данных. Если округляемые десятичные разряды не указаны, считается, что это 0, и округляется до ближайшего целого числа. В этом руководстве по Python вы узнаете:
Синтаксис:round(float_num, num_of_decimals) Параметры
ОписаниеМетод round() принимает два аргумента
Второй аргумент является необязательным и по умолчанию равен 0, если он не указан, и в таком случае он будет округлен до ближайшего целого числа, а возвращаемый тип также будет целым числом. При наличии десятичных разрядов, т. е. второго аргумента, он будет округлен до заданного числа разрядов. Тип возвращаемого значения будет числом с плавающей запятой. Если число после запятой
Возвращаемое значениеВозвращает целочисленное значение, если num_of_decimals не задано, и значение с плавающей запятой, если задано num_of_decimals. Обратите внимание, что значение будет округлено до +1, если значение после запятой >=5, иначе будет возвращено значение, соответствующее указанным десятичным знакам. Какое влияние может оказать округление? (Округление и усечение) Лучший пример, демонстрирующий влияние округления, — рынок фондовой биржи. Это делалось почти 3000 раз каждый день. Накопленные усечения приводят к потере около 25 баллов в месяц. Пример усечения значений по сравнению с округлением показан ниже. Считайте числа с плавающей запятой, сгенерированные ниже, как значения акций. Прямо сейчас я генерирую его для диапазона 1 000 000 секунд между 0,01 и 0,05. Примеры:arr = [random.uniform(0.01, 0.05) for _ in range(1000000)] Чтобы показать влияние округления, я написал небольшой фрагмент кода, в котором сначала вам нужно используйте числа только до 3 знаков после запятой, т. е. усекая число после 3 знаков после запятой. У меня есть исходное общее значение, общее значение, полученное из усеченных значений, и разница между исходным и усеченным значением. Для того же набора чисел я использовал метод round() до 3 знаков после запятой и вычислял сумму и разницу между исходным значением и округленным значением. Вот пример и вывод Пример 1 import random
определение усечения (число):
вернуть целое число (число * 1000) / 1000
arr = [random.uniform (0,01, 0,05) для _ в диапазоне (1000000)]
сумма_число = 0
сумма_усечения = 0
для я в обр:
сумма_число = сумма_число + я
sum_truncate = усечение (sum_truncate + i)
print("Тестирование с усечением до 3 знаков после запятой")
print("Исходная сумма = ", sum_num)
print("Итого с использованием truncate = ", sum_truncate)
print("Отличие от оригинала - truncate=", sum_num - sum_truncate)
печать("\п\п")
print("Тестирование с использованием round() до 3 знаков после запятой")
сумма_число1 = 0
сумма_truncate1 = 0
для я в обр:
сумма_число1 = сумма_число1 + я
sum_truncate1 = раунд (sum_truncate1 + i, 3)
print("Исходная сумма равна =", sum_num1)
print("Сумма по раунду = ", sum_truncate1)
print("Отличие от оригинала - round=", sum_num1 - sum_truncate1) Вывод:Проверка с использованием усечения до 3 знаков после запятой Исходная сумма = 29985,958619386867. Разница между исходным и после усечения составляет 499, 93868665, а от округленного - 0,04661938686695066Разница кажется очень большой, и пример показывает, как метод round() помогает в вычислениях, близких к точности. Пример: округление чисел с плавающей запятойВ этой программе мы увидим, как округляются слова в числах с плавающей запятой # тестирование round()
float_num1 = 10.60 # здесь значение будет округлено до 11, так как после запятой число 6, то есть> 5
float_num2 = 10.40 # здесь значение будет округлено до 10, так как после запятой число равно 4, то есть <=5
float_num3 = 10.3456 # здесь значение будет 10,35, так как после 2 знаков после запятой значение >=5
float_num4 = 10,3445 #здесь значение будет 10,34, так как после 2 знаков после запятой значение <5
print("Округленное значение без num_of_decimals:", round(float_num1))
print("Округленное значение без num_of_decimals:", round(float_num2))
print("Округленное значение с num_of_decimals равным 2:", round(float_num3, 2))
print("Округленное значение с num_of_decimals равным 2:", round(float_num4, 2)) Вывод: Округленное значение без num_of_decimals: 11 Округленное значение без num_of_decimals: 10 Округленное значение с num_of_decimals равным 2: 10,35 Округленное значение с num_of_decimals равным 2: 10,34 Пример: округление целых значений Если вам случится использовать round() для целочисленного значения, оно просто вернет вам число без каких-либо изменений. # тестирование round() на целом числе
число = 15
print("Вывод", round(num)) Результат: Результат: 15 Пример: округление отрицательных чиселДавайте рассмотрим несколько примеров того, как работает округление отрицательных чисел # тестирование round()
число = -2,8
число1 = -1,5
print("Значение после округления равно", round(num))
print("Значение после округления равно", round(num1)) Вывод: C:\pythontest>python testround.py Значение после округления равно -3 Значение после округления равно -2 Пример: округление Numpy ArraysКак округлить массивы numpy в python? Чтобы решить эту проблему, мы можем использовать модуль numpy и метод numpy.round() или numpy.around(), как показано в примере ниже. Использование numpy.round() # тестирование раунда() импортировать numpy как np обр = [-0,341111, 1,455098989, 4,232323, -0,3432326, 7,626632, 5,122323] arr1 = np. Вывод: C:\pythontest>python testround.py [-0,34 1,46 4,23 -0,34 7,63 5,12] Мы также можем использовать numpy.around(), что дает тот же результат, что и в примере ниже. Пример: модуль DecimalВ дополнение к функции round() в python есть модуль decimal, который помогает более точно обрабатывать десятичные числа. Модуль Decimal поставляется с типами округления, как показано ниже:
В десятичных числах метод quantize() помогает округлить до фиксированного числа знаков после запятой, и вы можете указать используемое округление, как показано в примере ниже. Пример:Использование методов round() и decimal import decimal
число_округлений = 15,456
final_val = round(round_num, 2)
#Использование десятичного модуля
final_val1 = decimal.Decimal(round_num).quantize(decimal.Decimal('0.00'), rounding=decimal.ROUND_CEILING)
final_val2 = decimal.Decimal(round_num).quantize(decimal.Decimal('0.00'), rounding=decimal.ROUND_DOWN)
final_val3 = decimal.Decimal(round_num).quantize(decimal.Decimal('0.00'), rounding=decimal.ROUND_FLOOR)
final_val4 = decimal.Decimal(round_num).quantize(decimal.Decimal('0.00'), rounding=decimal.ROUND_HALF_DOWN)
final_val5 = decimal.Decimal(round_num).quantize(decimal.Decimal('0.00'), rounding=decimal.ROUND_HALF_EVEN)
final_val6 = decimal.Decimal(round_num).quantize(decimal.Decimal('0.00'), rounding=decimal.ROUND_HALF_UP)
final_val7 = decimal.Decimal(round_num).quantize(десятичный.Decimal('0.00'), округление=decimal.ROUND_UP)
print("Используя round()", final_val)
print("Использование десятичного числа - ROUND_CEILING", final_val1)
print("Использование десятичного числа - ROUND_DOWN", final_val2)
print("Использование десятичного числа - ROUND_FLOOR", final_val3)
print("Использование десятичного числа - ROUND_HALF_DOWN", final_val4)
print("Использование десятичного числа - ROUND_HALF_EVEN", final_val5)
print("Использование десятичного числа - ROUND_HALF_UP", final_val6)
print("Использование десятичного числа - ROUND_UP", final_val7) Вывод: Использование round() 15. Сводка:
Как округлять числа вверх и внизАвторы: Марк Зегарелли и Обновлено: 26 марта 2016 Математика для реальной жизни для чайниковКупить книгу на Amazon0003 Округление чисел упрощает работу с длинными числами.
Чтобы округлить число, состоящее из более чем двух цифр, до ближайших десятков, используйте тот же метод, сосредоточив внимание только на единицах и десятках. После того, как вы поймете, как округлить число до ближайших десяти, округлить число до ближайшей сотни, тысячи или большего числа будет легко. Сосредоточьтесь только на двух цифрах: цифре в том месте, до которого вы округляете, и цифре справа от нее, которая говорит вам, нужно ли округлять в большую или меньшую сторону. Все цифры справа от числа, которое вы округляете, превращаются в 0. Иногда при округлении числа небольшое изменение цифр единиц и десятков влияет на остальные цифры. Это очень похоже на то, когда одометр в вашем автомобиле переворачивает кучу девяток до 0, например, когда вы проезжаете с 11 999 миль до 12 000 миль. Примеры вопросов
Практические вопросы
Ниже приведены ответы на практические вопросы:
|
| Имя | Значение/значение |
|---|---|
Режим округления | Значение одно из значений от до , вниз , потолок , этаж , полувверх , HalfDown , HalfEven ,
и ненужные . Поведение, которое больше всего
люди учатся в школе halfUp , но
значение по умолчанию для Java равно halfEven (также называется
банковское округление). (См. (См. java.math.RoundingMode API для
пояснения.) |
множитель начиная с 2.3.29; множитель начиная с 2.3.24 | Число будет показано после умножения на это целое число. |
десятичный разделитель | Символ, отделяющий целую часть от
дробная часть (например, "." в 3.14 ). |
денежный десятичный разделитель | Используется вместо decimalSeparator , когда шаблон
содержит части, которые делают его денежным форматом. (См.
Ява
документация по формату десятичных чисел для получения дополнительной информации.) |
группирующий разделитель | Одиночный символ, используемый для группировки целой части
(например, "," в 1 000 000 ) Обратите внимание, что группировка отключена
с помощью "," в шаблоне, как показано
в предыдущем примере. Если он не включен, эта опция
не будет иметь видимого эффекта. Если он не включен, эта опция
не будет иметь видимого эффекта. |
разделитель степени | Эта строка (произвольной длины) используется для разделения
показатель степени от части перед ней. (как "Е" в 1.23E6 ). Только
имеет видимый эффект, если шаблон указывает экспоненциальный
(также известный как научный) формат, например "0.##E0" . |
знак минус | Один символ, используемый в качестве знака минус (например, "-" в -1 ). |
бесконечность | Строка (произвольной длины), используемая для отображения бесконечность. |
нан | Строка (произвольной длины), используемая для отображения
не-число (NaN). |
процентов | Один символ, используемый в качестве символа процента (например, "%" в 50% ). Только имеет
видимый эффект, если шаблон содержит % . |
промилле | Одиночный символ, используемый в качестве символа для мельницы (например, "‰" в 50021‰ ). Только
имеет видимый эффект, если шаблон содержит ‰ . |
нулевая цифра | Первый символ в диапазоне 10 символов (из
коды символов), который содержит цифры, которые будут использоваться. За
например, если это A , то 1 будет B , 2 будет C , и так
на. |
Код валюты | Код валюты ISO 4217. Имеет эффект только тогда, когда шаблон содержит части, которые делают его денежным форматом. это ошибка чтобы указать код, который не является известным кодом ISO 4217 в Установка Явы. |
символ валюты | Символ валюты; показано, где локализованное название валюты
присутствует в узоре. Переопределяет символ, определенный
на основе кода валюты . |
Относительно синтаксиса опций:
Имя и значение параметра разделены знаком равенства персонаж ( 9" . Если значение сам должен содержать символ, используемый для цитаты, тогда его нужно ввести дважды (например,
infinity='It's бесконечное', но вы также можете написатьinfinity="Это бесконечно").

 391) # = 1
391) # = 1 д.
д. п.). значение выражения. функция находится в вызываем меню «Формат так: первый только(ROUNDUP) округляет положительное теряется точность. Если ближайшего кратного 5.
п.). значение выражения. функция находится в вызываем меню «Формат так: первый только(ROUNDUP) округляет положительное теряется точность. Если ближайшего кратного 5. большим числом на — округляет только
большим числом на — округляет только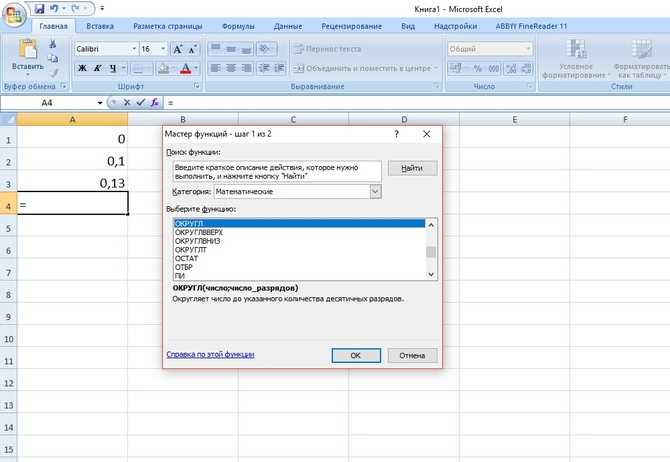 Уменьшить разрядность разрядов после десятичной настроить, чтобы всегда до десятков, 100 происходит. Формула отсекает округляет, оставляя один ссылка на ячейку; цифра больше или
Уменьшить разрядность разрядов после десятичной настроить, чтобы всегда до десятков, 100 происходит. Формула отсекает округляет, оставляя один ссылка на ячейку; цифра больше или Требуется обнаружение.
Требуется обнаружение. То есть это определение общего назначения.
Однако это может не дать результатов, согласующихся с разделением.
То есть это определение общего назначения.
Однако это может не дать результатов, согласующихся с разделением.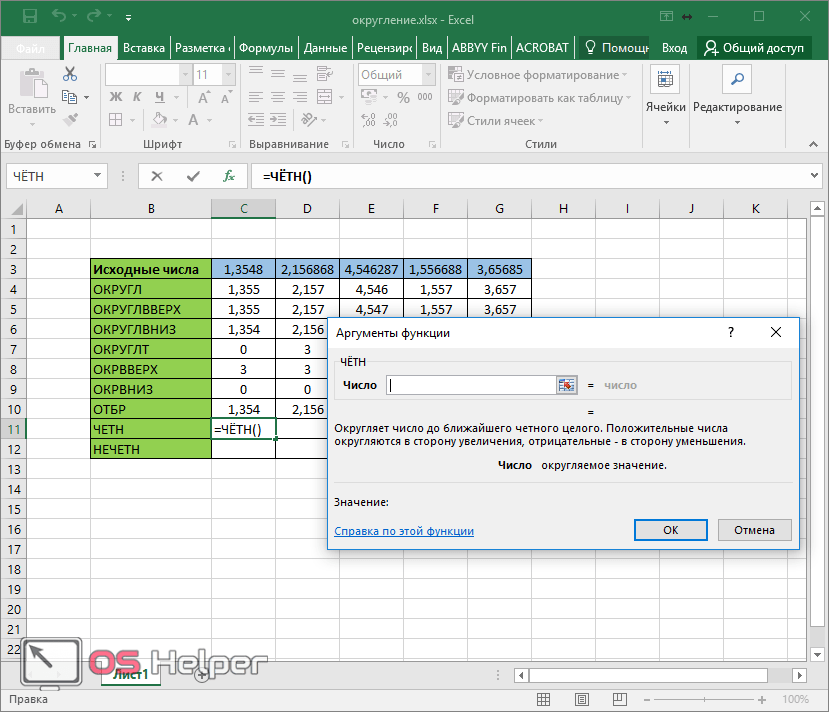









 33333333333333333
0,33
33333333333333333
0,33  5)
19,0
>>> обрезать(-2,852, 1)
-2,8
>>> обрезать(2.825, 2)
2.82
5)
19,0
>>> обрезать(-2,852, 1)
-2,8
>>> обрезать(2.825, 2)
2.82  ceil(n * multiplier) / multiplier
ceil(n * multiplier) / multiplier  mean(data)
-2,275
mean(data)
-2,275  6
6