Округление в геодезии | ГЕОДЕЗИСТ
GeoDemon сказал(а):
Давайте посмотрим, как может подвести «школьное» округление. Отвлечемся от геодезии и обратимся к глобальному потеплению.stout сказал(а):
Видимо я учился в другой стране или другом измерении. Только что опросил всех своих сотрудников, оказалось что они тоже в моем измерении учились)))…14 издание справочника Выгодского вышло в 1962г и ему уже было на тот момент 21 год.
Нажмите, чтобы раскрыть…
Раньше ведь не как сейчас, все по одной методике учились. Или я не прав?Нажмите, чтобы раскрыть…
Откроем прогноз погоды, например в Яндексе, за 10 дней (для корректности — можно по нескольким городам), и высчитаем сначала среднюю суточную температуру, а затем, из суточных — среднюю за декаду. Округляем до целых (с такой точностью нам даны значения)
Можно заметить, что если обе температуры четные либо нечетные, то и среднесуточная будет либо четной, либо нечетной, в общем — 50\50. А если одна (ночная, например) четная, а другая (дневная) — нечетная, то округленное среднее будет всегда четным, причем при «школьном» округлении — 100% в большую сторону, а «по Гауссу» — 50\50 в большую либо меньшую. Таким образом, при «школьном» округлении возникает систематическая ошибка, направленная на увеличение абсолютных значений. Понятно, округляем всегда в большую сторону, вот и ползет величина все больше и больше.
И среднедекадная из «школьных» значений будет несколько выше средней из всех срочных температур, то есть неправильной. А среднедекадная из величин «до ближайшего четного» — вполне совпадет.
И в кадастровых делах округление по Гауссу будет оправданным. из тех же соображений. Ведь мы берем вычисленные координаты углов с заданной точностью, как данность, отбрасывая посчитанные программой тысячные и десятитысячные доли. И по этим округленным координатам уже вычисляем площадь и длины сторон. Другое дело, что «точное значение длины стороны участка» — в значительной степени величина умозрительная.
Так что разные способы округления вполне законны. Надо только знать, для решения каких задач какой применяется.
И я не верю, чтобы в вузах и техникумах этому не учили. Просто, такую скучную и абстрактную материю, как правила производства вычислений никто не запоминает. Мы же на счетах считать не будем, нам электронный друг подсчитает, так что зачем мозги фигней забивать.
Я и сам, будучи молодым специалистом, как-т о рьяно доказывал, что округлять надо в большую сторону, пока меня не ткнули носом в мой же институтский учебник геодезии, лежащий у меня на столе.
geodesist.ru
7. Правила округления
В результате любых измерений, прямых или косвенных, получаются приближенные числа. Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой слева. Значащие цифры, составляющие число могут быть верными, сомнительными и неверными. Цифра называется верной, если погрешность числа меньше половины единицы разряда этой цифры. Цифры, стоящие левее верной цифры, также будут верными. Если разряд цифры совпадает с разрядом первой значащей цифры погрешности, то цифра называется сомнительной. Цифры, стоящие справа от сомнительной будут неверными.
При выполнении расчетов нужно придерживаться следующих правил:
1) В лабораторных работах исходными данными для вычислений служат результаты прямых измерений, последняя цифра которых обычно сомнительная.
2) Физические константы или табличные данные содержат только верные числа, а погрешность табличных данных, если она не указана, считают равной половине разряда последней значащей цифры.
3) При округлении, если цифра, расположенная за оставляемой, меньше 5, то ее просто отбрасывают, иначе оставляемую цифру увеличивают на единицу. Если отбрасываемая цифра равна 5, а следующие за ней отброшенные цифры ненулевые, то оставляемую цифру увеличивают на единицу. Если же отбрасываемая цифра равна 5, а следующие за ней цифры среди отброшенных равны нулю, то наименьшая ошибка достигается при округлении по правилу Гаусса до ближайшего четного числа. Пример: 2,54≈2,5; 5,6500≈5,6; 8,751≈8,8.
4) При сложении и вычитании результат округляется до наименьшего разряда с наименьшим количеством значащих цифр. Пример: 2,17+3,3=5,5.
5)
При умножении и делении в результате
сохраняют столько же значащих цифр,
сколько их имеется в числе с наименьшим
числом значащих цифр. Исключение
составляет случай, когда один из
сомножителей начинается с 1, а второй,
содержащий наименьшее количество
значащих цифр, – с другой цифры. Тогда
сохраняют на одну цифру больше, чем в
числе с наименьшим количеством значащих
цифр. Пример: 59
0,0273=1,6.
6)
При возведении в любую степень (в том
числе и дробную) нужно сохранять столько
значащих цифр, сколько их содержится в
возводимом числе. Пример: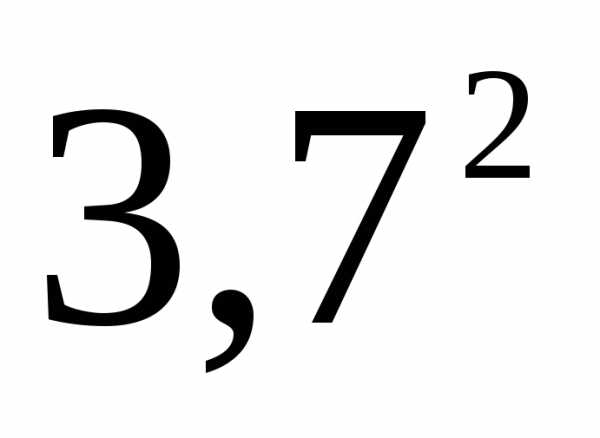 
7) При вычислении промежуточных результатов следует сохранять одной цифрой больше, чем этого требуют сформулированные выше правила. В конечном результате запасная цифра отбрасывается.
8) Если данные имеют излишние младшие десятичные разряды (при сложении и вычитании) или больше значащих цифр, чем другие (при умножении, делении, возведении в степень), то их предварительно нужно округлить, сохраняя одну запасную цифру.
9) Нахождение числа из таблиц считается за отдельное действие, и если оно является промежуточным, то берется запасная цифра.
При окончательной записи результата необходимо опираться на следующие правила:
1.
Выполнить предварительную запись
окончательного результата измерения
в виде (17)
и
вынести за общую скобку одинаковые
порядки среднего и погрешности, т.е.
множитель вида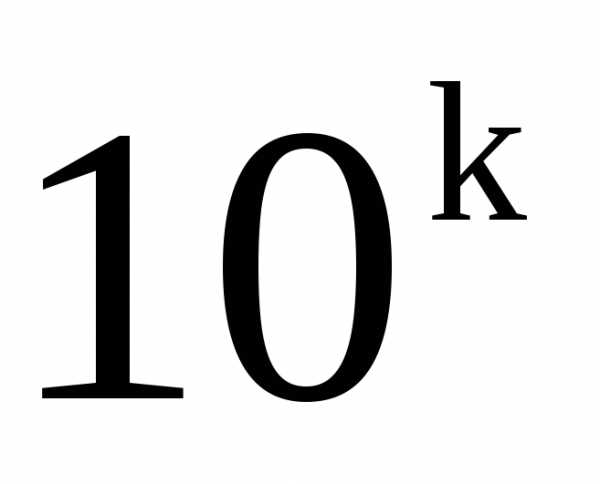 
,
где k – целое число. Числа в скобках
переписать в десятичном виде с
использованием запятой, убрав тем самым
оставшиеся порядковые множители.
2. Округлить в скобках число, соответствующее погрешности: до двух значащих цифр, если первая из них – 1 или 2, и до одной значащей цифры — в противном случае.
3. Округлить в скобках числовое значение среднего арифметического до цифры того же порядка, что и значение погрешности после ее округления.
4. Окончательно записать с учетом выполненных округлений. Общий порядок и единицы измерения величины приводят за скобками – получена стандартная форма записи, которая содержит только достоверные, т.е. надежно измеренные, цифры.
Например:
пусть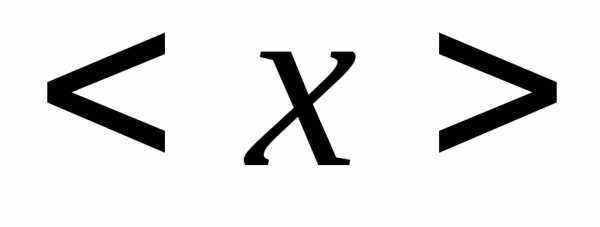 
=73,647мм,
а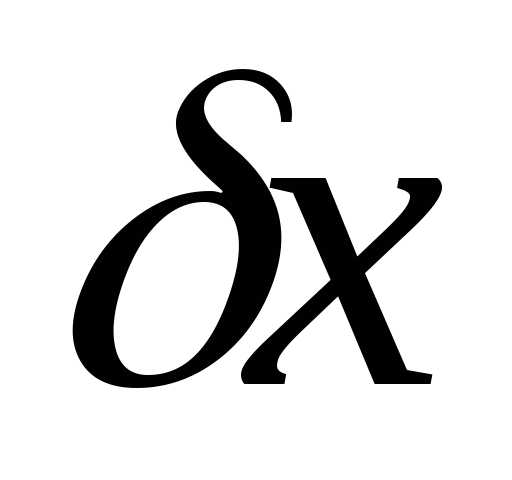
=0,039мм.
Округляем до первой значащей цифры и
переводим в метры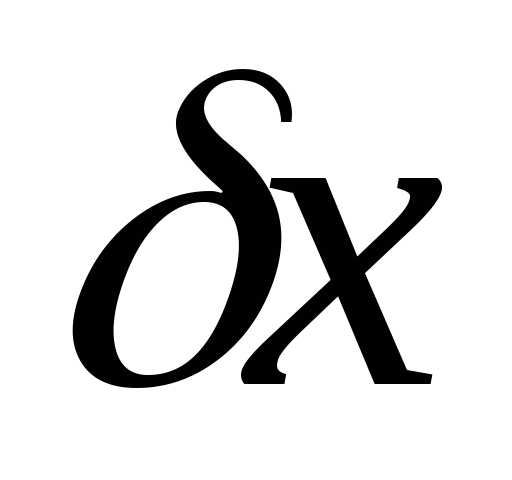
=0,04мм=0,04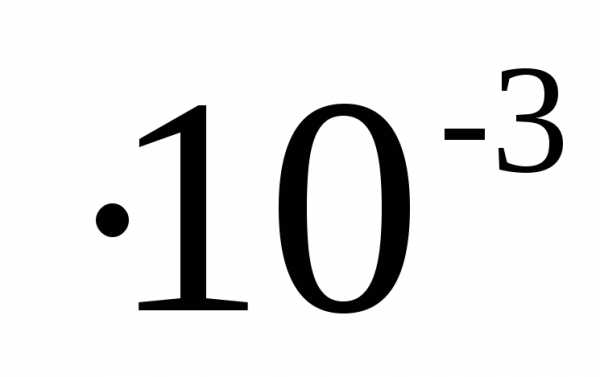
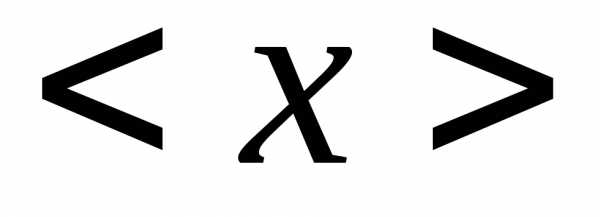округляем до цифры того же разряда что
и погрешность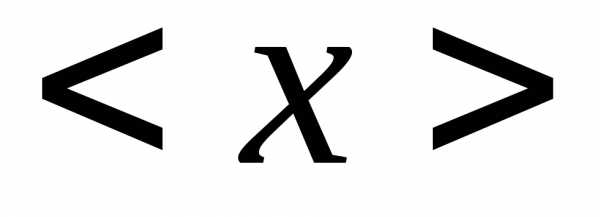
=73,65мм=73,65
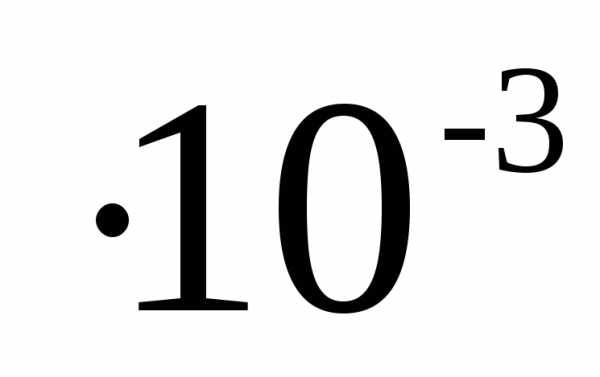м.
Тогда окончательно получим: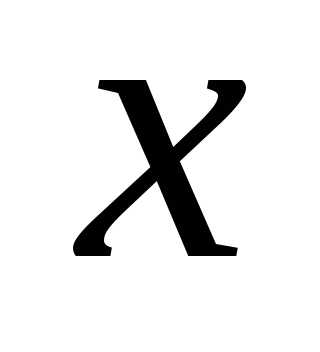 
=(73,65
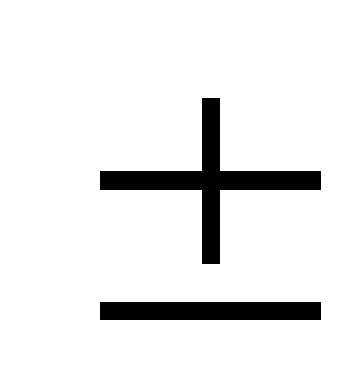0,04)
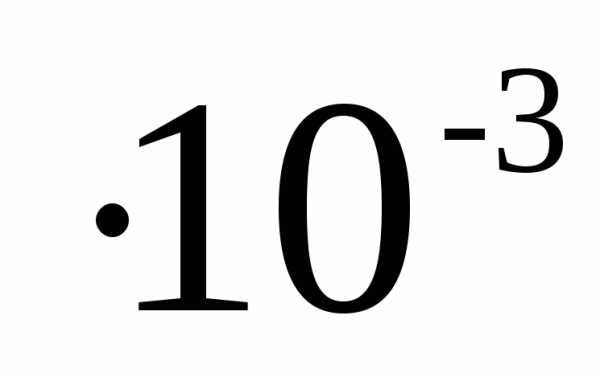м.
studfiles.net
Округление чисел | МобиСтрой
Чтобы не оперировать с лишними цифрами, затрудняющими вычисления, но не характеризующими требуемую точность, отдельные числовые значения исходных данных следует округлять. Правила округления одинаковы для целых и дробных чисел.
Округление числа представляет собой отбрасывание цифр справа до определенного разряда с возможным изменением цифры этого разряда.
Пример. Округление числа 132,584 до сотых долей единицы (до второго разряда десятичных знаков) даст результат 132,58. Округление этого же числа до десятых долей единицы (до первого разряда десятичных знаков) даст результат 132,6; округление данного числа до целого (до разряда единиц) даст результат 133; округление до разряда десятков даст результат 13-Ю или 1,3-10
При геодезических вычислениях применяют следующие правила округления:
Если первая из отбрасываемых цифр (считая слева направо) меньше 5, то последняя сохраняемая цифра не меняется.
Примеры.
Округление числа 12,23 до первого десятичного знака даст результат 12,2.
Округление числа 0,02499 до второго десятичного знака даст результат 0,02.
Округление числа 8449 до разряда сотен даст результат 84« 102.
Округление числа 12 456 до разряда тысяч даст результат 12-Ю3.
Если первая из отбрасываемых цифр (считая слева направо) больше 5, то последнюю сохраняемую цифру увеличивают на единицу.
Примеры.
Округление числа 24,6 до целых единиц даст результат 25. Округление числа 0,2361 до сотых долей (до второго разряда десятичных знаков) даст результат 0,24.
Округление числа 1483 до целых сотен даст результат 15-102.
Когда отбрасываемая часть числа ровно 5, то последнюю сохраняемую цифру увеличивают на единицу, если она нечетная, и оставляют без изменения, если она четная (т. е. цифра разряда, до которого округляют число, в данном случае всегда должна быть четной).
Примеры.
Округление числа 4,55 до десятых долей даст результат 4,6.
Округление числа 122,5 до целых единиц даст результат 122.
Округление числа 0,0695 до тысячных долей единицы (до третьего разряда десятичных знаков) даст результат 0,070 или 70-10-3.
Особо следует выделить положение, когда отбрасываемая цифра 5 образовалась в результате предварительного округления цифр в последующих за ней разрядах. В этом случае необходимо действовать согласно следующим правилам:
если отбрасываемая цифра 5 получилась в результате предыдущего округления в большую сторону, то последняя цифра разряда, до которого округляют число, сохраняется; например, округление до первого десятичного знака числа 0,15, полученного после округления до двух десятичных знаков числа 0,1499, даст^ результат 0,1;
если отбрасываемая цифра 5 получилась в результате предыдущего округления в меньшую сторону, то последнюю цифру разряда, до которого округляют число, увеличивают на единицу; например, округление до одного десятичного знака числа 0,25, полученного в результате предыдущего округления числа 0,2501, даст результат 0,3.
В связи с этим округление приближенных чисел необходимо выполнять сразу до требуемого разряда, а не по этапам. Так, например, округление числа 565,46 до разряда целых единиц непосредственно дает результат 565 (правильный). Округление по этапам могло бы привести к ошибке, а именно: 1-й этап округления числа 565,46 до десятых долей дал бы результат 565,5; 2-й этап округления числа 565,5 до целых единиц дал бы результат 566 (неправильный).
www.mobigeo.ru
Правило округления чисел
В приближенных вычислениях зачастую приходится округлять некоторые числа, как приближенные, так и точные, то есть убирать одну или несколько конечных цифр. Для того чтобы обеспечить наибольшую близость отдельного округленного числа к округляемому числу, следует соблюдать некоторые правила.
Первое правилоЕсли первая из отделяемых цифр больше, чем число 5, то последняя из оставляемых цифр усиливается, иначе говоря, увеличивается на единицу. Усиление так же предполагается и тогда, когда первая из убираемых цифр равна 5, а за ней имеется одна или некоторое количество значащих цифр.
Число 25,863 округлённо записывается как – 25,9.
В данном случае цифра 8 будет усилена до 9, так как первая отсекаемая цифра 6, больше чем 5.
Число 45,254 округлённо записывается как – 45,3.
Здесь цифра 2 будет усилена до 3, так как первая отсекаемая цифра равна 5, а за ней следует значащая цифра 1.
В случае если первая из отсекаемых цифр меньше чем 5, то усиления не производится.
Число 46,48 округлённо записывается как – 46.
Число 46 наиболее близко к округляемому числу, чем 47.
Если отсекается цифра 5, а за ней не имеется значащих цифр, то округление выполняется на ближайшее четное число, другими словами, последняя оставляемая цифра остаётся неизменной, если она четная, и усиливается в случае, если она нечетная.
Число 0,0465 округлённо записывается как – 0,046.
В данном случае усиления не делается, так как последняя оставляемая цифра 6 является чётной.
Число 0,935 округлённо записывается как – 0,94.
Последняя оставляемая цифра 3 усиливается, так как она является нечётной.
Примеры округления чисел:
6,527 → 6,5 |
2,195 → 2,2 |
0,950 → 1,0 |
0,850 → 0,8 |
0,456 → 0,5 |
1,450 → 1,4 |
4,851 → 4,9 |
0,05 → 0,0 |
simple-math.ru
Правила округления Википедия
Округление — замена числа на его приближённое значение (с определённой точностью), записанное с меньшим количеством значащих цифр. Модуль разности между заменяемым и заменяющим числом называется ошибкой округления.
Округление применяется для представления значений и результатов вычислений с тем количеством знаков, которое соответствует реальной точности измерений или вычислений, либо той точности, которая требуется в конкретном приложении. Округление в ручных расчётах также может использоваться для упрощения вычислений в тех случаях, когда погрешность, вносимая за счёт ошибки округления, не выходит за границы допустимой погрешности расчёта.
Общий порядок округления и терминология[ | ]
- Округление числа, записанного в позиционной системе счисления с M знаками дробной части, может производиться «до K-го знака после запятой», где K ≤ M. При таком округлении в записи числа отбрасываются справа (M-K) значащих цифр, а K-я цифра после запятой может измениться (см. #Методы). Применяется также терминология с указанием единицы наименьшей десятичной доли, сохраняющейся у округлённого числа, то есть «округление до десятых», «…до сотых», «…до тысячных» и т. д. (соответствует округлению до одного, двух, трёх и так далее знаков после запятой). Частный случай, когда K=0, называется «округлением до целого».
- Когда при округлении отбрасываются значащие цифры целой части числа, говорят об «округлении до десятков» (сотен, тысяч и так далее), отбрасывая, соответственно, один, два, три и более знака. При таком округлении отбрасываемые цифры целой части числа заменяются на нули.
- Для чисел, представленных в нормализованном виде, говорят об «округлении до K (значащих) цифр». При этом мантисса числа сохраняет K значащих цифр, остальные цифры справа отбрасываются.
Методы[ | ]
В разных сферах могут применяться различные методы округления. Во всех этих методах «лишние» знаки обнуляют (отбрасывают), а предшествующий им знак корректируется по какому-либо правилу.
- Округление к ближайшему целому — наиболее часто используемое округление, при котором число округляется до целого, модуль разности с которым у этого числа минимален. В общем случае, когда число в десятичной системе округляют до N-го знака, правило может быть сформулировано следующим образом:
- если N+1 знак < 5, то N-й знак сохраняют, а N+1 и все последующие обнуляют;
- если N+1 знак ≥ 5, то N-й знак увеличивают на единицу, а N+1 и все последующие обнуляют;
- Например: 11,9 → 12; −0,9 → −1; −1,1 → −1; 2,5 → 3.
- Максимальная дополнительная абсолютная погрешность, вносимая при таком округлении (погрешность округления), составляет ±0,5 последнего сохраняемого разряда.
- Округление к меньшему по модулю (округление к нулю, целое англ. fix, truncate, integer) — самое «простое» округление, поскольку после обнуления «лишних» знаков предшествующий знак сохраняют, то есть технически оно состоит в отбрасывании лишних знаков. Например, 11,9 → 11; −0,9 → 0; −1,1 → −1). При таком округлении может вноситься погрешность в пределах единицы последнего сохраняемого разряда, причём в положительной части числовой оси погрешность всегда отрицательна, а в отрицательной — положительна.
- Округление к большему (округление к +∞, округление вверх, англ. ceiling — досл. «потолок») — если обнуляемые знаки не равны нулю, предшествующий знак увеличивают на единицу, если число положительное, или сохраняют, если число отрицательное. В экономическом жаргоне — округление в пользу продавца, кредитора (лица, получающего деньги). В частности, 2,6 → 3, −2,6 → −2. Погрешность округления — в пределах +1 последнего сохраняемого разряда.
- Округление к меньшему (округление к −∞, округление вниз, англ. floor — досл. «пол») — если обнуляемые знаки не равны нулю, предшествующий зна
ru-wiki.ru
Как округлять числа в большую и меньшую сторону функциями Excel
Округляют числа в Excel несколькими способами. С помощью формата ячеек и с помощью функций. Эти два способа следует различать так: первый только для отображения значений или вывода на печать, а второй способ еще и для вычислений и расчетов.
С помощью функций возможно точное округление, в большую или меньшую сторону, до заданного пользователем разряда. А полученные значения в результате вычислений, можно использовать в других формулах и функциях. В то же время округление с помощью формата ячеек не даст желаемого результата, и результаты вычислений с такими значениями будут ошибочны. Ведь формат ячеек, по сути, значение не меняет, меняется лишь его способ отображения. Чтобы в этом быстро и легко разобраться и не совершать ошибок, приведем несколько примеров.
Как округлить число форматом ячейки
Впишем в ячейку А1 значение 76,575. Щелкнув правой кнопкой мыши, вызываем меню «Формат ячеек». Сделать то же самое можно через инструмент «Число» на главной странице Книги. Или нажать комбинацию горячих клавиш CTRL+1.
Выбираем числовой формат и устанавливаем количество десятичных знаков – 0.
Результат округления:
Назначить количество десятичных знаков можно в «денежном» формате, «финансовом», «процентном».
Как видно, округление происходит по математическим законам. Последняя цифра, которую нужно сохранить, увеличивается на единицу, если за ней следует цифра больше или равная «5».
Особенность данного варианта: чем больше цифр после запятой мы оставим, тем точнее получим результат.
Как правильно округлить число в Excel
С помощью функции ОКРУГЛ() (округляет до необходимого пользователю количества десятичных разрядов). Для вызова «Мастера функций» воспользуемся кнопкой fx. Нужная функция находится в категории «Математические».
Аргументы:
- «Число» — ссылка на ячейку с нужным значением (А1).
- «Число разрядов» — количество знаков после запятой, до которого будет округляться число (0 – чтобы округлить до целого числа, 1 – будет оставлен один знак после запятой, 2 – два и т.д.).
Теперь округлим целое число (не десятичную дробь). Воспользуемся функцией ОКРУГЛ:
- первый аргумент функции – ссылка на ячейку;
- второй аргумент – со знаком «-» (до десятков – «-1», до сотен – «-2», чтобы округлить число до тысяч – «-3» и т.д.).
Как округлить число в Excel до тысяч?
Пример округления числа до тысяч:
Формула: =ОКРУГЛ(A3;-3).
Округлить можно не только число, но и значение выражения.
Допустим, есть данные по цене и количеству товара. Необходимо найти стоимость с точностью до рубля (округлить до целого числа).
Первый аргумент функции – числовое выражение для нахождения стоимости.
Как округлить в большую и меньшую сторону в Excel
Для округления в большую сторону – функция «ОКРУГЛВВЕРХ».
Первый аргумент заполняем по уже знакомому принципу – ссылка на ячейку с данными.
Второй аргумент: «0» — округление десятичной дроби до целой части, «1» — функция округляет, оставляя один знак после запятой, и т.д.
Формула: =ОКРУГЛВВЕРХ(A1;0).
Результат:
Чтобы округлить в меньшую сторону в Excel, применяется функция «ОКРУГЛВНИЗ».
Пример формулы: =ОКРУГЛВНИЗ(A1;1).
Полученный результат:
Формулы «ОКРУГЛВВЕРХ» и «ОКРУГЛВНИЗ» используются для округления значений выражений (произведения, суммы, разности и т.п.).
Как округлить до целого числа в Excel?
Чтобы округлить до целого в большую сторону используем функцию «ОКРУГЛВВЕРХ». Чтобы округлить до целого в меньшую сторону используем функцию «ОКРУГЛВНИЗ». Функция «ОКРУГЛ» и формата ячеек так же позволяют округлить до целого числа, установив количество разрядов – «0» (см.выше).
В программе Excel для округления до целого числа применяется также функция «ОТБР». Она просто отбрасывает знаки после запятой. По сути, округления не происходит. Формула отсекает цифры до назначенного разряда.
Сравните:
Второй аргумент «0» — функция отсекает до целого числа; «1» — до десятой доли; «2» — до сотой доли и т.д.
Специальная функция Excel, которая вернет только целое число, – «ЦЕЛОЕ». Имеет единственный аргумент – «Число». Можно указать числовое значение либо ссылку на ячейку.
Недостаток использования функции «ЦЕЛОЕ» — округляет только в меньшую сторону.
Округлить до целого в Excel можно с помощью функций «ОКРВВЕРХ» и «ОКРВНИЗ». Округление происходит в большую или меньшую сторону до ближайшего целого числа.
Пример использования функций:
Второй аргумент – указание на разряд, до которого должно произойти округление (10 – до десятков, 100 – до сотен и т.д.).
Округление до ближайшего целого четного выполняет функция «ЧЕТН», до ближайшего нечетного – «НЕЧЕТ».
Пример их использования:
Почему Excel округляет большие числа?
Если в ячейки табличного процессора вводятся большие числа (например, 78568435923100756), Excel по умолчанию автоматически округляет их вот так: 7,85684E+16 – это особенность формата ячеек «Общий». Чтобы избежать такого отображения больших чисел нужно изменить формат ячейки с данным большим числом на «Числовой» (самый быстрый способ нажать комбинацию горячих клавиш CTRL+SHIFT+1). Тогда значение ячейки будет отображаться так: 78 568 435 923 100 756,00. При желании количество разрядов можно уменьшить: «Главная»-«Число»-«Уменьшить разрядность».
exceltable.com
Погрешность — округление — Большая Энциклопедия Нефти и Газа, статья, страница 1
Погрешность — округление
Cтраница 1
Погрешность округления может быть еще несколько уменьшена выбором главного элемента по всей матрице. Однако точность при этом возрастает незначительно, а расчет заметно усложняется. [1]
Погрешность округления возникает при усечении разрядной сетки процессора с предварительной поправкой на остаток — путем добавления 1 в старший из отбрасываемых разрядов. [2]
Погрешность округлений в процессе вычислений увеличивается ( накапливается) и может существенно повлиять на точность результатов. Поэтому при определении разрядности ММЭВМ на этапе проектирования в зависимости от требуемой точности вычислений обычно задаются максимальным значением инструментальной погрешности ЭВМ. [3]
Погрешности округления при арифметических вычислениях распределены равномерно. [4]
Погрешности округления при решении по методу итераций сказываются значительно меньше, чем при решении по методу Гаусса. Кроме того, случайные ошибки в процессе итераций самоисправляются на следующем шаге уточнения решений. [6]
Погрешность округления обусловлена тем, что любые вычисления на ЭВМ или ручные расчеты выполняются с ограниченным числом значащих цифр. При выполнении одной арифметической операции с числами погрешность округления лежит в пределах единицы младшего сохраняемого разряда. Так ЭВМ оперирует с числами, содержащими обычно 10 — 12 разрядов, поэтому погрешность единичного округления здесь Д10 — 10 — — 10 — 12 пренебрежимо мала по сравнению с неустранимой погрешностью. При расчетах на ЭВМ могут выполняться миллиарды операций, однако если нет систематических причин для накопления погрешностей округления, то их увеличение происходит не слишком существенно, поскольку при различных операциях погрешности будут иметь разные знаки и компенсировать друг друга. Тем не менее если численный метод таков, что возникают систематические причины накопления погрешностей округления, то очень быстро суммарная погрешность возрастает до катастрофических размеров и сделает невозможным получение достоверного результата. Такие условия возникают, например, при вычитании близких по величине чисел. [7]
Погрешность округления обусловлена ограничениями на представление чисел в используемой ЭВМ, так как для любой из них число значащих цифр, запоминаемых и используемых в вычислениях, ограниченно. [8]
Погрешность округления при отсчете значительно влияет на точность измерения угла теодолитом. С учетом этой погрешности определим среднюю квадратическую погрешность измерения угла теодолитом с металлическим лимбом. [9]
Погрешность округления 3 возникает а связи с неточностью численных значений коэффициентов Лагранжа. [10]
Погрешности округления являются основным источником операционных погрешностей, так как все исходные данные и результаты вычислений округляются в ПМК до г цифр мантиссы и при выполнении нескольких операций погрешности накапливаются вследствие как округления, так и увеличения погрешности результата операций над округленными значениями операндов. [11]
Погрешность округления возникает вследствие того, что в ЭВМ число представляется некоторым количеством значащих цифр. Если исходные данные или результат вычислений имеют больше цифр, то они округляются. Погрешность округления должна быть оценена. [12]
Погрешность округления может быть еще несколько уменьшена выбором главного элемента по всей матрице. Однако точность при этом возрастает незначительно, а расчет заметно усложняется. [13]
Погрешности округления в методе итераций сказываются значительно меньше, чем в методе Гаусса. [14]
Погрешность округления не превосходит пяти единиц первого отброшенного разряда. [15]
Страницы: 1 2 3 4
www.ngpedia.ru