Как найти в Python остаток от деления?
Python — простой и современный язык для написания кода. В нем есть мощные библиотеки, которые могут оценивать любое выражение. Python — главный конкурент Matlab и Octave. Запуская Python в интерактивном режиме, пользователь может легко найти оставшуюся часть раздела. Но это еще не все! Python может быть мощным калькулятором.
Понятие оператора
Чтобы легко найти остальную часть деления в Python, вам нужно понять некоторые определения. Оператор: знак или строка, позволяющая выполнять математические, побитовые, логические и другие вычисления. Выражения или числа, введенные пользователем для поиска остатка, комбинации или сравнения в Python 3, называются операндами.
Подразделяются на следующие типы операторов:
- операторы присваивания;
- арифметика;
- логические;
- сравнения;
- членство;
- личность.
- мало по малу;
Проще говоря, в примере «15-5» оператором является знак «-», операнды — 15 и 5. Это арифметическая операция с целыми числами. Если мы примем во внимание выражение «Истина и Истина», то здесь будет оператор «И», а операнды — «Истина» и «Истина». Этот пример можно отнести к логическому типу.
Это арифметическая операция с целыми числами. Если мы примем во внимание выражение «Истина и Истина», то здесь будет оператор «И», а операнды — «Истина» и «Истина». Этот пример можно отнести к логическому типу.
Целые и вещественные числа. Математические операции и вывод результата
Если мы рассматриваем математические операции над целыми и дробными числами, то это операторы +, -, *, /, **, //,%. С первыми тремя все понятно. Они обозначают соответственно сложение, вычитание, умножение. Оператор ** указывает на необходимость возведения в степень.
Одиночное (/) и двойное (//) деление различаются. Если первое дает действительное число в решении, второе необходимо, чтобы найти целую часть деления. Например, 9 // 4 = 2. Этот оператор соответствует функции div в Turbo Pascal. Но закономерность есть. Знак «/» напечатает целое число в результате, если и делитель, и делимое являются целыми числами. Чтобы найти остаток от деления в Python, вам нужно использовать оператор «%». По аналогии с тем же «Турбо Паскалем» «%» сравним с функцией мода. Например, 9% 2 = 1, то есть в Python остаток от деления в данном случае равен 1. Рассмотрим еще несколько примеров.
Например, 9% 2 = 1, то есть в Python остаток от деления в данном случае равен 1. Рассмотрим еще несколько примеров.
Для деления без остатка Python предлагает использовать функцию divmod (x, y). В этом случае x — делимое, y — делитель. Для divmod (9,3) программа выдает следующий результат (3,0). Это означает, что все деление равно 3, а остаток равен 0.
Математические операции могут выполняться без присвоения значения переменной. Затем результат выводится автоматически. Если ваш код содержит присвоение переменной, вы можете отобразить результат на экране с помощью оператора печати.
Модуль math
Для удобства пользователей разработчики предлагают мощный математический модуль, который может работать с любым типом чисел и выполнять дополнительные функции.
Для подключения библиотеки необходимо в начале кода программы написать следующую строку: import math. Эта команда позволит вам загрузить в программный код все функции, доступные в математическом модуле. Итак, чтобы подключить конкретный блок из библиотеки, нужно постоянно его регистрировать. Например, x = math.ceil (5.6).
Итак, чтобы подключить конкретный блок из библиотеки, нужно постоянно его регистрировать. Например, x = math.ceil (5.6).
Если программа будет часто использовать один и тот же блок, вы можете только импортировать его. Например, вам нужно округлить до ближайшего целого числа. Тогда код записывается следующим образом: из math import ceil или из math import *. В обоих случаях это не повлияет на дополнительный код округления.
Стандартные функции арифметики в Python
Чтобы вычислить остаток от целочисленного деления в Python, не всегда необходимо загружать математическую библиотеку. Некоторые функции интегрированы.
Интегрированные функции | Их цель | Примеры |
целое число (х) | Преобразует действительное число в целое, т. Е. Дробная часть «усекается». | интервал (5.3) >>> 5 интервал (5.6) >>> 5 интервал (5,987) >>> 5 |
круглый (х) | Выражение округляется до ближайшего целого числа. | круглый (5,4) >>> 5,0 круглый (5,7) >>> 6,0 круглый (5.5) >>> 6.0 круглый (5,987) >>> 6,0 |
круглый (х, п) | Используется для округления дробной части до n десятичных знаков | круглый (5.8776.2) >>> 5,88 круглый (5.9876.3) >>> 5,988 |
брюшной (х) | Найдите форму выражения | брюшной пресс (-7) >>> 7 брюшной пресс (7,8) >>> 7,8 абс (-66,55) >>> 66,55 |
Функции, для которых библиотека должна быть связана (сначала необходимо ввести из математического импорта *), показаны в следующей таблице.
Функции | Их цель |
потолок (x) | Функция нужна для округления числа до большего целого числа («вверх») |
самолет (x) | Функция нужна для округления числа до наименьшего целого числа («вниз») |
квадрат (x) | Вычислить корень числа |
регистр (х) | Требовалось найти логарифм. |
а также | Возвращает основание натурального логарифма |
грех (х) | Вычислить тригонометрические функции, где x в радианах |
cos (x) | |
загар (х) | |
asin (х) | |
acos (x) | |
атан (х) | |
atan2 (х, у) | Найдите полярный угол точки, заданной x и y |
градусы (x) | Требуется для преобразования угла из радиан в градусы |
радианы (х) | Функция, необходимая для преобразования угла из градусов в радианы |
пи | Печатает значение константы π |
В качестве примера ниже приведен код, в котором используются математические операторы.
Результат отображается следующим образом.
В математическом модуле есть много других функций. Здесь перечислены наиболее распространенные.
Остаток от деления Python, операторы Python
Статья содержит описание основных операторов языка python, таких как остаток от деления python, логические, побитовые операторы и т.д. Приведены примеры использования операторов и пояснены некоторые тонкости их использования.
Содержание
- Введение в операторы Python
- Арифметические операторы Python
- Сложение
- Вычитание
- Умножение
- Деление
- Возведение в степень
- Деление без остатка
- Деление по модулю (остаток от деления)
- Операторы сравнения
- Оператор «меньше»
- Оператор «больше»
- Оператор «меньше или равно»
- Оператор «больше или равно»
- Оператор «равно»
- Оператор «не равно»
- Операторы присваивания
- Простое присваивание
- Сложение и присваивание
- Вычитание и присваивание
- Деление и присваивание
- Умножение и присваивание
- Деление по модулю и присваивание
- Возведение в степень и присваивание
- Деление с остатком и присваивание
- Логические операторы python
- И (and)
- Или (or)
- Не (not)
- Операторы принадлежности (членства)
- В (in)
- Нет в (not in)
- Операторы тождественности
- Это (is)
- Это не (is not)
- Битовые операторы python
- Бинарное «и»
- Бинарное «или»
- Бинарное «или нет»
- Инвертирующий оператор
- Бинарный сдвиг влево
- Бинарный сдвиг вправо
Введение в операторы Python
В языке программирования python, как и во всех остальных, есть различные операторы. Большинство из них выглядят стандартно и привычно: арифметические операции везде обозначаются одинаково, а, например, для остатка от деления в python зарезервирован знак %. Но рассмотрим же подробнее все стандартные и наиболее часто используемые операторы языка python.
Большинство из них выглядят стандартно и привычно: арифметические операции везде обозначаются одинаково, а, например, для остатка от деления в python зарезервирован знак %. Но рассмотрим же подробнее все стандартные и наиболее часто используемые операторы языка python.
Операторы языка Питон подразделяются на 7 видов:
- Знаки арифметических операций
- Сравнительные
- Присваивающие
- Логические
- Операторы принадлежности (или членства, или вложенности)
- Тождественные
- Битовые (или бинарные)
Арифметические операторы Python
Данные операторы выполняют операции сложения, умножения, вычитания, деления, вычисления остатка от деления и возведения в степень над числами. Сложение и умножение также работает и для строк.
Рассмотрим примеры работы различных операторов (в качестве среды разработки в примерах используется Visual Studio 2019). Синтаксис python позволяет сразу же вычислять результат операции без присвоения его какой-либо переменной; это свойство будет использовано в некоторых примерах. Также не нужно производить import каких-либо библиотек: все основные команды python являются стандартными и зарезервированными.
Также не нужно производить import каких-либо библиотек: все основные команды python являются стандартными и зарезервированными.
Сложение
Складываем один и два:
Копировать Скопировано Use a different Browser
print(1 + 2) # Вывод: 3
Вычитание
Вычитаем из четырёх два:
Копировать Скопировано Use a different Browser
print(4 - 2) # Вывод: 2
Умножение
Умножаем десять на пять:
Копировать Скопировано Use a different Browser
print(10 * 5) # Вывод: 50
Деление
Делим двадцать четыре на шесть:
Копировать Скопировано Use a different Browser
print(24 / 6) # Вывод: 4.0
Примечание. Результат деления в Python 3 и выше всегда приводится к типу float (число с плавающей запятой), который требует большее количество памяти, чем, например, целочисленный тип int, в связи с чем деление (и другие операции) в питон работает медленнее, чем в более низкоуровневых языках.
Возведение в степень
Возводим семь во вторую степень (или в квадрат):
Копировать Скопировано Use a different Browser
print(7 ** 2) # Вывод: 49
Деление без остатка
Ищем целую часть от деления семи на два:
Копировать Скопировано Use a different Browser
print(7 // 2) # Вывод: 3
Примечание. Python отличается от других языков тем, что в нём результат целочисленного деления может быть как целым числом, так и числом с плавающей запятой. Например, если поделить число типа int на число типа float, то результатом будет число типа float:
Копировать Скопировано Use a different Browser
print(70 // 2.0) # Вывод: 35.0
Одно из чисел вещественное в этом — в этом и состоит загвоздка. В таком случае ответ обязан быть вещественным числом.
Деление по модулю (остаток от деления)
Ищем остаток от деления семи на два:
Копировать Скопировано Use a different Browser
print(7 % 2) # Вывод: 1
Операторы сравнения
Эти операторы сравнивают 2 значения (строковые или числовые). Любой из операторов данного типа возвращает булевое значение — True или False.
Любой из операторов данного типа возвращает булевое значение — True или False.
Оператор «меньше»
Копировать Скопировано Use a different Browser
print(13 < 15) # Вывод: True
13 меньше, чем 15 — это верно.
Копировать Скопировано Use a different Browser
print(13 < 12) # Вывод: False
13 меньше, чем 12 — это не верно.
Оператор «больше»
Копировать Скопировано Use a different Browser
print(13 > 13) # Вывод: False
13 меньше, чем 13 — это не верно.
Копировать Скопировано Use a different Browser
print(13 > 10) # Вывод: True
13 меньше, чем 10 — это верно.
Оператор «меньше или равно»
Копировать Скопировано Use a different Browser
print(13 <= 17) # Вывод: True
13 меньше или равно 17 — это верно.
Копировать Скопировано Use a different Browser
print(13 <= 1) # Вывод: False
13 меньше или равно 1 — это не верно.
Оператор «больше или равно»
Копировать Скопировано Use a different Browser
print(13 >= 13) # Вывод: True
13 большее или равно 13 — это верно.
Копировать Скопировано Use a different Browser
print(13 >= 17) # Вывод: False
13 большее или равно 17 — это не верно.
Оператор «равно»
Копировать Скопировано Use a different Browser
print(13 == 13) # Вывод: True
13 равно 13 — это верно.
Копировать Скопировано Use a different Browser
print(13 == 14) # Вывод: False
13 равно 14 — это не верно.
Оператор «не равно»
Копировать Скопировано Use a different Browser
print(13 != 13) # Вывод: False
13 не равно 13 — это не верно.
Копировать Скопировано Use a different Browser
print(13 != 14) # Вывод: True
13 не равно 14 — это верно.
Операторы присваивания
Эти операторы присваивают значение правого операнда левому. Только один-единственный оператор просто присваивает значение — это знак «=» (равно). Все остальные предварительно выполняют какое-либо арифметическое действие между двумя операндами, и получившийся результат записывается в левый операнд.
Простое присваивание
Присвоим переменным значения, с которыми будут работать другие операторы дальше:
Копировать Скопировано Use a different Browser
a = 100 b = 25 print(a, b) # Вывод: 100 25
Сложение и присваивание
Значение переменной b складывается со значением переменной a, после чего результат записывается в a:
Копировать Скопировано Use a different Browser
a += b print(a) # Вывод: 125
Вычитание и присваивание
Значение переменной b вычитается из значения переменной a, после чего результат записывается в a:
Копировать Скопировано Use a different Browser
a -= b print(a) # Вывод: 75
Деление и присваивание
Значение переменной a делится на значение переменной b, после чего результат записывается в a:
Копировать Скопировано Use a different Browser
a /= b print(a) # Вывод: 4.0
Умножение и присваивание
Значение переменной a умножается на значение переменной b, после чего результат записывается в a:
Копировать Скопировано Use a different Browser
a *= b print(a) # Вывод: 2500
Деление по модулю и присваивание
Значение переменной a делится на значение переменной b, после чего остаток от деления записывается в a:
Копировать Скопировано Use a different Browser
a %= b print(a) # Вывод: 0 a = 68 b = 23 a %= b print(a) # Вывод: 22
Возведение в степень и присваивание
Значение переменной a возводится в степень, равную значению переменной b, после чего результат записывается в a:
Копировать Скопировано Use a different Browser
a **= b print(a) # Вывод: 100000000000000000000000000000000000000000000000000
Деление с остатком и присваивание
Значение переменной a делится на значение переменной b, после чего целая часть результата деления записывается в a:
Копировать Скопировано Use a different Browser
a //= b print(a) # Вывод: 4 a = 68 b = 23 a //= b print(a) # Вывод: 2
Логические операторы python
Логических операторов в python, как и в математической логике, всего 3 — «и», «или», «не», в Python это их английские аналоги — and, or, not. Результат выполнения этих операций соответствует таблице истинности.
Результат выполнения этих операций соответствует таблице истинности.
И (and)
Копировать Скопировано Use a different Browser
a = (1 + 3 == 4) and (2 * 2 == 6) print(a) # Вывод: False
Результатом этой операции оказалось False, так как для оператора and необходимо, чтобы оба операнда были равны True. Тогда и только тогда вернётся True.
Или (or)
Копировать Скопировано Use a different Browser
a = (1 + 3 == 4) or (2 * 2 == 6) print(a) # Вывод: True
Результатом этой операции оказалось True, ведь для оператора «or» достаточно, чтобы лишь один из операндов был равен True.
Не (not)
Копировать Скопировано Use a different Browser
a = (1 + 3 == 4) and not (2 * 2 == 6) print(a) # Вывод: True
Так как наш «неверный» правый операнд в результате применения к нему операции not изменил своё значение на True, то верным стало и всё выражение целиком.
Операторы принадлежности (членства)
Эти операторы проверяют, существует ли заданное значение в известном списке, словаре, кортеже или строке. Можно сказать, что таковых в питон всего 2 — это in и его отрицание not in. Соответственно, in вернёт True в случае наличия элемента в последовательности, а not in, наоборот, вернёт False, если данный элемент есть в последовательности, и True, если его нет.
В (in)
Копировать Скопировано Use a different Browser
a = "abc" in "abcdef" print(a) # Вывод: True
Строка «abc» является подстрокой строки «abcdef», соответственно, являясь подпоследовательностью данной последовательности.
Копировать Скопировано Use a different Browser
a = 10 in (1, 7, 13, 6) print(a) # Вывод: False
Числа 10 нет в этом списке, потому мы и видим False.
Нет в (not in)
Копировать Скопировано Use a different Browser
a = 10 not in (1, 7, 13, 6) print(a) # Вывод: True
Элемента 10 нет в данном списке, поэтому операция вернёт True. А если он будет:
А если он будет:
Копировать Скопировано Use a different Browser
a = 10 not in (1, 7, 13, 6, 10) print(a) # Вывод: False
В этом списке уже есть значение 10, поэтому оператор непринадлежности возвращает False.
Копировать Скопировано Use a different Browser
a = "abc" not in "abcdef" print(a) # Вывод: False
Операторы тождественности
Их, как и операторов принадлежности, всего два, и один из них является отрицанием другого. Оператор в python is сравнивает положение двух объектов в памяти и выясняет, один и тот же ли это объект, в случае успеха возвращая True. Оператор not is вернёт True, если проверка показала, что сравниваемые объекты являются разными (имеют разное расположение в памяти).
Это (is)
Копировать Скопировано Use a different Browser
print("10" is '10')
# Вывод:
True
Разные кавычки не влияют на результат выполнения операции, так как это в любом случае строка, один и тот же объект. 2)
# Вывод:
3
2)
# Вывод:
3
Инвертирующий оператор
Копировать Скопировано Use a different Browser
print(~1) # Вывод: -2
Бинарный сдвиг влево
Копировать Скопировано Use a different Browser
print(1 << 2) # Вывод: 4
Бинарный сдвиг вправо
Копировать Скопировано Use a different Browser
print(1 >> 2) # Вывод: 0
Узнаем как найти в Python остаток от деления?
Python – простой, современный язык для написания кода. Он обладает мощными библиотеками, способными вычислить любое выражение. Python выступает основным конкурентом для Matlab и Octave. Запустив в интерактивном режиме Python, остаток от деления пользователь сможет найти без труда. Но это еще не все! «Питон» может выступить мощным калькулятором.
Понятие оператора
Чтобы без труда найти в Python остаток от деления, нужно разобраться с некоторыми определениями. Оператор – знак или строка, позволяющие произвести математическое, побитовое, логическое и другое вычисление. Выражения или числа, вводимые пользователем, чтобы найти в Python 3 остаток от деления, тождественность сочетания или сравнения, называются операндами.
Оператор – знак или строка, позволяющие произвести математическое, побитовое, логическое и другое вычисление. Выражения или числа, вводимые пользователем, чтобы найти в Python 3 остаток от деления, тождественность сочетания или сравнения, называются операндами.
Разделяют следующие виды операторов:
- арифметические;
- побитовые;
- логические;
- операторы присваивания;
- сравнения;
- членства;
- тождественности.
Проще говоря, в примере «15 — 5» оператором является знак «–», операндами – 15 и 5. Это арифметическая операция с целыми числами. Если взять к рассмотрению выражение «True and True», то оператором здесь выступает «and», а операндами – «True» и «True». Этот пример можно отнести к логическому типу.
Целые и вещественные числа. Математические операции и вывод результата
Если рассматривать математические операции над целыми и дробными числами, то операторами выступают +, -, *, /, **, //, %. С первыми тремя всё понятно. Они обозначают, соответственно, сложение, вычитание, умножение. Оператор «**» указывает на необходимость возведения в степень.
Они обозначают, соответственно, сложение, вычитание, умножение. Оператор «**» указывает на необходимость возведения в степень.
Знаки одинарного (/) и двойного (//) деления отличаются. Если первый выдает в решении вещественное число, то второй необходим для нахождения целой части от деления. К примеру, 9 // 4 = 2. Этот оператор соответствует функции div в Turbo Pascal. Но есть закономерность. Знак «/» выведет целое число как результат, если и делитель, и делимое – также целые. Чтобы найти в Python остаток от деления, нужно воспользоваться оператором «%». По аналогии с тем же «Турбо Паскалем» «%» сопоставим с функцией mod. К примеру, 9%2 = 1, т.е. в Python остаток от деления в данном случае равняется 1. Рассмотрим еще примеры.
Чтобы произвести деление без остатка, Python предлагает воспользоваться функцией divmod(х,у). В данном случае х – делимое, у – делитель. Для выражения divmod (9,3) программа выдаст следующий результат (3,0). Это означает, что целая часть от деления равняется 3, а остаток – 0.
Математические операции можно выполнять без присваивания значения переменной. Тогда результат выдается автоматически. Если же код содержит присваивание переменной, то вывести результат на экран можно посредством оператора print.
Модуль math
Для удобства пользователей разработчики предлагают мощный модуль math, способный работать с любыми типами чисел и выполнять дополнительные функции.
Чтобы подключить библиотеку, нужно прописать в начале программного кода следующую строку: import math. Такая команда позволит подгрузить в программный код все функции, имеющиеся в модуле math. Тогда для подключения определенного блока из библиотеки нужно постоянно прописывать его. К примеру, x = math.ceil(5.6).
Если в программе будет часто использоваться один и тот же блок, то можно импортировать только его. К примеру, нужно произвести ряд округлений до ближайшего целого числа в большую сторону. Тогда код прописывается следующим образом: from math import ceil или from math import *. В обоих случаях дальнейший код по округлению результата не изменится.
В обоих случаях дальнейший код по округлению результата не изменится.
Стандартные функции арифметики в Python
Чтобы вычислить в Python остаток от целочисленного деления, не всегда нужно подгружать библиотеку math. Некоторые функции являются встроенными.
Встроенные функции | Их назначение | Примеры |
int(x) | Превращает вещественное число в целое, т.е. дробная часть «отсекается». | int(5.3) >>> 5 int(5.6) >>>5 int(5.987) >>> 5 |
round(x) | Происходит округление выражения до ближайшего целого. | round(5.4) >>>5.0 round(5.7) >>>6.0 round(5.5) >>>6.0 round(5.987) >>>6.0 |
round(x, n) | Используется для округления дробной части до n знаков после запятой | round(5. 5.88 round(5.9876,3) >>> 5.988 |
abs(x) | Находит модуль выражения | abs(-7) >>>7 abs(7.8) >>>7.8 abs(-66.55) >>>66.55 |
Функции, для которых необходимо подключение библиотеки (нужно изначально вписать from math import *), можно увидеть в следующей таблице.
Функции | Их назначение |
ceil(x) | Функция необходима для округления числа до большего целого («вверх») |
floor(x) | Функция требуется, чтобы округлить число до меньшего целого («вниз») |
sqrt(x) | Вычисляет корень из числа |
log(x) | Необходима для нахождения логарифма. Если указать основание, то и вычисление будет соответствующим. |
e | Выводит основание натурального логарифма |
sin(x) | Вычисление тригонометрических функций, где х выражен в радианах |
cos(x) | |
tan(x) | |
asin(x) | |
acos(x) | |
atan(x) | |
atan2(x,y) | Находит полярный угол точки, координаты которой задаются х и у |
degrees(x) | Необходима для преобразования угла из радиан в градусы |
radians(x) | Функция, необходимая для преобразования угла, заданного в градусах, в радианы |
pi | Выводит значение константы π |
В качестве примера ниже приведен код с использованием математических операторов.
Результат выведен следующим образом.
В модуле math гораздо больше функций. Здесь указаны наиболее встречающиеся.
Как обозначается целочисленное деление python
Остаток от деления в Python 3 и целая часть при делении
Python — популярный высокоуровневый язык программирования. Он обладает большим набором инструментов, имеет динамическую типизацию и используется для решения любых видов задач.
Деление в Python разделяется на три вида: обычное, целочисленное и взятие остатка. Программисту не нужно заботиться о типах операндов, Python сам определяет их и приводит результат к нужному виду. Как это делается, разберемся в этой статье.
Оператор деления
Деление в Python обозначается косой чертой «/». Примечательно, что результат в консоле всегда приводится к типу «float», даже если оба операнда были целочисленного типа, об этом свидетельствует появление «.0» у полученного значения.
Это появилось в 3-ей версии Python, ранее результатом деления целых чисел было только целое число, чтобы получить дробный результат, программисты явно указывали одному из операндов тип «float», в противном случае дробная часть просто отбрасывалась.
Важно понимать, что деление в Python, как и другие операции, работает медленнее, чем в более низкоуровневых языках программирования. Это связано с высоким уровнем автоматизации и абстракции, из-за динамической типизации интерпретатор вынужден приводить числа к дробному типу «float», который требует большего количества памяти.
Деление в представлении человека отличается от его представления в компьютере. Компьютер устроен так, что все арифметические операции могут выполняться только через сложение. Это значит, что быстрее всего выполняется сложение, затем вычитание, где необходимо менять знак операндов, умножение, где число складывается много раз. Деление выполняется дольше всех, потому что помимо многократно повторяющейся операции сложения необходимо также менять знак операндов, что требует больше памяти и действий.
Из примера видно, что не смотря на то, что во всех случаях операция была между целыми числами, результатом деления в Python 3 является вещественное число. В первом случае мы даже специально использовали приведение к типу int.
В первом случае мы даже специально использовали приведение к типу int.
Деление без остатка
Чтобы выполнить деление на цело в Python, можно воспользоваться целочисленным делением. В этом случае результатом будет целое число, без остатка. Целочисленное деление в Python обозначается двумя косыми чертами «//».
В отличие от других языков программирования Python позволяет результату целочисленного деления быть как целым (int), так и дробным (float) числом. В обоих случаях дробная часть отбрасывается и получается число с окончанием «.0».
Примеры нахождения целой части от деления:
В первых двух случаях деление осуществлялось между целыми числами. Поэтому в результате было получено целое число. В третьем примере одно из чисел вещественное. В этом случае в результате получаем так же вещественное число (типа float), после запятой у которого 0.
Остаток
Для получения остатка от деления в Python 3 используется операция, обозначающаяся символом процента «%». Остаток — это оставшаяся после целочисленного деления часть числа. Операция взятия остатка используется для решения различных видов задач.
Остаток — это оставшаяся после целочисленного деления часть числа. Операция взятия остатка используется для решения различных видов задач.
Определение остатка от деления очень часто используется в программах для нахождения, допустим, чётных чисел. Или, например, если обработка данных выполняется в цикле, и нужно выводить в консоль сообщение о ходе обработки не каждый раз, а на каждой 10-ой итерации.
Вот пример вывода чётных чисел из списка в консоль:
Проблемы чисел с плавающей точкой
Компьютер устроен так, что на аппаратном уровне понимает только две цифры: один и ноль. Из-за этого при делении и других операциях с дробями часто возникают проблемы. Например, 1/10 в двоичном представлении является неправильной бесконечной дробью. Её нельзя написать полностью, поэтому приходится округлять, а выбор значения при округлении ограничен нулем и единицей.
Что говорить о делении, если ошибки возникают и при операции сложения. Если сложить число «0.1» с самим собой четырнадцать раз, то получиться 1. 400…01. Откуда взялась эта единица? Она появилась при переводе числа из двоичного вида в десятичный.
400…01. Откуда взялась эта единица? Она появилась при переводе числа из двоичного вида в десятичный.
Более технически сложное деление приводит к подобным неточностям гораздо чаще. Обычно Python округляет результат так, что пользователь не замечает этой проблемы, но если получается достаточно длинное число, то проблема проявляется.
Деление комплексных чисел
Комплексные числа — это числа вида «a + b·i». Они занимают наивысшую ступень в иерархии чисел, арифметические операции над ними существенно отличаются от операций над обычными числами.
Деление комплексного числа на обычное меняет лишь длину радиус вектора, но не его направление.
Сокращенные операции деления
Чтобы упростить жизнь программистов, разработчики Python включили в язык «сокращенные операции». Их используют если надо выполнить операцию над переменной и полученный результат записать в эту же переменную. То, что записывается в длинной форме, можно записать в более короткой по следующим правилам:
| Полная форма | Краткая форма | |
| Деление | a = a / b | a /= b |
| Целая часть | a = a // b | a //=b |
| Остаток | a = a % b | a %= b |
Деление на ноль
Если попробовать в Python выполнить деление на 0, то мы получим исключение ZeroDivisionError.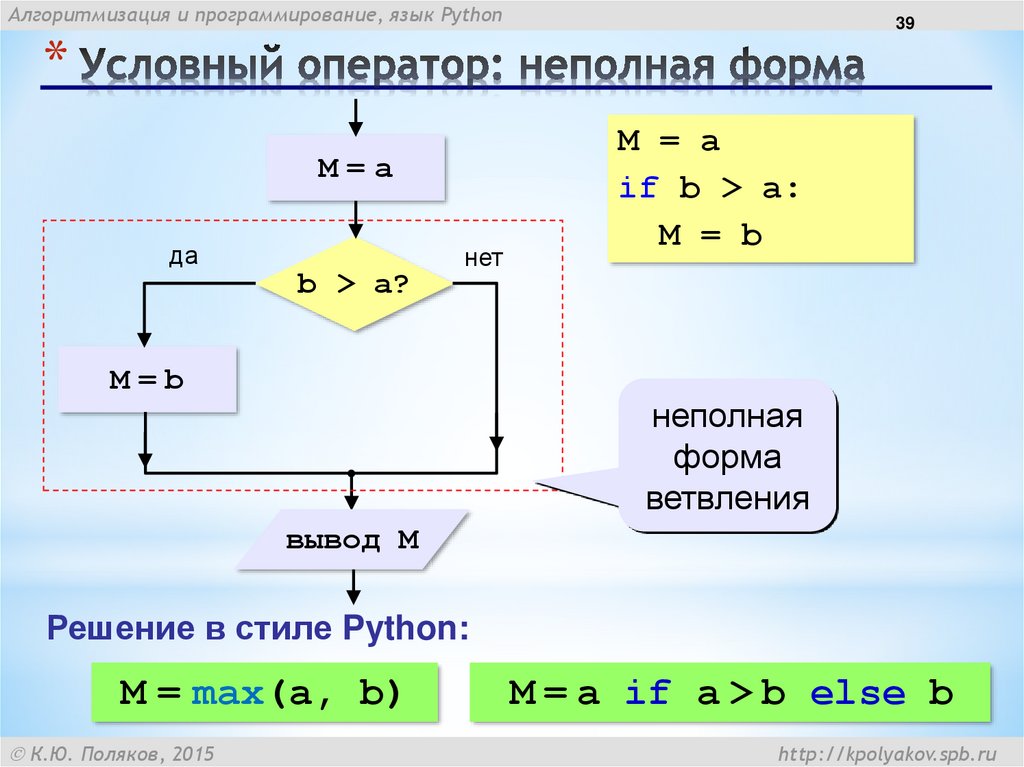
Исключение следует обрабатывать, это можно сделать так:
Но в этом случае мы обрабатываем все исключения. Зачастую так делать не совсем корректно. Мы знаем, что в нашем коде возможно деление на 0 и, чтобы отловить именно эту ошибку, следует заменить except Exception as e: на except ZeroDivisionError as e: .
Но можно и проверять перед выполнением операции, что делитель не равен 0. Например так:
Mod и div в питоне
Python – простой, современный язык для написания кода. Он обладает мощными библиотеками, способными вычислить любое выражение. Python выступает основным конкурентом для Matlab и Octave. Запустив в интерактивном режиме Python, остаток от деления пользователь сможет найти без труда. Но это еще не все! «Питон» может выступить мощным калькулятором.
Понятие оператора
Чтобы без труда найти в Python остаток от деления, нужно разобраться с некоторыми определениями. Оператор – знак или строка, позволяющие произвести математическое, побитовое, логическое и другое вычисление. Выражения или числа, вводимые пользователем, чтобы найти в Python 3 остаток от деления, тождественность сочетания или сравнения, называются операндами.
Выражения или числа, вводимые пользователем, чтобы найти в Python 3 остаток от деления, тождественность сочетания или сравнения, называются операндами.
Разделяют следующие виды операторов:
- арифметические;
- побитовые;
- логические;
- операторы присваивания;
- сравнения;
- членства;
- тождественности.
Проще говоря, в примере «15 — 5» оператором является знак «–», операндами – 15 и 5. Это арифметическая операция с целыми числами. Если взять к рассмотрению выражение «True and True», то оператором здесь выступает «and», а операндами – «True» и «True». Этот пример можно отнести к логическому типу.
Целые и вещественные числа. Математические операции и вывод результата
Если рассматривать математические операции над целыми и дробными числами, то операторами выступают +, -, *, /, **, //, %. С первыми тремя всё понятно. Они обозначают, соответственно, сложение, вычитание, умножение.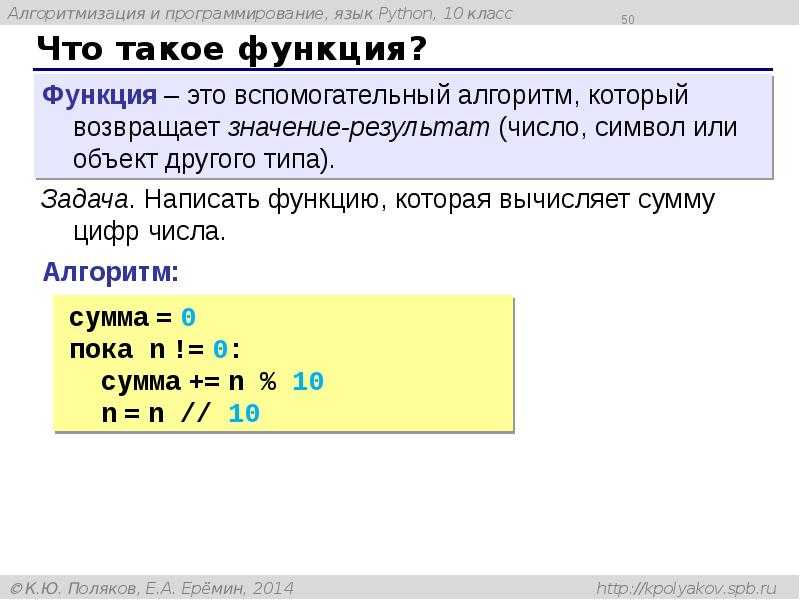 Оператор «**» указывает на необходимость возведения в степень.
Оператор «**» указывает на необходимость возведения в степень.
Знаки одинарного (/) и двойного (//) деления отличаются. Если первый выдает в решении вещественное число, то второй необходим для нахождения целой части от деления. К примеру, 9 // 4 = 2. Этот оператор соответствует функции div в Turbo Pascal. Но есть закономерность. Знак «/» выведет целое число как результат, если и делитель, и делимое – также целые. Чтобы найти в Python остаток от деления, нужно воспользоваться оператором «%». По аналогии с тем же «Турбо Паскалем» «%» сопоставим с функцией mod. К примеру, 9%2 = 1, т.е. в Python остаток от деления в данном случае равняется 1. Рассмотрим еще примеры.
Чтобы произвести деление без остатка, Python предлагает воспользоваться функцией divmod(х,у). В данном случае х – делимое, у – делитель. Для выражения divmod (9,3) программа выдаст следующий результат (3,0). Это означает, что целая часть от деления равняется 3, а остаток – 0.
Математические операции можно выполнять без присваивания значения переменной. Тогда результат выдается автоматически. Если же код содержит присваивание переменной, то вывести результат на экран можно посредством оператора print.
Тогда результат выдается автоматически. Если же код содержит присваивание переменной, то вывести результат на экран можно посредством оператора print.
Модуль math
Для удобства пользователей разработчики предлагают мощный модуль math, способный работать с любыми типами чисел и выполнять дополнительные функции.
Чтобы подключить библиотеку, нужно прописать в начале программного кода следующую строку: import math. Такая команда позволит подгрузить в программный код все функции, имеющиеся в модуле math. Тогда для подключения определенного блока из библиотеки нужно постоянно прописывать его. К примеру, x = math.ceil(5.6).
Если в программе будет часто использоваться один и тот же блок, то можно импортировать только его. К примеру, нужно произвести ряд округлений до ближайшего целого числа в большую сторону. Тогда код прописывается следующим образом: from math import ceil или from math import *. В обоих случаях дальнейший код по округлению результата не изменится.
Стандартные функции арифметики в Python
Чтобы вычислить в Python остаток от целочисленного деления, не всегда нужно подгружать библиотеку math. Некоторые функции являются встроенными.
Некоторые функции являются встроенными.
Превращает вещественное число в целое, т.е. дробная часть «отсекается».
Происходит округление выражения до ближайшего целого.
Используется для округления дробной части до n знаков после запятой
Находит модуль выражения
Функции, для которых необходимо подключение библиотеки (нужно изначально вписать from math import *), можно увидеть в следующей таблице.
Функция необходима для округления числа до большего целого («вверх»)
Функция требуется, чтобы округлить число до меньшего целого («вниз»)
Вычисляет корень из числа
Необходима для нахождения логарифма. Если указать основание, то и вычисление будет соответствующим.
Выводит основание натурального логарифма
Вычисление тригонометрических функций, где х выражен в радианах
Находит полярный угол точки, координаты которой задаются х и у
Необходима для преобразования угла из радиан в градусы
Функция, необходимая для преобразования угла, заданного в градусах, в радианы
Выводит значение константы π
В качестве примера ниже приведен код с использованием математических операторов.
Результат выведен следующим образом.
В модуле math гораздо больше функций. Здесь указаны наиболее встречающиеся.
Числа в Python 3: целые, вещественные, комплексные. Работа с числами и операции над ними.
Целые числа (int)
Числа в Python 3 ничем не отличаются от обычных чисел. Они поддерживают набор самых обычных математических операций:
| x + y | Сложение |
| x — y | Вычитание |
| x * y | Умножение |
| x / y | Деление |
| x // y | Получение целой части от деления |
| x % y | Остаток от деления |
| -x | Смена знака числа |
| abs(x) | Модуль числа |
| divmod(x, y) | Пара (x // y, x % y) |
| x ** y | Возведение в степень |
| pow(x, y[, z]) | x y по модулю (если модуль задан) |
Также нужно отметить, что целые числа в python 3, в отличие от многих других языков, поддерживают длинную арифметику (однако, это требует больше памяти).
Битовые операции
Над целыми числами также можно производить битовые операции
Дополнительные методы
int.bit_length() — количество бит, необходимых для представления числа в двоичном виде, без учёта знака и лидирующих нулей.
int.to_bytes(length, byteorder, *, signed=False) — возвращает строку байтов, представляющих это число.
Системы счисления
Те, у кого в школе была информатика, знают, что числа могут быть представлены не только в десятичной системе счисления. К примеру, в компьютере используется двоичный код, и, к примеру, число 19 в двоичной системе счисления будет выглядеть как 10011. Также иногда нужно переводить числа из одной системы счисления в другую. Python для этого предоставляет несколько функций:
- int([object], [основание системы счисления]) — преобразование к целому числу в десятичной системе счисления. По умолчанию система счисления десятичная, но можно задать любое основание от 2 до 36 включительно.

- bin(x) — преобразование целого числа в двоичную строку.
- hex(х) — преобразование целого числа в шестнадцатеричную строку.
- oct(х) — преобразование целого числа в восьмеричную строку.
Вещественные числа (float)
Вещественные числа поддерживают те же операции, что и целые. Однако (из-за представления чисел в компьютере) вещественные числа неточны, и это может привести к ошибкам:
Для высокой точности используют другие объекты (например Decimal и Fraction)).
Также вещественные числа не поддерживают длинную арифметику:
Простенькие примеры работы с числами:
Дополнительные методы
float.as_integer_ratio() — пара целых чисел, чьё отношение равно этому числу.
float.is_integer() — является ли значение целым числом.
float.hex() — переводит float в hex (шестнадцатеричную систему счисления).
classmethod float.fromhex(s) — float из шестнадцатеричной строки.
Помимо стандартных выражений для работы с числами (а в Python их не так уж и много), в составе Python есть несколько полезных модулей.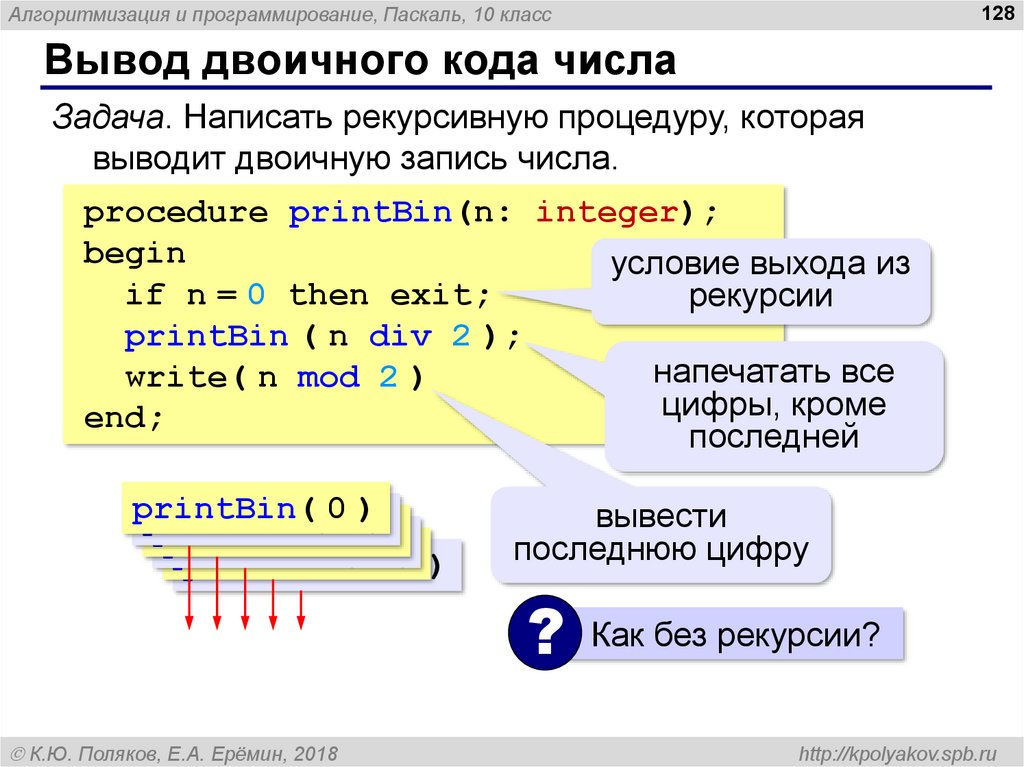
Модуль math предоставляет более сложные математические функции.
Модуль random реализует генератор случайных чисел и функции случайного выбора.
Комплексные числа (complex)
В Python встроены также и комплексные числа:
Также для работы с комплексными числами используется также модуль cmath.
Python — популярный высокоуровневый язык программирования. Он обладает большим набором инструментов, имеет динамическую типизацию и используется для решения любых видов задач.
Деление в Python разделяется на три вида: обычное, целочисленное и взятие остатка. Программисту не нужно заботиться о типах операндов, Python сам определяет их и приводит результат к нужному виду. Как это делается, разберемся в этой статье.
Оператор деления
Деление в Python обозначается косой чертой «/». Примечательно, что результат в консоле всегда приводится к типу «float», даже если оба операнда были целочисленного типа, об этом свидетельствует появление «.0» у полученного значения.
Это появилось в 3-ей версии Python, ранее результатом деления целых чисел было только целое число, чтобы получить дробный результат, программисты явно указывали одному из операндов тип «float», в противном случае дробная часть просто отбрасывалась.
Важно понимать, что деление в Python, как и другие операции, работает медленнее, чем в более низкоуровневых языках программирования. Это связано с высоким уровнем автоматизации и абстракции, из-за динамической типизации интерпретатор вынужден приводить числа к дробному типу «float», который требует большего количества памяти.
Деление в представлении человека отличается от его представления в компьютере. Компьютер устроен так, что все арифметические операции могут выполняться только через сложение. Это значит, что быстрее всего выполняется сложение, затем вычитание, где необходимо менять знак операндов, умножение, где число складывается много раз. Деление выполняется дольше всех, потому что помимо многократно повторяющейся операции сложения необходимо также менять знак операндов, что требует больше памяти и действий.
Из примера видно, что не смотря на то, что во всех случаях операция была между целыми числами, результатом деления в Python 3 является вещественное число. В первом случае мы даже специально использовали приведение к типу int.
Деление без остатка
Чтобы выполнить деление на цело в Python, можно воспользоваться целочисленным делением. В этом случае результатом будет целое число, без остатка. Целочисленное деление в Python обозначается двумя косыми чертами «//».
В отличие от других языков программирования Python позволяет результату целочисленного деления быть как целым (int), так и дробным (float) числом. В обоих случаях дробная часть отбрасывается и получается число с окончанием «.0».
Примеры нахождения целой части от деления:
В первых двух случаях деление осуществлялось между целыми числами. Поэтому в результате было получено целое число. В третьем примере одно из чисел вещественное. В этом случае в результате получаем так же вещественное число (типа float), после запятой у которого 0.
Остаток
Для получения остатка от деления в Python 3 используется операция, обозначающаяся символом процента «%». Остаток — это оставшаяся после целочисленного деления часть числа. Операция взятия остатка используется для решения различных видов задач.
Определение остатка от деления очень часто используется в программах для нахождения, допустим, чётных чисел. Или, например, если обработка данных выполняется в цикле, и нужно выводить в консоль сообщение о ходе обработки не каждый раз, а на каждой 10-ой итерации.
Вот пример вывода чётных чисел из списка в консоль:
Проблемы чисел с плавающей точкой
Компьютер устроен так, что на аппаратном уровне понимает только две цифры: один и ноль. Из-за этого при делении и других операциях с дробями часто возникают проблемы. Например, 1/10 в двоичном представлении является неправильной бесконечной дробью. Её нельзя написать полностью, поэтому приходится округлять, а выбор значения при округлении ограничен нулем и единицей.
Что говорить о делении, если ошибки возникают и при операции сложения. Если сложить число «0.1» с самим собой четырнадцать раз, то получиться 1.400…01. Откуда взялась эта единица? Она появилась при переводе числа из двоичного вида в десятичный.
Более технически сложное деление приводит к подобным неточностям гораздо чаще. Обычно Python округляет результат так, что пользователь не замечает этой проблемы, но если получается достаточно длинное число, то проблема проявляется.
Деление комплексных чисел
Комплексные числа — это числа вида «a + b·i». Они занимают наивысшую ступень в иерархии чисел, арифметические операции над ними существенно отличаются от операций над обычными числами.
Деление комплексного числа на обычное меняет лишь длину радиус вектора, но не его направление.
Сокращенные операции деления
Чтобы упростить жизнь программистов, разработчики Python включили в язык «сокращенные операции». Их используют если надо выполнить операцию над переменной и полученный результат записать в эту же переменную. То, что записывается в длинной форме, можно записать в более короткой по следующим правилам:
То, что записывается в длинной форме, можно записать в более короткой по следующим правилам:
| Полная форма | Краткая форма | |
| Деление | a = a / b | a /= b |
| Целая часть | a = a // b | a //=b |
| Остаток | a = a % b | a %= b |
Деление на ноль
Если попробовать в Python выполнить деление на 0, то мы получим исключение ZeroDivisionError.
Исключение следует обрабатывать, это можно сделать так:
Но в этом случае мы обрабатываем все исключения. Зачастую так делать не совсем корректно. Мы знаем, что в нашем коде возможно деление на 0 и, чтобы отловить именно эту ошибку, следует заменить except Exception as e: на except ZeroDivisionError as e: .
Но можно и проверять перед выполнением операции, что делитель не равен 0. Например так:
Операторы Python
В этом руководстве речь пойдет об операторах языка программирования Python. Вы узнаете об арифметических, логических и битовых операторах, а также операторах сравнения, присваивания, принадлежности, тождественности и их синтаксисе. Все это будет проиллюстрировано примерами.
Вы узнаете об арифметических, логических и битовых операторах, а также операторах сравнения, присваивания, принадлежности, тождественности и их синтаксисе. Все это будет проиллюстрировано примерами.
Оператор в Python — это символ, который выполняет операцию над одним или несколькими операндами.
Операндом выступает переменная или значение, над которыми проводится операция.
Введение в операторы Python
Операторы Python бывают 7 типов:
- Арифметические операторы
- Операторы сравнения
- Операторы присваивания
- Логические операторы
- Операторы принадлежности
- Операторы тождественности
- Битовые операторы
Арифметические операторы Python
Этот тип включает операторы для проведения базовых арифметических операций.
Сложение (+)
Складывает значение по обе стороны оператора.
Пример:
Вычитание (-)
Вычитает значение правой стороны из значения в левой.
Пример:
Умножение (*)
Перемножает значения с обеих сторон оператора.
Пример:
Деление (/)
Делит значение левой стороны на значение правой. Тип данных результата деления — число с плавающей точкой.
Пример:
Возведение в степень (**)
Возводит первое число в степень второго.
Пример:
Деление без остатка (//)
Выполняет деление и возвращает целочисленное значение частного, убирая цифры после десятичной точки.
Пример:
Деление по модулю (остаток от деления) (%)
Выполняет деление и возвращает значение остатка.
Пример:
Операторы сравнения
Операторы сравнения в Python проводят сравнение операндов. Они сообщают, является ли один из них больше второго, меньше, равным или и то и то.
Меньше (
Этот оператор проверяет, является ли значение слева меньше, чем правое.
Пример:
Больше (>)
Проверяет, является ли значение слева больше правого.
Пример:
Меньше или равно (
Проверяет, является ли левая часть меньше или равной правой.
Пример:
Больше или равно (>=)
Проверяет, является ли левая часть больше или равной правой.
Пример:
Равно (==)
Этот оператор проверяет, равно ли значение слева правому. 1 равна булевому True , а 2 (двойка) — нет. 0 равен False .
Пример:
Не равно (!=)
Проверяет, не равно ли значение слева правому. Оператор <> выполняет ту же задачу, но его убрали в Python 3.
Когда условие выполнено, возвращается True . В противном случае — False . Это возвращаемое значение можно использовать в последующих инструкциях и выражениях.
Пример:
Операторы присваивания
Оператор присваивания присваивает значение переменной. Он может манипулировать значением до присваивания. Есть 8 операторов присваивания: 1 простой и 7 с использованием арифметических операторов.
Есть 8 операторов присваивания: 1 простой и 7 с использованием арифметических операторов.
Присваивание (=)
Присваивает значение справа левой части. Стоит обратить внимание, что == используется для сравнения, а = — для присваивания.
Пример:
Сложение и присваивание (+=)
Суммирует значение обеих сторон и присваивает его выражению слева. a += 10 — это то же самое, что и a = a + 10 .
То же касается и все остальных операторов присваивания.
Пример:
Вычитание и присваивание (-=)
Вычитает значение справа из левого и присваивает его выражению слева.
Пример:
Деление и присваивание (/=)
Делит значение слева на правое. Затем присваивает его выражению слева.
Пример:
Умножение и присваивание (*=)
Перемножает значения обеих сторон. Затем присваивает правое левому.
Пример:
Деление по модулю и присваивание (%=)
Выполняет деление по модулю для обеих частей. Результат присваивает левой части.
Результат присваивает левой части.
Пример:
Возведение в степень и присваивание (**=)
Выполняет возведение левой части в степень значения правой части. Затем присваивает значение левой части.
Пример:
Деление с остатком и присваивание (//=)
Выполняет деление с остатком и присваивает результат левой части.
Пример:
Это один из важных операторов Python
Логические операторы Python
Это союзы, которые позволяют объединять по несколько условий. В Python есть всего три оператора: and (и), or (или) и not (не).
И (and)
Если условия с двух сторон оператора and истинны, тогда все выражение целиком считается истинным.
Пример:
Или (or)
Выражение ложно, если оба операнда с двух сторон ложные. Если хотя бы одно из них истинное, то и все выражение истинно.
Пример:
Не (not)
Этот оператор инвертирует булевые значения выражения.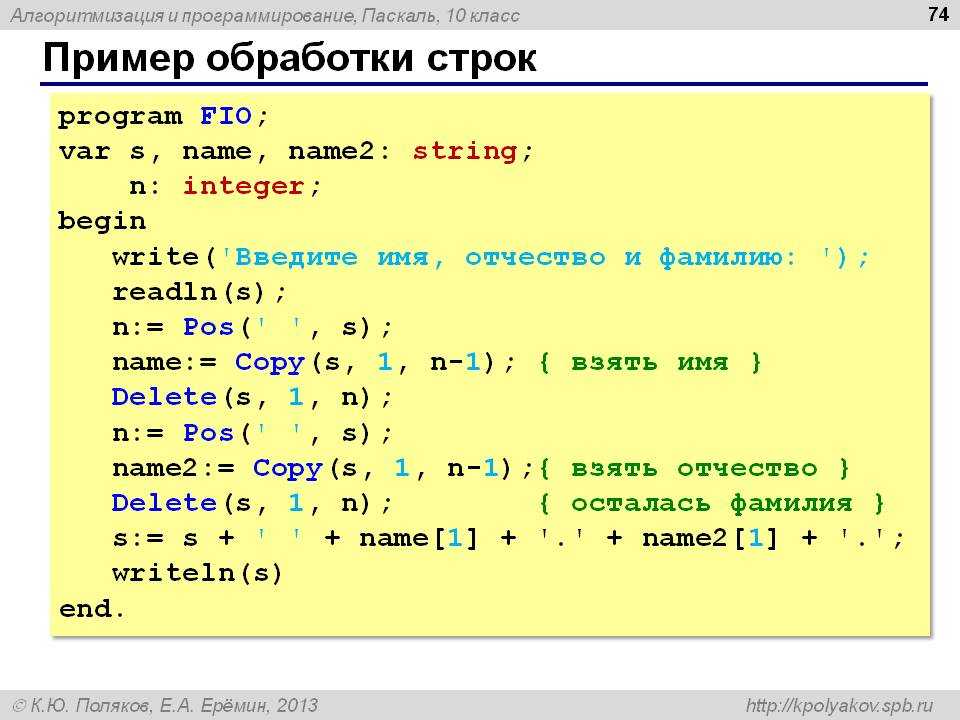 True превращается в False и наоборот. В примере внизу булево значение 0 — False . Поэтому оно превращается в True .
True превращается в False и наоборот. В примере внизу булево значение 0 — False . Поэтому оно превращается в True .
Пример:
Операторы принадлежности
Эти операторы проверяют, является ли значение частью последовательности. Последовательность может быть списком, строкой или кортежем. Есть всего два таких оператора: in и not in .
Проверяет, является ли значение членом последовательности. В этом примере видно, что строки fox нет в списке питомцев. Но cat — есть, поэтому она возвращает True . Также строка me является подстрокой disappointment . Поэтому она вернет True .
Пример:
Нет в (not in)
Этот оператор проверяет, НЕ является ли значение членом последовательности.
Пример:
Операторы тождественности
Эти операторы проверяют, являются ли операнды одинаковыми (занимают ли они одну и ту же позицию в памяти).
Это (is)
Если операнды тождественны, то вернется True . В противном случае — False . )
)
Проводит побитовую операцию xor (исключающее или) на двух значениях. Здесь результатом ИЛИ НЕ для 10 (2) и 11 (3) будет 01 (1).
Пример:
Инвертирующий оператор (
Он возвращает инвертированные двоичные числа. Другими словами, переворачивает биты. Битовая 2 — это 00000010 . Ее инвертированная версия — 11111101 . Это бинарная -3 . Поэтому результат -3 . Похожим образом
1 равняется -2 .
Пример:
Еще раз, инвертированная -3 — это 2 .
Бинарный сдвиг влево (
Он сдвигает значение левого операнда на позицию, которая указана справа. Так, бинарная 2 — это 10 . 2 сдвинет значение на две позиции влево и выйдет 1000 — это бинарная 8 .
Пример:
Бинарный сдвиг вправо (>>)
Сдвигает значение левого оператора на позицию, указанную справа. Так, бинарная 3 — это 11 . 3 >> 2 сдвинет значение на два положение вправо. Результат — 00 , то есть 0 . 3 >> 1 сдвинет на одну позицию вправо, а результатом будет 01 — бинарная 1 .
Пример:
Выводы
В этом уроке были рассмотрены все 7 типов операторов Python. Для каждого был предложен пример в IDE. Для понимания особенностей работы операторов нужно продолжать с ними работать, использовать в условных конструкциях и объединять.
Числа: целые, вещественные, комплексные
Числа в Python 3: целые, вещественные, комплексные. Работа с числами и операции над ними.
Целые числа (int)
Числа в Python 3 ничем не отличаются от обычных чисел. Они поддерживают набор самых обычных математических операций:
| x + y | Сложение |
| x — y | Вычитание |
| x * y | Умножение |
| x / y | Деление |
| x // y | Получение целой части от деления |
| x % y | Остаток от деления |
| -x | Смена знака числа |
| abs(x) | Модуль числа |
| divmod(x, y) | Пара (x // y, x % y) |
| x ** y | Возведение в степень |
| pow(x, y[, z]) | x y по модулю (если модуль задан) |
Также нужно отметить, что целые числа в python 3, в отличие от многих других языков, поддерживают длинную арифметику (однако, это требует больше памяти).
Битовые операции
Над целыми числами также можно производить битовые операции
Дополнительные методы
int.bit_length() — количество бит, необходимых для представления числа в двоичном виде, без учёта знака и лидирующих нулей.
int.to_bytes(length, byteorder, *, signed=False) — возвращает строку байтов, представляющих это число.
classmethod int.from_bytes(bytes, byteorder, *, signed=False) — возвращает число из данной строки байтов.
Системы счисления
Те, у кого в школе была информатика, знают, что числа могут быть представлены не только в десятичной системе счисления. К примеру, в компьютере используется двоичный код, и, к примеру, число 19 в двоичной системе счисления будет выглядеть как 10011. Также иногда нужно переводить числа из одной системы счисления в другую. Python для этого предоставляет несколько функций:
- int([object], [основание системы счисления]) — преобразование к целому числу в десятичной системе счисления.
 По умолчанию система счисления десятичная, но можно задать любое основание от 2 до 36 включительно.
По умолчанию система счисления десятичная, но можно задать любое основание от 2 до 36 включительно. - bin(x) — преобразование целого числа в двоичную строку.
- hex(х) — преобразование целого числа в шестнадцатеричную строку.
- oct(х) — преобразование целого числа в восьмеричную строку.
Вещественные числа (float)
Вещественные числа поддерживают те же операции, что и целые. Однако (из-за представления чисел в компьютере) вещественные числа неточны, и это может привести к ошибкам:
Для высокой точности используют другие объекты (например Decimal и Fraction)).
Также вещественные числа не поддерживают длинную арифметику:
Простенькие примеры работы с числами:
Дополнительные методы
float.as_integer_ratio() — пара целых чисел, чьё отношение равно этому числу.
float.is_integer() — является ли значение целым числом.
float.hex() — переводит float в hex (шестнадцатеричную систему счисления).
classmethod float.fromhex(s) — float из шестнадцатеричной строки.
Помимо стандартных выражений для работы с числами (а в Python их не так уж и много), в составе Python есть несколько полезных модулей.
Модуль math предоставляет более сложные математические функции.
Модуль random реализует генератор случайных чисел и функции случайного выбора.
Комплексные числа (complex)
В Python встроены также и комплексные числа:
Также для работы с комплексными числами используется также модуль cmath.
Арифметические операции
На этом занятии рассмотрим виды и работу арифметических операторов в Python. И как уже говорили, в этом языке имеется три базовых типа для представления чисел:
- int – для целочисленных значений;
- float – для вещественных;
- complex – для комплексных.
И введем несколько определений:
Операнд – то, к чему применяется оператор. Например, в умножении 5 * 2 есть два операнда: левый операнд равен 5, а правый операнд равен 2. Иногда их называют «аргументами» вместо «операндов».
Иногда их называют «аргументами» вместо «операндов».
Унарным называется оператор, который применяется к одному операнду.
Обратите внимание как записаны два оператора в одну строчку: они разделены точкой с запятой. Так тоже можно делать. Если каждый оператор начинается с новой строки, то точку с запятой ставить не обязательно, если пишем несколько операторов в одну строчку, то они разделяются точкой с запятой.
Бинарным называется оператор, который применяется к двум операндам.
Тот же минус существует и в бинарной форме:
Раз мы начали говорить об операциях + и -, то продолжим и отметим, что, в общем случае, можно использовать унарный плюс и минус, например:
Конечно, +a это то же самое, что и a, поэтому, в основном, используется унарный минус. По приоритету унарные операции выше бинарных операций. Например, вот такая запись:
означает, что число –a возводится в степень 2, то есть, унарный минус имеет больший приоритет, чем бинарная операция ** возведения в степень.
Если же используются бинарные сложение и вычитание:
то их приоритет становится наименьшим среди всех арифметических операций (они выполняются в последнюю очередь).
Следующая бинарная операция умножение работает так, как мы привыкли ее использовать в математике:
Здесь сначала выполнится умножение, а затем – сложение. Если необходимо изменить приоритет выполнения операций, то используются круглые скобки:
Далее, деление двух чисел (или переменных) можно выполнить двумя способами. Первый – традиционный, делает деление, привычное в математике, например:
получим ожидаемый результат 1,5. Однако те из вас, кто имеет опыт программирования на таких языках как С++ или Java, знают, что при делении двух целочисленных значений, результат также получался целочисленным. Но в Python это не так! Его арифметические операции работают в соответствии с классическими правилами математики и деление здесь – это всегда полноценное деление двух значений, какими бы они ни были.
Однако, если все же требуется выполнить целочисленное деление (то есть, с отбрасыванием дробной части), то используется такой оператор:
И, как видите, теперь результат 1, а не 1,5. Причем, это целочисленное деление будет выполняться и с вещественными числами:
Вот такие два оператора деления существуют в Python.
Если же хотим вычислить остаток от целочисленного деления, то используется оператор:
С положительными целыми числами он работает также как и во многих других языках программирования. Например,
и так далее, мы будем получать числа от 0 до 4. Но с отрицательными числами вычисления будут отличаться от того же языка С++. Например,
Почему так? Дело в том, что когда то давно инженеры фирмы Intell неверно математически реализовали данную операцию. И язык С++ как наследник этой интеловской архитектуры реализует данную операцию путем вынесения знака «-» за скобки и вычисления обычного остатка от деления. Язык же Python делает это так, как принято в математике. Сначала находится ближайшее наименьшее число кратное 5. Это число -10 (для числа -9) и остаток берется как разность между этими числами:
Сначала находится ближайшее наименьшее число кратное 5. Это число -10 (для числа -9) и остаток берется как разность между этими числами:
то есть, остатки всегда будут положительными в диапазоне от 0 до 4, как это и должно быть по математике.
Все рассмотренные операторы (*, /, //, %) имеют одинаковый приоритет и выполняются слева-направо. То есть, если записать
то это следует интерпретировать как формулу
Следующая операция – возведение в степень. В самом простом варианте она записывается так:
здесь x, y могут быть и дробными числами. Например:
Это будет соответствовать извлечению квадратного корня из 1,96. Если запишем такую конструкцию:
то получим кубический корень из 27. Причем, обратите внимание, круглые скобки у степени здесь обязательны, т.к. приоритет операции ** выше, чем у деления. Если записать вот так:
то это будет эквивалентно такому выражению:
Вот на это следует обращать внимание. И еще один нюанс. Операция возведения в степень выполняется справа-налево. То есть, если записать вот такую строчку:
То есть, если записать вот такую строчку:
Это будет эквивалентно степени:
Сначала (справа) вычисляется 3**2 = 9, а затем, 2**9 = 512. Все остальные арифметические операции работают слева-направо.
Используя оператор присваивания совместно с арифметическими операторами, можно выполнять некоторые полезные арифметические преобразования переменных. Например, очень часто требуется увеличить или уменьшить некую переменную на определенное число. Это можно сделать вот так:
Но, можно и короче, вот так:
Они довольно часто используются в программировании. Также, помимо сложения и вычитания, можно записывать и такие выражения:
То есть, здесь до оператора присваивания можно записывать любую арифметическую операцию.
Все рассмотренные арифметические операции можно выполнять и с комплексными числами:
Кроме операции целочисленного деления // и вычисления остатка от деления %. Дополнительно у объектов комплексных чисел есть свойства:
для взятия действительной и мнимой части. И полезный метод:
И полезный метод:
для получения комплексно-сопряженного числа.
В языке Python имеются встроенные функции для работы с числами. Наиболее полезные, следующие:
Также в языке Python имеется стандартная библиотека math, которая содержит большое количество стандартных математических функций. Чтобы ей воспользоваться, необходимо вначале программы подключить эту библиотеку. Делается это с помощью ключевого слова import, за которым указывается имя библиотеки:
Целочисленное деление в Python
Как вы знаете, в Python есть два способа делить целые числа.
Оператор / при делении целого числа на целое возвращает результат типа float.
А оператор // при делении целого на целое возвращает целое с округлением вниз, по-английски этот оператор еще называют floor division.
Копалась в истории языка и узнала, что изначально деление целых чисел в Python было только целочисленное, и для него Гвидо использовал символ / . Но быстро стало понятно, что в языке, где программист не объявляет типы явно, использование такого символа неудобно и будет приводить к обилию ошибок в программах.
Поэтому часть сообщества (включая Гвидо) настаивала на том, что оператором целочисленного деления нужно выбрать символ // , а оператор деления, который возвращает тип float, должен быть /. Другие разработчики говорили, что целочисленное деление нужно писать как /, аргументируя это тем, что «научиться обращаться с целочисленным делением — это как обряд инициации для начинающих программистов», да и в C целочисленное деление пишется именно так.
Вот что Гвидо пишет об этом в своем блоге (в моем вольном переводе):
Чтобы услышать мнение человека, далекого от программирования, я спросил свою подругу, которая занималась средневековой английской литературой. Разговор был примерно такой:
Я: Вот ты берешь два целых числа. Хорошо?
Она: Хорошо!
Я: Теперь ты можешь их сложить, вычесть, умножить в программе, правильно?
Она: Хм, конечно!
Я: А теперь предположим, что ты их делишь…
Она: Но в этом нет смысла! Целые числа образуют кольцо, а не поле. Ты ведь сказал, что взял эти числа из Z, верно?
Я: Ага.
Вот и все. Это точка зрения непрограммиста (с которой мне удобно согласиться). Целочисленное деление — это чушь и его не нужно писать как «/», даже если в C делают именно так;-)
Действительно, с точки зрения непрограммиста, целочисленное деление довольно странная история, ведь над целыми числами, как и над матрицами, нет деления в принципе!
Арифметические операции
Все числовые типы, кроме сложных, поддерживают следующие операции согласно их приоритетам выполнения:
- x + y
Результатом будет сумма чисел x и у - x — y
Результатом будет разница чисел x и у - x * y
Результатом будет произведение чисел x и у - x / y
Результатом будет частное чисел x и у - x // y
Результатом будет деление x / y с округлением результата до ближайшего целого в меньшую сторону. Операцию называют «целочисленным делением».
Результирующее значение является целым целым числом, хотя тип результата не обязательно является int .
Результат всегда округляется до минус бесконечности:
1 // 2 равно 0 ,
(-1) // 2 равно -1 ,
1 // (-2) равно -1 ,
(-1) // (-2) равно 0 . - x % y
Результатом будет остаток от деления чисел x / y . - -x
Результатом будет отрицательное значение x . - +x
В результате число x останется без изменений. - abs(x)
Результатом будет абсолютное значение или величина x . - int(x)
В результате число x преобразуется в целое число int .
В качестве аргумента допускается использовать принятые числовые литералы включающие цифры от 0 до 9 или любой эквивалент Юникода.
Преобразование вещественного числа в целое число может округляться или усекаться, как в C. Для четко определенных преобразований используйте math.floor() и math.ceil() - float(x)
В результате число x преобразуется в число с плавающей точкой float .
В качестве аргумента допускается использовать принятые числовые литералы включающие цифры от 0 до 9 или любой эквивалент Юникода.
Функция также принимает строки 'nan' — не число и 'inf' — положительная или отрицательная бесконечность, с необязательным префиксом + или — . - complex(real, image)
Результатом будет комплексное число с вещественной частью real , мнимой частью image .
В качестве аргумента допускается использовать принятые числовые литералы включающие цифры от 0 до 9 или любой эквивалент Юникода. - c.conjugate()
Результатом будет сопряженное комплексное число с . - divmod(x, y)
Результатом будет пара (x // y, x % y) . - pow(x, y)
Результатом будет число x в степени у . Python определяет 0 ** 0 как равное 1 , как это обычно бывает для языков программирования. - x ** y
Результатом будет число x в степени у . Python определяет pow(0, 0) как равное 1 , как это обычно бывает для языков программирования.
Python определяет pow(0, 0) как равное 1 , как это обычно бывает для языков программирования.
Внимание!. Комплексным числам (тип complex ) недоступны операции: // — деление без остатка , % — остаток от деления, int() , float() , divmod() .
Примеры использования:Синтаксис арифметических выражений прост. Операторы + , — , * и / работают так же, как и в большинстве других языков программирования, круглые скобки () могут быть использованы для группировки выражений.
Целые числа, например 2, 4, 20 имеют тип int , числа с дробной частью, например 5.0, 1.6 имеют тип float .
Деление / всегда возвращает тип float (число с плавающей запятой). Для получения целой части числа, полученного в результате деления ( floor division — округление результата до ближайшего целого в меньшую сторону) вы можете использовать оператор // , для расчета остатка вы можете использовать оператор %
С помощью Python можно использовать оператор ** для вычисления степеней
Знак равенства = используется для присвоения значения переменной.
Если переменная не определена, т. е. ей не присвоено значение, попытка использовать ее приведет к ошибке.
Существует полная поддержка операций с плавающей запятой, операции с числами смешанного типа преобразуют результат в число с плавающей точкой.
В интерактивном режиме последнее печатное выражение присваивается переменной _ — символ подчеркивания. Это означает, что при использовании Python в качестве калькулятора несколько проще продолжить вычисления, например:
Переменная _ должна рассматриваться как доступная только для чтения. Не присваивайте ей явно значение, иначе вы создадите независимую локальную переменную с тем же именем, маскируя встроенную переменную с ее магическим поведением. Эта магическая переменная нередко используется в коде для скрытия неиспользуемых данных.
Помимо int и float , Python поддерживает другие типы чисел, такие как Decimal и Fraction . Python также имеет встроенную поддержку комплексных complex чисел и использует суффикс j или J для обозначения мнимой части, например, 3+5j .
Операторы в Python
В этой статье мы поговорим про различные операторы в Python. Мы на примерах разберем арифметические, битовые и логические операторы, а также операторы присваивания и сравнения. Кроме того, мы рассмотрим операторы принадлежности и идентичности, такие как is, is not и in, not in.
Арифметические операторы
Python реализует семь основных бинарных арифметических операторов, два из которых могут использоваться как унарные операторы. Они приведены в следующей таблице:
| Оператор | Название | Описание |
|---|---|---|
| a + b | Сложение | Сумма a и b |
| a — b | Вычитание | Разность a и b |
| a * b | Умножение | Произведение a и b |
| a / b | Деление | Частное a и b |
| a // b | Целочисленное деление | Деление a на b без остатка (дробная часть отбрасывается) |
| a % b | Взятие модуля | Целый остаток от деления a на b |
| a ** b | Возведение в степень | a, возведенное в степень b |
| -a | Отрицание | Отрицательное значение a |
| +a | Унарный плюс | а без изменений (используется редко) |
Эти операторы можно использовать и комбинировать интуитивно понятным образом, используя стандартные круглые скобки для группировки операций. К примеру, это может выглядеть так:
К примеру, это может выглядеть так:
# сложение, вычитание, умножение (4 + 8) * (6.5 - 3) # 42.0
Целочисленное деление — это обычное деление, только с усечённой дробной частью:
# Деление print(11 / 2) # 5.5 # Целочисленное деление print(11 // 2) # 5
Оператор целочисленного деления был добавлен в Python 3. Если вы работаете в Python 2, вы должны знать, что стандартный оператор деления (/) действует как оператор целочисленного деления для целых чисел и как обычный оператор деления для чисел с плавающей запятой.
Наконец, упомянем ещё один арифметический оператор, который был добавлен в Python 3. 5. Это оператор
5. Это оператор a @ b, предназначенный для указания матричного произведения a и b для использования в различных пакетах линейной алгебры.
Английский для программистов
Наш телеграм канал с тестами по английскому языку для программистов. Английский это часть карьеры программиста. Поэтому полезно заняться им уже сейчас
Подробнее
×
Битовые операторы
В дополнение к стандартным числовым операциям в Python есть операторы для выполнения побитовых логических операций над целыми числами. Они используются гораздо реже стандартных арифметических операций, но знать их полезно. Шесть побитовых операторов сведены в следующую таблицу:
| Оператор | Название | Описание |
|---|---|---|
| a & b | Логическое И | Биты, определенные как в a, так и в b |
| a | b | Логическое ИЛИ | Биты, определенные в a или b или в обоих |
| a ^ b | Исключающее ИЛИ | Равен 1, если только a или только b равно 1 |
| a << b | Побитовый сдвиг влево | Сдвинуть биты a влево на b единиц |
| a >> b | Побитовый сдвиг вправо | Сдвинуть биты a вправо на b единиц |
| ~a | Логическое НЕ | Отрицание a |
Эти побитовые операторы имеют смысл только с точки зрения двоичного представления чисел. Это можно увидеть, используя встроенную функцию
Это можно увидеть, используя встроенную функцию bin:
bin(10) # '0b1010'
Результат имеет префикс 0b, что указывает на двоичное представление. Остальные цифры означают, что число 10 выражается как сумма 1⋅23+0⋅22+1⋅21+0⋅20. Точно так же мы можем написать:
bin(4) # '0b100'
Теперь, используя логическое ИЛИ, мы можем найти число, которое объединяет биты 4 и 10:
4 | 10 # 14 bin(4 | 10) # '0b1110'
Эти побитовые операторы не так полезны, как стандартные арифметические операторы, но стоит увидеть их хотя бы раз, чтобы понять, какой класс операций они выполняют. b), на самом деле имея в виду возведение в степень (т. е.
b), на самом деле имея в виду возведение в степень (т. е. a ** b).
Операторы присваивания
Мы видели, что переменным можно присваивать значение с помощью оператора =. Например, следующим образом:
a = 24 print(a) # 24
Мы можем использовать эти переменные в выражениях с любым из упомянутых ранее операторов. Например, чтобы добавить 2 к a, мы пишем:
a + 2 # 26
Мы можем захотеть обновить переменную a новым значением. В этом случае мы могли бы объединить сложение и присваивание и написать a = a + 2. Поскольку этот тип комбинированной операции и присваивания очень распространен, Python включает встроенные операторы обновления для всех арифметических операций:
a += 2 # эквивалентно a = a + 2 print(a) # 26
Расширенный оператор присваивания есть для каждого из бинарных операторов, перечисленных ранее. = b a <<= b a >>= b
= b a <<= b a >>= b
Каждый из этих операторов эквивалентен применению соответствующего оператора с последующим присваиванием. То есть для любого оператора ■ выражение a ■= b эквивалентно a = a ■ b с небольшой оговоркой.
Для изменяемых объектов, таких как списки, массивы или датафреймы, эти расширенные операции присваивания на самом деле немного отличаются от своих более подробных аналогов. Они изменяют содержимое исходного объекта, а не создают новый объект для хранения результата. Но это тонкости, в целом же укороченная версия работает так же, как и полная, но экономит кучу вашего времени.
Операторы сравнения
Другой тип операций, который может быть очень полезным, — это сравнение различных переменных. Для этого в Python реализованы стандартные операторы сравнения, которые возвращают логические значения True или False. Операции сравнения представлены в следующей таблице:
| Оператор | Описание |
|---|---|
| a == b | a равняется b |
| a < b | a строго меньше чем b |
| a <= b | a меньше либо равно b |
| a != b | a не равняется b |
| a > b | a строго больше чем b |
| a >= b | a больше либо равно b |
Эти операторы сравнения можно комбинировать с арифметическими и побитовыми операторами, чтобы осуществлять самые разнообразные операции над числами. Например, мы можем проверить, является ли число нечетным, проверив, что остаток от деления на 2 возвращает 1:
Например, мы можем проверить, является ли число нечетным, проверив, что остаток от деления на 2 возвращает 1:
# 25 - нечетное число 25 % 2 == 1 # True # 66 - нечетное число 66 % 2 == 1 # False
Мы можем объединить несколько сравнений, чтобы проверить более сложные отношения:
# проверяем, находится ли a между 15 и 30 a = 25 15 < a < 30 # True
И, чтобы у вас немного закружилась голова, взгляните на это сравнение:
-1 == ~0 # True
Напомним, что ~ — это оператор инвертирования битов, и, очевидно, когда вы инвертируете все биты нуля, вы получите -1. Если вам интересно, почему это так, посмотрите схему кодирования целых чисел с дополнением до двух, которую Python использует для кодирования целых чисел со знаком, и подумайте, что происходит, когда вы начинаете переворачивать все биты целых чисел, закодированных таким образом.
Если вам интересно, почему это так, посмотрите схему кодирования целых чисел с дополнением до двух, которую Python использует для кодирования целых чисел со знаком, и подумайте, что происходит, когда вы начинаете переворачивать все биты целых чисел, закодированных таким образом.
От редакции Pythonist: об операторе != можно почитать в статье «Оператор неравенства != в Python».
Логические операторы
При работе с логическими значениями Python предоставляет операторы для объединения значений с использованием стандартных понятий «и», «или» и «не». Эти операторы ожидаемо представлены словами and, or и not:
x = 4 (x < 6) and (x > 2) # True (x > 10) or (x % 2 == 0) # True not (x < 6) # False
Поклонники булевой алгебры могут заметить, что оператор исключающего ИЛИ не включен. Он, конечно, может быть построен несколькими способами путем составления других операторов. Или же вы можете использовать хитрый трюк:
Он, конечно, может быть построен несколькими способами путем составления других операторов. Или же вы можете использовать хитрый трюк:
# (x > 1) xor (x < 10) (x > 1) != (x < 10) # False
Иногда в языке возникает путаница: когда использовать логические операторы (and, or, not), а когда побитовые (&, |, ~). Ответ кроется в их названиях: логические операторы следует использовать, когда вы хотите вычислить логические значения (т.е. истинность или ложность) утверждений. Побитовые операции следует использовать, когда вы хотите работать с отдельными битами или компонентами рассматриваемых объектов.
Операторы принадлежности и идентичности
Помимо and, or и not, Python также имеет операторы для проверки принадлежности и идентичности. Они следующие:
Они следующие:
| Оператор | Описание |
|---|---|
| a is b | Возвращает True, если a и b — идентичные объекты |
| a is not b | Возвращает True, если a и b — не идентичные объекты |
| a in b | Возвращает True, если a содержится в b |
| a not in b | Возвращает True, если a не содержится в b |
Операторы is и is not проверяют идентичность объекта. Идентичность объекта отличается от равенства, как мы видим здесь:
a = [1, 2, 3] b = [1, 2, 3] a == b # True a is b # False a is not b # True
Как выглядят одинаковые объекты? Вот пример:
a = [1, 2, 3] b = a a is b # True
Разница между этими двумя случаями в том, что в первом a и b указывают на разные объекты, а во втором они указывают на один и тот же объект. Оператор
Оператор is проверяет, указывают ли две переменные на один и тот же контейнер (объект), а не на то, что содержит контейнер.
Новички часто испытывают искушение использовать is, хотя на самом деле имеют в виду ==. Подробнее о разнице между == и is можно почитать в статье «Чем == отличается от is?«.
Операторы принадлежности проверяют принадлежность к составным объектам. Так, например, мы можем написать:
1 in [1, 2, 3] # True 2 not in [1, 2, 3] # False
Эти операции членства являются примером простоты Python по сравнению с языками более низкого уровня, такими как C. В языке C членство обычно определяется путем ручного построения цикла по списку и проверки равенства каждого значения. В Python вы просто печатаете то, что хотите узнать, в манере, напоминающей простой текст.
Заключение
Итак, сегодня мы разобрали на примерах различные операторы в Python. Надеемся вам было полезно! Успехов в написании кода!
Перевод статьи «Basic Python Semantics: Operators».
Операторы в Python
Назад в начало
В языке программирования Python есть арифметические, логические и операторы сравнения.
Сложение:
# Cложение
print(10 + 30)
# Вывод
>> 40
Вычитание:
# Вычитание
print(30 — 20)
# Вывод
>> 10
Умножение:
# Умножение
print(2 * 9)
# Вывод
>> 18
Деление:
# Деление
print(100 / 25)
# Вывод
>> 4
Кроме всем знакомой четверки есть и несколько экзотических операторов: взятие остатка от деления, деление нацело, возведение в степень.
Взятие остатка от деления:
# Взятие остатка от деления на 2
print(0 % 2)
print(1 % 2)
print(2 % 2)
print(3 % 2)
print(4 % 2)
# Вывод
>> 0 # 0 % 2
>> 1 # 1 % 2
>> 0 # 2 % 2
>> 1 # 3 % 2
>> 0 # 4 % 2
# Взятие остатка от деления на 3
print(0 % 3)
print(1 % 3)
print(2 % 3)
print(3 % 3)
print(4 % 3)
print(5 % 3)
print(6 % 3)
# Вывод
>> 0 # 0 % 3
>> 1 # 1 % 3
>> 2 # 2 % 3
>> 0 # 3 % 3
>> 1 # 4 % 3
>> 2 # 5 % 3
>> 0 # 6 % 3
Деление нацело:
# Деление нацело на 10
print(91 // 10)
print(85 // 10)
print(16 // 10)
print(8 // 10)
# Вывод
>> 9 # 91 // 10
>> 8 # 85 // 10
>> 1 # 16 // 10
>> 0 # 8 // 10
# Деление нацело на 2
print(14 // 2)
print(15 // 2)
print(7 // 2)
print(6 // 2)
# Вывод
>> 7 # 14 // 2
>> 7 # 15 // 2
>> 3 # 7 // 2
>> 3 # 6 // 2
Возведение в степень:
# Возведение в степень числа 2
print(2 ** 0) # 1
print(2 ** 1) # 2
print(2 ** 2) # 2 * 2
print(2 ** 3) # 2 * 2 * 2
print(2 ** 4) # 2 * 2 * 2 * 2
# Вывод
>> 1
>> 2
>> 4
>> 8
>> 16
Операторы сравнения (╮°-°)╮ могут возвращать всего два результата: True и False.
Оператор равенства == возвращает True, если числа равны, и False в противном случае.
a = 10
b = 10
print(a == b)
# Вывод
>> True
a = 8
b = 7
print(a == b)
# Вывод
>> False
Оператор неравенства != возвращает True, если числа не равны, и False в противном случае.
a = 8
b = 7
print(a != b)
# Вывод
>> True
Оператор больше > возвращает True, если первое число больше второго, и False в противном случае.
a = 8
b = 7
print(a > b)
print(b > a)
# Вывод
>> True # a > b
>> False # b > a
Оператор меньше
c = 100
d = 200
print(c
print(d
# Вывод
>> True # c
>> False # d
Оператор меньше или равно
Оператор больше или равно >= возвращает True, если первое число больше второго или равно ему, и False в противном случае.
c = 200
d = 200
print(c >= d)
print(d
# Вывод
>> True # c >= d
>> True # d
Иногда требуются выполнение нескольких операторов сравнения сразу. Для таких целей существует оператор and (оператор логического умножения, конъюнкция).
print(10 > 0 and 5 > 0)
print(10 % 2 == 0 and 12 % 2 == 0) # оба числа четные
# Вывод:
>> True
>> True
Если хотя бы один из операторов равен False, то результат оператора будет равен False. Конъюкция истинна в том случае, когда все условия истинны.
print(10 > 100 and 5 > 0 and 10 > 0) # False
# Вывод:
>> False
Логическое сложение (дизъюнкция) или оператор or требует выполнения ХОТЯ БЫ одного условия.
print(10 > 100 or 5 > 100 or 10 > 0) # True
print(1 == 0 or 2 == 0) # False, оба условия ложны
# Вывод:
>> True
>> False
Последний из операторов — это оператор инверсии not. Оператор not изменяет (инвертирует) значение на противоположное.
Оператор not изменяет (инвертирует) значение на противоположное.
print(not False) # True
print(not True) # False
print(not 2 == 0) # True
# Вывод:
>> True
>> False
>> True
Оператор not выполняется в приоритете.
print(not 1 == 0 or 2 == 0) # True, значение первого условия инвертировано
# Вывод:
>> True
1. Одинаковая четность
Даны два целых числа: A, B. Проверить истинность высказывания: «Числа A и B имеют одинаковую четность».
# Ввод:
>> 0
>> 1
# Вывод:
>> False
# Ввод:
>> 2
>> 10
# Вывод:
>> True
2. Одно положительное
Даны три целых числа: A, B, C. Проверить истинность высказывания: «Хотя бы одно из чисел A, B, C положительное».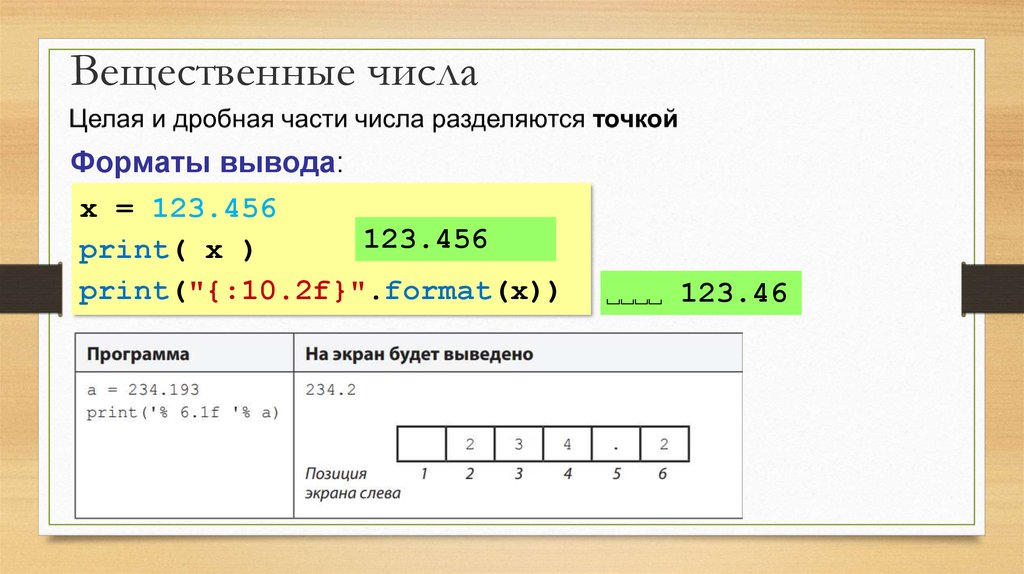
# Ввод:
>> 0
>> -1
>> -10
# Вывод:
>> False
# Ввод:
>> -1
>> 1
>> 0
# Вывод:
>> True
3. Последняя цифра
Дано натуральное число. Выведите его последнюю цифру.
# Ввод:
>> 2345678
# Вывод:
>> 8
# Ввод:
>> 19
# Вывод:
>> 9
4. Цифры двузначного
Дано двузначное число. Найдите сумму его цифр.
# Ввод:
>> 22
# Вывод:
>> 4
# Ввод:
>> 99
# Вывод:
>> 18
5. Цифры трехзначного
Дано трехзначное число. Найдите сумму его цифр.
# Ввод:
>>123
# Вывод:
>> 6
# Ввод:
>> 332
# Вывод:
>> 8
6. Разные цифры
Разные цифры
Дано трехзначное число. Проверить истинность высказывания: «Все цифры данного числа различны».
# Ввод:
>> 123
# Вывод:
>> True
# Ввод:
>> 332
# Вывод:
>> False
7. Часы (финальный босс)
С начала суток прошло N секунд (N — целое). Найти количество часов, минут и секунд на электронных часах.
# Ввод:
>> 1000
# Вывод:
>> 0 16 40
# Ввод:
>> 10000
# Вывод:
>> 2 46 40
# Ввод:
>> 85001
# Вывод:
>> 23 36 41
python — Найти остаток от деления числа
Asked
Изменено 4 месяца назад
Просмотрено 707k раз
Как я могу найти остаток от деления числа в Python?
Например:
Если число равно 26, а разделенное число равно 7, то остаток от деления равен 5.
(поскольку 7+7+7=21 и 26-21=5.)
- python
- по модулю
- целочисленное деление
1
вы ищете оператор по модулю:
a % b
например:
>>> 26 % 7 5
Конечно, может быть, они хотели, чтобы вы сами реализовали это, что тоже не составило бы особого труда.
2
Остаток от деления можно узнать с помощью оператора % :
>>> 26%7 5
Если вам нужно и частное, и модуль, есть встроенная функция divmod :
>>> секунды = 137 >>> минуты, секунды= divmod(секунды, 60)
0
26 % 7 (вы получите остаток)
26 / 7 (вы получите делитель, может быть числом с плавающей запятой)
26 // 7 (вы получите делитель, только целое число)
1
Если вы хотите получить частное и остаток в одной строке кода (более общий вариант использования), используйте:
частное, остаток = divmod(делимое, делитель) #или же разделмод (26, 7)
1
В Python 3. 7 появилась новая функция
7 появилась новая функция math.remainder() :
из остатка импорта математики печать (остаток (26,7))
Вывод:
-2.0 # не 5
Обратите внимание, как указано выше, это не то же самое, что % .
Ссылка на документацию:
мат. остаток (х, у)
Возвращает остаток x в стиле IEEE 754 с уважение к ю. Для конечного x и конечного отличного от нуля y это разница x — n*y, где n — целое число, ближайшее к точному значению частного x / y. Если x / y находится ровно посередине между двумя последовательных целых чисел, для n используется ближайшее четное целое число. остаток r = остаток (x, y), таким образом, всегда удовлетворяет абс (r) <= 0,5 * абс(у).
Особые случаи следуют IEEE 754: в частности, остаток(x, math.inf) является x для любого конечного x, а остаток (x, 0) и остаток (math.inf, x) поднять ValueError для любого не-NaN x. Если результат остатка операция равна нулю, этот ноль будет иметь тот же знак, что и x.
На платформах, использующих двоичные числа с плавающей запятой IEEE 754, результат этого операция всегда точно представима: ошибка округления невозможна. представил.
Issue29962 описывает обоснование создания новой функции.
1
Если вы хотите избежать модуля, вы также можете использовать комбинацию четырех основных операций 🙂
26 - (26 // 7 * 7) = 5
Используйте % вместо / при делении. Это вернет вам остаток. Итак, в вашем случае
26% 7 = 5
Мы можем решить это с помощью оператора модуля (%)
26 % 7 = 5;
но 26/7 = 3, потому что это даст частное, но оператор% даст остаток.
1
Модуль будет правильным ответом, но если вы делаете это вручную, это должно сработать.
число = ввод ("Введите число:")
div = input("Введите делитель:")
в то время как число >= дел:
число -= дел. напечатать номер
напечатать номер
1
Остаток можно найти с помощью оператора по модулю Пример
а=14 б=10 печать (а% б)
Будет напечатано 4
1
Если вам нужен остаток от задачи на деление, просто используйте настоящие правила остатка, как в математике. Конечно, это не даст вам десятичного вывода.
валон = 8 валдва = 3 х = валон / валтво r = valone - (valtwo * x) print "Ответ: %s с остатком %s" % (x, r)
Если вы хотите сделать это в формате калькулятора, просто замените valone = 8 с valone = int(input("Value One")) . Сделайте то же самое с valtwo = 3 , но, очевидно, с другими переменными.
1
Вот целочисленная версия остатка в Python, которая должна давать те же результаты, что и оператор «%» в C:
по умолч. остаток(n, d):
return (-1, если n < 0, иначе 1) * (абс (n) % абс (d))
Ожидаемые результаты:
Остаток(123, 10) == 3 остаток(123, -10) == 3 остаток(-123, 10) == -3 остаток(-123, -10) == -3
вы можете определить функцию и вызвать ее остаток с двумя значениями, такими как rem (число1, число2), которая возвращает число1% число2 затем создайте время и установите для него значение true, затем распечатайте два входа для вашей функции, содержащие номера 1 и 2, затем напечатайте (rem (число1, число2)
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
python - Как мне делить без остатка, если я беру случайные целые числа?
Задавать вопрос
Спросил
Изменено 1 год, 10 месяцев назад
Просмотрено 818 раз
Я еще новичок в программировании.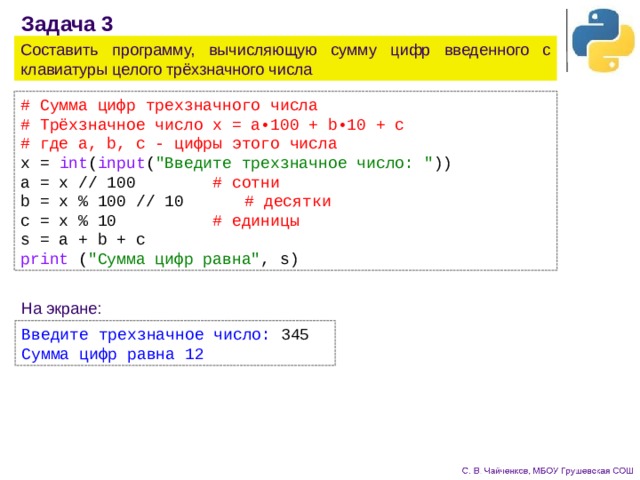 Я хотел запрограммировать полный скрипт, в котором я могу выбирать операторы и получать 2 случайных числа и так далее.
Это сработало, но если я хочу что-то разделить, есть некоторые вычисления, такие как 59: 6 = с примерно 9 цифрами после запятой.
В конце концов, я закончил с этим кодом для разделительной части
Я хотел запрограммировать полный скрипт, в котором я могу выбирать операторы и получать 2 случайных числа и так далее.
Это сработало, но если я хочу что-то разделить, есть некоторые вычисления, такие как 59: 6 = с примерно 9 цифрами после запятой.
В конце концов, я закончил с этим кодом для разделительной части
def Division():
х = случайный (1, 100)
у = случайный (1, 10)
a = int(input("Задача: что такое " + str(x) + ":" + str(y) + "?\n"))
б = х / у
г = раунд (б, 0)
если а == г:
распечатать("Хорошо!")
Начало()
еще:
print("Неверно! Правильный ответ: " + str(g))
Начало()
Это не лучшее решение, которое я знаю, но я хочу только вычислить без остатка, но не знаю как. Какие-нибудь советы?
Весь мой код, если хотите проверить:
из случайного импорта randint
защита плюс():
х = рандом (1, 1000)
у = рандинт (1, 1000)
a = int(input("Задача: что такое " + str(x) + "+" + str(y) + "?\n"))
б = х + у
если а == х+у:
распечатать("Хорошо!")
Начало()
еще:
print("Неверно! Правильный ответ: " + str(b))
Начало()
деф минус():
х = случайный (1, 100)
у = случайный (1, 100)
если х < у:
минус()
еще:
Распечатать()
a = int(input("Задача: что такое " + str(x) + "-" + str(y) + "?\n"))
б = х - у
если а == х-у:
распечатать("Хорошо!")
Начало()
еще:
print("Неверно! Правильный ответ: " + str(b))
Начало()
умножение по определению():
х = случайный (1, 10)
у = случайный (1, 10)
a = int(input("Задача: что такое " + str(x) + "*" + str(y) + "?\n"))
б = х * у
если а == х*у:
распечатать("Хорошо!")
Начало()
еще:
print("Неверно! Правильный ответ: " + str(b))
Начало()
деф деление():
х = случайный (1, 100)
у = случайный (1, 10)
a = int(input("Задача: что такое " + str(x) + ":" + str(y) + "?\n"))
б = х / у
г = раунд (б, 0)
если а == г:
распечатать("Хорошо!")
Начало()
еще:
print("Неверно! Правильный ответ: " + str(g))
Начало()
деф старт():
v = input("Какой оператор вы хотите использовать? (+, -, *, :): ")
если v == '+':
плюс()
Элиф v == '-':
минус()
Элиф v == '*':
умножение()
Элиф v == ':':
разделение()
еще:
print(">>> Конец. ..")
Начало()
..")
Начало()
- python
- python-3.x
- math
- случайный
- разделить
3
Случайным образом выберите результат деления и один из делителей, затем перемножьте их, чтобы получить первое число. Например, если вы генерируете 6 и 4, запросите 24/6.
def Division():
б = случайный (1, 10)
у = случайный (1, 10)
х = б * у
a = int(input("Задача: что такое " + str(x) + ":" + str(y) + "?\n"))
если а == б:
распечатать("Хорошо!")
Начало()
еще:
print("Неверно! Правильный ответ: " + str(b))
Начало()
0
вы ищете оператор div, который в python равен // пример: 5 // 2 == 2
Редактировать: Я снова прочитал ваш вопрос, в этом случае вам нужно генерировать случайные числа немного по-другому
g = randint(1, 10) у = случайный (1, 10) х = г * у
, поэтому ответ g вычисляется до x, а y после этого со случайным y,g вы вычисляете x, который ограничен в (1,100)
4
Альтернативный (и значительно менее полезный здесь) вариант по сравнению с теми, которые были предоставлены, — использовать модуль дробей : вы можете задать ему числитель и знаменатель (или строковую дробь), и он автоматически упростит дробь:
>>> дроби.Дробь(32, 8) Дробь(4, 1) >>> дроби.Дробь(32, 9) Дробь(32, 9) >>> дроби.Дробь(32, 10) Дробь(16, 5)
Дроби, упрощающие до знаменателя 1 — целые числа.
2
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Оператор по модулю и деление по полу в Python
В дополнение к обычным операторам сложения, вычитания, умножения и деления стандартная библиотека Python включает некоторые арифметические операторы, с которыми вы, возможно, менее знакомы. В этом посте я расскажу о модуле (
В этом посте я расскажу о модуле ( % ) и этажное подразделение ( // ), а также некоторые распространенные ошибки, связанные с ними.
Что делают деление по модулю и полу?
Модуль по модулю
Оператор по модулю используется для выполнения евклидова деления. Вы почти наверняка узнали о евклидовом делении в школе, даже если не знали, как оно называется.
При выполнении евклидова деления вы начинаете с делимого (число, которое вы хотите разделить) и делителя (число, на которое нужно разделить делимое). Допустим, 10 и 3 .
В том, что мы могли бы назвать «стандартным делением», результатом 10/3 является повторяющееся 3,333 или 3 и треть. В евклидовом делении нас не интересуют числа после запятой. Нам важен целочисленный результат деления (в данном случае 3 ), который называется частным .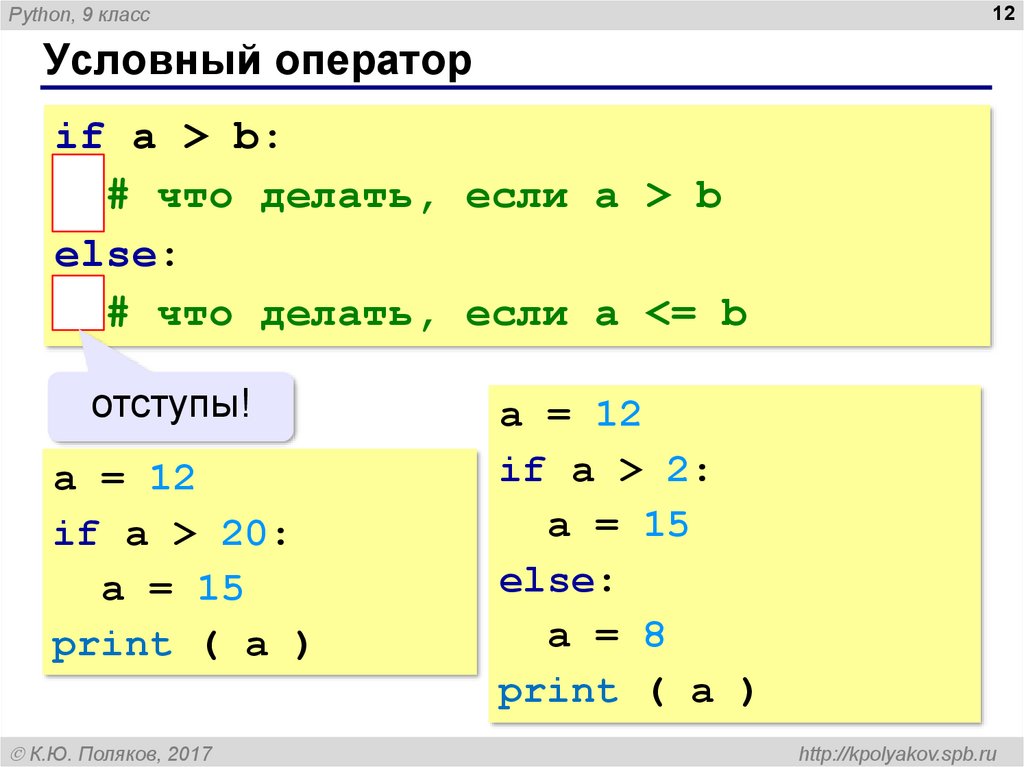 Сумма, оставшаяся после деления, называется 9.0090 остаток , который в данном случае равен
Сумма, оставшаяся после деления, называется 9.0090 остаток , который в данном случае равен 1 .
Чтобы дать вам еще один пример, 11 / 3 дает нам частное 3 и остаток 2 .
В Python оператор по модулю просто возвращает остаток:
>>> 10 % 3 1 >>> 11 % 3 2
Поэтажное деление
Поэтажное деление также используется для выполнения евклидова деления, но, в отличие от оператора по модулю, деление по этажам дает частное , а не остаток.
Рассмотрим пару примеров:
>>> 10 // 3 3 >>> 9 // 2 4
Мы можем создать небольшую функцию для вывода полного результата евклидова деления, например:
def euclidean_division(x, y):
частное = х // у
остаток = х % у
print(f"{частное} остаток {остаток}")
euclidean_division(10, 3) # 3 остаток 1
euclidean_division(11, 3) # 3 остаток 2
Однако есть проблема. Что происходит, когда мы вызываем нашу функцию с отрицательными числами?
>>> евклидов_дивизион (10, -3) -4 остаток -2
Это выглядит неправильно.
-3 умножить на -4 равно 12 , что больше, чем 10 . В результате мы должны были получить -3 остаток 1 . Так что же происходит?
Это вина деления пола
Картина, которую я нарисовал для вас ранее о евклидовом делении, не совсем точна. Для положительных целых чисел деление по полу и по модулю работает точно так же, как евклидово деление, но все становится сложнее, когда дело доходит до отрицательных чисел.
Это связано с округлением. Если мы посмотрим на документацию Python по арифметическим операторам, мы найдем подсказку о том, что происходит:
[T] он результат [деления пола] — это результат математического деления с применением к результату функции «пол».
Итак, давайте посмотрим на документацию по функции floor .
Возвращает нижний предел x, наибольшее целое число, меньшее или равное x.
И вот в чем проблема.
-4 считается менее повторяющимся, чем -3,333 . Это левее на числовой прямой. Это означает, что деление этажа всегда будет округляться от нуля для отрицательных чисел и до нуля для положительных чисел.
>>> 10 // 3 3 # 3,333 раунда в ноль >>> 10 // -3 -4 # -3,333 раунда от нуля >>> 9 // 2 4 # 4,5 раунда в ноль >>> 9 // -2 -5 # -4,5 раунда до нуля
Так в чем проблема с модулем?
Мы выяснили, почему мы получаем неожиданные результаты от деления на пол и отрицательных чисел, но наш остаток также оказался не таким, как мы ожидали. Так почему же?
Оказывается, деление по модулю и деление на пол являются тесно связанными операторами, о которых вы могли прочитать, если немного заглянули в документацию. Модульное и напольное деление связаны следующим тождеством: x = (x // y) * y + (x % y) .
Это означает, что результат деления этажа напрямую влияет на результат операции по модулю. Мы можем изменить вышеприведенное так: (х % у) = х - (х // у) * у .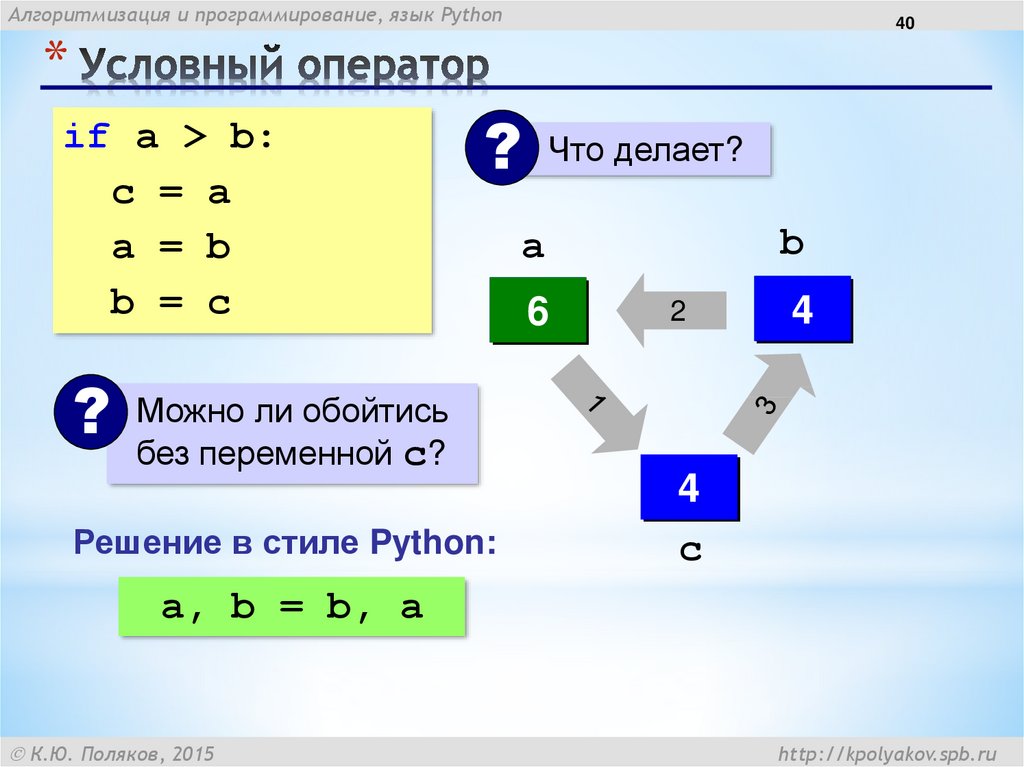
Давайте попробуем один из наших предыдущих примеров, 10 % -3 :
10 % -3 = 10 - (-3) * (10 // -3) 10 % -3 = 10 - (-3) * (-4) # Помните, здесь деление пола округляется от нуля 10 % -3 = 10 - 12 10 % -3 = -2
И мы получаем точно такой же результат, как и раньше: 10 % -3 = -2 .
Несколько заключительных замечаний
В этом заключительном разделе я просто хочу упомянуть еще несколько интересных вещей о делении по модулю и полу. Однако, прежде чем я углублюсь в это, я думаю, важно отметить, что реализация деления по полу и по модулю в Python не является ошибкой. Однако я считаю важным понимать, когда и как такие реализации отличаются от нашего интуитивного понимания, потому что тогда мы сможем использовать эту реализацию как инструмент, и она перестанет быть источником, возможно, неприятных ошибок.
Преобразование типов
Одна из интересных особенностей деления на пол в Python заключается в том, что оно не обязательно производит число с плавающей запятой. Фактически, во всех наших примерах результатом было целое число. Это полностью отличается от стандартного деления в Python, которое всегда дает число с плавающей запятой.
Фактически, во всех наших примерах результатом было целое число. Это полностью отличается от стандартного деления в Python, которое всегда дает число с плавающей запятой.
Оператор по модулю работает так же, возвращая целое число, если оба операнда были целыми числами.
Если любой из операндов является числом с плавающей запятой, деление по модулю и по полу даст число с плавающей запятой.
Использование чисел с плавающей запятой
Хотя все примеры в этом посте были целыми числами, вполне возможно использовать числа с плавающей запятой для любого операнда, и они работают точно так же, они просто дают число с плавающей запятой.
Пример из документации: 3,14 % 0,7 , что даст 0,34 .
Комплексные числа
Комплексные числа — это числа с действительной и мнимой частями. Здесь их стоит отметить только потому, что ни модульное деление, ни деление на пол не могут принимать комплексное число в качестве операнда. Попытка использовать комплексное число для деления на пол или операций по модулю приведет к повышению
Попытка использовать комплексное число для деления на пол или операций по модулю приведет к повышению Ошибка типа .
Резюме
- Для положительных чисел деление по полу и по модулю работает как евклидово деление, получая частное и остаток соответственно.
- Для отрицательных чисел обе операции приведут к несколько неожиданным результатам.
- Полное деление всегда округляется от нуля для отрицательных чисел, поэтому
-3,5будет округлено до-4, но к нулю для положительных чисел, поэтому3,5будет округлено до3. - Деление по полу и по модулю связаны следующим тождеством:
x = (x // y) * y + (x % y), поэтому модуль также дает неожиданные результаты для отрицательных чисел, а не только для деления по полу. .
Я надеюсь, что вы узнали что-то новое, и если вы хотите еще больше улучшить свои навыки Python, ознакомьтесь с нашим полным курсом Python.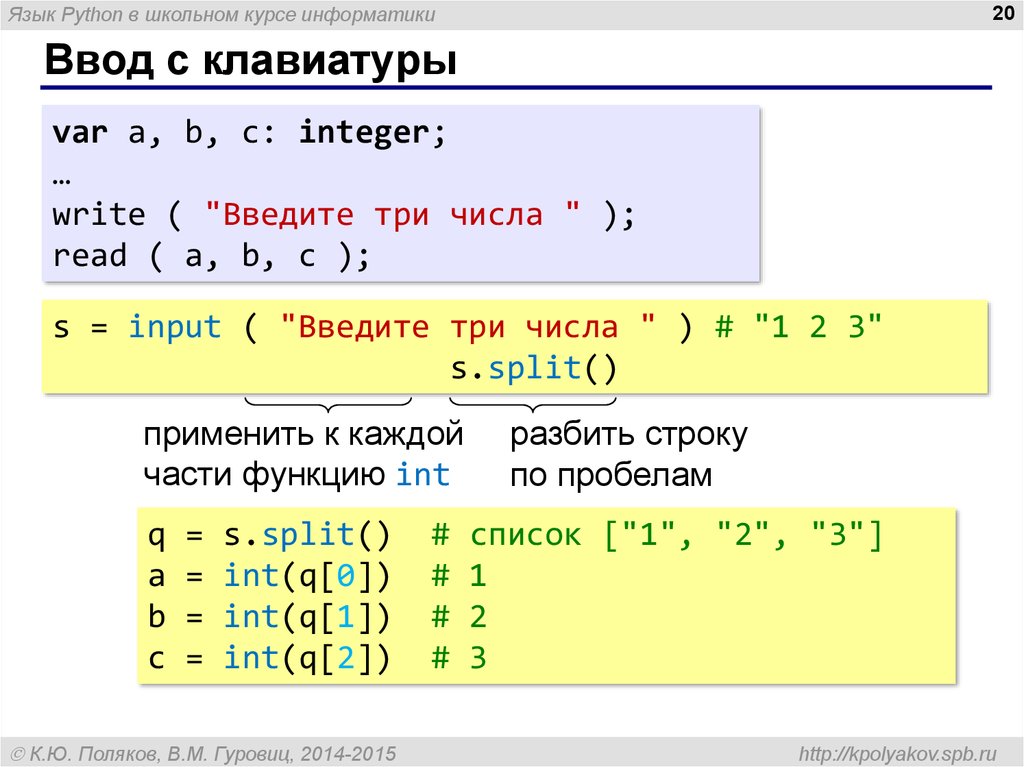
элементарная теория чисел. Является ли целочисленное деление однозначно определенным в математике?
Спросил
Изменено 7 лет назад
Просмотрено 4k раз
$\begingroup$
В настоящее время я изучаю программирование на Java, и меня немного потрясла концепция целочисленного деления. Я предполагаю, что это просто вопрос привыкания к тому, что $1/2=0$, но я боюсь, что это может занять некоторое время, учитывая, что это свойство оператора деления (/) несовместимо с математикой.
Или это? Чтение раздела Википедии о делении целых чисел, кажется, подразумевает, что это неоднозначное понятие (см. следующую ссылку). Утверждение о том, что множество целых чисел не замкнуто при делении (т. е. целочисленное деление может дать элементы, которые не являются целыми числами), имеет для меня смысл, как и вариант 2 в следующем списке. Однако список меня озадачивает. Его существование подразумевает, что у нас есть выбор в этом вопросе, и что один из них (вариант 4) позволяет вам назвать «$1/2=0$» истинным утверждением.
Однако список меня озадачивает. Его существование подразумевает, что у нас есть выбор в этом вопросе, и что один из них (вариант 4) позволяет вам назвать «$1/2=0$» истинным утверждением.
Значит, целочисленное деление — дело вкуса? Может ли «$1/2=0$» быть истинным утверждением даже в строгом математическом смысле, в зависимости от того, как вы его интерпретируете?
- элементарная теория чисел
$\endgroup$
7
$\begingroup$
Все зависит от того, что вы хотите, чтобы ваша операция "разделения" выполнялась. Другими словами, каким свойствам он должен удовлетворять. В действительных числах (или рациональных, или комплексных и т. д.) наиболее существенное свойство связывает $/$ с $\times$:
Деление обратно умножению: $a/b = c$ тогда и только тогда, когда $b \times c = a$.
Однако даже в привычных системах счисления операция не закрыта.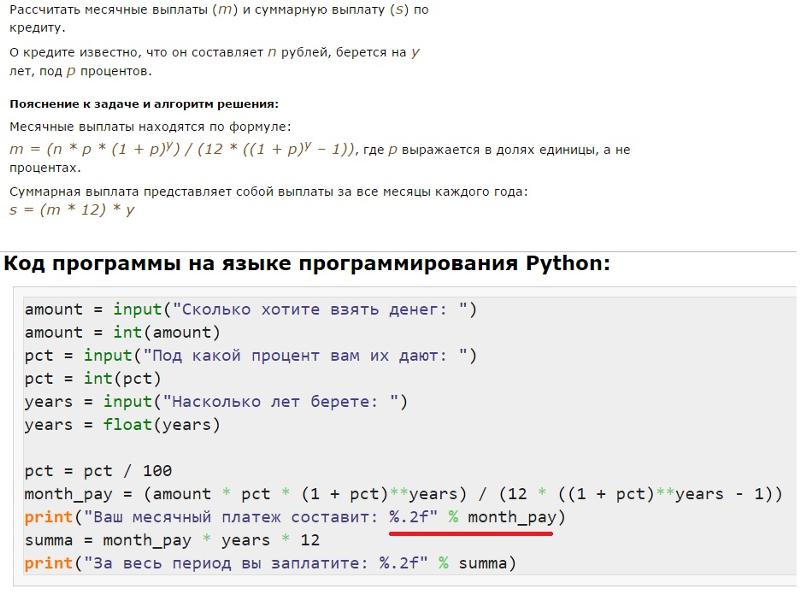 $a/0$ не определено (поскольку не существует действительного (или рационального, или комплексного) $c$ такого, что $0 \times c = a$. Ситуация еще более ограничена в целых числах, где $a/b$ может только быть определено, когда $b$ делит $a$
$a/0$ не определено (поскольку не существует действительного (или рационального, или комплексного) $c$ такого, что $0 \times c = a$. Ситуация еще более ограничена в целых числах, где $a/b$ может только быть определено, когда $b$ делит $a$
Операция «целочисленное деление» (существующая во многих компьютерных приложениях с использованием одного и того же символа «$/$») фиксирует свойство замыкания (то есть $a/b$ определяется для всех целых чисел, за исключением случаев, когда $b=0$), но в целом не имеет свойства Inverse. ИМХО, должно быть отдельное обозначение, такое как функция «Частное» в Mathematica:
Частное[a,b] = целочисленное частное $a$ и $b$, примерно, сколько целых раз $b$ входит в $a$.
Когда вы говорите о согласованности, это всегда относится к свойствам операции. Частное не обладает теми же свойствами, что и $/$, и является четко определенной функцией целых чисел (кроме случаев, когда делитель равен $0$).
Надеюсь, это поможет!
$\endgroup$
4
$\begingroup$
Вспомните истинный смысл деления: мы говорим, что $a/b=c$ тогда и только тогда, когда $a = b \cdot c$.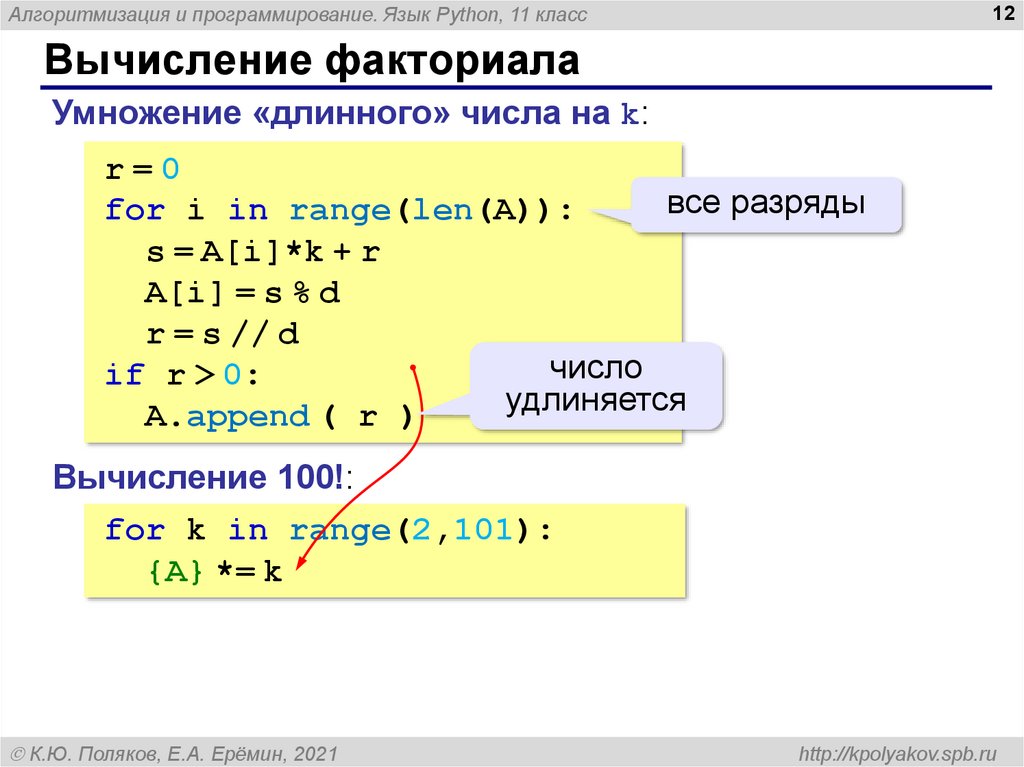 Но поскольку не существует целого числа $z$, такого что $2z = 1$, это означает, что простое определение деления целых чисел по необходимости является неполным: $1/2$ в этом смысле просто не существует.
Но поскольку не существует целого числа $z$, такого что $2z = 1$, это означает, что простое определение деления целых чисел по необходимости является неполным: $1/2$ в этом смысле просто не существует.
С другой стороны, есть довольно простое решение, которое на самом деле также предоставляется распространенными языками программирования: Вы можете определить деление как деление с остатком, то есть: Мы говорим, что $a/b$ равно $q$ с остатком $r$ тогда и только тогда, когда $a = bq + r$. Указав, что, например, $0 \le r < b$, это определение дает уникальные результаты для всех $a$ и $b \neq 0$, а значение $q$ равно для натуральных $a$ и $b$ , ровно $\mathtt{a/b}$ для большинства языков программирования. В языках, производных от C (например, Java), остаток $r$ задается как $\mathtt{a\%b}$.
$\endgroup$
3
$\begingroup$
Как уже упоминалось, математическая нотация сильно перегружена, когда один символ может использоваться для нескольких потенциально несовместимых понятий. Правильное понятие (обычно) дается или может быть выведено из контекста, по крайней мере, до необходимого уровня детализации. Языки программирования усугубляют эту проблему.
Правильное понятие (обычно) дается или может быть выведено из контекста, по крайней мере, до необходимого уровня детализации. Языки программирования усугубляют эту проблему.
В конце концов, любой символ может означать что угодно, если вы даете определение. Тем не менее, целочисленное деление не является специальным изобретением, хотя, возможно, оно неправильно реализовано в большинстве языков программирования. Взяв «основное свойство» деления Шона, мы можем ослабить его до другого свойства, полностью характеризующего целочисленное деление. Пусть $b$ — натуральное число, а $a$ и $c$ — любые целые числа. Тогда следующее свойство (связность или присоединение Галуа) характеризует целочисленное деление:
$$\textrm{forall}a \textrm{ и } c\quad a\times{}b \leq c\quad \textrm{тогда и только тогда, когда}\quad a \leq c/b$$
Обратите внимание, что это также эквивалентно
$$\textrm{forall}a \textrm{ и } c\quad a\times{}b \gt c\quad \textrm{тогда и только тогда, когда}\quad a \gt c/b$$
Так что же должно быть $5/3$? Если мы скажем $0$, то для всех $a$, $a \gt 5/3 = 0$ следует $a\times{}3 \gt 5$, что неверно для $a=1$..files/image030.png) Если мы скажем $2$, то для всех $a$, $a \leq 5/3 = 2$ следует $a\times{}3 \leq 5$, что неверно для $a=2$. $a=1$ удовлетворяет этому свойству. Что еще интереснее, определите, какой должна быть $(-5)/3$, и сравните ее с вашим любимым языком программирования.
Если мы скажем $2$, то для всех $a$, $a \leq 5/3 = 2$ следует $a\times{}3 \leq 5$, что неверно для $a=2$. $a=1$ удовлетворяет этому свойству. Что еще интереснее, определите, какой должна быть $(-5)/3$, и сравните ее с вашим любимым языком программирования.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. Оператор остатка
Оператор остаткаPython | 8 примеров оператора остатка Пайтона
Остаточные операторы Python используются для вычисления некоторых операндов. Операторы — это специальные символы, которые используются с операндами для выполнения некоторых операций, таких как сложение, вычитание, деление и т. д. Операторы могут обозначаться как «+» для сложения, «-» для вычитания, «/» для деления, «*» для умножения и т. д. В Python оператор модуля представляет собой символ процента ('%'), который также известен как оператор остатка Python, тогда как существует оператор деления для целого числа как '//', который также работает только с целочисленными операндами возвращает остаток, но в целых числах. Точно так же оператор остатка Python или оператор модуля также возвращает остаток при разделении двух операндов, т. Е. Один операнд делится с другим операндом, что приводит к остатку. Этот оператор остатка используется как для целых чисел, так и для чисел с плавающей запятой.
Синтаксис:
x % y
Дивиденд % Делитель: Остаток получается при делении x на y. Остаток будет целым числом, если оба делимых являются целыми числами. Остаток будет числом с плавающей запятой, если один из делимых или делителей является числом с плавающей запятой.
Примеры оператора напоминания Python
Ниже приведены различные примеры оператора напоминания Python.
Пример №1
Код:
х = 5
у = 2
г = х % у
print ('Remainder is:', r) Вывод:
Объяснение: В приведенном выше примере x = 5 , y = 2, поэтому 5 % 2 , 2 входит в 5 два раза, что дает 4 , поэтому остаток равен 5 – 4 = 1. В Python остаток получается с помощью функции numpy.ramainder() в numpy. Он возвращает остаток от деления двух массивов и возвращает 0, если массив делителей равен 0 (ноль) или если оба массива имеют массив целых чисел. Эта функция также используется для отдельных номеров.
Эта функция также используется для отдельных номеров.
Пример #2
Код:
импортировать numpy как np
п1 = 6
п2 = 4
г = np.остаток (n1, n2)
print ("Дивиденд равен:", n1)
print ("Делитель равен:", n2)
print ("Остаток: ", r) Вывод:
Объяснение: В приведенном выше примере используется функция numpy.remainder() для данного делимого и делителя, чтобы найти остатки двух, что работает аналогично модульный оператор. В этом примере это 6 % 4, 4 входит в 6, один раз, что дает 4, поэтому остаток 6 - 4 = 2.
Пример #3
Код:
импортировать numpy как np
arr1 = np.массив ([7, -6, 9])
массив2 = np.массив ([3, 4, 3])
rem_arr = np.remainder (arr1, arr2)
print ("Массив дивидендов: ", arr1)
print ("Массив делителей: ", arr2)
print ("Массив остатка: ", rem_arr) Вывод:
Объяснение: В приведенном выше примере функция numpy. remainder() может использоваться в списке элементов для вычисления остатка соответствующий элемент в списке или массиве элементов. у нас есть два массива [7 -6 9] и [3 4 3], поэтому 7 % 3,3 переходит в 7 два раза, поэтому остаток равен 1, -6 % 4, 4 входит в 6 один раз, поэтому остаток равен 2, 9 % 3, 3 идет в 9 три раза, так что остаток равен 0. Массив значений остатка будет [1 2 0].
remainder() может использоваться в списке элементов для вычисления остатка соответствующий элемент в списке или массиве элементов. у нас есть два массива [7 -6 9] и [3 4 3], поэтому 7 % 3,3 переходит в 7 два раза, поэтому остаток равен 1, -6 % 4, 4 входит в 6 один раз, поэтому остаток равен 2, 9 % 3, 3 идет в 9 три раза, так что остаток равен 0. Массив значений остатка будет [1 2 0].
Пример #4
Оператор остатка или оператор по модулю используется для нахождения четных или нечетных чисел. Ниже приведен фрагмент кода для печати нечетных чисел от 0 до 20.
Код:
для числа в диапазоне (1, 20):
если (число% 2 != 0):
печать (число) Вывод:
Объяснение: В приведенном выше примере с использованием оператора по модулю он выводит из кода нечетные числа от 0 до 20; если число делится на 2 и в остатке получается 0, то мы говорим это как четное число; иначе его нечетное число. Если число равно 2, то 2 % 2 дает остаток 0, так что теперь это четное число, а не нечетное; если число равно 3, то 3% 2 дает остаток 1, который 2 переходит в 3 один раз, поэтому дает 2, а остаток 3 - 2 = 1, что не равно нулю, поэтому заданное число 3 нечетно, и с помощью цикла for он будет проверять до 20 чисел и вывести все нечетные числа от 0 до 20. Оператор по модулю или оператор остатка также используется для чисел с плавающей запятой, в отличие от оператора деления ( // ), который используется только для целых чисел и дает остаток также в целочисленной форме.
Если число равно 2, то 2 % 2 дает остаток 0, так что теперь это четное число, а не нечетное; если число равно 3, то 3% 2 дает остаток 1, который 2 переходит в 3 один раз, поэтому дает 2, а остаток 3 - 2 = 1, что не равно нулю, поэтому заданное число 3 нечетно, и с помощью цикла for он будет проверять до 20 чисел и вывести все нечетные числа от 0 до 20. Оператор по модулю или оператор остатка также используется для чисел с плавающей запятой, в отличие от оператора деления ( // ), который используется только для целых чисел и дает остаток также в целочисленной форме.
Пример #5
Код:
a = input("Дивиденд:\n")
фа = поплавок (а)
b = input("Делитель:\n")
fb = плавающая (b)
fr = fa % fb
print ("Остаток равен", fr) Вывод:
Пример #6
В Python оператор по модулю можно использовать и для отрицательных чисел, что дает тот же остаток, что и для положительных чисел, но отрицательный знак делителя в остатке будет тот же.
Code:
print(-5 % 3)
Output:
Code:
print(5 % -3)
Output:
Logic За кодом:
- -5 % 3 = (1 -2*3) % 3 = 1
- 5 % -3 = (-1 * -2 * -3) % 3 = -1
Объяснение: Эти отрицательные числа используют функцию fmod() для нахождения остатка; если какое-либо из чисел среди делимого или делителя отрицательное, то мы можем даже использовать функцию fmod() математической библиотеки, и это также можно использовать для нахождения остатка чисел с плавающей запятой.
Пример #7
Код:
импортировать математику а = -10 б = 3 print(math.fmod(a,b))
Вывод:
Объяснение: В Python оператор по модулю выдает ошибку, когда делитель равен нулю (0). Обычно это дает ZeroDivisionError, поскольку мы знаем, что любое число, деленное на ноль, равно бесконечности (∞).
Пример #8
Код:
p = 10 д = 0 г = р % д печать (г)
Приведенный выше код выдает ошибку, как показано на снимке экрана ниже.
Вывод:
Код:
p = 10
д = 0
пытаться:
рем = p * q
печать (рем)
кроме ZeroDivisionError как zde:
print("Невозможно разделить на 0") Эту ошибку можно отловить с помощью блоков try-except, как показано на снимке экрана ниже.
Вывод:
Заключение
В Python оператор по модулю — это оператор для получения остатка от деления двух чисел, известного как делимое и делитель. Этот оператор можно использовать для нахождения остатка как целых чисел, так и чисел типа данных с плавающей запятой. Оператор по модулю также является одним из математических операторов, таких как сложение (+), вычитание (-), деление (//) и т. д. Оператор деления используется только для целых чисел, в отличие от оператора по модулю.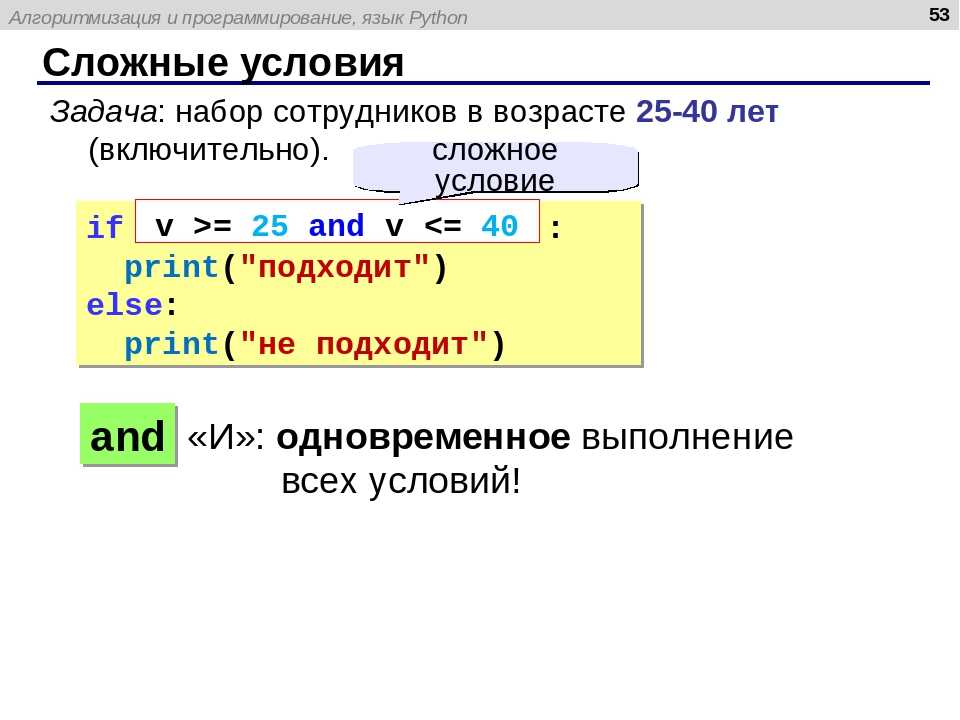 И если делитель равен нулю, мы можем обработать его, обработав исключение, используя блок try-except для вывода ошибки.
И если делитель равен нулю, мы можем обработать его, обработав исключение, используя блок try-except для вывода ошибки.
Рекомендуемые статьи
Как использовать оператор % — Real Python
Смотреть сейчас Это руководство содержит соответствующий видеокурс, созданный командой Real Python. Посмотрите его вместе с письменным учебным пособием, чтобы углубить свое понимание: Python Modulo: Использование оператора %
Python поддерживает широкий спектр арифметических операторов, которые вы можете использовать при работе с числами в своем коде. Одним из таких операторов является оператор по модулю ( % ), который возвращает остаток от деления двух чисел.
В этом уроке вы узнаете:
- Как по модулю работает в математике
- Как использовать оператор по модулю Python с различными числовыми типами
- Как Python вычисляет результаты операции по модулю
- Как переопределить
.в ваших классах, чтобы использовать их с оператором по модулю __mod__()
__mod__() - Как использовать оператор модуля Python для решения реальных проблем
Оператор по модулю Python иногда можно упустить из виду. Но хорошее понимание этого оператора даст вам бесценный инструмент в вашем наборе инструментов Python.
Бесплатный бонус: Нажмите здесь, чтобы получить шпаргалку по Python и изучить основы Python 3, такие как работа с типами данных, словарями, списками и функциями Python.
Модуль в математике
Срок по модулю происходит из раздела математики, называемого модульной арифметикой. Модульная арифметика имеет дело с целочисленной арифметикой на круговой числовой строке с фиксированным набором чисел. Все арифметические операции, выполняемые на этой числовой прямой, будут повторяться, когда они достигнут определенного числа, называемого модулем .
Классическим примером модуля по модулю в модульной арифметике являются двенадцатичасовые часы. Двенадцатичасовые часы имеют фиксированный набор значений от 1 до 12. При счете на двенадцатичасовых часах вы считаете до модуля 12, а затем возвращаетесь к 1. Двенадцатичасовые часы можно классифицировать как « по модулю 12», иногда сокращается до «мод 12».
Двенадцатичасовые часы имеют фиксированный набор значений от 1 до 12. При счете на двенадцатичасовых часах вы считаете до модуля 12, а затем возвращаетесь к 1. Двенадцатичасовые часы можно классифицировать как « по модулю 12», иногда сокращается до «мод 12».
Оператор по модулю используется, когда вы хотите сравнить число с модулем и получить эквивалентное число, ограниченное диапазоном модуля.
Например, вы хотите определить, какое время будет девять часов после 8:00 утра. В двенадцатичасовом формате вы не можете просто прибавить 9 к 8, потому что вы получите 17. Вам нужно взять результат, 17, и используйте mod , чтобы получить его эквивалентное значение в двенадцатичасовом контексте:
8 часов + 9 = 17 часов 17 по модулю 12 = 5
17 mod 12 возвращает 5 . Это означает, что девять часов после 8:00 — это 17:00. Вы определили это, взяв число 17 и применив его к контексту mod 12 .
Теперь, если подумать, 17 и 5 эквивалентны в контексте mod 12 . Если бы вы посмотрели на часовую стрелку в 5:00 и 17:00, она была бы в том же положении. В модульной арифметике есть уравнение, описывающее эту связь:
а ≡ б (mod n)
Это уравнение гласит: « a и b конгруэнтны по модулю n ». Это означает, что a и b эквивалентны в mod n , поскольку они имеют одинаковый остаток при делении на n . В приведенном выше уравнении n является модулем как для a , так и для b . Используя значения 17 и 5 , полученные ранее, уравнение будет выглядеть так:
17 ≡ 5 (mod 12)
Это гласит: « 17 и 5 конгруэнтны по модулю 12 ». 17 и 5 имеют одинаковый остаток 5 при делении на 12 . Таким образом, в
Таким образом, в mod 12 числа 17 и 5 эквивалентны.
Вы можете подтвердить это делением:
17/12 = 1 р 5 5/12 = 0 R 5
Обе операции имеют одинаковый остаток, 5 , поэтому они эквивалентны по модулю 12 .
Может показаться, что это слишком много математических вычислений для оператора Python, но эти знания подготовят вас к использованию оператора по модулю в примерах, приведенных далее в этом руководстве. В следующем разделе вы познакомитесь с основами использования оператора модуля Python с числовыми типами int и float .
Удалить рекламу
Основы Python Modulo Operator
Оператор по модулю, как и другие арифметические операторы, может использоваться с числовыми типами int и float . Как вы увидите позже, его также можно использовать с другими типами, такими как math., 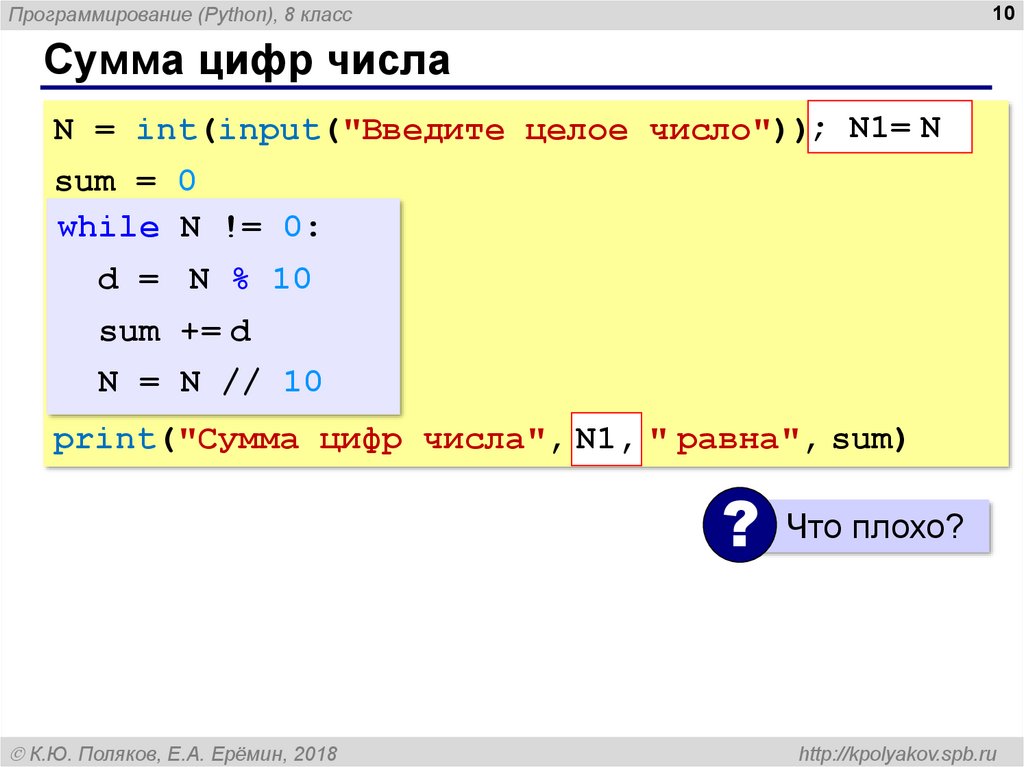 fmod()
fmod() decimal.Decimal и вашими собственными классами.
Оператор по модулю С
int Большую часть времени вы будете использовать оператор по модулю с целыми числами. Оператор по модулю при использовании с двумя положительными целыми числами вернет остаток от стандартного евклидова деления:
.>>>
>>> 15 % 4 3 >>> 17 % 12 5 >>> 240 % 13 6 >>> 10 % 16 10
Будьте осторожны! Как и в случае с оператором деления (/), Python вернет ZeroDivisionError , если вы попытаетесь использовать оператор по модулю с делителем 0 :
>>>
>>> 22 % 0 ZeroDivisionError: целочисленное деление или по модулю на ноль
Далее вы познакомитесь с использованием оператора по модулю с числом с плавающей запятой .
Модульный оператор С
поплавком Аналогично int , оператор по модулю, используемый с float , вернет остаток от деления, но как float значение:
>>>
>>> 12,5 % 5,5 1,5 >>> 17,0 % 12,0 5,0
Альтернативой использованию float с оператором по модулю является использование math. для выполнения операций по модулю над  fmod()
fmod() значениями float :
>>>
>>> импорт математики >>> math.fmod(12.5, 5.5) 1,5 >>> math.fmod(8.5, 2.5) 1,0
Официальная документация по Python предлагает использовать math.fmod() вместо оператора по модулю Python при работе с значениями с плавающей запятой из-за того, как math.fmod() вычисляет результат операции по модулю. Если вы используете отрицательный операнд, вы можете увидеть разные результаты между math.fmod(x, y) и x % y . В следующем разделе вы более подробно изучите использование оператора по модулю с отрицательными операндами.
Как и другие арифметические операторы, оператор по модулю и math.fmod() может столкнуться с проблемами округления и точности при работе с арифметикой с плавающей запятой:
>>>
>>> 13,3 % 1,1 0,09999999999999964 >>> импортировать математику >>> math.fmod(13.3, 1.1) 0,09999999999999964
Если для вашего приложения важна точность операций с плавающей запятой, вы можете использовать оператор по модулю с decimal.Decimal . Вы увидите это позже в этом уроке.
Оператор по модулю с отрицательным операндом
Все операции по модулю, которые вы видели до этого момента, использовали два положительных операнда и возвращали предсказуемые результаты. Когда вводится отрицательный операнд, все становится сложнее.
Как оказалось, способ, которым компьютеры определяют результат операции по модулю с отрицательным операндом, оставляет неоднозначность относительно того, должен ли остаток принимать знак делимого (число, которое делят) или знак делителя (число, на которое делится делимое). Разные языки программирования обрабатывают это по-разному.
Например, в JavaScript остаток будет иметь знак делимого:
8 % -3 = 2
Остаток в этом примере, 2 , положителен, поскольку принимает знак делимого, 8 . В Python и других языках вместо знака делителя будет стоять остаток:
В Python и других языках вместо знака делителя будет стоять остаток:
8 % -3 = -1
Здесь видно, что остаток -1 принимает знак делителя -3 .
Вам может быть интересно, почему остаток в JavaScript равен 2 , а остаток в Python равен -1 . Это связано с тем, как разные языки определяют результат операции по модулю. Языки, в которых остаток принимает знак делимого, используют следующее уравнение для определения остатка:
г = а - (п * усечение (а/п))
В этом уравнении три переменные:
-
rостаток. -
a— дивиденды. -
n— делитель.
trunc() в этом уравнении означает, что используется усеченное деление , которое всегда округляет отрицательное число до нуля. Для получения дополнительной информации см. этапы операции по модулю ниже с использованием
этапы операции по модулю ниже с использованием 8 в качестве делимого и -3 в качестве делителя:
г = 8 - (-3 * усечение (8/-3)) r = 8 - (-3 * усечение (-2,666666666667)) r = 8 - (-3 * -2) # Округление до 0 г = 8 - 6 г = 2
Здесь вы можете увидеть, как такой язык, как JavaScript, получает остаток 2 . Python и другие языки, в которых остаток принимает знак делителя, используют следующее уравнение:
г = а - (п * этаж (а/п))
floor() в этом уравнении означает, что используется деление этажей . С положительными числами деление на пол возвращает тот же результат, что и усеченное деление. Но с отрицательным числом деление на пол округлит результат в меньшую сторону от нуля:
р = 8 - (-3 * этаж(8/-3)) г = 8 - (-3 * пол (-2,666666666667)) r = 8 - (-3 * -3) # Округление от 0 г = 8 - 9 г = -1
Здесь вы можете видеть, что результат равен -1 .
Теперь, когда вы понимаете, откуда берется разница в остатке, вам может быть интересно, почему это имеет значение, если вы используете только Python. Как оказалось, не все операции по модулю в Python одинаковы. В то время как модуль, используемый с типами int и float , будет принимать знак делителя, другие типы не будут.
Вы можете увидеть пример этого, сравнив результаты 8.0 % -3.0 и math.fmod(8.0, -3.0) :
>>>
>>> 8,0 % -3 -1,0 >>> импортировать математику >>> math.fmod(8.0, -3.0) 2.0
math.fmod() принимает знак делимого с использованием усеченного деления, тогда как float использует знак делителя. Позже в этом руководстве вы увидите еще один тип Python, в котором используется знак делимого, 9.0039 десятичный. Десятичный .
Удалить рекламу
Оператор по модулю и
divmod() Python имеет встроенную функцию divmod() , которая внутри использует оператор по модулю.
divmod() принимает два параметра и возвращает кортеж, содержащий результаты деления на пол и по модулю с использованием предоставленных параметров.
Ниже приведен пример использования divmod() с 37 и 5 :
>>>
>>> раздел мод(37, 5) (7, 2) >>> 37 // 5 7 >>> 37 % 5 2
Вы видите, что divmod(37, 5) возвращает кортеж (7, 2) . 7 является результатом деления этажей 37 и 5 . 2 является результатом 37 по модулю 5 .
Ниже приведен пример, в котором второй параметр является отрицательным числом. Как обсуждалось в предыдущем разделе, когда оператор по модулю используется с int , остаток примет знак делителя:
>>>
>>> divmod(37, -5) (-8, -3) >>> 37//-5 -8 >>> 37 % -5 -3 # Результат имеет знак делителя
Теперь, когда у вас была возможность увидеть, как оператор по модулю используется в нескольких сценариях, важно взглянуть на то, как Python определяет приоритет оператора по модулю при использовании с другими арифметическими операторами.
Приоритет оператора по модулю
Как и для других операторов Python, для оператора по модулю существуют особые правила, определяющие его приоритет при вычислении выражений. Оператор по модулю ( % ) имеет тот же уровень приоритета, что и операторы умножения ( * ), деления (/) и деления на пол ( // ).
Взгляните на пример приоритета оператора по модулю ниже:
>>>
>>> 4 * 10 % 12 - 9 -5
И операторы умножения, и операторы по модулю имеют одинаковый уровень приоритета, поэтому Python будет оценивать их слева направо. Вот шаги для вышеуказанной операции:
-
4 * 10оценивается, в результате получается40 % 12 - 9. -
40 % 12оценивается, в результате получается4 - 9. -
4 - 9оценивается, в результате получается-5.
Если вы хотите переопределить приоритет других операторов, вы можете использовать круглые скобки для заключения операции, которую вы хотите оценить первой:
>>>
>>> 4 * 10 % (12 - 9) 1
В этом примере сначала оценивается (12 - 9) , затем 4 * 10 и, наконец, 40 % 3 , что равно 1 .
Python Modulo Operator на практике
Теперь, когда вы ознакомились с основами оператора по модулю Python, вы посмотрите на несколько примеров его использования для решения реальных задач программирования. Иногда может быть трудно определить, когда использовать оператор по модулю в вашем коде. Приведенные ниже примеры дадут вам представление о множестве способов его использования.
Как проверить, является ли число четным или нечетным
В этом разделе вы увидите, как можно использовать оператор по модулю, чтобы определить, является ли число четным или нечетным. Используя оператор по модулю с модулем
Используя оператор по модулю с модулем 2 , вы можете проверить любое число, чтобы увидеть, делится ли оно без остатка на 2 . Если оно делится без остатка, то это четное число.
Взгляните на is_even() , который проверяет, является ли параметр num четным:
по определению is_even(число):
вернуть число% 2 == 0
Здесь число % 2 будет равно 0 , если число четное, и 1 , если число нечетное. Проверка на 0 вернет логическое значение True или False в зависимости от того, является ли число четным.
Проверка нечетных чисел очень похожа. Чтобы проверить нечетное число, вы инвертируете проверку на равенство:
по определению is_odd(число):
вернуть число% 2 != 0
Эта функция вернет Истинно , если число % 2 не равно 0 , что означает, что есть остаток, доказывающий, что число является нечетным числом. Теперь вам может быть интересно, можете ли вы использовать следующую функцию, чтобы определить, является ли
Теперь вам может быть интересно, можете ли вы использовать следующую функцию, чтобы определить, является ли число нечетным числом:
по определению is_odd(число):
вернуть число% 2 == 1
Ответ на этот вопрос да и нет. Технически эта функция будет работать так же, как Python вычисляет по модулю с целыми числами. Тем не менее, вам следует избегать сравнения результата операции по модулю с 1 , поскольку не все операции по модулю в Python возвращают один и тот же остаток.
Вы можете понять почему в следующих примерах:
>>>
>>> -3 % 2 1 >>> 3 % -2 -1
Во втором примере остаток принимает знак отрицательного делителя и возвращает -1 . В этом случае логическая проверка 3 % -2 == 1 вернет False .
Однако, если вы сравните операцию по модулю с 0 , тогда не имеет значения, какой из операндов отрицательный. Результат всегда будет
Результат всегда будет True , если это четное число:
>>>
>>> -2 % 2 0 >>> 2 % -2 0
Если вы придерживаетесь сравнения операции Python по модулю с 0 , то у вас не должно возникнуть проблем с проверкой четных и нечетных чисел или любых других кратных чисел в вашем коде.
В следующем разделе вы увидите, как можно использовать оператор по модулю с циклами для управления потоком вашей программы.
Удалить рекламу
Как запускать код через определенные промежутки времени в цикле
С помощью оператора Python по модулю вы можете запускать код через определенные промежутки времени внутри цикла. Это делается путем выполнения операции по модулю с текущим индексом цикла и модулем. Число модуля определяет, как часто в цикле будет выполняться специфичный для интервала код.
Вот пример:
по определению split_names_into_rows (name_list, модуль = 3):
для индекса, имя в перечислении (name_list, start = 1):
печать (f"{имя:-^15} ", конец="")
если модуль индекса% == 0:
Распечатать()
Распечатать()
Этот код определяет split_names_into_rows() , который принимает два параметра.
name_list — это список имен, которые должны быть разбиты на строки. модуль устанавливает модуль для операции, эффективно определяя, сколько имен должно быть в каждой строке. split_names_into_rows() зациклится на name_list и начнет новую строку после достижения значения модуля .
Прежде чем более подробно разобрать функцию, взгляните на нее в действии:
>>>
>>> имена = ["Пикард", "Рикер", "Трой", "Крашер", "Ворф", "Дата", "Ла Форж"] >>> split_names_into_rows(имена) ----Пикард----- -----Рикер----- -----Троя------ ----Дробилка---- -----Ворф------ -----Дата------ ---Ла Форж----
Как видите, список имен разбит на три строки, максимум три имени в каждой строке. модуль по умолчанию 3 , но вы можете указать любое число:
>>>
>>> split_names_into_rows(имена, модуль=4) ----Пикард----- -----Райкер----- -----Трои------ ----Крашер---- -----Ворф------ -----Дата------ ---Ла Форж---- >>> split_names_into_rows(имена, модуль=2) ----Пикард----- -----Рикер----- ----- Трой ------ ---- Дробилка ---- -----Ворф------ -----Данные------ ---Ла Форж---- >>> split_names_into_rows(имена, модуль=1) ----Пикард----- -----Рикер----- ----- Трой ------- ----Дробилка---- -----Ворф------ -----Данные------ ---Ла Форж----
Теперь, когда вы увидели код в действии, вы можете понять, что он делает.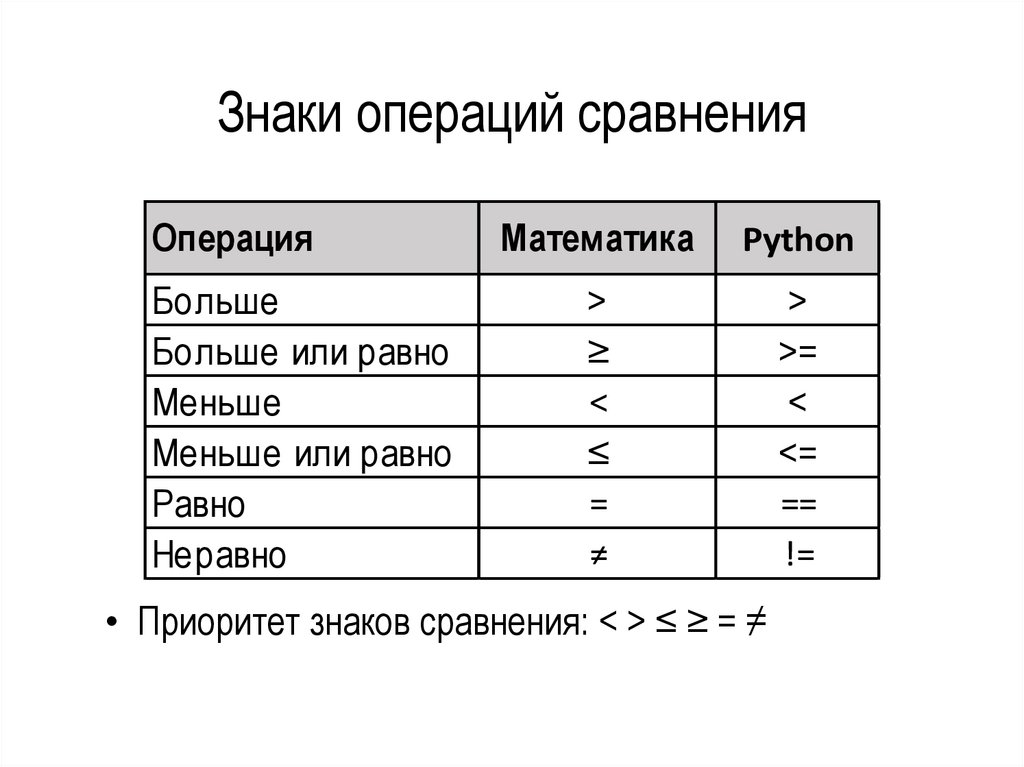 Во-первых, он использует
Во-первых, он использует enumerate() для перебора name_list , присваивая текущий элемент списка name , а значение счетчика index . Вы можете видеть, что необязательный аргумент start для enumerate() установлен на 1 . Это означает, что счет индекса начнется с 1 вместо 0 :
print() сделать следующее:- Вывести не менее
15символов, даже если строка короче 15 символов. - Выровнять строку по центру.
- Заполните любой пробел справа или слева от строки символом дефиса (
-).
Теперь, когда имя напечатано в строке, взгляните на основную часть split_names_into_rows() :
, если модуль индекса % == 0:
Распечатать()
Этот код берет текущую итерацию с индексом и с помощью оператора по модулю сравнивает его с по модулю . Если результат равен
Если результат равен 0 , то он может запускать код, зависящий от интервала. В этом случае функция вызывает print() для добавления новой строки, с которой начинается новая строка.
Приведенный выше код является только одним примером. Использование шаблона index % modulus == 0 позволяет вам запускать другой код через определенные промежутки времени в ваших циклах. В следующем разделе вы разовьете эту концепцию немного дальше и рассмотрите циклическую итерацию.
Как создать циклическую итерацию
Циклическая итерация описывает тип итерации, которая сбрасывается после достижения определенной точки. Как правило, этот тип итерации используется для ограничения индекса итерации определенным диапазоном.
Вы можете использовать оператор по модулю для создания циклической итерации. Взгляните на пример использования библиотеки черепахи для рисования фигуры:
импортная черепаха
импортировать случайный
определение draw_with_cyclo_iteration():
colors = ["зеленый", "голубой", "оранжевый", "фиолетовый", "красный", "желтый", "белый"]
черепаха. bgcolor("grey8") # Шестнадцатеричный: #333333
черепаха.penddown()
черепаха.pencolor(random.choice(colors)) # Первый цвет случайный
i = 0 # Начальный индекс
пока верно:
i = (i + 1) % 6 # Обновить индекс
черепаха.pensize(i) # Установить размер пениса равным i
черепаха.вперед(225)
черепаха.право(170)
# Выберите случайный цвет
если я == 0:
черепаха.pencolor(случайный.выбор(цвета))
bgcolor("grey8") # Шестнадцатеричный: #333333
черепаха.penddown()
черепаха.pencolor(random.choice(colors)) # Первый цвет случайный
i = 0 # Начальный индекс
пока верно:
i = (i + 1) % 6 # Обновить индекс
черепаха.pensize(i) # Установить размер пениса равным i
черепаха.вперед(225)
черепаха.право(170)
# Выберите случайный цвет
если я == 0:
черепаха.pencolor(случайный.выбор(цвета))
Приведенный выше код использует бесконечный цикл для рисования повторяющейся формы звезды. После каждых шести итераций он меняет цвет пера. Размер пера увеличивается с каждой итерацией до тех пор, пока i не сбрасывается обратно на 0 . Если запустить код, то должно получиться что-то похожее на это:
Важные части этого кода выделены ниже:
импортная черепаха
импортировать случайный
определение draw_with_cyclo_iteration():
colors = ["зеленый", "голубой", "оранжевый", "фиолетовый", "красный", "желтый", "белый"]
черепаха. bgcolor("grey8") # Шестнадцатеричный: #333333
черепаха.penddown()
черепаха.pencolor(случайный.выбор(цвета))
i = 0 # Начальный индекс
пока верно:
i = (i + 1) % 6 # Обновить индекс
черепаха.pensize(i) # Установить размер пениса равным i
черепаха.вперед(225)
черепаха.право(170)
# Выберите случайный цвет
если я == 0:
черепаха.pencolor(случайный.выбор(цвета))
bgcolor("grey8") # Шестнадцатеричный: #333333
черепаха.penddown()
черепаха.pencolor(случайный.выбор(цвета))
i = 0 # Начальный индекс
пока верно:
i = (i + 1) % 6 # Обновить индекс
черепаха.pensize(i) # Установить размер пениса равным i
черепаха.вперед(225)
черепаха.право(170)
# Выберите случайный цвет
если я == 0:
черепаха.pencolor(случайный.выбор(цвета))
Каждый раз в цикле i обновляется на основе результатов (i + 1) % 6 . Это новое значение i используется для увеличения .pensize с каждой итерацией. Как только i достигнет 5 , (i + 1) % 6 будет равно 0 , а i вернется к 0 .
Вы можете увидеть этапы итерации ниже для большего пояснения:
я = 0 : (0 + 1) % 6 = 1 я = 1 : (1 + 1) % 6 = 2 я = 2 : (2 + 1) % 6 = 3 я = 3 : (3 + 1) % 6 = 4 я = 4 : (4 + 1) % 6 = 5 i = 5 : (5 + 1) % 6 = 0 # Сброс
Когда i сбрасывается обратно на 0 , . изменяется на новый случайный цвет, как показано ниже: pencolor
pencolor
, если я == 0:
черепаха.pencolor(случайный.выбор(цвета))
Код в этом разделе использует 6 в качестве модуля, но вы можете установить его на любое число, чтобы настроить, сколько раз цикл будет повторяться перед сбросом значения i .
Удалить рекламу
Как конвертировать единицы
В этом разделе вы узнаете, как использовать оператор по модулю для преобразования единиц измерения. В следующих примерах берутся более мелкие единицы и преобразуются в более крупные без использования десятичных знаков. Оператор по модулю используется для определения любого остатка, который может существовать, когда меньшая единица не делится без остатка на большую единицу.
В этом первом примере вы конвертируете дюймы в футы. Оператор по модулю используется для получения оставшихся дюймов, которые неравномерно делятся на футы. Оператор деления пола (
Оператор деления пола ( // ) используется для округления общего числа футов в меньшую сторону:
по определению convert_inches_to_feet (всего_дюймов):
дюймы = общее количество дюймов % 12
футы = общее количество дюймов // 12
print(f"{total_inches} дюймов = {футов} футов и {дюймов} дюймов")
Вот пример используемой функции:
>>>
>>> конвертировать_дюймы_в_футы (450) 450 дюймов = 37 футов и 6 дюймов
Как видно из вывода, 450 % 12 возвращает 6 , то есть оставшиеся дюймы, которые не были равномерно разделены на футы. Результатом 450 // 12 будет 37 , то есть общее количество футов, на которое поровну были поделены дюймы.
В следующем примере вы можете пойти дальше. convert_minutes_to_days() принимает целое число total_mins , представляющее количество минут, и выводит период времени в днях, часах и минутах:
по определению convert_minutes_to_days(total_mins):
дней = общее количество минут // 1440
дополнительные_минуты = общие_минуты % 1440
часы = дополнительные_минуты // 60
минуты = экстра_минуты % 60
print(f"{total_mins} = {дней} дней, {часов} часов и {минут} минут")
Разобравшись, можно увидеть, что функция делает следующее:
- Определяет общее количество дней без остатка с помощью
total_mins // 1440, где1440— количество минут в сутках - Вычисляет любые оставшиеся
extra_minutesсtotal_mins % 1440 - Использует
extra_minutes, чтобы получитьчасов, которые делятся без остатка, и любые дополнительныеминут
Ниже показано, как это работает:
>>>
>>> конвертировать_минуты_в_дни(1503) 1503 = 1 день, 1 час и 3 минуты.>>> конвертировать_минуты_в_дни(3456) 3456 = 2 дня, 9часов и 36 минут >>> конвертировать_минуты_в_дни(35000) 35000 = 24 дня, 7 часов и 20 минут
Хотя приведенные выше примеры относятся только к преобразованию дюймов в футы и минут в дни, вы можете использовать любой тип единиц измерения с оператором по модулю для преобразования меньших единиц в большие.
Примечание : оба приведенных выше примера можно изменить, чтобы использовать divmod() , чтобы сделать код более кратким. Если вы помните, divmod() возвращает кортеж, содержащий результаты деления на пол и по модулю с использованием предоставленных параметров.
Ниже операторы деления пола и деления по модулю заменены на divmod() :
def convert_inches_to_feet_updated(total_inches):
футы, дюймы = divmod(total_inches, 12)
print(f"{total_inches} дюймов = {футов} футов и {дюймов} дюймов")
Как видите, divmod(total_inches, 12) возвращает кортеж, который распаковывается на футов и дюймов .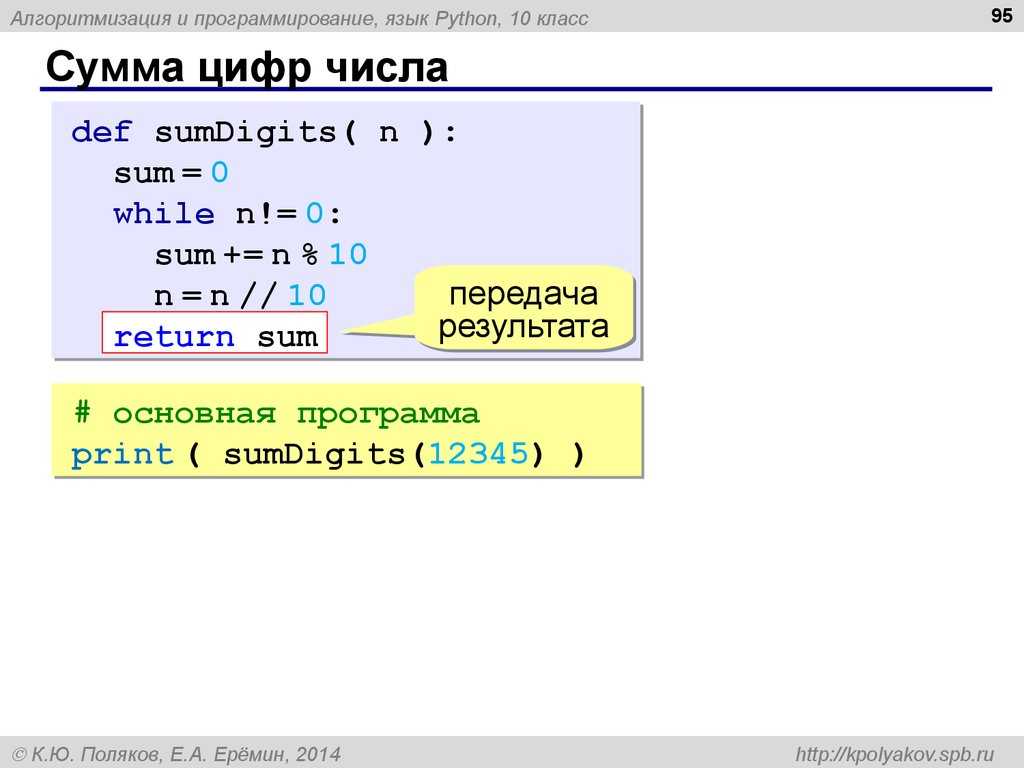
Если вы попробуете эту обновленную функцию, вы получите те же результаты, что и раньше:
>>>
>>> конвертировать_дюймы_в_футы(450) 450 дюймов = 37 футов и 6 дюймов >>> convert_inches_to_feet_updated(450) 450 дюймов = 37 футов и 6 дюймов
Вы получаете тот же результат, но теперь код стал более лаконичным. Вы также можете обновить convert_minutes_to_days() :
def convert_minutes_to_days_updated(total_mins):
дней, дополнительные_минуты = divmod(total_mins, 1440)
часы, минуты = divmod(extra_minutes, 60)
print(f"{total_mins} = {дней} дней, {часов} часов и {минут} минут")
Используя divmod() , функция легче читается, чем предыдущая версия, и возвращает тот же результат:
>>>
>>> convert_minutes_to_days(1503) 1503 = 1 день, 1 час и 3 минуты. >>> convert_minutes_to_days_updated(1503) 1503 = 1 день, 1 час и 3 минуты.
Использование divmod() необязательно во всех ситуациях, но здесь это имеет смысл, так как при расчетах преобразования единиц измерения используются как деление по полу, так и деление по модулю.
Теперь, когда вы узнали, как использовать оператор по модулю для преобразования единиц измерения, в следующем разделе вы узнаете, как можно использовать оператор по модулю для проверки простых чисел.
Как определить, является ли число простым числом
В следующем примере вы увидите, как можно использовать оператор по модулю Python, чтобы проверить, является ли число простым числом . Простое число — это любое число, которое содержит только два делителя: 1 и само себя. Некоторые примеры простых чисел: 2 , 3 , 5 , 7 , 23 , 29 , 59 , 83 и 97 .
Приведенный ниже код представляет собой реализацию определения простоты числа с помощью оператора по модулю:
по определению check_prime_number (число):
если число < 2:
print(f"{число} должно быть больше или равно 2, чтобы быть простым. ")
возвращаться
факторы = [(1, число)]
я = 2
в то время как я * я <= число:
если число% я == 0:
factor.append((i, число//i))
я += 1
если len(факторы) > 1:
print(f"{num} не простое число. Оно имеет следующие факторы: {factors}")
еще:
print(f"{число} — простое число")
")
возвращаться
факторы = [(1, число)]
я = 2
в то время как я * я <= число:
если число% я == 0:
factor.append((i, число//i))
я += 1
если len(факторы) > 1:
print(f"{num} не простое число. Оно имеет следующие факторы: {factors}")
еще:
print(f"{число} — простое число")
Этот код определяет check_prime_number() , который принимает параметр num и проверяет, является ли это простым числом. Если это так, то отображается сообщение о том, что число является простым числом. Если это не простое число, то выводится сообщение со всеми множителями числа.
Примечание: Приведенный выше код — не самый эффективный способ проверки простых чисел. Если вам интересно копнуть глубже, ознакомьтесь с решетом Эратосфена и решетом Аткина, где приведены примеры более эффективных алгоритмов поиска простых чисел.
Перед тем, как присмотреться к функции, вот результаты с использованием некоторых других чисел:
>>>
>>> check_prime_number(44) 44 не простое число.Он имеет следующие множители: [(1, 44), (2, 22), (4, 11)] >>> check_prime_number(53) 53 простое число >>> check_prime_number(115) 115 не простое число. Он имеет следующие факторы: [(1, 115), (5, 23)] >>> check_prime_number(997) 997 это простое число
Покопавшись в коде, вы можете увидеть, что он начинается с проверки наличия число меньше 2 . Простые числа могут быть только больше или равны 2 . Если число меньше, чем 2 , то продолжать работу функции не нужно. Это будет print() сообщение и возвратит :
, если число < 2:
print(f"{число} должно быть больше или равно 2, чтобы быть простым.")
возвращаться
Если число больше, чем 2 , то функция проверяет, является ли число простым числом. Чтобы проверить это, функция выполняет итерацию по всем числам между 9 и0039 2 и квадратный корень из , число , чтобы увидеть, делится ли оно на , число . Если одно из чисел делится без остатка, то множитель найден, и
Если одно из чисел делится без остатка, то множитель найден, и число не может быть простым числом.
Вот основная часть функции:
факторов = [(1, число)]
я = 2
в то время как я * я <= число:
если число% я == 0:
factor.append((i, число//i))
я += 1
Здесь многое предстоит распаковать, так что давайте пошагово.
Во-первых, 9Список 0039 факторов создается с начальными факторами (1, число) . Этот список будет использоваться для хранения любых других найденных факторов:
факторов = [(1, число)]
Затем, начиная с 2 , код увеличивает i , пока не достигнет квадратного корня из числа . На каждой итерации он сравнивает num с i , чтобы проверить, делится ли оно без остатка. Код нужно проверить только до квадратного корня из 9 включительно.0039 число , потому что он не будет содержать никаких факторов выше этого:
я = 2
в то время как я * я <= число:
если число% я == 0:
factor. append((i, число//i))
я += 1
append((i, число//i))
я += 1
Вместо того, чтобы пытаться определить квадратный корень из числа , функция использует цикл while , чтобы проверить, является ли i * i <= число . Пока i * i <= num , цикл не достиг квадратного корня из num .
Внутри цикла while оператор по модулю проверяет, число делится без остатка на i :
факторов = [(1, число)]
i = 2 # Начать начальный индекс с 2
в то время как я * я <= число:
если число% я == 0:
factor.append((i, число//i))
я += 1
Если число делится без остатка на i , то i является множителем число , и кортеж множителей добавляется в список факторов .
После завершения цикла while код проверяет, не были ли найдены какие-либо дополнительные факторы:
, если len(факторы) > 1:
print(f"{num} не простое число. Оно имеет следующие факторы: {factors}")
еще:
print(f"{число} — простое число")
Оно имеет следующие факторы: {factors}")
еще:
print(f"{число} — простое число")
Если в списке факторов существует более одного кортежа, то число не может быть простым числом. Для непростых чисел распечатываются множители. Для простых чисел функция выводит сообщение о том, что num является простым числом.
Удалить рекламу
Как реализовать шифры
Оператор по модулю Python можно использовать для создания шифров. Шифр — это тип алгоритма для выполнения шифрования и дешифрования входных данных, обычно текста. В этом разделе вы рассмотрите два шифра: шифр Цезаря и шифр Виженера .
Шифр Цезаря
Первый шифр, который вы увидите, — это шифр Цезаря, названный в честь Юлия Цезаря, который использовал его для тайной передачи сообщений. Это шифр замены, который использует замену букв для шифрования строки текста.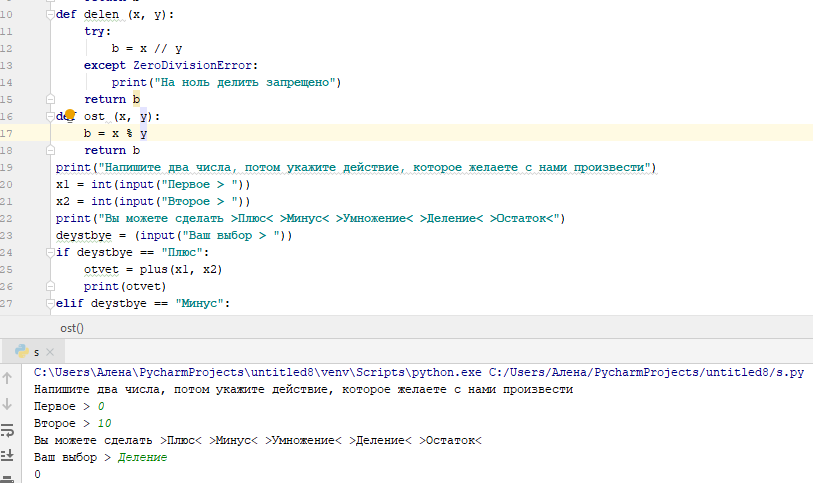
Шифр Цезаря работает, беря зашифрованную букву и сдвигая ее на определенное количество позиций влево или вправо в алфавите. Какая бы буква ни находилась в этой позиции, она используется как зашифрованный символ. Это же значение сдвига применяется ко всем символам в строке.
Например, если сдвиг был 5 , то A сдвинется на пять букв вверх и станет F , B станет G и так далее. Ниже вы можете увидеть процесс шифрования текста REALPYTHON со сдвигом 5 :
В результате получается шифр WJFQUDYMTS .
Расшифровка шифра выполняется обратным сдвигом. Процессы шифрования и дешифрования можно описать следующими выражениями, где char_index — индекс символа в алфавите:
зашифрованный_индекс_символа = (индекс_символа + сдвиг)% 26 decrypted_char_index = (char_index - сдвиг) % 26
Этот шифр использует оператор по модулю, чтобы гарантировать, что при сдвиге буквы индекс будет циклически повторяться, если будет достигнут конец алфавита. Теперь, когда вы знаете, как работает этот шифр, взгляните на его реализацию:
Теперь, когда вы знаете, как работает этот шифр, взгляните на его реализацию:
строка импорта
def caesar_cipher (текст, сдвиг, расшифровка = ложь):
если не text.isascii() или не text.isalpha():
поднять ValueError("Текст должен быть ASCII и не содержать цифр."
нижний регистр = строка.ascii_lowercase
верхний регистр = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower():
индекс = нижний регистр.индекс (символ)
результат += нижний регистр[(индекс + сдвиг)% 26]
еще:
индекс = верхний регистр.индекс (символ)
результат += верхний регистр[(индекс + сдвиг)% 26]
вернуть результат
Этот код определяет функцию с именем caesar_cipher() , которая имеет два обязательных параметра и один необязательный параметр:
-
текст— это текст, который нужно зашифровать или расшифровать.
-
сдвиг— количество позиций для сдвига каждой буквы. -
расшифровать— логическое значение, указывающее, следует ли расшифровывать текст
расшифровать включен, так что одну функцию можно использовать для обработки как шифрования, так и дешифрования. Эта реализация может обрабатывать только буквенные символы, поэтому функция сначала проверяет, что текст — буквенный символ в кодировке ASCII:
def caesar_cipher (текст, сдвиг, расшифровка = ложь):
если не text.isascii() или не text.isalpha():
поднять ValueError("Текст должен быть ASCII и не содержать цифр."
Затем функция определяет три переменные для хранения строчных символов ASCII, прописных символов ASCII и результатов шифрования или дешифрования:
нижний регистр = string.ascii_lowercase # "abcdefghijklmnopqrstuvwxyz" uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ" результат = ""
Далее, если функция используется для расшифровки текста , то она умножает сдвиг на -1 , чтобы сдвинуть назад:
если расшифровать:
сдвиг = сдвиг * -1
Наконец, caesar_cipher() перебирает отдельные символы в text и выполняет следующие действия для каждого char :
- Проверить, является ли
charстрочными или прописными буквами. - Получить индекс
символовв спискахнижнего регистраиливерхнего регистраASCII. - Добавьте сдвиг
- Используйте
% 26, чтобы убедиться, что сдвиг вернется к началу алфавита. - Добавить символ шифрования к строке
результата.
После того, как цикл завершит перебор значения text , значение результат возвращается:
для символов в тексте:
если char.islower():
индекс = нижний регистр.индекс (символ)
результат += нижний регистр[(индекс + сдвиг)% 26]
еще:
индекс = верхний регистр.индекс (символ)
результат += верхний регистр[(индекс + сдвиг)% 26]
вернуть результат
Вот еще раз полный код:
строка импорта
def caesar_cipher (текст, сдвиг, расшифровка = ложь):
если не text.isascii() или не text.isalpha():
поднять ValueError("Текст должен быть ASCII и не содержать цифр."
нижний регистр = строка.ascii_lowercase
верхний регистр = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower():
индекс = нижний регистр.индекс (символ)
результат += нижний регистр[(индекс + сдвиг)% 26]
еще:
индекс = верхний регистр. индекс (символ)
результат += верхний регистр[(индекс + сдвиг)% 26]
вернуть результат
индекс (символ)
результат += верхний регистр[(индекс + сдвиг)% 26]
вернуть результат
Теперь запустите код в Python REPL, используя текст meetMeAtOurHideOutAtTwo со сдвигом 10 :
>>>
>>> caesar_cipher("meetMeAtOurHideOutAtTwo", 10)
деревоWoKdYebRsnoYedKdDgy
Зашифрованный результат: woodWoKdYebRsnoYedKdDgy . Используя этот зашифрованный текст, вы можете запустить расшифровку, чтобы получить исходный текст:
>>>
>>> caesar_cipher("woodWoKdYebRsnoYedKdDgy", 10, decrypt=True)
встретиться со мной внашемHideOutAtTwo
Шифр Цезаря интересно поиграть для введения в криптографию. Хотя шифр Цезаря редко используется сам по себе, он является основой для более сложных шифров замены. В следующем разделе вы познакомитесь с одним из потомков шифра Цезаря, шифром Виженера.
Шифр Виженера
Шифр Виженера представляет собой полиалфавитный шифр замены. Для выполнения шифрования он использует разные шифры Цезаря для каждой буквы входного текста. Шифр Виженера использует ключевое слово, чтобы определить, какой шифр Цезаря следует использовать для нахождения шифровальной буквы.
Для выполнения шифрования он использует разные шифры Цезаря для каждой буквы входного текста. Шифр Виженера использует ключевое слово, чтобы определить, какой шифр Цезаря следует использовать для нахождения шифровальной буквы.
Вы можете увидеть пример процесса шифрования на следующем изображении. В этом примере входной текст REALPYTHON зашифрован с использованием ключевого слова MODULO :
Для каждой буквы входного текста REALPYTHON используется буква из ключевого слова MODULO , чтобы определить, какой столбец шифра Цезаря следует выбрать. Если ключевое слово короче входного текста, как в случае с MODULO , то буквы ключевого слова повторяются до тех пор, пока не будут зашифрованы все буквы входного текста.
Ниже приведена реализация шифра Виженера. Как вы увидите, оператор по модулю используется в функции дважды:
. строка импорта
def vigenere_cipher (текст, ключ, расшифровка = ложь):
если не text. isascii() или не text.isalpha() или не text.isupper():
поднять ValueError("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, char в перечислении (текст):
текущий_ключ = ключ [i% len (ключ)]
char_index = верхний регистр.index(char)
key_index = верхний регистр.index(current_key)
если расшифровать:
индекс = индекс_символа - индекс_ключа + 26
еще:
индекс = индекс_символа + индекс_ключа
результаты += верхний регистр[индекс% 26]
возвращать результаты
isascii() или не text.isalpha() или не text.isupper():
поднять ValueError("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, char в перечислении (текст):
текущий_ключ = ключ [i% len (ключ)]
char_index = верхний регистр.index(char)
key_index = верхний регистр.index(current_key)
если расшифровать:
индекс = индекс_символа - индекс_ключа + 26
еще:
индекс = индекс_символа + индекс_ключа
результаты += верхний регистр[индекс% 26]
возвращать результаты
Вы могли заметить, что подпись для vigenere_cipher() очень похожа на caesar_cipher() из предыдущего раздела:
def vigenere_cipher (текст, ключ, расшифровка = ложь):
если не text.isascii() или не text.isalpha() или не text.isupper():
поднять ValueError("Текст должен быть в верхнем регистре ASCII без цифр. ")
верхний регистр = строка.ascii_uppercase
результаты = ""
")
верхний регистр = строка.ascii_uppercase
результаты = ""
Основное отличие состоит в том, что вместо параметра shift используется vigenere_cipher() принимает параметр key , который является ключевым словом, используемым при шифровании и дешифровании. Другим отличием является добавление text.isupper() . Основываясь на этой реализации, vigenere_cipher() может принимать только вводимый текст, набранный прописными буквами.
Аналогично caesar_cipher() , vigenere_cipher() перебирает каждую букву входного текста, чтобы зашифровать или расшифровать его:
для i, символ в перечислении (текст):
текущий_ключ = ключ [i% len (ключ)]
В приведенном выше коде вы можете увидеть первое использование функции по модулю:
current_key = ключ [i % len (ключ)]
Здесь значение current_key определяется на основе индекса, возвращенного из i % len(key) . Этот индекс используется для выбора буквы из строки
Этот индекс используется для выбора буквы из строки ключа , например M из MODULO .
Оператор по модулю позволяет использовать ключевое слово любой длины независимо от длины текст для шифрования. Как только индекс i , индекс зашифрованного в данный момент символа, сравняется с длиной ключевого слова, он начнется с начала ключевого слова.
Для каждой буквы входного текста несколько шагов определяют, как его зашифровать или расшифровать:
- Определите
char_indexна основе индексаcharвнутриверхнего регистра. - Определить
key_indexна основе индексаcurrent_keyвнутриверхний регистр. - Используйте
char_indexиkey_index, чтобы получить индекс для зашифрованного или расшифрованного символа.
Взгляните на эти шаги в приведенном ниже коде:
char_index = верхний регистр.index(char) key_index = верхний регистр.index(current_key) если расшифровать: индекс = индекс_символа - индекс_ключа + 26 еще: индекс = индекс_символа + индекс_ключа
Вы видите, что индексы для расшифровки и шифрования вычисляются по-разному. Вот почему 9В этой функции используется расшифровка 0039 . Таким образом, вы можете использовать функцию как для шифрования, так и для расшифровки.
После определения индекса вы находите второе использование функции по модулю:
результатов += верхний регистр[индекс % 26]
index % 26 гарантирует, что index символа не превышает 25 , таким образом гарантируя, что он останется внутри алфавита. С помощью этого индекса зашифрованный или расшифрованный символ выбирается из прописные и добавленные к результаты .
Вот еще раз полный код шифра Виженера:
строка импорта
def vigenere_cipher (текст, ключ, расшифровка = ложь):
если не text. isascii() или не text.isalpha() или не text.isupper():
поднять ValueError("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, char в перечислении (текст):
текущий_ключ = ключ [i% len (ключ)]
char_index = верхний регистр.index(char)
key_index = верхний регистр.index(current_key)
если расшифровать:
индекс = индекс_символа - индекс_ключа + 26
еще:
индекс = индекс_символа + индекс_ключа
результаты += верхний регистр[индекс% 26]
возвращать результаты
isascii() или не text.isalpha() или не text.isupper():
поднять ValueError("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, char в перечислении (текст):
текущий_ключ = ключ [i% len (ключ)]
char_index = верхний регистр.index(char)
key_index = верхний регистр.index(current_key)
если расшифровать:
индекс = индекс_символа - индекс_ключа + 26
еще:
индекс = индекс_символа + индекс_ключа
результаты += верхний регистр[индекс% 26]
возвращать результаты
Теперь запустите его в Python REPL:
>>>
>>> vigenere_cipher(text="REALPYTHON", key="MODULO") ДСДФАМФВРХ >>> зашифровано = vigenere_cipher(text="REALPYTHON", key="MODULO") >>> печать (в зашифрованном виде) ДСДФАМФВРХ >>> vigenere_cipher(зашифровано, "MODULO", расшифровать=True) РЕАЛПИТОН
Красиво! Теперь у вас есть работающий шифр Виженера для шифрования текстовых строк.
Удалить рекламу
Python Modulo Operator Advanced Uses
В этом заключительном разделе вы поднимете свои знания оператора по модулю на новый уровень, используя его с decimal.Decimal . Вы также узнаете, как добавить .__mod__() в свои пользовательские классы, чтобы их можно было использовать с оператором по модулю.
Использование оператора модуля Python с
decimal.Decimal Ранее в этом руководстве вы видели, как можно использовать оператор по модулю с числовыми типами, такими как int и float 9.0040, а также с math.fmod() . Вы также можете использовать оператор по модулю с Decimal из модуля decimal . Вы используете decimal.Decimal , когда хотите дискретно контролировать точность арифметических операций с плавающей запятой.
Вот несколько примеров использования целых чисел с десятичным числом . и оператор по модулю: Десятичное число
Десятичное число
>>>
>>> импорт десятичного
>>> decimal.Decimal(15) % decimal.Decimal(4)
Десятичный ('3')
>>> decimal.Decimal(240) % decimal.Decimal(13)
Десятичный ('6')
Вот некоторые числа с плавающей запятой, используемые с десятичным числом . Десятичное число и оператор по модулю:
>>>
>>> decimal.Decimal("12.5") % decimal.Decimal("5.5")
Десятичный ('1,5')
>>> decimal.Decimal("13.3") % decimal.Decimal("1.1")
Десятичный ('0,1')
Все операции по модулю с десятичным числом . Десятичное число возвращает те же результаты, что и другие числовые типы, за исключением случаев, когда один из операндов отрицательный. В отличие от int и float , но, как и math.fmod() , decimal.Decimal использует знак делимого для результатов.
Взгляните на приведенные ниже примеры, сравнивающие результаты использования оператора по модулю со стандартными значениями int и float и с десятичным числом . : Decimal
Decimal
>>>
>>> -17 % 3
1 # Знак делителя
>>> decimal.Decimal(-17) % decimal.Decimal(3)
Decimal(-2) # Знак делимого
>>> 17 % -3
-1 # Знак делителя
>>> decimal.Decimal(17) % decimal.Decimal(-3)
Decimal("2") # Знак делимого
>>> -13,3 % 1,1
1.0000000000000004 # Знак делителя
>>> decimal.Decimal("-13.3") % decimal.Decimal("1.1")
Decimal("-0.1") # Знак делимого
По сравнению с math.fmod() , decimal.Decimal будет иметь тот же знак, но точность будет другой:
>>>
>>> decimal.Decimal("-13.3") % decimal.Decimal("1.1")
Десятичный ("-0,1")
>>> math.fmod(-13.3, 1.1)
-0,09999999999999964
Как видно из приведенных выше примеров, работа с decimal.Decimal и оператором по модулю аналогична работе с другими числовыми типами. Просто нужно иметь в виду, как он определяет знак результата при работе с отрицательным операндом.
В следующем разделе вы узнаете, как переопределить оператор по модулю в своих классах, чтобы настроить его поведение.
Использование оператора по модулю Python с пользовательскими классами
Модель данных Python позволяет переопределять встроенные методы объекта Python для настройки его поведения. В этом разделе вы узнаете, как переопределить .__mod__() , чтобы вы могли использовать оператор по модулю со своими собственными классами.
В этом примере вы будете работать с Ученик класса. Этот класс будет отслеживать количество времени, которое студент изучил. Вот начальный класс Студент :
класс Студент:
def __init__(я, имя):
self.name = имя
self.study_sessions = []
def add_study_sessions (я, сеансы):
self.study_sessions += сеансы
Класс Student инициализируется параметром name и начинается с пустого списка study_sessions , который будет содержать список целых чисел, представляющих минуты обучения за сеанс. Есть также .add_study_sessions() , который принимает параметр sessions , который должен быть списком учебных сессий для добавления к study_sessions .
Теперь, если вы помните из раздела о преобразовании единиц выше, convert_minutes_to_day() использовал оператор по модулю Python для преобразования total_mins в дни, часы и минуты. Теперь вы реализуете модифицированную версию этого метода, чтобы увидеть, как вы можете использовать свой пользовательский класс с оператором по модулю:
по определению total_study_time_in_hours (студент, total_mins):
часы = общее количество минут // 60
минуты = общее количество минут % 60
print(f"{student.name} учился {hours} часов и {minutes} минут")
Вы можете использовать эту функцию с классом Учащийся для отображения общего количества часов, отработанных Учащимся . В сочетании с классом Student выше код будет выглядеть так:
класс Студент:
def __init__(я, имя):
self.name = имя
self.study_sessions = []
def add_study_sessions (я, сеансы):
self.study_sessions += сеансы
def total_study_time_in_hours (студент, total_mins):
часы = общее количество минут // 60
минуты = общее количество минут % 60
print(f"{student. name} учился {hours} часов и {minutes} минут")
name} учился {hours} часов и {minutes} минут")
Если вы загрузите этот модуль в Python REPL, вы можете использовать его следующим образом:
>>>
>>> Джейн = Студент("Джейн")
>>> jane.add_study_sessions([120, 30, 56, 260, 130, 25, 75])
>>> total_mins = сумма(jane.study_sessions)
>>> total_study_time_in_hours(Джейн, total_mins)
Джейн училась 11 часов 36 минут
Приведенный выше код выводит общее количество часов обучения jane . Эта версия кода работает, но требует дополнительного шага суммирования study_sessions , чтобы получить total_mins перед вызовом total_study_time_in_hours() .
Вот как вы можете изменить класс Student , чтобы упростить код:
класс Студент:
def __init__(я, имя):
self.name = имя
self.study_sessions = []
def add_study_sessions (я, сеансы):
self.study_sessions += сеансы
def __mod__(я, другой):
возвращаемая сумма (self. study_sessions) % другое
def __floordiv__(я, другой):
возвращаемая сумма (self.study_sessions) // другое
study_sessions) % другое
def __floordiv__(я, другой):
возвращаемая сумма (self.study_sessions) // другое
Переопределяя .__mod__() и .__floordiv__() , вы можете использовать экземпляр Student с оператором по модулю. Вычисление sum() из study_sessions также включено в класс Student .
С этими изменениями вы можете использовать экземпляр Student непосредственно в total_study_time_in_hours() . Поскольку total_mins больше не нужен, его можно удалить:
по определению total_study_time_in_hours (студент):
часов = студент // 60
минут = студент% 60
print(f"{student.name} учился {hours} часов и {minutes} минут")
Вот полный код после доработок:
класс Студент:
def __init__(я, имя):
self.name = имя
self.study_sessions = []
def add_study_sessions (я, сеансы):
self. study_sessions += сеансы
def __mod__(я, другой):
возвращаемая сумма (self.study_sessions) % другое
def __floordiv__(я, другой):
возвращаемая сумма (self.study_sessions) // другое
def total_study_time_in_hours (студент):
часов = студент // 60
минут = студент% 60
print(f"{student.name} учился {hours} часов и {minutes} минут")
study_sessions += сеансы
def __mod__(я, другой):
возвращаемая сумма (self.study_sessions) % другое
def __floordiv__(я, другой):
возвращаемая сумма (self.study_sessions) // другое
def total_study_time_in_hours (студент):
часов = студент // 60
минут = студент% 60
print(f"{student.name} учился {hours} часов и {minutes} минут")
Теперь, вызвав код в Python REPL, вы увидите, что он намного лаконичнее:
>>>
>>> Джейн = Студент("Джейн")
>>> jane.add_study_sessions([120, 30, 56, 260, 130, 25, 75])
>>> total_study_time_in_hours(Джейн)
Джейн училась 11 часов 36 минут
Переопределяя .__mod__() , вы позволяете своим пользовательским классам вести себя как встроенные числовые типы Python.
Удалить рекламу
Вывод
На первый взгляд оператор по модулю в Python может не привлечь вашего внимания. Тем не менее, как вы видели, в этом скромном операторе так много всего. От проверки четных чисел до шифрования текста с помощью шифров — вы видели множество различных применений оператора по модулю.
От проверки четных чисел до шифрования текста с помощью шифров — вы видели множество различных применений оператора по модулю.
Из этого туториала вы узнали, как:
- Используйте оператор по модулю с
int,float,math.fmod(),divmod()идесятичный.Десятичный - Вычислить результаты операции по модулю
- Решите реальных задач с помощью оператора по модулю
- Переопределить
.__mod__()в ваших собственных классах, чтобы использовать их с оператором по модулю
Благодаря знаниям, которые вы получили в этом руководстве, вы теперь можете с большим успехом начать использовать оператор по модулю в своем собственном коде. Удачного питона!
Смотреть сейчас Это руководство содержит связанный с ним видеокурс, созданный командой Real Python.

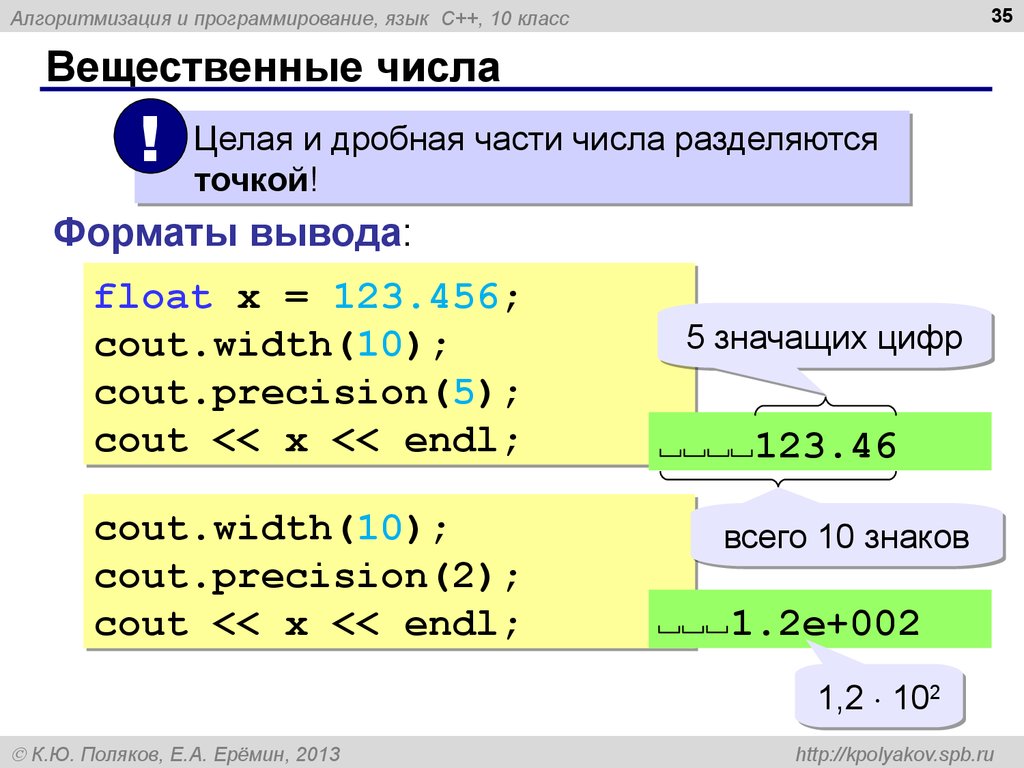
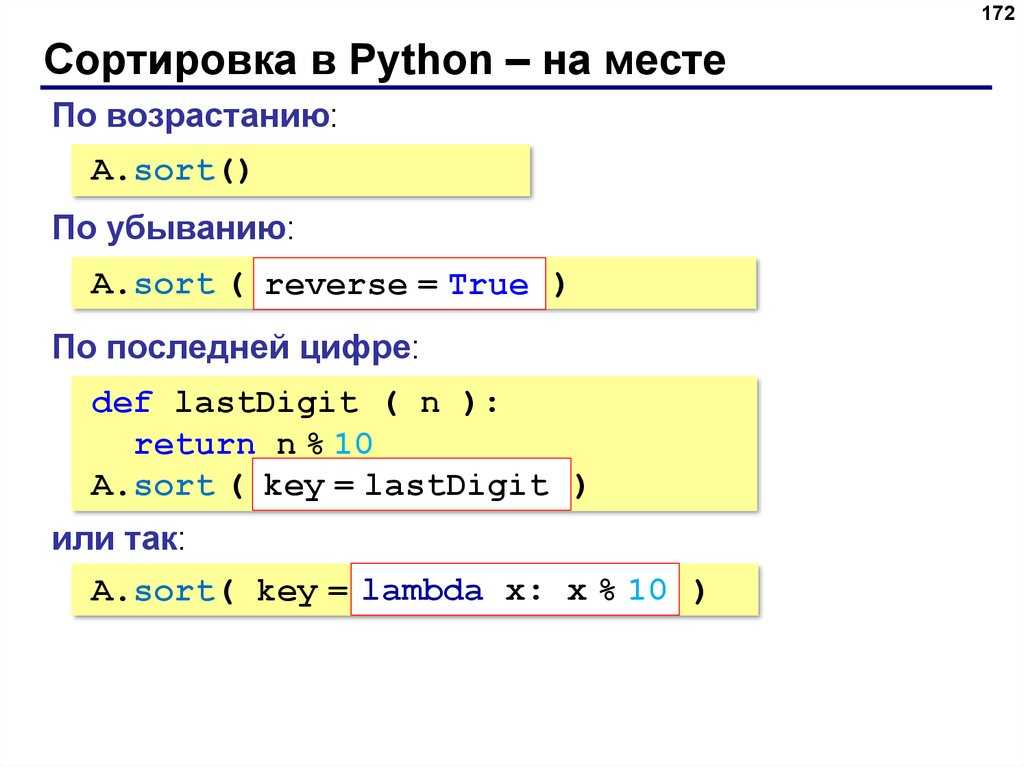 Если указать базу, расчет будет соответствующим.
Если указать базу, расчет будет соответствующим. 0
0
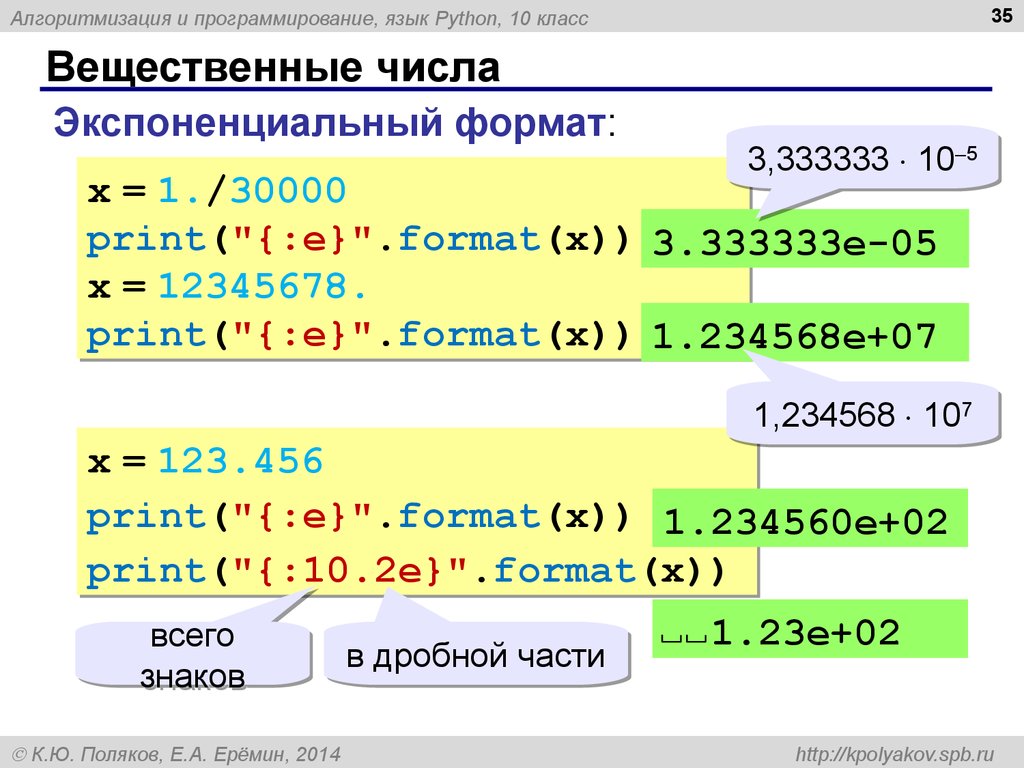 8776,2) >>>
8776,2) >>>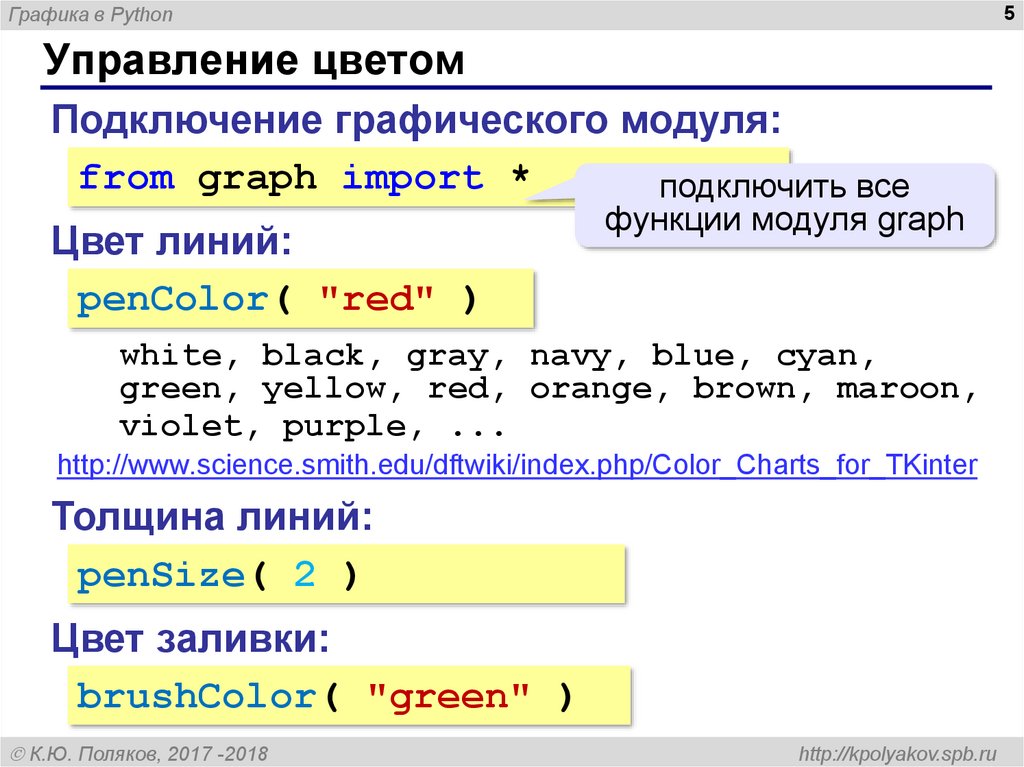
 По умолчанию система счисления десятичная, но можно задать любое основание от 2 до 36 включительно.
По умолчанию система счисления десятичная, но можно задать любое основание от 2 до 36 включительно.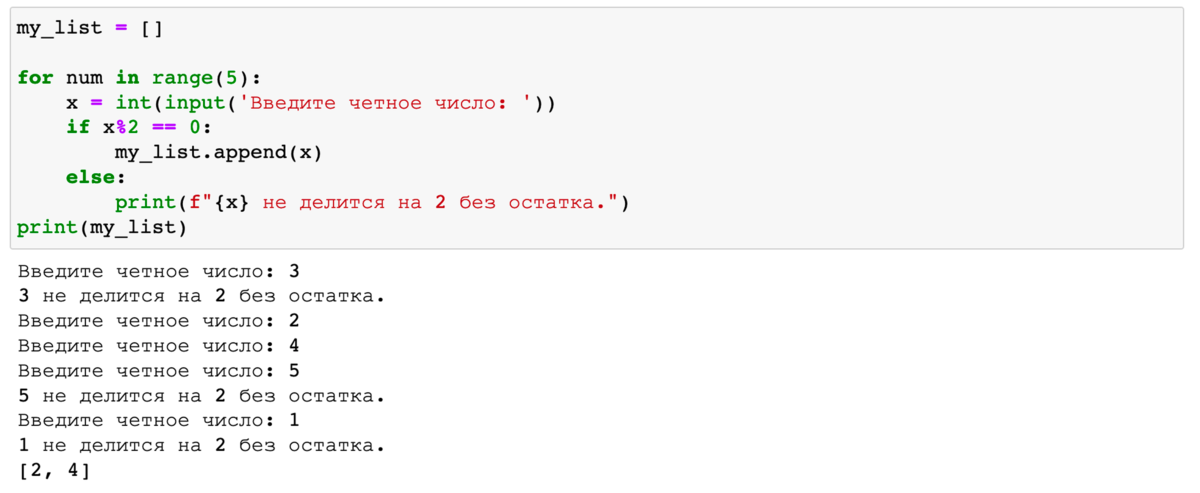

 Python определяет pow(0, 0) как равное 1 , как это обычно бывает для языков программирования.
Python определяет pow(0, 0) как равное 1 , как это обычно бывает для языков программирования.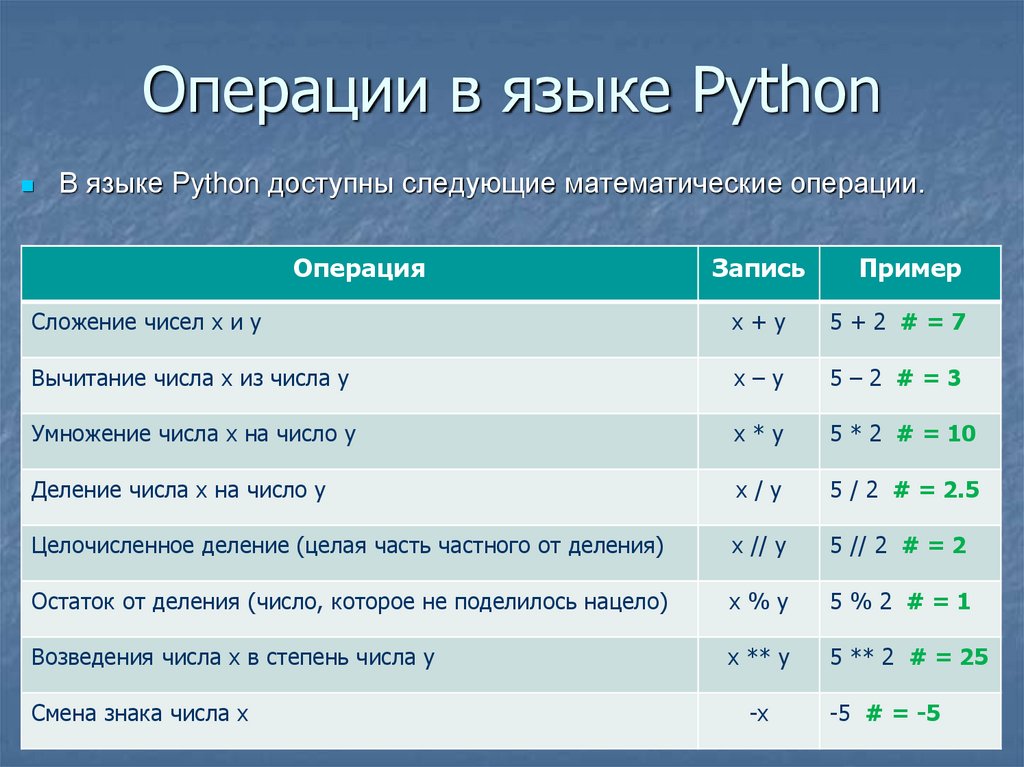
 напечатать номер
напечатать номер
 ..")
Начало()
..")
Начало()
 Дробь(32, 8)
Дробь(4, 1)
>>> дроби.Дробь(32, 9)
Дробь(32, 9)
>>> дроби.Дробь(32, 10)
Дробь(16, 5)
Дробь(32, 8)
Дробь(4, 1)
>>> дроби.Дробь(32, 9)
Дробь(32, 9)
>>> дроби.Дробь(32, 10)
Дробь(16, 5)
 __mod__()
__mod__()  fmod(13.3, 1.1)
0,09999999999999964
fmod(13.3, 1.1)
0,09999999999999964

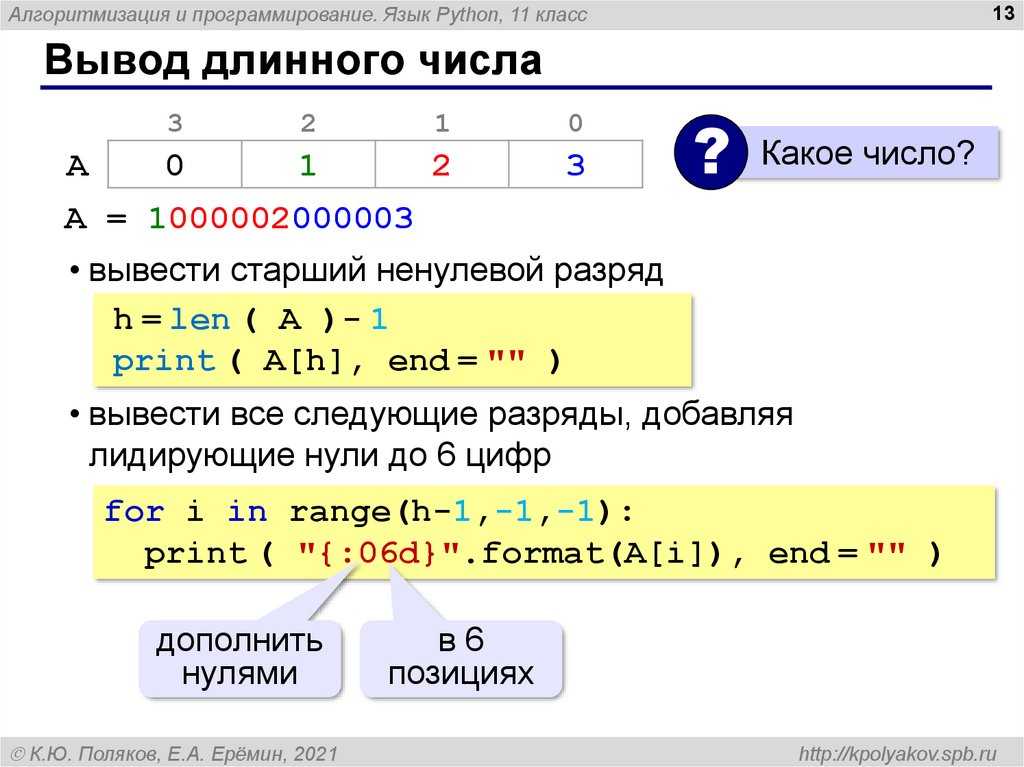 bgcolor("grey8") # Шестнадцатеричный: #333333
черепаха.penddown()
черепаха.pencolor(random.choice(colors)) # Первый цвет случайный
i = 0 # Начальный индекс
пока верно:
i = (i + 1) % 6 # Обновить индекс
черепаха.pensize(i) # Установить размер пениса равным i
черепаха.вперед(225)
черепаха.право(170)
# Выберите случайный цвет
если я == 0:
черепаха.pencolor(случайный.выбор(цвета))
bgcolor("grey8") # Шестнадцатеричный: #333333
черепаха.penddown()
черепаха.pencolor(random.choice(colors)) # Первый цвет случайный
i = 0 # Начальный индекс
пока верно:
i = (i + 1) % 6 # Обновить индекс
черепаха.pensize(i) # Установить размер пениса равным i
черепаха.вперед(225)
черепаха.право(170)
# Выберите случайный цвет
если я == 0:
черепаха.pencolor(случайный.выбор(цвета))
 bgcolor("grey8") # Шестнадцатеричный: #333333
черепаха.penddown()
черепаха.pencolor(случайный.выбор(цвета))
i = 0 # Начальный индекс
пока верно:
i = (i + 1) % 6 # Обновить индекс
черепаха.pensize(i) # Установить размер пениса равным i
черепаха.вперед(225)
черепаха.право(170)
# Выберите случайный цвет
если я == 0:
черепаха.pencolor(случайный.выбор(цвета))
bgcolor("grey8") # Шестнадцатеричный: #333333
черепаха.penddown()
черепаха.pencolor(случайный.выбор(цвета))
i = 0 # Начальный индекс
пока верно:
i = (i + 1) % 6 # Обновить индекс
черепаха.pensize(i) # Установить размер пениса равным i
черепаха.вперед(225)
черепаха.право(170)
# Выберите случайный цвет
если я == 0:
черепаха.pencolor(случайный.выбор(цвета))
 >>> конвертировать_минуты_в_дни(3456)
3456 = 2 дня, 9часов и 36 минут
>>> конвертировать_минуты_в_дни(35000)
35000 = 24 дня, 7 часов и 20 минут
>>> конвертировать_минуты_в_дни(3456)
3456 = 2 дня, 9часов и 36 минут
>>> конвертировать_минуты_в_дни(35000)
35000 = 24 дня, 7 часов и 20 минут
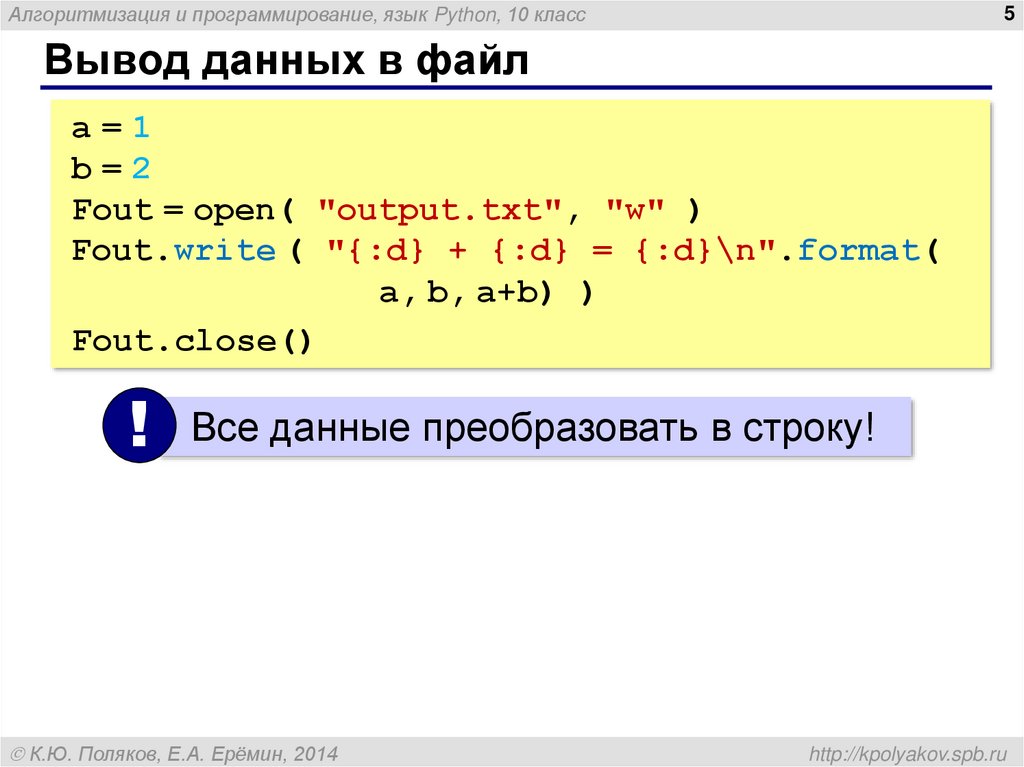
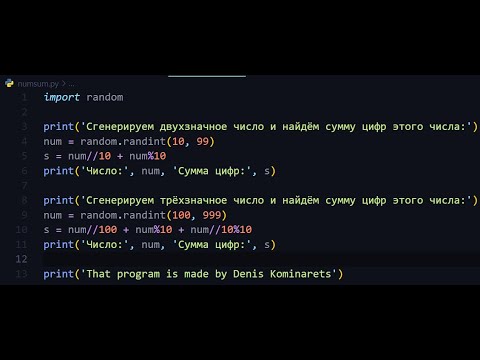 ")
возвращаться
факторы = [(1, число)]
я = 2
в то время как я * я <= число:
если число% я == 0:
factor.append((i, число//i))
я += 1
если len(факторы) > 1:
print(f"{num} не простое число. Оно имеет следующие факторы: {factors}")
еще:
print(f"{число} — простое число")
")
возвращаться
факторы = [(1, число)]
я = 2
в то время как я * я <= число:
если число% я == 0:
factor.append((i, число//i))
я += 1
если len(факторы) > 1:
print(f"{num} не простое число. Оно имеет следующие факторы: {factors}")
еще:
print(f"{число} — простое число")
 Он имеет следующие множители: [(1, 44), (2, 22), (4, 11)]
>>> check_prime_number(53)
53 простое число
>>> check_prime_number(115)
115 не простое число. Он имеет следующие факторы: [(1, 115), (5, 23)]
>>> check_prime_number(997)
997 это простое число
Он имеет следующие множители: [(1, 44), (2, 22), (4, 11)]
>>> check_prime_number(53)
53 простое число
>>> check_prime_number(115)
115 не простое число. Он имеет следующие факторы: [(1, 115), (5, 23)]
>>> check_prime_number(997)
997 это простое число
 append((i, число//i))
я += 1
append((i, число//i))
я += 1
 Оно имеет следующие факторы: {factors}")
еще:
print(f"{число} — простое число")
Оно имеет следующие факторы: {factors}")
еще:
print(f"{число} — простое число")

 ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результат = ""
ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результат = ""

 индекс (символ)
результат += верхний регистр[(индекс + сдвиг)% 26]
вернуть результат
индекс (символ)
результат += верхний регистр[(индекс + сдвиг)% 26]
вернуть результат
 isascii() или не text.isalpha() или не text.isupper():
поднять ValueError("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, char в перечислении (текст):
текущий_ключ = ключ [i% len (ключ)]
char_index = верхний регистр.index(char)
key_index = верхний регистр.index(current_key)
если расшифровать:
индекс = индекс_символа - индекс_ключа + 26
еще:
индекс = индекс_символа + индекс_ключа
результаты += верхний регистр[индекс% 26]
возвращать результаты
isascii() или не text.isalpha() или не text.isupper():
поднять ValueError("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, char в перечислении (текст):
текущий_ключ = ключ [i% len (ключ)]
char_index = верхний регистр.index(char)
key_index = верхний регистр.index(current_key)
если расшифровать:
индекс = индекс_символа - индекс_ключа + 26
еще:
индекс = индекс_символа + индекс_ключа
результаты += верхний регистр[индекс% 26]
возвращать результаты
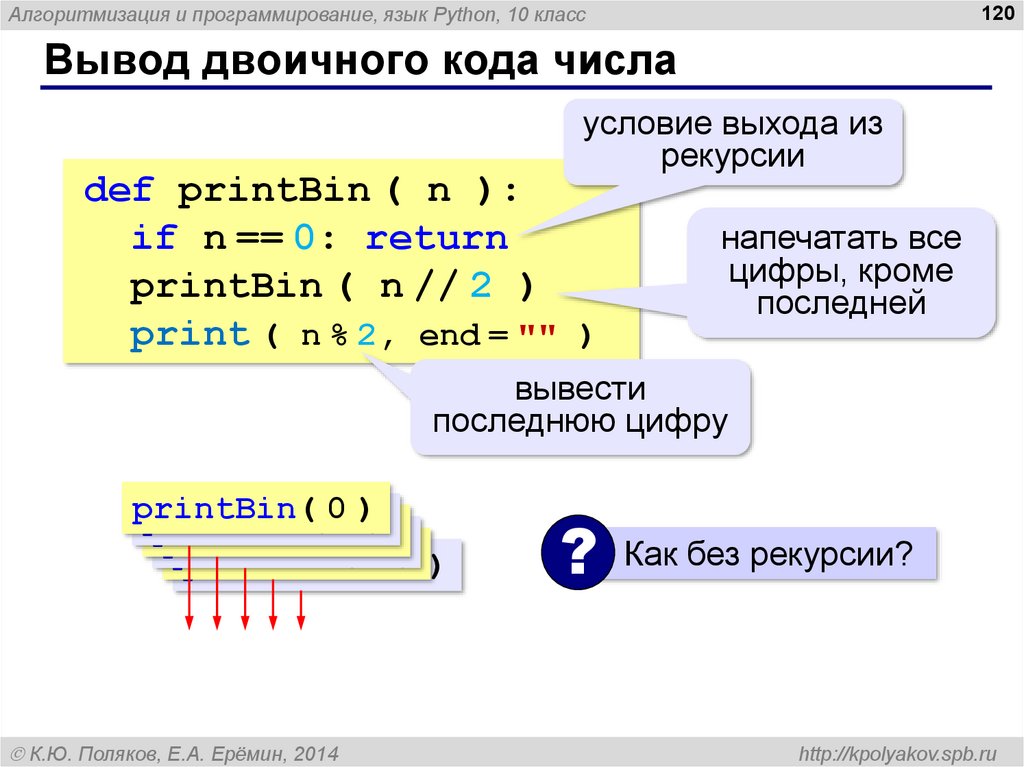 ")
верхний регистр = строка.ascii_uppercase
результаты = ""
")
верхний регистр = строка.ascii_uppercase
результаты = ""
 index(char)
key_index = верхний регистр.index(current_key)
если расшифровать:
индекс = индекс_символа - индекс_ключа + 26
еще:
индекс = индекс_символа + индекс_ключа
index(char)
key_index = верхний регистр.index(current_key)
если расшифровать:
индекс = индекс_символа - индекс_ключа + 26
еще:
индекс = индекс_символа + индекс_ключа
 isascii() или не text.isalpha() или не text.isupper():
поднять ValueError("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, char в перечислении (текст):
текущий_ключ = ключ [i% len (ключ)]
char_index = верхний регистр.index(char)
key_index = верхний регистр.index(current_key)
если расшифровать:
индекс = индекс_символа - индекс_ключа + 26
еще:
индекс = индекс_символа + индекс_ключа
результаты += верхний регистр[индекс% 26]
возвращать результаты
isascii() или не text.isalpha() или не text.isupper():
поднять ValueError("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, char в перечислении (текст):
текущий_ключ = ключ [i% len (ключ)]
char_index = верхний регистр.index(char)
key_index = верхний регистр.index(current_key)
если расшифровать:
индекс = индекс_символа - индекс_ключа + 26
еще:
индекс = индекс_символа + индекс_ключа
результаты += верхний регистр[индекс% 26]
возвращать результаты
 name} учился {hours} часов и {minutes} минут")
name} учился {hours} часов и {minutes} минут")
 study_sessions) % другое
def __floordiv__(я, другой):
возвращаемая сумма (self.study_sessions) // другое
study_sessions) % другое
def __floordiv__(я, другой):
возвращаемая сумма (self.study_sessions) // другое
 study_sessions += сеансы
def __mod__(я, другой):
возвращаемая сумма (self.study_sessions) % другое
def __floordiv__(я, другой):
возвращаемая сумма (self.study_sessions) // другое
def total_study_time_in_hours (студент):
часов = студент // 60
минут = студент% 60
print(f"{student.name} учился {hours} часов и {minutes} минут")
study_sessions += сеансы
def __mod__(я, другой):
возвращаемая сумма (self.study_sessions) % другое
def __floordiv__(я, другой):
возвращаемая сумма (self.study_sessions) // другое
def total_study_time_in_hours (студент):
часов = студент // 60
минут = студент% 60
print(f"{student.name} учился {hours} часов и {minutes} минут")