Как нам получить остаток от деления в Python 3?
Что представляет собой программа? Код и числа. Необходимые операции для чисел являются важным аспектом в программировании на любом языке. Какие же они бывают эти числа? Целочисленные, вещественные и комплексные. Для целых определены операции + , — , * , **. Для того чтобы получить остаток от деления Python и получить вещественное число, мы присваиваем знак \.
Из этой статьи вы узнаете:
Целые числа (int)
Вещественные числа (float)
Комплексные числа (из высшей математики)
Ребят, всем привет. Сегодня мы с вами поговорим о важной детали в программировании, о числах и взаимодействиях с ними.
Я открыл небольшой раздел «Примеры программ». В большей степени для себя. Так как хочу хранить в памяти как можно больше информации по строению кода. Для того чтобы быстро вспомнить, я решил выкладывать в ленте куски кода и примеры ПО.
Так что пользуйтесь, друзья.
Из истории. В V веке в Индии появилась система записи, которую мы знаем как арабские цифры и активно используем сейчас. Это был набор из 9 цифр от 1 до 9. Каждая цифра записывалась так, чтобы ей соответствовало количество углов. Например, в цифре 1 — один угол, в цифре 2 — два угла, в цифре 3 — три. И так до 9. Нуля еще не существовало, он появился позже. Вместо него просто оставляли пустое место.
Целые числа (int)
С целыми числами я думаю все понятно, обычные арифметические операции, остаток от деления, модуль числа и возведение в степень.
| x + y | Сложение |
| x — y | Вычитание |
| x * y | Умножение |
| x / y | Деление |
| x // y | Получение целой части от деления |
| x % y | Остаток от деления |
| -x | Смена знака числа |
| abs (x) | Модуль числа |
| divmod (x, y) | Пара (x // y, x % y) |
| x ** y | Возведение в степень |
| pow (x, y[, z]) | xy по модулю (если модуль задан) |
В среде разработки Arduino практически всё то же самое.
Вот то, что даст нам интерпретатор:
>>> 255 + 34 289 >>> 5 * 2 10 >>> 20 / 3 6.666666666666667 >>> 20 // 3 6 >>> 20 % 3 2 >>> 3 ** 4 81 >>> pow(3, 4) 81 >>> pow(3, 4, 27) 0 >>> 3 ** 150 369988485035126972924700782451696644186473100389722973815184405301748249
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | >>> 255 + 34 289 >>> 5 * 2 10 >>> 20 / 3 6.666666666666667 >>> 20 // 3 6 >>> 20 % 3 2 >>> 3 ** 4 81 >>> pow(3, 4) 81 >>> pow(3, 4, 27) 0 >>> 3 ** 150 369988485035126972924700782451696644186473100389722973815184405301748249 |
Вещественные числа (float)
То же самое что и целые, но имеют цифры после запятой. Мы можем манипулировать десятыми, сотыми и тысячными.
Сразу оговорюсь, с ними надо быть очень аккуратными и внимательными, так как такие числа могут давать погрешность и накопить ошибку.
Ответ интерпретатора:
>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 0.9999999999999999
>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 0.9999999999999999 |
Слишком мега длинные числа интерпретатор не поддерживает.
>>> a = 3 ** 1000 >>> a + 0.1 Traceback (most recent call last): File «», line 1, in OverflowError: int too large to convert to float
>>> a = 3 ** 1000 >>> a + 0.1 Traceback (most recent call last): File «», line 1, in OverflowError: int too large to convert to float |
Примеры с числами:
>>> c = 150 >>> d = 12.9 >>> c + d 162.9 >>> p = abs(d — c) # Модуль числа >>> print(p) 137.1 >>> round(p) # Округление 137
>>> c = 150 >>> d = 12.9 >>> c + d 162.9 >>> p = abs(d — c) # Модуль числа >>> print(p) 137.1 >>> round(p) # Округление 137 |
Для работы с числами есть ещё полезные модули, помогающие в расчетах.
Модуль math предоставляет более сложные математические функции. Такие как квадратный корень, логарифмы, пи и т.д.
>>> import math >>> math.pi 3.141592653589793 >>> math.sqrt(85) 9.219544457292887
>>> import math >>> math.pi 3.141592653589793 >>> math.sqrt(85) 9.219544457292887 |
И можно замутить любое случайное число с помощью модуля random. Я не до конца понимаю его значение, может кто использовал??
>>> import random >>> random.random() 0.15651968855132303
>>> import random >>> random.random() 0.15651968855132303 |
И наконец…
Комплексные числа (из высшей математики)
В общих чертах код будет примерно таким:
>>> x = complex(1, 2) >>> print(x) (1+2j) >>> y = complex(3, 4) >>> print(y) (3+4j) >>> z = x + y >>> print(x) (1+2j) >>> print(z) (4+6j) >>> z = x * y >>> print(z) (-5+10j) >>> z = x / y >>> print(z) (0.44+0.08j) >>> print(x.conjugate()) # Сопряжённое число (1-2j) >>> print(x.imag) # Мнимая часть 2.0 >>> print(x.real) # Действительная часть 1.0 >>> print(x > y) # Комплексные числа нельзя сравнить Traceback (most recent call last): File «», line 1, in TypeError: unorderable types: complex() > complex() >>> print(x == y) # Но можно проверить на равенство False >>> abs(3 + 4j) # Модуль комплексного числа 5.0 >>> pow(3 + 4j, 2) # Возведение в степень (-7+24j)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | >>> x = complex(1, 2) >>> print(x) (1+2j) >>> y = complex(3, 4) >>> print(y) (3+4j) >>> z = x + y >>> print(x) (1+2j) >>> print(z) (4+6j) >>> z = x * y >>> print(z) (-5+10j) >>> z = x / y >>> print(z) (0.44+0.08j) >>> print(x.conjugate()) # Сопряжённое число (1-2j) >>> print(x.imag) # Мнимая часть 2.0 >>> print(x.real) # Действительная часть 1.0 >>> print(x > y) # Комплексные числа нельзя сравнить Traceback (most recent call last): File «», line 1, in TypeError: unorderable types: complex() > complex() >>> print(x == y) # Но можно проверить на равенство False >>> abs(3 + 4j) # Модуль комплексного числа 5.0 >>> pow(3 + 4j, 2) # Возведение в степень (-7+24j) |
Если кто знает, скажите пожалуйста, в каких задачах применяются такие числа?
Подписывайтесь на новости блога. Если есть какие-то вопросы и предложения, вы знаете куда писать.
С уважением, ваш Гридин Семён
kip-world.ru
Как найти в Python остаток от деления?
Python – простой, современный язык для написания кода. Он обладает мощными библиотеками, способными вычислить любое выражение. Python выступает основным конкурентом для Matlab и Octave. Запустив в интерактивном режиме Python, остаток от деления пользователь сможет найти без труда. Но это еще не все! «Питон» может выступить мощным калькулятором.

Понятие оператора
Чтобы без труда найти в Python остаток от деления, нужно разобраться с некоторыми определениями. Оператор – знак или строка, позволяющие произвести математическое, побитовое, логическое и другое вычисление. Выражения или числа, вводимые пользователем, чтобы найти в Python 3 остаток от деления, тождественность сочетания или сравнения, называются операндами.
Разделяют следующие виды операторов:
- арифметические;
- побитовые;
- логические;
- операторы присваивания;
- сравнения;
- членства;
- тождественности.
Проще говоря, в примере «15 — 5» оператором является знак «–», операндами – 15 и 5. Это арифметическая операция с целыми числами. Если взять к рассмотрению выражение «True and True», то оператором здесь выступает «and», а операндами – «True» и «True». Этот пример можно отнести к логическому типу.
Целые и вещественные числа. Математические операции и вывод результата
Если рассматривать математические операции над целыми и дробными числами, то операторами выступают +, -, *, /, **, //, %. С первыми тремя всё понятно. Они обозначают, соответственно, сложение, вычитание, умножение. Оператор «**» указывает на необходимость возведения в степень.
Знаки одинарного (/) и двойного (//) деления отличаются. Если первый выдает в решении вещественное число, то второй необходим для нахождения целой части от деления. К примеру, 9 // 4 = 2. Этот оператор соответствует функции div в Turbo Pascal. Но есть закономерность. Знак «/» выведет целое число как результат, если и делитель, и делимое – также целые. Чтобы найти в Python остаток от деления, нужно воспользоваться оператором «%». По аналогии с тем же «Турбо Паскалем» «%» сопоставим с функцией mod. К примеру, 9%2 = 1, т.е. в Python остаток от деления в данном случае равняется 1. Рассмотрим еще примеры.
Чтобы произвести деление без остатка, Python предлагает воспользоваться функцией divmod(х,у). В данном случае х – делимое, у – делитель. Для выражения divmod (9,3) программа выдаст следующий результат (3,0). Это означает, что целая часть от деления равняется 3, а остаток – 0.
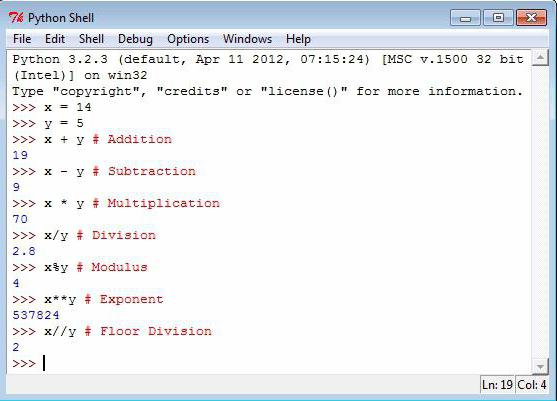
Математические операции можно выполнять без присваивания значения переменной. Тогда результат выдается автоматически. Если же код содержит присваивание переменной, то вывести результат на экран можно посредством оператора print.
Модуль math
Для удобства пользователей разработчики предлагают мощный модуль math, способный работать с любыми типами чисел и выполнять дополнительные функции.
Чтобы подключить библиотеку, нужно прописать в начале программного кода следующую строку: import math. Такая команда позволит подгрузить в программный код все функции, имеющиеся в модуле math. Тогда для подключения определенного блока из библиотеки нужно постоянно прописывать его. К примеру, x = math.ceil(5.6).
Если в программе будет часто использоваться один и тот же блок, то можно импортировать только его. К примеру, нужно произвести ряд округлений до ближайшего целого числа в большую сторону. Тогда код прописывается следующим образом: from math import ceil или from math import *. В обоих случаях дальнейший код по округлению результата не изменится.
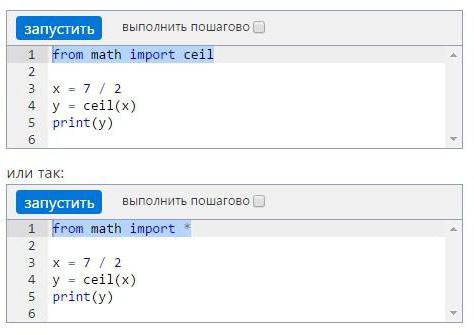
Стандартные функции арифметики в Python
Чтобы вычислить в Python остаток от целочисленного деления, не всегда нужно подгружать библиотеку math. Некоторые функции являются встроенными.
Встроенные функции | Их назначение | Примеры |
int(x) | Превращает вещественное число в целое, т.е. дробная часть «отсекается». | int(5.3) >>> 5 int(5.6) >>>5 int(5.987) >>> 5 |
round(x) | Происходит округление выражения до ближайшего целого. | round(5.4) >>>5.0 round(5.7) >>>6.0 round(5.5) >>>6.0 round(5.987) >>>6.0 |
round(x, n) | Используется для округления дробной части до n знаков после запятой | round(5.8776,2) >>> 5.88 round(5.9876,3) >>> 5.988 |
abs(x) | Находит модуль выражения | abs(-7) >>>7 abs(7.8) >>>7.8 abs(-66.55) >>>66.55 |
Функции, для которых необходимо подключение библиотеки (нужно изначально вписать from math import *), можно увидеть в следующей таблице.
Функции | Их назначение |
ceil(x) | Функция необходима для округления числа до большего целого («вверх») |
floor(x) | Функция требуется, чтобы округлить число до меньшего целого («вниз») |
sqrt(x) | Вычисляет корень из числа |
log(x) | Необходима для нахождения логарифма. Если указать основание, то и вычисление будет соответствующим. |
e | Выводит основание натурального логарифма |
sin(x) | Вычисление тригонометрических функций, где х выражен в радианах |
cos(x) | |
tan(x) | |
asin(x) | |
acos(x) | |
atan(x) | |
atan2(x,y) | Находит полярный угол точки, координаты которой задаются х и у |
degrees(x) | Необходима для преобразования угла из радиан в градусы |
radians(x) | Функция, необходимая для преобразования угла, заданного в градусах, в радианы |
pi | Выводит значение константы π |
В качестве примера ниже приведен код с использованием математических операторов.
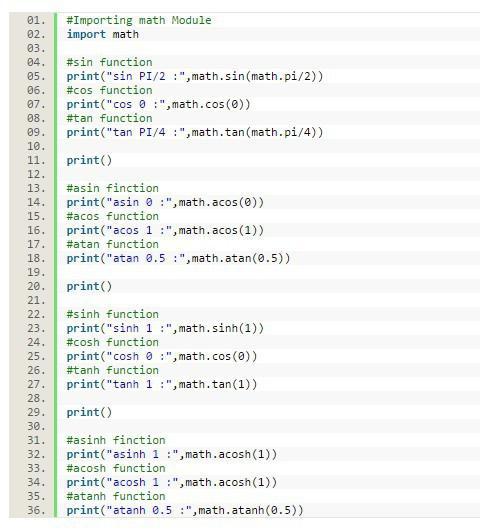
Результат выведен следующим образом.
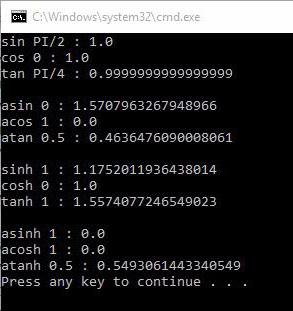
В модуле math гораздо больше функций. Здесь указаны наиболее встречающиеся.
fb.ru
Вещественные и комплексные числа в Python: системы счисления и операции
Для обработки данных, связанных с количественной информацией, а также для выполнения арифметических операций в языке программирования Python используются различные виды чисел: целые, вещественные и комплексные. Стандартная библиотека Python содержит массу полезных методов, позволяющих легко взаимодействовать с численными типами данных.
Целые числа
Самой простой и наиболее часто используемой разновидностью чисел в языке Python, как и во многих других средствах программирования является целочисленный тип данных. Для его представления используются цифровые значения, которые, как правило, присваиваются определенным переменным. Ниже обозначен пример задания целых чисел в программе, где создается целая переменная под именем i, а затем выводится на экран ее значение и тип:
i = 42 # целое число
print("i = " + str(i))
print(type(i))
i = 42
<type 'int'>Вещественные числа
Для того чтобы записать действительное число в Python есть числа с плавающей точкой. Работая в программе с подобными величинами, можно получать более точные данные при арифметических подсчетах. Чтобы инициализировать объект, который содержит вещественное число, необходимо присвоить ему значение, где целая и дробная части разделены символом точки. В данном примере показано создание переменной f:
f = 3.14 # вещественное число
print("f = " + str(f))
print(type(f))
f = 3.14
<type 'float'>Комплексные числа
В языке программирования Python также поддерживается работа с комплексными числами. Подобная информация представлена в виде пары значений: действительной и мнимой части, которые разделяются символом операции сложения. Также в завершении мнимой составной части комплексного числа обязательно должна стоять буква j. В следующем фрагменте кода демонстрируется создание комплексной переменной c и выводится вся информация о ней:
c = 1 + 2j # комплексное число
print("c = " + str(c))
print(type(c))
c = (1+2j)
<type 'complex'>Можно получить действительную и мнимую часть чисел отдельно. Для этого следует использовать real и image:
c = (1+2j) print(c.real) print(c.imag) 1.0 2.0
Системы счисления
Помимо общепринятой десятичной системы счисления, Python поддерживает приведение цифровых данных к двоичному, восьмеричному и шестнадцатеричному представлению. Чтобы начать работать с подобными числами, необходимо инициализировать переменные при помощи констант, обладающих префиксами 0b, 0o и 0x соответственно выбранному типу. В программе ниже создаются и выводятся на экран данные в различных системах:
b = 0b110101 # число в двоичной системе
o = 0o342 # число в восьмеричной системе
x = 0x1FE9 # число в шестнадцатеричной системе
print("b = " + str(b))
print("o = " + str(o))
print("x = " + str(x))
b = 53
o = 226
x = 8169Приведение типов
Используя стандартные средства языка Python, можно достаточно легко менять типовую принадлежность практически любой переменной. Для этого существуют методы, такие как int, float, complex, bin, oct, hex. Три последние функции позволяют перевести число либо переменную в десятичную, восьмеричную и шестнадцатеричную систему соответственно. Следующий фрагмент кода демонстрирует работу всех шести вышеописанных методов:
i = int(67.23) # вещественное число усекается до целого
f = float('1304') # строка становится вещественным числом
c = complex(2, 6) # формируется комплексное число
b = bin(42) # перевод числа в двоичную систему
o = oct(993) # перевод числа в восьмеричную систему
x = hex(4152) # перевод числа в шестнадцатеричную систему
print("i = " + str(i))
print("f = " + str(f))
print("c = " + str(c))
print("b = " + str(b))
print("o = " + str(o))
print("x = " + str(x))
i = 67
f = 1304.0
c = (2+6j)
b = 0b101010
o = 01741
x = 0x1038Операции над числами
Манипуляции над числовыми значениями в языке программирования Python выполняются благодаря множеству различных операций, символьные обозначения которых, как правило, совпадают с аналогами из традиционной математики. Таким образом, можно прибавлять, отнимать, умножать, делить, находить остаток от деления и возводить в степень числовые значения любых разновидностей. Ознакомиться с основными типами операций, которые выполняются над цифровыми значениями, можно из следующей небольшой таблицы:
| Операция | |
| a + b | Сложение a и b |
| a – b | Разница между a и b |
| a * b | Умножение a на b |
| a / b | Деление a на b |
| a % b | Остаток от деления a на b |
| a // b | Целая часть от деления a и b |
| a ** b | Возведение a в степень b |
Помимо вышеперечисленных арифметических действий, над числами можно осуществлять битовые операции, которые задействуют их двоичное представление. Перечень подобных операций представлен в следующей таблице, где можно найти назначение каждой из них:
| Операция | Назначение |
| a & b | Побитовое И для a и b |
| a | b | Побитовое ИЛИ для a и b |
| a ^ b | Исключающее ИЛИ для a и b |
| ~a | Инверсия битов для a |
| a << b | Побитовый сдвиг влево для a на b |
| a >> b | Побитовый сдвиг вправо для a на b |
Также для более эффективной обработки числовых данных в Python были добавлены особые методы, позволяющие всего за одно действие осуществлять множество сложных операций. К наиболее популярным из них относятся методы, предназначенные для быстрого нахождения квадратного корня, модуля, а также округления числа. Чтобы воспользоваться некоторыми арифметическими функциями, необходимо подключить стандартную библиотеку math при помощи вызова import math. Список популярных методов представлен в данной таблице:
| Метод | Назначение |
| sqrt(a) | Квадратный корень из a |
| log(a) | Натуральный логарифм из a |
| fabs(a) | Возвращает модуль a |
| round(a) | Округляет a до ближайшего целого |
| round(a, b) | Округляет a до b знаков после точки |
| floor(a) | Округляет a до меньшего целого значения |
| ceil(a) | Округляет a до большего целого значения |
| isfinite(a) | Проверяет, является ли a числом |
| modf(a) | Возвращает целую и дробную части a |
| sin(a) | Синус угла a, указанного в радианах |
| cos(a) | Косинус угла a, указанного в радианах |
| tan(a) | Тангенс угла a, указанного в радианах |
Функция fabs модуля math вначале пытается привести аргумент к вещественному типу (float), и только потом вычисляет модуль. Для вычисления модуля числа так же есть стандартная функция abs.
Ввод числа с клавиатуры
Для того чтобы получить числовые данные от пользователя используется стандартный метод input. Его вызов позволяет получать ввод информации с клавиатуры, который выполняется во время запуска программы на компьютере. В качестве аргумента для этого метода можно использовать строку, предлагающую пользователю ввести числовые сведения. Ниже показан пример того, как ввести в Pyhon с клавиатуры число. Переменная n получает значение и отображается на экране с помощью print:
n = input("Press n: ")
print("n = " + str(n))
Press n: 10
n = 10Максимальное значение
Получить максимальное значение целочисленной переменной, которое поддерживается в текущей версии языка Python можно с помощью переменной sys.maxsize. Как правило, на разных компьютерах это число совпадать не будет из-за разной архитектуры процессоров. На данный момент из Python были убраны любые ограничения, касающиеся размерности вводимых величин. Вывести на экран максимальное число в Python можно следующим образом:
import sys print(sys.maxsize) 9223372036854775807
Заключение
Для обработки числовых данных в языке программирования Python используются цифровые константы трех видов: целые, вещественные и комплексные. Стандартные математические операции над числами, как правило, выполняются при помощи набора общепринятых знаков сложения, вычитания, умножения и деления. Для выполнения специфических действий над числовыми величинами используются различные методы из стандартной библиотеки Python.
all-python.ru
Некоторые основные понятия — Практическое применение численных методов на языке Python
Мы рассмотрели несколько простых примеров, иллюстрирующих использование Python для решения простейших математических задач. Прежде чем мы перейдем к более сложным и достаточно реалистичным примерам, рассмотрим некоторые понятия, которые будут часто использоваться в следующих главах: переменные, объекты. Кроме того рассмотрим такие понятия, как ошибки округления, приоритет арифметических операций, деление целых чисел. Также получим чуть больше информации о функционале Python при работе с массивами, построении графиков и выводе результатов.
Интерактивное использование Python
Python можно использовать интерактивно, т.е. мы можем не писать
сначала сценарий и запускать его, выполнять операторы и выражения в оболочке Python. Мы рекомендуем использовать оболочку IPython (на
наш взгляд — лучшая из альтернативных оболочек Python). При
использовании IDE Spyder, IPython доступен при запуске в правом
нижнем окне. Следуя подсказке IPython In [1] (подсказка — это так
называемый знак готовности, т.е. программа предлагает вводить
команды), мы можем выполнять вычисления
In [1]: 2+2 Out[1]: 4 In [2]: 2*4 Out[2]: 8 In [3]: 10/2 Out[3]: 5 In [4]: 4**4 Out[4]: 256
Ответу интерпретатора IPython предшествует Out [q]:, где q —
номер соответствующей входной строки.
Заметим, что, как и в сценарии, можно выполнить команду from math import * для использования, например, pi или
математических функций. Также можно импортировать и другие модули,
когда они понадобятся.
Можно также определять переменные и использовать формулы интерактивно:
In [1]: v0 = 5 In [2]: g = 9.81 In [3]: t = 0.6 In [4]: y = v0*t - 0.5*g*t**2 In [5]: print y 1.2342
Иногда может понадобиться повторить команду, которую уже выполняли ранее. Для этого можно воспользоваться стрелкой вверх на клавиатуре. Нажав эту клавишу один получим предыдущую команду, два раза — команду перед этой и т.д. С помощью стрелки вниз мы будем пробегать вперед по истории команд. Также можно поправить выбранную команду перед ее выполнением.
Арифметические операции, круглые скобки и ошибки округления
Как известно арифметические операции +, -, *, / и ** имеют приоритет выполнения. Python обрабатывает операции слева
направо, вычисляя один операнд (часть выражения между двумя
последовательными + или -). Внутри каждого операнда операция ** выполняется перед * или /. Рассмотрим выражение x = 2*4**3 + 10*2 - 1.0/4. В нем три операнда, и Python
начинает обрабатывать их слева. В первом операнде 2*4**3 интерпретатор сначала вычислит 4**3, что даст 64, затем
результат умножается на 2. Получаем 128. Следующий операнд 10*2, т.е. 20. Затем два операнда складываются, что дает 148. Результат вычисления последнего операнда равен 0.25. Таким образом значение переменной x становится равным 147.75.
Отметим, что круглые скобки используются для группировки
операндов. Пусть x = 4 получим результат деления числа 1.0 на x+1. Приведем варианты записи в интерпретаторе Python:
In [1]: 1.0/x+1 Out[1]: 1.25 In [2]: 1.0/(x+1) Out[2]: 0.2
При первой попытке выполнено сначала деление 1.0 на x, к
которому затем прибавляется 1. Python не воспринимает x+1 как
знаменатель. Во второй попытке мы воспользовались круглыми скобками,
чтобы сгруппировать знаменатель. Так как большинство чисел в памяти
компьютера могут быть представлены только приближенно, иногда может
получаться не точное значение, что обусловлено ошибками округления.
Переменные и объекты
Переменные в Python имеют некоторый тип. Если мы запишем x = 2 в
сценарии Python, то x становится целой переменной, т.е. переменной
типа int (целое число). Аналогично, выражение x = 2.0 означает, что x переменная типа float (действительное число). В любом случае, Python
воспринимает x как объект типа int или float. Узнать тип
объекта x можно с помощью команды type(x). Еще один основной
тип переменной — это тип
x = "This is the text" y = 'This is the text'
Оба оператора создают объекты типа str.
При необходимости можно преобразовывать типы. Если, например, x — объект типа int, с помощью выражения y = float(x) мы
создаем объект с плавающей точкой. Аналогично можно получить целое
число из типа float, воспользовавшись int(x). Преобразование
типов может осуществлятся автоматически, как будет показано чуть ниже.
alpha в имени переменной в сценарии. Если,
например, вычисляем число овец (sheep), то одним из подходящих имен
для переменной может быть no_of_sheep. Такие имена переменных
делают более читабельным код программы. Имена переменных могут
содержать цифры и знак подчеркивания, но не могут начинаться с
цифры. Буквы могут быть строчными и прописными, в Python они
отличаются. Отметим, что некоторые имена в Python зарезервированы и мы
не можем их использовать в качестве имен переменных. Вот некоторые
примеры: forwhile, else, global, return и elif. Если мы случайно используем зарезервированное слово в
качестве имени переменных, то получим сообщение об ошибке.Выражение x = 2 присваивает значение 2 переменной x. Как
можно увеличить x на 4? Мы можем воспользоваться выражением x = x + 4 или выражением (дающим более быстрые вычисления) x += 4. Аналогично, x -= 4 уменьшает значение переменной x на 4, x *= 4 умножает x` на 4, ``x /= 4 делит x на 4,
обновляя значение переменной
Что произойдет, если x = 2, т.е. объект типа int, и мы к нему
прибавим 4.0 (объект типа float)? Будет иметь место автоматическое преобразование типов и новое x примет значение 6.0, т.е. станет объектом типа float.
In [1]: x = 2 In [2]: type(x) Out[2]: int In [3]: x = x +4.0 In [4]: x Out[4]: 6.0 In [5]: type(x) Out[5]: float
Отметим, что можно использовать выражение 2., чтобы указать, что
объект типа float.
Целочисленное деление
Следует обратить внимание на еще одну проблему — целочисленное деление. Рассмотрим пример деления числа 1 на 4:
In [1]: 1/4 Out[1]: 0 In [2]: 1.0/4 Out[2]: 0.25
Представлены два способа выполнения этой операции, при этом второй вариант дает правильный результат.
В Python версии 2 первый вариант дает результат так называемого целочисленного деления. В этом случае все десятичные знаки
отбрасываются, т.е. результат округляется до ближайшего меньшего
целого числа. Чтобы избежать этого мы можем явно указать десятичную
точку либо в числителе, либо в знаменателе, либо в обоих
операндах. Если числитель или знаменатель являются переменными,
т.е. мы вычисляем выражение 1/x, то, чтобы получить результат типа float, можно записать 1/float(x).
В Python версии 3 операция float, а для
целочисленного деления используется только операция // (// также есть в Python версии 2).
Форматированный вывод текста и чисел
В результате научных вычислений часто на печать выводится текст,
содержащий числа. Естественно желание контролировать формат вывода
числа. Например, мы хотим вывести число 1/3 как 0.33 или в
виде 3.3333e-1 (\(3.3333 \times 10^{-1}\)). Команда print — основной инструмент для вывода текста и чисел, обеспечивающий
полное управление форматированием. Первый аргумент команды print — это строка с определенным синтаксисом, задающим формат вывода, так
называемый printf-синтаксис. Такое название происходит от функции printf из языка программирования C, где такой синтаксис был введен
впервые.
Предположим, мы имеем действительное число 12.39486, целое число 23, и текст “сообщение”, которые мы хотим вывести на печать двумя способами:
real=12.394, integer=23, string=сообщение real=1.239e+01, integer= 23, string=сообщение
В первом варианте действительное число выведено в десятичной записи 12.394, а
во втором в научной записи (с плавающей точкой) 1.239e+01. Целое
число в первом варианте выведено в компактном виде, а во втором
варианте в текстовом поле из четырех символов.
Следующий сценарий (formatted_print.py) использует printf-синтаксис для
управления форматированным выводом:
# -*- coding: utf-8 -*- real = 12.29486 integer = 23 string = 'сообщение' print "real=%.3f, integer=%d, string=%s" % (real, integer, string) print "real=%4.3e, integer=%3d, string=%s" % (real, integer, string)
Вывод команды print — это строка, содержащая текст и набор
переменных, вставляемых в текст в местах отмеченных символом %. После % идет определение формата, например %f (для
действительных чисел), %d (для целых чисел) или %s (для
строк). Формат вида %4.3f означает, что действительное число
выводится в десятичной записи, с тремя знаками после запятой, в поле
из 4 символов. Вариант .3f означает вывод числа в наименьшем
возможном поле, в десятичной записи, с тремя знаками после
запятой. Замена f на e или E приводит к выводу в научном
формате: 1.239e+01 или 1.239E+01. Запись %4d означает
вывод целого числа в текстовом поле из четырех
символов. Действительные числа также могут выводится форматом %g,
который используется для автоматического выбора между десятичным и
научным форматом, дающим более компактную запись (научный формат
удобен для очень маленьких и очень больших чисел).
Типичный пример, когда требуется printf-синтаксис для вывода, когда нужно напечатать выровненные колонки. Предположим мы хотим напечатать колонку значений \(t\) и колонку с соответствующими значениями функции \(f(t) = t\sin t\). Простейший вариант
# -*- coding: utf-8 -*- from math import sin t = 0 dt = 0.55 t += dt; f = t*sin(t) print t, f t += dt; f = t*sin(t) print t, f t += dt; f = t*sin(t) print t, f
дает следующий результат
0.55 0.287477975912 1.1 0.980328096068 1.65 1.64482729695
Обратите внимание на то, что колонки не выровнены, что дает
нечитабельный вывод. Добавив в функцию print следующий аргумент '%6.2f %8.3f' %(t, f), мы управляем шириной каждой колонки и
количеством знаков после запятой:
0.55 0.287 1.10 0.980 1.65 1.645
Современная альтернатива printf-синтаксису
В современном Python отдается предпочтение использованию метода format. Например
print 'При t = {t:g} с, y = {y:.2f} м'.format(t=t, y=y)
соответствует следующему printf-синтаксису:
print 'При t = %g с, y = %.2f м' % (t, y)
Область, куда помещается значение переменной, теперь задается
фигурными скобками, а в методе format перечисляем имена
переменных внутри фигурных скобок и соответствующие им имена
переменных в программе.
Так как printf-синтаксис широко распространен в во многих языках программирования, мы будем использовать его. Однако уже во многих программах на Python вы можете встретить новый способ форматирования вывода, поэтому мы привели его здесь.
Массивы
В сценарии ball_plot.py из раздела
Программа на Python с векторизацией и построением графиков мы использовали массивы NumPy. Такие
массивы создаются и обрабатываются в соответствии с некоторыми
правилами, при этом управлять массивами можно как целиком, так и
отдельными элементами массива.
Рассмотрим такой пример: предположим у нас есть данные о росте четырех
человек. Эти данные мы можем сохранить в массиве с именем h следующим образом:
h = zeros(4) h[0] = 1.60 h[1] = 1.75 h[2] = 1.82 h[3] = 1.72
Здесь элементами массива являются h[0], h[1] и т.д. Самая
первая строка в приведенном фрагменте кода
дает указание Python зарезервировать, или выделить, пространство в
памяти для массива h из четырех элементов с начальными значениями
равными 0. Следующие четыре строки заменяют нулевые значения элементов
массива заданными. Элементы, как правило, индексируются с 0.
Используя двоеточие, мы можем получать срез массива. Например, чтобы
создать новый массив из двух элементов h[1] и h[2], мы можем
использовать следующую конструкцию slice_h = h[1:3]. Отметим, что
определение 1:3 означает индексы 1 и 2, т.е. последний
индекс в определении среза не включается. Полученный массив slice_h, индексируется стандартно с 0. Доступ к самому последнему элементу
массива можно получить следующим образом h[-1].
Копирование массива требует осторожности, так как запись new_h =
h означает присваивание ссылки, т.е. в этом случае, когда мы будем
изменять значения элементов массива h, будут изменяться значения
соответствующих элементов массива new_h.
Построение графиков
Иногда нам нужно построить графики двух функций на одном
рисунке. Предположим у нас есть массив h, заданный выше и массив H. График с двумя кривыми можно построить следующим образом
(сценарий plotting_two.py):
# -*- coding: utf-8 -*- import numpy as np import matplotlib.pyplot as plt h = np.zeros(4) h[0] = 1.60; h[1] = 1.75; h[2] = 1.82; h[3] = 1.72 H = np.zeros(4) H[0] = 0.60; H[1] = 0.30; H[2] = 1.90; H[3] = 1.99 numbers = np.zeros(4) numbers[0] = 1; numbers[1] = 2; numbers[2] = 3; numbers[3] = 4 plt.plot(numbers, h, numbers, H) plt.xlabel(u'Номер по порядку') plt.ylabel(u'Значение') plt.show()
Результат работы сценария представлен на рисунке
Рисунок 2. График, построенный с помощью сценария plotting_two.py
Две кривые на одном графике можно построить и другим способом,
используя две команды plot. Например, вы можете построить первую
кривую
plot(numbers, h)
hold('on')
Затем можно выполнить различные команды и вычисления в сценарии перед построением второй кривой
plot(numbers, H)
hold('off')
Мы здесь использовали функцию hold: hold('on') сообщает
Python, чтобы следующие кривые строились в том же окне. Python
выполняет это до тех пор пока не появится команда hold('off'). Если не использовать команды hold('on') и hold('off'), то вторая команда построения кривой перепишет первую,
т.е. появится только вторая кривая.
В случае, когда необходимо построить две кривые на отдельных графиках можно построить стандартно первую кривую
затем выполнить следующие команды
figure() plot(numbers, H)
Стандартно Python при построении графиков рисует прямые отрезки между точками со значениями. Можно также организовать другие способы вывода. Например, команда
построит только точки значений отмеченные символом * (можно
использовать также другие символы).
Кроме того, Python позволяет добавлять дополнительную информацию на графики. Например, можно добавить легенду с помощью следующей команды
или название графика
Команда
axis([xmin, xmax, ymin, ymax])
задает область построения графика: для оси \(x\) участок от xmin до xmax, для оси \(y\) участок от ymin до ymax
Сохранение графика в фалы соответствующих форматов можно выполнить с помощью следующих команд:
savefig('pic.png')
savefig('pic.jpg')
savefig('pic.gif')
savefig('pic.eps')
savefig('pic.pdf')
Матрицы
Для линейной алгебры могут понадобится стандартные операции, например,
умножение матрицы на вектор. Для этого можно использовать специальный
тип. Например, мы хотим вычислить вектор \(\mathbf{y}\) следующим
образом \(\mathbf{y} = \mathbf{A}\mathbf{x}\), где
\(\mathbf{A}\) — матрица размера \(2\times 2\),
\(\mathbf{x}\) — вектор. Это можно реализовать следующим образом
(сценарий mat_vec_mult.py)
# -*- coding: utf-8 -*- from numpy import zeros, mat, transpose x = zeros(2) x = mat(x) x = transpose(x) x[0] = 1.0; x[1] = 3.0 A = zeros((2,2)) A = mat(A) A[0,0] = 1.0; A[0,1] = 2.0 A[1,0] = 3.0; A[1,1] = 4.0 y = A*x print y
Здесь сначала x создан как объект типа array, затем тип
переменной x преобразован в тип matrix с помощью команды mat(x). Далее матрица-строка x преобразована в матрицу столбец
с помощью операции транспонирования transpose(x). Создана матрица A как массив размерности
slemeshevsky.github.io
Pythonicway — Операторы в Python
- Details
- Hits: 424179
Что такое оператор?
Говоря простым языком, в выражении 2 + 3, числа «2» и «3» называются операндами, знак «+» оператором. В языке программирования Python существуют следующие типы операторов:
Рассмотрим их по порядку.
| Оператор | Описание | Примеры |
|---|---|---|
| + | Сложение — Суммирует значения слева и справа от оператора |
15 + 5 в результате будет 20 |
| — | Вычитание — Вычитает правый операнд из левого | 15 — 5 в результате будет 10 20 — -3 в результате будет 23 13.4 — 7 в результате будет 6.4 |
| * | Умножение — Перемножает операнды | 5 * 5 в результате будет 25 7 * 3.2 в результате будет 22.4 -3 * 12 в результате будет -36 |
| / | Деление — Делит левый операнд на правый | 15 / 5 в результате будет 3 5 / 2 в результате будет 2 (В Python 2.x версии при делении двух целых чисел результат будет целое число) 5.0 / 2 в результате будет 2.5 (Чтобы получить «правильный» результат хотя бы один операнд должен быть float) |
| % | Деление по модулю — Делит левый операнд на правый и возвращает остаток. | 6 % 2 в результате будет 0 7 % 2 в результате будет 1 13.2 % 5 в результате 3.2 |
| ** | Возведение в степень — возводит левый операнд в степень правого | 5 ** 2 в результате будет 25 2 ** 3 в результате будет 8 -3 ** 2 в результате будет -9 |
| // | Целочисленное деление — Деление в котором возвращается только целая часть результата. Часть после запятой отбрасывается. | 12 // 5 в результате будет 2 4 // 3 в результате будет 1 25 // 6 в результате будет 4 |
| Оператор | Описание | Примеры |
|---|---|---|
| == | Проверяет равны ли оба операнда. Если да, то условие становится истинным. | 5 == 5 в результате будет True True == False в результате будет False «hello» == «hello» в результате будет True |
| != | Проверяет равны ли оба операнда. Если нет, то условие становится истинным. | 12 != 5 в результате будет True False != False в результате будет False «hi» != «Hi» в результате будет True |
| <> | Проверяет равны ли оба операнда. Если нет, то условие становится истинным. |
12 <> 5 в результате будет True. Похоже на оператор != |
| > | Проверяет больше ли значение левого операнда, чем значение правого. Если да, то условие становится истинным. | 5 > 2 в результате будет True. True > False в результате будет True. «A» > «B» в результате будет False. |
| < | Проверяет меньше ли значение левого операнда, чем значение правого. Если да, то условие становится истинным. | 3 < 5 в результате будет True. True < False в результате будет False. «A» < «B» в результате будет True. |
| >= | Проверяет больше или равно значение левого операнда, чем значение правого. Если да, то условие становится истинным. | 1 >= 1 в результате будет True. 23 >= 3.2 в результате будет True. «C» >= «D» в результате будет False. |
| <= | Проверяет меньше или равно значение левого операнда, чем значение правого. Если да, то условие становится истинным. | 4 <= 5 в результате будет True. 0 <= 0.0 в результате будет True. -0.001 <= -36 в результате будет False. |
| Оператор | Описание | Примеры |
|---|---|---|
| = | Присваивает значение правого операнда левому. | c = 23 присвоит переменной с значение 23 |
| += | Прибавит значение правого операнда к левому и присвоит эту сумму левому операнду. |
с = 5 |
| -= | Отнимает значение правого операнда от левого и присваивает результат левому операнду. |
с = 5 |
| *= | Умножает правый операнд с левым и присваивает результат левому операнду. |
с = 5 |
| /= | Делит левый операнд на правый и присваивает результат левому операнду. | с = 10 а = 2 с /= а равносильно: с = с / а. c будет равно 5 |
| %= | Делит по модулю операнды и присваивает результат левому. | с = 5 а = 2 с %= а равносильно: с = с % а. c будет равно 1 |
| **= | Возводит в левый операнд в степень правого и присваивает результат левому операнду. | с = 3 а = 2 с **= а равносильно: с = с ** а. c будет равно 9 |
| //= | Производит целочисленное деление левого операнда на правый и присваивает результат левому операнду. | с = 11 а = 2 с //= а равносильно: с = с // а. c будет равно 5 |
Побитовые операторы предназначены для работы с данными в битовом (двоичном) формате. Предположим, что у нас есть два числа a = 60; и b = 13. В двоичном формате они будут иметь следующий вид:
a = 0011 1100
b = 0000 1101
| Оператор | Описание | Примеры |
|---|---|---|
| & | Бинарный «И» оператор, копирует бит в результат только если бит присутствует в обоих операндах. | (a & b) даст нам 12, которое в двоичном формате выглядит так 0000 1100 |
| | | Бинарный «ИЛИ» оператор копирует бит, если тот присутствует в хотя бы в одном операнде. | (a | b) даст нам 61, в двоичном формате 0011 1101 |
| ^ | Бинарный «Исключительное ИЛИ» оператор копирует бит только если бит присутствует в одном из операндов, но не в обоих сразу. | (a ^ b) даст нам 49, в двоичном формате 0011 0001 |
| ~ | Бинарный комплиментарный оператор. Является унарным (то есть ему нужен только один операнд) меняет биты на обратные, там где была единица становиться ноль и наоборот. | (~a ) даст в результате -61, в двоичном формате выглядит 1100 0011. |
| << | Побитовый сдвиг влево. Значение левого операнда «сдвигается» влево на количество бит указанных в правом операнде. | a << 2 в результате даст 240, в двоичном формате 1111 0000 |
| >> | Побитовый сдвиг вправо. Значение левого операнда «сдвигается» вправо на количество бит указанных в правом операнде. | a >> 2 даст 15, в двоичном формате 0000 1111 |
| Оператор | Описание | Примеры |
|---|---|---|
| and | Логический оператор «И». Условие будет истинным если оба операнда истина. |
True and True равно True. |
| or | Логический оператор «ИЛИ». Если хотя бы один из операндов истинный, то и все выражение будет истинным. | True or True равно True. True or False равно True. False or True равно True. False or False равно False. |
| not | Логический оператор «НЕ». Изменяет логическое значение операнда на противоположное. | not True равно False. not False равно True. |
В добавок к перечисленным операторам, в Python присутствуют, так называмые, операторы членства, предназначенные для проверки на наличие элемента в составных типах данных, таких, как строки, списки, кортежи или словари:
| Оператор | Описание | Примеры |
|---|---|---|
| in | Возвращает истину, если элемент присутствует в последовательности, иначе возвращает ложь. | «cad» in «cadillac» вернет True. 1 in [2,3,1,6] вернет True. «hi» in {«hi»:2,»bye»:1} вернет True. 2 in {«hi»:2,»bye»:1} вернет False (в словарях проверяется наличие в ключах, а не в значениях). |
| not in | Возвращает истину если элемента нет в последовательности. | Результаты противоположны результатам оператора in. |
Операторы тождественности сравнивают размещение двух объектов в памяти компьютера.
| Оператор | Описание | Примеры |
|---|---|---|
| is | Возвращает истину, если оба операнда указывают на один объект. | x is y вернет истину, если id(x) будет равно id(y). |
| is not | Возврашает ложь если оба операнда указывают на один объект. | x is not y, вернет истину если id(x) не равно id(y). |
Приоритет операторов в Python
В следующей таблице описан приоритет выполнения операторов в Python от наивысшего (выполняется в первую очередь) до наинизшего.
| Оператор | Описание |
|---|---|
| ** | Возведение в степень |
| ~ + — | Комплиментарный оператор |
| * / % // | Умножение, деление, деление по модулю, целочисленное деление. |
| + — | Сложение и вычитание. |
| >> << | Побитовый сдвиг вправо и побитовый сдвиг влево. |
| & | Бинарный «И». |
| ^ | | Бинарный «Исключительное ИЛИ» и бинарный «ИЛИ» |
| <= < > >= | Операторы сравнения |
| <> == != | Операторы равенства |
| = %= /= //= -= += *= **= | Операторы присваивания |
| is is not | Тождественные операторы |
| in not in | Операторы членства |
| not or and | Логические операторы |
pythonicway.com
