Интерактивный учебник языка Python
1. Множества
Множество в языке Питон — это структура данных, эквивалентная множествам в математике. Множество может состоять из различных элементов, порядок элементов в множестве неопределен. В множество можно добавлять и удалять элементы, можно перебирать элементы множества, можно выполнять операции над множествами (объединение, пересечение, разность). Можно проверять принадлежность элемента множеству.
В отличие от массивов, где элементы хранятся в виде последовательного списка, в множествах порядок хранения элементов неопределен (более того, элементы множества хранятся не подряд, как в списке, а при помощи хитрых алгоритмов). Это позволяет выполнять операции типа “проверить принадлежность элемента множеству” быстрее, чем просто перебирая все элементы множества.
Элементами множества может быть любой неизменяемый тип данных:
числа, строки, кортежи. Изменяемые типы данных не могут быть
элементами множества, в частности, нельзя сделать элементом
множества список (но можно сделать кортеж) или другое множество.
Задание множеств
Множество задается перечислением всех его элементов в фигурных скобках.
Исключением явлеется пустое множество, которое можно создать при помощи
функции set(). Если функции set передать в качестве
параметра список, строку или кортеж, то она вернёт множество, составленное из элементов
списка, строки, кортежа. Например:
A = {1, 2, 3}
A = set('qwerty')
print(A)выведет {'e', 'q', 'r', 't', 'w', 'y'}.
Каждый элемент может входить в множество только один раз, порядок задания элементов неважен. Например, программа:
A = {1, 2, 3}
B = {3, 2, 3, 1}
print(A == B)выведет True, так как A и B — равные
множества.
Каждый элемент может входить в множество только один раз. set('Hello') вернет множество из четырех элементов: {'H', 'e', 'l', 'o'}.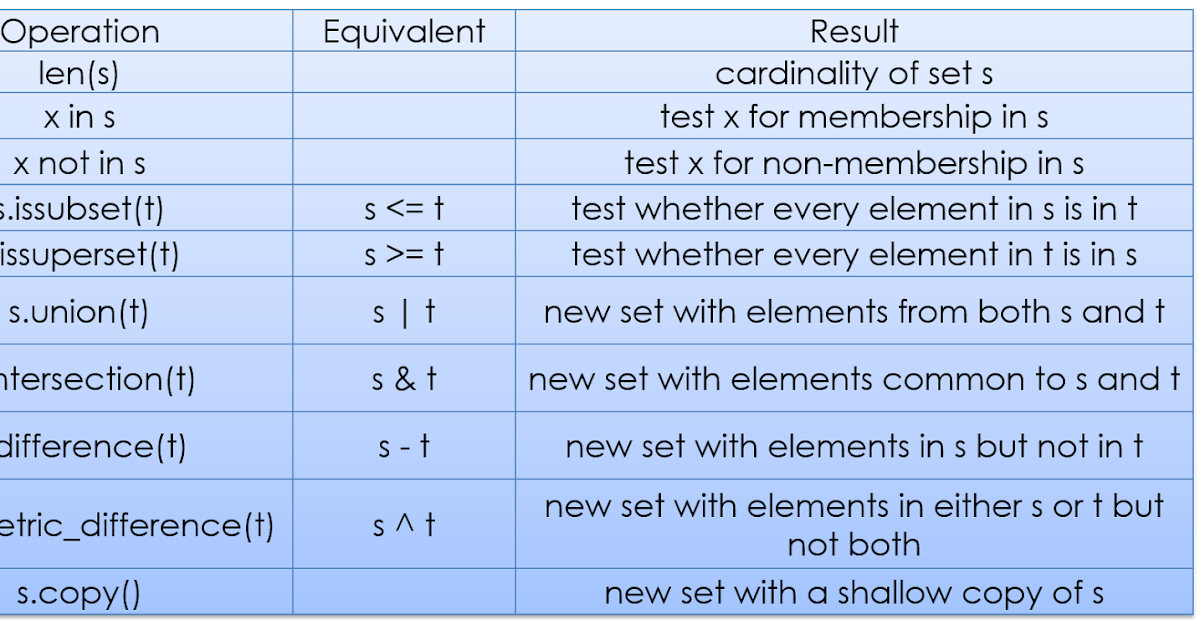
Работа с элементами множеств
Узнать число элементов в множестве можно при помощи функции len.
Перебрать все элементы множества (в неопределенном порядке!) можно при помощи цикла
primes = {2, 3, 5, 7, 11}
for num in primes:
print(num)Проверить, принадлежит ли элемент множеству можно при помощи операции in, возвращающей значение типа bool.
Аналогично есть противоположная операция not in.
Для добавления элемента в множество есть метод add:
A = {1, 2, 3}
print(1 in A, 4 not in A)
A.add(4)Для удаления элемента x из множества есть два метода: discard и remove. Их поведение различается
только в случае, когда удаляемый элемент отсутствует в множестве.
В этом случае метод discard не делает ничего, а метод KeyError.
Наконец, метод pop удаляет из множества один случайный
элемент и возвращает его значение. Если же множество пусто, то генерируется
исключение
Если же множество пусто, то генерируется
исключение KeyError.
Из множества можно сделать список при помощи функции list.
Операции с множествами
С множествами в питоне можно выполнять обычные для математики операции над множествами.
A | B A.union(B) | Возвращает множество, являющееся объединением множеств | |
A |= B A.update(B) | Добавляет в множество | |
A & B A.intersection(B) | Возвращает множество, являющееся пересечением множеств | |
A &= B A.intersection_update(B) | Оставляет в множестве | Записывает в |
A <= B A.issubset(B) | Возвращает | |
A >= B A.issuperset(B) | Возвращает | |
A < B | Эквивалентно | |
A > B | A >= B and A != B |
Ссылки на задачи доступны в меню слева. Эталонные решения теперь доступны на странице самой задачи.
Python и теория множеств / Хабр
В Python есть очень полезный тип данных для работы с множествами – это set. Об этом типе данных, примерах использования, и небольшой выдержке из теории множеств пойдёт речь далее.
Об этом типе данных, примерах использования, и небольшой выдержке из теории множеств пойдёт речь далее.
Следует сразу сделать оговорку, что эта статья ни в коем случае не претендует на какую-либо математическую строгость и полноту, скорее это попытка доступно продемонстрировать примеры использования множеств в языке программирования Python.
- Множество
- Множества в Python
- Хешируемые объекты
- Свойства множеств
- Принадлежность множеству
- Мощность множества
- Перебор элементов множества
- Отношения между множествами
- Равные множества
- Непересекающиеся множества
- Подмножество и надмножество
- Операции над множествами
- Объединение множеств
- Добавление элементов в множество
- Пересечение множеств
- Разность множеств
- Удаление элементов из множества
- Симметрическая разность множеств
- Заключение
- Полезные ссылки
Множество
Множество – это математический объект, являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества. Или другими словами:
Или другими словами:
Множество – это не более чем неупорядоченная коллекция уникальных элементов.
Что значит неупорядоченная? Это значит, что два множества эквивалентны, если содержат одинаковые элементы.
Элементы множества должны быть уникальными, множество не может содержать одинаковых элементов. Добавление элементов, которые уже есть в множестве, не изменяет это множество.
Множества, состоящие из конечного числа элементов, называются конечными, а остальные множества – бесконечными. Конечное множество, как следует из названия, можно задать перечислением его элементов. Так как темой этой статьи является практическое использование множеств в Python, то я предлагаю сосредоточиться на конечных множествах.
Множества в Python
Множество в Python можно создать несколькими способами. Самый простой – это задать множество перечислением его элементов в фигурных скобках:
fruits = {"banana", "apple", "orange"}Единственное ограничение, что таким образом нельзя создать пустое множество.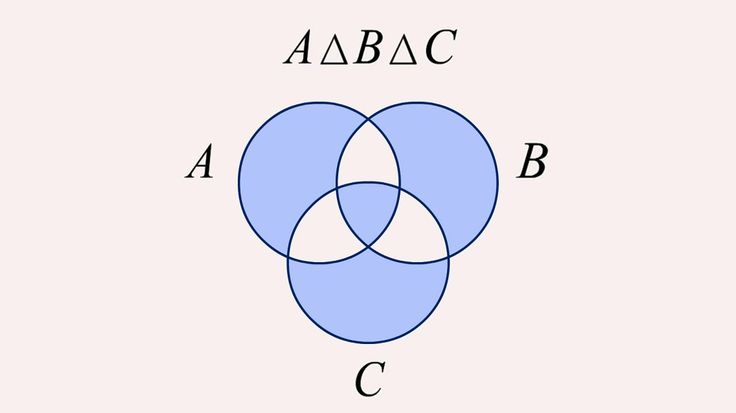 Вместо этого будет создан пустой словарь:
Вместо этого будет создан пустой словарь:
wrong_empty_set = {}
print(type(wrong_empty_set))
# Вывод
<class "dict">Для создания пустого множества нужно непосредственно использовать set():
correct_empty_set = set() print(type(correct_empty_set)) # Вывод <class "set">
Также в set() можно передать какой-либо объект, по которому можно проитерироваться (Iterable):
color_list = ["red", "green", "green", "blue", "purple", "purple"]
color_set = set(color_list)
print(color_set)
# Вывод (порядок может быть другим):
{"red", "purple", "blue", "green"}Ещё одна возможность создания множества – это использование set comprehension. Это специальная синтаксическая конструкция языка, которую иногда называют абстракцией множества по аналогии с
numbers = [1, 2, 2, 2, 3, 3, 4, 4, 5, 6]
# Единственное отличие со списковыми включениями - это
# использование фигурных скобок вместо квадратных
even_numbers = {
number for number in numbers
if number % 2 == 0
}
print(even_numbers)
# Вывод (порядок может быть другим):
{2, 4, 6}Хешируемые объекты
Существует ограничение, что элементами множества (как и ключами словарей) в Python могут быть только так называемые хешируемые (Hashable) объекты. Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (
Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (
# Множество кортежей (tuple)
records = {
("Москва", 17_200_000),
("Санкт-Петербург", 5_400_000),
("Новосибирск", 1_600_000),
("Москва", 17_200_000),
}
for city, population in records:
print(city)
# Вывод (порядок может быть другим):
Москва
Новосибирск
Санкт-ПетербургОбъекты пользовательских классов являются хешируемыми по умолчанию. Но практического смысла чаще всего в этом мало из-за того, что сравнение таких объектов выполняется по их адресу в памяти, т.е. невозможно создать два «равных» объекта.
class City:
def __init__(self, name: str):
self. name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}
name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}Скорее всего мы предполагаем, что объекты City("Moscow") должны быть равными, и следовательно в множестве cities должен находиться один объект.
Этого можно добиться, если определить семантику равенства для объектов класса City:
class City:
def __init__(self, name: str):
# Атрибут name не должен изменяться, пока объект существует
# Для простоты пометим этот атрибут как внутренний
self._name = name
def __hash__(self) -> int:
""" Хеш от объекта
"""
return hash((self._name, self.__class__))
def __eq__(self, other) -> bool:
""" Определяем семантику равентсва (оператор ==)
"""
if not isinstance(other, self. __class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'
__class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'Чтобы протокол хеширования работал без явных и неявных логических ошибок, должны выполняться следующие условия:
- Хеш объекта не должен изменяться, пока этот объект существует
- Равные объекты должны возвращать одинаковый хеш
moscow = City("Moscow")
moscow_again = City("Moscow")
print(moscow == moscow_again and hash(moscow) == hash(moscow_again))
# Вывод:
True
# Теперь множество городов работает более логично и интуитивно
cities = {City("Moscow"), City("Kazan"), City("Moscow")}
print(cities)
# Вывод (порядок может быть другим):
{City("Kazan"), City("Moscow")}Свойства множеств
Тип set в Python является подтипом Collection (про коллекции), из данного факта есть три важных следствия:
- Определена операция проверки принадлежности элемента множеству
- Можно получить количество элементов в множестве
- Множества являются iterable-объектами
Принадлежность множеству
Проверить принадлежит ли какой-либо объект множеству можно с помощью оператора in. Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за
Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за O(1) с теми же оговорками, которые существуют для хеш-таблиц.
tremendously_huge_set = {"red", "green", "blue"}
if "green" in tremendously_huge_set:
print("Green is there!")
else:
print("Unfortunately, there is no green...")
# Вывод:
Green is there!
if "purple" in tremendously_huge_set:
print("Purple is there!")
else:
print("Unfortunately, there is no purple...")
# Вывод:
Unfortunately, there is no purple...Мощность множества
Мощность множества – это характеристика множества, которая для конечных множеств просто означает количество элементов в данном множестве. Для бесконечных множеств всё несколько сложнее.
even_numbers = {i for i in range(100) if i % 2 == 0}
# Мощность множества
cardinality = len(even_numbers)
print(cardinality)
# Вывод:
50Перебор элементов множества
Как уже было отмечено выше, множества поддерживают протокол итераторов, таким образом любое множество можно использовать там, где ожидается iterable-объект.
colors = {"red", "green", "blue"}
# Элементы множества можно перебрать с помощью цикла for
for color in colors:
print(color)
# Вывод (порядок может быть другим):
red
green
blue
# Множества можно использовать там, где ожидается iterable-объект
color_counter = dict.fromkeys(colors, 1)
print(color_counter)
# Вывод (порядок может быть другим):
{"green": 1, "red": 1, "blue": 1}Отношения между множествами
Между множествами существуют несколько видов отношений, или другими словами взаимосвязей. Давайте рассмотрим возможные отношения между множествами в этом разделе.
Равные множества
Тут всё довольно просто – два множества называются равными, если они состоят из одних и тех же элементов. Как следует из определения множества, порядок этих элементов не важен.
my_fruits = {"banana", "apple", "orange", "orange"}
your_fruits = {"apple", "apple", "banana", "orange", "orange"}
print(my_fruits == your_fruits)
# Вывод:
TrueНепересекающиеся множества
Если два множества не имеют общих элементов, то говорят, что эти множества не пересекаются. Или другими словами, пересечение этих множеств является пустым множеством.
Или другими словами, пересечение этих множеств является пустым множеством.
even_numbers = {i for i in range(10) if i % 2 == 0}
odd_numbers = {i for i in range(10) if i % 2 == 1}
# Очевидно, что множества чётных и нечётных чисел не пересекаются
if even_numbers.isdisjoint(odd_numbers):
print("Множества не пересекаются!")
# Вывод:
Множества не пересекаются!Подмножество и надмножество
Подмножество множества S – это такое множество, каждый элемент которого является также и элементом множества S. Множество S в свою очередь является надмножеством исходного множества.
# Множество чисел Фибоначчи меньших 100
fibonacci_numbers = {0, 1, 2, 3, 34, 5, 8, 13, 21, 55, 89}
# Множество натуральных чисел меньших 100
natural_numbers = set(range(100))
# Множество чисел Фибоначчи является подмножеством множества
# натуральных чисел
if fibonacci_numbers.issubset(natural_numbers):
print("Подмножество!")
# Вывод:
Подмножество!
# В свою очередь множество натуральных чисел является
# надмножеством множества чисел Фибоначчи
if natural_numbers. issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!
issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!Пустое множество является подмножеством абсолютно любого множества.
empty = set()
# Методы issubset и issuperset могут принимать любой iterable-объект
print(
empty.issubset(range(100))
and empty.issubset(["red", "green", "blue"])
and empty.issubset(set())
)
# Вывод:
TrueСамо множество является подмножеством самого себя.
natural_numbers = set(range(100))
if natural_numbers.issubset(natural_numbers):
print("Подмножество!")
# Вывод:
Подмножество!Операции над множествами
Рассмотрим основные операции, опредяляемые над множествами.
Объединение множеств
Объединение множеств – это множество, которое содержит все элементы исходных множеств. В Python есть несколько способов объединить множества, давайте рассмотрим их на примерах.
my_fruits = {"apple", "orange"}
your_fruits = {"orange", "banana", "pear"}
# Для объединения множеств можно использовать оператор `|`,
# оба операнда должны быть объектами типа set
our_fruits = my_fruits | your_fruits
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Также можно использовать ментод union. # Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}Добавление элементов в множество
Добавление элементов в множество можно рассматривать как частный случай объединения множеств за тем исключением, что добавление элементов изменяет исходное множество, а не создает новый объект. Добавление одного элемента в множество работает за O(1).
colors = {"red", "green", "blue"}
# Метод add добаляет новый элемент в множество
colors.add("purple")
# Добавление элемента, который уже есть в множестве, не изменяет
# это множество
colors.add("red")
print(colors)
# Вывод (порядок может быть другим):
{"red", "green", "blue", "purple"}
# Метод update принимает iterable-объект (список, словарь, генератор и т.п.)
# и добавляет все элементы в множество
numbers = {1, 2, 3}
numbers. update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}
update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}Пересечение множеств
Пересечение множеств – это множество, в котором находятся только те элементы, которые принадлежат исходным множествам одновременно.
def is_prime(number: int) -> bool:
""" Возвращает True, если number - это простое число
"""
assert number > 1
return all(number % i for i in range(2, int(number**0.5) + 1))
def is_fibonacci(number: int) -> bool:
""" Возвращает True, если number - это число Фибоначчи
"""
assert number > 1
a, b = 0, 1
while a + b < number:
a, b = b, a + b
return a + b == number
# Множество простых чисел до 100
primes = set(filter(is_prime, range(2, 101)))
# Множество чисел Фибоначчи до 100
fibonacci = set(filter(is_fibonacci, range(2, 101)))
# Множество простых чисел до 100, которые одновременно являются
# числами Фибоначчи
prime_fibonacci = primes.intersection(fibonacci)
# Или используя оператор `&`, который определён для множеств
prime_fibonacci = fibonacci & primes
print(prime_fibonacci)
# Вывод (порядок может быть другим):
{2, 3, 5, 13, 89}При использовании оператора & необходимо, чтобы оба операнда были объектами типа set. Метод
Метод intersection, в свою очередь, принимает любой iterable-объект. Если необходимо изменить исходное множество, а не возращать новое, то можно использовать метод intersection_update, который работает подобно методу intersection, но изменяет исходный объект-множество.
Разность множеств
Разность двух множеств – это множество, в которое входят все элементы первого множества, не входящие во второе множество.
i_know: set = {"Python", "Go", "Java"}
you_know: dict = {
"Go": 0.4,
"C++": 0.6,
"Rust": 0.2,
"Java": 0.9
}
# Обратите внимание, что оператор `-` работает только
# для объектов типа set
you_know_but_i_dont = set(you_know) - i_know
print(you_know_but_i_dont)
# Вывод (порядок может быть другим):
{"Rust", "C++"}
# Метод difference может работать с любым iterable-объектом,
# каким является dict, например
i_know_but_you_dont = i_know.difference(you_know)
print(i_know_but_you_dont)
# Вывод:
{"Python"}Удаление элементов из множества
Удаление элемента из множества можно рассматривать как частный случай разности, где удаляемый элемент – это одноэлементное множество. Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность
Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность O(1).
fruits = {"apple", "orange", "banana"}
# Удаление элемента из множества. Если удаляемого элемента
# нет в множестве, то ничего не происходит
fruits.discard("orange")
fruits.discard("pineapple")
print(fruits)
# Вывод (порядок может быть другим):
{"apple", "banana"}
# Метод remove работает аналогично discard, но генерирует исключение,
# если удаляемого элемента нет в множестве
fruits.remove("pineapple") # KeyError: "pineapple"Также у множеств есть метод differenсe_update, который принимает iterable-объект и удаляет из исходного множества все элементы iterable-объекта. Этот метод работает аналогично методу difference, но изменяет исходное множество, а не возвращает новое.
numbers = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
even_numbers_under_100 = (i for i in range(1, 101) if i % 2 == 0)
numbers. , также существует два специальных метода –
, также существует два специальных метода – symmetric_difference и symmetric_difference_update. Оба этих метода принимают iterable-объект в качестве аргумента, отличие же состоит в том, что symmetric_difference возвращает новый объект-множество, в то время как symmetric_difference_update изменяет исходное множество.non_positive = {-3, -2, -1, 0}
non_negative = range(4)
non_zero = non_positive.symmetric_difference(non_negative)
print(non_zero)
# Вывод (порядок может быть другим):
{-1, -2, -3, 1, 2, 3}
# Метод symmetric_difference_update изменяет исходное множество
colors = {"red", "green", "blue"}
colors.symmetric_difference_update(["green", "blue", "yellow"])
print(colors)
# Вывод (порядок может быть другим):
{"red", "yellow"}
Заключение
Я надеюсь, мне удалось показать, что Python имеет очень удобные встроенные средства для работы с множествами. На практике это часто позволяет сократить количество кода, сделать его выразительнее и легче для восприятия, а следовательно и более поддерживаемым. Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Полезные ссылки
Множества (Статья на Википедии)
Документация по типу set
Iterable-объекты (Глоссарий Python)
Hashable-объекты (Глоссарий Python)
Sets in Python
Set Theory: the Method To Database Madness
Python и теория множеств / Хабр
В Python есть очень полезный тип данных для работы с множествами – это set. Об этом типе данных, примерах использования, и небольшой выдержке из теории множеств пойдёт речь далее.
Следует сразу сделать оговорку, что эта статья ни в коем случае не претендует на какую-либо математическую строгость и полноту, скорее это попытка доступно продемонстрировать примеры использования множеств в языке программирования Python.
- Множество
- Множества в Python
- Хешируемые объекты
- Свойства множеств
- Принадлежность множеству
- Мощность множества
- Перебор элементов множества
- Отношения между множествами
- Равные множества
- Непересекающиеся множества
- Подмножество и надмножество
- Операции над множествами
- Объединение множеств
- Добавление элементов в множество
- Пересечение множеств
- Разность множеств
- Удаление элементов из множества
- Симметрическая разность множеств
- Заключение
- Полезные ссылки
Множество
Множество – это математический объект, являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества. Или другими словами:
Или другими словами:
Множество – это не более чем неупорядоченная коллекция уникальных элементов.
Что значит неупорядоченная? Это значит, что два множества эквивалентны, если содержат одинаковые элементы.
Элементы множества должны быть уникальными, множество не может содержать одинаковых элементов. Добавление элементов, которые уже есть в множестве, не изменяет это множество.
Множества, состоящие из конечного числа элементов, называются конечными, а остальные множества – бесконечными. Конечное множество, как следует из названия, можно задать перечислением его элементов. Так как темой этой статьи является практическое использование множеств в Python, то я предлагаю сосредоточиться на конечных множествах.
Множества в Python
Множество в Python можно создать несколькими способами. Самый простой – это задать множество перечислением его элементов в фигурных скобках:
fruits = {"banana", "apple", "orange"}Единственное ограничение, что таким образом нельзя создать пустое множество. Вместо этого будет создан пустой словарь:
Вместо этого будет создан пустой словарь:
wrong_empty_set = {}
print(type(wrong_empty_set))
# Вывод
<class "dict">Для создания пустого множества нужно непосредственно использовать set():
correct_empty_set = set() print(type(correct_empty_set)) # Вывод <class "set">
Также в set() можно передать какой-либо объект, по которому можно проитерироваться (Iterable):
color_list = ["red", "green", "green", "blue", "purple", "purple"]
color_set = set(color_list)
print(color_set)
# Вывод (порядок может быть другим):
{"red", "purple", "blue", "green"}Ещё одна возможность создания множества – это использование set comprehension. Это специальная синтаксическая конструкция языка, которую иногда называют абстракцией множества по аналогии с list comprehension (Списковое включение).
numbers = [1, 2, 2, 2, 3, 3, 4, 4, 5, 6]
# Единственное отличие со списковыми включениями - это
# использование фигурных скобок вместо квадратных
even_numbers = {
number for number in numbers
if number % 2 == 0
}
print(even_numbers)
# Вывод (порядок может быть другим):
{2, 4, 6}Хешируемые объекты
Существует ограничение, что элементами множества (как и ключами словарей) в Python могут быть только так называемые хешируемые (Hashable) объекты. Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) – хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы.
Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) – хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы.
# Множество кортежей (tuple)
records = {
("Москва", 17_200_000),
("Санкт-Петербург", 5_400_000),
("Новосибирск", 1_600_000),
("Москва", 17_200_000),
}
for city, population in records:
print(city)
# Вывод (порядок может быть другим):
Москва
Новосибирск
Санкт-ПетербургОбъекты пользовательских классов являются хешируемыми по умолчанию. Но практического смысла чаще всего в этом мало из-за того, что сравнение таких объектов выполняется по их адресу в памяти, т.е. невозможно создать два "равных" объекта.
class City:
def __init__(self, name: str):
self. name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}
name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}Скорее всего мы предполагаем, что объекты City("Moscow") должны быть равными, и следовательно в множестве cities должен находиться один объект.
Этого можно добиться, если определить семантику равенства для объектов класса City:
class City:
def __init__(self, name: str):
# Атрибут name не должен изменяться, пока объект существует
# Для простоты пометим этот атрибут как внутренний
self._name = name
def __hash__(self) -> int:
""" Хеш от объекта
"""
return hash((self._name, self.__class__))
def __eq__(self, other) -> bool:
""" Определяем семантику равентсва (оператор ==)
"""
if not isinstance(other, self. __class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'
__class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'Чтобы протокол хеширования работал без явных и неявных логических ошибок, должны выполняться следующие условия:
- Хеш объекта не должен изменяться, пока этот объект существует
- Равные объекты должны возвращать одинаковый хеш
moscow = City("Moscow")
moscow_again = City("Moscow")
print(moscow == moscow_again and hash(moscow) == hash(moscow_again))
# Вывод:
True
# Теперь множество городов работает более логично и интуитивно
cities = {City("Moscow"), City("Kazan"), City("Moscow")}
print(cities)
# Вывод (порядок может быть другим):
{City("Kazan"), City("Moscow")}Свойства множеств
Тип set в Python является подтипом Collection (про коллекции), из данного факта есть три важных следствия:
- Определена операция проверки принадлежности элемента множеству
- Можно получить количество элементов в множестве
- Множества являются iterable-объектами
Принадлежность множеству
Проверить принадлежит ли какой-либо объект множеству можно с помощью оператора in. Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за
Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за O(1) с теми же оговорками, которые существуют для хеш-таблиц.
tremendously_huge_set = {"red", "green", "blue"}
if "green" in tremendously_huge_set:
print("Green is there!")
else:
print("Unfortunately, there is no green...")
# Вывод:
Green is there!
if "purple" in tremendously_huge_set:
print("Purple is there!")
else:
print("Unfortunately, there is no purple...")
# Вывод:
Unfortunately, there is no purple...Мощность множества
Мощность множества – это характеристика множества, которая для конечных множеств просто означает количество элементов в данном множестве. Для бесконечных множеств всё несколько сложнее.
even_numbers = {i for i in range(100) if i % 2 == 0}
# Мощность множества
cardinality = len(even_numbers)
print(cardinality)
# Вывод:
50Перебор элементов множества
Как уже было отмечено выше, множества поддерживают протокол итераторов, таким образом любое множество можно использовать там, где ожидается iterable-объект.
colors = {"red", "green", "blue"}
# Элементы множества можно перебрать с помощью цикла for
for color in colors:
print(color)
# Вывод (порядок может быть другим):
red
green
blue
# Множества можно использовать там, где ожидается iterable-объект
color_counter = dict.fromkeys(colors, 1)
print(color_counter)
# Вывод (порядок может быть другим):
{"green": 1, "red": 1, "blue": 1}Отношения между множествами
Между множествами существуют несколько видов отношений, или другими словами взаимосвязей. Давайте рассмотрим возможные отношения между множествами в этом разделе.
Равные множества
Тут всё довольно просто – два множества называются равными, если они состоят из одних и тех же элементов. Как следует из определения множества, порядок этих элементов не важен.
my_fruits = {"banana", "apple", "orange", "orange"}
your_fruits = {"apple", "apple", "banana", "orange", "orange"}
print(my_fruits == your_fruits)
# Вывод:
TrueНепересекающиеся множества
Если два множества не имеют общих элементов, то говорят, что эти множества не пересекаются. Или другими словами, пересечение этих множеств является пустым множеством.
Или другими словами, пересечение этих множеств является пустым множеством.
even_numbers = {i for i in range(10) if i % 2 == 0}
odd_numbers = {i for i in range(10) if i % 2 == 1}
# Очевидно, что множества чётных и нечётных чисел не пересекаются
if even_numbers.isdisjoint(odd_numbers):
print("Множества не пересекаются!")
# Вывод:
Множества не пересекаются!Подмножество и надмножество
Подмножество множества S – это такое множество, каждый элемент которого является также и элементом множества S. Множество S в свою очередь является надмножеством исходного множества.
# Множество чисел Фибоначчи меньших 100
fibonacci_numbers = {0, 1, 2, 3, 34, 5, 8, 13, 21, 55, 89}
# Множество натуральных чисел меньших 100
natural_numbers = set(range(100))
# Множество чисел Фибоначчи является подмножеством множества
# натуральных чисел
if fibonacci_numbers.issubset(natural_numbers):
print("Подмножество!")
# Вывод:
Подмножество!
# В свою очередь множество натуральных чисел является
# надмножеством множества чисел Фибоначчи
if natural_numbers. issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!
issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!Пустое множество является подмножеством абсолютно любого множества.
empty = set()
# Методы issubset и issuperset могут принимать любой iterable-объект
print(
empty.issubset(range(100))
and empty.issubset(["red", "green", "blue"])
and empty.issubset(set())
)
# Вывод:
TrueСамо множество является подмножеством самого себя.
natural_numbers = set(range(100))
if natural_numbers.issubset(natural_numbers):
print("Подмножество!")
# Вывод:
Подмножество!Операции над множествами
Рассмотрим основные операции, опредяляемые над множествами.
Объединение множеств
Объединение множеств – это множество, которое содержит все элементы исходных множеств. В Python есть несколько способов объединить множества, давайте рассмотрим их на примерах.
my_fruits = {"apple", "orange"}
your_fruits = {"orange", "banana", "pear"}
# Для объединения множеств можно использовать оператор `|`,
# оба операнда должны быть объектами типа set
our_fruits = my_fruits | your_fruits
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Также можно использовать ментод union. # Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}Добавление элементов в множество
Добавление элементов в множество можно рассматривать как частный случай объединения множеств за тем исключением, что добавление элементов изменяет исходное множество, а не создает новый объект. Добавление одного элемента в множество работает за O(1).
colors = {"red", "green", "blue"}
# Метод add добаляет новый элемент в множество
colors.add("purple")
# Добавление элемента, который уже есть в множестве, не изменяет
# это множество
colors.add("red")
print(colors)
# Вывод (порядок может быть другим):
{"red", "green", "blue", "purple"}
# Метод update принимает iterable-объект (список, словарь, генератор и т.п.)
# и добавляет все элементы в множество
numbers = {1, 2, 3}
numbers. update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}
update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}Пересечение множеств
Пересечение множеств – это множество, в котором находятся только те элементы, которые принадлежат исходным множествам одновременно.
def is_prime(number: int) -> bool:
""" Возвращает True, если number - это простое число
"""
assert number > 1
return all(number % i for i in range(2, int(number**0.5) + 1))
def is_fibonacci(number: int) -> bool:
""" Возвращает True, если number - это число Фибоначчи
"""
assert number > 1
a, b = 0, 1
while a + b < number:
a, b = b, a + b
return a + b == number
# Множество простых чисел до 100
primes = set(filter(is_prime, range(2, 101)))
# Множество чисел Фибоначчи до 100
fibonacci = set(filter(is_fibonacci, range(2, 101)))
# Множество простых чисел до 100, которые одновременно являются
# числами Фибоначчи
prime_fibonacci = primes.intersection(fibonacci)
# Или используя оператор `&`, который определён для множеств
prime_fibonacci = fibonacci & primes
print(prime_fibonacci)
# Вывод (порядок может быть другим):
{2, 3, 5, 13, 89}При использовании оператора & необходимо, чтобы оба операнда были объектами типа set. Метод
Метод intersection, в свою очередь, принимает любой iterable-объект. Если необходимо изменить исходное множество, а не возращать новое, то можно использовать метод intersection_update, который работает подобно методу intersection, но изменяет исходный объект-множество.
Разность множеств
Разность двух множеств – это множество, в которое входят все элементы первого множества, не входящие во второе множество.
i_know: set = {"Python", "Go", "Java"}
you_know: dict = {
"Go": 0.4,
"C++": 0.6,
"Rust": 0.2,
"Java": 0.9
}
# Обратите внимание, что оператор `-` работает только
# для объектов типа set
you_know_but_i_dont = set(you_know) - i_know
print(you_know_but_i_dont)
# Вывод (порядок может быть другим):
{"Rust", "C++"}
# Метод difference может работать с любым iterable-объектом,
# каким является dict, например
i_know_but_you_dont = i_know.difference(you_know)
print(i_know_but_you_dont)
# Вывод:
{"Python"}Удаление элементов из множества
Удаление элемента из множества можно рассматривать как частный случай разности, где удаляемый элемент – это одноэлементное множество. Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность
Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность O(1).
fruits = {"apple", "orange", "banana"}
# Удаление элемента из множества. Если удаляемого элемента
# нет в множестве, то ничего не происходит
fruits.discard("orange")
fruits.discard("pineapple")
print(fruits)
# Вывод (порядок может быть другим):
{"apple", "banana"}
# Метод remove работает аналогично discard, но генерирует исключение,
# если удаляемого элемента нет в множестве
fruits.remove("pineapple") # KeyError: "pineapple"Также у множеств есть метод differenсe_update, который принимает iterable-объект и удаляет из исходного множества все элементы iterable-объекта. Этот метод работает аналогично методу difference, но изменяет исходное множество, а не возвращает новое.
numbers = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
even_numbers_under_100 = (i for i in range(1, 101) if i % 2 == 0)
numbers. , также существует два специальных метода –
, также существует два специальных метода – symmetric_difference и symmetric_difference_update. Оба этих метода принимают iterable-объект в качестве аргумента, отличие же состоит в том, что symmetric_difference возвращает новый объект-множество, в то время как symmetric_difference_update изменяет исходное множество.non_positive = {-3, -2, -1, 0}
non_negative = range(4)
non_zero = non_positive.symmetric_difference(non_negative)
print(non_zero)
# Вывод (порядок может быть другим):
{-1, -2, -3, 1, 2, 3}
# Метод symmetric_difference_update изменяет исходное множество
colors = {"red", "green", "blue"}
colors.symmetric_difference_update(["green", "blue", "yellow"])
print(colors)
# Вывод (порядок может быть другим):
{"red", "yellow"}
Заключение
Я надеюсь, мне удалось показать, что Python имеет очень удобные встроенные средства для работы с множествами. На практике это часто позволяет сократить количество кода, сделать его выразительнее и легче для восприятия, а следовательно и более поддерживаемым. Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Полезные ссылки
Множества (Статья на Википедии)
Документация по типу set
Iterable-объекты (Глоссарий Python)
Hashable-объекты (Глоссарий Python)
Sets in Python
Set Theory: the Method To Database Madness
Python и теория множеств / Хабр
В Python есть очень полезный тип данных для работы с множествами – это set. Об этом типе данных, примерах использования, и небольшой выдержке из теории множеств пойдёт речь далее.
Следует сразу сделать оговорку, что эта статья ни в коем случае не претендует на какую-либо математическую строгость и полноту, скорее это попытка доступно продемонстрировать примеры использования множеств в языке программирования Python.
- Множество
- Множества в Python
- Хешируемые объекты
- Свойства множеств
- Принадлежность множеству
- Мощность множества
- Перебор элементов множества
- Отношения между множествами
- Равные множества
- Непересекающиеся множества
- Подмножество и надмножество
- Операции над множествами
- Объединение множеств
- Добавление элементов в множество
- Пересечение множеств
- Разность множеств
- Удаление элементов из множества
- Симметрическая разность множеств
- Заключение
- Полезные ссылки
Множество
Множество – это математический объект, являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества. Или другими словами:
Или другими словами:
Множество – это не более чем неупорядоченная коллекция уникальных элементов.
Что значит неупорядоченная? Это значит, что два множества эквивалентны, если содержат одинаковые элементы.
Элементы множества должны быть уникальными, множество не может содержать одинаковых элементов. Добавление элементов, которые уже есть в множестве, не изменяет это множество.
Множества, состоящие из конечного числа элементов, называются конечными, а остальные множества – бесконечными. Конечное множество, как следует из названия, можно задать перечислением его элементов. Так как темой этой статьи является практическое использование множеств в Python, то я предлагаю сосредоточиться на конечных множествах.
Множества в Python
Множество в Python можно создать несколькими способами. Самый простой – это задать множество перечислением его элементов в фигурных скобках:
fruits = {"banana", "apple", "orange"}Единственное ограничение, что таким образом нельзя создать пустое множество. Вместо этого будет создан пустой словарь:
Вместо этого будет создан пустой словарь:
wrong_empty_set = {}
print(type(wrong_empty_set))
# Вывод
<class "dict">Для создания пустого множества нужно непосредственно использовать set():
correct_empty_set = set() print(type(correct_empty_set)) # Вывод <class "set">
Также в set() можно передать какой-либо объект, по которому можно проитерироваться (Iterable):
color_list = ["red", "green", "green", "blue", "purple", "purple"]
color_set = set(color_list)
print(color_set)
# Вывод (порядок может быть другим):
{"red", "purple", "blue", "green"}Ещё одна возможность создания множества – это использование set comprehension. Это специальная синтаксическая конструкция языка, которую иногда называют абстракцией множества по аналогии с list comprehension (Списковое включение).
numbers = [1, 2, 2, 2, 3, 3, 4, 4, 5, 6]
# Единственное отличие со списковыми включениями - это
# использование фигурных скобок вместо квадратных
even_numbers = {
number for number in numbers
if number % 2 == 0
}
print(even_numbers)
# Вывод (порядок может быть другим):
{2, 4, 6}Хешируемые объекты
Существует ограничение, что элементами множества (как и ключами словарей) в Python могут быть только так называемые хешируемые (Hashable) объекты.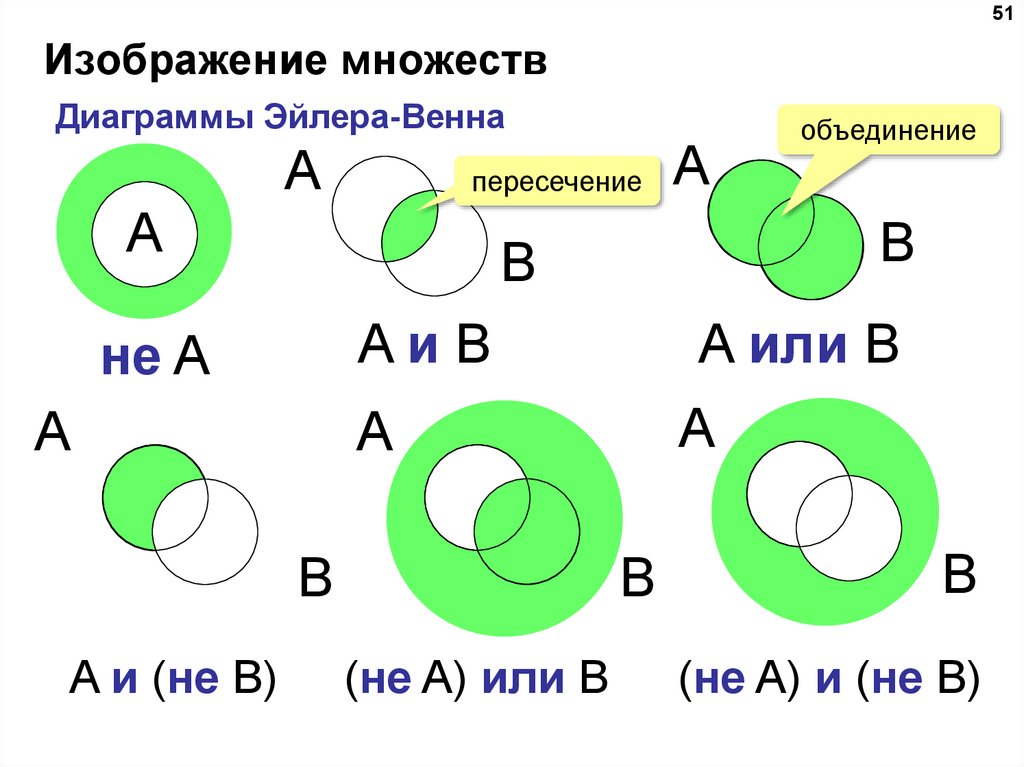 Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) – хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы.
Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) – хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы.
# Множество кортежей (tuple)
records = {
("Москва", 17_200_000),
("Санкт-Петербург", 5_400_000),
("Новосибирск", 1_600_000),
("Москва", 17_200_000),
}
for city, population in records:
print(city)
# Вывод (порядок может быть другим):
Москва
Новосибирск
Санкт-ПетербургОбъекты пользовательских классов являются хешируемыми по умолчанию. Но практического смысла чаще всего в этом мало из-за того, что сравнение таких объектов выполняется по их адресу в памяти, т.е. невозможно создать два "равных" объекта.
class City:
def __init__(self, name: str):
self. name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}
name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}Скорее всего мы предполагаем, что объекты City("Moscow") должны быть равными, и следовательно в множестве cities должен находиться один объект.
Этого можно добиться, если определить семантику равенства для объектов класса City:
class City:
def __init__(self, name: str):
# Атрибут name не должен изменяться, пока объект существует
# Для простоты пометим этот атрибут как внутренний
self._name = name
def __hash__(self) -> int:
""" Хеш от объекта
"""
return hash((self._name, self.__class__))
def __eq__(self, other) -> bool:
""" Определяем семантику равентсва (оператор ==)
"""
if not isinstance(other, self. __class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'
__class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'Чтобы протокол хеширования работал без явных и неявных логических ошибок, должны выполняться следующие условия:
- Хеш объекта не должен изменяться, пока этот объект существует
- Равные объекты должны возвращать одинаковый хеш
moscow = City("Moscow")
moscow_again = City("Moscow")
print(moscow == moscow_again and hash(moscow) == hash(moscow_again))
# Вывод:
True
# Теперь множество городов работает более логично и интуитивно
cities = {City("Moscow"), City("Kazan"), City("Moscow")}
print(cities)
# Вывод (порядок может быть другим):
{City("Kazan"), City("Moscow")}Свойства множеств
Тип set в Python является подтипом Collection (про коллекции), из данного факта есть три важных следствия:
- Определена операция проверки принадлежности элемента множеству
- Можно получить количество элементов в множестве
- Множества являются iterable-объектами
Принадлежность множеству
Проверить принадлежит ли какой-либо объект множеству можно с помощью оператора in. Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за
Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за O(1) с теми же оговорками, которые существуют для хеш-таблиц.
tremendously_huge_set = {"red", "green", "blue"}
if "green" in tremendously_huge_set:
print("Green is there!")
else:
print("Unfortunately, there is no green...")
# Вывод:
Green is there!
if "purple" in tremendously_huge_set:
print("Purple is there!")
else:
print("Unfortunately, there is no purple...")
# Вывод:
Unfortunately, there is no purple...Мощность множества
Мощность множества – это характеристика множества, которая для конечных множеств просто означает количество элементов в данном множестве. Для бесконечных множеств всё несколько сложнее.
even_numbers = {i for i in range(100) if i % 2 == 0}
# Мощность множества
cardinality = len(even_numbers)
print(cardinality)
# Вывод:
50Перебор элементов множества
Как уже было отмечено выше, множества поддерживают протокол итераторов, таким образом любое множество можно использовать там, где ожидается iterable-объект.
colors = {"red", "green", "blue"}
# Элементы множества можно перебрать с помощью цикла for
for color in colors:
print(color)
# Вывод (порядок может быть другим):
red
green
blue
# Множества можно использовать там, где ожидается iterable-объект
color_counter = dict.fromkeys(colors, 1)
print(color_counter)
# Вывод (порядок может быть другим):
{"green": 1, "red": 1, "blue": 1}Отношения между множествами
Между множествами существуют несколько видов отношений, или другими словами взаимосвязей. Давайте рассмотрим возможные отношения между множествами в этом разделе.
Равные множества
Тут всё довольно просто – два множества называются равными, если они состоят из одних и тех же элементов. Как следует из определения множества, порядок этих элементов не важен.
my_fruits = {"banana", "apple", "orange", "orange"}
your_fruits = {"apple", "apple", "banana", "orange", "orange"}
print(my_fruits == your_fruits)
# Вывод:
TrueНепересекающиеся множества
Если два множества не имеют общих элементов, то говорят, что эти множества не пересекаются. Или другими словами, пересечение этих множеств является пустым множеством.
Или другими словами, пересечение этих множеств является пустым множеством.
even_numbers = {i for i in range(10) if i % 2 == 0}
odd_numbers = {i for i in range(10) if i % 2 == 1}
# Очевидно, что множества чётных и нечётных чисел не пересекаются
if even_numbers.isdisjoint(odd_numbers):
print("Множества не пересекаются!")
# Вывод:
Множества не пересекаются!Подмножество и надмножество
Подмножество множества S – это такое множество, каждый элемент которого является также и элементом множества S. Множество S в свою очередь является надмножеством исходного множества.
# Множество чисел Фибоначчи меньших 100
fibonacci_numbers = {0, 1, 2, 3, 34, 5, 8, 13, 21, 55, 89}
# Множество натуральных чисел меньших 100
natural_numbers = set(range(100))
# Множество чисел Фибоначчи является подмножеством множества
# натуральных чисел
if fibonacci_numbers.issubset(natural_numbers):
print("Подмножество!")
# Вывод:
Подмножество!
# В свою очередь множество натуральных чисел является
# надмножеством множества чисел Фибоначчи
if natural_numbers. issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!
issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!Пустое множество является подмножеством абсолютно любого множества.
empty = set()
# Методы issubset и issuperset могут принимать любой iterable-объект
print(
empty.issubset(range(100))
and empty.issubset(["red", "green", "blue"])
and empty.issubset(set())
)
# Вывод:
TrueСамо множество является подмножеством самого себя.
natural_numbers = set(range(100))
if natural_numbers.issubset(natural_numbers):
print("Подмножество!")
# Вывод:
Подмножество!Операции над множествами
Рассмотрим основные операции, опредяляемые над множествами.
Объединение множеств
Объединение множеств – это множество, которое содержит все элементы исходных множеств. В Python есть несколько способов объединить множества, давайте рассмотрим их на примерах.
my_fruits = {"apple", "orange"}
your_fruits = {"orange", "banana", "pear"}
# Для объединения множеств можно использовать оператор `|`,
# оба операнда должны быть объектами типа set
our_fruits = my_fruits | your_fruits
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Также можно использовать ментод union. # Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}Добавление элементов в множество
Добавление элементов в множество можно рассматривать как частный случай объединения множеств за тем исключением, что добавление элементов изменяет исходное множество, а не создает новый объект. Добавление одного элемента в множество работает за O(1).
colors = {"red", "green", "blue"}
# Метод add добаляет новый элемент в множество
colors.add("purple")
# Добавление элемента, который уже есть в множестве, не изменяет
# это множество
colors.add("red")
print(colors)
# Вывод (порядок может быть другим):
{"red", "green", "blue", "purple"}
# Метод update принимает iterable-объект (список, словарь, генератор и т.п.)
# и добавляет все элементы в множество
numbers = {1, 2, 3}
numbers. update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}
update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}Пересечение множеств
Пересечение множеств – это множество, в котором находятся только те элементы, которые принадлежат исходным множествам одновременно.
def is_prime(number: int) -> bool:
""" Возвращает True, если number - это простое число
"""
assert number > 1
return all(number % i for i in range(2, int(number**0.5) + 1))
def is_fibonacci(number: int) -> bool:
""" Возвращает True, если number - это число Фибоначчи
"""
assert number > 1
a, b = 0, 1
while a + b < number:
a, b = b, a + b
return a + b == number
# Множество простых чисел до 100
primes = set(filter(is_prime, range(2, 101)))
# Множество чисел Фибоначчи до 100
fibonacci = set(filter(is_fibonacci, range(2, 101)))
# Множество простых чисел до 100, которые одновременно являются
# числами Фибоначчи
prime_fibonacci = primes.intersection(fibonacci)
# Или используя оператор `&`, который определён для множеств
prime_fibonacci = fibonacci & primes
print(prime_fibonacci)
# Вывод (порядок может быть другим):
{2, 3, 5, 13, 89}При использовании оператора & необходимо, чтобы оба операнда были объектами типа set. Метод
Метод intersection, в свою очередь, принимает любой iterable-объект. Если необходимо изменить исходное множество, а не возращать новое, то можно использовать метод intersection_update, который работает подобно методу intersection, но изменяет исходный объект-множество.
Разность множеств
Разность двух множеств – это множество, в которое входят все элементы первого множества, не входящие во второе множество.
i_know: set = {"Python", "Go", "Java"}
you_know: dict = {
"Go": 0.4,
"C++": 0.6,
"Rust": 0.2,
"Java": 0.9
}
# Обратите внимание, что оператор `-` работает только
# для объектов типа set
you_know_but_i_dont = set(you_know) - i_know
print(you_know_but_i_dont)
# Вывод (порядок может быть другим):
{"Rust", "C++"}
# Метод difference может работать с любым iterable-объектом,
# каким является dict, например
i_know_but_you_dont = i_know.difference(you_know)
print(i_know_but_you_dont)
# Вывод:
{"Python"}Удаление элементов из множества
Удаление элемента из множества можно рассматривать как частный случай разности, где удаляемый элемент – это одноэлементное множество.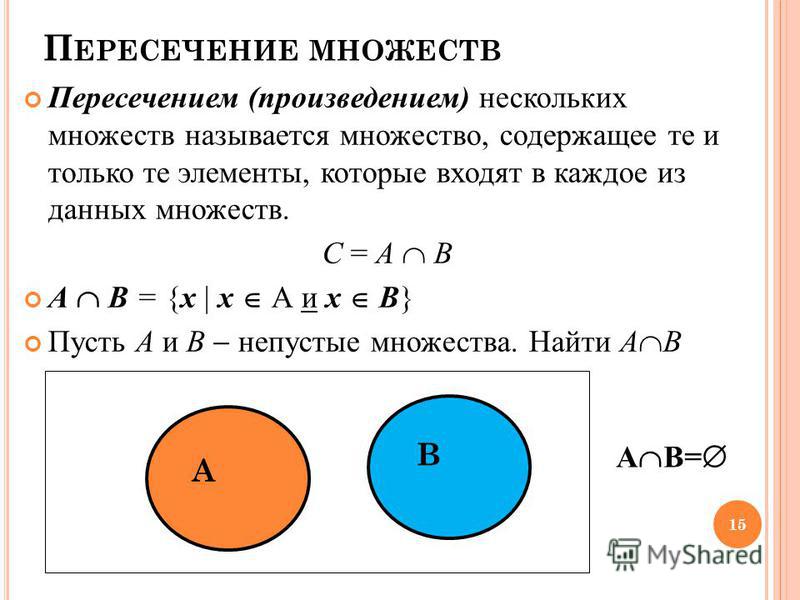 Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность
Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность O(1).
fruits = {"apple", "orange", "banana"}
# Удаление элемента из множества. Если удаляемого элемента
# нет в множестве, то ничего не происходит
fruits.discard("orange")
fruits.discard("pineapple")
print(fruits)
# Вывод (порядок может быть другим):
{"apple", "banana"}
# Метод remove работает аналогично discard, но генерирует исключение,
# если удаляемого элемента нет в множестве
fruits.remove("pineapple") # KeyError: "pineapple"Также у множеств есть метод differenсe_update, который принимает iterable-объект и удаляет из исходного множества все элементы iterable-объекта. Этот метод работает аналогично методу difference, но изменяет исходное множество, а не возвращает новое.
numbers = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
even_numbers_under_100 = (i for i in range(1, 101) if i % 2 == 0)
numbers. , также существует два специальных метода –
, также существует два специальных метода – symmetric_difference и symmetric_difference_update. Оба этих метода принимают iterable-объект в качестве аргумента, отличие же состоит в том, что symmetric_difference возвращает новый объект-множество, в то время как symmetric_difference_update изменяет исходное множество.non_positive = {-3, -2, -1, 0}
non_negative = range(4)
non_zero = non_positive.symmetric_difference(non_negative)
print(non_zero)
# Вывод (порядок может быть другим):
{-1, -2, -3, 1, 2, 3}
# Метод symmetric_difference_update изменяет исходное множество
colors = {"red", "green", "blue"}
colors.symmetric_difference_update(["green", "blue", "yellow"])
print(colors)
# Вывод (порядок может быть другим):
{"red", "yellow"}
Заключение
Я надеюсь, мне удалось показать, что Python имеет очень удобные встроенные средства для работы с множествами. На практике это часто позволяет сократить количество кода, сделать его выразительнее и легче для восприятия, а следовательно и более поддерживаемым. Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Полезные ссылки
Множества (Статья на Википедии)
Документация по типу set
Iterable-объекты (Глоссарий Python)
Hashable-объекты (Глоссарий Python)
Sets in Python
Set Theory: the Method To Database Madness
Python и теория множеств / Хабр
В Python есть очень полезный тип данных для работы с множествами – это set. Об этом типе данных, примерах использования, и небольшой выдержке из теории множеств пойдёт речь далее.
Следует сразу сделать оговорку, что эта статья ни в коем случае не претендует на какую-либо математическую строгость и полноту, скорее это попытка доступно продемонстрировать примеры использования множеств в языке программирования Python.
- Множество
- Множества в Python
- Хешируемые объекты
- Свойства множеств
- Принадлежность множеству
- Мощность множества
- Перебор элементов множества
- Отношения между множествами
- Равные множества
- Непересекающиеся множества
- Подмножество и надмножество
- Операции над множествами
- Объединение множеств
- Добавление элементов в множество
- Пересечение множеств
- Разность множеств
- Удаление элементов из множества
- Симметрическая разность множеств
- Заключение
- Полезные ссылки
Множество
Множество – это математический объект, являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества. Или другими словами:
Или другими словами:
Множество – это не более чем неупорядоченная коллекция уникальных элементов.
Что значит неупорядоченная? Это значит, что два множества эквивалентны, если содержат одинаковые элементы.
Элементы множества должны быть уникальными, множество не может содержать одинаковых элементов. Добавление элементов, которые уже есть в множестве, не изменяет это множество.
Множества, состоящие из конечного числа элементов, называются конечными, а остальные множества – бесконечными. Конечное множество, как следует из названия, можно задать перечислением его элементов. Так как темой этой статьи является практическое использование множеств в Python, то я предлагаю сосредоточиться на конечных множествах.
Множества в Python
Множество в Python можно создать несколькими способами. Самый простой – это задать множество перечислением его элементов в фигурных скобках:
fruits = {"banana", "apple", "orange"}Единственное ограничение, что таким образом нельзя создать пустое множество.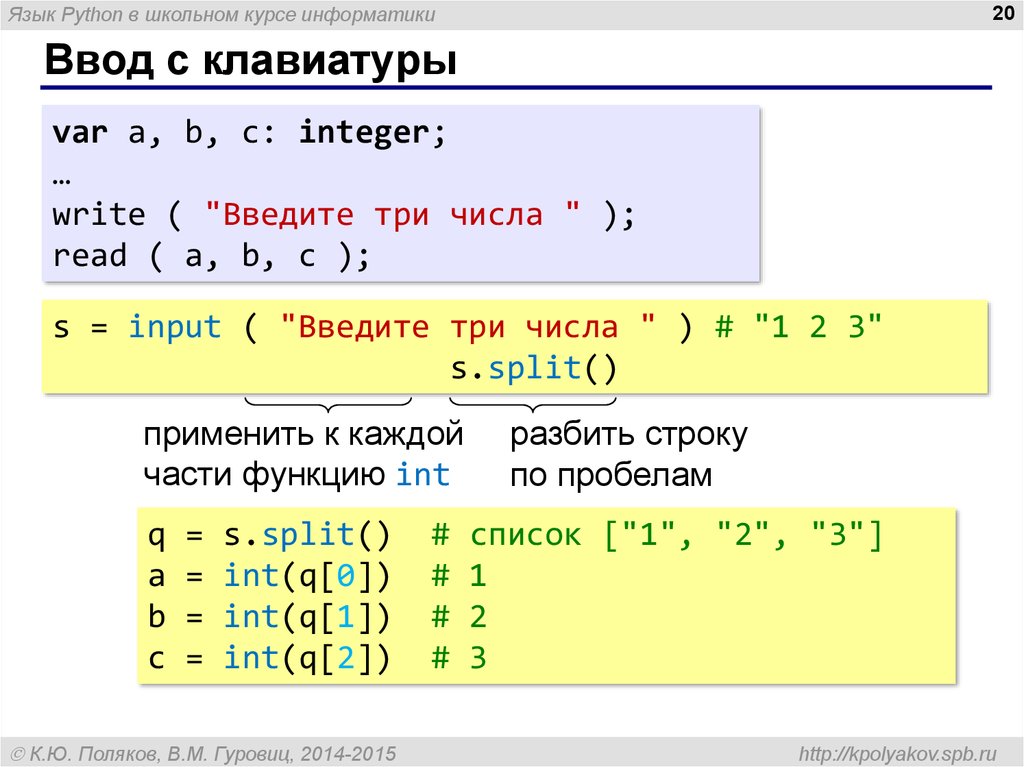 Вместо этого будет создан пустой словарь:
Вместо этого будет создан пустой словарь:
wrong_empty_set = {}
print(type(wrong_empty_set))
# Вывод
<class "dict">Для создания пустого множества нужно непосредственно использовать set():
correct_empty_set = set() print(type(correct_empty_set)) # Вывод <class "set">
Также в set() можно передать какой-либо объект, по которому можно проитерироваться (Iterable):
color_list = ["red", "green", "green", "blue", "purple", "purple"]
color_set = set(color_list)
print(color_set)
# Вывод (порядок может быть другим):
{"red", "purple", "blue", "green"}Ещё одна возможность создания множества – это использование set comprehension. Это специальная синтаксическая конструкция языка, которую иногда называют абстракцией множества по аналогии с list comprehension (Списковое включение).
numbers = [1, 2, 2, 2, 3, 3, 4, 4, 5, 6]
# Единственное отличие со списковыми включениями - это
# использование фигурных скобок вместо квадратных
even_numbers = {
number for number in numbers
if number % 2 == 0
}
print(even_numbers)
# Вывод (порядок может быть другим):
{2, 4, 6}Хешируемые объекты
Существует ограничение, что элементами множества (как и ключами словарей) в Python могут быть только так называемые хешируемые (Hashable) объекты. Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) – хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы.
Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) – хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы.
# Множество кортежей (tuple)
records = {
("Москва", 17_200_000),
("Санкт-Петербург", 5_400_000),
("Новосибирск", 1_600_000),
("Москва", 17_200_000),
}
for city, population in records:
print(city)
# Вывод (порядок может быть другим):
Москва
Новосибирск
Санкт-ПетербургОбъекты пользовательских классов являются хешируемыми по умолчанию. Но практического смысла чаще всего в этом мало из-за того, что сравнение таких объектов выполняется по их адресу в памяти, т.е. невозможно создать два "равных" объекта.
class City:
def __init__(self, name: str):
self. name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}
name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}Скорее всего мы предполагаем, что объекты City("Moscow") должны быть равными, и следовательно в множестве cities должен находиться один объект.
Этого можно добиться, если определить семантику равенства для объектов класса City:
class City:
def __init__(self, name: str):
# Атрибут name не должен изменяться, пока объект существует
# Для простоты пометим этот атрибут как внутренний
self._name = name
def __hash__(self) -> int:
""" Хеш от объекта
"""
return hash((self._name, self.__class__))
def __eq__(self, other) -> bool:
""" Определяем семантику равентсва (оператор ==)
"""
if not isinstance(other, self. __class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'
__class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'Чтобы протокол хеширования работал без явных и неявных логических ошибок, должны выполняться следующие условия:
- Хеш объекта не должен изменяться, пока этот объект существует
- Равные объекты должны возвращать одинаковый хеш
moscow = City("Moscow")
moscow_again = City("Moscow")
print(moscow == moscow_again and hash(moscow) == hash(moscow_again))
# Вывод:
True
# Теперь множество городов работает более логично и интуитивно
cities = {City("Moscow"), City("Kazan"), City("Moscow")}
print(cities)
# Вывод (порядок может быть другим):
{City("Kazan"), City("Moscow")}Свойства множеств
Тип set в Python является подтипом Collection (про коллекции), из данного факта есть три важных следствия:
- Определена операция проверки принадлежности элемента множеству
- Можно получить количество элементов в множестве
- Множества являются iterable-объектами
Принадлежность множеству
Проверить принадлежит ли какой-либо объект множеству можно с помощью оператора in. Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за
Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за O(1) с теми же оговорками, которые существуют для хеш-таблиц.
tremendously_huge_set = {"red", "green", "blue"}
if "green" in tremendously_huge_set:
print("Green is there!")
else:
print("Unfortunately, there is no green...")
# Вывод:
Green is there!
if "purple" in tremendously_huge_set:
print("Purple is there!")
else:
print("Unfortunately, there is no purple...")
# Вывод:
Unfortunately, there is no purple...Мощность множества
Мощность множества – это характеристика множества, которая для конечных множеств просто означает количество элементов в данном множестве. Для бесконечных множеств всё несколько сложнее.
even_numbers = {i for i in range(100) if i % 2 == 0}
# Мощность множества
cardinality = len(even_numbers)
print(cardinality)
# Вывод:
50Перебор элементов множества
Как уже было отмечено выше, множества поддерживают протокол итераторов, таким образом любое множество можно использовать там, где ожидается iterable-объект.
colors = {"red", "green", "blue"}
# Элементы множества можно перебрать с помощью цикла for
for color in colors:
print(color)
# Вывод (порядок может быть другим):
red
green
blue
# Множества можно использовать там, где ожидается iterable-объект
color_counter = dict.fromkeys(colors, 1)
print(color_counter)
# Вывод (порядок может быть другим):
{"green": 1, "red": 1, "blue": 1}Отношения между множествами
Между множествами существуют несколько видов отношений, или другими словами взаимосвязей. Давайте рассмотрим возможные отношения между множествами в этом разделе.
Равные множества
Тут всё довольно просто – два множества называются равными, если они состоят из одних и тех же элементов. Как следует из определения множества, порядок этих элементов не важен.
my_fruits = {"banana", "apple", "orange", "orange"}
your_fruits = {"apple", "apple", "banana", "orange", "orange"}
print(my_fruits == your_fruits)
# Вывод:
TrueНепересекающиеся множества
Если два множества не имеют общих элементов, то говорят, что эти множества не пересекаются. Или другими словами, пересечение этих множеств является пустым множеством.
Или другими словами, пересечение этих множеств является пустым множеством.
even_numbers = {i for i in range(10) if i % 2 == 0}
odd_numbers = {i for i in range(10) if i % 2 == 1}
# Очевидно, что множества чётных и нечётных чисел не пересекаются
if even_numbers.isdisjoint(odd_numbers):
print("Множества не пересекаются!")
# Вывод:
Множества не пересекаются!Подмножество и надмножество
Подмножество множества S – это такое множество, каждый элемент которого является также и элементом множества S. Множество S в свою очередь является надмножеством исходного множества.
# Множество чисел Фибоначчи меньших 100
fibonacci_numbers = {0, 1, 2, 3, 34, 5, 8, 13, 21, 55, 89}
# Множество натуральных чисел меньших 100
natural_numbers = set(range(100))
# Множество чисел Фибоначчи является подмножеством множества
# натуральных чисел
if fibonacci_numbers.issubset(natural_numbers):
print("Подмножество!")
# Вывод:
Подмножество!
# В свою очередь множество натуральных чисел является
# надмножеством множества чисел Фибоначчи
if natural_numbers. issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!
issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!Пустое множество является подмножеством абсолютно любого множества.
empty = set()
# Методы issubset и issuperset могут принимать любой iterable-объект
print(
empty.issubset(range(100))
and empty.issubset(["red", "green", "blue"])
and empty.issubset(set())
)
# Вывод:
TrueСамо множество является подмножеством самого себя.
natural_numbers = set(range(100))
if natural_numbers.issubset(natural_numbers):
print("Подмножество!")
# Вывод:
Подмножество!Операции над множествами
Рассмотрим основные операции, опредяляемые над множествами.
Объединение множеств
Объединение множеств – это множество, которое содержит все элементы исходных множеств. В Python есть несколько способов объединить множества, давайте рассмотрим их на примерах.
my_fruits = {"apple", "orange"}
your_fruits = {"orange", "banana", "pear"}
# Для объединения множеств можно использовать оператор `|`,
# оба операнда должны быть объектами типа set
our_fruits = my_fruits | your_fruits
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Также можно использовать ментод union. # Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}Добавление элементов в множество
Добавление элементов в множество можно рассматривать как частный случай объединения множеств за тем исключением, что добавление элементов изменяет исходное множество, а не создает новый объект. Добавление одного элемента в множество работает за O(1).
colors = {"red", "green", "blue"}
# Метод add добаляет новый элемент в множество
colors.add("purple")
# Добавление элемента, который уже есть в множестве, не изменяет
# это множество
colors.add("red")
print(colors)
# Вывод (порядок может быть другим):
{"red", "green", "blue", "purple"}
# Метод update принимает iterable-объект (список, словарь, генератор и т.п.)
# и добавляет все элементы в множество
numbers = {1, 2, 3}
numbers. update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}
update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}Пересечение множеств
Пересечение множеств – это множество, в котором находятся только те элементы, которые принадлежат исходным множествам одновременно.
def is_prime(number: int) -> bool:
""" Возвращает True, если number - это простое число
"""
assert number > 1
return all(number % i for i in range(2, int(number**0.5) + 1))
def is_fibonacci(number: int) -> bool:
""" Возвращает True, если number - это число Фибоначчи
"""
assert number > 1
a, b = 0, 1
while a + b < number:
a, b = b, a + b
return a + b == number
# Множество простых чисел до 100
primes = set(filter(is_prime, range(2, 101)))
# Множество чисел Фибоначчи до 100
fibonacci = set(filter(is_fibonacci, range(2, 101)))
# Множество простых чисел до 100, которые одновременно являются
# числами Фибоначчи
prime_fibonacci = primes.intersection(fibonacci)
# Или используя оператор `&`, который определён для множеств
prime_fibonacci = fibonacci & primes
print(prime_fibonacci)
# Вывод (порядок может быть другим):
{2, 3, 5, 13, 89}При использовании оператора & необходимо, чтобы оба операнда были объектами типа set.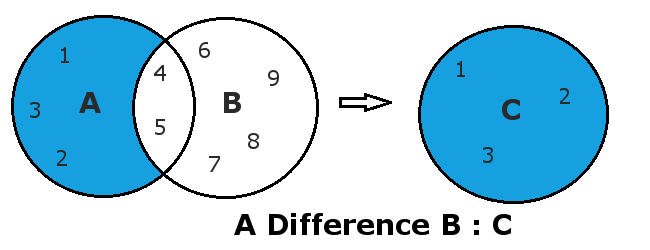 Метод
Метод intersection, в свою очередь, принимает любой iterable-объект. Если необходимо изменить исходное множество, а не возращать новое, то можно использовать метод intersection_update, который работает подобно методу intersection, но изменяет исходный объект-множество.
Разность множеств
Разность двух множеств – это множество, в которое входят все элементы первого множества, не входящие во второе множество.
i_know: set = {"Python", "Go", "Java"}
you_know: dict = {
"Go": 0.4,
"C++": 0.6,
"Rust": 0.2,
"Java": 0.9
}
# Обратите внимание, что оператор `-` работает только
# для объектов типа set
you_know_but_i_dont = set(you_know) - i_know
print(you_know_but_i_dont)
# Вывод (порядок может быть другим):
{"Rust", "C++"}
# Метод difference может работать с любым iterable-объектом,
# каким является dict, например
i_know_but_you_dont = i_know.difference(you_know)
print(i_know_but_you_dont)
# Вывод:
{"Python"}Удаление элементов из множества
Удаление элемента из множества можно рассматривать как частный случай разности, где удаляемый элемент – это одноэлементное множество. Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность
Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность O(1).
fruits = {"apple", "orange", "banana"}
# Удаление элемента из множества. Если удаляемого элемента
# нет в множестве, то ничего не происходит
fruits.discard("orange")
fruits.discard("pineapple")
print(fruits)
# Вывод (порядок может быть другим):
{"apple", "banana"}
# Метод remove работает аналогично discard, но генерирует исключение,
# если удаляемого элемента нет в множестве
fruits.remove("pineapple") # KeyError: "pineapple"Также у множеств есть метод differenсe_update, который принимает iterable-объект и удаляет из исходного множества все элементы iterable-объекта. Этот метод работает аналогично методу difference, но изменяет исходное множество, а не возвращает новое.
numbers = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
even_numbers_under_100 = (i for i in range(1, 101) if i % 2 == 0)
numbers. , также существует два специальных метода –
, также существует два специальных метода – symmetric_difference и symmetric_difference_update. Оба этих метода принимают iterable-объект в качестве аргумента, отличие же состоит в том, что symmetric_difference возвращает новый объект-множество, в то время как symmetric_difference_update изменяет исходное множество.non_positive = {-3, -2, -1, 0}
non_negative = range(4)
non_zero = non_positive.symmetric_difference(non_negative)
print(non_zero)
# Вывод (порядок может быть другим):
{-1, -2, -3, 1, 2, 3}
# Метод symmetric_difference_update изменяет исходное множество
colors = {"red", "green", "blue"}
colors.symmetric_difference_update(["green", "blue", "yellow"])
print(colors)
# Вывод (порядок может быть другим):
{"red", "yellow"}
Заключение
Я надеюсь, мне удалось показать, что Python имеет очень удобные встроенные средства для работы с множествами. На практике это часто позволяет сократить количество кода, сделать его выразительнее и легче для восприятия, а следовательно и более поддерживаемым. Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Полезные ссылки
Множества (Статья на Википедии)
Документация по типу set
Iterable-объекты (Глоссарий Python)
Hashable-объекты (Глоссарий Python)
Sets in Python
Set Theory: the Method To Database Madness
Множества в Python - CodeChick
В этом руководстве вы узнаете всё о множествах в Python: как их создавать, как добавлять и удалять элементы и т. д.
Множество — неупорядоченный набор элементов. Каждый элемент в множестве уникален (т. е. повторяющихся элементов нет) и неизменяем.
Само по себе множество можно изменять, то есть удалять или добавлять элементы.
Множества удобно использовать для выполнения математических операций: объединение, пересечение, симметрическая разность и т. д.
Как создать множество
Множество объявляется так: элементы помещаются в фигурные скобки {} и разделяются запятыми. Сделать это можно и с помощью встроенной функции
Сделать это можно и с помощью встроенной функции set().
Внутри множества может быть любое количество элементов любого типа (целые числа, числа с плавающей точкой, кортежи, строки и т. д.). Внутрь множества нельзя помещать элементы изменяемых типов: списки, другие множества или словари.
# Разные виды множеств
# Множество с целыми числами
my_set = {1, 2, 3}
print(my_set)
# Множество с разными типами данных
my_set = {1.0, "Привет", (1, 2, 3)}
print(my_set)Вывод:
{1, 2, 3}
{1.0, (1, 2, 3), 'Привет'}# Внутри множества не может быть одинаковых элементов
# Вывод: {1, 2, 3, 4}
my_set = {1, 2, 3, 4, 3, 2}
print(my_set)
# Аргументом функции set() может быть список
# Вывод: {1, 2, 3}
my_set = set([1, 2, 3, 2])
print(my_set)
# Внутри множества не может быть изменяемых объектов
# В этом множестве [3, 4] — изменяемый список
# Поэтому следующая строка вызовет ошибку
my_set = {1, 2, [3, 4]}Вывод:
{1, 2, 3, 4}
{1, 2, 3}
Traceback (most recent call last):
File "<string>", line 15, in <module>
my_set = {1, 2, [3, 4]}
TypeError: unhashable type: 'list'Создание пустого множество — дело хитрое.
Пустые фигурные скобки {} — это словарь. Чтобы объявить пустое множество, нужно использовать функцию set() без аргументов.
# Обратим внимание на объявление пустого множества
# Объявление с помощью {}
a = {}
# Проверка типа a
print(type(a))
# Объявление с помощью set()
a = set()
# Проверка типа a
print(type(a))Вывод:
<class 'dict'>
<class 'set'>
Как изменять множество
Множества изменяемы и не упорядочены. Поэтому в индексации нет никакого смысла.
Так что получить доступ к элементам с помощью индексов или срезов не получится. Множества просто не поддерживают эти операции.
Чтобы добавить один элемент, нужно использовать метод add(). Если нужно добавить несколько элементов — метод update(). Метод update() принимает в качестве аргументов кортежи, списки или другие множества. Во всех случаях следует избегать одинаковых элементов.
Во всех случаях следует избегать одинаковых элементов.
# создаем my_set
my_set = {1, 3}
print(my_set)
# вызов my_set[0] приведет к ошибке
# TypeError: 'set' object does not support indexing
# добавляем элемент
# Вывод: {1, 2, 3}
my_set.add(2)
print(my_set)
# добавляем несколько элементов
# Вывод: {1, 2, 3, 4}
my_set.update([2, 3, 4])
print(my_set)
# добавляем список и множество
# Вывод: {1, 2, 3, 4, 5, 6, 8}
my_set.update([4, 5], {1, 6, 8})
print(my_set)Вывод:
{1, 3}
{1, 2, 3}
{1, 2, 3, 4}
{1, 2, 3, 4, 5, 6, 8}Как удалять элементы из множества
Определенный элемент множества можно удалить с помощью методов discard() и remove().
Разница между ними вот в чем. Если элемент, который вы хотите удалить с помощью discard(), отсутствует в множестве — оно не изменится. А вот
А вот remove() вызовет ошибку, если элемента нет в множестве.
# разница между discard() и remove()
# создаем my_set
my_set = {1, 3, 4, 5, 6}
print(my_set)
# удаление элемента
# с помощью discard
# Вывод: {1, 3, 5, 6}
my_set.discard(4)
print(my_set)
# удаление элемента
# с помощью remove
# Вывод: {1, 3, 5}
my_set.remove(6)
print(my_set)
# удаление элемента,
# отсутствующего в my_set,
# с помощью discard
# Вывод: {1, 3, 5}
my_set.discard(2)
print(my_set)
# При удалении элемента,
# отсутствующего в my_set,
# с помощью remove
# вы получите ошибку.
# Вывод: KeyError
my_set.remove(2)Вывод:
{1, 3, 4, 5, 6}
{1, 3, 5, 6}
{1, 3, 5}
{1, 3, 5}
Traceback (most recent call last):
File "<string>", line 28, in <module>
KeyError: 2Удалить и вернуть элемент мы можем с помощью метода pop().
Так как множество — неупорядоченный тип данных, невозможно определить, какой из элементов будет удален. Это произойдет случайным образом.
Удалить все элементы из множества можно с помощью метода clear().
# cоздаем my_set
# Вывод: множество уникальных элементов
my_set = set("Приветмир")
print(my_set)
# pop элемента
# Вывод: случайный элемент
print(my_set.pop())
# pop еще одного элемента
my_set.pop()
print(my_set)
# очищаем my_set
# Вывод: set()
my_set.clear()
print(my_set)Вывод:
{'П', 'и', 'р', 'т', 'е', 'м', 'в'}
П
{'р', 'т', 'е', 'м', 'в'}
set()Операции со множествами
Множества можно использовать для выполнения математических операций вроде объединения, пересечения, симметрической разности и т. д. Сделать это можно с помощью операторов и методов.
Рассмотрим два множества и проведем с ними разные операции.
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8}Объединение
Результат бъединения A и B — множество, содержащее в себе все элементы множеств A и B.
Операцию объединения можно произвести двумя способами: с помощью оператора | и метода union().
# Операция объединения двух множеств
# Создаем множества A и B
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8}
# Используем оператор |
# Вывод: {1, 2, 3, 4, 5, 6, 7, 8}
print(A | B)Вывод:
{1, 2, 3, 4, 5, 6, 7, 8}Попробуйте ввести следующие примеры в консоль:
# используем функцию union
>>> A.union(B)
{1, 2, 3, 4, 5, 6, 7, 8}
# используем функцию union с B
>>> B.union(A)
{1, 2, 3, 4, 5, 6, 7, 8}Пересечение
Результат пересечения A и B — множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам
Операцию объединения можно произвести двумя способами: с помощью оператора & и метода intersection().
# Пересечение множеств
# Создаем множества A и B
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8}
# Используем оператор &
# Вывод: {4, 5}
print(A & B)Вывод:
{4, 5}Попробуйте ввести следующие примеры в консоль:
# использование метода intersection с A
>>> A.intersection(B)
{4, 5}
# использование метода intersection с B
>>> B.intersection(A)
{4, 5}Разность
Результат разности множеств B и A — множество элементов, содержащихся только в A. Следовательно, B-A = множество элементов, содержащихся только в B.
Операцию объединения можно произвести двумя способами: с помощью оператора - и метода difference().
# Разность двух множеств
# Создаем множества A и B
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8}
# Используем оператор - с A
# Вывод: {1, 2, 3}
print(A - B)Вывод:
{1, 2, 3}Попробуйте ввести следующие примеры в консоль:
# Использование функции difference с A
>>> A. B)
B)
Вывод:
{1, 2, 3, 6, 7, 8}Попробуйте ввести следующие примеры в консоль:
# Использование функции symmetric_difference с A
>>> A.symmetric_difference(B)
{1, 2, 3, 6, 7, 8}
# Использование функции symmetric_difference с B
>>> B.symmetric_difference(A)
{1, 2, 3, 6, 7, 8}Методы множеств
У множеств много методов, некоторые мы уже обсудили выше. Вот полный список методов объекта set:
Метод | Описание |
| Добавляет элемент в множество |
| Удаляет все элементы из множества |
| Возвращает копию множества |
| Возвращает новое множество — разность двух или более множеств |
| Удаляет все элементы одного набора из другого |
| Удаляет элемент, если он содержится в множестве (если элемента в множестве нет, то ничего не происходит) |
| Возвращает новое множество — пересечение двух множеств |
| Добавляет в множество пересечение с другим множеством или с самим собой |
| Возвращает |
| Возвращает |
| Возвращает |
| Удаляет и возвращает случайный элемент множества. |
| Удаляет определенный элемент множества. Если элемент отсутствует в множестве, то возвращает ошибку KeyError |
| Возвращает новое множество — симметрическую разность двух множеств |
| Добавляет в множество симметрическую разницу с другим множеством или с самим собой |
| Возвращает новое множество — объединение множеств |
| Добавляет в множество объединение с другим множеством или с самим собой |
Несколько операций со множествами
Проверка на вхождение
Мы можем проверить, есть ли элемент в множестве. Сделать это можно с помощью ключевого слова in.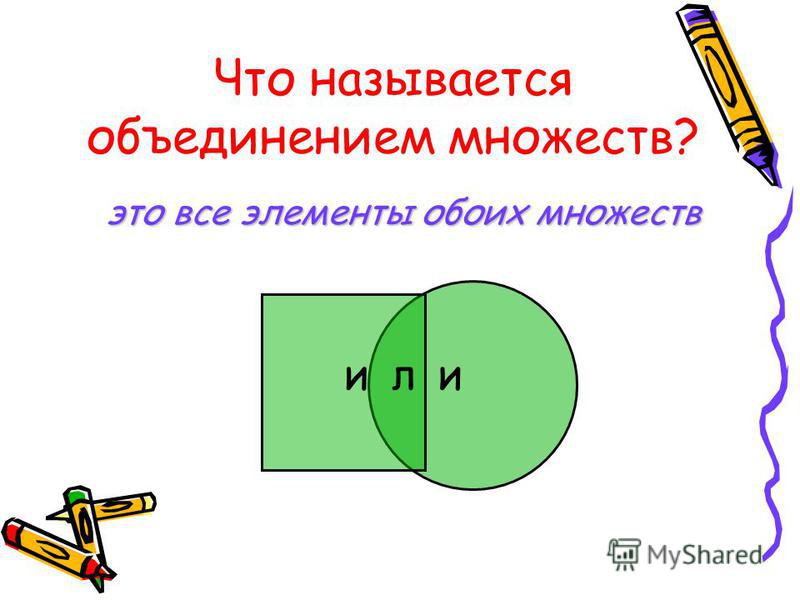
# Использование ключевого слова in
# Создаем множество my_set
my_set = set("яблоко")
# Проверяем, есть ли 'о' в множестве
# Вывод: True
print('о' in my_set)
# Проверяем, отсутствует ли 'к' в множестве
# Output: False
print('к' not in my_set)Вывод:
True
False
Итерирование по множеству
Множество можно перебрать с помощью цикла for.
for letter in set("яблоко"):
print(letter) Вывод:
я
о
л
к
б
Встроенные функции множеств
Функция | Описание |
| Возвращает |
| Возвращает |
| Возвращает перечисляемый объект. В нем в виде пар содержатся значения и индексы всех элементов множества |
| Возвращает длину (количество элементов) множества |
| Возвращает наибольший элемент множества |
| Возвращает наименьший элемент множества |
| Возвращает отсортированный список, в котором находятся элементы множества (само множество не сортируется) |
| Возвращает сумму всех элементов множества |
Frozenset
Frozenset — класс, имеющий характеристики множества. Отличие состоит в том, что frozenset после объявления неизменяем.
Кортеж — неизменяемый список, frozenset — неизменяемое множество.
Множества изменяемы, поэтому не могут использоваться в качестве ключей словаря. Frozenset же неизменяемы — их можно использовать в качестве ключей словаря.
Этот тип данных поддерживает следующие методы: copy(), difference(), intersection(), isdisjoint(), issubset(), issuperset(), symmetric_difference() и union(). Так как он неизменяем, методы add() и remove() с ним не работают.
# Frozenset # Создаем множества A и B A = frozenset([1, 2, 3, 4]) B = frozenset([3, 4, 5, 6])
Попробуйте ввести следующие примеры в консоль:
>>> A.isdisjoint(B)
False
>>> A.difference(B)
frozenset({1, 2})
>>> A | B
frozenset({1, 2, 3, 4, 5, 6})
>>> A. add(3)
...
AttributeError: 'frozenset' object has no attribute 'add'
```
add(3)
...
AttributeError: 'frozenset' object has no attribute 'add'
```Функция Union() в Python - GeeksforGeeks
Набор Python Метод Union() возвращает новый набор, содержащий все элементы исходного набора.
Объединение двух заданных множеств — это множество, содержащее все элементы обоих множеств. Объединение двух заданных множеств A и B — это множество, состоящее из всех элементов A и всех элементов B, таких, что ни один элемент не повторяется.
Python Set Union () Синтаксис метода:Символ для обозначения объединения множеств - 'U'
Пример метода Python set Union():Синтаксис: SET1.Union (SET2, SET3, SET4….)
. Параметры: Зеро или больше сет
: Зеро или больше сет. Возврат: Возвращает набор, который представляет собой объединение всех наборов (набор1, набор2, набор3…) с набором1.
Он возвращает копию set1, только если параметр не передан.
Python3
|
Output:
A U B: {2, 4, 5, 6, 7, 8} Example 1: Working with
Python set Union() methodsPython3
|
Выход
набор1 U набор2 : {2, 4, 5, 6, 7, 8}
набор1 U набор2 U набор3 : {2, 4, 5, 6, 7, 8, 9, 10} Вывод:
набор1 U набор2 : {2, 4, 5, 6, 7, 8}
set1 U set2 U set3 : {2, 4, 5, 6, 7, 8, 9, 10} Пример 2. Объединение множеств Python с использованием | Оператор
Мы можем использовать «|» Оператор нахождения объединения множеств.
Python3
|
Выход
set1 U set2 : {2, 4, 5, 6, 7, 8}
набор1 U набор2 U набор3 : {2, 4, 5, 6, 7, 8, 9, 10} Вывод:
набор1 U набор2 : {2, 4, 5, 6, 7, 8}
набор1 U набор2 U набор3 : {2, 4, 5, 6, 7, 8, 9, 10} Example 3 : Python Set Union() Method on String Python3
|
Output
A U B: {'za', 'ab' , 'dd', 'dz', 'ba', 'cd'} Пример 4. Метод Python Set Union() для множественного набора (с 3 наборами). Python3
|
Python Set Union с кодами и примерами составные части. Python решил сделать реализацию математических наборов внутренней структурой данных из-за ее важности. В этой статье мы узнаем, как найти объединение между двумя наборами с помощью метода set union() в python. Но сначала давайте рассмотрим, что такое множества и что мы имеем в виду, когда говорим «объединение двух множеств».
Что такое множество в Python? Фигурные скобки используются для представления наборов, которые являются одной из четырех основных структур данных Python. Наборы, как и списки, могут хранить данные любого типа (строки, целые числа, числа с плавающей запятой), а также смесь типов данных. Однако имеет логичный смысл группировать в наборе только связанные вещи. Вам может быть интересно, в чем разница между структурами данных словаря и набора, поскольку они обе используют фигурные скобки для описания себя. Решение простое: словари хранят данные в виде пар ключ-значение, а наборы — нет.
Давайте подробнее рассмотрим наборы с технической точки зрения. Наборы являются изменчивыми, повторяемыми и не допускают существования в них повторяющихся элементов. Важно отметить, что, поскольку наборы неупорядочены , мы не можем использовать индексы для доступа к их элементам, как мы делаем со списками. На самом деле, по сравнению с другими структурами данных, наборы дают значительное преимущество. Внутри наборы используют структуру данных, называемую хэш-таблицей , которая обеспечивает оптимальную технику определения того, входит ли определенный элемент в набор. Этот подход быстрее, чем самый эффективный алгоритм поиска. Давайте посмотрим на некоторые примеры наборов Python.
Например:
setA = { "a", "b", "c"}
печать (набор)
# Добавляем элемент в набор
setA.добавить ("д")
печать (набор)
Вывод:
{'c', 'b', 'a'}
{'в', 'г', 'б', 'а'}
Что такое объединение множеств?
Объединение любых двух или более наборов дает совершенно новый набор, который включает смесь элементов из всех наборов .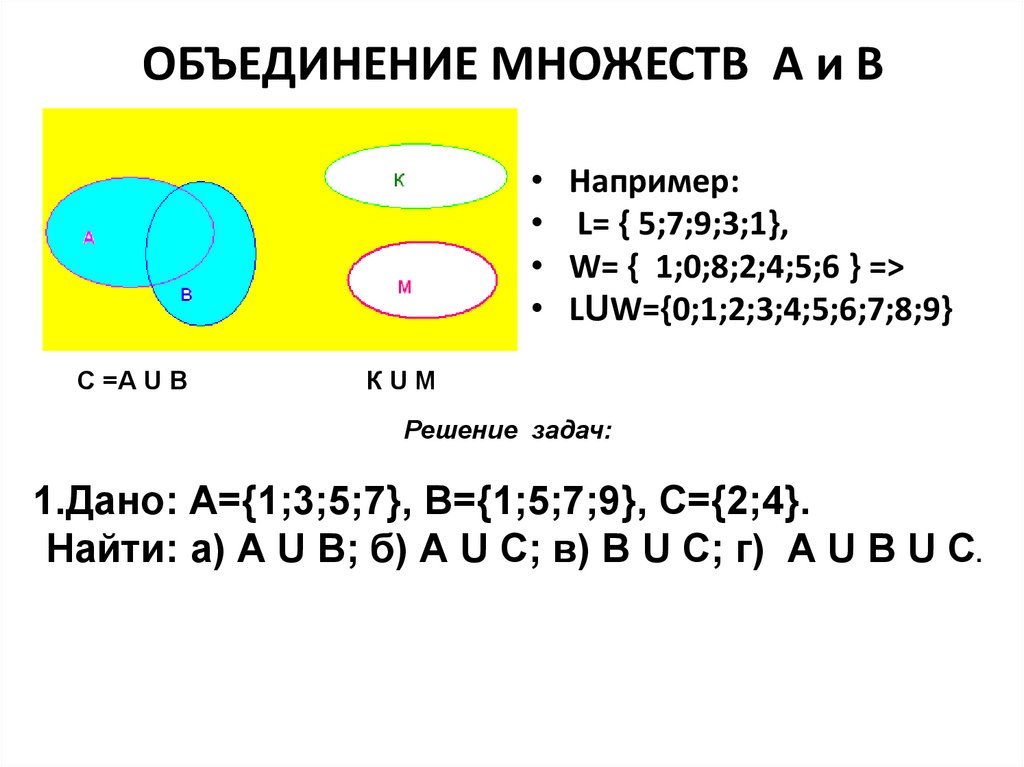 Другими словами, объединение двух или более множеств — это множество из все отдельные элементы присутствуют во всех наборах . Слово « или » используется для обозначения объединения наборов. Рассмотрим два множества A и B. Все элементы, которые присутствуют либо в A, либо в B, либо в обоих множествах, будут присутствовать в объединении A и B. Объединение множеств представлено символом «U». Операция над множествами, часто известная как объединение множеств, записывается как:
Другими словами, объединение двух или более множеств — это множество из все отдельные элементы присутствуют во всех наборах . Слово « или » используется для обозначения объединения наборов. Рассмотрим два множества A и B. Все элементы, которые присутствуют либо в A, либо в B, либо в обоих множествах, будут присутствовать в объединении A и B. Объединение множеств представлено символом «U». Операция над множествами, часто известная как объединение множеств, записывается как:
A ∪ B = {x: x ∈ A или x ∈ B}. Здесь x — элемент, присутствующий в обоих множествах, A и B.
Давайте лучше поймем эту концепцию на примере:
Если A = { 23, 453, 43, 66, 21} и B = { 43, 785, 12, 35, 23, 545}
Тогда A U B = {23, 453, 43, 66, 21, 43, 785, 12, 35, 545}
Вы также можете визуализировать эту концепцию с помощью диаграммы Венна, как показано ниже:
Найти союз наборов в Python? Теперь, когда мы знаем, что такое множества и что такое объединение множеств, давайте теперь узнаем, как найти объединение множеств в Python. К счастью для нас, Python предоставляет нам две реализации, которые позволяют найти объединение: одна встроенная функция, а другая переопределенный оператор. Итак, без лишних слов, давайте рассмотрим каждый из этих подходов один за другим.
К счастью для нас, Python предоставляет нам две реализации, которые позволяют найти объединение: одна встроенная функция, а другая переопределенный оператор. Итак, без лишних слов, давайте рассмотрим каждый из этих подходов один за другим.
Это встроенный метод в python, предназначенный для поиска объединения любого заданного количества наборов. Эта функция реализует оператор объединения, а для требуется набор, по которому можно вызвать функцию . Остальные наборы передаются функции в качестве аргументов. Значение, возвращаемое этой функцией, представляет собой новый набор, являющийся объединением набора, для которого вызывается функция, и всех наборов, которым передается аргумент. . Обратите внимание, что эта функция не вносит изменений в исходные наборы .
Например, предположим, что у нас есть два набора (A и B), и мы хотим найти AUB. Итак, синтаксис будет выглядеть примерно так:
Итак, синтаксис будет выглядеть примерно так:
A.union(B) # Оператор 1 B.union(A) # Заявление 2
Обратите внимание, что оба оператора, а именно оператор 1 и оператор 2, дадут один и тот же результат. Давайте теперь посмотрим на код, чтобы лучше понять использование этой функции. Обратите внимание, как мы использовали его, чтобы найти объединение более чем двух множеств.
Код Python:
A = {1, 2, 3, 4} #Set A
B = {2, 5, 6, 7} #Набор B
С = {7, 8, 9, 10} #Набор С
D = {11, 12, 13, 14} # Установить D
# Е = А У В
E = A.union(B) # Утверждение 1
# F = А У Б У С У Д
F = A.union(B, C, D) # Утверждение 2
print("A U B: " +str(E))
print("A U B U C U D: " +str(F))
Вывод:
A U B: {1, 2, 3, 4, 5, 6, 7}
А У Б У Ц У Д: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}
2) Использование | оператор
Этот метод делает то же самое, что и предыдущая встроенная функция. Здесь вместо вызова функции используется оператор | . Посмотрите на код ниже, объединение двух или более наборов можно найти с помощью этого оператора,
Здесь вместо вызова функции используется оператор | . Посмотрите на код ниже, объединение двух или более наборов можно найти с помощью этого оператора,
Код Python:
A = {1, 2, 3, 4} #Set A
B = {2, 5, 6, 7} #Набор B
С = {7, 8, 9, 10} #Набор С
D = {11, 12, 13, 14} # Установить D
# Е = А У В
Е = А|В
# F = А У Б У С У Д
Ф = А|В|С|D
print("A U B: " +str(E))
print("A U B U C U D: " +str(F))
Вывод:
A U B: {1, 2, 3, 4, 5, 6, 7}
А У Б У Ц У Д: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}
Заключение
Python известен своим простым синтаксисом, похожим на английский язык. Python поставляется с огромным количеством встроенных функций, которые можно использовать для выполнения многих распространенных операций с множествами. В этой статье был описан оператор объединения множеств и его реализация в Python. Есть еще две основные операции над множествами пересечение и разница . Мы настоятельно рекомендуем вам узнать об обеих этих операциях.
Мы настоятельно рекомендуем вам узнать об обеих этих операциях.
Python Set Union (union, | & |= , update) с примером
В этом руководстве мы узнаем о различных способах выполнения операции union над двумя или более наборами в python.
В теории множеств объединение двух или более множеств — это множество, содержащее все элементы (различные), присутствующие во всех множествах. Например:
А = {1, 2, 3, 4, 5}
В = {4, 5, 6, 7, 8, 9}
Союз А и Б: -
A U B = {1, 2, 3, 4, 5, 6, 7, 8, 9} Python Set Union : В Python существует четыре различных способа выполнения операции union над сбором наборы, они следующие:
- Union Method
- | Оператор Метод обновления
- |= Оператор
Этот метод используется для возврата объединения набора и набора элементов из одной или нескольких итераций, таких как строка, список, набор. Этот метод принимает произвольное количество итерируемых объектов в качестве аргумента, что означает, что может быть передан один или несколько итерируемых объектов. Если передается итерируемый объект, отличный от набора, он сначала преобразует итерируемый объект в объект набора, а затем выполняет операцию объединения. Он возвращает только что созданный набор, который содержит все элементы (различные), присутствующие во всех итерируемых объектах.
Этот метод принимает произвольное количество итерируемых объектов в качестве аргумента, что означает, что может быть передан один или несколько итерируемых объектов. Если передается итерируемый объект, отличный от набора, он сначала преобразует итерируемый объект в объект набора, а затем выполняет операцию объединения. Он возвращает только что созданный набор, который содержит все элементы (различные), присутствующие во всех итерируемых объектах.
Синтаксис : < Установить объект >.union( *<итерируемый объект> ) : < Установить объект >
Пример: # Python Set Union
# создаем объект set и присваиваем его переменной A
А = {1,2,3,4,5} # создаем объект set и присваиваем его переменной B
В = {4,5,6,7,8,9} # вызвать метод union, чтобы получить объединение множества A и B и присвоить его переменной S
S = А.  союз(В) # вывести все значения множества A, B и S
печать('А : ',А)
печать('В : ',В)
print('Союз B : ',S) # создать объект списка и присвоить его переменной L
Л = [11,12,13,14,15] # вызвать метод объединения, чтобы получить объединение множества A, B и списка L и присвоить его переменной S
S = A.union(B,L) # вывести все значения множества A, B, S и списка L
печать('А : ',А)
печать('В : ',В)
печать('Л : ',Л)
print('A Union B Union L : ',S)
союз(В) # вывести все значения множества A, B и S
печать('А : ',А)
печать('В : ',В)
print('Союз B : ',S) # создать объект списка и присвоить его переменной L
Л = [11,12,13,14,15] # вызвать метод объединения, чтобы получить объединение множества A, B и списка L и присвоить его переменной S
S = A.union(B,L) # вывести все значения множества A, B, S и списка L
печать('А : ',А)
печать('В : ',В)
печать('Л : ',Л)
print('A Union B Union L : ',S)
Этот оператор используется для возврата объединения двух или более наборов точно так же, как метод union() . Разница между | оператор и union() метод заключается в том, что первый может работать только с объектами набора, а второй может работать с любыми итерируемыми объектами, такими как список, строка, набор.
Синтаксис : < Установить объект 1 > | < Установить объект 2 > | <Установить объект 2>… : <Установить объект>
Пример: # Python Set Union
# создаем объект set и присваиваем его переменной A
А = {1,2,3,4,5} # создаем объект set и присваиваем его переменной B
В = {4,5,6,7,8,9} # использовать | оператор, чтобы получить объединение множества A и B и присвоить его переменной S
С = А | Б # вывести все значения множества A, B и S
печать('А : ',А)
печать('В : ',В)
print('Союз B : ',S) # создаем объект set и присваиваем его переменной C
С = {7,8,9,10,11,12} # использовать | оператор, чтобы получить объединение множества A, B и C и присвоить его переменной S
С = А | Б | С # вывести все значения множества A, B, C и S
печать('А : ',А)
печать('В : ',В)
печать('С : ',С)
print('A Union B Union C : ',S) # создать объект списка и присвоить его переменной L
Л = [11,12,13,14,15] # использовать | оператор для получения объединения набора A и списка L
С = А | л
# TypeError вызывается как | оператор работает только с установленными операндами
Этот метод используется для возврата объединения набора и набора элементов из одной или нескольких итераций, таких как строка, список, набор. Он очень похож на метод union() , с той разницей, что если метод union() создает и возвращает новый набор, содержащий все элементы (различные), присутствующие во всех итерациях, метод update() обновляет набор, в котором этот метод вызывается со всеми отдельными элементами, присутствующими во всех итерациях.
Он очень похож на метод union() , с той разницей, что если метод union() создает и возвращает новый набор, содержащий все элементы (различные), присутствующие во всех итерациях, метод update() обновляет набор, в котором этот метод вызывается со всеми отдельными элементами, присутствующими во всех итерациях.
Синтаксис : < Установить объект >.update( *<итерируемый объект> )
Пример: # Python Set Union
# создаем объект set и присваиваем его переменной A
А = {1,2,3,4,5} # создаем объект set и присваиваем его переменной B
В = {4,5,6,7,8,9} # вызовите метод update, чтобы получить объединение наборов A и B, обновив набор A
А.обновить(Б) # вывести все значения множества A
print('Союз B : ',A) # создать объект списка и присвоить его переменной L
Л = [11,12,13,14,15] # вызовите метод обновления, чтобы получить объединение множества A, B и списка L, обновив множество A
А.  обновить(B,L) # вывести все значения множества A
print('A Union B Union L : ',A)
обновить(B,L) # вывести все значения множества A
print('A Union B Union L : ',A)
Этот оператор используется для возврата объединения двух или более наборов точно так же, как метод update() . Разница между методом |= operator и update() заключается в том, что первый может работать только с объектами набора, а второй может работать с любыми итерируемыми объектами, такими как список, строка, набор.
Синтаксис : < Установить объект 1 > |= < Установить объект 2 > | < Установить объект 2>…
Пример: # Python Set Union
# создаем объект set и присваиваем его переменной A
А = {1,2,3,4,5} # создаем объект set и присваиваем его переменной B
В = {4,5,6,7,8,9} # используйте оператор |=, чтобы получить объединение наборов A и B, обновив набор A
А |= В # вывести все значения множества A
print('Союз B : ',A) # создаем объект set и присваиваем его переменной A
А = {1,2,3,4,5} # создаем объект set и присваиваем его переменной C
С = {7,8,9,10,11,12} # используйте оператор |=, чтобы получить объединение наборов A, B и C, обновив набор A
А |= В | С # вывести все значения множества A
print('A Union B Union C : ',A) # создать объект списка и присвоить его переменной L
Л = [11,12,13,14,15] # используйте оператор |=, чтобы получить объединение множества A и списка L
А |= Л
# TypeError возникает, поскольку оператор |= работает только с установленными операндами
- метод объединения Документы Метод обновления
- Документы
Это все, что касается Python Set Union with Example. Если вам понравилось, пожалуйста, поделитесь своими мыслями в разделе комментариев и поделитесь им с другими.
Если вам понравилось, пожалуйста, поделитесь своими мыслями в разделе комментариев и поделитесь им с другими.
Предыдущий
Операции над множествами в Python (объединение, пересечение, симметричная разность и т. д.)
В Python множество представляет собой набор непересекающихся элементов (уникальных элементов). Он может выполнять операции над множествами, такие как объединение, пересечение, разность, симметричная разность и так далее.
- Встроенные типы — Установить тип — Документация по Python 3.9.7
- Набор (математика) - Википедия
В этой статье описывается следующее содержимое.
Основные операции:
- Создание объекта
set:{},set() - Комплект понимания
- Получить количество элементов в наборе:
len() - Добавить элемент в набор:
add() - Удалить элемент из набора: 9 оператор,
симметричная_разность() - Проверить, является ли A подмножеством B: оператор
<=,issubset() - Проверить, является ли A надмножеством B:
>=оператор,issuperset() - Проверить, не пересекаются ли A и B:
isdisjoint()
Тип set — это изменяемый тип, который может добавлять и удалять элементы. Python также предоставляет тип
Python также предоставляет тип frostset , который имеет методы для операций с множествами, такие как устанавливает , но неизменен. замороженный набор нельзя изменить, добавив или удалив элементы.
Создание
Set Объект: {} , Set () Создайте
Set Объект с вьющимися скобками {} SET Объекты могут быть созданы на участках. {} .
Если есть повторяющиеся значения, они игнорируются, и в качестве элементов остаются только уникальные значения.
с = {1, 2, 2, 3, 1, 4}
печать(и)
печать (тип (ы))
# {1, 2, 3, 4}
# <класс 'набор'>
источник: set.py
set может иметь элементы разных типов, но не может иметь изменяемые объекты, такие как list .
Тип set неупорядочен, поэтому порядок, в котором он был создан, не сохраняется.
с = {1.23, 'abc', (0, 1, 2), 'abc'}
печать(и)
# {(0, 1, 2), 1. 23, 'абв'}
# с = {[0, 1, 2]}
# TypeError: unhashable type: 'list'
23, 'абв'}
# с = {[0, 1, 2]}
# TypeError: unhashable type: 'list'
источник: set.py
Даже если типы разные, например int и float , они считаются дубликатами, если значения равны.
с = {100, 100,0}
печать(и)
# {100}
источник: set.py
Поскольку пустой {} считается словарем dict , пустой набор может быть создан с помощью set() , описанного далее.
с = {}
печать(и)
печать (тип (ы))
# {}
# <класс 'дикт'>
источник: set.py
Создайте объект
set с помощью set() Объекты set также можно создать с помощью set() .
При указании итерируемого объекта, такого как список или кортеж, в качестве аргумента создается объект set , в котором исключаются повторяющиеся элементы и остаются только уникальные значения.
л = [1, 2, 2, 3, 1, 4]
печать (л)
печать (тип (л))
# [1, 2, 2, 3, 1, 4]
# <класс 'список'>
s_l = набор (л)
печать (s_l)
печать (тип (s_l))
# {1, 2, 3, 4}
# <класс 'набор'>
источник: set.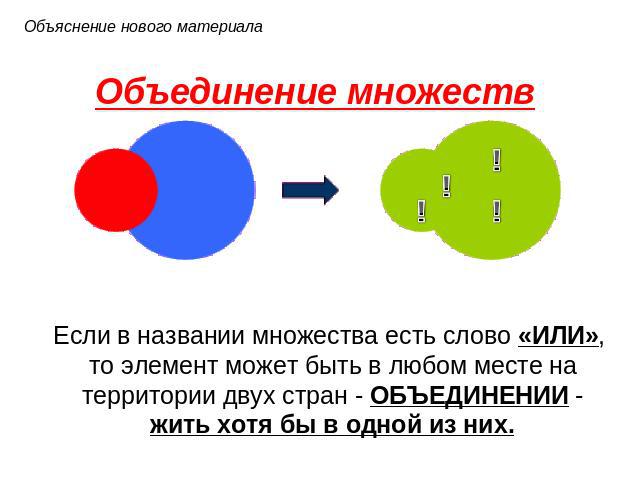 py
py
Для неизменного замороженного набора используйте замороженный набор () .
fs_l = замороженный набор (l)
печать (fs_l)
печать (тип (fs_l))
# замороженный набор({1, 2, 3, 4})
# <класс 'замороженный набор'>
источник: set.py
Если аргумент опущен, создается пустой набор .
с = установить() печать(и) печать (тип (ы)) # установлен() # <класс 'набор'>
источник: set.py
Вы можете использовать set() для удаления повторяющихся элементов из списка или кортежа, но исходный порядок не сохраняется.
Используйте list() и tuple() для преобразования набора в список или кортеж.
- Преобразование списка и кортежа друг в друга в Python
л = [2, 2, 3, 1, 3, 4] l_unique = список (набор (l)) печать (l_unique) # [1, 2, 3, 4]
источник: set.py
См. следующую статью об удалении повторяющихся элементов в исходном порядке или извлечении только повторяющихся элементов.
- Удалить/извлечь повторяющиеся элементы из списка в Python
Включение множеств
Python обеспечивает включение множеств, а также включение списков. Используйте фигурные скобки {} вместо квадратных скобок [] .
с = {i**2 для i в диапазоне (5)}
печать(и)
# {0, 1, 4, 9, 16}
источник: set.py
См. следующую статью для получения дополнительной информации о включении списков.
- Включение списков в Python
Получить количество элементов в наборе:
len() Количество элементов множества можно получить с помощью встроенной функции len() .
с = {1, 2, 2, 3, 1, 4}
печать(и)
печать (длина (ы))
# {1, 2, 3, 4}
№ 4
источник: set.py
Если вы хотите подсчитать количество вхождений в списке с повторяющимися элементами, см. следующую статью.
- Подсчет элементов в списке с коллекциями. Счетчик в Python
Добавить элемент в набор:
add() Используйте метод add() для добавления элемента в набор.
с = {0, 1, 2}
с.добавить(3)
печать(и)
# {0, 1, 2, 3}
источник: set.py
Удалить элемент из набора:
discard() , remove() , pop() , clear() Использовать discard() 7 9048 , remove() , pop() и clear() методы для удаления элемента из набора.
Метод discard() удаляет элемент, указанный аргументом. Если указано значение, не существующее в наборе, никаких действий не предпринимается.
с = {0, 1, 2}
s.discard(1)
печать(и)
# {0, 2}
с = {0, 1, 2}
s.discard(10)
печать(и)
# {0, 1, 2}
источник: set.py
Метод remove() также удаляет элемент, указанный аргументом, но вызывает ошибку KeyError , если указано значение, не существующее в наборе.
с = {0, 1, 2}
с.удалить(1)
печать(и)
# {0, 2}
# с = {0, 1, 2}
# с.удалить(10)
# KeyError: 10
источник: set.py
Метод pop() удаляет элемент из набора и возвращает его значение. Вы не можете выбрать, какие значения удалить. Выдает ошибку
Вы не можете выбрать, какие значения удалить. Выдает ошибку KeyError , если набор пуст.
с = {2, 1, 0}
v = s.pop()
печать(и)
печать (v)
# {1, 2}
# 0
с = {2, 1, 0}
печать (s.pop())
# 0
печать (s.pop())
№ 1
печать (s.pop())
№ 2
# печать(s.pop())
# KeyError: 'извлечь из пустого множества'
источник: set.py
Метод clear() удаляет все элементы из набора и очищает его.
с = {0, 1, 2}
с.очистить()
печать(и)
# установлен()
источник: set.py
Союз:
| оператор, объединение() Вы можете получить союз с | Оператор или метод union() .
с1 = {0, 1, 2}
с2 = {1, 2, 3}
с3 = {2, 3, 4}
s_union = s1 | с2
печать (s_union)
# {0, 1, 2, 3}
s_union = s1.union(s2)
печать (s_union)
# {0, 1, 2, 3}
источник: set.py
Для union() можно указать несколько аргументов.
Кроме того, не только set , но также списки и кортежи, которые можно преобразовать в set с помощью set() можно указать в качестве аргументов. То же самое относится и к следующим методам.
То же самое относится и к следующим методам.
s_union = s1.union(s2, s3)
печать (s_union)
# {0, 1, 2, 3, 4}
s_union = s1.union(s2, [5, 6, 5, 7, 5])
печать (s_union)
# {0, 1, 2, 3, 5, 6, 7}
источник: set.py
Пересечение: оператор
и , пересечение() Вы можете получить пересечение с помощью оператора и или метода пересечения() .
s_intersection = s1 и s2
печать (s_intersection)
# {1, 2}
s_intersection = s1.intersection(s2)
печать (s_intersection)
# {1, 2}
s_intersection = s1.intersection(s2, s3)
печать (s_intersection)
# {2}
9с2
печать (s_симметричная_разница)
# {0, 3}
s_symmetric_difference = s1.symmetric_difference(s2)
печать (s_симметричная_разница)
# {0, 3}
источник: set.py
Проверить, является ли A подмножеством B:
<= оператор, issubset() Чтобы проверить, является ли A подмножеством B, т. е. все ли элементы A содержатся в B используйте оператор <= или метод issubset() .
с1 = {0, 1}
с2 = {0, 1, 2, 3}
печать (s1 <= s2)
# Истинный
печать (s1.issubset (s2))
# Истинный
источник: set.py
Как оператор <= , так и метод issubset() возвращают True для эквивалентных наборов.
Чтобы проверить, является ли набор правильным подмножеством, используйте оператор < , который возвращает False для эквивалентных наборов.
печать (s1 <= s1) # Истинный печать (s1.issubset (s1)) # Истинный печать (s1 < s1) # ЛОЖЬ
источник: set.py
Проверить, является ли A надмножеством B:
>= оператор, issuperset() Чтобы проверить, является ли A надмножеством B, т. е. все ли элементы B содержатся в A, используйте оператор >= или issuperset() .
с1 = {0, 1}
с2 = {0, 1, 2, 3}
печать (s2 >= s1)
# Истинный
печать (s2.issuperset (s1))
# Истинный
источник: set.py
Как оператор >= , так и метод issuperset() возвращают True для эквивалентных наборов.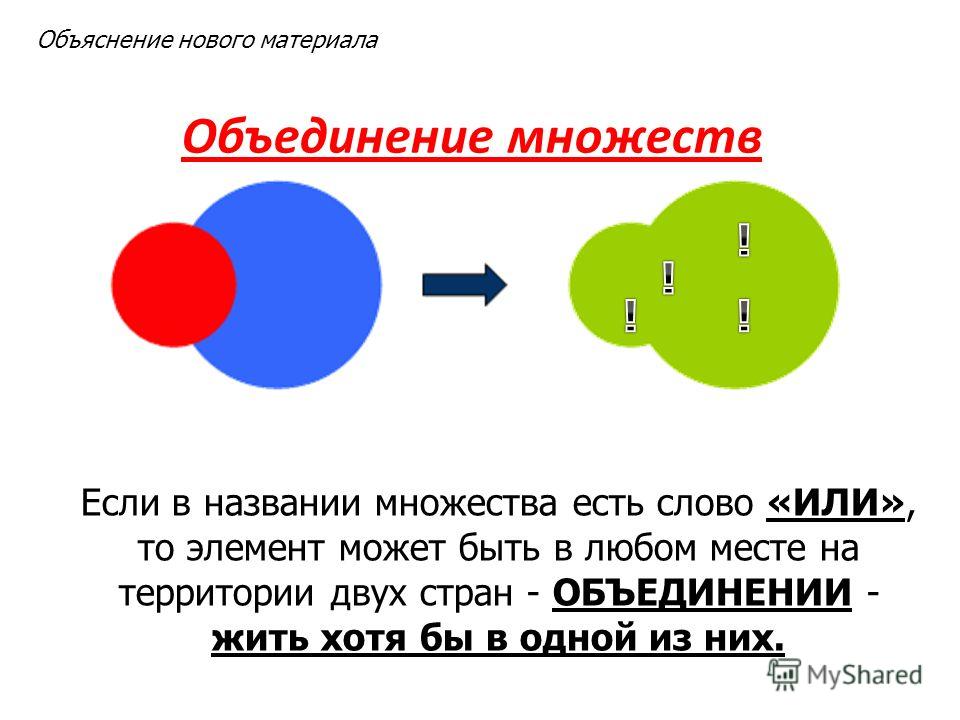
Чтобы проверить, является ли набор надлежащим надмножеством, используйте 9Оператор 0047 > , который возвращает False для эквивалентных наборов.
печать (s1 >= s1) # Истинный печать (s1.issuperset (s1)) # Истинный печать (s1 > s1) # ЛОЖЬ
источник: set.py
Проверить, не пересекаются ли A и B:
isdisjoint() Чтобы проверить, не пересекаются ли A и B, т. е. нет ли у A и B общих элементов, используйте isdisjoint() Метод .
с1 = {0, 1}
с2 = {1, 2}
с3 = {2, 3}
печать (s1.isdisjoint (s2))
# ЛОЖЬ
печать (s1.isdisjoint (s3))
# Истинный
источник: set.py
Python Set Operations | союз | пересечение
Набор Python может использоваться для различных операций Python Set . Существуют разные типы операций, используемые с наборами Python. В этом уроке Python мы сосредоточимся на этих операциях и узнаем, как их использовать.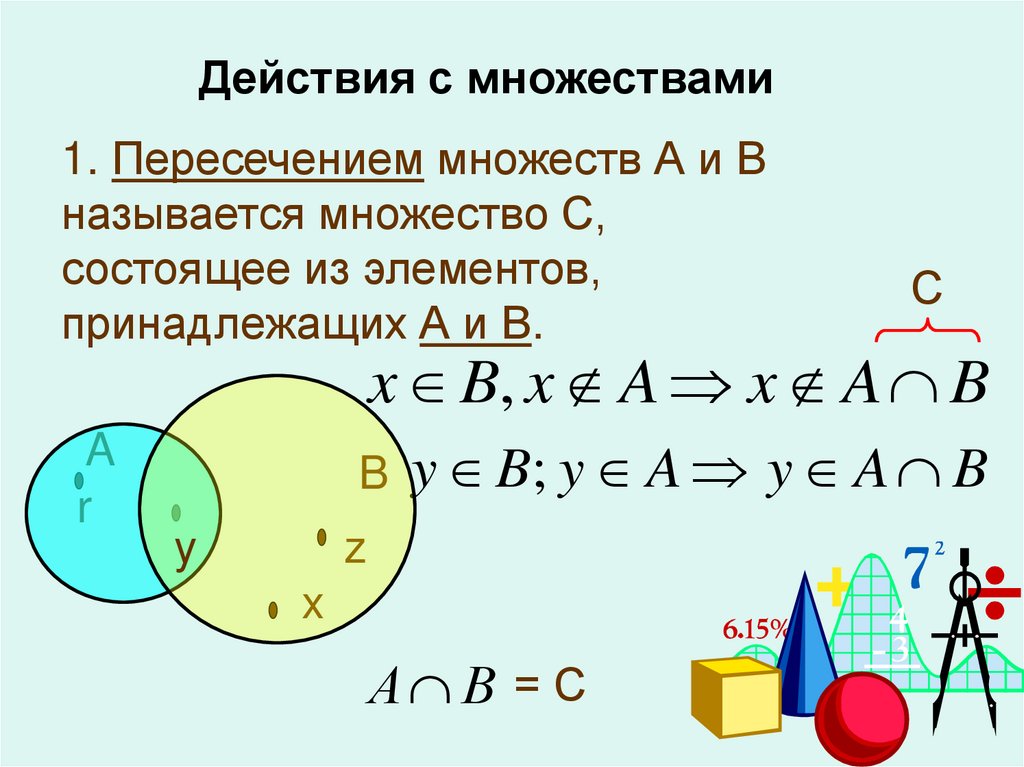 Мы увидим, когда мы сможем использовать эти Python Set Operations в наших кодах.
Мы увидим, когда мы сможем использовать эти Python Set Operations в наших кодах.
Так что же это за операции и используемые с ними операторы. Это: 9“ Оператор
Содержание
Первый оператор, используемый с наборами Python, это « | » оператор. С помощью этого оператора мы объединяем два набора вместе. Мы можем сделать ту же работу с помощью python union method .
Ниже мы объединим два набора чисел с помощью «|» оператор.
числа1 = {1,2,3}
числа2 = {2,3,7,10,15}
печать (числа1 | числа2) Вывод этого кода будет:
{1, 2, 3, 7, 10, 15} Тот же код может быть написан с помощью метода Python Union ниже:
Вы также можете посмотреть видео этого урока.
youtube.com/embed/sY0Ykd-coIs?start=4&feature=oembed&enablejsapi=1&origin=https://ipcisco.com" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen="">
числа1 = {1,2,3}
числа2 = {2,3,7,10,15}
print(numbers1.union(numbers2))
{1, 2, 3, 7, 10, 15}
Опять же, мы можем использовать этот оператор для комбинирования наборов строк, как показано ниже:
dwarves1", ""inwalin} dwarves1", ""Thor}
dwarves2 = {"Гимли", "Бофур", "Торин"}
print(dwarves1 | dwarves2)
На выходе мы увидим комбинацию этих наборов. Как вы можете видеть ниже, двойные предметы будут только один раз в новом наборе. Другими словами, «Торин» будет только один раз в этом новом наборе.
{'balin', 'dwalin', 'bofur', 'thorin', 'gimli'}
Другой, используемый с сетями Python is ‘ & ». оператор. С помощью этого оператора мы можем найти общие элементы в двух наборах вместе. Мы можем сделать ту же работу с помощью метода пересечения Python .
оператор. С помощью этого оператора мы можем найти общие элементы в двух наборах вместе. Мы можем сделать ту же работу с помощью метода пересечения Python .
числа1 = {1,2,3}
числа2 = {2,3,7,10,15}
печать (числа1 и числа2)
Вывод этого кода Python будет похож на beloe, потому что общие элементы в обоих наборах — 2 и 3. наборов.
dwarves1 = {"Торин", "Балин", "Двалин"}
dwarves2 = {"Гимли", "Бофур", "Торин"}
print(dwarves1 & dwarves2)
{'Торин'}
«-» оператор используется для нахождения разности двух наборов с, если он используется с наборами. Та же работа выполняется с помощью метода различий , используемого в python. Например, если мы хотим найти элементы только в наборе1, но не в наборе2, мы используем код (набор1-набор2). Приведем пример, чтобы лучше понять.
числа1 = {1,2,3}
числа2 = {2,3,7,10,15}
print(числа2-числа1)
{10, 15, 7}
В этом коде Python мы получили разницу двух наборов. Вывод этого кода показывает, что элементы находятся в числах2, но не в числах1. Итак, в новом наборе убраны общие предметы.
Мы можем сделать то же самое с помощью разностного метода.
числа1 = {1,2,3}
числа2 = {2,3,7,10,15}
print(numbers2.difference(numbers1)) {10, 15, 7}
Если мы используем числа1-числа2, на этот раз вывод будет другим. И использование разностного метода также будет изменено.
числа1 = {1,2,3}
числа2 = {2,3,7,10,15}
print(числа1-числа2)
числа1 = {1,2,3}
числа2 = {2,3,7,10,15}
print(numbers1.difference(numbers2))
^ Оператор — метод Python Set Symetric Difference 9числа2)
Как вы можете видеть ниже, вывод этого кода даст нам элементы, которые не являются общими в обоих наборах.
{22, 56, 12, 92}
Мы можем выполнить ту же работу, используя метод симметричной_разности.
числа1 = {17,22,80}
числа2 = {12,17,56,80,92}
print(numbers1.symmetric_difference(numbers2)) {22, 56, 12, 92}
Приведенное ниже использование также даст тот же результат. Но предметы в наборе могут быть в другом порядке.
числа1 = {17,22,80}
числа2 = {12,17,56,80,92}
print(numbers2.symmetric_difference(numbers1))
{12, 22, 56, 92} Неупорядоченный набор элементов называется set в Python. Любой элемент может быть добавлен или удален из установить , но значение любого элемента в установить не может быть изменено, как кортеж. Каждый предмет в наборе должен быть уникальным. Набор не содержит никакого индекса, такого как список или кортеж, поэтому к каждому элементу набора нельзя получить доступ по индексу, подобному списку или кортежу.
 Наборы в основном используются для различных типов математических операций в Python, таких как объединение, пересечение, разность и т. д. Различные символы используются для выполнения разных типов операций. Труба ( | ) используется для union операция на наборах . В этом руководстве объясняется, как объявить наборы и выполнить над ними операцию union .
Наборы в основном используются для различных типов математических операций в Python, таких как объединение, пересечение, разность и т. д. Различные символы используются для выполнения разных типов операций. Труба ( | ) используется для union операция на наборах . В этом руководстве объясняется, как объявить наборы и выполнить над ними операцию union .Предварительное условие:
Прежде чем приступить к этому руководству, важно прояснить концепцию операции объединения. Новый набор формируется путем объединения общих и необычных элементов двух или более наборов с помощью операции объединения. Как правило, символ ‘U’ используется для обозначения операции объединения.
Например:
Есть два набора, A и B.
Набор, A = {79, 34, 99, 23, 61}
Набор, B = {26, 99, 61, 55}
Тогда, AUB = {34, 99, 55, 23, 26, 61, 79 }
Графическое представление вышеуказанной операции объединения показано ниже.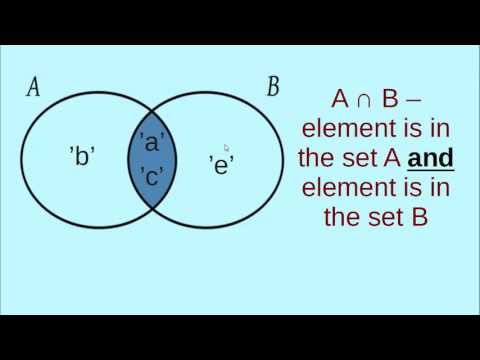 Здесь 99 и 61 являются общими в обоих наборах.
Здесь 99 и 61 являются общими в обоих наборах.
Пример 1: Применение операции объединения к наборам числовых данных
В следующем примере определены два числовых набора, A и B. Три значения являются общими в этих наборах. Это 7, 9, и 11.
#!/usr/bin/env python3
# Определить два набора, A и B
A = { 10, 20, 7 ,9, 11, 15 }
B = { 11, 3, 7 , 9, 25 }
# Результат объединения A и B
print("Выход A U B равен :\n", A | B)
Вывод:
После запуска скрипта появится следующий вывод .
Пример 2: Применение операции объединения к наборам данных символов
В следующем примере показано использование операторов объединения к трем наборам символов. Это наборы A, B и C. Здесь набор A содержит четыре символа, набор B содержит три символа, а набор C содержит четыре символа. Два символа, «C» и «R», присутствуют во всех трех наборах. Итак, новый набор после операции объединения будет содержать 4+1+2=7 символов.
Итак, новый набор после операции объединения будет содержать 4+1+2=7 символов.
#!/usr/bin/env python3
# Определить три набора символов, A, B и C
A = { 'A', 'C', 'E', 'R' }
B = { ' B','C', 'R' }
C = { 'C','G', 'R', 'X' }
# Объединение выходных данных A, B и C
print("Вывод of (A U B U C) is :\n", A | B | C)
Вывод:
После запуска сценария появится следующий вывод.
Пример 3: Применение операции объединения к наборам строковых данных
Как операцию объединения можно выполнить для двух наборов строковых данных и выполнить итерацию значений конечного набора после операции объединения с помощью цикла, показано ниже. пример. Здесь два множества, A и B, содержат имена людей. После применения объединения к этим наборам результат сохраняется в переменной C. Затем цикл for используется для итерации значений набора C, подобного списку или кортежу, и печати значения в каждой строке.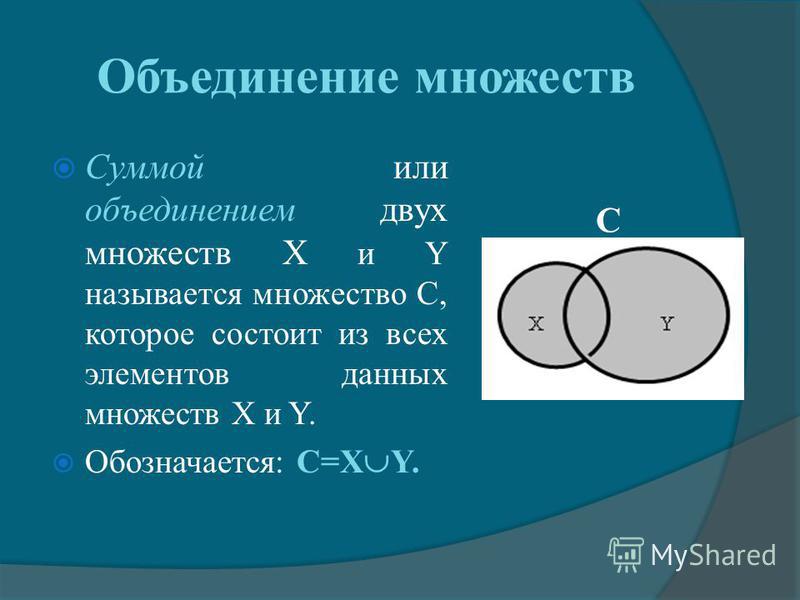
#!/usr/bin/env python3
# Определить два набора строк, A и B
A = { 'Джойя Хасан', 'Ахмед Али', 'Ээлла Назир', 'Рита Хоссейн' }
B = { 'Mehr Afroz', 'Ahmed Ali', 'Rita Hossain', 'Zinnia Rahman' }
# Применить операцию объединения к A и B, сохранить результат в C
C = A | B
# Набор для печати A
print("Set A:", A)
# Набор для печати B
print("\nSet B:", B)
# Сообщение для печати
print("\nЭлементы после применения СОЮЗ:\n")
# Итерировать каждый элемент набора C
для val в C:
# Вывести каждый элемент
print(val)
Вывод:
Здесь оба набора содержат четыре значения, и два значения являются общими в наборах A и B. Это «Ахмед Али» и «Рита Хоссейн» . Итак, множество C будет содержать шесть значений. Следующий вывод появится после запуска скрипта.
Пример 4: Применение операции объединения с использованием метода union()
union() 9Метод 0004 можно использовать как альтернативу оператору ‘|’ для выполнения операций объединения наборов.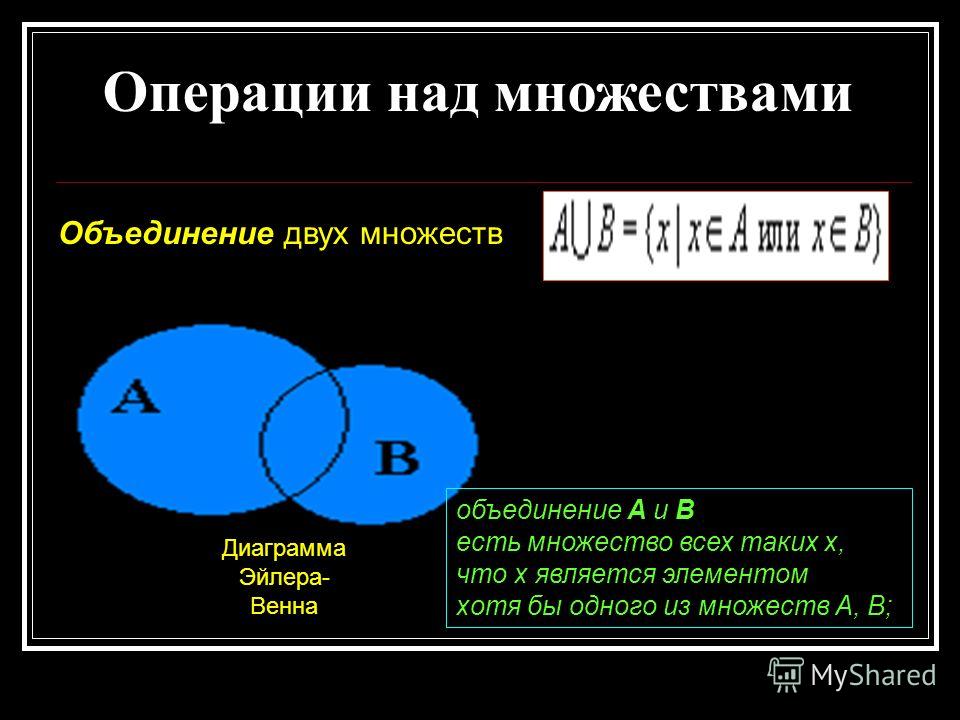 В следующем скрипте два набора строковых значений определяются как A и B . Значения ‘PHP’ и ‘Laravel’ являются общими в обоих наборах. Переменная C содержит набор после применения операции объединения с использованием метода union() . Здесь печатаются значения трех наборов, а цикл for используется для повторения значений набора C, как в предыдущем примере.
В следующем скрипте два набора строковых значений определяются как A и B . Значения ‘PHP’ и ‘Laravel’ являются общими в обоих наборах. Переменная C содержит набор после применения операции объединения с использованием метода union() . Здесь печатаются значения трех наборов, а цикл for используется для повторения значений набора C, как в предыдущем примере.
#!/usr/bin/env python3
# Определить два набора строк, A и B
A = { 'PHP', 'Java', 'Laravel', 'C#' }
B = { 'Angular' ,'PHP', 'Javascript', 'Laravel' }
# Применить метод union() к A и B, сохранить результат в C
C = A.union(B)
# Набор для печати A
print(" Набор A:", A)
# Печать набора B
print("\nSet B:", B)
# Сообщение печати
print("\nЭлементы после применения метода union():\n")
# Итерировать каждый элемент набора C
для val в C:
# Напечатать каждый элемент
print(val)
Вывод:
После применения операции объединения набор C будет содержать шесть значений.

 = B
A.symmetric_difference_update(B)
= B
A.symmetric_difference_update(B) name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}
name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")} __class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'
__class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")' issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!
issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество! # Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"} update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}
update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9} , также существует два специальных метода –
, также существует два специальных метода –  Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.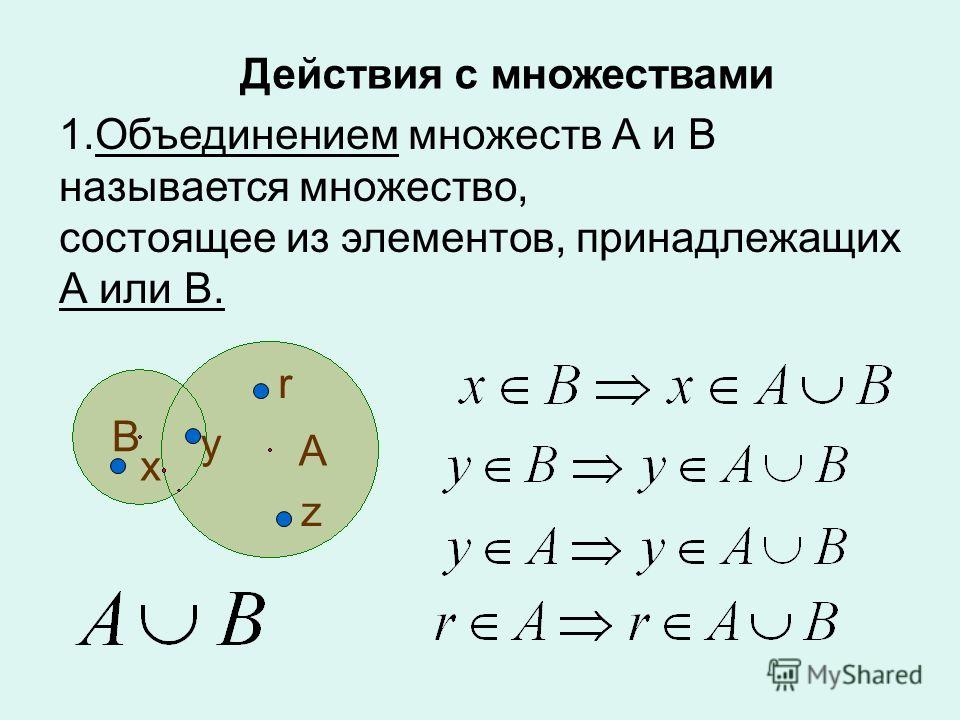 name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}
name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")} __class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'
__class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")' issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!
issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество! # Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"} update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}
update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9} , также существует два специальных метода –
, также существует два специальных метода –  Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.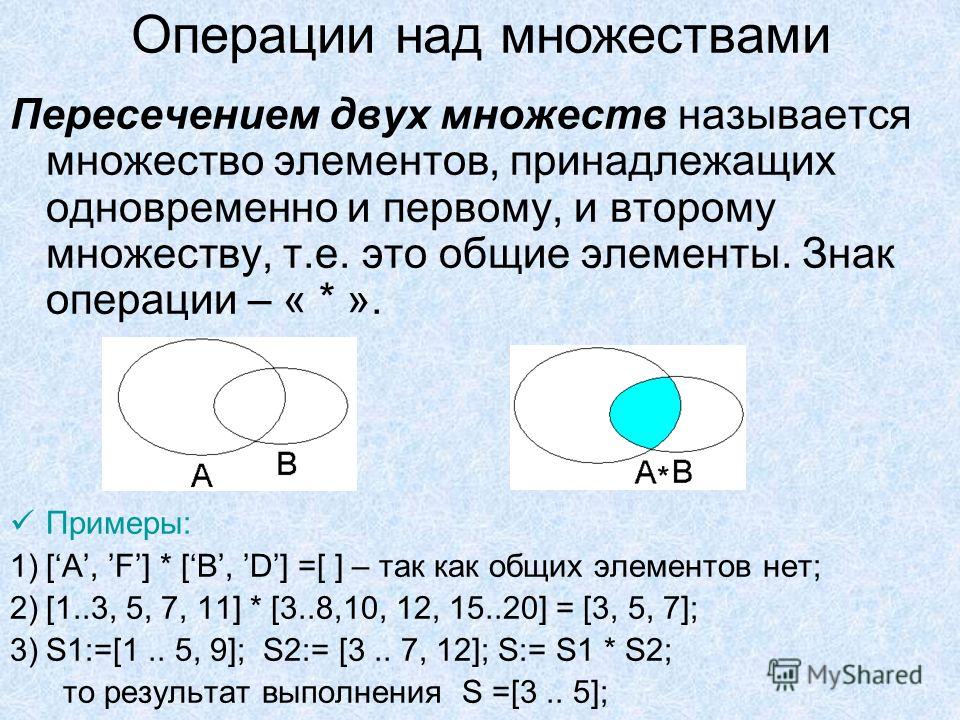 name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}
name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")} __class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'
__class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")' issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!
issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество! # Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"} update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}
update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9} , также существует два специальных метода –
, также существует два специальных метода –  Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения. name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}
name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}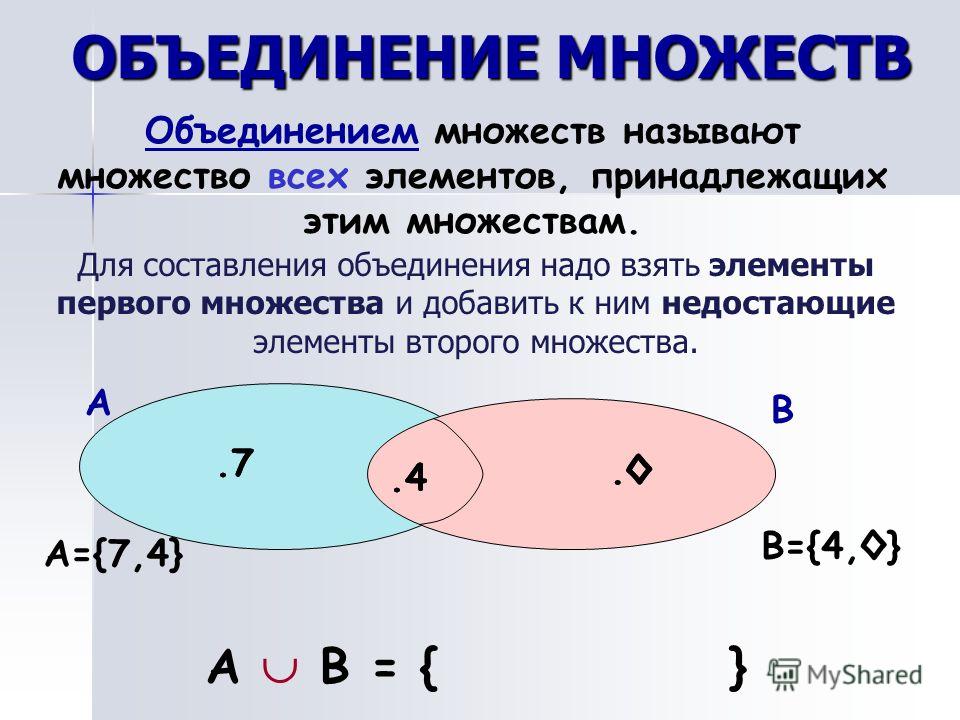 __class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'
__class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'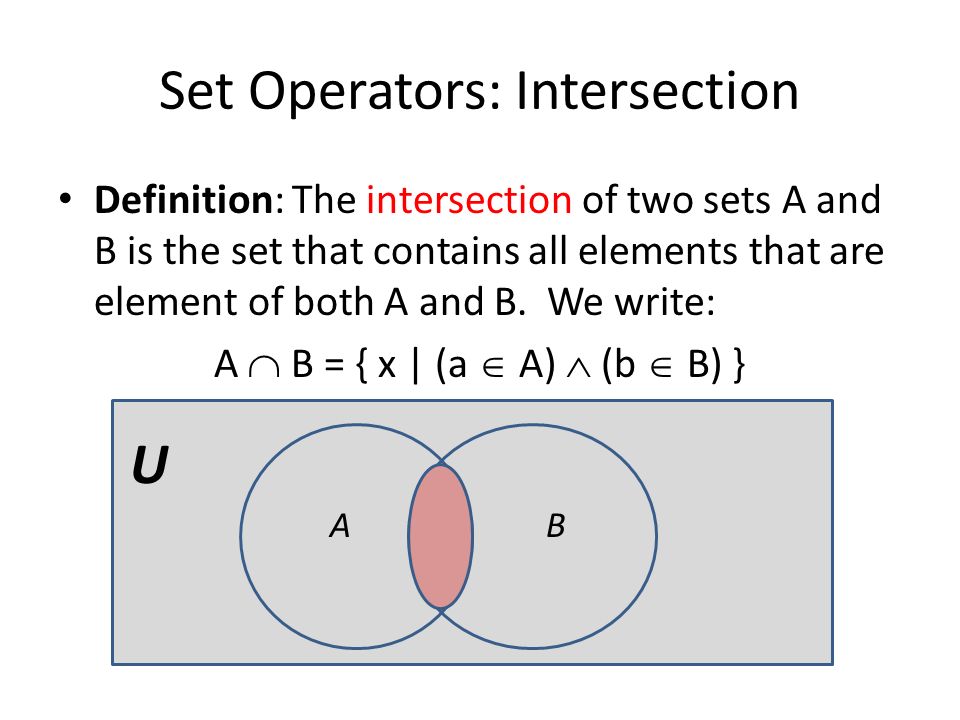 issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!
issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество! # Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"} update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}
update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9} , также существует два специальных метода –
, также существует два специальных метода –  Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.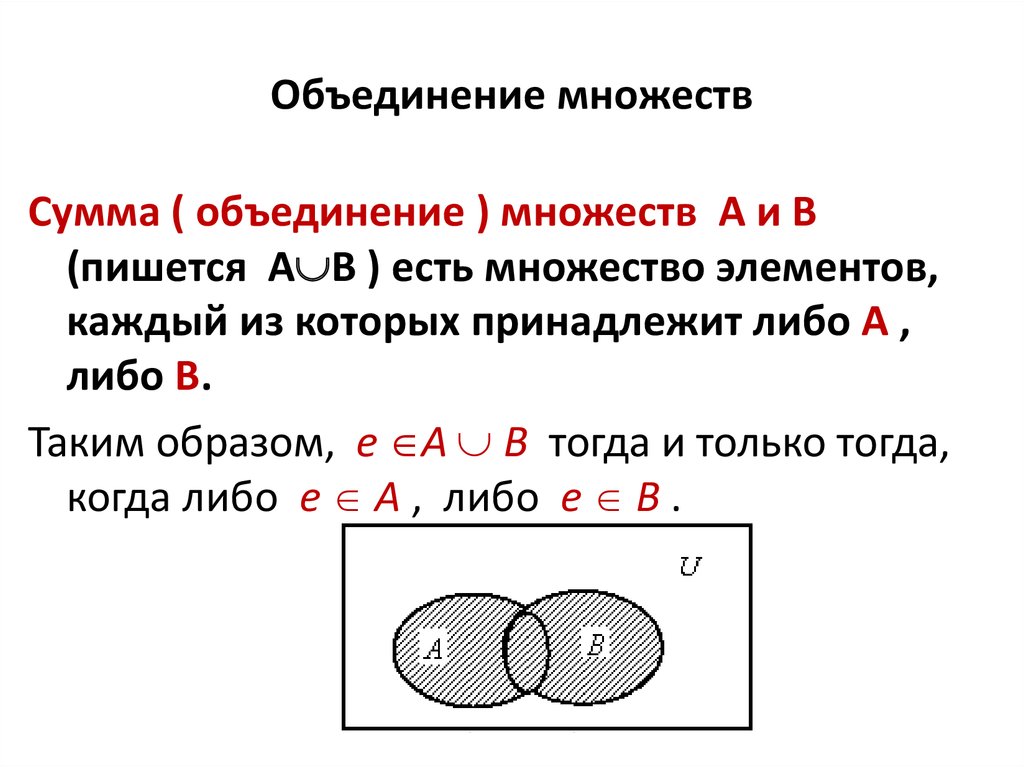 Сделать это можно и с помощью встроенной функции
Сделать это можно и с помощью встроенной функции 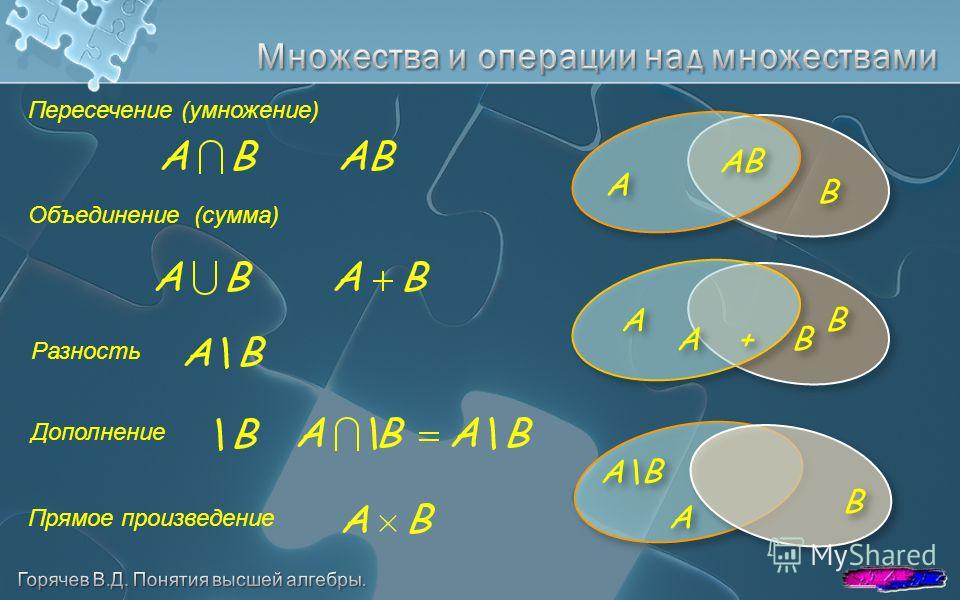
 Во всех случаях следует избегать одинаковых элементов.
Во всех случаях следует избегать одинаковых элементов.  А вот
А вот 


 B)
B) Если множество пусто, то возвращает ошибку KeyError
Если множество пусто, то возвращает ошибку KeyError Если множество пустое, возвращает
Если множество пустое, возвращает  add(3)
...
AttributeError: 'frozenset' object has no attribute 'add'
```
add(3)
...
AttributeError: 'frozenset' object has no attribute 'add'
``` Он возвращает копию set1, только если параметр не передан.
Он возвращает копию set1, только если параметр не передан.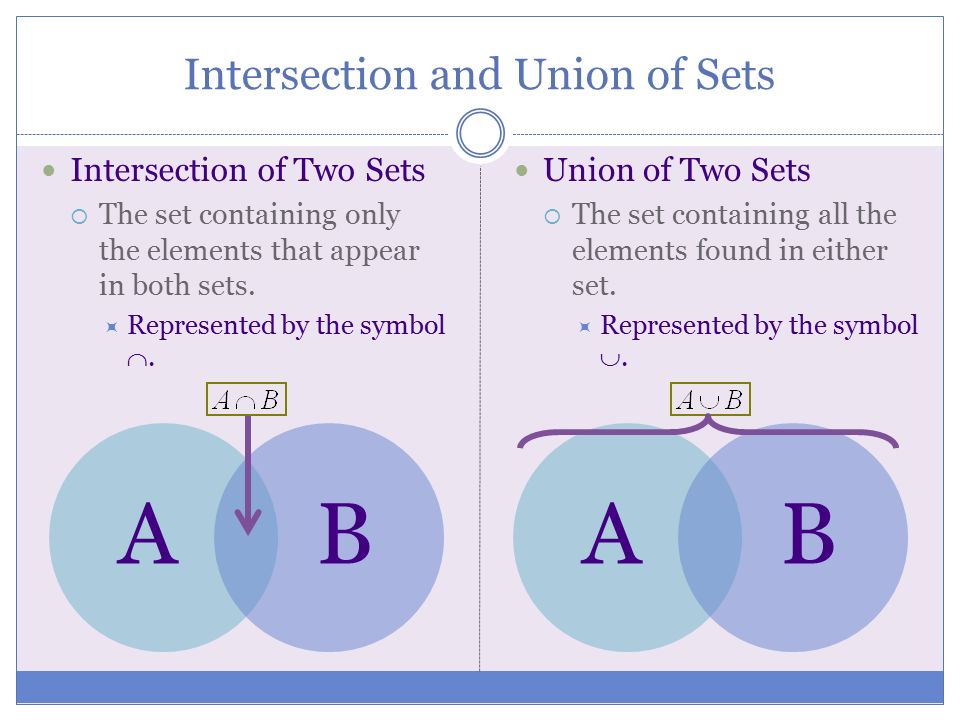 UNION (SET2))
UNION (SET2))  , set1 |set2 | set3)
, set1 |set2 | set3) 
 union(B).union(c))
union(B).union(c))  23, 'абв'}
# с = {[0, 1, 2]}
# TypeError: unhashable type: 'list'
23, 'абв'}
# с = {[0, 1, 2]}
# TypeError: unhashable type: 'list'