Рекурсивный алгоритм это: НОУ ИНТУИТ | Лекция | Рекурсия и рекурсивные алгоритмы

Рекурсивный алгоритм | это… Что такое Рекурсивный алгоритм?

Реку́рсия — метод определения класса объектов или методов предварительным заданием одного или нескольких (обычно простых) его базовых случаев или методов, а затем заданием на их основе правила построения определяемого класса, ссылающегося прямо или косвенно на эти базовые случаи.

Другими словами, рекурсия — способ общего определения объекта или действия через себя, с использованием ранее заданных частных определений. Рекурсия используется, когда можно выделить самоподобие задачи.

Определение в логике, использующее рекурсию, называется индуктивным (см., например, Натуральное число).

Содержание 1 Примеры 2 Рекурсия в программировании 2.1 Функции 2.2 Данные 3 Рекурсия в физике 4 Рекурсия в лингвистике 5 Цитаты 6 Юмор 7 См. также 8 Ссылки

Примеры

• Метод Гаусса — Жордана для решения Системы линейных алгебраических уравнений является рекурсивным.
• Факториал целого неотрицательного числа n обозначается n! и определяется как

  при n > 0 и n! = 1 при n = 0

• Числа Фибоначчи определяются с помощью рекуррентного соотношения:

  Первое и второе числа Фибоначчи равны 1

  Для n > 2, n − e число Фибоначчи равно сумме (n − 1)-го и (n − 2)-го чисел Фибоначчи

• Практически все геометрические фракталы задаются в форме бесконечной рекурсии. (например, треугольник Серпинского).
• Задача «Ханойские башни». Её содержательная постановка такова:

  В одном из буддийских монастырей монахи уже тысячу лет занимаются перекладыванием колец. Они располагают тремя пирамидами, на которых надеты кольца разных размеров. В начальном состоянии 64 кольца были надеты на первую пирамиду и упорядочены по размеру. Монахи должны переложить все кольца с первой пирамиды на вторую, выполняя единственное условие — кольцо нельзя положить на кольцо меньшего размера. При перекладывании можно использовать все три пирамиды. Монахи перекладывают одно кольцо за одну секунду. Как только они закончат свою работу, наступит конец света.

  Рекурсивный вариант решения задачи можно описать так:

Алгоритм по передвижению башни, алгоритм передвинет нужное количество дисков из пирамиды «источник» на пирамиду «задание» используя «запасную» пирамиду.

Если число дисков равно одному, тогда:

• Передвиньте диск из источника в задание

В противном случае:

• Рекурсивно передвиньте все диски кроме одного из источника в запас, используя задание как запас
• Передвиньте оставшийся диск из источника в задание
• Передвиньте все диски из запаса в задание используя источник как запас

Рекурсия в программировании

Функции

В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная рекурсия), например, функция

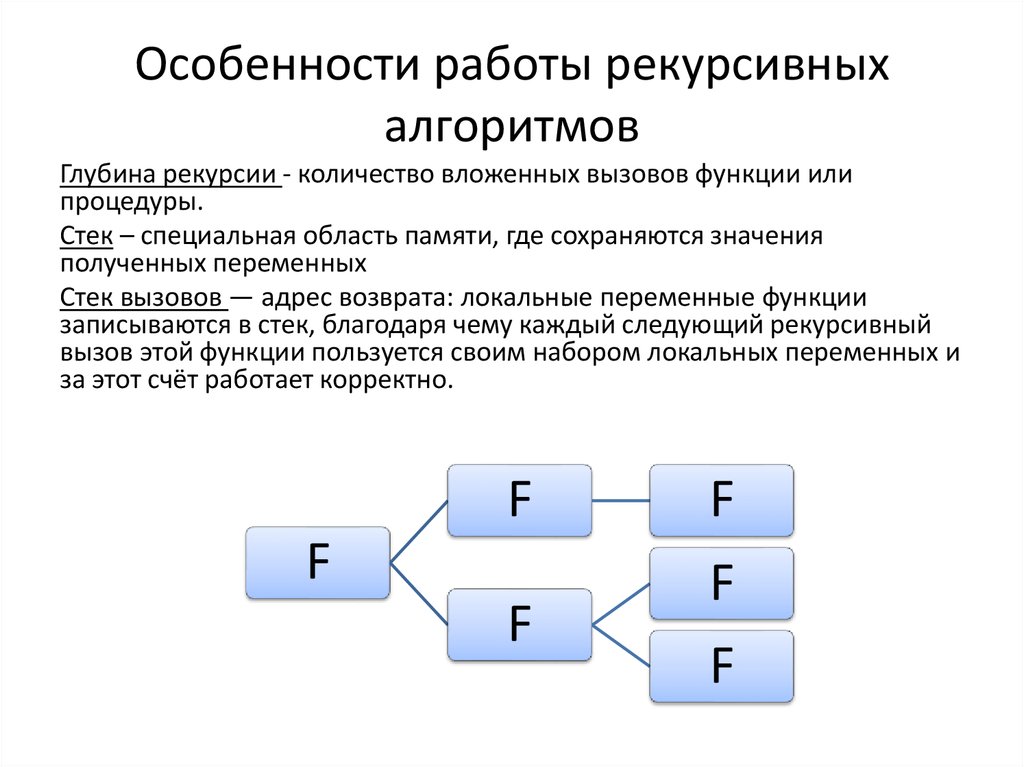
A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.

Мощь рекурсивного определения объекта в том, что такое конечное определение способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.

Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за этот счёт работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что рекурсивные вызовы не бесплатны — на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.

Впрочем, имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного и/или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивают выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. К сожалению, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Lisp), описание которого содержит все необходимые сведения.

• См. также Примеры реализации функции факториал

Данные

Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):

 class element_of_list
 {
   element_of_list *next; /* ссылка на следующий элемент того же типа */
   int data; /* некие данные */
 };

Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.

Рекурсия в физике

Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из затухающих отражений зеркал.

Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.

Рекурсия в лингвистике

Способность языка порождать вложенные предложения и конструкции. Базовое предложение кошка съела мышь может быть за счет рекурсии расширено как Ваня догадался, что кошка съела мышь, далее как Катя знает, что Ваня догадался, что кошка съела мышь и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку (хотя в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Д. Эверетт). О рекурсии в лингвистике, ее разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е.А.Лодатко «Рекурсивные лингвистические структуры» (см.: Рекурсивные лингвистические структуры)

Цитаты

Итерация от человека. Рекурсия — от Бога. — Л. Питер Дойч^[1]

Юмор

Большая часть всех шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода. Известные высказывания: ‘Чтобы понять рекурсию, нужно сначала понять рекурсию’, ‘Чтобы что-то сделать, надо что-то сделать’, ‘Для приготовления салата необходимы: огурцы, помидоры, салат’. Весьма популярна шутка о рекурсии, напоминающая словарную статью:

рекурсия 

см. рекурсия

Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:

• Рассказ про Йона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки».
• Рассказ о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).

Русская народная сказка-песня «У попа была собака…» являет пример рекурсии:

У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:

«У попа была собака, он её любил,

Она съела кусок мяса, он её убил,

В землю закопал,

Надпись написал:

«У попа была собака, он её любил,

Она съела кусок мяса, он её убил,

В землю закопал,

Надпись написал:

…

См.

также

• Индукция
• Математическая индукция
• Корекурсия
• Рекуррентная последовательность (возвратная последовательность)

Ссылки

1. ↑ * Дональд Кнут Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4

• Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1

Рекурсивный алгоритм | это… Что такое Рекурсивный алгоритм?

Реку́рсия — метод определения класса объектов или методов предварительным заданием одного или нескольких (обычно простых) его базовых случаев или методов, а затем заданием на их основе правила построения определяемого класса, ссылающегося прямо или косвенно на эти базовые случаи.

Другими словами, рекурсия — способ общего определения объекта или действия через себя, с использованием ранее заданных частных определений. Рекурсия используется, когда можно выделить самоподобие задачи.

Определение в логике, использующее рекурсию, называется индуктивным (см., например, Натуральное число).

Содержание 1 Примеры 2 Рекурсия в программировании 2.1 Функции 2.2 Данные 3 Рекурсия в физике 4 Рекурсия в лингвистике 5 Цитаты 6 Юмор 7 См. также 8 Ссылки

Примеры

• Метод Гаусса — Жордана для решения Системы линейных алгебраических уравнений является рекурсивным.
• Факториал целого неотрицательного числа n обозначается n! и определяется как

  при n > 0 и n! = 1 при n = 0

• Числа Фибоначчи определяются с помощью рекуррентного соотношения:

  Первое и второе числа Фибоначчи равны 1

  Для n > 2, n − e число Фибоначчи равно сумме (n − 1)-го и (n − 2)-го чисел Фибоначчи

• Практически все геометрические фракталы задаются в форме бесконечной рекурсии. (например, треугольник Серпинского).
• Задача «Ханойские башни». Её содержательная постановка такова:

  В одном из буддийских монастырей монахи уже тысячу лет занимаются перекладыванием колец. Они располагают тремя пирамидами, на которых надеты кольца разных размеров. В начальном состоянии 64 кольца были надеты на первую пирамиду и упорядочены по размеру. Монахи должны переложить все кольца с первой пирамиды на вторую, выполняя единственное условие — кольцо нельзя положить на кольцо меньшего размера. При перекладывании можно использовать все три пирамиды. Монахи перекладывают одно кольцо за одну секунду. Как только они закончат свою работу, наступит конец света.

  Рекурсивный вариант решения задачи можно описать так:

Алгоритм по передвижению башни, алгоритм передвинет нужное количество дисков из пирамиды «источник» на пирамиду «задание» используя «запасную» пирамиду.

Если число дисков равно одному, тогда:

• Передвиньте диск из источника в задание

В противном случае:

• Рекурсивно передвиньте все диски кроме одного из источника в запас, используя задание как запас
• Передвиньте оставшийся диск из источника в задание
• Передвиньте все диски из запаса в задание используя источник как запас

Рекурсия в программировании

Функции

В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная рекурсия), например, функция A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.

Мощь рекурсивного определения объекта в том, что такое конечное определение способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.

Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за этот счёт работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что рекурсивные вызовы не бесплатны — на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.

Впрочем, имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного и/или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивают выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. К сожалению, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Lisp), описание которого содержит все необходимые сведения.

• См. также Примеры реализации функции факториал

Данные

Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):

 class element_of_list
 {
   element_of_list *next; /* ссылка на следующий элемент того же типа */
   int data; /* некие данные */
 };

Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.

Рекурсия в физике

Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из затухающих отражений зеркал.

Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.

Рекурсия в лингвистике

Способность языка порождать вложенные предложения и конструкции. Базовое предложение кошка съела мышь может быть за счет рекурсии расширено как Ваня догадался, что кошка съела мышь, далее как Катя знает, что Ваня догадался, что кошка съела мышь и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку (хотя в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Д. Эверетт). О рекурсии в лингвистике, ее разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е.А.Лодатко «Рекурсивные лингвистические структуры» (см.: Рекурсивные лингвистические структуры)

Цитаты

Итерация от человека. Рекурсия — от Бога. — Л. Питер Дойч^[1]

Юмор

Большая часть всех шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода. Известные высказывания: ‘Чтобы понять рекурсию, нужно сначала понять рекурсию’, ‘Чтобы что-то сделать, надо что-то сделать’, ‘Для приготовления салата необходимы: огурцы, помидоры, салат’. Весьма популярна шутка о рекурсии, напоминающая словарную статью:

рекурсия 

см. рекурсия

Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:

• Рассказ про Йона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки».
• Рассказ о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).

Русская народная сказка-песня «У попа была собака…» являет пример рекурсии:

У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:

«У попа была собака, он её любил,

Она съела кусок мяса, он её убил,

В землю закопал,

Надпись написал:

«У попа была собака, он её любил,

Она съела кусок мяса, он её убил,

В землю закопал,

Надпись написал:

…

См.

также

• Индукция
• Математическая индукция
• Корекурсия
• Рекуррентная последовательность (возвратная последовательность)

Ссылки

1. ↑ * Дональд Кнут Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4

• Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1

Объяснение

алгоритмов #1: Рекурсия | by Claudia Ng

Поймите, когда и как использовать рекурсивные решения с примерами на Python

Это первая статья из серии, посвященной объяснению алгоритмов с примерами на Python. Это предназначено для начинающих специалистов по данным и инженеров-программистов или тех, кто хочет освежить в памяти алгоритмы при подготовке к собеседованиям по программированию.

Изображение Gerd Altmann с сайта Pixabay

Рекурсия — это фундаментальная концепция в программировании при изучении структур данных и алгоритмов. В этой статье я объясню, что такое рекурсия, когда ее использовать, и рассмотрю несколько примеров, написанных на Python 3.9.0005

Что такое рекурсия?

Рекурсия — это когда функция или метод вызывает саму себя и необходима для парадигмы «разделяй и властвуй», где идея состоит в том, чтобы разделить большие проблемы на более мелкие подзадачи, а подзадача — это некоторая постоянная часть исходной проблемы. Принцип работы рекурсии заключается в решении небольших подзадач по отдельности, а затем в объединении результатов для получения окончательного решения.

Когда используется рекурсия?

Рекурсия часто используется для задач, которые носят рекурсивный характер. Сюда входят графы, деревья и структуры данных, которые имеют отношение родитель-потомок. Некоторыми каноническими примерами задач рекурсии являются вычисление n-го числа Фибоначчи, вычисление факториала числа и преобразование десятичных чисел в двоичные числа.

Зачем мне использовать рекурсию?

При правильном использовании рекурсивное решение обычно приводит к более чистому коду, который легче читать. Это более интуитивно понятно при решении рекурсивных по своей природе решений, как мы увидим позже на примерах. Однако имейте в виду, что рекурсивные решения могут быть менее эффективными с точки зрения использования памяти, и если память вашего компьютера исчерпана или стек вашей функции слишком велик до достижения базового случая, это вызовет ошибку переполнения стека.

Как создать рекурсивный алгоритм?

Чтобы написать рекурсивный алгоритм, сначала нужно разбить задачу на две части: первая — базовый случай, а вторая — рекурсивный шаг:

1. Базовый случай: Базовый случай относится к условию, что необходимо выполнить, чтобы прекратить вызов рекурсивной функции. Это конечное состояние или последний случай, который необходимо оценить перед завершением рекурсивной функции и возвратом результата. Без базового случая ваша рекурсивная функция зациклилась бы на бесконечном цикле и никогда не завершилась бы!
2. Рекурсивный шаг: Это часть кода, выполняющая рекурсивные вызовы одной и той же функции для вычисления результатов с использованием входных данных, которые обновляются при каждом рекурсивном вызове. Каждая итерация должна приближать вас к базовому варианту.

Примеры #1: Определение n-го ряда Фибоначчи с помощью рекурсии

В ряду Фибоначчи первый и второй члены ряда равны 0 и 1 соответственно. Чтобы вычислить число в позиции n, вы можете взять сумму двух предыдущих членов, то есть число в позиции (n-1) + число в позиции (n-2). Ряд Фибоначчи F может быть представлен математически следующим образом:

• F(1) = 0
• F(2) = 1
• F(n) = F(n-1) + F(n-2)

Мы определим функцию fibonacci() который принимает число n в качестве аргумента и возвращает число в позиции n в ряду Фибоначчи. Эту проблему можно решить несколькими способами, но в рекурсивном решении мы можем разбить задачу на следующие две части:

1. Базовый случай: , если n равно 1, вернуть 0, начиная с первого члена ряда Фибоначчи. равно 0. Если n равно 2, вернуть 1, так как второй член ряда равен 1.
2. Шаг рекурсии: для всех остальных значений n мы можем вычислить число в позиции n, сложив два предыдущих члена: Фибоначчи(n-1) + Фибоначчи(n-2).

Ниже приведена реализация Python рекурсивного решения для вычисления n-го числа в ряду Фибоначчи:

 def fibonacci(n): 
, если n == 1: 
 возвращает 0 
, если n == 2: 
 возвращает 1 
 return fibonacci(n-1) + fibonacci(n-2) 

Пример #2: Вычисление n-го факториала

Факториал n-го числа — это произведение всех целых чисел от 1 до n. Например, факториал числа 5 равен 5! = 1 * 2 * 3 * 4 * 5 = 120 . Обратите внимание, что факториал 0 равен 1, а факториал отрицательных чисел не определен.

Мы определим функцию factorial() , которая принимает число n в качестве аргумента и возвращает факториал n . Чтобы решить эту проблему с помощью рекурсии, мы должны разбить ее на следующие два случая:0005

1. Базовый случай: , если n = 0 или 1, вернуть 1. Если n < 0, вернуть ошибку, поскольку факториал для отрицательных чисел не определен.
2. Рекурсивный шаг: умножить n на результат предыдущего члена, т.е. n * factorial(n-1) .

Ниже приведена реализация Python рекурсивного решения для вычисления n-го факториала:

 def factorial(n): 
 if (n == 0 или n == 1): 
 вернуть 1 
, если n < 0: 
 поднять Exception("n должно быть положительным. Факториал отрицательного числа не определен.") 
 return n * factorial(n - 1) 

Пример №3: Отображение десятичного целого числа в виде двоичного Часто используется система счисления с основанием 2.

Один из способов преобразования десятичного числа в двоичное — это разделить число на 2 и записать остаток на каждом шаге, а затем записать остаток в обратном порядке (снизу вверх) и это двоичный эквивалент вашего целого числа. Например, десятичное число 36 в двоичном виде равно:

36 / 2 = 18 R 0 → 18 / 2 = 9 R 0 → 9/ 2 = 4 R 1 → 4/ 2 = 2 R 0 → 2 / 2 = 1 R 0 → 1/ 2 = 0 R 1

Собирая остатки в обратном порядке, мы получаем 100100 как двоичное число для десятичного числа 36.

Мы определим функцию convert_to_binary() , которая принимает десятичное число n и возвращает двоичное число в виде списка целых чисел. Чтобы решить эту задачу рекурсивно, мы можем разбить ее на две части:

1. Базовый случай: Если n равно 0, вернуть список с целым числом 0. Если n равно 1, вернуть список с целым числом 1.
2. Рекурсивный шаг: Вызов функции convert_to_binary () на частное (число n разделить на 2) и отслеживать остаток от этой операции.

Ниже приведена реализация Python рекурсивной функции для преобразования десятичных чисел в двоичные числа:

 def convert_to_binary(n): 
, если n == 0: 
, возврат [0] 
 elif n == 1: 
, возврат [1] 
 остатков = convert_to_binary(n // 2) 
 остатков.расширить ([n % 2]) 
 возврат остатков 

Заключение

Рекурсия является фундаментальной концепцией программирования и популярна на собеседованиях по программированию. Некоторыми распространенными вариантами использования рекурсии являются структуры данных с отношениями родитель-потомок. Ключ к написанию рекурсивного решения состоит в том, чтобы сначала определить базовый случай, а затем подумать о рекурсивном шаге. Рекурсивный часто приводит к более чистому коду, но может быть не таким эффективным с точки зрения памяти.

Подробнее из этой серии «Объяснение алгоритмов»: №1: рекурсия (текущая статья), №2: сортировка, №3: поиск, №4: жадные алгоритмы, №5: динамическое программирование, №6: обход дерева.

6.2. Свойства рекурсивных функций — CISC 187 для чтения курса Обзор

Все рекурсивные алгоритмы должны реализовывать 3 свойства:

1. Рекурсивный алгоритм должен иметь базовый случай .

2. Рекурсивный алгоритм должен изменить свое состояние и двигаться к базе случай.

3. Рекурсивный алгоритм должен вызывать сам себя.

Базовым вариантом является условие что позволяет алгоритму остановить рекурсию и начать процесс возврата к исходной вызывающей функции. Этот процесс иногда называют раскручиванием стека . Базовым случаем обычно является проблема, которая достаточно мала, чтобы решить ее напрямую. В накапливается алгоритм базовым случаем является пустой вектор.

Второе свойство требует изменения чего-либо в рекурсивном функция, которая при последующих вызовах перемещает состояние программы ближе к базовому варианту. Изменение состояния означает, что некоторые данные, используемые алгоритмом, изменяются. Обычно данные, которые представляет, что наша проблема каким-то образом становится меньше. В накапливать алгоритма наша первичная структура данных является вектором, поэтому мы должны сосредоточить наши усилия по изменению состояния вектора. Поскольку базовым случаем является пустой вектор, естественным переходом к базовому варианту является сокращение вектора.

Наконец, рекурсивный алгоритм должен вызывать сам себя. Это очень определение рекурсии. Рекурсия — сбивающее с толку понятие для многих начинающих программистов. Как начинающий программист, вы узнали, что функции хороши тем, что вы можете взять большую проблему и разбить ее в более мелкие проблемы. Небольшие проблемы можно решить, написав Функция для решения каждой проблемы. Когда мы говорим о рекурсии, может показаться что мы говорим о себе кругами. У нас есть проблема, которую нужно решить с функцией, но эта функция решает проблему, вызывая саму себя! Но логика вовсе не круговая; логика рекурсии — это элегантное выражение решения проблемы путем разбиения ее на меньшие и более легкие проблемы.

В оставшейся части этой главы мы рассмотрим другие примеры рекурсия. В каждом случае мы сосредоточимся на разработке решения для задачу, используя три свойства рекурсивных функций.

Самопроверка

sc-1-1: Сколько рекурсивных вызовов выполняется при вычислении суммы вектора {2,4,6,8,10}?

• 6
• Хороший выбор: наш пример с накоплением вызывается один раз для каждого элемента плюс пустой вектор.
• 5
• Последний вызов для накопления всегда является пустым вектором
• 4
• первый рекурсивный вызов передает вектор {4,6,8,10}, второй {6,8,10} и так далее, пока вектор не станет пустым.
• 3
• Этого звонка не хватило бы, чтобы охватить все номера на векторе

2.2″ data-multipleanswers=»false»>

sc-1-2: Предположим, вы собираетесь написать рекурсивную функцию для вычисления факториала числа. fact(n) возвращает n * n-1 * n-2 * … Где факториал нуля определен равным 1. Какой базовый случай был бы наиболее подходящим?

• n == 0
• Хотя это сработает, есть лучшие и немного более эффективные варианты. поскольку факт (1) и факт (0) совпадают.
• n == 1
• Хороший выбор, но что произойдет, если вы вызовете fact(0)?
• n >= 0
• Этот базовый случай будет верен для всех чисел больше нуля, поэтому факт любого положительного числа будет равен 1.
• n <= 1
• Хорошо, это самый эффективный способ, который даже предотвращает сбой вашей программы, если вы попытаетесь вычислить факториал отрицательного числа.

  No related posts.