Что выбрать — блочный или рекурсивный арбалет?
Вы узнаете об основных отличиях блочных и рекурсивных арбалетов, о принципах их работы, о плюсах и минусах, а также о том, как выбрать арбалет для охоты или развлечения.
Все современные арбалеты делятся на два класса: рекурсивные и блочные.
Как их отличить?
По сути, арбалеты различаются устройством плеч. На любом блочном арбалете установлены эксцентрики, или блоки.Блоки соединяются тетивой. Также есть два троса, каждый из которых соединяет блок с противоположным плечом. Тросы располагаются в специальном пазу, располгающемся в корпусе арбалета.
У рекурсивного арбалета есть плечи и тетива, которая их соединяет. Плечи имеют обратный сгиб, отсюда и его название — рекурсивный.
Чем отличается принцип работы блочного арбалета от рекурсивного?
И в том, и в другом случае плечи арбалета сгибаются и накапливают энергию. В момент выстрела плечи резко распрямляются, передавая накопленную энергию стреле.
Рекурсивный арбалет
По мере того, как сгибаются плечи, усилие натяжения непрерывно растет и становится максимальным в момент фиксации тетивы спусковым механизмом. То есть, спусковой механизм рекурсивного арбалета испытывает нагрузку в 43 кг. В момент выстрела спусковой механизм высвобождает тетиву. Плечи распрямляются и передают через тетиву всю накопленную энергию стреле. Таким образом, понятно, что у рекурсивных арбалетов на скорость вылета стрелы влияет усилие натяжения плечей.
Блочный арбалет
Когда вы взводите тетиву, она проворачивает блоки. Блоки тянут на себя тросы, которые, в свою очередь, сгибают плечи. Усилие натяжения растет, но в самом конце хода тетивы усилие вдруг сбрасывается более, чем на 60%. Это провернулись блоки и так распределили нагрузку, что вместо 43 кг замок держит максимум 15. Этот эффект называется «сброс». Что происходит в момент выстрела? Спусковой механизм высвобождает тетиву, плечи распрямляются, блоки проворачиваются назад и дают стреле дополнительный импульс, который значительно ее ускоряет. Таким образом, у блочных арбалетов на скорость вылета стрелы влияет не только напряжение и форма плеч, но и размер и форма блоков.
Этот эффект называется «сброс». Что происходит в момент выстрела? Спусковой механизм высвобождает тетиву, плечи распрямляются, блоки проворачиваются назад и дают стреле дополнительный импульс, который значительно ее ускоряет. Таким образом, у блочных арбалетов на скорость вылета стрелы влияет не только напряжение и форма плеч, но и размер и форма блоков.
Преимущества рекурсивного арбалета:
1. Вес рекурсивных плечей небольшой, поэтому центр тяжести арбалета смещен к стрелку, а нек плечам арбалета. Благодаря этому удержание арбалета становится очень комфортным.
2. Конструкция состоит всего из нескольких деталей. Очевидно, чем меньше деталей, тем меньше поломок. Поэтому рекурсивный арбалет очень надежный.
3. Не требует специальных настроек плечей (в отличие от блочного, где надо следить за синхронизацией блоков).
4. Рекурсивный арбалет проще в эксплуатации. Заменить тетиву можно прямо в полевых условиях (у блочного придется обращаться в специальную мастерскую).
Недостатки рекурсивного арбалета:
1. Скорость вылета стрелы ниже, чем у блочных.
2. Широкие плечи, что не слишком удобно при переноске, транспортировке.
3. При взведении тетивы руками очень просто совершить ошибку и установить ее с перекосом вправо или влево (в зависимости от рабочей руки). А это значит, что стрела полетит правее или левее. Поэтому взводить рекурсивные арбалеты желательно только со специальным натяжителем.
1. Высокая скорость вылета стрелы при небольшом натяжении плечей. Блочный арбалет мощнее.
2. Плечи блочного арбалета компактнее. Удобно при перевозке, переноске, хранении, нахождении в замкнутом пространстве, например — в засидке. С такой конструкцией проще передвигаться по зарослям.
3. Эффект «сброса» блочного арбалета, когда при взведении тетивы падает сила напряжения, дает сразу несколько преимуществ. Арбалет проще взвести. Нагрузка на замок меньше, чему рекурсивного, поэтому поломок меньше.
Арбалет проще взвести. Нагрузка на замок меньше, чему рекурсивного, поэтому поломок меньше.
Недостатки блочного арбалета:
1. Конструкция сложнее, потому блочные менее пригодны для полевых условий.
2. Требуют специальной настройки положения блоков после замены тросов, не говоря уж о необходимости замены самих тросов рано или поздно.
3. Центр тяжести немного дальше, это делает прицеливание чуть менее комфортным. Это не касается блочных арбалетов с обратными плечами.
Какой же выбрать?
Лучше всего отталкиваться от применения арбалета. Если вам нужен арбалет для стрельбы по мишеням — на даче, в тире, на природе, то лучше брать небольшой рекурсивный арбалет. Он легкий, простой, недорогой, с ним не надо заморачиваться ни с настройкой, ни с ремонтом. С ним можно комфортно прогуляться по лесу. Он подойдет для охоты на мелкого зверя (лисица, заяц) и птицу.
Если вам нужен арбалет для серьезной охоты, то судить нужно по критерию скорости вылета стрелы. Оба типа арбалетов могут дать достаточную скорость. Тут выбор встает такой: либо взять максимально мощный и компактный блочный арбалет, либо максимально надежный рекурсивный.
Оба типа арбалетов могут дать достаточную скорость. Тут выбор встает такой: либо взять максимально мощный и компактный блочный арбалет, либо максимально надежный рекурсивный.
Если вы предпочитаете рядовые выезды на охоту раз в несколько дней, лучше взять блочный арбалет. Его удобно упаковать в чехол и бросить в машину. А если вы собрались в долговременный поход в дикую природу, то берите собой легковесный рекурсивный арбалет. Кстати, большинство охотников выбирают блочные арбалеты.
По материалам «Интерлопер»
Новости поискаНа главную
Рекурсия | это… Что такое Рекурсия?
У этого термина существуют и другие значения, см. Рекурсия (значения).
Визуальная форма рекурсии (эффект Дросте)
Рекурсивное изображение экрана
Визуальная форма рекурсии страницы Википедии
Реку́рсия — процесс повторения элементов самоподобным образом.
Термин «рекурсия» используется в различных специальных областях знаний — от лингвистики до логики, но наиболее широкое применение находит в математике и информатике. В математике и информатике рекурсия имеет отношение к методу определения функций: рекурсивно заданная функция в своём определении содержит себя, в частности, рекурсивной является функция, заданная рекуррентной формулой. Таким образом, можно одним выражением дать бесконечный набор способов вычисления функции, определить множество объектов через самого себя с использованием ранее заданных частных определений.
С рекурсией тесно связана математическая индукция: она является естественным способом доказательства свойств функций на натуральных числах, рекурсивно заданных через свои меньшие значения.
Содержание
|
В математике
Треугольник Серпинского
- Метод Гаусса — Жордана для решения систем линейных алгебраических уравнений является рекурсивным.
- Факториал целого неотрицательного числа n (обозначается ) определяется как
- при и при
- Числа Фибоначчи определяются с помощью рекуррентного соотношения:
- Первое и второе числа Фибоначчи равны 1
- Для , -e число Фибоначчи равно сумме -го и -го чисел Фибоначчи
- Практически все геометрические фракталы задаются в форме бесконечной рекурсии (например, треугольник Серпинского).
В программировании
Функции
Блок схема рекурсивного алгоритма решения Ханойской башни.
В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (
 Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.
Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.Преимущество рекурсивного определения объекта заключается в том, что такое конечное определение теоретически способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.
Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за счёт этого работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого, обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.
Имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивается выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. Однако, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Scheme (диалект языка Lisp), описание которого содержит все необходимые сведения.
Любую рекурсивную функцию можно заменить циклом и стеком.
См. также: Примеры реализации функции факториал в Викиучебнике
Данные
Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):
Подобные структуры используются при описании списков и графов. Пример описания списка (C++):
struct element_of_list
{
element_of_list *next; /* ссылка на следующий элемент того же типа */
int data; /* некие данные */
};
Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.
В физике
Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из уменьшающихся отражений зеркал.
Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.
В лингвистике
См. также: Рекурсия (лингвистика)
Способность языка порождать вложенные предложения и конструкции. Базовое предложение «кошка съела мышь» может быть за счёт рекурсии расширено как Ваня догадался, что кошка съела мышь, далее как Катя знает, что Ваня догадался, что кошка съела мышь и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку. Однако, в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Дэниэл Эверетт (англ.)[1].
Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку. Однако, в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Дэниэл Эверетт (англ.)[1].
В культуре
См. также: Mise en abyme и Эффект Дросте
Большая часть шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода, например, известно высказывание: «чтобы понять рекурсию, нужно сначала понять рекурсию».
Весьма популярна шутка о рекурсии, напоминающая словарную статью:
- рекурсия
- см. рекурсия
Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:
- рассказ про Йона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки»:
Нашёл следующие краткие сведения:
«СЕПУЛЬКИ — важный элемент цивилизации ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКАРИИ».
Я последовал этому совету и прочёл:
«СЕПУЛЬКАРИИ — устройства для сепуления (см.)».
Я поискал «Сепуление»; там значилось:
«СЕПУЛЕНИЕ — занятие ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКИ».Лем С. «Звёздные дневники Ийона Тихого. Путешествие четырнадцатое.»
- Рассказ из «Кибериады» о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).
- Рекурсивные акронимы: GNU (GNU Not Unix), PHP (PHP: Hypertext Preprocessor) и т. д.
См. также
- Математическая индукция
- Корекурсия
- Рекуррентная формула
- Возвратная последовательность
- Докучная сказка
- Рефлексивное отношение
- Порочный круг
Примечания
- ↑ О рекурсии в лингвистике, её разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е.
 А. Лодатко «Рекурсивные лингвистические структуры»
А. Лодатко «Рекурсивные лингвистические структуры»
в кембриджском словаре английского языка
Примеры рекурсии
рекурсии
Хитрость в том, что эти три вещи подпитывают друг друга, иногда рекурсивно способами.
Из проводного
Несмотря на наше незнание причин, антидепрессанты остаются незаменимым бальзамом для миллионов людей, позволяющим им вырваться из замкнутого круга горя.
Из проводного
Рекурсивное мышление имеет решающее значение для всех человеческих групп; рекурсии в языке нет.
От NPR
Он говорит, что первый может избежать проблемы, не запуская рекурсивный , но что насчет второго?
Из Арс Техника
Их подход к рекурсивному обобщению из краудсорсинга имеет интригующий потенциал.
Из Phys.Org
Их трудно остановить, потому что они часто направляются через рекурсивных провайдеров.
Из Арс Техника
Но «самое забавное в этом определении то, что рекурсивно », — говорит он.
Из Phys.Org
Вычислительная эффективность была улучшена за счет отказа от традиционного рекурсивного поиска .
Из Кембриджского корпуса английского языка
Надо сначала переделать рекурсивные определения типов как фиксированные точки так называемых базовых функторов.
Из Кембриджского корпуса английского языка
Здесь необходимо упомянуть еще один аспект ленивых рекурсивных типов данных.
Из Кембриджского корпуса английского языка
Теперь мы можем определить рекурсивный алгоритм на основе этой двухфазной спецификации и доказать его корректность.
Из Кембриджского корпуса английского языка
Это позволяет избежать написания явных пунктов «обработки исключений» для каждого рекурсивного вызова gfpt.
Из Кембриджского корпуса английского языка
Все рекурсивные вызовы сохраняют сжимаемость и замыкание типов аргументов.
Из Кембриджского корпуса английского языка
В оставшейся части этого раздела рассматриваются еще два варианта алгоритма gfp, которые более точно соответствуют хорошо известным алгоритмам подтипирования для рекурсивные типов.
Из Кембриджского корпуса английского языка
Любые ограничения, исключающие этот пример, должны исключать примитивные рекурсивные типы экземпляров; трудно понять, что останется при таких ограничениях.
Из Кембриджского корпуса английского языка
Эти примеры взяты из корпусов и источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Переводы recursive
на китайский (традиционный)
回歸的, 遞迴的…
Подробнее
на китайском (упрощенном)
回归的, 递归的…
Узнать больше
Нужен переводчик?
Получите быстрый бесплатный перевод!
Как произносится рекурсивное ?
Обзор
повторяющийся
повторяющийся
повторяющийся номер
рекурсия
рекурсивный
рекурсивно БЕТА
изогнутый БЕТА
отвод
бунтующий
Проверьте свой словарный запас с помощью наших веселых викторин по картинкам
- {{randomImageQuizHook.
 copyright1}}
copyright1}} - {{randomImageQuizHook.copyright2}}
Авторы изображений
Пройди тест сейчас
Слово дня
Пи
Великобритания
Ваш браузер не поддерживает аудио HTML5
/paɪ/
НАС
Ваш браузер не поддерживает аудио HTML5
/paɪ/
число (приблизительно 3,14), используемое для расчета размера кругов
Об этом
Блог
Нет недостатка в фразах (Язык больших сумм или чисел, часть 2)
Подробнее
Новые Слова
Хлебфляция
В список добавлено больше новых слов
Наверх
Содержание
EnglishExamplesTranslations
recursive — определение и значение
- Определить
- Связать
- Список
- Обсудить
- См.
- Услышать
- и Любовь
Определения
из Словаря английского языка American Heritage®, 5-е издание.
- прилагательное Относящийся к повторяющемуся процессу, выходные данные которого на каждой стадии применяются в качестве входных данных на последующей стадии.
- прилагательное Математика Относящаяся к последовательной формуле или функции, в которой задан первый термин или первый набор терминов, но в которой последующие термины определяются по отношению к предшествующим терминам.

- прилагательное Компьютеры Относящийся к алгоритму или процедуре, которая ссылается на себя в своем определении или вызывает себя при своем выполнении.
- прилагательное Лингвистика Относящийся к рекурсии или характеризующийся ею.
- прилагательное опираясь на себя, ссылаясь назад.
- прилагательное математика, несопоставимая выражения, каждый член которого определяется применением формулы к предшествующим терминам
- прилагательное вычисление, несопоставимое программы или функции, которая вызывает сама себя
- прилагательное вычислительная теория, несопоставимая, функции , которая может быть вычислена с помощью теоретической модели компьютера за конечное время
- прилагательное вычислительная теория, несопоставимая, множества , характеристическая функция которого является рекурсивной (4)
из WordNet 3.
 0 Copyright 2006 Принстонского университета. Все права защищены.
0 Copyright 2006 Принстонского университета. Все права защищены.- прилагательное рекурсии или относящейся к ней
Этимологии
Извините, этимологии не найдено.
Поддержка
Помогите поддержать Wordnik (и сделайте эту страницу свободной от рекламы), приняв слово рекурсивный.
Примеры
Что делает его рекурсивным , так это то, что мы возвращаемся к предыдущим шагам, таким как исследование или редактирование.
Рекурсивный процесс « Пишите что угодно
Когда моя конечная точка JSON возвращает список строк, которые должны быть отображены по очереди, возможно, 10 лучших текущих сообщений в блоге, я вызываю рекурсивную функцию отображения , которая выполняет простую задачу отображения каждой по очереди.
Домашняя страница сайта
Я в этом почти уверен, но подождите, сначала яйца были от кур, а те тоже от яиц….
 не могу думать, застрял в рекурсивном цикле ….
не могу думать, застрял в рекурсивном цикле ….Думай о прогрессе » Фрист и Хастерт позволили производителям вакцин написать свой собственный многомиллиардный розыгрыш
По доброй воле я создал длинную серию того, что можно назвать рекурсивными петлями легковерия, которые принесли мне бесконечный источник инвесторов.
Берни Мэдофф — Письмо с объяснением?
В 1980-х годах на уроках C++ в университете я изучил мощную технику кодирования, называемую рекурсивными алгоритмами.
Томас Глосер: Рекурсивные циклы — Давос, 2007 г.
Файл XSLT в этом проекте может помочь вам понять вызов рекурсивных шаблонов , а также дать представление о том, как использовать встроенные функции.
The Code Project Последние статьи
Кроме того, для каждого из них вы найдете класс «драйвер» в пакете по умолчанию, который просто вызывает рекурсивную и итеративную реализации, а затем отображает измерения, возвращаемые интерфейсом SimpleMeasurement, которые должна предложить каждая такая реализация.


 1 Функции
1 Функции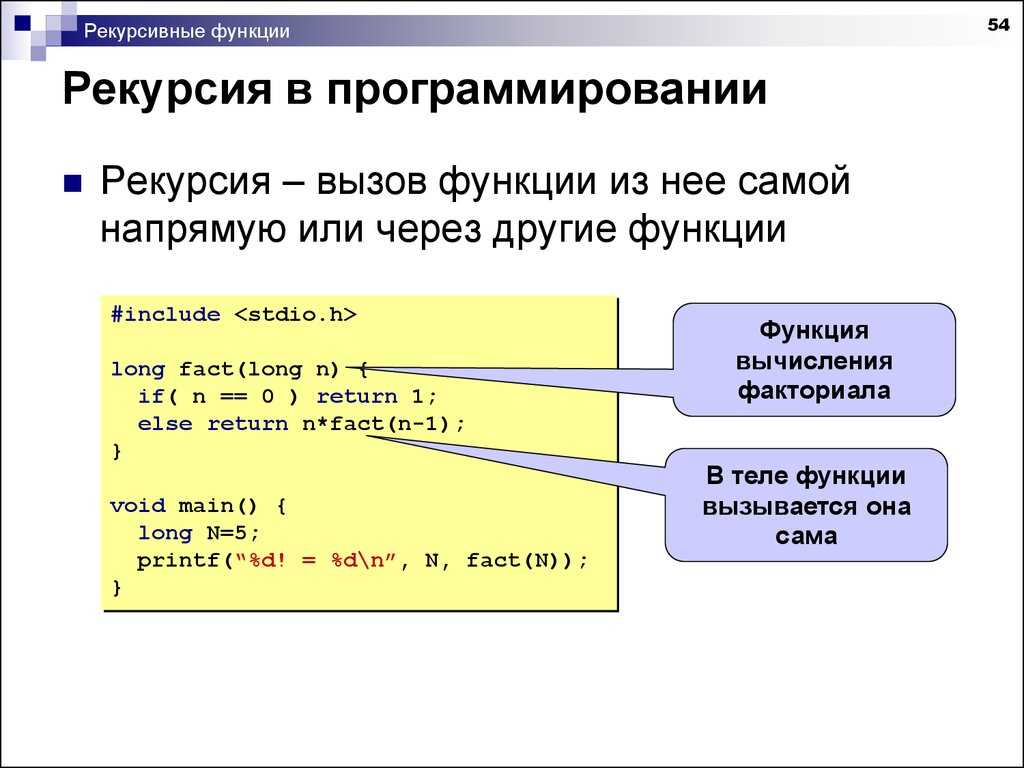 ) с планеты Энтеропия (см.). См. СЕПУЛЬКАРИИ».
) с планеты Энтеропия (см.). См. СЕПУЛЬКАРИИ». А. Лодатко «Рекурсивные лингвистические структуры»
А. Лодатко «Рекурсивные лингвистические структуры» copyright1}}
copyright1}}
 не могу думать, застрял в рекурсивном цикле ….
не могу думать, застрял в рекурсивном цикле ….