Рекурсия это в программировании – Рекурсия. Тренировочные задачи / Habr

это что? Рекурсия в программировании (примеры)

Рекурсии являются интересными событиями сами по себе, но в программировании они представляют особенную важность в отдельных случаях. Впервые сталкиваясь с ними, довольно значительное количество людей имеют проблемы с их пониманием. Это связано с огромным полем потенциального применения самого термина в зависимости от контекста, в котором «рекурсия» используется. Но можно надеяться, что эта статья поможет избежать возможного недоразумения или непонимания.

Что такое «рекурсия» вообще?

Слово «рекурсия» имеет целый спектр значений, которые зависят от области, в которой оно применяется. Универсальное обозначение является таким: рекурсии — это определения, изображения, описания объектов или процессов в самих объектах. Возможны они только в тех случаях, когда объект является частью самого себя. По-своему определяют рекурсию математика, физика, программирование и ряд других научных дисциплин. Практическое применение она нашла в работе информационных систем и физических экспериментах.

Что подразумевают под рекурсией в программировании?

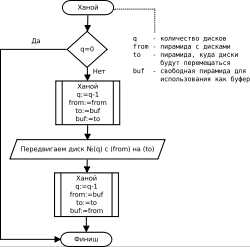Рекурсивными ситуациями, или рекурсией в программировании, называют моменты, когда процедура или функция программы вызывает саму себя. Как бы странно для тех, кто начал изучать программирование, это ни звучало, здесь нет ничего странного. Следует запомнить, что рекурсии – это не сложно, и в отдельных случаях они заменяют циклы. Если компьютеру правильно задать вызов процедуры или функции, он просто начнёт её выполнять.

Рекурсия может быть конечной или бесконечной. Для того чтобы первая прекратила сама себя вызывать, в ней же должны быть условия прекращения. Это может быть уменьшение значения переменной и при достижении определённого значения остановка вызова и завершение программы/переход к последующему коду, в зависимости от потребностей достичь определённых целей. Под бесконечной рекурсией подразумевают, что она будет вызываться, пока будет работать компьютер или программа, в которой она работает.

Возможна также организация сложной рекурсии с помощью двух функций. Допустим, есть А и Б. Функция А имеет в своем коде вызов Б, а Б, в свою очередь, указывает компьютеру на необходимость выполнить А. Сложные рекурсии – это выход из целого ряда сложных логических ситуаций для компьютерной логики.

Если читающий эти строки изучал программные циклы, то он, наверное, уже заметил схожесть между ними и рекурсией. В целом они действительно могут выполнять похожие или идентичные задания. С помощью рекурсии удобно делать имитацию работы цикла. Особенно это полезно там, где сами циклы использовать не очень удобно. Схема программной реализации не сильно различается у разных высокоуровневых языков программирования. Но всё же рекурсия в «Паскале» и рекурсия в С или другом языке имеет свои особенности. Может она быть успешно реализована и в низкоуровневых языках вроде «Ассемблера», но это является более проблематичным и затратным по времени.

Деревья рекурсии

Что такое «дерево» в программировании? Это конечное множество, состоящее как минимум из одного узла, который:

1. Имеет начальный специальный узел, который называют корнем всего дерева.
2. Остальные узлы находятся в количестве, отличном от нуля, попарно непересекающихся подмножеств, при этом они тоже являются деревом. Все такие формы организации называют поддеревьями главного дерева.

Другими словами: деревья содержат поддеревья, которые содержат ещё деревья, но в меньшем количестве, чем предыдущее дерево. Так продолжается до тех пор, пока в одном из узлов не останется возможности продвигаться далее, и это будет обозначать конец рекурсии. Есть ещё один нюанс насчет схематического изображения: обычные деревья растут снизу вверх, а в программировании они рисуются наоборот. Узлы, не имеющие продолжения, называются конечными узлами. Для удобства обозначения и для удобства используется генеалогическая терминология (предки, дети).

Зачем она применяется в программировании?

Своё применение рекурсия в программировании нашла в решении целого ряда сложных задач. Если необходимо сделать только один вызов, то более легким является применение интеграционного цикла, но при двух и более повторах, чтобы избежать построения цепочки и сделать их выполнение в виде дерева, и применяются рекурсивные ситуации. Для широкого класса задач организация вычислительного процесса таким способом является наиболее оптимальной с точки зрения потребления ресурсов. Так, рекурсия в «Паскале» или другом любом высокоуровневом языке программирования представляет собой вызов функции или процедуры до выполнения условий, независимо от количества внешних вызовов. Другими словами, в программе может быть только одно обращение к подпрограмме, но происходить оно будет до определённого заранее момента. В некотором роде это аналог цикла со своей спецификой использования.

Отличия рекурсии в различных языках программирования

Несмотря на общую схему реализации и конкретное применение в каждом отдельном случае, рекурсия в программировании имеет свои особенности. Это может привести к сложности во время поиска необходимого материала. Но всегда следует помнить: если язык программирования вызывает функции или процедуры, значит, и вызов рекурсии — дело осуществимое. Но наиболее значимые её отличия проявляются при использовании низких и высоких языков программирования. Особенно это касается возможностей программной реализации. Исполнение в конечном итоге зависит от того, какая задача поставлена, в соответствии с ней и пишется рекурсия. Функции и процедуры используются разные, но их цель всегда одна – заставить вызвать самих себя.

Рекурсия – это легко. Как просто запомнить содержание статьи?

Для начинающих понять её, может быть, поначалу сложно, поэтому нужны примеры рекурсии или хотя бы один. Поэтому следует привести небольшой пример из бытовой жизни, который поможет понять саму суть этого механизма достижения целей в программировании. Возьмите два или больше зеркал, поставьте их так, чтобы в одном отображались все остальные. Можно увидеть, что зеркала отображают себя многократно, создавая эффект бесконечности. Вот рекурсии — это, образно говоря, отражения (их будет множество). Как видите, понять несложно, было бы желание. А изучая материалы по программированию, далее можно понять, что рекурсия – это ещё и очень легко выполнимая задача.

fb.ru

Рекурсия в программировании

Рекурсии представляют собой довольно интересные события, однако в программировании они являются особенной важностью в отдельных случаях. У людей, которые впервые сталкиваются с ними, часто возникают проблемы с их пониманием.

Как правило, это связано с обширной сферой потенциального использования самого термина в зависимости от контекста, в котором «рекурсия» применяется. Однако можно надеяться, что данная статья позволит избежать различных недоразумений или непониманий.

Что означает термин «рекурсия»?

Слово «рекурсия» обладает целым спектром значений, которые связаны с областью, где оно используется. Универсальным обозначением является то, что данный термин представляет собой определения, изображения, описания объектов либо процессов в самих объектах. Они наблюдаются тогда, когда объект выступает частью самого себя. В различных науках, таких как математика, программирование, физика и других по-своему определяется рекурсия. Практическое использование она находит в работе информационных систем, а также физических экспериментах.

Что означает рекурсия в программировании?

Рекурсивными ситуациями в программировании называют такие моменты, когда процедура или функция программы вызываются самостоятельно. В данном случае нет ничего странного. Необходимо отметить, что рекурсии не вызывает сложностей, и в отдельных случаях способны заменить циклы. При правильном задании компьютеру вызова процедуры или функции он просто начинает ее выполнять. Рекурсия способна быть конечной или бесконечной.

Чтобы первая перестала самостоятельно себя вызывать, в ней же должны быть условия прекращения. Ними могут выступать уменьшение значения переменной, в результате чего при достижении конкретного значения осуществляется остановка вызова и завершение программы/переход к последующему коду. Все зависит от необходимости достичь определенных целей. Бесконечная рекурсия предусматривает то, что она будет вызываться до тех пор, пока будет функционировать компьютер или программа.

Кроме того, существует организация сложной рекурсии, которая происходит при использовании двух функций. Например, есть А и Б. Функция А предусматривает в своем коде вызов Б, который, в свою очередь, говорит компьютеру о необходимости выполнения А. Сложные рекурсии являются выходом из целого ряда сложных логических ситуаций, которые возникают в компьютерной логике. Если пользователь хорошо знаком с программными циклами, он, наверняка, уже замечал схожесть между ними, а также рекурсией. Таким образом, они на самом деле способны осуществлять похожие или аналогичные задания.

При помощи рекурсии можно выполнять имитацию работы цикла. Это, как правило, полезно в том случае, когда сами циклы применять не очень удобно. Схема программной реализации не особо отличается у различных высокоуровневых языков программирования. Однако рекурсия в «Паскале», в С или другом языке программирования обладает своими особенностями. Ее можно с успехом реализовать и в низкоуровневых языках, к примеру, «Ассемблера», однако это несколько проблематично и требует больших затрат по времени.

Деревья рекурсии Что означает «дерево» в программировании? Оно представляет собой конечное множество, которое состоит как минимум из одного узла.

Должны соблюдаться следующие условия:

• присутствует начальный специальный узел, который является корнем всего дерева.
• остальных узлов насчитывается количество, отличное от нуля.

Они отличаются от попарно непересекающихся подмножеств и тоже являются деревом. Данные формы организации имеют названия поддеревьев главного дерева. Таким образом, деревья включают поддеревья, содержащие еще деревья, однако их меньше, чем предыдущее дерево. Такая ситуация продолжается до того момента, пока в одном узле не останется возможность продвинуться дальше. Это и будет означать окончание рекурсии. Существует еще один нюанс, который связан со схематическим изображением. Итак, обыкновенные деревья растут снизу вверх, однако в программировании они изображаются наоборот. Узлы, которые не имеют продолжения, являются конечными узлами. Чтобы обеспечить удобство обозначения, применяется генеалогическая терминология (предки, дети).

Зачем она используется в программировании?

Рекурсия нашла свое применение в программировании при решении множества сложных задач. Если требуется совершить лишь один вызов, наиболее оптимальным вариантом является использование интеграционного цикла, однако при двух и более повторах, во избежание построения цепочки и обеспечение их выполнения в виде дерева, применяются рекурсивные ситуации. Что касается широкого класса задач, такая организация вычислительного процесса считается самой удачной с точки зрения потребления ресурсов.

Таким образом, рекурсия в «Паскале» или другом высокоуровневом языке программирования является вызовом функции или процедуры до выполнения условий. Причем количество внешних вызовов не имеет значение. Таким образом, в программе может быть лишь одно обращение к подпрограмме, однако выполняться оно будет до конкретного момента, который определен заранее. Это так называемый аналог цикла с собственной спецификой использования.

Различие рекурсии в различных языках программирования

Конечно, рекурсия имеет общую схему реализации и определенное использование в каждом отдельном случае, однако в программировании она обладает собственными особенностями. Иногда это приводит к некоторым трудностям в процессе поиска требуемого материала. Так или иначе, всегда необходимо помнить: когда язык программирования вызывает функции или процедуры, это означает, что и вызов рекурсии вполне осуществим. Ее отличия, которые имеют первостепенное значение, проявляются во время использования низких и высоких языков программирования.

Как правило, это связано с возможностями программной реализации. Исполнение в результате зависит от того, какую задачу следует решить, в соответствии с ней и пишется рекурсия. Стоит отметить, что функции и процедуры применяются различные, однако их цель всегда одна. Она заключается в том, чтобы заставить вызвать самих себя.

Рекурсия – это просто. Возможно, для начинающих ее понять поначалу будет сложно. Именно поэтому требуются примеры рекурсии или один из них. Необходимо привести пример из бытовой жизни, который способен лучше всего понять саму суть данного механизма достижения целей в области программирования. Понадобится взять два или больше зеркал, установить их таким способом, чтобы в одном отражались все остальные. В таком случае можно увидеть, что зеркала отображают себя многократно, обеспечивая эффект бесконечности. Таким образом, рекурсия представляет собой отражения. Как видно из примера, представленного выше, их будет множество.

Из всего вышесказанного можно сделать вывод, что понять рекурсию просто, для этого необходимо лишь желание. При изучению материалов по программированию, можно понять, что рекурсия является легко выполнимой задачей.

bezwindowsa.ru

Что такое рекурсия?

20

В осточноукраинский национальный университет имени Владимира Даля

Рекурсия

Информатика и компьютерная техника

© Велигура А.В., кафедра экономической кибернетики, 2004

Рекурсия — мощный метод программирования, который позволяет разбить задачу на части все меньшего и меньшего размера до тех пор, пока они не станут настолько малы, что решение этих подзадач сведется к набору простых операций.

После того, как вы приобретете опыт применения рекурсии, вы будете обнаруживать ее повсюду. Многие программисты, недавно овладевшие рекурсией, увлекаются, и начинают применять ее в ситуациях, когда она является ненужной, а иногда и вредной.

Рекурсия происходит, если функция или подпрограмма вызывает сама себя. Прямая рекурсия (direct recursion) выглядит примерно так:

Function Factorial(num As Long) As Long

Factorial = num * Factorial(num — 1)

End Function

В случае косвенной рекурсии(indirectrecursion) рекурсивная процедура вызывает другую процедуру, которая, в свою очередь, вызывает первую:

Private Sub Ping(num As Integer)

Pong(num — 1)

End Sub

Private Sub Pong(num As Integer)

Ping(num / 2)

End Sub

Рекурсия полезна при решении задач, которые естественным образом разбиваются на несколько подзадач, каждая из которых является более простым случаем исходной задачи. Можно представить дерево в виде «ствола», на котором находятся два дерева меньших размеров. Тогда можно написать рекурсивную процедуру для рисования деревьев:

Private Sub DrawTree()

Нарисовать «ствол»

Нарисовать дерево меньшего размера, повернутое на -45 градусов

Нарисовать дерево меньшего размера, повернутое на 45 градусов

End Sub

Хотя рекурсия и может упростить понимание некоторых проблем, люди обычно не мыслят рекурсивно. Они обычно стремятся разбить сложные задачи на задачи меньшего объема, которые могут быть выполнены последовательно одна за другой до полного завершения. Например, чтобы покрасить изгородь, можно начать с ее левого края и продолжать двигаться вправо до завершения. Вероятно, во время выполнения подобной задачи вы не думаете о возможности рекурсивной окраски — вначале левой половины изгороди, а затем рекурсивно — правой.

Для того чтобы думать рекурсивно, нужно разбить задачу на подзадачи, которые затем можно разбить на подзадачи меньшего размера. В какой‑то момент подзадачи становятся настолько простыми, что могут быть выполнены непосредственно. Когда завершится выполнение подзадач, большие подзадачи, которые из них составлены, также будут выполнены. Исходная задача окажется выполнена, когда будут все выполнены образующие ее подзадачи.

1. Опасности рекурсии

   1. Бесконечная рекурсия

Наиболее очевидная опасность рекурсии заключается в бесконечной рекурсии. Если неправильно построить алгоритм, то функция может пропустить условие остановки рекурсии и выполняться бесконечно. Проще всего совершить эту ошибку, если просто забыть о проверке условия остановки, как это сделано в следующей ошибочной версии функции факториала. Поскольку функция не проверяет, достигнуто ли условие остановки рекурсии, она будет бесконечно вызывать сама себя.

Private Function BadFactorial(num As Integer) As Integer

BadFactorial = num * BadFactorial (num — 1)

End Function

Функция также может вызывать себя бесконечно, если условие остановки не прекращает все возможные пути рекурсии. В следующей ошибочной версии функции факториала, функция будет бесконечно вызывать себя, если входное значение — не целое число, или если оно меньше 0. Эти значения не являются допустимыми входными значениями для функции факториала, поэтому в программе, которая использует эту функцию, может потребоваться проверка входных значений. Тем не менее, будет лучше, если функция выполнит эту проверку сама.

Private Function BadFactorial2(num As Double) As Double

If num = 0 Then

BadFactorial2 = 1

Else

BadFactorial2 = num * BadFactorial2(num-1)

End If

End Function

Следующая версия функции Fibonacciявляется более сложным примером. В ней условие остановки рекурсии прекращает выполнение только нескольких путей рекурсии, и возникают те же проблемы, что и при выполнении функцииBadFactorial2, если входные значения отрицательные или не целые.

Private Function BadFib(num As Double) As Double

If num = 0 Then

BadFib = 0

Else

BadFib = BadPib(num — 1) + BadFib (num — 2)

End If

End Function

И последняя проблема, связанная с бесконечной рекурсией, заключается в том, что «бесконечная» на самом деле означает «до тех пор, пока не будет исчерпано стековое пространство». Даже корректно написанные рекурсивные процедуры будут иногда приводить к переполнению стека и аварийному завершению работы. Следующая функция, которая вычисляет сумму N + (N — 1) + … + 2 +1, приводит к исчерпанию стекового пространства при больших значенияхN. Наибольшее возможное значениеN, при котором программа еще будет работать, зависит от конфигурации вашего компьютера.

Private Function BigAdd(N As Double) As Double

If N <= 1 Then

BigAdd = 1

Else

BigAdd=N + BigAdd(N — 1)

End If

End Function

Программа BigAddна диске с примерами демонстрирует этот алгоритм. Проверьте, насколько большое входное значение вы можете ввести в этой программе до того, как наступит переполнение стека на вашем компьютере.

studfiles.net

Рекурсия — Lurkmore

Анонимус! Альтернативное мнение также имеется в смехуечках.

«	To iterate is human, to recurse, divine	»
— James O. Coplien, Bell Labs

Это, например, рекурсия. А может быть, даже фрактал.

Рекурсия — см. «Рекурсия».

Рекурсией программисты на своём мунспике называют вызов функцией самой себя прямо (в теле функции расположен вызов себя) или косвенно (функция вызывает функцию, которая вызывает функцию, которая… и в одной из этих функций расположен вызов самой первой функции). У хорошей, годной рекурсии должно быть и условие для выхода из рекурсии, иначе получается зацикливание. Типичным примером функций, использующих рекурсию, являются вычисление факториала и функция Аккермана. В более общем смысле, включение некоторой сущностью самой себя целиком (см. пример с зеркалами ниже). Более сложный вариант: «Чтобы понять рекурсию, нужно сперва понять рекурсию».

Помимо своего матанного и программистского значения, рекурсия — мем, используемый в наших интернетах в основном среди читателей башорга. Уйдя в массы, мем утратил своё специфичное значение и используется для описания любой рвущей шаблон ситуации. Чаще всего слово «рекурсия» всплывает ассоциацией в мозгу планктонины либо при упоминании бесконечности как меры мощности множества, либо при столкновении с логическим парадоксом (так, зарегистрированы случаи непроизвольного произнесения слова «рекурсия» при упоминании парадокса лжеца).

[править] Наблюдение рекурсии

«	Это как тако внутри тако? Да, это такое тако внутри тако внутри супер-тако внутри ресторана «Тако Белл» внутри KFC в супермаркете внутри сна.	»
— South Park

Ещё один

Вообще древнейший из примеров применения рекурсии IRL связан ещё с изобретением зеркала. Установив два зеркала параллельно и строго напротив друг друга, внутри можно увидеть классическую рекурсию. А при особом упорстве и склонности к магии — и неиллюзорную кучу глюков. Но мы же не ищем лёгких путей. Поэтому если вам внезапно нечем будет себя занять, то можете поэкспериментировать и с другими методами получения рекурсии:

• Просто включите веб-камеру и наведите её на экран монитора. Или просто обычную видеокамеру, наведя на показывающий с неё телевизор. В последнем случае (повращав камеру) можно убедиться в том, что даже телевизор способен неиллюзорно тормозить.
• Тот же самый спецэффект можно получить и с меньшим бюджетом, воспользовавшись программой записи видео с экрана (или программой-лупой).
• Также её можно наблюдать в игре Portal, если создать два портала один перед другим.
• Кстати об играх. В The Stanley Parable в одной из концовок ГГ слышит, как голос в его голове (закадровый рассказчик) говорит о том, что ГГ его слышит.
• А ещё можно поюзать Radmin или что-то подобное для управления удаленным десктопом и приконнектиться к локалхосту.
• Православный и легкодоступный способ.

На своем компе активируем Team Viewer. Заходим на отдаленную машину через удаленное подключение к рабочему столу. На удаленной машине также запускаем Team Viewer Подключаемся к своему исходному компу. Получите каноничную рекурсию и, если комп слабый, нарастающие тормоза системы.

• Если и этого нет под рукой, то подобную рекурсию можно произвести вручную. Откройте любой графический редактор (например, тот же MS Paint) и с детским задором, высунув язык, без остановки поочерёдно жмакайте на клавиатуре Print Screen и Ctrl+V.
• Человека от обезьяны отличает отнюдь не абстрактное мышление, как любили догматически утверждать марксисты, а способность к мышлению рекурсивному.

Можно получить и слуховую форму рекурсии. Для этого просто дозвонитесь на любое принимающее в данный момент звонки радио с сотового и вместо того, чтобы (по настоятельным просьбам RJ) увернуть громкость приёмника, наоборот, прибавьте. Трети секунды задержки, которую гуляет Ваш голос вместе с самим сигналом станции в глубинах сотовых сетей, будет вполне достаточно для наблюдения полноценной звуковой рекурсии.

[править] Рекурсия и цикл

Не стоит путать рекурсию и цикл (возможно, бесконечный). Отрицательный пример — тоже пример, рассмотрим выражение:

1. Начальник всегда прав. 2. Если начальник не прав, смотреть п. 1.

Оно является циклом с плохим условием, а не рекурсией. Дональд Кнут гарантирует. Можно ли это переделать в рекурсию? Да:

Приказ № 1. Начальник всегда прав. Если начальник не прав, см. Приказ № 1.

С точки зрения процесса, это по-прежнему цикл. Чтобы процесс стал рекурсивным, можно сделать так:

п1. Если начальник не прав, то см. п1. и начальник всегда прав.

Более понятный вариант:

«	111: А можешь мне, как гуманитарию, объяснить разницу между бесконечным циклом и бесконечной рекурсией? 222: Но вот смотри: «У царя был двор, во дворе стоял кол, На колу мочало, начинай сначала» — это бесконечный цикл. «У попа была собака, он ее любил, Она съела кусок мяса — он ее убил, В яму закопал, крест поставил, написал: …» — это бесконечная рекурсия.	»
— anekdot.ru

Не следует также путать рекурсию и заколдованный круг (также известный как «тупик» или «взаимная блокировка»). Отличие между ними в том, что рекурсия не имеет точки выхода, а тупик — точки входа. Именно к взаимным блокировкам относится кое-что по тексту статьи. Это не может быть рекурсией, так как не предполагает повторяющихся действий. Исхитрившись один раз добыть пароль из ящика, мы разрываем круг. Ведь никому не придёт в голову обозвать рекурсией цикл while (false)?.. Подобная ситуация также известна как проблема курицы и яйца.

Примеры:

• «Установите драйвера для CD-ROM, находящиеся на нашем компакт-диске».
• «Для выхода в Интернет скачайте из Интернета нашу программу».
• «Windows не смог найти драйверы для устройства Модем. Поискать в интернете?»
• PKUNZIP.ZIP
• «Keyboard not found. Press F1 to continue» (BIOS). (спойлер: На самом деле это — лаконичная просьба подключить клавиатуру.)
• «Если у Вас украли кредитную карту, позвоните по телефону, указанному на оборотной стороне кредитной карты».
• «Смысл жизни — в достижении её цели, цель жизни — в наполнении её смыслом» (или, как вариант, — «Смысл жизни в том, чтобы найти смысл жизни»).
• «Уйти, себя избавить памяти о близких, чтобы, уйдя, избавить память близких о себе»
• При Советской власти в крупных городах (>100000) наняться на работу можно было только при предоставлении справки о прописке, а прописаться можно было только при наличии справки с места работы, что доставляло субъекту множество разных эмоций.
• Рассказ Айзека Азимова «…Вставьте шплинт А в гнездо Б…» (спойлер: о роботе, который должен был складывать других роботов и механизмы по инструкциям, записанным у него в памяти, но самого робота нужно было тоже складывать по прилагающейся к нему инструкции.)

[править] Примеры рекурсии

Таки да, это не единичный случай.

• Бюрократия разрастается, чтобы удовлетворить нужды разрастающейся бюрократии.
• Программа «Средство отправки отчетов об ошибках» неожиданно завершила работу. Отправить отчет об этой ошибке?
• Библии можно верить, потому что в Библии написано, что Библии можно верить.
• При вводе в Google слова «рекурсия», он будет говорить: «Возможно, вы имели в виду: рекурсия».
• Тренинги личностного роста: «чтобы добиться уверенности в себе, надо начать верить в себя».

Кстати, пример с клавиатурой немного особенный: USB-клавиатура иногда всё же может послать на материнскую плату нужный сигнал при нажатии кнопки F1.

[править] В кино и мультипликации

«	Учёные доказали, что утверждения, начинающиеся со слов «учёные доказали», никогда ими не доказывались.	»
— Рекурсия и взаимоисключающие параграфы

• В фильме «12 друзей Оушена» представлен интересный пример рекурсии: Джулия Робертс сыграла героиню, которая по сюжету фильма некоторое время неубедительно играла Джулию Робертс.
• В сериале «Сверхъестественное» в восемнадцатой серии четвертого сезона предсказатель предсказывает то, что он предскажет… И когда Дин читает рукопись предсказания, он недоумевает. Дин: «Я сижу в прачечной и читаю о себе, сидящем в прачечной и читающем о себе, сидящем в прачечной…»
• В этом вашем «Хаусе» в конце второго сезона Хаус видит галлюцинацию, в которой он, в свою очередь, тоже видит галлюцинацию. Кто смотрел, поймёт.
• В фильме «Быть Джоном Малковичем» Джон Малкович, роль которого играет Джон Малкович, проникает в сознание Джона Малковича, в котором он (спойлер: обнаруживает кучу Джонов Малковичей).
• В фильме «Адаптация», поставленном по сценарию Чарли Кауфмана, Чарли Кауфман пишет сценарий про то, как Чарли Кауфман пишет сценарий.
• В фильме «Космические яйца» два мудозвона, не зная, что делать дальше по сюжету, решают посмотреть кино «Космические яйца».
• В серии «Most Wanted» Бивис говорит: «Я сделаю татуировку в виде задницы на моей заднице».

Тот самый кадр из «Паранойи». Video Feedback в действии.

• В фильме «Паранойя», в момент настройки главным героем камеры наблюдения (на 1:09:52), можно обнаружить рекурсию (скрин прилагается).
• В одной из серий киножурнала «Ералаш» есть абсолютно тупой эпизод, где лоли сломя голову мчится домой к зомбоящику, сметая всё на своём пути, чтобы посмотреть всё тот же киножурнал «Ералаш»
• Что, видимо, спизжено из заставки к Симпсонам, где Симпсоны сломя голову разными путями добираются домой смотреть «Симпсонов». В одном из couch gag показывается, что вселенная Симпсонов находится внутри атома, находящегося в голове Гомера Симпсона. И да, эту заставку он видит по телевизору.
• И ещё: «Симпсоны» — мультик в мире «Футурамы», а «Футурама» — мультик в мире «Симпсонов».
• Ну, «Начало» же! «Inception», десу! Весь фильм главные герои только и занимаются тем, что смотрят сон, в котором смотрят сон, в котором смотрят сон (просто так можно ужать час в минуту)
• В фильме «В пасти безумия» Джона Карпентера про глобальный пиздец главный герой в конце идет в кинотеатр смотреть фильм «В пасти безумия». Да и вообще, кино местами повествует самое себя, когда герои читают отрывки книги, по которой снят этот фильм.
• В серии Гриффинов 8×11 Питер не понимает, почему у Мег в спальне преступник, и поэтому он берет телепрограмму и смотрит в описание серии, в которой он находится.
• В махо-сёдзе «Cardcaptor Sakura» (в OVAшке) сам сериал оказывается результатом режиссёрских трудов подруги Сакуры, отправленных на телевидение.
• В фильме «Наказание» одна из героинь меняется сознанием с телом матери девятнадцатилетней давности, проживает её тогдашнюю жизнь и меняется сознанием уже с собой. И таких примеров в фильме масса.
• В фильме Немое кино, созданном в жанре немого кино, рассказывается о попытке снять немое кино.
• Одна из серий «Масяни» «День сурком» состоит из рекурсии чуть более, чем полностью.
• Да и сам «День сурка» является не бесконечным циклом, а рекурсией, из которой ГГ всё же, начитавшись достаточно книг и наигравшись на пианино, сумел выйти через хороший, годный пикап.
• В пиндостанском шоу «1000 способов умереть» один из героев смотрит по телевизору «1000 способов умереть».
• В фильме «Частный детектив, или операция „Кооперация“» в конце невъебенно счастливый Харатьян на крутой тачке подвозит папу своего героя к кинотеатру с афишей сего же фильма.
• Сюжет фильма «Новый кошмар Уэса Крейвена» заключается в том, что во время съёмок нового фильма про Фредди Крюгера начинают погибать люди из съёмочной группы. В финальной сцене главная героиня находит сценарий только что закончившегося фильма.
• В клипе группы Nero «Me And You» парень находит в подсобке торгового-развлекательного центра заброшенный игровой автомат. В конце игры парень видит в ней себя самого стоящим за игровым автоматом.
• В одной из серий «Чёрного Плаща» Гога рекламирует по телевизору кукурузные хлопья, на коробке которых изображено, как Гога рекламирует кукурузные хлопья, на коробке которых изображено, как Гога рекламирует кукурузные хлопья. Ну ты понел.
• В одной из серий «Бригады» Саша Белый видит, как возле ресторана снимают кино про бандитов под названием «Бригада». При выходе он замечает, как бандитов на съёмочной площадке по сценарию скручивает ОМОН. Буквально через несколько секунд то же самое происходит с Сашей Белым и его бригадой.
• Некоторые эпизоды сериала «Доктор Кто» буквально состоят из чистой рекурсии — например, машина времени материализуется внутри самой себя. В Рождественском эпизоде 2014 года также присутствует рекурсия: (спойлер: герои просыпаются, чтобы понять, что спят, снова просыпаются и так много раз.).
• Ещё в советском фильме «31 июня», снятом по нетленке Джона Бойнтона Пристли, есть забавный момент, когда главный герой находит на столике томик Пристли с произведением, по которому снято кино… и ловит от этого истинное наслаждение, когда до него доходит непередаваемое ощущение попаданца.
• Впоследствии эту шутку скопировали в ремейке «Графа Монте-Кристо», где в конце фильма граф Туманский к вящему удовольствию главзлодея дарит ему книгу, по мотивам которой снят фильм.
• В ещё одном идейно правильном кино про Алису Коля Герасимов в будущем «станет самым обыкновенным инженером и изобретёт самую обыкновенную машину времени»… с использования которой именно им и начинается сюжет кино. Больше всего доставляет то, что предсказание это добуквенно соответствует книжке, по которой снят фильм.
• В мультсериале про Кота Леопольда есть эпизод, где главный герой смотрит по телевизору этот же мультсериал.
• Терминатор же. В далёком будущем Джон Коннор знает, как бороться с машинами, поэтому Скайнет раз за разом посылает в прошлое терминаторов-убийц. Уничтожая их, Коннор и получает столь опасные для машин навыки.
• Сюжет британского хоррора «Треугольник» есть рекурсия верхом на рекурсии и рекурсией же погоняющая. Любители идеи «петли времени» вполне могут посмотреть.
• Кино 2015 года «Он снова здесь» о воскресшем Гитлере снято по одноимённой книге. Книга фигурирует в сюжете фильма, причём герои опять-таки решают экранизировать её, в результате чего (спойлер: концовка фильма оказывается действом на съёмочной площадке.)

[править] Из жизни братьев наших меньших

xkcd о рекурсии

• Хаскель состоит из рекурсии чуть менее, чем полностью.
• Scheme же состоит из рекурсии чуть более, чем полностью.
• Реакция на слово «рекурсия» типичного ПеХаПе-программиста.
• В этом вашем OCaml есть специальное слово «rec», которое вставляется перед названием функции, если программист хочет показать, что она будет рекурсивной.
• В Фортране тоже: функция рекурсивна, если имеет атрибут recursive; в противном случае имя функции — это идентификатор возвращаемого значения.

Показанные в этом разделе примеры у программистов называют «бесконечным рекурсивным циклом», а в программировании к рекурсии (которая и так может быть банальным «добавить к Х единичку каждый цикл», то есть Х=Х+N) еще и прописывается «пока не…», оно же «условие выхода из рекурсии».

[править] В архитектуре

На западном фасаде Исаакиевского собора в Петербурге расположилась огромная статуя архитектора Монферрана, который держит в руке модель построенного им собора (по-видимому, с такой же статуей на западном портике). Алсо, внутри собора на иконостасе преподобный Исаакий держит в левой руке свиток, на развёрнутой части которого изображён Исаакиевский собор (с таким иконостасом и свитком внутри и т. д.).

[править] В законодательстве

• Из Земельного кодекса Российской Федерации (ст. 5):

• Прошедшему обряд посвящения в полицейские, чтобы получить форму, нужно предъявить удостоверение, где он сфотографирован в форме.

• Народные депутаты Верховной Рады отличили эротику от порнографии, обосновав, что: «…продукция порнографического характера — продукция, которая содержит порнографию».

• Из статьи 264 Уголовного кодекса: «Под другими механическими транспортными средствами в настоящей статье понимаются троллейбусы, а также трактора и иные самоходные машины, мотоциклы и иные механические транспортные средства».

[править] В геральдике

Первым в этом списке, естественно, идет российский герб. Причем, естественно, только современный его вариант. Скипетр, который орёл держит в правой лапе, увенчан небольшим двуглавым орлом, который в свою очередь также держит скипетр…

[править] В гидравлике

Эпическая рекурсия: сжатие гидравлического пресса в гидравлическом прессе гидравлическим прессом

[править] В музыке

Рекурсивный клип: Gabin — «Doo Uap Doo Uap Doo Uap» Еще один: Kylie Minogue — «Come Into My World» Björk — «Bachelorette», рекурсия с глубиной вложенности 3

• Pink Floyd, альбом «Ummagamma», 1969 год/
• Ирландский расовый Bog Down in the Valley.
• Верный пример рекурсии из этого вашего Сплина:

И мудрец сошел с ума, набрал 01, И по вызову явился незнакомый господин. И господин сошел с ума, набрал 01, И по вызову явился незнакомый господин. И господин сошел с ума, набрал 01, И по вызову явился незнакомый господин. И господин сказал…[1]

И ещё «Человек и дерево»:

Человек, проглотивший дерево, превращается в дерево, проглотившее человека. Человек, который проглотил дерево, превращается в дерево, проглотившее человека.

• Песня «Человек» советской группы «Центр». Чтобы понять, надо прослушать целиком.

• Детская песенка:

У попа была собака, Он её любил. Она съела кусок мяса, Он её убил. В землю закопал, Надпись написал: «У попа была собака…»

А также целый жанр докучных сказок.

• Незабвенная «Put The Lime In The Coconut»

• А еще у Наутилуса песня «Ни кому ни кабельность»:

Я набрал знакомый номер, а в нём короткие гудки, это — мой телефонный номер, видимо, с кем-то уже говорю

• У Максима Леонидова в песне «Девочка-виденье» есть такие слова:

Я оглянулся посмотреть, не оглянулась ли она, Чтоб посмотреть, не оглянулся ли я

• У Высоцкого в «Песне о мангустах» (надо слушать целиком)

• Классическая музыка тоже отличилась, изобретя канон, то есть музыкальное произведение, в котором основная тема повторяется во всех голосах, но с разными задержками. При ближайшем рассмотрении такие произведения выглядят как попытка автора включить в произведение это же произведение, но со сдвигом по фазе и, иногда, тональности, со вполне очевидным фейлом типа «переполнение стека» и последующими попытками из этого выкрутиться.

[править] В Педивикии

Рекурсия в классической фотографии: Д. Бальтерманц — маршал С. Буденный у любимого портрета.

Копипаста оттуда:

Введение в вопрос: в 2006 году в одной из статей Википедии был создан (разными участниками в течение примерно полугода) некий текст. Через некоторое время его принялись копировать авторы статей в реферируемых журналах. При внимательном изучении статьи выяснилось, что источниками текст толком и не подтверждён — были проставлены запросы. Нетрудно догадаться, что запросы были заменены теми самыми источниками, которые из Википедии текст и взяли, благо, совпадение текстов по понятным причинам очень близкое:). Я указал, что в данной ситуации эти источники не являются авторитетными, так как сами заимствовали текст из Википедии. Были высказаны возражения, которые вкратце можно передать как «ВАК — это серьёзно, там всё всегда проверяется, ничего неправильного там опубликовано быть не может, дата публикации ни о чём не говорит, статья в научном журнале — бесспорный абсолютный АИ».

В зависимости от ориентации, развитие баттхерта, расширение рек поноса до ширины Енисея, участие, учащение периода рекурсии возможно тут.

Собственно статья, по поводу которой шли метания говн — Содружество непризнанных государств.

[править] В книгах

• В повести Пейсателя «Царь, царевич, король, королевич…» есть доставляющий эпизод (в отличие от самой книги), где персонажи решают пролистать повесть «Царь, царевич, король, королевич…», чтобы узнать будущие события:

Пока я размышлял, стоит ли принимать такие странные извинения, Кубатай полистал книжку и громко, выразительно прочитал: — «Пока я размышлял, стоит ли принимать такие странные извинения, Кубатай полистал книжку и громко, выразительно прочитал: — Пока я размышлял, стоит ли принимать такие странные извинения, Кубатай полистал книжку и громко, выразительно прочитал: — Пока я размышлял…» Быстрым движением Холмс выхватил у Кубатая томик.

Люди бывают свиньи, шакалы и люди.

• Из литературных анекдотов, ошибочно приписываемых Д. Хармсу:

Гоголь переоделся Пушкиным, пришел к Пушкину и позвонил. Пушкин открыл ему и кричит: «Смотри, Арина Родионовна, я пришел!»

В юридической атмосфере почти невозможно дышать. Этот воздух<…> На ней лежала та самая распечатка. Я открыл первую страницу. Первым предложением было «В юридической атмосфере почти невозможно дышать. Этот воздух…»

• Аналогично у юмориста Аркадия Арканова в книжке «Рукописи не возвращаются»: в финале появляется тетрадь с романом, который начинается с тех же слов, что и книга.

В помещении редакции журнала «Поле-полюшко» частенько пахло газом.<…> «В печенках они у меня со своей литературой!» — подумал Рапсод Мургабович, машинально раскрыл тетрадь в красном кожаном переплете и прочитал: «В помещении редакции журнала „Поле-полюшко“ частенько пахло газом…»

И дальше картина моя без загвоздки по струнам-канатам, аж звездам к ногам. Я вижу — здесь стоял Маяковский, стоял и стихи слагал по слогам.

Черный Король мне снится. Но он спит и видит во сне, будто я сплю и вижу во сне, что он спит и видит меня во сне… Видно, я никогда не доберусь до конца.

• У Антуана де Сент-Экзюпери в «Маленьком принце», правда, с выходом из рекурсии:

— Что это ты делаешь? — спросил Маленький принц. — Пью, — мрачно ответил пьяница. — Зачем? — Чтобы забыть. — О чем забыть? — спросил Маленький принц; ему стало жаль пьяницу. — Хочу забыть, что мне совестно, — признался пьяница и повесил голову. — Отчего же тебе совестно? — спросил Маленький принц, ему очень хотелось помочь бедняге. — Совестно пить! — объяснил пьяница, и больше от него нельзя было добиться ни слова.

• Создатели Death Note выпускали мангу Bakuman в журнале «Weekly Shonen Jump», в нем же выпускали свои произведения и ГГ манги.

[править] Рекурсивные акронимы

Про PHP
PHP — от англ. Personal home page — личная домашняя страничка. Так-то! Впоследствии для пущей солидности была изобретена другая интерпретация: PHP: Hypertext Preprocessor. Она содержит рекурсию вовсе не потому, что PHP-разработчики любят рекурсию, а скорее потому, что подогнать нормальный акроним к имеющимся буквам было весьма затруднительно.

Про PNG
Официально PNG — Portable network graphics. Однако формат создавался как альтернатива патентнотролльскому GIF, поэтому на самом деле верна неофициальная интерпретация.

Бородатые линуксоиды обожают рекурсивные бэкронимы:

• Linux — Linux is not unix
• GNU — GNU is not unix
• WINE — WINE is not an emulator
• PINE — PINE is not elm
• LAME — LAME ain’t an MP3 encoder
• Gajim — Gajim is a jabber instant messenger
• PNG — PNG is not GIF
• Hurd — HIRD of Unix-Replacing Daemons, где HIRD — HURD of Interfaces Representing Depth.

В общем, и Микрософт тоже:

• XNA — XNA’s not acronymed

Внезапно:

• VISA — Visa International Service Association
• АСКА — акционерная страховая компания «АСКА»
• VES — VES Electric Spain
• FGHI — FGHI Global Headlight Ignited

[править] В программировании

• Простейший пример рекурсивной функции, вычисляющей факториал на Common Lisp’е:

(defun fact (x) (if (> x 1) (* x (fact (- x 1))) 1))

• И рекурсия на BASIC’е:

• И двойная на C:

uint f(uint x) {
  return x?--x?f(--x)+f(++x):++x:x;;
}

[править] В браузере

chrome://browser/content/browser.xul

Потом снова и снова…

[править] С миру по нитке

Подпольная рекурсия

Требуется расклейщик объявлений для расклейки объявлений о приеме на работу расклейщиков объявлений.

Бомба всегда падает в эпицентр.

<DaGGeR> У нас на обед — салат «Рекурсивный» : помидоры, огурцы, салат.

100219

мама папе: а это что за рваные деньги тут лежат?
папа: ну скопились рваные деньги. А скотча, чтобы заклеить, дома нет. А чтобы купить скотч, нужны деньги. А они рваные, нужно сначала заклеить. Вот и лежат…

416177

1: Я подумаю. Иди потролль кого-нибудь. 2: Я подумаю. Иди потролль кого-нибудь.

— Ты где деньги берёшь? — Жена даёт. — А жена где берёт? — Из тумбочки. — А в тумбочку кто кладёт? — Я кладу.

В: Какой вопрос может являться ответом сам на себя? О: «Какой вопрос может являться ответом сам на себя?»

Parchom: «Цена на на топливо выросла потому что увеличилась цена на топливо, которое используют бензововозы при доставке топлива.»

420965

Что означает «Б» в имени Бенуа Б. Мандельброта? — Бенуа Б. Мандельброт.

Шутеечка про «Отца фрактальной геометрии»

• Рекурсия в качестве источника лулзов не столь новое изобретение. Цитата из книги английского математика Дж. Литлвуда «Mathematician’s miscellany», выпущенной в 1957 году:

Однажды научный журнал Spectator объявил среди читателей конкурс на тему «Что бы вы с наибольшим удовольствием прочли, раскрыв утреннюю газету?». Приз получил ответ: Наш второй конкурс. Первый приз во втором конкурсе этого года присуждён мистеру Артуру Робинсону, остроумный ответ которого без натяжки должен быть признан наилучшим. Его ответ на вопрос «Что бы вы с наибольшим удовольствием прочли, раскрыв утреннюю газету?» был озаглавлен «Наш второй конкурс», и состоял в следующем: «Первый приз во втором конкурсе этого года присуждён мистеру Артуру Робинсону, остроумный ответ которого без натяжки должен быть признан наилучшим. Его ответ на вопрос „Что бы вы с наибольшим удовольствием прочли, раскрыв утреннюю газету?“ был озаглавлен „Наш второй конкурс“, но из-за лимитирования бумаги мы не можем напечатать его полностью.»

пруф

• Известно, что в системах с ограниченным объёмом оперативной памяти (компьютер, мозг быдлокодера…) неограниченная или недостаточно ограниченная рекурсия может привести к stack overflow с малопредсказуемыми, но не всегда неприятными последствиями. Знатоки Хацкеля обычно дружелюбно поплёвывают в данную сторону людей лямбдой.
• Логический парадокс «я лгу» косвенно относится к рекурсии. Это так называемые автореферентные выражения.
• Простейший пример косвенной рекурсии — про бабочку и китайского философа Чжуан Цзы. Философ спит, и ему снится, что он бабочка, которая спит и ей снится, что она философ, который спит и ему снится, что он бабочка, которая спит и ей снится… Аналогичный пример присутствует у Кэрролла в «Алисе в Зазеркалье»: Алиса спит и видит во сне Чёрного Короля, который спит и видит во сне Алису, которая спит и видит Короля…
• Радиолюбители знают, что принцип рекурсии лежит в основе таких устройств, как мультивибратор и триггер.
• Во многих видеоиграх на принципе рекурсии основаны пасхалки, в которых упоминается название данной игры в контексте игровой же вселенной.
• Всем похуй, что всем похуй.
• Парадокс Рассела (того самого, известного своим чайником): содержит ли себя в качестве элемента множество всех множеств, которые не содержат себя в качестве элемента? Решение парадокса
• Рекурсией часто пользуется Капитан Очевидность.
• Ложные пробуждения (человек просыпается, делает какие-то обычные действия, пребывая в уверенности, что это реальность, а затем просыпается снова — в этот раз, как правило, по-настоящему. Некоторые «просыпаются» и по три раза, и даже больше, такой вот ночной кошмар)
• Фобофобия — страх возникновения фобии. Носители могут бояться смотреть любые фильмы/читать книги/выходить гулять, так как боятся начать шарахаться от… они и сами еще не знают, что станет поводом для их причины похода к психиатру, такой вот Лавкрафт-стайл.

1	3	yes	Показать	Скрыть
Рекурсивная рекурсия на Гугле. Ещё один пример рекурсии. Гуглорекурсия #2 (смотрим первые пункты в списке суджестов). Ещё когда фотошопов не было. Рекурсия в искусстве: Мауриц Эшер. Рисунок в рисунке Эшера Вложенный в кота кот. Сёнэн Джамп поясняет. Кот, вложенный в монитор. Рекурсия и сиськи — Гитлер не был таким уж злодеем: в конце концов, он убил Гитлера. — Да, но он также убил парня, что убил Гитлера. Далее в тред врывается Капитан.

1. ↑ В последней строке мы наблюдаем выход из рекурсии.

	Рекурсия ⊆ Рекурсия

lurkmore.to

Что такое рекурсия в программировании – рекурсивный алгоритм

Тренировочные задачи на рекурсию

В этом листке собраны тренировочные задачи. Их решение необязательно, но рекомендуется тем, кто плохо освоил задачи на рекурсию. Также в этом листке есть несколько довольно сложных задач, которые могут быть интересны всем. Задачи из этого листка не учитываются при выставлении оценок.

Задачи можно сдавать на языках C++ и Python, поэтому если вы хотите попрактиковаться в другом языке, то тоже можете сдавать задачи.

В задачах этого листка нельзя использовать циклы и массивы. Также могут быть и другие ограничения в каких-то конкретных задачах (например, запрет использования строк в арифметических задачах, запрет использования срезов в решениях на питоне).

Задачи проверяются только автоматически и сразу же получают OK при прохождении всех тестов. Однако, если при последующей проверке кода будет выявлено нарушение вышеизложенных требований или будут другие замечания к решению, статус OK может быть изменен.

A: От 1 до n

Дано натуральное число \(n\). Выведите все числа от 1 до \(n\).

B: От A до B

Даны два целых числа A и В (каждое в отдельной строке). Выведите все числа от A до B включительно, в порядке возрастания, если , или в порядке убывания в противном случае.

C: Функция Аккермана

В теории вычислимости важную роль играет функция Аккермана \(A(m, n)\), определенная следующим образом: \[ A(m, n) = \begin{cases} n + 1 & m = 0\\ A(m — 1, 1)& m > 0, n = 0\\ A(m — 1, A(m, n — 1))& m > 0, n > 0\\ \end{cases} \]

Даны два целых неотрицательных числа \(m\) и \(n\), каждое в отдельной строке. Выведите \(A(m, n)\).

D: Точная степень двойки

Дано натуральное число N. Выведите слово , если число N является точной степенью двойки, или слово в противном случае.

Операцией возведения в степень пользоваться нельзя!

E: Сумма цифр числа

Дано натуральное число N. Вычислите сумму его цифр.

При решении этой задачи нельзя использовать строки, списки, массивы (ну и циклы, разумеется).

F: Цифры числа справа налево

Дано натуральное число N. Выведите все его цифры по одной, в обратном порядке, разделяя их пробелами или новыми строками.

При решении этой задачи нельзя использовать строки, списки, массивы (ну и циклы, разумеется). Разрешена только рекурсия и целочисленная арифметика.

G: Цифры числа слева направо

Дано натуральное число N. Выведите все его цифры по одной, в обычном порядке, разделяя их пробелами или новыми строками.

При решении этой задачи нельзя использовать строки, списки, массивы (ну и циклы, разумеется). Разрешена только рекурсия и целочисленная арифметика.

H: Проверка числа на простоту

Дано натуральное число \(n>1\). Проверьте, является ли оно простым. Программа должна вывести слово , если число простое и , если число составное. Алгоритм должен иметь сложность \(O(\sqrt{n})\).

Указание. Понятно, что задача сама по себе нерекурсивна, т.к. проверка числа \(n\) на простоту никак не сводится к проверке на простоту меньших чисел. Поэтому нужно сделать еще один параметр рекурсии: делитель числа, и именно по этому параметру и делать рекурсию.

I: Разложение на множители

Дано натуральное число \(n>1\). Выведите все простые делители этого числа в порядке неубывания с учетом кратности. Алгоритм должен иметь сложность \(O(\sqrt{n})\).

J: Палиндром

Дано слово, состоящее только из строчных латинских букв. Проверьте, является ли это слово палиндромом. Выведите или .

При решении этой задачи нельзя пользоваться циклами, в решениях на питоне нельзя использовать срезы с шагом, отличным от 1.

Ввод	Вывод
radar	YES
yes	NO

K: Вывести нечетные числа последовательности

Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Выведите все нечетные числа из этой последовательности, сохраняя их порядок.

В этой задаче нельзя использовать глобальные переменные и передавать какие-либо параметры в рекурсивную функцию. Функция получает данные, считывая их с клавиатуры. Функция не возвращает значение, а сразу же выводит результат на экран. Основная программа должна состоять только из вызова этой функции.

L: Вывести члены последовательности с нечетными номерами

Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Выведите первое, третье, пятое и т.д. из введенных чисел. Завершающий ноль выводить не надо.

В этой задаче нельзя использовать глобальные переменные и передавать какие-либо параметры в рекурсивную функцию. Функция получает данные, считывая их с клавиатуры. Функция не возвращает значение, а сразу же выводит результат на экран. Основная программа должна состоять только из вызова этой функции.

M: Максимум последовательности

Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите наибольшее значение числа в этой последовательности.

В этой задаче нельзя использовать глобальные переменные и передавать какие-либо параметры в рекурсивную функцию. Функция получает данные, считывая их с клавиатуры. Функция возвращает единственное значение: максимум считанной последовательности. Гарантируется, что последовательность содержит хотя бы одно число (кроме нуля).

N: Среднее значение последовательности

Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите среднее значение элементов этой последовательности (без учета последнего нуля).

В этой задаче нельзя использовать глобальные переменные. Функция получает данные, считывая их с клавиатуры, а не получая их в виде параметра. В программе на языке Python функция возвращает кортеж из пары чисел: число элементов в последовательности и их сумма. В программе на языке C++ результат записывается в две переменные, которые передаются в функцию по ссылке.

Гарантируется, что последовательность содержит хотя бы одно число (кроме нуля).

Ввод	Вывод
1 7 9 0	5.666666666666667

O: Второй максимум

Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите значение второго по величине элемента в этой последовательности, то есть элемента, который будет наибольшим, если из последовательности удалить наибольший элемент.

В этой задаче нельзя использовать глобальные переменные. Функция получает данные, считывая их с клавиатуры, а не получая их в виде параметра. В программе на языке Python функция возвращает результат в виде кортежа из нескольких чисел и функция вообще не получает никаких параметров. В программе на языке C++ результат записывается в переменные, которые передаются в функцию по ссылке. Других параметров, кроме как используемых для возврата значения, функция не получает.

Гарантируется, что последовательность содержит хотя бы два числа (кроме нуля).

Ввод	Вывод
1 7 9 0	7
1 2 2 1 0	2

P: Количество элементов, равных максимуму

Дана последовательность натуральных чисел (одно число в строке), завершающаяся числом 0. Определите, какое количество элементов этой последовательности, равны ее наибольшему элементу.

В этой задаче нельзя использовать глобальные переменные. Функция получает данные, считывая их с клавиатуры, а не получая их в виде параметра.

В программе на языке Python функция возвращает результат в виде кортежа из нескольких чисел и функция вообще не получает никаких параметров. В программе на языке C++ результат записывается в переменные, которые передаются в функцию по ссылке. Других параметров, кроме как используемых для возврата значения, функция не получает.

Гарантируется, что последовательность содержит хотя бы одно число (кроме нуля).

Ввод	Вывод
1 7 9 0	1
1 3 3 1 0	2

Q: Количество единиц

Дана последовательность натуральных чисел (одно число в строке), завершающаяся двумя числами 0 подряд. Определите, сколько раз в этой последовательности встречается число 1. Числа, идущие после двух нулей, необходимо игнорировать.

В этой задаче нельзя использовать глобальные переменные и параметры, передаваемые в функцию. Функция получает данные, считывая их с клавиатуры, а не получая их в виде параметров.

R: Треугольная последовательность

Дана монотонная последовательность, в которой каждое натуральное число k встречается ровно k раз: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, …

По данному натуральному n выведите первые n членов этой последовательности. Попробуйте обойтись только одним циклом for.

Ввод	Вывод
2	1 2
5	1 2 2 3 3

S: Заданная сумма цифр

Даны натуральные числа \(k\) и \(s\). Определите, сколько существует \(k\)-значных натуральных чисел, сумма цифр которых равна \(d\). Запись натурального числа не может начинаться с цифры 0.

В этой задаче можно использовать цикл для перебора всех цифр, стоящих на какой-либо позиции.

T: Без двух нулей

Даны числа \(a\) и \(b\). Определите, сколько существует последовательностей из \(a\) нулей и \(b\) единиц, в которых никакие два нуля не стоят рядом.

U: Разворот числа

Дано число \(n\), десятичная запись которого не содержит нулей. Получите число, записанное теми же цифрами, но в противоположном порядке.

При решении этой задачи нельзя использовать циклы, строки, списки, массивы, разрешается только рекурсия и целочисленная арифметика.

Фунция должна возвращать целое число, являющееся результатом работы программы, выводить число по одной цифре нельзя.

steptosleep.ru

это… Что такое Рекурсия? 💯 ✅

Рекурсивное изображение экрана Визуальная форма рекурсии страницы Википедии

Реку́рсия — процесс повторения элементов самоподобным образом. Например, если два зеркала установить друг напротив друга, то возникающие в них вложенные отражения суть одна из форм бесконечной рекурсии.

Термин «рекурсия» используется в различных специальных областях знаний — от лингвистики до логики, но наиболее широкое применение находит в математике и информатике. В математике и информатике рекурсия имеет отношение к методу определения функций: рекурсивно заданная функция в своём определении содержит себя, в частности, рекурсивной является функция, заданная рекуррентной формулой. Таким образом, можно одним выражением дать бесконечный набор способов вычисления функции, определить множество объектов через самого себя с использованием ранее заданных частных определений.

С рекурсией тесно связана математическая индукция: она является естественным способом доказательства свойств функций на натуральных числах, рекурсивно заданных через свои меньшие значения.

В математике

В программировании

Функции

В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная или косвенная рекурсия), например, функция вызывает функцию , а функция  — функцию . Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.

Преимущество рекурсивного определения объекта заключается в том, что такое конечное определение теоретически способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.

Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за счёт этого работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого, обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.

Имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивается выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. Однако, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Scheme (диалект языка Lisp), описание которого содержит все необходимые сведения.

Любую рекурсивную функцию можно заменить циклом и стеком.

Данные

Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):

 struct element_of_list
 {
   element_of_list *next; /* ссылка на следующий элемент того же типа */
   int data; /* некие данные */
 };

Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.

В физике

Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из уменьшающихся отражений зеркал.

Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.

В лингвистике

См. также: Рекурсия (лингвистика)

Способность языка порождать вложенные предложения и конструкции. Базовое предложение «кошка съела мышь» может быть за счёт рекурсии расширено как Ваня догадался, что кошка съела мышь, далее как Катя знает, что Ваня догадался, что кошка съела мышь и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку. Однако, в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Дэниэл Эверетт (англ.)^[1].

В культуре

Большая часть шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода, например, известно высказывание: «чтобы понять рекурсию, нужно сначала понять рекурсию».

Весьма популярна шутка о рекурсии, напоминающая словарную статью:

Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:

• рассказ про Йона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки»:

Нашёл следующие краткие сведения:
«СЕПУЛЬКИ — важный элемент цивилизации ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКАРИИ».
Я последовал этому совету и прочёл:
«СЕПУЛЬКАРИИ — устройства для сепуления (см.)».
Я поискал «Сепуление»; там значилось:
«СЕПУЛЕНИЕ — занятие ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКИ».

Лем С. «Звёздные дневники Ийона Тихого. Путешествие четырнадцатое.»

• Рассказ из «Кибериады» о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).
• Рекурсивные акронимы: GNU (GNU Not Unix), PHP (PHP: Hypertext Preprocessor) и т. д.

См. также

Примечания

dal.academic.ru

это… Что такое Рекурсия? 💯 ✅

Рекурсивное изображение экрана Визуальная форма рекурсии страницы Википедии

Реку́рсия — процесс повторения элементов самоподобным образом. Например, если два зеркала установить друг напротив друга, то возникающие в них вложенные отражения суть одна из форм бесконечной рекурсии.

Термин «рекурсия» используется в различных специальных областях знаний — от лингвистики до логики, но наиболее широкое применение находит в математике и информатике. В математике и информатике рекурсия имеет отношение к методу определения функций: рекурсивно заданная функция в своём определении содержит себя, в частности, рекурсивной является функция, заданная рекуррентной формулой. Таким образом, можно одним выражением дать бесконечный набор способов вычисления функции, определить множество объектов через самого себя с использованием ранее заданных частных определений.

С рекурсией тесно связана математическая индукция: она является естественным способом доказательства свойств функций на натуральных числах, рекурсивно заданных через свои меньшие значения.

В математике

В программировании

Функции

В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная или косвенная рекурсия), например, функция вызывает функцию , а функция  — функцию . Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.

Преимущество рекурсивного определения объекта заключается в том, что такое конечное определение теоретически способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.

Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за счёт этого работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого, обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.

Имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивается выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. Однако, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Scheme (диалект языка Lisp), описание которого содержит все необходимые сведения.

Любую рекурсивную функцию можно заменить циклом и стеком.

Данные

Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):

 struct element_of_list
 {
   element_of_list *next; /* ссылка на следующий элемент того же типа */
   int data; /* некие данные */
 };

Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.

В физике

Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из уменьшающихся отражений зеркал.

Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.

В лингвистике

См. также: Рекурсия (лингвистика)

Способность языка порождать вложенные предложения и конструкции. Базовое предложение «кошка съела мышь» может быть за счёт рекурсии расширено как Ваня догадался, что кошка съела мышь, далее как Катя знает, что Ваня догадался, что кошка съела мышь и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку. Однако, в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Дэниэл Эверетт (англ.)^[1].

В культуре

Большая часть шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода, например, известно высказывание: «чтобы понять рекурсию, нужно сначала понять рекурсию».

Весьма популярна шутка о рекурсии, напоминающая словарную статью:

Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:

• рассказ про Йона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки»:

Нашёл следующие краткие сведения:
«СЕПУЛЬКИ — важный элемент цивилизации ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКАРИИ».
Я последовал этому совету и прочёл:
«СЕПУЛЬКАРИИ — устройства для сепуления (см.)».
Я поискал «Сепуление»; там значилось:
«СЕПУЛЕНИЕ — занятие ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКИ».

Лем С. «Звёздные дневники Ийона Тихого. Путешествие четырнадцатое.»

• Рассказ из «Кибериады» о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).
• Рекурсивные акронимы: GNU (GNU Not Unix), PHP (PHP: Hypertext Preprocessor) и т. д.

См. также

Примечания

brokgauz.academic.ru

No related posts.