Как округлять числа правильно?
Поможем понять и полюбить математику
Начать учиться
237.9K
Если хорошо изучить тему приближенных значений — можно объяснить любому взрослому, почему ты поздно пришел домой или забыл дневник. Спойлер: точной договоренности нет — есть приблизительная. А теперь по порядку о правилах математического округления.
Приближенные значения
В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.
У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин иногда можно использовать приближенные значения.
Поэтому вместо точных значений величин иногда можно использовать приближенные значения.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Примерчики
Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.
Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.
Если длина платья 1 м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.
Приближенное значение — число, которое получилось после округления.
Для записи результата округления используют знак «приблизительно равно» — ≈.
Округлить можно любое число — для всех чисел работают одни и те же правила.
Округлить число значит сократить его значение до нужного разряда, например, до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Округление натуральных чисел
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.
Особенности натуральных чисел:
- Наименьшее натуральное число: единица (1).
- Наибольшего натурального числа не существует. Натуральный ряд бесконечен.
- У натурального ряда каждое следующее число больше предыдущего на единицу: 1, 2, 3, 4, 5, 6, 7.

Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.
Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.
Правила округления чисел:
- Подчеркнуть цифру разряда, до которого надо округлить число.
- Отделить все цифры справа от этого разряда вертикальной чертой.
- Если справа от подчеркнутой цифры стоит 0,1, 2, 3 или 4 — все цифры, которые отделены справа, заменяем нулями. Цифру разряда, до которой округляли, оставляем без изменений.
- Если справа от подчеркнутой цифры стоит 5, 6, 7, 8 или 9 — все цифры, которые отделены справа, заменяем нулями.

Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.
После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.
Теперь округлим 756 485 до сотен:
Округлим число 123 до десятков: 123 ≈ 120.
Округлим число 3581 до сотен: 3581 ≈ 3580.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.
Примеры:
- как округлить число 697 до десятков — 697 ≈ 700;
- как округлить число 980 до сотен — 980 ≈ 1000.
Иногда уместно записать округленный результат с сокращениями «тыс. » (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:
» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:
- 7 882 000 = 7 882 тыс.
- 1 000 000 = 1 млн.
Округление десятичных дробей
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Есть два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10 000 и т. д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,7
- 9,891
При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:
И у каждой из этих частей есть свои разряды:
Разряды целой части:
- разряд единиц;
- разряд десятков;
- разряд сотен;
- разряд тысяч.
Разряды дробной части:
- разряд десятых;
- разряд сотых;
Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.
Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248. При этом у каждой из них есть свои разряды, которые важно не перепутать:
Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.
Цифра, которая записана в данном разряде:
- не меняется, если следующая за ней справа цифра — 0,1, 2, 3 или 4;
- увеличивается на единицу, если за ней справа следует цифра — 5, 6, 7, 8 или 9.
Как округлить до десятых. Оставить одну цифру после запятой, остальные отбросить. Согласно правилу выше, если первая отбрасываемая цифра — 0, 1, 2, 3 или 4, то цифра после запятой остается той же. Если мы отбрасываем цифру 5, 6, 7, 8 или 9 — цифра после запятой увеличивается на единицу.
Как округлить до сотых. Оставить две цифры после запятой, остальные отбросить. И снова не забываем про правило: если следующая цифра 0, 1, 2, 4 — цифра в разряде сотых остается неизменной. Если же это 5, 6, 7, 8 или 9, то цифра в разряде сотых увеличится на 1.
Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.
Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.
Пример 1
256,43 ≈ 256,4 — округление до десятых;
4,578 ≈ 4,58 — округление до сотых;
17,935 ≈ 18 — округление до целых.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра слева в предыдущем разряде увеличивается на 1.
Пример 2
79,7 ≈ 80 — округление до десятков;
0,099 ≈ 0,10 — округление до сотых.
Математическое округление и его правила быстро запомнится, если не лениться решать примеры и задачки из учебников 5 класса.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
434.3K
График линейной функции, его свойства и формулы
194.2K
Факториал
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
§ Округление чисел. Правила округления натуральных чисел
Округление чисел Округление десятичных дробей
Числа округляют, когда полная точность не нужна или невозможна.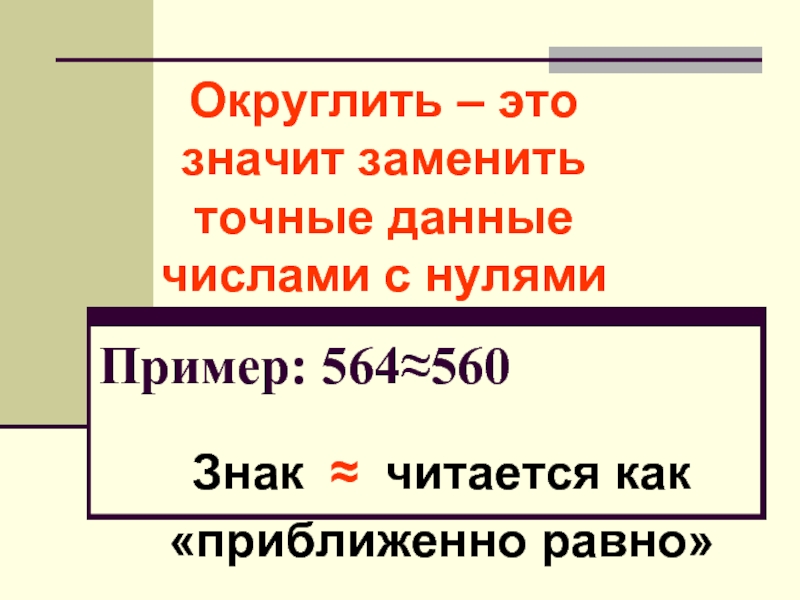
Запомните!
Округлить число до определенной цифры (знака), значит заменить его близким по значению числом с нулями на конце.
Натуральные числа округляют до десятков, сотен, тысяч и т.д. Названия цифр в разрядах натурального числа можно вспомнить в теме натуральные числа.
В зависимости от того, до какого разряда надо округлить число, мы заменяем нулями цифру в разрядах единиц, десятков и т.д.
Если число округляется до десятков, то нулями заменяем цифру в разряде единицы.
Если число округляется до сотен, то цифра ноль должна стоять и в разряде единиц, и в разряде десятков.
Запомните!
Число, полученное при округлении, называют приближённым значением данного числа.
Записывают результат округления после специального знака «≈». Этот знак читается как «приближённо равно».
При округлении натурального числа до какого-либо разряда надо воспользоваться правилами округления.
- Подчеркнуть цифру разряда, до которого надо округлить число.
- Отделить все цифры, стоящие справа этого разряда вертикальной чертой.
- Если справа от подчёркнутой цифры стоит цифра 0, 1, 2, 3 или 4 , то все цифры, которые отделены справа, заменяются нулями. Цифру разряда, до которой округляли, оставляем без изменений.
- Если справа от подчёркнутой цифры стоит цифра 5, 6, 7, 8 или 9 , то все цифры, которые отделены справа, заменяются нулями, а к цифре разряда, до которой округляли, прибавляется 1.
Поясним на примере. Округлим 57 861 до тысяч. Выполним первые два пункта из правил округления.
После подчёркнутой цифры стоит цифра 8, значит к цифре разряда тысяч (у нас это 7) прибавим 1, а все цифры, отделённые вертикальной чертой заменим нулями.
Теперь округлим 756 485 до сотен.
Округлим 364 до десятков.
36|4 ≈ 360 — в разряде единиц стоит 4, поэтому мы оставляем 6 в разряде десятков без изменений.
На числовой оси число 364 заключено между двумя «круглыми» числами 360 и 370. Эти два числа называют приближёнными значениями числа 364 с точностью до десятков.
Число 360 — приближённое значение с недостатком, а число 370 — приближённое значение с избытком.
В нашем случае, округлив 364 до десятков, мы получили, 360 — приближённое значение с недостатком.
Округлённые результаты часто записывают без нулей, добавляя сокращения «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард).
Примеры:
- 8 659 000 = 8 659 тыс.
- 3 000 000 = 3 млн.
Округление также применяется для прикидочной проверки ответа в вычислениях.
Пусть нам нужно посчитать:
794 · 52 =
До точного вычисления сделаем прикидку ответа, округлив множители до наивысшего разряда.
794 · 52 ≈ 800 · 50 ≈ 40 000
Делаем вывод, что ответ будет близок к 40 000.
794 · 52 = 41 228
Аналогично можно выполнять прикидку округлением и при делении чисел.
Округление чисел Округление десятичных дробей
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».
Оставить комментарий:
| Отправить |
Округление чисел: правила и примеры для дробей и сумм
Например, 341, округленное до ближайшей сотни, равно 300. Это потому, что 341 по значению ближе к 300, чем к 400. При округлении до ближайшего доллара 1,89 доллара становится 2,09 доллара, потому что 1 доллар. ближе к 2 долларам США, чем к 1 доллару США
При округлении до ближайшего доллара 1,89 доллара становится 2,09 доллара, потому что 1 доллар. ближе к 2 долларам США, чем к 1 доллару США
Правила округления
Вот общее правило округления:
- Если за округляемым числом следует 5, 6, 7, 8 или 9, округляйте число в большую сторону. Пример: 38, округленное до десятых, равно 40 1
- Если за округляемым числом следует 0, 1, 2, 3 или 4, округлите число в меньшую сторону. Пример: 33 при округлении до десятых равно 30
До чего вы округляете?
При округлении числа сначала нужно спросить: до чего вы его округляете? Числа можно округлить до ближайших десятков, сотен, тысяч и т. д.
Рассмотрим число 4827.
- 4,827 округлить до десятых будет 4,830
- 4,827 округлить до ближайшей сотни получится 4,800
- 4,827 округлить до ближайшей тысячи будет 5,000 . Вот еще несколько примеров:
- 34 округлить до десятых будет 30
- 6,809 округление до ближайшей сотни равно 6,800
- 1,951 округление до ближайшей тысячи равно 2,000
Округление и дроби
Округление дробей работает точно так же, как округление целых чисел .
 Разница лишь в том, что округление производится не до десятков, сотен, тысяч и т. д., а до десятых, сотых, тысячных и т. д.
Разница лишь в том, что округление производится не до десятков, сотен, тысяч и т. д., а до десятых, сотых, тысячных и т. д.- 7,8199 округлить до десятых 7,8
- 1,0621 округлить до сотых 1,06
- 3.8792 округлить до тысячных будет 3.879
Вот совет: до не путайтесь при округлении длинных десятичных дробей, смотрите только на число в том месте, до которого вы округляете, и на число, которое следует за ним. Например, чтобы округлить 5,3824791401 до сотых, просто посмотрите на число в сотых долях — 8 — и на следующее за ним число — 2. Тогда вы можете легко округлить его до 5,38.
Округление и суммирование
Округление сделать суммы легко. Например, в продуктовом магазине вы можете купить товары по следующим ценам:
- 2,25 доллара
- 0,88 доллара
- 2,69 доллара
Если вы хотите узнать, сколько они будут стоить, вы можете сложить цены с помощью ручку и бумагу или попробуйте сложить их в уме.
 Или вы можете сделать это простым способом — округлить до ближайшего доллара, например:
Или вы можете сделать это простым способом — округлить до ближайшего доллара, например:- 2 доллара
- 1 доллар
- 3 доллара
Округляя, можно легко вычислить, что вам потребуется около 6 долларов, чтобы заплатить за продукты. Это довольно близко к точному числу в 5,82 доллара.
Как видите, при нахождении круглой суммы быстрее всего округлить числа перед их сложением.
1. Некоторые статистики предпочитают округлять 5 до ближайшего четного числа. В результате примерно в половине случаев 5 будет округляться в большую сторону, а примерно в половине случаев — в меньшую. Таким образом, 26,5, округленное до ближайшего четного числа, будет равно 26 — оно будет округлено в меньшую сторону. И 77,5, округленное до ближайшего четного числа, будет 78 — оно будет округлено в большую сторону.
База данных Fact Monster/Information Please®, © 2008 Pearson Education, Inc. Все права защищены.
Методы округления
Существует множество способов округления чисел.
 ..
.. Во-первых, что такое «Округление»?
Округление означает сделать число проще , но сохранить его значение близким к тому, что было. Результат менее точен, но проще в использовании.
Пример: 7,3 раунда до 7
Поскольку 7,3 ближе к 7, чем к 8
(Примечание: в этих примерах мы округляем до целых чисел, но можем округлять до десятков, десятых и т. д.)
А как насчет 7.5 ? Ближе к 7 или ближе к 8?
7.5 находится на полпути между ними, так что же нам делать?
Half Round Up (общий метод округления)
Общий метод округления состоит в том, чтобы сделать 0,5 к до , поэтому 7,5 раундов до 8
7,5 обычно округляется до 8
Но это не закон или что-то в этом роде, это просто то, что люди обычно делают, и мы получаем это:
- 7,6 раундов до 8
- 7,5 патронов до 8
- 7,4 округления до 7
Узнайте больше об этом методе в округлении чисел.

Полукруглая вниз
Но 5 может заменить , если мы захотим. В этом случае 7,5 округляется до 7, и мы получаем:
- 7,6 раундов до 8
- 7,5 раундов до 7
- 7,4 округления до 7
Но мы всегда должны информировать людей о том, что мы используем «Half Round Down».
Зачем снижать 0.5? Может быть, в наших числах много 0,5, и мы хотим посмотреть, как округление в меньшую сторону повлияет на наши результаты.
Поиграйте… попробуйте различные методы округления в инструменте округления.
Отрицательные числа
А как же -7,5 ?
- Округляет до -8 (и идет ли это «вверх» или «вниз»?),
- Или округляется до -7 ?
Помогите! Я смущен!
На самом деле весь мир запутался в округлении отрицательных чисел… одни компьютерные программы округляют от -7,5 до -8, другие до -7
Но мы можем согласиться, что здесь , что «вверх» означает движение в положительном направлении, как в этой числовой строке:
Half Round Up (включая отрицательные числа)
Получаем вот это:
- 7,6 раундов до 8
- 7,5 патронов до 8
- 7,4 округления до 7
- -7,4 раунда до -7
- -7,5 патронов до -7
- -7,6 округляется до -8
Половина округления вниз (включая отрицательные числа)
Когда мы округляем 0,5 до получаем это:
- 7,6 раундов до 8
- 7,5 раундов до 7
- 7,4 округления до 7
- -7,4 раунда до -7
- -7,5 раундов до -8
- -7,6 округляется до -8
«Симметричное» округление
Но, может быть, вы думаете, что «7,5 округляется до 8, поэтому -7,5 должно превратиться в -8», что красиво и симметрично.

Вам повезло, потому что это округление до или от нуля :
Половина раунда от 0
Для этого метода число округляется до 0,5, так что оно будет на дальше от нуля , например:
- 7,6 раундов до 8
- 7,5 раундов до 8
- 7,4 раунда до 7
- -7,4 патронов до -7
- -7,5 раундов до -8
- -7,6 раундов до -8
Круглая половина к 0
Или мы можем округлить число до нуля на 0,5, например:
- 7,6 раундов до 8
- 7,5 патронов до 7
- 7,4 раунда до 7
- -7,4 патронов до -7
- -7,5 патронов до -7
- -7,6 раундов до -8
Но быть последовательным может быть плохо
Выбор любого из этих методов может быть плохим!
Представьте, что вы складываете длинный список чисел. Вы решаете округлить каждое число, чтобы сделать это быстрее. Если 0,5 много, все они округляются, и ваш ответ будет иметь смещение .

Пример: Сложите эти числа до и после округления: 5,5, 7,5, 6,5, 9,5
Перед округлением: 5,5 + 7,5 + 6,5 + 9,5 = 29
После округления: 6 + 8 + 7 + 10 = 0 31 31
Расчет был намного проще, но ответ сместился до много!
Как мы можем остановить округление в одном направлении?
Мы можем решить округлить до четных (или нечетных) чисел , или мы можем просто выбрать случайным образом .
Округление до четного (банковское округление)
Округляем 0,5 до ближайшего даже цифра
Пример:
7,5 раундов до до 8 (поскольку 8 — четное число)
но 6,5 раундов вниз с до 6 (поскольку 6 — четное число)
Остальные числа (не оканчивающиеся на 0,5) округляются до ближайшего, как обычно, поэтому:
- 7,6 раундов до 8
- 7,5 раундов до до 8 (поскольку 8 — четное число)
- 7,4 округления до 7
- 6,6 раундов до 7
- 6,5 раундов вниз с до 6 (поскольку 6 — четное число)
- 6,4 округления до 6
- и т.
 д.
д.
Округлить до нечетного
То же, что «Округлить до четного», но 0,5 приближается к нечетным числам
Пример:
7,5 округлить до 7 (поскольку 7 — нечетное число)
, но 6,5 округлить до до 7 (поскольку 7 — нечетное число)
Раунд случайным образом
Мы также можем произвольно округлять 0,5 в большую или меньшую сторону, но как? Подбрасывая монетку? Или функция компьютера?
С большим списком чисел это может дать хорошие результаты, но каждый раз дает другой ответ (если только мы не используем фиксированный список случайных выборов).
Пол и потолок
Есть два других метода, которые даже не учитывают 0,5. Их называют напольными и потолочными.
Этаж дает нам ближайшее целое число ниже (и потолок поднимается).
Пример: Каковы пол и потолок 2,31?
Этаж 2.31 это 2
Верхний предел 2.31 3Этаж
При использовании «пола» все цифры идут вниз, независимо от того, какая цифра отброшена:
Пример: 7,8 уменьшается до 7
то же самое происходит и с 7,2, 7,5, 7,9 и т.
 д.
д.И 7 тоже превращается в 7.
Потолок
И «потолок» поднимается:
Пример: 7.1 становится 8
, то же самое происходит с 7.2, 7.5, 7.8 и т. д.
Но 7 остается на 7 .
Резюме
Номер Половина
UPПоловина Половина
ВАШ 0Половина
до 0Пол. 8 8 8 8 8 8 8 8 82 9
7,6 8 8 8 8 8 8 7 8 7,5 8 7 8 7 8 7 909078 882 82
7.  4
47 7 7 7 7 7 909078 282 72
7 7 7 7 7 7 7 7 7 -7 -7 -7 -7 -7 -7 -7 -72 — 7 -72 — 7 -7,4 -7 -7 -7 -7 -7 -7 1 -8
2 2 -7,5 -7 -8 -8 -7 -8 -7 -8 -7 -7,6 -8 -8 -8 -8 -8 -8 1 -8
2 2 -8 -8 -8 -8 -8 -8 -8 -82 — Округление до десятков, десятых, сколько угодно.




 Разница лишь в том, что округление производится не до десятков, сотен, тысяч и т. д., а до десятых, сотых, тысячных и т. д.
Разница лишь в том, что округление производится не до десятков, сотен, тысяч и т. д., а до десятых, сотых, тысячных и т. д.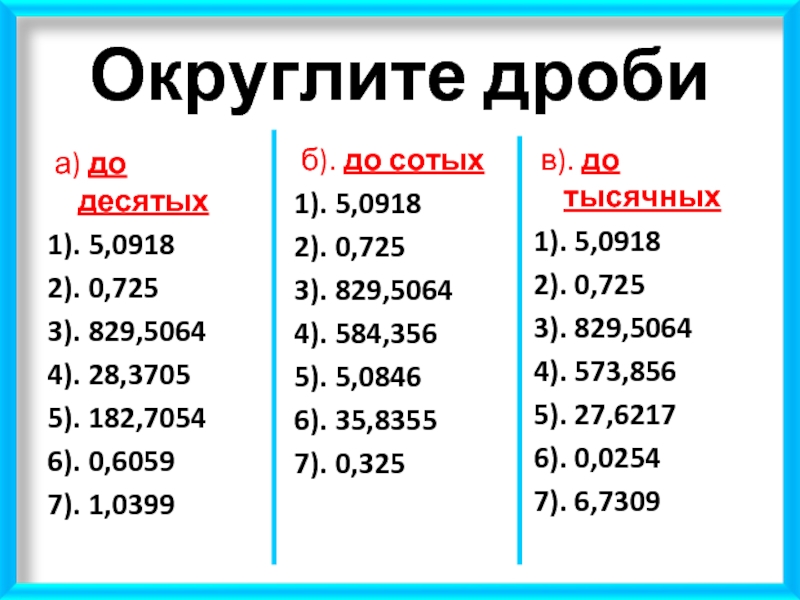 Или вы можете сделать это простым способом — округлить до ближайшего доллара, например:
Или вы можете сделать это простым способом — округлить до ближайшего доллара, например: ..
.. 


 д.
д. д.
д. 4
4