Способы округления чисел: МЕТОДЫ ОКРУГЛЕНИЯ

Как округлять числа правильно?

Приближенные значения

В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.

У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин иногда можно использовать приближенные значения.

Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!

Примерчики

1. Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.

2. Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.

3. Если длина платья 1 м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.

Приближенное значение — число, которое получилось после округления.

Для записи результата округления используют знак «приблизительно равно» — ≈.

Округлить можно любое число — для всех чисел работают одни и те же правила.

Округлить число значит сократить его значение до нужного разряда, например, до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Округление натуральных чисел

Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое.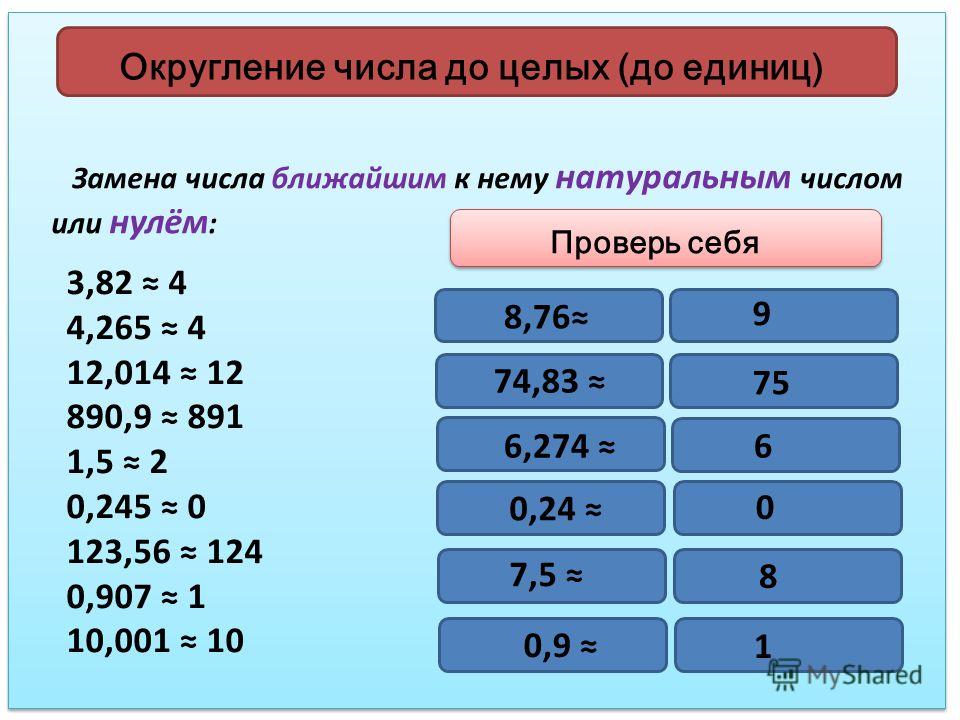 Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.

Особенности натуральных чисел:

• Наименьшее натуральное число: единица (1).
• Наибольшего натурального числа не существует. Натуральный ряд бесконечен.
• У натурального ряда каждое следующее число больше предыдущего на единицу: 1, 2, 3, 4, 5, 6, 7.

Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.

Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.

Правила округления чисел:

 

1. Подчеркнуть цифру разряда, до которого надо округлить число.


2. Отделить все цифры справа от этого разряда вертикальной чертой.


3. Если справа от подчеркнутой цифры стоит 0,1, 2, 3 или 4 — все цифры, которые отделены справа, заменяем нулями. Цифру разряда, до которой округляли, оставляем без изменений.


4. Если справа от подчеркнутой цифры стоит 5, 6, 7, 8 или 9 — все цифры, которые отделены справа, заменяем нулями. К цифре разряда, до которой округляли, прибавляем 1.

Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.

После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.

Теперь округлим 756 485 до сотен:

Округлим число 123 до десятков: 123 ≈ 120.

Округлим число 3581 до сотен: 3581 ≈ 3580.

Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.

Примеры:

• как округлить число 697 до десятков — 697 ≈ 700;
• как округлить число 980 до сотен — 980 ≈ 1000.

Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:

• 7 882 000 = 7 882 тыс.
• 1 000 000 = 1 млн.

Округление десятичных дробей

Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Есть два формата записи:

• обыкновенный вид — 1/2 или a/b,
• десятичный вид — 0,5.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10 000 и т. д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,7
• 6,35
• 9,891

При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:

Разряды целой части:

• разряд единиц;
• разряд десятков;
• разряд сотен;
• разряд тысяч.

Разряды дробной части:

• разряд десятых;
• разряд сотых;
• разряд тысячных.

Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.

Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248. При этом у каждой из них есть свои разряды, которые важно не перепутать:

Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.

То число, к которому дробь ближе, называют округленным значением числа.

Цифра, которая записана в данном разряде:

• не меняется, если следующая за ней справа цифра — 0,1, 2, 3 или 4;
• увеличивается на единицу, если за ней справа следует цифра — 5, 6, 7, 8 или 9.

Как округлить до десятых. Оставить одну цифру после запятой, остальные отбросить.

Согласно правилу выше, если первая отбрасываемая цифра — 0, 1, 2, 3 или 4, то цифра после запятой остается той же. Если мы отбрасываем цифру 5, 6, 7, 8 или 9 — цифра после запятой увеличивается на единицу.

Как округлить до сотых. Оставить две цифры после запятой, остальные отбросить. И снова не забываем про правило: если следующая цифра 0, 1, 2, 4 — цифра в разряде сотых остается неизменной. Если же это 5, 6, 7, 8 или 9, то цифра в разряде сотых увеличится на 1.

Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.

Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.

Пример 1

256,43 ≈ 256,4 — округление до десятых;

4,578 ≈ 4,58 — округление до сотых;

17,935 ≈ 18 — округление до целых.

Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра слева в предыдущем разряде увеличивается на 1.

Пример 2

79,7 ≈ 80 — округление до десятков;

0,099 ≈ 0,10 — округление до сотых.

Математическое округление и его правила быстро запомнится, если не лениться решать примеры и задачки из учебников 5 класса.

Округление числа в Excel

Excel

Формулы и функции

Другие функции

Другие функции

Округление числа в Excel

Excel для Microsoft 365 Excel для Интернета Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше

Предположим, что необходимо округить число до ближайшего целого, так как десятичная часть не имеет для вас значения. Или вы хотите округление числа до кратного 10, чтобы упростить аппроксимацию сумм.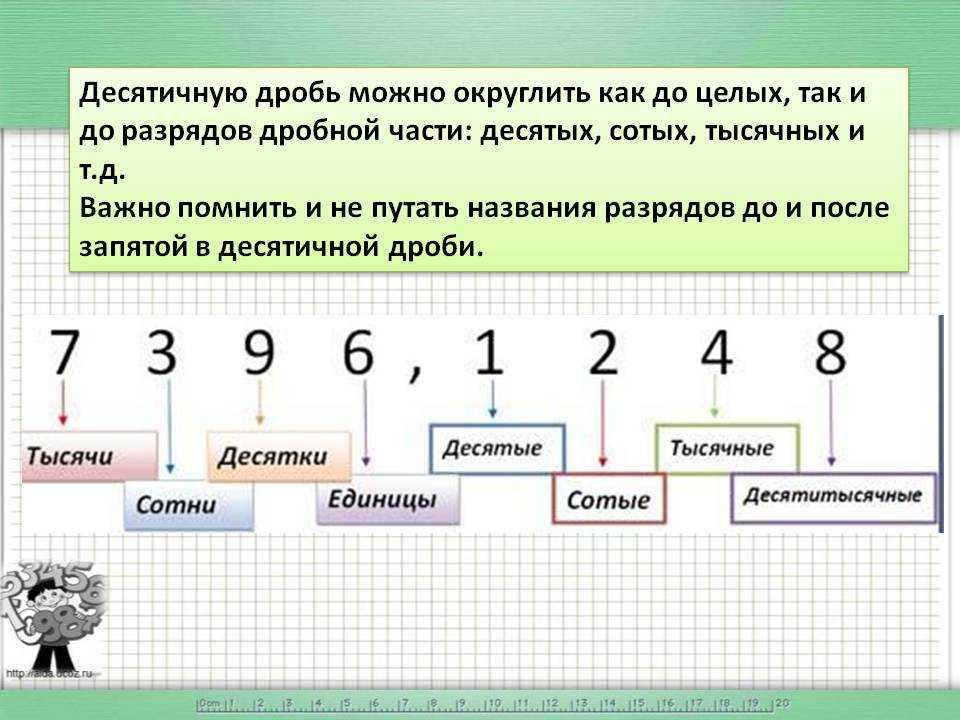

Существует несколько способов округлки числа.

Изменение количества знаков после запятой без изменения значения

На листе

1. Выделите ячейки, формат которых требуется изменить.

2. Чтобы после запятой отображалось больше или меньше знаков, на вкладке Главная в группе Число нажмите кнопку Увеличить разрядность или Уменьшить разрядность .

Во встроенном числовом формате

1. org/ListItem»>

   На вкладке Главная в группе Число щелкните стрелку рядом со списком числовых форматов и выберите пункт

   Другие числовые форматы.

2. В списке Категория выберите значение Денежный, Финансовый, Процентный или Экспоненциальный в зависимости от типа данных.

3. В поле Число десятичных знаков введите требуемое число знаков после запятой.

Округление числа вверх

Используйте функцию ОКРУГЛВВЕРХ. В некоторых случаях может потребоваться использовать функции ЧЁТН и НЕЧЁТ для округления вверх до ближайшего четного или нечетного числа.

Округление числа вниз

Используйте функцию ОКРУГЛВНИЗ.

Округление числа до ближайшего значения

Используйте функцию ОКРУГЛ.

Округление числа до ближайшего дробного значения

Используйте функцию ОКРУГЛ.

Округление числа до указанного количества значимых разрядов

Значимые разряды — это разряды, которые влияют на точность числа.

В примерах этого раздела используются функции ОКРУГЛ, ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ. Они показывают способы округления положительных, отрицательных, целых и дробных чисел, но приведенные примеры охватывают лишь небольшую часть возможных ситуаций.

В приведенном ниже списке содержатся общие правила, которые необходимо учитывать при округлении чисел до указанного количества значимых разрядов. Вы можете поэкспериментировать с функциями округления и подставить собственные числа и параметры, чтобы получить число с нужным количеством значимых разрядов.

• Округляемые отрицательные числа прежде всего преобразуются в абсолютные значения (значения без знака «минус»). После округления знак «минус» применяется повторно. Хотя это может показаться нелогичным, именно так выполняется округление. Например, при использовании функции ОКРУГЛВНИЗ для округления числа -889 до двух значимых разрядов результатом является число -880. Сначала -889 преобразуется в абсолютное значение (889). Затем это значение округляется до двух значимых разрядов (880). После этого повторно применяется знак «минус», что дает в результате -880.

• При применении к положительному числу функции ОКРУГЛВНИЗ оно всегда округляется вниз, а при применении функции ОКРУГЛВВЕРХ — вверх.

• Функция ОКРУГЛ округляет дробные числа следующим образом: если дробная часть больше или равна 0,5, число округляется вверх. Если дробная часть меньше 0,5, число округляется вниз.

• Функция ОКРУГЛ округляет целые числа вверх или вниз аналогичным образом, при этом вместо делителя 0,5 используется 5.

• В общем при округлении числа без дробной части (целого числа) необходимо вычесть длину числа из нужного количества значимых разрядов. Например, чтобы округлить 2345678 вниз до 3 значимых разрядов, используется функция ОКРУГЛВНИЗ с параметром -4: = ОКРУГЛВНИЗ(2345678,-4). При этом число округляется до значения 2340000, где часть «234» представляет собой значимые разряды.

Округление числа до заданного кратного

Иногда может потребоваться округлить значение до кратного заданному числу. Например, допустим, что компания поставляет товары в ящиках по 18 единиц. С помощью функции ОКРУГЛТ можно определить, сколько ящиков потребуется для поставки 204 единиц товара. В данном случае ответом является 12, так как число 204 при делении на 18 дает значение 11,333, которое необходимо округлить вверх. В 12-м ящике будет только 6 единиц товара.

Может также потребоваться округлить отрицательное значение до кратного отрицательному или дробное — до кратного дробному. Для этого также можно применять функцию ОКРУГЛТ.

Округление чисел

Сегодня мы рассмотрим довольно скучную тему, без понимания которой двигаться дальше не представляется возможным. Эта тема называется «округление чисел» или по-другому «приближённые значения чисел».

Приближённые значения

Приближённые (или приблизительные) значения применяются тогда, когда точное значение чего-то найти невозможно, или же не важно чтобы это значение было точным для исследуемого предмета.

Например, на словах можно сказать, что в городе проживает полмиллиона человек, но это высказывание не будет истинным, поскольку количество человек в городе меняется — люди приезжают и уезжают, рождаются и умирают. Поэтому правильнее будет сказать, что в городе проживает приблизительно полмиллиона человек.

Ещё пример. В девять утра начинаются занятия. Мы вышли из дома в 8:30. Через некоторое время по дороге мы встретили своего товарища, который спросил у нас сколько сейчас времени. Когда мы выходили из дома было 8:30, на дорогу мы потратили какое-то неизвестное время. Мы не знаем сколько сейчас времени, поэтому отвечаем товарищу: «сейчас приблизительно около девяти часов».

В математике приближенные значения указываются с помощью специального знака. Выглядит он следующим образом:

Читается как «приближённо (приблизительно) равно».

Чтобы указать приближённое (приблизительное) значение, прибегают к такому действию как округление чисел.

---

Округление чисел

Для нахождения приближенного значения применяется такое действие как округление чисел.

Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулём. Например, следующие числа являются круглыми:

10, 20, 30, 100, 300, 700, 1000

Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числá.

Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак. По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.

На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.

Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.

Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, то надо понимать, что от нас требуют найти ближайшее круглое число от числá 17. Причём в ходе этого поиска возможно изменения коснутся и той цифры, которая располагается в разряде десятков числá 17 (т.е цифры 1).

Предстáвим числа от 10 до 20 с помощью следующего рисунка:

На рисунке видно, что для числá 17 ближайшее круглое число это число 20. Значит ответ к задаче таким и будет: «17 приближённо равно 20″

17 ≈ 20

Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.

Попробуем найти приближённое число для числа 12. Для этого снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приближённо равно 10

12 ≈ 10

Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так получилось мы расскажем позже.

Попробуем найти ближайшее число для числá 15. Снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать бóльшее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20

15 ≈ 20

Округлять можно и большие числа. Естественно, для них делать рисунки и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.

Итак, мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:

Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56

Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60

Значит при округлении числа 1456 до разряда десятков полýчим 1460

1456 ≈ 1460

Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самогó разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.

Округлять числа можно не только до разряда десятков. Округлять число можно до разряда сотен, тысяч, десятков тысяч и так далее.

После того, как станóвится ясно, что округление это ни что иное как поиск ближáйшего числá, можно применять готовые правила, которые значительно облегчают округление чисел.

---

Первое правило округления

В предыдущих примерах мы видели, что округляя число до определенного разряда, младшие разряды заменяются нулями. Цифры, которые заменяются нулями, называют отбрасываемыми цифрами.

Первое правило округления выглядит следующим образом:

Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Например, округлим число 123 до разряда десятков.

В первую очередь находим сохраняемую цифру. Для этого надо прочитать самó задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 123 до разряда десятков.

Видим, что в разряде десятков нахóдится двойка. Значит сохраняемой цифрой является цифра 2

Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после двойки это цифра 3. Значит цифра 3 является первой отбрасываемой цифрой.

Теперь применяем правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Так и делаем. Оставляем без изменения сохраняемую цифру, а все младшие разряды заменяем нулями. Другими словами, всё что следует после цифры 2 заменяем нулями (точнее нулём):

123 ≈ 120

Значит при округлении числа 123 до разряда десятков, получаем приближённое ему число 120.

---

Теперь попробуем округлить то же самое число 123, но уже до разряда сотен.

Нам требуется округлить число 123 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 1, поскольку мы округляем число до разряда сотен.

Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после единицы это цифра 2. Значит цифра 2 является первой отбрасываемой цифрой:

Теперь применим правило. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Так и делаем. Оставляем без изменения сохраняемую цифру, а все младшие разряды заменяем нулями. Другими словами, всё что следует после цифры 1 заменяем нулями:

123 ≈ 100

Значит при округлении числа 123 до разряда сотен, получаем приближённое ему число 100.

---

Пример 3. Округлить число 1234 до разряда десятков.

Здесь сохраняемая цифра это 3. А первая отбрасываемая цифра это 4. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит оставляем сохраняемую цифру 3 без изменений, а всё что располагается после неё заменяем нулём:

1234 ≈ 1230

---

Пример 4. Округлить число 1234 до разряда сотен.

Здесь сохраняемая цифра это 2. А первая отбрасываемая цифра это 3. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит оставляем сохраняемую цифру 2 без изменений, а всё что располагается после неё заменяем нулями:

1234 ≈ 1200

---

Пример 3. Округлить число 1234 до разряда тысяч.

Здесь сохраняемая цифра это 1. А первая отбрасываемая цифра это 2. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит оставляем сохраняемую цифру 1 без изменений, а всё что располагается после неё заменяем нулями:

1234 ≈ 1000

---

Второе правило округления

Второе правило округления выглядит следующим образом:

Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Например, округлим число 675 до разряда десятков.

В первую очередь находим сохраняемую цифру. Для этого надо прочитать само задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 675 до разряда десятков.

Видим, что в разряде десятков находится семёрка. Значит сохраняемой цифрой является цифра 7

Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после семёрки это цифра 5. Значит цифра 5 является первой отбрасываемой цифрой.

Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

У нас первая из отбрасываемых цифр это 5. Значит мы должны увеличить на единицу сохраняемую цифру 7, а всё что следует после неё заменить нулём:

675 ≈ 680

Значит при округлении числа 675 до разряда десятков, получаем приближённое ему число 680.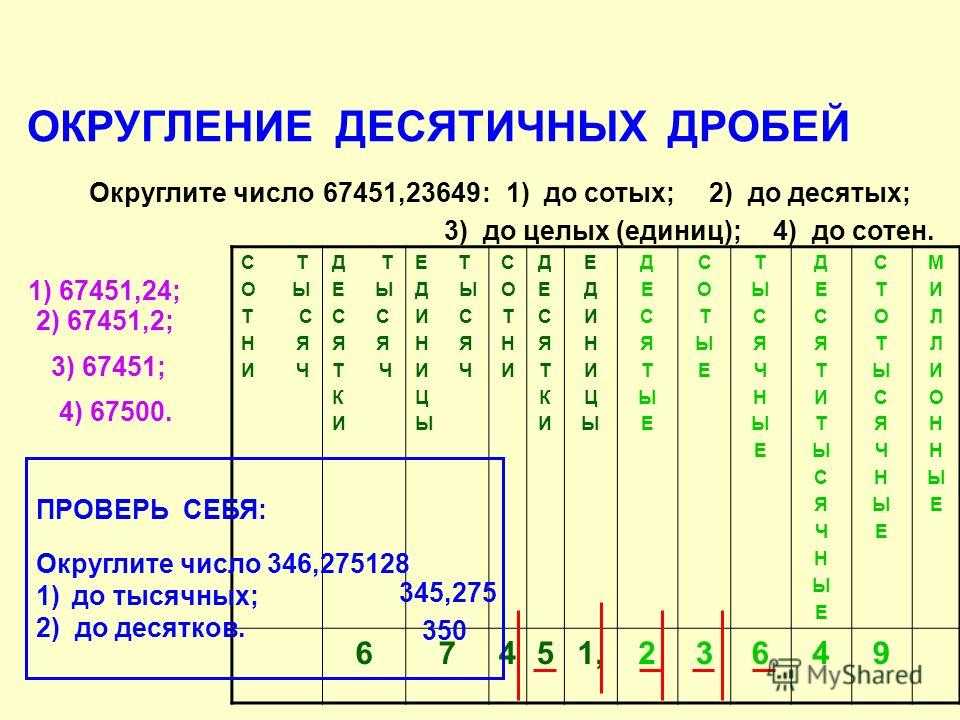

---

Теперь попробуем округлить то же самое число 675, но уже до разряда сотен.

Нам требуется округлить число 675 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 6, поскольку мы округляем число до разряда сотен:

Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после шестёрки это цифра 7. Значит цифра 7 является первой отбрасываемой цифрой:

Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

У нас первая из отбрасываемых цифр это 7. Значит мы должны увеличить на единицу сохраняемую цифру 6, а всё что следует после неё заменить нулями:

675 ≈ 700

Значит при округлении числа 675 до разряда сотен, получаем приближённое ему число 700.

---

Пример 3. Округлить число 9876 до разряда десятков.

Здесь сохраняемая цифра это 7. А первая отбрасываемая цифра это 6. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит увеличиваем на единицу сохраняемую цифру 7, а всё что располагается после неё заменяем нулём:

9876 ≈ 9880

---

Пример 4. Округлить число 9876 до разряда сотен.

Здесь сохраняемая цифра это 8. А первая отбрасываемая цифра это 7. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит увеличиваем на единицу сохраняемую цифру 8, а всё что располагается после неё заменяем нулями:

9876 ≈ 9900

---

Пример 5. Округлить число 9876 до разряда тысяч.

Здесь сохраняемая цифра это 9. А первая отбрасываемая цифра это 8. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит увеличиваем на единицу сохраняемую цифру 9, а всё что располагается после неё заменяем нулями:

9876 ≈ 10000

---

Пример 6. Округлить число 2971 до сотен.

При округлении этого числа до сотен следует быть внимательным, поскольку сохраняемая цифра здесь 9, а первая отбрасываемая цифра это 7. Значит цифра 9 должна увеличиться на единицу. Но дело в том, что после увеличения девятки на единицу получится 10, а это цифра не вместится в разряд сотен нового числа.

В этом случае, в разряде сотен нового числа надо записать 0, а единицу перенести на следующий разряд и сложить с цифрой, которая там находится. Далее заменить все цифры после сохраняемой нулями:

2971 ≈ 3000

---

Округление десятичных дробей

При округлении десятичных дробей следует быть особенно внимательным, поскольку десятичная дробь состоит из целой и дробной части. И каждая из этих двух частей имеет свои разряды:

Разряды целой части:

• разряд единиц;
• разряд десятков;
• разряд сотен;
• разряд тысяч.

Разряды дробной части:

• разряд десятых;
• разряд сотых;
• разряд тысячных

Рассмотрим десятичную дробь 123,456 — сто двадцать три целых четыреста пятьдесят шесть тысячных. Здесь целая часть это 123, а дробная часть 456. При этом у каждой из этих частей есть свои разряды. Очень важно не путать их:

Для целой части применяются те же правила округления, что и для обычных чисел. Отличие в том, что после округления целой части и замены нулями всех цифр после сохраняемой цифры, дробная часть полностью отбрасывается.

Например, округлим дробь 123,456 до разряда десятков. Именно до разряда десятков, а не разряда десятых. Очень важно не перепутать эти разряды. Разряд десятков располагается в целой части, а разряд десятых в дробной.

Итак, мы должны округлить 123,456 до разряда десятков. Сохраняемая цифра здесь это 2, а первая из отбрасываемых цифр это 3

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. А что делать с дробной частью? Её просто отбрасывают (убирают):

123,456 ≈ 120

---

Теперь попробуем округлить ту же самую дробь 123,456 до разряда единиц. Сохраняемая цифра здесь будет 3, а первая из отбрасываемых цифр это 4, которая находится в дробной части:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. Оставшаяся дробная часть будет отброшена:

123,456 ≈ 123,0

Ноль, который остался после запятой тоже можно отбросить. Значит окончательный ответ будет выглядеть следующим образом:

123,456 ≈ 123,0 ≈ 123

---

Теперь займёмся округлением дробных частей. Для округления дробных частей справедливы те же правила, что и для округления целых частей. Попробуем округлить дробь 123,456 до разряда десятых. В разряде десятых располагается цифра 4, значит она является сохраняемой цифрой, а первая отбрасываемая цифра это 5, которая находится в разряде сотых:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит сохраняемая цифра 4 увеличится на единицу, а остальная часть заменится нулями

123,456 ≈ 123,500

---

Попробуем округлить ту же самую дробь 123,456 до разряда сотых. Сохраняемая цифра здесь это 5, а первая из отбрасываемых цифр это 6, которая находится в разряде тысячных:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит сохраняемая цифра 5 увеличится на единицу, а остальная часть заменится нулями

123,456 ≈ 123,460

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

Методы округления

Существует множество способов округления чисел. ..

Во-первых, что такое «Округление»?

Округление означает сделать число проще , но сохранить его значение близким к тому, что было. Результат менее точен, но проще в использовании.

Пример: 7,3 округляется до 7

Поскольку 7,3 ближе к 7, чем к 8

(Примечание: в этих примерах мы округляем до целых чисел, но можем округлять до десятков, десятых и т. д.)

А как насчет 7.5 ? Ближе к 7 или ближе к 8?

7.5 находится на полпути между ними, так что же нам делать?

Half Round Up (общий метод округления)

Общий метод округления состоит в том, чтобы сделать 0,5 к до , поэтому 7,5 округляется до 8

7.5 обычно округляется до 8

Но это не закон или что-то в этом роде, это просто то, что люди обычно делают, и мы получаем это:

• 7,6 патронов до 8
• 7,5 патронов до 8
• 7,4 округления до 7

Узнайте больше об этом методе в округлении чисел.

Полукруглая вниз

Но 5 может заменить , если мы захотим. В этом случае 7,5 округляется до 7, и мы получаем:

.

• 7,6 патронов до 8
• 7,5 раундов до 7
• 7,4 округления до 7

Но мы всегда должны информировать людей о том, что мы используем «Полукруглый в меньшую сторону».

Зачем снижать 0,5? Может быть, в наших числах много 0,5, и мы хотим посмотреть, как округление в меньшую сторону повлияет на наши результаты.

Поиграйте… попробуйте различные методы округления в инструменте округления.

Отрицательные числа

А как насчет -7,5 ?

• Округляет до -8 (и идет ли это «вверх» или «вниз»?),
• Или округляется до -7 ?

Помогите! Я сбит с толку!

На самом деле весь мир запутался в округлении отрицательных чисел… одни компьютерные программы округляют от -7,5 до -8, другие до -7

Но мы можем согласиться, что здесь , что «вверх» означает движение в положительном направлении, как в этой числовой строке:

Half Round Up (включая отрицательные числа)

Получаем вот это:

• 7,6 раундов до 8
• 7,5 патронов до 8
• 7,4 округления до 7
• -7,4 раунда до -7
• -7,5 патронов до -7
• -7,6 округляется до -8

Половина округления вниз (включая отрицательные числа)

Когда мы округляем 0,5 до , мы получаем это:

• 7,6 патронов до 8
• 7,5 раундов до 7
• 7,4 округляет до 7
• -7,4 раунда до -7
• -7,5 раундов до -8
• -7,6 округляется до -8

 

«Симметричное» округление

Но, может быть, вы думаете, что «7,5 округляется до 8, поэтому -7,5 должно превратиться в -8», что красиво и симметрично.

Что ж, вам повезло, потому что это с округлением до или от нуля :

Половина раунда от 0

В этом методе число округляется до 0,5, так что дальше от нуля , например:

• 7,6 раундов до 8
• 7,5 раундов до 8
• 7,4 раунда до 7
• -7,4 патронов до -7
• -7,5 раундов до -8
• -7,6 раундов до -8

Круглая половина к 0

Или мы можем округлить число до нуля на 0,5, например:

• 7,6 раундов до 8
• 7,5 патронов до 7
• 7,4 раунда до 7
• -7,4 патронов до -7
• -7,5 патронов до -7
• -7,6 раундов до -8

Но быть последовательным может быть плохо

Однако выбор любого из этих методов может быть плохим!

Представьте, что вы складываете длинный список чисел. Вы решаете округлить каждое число, чтобы сделать это быстрее. Если 0,5 много, все они округляются, и ваш ответ будет иметь смещение .

Пример: Сложите эти числа до и после округления: 5,5, 7,5, 6,5, 9,5

До округления: 5,5 + 7,5 + 6,5 + 9,5 = 29

После округления: 6 + 8 + 7 + 10 = 0 91 3

Расчет был намного проще, но ответ сместился вверх сильно!

Как мы можем остановить округление в одном направлении?

Мы можем округлить до четных (или нечетных) чисел или просто выбрать случайно .

Округлить до четного (банковское округление)

Округляем 0,5 до ближайшего даже цифра

Пример:

7,5 округляет до до 8 (поскольку 8 — четное число)

, но 6,5 округляет до до 6 (поскольку 6 — четное число4) 9000

Остальные числа (не заканчивающиеся на 0,5) округляются до ближайшего, как обычно, поэтому:

• 7,6 патронов до 8
• 7,5 раундов до до 8 (поскольку 8 — четное число)
• 7,4 округления до 7
• 6,6 патронов до 7
• 6,5 раундов вниз с до 6 (поскольку 6 — четное число)
• 6,4 раунда до 6
• и т. д.

Округлить до нечетного

То же, что и «Округлить до четного», но 0,5 приближается к нечетным числам

Пример:

7,5 округляется до 7 (поскольку 7 — нечетное число)

, но 6,5 округляет до до 7 (поскольку 7 — нечетное число)

Раунд случайным образом

Мы также можем произвольно округлять 0,5 в большую или меньшую сторону, но как? Подбрасывая монетку? Или функция компьютера?

С большим списком чисел это может дать хорошие результаты, но каждый раз дает другой ответ (если только мы не используем фиксированный список случайных вариантов).

Пол и потолок

Есть два других метода, которые даже не учитывают 0,5. Их называют напольными и потолочными.

Этаж дает нам ближайшее целое число меньше (и потолок поднимается).

Пример: Каковы пол и потолок 2.31?

Этаж 2.31 2
Верхний 2.31 3

Этаж

При использовании «floor» все цифры идут вниз, независимо от того, какая цифра отброшена:

Пример: 7,8 уменьшается до 7

то же самое происходит с 7,2, 7,5, 7,9 и т. д.

И 7 тоже превращается в 7.

Потолок

И «потолок» поднимается вверх:

Пример: 7.1 увеличивается до 8

, то же самое происходит и с 7.2, 7.5, 7.8 и т. д.

Но 7 остается равным 7 .

 

Резюме

Number	Half Up	Half Down	Half Away 0	Half To 0	Half Even	Half Odd	Floor	Ceiling
8	8	8	8	8	8	8	8	2 9
7,6	8	8	8	8	8	8	8	2 7	2
7,5	8	7	8	7	8	7	8	2 7	2
7. 4	7	7	7	7	7	7	7	8	2
7	7	7	7	7	7	7	7	6 9 2
-7	-7	-7	-7	-7	-7	-7	-7	2	2
-7,4	-7	-7	-7	-7	-7	-7	-8	-7
-7,5	-7	-8	-8	-7	-8	-7	-8	2
-7,6	-8	-8	-8	-8	-8	-8	-8	2	-8
-8	-8	-8	-8	-8	-8	-8	-8	-8

 

Округление до десятков, десятых, сколько угодно.

..

В наших примерах мы округлили до целых чисел, но вы можете округлить до десятков, десятых и т. д.:

Пример: «Половина округления вверх» до

десятков (ближайшие 10):

25 округлений до 30

24,97 округлений до 20

Пример: «Half Round Up» до

сотых (ближайшая 1/100):

0,5168 округляет до 0,52

1,41119 округляет до 1,41

 

Правила округления чисел и примеры составляет 5 или больше.

Округление чисел дает ваши числа, близкие по значению к начальным числам, но менее точные. Например, округление 241 до ближайших десяти дает 240. Округление 243 до ближайших десяти также дает 240, а 246 округляет до 250. Вот правила округления чисел и сумм. Также узнайте об округлении значащих цифр.

Правила округления чисел

Вас может удивить, что существует множество различных способов округления чисел. Каждый метод имеет свои правила, преимущества и недостатки. Однако наиболее распространен метод округления в большую сторону, когда за рассматриваемой цифрой следует цифра 5 или выше:

• Округление в большую сторону, если за цифрой, которую вы округляете, следует цифра 5, 6, 7, 8 или 9. Для например, 48, округленное до десятых, будет равно 50.
• Округлите в меньшую сторону, если за округляемой цифрой следует 0, 1, 2, 3 или 4. Например, 23, округленное до ближайших 10, будет 20.

Вот стишок, который поможет вам запомнить:

Найди свое место,
посмотри по соседству.
5 или выше, добавьте еще один.

В поисках своего места

Сначала решите, к какому месту вы будете округлять, будь то ближайшее, десятое, единица, десять, сто, тысяча и так далее. Вот несколько примеров:

• 3947 округлить до десятых будет 3950
• 3947 округлить до ближайшей сотни будет 3900
• 3947 округление до ближайшей тысячи равно 4000

Обратите внимание, что все цифры справа от округляемого места становятся нулями. Точно так же работает округление десятичных дробей. Например:

• 21.0538 округлый до ближайшей десятой — 21,1
• 21,0538 округлый до ближайшей сотни — 21,05
• 21. 0538 округлый до ближайшей тысячи. не добавлять нули справа от запятой.

  Рабочие листы для округления чисел

  Практика округления чисел с помощью этих рабочих листов, доступных в виде файлов PDF, Google Apps или PNG для загрузки или печати.

  Суммы раундов – Деньги

  Денежные суммы обычно идут до сотого места (в зависимости от вашей страны). Округление сумм делает оценку стоимости предметов намного проще, чем ходить с калькулятором.

  Например, если вы хотите узнать, сколько стоят три предмета:

  • 2,25 доллара
  • $ 2,68
  • $ 0,88

  Округление цифры делает математику простым:

  • $ 2,00
  • $ 3,00
  • $ 1,00

  Добавление 2 + 3 + 1 В своей головке дает вам общее количество 6. предметы стоят около 6 долларов США (фактическая стоимость составляет 5,81 доллара США). Если предметы облагаются налогом, простой способ приблизиться к окончательной стоимости всегда округляется!

  Правила округления отрицательных чисел

  Правила округления отрицательных чисел различаются в зависимости от дисциплины. Вот некоторые распространенные методы:

  • Половина округления от нуля : Например, 23,5 раунда до 24 и -23,5 раунда до -24. Этот метод распространен в науке, в коммерции и в бинарных компьютерах, потому что он прост и симметрично работает с положительными и отрицательными числами.
  • Округление половины до нуля : Например, 23,5 округляется до 23 и -23,5 округляется до -23.
  • Округлить наполовину до (в сторону положительной бесконечности): например, 23,5 округления до 24 и -23,5 округления до -23.
  • Округлить наполовину вниз (в сторону отрицательной бесконечности): например, 23,5 округления до 23 и -23,5 округления до -24.
  • Округлить половину до четного : Например, 23,5 и 24,5 округлить до 24, а -23,5 -24,5 округлить до -24.
  • Половина округляется до нечетного : Здесь 22,5 и 23,5 округляются до 23, а 24,5 округляются до 25. И -22,5, и -23,5 округляются до -23, а -24,5 округляются до -25.

  Правила округления значащих цифр

  Ученые, инженеры и другие специалисты, выполняющие измерения, сообщают окончательные значения, используя значащие цифры.

  • Если первая незначащая цифра меньше 5, младшая значащая цифра остается неизменной.
  • Если первая незначащая цифра больше 5, увеличьте младшую значащую цифру на 1.
  • Однако, если первая незначащая цифра равна 5, младшая значащая цифра либо останется неизменной, либо увеличится на 1. Округление вводит ошибку, поэтому один из распространенных методов ее компенсации — увеличение младшей значащей цифры на 1, если она нечетная, и оставление ее неизменной, если она четная.

  При выполнении вычислений, состоящих из нескольких шагов, обычно лучше избегать округления, пока не будет получен окончательный ответ.

  Ссылки

  • Борман, Фил; Чатфилд, Марион (2015). «Избегайте опасностей использования округленных данных». Журнал фармацевтического и биомедицинского анализа . 115: 506–507. doi: 10.1016/j.jpba.2015.07.021
  • Хайэм, Николас Джон (2002). Точность и устойчивость численных алгоритмов . ISBN 978-0-89871-521-7.
  • Кулиш, Ульрих В. (1977). «Математические основы компьютерной арифметики». Транзакции IEEE на компьютерах . С-26 (7): 610–621. doi:10.1109/TC.1977.1674893
  • Ланкхэм, Исайя; Нахтергаэле, Бруно; Шиллинг, Энн (2016). Линейная алгебра как введение в абстрактную математику . Всемирная научная. ISBN 978-981-4730-35-8.

  Округление чисел — правила, примеры округления чисел

  Округление чисел означает корректировку цифр числа таким образом, чтобы получить приблизительное значение. Это значение является более простым представлением данного числа. Например, население города можно было бы легко выразить как 700 000, а не 69 человек.8869. Округление чисел упрощает расчеты, в результате получается цифра, которую легко запомнить. Однако округление чисел производится только для тех чисел, точное значение которых не имеет большого значения.

  Давайте узнаем больше об округлении чисел, чтобы лучше понять, как округлить число до ближайших десятков, сотен, тысяч и так далее.

  1.	Что такое округление чисел?
  2.	Правила округления чисел
  3.	Как округлять целые числа?
  4.	Как округлить дроби?
  5.	Как округлить десятичные числа?
  6.	Часто задаваемые вопросы об округлении чисел

  Что такое округление чисел?

  Округление числа означает процесс упрощения числа таким образом, чтобы его значение оставалось близким к прежнему. Результат, полученный после округления числа, менее точен, но более удобен в использовании. Округляя число, мы учитываем разрядное значение цифр в числе.

  Давайте разберемся с концепцией округления на примере. Сьюзан преодолела расстояние в 2,05 мили, которое она отметила примерно как 2 мили. Как она оценила приблизительное значение пройденного ею расстояния? Почему она не записала свое расстояние как 3 мили? Указание приблизительного и более простого значения для данного числа помогает упростить анализ и расчеты при использовании этого числа. Здесь Сьюзен отметила, что проще вести учет пройденного ею расстояния.

  Числа можно округлять до разных цифр, например, их можно округлять до ближайших десятков, сотен, тысяч и так далее. Например, 541, округленное до ближайшей сотни, равно 500, потому что 541 гораздо ближе к 500, чем к 600. При округлении числа нам нужно знать ответ на вопрос: «До чего мы округляем число?» Предположим, нам нужно округлить число 7456. Если 7456 округлить до десятых, получится 7460, а если 7456 округлить до ближайшей тысячи, то получится 7000. Несколько подобных примеров приведены ниже.

  Округление чисел до ближайших десятков

  Округление чисел до ближайших десятков означает, что нам нужно проверить цифру справа от разряда десятков, то есть разряда единиц. Например, когда мы округляем число 7486 до ближайших десяти, оно становится 7490.

  Округление чисел до ближайшей сотни

  Округление чисел до ближайшей сотни означает, что нам нужно проверить цифру справа от разряда сотен, что есть, разряд десятков. Например, если 7456 округлить до ближайшей сотни, получится 7500.

  Округление в большую и меньшую сторону

  Хотя округление является общим термином, мы обычно используем термины «округление в большую сторону» или «округление в меньшую сторону», чтобы указать, увеличилось или уменьшилось число после округления. Когда округленное число увеличивается, то говорят, что данное число округляется в большую сторону, а если округляемое число уменьшается, то говорят, что оно округляется в меньшую сторону.

  Правила округления чисел

  Как решить, какое значение является более подходящим среди различных приближенных значений числа? Должны ли мы выбрать число больше заданного числа или выбрать меньшее?

  Есть несколько основных правил, которые необходимо соблюдать при округлении чисел.

  • Сначала нам нужно узнать, какая у нас цифра округления. Эта цифра в конечном итоге будет затронута.
  • После этого нужно проверить цифру справа от этого места, которая решит судьбу цифры округления.
  • Если цифра справа меньше 5, мы не меняем цифру округления. Однако все цифры справа от цифры округления меняются на 0,9.0046
  • Если цифра справа 5 или больше 5, мы увеличиваем цифру округления на 1, а все цифры справа от цифры округления меняем на 0.

  Пример:

  a.) Если счет в мебельном магазине составляет 3257 долларов, как округляется значение этой суммы до ближайших десяти?

  б. ) Если счет доходит до 3284 долларов, каково будет значение этой суммы, округленное до ближайших десяти?

  Решение:

  а) 3257 долларов необходимо округлить до десяти. Итак, давайте отметим цифру в разряде десятков, то есть 5. Теперь давайте проверим число справа, которое в данном случае равно 7. Поскольку 7 больше 5, мы заменим 5 на 6, и все цифры справа станут 0. Таким образом, 3257 долларов округляются до 3260 долларов.

  b .) Здесь 3284 доллара необходимо округлить до десяти. Итак, давайте отметим цифру в разряде десятков, то есть 8. Теперь давайте проверим число справа, которое в данном случае равно 4. Поскольку 4 меньше 5, 8 останется без изменений, а остальные цифры справа изменятся на 0. Таким образом, 3284 доллара округляются до 3280 долларов.

  Как округлять целые числа?

  Целые числа округляются в соответствии с указанными выше правилами. Применим правила на примере.

  Пример: Округлите 7234 до ближайшей сотни.

  • Шаг 1: Отметьте разряд, до которого необходимо округлить число. Здесь 7234 нужно округлить до ближайшей сотни. Итак, мы отмечаем 2, которые находятся в разряде сотен.
  • Шаг 2: Обратите внимание и подчеркните цифру справа от 2, то есть разряд десятков. Здесь это 3, поэтому мы обозначим его как: 7 2 3 4
  • Шаг 3: Сравните подчеркнутую цифру с 5.
  • Шаг 4: Если число меньше 5, все цифры справа от него, включая его, будут заменены на 0, а цифра в разряде сотен (2) останется неизменной. Следовательно, 7234 будет округлено до 7200.

  Примечание. Если число справа от 2 равно 5 или больше 5, то все цифры справа от 2 станут 0, а 2 будет увеличено на 1, изменив его на 3. Например, если данный число было 7268, то оно будет округлено до 7300 (до ближайшей сотни).

  Как округлять дроби?

  Дроби — это числовые значения, представляющие часть целого. Они записываются в виде (p/q), где q не равно нулю. Простое правило округления дробей до ближайшего целого числа состоит в том, чтобы сравнивать правильные дроби с 1/2. В случае, если это неправильная дробь, нам нужно изменить ее на смешанную дробь, а затем сравнить дробную часть с 1/2. Мы округлить дробь, если она равна или больше 1/2, и округлить вниз, если она меньше 1/2. Давайте разберемся с округлением дробей до ближайшего целого числа на следующем примере.

  Пример: Округлить данные дроби до целого числа:

  а.) 3/4

  б.) \(6 \dfrac{2}{5}\)

  в.) 21/5

  Решение:

  а) Правильную дробь можно округлить до ближайшего целого числа, следуя простому правилу сравнения ее с 1/2. Поскольку 3/4 больше 1/2, оно будет округлено до 1,9.0004

  б.) \(6 \dfrac{2}{5}\) — смешанная дробь. Здесь мы оставим целую часть числа в стороне и сравним дробную часть с 1/2. Итак, оставив 6 в стороне, мы проверим, больше или меньше 2/5 1/2. Поскольку 2/5 меньше 1/2, округлим данную смешанную дробь до 6.

  в.) 21/5 — неправильная дробь, поэтому преобразуем ее в смешанную дробь. Это сделает его \(4 \dfrac{1}{5}\). Теперь мы оставим в стороне целую часть числа и сравним дробную часть с 1/2. Итак, оставив 4 в стороне, мы проверим, больше или меньше 1/2 1/5. Так как 1/5 меньше 1/2, округлим данную дробь до 4.

  Как округлять десятичные числа?

  Десятичное число представляет собой комбинацию целой части числа и дробной части, разделенных десятичной точкой. Округление десятичных чисел работает так же, как мы округляем целые числа, хотя нам нужно знать значения десятичных разрядов всех цифр в заданном числе. Это относится к цифрам, указанным до десятичной точки, а также к цифрам, данным после десятичной точки. Обратите внимание на таблицу десятичных разрядов, чтобы лучше понять это.

  Обычно мы округляем десятичные числа до ближайших десятых, сотых, тысячных и т. д., которые представляют разряды после запятой. Однако иногда нам даже нужно округлить десятичную дробь до ближайшего целого числа. В этом случае мы проверяем разряд десятых. Если оно равно или больше 5, то данное число округляется в большую сторону, а если десятый разряд меньше 5, то данное число округляется в меньшую сторону.

  Пример 1: Округлите 5,62 до ближайшего целого числа.

  Решение: Так как нам нужно округлить это десятичное число до ближайшего целого числа, мы проверим разряд десятых. В данном случае десятая цифра равна 6, что больше 5. Значит, число будет округлено до 6. Другими словами, 5,62 ≈ 6

  В остальных случаях, когда нужно округлить десятичные дроби до ближайших десятых , сотых или тысячных, нам нужно запомнить простое правило пометки числа, до которого мы округляем, и проверки числа справа от него. Например, когда мы округляем десятичные числа до ближайших сотых, нам нужно проверять разряд тысячных. Точно так же, если нам нужно округлить десятичные числа до ближайших десятых, нам нужно проверить сотые доли. Если проверяемое число меньше 5, то число округления остается неизменным, а следующие цифры заменяются на 0. Если же проверяемое число равно 5 или больше 5, то число округления увеличивается на 1. и следующие цифры заменяются на 0. Давайте разберемся в этом на примере.

  Пример 2: Округлите 0,439 до сотых.

  Решение: В данном случае цифра справа от сотых, то есть тысячных, равна 9, что больше 5. Значит, к цифре, стоящей в сотых, прибавим 1, что 3 + 1 = 4, и запишите 0 цифрами справа. Таким образом, 0,439 будет округлено до 0,44

  Примечание: Следует отметить, что , когда мы округляем десятичное число до сотых, говорят, что круглая десятичная дробь верна до двух знаков после запятой. Другими словами, если нас просят округлить число до двух знаков после запятой, значит, нужно округлить его до ближайших сотых. Точно так же, когда нас просят округлить число до одного десятичного знака, это означает, что нам нужно округлить его до ближайших десятых .

  Советы по округлению чисел:

  Следующие советы помогут решить вопросы, связанные с округлением чисел.

  • При округлении чисел всегда нужно проверять цифру справа от округляемого числа. Если оно меньше 5, число округления остается прежним, а следующие цифры меняются на 0. Если цифра справа равна или больше 5, мы увеличиваем цифру округления на 1, а следующие числа меняем на 0.
  • Когда мы округляем десятичные числа, мы обычно сталкиваемся с такими терминами, как округление до ближайших десятых, сотых, тысячных и так далее.
  • Когда нас просят округлить число до одного знака после запятой, значит нужно округлить до ближайших десятых, аналогично, когда нас просят округлить число до двух знаков после запятой, значит нужно округлить это с точностью до сотых.
  • Когда округляемое число увеличивается, говорят, что данное число округляется в большую сторону, а если округляемое число уменьшается, то говорят, что оно округляется в меньшую сторону.

  См. также

  Ознакомьтесь со следующими ссылками, связанными с округлением чисел.

  • Что такое числа?
  • Номер строки

  Часто задаваемые вопросы об округлении чисел

  Что такое округление чисел в математике?

  Округление числа означает преобразование числа в более простое значение таким образом, чтобы его значение оставалось близким к тому, что было. Округление чисел упрощает вычисления и преобразует цифры в приблизительное значение, которое легче запомнить. Например, если население города составляет 69 человек.2 769, то его можно округлить до 700 000, и будет легче запомнить примерную цифру 700 000, а не реальную цифру.

  Каковы правила округления десятичных чисел?

  Есть несколько основных правил, которым необходимо следовать при округлении десятичных чисел. Они аналогичны округлению других чисел, однако нам нужно знать десятичные разряды всех цифр в заданном числе. Это относится к цифрам, указанным до десятичной точки, а также к цифрам, данным после десятичной точки. Другими словами, мы обычно округляем десятичные числа до ближайших десятых, сотых, тысячных и т. д., которые представляют разряды после запятой. Иногда мы даже округляем десятичную дробь до ближайшего целого числа. Во всех этих случаях мы используем следующие правила.

  • Сначала нам нужно узнать, какая у нас цифра округления. Эта цифра в конечном итоге будет затронута.
  • После этого нужно проверить цифру справа от этого места, которая решит судьбу цифры округления.
  • Если цифра справа меньше 5, мы не меняем цифру округления. Однако все цифры справа от цифры округления заменяются на 0.
  • Если цифра справа 5 или больше 5, мы увеличиваем цифру округления на 1, а все цифры справа от цифры округления меняем на 0.

  Например, если нам нужно округлить 0,476 до ближайших десятых, это означает, что мы будем проверять цифру справа от нее, которая является цифрой сотых. В данном случае это 7, что больше 5. Следовательно, 0,476 будет округлено до 0,5 с точностью до десятых.

  Что такое 62 Округлить до ближайшего десятка?

  Когда 62 округляется до ближайших 10, нам нужно проверить цифру на единицу. Здесь это 2, что меньше 5. Значит, 6 останется прежним, а 2 изменится на 0. Следовательно, 62, округленное до десятка, будет 60.

  Где мы используем округление чисел в реальной жизни?

  В реальной жизни мы обычно округляем числа, когда точное значение не так важно. Например, если мы хотим узнать приблизительную сумму, которую мы потратили в продуктовом магазине, или сумму при оценке бюджета, или при выражении более крупных цифр, таких как население города. Мы оцениваем сумму до более простых чисел, чтобы расчет стал проще. Например, если мы знаем, что наши ежемесячные расходы составят около 59 долларов.0, мы можем легко округлить число до 600 долларов, что легче запомнить.

  Как округлить числа до десятых?

  Если нам нужно округлить десятичные числа до ближайших десятых, нам нужно проверить цифру справа от цифры на десятом разряде, который является сотым разрядом. Если число в сотом разряде меньше 5, то число округления остается неизменным, а следующие цифры заменяются на 0. Если же проверяемое число равно 5 или больше 5, то число округления увеличивается на 1, а следующие цифры заменяются на 0. Например, чтобы округлить 56,73 до десятых, мы проверим цифру в сотых долях, которая в данном случае равна 3. Поскольку 3 меньше 5, 7 останется прежним, а следующие цифры станут 0. Итак, 56,73, округленное до ближайших десятых, станет 56,7

  Какова цель округления чисел?

  Округление чисел означает корректировку цифр числа таким образом, чтобы получить приблизительный результат. Округление числа дает приблизительное значение, которое является более простым и коротким представлением данного числа. Например, если население города составляет 498 821 человек, было бы проще выразить его как 500 000 человек. Это помогает упростить расчеты с цифрой, которую легко запомнить и записать. Однако округление чисел производится в тех случаях, когда точное значение не имеет большого значения.

  Что такое округление чисел до ближайших десяти?

  Когда мы округляем числа до ближайших десятков, мы сначала отмечаем цифру в разряде десятков. Затем мы наблюдаем за разрядом единиц, который находится справа от столбца десятков. По правилам, если цифра в разряде единиц 5 или больше 5, к цифре в разряде десятков прибавляем 1, то есть увеличиваем разряд десятков на 1 и пишем 0 во всех цифрах справа . Однако, если цифра в разряде единиц меньше 5, мы пишем 0 в разряде единиц и во всех разрядах справа от него, а разряд десятков остается прежним. Например, если нам нужно округлить 389до ближайшего десятка, мы проверим цифру в разряде единиц. В данном случае это 9, что больше 5. Таким образом, 8 изменится на 9, а 389 будет округлено до 390.

  Как округлить числа до ближайших 100?

  Чтобы округлить числа до ближайшей сотни, нам нужно проверить цифру справа от нее, которая соответствует разряду десятков. Например, если нам нужно округлить 3270 до ближайших 100, мы проверим разряд десятков.

  No related posts.