Способы округления: МЕТОДЫ ОКРУГЛЕНИЯ

Как округлять числа: руководство с примерами

15 марта 2021ЛикбезОбразование

Вспоминаем полезное правило из школьной программы.

Поделиться

0

Что такое округление числа

Округление — это замена числа близким по значению, у которого на конце стоит ноль. Тогда исходное число и станет круглым. Например, круглыми являются числа 10, 20, 100, 730, 1 420, 15 000.

Результат округления называется приближённым значением данного числа и указывается после знака ≈ («приблизительно равно»).

Как округлять числа

Натуральные числа

Все числа, в которых больше одного знака, имеют разряды. Это место, на котором в числе стоит та или иная цифра. Например, в числе 342 три разряда: сотен (три сотни), десятков (четыре десятка) и единиц (две единицы). Соответственно, округлять числа можно до десятков, сотен, тысяч и так далее.

При округлении цифры в ненужных нам разрядах заменяются нулями (по сути, отбрасываются), а цифра в нужном разряде либо изменяется в большую сторону, либо остаётся неизменной. Это зависит от того, какая цифра стоит за ней. Если от 0 до 4, то ничего не происходит. Если от 5 до 9, тогда к разряду прибавляется единица.

Возьмём число 21 769. Его можно округлить следующим образом:

• До десятков. Находим количество десятков в числе 21 769 — их шесть. За шестёркой стоит цифра 9, значит, при округлении разряд десятков увеличится на один. То есть ответ — 21 770.
• До сотен. Находим количество сотен в числе 21 769 — их семь. Теперь проверяем цифру за семёркой — это 6, соответственно, к разряду сотен прибавляем единицу. Результат — 21 800.
• До тысяч. Находим количество тысяч — их 21. За единицей стоит семёрка, значит, при округлении числа разряд тысяч увеличиваем на один и получаем 22 000.

Дробные числа

При округлении дробей действуют точно такие же правила, как и при округлении натуральных чисел. Только нужно быть более внимательным, потому что разрядов в дробях больше — они есть и в целой части (единицы, десятки, сотни, тысячи и т. д.), и в дробной (десятые, сотые, тысячные и т. д.).

Например, возьмём десятичную дробь 45,836. Её можно округлить так:

• до сотых → 45,84;
• до десятых → 45,8;
• до целого → 46;
• до десятков → 50.

Когда пригодится округление чисел

Округление помогает в самых разных случаях. Например, когда нужно прикинуть результат умножения больших чисел. Допустим, вы хотите представить, сколько будет 738 × 46. По правилам округления, это приблизительно равно 700 × 50. Получается: 738 × 46 ≈ 700 × 50 ≈ 35 000. А точный результат умножения равен 33 948.

Правила округления чисел пригодятся не только при решении задачек, но и когда нужно примерно рассчитать стоимость чего‑то, чтобы понять, укладывается ли она в ваш бюджет или нет.

Также к округлению прибегают, когда абсолютная точность просто не важна. Например, если знакомые из другого города спросят вас, сколько людей живёт в вашем, вы вряд ли будете называть число до десятков и единиц, даже если знаете его. Вы, скорее, скажете, что в нём живёт «примерно четыреста тысяч» или «около миллиона» человек.

Читайте также 🧐

• Какого числа не хватает? 10 интересных заданий на поиск закономерностей
• Простой математический лайфхак, как быстро высчитать процент от числа
• Гимнастика для ума: 10 увлекательных задач с числами

примеры, правильный способ работы с десятичными дробями и целыми значениями

Математика

12.11.21

16 мин.

Некоторые операции в дисциплинах с физико-математическим уклоном не всегда приводят к целочисленному результату. Для удобства вычислений значения рекомендуется округлять. Однако не все молодые математики умеют это правильно делать. В этом случае специалисты рекомендуют воспользоваться алгоритмом округления чисел в 5 классе, примеры которого нужно разобрать, используя практический подход.

Общие сведения

Округление — математическая операция, которую каждый человек использует в повседневной жизни. Например, расстояние от дома до остановки составляет 608 м. Однако люди не произносят это значение, а округляют его до 600 метров. Из примера можно сделать вывод, что округлением числа является приближение его к более простой форме для восприятия человеком. Оно обозначается символом ≈ (608 ≈ 600). Читается последняя запись следующим образом: числовое значение «608» приближенно равно «600».

Округлять можно не только целые значения, но и дробные. В последнем случае берется десятичная дробь и указывается, до какой доли нужно осуществить операцию. Ее можно округлить до целочисленного значения. Чтобы выполнить эту операцию, нужно знать правила округления чисел.

Правила округления

Операция приближенной записи числа применяется, когда нет необходимости использовать точное значение

. Это утверждение справедливо при решении задач с использованием не только целых значений, но и десятичных дробей. Для каждого вида чисел используются свои методики, которые немного похожи. Следует отметить, что при математических расчетах целые величины округляются реже, чем дробные.

Однако необходимо знать все правила, поскольку знания помогут выполнять математические операции за короткий промежуток времени. После тренировок навык округления любого числа будет выполняться в автоматическом режиме, т. е. алгоритмы будут использоваться на подсознательном уровне.

Проверка правильности выполнения операции осуществляется посредством онлайн-округлителей любых числовых значений.

Для начала, чтобы идти от простого к сложному, следует рассмотреть методику поиска приближенных величин для целых чисел.

Для целых чисел

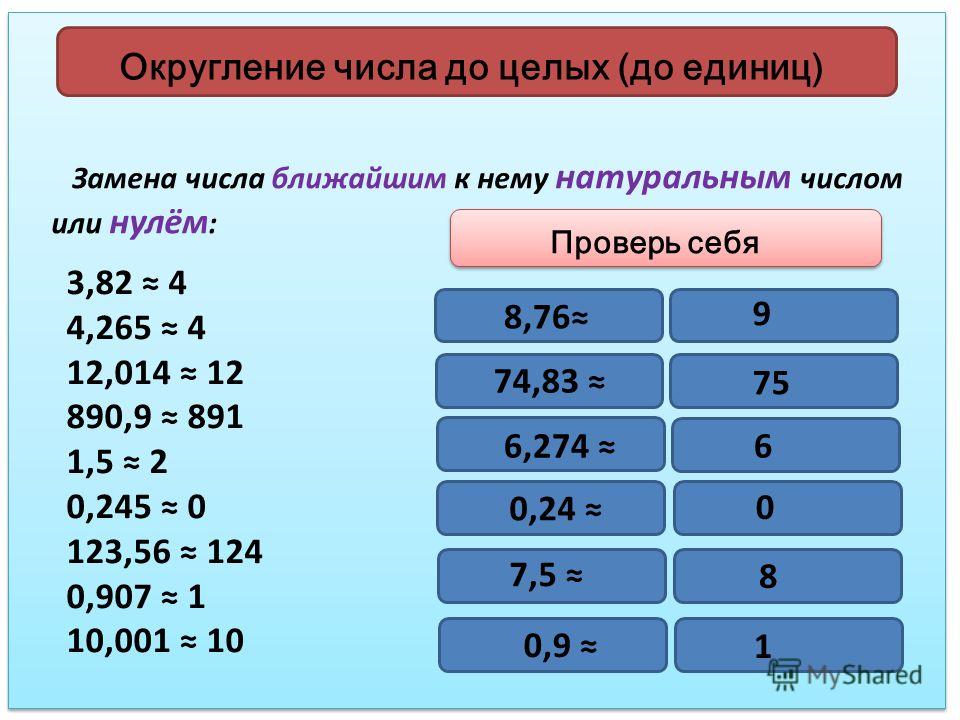
Рассматривается математическая операция округления натуральных чисел в 5 классе средней образовательной школы. Алгоритм, позволяющий округлять целые числа, имеет следующий вид:

1. Найти разряд, до которого следует выполнить операцию.
2. Анализируется значение цифры, находящейся справа.
3. Если оно меньше 5, то 1 не прибавляется к значению в первом пункте.
4. При равенстве величины, которая находится справа, одному из значений (5, 6, 7, 8, 9), цифру в 1 пункте следует увеличить на 1.
5. Остальные цифры, находящиеся после разряда в первом пункте, заменяются нулевыми значениями.

Для примера следует выполнить операцию нахождения приближенного значения 987. Если задача заключается в округлении до десятых, то результат вычисляется следующим образом:

1. Искомая величина: 8.
2. Цифра справа: 7.
3. Результат: 987 ≈ 990.

Чтобы получить приближенную величину до сотых, нужно произвести такую процедуру: 987 ≈ 1000. На начальном этапе требуется записать «9». Справа от нее — 8. Итоговый результат: 9 + 1 = 10. Далее следует заменить «87» нулями, т. е. 1000. Ответ: 1000.

Однако существует и другой пример, в котором приближенное значение получается меньше исходного. Например, требуется найти ближайшие числа к 1234. Решать следует таким способом:

1. До десятков: 1230.
2. До сотых: 1200.
3. До тысячных: 1000.

Все значения получились меньше исходного «1234». Такая методика округления является правильной не во всех случаях.

Показывает это простая задача, связанная с копированием информации с компьютера на съемный жесткий диск. Например, емкость переносного винчестера составляет 2 Тб (терабайта). На него требуется скинуть данные со всего офиса, занимающие 4,2 Тб.

Необходимо определить количество переносных винчестеров. Для решения задачи требуется воспользоваться алгоритмом:

1. Расчет количества: 4,2 / 2 = 2,1.
2. Округление: 2,1 ≈ 2.

Если проверить результат, то получится такое выражение: 4,2 — 2 * 2 ≈ 0,2 (Тб) ≈ 200 Гб. Последняя величина является остатком. Следовательно, необходимо использовать еще один винчестер, чтобы записать 200 Гб.

Пример с резервированием информации значит, что округлять необходимо в большую и в меньшую сторону в зависимости от поставленной задачи.

Для дробных значений

Десятичные дроби округляются так же, как и целые натуральные числа. При этом учитываются цифры после запятой. Методика поиска приближенной величины имеет такой вид:

1. Идентифицировать разряд, до которого следует получить приближенную величину.
2. Определить справа исходное значение, которое влияет на результат.
3. Если величина во втором пункте меньше «5», то дробь остается без изменения. При этом все остальные цифры не пишутся.
4. К разряду в первом пункте прибавляется 1 при равенстве числового значения во втором пункте 5, 6, 7, 8 или 9. Остальные значения заменяются нулями, которые не пишутся по свойству десятичных дробей.

Основное свойство десятичной дроби: если после запятой прописать любое количество нулей, то дробь останется неизменной, т. е. 1,2564 = 1,256400000000000000000000.

Для примера нужно найти приближенные величины следующей десятичной дроби: 2,3589. Для этого следует воспользоваться таким алгоритмом:

1. До тысячных: 2,359.
2. До сотых: 2,36.
3. До десятых: 2,4.
4. До целых: 2.

Очень часто такие операции необходимо применять при расчетах физических величин, исследовании функций и т. д.

Таким образом, округление чисел является очень важной операцией, которая применяется не только в науках с физико-математическим уклоном, но и в различных жизненных ситуациях.

Некоторые операции в дисциплинах с физико-математическим уклоном не всегда приводят к целочисленному результату. Для удобства вычислений значения рекомендуется округлять. Однако не все молодые математики умеют это правильно делать. В этом случае специалисты рекомендуют воспользоваться алгоритмом округления чисел в 5 классе, примеры которого нужно разобрать, используя практический подход.

Общие сведения

Округление — математическая операция, которую каждый человек использует в повседневной жизни. Например, расстояние от дома до остановки составляет 608 м. Однако люди не произносят это значение, а округляют его до 600 метров. Из примера можно сделать вывод, что округлением числа является приближение его к более простой форме для восприятия человеком. Оно обозначается символом ≈ (608 ≈ 600). Читается последняя запись следующим образом: числовое значение «608» приближенно равно «600».

Округлять можно не только целые значения, но и дробные. В последнем случае берется десятичная дробь и указывается, до какой доли нужно осуществить операцию. Ее можно округлить до целочисленного значения. Чтобы выполнить эту операцию, нужно знать правила округления чисел.

Правила округления

Операция приближенной записи числа применяется, когда нет необходимости использовать точное значение. Это утверждение справедливо при решении задач с использованием не только целых значений, но и десятичных дробей. Для каждого вида чисел используются свои методики, которые немного похожи. Следует отметить, что при математических расчетах целые величины округляются реже, чем дробные.

Однако необходимо знать все правила, поскольку знания помогут выполнять математические операции за короткий промежуток времени. После тренировок навык округления любого числа будет выполняться в автоматическом режиме, т.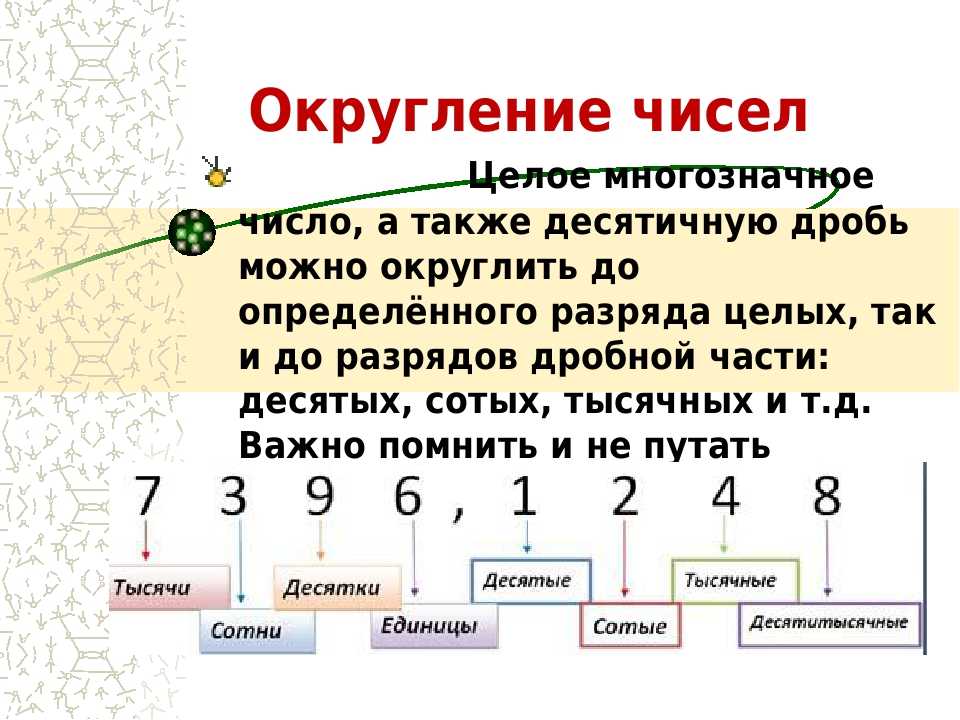 е. алгоритмы будут использоваться на подсознательном уровне.

Проверка правильности выполнения операции осуществляется посредством онлайн-округлителей любых числовых значений. Для начала, чтобы идти от простого к сложному, следует рассмотреть методику поиска приближенных величин для целых чисел.

Для целых чисел

Рассматривается математическая операция округления натуральных чисел в 5 классе средней образовательной школы. Алгоритм, позволяющий округлять целые числа, имеет следующий вид:

1. Найти разряд, до которого следует выполнить операцию.
2. Анализируется значение цифры, находящейся справа.
3. Если оно меньше 5, то 1 не прибавляется к значению в первом пункте.
4. При равенстве величины, которая находится справа, одному из значений (5, 6, 7, 8, 9), цифру в 1 пункте следует увеличить на 1.
5. Остальные цифры, находящиеся после разряда в первом пункте, заменяются нулевыми значениями.

Для примера следует выполнить операцию нахождения приближенного значения 987. Если задача заключается в округлении до десятых, то результат вычисляется следующим образом:

1. Искомая величина: 8.
2. Цифра справа: 7.
3. Результат: 987 ≈ 990.

Чтобы получить приближенную величину до сотых, нужно произвести такую процедуру: 987 ≈ 1000. На начальном этапе требуется записать «9». Справа от нее — 8. Итоговый результат: 9 + 1 = 10. Далее следует заменить «87» нулями, т. е. 1000. Ответ: 1000.

Однако существует и другой пример, в котором приближенное значение получается меньше исходного. Например, требуется найти ближайшие числа к 1234. Решать следует таким способом:

1. До десятков: 1230.
2. До сотых: 1200.
3. До тысячных: 1000.

Все значения получились меньше исходного «1234». Такая методика округления является правильной не во всех случаях.

Показывает это простая задача, связанная с копированием информации с компьютера на съемный жесткий диск. Например, емкость переносного винчестера составляет 2 Тб (терабайта). На него требуется скинуть данные со всего офиса, занимающие 4,2 Тб. Необходимо определить количество переносных винчестеров. Для решения задачи требуется воспользоваться алгоритмом:

1. Расчет количества: 4,2 / 2 = 2,1.
2. Округление: 2,1 ≈ 2.

Если проверить результат, то получится такое выражение: 4,2 — 2 * 2 ≈ 0,2 (Тб) ≈ 200 Гб. Последняя величина является остатком. Следовательно, необходимо использовать еще один винчестер, чтобы записать 200 Гб.

Пример с резервированием информации значит, что округлять необходимо в большую и в меньшую сторону в зависимости от поставленной задачи.

Для дробных значений

Десятичные дроби округляются так же, как и целые натуральные числа. При этом учитываются цифры после запятой. Методика поиска приближенной величины имеет такой вид:

1. Идентифицировать разряд, до которого следует получить приближенную величину.
2. Определить справа исходное значение, которое влияет на результат.
3. Если величина во втором пункте меньше «5», то дробь остается без изменения. При этом все остальные цифры не пишутся.
4. К разряду в первом пункте прибавляется 1 при равенстве числового значения во втором пункте 5, 6, 7, 8 или 9. Остальные значения заменяются нулями, которые не пишутся по свойству десятичных дробей.

Основное свойство десятичной дроби: если после запятой прописать любое количество нулей, то дробь останется неизменной, т. е. 1,2564 = 1,256400000000000000000000.

Для примера нужно найти приближенные величины следующей десятичной дроби: 2,3589. Для этого следует воспользоваться таким алгоритмом:

1. До тысячных: 2,359.
2. До сотых: 2,36.
3. До десятых: 2,4.
4. До целых: 2.

Очень часто такие операции необходимо применять при расчетах физических величин, исследовании функций и т. д.

Таким образом, округление чисел является очень важной операцией, которая применяется не только в науках с физико-математическим уклоном, но и в различных жизненных ситуациях.

Округление чисел: правила и примеры для дробей и сумм

Например, 341, округленное до ближайшей сотни, равно 300. Это потому, что 341 по значению ближе к 300, чем к 400. При округлении до ближайшего доллара 1,89 доллара становится 2,09 доллара, потому что 1 доллар. ближе к 2 долларам США, чем к 1 доллару США

Правила округления

Вот общее правило округления:

• Если за округляемым числом следует 5, 6, 7, 8 или 9, округляйте число в большую сторону. Пример: 38, округленное до десятых, равно 40 ¹
• Если за округляемым числом следует 0, 1, 2, 3 или 4, округлите число в меньшую сторону. Пример: 33 при округлении до десятых равно 30

До чего вы округляете?

При округлении числа сначала нужно спросить: до чего вы его округляете? Числа можно округлить до ближайших десятков, сотен, тысяч и т. д.

Рассмотрим число 4827.

• 4 827 округлить до десятых равно 4 830
• 4 827 округлить до сотых равно 4 800
• 4 827 округлить до ближайшей тысячи получится 5 000

. Вот еще несколько примеров:

• 34 округлить до десятых будет 30
• 6,809 округление до ближайшей сотни равно 6,800
• 1,951 округление до ближайшей тысячи равно 2,000

Округление и дроби

Округление дробей работает точно так же, как округление целых чисел . Единственное отличие состоит в том, что вместо десятков, сотен, тысяч и так далее вы округляете до десятых, сотых, тысячных и так далее.

• 7,8199 округлить до десятых 7,8
• 1,0621 округлить до сотых 1,06
• 3.8792 округлить до тысячных будет 3.879

Вот совет: до не путайтесь при округлении длинных десятичных дробей, смотрите только на число в том месте, до которого вы округляете, и на число, которое следует за ним. Например, чтобы округлить 5,3824791401 до сотых, просто посмотрите на число в сотых долях — 8 — и на следующее за ним число — 2. Тогда вы можете легко округлить его до 5,38.

Округление и суммирование

Округление сделать суммы легко. Например, в продуктовом магазине вы можете найти товары по следующим ценам:

• 2,25 доллара
• 0,88 доллара
• 2,69 доллара

Если вы хотите узнать, сколько они будут стоить, вы можете сложить цены с помощью ручку и бумагу или попробуйте сложить их в уме. Или вы можете сделать это простым способом — округлить до ближайшего доллара, например:

• 2 доллара
• 1 доллар
• 3 доллара

Округляя, можно легко вычислить, что вам потребуется около 6 долларов, чтобы заплатить за продукты. Это довольно близко к точному числу в 5,82 доллара.

Как видите, при нахождении круглой суммы быстрее всего округлить числа перед их сложением.

1. Некоторые статистики предпочитают округлять 5 до ближайшего четного числа. В результате примерно в половине случаев 5 будет округляться в большую сторону, а примерно в половине случаев — в меньшую. Таким образом, 26,5, округленное до ближайшего четного числа, будет равно 26 — оно будет округлено в меньшую сторону. И 77,5, округленное до ближайшего четного числа, будет 78 — оно будет округлено в большую сторону.

База данных Fact Monster/Information Please®, © 2008 Pearson Education, Inc. Все права защищены.

Калькулятор методов округления

Базовый калькулятор

Калькулятор методов округления

Метод:

Округлить наполовину вверхОкруглить наполовину внизОкруглить наполовину к нулюОкруглить наполовину от нуляОкруглить наполовину четно (банкиры)Округлить наполовину нечетноОкруглить наполовину в случайном порядкеОкруглить все вверх (потолок)Округлить все вниз (пол)

раунд:

до:

млн. Сотни миллионов миллионов миллионов миллионов сотней тысяч тысяч тысяч тысяч. Миллионные (6)Десятимиллионные (7)Стомиллионные (8)Миллиардные (9)
Округлить до ближайшего разряда

Ответ:

1,2

Округление до , ближайшего 0,1 или
до десятых долей .

Метод: Округление средних значений в сторону положительной бесконечности

Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.

Получить виджет для этого калькулятора

© Calculator Soup

Поделитесь этим калькулятором и страницей

Использование калькулятора

Округляйте числа и десятичные дроби, используя правила половинного значения выбранного вами метода округления. Включает в себя методы скругления наполовину вверх и скругления наполовину вниз, а также скругление потолка и пола.

Методы округления

Существует несколько методов округления чисел. Используемый вами метод зависит от того, почему вы округляете числа, и от обычных правил округления для типов чисел, с которыми вы работаете.

Типичные методы округления:

• Круглая половинка вверх
• Круглая половина вниз
• Круглая половина к нулю
• Половина раунда от нуля
• Round Half Even (банковские правила)
• Круглый Половина Нечетный
• Круглый полуслучайный
• Круглый (потолок)
• Округлить все вниз (пол)

Округление в большую и меньшую сторону выполняется довольно просто, если только вы не имеете дело с числами, лежащими ровно посередине между числами, до которых вы округляете. Например, финансовые расчеты могут привести к таким цифрам, как 24 765 долларов США. Округлили бы вы 5 до 77 центов или до 76 центов?

Или при вычислении площади круга вам может понадобиться округлить значение числа пи (3,1415926535898. ..) до определенного десятичного разряда перед вычислением.

Пример округления

Допустим, у вас есть набор измерений с точностью до двух знаков после запятой, но вам нужны числа с точностью до одного знака после запятой. Вы должны округлить десятичную дробь в сотых до десятых.

Набор данных

1.11

1.12

1.13

1.14

1.15

1.16

1.17

1.18

1.19

Вы отбрасываете все цифры справа от десятых, чтобы все значения стали 1,1? Нет, потому что 1.1 не является достоверным представлением набора данных. Вместо этого вы округляете каждое число до ближайшего значения.

Возьмите первую точку данных: вы округляете 1,11 до 1,1 или до 1,2? Первый шаг — оценить, ближе ли значение 1,11 к 1,1 или 1,2. Это ближе к 1,1, поэтому вы округляете 1,11 до 1,1.

Что насчет 1.18 — это ближе к 1.1 или 1.2? Поскольку оно ближе по значению к 1,2, вы должны округлить до 1,2.

Вы можете видеть, что 1.15 находится ровно посередине между 1.1 и 1.2. Каждое число ниже 1,15 ближе к 1,1, поэтому округляйте в меньшую сторону. Каждое число выше 1,15 ближе к 1,2, поэтому округляйте в большую сторону. А как же 1.15?

1,1

1,11

1,12

1,13

1,14

1,15

1.16

1.17

1.18

1.19

1.2

Описанные ниже методы округления были разработаны для обработки средней точки и, теоретически, минимизации накопленных ошибок округления. В реальных ситуациях выбранный метод округления зависит от применения математики, а также от задействованных языков программирования. Калькулятор округления в CalculatorSoup использует общий метод округления до половины от нуля.

Типы округления

В следующих пояснениях показано, как округлить среднее десятичное значение 1,15 до 1 в десятых долях. x — это округляемое число.

Круглая половинка вверх

Половинчатые значения округляются до положительной бесконечности.

• х
• x >= 5 округлить вверх

Для положительных чисел:

• 1,149 патронов до 1,1
• 1150 патронов до 1,2
• 1,151 патрона до 1,2

Для отрицательных чисел:

• -1,149 патронов до -1,1
• -1,150 патронов до -1,1 до
• -1,151 патронов до -1,2

Круглая половина вниз

Половинчатые значения округляются в меньшую сторону до отрицательной бесконечности.

• х
• x > 5 округлить вверх

Для положительных чисел:

• 1,149 патронов до 1,1
• 1.150 патронов на 1.1 вниз
• 1,151 патрона до 1,2

Для отрицательных чисел:

• -1,149 патронов до -1,1
• -1,150 раундов до -1,2 вниз, более отрицательное
• -1,151 раундов до -1,2

Круглая половина к нулю

Половинчатые значения округляются до нуля . Это правило округления действует симметрично около 0,

.

• Для положительных чисел, x
• Для отрицательных чисел x >= 5 округлить до нуля

Для положительных чисел:

• 1,149 патронов до 1,1
• 1.150 раундов на 1.1 вниз, в сторону 0
• 1,151 патрона до 1,2

Для отрицательных чисел:

• -1,149 патронов до -1,1
• -1,150 раундов до -1,1 вверх, в сторону 0
• -1,151 патронов до -1,2

Половина раунда от нуля

Округление промежуточных значений от нуля . Это правило округления действует симметрично около 0,

.

• Для положительных чисел, x >= 5 округлить вверх, от нуля
• Для отрицательных чисел x >= 5 округлить в меньшую сторону от нуля

Для положительных чисел:

• 1,149 патронов до 1,1
• 1. 150 патронов на 1.2 вверх, от 0
• 1,151 патрона до 1,2

Для отрицательных чисел:

• -1,149 патронов до -1,1
• -1.150 раундов до -1.2 вниз, от 0
• -1,151 патронов до -1,2

Round Half Even (банковские правила)

Половинчатые значения округляются до ближайшего четного значения .

Обратите внимание, что 1,150 округляется до четного значения 1,2, а 1,250 округляется до четного значения 1,2

• х
• x = 5 округлить до ближайшего четного (нечетного) значения
• x > 5 раундов от нуля

Для положительных чисел:

• 1,149 патронов к 1,1 и 1,249 патронов к 1,2
• 1.150 раундов до 1.2 и 1.250 раундов до 1.2 ближайшее четное значение
• 1,151 патрона на 1,2 и 1,251 патрона на 1,3

Для отрицательных чисел:

• -1,149 раундов до -1,1 и -1,249 раундов до -1,2
• -1,150 раундов до -1,2 и -1,250 раундов до -1,2 ближайшее четное значение
• -1,151 раунда до -1,2 и -1,251 раунда до -1,3

Круглая половина Нечетная

Половинчатые значения округляются до ближайшего нечетного значения .

Обратите внимание, что 1,150 округляется до нечетного значения 1,1, а 1,250 округляется до нечетного значения 1,3

• х
• x = 5 округлить до ближайшего нечетного (нечетного) значения
• x > 5 раундов от нуля

Для положительных чисел:

• 1,149 патронов к 1,1 и 1,249 патронов к 1,2
• 1,150 раундов до 1,1 и 1,250 раундов до 1,3 ближайшего нечетного значения
• 1,151 патрона на 1,2 и 1,251 патрона на 1,3

Для отрицательных чисел:

• -1,149 патронов до -1,1 и -1,249 патронов до -1,2
• От -1,150 раунда до -1,1 и от -1,250 раунда до -1,3 ближайшего нечетного значения
• -1,151 раунда до -1,2 и -1,251 раунда до -1,3

Круглый, полуслучайный

Округлить промежуточные значения в соответствии со случайно выбранным методом Округлить наполовину вверх или Округлить наполовину вниз.

Круглый (потолок)

Округлить все значения в большую сторону. 1.150 патронов к 2 и -1.150 патронов к -1.

• 1,7 раунда до 2
• 1,5 раунда до 2
• 1,3 раунда до 2
• -1,3 раунда до -1
• -1,5 раунда до -1
• -1,7 раунда до -1

Скругление вниз (пол)

Округлите все значения в меньшую сторону. 1.150 патронов к 1 и -1.150 патронов к -2.

• 1,7 раунда до 1
• 1,5 раунда до 1
• 1,3 раунда до 1
• -1,3 раунда до -2
• -1,5 раунда до -2
• -1,7 раунда до -2

Дополнительная литература

участника Википедии, «Округление», Википедия, Бесплатная энциклопедия, https://en.