Связные списки
Связный список является простейшим типом данных динамической структуры, состоящей из элементов (узлов). Каждый узел включает в себя в классическом варианте два поля:
- данные (в качестве данных может выступать переменная, объект класса или структуры и т. д.)
- указатель на следующий узел в списке.
Элементы связанного списка можно помещать и исключать произвольным образом.
Доступ к списку осуществляется через указатель, который содержит адрес первого элемента списка, называемый корнем списка.
Классификация списков
По количеству полей указателей различают однонаправленный (односвязный) и двунаправленный (двусвязный) списки.
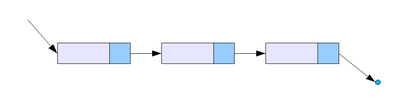
Связный список, содержащий только один указатель на следующий элемент, называется односвязным.
По способу связи элементов различают линейные и циклические списки.
Связный список, в котором, последний элемент указывает на NULL, называется линейным.
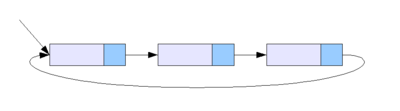
Связный список, в котором последний элемент связан с первым, называется циклическим.
Виды списков
Таким образом, различают 4 основных вида списков.
- Односвязный линейный список (ОЛС).
Каждый узел ОЛС содержит 1 поле указателя на следующий узел. Поле указателя последнего узла содержит нулевое значение (указывает на NULL).
- Односвязный циклический список (ОЦС).
Каждый узел ОЦС содержит 1 поле указателя на следующий узел. Поле указателя последнего узла содержит адрес первого узла (корня списка).
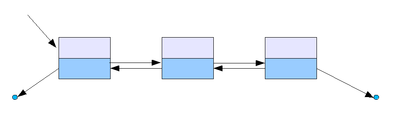
- Двусвязный линейный список (ДЛС).
Каждый узел ДЛС содержит два поля указателей: на следующий и на предыдущий узел. Поле указателя на следующий узел последнего узла содержит нулевое значение (указывает на NULL). Поле указателя на предыдущий узел первого узла (корня списка) также содержит нулевое значение (указывает на NULL).
- Двусвязный циклический список (ДЦС).
Каждый узел ДЦС содержит два поля указателей: на следующий и на предыдущий узел. Поле указателя на следующий узел последнего узла содержит адрес первого узла (корня списка). Поле указателя на предыдущий узел первого узла (корня списка) содержит адрес последнего узла.
Сравнение массивов и связных списков
| Массив | |
| Выделение памяти осуществляется единовременно под весь массив до начала его использования | Выделение памяти осуществляется по мере ввода новых элементов |
| При удалении/добавлении элемента требуется копирование всех последующих элементов для осуществления их сдвига | Удаление/добавление элемента осуществляется переустановкой указателей, при этом сами данные не копируются |
| Для хранения элемента требуется объем памяти, необходимый только для хранения данных этого элемента | Для хранения элемента требуется объем памяти, достаточный для хранения данных этого элемента и указателей (1 или 2) на другие элементы списка |
| Доступ к элементам может осуществляться в произвольном порядке | Возможен только последовательный доступ к элементам |
Назад: Структуры данных
prog-cpp.ru
Коты в коробках / OTUS. Онлайн-образование corporate blog / Habr
И снова здравствуйте! В преддверии старта курса «Разработчик Python» подготовили для вас небольшой авторский материал о связных списках на Python.Python очень удобный и многогранный язык, но по умолчанию не имеет такой структуры данных как связный список или LinkedList. Сегодня я поделюсь своими наработками на эту тему и расскажу немного о том, что из себя представляет эта структура данных. Эта статья будет интересна тем, кто впервые сталкивается с темой связных списков и хочет понять, как они работают с алгоритмической точки зрения.
Что такое LinkedList?
LinkedList или связный список – это структура данных. Связный список обеспечивает возможность создать двунаправленную очередь из каких-либо элементов. Каждый элемент такого списка считается узлом. По факту в узле есть его значение, а также две ссылки – на предыдущий и на последующий узлы. То есть список «связывается» узлами, которые помогают двигаться вверх или вниз по списку. Из-за таких особенностей строения из связного списка можно организовать стек, очередь или двойную очередь.
Что мы будем делать со связным списком:
- Проверять содержится ли в нем тот или иной элемент;
- Добавлять узлы в конец;
- Получать значение узла по индексу;
- Удалять узлы.
На самом деле опций по работе с ними гораздо больше, но остановимся мы именно на реализации этих основных шагов. Поняв, по какому принципу они строятся, вы сами с легкостью сможете реализовать свои собственные методы.
Начать придется с создания двух классов:
class Box:
def __init__ (self,cat = None):
self.cat = cat
self.nextcat = None
class LinkedList:
def __init__(self):
self.head = NoneВ общем случае, у нас получился узел, у которого есть внутри какое-то значение – кот, и ссылка на следующий узел. То есть в классе Box, соответственно, есть кот и ссылка на следующую коробку. Как и у любого списка, у связного тоже есть начало, а именно head. Поскольку изначально там ничего нет, начальному элементу присваивается значение None.
Содержится ли элемент в списке
Начнем с простого. Чтобы проверить есть ли какой-то определенный кот в одной из последовательно расположенных коробок, нужно пройтись циклом по всему списку, сверяя имеющееся значение со значениями элемента в списке.
def contains (self, cat):
lastbox = self.head
while (lastbox):
if cat == lastbox.cat:
return True
else:
lastbox = lastbox.nextcat
return FalseДобавить узел в конец списка
Для начала новую коробку нужно создать, а уже в нее поместить нового кота. После необходимо проверять начиная с начала связного списка, есть ли в текущем узле ссылка на следующий и если она есть, то переходить к нему, в противном случае узел — последний, значит нужно создавать ссылку на следующий узел и помещать в него ту самую новую коробку, которую мы создали.
def addToEnd(self, newcat): newbox = Box(newcat) if self.head is None: self.head = newbox return lastbox = self.head while (lastbox.nextcat): lastbox = lastbox.nextcat lastbox.nextcat = newbox
Получить узел по индексу
По индексу catIndex мы хотим получить узел-коробку, но поскольку как такового индекса у узлов не предусмотрено, нужно придумать какую-то замену, а именно переменную, которая будет выполнять роль индекса. Эта переменная – это boxIndex. Мы проходимся по всему списку и сверяем «порядковый номер» узла, и при совпадении его с искомым индексом – выдаем результат.
def get(self, catIndex): lastbox = self.head boxIndex = 0 while boxIndex <= catIndex: if boxIndex == catIndex: return lastbox.cat boxIndex = boxIndex + 1 lastbox = lastbox.nextcat
Удалить узел
Здесь мы рассмотрим удаление элемента не по индексу, а по значению, чтобы внести хоть какое-то разнообразие.
Поиск начинается с головы списка, то есть с первой по счету коробки, и продолжается, пока коробки не закончатся, то есть пока headcat не станет None. Мы проверяем соответствует ли значение, хранящееся в текущем узле, тому, которое мы хотим удалить. Если нет, то мы просто идем дальше. Однако, если соответствует, то мы удаляем его и «перепривязываем» ссылки, то есть мы удаляем N-ую коробку, при этом коробка N-1 теперь ссылается на коробку N+1.
def removeBox(self,rmcat):
headcat = self.head
if headcat is not None:
if headcat.cat==rmcat:
self.head = headcat.nextcat
headcat = None
return
while headcat is not None:
if headcat.cat==rmcat:
break
lastcat = headcat
headcat = headcat.nextcat
if headcat == None:
return
lastcat.nextcat = headcat.nextcat
headcat = NoneВот и все, спасибо, что ознакомились с материалом! На самом деле структура LinkedList это не сложно, и важно понимать, как она работает изнутри. Конечно, на Python ее можно было бы реализовать и в lambda-выражениях, это заняло бы гораздо меньше места, однако здесь я преследовала целью объяснить ее строение, и принцип ее работы на Python максимально подробно, а не гнаться за оптимизацией.
habr.com
О выборе структур данных для начинающих / Habr
Часть 1. Линейные структуры
Когда вам нужен один объект, вы создаёте один объект. Когда нужно несколько объектов, тогда есть несколько вариантов на выбор. Я видел, как многие новички в коде пишут что-то типа такого:
// Таблица рекордов
int score1 = 0;
int score2 = 0;
int score3 = 0;
int score4 = 0;
int score5 = 0;Это даёт нам значение пяти рекордов. Этот способ неплохо работает, пока вам не потребуется пятьдесят или сто объектов. Вместо создания отдельных объектов можно использовать массив.
// Таблица рекордов const int NUM_HIGH_SCORES = 5; int highScore[NUM_HIGH_SCORES] = {0};
Будет создан буфер из 5 элементов, вот такой:
Заметьте, что индекс массива начинается с нуля. Если в массиве пять элементов, то они будут иметь индексы от нуля до четырёх.
Недостатки простого массива
Если вам нужно неизменное количество объектов, то массив вполне подходит. Но, допустим, вам нужно добавить в массив ещё один элемент. В простом массиве этого сделать невозможно. Допустим, вам нужно удалить элемент из массива. В простом массиве это так же невозможно. Вы привязаны к одному количеству элементов. Нам нужен массив, размер которого можно менять. Поэтому нам лучше выбрать…
Динамический массив — это массив, который может менять свой размер. Основные языки программирования в своих стандартных библиотеках поддерживают динамические массивы. В C++ это vector. В Java это ArrayList. В C# это List. Все они являются динамическими массивами. В своей сути динамический массив — это простой массив, однако имеющий ещё два дополнительных блока данных. В них хранятся действительный размер простого массива и объём данных, который может на самом деле храниться в простом массиве. Динамический массив может выглядеть примерно так:
// Внутреннее устройство класса динамического массива
sometype *internalArray;
unsigned int currentLength;
unsigned int maxCapacity;Элемент internalArray указывает на динамически размещаемый буфер. Действительный массив буфера хранится в maxCapacity. Количество использовуемых элементов задаётся currentLength.
Добавление к динамическому массиву
При добавлении объекта к динамическому массиву происходит несколько действий. Класс массива проверяет, достаточно ли в нём места. Если currentLength < maxCapacity, то в массиве есть место для добавления. Если места недостаточно, то размещается больший внутренний массив, и всё копируется в новый внутренний массив. Значение maxCapacity увеличивается до нового расширенного значения. Если места достаточно, то добавляется новый элемент. Каждый элемент после точки вставки должен быть скопирован на соседнее место во внутреннем массиве, и после завершения копирования пустота заполняется новым объектом, а значение currentLength увеличивается на единицу.
Поскольку необходимо перемещать каждый объект после точки вставки, то наилучшим случаем будет добавление элемента к концу. При этом нужно перемещать ноль элементов (однако внутренний массив всё равно требует расширения). Динамический массив лучше всего работает при добавлении элемента в конец, а не в середину.
При добавлении объекта к динамическому массиву каждый объект может переместиться в памяти. В таких языках, как C и C++, добавление к динамическому массиву означает, что ВСЕ указатели на объекты массива становятся недействительными.
Удаление из динамического массива
Удаление объектов требует меньше работы, чем добавление. Во-первых, уничтожается сам объект. Во-вторых, каждый объект после этой точки сдвигается на один элемент. Наконец, currentLength уменьшается на единицу.
Как и при добавлении к концу массива, удаление из конца массива является наилучшим случаем, потому что при этом нужно перемещать ноль объектов. Также стоит заметить, что нам не нужно изменять размер внутреннего массива, чтобы сделать его меньше. Выделенное место может оставаться таким же, на случай, если мы позже будем добавлять объекты.
Удаление объекта из динамического массива приводит к смещению в памяти всего после удалённого элемента. В таких языках, как C и C++, удаление из динамического массива означает, что указатели на всё после удалённого массива становятся недействительными.
Недостатки динамических массивов
Допустим, массив очень велик, а вам нужно часто добавлять и удалять объекты. При этом объекты могут часто копироваться в другие места, а многие указатели становиться недействительными. Если вам нужно вносить частые изменения в середине динамического массива, то для этого есть более подходящий тип линейной структуры данных…
Массив — это непрерывный блок памяти, и каждый элемент его расположен после другого. Связанный список — это цепочка объектов. Связанные списки тоже присутствуют в стандартных библиотеках основных языков программирования. В C++ они называются list. В Java и C# это LinkedList. Связанный список состоит из серии узлов. Каждый узел выглядит примерно так:
// Узел связанного списка
sometype data;
Node* next;Он создаёт структуру такого типа:
Каждый узел соединяется со следующим.
Добавление к связанному списку
Добавление объекта к связанному списку начинается с создания нового узла. Данные копируются внутрь узла. Затем находится точка вставки. Указатель нового узла на следующий объект изменяется так, чтобы указывать на следующий за ним узел. Наконец, узел перед новым узлом изменяет свой указатель, чтобы указывать на новый узел.
Удаление из связанного списка
При удалении объекта из связанного списка находится узел перед удаляемым узлом. Он изменяется таким образом, чтобы указывать на следующий после удалённого объекта узел. После этого удалённый объект можно безопасно стереть.
Преимущества связанного списка
Самое большое преимущество связанного списка заключается в добавлении и удалении объектов из списка. Внесение изменений в середину списка выполняется очень быстро. Помните, что динамический массив теоретически мог вызывать смещение каждого элемента, а связанный список сохраняет каждый другой объект на своём месте.
Недостатки связанного списка
Вспомните, что динамический массив — это непрерывный блок памяти.
Если вам нужно получить пятисотый элемент массива, то достаточно просто посмотреть на 500 «мест» вперёд. В связанном списке память соединена в цепочку. Если вам нужно найти пятисотый элемент, то придётся начинать с начала цепочки и следовать по её указателю к следующему элементу, потом к следующему, и так далее, повторяя пятьсот раз.
Произвольный доступ к связанному списку выполняется очень медленно.
Ещё один серьёзный недостаток связанного списка не особо очевиден. Каждому узлу необходимо небольшое дополнительное место. Сколько ему нужно места? Можно подумать, что для него нужен только размер указателя, но это не совсем так. При динамическом создании объекта всегда существует небольшой запас. Некоторые языки программирования, например, C++, работают со страницами памяти. Обычно страница занимает 4 килобайта. При использовании операторы добавления и удаления, размещается целая страница памяти, даже если вам нужно использовать только один байт.
В Java и C# всё устроено немного иначе, в них есть специальные правила для небольших объектов. Для этих языков не требуется вся 4-килобайтная страница памяти, но всё равно у них есть небольшой запас. Если вы используете стандартные библиотеки, то о втором недостатке волноваться не нужно. Они написаны таким образом, чтобы минимизировать занимаемое впустую место.
Эти три типа (массив, динамический массив и связанный список) создают основу почти для всех более сложных контейнеров данных. При учёбе в колледже одним из первых заданий в изучении структур данных становится собственная реализация классов динамического массива и связанного списка.
Эти структуры являются в программировании фундаментальными. Не важно, какой язык вы будете изучать, для работы с данными вы будете их использовать.
Часть 2. Линейные структуры данных с конечными точками
Представьте, что у вас есть куча листов бумаги.
Мы кладём один лист в стопку. Теперь мы можем получить доступ только к верхнему листу.
Мы кладём ещё один лист в стопку. Предыдущий лист теперь скрыт и доступ к нему невозможен, мы можем использовать верхний лист. Когда мы закончим с верхним листом, мы можем убрать его со стопки, открыв доступ к лежащему под ним.
В этом заключается идея стека. Стек — это структура LIFO. Это расшифровывается как Last In First Out («последним вошёл, первым вышел»). При добавлении и удалении из стека последний добавленный элемент будет первым удаляемым.
Для стека нужно всего три операции: Push, Pop и Top.
Push добавляет объект в стек. Pop удаляет объект из стека. Top даёт самый последний объект в стеке. Эти контейнеры в большинстве языков являются частью стандартных библиотек. В C++ они называются stack. В Java и C# это Stack. (Да, единственная разница в названии с заглавной буквы.) Внутри стек часто реализуется как динамический массив. Как вы помните из этой структуры данных, самыми быстрыми операциями на динамических массивах являются добавление и удаление элементов из конца. Поскольку стек всегда добавляет и удаляет с конца, обычно push и pop объектов в стеке выполняется невероятно быстро.
Представьте, что вы стоите в очереди за чем-то.
Первого человека в очереди обслуживают, после чего он уходит. Потом обслуживается и уходит второй в очереди. Другие люди подходят к очереди и встают в её конец. Вот в этом заключается идея структуры данных «очередь».
Очередь — это структура FIFO (First In First Out, «первым зашёл, первым вышел»).
При добавлении и удалении из очереди первый добавляемый элемент будет первым извлекаемым. Очереди нужно только несколько операций: Push_Back, Pop_Front, Front и Back. Push_Back добавляет элемент к концу очереди. Pop_Front удаляет элемент из начала очереди. Front и Back позволяют получить доступ к двум концам очереди.
Программистам часто нужно добавлять или удалять элементы из обоих концов очереди. Такая структура называется двухсторонней очередью (double ended queue, deque). В этом случае добавляется ещё пара операций: Push_Front и Pop_Back. Эти контейнеры тоже включены в большинство основных языков. В C++ это queue и deque. Java определяет интерфейсы для очереди и двухсторонней очереди, а затем реализует их через LinkedList. В C# есть класс Queue, но нет класса Deque.
Внутри очередь и двухсторонняя очередь могут быть устроены довольно сложно. Поскольку объекты могут поступать и извлекаться с любого конца, внутренний контейнер должен уметь наращивать и укорачивать очередь с начала и с конца. Во многих реализациях используются множественные страницы памяти. Когда любой из концов разрастается за пределы текущей страницы, добавляется дополнительная страница. Если страница больше не нужна, то она удаляется. В Java используется следующий способ: для связанного списка требуется немного дополнительной памяти, а не страниц памяти, но для этого языка такая реализация вполне работает.
Это очень распространённая вариация очереди. Очередь с приоритетом очень похожа на обычную очередь.
Программа добавляет элементы с конца и извлекает элементы из начала. Разница в том, что можно задавать приоритеты определённым элементам очереди. Все самые важные элементы обрабатываются в порядке FIFO. Потом в порядке FIFO обрабатываются элементы с более низким приоритетом. И так повторяется, пока не будут обработаны в порядке FIFO элементы с самым низким приоритетом.
При добавлении нового элемента с более высоким приоритетом, чем остальная часть очереди, он сразу же перемещается в начало очереди. В C++ эта структура называется priority_queue. В Java это PriorityQueue. В стандартной библиотеке C# очереди с приоритетом нет. Очереди с приоритетом полезны не только для того, чтобы встать первым на очереди к принтеру организации. Их можно использовать для удобной реализации алгоритмов, например, процедуры поиска A*. Наболее вероятным результатам можно отдать более высокий приоритет, менее вероятным — более низкий. Можно создать собственную систему для сортировки и упорядочивания поиска A*, но намного проще использовать встроенную очередь с приоритетом.
Стеки, очереди, двухсторонние очереди и очереди с приоритетом можно реализовать на основе других структур данных. Это не фундаментальные структуры данных, но их часто используют. Они очень эффективны, когда нужно работать только с конечными элементами данных, а серединные элементы не важны.
Часть 3. Деревья и кучи.
Деревья данных очень полезны во многих случаях. В разработке видеоигр структуры деревьев используются для подразделения пространства, позволяющего разработчику быстро находить находящиеся рядом объекты без необходимости проверки каждого объекта в игровом мире. Даже несмотря на то, что структуры деревьев являются фундаментальными в информатике, на практике в большинстве стандартных библиотек нет непосредственной реализации контейнеров на основе деревьев. Я подробно расскажу о причинах этого.
Дерево — это… дерево. У настоящего дерева есть корень, ветви, а на концах ветвей есть листья.
Структура данных дерева начинается с корневого узла. Каждый узел может разветвляться на дочерние узлы. Если у узла нет дочерних элементов, то он называется узлом листа. Когда деревьев несколько, это называется лесом. Вот пример дерева. В отличие от настоящих деревьев они растут сверху вниз: корневой узел обычно рисуется сверху, а листья — внизу.
Одним из первых возникает вопрос: сколько каждый узел может иметь дочерних элементов?
Многие деревья имеют не больше двух дочерних узлов. Они называются двоичными деревьями. На примере выше показано двоичное дерево. Обычно дочерние элементы называются левым и правым дочерними узлами. Ещё одним распространённым в играх типом деревьев является дерево с четырьмя дочерними узлами. В дереве квадрантов (quadtree), которое можно использовать для покрытия сетки, дочерние узлы обычно называются по закрываемому ими направлению: NorthWest (северо-запад) или NW, NorthEast (северо-восток) или NE, SouthWest (юго-запад) или SW и SouthEast (юго-восток) или SE.
Деревья используются во многих алгоритмах (я уже упоминал о двоичных деревьях). Существуют сбалансированные и несбалансированные деревья. Бывают красно-чёрные деревья, АВЛ-деревья, и многие другие.
Хотя теория деревьев и удобна, она страдает от серьёзных недостатков: места для хранения и скорости доступа. Каким способом лучше всего хранить дерево? Наиболее простым способом является построение связанного списка, он же оказывается самым худшим. Предположим, что нам нужно построить сбалансированное двоичное дерево. Мы начинаем со следующей структуры данных:
// Узел дерева
Node* left;
Node* right;
sometype data;Достаточно просто. Теперь представим, что в нём нужно хранить 1024 элемента. Тогда для 1024 узлов придётся хранить 2048 указателей.
Это нормально, указатели малы и можно обойтись небольшим пространством.
Вы можете помнить, что при каждом размещении объекта он занимает небольшую часть дополнительных ресурсов. Точное количество дополнительных ресурсов зависит от библиотеки используемого вами языка. Многие популярные компиляторы и инструменты могут использовать различные варианты — от всего лишь нескольких байтов для хранения данных до нескольких килобайтов, позволяющих упростить отладку. Я работал с системами, в которых размещение занимает не меньше 4 КБ памяти. В этом случае 1024 элементов потребуют около 4 МБ памяти. Обычно ситуация не настолько плоха, но дополнительные затраты на хранение множества мелких объектов нарастают очень быстро.
Вторая проблема — скорость. Процессорам «нравится», когда объекты находятся в памяти рядом друг с другом. У современных процессоров есть участок очень быстрой памяти — кэш — который очень хорошо справляется с большинством данных. Когда программе требуется один фрагмент данных, кэш загружает этот элемент, а также элементы рядом с ним. Когда данные не загружены в очень быструю память (это называется «промахом кэша»), программа приостанавливает свою работу, и ждёт загрузки данных. В самом очевидном формате, когда каждый элемент дерева хранится в собственном участке памяти, ни один из них не находится рядом с другим. Каждый раз при обходе дерева программа приостанавливается.
Если создание дерева напрямую связано с такими проблемами, то стоит выбрать структуру данных, работающую как дерево, но не обладающую его недостатками. И эта структура называется…
Чтобы вас запутать, скажу, что существует два вида куч.
Первая — это куча в памяти. Это большой блок памяти, в котором хранятся объекты. Но я буду говорить о другой куче.
Структура данных «куча» — это, в сущности, то же самое, что и дерево. У неё есть корневой узел, у каждого узла есть дочерние узлы, и так далее. Куча добавляет ограничения, её сортировка всегда должна выполняться в определённом порядке. Необходима функция сортировки — обычно оператор «меньше чем».
При добавлении или удалении объектов из кучи структура сортирует себя, чтобы стать «полным» деревом, в котором каждый уровень дерева заполнен, за исключением, возможно, только последнего ряда, где всё должно быть смещено в одну сторону. Это позволяет очень эффективно обеспечить пространство для хранения и поиск по куче.
Кучи можно хранить в простом или динамическом массиве, то есть на её размещение тратится мало места. В C++ есть такие функции, как push_heap() и pop_heap(), позволяющие реализовать кучи в собственном контейнере разработчика. В стандартных библиотеках Java и C# нет похожего функционала. Вот дерево и куча с одинаковой информацией:
Это простые, фундаментальные и очень полезные структуры данных. Многие считают, что они должны присутствовать в стандартных библиотеках. За несколько секунд в поисковике вы можете найти тысячи реализаций деревьев.
Оказывается, что хотя деревья очень полезны и фундаментальны, существуют более хорошие контейнеры. Есть более сложные структуры данных, обладающие преимуществами дерева (стабильность и форма) и преимуществами кучи (пространство и скорость). Более совершенные структуры данных обычно являются сочетанием таблиц данных с таблицами поиска. Две таблицы в сочетании обеспечивают быстрый доступ, быстрое изменение, и хорошо проявляются себя и в плотных, и в неплотных ситуациях. Они не требуют переноса элементов при добавлении и удалении элементов, не потребляют излишней памяти и не фрагментируют память при расширенном использовании.
Важно знать о структурах данных «дерево», потому что в работе вам часто придётся их использовать. Также важно знать, что эти структуры данных при прямой реализации имеют недостатки. Вы можете реализовывать собственные структуры деревьев, просто знайте, что существуют более компактные типы. Зачем же я рассказал о них, если они на самом деле не используются в стандартных библиотеках? Они применяются в качестве внутренних структур в нашей следующей теме:
Часть 4. Нелинейные структуры данных.
Эти структуры данных отличаются от массивов и списков. Массивы — это последовательные контейнеры. Элементы в них расположены по порядку. При добавлении нескольких элементов в определённом порядке, они остаются в этом порядке.
Нелинейные структуры данных необязательно остаются в том порядке, в котором их добавляют. При добавлении или удалении элементов может измениться порядок других элементов. Внутри они состоят из деревьев и куч, рассмотренных в предыдущей части.
Существует много вариаций таких структур данных. Самыми базовыми являются словарь данных, а также упорядоченное и неупорядоченное множества.
Обычный словарь состоит из набора слов (ключа) и определения (значения). Поскольку ключи находятся в алфавитном порядке, любой элемент можно найти очень быстро.
Если словари не были бы отсортированы, то поиск слов в них был невероятно сложным.
Существует два основных способа сортировки элементов в словаре: сравнение или хэш. Традиционное упорядочивание сравнением обычно более интуитивно. Оно похоже на порядок бумажном словаре, где всё отсортировано по алфавиту или по числам.
При сортировке элементов таким образом может потребоваться функция сравнения. Обычно эта функция по умолчанию является оператором «меньше чем», например a < b.
Второй способ сортировки элементов — использование хэша. Хэш — это просто способ преобразования блока данных в одно число. Например, строка «blue» может иметь хэш 0xa66b370d, строка «red» — хэш 0x3a72d292. Когда словарь данных использует хэш, он обычно считается неотсортированным. В действительности он всё равно отсортирован по хэшу, а не по удобному человеку критерию. Словарь данных работает тем же образом. Есть небольшая разница в скорости между использованием словарей с традиционной сортировкой и сортировкой по хэшу. Различия так малы, что их можно не учитывать.
В C++ есть семейство контейнеров map/mutimap или unordered_map/unordered_multimap. В Java семейство называется HashMap, TreeMap или LinkedHashMap. В C# это Dictionary или SortedDictionary. Каждое из них имеет собственные особенности реализации, например сортировка по хэшу или сравнением, допущение дубликатов, но в целом концепция одинакова. Заметьте, что в каждой из стандартных библиотек имеется их упорядоченная версия (в которой задаётся сравнение) и неупорядоченная версия (где используется хэш-функция). После добавления элементов в словарь данных вы сможете изменять значения, но не ключ.
Вернёмся к аналогии с бумажным словарём: можно менять определение слова, не перемещая слово в книге; если изменить написание слова, то придётся удалять первое написание и повторно вставлять слово с новым написанием. Подробности работы вы можете узнать в учебниках. Достаточно знать, что словари очень быстры при поиске данных, и могут быть очень медленными при добавлении или удалении значений.
Упорядоченное множество — это почти то же самое, что и словарь. Вместо ключа и значения в нём есть только ключ. Вместо традиционного словаря со словами и определениями там только слова. Множества полезны, когда вам нужно хранить только слова без дополнительных данных. В C++ семейство структур называется set/multiset или unordered_set/unordered_multiset. В Java это HashSet, TreeSet или LinkedHashSet. В C# они называются HashSet и SortedSet.
Как и в случае со словарями, существуют упорядоченные версии (где задаётся сравнение) и неупорядоченные версии (где используется хэш-функция). После добавления ключа его тоже нельзя изменять. Вместо этого нужно удалить старый объект и вставить новый. Часто они реализуются точно так же, как словарь данных, просто хранят только значение. Поскольку они реализуются так же, то они имеют те же характеристики. В множествах очень быстро ищутся и находятся значения, но они медленно работают при добавлении и удалении элементов.
Классы контейнеров словарей данных, упорядоченных и неупорядоченных множеств очень полезны для быстрого поиска данных. Часто они реализуются как деревья или хэш-таблицы, которые очень эффективны в этом отношении. Используйте их тогда, когда требуется один раз создать данные и часто ссылаться на них. Они не так эффективны при добавлении и удалении элементов. Внесение изменений в контейнер может вызвать смещение или изменение порядка внутри него. Если вам необходимо следовать этому паттерну использования, то лучше выбрать упорядоченный связанный список.
Часть 5. Правильный выбор структур данных.
В предыдущих частях мы перечислили самые часто используемые структуры данных.
Вкратце повторим их.
Существуют линейные структуры: массив, динамический массив и связанный массив. Они линейны потому, что остаются в том порядке, в котором из расположили. Массивы очень быстры при произвольном доступе и имеют относительно неплохую производительность при добавлении и удалении из конца. Связанный список очень хорош при частом добавлении и удалении из середины.
Есть линейные структуры данных с конечными точками: семейство стеков и очередей. Оба они работают примерно так же, как их аналоги в реальном мире. В стеке, например, в стопке тарелок или в стеке данных, можно «затолкнуть» (push) что-нибудь наверх, можно получить доступ к верхнему элементу и можно «столкнуть» (pop) этот элемент. Очередь, так же как очередь людей, работает добавлением к концу линии и удалением с начала линии.
Затем существуют нелинейные структуры данных: словарь данных, упорядоченное и неупорядоченное множество. Все они внутренне нелинейны, порядок, в котором вы добавляете их, в сущности, не связан с порядком, в котором вы получаете их обратно. Словарь данных работает примерно так же, как настоящий бумажный словарь. У него есть ключ (слово, которое мы ищем) и значение (определение слова). Упорядоченное множество — это точно то же, что и словарь данных, содержащий ключи, но не значения, и отсортированный. Неупорядоченное множество — это просто «мешок» с объектами. Название немного сбивает с толку, потому что на самом деле они упорядочены, просто способ упорядочивания неудобен для человека. Все эти структуры идеальны для быстрого поиска.
Бо́льшую часть времени программистам приходится итеративно обрабатывать наборы данных.
Обычно нас не волнует порядок, в котором находится набор, мы просто начинаем с начала и посещаем каждый элемент. В этой очень частой ситуации выбор структуры данных на самом деле не важен.
Если возникают сомнения, то наилучшим выбором обычно является динамический массив. Он может разрастаться до любого объёма, при этом он относительно нейтрален, что позволяет довольно просто заменить его позже на другую структуру данных. Но иногда структура очень важна.
Одна из самых частых задач в играх — поиск пути: необходимо найти маршрут из точки А в точку Б. Один из наиболее распространённых алгоритмов поиска пути — это A*. В алгоритме A* существует структура данных, содержащая частичные пути. Структура сортируется таким образом, чтобы наиболее вероятный частичный путь находился в передней части контейнера. Этот путь оценивается, и если он не является законченным, алгоритм превращает этот частичный путь в несколько частичных путей большего размера, а потом добавляет их в контейнер.
Использование динамического массива в качестве этого контейнера будет плохим выбором по нескольким причинам. Во-первых, удаление элементов из начала динамического массива — это одна из самых медленных операций, которые мы можем выполнить. Во-вторых, повторная сортировка динамического массива после каждого добавления также может быть медленной. Как вы можете помнить из сказанного выше, существует структура данных, оптимизированная для такого типа доступа. Мы удаляем с начала и добавляем с конца, а автоматическая сортировка выполняется на основании того, какой путь является лучшим. Идеальным выбором для контейнера путей A* является очередь с приоритетом, она встроена в язык и полностью обеспечивает отладку.
Выбор структуры данных в основном зависит от паттерна использования.
Динамический массив — выбор по умолчанию
В случае сомнений используйте динамический массив. В C++ это vector. В Java он называется ArrayList. В C# это List. В общем случае динамический массив — это то, что нужно. У него хорошая скорость для большинства операций, и неплохая скорость для всех остальных. Если вы выясните, что вам нужна другая структура данных, то с него перейти будет легче всего.
Стек — только один конец
Если вы используете добавление и удаление только с одного конца, то выбирайте стек. Это stack в C++, Stack в Java и C#. Существует много алгоритмов, использующих стековую структуру данных. Первый, который приходит мне в голову — это двухстековый калькулятор. Численные задачи, такие как «Ханойские башни», можно решить с помощью стека. Но, вероятно, вы не будете использовать эти алгоритмы в своей игре. Однако игровые инструменты часто выполняют парсинг данных, а парсеры активно используют стековые структуры данных, чтобы обеспечить правильное сочетание пар элементов. Если вы работаете с широким диапазоном типов ИИ, то стековая структура данных будет невероятно полезна для семейства автоматов, называемых автоматом с магазинной памятью (pushdown automaton).
Семейство очередей — первый вошёл, первый вышел.
Если вы добавляете и удаляете только с обоих концов, то используйте или очередь, или двухстороннюю очередь. В C++ это queue или deque. В Java можно использовать интерфейсы Queue или Deque, оба они реализованы с помощью LinkedList. В C# есть класс Queue, но нет встроенной Deque. Если вам нужно, чтобы важные события происходили первыми, но в остальном всё происходило по порядку, то выберите очередь с приоритетом. В C++ это priority_queue, в Java это PriorityQueue. В C# нужно реализовывать её самостоятельно.
Нелинейные структуры — быстрый поиск.
Если вы создаёте стабильную группу элементов, и в основном выполняете произвольный поиск, то стоит выбрать одну из нелинейных структур. Некоторые из них хранят пары данных, в других содержатся отдельные данные. Некоторые из них отсортированы в полезном виде, другие упорядочены в удобном для компьютера порядке. Если попробовать создать список всех их сочетаний, то придётся писать отдельную статью (или можете перечитать предыдущую часть).
Связанный список — частые изменения с сохранением порядка
Если вы часто изменяете середину контейнера, и вам нужно обходить список только последовательно, то используйте связанный список. В C++ он называется list. В Java и C# это LinkedList. Связанный список — это отличный контейнер для случаев, когда данные только поступают и должны содержаться в порядке, или когда вам нужно периодически сортировать и перемещать элементы.
Выбор подходящей структуры данных может сильно повлиять на скорость работы алгоритмов. Понимание основных структур данных, их преимуществ и недостатков, поможет вам в использовании наиболее эффективной структуры для любой задачи. Рекомендую вам в конечном итоге изучить их подробно. Полное изучение этих структур данных в колледже по специальности «Информатика» обычно занимает несколько недель. Надеюсь, вы уяснили основные структуры данных и сможете выбрать подходящую без долгой учёбы в колледже.
На этом статья завершается. Благодарю за чтение.
habr.com
Разворот односвязного списка. Swift Edition / Habr
Ни для кого не секрет, что одна из любимых забав для разработчика программного обеспечения – прохождение собеседований с работодателями. Все мы занимаемся этим время от времени и совершенно по разным причинам. Причем самая очевидная из них – поиск работы – думаю, не самая распространенная. Посещение интервью – это неплохой способ держать себя в форме, повторять забытые основы и узнавать что-то новое. А в случае успеха, еще и повышать уверенность в своих силах. Нам становится скучно, мы выставляем себе статус «открыт для предложений» в какой-нибудь «деловой» социальной сети вроде «LinkedIn» – и армия менеджеров человеческих ресурсов уже атакует наши ящики для входящих сообщений.В процессе, пока весь этот бедлам творится, мы сталкиваемся со множеством вопросов, которые, как говорят по ту сторону подразумеваемо-обвалившегося занавеса, «ring a bell», а их подробности скрылись за туманом войны. Вспоминаются они чаще всего лишь на зачетах по алгоритмам и структурам данных (лично у меня таких вовсе не было) и собственно собеседованиях.
Один из самых распространенных вопросов на собеседовании на должность программиста любой специализации – это списки. Например, односвязные списки. И связанные с ними базовые алгоритмы. Например, разворот. И обычно это происходит как-то так: «Хорошо, а как бы вы развернули односвязный список?» Главное – застать этим вопросом соискателя врасплох.
Собственно, это все и привело меня к мысли написать этот небольшой обзор для постоянного напоминания и назидания. Итак, шутки в сторону, behold!
Односвязный список
Связный список – это одна из базовых структур данных. Каждый элемент (или узел) ее состоит из, собственно, хранимых данных и ссылок на соседние элементы. Односвязный список хранит ссылку только на следующий элемент в структуре, а двусвязный – на следующий и предыдущий. Такая организация данных позволяет им располагаться в любой области памяти (в отличие от, например, массива, все элементы которого должны располагаться в памяти один за другим).
Про списки можно много чего еще сказать, конечно: они могут быть кольцевыми (т.е. последний элемент хранит ссылку на первый) или нет (т.е. ссылка у последнего элемента отсутствует). Списки могут быть типизированными, т.е. содержать данные одного типа, или нет. И прочее, и прочее.
Лучше попробуем написать немного кода. Например, как-нибудь так можно представить узел списка:
final class Node<T> {
let payload: T
var nextNode: Node?
init(payload: T, nextNode: Node? = nil) {
self.payload = payload
self.nextNode = nextNode
}
}
«Generic»–тип, который в поле
payload способен хранить полезную нагрузку любого типа.Сам список исчерпывающе идентифицируется своим первым узлом:
final class SinglyLinkedList<T> {
var firstNode: Node<T>?
init(firstNode: Node<T>? = nil) {
self.firstNode = firstNode
}
}
Первый узел объявлен опциональным, потому что список вполне может быть и пустым.
По идее, конечно, в классе надо реализовать все необходимые методы – вставка, удаление, доступ к узлам и пр., но мы этим займемся как-нибудь в другой раз. Заодно проверим, будет ли использование struct (на что нас активно поощряют «Apple» своим примером) более выгодным выбором, и, возможно, вспомним о «Copy-on-write»-подходе.
Разворот односвязного списка
Первый способ. Цикл
Пора заняться делом, ради которого мы сегодня здесь собрались! А наиболее эффективно им заняться можно двумя способами. Первый – это простой цикл, от первого до последнего узла.
Цикл работает с тремя переменными, которым перед началом присваивается значение предыдущего, текущего и следующего узла. (В этот момент значение предыдущего узла, естественно, пустое.) Цикл начинается с проверки того, что следующий узел – не пустой, и, если это так, выполняется тело цикла. В цикле не происходит никакой магии: у текущего узла полю, ссылающемуся на следующий элемент, присваивается ссылка на предыдущий (на первой итерации значение ссылки, соответственно, обнуляется, что соответствует положению дел в последнем узле). Ну и дальше переменным соответствующим предыдущему, текущему и следующему узлу присваиваются новые значения. После выхода из цикла текущему (т.е. вообще последнему итерируемому) узлу присваивается новое значение ссылки на следующий узел, т.к. выход из цикла происходит как раз в момент, когда последний узел в списке становится текущим.
На словах, конечно, все это звучит странно и непонятно, поэтому лучше посмотрим код:
extension SinglyLinkedList {
func reverse() {
var previousNode: Node<T>? = nil
var currentNode = firstNode
var nextNode = firstNode?.nextNode
while nextNode != nil {
currentNode?.nextNode = previousNode
previousNode = currentNode
currentNode = nextNode
nextNode = currentNode?.nextNode
}
currentNode?.nextNode = previousNode
firstNode = currentNode
}
}
Для проверки воспользуемся списком узлов, полезная нагрузка которых представляют собой простые целочисленные идентификаторы. Создадим список из десяти элементов:
let node = Node(payload: 0) // T == Int
let list = SinglyLinkedList(firstNode: node)
var currentNode = node
var nextNode: Node<Int>
for id in 1..<10 {
nextNode = Node(payload: id)
currentNode.nextNode = nextNode
currentNode = nextNode
}
Вроде все хорошо, но мы с вами люди, а не компьютеры, и нам хорошо бы получить визуальное доказательство корректности созданного списка и описанного выше алгоритма. Пожалуй, простого вывода на печать будет достаточно. Чтобы вывод сделать читаемым, добавим реализации протокола
CustomStringConvertible узлу с целочисленным идентификатором:extension Node: CustomStringConvertible where T == Int {
var description: String {
let firstPart = """
Node \(Unmanaged.passUnretained(self).toOpaque()) has id \(payload) and
"""
if let nextNode = nextNode {
return firstPart + " next node \(nextNode.payload)."
} else {
return firstPart + " no next node."
}
}
}
…И соответствующему списку, чтобы вывести все узлы по порядку:
extension SinglyLinkedList: CustomStringConvertible where T == Int {
var description: String {
var description = """
List \(Unmanaged.passUnretained(self).toOpaque())
"""
if firstNode != nil {
description += " has nodes:\n"
var node = firstNode
while node != nil {
description += (node!.description + "\n")
node = node!.nextNode
}
return description
} else {
return description + " has no nodes."
}
}
}
Строковое представление наших типов будет содержать адрес в памяти и целочисленный идентификатор. С помощью них организуем вывод на печать сгенерированного списка из десяти узлов:
print(String(describing: list))
/*
List 0x00006000012e1a60 has nodes:
Node 0x00006000012e2380 has id 0 and next node 1.
Node 0x00006000012e8d40 has id 1 and next node 2.
Node 0x00006000012e8d20 has id 2 and next node 3.
Node 0x00006000012e8ce0 has id 3 and next node 4.
Node 0x00006000012e8ae0 has id 4 and next node 5.
Node 0x00006000012e89a0 has id 5 and next node 6.
Node 0x00006000012e8900 has id 6 and next node 7.
Node 0x00006000012e8a40 has id 7 and next node 8.
Node 0x00006000012e8a60 has id 8 and next node 9.
Node 0x00006000012e8820 has id 9 and no next node.
*/
Развернем этот список и выведем его на печать снова:
list.reverse()
print(String(describing: list))
/*
List 0x00006000012e1a60 has nodes:
Node 0x00006000012e8820 has id 9 and next node 8.
Node 0x00006000012e8a60 has id 8 and next node 7.
Node 0x00006000012e8a40 has id 7 and next node 6.
Node 0x00006000012e8900 has id 6 and next node 5.
Node 0x00006000012e89a0 has id 5 and next node 4.
Node 0x00006000012e8ae0 has id 4 and next node 3.
Node 0x00006000012e8ce0 has id 3 and next node 2.
Node 0x00006000012e8d20 has id 2 and next node 1.
Node 0x00006000012e8d40 has id 1 and next node 0.
Node 0x00006000012e2380 has id 0 and no next node.
*/
Можно заметить, что адреса в памяти списка и узлов не изменились, а узлы списка напечатались в обратном порядке. Ссылки на следующий элемент узла теперь указывают на предыдущий (т.е., например, следующий элемент узла «5» теперь не «6», а «4»). И это означает, что у нас получилось!
Второй способ. Рекурсия
Второй известный способ сделать такой же разворот основан на рекурсии. Для его реализации объявим функцию, которая принимает первый узел списка, а возвращает уже «новый» первый узел (который до этого был последним).
Параметр и возвращаемое значение – опциональные, потому что внутри этой функции она вызывается снова и снова на каждом следующем узле, пока тот не будет пустым (т.е. пока не достигнут конец списка). Соответственно, в теле функции необходимо проверить не пуст ли узел, на котором вызвана функция и имеется ли у этого узла следующий. Если нет, то функция возвращает то же, что было передано в аргумент.
Вообще-то я честно попытался описать полный алгоритм словами, но в итоге стер почти все, потому что результат было бы невозможно понять. Рисовать блок-схемы и формально описывать шаги алгоритма – также в данном случае, думаю, смысла не имеет, потому что нам с вами будет удобней просто прочитать и попробовать осмыслить код на «Swift»:
extension SinglyLinkedList {
func reverseRecursively() {
func reverse(_ node: Node<T>?) -> Node<T>? {
guard let head = node else { return node }
if head.nextNode == nil { return head }
let reversedHead = reverse(head.nextNode)
head.nextNode?.nextNode = head
head.nextNode = nil
return reversedHead
}
firstNode = reverse(firstNode)
}
}
Сам алгоритм «обернут» методом типа собственно списка, для удобства вызова.
Выглядит покороче, но, на мой взгляд, сложнее для понимания.
Вызовем этот метод на результате предыдущего разворота и выведем на печать новый результат:
list.reverseRecursively()
print(String(describing: list))
/*
List 0x00006000012e1a60 has nodes:
Node 0x00006000012e2380 has id 0 and next node 1.
Node 0x00006000012e8d40 has id 1 and next node 2.
Node 0x00006000012e8d20 has id 2 and next node 3.
Node 0x00006000012e8ce0 has id 3 and next node 4.
Node 0x00006000012e8ae0 has id 4 and next node 5.
Node 0x00006000012e89a0 has id 5 and next node 6.
Node 0x00006000012e8900 has id 6 and next node 7.
Node 0x00006000012e8a40 has id 7 and next node 8.
Node 0x00006000012e8a60 has id 8 and next node 9.
Node 0x00006000012e8820 has id 9 and no next node.
*/
Из вывода видно, что все адреса в памяти снова не изменились, а узлы теперь следуют в первоначальном порядке (т.е. «развернулись» еще раз). А это означает, что мы снова справились!
Выводы
Если взглянуть на методы разворота внимательно (или провести эксперимент с подсчетом вызовов), можно заметить, что цикл в первом случае и внутренний (рекурсивный) вызов метода во втором случае происходят на один раз меньше, чем количество узлов в списке (в нашем случае, девять раз). Также можно обратить внимание на то, что происходит вокруг цикла в первом случае – та же череда присваиваний – и на первый, не рекурсивный, вызов метода во втором случае. Получается, что в обоих случаях «круг» повторяется ровно десять раз для списка из десяти узлов. Таким образом, мы имеем линейную сложность для обоих алгоритмов – O(n).
Вообще говоря, два описанных алгоритма считаются наиболее эффективными для решения данной задачи. Что касается вычислительной сложности, то возможность придумать алгоритм с более низким ее значением, не представляется возможным: так или иначе необходимо «посетить» каждый узел для присваивания нового значения для хранимой внутри ссылки.
Еще одна характеристика, которую стоит упомянуть – это «сложность по выделяемой памяти». Оба предложенных алгоритма создают фиксированное число новых переменных (три в первом случае и одна – во втором). Это означает, что объем выделяемой памяти не зависит от количественной характеристики входных данных и описывается константной функцией – O(1).
Но, на самом деле, во втором случае это не так. Опасность рекурсии в том, что для каждого рекурсивного вызова на стеке выделяется дополнительная память. В нашем случае глубина рекурсии соответствует количеству входных данных.
И наконец, я решил поэкспериментировать еще немного: простым и примитивным способом замерил абсолютное время выполнения двух методов для разного количества входных данных. Вот так:
let startDate = Date().timeIntervalSince1970
// list.reverse() / list.reverseRecursively()
let finishDate = Date().timeIntervalSince1970
let runningTime = finishDate – startDate // Seconds
И вот что у меня получилось (это «сырые» данные из «Playground»):
(Бóльшие значения мой компьютер, к сожалению, уже не осилил.)
Что можно увидеть из таблицы? Пока ничего особенного. Хотя уже заметно, что рекурсивный метод ведет себя чуть хуже при относительно малом количестве узлов, но где-то между 100 и 1000 начинает показывать себя лучше.
Также я попробовал тот же простой тест внутри полноценного «Xcode»-проекта. Результаты получились такие:
Во-первых, стоит упомянуть, что результаты получены после активации режима «агрессивной» оптимизации, направленной на скорость исполнения (-Ofast), отчасти поэтому числа столь малы. Также интересно то, что в этом случае рекурсивный метод показал себя чуть лучше, наоборот, лишь на очень малых размерах входных данных, а уже на списке из 100 узлов, метод проигрывает. Из 100000 – он и вовсе заставил программу завершиться аварийно.
Заключение
Я постарался осветить довольно классическую тему с точки зрения своего любимого на данный момент языка программирования и, надеюсь, вам было любопытно следить за прогрессом также, как и мне самому. А еще я очень рад, если вам удалось узнать и что-нибудь новое – тогда я точно не зря потратил время на эту статью (вместо того, чтобы сидеть и смотреть сериалы).
Если у кого-то есть желание отслеживать мою общественную активность, вот ссылка на мой «Twitter», где первым делом появляются ссылки на мои новые посты и еще немного, сверх того.
habr.com
Почему на собеседованиях так часто спрашивают про связные списки / Habr
Примечание переводчика: оригинальная статья опубликована в серии твитовВероятно, вы уже читали кучу объяснений, почему обработка связных списков — плохой вопрос для собеседования. Я же в первую очередь хочу объяснить, откуда он вообще взялся. Всем пристегнуться, погружаемся в теорию игр ИСТОРИЮ!
Хотя индустрия программного обеспечения процветала в 80-е годы, но действительно взлетела в 90-е. В это десятилетие число работников отрасли в США утроилось и превысило миллион человек. Со взрывным ростом пришла необходимость нанимать массу сотрудников и оценивать их.
Что нужно оценить? Ну, в первую очередь, знание языков. Согласно TIOBE, в 1986−2006 годы самым популярным языком в мире был C, далее следовал C++. К 2006 году Java вышла на первое место, но C остался рядом.
C работал близко к железу без лишних абстракций. Пустой словарь Python расходует аж 288 байт, то есть 5% всего объёма памяти первого поколения Apple II. Абстракции слишком дороги, слишком много накладных расходов. Если вам нужна сложная структура данных, вы должны построить её самостоятельно с помощью массивов, структур и указателей.
(C++ оказался получше в этом отношении, поскольку там появилась стандартная библиотека шаблонов, но её официально приняли только в 1998 году, а повсеместно использовать начали гораздо позже. Помню, как читал аргументы о накладных расходах даже в 2005 году).
Связные списки — необходимая структура данных, которая позволяет производить динамическое выделение памяти с меньшими рисками переполнения буфера. И нужно было писать эти связные списки вручную. Это означает, что вы должны были вручную манипулировать указателями в связных списках.
Другими словами, в 90-е годы вопрос «Как развернуть связный список» — это не проверка алгоритмического мышления или знания структур данных, это вопрос «Вы программировали на C?». Если да, то для вас ответ тривиален. Если нет, ответить (в идеале) невозможно.
В настоящее время большинство из нас не программирует на C. Но устаревший вопрос не исчез, а модифицировался. Я подозреваю, причина в том, что огромное количество программистов продолжали задавать и задавать его, не понимая исторического контекста и причин, почему этот вопрос появился.
Вероятно, ситуацию помог зацементировать бестселлер «Взлом собеседования по программированию». Её автор Гейл Лакман Макдауэлл работала по специальности в 2000−2008 годы и, вероятно, написала книгу на основе собственного опыта. Книга стала настольным справочником компаний, которые проводят собеседования — и связные списки укрепились в списке стандартных вопросов.
Без исторического контекста связные списки стали преподносить как вопрос на «навыки решения проблем». Но это полностью противоречит изначальной цели: если вы проверяете знание языка, вы не хотите, чтобы на вопрос могли ответить (то есть «решить проблему») люди, не знакомые с этим языком.
Например, вопрос «Определите, есть ли в связном списке цикл». Предполагается, что кандидат должен придумать решение типа «черепаха и заяц», опубликованное в обильно цитируемой научной статье 1967 года. Вы просите кандидата повторить научное исследование за 30 минут!
Возможно, когда мы перешли к вопросам типа «решение проблем», то откалибровали сложность, взяв связные списки в качестве ориентира. Что совершенно искажает шкалу.
(Кстати: ещё один аргумент для связных списков — это «проверка фундаментальных знаний информатики». Ну если так, то почему у всех не спрашивают про детерминированные конечные автоматы? Теорему Райса? Как работает компилятор? Структуры данных — очень небольшая часть компьютерной науки и часто нерепрезентативная).
Подводя итог, вопрос о связном списке был хорошей проверкой умения писать на С, а теперь стал плохой проверкой «Умеете ли вы решать проблемы?»
Мораль: подумайте ещё раз о том, чтобы задавать вопросы по связным спискам в собеседовании.
Ещё одна мораль: из истории можно многому научиться.
(Третья мораль: если видите наполовину завершённую статью и думаете «Эх, легче запустить проект в серии твитов», это ловушка, не попадайтесь в неё)
habr.com
Связные списки в функциональном стиле / Habr
Рассмотрим вариант реализации связных списков через замыкания.Для обозначения списков будем использовать нотацию, похожую на Haskell: x:xs, где x — начало списка (head), xs — продолжение (tail).
В качестве языка реализации я выбрал JavaScript.
Конструируем список
Для работы со связными списками необходимы следующие базовые примитивы:
nil — пустой список, prepend (cons) — функция вставки в начало списка, head и tail.Создание списка из двух элементов выглядит следующим образом:
prepend('a', prepend('b', nil))
// 'a' -> 'b' -> nil
Реализация функции
prepend:function prepend(x, xs) {
return function (select) {
return select(x, xs)
}
}
Функция
select нужна для доступа к свободным переменным (x:xs).Реализация head и tail сводится к вызову функции-списка с нужным значением select:
function select_head(x, xs) { return x }
function select_tail(x, xs) { return xs }
function head(a) { return a(select_head) }
function tail(a) { return a(select_tail) }
Осталось реализовать пустой список (
nil):function nil() { return nil }
Таким образом,
head(nil) === tail(nil) === nil.Пример использования
Несложная программа, иллюстрирующая конструирование и обход списка:
var a = prepend('a', prepend('b', nil))
// 'a' -> 'b' -> nil
head(a) // => 'a'
head(tail(a)) // => 'b'
head(tail(tail(a))) // => nil
while (a !== nil) {
console.log(head(a))
a = tail(a)
}
Функции высшего порядка
Для получившейся структуры данных можно реализовать функции высшего порядка, например,
map:function map(fn, a) {
if (a === nil) return nil
return prepend(fn(head(a)), map(fn, tail(a)))
}
Это позволит работать с нашими списками в функциональном стиле:
var a = prepend(1, prepend(2, prepend(3, nil)))
// 1 -> 2 -> 3 -> nil
function power_of_2(x) { return 1 << x }
var b = map(power_of_2, a)
// 2 -> 4 -> 8 -> nil
Другие ассоциированные функции (
filter, reduce) предлагаются читателю в качестве домашнего задания.Такие дела™
При написании статьи ни один массив не пострадал.
Предвосхищая картинку про троллейбус из хлеба: это, безусловно, не прикладное решение. Более того, на работе за такой коммит могут легко и непринужденно оторвать руки. Что с этим знанием делать дальше — решать вам.
GitHub: github.com/mvasilkov/functional-js
habr.com
Односвязный список — это… Что такое Односвязный список?
- Односвязный список
В информатике, cвя́зный спи́сок — структура данных, состоящая из узлов, каждый из которых содержит как собственные данные, так и одну или две ссылки («связки») на следующее и/или предыдущее поле. Принципиальным преимуществом перед массивом является структурная гибкость: порядок элементов связного списка может не совпадать с порядком расположения элементов данных в памяти компьютера, а порядок обхода списка всегда явно задаётся его внутренними связями.
Виды связных списков
Линейный связный список
Односвязный список

В односвязном списке можно передвигаться только в сторону конца списка. Узнать адрес предыдущего элемента из данного невозможно.
Двусвязный список

По двусвязному списку можно передвигаться в любом направлении — как к началу, так и к концу. В этом списке проще производить удаление и перестановку элементов, т.к. всегда известны адреса тех элементов списка, указатели которых направлены на изменяемый элемент.
XOR-связный список
Кольцевой связный список
Разновидностью связных списков является кольцевой (циклический, замкнутый) список. Он тоже может быть односвязным или двусвязным. Последний элемент кольцевого списка содержит указатель на первый, а первый (в случае двусвязного списка) — на последний.

Список с пропусками
Развёрнутый связный список
Достоинства
- лёгкость добавления и удаления элементов
- размер ограничен только объёмом памяти компьютера и разрядностью указателей
Недостатки
- сложность определения адреса элемента по его индексу (номеру) в списке
- на поля-указатели (указатели на следующий и предыдущий элемент) расходуется дополнительная память (в массивах, например, указатели не нужны)
- работа со списком медленнее, чем с массивами, так как к любому элементу списка можно обратиться, только пройдя все предшествующие ему элементы
- элементы списка могут быть расположены в памяти разреженно, что окажет негативный эффект на кэширование процессора
- над связными списками гораздо труднее (хотя и в принципе возможно) производить параллельные векторные операции, такие как вычисление суммы
См. также
Wikimedia Foundation. 2010.
- Односвязное пространство
- Односвязность
Смотреть что такое «Односвязный список» в других словарях:
Связный список — В информатике, связный список базовая динамическая структура данных, состоящая из узлов, каждый из которых содержит как собственно данные, так и одну или две ссылки («связки») на следующий и/или предыдущий узел списка.[1] Принципиальным… … Википедия
Двусвязный список — В информатике, cвязный список структура данных, состоящая из узлов, каждый из которых содержит как собственные данные, так и одну или две ссылки («связки») на следующее и/или предыдущее поле. Принципиальным преимуществом перед массивом является… … Википедия
Связанный список — В информатике, cвязный список структура данных, состоящая из узлов, каждый из которых содержит как собственные данные, так и одну или две ссылки («связки») на следующее и/или предыдущее поле. Принципиальным преимуществом перед массивом является… … Википедия
Линейный список — У этого термина существуют и другие значения, см. Список. Разновидность связного списка односвязный список, содержащий 3 элемента Линейный однонаправленный список это структура данных, состоящая из элементов одног … Википедия
Развёрнутый связный список — список, каждый физический элемент которого содержит несколько логических (обычно в виде массива, что … Википедия
Развёрнутый связанный список — список, каждый физический элемент которого содержит несколько логических (обычно в виде массива, что позволяет ускорить доступ к отдельным элементам). Позволяет значительно уменьшить размер памяти и увеличить производительность по сравнению с… … Википедия
Развернутый связанный список — Развёрнутый связанный список список, каждый физический элемент которого содержит несколько логических (обычно в виде массива, что позволяет ускорить доступ к отдельным элементам). Позволяет значительно уменьшить размер памяти и увеличить… … Википедия
Сортировка связного списка — Сортировка связного списка. Подавляющее большинство алгоритмов сортировки требует для своей работы возможности обращения к элементам сортируемого списка по их порядковым номерам (индексам). В связных списках, где элементы хранятся неупорядоченно … Википедия
Коллекция (программирование) — У этого термина существуют и другие значения, см. Коллекция. Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторитетные исто … Википедия
Коллекция данных — Коллекция в программировании программный объект, содержащий в себе, тем или иным образом, набор значений одного или различных типов, и позволяющий обращаться к этим значениям. Коллекция позволяет записывать в себя значения и извлекать их.… … Википедия
Книги
- Структуры и алгоритмы обработки данных. Линейные структуры. Учебное пособие, Апанасевич Сергей Александрович. Учебное пособие содержит 6 лабораторных работ, посвященных линейным структурам данных. Среди них динамические массивы, односвязный линейный список, стек, очередь, множества. В лабораторных… Подробнее Купить за 1691 руб
- Структуры и алгоритмы обработки данных. Линейные структуры. Учебное пособие, Апанасевич Сергей Александрович. Учебное пособие содержит 6 лабораторных работ, посвященных линейным структурам данных. Среди них динамические массивы, односвязный линейный список, стек, очередь, множества. В лабораторных… Подробнее Купить за 1120 грн (только Украина)
- Структуры и алгоритмы обработки данных Линейные структуры Учебное пособие, Апанасевич С.. Учебное пособие содержит 6 лабораторных работ, посвященных линейным структурам данных. Среди них динамические массивы, односвязный линейный список, стек, очередь, множества. В лабораторных… Подробнее Купить за 1053 руб
dic.academic.ru