Double, Float — не вещественные числа / Хабр
Во многих источниках тип double и float, числа с плавающей запятой/точкой зачем-то называют вещественными. Такое чувство что кто-то когда-то совершил ошибку или не внимательно написал эту глупость и все как один начали её повторять, совершенно не задумываясь о чём они говорят.
Ладно это были бы просто троечники студенты и любители, так эту ошибку говорят и те, кто обучают специалистов. И эта проблема терминологии не одного ЯП, их правда много (Java, C++, C#, Python, JS и т.д.) везде, где бы я не искал, всегда находятся статьи, ответы, лекции, где дробные числа называют вещественными!
Вот ОЧЕНЬ МАЛЕНЬКАЯ выборка:
https://javarush.ru/quests/lectures/questsyntaxpro.level04.lecture06 — JavaRush
https://docs-python.ru/tutorial/osnovnye-vstroennye-tipy-python/tip-dannyh-float-veschestvennye-chisla/ — Docs Python3
http://cppstudio.com/post/310/ — CppStudio
https://ejudge.
 ru/study/3sem/sem07.pdf — Ejudge
ru/study/3sem/sem07.pdf — Ejudgehttps://ru.wikipedia.org/wiki/Система_типов_Си — даже всеми любимая Wikipedia!
Ещё раз повторюсь это очень маленькая выборка, можете набрать в гугл поиске, по ключевым словам, и удостовериться что их полно.
Начнём с простого, что такое вещественное число коим называют double и float. Будет немного формул, но не пугайтесь, прочитайте пожалуйста до конца, они очень простые, к каждой я даю интуитивное объяснение.
Вещественное число
Определение можете прочитать в Википедии или дочитать до конца мою статью, где я простым языком скажу или вы сами поймёте, но нужно проследить за мыслью, которую я хочу донести до вас. Я напишу формулой из теории множеств:
R = Q ∪ I
Где, R — множество вещественных чисел;
Q — множество рациональных чисел;
I — множество иррациональных чисел.
Так же Q ⊂ R и I ⊂ R.
Расшифровка тем, кто не очень с теорией множеств. Вещественные числа эта числа которые включают в себя Рациональные и Иррациональные числа (R = Q ∪ I), т. к. Вещественные числа включают их в себя, то Рациональные числа и Иррациональные числа являются подмножеством множества Вещественных (Q ⊂ R и I ⊂ R), причём строго, то есть Q != R и I != R, это очевидная мысль, но её требуется подчеркнуть.
к. Вещественные числа включают их в себя, то Рациональные числа и Иррациональные числа являются подмножеством множества Вещественных (Q ⊂ R и I ⊂ R), причём строго, то есть Q != R и I != R, это очевидная мысль, но её требуется подчеркнуть.
Теперь к самому интересному, какие числа называются Рациональными и Иррациональными (представляю себя преподавателем начальных курсов технических вузов).
Рациональные
Начнём с Рациональных, возьмём определение из википедии.
Рациональное число (от лат. ratio «отношение, деление, дробь») — число, которое можно представить в виде обыкновенной дроби m/n, где m — целое число, а n — натуральное.
Так же стоит отметить, что Рациональные включают в себя Целые и Натуральные числа (-1, 0, 1, 2 …) их можно выразить в виде дроби, 1 = 1/1, 2 = 2/1, -1 = -1/1, 0 = 0/1 и т.д.
Почему это важно? Потому что Иррациональные числа не включают в себя Целые и Натуральные числа, это отдельный класс чисел.
Иррациональные
Берём определение из Википедии.
Иррациональное число — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде обыкновенной дроби m/n, где m,n — целые числа, n != 0. Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.
Так же приведу примеры иррациональных чисел, чтобы стало понятно: π (число пи), e (число Эйлера), √2.
Вы начали что-то подозревать? Если нет я помогу вам.
Первое предложение определения — это то, о чём я вам говорил, то, что Иррациональные числа — это отдельный класс чисел и он не включает в себя Целые и Натуральные.
Но самое важное здесь это второе предложение «Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.».
Что это значит? Заметили, что в примерах я дал вам буквенное обозначение? Это не просто так, это представление иррационального числа, ВАЖНО — сама запись π это не само иррациональное число, это всего лишь его представление, и оно является чем угодно, но не иррациональным числом. Само Иррациональное число оно бесконечно. Понимаете?
Само Иррациональное число оно бесконечно. Понимаете?
То есть его невозможно записать по определению. Никакой памяти в компьютере не хватит чтобы его записать. Это невозможно!
И мало того что в большинстве (я не проверял прям на всех, но очень сомневаюсь, что хотя бы в одном это есть) языков в которых используется термин Вещественный тип нельзя чисто синтаксически сделать запись по типу: «double a = π», попросту будет ошибка компиляции, так ещё если и возможно с помощью латинских букв подключая библиотеки, то в конечном-то итоге эта переменная будет ссылаться на конечное представление, а то есть рациональное этого иррационального числа!
Всё с чем мы можем работать это ТОЛЬКО РАЦИОНАЛЬНЫЕ ЧИСЛА, представления иррациональных чисел они ТОЖЕ рациональные и ТОЛЬКО рациональные. Они большие, они могут быть ооооочень большими, но они всё равно рациональные!
R = Q ∪ I, если мы исключаем I из-за невозможности работы с ними в прямом смысле без представлений получается R’ = R\I, R’ = Q, а Q у нас рациональные числа.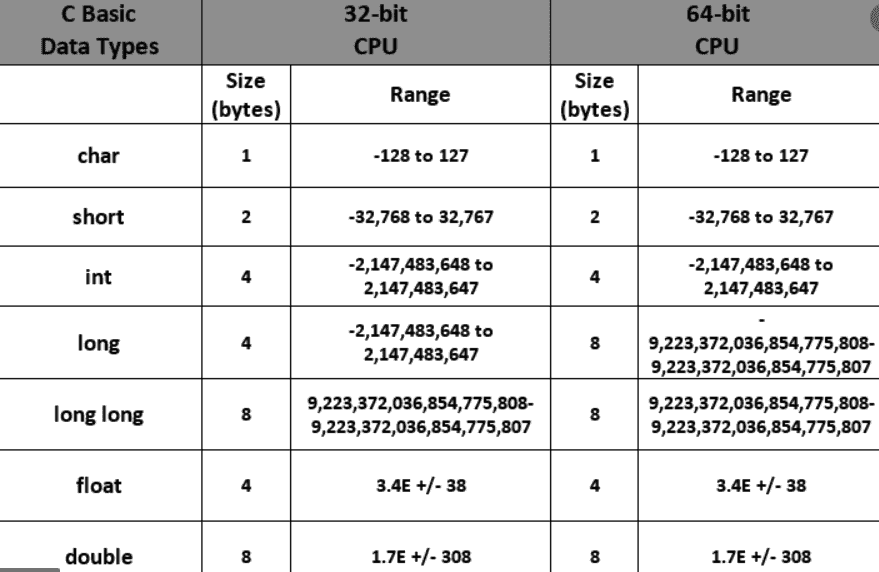
Так почему же так много людей и весьма неглупых всё ещё допускают эту простую ошибку? Эту ошибку можно было описать в пару предложений, но я хотел донести до вас последовательно как к этому прийти, используя общепринятую терминологию.
Спасибо.
P.S. Это моя оригинальная статья AfterWing, не является переводом, доработкой другой какой-либо статьи на русском/английском и др. языках.
Преобразование типов данных в Python 3
24 ноября, 2016 12:10 пп 130 503 views | Комментариев нетPython | Amber | Комментировать запись
Типы данных в Python позволяют классифицировать данные, определить значения, которые можно присвоить, и операции, которые можно выполнить с этими данными. В программировании бывает необходимо конвертировать один тип данных в другой, чтобы получить доступ к другим функциям: например, склеить числовые значения со строками или представить целые числа в виде десятичных.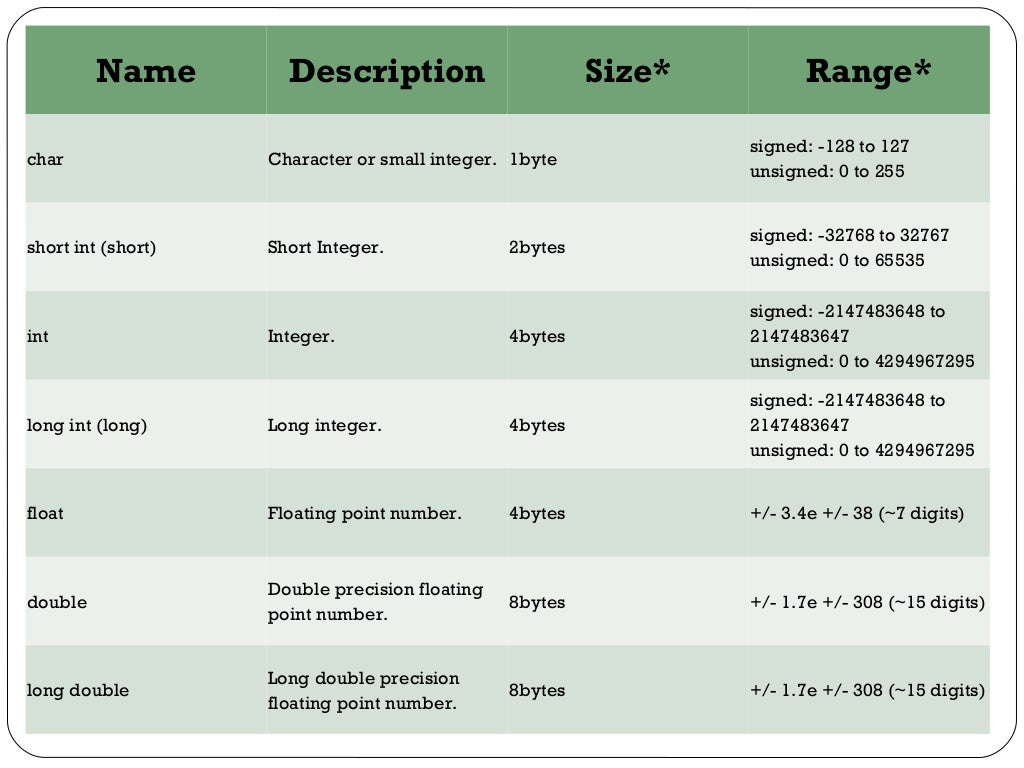
Данное руководство научит вас преобразовывать числа, строки, кортежи и списки.
Читайте также: Типы данных в Python 3
Преобразование числовых типов
В Python существует два числовых типа данных: целые числа и числа с плавающей точкой. Для преобразования целых чисел в числа с плавающей точкой и наоборот Python предоставляет специальные встроенные методы.
Преобразование целых чисел в числа с плавающей точкой
Метод float() преобразовывает целые числа в числа с плавающей точкой. Число указывается в круглых скобках:
float(57)
Это преобразует число 57 в 57.0.
Также можно использовать переменные. Объявите переменную f = 57, а затем выведите число с плавающей точкой:
f = 57
print(float(f))
57.0
Преобразование чисел с плавающей точкой в целые числа
Встроенная функция int() предназначена для преобразования чисел с плавающей точкой в целые числа.
Функция int() работает так же, как и float().
int(390.8)
Число 390.8 преобразуется в 390.
Эта функция также может работать с переменными. Объявите переменные:
b = 125.0
c = 390.8
Затем преобразуйте и отобразите их:
print(int(b))
print(int(c))
125
390
Чтобы получить целое число, функция int() отбрасывает знаки после запятой, не округляя их (потому 390.8 не преобразовывается в 391).
Преобразование чисел с помощью деления
При делении Python 3 может преобразовать целое число в число с плавающей точкой (в Python 2 такой функции нет). К примеру, разделив 5 на 2, вы получите 2.5.
a = 5 / 2
Python не преобразовывает тип данных во время деления; следовательно, деля целое число на целое число, в результате вы получили бы целое число, 2.
Читайте также: Python 2 vs Python 3: краткий обзор и практические соображения
Преобразование строк
Строка – это последовательность из одного или больше символов (цифр, букв и других символов). Строки – очень распространённый тип данных в программировании. Существует много способов преобразования строк.
Строки – очень распространённый тип данных в программировании. Существует много способов преобразования строк.
Читайте также: Основы работы со строками в Python 3
Преобразование чисел в строки
Чтобы конвертировать число в строку, используйте метод str(). Поместите число или переменную в круглые скобки.
Попробуйте преобразовать целое число, например:
str(12)
Запустив метод str(12) в интерактивной оболочке Python (с помощью команды python), вы получите вывод:
'12'
Кавычки означают, что теперь 12 является строкой, а не числом.
Особенно полезно преобразовывать числа в строки, используя переменные. К примеру, можно отследить, сколько строк кода в день пишет тот или иной пользователь. Если пользователь пишет больше 50 строк, программа отправит ему поощрительное сообщение.
user = "Michael"
lines = 50
print("Congratulations, " + user + "! You just wrote " + lines + " lines of code.
Запустив этот код, вы получите ошибку:
TypeError: Can't convert 'int' object to str implicitly
Python не может склеивать строки с числами, потому нужно преобразовать значение lines в строку.
user = "Michael"
lines = 50
print("Congratulations, " + user + "! You just wrote " + str(lines) + " lines of code.")
Теперь, запустив код, вы увидите:
Congratulations, Michael! You just wrote 50 lines of code.
Метод str() может преобразовать в строку и число с плавающей точкой. Поместите в круглые скобки число или переменную:
print(str(421.034))
f = 5524.53
print(str(f))
421.034
5524.53
Попробуйте выполнить конкатенацию строки и преобразованного в строку числа:
f = 5524.53
print("Michael has " + str(f) + " points.")
Michael has 5524.53 points.
Преобразование строк в числа
Строки можно преобразовать в числа с помощью методов int() и float()
Если в строке нет десятичных знаков, лучше преобразовать её в целое число. Для этого используется int().
Для этого используется int().
Попробуйте расширить предыдущий пример кода, который отслеживает количество написанных строк. Пусть программа отслеживает, сколько строк пишет пользователь каждый день.
lines_yesterday = "50"
lines_today = "108"
lines_more = lines_today - lines_yesterday
print(lines_more)
TypeError: unsupported operand type(s) for -: 'str' and 'str'
При запуске возникла ошибка, поскольку Python не может выполнить сложение строк. Преобразуйте строки в числа и попробуйте снова запустить программу:
lines_yesterday = "50"
lines_today = "108"
lines_more = int(lines_today) - int(lines_yesterday)
print(lines_more)
58
Значение переменной lines_more – это число, в данном случае это 58.
Также можно преобразовать числа в предыдущем примере в числа с плавающей точкой. Для этого используйте метод float() вместо int().
К примеру, очки начисляются в десятичных значениях.
total_points = "5524. 53"
53"
new_points = "45.30"
new_total_points = total_points + new_points
print(new_total_points)
5524.5345.30
В данном случае оператор + склеивает две строки, а не складывает числа. Потому в результате получилось довольно странное значение.
Конвертируйте эти строки в числа с плавающей точкой, а затем выполните сложение.
total_points = "5524.53"
new_points = "45.30"
new_total_points = float(total_points) + float(new_points)
print(new_total_points)
5569.83
Как видите, теперь программа возвращает ожидаемый результат.
Если вы попробуете преобразовать строку с десятичными значениями в целое число, вы получите ошибку:
f = "54.23"
print(int(f))
ValueError: invalid literal for int() with base 10: '54.23'
Преобразование в кортежи и списки
Чтобы преобразовать данные в кортеж или список, используйте методы tuple() и list() соответственно. В Python:
- Список – это изменяемая упорядоченная последовательность элементов, взятая в квадратные скобки ([ ]).

- Кортеж – неизменяемая упорядоченная последовательность элементов, взятая в круглые скобки.
Преобразование списка в кортеж
Преобразовывая список в кортеж, вы можете оптимизировать программу. Для преобразования в кортеж используется метод tuple().
print(tuple(['pull request', 'open source', 'repository', 'branch']))
('pull request', 'open source', 'repository', 'branch')
Выведенные на экран данные являются кортежем, а не списком, поскольку они взяты в круглые скобки.
Попробуйте использовать tuple() с переменной:
sea_creatures = ['shark', 'cuttlefish', 'squid', 'mantis shrimp']
print(tuple(sea_creatures))
В кортеж можно преобразовать любой итерируемый тип, включая строки:
print(tuple('Michael'))
('M', 'i', 'c', 'h', 'a', 'e', 'l')
Конвертируя в кортеж числовой тип данных, вы получите ошибку:
print(tuple(5000))
TypeError: 'int' object is not iterable
Преобразование в списки
Вы можете преобразовать кортеж в список, чтобы сделать его изменяемым.
Обратите внимание: при этом в методах list() и print() используется две пары круглых скобок. Одни принадлежать собственно методу, а другие – кортежу.
print(list(('blue coral', 'staghorn coral', 'pillar coral')))
['blue coral', 'staghorn coral', 'pillar coral']
Если данные, которые вывел метод print, заключены в квадратные скобки, значит, кортеж преобразовался в список.
Чтобы избежать путаницы с круглыми скобками, можно создать переменную:
coral = ('blue coral', 'staghorn coral', 'pillar coral')
list(coral)
Строки тоже можно преобразовывать в списки:
print(list('Michael'))
['M', 'i', 'c', 'h', 'a', 'e', 'l']
Заключение
Теперь вы умеете преобразовывать различные типы данных Python с помощью встроенных методов, благодаря чему код вашей программы может стать более гибким.
Тип поплавковый | Microsoft Узнайте
Редактировать Твиттер LinkedIn Фейсбук Электронная почта- Статья
Числа с плавающей запятой используют формат IEEE (Институт инженеров по электротехнике и электронике). Значения одинарной точности с типом float имеют 4 байта, состоящие из знакового бита, 8-битной двоичной экспоненты с избыточным значением 127 и 23-битной мантиссы. Мантисса представляет собой число от 1,0 до 2,0. Поскольку старший бит мантиссы всегда равен 1, он не сохраняется в числе. Это представление дает диапазон примерно от 3,4E-38 до 3,4E+38 для типа float.
Вы можете объявить переменные как float или double, в зависимости от потребностей вашего приложения. Принципиальные различия между этими двумя типами заключаются в значимости, которую они могут представлять, требуемой памяти и их диапазоне. В следующей таблице показана взаимосвязь между значимостью и требованиями к хранению.
Типы с плавающей запятой
| Тип | Значащие цифры | Количество байтов |
|---|---|---|
| с плавающей запятой | 6 — 7 | 4 |
| двойной | 15 — 16 | 8 |
Переменные с плавающей запятой представлены мантиссом, которая содержит значение числа, и показателем степени, который содержит порядок величины числа.
В следующей таблице показано количество битов, выделенных для мантиссы, и показатель степени для каждого типа с плавающей запятой. Старшим битом любого float или double всегда является бит знака. Если это 1, число считается отрицательным; в противном случае оно считается положительным числом.
Длины показателей и мантиссы
| Тип | Длина экспоненты | Длина мантиссы |
|---|---|---|
| поплавок | 8 бит | 23 бита |
| двойной | 11 бит | 52 бита |
Поскольку показатели степени хранятся в беззнаковой форме, показатель степени смещается на половину его возможного значения. Для типа float смещение равно 127; для типа double это 1023. Фактическое значение экспоненты можно вычислить, вычитая значение смещения из значения экспоненты.
Мантисса хранится в виде двоичной дроби, большей или равной 1 и меньшей 2. Для типов float и double в мантиссе в самом старшем разряде подразумевается ведущая 1, поэтому на самом деле мантиссы равны 24. и 53 бита соответственно, хотя самый старший бит никогда не сохраняется в памяти.
и 53 бита соответственно, хотя самый старший бит никогда не сохраняется в памяти.
Вместо только что описанного метода хранения пакет с плавающей запятой может хранить двоичные числа с плавающей запятой как денормализованные числа. «Денормализованные числа» — это ненулевые числа с плавающей запятой с зарезервированными значениями экспоненты, в которых старший бит мантиссы равен 0. Используя денормализованный формат, диапазон числа с плавающей запятой может быть расширен за счет точности. Вы не можете контролировать, представлено ли число с плавающей запятой в нормализованной или денормализованной форме; пакет с плавающей запятой определяет представление. Пакет с плавающей запятой никогда не использует денормализованную форму, если показатель степени не становится меньше минимума, который может быть представлен в нормализованной форме.
В следующей таблице показаны минимальные и максимальные значения, которые вы можете хранить в переменных каждого типа с плавающей запятой. Значения, перечисленные в этой таблице, относятся только к нормализованным числам с плавающей запятой; денормализованные числа с плавающей запятой имеют меньшее минимальное значение. Обратите внимание, что числа, хранящиеся в 80 x 87 регистрах, всегда представлены в 80-битной нормализованной форме; числа могут быть представлены в денормализованной форме только при сохранении в 32-битных или 64-битных переменных с плавающей запятой (переменные типа float и типа long).
Значения, перечисленные в этой таблице, относятся только к нормализованным числам с плавающей запятой; денормализованные числа с плавающей запятой имеют меньшее минимальное значение. Обратите внимание, что числа, хранящиеся в 80 x 87 регистрах, всегда представлены в 80-битной нормализованной форме; числа могут быть представлены в денормализованной форме только при сохранении в 32-битных или 64-битных переменных с плавающей запятой (переменные типа float и типа long).
Диапазон типов с плавающей запятой
| Тип | Минимальное значение | Максимальное значение |
|---|---|---|
| поплавок | 1.175494351 Э — 38 | 3.402823466 Е + 38 |
| двойной | 2.2250738585072014 Э — 308 | 1.7976931348623158 Е + 308 |
Если точность важнее хранения, рассмотрите возможность использования типа float для переменных с плавающей запятой. И наоборот, если точность является наиболее важным критерием, используйте тип double.
И наоборот, если точность является наиболее важным критерием, используйте тип double.
Переменные с плавающей запятой могут быть преобразованы в более значимый тип (из типа float в тип double). Продвижение часто происходит, когда вы выполняете арифметические действия над переменными с плавающей запятой. Эта арифметика всегда выполняется с такой же высокой степенью точности, как и переменная с наивысшей степенью точности. Например, рассмотрим следующие объявления типов:
float f_short; двойной f_long; длинный двойной f_longer; f_short = f_short * f_long;
В предыдущем примере переменная f_short преобразуется в тип double и умножается на f_long ; затем результат округляется до типа float перед присвоением f_short .
В следующем примере (в котором используются объявления из предыдущего примера) арифметические операции над переменными выполняются с точностью до числа с плавающей запятой (32 бита); затем результат преобразуется в тип double:
f_longer = f_short * f_short;
См.
 {38}}3,4∗1038 . Если мы хотим сохранить число с более высокими значениями точности, чем заданный диапазон числа с плавающей запятой, мы можем использовать двойное число, которое имеет более высокий диапазон, чем число с плавающей запятой.
{38}}3,4∗1038 . Если мы хотим сохранить число с более высокими значениями точности, чем заданный диапазон числа с плавающей запятой, мы можем использовать двойное число, которое имеет более высокий диапазон, чем число с плавающей запятой.Использование числа с плавающей запятой
Значения с плавающей запятой лучше по производительности по сравнению со значениями типа double. Обработка значений с плавающей запятой происходит быстрее из-за их внутренней реализации, значение с плавающей запятой потребляет 90 190 половину пропускной способности памяти 90 191 по сравнению с двойной, по этой причине является хорошим решением использовать число с плавающей запятой чаще, когда требование равно или менее 7-значной точности, более чем в два раза.
Поскольку для графических библиотек требуется чрезвычайно высокая вычислительная мощность , значения с плавающей запятой также предпочтительны в графической библиотеке из-за их преимущества в производительности по сравнению со значениями типа double.
Программисты также предпочитают хранить записи валют в числах с плавающей запятой из-за их возможности определять количество знаков после запятой с некоторыми дополнительными параметрами .
Float vs Double и Int
Значения с плавающей запятой и значения типа double служат одной и той же цели хранения значений с плавающей запятой. Основное различие между ними заключается в их диапазоне и объеме памяти. Размер double в С++ составляет 64 бита (т.е. 8 байтов), что составляет дважды типа данных с плавающей запятой. Если мы хотим хранить значения с точностью от 15 до 16 знаков после запятой, то предпочтительным выбором будет double, а не float в C++.
Тип int известен как встроенный целочисленный тип данных, который используется для хранения целых чисел. Он служит совершенно другой цели, чем поплавок. Размер int в С++ составляет 32 бита (т.е. 4 байта).
Пример 1: Float в C++
Рассмотрим следующий пример, в котором переменная типа float создается и печатается с помощью C++.
Пример кода —
Вывод —
В приведенной выше программе мы объявили переменную типа float с именем numFloat и присвоили ей плавающее значение 5,6937. Затем мы напечатали значение внутри этой переменной numFloat. Этот код демонстрирует базовое использование float в C++.
Функция setprecision()
В C++ мы можем использовать функцию setprecision(), чтобы указать количество значений с десятичной точкой в наших значениях с плавающей запятой для печати с помощью cout. Ниже приведены примеры некоторых чисел с плавающей запятой с числом точности — 9.0003
Функция setprecision() — это часть библиотеки iomanip на C++, которую нам нужно импортировать в наш код. iomanip означает манипулирование вводом-выводом.
Пример 2: Использование setprecision() для чисел с плавающей запятой
Ниже приведен пример кода, показывающий использование функции setprecision() в программе для установки количества значений с десятичной точкой в нашей программе.
Пример кода —
Выходные данные —
Рассмотрим приведенный выше пример кода, в котором мы использовали метод setprecision() из библиотеки iomanip, чтобы установить количество значений числа для его печати с помощью cout. Как вы можете видеть в приведенном выше примере, мы присвоили переменной numFloat значение 15,639.7. Здесь, если мы передали значение 4 в качестве аргумента функции setprecision(), то мы получим вывод, что 15,64 состоит из 4 цифр, данное значение генерируется путем округления числа. Если мы передали значение 3 в качестве аргумента, то мы получим вывод как 15,6, что является значением с точностью до 3 цифр, как вы можете видеть в выводе. Таким образом, мы можем использовать эти способы для установки точности значений float в C++.
Работа с экспоненциальными числами
Мы можем использовать число с плавающей запятой в C++ для представления экспоненциальных чисел. Например, для представления 21000 (т. {3}}213) можно сохранить следующим образом.
{3}}213) можно сохранить следующим образом.
Этот формат чисел называется научным форматом, где мы используем e+ для обозначения экспоненты. Число перед e+ является основанием, тогда как число после e+ является показателем степени данного числа.
Этот научный формат также используется для демонстрации чисел, выходящих за пределы диапазона точности. Как мы видели ранее, диапазон точности для значений с плавающей запятой составляет 7 цифр, поэтому числа выше этого хранятся в научном формате. Например, сохраненное число 2100000 отображается как 2.1e+06. здесь базовое значение равно 2,1, а показатель степени равен 6,9.0003
Пример кода —
Вывод —
Как вы можете видеть в приведенном выше примере кода, здесь демонстрация научного формата дается с двумя примерами. Прежде всего объявляется переменная numFloat типа float, и ей присваивается номер научного формата, который получается равным 21000. При второй инициализации той же переменной numFloat присваивается значение, превышающее диапазон типа float, при печати мы можем убедитесь, что он хранится в научном формате.

 ru/study/3sem/sem07.pdf — Ejudge
ru/study/3sem/sem07.pdf — Ejudge