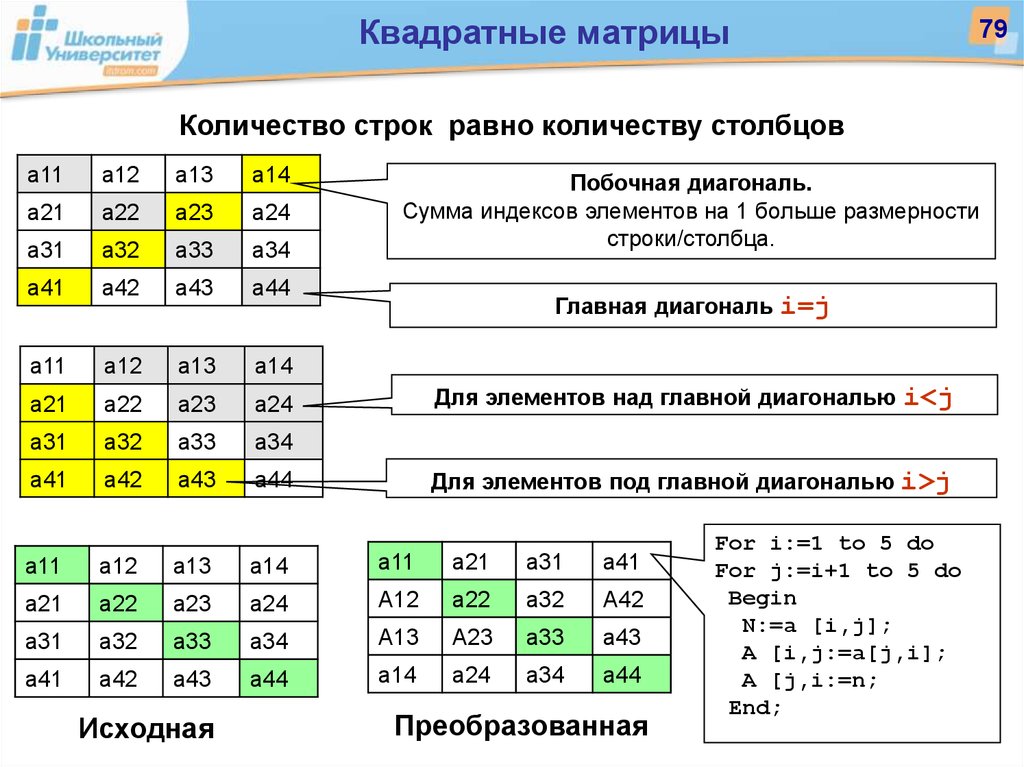
Как транспонировать матрицу в Python (с библиотеками и без них)
Перевод статьи «Transpose a Matrix».
Сегодня мы хотим разобрать, как транспонировать матрицу в Python. Однако сначала давайте рассмотрим, что представляет из себя матрица сама по себе и в чём заключается процесс транспонирования.
Итак, матрица состоит из строк и столбцов. Создать матрицу можно по-разному, но самый простой способ – использовать вложенные списки, как показано ниже:
matrix = [[1, 2, 4], [31, 17, 15]]
Внутренние списки представляют собой строки, а каждый элемент внутри списка называется столбцом. Итак, в приведенном выше примере у нас есть две строки и три столбца, т.е. мы имеем дело с матрицей 2 на 3. Стоит помнить, что индексация Python начинается с нуля.
Транспонирование матрицы означает, что мы меняем строки на столбцы или столбцы на строки. Теперь давайте обсудим различные методы транспонирования матрицы.
Теперь давайте обсудим различные методы транспонирования матрицы.
Метод 1. Транспонирование матрицы с помощью NumPy transpose()
Первый метод, который мы разберем, — это использование библиотеки NumPy. NumPy в основном работает с массивами в Python, а для транспонирования мы можем вызвать метод transpose().
Давайте разберем всё по порядку. Для начала нам нужно импортировать модуль NumPy как np.
Дальше, в ячейке номер [25] мы создаем массив NumPy с именем arr_matrix.
В ячейке номер [26] мы вызываем метод transpose() для нашей матрицы – объекта arr_matrix, который мы создали ранее.
В ячейке номер [27] мы выводим на экран исходную матрицу arr_matrix.
А в ячейке номер [28] – транспонированную матрицу arr_transpose. Можем заметить, что в результате мы получили именно то, что нам было нужно – транспонированную матрицу.
Метод 2. Использование метода numpy.
 transpose()
transpose()Мы также можем транспонировать матрицу в Python с помощью numpy.transpose(). При этом мы передаем матрицу в метод transpose() в качестве аргумента.
В ячейке номер [29] мы создаем матрицу, используя массив NumPy, с именем arr_matrix.
Далее мы передаем arr_matrix в метод transpose() и сохраняем результат в новую переменную arr_transpose.
В ячейке номер [31] мы печатаем исходную матрицу arr_matrix.
А дальше мы выводим на экран транспонированную матрицу arr_transpose. Получаем результат аналогичный тому, что получили в первом примере.
Метод 3. Транспонирование матрицы с использованием библиотеки SymPy
Применение библиотеки SymPy – это еще один подход к транспонированию матрицы. Эта библиотека использует символьную математику для решения алгебраических задач.
Сначала нам, конечно же, нужно импортировать библиотеку SymPy. Она не поставляется вместе с Python по умолчанию, поэтому вы должны установить её в своей системе, иначе код не будет работать.
В ячейке номер [34] мы создаем матрицу с помощью библиотеки sympy.
Дальше, в ячейке [35], мы вызываем transpose (T) при помощи точечного оператора и сохраняем результаты в новую переменную sympy_transpose.
В ячейке номер [36] мы печатаем исходную матрицу matrix. А в ячейке номер [37] – транспонированную матрицу sympy_transpose. Как видим, у нас получилась транспонированная матрица.
Метод 4. Транспонирование матрицы с использованием вложенного цикла
В Python матрицу можно транспонировать и без применения каких-либо библиотек. Для этого нам придется использовать вложенные циклы.
Мы создаем одну матрицу, а затем вторую (того же размера, что и первая) — для сохранения результатов после транспонирования. При этом важно отметить, что мы далеко не всегда знаем размерность исходной матрицы. Поэтому матрицу для результата мы создаем не напрямую, а используя размер исходной.
В ячейке номер [38] мы создаем матрицу и выводим ее на экран.
В следующей ячейке мы применяем «питонический» способ узнать размерность транспонированной матрицы, используя исходную. А именно — используем генератор списков со вложенными циклами for.
В ячейке [40] мы запускаем два цикла for. Внешний цикл предназначен для строк, а вложенный – для столбцов.
В ячейке номер [41] мы выводим исходную матрицу Matrix. А в ячейке [42] — транспонированную матрицу trans_Matrix.
Метод 5. Использование генератора списка
Следующий метод, который мы разберем, — это использование генератора списка. Этот метод похож на предыдущий с использованием вложенных циклов, но он более «питонический». Можно сказать, что это более продвинутый способ транспонирования матрицы в одной строке кода без использования библиотек.
Сначала мы создаем матрицу m, используя вложенные списки.
Затем в ячейке номер [44] мы используем вложенные циклы, как и в предыдущем примере. Однако здесь мы делаем это в одну строчку, используя генератор списков. Более того, тут нет никакой необходимости менять индексы
Более того, тут нет никакой необходимости менять индексы [j] [i] местами, как мы это делали в предыдущий раз.
В следующей ячейке мы выводим исходную матрицу m. После этого в ячейке номер [42] выводим транспонированную матрицу trans_m. Как видим, желаемый результат получен.
Метод 6. Транспонирование матрицы с помощью pymatrix
Pymatrix – ещё одна облегченная библиотека для матричных операций в Python. Мы можем выполнить транспонирование и с её помощью.
В ячейке номер [43] мы импортируем библиотеку pymatrix. Она не поставляется вместе с Python по умолчанию, поэтому, чтобы код работал корректно, нужно установить ее в своей системе перед использованием.
Затем при помощи библиотеки pymatrix мы создаем матрицу (в ячейке [44]).
В ячейке номер [45] вызываем метод trans() для нашей матрицы и сохраняем результаты в новую переменную pymatrix_transpose.
Потом мы выводим на экран исходную матрицу matrix. А в ячейке номер [47] выводим уже транспонированную матрицу
А в ячейке номер [47] выводим уже транспонированную матрицу pymatrix_transpose. Как видим, код отработал правильно.
Метод 7. Использование метода zip
Zip – еще один метод транспонирования матрицы.
В ячейке номер [63] мы создаем новую матрицу, используя вложенные списки.
В ячейке номер [64] мы передаем матрицу в zip с помощью оператора *. Мы вызываем каждую строку, а затем преобразуем эту строку в новый список, который становится транспонированной матрицей.
Заключение
Итак, сегодня мы рассмотрели, как транспонировать матрицу в Python. Мы разобрали различные методы, которые могут помочь нам в транспонировании матрицы (с использованием библиотек и без них).
Мы также познакомились с несколькими новыми библиотеками, такими как pymatrix и sympy.
Надеемся, теперь у вас не осталось вопросов о том, как транспонировать матрицу. Более того, вы можете выбрать наиболее подходящий способ для решения этой задачи.
Линейная алгебра на Python.
 [Урок 2].Транспонирование Матрицы
[Урок 2].Транспонирование МатрицыВ этом уроке мы рассмотрим операцию “транспонирование матрицы” и как она выполняется на Python. Также разберем на примерах свойства этой операции.
Транспонирование матрицыТранспонирование матрицы – это процесс замены строк матрицы на ее столбцы, а столбцов соответственно на строки. Полученная в результате матрица называется транспонированной. Символ операции транспонирования – буква T.
➣ Численный пример
Для исходной матрицы:
Транспонированная будет выглядеть так:
➤ Пример на Python
Решим задачу транспонирования матрицы на Python. Создадим матрицу A:
>>> A = np.matrix('1 2 3; 4 5 6')
>>> print(A)
[[1 2 3]
[4 5 6]]Транспонируем матрицу с помощью метода transpose():
>>> A_t = A.transpose() >>> print(A_t) [[1 4] [2 5] [3 6]]
Существует сокращенный вариант получения транспонированной матрицы, он очень удобен в практическом применении:
>>> print(A.T) [[1 4] [2 5] [3 6]]
Рассмотрим на примерах свойства транспонированных матриц. Операции сложения и умножение матриц, а также расчет определителя более подробно будут рассмотрены в последующих уроках.
Свойство 1. Дважды транспонированная матрица равна исходной матрице:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2 3; 4 5 6')
>>> print(A)
[[1 2 3]
[4 5 6]]
>>> R = (A.T).T
>>> print(R)
[[1 2 3]
[4 5 6]]Свойство 2. Транспонирование суммы матриц равно сумме транспонированных матриц:
➣ Численный пример
➤Пример на Python
>>> A = np.matrix('1 2 3; 4 5 6') >>> B = np.matrix('7 8 9; 0 7 5') >>> L = (A + B).T >>> R = A.T + B.T >>> print(L) [[ 8 4] [10 12] [12 11]] >>> print(R) [[ 8 4] [10 12] [12 11]]
Свойство 3. Транспонирование произведения матриц равно произведению транспонированных матриц расставленных в обратном порядке:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> L = (A.dot(B)).T
>>> R = (B.T).dot(A.T)
>>> print(L)
[[19 43]
[22 50]]
>>> print(R)
[[19 43]
[22 50]]В данном примере, для умножения матриц, использовалась функция dot() из библиотеки Numpy.
Свойство 4. Транспонирование произведения матрицы на число равно произведению этого числа на транспонированную матрицу:
Транспонирование произведения матрицы на число равно произведению этого числа на транспонированную матрицу:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2 3; 4 5 6')
>>> k = 3
>>> L = (k * A).T
>>> R = k * (A.T)
>>> print(L)
[[ 3 12]
[ 6 15]
[ 9 18]]
>>> print(R)
[[ 3 12]
[ 6 15]
[ 9 18]]Свойство 5. Определители исходной и транспонированной матрицы совпадают:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> A_det = np.linalg.det(A)
>>> A_T_det = np.linalg.det(A.T)
>>> print(format(A_det, '.9g'))
-2
>>> print(format(A_T_det, '.9g'))
-2Ввиду особенностей Python при работе с числами с плавающей точкой, в данном примере вычисления определителя рассматриваются только первые девять значащих цифр после запятой (за это отвечает параметр ‘.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Транспонирование и умножение матриц на Python
В этом уроке мы напишем программы на Python для транспонирования и умножения матриц и вывода результатов.
Прежде чем писать программу транспонирования матрицы на Python, давайте сначала посмотрим на обзор транспонирования.
Транспонирование матрицы
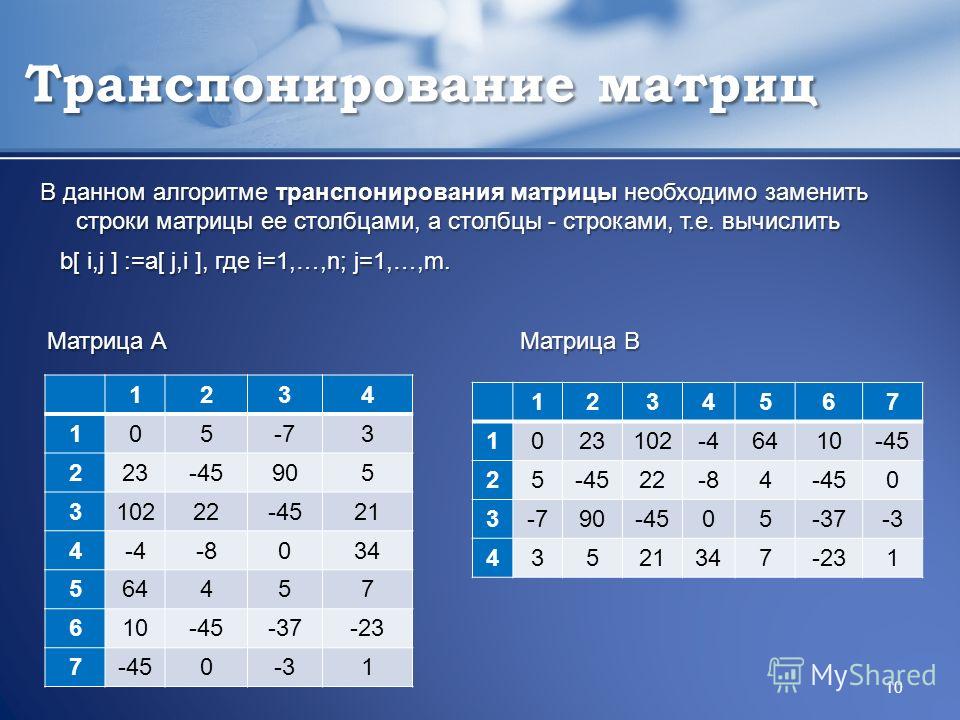
Если вы заменяете строки матрицы столбцом той же матрицы, это называется транспонированием матрицы. Обозначается как X’. Например: Элемент в i-й строке и j-м столбце в X будет помещен в j-ю строку и i-й столбец в X’.
Пример: Предположим, мы взяли следующую матрицу A:
A = [[5, 4, 3]
[2, 4, 6]
[4, 7, 9]
[8, 1, 3]]
At будет транспонированием указанной выше матрицы, т. е. A [i] [j] = At [j] [i], и поэтому At должно быть:
В = [5, 2, 4, 8] [4, 4, 7, 1] [3, 6, 9, 3]
Программа Python для транспонирования матрицы
Теперь мы напишем программу на Python для транспонирования входной заданной матрицы, где мы выполняем операцию, как мы выполнили в приведенном выше примере. Чтобы выполнить операцию транспонирования матрицы, мы будем использовать метод вложенного цикла for.
Давайте разберемся с использованием и реализацией этого метода на следующем примере.
Пример:
# Define a matrix A
A = [[5, 4, 3],
[2, 4, 6],
[4, 7, 9],
[8, 1, 3]]
# Define an empty matrix of reverse order
transResult = [[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]]
# Use nested for loop on matrix A
for a in range(len(A)):
for b in range(len(A[0])):
transResult[b][a] = A[a][b] # store transpose result on empty matrix
# Printing result in the output
print("The transpose of matrix A is: ")
for res in transResult:
print(res)
Выход:
The transpose of matrix A is: [5, 2, 4, 8] [4, 4, 7, 1] [3, 6, 9, 3]
Умножение матриц
В этом разделе мы напишем программу на Python для умножения двух входных матриц и выведем результат на выходе.
Прежде чем писать программу на Python, давайте сначала посмотрим на обзор умножения двух матриц.
Умножение матриц — это бинарная операция, в которой используется пара матриц для создания другой матрицы. Элементы в матрице умножаются в соответствии с элементарной арифметикой.
При умножении двух матриц элементы строки первой матрицы умножаются на элементы столбца второй матрицы.
Пример: предположим, что мы взяли следующие две матрицы A и B:
A = [[5, 4, 3] [2, 4, 6] [4, 7, 9]] and, B = [[3, 2, 4] [4, 3, 6] [2, 7, 5]]
C будет объединением двух указанных выше матриц, т. е. C = A + B, и поэтому C должно быть:
C = [[37, 43, 59]
[34, 58, 62]
[58, 92, 103]]
Как мы видим, результирующая матрица C, также известная как произведение матриц, имеет то же количество строк, что и первая матрица (матрица A), и такое же количество столбцов, как и вторая матрица (матрица B). Мы также знаем этот тип умножения матриц как скалярное произведение матриц.
Мы также знаем этот тип умножения матриц как скалярное произведение матриц.
Умножение двух матриц
Теперь мы напишем программу Python для умножения двух матриц, где мы выполняем умножение, как мы это делали в приведенном выше примере. Мы можем использовать различные методы для написания такой программы на Python, но в этом руководстве будем использовать только следующие два метода:
- Использование метода вложенного цикла.
- Использование метода понимания вложенного списка.
В обоих методах мы напишем пример программы, чтобы понять их реализацию для умножения двух матриц.
Способ 1: Использование метода вложенного цикла
В этом методе мы собираемся использовать вложенный цикл for для двух матриц, выполнять над ними умножение и сохранять результат умножения в третьей матрице в качестве итогового значения.
Давайте разберемся с реализацией этого метода на следующем примере.
Пример:
# Define two matrix A and B in program
A = [[5, 4, 3],
[2, 4, 6],
[4, 7, 9]]
B = [[3, 2, 4],
[4, 3, 6],
[2, 7, 5]]
# Define an empty matrix to store multiplication result
multiResult = [[0, 0, 0],
[0, 0, 0],
[0, 0, 0]]
# Using nested for loop method on A & B matrix
for m in range(len(A)):
for n in range(len(B[0])):
for o in range(len(B)):
multiResult[m][n] += A[m][o] * B[o][n] # Storing multiplication result in empty matrix
# Printing multiplication result in the output
print("The multiplication result of matrix A and B is: ")
for res in multiResult:
print(res)
Выход:
The multiplication result of matrix A and B is: [37, 43, 59] [34, 58, 62] [58, 92, 103]
Способ 2: Использование метода понимания вложенного списка
В этом методе мы будем использовать понимание вложенного списка, чтобы получить результат умножения двух входных матриц. При использовании в программе метода понимания списка мы также будем использовать «zip в Python» для вложенного списка. Давайте разберемся с реализацией этого метода на следующем примере.
При использовании в программе метода понимания списка мы также будем использовать «zip в Python» для вложенного списка. Давайте разберемся с реализацией этого метода на следующем примере.
Пример:
# Define two matrix A & B in the program
A = [[5, 4, 3],
[2, 4, 6],
[4, 7, 9]]
B = [[3, 2, 4],
[4, 3, 6],
[2, 7, 5]]
# Using nested list method with zip in Python
multiResult = [[sum(a * b for a, b in zip(Arow, Bcol))
for Bcol in zip(*B)]
for Arow in A]
# Printing multiplication result in the output
print("The multiplication result of matrix A and B is: ")
for res in multiResult:
print(res)
Выход:
The multiplication result of matrix A and B is: [37, 43, 59] [34, 58, 62] [58, 92, 103]
119401cookie-checkТранспонирование и умножение матриц на Pythonyes
Транспонировать матрицу в одну строку в Python
Посмотреть обсуждение
Улучшить статью
Сохранить статью
- Уровень сложности: Easy
- Последнее обновление: 24 Дек, 2021
Посмотреть обсуждение
Улучшить статью
Сохранить статью
Транспонирование матрицы — это задача, которую мы все можем очень легко выполнить в python (используя вложенный цикл). Но есть несколько интересных способов сделать то же самое в одной строке.
Но есть несколько интересных способов сделать то же самое в одной строке.
В Python мы можем реализовать матрицу как вложенный список (список внутри списка). Каждый элемент рассматривается как строка матрицы. Например, m = [[1, 2], [4, 5], [3, 6]] представляет собой матрицу из 3 строк и 2 столбцов.
Первый элемент списка – m[0] и элемент первой строки, первого столбца – m[0][0] .
- Использование понимания вложенного списка: Вложенное понимание списка используется для перебора каждого элемента в матрице. В данном примере мы перебираем каждый элемент матрицы (m) в основном столбце и присваиваем результат матрице rez, которая является транспонированной m.
m=[[1,2],[3,4],[5,6]]дляRowвM:Print(ROW)9004 ]
] дляjinrange(len(m))]foriinrange(len(m[0] ))]print("\n")forrowinrez:print(row)Выход:
[1, 2] [3, 4] [5, 6] [1, 3, 5] [2, 4, 6]
- Использование zip: Zip возвращает итератор кортежей, где i-й кортеж содержит i-й элемент из каждой из последовательностей аргументов или итерируемых объектов.
 В этом примере мы разархивируем наш массив с помощью *, а затем сжимаем его, чтобы получить транспонирование.
В этом примере мы разархивируем наш массив с помощью *, а затем сжимаем его, чтобы получить транспонирование.матрица=[(1,2,3),(4,5,6),(7,8,9),(10,11,12)]forrowinmatrix:print(row)print("\n")t_matrix=zip(*matrix)forrowвT_MATRIX:Печать(ряд)Выход:
Выход:
:
(1, 2, 3) (4, 5, 6) (7, 8, 9) (10, 11, 12) (1, 4, 7, 10) (2, 5, 8, 11) (3, 6, 9, 12)
Примечание.
 Если вы хотите получить результат в виде [[1,4,7,10][2,5,8,11][3,6,9,12]] , вы можете использовать t_matrix=map( список, zip(*матрица)).
Если вы хотите получить результат в виде [[1,4,7,10][2,5,8,11][3,6,9,12]] , вы можете использовать t_matrix=map( список, zip(*матрица)).
- Использование numpy: NumPy — это пакет обработки массивов общего назначения, предназначенный для эффективного управления большими многомерными массивами. Метод транспонирования возвращает транспонированное представление переданной многомерной матрицы.
импортnumpymatrix=[[1,2,3],[4,5,6]]print(matrix)print("\n")print(numpy. transpose(matrix))
transpose(matrix)) Or, simply используя «.T» после переменной
importnumpy as npmatrix=np.array([[1,2,3],[4,5,6]])Печать(Матрикс). распечатать(матрица.T)Вывод:
[[1 2 3] [4 5 6]] [[1 4] [2 5] [3 6]]
Примечание. «.T» работает только с массивами numpy
Эта статья написана Mayank Rawat и просто изменена Md. Т. Транспонирование матрицы в python может быть реализовано различными способами, такими как вложенные циклы, понимание вложенного списка, функция zip() и функция transpose() библиотеки NumPy.
Т. Транспонирование матрицы в python может быть реализовано различными способами, такими как вложенные циклы, понимание вложенного списка, функция zip() и функция transpose() библиотеки NumPy.
Scope
Статья содержит такие темы, как
- Введение в транспонирование матрицы в Python.
- транспонировать матрицу с помощью вложенного цикла, транспонировать матрицу с помощью понимания вложенного списка, транспонировать матрицу с помощью Zip, транспонировать матрицу с помощью библиотеки NumPy.
Каждая из тем четко объяснена с диаграммами и примерами, где это необходимо.
Введение в транспонирование матрицы в Python
Прежде чем научиться транспонировать матрицу в Python, мы должны сначала понять матрицу и транспонировать матрицу.
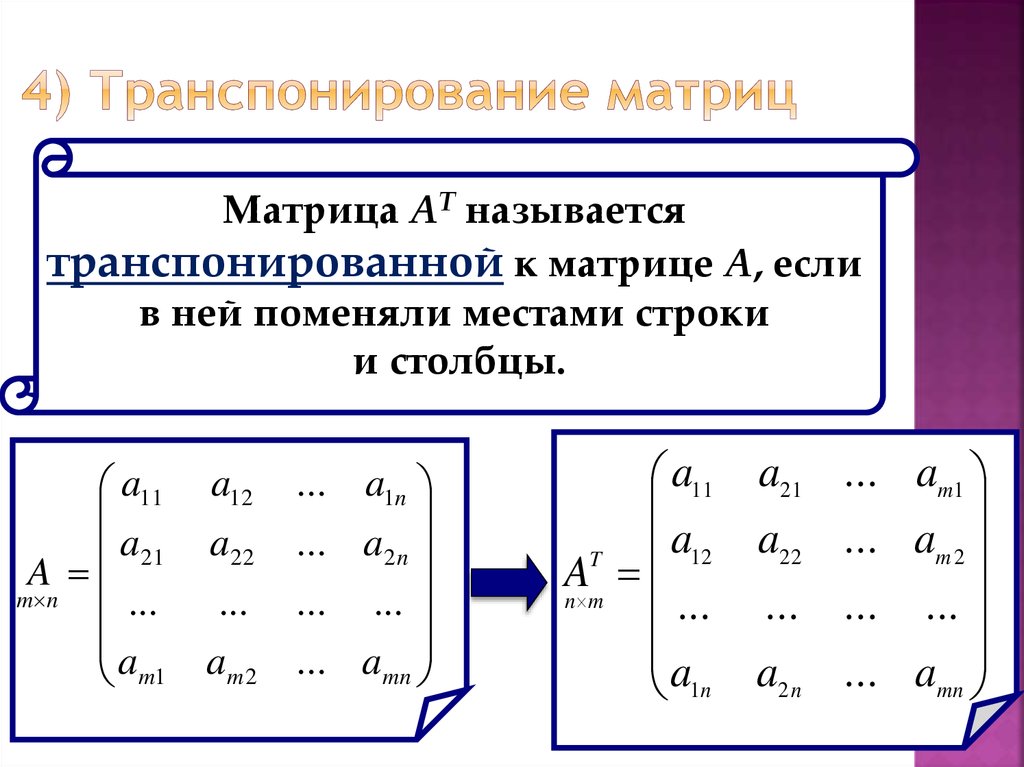
Матрица представляет собой прямоугольный массив некоторых данных (чисел, букв или других объектов), расположенных в виде строк и столбцов. Матрица состоит из строк и столбцов. Если количество строк N и количество столбцов M . Тогда мы говорим, что матрица представляет собой матрицу N x M .
Обратитесь к изображению ниже, чтобы увидеть, как матрица представлена с помощью индексов.
Если количество строк N и количество столбцов M . Тогда мы говорим, что матрица представляет собой матрицу N x M .
Обратитесь к изображению ниже, чтобы увидеть, как матрица представлена с помощью индексов.
Транспонированная матрица есть не что иное, как матрица, полученная путем замены строк на столбцы и столбцов на строки. Если матрица изначально равна 9Т. ::: :::section.{tip}
Теперь в python матрица может быть реализована с помощью вложенных списков. Пример: матрица = [[1, 2], [2, 3], [3, 4]] Как мы видим, матрица имеет 3 строки и 2 столбца, поэтому это матрица 3x2. Мы можем визуализировать матрицу как:
[
[1, 2],
[2, 3],
[3, 4]
]
После транспонирования матрица имеет 2 строки и 3 столбца, поэтому она становится матрицей 2x3. Транспонирование матрицы будет выглядеть так, как показано ниже:
[
[1, 2, 3],
[2, 3, 4]
]
Транспонирование матрицы в Python может быть реализовано различными способами. Давайте теперь обсудим их один за другим.
:::
Давайте теперь обсудим их один за другим.
:::
Транспонирование матрицы с использованием вложенного цикла
Как мы видели, мы можем реализовать матрицу с помощью вложенных списков (списков внутри списка). Итак, мы можем использовать вложенный цикл (цикл внутри другого цикла). Запустив два цикла (используя переменные I и j), мы можем изменить значение, присутствующее в i-й строке и j-м столбце, на j-ю строку и i-й столбец. Обратитесь к приведенному ниже коду для лучшего понимания.
# инициализация матрицы (3 x 2).
матрица = [[1, 2], [2, 3], [3, 4]]
# инициализируем другую матрицу (2 x 3) для сохранения результата.
транспонировать = [[0, 0, 0], [0, 0, 0]]
# итерация строк, а затем столбцов каждой строки
для i в диапазоне (len (матрица)):
для j в диапазоне (len (матрица [0])):
транспонировать [j] [i] = матрица [i] [j]
печатать (транспонировать)
Вывод:
[[1, 2, 3], [2, 3, 4]]
Здесь мы помещаем элемент matrix[i][j] в транспозицию[j][i].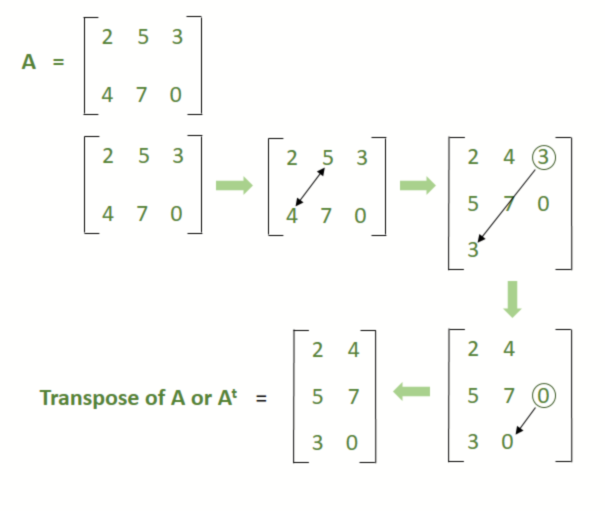
Транспонирование матрицы с использованием понимания вложенных списков
Мы видели, как транспонировать матрицу в python с помощью вложенных циклов, но мы также можем использовать питонический способ (более короткий). Понимание списков (создание списков на основе существующих итерируемых объектов) очень часто используется в этих сценариях, поскольку понимание списков помогает нам писать краткие коды (коды, которые занимают меньше места). Обратитесь к приведенному ниже коду для лучшего понимания.
# инициализация матрицы (3 x 2).
матрица = [[1, 2], [2, 3], [3, 4]]
транспонировать = [[матрица [j] [i]
для j в диапазоне (len (матрица))] для i в диапазоне (len (матрица [0]))]
печатать (транспонировать)
Вывод:
[[1, 2, 3], [2, 3, 4]]
Транспонирование матрицы с помощью Zip
Мы также можем получить транспонирование матрицы в python, используя функцию map() и функцию zip().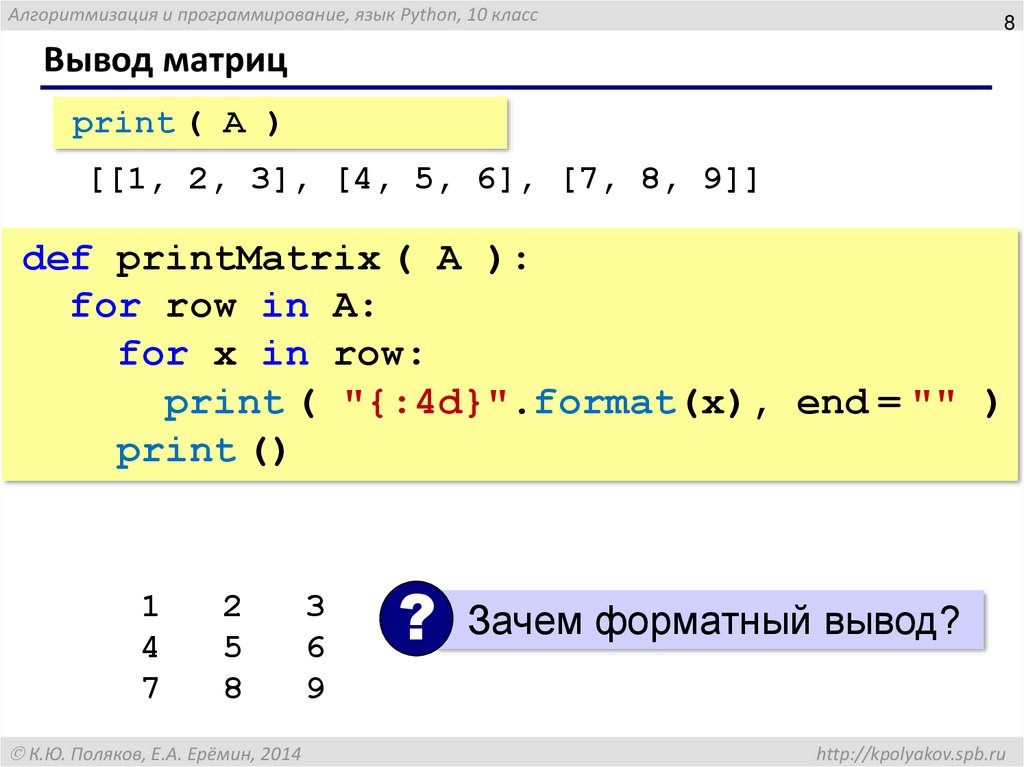
Примечание:
- map() — это функция, которая работает как итератор, она возвращает результат после применения предоставленной функции к каждому из своих итерируемых элементов.
- zip(iterable) также является функцией, которая принимает итерируемые объекты в качестве аргументов и возвращает итератор.
Давайте посмотрим код для лучшего понимания.
# инициализация матрицы (3 x 2).
матрица = [[1, 2], [2, 3], [3, 4]]
транспонировать = карта (список, zip (* матрица))
для i в транспонировании:
печать (я)
Вывод:
[1, 2, 3] [2, 3, 4]
Транспонирование матрицы с использованием библиотеки NumPy
До сих пор мы видели все встроенные методы транспонирования матрицы в Python. Мы можем использовать библиотеку NumPy, созданную для работы с массивами. Библиотека NumPy помогает нам работать с большими наборами данных и поддерживает различные методы, помогающие нам эффективно работать с многомерными массивами. Мы будем использовать функцию transpose() библиотеки NumPy. Давайте посмотрим код для лучшего понимания.
Мы будем использовать функцию transpose() библиотеки NumPy. Давайте посмотрим код для лучшего понимания.
импорт numpy # инициализация матрицы (3 x 2). матрица = [[1, 2], [2, 3], [3, 4]] печать (numpy.transpose (матрица))
Вывод:
[[1 2 3] [2 3 4]]
Примечание: Поскольку NumPy — это внешняя библиотека, нам нужно установить NumPy с помощью команды pip install NumPy.
Для квадратной матрицы
В результате транспонирования квадратной матрицы получается другая квадратная матрица, поскольку число строк и столбцов одинаково. Возьмем пример квадратной матрицы (NxN):
# инициализация матрицы (3 x 3).
матрица = [[1, 2, 3], [12, 13, 14], [23, 24, 25]]
транспонировать = [[матрица [j] [i]
для j в диапазоне (len (матрица))] для i в диапазоне (len (матрица [0]))]
печатать (транспонировать)
Вывод:
[[1, 12, 23], [2, 13, 24], [3, 14, 25]]
Для прямоугольной матрицы
Как мы знаем, транспонирование матрицы NxM приведет к матрице NxM. Поскольку N и M имеют разные значения, матрица не считается прямоугольной матрицей. Возьмем пример матрицы 2x5:
Поскольку N и M имеют разные значения, матрица не считается прямоугольной матрицей. Возьмем пример матрицы 2x5:
# инициализация матрицы (2 x 5).
матрица = [[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]]
транспонировать = [[матрица [j] [i]
для j в диапазоне (len (матрица))] для i в диапазоне (len (матрица [0]))]
печатать (транспонировать)
Вывод:
[[1, 6], [2, 7], [3, 8], [4, 9], [5, 10]]
Заключение
- Матрица представляет собой прямоугольный массив некоторых данных (чисел, букв или других объектов), расположенных в виде строк и столбцов. 9Т.
- Если матрица изначально имеет размер N x M , то после транспонирования матрица становится M x N .
- Транспонирование матрицы в python может быть реализовано с использованием вложенных циклов, понимания вложенного списка, функции zip() и функции transpose() библиотеки NumPy. Список
— транспонирование матрицы в Python
Задавать вопрос
Спросил
Изменено 1 год, 4 месяца назад
Просмотрено 170 тысяч раз
156
Новинка! Сохраняйте вопросы или ответы и организуйте свой любимый контент.
Узнать больше.
Здесь уже есть ответы на этот вопрос :
Транспонировать список списков (14 ответов)
Закрыт 8 месяцев назад.
Я пытаюсь создать функцию транспонирования матрицы для Python, но не могу заставить ее работать. скажи у меня
theArray = [['a','b','c'],['d','e','f'],['g','h','i']]
, и я хочу, чтобы моя функция выдавала
newArray = [['a','d','g'],['b','e','h'],['c', ' ф', 'и']]
Другими словами, если бы я печатал этот двумерный массив в виде столбцов и строк, я бы хотел, чтобы строки превратились в столбцы, а столбцы в строки.
Я сделал это до сих пор, но это не работает
def matrixTranspose(anArray):
транспонированный = [Нет] * len (массив [0])
для t в диапазоне (len (anArray)):
для tt в диапазоне (len (anArray [t])):
транспонированный [t] = [Нет] * len (массив)
транспонированный[t][tt] = массив[tt][t]
печать транспонирована
- питон
- список
- многомерный массив
0
Python 2:
>>> theArray = [['a','b','c'],['d','e','f'],['g','h', 'я']]
>>> zip(*массив)
[('a', 'd', 'g'), ('b', 'e', 'h'), ('c', 'f', 'i')]
Python 3:
>>> [*zip(*theArray)]
[('a', 'd', 'g'), ('b', 'e', 'h'), ('c', 'f', 'i')]
9
>>> theArray = [['a','b','c'],['d','e','f'],['g','h','i']] >>> [список(i) для i в zip(*theArray)] [['a', 'd', 'g'], ['b', 'e', 'h'], ['c', 'f', 'i']]
генератор списков создает новый двумерный массив с элементами списка вместо кортежей.
2
Если ваши строки не равны, вы также можете использовать карту :
>>> неровный = [['a','b','c'],['d','e'],[' г','ч','и']]
>>> карта(Нет,*нечетная)
[('a', 'd', 'g'), ('b', 'e', 'h'), ('c', None, 'i')]
Редактировать: в Python 3 функциональность карты изменена, вместо нее можно использовать itertools.zip_longest :
Источник: Что нового в Python 3.0
>>> импорт itertools
>>> неравномерный = [['a','b','c'],['d','e'],['g','h','i']]
>>> список(itertools.zip_longest(*uneven))
[('a', 'd', 'g'), ('b', 'e', 'h'), ('c', None, 'i')]
0
Намного проще с numpy:
>>> arr = np.array([[1,2,3],[4,5,6],[7,8,9]])
>>> обр.
массив([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
>>> обр.Т
массив([[1, 4, 7],
[2, 5, 8],
[3, 6, 9]])
>>> theArray = np.array([['a','b','c'],['d','e','f'],['g','h','i' ]])
>>> массив
массив([['а', 'б', 'с'],
['д', 'е', 'ф'],
['г', 'ч', 'и']],
dtype='|S1')
>>> theArray. T
массив([['а', 'г', 'г'],
['б', 'е', 'ч'],
['с', 'ф', 'и']],
dtype='|S1')
T
массив([['а', 'г', 'г'],
['б', 'е', 'ч'],
['с', 'ф', 'и']],
dtype='|S1')
Проблема с исходным кодом заключалась в том, что вы инициализировали transpose[t] для каждого элемента, а не только один раз в строке:
def matrixTranspose(anArray):
транспонированный = [Нет] * len (массив [0])
для t в диапазоне (len (anArray)):
транспонированный [t] = [Нет] * len (массив)
для tt в диапазоне (len (anArray [t])):
транспонированный[t][tt] = массив[tt][t]
печать транспонирована
Это работает, хотя есть и другие способы Pythonic для выполнения тех же задач, в том числе @J.F. 9Приложение 0043 zip .
1
Чтобы завершить ответ Дж. Ф. Себастьяна, если у вас есть список списков разной длины, ознакомьтесь с этим замечательным сообщением от ActiveState. Короче:
Встроенная функция zip выполняет аналогичную работу, но усекает результат до длины кратчайшего списка, поэтому некоторые элементы из исходного данные могут быть потеряны впоследствии.
Для обработки списка списков разной длины используйте:
def transposed(lists): если нет списков: вернуть [] карта возврата (лямбда * строка: список (строка), * списки) def transposed2 (списки, defval = 0): если нет списков: вернуть [] карта возврата (лямбда *строка: [элемент или defval для элемента в строке], *списки)
2
«Лучший» ответ уже отправлен, но я решил добавить, что вы можете использовать вложенные списки, как показано в учебнике по Python.
Вот как можно получить транспонированный массив:
def matrixTranspose(matrix):
если не матрица: вернуть []
return [[ row[ i ] для строки в матрице ] для i в диапазоне ( len ( матрица [ 0 ] ) ) ]
Этот сохранит прямоугольную форму, так что последующие транспонирования получат правильный результат:
импорт itertools деф транспонировать (list_of_lists): список возврата (itertools.izip_longest (* list_of_lists, fillvalue = ' '))
вы можете попробовать это с пониманием списка, как показано ниже ,'Здравствуй']] n = len (матрица) транспонировать = [[строка [i] для строки в матрице] для i в диапазоне (n)] print (transpose)
Если вы хотите транспонировать матрицу типа A = np. array([[1,2],[3,4]]), то вы можете просто использовать A.T, но для вектора вида a = [1,2], a.T не возвращает транспонирование! и вам нужно использовать a.reshape(-1, 1), как показано ниже
array([[1,2],[3,4]]), то вы можете просто использовать A.T, но для вектора вида a = [1,2], a.T не возвращает транспонирование! и вам нужно использовать a.reshape(-1, 1), как показано ниже
импортировать numpy как np
а = np.массив ([1,2])
print('a.T не транспонирует Python!\n','a = ',a,'\n','a.T = ', a.T)
print('Транспонировать вектор a: \n',a.reshape(-1, 1))
А = np.массив([[1,2],[3,4]])
print('Транспонировать матрицу A: \n',A.T)
Вы можете сделать это, просто используя понимание Python.
обр = [
['а', 'б', 'в'],
['д', 'е', 'ф'],
['г', 'ч', 'и']
]
транспонировать = [[arr[y][x] для y в диапазоне (len(arr))] для x в диапазоне (len(arr[0]))]
2
def matrixTranspose(anArray):
транспонированный = [Нет] * len (массив [0])
для i в диапазоне (len (транспонированном)):
транспонированный [i] = [Нет] * len (транспонированный)
для t в диапазоне (len (anArray)):
для tt в диапазоне (len (anArray [t])):
транспонированный[t][tt] = массив[tt][t]
возврат транспонированный
theArray = [['a','b','c'],['d','e','f'],['g','h','i']]
матрица печати транспонировать (массив)
импортировать numpy как np #Import Numpy
m=int(input("Введите строку")) #Input Номер строки
n=int(input("Введите столбец")) #Введите номер столбца
a=[] #Пустая матрица
для i в диапазоне (м): #Row Input
b=[] #Пустой список
для j в диапазоне (n): # столбец Ввод
j=int(input("Введите число в Карман ["+str(i)+"]["+str(j)+"]")) #sow Номер столбца строки
b. append(j) #addVlaue в список
a.append(b)#Добавить список в матрицу
a=np.array(a)#convert 1matrix as Numpy
b=a.transpose()#транспонировать с помощью Numpy
print(a) #Печать матрицы
print(b)#print Транспонировать матрицу
append(j) #addVlaue в список
a.append(b)#Добавить список в матрицу
a=np.array(a)#convert 1matrix as Numpy
b=a.transpose()#транспонировать с помощью Numpy
print(a) #Печать матрицы
print(b)#print Транспонировать матрицу
#генерировать матрицу
матрица=[]
m=input('введите количество строк, m =')
n=input('введите количество столбцов, n = ')
для я в диапазоне (м):
матрица.дополнение([])
для j в диапазоне (n):
elem=input('введите элемент:')
матрица[i].append(элемент)
#печатать матрицу
для я в диапазоне (м):
для j в диапазоне (n):
матрица печати [i][j],
напечатать '\п'
# сгенерировать транспонировать
транспонировать=[]
для j в диапазоне (n):
транспонировать.append([])
для i в диапазоне (м):
ent=матрица[i][j]
транспонировать[j].append(ent)
#print транспонировать
для i в диапазоне (n):
для j в диапазоне (м):
печатать транспонировать[i][j],
напечатать '\n'
а=[]
def showmatrix (a, m, n):
для i в диапазоне (м):
для j в диапазоне (n):
k=int(input("введите число")
а. добавить (к)
напечатать (а [я] [j]),
печать('\т')
def showtranspose (a, m, n):
для j в диапазоне (n):
для я в диапазоне (м):
распечатать (а [я] [j]),
печать('\т')
а=((89,45,50),(130,120,40),(69,79,57),(78,4,8))
print("данная матрица порядка 4x3 равна:")
показать матрицу (а, 4, 3)
print("Транспонировать матрицу:")
показать транспонирование (а, 4, 3)
добавить (к)
напечатать (а [я] [j]),
печать('\т')
def showtranspose (a, m, n):
для j в диапазоне (n):
для я в диапазоне (м):
распечатать (а [я] [j]),
печать('\т')
а=((89,45,50),(130,120,40),(69,79,57),(78,4,8))
print("данная матрица порядка 4x3 равна:")
показать матрицу (а, 4, 3)
print("Транспонировать матрицу:")
показать транспонирование (а, 4, 3)
0
по определению транспонировать (матрица):
х=0
транс=[]
б = len (матрица [0])
а б!=0:
транс.присоединить([])
б-=1
для списка в матрице:
для элемента в списке:
транс[x].append(элемент)
х+=1
х=0
вернуть транс
деф транспонировать (матрица):
списокСписков = []
для строки в диапазоне (len (матрица [0])):
столбец = []
для столбца в диапазоне (len (матрица)):
colList.append (матрица [столбец] [строка])
listOfLists.append (список столбцов)
вернуть listOfLists
1
`
деф транспонировать(м):
return(list(map(list,list(zip(*m))))) `Эта функция вернет программу транспонирования
Python для транспонирования матрицы:
row,col = map(int,input().

 transpose()
>>> print(A_t)
[[1 4]
[2 5]
[3 6]]
transpose()
>>> print(A_t)
[[1 4]
[2 5]
[3 6]] matrix('1 2 3; 4 5 6')
>>> B = np.matrix('7 8 9; 0 7 5')
>>> L = (A + B).T
>>> R = A.T + B.T
>>> print(L)
[[ 8 4]
[10 12]
[12 11]]
>>> print(R)
[[ 8 4]
[10 12]
[12 11]]
matrix('1 2 3; 4 5 6')
>>> B = np.matrix('7 8 9; 0 7 5')
>>> L = (A + B).T
>>> R = A.T + B.T
>>> print(L)
[[ 8 4]
[10 12]
[12 11]]
>>> print(R)
[[ 8 4]
[10 12]
[12 11]] ]
]  В этом примере мы разархивируем наш массив с помощью *, а затем сжимаем его, чтобы получить транспонирование.
В этом примере мы разархивируем наш массив с помощью *, а затем сжимаем его, чтобы получить транспонирование.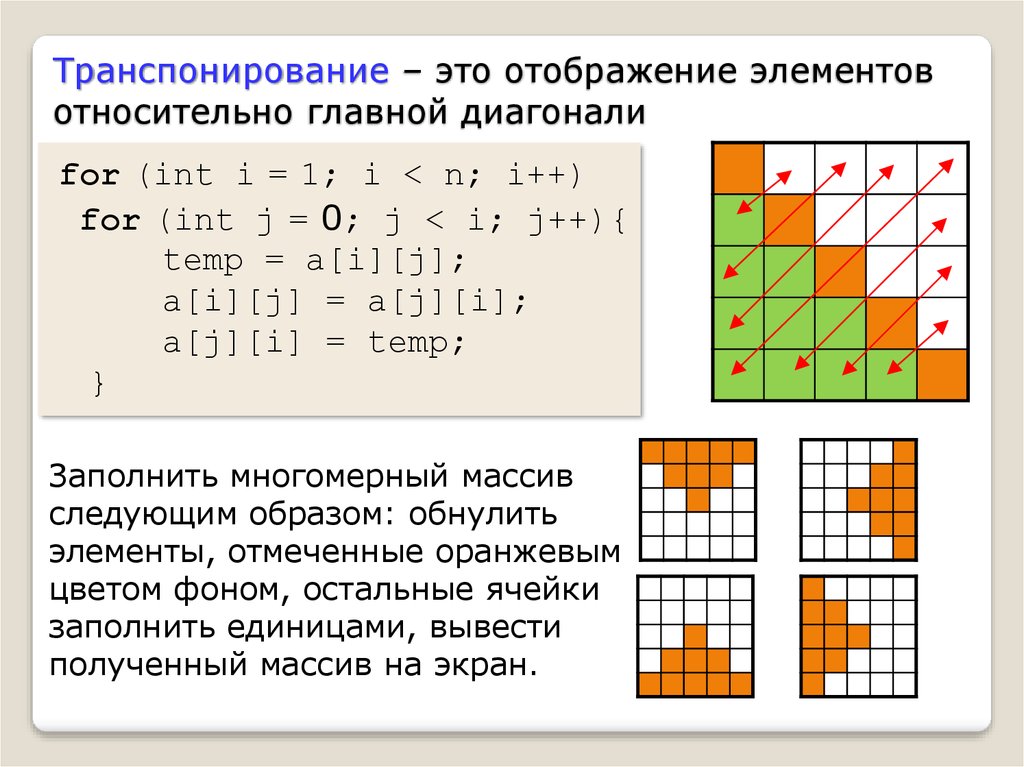 Если вы хотите получить результат в виде [[1,4,7,10][2,5,8,11][3,6,9,12]] , вы можете использовать t_matrix=map( список, zip(*матрица)).
Если вы хотите получить результат в виде [[1,4,7,10][2,5,8,11][3,6,9,12]] , вы можете использовать t_matrix=map( список, zip(*матрица)). transpose(matrix))
transpose(matrix))  T
массив([['а', 'г', 'г'],
['б', 'е', 'ч'],
['с', 'ф', 'и']],
dtype='|S1')
T
массив([['а', 'г', 'г'],
['б', 'е', 'ч'],
['с', 'ф', 'и']],
dtype='|S1')
 append(j) #addVlaue в список
a.append(b)#Добавить список в матрицу
a=np.array(a)#convert 1matrix as Numpy
b=a.transpose()#транспонировать с помощью Numpy
print(a) #Печать матрицы
print(b)#print Транспонировать матрицу
append(j) #addVlaue в список
a.append(b)#Добавить список в матрицу
a=np.array(a)#convert 1matrix as Numpy
b=a.transpose()#транспонировать с помощью Numpy
print(a) #Печать матрицы
print(b)#print Транспонировать матрицу
 добавить (к)
напечатать (а [я] [j]),
печать('\т')
def showtranspose (a, m, n):
для j в диапазоне (n):
для я в диапазоне (м):
распечатать (а [я] [j]),
печать('\т')
а=((89,45,50),(130,120,40),(69,79,57),(78,4,8))
print("данная матрица порядка 4x3 равна:")
показать матрицу (а, 4, 3)
print("Транспонировать матрицу:")
показать транспонирование (а, 4, 3)
добавить (к)
напечатать (а [я] [j]),
печать('\т')
def showtranspose (a, m, n):
для j в диапазоне (n):
для я в диапазоне (м):
распечатать (а [я] [j]),
печать('\т')
а=((89,45,50),(130,120,40),(69,79,57),(78,4,8))
print("данная матрица порядка 4x3 равна:")
показать матрицу (а, 4, 3)
print("Транспонировать матрицу:")
показать транспонирование (а, 4, 3)
